ISSN 2307–3489 (Print), ІSSN 2307–6666 (Online)

Наука та прогрес транспорту. Вісник Дніпропетровського
національного університету залізничного транспорту, 2017, № 2 (68)

ІНФОРМАЦІЙНО-КОМУНІКАЦІЙНІ ТЕХНОЛОГІЇ ТА МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ

Вступ

У промислово розвинених країнах, до яких належить і Україна, залізничний транспорт належить до сфери матеріального виробництва, своєрідною продукцією якого є пасажирські, вантажні та змішані вантажо-пасажирські перевезення. За будь-яких обставин безпека руху залізничного транспорту є одним з найважливіших питань його експлуатації. При цьому особливі вимоги висуваються до геометрії залізничної колії.

Улаштування рейкової колії на кривих її ділянках має низку особливостей, зумовлених специфікою взаємодії колії і рухомого складу, змінами конфігурації колії на криволінійних ділянках і наявністю так званих перехідних кривих, які з’єднують кругові криві з прилягаючими прямими рейками або з’єднують кругові криві різних радіусів кривини. Відомо, що призначенням перехідних кривих є забезпечення плавної зміни кривини в місцях з’єднання ділянок колії з різними сталими кривинами рейок.

Проектантами залізничної колії особлива увага приділяється улаштуванню перехідних ділянок при високих швидкостях руху потягів, застосуванні колійних кривих малого радіуса, при русі рухомого складу великої ваги та значної бази між колесами. У сучасних умовах, коли швидкість пасажирських потягів сягає 200 км/год і більше, вимоги до якості перехідних кривих суттєво зростають.

Підвищення швидкості руху поїздів, їх вантажопідйомності та забезпечення безпеки руху на криволінійних ділянках колії значною мірою визначається геометричною досконалістю перехідних кривих цих ділянок. Геометричне моделювання перехідних кривих залізничних колій є важливим науково-технічним завданням.

Наукові дослідження в галузях прикладної та обчислювальної геометрії, комп’ютерної графіки останнім часом досягли значних успіхів у сфері аналітичного подання обводів і поверхонь різних технічних деталей та їх візуалізації за допомогою ЕОМ. Це дає можливість сподіватися, що застосування досягнень цієї галузі науки до геометричного моделювання перехідних кривих залізничної колії дозволить підвищити якість їх проектування і сприятиме підвищенню безпеки руху на цих дуже важливих і одночасно небезпечних ділянках шляху.

Таким чином, розв’язання задачі, яка поставлена в цій роботі, а саме: вдосконалення методів геометричного моделювання перехідних кривих залізничної колії, є актуальним, воно має не тільки важливе теоретичне, й практичне значення.

Аналіз останніх досліджень і публікацій. Основи теорії перехідних кривих на залізниці були закладені на початку минулого століття і набули подальшого розвитку в роботах вітчизняних і закордонних дослідників [1, 4, 8, 9, 12, 15–19, 22–25]. У цих роботах пропонується перехідні криві подавати клотоїдами, кардіоїдами, радіоїдами. параболами різних степенів, лемніскатами Бернуллі, мажорантними, пружними, швидкісними та іншими математичними кривими.

У літературі приділено достатньо уваги питанню моделювання кривих ліній для різних практичних додатків, у тому числі і тих, які застосовуються при описі кривих, придатних для подання залізничної колії [2, 3, 11, 15, 20]. Автори цих робіт застосовують явну, неявну, параметричну форми опису кривих.

Моделюванню криволінійних обводів у натуральній параметризації присвячені публікації [3, 11, 13, 14]. У роботах [3, 14] розглянуті питання геометричного моделювання кривих ліній з кубічним розподілом кривини в залежно від довжини дуги.

Останніми роками в залізничній справі значна увага приділяється розробці проектів високошвидкісних залізничних шляхів. Про це свідчать, зокрема, наступні публікації вітчизняних науковців [5–7, 10]. Як вище відмічалося, підвищення швидкісного режиму руху поїздів вимагає застосування більш ретельних підходів до геометричного моделювання перехідних кривих, де одним із основних чинників є розподіл кривини кривої. Саме це послужило основним мотивом для розробки нового методу моделювання перехідних ділянок залізничних шляхів із застосуванням натуральної параметризації кривих, що їх подають.

Мета

Метою цієї статті є подальший розвиток методу геометричного моделювання перехідних кривих залізничних колій, які будуються на місцевості, рельєф якої зумовлює певні обмеження на геометрію перехідної кривої, яка влаштовується між прямолінійною та круговою ділянками залізничної колії.

Зрозуміло, що питання моделювання перехідних кривих не є новим. Його вирішенню присвячено достатньо публікацій як у вітчизняній, так і зарубіжній літературі. Автори багатьох робіт, які розглядають це дуже важливе для залізничного транспорту питання, використовують різні математичні криві для забезпечення плавної, не стрибкоподібної зміни кривини в місцях переходу від прямолінійних ділянок шляхів до кругових.

Ця робота є продовженням досліджень, які виконуються авторами з геометричного моделювання кривих ліній із застосуванням заданих законів розподілу кривини та заданими значеннями кривини в граничних точках [3, 11, 13–15].

Методика

У практиці будівництва залізничних шляхів непоодинокі випадки, коли у зв'язку з рельєфом місцевості або через інші які-небудь причинами необхідно прокладати колію на обмеженій за розмірами ділянці місцевості. Під обмеженням будемо розуміти наявну в розпорядженні проектанта відстань від початку перехідної кривої на прямолінійній ділянці колії до дотичної, проведеної до кругової ділянки шляху. При цьому дотична до кругової ділянки проводиться перпендикулярно до передбачуваного продовження прямолінійної рейки шляху (рис.1).

Автори цієї роботи пропонують моделювати плоскі перехідні криві з використанням їх натуральної параметризації, яка передбачає наявність залежностей декартових координат модельованої кривої від довжини її дуги.

Побудову перехідної ділянки шляху здійснюватимемо з використанням кривої, кривина якої описується кубічною залежністю від довжини її дуги s:

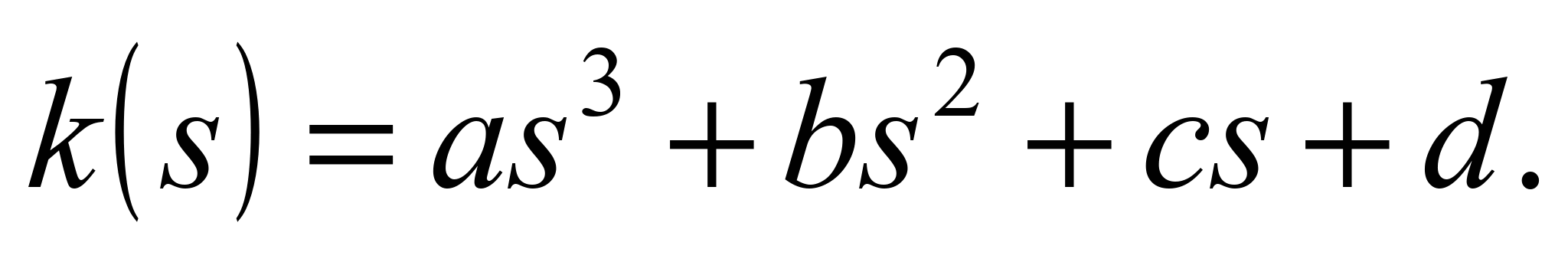(1)

Коефіцієнти a, b, c і d цієї залежності визначаються в процесі моделювання кривої.

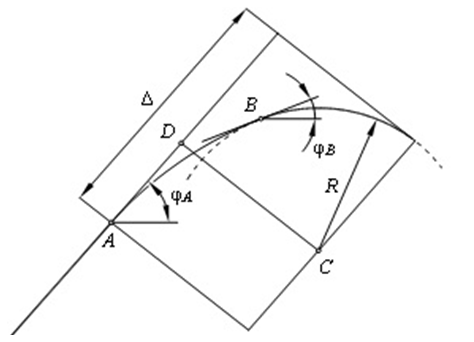
Рис. 1. До устрою перехідної кривої

Fig. 1. To the structure of the transition curve

При розв’язанні питання визначення невідомих коефіцієнтів залежності (1) за граничні умови приймається, що в початковій точці перехідної кривої її кривина дорівнює нулю, а в кінцевій точці – величині оберненій радіусу кругової ділянки шляху. Також приймається, що в початковій і кінцевій точках перехідної кривої похідна від її кривини по довжині дуги дорівнює нулю.

За означених граничних умов, можна встановити, що коефіцієнти c і d мають дорівнювати нулю.

Коефіцієнти а і b визначаються за умови, що відомі координати кінцевої точки прямолінійної ділянки шляху, кут його нахилу до горизонтальної осі, а також радіус кола, що описує кругову ділянку шляху.

Відомою є також і величина Δ, яка обумовлюється обмеженими розмірами ділянки місцевості, де мають бути прокладені рійки залізничного шляху.

Відзначимо, що для побудови перехідної кривої необхідно, крім коефіцієнтів a і b, також знати довжину дуги S цієї кривої.

З диференціальної геометрії відомо, що диференціал кута, утвореного між дотичною до кривої та віссю абсцис, визначається добутком диференціала довжини дуги на її кривину

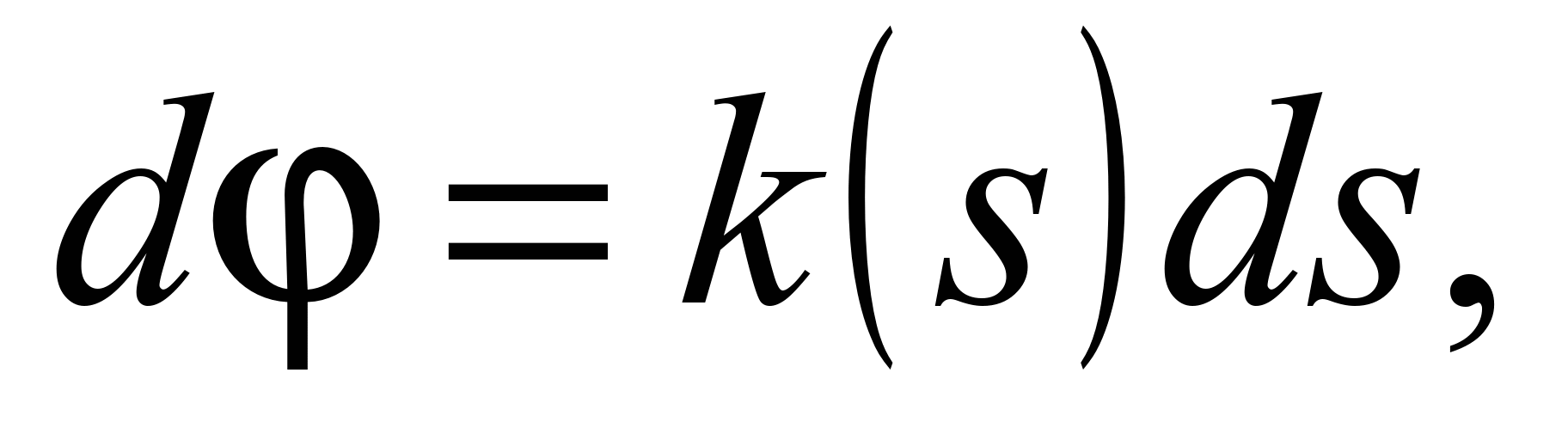
де 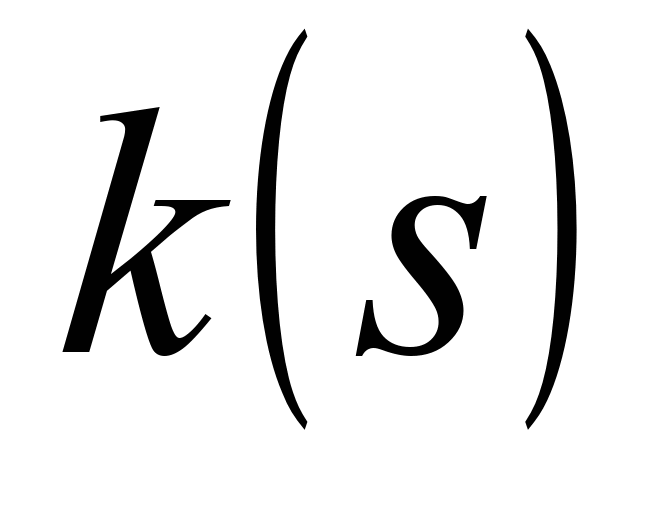– кривина кривої.

Інтегруванням цього виразу можна визначити залежність розподілу кута нахилу дотичної до кривої від довжини її дуги

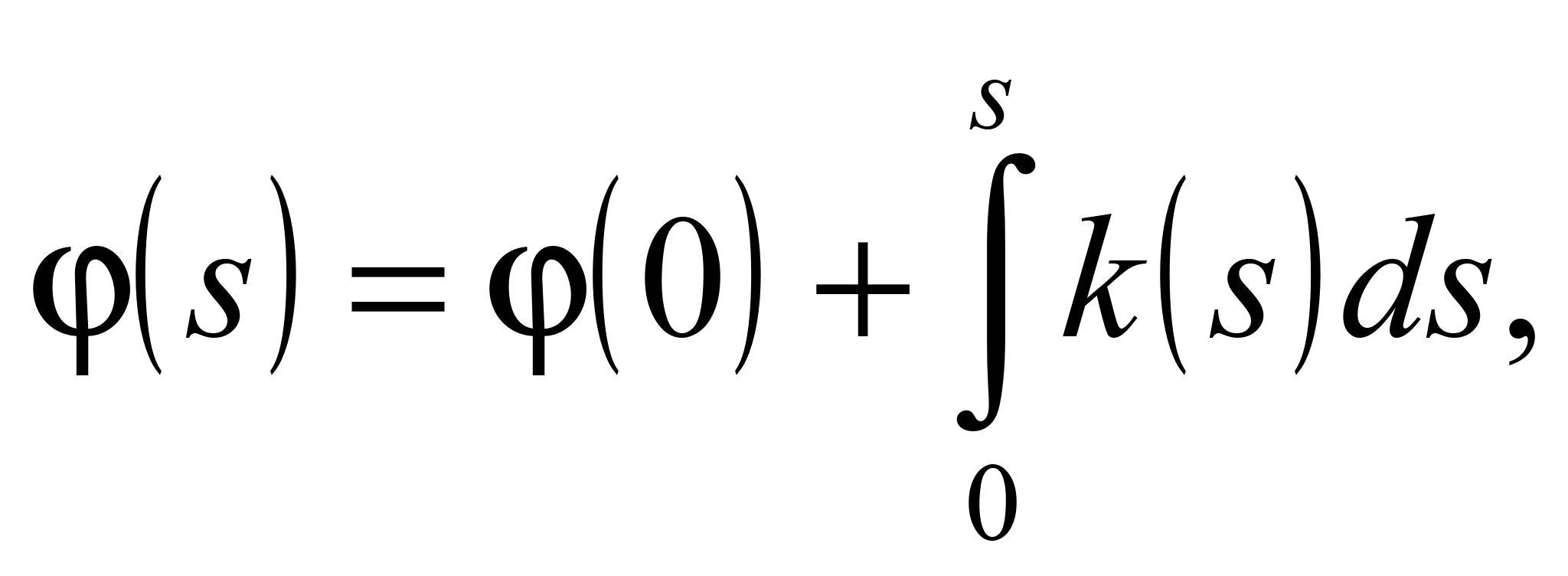
де φ(0) – кут нахилу дотичної в початковій точці кривої, тобто в точці А (див. рис. 1).

З урахуванням граничних умов, які застосовуються до закону розподілу кривини для нашого випадку, остаточно отримаємо наступну залежність розподілу кута нахилу дотичної до кривої від її довжини:

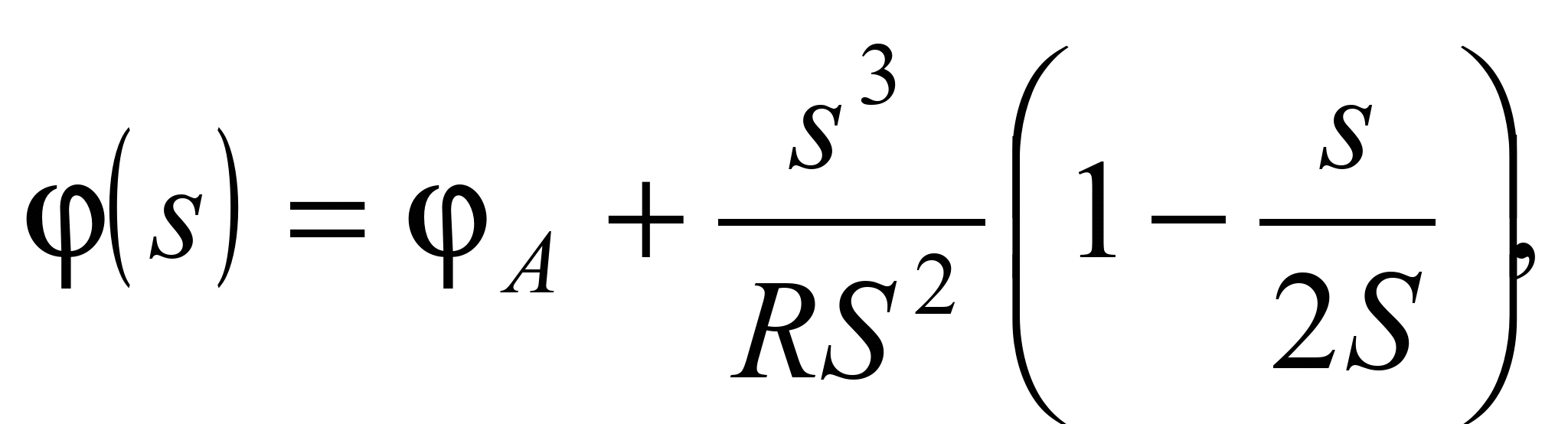(2)

де S – довжина дуги перехідної кривої між точками А і В, яка на початку моделювання є величиною невідомою.

Зазначимо, що на цьому кроці моделювання також невідомими є координати точки В. Але із залежності (2) можна при 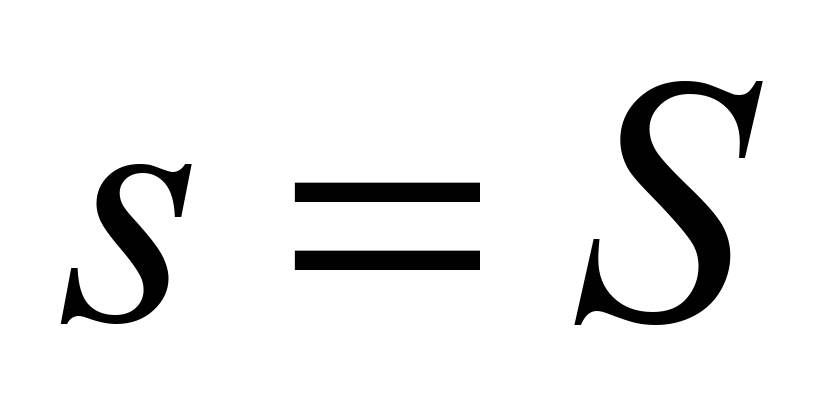знайти вираз для обчислення кута в кінцевій точці перехідної кривої:

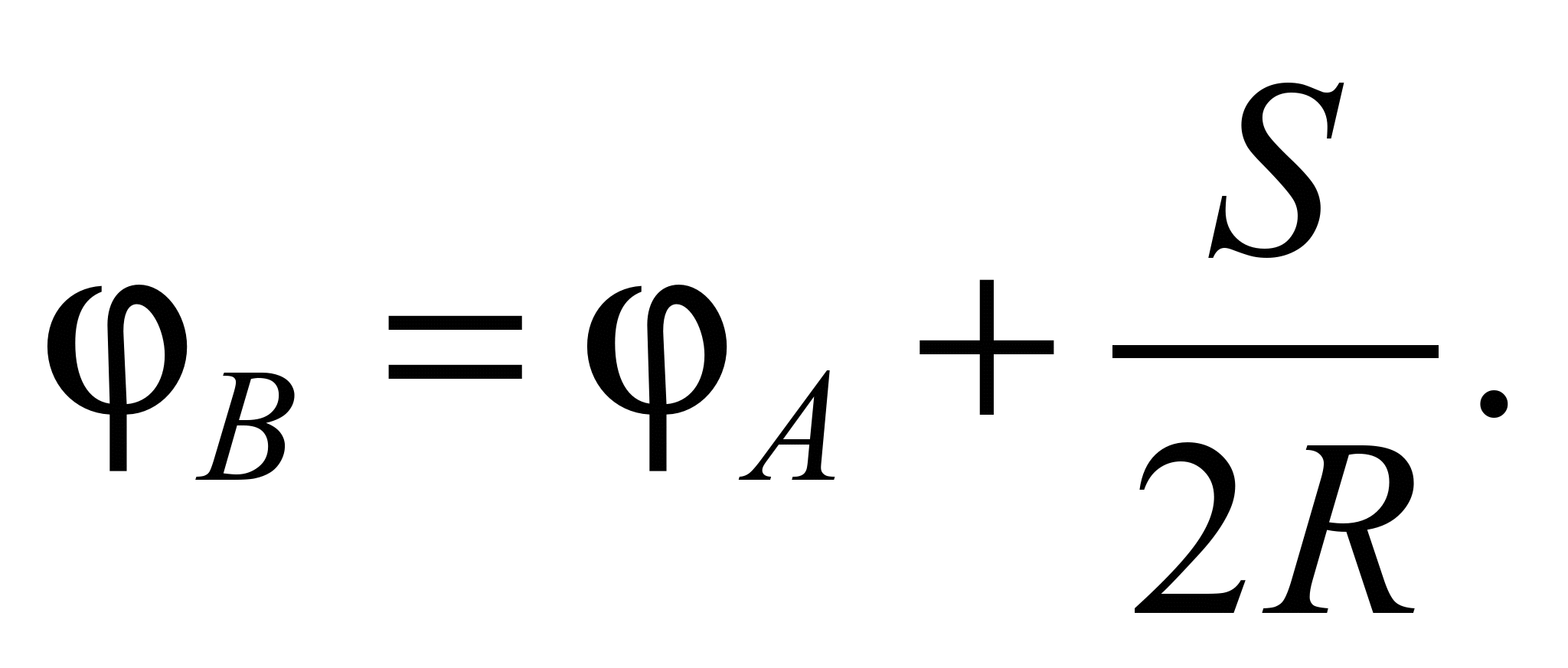(3)

Координати точки В – кінцевої точки перехідної кривої, яка подається в натуральній параметризації, визначаються за виразами:

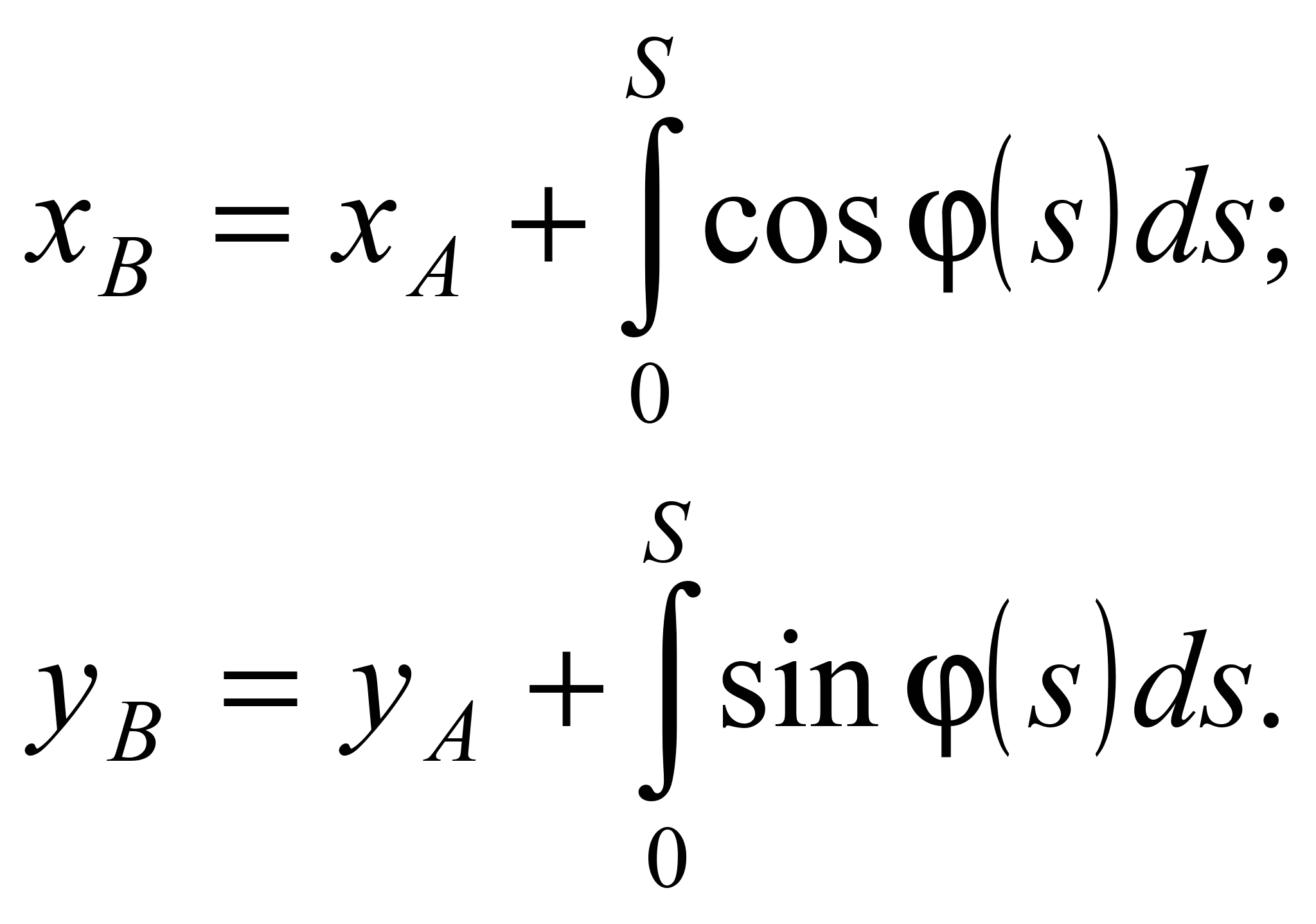(4)

Аналізуючи вирази (2)–(4) можна прийти до висновку, що в них єдиною невідомою величиною є довжина дуги перехідної кривої .

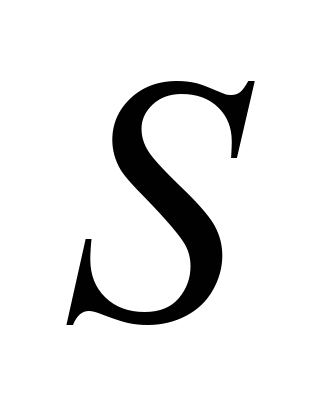Довжину цієї дуги можна визначити числовим методом, зокрема, методом мінімізації функціонала, за який візьмемо відстань між центром С кола кругової ділянки та точкою C´, яка визначається тимчасово під час роботи алгоритму мінімізації. Вказаний функціонал може бути записаним наступним чином

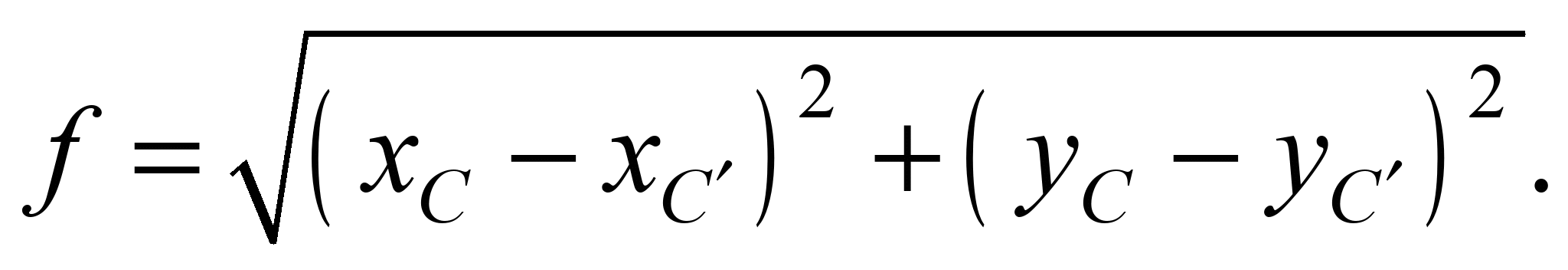(5)

Для мінімізації цього функціонала в роботі застосовано високоефективний алгоритм, запропонований Хуком–Дживсом [21].

Отже, задавшись деякою величиною довжини перехідної кривої, можна визначити за формулами (4) координати деякої проміжної точки В. За перше наближення довжини перехідної кривої береться частка від величини обмеження Δ. Координати точки С – центра кола кругової ділянки визначаються за формулами:

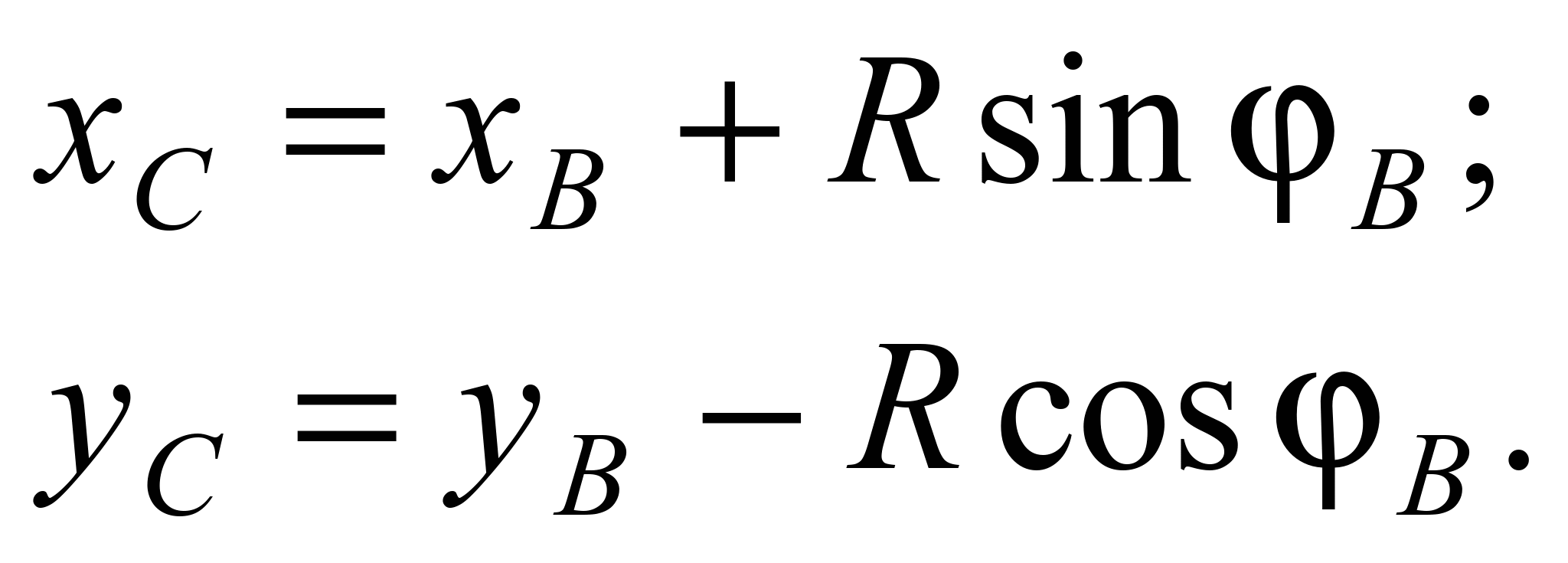
З іншого боку ці координати можна розрахувати за наступними виразами:

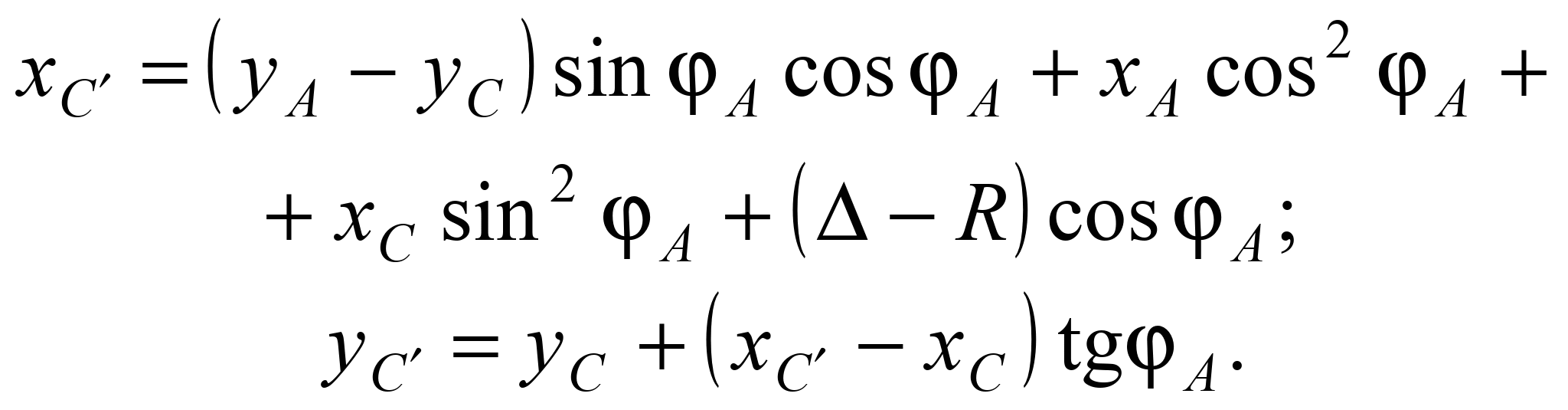
На підставі запропонованого підходу до геометричного моделювання перехідних кривих на обмеженій ділянці розроблено програму розрахунків і візуалізації отриманих результатів на екрані ПЕОМ.

Результати

На рис. 2 у графічному вигляді наведено результати розв’язання тестової задачі, пов’язаної з моделюванням перехідної кривої на обмеженій ділянці. Прямолінійна ділянка шляху має кут нахилу до осі х, який дорівнює 60°; вона закінчується в точці А. Необхідно побудувати перехідну криву між прямолінійною та круговою ділянками колії. Радіус кругової ділянки дорівнює 500 м. Обмеженням для моделювання перехідної кривої виступає відрізок DM, який відповідає параметру Δ (див. рис. 1). У розглянутому прикладі Δ = 850 м.

Результатом моделювання є побудована перехідна крива, яка починається в точці А і закінчується в знайденій точці В. Були розраховані координати точки С, яка є центром кругової ділянки шляху. Відрізок ВЕ, дотичний до кола кругової ділянки, є додатковим візуальним підтвердженням того, що відрізок СВ, проведений із точки В (точки початку кругової ділянки), є перпендикулярним до дотичної ВЕ.

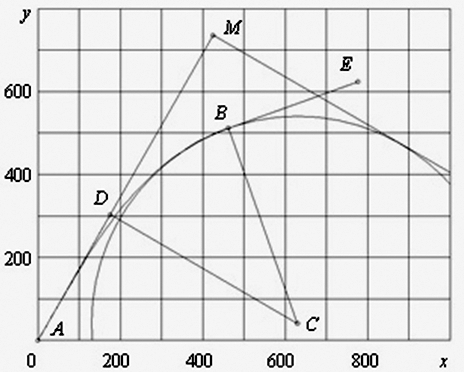
Рис. 2. Тестовий приклад побудови перехідної
кривої на обмеженій ділянці

Fig. 2. The test example of construction of transition curve in a limited area

Таким чином, точка В є закінченням перехідної кривої та початком кругової ділянки шляху, який моделюється на обмеженій ділянці місцевості.

Наведемо величини координат точок С і С', які були отримані при розв’язанні в цієї тестової задачі:

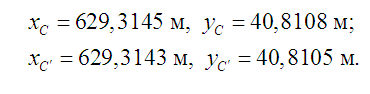
Величина похибки, яка розраховувалася за формулою (5), в тестовій задачі становила 0,3675 мм.

Наукова новизна та
практична значимість

Наукова новизна полягає в удосконаленні підходу до геометричного моделювання перехідних кривих між прямолінійними та круговими рійками залізничного шляху в умовах обмеженої ділянки на основі застосування кубічного розподілу кривини перехідної кривої від довжини її дуги та відомими її значеннями в початковій та кінцевій точках.

Запропонований метод моделювання перехідних кривих може бути застосованим при проектуванні не тільки залізничного шляху, але й криволінійних обводів технічних виробів різного конструктивного оформлення та цільового призначення.

Висновки

Проведені розрахункові дослідження підтвердили працездатність запропонованого підходу до моделювання перехідних кривих між прямолінійними та круговими ділянками за наявності обмежень на місцевості. Метод може бути поширений на побудову перехідної кривої між двома круговими ділянками залізничної колії.

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1. Амелин, С. В. Путь и путевое хозяйство / С. В. Амелин, Л. М. Дановский. – Москва : Транспорт, 1986. – 215 c.

2. Бадаєв, С. Ю. Криволінійний сегмент на основі інтегральної кривої / С. Ю. Бадаєв, Є. О. Боровік // Прикладна геометрія та інженерна графіка : міжвідом. наук.-техн. зб. / Київ. держ. техн. ун-т буд-ва і архітектури. – Киів, 2009. – Вип. 81. – С. 213–217.

3. Борисенко, В. Д. Геометричне моделювання плоского криволінійного обводу із застосуванням кубічного закону розподілу його кривини / В. Д. Борисенко, С. А. Устенко, В. С. Комар // Прикладна геометрія та інженерна графіка : міжвідом. наук.-техн. зб. / Київ. держ. техн. ун-т буд-ва і архітектури. – Киів, 2008. – Вип. 79. – С. 52–57.

4. Ельфимов, Г. В. Теория переходных кривых / Г. В. Ельфимов. – Москва : Трансжелдориздат, 1948. – 31 с.

5. Курган, М. Б. Основні вимоги до вибору радіусів кривих при проектуванні високошвидкісних магістралей / М. Б. Курган, Р. Б. Новік // Проблемы и перспективы развития железнодорожного транспорта : тез. 74 Междунар. науч.-практ. конф. (Днепропетровск, 15–16 мая 2014 г.). – Днепропетровск, 2014. – С. 270–271.

6. Курган, М. Б. Основні вимоги до вибору форми і довжини перехідних кривих при проектуванні високошвидкісних магістралей / М. Б. Курган, Д. М. Курган // Проблемы и перспективы развития железнодорожного транспорта : тез. 74 Междунар. науч.-практ. конф. (Днепропетровск, 15–16 мая 2014 г.). – Днепропетровск, 2014. – С. 253–254.

7. Курган, М. Б. Перебудова кривих для впровадження швидкісного руху пасажирських поїздів / М. Б. Курган, М. А. Гусак, Н. П. Хмелевська // Вісн. Дніпропетр. нац. ун-ту залізн. трансп. ім. акад.
   В. Лазаряна. – Дніпропетровськ, 2012. – Вип. 40. – С. 90–97.

8. Лагута, В. В. Удосконалення проектування кривих залізничної колії в плані : автореф. дис. … канд. техн. наук : 05.22.06 / Лагута Василь Васильович ; Дніпропетр. держ. техн. ун-т залізн. трансп. – Дніпропетровськ, 2002. – 18 с.

9. Лазарян, В. А. О форме переходной кривой (Теоретические основы выбора рациональной формы переходной кривой) / В. А. Лазарян // Динамика транспортных средств. – Киев : Наук. думка, 1985. – С. 10–24.

10. Миронов, В. С. Радиусы круговых кривых для скоростных железных дорог при использовании вагонов с наклоном кузова / В. С. Миронов, Т. А. Руденко // Вестн. трансп. Поволжья. – 2014. – № 3 (45). – С. 44–50.

11. Моделювання плоских кривих у натуральній параметризації / В. Борисенко, О. Агарков, К. Палько, М. Палько // Геометричне моделювання та інформаційні технології. – 2016. – № 1. – С. 21–27.

12. Проценко, А. И. Методика расчета на ЭВМ сложных железнодорожных кривых при текущем содержании пути / А. И. Проценко, В. Б. Бредюк // Сб. тр. Новосиб. ин-та инженеров трансп. – Новосибирск, 1971. – Вып. 130. – С. 48–53.

13. Устенко, С. А. Геометричне моделювання кривих ліній із заданою кривиною в граничних точках /
    С. А. Устенко, С. В. Діданов, О. Ю. Агарков // Прикладна геометрія та інженерна графіка : міжвідом. наук.-техн. зб. / Київ. держ. техн. ун-т буд-ва і архітектури. – Киів, 2011. – Вип. 87. – С. 404–409.

14. Устенко, С. А. Дослідження кривих ліній, заданих кубічним розподілом кривини / С. А. Устенко, С. В. Діданов, О. Ю. Агарков // Наука та прогрес транспорту. – 2014. – № 2 (50). – С. 164–172. doi: 10.15802/stp2014/23797.

15. Устенко, С. А. Метод побудови просторової перехідної кривої / С. А. Устенко, С. В. Діданов // Наука та прогрес транспорту. – 2013. – № 2 (44). – С. 124–128. doi: 10.15802/stp2013/11394.

16. Чернышев, М. А. Железнодорожный путь / М. А. Чернышев, З. Л. Крейнис. – Москва : Транспорт, 1985. – 302 с.

17. Шахунянц, Г. М. Проектирование железнодорожного пути / Г. М. Шахунянц. – Москва : Транспорт, 1972. – 140 c.

18. A numerical study of cubic parabolas on railway transition curves / T.-I Shen, Ch.-H. Chang, K.-Yu. Chang, Ch.-Ch. Lu // J. of Marine Science and Technology. – 2013. – Vol. 21, No. 2. – P. 191–197. doi: 10.6119/JMST-012-0403-1.

19. Eliou, N. A new, simple and accurate transition curve type, for use in road and railway alignment design / N. Eliou, G. Kaliabetsos // European Transport Research Review. – 2014. – Vol. 6. – Iss. 2. – P. 171–179.
    doi 10.1007/s12544-013-0119-8.

20. Farin, G. Curves and surfaces for computer-aided geometric design: a practical guide / G. Farin. – 4 ^th ed. – Academic Press Inc., 1997. – 447 p.

21. Hooke, R. "Direct Search" Solution of Numerical and Statistical Problems / R. Hooke, T. A. Jeeves // J. of the ACM. – 1961. – Vol. 8. – Iss. 2. – P. 212–229. doi: 10.1145/321062.321069.

22. Lipicnik, M. New form of Road/Railway Transition Curve / M. Lipicnik // J. of Transportation Engineering. – 1998. – Vol. 124. – Iss. 6. – P. 546–556. doi: 10.1061/(asce)0733-947x(1998)124:6(546).

23. Long, X.-Y. Dynamic analysis of railway transition curves / X.-Y. Long, Q.-C. Wei1, F.-Y. Zheng // Proc. of the Institution of Mechanical Engineers, Part F: J. of Rail and Rapid Transit. – 2010. – Vol. 224. – Iss. 1. –
    P. 1–14. doi: 10.1243/09544097jrrt287.

24. Tari, E. A new transition curve with enhanced properties / E. Tari, O. Baykal // Canadian J. of Civil Engineering. – 2005. – Vol. 32. – Iss. 5. – P. 913–923. doi: 10.1139/l05-051.

25. Transition Curve Modelling with Kinematical Properties: Research on Log-Aesthetic Curves / A. Arslan,
    E. Tari, R. Ziatdinov, R. I. Nabiyev // Computer Aided Design & Applications. – 2014 – Vol. 11. – Iss. 5. –
    P. 509–517. doi: 10.1080/16864360.2014.902680.

В. Д. БОРИСЕНКО^1*, С. А. УСТЕНКО^2*

^1*Каф. «Компьютерная инженерия», Николаевский национальный университет
имени В. О. Сухомлинского, ул. Никольская, 24, Николаев, Украина, 54030,
тел. +38 (0512) 71 30 25, тел. +38 (063) 304 75 26,
эл. почта borisenko.valery@gmail.com, ORCID 0000-0002-0857-0708
^2*Каф. «Компьютерная инженерия», Николаевский национальный университет
имени В. О. Сухомлинского, ул. Никольская, 24, Николаев, Украина, 54030,
тел. +38 (063) 479 90 61, эл. почта ustenko.s.a@gmail.com,
ORCID 0000-0003-4968-1233

МОДЕЛИРОВАНИЕ ПЕРЕХОДНОЙ КРИВОЙ

НА ОГРАНИЧЕННОМ УЧАСТКЕ МЕСТНОСТИ

Цель. В статье необходимо рассмотреть дальнейшее развитие метода геометрического моделирования переходных кривых, которые размещаются между прямолинейными и круговыми участками железнодорожных путей и создаются на местностях, рельеф которых обусловливает определенные ограничения на размеры переходных кривых железнодорожного пути. Методика. Уравнение переходной кривой берется в параметрическом виде, где в качестве параметра указывается длина дуги моделируемой кривой. В качестве исходных данных при моделировании переходной кривой используются координаты начальной ее точки и угол наклона в ней касательной, радиус окружности круговой участка и параметр, который выступает в качестве ограничения при размещении участка железнодорожного пути. Переходная кривая моделируется при условии, что распределение ее кривизны от длины дуги – натурального параметра – описывается кубической зависимостью. Эта зависимость содержит четыре неизвестных коэффициента, неизвестной также является длина дуги. Коэффициенты кубической зависимости и длина дуги переходной кривой, координаты ее конечной точки, угол наклона в ней касательной определяются в процессе моделирования переходной кривой. Применение граничных условий, положений дифференциальной геометрии применительно к распределению угла наклона касательной к моделируемой кривой (от начальной до конечных точек переходной кривой и расчета координат конечной точки кривой) позволяет свести задачу моделирования переходной кривой к определению длины дуги этой кривой. Непосредственно длина переходной кривой находится в процессе минимизации отклонения центра окружности кругового участка пути от его текущего значения, получаемого при поиске длины дуги. Результаты. Проведенный вычислительный эксперимент доказал возможность моделирования переходной кривой между прямолинейными и круговыми рельсами железнодорожного пути на участке местности ограниченного размера. Научная новизна. Авторами разработан метод геометрического моделирования переходных кривых между прямолинейными и круговыми участками железнодорожного пути в условиях ограниченных размеров местности, на которой прокладываются рельсы. Переходная кривая представляется в натуральной параметризации с применением кубической зависимости распределения кривизны от длины ее дуги. Практическая значимость. Предложенный метод моделирования переходных кривых в условиях ограниченных размеров местности позволяет с высокой точностью получать эти кривые в широком диапазоне варьирования геометрических параметров прямолинейных и круговых участков железнодорожного пути и параметра, который выступает ограничением при моделировании переходной кривой. Метод можно рекомендовать в практику строительства железнодорожных путей.

Ключевые слова: геометрическое моделирование; переходная кривая; ограниченный участок; кривизна кривой; кубическая зависимость; распределение кривизны

V. D. BORISENKO^1*, S. A. USTENKO^2*

^1*Dep. «Computer Engineering», V. A. Suhomlinskiy Nikolayev National University,
Nikolskaya St., 24, Nikolayev, Ukraine, 54030, tel. +38 (0512) 71 30 25,
tel. +38 (063) 304 75 26, e-mail borisenko.valery@gmail.com, ORCID 0000-0002-0857-0708
^1*Dep. «Computer Engineering», V. A. Suhomlinskiy Nikolayev National University,
Nikolskaya St., 24, Nikolayev, Ukraine, 54030, tel. + 38 (063) 479 90 61,
e-mail ustenko.s.a@gmail.com, ORCID 0000-0003-4968-1233

modeling the transition curve

on a limited terain

Purpose. The article highlights further development of the method of geometric modelling of transition curves, which are placed between rectilinear and circular sections of railway tracks and are created in localities, the relief of which causes certain restrictions on the size of the transition curves of the railway track. Methodology. The equation of the transition curve is taken in parametric form, in which the length of the arc of the modelled curve is used as a parameter. As initial data in the modelling of the transition curve, the coordinates of its initial point and the angle of inclination in it are tangent, the radius of the circumference of the circular section and the parameter that is used as a constraint when placing a section of the railway track. The transition curve is modelled under the condition that the distribution of its curvature from the length of the arc - the natural parameter - is described by a cubic dependence. This dependence contains four unknown coefficients; the unknown is also the length of the arc. The coefficients of the cubic dependence and the length of the arc of the transition curve, the coordinates of its end point, the angle of inclination in it of the tangent are determined during the simulation of the transition curve. The application of boundary conditions and methods of differential geometry with respect to the distribution of the slope angle of the tangent to the simulated curve (from the initial to the end points of the transition curve and the calculation of the coordinates of the end point of the curve) allows us to reduce the problem of modelling the transition curve to determine the arc length of this curve. Directly the length of the transition curve is in the process of minimizing the deviation of the circumference of the circular path from its current value obtained when searching for the arc length. Findings. As a result of the computational experiment, the possibility of modelling a transition curve between a rectilinear and circular rail track in a region of a limited size has been proved. Originality. Authors developed a method for geometric modelling of transition curves between a rectilinear and circular section of a railway track in conditions of limited terrain size, on which rails are laid. The transition curve is represented in the natural parameterization, using the cubic dependence of the curvature distribution on the length of its arc. Practical value. The proposed method of modelling the transition curves in conditions of limited terrain size allows obtaining these curves with a high accuracy in a wide range of geometric parameters of rectilinear and circular sections of the railway track and a parameter that acts as a constraint in the modelling of the transition curve. The method can be recommended in the practice of building railways.

Keywords: geometric modelling; transition curve; limited area; the curvature of the curve; a cubic dependence; curvature distribution

REFEReNCEs

1. Amelin, S. V., & Danovskiy, L. M. (1986). Put i putevoye khozyaystvo. Moscow: Transport.

2. Badaiev, S. Y., Borovik, Y. O. (2009). Kryvoliniinyi sehment na osnovi intehralnoi kryvoi. Applied Geometry and Graphics, 81, 213-217.

3. Borysenko, V. D., Ustenko, S. A., & Komar, V. S. (2008). Heometrychne modeliuvannia ploskoho kryvoliniinoho obvodu iz zastosuvanniam kubichnoho zakonu rozpodilu ioho kryvyny. Applied Geometry and Graphics, 79, 52-57.

4. Yelfimov, G. V. (1948). Teoriya perekhodnykh krivykh. Moscow: Transzheldorizdat.

5. Kurhan, M. B., & Novik, R. B. (2014). Osnovni vymohy do vyboru radiusiv kryvykh pry proektuvanni vysokoshvydkisnykh mahistralei. Proceedings of the 74 International Scientific & Practical Conference The problems and prospects of railway transport development, May 15-16, 2014, Dnipropetrovsk. 270-271.

6. Kurhan, M. B., Kurhan, D. M. (2014). Osnovni vymohy do vyboru formy i dovzhyny perekhidnykh kryvykh pry proektuvanni vysokoshvydkisnykh mahistralei. Proceedings of the 74 International Scientific & Practical Conference The problems and prospects of railway transport development, May 15-16, 2014, Dnipropetrovsk. 253-254.

7. Kurhan, M. B., Husak, M. A., & Khmelevska, N. P. (2012). Reconstruction of curves for introduction of highspeed traffic of passenger train. Bulletin of Dnipropetrovsk National University of Railway Transport, 40, 90-97.

8. Laguta, V. V. (2002). Improvement of designing of the railway curves in a plan. (PhD thesis). Available from Dnipropetrovsk National University of Railway Transport named after Academician V. Lazaryan, Dnipropetrovsk.

9. Lazaryan, V. A. (1985). O forme perekhodnoy krivoy (Teoreticheskiye osnovy vybora ratsionalnoy formy perekhodnoy krivoy). Dinamika transportnykh sredstv (pp. 10-24). Kyiv: Naukova dumka.

10. Mironov, V. S., & Rudenko, T. A. (2014). Radii of circular curves for high-speed railways when using railway tilting cars. Vestnik transporta Povolzhya, 3(45), 44-50.

11. Borysenko, V., Agarkov, O., Palko, K., & Palko, M. (2016). Modeling of curves in the natural parametrization. Heometrychne modeliuvannia ta informatsiini tekhnolohii, 1, 21-27.

12. Protsenko, A. I., & Bredyuk V. B. (1971). Metodika rascheta na EVM slozhnykh zheleznodorozhnykh krivykh pri tekushchem soderzhanii puti. Sbornik trudov NIIZHT, 130, 48-53.

13. Ustenko, S. A., Didanov, S. V., & Aharkov, O. Y. (2011). Heometrychne modelyuvannya kryvykh liniy iz zadanoyu kryvynoyu v hranychnykh tochkakh. Applied Geometry and Graphics, 87, 404-409.

14. Ustenko, S. A., Didanov, S. V., & Aharkov, O. Y. (2014). Investigation of curves set by cubic distribution of curvature. Science and Transport Progress, 2(50), 164-172. doi: 10.15802/stp2014/23797

15. Ustenko, S. A., & Didanov, S. V. (2013). Method of construction spatial transition curve. Science and Transport Progress, 2(44), 124-128. doi: 10.15802/stp2013/11394

16. Chernyshev, M. A., & Kreynis, Z. L. (1985). Zheleznodorozhnyy put. Moscow: Transport.

17. Shakhunyants, G. M. (1972). Proyektirovaniye zheleznodorozhnogo puti. Moscow: Transport.

18. Shen, T.-I, Chang, C.-H., Chang, K.-Y., & Lu, C. C. (2013). A numerical study of cubic parabolas on railway transition curves. Journal of Marine Science and Technology, 21(2), 191-197. doi: 10.6119/JMST-012-0403-1

19. Eliou, N., & Kaliabetsos, G. (2014). A new, simple and accurate transition curve type, for use in road and railway alignment design. European Transport Research Review, 6(2), 171-179. doi: 10.1007/s12544-013-0119-8

20. Farin, G. (1997). Curves and surfacts for computer-aided geometric design: a practical guide (4th ed.). London: Academic Press Inc.

21. Hooke, R., & Jeeves, T. A. (1961). Direct search solution of numerical and statistical problems. Journal of the ACM, 8(2), 212-229. doi: 10.1145/321062.321069

22. Lipicnik, M. (1998). New form of road/railway transition curve. Journal of Transportation Engineering, 124(6), 546-556. doi: 10.1061/(asce)0733-947x(1998)124:6(546)

23. Long, X.-Y., Wei, Q.-C., & Zheng, F.-Y. (2010). Dynamic analysis of railway transition curves. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 224(1), 1-14.

24. Tari, E., & Baykal, O. (2005). A new transition curve with enhanced properties. Canadian Journal of Civil Engineering, 32(5), 913-923. doi: 10.1139/l05-051

25. Arslan, A., Tari, E., Ziatdinov, R., & Nabiyev, R. I. (2014). Transition Curve Modelling with Kinematical Properties: Research on Log-Aesthetic Curves. Computer-Aided Design & Applications, 11(5), 509-517. doi: 10.1080/16864360.2014.902680

Стаття рекомендована до публікації д.т.н., проф. І. І. Коваленком (Україна); д.т.н., проф.
A. A. Ставинським (Україна); науковим комітетом X Міжнародної науково-практичної конференції «Сучасні інформаційні та комунікаційні технології на транспорті, в промисловості та освіті-2016»

Надійшла до редколегії: 01.12.2016

Прийнята до друку: 02.03.2017

doi 10.15802/stp2017/99942 © В. Д. Борисенко, С. А. Устенко, 2017