ISSN 2307–3489 (Print), ІSSN 2307–6666 (Online)

Наука та прогрес транспорту. Вісник Дніпропетровського
національного університету залізничного транспорту, 2017, № 1 (67)

автоматизовані системи управління на транспорті

Introduction

The existing system of automatic locomotive signaling of continuous action (ALSC) has been developed and started to operate more than 40 years ago. It was built using electromagnetic relay with a numeric code, and has significant disadvantages in spite of a series of upgrades.

The disadvantages of the system include: the limited informative value (three code dispatches and five signal indications on locomotive light-signal); indications of the locomotive light-signal do not reflect the speed limit of passing of traffic guide lights and station lights, depending on the length of the block section and the required speed limit on it; low reliability of locomotive devices is due to the coding by amplitude modulated signal, which has low interference immunity. It is subjected to changes in the duration of the pulses and pauses, which causes failures when applying the codes for a locomotive. The system can receive codes from the next track. It is impossible to use it on the high-speed sections because of the low information content and large inertia [2, 24].

ALSC signaling occurs in specific conditions, peculiar only to this system. Firstly, the signal in each track circuit is transmitted only from its own source and its level in the rails continuously increasing as the train moves. Secondly, the locomotive transition from the one track circuit to another is accompanied by a short interruption in the track signal reception and a dramatic decrease of signal current in the rails. In addition, track circuits, connecting the moving locomotive with the signal transmitter are simultaneously used both in the auto-lock system and on the electrified railways to pass the reverse traction current. The sources of harmonic interferences are the traction substations and the networks of direct and alternating current, as well as the traction drive of locomotive. This particularly applies to electric drives with asynchronous traction motors widely used in recent years [8].

The problems of protection from the main sources of interference at the railway transport, which lead to failures in the operation of signaling and communication equipment, their research and identification, were considered in numerous scientific studies, but they are still relevant [23].

It is known that the amplitude modulation which is used in ALSC for transmission of numeric code combination has low interference immunity as compared to the frequency and phase one. This is explained by the so-called passive pauses, i.e. the lack of signals in the pauses. As a result, upon the receipt of code combination the total signal energy in a cycle is proportional to the ratio of the total duration of all pulses and the duration of code combination. Thus, the difference in energy level of different ALSC codes is from 6 to 11 dB.

Applicable coding principle also has some disadvantages, which do not allow the use of well-known schemes for constructing an optimal receiver. Discrete signal transmission theory is based on the concept of a symbol having a predetermined duration, frequency, and it is not applied to code combinations of the ALSC system. Consequently, it is impossible to use the systems of clock and frame synchronizations, pulse distortion equalizers. For this reason, the interference immunity is reduced almost by 6 dB.

Another factor influencing the interference immunity of ALSC receivers is the signal degradation associated with the carrier frequency. As a rule, filter systems of data transmission in the signals should contain at least eight periods of carrier for each symbol. The exception is the systems with the minimum phase modulation types, operable with a signal/interference ratio at least 20 dB, which cannot be achieved in the channel ALSC. The pulse duration «RY» transmitter KPT-5 is about 0.23 seconds. When a carrier frequency of 25 Hz in a pulse will be at least six periods. The amount of signal degradation in this case is 0.8, i.e. its capacity is reduced by 2 dB.

The amount of losses of the interference immunity of the system is 14 dB. Accordingly, the error probability is increased tenfold as compared to the optimal receiver.

The analysis shows that in ALSC system especially at a frequency of 25 Hz it in principle impossible to obtain high interference immunity [7].

In addition, the railway lines almost always have a longitudinal traction current asymmetry that arises, for example, when breaking the wire rail-bonds or when connecting to one of the rails the earthings of traffic lights supports, masts, and other metal constructions. Therefore, with the electric traction the track transformer core is magnetized by the traction current. During the train movement the current value is changing, and the parasitic modulation of signal current by the traction one takes place. In connection with this the increase in signal current is not always effective and sometimes it results in increase of ALSC failures. It should be noted that with the advent of more powerful locomotives, this phenomenon has become even more pronounced [19, 20].

Purpose

In view of the above mentioned the work is aimed to study the possibility of using the frequency methods (Fourier transform and wavelet decomposition) to increase the reliability and credibility of extraction the informational component of the received code from amplitude-modulated ALSC signals under the action of various types of interferences. The implementation of this research in the future may be the basis for the development of a new receiver of the ALSC system with improved interference immunity.

Methodology

In the existing ALSC system the principle of operation of decoding devices is based on the analysis of amplitude and time characteristics of the received signal. Information value is the number of pulses in the signal, and the protective one is a long interval at the end of the code. On this basis, shortening or lengthening pulses and intervals, filling the long interval or numerical distortions can lead to incorrect reception of the code [3, 6].

Often the information, which is not noticeable in the time representation of the signal, is shown in its frequency representation. Using the Fourier transform (FT) one can study the noisy ALSC code signal comprising interferences from various sources. With the use of FT, a signal is decomposed into elementary harmonic vibrations with different frequencies and all the necessary properties and formulas are expressed using one basis function exp(jωt) or two real functions sin(ωt) and cos(ωt). This gives the spectral information about the signal and describes its behavior in the frequency domain [16, 17, 21, 22].

The Fourier transform is described by the formula:

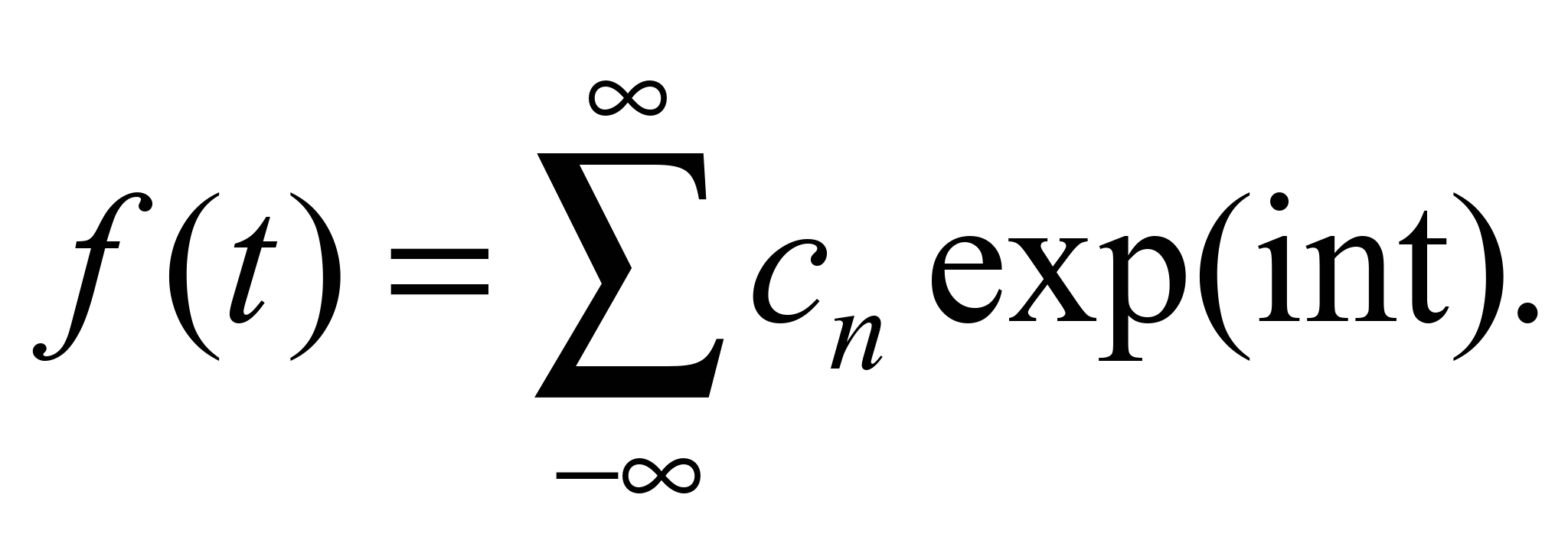
in which the basis function is:

,

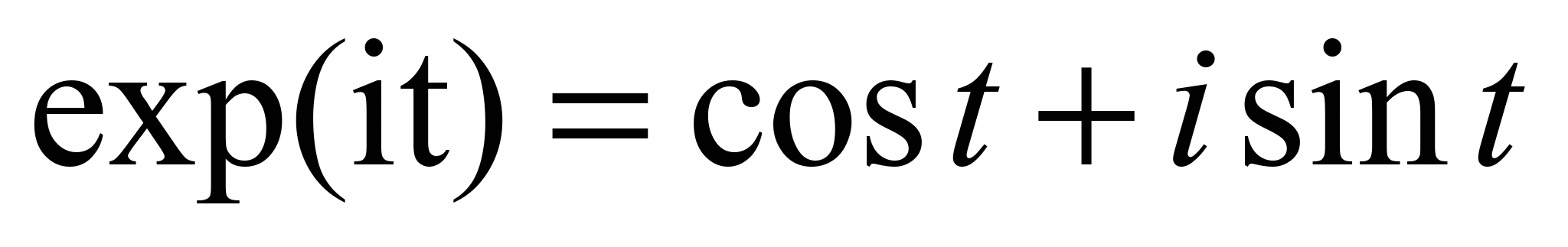As a result of the ALSC signal decomposition it is obtained the basic carrier frequency 25, 50 or 75 Hz (depending on the type of track circuits) and interference frequency. Based on the method of correlation reception according to spectral feature in the amplitude-frequency dependence appropriate ALSC codes can be recognized. But it should be noted that the FT makes it possible to determine the frequency content of the signals, but one cannot determine at what time point there is one or another frequency. This makes the method of spectral analysis unusable for processing of noisy non-periodic signals containing interferences, for which the value of occurrence time is of paramount importance. Moreover, the interferences coinciding in frequency with the desired signal will be decoded as the code elements, which in turn may lead to incorrect representation of signal indication on locomotive traffic light.

In case of decoding the ALSC code signal a significant information load carries the temporal localization of the spectral components and the corresponding time-frequency signal representation, which can be implemented using the wavelet decomposition (WD). As compared to the signal decomposition in Fourier series the wavelets can represent local features of the signal much more accurately and to provide a two-dimensional scan, in which the frequency and the coordinates are regarded as independent variables. This makes it possible to analyze the signal in two spaces at the same time.

The wavelet decomposition is described by the formula:

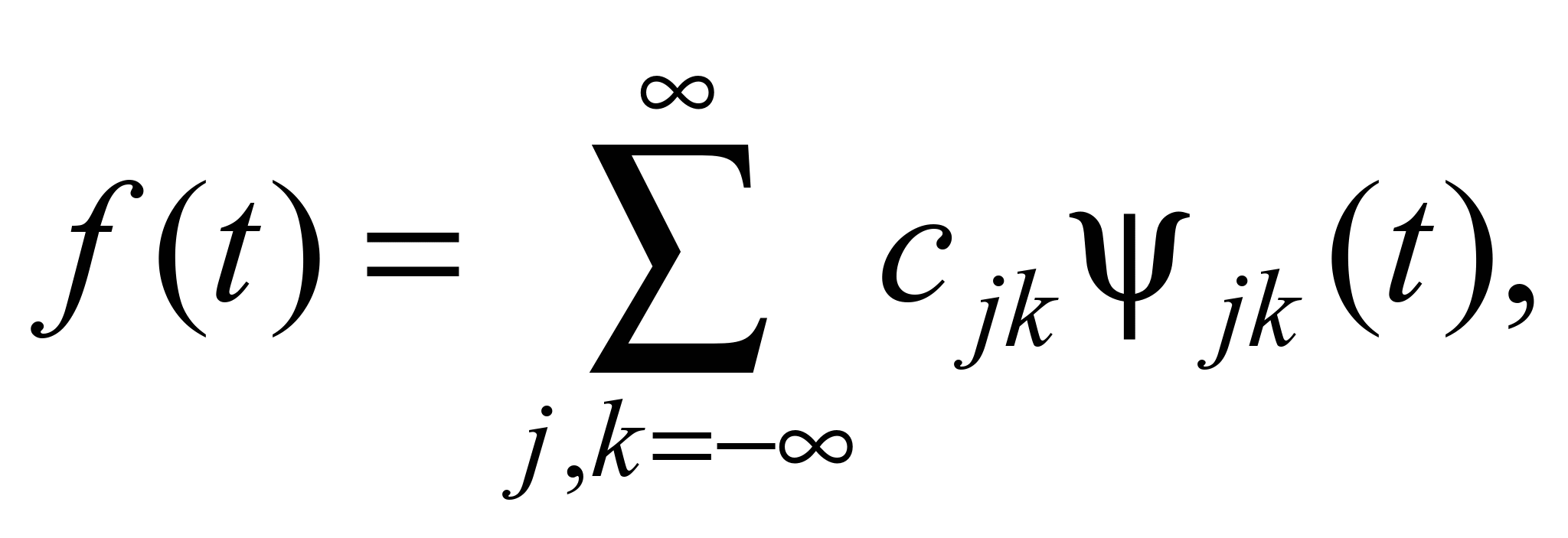
with arbitrary parameters of basis function (which is also called the mother wavelet) – scaling factor j, and the shift parameter k:

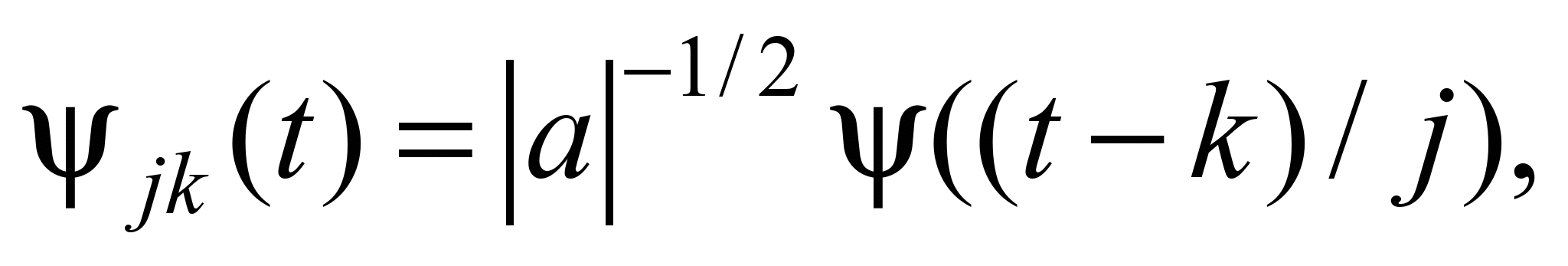
In addition to Fourier transform one can use for signal processing the Short Time Fourier Transform, which is the time, frequency and amplitude function. However, considering the «Heisenberg Uncertainty Principle», this method of processing does not give the opportunity to measure the frequency and time with high accuracy. In turn, the wavelet decomposition makes it possible to reduce the influence of «Heisenberg uncertainty principle» on the obtained time-frequency representation of the signal, where the shift of mother wavelet can be considered as the time elapsed from the time t=0 (since it shows the wavelet location in time), and the scale is the quantity inverse to the frequency.

By analyzing the time intervals equal to the duration of pulses and frequency components contained in it, it is possible to fix the presence of the corresponding code. At this the interference frequency appearing outside the time pulse intervals, even repeating the basic carrier frequency will not carry a critical information load, which in turn will prevent erroneous decryption of the code [4, 12, 14].

Findings

Firstly, it was taken the signal containing in-formation on a green signal indication (G code), without interferences, obtained in the actual operating conditions (Fig. 1). Using the MATLAB programs let us carry out the Fourier transform (Fig. 2) [9, 10, 11] on this signal. Analyzing the Fig. 2, we can see the maximum amplitude surge is at the frequency of 50 Hz and the signal current harmonics is at the frequencies multiples of 50. Since this signal has the correct amplitude and time parameters, we accept it as a reference.

Further we expand this signal by continuous one-dimensional wavelet decomposition with the help of MATLAB pack (Fig. 3), using the Daubechies wavelet with a center frequency of 0.7143 Hz.

In the first field is the amplitude-time characteristic of the signal, in the second field is the wavelet spectrum in which using the color gradation are shown:

• the minimal frequencies, which are present in the signal using dark brown color;

• maximal frequencies (in this case 50 Hz) that are present in the signal using the milky white color.

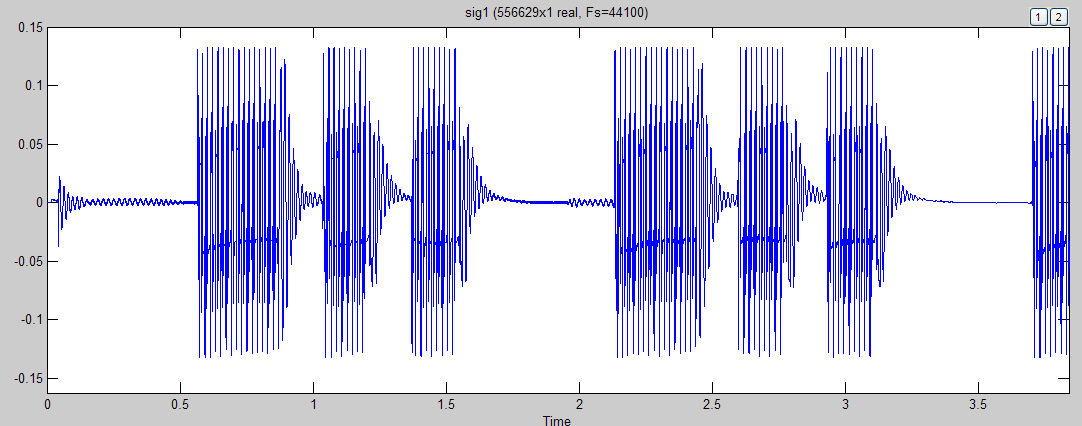
Fig. 1. Code of green fire

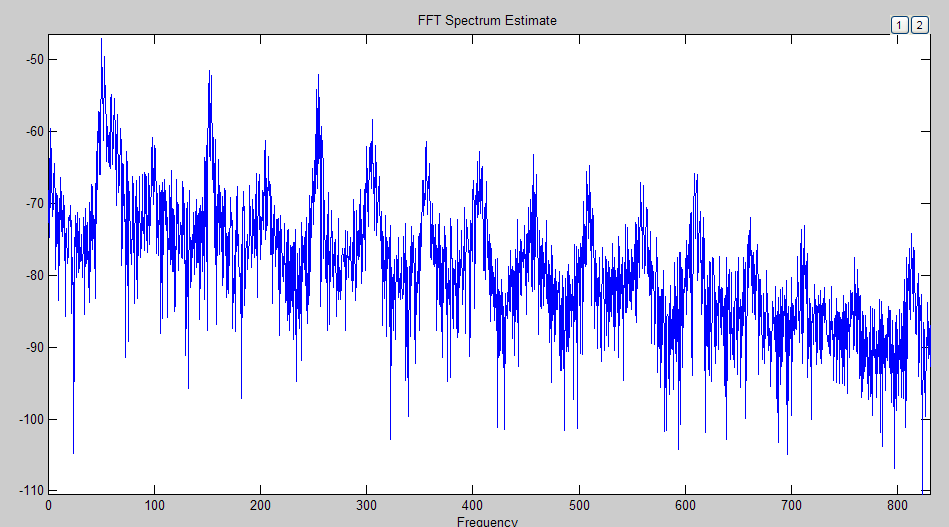
Fig. 2. The spectral composition of green fire code

It can be seen that the entire period of time interval of the code G pulse is filled with the maximal frequency (50 Hz). Time intervals of pauses are not sharp; the signal frequency is reduced and gradually comes to zero. This informs that the signal current in these sections (almost black sections of the spectrum) disappeared.

As in the case of Fourier transform, the wavelet function is characterized by coefficients. But in this case, we are talking about the scale factors (scale), which are visualized in the third field of the Fig. 3. Local maxima of these coefficients are in the fourth field of the Figures. If we draw an analogy with the time-frequency dependency, then the scale will be the reverse value to the frequency, since the small scales correspond to the upper frequencies of the analyzed signal, and the large scales – to the lower frequencies.

This dependence is easy to trace in the Fig. 4. Here on the scale of the range 1-97 pulses and pauses of green code are clearly visible, and on the scale of the range 129-577 pauses are filled with tapered continuous graph of dark brown color. This indicates the presence of low-frequency interferences, which are not essential for decoding the code almost in the entire time interval of the signal current presence [15].

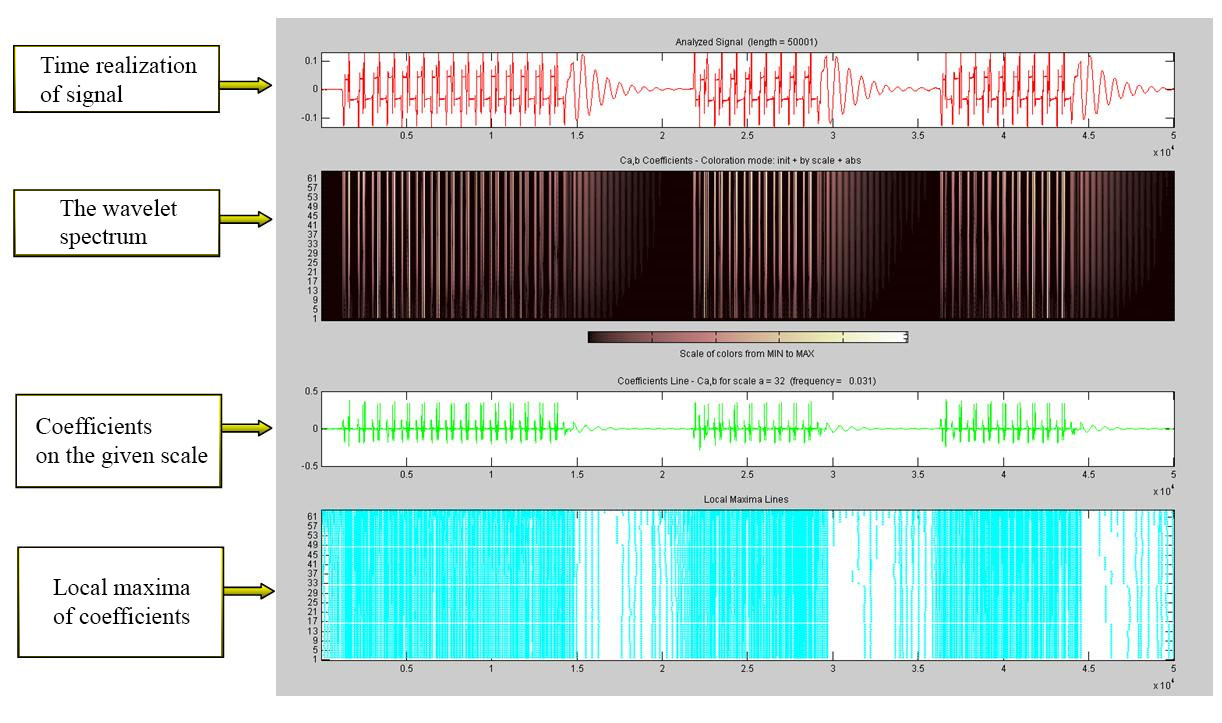
Fig. 3. The spectral composition of green fire code
in continuous one-dimensional wavelet decomposition

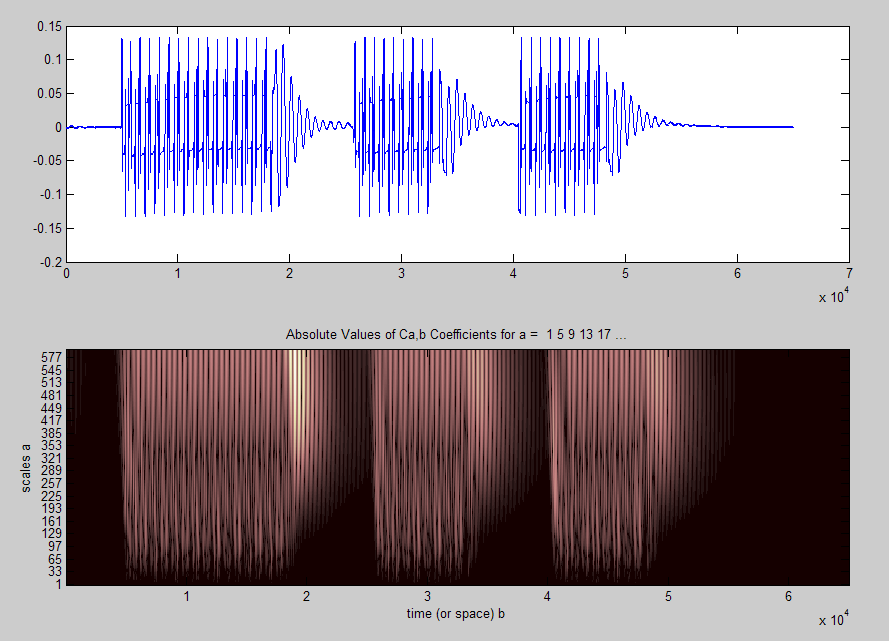
Fig. 4. Time-frequency dependence of green fire code
during continuous one-dimensional wavelet decomposition

The Fig. 5 shows noisy signal in comparison with the reference one, which contains information about green signal indication (G code) obtained under real operating conditions. The figure shows that there is high amplitude of interference, the time of occurrence of which coincides with the time slot of the G code intervals, resulting in their considerable distortions. Using MATLAB let us carry out the Fourier transform on this signal (Fig. 6). Analyzing the Figure 6, it can be noted that some part of interferences has significant spikes at higher frequencies of 380, 620, 1020 Hz, which cannot result in erroneous decoding of code, and the other part of interferences coincides with the carrier frequency of 50 Hz, which could have a fundamental importance to identify the boundaries of the intervals and pauses.

Let us apply continuous one-dimensional wavelet decomposition with the help of MATLAB package (Fig. 7) to the one period of G code using the Daubechies wavelet as in the first example. In this Figure it is clearly seen that the first pause of the G code is filled by the interferences, which coincide with the carrier frequency of 50 Hz (white-milky color of the verticals). Having the ability to monitor the frequency, which is not localized in time, the interference data may cause incorrect decryption of the code. Wavelet analysis gives the possibility to track the presence of the carrier frequency in relation to the time of existence of the spectral component that enables more correct signal decoding.

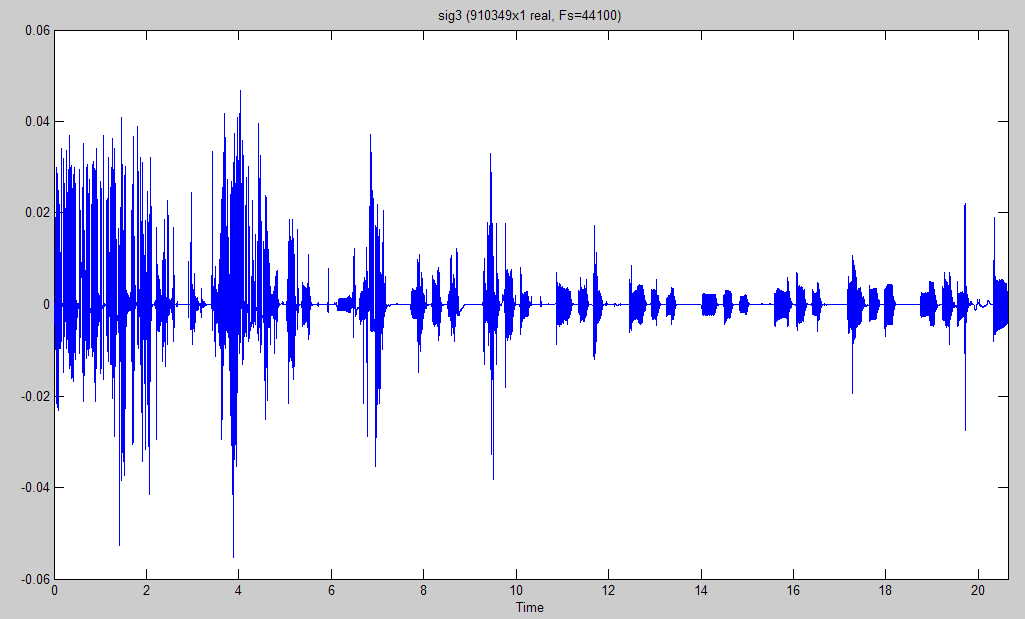
Fig. 5. The green light code containing significant interferences

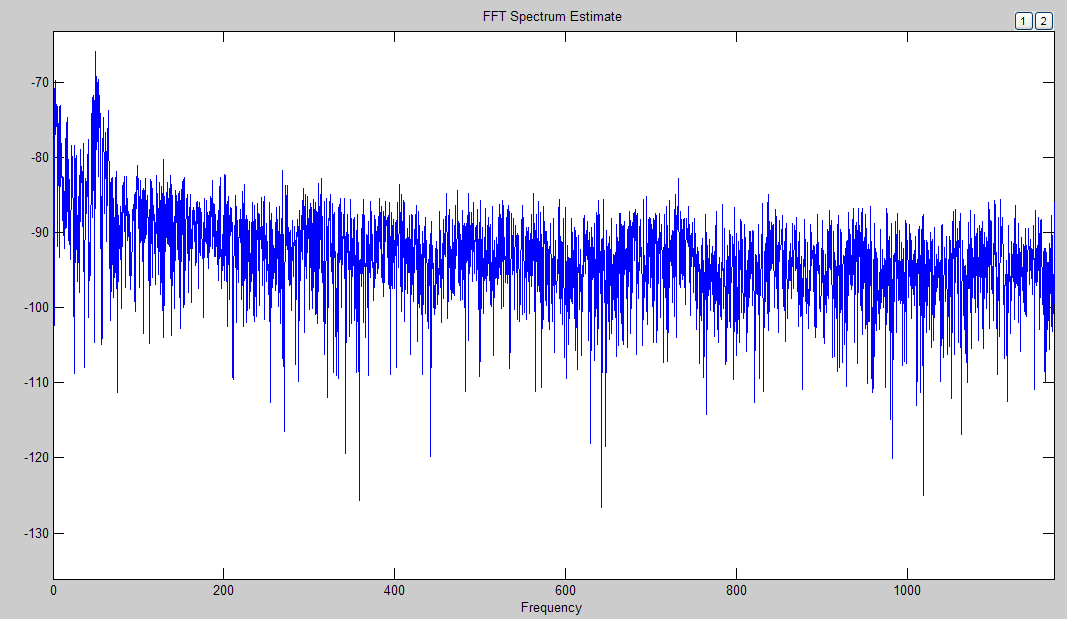
Fig. 6. The spectral composition of the green light code
containing significant interferences

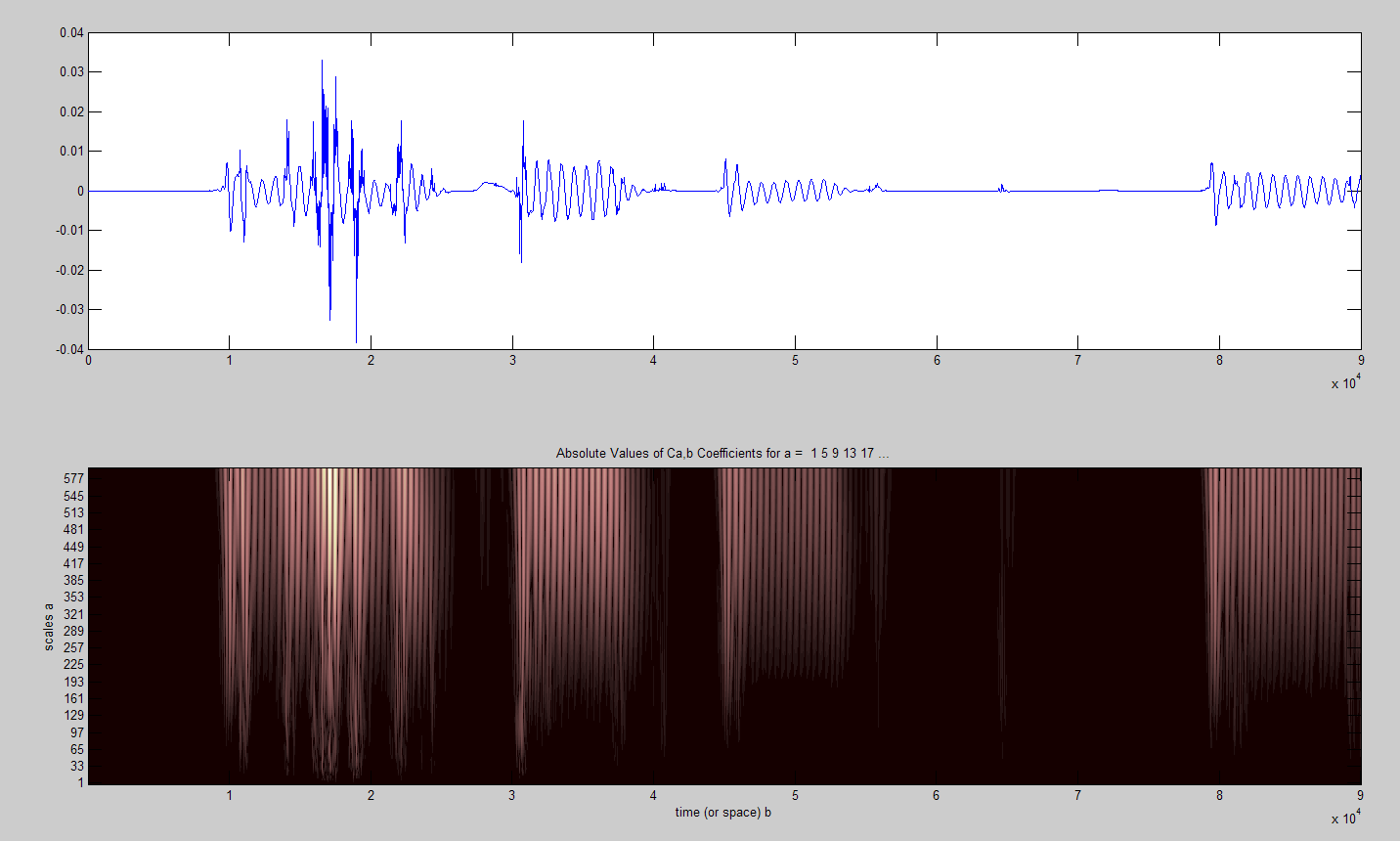
Fig. 7. Time-frequency dependence of green fire code
with interferences during continuous one-dimensional wavelet transformation

Originality and practical value

Upgrading existing ALSC system involves replacing relay by the microprocessor hardware, which has a huge number of advantages. In turn, the digital processing of the received code signal increases reliability that reduces the number of failures in the system operation.

Digital processing of the signal involves the use of a mathematical tool to convert the signal in order to obtain more information about it, which is not available in its original form. Among many well-known signal transformations, such as the Short Time Fourier Transform, Wigner transform and others, the most popular is the classical Fourier transform. By Fourier series expansion of the signal one can determine the value of amplitude and phase both of the studied signal and the interferences, affecting the work of ALSC devices, as well as the distribution density of probability of the code signals, interferences and their statistical characteristics [1, 5, 13]. But there are some disadvantages of this analysis:

• the limited informative value of the nonstationary signal analysis and the fact that it is almost impossible to analyze their peculiarities (breaks, steps, peaks, etc.), since their «dissipation» in the entire frequency range of the spectrum takes place;

• representation of the global information about the frequencies of the studied signal and the lack of representation of the local signal properties with rapid temporal changes in its spectral composition.

Therefore, it is necessary a mathematical optimal signal processing method that can take into account these drawbacks. In this article the wavelet decomposition is considered as a possible alternative, which has all the advantages of Fourier transforms, but it has a number of advantages:

– wavelet bases can be well localized in both frequency and time;

– wavelet bases can be represented by variety of basic functions, the properties of which are focused on the solution of various problems.

This article WD is used to analyze the ALSC signal code, the expansion of the reference and the noisy G code followed by conclusions about the peculiarities of this expansion is carried out. Based on the above mentioned method of the code signal study one can develop a dynamic model of receiver and ALSC decoder, in which the module of digital signal processing applying the wavelet decomposition will be used. This will increase the interference immunity of the locomotive ALSC devices as a whole.

Conclusions

Sending messages about the signals of track traffic lights or the block sections vacancy using the ALSC to the moving locomotive is carried out by electrical signals which are transmitted along the rails and are perceived by the locomotive receiver. The messages during transmission are subjected to distortions that may occur when converting a message during transmission or reception and under the influence of interferences.

Considerable part of interferences may enter the frequency range of the useful signal component and lead to failures in the ALSC operation. Signal decoding and analyzing it in the amplitude-frequency domain, which can be carried out using the FT does not provide comprehensive information about the received code. Information on the signal local features can be obtained by expanding it in the time-frequency domain using WD.

However, wavelet analysis cannot always substitute the Fourier analysis. Many theorems of wavelet analysis are proved by Fourier expansions. Thus, these two types of analysis are rather complementary than mutually exclusive. Improvement of decoding principles by using modern technical devices and methods of digital signal processing are promising for the development of ALSC receiver with high reliability of noisy signals reception [18].

LIST OF REFERENCE LINKS

1. Алексеев, К. А. Очерк «Вокруг CWT» [Electronic resource] / К. А. Алексеев. – Available at: http://matlab.exponenta.ru/wavelet/book3/index.php. – Title from the screen. – Accessed : 30.01.2017.

2. Ананьева, О. М. Прием сигналов АЛСН в условиях действия двухкомпонентной помехи /
   О. М. Ананьева, М. Г. Давиденко // Інформ.-керуючі системи на залізн. трансп. – 2015. – Вип. 5. –
   С. 52–56. doi: 10.18664/ikszt.v0i5.55748.

3. Ананьева, О. М. Синтез нелинейного приемника сигналов АЛСН в условиях действия аддитивной двухкомпонентной помехи / О. М. Ананьева, М. Г. Давиденко // Інформ.-керуючі системи на залізн. трансп. – 2015. – № 6. – С. 46–50. doi: 10.18664/ikszt.v0i6.60191.

4. Астафьева, Н. М. Вейвлет-анализ: основы теории и примеры применения / Н. М. Астафьева // Успехи физических наук. – 1996. – Т. 166, № 11. – С. 1145–1170. doi: 10.3367/UFNr.0166.199611a.1145.

5. Баскаков, С. И. Радиотехнические цепи и сигналы / С. И. Баскаков. – Москва : Высш. шк., 2000. – 448с.

6. Бойник, А. Б. Корреляционный прием и дешифрация кода АЛСН по спектральному признаку /
   А. Б. Бойник, М. Н. Чепцов, А. М. Трунаев // Інформ.-керуючі системи на залізн. трансп. – 2008. – № 2. – С. 64–68.

7. Бушуев, В. И. Явление феррорезонанса в фазочувствительных рельсовых цепях частотой 50 Гц /
   В. И. Бушуев, С. В. Бушуев // Автоматика, связь, информатика. – 2004. – № 3. – С. 31–32.

8. Гаврилюк, В. И. Испытания новых типов подвижного состава на электромагнитную совместимость с устройствами сигнализации и связи / В. И. Гаврилюк, В. И. Щека, В. В. Мелешко // Наука та прогрес транспорту. – 2015. – № 5 (59). – С. 7–15. doi: 10.15802/stp2015/55352.

9. Дремин, И. М. Вейвлеты и их использование / И. М. Дремин, О. В. Иванов, В. А. Нечитайло // Успехи физических наук. – 2001. – Т. 171, № 5. – С. 465–501. doi: 10.3367/UFNr.0171.200105a.0465.

10. Дьяконов, В. П. Вейвлет-анализ в MATLAB реальных осциллограмм [Electronic resource] / В. П. Дьяконов // Измерения в технике и связи. – С. 19–25. – Available at: http://www.tmi-s.com/upload/kipis_articles/article_Dyakonov_3-2010.pdf. – Title from the screen. – Accessed : 27.01.2017.

11. Дьяконов, В. MATLAB. Обработка сигналов и изображений : спец. справ. / В. Дьяконов, И. Абраменкова. – Санкт-Петербург : Питер, 2002. – 608 с.

12. Илюшин, Я. А. Теория и применение вейвлетов / Я. А. Илюшин // Вейвлеты. – 2009. – 1 эл. опт. диск (CD-ROM).

13. Каганов, В. И. Радиотехника+компьютер+Math CAD / В. И. Каганов. – Москва : Горячая линия, 2001. –413 с.

14. Левкович-Маслюк, Л. Введение в вейвлет-анализ : учеб. курс / Л. Левкович-Маслюк, А. Переберин. – Москва : ГрафиКон’99, 1999. – 218 с.

15. Мистецкий, В. Разработка. Непрерывное wavelet преобразование [Electronic resource] / В. Мистецкий // Хабрахабр. – 2010. – Available at: https://habrahabr.ru/post/103899/. – Title from the screen. – Accessed : 17.01.2017.

16. Новиков, Л. В. Основы вейвлет-анализа сигналов : учеб. пособие / Л. В. Новиков. – Санкт-Петербург : ИАнП РАН. –1999. – 152 с.

17. Смоленцев, Н. К. Основы теории вейвлетов. Вейвлеты в MATLAB / Н. К. Смоленцев. – Москва : ДМК Пресс, 2005. – 304 с.

18. Cотник, В. О. Нейромережева модель розпізнавання тривалості імпульсів та інтервалів кодів АЛСН /
    В. О. Cотник, М. М. Бабаєв, М. М. Чепцов // Зб. наук. пр. Донец. ін-ту залізн. трансп. – Донецьк, 2013. – Вип. 36. – С. 67–78.

19. Чепцов, М. Н. Метод определения параметров безопасности программного обеспечения в микропроцессорных системах управления движением поездов / М. Н. Чепцов // Зб. наук. пр. Донец. ін-ту залізн. трансп. – Донецьк, 2005. – Вип. 2. – С. 39–45.

20. Djukanovic, S. A Parametric Method for Multicomponent Interference Suppression in Noise Radars / S. Djukanovic, V. Popovic // IEEE Transactions on Aerospace and Electronic Systems. – 2012. – Vol. 48. – Iss. 3. – P. 2730–2738. doi: 10.1109/taes.2012.6237624.

21. Lewalle, J. Введение в анализ данных с применением непрерывного вейвлет-преобразования [Electronic resource] / J. Lewalle ; пер. с англ. Грибунина В. Г – Available at: http://www.autex.spb.su/download/wavelet/books/lewalle.pdf. – Title from the screen. – Accessed : 27.01.2017.

22. Polikar, R. Введение в вейвлет-преобразование [Electronic resource] / R. Polikar ; пер. с англ. Грибунина В. Г. – Available at: http://www.autex.spb.su/download/wavelet/books/tutorial.pdf. – Title from the screen. – Accessed : 27.01.2017.

23. Said, A. A New Fast and Efficient Image Codec Based on Set Partitioning in Hierarchical Trees / А. Said,
    W. A. Pearlman // Transactions on Circuits and Systems for Video Technology. – 1996. – Vol. 6. – Iss. 3. –
    P. 243–250. doi: 10.1109/76.499834.

24. Study of transmission lines effect on the system operation of continuous automatic cab signaling /
    O. O. Hololobova, V. I. Havryliuk, M. O. Kovryhin, S. Yu. Buriak // Наука та прогрес транспорту. – 2014. – № 5 (53) – С. 17–28. doi: 10.15802/stp2014/30833.

О. О. ГОЛОЛОБОВА^1*, В. І. ГАВРИЛЮК²

^1*Каф. «Автоматика, телемеханіка та зв’язок», Дніпропетровський національний університет залізничного
транспорту імені академіка В. Лазаряна, вул. Лазаряна, 2, Дніпро, Україна, 49010, тел. +38 (056) 373 15 04,
ел. пошта gololobova_oksana@i.ua, ORCID 0000-0003-1857-8196
²Каф. «Автоматика, телемеханіка та зв’язок», Дніпропетровський національний університет залізничного
транспорту імені академіка В. Лазаряна, вул. Лазаряна, 2, Дніпро, Україна, 49010, тел. +38 (056) 373 15 04,
ел. пошта gvi_dp@mail.ru, ORCID 0000-0001-9954-4478

ЗАСТОСУВАННЯ ПЕРЕТВОРЕННЯ

ФУР’Є І ВЕЙВЛЕТ-ПЕРЕТВОРЕННЯ

ДЛЯ ДЕШИФРАЦІЇ КОДУ АЛСН

Мета. Існуюча система автоматичної локомотивної сигналізації (АЛС) була розроблена в кінці минулого століття. У даній системі використовується принцип числового коду, реалізований на базі релейної техніки, у зв’язку з чим вона схильна до впливу різних перешкод. За минулі роки система була неодноразово модернізована, але причини збоїв та відмов у її роботі, як і раніше, залишаються предметом досліджень. Відомо, що частотна і фазова модуляція сигналу має вищу завадостійкість у порівнянні з амплітудною модуляцією. Тому в роботі була поставлена мета – дослідити можливість застосування частотних методів, таких як розкладання в ряд Фур’є та вейвлет-перетворення для вилучення із сигналів АЛС інформаційної складової про прийнятий код в умовах дії різних перешкод. Методика. За допомогою дослідження сигналу в частотній області можна витягти інформацію, недоступну в тимчасовому поданні сигналу. Для цієї мети було використано вейвлет-перетворення, яке дає можливість представляти локальні особливості сигналу та забезпечувати частотно-часове розкладання відразу в двох просторах. Завдяки високій точності представлення сигналу з’являється можливість аналізувати тимчасову локалізацію спектральних компонентів і виключити складові перешкод, навіть у разі збігу частоти перешкоди з частотою сигналу. Результати. Для порівняння інформативності методів розкладання Фур’є та вейвлет-перетворення було досліджено за допомогою програмного пакету MATLAB еталонний та зашумленний сигнал коду зеленого вогню. Докладний аналіз отриманих спектральних характеристик показав, що вейвлет-перетворення дає більш коректну дешифрацію сигналу. Наукова новизна. Заміна електромагнітних реле в системі АЛС на мікропроцесорну апаратуру передбачає застосування будь-якого математичного інструменту для дешифрування коду з метою отримання про нього додаткової інформації. Найчастіше, як математичний інструмент, використовується класичне перетворення Фур’є. Але, в силу наявності ряду недоліків в даному методі, було запропоновано використовувати вейвлет-перетворення, яке має ряд переваг і враховує недоліки перетворення Фур’є. Практична значимість. Наведений метод дослідження кодового сигналу можна покласти в основу розробки динамічної моделі приймача і дешифратора АЛС із використанням модуля цифрової обробки, що дасть можливість підвищити надійність та достовірність вилучення інформаційної складової коду.

Ключові слова: автоматична локомотивна сигналізація; перетворення Фур’є; вейвлет-перетворення; завадостійкість; амплітудна модуляція; зрушення; масштаб; частотно-тимчасова область

о. а. гололобова^1*, в. И. гаврилюк²

^1*Каф. «Автоматика, телемеханика и связь», Днепропетровский национальный университет железнодорожного
транспорта имени академика В. Лазаряна, ул. Лазаряна, 2, Днипро, Украина, 49010, тел. +38 (056) 373 15 04,
эл. почта gololobova_oksana@i.ua, ORCID 0000-0003-1857-8196
²Каф. «Автоматика, телемеханика и связь», Днепропетровский национальный университет железнодорожного
транспорта имени академика В. Лазаряна, ул. Лазаряна, 2, Днипро, Украина, 49010, тел. +38 (056) 373 15 04,
эл. почта gvi_dp@mail.ru, ORCID 0000-0001-9954-4478

Применение преобразования фурье

и вейвлет-преобразования

для дешифрации кода АЛСН

Цель. Существующая система автоматической локомотивной сигнализации (АЛС) была разработана в конце прошлого века. В данной системе используется принцип числового кода, реализованный на базе релейной техники, в связи с чем она подвержена влиянию различных помех. За прошедшие годы система была неоднократно модернизирована, но причины сбоев и отказов в ее работе по-прежнему остаются предметом исследований. Известно, что частотная и фазовая модуляция сигнала имеет более высокую помехоустойчивость в сравнении с амплитудной модуляцией. Поэтому в работе была поставлена цель – исследовать возможность применения частотных методов, таких как разложение в ряд Фурье и вейвлет-преобразование для извлечения из сигналов АЛС информационной составляющей о принимаемом коде в условиях действия различных помех. Методика. С помощью исследования сигнала в частотной области можно извлечь информацию, недоступную во временном представлении сигнала. Для этой цели было использовано вейвлет-преобразование, которое дает возможность представлять локальные особенности сигнала и обеспечивать частотно-временное разложение сразу в двух пространствах. Благодаря высокой точности представления сигнала появляется возможность анализировать временную локализацию спектральных компонент и исключить составляющие помех, даже в случае совпадения частоты помехи с несущей частотой сигнала. Результаты. Для сравнения информативности методов разложения Фурье и вейвлет-преобразования был исследован с помощью программного пакета MATLAB эталонный и зашумленный сигнал кода зеленого огня. Подробный анализ полученных спектральных характеристик показал, что вейвлет-преобразование дает более корректную дешифрацию сигнала. Научная новизна. Замена электромагнитных реле в системе АЛС на микропроцессорную аппаратуру предполагает применение какого-либо математического инструмента для дешифрации кода с целью получения о нем дополнительной информации. Чаще всего, как математический инструмент, используется классическое преобразование Фурье. Но, в силу наличия ряда недостатков в данном методе, было предложено использовать вейвлет-преобразование, которое имеет ряд преимуществ и учитывает недостатки преобразования Фурье. Практическая значимость. Приведенный метод исследования кодового сигнала можно положить в основу разработки динамической модели приемника и дешифратора АЛС с использованием модуля цифровой обработки, что даст возможность повысить надежность и достоверность извлечения информационной составляющей кода.

Ключевые слова: автоматическая локомотивная сигнализация; преобразование Фурье; вейвлет-преобразование; помехоустойчивость; амплитудная модуляция; сдвиг; масштаб; частотно-временная область

REFERENCES

1. Alekseev, K. A. Ocherk «Vokrug CWT». (n.d.). Retrieved from http://matlab.exponenta.ru/wavelet/book3/index.php

2. Аnan’yevа, O. M., & Davidenko M. G. (2015). The reception of the signals of continuous automatic cab signaling (CACS) under the conditions of two-component interference effect. Information and Control Systems at Railway Transport, 5, 52-56. doi: 10.18664/ikszt.v0i5.55748

3. Аnan’yevа, O. M., & Davidenko, M. G. (2015). Synthesis of the nonlinear receiver of CACS signals in the conditions of the additive two-component interference. Information and Control Systems at Railway Transport, 6, 46-50. doi: 10.18664/ikszt.v0i6.60191

4. Astaf’eva, N. M. (1996). Wavelet analysis: basic theory and some applications. Uspekhi Fizicheskikh Nauk, 11(166), 1145-1170. doi: 10.3367/UFNr.0166.199611a.1145

5. Baskakov, S. I. (2000). Radiotekhnicheskiye tsepi i signaly. Moscow: Vysshaya shkola.

6. Boynik, A. B., Cheptsov, M. N., & Trunaev, A. M. (2008). Korrelyatsionnyy priyem i deshifratsiya koda ALSN po spektralnomu priznaku. Information and Control Systems at Railway Transport, 2, 64-68.

7. Bushuev, V. I., & Bushuev, S. V. (2004). Yavleniye ferrorezonansa v fazochuvstvitelnykh relsovykh tsepyakh chastotoy 50 Gts. Automation, Communication and Informatics, 3, 31-32.

8. Havrilyuk, V. I., Shcheka, V. I., & Meleshko, V. V. (2015). Testing New Types of Rolling Stock for Electromagnetic Compatibility with Signaling and Communication Devices. Science and Transport Progress, 5(59), 7-15. doi: 10.15802/stp2015/55352

9. Dremin, I. M., Ivanov, O. V., & Nechitailo, V. A. (2001). Wavelets and their uses. Uspekhi Fizicheskikh Nauk, 5(171), 465-501. doi: 10.3367/UFNr.0171.200105a.0465

10. Dyakonov, V. (2010). Wavelet signal analysis of actual oscillograms using Math. Test & Measuring Instruments and Systems, 3, 19-25. Retrieved from http://www.tmi-s.com/upload/kipis_articles/article_Dyakonov_3-2010.pdf

11. Dyakonov, V. & Abramenkova, I. (2002). MATLAB. Obrabotka signalov i izobrazheniy: spetsialnyy spravochnik. Saint Petersburg: Piter.

12. Ilyushin, Y. A. (2009). Teoriya i primeneniye veyvletov. [CD].

13. Kaganov, V. I. (2001). Radiotekhnika+kompyuter+Math CAD. Moscow: Goryachaya liniya.

14. Levkovich-Maslyuk, L., & Pereberin, A. (1999). Vvedeniye v veyvlet-analiz. Moscow: GrafiKon’99.

15. Mistetskiy, V. (2010). Razrabotka. Nepreryvnoye wavelet preobrazovaniye. Habrahabr. Retrieved from https://habrahabr.ru/post/103899/

16. Novikov, L. V. (1999). Osnovy veyvlet-analiza signalov. St. Petersburg: IAI RAS.

17. Smolentsev, N. K. (2005). Osnovy teorii veyvletov. Veyvlety v MATLAB. Moscow: DMK Press.

18. Cotnyk, V. O., Babaiev, M. M., & Cheptsov, M. M. (2013). Neiromerezheva model rozpiznavannia tryvalosti impulsiv ta intervaliv kodiv ALSN. Zbirnik naukovih prac' of Donetsk Railway Transport Institute, 36, 67-78.

19. Cheptsov, M. M. (2005). The method of determination of parameters software safety in microsystems by moving the trains. Zbirnik naukovih prac' of Donetsk Railway Transport Institute, 2, 39-45.

20. Djukanovic, S., & Popovic, V. (2012). A Parametric Method for Multicomponent Interference Suppression in Noise Radars. IEEE Transactions on Aerospace and Electronic Systems, 48(3), 2730-2738. doi: 10.1109/taes.2012.6237624

21. Lewalle, J. (n.d.) Vvedeniye v analiz dannykh s primeneniyem nepreryvnogo veyvlet-preobrazovaniya (V. G. Gribunin, Trans.). Saint Petersburg Autex. Retrieved from http://www.autex.spb.su/download/wavelet/books/lewalle.pdf

22. Polikar, R. (n.d.) Vvedeniye v veyvlet-preobrazovaniye (V. G. Gribunin, Trans.). St. Petersburg: Autex. Retrieved from http://www.autex.spb.su/download/wavelet/books/tutorial.pdf

23. Said, A., & Pearlman, W. A. (1996). A New Fast and Efficient Image Codec Based on Set Partitioning in Hierarchical Trees. Transactions on Circuits and Systems for Video Technology, 6(3), 243-250. doi: 10.1109/76.499834

24. Hololobova, O. O., Havryliuk, V. I., Kovryhin, M. O., & Buriak, S. Y. (2014). Study of transmission lines effect on the system operation of continuous automatic cab signaling. Science and Transport Progress, 5(53), 17-28. doi: 10.15802/stp2014/30833

Prof. A. V. Kovalenko, D. Sc. (Phys.-Math.); Associate Prof. V. I. Profatilov, Ph.D. (Tech.) recommended this article to be published)

Accessed: Oct. 12, 2016

Received: Jan. 04, 2017

doi 10.15802/stp2017/92771 © O. O. Hololobova, V. I. Gavryliuk, 2017