Н. Н. БЕЛЯЕВ1*, М. О. ОЛАДИПО2*
Введение
Транспортировка
угля в Нигерии осуществляется
железнодорожным транспортом (рис. 1),
поскольку страна имеет достаточно
хорошо развитую сеть железных дорог.
Однако, транспортировка угля осуществляется
в полувагонах, вследствие чего происходит
вынос угольной пыли [6, 12, 14]. При таком
выносе угольной пыли происходит
интенсивное загрязнение транспортного
коридора и прилегающей территории.

Рис. 1. Перевозка угля в Нигерии
Fig. 1.
Transportation of
coal in
Nigeria
Особенно
опасен такой процесс загрязнения, когда
состав проходит через железнодорожные
станции (рис. 2), вблизи селитебных зон
или по территории промышленных объектов
[13, 15]. В этой связи возникает важная
задача по прогнозированию интенсивности
загрязнения транспортного коридора и
примагистральной территории при
перевозке угля [13, 16, 17].

Рис. 2. Железнодорожная
станция Enugu
(Нигерия):
1
– место «входа» состава с углем в
расчетную область
Fig. 2. Railway
station Enugu (Nigeria): 1 – «entry»
point of the train with coal into the computational region
Анализ
литературных источников, посвященных
этой проблеме, показал, что для
прогнозирования процесса загрязнения
воздушной среды используется модель
Гаусса [3, 5, 8], реализованная в виде кода
«AERMOD» [10]. Данный пакет
программ позволяет рассчитать загрязнение
окружающей среды в приближении «постоянно
действующий точечный источник». Модель
Гаусса является эффективным инструментом
оценки уровня загрязнения воздушной
среды, но не учитывает профиль скорости
ветра, движение источника эмиссии.
Применение CFD моделей для решения этой
задачи требует использования мощных
компьютеров и значительных затрат
времени на получение прогнозных данных.
В этой связи, важно отметить, что
актуальной задачей является разработка
эффективных численных моделей,
позволяющих учитывать основные
физические факторы, влияющие на
формирование зоны загрязнения в
транспортном коридоре при движении
состава с углем и разработка методов
по минимизации выноса угольной пыли
из полувагонов [4, 6, 16].
Цель
Целью
данной работы является разработка 3D
численной модели для прогноза уровня
загрязнения атмосферы при эмиссии
пылевых загрязнений из полувагонов.
Ставится задача создания модели, которая
позволяла бы учитывать основные
физические факторы рассеивания пыли
в атмосфере, движение источника эмиссии
(состав с углем) и при этом требовала
бы малых затрат компьютерного времени
при практической реализации (эта модель
группы «screening models»).
Математическая
модель. Прогноз уровня загрязнения
атмосферы при выносе пылевых загрязнений
из полувагона осуществляется на базе
фундаментального уравнения массопереноса
[1, 2, 7, 9, 11]:
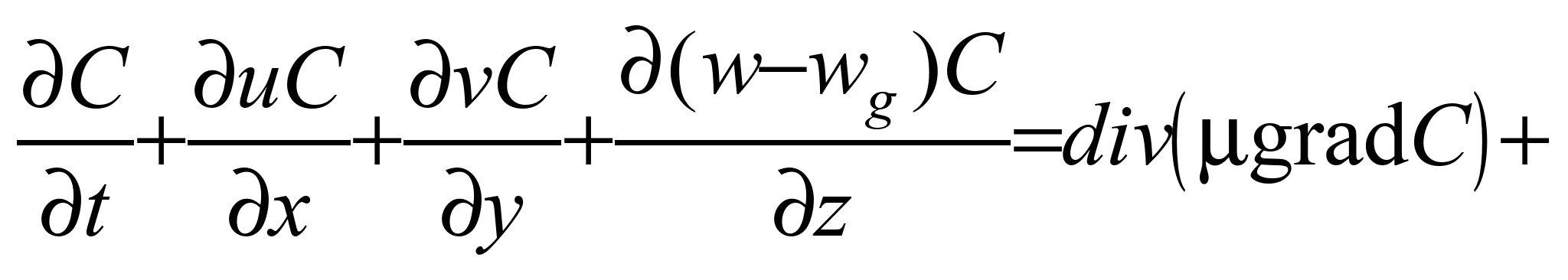
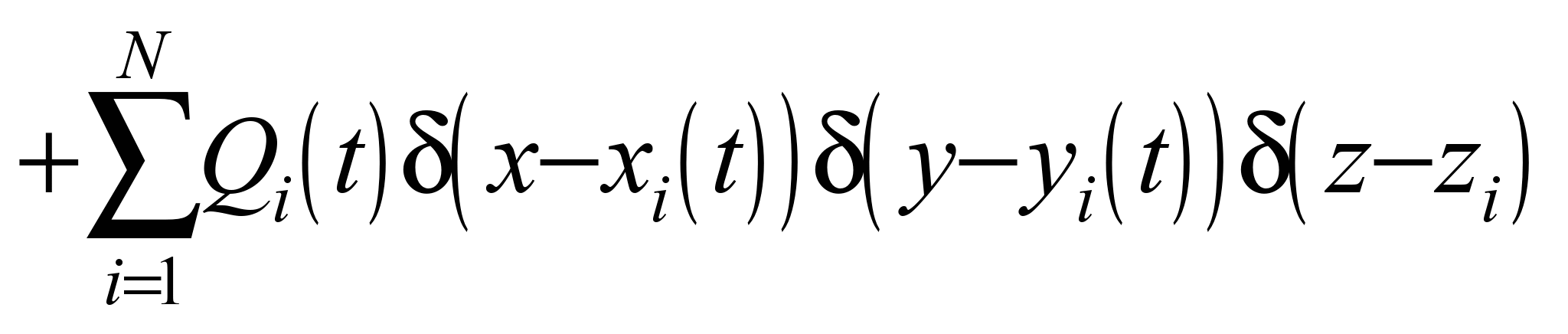 , (1)
, (1)
где
 – концентрация загрязняющего
вещества (пылевой загрязнитель);
– концентрация загрязняющего
вещества (пылевой загрязнитель);
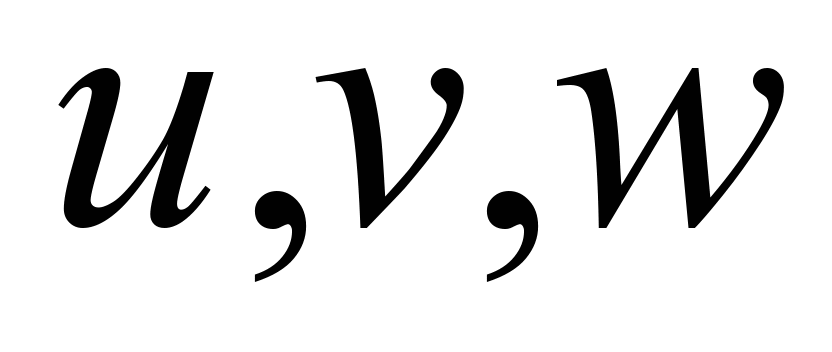 – компоненты вектора скорости воздушного
потока;
– компоненты вектора скорости воздушного
потока;
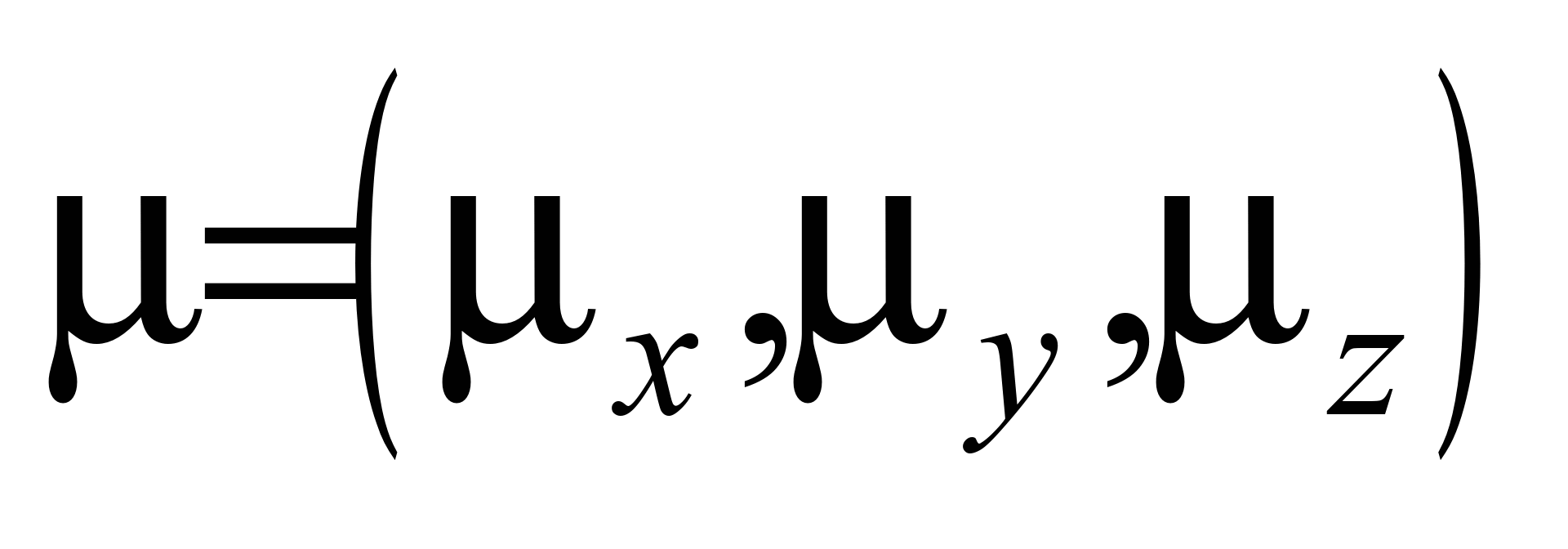 – коэффициенты атмосферной турбулентной
диффузии;
– коэффициенты атмосферной турбулентной
диффузии;
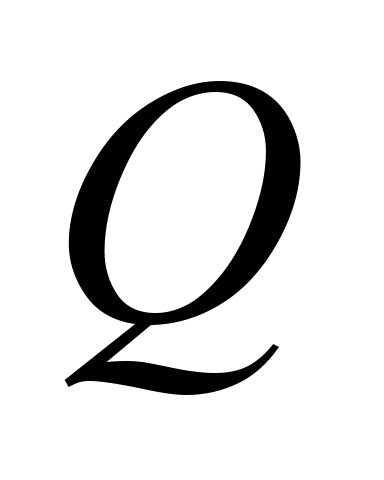 – интенсивность выброса загрязнителя
от «насыпи» в полувагоне;
– интенсивность выброса загрязнителя
от «насыпи» в полувагоне;
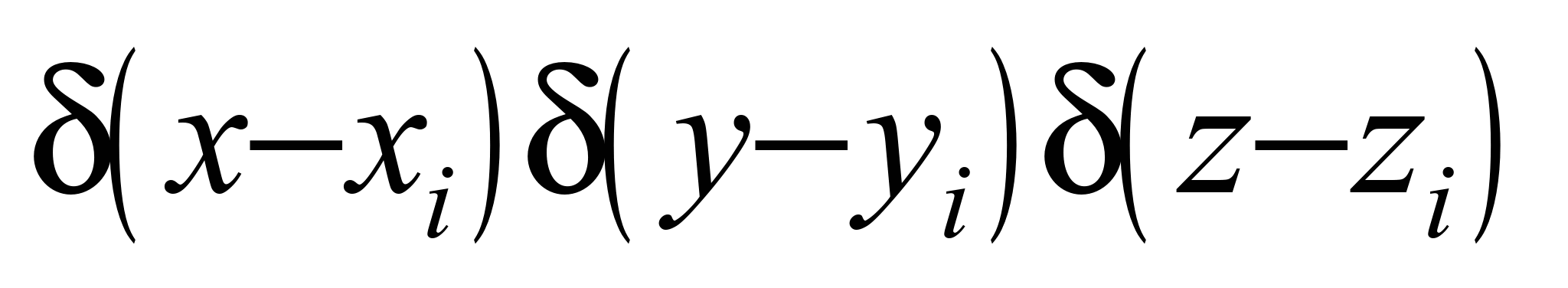 – дельта-функция Дирака;
– дельта-функция Дирака;
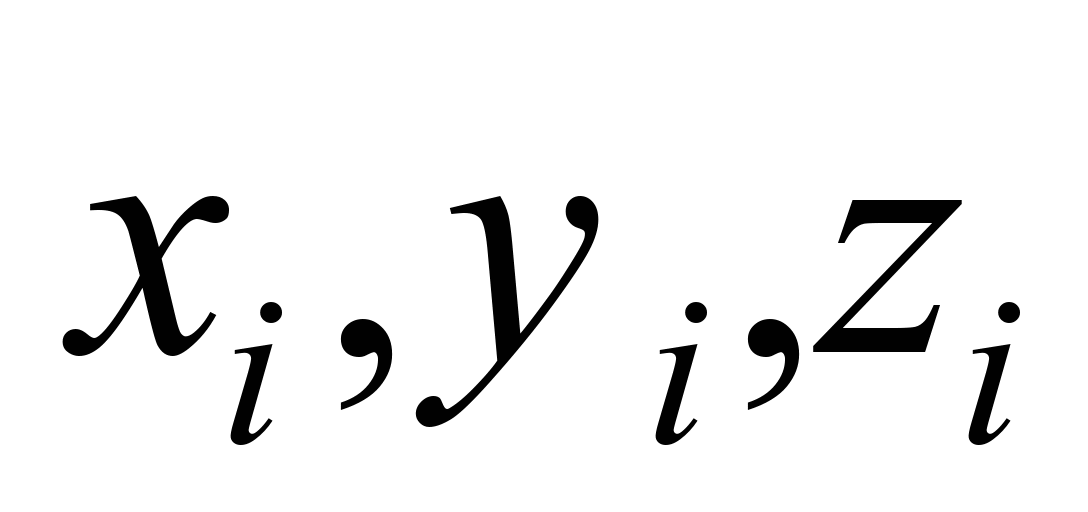 – координаты источника выброса;
– координаты источника выброса;
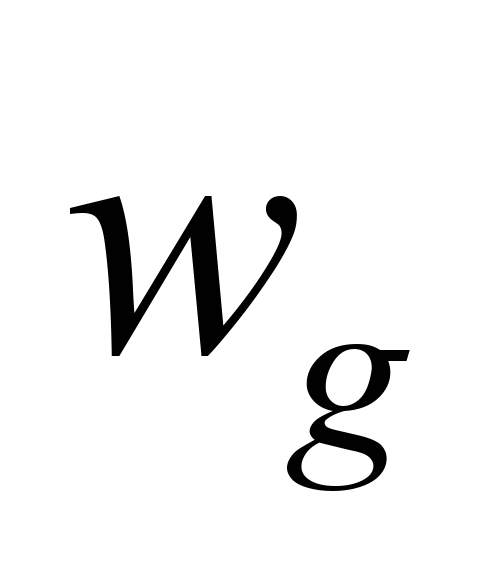 – скорость гравитационного оседания
пыли; t – время.
– скорость гравитационного оседания
пыли; t – время.
Постановка
краевых условий для данного уравнения
рассмотрена в работах [1, 2, 7, 9]. Отметим,
что координаты источника эмиссии
(полувагонов с углем) зависят от времени.
Таким образом, с помощью задания
зависимости
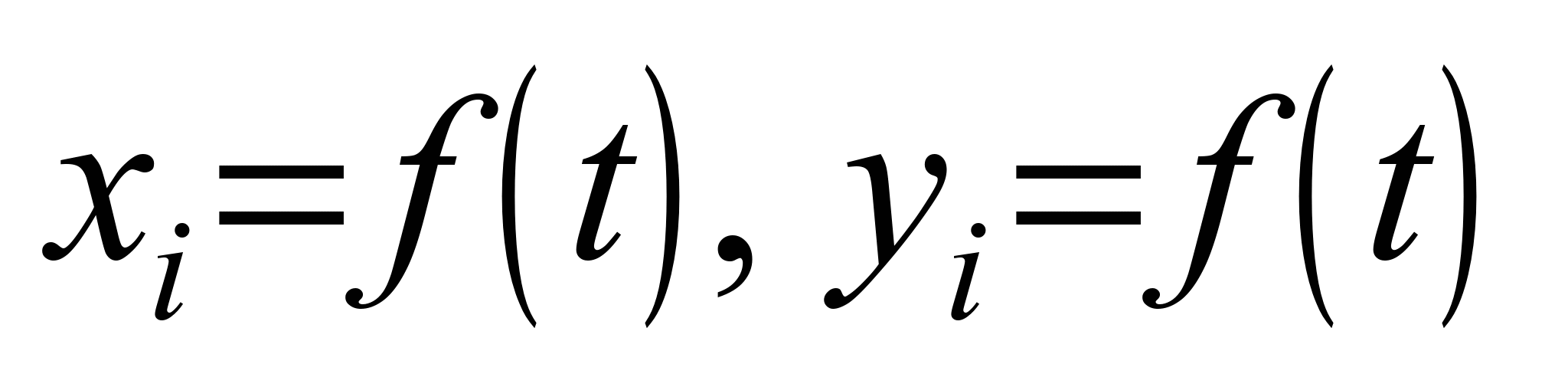 можно моделировать изменения положения
вагонов в расчетной области с течением
времени, то есть моделировать
движение состава с углем.
можно моделировать изменения положения
вагонов в расчетной области с течением
времени, то есть моделировать
движение состава с углем.
В
разработанной численной модели
используются следующие зависимости
для задания профиля ветра и вертикального
коэффициента атмосферной диффузии [3,
5]:
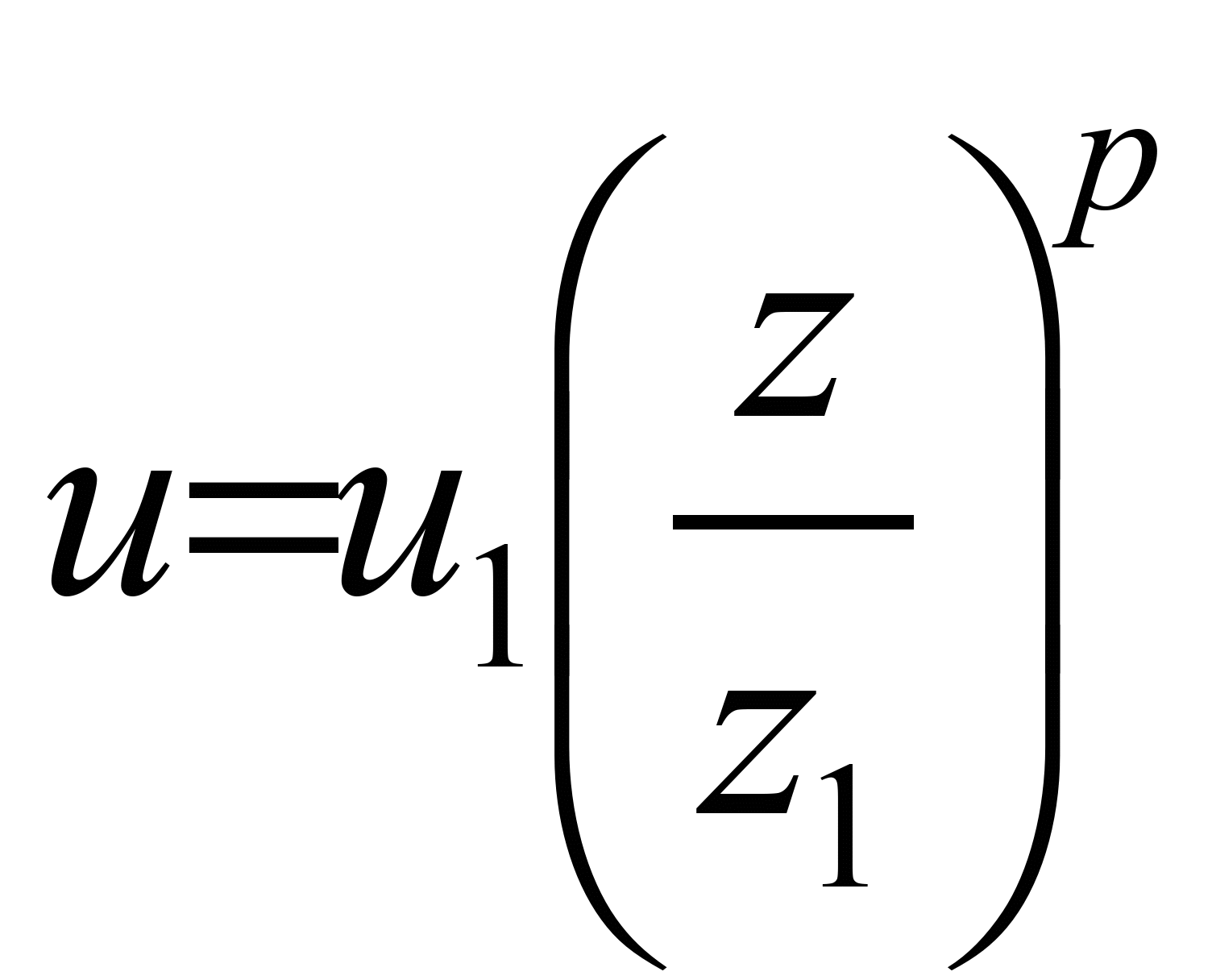 ,
,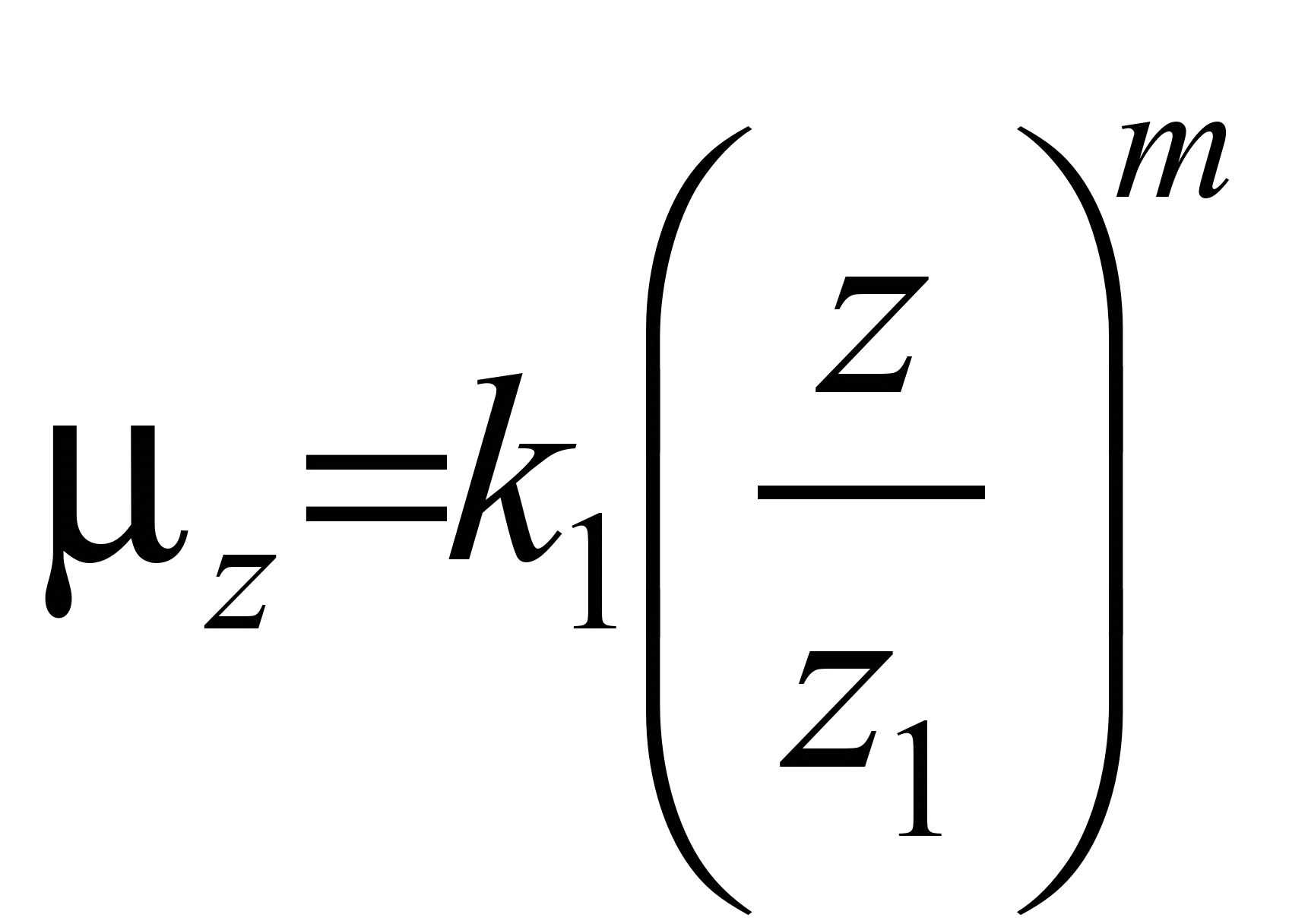 ,
,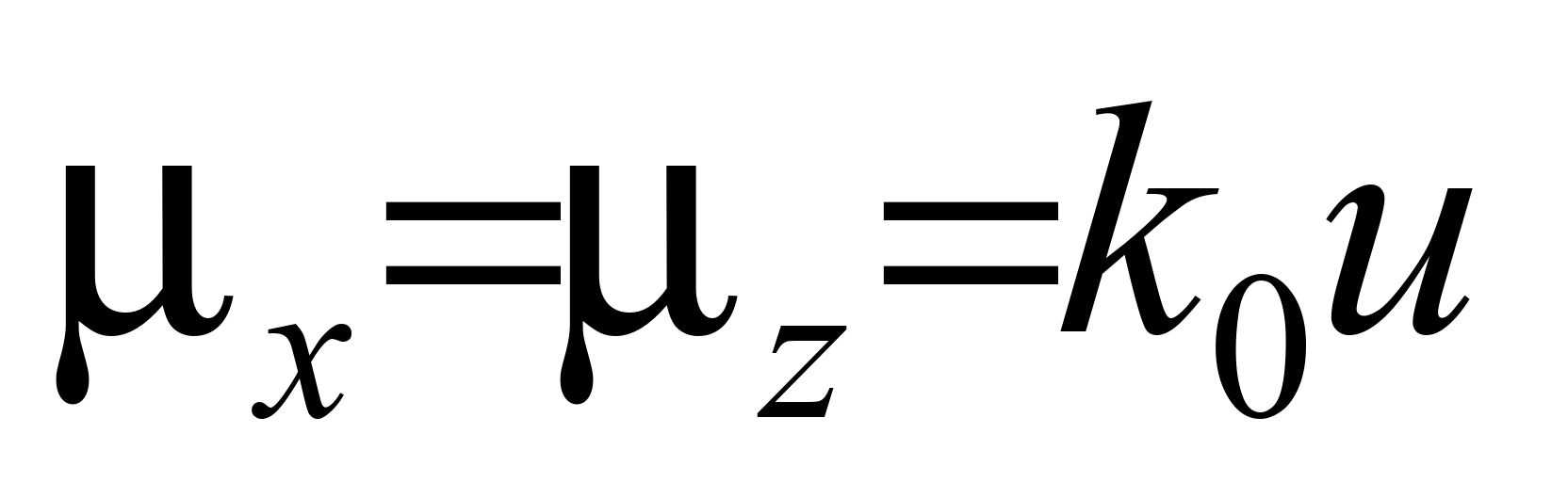 , (2)
, (2)
где u1
– скорость ветра на высоте z1
(принимается
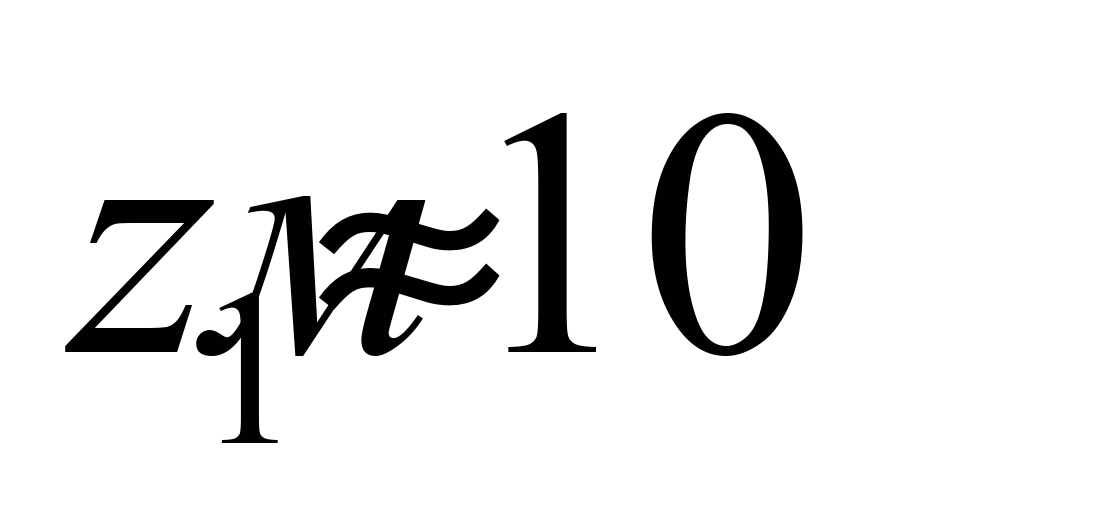 );
);
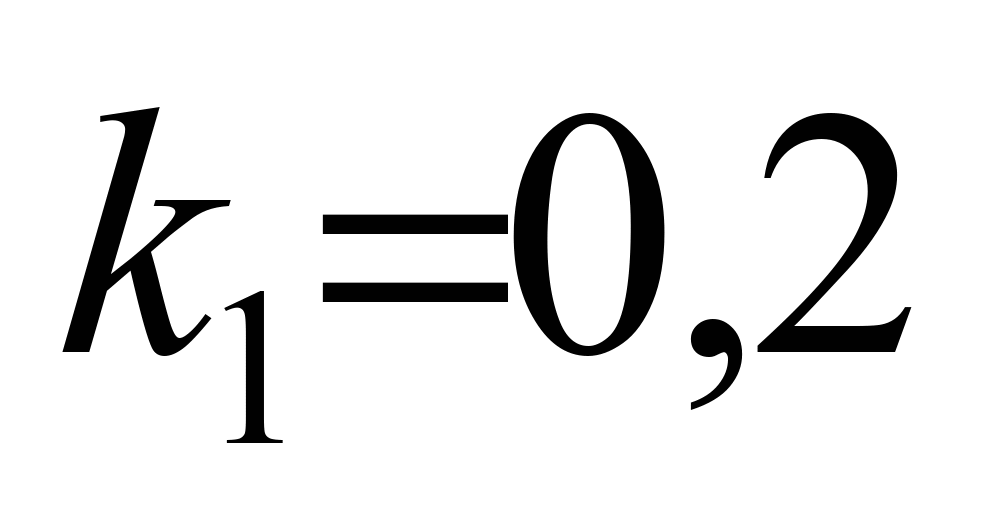 ;
;
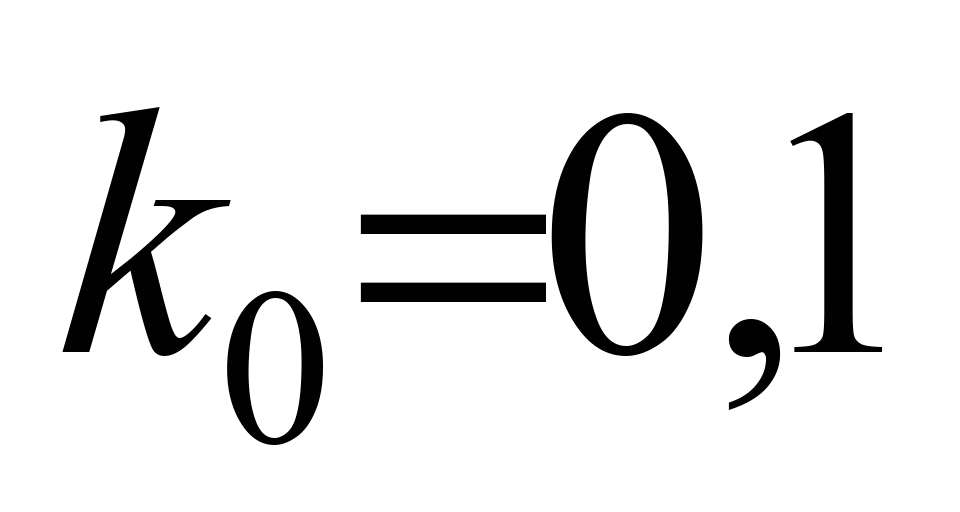 ;
;
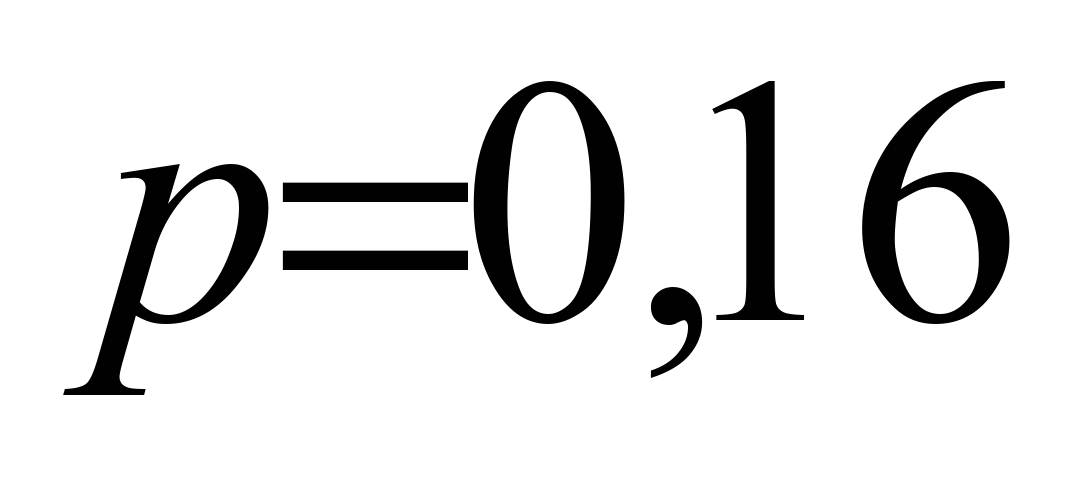 ;
;
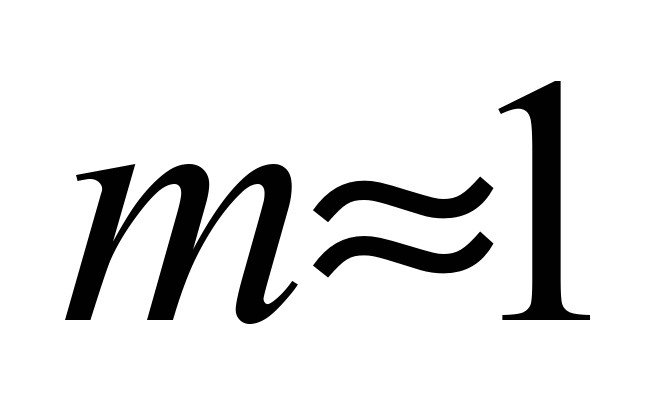 .
.
Численное
решение. Для численного интегрирования
уравнения (1) используются неявные
разностные схемы [1, 2, 9, 11]. Предварительно
данное уравнение расщепляется на
дифференциальном уровне на
последовательность следующих уравнений:
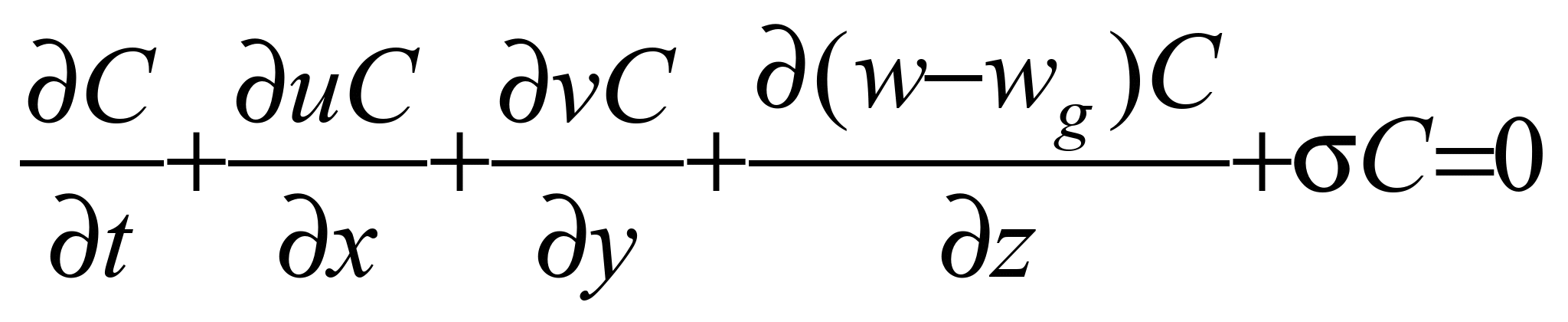 ,
,
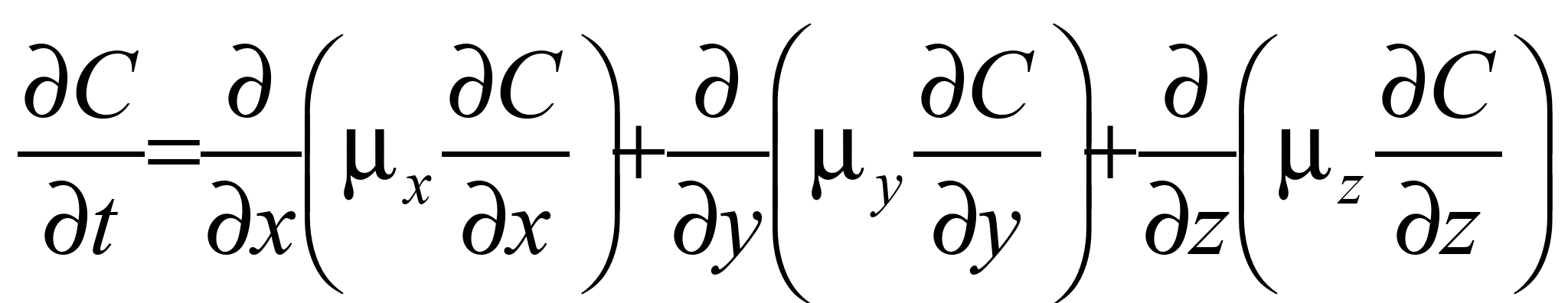 ,
,
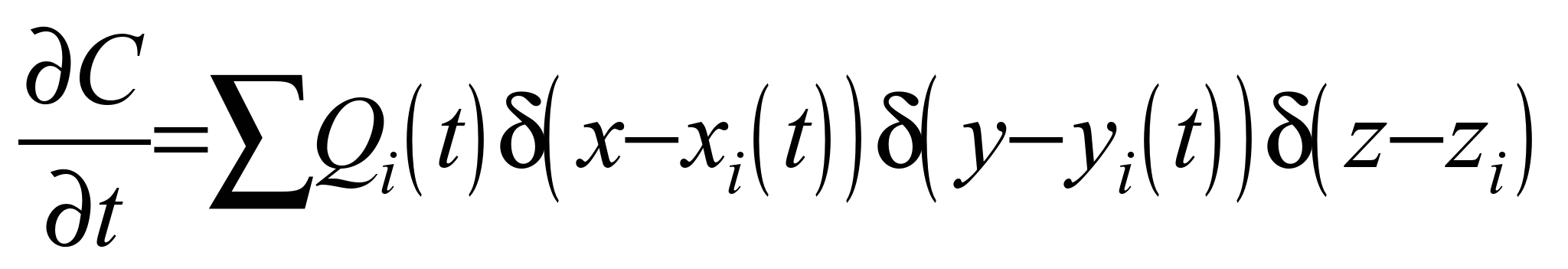 .
.
Первое
уравнение данной системы описывает
перенос пыли по траекториям. Второе
уравнение описывает перенос пыли за
счет атмосферной турбулентной диффузии.
Третье уравнение учитывает изменение
концентрации пыли в атмосферном воздухе
под действием источников эмиссии (вынос
пыли из полувагонов). Численное
интегрирование этих уравнений выполняется
на прямоугольной разностной сетке. Для
численного интегрирования первого
уравнения этой системы используется
попеременно-треугольная неявная
разностная схема. Для численного
интегрирования второго уравнения
данной системы используется метод
суммарной аппроксимации. Для численного
интегрирования третьего уравнения
используется метод Эйлера.
Применяемая
неявная попеременно-треугольная
разностная схема строиться таким
образом, чтобы на каждом шаге расщепления
неизвестное значение концентрации
пыли определялось по явной схеме
бегущего счета [1, 2]. Это позволяет
получить простые рекуррентные
соотношения, которые удобны для
программирования. Для программной
реализации разработанной численной
модели использовался FORTRAN. Создан
специализированный код «Coal
Dust Emission».
Для
проведения расчетов на базе этого кода
необходимо задать:
1. Класс
устойчивости атмосферы.
2. Профиль
скорости ветра.
3. Скорость
движения состава, направление движения.
4. Интенсивность
выделения пыли от насыпи в полувагоне.
Отметим,
что время расчета 3D задачи
и задачи массопереноса составляет
порядка 6 сек. Таким образом, разработанный
код позволяет быстро проводить серийные
расчеты в течение одного рабочего дня.
Результаты
Пример
практического использования разработанного
кода «Coal Dust
Emission» показан ниже.
Рассматривался процесс движения состава
с углем на железнодорожной станции
Enugu (Нигерия). Ставилась задача по
определению интенсивности загрязнения
транспортного коридора при вхождении
состава с углем на станцию. На рис.
2 (позиция 1) показана точка «входа»
состава на станцию. Стрелкой, на данном
рисунке, показано направление движения
состава.
На
последующих рисунках показана зона
пылевого загрязнения (уровень z =
1,7 м) для различных моментов времени.

Рис. 3. Зона пылевого
загрязнения
на станции Enugu
(t = 15
c)
Fig. 3. Dust-polluted zone
at the Enugu station (t = 15
sec)
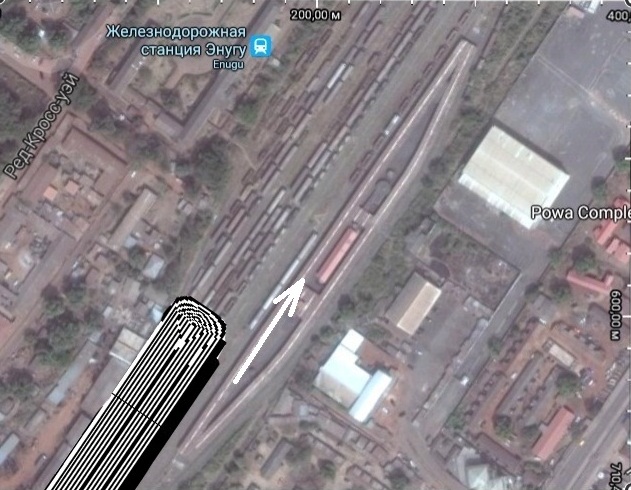
Рис. 4. Зона пылевого
загрязнения
на станции Enugu
(t = 37
c)
Fig. 4. Dust-polluted zone
at
the Enugu station (t = 37 sec)
Как
видно из представленных рисунков, при
движении состава формируется обширная
зона пылевого загрязнения. Это значит,
что под влияние источника эмиссии пыли
попадают работники станции – монтеры
пути, сцепщики, сигналисты и т.д. Также
очевидно, что пылевое загрязнение может
проникнуть внутрь вагонов, находящихся
рядом составов. В этой связи возникает
важная задача по минимизации выноса
угольной пыли из полувагонов. Ниже
рассматривается новый подход к решению
этой задачи.
Рабочая
гипотеза. Для минимизации выноса
угольной пыли из полувагона предлагается
осуществить геометрическое воздействие
на воздушный поток, который обтекает
полувагон с грузом угля. Для этого
рекомендуется установить на полувагон
дополнительные борта специальной
формы, например, как показано на рис. 5
(борт типа «внутреннее крыло»). Для
обоснования, предложенной конструкции
борта, проведем рассуждения с
использованием методов системного
анализа. Для этой цели рассмотрим
эмпирическую зависимость для оценки
интенсивности пылевыделения от
поверхности угля в полувагоне. Эта
зависимость имеет вид [6]:
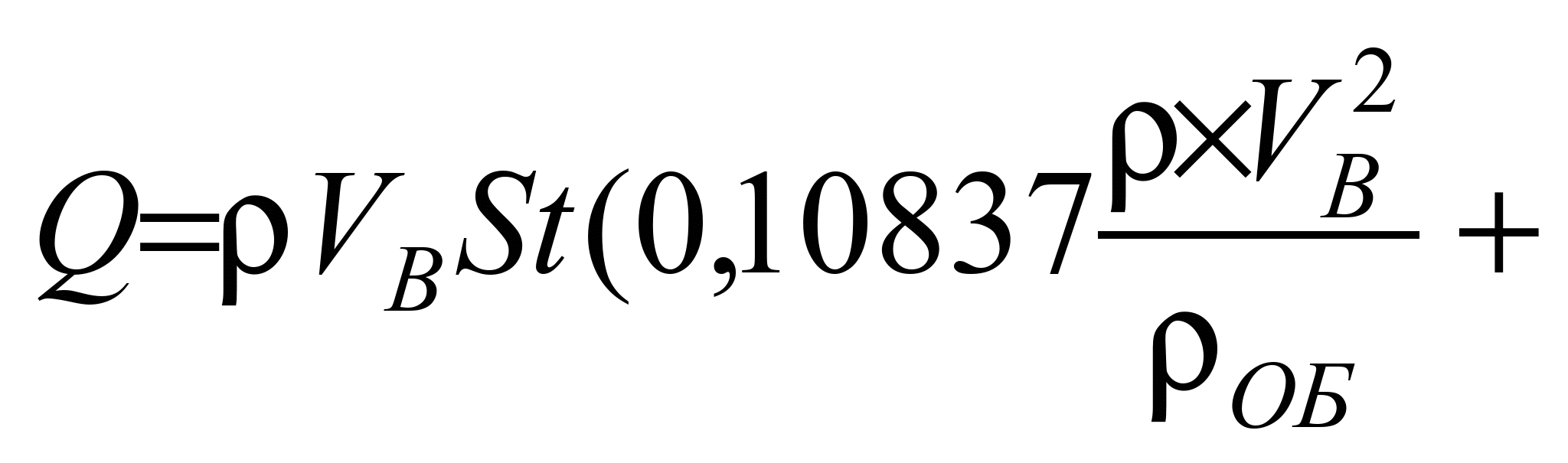
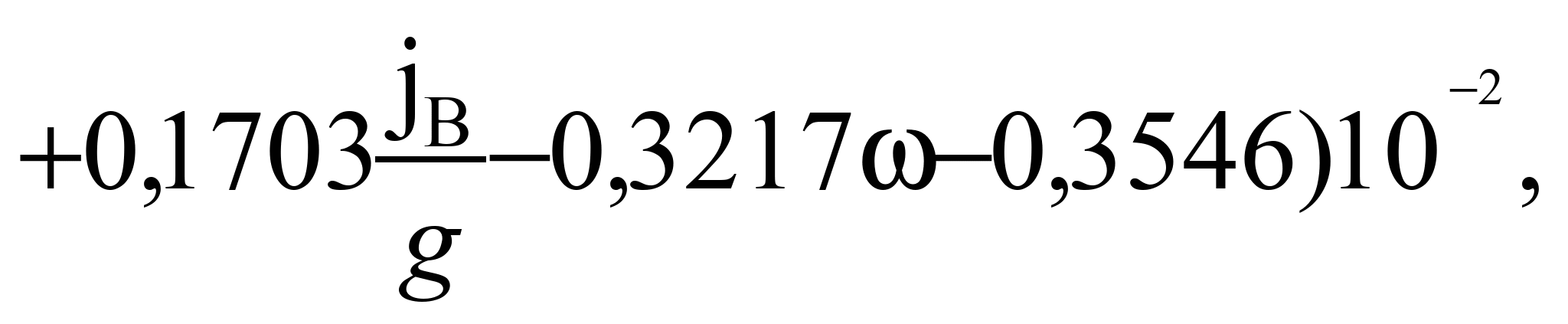 (3)
(3)
где
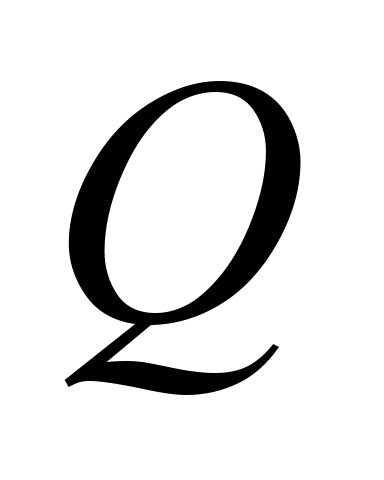 – потери угля при транспортировке;
– потери угля при транспортировке;
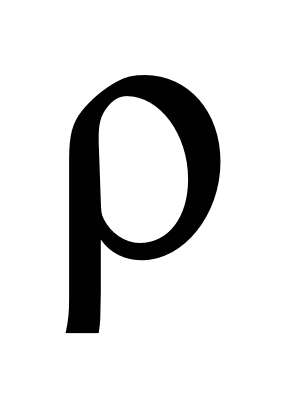 – плотность воздуха;
– плотность воздуха;
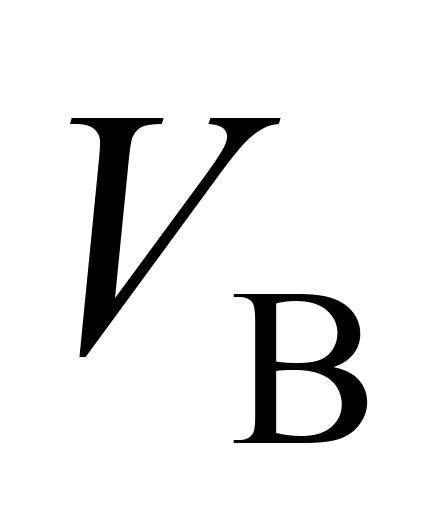 – скорость воздуха вблизи обтекаемой
поверхности;
– скорость воздуха вблизи обтекаемой
поверхности;
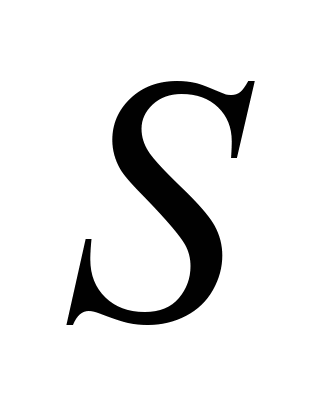 – площадь поверхности, из которой
выдувается груз;
– площадь поверхности, из которой
выдувается груз;
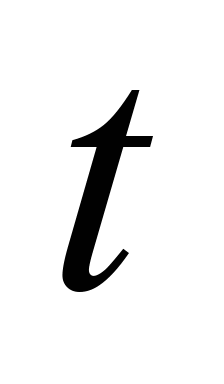 – продолжительность процесса выдувания
груза;
– продолжительность процесса выдувания
груза;
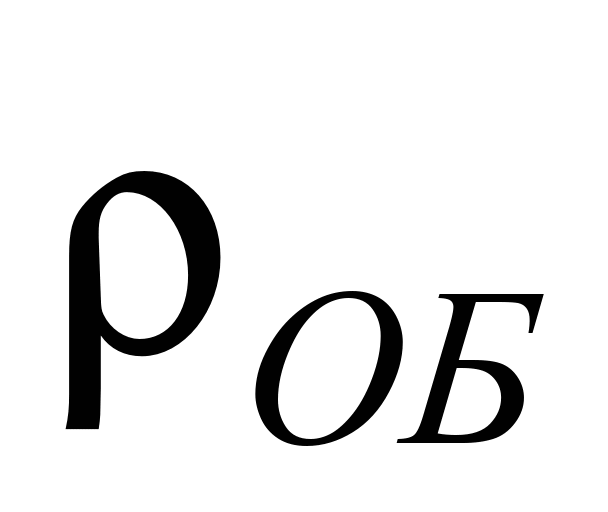 – объемная масса груза;
– объемная масса груза;
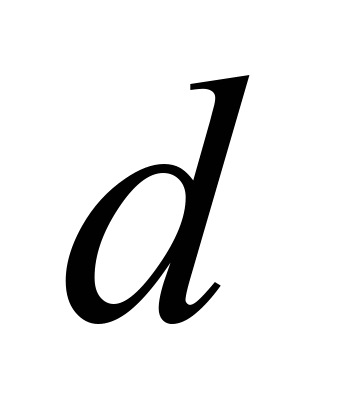 – средний диаметр частиц груза;
– средний диаметр частиц груза;
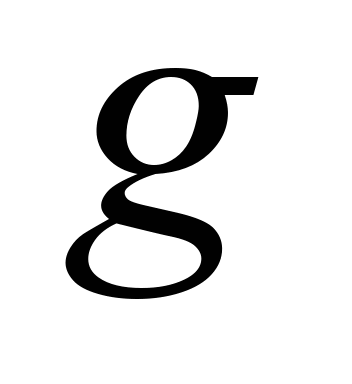 – ускорение свободного падения;
– ускорение свободного падения;
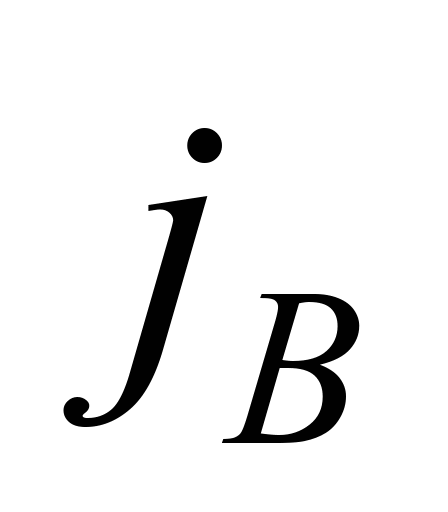 – ускорение вертикальных колебаний
вагона;
– ускорение вертикальных колебаний
вагона;
 – влажность воздуха.
– влажность воздуха.
Зависимость
(3) достаточно «полно» учитывает те
факторы, которые определяют интенсивность
эмиссии пыли от поверхности груза. Это
дает нам определенный ключ к решению
задачи – если необходимо изменить
интенсивность пылевыделения, надо
«воздействовать» на конкретный фактор,
увеличить его или уменьшить в зависимости
от того, с каким знаком «плюс» или
«минус» входит в формулу (3) этот фактор.
Например, если изменить влажность груза
(параметр
 )
и ее увеличить, то интенсивность
пылевыделения – уменьшится, так
как в формулу (3) данный параметр
входит со знаком «минус». На практике
такой подход реализуется путем подачи
воды на поверхность груза перед его
отправкой, то есть путем
увлажнения угля. Аналогично рассуждая,
мы приходим к выводу, что если уменьшить
скорость воздушного потока
)
и ее увеличить, то интенсивность
пылевыделения – уменьшится, так
как в формулу (3) данный параметр
входит со знаком «минус». На практике
такой подход реализуется путем подачи
воды на поверхность груза перед его
отправкой, то есть путем
увлажнения угля. Аналогично рассуждая,
мы приходим к выводу, что если уменьшить
скорость воздушного потока
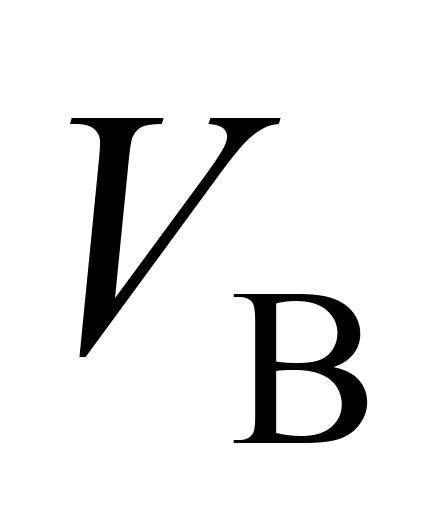 вблизи обтекаемой поверхности (локальная
скорость), то можно уменьшить интенсивность
пылевыделения. Поэтому, для минимизации
интенсивности пылевыделения при
перевозке угля, будем «воздействовать»
на этот параметр. Воздействие будем
проводить в направлении уменьшения
параметра
вблизи обтекаемой поверхности (локальная
скорость), то можно уменьшить интенсивность
пылевыделения. Поэтому, для минимизации
интенсивности пылевыделения при
перевозке угля, будем «воздействовать»
на этот параметр. Воздействие будем
проводить в направлении уменьшения
параметра
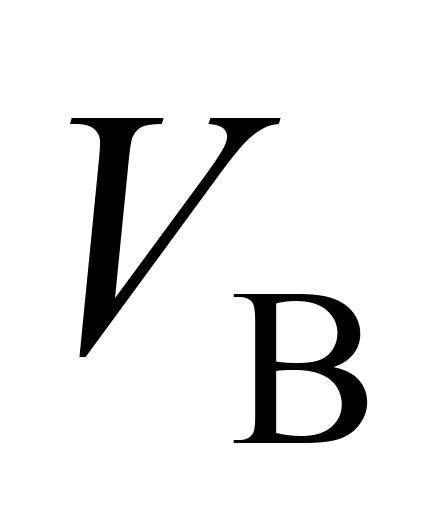 .
Например, такое воздействие можно
осуществить геометрическим путем –
то есть, как указывалось выше, применить
дополнительный борт с «внутренним
крылом» (рис. 5).
.
Например, такое воздействие можно
осуществить геометрическим путем –
то есть, как указывалось выше, применить
дополнительный борт с «внутренним
крылом» (рис. 5).
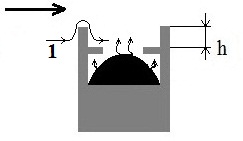
Рис. 5.
Дополнительный борт типа
«внутреннее
крыло»:
1
– линия тока
Fig. 5. Additional board of
«inner wing» type:
1 –
stream line
При
использовании такой конструкции
происходит удлинение линий тока частиц
воздуха, входящих внутрь полувагона,
а значит – происходит локальное
уменьшение скорости
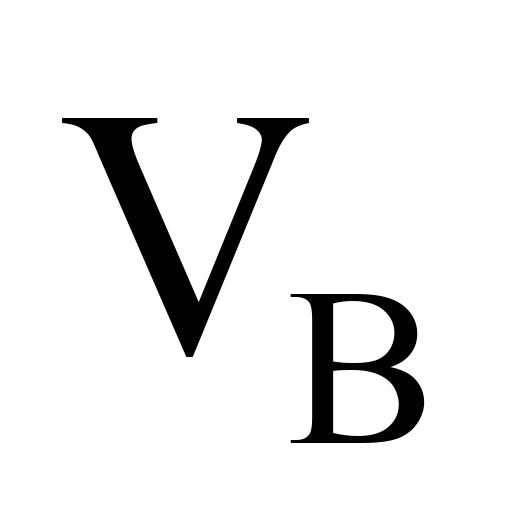 воздушного потока. То есть при применении
такого борта происходит геометрическое
воздействие на воздушный поток.
воздушного потока. То есть при применении
такого борта происходит геометрическое
воздействие на воздушный поток.
Для
подтверждения рабочей гипотезы был
проведен физический эксперимент в
лаборатории кафедры «Гидравлика и
водоснабжение» Днепропетровского
национального университета железнодорожного
транспорта имени академика В. Лазаряна.
Результаты физического эксперимента
представлены ниже.
На
рис. 6 представлены результаты эксперимента
по оценке размеров зоны загрязнения,
если используется полувагон без
дополнительных бортов с «шапкой груза».
Как
видно из рис. 6, возле
полувагона сформировалась обширная
зона загрязнения, длина которой
составляет более четырех «калибров».
Видно, что произошел вынос различных
фракций угля. Более крупные фракции
осели вблизи вагона.
Данный
эксперимент подтверждает, что при
использовании полувагонов без
дополнительных бортов, формируется
большая зона загрязнения в транспортном
коридоре и за его пределами.

Рис. 6.
Зона загрязнения при отсутствии
дополнительных бортов на модели
полувагона:
1
– модель вагона; 2
– «шапка груза»;
3
– зона загрязнения
Fig. 6. Pollution
zone in the absence of additional boards at the model of gondola
car: 1 – model of the car; 2 – «cargo
cap»;
3 – pollution zone
На
рис. 7 показана модель полувагона с
дополнительными бортами типа «внутреннее
крыло», а на рис. 8 представлены результаты
эксперимента по оценке зоны загрязнения
за таким полувагоном.

Рис. 7.
Модель полувагона с дополнительными
бортами типа «внутреннее крыло»:
1
– «внутреннее крыло»
Fig. 7. Gondola car model
with additional boards,
type «inner
wing»:
1 – «inner
wing»

Рис. 8.
Зона загрязнения при использовании
дополнительных бортов типа «внутреннее
крыло»:
1
– модель вагона; 2
– зона загрязнения
Fig. 8. Pollution
zone at
additional boards usage, type «inner
wing»:
1 –the car model; 2 – pollution zone
Как
видно из рис. 8, формирующаяся зона
загрязнения значительно меньше как по
площади, так и по интенсивности. Также
видно, что в отличие от предыдущего
варианта (то есть вагон без дополнительных
бортов), здесь произошел вынос, в
основном, мелких фракций угля.
Таким
образом, результаты проведенных
экспериментов подтверждают выдвинутую
рабочую гипотезу о возможной минимизации
выноса угольной пыли из полувагона за
счет использования дополнительных
бортов типа «внутреннее крыло».
Научная новизна
и практическая
значимость
Создана
3D численная модель, позволяющая
рассчитывать динамику загрязнения
воздушной среды при движении
железнодорожного состава с углем.
Предложенная модель дает возможность
при моделировании учесть наиболее
существенные физические факторы,
влияющие на процесс рассеивания пылевых
загрязнений в атмосфере.
Особенностью
предложенной численной модели является
использование стандартной исходной
информации, быстрота в получении
расчетных данных и удобство анализа
получаемых результатов прогноза.
Для
минимизации процесса выноса угольной
пыли из полувагона предложено использовать
дополнительные борта типа «внутреннее
крыло».
Представлены
результаты физического эксперимента,
подтверждающие эффективность такого
подхода.
Выводы
Рассмотрена
эффективная 3D численная
модель, которая относится к классу
«screening models»
для расчета динамики загрязнения
атмосферы при перевозке угля
железнодорожным транспортом. Модель
позволяет рассчитать процесс загрязнения
атмосферного воздуха с учетом
метеоситуации, скорости движения
состава, интенсивности пылевыделения.
Дальнейшее
совершенствование модели следует
проводить в направлении их развития
для расчета аэродинамики обтекания
состава на базе уравнений Навье-Стокса
и уравнений массопереноса.
СПИСОК использованных
источников
Беляев,
Н. Н. Математическое моделирование в
задачах экологической безопасности
и мониторинга чрезвычайных ситуаций
: монография / Н.
Н. Беляев, Е. Ю. Гунько,
П. Б. Машихина. –
Днепропетровск : Акцент ПП, 2013. – 159 с.
Беляев,
Н. Н. Моделирование аварийного загрязнения
атмосферы при чрезвычайной ситуации
в хранилище твердого ракетного топлива
/ Н. Н. Беляев, А. В. Берлов,
А. В. Шевченко // Наука та
прогрес транспорту. – 2014. – №
5 (53). – С. 29–38.
doi: 10.15802/stp2014/29973.
Берлянд, М. Е.
Прогноз и регулирование загрязнения
атмосферы / М. Е. Берлянд. – Ленинград
: Гидрометеоиздат, 1985. – 273 с.
Берлянд,
М. Е. Современные проблемы атмосферной
диффузии и загрязнения атмосферы / М.
Е. Берлянд. – Ленинград
: Гидрометеоиздат, 1975. – 448 с.
Бруяцкий,
Е. В. Теория атмосферной
диффузии радиоактивных выбросов / Е.
В. Бруяцкий. – Киев : Ин-т гидромеханики
НАН Украины, 2000. – 443 с.
Воробйов,
Є. О. Запобігання
забруднення повітря пилом під час
транспортування вугілля / Є. О. Воробйов,
М. О. Ніколенко, І. О. Худякова // Вісті
АДІ ДВНЗ «ДонНТУ». – Горлівка, 2005. – №
1. – С. 34–38.
Марчук,
Г. И. Математическое моделирование в
проблеме окружающей среды / Г. И. Марчук.
– Москва : Наука,
1982. – 320 с.
Уорк,
К. Загрязнение воздуха. Источники и
контроль / К. Уорк, С. Уорнер. – Москва
: Мир, 1980. – 539 с.
Численное
моделирование распространения
загрязнения в окружающей среде / М. З.
Згуровский, В. В. Скопецкий, В. К. Хрущ,
Н. Н. Беляев. – Киев :
Наук. думка, 1997. – 368 с.
AERMOD:
Description of
model formulation
[Электронный ресурс]. – USA,
North Carolina,
2004. – 91 p. – Режим доступа:https://www3.epa.gov/scram001/7thconf/aermod/aermod_mfd.pdf. –
Загл. с экрана. – Проверено : 23.01.2017.
Biliaiev,
M. Numerical Simulation of Indoor Air Pollution and Atmosphere
Pollution for Regions Having Complex Topography / M. Biliaiev //
NATO Science for Peace and Security Series C: Environmental
Security. – 2012. – P. 87–91. doi:
10.1007/978-94-007-1359-8_15.
Coal
dust emissions: From environmental control to risk minimization by
underground transport. An applicative case-study /
B. Fabiano, F. Curro, A. P. Reverberi, E. Palazzi // Process
Safety and Environmental Protection.
– 2014. – Vol. 92. – Iss. 2. – P. 150–159. doi:
10.1016/j.psep.2013.01.002.
Diesel
and Gasoline Engine Exhausts and Some Nitroarenes : IARC Monographs
on the Evaluation of Carcinogenic Risks to Humans. –
Lyon, 2012. – Vol.
105. – 714 p.
Emmitt,
G. D. Fugitive coal dust: An old problem demanding new solutions /
G. D. Emmitt // Port Technology
International. – 1999;9:1.
Full
cost accounting for the life cycle of coal / P. R. Epstein, J. J.
Buonocore, K. Eckerle [et al.] // Annals
of the New York Academy of Sciences. –
2011. – Vol. 1219. – Iss. 1. – P. 73–98. doi:
10.1111/j.1749-6632.2010.05890.x.
Initial
Report on the Independent Review of Rail Coal Dust Emissions
Management Practices in the NSW Coal Chain / Chief Scientist &
Engineer. – Sydney
NSW, Australia, 2015. – 75 p.
Szabo,
M. F. Environmental assessment of coal
transportation / M. F. Szabo. –
Cincinnati, Ohio : Environmental
Protection Agency, 1978. – 142 р.
М. М. БІЛЯЄВ1*,
М. О.
ОЛАДІПО2*
1*Каф. «Гідравліка
та водопостачання», Дніпропетровський
національний університет залізничного
транспорту
імені академіка В. Лазаряна,
вул. Лазаряна, 2, Дніпро, Україна, 49010,
тел. +38 (056) 273 15 09,
ел. пошта
gidravlika2013@mail.ru,
ORCID 0000-0002-1531-7882
2*Каф.
«Гідравліка та водопостачання»,
Дніпропетровський національний
університет залізничного транспорту
імені академіка В. Лазаряна, вул.
Лазаряна, 2, Дніпро, Україна, 49010, тел.
+38 (056) 273 15 09,
ел. пошта
Oladipo.toye@outlook.com,
ORCID 0000-0001-7945-6657
РОЗРАХУНОК ДИНАМІКИ ЗАБРУДНЕННЯ
примагістральної ТЕРИТОРІЇ
ПІД ЧАС
ПЕРЕВЕЗЕННЯ ВУГІЛЛЯ
Мета.
Наукова робота передбачає розробку 3D
чисельної моделі для прогнозу забруднення
атмосфери при транспортуванні сипучих
вантажів у залізничному вагоні. Методика.
Для вирішення поставленої задачі
розроблена тривимірна чисельна модель,
заснована на застосуванні рівняння
переносу пилових забруднень в
атмосферному повітрі під дією вітру
та атмосферної турбулентної дифузії.
Для чисельного інтегрування моделюючого
рівняння переносу пилу використовувалася
неявна різницева схема. При побудові
різницевої схеми здійснюється попереднє
розщеплення вихідного рівняння переносу
на послідовність розв’язання трьох
рівнянь. Перше з них враховує перенесення
пилу по траєкторіях, друге рівняння –
перенесення пилу під дією атмосферної
турбулентної дифузії, а третє рівняння
– зміна концентрації пилу в атмосферному
повітрі за рахунок її емісії з вагонів.
Невідоме значення концентрації
забруднювача на кожному кроці розщеплення
визначається за явною схемою – методу
біжучого рахунку, що забезпечує просту
чисельну реалізацію рівнянь розщеплення.
Розроблена чисельна модель становить
основу спеціалізованої комп’ютерної
програми. На основі побудованої чисельної
моделі проведено обчислювальний
експеримент по оцінці рівня забруднення
атмосфери на залізничній станції під
час руху потяга з вугіллям. Результати.
Розроблено 3D чисельну модель, яка
відноситься до класу «screning models». Дана
модель враховує основні фізичні фактори,
що впливають на процес розсіювання
пилових забруднень в атмосфері при
транспортуванні вугілля. Запропонована
чисельна модель вимагає невеликих
витрат комп’ютерного часу при практичній
реалізації на комп’ютерах малої та
середньої потужності. Ця модель може
використовуватися для оперативних
розрахунків динаміки забруднення
атмосферного повітря при перевезенні
вугілля залізничним транспортом.
Виконано розрахунки по визначенню
концентрації забруднювача та формуванню
зони забруднення на станції Enugu.
Представлені результати фізичного
експерименту, що дозволяють рекомендувати
застосування додаткових бортів
спеціальної форми для мінімізації
виносу вугільного пилу з напіввагонів.
Наукова новизна.
Авторами створена 3D чисельна модель,
що дозволяє врахувати істотні фізичні
фактори, що впливають на процес
розсіювання пилу в атмосфері. Модель
дозволяє розраховувати формування зон
забруднення при перевезенні вугілля
залізничним транспортом. Практична
значимість. Розглянута
ефективна чисельна модель класу
«screening models» для експрес-розрахунку
рівня забруднення атмосфери при
транспортуванні вугілля залізничним
транспортом. Модель може бути застосована
при розробці заходів із охорони
навколишнього середовища при експлуатації
залізничного транспорту. Запропонована
модель дозволяє оперативно розрахувати
3D перенесення пилу в атмосферному
повітрі.
Ключові слова:
забруднення атмосфери;
залізничний транспорт; перевезення
вугілля; чисельне моделювання
M. M. BILIAIEV1*,
M. O. OLADIPO2*
1*Dep.
«Hydraulics and Water Supply», Dnipropetrovsk National University
of Railway Transport named
after Academician V. Lazaryan,
Lazaryan St., 2, Dnipro, Ukraine, 49010, tel. +38 (056)
273 15
09,
e-mail gidravlika2013@mail.ru,
ORCID 0000-0002-1531-7882
2*Dep.
«Hydraulics and Water Supply», Dnipropetrovsk National University
of Railway Transport named
after Academician V. Lazaryan,
Lazaryan St., 2, Dnipro, Ukraine, 49010, tel. +38 (056)
273 15 09,
e-mail Oladipo.toye@outlook.com,
ORCID 0000-0001-7945-6657
CALCULATION OF POLLUTION
DYNAMICS
NEAR RAILWAY TERRITORY
DURING
COAL TRANSPORTATION
Purpose.
The article is aimed to develop
3D numerical model for the prediction of atmospheric pollution
during transportation of bulk cargo in the railway car. Methodology.
To
solve this problem, it was developed three-dimensional numerical
model, based on the use of the transport equation of dust pollution
in the air by the wind and atmospheric turbulent diffusion. For the
numerical integration of the simulating equation of the dust
transport the implicit difference scheme was used. When constructing
a difference scheme, it was carried out prior splitting of the
original transport equation into the sequence of solutions of three
equations. The first of them takes into account the transport of
dust in paths, the second equation –
dust transport under the influence of atmospheric turbulent
diffusion, and the third equation –change
of the dust concentration in the air due to its emissions from the
cars.
Unknown
value of the pollutant concentration at every step of splitting is
determined by the explicit scheme – the method of running account,
which provides a simple numerical implementation of splitting
equations. The developed numerical model is the basis for
specialized computer program. On the basis of the constructed
numerical model we carried out a computational experiment to assess
the level of air pollution at the railway station during the motion
of train with coal. Findings.
Authors
developed 3D numerical model, which belongs to the class of
«screening models». This model takes into account the main
physical factors affecting the process of dispersion of dust
pollution in the atmosphere during coal transportation. The proposed
numerical model requires low cost of computer time in the practical
implementation on small and medium-power computers. This model can
be used for rapid calculations of the dynamics of air pollution when
transporting coal by rail. Calculations to determine the pollutant
concentration and formation of the contamination zone at Enugu
station were performed. The results of physical experiment, allow us
to recommend the use of additional specially shaped boards to
minimize the removal of coal dust from gondola cars. Originality.
It
was created
3D
numerical model that makes it possible to take into account
significant physical factors that influence the process of dust
dispersion in the atmosphere. The model allows calculating the
formation of pollution zones during transportation of coal by rail.
Practical
value.
The
effective numerical model of the class «screening models» for
rapid calculation of the level of air pollution from coal transport
by rail
was considered.
The model can be applied in the development of environmental
protection measures in the operation of rail transport. The proposed
model allows you to quickly calculate the 3D transfer of dust in the
air.
Keywords:
air pollution; railway
transport; coal transportation; numerical simulation
References
Biliaiev, M. M., Gunko,
Y. Y., &
Mashikhina, P.
B. (2013). Matematicheskoye
modelirovaniye v zadachakh ekologicheskoy bezopasnosti i
monitoringa chrezvychaynykh situatsiy.
Dnipropetrovsk: Aktsent PP.
Biliaiev,
M. M., Berlov, O. V., & Shevchenko, A. V. (2014). Simulation of
the accidental pollution after the emergency in to the storage of
rocket solid propellant. Science and
Transport Progress, 5(53), 29-38.
doi:10.15802/stp2014/29973
Berlyand,
M. Y. (1985). Prognoz i regulirovaniye
zagryazneniya atmosfery. Leningrad:
Gidrometeoizdat.
Berlyand,
M. Y. (1975). Sovremennyye problemy
atmosfernoy diffuzii i zagryazneniya atmosfery.
Leningrad: Gidrometeoizdat.
Bruyatskiy,
Y. V. (2000). Teoriya atmosfernoy
diffuzii radioaktivnykh vybrosov.
Kyiv: Institut gidromekhaniki NAN Ukrainy.
Vorobyov,
Y. O., Nikolenko, M.
O., & Khudyakova, I. O. (2005). Zapobihannia zabrudnennia
povitria pylom pid chas transportuvannia vuhillia. Visti
ADI DVNZ «DonNTU», 1, 34-38.
Marchuk,
G. I. (1982).
Matematicheskoye modelirovaniye v
probleme okruzhayushchey sredy.
Moscow: Nauka.
Wark,
K., &
Warner, C.
F. (1980).
Zagryazneniye vozdukha. Istochniki i
kontrol. Moscow:
Mir.
Zgurovskiy,
M. Z.,
Skopetskiy, V.
V., Khrushch,
V. K., &
Biliaiev, M. M. (1997).
Chislennoye
modelirovaniye
rasprostraneniya
zagryazneniya
v
okruzhayushchey
srede.
Kyiv: Naukova
dumka.
U.S.
Environmental Protection Agency. (2004).
AERMOD: Description of model
formulation,
No. EPA-454/R-03-004.
USA, North Carolina. Retrieved
from https://www3.epa.gov/scram001/7thconf/aermod/aermod_mfd.pdf
Biliaiev,
M. M., &
Kharytonov, M. M.
(2011).
Numerical Simulation of Indoor Air
Pollution and Atmosphere Pollution for Regions Having Complex
Topography. NATO Science for Peace and
Security,
series C: Environmental Security,
87-91. doi: 10.1007/978-94-007-1359-8_15
Fabiano,
B., Curro, F., Reverberi, A. P., & Palazzi, E. (2014). Coal
dust emissions: From environmental control to risk minimization by
underground transport. An applicative case-study.
Process
Safety and Environmental
Protection,
92(2),
150-159. doi: 10.1016/j.psep.2013.01.002
IARC
Monographs on the Evaluation of Carcinogenic Risks to Humans.
(2012). Diesel and Gasoline Engine
Exhausts and Some Nitroarenes, 105.
Lyon: International Agency for Research on Cancer.
Emmitt,
G. D. (1999). Fugitive coal dust: An old problem demanding new
solutions. Port Technology
International, 9, 1.
Epstein,
P. R., Buonocore, J. J., Eckerle, K., Hendryx, M., Stout III, B.
M., Heinberg, R., … & Glustrom, L. (2011). Full cost
accounting for the life cycle of coal. Annals
of the New York Academy of Sciences, 1219(1),
73–98. doi: 10.1111/j.1749-6632.2010.05890.x
NSW
Chief Scientist & Engineer. (2015). Initial
Report on the Independent Review of Rail Coal Dust Emissions
Management Practices in the NSW Coal Chain.
Sydney: NSW. Retrieved from
http://www.chiefscientist.nsw.gov.au/__data/assets/pdf_file/0009/79884/Initial-Report_Review-rail-coal-dust-emissions.pdf
Szabo,
M. F. (1978). Environmental assessment
of coal transportation. Cincinnati,
Ohio: Environmental Protection Agency.
Статья
рекомендована к публикации д.физ.-мат.н.,
проф. C. А. Пичуговым
(Украина);
д.т.н., проф. С. З. Полищуком
(Украина)
Поступила
в редколлегию: 30.11.2016
Принята
к печати: 12.01.2017
, (1)
– концентрация загрязняющего
вещества (пылевой загрязнитель);
– компоненты вектора скорости воздушного
потока;
– коэффициенты атмосферной турбулентной
диффузии;
– интенсивность выброса загрязнителя
от «насыпи» в полувагоне;
– дельта-функция Дирака;
– координаты источника выброса;
– скорость гравитационного оседания
пыли; t – время.
можно моделировать изменения положения
вагонов в расчетной области с течением
времени, то есть моделировать
движение состава с углем.
,
,
, (2)
);
;
;
;
.
,
,
.
(3)
– потери угля при транспортировке;
– плотность воздуха;
– скорость воздуха вблизи обтекаемой
поверхности;
– площадь поверхности, из которой
выдувается груз;
– продолжительность процесса выдувания
груза;
– объемная масса груза;
– средний диаметр частиц груза;
– ускорение свободного падения;
– ускорение вертикальных колебаний
вагона;
– влажность воздуха.
)
и ее увеличить, то интенсивность
пылевыделения – уменьшится, так
как в формулу (3) данный параметр
входит со знаком «минус». На практике
такой подход реализуется путем подачи
воды на поверхность груза перед его
отправкой, то есть путем
увлажнения угля. Аналогично рассуждая,
мы приходим к выводу, что если уменьшить
скорость воздушного потока
вблизи обтекаемой поверхности (локальная
скорость), то можно уменьшить интенсивность
пылевыделения. Поэтому, для минимизации
интенсивности пылевыделения при
перевозке угля, будем «воздействовать»
на этот параметр. Воздействие будем
проводить в направлении уменьшения
параметра
.
Например, такое воздействие можно
осуществить геометрическим путем –
то есть, как указывалось выше, применить
дополнительный борт с «внутренним
крылом» (рис. 5).
воздушного потока. То есть при применении
такого борта происходит геометрическое
воздействие на воздушный поток.