ISSN
2307–3489 (Print), ІSSN
2307–6666
(Online)
Наука
та прогрес транспорту. Вісник
Дніпропетровського
національного університету залізничного
транспорту, 2016,
№
6
(66)
екологія
на ТРАНСПОРТі
УДК
502.3:504.5:621.43.068.4
Н. Н. БЕЛЯЕВ1*, Е. С. СЛАВИНСКАЯ2*,
р. В. КИРИЧЕНКО3*
1*Каф. «Гидравлика
и водоснабжение», Днепропетровский
национальный университет железнодорожного
транспорта имени академика В. Лазаряна,
ул. Лазаряна, 2, Днипро, Украина, 49010, тел.
+38 (056) 273 15 09, эл. почта gidravlika2013@mail.ru,
ORCID 0000-0002-1531-7882
2*Каф.
«Управление производством и имуществом»,
Национальный транспортный университет,
ул. Суворова, 1, Киев, Украина, 01010, тел.
+38 (044) 280 82 03, эл. почта gidravlika2013@mail.ru, ORCID
0000-0001-5163-5645
3*Каф. «Управление
производством и имуществом», Национальный
транспортный университет, ул. Суворова,
1, Киев, Украина, 01010, тел. +38 (044) 280 82 03, эл.
почта gidravlika2013@mail.ru,
ORCID 0000-0001-9918-3895
ЧИСЛЕННЫЕ МОДЕЛИ ДЛЯ ПРОГНОЗА
ЗАГРЯЗНЕНИЯ АТМОСФЕРНОГО ВОЗДУХА
ВЫБРОСАМИ АВТОТРАНСПОРТА
Цель.
Научная работа предполагает: 1) разработку
3D численных моделей,
которые позволяют рассчитывать процесс
загрязнения атмосферного воздуха
выбросами автотранспорта; 2) создание
моделей, которые давали бы возможность
прогнозировать уровень загрязнения
атмосферного воздуха в условиях городской
застройки. Методика.
Для решения задачи по
оценке уровня загрязнения атмосферного
воздуха выбросами автотранспорта
используются фундаментальные уравнения
аэродинамики и массопереноса. Для
решения дифференциальных уравнений
аэродинамики и массопереноса используются
конечно-разностные методы. Для численного
интегрирования уравнения потенциала
скорости применяется метод условной
аппроксимации. Уравнение для потенциала
скорости, записанное в разностном виде,
расщепляется на два уравнения, причем
на каждом шаге расщепления неизвестное
значение потенциала скорости определяется
по явной схеме бегущего счета, при этом
сама разностная схема – неявная. Для
численного интегрирования уравнения
рассеивания выбросов в атмосфере
применяется неявная попеременно-треугольная
разностная схема расщепления. Выбросы
от автотрассы моделируются серией
точечных источников заданной интенсивности.
Разработанные численные модели составляют
основу созданного пакета прикладных
программ. Результаты.
Разработаны 3D
численные модели, которые относятся к
классу «diagnostic models».
Данные модели учитывают основные
физические факторы, влияющие на процесс
рассеивания вредных веществ в атмосфере
при выбросах от автотранспорта в городе.
На основе построенных численных моделей
проведен вычислительный эксперимент
по оценке уровня загрязнения воздушной
среды на улице. Научная
новизна. Авторами
разработаны численные модели, которые
позволяют рассчитать 3D
аэродинамику ветрового потока в условиях
городской застройки и процесс массопереноса
выбросов от автотрассы. Выполнены
расчеты по определению зоны загрязнения,
которая формируется возле зданий,
расположенных вдоль автомагистрали.
Практическая значимость.
В работе рассмотрены
эффективные численные модели, которые
могут быть применены при разработке
мероприятий по охране окружающей среды
при эксплуатации автомобильного
транспорта в городе. Разработанные
модели позволяют оценить размеры, форму
и интенсивность зоны загрязнения возле
автомагистрали.
Ключевые слова:
загрязнение атмосферы;
автотранспорт; численное моделирование
Введение
В
настоящее время усилился интерес к
разработке моделей для оценки уровня
загрязнения воздушной среды выбросами
автотранспорта (рис. 1)
[1, 2, 13, 15, 16]. Это связано
с тем, что применение
метода физического моделирования [14]
требует значительных материальных
затрат, времени на проведение эксперимента,
обработку и анализ полученных результатов.
При
использовании метода математического
моделирования наиболее часто применяются
эмпирические и аналитические модели
[3–5, 7, 9]. Такие модели
дают возможность оперативно получать
данные о возможном уровне загрязнения
атмосферного воздуха, но не учитывают
самый главный фактор – наличия зданий,
которые деформируют поле скорости
ветрового потока и вследствие этого
формирующиеся зоны загрязнения в
атмосфере.
Поэтому
в мире активно развивается численное
моделирование процесса загрязнения
атмосферного воздуха выбросами
автотранспорта [1, 2, 16]. Однако в Украине
существует определенный дефицит
численных моделей, ориентированных на
решение задач рассматриваемого класса.

Рис. 1. Выбросы от автотранспорта
Fig. 1.
Emissions
from
motor
vehicles
Цель
Целью
данной работы является разработка 3D
CFD моделей для прогноза
уровня загрязнения атмосферного воздуха
в условиях застройки выбросами
автомобилей. Ставится задача создания
моделей, которые давали бы возможность
оперативно прогнозировать уровень
загрязнения атмосферного воздуха и
оценивать влияние автотранспорта на
степень этого загрязнения.
Методика
Для
решения задачи по прогнозу уровня
загрязнения атмосферного воздуха
выбросами автотранспорта будут
использоваться фундаментальные
уравнения аэродинамики и массопереноса.
Для численного интегрирования
моделирующих уравнений будут применяться
конечно-разностные методы.
Математическая
модель.
Модель аэродинамики. Оценка
уровня загрязнения атмосферного воздуха
выбросами от автотранспорта будет
осуществлена с учетом застройки
примагистральной территории. Поэтому,
для решения такой задачи необходимо
определить поле скорости ветрового
потока при наличии застройки. Для
решения этой задачи будем применять
модель идеальной жидкости. Если сделать
предположение о безвихревом воздушном
потоке, то моделирующее уравнение будет
иметь вид [10, 12]:
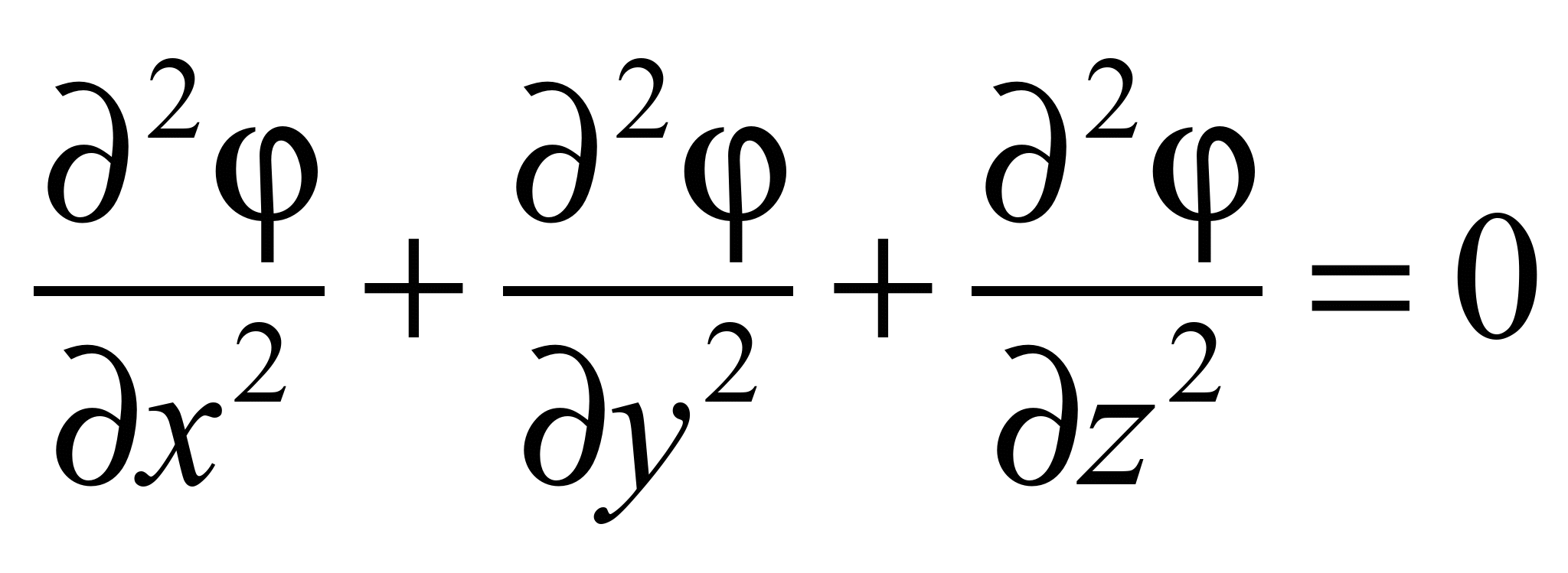 , (1)
, (1)
где
 – потенциал скорости.
– потенциал скорости.
Компоненты
вектора скорости воздушного потока
определяется такими соотношениями:
 ,
,
 ,
,
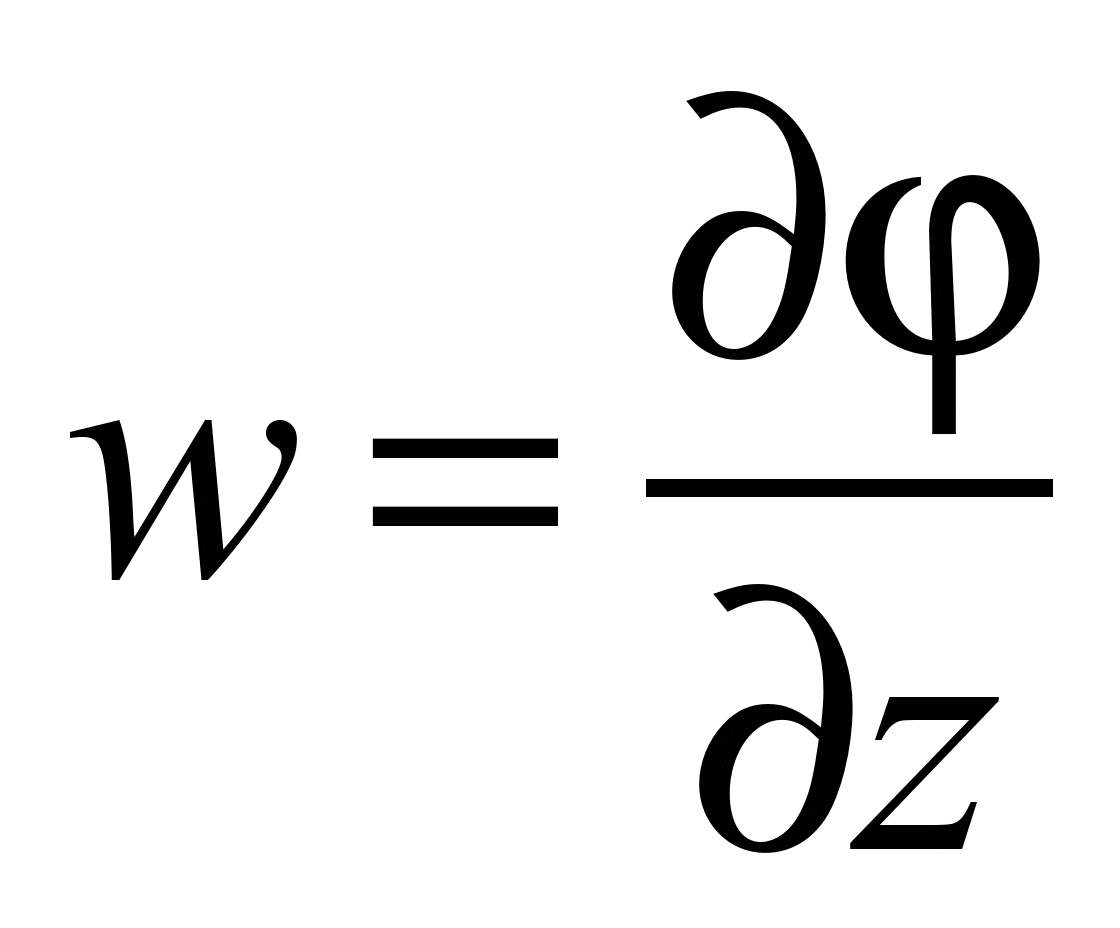 .
.
Постановка
краевых условий для данного уравнения
рассматривается в работе [10].
Модель
массопереноса. Для моделирования
рассеивания выбросов от автомобилей
в атмосферном воздухе будем использовать
следующее уравнение [1, 6, 10,
11]:
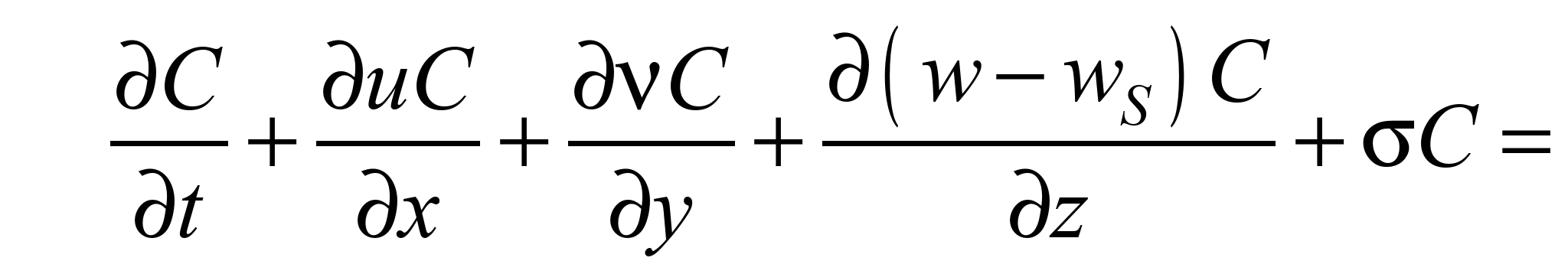

 (2)
(2)
где С –
концентрация вредного вещества в
атмосферном воздухе;
 – компоненты вектора скорости движения
воздушной среды;
– компоненты вектора скорости движения
воздушной среды;
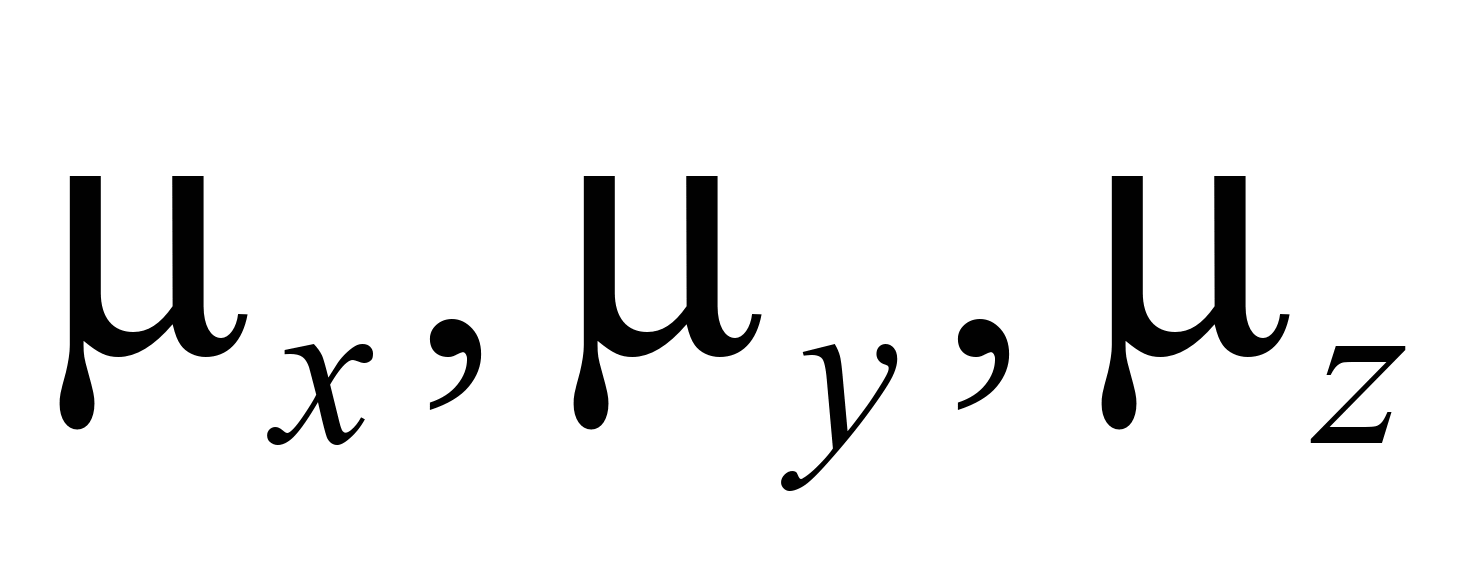 – коэффициенты атмосферной турбулентной
диффузии;
– коэффициенты атмосферной турбулентной
диффузии;
 – коэффициент, учитывающий изменение
концентрации за счет химических реакций,
протекающих в атмосфере и вымывания
вредного вещества осадками [5];
t – время;
– коэффициент, учитывающий изменение
концентрации за счет химических реакций,
протекающих в атмосфере и вымывания
вредного вещества осадками [5];
t – время;
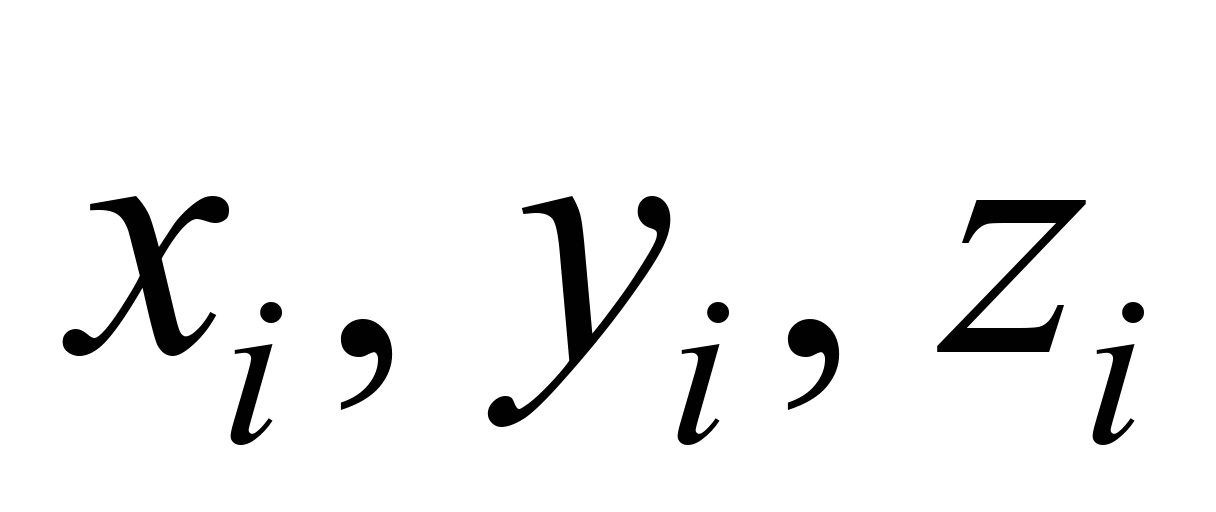 – координаты расположения точечного
источника выделения примеси (место
расположения автомобилей);
– координаты расположения точечного
источника выделения примеси (место
расположения автомобилей);
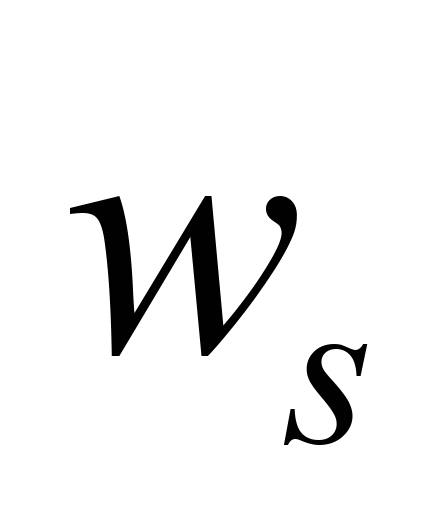 – скорость гравитационного оседания
загрязнителя;
– скорость гравитационного оседания
загрязнителя;
 – интенсивность эмиссии точечного
источника (интенсивность выброса от
автомобилей);
– интенсивность эмиссии точечного
источника (интенсивность выброса от
автомобилей);
 – обозначение дельта-функции Дирака.
– обозначение дельта-функции Дирака.
Таким
образом, загрязнение примагистральной
территории от автотранспорта моделируется
серией точечных источников заданной
интенсивности. Поскольку выбросы от
автомобилей содержат различные вредные
вещества, уравнение (2)
необходимо использовать для рассеивания
каждого конкретного вредного вещества.
Постановка
граничных и начальных условий для
уравнения массопереноса рассмотрено
в работах [1, 10].
На
входе в расчетную область задаются
следующие значения параметров [5, 6]:
 ,
, ,
,
 ,
,
 ,
,
где u1
– скорость ветра на высоте z1
(принимается
 );
);
 ;
;
 ;
;
 ;
;
 .
.
С
помощью маркеров в дискретной модели
задается положение автомагистрали,
интенсивность выбросов от автомобилей
и положение зданий в расчетной области.
Это позволяет очень быстро формировать
«геометрию» расчетной области, то
есть положение зданий, их форму,
положение автомагистралей и т.д.
Для
решения дифференциальных уравнений
аэродинамики и массопереноса используются
конечно-разностные методы. Так для
численного интегрирования уравнения
для потенциала скорости применяется
метод условной аппроксимации [8].
Предварительно, уравнение (1) записывается
в эволюционном виде:
 , (3)
, (3)
здесь
 – фиктивное время.
– фиктивное время.
При
 решение уравнения (3)
будет стремиться к «установлению», то
есть к решению уравнения (1).
решение уравнения (3)
будет стремиться к «установлению», то
есть к решению уравнения (1).
Разностные
уравнения для численного решения (3),
на каждом дробном шаге расщепления,
имеют вид [8]:
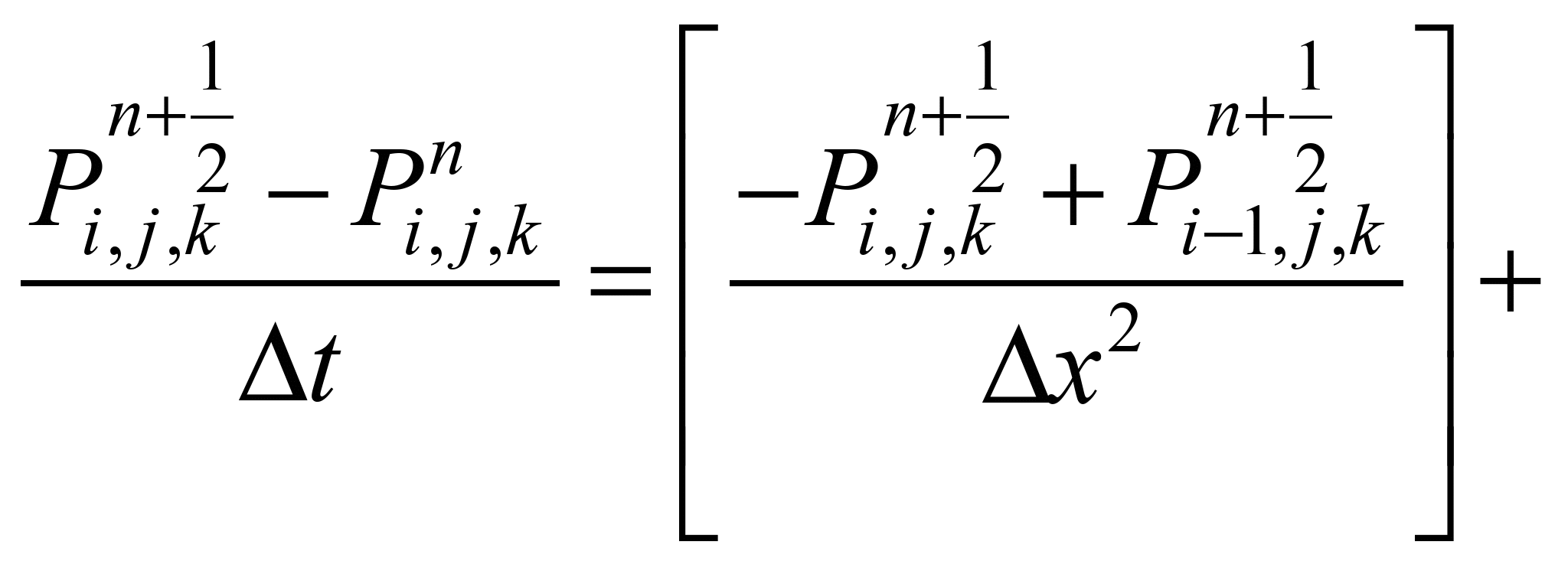



На
каждом шаге расщепления расчет
неизвестной величины потенциала
скорости идет по явной формуле – методу
бегущего счета.
Перед
началом численного интегрирования
уравнения (3) задается
поле потенциала скорости для «начального»
момента фиктивного времени. Процесс
расчета поля потенциала скорости
заканчивается при выполнении условия:
 ,
,
где
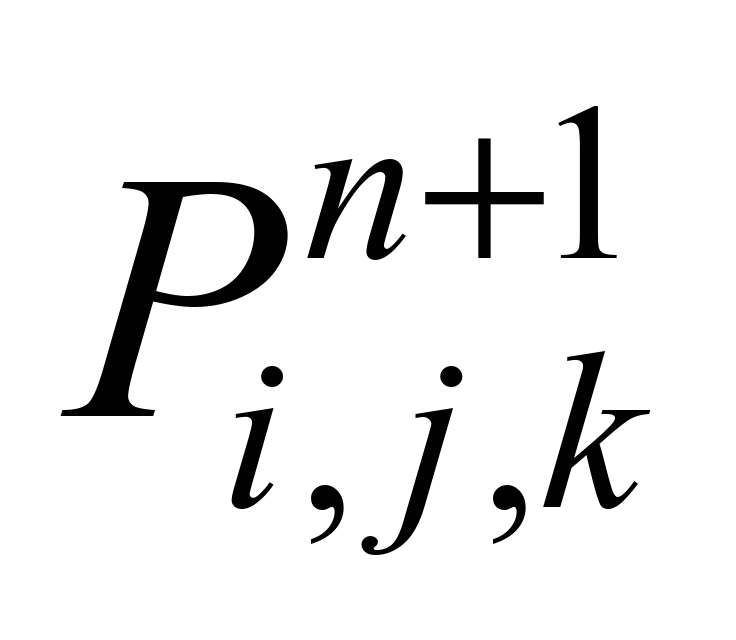 – новое приближение величины потенциала
скорости;
– новое приближение величины потенциала
скорости;
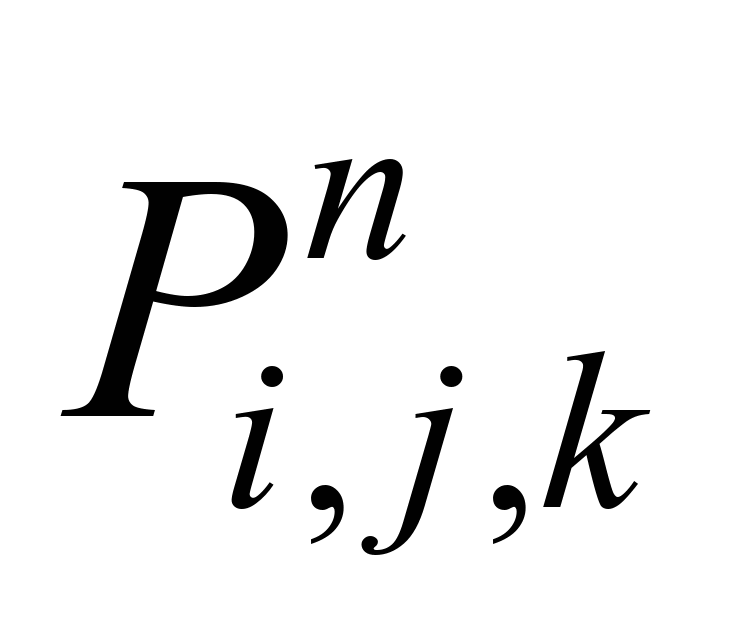 – предыдущее значение величины
потенциала скорости; ε – малое
число.
– предыдущее значение величины
потенциала скорости; ε – малое
число.
После
расчета поля потенциала скорости
осуществляется расчет компонент вектора
скорости воздушного потока
на гранях разностных ячеек по
зависимостям:
 ,
,
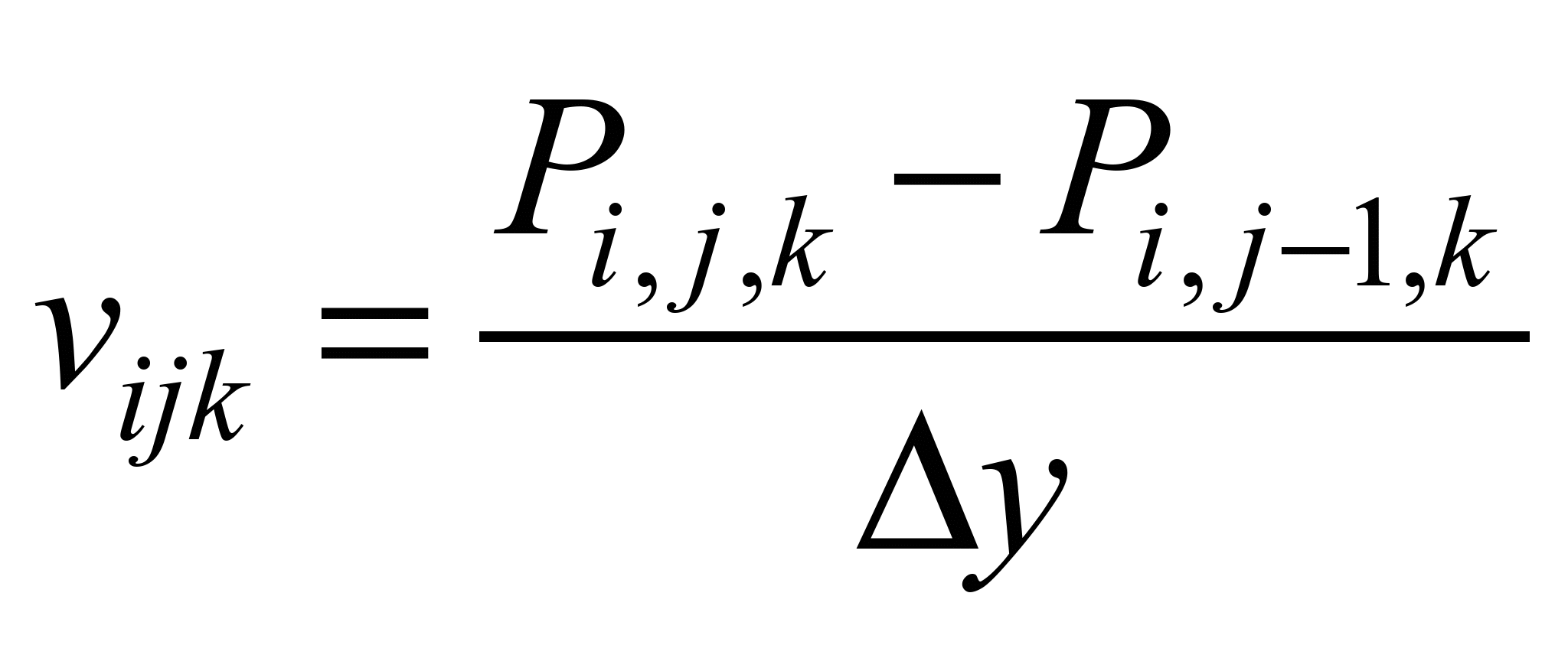 ,
,
 .
.
После
решения задачи аэродинамики – определения
поля скорости воздушного потока
– решается задача массопереноса
загрязняющих веществ от автомагистрали.
Для численного интегрирования уравнения
массопереноса используется
попеременно-треугольная
разностная схема [10].
Построение этой разностной схемы
осуществляется путем расщепления
решения исходного уравнения массопереноса
(2) на последовательность
разностных уравнений более простой
структуры, из которых неизвестное
значение концентрации примеси
определяется методом бегущего счета.
Результаты
Ниже
представлены результаты решения задачи
по оценке уровня загрязнения атмосферного
воздуха вблизи двух зданий. Рядом со
зданиями планируется строительство
автомагистрали (рис. 2).
Как видно из рис. 2.
автомагистраль огибает первое здание
(позиция 1,
рис.
2), которое имеет Г-образную форму.
Интенсивность эмиссии СО от
автомагистрали задается с помощью
дельта-функции Дирака, то
есть набором точечных источников
эмиссии, расположенных по трассе
автомагистрали. Ставилась задача оценки
размеров, формы зоны загрязнения возле
автомагистрали.

Рис. 2.
Расчетная схема:
1,
2
–здания, 3
– автомагистраль
Fig. 2. Sketch of
computational region:
1,
2 –
buildings, 3
–
highway
На
последующих рисунках представлена
зона загрязнения атмосферного воздуха
в расчетной области для двух различных
уровней по высоте. На рис. 3
показана зона загрязнения на уровне z
= 3 м. Из этого рисунка хорошо видно, что
первое здание полностью попадает в
зону влияния автомагистрали. Между
зданиями формируется подзона с большим
градиентом концентрации примеси.
На
рис. 4 показана зона
загрязнения атмосферного воздуха на
более высоком уровне – z
= 7,5 м (высота зданий 6 м). Сравнивая рис.
3 и рис.
4 можно заметить различия в характере
распределения в концентрации примеси
на разных высотах. Так на большей высоте
зона загрязнения более «разрежена»,
что объясняется тем, что на данной
высоте происходит более интенсивный
снос примеси ветровым потоком. На этой
высоте позиция второго здания
(прямоугольное здание – позиция 2, рис.
2) не видна. Позиция первого здания
четко не очерчена, но видно определенное
«поджатие» зоны загрязнения в районе
между автомагистралью и первым зданием.

Рис. 3. Зона загрязнения
возле зданий
(уровень
z = 3 м)
Fig. 3. Pollution
area near the
buildings (z
= 3 m)

Рис. 4. Зона загрязнения
возле зданий
(уровень
z = 7,5
м)
Fig. 4. Pollution area near
the buildings (z = 7,5 m)
Отметим,
что на решение задачи потребовалось
около 10 с компьютерного
времени.
Научная новизна
и практическая
значимость
Созданы
3D численные модели,
позволяющие рассчитывать формирование
зон загрязнений в условиях застройки
выбросами от автотранспорта. Представленные
3D численные модели
основаны на применении фундаментальных
уравнений аэродинамики и массопереноса.
Особенностью
разработанных моделей является
использование стандартной метеорологической
информации, быстрота в получении
расчетных данных и удобство анализа
получаемых результатов прогноза.
Выводы
Предложены
численные 3D модели для
оценки уровня загрязнения атмосферного
воздуха выбросами от автотранспорта.
Особенностью предложенных численных
моделей является возможность
прогнозирования уровня загрязнения
атмосферного воздуха в условиях
застройки. Решение аэродинамической
задачи по определению поля скорости
воздушного потока, при наличии зданий,
основывается на численном интегрировании
уравнения для потенциала скорости.
Оценка уровня загрязнения атмосферного
воздуха осуществляется на базе уравнения
массопереноса, которое учитывает
конвективный и диффузионный перенос
примеси в атмосфере. Выбросы от автотрассы
моделируются серией точечных источников,
которые задаются с помощью дельта-функции
Дирака. Предложенные модели дают
возможность оперативно получить
информацию об уровне загрязнения
атмосферного воздуха в
районах, где проходят автомагистрали.
Дальнейшее
совершенствование моделей следует
проводить в направлении создания
численной модели, учитывающей химическую
трансформацию выбросов в атмосфере.
СПИСОК использованных
источников
Беляев,
Н.
Н.
Моделирование загрязнения атмосферного
воздуха выбросами автотранспорта на
улицах городов : монография / Н. Н.
Беляев, Т. И. Русакова, П. С. Кириченко.
– Днепропетровск : Акцент ПП, 2014. – 159
с.
Беляев,
Н. Н. CFD
прогнозирование процесса загрязнения
воздушной среды на улицах / Н. Н. Беляев,
Т. И. Русакова // Екологія
і природокористування : зб. наук. пр.
ін-ту проблем природокористування та
екології НАН України. – Дніпропетровськ,
2013. – Вип. 17. – С. 188–194.
Берлянд,
М. Е. Прогноз и регулирование загрязнения
атмосферы / М. Е. Берлянд. – Ленинград
:
Гидрометеоиздат, 1985. – 273 с.
Берлянд,
М. Е. Современные проблемы атмосферной
диффузии и загрязнения атмосферы / М.
Е. Берлянд.
– Ленинград
:
Гидрометеоиздат, 1975. – 448 с.
Бруяцкий,
Е.
В. Теория
атмосферной диффузии радиоактивных
выбросов / Е. В. Бруяцкий. – Киев
: Ин-т гидромеханики НАН Украины, 2000. –
443 с.
Марчук,
Г.
И.
Математическое моделирование в проблеме
окружающей среды / Г. И. Марчук.–
Москва
: Наука,
1982. – 320 с.
Рудаков,
Д. В. Модель рассеивания примеси в
приземном слое атмосферы над поверхностью
со сложным рельефом / Д. В. Рудаков
//
Вісн.
Дніпропетр.
нац. ун-ту. Серія: Механіка. –
Дніпропетровськ, 2004. – № 6, вип. 8, т. 1.
– С. 89–97.
Самарский,
А.
А. Теория
разностных схем / А.
А. Самарский.
– Москва : Наука, 1983. – 616 с.
Уорк,
К. Загрязнение воздуха. Источники и
контроль / К. Уорк, С. Уорнер.
– Москва : Мир, 1980. – 539 с.
Численное
моделирование распространения
загрязнения в окружающей среде / М. З.
Згуровский, В. В. Скопецкий, В. К. Хрущ,
Н. Н. Беляев. – Київ
: Наук.
думка, 1997. – 368 с.
Berlov,
O. V. Atmosphere
protection in case of emergency during
transportation
of dangerous cargo /
O.
V. Berlov
// Наука та прогрес транспорту. – 2016.
– № 1
(61).
– С. 48–54.
doi:
10.15802/stp2016/60953.
Biliaiev,
M. Numerical Simulation of Indoor Air Pollution and Atmosphere
Pollution for Regions Having Complex Topography / M. Biliaiev
// NATO
Science for Peace and Security Series C: Environmental Security.
– 2011. – P. 87–91. doi: 10.1007/978-94-007-1359-8_15.
Mitran,
G. The identification of major factors from road traffic which
produce the air pollution and presentation of the current stage of
the research in road traffic modeling and air pollution from road
vehicles / G. Mitran // PhD Scientific Report No. 1 /
University
of Pitesti. – Pitesti, Romania, 2011. – P. 60–63.
Ooka,
R. Wind – tunnel test of gaseous diffusion in street canyon with
thermal stratificution / R. Ooka, S. Murakami, S. Iizuka / Wind
Engeneering into the 21st Century. – 1999. – Vol. 2. – P.
781–786.
Sathe,
Y. V. Air Quality Modeling in Street Canyons of Kolhapur City,
Maharashtra, India / Y. V. Sathe // Universal J. of Environmental
Research and Technology. – 2012. – Vol. 2. – Iss. 2. – P.
97–105.
Xianxiang,
Li. Large-Eddy Simulation of Wind Flow and Air Pollutant Transport
inside Urban Street Canyons of Different Aspect Rations / Li
Xianxiang // Posgraduated Thesis
/
University of Hong Kong – Pokfulam,
Hong Kong,
2008. – P. 205.
doi: 10.5353/th_b4068732.
М. М. БІЛЯЄВ1*,
О. С. СЛАВІНСЬКА2*,
Р. В. КИРИЧЕНКО3*
1*Каф.
«Гідравліка та водопостачання»,
Дніпропетровський національний
університет залізничного транспорту
імені академіка В. Лазаряна, вул.
Лазаряна, 2, Дніпро, Україна, 49010, тел.
+38 (056) 273
15 09,
ел. пошта gidravlika2013@mail.ru, ORCID
0000-0002-1531-7882
2*Каф.
«Управління виробництвом та майном»,
Національний транспортний університет,
вул. Суворова, 1, Київ, Україна, 01010, тел.
+38 (044) 280
82 03,
ел. пошта gidravlika2013@mail.ru, ORCID
0000-0001-5163-5645
3*Каф.
«Управління виробництвом та майном»,
Національний транспортний університет,
вул. Суворова, 1, Київ, Україна, 01010, тел.
+38 (044) 280
82 03,
ел. пошта gidravlika2013@mail.ru, ORCID 0000-0001-9918-3895
ЧИСЕЛЬНІ МОДЕЛІ ДЛЯ ПРОГНОЗУ
забруднення атмосферного повітря
викидами АВТОТРАНСПОРТУ
Мета.
Наукова робота передбачає: 1) розробку
3D чисельних моделей, які дозволяють
розраховувати процес забруднення
атмосферного повітря викидами
автотранспорту; 2) створення моделей,
які давали б можливість прогнозувати
рівень забруднення атмосферного повітря
в умовах міської забудови. Методика.
Для розв’язання задачі з оцінки рівня
забруднення атмосферного повітря
викидами автотранспорту використовуються
фундаментальні рівняння аеродинаміки
і масопереносу. Для розв’язання
диференціальних рівнянь аеродинаміки
і масопереносу використовуються
кінцево-різницеві методи. З метою
чисельного інтегрування рівняння для
потенціалу швидкості застосовується
метод умовної апроксимації. Рівняння
для потенціалу швидкості, записане в
різницевому вигляді, розщеплюється на
два рівняння, причому на кожному кроці
розщеплення невідоме значення потенціалу
швидкості визначається за явною схемою
біжучого рахунку, при цьому сама
різницева схема – неявна. Для чисельного
інтегрування рівняння розсіювання
викидів в атмосфері застосовується
неявна поперемінно-трикутна різницева
схема розщеплення. Викиди від автотраси
моделюються серією точкових джерел
заданої інтенсивності. Розроблені
чисельні моделі складають основу
створеного пакета прикладних програм.
Результати.
Розроблені 3D чисельні моделі, які
відносяться до класу «diagnostic models». Дані
моделі враховують основні фізичні
фактори, що впливають на процес
розсіювання шкідливих речовин в
атмосфері при викидах від автотранспорту
в місті. На основі побудованих чисельних
моделей проведено обчислювальний
експеримент із оцінки рівня забруднення
повітряного середовища на вулиці.
Наукова новизна.
Авторами розроблено чисельні моделі,
які дозволяють розрахувати 3D аеродинаміку
вітрового потоку в умовах міської
забудови та процес масопереносу викидів
від автотраси. Виконано розрахунки по
визначенню зони забруднення, яка
формується біля будівель, розташованих
вздовж автомагістралі. Практична
значимість. В роботі
розглянуті ефективні чисельні моделі,
які можуть бути застосовані при розробці
заходів із охорони навколишнього
середовища при експлуатації автомобільного
транспорту в місті. Розроблені моделі
дозволяють оцінити розміри, форму та
інтенсивність зони забруднення біля
автомагістралі.
Ключові слова:
забруднення атмосфери; автотранспорт;
чисельне моделювання
M. M. BILIAIEV1*,
O. S. SLAVINSKA2*,
R. V. KYRYCHENKO3*
1*Dep.
«Hydraulics and Water Supply», Dnipropetrovsk National University
of Railway Transport named after
Academician
V. Lazaryan, Lazaryan St., 2, Dnipro, Ukraine, 49010, tel. +38 (056)
273 15
09,
e-mail
gidravlika2013@mail.ru, ORCID 0000-0002-1531-7882
2*Dep.
«Manufacturing and Property Management», National Transport
University of Ukraine, Suvorov
St., 1, Kyiv,
Ukraine,
01010, tel. +38 (044) 280 82 03, e-mail gidravlika2013@mail.ru,
ORCID 0000-0001-5163-5645
3*Dep.
«Manufacturing and Property Management», National Transport
University of Ukraine, Suvorov
St., 1, Kyiv,
Ukraine,
01010, tel. +38 (044) 280 82 03, e-mail gidravlika2013@mail.ru,
ORCID 0000-0001-9918-3895
NUMERICAL PREDICTION MODELS
FOR AIR
POLLUTION BY MOTOR
VEHICLE EMISSIONS
Purpose.
Scientific work involves: 1) development of 3D numerical models that
allow calculating the process of air pollution by motor vehicles
emissions; 2) creation of models which would allow predicting the
air pollution level in urban areas. Methodology. To solve the
problem upon assessing the level of air pollution by motor vehicles
emissions fundamental equations of aerodynamics and mass transfer
are used. For the solution of differential equations of aerodynamics
and mass transfer finite-difference methods are used. For the
numerical integration of the equation for the velocity potential the
method of conditional approximations is applied. The equation for
the velocity potential written in differential form, splits into two
equations, where at each step of splitting an unknown value of the
velocity potential is determined by an explicit scheme of running
computation, while the difference scheme is implicit one. For the
numerical integration of the emissions dispersion equation in the
atmosphere applies the implicit alternating-triangular difference
scheme of splitting. Emissions from the road are modeled by a series
of point sources of given intensity. Developed numerical models form
is the basis of the created software package. Findings. 3D
numerical models were developed; they belong to the class of
«diagnostic models». These models take into account main physical
factors that influence the process of dispersion of harmful
substances in the atmosphere when emissions from vehicles in the
city occur. Based on the constructed numerical models the
computational experiment was conducted to assess the level of air
pollution in the street. Originality. Authors have developed
numerical models that allow to calculate the 3D aerodynamics of the
wind flow in urban areas and the process of mass transfer emissions
from the highway. Calculations to determine the area of
contamination, which is formed near the buildings, located along the
highway were carried out. Practical value. Efficient
numerical models that can be applied when developing activities for
environmental protection in the operation of road transport in the
city. The developed models allow to estimate the size, shape, and
intensity of the contamination zone near the highway.
Keywords:
air pollution; vehicles; numerical simulation
References
Biliaiev M.M., Rusakova T.I.,
Kyrychenko P.S. Modelirovaniye
zagryazneniya atmosfernogo vozdukha vybrosami avtotransporta na
ulitsakh gorodov [Simulation
of air pollution emissions by vehicles in city streets].
Dnepropetrovsk, Aktsent PP Publ., 2014, 159 p.
Biliaiev
M.M., Rusakova T.I. CFD prognozirovaniye protsessa zagryazneniya
vozdushnoy sredy na ulitsakh [CFD prediction
of air pollution process in the streets].
Zbirnyk naukovykh prats instytutu
problem pryrodokorystuvannia ta ekolohii NAN Ukrainy «Ekolohiia i
pryrodokorystuvannia» [Bulletin of
Institute of Natural Resources and Ecology
of NAS of Ukraine «Ecology and
Environmental Sciences»], 2013, issue 17, pp. 188-194.
Berlyand
M.Ye. Prognoz i regulirovaniye
zagryazneniya atmosfery [Prediction
and regulation of air pollution]. Leningrad, Gidrometeoizdat Publ.,
1985. 273 p.
Berlyand
M.Ye. Sovremennyye problemy
atmosfernoy diffuzii i zagryazneniya atmosfery [Contemporary
problems of atmospheric diffusion and air pollution].
Leningrad, Gidrometeoizdat Publ., 1975. 448 p.
Bruyatskiy
Ye.V. Teoriya atmosfernoy diffuzii
radioaktivnykh vybrosov [The theory
of atmospheric diffusion of radioactive emissions]. Kiev, Institut
gidromekhaniki NAN Ukrainy Publ., 2000. 443 p.
Marchuk
G.I. Matematicheskoye modelirovaniye v
probleme okruzhayushchey sredy
[Mathematical modeling in the environmental problem]. Moscow, Nauka
Publ., 1982. 320 p.
Rudakov
D.V. Model rasseivaniya primesi v prizemnom sloye atmosfery nad
poverkhnostyu so slozhnym relefom [Model of impurity dispersion in
the ground layer over a surface with complex terrain]. Visnyk
Dnipropetrovskoho natsionalnoho universytetu. Seriia: Mekhanika
[Bulletin of Oles Honchar Dnipropetrovsk National University.
Series: Mechanics], 2004, no. 6, issue 8, vol. 1, pp. 89-97.
Samarskiy
A.A. Teoriya raznostnykh skhem
[The theory of difference schemes]. Moscow, Nauka Publ., 1983. 616
p.
Uork
K., Uorner S. Zagryazneniye vozdukha.
Istochniki i kontrol [Air pollution.
Sources and control]. Moscow, Mir Publ., 1980. 539 p.
Zgurovskiy
M.Z., Skopetskiy V.V., Khrushch V.K., Biliaiev M.M. Chislennoye
modelirovaniye rasprostraneniya zagryazneniya v okruzhayushchey
srede [Numerical modelling of
pollution spreading in the environment]. Kyiv,
Naukova dumka Publ., 1997. 368 p.
Berlov
O. V. Atmosphere protection in case of
emergency during transportation
of dangerous cargo. Nauka
ta prohres transportu – Science and Transport Progress,
2016, no. 1 (61), pp. 48-54. doi: 10.15802/stp2016/60953.
Biliaiev
M. Numerical Simulation of Indoor Air Pollution and Atmosphere
Pollution for Regions Having Complex Topography. NATO
Science for Peace and Security Series C: Environmental Security,
2011, pp. 87-91. doi: 10.1007/978-94-007-1359-8_15.
Mitran
G. The identification of major factors from road traffic which
produce the air pollution and presentation of the current stage of
the research in road traffic modeling and air pollution from road
vehicles. PhD Scientific Report No. 1.
University of Pitesti. Pitesti, Romania,
2011, pp. 60-63.
Ooka
R., Murakami S., Iizuka S. Wind – tunnel test of gaseous
diffusion in street canyon with thermal stratification. Wind
Engeneering into the 21st Century,
1999, vol. 2, pp. 781-786.
Sathe
Y.V. Air Quality Modeling in Street Canyons of Kolhapur City,
Maharashtra, India. Universal Journal
of Environmental Research and Technology,
2012, vol. 2, issue 2, pp. 97-105.
Xianxiang
Li. Large-Eddy Simulation of Wind Flow and Air Pollutant Transport
inside Urban Street Canyons of Different Aspect Rations.
Posgraduated Thesis. University of Hong Kong, Pokfulam,
Hong Kong, 2008. P. 205. doi:
10.5353/th_b4068732.
Статья
рекомендована к публикации д.физ.-мат.н.,
проф. C. А. Пичуговым
(Украина); д.т.н., проф. С. З. Полищуком
(Украина)
Поступила
в редколлегию: 01.09.2016
Принята
к печати: 01.12.2016
doi
© Н. Н. Беляев, Е. С. Славинская,
Р. В. Кириченко, 2016
, (1)
![]() – потенциал скорости.
– потенциал скорости.![]() ,
,
![]() ,
,
.
![]()
![]() (2)
(2)![]() – компоненты вектора скорости движения
воздушной среды;
– компоненты вектора скорости движения
воздушной среды;
– коэффициенты атмосферной турбулентной
диффузии;
![]() – коэффициент, учитывающий изменение
концентрации за счет химических реакций,
протекающих в атмосфере и вымывания
вредного вещества осадками [5];
t – время;
– коэффициент, учитывающий изменение
концентрации за счет химических реакций,
протекающих в атмосфере и вымывания
вредного вещества осадками [5];
t – время;
– координаты расположения точечного
источника выделения примеси (место
расположения автомобилей);
– скорость гравитационного оседания
загрязнителя;
![]() – интенсивность эмиссии точечного
источника (интенсивность выброса от
автомобилей);
– интенсивность эмиссии точечного
источника (интенсивность выброса от
автомобилей);
![]() – обозначение дельта-функции Дирака.
– обозначение дельта-функции Дирака. ,
, ,
,![]() ,
,
![]() ,
,![]() );
);
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.![]() , (3)
, (3)![]() – фиктивное время.
– фиктивное время.![]() решение уравнения (3)
будет стремиться к «установлению», то
есть к решению уравнения (1).
решение уравнения (3)
будет стремиться к «установлению», то
есть к решению уравнения (1).


![]() ,
,
– новое приближение величины потенциала
скорости;
– предыдущее значение величины
потенциала скорости; ε – малое
число.
![]() ,
,,
![]() .
.

