ISSN
2307–3489 (Print), ІSSN
2307–6666
(Online)
Наука
та прогрес транспорту. Вісник
Дніпропетровського
національного університету залізничного
транспорту, 2016,
№
4
(64)
рухомий
склад і тяга поїздів
UDC [629.4.027.5:543.1]-047.58
S. V.
MYAMLIN1,
O. A.
KIRILCHUK2*,
V. S.
METYZHENKO3
1Dep. «Car and Car
Facilities», Dnipropetrovsk National University of Railway Transport
named after Academician
V. Lazaryan,
Lazaryan St., 2, Dnipro, Ukraine, 49010, tel./fax +38 (056) 776 84
98, e-mail sergeymyamlin@gmail.com,
ORCID 0000-0002-7383-9304
2*Dep.
«Car and Car Facilities», Dnipropetrovsk National University of
Railway Transport named after Academician
V. Lazaryan, Lazaryan
St., 2, Dnipro, Ukraine, 49010, tel./fax +38 (056) 776 82 27, e-mail
kirilchuk.o@mail.ru,
ORCID 0000-0002-0565-1692
3Dep.
«Car and Car Facilities», Dnipropetrovsk National University of
Railway Transport named after Academician
V. Lazaryan, Lazaryan
St., 2, Dnipro, Ukraine, 49010, tel./fax +38 (099) 709 85 34, e-mail
VladR.K.I.S.M@yandex.ua,
ORCID 0000-0001-5318-7559
MATHEMATICAL MODEL OF WHEELSET OSCILLATIONS
WITH INDEPENDENT WHEEL
ROTATION IN
THE HORIZONTAL PLANE
Purpose. The
work is devoted to the study of horizontal oscillation and the
assessment of the motion stability of a single wheelset with
independent wheel rotation, and to the comparison of stability
indicators of the typical wheelset and the wheelset with independent
wheel rotation. This is connected with the necessity to increase
traffic speed of rolling stock, improve road safety and comfort of
passengers. Methodology.
To achieve this purpose we used the methods of mathematical
simulation of railway rolling stock dynamics, as well as the linear
algebra methods to assess the stability of solutions of the linear
homogeneous differential equations. Findings.
To solve the set
task the design model of a single wheelset with independent wheel
rotation was created. The wheelset is not a single solid body; each
of the wheelset axles has a surplus degree of freedom. Thus, we
obtained the system with 4 degrees of freedom. The design model
allowed to obtain the system of linear homogeneous differential
equations describing the oscillations of the represented wheelset in
a horizontal plane on a straight track section. On the basis of the
computer modeling were calculated the eigenvalues of the differential
equation system coefficients and the asymptotic stability analysis of
the wheelset motion with independent wheel rotation. The increment
and the frequency of fluctuations were compared with similar
indicators for the standard wheelset. The authors also discussed
non-oscillatory forms of the wheelset motion and the issues of
wheelset self-centering on the track. Originality.
The result of the work is the mathematical model of the sinuous
movement of a single wheelset, in two-dimensional formulation, with
independent wheel rotation and the estimate of the dynamic indices
during its motion on a straight track section without any
irregularities. There were also proposed the ways to ensure the
self-centering on the track of the wheelset with independent wheel
rotation. Practical
value. The
developed mathematical model of the single wheelset motion with
independent wheel rotation can be used to create the advanced designs
of railway running gear of cars.
Keywords:
wheelset; sinuous movement; independent wheel rotation; horizontal
oscillations; rolling stock; motion stability
Introduction
During
movement along the track the car components perform complex
oscillations. These oscillations are caused by dynamic forces and by
the track irregularities, gaps on the rail junctions, wheel bearing
surface conicity, as well as the irregularities on wheel bearing
surface, variability of physical properties of track and wheelset
materials, spring suspension type, changes of car speed, etc. [1,
2, 4, 5].
This paper examines in detail the oscillations caused by wheel
bearing surface conicity.
Analyzing the movement of the
wheelset on the rail track it is not difficult to see that it moves
not only progressively along the track axis, but also makes lateral
and rotational movements around its vertical axis. The conical wheel
bearing surface causes the alternate lead of one wheel in relation
to the other, herewith the geometric center of the wheelset axle
deviates from the track central axis and at the same time the
wheelset axle is rotated from the perpendicular to the track center
position [6, 9, 10, 13]. So during the motion the wheelset traces
out a complex wavy trajectory. This motion was first described in
1883 by Klingel [3]. In this regard, at high speed the train becomes
unstable, there are lateral oscillations and the motion quality
becomes unsatisfactory. There is a danger of derailment.
Purpose
The purpose of the work is to
study horizontal oscillation and to assess the motion stability of a
single wheelset with independent wheel rotation, as well as to
compare the stability indicators of the typical wheelset and the
wheelset with independent wheel rotation.
Methodology
To achieve this purpose we
developed the design model and composed the mathematical model
describing the oscillations of a single wheelset with independent
wheel rotation and in a horizontal plane. After that we analyzed the
asymptotic solutions stability of linear homogeneous differential
equations describing the oscillations of a single wheelset with
independent wheel rotation in a horizontal plane on a straight track
section.
Findings
The wheelset
consists of two wheels firmly fixed on the relevant axle shafts. The
axle shafts are connected with bearing units. Thus the wheelset may
be represented as a single solid body, but the axle shafts can be
rotated in a longitudinal plane on each other (have surplus degree
of freedom). In the proposed mathematical
model of
the single
wheelset motion,
the friction in
the bearing
unit is
ignored. To
describe the motion of the wheelset with independent wheel rotation
on the straight track section, we should calculate the rail-wheel
interaction forces. In 1926, F. Carter found that the tangential
force of contact wheel-rail interaction is proportional to the
relative slip (creep) of the contacting bodies [3,
7, 8, 11]. The tangential force
projections onto the longitudinal and transversal axis are,
respectively:
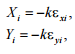 (1)
(1)
where
εxi,
εyi
–
relative ship towards x-axis and y-axis, respectively; k
– creep coefficient (according to Carter’s hypothesis we
consider that the proportionality coefficients between longitudinal
slip and longitudinal force and between lateral slip and lateral
force are equal).
Design model of wheelset with
independent wheel rotation is shown in Fig.1.
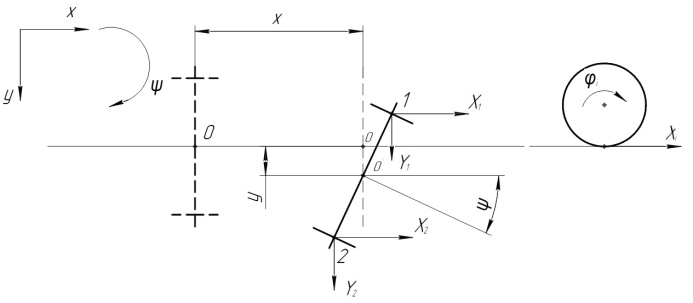
Fig.
1. Design model of
wheelset
with
independent wheel
rotation
The wheelset
with independent
wheel rotation
moves at
a speed
V. According
to the
above design
model (Fig.
1) the wheelset
position is
determined by
the lateral
swaying y,
the hunting
angle ψ,
and the
additional angle
of rotation
of each
of wheelset
axle shaft in the
longitudinal
plane φ1,
φ2,
so the
angular velocity
of each
axle shaft is:
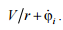
Thus,
we consider a
system with
four degrees
of freedom.
We accept that the hunting angle of the
wheelset is small enough. The relative slip εxi,
εyi can
be determined by the formulas:
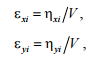
where ηxi,
ηyi
– slip velocity at the wheel-rail
contact points;
The slip rate is determined as
the difference between the rail and the wheel speeds:
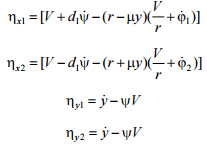
where μ
– wheel tread
grade; r
– rim radius
on neutral
axis.
The
relative slip
is:
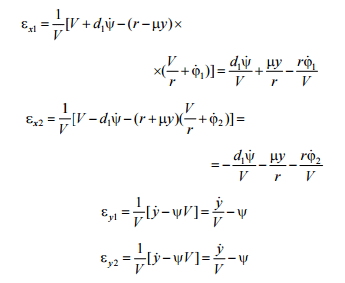
Herewith we
ignore the summand
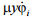 ,
given that it is by several orders of magnitude smaller than the
others.
,
given that it is by several orders of magnitude smaller than the
others.
Let us substitute the slip
expressions into the formula 1 and we obtain the expression:
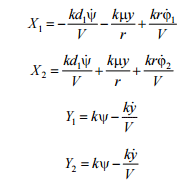
Then
the principal
moment acting
on the
vertical axis
is:
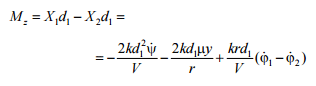
The principal vector in the
transversal direction is equal to:
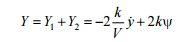
The
moment acting
transversely on
the axle
shafts
respectively:
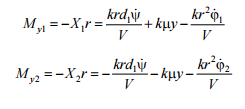
The motion equations:
 (2)
(2)
The resulting system of
equations describes the motion of a single wheelset on a straight
track section.
To assess the stability of the
motion of the single wheelset with independent wheel rotation, we
write the equation 2 in matrix form:
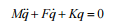 (3)
(3)
where
q – вектор обобщенных координат.
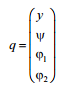
М –
matrix of
inertial
coefficients;
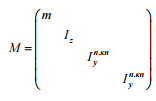
F
– matrix of damping coefficients;
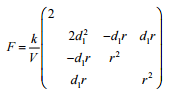
К –
coefficient
matrix of
the movements;
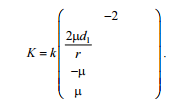
To
determine the
eigenvalues of
the coefficient
matrix the
system of equations
3 can be
written as:
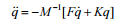
After
some
transformations
we obtain:
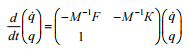
Thus, calculation of the
eigenvalues of the coefficient matrix for different speeds and
different values of the wheel rate allows obtaining the diagrams of
oscillation increment and frequency dependency on speed (Fig. 3, 4).
1 – Wheelset with independent
wheel rotation;
2 – Standard wheelset.
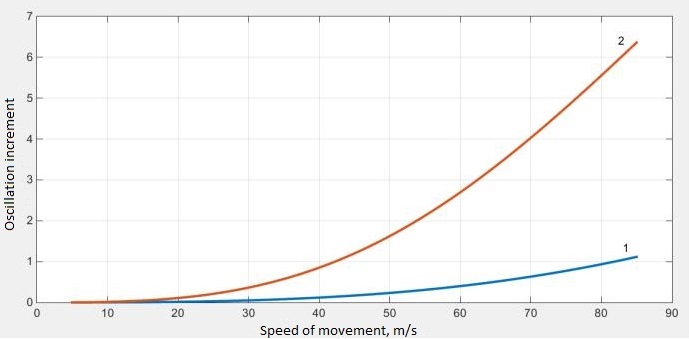
Fig.2.
Dependency of oscillation increment on speed
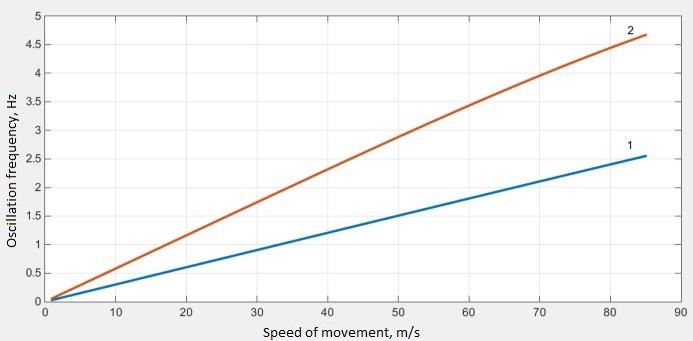
Fig.
3. Dependency of oscillation frequency on speed
The obtained results indicate
that for the wheelset with independent wheel rotation the form of
hunting oscillations and swaying remains. Herewith the oscillation
frequency at the same speed is half that of the standard wheelset.
Oscillation increment is 5.5 times less than for the standard
wheelset, although it remains positive over the entire range of the
examined velocities. This indicates that the use of wheelsets with
independent wheel rotation will increase the car movement stability
at high speeds. However wheelset with independent wheel rotation is
also characterized by non-oscillatory movement forms. In this
regard, under certain conditions the wheelset loses its
self-centering in the track that is its significant disadvantage.
One of the variants to ensure wheelset self-centering in the track
is the use of resistance element to the relative rotation of the
wheelset axle-shafts [12]. During the relative rotation of the
wheelset axle-shafts such an element will create a moment of
resistance in an effort to equal the angular velocities of the
axle-shafts. This will lead to the wheelset rotation around the
vertical axis in such a way that the wheelset will tend to take the
central position in relation to the track axis [14, 15]. Of course,
to confirm this assumption it is necessary to conduct experiments on
a physical model or prototype of the wheelset as part of a bogie and
a car.
Originality
and practical
value
The result of the work is the
mathematical model of the sinuous movement of a single wheelset with
independent wheel rotation and the estimate of the dynamic indices
during its motion on a straight track section without any
irregularities. The developed mathematical model of the motion of
the single wheelset with independent wheel rotation can be used to
create the advanced designs of railroad car undercarriage at the
stage of selection of running gear parameters using mathematical
modeling.
Conclusions
As a result of comparison of
the increment and the oscillation frequency of a single wheelset,
standard and with independent wheel rotation, it was found that the
use of wheelsets with independent wheel rotation allows achieving
higher dynamic qualities of movement. However, this requires
experimental verification on the stand or dynamic tests on the line.
LIST OF REFERENCE LINKS
Вериго, М. Ф. Взаимодействие
пути и подвижного состава / М. Ф. Вериго,
А. Я. Коган. – Москва :Транспорт, 1986. –
560 с.
Дьомін, Ю. В. Основи динаміки
вагонів : навч.
посібник / Ю. В. Дьомін, Г. Ю. Черняк. –
Киів : КУЕТТ, 2003. – 270
с.
Компьютерное
моделирование ходовой динамики и
износа колес грузового локомотива
с
радиальной установкой колесных пар /
Г. С. Михальченко, В. Н. Языков, В. С.
Коссов, А. В. Спиров // Вісн. Дніпропетр.
нац. ун-ту залізн. трансп. ім. акад. В.
Лазаряна. – Дніпропетровськ, 2004. –
Вип. 5. – С. 139–142.
Лазарян, В.
А. Динамика вагонов / В.
А. Лазарян. – Москва :
Транспорт, 1964. – 256 с.
Лазарян, В. А. Динамика транспортных
средств / В. А. Лазарян. – Киев : Наук.
думка, 1985. – 528 с.
Математическое моделирование
колебаний рельсовых транспортных
средств / В. Ф. Ушкалов, Л. М. Резников,
В. С. Иккол [и др.]. – Киев : Наук. думка,
1989. – 240 с.
Математическое
описание силового взаимодействия
колес и рельсов / Л. Н. Дегтярева, Ю.
И. Осенин, С. В. Мямлин // Вісн. Дніпропетр.
нац. ун-ту залізн. трансп. ім. акад. В.
Лазаряна. – Дніпропетровськ, 2009. –
Вип. 28. – С. 21–24.
Михайлов, Е. В. Анализ путей
снижения из-носа в системе «гребень
колеса-рельс» / Е. В. Михайлов, С. А.
Семенов // Вісн. СНУ ім. В.
Даля. – 2012. – Ч. 1, № 5 (176). –
С. 71–76.
Мусаев, Ж. С. Сравнительный
анализ продольной динамики железнодорожных
экипажей при переходных режимах / Ж.
С. Мусаев, В. Г. Солоненко, Т. М. Дюсенгалиева
// Вестн. МГТУ им. Н. Э.
Баумана. Изв. высш.
учеб. за-ведений.
Машиностроение. – 2013. – № 1. – С.
33–37.
Основные динамические
показатели пассажирского вагона / Ю.
М. Федюшин, А. Н. Пшинько, С. В. Мямлин [и
др.] // Вісн. Дніпропетр. нац. ун-ту залізн.
трансп. ім. акад. В. Лазаряна. –
Дніпропетровськ, 2005. –
Вип.
7. –
С.
91–94.
Malavasi, G. Contact Forces and
Running Stability of Railway Vehicles /
G. Malavasi //
Intern. J. of Railway Technology.
– 2014. – Vol.
3. – Iss. 1. – P. 121–132. doi:
10.4203/ijrt.3.1.6.
Manashkin, L. A. To the question of
modeling of wheels and rails wear processes / L.
A. Manashkin, S. V. Myamlin
// Наука та
прогрес транспорту.
– 2013. – № 3 (45).
– С. 119–124. doi:
10.15802-/stp2013/14791.
Myamlin, S.
V. Investigation of dynamic charac-teristics of gondola cars on
perspective bogies / S. V.
Myamlin, V.
M.
Bubnov, Ye.
O. Pysmennyi // Наука
та
прогрес
транспорту.
– 2014. – № 5 (53). – С.
126–137. doi: 10.158022/stp2014-/30789.
Rozenblat, G. M. On the stability
of motion of a railway wheel pair / G. M. Rozenblat // Doklady
Physics. – 2012. – Vol.
57. – Iss. 2. – P. 87–91. doi: 10.1134/S1028335812020085.
Vil’ke, V. G. Stability of the
Rectilinear Motion of a Railway Wheelset
/ V. G. Vil’ke, B. A. Maksimov, S. A.
Popov // Moscow
University Mechanics Bulletin. – 2010. – Vol. 65. – Iss. 2. –
P. 31–37. doi:
10.3103/S0027133015020020.
С. В. МЯМЛІН1,
О. А.
КИРИЛЬЧУК2*,
В. С. МЕТИЖЕНКО3
1Каф.
«Вагони та вагонне господарство»,
Дніпропетровський національний
університет залізничного
транспорту
імені академіка В.
Лазаряна, вул. Лазаряна,
2, Дніпропетровськ,
Україна, 49010, тел. +38
(056) 776 84
98,
ел. пошта
sergeymyamlin@gmail.com, ORCID 0000-0002-7383-9304
2*Каф.
«Вагони та вагонне господарство»,
Дніпропетровський національний
університет залізничного
транспорту
імені академіка В.
Лазаряна, вул. Лазаряна,
2, Дніпропетровськ,
Україна, 49010, тел. +38
(056) 776 82
27,
ел. пошта
kirilchuk.o@mail.ru,
ORCID 0000-0002-0565-1692
3Каф.
«Вагони та вагонне господарство»,
Дніпропетровський національний
університет залізничного
транспорту
імені академіка В.
Лазаряна, вул. Лазаряна,
2, Дніпропетровськ,
Україна, 49010, тел. +38
(099) 709 85
34,
ел. пошта
VladR.K.I.S.M@yandex.ua,
ORCID 0000-0001-5318-7559
МАТЕМАТИЧНА МОДЕЛЬ КОЛИВАНЬ КОЛІСНОЇ
ПАРИ
З НЕЗАЛЕЖНИМ ОБЕРТАННЯМ КОЛІС
В ГОРИЗОНТАЛЬНІЙ ПЛОЩИНІ
Мета.
Робота присвячена дослідженню
горизонтальних коливань і оцінці
стійкості руху одиночної колісної пари
з незалежним обертанням коліс, а також
порівнянню показників стійкості типової
колісної пари і колісної пари з незалежним
обертанням коліс. Це пов’язано з
необхідністю підвищення швидкостей
руху рухомого складу, підвищенням
показників безпеки руху, а також
покращенням комфорту перевезення
пасажирів. Методика.
Для досягнення поставленої мети
використані методи математичного
моделювання динаміки залізничного
рухомого складу, а також методи лінійної
алгебри – для оцінки стійкості розв’язку
системи лінійних однорідних диференціальних
рівнянь. Результати.
Для вирішення поставленої задачі була
побудована розрахункова схема одиночної
колісної пари з незалежним обертанням
коліс. Колісна пара представлена єдиним
твердим тілом, проте кожна з півосей
колісної пари має додаткові ступені
свободи. Таким чином, отримали систему
з 4 ступенями свободи. На основі
розрахункової схеми була отримана
система лінійних однорідних диференціальних
рівнянь, що описує коливання представленої
колісної пари в горизонтальній площині
на прямій ділянці шляху. З використання
ЕОМ були обчислені власні числа матриці
коефіцієнтів системи диференційних
рівнянь і виконаний аналіз асимптотичної
стійкості руху колісної пари з незалежним
обертанням коліс. Інкремент і частоту
коливань порівнювали з аналогічними
показниками для типової колісної пари.
Також розглянуті неколивальні форми
руху колісної пари і питання самостійного
центрування колісної пари в колії.
Наукова новизна.
За результатами роботи розроблена
математична модель звивистого руху
одиночної колісної пари в плоскій
постановці задачі з незалежним обертанням
коліс і виконана оцінка динамічних
характеристик при її русі по прямій
ділянці шляху без нерівностей. Також
розглянуті способи забезпечення
самостійного центрування в колії
колісної пари з незалежним обертанням
коліс. Практична
значимість. Розроблена
авторами математична модель руху
одиночної колісної пари з незалежним
обертанням коліс може бути використана
при створенні перспективних конструкцій
ходових частин вагонів.
Ключові слова: колісна пара;
звивистий рух; залежне обертання коліс;
горизонтальні коливання; рухомий склад;
стійкість руху
С. В. МЯМЛИН1,
О. А. КИРИЛЬЧУК2*,
В. С. МЕТЫЖЕНКО3
1Каф. «Вагоны
и вагонное хозяйство», Днепропетровский
национальный университет железнодорожного
транспорта имени академика В.Лазаряна,
ул. Лазаряна, 2, Днепропетровск, Украина,
49010, тел. +38 (056) 776 84 98,
эл.
почта sergeymyamlin@gmail.com, ORCID 0000-0002-7383-9304
2*Каф.
«Вагоны и вагонное хозяйство»,
Днепропетровский национальный
университет железнодорожного
транспорта
имени академика В.Лазаряна, ул. Лазаряна,
2, Днепропетровск, Украина, 49010, тел. +38
(056) 776 82 27,
эл. почта kirilchuk.o@mail.ru,
ORCID 0000-0002-0565-1692
3Каф.
«Вагоны и вагонное хозяйство»,
Днепропетровский национальный
университет железнодорожного
транспорта
имени академика В.Лазаряна, ул. Лазаряна,
2, Днепропетровск, Украина, 49010, тел. +38
(099) 709 85 34,
эл. почта VladR.K.I.S.M@yandex.ua,
ORCID 0000-0001-5318-7559
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ КОЛЕБАНИЙ
КОЛЕСНОЙ ПАРЫ
С НЕЗАВИСИМЫМ ВРАЩЕНИЕМ
КОЛЕС
В ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТИ
Цель.
Работа посвящена исследованию
горизонтальных колебаний и оценке
устойчивости движения одиночной
колесной пары с независимым вращением
колес, а также сравнению показателей
устойчивости типовой колесной пары и
колесной пары с независимым вращением
колес. Это связано с необходимостью
повышения скоростей движения подвижного
состава, увеличением показателей
безопасности движения, а также
улучшением комфорта перевозки пассажиров.
Методика.
Для достижения поставленной цели
использованы методы математического
моделирования динамики железнодорожного
подвижного состава, а также методы
линейной алгебры – для оценки устойчивости
решения системы линейных однородных
дифференциальных уравнений. Результаты.
Для решения поставленной задачи была
построена расчетная схема одиночной
колёсной пары с независимым вращением
колес. Колесная пара представлена
единым твердым телом, каждая из полуосей
колесной пары имеет дополнительные
степени свободы. Таким образом, получили
систему с 4 степенями свободы. На основе
расчетной схемы была получена система
линейных однородных дифференциальных
уравнений, описывающая колебания
представленной колесной пары в
горизонтальной плоскости на прямом
участке пути. С использованием ЭВМ
вычислены собственные числа матрицы
коэффициентов системы дифференциальных
уравнений и выполнен анализ асимптотической
устойчивости движения колесной пары
с независимым вращением колес. Инкремент
и частоту колебаний сравнивали с
аналогичными показателями для типовой
колесной пары. Также рассмотрены
неколебательные формы движения колесной
пары и вопросы самостоятельного
центрирования колесной пары в колее.
Научная новизна. По
результатам работы разработана
математическая модель извилистого
движения одиночной колесной пары в
плоской постановке задачи с независимым
вращением колес и выполнена оценка
динамических показателей при ее движении
по прямому участку пути без неровностей.
Также рассмотрены способы обеспечения
самостоятельного центрирования в колее
колесной пары с независимым вращением
колес. Практическая
значимость. Разработанная
авторами математическая модель движения
одиночной колесной пары с независимым
вращением колес может быть использована
при создании перспективных конструкций
ходовых частей вагонов.
Ключевые слова: колесная
пара; извилистое движение; зависимое
вращение колес; горизонтальные колебания;
подвижной состав; устойчивость движения
REFERENCES
Verigo M.F., Kogan A.Ya.
Vzaimodeystviye puti i podvizhnogo
sostava [Interaction of track and
rolling stock]. Moscow, Transport Publ., 1986. 560 p.
Domin Yu.V., Cherniak H.Yu. Osnovy
dynamiky vahoniv [Fundamentals of car
dynamics]. Kyiv, KUETT Publ., 2003. 270 p.
Mikhalchenko G.S., Yazykov V.N.,
Kossov V.S., Spirov A.V. Kompyuternoye modelirovaniye khodovoy
dinamiki i iznosa koles gruzovogo lokomotiva s radialnoy ustanovkoy
kolesnykh par [Computer simulation of the dynamics and wear of the
freight locomotive wheels with radial layout of wheel sets]. Vіsnyk
Dnіpropetrovskoho natsionalnoho universytetu zalіznychnoho
transportu іmeni akademika V. Lazaryana
[Bulletin of Dnipropetrovsk National University of Railway
Transport named after Academician V. Lazaryan], 2004, issue 5, pp.
139-142.
Lazaryan V.A. Dinamika
vagonov [Car dynamics]. Moscow,
Transport Publ., 1964. 256 p.
Lazaryan V.A. Dinamika
transportnykh sredstv [Dynamics of
vehicles]. Kyiv, Naukova dumka Publ., 1985. 528 p.
Ushkalov V.F., Reznikov L.M., Ikkol
V.S. Matematicheskoye modelirovaniye
kolebaniy relsovykh transportnykh sredstv
[Mathematical modeling of rail vehicles oscillations]. Kyiv,
Naukova dumka Publ., 1989. 240 p.
Degtyareva L.N., Osenin Yu.I.,
Myamlin S.V. Matematicheskoye opisaniye silovogo vzaimodeystviya
koles i relsov [Mathematical description of the force interaction
of wheels and rails]. Vіsnyk
Dnіpropetrovskoho natsionalnoho universytetu zalіznychnoho
transportu іmeni akademika V. Lazaryana
[Bulletin of Dnipropetrovsk National University of Railway
Transport named after Academician V. Lazaryan], 2009, issue 28, pp.
21-24.
Mikhaylov Ye.V., Semenov S.A.
Analiz putey snizheniya iznosa v sisteme «greben kolesa-rels»
[Analysis of ways to reduce the wear in the system, «wheel
flange-rail»]. Vіsnyk
Skhidnoukrainskoho natsionalnoho universytetu imeni V. Dalia
[Volodymyr Dahl East Ukrainian National University], 2012, part 1,
no. 5 (176), pp. 71-76.
Musayev Zh.S., Solonenko V.G.,
Dyusengalieva T.M. Sravnitelnyy analiz prodolnoy dinamiki
zheleznodorozhnykh ekipazhey pri perekhodnykh rezhimakh
[Comparative analysis of longitudinal dynamics of railway vehicles
during transient conditions]. Vestnik
MGTU imeni N. E. Baumana. Izvestiya vysshikh uchebnykh zavedeniy.
Mashinostroyeniye –
Bulletin of Bauman Moscow State Technical University,
2013, no. 1, pp. 33-37.
Fedyushin Yu.M., Pshinko A.N.,
Myamlin S.V., Donchenko A.V., Loboyko L.M. Osnovnyye dinamicheskiye
pokazateli passazhirskogo vagona [The basic dynamic performance of
passenger car]. Vіsnyk
Dnіpropetrovskoho natsionalnoho universytetu zalіznychnoho
transportu іmeni akademika V. Lazaryana
[Bulletin of Dnipropetrovsk National University of Railway
Transport named after Academician V. Lazaryan], 2005, issue 7, pp.
91-94.
Malavasi G. Contact Forces and
Running Stability of Railway Vehicles. International
Journal of Railway Technology, 2014,
vol. 3, issue
1, pp. 121-132. doi: 10.4203/ijrt.3.1.6.
Manashkin L.A., Myamlin
S.V.
To the question of
modeling of wheels and rails wear processes.
Nauka
ta prohres transportu –
Science and Transport Progress, 2013, no. 3
(45),
pp. 119-124. doi: 10.15802/stp2013/14791.
Myamlin S.V., Bubnov V.M., Pysmennyi Ye.O.
Investigation of dynamic characteristics of gondola cars on
perspective bogies. Nauka ta prohress transportu – Science and
Transport Progress, 2014, no. 5 (53), pp. 126-137. doi:
10.158022/stp2014/30789.
Rozenblat G.M. On the stability of
motion of a railway wheel pair. Doklady
Physics, 2012, vol. 57, issue 2, pp.
87-91. doi: 10.1134/S1028335812020085.
Vil’ke V.G., Maksimov B.A., Popov
S.A. Stability of the Rectilinear Motion
of a Railway Wheelset. Moscow
University Mechanics Bulletin, 2010,
vol. 65, issue 2, pp. 31-37. doi: 10.3103/S0027133015020020.
Prof. V.
L. Horobets., D. Sc. (Tech.)
(Ukraine) recommended this article to be published
Accessed: 17 May, 2016
Received:
01 Aug., 2016
doi © S. V.
Myamlin, O. A. Kirilchuk, V. S. Metyzhenko, 2016
(1)
,
given that it is by several orders of magnitude smaller than the
others.
(2)
(3)