ISSN 2307–3489 (Print), ІSSN 2307–6666 (Online)

Наука та прогрес транспорту. Вісник Дніпропетровського
національного університету залізничного транспорту, 2016, № 4 (64)

рухомий склад і тяга поїздів

Введение

Продольные силы, испытываемые вагоном и грузом, а, соответственно, и убытки от повреждений, достигают своих наибольших величин при соударениях. Поэтому, основная задача защиты длинномерных и крупноразмерных грузов от динамических воздействий при перевозке состоит в уменьшении ударных нагрузок, передаваемых грузу при соударениях вагонов в процессе сортировочной и маневровой работы. Решение задачи определения характера и величин действующих на грузы сил и ускорений, вызывает необходимость исследования сложных механических систем, включающих в себя вагоны или сцепы вагонов с грузом и взаимодействующие с ними другие единицы подвижного состава (локомотивы, вагоны, группы вагонов).

Анализ предыдущих исследований. Теоретическими исследованиями в области крепления грузов на подвижном составе железных дорог занимались ученые и специалисты А. Д. Малов, Г. П. Ефимов, Н. Г. Гончаров, Г. П. Гриневич, Б. М. Хотин, Е. Н. Гохбом и другие [2–8]. Общей чертой всех названных работ является то, что вопросы выбора типа крепления, его конструкции и расчета на прочность при перевозке длинномерных и крупногабаритных грузов решаются исходя из существующих традиционных конструктивных схем крепления груза с использованием упоров, стоек, растяжек и обвязок. Крепление длинномерных грузов на сцепах из нескольких вагонов принципиального отличия в аспекте продольной динамики не имеет, поскольку турникетная опора на одном из опорных вагонов обеспечивает жесткое крепление груза. Прочность такого рода крепления обеспечивается при соударениях вагонов со скоростями не более 5−6 км/ч. При этом ускорения груза достигают величин 2−3 g и более.

Совершенствованию методов расчета передаваемых грузам при соударениях вагонов продольных инерционных сил посвящен ряд работ А. Д. Малова, В. А. Каблукова, И. К. Мороза, А. В. Шатунова, В. А. Калашника, Б. Г. Кеглина, Е. Ф. Стуся, Г. Б. Крайзгура, Г. В. Костина, В. А. Лазаряна, Е. П. Блохина, Л. А. Манашкина и др. [2–8].

Цель

Обеспечение сохранности вагонов и длинномерных грузов в процессе перевозки требует совершенствования методики определения параметров ТКУ.

Методика

Исследования выполнены методом теории колебаний механических систем с конечным числом степеней свободы, с использованием математического моделирования актуального в настоящее время способа исследования вагонных конструкций [5, 10–13].

Платформы сцепа и груза считаются абсолютно жесткими телами, а межвагонные соединения и опоры ТКУ упругими связями постоянной жесткости сухим трением. Для получения движения системы используем принцип Даламбера.

Расчетная схема соударения сцепа с неподвижной преградой (группы заторможенных выгонов) показано на рис. 1.

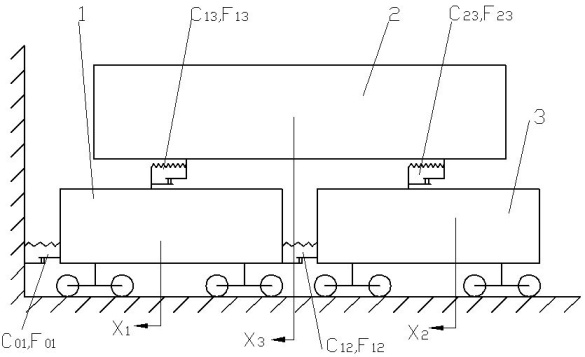
Рис. 1. Расчетная схема соударения

Fig. 1. The calculation model of impact

В начальный момент набегания сцепа на преграду платформа 1 получает жесткий удар, сила которого при любой скорости соударения V₀ к началу деформации упругой связи С₀₁ практически мгновенно возрастает до величины силы трения F₀₁. В результате платформа 1 как жесткое тело приобретает ускорение x₁, зависящее от степени участия в ударе каждой из масс системы. Возможны следующие варианты взаимодействия тел.

Все три массы системы жестко соединены между собой силами сухого трения в единое тело и на первом этапе движутся совместно (x¹ = x² = x³). Условия, при которых возникает такое движение, могут быть представлены в виде:

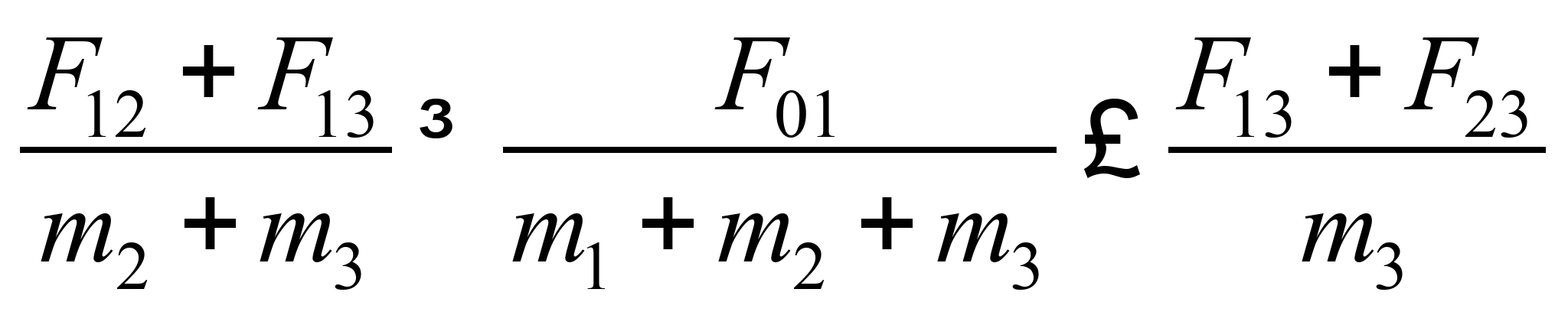. (1)

Рассматриваемое движение описывается уравнением:

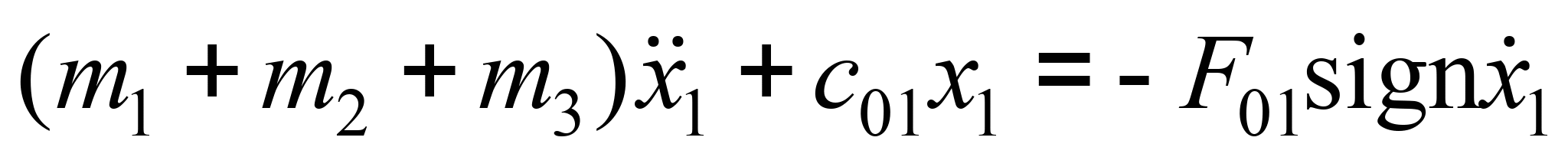. (2)

Характер движения сохраняется, пока выполняется следующие условие x¹ ≥ 0:

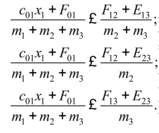(3)

При нарушении первого, второго или третьего неравенства (3) начинает двигаться отдельно первая, вторая или третья массы системы соответственно.

Платформы 1 и 2 жестко соединены между собой силами сухого трения в единое тело и на первом этапе движутся совместно (x₁ = x₂), а груз 3 начинает проскальзывать относительно их. Условия возникновения такого движения в момент удара определяются неравенствами:

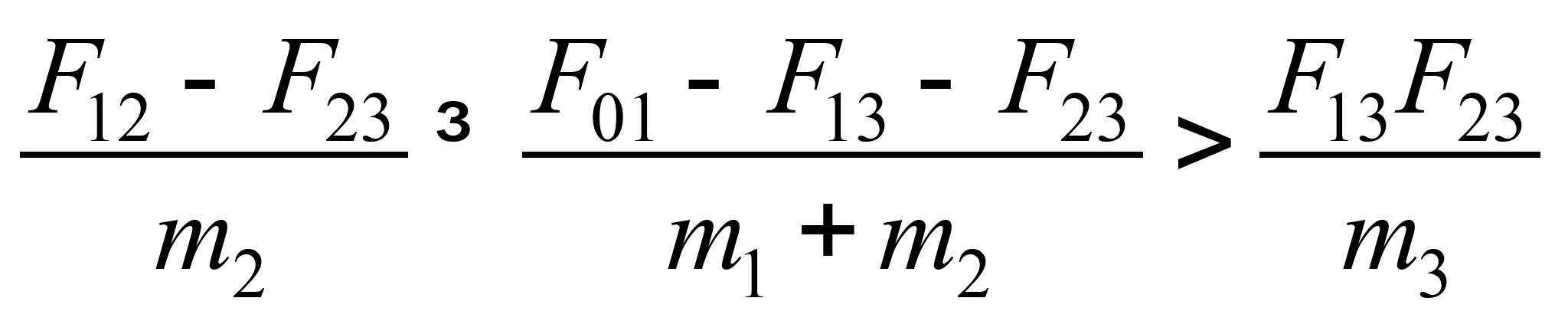. (4)

Оно описывается следующими уравнениями:

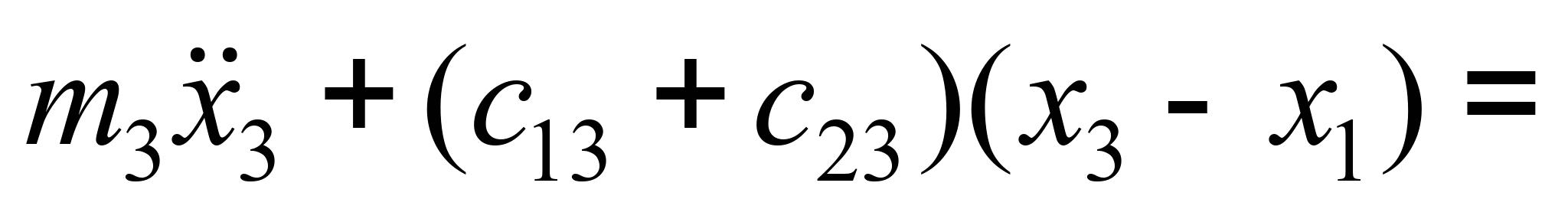
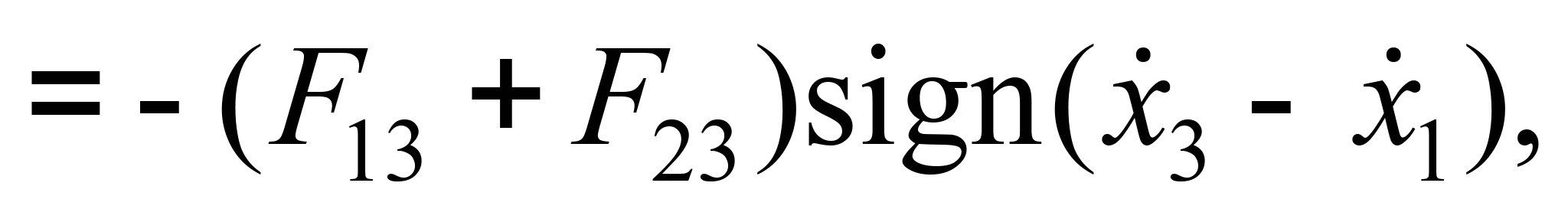(5)

где

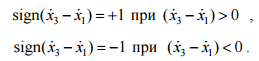
Рассматриваемый вид движения происходит до тех пор, пока соблюдаются условия x₁≥0; (x₃ – x₁) ≥0:

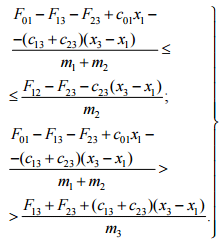(6)

При нарушении первого неравенства в полученных условиях возникает относительное перемещение платформ 1 и 2, при нарушении второго – все три массы начинают двигаться совместно.

Массы 1 и 3 жестко связаны между собой силами сухого трения в единое тело и на первом этапе движутся совместно (x₁ = x₃), а платформа 2 начинает проскальзывать относительно их. Условия, при которых возникает такое движение, могут быть получены в виде:

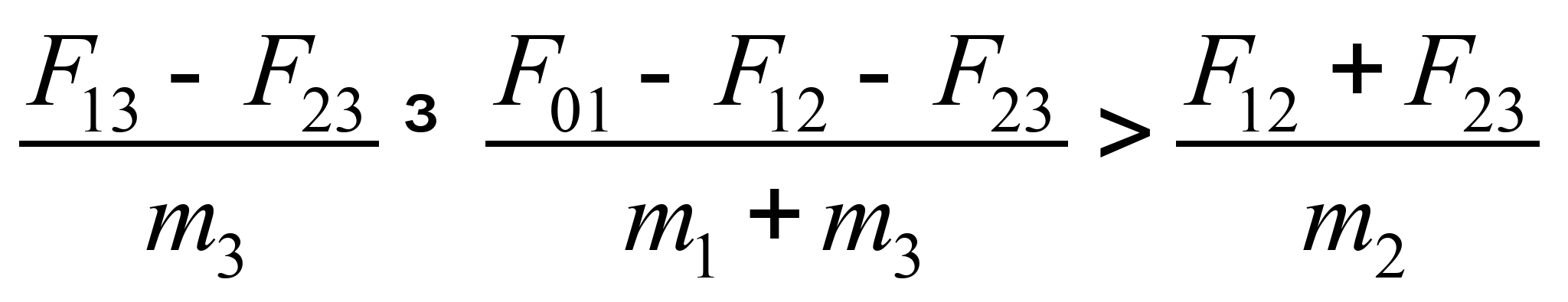. (7)

Рассматриваемое движение описывается уравнениями:

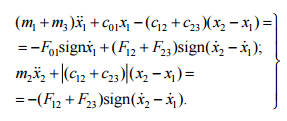(8)

Этот вид движения происходит только при соблюдении следующих условий (при ):

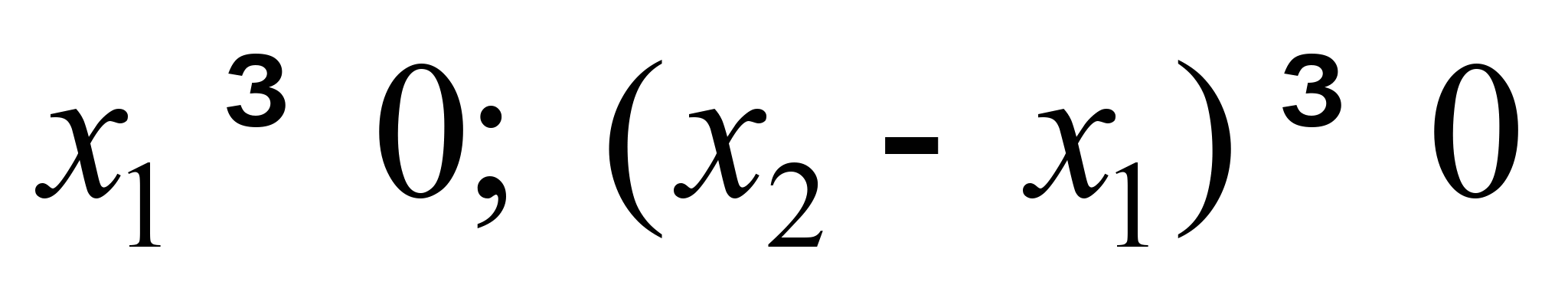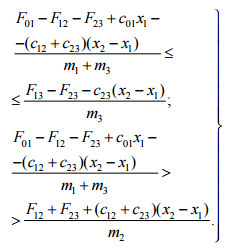(9)

В случае нарушения первого неравенства в условиях (9) возникает относительное перемещение масс 1 и 3, при нарушении второго – все три массы начинают двигаться совместно.

Массы 2 и 3 жестко связаны между собой силами сухого трения в единое тело и на первом этапе движутся совместно (x₂ = x₃), а платформа 1 начинает проскальзывать относительно их. Условия, при которых возникает рассматриваемое движение, можно представить в виде:

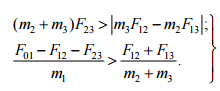(10)

Оно описывается следующими уравнениями:

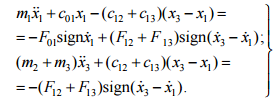(11)

Характер движения сохраняется до тех пор, пока выполняются условия при x¹ ≥ 0, (x³ – x¹) ≥ 0:

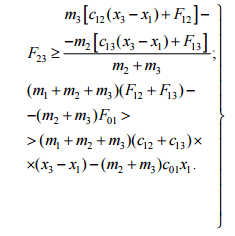(12)

В случае нарушения первого неравенства в условиях (12) возникает относительное перемещение масс 2 и 3, при нарушении второго – все три массы начинают двигаться совместно.

Все три массы системы имеют перемещения относительно друг друга. Такое движение возникает в случаях, когда не выполняется ни одно из условий (1), (4), (7), (10) в начале движения или нарушаются первые неравенства в условиях (6), (9), (12). Дифференциальные уравнения этого вида движения имеют вид (13). Рассматриваемый характер движения сохраняется до возникновения условий для жесткого соединения каких-либо масс силами трения.

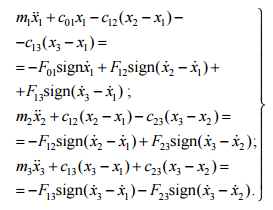(13)

Порядок расчетов по приведенным уравнениям может быть принят следующим:

а) по формулам (1), (4), (7), (10) определяется характер движения на его начальном этапе;

б) по выявленному характеру движения производится интегрирование соответствующих уравнений при начальных условиях:

.

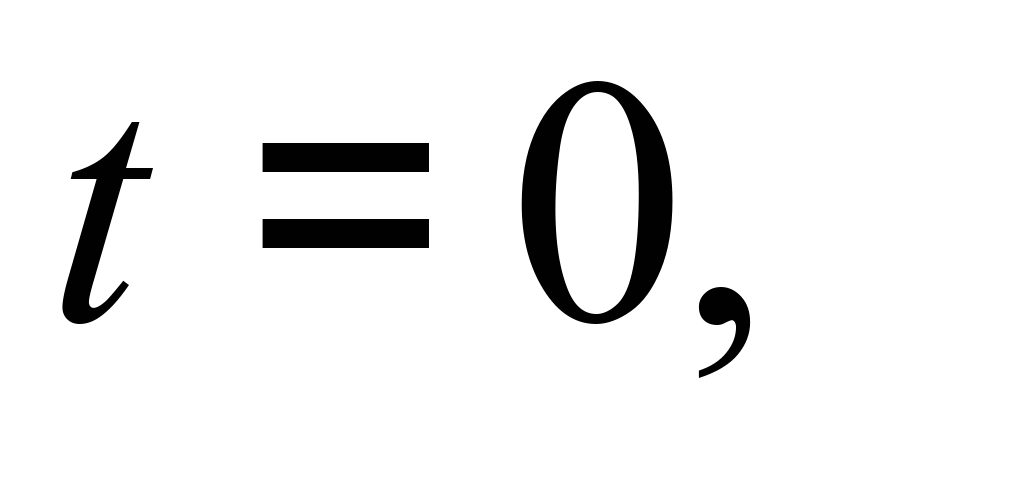
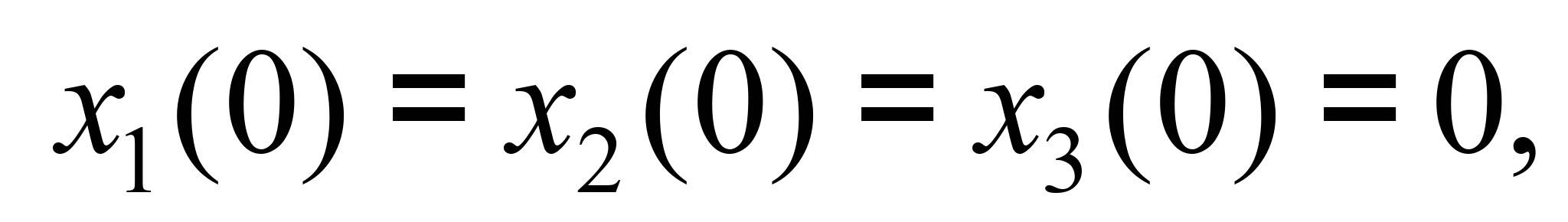
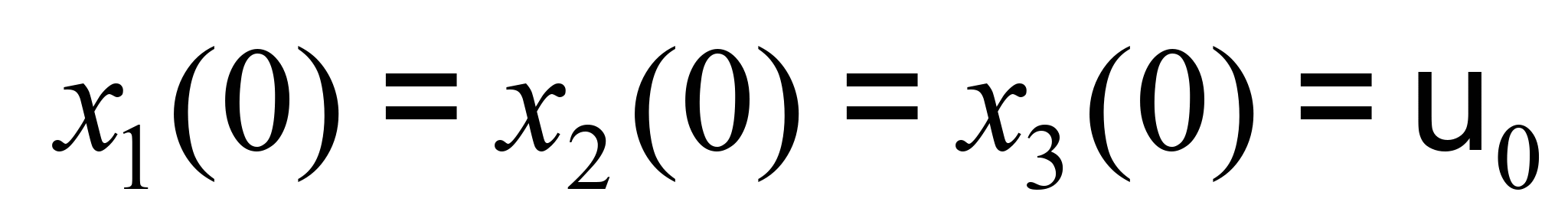Интегрирование ведется до тех пор, пока соблюдаются условия, соответствующие этому характеру движения;

в) при нарушении характера движения используется другая, соответствующая этому нарушению система уравнений и производится ее интегрирование при начальных условиях, равных значениям параметров в конечный момент предыдущего этапа. Интегрирование производится, пока не нарушатся условия, определяющие характер движения на рассматриваемом этапе;

г) работы по п. в продолжаются до прекращения роста значений x_{1 ;} (x₃ – x₁); (x₂ – x₁);

д) проверяется соответствие максимальных величин полученных относительных перемещений x₁; (x₃ – x₁); (x₃ – x₂); (x₂ – x₁) заданным конструктивным ограничениям (указанные перемещения не должны превышать допускаемых значений). Если это условие не выполняется, то либо рассматриваемый расчетный вариант, определяемый сочетанием параметров системы и скорости соударения, признается неприемлемым (не удовлетворяющим ограничениям), либо решается вопрос об учете собственной упругости масс сцепа;

е) в случае удовлетворения полученных относительных перемещений установленным ограничениям максимальные значения усилий, характеризующих повреждаемость груза, определяются из формул:

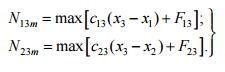(14)

Результаты

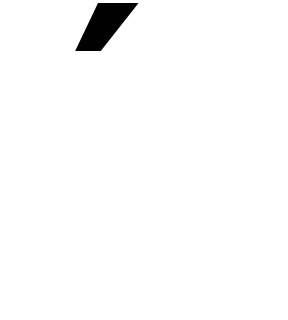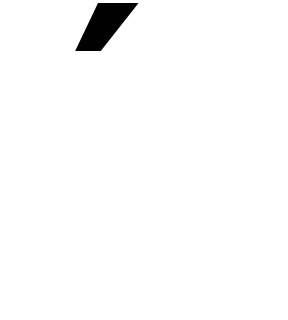По изложенной методике были проведены расчеты по определению динамических воздействий на перевозимый длинномерный груз при соударении сцепа с неподвижной преградой. Для расчета было принято: m₁ = m₂ =2,210⁴ кг (что соответствует массе порожней четырехосной платформы); m₃ =12,0210⁴ кг (соответствует примерно полному использованию грузоподъемности двух платформ); с₀₁=с₁₂=8,5 МН/м (соответствует жесткости двух последовательно работающих поглощающих аппаратов автосцепки); F₀₁ = F₁₂ = 0,2 МН (cоответствует предварительной затяжке поглощаемого аппарата); v₀ = 2 м/c (примерно соответствует перспективной норме скорости соударения). Допускаемые значения относительных перемещений (зазоры в связях) принимались равными: х₁ = (х₂ – х₁) = 0,15 м (примерно соответствует удвоенному ходу поглощающего аппарата с учетом зазоров и деформаций жестких тел);

(х₃ – х₁) = (х₃ – х₂) = 0,5 м.

Расчет с использованием программы интегрирования дифференциальных уравнений методом Рунге–Кутта четвертого порядка. Рассматривались 4 комбинации коэффициентов трения: ₁₃ = ₂₃ = 0,1; ₁₃ = ₂₃ = 0,3;

₁₃ = ₂₃ = 0,5; ₁₂ = 0,1, ₂₃ = 0,55.

Проверка выполнения условий (1), (4), (7), (10) показала, что движение сцепа в начальный момент соударения при всех сочетаниях коэффициентов трения между грузом и платформами, кроме первого (при ₁₃ = ₂₃ = 0,1), начинается с совместного движения всех трех масс. При первом сочетании указанных коэффициентов платформы 1 и 2 начинают двигаться совместно, а груз относительно их проскальзывает. Результаты расчета по определению относительных перемещений элементов системы и усилий N₁₃ и N₂₃ с учетом ограничений по зазорам в турникетно крепежных устройствах и поглощающих аппаратах представлены в табл. 1.

Таблица 1

Результаты расчетов

Table 1

Calculations date

Варьируемые параметры				Относительные перемещения, м			N13 МН	N23 МН
с13 МН/м	с23 МН/м	F12 МН	F23 МН	х1	х3–х1	х3 – х2
0	0,5	0,06 0,18 0,30 0,06	0,06 0,18 0,30 0,33	– 0,129 0,144 0,118	>>0,500 0,509 0,380 0,508	>>0,500 0,509 0,380 0,508	– 0,18 0,30 0,05	– 0,4194 0,4634 0,5615
	4	0,06 0,18 0,30 0,06	0,06 0,18 0,30 0,33	0,117 0,130 0,144 0,118	0,378 0,306 0,255 0,320	0,268 0,211 0,161 0,206	0,06 0,18 0,30 0,06	1,1320 1,0235 1,0446 1,1559
	8	0,06 0,18 0,30 0,06	0,06 0,18 0,30 0,33	0,117 0,130 0,147 0,133	0,293 0,226 0,220 0,267	0,162 0,121 0,110 0,137	0,06 0,18 0,30 0,06	1,2534 1,1487 1,1830 1,4287
0,5	0,5	0,06 0,18 0,30 0,06	0,06 0,18 0,30 0,33	– 0,131 0,146 0,120	>>0,500 0,437 0,326 0,431	>>0,500 0,396 0,279 0,382	– 0,39 0,46 0,27	– 0,37 0,4396 0,5211

Окончание табл. 1

End of table 1

Варьируемые параметры				Относительные перемещения, м			N13 МН	N23 МН
с13 МН/м	с23 МН/м	F12 МН	F23 МН	х1	х3–х1	х3 – х2
4	4	0,06 0,18 0,30 0,06	0,06 0,18 0,30 0,33	>>0,150 >>0,150 >>0,150 >>0,150	– – – –	– – – –	– – – –	– – – –
8	8	0,06 0,18 0,30 0,06	0,06 0,18 0,30 0,33	>>0,150 >>0,150 >>0,150 >>0,150	– – – –	– – – –	– – – –	– – – –

^Не удовлетворяет ограничениям по зазорам в поглощающих аппаратах или ТКУ.

Научная новизна и практическая
значимость

Исследовано соударение сцепа вагонов с размещенным длинномерным грузом с учетом сухого трения в опорах. Преведенную методику следует иметь ввиду при расчете параметров ТКУ с сухим трением.

Выводы

Как видно из полученных данных, рациональная схема ТКУ должна обеспечивать минимальную жесткость на первой по ходу движения платформе и жесткость, подбираемую исходя из ограничений по зазорам в ТКУ и поглощающих аппаратах, на задней платформе. Такое сочетание должно сохраняться независимо от направления при ударе. Наименьшие силы удара, действующие на груз, возникают при средних значениях коэффициентов трения в ТКУ. Эти выводы могут быть уточнены путём оптимизации упругих и демпфирующих параметров с применением методов математического программирования.

Список использованных источников

1. Васильев, С. М. Параметры подвижных турникетно-крепёжных устройств для перевозки длинномерных грузов на железнодорожном подвижном составе : дис. … канд. техн. наук : 05.22.08 / Степан Михайлович Васильев ; БелГУТ. – Гомель, 2011. – 128 с.

2. Исследование с помощью ЭВМ нагрузок, действующих на вагоны и амортизированные грузы при соударении сцепов и пуске в ход грузовых поездов / Л. А. Манашкин, Б. С. Ратнер, А. В. Юрченко, Н. И. Грановская // Тр. ДИИТ. – Днепропетровск, 1978. – Вып. 199/25 : Проблемы механики наземного транспорта. – С. 87–93.

3. Лазарян, В. А. Моделирование соударения сцепов из вагонов с подвижными хребтовыми балками / В. А. Лазарян, Е. П. Блохин, Л. А. Манашкин // Тр. ДИИТ. – Днепропетровск, 1968. – Вып. 76. – С. 26–33.

4. Мямлин, С. В. Построение математической модели фрикционно-полимерного поглощающего аппарата / С. В. Мямлин, Н. Е. Науменко // Вісн. Дніпропетр. нац. ун-ту залізн. трансп. ім. акад. В. Лазаряна. – Дніпропетровськ, 2008. – Вип. 24. – С. 25–33.

5. Никольский, Л. Н. Амортизаторы удара подвижного состава / Л. Н. Никольский, Б. Г. Кеглин. – Москва : Машиностроение, 1986. – 144 с.

6. Размещение и крепление грузов в вагонах / А. Д. Малов, Г. П. Ефимов, О. И. Михайлов, Г. М. Штейнфер. – Москва : Транспорт, 1980. – 328 с.

7. Совершенствование способов размещения и крепления грузов в вагонах / под ред. А. Д. Малова. – Москва : Транспорт, 1970. – 136 с.

8. Спиридонов, Б. К. Аналитическое определение динамических силовых характеристик катковых опор турникетно-крепежных устройств / Б. К. Спиридовнов, А. Д. Железняков ; БелИИЖТ. – Гомель, 1982. – 14 с. – Деп. в ЦНИИT МПС 1982, № 2094.

9. Спиридонов, Б. К. Применение подвижных турникетно-крепежных устройств для перевозки длинномерных строительных конструкций железнодорожным транспортом / Б. К. Спиридонов, А. Д. Железняков, Л. П. Целковикова ; БелИИЖТ. – Гомель, 1982. – 13 с. – Деп. в ЦНИИТ МПС 1982, № 2093.

10. A selected review on the negative externalities of the freight transportation: Modeling and pricing / E. Demir, Y. Huang, S. Scholts, T. Van Woensel // Transportation Research Part E: Logistics and Transportation Review. – 2015. – Vol. 77. – P. 95–114. doi:10.1016/j.tre.2015.02.020.

11. Chou, M. Modeling and model validation of heavy-haul trains equipped with electronically controlled pneumatic brake systems / M. Chou, X. Xia, C. Kayser // Control Engineering Practice. – 2007. – Vol. 15. – Iss. 4. – P. 501–509. doi:10.1016/j.conengprac.2006.09.006.

12. Fahmy Aly, M. H. Computer applications in railway operation / M. H. Fahmy Aly, H. Hemeda, M. A. El-sayed // Alexandria Engineering J. – 2016. – Vol. 55. – Iss. 2. – P. 1573–1580. doi:10.1016/j.aej.2015.12.028.

13. Simulation of venting and leaks from pressure vessels / R. Kanes, A. Basha, L. N. Véchot, M. Castier // J. of Loss Prevention in the Process Industries. – 2016. – Vol. 40. – Р. 563–577. doi:10.1016/j.jlp.2016.02.011.

С. М. ВАСІЛЬЄВ^1*, А. Д. ЖЕЛЄЗНЯКОВ², Л. П. ЦЕЛКОВІКОВА³

^1*Каф. «Вагони», Білоруський державний університет транспорту, вул. Кірова, 34, Гомель, Білорусь, 246653,
+37 (529) 634 78 58, ел. пошта stepangomel@mail.ru, ORCID 0000-0003-3656-1603
²Каф. «Вагони», Білоруський державний університет транспорту, вул. Кірова, 34, Гомель, Білорусь, 246653,
+37 (523) 277 71 48, ORCID 0000-0002-0117-1309
³ГНДЛ ТТОРЕПС, Білоруський державний університет транспорту, вул. Кірова, 34, Гомель, Білорусь, 246653,
+37 (523) 295 39 08, ел. пошта Ilin_maksimka@list.ru, ORCID 0000-0002-1499-7257

МОДЕЛЮВАННЯ зіткнень ВАГОНІВ

ПРИ сухому терті в опорАХ ВАНТАЖУ

Мета. У статті необхідно дослідити: 1) переміщення довгомірного вантажу, що перевозиться на зчепі двох залізничних платформ, обладнаних турнікетно-кріпильними пристроями (TКП); 2) дію сил на вантаж із боку TКП. Методика. Дослідження виконані методом теорії коливань механічних систем із кінцевим числом ступенів свободи. Результати. Авторами отримано раціональні параметри TКП при сухому терті в опорах, які забезпечують найменші сили, що діють на вантаж у результаті зіткнення. Наукова новизна. Ранні дослідження динаміки систем «вагон–вантаж» із рухомими TКП здійснювалися з недостатньою точністю. При розгляді подібних завдань вдавалися до значного спрощення розрахункових схем. Використання таких пристроїв дозволяє робити опори довгомірного вантажу на вагони рухливо-центрованими. TКП допускають більш або менш значний зсув вантажу відносно опорних вагонів у поздовжньому напрямку. Після удару забезпечується повернення вантажу в початкове положення. Поворотна сила в таких пристроях утворюється або за рахунок пружних властивостей TКП, або за рахунок підвищення рівня центру мас, що спираються на них. Процес повернення відбувається кінематичним шляхом при горизонтальному відхиленні TКП з рівноважного положення. Рішення задачі визначення характеру та величин, що діють на вантажі сил і прискорень, реалізовано адекватною реальним умовам математичною моделлю. Враховано обмеження по зазорам у TКП та поглинаючих апаратах вагонів. Практична значимість. Проведене дослідження дозволить розрахувати параметри реальних TКП, що призведе до зниження пошкоджуваності довгомірних вантажів, які перевозяться на зчепах залізничних платформ.

Ключові слова: довгомірний вантаж; турнікетно-кріпильний пристрій; математичне моделювання; пошкоджуваність вантажу

S. M. VASILYEU^1*, A. D. ZHELEZNYAKOV², L. P. TSELKOVIKOVA³

^1*Dep. «Cars», Belarusian State University of Transport, Kirov St., 34, Gomel, Belarus, 246653, tel. +37 (529) 634 78 58,
e-mail stepangomel@mail.ru, ORCID 0000-0003-3656-1603
²Dep. «Cars», Belarusian State University of Transport, Kirov St., 34, Gomel, Belarus, 246653, tel. +37 (523) 277 71 48,
ORCID 0000-0002-0117-1309
³Dep. TTOREPS, Belarusian State University of Transport, Kirov St., 34, Gomel, Belarus, 246653, tel. +37 (523) 295 39 08,
e-mail Ilin_maksimka@list.ru, ORCID 0000-0002-1499-7257

CARS IMPACT SIMULATION at dry friction

IN CARGO SUPPORTS

Purpose. The study investigates: 1) long cargo movements, carried on coupling of two railway platforms equipped with turnstile-fastening devices (TFD); 2) the forces acting on the cargo by the TFD. Methodologhy. Research were carried out using oscillations theory of mechanical systems with a finite number of degrees of freedom. Findings. Authors obtained rational parameters of TFD at dry friction in supports, which provide the smallest forces acting on the cargo as a result of impact. Oringinality. Early studies of «car – cargo» system dynamics with moving TFD were carried out with insufficient accuracy. When considering such tasks one resorted to a significant simplification of the calculation schemes. The use of such devices allows producing supports of long cargo for cars movable-centered ones. TED allow more or less significant shift of the cargo relatively to support cars in the longitudinal direction. After impact the return of the goods in the original position is ensured. Restoring force in such devices is formed either by the elastic properties of TED, either by increasing the center level relying on them masses. The return process takes place by the kinematic way when horizontal deflection of TFD from the equilibrium position. The solution of the problem to determine the nature and magnitudes acting on the cargo forces and accelerations is implemented by mathematical model, adequate to real conditions. Gaps limitations and absorbing apparatuses of the cars in TFD are taken into account. Practical value. This study will allow to calculate the parameters of real TFD that will reduce the damage of long cargo transported on coupling of railway platforms.

Keywords: long cargo; turnstile-fastening device; mathematical modeling; damage of goods

REFERENCES

1. Vasilyev S.M. Parametry podvizhnykh turniketno-krepezhnykh ustroystv dlya perevozki dlinnomernykh gruzov na zheleznodorozhnom podvizhnom sostave. Dokt. Diss. [Parameters of moving turnstile-mounting devices for long cargo carrying on railway rolling stock. Doct. Diss.]. Gomel, 2011. 168 p.

2. Manashkin L.A., Ratner B.S., Yurchenko A.V., Granovskaya N.I. Issledovaniye s pomoshchyu EVM nagruzok, deystvuyushchikh na vagony i amortizirovannyye gruzy pri soudarenii stsepov i puske v khod gruzovykh poyezdov [Research using DCM loads, acting on the cars and elastic cargo at collision of tractive connections and starting freight trains]. Trudy DIIT: Problemy mekhaniki nazemnogo transporta [Proc. of DIIT: Mechanics issues of land transport], 1978, vol. 199/25, pp. 87-93.

3. Lazaryan V.A., Blokhin Ye.P., ManashkinL.A. Modelirovaniye soudareniya stsepov iz vagonov s podvizhnymi khrebtovymi balkami [Modeling tractive connections collision of cars with backframes]. Trudy DIIT [Proc. of DIIT], 1968, vol. 76, pp. 26-33.

4. Myamlin S.V., Naumenko N.Ye. Postroyeniye matematicheskoy modeli friktsionno-polimernogo pogloshchayushchego apparata [The mathematical model of frictional-plastic absorbing machine]. Visnyk Dnipropetrovskoho natsionalnoho universytetu zaliznychnoho transportu imeni akademika V. Lazariana [Bulletin of Dnipropetrovsk National University of Railway Transport named after Academician V. Lazaryan], 2008, issue 24, pp. 25-33.

5. Nikolskiy L.N., Keglin B.G. Amortizatory udara podvizhnogo sostava [Shock damper of rolling stock]. Moscow, Mashinostroeniye Publ., 1986. 144 p.

6. Malov A.D., Yefimov G.P., Mikhaylov O.I., Shteynfer G.M. Razmeshcheniye i krepleniye gruzov v vagonakh [Placing and securing of cargo in cars]. Moscow, Transport Publ., 1980. 328 p.

7. MalovA.D. Sovershenstvovaniye sposobov razmeshcheniya i krepleniya gruzov v vagonakh [Improvement of methods for cargo placement and securing in cars]. Moscow, Transport Publ., 1970. 136 p.

8. Spiridonov B.K., ZheleznyakovA.D. Analiticheskoye opredeleniye dinamicheskikh silovykh kharakteristik katkovykh opor turniketno-krepezhnykh ustroystv [Analytical determination of the dynamic and power characteristics of the expansion roller in turnstile-mounting devices]. Gomel, 1982. No. 2094. 14 p.

9. Spiridonov B.K., Zheleznyakov A.D., Tselkovikova L.P. Primeneniye podvizhnykh turniketno-krepezhnykh ustroystv dlya perevozki dlinnomernykh stroitelnykh konstruktsiy zheleznodorozhnym transportom [Application of mobile turnstile-mounting devices for carrying the long building constructions by railway transport]. Gomel, 1982. No. 2093. 13 p.

10. Demir E., Huang Y., Scholts S., Van Woensel T. A selected review on the negative externalities of the freight transportation: Modeling and pricing. Transportation Research Part E: Logistics and Transportation Review, 2015, vol. 77, pp. 95-114. doi:10.1016/j.tre.2015.02.020.

11. Chou M., Xia X., Kayser C. Modelling and model validation of heavy-haul trains equipped with electronically controlled pneumatic brake systems. Control Engineering Practice, 2007, vol. 15, issue 4, pp. 501-509. doi:10.1016/j.conengprac.2006.09.006.

12. Fahmy Aly M.H., Hemeda H., El-sayed M. A. Computer applications in railway operation. Alexandria Engineering Journal, 2016, vol. 55, issue 2, pp. 1573-1580. doi:10.1016/j.aej.2015.12.028/.

13. Kanes R., Basha A., Véchot L. N., Castier M. Simulation of venting and leaks from pressure vessels. Journal of Loss Prevention in the Process Industries, 2016, vol. 40, pp. 563-577. doi:10.1016/j.jlp.2016.02.011.

Статья рекомендована к публикации д.т.н., проф. А. В. Путято (Беларусь); д.т.н., проф.
С. В. Мямлиным (Украина)

Поступила в редколлегию: 22.03.2016

Принята к печати: 20.07.2016

doi © С. М. Васильев, А. Д. Железняков, Л. П. Целковикова, 2016