ISSN 2307–3489 (Print), ІSSN 2307–6666 (Online)

Наука та прогрес транспорту. Вісник Дніпропетровського
національного університету залізничного транспорту, 2016, № 3 (63)

Introduction

Modern technology construction method of underground pipelines enables building of sewer pipelines for lengths of over 500 m. It is possible to make this without disturbing the existing infrastructure. One of the most common methods is the microtunneling technology. This technology allows drilling the microtunnel hole by drilling machine where, after loosening the soil with high-pressure water, excavated material is transported to the surface of the ground. The pipe jacking is pressed in place of the removed soil. This technology and the various methods of calculation are given in the book [6] and in the article [10]. Microtunnel execution is preceded by the construction of the starting shaft and receiving shaft. Before the implementation of microtunnel the full recognition of geological and engineering on the planned route should be performed. Unfortunately even that it is not possible to provide all the possible complications you may encounter during the implementation of the collector using microtunnelling. Commonly used methods of static analysis jacking pipes describe the most common situations without considering exceptional situations such as the heterogeneity of ground. Such situation is considered by the authors of the study. The analysis is made for partially realized microtunnel with a total length of 300 m. The steel pipe has a diameter of 2 000 mm and thickness of 12 mm. Steel pipe will be a protective tube for the pipeline made under the river leading to a large sewage-treatment plant.

Physical model. In this article an influence the heterogeneity of soil and a flexural rigidity of the pipe on the bending moments where presented. In order to solve this problem, it was divided into two stages. The first stage estimated the force on the pipe jacking and the second stage included the analysis the heterogeneity of soil on bending moments. The problem is shown in Fig. 1.

The loads acting transversely to the axis of the pipe. Modern analysis of static tunnels needs to determine static scheme including the interactions between the soil and pipe jacking. It is important to choice the characteristics of elastic microtunnel structures and to determine geotechnical parameters of soil medium. Microtunnel in selected cross-sections is considered. In order to perform the analysis the following two distinctive sections were chosen (Fig. 2).

On the basis of guidelines [1], [5] the load diagram of the steel pipelines for a microtunnel was adopted which is illustrated in Fig. 3.

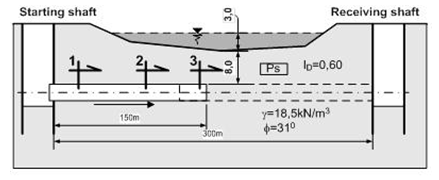
Fig. 1. Illustration showing the reported problem

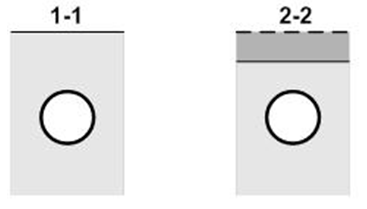
Fig. 2. The characteristic sections of computing

According to various proposals the width of the solid ground was determined. It was a load on the pipeline. The load induces a state of stress in the walls of the pipe. It should be noted that the drilling of microtunnel change the state of stress in the ground. This was confirmed by the research field and the numerical calculations. During the drill microtunnel occurs reduction of the load ground on the pipeline. This is a consequence of loosening the soil in the area of vaults and transfer loads to the ground on both sides of the pipe. This phenomenon was studied among others by Terzaghi and Houskawa based on the theory of the silo. The necessary condition to reduce the load is large vertical deformation in the key course. Using appropriate technological solutions in the implementation of microtunneling seeks to reduce the vertical movements to a minimum, which results in that only a small portion of the angle of internal friction is mobilized in the plane of shear. It is known that already at 10% of the value of the vertical movement is mobilized half of the angle of friction. This phenomenon allowing appoint an increased load on the ground in areas of the lateral pipe. According to silo theory (Terzaghi) 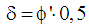was accepted. The results of calculating the width of the ground solids of different proposals was illustrated in Fig. 4. The values of the vertical and horizontal loads were calculated according to the following relationships.

Vertical load acting on the ground pipe

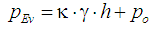(1)

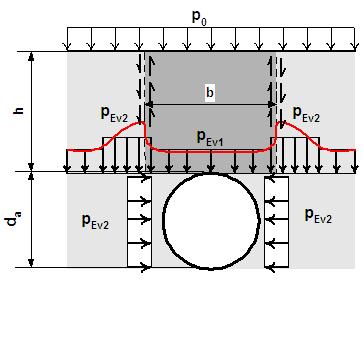
Fig. 3. The load diagram
of the pipelines microtunnel by [5, 1]

Where:  – volume weight of soil overburden conductor;  – reduction factor taking into account the stress distribution after completing of microtunnel; h – thickness of the soil on the pipeline.

The reduction factor  from the expression was determined:

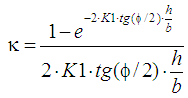(2)

where K1 – coefficient of earth pressure on the wall of the silo, K11,0;

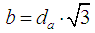
The horizontal earth pressure at the height of the key course of the pipe was calculated by the following expression:

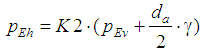(3)

Where

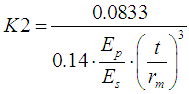(4)

and t is the wall thickness of the pipe, r_m – radius in the middle of the wall thickness, E_p is the modulus of elasticity of the pipe material, E_s – the modulus of elasticity of soil.

A common approach are the guidelines contained in the ATV 161 E [1], so for numerical analysis the width of the ground solid b = (3)^0.5 × d_a was assumed. The load on the Terzaghi assumptions is shown below (Fig. 5). In the analysis the distributions of internal forces for the various static diagrams were compared. The loads for different schemes are shown below (Fig.6, 7).

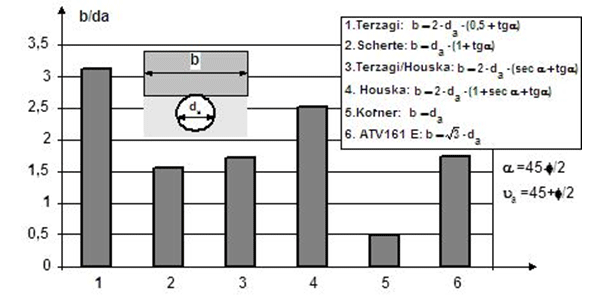
Fig. 4. Comparison of the calculated b by different authors

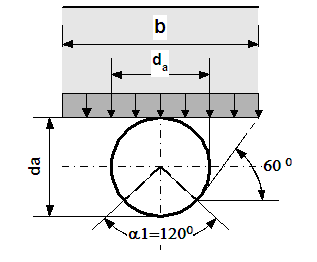
Fig. 5. The load a underground pipe with solid ground

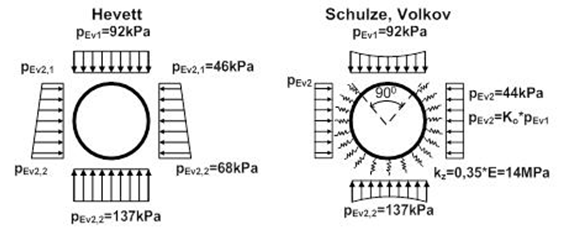
Fig. 6. The loads on a underground pipe by Hevett, Schultze, Volkov

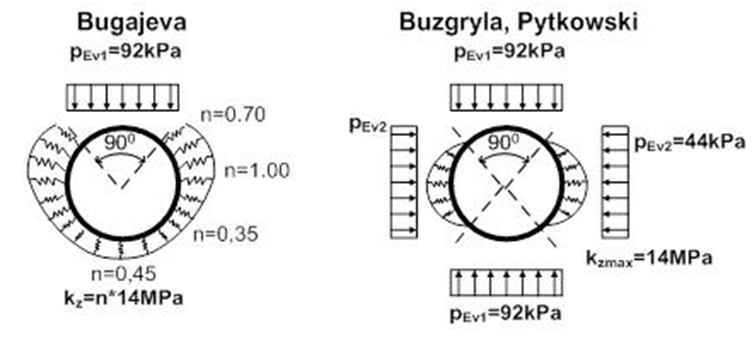
Fig. 7. The loads on a underground pipe by Bugajeva, Buzgryla, Pytkowski

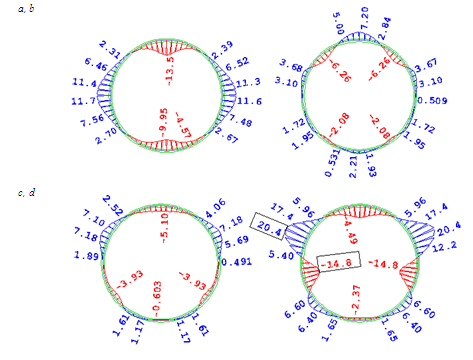
Fig. 8. The bending moment in cross-section
from the ground pressure and weight of the pipe by:
a − Hevett, b − Schulze, Volkov, c − Bugajeva, d − Buzgryla, Pytkowski

Findings

Internal force diagrams for different schemes are shown below (Fig.8). The results were compared to the values calculated according to [1], which is presented in Table 1.

The presented results of calculations have shown that there are large differences in the values of the internal forces determined on the basis of proposals from different authors and they cannot be directly compared. Differences result directly from the assumptions regarding the scope and distribution of elastic supports describing the interaction of soil – pipe. The consequence of these assumptions is the distribution of soil along the perimeter of the steel tube, which also generates different distributions of internal forces. In order to verify the above conclusions, numerical analysis using finite element modeling system and geotechnical calculations Sofistik -Talpa [16] were performed. Numerical model was made in the plane strain. The calculations were made in several stages the state of stress and strain as the initial condition for the next stage of the calculation. The model of Coulomb – Mohr’s with non-associated flow rule in plasticity was calculated. For the analysis, the following parameters were taken: angle of internal friction of soil  = 31^o, cohesion c_u = 0 kPa, the volume density of soil  = 18,5 kN/m³. In the contact zone of the soil – pipe, special contact elements were used which were assigned a variable

coefficient of friction. Contact elements do not carry the tensile forces. In order to take account of the effect of a breach in the soil zone drilling area, the model is divided into various material parameters. It allowed to map the loosening of the soil and its effect on the internal forces in the cross section of the pipe.

Table 1

The bending moments in the pipe jacking

Bending moments	ATV 161	Hevett	Schulze, Volkov	Bugajeva	Buzgryla, Pytkowski
		kNm	kNm	kNm	kNm	kNm
ME1- key course	-16,61	-13,50	7,20	-5,10	-10,30
ME2- side wall	17,38	11,70	0	0	-12,20
ME3- invert	-17,52	-9,95	2,21	-0,63	-2,37
Legend

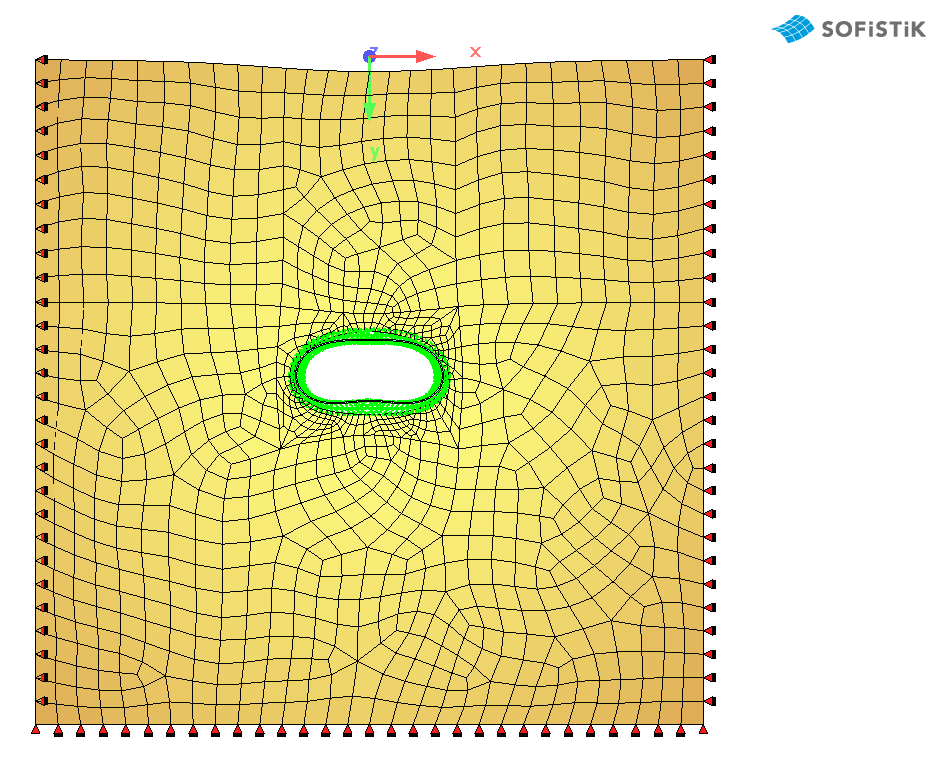
Fig. 9. An example of a numerical (FEM) model
of the interaction of soil – pipe

In Fig. 10 one can see that the internal forces are significantly different from the values determined by guidelines [1]. We can conclude that the graph of internal forces has a similar distribution as in the proposal Hevetta. In the case of the analysis the flexural rigidity of the pipe is very important. In order to grasp this fact, numerical analysis controlling two parameters was made. First parameter was the change of modulus of elasticity in the zone of potential loosening of the soil and secend parameter was the change in the flexural rigidity of pipe. For the analysis of the interaction pipe – soil has been introduced a replacing flexural rigidity of the pipe as a function of strain. Vertical displacement of the pipe was calculated by the theory of second order. It was shown in the Fig. 13.

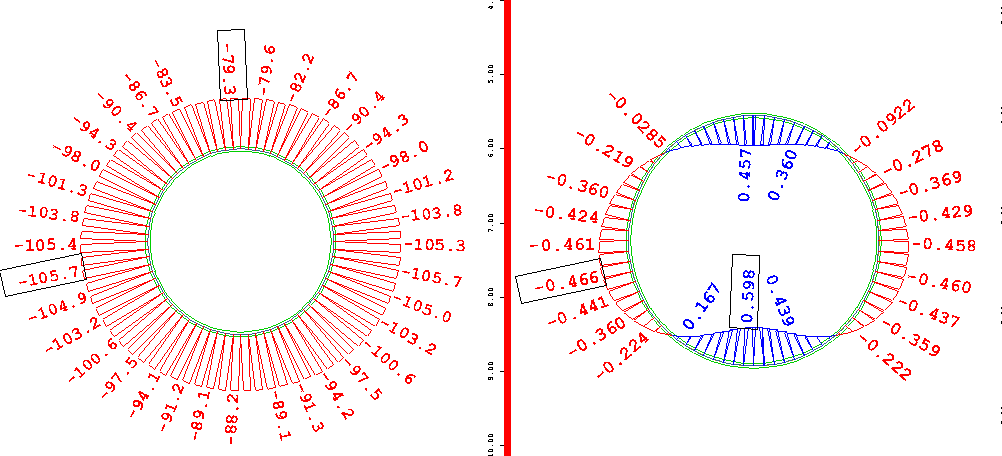
Fig. 10. Internal force diagrams without loosening of the soil in the area around the pipe,
(E = 100 kPa). Steel pipe Dz = 2500 mm, t = 25 mm

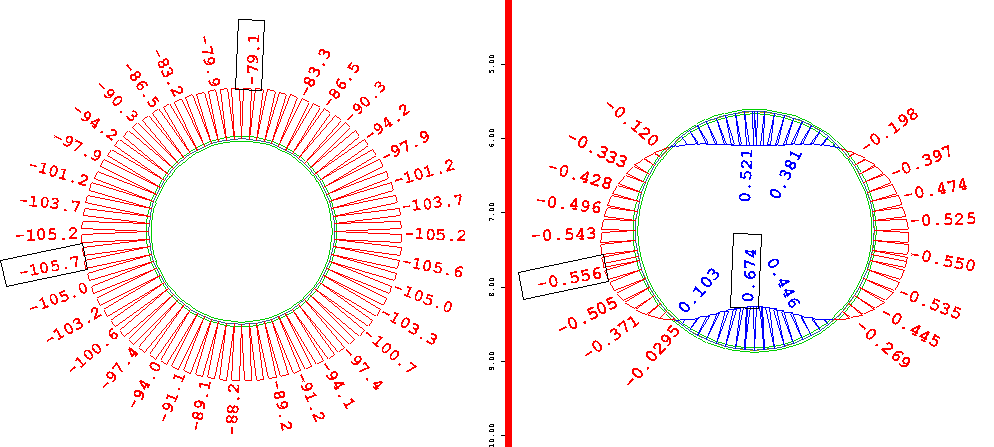
Fig. 11. Internal forces diagrams without loosening the soil in the area around the pipe,
(E = 50 kPa). Steel pipe Dz = 2 500 mm, t = 25 mm

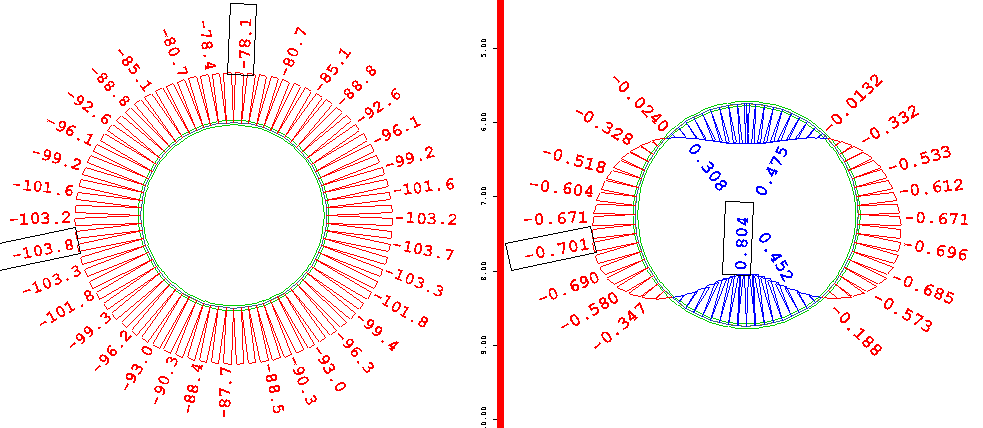
Fig. 12. Internal forces diagrams without loosening the soil in the area around the pipe, (E = 25 kPa).
Steel pipe Dz = 2500 mm, t = 25 mm

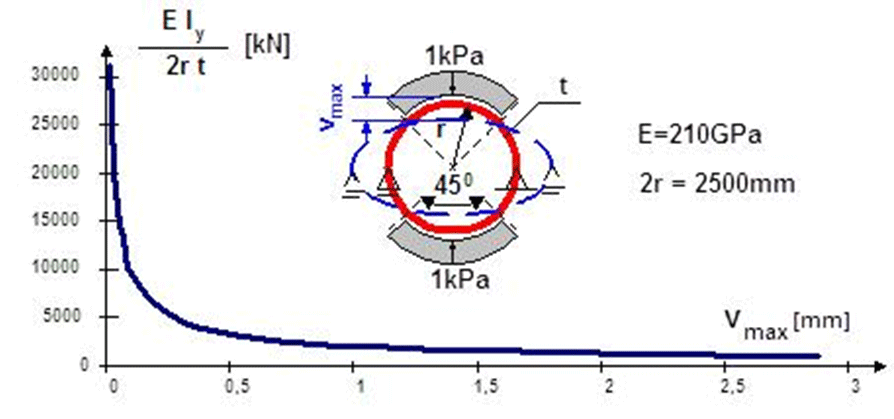
Fig. 13. The replacing flexural rigidity the pipe

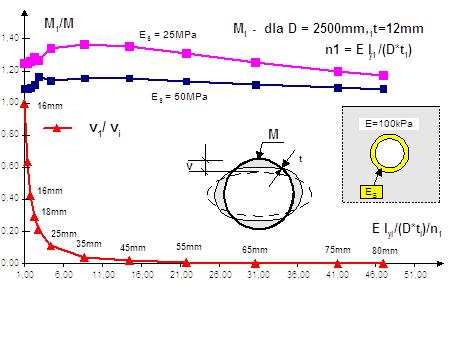
Fig. 14. The increment of the bending moment M in key course as a function
of a flexural rigidity the steel pipe and soil stiffness

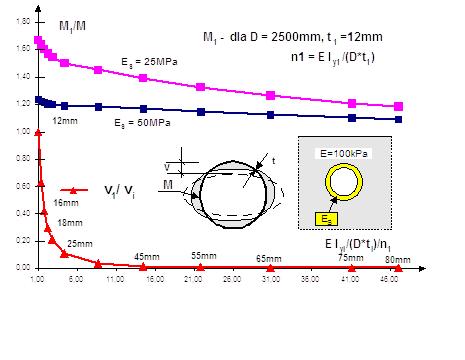
Fig. 15. The increment of the bending moment M in side wall as a function
of a flexural rigidity the steel pipe and soil stiffness

The obtained results clearly show the influence of flexural rigidity of the pipe on the internal forces. The bending moments in the steel pipe with the wall thickness between 12 mm – 35 mm are quite different. They are much smaller than the value calculated on the basis of the guidelines [1]. The formulas for the bending moments in [1] are independent of the deformability pipe.

Conclusions

The obtained results showed the influence of flexural rigidity and the soil stiffness on the size of the bending moments in the steel of pipe jacking. They depend on the interaction of soil – steel pipe. On the basis of Fig.14 with the modulus of elasticity of the soil Es = 50 MPa, the increase of the bending moment in the key course of the pipe is practically not variable independently of the wall thickness of the steel pipe. A similar example was found for bending moments in the side wall tunnel (Fig. 15). The construction steel pipe jacking behaves quite different, when the modulus of soil Es is smaller (Es = 25 MPa). The increase of the bending moment in the key course according to the rigidity of the tube can be up to 15% (Fig. 14). In the case of the increase of the bending moment side wall, it may be as high as 41.5% (Fig. 15).

LIST OF REFERENCE LINKS

1. ATV 161 E. Structural calculation driven pipes : German ATV Standards Wastewater-Waste. – Hennef : GFA, 1990.

2. Brzoska, Z. Statyka i stateczność konstrukcji prętowych i cienkościennych / Z. Brzoska. – War-szawa : PWN, 1961.

3. Buckling of steel shells – European Design Recommendations / Edited by J. Michael Rotter and Herbert Schmidt. – 2013. – 408 р.

4. Hornung, K. Statik eruberddeckter Rohde / K. Ho-rnung, D. Kitel. – Berlin : Bauverlag GMBH, 1989.

5. Glinicki, S. Budownictwo podziemne / S. Gli-nicki. – Politechnika Białostocka, 1994.

6. Madryas, C. Konstrukcje przewodów kanaliza-cyjnych / C. Madryas, A. Kolonko, L. Wysocki. – Wrocław : Oficyna Wydawnicza Politechniki Wrocławskiej, 2002. – 377 p.

7. Mendera, Z., Interakcyjne kryteria stateczności płyt i powłok metalowych w złożonych stanach naprężenia / Z. Mendera // Inżynieria i Budo-wnictwo. – 1993. – №. 2. – P. 50–53.

8. Mendera, Z. Stateczność stalowych powłok walcowych ściskanych podłużnie / Z. Mendera // Inżynieria i Budownictwo. – 2000. – №. 4/5. – P. 240–243.

9. Murzewski, J. Stalowe belki powłokowe / J. Mur-zewski, J. Siepak. – Kraków : Politechnika Krakowska, 1978.

10. Kuliczkowski, A. Projektowanie konstrukcji prze-wodów kanalizacyjnych. – Kielce : Politechnika Świętokrzyska, 1993. – W. I, №. 222. – 290 p.

11. PN-EN 1991-1-3:2005. Eurokod 1. Oddziaływania na konstrukcje. Część 1–3 : Oddziaływania ogólne. Obciążenie śniegiem.

12. PN-EN 1993-1-5. Projektowanie konstrukcji stalowych. Część 1-5 : Blachownice, PKN. – Warszawa, 2008.

13. PN-EN 1993-1-1. Projektowanie konstrukcji stalowych. Część 1-1 : Reguły ogólne i reguły dla budynków, PKN. – Warszawa, 2008.

14. PN-EN 1993-1-6. Projektowanie konstrukcji stalowych. Część 1-6 : Wytrzymałość i state-czność konstrukcji powłokowych, PKN. – War-szawa, 2008.

15. Samuelson, L. A. Shell stability handbook / L. A. Samuelson, S. F. Eggwertz. – London ; New York : Elsevier, 1992. – 303 p.

16. Sofistik v 2014, Licencja: Rajmund Ignatowicz.

17. Timoszenko, S. P. Ustojcziwost’ uprugich system / S. P. Timoszenko. – Moskwa : GITTL, 1955. – 568 p.

К. Горскі^1*, Р. Л. Ігнатович^2*

^1*Каф. «Цивільна та інженерна геологія», Познаньський університет
природничих наук, вул. Піатковська, 94, Познань, Польща, 60-649,
ел. пошта kgorski@up.poznan.pl
^2*Каф. «Металеві конструкції», Вроцлавський технологічний
університет, Грюнвальдська пл., 11, Вроцлав, Польща,
50-377, ел. пошта rajmund.ignatowicz@pwr.edu.pl

НАПРУГА СТАЛЕВОЇ ТРУБИ, ПРОКЛАДЕНОЇ

В УМОВАХ НЕДОСКОНАЛОСТІ ТРУБ ТА

НЕОДНОРІДНОСТІ ГРУНТУ

Мета. У дослідженні необхідно вивчити питання впливу локальних неоднорідностей ґрунту на внутрішні сили в сталевій трубі. Методика. Автори представили відмінності в розподілі ґрунтового тиску на труби. Одним із найбільш поширених методів є технологія мікротунелювання. Приклади чисельного аналізу були розраховані методом скінченних елементів (МСЕ). Результати. Встановлені дані чисельного аналізу представлені для обраних ґрунтових умов. Був також показаний розподіл внутрішніх сил у гнучкій секції сталевої труби. Наукова новизна та практична значимість. Отримані результати чітко показують вплив згинальної жорсткості труби на внутрішні сили, на величину згинальних моментів у сталі вдавлених труб. Вони залежать від взаємодії грунт–сталева труба.

Ключові слова: сталеві труби; метод кінцевих елементів; мікротунелювання; грунт

К. Горски^1*, Р. Л. Игнатович^2*

^1*Каф. «Гражданская и инженерная геология», Познаньский университет
естественных наук, ул. Пиатковска, 94, Познань, Польша, 60-649,
эл. почта kgorski@up.poznan.pl
^2*Каф. «Металлические конструкции», Вроцлавский технологический
университет, Грюнвальдская пл., 11, Вроцлав, Польша, 50-377,
эл. почта rajmund.ignatowicz@pwr.edu.pl

НАПРЯЖЕНИЕ СТАЛЬНОЙ ТРУБЫ,

ПРОЛОЖЕННОЙ В УСЛОВИЯХ

НЕСОВЕРШЕНСТВА ТРУБ

И НЕОДНОРОДНОСТИ ГРУНТА

Цель. В исследовании необходимо изучить вопросы влияния локальных неоднородностей грунта на внутренние силы в стальной трубе. Методика. Авторы представили различия в распределении грунтового давления на трубы. Одним из наиболее распространенных методов является технология микротоннелирования. Примеры численного анализа были рассчитаны методом конечных элементов (МКЭ). Результаты. Установленные данные численного анализа представлены для выбранных грунтовых условий. Также показано распределение внутренних сил в гибкой секции стальной трубы. Научная новизна и практическое значение. Полученные результаты четко показывают влияние изгибной жесткости трубы на внутренние силы, на величину изгибающих моментов в стали вдавленных труб. Они зависят от взаимодействия почва–стальная труба.

Ключевые слова: стальные трубы; метод конечных элементов; микротоннелирование; грунт

Prof. V. D. Petrenko, D. Sc. (Tech.) (Ukraine) recommended this article to be published

Accessed: Feb., 29. 2016

Received: May, 31. 2016

doi 10.15802/stp2016/74764
© K. Górski, R. L. Ignatowicz, 2016