ISSN 2307–3489 (Print), ІSSN 2307–6666 (Online)

Наука та прогрес транспорту. Вісник Дніпропетровського
національного університету залізничного транспорту, 2021, № 1 (91)

Експлуатація та ремонт засобів транспорту

Introduction

Bringing the tourism industry to the modern level needs support in the form of new transport technologies. This thesis is relevant not only for countries with a large number of tourist locations, but primarily for countries such as Ukraine, Canada, USA, where in order to get to them you need to cover long distances using different modes of transport. However, transport cannot only be an aid to tourism, but also play a key role in tourism activities. For example, the English pastor Thomas Cook, from whom the history of modern tourism is derived, for the first time organized a rail journey from Liverpool to London. Then in 1843 he organized boat trips on the Thames. Almost at the same time on the American continent on the legendary wheeled steamer «Mississippi», the company «American Express» opened regular tours on the Mississippi. Similar cruises began to take place on the Nile, Rhine, and Danube. There are many water travel routes in the United States and Canada, such as cruises to observe marine mammals, for example, whales, orcas, or polar bears. However, to get to the ocean coast you need to use other modes of transport. The sphere of water tourism is rapidly developing in Ukraine as well. Thus, the number of cruises on the Black Sea and the Danube River increases annually in the port of Odessa. But to get to Odessa from such big cities as Kyiv or Lviv it is necessary to overcome considerable distances. Therefore, in order for these routes not to lose their attractiveness and in order to attract new customers, it is necessary to introduce new transport technologies.

Under these conditions, it is advisable to use high-speed rail transport as an auxiliary mode of transport, which is the main passenger transport in Ukraine. Thus, such trips are intermodal passenger traffic. Thus, the urgent task is the formation of modern technologies for managing intermodal passenger traffic with the involvement of high-speed rail transport.

Due to the relevance of this topic, it is becoming an increasingly popular object of research in recent years. One of the main directions of research in this area is the formulation and solution of problems related to the optimization of train planning. In [2], based on the analysis of the railway system in the Paris region of France, the problem of operational re-planning is solved, in which stops on railway lines can be missed by trains in case of limited traffic disruptions. For this purpose, a model of linear programming is presented, the objective function of which minimizes both the time of restoration of the traffic schedule and the waiting time of passengers. However, this model is only aimed at overcoming the problems associated with the malfunction of the transport system. [13] proposes a solution to the problem of planning the operation of high-speed rail lines by simultaneously optimizing the schedule of trains and their binding to passenger platforms at stations using the Lagrange relaxation method. However, this approach allows reducing the train movement time by only a small amount. In [3] using the model of mixed programming, the problem of simultaneous optimization of the operational schedule of traffic and stops of suburban trains is solved. However, this model is aimed only at reducing the waiting time of the passenger in case of train delay. [10] also solves the problem of optimizing stops and train schedules taking into account the probability of delays. However, the model does not take into account the data on passenger traffic. In [6], to reduce the waiting time for trains by passengers, a model based on a hybrid methodology for modeling discrete events is proposed, but this model is focused on use in subways and not on trunk lines. [1] proposed a model for constructing train schedules based on optimizing the number of stops, but this model is also focused on urban rail transport. In [14], a model of mixed integer programming is proposed to automate the process of constructing train schedules on high-speed lines in China. However, this model does not solve the problem of attracting passenger traffic, and its main focus is to optimize the use of rolling stock. In [12] the model of mixed integer programming which allows to minimize the general time of movement of day trains is resulted. However, this model is also not aimed at solving the problem of increasing comfort for passengers. Its purpose is to reduce the impact of high-speed railway maintenance processes on high-speed trains by changing their routes. In [11] the possibility of applying an integrated approach to the optimization of intermodal transportation in the implementation of transport links between the Japanese cities of Miyazaki and Fukuoka is considered. It is proposed to introduce an operational integrated schedule of railway and road transport and its operational adjustment, the introduction of a single ticket and even the coordination of the design of rolling stock in the design of trains and buses. However, the practical implementation of such developments is associated with significant difficulties. In [8] the possibility of optimizing the trajectory of the passenger on the basis of improving the technology of processing and exchange of information in the intermodal transport system, including rail and air transport is studied. However, this study primarily focuses on adjusting intermodal operations in the event of delays and does not take into account the dynamics of passenger traffic.

Thus, the tasks of optimizing the functioning of high-speed rail systems in the implementation of intermodal rail transport are relevant. However, in the context of the use of high-speed rail transport as an aid in the implementation of tourist travel, considerable attention should be paid to the attractiveness of transport services for passengers. To this end, it is necessary to investigate the factors influencing the attractiveness of the use of high-speed rail transport in intermodal transport and the corresponding impact of these factors on the dynamics of passenger traffic.

Purpose

The purpose of the work is to improve the technology of intermodal passenger transport with the involvement of high-speed rail transport in terms of tourist travel.

To achieve this goal, the following tasks were set:

– To analyze the technology of passenger intermodal transportation with the involvement of railway trains as an auxiliary mode of transport. To determine the parameters of the process of realization of the railway part of the route, which are the main factors influencing the attractiveness of tourist travel in general.

– To form an optimization model of high-speed trains route management in the direction of tourist passenger traffic. In order to provide the optimization model with the initial data to form a model for forecasting passenger traffic on the high-speed line.

– Carry out modeling using the formed models and analyze the results.

Methodology

An important aspect of the process of formation of modern technology for managing of high-speed railway transport operation is the possibility of applying the latest methods that use mathematical apparatus related to the branch of artificial intelligence or related fields. This approach is not a matter of time or a tribute to fashion, but a vital necessity, as it is the only way to overcome the obstacles associated with, for example, obtaining qualitative forecasts or combinatorial complexity when performing calculations on real models of large dimensions.

Formation of railway transport management technology at realization of intermodal transportations in the conditions of development of tourism

Analysis of the technology of intermodal transportation with the involvement of railway transport in terms of tourist passenger traffic.

High-speed rail systems require careful technical planning and decision-making on the basic elements and modes of operation. These elements have a complex relationship. Failure to take into account at least one factor may call into question the possibility of the existence of such a system.

Recently, in many developed countries, the availability of high-speed rail transport is becoming another impetus for the further development of tourism. For example, high-speed rail transport participates in the implementation of intermodal passenger transport in the implementation of tourist cruises using water transport (Fig. 1).

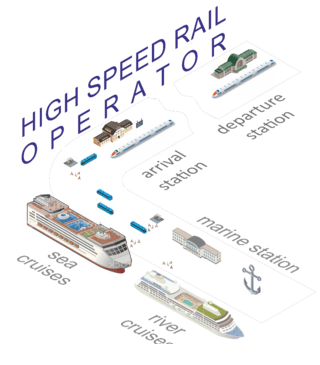
Fig. 1. The scheme of interaction between modes
of transport during intermodal
transportation in the service
of tourist passenger traffic

In order for the tourist flow not to decrease, it is necessary to make this trip attractive for the tourist. According to the results of research [9], it was established which factors affect the attractiveness of tourist travel using high-speed rail transport (Fig. 2).

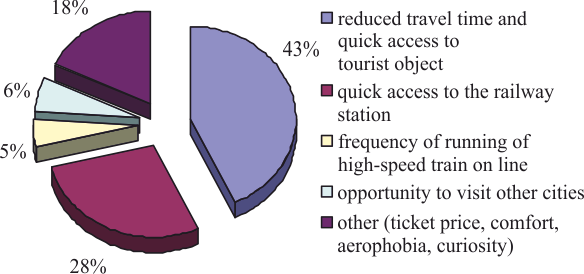
Fig. 2. Significance of factors influencing the decision
to make tourist trips using high-speed rail transport

Thus, since high-speed lines already exist, we first identify the factors that directly affect the decision to make a tourist trip. Thus, the second most important factor (28%) is the time of access to the railway station, which depends on the density of stops on the line or the availability of convenient bus routes to get to the railway station. The most important factor (43%) is the total duration of travel using ancillary modes of transport to move to a tourist location or change to tourist modes of transport (water transport).

However, it should be noted that the total duration of the trip includes the time of access to the railway station. Thus, to increase the attractiveness of travel, it is necessary to develop mechanisms to influence these two factors: the time of access to the railway station and the time of the high-speed train.

Passengers' access times and, accordingly, the total travel time are related. In turn, they also depend on many factors, such as the area covered by the zone, which depends on the density of the stations. The speed of trains depends on the density of stops on the line. The attractiveness of the trip is also influenced by the frequency and population of trains. They, in turn, depend on the number of working fleet of trains, line capacity and tariffs and other economic factors. The study of the seriousness and sophistication of such interrelated complexity encourages careful elaboration of decision-making procedures for the planning, design and operation of such lines and the continuous comprehensive monitoring of their operation.

Thus, the travel time to the tourist location or to the tourist mode of transport consists of the time of access (arrival by other modes of transport) of passengers to the railway line, the travel time by rail and the transfer time between rail and water transport. The transfer time depends primarily on the consistency of the schedules of these modes of transport and the time to overcome the distance between the terminals. However, first of all, it is necessary to single out the factors directly related to railway transport – the time of access of passengers to the railway line and the time in the movement of a high-speed train. You can use the utility function to quantify the attractiveness of a trip. Linear utility functions are often used as a utility function in such problems [7].

In Fig. 3, the general function of the usefulness of travel for the passenger is represented by a linear relationship (3). The dependence of utility on access time to the railway station, which, in turn, depends on the number of stops on the line, in some studies is presented as a convex function (1). Then the difference between curves (3) and (1) is a concave curve (2). It represents a utility function of the duration of the trip, which depends on the speed, which, in turn, depends on the number of stops on the line.

Fig. 3. The dependence of the usefulness of a tourist trip on the number of stops on
the route of a high-speed train

This feature is obviously declining. However, we also argue that this concave shape of this curve is correct, because the greater elasticity in the initial section of the speed reduction is in line with the psychology of tourists, as small changes in travel duration have little effect on decision-making. To specify the utility function more precisely, it is proposed to build it on the basis of a five-parameter logistic function [5]. This approach will make it possible to give it the desired shape, taking into account the importance of utility and elasticity at certain points in the field of its calculation.

Increasing the speed of trains on the line through technical modernization of tracks, automation and rolling stock is often impossible or economically impractical. Under such conditions, a rational way to achieve this goal is the formation of methods for organizing the movement of high-speed trains and the development on their basis of appropriate management technology.

One of the methods that allow to reduce the movement time of passenger trains is the method of «skip stop».

The idea of the method is that express trains of several types run on the line, during the stop operation each train visits only a fixed subset of stations. Skipping several stations allows you to reduce the cycle time and increase the route speed.

Formation of the optimization model of management of routes of high-speed trains on a direction in the conditions of service of a tourist passenger flow.

Skip-stop technology allows you to increase the route speed on the line and reduce the frequency of stops compared to the standard scheme of the organization; however, at the same time it can complicate the planning process. In addition, this technology may result in the lack of direct communication between some stations on the route, but due to the increase in speed, the line capacity is increased. However, passengers who do not leave at the final station of the route do not belong to the tourist passenger flow, and therefore for them the speed has little effect on the level of usefulness. For most of these passengers, it makes little difference whether a train belongs to the InterCity+, InterCity or regular interregional trains. Thus, although these passengers can be transported by other categories of trains, it is still necessary to minimize the loss of passenger traffic for high-speed rail companies and maximize profits by attracting new passengers. Thus, the objective function of the model, which represents the profit of the railway operator, can be written as follows:

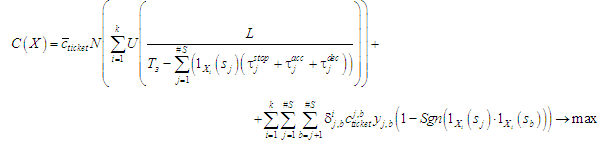,(1)

where – indicator of functions that return the value 1 in the case of belonging to the station s_j or station s_b to the set of stops X_i i-th train; X – vector of Boolean variables corresponding to the inclusion of stops at the stations of the route of all trains on the line; X_i – an elements subset of the vector of Boolean variables corresponding to the inclusion of stops at route stations for the i-th train; k – the number of routes and trains on the line; – stop time according to the schedule at the j-th station of the route; – additional time for acceleration after stopping at the j-th station of the route; – additional time for braking before stopping at the j-th station of the route; – passenger traffic between stations j and b; s_j,s_b– elements of the plurality of stations representing the j-th and b-th stations of the route, respectively; – a variable factor that determines the relative share of the total passenger traffic between stations j and b, which is transported by the i-th train on the line; #S – power (number of elements) of the set of route stations; T_з– the time the train is in motion, provided that all stops are included in the route; L – route length; – the average ticket price for a tourist (passenger who goes to the final station of the route); – ticket price between stations j and b; U(…) – a function that returns the value of utility depending on the route speed of the train; N(…) – linear function that returns the value of passenger traffic depending on the value of utility; Sgn(…) – sign function.

This objective function is represented by a criterion that expresses the income of the company-operator of high-speed rail transport from the sale of tickets in terms of tourist passenger traffic. This objective function is subject to optimization with the following restrictions:

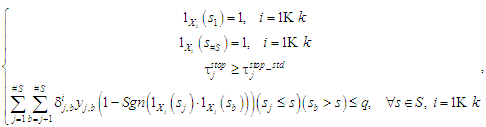(2)

where 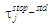– standard stop time according to the schedule at the j-th station of the route; q – passenger capacity of one high-speed train on the line.

The first and second restrictions prevent the exclusion of stations corresponding to the starting and ending points of passengers. The third restriction prevents the reduction of train stops at stations below the normative values. The fourth restriction prevents the current number of passengers from being exceeded after the disembarkation operations at each station of the route for each train. Thus, this objective function and the system of constraints represent a mathematical model of mixed-integer programming. The elements of the variable vector  represent the relative shares of passenger traffic and can take any value in the range from 0 to 1. In fact, with the help of a vector  we can get a detailed plan of ticket sales at all stations of each train, which is important when planning speed on the line. Integer constraints are imposed on vector elements, as they can only take a value of 1 or 0, which corresponds to the presence or absence of a stop at a given station, respectively. To solve problems of this type, specific algorithms based on combinatorics, graph theory, etc. are developed. In addition, to optimize the model and obtain the result it is necessary to have high-quality forecast data of passenger flows.

Formation of the forecast model.

The initial data for solving the forecasting problem are the historical data of passenger flows between the stations of the railway line on which high-speed trains run, which are time series. Models based on the modern mathematical apparatus of neural networks are a powerful tool, which is suitable for solving time series forecasting problems. However, the difficulty is that the historical data of correspondence of passenger flows can be represented not by ordinary time series, but by multidimensional ones. Theoretically, they can be predicted separately, but in this case, it is necessary to create a number of individual models that will be equal to the dimensions of the multidimensional time series, and also to configure or train them separately. But the main disadvantage of this approach is that in this case, the relationship between the data of parallel series will be impossible to take into account. Predicting multidimensional time series is a non-trivial problem that is almost impossible to solve even with the use of modern neural networks of standard architectures. Although there are classical, regression-based models, such as the vector autoregressive model (VARM). Regression models are unable to predict data that, for example, are affected by seasonal factors, and have many other limitations. At the present level, such a problem can be solved only by using the latest developments in the field of artificial intelligence. In 2014, a model called the Generative Adversarial Networks (GAN) [4] was proposed. This model is based on the original algorithm of machine learning without a teacher, which is implemented on a structure of two parallel convolutional neural networks, which are configured to work against each other. One neural network, called a generator, generates new instances of data, and the other, a discriminator, evaluates them for authenticity. Thus, the discriminator decides whether each copy of the data it is considering belongs to the training data set or not. This model was developed for processing graphic images. However, multidimensional time series can also be represented as graphical images. The numbers of pixel lines correspond to the numbers of elementary (one-dimensional) time series, the numbers of pixel columns correspond to consecutive moments of time, the numerical values of the elements of time series represent the intensity of pixels (shades of gray). The generator network (G) generates images using data matrices that contain random noise. The discriminator network (D) (Fig. 4) receives the generated images and «real» images, which were obtained on the basis of historical data of time series of passenger flows. The purpose of the generator is to learn to generate such images that the discriminator will consider true and the purpose of the discriminator is to learn to recognize «fake» images. As a result of parallel training of both networks the generator gets ability to generate such images which the discriminator recognizes as «real». These images pass through the discriminator and are interpreted as multivariate time series forecast data.

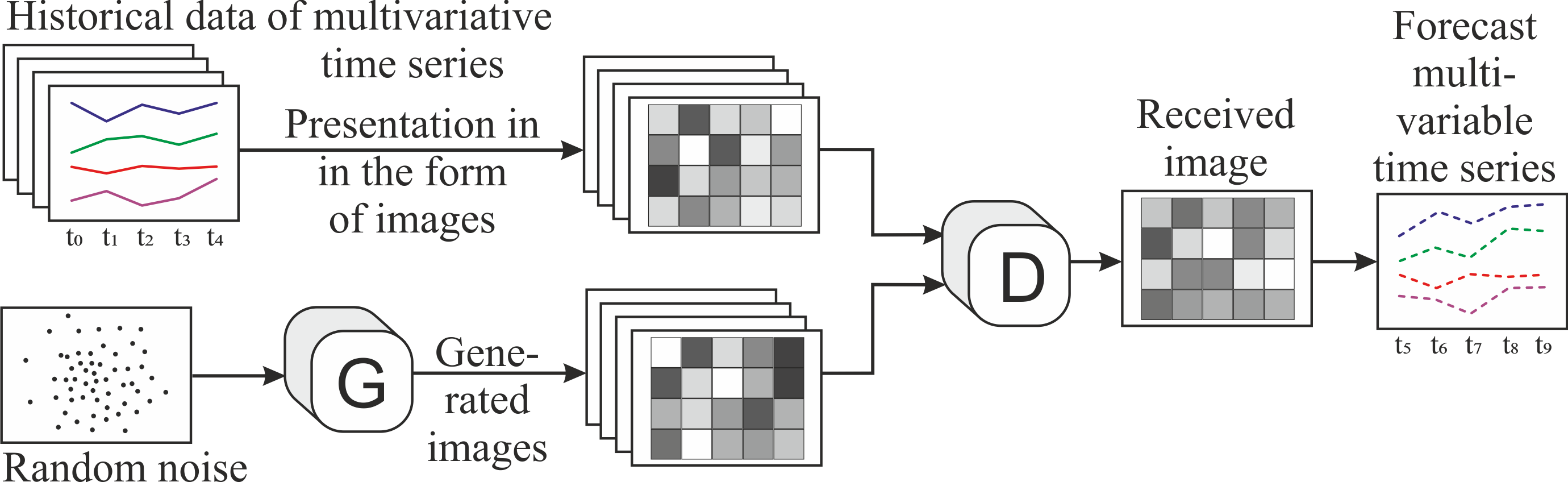
Fig. 4. Scheme of functioning of the multivariate time series forecasting model on the basis
of generative-adversarial network

The proposed forecast model based on the generative-adversarial network was implemented in the Matlab environment. The simulation was performed using real data on passenger flows on the line connecting Kyiv-Pasazhyrskyi and Odesa-Holovna stations. Fig. 5 shows the dynamics of assessing the quality of the generator and discriminator networks during training. This graph shows that the process of setting up both networks went well, because the discriminatory network dominates over the generator and at the same time, their estimates do not approach the extreme limits (0 or 1). The gradual decrease in the amplitudes of oscillations also indicates the stabilization of both networks.

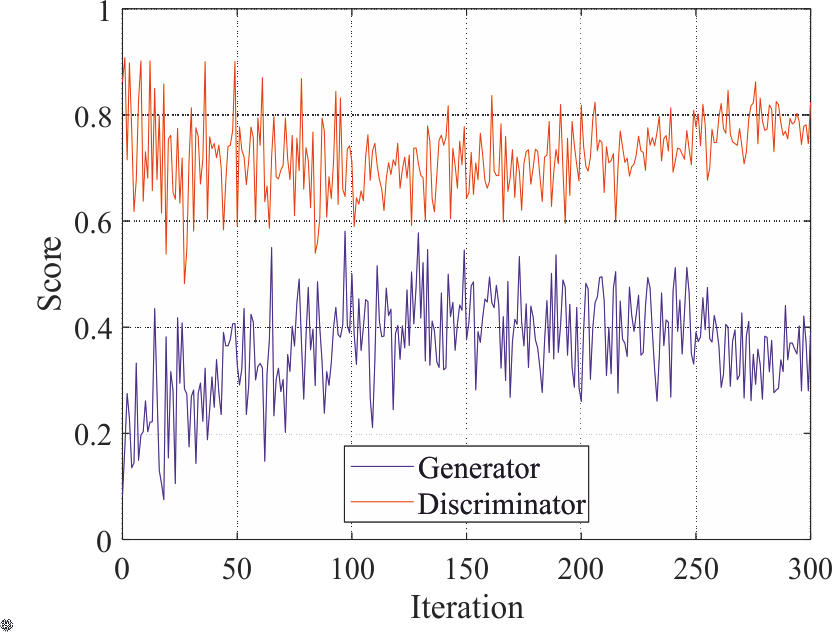
Fig. 5. Dynamics of quality assessments of generator and discriminatory networks during training

Table 1 shows the actual data of correspondence of passenger flows between stations and forecast data obtained using the formed model for April 24, 2019, as well as actual data for the previous week.

Table 1

Correspondence of passenger flows between stations on the line

#	station of boarding	station of unboarding	17.04	18.04	19.04	20.04	21.04	22.04	23.04	24.04
			fact							fact	forecast	diff.
1	Kyiv-Pass.	Vinnytsia	26	43	44	46	47	47	44	29	33	4
2	Kyiv-Pass.	Zhmerynka	17	29	28	21	20	10	30	18	18	0
3	Kyiv-Pass.	Vapniarka	22	32	24	36	24	13	31	20	17	–3
4	Kyiv-Pass.	Podilsk	21	33	36	36	39	43	44	20	20	0
5	Kyiv-Pass.	Odesa	375	703	698	693	757	672	713	407	402	–5
6	Vinnytsia	Zhmerynka	29	49	40	45	47	36	44	25	27	2
7	Vinnytsia	Vapniarka	27	56	34	47	60	43	59	28	24	–4
8	Vinnytsia	Podilsk	11	6	16	13	15	24	21	10	11	1
9	Vinnytsia	Odesa	294	361	375	329	372	462	368	246	241	–5
10	Zhmerynka	Vapniarka	20	45	42	46	46	27	48	32	32	0
11	Zhmerynka	Podilsk	22	18	27	27	36	35	23	22	22	0
12	Zhmerynka	Odesa	68	176	121	97	191	142	145	94	91	–3
13	Vapniarka	Podilsk	15	33	39	39	28	28	32	16	19	3
14	Vapniarka	Odesa	96	166	174	177	179	171	170	97	100	3
15	Podilsk	Odesa	87	142	140	139	162	144	149	84	84	0

The mean absolute percentage error used to assess the quality of the time series forecast was MAPE = 5.9583%. This accuracy of the forecast is sufficient to develop a scheme of routes of high-speed passenger trains.

Model optimization.

An abstract line with 15 stations was chosen as the initial data for optimization of the formed model. The average distance between the stations is 40 km. The average values of stop, acceleration and deceleration times are 1 min, 6 min and 7 min, respectively. The running speed of the train is 160 km/h. Table 2 shows the data on the correspondence of passenger flows between stations on the line.

Table 2

Correspondence of passenger flows between stations on the line

to from	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1	–	20	16	13	11	12	9	3	5	2	4	11	2	13	489
2	–	–	23	11	5	15	3	4	3	1	5	5	5	12	21
3	–	–	–	12	16	12	1	12	5	5	5	6	5	5	24
4	–	–	–	–	5	7	18	7	8	6	8	2	1	1	12
5	–	–	–	–	–	12	9	18	5	2	3	1	5	3	12
6	–	–	–	–	–	–	2	11	15	11	5	5	16	5	20
7	–	–	–	–	–	–	–	12	11	5	11	18	5	8	13
8	–	–	–	–	–	–	–	–	11	12	14	5	11	11	11
9	–	–	–	–	–	–	–	–	–	17	5	18	5	14	13
10	–	–	–	–	–	–	–	–	–	–	18	23	12	6	11
11	–	–	–	–	–	–	–	–	–	–	–	2	4	2	18
12	–	–	–	–	–	–	–	–	–	–	–	–	5	1	17
13	–	–	–	–	–	–	–	–	–	–	–	–	–	12	19
14	–	–	–	–	–	–	–	–	–	–	–	–	–	–	20
15	–	–	–	–	–	–	–	–	–	–	–	–	–	–	–

Since the objective function and the constraint system represent a model of mixed-integer programming, this problem belongs to the problems of combinatorial optimization, and, therefore, its solution requires a search of a large number of variants of vectors of control variables. The vector of variables must contain information about the presence of a stop at all 13 stations (there are always stops at the start and end stations). Then, when planning the routes of only two trains at the same time, the number of possible variants of the train running plan will be:

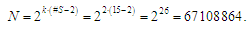(3)

Since there are no general effective exact methods of solution for combinatorial optimization problems of large dimension, it is expedient to apply modern approximate metaheuristic methods, which include, for example, the method of genetic algorithm (GA). The GA method is a method of stochastic search, the effectiveness of which is due to the reproduction of mechanisms for the development of adaptation and transmission of heredity of living nature, such as selection, crossing and mutation. Thus, for the use of GA, the solution must be represented as a chromosome. In this case, the chromosome contains genes containing Boolean variables that carry information about the presence or absence of stops at the route stations of each of the trains.

To optimize the model, we used a floating-point genetic algorithm (FPGA) with integer constraints imposed on some variables. Fig. 6 shows the dynamics of convergence of the objective function during the execution of the genetic algorithm using a software product implemented in Matlab.

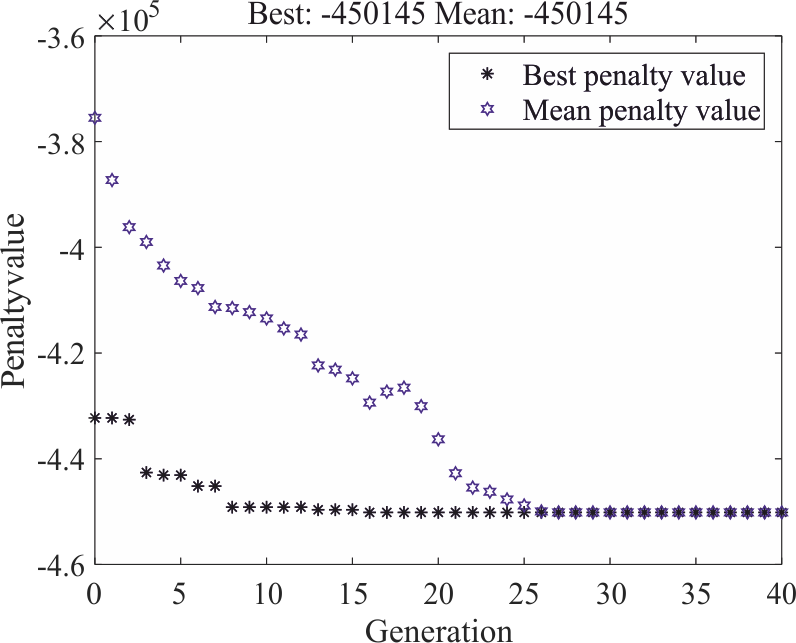
Fig. 6. Dynamics of convergence of the objective function
of the genetic algorithm during model optimization

Since the standard GA procedures provide for the minimization of the objective function, and the objective function of the developed model is subject to maximization, the minimization of this function, taken with a minus sign, was carried out. Fig. 7 shows a diagram of the running of two high-speed trains on the line in terms of the use of railway transport as an auxiliary in intermodal passenger traffic in the service of tourist passenger traffic.

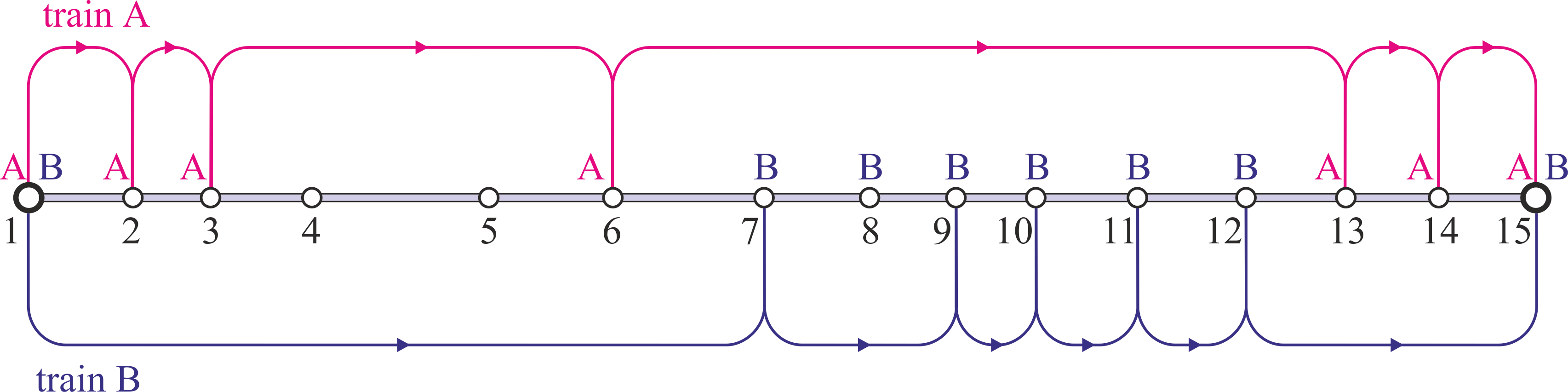
Fig. 7. Scheme of running two high-speed trains on the line,
obtained as a result of model optimization

The optimization results indicate that the formed model allows to save up to 90% of the potential tourist passenger traffic and to process about 50% of the passenger traffic between the intermediate stations of the route.

Findings

The possibility of further development of tourism and achievement of new quality standards in any country requires modern transport. For high-quality organization of cruises on sea and river vessels, it is necessary to provide fast and comfortable delivery of passengers using other modes of transport. Thus, high-quality organization of tourist trips is impossible without modern technologies for managing intermodal passenger traffic. An important role in organizing such trips can play high-speed passenger transport as an ancillary mode of transport. However, the success of its use in this role depends on the ability to organize its work in such a way as not to reduce the tourist attractiveness of the trip as a whole. In the analysis of factors influencing the attractiveness of the use of trains as ancillary transport, it was found that the key factor is the time of the high-speed train. The introduction of modern technical means to increase the running speed of trains on the line may be impossible or impractical. Under such conditions, a rational way to solve the problem is to develop technology for planning high-speed train routes based on the method of skipping stops. The formed mathematical model is aimed at preserving the tourist passenger flow and at the same time the maximum processing of passenger flows between intermediate stations of train routes. This approach will not only provide comfortable conditions for transporting tourists, but will also allow railway operators to maintain the level of profitability of transportation. A linear utility function was used to numerically represent attractiveness. In order to obtain high-quality initial data for calculations, a high-precision forecast model was formed. The use of modern artificial intelligence technologies, such as generative adversarial networks, has ensured high accuracy of forecasting and overcoming the difficulties associated with multivariate time series. The use of a modern mathematical apparatus of genetic algorithms made it possible to find a vector of variables in which the extremum of the objective function is achieved with sufficient accuracy. Confident convergence of the genetic algorithm in the process of solving the problem (Fig. 6) indicates the adequacy of the formed model.

Originality and practical value

It should be noted that the method of skipping stops has been used before, but mainly as a temporary regulatory measure without a certain mathematical basis. However, in this study, it is used as part of a mathematical model of mixed-integer programming. It allows to actually get a compromise solution, which is the basis for building a scheme of operation of high-speed trains. This approach provides an opportunity to maximize the involvement of tourist passenger traffic in the implementation of intermodal transport and maintaining the profitability of high-speed rail operators. Building a forecast model based on the generative-adversarial neural network, the primary purpose of which is image processing, to obtain accurate predictions of passenger flow parameters based on the data of multi-variable time series is also a new scientific approach.

Conclusions

1. The analysis of tourist trips with the use of water modes of transport revealed the need to improve the technology of intermodal passenger transport to improve the performance of high-speed trains in the case of their use as ancillary transport. It was found that the main factor influencing the attractiveness of tourist travel using trains as ancillary transport is the duration of the trip. It in turn depends on the precinct speed.

To numerically assess the dependence of the attractiveness of a tourist trip on the speed of the train, the use of the utility function is proposed.

2. In order to increase the route speed of high-speed trains, it is proposed to improve the technology of planning their work on the basis of the method of skipping stops. Based on the use of this method, a mathematical model of mixed-integer programming is formed, which simultaneously provides the attractiveness of tourist travel and profitability for railway operators. In order to provide the optimization model with high-quality initial data, a model of passenger traffic forecasting is formed on the basis of modern neural network technology, the error of which exceeds 6%.

3. Given the significant combinatorial complexity of the problem, to optimize the existing model, it was proposed to use the mathematical apparatus of genetic algorithms. To this end, software has been developed in the Matlab environment. The optimization results indicate that the formed model allows to save up to 90% of the potential tourist passenger traffic and to process about 50% of the passenger traffic between the intermediate stations of the route.

LIST OF REFERENCE LINKS

1. Abdelhafiez E. A., Salama M. R., Shalaby M. A. Minimizing passenger travel time in URT system adopting skip-stop strategy. Journal of Rail Transport Planning & Management. 2017. Vol. 7. Iss. 4. P. 277–290.
   DOI: 10.1016/j.jrtpm.2017.11.001

2. Altazin E., Dauzère-Pérès S., Ramond F., Tréfond S. Rescheduling through stop-skipping in dense railway systems. Transportation Research Part C : Emerging Technologies. 2017. Vol. 79. P. 73–84. DOI: 10.1016/j.trc.2017.03.012

3. Dong X., Li D., Yin Y., Ding S., Cao Z. Integrated optimization of train stop planning and timetabling for commuter railways with an extended adaptive large neighborhood search metaheuristic approach.
   Transportation Research Part C : Emerging Technologies. 2020. Vol. 117. P. 102681. DOI: 10.1016/j.trc.2020.102681

4. Goodfellow I., Pouget-Abadie J., Mirza M., Xu B., Warde-Farley D., Ozair S., Courville A., Bengio Y. Generative Adversarial Networks. Advances in Neural Information Processing Systems 27 (NIPS 2014). 2014. P. 2672–2680.

5. Gottschalk P. G., Dunn J. R. The five-parameter logistic : A characterization. Analytical Biochemistry. 2005. Vol. 343. Iss. P. 54–65. DOI: 10.1016/j.ab.2005.04.035

6. Hassannayebi E., Boroun M., Alaei Jordehi S., Kor H. Train schedule optimization in a high-speed railway system using a hybrid simulation and meta-model approach. Computers & Industrial Engineering. 2019. Vol. 138. P. 106110. DOI: 10.1016/j.cie.2019.106110

7. Li Z., Hensher D. A. Crowding and public transport: A review of willingness to pay evidence and its relevance in project appraisal. Transport Policy. 2011. Vol. 18. Iss. 6. P. 880–887. DOI: 10.1016/j.tranpol.2011.06.003

8. Milbredt O., Rudolph F., Grunewald E., Christ T. Evaluating conditions and impact of intermodal traffic management involving airports and railways. Transportation Research Procedia. 2017. Vol. 25. P. 1735–1744. DOI:10.1016/j.trpro.2017.05.132

9. Pagliara F., Valeri E., de Abreu e Silva J. Is there an impact of High Speed Rail on tourism? 13th WCTR. 2013. P. 1–16.

10. Yang L., Qi J., Li S., Gao Y. Collaborative optimization for train scheduling and train stop planning on high-speed railways. Omega. 2016. Vol. 64. P. 57–76. DOI: 10.1016/j.omega.2015.11.003

11. Yashiro R., Kato H. Success factors in the introduction of an intermodal passenger transportation system connecting high-speed rail with intercity bus services. Case Studies on Transport Policy. 2019. Vol. 7. Iss. 4. P. 708–717. DOI: 10.1016/j.cstp.2019.10.001

12. Zhang C., Gao Y., Yang L., Kumar U., Gao Z. Integrated optimization of train scheduling and maintenance planning on high-speed railway corridors. Omega. 2019. Vol. 87. P. 86–104. DOI: 10.1016/j.omega.2018.08.005

13. Zhang Q., Lusby R., Shang P., Zhu X. Simultaneously re-optimizing timetables and platform schedules under planned track maintenance for a high-speed railway network. Transportation Research Part C : Emerging Technologies. 2020. Vol. 121. P. 102823. DOI: 10.1016/j.trc.2020.102823

14. Zhong Q., Lusb, R. M., Larsen J., Zhang Y., Peng Q. Rolling stock scheduling with maintenance requirements at the Chinese High-Speed Railway. Transportation Research Part B : Methodological. 2019. Vol. 126. P. 24–44. DOI: 10.1016/j.trb.2019.05.013

Т. В. БУТЬКО¹, В. М. ПРОХОРОВ^2*, Л. О. ПАРХОМЕНКО³, А. О. ПРОКОПОВ⁴

¹Каф. «Управління експлуатаційною роботою», Український державний університет
залізничного транспорту, пл. Феєрбаха, 7, Харків, Україна, 61050, тел. +38 (057) 730 10 89,
ел. пошта uermp@ukr.net, ORCID 0000-0003-1082-599X
^2*Каф. «Управління експлуатаційною роботою», Український державний університет
залізничного транспорту, пл. Феєрбаха, 7, Харків, Україна, 61050, тел. +38 (099) 420 45 28,
ел. пошта vicmmx@gmail.com, ORCID 0000-0001-8963-6467
³Каф. «Управління експлуатаційною роботою», Український державний університет
залізничного транспорту, пл. Феєрбаха, 7, Харків, Україна, 61050, тел. +38 (057) 730 10 88,
ел. пошта l.o.parkhomenko@kart.edu.ua, ORCID 0000-0003-1647-7746
⁴Каф. «Управління вантажною та комерційною роботою», Український державний
університет залізничного транспорту, пл. Феєрбаха, 7, Харків, Україна, 61050,
тел. +38 (057) 730 10 88, ел. пошта prokopovartem1301@gmail.com,
ORCID 0000-0001-7324-4047

Удосконалення технології пасажирських

інтермодальних перевезень із залученням

залізничного транспорту в умовах

розвитку туризму

Мета. За основну мету автори ставлять визначення та методичне обґрунтування шляхів підвищення ефективності пасажирських інтермодальних перевезень із залученням швидкісних поїздів як допоміжного виду транспорту в умовах здійснення морських та річкових туристичних подорожей. Методика. У процесі дослідження було використано: метод факторного аналізу – для визначення факторів, що впливають на привабливість здійснення туристичних подорожей із використанням швидкісних поїздів як допоміжного транспорту; метод пропуску зупинок – для з’ясування шляхів підвищення ефективності використання швидкісних поїздів як допоміжного виду транспорту під час здійснення туристичних подорожей; методи побудови та навчання генеративно-змагальних нейронних мереж – для формування моделі прогнозування пасажиропотоків, на основі історичних даних мультиваріативних часових рядів; метод генетичних алгоритмів – для оптимізації моделі змішано-цілочисельного програмування, яка дозволяє отримати оптимальну схему курсування швидкісних поїздів на лінії. Результати. Із метою збереження привабливості здійснення туристичних подорожей та підвищення маршрутної швидкості поїздів запропоновано вдосконалення технології планування їх роботи на основі методу пропуску зупинок. Сформовано математичну модель змішано-цілочисельного програмування, яка одночасно забезпечує привабливість здійснення туристичних подорожей та рентабельність для залізничних операторів. Для підготовки вихідних даних розроблено метод прогнозування пасажиропотоків на основі мультиваріативних часових рядів. Процедуру оптимізації сформованої моделі було реалізовано у вигляді програмного забезпечення мовою Matlab. Наукова новизна. У роботі набув подальшого розвитку метод пропуску зупинок, який уперше було застосовано для вдосконалення технології інтермодальних пасажирських перевезень. Запропоновано оригінальний метод прогнозування пасажиропотоків на основі мультиваріативних часових рядів із використанням сучасної моделі генеративно-змагальних нейронних мереж. Практична значимість. Отримані результати спрямовані на вдосконалення методичних підходів до формування сучасних технологій інтермодальних пасажирських перевезень та реалізації потенціалу швидкісного залізничного транспорту як основи всебічного розвитку туризму.

Ключові слова: інтермодальні пасажирські перевезення; швидкісні залізничні пасажирські перевезення; метод пропуску зупинок; генетичні алгоритми; нейронні мережі; прогнозування мультиваріативних часових рядів; розвиток туризму

REFERENCES

1. Abdelhafiez, E. A., Salama, M. R., & Shalaby, M. A. (2017). Minimizing passenger travel time in URT system adopting skip-stop strategy. Journal of Rail Transport Planning & Management, 7(4), 277-290. DOI: 10.1016/j.jrtpm.2017.11.001 (in English)

2. Altazin, E., Dauzère-Pérès, S., Ramond, F., & Tréfond, S. (2017). Rescheduling through stop-skipping in dense railway systems. Transportation Research Part C: Emerging Technologies, 79, 73-84. DOI: 10.1016/j.trc.2017.03.012 (in English)

3. Dong, X., Li, D., Yin, Y., Ding, S., & Cao, Z. (2020). Integrated optimization of train stop planning and timetabling for commuter railways with an extended adaptive large neighborhood search metaheuristic approach. Transportation Research Part C: Emerging Technologies, 117, 102681. DOI: 10.1016/j.trc.2020.102681 (in English)

4. Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., Courville, A., & Bengio, Y. (2014). Generative Adversarial Networks. Advances in Neural Information Processing Systems 27 (NIPS 2014), 2672-2680. (in English)

5. Gottschalk, P. G., & Dunn, J. R. (2005). The five-parameter logistic: A characterization and comparison with the four-parameter logistic. Analytical Biochemistry, 343(1), 54-65. DOI: 10.1016/j.ab.2005.04.035 (in English)

6. Hassannayebi, E., Boroun, M., Alaei Jordehi, S., & Kor, H. (2019). Train schedule optimization in a high-speed railway system using a hybrid simulation and meta-model approach. Computers & Industrial Engineering, 138, 106110. DOI: 10.1016/j.cie.2019.106110 (in English)

7. Li, Z., & Hensher, D. A. (2011). Crowding and public transport: A review of willingness to pay evidence and its relevance in project appraisal. Transport Policy, 18(6), 880-887. DOI: 10.1016/j.tranpol.2011.06.003 (in English)

8. Milbredt, O., Rudolph, F., Grunewald, E., & Christ, T. (2017). Evaluating conditions and impact of intermodal traffic management involving airports and railways. Transportation Research Procedia, 25, 1735-1744. DOI: 10.1016/j.trpro.2017.05.132 (in English)

9. Pagliara, F., Valeri, E., de Abreu e Silva, J. (2013). Is there an impact of High Speed Rail on tourism? 13th WCTR, 1-16. (in English)

10. Yang, L., Qi, J., Li, S., & Gao, Y. (2016). Collaborative optimization for train scheduling and train stop planning on high-speed railways. Omega, 64, 57-76. DOI: 10.1016/j.omega.2015.11.003 (in English)

11. Yashiro, R., & Kato, H. (2019). Success factors in the introduction of an intermodal passenger transportation system connecting high-speed rail with intercity bus services. Case Studies on Transport Policy, 7(4), 708-717. DOI: 10.1016/j.cstp.2019.10.001 (in English)

12. Zhang, C., Gao, Y., Yang, L., Kumar, U., & Gao, Z. (2019). Integrated optimization of train scheduling and maintenance planning on high-speed railway corridors. Omega, 87, 86-104. DOI: 10.1016/j.omega.2018.08.005 (in English)

13. Zhang, Q., Lusby, R. M., Shang, P., & Zhu, X. (2020). Simultaneously re-optimizing timetables and platform schedules under planned track maintenance for a high-speed railway network. Transportation Research Part C: Emerging Technologies, 121, 102823. DOI: 10.1016/j.trc.2020.102823 (in English)

14. Zhong, Q., Lusby, R. M., Larsen, J., Zhang, Y., & Peng, Q. (2019). Rolling stock scheduling with maintenance requirements at the Chinese High-Speed Railway. Transportation Research Part B: Methodological, 126, 24-44. DOI: 10.1016/j.trb.2019.05.013 (in English)

Received: Oct. 09,2020

Accepted: Feb. 08,2021

Creative Commons Attribution 4.0 International

doi: 10.15802/stp2021/228106
© T. V. Butko, V. M. Prokhorov, L. O. Parkhomenko, A. O. Prokopov, 2021