ISSN 2307–3489 (Print), ІSSN 2307–6666 (Online)

Наука та прогрес транспорту. Вісник Дніпропетровського
національного університету залізничного транспорту, 2021, № 1 (91)

РУХОМИЙ СКЛАД І ТЯГА ПОЇЗДІВ

Вступ

Плідне функціонування транспортної галузі зумовлює необхідність упровадження в експлуатацію сучасних транспортних засобів. Оскільки основний сегмент перевізного процесу відведено залізничному транспорту, то до створення сучасних конструкцій вагонів потрібно перед’являтися особливі умови. Зокрема це стосується їх несучих конструкцій.

Важливим напрямом створення перспективних вантажних вагонів є оптимізація їх несучих конструкцій. Це дозволило б зменшити їх матеріалоємність за умови дотримання вантажопідйомності не нижче за відповідні конструкцій вагонів-прототипів. Таке рішення сприятиме зменшенню витрат на виготовлення вагонів, їх експлуатацію, а також підвищенню ефективності перевізного процесу.

Визначення динамічної навантаженості піввагона моделі С70 з урахуванням різної висоти центра ваги наведено у [8]. Розрахункові сили, які діють на кузов вагона, установлено на підставі нормативних стандартів для залізниць Китаю.

З’ясування основних динамічних показників вантажних вагонів з урахуванням поперечних зміщень візків описано в [7]. Отримано дані, які дозволяють оцінити вплив поперечного зміщення візків вагона на показники безпеки руху.

Однак задачу визначення вертикальної навантаженості несучих конструкцій вагонів з урахуванням зменшення їх матеріалоємності в цих роботах не розглянуто.

Дослідженню динаміки рухомого складу з використанням експериментального вагона-лабораторії присвячено роботу [5]. Розглянуто можливу силову дію на рейку та колесо рухомого складу під час проходження складної ділянки колії.

Оцінку динамічних якостей вантажних вагонів на візках перспективної моделі наведено в [14]. Отримано експериментальні залежності основних динамічних показників руху піввагонів із використанням візків моделі 18–9771, яка має різні параметри ковзунів. Це дає можливість вибору параметрів ковзунів для отримання найбільшого ефекту зі зниження динамічної навантаженості як вагона, так і колії.

Однак у цих роботах приділено увагу поліпшенню показників динаміки вагонів шляхом використання нових або модернізованих типів візків. При цьому не взято до уваги несучі конструкції вагонів.

Особливості модернізації кузовів вантажних вагонів на сучасному етапі розвитку транспортної галузі описано в [15]. Метою такої модернізації є подовження строку експлуатації вагона. Також у роботі запропоновано вдосконалення системи діагностики технічного стану модернізованих кузовів вагонів.

Заходів щодо оптимізації кузова вагона з метою зменшення матеріалоємності в роботі не запропоновано.

Структурно-динамічний аналіз вантажного вагона подано в [13]. Розрахунок проведено за методом скінченних елементів. При цьому розглянуто багаторівневу систему вільності вагона.

Результати визначення динамічної навантаженості піввагона під час перевезення на залізничному поромі наведено в [9, 11]. При цьому розглянуто випадок жорсткого закріплення кузова відносно палуби, тобто відсутність власного ступеня вільності під час коливань залізничного порома.

Важливо зазначити, що в цих роботах не взято до уваги визначення вертикальної динаміки та оцінку ходу вагона.

Дослідження впливу осьового навантаження на динамічні показники піввагонів, а також показники їх взаємодії з колією описано в [16]. Проведено математичне та комп’ютерне моделювання динамічної навантаженості піввагона під час руху зі швидкостями в діапазоні від 50 до 90 км/год в кривих радіусами 350 і 600 м.

Визначення міцності кузова піввагона з урахуванням отриманих результатів динамічної навантаженості в роботі не проведено.

Результати втомного аналізу кузова вагона серії S (g) mmns наведено в [17]. Розрахунок здійснено за методом скінченних елементів. Розроблено та верифіковано тривимірні моделі досліджуваних вагонів та визначено показники їх міцності.

Однак питанню оптимізації кузова вагона з метою зменшення матеріалоємності в цій роботі уваги не приділено.

Мета

Основною метою статті є дослідження вертикальної динаміки несучих конструкцій вантажних вагонів з круглих труб. Це дозволить обґрунтувати доцільність упровадження круглих труб як несучих елементів кузовів вагонів та визначити вплив цього вдосконалення на безпеку руху. Для досягнення зазначеної мети потрібно виконати такі завдання:

– створити розрахункову схему несучої конструкції вантажного вагона для визначення основних показників динаміки;

– визначити основні показники динаміки вантажних вагонів із круглих труб;

– провести аналіз отриманих результатів щодо визначення основних показників динаміки вантажних вагонів із круглих труб.

Методика

Для зменшення матеріалоємності несучих конструкцій вагонів запропоновано впровадити як конструкційні елементи круглі труби [10, 12]. Таке технічне рішення обґрунтовано проведеними розрахунками на міцність. При цьому дослідження проведено для основних типів вантажних вагонів: піввагон, критий вагон, вагон-платформа та вагон-хопер (рис. 1).

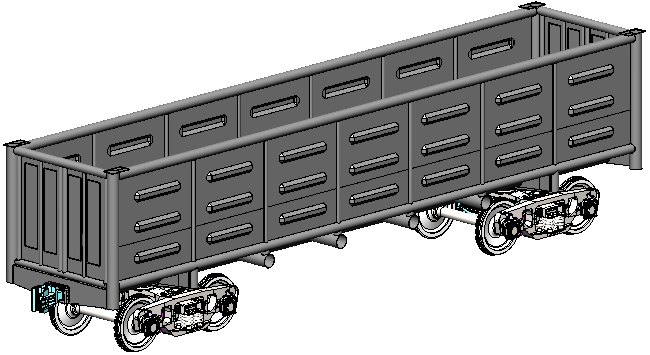
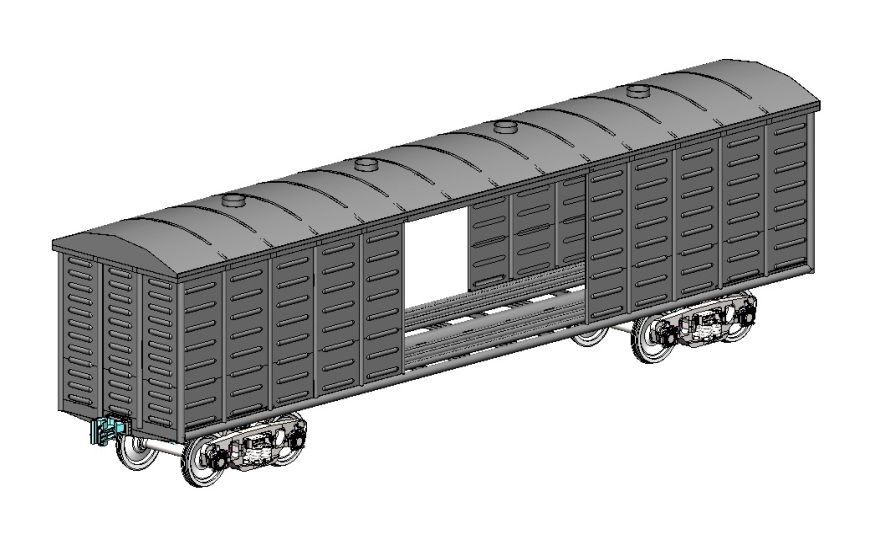
Просторові комп’ютерні моделі вантажних вагонів з урахуванням запропонованих рішень наведено на рис. 2.

Для визначення основних показників динаміки запропонованих конструкцій вагонів проведено розрахунки, для чого використано математичну модель, наведену в [3].

Вагон при цьому розглянуто як систему з трьох твердих тіл – несучої конструкції та двох візків моделі 18–100 з ресорними комплектами, які мають жорсткість та коефіцієнт відносного тертя.

Ураховано, що на систему накладено такі зв’язки:

– переміщення кузова та візків вагона-платформи уздовж осі колії однакові: q₁ = q₃ = q₅;

– колісні пари рухаються без проковзування: Ψr_ij = xr_ij/R, (r, i, j = 1, 2), де R – радіус колеса, 0,475 м;

– через відсутність пружних елементів у буксовому підвішуванні підстрибування візків визначають підстрибуванням колісних пар.

а – а                                                                    б – b

в – c                                                                                          г – d

Рис. 1. Досліджувані типи вантажних вагонів:
а – піввагон; б – критий вагон; в – вагон-платформа; г – вагон-хопер

Fig. 1. Types of freight cars under study:
a – gondola car; b – covered car; c – flat car; d – hopper car

а – a                                                                               б – b

в – c                                                                              г – d

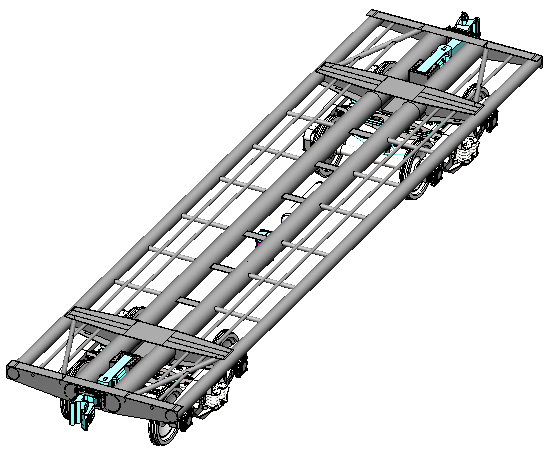
Рис. 2. Комп’ютерні моделі залізничних вагонів, несучі елементи
кузовів яких виконано з труб круглого перерізу:
а – піввагон; б – критий вагон; в – вагон-платформа; г – вагон-хопер

Fig. 2. Computer models of railway cars, supporting elements of bodies of which are made of round section pipes:
a – gondola car; b – covered car; c – flat car; d – hopper car

Результати

Дослідження проведено в плоскій системі координат. Прийнято припущення, що вагон рухається пружно-в’язкою колією так, що реакції колії пропорційні як її деформації, так і швидкості цієї деформації [3]. Ураховано, що вагони рухаються в порожньому стані. Розрахункова модель вагона наведена на рис. 3.

Рис. 3. Розрахункова схема вантажного вагона

Fig. 3. Estimated scheme of freight car

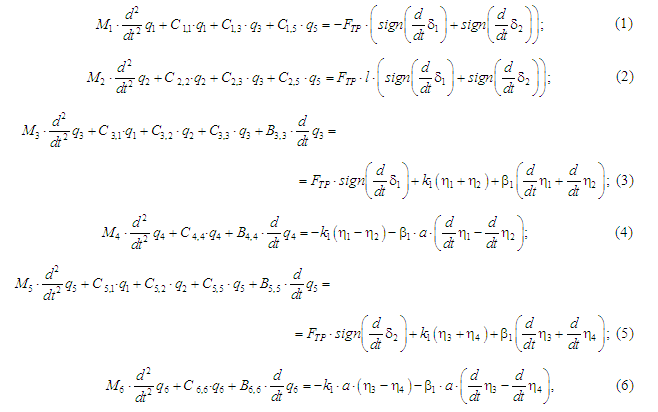
де М₁, М₂ – відповідно маса та момент інерції несучої конструкції вагона-платформи; М₃, М₄ – відповідно маса та момент інерції першого за ходом руху візка; М₅, М₆ – відповідно маса та момент інерції другого за ходом руху візка; С_i,j – характеристики пружності елементів коливальної системи, які визначають значеннями коефіцієнтів жорсткості пружин k_T; B_i,j – функція розсіювання; а – половина бази візка; k₁ – жорсткість колії; β₁ – коефіцієнт демпфування; η_i(x) – функція, яка описує нерівність рейкової колії; δ_i – деформації пружних елементів ресорного підвішування; F_ТР – сила абсолютного тертя в ресорному комплекті.

Стикову нерівність описано періодичною функцією [3]:

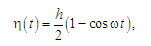₍₇₎

де h – глибина нерівності; ω – частота коливань, яку визначають за формулою ω=2πV/L (V – швидкість руху вагона, L – довжина нерівності).

Розв’язок математичної моделі здійснено в програмному комплексі MathCad за методом Рунге–Кутта [4, 6, 18].

Початкове переміщення та швидкості взято рівними нулю. Вхідними параметрами моделі є технічні характеристики кузовів вагонів, ресорного підвішування, а також збурюючої дії. Під час проведення розрахунків ураховано параметри ресорного підвішування візка моделі 18–100.

Інерційні коефіцієнти несучих конструкцій вагонів, які враховано під час визначення динамічної навантаженості у вертикальній площині, наведено в табл. 1. Ці коефіцієнти визначено за допомогою опцій програмного комплексу SolidWorks.

Розрахунок проведено за швидкості руху вагонів 80 км/год. Результати розрахунків наведено в табл. 2, а також на рис. 4–7.

Отже, для піввагона, критого вагона, а також вагона-хопера прискорення в центрі мас несучої конструкції перебуває в межах 0,4 g, а вагона-платформи – 0,5 g.

Отримані результати дозволяють зробити висновок, що показники динаміки вагонів перебувають у межах допустимих [1, 2].

Прискорення, які діють на несучі конструкції вагонів із круглих труб, майже не відрізняються від тих, що отримані для вагонів-прототипів (рис. 8).

При цьому хід вагонів оцінено як «відмінний» – піввагон, критий вагон, вагон-хопер та «добрий» – вагон-платформа (рис. 9).

Таблиця 1

Інерційні коефіцієнти несучих конструкцій вагонів для визначення
динамічної навантаженості у вертикальній площині

Table 1

Inertial coefficients of supporting structures of cars for determination
of dynamic loading in the vertical plane

Тип вагона	Маса, т	Момент інерції, т ∙ м2	Відсоток зменшення маси порівняно з вагоном-прототипом
Піввагон	14,6	266,1	6,0
Критий вагон	14,7	307,9	4,0
Вагон-платформа	11,0	101,4	4,0
Вагон-хопер	14,8	230,2	5,0

Таблиця 2

Динамічні показники досліджуваних вагонів під час руху в порожньому стані

Table 2

Dynamic indicators of the cars under study when moving in empty state

Показник	Значення
	ПВ	КВ	ВПФ	ВХ
Прискорення кузова, м/с2	4,1	4,07	5,2	4,05
Сила в ресорному підвішуванні першого візка, кН	41,0	41,4	40,3	41,3
Сила в ресорному підвішуванні другого візка, кН	41,0	41,4	40,3	41,3
Коефіцієнт динаміки першого візка	0,52	0,5	0,72	0,5
Коефіцієнт динаміки другого візка	0,52	0,5	0,72	0,5
ПВ – піввагон; КВ – критий вагон; ВПФ – вагон-платформа; ВХ – вагон-хопер

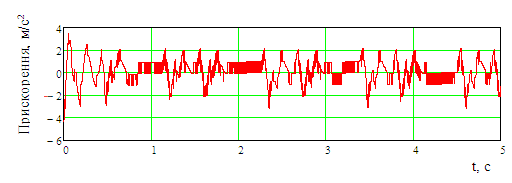
Рис. 4. Прискорення, які діють на несучу конструкцію піввагона

Fig. 4. Accelerations acting on the supporting structure of the gondola

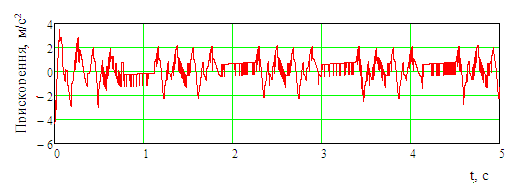
Рис. 5. Прискорення, які діють на несучу конструкцію критого вагона

Fig. 5. Accelerations acting on the supporting structure of the covered car

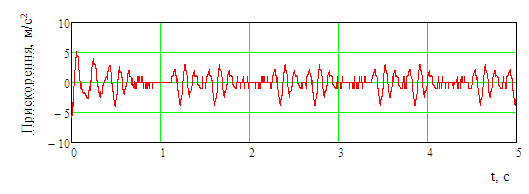
Рис. 6. Прискорення, які діють на несучу конструкцію вагона-платформи

Fig. 6. Accelerations acting on the supporting structure of the flat car

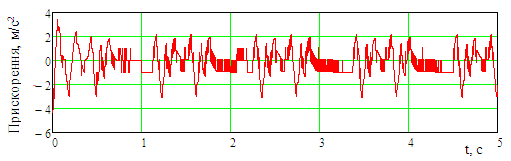
Рис. 7. Прискорення, які діють на несучу конструкцію вагона-хопера

Fig. 7. Accelerations acting on the supporting structure of the hopper car

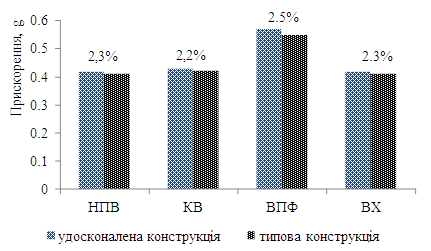
Рис. 8. Порівняльний аналіз прискорень, які діють на несучі конструкції вагонів

Fig. 8. Comparative analysis of accelerations acting on the supporting structures of cars

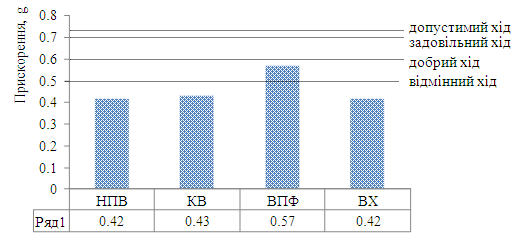
Рис. 9. Прискорення, які діють на несучі конструкції вагонів із круглих труб

Fig. 9. Accelerations acting on the supporting structures of cars made of round pipes

Проведені дослідження доводять доцільність упровадження круглих труб для несучих елементів вагонів.

Наукова новизна та практична
значимість

У роботі вперше здійснено математичне моделювання динамічної навантаженості несучих конструкцій вагонів із круглих труб та отримано основні показники їх динаміки.

Проведені дослідження сприятимуть створенню рекомендацій щодо проектування несучих конструкцій вагонів із круглих труб, а також можуть бути корисними напрацюваннями для створення інноваційних конструкцій вагонів.

Висновки

1. Створено розрахункову схему несучої конструкції вантажного вагона для визначення основних показників динаміки. Дослідження проведено в плоскій системі координат. Модель враховує переміщення вагона по стиковій нерівності. При цьому досліджено рух вагонів у порожньому стані.

2. Визначено основні показники динаміки вантажних вагонів із круглих труб: прискорення, які діють на несучу конструкцію в центрі мас, сили, що діють у ресорному підвішуванні візків, коефіцієнти динаміки.

3. Проведено аналіз отриманих результатів щодо визначення основних показників динаміки вантажних вагонів із круглих труб. При цьому для піввагона, критого вагона, а також вагона-хопера прискорення в центрі мас несучої конструкції перебувають у межах 0,4 g, а вагона-платформи – 0,5 g.

Прискорення, які діють на несучі конструкції вагонів із круглих труб, майже не відрізняються від прискорень для вагонів-прототипів, а хід вагонів оцінено як «відмінний» – піввагон, критий вагон, вагон-хопер та «добрий» – вагон-платформа.

Установлено, що отримані показники динаміки вагонів із круглих труб перебувають у межах допустимих.

Викладене вказує на доцільність упровадження несучих елементів вагонів із круглих труб.

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1. ГОСТ 33211-2014. Вагоны грузовые. Требования к прочности и динамическим качествам. [Действителен от 2016-07-01]. Москва, 2016. 54 с.

2. ДСТУ 7598:2014. Вагони вантажні. Загальні вимоги до розрахунків та проектування нових і модернізованих вагонів колії 1520 мм (несамохідних). [Чинний від 2015-07-01]. Київ, 2015. 250 с.

3. Дьомін Ю. В. Залізнична техніка міжнародних транспортних систем (вантажні перевезення). Київ : Юніком-Прес, 2001. 342 с.

4. Дьяконов В. MATHCAD 8/2000 : специальный справочник. Санкт-Петербург : Издательство «Питер», 2000. 592 c.

5. Ермоленко И. Ю., Железняк В. Н. Исследование динамики подвижного состава с использованием экспериментального вагона-лаборатории при движении по сложным участкам дороги ВСЖД. Современные технологии. Системный анализ. Моделирование. 2016. № 4 (52). С. 199–203.

6. Кирьянов Д. В. Mathcad 13. Санкт-Петербург : БХВ-Петербург, 2006. 608 c.

7. Луханин Н. И., Мямлин С. В., Недужая Л. А., Швец А. А. Динамика грузовых вагонов с учетом поперечного смещения тележек. Збірник наукових праць ДонІЗТ. 2012. № 29. С. 234–241.

8. Chao C., Mei H., Yanhui H. Study of Railway Freight Vehicle Body’s Dynamic Model Based on Goods Loading Technical Standards. Procedia Engineering. 2012. Vol. 29. P. 3572–3577. DOI: 10.1016/j.proeng.2012.01.533

9. Fomin O., Gerlici J., Lovska A., Kravchenko K., Prokopenko P., Fomina A., Hauser V. Durability Determination of the Bearing Structure of an Open Freight Wagon Body Made of Round Pipes during its Transportation on the Railway Ferry. Communications – Scientific letters of the University of Zilina. 2019. Vol. 21. Iss. 1. P. 28–34. DOI: 10.26552/com.c.2019.1.28-34

10. Fomin O., Gerlici J., Lovskaya A., Kravchenko K., Prokopenko P., Fomina A., Hauser V. Research of the strength of the bearing structure of the flat wagon body from round pipes during transportation on the railway ferry. MATEC Web of Conferences. 2018. Vol. 235. P. 1–5. DOI: 10.1051/matecconf/201823500003

11. Fomin O., Lovska A., Masliyev V., Tsymbaliuk A., Burlutski O. Determining strength indicators for the bearing structure of a covered wagon's body made from round pipes when transported by a railroad ferry. Eastern-European Journal of Enterprise Technologies. 2019. Vol. 1. Iss. 7 (97). P. 33–40. DOI: 10.15587/1729-4061.2019.154282

12. Fomin O. V., Lovska A. O., Plakhtii O. A., Nerubatskyi V. P. The influence of implementation of circular pipes in load-bearing structures of bodies of freight cars on their physico-mechanical properties. Naukovyi Visnyk Natsionalnoho Hirnychoho Universytetu. 2017. № 6. P. 89–96.

13. Haraka S. S., Sharma S. C., Harsha S. P. Structural dynamic analysis of freight railway wagon using finite element method. Procedia Materials Science. 2014. Vol. 6. P. 1891–1898. DOI: 10.1016/j.mspro.2014.07.221

14. Myamlin S., Neduzha L., Lunys O. Estimation of dynamic qualities of freight wagons on bogies of a perspective model. IX International conference. 2017. P. 459–471.

15. Płaczek M., Wróbel A., Buchacz A. A concept of technology for freight wagons modernization. IOP Conference Series : Materials Science and Engineering. 2016. Vol. 161. P. 1–13. DOI: 10.1088/1757-899X/161/1/012107

16. Shvets A. O., Bolotov О. О. Influence of loading from the axle of a gondola car on its dynamic indicators and railway track. Наука та прогрес транспорту. 2019. № 1 (79). С. 151–166. DOI: 10.15802/stp2019/158127

17. Stoilov V., Slavchev S., Purgic S. Study of fatigue in welded joints and stress notches of wagon series S(g)mmns with methods of UIC and DVS 1612. URL: http://www.mech-ing.com/journal/Archive/2012/9/nano/82_Stoilov%20d1%20en_tm'12.pdf

18. Vatulia G., Komagorova S., Pavliuchenkov M. Optimization of the truss beam. Verification of the calculation results. MATEC Web of Conferences. 2018. Vol. 230. P. 1–8. DOI: 10.1051/matecconf/201823002037

O. V. FOMIN¹, A. O. LOVSKA^2*

¹Dep. «Cars and Carriage Facilities», State Economy and Technology University of Transport,
Kyrylivska St., 19, Kyiv, Ukraine, 03049, tel. +38 (067) 813 97 88, e-mail fomin1985@list.ru,
ORCID 0000-0003-2387-9946
^2*Dep. «Wagon Engineering and Product Quality», Ukrainian State University of Railway Transport,
Feuerbach Sq., 7, Kharkiv, Ukraine, 61500, tel. +38 (057) 730 10 35,
e-mail alyonalovskaya.vagons@gmail.com, ORCID 0000-0002-8604-1764

Research of the Vertical Dynamics of the Supporting

Structures of Freight Cars Made of Round Pipes

Purpose. This study is aimed at determining the vertical dynamics of supporting structures of freight cars made of round pipes. Methodology. Mathematical modeling of the dynamic loading of the supporting structures of the main types of freight cars made of round pipes (gondola car, covered car, flat car, hopper car) was carried out. The studies were carried out in a plane coordinate system – the XZ plane. At the same time, it was taken into account that the car is moving in an elastic-viscous track so that the reactions of the track are proportional to both its deformation and the rate of this deformation. The studies were carried out for the case of empty cars. The joint inequality is described by a periodic function. The calculation was performed at a speed of 80 km/h. Differential equations of motion were solved in the MathCad software package using the Runge-Kutta method. Findings. Based on the mathematical modeling of the dynamic loading of the supporting structures of cars made of round pipes, the main indicators of their dynamics were obtained: accelerations acting on the supporting structures in the mass center, forces acting in the spring suspension of bogies, dynamics coefficients. For gondola car, covered car, and hopper car, the acceleration at the mass center of the supporting structure is within 0.4 g, and for a flat car – 0.5 g. It was found that the obtained indicators of the dynamics of cars made of round pipes are within the permissible limits. The accelerations acting on the supporting structures of cars made of round pipes are almost the same as those obtained for prototype cars. At the same time, the motion of cars is assessed as «excellent» for gondola car, covered car, and hopper car and «good» for flat car. Originality. Mathematical modeling of the dynamic loading of the supporting structures of cars from round pipes was carried out and the main indicators of their dynamics were obtained. Practical value. The research carried out will contribute to the creation of recommendations for the design of supporting structures of freight cars of round pipes, and can also be useful developments in the creation of innovative car designs.

Keywords: car; supporting structure; dynamic loading; vertical dynamics; transport mechanics

REFEReNCEs

1. Vagony gruzovye. Trebovaniya k prochnosti i dinamicheskim kachestvam, 54 GOST 33211-2014 (2016). (in Russian)

2. Vagoni vantazhni. Zagalni vimogi do rozrahunkiv ta proektuvannya novih i modernizovanih vagoniv koliyi 1520 mm (nasamohidnih), 250 DSTU 7598:2014 (2015). (in Ukraіnian)

3. Domin, Yu. V. (2001). Zaliznychna tekhnika mizhnarodnykh transportnykh system (vantazhni perevezennya). Kiev: Yunikom-Pres. (in Ukraіnian)

4. Dyakonov, V. (2000). MATHCAD 8/2000: spetsialnyy spravochnik. St. Petersburg: Izdatelstvo «Piter». (in Russian)

5. Yermolenko, I. Yu., & Zheleznyak, V. N. (2016). Issledovanie dinamiki podvizhnogo sostava s ispolzovaniem eksperimentalnogo vagona-laboratorii pri dvizhenii po slozhnym uchastkam dorogi VSZhD. Modern Technologies system. Analysis. Modeling, 4(52), 199-203. (in Russian)

6. Kiryanov, D. V. (2006). Mathcad 13. St. Petersburg: BKhV-Peterburg. (in Russian)

7. Lukhanyn, M. I., Myamlin, S. V., Neduzha, L. A., & Shvets, A. O. (2012). Freight Cars Dynamics Taking into Account Transversal Displacement of the Bogies. Zbirnyk naukovykh prats DonIZT, 29, 234-241. (in Russian)

8. Chao, C., Mei, H., & Yanhui, H. (2012). Study of Railway Freight Vehicle Body’s Dynamic Model Based on Goods Loading Technical Standards. Procedia Engineering, 29, 3572-3577. DOI: 10.1016/j.proeng.2012.01.533 (in English)

9. Fomin, O., Gerlici, J., Lovska, A., Kravchenko, K., Prokopenko, P., Fomina, A., & Hauser, V. (2019). Durability Determination of the Bearing Structure of an Open Freight Wagon Body Made of Round Pipes during its Transportation on the Railway Ferry. Communications-Scientific Letters of the University of Zilina, 21(1), 28-34. DOI: 10.26552/com.c.2019.1.28-34 (in English)

10. Fomin, O., Gerlici, J., Lovskaya, A., Kravchenko, K., Prokopenko, P., Fomina, A., & Hauser, V. (2018). Research of the strength of the bearing structure of the flat wagon body from round pipes during tran-sportation on the railway ferry. MATEC Web of Conferences, 235, 1-5. DOI: 10.1051/matecconf/201823500003 (in English)

11. Fomin, O., Lovska, A., Masliyev, V., Tsymbaliuk, A., & Burlutski, O. (2019). Determining strength indicators for the bearing structure of a covered wagon's body made from round pipes when transported by a railroad ferry. Eastern-European Journal of Enterprise Technologies, 1(7(97)), 33-40. DOI: 10.15587/1729-4061.2019.154282 (in English)

12. Fomin, O. V., Lovska, A. O., Plakhti,i O. A., & Nerubatskyi, V. P. (2017). The influence of implementation of circular pipes in load-bearing structures of bodies of freight cars on their physico-mechanical properties. Naukovyi Visnyk Natsionalnoho Hirnychoho Universytetu, 6, 89-96. (in English)

13. Haraka, S. S., Sharma, S. C., & Harsha, S. P. (2014). Structural dynamic analysis of freight railway wagon using finite element method. Procedia Materials Science, 6, 1891-1898.
    DOI: 10.1016/j.mspro.2014.07.221 (in English)

14. Myamlin, S., Neduzha, L., & Lunys, O. (2017). Estimation of dynamic qualities of freight wagons on bogies of a perspective model. IX International conference, 459-471. (in English)

15. Płaczek, M., Wróbel, A., & Buchacz, A. (2016). A concept of technology for freight wagons modernization. IOP Conference Series: Materials Science and Engineering, 161, 1-13. DOI: 10.1088/1757-899X/161/1/012107 (in English)

16. Shvets, A. O., & Bolotov, О. О. (2019). Influence of loading from the axle of a gondola car on its dynamic indicators and railway track. Science and Transport Progress, 1(79), 151-166. DOI: 10.15802/stp2019/158127 (in English)

17. Stoilov, V., Slavchev, S., & Purgic, S. Study of fatigue in welded joints and stress notches of wagon series s (g)mmns with methods of UIC and DVS 1612. Retrieved from http://www.mech-ing.com/journal/Archive/2012/9/nano/82_Stoilov%20d1%20en_tm'12.pdf (in English)

18. Vatulia, G., Komagorova, S., & Pavliuchenkov, M. (2018). Optimization of the truss beam. Verification of the calculation results. MATEC Web of Conferences, 230, 1-8. DOI: 10.1051/matecconf/201823002037 (in English)

Надійшла до редколегії: 02.10.2020

Прийнята до друку: 02.02.2021

Creative Commons Attribution 4.0 International

doi: 10.15802/stp2021/227223
© О. В. Фомін, А. О. Ловська, 2021