ISSN
2307–3489 (Print), ІSSN
2307–6666
(Online)
Наука
та прогрес транспорту. Вісник
Дніпропетровського
національного університету залізничного
транспорту, 2020, № 6 (90)
екологія
Та промислова безпека
UDC
504.5:[628.3:519.87]
M. M. BILIAIEV1*,
M. V. LEMESH2,
O. Y. Gunko3,
V. O. ZADOIA4,
P. B. MASHYKHINA5,
Z. M. YAKUBOVSKA6
1*Dep.
«Hydraulics and Water Supply», Dnipro National University
of
Railway Transport named after Academician V. Lazaryan, Lazaryana St.,
2,
Dnipro, Ukraine, 49010, tel. +38 (056) 273 15 09,
e-mail
water.supply.treatment@gmail.com,
ORCID 0000-0002-1531-7882
2Dep.
«Hydraulics and Water Supply», Dnipro National University
of
Railway Transport named after Academician V. Lazaryan, Lazaryana St.,
2,
Dnipro, Ukraine, 49010, tel. +38 (056) 273 15 09,
e-mail
water.supply.treatment@gmail.com,
ORCID 0000-0002-1230-8040
3Dep.
«Hydraulics and Water Supply», Dnipro National University
of
Railway Transport named after Academician V. Lazaryan, Lazaryana St.,
2,
Dnipro, Ukraine, 49010, tel. +38 (056) 273 15
09,
e-mail water.supply.treatment@gmail.com,
ORCID
0000-0001-9257-763X
4Dep.
«Economics and Management», Dnipro National University
of
Railway Transport named after Academician V. Lazaryan, Lazaryana St.,
2,
Dnipro, Ukraine, 49010, tel. +38 (096) 469 60 09,
e-mail
v.a.zadoya@gmail.com,
ORCID 0000-0001-9408-4978
5Dep.
«Hydraulics and Water Supply», Dnipro National University
of
Railway Transport named after Academician V. Lazaryan, Lazaryana St.,
2,
Dnipro, Ukraine, 49010, tel. +38 (056) 273 15 09,
e-mail
water.supply.treatment@gmail.com,
ORCID 0000-0003-3057-9204
6Dep.
«Power Engineering», Ukrainian State University of Chemical
Technology, Haharina Av., 8, Dnipro, Ukraine, 49000,
tel. +38
(056) 753 56 38, e-mail zinaidaya25@gmail.com,
ORCID 0000-0002-9893-3479
3D modeling of biological wastewater
treatment in
aeration tank
Purpose. The main purpose of the article is to
develop a 3D CFD model for modeling the process of biological
wastewater treatment in an aeration tank. Methodology. For
mathematical modeling of the process of biological wastewater
treatment in the reactor, taking into account the flow hydrodynamics,
geometric shape of the aeration tank, convective-diffusion transfer
of the substrate and activated sludge, a 3D CFD model was built. The
model is based on the three-dimensional equation of motion of an
ideal liquid and the equation of mass conservation for the substrate,
activated sludge. The field of sewage flow rate in the aeration tank
is calculated based on the velocity potential equation. The
process of biological transformation of the substrate is calculated
on the basis of the Monod model. The splitting scheme was used for
numerical integration of the equations of convective-diffusion
transfer of activated sludge and substrate. The splitting is carried
out in such a way to take into account the transfer of substrate
(activated sludge) in only one direction at each step of splitting.
The calculation of the unknown value of the substrate (activated
sludge) concentration is carried out according to an explicit scheme.
The Richardson method is used to numerically integrate the
three-dimensional equation for the velocity potential, and the
unknown value of the velocity potential is calculated by an explicit
formula. Euler's method is used for numerical integration of
equations describing the process of substrate transformation and
change in activated sludge concentration (Monod model). Findings.
The software implementation of the constructed 3D CFD model is
carried out. A description of the structure of the developed software
package is provided. The results of a computer experiment to study
the process of wastewater treatment in an aeration tank with
additional elements are presented. Originality. A new
multifactor 3D CFD model has been developed, which allows quick
assessing the efficiency of biological treatment in an aeration tank.
Practical value. The constructed 3D CFD model can be used to
analyze the efficiency of the aeration tank under different operating
conditions at the stage of sketch design of wastewater treatment
systems.
Keywords:
water treatment; biological water
treatment; mathematical modeling; aeration tank; Monod model
Introduction
To determine the efficiency of
biological wastewater treatment at the design stage of aeration
tanks, it is necessary to use special mathematical models [3, 4, 6].
Nowadays, balance, empirical and analytical models are most often
used to solve this problem [1–5, 7–17]. But in some cases, these
models cannot provide a reliable result, because they do not take
into account primarily the geometric shape of the reactor and the
process of hydrodynamics, as well as a number of other parameters.
In this regard, the problem of the development of mathematical
models that allow theoretical investigation of the process of
biological wastewater treatment in aeration tanks, taking into
account the most important factors is relevant [1, 2, 6–10].
Purpose
The work is aimed to develop a
three-dimensional CFD-model of the process of biological wastewater
treatment in aeration tanks. The model must perform real-time
calculation. In addition, the model should be acceptable for
implementation on low- and medium-power computers.
Methodology
To model the biological
wastewater treatment in the aeration tank the following equations
are used:
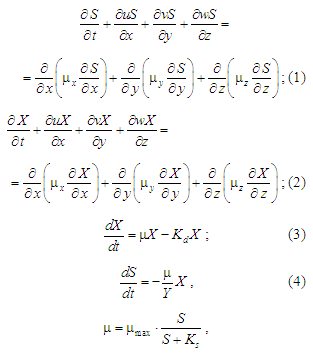
where
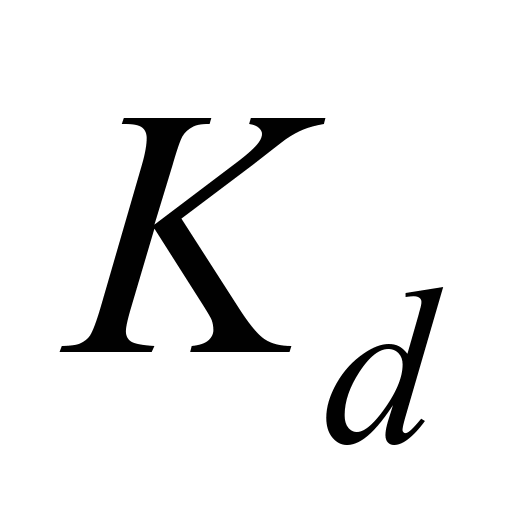 – extinction coefficient of activated sludge;
– extinction coefficient of activated sludge;
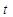 – time;
– time;
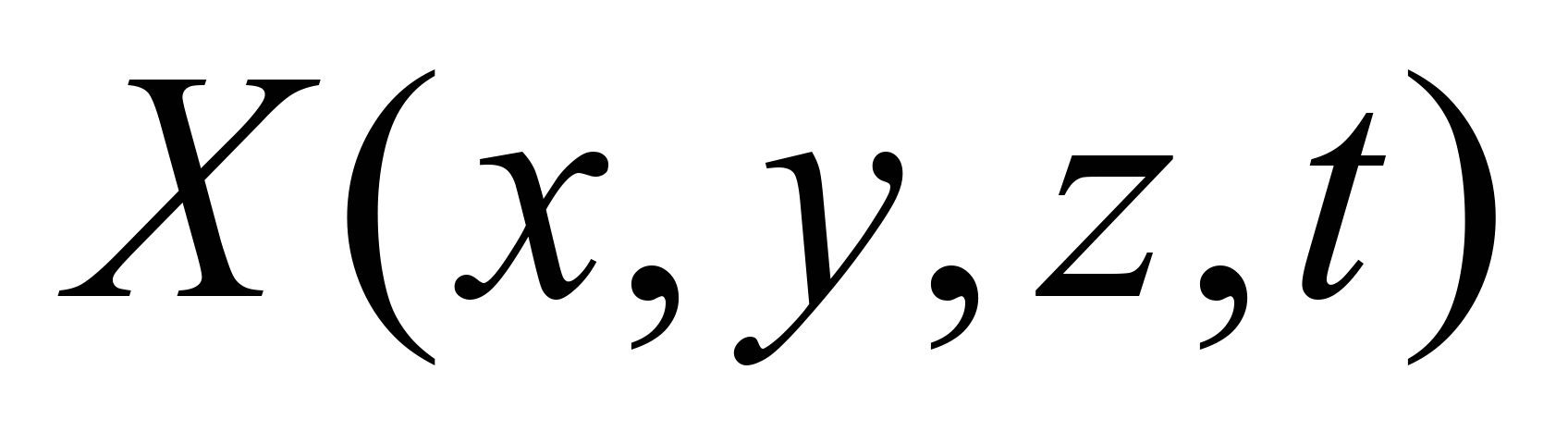 – concentration of activated sludge in the bioreactor;
– concentration of activated sludge in the bioreactor;
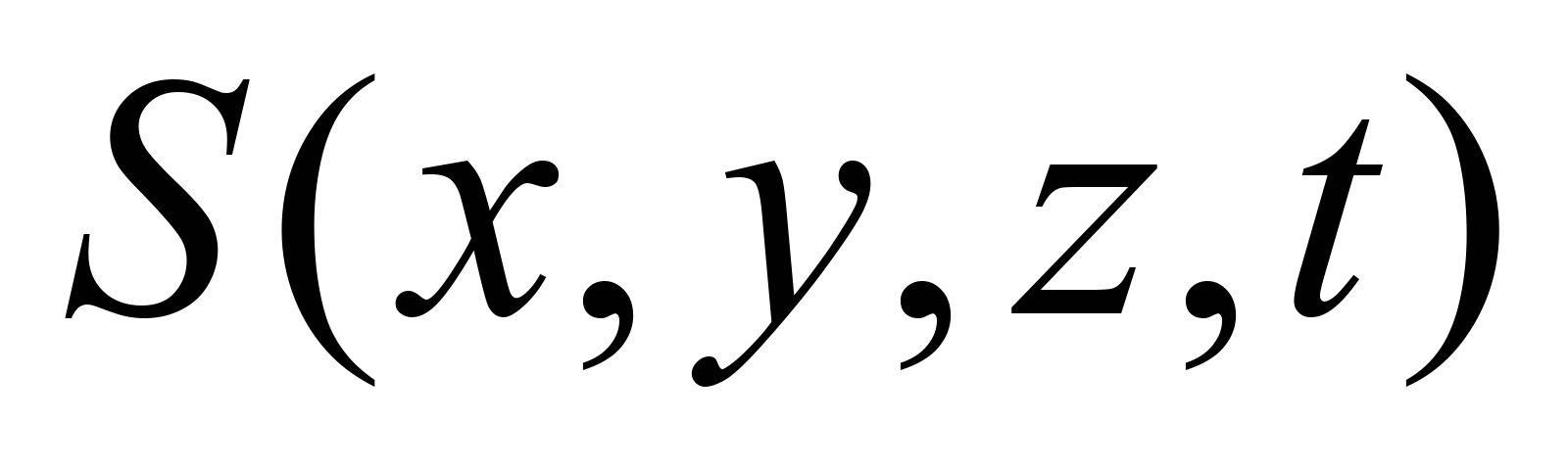 – substrate concentration in the bioreactor;
– substrate concentration in the bioreactor;
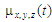 – empirical parameter;
– empirical parameter;
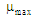 – parameter in the Mono model;
– parameter in the Mono model;
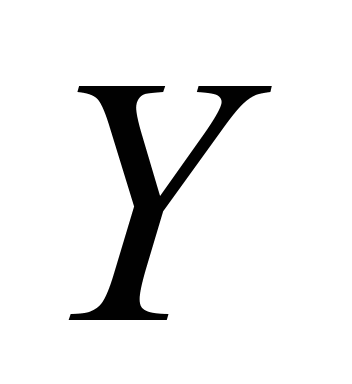 – empirical parameter;
– empirical parameter;
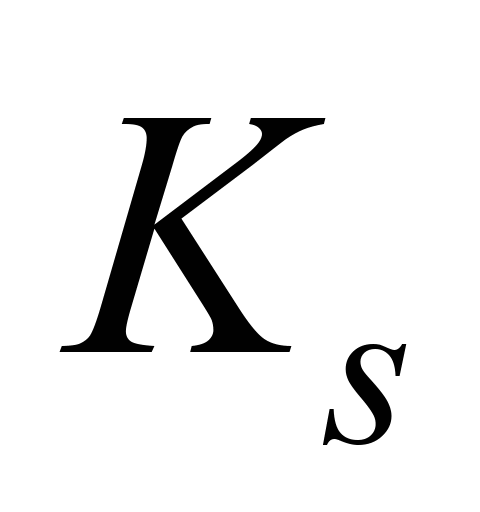 – parameter in the Mono model;
– parameter in the Mono model;
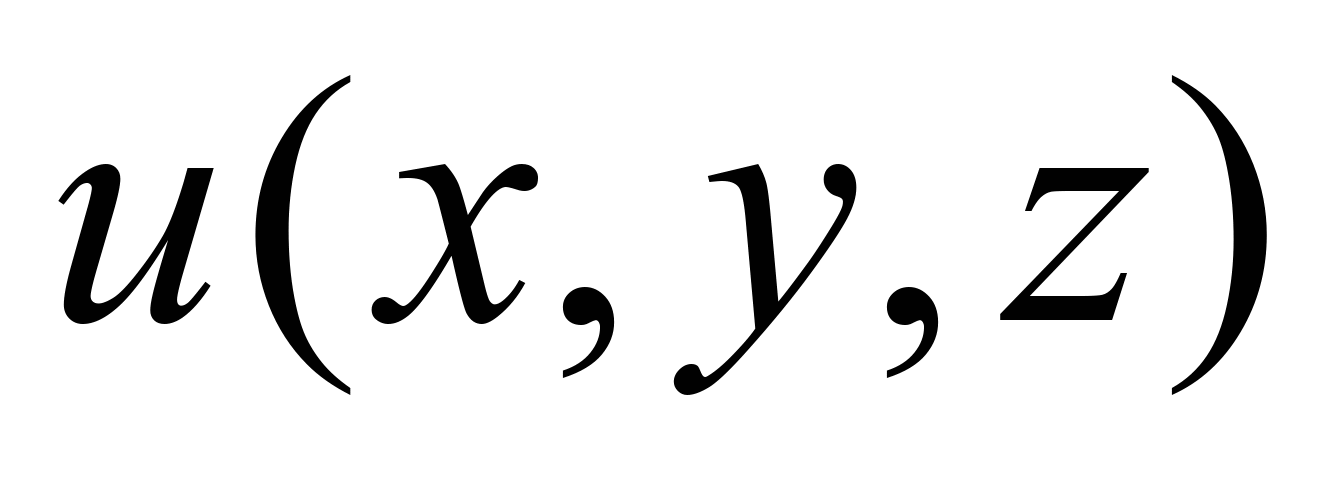 ,
,
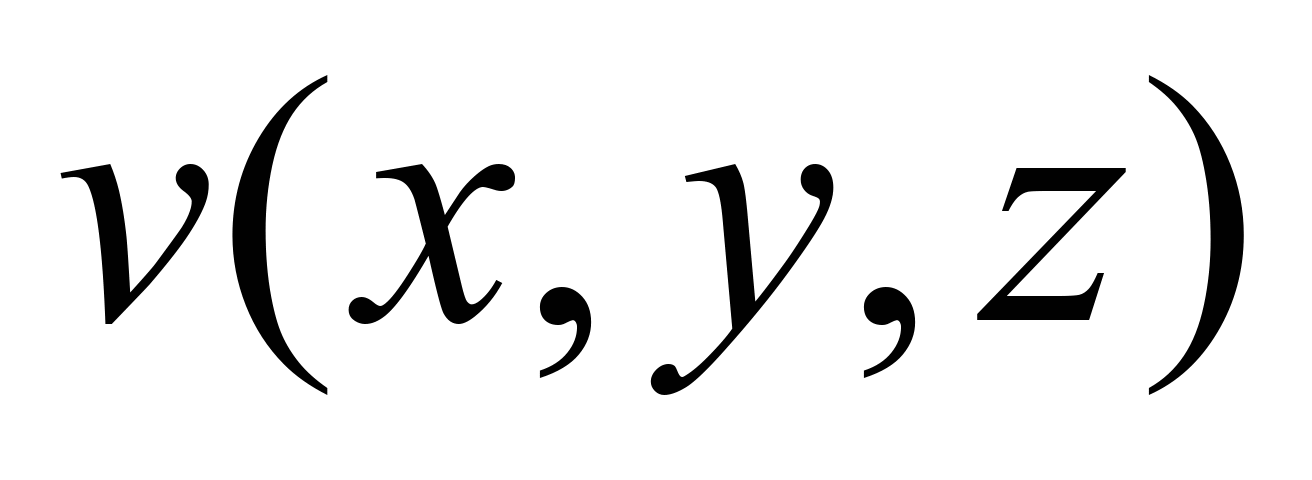 ,
,
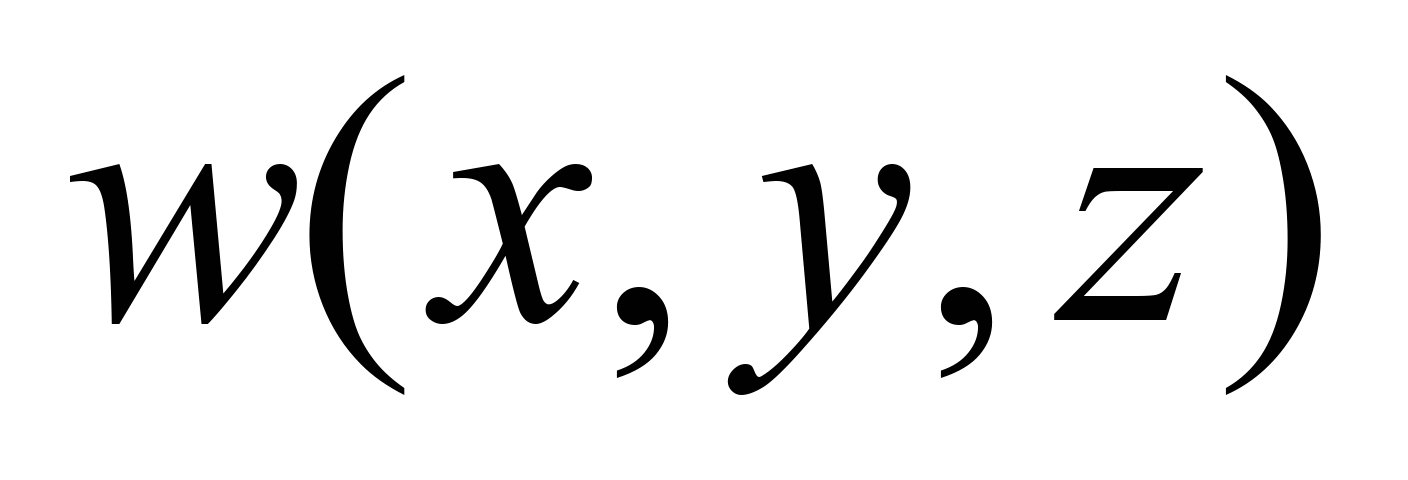 –
components of the water flow rate in the bioreactor, in the
direction of the axes
–
components of the water flow rate in the bioreactor, in the
direction of the axes
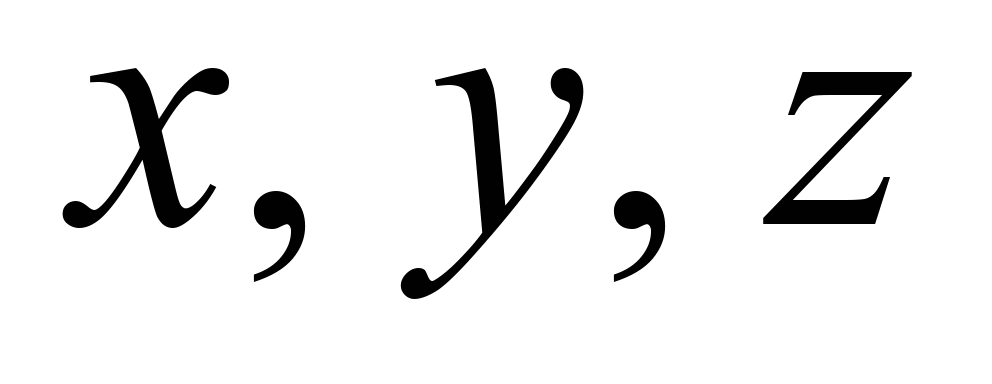 ,
respectively;
,
respectively;
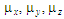 – diffusion
coefficients, respectively, in the direction
– diffusion
coefficients, respectively, in the direction
 ;
;
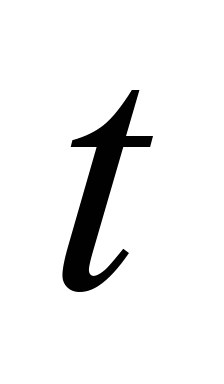 – time.
– time.
Let us note
that the diffusion coefficients
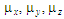 are different values, but in the scientific literature there is a
significant shortage of data on their values. Therefore, in
practice, the calculations are carried out under the condition
are different values, but in the scientific literature there is a
significant shortage of data on their values. Therefore, in
practice, the calculations are carried out under the condition
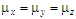 .
Determining these parameters experimentally is a rather
difficult task.
.
Determining these parameters experimentally is a rather
difficult task.
For
practical use of equations of model (1) – (4) it is necessary to
calculate the non-uniform flow velocity field in the reactor, i.e.
to determine the parameters
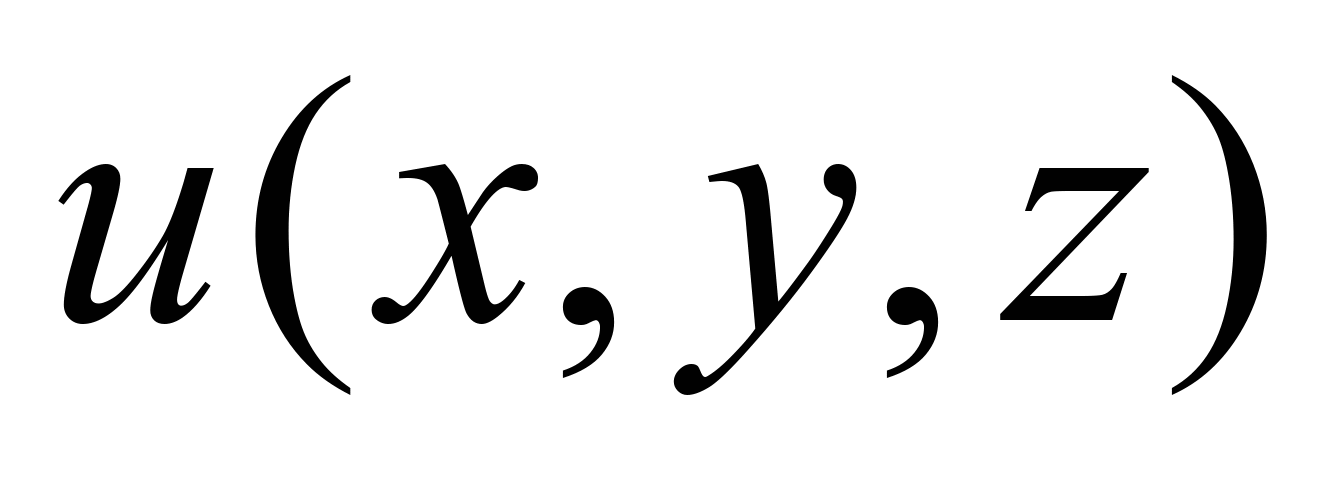 ,
,
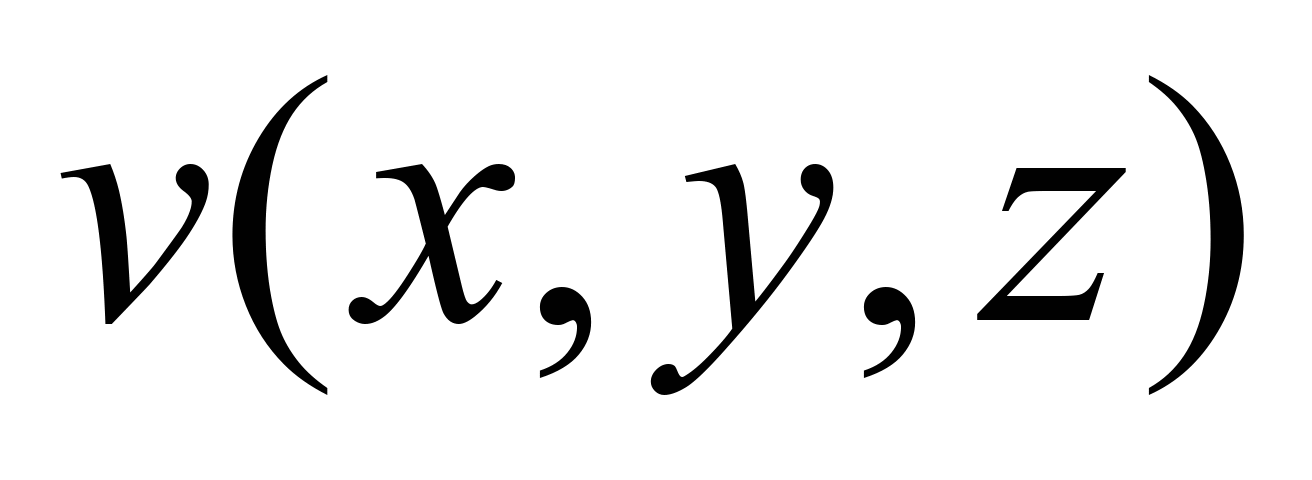 ,
,
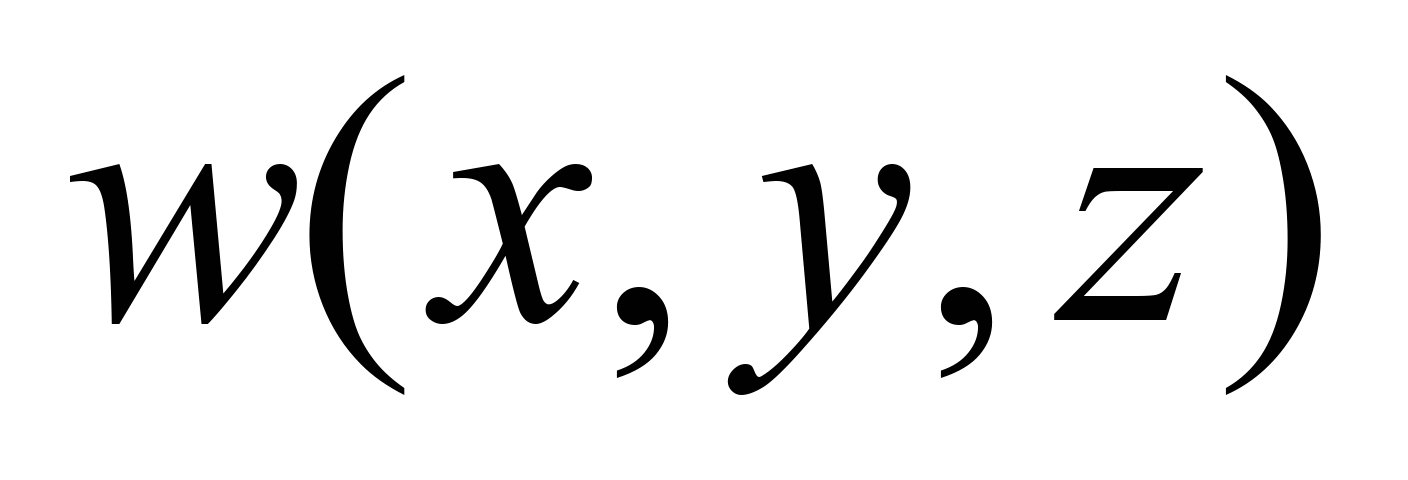 ,
under the action of these parameters there is a convective transfer
of substrate and activated sludge in the bioreactor. To calculate
the non-uniform flow velocity field in the bioreactor, we use the
3D equation for the velocity potential:
,
under the action of these parameters there is a convective transfer
of substrate and activated sludge in the bioreactor. To calculate
the non-uniform flow velocity field in the bioreactor, we use the
3D equation for the velocity potential:
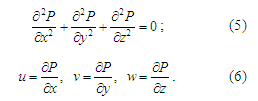
The
boundary conditions for modeling equations are as follows:
– on
the surfaces of the building, solid walls, upper surface:
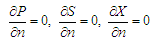 ,
,
where 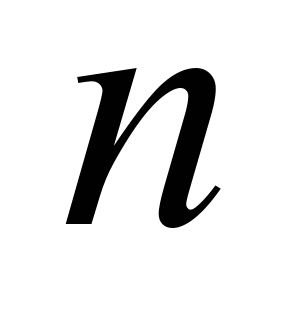 – outward normal to a surface;
– outward normal to a surface;
– at
the entrance boundary:
 ,
where
,
where
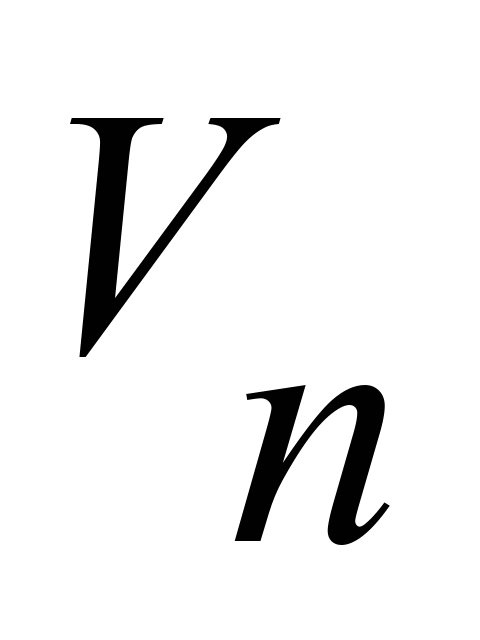 – flow
velocity;
– flow
velocity;
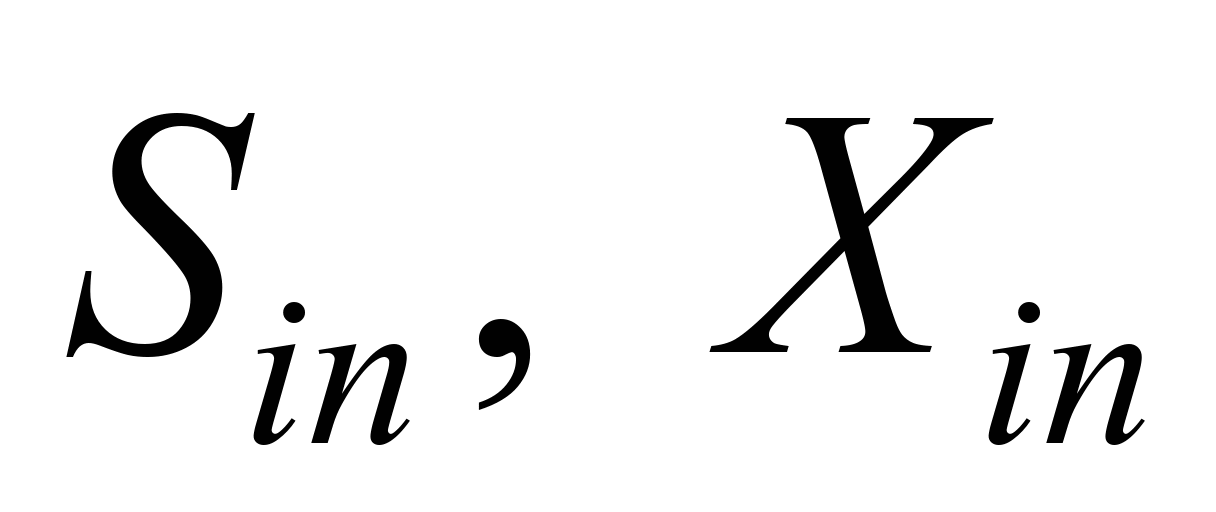 – known concentration;,
– known concentration;,
– at
the boundary of outflow of the building:
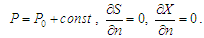
CFD
model.
The
method of solving the mass transfer equations from system (1)
– (2) will
be considered using the example only for the substrate transfer
equation. The equation for the transfer of activated sludge has a
similar form. The three-dimensional equation for the substrate
transfer from the system (1) is split into a system of
one-dimensional equations as follows:

Equations
from system (7) describe the process of substrate transfer in the
directions of the x,
y,
z
axes.
The
difference equations that make it possible to solve the
system of equations (7) are as follows:
– step
1 for
the first equation:
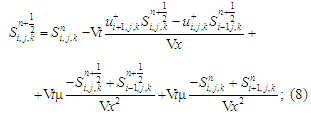
– step 2
for the first equation:
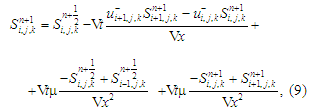
where
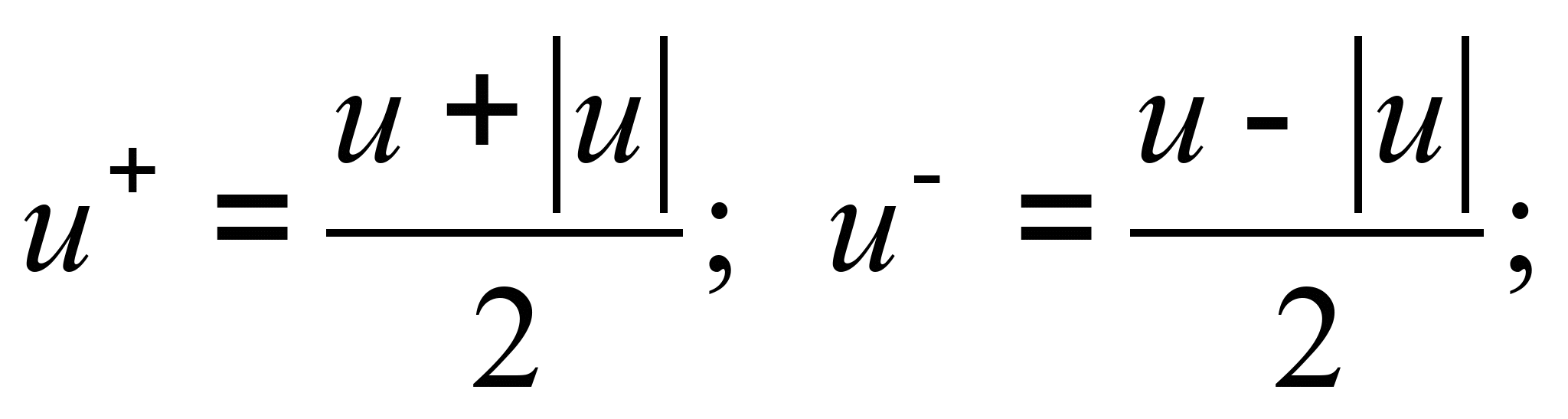
– step 1
for the second equation:
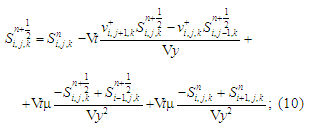
– step 2
for the second equation:
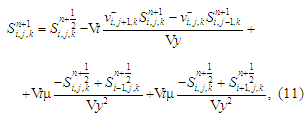
where
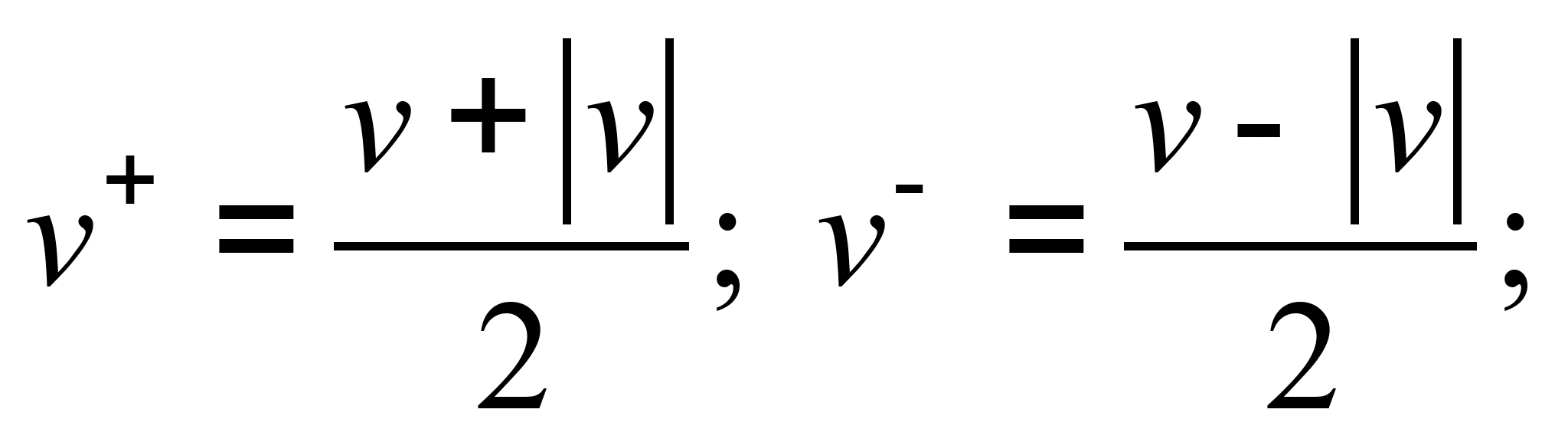
– step
1 for the third equation:
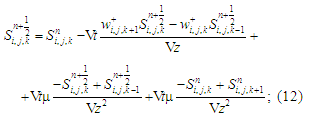
– step 2
the third equation:
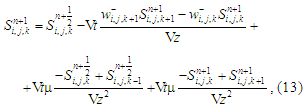
where
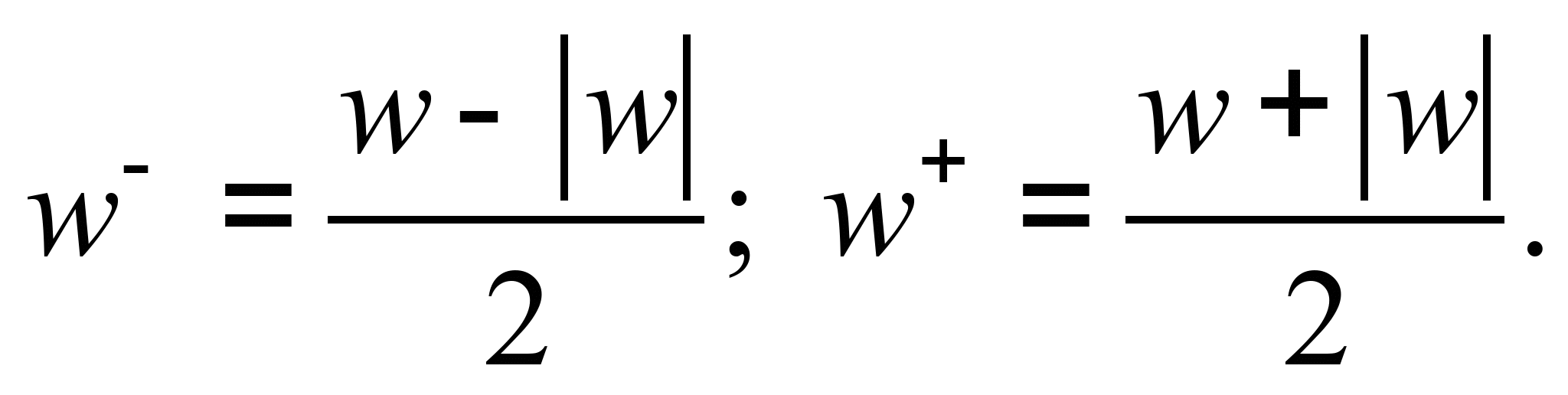
We solve the
equation of activated sludge transfer from system (2) according to a
similar finite-difference scheme. After solving the transfer
equations for X
and S,
for each difference cell, we solve equations (3) – (4) using
the Euler method. That is, we determine new values
of the
substrate
and
activated sludge concentration due to their biological interaction.
Difference expressions have the form:
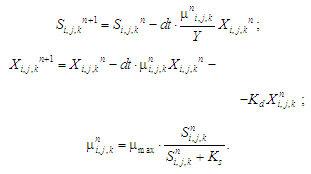
Next,
in a new time step, we repeat the calculation of the change in the
concentration of substrate and activated sludge in each difference
cell due to their movement, diffusion and biological interaction.
To construct a local
one-dimensional scheme for solving equation (5), we perform the
following transformations. First, let us present this equation as:
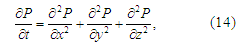
where
t
– fictitious time.
Then, we split equation (14) as
follows:
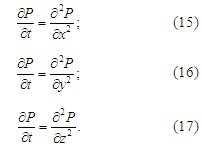
The
calculated dependencies (Richardson's method) for determining the
unknown value P
based on equation (15) have the form:
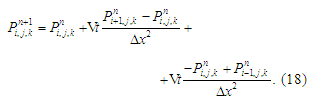
The
calculated dependencies for determining the unknown value P
based on equation (16) have the form:
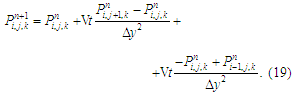
The
calculated dependencies for determining the unknown value of Р
based on equation (17) have the form:
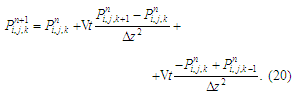
The calculation according to
these dependencies ends when the condition is met:
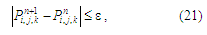
where ε –
small number; n
– iteration number.
At
the next stage we determine the flow velocity:
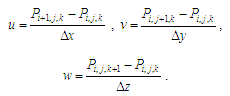
FORTRAN was used to encode the
difference equations. The BIO-3К code has been created. To use it,
one needs to specify the following input data:
– concentration of the
substrate entering the bioreactor and its change over time;
– concentration and
consumption of activated sludge entering the bioreactor and its
change over time;
– dimensions of the
bioreactor, its geometric shape;
– values of Monod model
parameters;
BIO-3K code includes the
following subroutines:
SLE3 – velocity potential
calculation in the bioreactor;
SLE3 – velocity field
calculation in the bioreactor;
SLМ33 – calculation of the
substrate concentration field in the bioreactor and its change over
time;
SLМ33 – calculation of the
concentration field of activated sludge in the bioreactor and its
change over time;
SLМ33 – calculation of
changes in the concentration of substrate and activated sludge in
the bioreactor according to the dependencies of the Monod model;
SLEM5 – print of the modeling
results.
Result of this code is the
concentration fields of the substrate and activated sludge in the
bioreactor and the change of these fields over time.
Findings
The following are the results
of solving the problem of evaluating the efficiency of a biological
reactor for wastewater treatment based on the developed
three-dimensional CFD model. The calculations are performed on the
basis of the following input data:
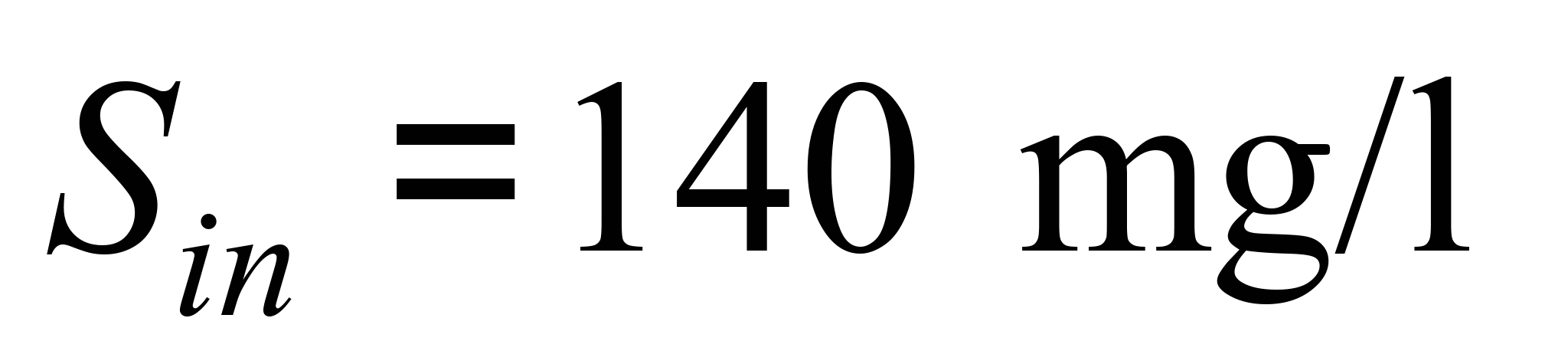 – the
concentration of the substrate (BODcomplete)
entering the structure;
– the
concentration of the substrate (BODcomplete)
entering the structure;
dimensions of the bioreactor
15mx4mx4m;
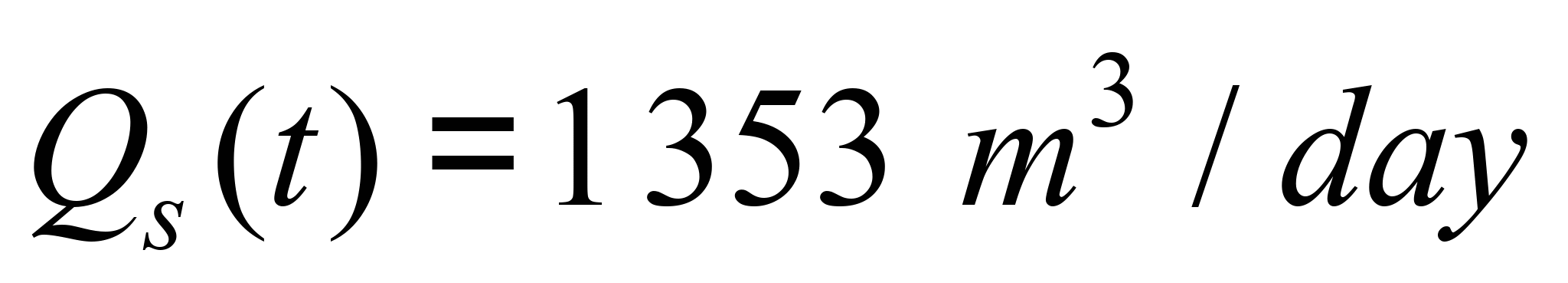 – wastewater
consumption;
– wastewater
consumption;
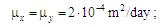
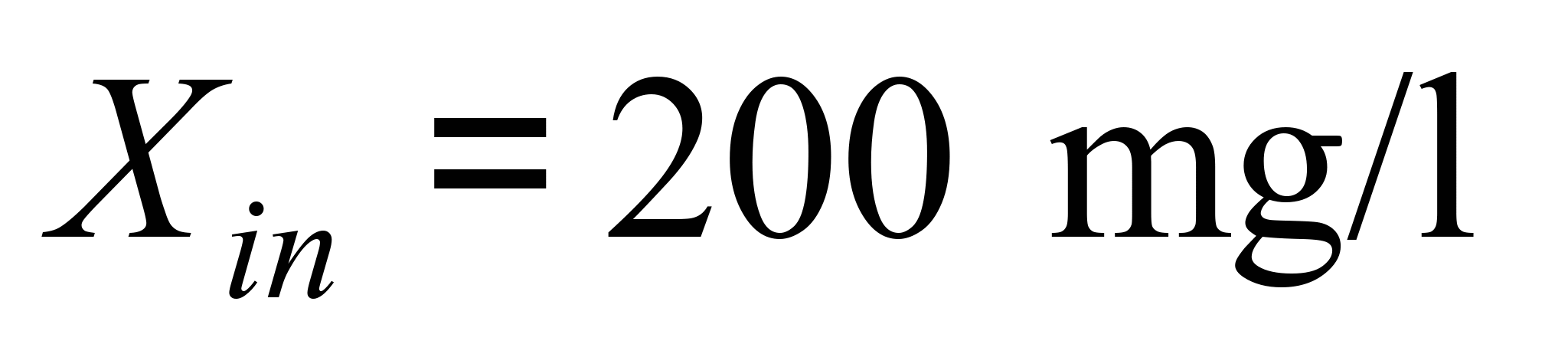 –concentration
of activated sludge entering the reactor;
–concentration
of activated sludge entering the reactor;
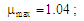
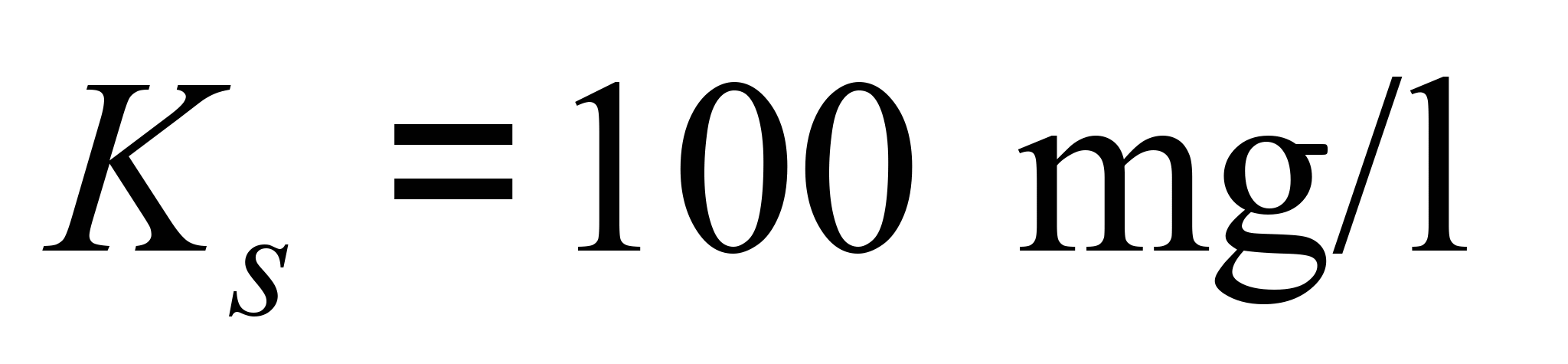 ;
;
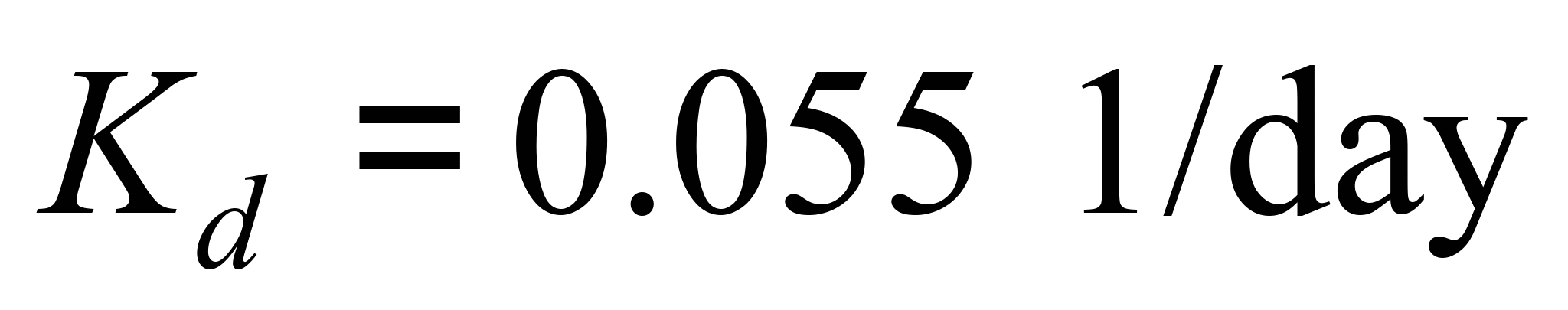 – coefficient
that takes into account the death of microorganisms;
– coefficient
that takes into account the death of microorganisms;
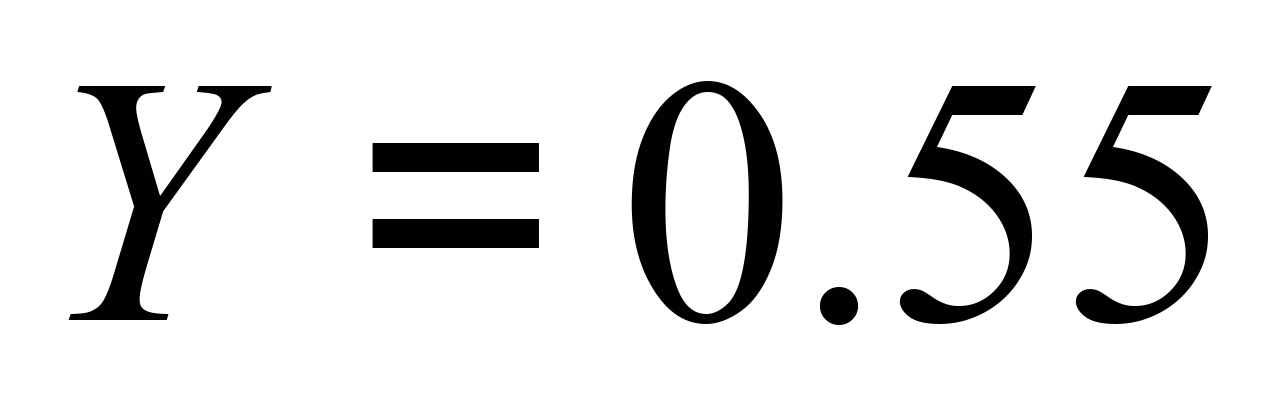 .
.
Initial
condition:
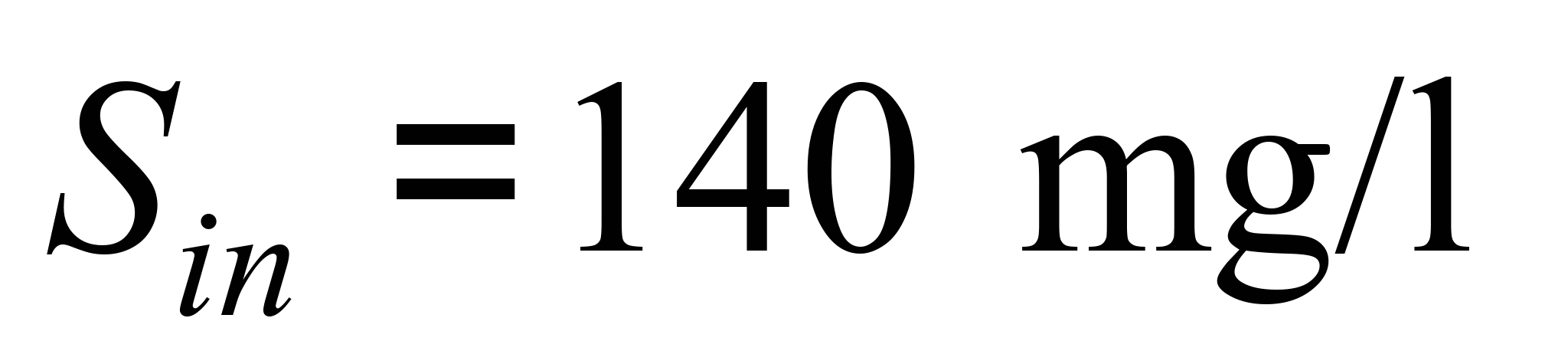 ,
,
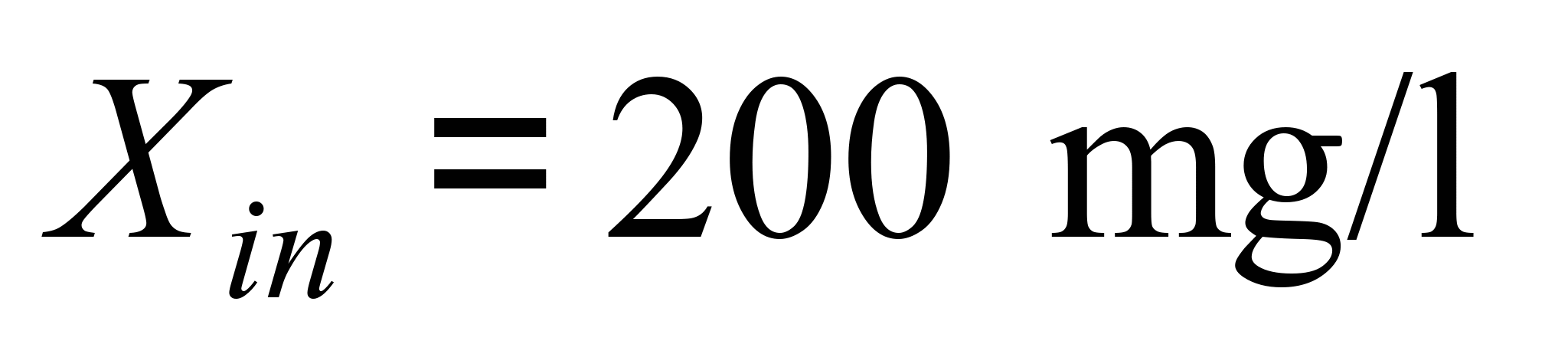 – concentration of substrate and activated sludge in the reactor
for the moment of time t = 0.
– concentration of substrate and activated sludge in the reactor
for the moment of time t = 0.
The following scenarios are
considered:
– scenario 1: the reactor
operates without additional elements inside the building;
– scenario 2: inside the
reactor there are two solid plates (calculation area is
multiconnected);
– scenario 3: the reactor has
three plates, but they have a gap.
Initial
condition:
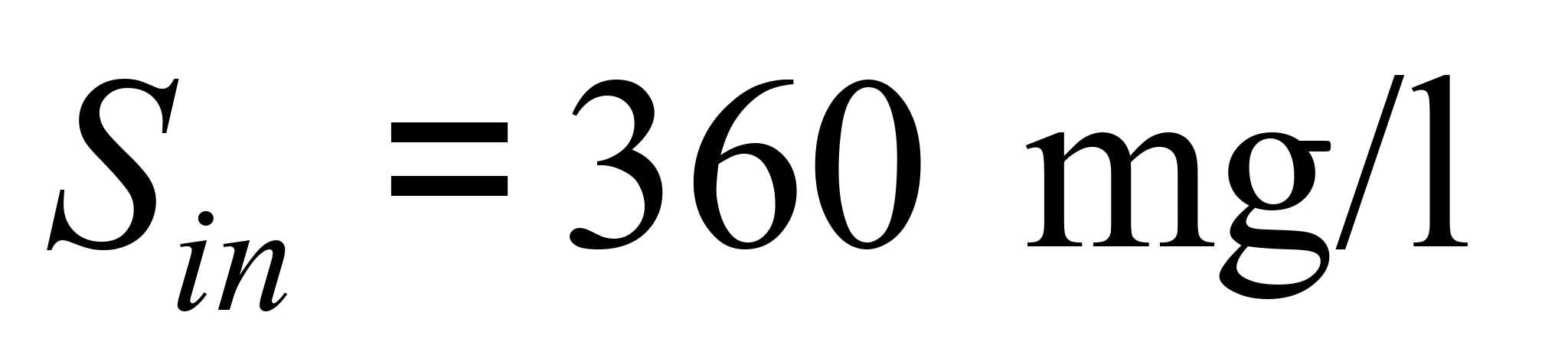 ,
,
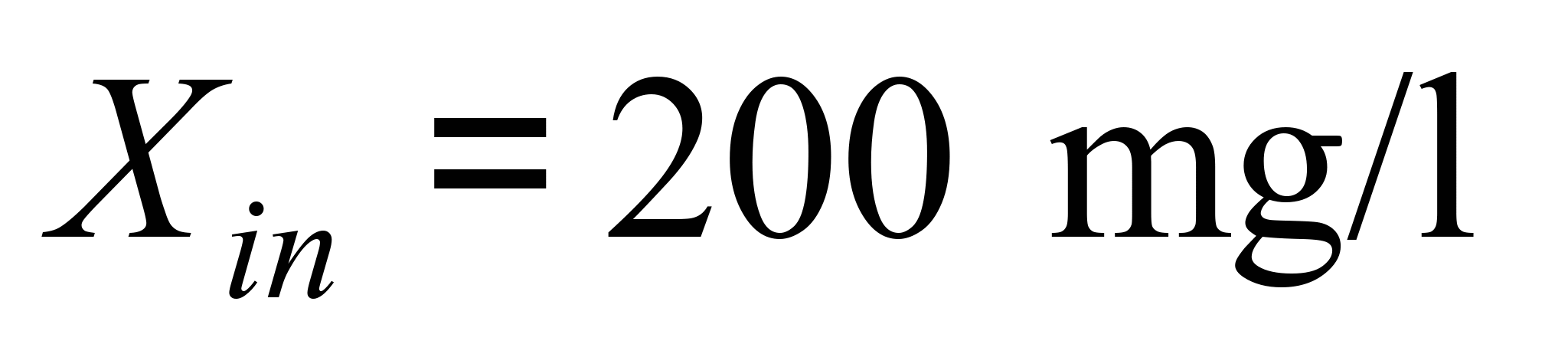 .
We study the process of substrate destruction in the reactor over
time according to the Monod model and taking into account mass
transfer.
.
We study the process of substrate destruction in the reactor over
time according to the Monod model and taking into account mass
transfer.
It should be noted that the
calculation of spatial flow in multiconnected domains is one of the
most complex problems of hydrodynamics.
Evaluation
of the bioreactor performance is determined by the substrate
concentration at the reactor outlet. Fig. 1–6 show the
distribution of substrate concentration in the bioreactor for all
scenarios, where each number indicates the concentration as a
percentage of the maximum concentration in the calculation area (the
time shown in the figures is dimensionless). The number 99
corresponds to the maximum value of the concentration in percent.
These values are printed in the INTEGER format, i.e. only the
integer value of the real number is printed. For example, if at some
point in the reactor the concentration is 61.95 %,
then the number 61 is printed. Since the three-dimensional problem
is being solved, the concentration is shown in different sections of
the bioreactor, the time is dimensionless.

Fig.
1. Distribution of substrate concentration
in the bioreactor,
cross section y = 2 m, t = 0.24
(scenario 1)

Fig.
2. Distribution of substrate concentration in the bioreactor, cross
section z = 2 m, t = 0.24 (scenario 1)

Fig.
3. Distribution of substrate concentration in the bioreactor, cross
section y = 2 m, t = 0.40 (scenario 1)

Fig.
4. Distribution of substrate concentration in the bioreactor, cross
section y = 2 m, t = 0.40 (scenario 2)
The figures
show that inside the reactor there is a significantly uneven
distribution of the substrate concentration,
i.e. the process of biological treatment is uneven. The use of
plates changes the concentration distribution in the structure,
which affects the performance of the reactor.
To analyze
the performance of the reactor Table 1 shows the substrate
concentration at the outlet for the time t
= 0.40.

Fig.
5. Distribution of substrate concentration in the bioreactor, cross
section z = 2 m, t = 0.40 (scenario 2)
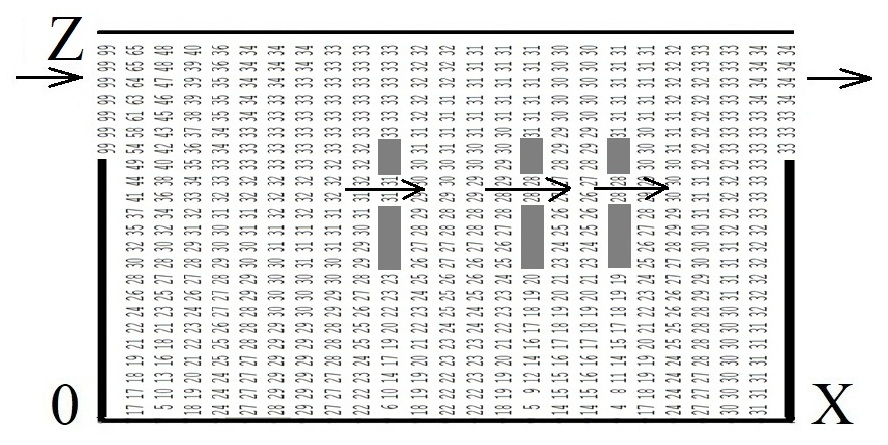
Fig.
6. Distribution of substrate concentration in the bioreactor, cross
section y = 2 m, t = 0.40 (scenario 3)
Table 1
Average
concentration of substrate
at the reactor outlet
|
Scenario
|
1
|
2
|
3
|
|
Concentration
|
147
mg/l
|
128
mg/l
|
118
mg/l
|
Analysis of data from table 1
shows that the use of plates makes it possible to increase the
performance of the biological reactor. That is, we have the
opportunity to control the process of wastewater treatment in the
bioreactor.
Originality
and practical value
A three-dimensional CFD model
has been developed to model the process of biological wastewater
treatment in an aeration tank. The potential motion model was used
to calculate the flow velocity field in the aeration tank. The
process of substrate and activated sludge transfer was determined
based on the mass transfer equation. The Monod model was used to
calculate the biological treatment process.
The constructed model can be
used at the stage of sketch design of structures for wastewater
treatment.
Conclusions
The article considers an
efficient CFD model that allows you to quickly calculate the process
of biological wastewater treatment in the aeration tank, in
particular in the presence of additional plates in the middle of the
reactor. To solve the problem, the fundamental equations of
continuum dynamics are used.
In the
future, it is planned to develop a three-dimensional CFD model based
on the Navier–Stokes equations.
LIST OF
Reference LINKS
Беляев
Н. Н., Нагорная Е. К. Математическое
моделирование массопереноса в
отстойниках систем водоотведения
: монография.
Днепропетровск : Новая идеология, 2012.
112 с.
Беляев
Н. Н., Козачина В. А.
Математическое моделирование
массопереноса в горизонтальных
отстойниках :
монография. Днепропетровск : Акцент
ПП, 2015. 115 с.
Василенко
О. А., Грабовський П. О., Ларкіна Г. М.,
Поліщук О. В., Прогульний В. Й. Реконструкція
і інтенсифікація споруд водопостачання
та водовідведення :
навч. посіб. Київ : ІВНВКП «Укргеліотек»,
2010. 272 с.
Карелин
Я. А., Жуков Д. Д., Журов В. Н., Репин Б. Н.
Очистка производственныхсточных
вод в аеротенках.
Москва : Стройиздат, 1973.
223 с.
Ласков
Ю. М., Воронов Ю. В., Калицун В. И. Примеры
расчетов канализационных сооружений.
Москва : Высшая
школа, 1981. 237 с.
Олійник О. Я., Айрапетян
Т. С. Моделювання очисних стічних вод
від органічних забруднень в
біореакторах-аеротенках зі зваженим
(вільно плаваючим) і закріпленим
біоценозом. Доповідь
НАН України. 2015. № 5.
С. 55–60. DOI: 10/15407/dopovidi2015.05.055
Alharbi
A. O. M. The biological treatment of wastewater : mathematical
models. Bulletin of the Australian
Mathematical Society.
2016. Vol. 94. Іss. 2. P. 347–348.
DOI: 10.1017/S0004972716000411
Amaral A., Gillot S.,
Garrido-Baserba M., Filali A., Karpinska A. M., Plósz B. G., …
Rosso D. Modelling gasliquid mass transfer in wastewater
treatment : when current knowledge needs to encounter engineering
practice and viceversa. Water
Science & Technology.
2019. Vol. 80.
Iss. 4. P. 607–619. DOI: 10.2166/wst.2019.253
Babaei
A., Azadi R., Jaafarzadeh N., Alavi N. Application and Kinetic
Evaluation of upflow Anaerobic biofilm Reactor for Nitrogen Removal
from Wastewater. Iranian Journal of
Environmental Health Science and Engineering.
2013. Vol. 10. Iss. 1. P. 1–8. DOI:
10.1186/1735-2746-10-20
Bomba A., Klymiuk Y.,
Prysiazhniuk I., Prysiazhniuk O., Safonyk A.
Mathematical modeling of wastewater treatment from multicomponent
pollution by through microporous filling.
AIP Conference Proceedings.
2016. Vol. 1773.
P. 040003-1–040003-11. DOI: 10.1063/1.4964966
Dapelo D.,
Bridgeman G. A CFD strategy to retrofit an anaerobic digester
to improve mixing performance in wastewater treatment. Water
Science & Technology. 2020. Vol.
81. Iss. 8. P. 1646–1657.
DOI: 10.2166/wst.2020.086
Gao
H., Stenstrom M. K. Development and applications in CFD modeling
for secondary settling tanks over the last three decades : A
review. Water Environment Research.
2019. Vol. 92. Iss. 6. P. 796–820.
DOI: 10.1002/wer.1279
Gao
H., Stenstrom M. K. Influence of Model Parameters and Inlet
Turbulence Boundary Specification Methods in Secondary Settling
Tanks : Computational Fluid Dynamics Study. Journal
of Environmental Engineering.
2020. Vol. 146. Iss. 5. P. 04020028-1–04020028-12. DOI:
10.1061/(ASCE)EE.1943-7870.0001689
Gao
H., Stenstrom M. K. Computational Fluid Dynamics Analysis for
Improving Secondary Settling Tank Performance. World
Environmental and Water Resources Congress 2020.
2020. P. 212–224. DOI: 10.1061/9780784482988.021
Griborio
A. Secondary Clarifier Modeling : A
Multi-Process Approach. Dissertation
and Theses. University of New Orleans
: USA, 2004. 440 p.
Mocanu
C. R., Mihaillescu R. Numerical Simulation Wastewater Treatment
Aeration Processes. U. P. B. Sci.
Bull., Series D. 2012. Vol. 74. Iss.
2. P. 191–198.
Pereda
M., Zamarreno J. M. Agent – based modeling of an activated sludge
process in batch reactor. 19th
Mediterrian Conference on Control and Automation Aquis.
2011. P. 1128–1133. DOI: 10.1109/med.2011.5983027
М. М. БІЛЯЄВ1*,
М. В. ЛЕМЕШ2,
О. Ю. Гунько3,
В. О. ЗАДОЯ4,
П. Б. МАШИХІНА5,
З. М. ЯКУБОВСЬКА6
1*Каф.
«Гідравліка та водопостачання»,
Дніпровський національний
університет
залізничного транспорту імені академі-ка
В. Лазаряна,
вул. Лазаряна, 2, Дніпро,
Україна, 49010, тел. +38 (056) 273 15 09,
ел. пошта
water.supply.treatment@gmail.com, ORCID 0000-0002-1531-7882
2Каф.
«Гідравліка та водопостачання»,
Дніпровський національний
університет
залізничного транспорту імені академіка
В. Лазаряна,
вул. Лазаряна, 2, Дніпро,
Україна, 49010, тел. +38 (056) 273 15 09,
ел. пошта
water.supply.treatment@gmail.com, ORCID 0000-0002-1230-8040
3Каф. «Гідравліка та
водопостачання», Дніпровський
національний
університет залізничного
транспорту імені академі-ка В. Лазаряна,
вул. Лазаряна, 2, Дніпро, Україна, 49010,
тел. +38 (056) 273 15 09,
ел. пошта
water.supply.treatment@gmail.com, ORCID
0000-0001-9257-763X
4Каф. «Економіка
та менеджмент», Дніпровський національний
університет залізничного транспорту
імені академіка В. Лазаряна,
вул. Лазаряна, 2, Дніпро, Україна, 49010,
тел. +38 (096) 469 60 09,
ел. пошта
v.a.zadoya@gmail.com, ORCID 0000-0001-9408-4978
5Каф.
«Гідравліка та водопостачання»,
Дніпровський національний
університет
залізничного транспорту імені академіка
В. Лазаряна,
вул. Лазаряна, 2, Дніпро,
Україна, 49010, тел. +38 (056) 273 15 09,
ел. пошта
water.supply.treatment@gmail.com, ORCID
0000-0003-3057-9204
6Каф. «Енергетика»,
Український державний хіміко-технологічний
університет, пр. Гагаріна, 8, Дніпро,
Україна, 49000, тел. +38 (056) 753 56 38,
ел. пошта
zinaidaya25@gmail.com,
ORCID
0000-0002-9893-3479
3D-МОДЕЛЮВАННЯ
БІОЛОГІЧНОГО ОчиЩЕННЯ
СТІЧНИХ ВОД В
АЕРОТЕНКУ
Мета.
Основною метою статті є розробка
тривимірної CFD-моделі для моделювання
процесу біологічного очищення стічних
вод в аеротенку. Методика.
Для математичного
моделювання процесу біологічного
очищення стічних вод у реакторі, з
урахуванням гідродинаміки потоку,
геометричної форми аеротенка,
конвективно-дифузійного переносу
субстрату та активного мулу, побудовано
тривимірну CFD-модель.
В основу моделі покладено тривимірне
рівняння руху ідеальної
рідини та рівняння збереження маси для
субстрату й активного мулу. Поле
швидкості потоку стічних вод в аеротенку
розраховано на базі рівняння для
потенціалу швидкості. Процес біологічного
перетворення субстрату розраховано
на базі моделі Monod. Для чисельного
інтегрування рівнянь конвективно-дифузійного
переносу активного мулу та субстрату
використано схему розщеплення.
Розщеплення здійснено так, щоб на
кожному кроці враховувався перенос
субстрату (активного мулу) лише в одному
напрямку. Розрахунок невідомої величини
концентрації субстрату (активного
мулу) виконано за явною схемою. Під час
чисельного інтегрування тривимірного
рівняння для потенціалу швидкості
використано метод Річардсона, розрахунок
невідомого значення потенціалу швидкості
здійснено за явною формулою. Для
чисельного інтегрування рівнянь, що
описують процес трансформації субстрату
та зміну концентрації активного мулу
(модель Monod), використано метод Ейлера.
Результати.
Здійснено програмну реалізацію
побудованої тривимірної
CFD-моделі. Описано структуру
розробленого пакету програм. Подано
результати проведеного комп’ютерного
експерименту з дослідження процесу
очищення стічних вод в аеротенку з
додатковими елементами. Наукова
новизна.
Розроблено нову багатофакторну
тривимірну CFD-модель, що дозволяє швидко
оцінити ефективність біологічного
очищення стічних вод в аеротенку.
Практична значимість.
Побудована CFD-модель
може бути використана для аналізу
ефективності роботи аеротенку за різних
умов експлуатації та на етапі ескізного
проектування систем очищення стічних
вод.
Ключові слова: очищення
води; біологічне очищення води;
математичне моделювання; аеротенк;
модель Monod
Н. Н. БЕЛЯЕВ1*,
М. В. ЛЕМЕШ2,
Е. Ю. Гунько3,
В. А. ЗАДОЯ4,
П. Б. МАШИХИНА5,
З. Н. ЯКУБОВСКАЯ6
1*Каф.
«Гидравлика и водоснабжение», Днипровский
национальный университет
железнодорожного
транспорта имени академика В. Лазаряна,
ул. Лазаряна, 2,
Днипро, Украина, 49010, тел.
+38 (056) 273 15 09,
эл. почта
water.supply.treatment@gmail.com, ORCID 0000-0002-1531-7882
2Каф.
«Гидравлика и водоснабжение», Днипровский
национальный университет
железнодорожного
транспорта имени академика В. Лазаряна,
ул. Лазаряна, 2,
Днипро, Украина, 49010, тел.
+38 (056) 273 15 09,
эл. почта
water.supply.treatment@gmail.com, ORCID 0000-0002-1230-8040
3Каф.
«Гидравлика и водоснабжение», Днипровский
национальный университет
железнодорожного
транспорта имени академика В. Лазаряна,
ул. Лазаряна, 2,
Днипро, Украина, 49010, тел.
+38 (056) 273 15 09,
эл. почта
water.supply.treatment@gmail.com, ORCID 0000-0001-9257-763X
4Каф.
«Экономика и менеджмент», Днипровский
национальный университет
железнодорожного
транспорта имени академика В. Лазаряна,
ул. Лазаряна, 2,
Днипро, Украина, 49010, тел.
+38 (096) 469 60 09,
эл. почта v.a.zadoya@gmail.com,
ORCID 0000-0001-9408-4978
5Каф.
«Гидравлика и водоснабжение», Днипровский
национальный университет
железнодорожного
транспорта имени академика В. Лазаряна,
ул. Лазаряна, 2,
Днипро, Украина, 49010, тел.
+38 (056) 273 15 09,
эл. почта
water.supply.treatment@gmail.com, ORCID
0000-0003-3057-9204
6Каф.
«Энергетика», Украинский государственный
химико-технологический
университет,
пр. Гагарина, 8, Днипро, Украина,
49000, тел. +38 (056) 753 56 38,
эл. почта
zinaidaya25@gmail.com,
ORCID
0000-0002-9893-3479
3D-моделирование
биологической
очистки сточных вод в
аэротенкЕ
Цель.
Основной целью статьи является разработка
трёхмерной CFD-модели для моделирования
процесса биологической очистки сточных
вод в аэротенке. Методика.
Для математического моделирования
процесса биологической очистки сточных
вод в реакторе, с учетом гидродинамики
потока, геометрической формы аэротенка,
конвективно-диффузионного переноса
субстрата и активного ила, построена
трёхмерная CFD-модель. В основу модели
положено трехмерное уравнение движения
идеальной жидкости и уравнение сохранения
массы для субстрата и активного ила.
Поле скорости потока
сточных вод в аэротенке рассчитано на
базе уравнения для потенциала скорости.
Процесс биологического превращения
субстрата рассчитано на базе модели
Monod. Для численного интегрирования
уравнений конвективно-диффузионного
переноса активного ила и субстрата
использована схема расщепления.
Расщепление осуществлено так, чтобы
на каждом шагу учитывался перенос
субстрата (активного ила) только в одном
направлении. Расчет неизвестной величины
концентрации субстрата (активного ила)
осуществлен по явной схеме. Для численного
интегрирования трехмерного уравнения
для потенциала скорости использован
метод Ричардсона, расчет неизвестного
значения потенциала скорости осуществлен
по явной формуле. Для численного
интегрирования уравнений, описывающих
процесс трансформации субстрата и
изменение концентрации активного ила
(модель Monod), использован метод Эйлера.
Результаты.
Осуществлена программная реализация
построенной трёхмерной
CFD -модели. Описана
структура разработанного пакета
программ. Представлены результаты
проведенного компьютерного эксперимента
по исследованию процесса очистки
сточных вод в аэротенке с дополнительными
элементами. Научная
новизна. Разработана
новая многофакторная трёхмерная
CFD-модель, позволяющая быстро оценить
эффективность биологической очистки
сточных вод в аэротенке. Практическая
значимость. Построенная
CFD-модель может быть использована для
анализа эффективности работы аэротенка
при различных условиях эксплуатации
и на этапе эскизного проектирования
систем очистки сточных вод.
Ключевые слова: очистка
воды; биологическая очистка воды;
математическое моделирование; аэротенк;
модель Monod
ReferenceS
Biliaiev,
N. N., & Kozachina, V. A. (2015). Modelirovaniye
massoperenosa v gorizontalnykh otstoynikakh:
monografiya. Dnepropetrovsk: Aktsent PP. (in Russian)
Biliaiev,
N. N., & Nagornaya, E. K. (2012). Matematicheskoye
modelirovaniye massoperenosa v otstoynikakh sistem vodootvedeniya:
monografiya. Dnepropetrovsk: Novaya ideologiya. (in Russian)
Vasilenko,
O. A.,
Grabovskiy, P. O., Larkina, G. M., Polishchuk, O. V., &
Progulny, V. Y. (2010). Rekonstruktsiya
i intensyfikatsiya sporud vodopostachannya ta vodovidvedennya:
navchalnyy posibnyk.
Kyiv: IVNVKP «Ukrgeliotek». (in Ukrainian)
Karelin,
Ya. A., Zhukov, D. D., Zhurov, V. N., & Repin, B. N. (1973).
Ochistka proizvodstvennykhstochnykh
vod v aerotenkakh. Moscow:
Stroyizdat. (in
Russian)
Laskov,
Yu. M., Voronov, Yu. V., & Kalitsun, V. I. (1981). Primery
raschetov kanalizatsionnykh sooruzheniy.
Moscow: Vysshaya shkola. (in Russian)
Oleynik,
A. Y., & Airapetyan, T. S. (2015). The modeling of the
clearance of waste waters from organic pollutions in
bioreactors-aerotanks with suspended (free flow) and fixed
biocenoses. Reports of the National
Academy of Sciences of Ukraine, 5,
55-60. DOI: 10.15407/dopovidi2015.05.055(in
Ukrainian)
Alharbi,
A. O. M. (2016). The biological treatment of wastewater:
mathematical models. Bulletin of the
Australian Mathematical Society,
94(2),
347-348. DOI: 10.1017/S0004972716000411 (in
English)
Amaral,
A., Gillot, S., Garrido-Baserba, M., Filali, A., Karpinska, A. M.,
Plósz, B. G., … Rosso, D. (2019). Modelling gas–liquid mass
transfer in wastewater treatment: when current knowledge needs to
encounter engineering practice and vice versa. Water
Science and Technology, 80(4),
607-619.
DOI: 10.2166/wst.2019.253
(in English)
Babaei,
A. A., Azadi, R., Jaafarzadeh, N., & Alavi, N. (2013).
Application and kinetic evaluation of upflow anaerobic biofilm
reactor for nitrogen removal from wastewater by Anammox process.
Iranian Journal of Environmental
Health Science and Engineering, 10(1),
1-8. DOI: 10.1186/1735-2746-10-20 (in English)
Bomba,
A., Klymiuk, Y., Prysiazhniuk, I., Prysiazhniuk, O., &
Safonyk, A. (2016). Mathematical modeling of wastewater
treatment from multicomponent pollution by through microporous
filling. AIP
Conference Proceedings,
1773,
040003-1-040003-11.
DOI: 10.1063/1.4964966 (in English)
Dapelo,
D., & Bridgeman, J. (2020). A CFD strategy to retrofit an
anaerobic digester to improve mixing performance in wastewater
treatment. Water Science and
Technology, 81(8), 1646-1657.
DOI: 10.2166/wst.2020.086
(in English)
Gao,
H., & Stenstrom, M. K. (2019). Development and applications in
computational fluid dynamics modeling for secondary settling tanks
over the last three decades: A review. Water
Environment Research, 92(6), 796-820.
DOI: 10.1002/wer.1279
(in English)
Gao,
H., & Stenstrom, M. K. (2020). Influence of Model Parameters
and Inlet Turbulence Boundary Specification Methods in Secondary
Settling Tanks: Computational Fluid Dynamics Study. Journal
of Environmental Engineering, 146(5),
04020028-1-04020028-12.DOI:
10.1061/(ASCE)EE.1943-7870.0001689
(in English)
Gao,
H., & Stenstrom, M. K. (2020). Computational Fluid Dynamics
Analysis for Improving Secondary Settling Tank Performance. World
Environmental and Water Resources Congress 2020,
212-224. DOI: 10.1061/9780784482988.021
(in English)
Griborio,
A. (2004). Secondary Clarifier
Modeling: A Multi-Process Approach.
Dissertation and Theses.
University of New Orleans: USA. (in English)
Mocanu,
C. R., & Mihaillescu, R. (2012). Numerical Simulation
Wastewater Treatment Aeration Processes.
U.
P. B. Sci. Bull., Series D, 74(2),
191-198. (in English)
Pereda,
M., & Zamarreno, J. M. (2011). Agent–based modeling of an
activated sludge process in batch reactor. 19th
Mediterrian Conference on Control and Automation Aquis
(рр. 1128-1133).
DOI: 10.1109/med.2011.5983027 (in English)
Received:
August 11, 2020
Accepted:
December 11, 2020
Creative
Commons Attribution 4.0 International
doi:
10.15802/stp2020/224619
©
M. M. Biliaiev,
M. V. Lemesh,
O. Y. Gunko,
V. O. Zadoia,P. B. Mashykhina,
Z. M. Yakubovska, 2020
– extinction coefficient of activated sludge;
– time;
– concentration of activated sludge in the bioreactor;
– substrate concentration in the bioreactor;
– empirical parameter;
– parameter in the Mono model;
– empirical parameter;
– parameter in the Mono model;
,
,
–
components of the water flow rate in the bioreactor, in the
direction of the axes
,
respectively;
– diffusion
coefficients, respectively, in the direction
;
– time.
are different values, but in the scientific literature there is a
significant shortage of data on their values. Therefore, in
practice, the calculations are carried out under the condition
.
Determining these parameters experimentally is a rather
difficult task.
,
,
,
under the action of these parameters there is a convective transfer
of substrate and activated sludge in the bioreactor. To calculate
the non-uniform flow velocity field in the bioreactor, we use the
3D equation for the velocity potential:
,
– outward normal to a surface;
,
where
– flow
velocity;
– known concentration;,
– the
concentration of the substrate (BODcomplete)
entering the structure;
– wastewater
consumption;
–concentration
of activated sludge entering the reactor;
;
– coefficient
that takes into account the death of microorganisms;
.
,
– concentration of substrate and activated sludge in the reactor
for the moment of time t = 0.
,
.
We study the process of substrate destruction in the reactor over
time according to the Monod model and taking into account mass
transfer.