ISSN 2307–3489 (Print), ІSSN 2307–6666 (Online)

Наука та прогрес транспорту. Вісник Дніпропетровського
національного університету залізничного транспорту, 2020, № 6 (90)

рухомий склад і тяга поїздів

Вступ

Безпека руху є неухильною вимогою до роботи залізничного транспорту. Значимість питань забезпечення безпеки руху зростає в умовах збільшення швидкостей руху поїздів, що впроваджують зараз в Україні [17]. Особливо важливим при цьому є визначення допустимих швидкостей руху, що пов’язано з оцінкою динамічних якостей рухомого складу. Таку оцінку здійснюють під час проведення приймальних випробувань, зокрема ходових динамічних і по впливу на колію. Замінити частину натурних випробувань комп’ютерним моделюванням неможливо, оскільки зменшення їх обсягу загрожує зменшенням вимог до безпеки руху та якості динамічних показників рухомого складу [2, 9, 16].

Математична модель рухомого складу є певною ідеалізацією реальної системи, деякі параметри якої недостатньо добре відомі. Під час випробувань нової конструкції рухомого складу можуть проявитися ті особливості, які не було враховано в математичній моделі. Експериментальні дослідження, хоча і є в достатній мірі надійними, але потребують значних коштів, тривалого часу й не здатні охопити всі ситуації, які можуть виникнути в експлуатації [19–21].

Теоретичні та експериментальні дослідження потрібно виконувати спільно. Експериментальні дослідження мають давати можливість уточнити основні положення та гіпотези, розрахункові схеми, а в разі необхідності виправити результати теоретичних досліджень та виконати необхідні перерахунки [2, 7, 12].

Взаємодію рухомого складу та верхньої будови колії визначають за такими факторами: наявність ухилів та кривих ділянок колії; вага, довжина та швидкість руху поїздів; потужність локомотивів. Але найбільші горизонтальні поперечні зусилля сприймають колеса від рейок саме на криволінійних ділянках колії. Ці зусилля, особливо в крутих кривих, можуть у декілька разів перевищувати зусилля, які виникають під час виляння екіпажа на прямих ділянках. До того ж у кривих із радіусом менше 800–600 м гребені деяких коліс під час руху притиснуті до зовнішньої рейки майже на всій довжині кривої. Основними зонами виходу з ладу рейок за дефектами контактно-втомного походження є криві ділянки. Переважна кількість аварій та катастроф поїздів, зумовлених недоліками міцності конструкцій колії, рухомого складу та втратою їх стійкості, відбувається також на кривих ділянках [8, 15, 22].

Загальновідомо, що втрату стійкості або сходження рухомого складу з рейок можна поділити на два види: вкочування колеса на зовнішню рейку та провал колісної пари (колеса) всередину колії за рахунок її розпирання. Різновидом сходження через вкочування колеса на рейку є сходження через неприпустимий поперечний угон (зсув) рейко-шпальної решітки (кут у плані) [9, 18].

Вкочування гребеня колеса на головку рейки або вістряка з подальшим провалом іншого колеса всередину колії найбільш імовірне в порожніх вагонах у кривих та навіть прямих ділянках колії, коли вагон витискається під час гальмування поїзда вгору й одночасно встановлюється в «ялинку» під дією набігаючих незагальмованих вагонів. Поперечна сила, яка при цьому виникає, притискає гребінь колеса до зношеної бокової грані головки рейки, а за наявності навіть незначного повороту рейки гребінь колеса по похилій площині бокової грані вкочується спочатку на головку рейки, а через кілька метрів зістрибує з рейки на шпали і далі на баластну призму [10, 13, 23].

За розташування вагонів під кутом один до одного в плані (в «ялинку») виникають поперечні горизонтальні складові поздовжніх сил, а за різниці висот їх автозчеплень – вертикальні складові, які створюють додаткове довантаження або розвантаження відповідних коліс екіпажа (рис. 1, а). Це впливає на величини бокових та вертикальних сил взаємодії, що визначають необхідні умови вкочування коліс на головку рейки. Різниця у висоті між поздовжніми осями автозчеплень у вантажному поїзді допускається не більше 80 мм (рис. 1, б) [1, 12, 13].

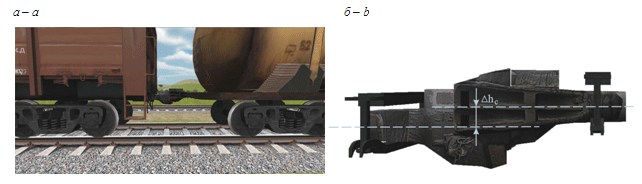
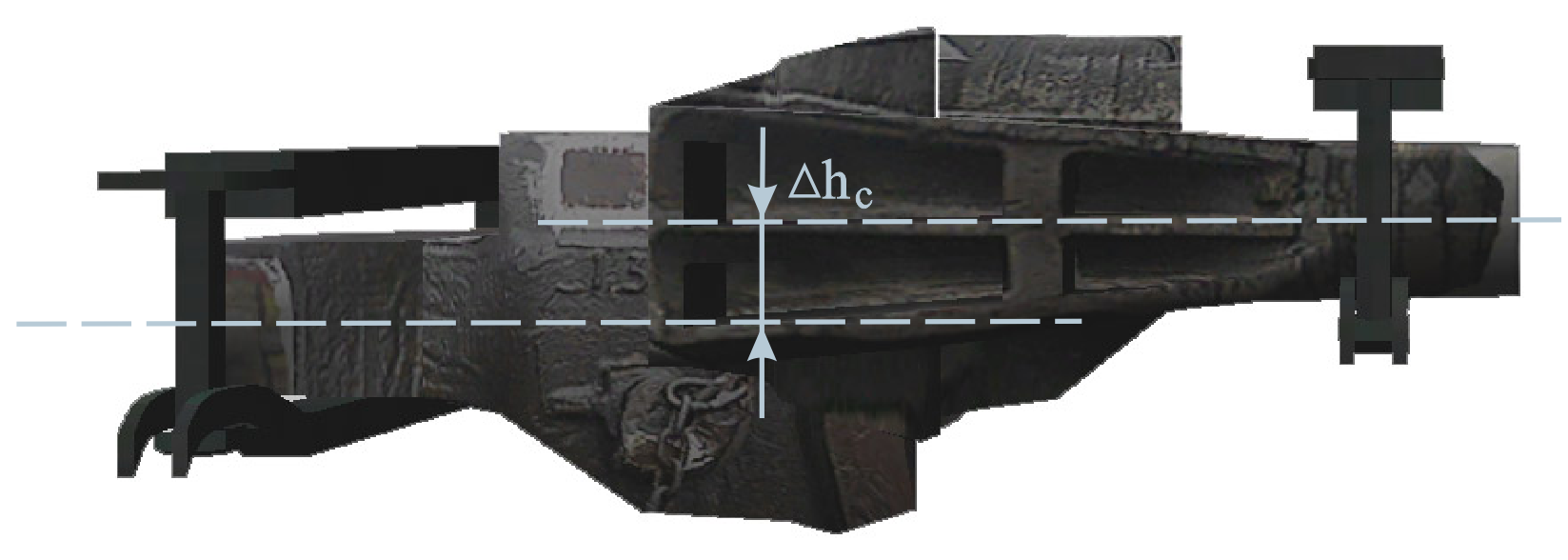
Рис. 1. З’єднання двох вагонів:
а – група частково завантажених або порожніх вагонів у хвості поїзда;
б – різниця рівнів осей автозчеплень

Fig. 1. Coupling of two cars:
a – a group of partially loaded or empty cars in the train tail;

b – difference between the axle levels of the of the automatic couplers

Сходження через вкочування колеса на рейку може трапитися в навантаженого вагона з рухомим вантажем за умови, якщо поїзд іде на вибігу (поздовжня сила в автозчепленні відсутня) і на внутрішній рейковій нитки є вертикальні нерівності. Центр тяжіння рухомого вантажу змінює своє положення, і навіть у плавній кривій перша по ходу колісна пара розвантажується та вкочується на рейку [9, 14].

Основною причиною сходження внаслідок провалу колеса всередину колії є неприпустима величина розширення колії, що виникає завдяки відтисканню гребенем колеса однієї з рейок. При цьому друге колесо провалюється всередину колії. Таке сходження можливе лише за однієї з умов або їх поєднання:

– головною умовою є дія великої поперечної бокової сили від колеса, яка здатна відтиснути рейку;

– недостатній опір такому відтисканню рейки внаслідок її недостатньої поперечної жорсткості;

– наявність ослаблених проміжних рейкових скріплень, які не забезпечують необхідну вертикальну та горизонтальну жорсткість.

Імовірність такого сходження вища в крутих кривих, на дерев’яних шпалах, на рейках із невисокою поперечною жорсткістю та в разі костильного скріплення внаслідок нахилу рейки гребенями. У такому випадку розпирання колії з провалом колеса відбувається за значно менших сила бокового впливу коліс, ніж сходження через зсув решітки на обох основних типах підрейкової основи. Чим менше завантаження вагона, тим імовірніше сходження через розпирання колії. У випадку завантаження вагонів до повної вантажопідйомності опір розпору значно більший [9].

На ділянках із дерев’яними шпалами та типовим костильним скріпленням, порівняно з ділянками із залізобетонними шпалами, істотно полегшене сходження рухомого складу через витискання екіпажів унаслідок можливості нахилу рейки через відрив внутрішньої кромки підошви рейки від підкладок. Під час руху візка з притиснутими до голівки рейки гребенями коліс відбувається підсмикування внутрішніх обшивних костилів та пружний нахил рейки з подальшим відновленням ширини колії після проходження такого візка. Чим більша сила бокового впливу гребенів коліс на головку рейки і чим менша вертикальна сила, тим на більшу величину підсмикуються внутрішні обшивні костилі [9, 15, 22].

Збільшення рівня сил взаємодії між залізничними екіпажами та колією можливе також у разі значного зносу колісних пар та рейок. Реборди підп’ятників і бокові грані п’ятників вантажних вагонів у процесі експлуатації зношуються, й утворюється горизонтальний люфт між ними, який у ряді випадків перевищує 5 мм. Шкворневий отвір також стає овальним. На ребордах підп’ятників у верхній їх частині та на бокових гранях п’ятників у нижній їх частині метал зношується від дії горизонтальних сил, відбувається заокруглення внутрішнього обрису верху реборд підп’ятників й низу п’ятників. За наявними правилами шкворень у вантажних вагонів не повинен працювати, а тим часом він зношується, згинається й навіть ламається, зминаючи отвір, куди його вставляють. Значення ексцентриситету в перерізі шкворня візка тільки через боковий знос підп’ятника та п’ятника може досягати 10 мм [11].

Конструкційні параметри рухомого складу та колії у свою чергу впливають на величину поперечних сил, які виникають від дії поздовжніх сил в автозчепленнях вагона. Пристрій автозчеплення, який експлуатують на вітчизняних залізницях, не має стабілізуючого шарніра у хвостовику. Радіус заокруглення хвостовика автозчеплення – 130 мм, а опорна плита, на яку передається поздовжня сила поїзда хвостовиком автозчеплення, має радіус заокруглення 150 мм. Теоретично стискальна сила автозчепленням передається опорній плиті в точці, й у разі перекосів екіпажів за схемою «ялинки» ця точка контакту переміщується поперек екіпажа (рис. 2). Парк вантажного рухомого складу містить велику кількість вагонів із подовженим терміном служби. Вантажні вагони, що перебувають в експлуатації в наш час, спроектовані й побудовані за різними редакціями норм їх розрахунку й проектування. Неточність розташування розетки на кінцевій балці деяких вагонів може перевищувати 14 мм. Для вантажних вагонів це значення реально може становити 20 мм [9, 10].

Рис. 2. Передача автозчепленням поздовжнього зусилля з ексцентриситетом

Fig. 2. Transmission of longitudinal force with eccentricity by automatic coupler

У роботі [8] розглянуто поперечне зміщення візків один відносно одного. Узято, що задній візок розташований по поздовжній осі колії, а передній має поперечне зміщення, що відповідає початковому куту повороту кузова в плані відносно осі колії в межах від 0,002 до 0,008 рад зі знаком «плюс», за якого збільшується кут набігання передньої колісної пари на рейку. Наведено теоретичні дослідження з визначення впливу поперечного зміщення візків на основні динамічні показники – коефіцієнт вертикальної динаміки, коефіцієнт стійкості, рамні сили, прискорення в зоні п’ятників. Проте в цій роботі не наведено вплив означеного зміщення на показники взаємодії рухомого складу з колією.

Мета

Робота спрямована на визначення впливу поперечного зміщення візка вантажного вагона з урахуванням величини швидкості руху на його основні динамічні показники та показники взаємодії рухомого складу з колією.

Методика

Кількісна оцінка динамічних показників може бути отримана методом математичного моделювання. Розрахункова схема вагона повинна відображати особливості взаємодії вагонів у складі потяга: можливість прояву всіх форм коливань кузова в просторі, передачі поздовжньої сили у вертикальному та горизонтальному напрямках від сусідніх вагонів, облік технічного стану окремих частин вагона та їх конструктивних особливостей, а також умов експлуатації – швидкість, рух по прямих і кривих ділянках залізничної колії, режим завантаження, вид вантажу, його розміщення й кріплення, вертикальні та горизонтальні нерівності колії [7, 12, 13].

Для проведення дослідження узято математичну модель просторових коливань вантажного вагона у вигляді багатомасової (кузов, дві надресорні балки, чотири бокові рами, чотири колісні пари) нелінійної механічної системи, яка рухається по інерційній, пружно-дисипативній колії [4]. У роботі [5] запропонована математична модель, що описує просторові коливання зчепу вагонів у складі потяга (рис. 3) у яких один рейковий екіпаж розглядають за повною розрахунковою схемою («нульовий»), а розрахункові схеми сусідніх вагонів, залежно від постановки задачі, спрощують по мірі віддалення від «нульового» екіпажа в обидві сторони.

Ця робота присвячена дослідженню впливу на основні динамічні показники та показники взаємодії рухомого складу з колією вантажних вагонів у кривих одного з чинників, а саме зміни кута повороту центральної осі кузова вагона 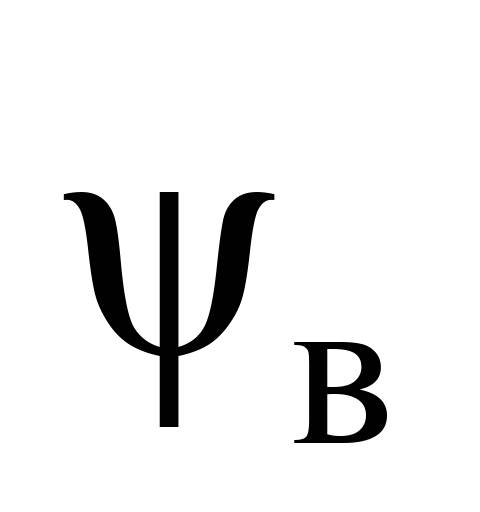. Вибір цього фактора як предмета дослідження пов’язаний із тим, що він залежить від величини поперечного зазору в рейковій колії. У свою чергу від цього зазору залежать відносні пружні й непружні проковзування коліс відносно рейок та величини відповідних сил, а також геометричні умови контактування коліс і рейок. Крім того, необхідна величина поперечного зазору визначає ширину рейкової колії.

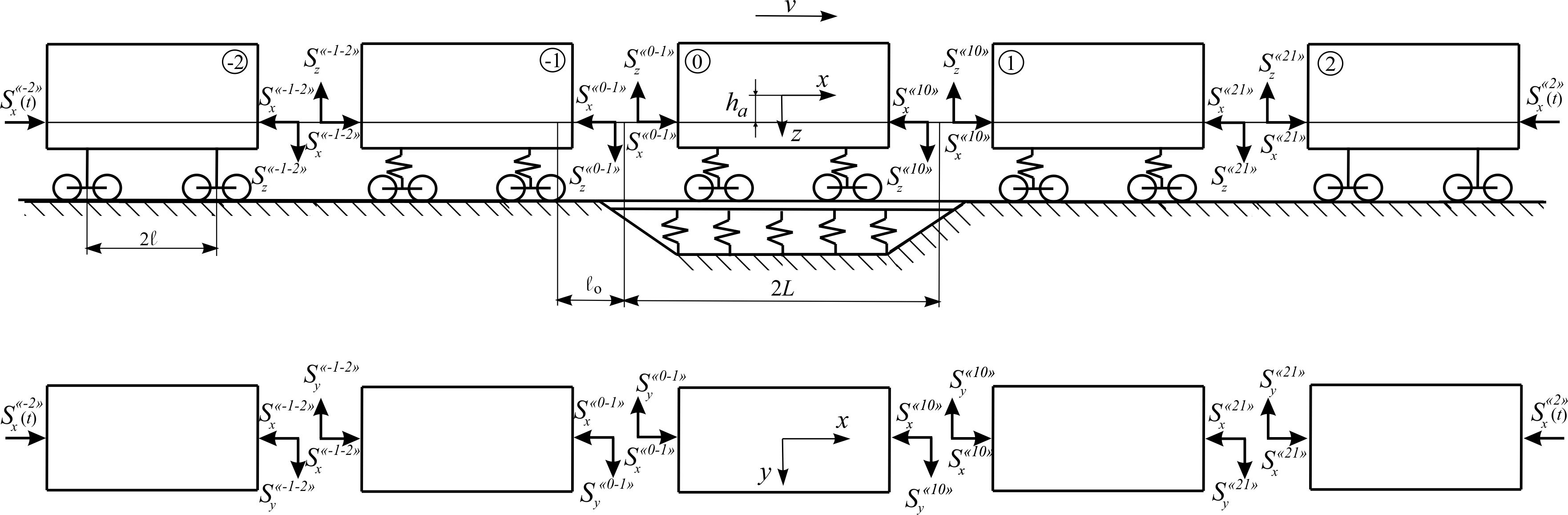
Рис. 3. Схема розташування зчепу вагонів у складі потяга в разі передачі поздовжнього зусилля

Fig. 3. Diagram of the coupler location in the train in case of transmission of longitudinal force

Під час розрахунків розглянуто зміну кута повороту центральної осі кузова вагона 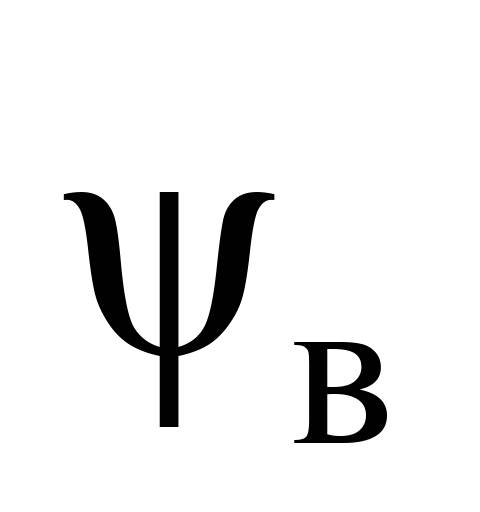, який призводить до поперечного зміщення візків відносно один одного, що є продовженням дослідження, наведеного в роботі [8]. Задній візок вантажного вагона розташований по поздовжній осі колії, а передній має поперечне зміщення, що відповідає куту повороту кузова в плані відносно осі колії в межах від 0 до 0,008 рад зі знаком «плюс», за якого збільшується кут набігання передньої колісної пари на зовнішню рейку (рис. 4).

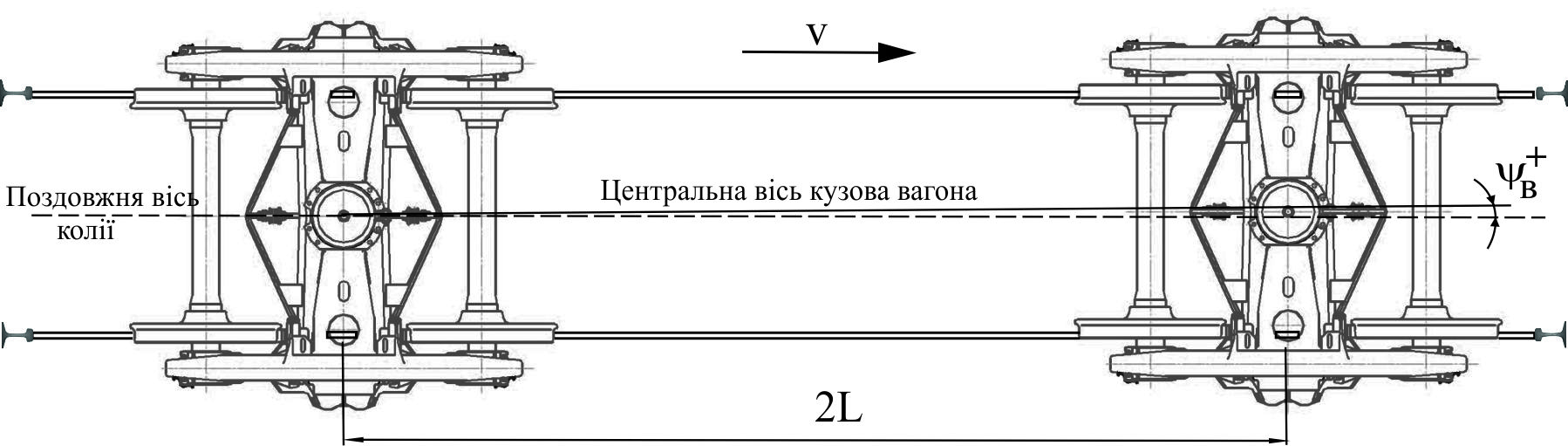
Рис. 4. Розташування візків вантажного вагона в рейковій колії

Fig. 4. Location of freight car bogies in the rail track

Як відомо, повний зазор у рейковій колії визначають за формулою [3]: 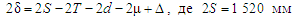, де 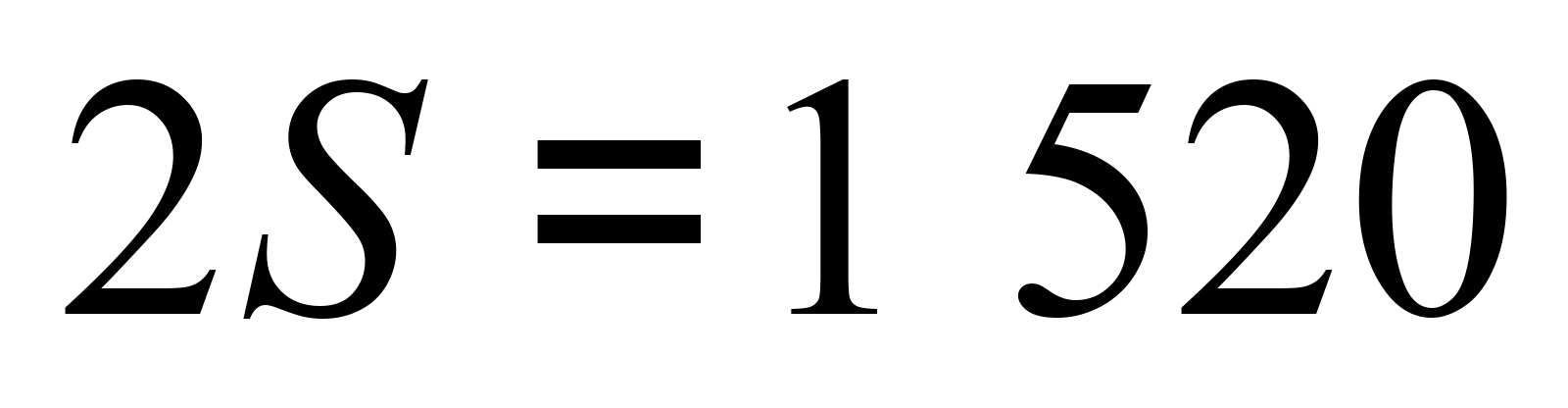мм – ширина рейкової колії; 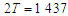мм мінімальна відстань між внутрішніми гранями гребенів коліс; 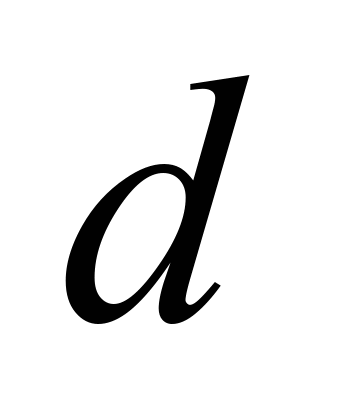– товщина гребеня колеса в розрахунковій площині, яка в процесі експлуатації змінюється від прийнятої номінальної 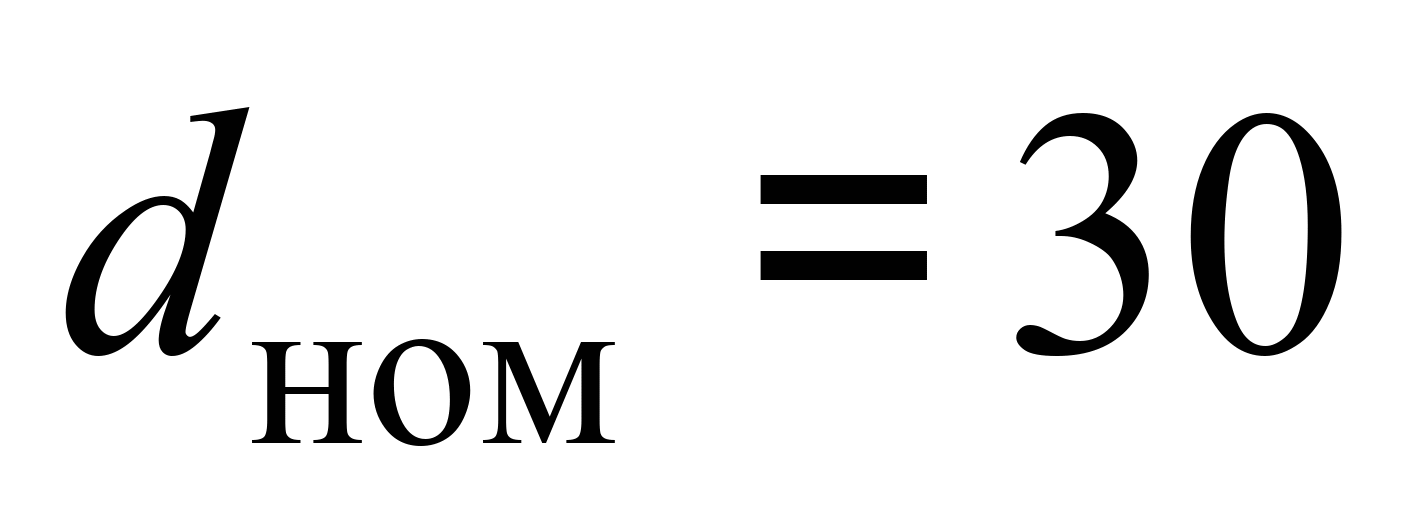мм до мінімального значення 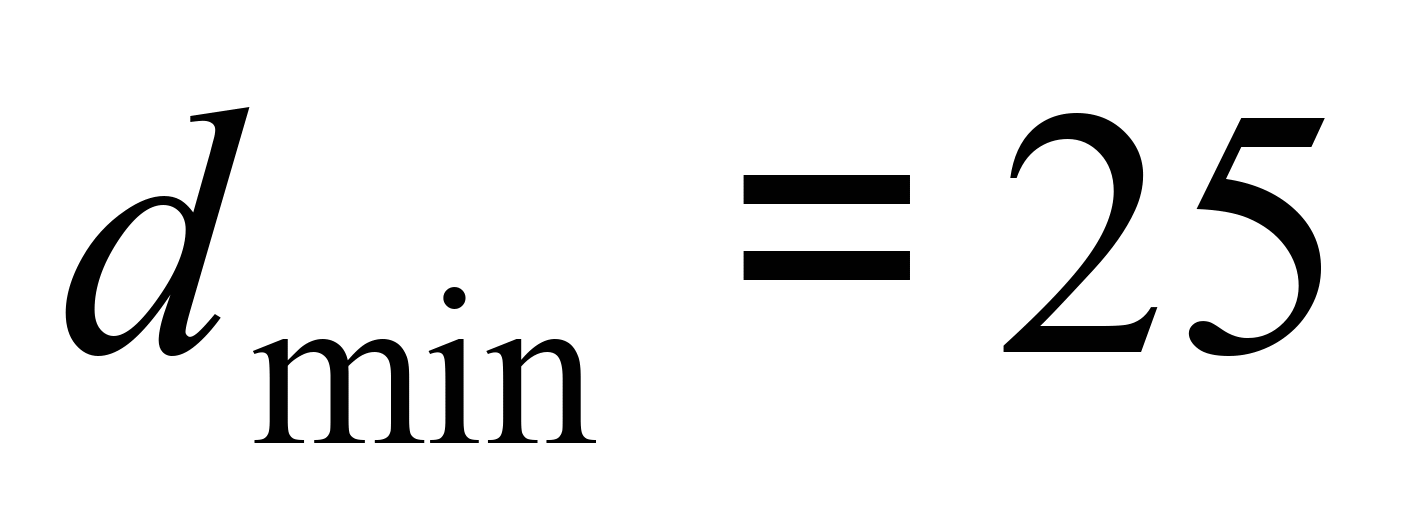мм; 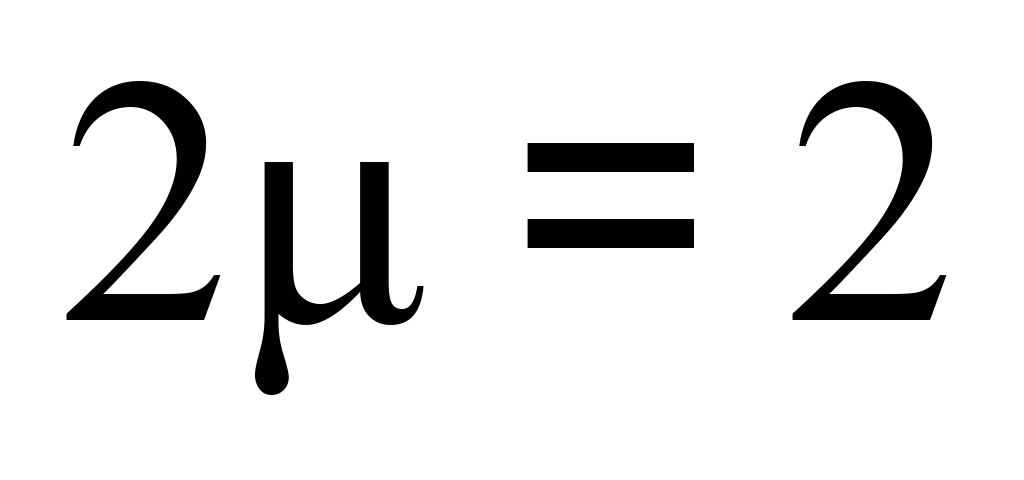мм – потовщення гребенів вагонних коліс, вище за розрахункову площину, 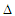– розширення рейкової колії.

Найбільша ширина колії допускається 1 548 мм, тобто 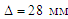. У цьому випадку за мінімальної товщини гребеня 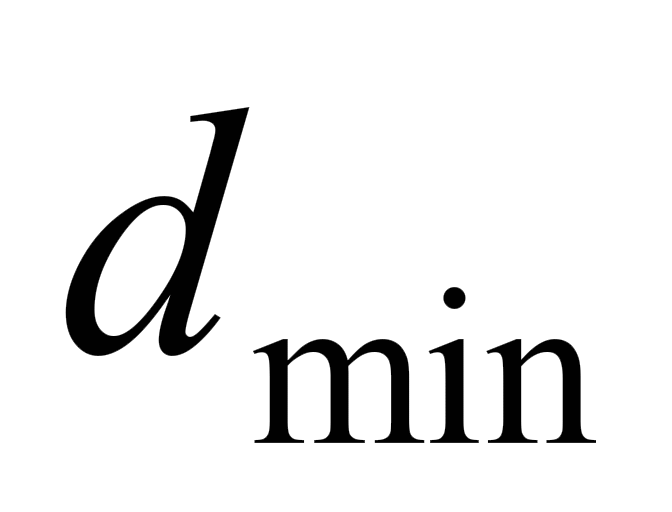та інших номінальних параметрів найбільше значення зазору в колії становитиме .

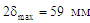Для більшої наочності отриманих результатів необхідно встановити залежність відповідних значень між повним зазором у рейковій колії 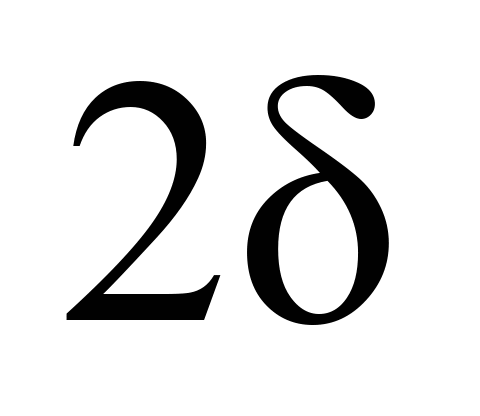та кутом повороту центральної осі кузова вагона 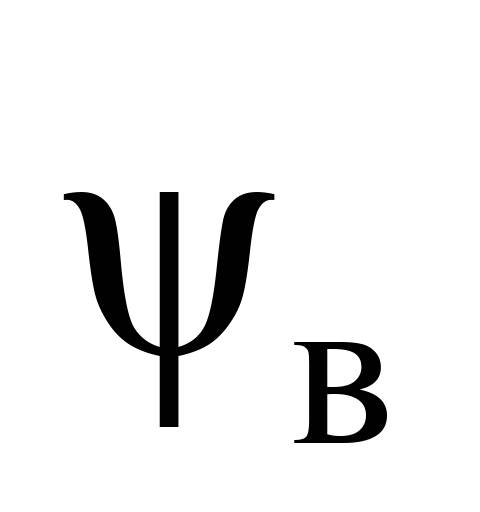. Ураховуючи геометричні розміри піввагона моделі 12–532 та залізничної колії, отримуємо, що за товщини гребеня 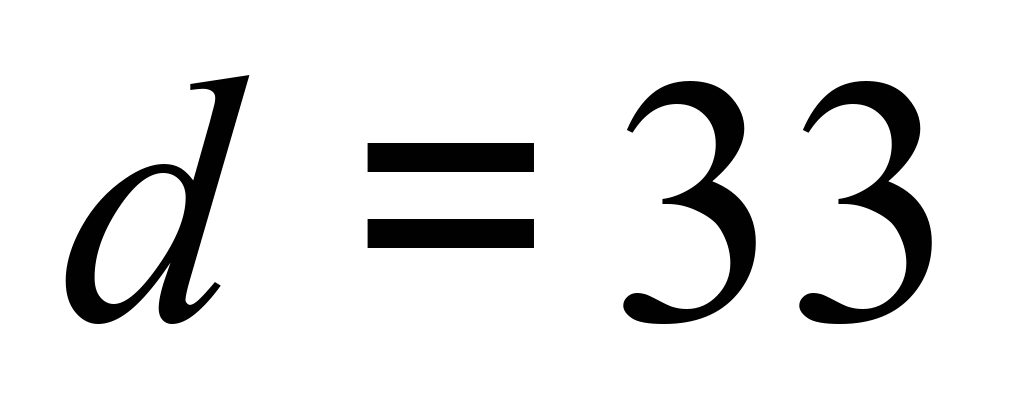мм і 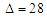повний зазор у колії 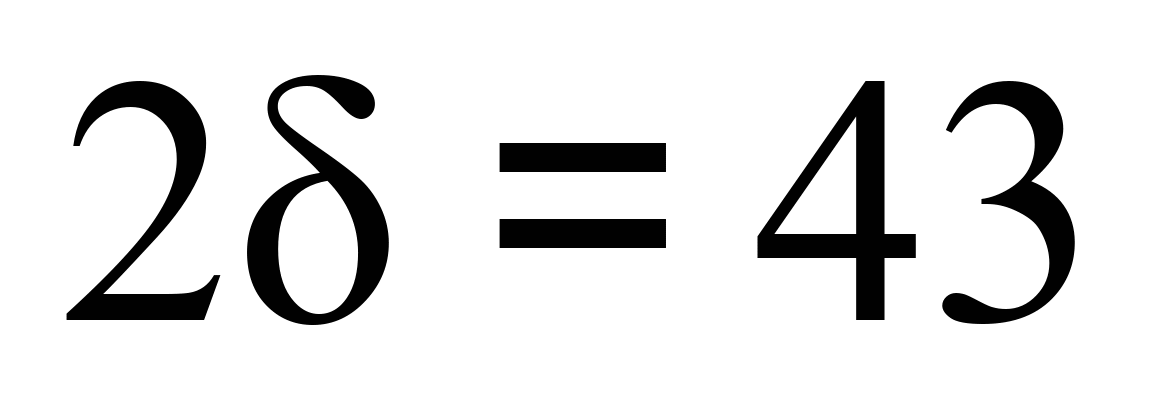мм та відповідно 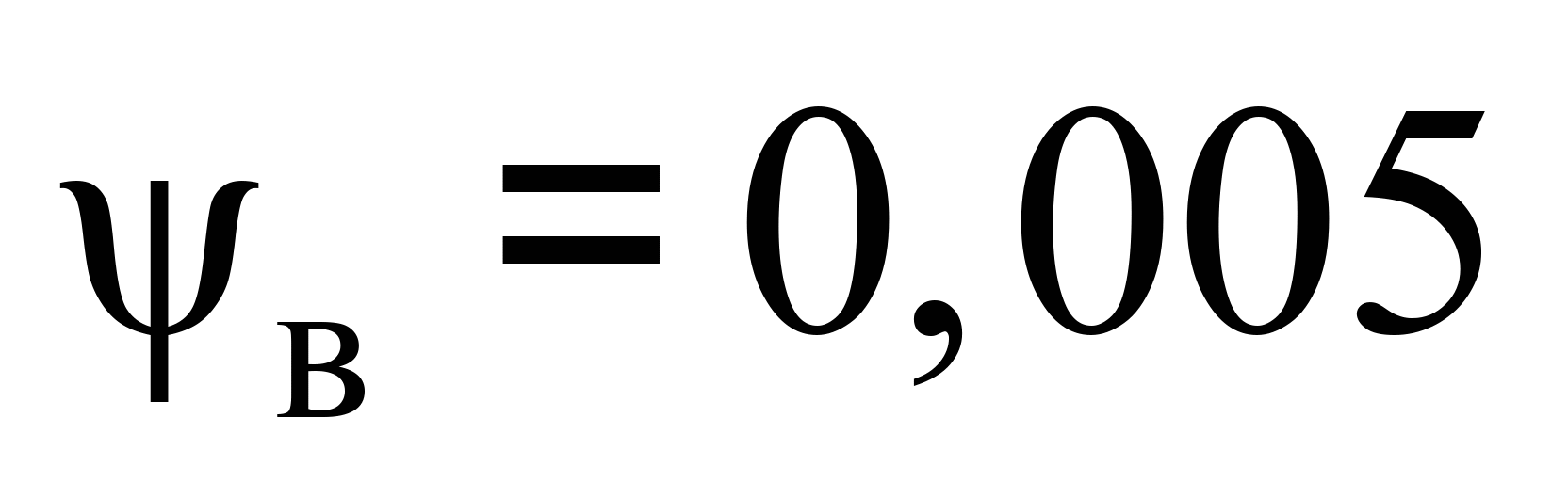рад. За номінальної товщини гребеня 30 мм – 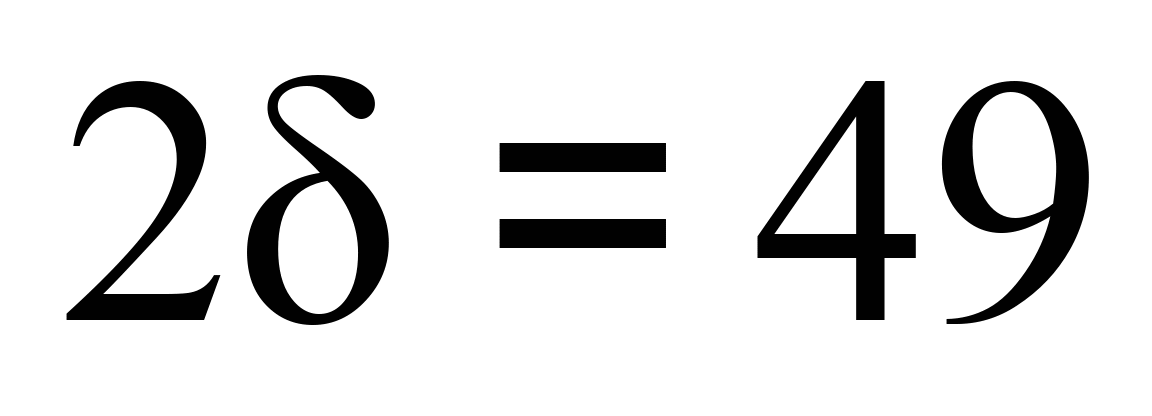мм, а 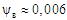рад. Повний зазор у рейковій колії 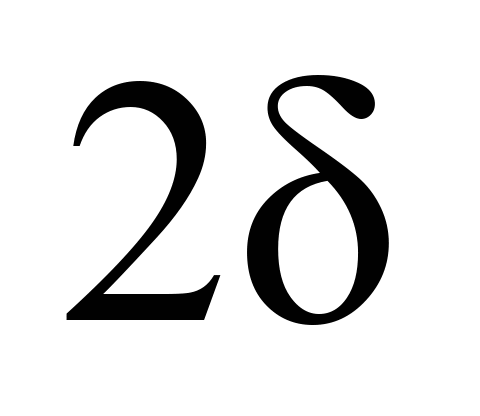може варіюватися від 0 до 59 мм, але кузов вагона може додатково обертатись за рахунок зношеності частин рухомого складу.

Сумарний вільний поперечний розбіг рами кузова вагона відносно осі колії в напрямному перерізі по шворню (за рахунок поперечних розбігів колісних пар у рейковій колії, рами візка відносно колісних пар, надресорної балки відносно рами (візка) і шворневої балки кузова відносно надресорної балки) нормативною документацією рекомендовано вважати для вантажних чотиривісних вагонів із безколисковим підвішуванням візків 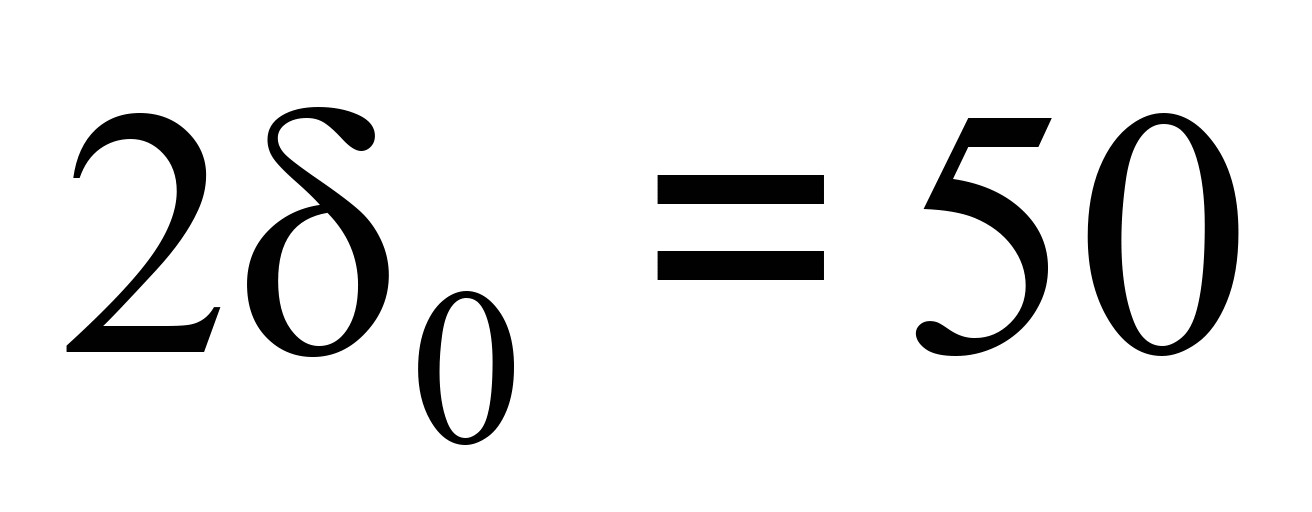мм. З урахуванням того, що боковий знос підп’ятника та п’ятника може досягати 10 мм, а неточність розташування розетки на кінцевій балці деяких вагонів – 20 мм, кут повороту центральної осі кузова вагона також становитиме 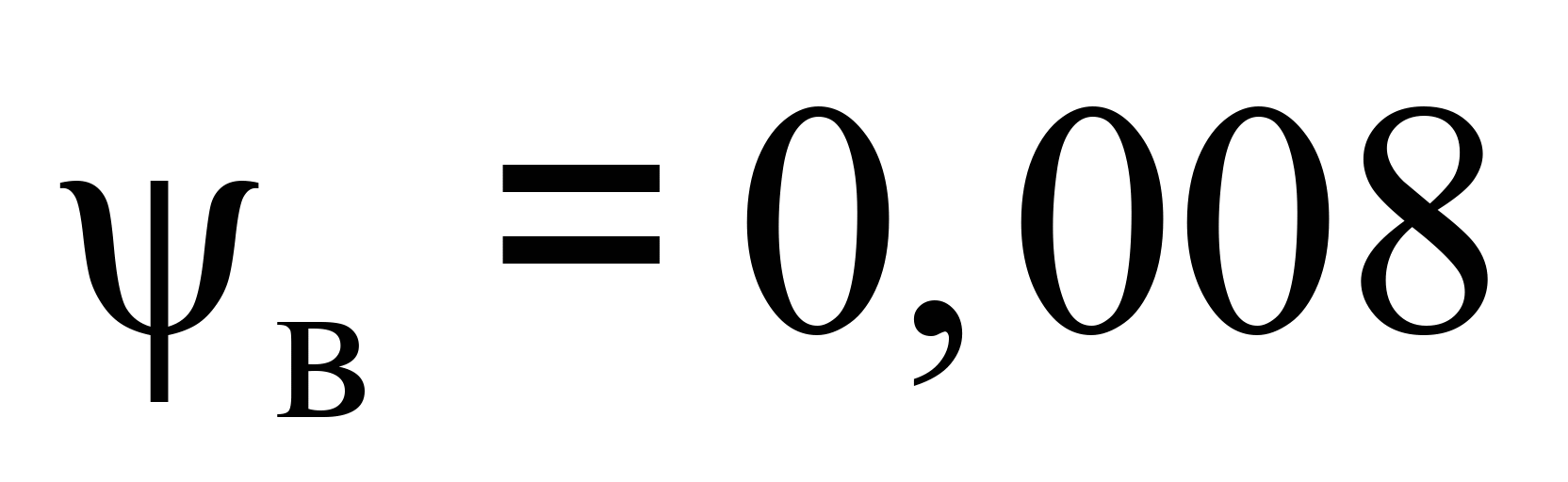 рад. Відповідність значень між 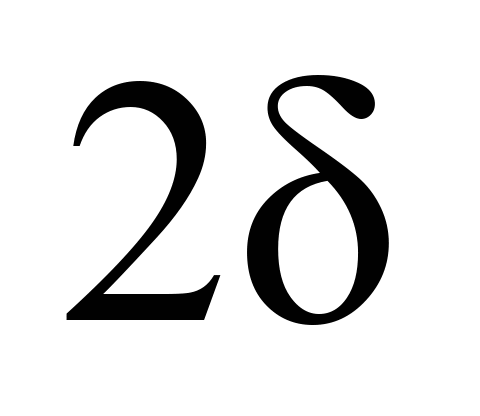, 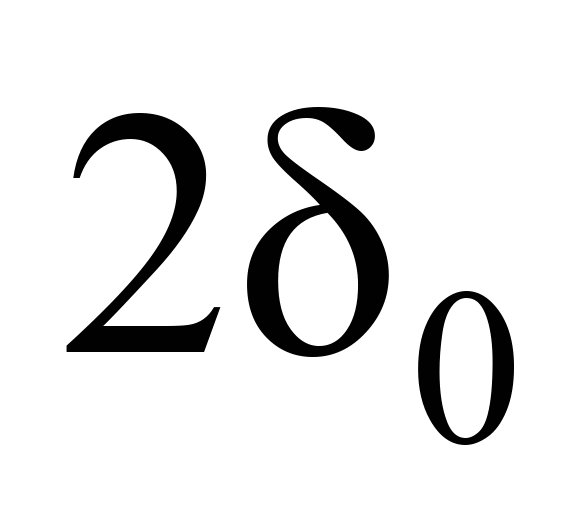й 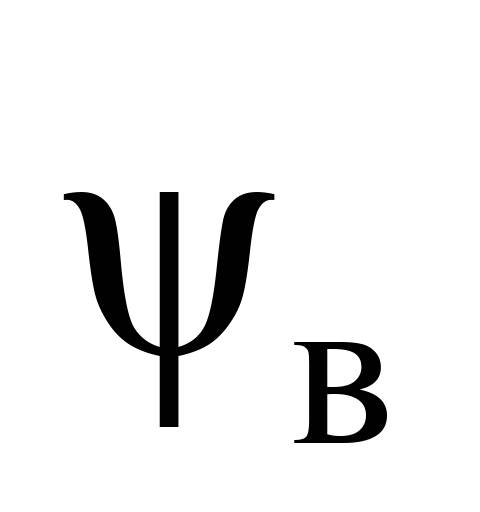наведені в табл. 1.

Таблиця 1

Відповідність значень досліджуваних параметрів

Table 1

Correspondence of values of parameters under study

Параметр	Відповідність між значеннями
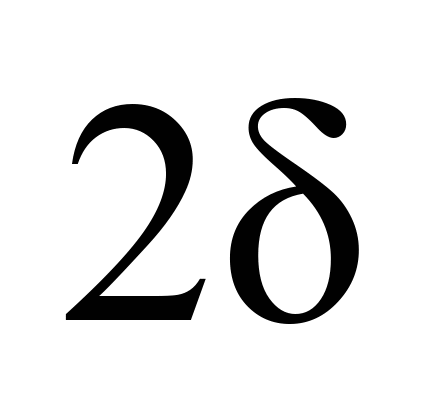, мм	0	9	17	26	35	43	52	59	59
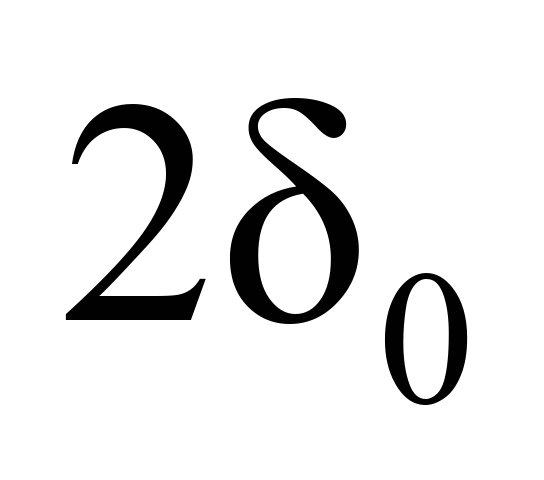, мм	0	9	17	26	35	43	52	60	69
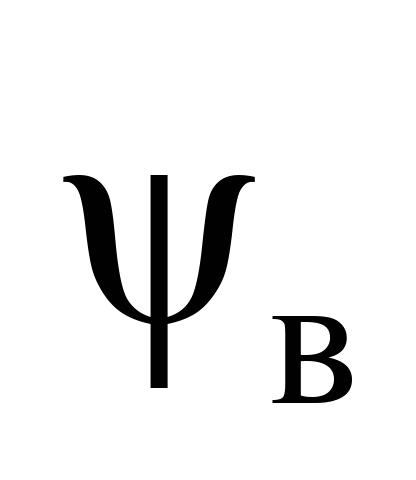, рад	0	0,001	0,002	0,003	0,004	0,005	0,006	0,007	0,008

Вихідні дані для теоретичного дослідження: рух піввагона моделі 12–532 з типовими візками 18–100 зі швидкостями в інтервалі від 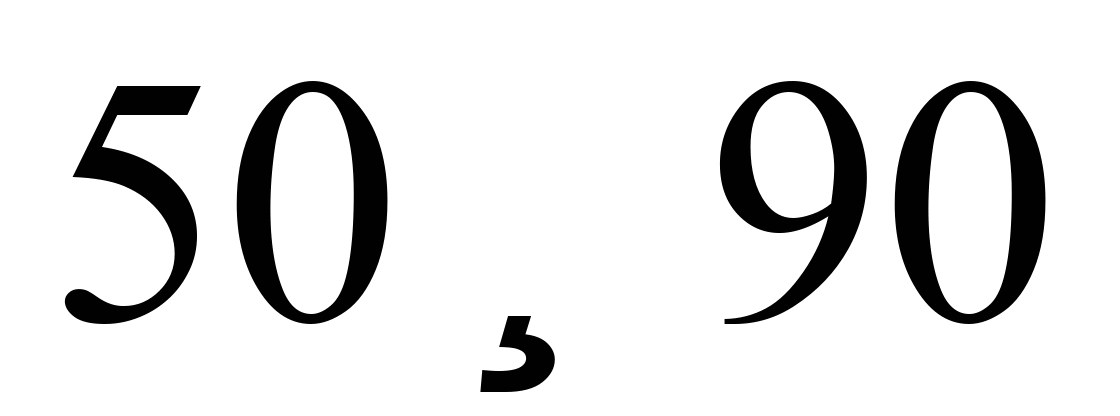 км/год в кривій радіусом 600 м із підвищеннями зовнішньої рейки 120 мм. Рейки – P65, шпали – дерев’яні, баласт – щебеневий. Досліджено стаціонарний рух із метою встановлення впливу тільки розглянутого фактора. Ходові частини вагона, поверхня кочення колеса й профіль головки рейки було передбачено в нормальному технічному стані.

Рівні оцінки та допустимі значення показників динамічних якостей вантажного рухомого складу відповідно до нормативної документації наведені в табл. 2 [6].

Таблиця 2

Рівні оцінки та допустимі значення показників динамічних якостей

Table 2

Levels of estimation and admissible values of indicators of dynamic qualities

Показник	Рівень оцінки	Допустимі значення
		порожній	завантажений
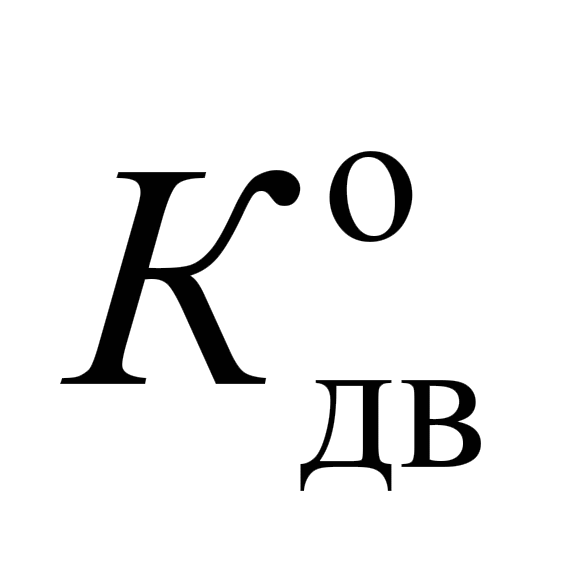
Максимальний коефіцієнт динамічної добавки обресорених частин (коефіцієнт вертикальної динаміки центрального ступеня підвішування)	відмінно	0,5	0,2
	добре	0,6	0,35
	задовільно	0,7	0,4
	припустимий	0,75	0,65

Продовження табл. 2

Continuation of Table 2

Показник	Рівень оцінки	Допустимі значення
		порожній	завантажений
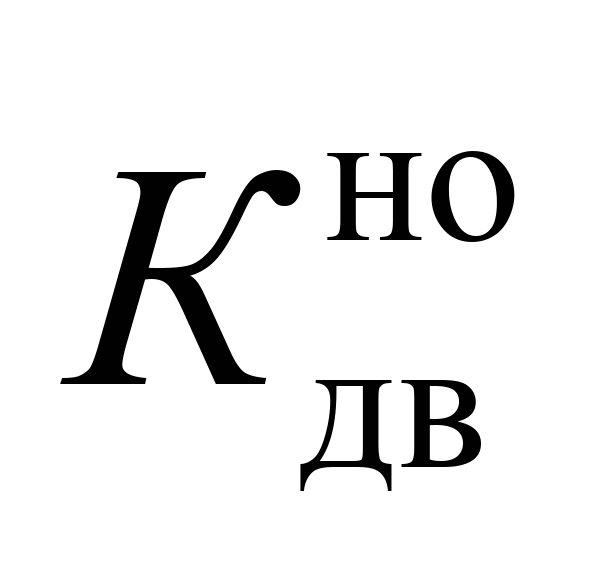
Максимальний коефіцієнт динамічної добавки необресорених частин (коефіцієнт вертикальної динаміки буксового ступеня підвішування)	відмінно	0,6	0,5
	добре	0,75	0,7
	задовільно	0,85	0,8
	припустимий	0,98	0,9
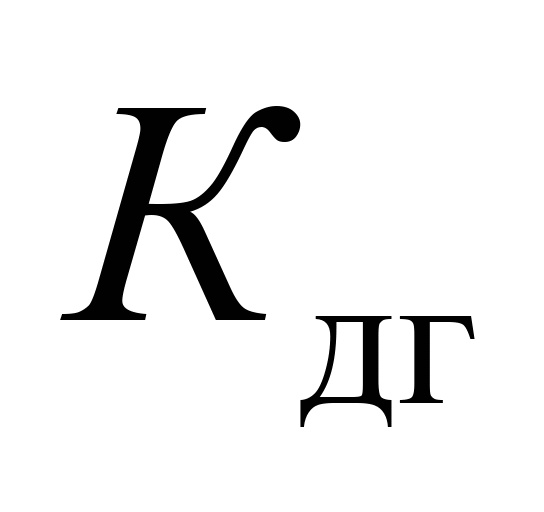
Максимальне відношення рамної сили до статичного осьового навантаження (коефіцієнт горизонтальної динаміки)	відмінно	0,25	0,2
	добре	0,3	0,25
	задовільно	0,38	0,3
	припустимий	0,4	0,38
Коефіцієнт стійкості від сходження колеса з рейок	припустимий	1,3

Результати

Динамічні сили та процеси, які діють у складових частинах візка або кузова вагона, вивчають за допомогою максимальних коефіцієнтів динамічної добавки обресорених і необресорених частин , максимального відношення рамної сили до статичного осьового навантаження та коефіцієнта стійкості від сходження колеса з рейок . Графіки зміни динамічних показників під час руху по кривій ділянці колії м наведені на рис. 5, 6.

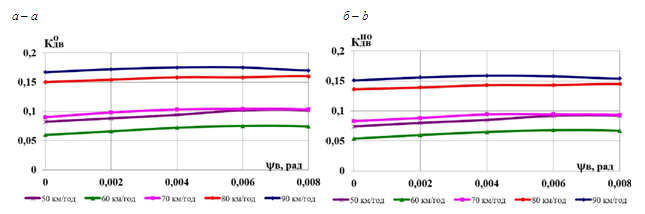
Рис. 5. Графіки зміни динамічних показників від швидкості руху:
а – коефіцієнта динамічної добавки обресорених частин;
б – коефіцієнта динамічної добавки необресорених частин

Fig. 5. Graphs of change of dynamic from the movement speed:
a – coefficient of dynamic additive of sprung parts;
b – coefficient of dynamic additive of unsprung parts

Як видно з рис. 5, зі збільшенням кута повороту кузова в плані відносно осі колії досліджувані динамічні коефіцієнти в цілому залишаються незмінними. У всьому інтервалі швидкостей показники 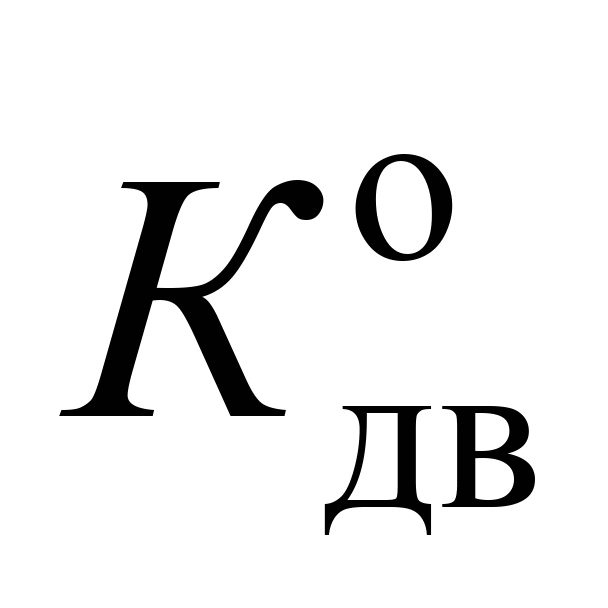(рис. 5, а), 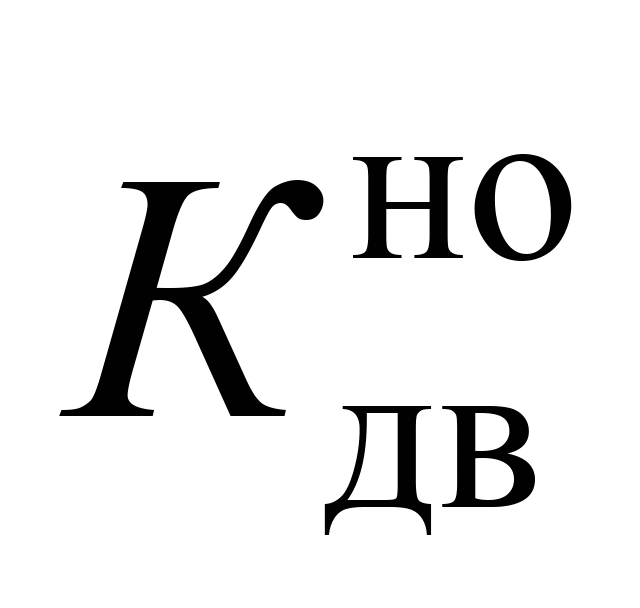(рис. 5, б) в разі збільшення 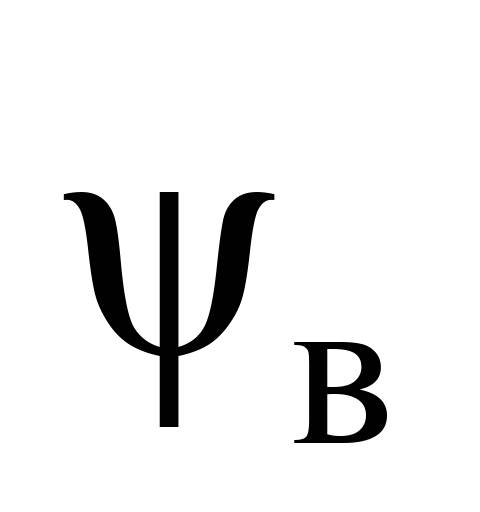від 0 до 0,008 рад не перевищують допустиму норму. Рівень оцінок – «відмінно» [6].

З отриманих результатів можна зробити висновок, що кут повороту кузова в плані відносно осі колії 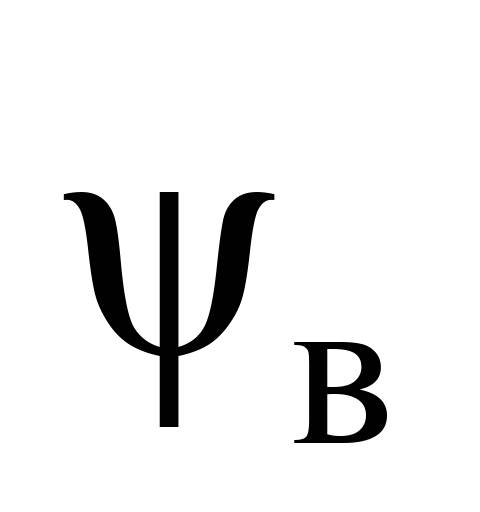в разі збільшення швидкості руху не викликає істотного збільшення показників вертикальної динаміки в буксовому та центральному ступенях підвішування, а їх значення не перевищують величин, визначених нормативною документацією.

Максимальне відношення рамної сили до статичного осьового навантаження 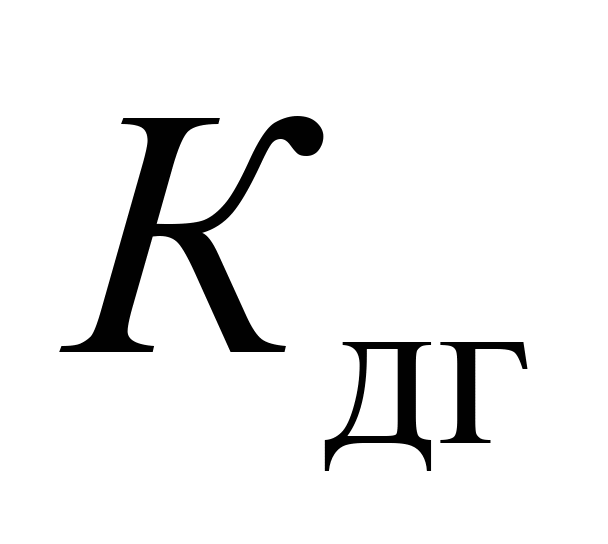(рис. 6, а) та коефіцієнт стійкості від сходження колеса з рейок 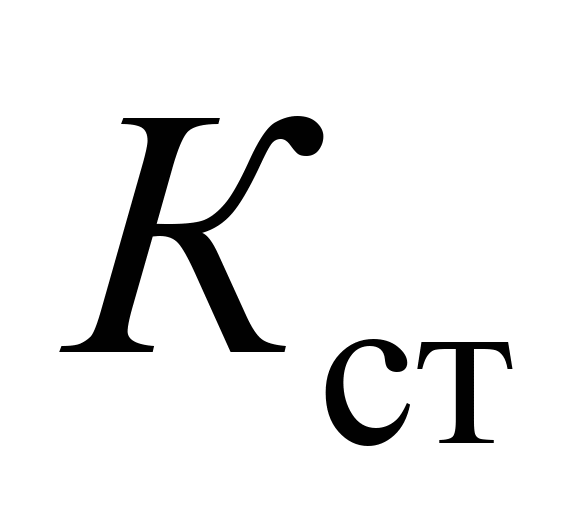(рис. 6, б) в разі збільшення 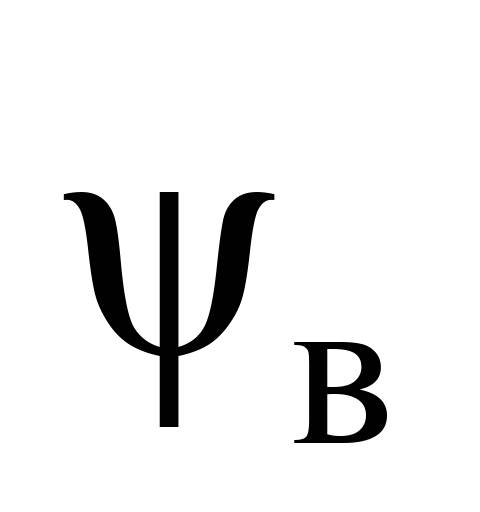не перевищують допустиму норму. Рівень оцінок для 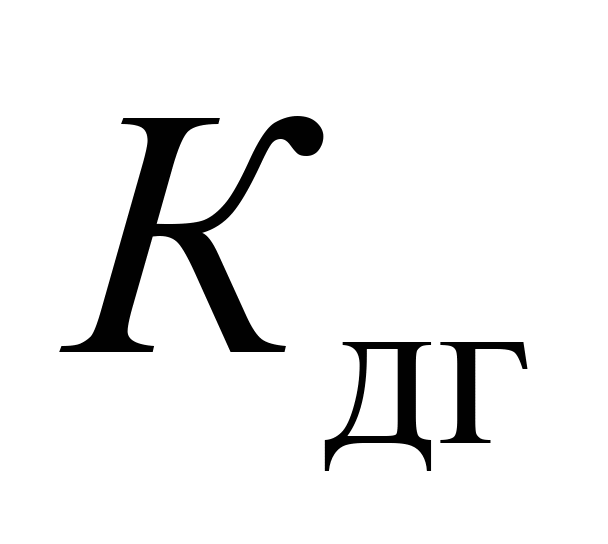– «відмінно», 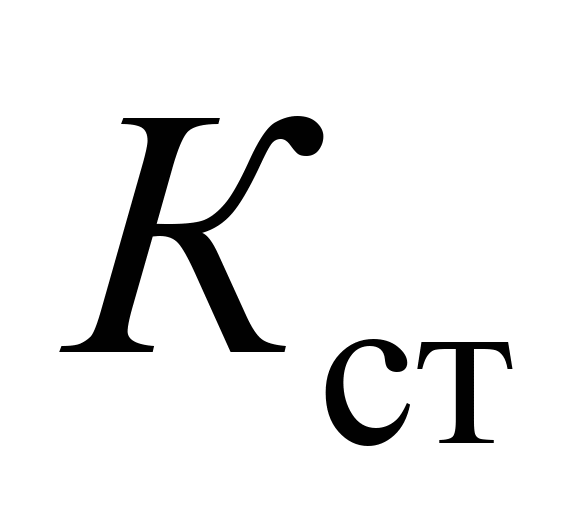– вище допустимого [6].

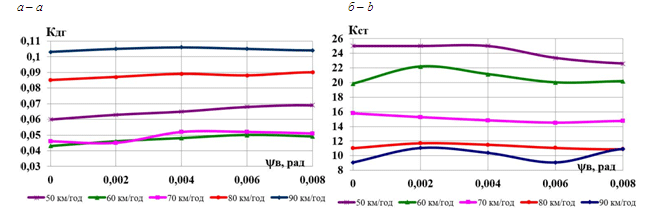
Рис. 6. Графіки зміни динамічних показників від швидкості руху:
а – максимального відношення рамної сили до статичного осьового навантаження;
б – коефіцієнта стійкості від сходження колеса з рейок

Fig. 6. Graphs of change of dynamic indicators from the movement speed:
a – maximum ratio of the frame force to the static axial load;
b – derailment stability coefficient

Hа рис. 7 показано вплив швидкості на показники взаємодії рухомого складу з колією в кривій м – бокової сили, що діє від колії на колесо та кромкового напруження в підошві рейки . Бокові сили , що діють від колії на колесо (горизонтальні сили) (рис. 7, а), зростають та мають максимум за рад і порівняно з допустимим значенням кН для забезпечення умови стійкості проти наповзання гребенів коліс на рейки не мають перевищень.

Кут повороту центральної осі кузова вагона в значній мірі залежить від сил взаємодії контактуючих тіл і їх відносних переміщень (відносних проковзувань). Ці сили й переміщення визначаються умовами взаємодії коліс рухомого складу та колії. Умови взаємодії тіл цієї системи залежать як від конструкції, технічного стану й режимів руху рухомого складу, так і від конструкції, стану й параметрів рейкової колії. Але саме за номінальної товщини гребеня колеса та за мм ( рад) отримано максимальні значення бокової сили . Порівняно з максимальною товщиною гребеня та рад ці значення більші в середньому на 9,5 %.

Рис. 7. Графіки зміни динамічних показників від швидкості руху:
а – бокової сили, що діє від колії на колесо;
б – кромкового напруження в підошві рейки

Fig. 7. Graphs of change of dynamic indicators from the movement speed:
a – lateral force acting from the track on the wheel;
b – edge stress in the rail base

Під час підвищення швидкостей руху поїздів зростає динамічний вплив на колію рухомого складу і, як наслідок, зростають напруження в кромках підошви рейок. Максимальні напруження, що виникають у кромках підошви рейки, використовують як критерій для встановлення допустимих швидкостей. Вони не повинні перевищувати 215 МПа до пропуску й 165 МПа після пропуску нормативного тоннажу для колії з нетермообробленими рейками Р65 [3]. Але у випадку розглянутої схеми розташування візків вантажного вагона в рейковій колії відбувається перерозподіл вертикальних та горизонтальних реакцій e зоні контакту колеса та рейки. За результатами обчислень, кромкові напруження (рис. 7, б) зростають у разі підвищення швидкості руху, але мають мінімум саме за рад в інтервалі швидкостей км/год та максимум за км/год. Проте отримані результати не перевищують допустимих значень для обох типів рейок [3].

Hа рис. 8 наведено коефіцієнти вертикальної й горизонтальної динаміки колії за силами взаємодії коліс із рейками.

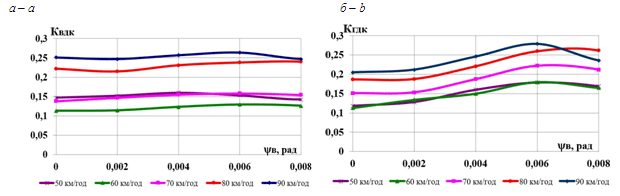
Рис. 8. Графіки зміни динамічних показників від швидкості руху:
а – коефіцієнта вертикальної динаміки колії за силами взаємодії коліс із рейками;
б – коефіцієнта горизонтальної динаміки колії за силами взаємодії коліс із рейками

Fig. 8. Graphs of change of dynamic indicators from the movement speed:
a – vertical dynamics coefficient of the track according to the interaction forces of the wheels and the rails;
b – horizontal dynamics coefficient of the track according to the interaction forces of the wheels and the rails

Допустиме значення коефіцієнта вертикальної динаміки колії розраховують відповідно до допустимого динамічного погонного навантаження на залізничну колію від групи осей візка 168 кН/м, воно становить для цього типу рухомого складу [3]. Коефіцієнт вертикальної динаміки колії (рис. 8, а) не перевищує допустимого значення. Коефіцієнт горизонтальної динаміки колії (рис. 8, б), який вважають критерієм безпеки від зсуву рейко-шпальної решітки, не перевищує допустимого значення та також має істотний максимум в усьому інтервалі розглянутих швидкостей за рад.

Hа рис. 9 наведено коефіцієнти стійкості рейко-шпальної решітки від угону (зсуву) та фактора зносу бокової грані бандажа колеса .

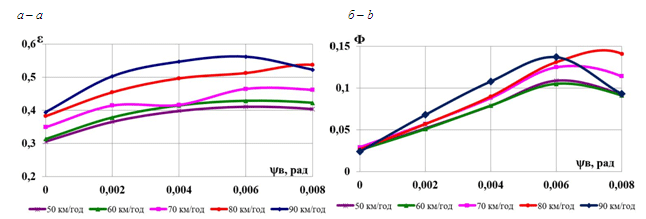
Рис. 9. Графіки зміни динамічних показників від швидкості руху:
а – коефіцієнта стійкості рейко-шпальної решітки від дії поперечних сил;
б – фактора зносу бокової грані бандажа колеса

Fig. 9. Graphs of change of dynamic indicators from speed of movement:
a – stability coefficient of the track panel from the action of lateral forces;
b – wear factor of the lateral edge of the wheel rim

Значення коефіцієнта стійкості рейко-шпальної решітки від дії поперечних сил 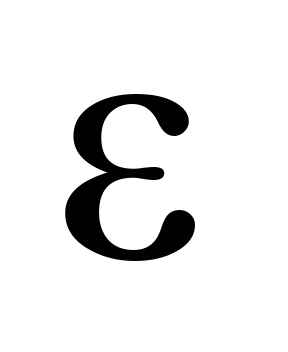(рис. 9, а) в колії зі щебеневим баластом за результатами розрахунку становить 0,3–0,56, що менше допустимої величини 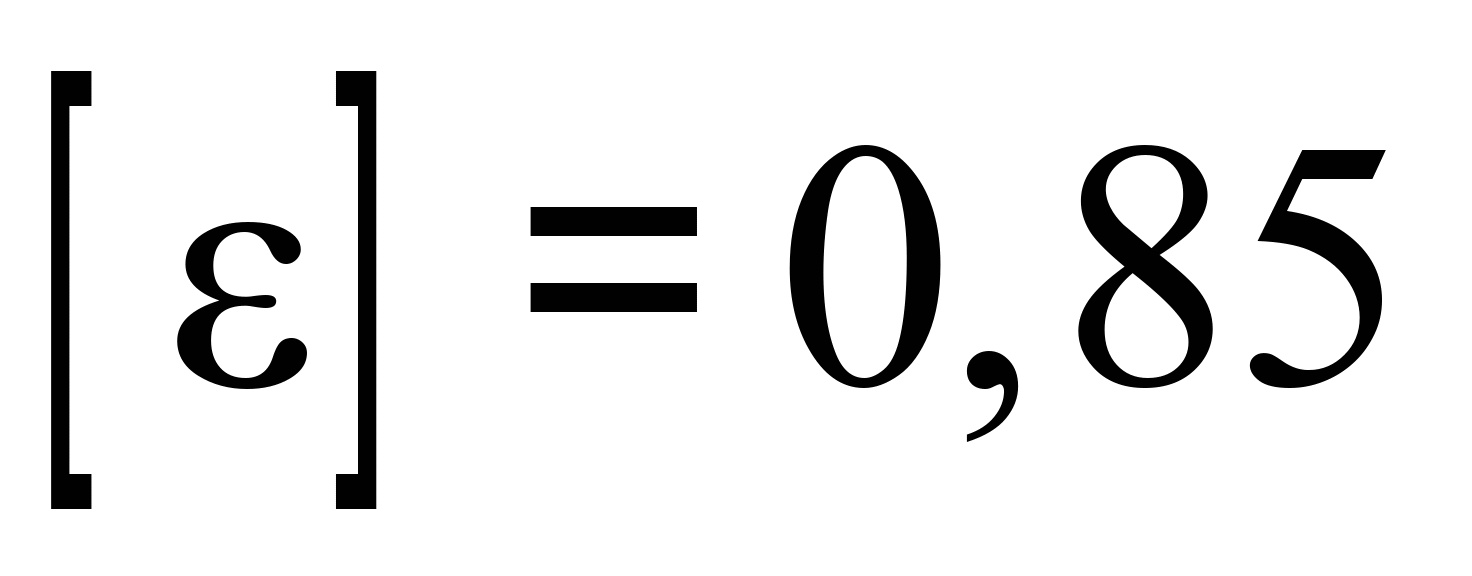[3].

Зі збільшенням швидкості руху (наприклад, за швидкостей 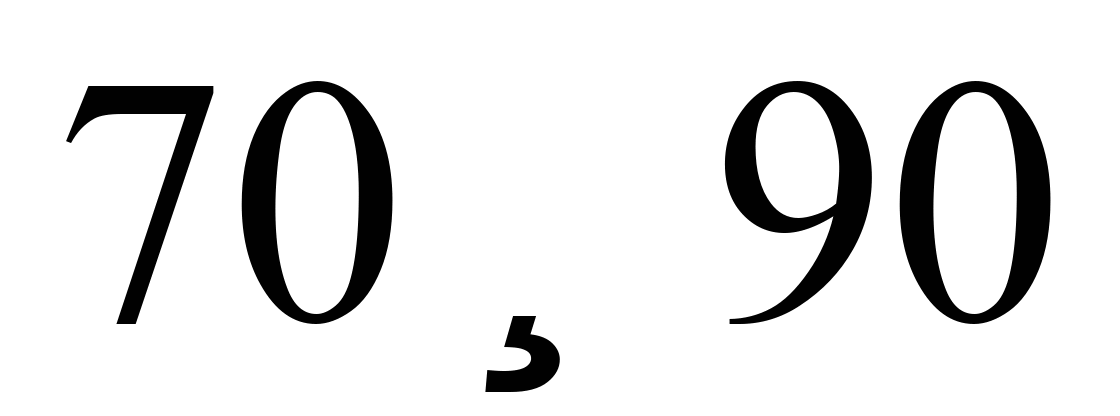км/год) значно зростає фактор зносу бокової грані бандажа колеса (рис. 9, б), відповідні значення за 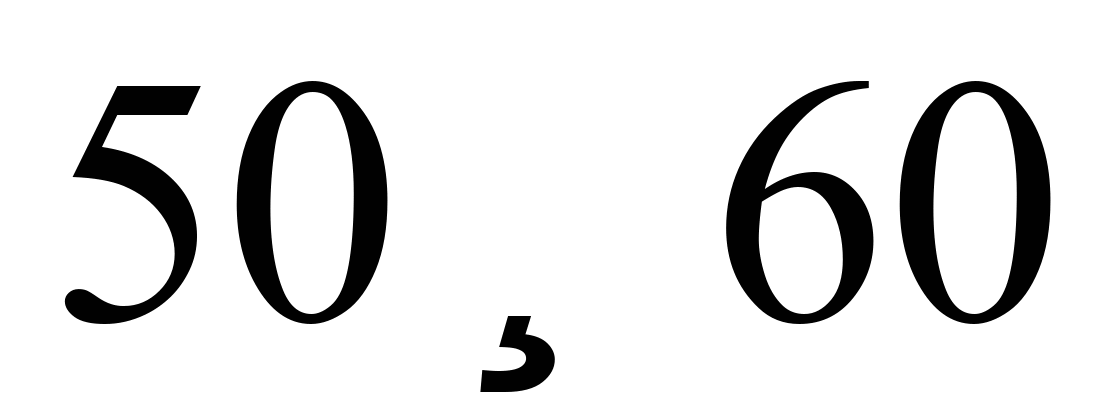 км/год збільшуються в середньому на 22,43 %. По мірі зростання 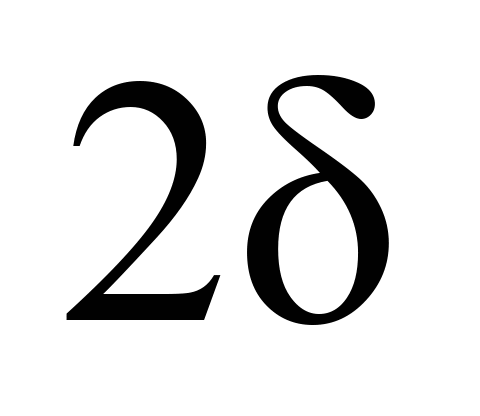від 52 до 59 мм показник зносу гребеня падає, що свідчить про зростання терміну служби колісної пари. Як видно з рис. 9, показники 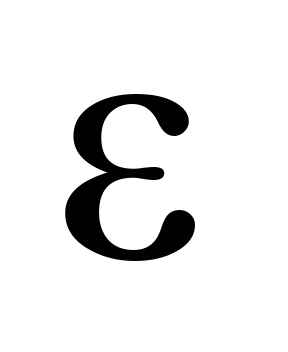та також мають максимуми за 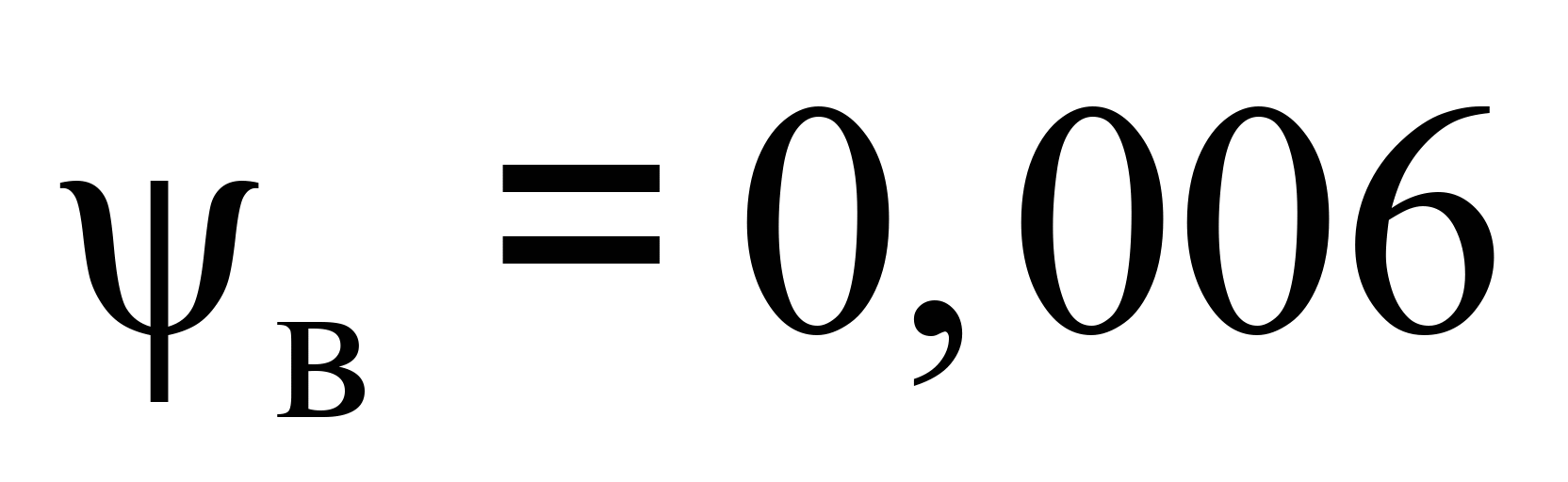рад.

На рис. 10 наведено відтискання підошви 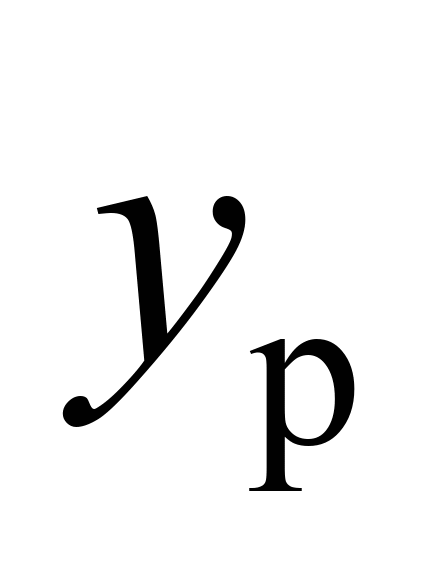та головки рейки 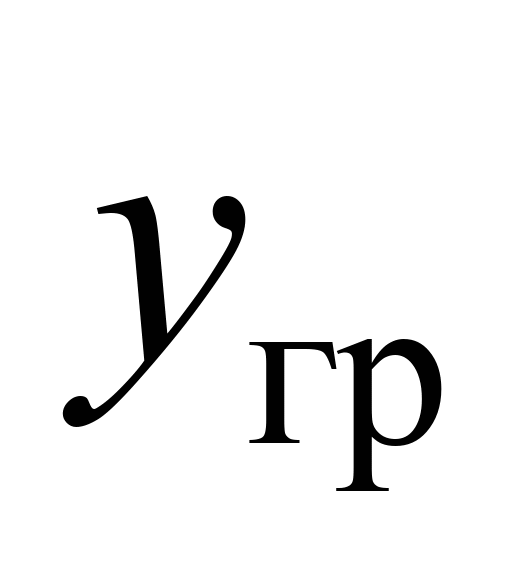, оскільки як на ділянках із дерев’яними шпалами існує висока ймовірність сходження через витискання екіпажів унаслідок можливості нахилу рейки.

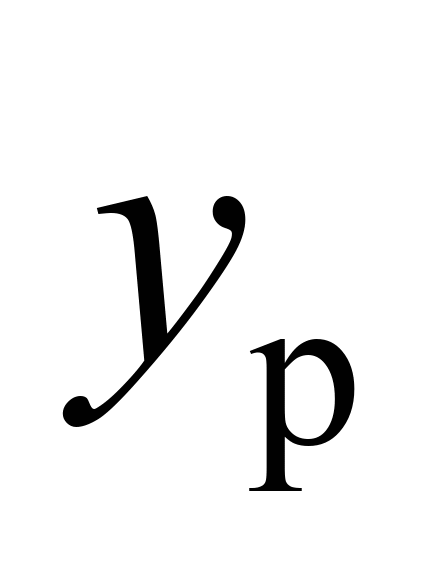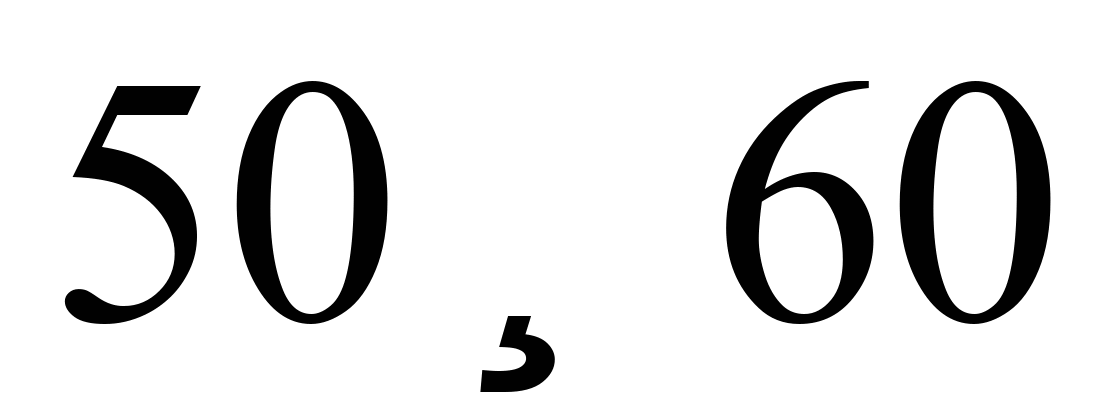Чим більша швидкість руху, тим на більшу величину підсмикуються внутрішні обшивні костилі (рис. 10, а). В інтервалі швидкостей км/год зростання відтискань підошви рейок у середньому становить 9,59 % на кожні 10 км/год, а за швидкостей 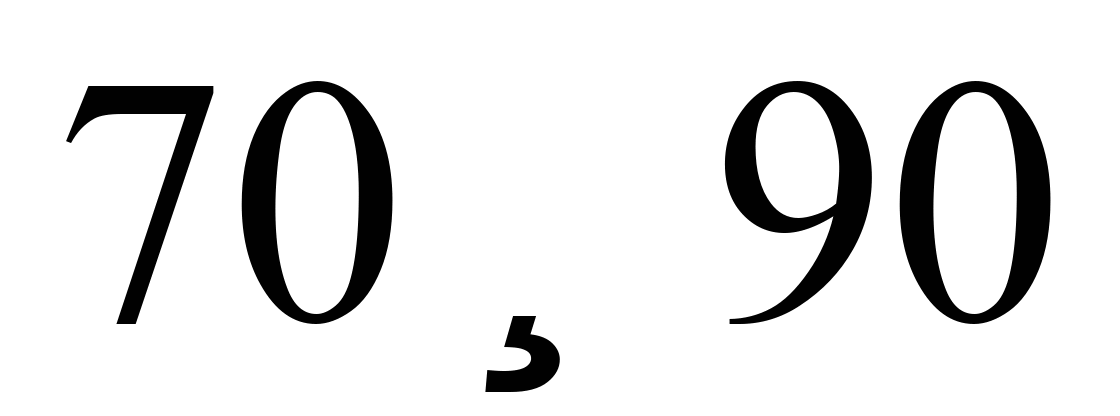км/год відповідні значення зростають у середньому на 21,1 %. 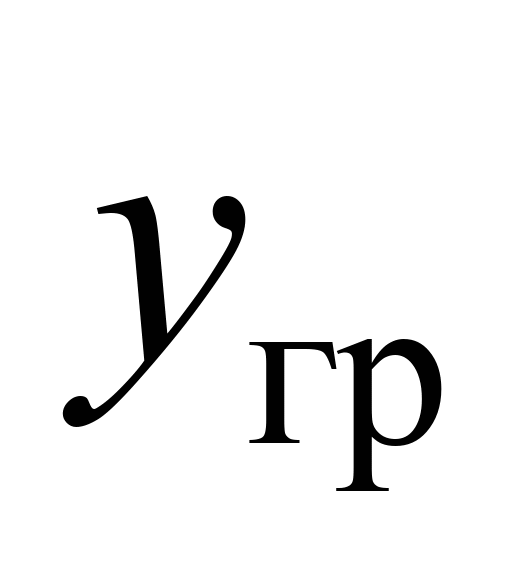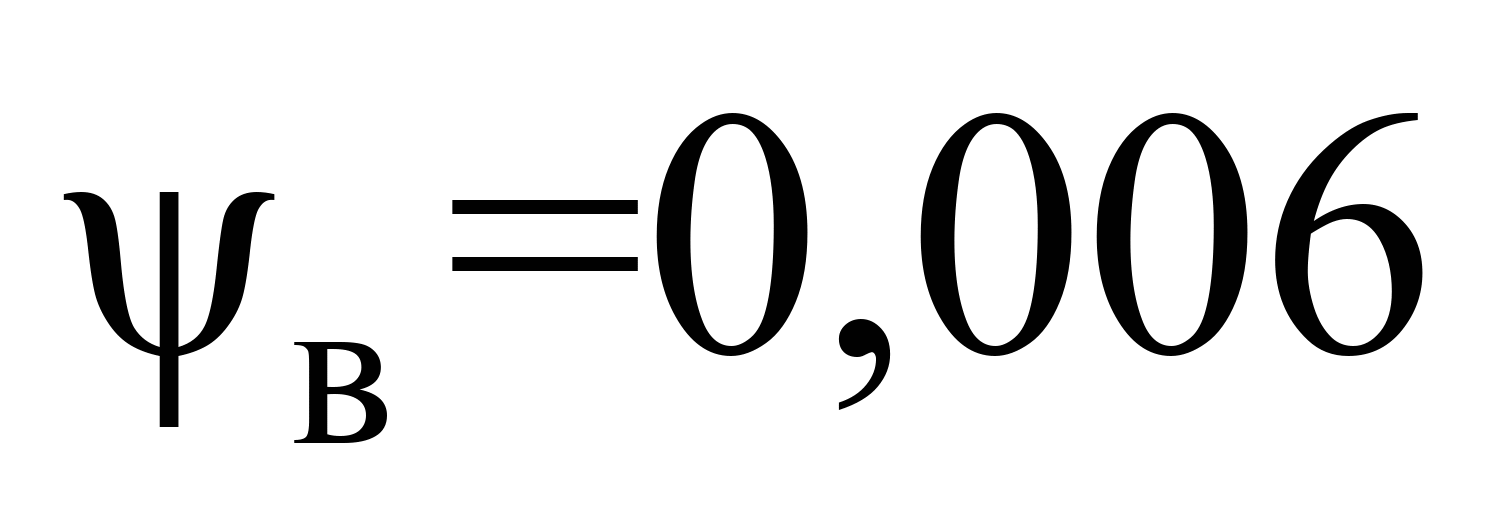Для відтискання головки рейки за результатами розрахунків такої чіткої залежності не отримано, але обидва показники мають максимальні значення за кута повороту центральної осі кузова вагона рад.

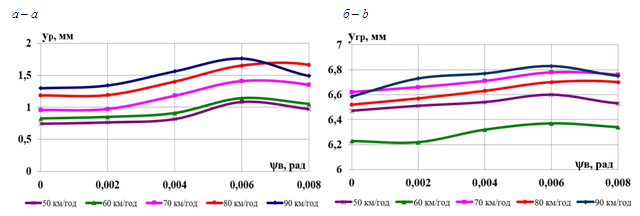
Рис. 10. Графіки зміни динамічних показників від швидкості руху:
а – відтискання підошви рейки; б – відтискання головки рейки

Fig. 10. Graphs of change of dynamic indicators from the movement speed:
a – squeezing of the rail base; b – squeezing of the rail head

У роботі [9] описано серію натурних експериментів зі сходження коліс із рейок через витискання екіпажів, розпирання та угону (зсуву) колії. Експерименти виконано за умови застосування дерев’яних і залізобетонних шпал, щебеневого, азбестового й піщаного баласту, добитих та підсмикнутих костилів. Схема проведення натурних експериментів зі сходження коліс з рейок через витискання вагона, розпирання та угону (зсуву) колії наведена на рис. 11.

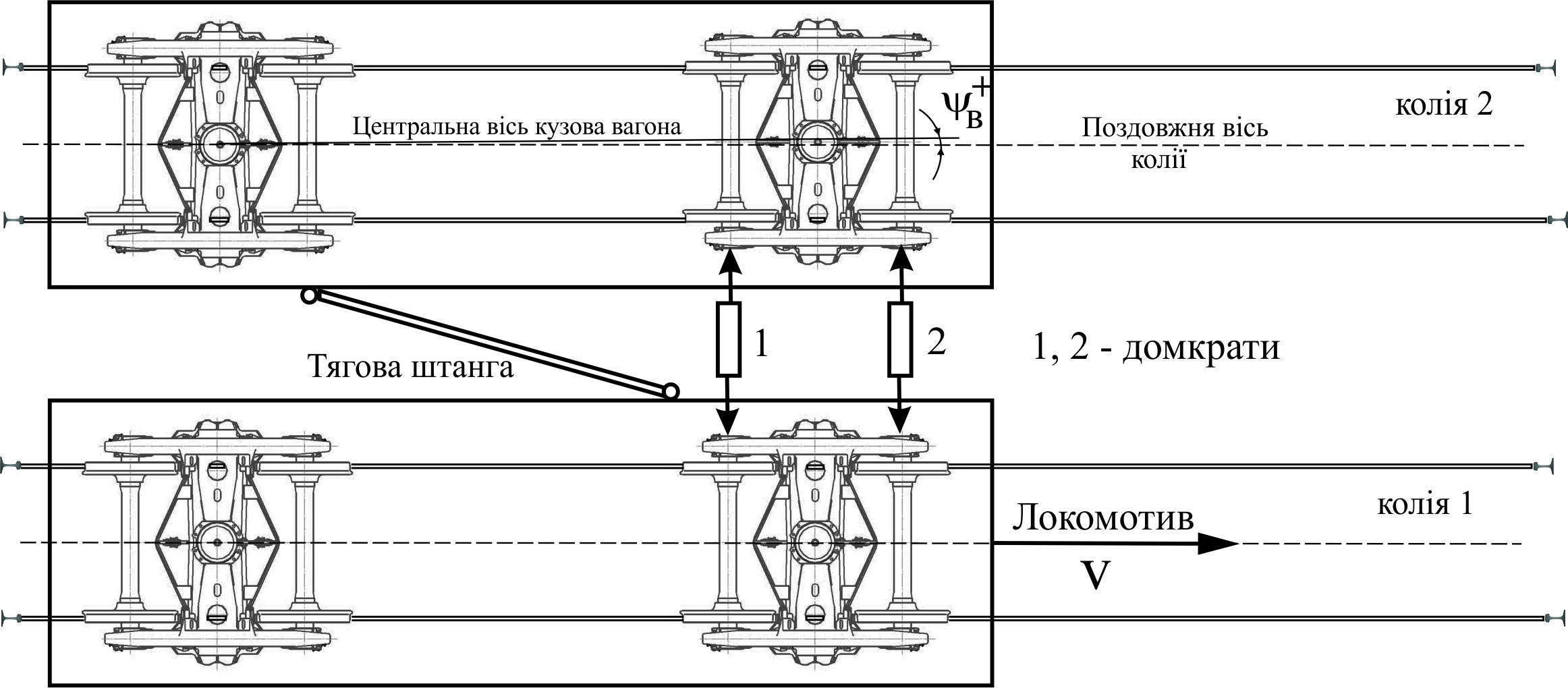
Рис. 11. Схема проведення натурних експериментів зі сходження коліс із рейок

Fig. 11. Scheme of field experiments on derailments

По першій колії двоколійної ділянки (рис. 11) локомотивом переміщав 4-вісний піввагон зі швидкістю 15–25 км/год, завантажений щебенем до 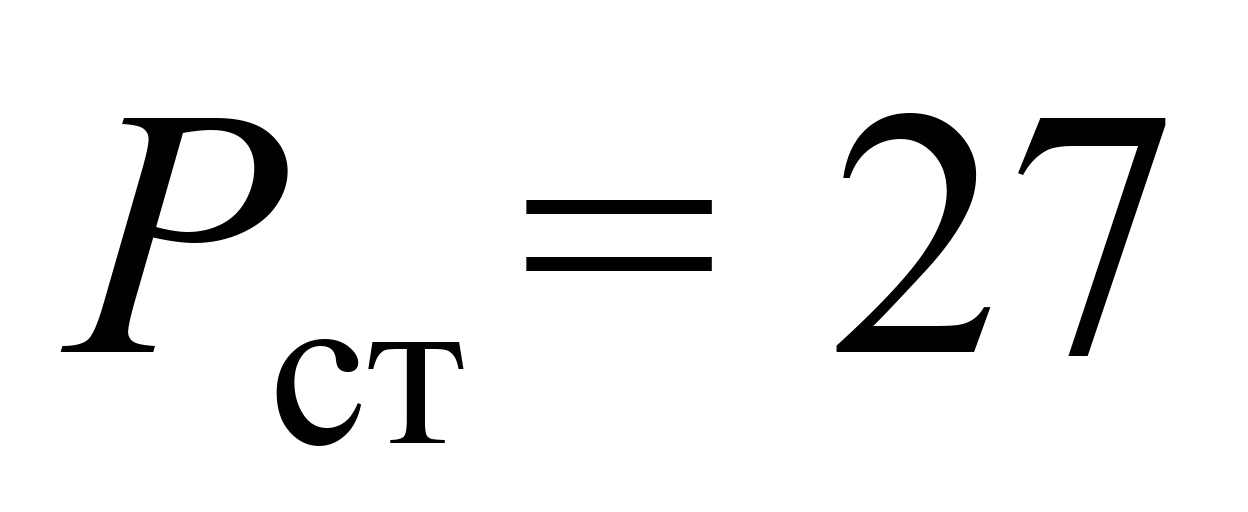т/вісь. По другій колії за допомогою штанги синхронно переміщався такий самий 4-вісний піввагон, але з меншим завантаженням. У кожну буксу були вмонтовані розпірні гідравлічні домкрати 1 і 2, що дозволяють на ходу встановлювати розпираючу силу від 0 до 392 кН (по 196 кН на одну вісь). Установлені вздовж колії прилади фіксували відтискання головки та підошви рейки, у т. ч. її нахил за одночасного вимірювання динамометричними колісними парами сил бокового горизонтального впливу коліс на рейки. Заїзди повторювали багаторазово з доведенням у ряді випадків до сходження коліс через розпирання або угон (зсув) колії. На прямих ділянках колії з дерев’яними шпалами з типовим костильним скріпленням для малозавантажених вагонів відтискання підошви не перевищувало 1–1,5 мм за відтискання головки рейки 5,0–6,0 мм.

Наведені в цьому дослідженні розрахунки були проведені за осьового навантаження вагона 21,4 т на вісь і в інтервалі швидкостей 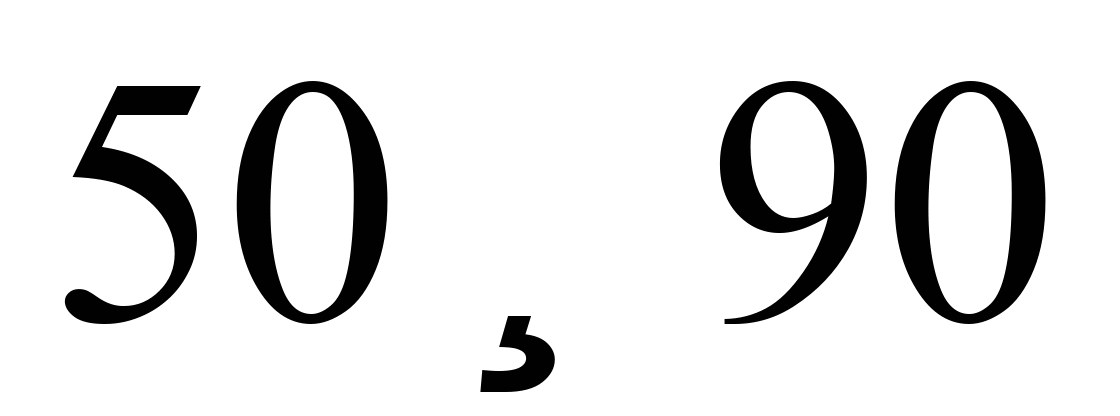км/год у кривій радіусом 600 м. Порівняння отриманих результатів розрахунку показує задовільну відповідність експериментальним даним за величинами .

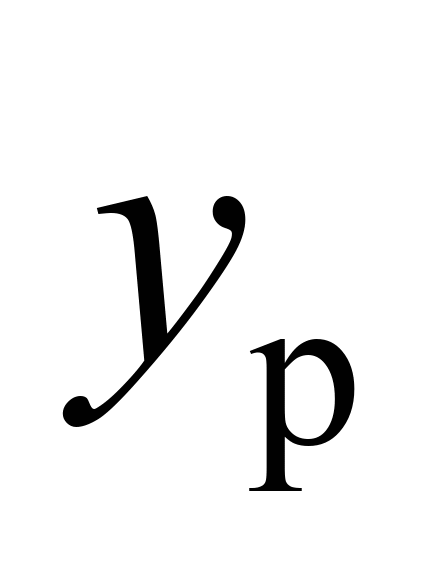Наукова новизна та практична
значимість

Доопрацьовано математичну модель зчепу вантажних вагонів у складі поїзда. У розрахункових схемах, що описують коливання вагонів, враховано особливості візків вантажних вагонів – забігання бокових рам. Модель дозволяє дослідити вплив зміни кута повороту центральної осі кузова вагона, що у свою чергу призводить до поперечного зміщення візків відносно один одного, на основні динамічні показники та показники взаємодії рухомого складу з колією. Уперше досліджено вплив поперечного зміщення візка з урахуванням зносів його деталей та вузлів під час руху на ділянках колії з нерівностями.

Це дослідження виконано в напрямі розвитку методів математичного моделювання динамічних процесів взаємодії рухомого складу та колії. Результати розрахунків можна застосовувати під час оцінювання впливу поперечного зміщення візка на динамічні якості рухомого складу та показники взаємодії рухомого складу з колією з урахуванням зносів деталей та вузлів візка під час руху в прямих і криволінійних ділянках колії з нерівностями.

Застосування отриманих результатів сприятиме підвищенню стійкості вантажного рухомого складу в умовах підвищення швидкостей руху, що у свою чергу дозволить розробити технічні умови для реалізації ресурсозбережних технологій транспортування вантажів, які відповідають вимогам безпеки руху поїздів.

Висновки

У статті представлено аналіз проведених теоретичних досліджень основних динамічних показників та показників взаємодії рухомого складу з колією на прикладі піввагонів моделі 12–532. На підставі проведених досліджень динамічної навантаженості вантажного рухомого складу за наявності поперечного зміщення візків можна зробити такі висновки:

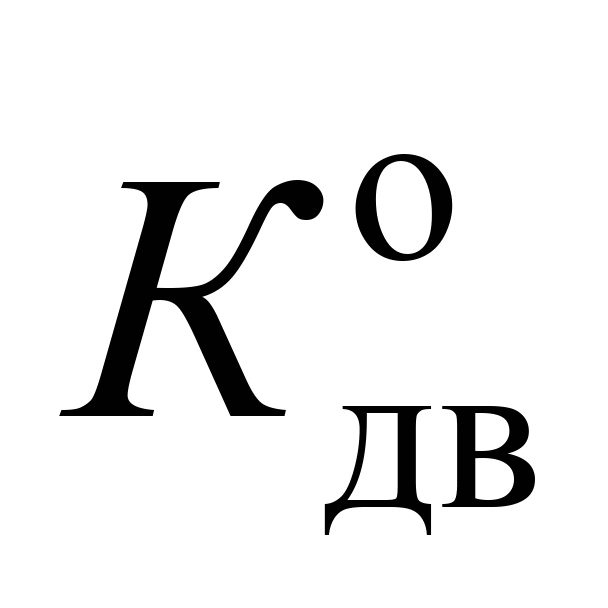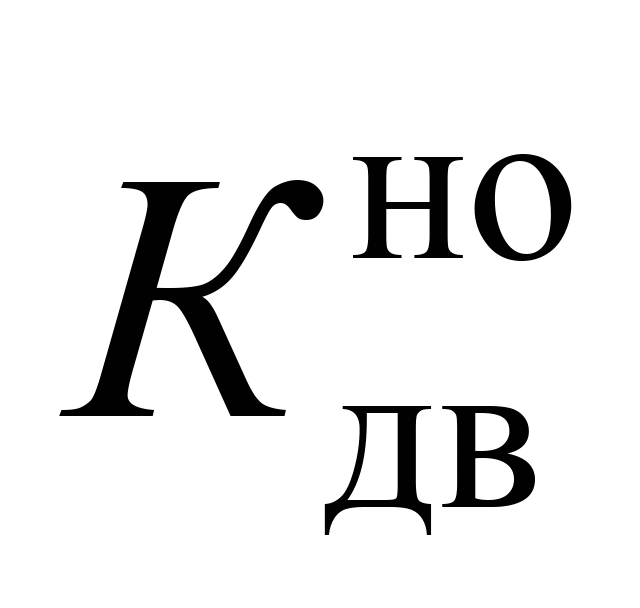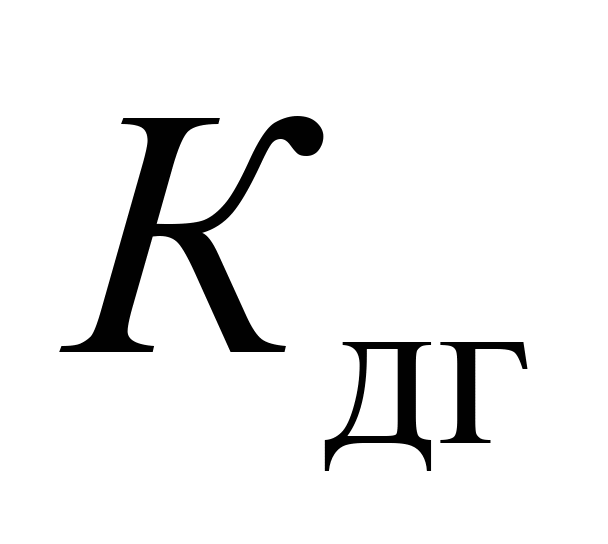– максимальні коефіцієнти динамічної добавки обресорених і необресорених частин , максимальне відношення рамної сили до статичного осьового навантаження та коефіцієнт стійкості від сходження колеса з рейок 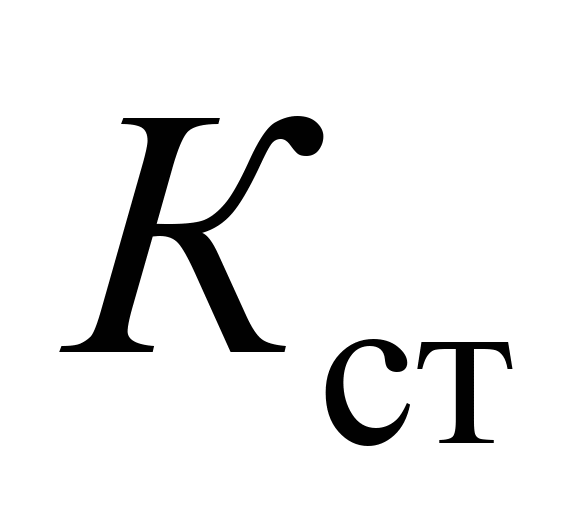більше залежать від швидкості руху, ніж від кута повороту центральної осі кузова вагона ;

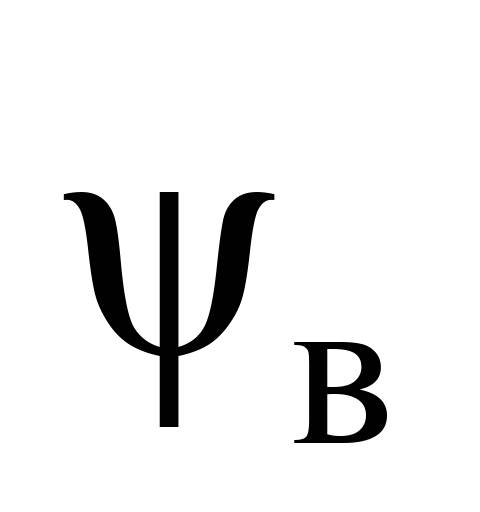– проаналізовані показники взаємодії рухомого складу з колією не перевищують нормативних значень та мають екстремуми за 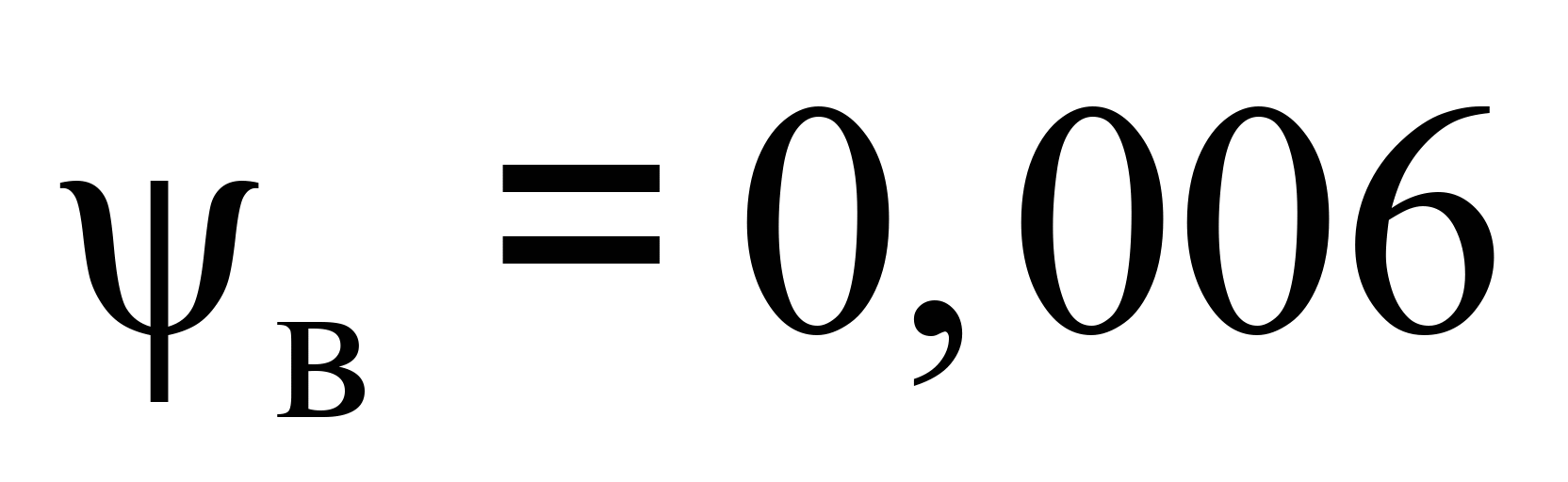рад;

– одночасне збільшення кута повороту центральної осі кузова вагона 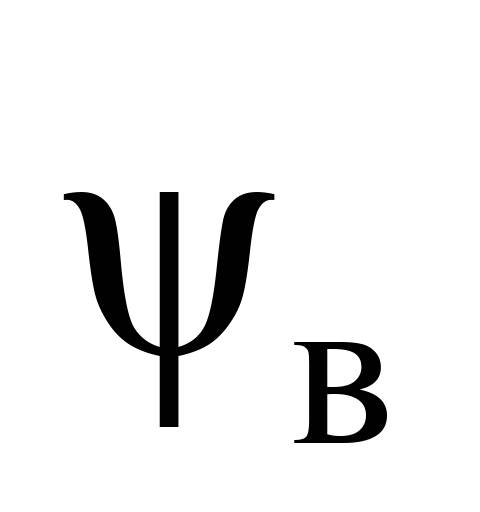та швидкості руху призводить до підвищення фактора зносу коліс та рейок;

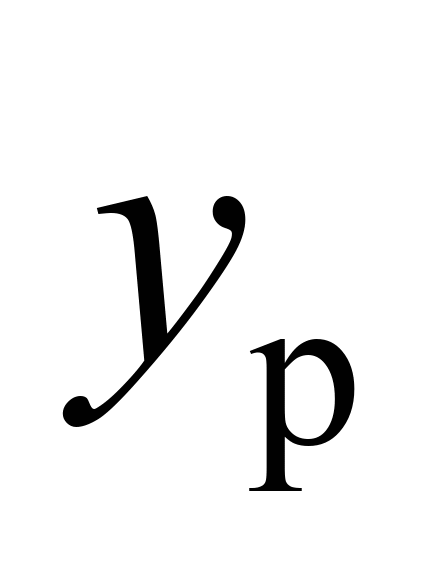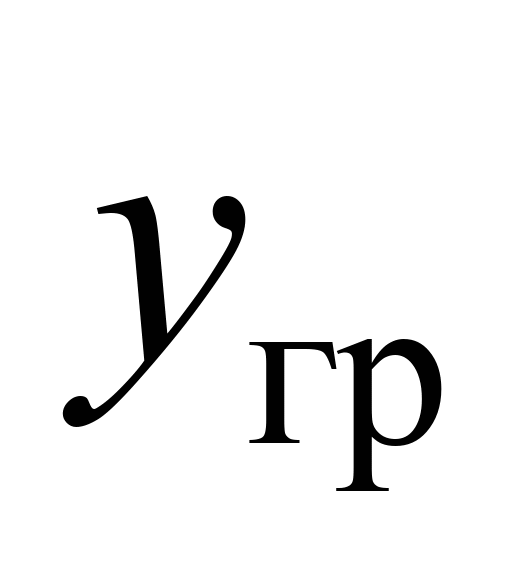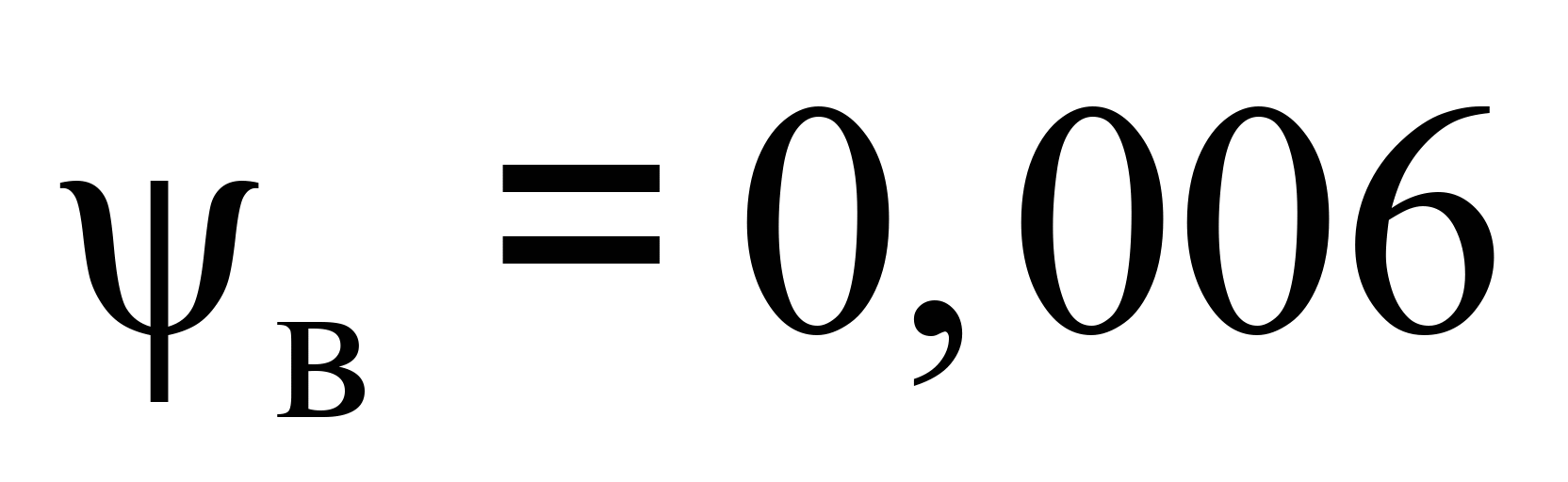– зі збільшенням швидкості руху відтискаються внутрішні обшивні костилі та головки рейок , обидва показники мають максимальні значення в разі кута повороту центральної осі кузова вагона рад;

– отримані результати розрахунків відповідають експериментальним даним за величинами відтискань підошви рейки .

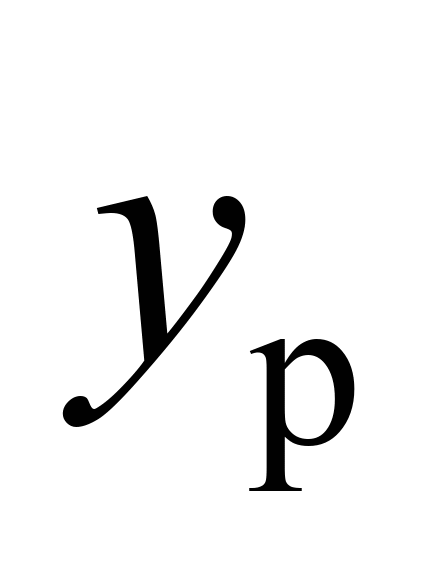СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1. Акулов А. С., Желєзнов К. І., Заболотний О. М., Пуларія А. Л., Чабанюк Є. В., Швець А. О. Розробка програмного комплексу «Тренажер оглядача вагонів». Вагонний парк. 2018. № 6 (138). С. 18–21.

2. Блохин Е. П., Коротенко М. Л., Луханин Н. И. Динамика подвижного состава и безопасность движения. Перспективи впровадження технічних засобів безпеки руху на залізницях України : зб. наук. пр. 10-ї наук.-практ. конф. (Київ, 8-10 верес. 2010 р.). Київ, 2010. С. 16–21.

3. Даніленко Е. І. Залізнична колія : підруч. для вищ. навч. закл. : у 2 т. Київ : Інпрес, 2010. Т. 2. 456 с.

4. Данович В. Д. Пространственные колебания вагонов на инерционном основании : дис. … д-ра техн. наук. Днепропетр. ин-т инж. ж.-д. трансп. Днепропетровск, 1981. 465 с.

5. Данович В. Д., Малышева А. А. Математическая модель пространственных колебаний сцепа пяти вагонов, движущихся по прямолинейному участку пути. Транспорт. Нагруженность и прочность подвижного состава : сб. науч. тр. Днепропетр. гос. техн. ун-т ж.-д. трансп. Днепропетровск, 1998. С. 62–69.

6. ДСТУ ГОСТ 33211:2017. Вагони вантажні. Вимоги до міцності та динамічних якостей (ГОСТ 33211-2014, IDТ). [Чинний від 2017-07-01]. Київ : УкрНДНЦ, 2017. 58 с.

7. Курган Д. М., Губар О. В., Гаврилов М. О. Методика інженерного розрахунку коефіцієнта стійкості проти вкочування колеса на рейку. Наука та прогрес транспорту. 2020. № 3 (87). С. 71–80. DOI: 10.15802/stp2020/208202

8. Луханин Н. И., Мямлин С. В., Недужая Л. А., Швец А. А. Динамика грузовых вагонов с учетом поперечного смещения тележек. Зб. наук. праць Донецького інституту заліз. тр-ту. 2012. Вип. 29. С. 234–241.

9. Лысюк В. С. Причины и механизмы схода колеса с рельса. Проблема износа колес и рельсов : 2-е изд., перераб. и доп. Москва : Транспорт, 2002. 215 с.

10. Мугинштейн Л. А., Ромен Ю. С. Влияние продольных сил на опасность сходов порожних вагонов в поездах. Вестник ВНИИЖТ. 2011. № 3. С. 3–6.

11. Мямлін С. В., Мурадян Л. А., Подосьонов Д. О. Підвищення надійності п'ятникового вузла вантажного вагону. Залізничний транспорт України. 2018. Вип. 1. С. 34–41.

12. Швець А. О. Визначення стійкості вантажних вагонів з урахуванням параметрів залізничної колії. Наука та прогрес транспорту. 2020. № 2 (86). С. 103–118. DOI: 10.15802/stp2020/203421

13. Швець А. О. Динаміка піввагонів від дії поздовжніх сил. Наука та прогрес транспорту. 2019. № 6 (84). С. 142–155. DOI: 10.15802/stp2019/195821

14. Cao T. N. T., Reddy J. N., Ang K. K., Luong V. H., Tran M. T., Dai J. Dynamic analysis of three-dimensional high-speed train-track model using moving element method. Advances in Structural Engineering. 2018. Vol. 21. Iss. 6. P. 862–876. DOI: 10.1177/1369433217733763

15. Hazrati Ashtiani I., Rakheja S., Ahmed A. Influence of friction wedge characteristics on lateral response and hunting of freight wagons with three-piece bogies. Proceedings of the Institution of Mechanical Engineers, Part F : Journal of Rail and Rapid Transit. 2017. Vol. 231. Iss. 8. P. 877–891. DOI: 10.1177/0954409716647095

16. Kampczyk A. Measurement of the Geometric Center of a Turnout for the Safety of Railway Infrastructure Using MMS and Total Station. Sensors. 2020. Vol. 20. Iss. 16. P. 1–35. DOI: 10.3390/s20164467

17. Kurhan M., Kurhan D. Providing the Railway Transit Traffic Ukraine–European Union. Pollack Perodica. 2019. Vol. 14. Iss. 2. P. 27–38. DOI: 10.1556/606.2019.14.2.3

18. Mei H., Leng W., Nie R., Tu R., Li Y., Dong J. Experimental research on the dynamic response characteristics of the transition subgrade induced by heavy-haul train passage. Proceedings of the Institution of Mechanical Engineers, Part F : Journal of Rail and Rapid Transit. 2019. Vol. 233. Iss. 9. P. 974–987. DOI: 10.1177/0954409718822924

19. Rezvani M. A., Mazraeh A. Dynamics and stability analysis of a freight wagon subjective to the railway track and wheelset operational conditions. European Journal of Mechanics – A/Solids. 2017. Vol. 61. P. 22–34. DOI: 10.1016/j.euromechsol.2016.08.011

20. Sysyn M., Nabochenko O., Kovalchuk V. Experimental investigation of the dynamic behavior of railway track with sleeper voids. Railway Engineering Science. 2020. Vol. 28. Iss. 3. P. 290–304. DOI: 10.1007/s40534-020-00217-8

21. Xing L. L., Wang Y. M., Dong X. Q. Effect of the Wheel/Rail contact geometry on the stability of railway vehicle. IOP Conference Series : Materials Science and Engineering. 2018. Vol. 392. Iss. 6. P. 1–11.
    DOI: 10.1088/1757-899X/392/6/062134

22. Ye Y., Ning J. Small-amplitude hunting diagnosis method for high-speed trains based on the bogie frame’s lateral–longitudinal–vertical data fusion, independent mode function reconstruction and linear local tangent space alignment. Proceedings of the Institution of Mechanical Engineers, Part F : Journal of Rail and Rapid Transit. 2019. Vol. 233. Iss. 10. P. 1050–1067. DOI: 10.1177/0954409718825412

23. Zhu T., Yang B., Yang C., Xiao S., Yang G., Yang B. The mechanism for the coupler and draft gear and its influence on safety during a train collision. Vehicle System Dynamics. 2018. Vol. 56. Iss. 9. P. 1375–1393. DOI: 10.1080/00423114.2017.1413198

А. А. Швец^1*

^1*Каф «Теоретическая и строительная механика», Днипровский национальный
университет железнодорожного транспорта имени академика В. Лазаряна,
ул. Лазаряна, 2, Днипро, Украина, 49010, тел. +38 (050) 214 14 19,
эл. почта angela_Shvets@ua.fm, ORCID 0000-0002-8469-3902

Влияние на динамику грузовых вагонов

поперечного смещения ТЕЛЕЖЕК

Цель. Работа направлена на определение влияния поперечного смещения тележки грузового вагона с учетом величины скорости движения на его основные динамические показатели и показатели взаимодействия подвижного состава с колеей. Методика. Количественная оценка динамических показателей получена методом математического и компьютерного моделирования. Расчетная схема учитывает особенности взаимодействия вагонов в составе поезда: возможность проявления всех форм колебаний кузова в пространстве, передачу продольной силы в вертикальном и горизонтальном направлениях от соседних вагонов, учет технического состояния отдельных частей вагона и их конструктивных особенностей, а также различные условия эксплуатации. Результаты. В процессе исследования применена математическая модель сцепа из пяти грузовых вагонов для изучения динамической нагруженности полувагона и пути. Проведена оценка основных динамических показателей и показателей взаимодействия подвижного состава с колеей в случае поперечного смещения тележки при движении по криволинейным участкам железнодорожного пути. Обосновано максимально возможные величины поперечного смещения тележки грузового вагона. Научная новизна. Доработана математическая модель сцепа грузовых вагонов в составе поезда. В расчетных схемах, описывающих колебания, учтены особенности тележек грузовых вагонов – забегания боковых рам. Модель позволяет исследовать влияние изменения угла поворота центральной оси кузова вагона, что в свою очередь приводит к поперечному смещению тележек относительно друг друга, на основные динамические показатели и показатели взаимодействия подвижного состава с колеей. Впервые исследовано влияние поперечного смещения тележки с учетом износов её деталей и узлов при движении на участках пути с неровностями. Практическая значимость. Результаты расчетов можно применять при оценке влияния поперечного смещения тележки на динамические качества подвижного состава и показатели взаимодействия подвижного состава с колеей с учетом износов деталей и узлов тележки при движении в прямых и криволинейных участках пути с неровностями. Применение полученных результатов будет способствовать повышению устойчивости грузового подвижного состава в условиях повышения скоростей движения, что в свою очередь позволит разработать технические условия для реализации ресурсосберегающих технологий транспортировки грузов, отвечающих требованиям безопасности движения поездов.

Ключевые слова: безопасность движения; динамические показатели; смещение тележек; полувагон; скорость движения

A. O. shvets^1*

^1*Dep. «Theoretical and Structural Mechanics», Dnipro National
University of Railway Transport named after Academician
V. Lazaryan, Lazaryana St., 2, Dnipro, Ukraine, 49010,
tel. +38 (050) 214 14 19, e-mail angela_Shvets@ua.fm,
ORCID 0000-0002-8469-3902

INFLUENCE of lateral displacement

of bogies ON THE FREIGHT car DYNAMICS

Purpose. The work is aimed at determining the influence of the lateral displacement of a freight car bogie, taking into account the value of the movement speed on its main dynamic indicators and interaction indicators of the rolling stock and the track. Methodology. The quantitative assessment of dynamic indicators was obtained by the method of mathematical and computer modeling. The design scheme of the car takes into account the interaction peculiarities of cars as part of the train: the possibility of all modes of body vibration in space, the transmission of longitudinal force from neighboring cars in vertical and horizontal directions, taking into account the technical condition of individual parts of the car and their design features, as well as various operating conditions. Findings. During the research, a mathematical model of a coupling of five freight cars was applied to study the dynamic loading of a gondola car and a track. Main dynamic and interaction indicators of the rolling stock and the track in case of transverse bogie displacement when moving along curved track sections assessment were assessed. The maximum possible values of the lateral displacement of the freight car bogie were substantiated. Originality. The mathematical model of the coupling of freight cars in the train has been improved. In the calculation schemes describing the vibrations of the cars, the peculiarities of the freight car bogies, lozenging of the bogie side frames are taken into account. The model makes it possible to study the effect of changing rotation angle of the central axis of the car body, which in turn leads to the lateral displacement of bogies relative to each other, on the main dynamic and interaction indicators of the rolling stock and the track. For the first time, the influence of transverse displacement of the bogie was investigated, taking into account the wear of its parts and assemblies when moving on track sections with unevenness. Practical value. The calculation results can be used to assess the influence of the bogie transverse displacement on the dynamic qualities of the rolling stock and interaction indicators of the rolling stock and the track, taking into account the wear of parts and units of the bogie when moving in straight and curved track sections with irregularities. The application of the results obtained will contribute to an increase in the stability of freight rolling stock in the conditions of increasing travel speeds, which in turn will allow developing technical conditions for the implementation of resource-saving technologies for transporting goods that meet the safety requirements of train traffic.

Keywords: traffic safety; dynamic indicators; displacement of bogies; gondola car; movement speed

REFERENCES

1. Akulov, A. S., Zhelieznov, K. I., Zabolotnyi, O. M., Pulariia, A. L., Chabaniuk, Ye. V., & Shvets, A. O. (2018). Development of the Software Complex «Simulator of the Railway Carriage Inspector». Vaghonnyj park, 6, 18-21. (in Ukrainian)

2. Blokhin, E. P., Korotenko, M. L., & Lukhanin, N. I. (2010). Rolling stock dynamics and traffic safety. In Perspektyvy vprovadzhennia tekhnichnykh zasobiv bezpeky rukhu na zaliznytsiakh Ukrainy: Tezisy X nauchno-prakticheskoy konferentsii (pp. 16-20). Kiev, 16-20. (in Russian)

3. Danilenko, E. I. (2010). Zaliznychna koliia. (Vol. 2). Kyiv: Inpres. (in Ukrainian)

4. Danovich, V. D. (1982). Spatial Cars Oscillations in Inertia Track. (Dysertatsiia doktora tekhnichnykh nauk). Dnepropetrovsk Institute of Railway Transport Engineering, Dnеpropetrovsk. (in Russian)

5. Danovich, V. D., & Malysheva, A. A. (1998). Mathematical Model of Spatial Oscillations of the Coupling of Five Cars Moving Along a Rectilinear Section of the Track. In Transport. Stress loading and durability of a rolling stock, 62-69. Dnepropetrovsk. (in Russian)

6. Vahony vantazhni. Vymohy do mitsnosti ta dynamichnykh yakostei, 58 DSTU 33211:2017 (2017). (in Ukrainian)

7. Kurhan, D. M., Hubar, O. V., & Havrilov, M. O. (2020). Methodology for engineering calculation of stability coefficient against wheel climbing on the rail. Science and Transport Progress, 3(87), 71-80.
   DOI: 10.15407/scin12.06.006 (in Ukrainian)

8. Lukhanin, N. I., Myamlin, S. V., Neduzhaya, L. A., & Shvets, A. A. (2012). Dinamika gruzovykh vagonov s uchetom poperechnogo smeshcheniya telezhek. Zbirnik naukovih prac' of Donetsk Railway Transport Institute, 29, 234-241. (in Russian)

9. Lysyuk, V. S. (2002). Prichiny i mekhanizmy skhoda kolesa s relsa. Problema iznosa koles i relsov. Moscow: Transport. (in Russian)

10. Muginshteyn, L. A., & Romen, Yu. S. (2011). Vliyanie prodolnykh sil na opasnost skhodov porozhnikh vagonov v poezdakh. Vestnik VNIIZhT, 3, 3-6. (in Russian)

11. Myamlin, S. V., Muradian, L. A., & Podosenov, D. O. (2018). Increase of reliability of thrust bearing of freight car. Railway transport of Ukraine, 1, 34-41. (in Ukrainian)

12. Shvets, A. O. (2020). Determination of the Stability of Freight Cars Taking Into Account the Railway Track Parameters. Science and Transport Progress, 2(86), 103-118. DOI: 10.15802/stp2019/195821 (in Ukrainian)

13. Shvets, A. O. (2019). Gondola cars dynamics from the action of longitudinal forces. Science and Transport
    Progress, 6(84), 142-155. DOI: 10.15802/stp2019/195821 (in Ukrainian)

14. Cao, T. N. T., Reddy, J., Ang, K. K., Luong, V. H., Tran, M. T., & Dai, J. (2017). Dynamic analysis of three-dimensional high-speed train-track model using moving element method. Advances in Structural Engineering, 21(6), 862-876. DOI: 10.1177/1369433217733763 (in English)

15. Hazrati Ashtiani, I., Rakheja, S., & Ahmed, A. (2016). Influence of friction wedge characteristics on lateral response and hunting of freight wagons with three-piece bogies. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 231(8), 877-891. DOI: 10.1177/0954409716647095 (in English)

16. Kampczyk, A. (2020). Measurement of the Geometric Center of a Turnout for the Safety of Railway Infrastructure Using MMS and Total Station. Sensors, 20(16), 1-35. DOI: 10.3390/s20164467 (in English)

17. Kurhan, M., & Kurhan, D. (2019). Providing the railway transit traffic Ukraine–European Union. Pollack
    Perodica, 14(2), 27-38. DOI: 10.1556/606.2019.14.2.3 (in English)

18. Mei, H., Leng, W., Nie, R., Tu, R., Li, Y., & Dong, J. (2019). Experimental research on the dynamic response characteristics of the transition subgrade induced by heavy-haul train passage. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 233(9), 974-987. DOI: 10.1177/0954409718822924 (in English)

19. Rezvani, M. A., & Mazraeh, A. (2017). Dynamics and stability analysis of a freight wagon subjective to the railway track and wheelset operational conditions. European Journal of Mechanics – A/Solids, 61, 22-34. DOI: 10.1016/j.euromechsol.2016.08.011 (in English)

20. Sysyn, M., Nabochenko, O., & Kovalchuk, V. (2020). Experimental investigation of the dynamic behavior of railway track with sleeper voids. Railway Engineering Science, 28(3), 290-304. DOI: 10.1007/s40534-020-00217-8 (in English)

21. Xing, L. L., Wang, Y. M., & Dong, X. Q. (2018). Effect of the Wheel/Rail contact geometry on the stability of railway vehicle. IOP Conference Series: Materials Science and Engineering, 392(6), 1-11. DOI: 10.1088/1757-899X/392/6/062134 (in English)

22. Ye, Y., & Ning, J. (2019). Small-amplitude hunting diagnosis method for high-speed trains based on the bogie frame’s lateral–longitudinal–vertical data fusion, independent mode function reconstruction and linear local tangent space alignment. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 233(10), 1050-1067. DOI: 10.1177/0954409718825412 (in English)

23. Zhu, T., Yang, B., Yang, C., Xiao, S., Yang, G., & Yang, B. (2017). The mechanism for the coupler and draft gear and its influence on safety during a train collision. Vehicle System Dynamics, 56(9), 1375-1393. DOI: 10.1080/00423114.2017.1413198 (in English)

Надійшла до редколегії: 03.08.2020

Прийнята до друку: 03.12.2020

Creative Commons Attribution 4.0 International

doi: 10.15802/stp2020/223519
© А. А. Швець, 2020