ISSN 2307–3489 (Print), ІSSN 2307–6666 (Online)

Наука та прогрес транспорту. Вісник Дніпропетровського
національного університету залізничного транспорту, 2020, № 5 (89)

ЕКОЛОГІЯ ТА ПРОМИСЛОВА БЕЗПЕКА

Введение

Повышение качества очистки сточных вод является важной проблемой. В технологических схемах очистки задействованы различные сооружения. При изменении объема сточных вод, которые поступают на очистные станции, и при изменении их состава возникает задача оценки эффективности работы очистных сооружений в новых условиях эксплуатации. Для этого широко используют математические модели разного уровня – эмпирические, регрессионные, аналитические, численные [3–5, 7–12]. Наиболее часто на практике используют эмпирические модели, которые позволяют быстро определить необходимые показатели работы очистного сооружения, но данные модели не могут быть использованы для расчета сооружений, которые имеют другую геометрию. С этой точки зрения наиболее эффективными являются CFD-модели [1, 2, 6–10]. Однако в настоящий момент в Украине имеется определенный дефицит CFD-моделей, поэтому актуальной проблемой является создание эффективных численных моделей расчёта сооружений по очистке сточных вод.

Цель

Основной целью данной работы является разработка CFD-модели процесса очистки сточных вод в отстойниках с дополнительными элементами.

Методика

Для математического моделирования процесса очистки сточных вод используют два класса математических моделей, на основе которых рассчитывают гидродинамику течения в сооружении. Первый класс моделей – это модели, которые основаны на уравнениях движения невязкой жидкости [1, 2]. Модели второго класса основаны на уравнениях Навье–Стокса. В данной работе будем использовать уравнения Навье–Стокса, записанные в переменных «завихренность – функция тока»:

где Re = V₀L/υ – число Рейнольдса (тут υ – кинематический коэффициент вязкости); y – функция тока; ω = ∂v/∂x-∂u/∂y – вихрь; u = ∂y/∂y; v = –∂y/∂x – компоненты вектора скорости водного потока; L – характерный размер; V₀ – характерная скорость.

Для расчета процесса распространения загрязнителя в очистном сооружении используем уравнение массопереноса [1, 2]:

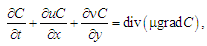(3)

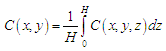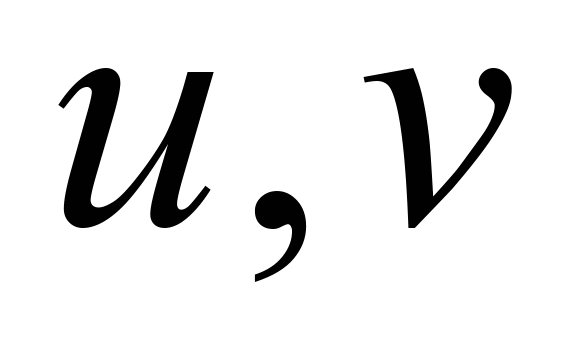где – усредненная концентрация загрязнителя; H – глубина сооружения; – компоненты скорости потока в направлении x, y соответственно; 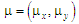– коэффициенты диффузии; 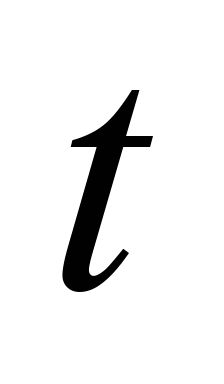– время.

Граничные условия для уравнения массопереноса (3) такие:

1. На входе:

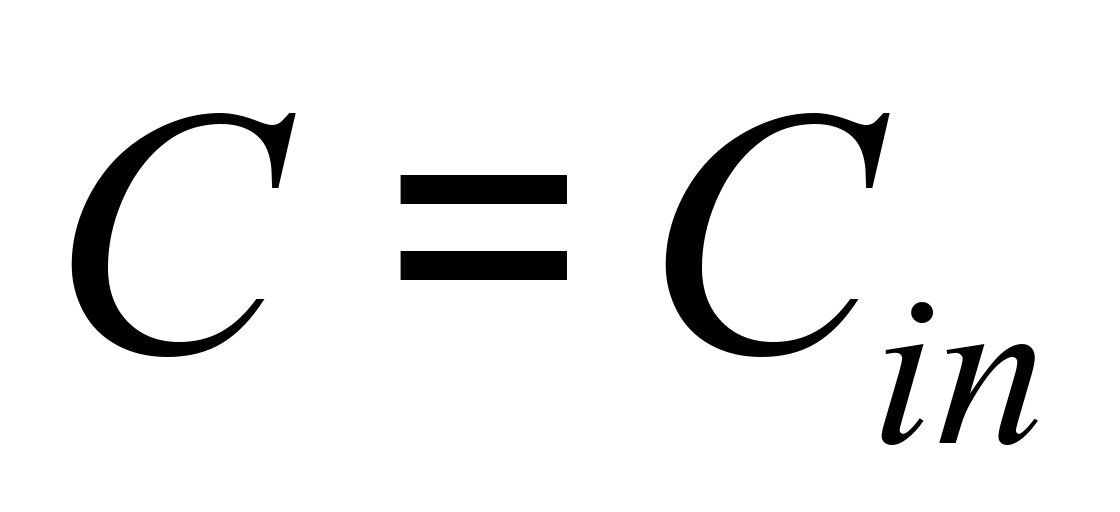, (4)

где C_in – известная концентрация загрязнителя.

2. На выходе:

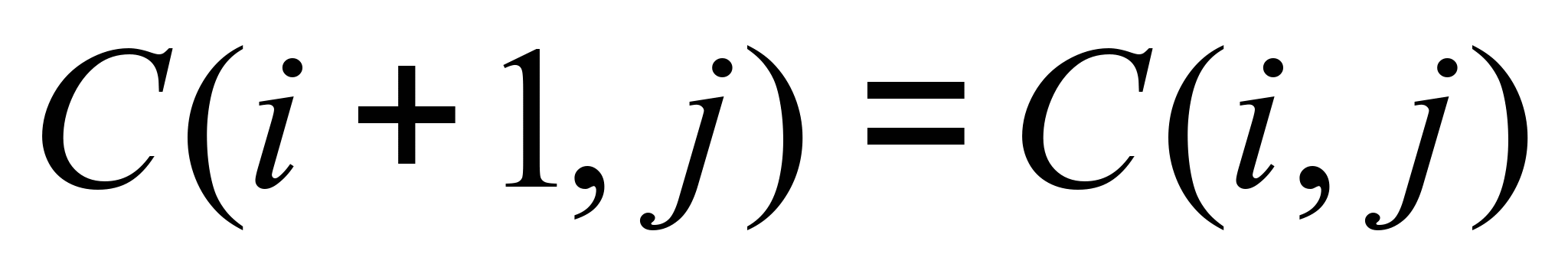, (5)

где C(i+1,j) – концентрация загрязнителя в последней вычислительной ячейке; C(i,j) – концентрация загрязнителя в предыдущей вычислительной ячейке.

3. На стенках:

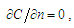
где 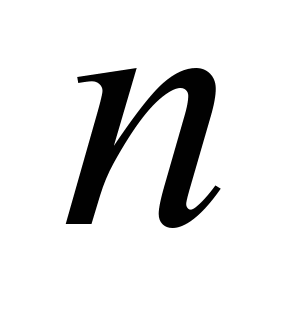является вектором нормали к границе.

Начальное условие:

,

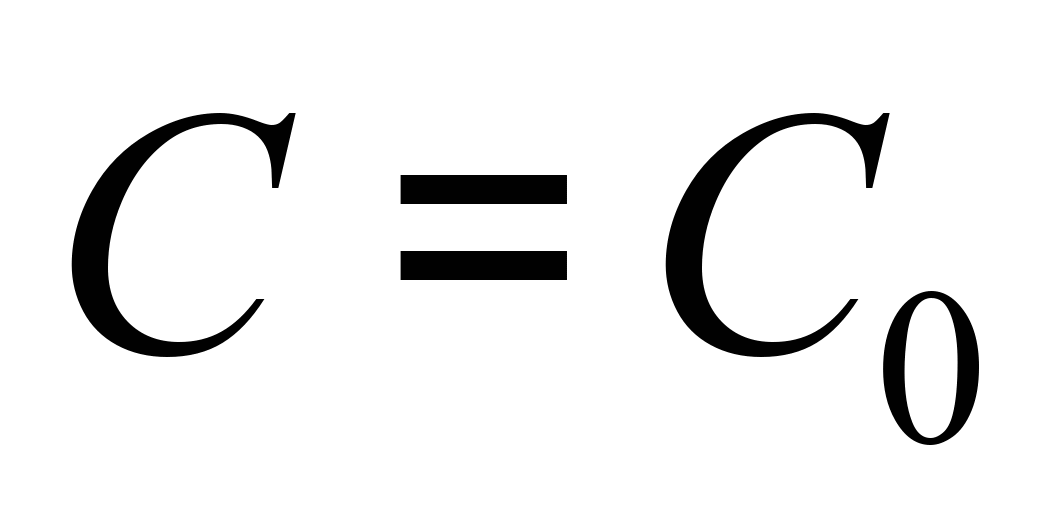где C₀ – концентрация загрязнителя в очистном сооружении на момент начала расчета.

Численная модель. Для интегрирования моделирующих уравнений будем использовать конечно-разностные методы. Рассмотрим сначала разностную схему расщепления для решения уравнения массопереноса. Исходное уравнение перед построением разностной схемы расщепляется на два уравнения следующим образом:

На следующем этапе выполняем аппроксимацию производных для каждого уравнения [1, 2]:

Производные, связанные со скоростью потока, записываем так:

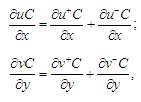
где .

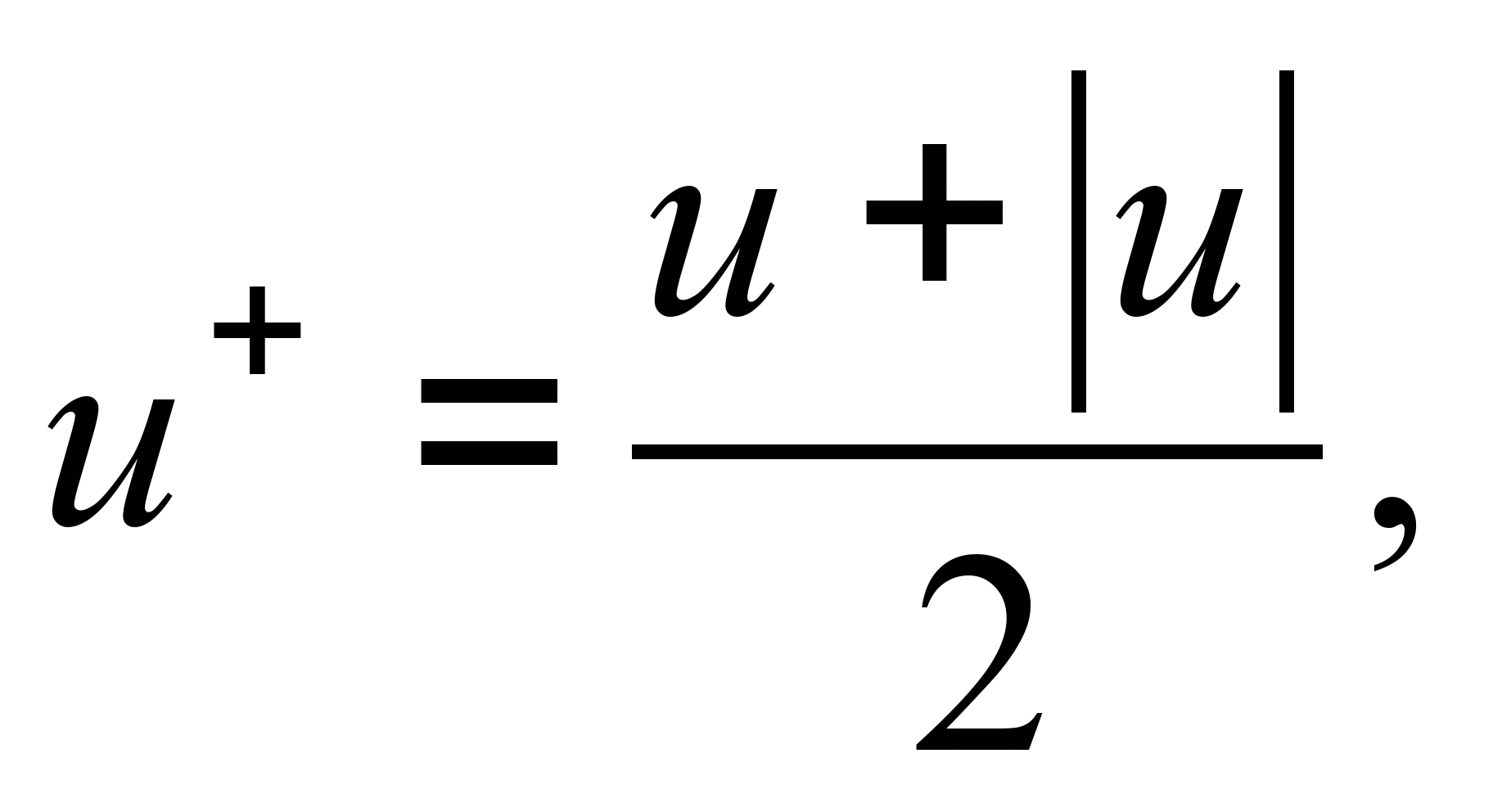
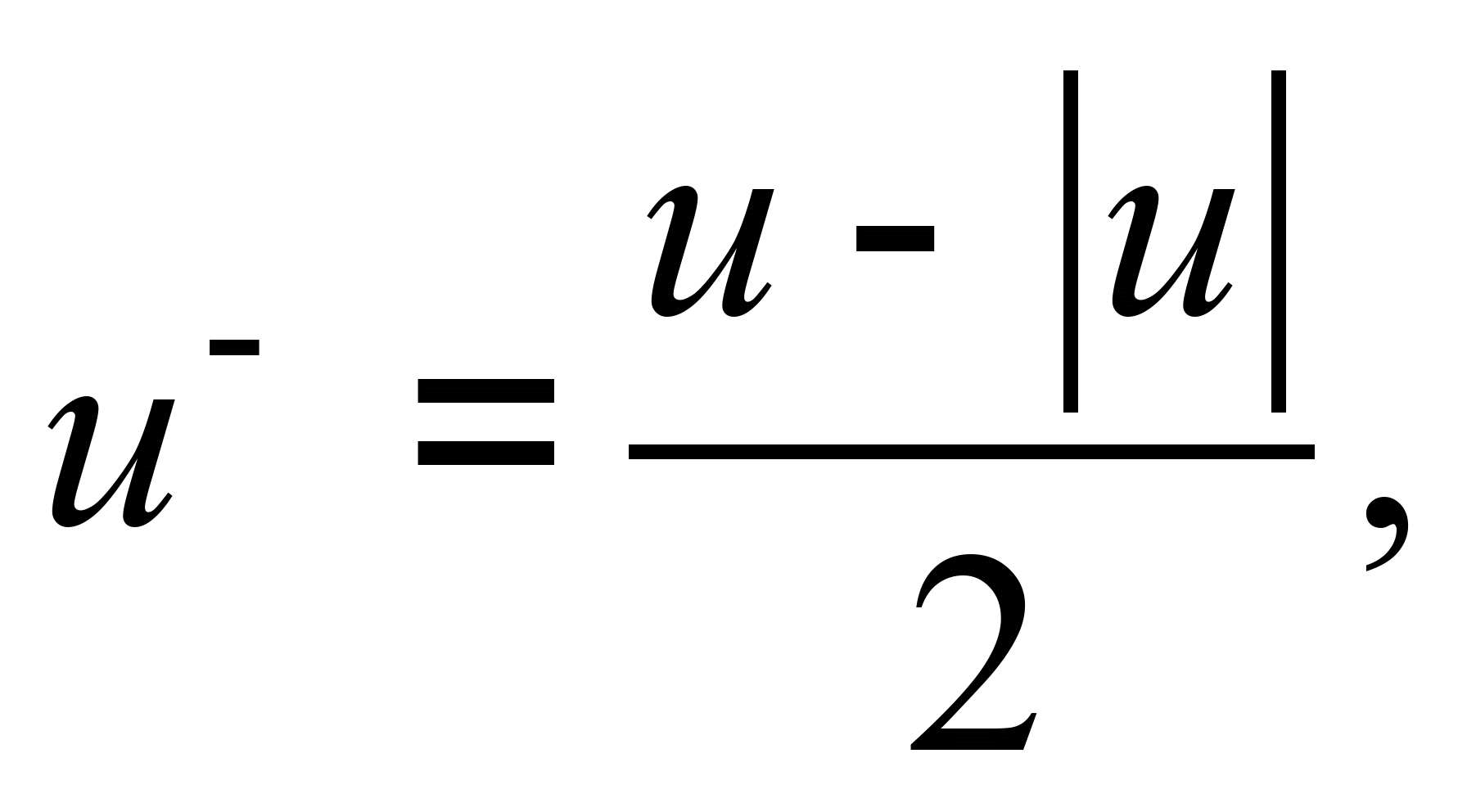
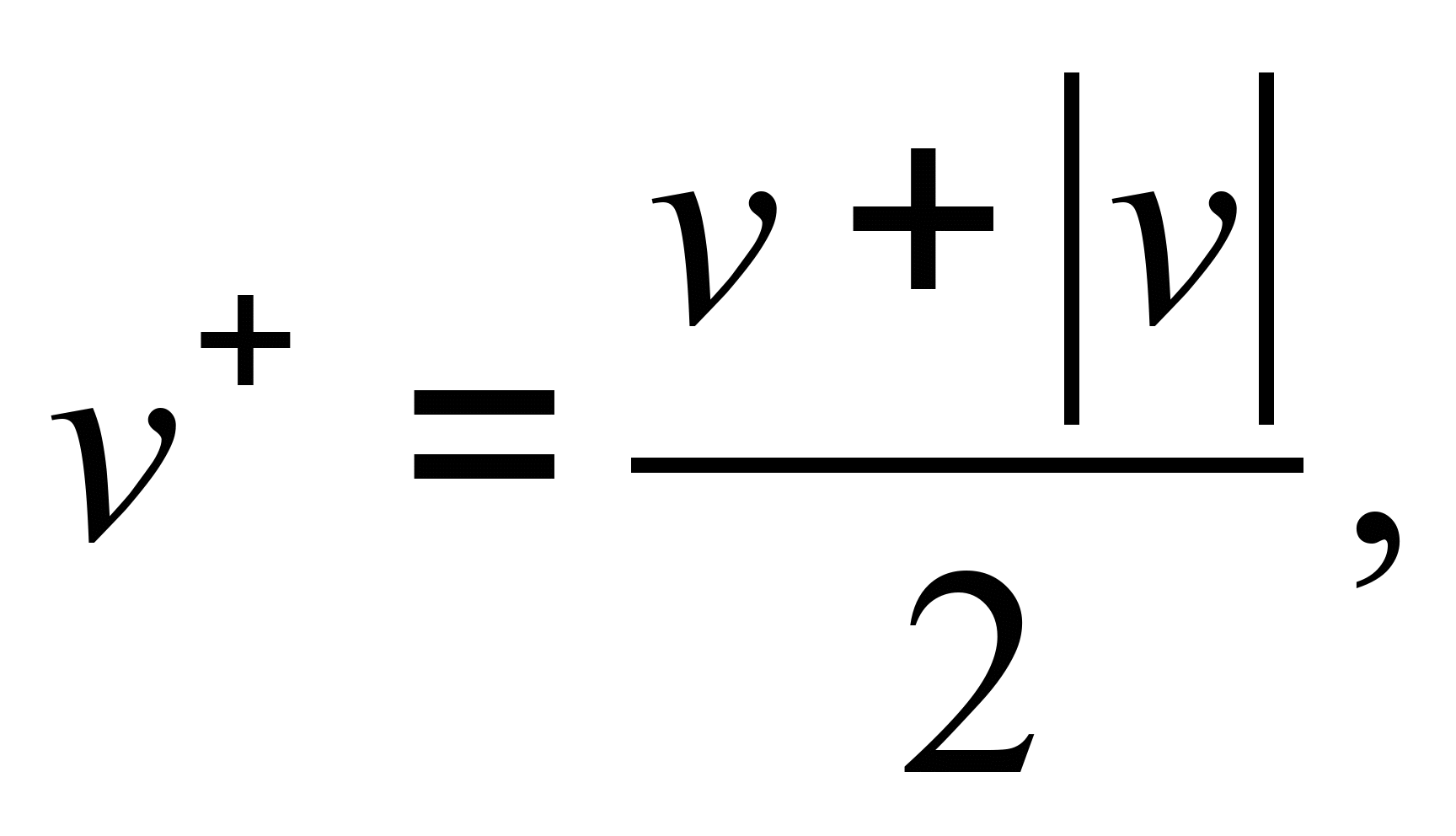
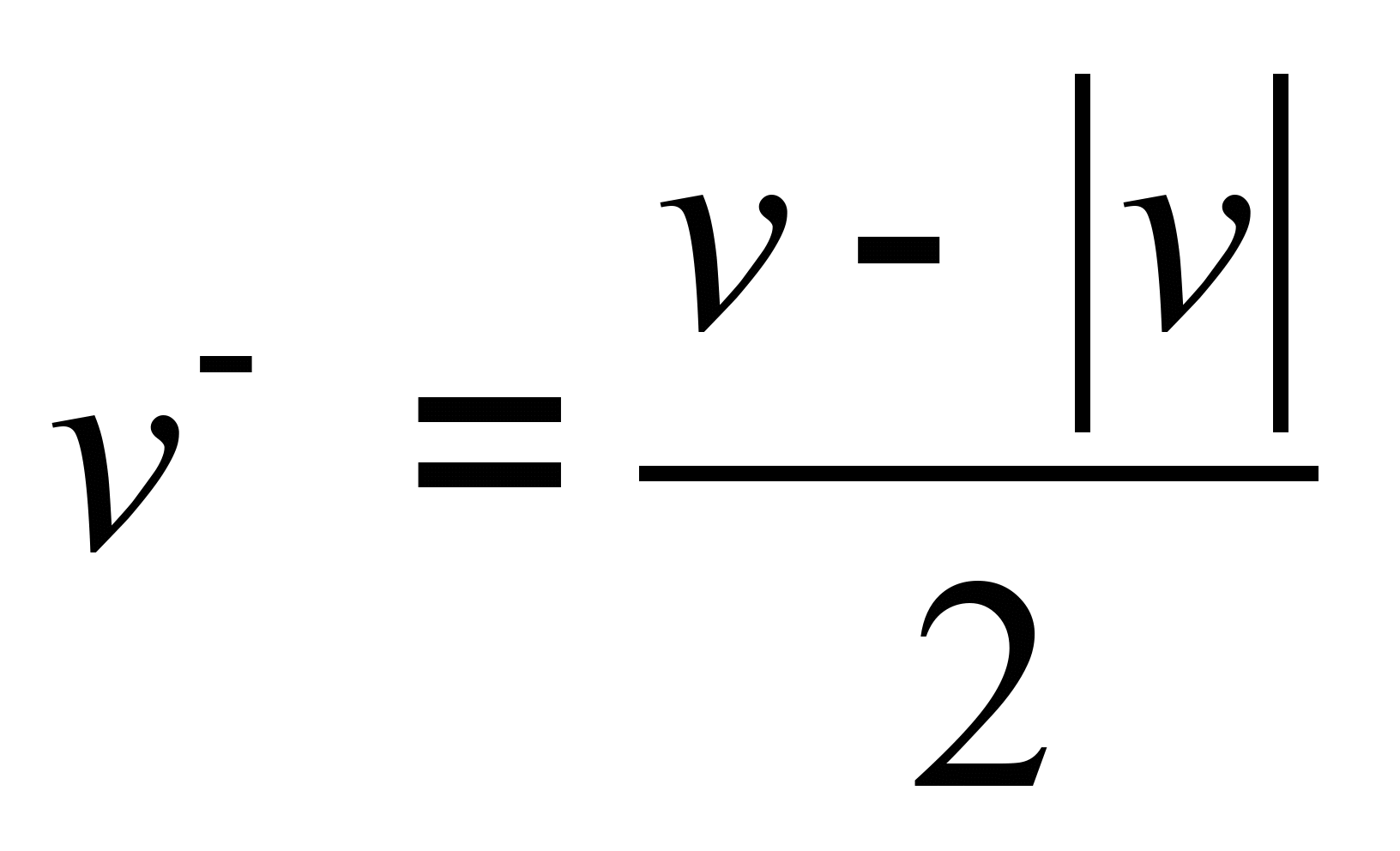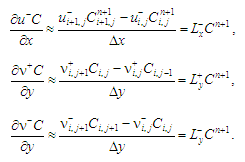
После проведения таких преобразований разностную схему расщепления представляем в виде:

– на первом этапе k = 1/2:

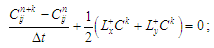(8)

– на втором этапе k = 1, c = n+1/2:

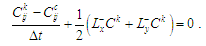(9)

Особенностью этой разностной схемы является то, что неизвестное значение концентрации загрязнителя находят на каждом шаге расщепления по явной формуле.

Аналогичный подход используем к построению разностной схемы для численного интегрирования уравнения переноса вихря:

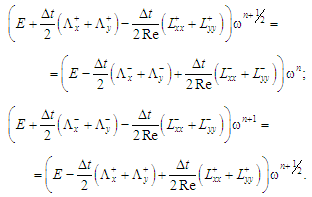
Обозначения разностных операторов, которые представлены в приведенной схеме, указаны в [1, 2]. При численном интегрировании уравнения для функции тока применяем разностную схему, описанную в работе [1].

Алгоритм проведения расчета. Построенная численная модель была реализована в виде пакета прикладных программ. Процедура расчета такая:

– этап №1: формируем вид расчетной области, задаем исходные параметры, определяющие массоперенос в очистном сооружении;

– этап №2: осуществляем расчет уравнения переноса вихря;

– этап №3: осуществляем расчет уравнения для функции тока;

– этап №4: осуществляем расчет поля скорости в очистном сооружении;

– этап №5: осуществляем расчет концентрации загрязнителя в очистном сооружении.

Необходимо отметить, что время решения задачи по оценке эффективности работы очистного сооружения на базе разработанной модели составляет порядка 15 с.

Результаты

На рис. 1 показано распределение концентрации загрязнителя в отстойнике, который имеет два входа и два выхода (плановая модель).

Расчет было выполнено для отстойника, форма которого существенно отличается от классического варианта, а именно: в отстойнике расположены две горизонтальные пластины и одна поперечная. Эти пластины изменяют гидродинамику потока и влияют на эффективность очистки воды в сооружении. Оценку эффективности очистки осуществляют по концентрации загрязнителя на выходе из отстойника. Как видно из представленного рисунка, концентрация загрязнителя на выходе из сооружения составляет порядка 22–29 %.

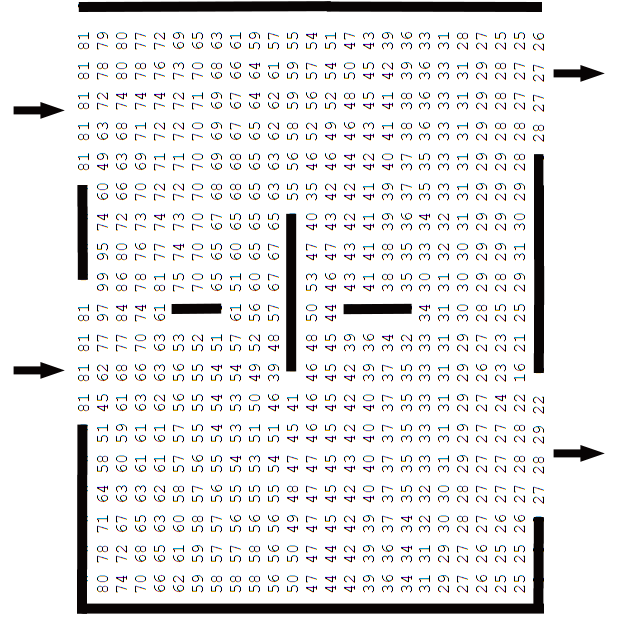
Рис. 1. Поле концентрации загрязнителя
в отстойнике

Fig. 1. Pollutant concentration field in the settler

Научная новизна и практическая
значимость

Разработана CFD-модель для расчета концентрации загрязнителя в сооружении используется для очистки сточных вод (отстойнике). Моделирующими уравнениями являются уравнения Навье–Стокса (для расчета гидродинамики течения в очистном сооружении) и двухмерное уравнение массопереноса, учитывающее конвективную и диффузионную составляющие переноса. Модель может быть использована для проведения серийных расчетов при проектировании новых очистных сооружений.

Выводы

В статье представлено описание эффективной CFD-модели, разработанной для расчета гидродинамики течения и массопереноса загрязнителя в отстойнике. Для решения задачи использованы фундаментальные двухмерные уравнения механики сплошной среды. Последующие работы в этой области будут связаны с разработкой гидродинамической 3D-модели.

Список использованных источников

1. Беляев Н. Н., Козачина В. А. Математическое моделирование массопереноса в горизонтальных отстойниках : монография. Днепропетровск : Акцент ПП, 2015. 115 с.

2. Беляев Н. Н., Нагорная Е. К. Математическое моделирование массопереноса в отстойниках систем водоотведения : монография. Днепропетровск : Новая идеология, 2012. 112 с.

3. Колобанов С. К., Ершов А. В., Кигель М. Е. Проектирование очистных сооружений канализации.
   Киев : Будівельник, 1997. 224 с.

4. Олейник Я. А., Калугин Ю. И., Степовая Н. Г., Зябликов С. М. Теоретический анализ процессов осаждения в системах биологической очистки сточных вод. Прикладна гідромеханіка. 2004. Т. 6 (78), № 4. С. 62–67.

5. Олійник О. Я, Айрапетян Т. С. Моделювання очисних стічних вод від органічних забруднень в біореакторах-аеротенках зі зваженим (вільно плаваючим) і закріпленим біоценозом. Доповідь НАН України. 2015. № 5. С. 55–60. DOI: 10/15407/dopovidi2015.05.055

6. Biliaiev M. M., Kozachyna V. A. Numerical determination of horizontal settlers performance. Наука та прогрес транспорту. 2015. № 4 (58). P. 34–43. DOI: 10.15802/STP2015/49201

7. Hadad H., Ghaderi J. Numerical Simulation of the Flow Pattern in the Aeration Tank of Sewage Treatment System by the Activated Sludge Process Using Fluent Program. Biological Forum – An International Journal. 2015. Vol. 7 (1). P. 382–393.

8. Luna F. D., Silva A. G., Fukumasu N. K., Bazan O., Gouveia J. H. A., Moraes D., … Vianna A. S. Fluid dynamics in continuous settler. Chemical Engineering Journal. 2019. Vol. 362. P. 712–720. DOI: 10.1016/j.cej.2019.01.088

9. Misra A., de Souza L. G. M., Illner M., Hohl L., Kraume M., Repke J.-U., Thévenin D. Simulating separation of a multiphase liquid-liquid system in a horizontal settler by CFD. Chemical Engineering Science. 2017. Vol. 167. P. 242–250. DOI: 10.1016/j.ces.2017.03.062

10. Panda S. K., Singh K. K., Shenoy K. T., Buwa V. V. Numerical simulations of liquid-liquid flow in a continuous gravity settler using OpenFOAM and experimental verification. Chemical Engineering Journal. 2017. Vol. 310. P. 120–133. DOI: 10.1016/j.cej.2016.10.102

11. Thaker A. H., Darekar M., Singh K. K., Buwa V. V. Experimental investigations of liquid–liquid disengagement in a continuous gravity settler. Chemical Engineering Research and Design. 2018. Vol. 139. P. 174–187. DOI: 10.1016/j.cherd.2018.09.031

12. Zhang H., Zheng S., Zhang X., Duan S., Li S. Optimizing the inclined plate settler for a high-rate microaerobic activated sludge process for domestic wastewater treatment : A theoretical model and experimental validation. International Biodeterioration & Biodegradation. 2020. Vol. 154. P. 105060. DOI: 10.1016/j.ibiod.2020.105060

В. А. козачина^1*, О. В. Громова², О. Ю. Гунько³, Л. Г. Татарко⁴

^1*Каф. «Гідравліка та водопостачання», Дніпровський національний університет
залізничного транспорту імені академіка В. Лазаряна, вул. Лазаряна, 2, Дніпро,
Україна, 49010, тел. +38 (056) 373 15 09,
ел. пошта v.kozachyna@gmail.com, ORCID 0000-0002-6894-5532
²Каф. «Архітектурне проєктування, землеустрій та будівельні матеріали»,
Дніпровський національний університет залізничного транспорту імені академіка
В. Лазаряна, вул. Лазаряна, 2, Дніпро, Україна, 49010, тел. +38 (095) 304 73 33,
ел. пошта Gromova_Elen_upbbm_diit@i.ua, ORCID 0000-0002-5149-4165
³Каф. «Гідравліка та водопостачання», Дніпровський національний університет
залізничного транспорту імені академіка В. Лазаряна, вул. Лазаряна, 2, Дніпро,
Україна, 49010, тел. +38 (056) 373 15 09,
ел. пошта water.supply.treatment@gmail.com, ORCID 0000-0001-9257-763X
⁴Каф. «Енергетика», Український державний хіміко-технологічний університет,
пр. Гагаріна, 8, Дніпро, Україна, 49005, тел. +38 (056) 753 56 38,
ел. пошта larisa.tatarko@gmail.com, ORCID 0000-0002-2080-6090

моделювання очиЩЕННЯ стічних вод

на базі CFD-моделі: експрес-розрахунок

Мета. У роботі передбачено розробку CFD-моделі для оцінки ефективності очищення стічних вод у горизонтальному відстійнику. CFD-модель може бути використана для розрахунку гідродинаміки течії і масопереносу в спорудах, що мають складну геометричну форму в області руху потоку стічних вод. Методика. Для чисельного моделювання процесу руху стічних вод у горизонтальному відстійнику використано дві математичні моделі. Перша модель застосована на рівняннях руху в'язкої нестисливої рідини – рівняннях Нав’є–Стокса. Ці рівняння записано у змінних «завихреність – функція потоку». Для розрахунку концентрації забруднювача в горизонтальному відстійнику використано двовимірне рівняння масопереносу. Для чисельного інтегрування цього рівняння застосовано кінцево-різницеву схему розщеплення. Розщеплення моделювального рівняння масопереносу проведено так, щоб на кожному дробовому кроці невідоме значення концентрації забруднювача визначати за явною формулою. Для чисельного інтегрування рівняння переносу вихору та рівняння для функції потоку (система рівнянь Нав’є–Стокса) використано кінцево-різницеві схеми розщеплення. Результати. На базі розробленої CFD-моделі створено комплекс комп’ютерних програм, що дозволяє визначати ефективність очищення води в горизонтальному відстійнику. Представлено результати проведеного обчислювального експерименту з оцінки ефективності очищення води у відстійнику з додатковими елементами у вигляді пластин. Наукова новизна. Створено ефективну CFD-модель, що дозволяє оперативно оцінювати ефективність очищення стічних вод у горизонтальному відстійнику з додатковими елементами. Ця модель враховує геометричну форму очисної споруди та найбільш значущі фізичні фактори, які впливають на ефективність очищення води в горизонтальних відстійниках: нерівномірне поле швидкості потоку стічних вод, процеси дифузії, різне положення вхідних і вихідних отворів очисної споруди. Практична значимість. Побудована CFD-модель належить до класу «діагностичних моделей» і може бути використана для оцінки ефективності очисних споруд на етапі їх ескізного проєктування.

Ключові слова: очищення стічних вод; чисельне моделювання; горизонтальний відстійник

V. А. Kozachyna^1*, O. V. Hromova², O. Y. Hunko³, L. H. Tatarko⁴

^1*Dep. «Hydraulics and Water Supply», Dnipro National University of Railway Transport
named after Academician V. Lazaryan, Lazaryana St., 2, Dnipro, Ukraine, 49010, tel. +38 (056) 373 15 09,
e-mail v.kozachyna@gmail.com, ORCID 0000-0002-6894-5532
²Dep. «Аrchitectural Design, Land Management and Building Materials», Dnipro National
University of Railway Transport named after Academician V. Lazaryan, Lazaryana St., 2,
Dnipro, Ukraine, 49010, tel. +38 (095) 304 73 33,
e-mail Gromova_Elen_upbbm_diit@i.ua, ORCID 0000-0002-5149-4165
³Dep. «Hydraulics and Water Supply», Dnipro National University of Railway Transport
named after Academician V. Lazaryan, Lazaryana St., 2, Dnipro, Ukraine, 49010,
tel. +38 (056) 373 15 09, e-mail water.supply.treatment@gmail.com,
ORCID 0000-0001-9257-763X
⁴Dep. «Energy», Ukrainian State University of Chemical Technology, Haharina Av., 8,
Dnipro, Ukraine, 49005, tel. +38 (056) 753 56 38,
e-mail larisa.tatarko@gmail.com, ORCID 0000-0002-2080-6090

Simulation of Waste WATER Treatment

based on CFD model: express calculation

Purpose. Development of CFD model to evaluate the efficiency of wastewater treatment in a horizontal settler. The CFD model can be used to calculate flow hydrodynamics and mass transfer in settlers with complex geometric shape in the area of wastewater flow. Methodology. For numerical simulation of the process of wastewater movement in a horizontal settler, two mathematical models are used. The first model is based on the motion equations of a viscous incompressible fluid – the Navier-Stokes equations. The Navier-Stokes equations are written in the variables «vorticity - flow function». A two-dimensional mass transfer equation is used to calculate the concentration of a pollutant in a horizontal settler. To numerically integrate the two-dimensional mass transfer equation, a finite-difference splitting scheme is used. The splitting of the modeling equation of mass transfer is carried out so that at each fractional step to determine the unknown value of the pollutant concentration by an explicit formula. For numerical integration of the vortex transfer equation and the equation for the flow function (the Navier-Stokes system of equations), finite-difference splitting schemes are used. Findings. Based on the developed CFD model, a complex of computer programs has been developed, which makes it possible to determine the efficiency of water treatment in a horizontal settler with additional elements. The results of a computational experiment to assess the efficiency of water treatment in a horizontal settler with additional elements in the form of plates are presented. Originality. An efficient CFD model has been created, which allows to quickly evaluate the efficiency of wastewater treatment in a horizontal settler with additional elements. The developed CFD model takes into account the geometric shape of the facility and the most significant physical factors, that influence the efficiency of the waste water treatment in horizontal settler: non-uniform flow velocity, diffusion, different position of inlet and outlet openings. Practical value. The developed CFD model belongs to the class of «diagnostic models» and can be used to assess the efficiency of treatment facilities at the stage of their preliminary design.

Keywords: waste waters treatment; numerical simulation; horizontal settler

LIST OF Reference LINKS

1. Biliaiev, N. N., & Kozachina, V. A. (2015). Modelirovaniye massoperenosa v gorizontalnykh otstoynikakh: monografiya. Dnepropetrovsk: Aktsent PP. (in Russian)

2. Biliaiev, N. N., & Nagornaya, E. K. (2012). Matematicheskoye modelirovaniye massoperenosa v otstoynikakh sistem vodootvedeniya: monografiya. Dnepropetrovsk: Novaya ideologiya. (in Russian)

3. Kolobanov, S. K., Yershov, A. V., & Kigel, M. Ye. (1997). Proektirovanie ochistnykh sooruzheniy kanalizatsii. Kiev: Budіvelnik. (in Russian)

4. Oleynik, Ya. A., Kalugin, Yu. I., Stepovaya, N. G., & Zyablikov, S. M. (2004). Teoreticheskiy analiz protsessov osazhdeniya v sistemakh biologicheskoy ochistki stochnykh vod. Prikladna gіdromekhanіka, 6(78(4)),
   62-67. (in Russian)

5. Oleynik, A. Y., & Airapetyan, T. S. (2015). The modeling of the clearance of waste waters from organic pollutions in bioreactors-aerotanks with suspended (free flow) and fixed biocenoses. Reports of the National Academy of Sciences of Ukraine, 5, 55-60. DOI: 10.15407/dopovidi2015.05.055 (in Ukrainian)

6. Biliaiev, M. M., & Kozachyna, V. A. (2015). Numerical determination of horizontal settlers performance. Science and Transport Progress, 4(58), 34-43. DOI: 10.15802/STP2015/49201 (in English)

7. Hadad, H., & Ghaderi, J. (2015). Numerical Simulation of the Flow Pattern in the Aeration Tank of Sewage Treatment System by the Activated Sludge Process Using Fluent Program. Biological Forum-An International Journal, 7(1), 382-393. (in English)

8. Luna, F. D. ., Silva, A. G., Fukumasu, N. K., Bazan, O., Gouveia, J. H. A., Moraes, D., … & Vianna, A. S. (2019). Fluid dynamics in continuous settler. Chemical Engineering Journal, 362, 712-720. DOI: 10.1016/j.cej.2019.01.088 (in English)

9. Misra, A., de Souza, L. G. M., Illner, M., Hohl, L., Kraume, M., Repke, J.-U., & Thévenin, D. (2017). Simulating separation of a multiphase liquid-liquid system in a horizontal settler by CFD. Chemical Engineering Science, 167, 242-250. DOI: 10.1016/j.ces.2017.03.062 (in English)

10. Panda, S. K., Singh, K. K., Shenoy, K. T., & Buwa, V. V. (2017). Numerical simulations of liquid-liquid flow in a continuous gravity settler using OpenFOAM and experimental verification. Chemical Engineering Journal, 310, 120-133. DOI: 10.1016/j.cej.2016.10.102 (in English)

11. Thaker, A. H., Darekar, M., Singh, K. K., & Buwa, V. V. (2018). Experimental investigations of liquid–liquid disengagement in a continuous gravity settler. Chemical Engineering Research and Design, 139, 174-187. DOI: 10.1016/j.cherd.2018.09.031 (in English)

12. Zhang, H., Zheng, S., Zhang, X., Duan, S., & Li, S. (2020). Optimizing the inclined plate settler for a high-rate microaerobic activated sludge process for domestic wastewater treatment: A theoretical model and experimental validation. International Biodeterioration & Biodegradation, 154, 105060. DOI: 10.1016/j.ibiod.2020.105060 (in English)

Поступила в редколегию: 05.06.2020

Принята к печати: 06.10.2020

Creative Commons Attribution 4.0 International
doi: 10.15802/stp2020/218310
© В. А. Козачина, Е. В. Громова,

Е. Ю. Гунько, Л. Г. Татарко, 2020