ISSN
2307–3489 (Print), ІSSN
2307–6666
(Online)
Наука
та прогрес транспорту. Вісник
Дніпропетровського
національного університету залізничного
транспорту, 2020, № 4 (88)
рухомий
склад і тяга поїздів
УДК
629.463.62:656.225
О.
В. Шатунов1*,
А. О. Швець2*
1*Каф.
«Вагони та вагонне господарство»,
Дніпровський національний
університет
залізничного транспорту імені академіка
В. Лазаряна,
вул. Лазаряна, 2, Дніпро,
Україна, 49010, тел.
+38 (067) 953 60 14,
ел. пошта shatunov220648@gmail.com,
ORCID 0000-0002-1115-0093
2*Каф. «Теоретична
та будівельна механіка», Дніпровський
національний
університет залізничного
транспорту імені академіка В. Лазаряна,
вул. Лазаряна, 2, Дніпро, Україна, 49010,
тел. +38 (050) 214 14 19,
ел. пошта
angela_Shvets@ua.fm, ORCID 0000-0002-8469-3902
динаміка
зчепу вагонів-Платформ
пІД ЧАС перевезеннЯ
довгомірного
вантажу
Мета.
У зв’язку з тенденцією до інтенсифікації
перевізного процесу в умовах підвищених
осьових навантажень та швидкостей руху
поїздів у статті передбачено дослідити
динамічну навантаженість зчепу двох
вагонів-платформ з довгомірним вантажем,
а також визначити динамічні сили
взаємодії під впливом квазістатичних
поздовжніх сил. Методика.
Основою дослідження є метод математичного
та комп’ютерного моделювання динамічної
навантаженості поздовжньо-згинальних
коливань штабеля вантажу довжиною 22 м,
розташованого на зчепі з двох
вагонів-платформ моделі 13–4012. Кінетична
й потенціальна енергії системи складені
з урахуванням кінетичної й потенціальної
енергії вантажу, які обчислюють за
відомими фундаментальними функціями.
Для визначення фундаментальних функцій
розв’язано задачі про згинальні
коливання вантажу як балки на двох
пружних опорах. Для визначення
фундаментальних функцій за поздовжніх
переміщень використано диференціальне
рівняння вільних поздовжніх коливань
стрижня постійного перетину. Теоретичні
дослідження проведені за умови руху
зчепу платформ із типовими візками
18–100 зі швидкостями в інтервалі від 60
до 100 км/год по прямій ділянці залізничної
колії. Результати.
У дослідженні взято до уваги рух зчепу
вагонів-платформ по синусоїдальній
нерівності довжиною 25 м і різною глибиною
у випадку дії поздовжніх стискних або
розтягальних сил, а також на вибігу. У
ході виконання теоретичних досліджень
і після проведення моделювання з
урахуванням процесів коливання
вагона-платформи й довгомірного вантажу,
за наявності квазістатичних поздовжніх
сил, отримано залежності основних
динамічних показників від величини
швидкості руху. Наукова
новизна. Для визначення
динамічної навантаженості зчепу
вагонів-платформ розроблено математичну
модель поздовжньо-згинальних коливань
у вертикальній площині системи штабель
вантажу – зчеп вагонів-платформ.
Запропонована математична модель дає
можливість теоретично
визначити динамічні показники системи
та забезпечити розроблення способів
транспортування довгомірних вантажів
відповідно вимог безпеки руху поїздів.
Практична значимість.
У результаті проведених теоретичних
досліджень вирішено актуальне та
практично важливе завдання визначення
навантаженості платформ зчепу під час
транспортування довгомірного вантажу,
що дозволить розробити технічні умови
для реалізації ресурсозбережних
технологій.
Ключові
слова: вагон-платформа;
довгомірний вантаж; динамічні показники;
зчеп вагонів; поздовжні сили; швидкість
руху
Вступ
Технічне
переоснащення залізничного транспорту
є досить складним, дорогим, але необхідним
завданням. У сучасний кризовий період
актуальним є вирішення питань, пов’язаних
із більш інтенсивним використанням
наявного рухомого складу. До числа
таких питань належать ресурсозбережні
способи транспортування довгомірних
вантажів на відкритому рухомому складі
[9, 14, 15].
Під час вибору типу
рухомого складу для перевезення того
чи іншого вантажу, як правило, доводиться
вирішувати досить принципове питання:
створювати спеціалізовані або
застосовувати універсальні вагони.
Однозначної відповіді не існує. Тільки
техніко-економічний розрахунок
конкретного способу транспортування
вантажу із застосуванням того чи іншого
типу універсального або спеціалізованого
рухомого складу дозволяє відповісти
на це питання [10, 12, 13].
У ряді випадків
перевезення досить жорстких довгомірних
вантажів виконують зчепами з трьох
вагонів, один із них (середній)
завантажений, а два інших – порожні
платформи – забезпечують прикриття
консолей вантажу, які виступають. Такі
перевезення вкрай неекономічні. Виникає
необхідність організації перевезень
таких вантажів на зчепах із двох вагонів
із максимально повним використанням
їх вантажопідйомності. Це стає можливим
тільки із застосуванням спеціальних
опорно-кріпильних пристроїв. Проблема
безпечного та раціонального перевезення
довгомірних вантажів на універсальному
рухомому складі пов’язана з вирішенням
декількох завдань, із яких основними
є:
– дослідження
статичної та динамічної навантаженості
елементів конструкції вагона-платформи
та оцінка її міцності;
– розробка
спеціальних опорно-кріпильних пристроїв;
– визначення
допустимої ваги вантажу, можливих його
габаритів і способів перевезення.
Аналіз принципових
схем кріпильних пристроїв дозволяє
відзначити, що розвиток їх конструкції
йде не тільки в напрямі підвищення
міцності, надійності, забезпечення
безперешкодного проходження кривих
ділянок колії та роботи ударно-тягових
приладів вагонів зчепу, але і в напрямі
надання турнікетним опорам демпфувальних
та зворотньо-поворотних властивостей
із метою зменшення впливу поздовжніх
інерційних сил на вантаж.
У зв’язку з цим
залишається актуальною розробка
методики теоретичних та експериментальних
досліджень навантаженості і відповідно,
оцінки міцності рухомого складу під
час транспортування довгомірних
вантажів, а також розробка способів їх
розміщення і кріплення [9].
Мета
З огляду на викладене
метою цього теоретичного дослідження
є вивчення динамічної навантаженості
зчепу з двох вагонів-платформ із
довгомірним вантажем, визначення
динамічних сил взаємодії під впливом
квазістатичних поздовжніх сил під час
руху по синусоїдальній нерівності з
різною глибиною.
Методика
Теоретичні
дослідження динамічної поздовжньої
навантаженості вагона (зчепу вагонів)
в експлуатації знайшли відображення
в багатьох роботах. Реалізовані при
цьому математичні моделі дають рішення,
які добре узгоджуються з експериментальними
даними [1, 5, 6].
Наведена в роботі
[9] методика розрахунку та оцінки
напруженого стану елементів рами вагона
за нештатних схем передачі навантаження
дозволяє вибрати раціональні
ресурсозбережні способи перевезення
довгомірних вантажів. Крім того,
досліджено спосіб транспортування
штабеля довгомірного вантажу на зчепі
з двох вагонів-платформ із застосуванням
комплекту багатооборотних металевих
опор. Специфікою кріплення є відсутність
обв’язок у рухомої опори, що забезпечує
передачу тягових та гальмівних зусиль
між платформами зчепу через їх
автозчеплення. Зміна бази зчепу в ході
роботи поглинальних апаратів під час
маневрів, проходження горба сортувальної
гірки не порушує кріплення вантажу,
тому що рухомий кінець штабеля компенсує
хід поглинальних апаратів вагона-платформи,
а розміщення обв’язок у площині опори
не викликає їх розтягнення за відносного
переміщення підлоги й вантажу на
переломах профілю колії.
Теоретичний аналіз
міцності конструкції вагона-платформи
за різних варіантів позаштатних
завантажень зчепу дозволив вибрати
найбільш доцільний спосіб розміщення
вантажу, який дозволяє за максимальної
ваги отримати значення напружень в
елементах вагона, що не перевищують
допустимих та забезпечують їх надійність
і безпеку руху.
У роботі
[9] наведено також
математичну модель поздовжньо-згинальних
коливань штабеля вантажу довжиною 22
м, розташованого на зчепі з двох
вагонів-платформ моделі 13–4012.
Розрахункова схема коливання зчепу
вагонів-платформ та штабеля довгомірного
вантажу у вертикальній поздовжній
площині симетрії представлена на рис.
1, де показані додатні напрямки переміщень
і кутів повороту, а позначення тіл
системи наведені в табл. 1.
Особливістю
цієї розрахункової схеми є необхідність
урахування зав’язок між штабелями –
опорами – рамами (підлогами) платформ.
Кожну платформу розглядають як систему
з трьох твердих тіл: рами 1,
двох візків 5
моделі 18–100 з ресорними комплектами
4, які
мають жорсткість
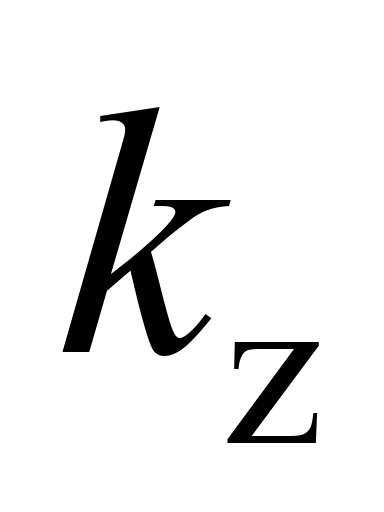 і коефіцієнт відносного тертя
і коефіцієнт відносного тертя
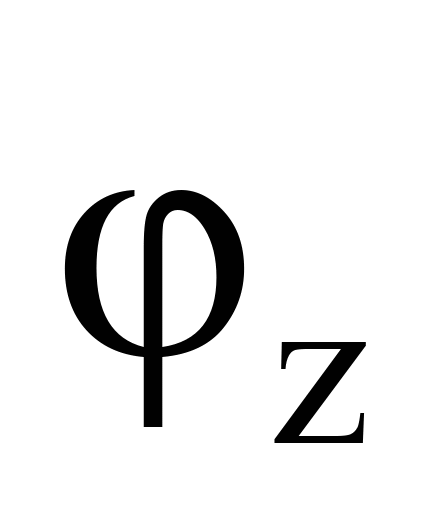 .
Рами платформ з’єднані між собою
автозчепленням 3
через поглинаючі апарати 2
з жорсткістю
.
Рами платформ з’єднані між собою
автозчепленням 3
через поглинаючі апарати 2
з жорсткістю
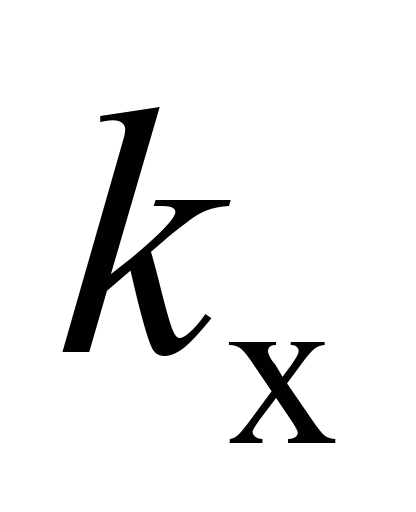 і коефіцієнтом відносного тертя
і коефіцієнтом відносного тертя
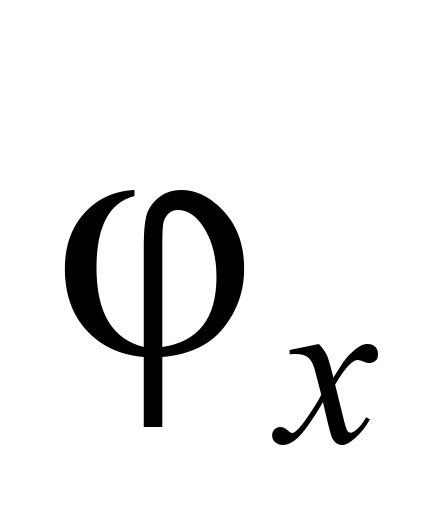 .
.
На
платформах розміщено штабель довгомірного
вантажу, що складається з нижнього 6
та верхнього 7
ярусів. Нижній ярус укладено на жорсткі
опори, одна з яких шарнірно-рухома 8,
а друга шарнірно-нерухома 9.
Опори 10
верхнього ярусу розглядають як пружні
з жорсткістю
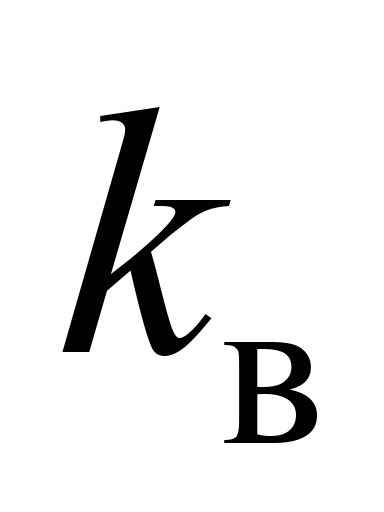 .
У процесі руху зчепу обидва яруси
роблять поздовжньо-згинальні коливання.
Передбачено, що ці коливання не пов’язані
між собою.
.
У процесі руху зчепу обидва яруси
роблять поздовжньо-згинальні коливання.
Передбачено, що ці коливання не пов’язані
між собою.
На рис. 1 уведено
такі позначення:
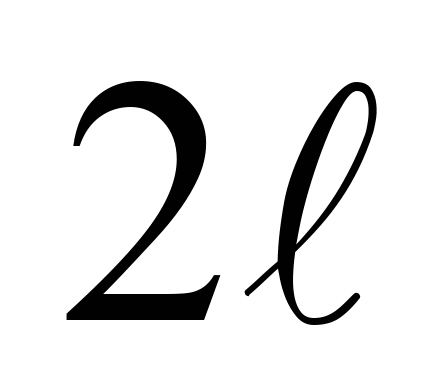 – база
вагона, 9,72 м;
– база
вагона, 9,72 м;
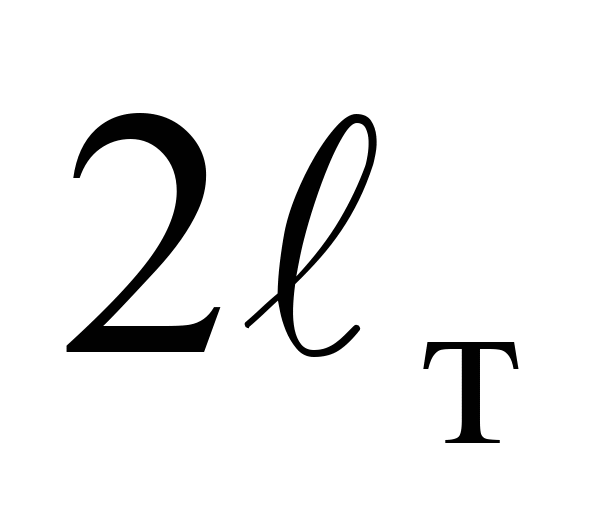 – база візка, 1,85 м;
– база візка, 1,85 м;
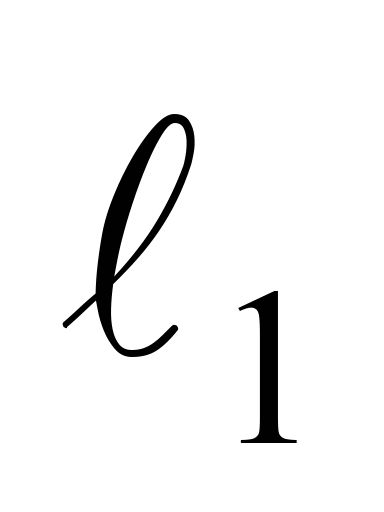 – відстань від шкворневого перетину
до осі зчеплення вагонів, 2,46 м;
– відстань від шкворневого перетину
до осі зчеплення вагонів, 2,46 м;
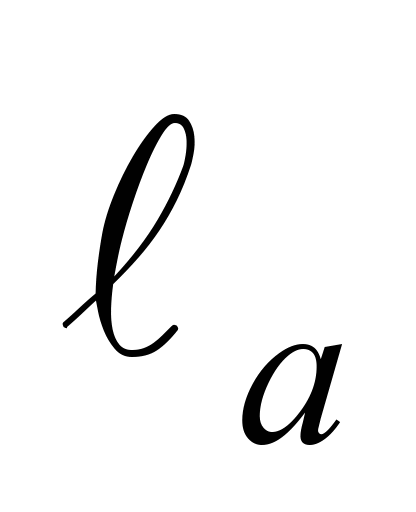 – відстань від осі зчеплення до осі
клина автозчеплення, 0,93 м;
– відстань від осі зчеплення до осі
клина автозчеплення, 0,93 м;
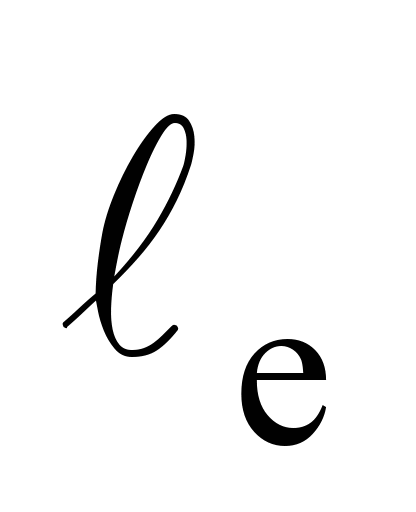 – ексцентриситет закріплення опор 8
та 9
відноснодо центра мас вагона в
поздовжньому напрямку, 0,81 м;
– ексцентриситет закріплення опор 8
та 9
відноснодо центра мас вагона в
поздовжньому напрямку, 0,81 м;
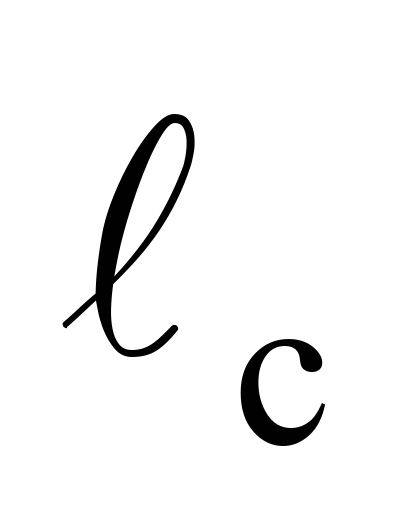 – відстань між пружними опорами
верхнього ярусу штабеля вантажу, 13,0 м;
– відстань між пружними опорами
верхнього ярусу штабеля вантажу, 13,0 м;
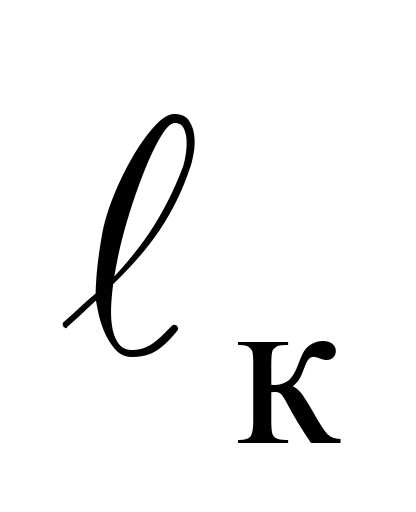 – довжина консольної частини верхнього
ярусу штабеля вантажу,
– довжина консольної частини верхнього
ярусу штабеля вантажу,
4,325 м.
У табл.
1 позначено через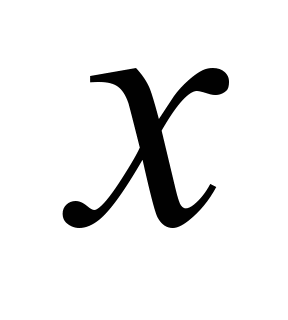 – посмикування,
– посмикування,
 –
підстрибування,
–
підстрибування,
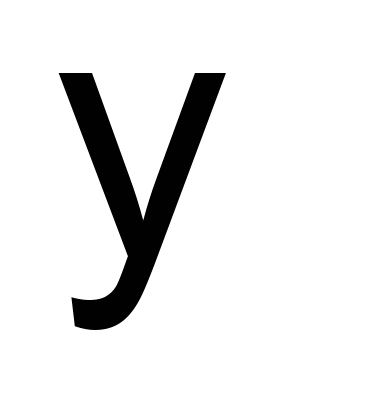 – кути поздовжньої хитавиці (позитивні
напрямки на рис. 2). Для
відзнаки переміщень передньої по ходу
руху платформи від задньої введені
індекси
– кути поздовжньої хитавиці (позитивні
напрямки на рис. 2). Для
відзнаки переміщень передньої по ходу
руху платформи від задньої введені
індекси
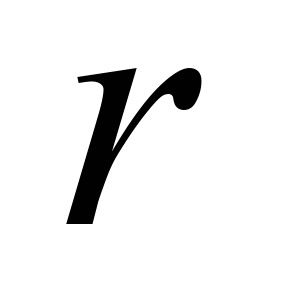 (
(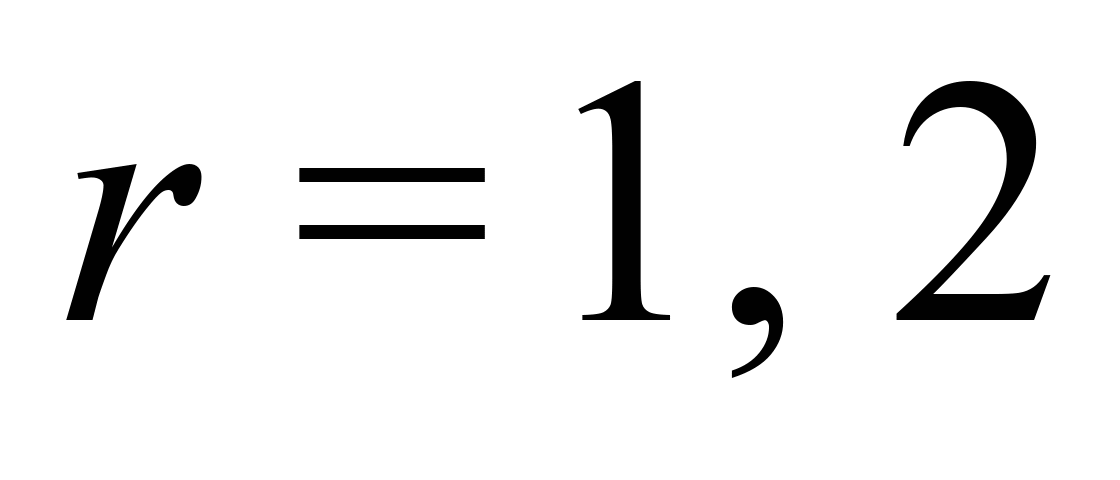 –
номер платформи у зчепі). Переміщення
візків позначені індексом
–
номер платформи у зчепі). Переміщення
візків позначені індексом
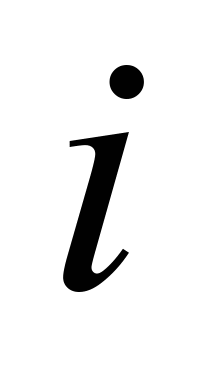 (
(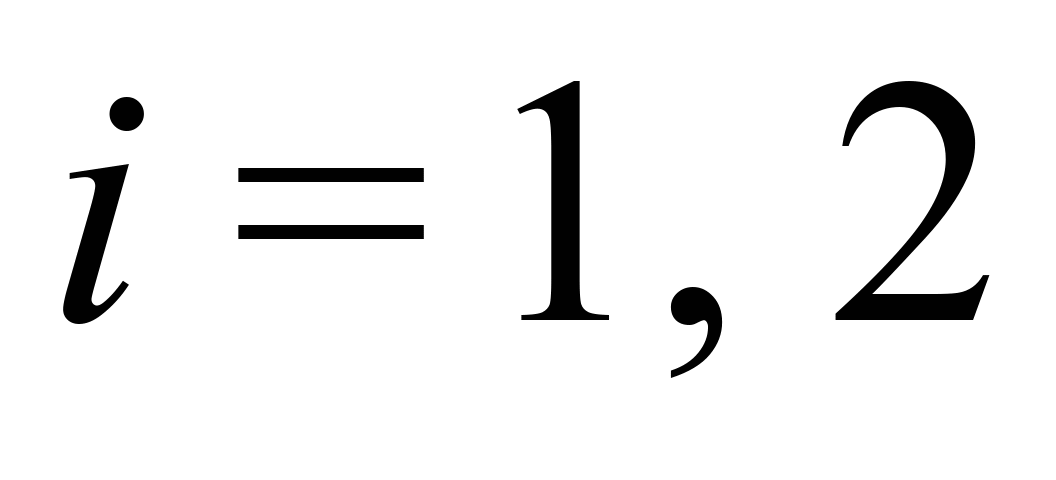 –
номер візка), переміщення колісних пар
– індексом
–
номер візка), переміщення колісних пар
– індексом
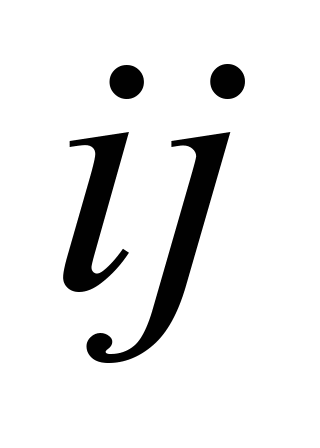 (
(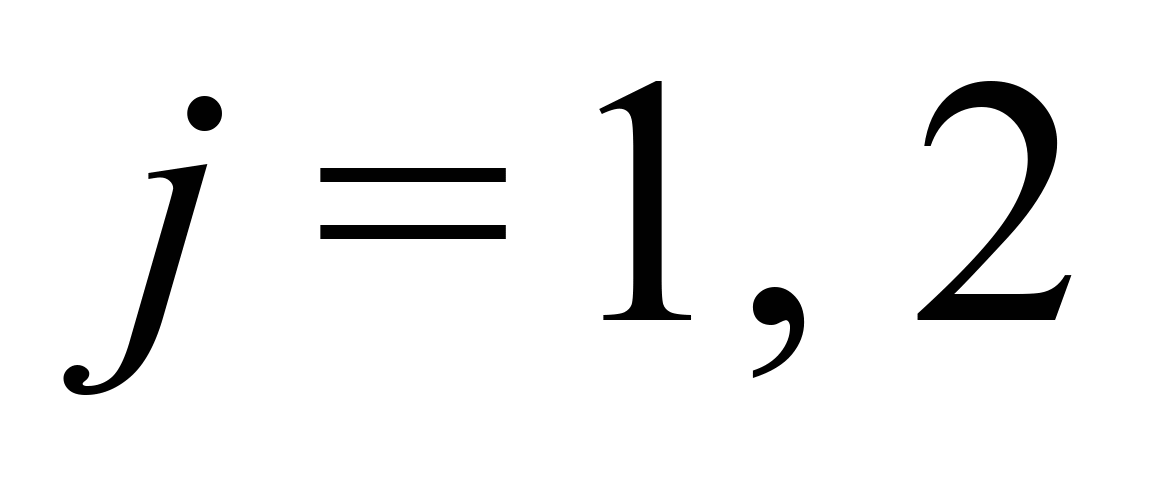 –
номер колісної пари у візку), переміщення
нижнього ярусу позначені індексом
–
номер колісної пари у візку), переміщення
нижнього ярусу позначені індексом
 ,
верхнього –
,
верхнього –
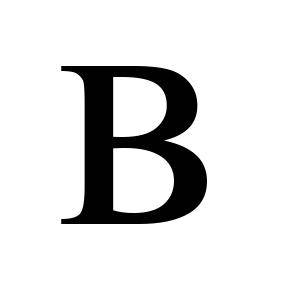 ,
переміщення балок як пружних тіл уздовж
осі
,
переміщення балок як пружних тіл уздовж
осі
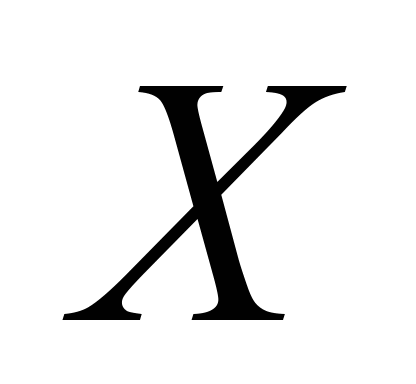 позначені через
позначені через
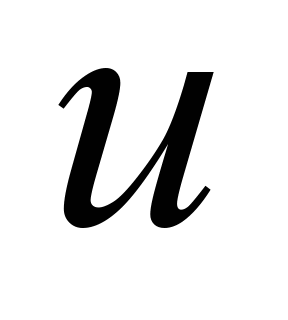 ,
уздовж осі
,
уздовж осі
 – через
– через
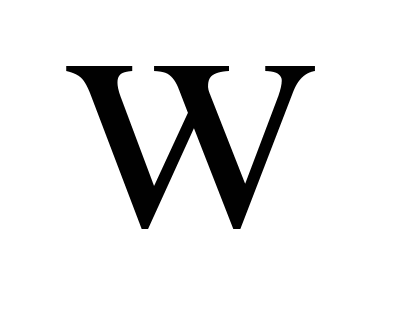 .
Переміщення ярусів позначені подвійно:
через
.
Переміщення ярусів позначені подвійно:
через
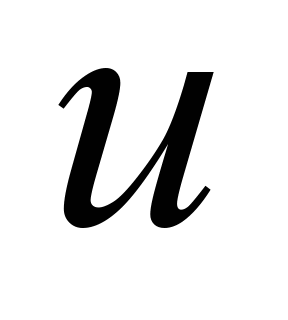 та
та
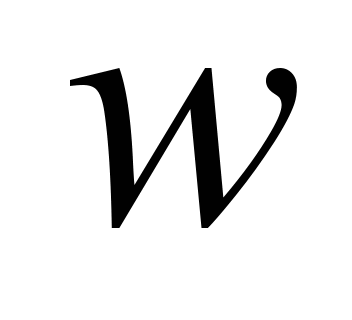 – переміщення пружного тіла, через
– переміщення пружного тіла, через
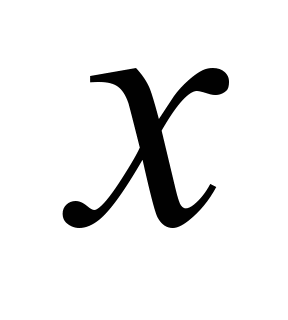 ,
,
 ,
,
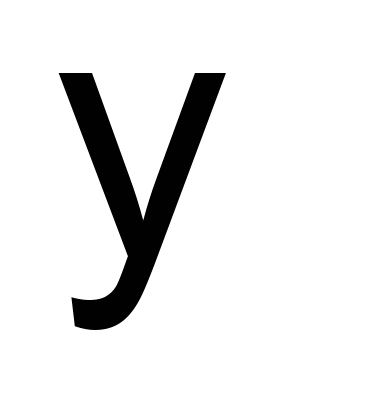 – твердого тіла.
– твердого тіла.
Колія у вертикальному
напрямку була взята пружно-в’язкою,
безінерційною.
Експерименти
показали, що під час коливань обох
ярусів штабеля проявляється переважно
перша форма коливань. Отже, для кожного
виду коливань за ярусами було взято до
уваги по одній узагальненій координаті.
Вертикальні переміщення нижнього ярусу
визначаються вертикальними переміщеннями
кузовів вагонів. Під час коливань
верхнього ярусу необхідно, крім першої
форми згинальних та поздовжніх коливань,
брати до уваги також коливання верхнього
ярусу як твердого тіла (підстрибування,
поздовжня хитавиця й посмикування).
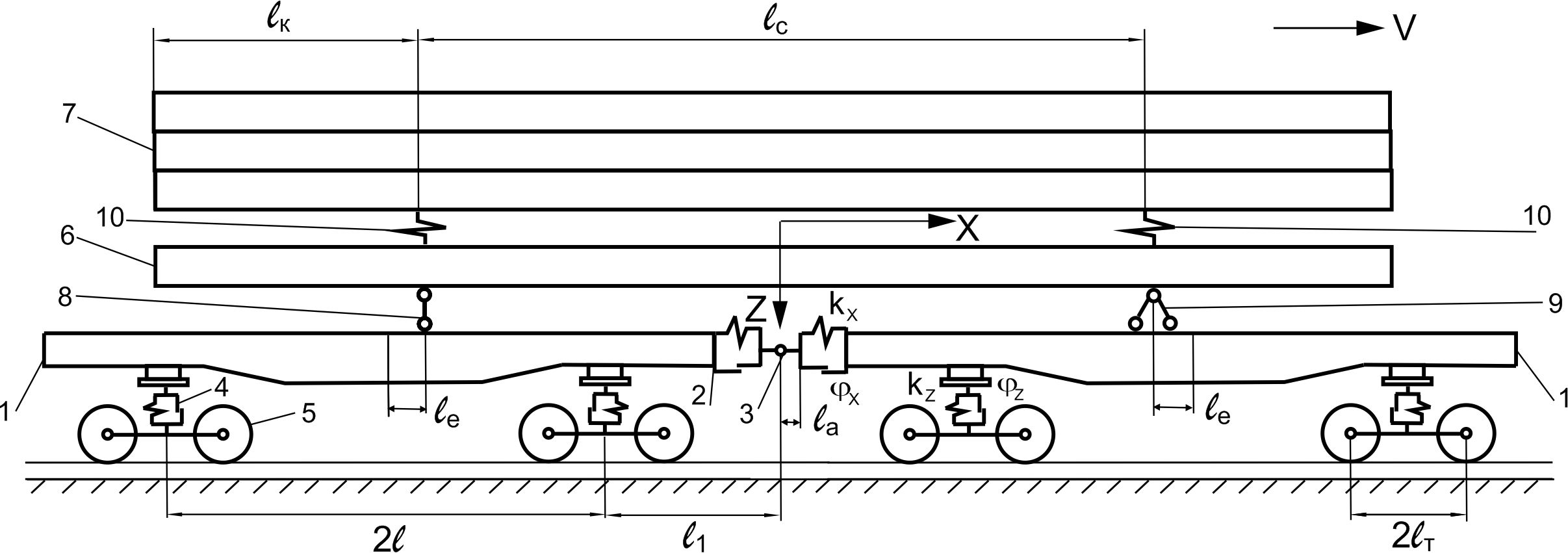
Рис. 1.
Розрахункова схема зчепу вагонів-платформ
зі штабелем довгомірного вантажу
Fig.
1. Computation
scheme of flat
cars coupling
with long stack of cargo
Таблиця 1
Лінійні
та кутові переміщення тіл системи
Table
1
Linear and
angular movements of system bodies
|
Тіла
системи
|
Переміщення
|
|
|
Лінійні
уздовж осей
|
Кутові
відносно осі
|
|
|
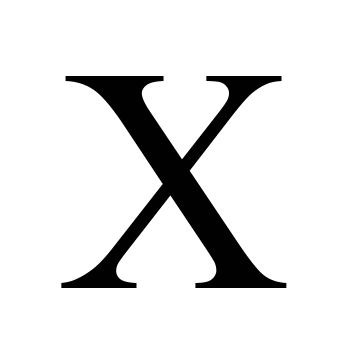
|

|

|
|
|
Перша
платформа
|
|
Рама
платформи
|
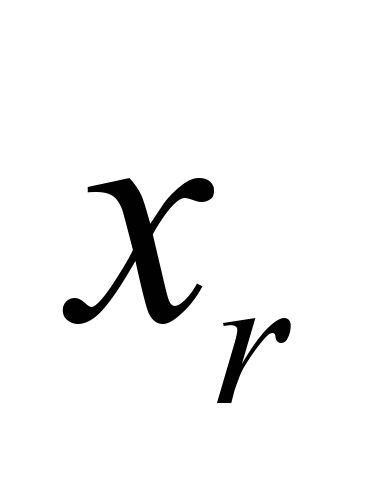
|
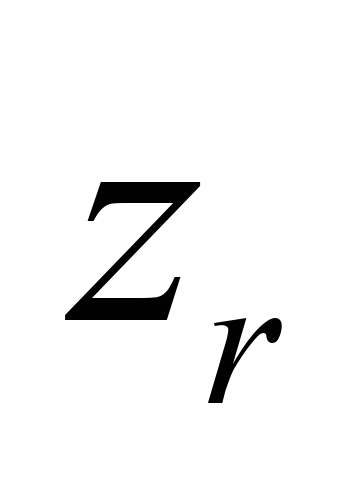
|
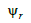
|
|
Візок
|
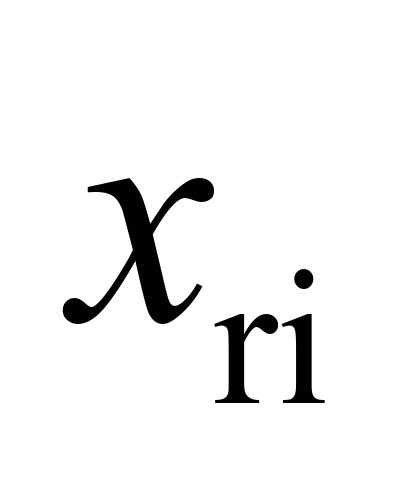
|
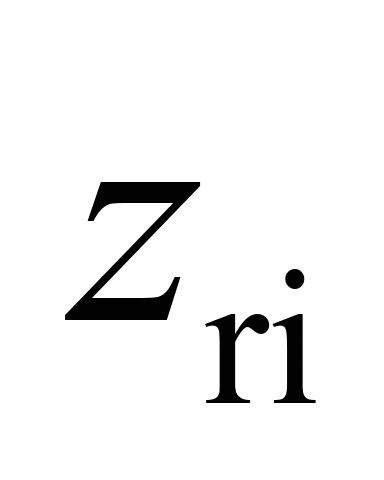
|
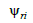
|
|
Колісні
пари
|
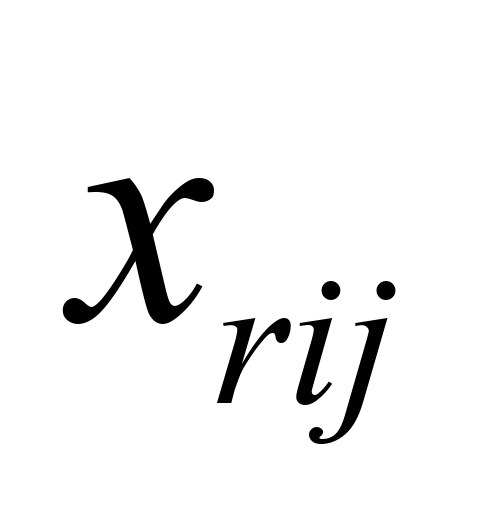
|

|
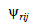
|
|
|
Друга
платформа
|
|
Рама
платформи
|
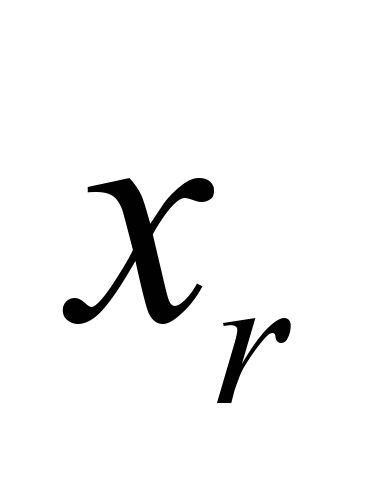
|
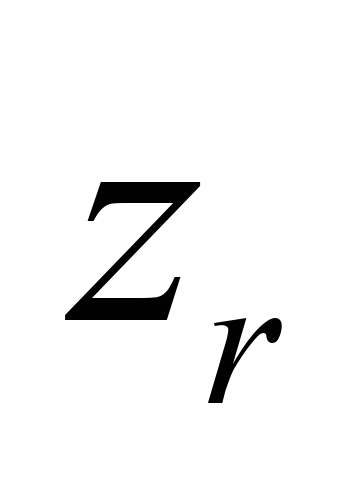
|
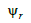
|
|
Візок
|
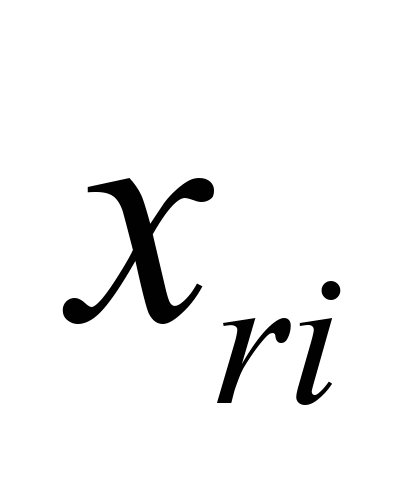
|
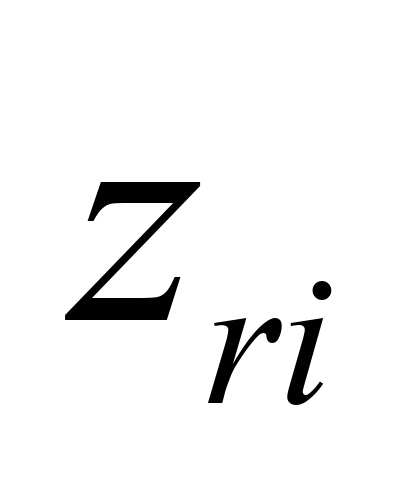
|
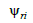
|
|
Колісні
пари
|
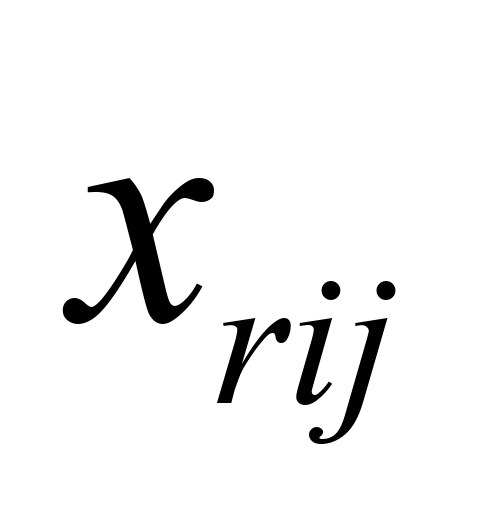
|

|
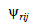
|
|
|
Штабель
|
|
Нижній
ярус
|
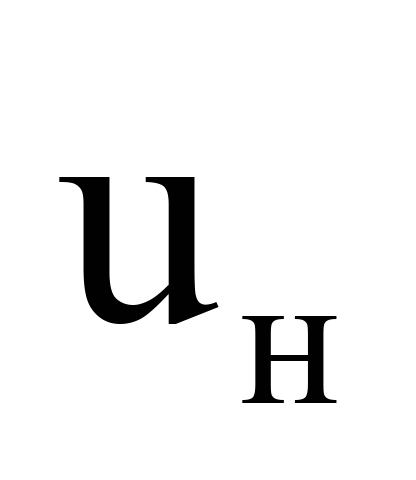 , ,
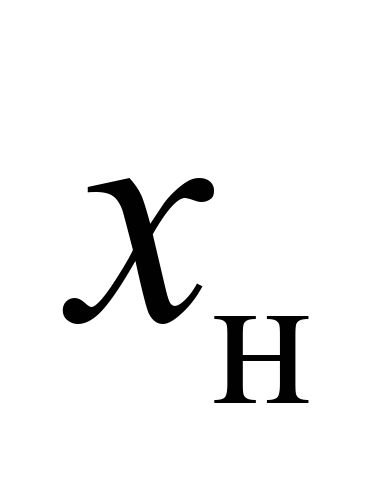
|
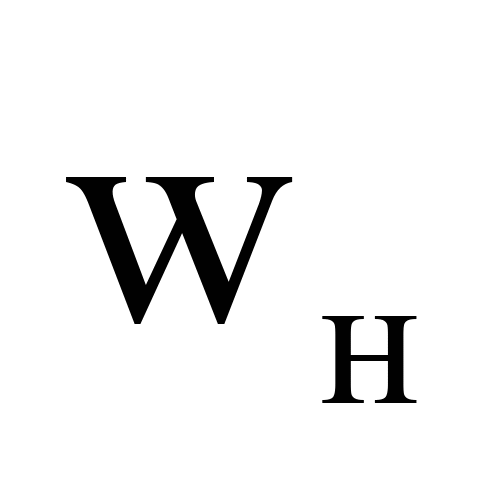 , ,

|
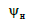
|
|
Верхній
ярус
|
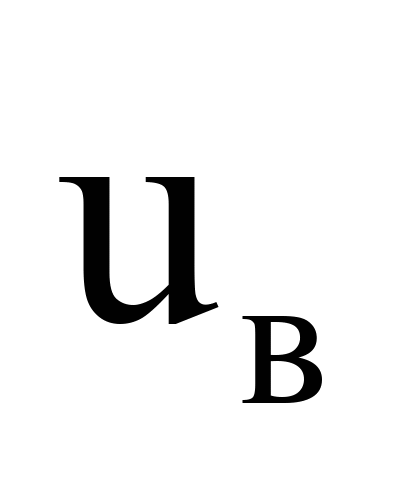 , ,
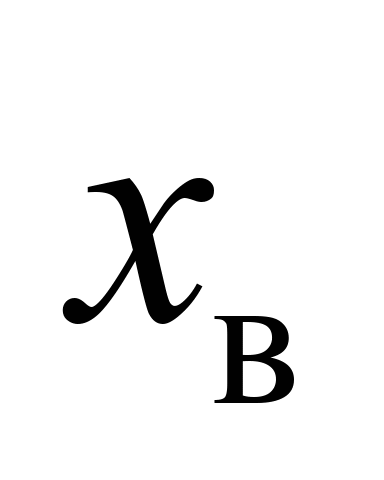
|
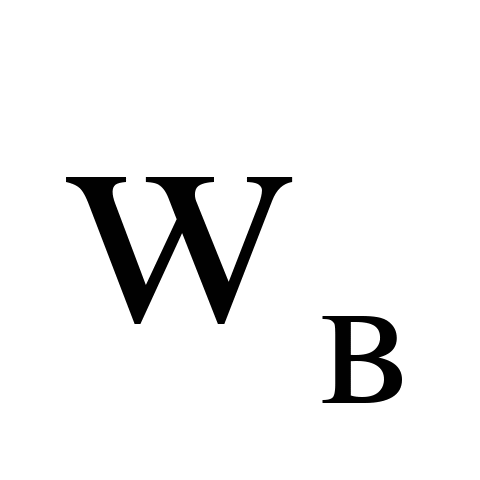 , ,
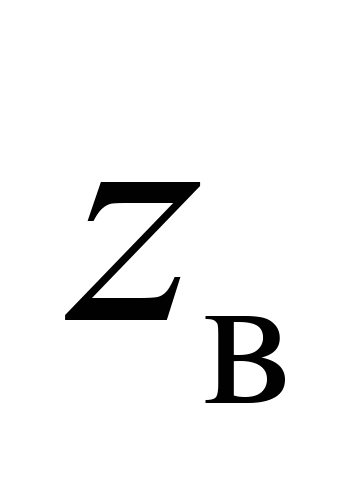
|
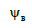
|
На систему накладені
такі наступні зв’язки:
– переміщення
всіх тіл першої платформи з нерухомою
опорою та балок штабеля уздовж осі
колії однакові:
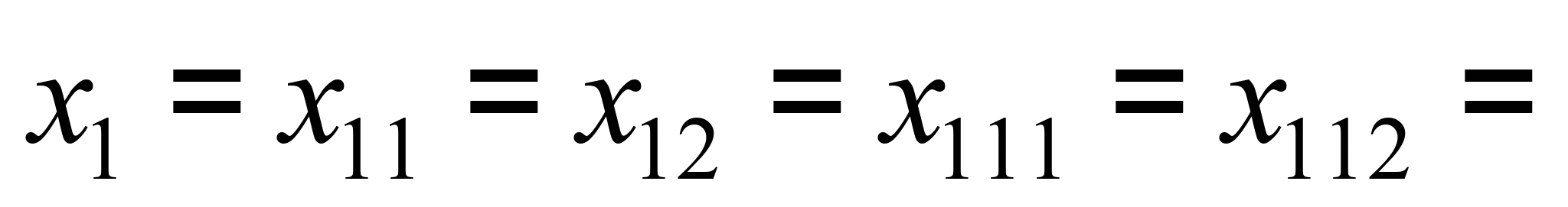
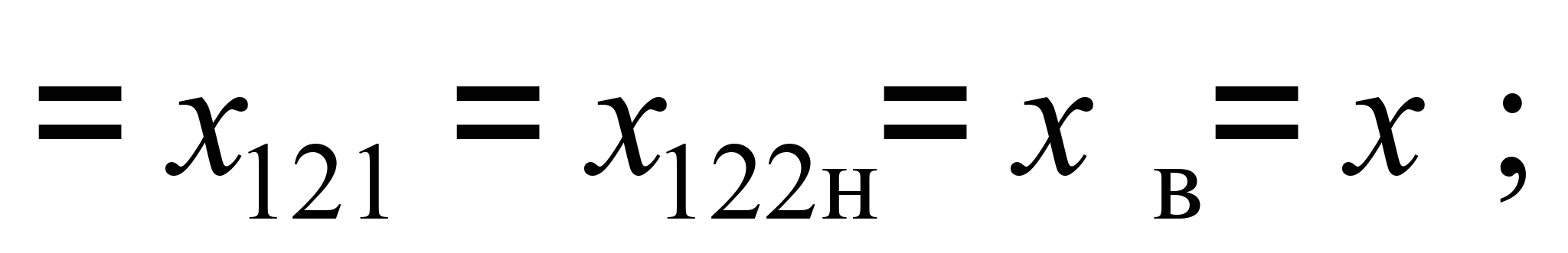 (1)
(1)
– переміщення
кузова й візків другої платформи уздовж
осі колії однакові:
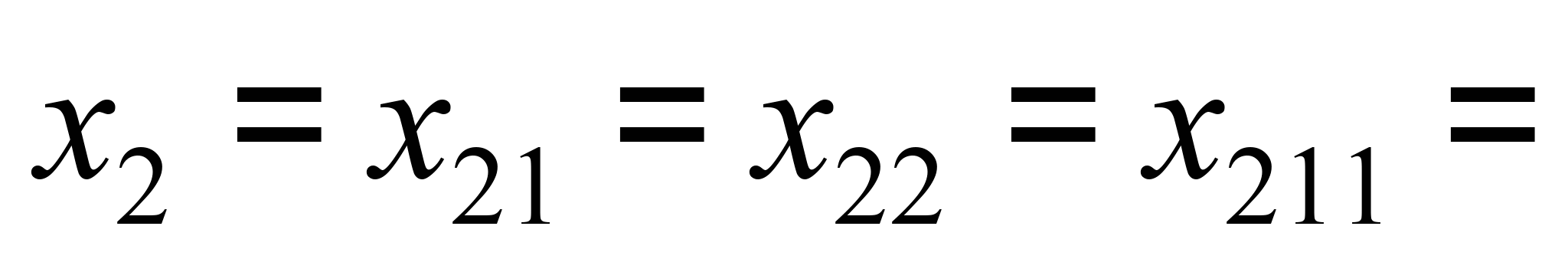
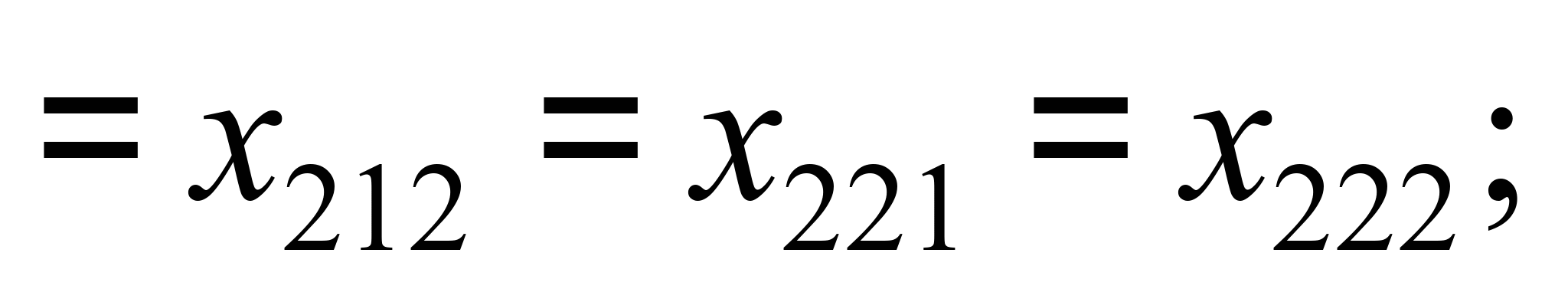 (2)
(2)
– колісні
пари рухаються без проковзування:
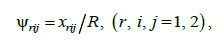 (3)
(3)
де
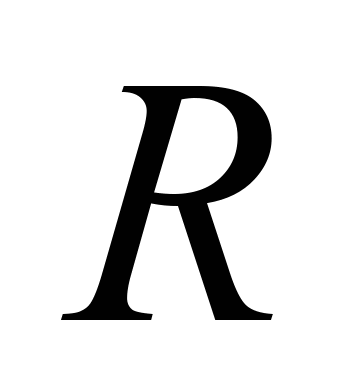 – радіус колеса, 0,475 м;
– радіус колеса, 0,475 м;
– через
відсутність пружних елементів у
буксовому підвішуванні підстрибування
та поздовжня хитавиця візків визначаються
підстрибуванням колісних пар:
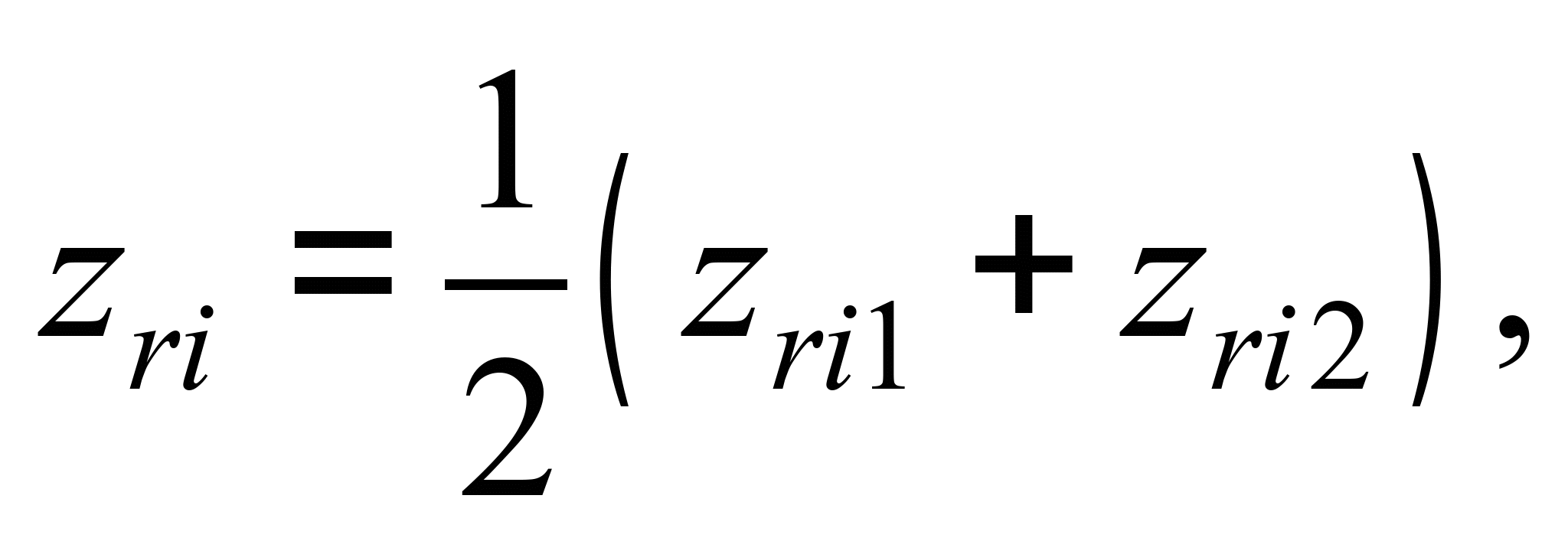 (4)
(4)
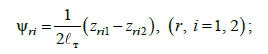 (5)
(5)
– підстрибування
та поздовжня хитавиця нижнього ярусу
визначається вертикальними переміщеннями
точок кузова в місцях обпирання.
Оскільки
опори нижнього ярусу розглянуто як
шарнірно-нерухомі (перша платформа) та
шарнірно-рухомі (друга платформа),
аналітичні вирази для визначення
підстрибування й поздовжньої хитавиці
можна отримати з рис. 3, а.
Вертикальні переміщення точок кузова
в місцях опор:
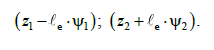 (6)
(6)
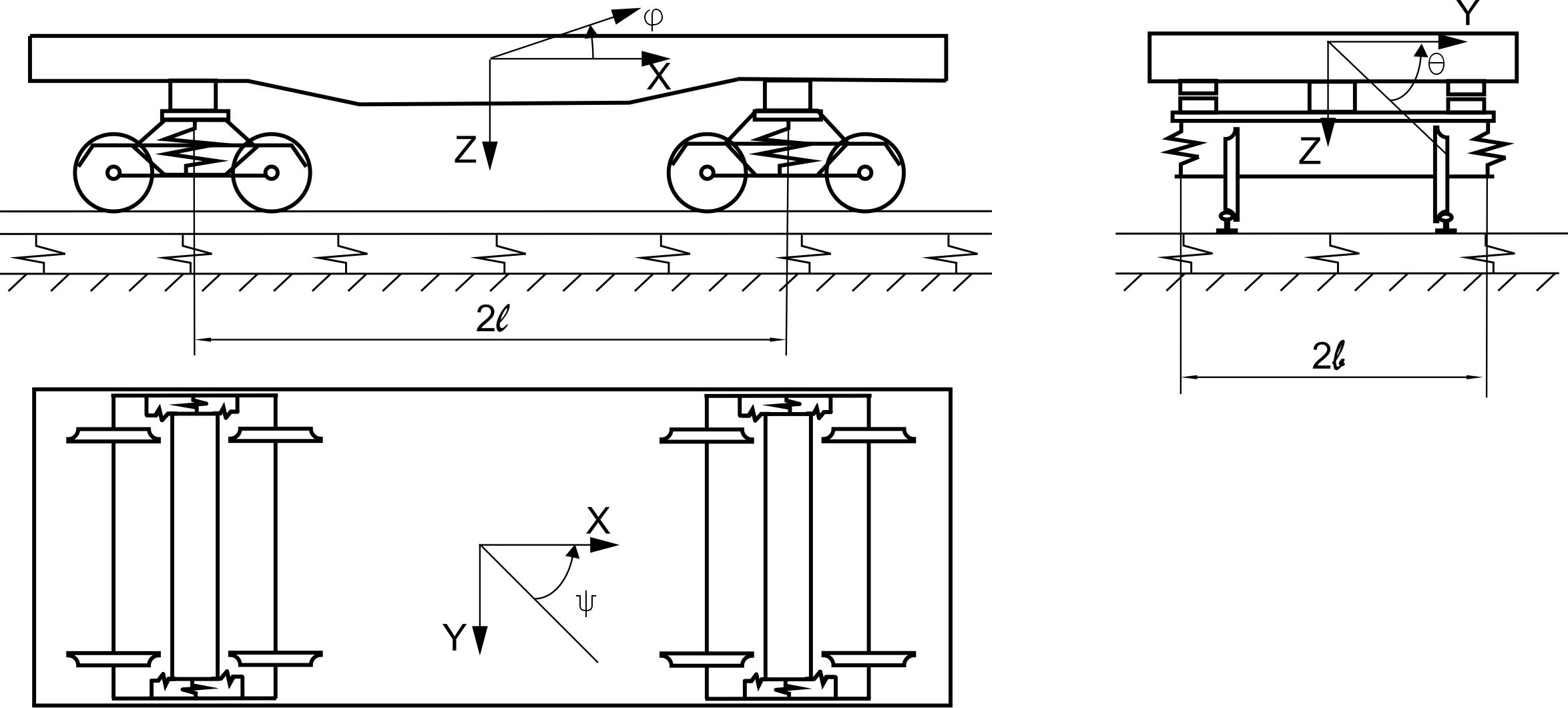
Рис. 2.
Розрахункова схема 4-вісного
вагона-платформи
Fig.
2. Calculation scheme of a 4-axle flat
car
Підстрибування й
поздовжня хитавиця нижнього ярусу як
твердого тіла дорівнюють:
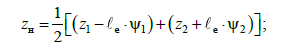 (7)
(7)
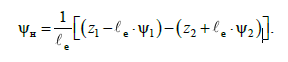 (8)
(8)
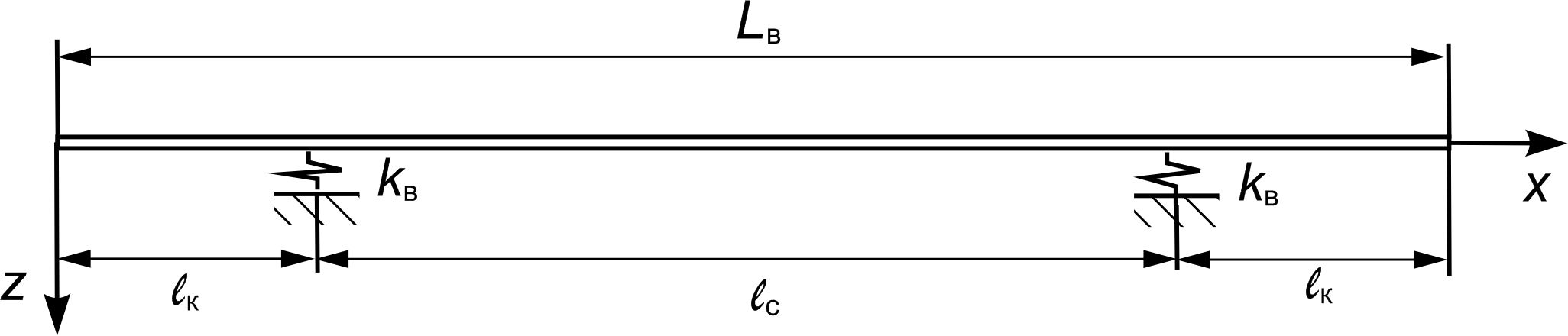
Верхній
ярус штабеля вантажу є пружною балкою,
що розташована на пружних опорах
і
здійснює згинальні та поздовжні
коливання (рис. 3, б).
Опора
 не рухається в поздовжньому напрямку,
а опора
не рухається в поздовжньому напрямку,
а опора
 має можливість такого переміщення
(рис. 3, в).
Передбачено, що опори є пружними тільки
у вертикальному напрямку.
має можливість такого переміщення
(рис. 3, в).
Передбачено, що опори є пружними тільки
у вертикальному напрямку.
а
– a
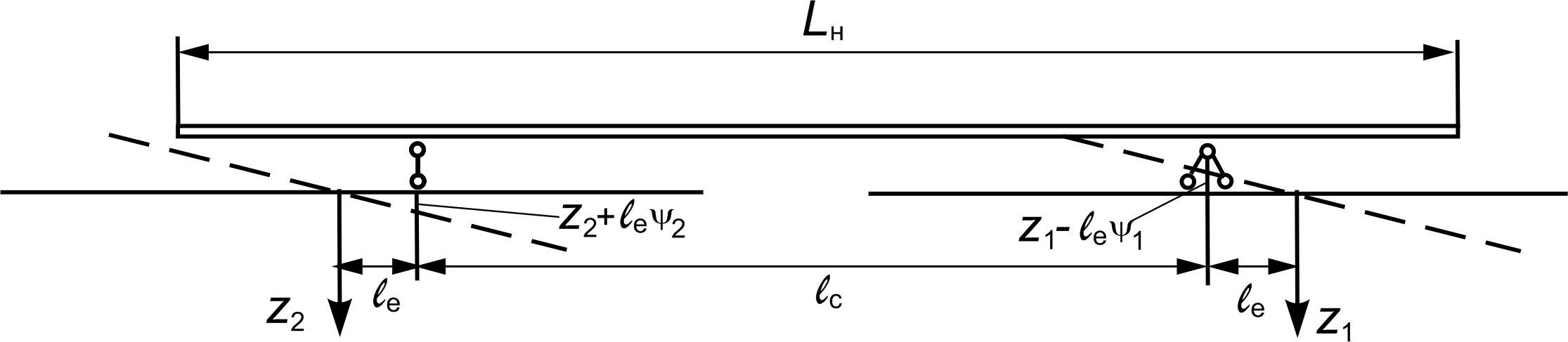
б
– b
в – c
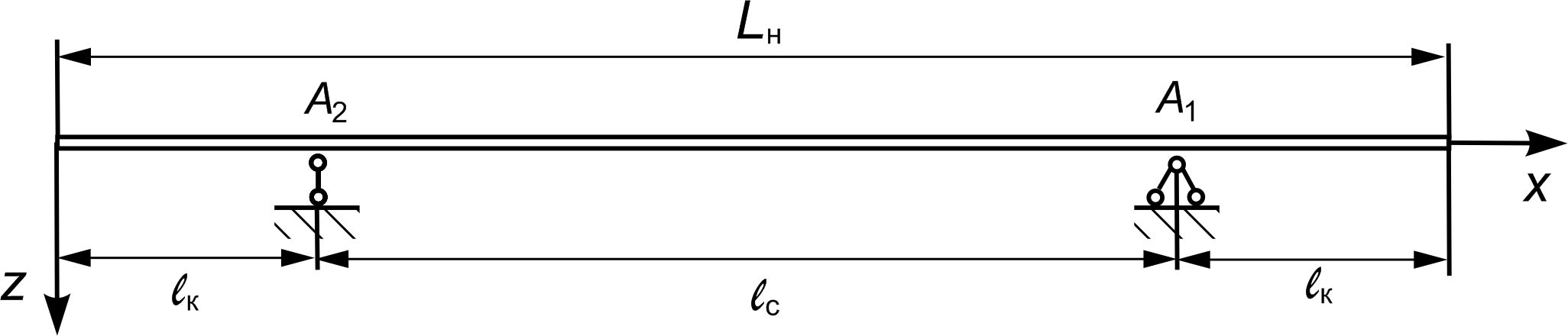
Рис.
3. Схематичне подання ярусів штабеля
довгомірного вантажу та їх опор:
а
– для визначення вертикальних переміщень
точок кузова в місцях опор;
б
– верхній ярус на пружних опорах;
в
– нижній ярус на жорстких опорах
Fig.
3. Schematic representation of the stack tiers of long cargo
and their supports:
a
–
to determine the vertical displacements of body points in the
support places;
b
– the upper tier on elastic supports; c
– the
lower tier on rigid supports
На рис.
3 позначено:
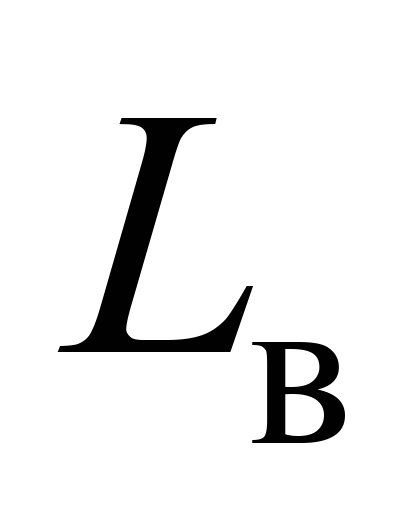 ,
,
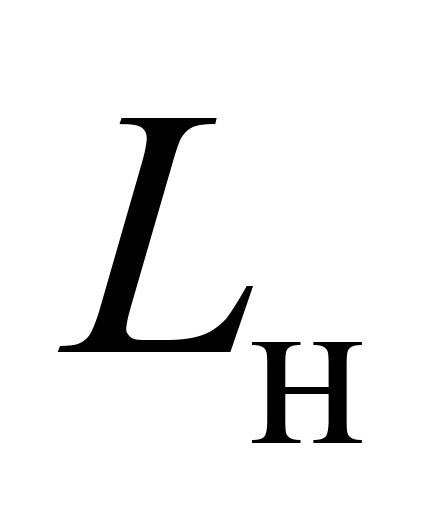 – довжина відповідно верхнього та
нижнього ярусів довгомірного вантажу,
які узято однаковими зі значенням 22 м;
– довжина відповідно верхнього та
нижнього ярусів довгомірного вантажу,
які узято однаковими зі значенням 22 м;
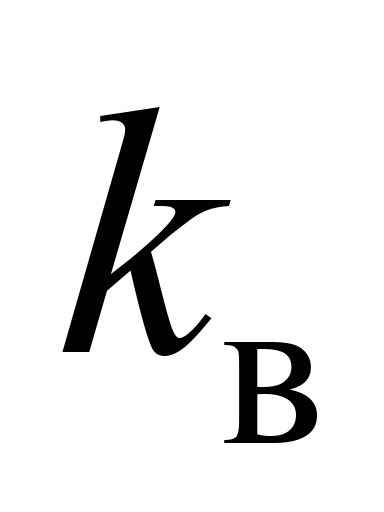 – жорсткість пружних опор верхнього
ярусу штабеля вантажу, 20 000 кН/м.
– жорсткість пружних опор верхнього
ярусу штабеля вантажу, 20 000 кН/м.
З
урахуванням накладених зв’язків та
узагальнених координат балок штабеля
як пружних тіл, механічна система має
двадцять ступенів свободи. За узагальнені
координати взято такі величини:
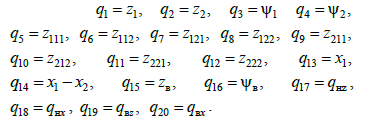
Розглянемо взаємні
переміщення верхнього та нижнього
ярусів вантажу. За вертикальних коливань
відбувається стискання пружних опор
першої і другої платформ на величину:
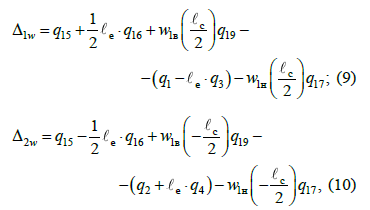
де
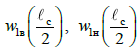 ,
– фундаментальні функції під час вигину
верхнього й нижнього ярусів, які
визначають із розв’язку задачі про
власні коливання відповідного ярусу
вантажу [8, 9].
,
– фундаментальні функції під час вигину
верхнього й нижнього ярусів, які
визначають із розв’язку задачі про
власні коливання відповідного ярусу
вантажу [8, 9].
Припускаємо, що в
поздовжньому напрямку взаємні переміщення
верхнього й нижнього ярусів на опорі
першої платформи відсутні, а мають
місце на опорі другої платформи:
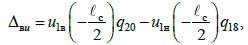 (11)
(11)
де
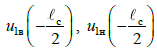 – фундаментальні функції під час
поздовжніх переміщень верхнього й
нижнього ярусів, які визначають із
розв’язку задачі про власні коливання
відповідного ярусу вантажу.
– фундаментальні функції під час
поздовжніх переміщень верхнього й
нижнього ярусів, які визначають із
розв’язку задачі про власні коливання
відповідного ярусу вантажу.
У процесі руху мають
місце взаємні переміщення нижнього
ярусу відносно другої платформи в
поздовжньому напрямку:
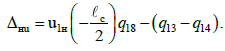 (12)
(12)
оскільки колія
передбачена пружно-в’язкою безінерційною,
будемо вважати, що розподілені параметри
колії можна замінити на зосереджені,
наведені до точок контакту коліс із
рейками. Вертикальні переміщення
наведених пружно-в’язких елементів
колії дорівнюють:
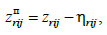 (13)
(13)
де
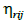 – поточна ордината геометричної
нерівності колії. Їх задають із
запізнюванням
– поточна ордината геометричної
нерівності колії. Їх задають із
запізнюванням
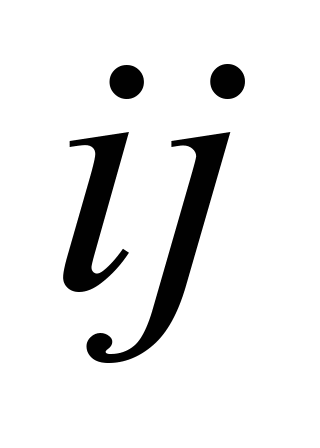 -ої
колісної пари відносно до першої
колісної пари першої платформи.
-ої
колісної пари відносно до першої
колісної пари першої платформи.
Взаємні переміщення
кузовів платформ у поздовжньому
напрямку визначають залежністю:
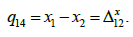 (14)
(14)
Поздовжню
силу, що діє на перший і другий вагон
зчепу з боку відкинутих частин поїзда
(рис. 4), позначено відповідно
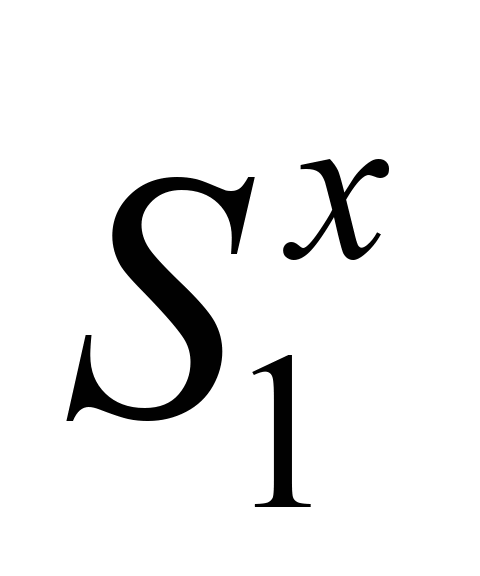 та
та
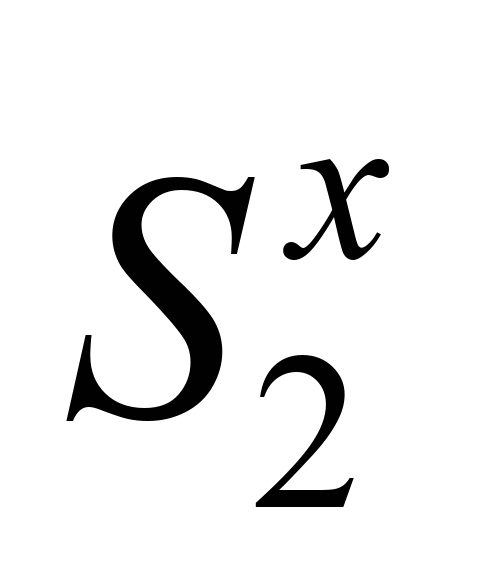 ,
значення яких у будь-який момент часу
визначають із розв’язку задачі
поздовжньої динаміки поїзда [2, 3, 11].
,
значення яких у будь-який момент часу
визначають із розв’язку задачі
поздовжньої динаміки поїзда [2, 3, 11].

Рис.
4. Розрахункова схема
зчепу з двох вагонів-платформ у складі
поїзда
Fig.
4. Computation
scheme of coupling
of two flat cars
in the train
Поздовжні
сили вважають позитивними, якщо вони
викликають розтягнення. Поздовжні сили
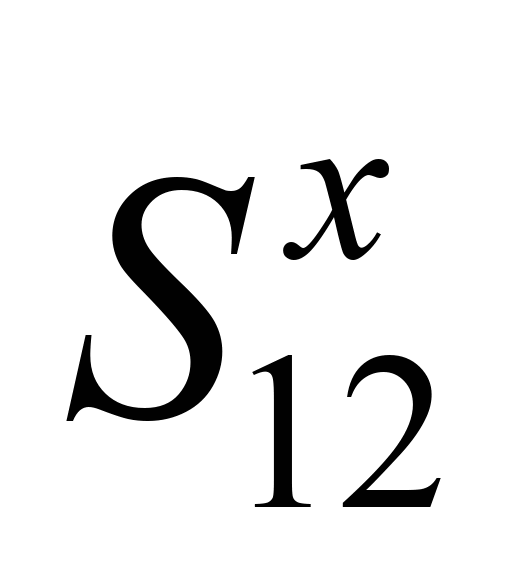 та
та
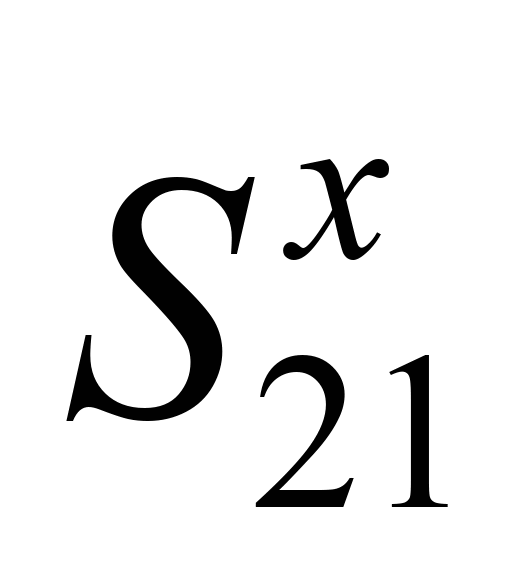 ,
які виникають у поглинальних апаратах
платформ зчепу, визначають відповідно
до [2, 3].
,
які виникають у поглинальних апаратах
платформ зчепу, визначають відповідно
до [2, 3].
Крім взаємних
поздовжніх переміщень платформ зчепу,
у процесі руху виникають також взаємні
вертикальні переміщення, які визначають
таким чином:
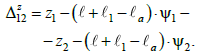 (15)
(15)
Під час цих переміщень
виникають вертикальні сили:
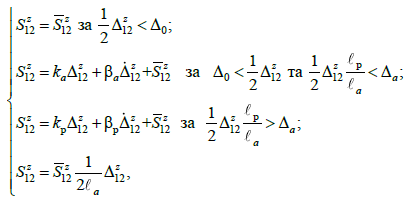 (16)
(16)
де
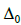 – зазор у контурі зачеплення, 0,005 м;
– зазор у контурі зачеплення, 0,005 м;
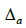 – зазор між тілами хвостовика
автозчеплення й обмежувальними
поличками розетки, 0,04 м;
– зазор між тілами хвостовика
автозчеплення й обмежувальними
поличками розетки, 0,04 м;
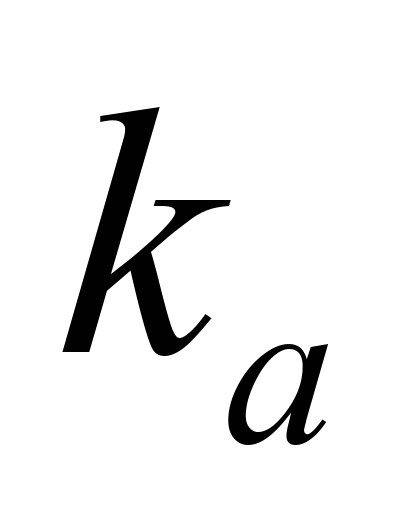 – вертикальна жорсткість пружин
центрувальної балочки, 26 000 кН/м;
– вертикальна жорсткість пружин
центрувальної балочки, 26 000 кН/м;
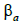 – коефіцієнт в’язкого тертя за
вертикальних переміщень автозчеплення
в межах вікна розетки;
– коефіцієнт в’язкого тертя за
вертикальних переміщень автозчеплення
в межах вікна розетки;
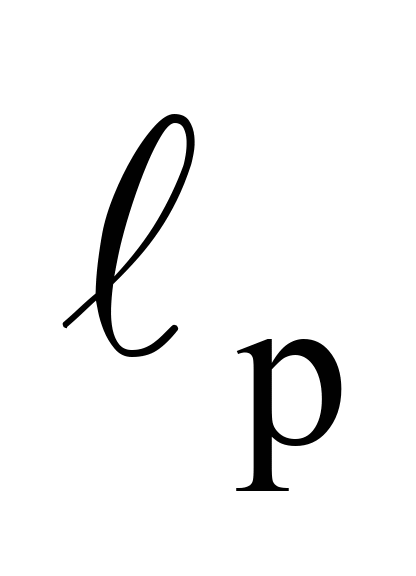 – відстань від осі клина автозчеплення
до ударної поверхні розетки, 0,43 м;
– відстань від осі клина автозчеплення
до ударної поверхні розетки, 0,43 м;
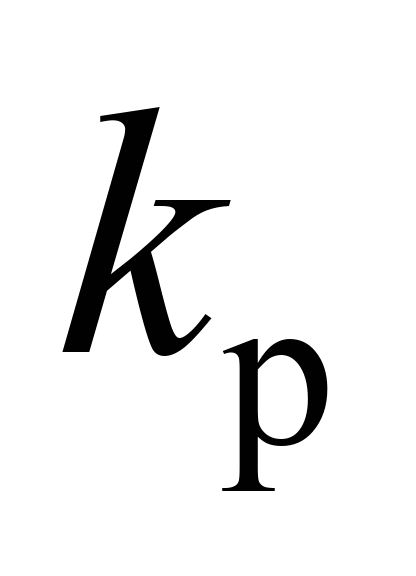 ,
,
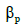 – відповідно вертикальна жорсткість
і коефіцієнт в’язкого
– відповідно вертикальна жорсткість
і коефіцієнт в’язкого
тертя розетки,
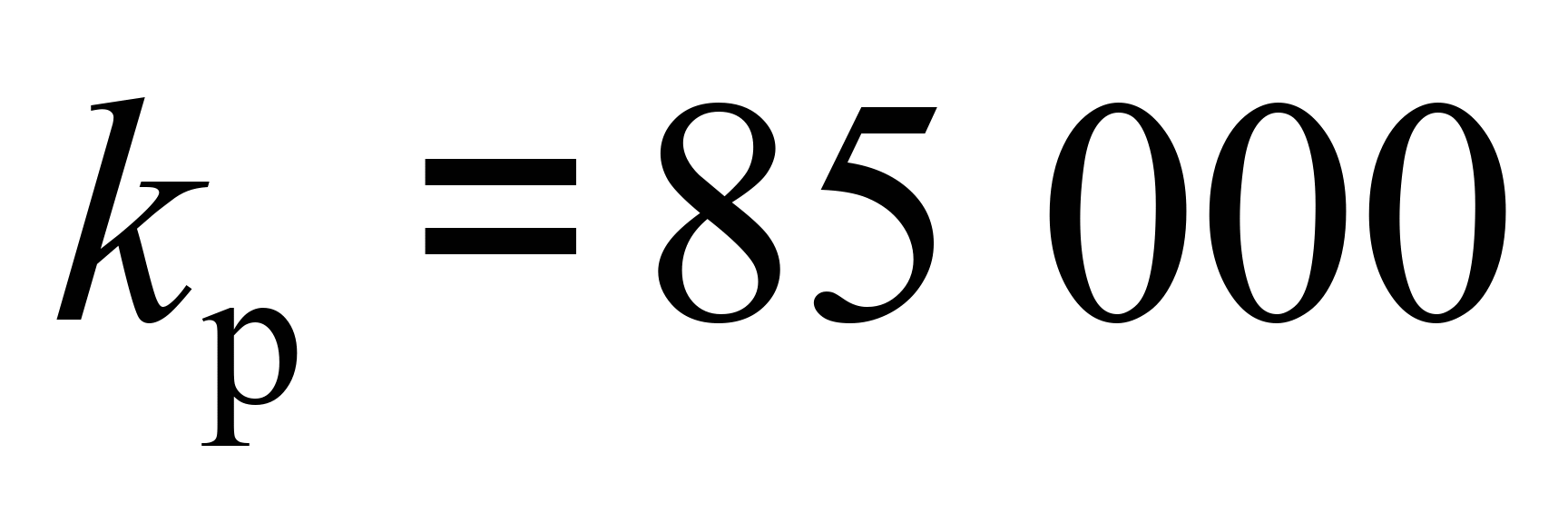 кН/м;
кН/м;
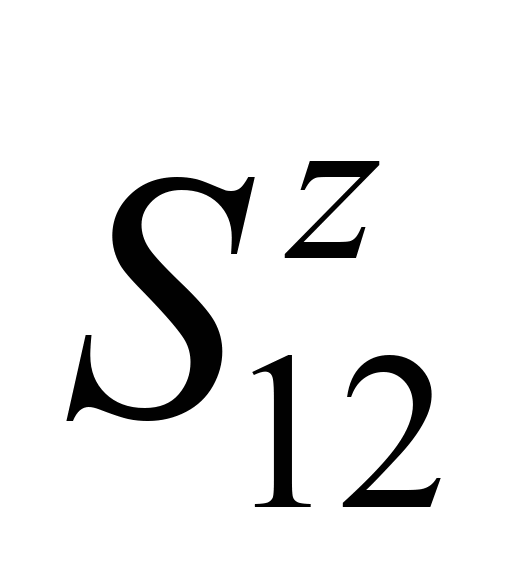 ,
,
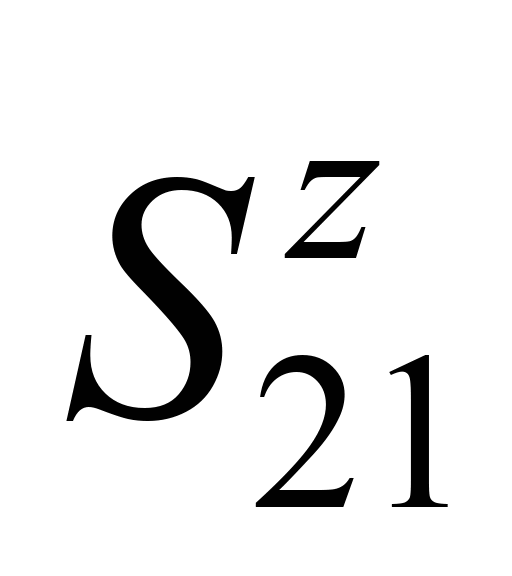 – вертикальна складова поздовжньої
сили в автозчепленні.
– вертикальна складова поздовжньої
сили в автозчепленні.
Визначимо
добавки до узагальнених сил (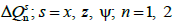 ),
які входять до правих частин диференціальних
рівнянь, що описують коливання кузовів
розглянутих вагонів. Добавки до
узагальнених сил, що входять до рівняння
першої платформи, описують залежностями
(17), а другої – (18):
),
які входять до правих частин диференціальних
рівнянь, що описують коливання кузовів
розглянутих вагонів. Добавки до
узагальнених сил, що входять до рівняння
першої платформи, описують залежностями
(17), а другої – (18):
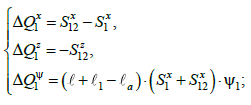 (17)
(17)
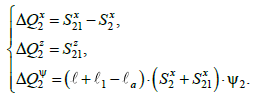 (18)
(18)
Диференціальні
рівняння коливання системи складені
з використанням рівняння Лагранжа II
роду:
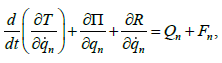 (19)
(19)
де
 ,
,
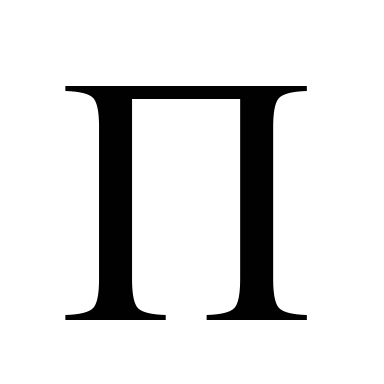 – кінетична й потенціальна енергії
системи;
– кінетична й потенціальна енергії
системи;
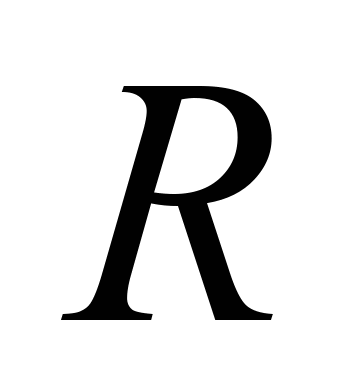 – функція розсіювання енергії системи;
– функція розсіювання енергії системи;
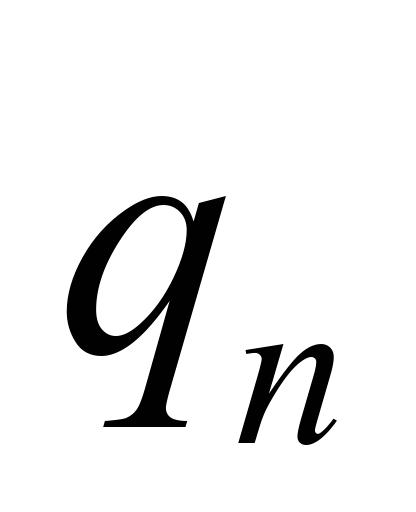 – узагальнені координати;
– узагальнені координати;
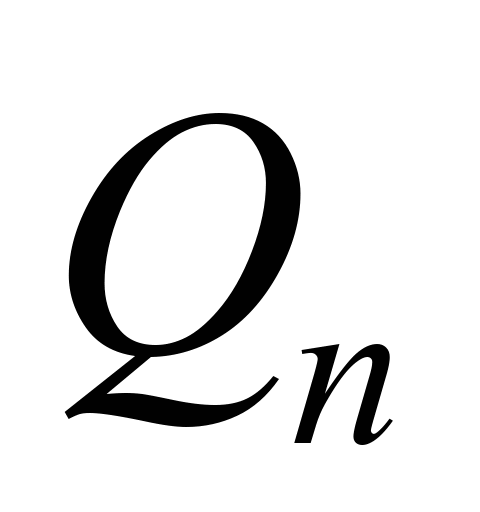 – відповідні їм узагальнені сили, що
є сумою сил взаємодії колеса й рейки
та сил, що діють у з’єднаннях між
вагонами під час руху поїзда;
– відповідні їм узагальнені сили, що
є сумою сил взаємодії колеса й рейки
та сил, що діють у з’єднаннях між
вагонами під час руху поїзда;
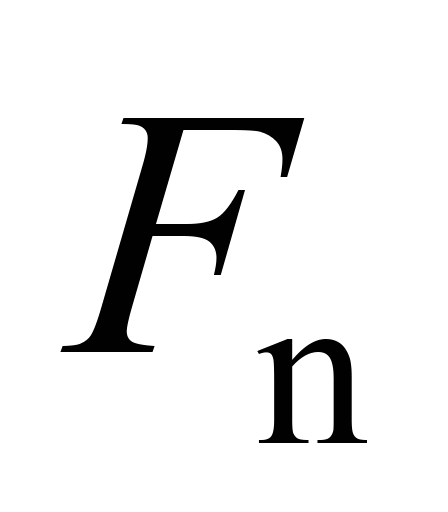 – зовнішні сили тяги або гальмування;
– зовнішні сили тяги або гальмування;
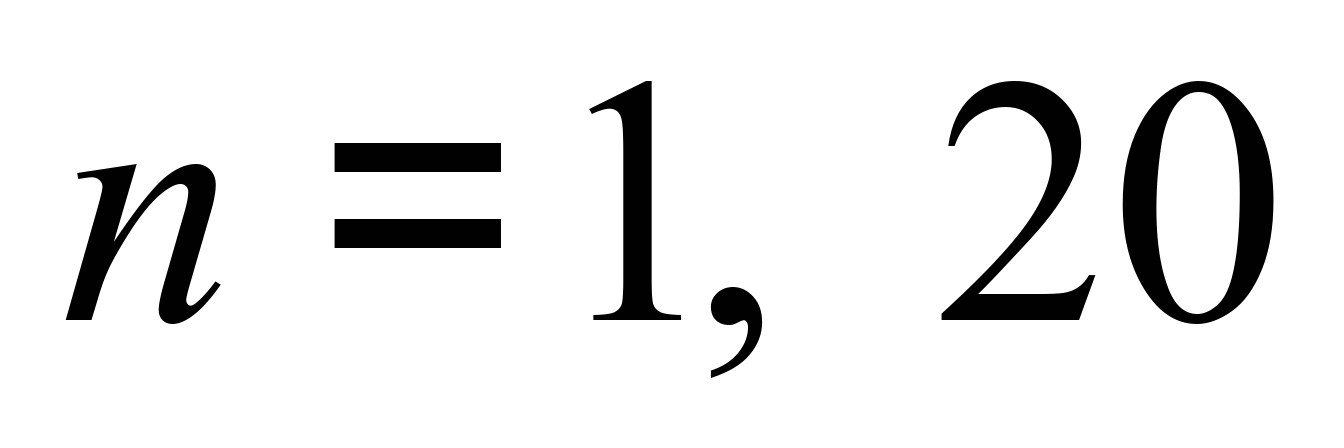 – число ступенів свободи.
– число ступенів свободи.
Кінетична та
потенціальна енергії системи визначено
за залежностями:
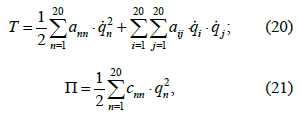
де
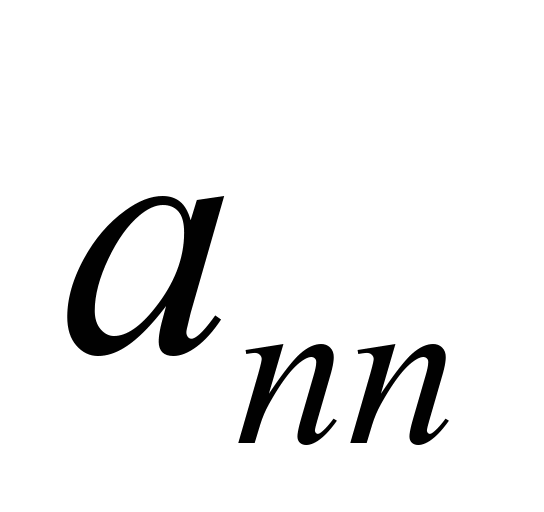 ,
,
 – інерційні коефіцієнти;
– інерційні коефіцієнти;
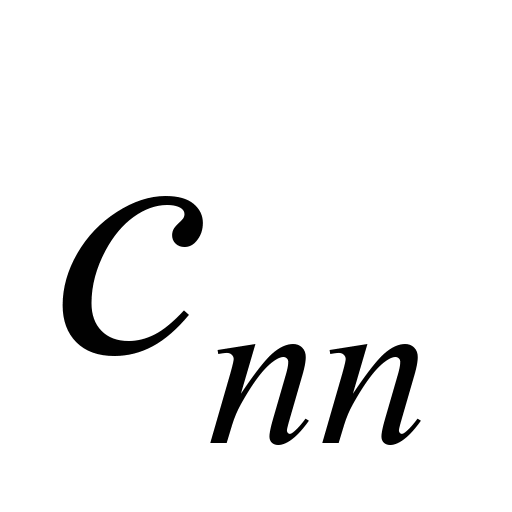 – коефіцієнти жорсткості;
– коефіцієнти жорсткості;
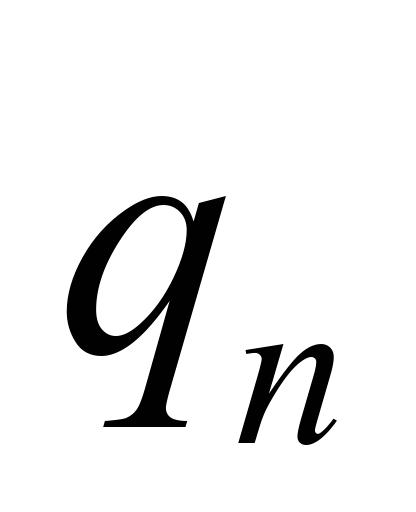 – узагальнені координати.
– узагальнені координати.
Функція розсіювання
енергії системи містить внутрішню
енергію розсіювання в матеріалі ярусів
довгомірного вантажу, вона пропорційна
відповідній кінетичній енергії та
дорівнює:
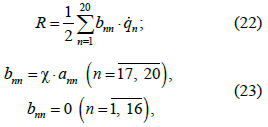
де
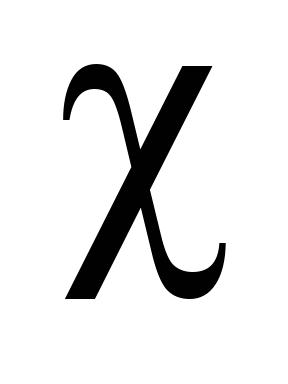 – коефіцієнт розсіювання енергії.
– коефіцієнт розсіювання енергії.
Кінетична й
потенціальна енергії системи складені
з урахуванням кінетичної й потенціальної
енергії вантажу, яку обчислюють за
відомими фундаментальними функціями.
Для визначення фундаментальних функцій
розв’язують задачу про згинальні
коливання вантажу як балки на двох
пружних опорах [8, 9].
Власні
частоти коливань верхнього ярусу на
двох пружних опорах як стрижня з
розподіленою рівномірно по довжині
погонною масою, визначають із розв’язання
характеристичного рівняння, записаного
в узагальнених функціях А. Н. Крилова
й отриманого шляхом розв’язання
диференційного рівняння вигину стержня
довжиною
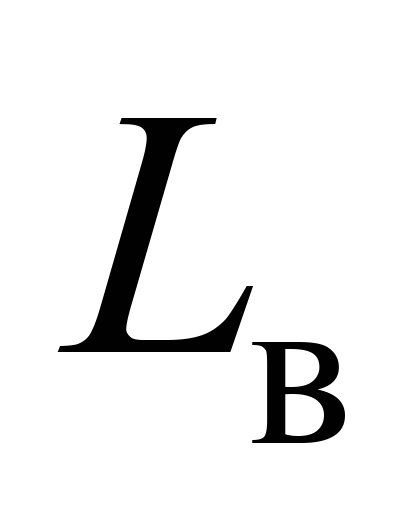 із зосередженими включеннями в
жорсткість. Характеристичне рівняння
системи:
із зосередженими включеннями в
жорсткість. Характеристичне рівняння
системи:
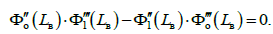 (24)
(24)
Цим
частотам відповідають власні форми,
які визначають виразом для фундаментальної
функції
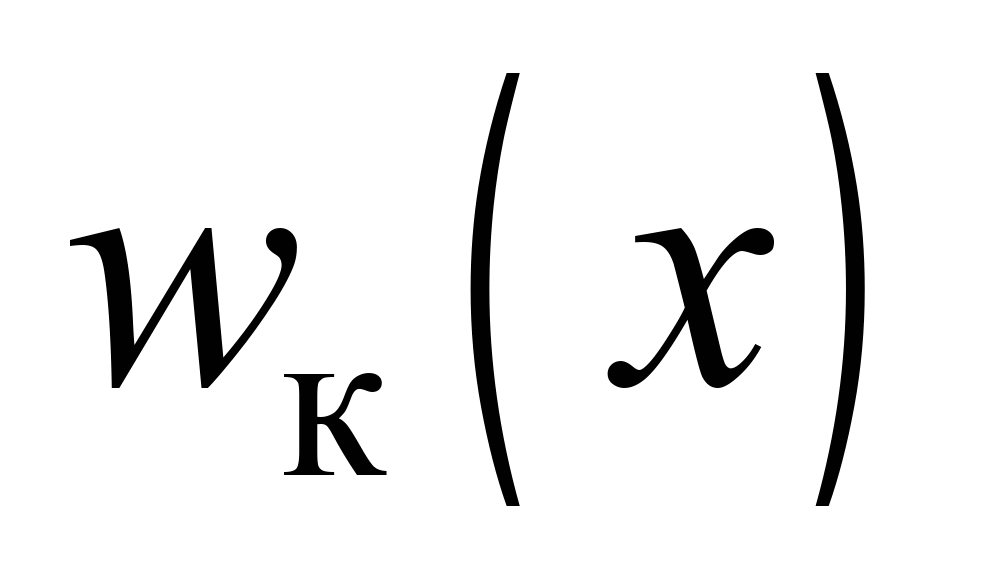 :
:
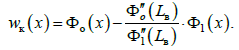 (25)
(25)
де
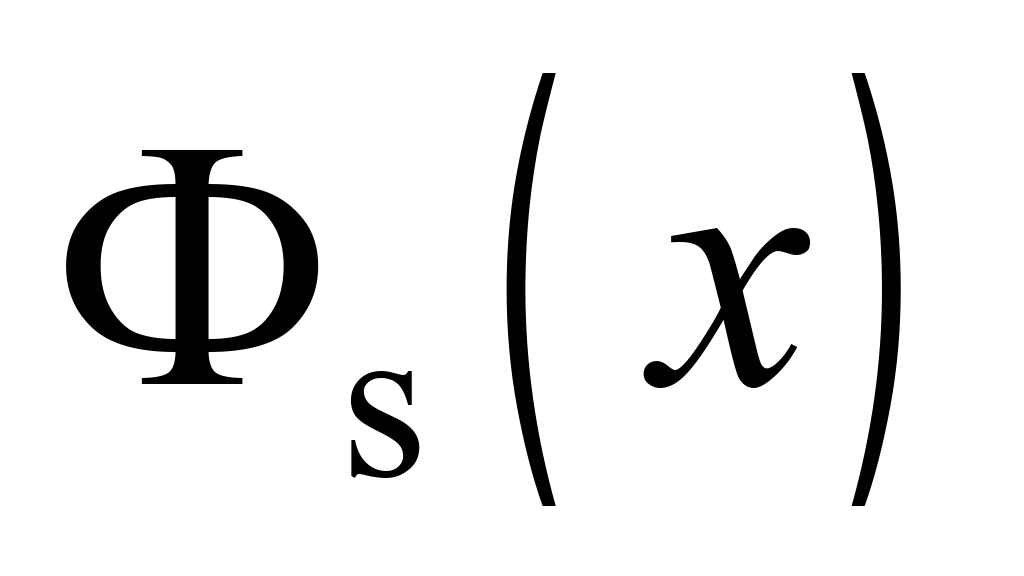 ,
,
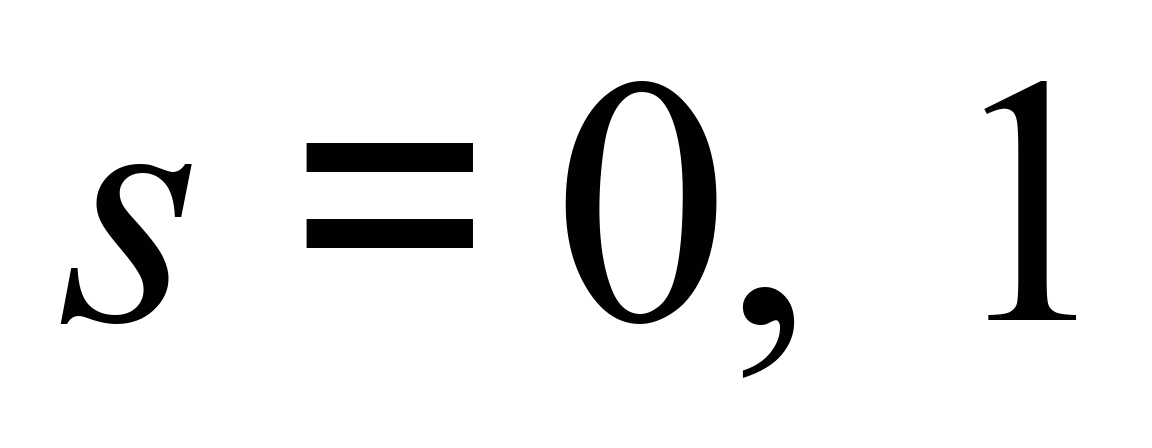 – узагальнені функції А. Н. Крилова,
що належить до класу сплайнів.
– узагальнені функції А. Н. Крилова,
що належить до класу сплайнів.
Граничний
перехід
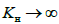 дає можливість визначити частоти й
форми коливань вільного нижнього ярусу
довжиною
дає можливість визначити частоти й
форми коливань вільного нижнього ярусу
довжиною
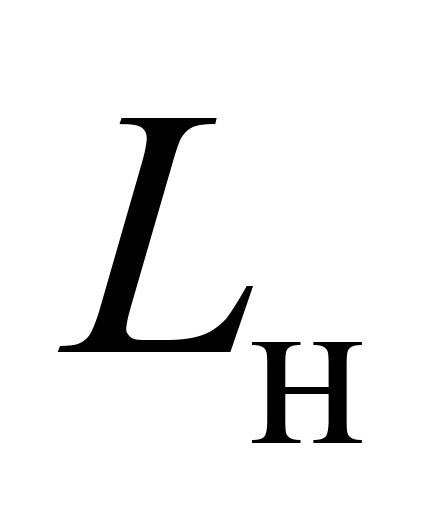 як стрижня на жорстких опорах. Після
визначення фундаментальних функцій
можна визначити переміщення верхнього
й нижнього ярусів. Оскільки розглянуто
одну форму згинальних коливань ярусів,
вирази для визначення переміщень мають
такий вигляд:
як стрижня на жорстких опорах. Після
визначення фундаментальних функцій
можна визначити переміщення верхнього
й нижнього ярусів. Оскільки розглянуто
одну форму згинальних коливань ярусів,
вирази для визначення переміщень мають
такий вигляд:
– для
верхнього ярусу:
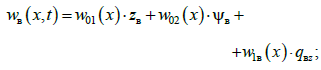 (26)
(26)
– для
нижнього ярусу:
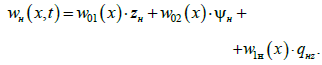 (27)
(27)
Оскільки в поздовжньому
напрямку опори верхнього та нижнього
ярусів вантажу працюють однаково
(жорсткість усіх опор у поздовжньому
напрямку не беруть до уваги), то поздовжні
коливання обох ярусів розглядають за
однаковою розрахунковою схемою. Для
визначення фундаментальних функцій
за поздовжніх переміщень використано
диференціальне рівняння вільних
поздовжніх коливань стрижня постійного
перетину в припущенні, що виникає
поздовжня реакція [8].
Фундаментальну
функцію
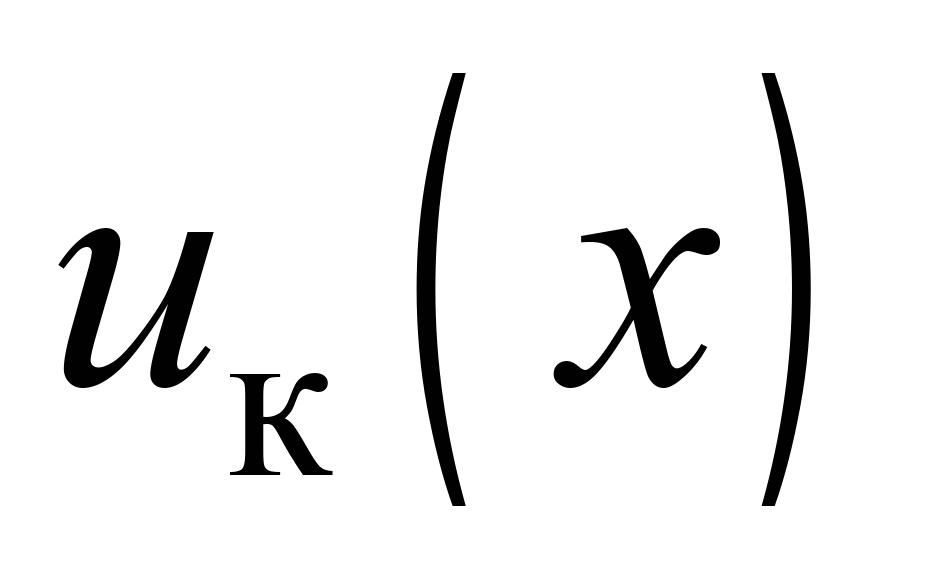 для поздовжніх переміщень верхнього
ярусу вантажу визначаються за виразом:
для поздовжніх переміщень верхнього
ярусу вантажу визначаються за виразом:
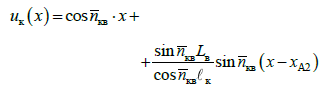 ,(28)
,(28)
де
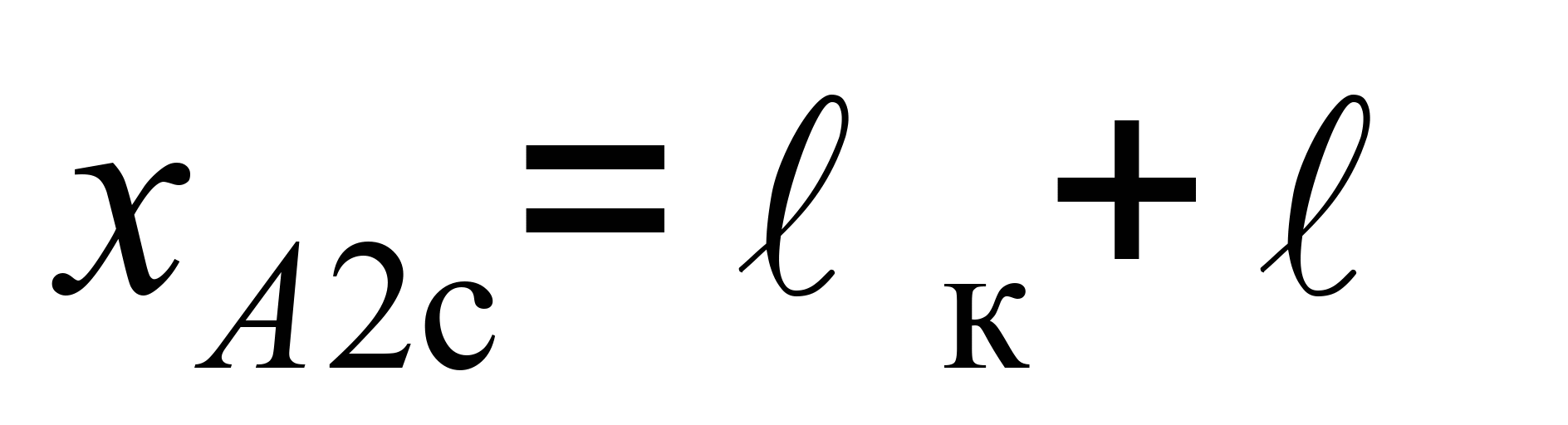 – координата опори нижнього ярусу
вантажу
– координата опори нижнього ярусу
вантажу
 уздовж осі
уздовж осі
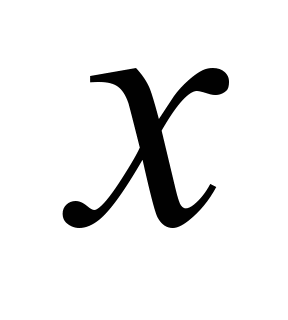 .
.
Характеристичне
рівняння задачі за поздовжніх коливань
має вигляд:
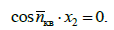 (29)
(29)
Розв’язок цього
рівняння має вигляд:
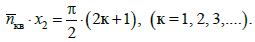 (30)
(30)
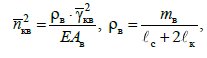 (31)
(31)
де
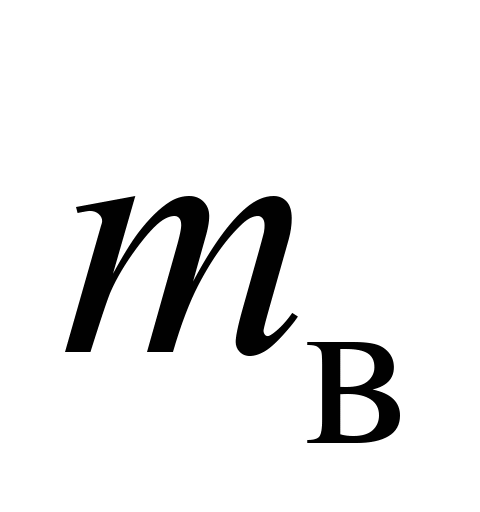 – маса верхнього ярусу вантажу;
– маса верхнього ярусу вантажу;
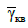 – частота
– частота
 -го
тону власних поздовжніх коливань
верхнього ярусу;
-го
тону власних поздовжніх коливань
верхнього ярусу;
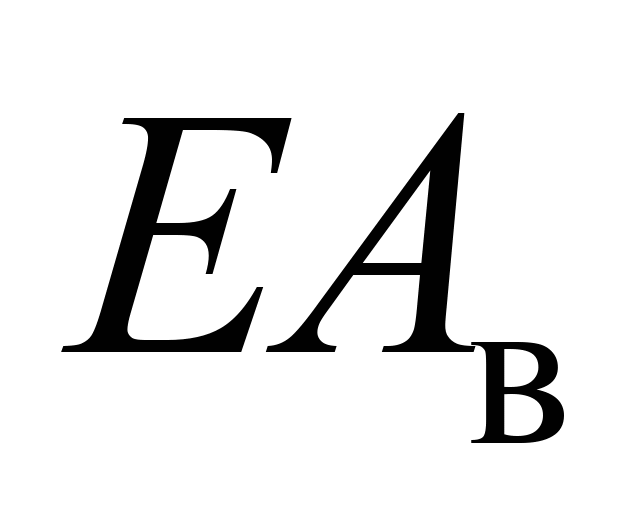 – жорсткість під час розтягування
верхнього ярусу вантажу.
– жорсткість під час розтягування
верхнього ярусу вантажу.
Для поздовжніх
переміщень нижнього ярусу вантажу
розв’язок здобувають за аналогічним
алгоритмом. Оскільки в розрахунках
береться до уваги одна форма поздовжніх
коливань стрижнів, то вирази для
визначення поздовжніх переміщень мають
такий вигляд:
– для
верхнього ярусу:
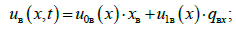 (31)
(31)
– для
нижнього ярусу:
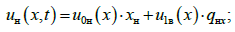 (32)
(32)
де
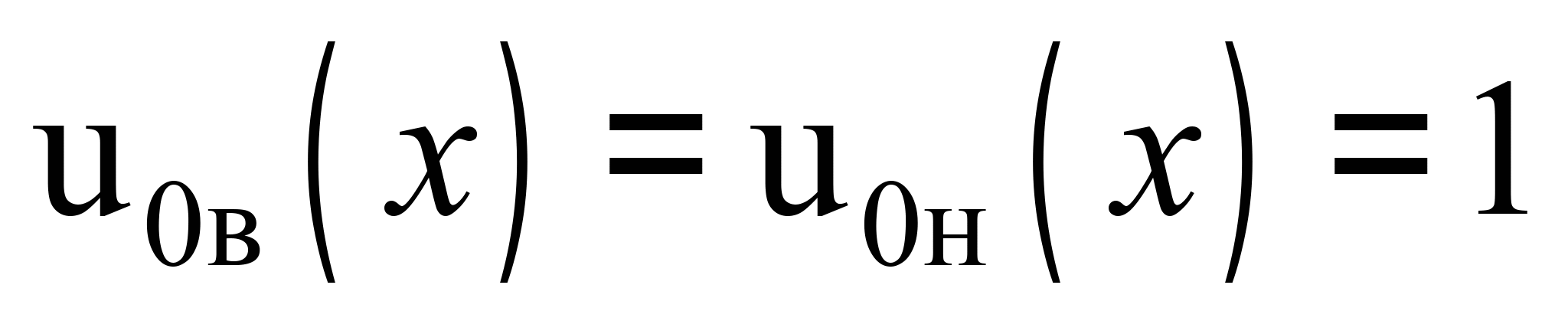 – фундаментальні функції за поздовжніх
переміщень ярусів як твердих тіл [8].
– фундаментальні функції за поздовжніх
переміщень ярусів як твердих тіл [8].
Параметри, які
використовують для визначення показників
динамічних якостей та власних частот
коливань штабелів довгомірного вантажу,
зведені в табл. 2.
Таблиця
2
Вихідні
дані для розрахунків
Table
2
Initial data for
calculations
|
Позна-
чення
|
Параметр
|
Значення
|
Розмірність
|
|
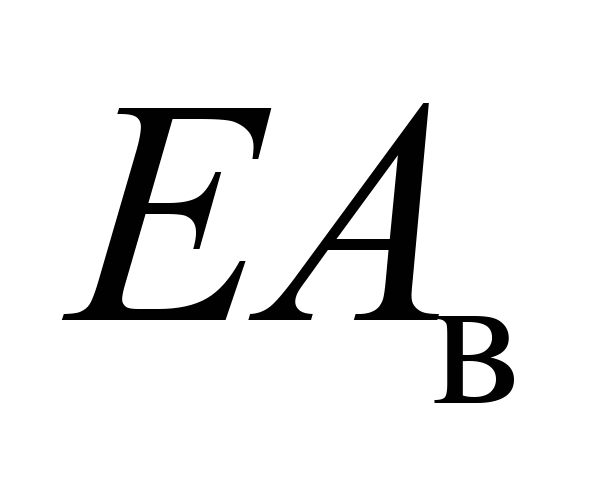
|
жорсткість
за розтягування верхнього ярусу
вантажу
|
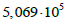
|
т
|
|
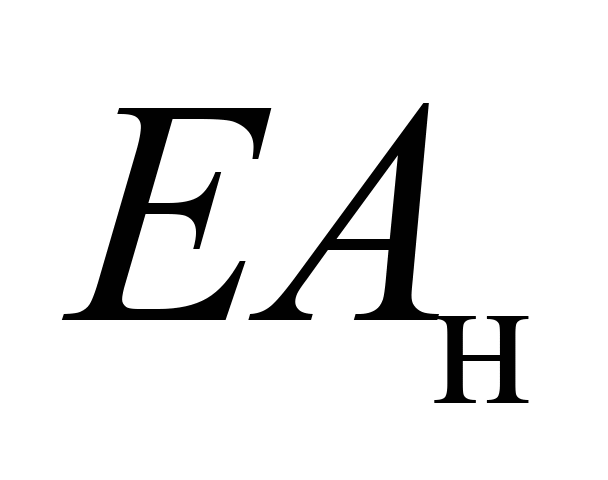
|
жорсткість
за розтягування нижнього ярусу
вантажу
|

|
т
|
|
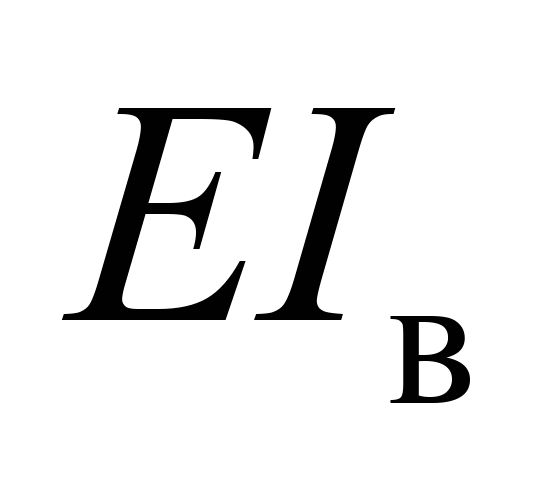
|
згинальна
жорсткість верхнього ярусу вантажу
|
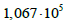
|
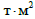
|
|

|
згинальна
жорсткість нижнього ярусу вантажу
|
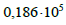
|
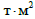
|
|
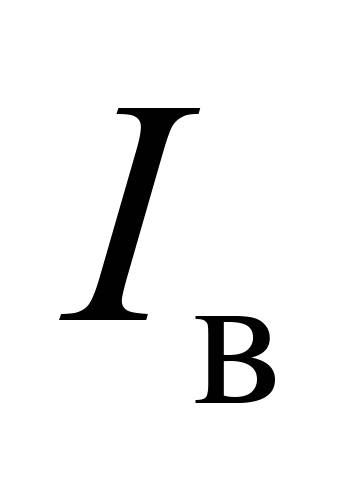
|
осьовий
момент інерції верхнього ярусу
вантажу
|
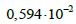
|
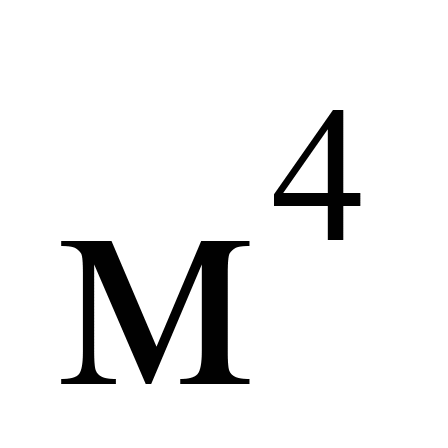
|
|
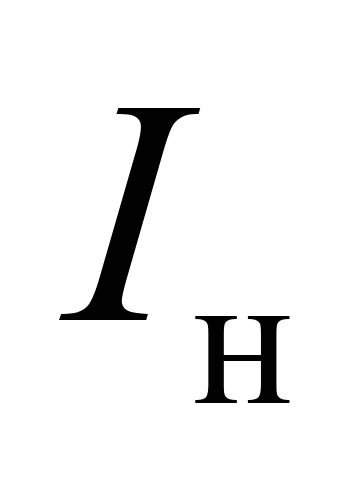
|
осьовий
момент інерції нижнього ярусу вантажу
|
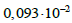
|
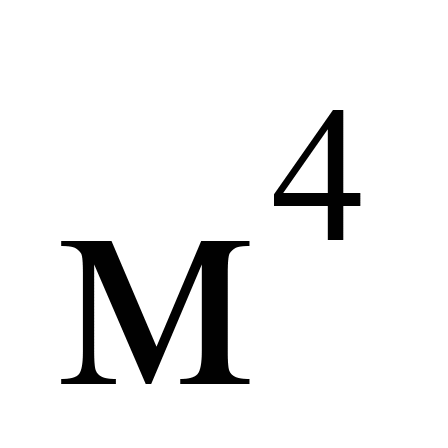
|
|
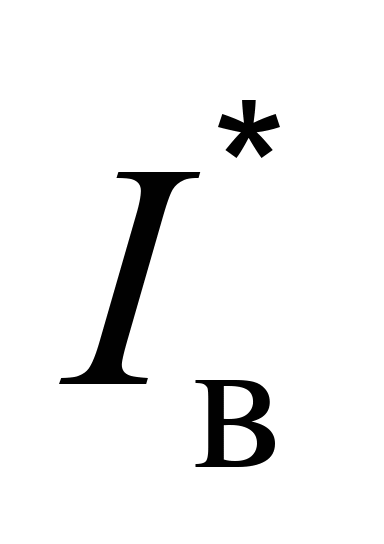
|
момент
інерції відносно центральної осі
верхнього ярусу вантажу
|
976,06
|
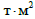
|
|
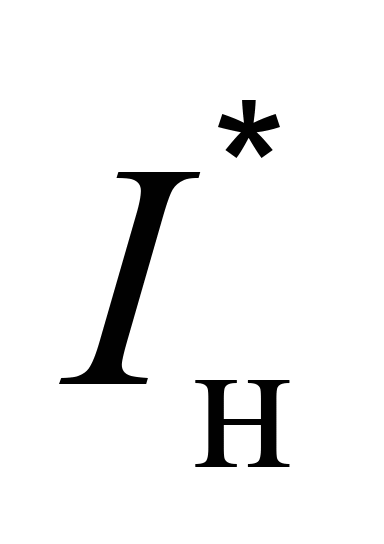
|
момент
інерції відносно центральної осі
нижнього ярусу вантажу
|
1774,67
|
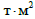
|
|
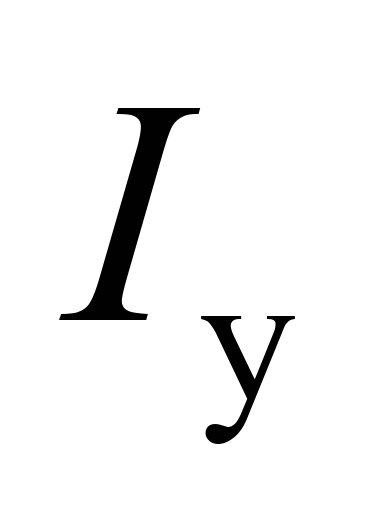
|
момент
інерції кузова платформи відносно
головної осі
|
270
|
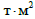
|
|
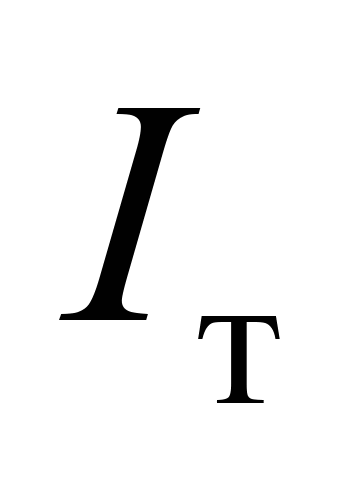
|
момент
інерції візка (без колісних пар та
надресорних балок)
|
27
|
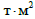
|
|
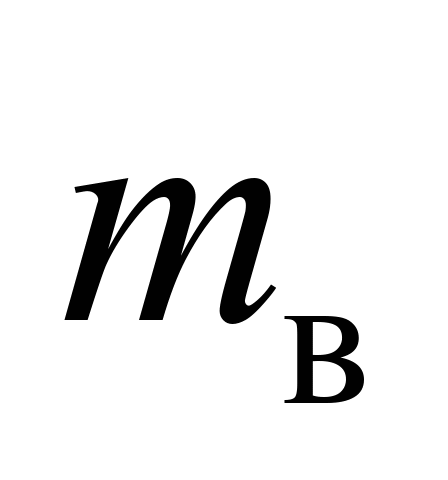
|
маса
верхнього ярусу вантажу
|
44,0
|
т
|
|
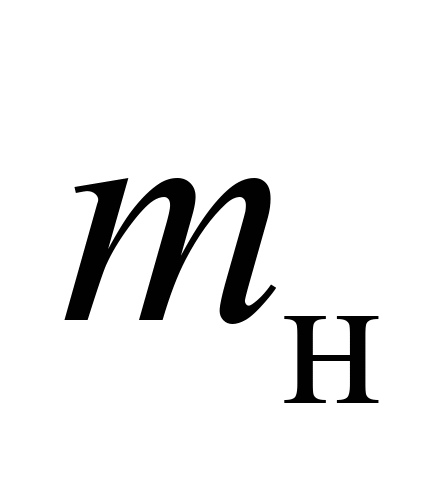
|
маса
нижнього ярусу вантажу
|
24,0
|
т
|
|
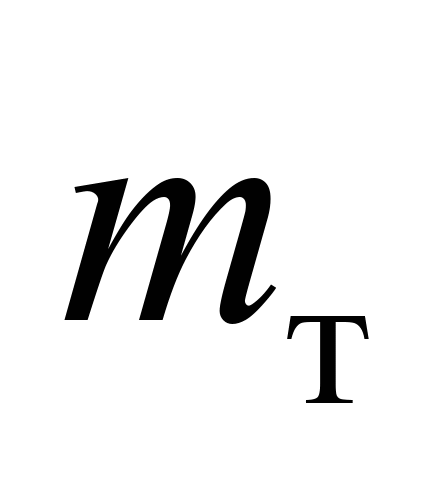
|
маса
візка
|
4,7
|
т
|
|
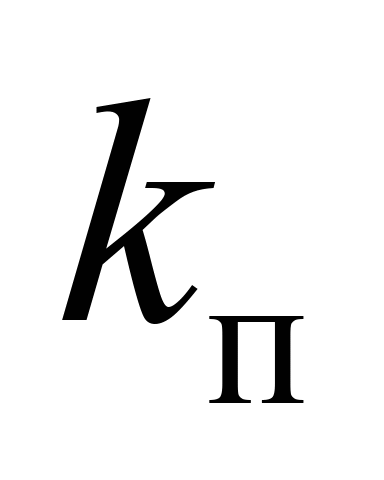
|
приведена
жорсткість колії
|
14160
|
кН/м
|
|
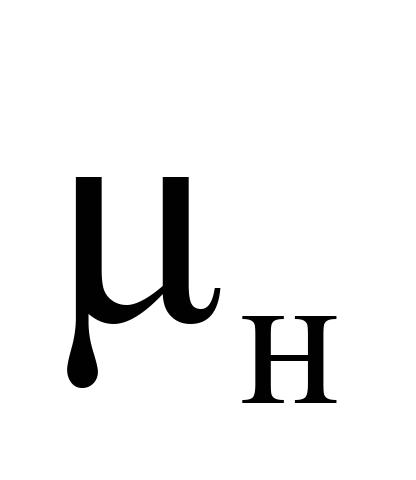
|
коефіцієнт
тертя пари сталь-сталь
|
0,3
|
|
|
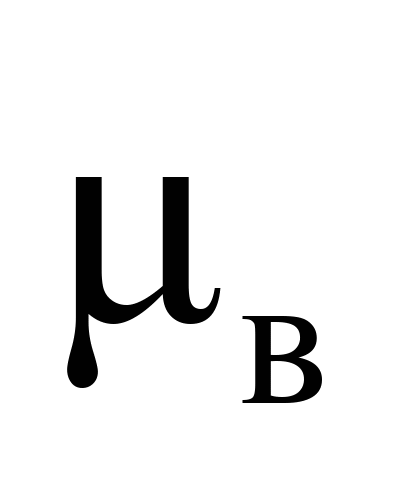
|
коефіцієнт
тертя пари сталь-дерево
|
0,4
|
|
Таблиця 3
Рівні
оцінки й допустимі значення показників
динамічних якостей
Table
3
Levels of
estimation and admissible values of dynamic qualities indicators
|
Показник
|
Рівень
оцінки
|
Допустимі
значення
|
|
|
|
порожній
|
завантажений
|
|
Максимальний
коефіцієнт динамічної добавки
обресорених частин (коефіцієнт
вертикальної динаміки центрального
ступеня підвішування)
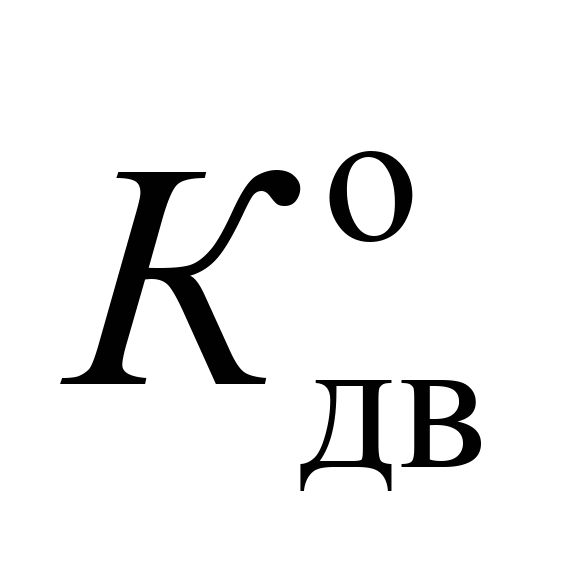
|
відмінно
|
0,5
|
0,2
|
|
добре
|
0,6
|
0,35
|
|
задовільно
|
0,7
|
0,4
|
|
допустимий
|
0,75
|
0,65
|
|
Максимальне
вертикальне прискорення обресорених
частин у частках від прискорення
вільного падіння
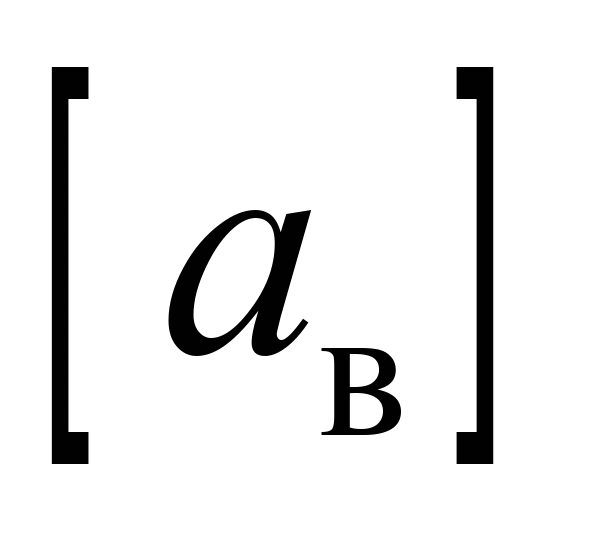
|
відмінно
|
0,5
|
0,2
|
|
добре
|
0,6
|
0,35
|
|
задовільно
|
0,7
|
0,45
|
|
допустимий
|
0,75
|
0,65
|
|
Коефіцієнт
стійкості від сходження колеса з
рейок
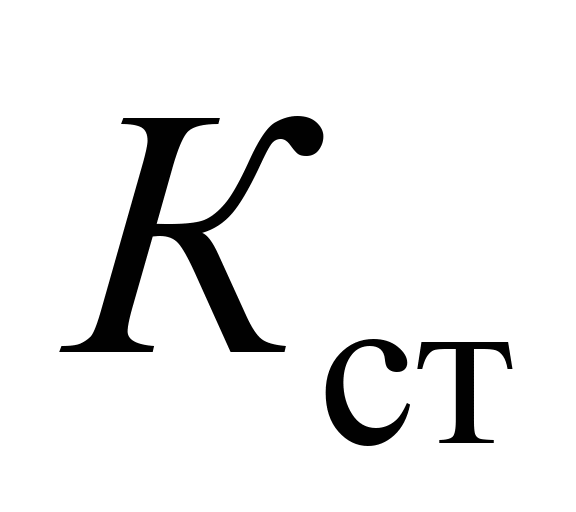
|
допустимий
|
1,3
|
|
Коефіцієнт
стійкості від сходження колеса з
рейок у разі дії стискних поздовжніх
сил
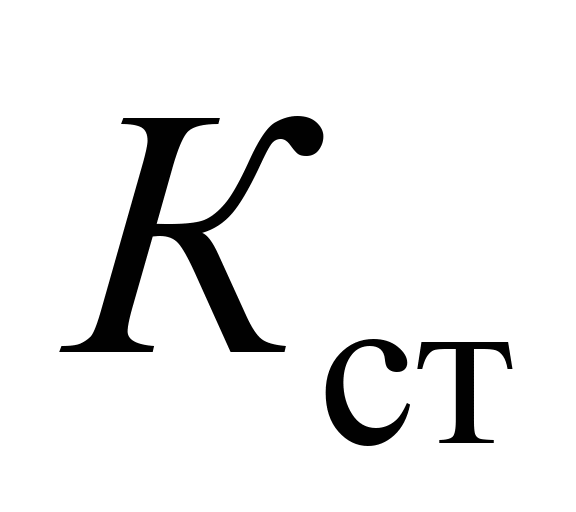
|
допустимий
|
1,2
|
Результати
Теоретичні дослідження
проведені за умови руху вагонів-платформ
моделі 13–4012 з типовими візками 18–100
зі швидкостями в інтервалі від 60 до 100
км/год на прямій ділянці залізничної
колії. Під час проведення теоретичних
досліджень динамічних показників
платформ зчепу як збурювання використано
випадкові вертикальні геометричні
нерівності колії. У досліджені взято
до уваги рух зчепу вагонів-платформ по
синусоїдальній нерівності довжиною
25 м і різною глибиною у випадку дії
поздовжніх стискних або розтягальних
сил, а також на вибігу.
Графіки
зміни досліджуваних динамічних
показників наведені на рис. 5–7. На
неведених графічних залежностях
представлено максимальні та мінімальні
значення: коефіцієнтів динамічної
добавки обресорених частин (вертикальної
динаміки в центральному ресорному
підвішуванні)
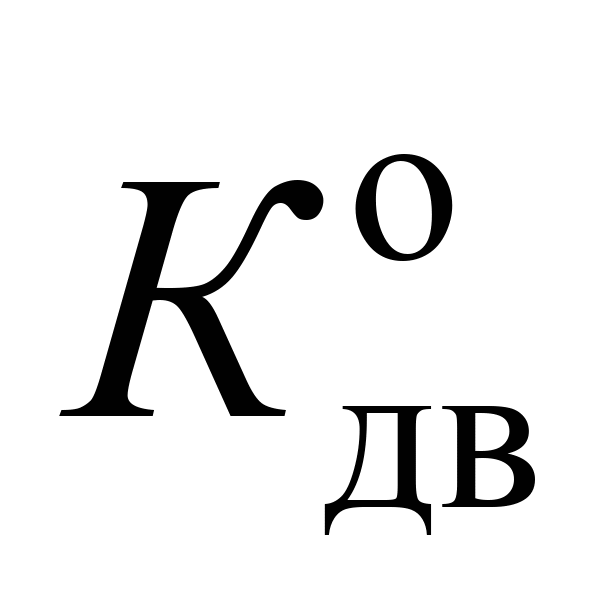 ;
коефіцієнтів вертикальної динаміки
колії за силами взаємодії коліс та
рейок
;
коефіцієнтів вертикальної динаміки
колії за силами взаємодії коліс та
рейок
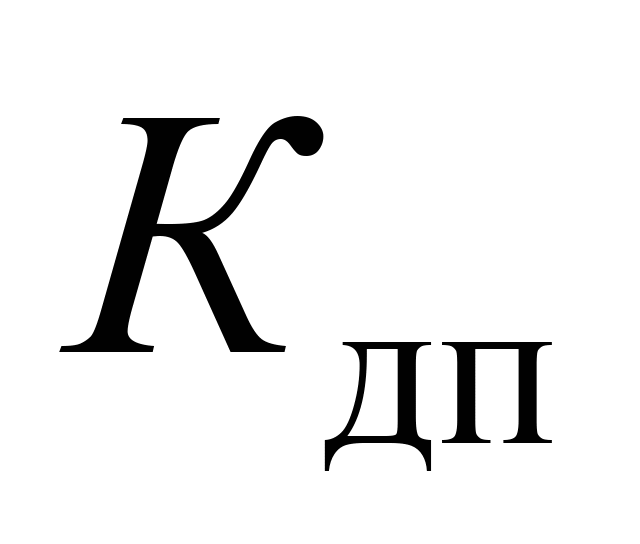 ;
вертикального прискорення обресорених
частин
;
вертикального прискорення обресорених
частин
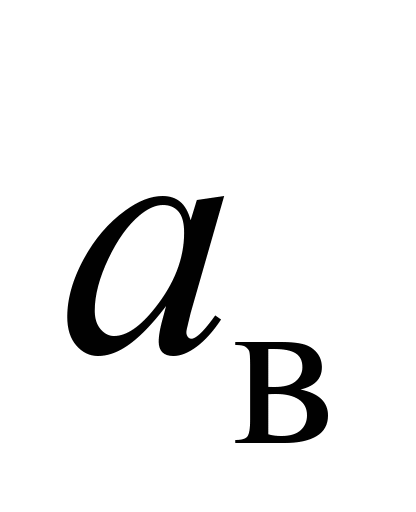 в частках від прискорення вільного
падіння
в частках від прискорення вільного
падіння
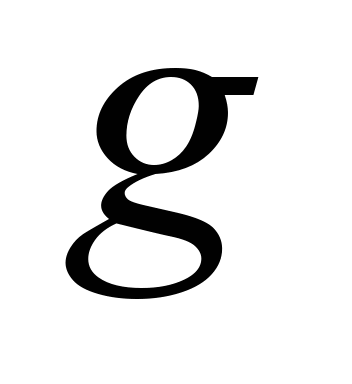 .
.
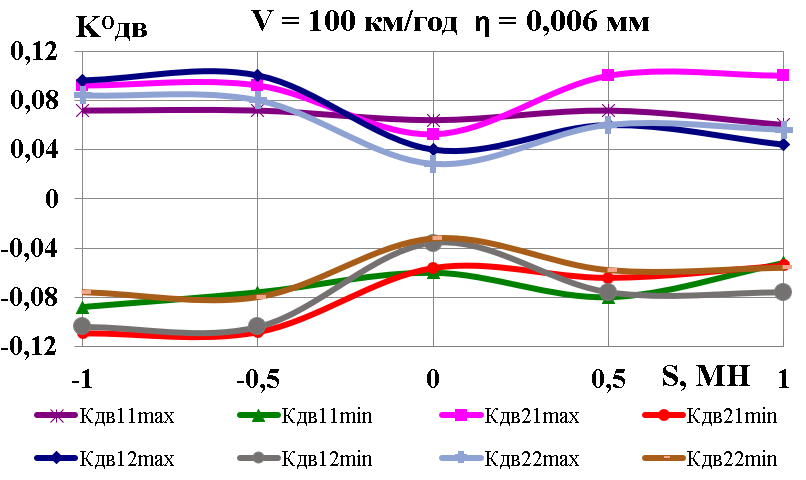
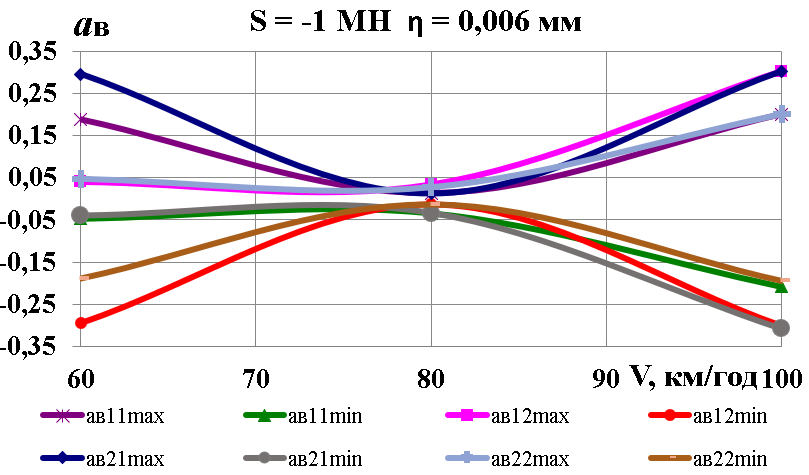
У
теоретичному дослідженні розглянуто
вплив квазістатичних поздовжніх
розтягальних та стискних сил у діапазоні
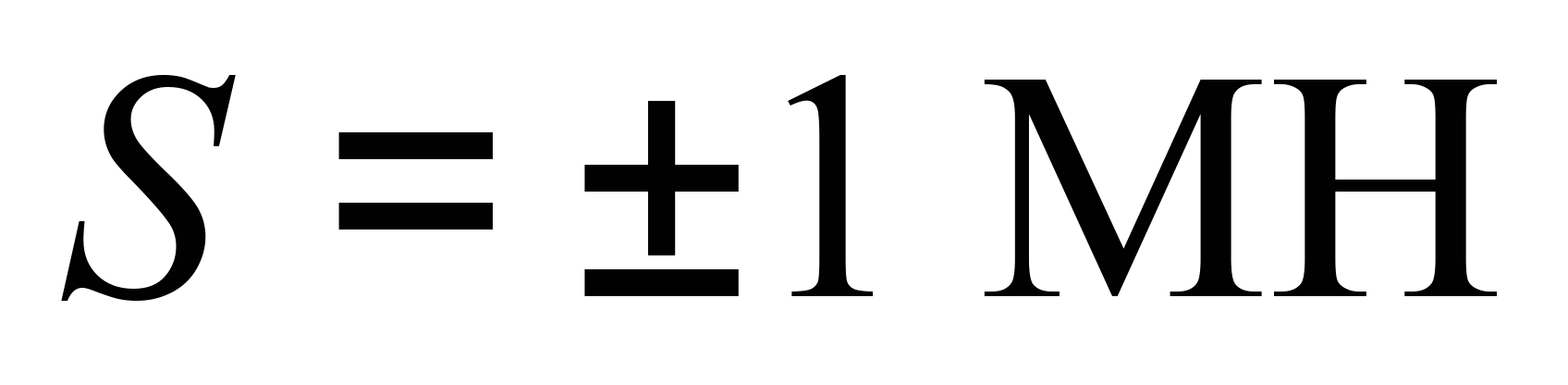 за швидкості 100 км/год та величини
синусоїдальної нерівності глибиною
за швидкості 100 км/год та величини
синусоїдальної нерівності глибиною
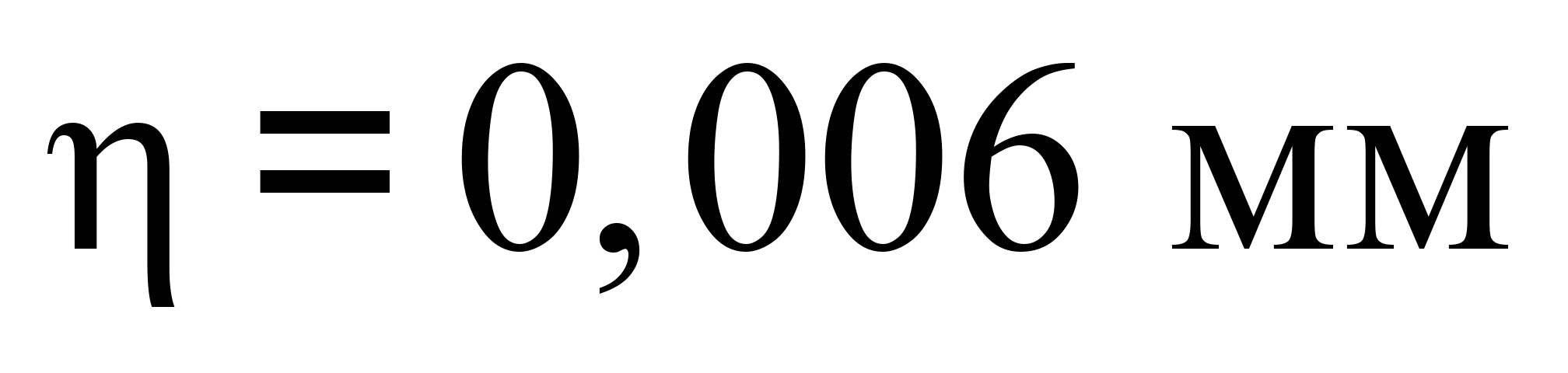 (рис.
5).
(рис.
5).
а
– a
б
– b
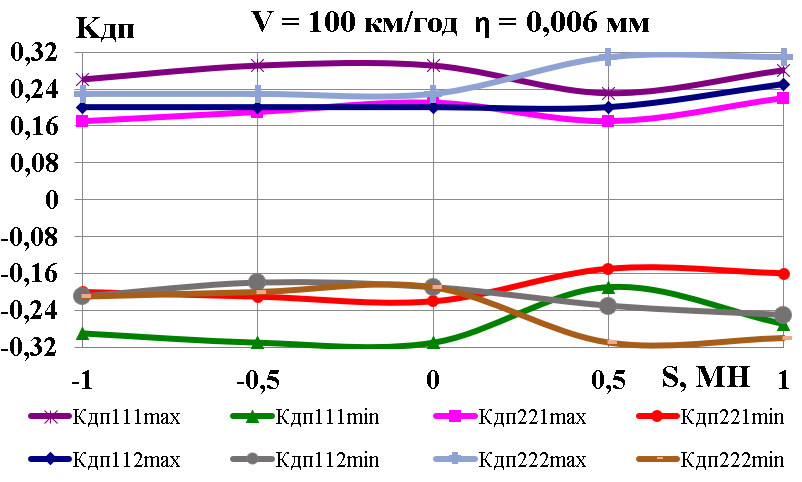
в – c
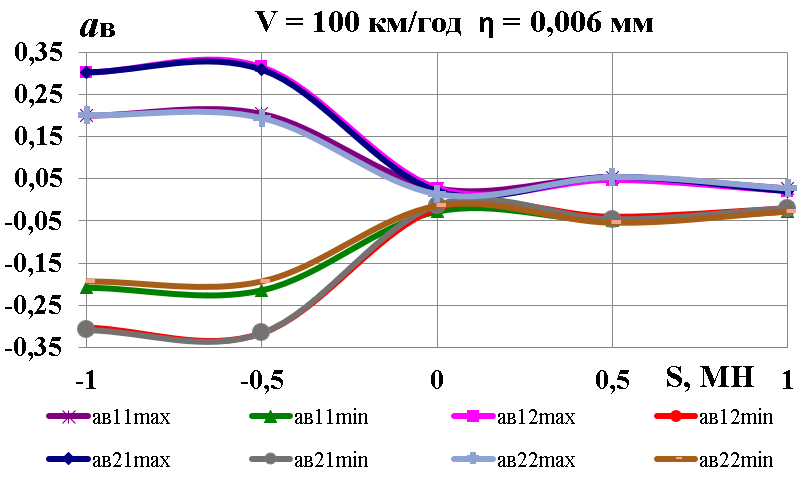
Рис.
5. Графіки залежності від швидкості
руху та глибини нерівності:
а
– коефіцієнти динамічної добавки
обресорених частин; б
– коефіцієнти вертикальної динаміки
колії
за силами взаємодії коліс та
рейок;
в
– вертикальні прискорення обресорених
частин
Fig.
5. Dependence graphs
on speed and depth of inequality:
a
– coefficients of dynamic addition of the
sprung
parts;
b
–
vertical
dynamics coefficients of the track according to the interaction
forces of wheels and rails;
c
– vertical accelerations of
the
sprung parts
Аналіз
отриманих результатів показує, що за
такої швидкості коефіцієнти вертикальної
динаміки за силами взаємодії коліс та
рейок
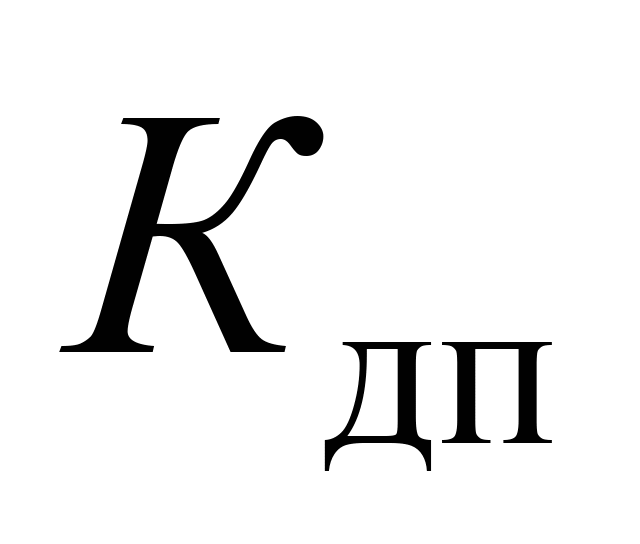 (рис. 5, б)
мало залежать від поздовжньої стискної
сили. Більшою мірою поздовжні сили
впливають на коефіцієнти динаміки в
центральному підвішуванні
(рис. 5, б)
мало залежать від поздовжньої стискної
сили. Більшою мірою поздовжні сили
впливають на коефіцієнти динаміки в
центральному підвішуванні
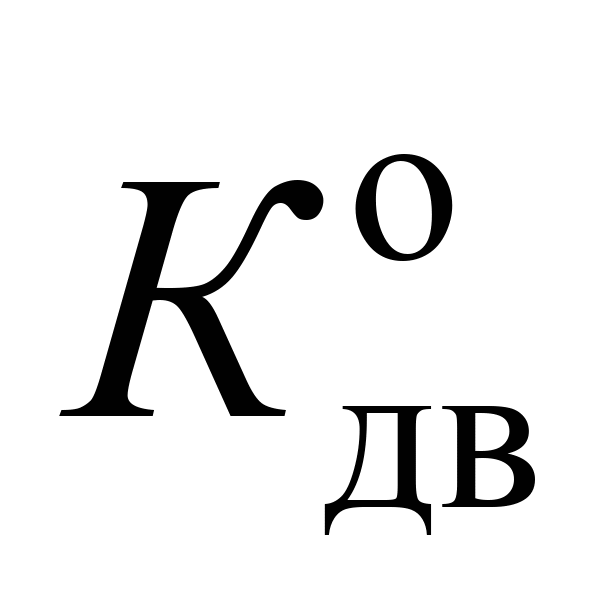 (рис. 5, а),
особливо на прискорення п’ятників
платформ
(рис. 5, а),
особливо на прискорення п’ятників
платформ
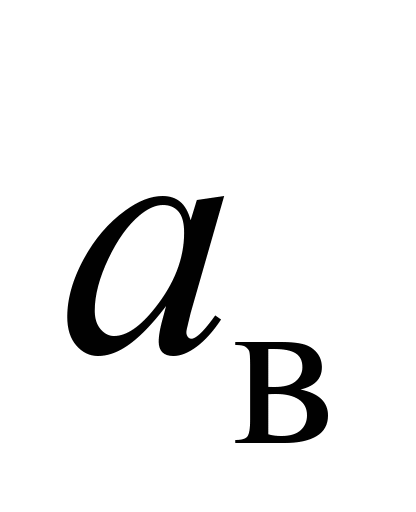 (рис.
5, в). У
разі дії поздовжньої стискної сили
значення цих параметрів збільшуються.
Зі зміною значення поздовжньої сили
від розтягання величиною 1 МН; 0,5 МН; 0 і
до стискання 0,5 МН; 1 МН значно змінюються
значення вертикального прискорення
обресорених частин
(рис.
5, в). У
разі дії поздовжньої стискної сили
значення цих параметрів збільшуються.
Зі зміною значення поздовжньої сили
від розтягання величиною 1 МН; 0,5 МН; 0 і
до стискання 0,5 МН; 1 МН значно змінюються
значення вертикального прискорення
обресорених частин
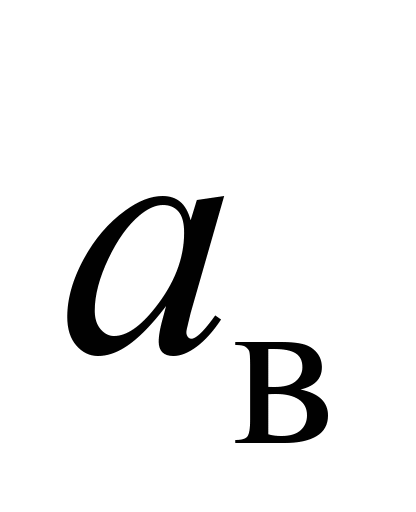 для заднього візка першої платформи
та переднього візка другої платформи
зчепу.
для заднього візка першої платформи
та переднього візка другої платформи
зчепу.
Відповідно
до допустимого динамічного погонного
навантаження на залізничну колію від
групи осей візка величиною 168 кН/м
допустиме значення коефіцієнта
вертикальної динаміки колії
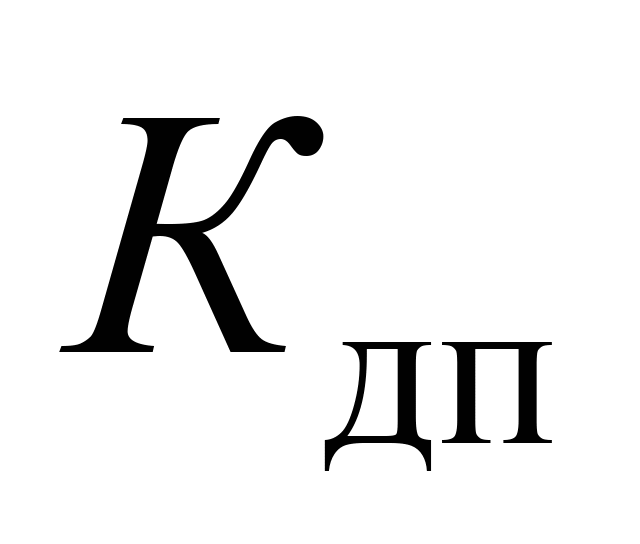 для досліджуваного типу рухомого складу
становить
для досліджуваного типу рухомого складу
становить
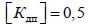 [4]. Коефіцієнт вертикальної
динаміки колії
[4]. Коефіцієнт вертикальної
динаміки колії
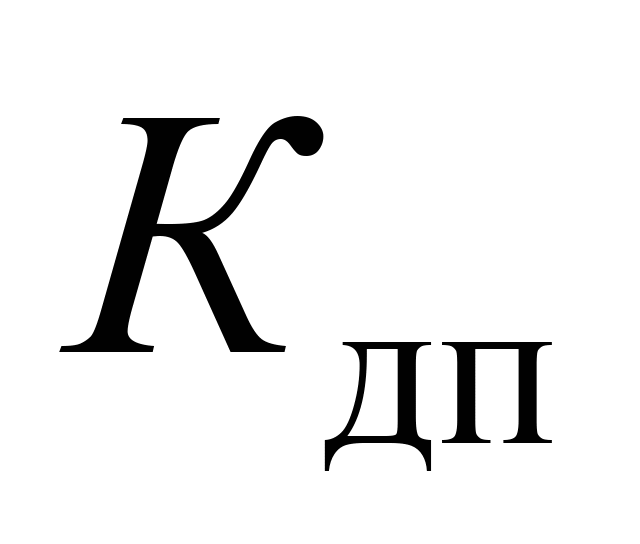 (рис. 5, б)
не перевищує допустимого значення.
(рис. 5, б)
не перевищує допустимого значення.
Рівень
оцінок:
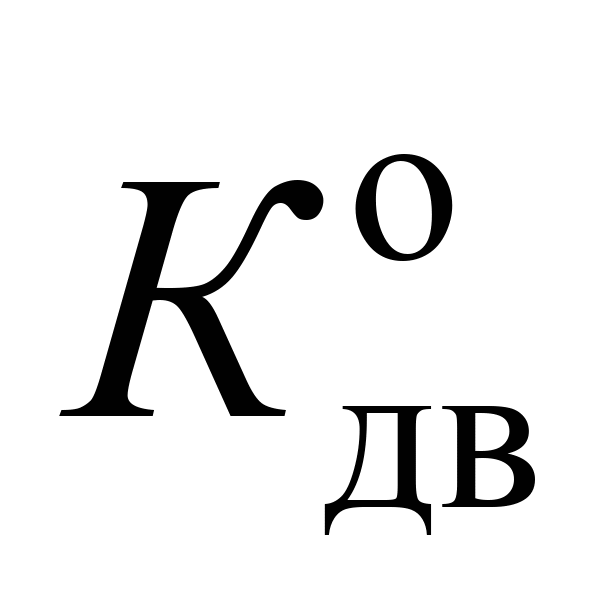 – «відмінно»,
– «відмінно»,
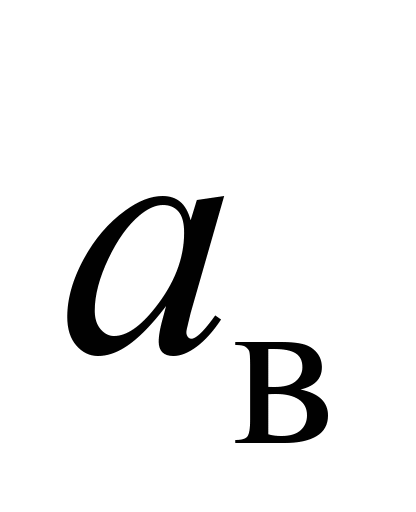 – «добре»,
– «добре»,
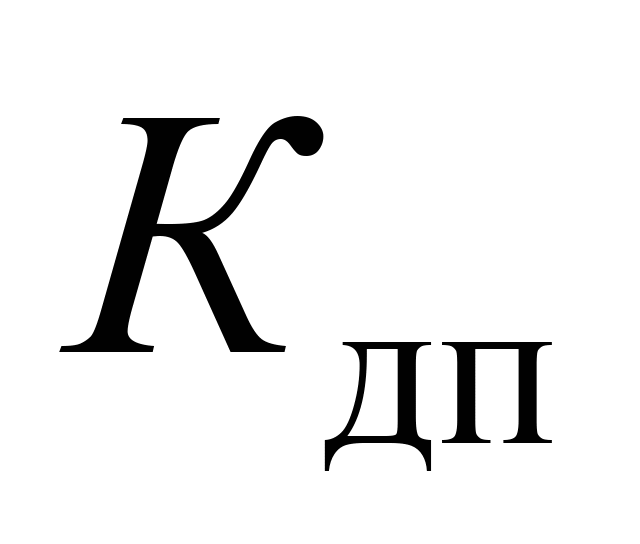 – менше допустимого значення [4,
7].
– менше допустимого значення [4,
7].
Hа рис. 6 наведено
залежності динамічних показників від
швидкості руху за глибини нерівності
колії 6 мм та за наявності стискної
поздовжньої сили величиною 1 МН.
Різке
зменшення коефіцієнтів динамічної
добавки обресорених частин (вертикальної
динаміки в центральному ресорному
підвішуванні)
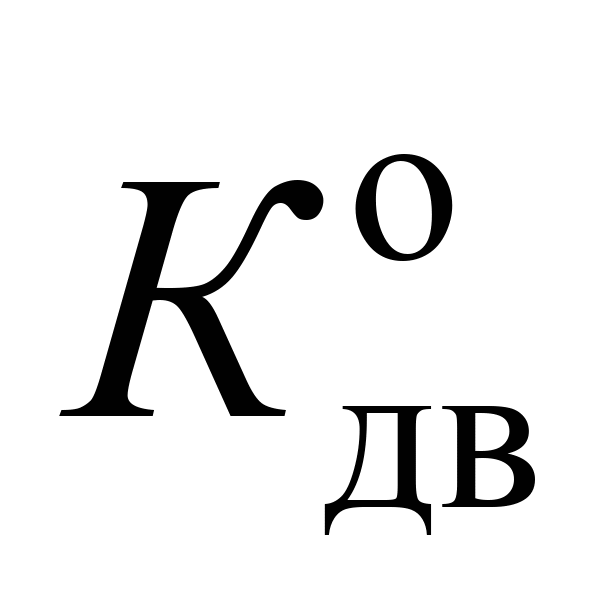 (рис. 6, а)
та показників вертикального прискорення
обресорених частин
(рис. 6, а)
та показників вертикального прискорення
обресорених частин
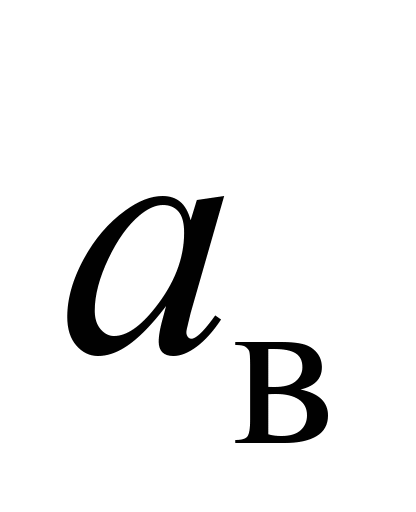 (рис. 6, г)
за швидкості 80 км/год пояснюється тим,
що за цієї швидкості галопування
платформ, викликане нерівністю колії
під дією моментів стискних сил, мають
різні знаки. Доказом цього є відсутність
екстремумів за швидкості руху 80
км/год на графіках залежності динамічних
показників за відсутності поздовжньої
стискної сили (рис. 6, б,
е).
(рис. 6, г)
за швидкості 80 км/год пояснюється тим,
що за цієї швидкості галопування
платформ, викликане нерівністю колії
під дією моментів стискних сил, мають
різні знаки. Доказом цього є відсутність
екстремумів за швидкості руху 80
км/год на графіках залежності динамічних
показників за відсутності поздовжньої
стискної сили (рис. 6, б,
е).
Рівень
оцінок: коефіцієнтів динамічної добавки
обресорених частин
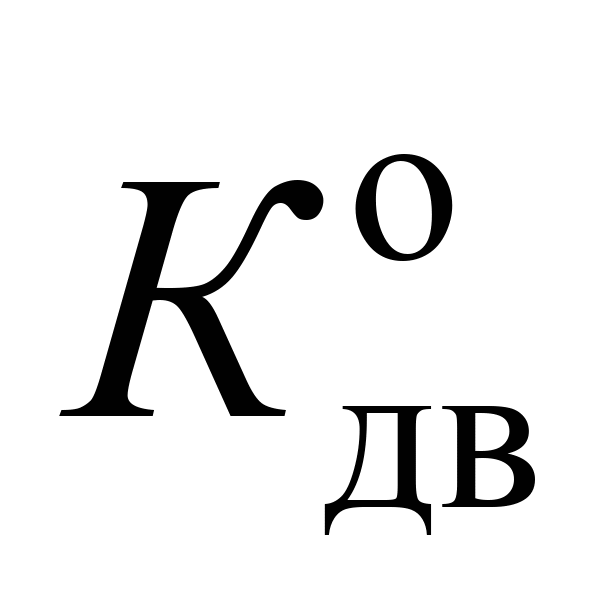 – «відмінно», коефіцієнтів вертикальної
динаміки за силами взаємодії коліс та
рейок
– «відмінно», коефіцієнтів вертикальної
динаміки за силами взаємодії коліс та
рейок
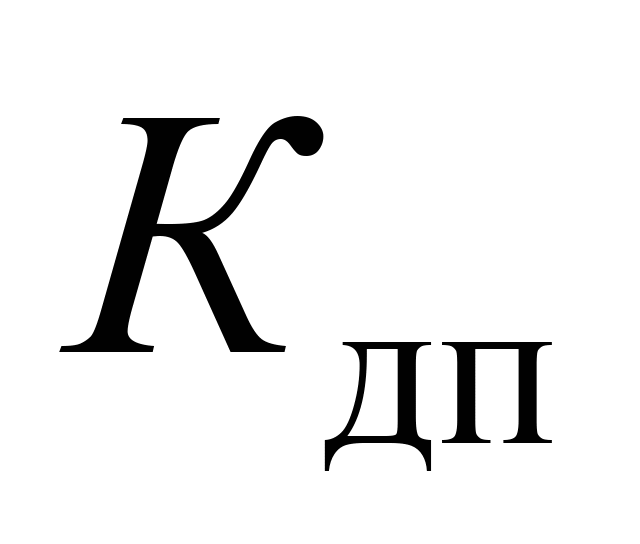 – менше допустимого значення,
вертикального прискорення обресорених
частин
– менше допустимого значення,
вертикального прискорення обресорених
частин
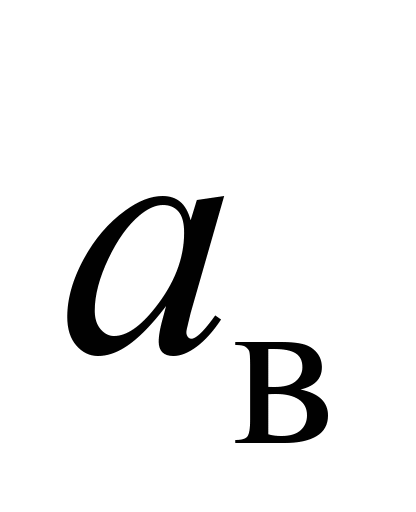 – у середньому «добре» в розглянутому
діапазоні швидкостей [4, 7].
– у середньому «добре» в розглянутому
діапазоні швидкостей [4, 7].
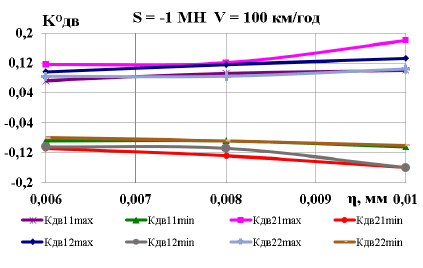
На рис. 7 наведені
залежності досліджуваних показників
за швидкості руху 100 км/год і стискної
сили 1 МН від глибини нерівності колії.
Як видно
з наведених графічних залежностей, із
ростом глибини нерівності показники
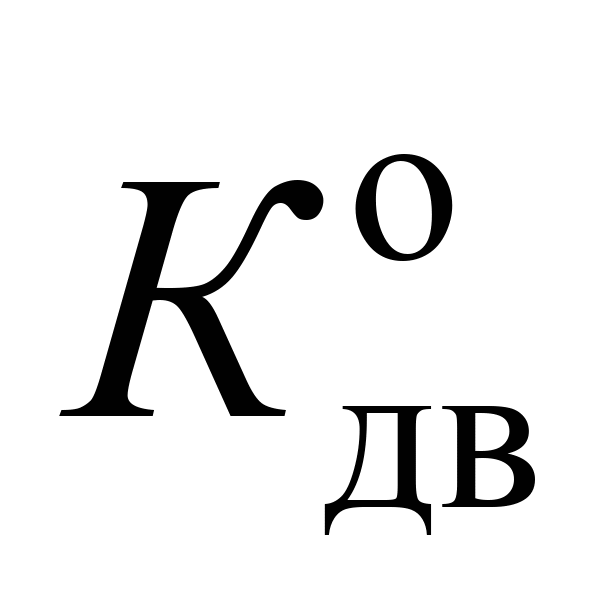 (рис. 7, а)
та
(рис. 7, а)
та
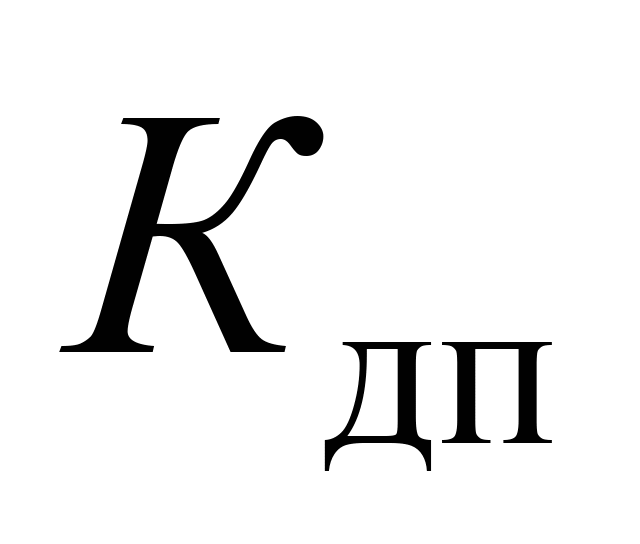 (рис. 7, б)
збільшуються. Однак можна відзначити,
що це збільшення несуттєве для
вертикального прискорення обресорених
частин
(рис. 7, б)
збільшуються. Однак можна відзначити,
що це збільшення несуттєве для
вертикального прискорення обресорених
частин
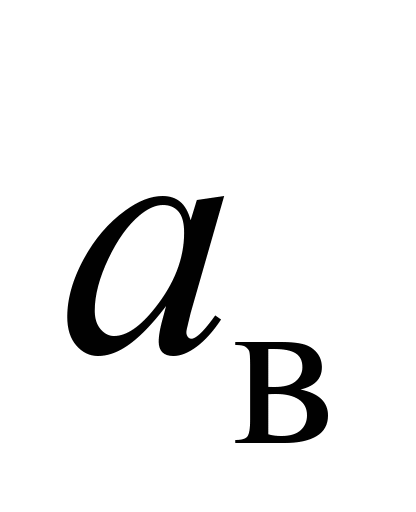 п’ятників платформ (рис. 7, в).
Значення
п’ятників платформ (рис. 7, в).
Значення
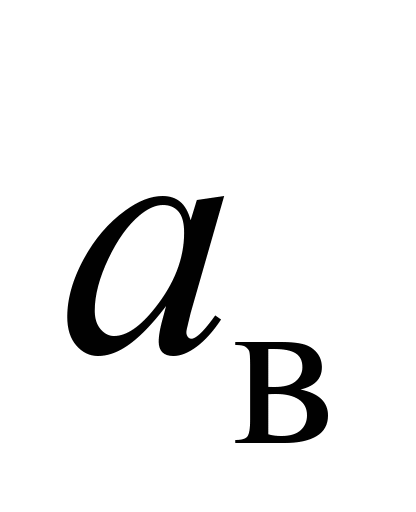 для заднього візка першої платформи
та переднього візка другої платформи
зчепу в разі збільшення глибини
синусоїдальної нерівності в середньому
у 1,5 раза вище.
для заднього візка першої платформи
та переднього візка другої платформи
зчепу в разі збільшення глибини
синусоїдальної нерівності в середньому
у 1,5 раза вище.
Рівень
оцінок: коефіцієнтів динамічної добавки
обресорених частин
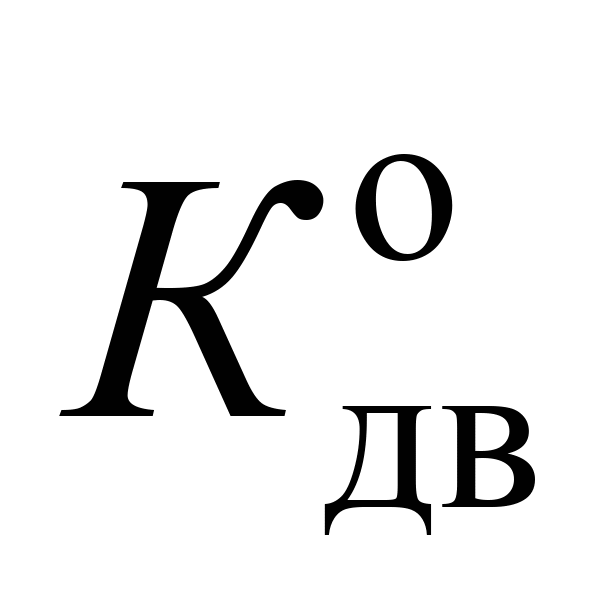 – «відмінно», коефіцієнтів вертикальної
динаміки за силами взаємодії коліс та
рейок
– «відмінно», коефіцієнтів вертикальної
динаміки за силами взаємодії коліс та
рейок
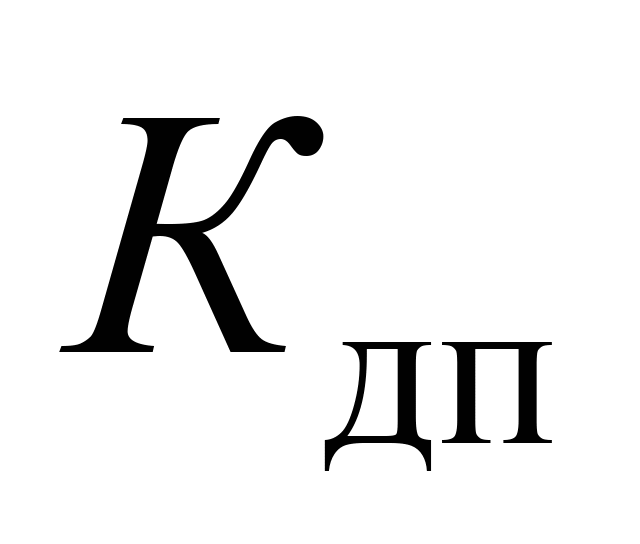 – менше допустимого значення,
вертикального прискорення обресорених
частин
– менше допустимого значення,
вертикального прискорення обресорених
частин
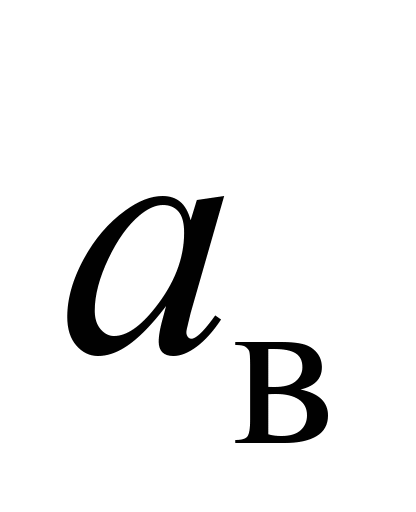 – у середньому «добре» [4, 7].
– у середньому «добре» [4, 7].
У ході
проведення теоретичних досліджень
установлено, що під час руху зчепу зі
швидкостями до 100 км/год мінімальні
значення коефіцієнта стійкості від
сходження колеса з рейок не нижче 1,5
(табл. 3). При цьому в діапазоні швидкостей
руху
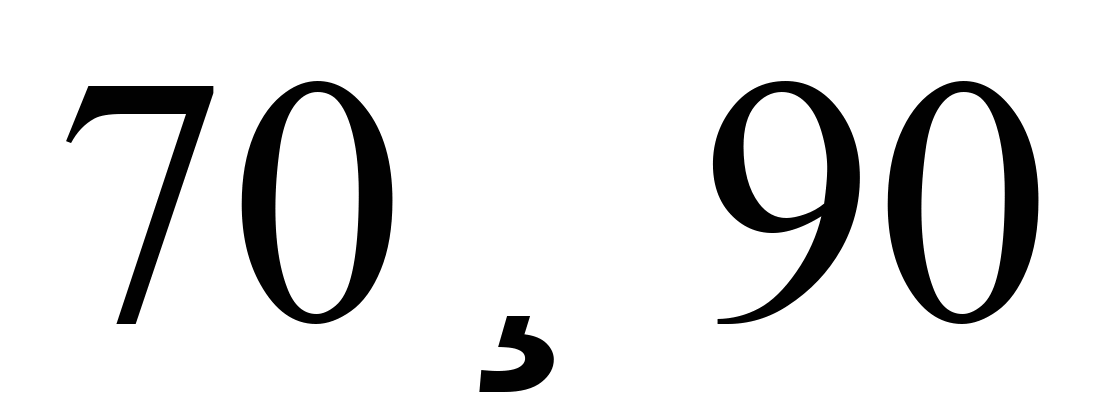 км/год коефіцієнт
км/год коефіцієнт
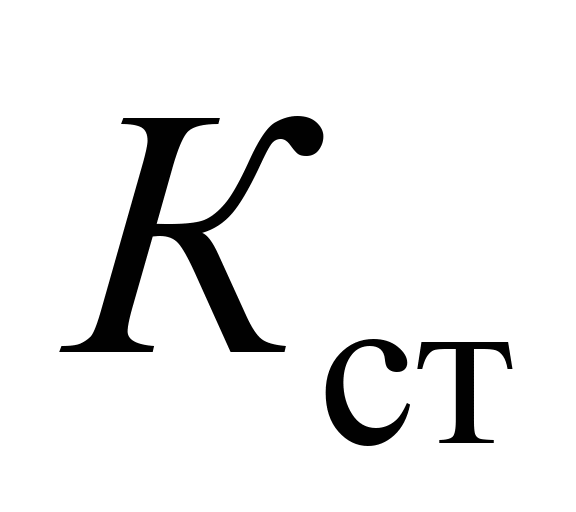 мінімальний, а поза цим діапазоном
збільшується. У кривих ділянках колії
мінімальний, а поза цим діапазоном
збільшується. У кривих ділянках колії
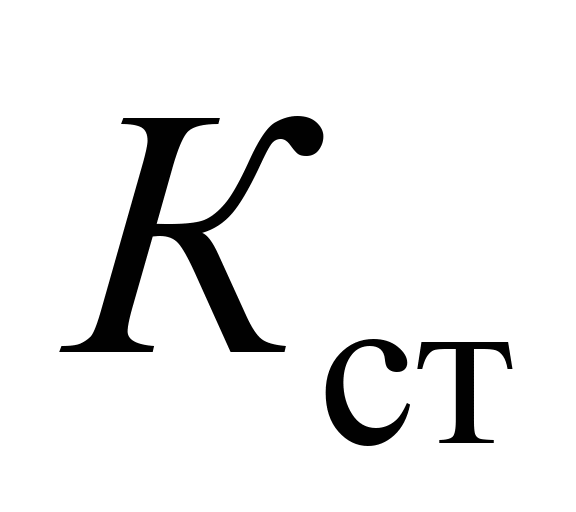 наближається до гранично допустимих
значень, тоді як на прямих має запас.
Для колісних пар, що набігають, за
швидкостей руху
наближається до гранично допустимих
значень, тоді як на прямих має запас.
Для колісних пар, що набігають, за
швидкостей руху
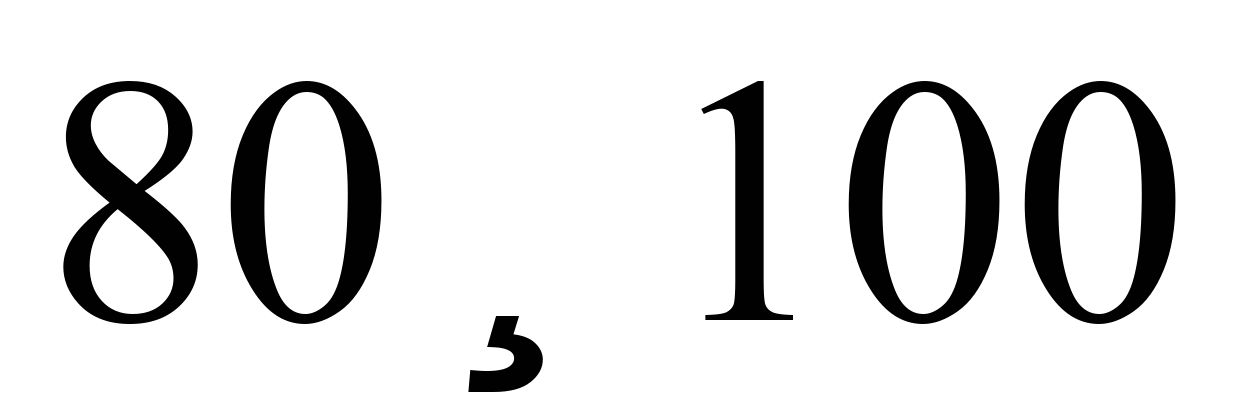 км/год коефіцієнт стійкості від сходження
колеса з рейок мало залежить від місця
знаходження колісної пари в зчепі .
Отримані результати свідчать про
забезпечення безпеки руху зчепу за
швидкостей до 100 км/год на прямих ділянках
залізничної колії.
км/год коефіцієнт стійкості від сходження
колеса з рейок мало залежить від місця
знаходження колісної пари в зчепі .
Отримані результати свідчать про
забезпечення безпеки руху зчепу за
швидкостей до 100 км/год на прямих ділянках
залізничної колії.
а
– a
б
– b
в
– c
г
– d
д
– e
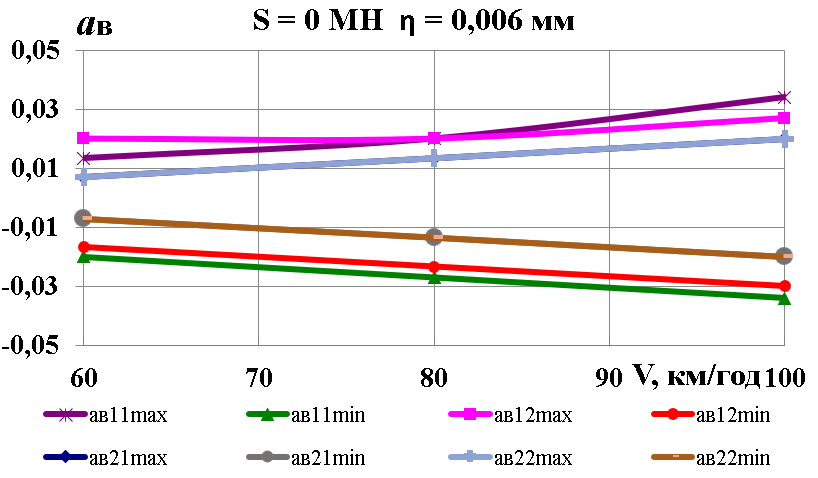
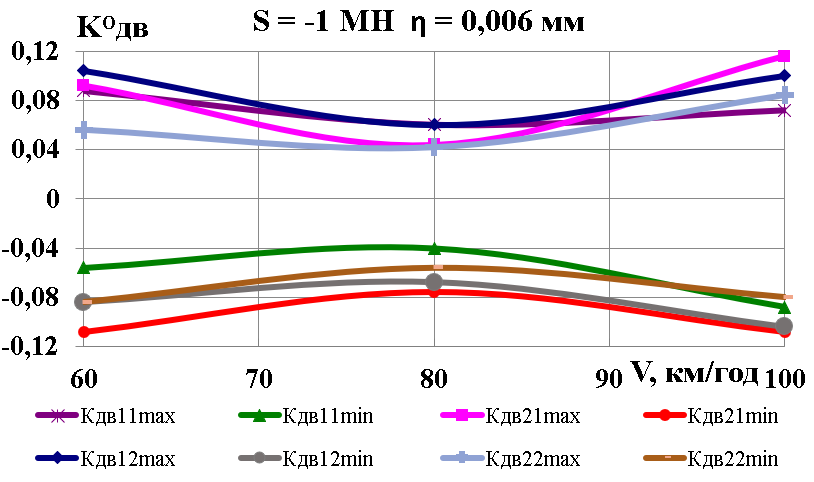
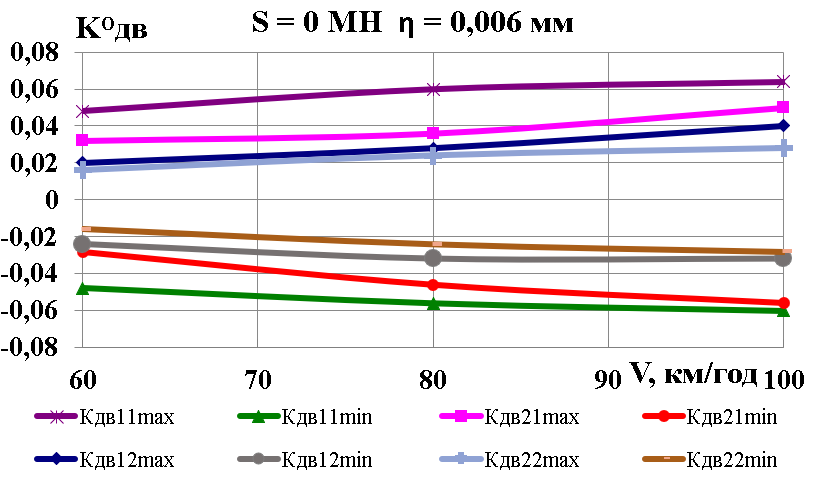
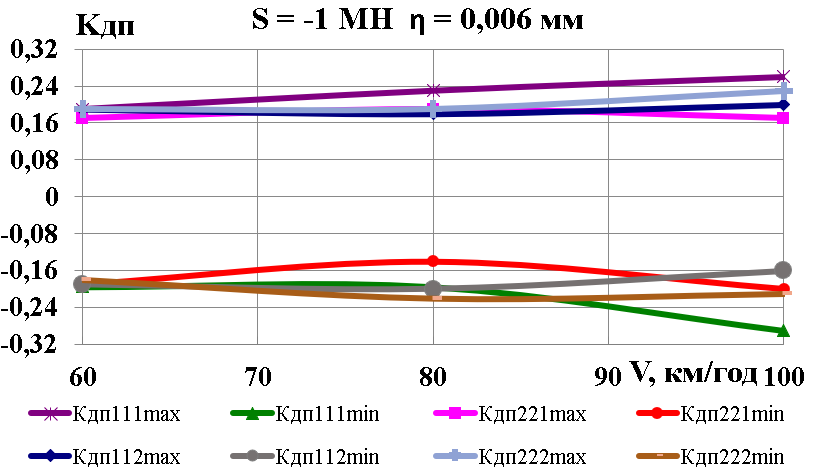
Рис.
6. Графіки залежності від поздовжньої
сили та глибини нерівності:
а,
б
– коефіцієнти динамічної добавки
обресорених частин;
в
–
коефіцієнти вертикальної динаміки
колії за силами взаємодії коліс та
рейок;
г,
д
– вертикальні прискорення обресорених
частин
Fig. 6. Dependence
graphs on the longitudinal force and depth of inequality:
a,
b – coefficients of
dynamic addition of the sprung parts;
c
–
vertical dynamics
coefficients of the track according to the interaction forces of
wheels and rails;
d,
e – vertical
accelerations of the sprung parts
а
– a
б
– b
в
– c
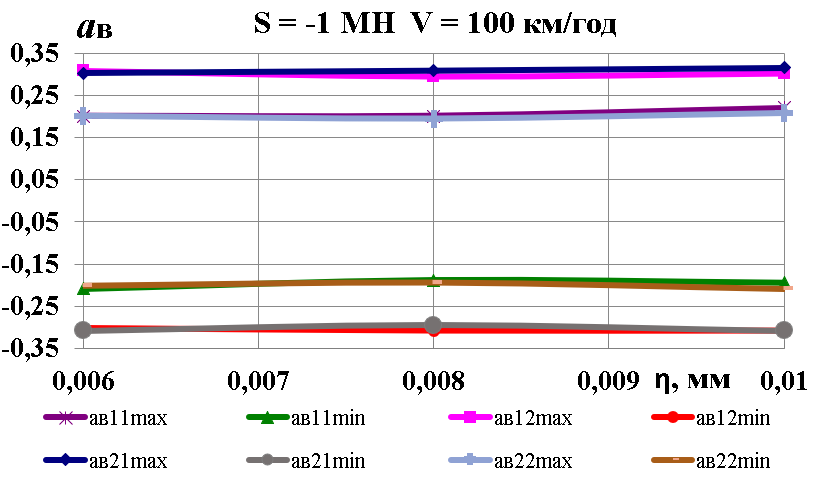
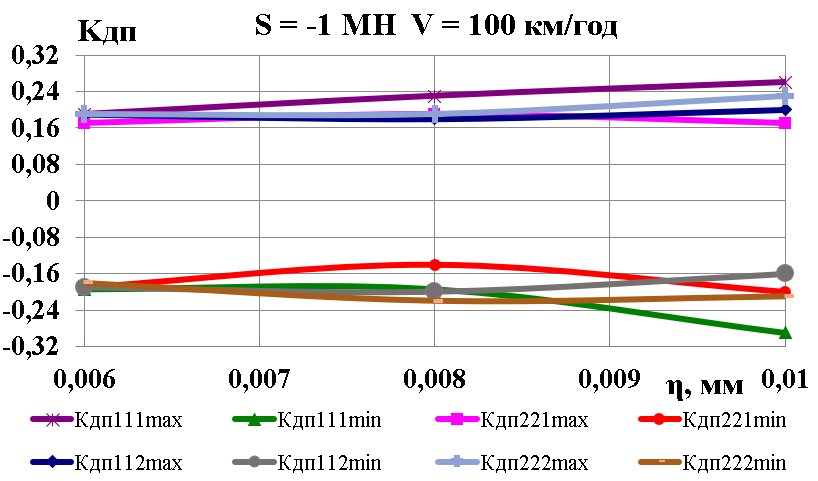
Рис.
7. Графіки залежності від швидкості
руху та поздовжньої сили:
а
– коефіцієнти динамічної добавки
обресорених частин;
б
– коефіцієнти вертикальної динаміки
колії за силами взаємодії коліс та
рейок;
в
– вертикальні прискорення обресорених
частин
Fig.
7. Dependence graphs
on speed and longitudinal force:
a
– coefficients of dynamic addition of the
sprung
parts;
b
– vertical dynamics coefficients of the track according to the
interaction forces of wheels and rails;
c
– vertical accelerations of the sprung parts
Наукова новизна
та практична
значимість
Виконаний комплекс
теоретичних досліджень дозволив
вирішити актуальне та практично важливе
завдання визначення навантаженості
платформ зчепу під час транспортування
довгомірного вантажу й розробити
технічні умови для реалізації
ресурсозбережних технологій.
Запропонована
математична модель оцінки динамічної
навантаженості поздовжньо-згинальних
коливань у вертикальній площині системи
штабель вантажу – зчеп вагонів-платформ
дає можливість теоретично визначити
динамічні показники системи та
забезпечити розроблення таких способів
транспортування довгомірних вантажів,
які відповідають вимогам безпеки руху
поїздів.
Висновки
У процесі
досліджень під час руху зчепу
вагонів-платформ, завантажених
довгомірним вантажем, було вивчено:
коефіцієнти динамічної добавки
обресорених частин (вертикальної
динаміки в центральному ресорному
підвішуванні)
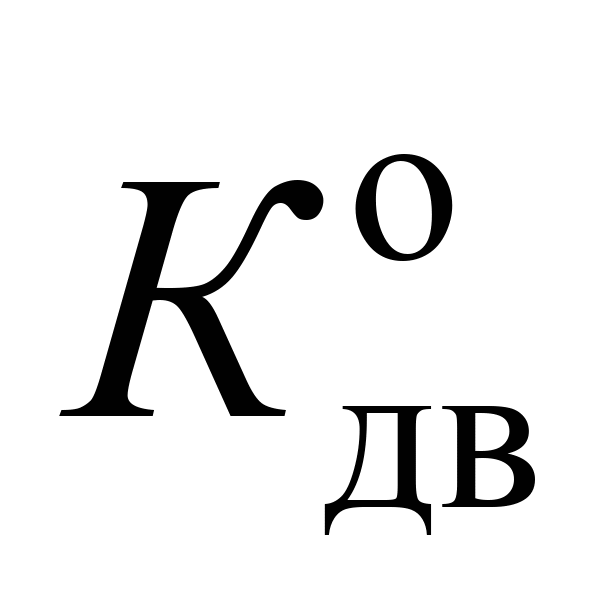 ;
коефіцієнти вертикальної динаміки
колії за силами взаємодії коліс та
рейок
;
коефіцієнти вертикальної динаміки
колії за силами взаємодії коліс та
рейок
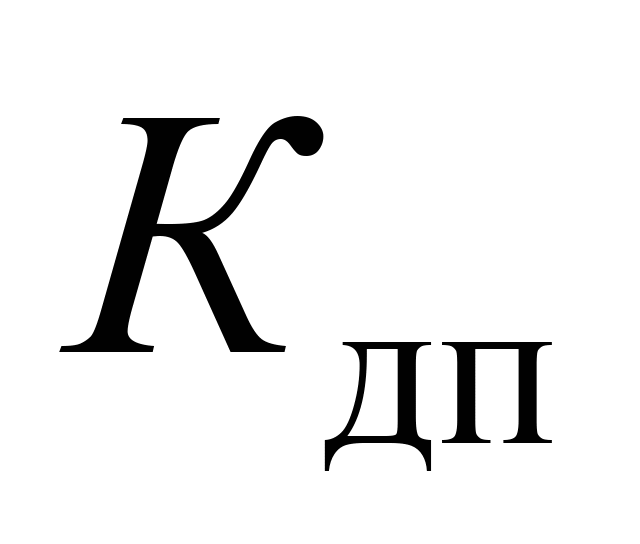 ;
вертикальне прискорення обресорених
частин
;
вертикальне прискорення обресорених
частин
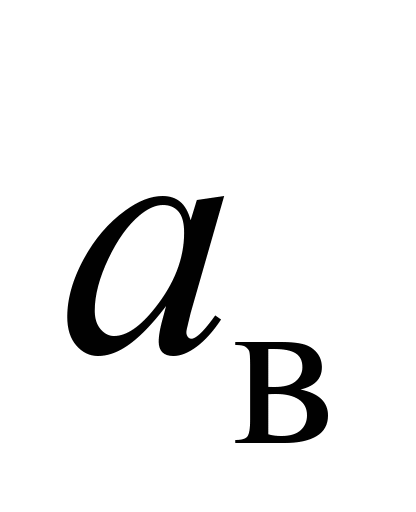 в частках від прискорення вільного
падіння
в частках від прискорення вільного
падіння
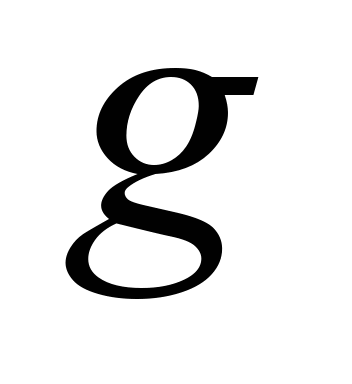 ,
а також частота коливань пакета
довгомірного вантажу.
,
а також частота коливань пакета
довгомірного вантажу.
На підставі аналізу
проведених теоретичних досліджень
динамічних якостей можна зробити такі
висновки:
– максимальні
значення коефіцієнта
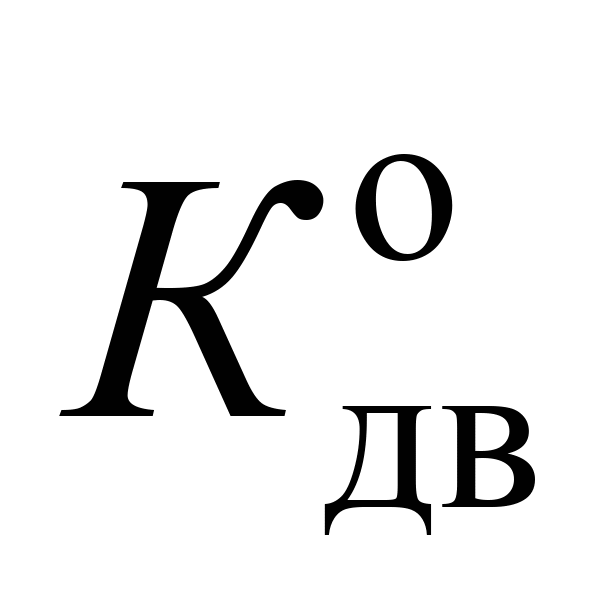 отримані за швидкості руху 100 км/год,
але їх величина не перевищує 0,35, що
свідчить про задовільні ходові якості
дослідного зчепу в разі вертикальних
коливань;
отримані за швидкості руху 100 км/год,
але їх величина не перевищує 0,35, що
свідчить про задовільні ходові якості
дослідного зчепу в разі вертикальних
коливань;
– за дії
поздовжньої стискної сили значно
збільшуються значення вертикального
прискорення обресорених частин
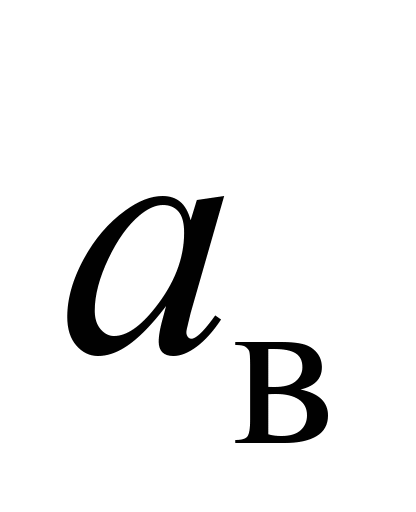 для заднього візка першої платформи
та переднього візка другої платформи
зчепу. Максимальні значення вертикальних
прискорень
для заднього візка першої платформи
та переднього візка другої платформи
зчепу. Максимальні значення вертикальних
прискорень
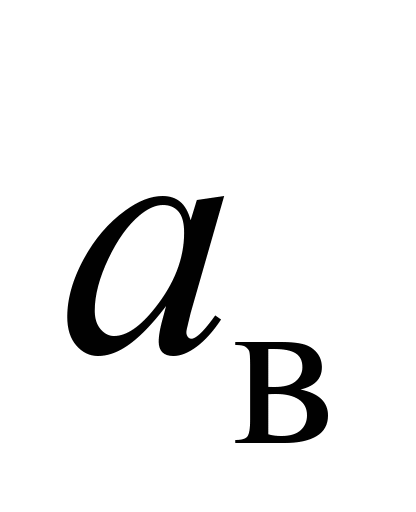 становлять 0,35, що не перевищує допустимих
для рівня оцінки «добре»;
становлять 0,35, що не перевищує допустимих
для рівня оцінки «добре»;
– коефіцієнти
вертикальної динаміки за силами
взаємодії коліс та рейок
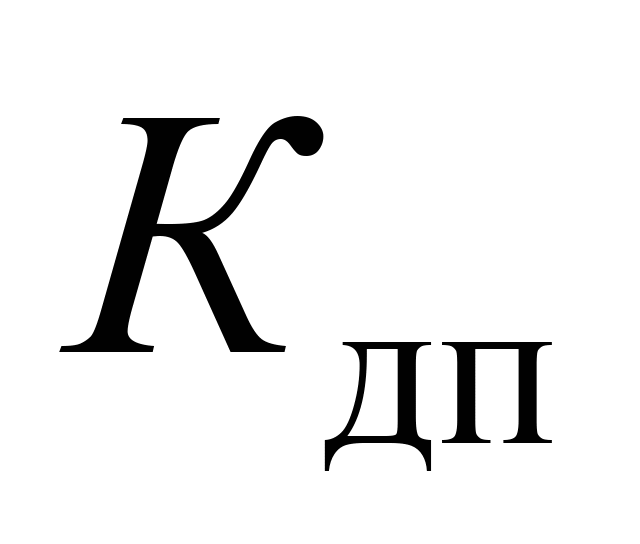 менше допустимого значення у всіх
розглянутих варіантах розрахунків;
менше допустимого значення у всіх
розглянутих варіантах розрахунків;
– значення
динамічних показників (коефіцієнти
динамічної добавки обресорених частин
і коефіцієнт стійкості колеса на
рейці, прискорення вагона й вантажу)
задовольняють безпеці руху зчепу,
завантаженого довгомірним вантажем,
у діапазоні швидкостей руху до 100
км/год на прямолінійній ділянці
залізничної колії.
СПИСОК ВИКОРИСТАНИХ
ДЖЕРЕЛ
Анисимов
П. С. Модель пространственных колебаний
платформы с длинномерным грузом.
Мир транспорта. 2013. № 4. С. 6–13.
Блохин Е.
П., Манашкин Л. А. Динамика поезда
(нестационарные продольные колебания)
: монография. Москва : Транспорт,
1982. 222 с.
Блохин Е.
П., Манашкин Л. А., Стамблер Е. Л., Маслеева
Л. Г., Михайличенко В. М., Грановская Н.
И. Расчеты и испытания тяжеловесных
поездов. Москва : Транспорт, 1986. 263 с.
Даніленко
Е. І. Залізнична колія
: підруч. для вищ. навч. закл. : у 2 т. Київ
: Інпрес, 2010. Т. 2. 456 с.
Данович В.
Д. Пространственные колебания вагонов
на инерционном основании : дис. …
д-ра техн. наук. Днепропетр. ин-т инж.
ж.-д. трансп. Днепропетровск,
1981. 465 с.
Данович В.
Д., Малышева А. А. Математическая модель
пространственных колебаний сцепа пяти
вагонов, движущихся по прямолинейному
участку пути. Транспорт. Нагруженность
и прочность подвижного состава : сб.
науч. тр. Днепропетр. гос. техн. ун-т
ж.-д. трансп. Днепропетровск, 1998. С. 62–69.
ДСТУ
ГОСТ 33211:2017. Вагони вантажні. Вимоги до
міцності та динамічних якостей (ГОСТ
33211-2014, IDТ).
[Чинний від 2017-07-01]. Київ : УкрНДНЦ, 2017.
58 с.
Лазарян В.
А., Конашенко С. И. Обобщённые функции
в задачах механики. Киев
: Наукова думка, 1974. 194 с.
Шатунов А.
В. Нагруженность
сцепа из двух платформ при ресурсосберегающем
способе транспортировки длинномерных
грузов : автореф. дис. … канд. техн.
наук. Днепропетр. ин-т инж. ж.-д. трансп.
Днепропетровск, 1992. 17
с.
Швець
А. О. Вплив поздовжнього та поперечного
зміщення центру ваги вантажу в піввагонах
на їх динамічні показники. Наука
та прогрес транспорту.
2018. № 5 (77). С. 115–128.DOI:
10.15802/stp2018/146432
Blochinas
E., Dailydka S., Lingaitis L., Ursuliak L. Nestacionarieji
ir kvazistatiniai geležinkelio traukinių judčjimo režimai.
Vilnius : Technika, 2016. 168 p. DOI:
10.3846/2321-m
Kurhan
M., Kurhan D. Providing the Railway Transit Traffic
Ukraine–European Union. Pollack
Periodica. Vol. 14. Iss. 2. P. 27–38.
DOI: 10.1556/606.2019.14.2.3
McKinnon
A. C.
Freight Transport Deceleration: Its
Possible Contribution to the Decarbonisation of Logistics.
Transport Reviews.
2016. Vol.
36. Iss.
4. P.
418–436.
DOI:
10.1080/01441647.2015.1137992
Shatunov
O. V., Shvets A. O. Study of dynamic indicators of flat wagon with
load centre
shift. Наука
та
прогрес
транспорту. 2019. №
2 (80). Р. 127–143. DOI:
10.15802/stp2019/165160
Shatunov
O. V., Shvets A. O., Kirilchuk O. A., Shvets A. O.
Research of Wheel-Rail Wear Due to
Non-Symmetrical Loading of a Flat Car.
Наука та
прогрес транспорту.
2019. № 4 (82). Р. 102–117.
DOI:
10.15802/stp2019/177457
А.
В. Шатунов1*,
А. А.
Швец2*
1*Каф.
«Вагоны и
вагонное хозяйство»,
Днипровский национальный
университет железнодорожного
транспорта имени академика В.
Лазаряна,
ул. Лазаряна, 2, Днипро,
Украина, 49010, тел. +38 (067) 953 60 14,
эл. почта
shatunov220648@gmail.com, ORCID 0000-0002-1115-0093
2*Каф.
«Теоретическая и строительная механика»,
Днипровский национальный
университет
железнодорожного транспорта имени
академика В. Лазаряна,
ул. Лазаряна, 2,
Днипро, Украина, 49010, тел.
+38 (050) 214 14 19,
эл. почта angela_Shvets@ua.fm, ORCID
0000-0002-8469-3902
ДИНАМИКА
сцепа вагонов-платформ
ПРИ перевозке
длинномерных грузов
Цель.
В связи с тенденцией к интенсификации
перевозочного процесса в условиях
повышенных осевых нагрузок и скоростей
движения поездов в статье предусмотрено
исследовать динамическую нагруженность
сцепа двух вагонов-платформ с длинномерным
грузом, а также определить динамические
силы взаимодействия под влиянием
квазистатических продольных сил.
Методика.
Основой исследования является метод
математического и компьютерного
моделирования динамической нагруженности
продольно-изгибных колебаний штабеля
груза длиной 22 м, расположенного на
сцепе из двух вагонов-платформ модели
13–4012. Кинетическая и потенциальная
энергии системы составлены с учетом
кинетической и потенциальной энергии
груза, которые вычисляют по известным
фундаментальным функциям. Для определения
фундаментальных функций решалась
задача о изгибных колебаниях груза как
балки на двух упругих опорах. Для
определения фундаментальных функций
при продольных перемещениях использовано
дифференциальное уравнение свободных
продольных колебаний стержня постоянного
сечения. Теоретические исследования
проведены при движении сцепа платформ
с типовыми тележками 18–100 со скоростями
в интервале от 60 до 100 км/ч на прямом
участке железнодорожного пути.
Результаты.
В исследовании принято во внимание
движение сцепа вагонов-платформ по
синусоидальной неровности длиной 25 м
и разной глубиной при действии продольных
сжимающих или растягивающих сил, а
также на выбеге. В ходе выполнения
теоретических исследований и после
проведения моделирования с учетом
процессов колебания вагона-платформы
и длинномерного груза, при наличии
квазистатических продольных сил,
получены зависимости основных
динамических показателей от величины
скорости движения. Научная
новизна. Для определения
динамической нагруженности сцепа
вагонов-платформ разработана
математическая модель продольно-изгибных
колебаний в вертикальной плоскости
системы штабель груза – сцеп
вагонов-платформ. Предложенная
математическая модель дает возможность
теоретически определить динамические
показатели системы и обеспечить
разработку способов транспортировки
длинномерных грузов в соответствии с
требованиями безопасности движения
поездов. Практическая
значимость. В результате
проведенных теоретических исследований
решена актуальная и практически важная
задача определения нагруженности
платформ сцепа при транспортировке
длинномерного груза, что позволит
разработать технические условия для
реализации ресурсосберегающих
технологий.
Ключевые
слова: вагон-платформа;
длинномерный груз; динамические
показатели; сцеп вагонов; продольные
силы; скорость движения
O.
V. Shatunov1*,
A. O. shvets2*
1*Dep.
«Cars and Car
Facilities»,
Dnipro National
University of Railway Transport named after
Academician V. Lazaryan,
Lazaryana St., 2, Dnipro, Ukraine,
49010, tel. +38 (067) 953 60 14,
e-mail shatunov220648@gmail.com,
ORCID 0000-0002-1115-0093
2*Dep.
«Theoretical
and Structural Mechanics»,
Dnipro National
University of Railway Transport named after
Academician
V. Lazaryan, Lazaryana St., 2, Dnipro, Ukraine,
49010, tel. +38 (050) 214 14 19,
e-mail angela_Shvets@ua.fm,
ORCID
0000-0002-8469-3902
FLAT
cars coupling
DYNAMICS
WHEN TRANSPORTING LONG CARGO
Purpose.
In connection with the tendency to
intensify the transportation process under conditions of increased
axial loads and train speeds the article aims to investigate the
dynamic loading of the coupling of two flat cars with a long
load, as well as to determine the dynamic forces of interaction
under the action of quasi-static longitudinal forces.
Methodology.
The research is based on the method of mathematical and
computer modeling of dynamic loading of longitudinal-and-flexural
vibrations of a 22 m long stack of cargo, located on the coupling of
two flat cars of 13-4012 model. The kinetic and potential energies
of the system are compiled taking into account the kinetic and
potential energies of the load, which are calculated using the known
fundamental functions. To determine the fundamental functions, the
problem of flexural vibrations of a load as a beam on two elastic
supports was solved. To determine the fundamental functions for
longitudinal displacements, the differential equation of free
longitudinal vibrations of a bar of constant cross section was used.
Theoretical studies were carried out when moving of flat cars with
typical bogies 18-100 at speeds in the range from 60 to 100 km/h on
a straight section of the railway track. Findings.
During the study it was taken into account the movement of
flat car coupling along a sinusoidal irregularity with a length of
25 m and different depths under the action of longitudinal
compressive or tensile forces, as well as during running out. In the
course of theoretical studies and after the modeling, taking into
account the oscillation processes of the flat car and long cargo, in
the presence of quasi-static longitudinal forces, the dependences of
the main dynamic indicators on the movement speed were obtained.
Originality.
To determine the dynamic loading of the flat car coupling, a
mathematical model of longitudinal-and-flexural vibrations in
the vertical plane of the cargo stack-platform car coupling system
has been developed. The proposed mathematical model makes it
possible to theoretically determine the dynamic parameters of the
system and ensure the development of methods for transporting long
cargo in accordance with the safety requirements of train traffic.
Practical value.
As a result of the theoretical studies, a relevant and practically
important problem of determining the loading of flat car coupling
during the transportation of long cargo was solved, which will allow
developing technical conditions for the implementation of
resource-saving technologies.
Keywords:
flat car; long cargo; dynamic indicators; coupling of cars;
longitudinal forces; movement speed
REFERENCES
Anisimov,
P. S. (2013). Model of spatial oscillations of a flat car with long
goods. Mir transporta,
4, 6-13. (in Russian)
Blokhin,
Ye. P., & Manashkin, L. A. (1982). Dinamika
poyezda (nestatsionarnyye prodolnyye kolebaniya):
monograph. Moscow: Transport. (in Russian)
Blokhin,
Ye. P., Manashkin, L. A., Stambler, Ye. L., Masleeva, L. G.,
Mikhaylichenko, V. M., & Granovskaya, N. I. (1986). Raschety
i ispytaniya tyazhelovesnykh poezdov.
Moscow: Transport. (in Russian)
Danilenko,
E. I. (2010). Zaliznychna
koliia.
(Vol. 2). Kyiv: Inpres. (in Ukrainian)
Danovich,
V. D. (1982). Spatial Cars
Oscillations in Inertia Track.
(Dysertatsiia doktora tekhnichnykh nauk). Dnepropetrovsk Institute
of Railway Transport Engineering, Dnеpropetrovsk. (in Russian)
Danovich,
V. D., & Malysheva, A. A. (1998). Mathematical Model of Spatial
Oscillations of the Coupling of Five Cars Moving Along a
Rectilinear Section of the Track. In
Transport. Stress loading and durability of a rolling stock,
62-69. Dnepropetrovsk.
(in Russian)
Vahony
vantazhni. Vymohy do mitsnosti ta dynamichnykh yakostei, 58 DSTU
33211:2017 (2017). (in Ukrainian)
Lazaryan,
V. A., & Konashenko, S. I. (1974). Obobshchennye
funktsii v zadachakh mekhaniki. Kiev:
Naukova dumka. (in Russian)
Shatunov,
A. V. (1992). Nagruzhennost
stsepa iz dvukh platform pri resursosberegayushchem sposobe
transportirovki dlinnomernykh gruzov.
(Extended
abstract of PhD dissertation).
Dnepropetrovsk Institute of Railway Transport Engineering,
Dnеpropetrovsk.
(in Russian)
Shvets,
A. O. (2018). Influence of the longitudinal and transverse
displacement of the center of gravity of the load in gondola cars
on their dynamic indicators. Science
and Transport Progress, 5(77),
115-128. DOI: 10.15802/stp2018/146432
(in Ukrainian)
Blochinas,
E., Dailydka, S., Lingaitis, L. P., & Ursuliak, L. (2015).
Nestacionarieji ir kvazistatiniai
geležinkelio traukinių judėjimo režimai. Vilnius
: Technika.
DOI: 10.3846/2321-m(in Lithuanian)
Kurhan,
M., & Kurhan, D. (2019). Providing the railway transit traffic
Ukraine–European Union. Pollack
Periodica, 14(2), 27-38. DOI:
10.1556/606.2019.14.2.3 (in
English)
McKinnon,
A. C. (2016). Freight Transport Deceleration: Its Possible
Contribution to the Decarbonisation of Logistics. Transport
Reviews, 36(4), 418-436.
DOI: 10.1080/01441647.2015.1137992 (in
English)
Shatunov,
O. V., & Shvets, A. О. (2019). Study of dynamic indicators of
flat wagon with load centre shift. Science
and Transport Progress, 2(80),
127-143. DOI:
10.15802/stp2019/165160
(in English)
Shatunov,
O. V., Shvets, A. O., Kirilchuk, O. A., & Shvets, A. O. (2019).
Research of Wheel-Rail Wear Due to Non-Symmetrical Loading of a
Flat Car. Science and Transport
Progress, 4(82),
102–117. DOI:
10.15802/stp2019/177457
Надійшла до
редколегії: 25.02.2020
Прийнята до друку:
27.07.2020
і коефіцієнт відносного тертя
.
Рами платформ з’єднані між собою
автозчепленням 3
через поглинаючі апарати 2
з жорсткістю
і коефіцієнтом відносного тертя
.
.
У процесі руху зчепу обидва яруси
роблять поздовжньо-згинальні коливання.
Передбачено, що ці коливання не пов’язані
між собою.
– база
вагона, 9,72 м;
– база візка, 1,85 м;
– відстань від шкворневого перетину
до осі зчеплення вагонів, 2,46 м;
– відстань від осі зчеплення до осі
клина автозчеплення, 0,93 м;
– ексцентриситет закріплення опор 8
та 9
відноснодо центра мас вагона в
поздовжньому напрямку, 0,81 м;
– відстань між пружними опорами
верхнього ярусу штабеля вантажу, 13,0 м;
– довжина консольної частини верхнього
ярусу штабеля вантажу,
– посмикування,
–
підстрибування,
– кути поздовжньої хитавиці (позитивні
напрямки на рис. 2). Для
відзнаки переміщень передньої по ходу
руху платформи від задньої введені
індекси
(
–
номер платформи у зчепі). Переміщення
візків позначені індексом
(
–
номер візка), переміщення колісних пар
– індексом
(
–
номер колісної пари у візку), переміщення
нижнього ярусу позначені індексом
,
верхнього –
,
переміщення балок як пружних тіл уздовж
осі
позначені через
,
уздовж осі
– через
.
Переміщення ярусів позначені подвійно:
через
та
– переміщення пружного тіла, через
,
,
– твердого тіла.