ISSN
2307–3489 (Print), ІSSN 2307–6666
(Online)
Наука та прогрес
транспорту. Вісник Дніпропетровського
національного університету залізничного
транспорту, 2020, № 4 (88)
НФОРМАЦІЙНО-КОМУНІКАЦІЙНІ
ТЕХНОЛОГІЇ ТА МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ
УДК 656.222.3:519.87
В. В. скалозуб1*, В. М. Ільман2*,
Б. Б. Білий3*
1*Каф.
«Комп’ютерні інформаційні технології»,
Дніпровський національний
університет
залізничного транспорту імені академіка
В. Лазаряна,
вул. Лазаряна, 2, Дніпро,
Україна, 49010, тел. +38 (056) 373 15 35,
ел. пошта
skalozub.vl.v@gmail.com, ORCID 0000-0002-1941-4751
2*Каф.
«Комп’ютерні інформаційні технології»,
Дніпровський національний
університет
залізничного транспорту імені академіка
В. Лазаряна,
вул. Лазаряна, 2, Дніпро,
Україна, 49010, тел. +38 (056) 373 15 35,
ел. пошта
valeriy_ilman@ukr.net,
ORCID 0000-0003-0983-8611
3*Каф. «Комп’ютерні
інформаційні технології», Дніпровський
національний
університет залізничного
транспорту імені академіка В. Лазаряна,
вул. Лазаряна, 2, Дніпро, Україна, 49010,
тел. +38 (056) 373 15 35,
ел. пошта hibarike@gmail.com,
ORCID 0000-0001-8324-4673
КОНСТРУКТИВНІ
БАГАТОШАРОВІ МОДЕЛІ
ДЛЯ ВПОРЯДКУВАННЯ
ПОСЛІДОВНОСТЕЙ
З УРАХУВАННЯМ СКЛАДНОСТІ
ОПЕРАЦІЙ
ФОРМУВАННЯ
Мета.
Основною метою статті є постановка
нової задачі планування процесів
функціонування сервісних систем, а
також розвиток конструктивних методів
моделювання складних процесів та систем
шляхом розробки багатошарової
конструктивної моделі з упорядкування
наборів неоднорідних послідовностей
замовлень (MLCРМ), яка враховує складність
операцій формування. Методика.
У роботі запропоновано постановку нової
задачі моделювання, що призначена для
впорядкування неоднорідних послідовностей
елементів (замовлень). Досліджувані
задачі поширені в логістичних,
технологічних, інформаційних, залізничних
та інших процесах. Головною та суттєвою
відмінністю запропонованих конструктивних
багатошарових моделей є введення до їх
складу додаткових структур конструювання,
що забезпечують можливості задавання
складності операцій формування, а також
додаткового аналізу властивостей
об’єктів, які формуються під час
реалізації розв’язків. Засобами MLCРМ
також реалізують процедури оптимального
керування процесами пошуку розв’язків.
Результати.
У статті на прикладі задачі з оптимального
формування-розформування багатогрупових
залізничних составів розроблено нову
багатошарову конструктивну модель
процесів оптимального планування задач
із упорядкування наборів неоднорідних
послідовностей замовлень. Також
запропоновано класифікацію ознак, які
визначають типи математичних моделей
процесів упорядкування. Наукова
новизна. Виконано
постановку нової науково-прикладної
задачі щодо планування сервісних систем,
уперше здійснено класифікацію ознак
класів математичних моделей процесів
упорядкування послідовностей замовлень
з вагою операцій. Отримали розвиток
контруктивно-продукційні моделі шляхом
створення багатошарових та паралельних
конструктивних структур моделювання
розформування-формування составів.
Практична значимість.
Цінність отриманих результатів
визначається широким спектром можливих
застосувань задачі з планування сервісних
систем. Запропоновані багатошарові
конструктивні структури моделювання
дозволяють удосконалити інструментарій
конструктивного моделювання. Побудована
модель процесів оптимального
розформування-формування составів
дозволяє отримати нову форму реалізації
зазначених технологічних процесів
залізничного транспорту.
Ключові слова:
конструктивне моделювання; багатошарові
моделі; паралельне конструювання;
неоднорідні послідовності замовлень;
упорядкування послідовностей; складність
операцій формування; багатогрупові
залізничні состави
Вступ
У
багатьох сучасних сферах діяльності,
зокрема в промислових та логістичних
технологіях, у певних математичних
методах аналізу та планування часто
постають задачі, які формально можуть
бути зведені до конструктивного (шляхом
побудови) оптимального впорядкування
елементів певних множин або недетермінованих
послідовностей замовлень (НПЗ) для
отримання визначених структур з
урахуванням складності операцій
процесів формування [1, 5, 6, 7, 10].
В [7] було досліджено
модель управління ланцюгами постачання
для сортування замовлень дистрибуційного
логістичного центру. Застосування
моделей групового сортування для вибору
функцій класифікації даних наведено
у [2]. Некласичні задачі, які зводяться
до конструктивного впорядкування
елементів, є важливими для практики
та мають значний теоретичний інтерес.
Їх розв’язання суттєво відрізняється
від розв’язання задач сортування та
ін. [11]. Важливим для подальшого аналізу
прикладом таких технологій є процеси
розформування-формування (РФ)
багатогрупових залізничних составів
(БГС) на станціях [1, 5].
Для
розв’язання задач упорядкування з
урахуванням складності операцій (УПСО),
їх ваги, необхідно виконати нові
змістовні та формальні постановки
задач, сформувати моделі операцій,
побудувати метрики для порівняння
станів процесів формування, а також
розробити спеціалізовані алгоритми
реалізації задач упорядкування з вагою.
У
роботі [6] запропоновано два методи
формалізації процесів проєктування
проблемно-орієнтованих пристроїв, які
представлені прямоспрямованим графом,
а також графом із підзадачею з вибору
множини оптимально реалізованих
функцій. У [4] розглянуто питання
формування потоків у мережах.
Конструктивні
моделі знаходять усе більш широке
застосування для відтворення та
дослідження широкого кола процесів
[7, 8, 9]. У роботі [8] було
запропоновано предметну (продукційну)
модель (КПМ) процесів конструювання
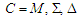 ,
яка містить:
,
яка містить:
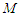 – неоднорідний носій,
– неоднорідний носій,
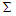 – список відносин та відповідних
операцій,
– список відносин та відповідних
операцій,
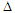 – набір засобів інформаційного
забезпечення конструктивної побудови
(правила, обмеження, умови початку та
завершення побудови моделей, онтологію
тощо). Складові наборів КПМ визначають
на основі дослідження допустимих
операцій процесів УПСО.
– набір засобів інформаційного
забезпечення конструктивної побудови
(правила, обмеження, умови початку та
завершення побудови моделей, онтологію
тощо). Складові наборів КПМ визначають
на основі дослідження допустимих
операцій процесів УПСО.
У
статті [9] представлено
напрями розвитку КПМ для процесів, які
розвиваються у змістовному предметному
напрямі формальних граматик, зокрема
в галузі онтологій [10].
У
нашій роботі запропоновано подальший
розвиток КПМ для розв’язання задач
моделювання РФ, що також призначені
для УПСО. Головною та суттєвою відмінністю
пропонованих у роботі конструктивних
багатошарових моделей (КШМ, або MLCРМ)
від КПМ є введення до них додаткових
структур конструювання, що забезпечують
можливості визначення складності
операцій формування (інших складових),
а також додаткового аналізу властивостей
(показники загальної складності
процесів, показники впорядкованості
заданої послідовності замовлень тощо)
структур, які формуються.
Із метою
явного виділення головних упорядкованих
складових процесів у моделях MLCРМ
запропоновано представляти їх системою
окремих шарів
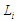 операцій конструювання, а саме:
операцій конструювання, а саме:
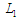 – шари оцінювання-перетворення даних;
L2 –
оцінювання станів процесу конструктивного
моделювання, відбір можливих операцій
або процедур перетворення структури
впорядкування;
– шари оцінювання-перетворення даних;
L2 –
оцінювання станів процесу конструктивного
моделювання, відбір можливих операцій
або процедур перетворення структури
впорядкування;
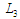 – генерація (породження)
наступних локальних вузлів моделі;
– генерація (породження)
наступних локальних вузлів моделі;
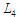 –
формування моделей оцінювання локальних
або глобальних властивостей;
–
формування моделей оцінювання локальних
або глобальних властивостей;
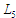 –
процедури оцінювання параметрів
моделей;
–
процедури оцінювання параметрів
моделей;
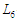 –
оптимізація процесу пошуку рішень.
Окремі шари
–
оптимізація процесу пошуку рішень.
Окремі шари
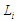 також можуть поєднувати кілька із
зазначених категорій операцій. Включення
до моделі MLCРМ шарових комплексів
також можуть поєднувати кілька із
зазначених категорій операцій. Включення
до моделі MLCРМ шарових комплексів
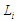 операцій конструювання утворює системну
модель CMLSI. Реалізація моделей процесів
УПСО засобами багатошарової моделі
CMLSI для задач РФ составів представляє
зміст нашої статті.
операцій конструювання утворює системну
модель CMLSI. Реалізація моделей процесів
УПСО засобами багатошарової моделі
CMLSI для задач РФ составів представляє
зміст нашої статті.
Мета
Основною
метою статті є розвиток конструктивних
методів моделювання складних процесів
та систем шляхом розробки багатошарової
конструктивної моделі CMLSI, призначеної
для аналізу та планування задач з УПСО,
зокрема РФ, у яких ураховано складність
(«вагу») операцій формування. У роботі
слід виконати постановку нової задачі
планування процесів функціонування
сервісних системи – виконання задачі
УПСО, а також запропонувати класифікацію
ознак, які визначають типи математичних
моделей наведених процесів.
Методика
Конкретизуємо
постановку задачі УПСО. Розглядаємо
множину послідовностей елементів
(in-потоки) та цільових послідовностей
елементів (out-потоки). Установлюємо
структури та складності операцій, а
також обмеження на ресурси системи
формування (обслуговування). Для відомих
множин та елементів in-потоків замовлень
(з їх визначеними властивостями –
індекс out-потоку, pos-індекс призначення,
вимірювані показники, припустимі
операції, пріоритет тощо) відома
сукупність операцій конструювання
out-потоків з оцінками відносної/абсолютної
складності (ваги). Також задаємо ресурси
та обмеження щодо можливостей процесів
конструювання вихідних потоків, умови
або вимоги завершення процедур
конструювання послідовностей out-потоків.
Можливе існування елементів з однаковим
індексом out-потоку та pos-індексом у
кількох in-потоках. Виконуємо умову
on-line, що означає можливість неодночасної
появи елементів in-потоків. Необхідно
сформувати модель процесу утворення
на основі заданої множини невпорядкованих
in-потоків замовлень множин, упорядкованих
за pos-індексами призначення out-потоків.
При цьому потрібно мінімізувати загальні
витрати на процеси УПСО конструювання,
а також ресурсних обмежень.
Схематично
зазначена постановка, безумовно,
визначає й типову постановку задачі
РФ одного состава на кількох залізничних
напрямах [1, 3, 5]. Інші приклади постановок
задач УПСО наведено у статті нижче.
Аналіз постановок задач, моделей та
процедур різноманітних технологічних
процесів, які реалізують із використанням
процесів конструктивного формування
впорядкованих за певними ознаками
елементів (замовлень, клієнтів, засобів
тощо), дозволяє визначити певну систему
ознак, за якими встановлюють категорії
математичних, інформаційних, логістичних
та інших моделей для дослідження та
планування процесів УПСО. Для
характеризування різноманітних процесів
із конструктивного впорядкування
сукупності послідовностей замовлень
проведемо класифікацію ознак
(властивостей), наявність або відсутність
яких призводить до окремих математичних
класів задач.
Таблиця
1
Класи
ознак математичних моделей процесів
УПСО
Table
1
Classes
of signs of
mathematical models of processes of the account of operations
complexity
|
Номер
|
Назва
ознаки
|
Описання
властивості
|
Приклади
моделей
|
|
1
(р1)
|
Структура
потоків
|
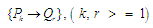
|
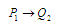
|
|
2
(р2)
|
Детерміновані/
стохастичні/ нечіткі/ невизначені
|
Задані
або відсутні показники
прямування
потоків елементів (імовірності,
ступені приналежності, ін.)
|
Для
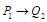 визначені визначені
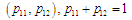
|
|
3
(р3)
|
Статичні/
динамічні
|
Урахування
часових властивостей операцій
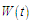
|
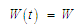
|
|
4
(р4)
|
Синхронні /
асинхронні
|
Одночасне
або неодгочасне отримання вхідних
послідовностей
|
Синхронні
(одночасне)
|
|
5
(р5)
|
Одноетапні
/
багатоетапні
|
Розподіленість
операцій та зон
обслуговування
за етапами, не всі зони постійно
доступні
|
Одноетапні
(під час розв’язання доступні всі
зони обробки)
|
|
6
(р6)
|
Без
втрат / із втратами
|
У
моделях із втратами не всі вхідні
елементи надходять до вихідних
послідовностей
|
Без
втрат
|
|
7
(р7)
|
Повні
/on-line / semi on-line
|
Наявність
даних про наступні послідовності
(відомі / не відомі / часткова
інформація)
|
Повні
|
Продовження
табл. 1
Continuation
of Table 1
|
Номер
|
Назва
ознаки
|
Описання
властивості
|
Приклади
моделей
|
|
8
(р8)
|
Число
виконавців (1/ багато )
|
Установлене
обмеження на число
незалежно
виконуваних операцій
|
Багато
|
|
9
(р9)
|
Число
зон обслуговування (1/ багато )
|
Задане
число зон обслуговування
потоків
замовлень
|
Багато
|
У
табл. 1 наведено ознаки класів математичних
моделей задач упорядкування, які певним
чином ураховують показники складності
(неоднорідності та вагу) операцій щодо
їх реалізації. Відповідно до табл. 1
класи математичних моделей процесів
упорядкування з урахуванням неоднорідності
(складності) операцій формування
визначають за переліком ознак або
властивостей чи їх комбінацій, тобто
за векторами виду
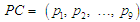 Кожнен із визначених таким чином класів
моделей буде мати відмінні від інших
математичні структури описання
вхідних/вихідних даних, представлення
результатів та процедур отримання
розв’язку. Ця класифікація ознак
показує широкий спектр можливих
застосувань запропонованої задачі
конструктивного впорядкування, вона
може бути продовжена.
Кожнен із визначених таким чином класів
моделей буде мати відмінні від інших
математичні структури описання
вхідних/вихідних даних, представлення
результатів та процедур отримання
розв’язку. Ця класифікація ознак
показує широкий спектр можливих
застосувань запропонованої задачі
конструктивного впорядкування, вона
може бути продовжена.
Укажемо
інші змістовні приклади деяких
технологічних процесів, які формально
можливо віднести до певних класів
конструктивних моделей відповідно до
табл. 1. Типовим прикладом стохастичних,
або нечітких, процесів упорядкування
є задач з формування черги хворих на
спеціалізоване лікування (операції
тощо). Вхідні потоки – це надходження
списків із різних джерел (від відділень
поліклініки та ін.), у яких указано
діагностичні фактори, необхідні
додаткові аналізи тощо. Необхідно
побудувати вихідну чергу, упорядковану
відповідно до лінгвістичних показників
(«негайно», «першочергово»,
«близько 12 днів», …). Зрозуміло, що за
такого впорядкування забезпечення
детермінованого порядку пацієнтів у
списку, що зростає за номерами, не
відповідає сутності процесу. В асинхронних
моделях передбачено впорядкування
кількох вхідних послідовностей
(наприклад, залізничних составів), які
надходять неодночасно до системи
формування.
Прикладом
процесів із втратами елементів вхідних
послідовностей є наведене вище завдання
РФ поїздів, коли деякі вагони вилучають
зі складу, переформовують інакше. Моделі
впорядкування послідовностей класу
semi on-line мають місце, коли до уваги беруть
інформацію про передісторію досліджуваних
(контрольованих) технологічних та інших
процесів. Наприклад, для підвищення
ефективності процесів РФ у [3] створено
базу знань структур «Шаблони формування».
Таким чином, за рахунок уведення
інтелектуальних моделей опису задач
та процедур пошуку подібних шаблонів
спрощують задачі РФ поїздів, які
представлено як задачі класу semi on-line.
Характеристики математичних моделей
процесів УПСО у табл. 1 показують, що
для кожного класу задач необхідно
створювати окремий клас конструктивних
моделей та відповідних процедур.
Результати
Дослідимо
формування конструктивних математичних
моделей процесів УПСО. Представимо
загальну структуру моделей задач УПСО
так:
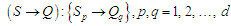 , (1)
, (1)
де
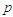 – кількість послідовностей in-seq,
– кількість послідовностей in-seq,
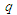 – число out-seq потоків моделей УПСО, що
відрізняються величинами
– число out-seq потоків моделей УПСО, що
відрізняються величинами
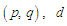 – граничне значення множин. Далі будемо
позначати структури моделей УПСО
– граничне значення множин. Далі будемо
позначати структури моделей УПСО
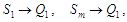 ,
,
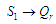 ,
тощо як
,
тощо як
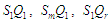 .
Послідовності
.
Послідовності
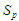 та
та
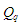 містять неподільні елементи
містять неподільні елементи
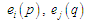 (замовлення), які позначають номерами
(замовлення), які позначають номерами
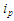 (вхідні невпорядковані) та
(вхідні невпорядковані) та
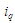 (вихідні впорядковані), а також індекси
призначення замовлень
(вихідні впорядковані), а також індекси
призначення замовлень
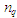 для
для
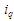 .
Між елементами out-seq потоків
.
Між елементами out-seq потоків
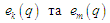 виконують звичайну умову впорядкування
відповідно до індексів pos-ind
виконують звичайну умову впорядкування
відповідно до індексів pos-ind
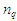
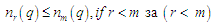
де
через
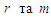 позначені номери елементів out-seq
позначені номери елементів out-seq
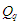 .
Установлено, що під час реалізації всі
структури моделей УПСО вигляду (1) можуть
бути зведені до основної базової
структури
.
Установлено, що під час реалізації всі
структури моделей УПСО вигляду (1) можуть
бути зведені до основної базової
структури
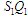 .
.
Представимо
результати розробки багатошарової
конструктивної структури моделі
впорядкування замовлень, подаючи процес
конструювання через параметри «зон
обслуговування (ЗО)
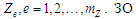 під час відображення процесів
конструктивного моделювання (побудови
розв’язку) визначають спеціальні
формальні компоненти, у яких відбувається
формування вихідних упорядкованих
послідовностей замовлень із початкових
невпорядкованих. Засобами аналізу
вмісту ЗО визначають усі властивості
процесу, можливі оператори перетворення
системи ЗО, які не призводять до порушення
системи обмежень моделі формування, а
також перевіряють умови закінчення
процесу конструювання.
під час відображення процесів
конструктивного моделювання (побудови
розв’язку) визначають спеціальні
формальні компоненти, у яких відбувається
формування вихідних упорядкованих
послідовностей замовлень із початкових
невпорядкованих. Засобами аналізу
вмісту ЗО визначають усі властивості
процесу, можливі оператори перетворення
системи ЗО, які не призводять до порушення
системи обмежень моделі формування, а
також перевіряють умови закінчення
процесу конструювання.
Розв’язання
задачі УПСО формують за певними етапами.
Структуру та всі характеристики процесу
конструювання відображають (зберігають)
у вигляді моделі орієнтованого графа
(графа розмітки, вершини якого містять
поточні структури
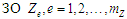 ,
а також значення їх показників складності
та впорядкованості, що наведені нижче).
Розмітка містить упорядкування
вузлів-станів процесу конструювання,
отримане на основі проходження етапів
конструювання. Вона являє собою дерево
вузлів (у загальному вигляді граф)
виконання операцій, або алгоритмів
формування впорядкування, кожна з
вершин розмітки має оцінку складності
(вагу). Ці оцінки питомі, загалом залежать
від кількості елементів
,
а також значення їх показників складності
та впорядкованості, що наведені нижче).
Розмітка містить упорядкування
вузлів-станів процесу конструювання,
отримане на основі проходження етапів
конструювання. Вона являє собою дерево
вузлів (у загальному вигляді граф)
виконання операцій, або алгоритмів
формування впорядкування, кожна з
вершин розмітки має оцінку складності
(вагу). Ці оцінки питомі, загалом залежать
від кількості елементів
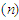 ,
які беруть участь в операціях і які
обробляють алгоритмами
,
які беруть участь в операціях і які
обробляють алгоритмами
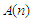 ,
зазначеними також у структурі (1).
,
зазначеними також у структурі (1).
Формалізуємо
оптимізаційну постановку задач УПСО
(1). Позначимо як
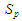 вхідні, а
вхідні, а
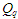 –вихідні послідовності замовлень з
елементами
–вихідні послідовності замовлень з
елементами
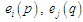 з їх визначеними властивостями, що
знаходяться на місцях
з їх визначеними властивостями, що
знаходяться на місцях
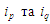 ,
причому відомі для
,
причому відомі для
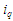 задані
індекси призначення замовлень
задані
індекси призначення замовлень
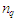 .
Різні
.
Різні
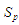 можуть мати елементи
можуть мати елементи
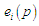 однаковим призначенням
однаковим призначенням
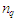 .
На різних місцях
.
На різних місцях
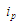 однієї послідовності
однієї послідовності
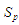 можуть бути елементи з однаковим
призначенням
можуть бути елементи з однаковим
призначенням
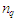 .
У встановленій множині різних вихідних
послідовностей
.
У встановленій множині різних вихідних
послідовностей
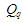 не може бути елементів з однаковим
призначенням. Задано також зони
обслуговування
не може бути елементів з однаковим
призначенням. Задано також зони
обслуговування
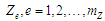 ,
де можуть міститися
,
де можуть міститися
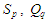 ,
а також їх модифікації, отримані під
час застосування операцій перетворення.
Вихідні послідовності
,
а також їх модифікації, отримані під
час застосування операцій перетворення.
Вихідні послідовності
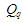 можуть міститися в певних або всіх
зонах
можуть міститися в певних або всіх
зонах
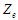 .
.
Якщо
для всіх зон
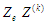 відомі
процедури доступу до елементів ЗО
відомі
процедури доступу до елементів ЗО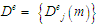 ,
тоді встановлюють певну групу,
послідовність (m)
елементів ЗО, якими можливо оперувати.
У цьому можливість застосування процедур
доступу залежить від кількості елементів
у групі. Серед процедур доступу
,
тоді встановлюють певну групу,
послідовність (m)
елементів ЗО, якими можливо оперувати.
У цьому можливість застосування процедур
доступу залежить від кількості елементів
у групі. Серед процедур доступу
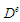 також
можуть бути процедури
також
можуть бути процедури
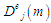 паралельного доступу, які забезпечують
незалежний доступ до окремих послідовностей
елементів (наприклад, із початку та з
кінця
паралельного доступу, які забезпечують
незалежний доступ до окремих послідовностей
елементів (наприклад, із початку та з
кінця
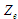 ).
Для ЗО задано множини допустимих
операцій перетворення
).
Для ЗО задано множини допустимих
операцій перетворення
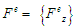 ,
за якими визначають правила формування
вмісту зон
,
за якими визначають правила формування
вмісту зон
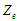 під
час застосування операцій
під
час застосування операцій
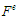 .
Також вважають заданими показники
складності, вагу операцій перетворення
.
Також вважають заданими показники
складності, вагу операцій перетворення
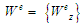 .
Виконання процедур перетворення ЗО
.
Виконання процедур перетворення ЗО
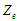 забезпечують
процеси-виконавці
забезпечують
процеси-виконавці 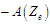 ,
кількість яких вважають відомою,
,
кількість яких вважають відомою,
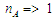 .
.
Виходячи
з уведених структур щодо представлення
та перетворення ЗО
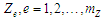 ,
для розв’язання задачі УПСО необхідно
визначити вид, аргументи та послідовність
виконання операторів
,
для розв’язання задачі УПСО необхідно
визначити вид, аргументи та послідовність
виконання операторів
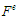 для окремих зон
для окремих зон
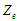 таким чином, щоб забезпечити впорядкування
таким чином, щоб забезпечити впорядкування
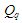 ,
отримати
,
отримати
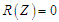 за мінімальних витрат на процес УПСО,
з урахуванням складності операцій
конструювання, а також ресурсних
обмежень, де
за мінімальних витрат на процес УПСО,
з урахуванням складності операцій
конструювання, а також ресурсних
обмежень, де
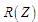 – загальна оцінка невпорядкованості
ЗО
– загальна оцінка невпорядкованості
ЗО
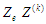 .
Процес упорядкування виконують
(конструюють) за кроками, або етапами.
Етапи складаються з виконання певних
незалежних одна від одної процедур
.
Процес упорядкування виконують
(конструюють) за кроками, або етапами.
Етапи складаються з виконання певних
незалежних одна від одної процедур
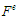 одним або кількома виконавцями
одним або кількома виконавцями
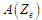 .
При цьому на етапі повинні бути виконані
всі процедури перетворення, допустимі
та відібрані заданим методом (визначений
нижче). Одночасність дії кількох
виконавців,
.
При цьому на етапі повинні бути виконані
всі процедури перетворення, допустимі
та відібрані заданим методом (визначений
нижче). Одночасність дії кількох
виконавців,
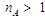 ,
визначає паралелізм у процесі формування
розв’язку щодо
,
визначає паралелізм у процесі формування
розв’язку щодо
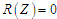 .
.
Показник
складності процесу УПСО
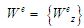 змістовно є оцінкою витрат часу, коштів
або фінансових та інших ресурсів, і
в цілому представляє вектор
змістовно є оцінкою витрат часу, коштів
або фінансових та інших ресурсів, і
в цілому представляє вектор
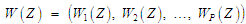 .
Також під час конструювання послідовностей
процедур
.
Також під час конструювання послідовностей
процедур
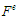 необхідно враховувати ресурсні обмеження
щодо процедур перетворення
необхідно враховувати ресурсні обмеження
щодо процедур перетворення
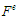 процесами
процесами
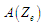 ,
а також допустимих значень
,
а також допустимих значень
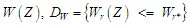 показників. Позначимо послідовності
допустимих операцій
показників. Позначимо послідовності
допустимих операцій
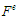 на етапах процесу формування впорядкування
через
на етапах процесу формування впорядкування
через
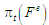 ,
а множину всіх таких послідовностей
як
,
а множину всіх таких послідовностей
як
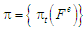 .
Задача оптимального УПСО для структури
(2) полягає в таком. Серед множини
.
Задача оптимального УПСО для структури
(2) полягає в таком. Серед множини
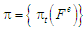 необхідно
визначити таку послідовність
необхідно
визначити таку послідовність
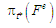 ,
для якої виконується умова:
,
для якої виконується умова:
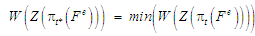 (2)
(2)
при
цьому
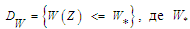 – це заданий вектор показників.
– це заданий вектор показників.
Визначимо
компоненти розвитку КПМ (1). Для
забезпечення можливостей розрахунку
параметрів складності в модифікованій
багатошаровій моделі CMLSI повинні бути
явно задані моделі конструювання ваги
терміналів:
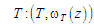 , (3)
, (3)
де
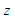 – зони обслуговування процесів.
– зони обслуговування процесів.
Модель
(3) показує, що процес конструювання
(ПК) визначається характеристиками зон
обслуговування
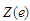 .
ПК явно представлено такою моделлю:
розмітка ПК
.
ПК явно представлено такою моделлю:
розмітка ПК 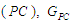 .
Ця розмітка
.
Ця розмітка
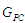 в загальному вигдяді є графом,
у якому позначено вузли
в загальному вигдяді є графом,
у якому позначено вузли
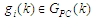 ,
де
,
де
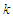 – етап
конструювання. Характеристики вузлів
– етап
конструювання. Характеристики вузлів
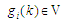 ,
де
,
де
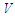 вузли
вузли
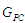 :
:
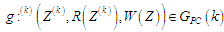 (4)
(4)
У
(4) позначено через
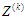 зміст зон обслуговування на етапі ПК
(
зміст зон обслуговування на етапі ПК
(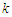 ).
).
У
виразі (4)
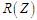 – загальна оцінка невпорядкованості
зон обслуговування
– загальна оцінка невпорядкованості
зон обслуговування
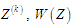 – оцінка складності (ваги) процедур
формування для вузла
– оцінка складності (ваги) процедур
формування для вузла
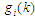 .
Зауважимо, що величину
.
Зауважимо, що величину
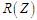 обчислюють на основі окремої моделі,
із використанням спеціальної міри
впорядкування, наведеної у статті
нижче. Уведення до моделі CMLSI структури
для оцінювання складності вузлів графа
GPC
забезпечує нові кількісні показники,
а також якісні можливості моделей
конструювання. У CMLSI стає можливим
оцінювати безпосередньо процес
конструювання (у завданнях УПСО це
загальна оцінка невпорядкованості
R(Z)) у
(4), а також використовувати такі оцінки
для цілеспрямованого вдосконалення
ПК.
обчислюють на основі окремої моделі,
із використанням спеціальної міри
впорядкування, наведеної у статті
нижче. Уведення до моделі CMLSI структури
для оцінювання складності вузлів графа
GPC
забезпечує нові кількісні показники,
а також якісні можливості моделей
конструювання. У CMLSI стає можливим
оцінювати безпосередньо процес
конструювання (у завданнях УПСО це
загальна оцінка невпорядкованості
R(Z)) у
(4), а також використовувати такі оцінки
для цілеспрямованого вдосконалення
ПК.
Оцінку
складності
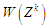 обчислюють за формулою:
обчислюють за формулою:
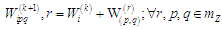 (5)
(5)
де
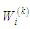 –
оцінка складності вузла
–
оцінка складності вузла
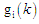 на етапі ПК (k),
на етапі ПК (k),
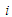 – номер вузла графа розміток на цьому
етапі конструювання;
– номер вузла графа розміток на цьому
етапі конструювання;
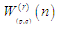 – оцінка складності операції перетворення
(алгоритму
– оцінка складності операції перетворення
(алгоритму
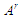 )
для зон (
)
для зон (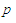 – вихідні,
– вихідні,
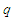 – результуючі), залежно
від кількості елементів, що беруть
участь в операції; причому вагу алгоритму
– результуючі), залежно
від кількості елементів, що беруть
участь в операції; причому вагу алгоритму
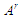 задають у моделі з терміналами
задають у моделі з терміналами
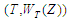 .
.
У
виразі (5)
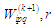 – вага вузла графа розмітки
– вага вузла графа розмітки
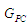 процесу конструювання на етапі
процесу конструювання на етапі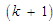 ,
який виходить із вузла
,
який виходить із вузла
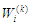 за допомогою застосування алгоритму
за допомогою застосування алгоритму
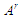 .
.
Для
відбору множини алгоритмів
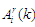 ,
які можуть бути застосовані до вузла
,
які можуть бути застосовані до вузла
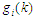 на етапі конструювання
на етапі конструювання
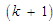 ,
розроблено метод багатошарової моделі
CMLSI, представлений окремою структурою
моделювання КПМ (або ж СРМ).
,
розроблено метод багатошарової моделі
CMLSI, представлений окремою структурою
моделювання КПМ (або ж СРМ).
З
урахуванням моделей (3) – (5) у цьому
розділі побудовано опис процесу
конструювання у вигляді графа розміток,
який дозволяє явно представляти й
оцінювати властивості процесу формування
висновку з вагою операцій, а також
уточнити й отримати розвиток КПМ [1, 6].
У
задачах УПСО існує ряд процесів, які
можуть проходити одночасно, паралельно.
Наприклад, побудова множин допустимих
операцій перетворення стану процесів
формування, побудова множин станів
графа розміток процесу конструювання,
пошук подібних шаблонів для вхідних
НПЗ та ін., які потребують додаткового
розв’язку у КПМ. Разом із тим реалізацію
таких паралельних методів конструювання
не передбачено у структурі КПМ (1) [8],
так само як розрахунки оцінок загальної
складності алгоритмів конструювання
КПМ. Ці можливості, поряд із багатошаровістю
моделі, у якій узгоджуються кілька
окремих КПМ, є змістом розвитку
конструктивного моделювання, виконаного
у статті.
Відповідно
до робіт [8, 9],
основна структура КПМ має такий вигляд:
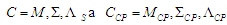 (6)
(6)
У
моделі (6):
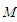 – предметний носій;
– предметний носій; 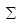 –
носій дій (операцій, операторів тощо)
та їх схема;
–
носій дій (операцій, операторів тощо)
та їх схема;
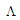 – представлення реалізацій; права
частина моделі є результатом трансформації
структури до конкретної предметної
області.
– представлення реалізацій; права
частина моделі є результатом трансформації
структури до конкретної предметної
області.
Реалізацію
процесу конструювання алгоритму
розв’язку виконують за рахунок розробки
спеціалізованих алгоритмів процесів
УПСО, створення відповідної системи
правил, розробки інших складових моделі
(6). Виконаємо розвиток багатошарової
паралельної структури CMLSI КПМ, що
враховує складність виконаних алгоритмів
відповідно до (3) – (6). У реальних задачах
конструювання подання процесів єдиною
структурою виду (6) може призводити до
значного ускладнення такої моделі. Для
зменшення в цілому конструктивного
опису будемо виконувати виділення
окремих підзадач відносно самостійних
(декомпозицію) та ін. Додатковою підставою
для створення багатошарової структури
моделі є те, що на практиці виділення
загальної формальної мети й подання
процесу конструювання, без реалізації
часткових задач, може бути досить
проблемним. Представимо модель
багатошарового конструювання, що
узагальнює (6), таким чином: уведемо
конструктивні моделі вигляду (6) для
часткових підзадач відповідно до
вихідної, розрізняючи їх індексами
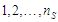 :
:
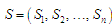 (7)
(7)
Розглядаючи
як мету реалізацію задачі УПСО, створюємо
опис структури графа розміток
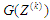 ,
що відображає етапи процесу конструювання,
наприклад, вигляду (3) – (6). Конструктивні
моделі шарів зв’язують через модель
процесу
,
що відображає етапи процесу конструювання,
наприклад, вигляду (3) – (6). Конструктивні
моделі шарів зв’язують через модель
процесу
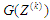 .
На відміну від КПМ, у моделях шарів
.
На відміну від КПМ, у моделях шарів
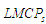 уведено термінали згідно з
(3), із вагою.
уведено термінали згідно з
(3), із вагою.
Загальна
структура багатошарової моделі MLCPM
або CMLSI має
вигляд:
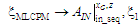 (8)
(8)
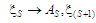
за
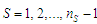 (9)
(9)
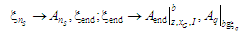 ,
,
за
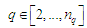 .
.
Конструктивні
моделі, які відповідають окремим шарам
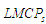 ,
можуть містити оператори
паралельного конструювання вигляду:
,
можуть містити оператори
паралельного конструювання вигляду:
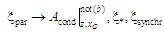 (10)
(10)
де
позначено
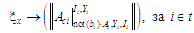 (11)
(11)
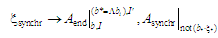 (12)
(12)
Продукція
(перетворення або відображення) (11)
показує, що модель процесу має паралельні
структури конструювання
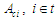 ,
які виконують до умови
,
які виконують до умови
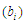 = true;
за подальших звернень до алгоритмів
= true;
за подальших звернень до алгоритмів
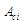 їх пропускають. Структура синхронізації
(12) перевіряє умови завершення всіх
паралельних алгоритмів (11), логічний
вираз
їх пропускають. Структура синхронізації
(12) перевіряє умови завершення всіх
паралельних алгоритмів (11), логічний
вираз
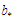 .
Якщо
.
Якщо
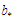 = true,
то (10) завершиться. У моделі
(8) – (12) позначено таке:
= true,
то (10) завершиться. У моделі
(8) – (12) позначено таке:
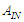 – алгоритм процесу формування внутрішніх
моделей
– алгоритм процесу формування внутрішніх
моделей
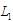 ;
;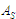 – алгоритм конструювання моделей шарів
– алгоритм конструювання моделей шарів
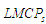 ;
;
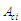 – алгоритм паралельного конструювання;
– алгоритм паралельного конструювання;
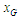 – представлення графа розміток ПК;
– представлення графа розміток ПК;
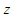 – зони обслуговування;
in_seq – набір вхідних послідовностей;
– зони обслуговування;
in_seq – набір вхідних послідовностей;
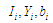 – параметри паралельних процесів (11);
– параметри паралельних процесів (11);
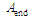 – алгоритм оцінки закінчення (11);
– алгоритм оцінки закінчення (11); 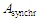 – алгоритм синхронізації закінчення;
– алгоритм синхронізації закінчення;
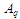 – алгоритм повтору моделей шарів
(q)(9).
– алгоритм повтору моделей шарів
(q)(9).
Модель
структури з правилами (8) – (12) і задає
багатошарову рекурсивну модель CMLSI.
Подальше
формування MLCPM для задачі УПСО полягає
в розробці конструктивних моделей
шарів
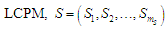 Для задачі УПСО загальна схема структури
процесу формування впорядкування НПЗ
така:
Для задачі УПСО загальна схема структури
процесу формування впорядкування НПЗ
така:
Е1.
Виконання процедур отримання, контролю
вхідних НПЗ відповідно до (1)
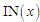
Е2.
Формування внутрішніх
моделей
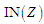 ,
представлених через зони
обслуговування
,
представлених через зони
обслуговування
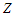 ,
далі позначено
,
далі позначено 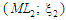 .
.
Е3.
Формування моделі для оцінки міри
впорядкування 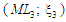 .
.
Е4.
Вимірювання оцінок міри
порядку
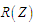 ,
за
,
за
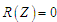 кінець.
кінець.
Е5.
Модель 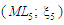 подає конструювання множини можливих
операторів (процедур) перетворень зон
подає конструювання множини можливих
операторів (процедур) перетворень зон
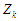 (можливе паралельне виконання).
(можливе паралельне виконання).
Е6.
Конструювання нового шару графа розміток
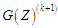 за допомогою можливих операторів,
за допомогою можливих операторів, 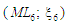 (можливе паралельне виконання).
(можливе паралельне виконання).
Е7.
Перехід до етапу E3.
Таким
чином, процес конструювання за схемою
(E1 – E7) у роботі представлено відповідно
до єдиної структури (8). При цьому у
вигляді модифікованих КПМ (6) (з урахуванням
уведення ваги терміналів відповідно
до (3)) будують конструктивні моделі
шарів для етапів E2 – E6.
На
рис. 1. представлена узагальнена
блок-схема багатошарової моделі MLCPM
процесів УПСО, яка відповідає (8). У ній
також позначено компоненти, виконання
яких можливе паралельно, із реалізацією
паралельних операторів конструювання
(10) – (12).

Рис. 1. Блок-схема багатошарової
моделі MLCPM
Fig. 1. Block diagram of the multilayer model MLCPM
Деталізуємо
змістовно окремі складові шарів моделі
MLCPM. Кожна з подальших складових
багатошарової моделі (8) може бути
представлена структурно, як на рис. 1:
1. Реалізація
процедур отримання та контролю вхідних
даних про структуру типу задачі
впорядкування, а також невпорядковані
послідовності замовлень (1)
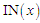
2. Формування
внутрішніх підмоделей [3] задачі
УПСО (ML2) і зворотного перетворення:
а) визначення
класу процесу перетворення за
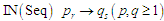 ;
;
б)
зведення
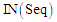 до структури
до структури
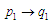 ;
;
в) формування
дійсних номерів груп (ДНГ) для
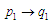 ;
;
г) формування
логічної нумерації груп (ЛНГ);
д) конструювання
скорочених ЛНГ (СЛНГ) для
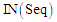 .
.
Використання
схеми бази знань шаблонів (БЗнШ) для
формування (підбору) подібних шаблонів,
для яких відомі оптимальні плани
впорядкування
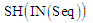 .
У разі повного збігу – завершити
розв’язання задачі.
.
У разі повного збігу – завершити
розв’язання задачі.
Результат:
ДНГ, ЛНГ, СЛНГ для 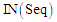 ;
;
е) у
разі перебування в БЗнШ
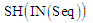 виконати конструювання оптимального
плану для
виконати конструювання оптимального
плану для
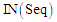 за шаблоном
за шаблоном
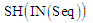 .
Перетворення необхідне у з’вязку з
тим, що кожній ЛНГ, СЛНГ відповідає
множині можливих вхідних послідовностей,
тому потрібен перехід від внутрішніх
моделей до дійсної вхідної послідовності,
також необхідно перейти від структури
.
Перетворення необхідне у з’вязку з
тим, що кожній ЛНГ, СЛНГ відповідає
множині можливих вхідних послідовностей,
тому потрібен перехід від внутрішніх
моделей до дійсної вхідної послідовності,
також необхідно перейти від структури
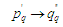 до вихідної структурі згідно з
до вихідної структурі згідно з
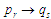 .
.
3. Модель
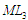 для розрахунку міри впорядкування
послідовності НПЗ за
для розрахунку міри впорядкування
послідовності НПЗ за
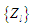 .
.
Вхідні
дані: розподіл елементів НПЗ за зонами
обслуговування
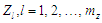 ;
граничне число виконавців конструювання
системної форми впорядкування
;
граничне число виконавців конструювання
системної форми впорядкування
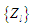 .
.
а) побудувати
шляхом конкатенації підпослідовностей,
збережених у зонах обслуговування
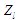 ,
усі можливі, з урахуванням допустимих
правил перетворення
(вставка в голову | «хвіст» |
з інвертуванням порядку та ін.),
послідовності
,
усі можливі, з урахуванням допустимих
правил перетворення
(вставка в голову | «хвіст» |
з інвертуванням порядку та ін.),
послідовності
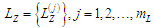 ;
;
б) розрахувати
оцінки складності з’єднання послідовностей
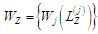 ;
;
в) використовуючи
метрику
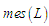 ,
вигляду (13)
,
вигляду (13)
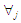 ,
розрахувати
,
розрахувати
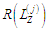 ;
;
г) побудувати
множину
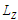 що містить послідовності
що містить послідовності
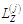 з
з
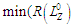 ;
;
д) конструювання
процесів п. п. 3. а
– 3. г
можливо виконати за допомогою паралельних
структур (10) – (12). Результатом
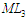 є множина оптимальних на етапі
є множина оптимальних на етапі
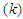 упорядкувань для зон
упорядкувань для зон
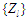 з оцінками складності з’єднань. Для
реалізації задач із розрахунку міри
впорядкування послідовності НПЗ
використовують функцію міри вигляду
(13), див. нижче.
з оцінками складності з’єднань. Для
реалізації задач із розрахунку міри
впорядкування послідовності НПЗ
використовують функцію міри вигляду
(13), див. нижче.
4. Модель
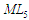 конструювання множин можливих операцій
(процедур) перетворення для
конструювання множин можливих операцій
(процедур) перетворення для
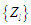 ,
з урахуванням
,
з урахуванням
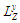 :
:
а) дані:
число виконавців (як окремий параметр
конкретної задачі УПСО); зони
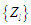 множин допустимих операцій (процедур)
перетворення в кожній
множин допустимих операцій (процедур)
перетворення в кожній
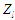 ;
;
б) у
кожній
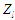 формуються набори міток щодо порушення
порядку, можливого поділу послідовності;
формуються набори міток щодо порушення
порядку, можливого поділу послідовності;
в) для
кожної точки поділу з урахуванням
можливих операторів конкатенації в
зонах
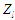 розглядають нові структури зон
обслуговування
розглядають нові структури зон
обслуговування
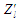 ,
отримані за рахунок приписування,
приєднання фрагментів, виділених у
всіх зонах
,
отримані за рахунок приписування,
приєднання фрагментів, виділених у
всіх зонах
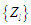 ;
;
г) розраховують
міри впорядкування в кожній із зон
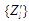 і
в системі впорядкування в цілому;
і
в системі впорядкування в цілому;
д) операторів
перестановок, які призводять до зростання
міри впорядкування, відбирають спільно
з методами поділу підпослідовностей
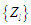 як множин процедур конструювання на
етапі
як множин процедур конструювання на
етапі
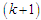 .
.
Конструювання
процесів п. п. 4. а
– 4. д
можливо виконати за допомогою паралельних
структур (10) – (12).
Результат:
множина операцій для побудови шару
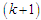 графа розміток.
графа розміток.
5 Модель
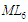 конструювання нового шару (етап
формування графа розміток) за допомогою
відібраних операторів (дані: зони
конструювання нового шару (етап
формування графа розміток) за допомогою
відібраних операторів (дані: зони
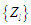 ;
число виконавців):
;
число виконавців):
а) для
кожного вузла графа розміток
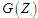 виконати всі операції перетворення
(перестановки);
виконати всі операції перетворення
(перестановки);
б) обчислити
показники складності для всіх нових
вузлів графа
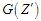 ,
використовуючи модель міри (13);
,
використовуючи модель міри (13);
в) побудувати
послідовності виконання операцій
перестановки для кожного з виконавців,
ураховуючи обмеження за
кількістю виконавців.
Конструювання
процесів формування моделі реалізації
п. п. 5. а
– 5. б можна
виконати за допомогою паралельних
структур (10) – (12).
Моделі
конструювання шарів
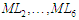 можуть бути представлені
засобами MLCPM за її схемою КПМ , а також
додатковими паралельними структурами
вигляду (10) – (12).
можуть бути представлені
засобами MLCPM за її схемою КПМ , а також
додатковими паралельними структурами
вигляду (10) – (12).
Для
реалізації моделі впорядкування УПСО
вигляду (1) найбільш важливою є задача
внутрішнього представлення процесів
конструювання, вимірювання ступеня
впорядкування станів системи
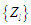 ,
розділення послідовностей заявок
окремих
,
розділення послідовностей заявок
окремих
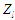 на частини, які використовують під час
формування нових вузлів графа розміток
на частини, які використовують під час
формування нових вузлів графа розміток
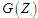 Процедури формування внутрішніх моделей
ДНГ, ЛНГ, СЛНГ представлені в роботах
[1, 3]. Вони дають можливість перейти від
фактичних індексів призначення заявок
до їх узагальнених кодів. Використання
внутрішніх кодів скорочує й уніфікує
розрахунки, дозволяє створювати шаблони
для баз знань (БЗнШ).
Процедури формування внутрішніх моделей
ДНГ, ЛНГ, СЛНГ представлені в роботах
[1, 3]. Вони дають можливість перейти від
фактичних індексів призначення заявок
до їх узагальнених кодів. Використання
внутрішніх кодів скорочує й уніфікує
розрахунки, дозволяє створювати шаблони
для баз знань (БЗнШ).
Центральною
ланкою конструктивної багатошарової
моделі (6), (8) процесів УПСО CMLSI є міра
впорядкування послідовності кодів
замовлень НПЗ, а саме
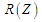 загальна оцінка невпорядкованості зон
обслуговування
загальна оцінка невпорядкованості зон
обслуговування
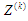 (4), яка є додатковим параметром графа
розміток
(4), яка є додатковим параметром графа
розміток
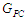 процесу конструювання. Важливо, що
показник
процесу конструювання. Важливо, що
показник
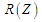 є спеціалізованим, уведеним безпосередньо
для задач УПСО типу РФ, як загальна
характеристика всього ПК. Для інших
задач конструктивного моделювання на
основі (8) необхідно використовувати
інші характеристики ПК.
є спеціалізованим, уведеним безпосередньо
для задач УПСО типу РФ, як загальна
характеристика всього ПК. Для інших
задач конструктивного моделювання на
основі (8) необхідно використовувати
інші характеристики ПК.
Для
вимірювання ступеня впорядкування
послідовності цілих чисел щодо зростання
{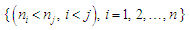 }
запропоновано характеристику міри
вигляду:
}
запропоновано характеристику міри
вигляду:
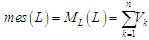 (13)
(13)
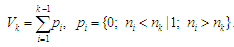
Для
зворотного впорядкування
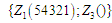 .
.
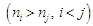 підраховують число порушень порядку
праворуч від позиції k.
підраховують число порушень порядку
праворуч від позиції k.
Модель
(13) задовольняє властивостям міри [2,
11]. Вона ефективно
забезпечує оцінку впорядкування для
прямого й зворотного прямування номерів,
що характеризують НПЗ.
Аналіз
і численні експерименти з реалізації
задач УПСО дозволили встановити деякі
загальні вимоги до вибору меж (до міток
поділу послідовностей кодів НПЗ), за
якими необхідно встановлювати частини
НПЗ (під ланцюжки) і використання
яких дозволяє спростити ПК та зменшити
обсяг перебору варіантів побудови
графа розміток GPC,
тобто до операторів ділення НПЗ –
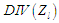 .
Процедури
.
Процедури
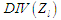 створюють вектор міток, що визначають
можливі під ланцюжки, на які поділяються
послідовності в
створюють вектор міток, що визначають
можливі під ланцюжки, на які поділяються
послідовності в
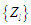 .
.
Загальною
змістовною властивістю операцій
відділення в числових послідовностях
(ланцюжках) є порушення щільної (без
пропусків номерів) нумерації елементів.
При цьому розглядають два види
впорядкування: за зростанням (up), за
спадною нумерацією (down). Мітки поділу
відповідають порушенню щільної
(up | down)
нумерації елементів. Такі мітки
забезпечують виконання операторів
перестановок: із початку зони (Head
(H)) в голову іншої (Н); із початку (Н) в
кінець (End (E)); із початку (Н) в кінець (E)
є інвертуванням елементів послідовності
(E.I.); також інші подібні оператори
перетворення.
Можливі
способи перестановок (з’єднання-поділу)
ланцюжків установлюють у структурах
моделі конструювання УПСО (8).
Наведемо
приклади конструювання векторів міток
поділу зон
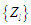 .
У наведених нижче послідовностях
номерів кодів НПЗ межі для поділу
ланцюжків визначають вертикальні
риски, установлені оператором
.
У наведених нижче послідовностях
номерів кодів НПЗ межі для поділу
ланцюжків визначають вертикальні
риски, установлені оператором
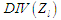 .
.
Розмітки
ланцюжків:
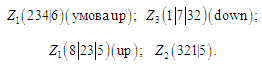
Упорядкування
за однакових номерів груп елементів
(приписування під ланцюжків в будь-якому
зручному та раціональному порядку:
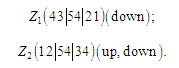
Послідовність
перестановок за мітками:
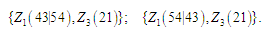
Упорядкування
на основі методу розриву щільної
числової послідовності з урахуванням
повтору номерів
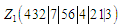 :
мітки розриву за умов up
| down.
:
мітки розриву за умов up
| down.
Повторні
номери в послідовності також є ознакою
міток розриву (у прикладі 2, 3, 4). З
урахуванням умови повтору номерів
отримана інша система міток розриву
зони
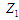 :
:
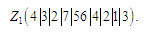
Будемо
називати мітки, отримані на основі (up
| down), мітками типу
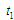 ;
мітки для умови повторів номерів назвемо
типу
;
мітки для умови повторів номерів назвемо
типу
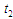 .
Для формування множин можливих операцій
перестановок частин
.
Для формування множин можливих операцій
перестановок частин
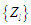 спочатку досліджують мітки типу t1,
якщо для них немає допустимих операторів
конкатенації – розглядають варіанти
поділу
спочатку досліджують мітки типу t1,
якщо для них немає допустимих операторів
конкатенації – розглядають варіанти
поділу
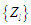 за мітками типу t2.
за мітками типу t2.
Як
приклад, послідовність виконання
операторів конструювання порядку така:
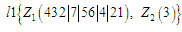 ;
;
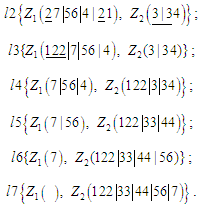
Приклади
показують зміст процесу конструювання
порядку УПСО на основі векторів міток
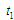 і
і
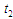 .
Обчислення показника міри (13) для
зазначеної послідовності етапів
демонструє збіжність процесу – зменшення
показників невпорядкованості до
.
Обчислення показника міри (13) для
зазначеної послідовності етапів
демонструє збіжність процесу – зменшення
показників невпорядкованості до
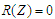 .
У табл. 2 наведено покрокове виконання
процедури впорядкування
послідовності замовлень
.
У табл. 2 наведено покрокове виконання
процедури впорядкування
послідовності замовлень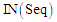 ,
коли використовують дві ЗО, указано
операції формування порядку, склад ЗО,
а також зміну загальної оцінки міри
невпорядкованості, яка зменшується до
,
коли використовують дві ЗО, указано
операції формування порядку, склад ЗО,
а також зміну загальної оцінки міри
невпорядкованості, яка зменшується до
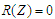 .
Дані таблиці демонструють застосування
показників (13) для планування процесу
впорядкування УПСО.
.
Дані таблиці демонструють застосування
показників (13) для планування процесу
впорядкування УПСО.
Наукова
новизна та практична
значимість
У
статті виконано постановку нової
науково-прикладної задачі з планування
сервісних систем. Уперше здійснено
класифікацію ознак класів математичних
моделей процесів упорядкування
послідовностей із вагою операцій.
Отримали розвиток конструктивно-продукційні
моделі шляхом створення багатошарових
та паралельних конструктивних структур
моделювання. Розроблено багатошарові
конструктивні моделі процесів РФ
залізничних составів.
Запропоновані
багатошарові конструктивні структури
моделювання дозволяють удосконалити
інструментарій конструктивного
моделювання, а побудована модель (6) –
(8) представляє нову форму реалізації
процесів оптимального РФ составів.
Розроблені моделі процесів УПСО є
придатними та ефективними для формалізації
широкого спектру задач аналізу та
оптимального планування технологічних
процесів залізничного транспорту,
логістичних та різноманітних інформаційних
систем.
Висновки
У
статті розв’язано науково-прикладну
задачу розвитку процесів конструктивного
моделювання шляхом розробки конструктивної
багатошарової моделі процесів
упорядкування РФ та неоднорідних
послідовностей замовлень (зокрема
залізничних составів), які мають
відмінність в урахуванні складності
операцій формування, процесів УПСО.
При цьому вперше виконано постановку
та структурну формалізацію задачі з
планування сервісних систем, яка може
бути зведена до моделі процесів УПСО.
Також здійснено класифікацію ознак
(властивостей) постановок задач
упорядкування НПЗ, наявність або
відсутність яких призводить до окремих
математичних класів задач конструктивного
моделювання. Класифікація ознак дозволяє
встановити широкий спектр можливих
прикладних та математичних застосувань
запропонованої задачі конструктивного
впорядкування УПСО.
Було
створено багатошарові й паралельні
конструктивні структури, розроблено
багатошарові конструктивні моделі
процесів оптимального розформування-формування
багатогрупових поїздів.
Запропоновані
у статті конструктивні моделі процесів
УПСО є універсальними для багатьох
технологічних додатків, заснованих на
процедурах оптимального впорядкування
складових компонентів за допомогою
неоднорідних систем операцій.
Таблиця
2
Виконання
процедури впорядкування
Table
2
Performing
of the ordering procedure
|
Номер
кроку
|
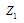
|
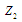
|
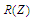
|
|
1
|
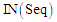
|
4
2 5 3 1
|
0
|
14
|
|
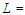
|
3
2 2 3 4
|
|
|
|
2
|
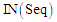
|
4
2 5 3
|
1
|
6
|
|
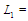
|
2
1 1 2
|
0
|
6
|
|
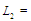
|
3
2 2 3
|
4
|
14
|
|
3
|
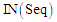
|
4
2 5
|
1
3
|
4
|
|
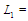
|
1
2 0
|
0
1
|
4
|
|
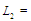
|
3
2 2
|
3
2
|
12
|
|
4
|
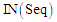
|
2
5
|
1
3 4
|
4
|
|
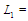
|
2
0
|
0
1 1
|
4
|
|
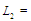
|
1
3
|
2
1 1
|
8
|
|
5
|
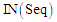
|
2
|
1
3 4 5
|
2
|
|
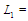
|
3
|
0
1 1 1
|
6
|
|
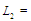
|
1
|
1
0 0 0
|
2
|
|
6
|
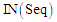
|
1
2
|
3
4 5
|
0
|
|
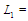
|
3
3
|
2
2 2
|
12
|
|
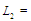
|
0
0
|
0
0 0
|
0
|
|
7
|
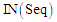
|
1
2 3 4 5
|
0
|
0
|
|
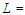
|
0
0 0 0 0
|
|
|
СПИСОК ВИКОРИСТАНИХ
ДЖЕРЕЛ
Бобровский
В. И., Сковрон И. Я., Дорош А. С., Демченко
Е. Б., Малашкин В. В., Болвановская Т. В.
Имитационное моделирование процесса
расформирования многогруппных составов
на двусторонней горке малой мощности.
Транспортні системи
та технології перевезень : зб. наук. пр.
Дніпропетр. нац. ун-ту залізн. трансп.
ім. акад. В. Лазаряна.
Дніпро, 2018. Вип. 15. С. 19–26.
DOI: 10.15802/tstt2018/150194
Кормен Т.,
Лейзерсон Ч., Ривест Р., Штайн К. Алгоритмы
: построение и анализ.
Пер. с англ. 2-е изд. Москва : Вильямс,
2005. 1296 с.
Скалозуб
В., Белый Б. Структура интеллектуальной
информационной технологии формирования
многогруппных составов. Транспортні
системи та технології перевезень.
2019. Вып. 17. С. 62–68.
DOI: 10.15802/tstt2019/178217
Holzhauser M.,
Krumke S. O., Thielen C. Maximum flows in generalized processing
networks. Journal of Combinatorial
Optimization. 2016. Vol. 33. Iss. 4.
P. 1226–1256. DOI: 10.1007/s10878-016-0031-y
Kozachenko D.,
Bobrovskiy V., Gera B., Skovron I., Gorbova A. An optimization
method of the multi-group train formation at flat yards.
International Journal of Rail
Transportation. 2020. P. 1–18.
DOI: 10.1080/23248378.2020.1732235
Kravchenko G.
Modeling the External Structure of a Fractals. EIOP
Conference Series : Earth and Environmental Science.
2017. Vol. 90. P. 1–8.
DOI: 10.1088/1755-1315/90/1/012100
Shang Zh., Li M.
Feature Selection Based on Grouped Sorting. 2016
9th International Symposium on Computational Intelligence and Design
(ISCID) (Hangzhou, 10–11 dec. 2016).
Hangzhou, 2016. P. 451–454.
DOI: 10.1109/ISCID.2016.1111
Shynkarenko V. I.,
Ilman V. M. Constructive-Synthesizing Structures and Their
Grammatical Interpretations. i. Generalized Formal
Constructive-Synthesizing Structure. Cybernetics
and Systems Analysis. 2014. Vol. 50.
Iss. 5. P. 655–662.
DOI: 10.1007/s10559-014-9655-z
Skalozub V., Ilman
V., Shynkarenko V. Ontological Support Formation for
Constructive-Synthesizing Modeling of Information Systems
Development Processes. Восточно-Европейский
журнал передовых технологий.
2018. Vol. 5, № 4 (95). Р. 55–63.
DOI: 10.15587/1729-4061.2018.143968
Stuart D.
Practical Ontologies for Information
Professionals. Language Arts &
Disciplines, 2016. 224 p.
DOI: 10.29085/9781783301522
Yadavalli V. S.
S., Balcou C. A supply chain management model to optimise the
sorting capability of a «third party logistics»
distribution centre. South African
Journal of Business Management. 2017.
Vol. 48. Iss. 1. P. 77–84.
DOI: 10.4102/sajbm.v48i1.22
Zhukovyts’kyy I.
Use of an automaton model for the designing of real-time information
systems in the railway stations. Transport
problems. 2017. Vol. 12. Iss. 4. P.
101–108. DOI: 10.20858/tp.2017.12.4.10
В. В. Скалозуб1*, В. М. Ильман2*,
Б. Б. БЕЛЫЙ3*
1*Каф.
«Компьютерные информационные технологии»,
Днипровский национальный
университет
железнодорожного транспорта имени
академика В. Лазаряна,
ул. Лазаряна, 2,
Днипро, Украина, 49010, тел. +38 (056) 373 15 35,
эл. почта skalozub.vl.v@gmail.com,
ORCID 0000-0002-1941-4751
2*Каф.
«Компьютерные информационные технологии»,
Днипровский национальный
университет
железнодорожного транспорта имени
академика В. Лазаряна,
ул. Лазаряна, 2,
Днипро, Украина, 49010, тел. +38 (056) 373 15 35,
эл. почта valeriy_ilman@ukr.net,
ORCID 0000-0003-0983-8611
3*Каф. «Компьютерные
информационные технологии», Днипровский
национальный
университет железнодорожного
транспорта имени академика В. Лазаряна,
ул. Лазаряна, 2, Днипро, Украина, 49010, тел.
+38 (056) 373 15 35,
эл. почта hibarike@gmail.com,
ORCID 0000-0001-8324-4673
КОНСТРУКТИВНЫЕ
МНОГОСЛОЙНЫЕ МОДЕЛИ
ДЛЯ УПОРЯДОЧЕНИЯ
ПОСЛЕДОВАТЕЛЬНОСТЕЙ
С УЧЕТОМ СЛОЖНОСТИ
ОПЕРАЦИЙ ФОРМИРОВАНИЯ
Цель. Основной
целью статьи является постановка новой
задачи по планированию процессов
функционирования сервисных систем, а
также развитие конструктивных методов
моделирования сложных процессов и
систем путем разработки многослойной
конструктивной модели по упорядочению
наборов неоднородных последовательностей
заказов (MLCРМ), которая учитывает сложность
операций формирования. Методика.
В работе предложена постановка новой
задачи моделирования, предназначенной
для упорядочения неоднородных
последовательностей элементов (заказов).
Исследуемые задачи распространены в
логистических, технологических,
информационных, железнодорожных и
других процессах. Главным и существенным
отличием предлагаемых конструктивных
многослойных моделей является введение
в их состав дополнительных структур
конструирования, обеспечивающих
возможности задания сложности операций
формирования, а также дополнительного
анализа свойств объектов, формирующихся
при реализации решений. Средствами
MLCРМ также реализуют процедуры оптимального
управления процессами поиска решений.
Результаты.
В статье на примере задачи по оптимальному
формированию-расформированию многогруппных
железнодорожных составов разработана
новая многослойная конструктивная
модель процессов оптимального планирования
задач по упорядочению наборов неоднородных
последовательностей заказов. Также
предложена классификация признаков,
которые определяют типы математических
моделей процессов упорядочения. Научная
новизна. Выполнено
постановку новой научно-прикладной
задачи по планированию сервисных систем,
впервые осуществлено классификацию
признаков классов математических
моделей процессов упорядочения
последовательностей заказов с весом
операций. Получили развитие
контруктивно-продукционные модели
путем создания многослойных и параллельных
конструктивных структур моделирования
расформирования-формировния составов.
Практическая значимость.
Ценность полученных результатов
определяется широким спектром возможных
применений задачи по планированию
сервисных систем. Предложенные
многослойные конструктивные структуры
моделирования позволяют усовершенствовать
инструментарий конструктивного
моделирования. Построенная модель
процессов оптимального
расформирования-формирования составов
позволяет получить новую форму реализации
указанных технологических процессов
железнодорожного транспорта.
Ключевые слова:
конструктивное моделирование; многослойные
модели; параллельное конструирование;
неоднородные последовательности
заказов; упорядочение последовательностей;
сложность операций формирования;
многогруппные железнодорожные составы
V. V. SKALOZUB1*,
V. M. ILMAN2*,
B. B. BILYI3*
1*Dep.
«Computer Information Technology», Dnipro National
University of
Railway Transport named after Academician V. Lazaryan,
Lazaryana
St., 2, Dnipro, Ukraine, 49010, tel. +38 (056) 373 15 35,
e-mail
skalozub.vl.v@gmail.com, ORCID 0000-0002-1941-4751
2*Dep.
«Computer Information Technology», Dnipro National
University of
Railway Transport named after Academician V. Lazaryan,
Lazaryana
St., 2, Dnipro, Ukraine, 49010, tel. +38 (056) 373 15 35,
e-mail
valeriy_ilman@ukr.net, ORCID 0000-0003-0983-8611
3*Dep.
«Computer Information Technology», Dnipro National
University of
Railway Transport named after Academician V. Lazaryan,
Lazaryana
St., 2, Dnipro, Ukraine, 49010, tel. +38 (056) 373 15 35,
e-mail
hibarike@gmail.com, ORCID 0000-0001-8324-4673
CONSTRUCTIVE
MULTI-LAYER MODELS FOR
ORDERING A SET OF SEQUENCES, TAKING
INTO
ACCOUNT THE COMPLEXITY
OPERATIONS OF FORMATION
Purpose. The aim of the article is to pose a new
task for planning the processes of service systems functioning, as
well as the development of constructive methods for modeling complex
processes and systems by developing multilayer constructive model for
ordering sets of inhomogeneous order sequences (MLCPM), which takes
into account the complexity of formation operations. Methodology.
The paper proposes the formulation of a new modeling problem,
designed for ordering heterogeneous sequences of elements (orders).
The studied results were used in logistics, technological,
information and other processes. The main and essential difference of
the proposed constructive multilayer models is the introduction of
additional design structures into their composition, which provides
the ability to set the complexity of the formation operations, as
well as the possibility of additional analysis of the properties of
objects that are formed during the adoption of decisions. Procedures
of optimal control of the processes of finding decision are also
being implemented by means of MLCRM. Findings. Using
the example of the problem of optimal making-
and breaking-up of multi-group trains, a new
multilayer constructive model of optimal planning processes for
ordering sets of heterogeneous order sequences has been developed.
The article proposes a classification of features that determine
the types of mathematical models of ordering processes. Originality.
The article formulates a new scientific and applied problem for
the planning of service systems, for the first time, the
classification of signs of mathematical model classes of ordering
processes of order sequences with the weight of operations was
carried out. In the article, constructive-production models were
developed, which was done by creating multilayer and parallel
structural modeling structures for making- and breaking-up of trains.
Practical value. The practical value of the results is
determined by a wide range of possible applications of the proposed
task for the planning of service systems. The proposed multilayer
structural modeling structures allow improving the tools of
constructive modeling. The constructed model of the processes of
optimal making- and breaking-up of trains allows obtaining a new form
of implementation of these technological processes of railway
transport.
Keywords: constructive modeling;
multilayer models; parallel construction;
heterogeneous orders sequences; sequence
ordering; complexity of formation
operations; multi-group railway trains
REFERENCES
Bobrovsky,
V., Skovron, I., Dorosh, A., Demchenko, Ye., Malashkin,
V., & Bolvanovska, T. (2018).
Simulation Modeling of the Process of Disbanding Multigroup
Compositions on a Double-Sided Low Power Hump.
Transport System and Transportation
Technologies,
15, 19-26.
DOI: 10.15802/tstt2018/150194
(in Russian)
Kormen, T.,
Leyzerson, C. I., Rivest, R. L., & Shtayn, K. (2011). Algoritmy:
Postroenie i analiz. Moskow: Williams.
(in Russian)
Skalozub,
V. V.,
& Bilyy,
B. B.
(2019).
Structure of intelectual information
technology for formation of multi-group train.
Transport Systems and Transportation
Technologies, 17,
62-68. DOI: 10.15802/tstt2019/178217
(in Russian)
Holzhauser, M.,
Krumke, S. O., & Thielen, C. (2016). Maximum flows in
generalized processing networks. Journal
of Combinatorial Optimization, 33(4),
1226-1256. DOI: 10.1007/s10878-016-0031-y
(in English)
Kozachenko, D.,
Bobrovskiy, V., Gera, B., Skovron, I., & Gorbova, A. (2020). An
optimization method of the multi-group train formation at flat
yards. International Journal of Rail
Transportation, 1-18.
DOI: 10.1080/23248378.2020.1732235
(in English)
Kravchenko, G.
(2017). Modeling the External Structure of a Fractals. EIOP
Conference Series: Earth and Environmental Science,
90, 1-8.
DOI: 10.1088/1755-1315/90/1/012100
(in English)
Shang, Zh.
& Li, M. (2016, December).
Feature Selection Based on Grouped Sorting. 2016
9th International Symposium on Computational Intelligence and Design
(ISCID) (pp.
451-454).
Hangzhou, China DOI: 10.1109/ISCID.2016.1111
(in English)
Shynkarenko, V.
I., & Ilman, V. M. (2014). Constructive-Synthesizing
Structures and Their Grammatical Interpretations. i. Generalized
Formal Constructive-Synthesizing Structure. Cybernetics
and Systems Analysis, 50(5), 655-662.
DOI: 10.1007/s10559-014-9655-z
(in English)
Skalozub, V.,
Ilman, V., & Shynkarenko, V. (2018). Ontological
support formation for constructive-synthesizing modeling of
information systems development processes. Eastern-European
Journal of Enterprise Technologies, 5(4(95)),
55-63.
DOI: 10.15587/1729-4061.2018.143968
(in English)
Stuart, D. (2016).
Practical Ontologies for Information
Professionals. Language
Arts & Disciplines.
DOI: 10.29085/9781783301522
(in English)
Yadavalli, V. S.
S., & Balcou, C. (2017). A supply
chain management model to optimise the sorting capability of a
«third party logistics” distribution centre. South
African Journal of Business Management, 48(1),
77-84. DOI: 10.4102/sajbm.v48i1.22
(in English)
Zhukovyts’kyy,
I. (2018). Use of an automaton model for the designing of real-time
information systems in the railway stations. Transport
Problems, 12(4), 101-108.
DOI: 10.20858/tp.2017.12.4.10
(in English)
Надійшла
до редколегії: 03.03.2020
Прийнята
до друку: 04.08.2020
Creative
Commons Attribution 4.0 International
doi:
10.15802/stp2020/213232
©
В. В. Скалозуб, В. М. Ільман, Б. Б.
Білий, 2020
,
яка містить:
– неоднорідний носій,
– список відносин та відповідних
операцій,
– набір засобів інформаційного
забезпечення конструктивної побудови
(правила, обмеження, умови початку та
завершення побудови моделей, онтологію
тощо). Складові наборів КПМ визначають
на основі дослідження допустимих
операцій процесів УПСО.
операцій конструювання, а саме:
– шари оцінювання-перетворення даних;
L2 –
оцінювання станів процесу конструктивного
моделювання, відбір можливих операцій
або процедур перетворення структури
впорядкування;
– генерація (породження)
наступних локальних вузлів моделі;
–
формування моделей оцінювання локальних
або глобальних властивостей;
–
процедури оцінювання параметрів
моделей;
–
оптимізація процесу пошуку рішень.
Окремі шари
також можуть поєднувати кілька із
зазначених категорій операцій. Включення
до моделі MLCРМ шарових комплексів
операцій конструювання утворює системну
модель CMLSI. Реалізація моделей процесів
УПСО засобами багатошарової моделі
CMLSI для задач РФ составів представляє
зміст нашої статті.