ISSN 2307–3489 (Print), ІSSN 2307–6666 (Online)

Наука та прогрес транспорту. Вісник Дніпропетровського
національного університету залізничного транспорту, 2020, № 3 (87)

Вступ

Залізничний транспорт є найважливішою галуззю країни, що відіграє ключову роль у її успішному розвитку. У сучасних умовах нестабільної економічної ситуації та жорсткої конкуренції у сфері перевезень питання підвищення якості послуг, які надає залізничний транспорт, є вкрай важливим.

Залізничні станції є одним із головних елементів транспортної інфраструктури країни, тому в наш час актуальним завданням є вдосконалення роботи станцій за безумовного забезпечення безпеки руху. Під час вирішення цього завдання необхідно враховувати, що залізничні станції є складною системою і містять велику кількість взаємодіючих елементів, на функціонування яких впливає значна кількість випадкових факторів.

Ефективним інструментом аналізу складних систем будь-якої природи, зокрема технічних, є математичне моделювання, оскільки при цьому з’являється можливість експериментувати не з реальною системою, а з її моделлю, переносячи отримані розрахункові рішення на досліджуваний об’єкт.

Існують універсальні імітаційні системи, розраховані на застосування в багатьох галузях діяльності, а також спеціалізовані, що мають більші можливості для відображення, дозволяють швидше й точніше створювати моделі для конкретних об’єктів та отримувати на них кращий набір результатів.

Значне визнання та застосування отримала імітаційна система ІСТРА [1], яка дозволяє будувати моделі транспортних об’єктів практично будь-якого розміру і складності. Засобом опису модельованого об’єкта в системі є спеціалізована мова моделювання, яка за своєю структурою та можливостями дуже близька до деяких мов програмування. Тому для розробки імітаційної моделі будь-якої залізничної системи дослідник повинен мати певний досвід у комп’ютерному програмуванні.

За кордоном набула поширення універсальна система імітаційного моделювання Arena компанії «Systems Modeling», що дозволяє будувати імітаційні моделі, опробувати їх і проводити аналіз результатів їх роботи. Це найбільш проста універсальна система. В основу моделі покладена система масового обслуговування (СМО), реалізованого в динаміці; при цьому основним результатом моделювання є характеристика черг, що виникають у системі.

Іншою універсальною системою моделювання, яку використовують для побудови імітаційних моделей широкого класу систем, є візуальне об’єктно-орієнтоване середовище з доданим специфічним сервісом eM–Plant Simulation.

У цьому середовищі рухомі об’єкти моделі переміщаються по згенерованій структурі, утворюючи в окремі моменти часу події, які визначаються параметрами об’єктів. За результатами роботи моделі виконують аналіз статистики – продуктивність, час зайнятості обладнання, використання накопичувачів.

Математичний апарат СМО також покладений в основу більшості спеціалізованих закордонних систем моделювання.

Для оптимізації міських транспортних потоків розроблені інструменти PASSER, PROGO, TSDWIN. До числа широко апробованих в інших країнах світу програмних продуктів, призначених для транспортного моделювання, належать пакети Trans Cad, TRPS, CUBE, CATURU, AIMSUN2, DRACULA, VISSIM. Указані моделі в основному використовують для досліджень організації руху в містах, вони вимагають адаптації до моделювання процесів на залізничному транспорті. Існує також досвід створення спеціалізованих систем для моделювання залізничних станцій OpenTrack (Швейцарія) [14], Villon (Словаччина) [11, 12], AnyLogic [8].

Серед вітчизняних розробок слід відзначити спеціалізовану ергатичну систему імітаційного моделювання [2], яка на відміну від наявних систем, дозволяє враховувати вплив людського фактора на процес керування роботою залізничної станції.

Існують також і вузькоспеціалізовані імітаційні комплекси. Одним з них є комплекс для визначення раціональних параметрів сортувального процесу [9], який дозволяє виконувати моделювання процесу розформування составів на сортувальній гірці з урахуванням її конструкції та ефективного режиму роботи маневрового тепловоза.

Відомо, що спеціалізовані імітаційні системи вимагають специфічних знань з їх використання, у більшості випадків є платними або не досить відомими для широкого кола дослідників, що не дозволяє застосовувати ці програмні продукти для вирішення поставлених завдань. У цьому зв’язку більшого розповсюдження в наш час набули універсальні імітаційні системи попри необхідність певного їх доопрацювання й адаптації під конкретний процес.

До числа таких універсальних систем моделювання належить продукт QPNet [15], до основних переваг якого, порівняно з подібними програмними комплексами, можна віднести високу продуктивність, наявність вбудованого редактора технологічного процесу, вільний доступ та її подальший розвиток, тобто система продовжує еволюціонувати.

Процес обслуговування об’єктів у транспортній системі в середовищі QPNet представлений мережею Петрі [16] – послідовністю позицій (станів) і переходів. При цьому переходи імітують обробку об’єктів протягом заданого часу, а позиції характеризують поточний стан системи й визначають умови переходів. Під час виконання умов перехід спрацьовує, у результаті чого змінюється поточне розмічання мережі.

У [5] розглянуто можливості використання апарату мереж Петрі для формалізації технології формування залізничних ступінчастих маршрутів із зерновими вантажами. Для моделювання залізничних технологічних процесів перевезень у моделі застосовано гібридні мережі Петрі із синтез-дугами з динамічними вагами. У цій роботі обґрунтовано надання якісних послуг залізничним перевізником в умовах дефіциту зерновозів та тягового рухомого складу за рахунок скорочення загального часу прямування зернових вантажів.

У [13] автори представили практичне застосування моделі функціонування станції на базі мереж Петрі для визначення затримок.

У роботах [6, 10] за допомогою імітаційного моделювання із застосуванням математичного апарату мереж Петрі автори спробували вирішити завдання підвищення ефективності сортувального процесу на сортувальній станції.

Також мережі Петрі використовують і для оптимізації роботи декількох залізничних станцій різного типу. Так, автори роботи [7] розробили імітаційну модель процесу взаємодії сортувальної та припортової станцій із метою пошуку раціональної технології обслуговування експортних вагонопотоків.

Мета

Незважаючи на значну наукову та практичну значимість проблеми вдосконалення роботи залізничних станцій, характер і ступінь впливу розмірів вагонопотоків на ємність колійного розвитку та взаємне розташування основних пристроїв на залізничних станціях із позиції системного підходу вивчені недостатньо. Відсутність універсальної методики виявлення ефективних технічних і технологічних параметрів залізничних станцій визначило мету цього дослідження, яка полягає у встановленні раціональних параметрів залізничної станції на основі імітаційного моделювання її процесу функціонування, що представлений мережею Петрі в середовищі QPNet на основі запропонованої методики техніко-економічного порівняння варіантів.

Методика

Сортувальний комплекс (СК) являє собою одну з головних підсистем залізничної станції, що забезпечує переробку вагонопотоків. До складу СК належать: парк прибуття (П), колії насуву, сортувальна гірка (СГ) та голова сортувального парку. Поїзди в розформування приймають у парк П, після чого на станції виконують ряд технологічних операцій із підготовки составів до розпуску на сортувальній гірці. Однією з основних операцій при цьому є технічне обслуговування (ТО), яке проводить бригада ПТО на коліях парку П. Тривалість ТО є випадковою величиною, яка, з одного боку, залежить від кількості оглядачів у бригаді ПТО та параметрів составів, а з іншої – суттєво впливає на показники функціонування сортувального комплексу та пов’язані з ними експлуатаційні витрати. У цьому зв’язку виникає оптимізаційна задача визначення раціональної кількості оглядачів у бригаді ПТО, за якої б забезпечувався мінімум експлуатаційних витрат. Для розв’язання вказаної задачі СК доцільно розглядати як СМО з випадковим вхідним потоком та випадковою тривалістю обслуговування; при цьому основними показниками функціонування такої системи є:

– кількість вимог в окремий момент часу у стані очікування обслуговування (у черзі) n_ч, у стані обслуговування n_обс, загалом у системі n_с;

– тривалість знаходження окремої вимоги у стані очікування t_оч, під обслуговуванням t_обс, у цілому в системі t_с.

Відомо, що для СМО з найпростішим вхідним потоком і показниковим законом розподілу тривалості обслуговування існують аналітичні вирази для визначення наведених показників [4]. У той же час визначення показників функціонування реальних транспортних об’єктів, як правило, здійснюється шляхом імітаційного моделювання їх роботи. Це пов’язано зі складністю технологічних процесів транспортних об’єктів та їх стохастичним характером.

Технологічний процес функціонування сортувального комплексу формалізується за допомогою мережі Петрі в програмному середовищі QPNet (рис. 1), яке дозволяє будувати мережі Петрі та змінювати параметри їх елементів в інтерактивному режимі, досліджувати функціонування дискретних моделей різної складності, накопичувати та зберігати результати моделювання у файлі, формат якого підтримується програмою для роботи з електронними таблицями MS Excel.

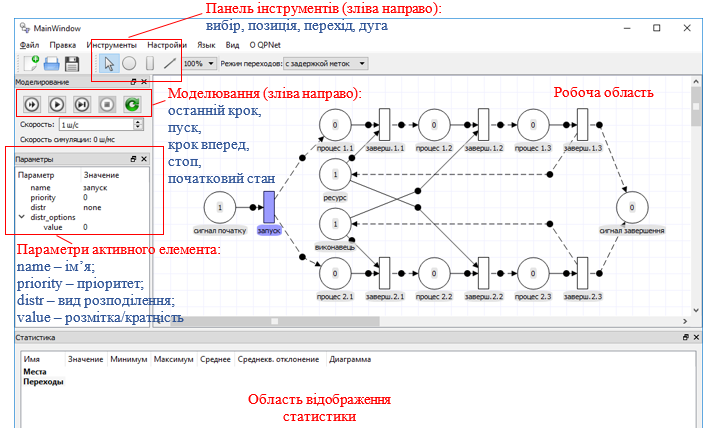
Рис. 1. Головне вікно системи імітаційного
моделювання QPNet

Fig. 1. The main window of the QPNet
simulation system

Технологічний процес функціонування СК у вигляді часової мережі Петрі представлений на рис. 2. Він складається з таких елементів:

1. позицій, за допомогою яких ведуть облік кількості:

– підхід поїздів – поїздів, що прибудуть на СК;

– очік. ТО – составів в черзі на технічне обслуговування;

– очік. розф. – составів в черзі на розформування на СГ;

– парк прибуття – составів в парку П;

– розформовано составів – розформованих составів за період моделювання;

– вимоги на осаджування – розформованих составів в поточному гірковому циклі.

Крім цього, позиції використовують для контролю зайнятості виконавців:

– бригада ПТО – оглядачів бригади ПТО;

– ман. лок. – гіркового локомотиву.

2. переходів, за допомогою яких виконують моделювання технологічних операцій сортувального комплексу:

– прибуття поїзда – прийом поїздів на СК з інтервалом I;

– ТО – технічне обслуговування состава на коліях парку П з тривалістю t_обс;

– розф. – розформування состава на сортувальній гірці з тривалістю t_р;

– осадж. – осаджування вагонів на коліях сортувального парку з тривалістю t_ос.

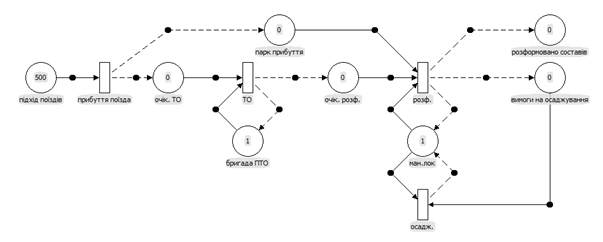
Рис. 2. Модель процесу функціонування сортувального комплексу у вигляді мережі Петрі

Fig. 2. Model of the process of sorting complex functioning in the form of Petri net

Розглянемо алгоритм функціонування розробленої моделі СК. Позиція «підхід поїздів» є джерелом надходження вимог у систему; при цьому моделювання відбувається до моменту досягнення заданої кількості вимог, які повинні бути обслуговані системою, що відповідає кількості міток в даній позиції.

Позиція «підхід поїздів» сполучається з переходом «прибуття поїзда» дугою з кратністю 1, тому цей перехід спрацьовує в разі наявності в попередній позиції хоча б одної мітки. Система QPNet дозволяє реалізувати часову затримку спрацювання переходу; при цьому можливо задати як детерміновану, так і випадкову тривалість затримки, розподілену за нормальним, експоненціальним або рівномірним законами (рис. 3).

Таким чином, на черговому кроці моделювання за наявності міток у позиції «підхід поїздів» спрацьовує перехід «прибуття поїзда», який забирає із вказаної позиції одну мітку. Ця мітка затримується в зазначеному переході на задану кількість кроків; при цьому перехід припиняє відбір нових міток на час затримки в ньому чергової мітки. Після вичерпання тривалості затримки перехід віддає мітки в кожну вихідну дугу відповідно до їх кратності. Так, перехід «прибуття поїзда» сполучається з позиціями «очікування ТО» та «парк прибуття» дугами з кратністю 1, тому після спрацювання цього переходу у вказані позиції буде додано по одній мітці. Ці позиції реалізують функцію лічильника кількості вимог у черзі на ТО та в парку П відповідно.

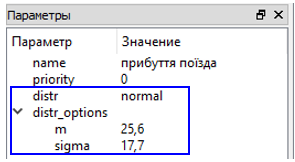
Рис. 3. Вікно вибору параметрів затримки
спрацьовування переходу

Fig. 3. The window for selecting the parameters of the transition response delay

Перехід «ТО» імітує процес технічного обслуговування состава та має 2 вхідні позиції: «очікування ТО» та «бригада ПТО», які сполучаються з цим переходом дугами з кратністю 1. Тому перехід «ТО» спрацює тільки в тому випадку, коли в обох вхідних позиціях буде мінімум по одній мітці – технічне обслуговування розпочнеться тільки тоді, коли в черзі на обслуговування є хоча б один состав та наявна вільна бригада ПТО. За виконання цієї умови перехід «ТО» забирає з його вхідних позицій по одній мітці та затримує їх проходження аналогічно до переходу «прибуття поїзда». Після спрацювання перехід «ТО» віддає по одній мітці у вихідні позиції-лічильники «бригада ПТО» та «очікування розформування», які обліковують кількість відповідно вільних бригад ПТО та готових до розформування составів.

Перехід «розформування» імітує розформування составів на СГ та має 3 вхідні позиції: «парк прибуття», «очікування розформування» та «маневровий локомотив», які сполучаються з цим переходом дугами з кратністю 1. Відповідно цей перехід спрацює лише у випадку наявності мінімум по 1 мітці в кожній вхідній позиції – розформування почнеться в разі наявності готового состава та вільного гіркового локомотива.

Відомо, що гірковий локомотив може виконувати як насув та розпуск составів, так і проводити осаджування вагонів на сортувальних коліях. У дослідженні взято, що локомотив відволікається на осаджування після розформування N_ц составів. Із цією метою в позиції «вимоги до осаджування» ведеться облік кількості составів, розформованих у поточному гірковому циклі. Ця позиція сполучається з переходом «осаджування» дугою, кратність якої дорівнює N_ц. Перехід «осаджування» імітує процес осаджування вагонів на сортувальних коліях та має пріоритет спрацювання перед іншими переходами (рис. 4).

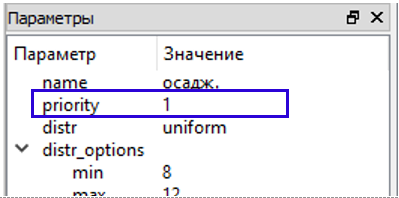
Рис. 4. Вікно для встановлення пріоритету
спрацювання переходу

Fig. 4. Window for setting the priority of the transition

Таким чином, у разі звільнення маневрового локомотива, за наявності в позиції «вимоги до осаджування» N_ц міток, спрацює пріоритетний перехід «осаджування», який забере N_ц міток із позиції «вимоги до осаджування», скидаючи до нуля лічильник розформованих у циклі составів, та одну мітку з позиції «маневровий локомотив», імітуючи відволікання маневрового локомотива на осаджування. При цьому перехід «розформування» буде заблоковано до моменту завершення затримки спрацювання переходу «осаджування» та подальшого за цим повернення мітки в позицію «маневровий локомотив».

Якщо міток у позиціях мережі недостатньо для спрацювання жодного переходу, моделювання припиняється. Після закінчення моделювання програмне середовище QPNet дозволяє зберегти динаміку зміни кількості міток у кожній позиції у вигляді набору кортежів (крок моделювання; нове значення кількості міток), на основі аналізу яких може бути визначена середня тривалість знаходження вимог T_п у парку П.

Слід відзначити, що QPNet має зручний візуальний інструментарій для статистичного аналізу. Використання вказаного інструментарію дозволяє на основі інтегральної функції розподілу випадкової величини кількості вимог у системі (позиція «парк прибуття») визначити потрібну кількість колій Z в парку П із заданою надійністю  (рис. 5).

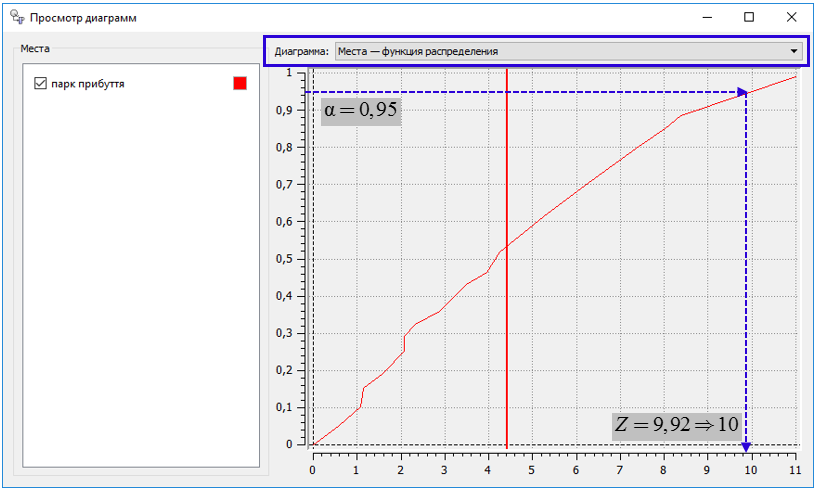
Рис. 5. Вікно з функцією розподілу випадкової
величини кількості вимог у системі й потрібною кількістю приймальних колій

Fig. 5. Window with the distribution function of the random variable of the number of requirements in the system and the required number of receiving tracks

Вибір ефективного варіанта оснащення СК може бути здійснений за мінімальною величиною модифікованих зведених витрат (МЗВ), які визначають на основі отриманих результатів моделювання за формулою [3]:

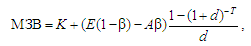(1)

де K – капітальні вкладення в оснащення СК, тис. грн; E – щорічні експлуатаційні витрати без урахування амортизаційних відрахувань, тис. грн; A – амортизаційні відрахування, тис. грн;  – норма податку на прибуток; d – мінімальна необхідна норма доходу на капітал; T – тривалість життєвого циклу проєкту, років.

Спрощено приймемо, що з постійних пристроїв СК за варіантами буде змінюватись лише кількість приймальних колій. Тоді капітальні вкладення можуть бути визначені так:

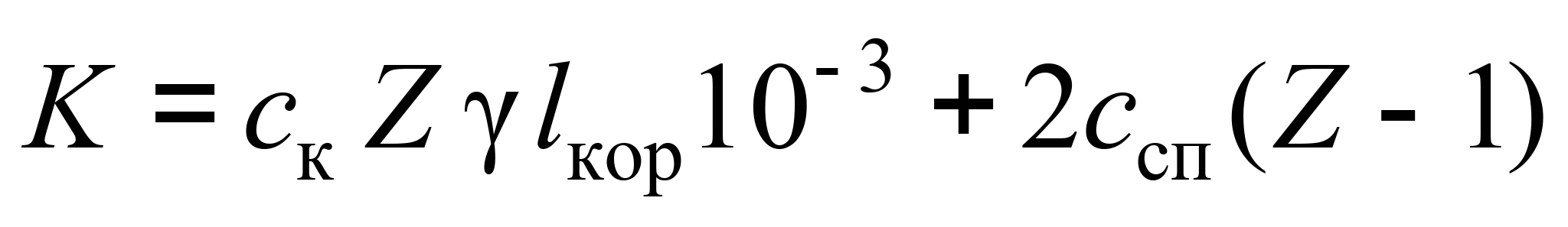, (2)

де Z – кількість колій у парку П;  – коефіцієнт, який показує відношення повної довжини колії до корисної; l_кор – корисна довжина колії в парку прибуття, м; c_к – вартість будівництва 1 км колії, тис. грн; c_сп – вартість укладання стрілочного переводу, тис. грн.

Амортизаційні відрахування визначають прямолінійним методом за формулою:

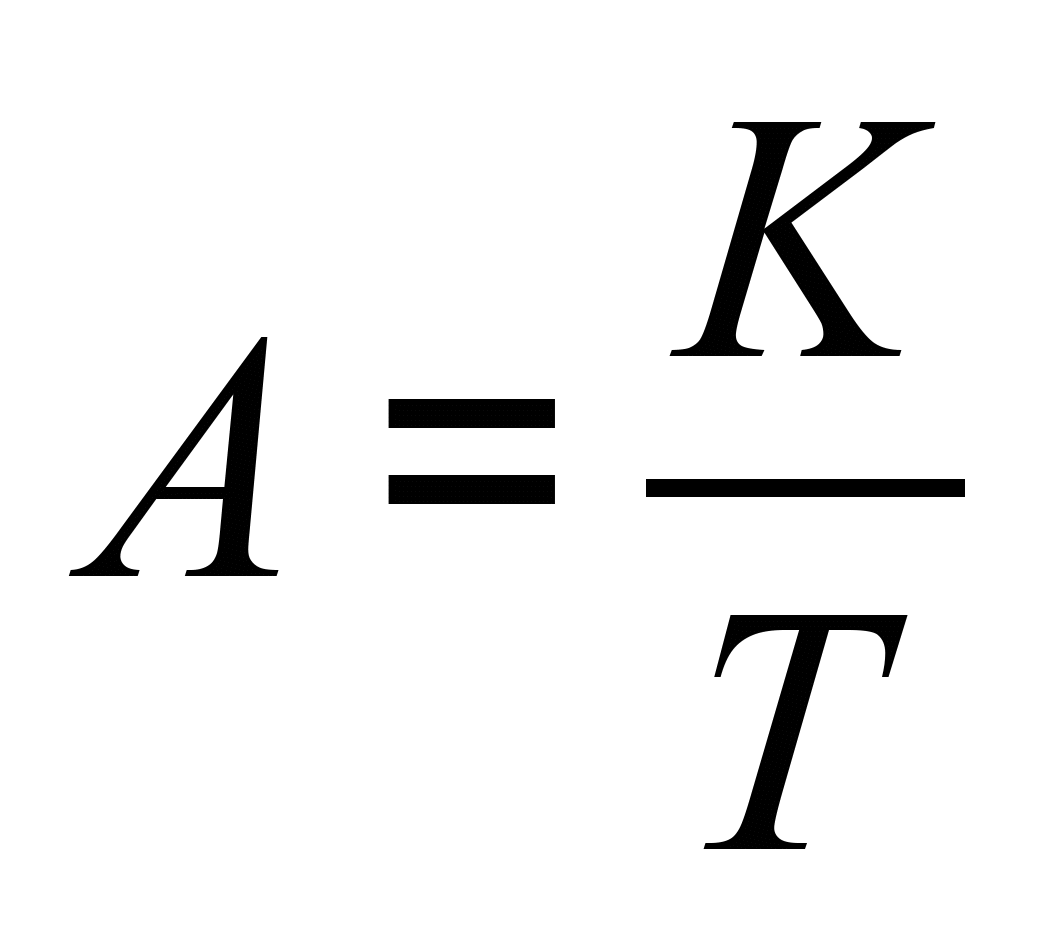. (3)

Щорічні експлуатаційні витрати визначають за формулою:

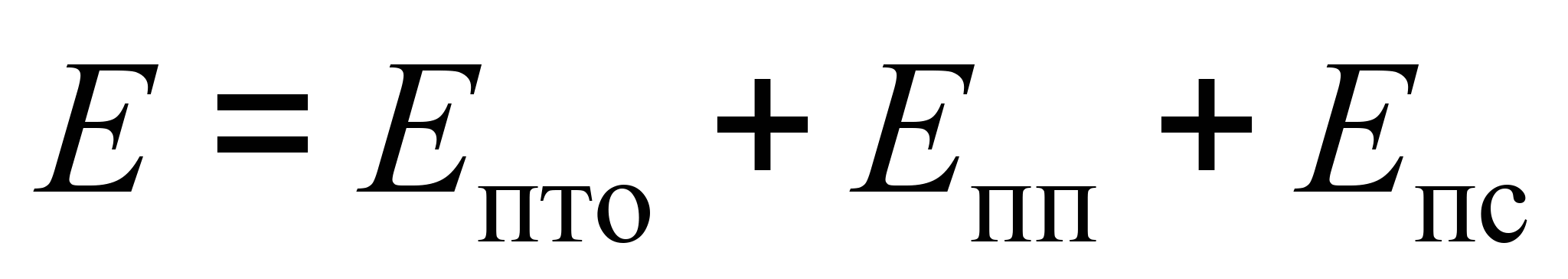, (4)

де E_пто – витрати на утримання бригади ПТО;
E_пп – витрати на утримання колій у парку прибуття; E_пс – витрати, пов’язані з тривалістю перебування составів на СК. Складові частини формули (4) можна знайти так:

– витрати, пов’язані з утриманням бригади ПТО:

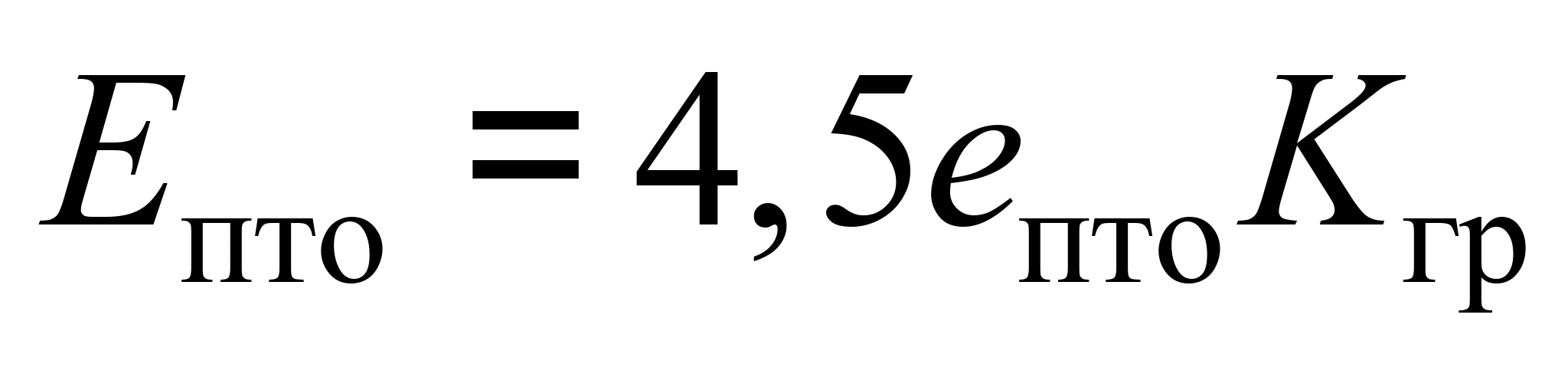, (5)

де e_пто – витрати на утримання однієї групи в бригаді ПТО, тис. грн; K_гр – кількість груп у бригаді ПТО;

– витрати, пов’язані з утриманням колій та стрілочних переводів парку П:

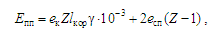(6)

де e_к – витрати на утримання 1 км станційних колій, тис. грн; e_сп – витрати на утримання одного стрілочного переводу, тис. грн;

– витрати, пов’язані з тривалістю перебування составів на СК:

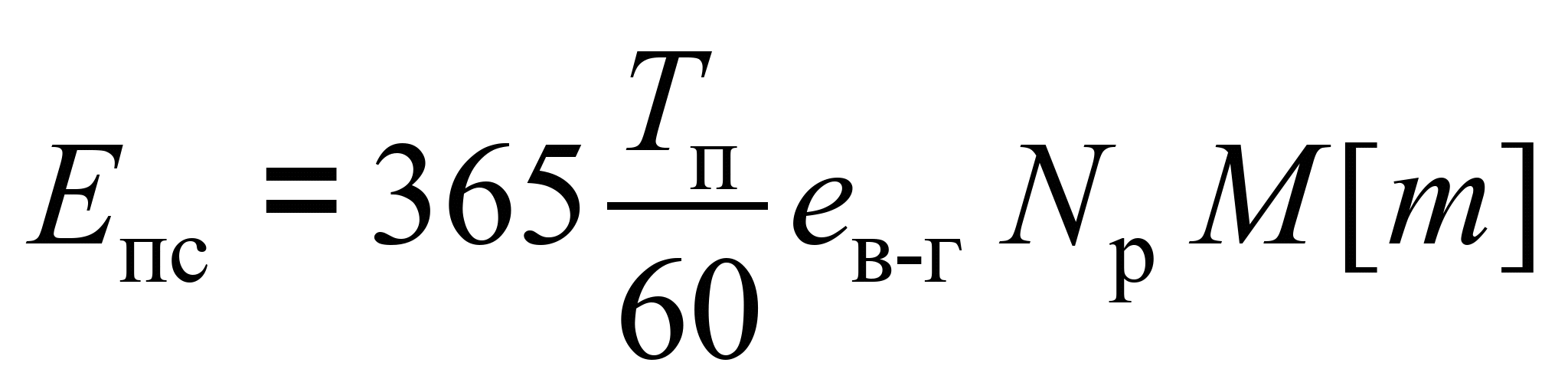, (7)

де T_п – середня тривалість перебування составів у парку П, хв; e_в-г – вартість однієї вагоно-години простою на станції, грн; N_р – кількість поїздів, які прибувають за добу, яку визначають так:

, (8)

де M[I] – середній інтервал прибуття поїздів, хв; M[m] – середня кількість вагонів у складі поїзда, ваг.

Результати

Із використанням розробленої моделі в роботі виконано дослідження впливу інтенсивності вхідного потоку поїздів  на показники функціонування сортувального комплексу. Під час моделювання було взято такі вихідні дані:

– інтервал прибуття поїздів – випадковий, розподілений за експоненціальним законом; величина M[I] варіювалась у межах від 20 до 80 хв;

– тривалість t_то технічного обслуговування – випадкова, розподілена за нормальним законом із параметрами: середнє значення M[t_то] = {27,0; 18,7; 14,5} хв, відповідно для K_гр = {2; 3; 4} груп; коефіцієнт варіації тривалості обслуговування v[t_то] = 0,2;

– тривалість розформування состава t_р на сортувальній гірці – випадкова, розподілена за рівномірним законом у межах M[t_р]  [18…22] хв;

– тривалість t_ос осаджування вагонів на сортувальних коліях – випадкова, розподілена за рівномірним законом у межах M[t_р]  [9…13] хв; при цьому осаджування виконується після розформування трьох составів, тобто N_ц = 3.

Результати моделювання обслуговування на СК потоку з 500 поїздів представлені в табл. 1; при цьому потрібна кількість приймальних колій Z визначена для рівня надійності  = 0,95.

Таблиця 1

Результати моделювання функціонування СК

Table 1

The results of modeling the functioning
of the sorting complex

M[I]	Kгр = 2 групи		Kгр = 3 групи		Kгр = 4 групи
		Z, кол.	Tп, хв	Z, кол.	Tп, хв	Z, кол.	Tп, хв
20	114	1654,44	104	1543,61	85	908,14
25	44	781,58	29	370,44	22	197,12
28	25	302,93	18	142,09	10	81,85
30	15	183,96	13	99,01	9	64,19
40	7	55,82	5	39,45	5	36,42
50	5	43,88	4	31,47	4	26,65
60	4	39,95	3	28,05	3	24,42
70	4	39,29	3	25,27	3	22,28
80	3	35,40	3	24,07	3	21,20

Як видно з таблиці, за значної нерівномірності прибуття поїздів, якою характеризується взятий випадковий вхідний потік вимог, розподілений за експоненціальним законом, зі скороченням інтервалу прибуття M[I] у межах від 30 до 20 хв спостерігається інтенсивне зростання потрібної кількості колій Z. Це пояснюється значним рівнем завантаження бригади ПТО та пов’язаним із цим зростанням черги составів Q (рис. 6).

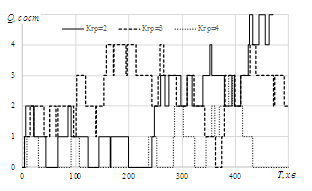
Рис. 6. Динаміка зміни черги составів у парку

Fig. 6. Dynamics of changing the train queue in the yard

Для економічного обґрунтування ефективного варіанта оснащення СК взято такі вихідні дані: T = 10 років;  = 0,18; d = 0,15;  = 1,1; c_к = 2 000,0 тис. грн; c_сп = 300,0 тис. грн.; e_к = 250,0 тис. грн; e_сп = 30,0 тис. грн; e_в-г = 3,0 грн.; l_кор = 850 м; M[m] = 50,0 ваг.

Значення величини МЗВ за варіантами оснащення сортувального комплексу представлено на рис. 7.

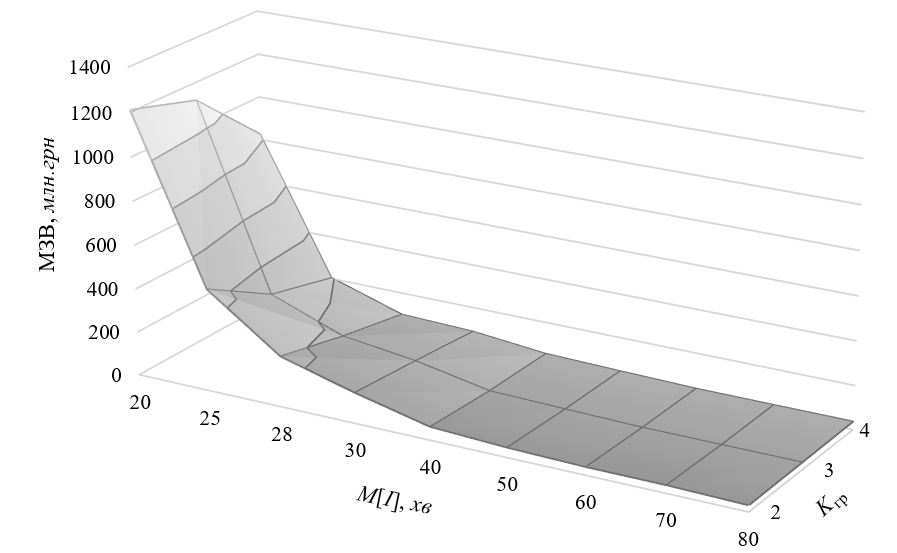
Рис. 7. Модифіковані зведені витрати
за варіантами оснащення сортувального комплексу

Fig. 7. Modified summarized costs according
to the variants for equipping the sorting complex

За розрахованою величиною МЗВ можна визначити граничні значення інтенсивності вхідного потоку поїздів , за яких кожен із розглянутих варіантів оснащення СК є ефективним (рис. 8).

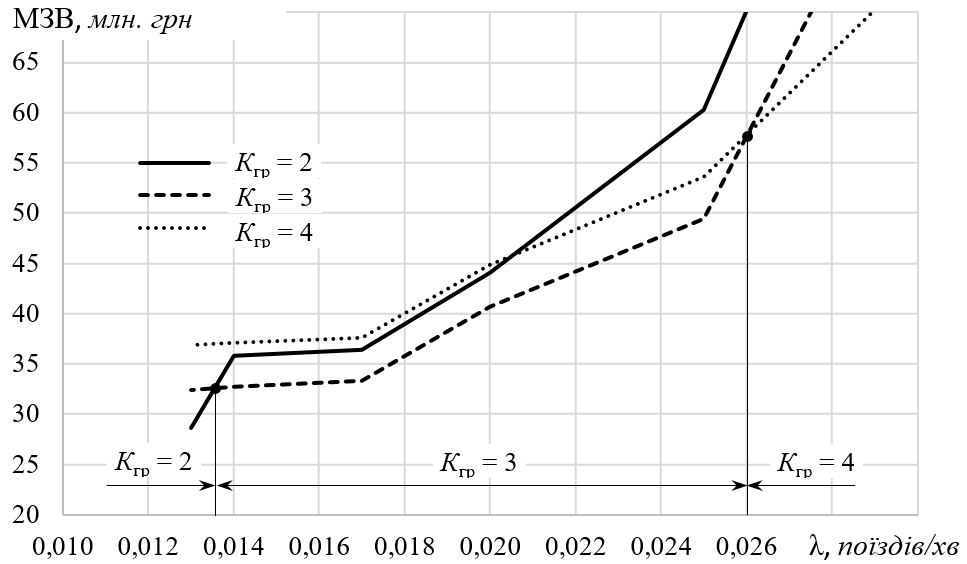
Рис. 8. Ефективність варіантів оснащення СК

Fig. 8. The efficiency of the variants for equipping the sorting complex

Відповідно до графіку на рис. 8 установлено, що за вхідного потоку до 1 поїзда/год технічний огляд доцільно виконувати двома групами у бригаді ПТО, а понад 2 поїзди/год – чотирма групами у бригаді ПТО. У випадку, коли вхідний потік коливається в межах 1–2 поїзди/год, раціонально утримувати у бригаді ПТО три групи.

Наукова новизна та практична
значимість

Наукова новизна полягає в удосконаленні імітаційної моделі сортувального комплексу, процес функціонування якого представлений часовою мережею Петрі, що, на відміну від інших моделей, дозволяє враховувати додатковий час зайнятості гіркового локомотива іншими операціями, не пов’язаними з розформуванням составів на сортувальній гірці безпосередньо.

Практична значимість представленої у роботі вдосконаленої імітаційної моделі сортувального комплексу полягає в можливості більш точно враховувати вплив технічного оснащення залізничної станції на показники її функціонування.

Висновки

Виконані в роботі аналіз та дослідження дозволили сформулювати такі висновки.

1. Для визначення достовірних показників функціонування будь-яких транспортних систем доцільно використовувати методи імітаційного моделювання.

2. Серед різноманіття імітаційних систем найбільш популярними є універсальні системи, які, на відміну від спеціалізованих, доступні більш широкому колу попри вимогу певного їх доопрацювання й адаптації під конкретний процес.

3. Запропоновані вдосконалення до часової мережі Петрі, за допомогою якої формалізовано процес функціонування сортувального комплексу, дозволять більш точно враховувати вплив технічного оснащення залізничної станції на показники її функціонування.

4. Розглянуто методику техніко-економічного обґрунтування варіантів оснащення сортувального комплексу.

5. Визначено ефективні техніко-технологічні параметри сортувального комплексу в різних експлуатаційних умовах роботи.

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1. Александров А. Э. Расчет и оптимизация транспортных систем с использованием моделей (теоретические основы, методология) : дис. … д-ра тех. наук : 05.22.08. Екатеринбург, 2008. 232 с.

2. Бобровский В. И., Козаченко Д. Н, Вернигора Р. В., Малашкин В. В. Функциональное моделирование работы железнодорожных станций : монография. Днепропетровск : ДНУЖТ, 2015. 269 с.

3. Виленский П. Л., Лившиц В. Н., Смоляк С. А. Оценка эффективности инвестиционных проектов. Теория и практика. Москва : Дело, 2004. 888 с.

4. Илесалиев Д. И., Абдувахитов, Ш. Р. Исследования функционирования контейнерного терминала. Транспорт : Наука, Техника, Управление. 2019. № 11. С. 59–62. DOI: 10.36535/0236-1914-2019-11-11

5. Ломотько Д. В., Арсененко Д. В. Створення ефективної технології формування залізничних маршрутів із зерновими вантажами за допомогою моделей на мережі Петрі. ІКСЗТ. 2018. № 6. С. 38–45. DOI: 10.18664/ikszt.voi6.151642

6. Шаповал Г. В., Шелехань Г. І., Занік І. В. Дослідження впливу поїздоутворення на ефективність сортувального процесу. Збірник наукових праць УкрДУЗТ. 2016. № 166. С. 68–78. DOI: 10.18664/1994-7852.166.2016.92849

7. Шелехань А. І., Продащук М. В. Удосконалення процесу взаємодії сортувальної та припортової станцій при обслуговуванні експортних вагонопотоків. Збірник наукових праць УкрДУЗТ. 2017. № 168. С. 10–18. DOI: 10.18664/1994-7852.168.2017.101565

8. AnyLogic. Железнодорожные перевозки. URL: https://www.anylogic.ru/rail-logistics/ (дата звернення 05.05.2020).

9. Demchenko E. B. Complex simulation model of train breaking-up process at the humps. Наука та прогрес транспорту. 2015. № 6 (60). P. 25–34. DOI: 10.15802/stp2015/57003

10. Dorda M., Teichmann D. Modelling of Freight Trains Classification Using Queueing System Subject to Breakdowns. Mathematical Problems in Engineering, 2013. Vol. 2013. P. 1–11. DOI: 10.1155/2013/307652

11. Lu Q., Dessouky M., Leachman R. C. Modeling Train Movements through Complex Rail Networks. ACM Transactions on Modeling and Computer Simulation (TOMACS). 2004. Vol. 14. Iss. 1. P. 48–75. DOI: 10.1145/974734.974737

12. Márton P., Žarnay M., Wenjian L. Development of computer simulation model of mudanjiang railway junction and its results. URL: http://frdsa.fri.uniza.sk/~zarnay/publications/SimulationTranspSystems/MartonZarnayLi-Zel2003.pdf (дата звернення 05.05.2020).

13. Milinkovic S., Markovic M., Veskovic S., Ivic M., Pavlovic N. A fuzzy Petri net model to estimate train delays. Simulation Modelling Practice and Theory. 2013. Vol. 33. Р. 144–157. DOI: 10.1016/j.simpat.2012.12.005

14. OpenTrack. Моделирование железнодорожных сетей. URL: http://www.opentrack.ch/opentrack/downloads/OpenTrack.Info_RU.pdf (дата звернення 05.05.2020).

15. Sourceforge. QPNet – Synchronous Petri Nets' emulator. URL: https://sourceforge.net/projects/qpnet/ (дата звернення 05.05.2020).

16. Zaitsev D. A. Petri Nets for Modeling and Computing. 2016. DOI: 10.4018/978-1-4666-9594-8

Е. Б. ДЕМЧЕНКО^1*, В. В. МАЛАШКИН^2*, И. Я. СКОВРОН^3*

^1*Каф. «Транспортные узлы», Днипровский национальный университет железнодорожного транспорта имени академика В. Лазаряна, ул. Лазаряна, 2, Днипро, Украина, 49010, тел. +38 (097) 799 16 75, эл. почта e.b.dmch@gmail.com, ORCID 0000-0003-1411-6744
^2*Каф. «Транспортные узлы», Днипровский национальный университет железнодорожного транспорта имени академика В. Лазаряна, ул. Лазаряна, 2, Днипро, Украина, 49010, тел. +38 (056) 793 19 13, эл. почта viacheslav.malashkin@gmail.com, ORCID 0000-0002-5650-1571
^3*Каф. «Транспортные узлы», Днипровский национальный университет железнодорожного транспорта имени академика В. Лазаряна, ул. Лазаряна, 2, Днипро, Украина, 49010, тел. +38 (095) 230 50 34, эл. почта norvoks@gmail.com, ORCID 0000-0003-0697-2698

ИССЛЕДОВАНИЕ ПАРАМЕТРОВ ЖЕЛЕЗНОДОРОЖНЫХ

СТАНЦИЙ С ИСПОЛЬЗОВАНИЕМ СЕТЕЙ ПЕТРИ

Цель. Эта работа заключается в определении рациональных параметров железнодорожной станции на основе имитационного моделирования её процесса функционирования, представленной сетью Петри в среде QPNet на основе предложенной методики технико-экономического сравнения вариантов. Методика. Авторы представили методику формализации процесса функционирования сортировочного комплекса с помощью сети Петри в среде QPNet. Особое внимание уделено формализации работы горочного локомотива. Разработана методика технико-экономического сравнения вариантов оснащения сортировочного комплекса, в основе которой лежит использование модифицированных приведенных расходов. Результаты. Авторы выполнили обзор существующих систем имитационного моделирования, которые бывают специализированными и универсальными. Специализированные имеют больше возможности для отображения, позволяют быстрее и точнее создавать модели для конкретных объектов, а также получать с их помощью лучший набор результатов. Вместе с тем большее признание получили именно универсальные системы, не взирая на требование определённой их доработки и адаптации под конкретный процесс, поскольку специализированные имитационные системы являются платными или недостаточно известными, что не позволяет широкому кругу исследователей использовать их для решения поставленных задач. В статье приведены результаты работы сортировочного комплекса при различном оснащении, установленные при моделировании его работы в среде QPNet. Полученные значения технико-технологических параметров сортировочного комплекса стали основой для определения рациональных мероприятий, направленных на повышение эффективности функционирования сортировочной станции в различных эксплуатационных условиях её работы. Научная новизна. Усовершенствовано имитационную модель сортировочного комплекса, процесс функционирования которого представлен временной сетью Петри, что, в отличие от других моделей, позволяет учитывать дополнительное время занятости горочного локомотива другими операциями, не связанными непосредственно с расформированием составов на сортировочной горке. Практическая значимость. Представленная в работе усовершенствованная имитационная модель сортировочного комплекса дает возможности более точно учитывать влияние технического оснащения железнодорожной станции на показатели её функционирования.

Ключевые слова: железнодорожная станция; имитационное моделирование; сеть Петри; оснащение станции; среда QPNet

Y. B. DEMCHENKO^1*, V. V. MALASHKIN^2*, I. Y. SKOVRON^3*

^1*Dep. «Stations and Junctions», Dnipro National University of Railway Transport named after Academician V. Lazaryan, Lazaryana St., 2, Dnipro, Ukraine, 49010, tel. +38 (097) 799 16 75, e-mail e.b.dmch@gmail.com, ORCID 0000-0003-1411-6744
^2*Dep. «Stations and Junctions», Dnipro National University of Railway Transport named after Academician V. Lazaryan, Lazaryana St., 2, Dnipro, Ukraine, 49010, tel. +38 (056) 793 19 13, e-mail viacheslav.malashkin@gmail.com, ORCID 0000-0002-5650-1571
^3*Dep. «Stations and Junctions», Dnipro National University of Railway Transport named after Academician V. Lazaryan, Lazaryana St., 2, Dnipro, Ukraine, 49010, tel. +38 (095) 230 50 34, e-mail norvoks@gmail.com, ORCID 0000-0003-0697-2698

INVESTIGATION OF THE PARAMETERS

OF RAILWAY STATIONS USING PETRI NETS

Purpose. The work is aimed to determine the rational parameters of a railway station based on the simulation modeling of its functioning process, presented by the Petri net in QPNet using the proposed methodology of technical and economic comparison of equipment options. Methodology. The authors presented a methodology for formalizing the functioning of the sorting complex using a Petri net in QPNet. Particular attention is paid to the formalization of the operation of the hump locomotive. Methodology of technical and economic comparison of equipment options for the sorting complex was developed. It is based on the use of modified summarized costs. Findings. The authors performed a review of existing simulation systems, which can be specialized and universal. Specialized ones have richer display capabilities, allow you to create models for specific objects faster and more accurately, and as a result you can get the best set of results with their help. At the same time, the universal systems gained greater recognition, despite the requirement of some refinement and adaptation to a specific process, since specialized simulation systems are paid or insufficiently advertised, which does not allow a wide circle of researchers to use them to solve the set tasks. The paper presents the operation results of sorting complex with various equipment, obtained by simulation in the QPNet. The obtained values of the technical and technological parameters of the sorting complex became the basis for determining rational measures aimed at improving the efficiency of the sorting station in various operating conditions. Originality lies in improving the simulation model of the sorting complex which functioning is represented by the temporary Petri net. This, unlike other models, allows you to take into account the additional time of hump locomotive occupation by other operations not directly related with trains breaking-up. Practical value of the improved simulation model of the sorting complex presented in the work lies in the ability to more accurately take into account the influence of the technical equipment parameters of the railway station on its performance.

Keywords: railway station; simulation modeling; Petri net; station equipment; QPNet

REFERENCES

1. Aleksandrov, A. E. (2008). Raschet i optimizatsiya transportnykh sistem s ispolzovaniem modeley (teoreticheskie osnovy, metodologiya). (Doctoral dissertation). Ekaterinburg. (in Russian)

2. Bobrovskiy, V. I., Kozachenko, D. N., Vernigora, R. V., & Malashkin, V. V. (2015). Functional modeling of the work of railway stations: monografiya. Dnipropetrovsk National University of Railway Transport named after Academician V. Lazaryan. (in Russian)

3. Vilenskiy, P. L., Livshits, V. N., & Smolyak, S. A. Otsenka effektivnosti investitsionnykh proektov. Teoriya i praktika. Moscow: Delo. (in Russian)

4. Ilesaliev, D. I., & Abduvahitov, Sh. R. (2019). Research functioning container terminal. Transport : science, equipment, management, 11, 59-62. DOI: 10.36535/0236-1914-2019-11-11 (in Russian)

5. Lomotko, D. V., & Arsenenko, D. V. (2018). Creating an effective technology for the formation railway routes with grain cargoes using models on the Petri net. Information and Control Systems on Railway Transport, 6, 38-45. DOI: 10.18664/ikszt.v0i6.151642 (in Ukrainian)

6. Shapoval, G. V., Shelekhan, G. I., & Zanik, I. V. (2016). Research of the train formation influence on the sorting process efficiency. Collection of Scientific Works of the Ukrainian State University of Railway Transport, 166, 68-78. DOI: 10.18664/1994-7852.166.2016.92849 (in Ukrainian)

7. Shelekhan, A. I., & Prodaschuk, M. V. (2017). Improvement of the interaction process of marshalling yards and portside stations at the service of exporting traffic volumes. Collection of Scientific Works of the Ukrainian State University of Railway Transport, 168, 10-18. DOI: 10.18664/1994-7852.168.2017.101565 (in Ukrainian)

8. AnyLogic. Rail simulation software. Retrieved from https://www.anylogic.ru/rail-logistics (in Russian)

9. Demchenko, E. B. (2015). Complex simulation model of train breaking-up process at the humps. Science and Transport Progress, 6(60), 25-34. DOI: 10.15802/stp2015/57003 (in English)

10. Dorda, M., & Teichmann, D. (2013). Modelling of Freight Trains Classification Using Queueing System Subject to Breakdowns. Mathematical Problems in Engineering, 2013, 1-11. DOI: 10.1155/2013/307652 (in English)

11. Lu, Q., Dessouky, M., & Leachman, R. C. (2004). Modeling train movements through complex rail networks. ACM Transactions on Modeling and Computer Simulation (TOMACS), 14(1), 48-75. DOI: 10.1145/974734.974737 (in English)

12. Márton, P., Žarnay, M., & Wenjian, L. (2014). Development of computer simulation model of Mudanjiang rail-way junction and its results. Retrieved from http://frdsa.fri.uniza.sk/~zarnay/publications/SimulationTranspSystems/MartonZarnayLi-Zel2003.pdf (in English)

13. Milinković, S., Marković, M., Vesković, S., Ivić, M., & Pavlović, N. (2013). A fuzzy Petri net model to estimate train delays. Simulation Modelling Practice and Theory, 33, 144-157. DOI: 10.1016/j.simpat.2012.12.005 (in English)

14. OpenTrack. Modelirovanie zheleznodorozhnykh setey. Retrieved from http://www.opentrack.ch/opentrack/downloads/OpenTrack.Info_RU.pdf. (in Russian)

15. Sourceforge. QPNet–Synchronous Petri Nets' emulator. Retrieved from https://sourceforge.net/projects/qpnet (in English)

16. Zaitsev, D. A. (2016). Petri Nets for Modeling and Computing.DOI: 10.4018/978-1-4666-9594-8 (in English)

Надійшла до редколегії: 31.01.2020

Прийнята до друку: 05.06.2020

Creative Commons Attribution 4.0 International

doi: 10.15802/stp2020/208551
© Є. Б. Демченко, В. В. Малашкін, І. Я. Сковрон, 2020