ISSN
2307–3489 (Print), ІSSN
2307–6666
(Online)
Наука
та прогрес транспорту. Вісник
Дніпропетровського
національного
університету залізничного транспорту,
2020, № 3 (87)
МаШИНОБУДУВАННЯ
УДК 621.434
П.
М. ГАЩУК1,
С. В. НІКІПЧУК2*
1Каф.
«Експлуатація транспортних
засобів та пожежно-рятувальної техніки»,
Львівський державний університет
безпеки життєдіяльності, вул. Клепарівська,
35,
Львів, Україна, 79007, тел. +38 (067) 476 84
83, ел. пошта petroh@meta.ua,
ORCID 0000-0002-2345-4879
2*Каф. «Експлуатація
та ремонт автомобільної техніки»,
Національний університет «Львівська
політехніка»,
вул. С. Бандери, 12, Львів,
Україна, 79013, тел. +38 (097) 217 23 15, ел. пошта
nikipch@gmail.com,
ORCID 0000-0003-2499-9990
ЕФЕКТИВНІСТЬ
РОБОЧИХ ЦИКЛІВ ДВИГУНА
ШВИДКОГО
ВНУТРІШНЬОГО ЗГОРЯННЯ
З ПОДОВЖЕНИМ
РОБОЧИМ ХОДОМ
Мета.
Ми передбачаємо в найбільш загальних
термінах дослідити ефективність робочих
циклів двигуна швидкого внутрішнього
згоряння з подовженим робочим ходом.
Подовження робочого ходу передбачено,
наприклад, у так званих двигунах Аткінсона
й Міллера, які як більш досконалі
протиставляють традиційному двигуну
Отто. Методика.
Різні робочі цикли задля виявлення їх
суто принципових особливостей, розглянуто
в ідеалізованому вигляді із застосуванням
понять умовної роботи циклу, кількісної
та якісної характеристик
робочого тіла. Результати.
З’ясовано, зокрема, таке: 1) щоб двигун
Аткінсона–Міллера виконував однакову
роботу з двигуном Отто, він повинен мати
помітно більший робочий об’єм; 2) у разі
наперед заданої механічної роботи
коефіцієнт корисної дії й хід розширення
циклу Аткінсона–Міллера зростають, аж
поки він не перетворюється на цикл
Гамфрі; 3) підвищення засобами Аткінсона
ефективності двигуна Отто супроводжується
тим більшим зростанням робочого об’єму,
чим ефективнішим є двигун від самого
початку. Наукова новизна.
Доведено, що за часткових навантаг
двигун Аткінсона може істотно втрачати
свою енергетичну ефективність. До того
ж, якщо в процесі віртуального конструювання
двигуна Аткінсона стають помітними
енергоощадні переваги циклу Гамфрі, то
в процесі уявного регулювання тяги
синтезованого двигуна такого кшталту
переваги цього циклу вже не простежуються.
Практична значимість.
Загалом існують підстави стверджувати,
що двигун Отто – це все-таки вигідний
технічний компроміс між двотактним
двигуном і двигуном Аткінсона. З одного
боку, зростання коефіцієнта корисної
дії двигуна швидкого внутрішнього
згоряння сприяє істотному заощадженню
пального та зниженню загроз довкіллю
упродовж життєвого циклу машини з
приводом від такого енергоощадного
двигуна. А з другого боку, втілення
енергоощадного
робочого
циклу Аткінсона–Міллера
супроводжуватиметься зростанням
масогабаритних розмірів двигуна й
негативно позначатиметься на властивостях
машини.
Ключові
слова: двигун швидкого
внутрішнього згоряння; подовжений
робочий хід; робочий цикл; двигун
Аткінсона–Міллера; двигун Отто;
енергетична ефективність; коефіцієнт
корисної дії
Вступ
У наш час енергетичну
ефективність та екологічність машин
будь-якого призначення співвідносять
вельми критично. Наприклад, дизельний
двигун ще відносно недавно значною
мірою сприймали як досконалу теплову
машину, оскільки йому серед інших
теплових машин потенційно притаманний
більший коефіцієнт корисної дії. Хоча
очевидно, що дизель – це теплова машина
повільного внутрішнього згоряння, що
не є ознакою енергетичної досконалості.
Високий ступінь стиснення пальної
суміші, звісно, сприяв підвищенню
коефіцієнта корисної дії дизеля, але
при цьому погіршував масогабаритні
критерії досконалості. Та найважливіше,
що ще й не видно було достатньо чітких
орієнтирів щодо його екологічного
вдосконалення. Тож дизельний двигун у
приводі мобільної машини, перш за все
через екологічні недоліки, поступився
місцем двигуну швидкого внутрішнього
згоряння. І зараз навіть не дуже цікаво
з’ясовувати, що стало визначальним:
тип і властивості пального чи принцип
роботи й будова двигуна.
Проблемним
з огляду на екологію є вимушене
використання карбоновмісних енергоносіїв.
Тож і швидке внутрішнє згоряння аж ніяк
не вичерпує екологічну проблему. Одним
із засобів істотного підвищення
ефективності класичного двигуна
швидкого внутрішнього згоряння (двигуна
Ніколауса–Августа Отто,
Nikolaus–August Otto Engine), як
вважають, є подовження робочого ходу
(процесу розширення робочого тіла).
Саме таке вдосконалення втілено в
двигунах Джеймса Аткінсона (James Atkinson
Engine) [5, 6] і Ральфа Міллера (Ralph Miller Engine)
[38–40].
Установлено,
що цикл із подовженим робочим ходом
(цикл із подовженим процесом розширення,
який називатимемо циклом Аткінсона–Міллера),
поза всяким сумнівом, сприяє підвищенню
енергетичної ефективності двигуна,
але ціною зменшення середнього
індикаторного тиску й потужності [31].
Ефективність цього циклу ретельно
вивчали стосовно двигуна Отто [17, 29]
двигуна Дизеля [9, 18,
19], обох паралельно [35, 41, 45],
у випадку застосування нетрадиційного
й альтернативного палива [28, 30, 36], у
системі гібридного приводу [32]. Усі ці
дослідження є цінним внеском у скарбничку
знань про потенційні можливості
вдосконалення теплових двигунів. Це
стосується й результатів дослідження
ефективності навіть дизельних двигунів
[7, 8, 42], які тепер практично не визнають
перспективними, оскільки ці результати
в певних аспектах можна перенести на
інші типи двигунів, яким поки що не
відмовлено у визнанні перспективності
застосування.
Цикл
Аткінсона–Міллера в різних стратегіях
реалізації все більше й більше привертає
увагу розробників двигунів з іскровим
запаленням для транспортних засобів
[17, 29, 44]. Це стосується й стаціонарного
енергопостачання [21, 37]. У роботі [37]
оцінено потенційні вигоди від застосування
концепції Міллера в малому газовому
двигуні, призначеному, наприклад, для
місцевого комбінованого продукування
і тепла, і механічної енергії.
З’ясувалося, що цикл Міллера порівняно
з традиційним циклом Отто сприяє
заощадженню палива на рівні 5…10 %, але
із супутньою втратою потужності. Більші
механічні втрати при цьому будуть
переважені енергоощадністю. Актуальним
є також дослідження шуму/вібрації та
довговічності. Когенерацію енергії
газовими двигунами на основі концепції
Міллера визнають ефективною й вигідною
також у більших масштабах [21]. Поряд із
газовим вигідним можна вважати
запровадження робочого циклу Міллера
також і в звичному бензиновому двигуні
[27, 46]. Але
прийнятність концепції Міллера
залежатиме від того, чи прийнятними
будуть втрати потужності.
У значній мірі
стратегія втілення принципу Міллера
визначається властивостями системи
керування газорозподілом [13–15]. Тож
інколи співвідносять різні варіанти
саме керування клапанами механізму
газорозподілу і організації циклу
Міллера з метою розпізнати кращий [43].
Особливе значення
мають дослідження теоретичного
спрямування [20, 23, 48]. За приклад раціонально
систематизованого аналізу можуть
правити роботи [20, 23], у яких цикл Мюллера
моделюють у термінах [4] обмежених у
часі термодинамічних процесів. При
цьому співвідносять енергетичну
ефективність та енергетичну продуктивність.
Теоретичні узагальнення містять також
роботи [25, 26, 47]. Високим рівнем теоретичності
відзначаються й дослідження [11, 34], у
яких беруть до уваги необоротність
циклів, ентропійність явища перетворення
теплоти на роботу, температурну
залежність теплоємності робочої
субстанції.
Проблема
вдосконалення теплового двигуна є
багатоаспектною. Власне, різні аспекти
вдосконалення теплового двигуна стали
предметом ретельного дослідження,
наприклад, у роботах [2, 3, 16, 22, 24]. Але
доцільним було б розглянути концепцію
подовженого робочого ходу
насамперед у більш загальних термінах,
зберігаючи наочність аналітичних
міркувань.
Мета
З огляду
на викладене мета статті – формалізовано
оцінити потенційну ефективність
технології зменшення відношення ходу
стискання пальної суміші до робочого
ходу поршня у двигуні швидкого
внутрішнього згоряння.
Методика
У процесі
аналізу доречно було б зважати на
енергетичну ефективність двигуна
(вимірювану коефіцієнтом корисної
дії), на можливу зміну його маси й
габаритів, на здатність сприймати
навантаження та на можливості змінювати
режими роботи за потреби. При цьому
доцільно використовувати найбільш
загальні теоретичні поняття, що не
містять надто конкретної інформації
та не обтяжують суть справи побічними
ефектами. Двигун Міллера за технічними
проявами близький до двигуна Аткінсона,
і тому є підстави знайти спосіб
протиставляти їх разом як один об’єкт
традиційному двигуну Ніколауса–Августа
Отто. За взірець підходу
до загального аналізу властивостей
теплової машини могла би правити логіка
Саді Карно (Saadi Carnot) [10],
яка, щоправда, стосується віртуальної
так званої двотемпературної теплової
машини (паливний елемент, на противагу
їй, зазначмо, називають однотемпературною
машиною). Але цілком продуктивним міг
би стати аналіз, що спирається й на інші
ідеальні термодинамічні цикли з
нескінченною тривалістю [1].
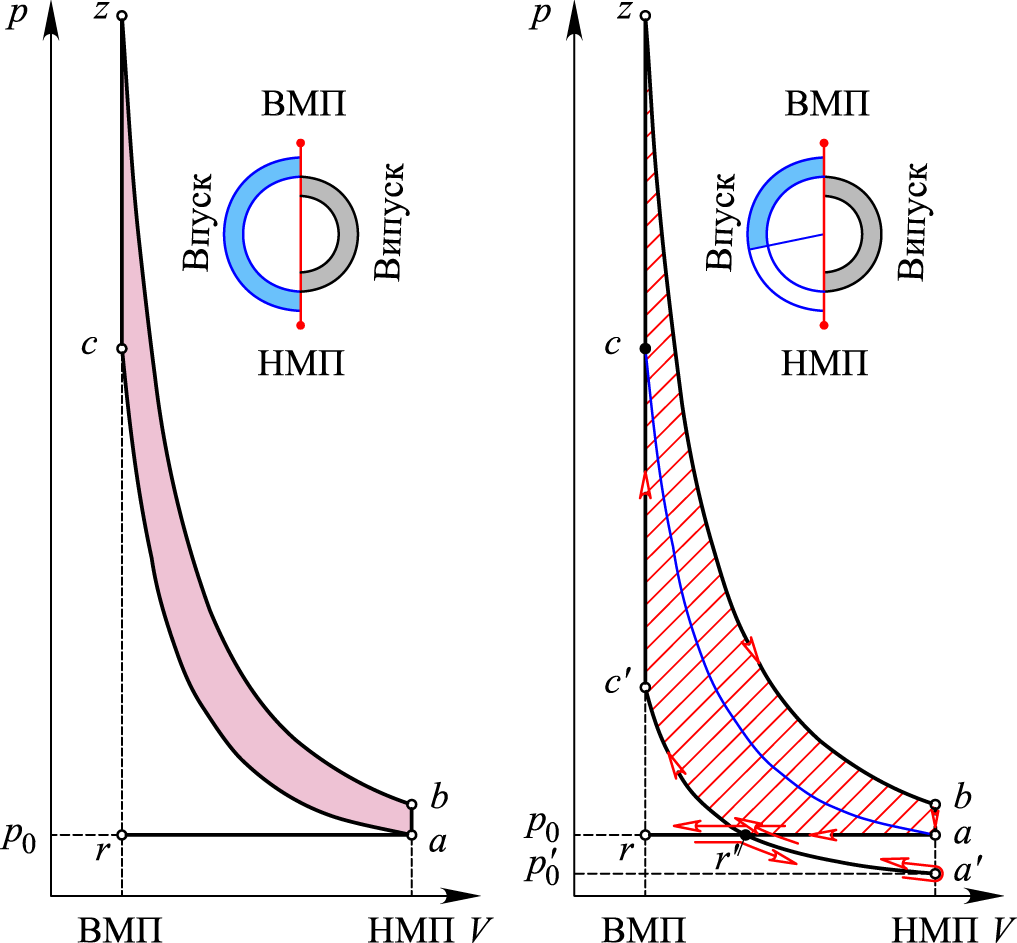
Розгляньмо
окремі варіації термодинамічного циклу
Отто, рис. 1 (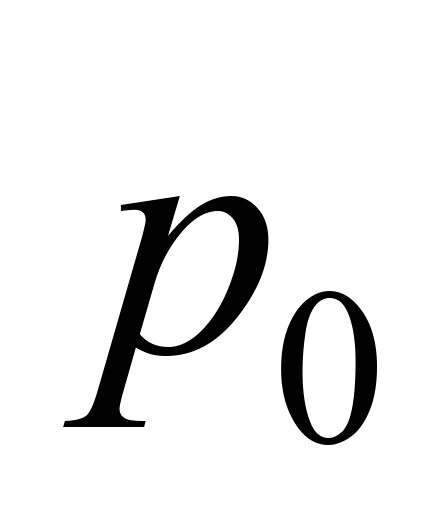 – тиск у довкіллі).
– тиск у довкіллі).
У звичайному циклі
Отто
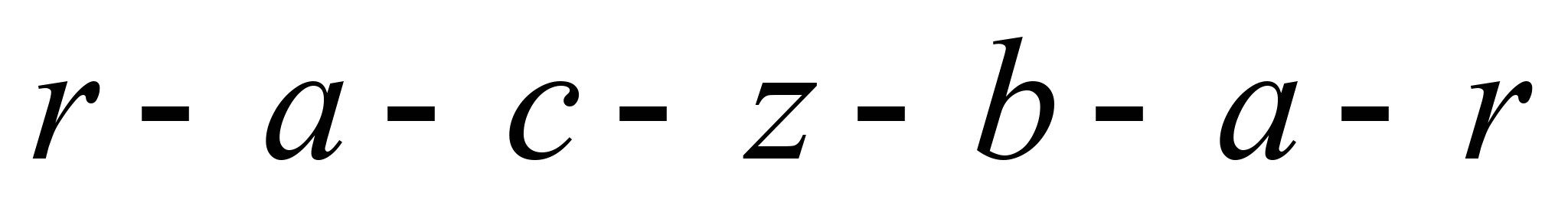 (рис. 1, а)
ділянки
(рис. 1, а)
ділянки
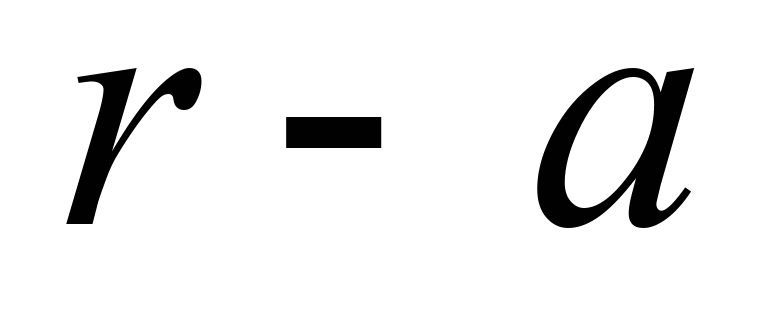 та
та
 імітують відповідно такт впускання
пальної суміші в робочий простір і такт
випускання відпрацьованих газів з
нього, а ділянка
імітують відповідно такт впускання
пальної суміші в робочий простір і такт
випускання відпрацьованих газів з
нього, а ділянка
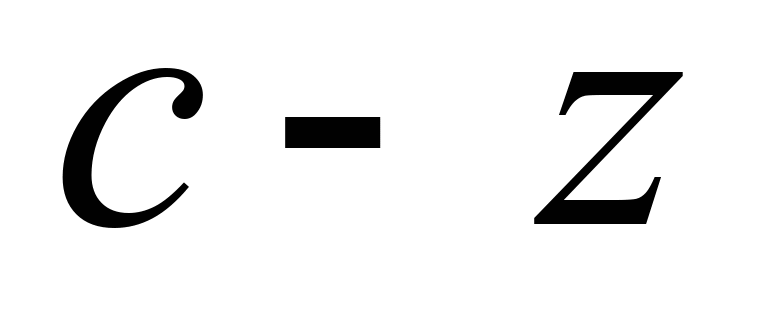 – процес згоряння суміші (процес
теплотворення). У 1947 році
американський інженер Ральф Міллер
запропонував зробити
такт стиснення в класичному двигуні
Отто механічно коротшим за такт робочого
ходу (за такт розширення), рис. 1, б:
у робочому тепловому циклі Міллера
(Miller Cycle)
– процес згоряння суміші (процес
теплотворення). У 1947 році
американський інженер Ральф Міллер
запропонував зробити
такт стиснення в класичному двигуні
Отто механічно коротшим за такт робочого
ходу (за такт розширення), рис. 1, б:
у робочому тепловому циклі Міллера
(Miller Cycle)
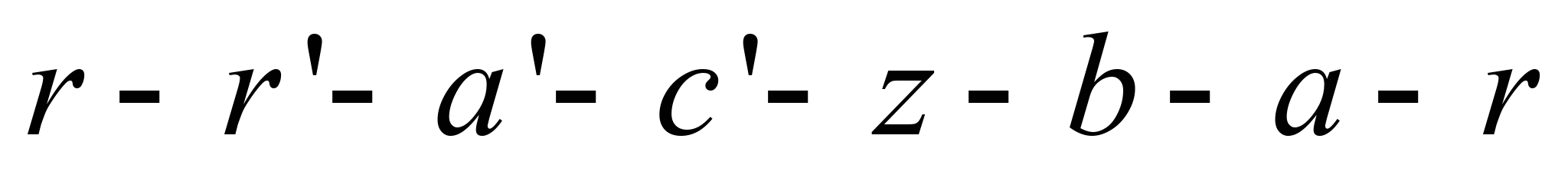 точка
точка
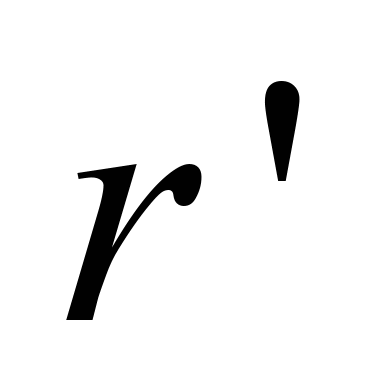 відповідає моменту закриття впускного
клапана; такт стискання робочого тіла
(ідеального газу) формально відображає
ділянка
відповідає моменту закриття впускного
клапана; такт стискання робочого тіла
(ідеального газу) формально відображає
ділянка
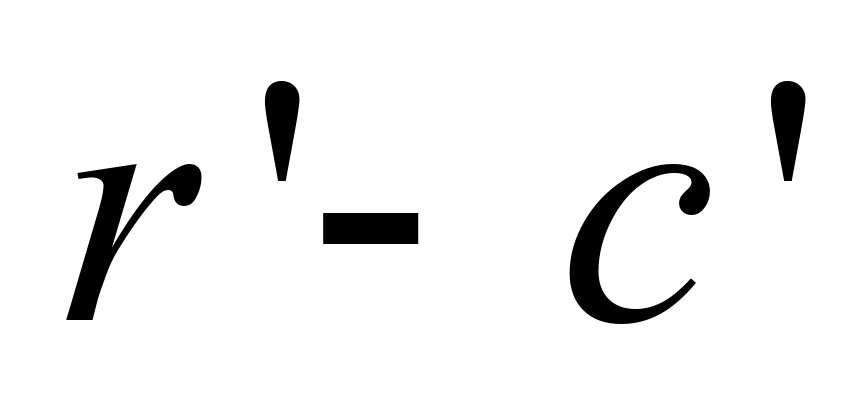 циклу, яка за переміщенням поршня
справді є коротшою за ділянку
циклу, яка за переміщенням поршня
справді є коротшою за ділянку
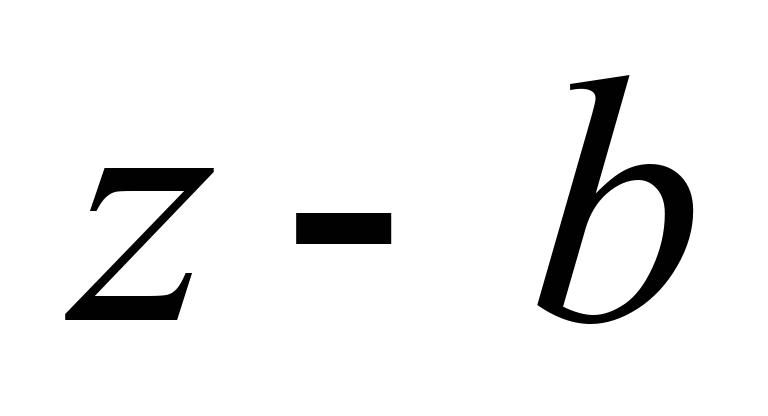 розширення (
розширення (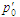 – тиск у циліндрі в кінці ходу поршня
до нижнього мертвого положення на такті
всмоктування). Того самого результату
можна досягнути, закриваючи впускний
клапан після НМП із великим запізненням,
виштовхуючи при цьому частину пальної
суміші назад у впускний колектор, рис.
1, в: у
робочому циклі
– тиск у циліндрі в кінці ходу поршня
до нижнього мертвого положення на такті
всмоктування). Того самого результату
можна досягнути, закриваючи впускний
клапан після НМП із великим запізненням,
виштовхуючи при цьому частину пальної
суміші назад у впускний колектор, рис.
1, в: у
робочому циклі
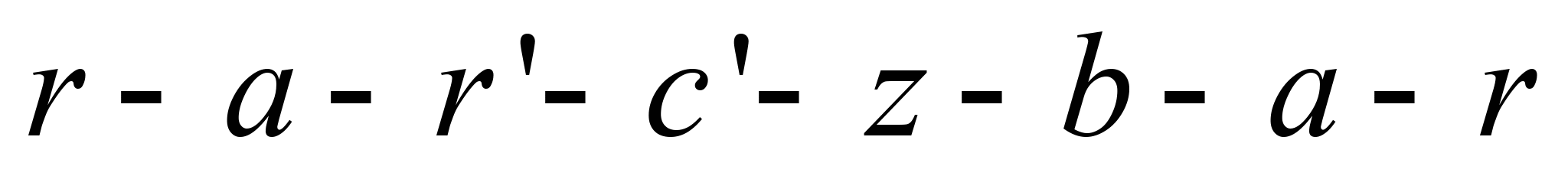 власне процес впускання пальної суміші
формально імітує ділянка
власне процес впускання пальної суміші
формально імітує ділянка
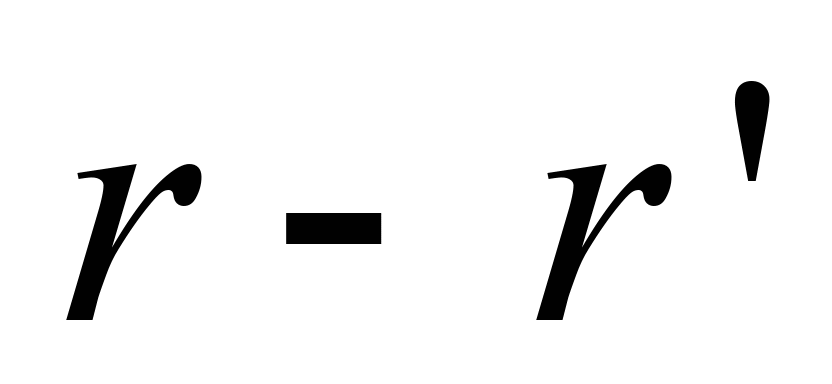 .
.
Впускний
клапан, зрештою, можна відкривати також
із запізненням, рис. 1, г:
у циклі
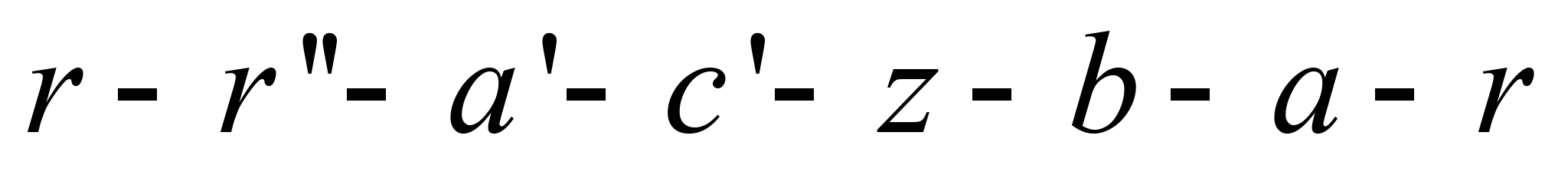 ділянка
ділянка
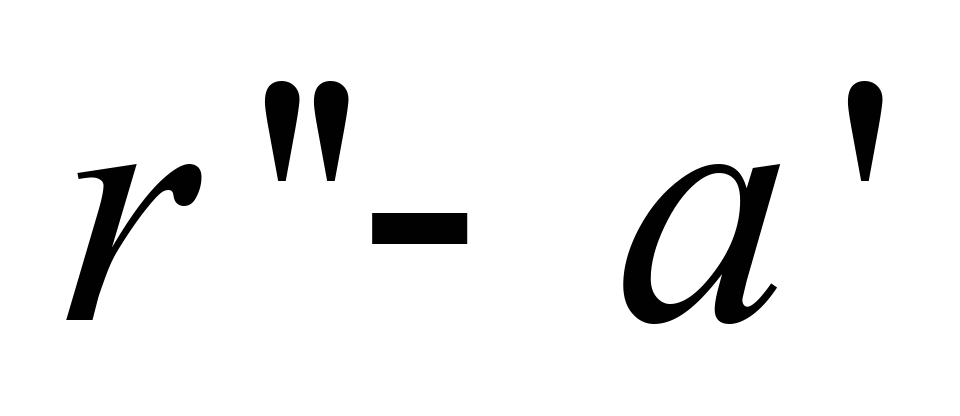 імітує власне процес впускання; площа
фігури
імітує власне процес впускання; площа
фігури
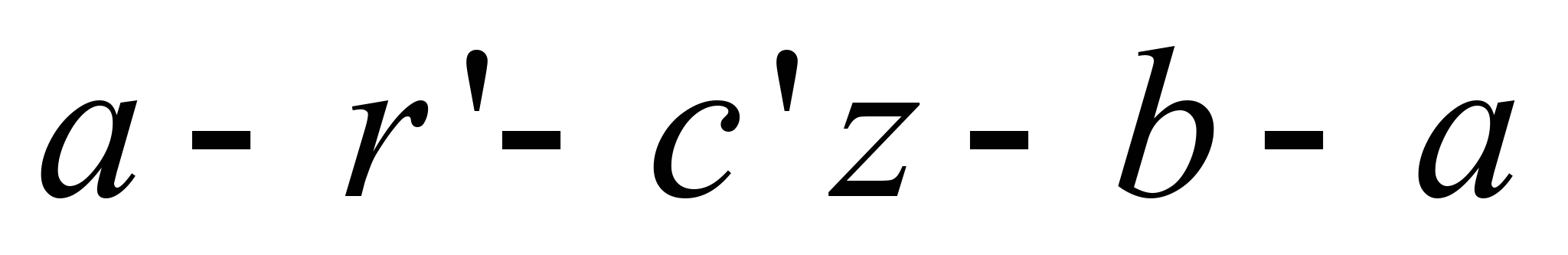 відповідає додатній роботі циклу, а
площа фігури
відповідає додатній роботі циклу, а
площа фігури
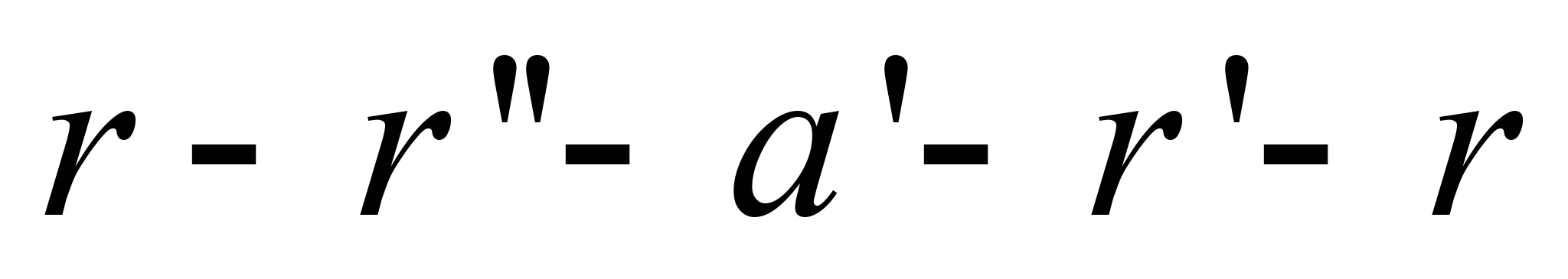 – від’ємній роботі. Зауважмо, на
наведених діаграмах ділянка розширення
– від’ємній роботі. Зауважмо, на
наведених діаграмах ділянка розширення
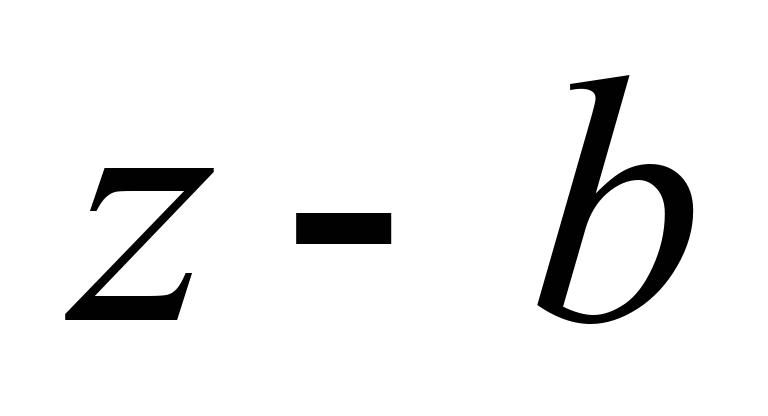 розташована довільно, без урахування
пропорцій між кількостями спожитої
суміші й показниками її якості.
розташована довільно, без урахування
пропорцій між кількостями спожитої
суміші й показниками її якості.
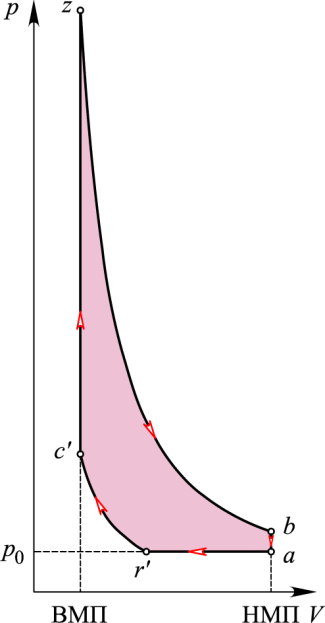
Загалом
циклові Міллера ( рис. 1, б
і в)
можна поставити у відповідність
теоретичний цикл
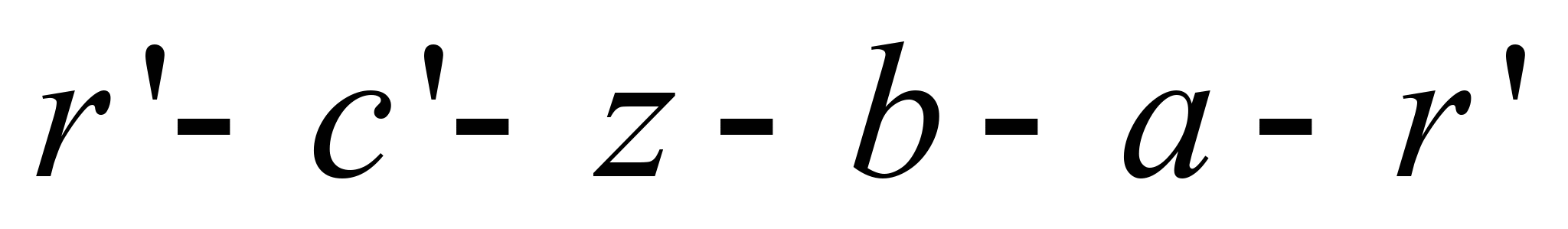 (рис. 2). У такому разі цикл Міллера (див.
рис. 2) можна беззастережно трактувати
як ще один важливий елементарний
термодинамічний поряд зі звичними
елементарними термодинамічними циклами
[1] Карно, Отто, Брайтона, Дизеля, Ериксона,
Сабате, Стирлінга. Хоча, з іншого боку,
він є ніби похідним від циклу Отто, є
його варіацією.
(рис. 2). У такому разі цикл Міллера (див.
рис. 2) можна беззастережно трактувати
як ще один важливий елементарний
термодинамічний поряд зі звичними
елементарними термодинамічними циклами
[1] Карно, Отто, Брайтона, Дизеля, Ериксона,
Сабате, Стирлінга. Хоча, з іншого боку,
він є ніби похідним від циклу Отто, є
його варіацією.
Двигун
Міллера за технічними проявами близький
до так званого двигуна Аткінсона, рис.
3: цикл роботи двигуна Аткінсона ідеалізує
та сама, зображена на рис. 2, діаграма,
що й цикл Міллера. Тут також стиск є
«коротшим» за розширення, але цього
разу завдяки особливому триланковому
хитневому механізмові. Можна казати,
що двигун Міллера – це примітивізоване
поєднання двигунів Аткінсона й Отто.
Але двигун Аткінсона в разі варіації
його схемних параметрів (рис. 4) потенційно
здатен реалізувати і структурно
складніший робочий цикл – із двома
парами мертвих положень поршня.
а
– a б
– b
в
– c г – d
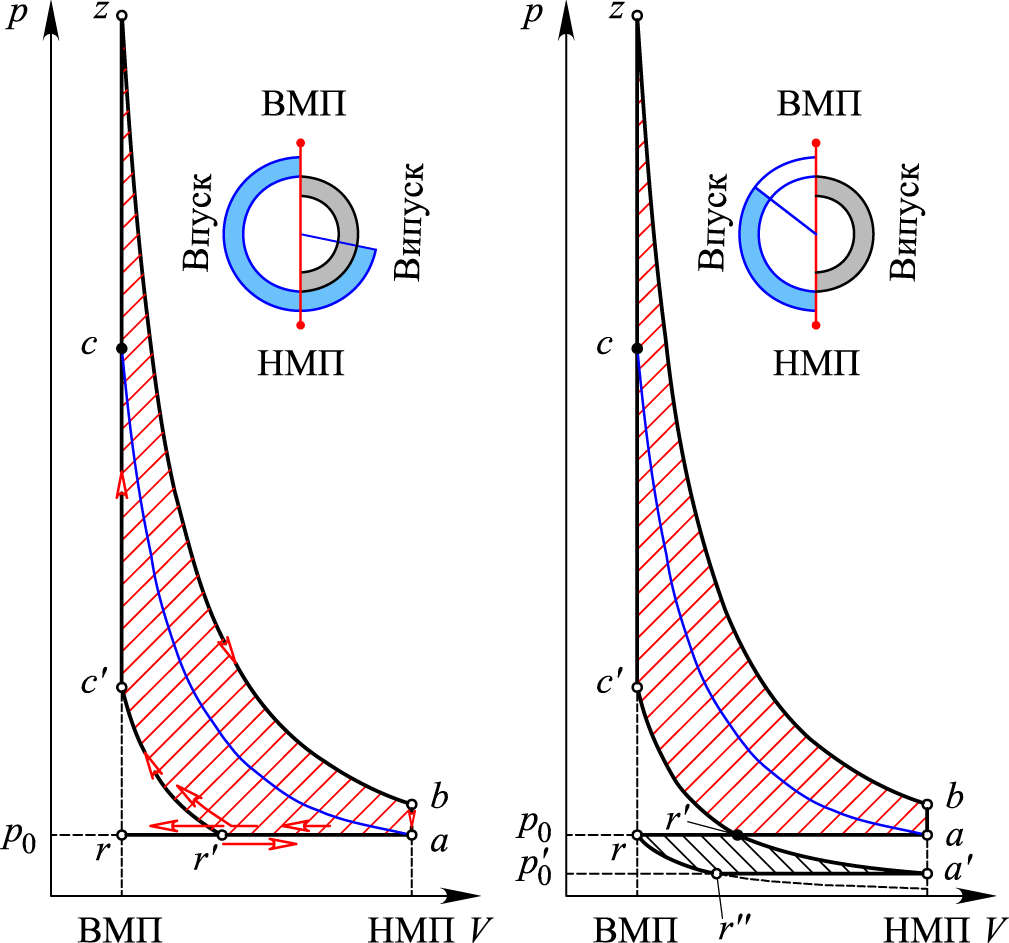
Рис. 1. Варіації
циклу Отто
Fig. 1. Otto cycle
variations
Якщо двигуни Отто
й Міллера чотири такти свого робочого
циклу здійснюють за два оберти
колінчастого вала, то традиційний
двигун Аткінсона реалізує свій робочий
цикл лише за один оберт вала (подібно
до того, як двотактний (двостадійний)
двигун утілює свій двотактний робочий
цикл також за один оберт вала). Це
дозволяє (рис. 4) застосувати безпосередній
(безредукторний) привід газорозподільного
механізму. Щоправда, схему двигуна
можна істотно модифікувати (рис. 5),
відводячи під робочий цикл усе-таки
два оберти вала.
|
|
|
Рис.
2. Цикл Аткінсона–Міллера
Fig.
2. Atkinson/Miller cycle
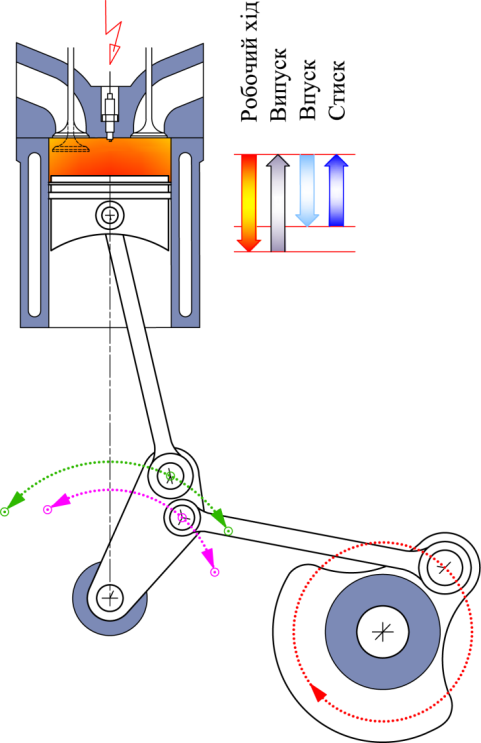
Рис.
3. Схема простого хитневого механізму
двигуна Аткінсона
Fig.
3. Scheme of a simple connecting rod gear
оf
Atkinson engine
|
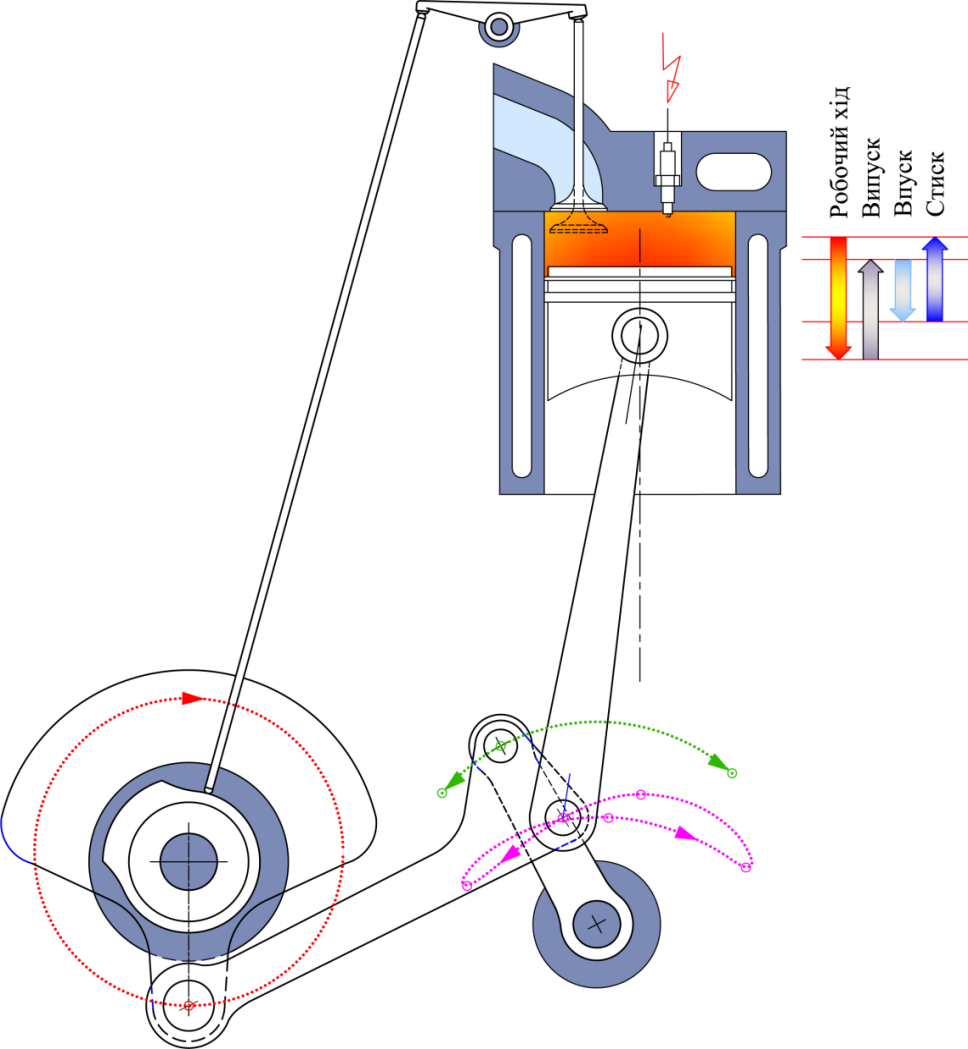
Рис. 4. Схема
хитневого механізму з двома верхніми
та двома нижніми мертвими положеннями
Fig. 4. Scheme of
the connecting rod gear with two upper and two lower dead center
positions
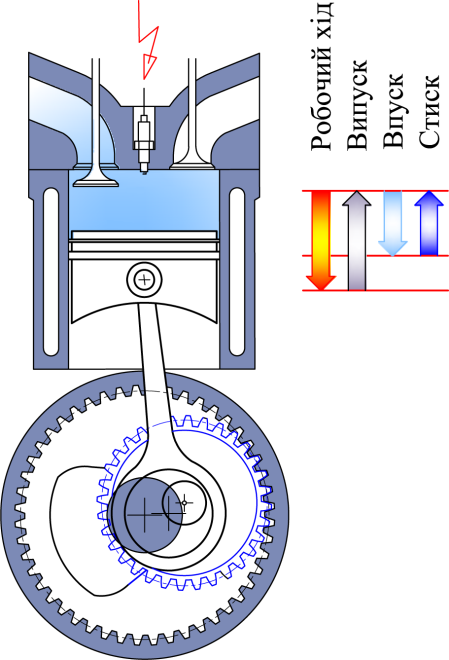
Рис. 5. Схема
планетарно-зубчастого хитневого
механізму
двигуна Аткінсона
Fig. 5. Scheme of
planetary gear mechanism
of Atkinson engine
Зауважмо,
двигун Аткінсона запатентовано
англійським інженером Джеймсом
Аткінсоном ще в 1886 році [5], щоб оминути,
як стверджують, перепони патенту
Ніколауса Отто. Та все ж він не набув
практичного визнання, а от до двигуна
Міллера ставлення практиків виявилося
більш доброзичливим.
Результати
Ефективність
швидкого теплотворення.
Хай задано теоретичний
цикл Отто
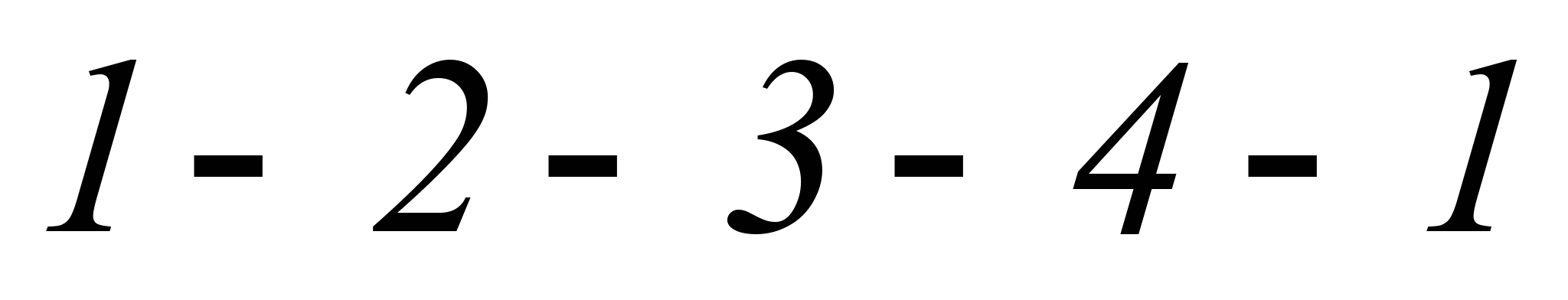 ,
який складають дві ізохори і дві
адіабати (ізоентропи), рис. 6 (
,
який складають дві ізохори і дві
адіабати (ізоентропи), рис. 6 (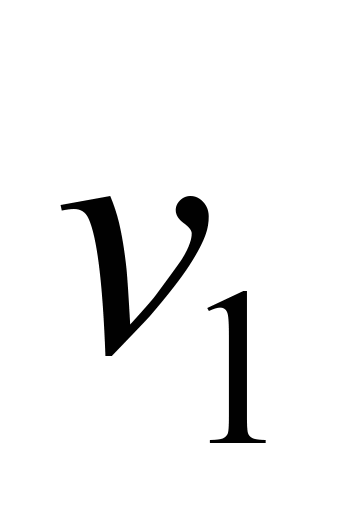 і
і
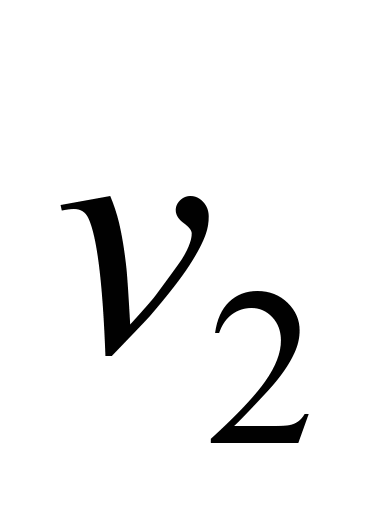 – питомі об’єми робочого простору й
камери згоряння). Робочим тілом є
ідеальний газ, стан якого визначає
рівняння
– питомі об’єми робочого простору й
камери згоряння). Робочим тілом є
ідеальний газ, стан якого визначає
рівняння
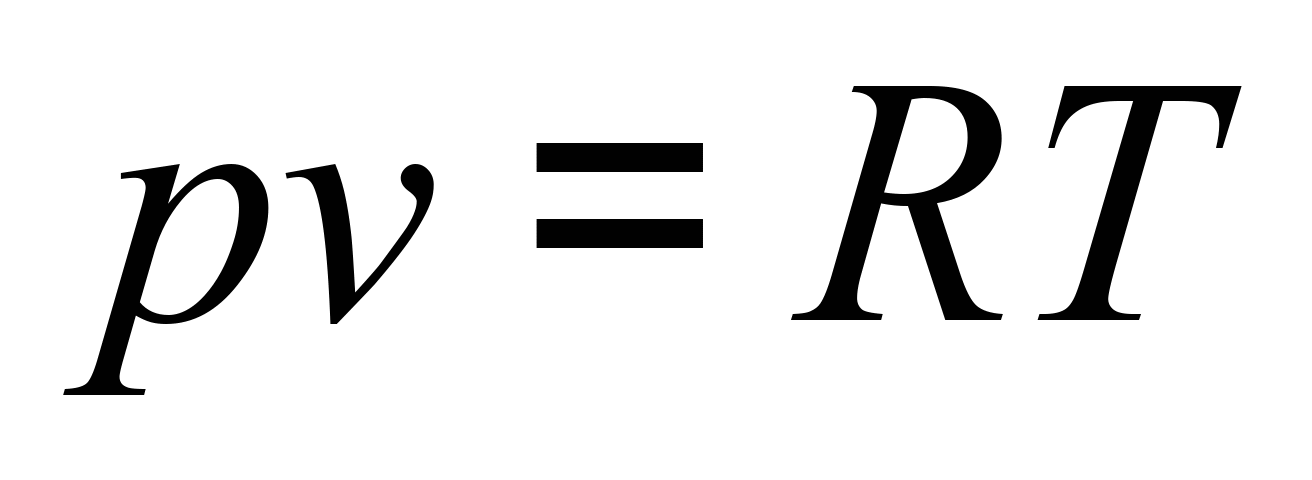 (
(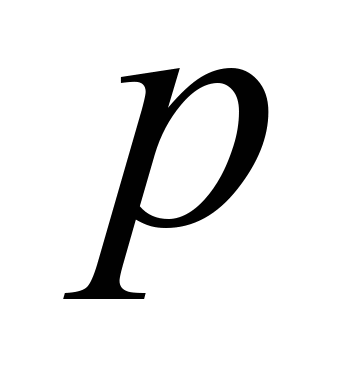 – тиск у робочому просторі,
– тиск у робочому просторі,
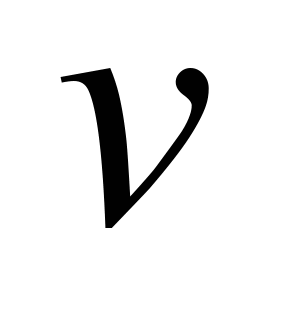 – питомий об’єм газу,
– питомий об’єм газу,
 – абсолютна температура газу,
– абсолютна температура газу,
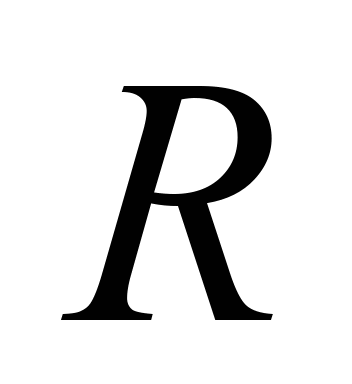 – газова стала). До одиниці маси робочого
тіла ізохорно підводиться (питома)
теплота
– газова стала). До одиниці маси робочого
тіла ізохорно підводиться (питома)
теплота
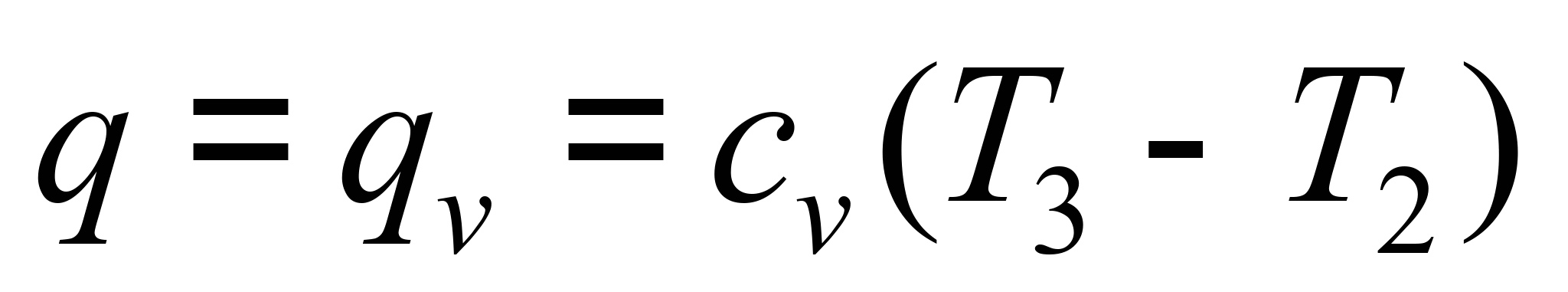 , (1)
, (1)
де
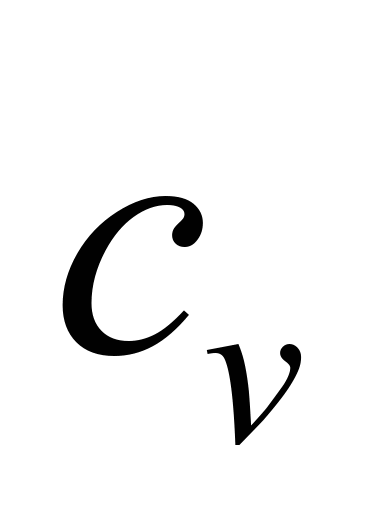 – незмінна питома теплоємність робочого
тіла за сталого об’єму;
– незмінна питома теплоємність робочого
тіла за сталого об’єму;
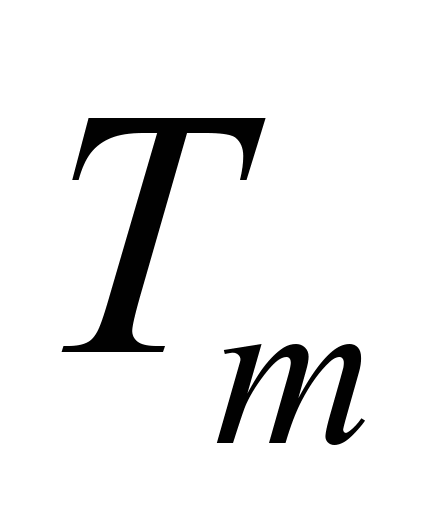 і
і
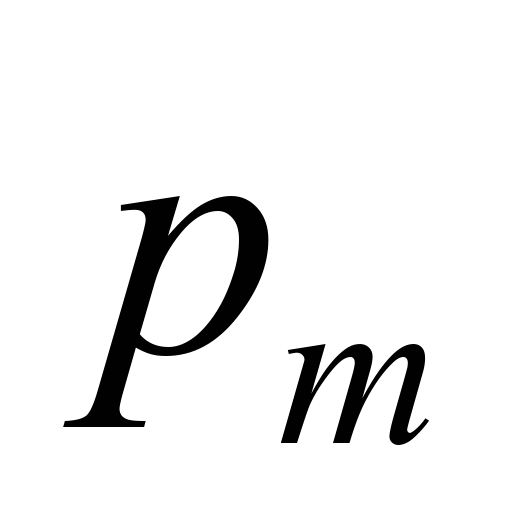 – температура й тиск, відповідні
точці
– температура й тиск, відповідні
точці
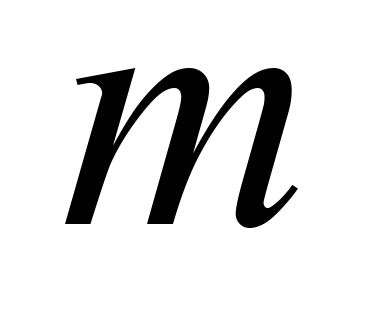 циклу. Цю ж кількість теплоти можна
підвести спочатку частиною
циклу. Цю ж кількість теплоти можна
підвести спочатку частиною
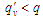 ізохорно, а потім частиною
ізохорно, а потім частиною
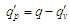 ізобарно:
ізобарно:
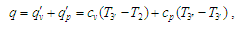 (2)
(2)
де
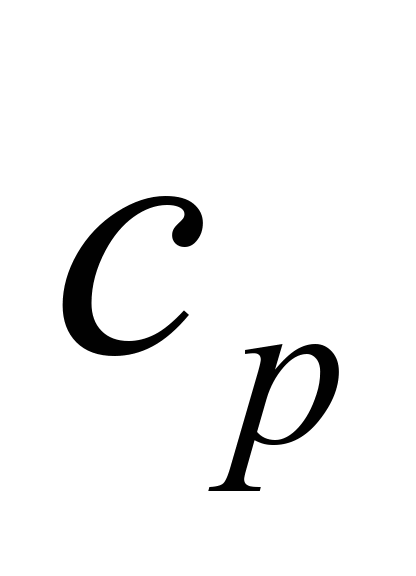 – незмінна питома теплоємність робочого
тіла за сталого тиску.
– незмінна питома теплоємність робочого
тіла за сталого тиску.
Прирівняємо
(1) і (2):
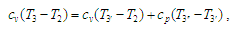
звідки
(перемножуючи ліву та праву частини
цієї рівності на
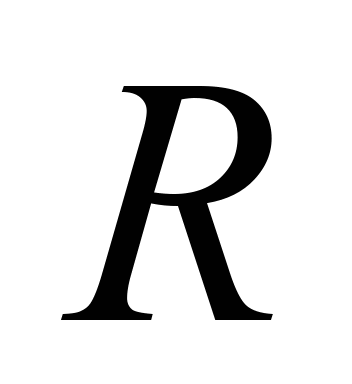 ,
беручи до уваги рівняння стану та
позначаючи
,
беручи до уваги рівняння стану та
позначаючи
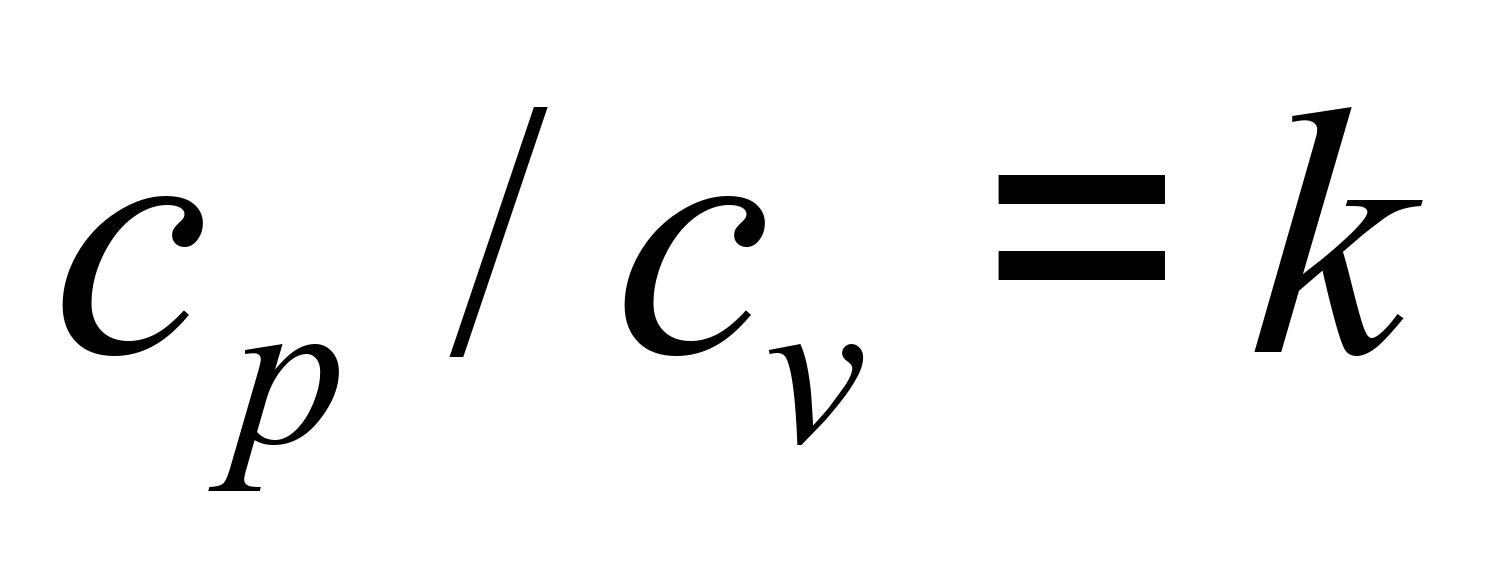 – показник адіабати) знайдемо:
– показник адіабати) знайдемо:
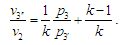
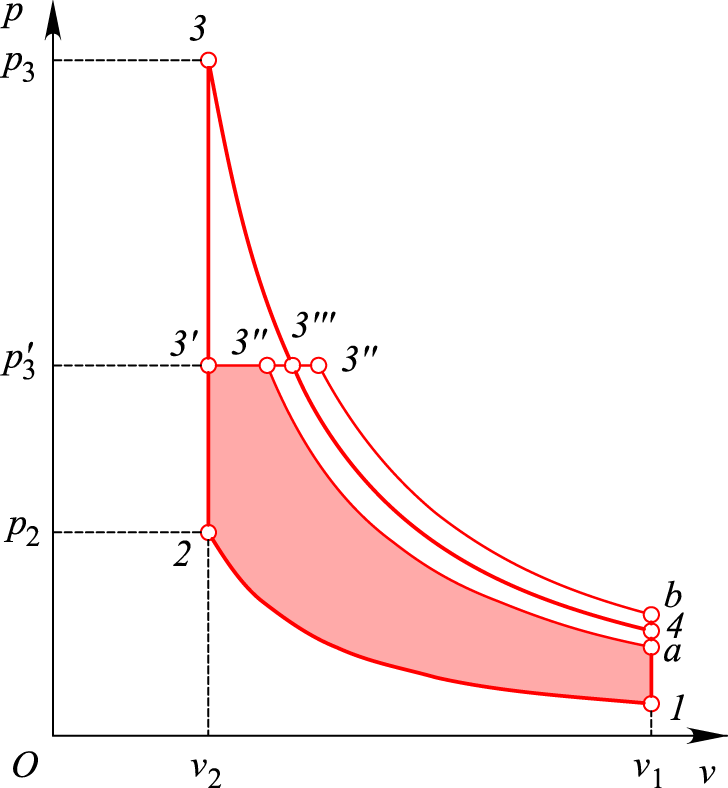
Рис. 6.
Порівняння циклів з ізохорним
та
ізохорно-ізобарним підведеннями
теплоти до робочого тіла
Fig. 6. Comparison
of cycles with isochoric
and isochoric-isobaric heat supply
to
the working fluid
Ізобара
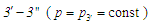 гіпотетично може не перетинати адіабату
гіпотетично може не перетинати адіабату
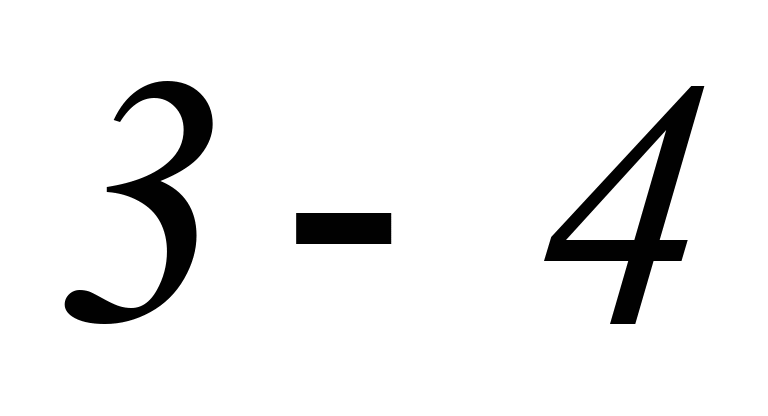 (як, наприклад, у разі циклу
(як, наприклад, у разі циклу
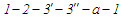 ),
а може перетнути її в точці
),
а може перетнути її в точці
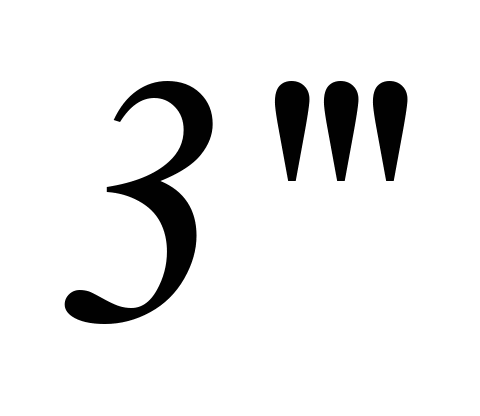 (як, наприклад, у разі циклу
(як, наприклад, у разі циклу
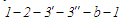 ),
якій відповідає рівність (рис. 6):
),
якій відповідає рівність (рис. 6):
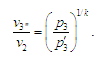
У першому
випадку (коли
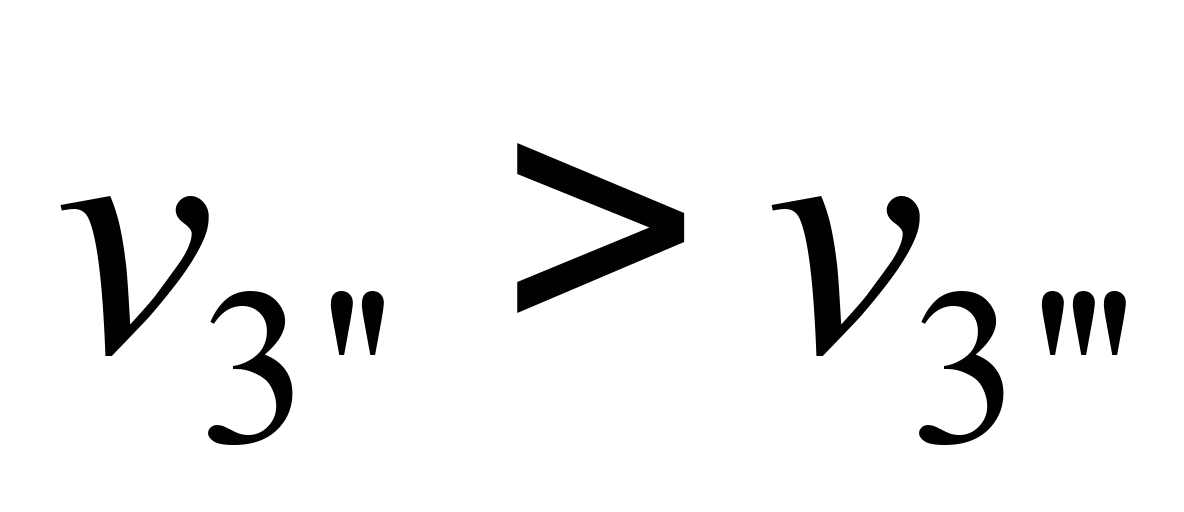 )
виділена на рис. 6 площа, що характеризує
механічну роботу циклу зі змішаним
підведенням теплоти, очевидно, менша
за площу фігури
)
виділена на рис. 6 площа, що характеризує
механічну роботу циклу зі змішаним
підведенням теплоти, очевидно, менша
за площу фігури 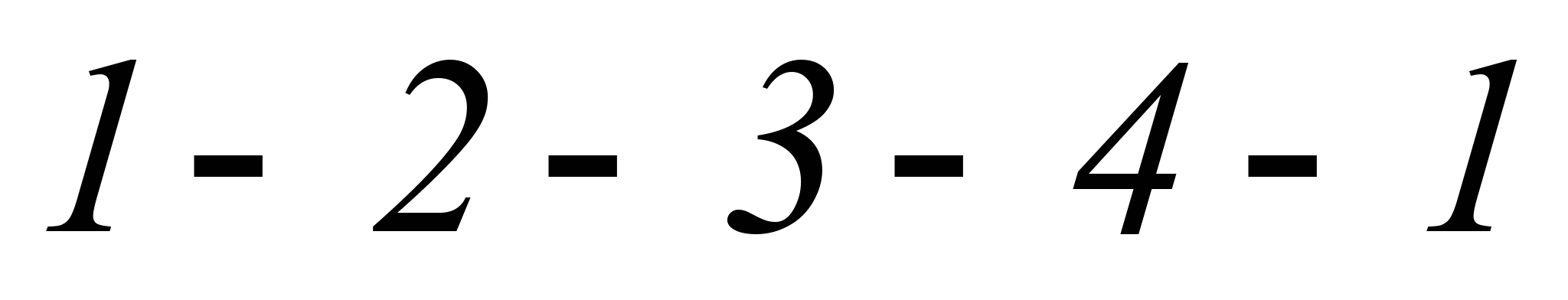 ,
що характеризує механічну роботу циклу
з ізохорним підведенням теплоти. Це
означає, що класичний цикл Отто
досконаліший за його ізобарну варіацію.
Але й у другому випадку (коли
,
що характеризує механічну роботу циклу
з ізохорним підведенням теплоти. Це
означає, що класичний цикл Отто
досконаліший за його ізобарну варіацію.
Але й у другому випадку (коли
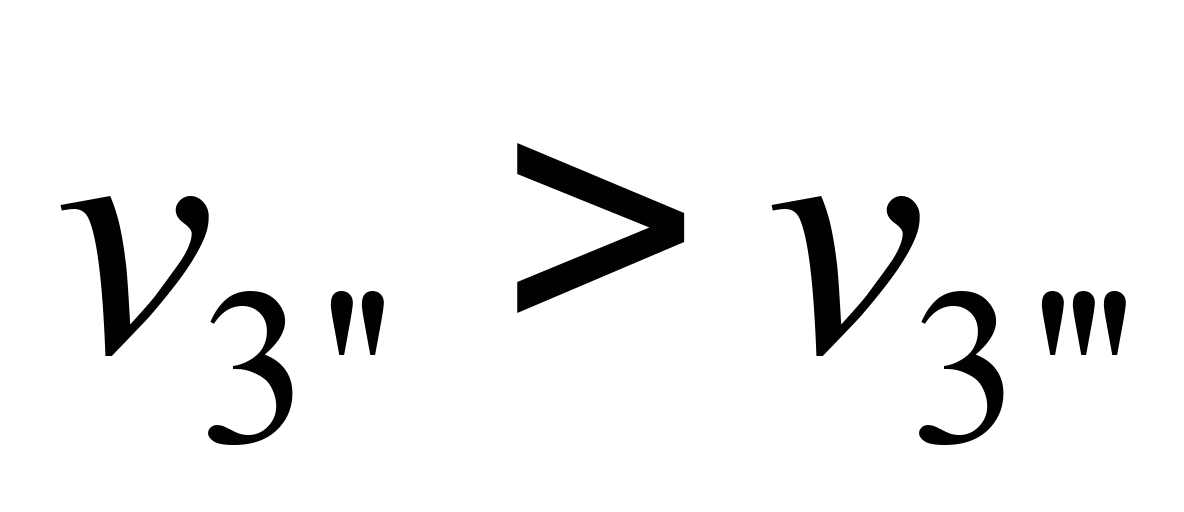 )
цей цикл залишається також досконалішим:
в ізохорному процесі
)
цей цикл залишається також досконалішим:
в ізохорному процесі
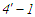 відводиться в довкілля більше теплоти,
ніж в ізохорному процесі
відводиться в довкілля більше теплоти,
ніж в ізохорному процесі
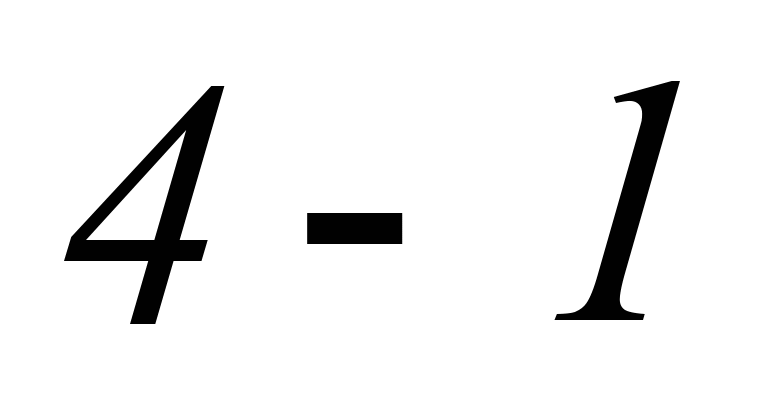 .
.
Тож
ізохорне підведення теплоти до робочого
тіла ефективніше за ізохорно-ізобарне.
Це теоретична вказівка на те, що вся
теплота повинна надійти в робочий
простір двигуна відразу з початком
такту робочого ходу і що досконалішим
є двигун саме швидкого внутрішнього
згоряння. Відтак достатньо надійне
втілення принципу HCCI–двигуна
(Homogeneous Charge Compression Ignition Engine; двигуна з
об’ємним згорянням) слід було б сприймати
як істотне досягнення [12, 33].
Порівняння
ефективності циклів Отто й
Аткінсона–Міллера. Зімітуймо
перетворення циклу Отто
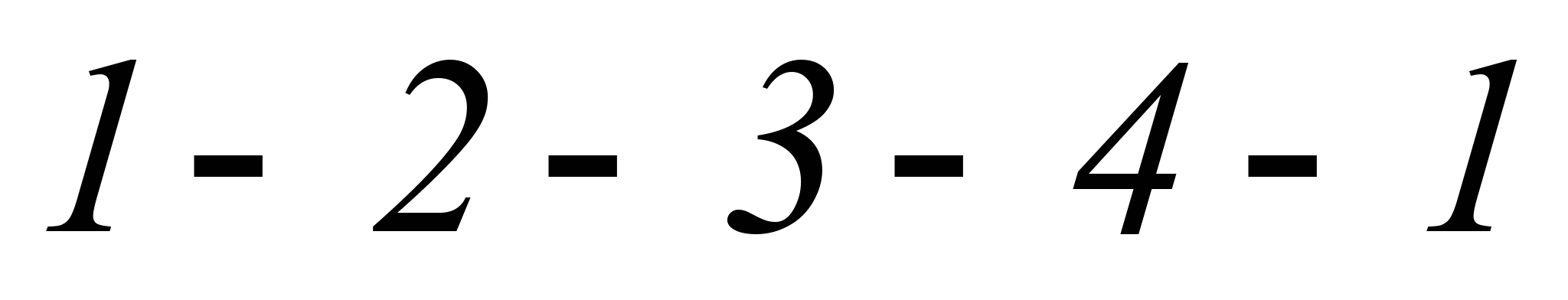 на цикл Аткінсона (Міллера)
на цикл Аткінсона (Міллера)
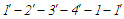 ,
рис. 7. Хай ідеться про номінальний режим
роботи двигуна, коли енергоємність
робочої суміші (робочого тіла) є
максимально можливою. Тож вважатимемо,
що масу
,
рис. 7. Хай ідеться про номінальний режим
роботи двигуна, коли енергоємність
робочої суміші (робочого тіла) є
максимально можливою. Тож вважатимемо,
що масу
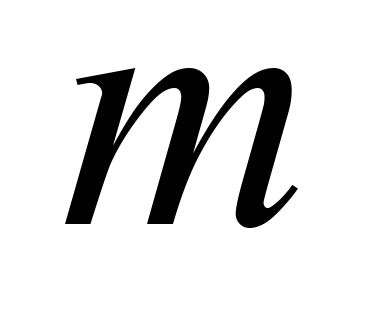 робочої суміші, яка потрапляє в робочий
простір двигуна Отто, і масу
робочої суміші, яка потрапляє в робочий
простір двигуна Отто, і масу
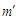 робочої суміші, яка потрапляє в робочий
простір двигуна Аткінсона (Міллера) на
номінальному режимі, співвідносять як
відповідні їм об’єми
робочої суміші, яка потрапляє в робочий
простір двигуна Аткінсона (Міллера) на
номінальному режимі, співвідносять як
відповідні їм об’єми
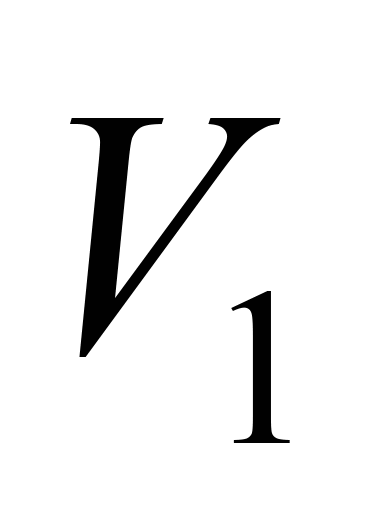 і
і
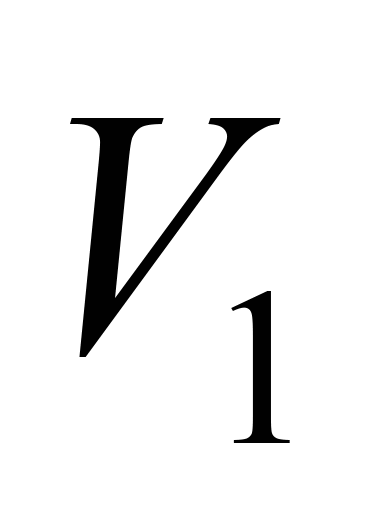 (залишки відпрацьованого робочого тіла
від попереднього циклу в камері
згоряння до уваги не беруться):
(залишки відпрацьованого робочого тіла
від попереднього циклу в камері
згоряння до уваги не беруться):
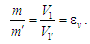 (3)
(3)
Якщо
ступінь стискування пальної суміші у
двигуні Отто становив
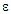 ,
то логічно зберегти його значення й у
двигуні Аткінсона:
,
то логічно зберегти його значення й у
двигуні Аткінсона:
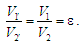 (4)
(4)
Ізоентропам
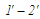 і
і
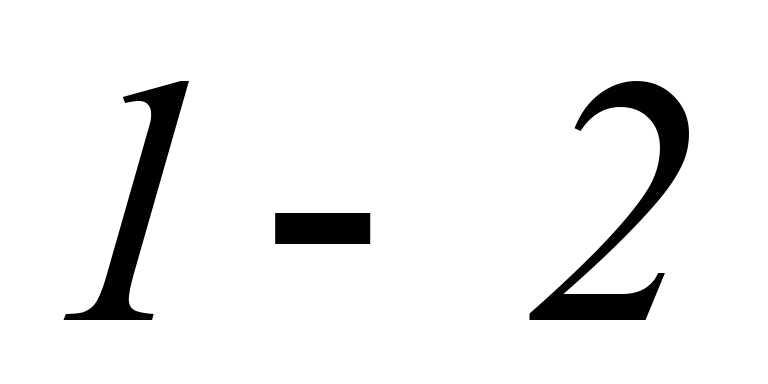 відповідають
співвідношення:
відповідають
співвідношення:
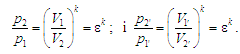
Тож
оскільки
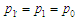 (
(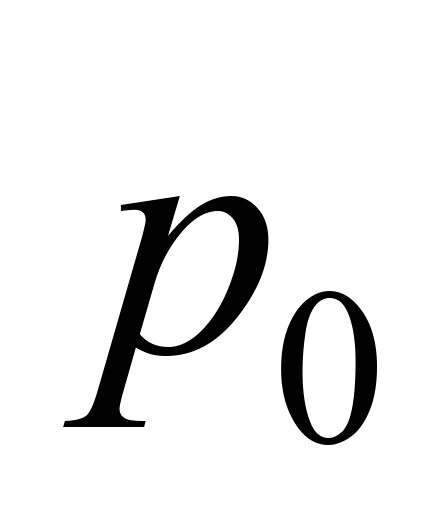 — тиск у довкіллі), то й
— тиск у довкіллі), то й
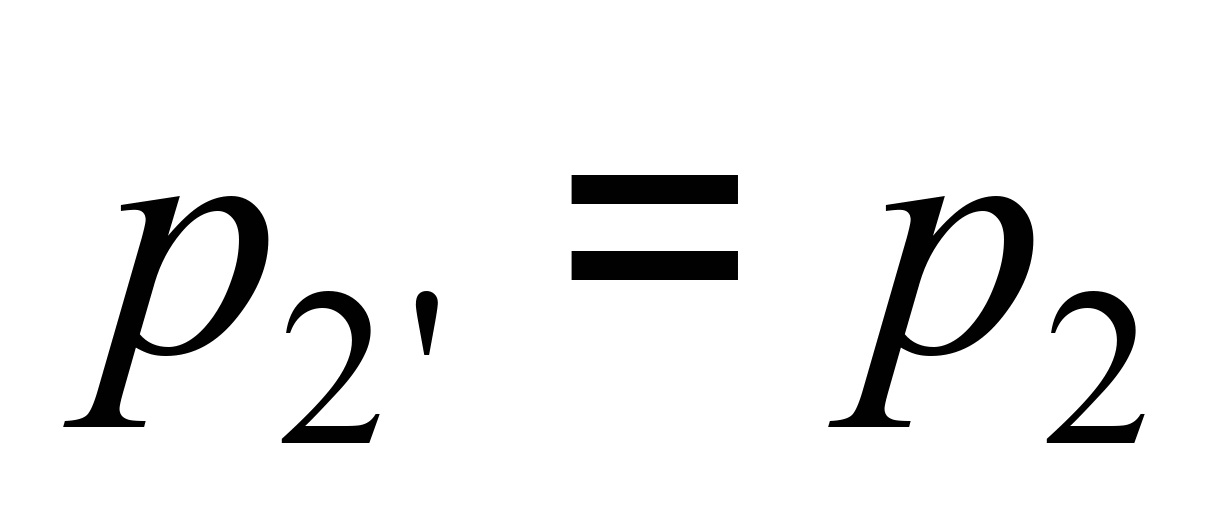 .
.
До робочих
тіл у циклах підводяться теплоти
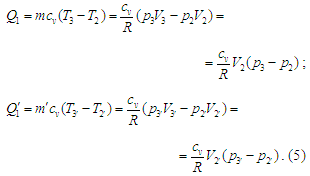
Тут узято
до уваги відповідні рівняння стану
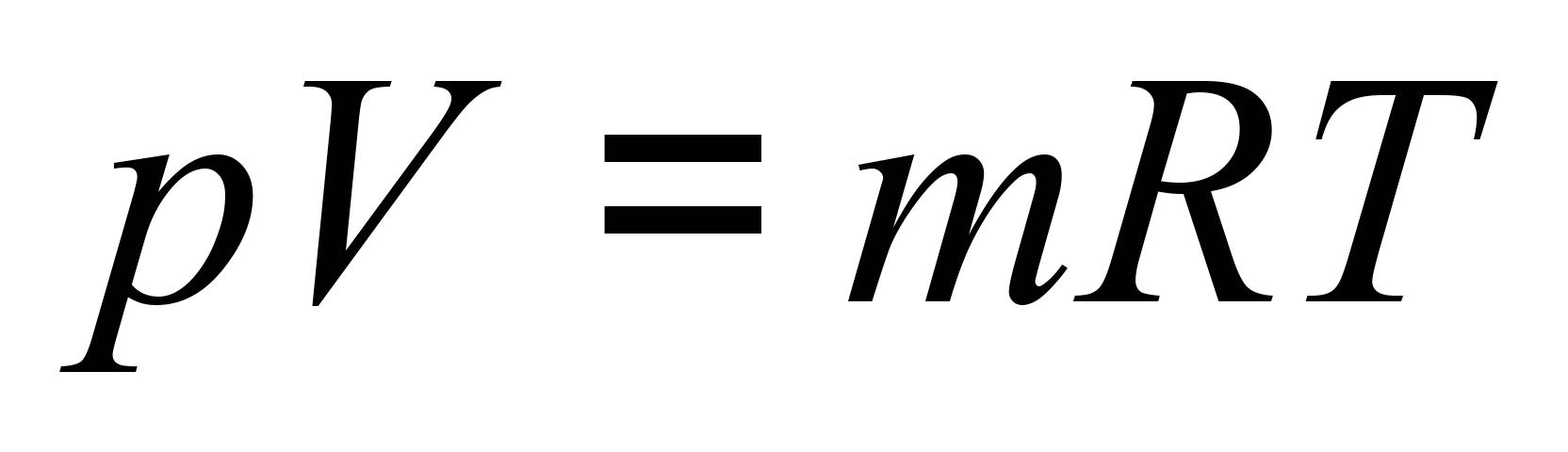 і
і
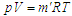 .
Є сенс вважати, що
.
Є сенс вважати, що
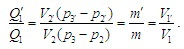
Тож
оскільки
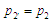 ,
то й
,
то й
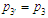 ,
див. (4) і рис. 7. Позначимо
,
див. (4) і рис. 7. Позначимо
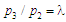 .
.
Величина
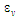 (див. (3) і рис. 7) у разі незмінності
параметра
(див. (3) і рис. 7) у разі незмінності
параметра
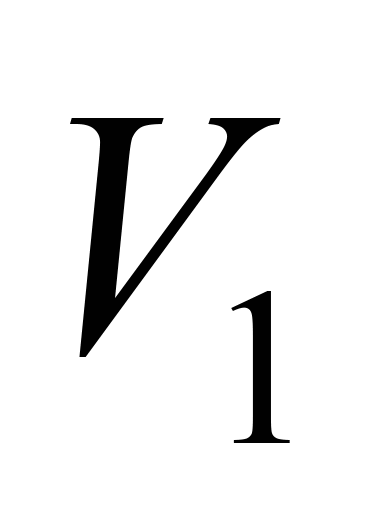 може збільшуватись від значення
може збільшуватись від значення
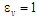 (що відповідає двигуну Отто) до значення
(що відповідає двигуну Отто) до значення
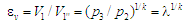
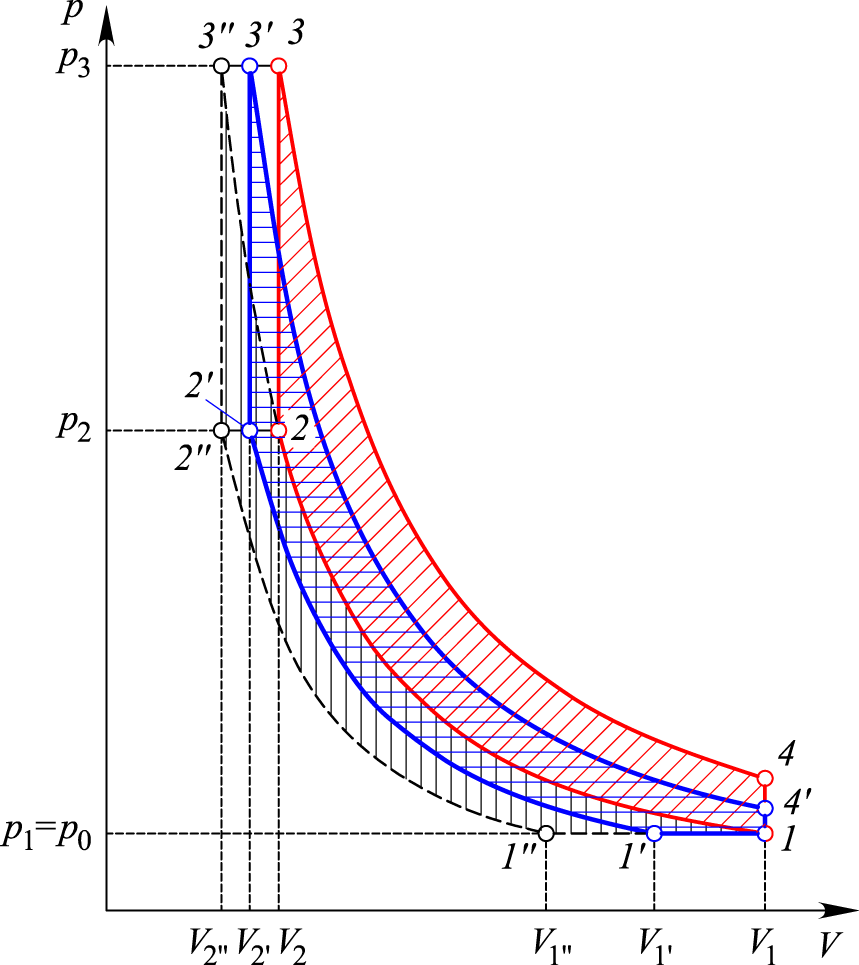
Рис. 7.
Порівняння циклів Отто й Аткінсона
Fig. 7. Comparison
of Otto and Atkinson cycles
(що
відповідає циклові
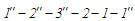 ,
властивому газотурбінному двигуну).
,
властивому газотурбінному двигуну).
Тож у
циклі Аткінсона впродовж ізохорного
процесу
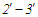 підводиться теплота (див. (5)):
підводиться теплота (див. (5)):
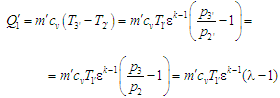 ,
(6)
,
(6)
тут узято
до уваги співвідношення:
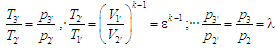 .
.
Натомість
в ізохорно-ізобарному процесі
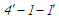 відводиться теплота:
відводиться теплота:
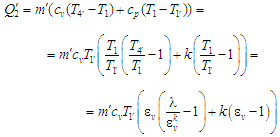 (7)
(7)
Тут узято
до уваги співвідношення:
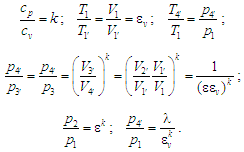
На підставі
(6) і (7) корисну дію циклу Аткінсона
визначатиме коефіцієнт:
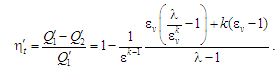 .
(8)
.
(8)
При цьому:
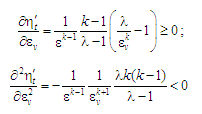 (9)
(9)
(згадаймо:
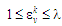 ).
Отже, залежність
).
Отже, залежність
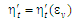 є монотонно зростаючою й опуклою догори
(її підграфік є опуклою фігурою).
Натомість корисну дію циклу Отто
визначає коефіцієнт:
є монотонно зростаючою й опуклою догори
(її підграфік є опуклою фігурою).
Натомість корисну дію циклу Отто
визначає коефіцієнт:
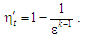 (10)
(10)
Зауважимо, що цикл,
який складають адіабатне (ізоентропне)
стискання, ізохорне нагрівання (унаслідок
спалювання палива в замкнутому об’ємі),
адіабатне (ізоентропне) розширення,
ізобарне охолодження, називають циклом
Гамфрі (Humphrey Cycle). За його допомогою
ідеалізовано описують робочий процес
клапанного пульсуючого повітряно-реактивного
двигуна.
Отож у
разі
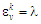 цикл Аткінсона вироджується у так
званий «газотурбінний» цикл (цикл
Гамфрі), для якого (див. (8), (9)):
цикл Аткінсона вироджується у так
званий «газотурбінний» цикл (цикл
Гамфрі), для якого (див. (8), (9)):
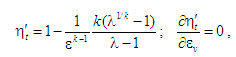
а в разі
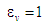 збігається з циклом Отто, для якого
збігається з циклом Отто, для якого
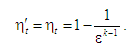
Робоче тіло в циклі
Отто, який узято за основу, виконує
роботу:
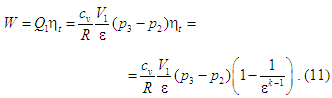
Робота
ж меншої кількості робочого тіла в
циклі Аткінсона, похідному від циклу
Отто, звісно, буде меншою
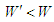 .
Щоб ці роботи стали однаковими, потрібно
синтезувати новий цикл Аткінсона зі
збільшеним робочим об’ємом
.
Щоб ці роботи стали однаковими, потрібно
синтезувати новий цикл Аткінсона зі
збільшеним робочим об’ємом
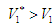 і, відповідно, більшою кількістю
підведеної теплоти
і, відповідно, більшою кількістю
підведеної теплоти
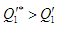 :
:
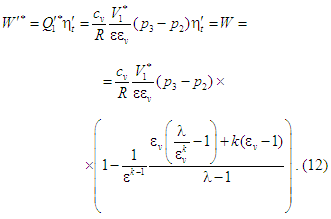
Відтак
із (11) і (12) випливає співвідношення:
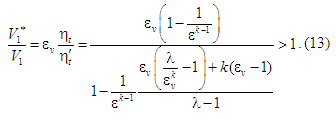
Вагоме
збільшення коефіцієнта корисної дії
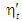 двигуна внутрішнього згоряння в разі
втілення циклу Аткінсона–Міллера на
основі циклу Отто потребує істотного
збільшення об’єму робочого простору.
Це можна проілюструвати на прикладі
ідеального двигуна з параметрами
двигуна внутрішнього згоряння в разі
втілення циклу Аткінсона–Міллера на
основі циклу Отто потребує істотного
збільшення об’єму робочого простору.
Це можна проілюструвати на прикладі
ідеального двигуна з параметрами
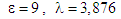 ,
(рис. 8, точки штрихової лінії відповідають
«газотурбінному» циклові Гамфрі). Зі
збільшенням
,
(рис. 8, точки штрихової лінії відповідають
«газотурбінному» циклові Гамфрі). Зі
збільшенням
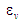 об’єм робочого простору зростає майже
лінійно пропорційно (рис. 8, а).
Натомість коефіцієнт корисної дії
об’єм робочого простору зростає майже
лінійно пропорційно (рис. 8, а).
Натомість коефіцієнт корисної дії
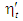 дуже чутливий до зміни і
дуже чутливий до зміни і
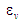 ,
і
,
і
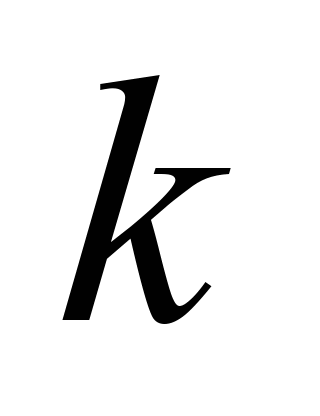 (рис 8, б).
У разі
(рис 8, б).
У разі
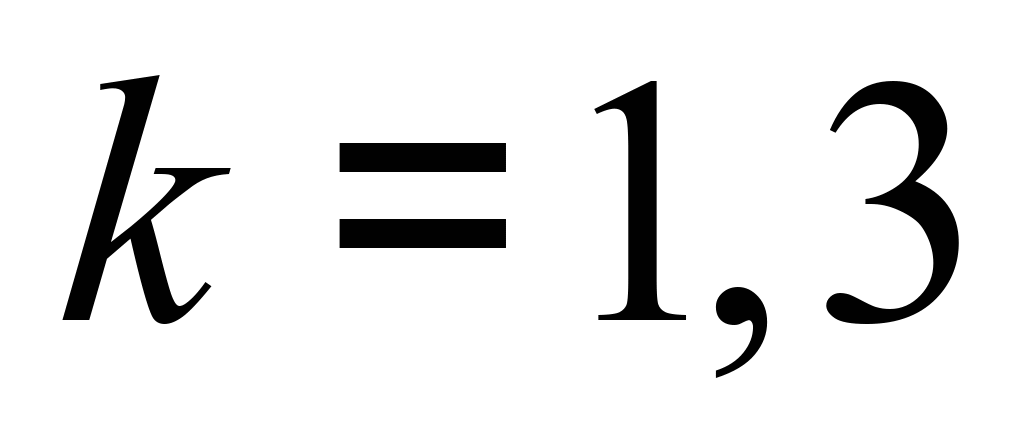 ,
наприклад, максимально можливе зростання
коефіцієнта корисної дії
,
наприклад, максимально можливе зростання
коефіцієнта корисної дії
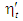 двигуна в 1,19 раза (приблизно на 20 % –
від значення 0,48, відповідного циклові
Отто, до значення 0,57, відповідного
«газотурбінному» циклові Аткінсона–Міллера)
потребує збільшення об’єму робочого
простору у 2,4 раза (рис. 8, в).
двигуна в 1,19 раза (приблизно на 20 % –
від значення 0,48, відповідного циклові
Отто, до значення 0,57, відповідного
«газотурбінному» циклові Аткінсона–Міллера)
потребує збільшення об’єму робочого
простору у 2,4 раза (рис. 8, в).
Не виходячи
за межі властивостей власне двигуна
внутрішнього згоряння, бездоганно й
вичерпно з’ясувати, чи доцільно таким
способом підвищувати його енергетичну
ефективність, ніяк не вдасться. З одного
боку, високий коефіцієнт корисної дії
теплового двигуна – це запорука істотних
заощаджень пального та помітного
зниження негативних впливів на довкілля
за увесь життєвий цикл будь-якої машини
з таким двигуном. Але певний сенс
таки має евристична гіпотеза: зростання
розмірів провокує зростання маси
настільки, що ставить під загрозу
міцність конструкції, а отже, виникає
потреба в підсиленні та відповідному
її ускладненні (маса конструкції зростає
пропорційно кубові лінійного розміру,
а от її міцність – пропорційно квадратові
лінійного розміру; можна казати, що
маса породжує ще масу). Очевидно, що
зайві габарити автомобіля, наприклад,
через надмірні розміри двигуна погіршують
його аеродинамічність і провокують
тим самим постійні додаткові витрати
енергії. Або ж вилучення з життєвого
чи вантажного простору автомобіля
частини його об’єму можна трактувати
як зазіхання на потенційну ефективність,
продуктивність автомобіля. Надлишкова
маса автомобіля породжує також зростання
опору коченню, погіршує його динамічність,
знижує безпечність у разі зіткнення з
перешкодою.
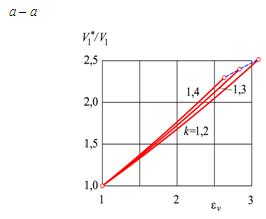
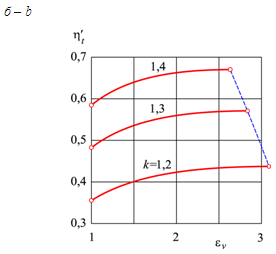

Рис. 8.
Взаємозв’язок між коефіцієнтом корисної
дії та робочим об’ємом ідеального
двигуна
Fig. 8. The
relationship between efficiency coefficient and
the displacement of an ideal engine
Формально (без
урахування можливих зв’язків між
параметрами, див. (13))
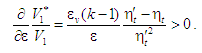
Зростання
стиску (ступеня стискування)
 нібито сприяє зростанню різниці між
габаритами двигунів Отто й Аткінсона.
Тобто підвищення засобами Аткінсона
ефективності двигуна Отто супроводжується
тим більшим зростанням робочого об’єму,
чим ефективнішим є двигун від самого
початку.
нібито сприяє зростанню різниці між
габаритами двигунів Отто й Аткінсона.
Тобто підвищення засобами Аткінсона
ефективності двигуна Отто супроводжується
тим більшим зростанням робочого об’єму,
чим ефективнішим є двигун від самого
початку.
Регулювання
тягових потенцій двигуна.
Розгляньмо тепер
теоретичний цикл Аткінсона окремо
(рис. 9). Хай ідеться, наприклад, про цикл
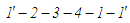 ,
у якому в механічну роботу перетворюється
певна номінальна кількість теплоти
,
у якому в механічну роботу перетворюється
певна номінальна кількість теплоти
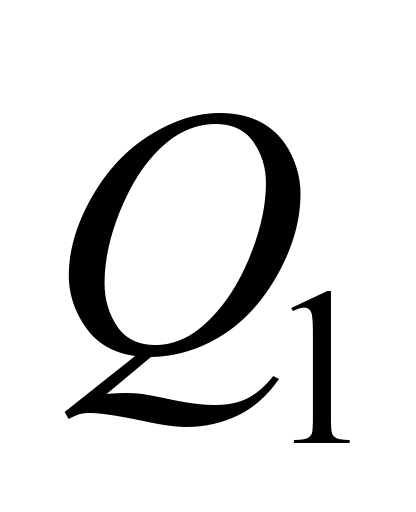 ,
що підводиться до робочого тіла в
ізохорному процесі
,
що підводиться до робочого тіла в
ізохорному процесі
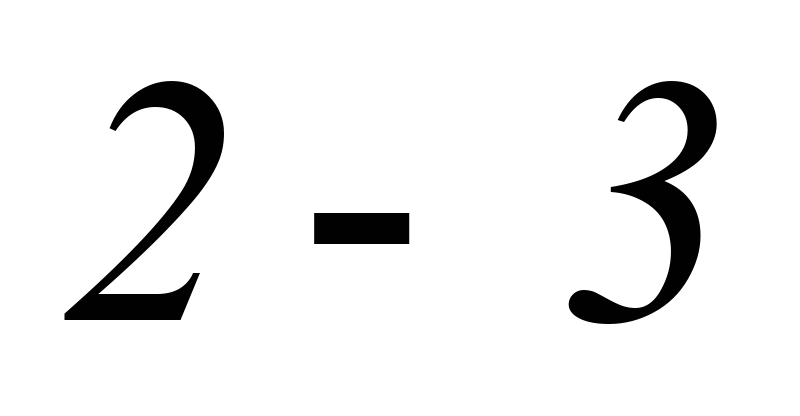 .
Якщо навантага на двигун зменшиться,
то кількість теплоти, яку слід підводити
до робочого тіла, звісно, також має
зменшитись. Вважатимемо, що це не
позначиться на значенні величини
.
Якщо навантага на двигун зменшиться,
то кількість теплоти, яку слід підводити
до робочого тіла, звісно, також має
зменшитись. Вважатимемо, що це не
позначиться на значенні величини
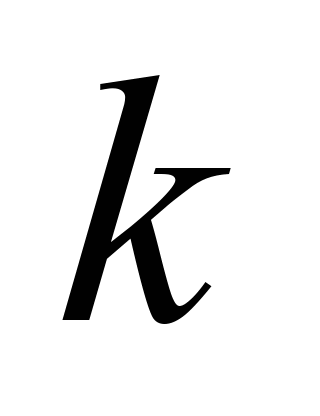 .
Тож буде реалізовано, наприклад, цикл
.
Тож буде реалізовано, наприклад, цикл
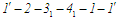 з підведенням теплоти в ізохорному
процесі
з підведенням теплоти в ізохорному
процесі
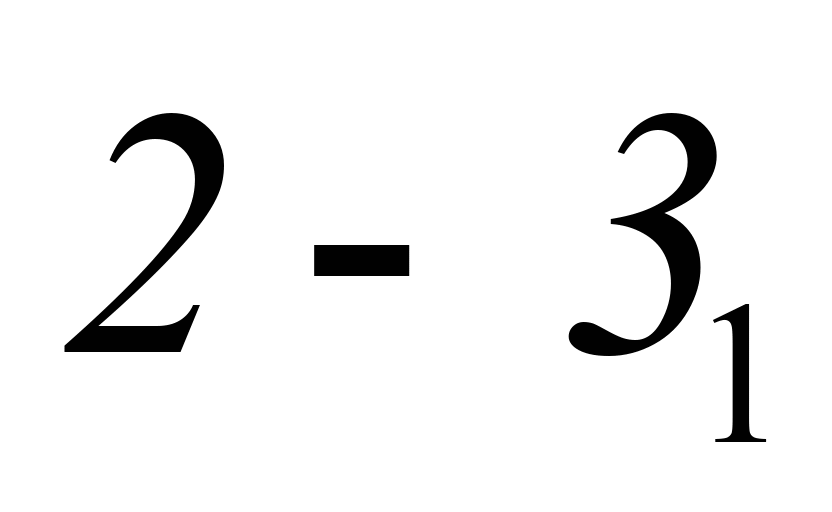 .
Кількість теплоти
.
Кількість теплоти
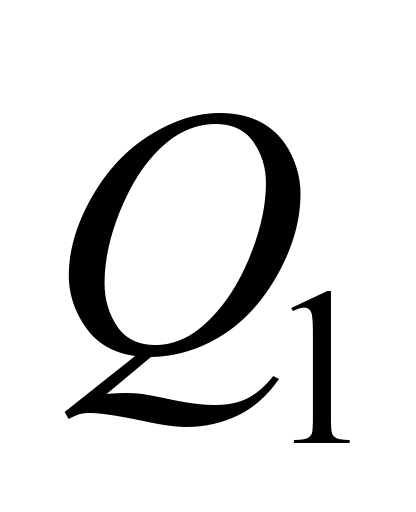 можна зменшувати без застережень, поки
не виникне граничний цикл
можна зменшувати без застережень, поки
не виникне граничний цикл
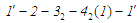 із суто ізобарним процесом
із суто ізобарним процесом
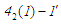 відведення теплоти
відведення теплоти
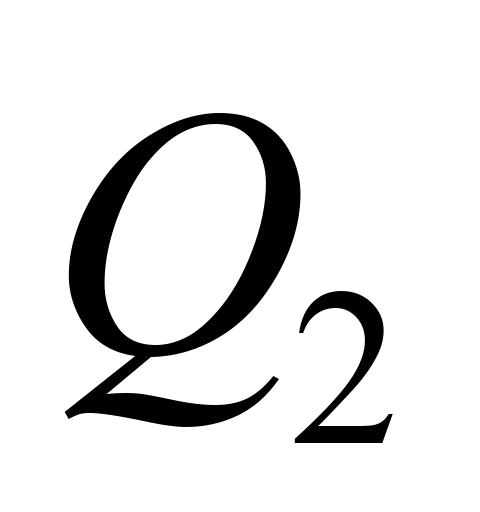 .
Цикл із ще меншим значенням
.
Цикл із ще меншим значенням
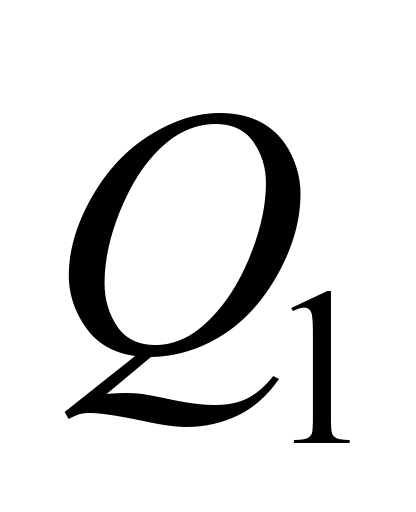 у принципі, не можливий. Наприклад, для
того щоб реалізувати цикл
у принципі, не можливий. Наприклад, для
того щоб реалізувати цикл
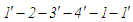 (який зображено ще й окремо), необхідно
було б у процесі
(який зображено ще й окремо), необхідно
було б у процесі
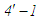 підводити додаткову теплоту
підводити додаткову теплоту
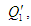 що свідчило б про втрату ефективності
двигуна.
що свідчило б про втрату ефективності
двигуна.
У реальному
двигуні внутрішнього згоряння можна
було б сподіватися на допомогу маховика,
який за достатньої кількості акумульованої
кінетичної енергії міг би за інерцією
допровадити поршень до нижнього мертвого
положення. Але в такому разі він (маховик)
мусив би поповнити свою енергію на
іншій ділянці процесу розширення
робочого тіла (можливо, у попередньому
циклі). Тож що теоретично, що практично
втрата енергетичної ефективності
двигуна Аткінсона у випадку малих
навантаг є неминучою. Звідси, зокрема,
випливає, що двигун Аткінсона, у якого
за номінальний править «газотурбінний»
цикл, неминуче губить свою перевагу за
будь-яких часткових навантаг. Натомість
змінюваність навантажень на енергетичній
ефективності двигуна Отто (10). ніяк не
позначатиметься. Відтак важко сказати,
що краще: реалізовувати дещо нижчу
ефективність, але постійно одну й ту
саму, чи мати можливість реалізовувати
вищу ефективність тільки
на номінальному режимі роботи двигуна,
але губити її на всіх інших режимах.
Мабуть,
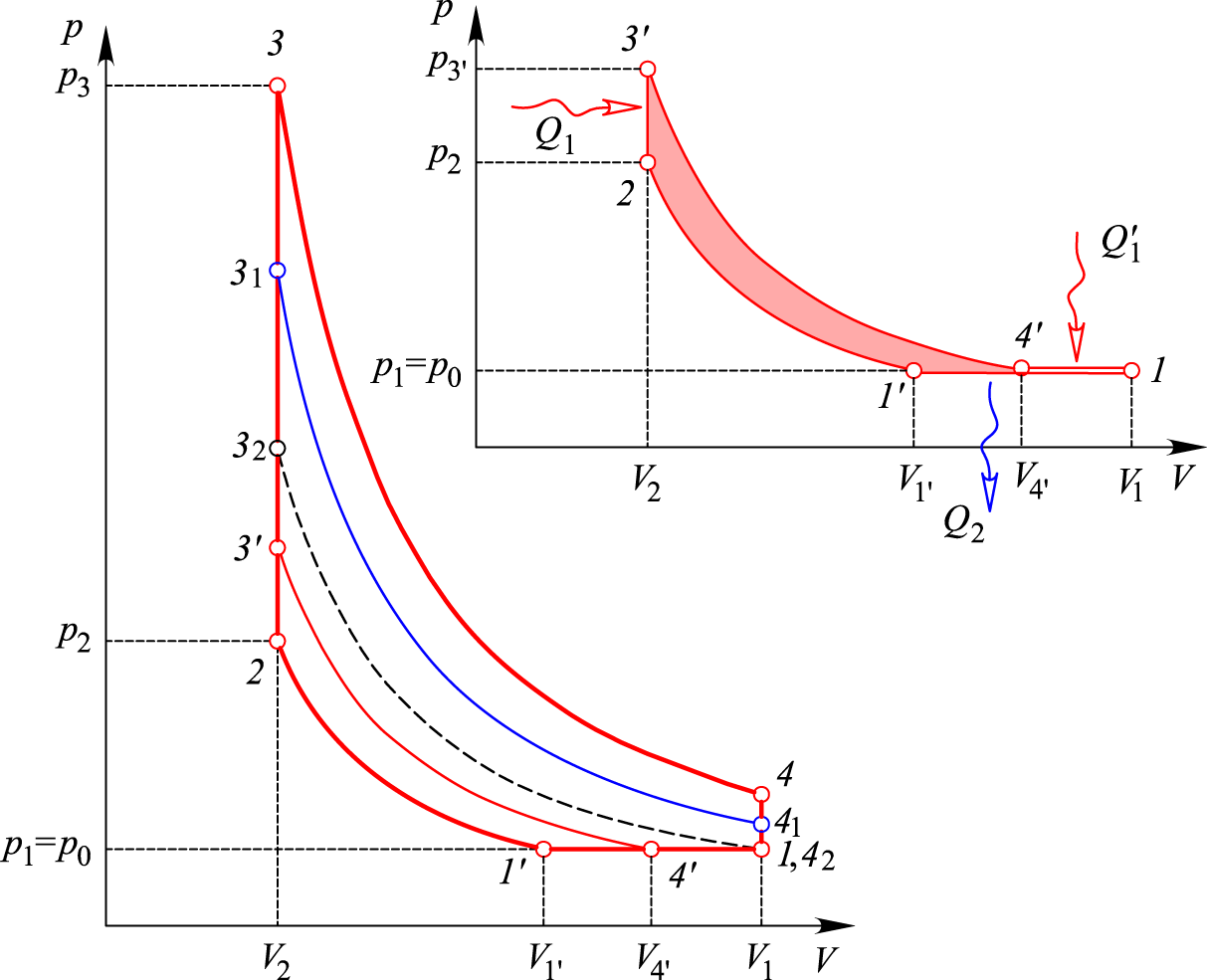
Рис. 9. Цикли
Аткінсона за різних навантаг на двигун
Fig. 9. Atkinson
cycles under different loads on the engine
двигун
Отто – це все-таки вигідний технічний
компроміс між двотактним двигуном і
двигуном Аткінсона.
Звернімося
до термодинамічного циклу
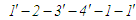 ,
що «оперує» теплотами:
,
що «оперує» теплотами:
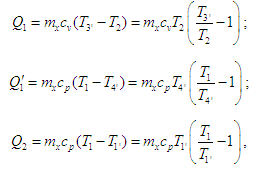 ;
;
де
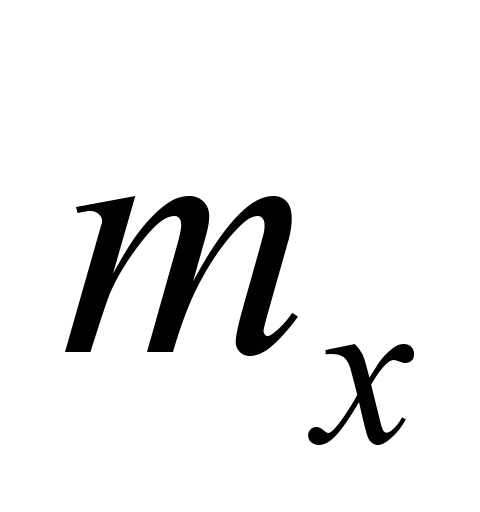 – маса робочого тіла на поточному
режимі роботи двигуна. Тож коефіцієнт
корисної дії циклу визначатиме формула:
– маса робочого тіла на поточному
режимі роботи двигуна. Тож коефіцієнт
корисної дії циклу визначатиме формула:
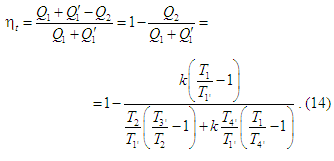
Вважатимемо
величину
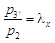 змінним параметром, що характеризує
навантагу на двигун. Беручи до уваги
рівняння адіабат, матимемо співвідношення:
змінним параметром, що характеризує
навантагу на двигун. Беручи до уваги
рівняння адіабат, матимемо співвідношення:
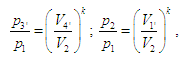
звідки
випливає рівність
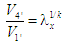 .
Дійсним є співвідношення:
.
Дійсним є співвідношення:
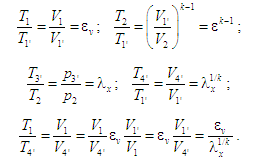
Тож
формулу (14) є підстави подати у вигляді:
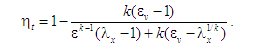
Відтак
виникає можливість унаочнити той факт,
що за часткових навантаг двигун може
істотно втрачати свою енергетичну
ефективність (рис. 10). Наприклад,
порівнюючи графік (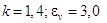 – двигун Аткінсона) і графік (
– двигун Аткінсона) і графік (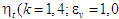 –двигун Отто), можна відзначити, що
помітне зростання ККД у разі достатньо
великих навантаг, коли
–двигун Отто), можна відзначити, що
помітне зростання ККД у разі достатньо
великих навантаг, коли
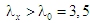 ,
супроводжується істотним його падінням
у разі малих навантаг, коли
,
супроводжується істотним його падінням
у разі малих навантаг, коли
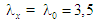 .
Зі зменшенням величини
.
Зі зменшенням величини
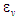 перевага двигуна Аткінсона стає менш
істотною, зате поширюється на більшу
множину режимів.
перевага двигуна Аткінсона стає менш
істотною, зате поширюється на більшу
множину режимів.
Кількість
робочого тіла, що потрапляє в робочий
простір двигуна, визначатимемо за
формулою:
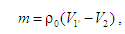
де
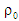 – умовна густина робочого тіла.
– умовна густина робочого тіла.
Позначмо
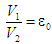 – незмінний параметр Змінюваний
параметр
– незмінний параметр Змінюваний
параметр
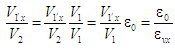 двигуна
Аткінсона не повинен би (умовно задля
уникнення детонації) перевищувати
регламентоване значення величини
двигуна
Аткінсона не повинен би (умовно задля
уникнення детонації) перевищувати
регламентоване значення величини
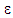 ,
яке притаманне також порівнюваному
двигуну Отто. Отож
,
яке притаманне також порівнюваному
двигуну Отто. Отож
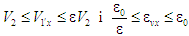 .
Це накладає відповідні обмеження на
можливості варіювання тяги двигуна
Аткінсона зміною параметра
.
Це накладає відповідні обмеження на
можливості варіювання тяги двигуна
Аткінсона зміною параметра
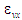 .
.
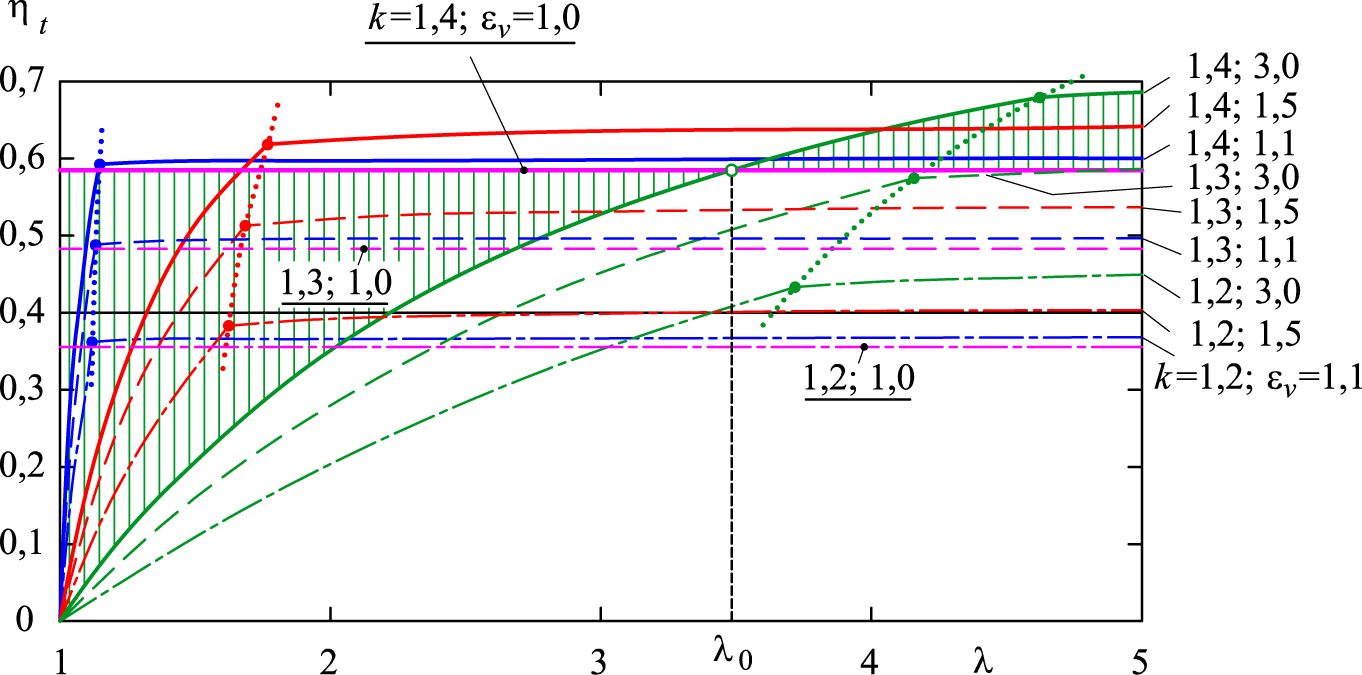
Рис. 10.
Ефективність циклів Аткінсона за різних
навантаг на двигун
Fig. 10. The
efficiency of Atkinson cycles at different loads on the
engine
Якщо
max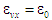 ,
то перевага двигуна Аткінсона над
двигуном Отто за енергоефективністю
на номінальному режимі й за достатньо
великих навантаг зменшується. Але при
цьому існуватиме можливість регулювати
часткові режими аж до марного ходу, не
використовуючи умовний цикл із
підведенням теплоти в кінці розширення
(рис. 9, верхня схема). Натомість у разі
,
то перевага двигуна Аткінсона над
двигуном Отто за енергоефективністю
на номінальному режимі й за достатньо
великих навантаг зменшується. Але при
цьому існуватиме можливість регулювати
часткові режими аж до марного ходу, не
використовуючи умовний цикл із
підведенням теплоти в кінці розширення
(рис. 9, верхня схема). Натомість у разі
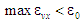 гіршою буде енергоефективність на
режимах часткових навантаг.
гіршою буде енергоефективність на
режимах часткових навантаг.
Розглядаючи
ідеальний цикл Аткінсона, (рис. 11,
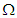 – область допустимих адіабат),
розрізнятимемо загальний (рис. 11, а)
та вироджений (рис. 11, б)
цикли. Задля унаочнення аналізу візьмімо
для прикладу
– область допустимих адіабат),
розрізнятимемо загальний (рис. 11, а)
та вироджений (рис. 11, б)
цикли. Задля унаочнення аналізу візьмімо
для прикладу
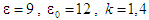
Стосовно
загального циклу
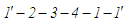 (рис. 11, а),
оперуючи співвідношеннями
(рис. 11, а),
оперуючи співвідношеннями
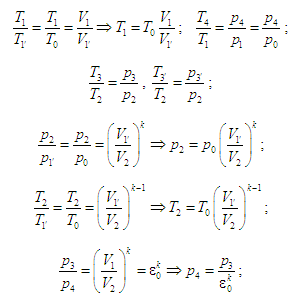
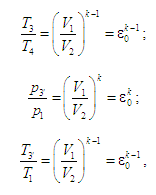
можна визначити
теплоту
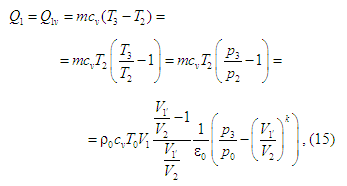
що підводиться до
робочого тіла, і теплоти
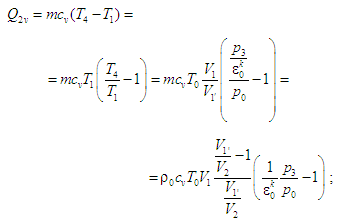
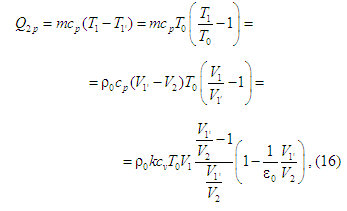
що
відводяться від нього. Відтак у циклі
буде виконана робота:
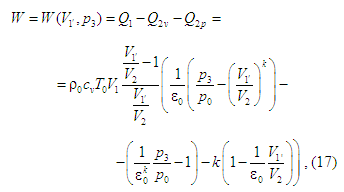
із
коефіцієнтом корисної дії:
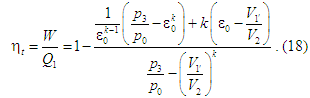
Стосовно
ж циклу
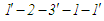 (у певному сенсі граничного) дійсними
є співвідношення:
(у певному сенсі граничного) дійсними
є співвідношення:
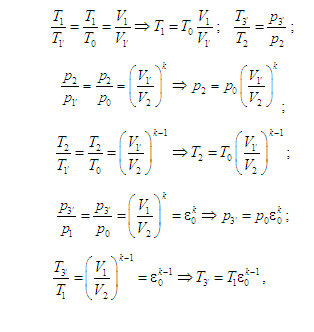
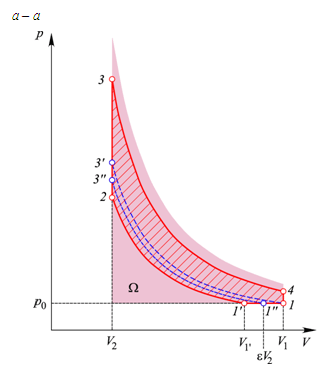
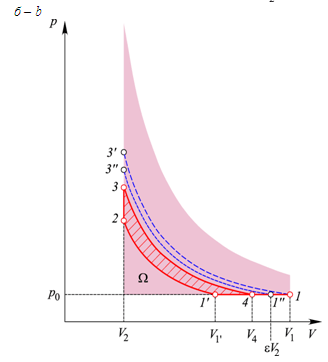
Рис. 11. Два
типи циклів Аткінсона
Fig. 11. Two types
of Atkinson cycles
а тому
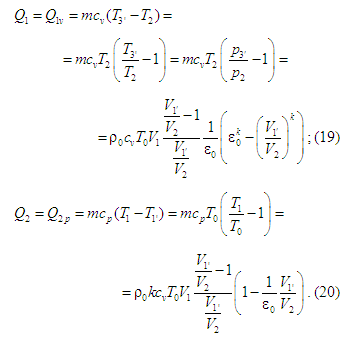
Вирази
(19) і (20) випливають також, як і слід було
сподіватись, із виразів (15) і (16) у разі
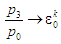 .
.
Формули
(17) і (18) мають сенс у разі
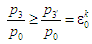 .
У разі ж
.
У разі ж
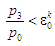 основний термодинамічний цикл (рис.
11, а)
вироджується у цикл із вимушеним
підведенням теплоти в кінці такту
розширення робочого тіла (рис. 9, схема
вгорі-праворуч, та рис. 11, б).
основний термодинамічний цикл (рис.
11, а)
вироджується у цикл із вимушеним
підведенням теплоти в кінці такту
розширення робочого тіла (рис. 9, схема
вгорі-праворуч, та рис. 11, б).
Співвідношення
(рис. 11, б)
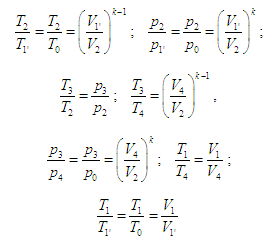
дають змогу визначити
такі величини:
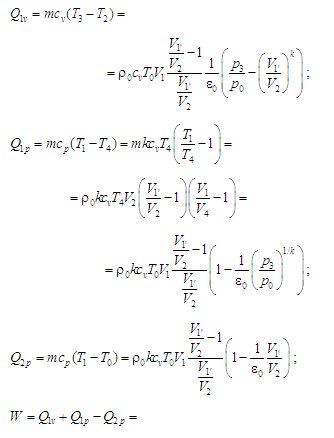
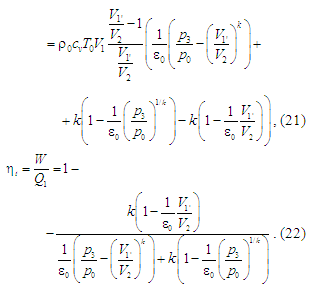 ;
;
Формули (21) і (22)
мають сенс у разі
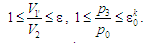
Характер
залежності умовної роботи циклу
Аткінсона
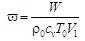
від параметрів
керування тягою двигуна
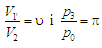
ілюструє
рис. 12. Величину
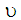 є сенс трактувати як кількісну
характеристику робочого тіла, а
величину
є сенс трактувати як кількісну
характеристику робочого тіла, а
величину
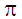 – як якісну характеристику. Вертикальна
пряма
– як якісну характеристику. Вертикальна
пряма
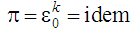 ділить діаграму на ліву частину, що
відповідає виродженим циклам, і праву,
яка відповідає загальним циклам.
Очевидно, що функція
ділить діаграму на ліву частину, що
відповідає виродженим циклам, і праву,
яка відповідає загальним циклам.
Очевидно, що функція
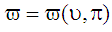 не належить до монотонних.
не належить до монотонних.
Загалом
немонотонною є й залежність коефіцієнта
корисної дії
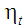 від прийнятих режимних (регулювальних)
параметрів (характеристик)
від прийнятих режимних (регулювальних)
параметрів (характеристик)
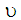 та
та
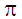 (рис. 13). Але за кожного фіксованого
значення параметра
(рис. 13). Але за кожного фіксованого
значення параметра
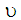 вона все ж монотонно зростаюча. Коефіцієнт
корисної дії
вона все ж монотонно зростаюча. Коефіцієнт
корисної дії
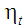 циклу Аткінсона, звісно, за певних
значень
циклу Аткінсона, звісно, за певних
значень
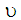 і
і
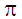 може перевищувати коефіцієнт корисної
дії
може перевищувати коефіцієнт корисної
дії
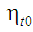 циклу Отто, якому відповідають задані
параметри
циклу Отто, якому відповідають задані
параметри
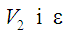 .
У разі
.
У разі
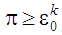 безперечно енергетично найефективнішими
є цикли з параметром
безперечно енергетично найефективнішими
є цикли з параметром
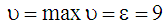 .
.
За потреби
керувати умовною роботою
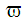 у бік її зменшення спочатку, за
можливості, доцільно досягнути й
зберігати максимальним значення
величини
у бік її зменшення спочатку, за
можливості, доцільно досягнути й
зберігати максимальним значення
величини
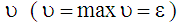 ,
зменшуючи тільки значення параметра
,
зменшуючи тільки значення параметра
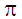 ,
аж доки далі не доведеться одночасно
зменшувати ще й значення величини
,
аж доки далі не доведеться одночасно
зменшувати ще й значення величини
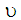 (рис. 14). Наприклад, у разі
(рис. 14). Наприклад, у разі
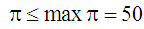 керувати роботою циклу доцільно вздовж
лінії
керувати роботою циклу доцільно вздовж
лінії
 .
У цьому прикладі коефіцієнт корисної
дії циклу Аткінсона досягає найбільшого
значення
.
У цьому прикладі коефіцієнт корисної
дії циклу Аткінсона досягає найбільшого
значення
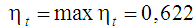 ,
що на 6 % є більшим за значення
,
що на 6 % є більшим за значення
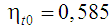 коефіцієнта корисної дії, відповідного
циклу Отто. Але при цьому розмір двигуна
Аткінсона в
коефіцієнта корисної дії, відповідного
циклу Отто. Але при цьому розмір двигуна
Аткінсона в
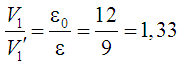 раза (на третину) буде більшим.
раза (на третину) буде більшим.
Тож якщо
в процесі конструювання двигуна
Аткінсона–Міллера стають помітними
енергоощадні переваги циклу Гамфрі,
то в процесі регулювання тяги синтезованого
двигуна такого кшталту переваги цього
циклу вже не простежуються. Справді
(рис. 13), режими, яким властиве співвідношення
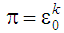 ,
загалом не мають переваги перед режимами,
яким властиві співвідношення
,
загалом не мають переваги перед режимами,
яким властиві співвідношення
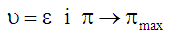 (
(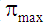 – фізично допустимі значення параметра
– фізично допустимі значення параметра
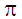 ).
).
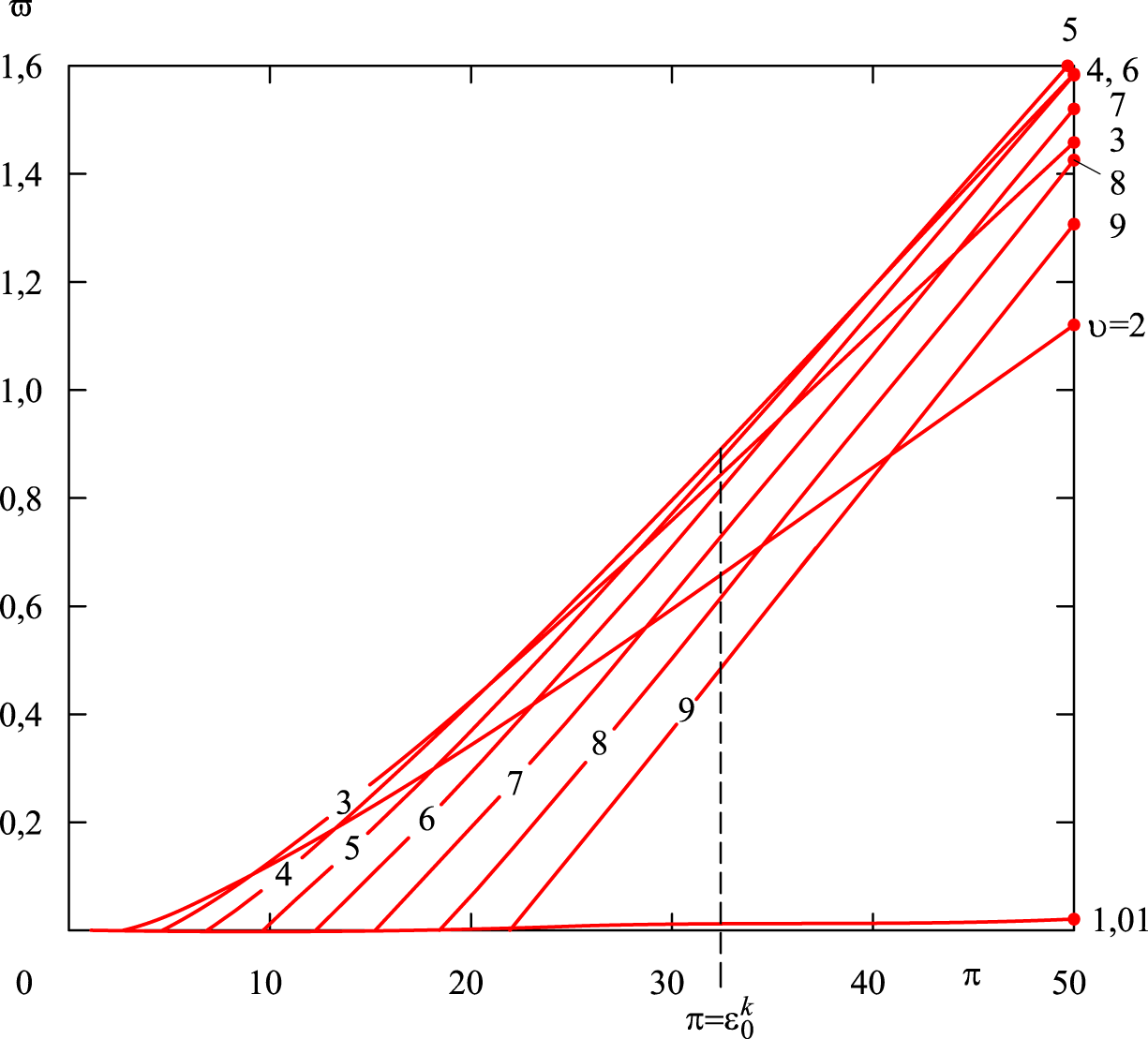
Рис. 12.
Залежність умовної роботи двигуна від
регулювальних параметрів
Fig. 12. Dependence
of conditional operation of the engine on adjustment parameters
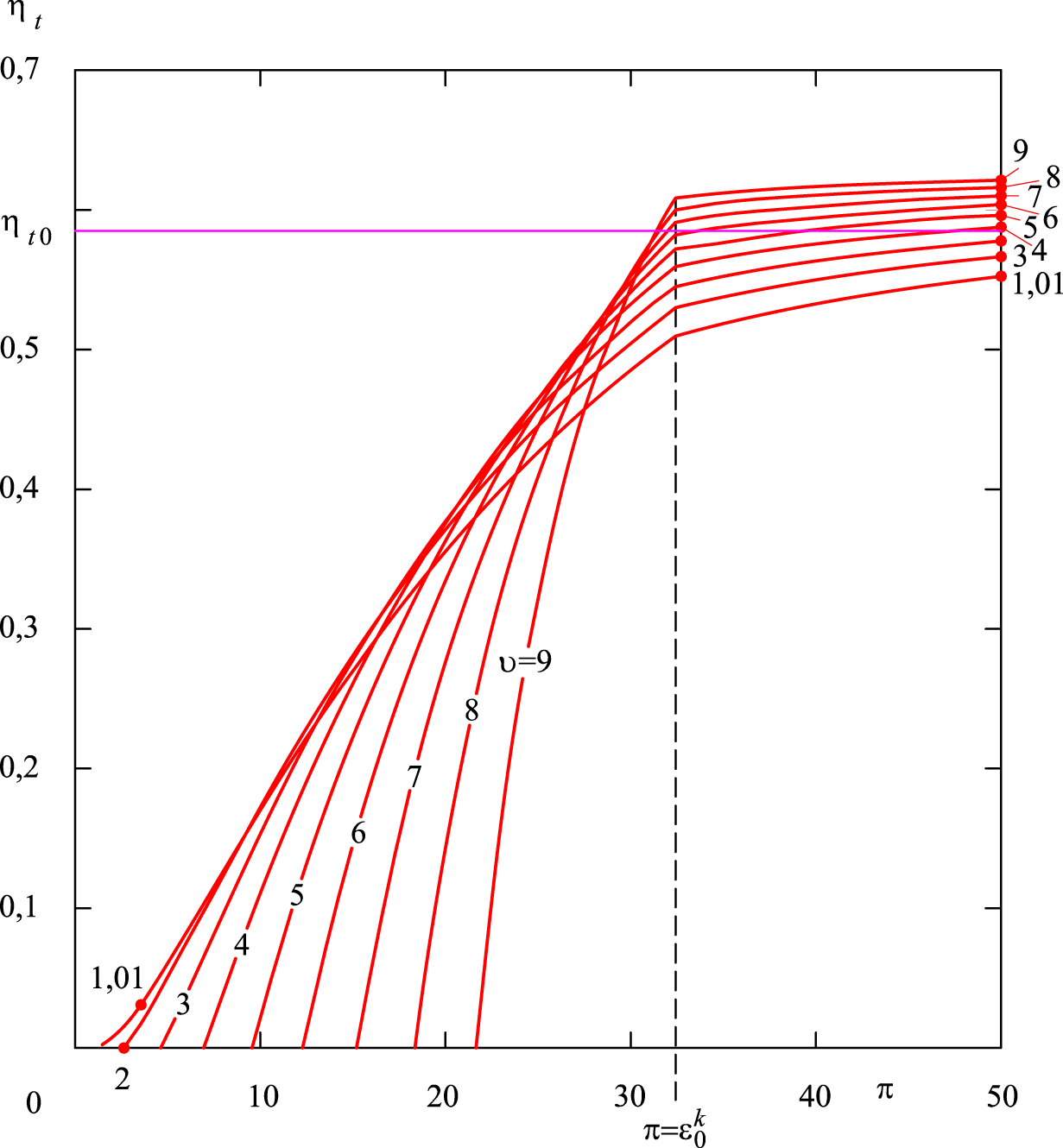
Рис. 13.
Залежність коефіцієнта корисної дії
двигуна від регулювальних параметрів
Fig. 13.
Dependence of efficiency coefficient of
the engine on adjustment parameters
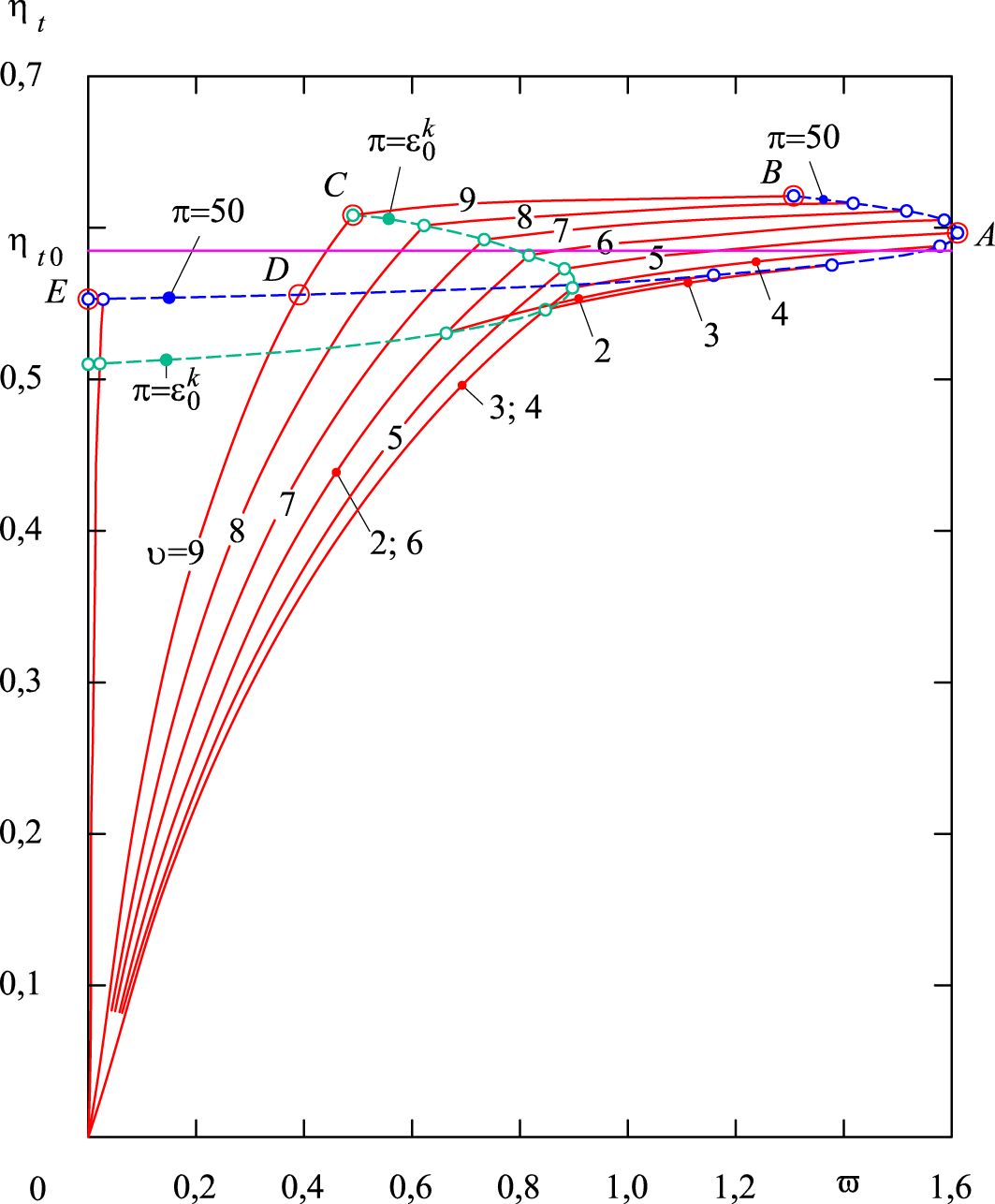
Рис. 14.
Взаємозумовленість ефективності
двигуна й регулювальних параметрів
Fig. 14.
Interdependence of engine efficiency and adjustment parameters
Об’єктивно не
вдасться побачити істинний рівень
досконалості двигуна, залишаючись у
рамках суто його власної парадигми, не
беручи до уваги нічого з того, що може
виявитися в системі, куди його залучать
працювати. Найважливішими системними
ознаками досконалості двигуна є ступінь
потенційної автономності, енергоощадність,
енергоефективність, екологічність,
масогабаритність. І всі ці ознаки так
чи інакше позначаться на властивостях
та ефективності машини з приводом від
цього двигуна.
При цьому доводиться
розрізняти конструктивні, робочі та
функційні масогабарити. Наприклад,
звичний двигун Аткінсона поступається
двигунові Отто як за конструктивними,
так і робочими масогабаритами, але є
привабливішим за функційними
масогабаритами – робочий цикл
здійснюється не за два, а за один оберт
його вала. Планетарно-зубчастий хитневий
механізм перетворює звичний двигун
Аткінсона на конструктивно компактніший,
але повний робочий цикл у ньому
здійснюватиметься вже за два оберти
вихідного вала. Та й за робочими
масогабаритами він все одно поступатиметься
двигуну Отто, як і, зрештою, двигун
Міллера.
Перелічені системні
ознаки досконалості двигуна в значній
мірі взаємопов’язані. Низька
енергоощадність негативно позначається
на екологічності та до певної міри
обмежує автономність. Підвищення ж
енергоощадності, вимірюваної коефіцієнтом
корисної дії, знижує тягові потенції
двигуна, його енергоефективність, тобто
здатність перетворити більше теплоти
на більшу кількість роботи. Взаємозв’язок
між енергоощадністю й енергоефективністю
відносно легко ідеалізувати й тим самим
унаочнити засобами аналізу термодинамічних
циклів, особливо на прикладі двигуна
Аткінсона–Міллера.
Наукова новизна
та практична
значимість
З’ясувалось, що
двигунові Аткінсона–Міллера справді
потенційно властиві вищі значення
коефіцієнта корисної дії порівняно з
двигуном Отто. Але при цьому зменшується
робота, яку цей двигун здатен продукувати
в робочому просторі такого самого
об’єму, що й у традиційного двигуна
Отто. Щоб відновити його тягові потенції,
доведеться збільшити робочий об’єм
(літраж), жертвуючи тим самим можливими
масогабаритними перевагами. При цьому
робочий об’єм формально вигідно
збільшувати, аж поки робочий цикл
Аткінсона–Міллера не виродиться в
цикл Гамфрі. Проте коли виникає потреба
зменшувати тягу двигуна Аткінсона–Міллера
в разі зменшення навантаги на його
валу, цикл Гамфрі перестає бути
привабливим.
З одного
боку, зростання коефіцієнта корисної
дії теплового двигуна сприяє істотному
заощадженню пального та зниженню загроз
довкіллю упродовж життєвого циклу
машини з приводом від такого
енергоощадного двигуна. Але зростання
масогабаритних розмірів двигуна
внаслідок утілення енергоощадного
робочого
циклу Аткінсона–Міллера
провокує
зростання маси двигуна настільки, що
ставить під загрозу міцність конструкції.
Тож виникає потреба в її підсиленні: у
першому наближенні маса конструкції
зростає пропорційно кубові лінійного
розміру, а от її міцність – пропорційно
квадратові лінійного розміру; можна
стверджувати, що кожна додаткова маса
породжує ще нову масу. Надлишкові,
зумовлені надмірними розмірами двигуна,
габарити автомобіля, наприклад,
погіршують його аеродинамічність і
провокують тим самим постійні додаткові
витрати енергії в процесі реалізації
транспортних функцій. Або ж вилучення
з життєвого чи вантажного простору
автомобіля частини його об’єму можна
трактувати як зниження потенційної
продуктивності автомобіля. Надмірна
маса автомобіля призводить також до
зростання опору коченню коліс, погіршує
його розгінну й гальмівну динамічність,
знижує рівень безпечності в разі
зіткнення з перешкодою. Отже, підвищення
таким способом коефіцієнта корисної
дії теплового двигуна насправді може
й не визнаватися як удосконалення через
оцінку набутих робочою чи транспортною
машиною експлуатаційних властивостей.
Масогабарити
практично завжди тлумачили як надзвичайно
вагому характеристику досконалості
двигуна. Турбонаддув, наприклад, спочатку
використовували саме для підвищення
потужності двигуна в рамках заданих
його масогабаритів. Це тільки згодом
наддув став ще й засобом підвищення
енергоефективності та екологічності.
Підвищення ж потужності шляхом збільшення
робочого об’єму вважалось не дуже
доречним через зростання матеріаломісткості
конструкції та поточних механічних
втрат енергії в процесі її функціювання.
Потужність за фіксованого робочого
об’єму підвищували радше збільшенням
номінальної частоти обертання
колінчастого вала. Щоправда, це призводило
до зростання масогабаритів трансмісії
робочої машини чи автомобіля.
Висновки
1. Швидке (аж до
миттєвого) внутрішнє згоряння пальної
суміші в тепловому двигуні є
найефективнішим процесом перетворення
теплоти на механічну роботу.
2. Використання
теорії ідеальних термодинамічних
циклів (так званих циклів із нульовою
потужністю) насправді дозволяє дуже
простими засобами коректно й наочно
пояснити та оцінити прояв енергетично
корисного ефекту від розширення робочого
ходу в двигуні швидкого внутрішнього
згоряння.
3. Підвищення
коефіцієнта корисної дії завдяки
подовженню робочого ходу поршня вимушено
супроводжується зростанням маси й
габаритів двигуна, і тому негативно
позначається на властивостях автомобіля
з приводом від такого двигуна. Наприклад,
коефіцієнт корисної дії циклу Аткінсона
може бути на 6 % більшим за значення
коефіцієнта корисної дії відповідного
циклу Отто. Але при цьому його характерний
розмір на третину виявиться більшим.
4. Енергоефективність
двигуна Аткінсона–Міллера порівняно
з двигуном Отто є помітною на режимах
великого навантаження. Але автомобільний
двигун зазвичай працює на так званих
часткових режимах.
5. Двигун Отто є
вигідним технічним компромісом між
двотактним двигуном і двигуном Аткінсона.
СПИСОК ВИКОРИСТАНИХ
ДЖЕРЕЛ
1. Гащук П.
М. Енергія та упорядкований
рух. Львів : Українські технології,
2004. 608 с.
2. Al-Sarkhi A.,
Akash B. A., Jaber J. O., Mohsen M. S., Abu-Nada E. Efficiency of
Miller engine at maximum power density. International
Communications in Heat and Mass Transfer. 2002. Vol. 29.
Iss. 8. P. 1159–1167. DOI: 10.1016/S0735-1933(02)00444-X
3. Al-Sarkhi A.,
Jaber J. O., Probert S. D. Efficiency of a Miller engine. Applied
Energy. 2006. Vol. 83. Iss. 4. P. 343–351.
DOI: 10.1016/j.apenergy.2005.04.003
4. Andresen B.,
Salamon P., Berry R. S. Thermodynamics in finite time.
Physics Today. 1984. Vol.
37. Iss. 9. P. 62–70. DOI: 10.1063/1.2916405
5. Atkinson
J. Gas engine : Patent 336505A US.
USA, 1886.
6. Atkinson
J. Gas engine : Patent 367496A US.
USA, 1887.
7. Benajes J.,
Novella R., Arthozoul S., Kolodziej C. Particle Size Distribution
Measurements from Early to Late Injection Timing Low Temperature
Combustion in a Heavy Duty Diesel Engine. SAE
International Journal of Fuels and Lubricants. 2010. Vol.
3. Iss. 1. P. 567–581. DOI: 10.4271/2010-01-1121
8. Benajes J.,
Serrano J. R., Molina S., Novella R. Potential of Atkinson cycle
combined with EGR for pollutant control in a HD diesel engine.
Energy Conversion and Management.
2009. Vol. 50. Iss. 1. P. 174–183.
DOI: 10.1016/j.enconman.2008.08.034
9. Brijesh P.,
Sreedhara S. Exhaust emissions and its control methods in
compression ignition engines : A review. International
Journal of Automotive Technology. 2013. Vol. 14. Iss. 2.
P. 195–206. DOI: 10.1007/s12239-013-0022-2
10. Carnot S.
Réflexions
sur la puissance motrice du feu et sur les machines propres à
développer cette puissance. Paris :
Gauthier-Villars, Imprimeur-Libraire, 1872. 102 p.
11. Chen L., Zhang
W., Sun F. Power, efficiency, entropy-generation rate and ecological
optimisation for a class of generalized irreversible universal
heatengine cycles. Applied Energy.
2007. Vol. 84. Iss. 5. P. 512–525.
DOI: 10.1016/j.apenergy.2006.09.004
12. Chen Z., Konno
M., Oguma M., Yanai T. Experimental study of CI natural-gas / DME
homogeneous charge engine. SAE Technical Paper
Series. 2000. Vol. 109. Iss. 3. P.
442–451.DOI: 10.4271/2000-01-0329
13. Clarke D.,
Smith W. J. S The Simulation,
Implementation and Analysis of the Miller Cycle Using an Inlet
Control Rotary Valve. SAE Technical Paper
Series. 1997. P. 61–70.
DOI: 10.4271/970336
14. Cornell S. O.,
Leman S. A. Engine valve actuation system
(Caterpillar) : Patent 7004122 US. USA, 2006.
15. Demirci
O. K.,
Uyumaz
A.,
Sarıdemir
S.
and Çinar
C.
Performance and Emission Characteristics of a Miller Cycle Engine.
International Journal of Automotive Technology
(IJAET). 2018.Vol/.7. Iss. 3. P. 107–116.
DOI: 10.18245/ijaet.486408
16. Ebrahimi R.
Effects of mean piston speed, equivalence ratio and cylinder wall
temperature on performance of an Atkinson engine. Mathematical
and Computer Modelling. 2011. Vol. 53. Iss. 5–6. P.
1289–1297. DOI: 10.1016/j.mcm.2010.12.015
17. Ebrahimi R.
Performance analysis of an irreversible Miller cycle with
considerations of relative air-fuel ratio and stroke length. Applied
Mathematical Modelling. 2012. Vol. 36. Iss. 9. P.
4073–4079. DOI: 10.1016/j.apm.2011.11.031
18. Edwards S.,
Frankle G., Wirbeleit F., Raab A. The Potential of a Combined Miller
Cycle and Internal EGR Engine for Future Heavy Duty Truck
Applications. SAE Technical Paper. 1998. P. 1–21.
DOI: 10.4271/980180
19. Ehleskog M.,
Gjirja S., Denbratt I. Effects of Variable Inlet Valve Timing and
Swirl Ratio on Combustion and Emissions in a Heavy Duty Diesel
Engine. SAE Technical Paper. 2012.
P. 1–12. DOI: 10.4271/2012-01-1719
20. Ebrahimi R.
Thermodynamic modeling of performance of a Miller cycle with engine
speed and variable specific heat ratio of working fluid. Computers
and Mathematics with Applications. 2011. Vol. 62. P.
2169–2176. DOI: 10.1016/j.camwa.2011.07.002
21. Fukuzawa Y.,
Kakuhama Y., Shimoda H., Endo H., Tanaka K. Development of High
Efficiency Miller Cycle Gas Engine. Mitsubishi
Heavy Industries. 2001. Vol. 38, No. 3. P. 146–150.
22. Ge Y., Chen L.,
Sun F., Wu C. Effects of heat transfer and variable specific heats
of working fluid on performance of a Miller cycle. International
Journal of Ambient Energy. 2005. Vol. 26. Iss. 4. P.
203–214. DOI: 10.1080/01430750.2005.9674991
23. Ge Y., Chen L.,
Sun F., Wu C. Effects of heat transfer and friction on the
performance of an irreversible air-standard Miller cycle.
International Communications in Heat and Mass Transfer.
2005. Vol. 32. Iss. 8. P. 1045–1056.
DOI: 10.1016/j.icheatmasstransfer.2005.02.002
24. Ge Y., Chen L.,
Sun F., Wu C. Reciprocating heat-engine cycles. Applied
Energy. 2005. Vol. 81. Iss. 4.
P. 397–408.
DOI: 10.1016/j.apenergy.2004.09.007
25. Gonca
G., Hocaoglu
M. F. Performance Analysis and Simulation of a Diesel – Miller
Cycle (DiMC) Engine. Arabian
Journal for Science and Engineering. 2019. Vol. 44.
P. 5811–5824. DOI: 10.1007/s13369-019-03747-4
26. Gonca G., Sahin
B., Ust Y. Investigation of Heat Transfer Influences on Performance
of Air-Standard Irreversible Dual-Miller Cycle. Journal
of Thermophysics and Heat Transfer. 2015. Vol. 29. Iss.
4. P. 678–683. DOI: 10.2514/1.T4512
27. Goto T.,
Hatamura K., Takizawa S., Hayama N., Abe H., Kanesaka H. Development
of V6 Miller Cycle Gasoline Engine. SAE
Technical Paper. 1994. P. 1–11.
DOI: 10.4271/940198
28. Grab-Rogaliński
K., Szwaja S., Tutak W. The Miller
Cycle Based IC Engine Fuelled with a CNG / Hydrogen. Journal
of KONES. Powertrain and Transport.
2014. Vol. 21. Iss. 4. P. 137–144.
DOI: 10.5604/12314005.1130459
29. Hatamura K.,
Hayakawa M., Goto T., Hitomi M. A study of the improvement effect of
Miller-cycle on mean effective pressure limit for high-pressure
supercharged gasoline engines. JSAE Review.
1997. Vol. 18. Iss. 2. P. 101–106.
DOI: 10.1016/S0389-4304(96)00069-0
30. Heikkilä J.,
Happonen M., Murtonen T., Lehto K., Sarjovaara T., Larmi M., …
Virtanen, A. Study of Miller timing on exhaust emissions of a
hydrotreated vegetable oil (HVO) – fueled diesel engine. Journal
of the Air & Waste Management Association 2012. Vol.
62. Iss. 11. P. 1305–1312.
DOI: 10.1080/10962247.2012.708383
31. Heywood J. B.
Ideal models of engine cycles.
Singapore : McGraw-Hill Education,
1988. 930 p.
32. Higuchi N.,
Sunaga Y., Tanaka M., Shimada H. Development of a New Two-Motor
Plug-In Hybrid System. SAE International
Journal of Alternative Powertrains. 2013. Vol. 2. Iss. 1.
P. 135–145. DOI: 10.4271/2013-01-1476
33. Kong S. C. A
study of natural gas / DME combustion in HCCI engines using CFD with
detailed chemical kinetics. Fuel.
2007. Vol. 86. Iss. 10. P. 1483–1489.
DOI: 10.1016/j.fuel.2006.11.015
34. Liu J., Chen J.
Optimum performance analysis of a class of typical irreversible heat
engines with temperature-dependent heat capacities of the working
substance. International Journal of Ambient
Energy. 2010. Vol. 31. Iss. 2. P. 59–70.
DOI: 10.1080/01430750.2010.9675103
35. Martins J.,
Uzuneanu K., Ribeiro B., Jasasky O. Thermodynamic Analysis of an
Over-Expanded Engine. SAE Technical Paper.
2004. P. 1–15. DOI: 10.4271/2004-01-0617
36. Martins M. E.
S., Lanzanova T. D. M. Full-load Miller cycle with ethanol and EGR :
Potential benefits and challenges. Applied
Thermal Engineering. 2015. Vol. 90. P. 274–285.
DOI: 10.1016/j.applthermaleng.2015.06.086
37. Mikalsen R.,
Wang Y. D., Roskilly A. P. A Comparison of Miller and Otto Cycle
Natural Gas Engines for Small Scale CHP Applications. Applied
Energy. 2009. Vol. 86. Iss. 6. P. 922–927.
DOI: 10.1016/j.apenergy.2008.09.021
38. Miller R. High
expansion, spark-ignited, gas burning, internal combustion engines :
US Patent 2773490A. USA, 1952, 1956.
39. Miller
R. Supercharged
Engine : US Patent
2817322A.
USA, 1957.
40. Miller R. H.
Supercharging and Internal Cooling Cycle for High Output.
Transactions ASME. 1947. Vol. 69.
P. 453–464.
41. Miller R. H.,
Lieberherr H. U. The Miller supercharging system for Diesel and gas
engines operating characteristics. CIMAC.
1957. P. 787–803.
42. Millo F.,
Gianoglio B. M., Delneri D. Computational Analysis of Internal and
External EGR Strategies Combined with Miller Cycle Concept for a Two
Stage Turbocharged Medium Speed Marine Diesel Engine. SAE
International Journal of Engines. 2011. Vol. 4. Iss. 1.
P. 1319–1330.DOI: 10.4271/2011-01-114
43. Mo H., Yongquan
H. Y., Xiaojian M. X., Zhuo B. Investigations on the Potential of
Miller Cycle for Performance Improvement of Gas Engine. Global
Journal of Researches in Engineering : B Automotive Engineering.
2016. Vol. 16. Iss. 1. P. 37–46.
44. Niculae M.,
Clenci A., Iorga-Simăn V., Niculescu R. An Overview on the
Miller-Atkinson Over-expansion Thermodynamic Cycle. IOP
Conf. Series : Materials Science and Engineering. 2019.
Vol. 564 P. 1–7.
DOI: 10.1088/1757-899X/564/1/012125
45. Ribeiro, B.
Martins, J. Direct Comparison of an Engine Working under Otto,
Miller and Diesel Cycles : Thermodynamic Analysis and Real Engine
Performance. SAE Technical Paper.
2007. P. 1–11. DOI: 10.4271/2007-01-0261
46. Wang Y., Lin
L., Roskilly A. P., Zeng S., Huang J., He Y., Huang X., Huang H.,
Wei H., Li S., Yang J. An analytic study of applying Miller cycle to
reduce NOx emission from petrol
engine. Applied Thermal Engineering.
2007. Vol. 27. Iss. 11–12. P. 1779–1789.
DOI: 10.1016/j.applthermaleng.2007.01.013
47. Wu C.,
Puzinauskas P. V., Tsai J. S. Performance analysis and optimization
of a supercharged Miller cycle Otto engine. Applied
Thermal Engineering. 2003. Vol. 23. Iss. 5. P. 511–521.
DOI: 10.1016/S1359-4311(02)00239-9
48. Zhao Y, Chen J.
Performance analysis of an irreversible Miller heat engine and its
optimum criteria. Applied Thermal Engineering.
2007. Vol. 27. P. 2051–2058.
DOI: 10.1016/j.applthermaleng.2006.12.002
П.
М. ГАЩУК1,
С. В. НИКИПЧУК2*
1Каф.
«Эксплуатация транспортных
средств и пожарно-спасательной техники»,
Львовский государственный университет
безопасности жизнедеятельности,
ул.
Клепаривская, 35, Львов, Украина, 79007,
тел. +38 (067) 476 84 83,
эл. почта
petroh@meta.ua,
ORCID 0000-0002-2345-4879
2*Каф.
«Эксплуатация и ремонта
автомобильной техники»,
Национальный
университет
«Львовская политехника», ул.
С. Бандеры, 12, Львов, Украина,
79013, тел.
+38 (097) 217 23 15, эл. почта nikipch@gmail.com,
ORCID 0000-0003-2499-9990
ЭФФЕКТИВНОСТЬ
РАБОЧИХ ЦИКЛОВ
ДВИГАТЕЛЯ БЫСТРОГО
ВНУТРЕННЕГО
СГОРАНИЯ С УДЛИНЕННЫМ
РАБОЧИМ
ХОДОМ
Цель.
Мы предусматриваем в
самых общих терминах исследовать
эффективность рабочих циклов двигателя
быстрого внутреннего сгорания с
удлиненным рабочим ходом. Удлинение
рабочего хода предусмотрено, например,
в так называемых двигателях Аткинсона
и Миллера, противопоставляемых как
более совершенных традиционному
двигателю Отто. Методика.
Разные рабочие циклы для выявления их
исключительно принципиальных особенностей
рассмотреные идеализированном виде с
применением понятий условной работы
цикла, количественной и
качественной характеристик
рабочего тела. Результаты.
Выяснено, в частности, следующее: 1)
чтобы двигатель Аткинсона–Миллера
выполнял одинаковую с двигателем Отто
работу, он должен иметь заметно больший
рабочий объем; 2) в случае заранее
заданного количества механической
работы коэффициент полезного действия
и ход расширения цикла Аткинсона—Миллера
растут до тех пор, пока цикл не превращается
в цикл Гамфри; 3) повышение средствами
Аткинсона эффективности двигателя
Отто сопровождается тем большим ростом
рабочего объема, чем более эффективным
является двигатель изначально. Научная
новизна. Доказано, что
при частичных нагрузках двигатель
Аткинсона может существенно терять
свою энергетическую эффективность. К
тому же, если в процессе виртуального
конструирования двигателя Аткинсона
становятся заметными энергоэкономные
преимущества цикла Гамфри, то в процессе
мнимого регулирования тяги синтезированного
двигателя такого типа преимущества
этого цикла уже не прослеживаются.
Практическая значимость.
В целом существуют основания утверждать,
что двигатель Отто – это все-таки
выгодный технический компромисс между
двухтактным двигателем и двигателем
Аткинсона. С одной стороны, увеличение
коэффициента полезного действия
двигателя быстрого внутреннего сгорания
способствует существенной экономии
горючего и снижению угроз окружающей
среде на протяжении жизненного цикла
машины с приводом от такого энергоэкономного
двигателя. Но с другой стороны,
воплощение
энергоэкономного
рабочего
цикла Аткинсона–Миллера
будет сопровождаться ростом
массогабаритных размеров двигателя и
отрицательно сказываться на свойствах
машины.
Ключевые
слова: двигатель быстрого внутреннего
сгорания; удлиненный рабочий ход;
рабочий цикл; двигатель Аткинсона–Миллера;
двигатель Отто; энергетическая
эффективность; коэффициент полезного
действия
P.
М. HASHCHUK1,
S. V. NIKIPCHUK2*
1Dep.
«Operation of vehicles and fire rescue equipment»,
Lviv State University of Life Safety,
Kleparivska St., 35, Lviv, Ukraine, 79007,
tel. +38 (067) 476 84 83,
е-mail petroh@meta.ua,
ORCID 0000-0002-2345-4879
2*Dep.
«Operation and
repair of
automotive vehicles»,
Lviv Polytechnic National University,
S. Bandera St., 12, Lviv, Ukraine,
79013, tel.
+38 (097) 217 23 15, е-mail nikipch@gmail.com,
ORCID 0000-0003-2499-9990
THE EFFICIENCY
OF WORKING CYCLES
IN THE RAPID INTERNAL COMBUSTION
ENGINE WITH THE
EXTENDED WORKING
STROKE
Purpose: The
investigation covers the efficiency of working cycles in the rapid
internal combustion engine with the extended working stroke. The
extended working stroke is applied in so-called Atkinson/Miller
engines that are considered to be more effective than traditional
Otto engines. Methodology. In order to identify purely
distinctive features of different working cycles, they were
investigated in an idealized form using the concepts of a
conditional working cycle, quantitative as well as qualitative
characteristics of the working fluid. Findings. The
investigation illustrates the following: 1) the Otto engine should
have a significantly larger displacement to function the same way as
the Atkinson/Muller engine; 2) if the mechanic work is
predetermined, the efficiency coefficient and the course of
expansion of the Atkinson-Miller cycle increase until it turns into
the Humphrey cycle; 3) the increase of Otto engine’s efficiency
using Attkinson’s means involves larger displacement if the engine
was efficient from the very beginning. Originality.
Attkinson’s engine may significantly lose its efficiency in energy
at partial loads. If in the process of virtual design of the
Atkinson engine the energy-saving advantages of Humphrey cycle
become noticeable, then in the process of imaginary regulation of
the thrust of an already synthesized engine of this type the
advantages of this cycle are no longer traceable. Practical
value. In general, the Otto engine could be considered as a
still profitable technical compromise between a two-stroke engine
and the Atkinson engine. On the one hand, increasing the efficiency
coefficient of a rapid internal combustion engine contributes to
significant fuel savings and environmental hazards reduction
throughout the life cycle of a machine driven by such an
energy-saving engine. But on the other hand, the implementation of
the energy-saving Atkinson/Miller working cycle will be accompanied
by an increase in the mass and size of the engine and will
negatively affect the properties of the machine.
Keywords: rapid
internal combustion engine; extended
working stroke; working cycle; Atkinson-Miller engine; Otto engine;
energy efficiency; efficiency
REFERENCES
Hashchuk, P. M.
Enerhiia ta uporiadkovanyi rukh.
Lviv: Ukrainski tekhnolohii.
DOI: http://hdl.handle.net/123456789/3790
(in English)
Al-Sarkhi, A.,
Akash, B. A., Jaber, J. O., Mohsen, M. S., & Abu-Nada, E.
(2002). Efficiency of Miller engine at maximum power density.
International Communications in Heat and Mass
Transfer, 29(8),
1159-1167. DOI: 10.1016/S0735-1933(02)00444-X
(in English)
Al-Sarkhi, A.,
Jaber, J. O., & Probert, S. D. (2006). Efficiency of a Miller
engine. Applied Energy, 83(4),
343-351. DOI: 10.1016/j.apenergy.2005.04.003
(in English)
Andresen, B.,
Salamon, P., & Berry, R. S. (1984). Thermodynamics in finite
time. Physics Today, 37(9),
62-70. DOI: 10.1063/1.2916405
(in English)
Atkinson,
J. (1886).
Gas engine: US 336505A.
Atkinson,
J. (1887). Gas engine:
US 367496A.
Benajes, J.,
Novella, R., Arthozoul, S., & Kolodziej, C. (2010). Particle
Size Distribution Measurements from Early to Late Injection Timing
Low Temperature Combustion in a Heavy Duty Diesel Engine. SAE
International Journal of Fuels and Lubricants,
3(1), 567-581. DOI: 10.4271/2010-01-1121
(in English)
Benajes, J.,
Serrano, J. R., Molina, S., & Novella, R. (2009). Potential of
Atkinson cycle combined with EGR for pollutant control in a HD
diesel engine. Energy Conversion and
Management, 50(1),
174-183. DOI: 10.1016/j.enconman.2008.08.034
(in English)
Brijesh, P., &
Sreedhara, S. (2013). Exhaust emissions and its control methods in
compression ignition engines: A review. International
Journal of Automotive Technology, 14(2),
195-206. DOI: 10.1007/s12239-013-0022-2 (in
English)
10. Carnot, S.
(1872). Réflexions
sur la puissance motrice du feu et sur les machines propres à
développer cette puissance. Paris: Gauthier-Villars,
Imprimeur-Libraire. (in English)
Chen, L.,
Zhang, W., & Sun, F. (2007). Power, efficiency,
entropy-generation rate and ecological optimisation for a class of
generalized irreversible universal heatengine cycles. Applied
Energy, 84(5), 512-525.
DOI: 10.1016/j.apenergy.2006.09.004
(in English)
Chen, Z.,
Konno, M., Oguma, M., & Yanai, T. (2000). Experimental study of
CI natural-gas/DME homogeneous charge engine. SAE
Technical Paper Series, 109(3),
442-451.
DOI: 10.4271/2000-01-0329
(in English)
Clarke, D., &
Smith, W. J. (1997). Simulation, Implementation and Analysis of the
Miller Cycle Using an Inlet Control Rotary Valve, Variable Valve
Actuation and Power Boost. SAE SAE Technical
Paper Series, 61-70. DOI: 10.4271/970336.
(in English)
Cornell, S. O.,
& Leman, S. A. (2006). Engine valve
actuation system (Caterpillar), US Patent 7004122.
Demirci,
O. K.,
Uyumaz,
A.,
Sarıdemir,
S.,
& Çinar,
C.
(2018). The Simulation, Implementation and Analysis of the Miller
Cycle Using an Inlet Control Rotary Valve. International
Journal of Automotive Technology (IJAET), 7(3),
107-116. DOI: 10.18245/ijaet.486408.
(in English)
Ebrahimi, R.
(2011). Effects of mean piston speed, equivalence ratio and cylinder
wall temperature on performance of an Atkinson engine. Mathematical
and Computer Modelling, 53(5-6),
1289-1297. DOI: 10.1016/j.mcm.2010.12.015
(in English)
Ebrahimi, R.
(2012). Performance analysis of an irreversible Miller cycle with
considerations of relative air-fuel ratio and stroke length. Applied
Mathematical Modelling, 36(9),
4073-4079. DOI: 10.1016/j.apm.2011.11.031 (in
English)
Edwards, S.,
Frankle, G., Wirbeleit, F., & Raab, A. (1998). The Potential of
a Combined Miller Cycle and Internal EGR Engine for Future Heavy
Duty Truck Applications, SAE Technical Paper,
1-21. DOI: 10.4271/980180 (in
English)
Ehleskog, M.,
Gjirja, S., & Denbratt, I. (2012). Effects of Variable Inlet
Valve Timing and Swirl Ratio on Combustion and Emissions in a Heavy
Duty Diesel Engine. SAE Technical Paper,
1-12. DOI: 10.4271/2012-01-1719 (in English)
Ebrahimi, R.
(2011). Thermodynamic modeling of performance of a Miller cycle with
engine speed and variable specific heat ratio of working fluid.
Computers and Mathematics with Applications,
62, 2169-2176.
DOI: 10.1016/j.camwa.2011.07.002
(in English)
Fukuzawa, Y.,
Kakuhama, Y., Shimoda, H., Endo, H., & Tanaka, K. (2001).
Development of High Efficiency Miller Cycle Gas Engine. Mitsubishi
Heavy Industries, 38(3), 146-150. (in English)
Ge, Y., Chen,
L., Sun, F., & Wu, C. (2005). Effects of heat transfer and
variable specific heats of working fluid on performance of a Miller
cycle. International Journal of Ambient
Energy, 26(4), 203-214.
DOI: 10.1080/01430750.2005.9674991
(in English)
Ge, Y., Chen,
L., Sun, F., & Wu, C. (2005). Effects of heat transfer and
friction on the performance of an irreversible air-standard Miller
cycle. International Communications in Heat
and Mass Transfer, 32(8),
1045-1056. DOI:
10.1016/j.icheatmasstransfer.2005.02.002
(in English)
Ge, Y., Chen,
L., Sun, F., & Wu, C. (2005). Reciprocating heat-engine cycles.
Applied Energy, 81(4),
397-408. DOI: 10.1016/j.apenergy.2004.09.007
(in English)
Gonca,
G., & Hocaoglu,
M. F. (2019). Performance Analysis and Simulation of a Diesel-Miller
Cycle (DiMC) Engine. Arabian
Journal for Science and Engineering, 44,
5811-5824. DOI: 10.1007/s13369-019-03747-4
(in
English)
Gonca, G.,
Sahin, B., & Ust, Y. (2015). Investigation of Heat Transfer
Influences on Performance of Air-Standard Irreversible Dual-Miller
Cycle. Journal of Thermophysics and Heat
Transfer, 29(4),
678-683. DOI: 10.2514/1.T4512
(in English)
Goto, T.,
Hatamura, K., Takizawa, S., Hayama, N., Abe, H., & Kanesaka, H.
(1994). Development of V6 Miller Cycle Gasoline Engine. SAE
Technical Paper, 1-11.
DOI: 10.4271/940198
(in English)
Grab-Rogaliński,
K., Szwaja, S., & Tutak, W.
(2014). The Miller Cycle Based IC Engine Fuelled with a
CNG/Hydrogen. Journal of KONES. Powertrain and
Transport, 21(4), 137-144.
DOI: 10.5604/12314005.1130459 (in English)
Hatamura, K.,
Hayakawa, M., Goto, T., & Hitomi, M. (1997). A study of the
improvement effect of Miller-cycle on mean effective pressure limit
for high-pressure supercharged gasoline engines. JSAE
Review, 18(2), 101-106.
DOI: 10.1016/S0389-4304(96)00069-0 (in English)
Heikkilä, J.,
Happonen, M., Murtonen, T., Lehto, K., Sarjovaara, T., Larmi, M., …
& Virtanen, A. (2012). Study of Miller timing on exhaust
emissions of a hydrotreated vegetable oil (HVO)-fueled diesel
engine. Journal of the Air & Waste
Management Association, 62(11),
1305-1312. DOI: 10.1080/10962247.2012.708383.
(in English)
Heywood, J. B.
(1988). Ideal models of engine cycles.
Singapore: McGraw-Hill Education.
(in English)
Higuchi, N.,
Sunaga, Y., Tanaka, M., & Shimada, H. (2013). Development of a
New Two-Motor Plug-In Hybrid System. SAE
International Journal of Alternative Powertrains,
2(1), 135-145. DOI: 10.4271/2013-01-1476
(in English)
Kong, S. C.
(2007). A study of natural gas/DME combustion in HCCI engines using
CFD with detailed chemical kinetics. Fuel,
86(10), 1483-1489.
DOI: 10.1016/j.fuel.2006.11.015
(in English)
Liu, J., &
Chen, J. (2010). Optimum performance analysis of a class of typical
irreversible heat engines with temperature-dependent heat capacities
of the working substance. International
Journal of Ambient Energy, 31(2),
59-70. DOI: 10.1080/01430750.2010.9675103
(in English)
Martins, J.,
Uzuneanu, K., Ribeiro, B., & Jasasky, O. (2004). Thermodynamic
Analysis of an Over-Expanded Engine. SAE
Technical Paper, 1-15. DOI:
10.4271/2004-01-0617 (in English)
Martins, M. E.
S., & Lanzanova, T. D. M. (2015). Full-load Miller cycle with
ethanol and EGR: Potential benefits and challenges. Applied
Thermal Engineering, 90,
274-285. DOI: 10.1016/j.applthermaleng.2015.06.086
(in English)
Mikalsen, R.,
Wang, Y. D., & Roskilly, A. P. (2009) A Comparison of Miller and
Otto Cycle Natural Gas Engines for Small Scale CHP Applications.
Applied Energy, 86(6),
922-927. DOI: 10.1016/j.apenergy.2008.09.021
(in English)
Miller, R.
(1952, 1956). High expansion, spark-ignited,
gas burning, internal combustion engines:
US Patent 2773490A.
39. Miller,
R. (1957). Supercharged
Engine:
US Patent
2817322A.
Miller, R. H.
(1947). Supercharging and Internal Cooling Cycle for High Output.
Transactions ASME,
69, 453-464. (in
English)
Miller, R. H.,
& Lieberherr, H. U. (1957). The Miller supercharging system for
Diesel and gas engines operating characteristics. CIMAC,
787–803. (in English)
Millo, F.,
Gianoglio B. M., & Delneri, D. (2011). Computational Analysis of
Internal and External EGR Strategies Combined with Miller Cycle
Concept for a Two Stage Turbocharged Medium Speed Marine Diesel
Engine. SAE International Journal of Engines,
4(1), 1319-1330.
DOI: 10.4271/2011-01-1142 (in English)
Mo, H.,
Yongquan, H. Y., Xiaojian, M. X., & Zhuo, B. (2016).
Investigations on the Potential of Miller Cycle for Performance
Improvement of Gas Engine. Global Journal of
Researches in Engineering: B Automotive Engineering,
16(1), 37-46.
(in English)
Niculae, M.,
Clenci, A., Iorga-Simăn, V., & Niculescu, R. (2019). An
Overview on the Miller-Atkinson Over-expansion Thermodynamic Cycle.
IOP Conf. Series:
Materials Science and Engineering, 564,
1-7. DOI: 10.1088/1757-899X/564/1/012125 (in
English)
Ribeiro, B., &
Martins, J. (2007). Direct Comparison of an Engine Working under
Otto, Miller and Diesel Cycles: Thermodynamic Analysis and Real
Engine Performance. SAE Technical Paper,
1-11. DOI: 10.4271/2007-01-0261 (in English)
Wang, Y, Lin,
L, Roskilly, A. P., Zeng, S, Huang, J, He, Y, Huang, X, Huang, H,
Wei, H, Li, S, & Yang, J. (2007). An analytic study of
applying Miller cycle to reduce NOx
emission from petrol engine. Applied Thermal
Engineering, 27(11-12),
1779-1789. DOI: 10.1016/j.applthermaleng.2007.01.013
(in English)
Wu,
C., Puzinauskas, P. V., & Tsai, J. S. (2003). Performance
analysis and optimization of a supercharged Miller cycle Otto
engine. Applied
Thermal Engineering,
23(5),
511-521.
DOI: 10.1016/S1359-4311(02)00239-9
(in English)
Zhao, Y, &
Chen, J. (2007) Performance analysis of an irreversible Miller heat
engine and its optimum criteria. Applied
Thermal Engineering, 27,
2051-2058. DOI: 10.1016/j.applthermaleng.2006.12.002
(in English)
Надійшла
до редколегії: 27.01.2020
Прийнята
до друку: 29.05.2020
– тиск у довкіллі).
(рис. 1, а)
ділянки
та
імітують відповідно такт впускання
пальної суміші в робочий простір і такт
випускання відпрацьованих газів з
нього, а ділянка
– процес згоряння суміші (процес
теплотворення). У 1947 році
американський інженер Ральф Міллер
запропонував зробити
такт стиснення в класичному двигуні
Отто механічно коротшим за такт робочого
ходу (за такт розширення), рис. 1, б:
у робочому тепловому циклі Міллера
(Miller Cycle)
точка
відповідає моменту закриття впускного
клапана; такт стискання робочого тіла
(ідеального газу) формально відображає
ділянка
циклу, яка за переміщенням поршня
справді є коротшою за ділянку
розширення (
– тиск у циліндрі в кінці ходу поршня
до нижнього мертвого положення на такті
всмоктування). Того самого результату
можна досягнути, закриваючи впускний
клапан після НМП із великим запізненням,
виштовхуючи при цьому частину пальної
суміші назад у впускний колектор, рис.
1, в: у
робочому циклі
власне процес впускання пальної суміші
формально імітує ділянка
.
ділянка
імітує власне процес впускання; площа
фігури
відповідає додатній роботі циклу, а
площа фігури
– від’ємній роботі. Зауважмо, на
наведених діаграмах ділянка розширення
розташована довільно, без урахування
пропорцій між кількостями спожитої
суміші й показниками її якості.
(рис. 2). У такому разі цикл Міллера (див.
рис. 2) можна беззастережно трактувати
як ще один важливий елементарний
термодинамічний поряд зі звичними
елементарними термодинамічними циклами
[1] Карно, Отто, Брайтона, Дизеля, Ериксона,
Сабате, Стирлінга. Хоча, з іншого боку,
він є ніби похідним від циклу Отто, є
його варіацією.