ISSN
2307–3489 (Print), ІSSN
2307–6666
(Online)
Наука
та прогрес транспорту. Вісник
Дніпропетровського
національного університету залізничного
транспорту, 2020, № 2 (86)
ЕКОЛОГІЯ
ТА ПРОМИСЛОВА БЕЗПЕКА
УДК
504.5:[628.334.5/.6:519.87]
В. Д. Петренко1,
М. І. Нетеса2,
О. Л. Тютькін3,
О. В. Громова4,
В.
І. Шинкаренко5,
В. А. козачина6*
1Каф.
«Мости та тунелі», Дніпровський
національний університет залізничного
транспорту імені академіка В. Лазаряна,
вул. Лазаряна, 2, Дніпро, Україна, 49010,
тел. +38 (056) 373 15 53, ел. пошта
petrenko.diit@gmail.com, ORCID 0000-0003-2201-3593
2Каф.
«Будівельне виробництво та геодезія»,
Дніпровський національний університет
залізничного транспорту імені академіка
В. Лазаряна, вул. Лазаряна, 2, Дніпро,
Україна, 49010, тел. +38 (067) 195 50 27, ел. пошта
andreynetesa@meta.ua, ORCID 0000-0003-1730-7642
3Каф.
«Мости та тунелі», Дніпровський
національний університет залізничного
транспорту імені академіка В. Лазаряна,
вул. Лазаряна, 2, Дніпро, Україна, 49010,
тел. +38 (056) 373 15 53, ел. пошта alexeytutkin@gmail.com,
ORCID 0000-0003-4921-4758
4Каф.
«Архітектурне проєктування, землеустрій
та будівельні матеріали», Дніпровський
національний
університет залізничного транспорту
імені академіка В. Лазаряна, вул. Лазаряна,
2, Дніпро, Україна, 49010, тел. +38 (095) 304 73 33,
ел. пошта Gromova_Elen_upbbm_diit@i.ua,
ORCID 0000-0002-5149-4165
5Каф.
«Комп’ютерні інформаційні технології»,
Дніпровський національний університет
залізничного транспорту імені академіка
В. Лазаряна, вул. Лазаряна, 2, Дніпро,
Україна, 49010, тел. +38 (056) 373 15 35, ел. пошта
shinkarenko_vi@ua.fm, ORCID
0000-0001-8738-7225
6*Каф.
«Гідравліка та водопостачання»,
Дніпровський національний університет
залізничного транспорту імені академіка
В. Лазаряна, вул. Лазаряна, 2, Дніпро,
Україна, 49010, тел. +38 (056) 273 15 09, ел. пошта
v.kozachyna@gmail.com,
ORCID 0000-0002-6894-5532
ЕКСПРЕС МОДЕЛЬ ДЛЯ РОЗРАХУНКУ
ПРОЦЕСУ ОЧИЩЕННЯ ВОДИ
Мета.
Використання фізичного експерименту
для дослідження процесів масопереносу
в спорудах систем водопостачання та
каналізації потребує значного часу та
є досить вартісним. Тому метою роботи
є розробка чисельних моделей для
проведення обчислювального експерименту
з дослідження процесу масопереносу в
піскоуловлювачах. Методика.
Для математичного
моделювання процесу масопереносу в
піскоуловлювачах використано двовимірні
рівняння Нав’є–Стокса та двовимірне
рівняння масопереносу домішки. Для
чисельного інтегрування рівнянь, що
описують рух в’язкої нестисливої
рідини, використано неявні різницеві
схеми розщеплення. Невідомі параметри
на кожному кроці розщеплення знайдено
за явною залежністю. Для чисельного
інтегрування двовимірного рівняння
масопереносу використано поперемінно–трикутну
різницеву схему розщеплення. Результати.
Для проведення обчислювального
експерименту на базі побудованої
чисельної моделі створено спеціалізований
код. Наведено результати обчислювальних
експериментів із дослідження процесу
масопереносу в піскоуловлювачах з
додатковими елементами. З’ясовано, що
ефективність очищення
води змінюється у випадку використання
додаткового елемента на дні піскоуловлювача.
Наукова новизна.
Побудовано чисельні моделі, що дають
можливість оперативно аналізувати та
прогнозувати ефективність роботи
піскоуловлювачів, які мають складну
геометричну форму. Ці моделі дозволяють
урахувати також гідродинаміку течії в
очисній споруді. Практична
значимість. Запропоновані
чисельні моделі можна
використовувати на етапі проектування
очисних споруд систем каналізації.
Ключові слова: очищення води;
чисельне моделювання; різницеві схеми;
піскоуловлювач; водокористування;
математичне моделювання
Вступ
У наш час у галузі
проектування систем водопостачання
та каналізації значну роль відіграє
метод математичного моделювання. Це
пов’язано з тим, що використання
фізичного моделювання, навіть у
лабораторних умовах, потребує значного
часу на постановку експерименту. Крім
цього, є значні труднощі в інтерпретації
результатів експериментальних
досліджень, що отримані, коли неможливо
провести експеримент із виконанням
тих чи інших критеріїв подібності. Тому
альтернативою фізичному експерименту
є метод математичного моделювання.
Сьогодні для моделювання та розрахунку
процесів масопереносу в системах
водопостачання та водовідведення
створені математичні моделі різних
класів [1, 2, 4, 6–12]. Найчастіше на практиці
використовують емпіричні та аналітичні
моделі. Вони дозволяють дуже швидко
отримати дані необхідні для проектування
будь-якої споруди в системах водопостачання
та водовідведення. Але в Україні існує
певний дефіцит моделей, що базуються
на чисельному інтегруванні фундаментальних
рівнянь механіки суцільного середовища,
які дозволяють, на відміну від емпіричних
та аналітичних моделей, під час проведення
обчислювального експерименту передати
геометричну форму споруди для дослідження
процесу масопереносу. Такі моделі є
прямою альтернативою фізичного
експерименту, окрім цього, не такими
вартісними, як витрати на постановку,
обладнання, проведення фізичного
експерименту.
Мета
Зважаючи на
викладене, метою цієї статті є побудова
CFD-моделі для розрахунку процесу
масопереносу в піскоуловлювачі, що має
складну геометричну форму. Під час
побудови математичної моделі враховано
найбільш суттєві фізичні фактори, при
цьому час розрахунку на базі моделі є
досить невеликим.
Методика
Піскоуловлювач є
важливим елементом у системах
водовідведення. Ефективність роботи
піскоуловлювача впливає на ефективність
роботи інших елементів – очисних
спорудах, що розташовані за піскоуловлювачем
у технологічній схемі очищення води.
Для підвищення ефективності роботи
піскоуловлювачів можна встановлювати
в них додаткові елементи або змінювати
їх геометричну форму. Для визначення
ефективності роботи таких модернізованих
піскоуловлювачів необхідно мати
ефективні математичні моделі. У нашій
роботі для цього використано такі
рівняння [2]:
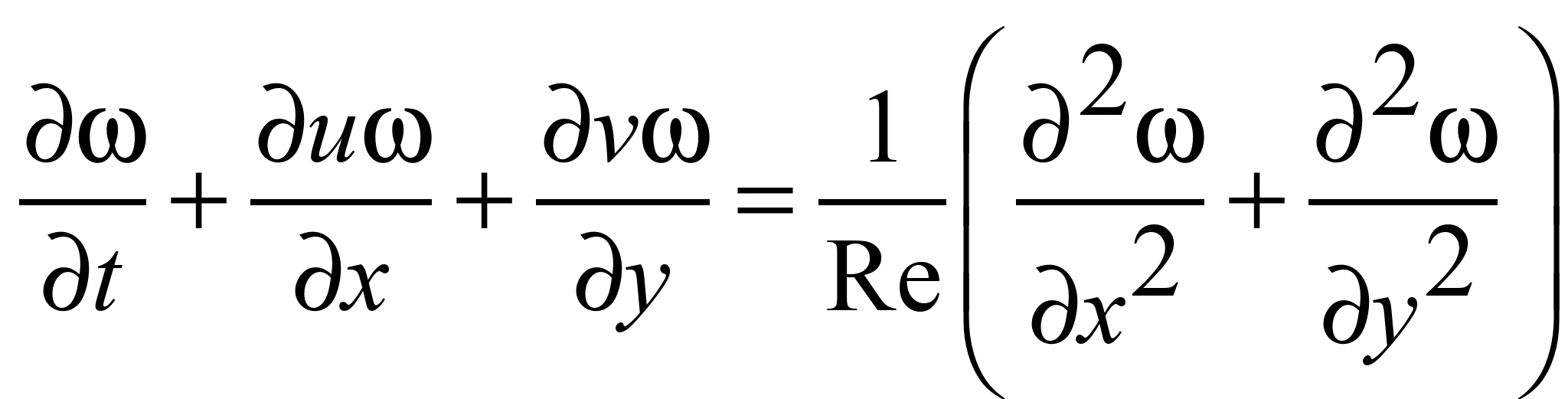 ; (1)
; (1)
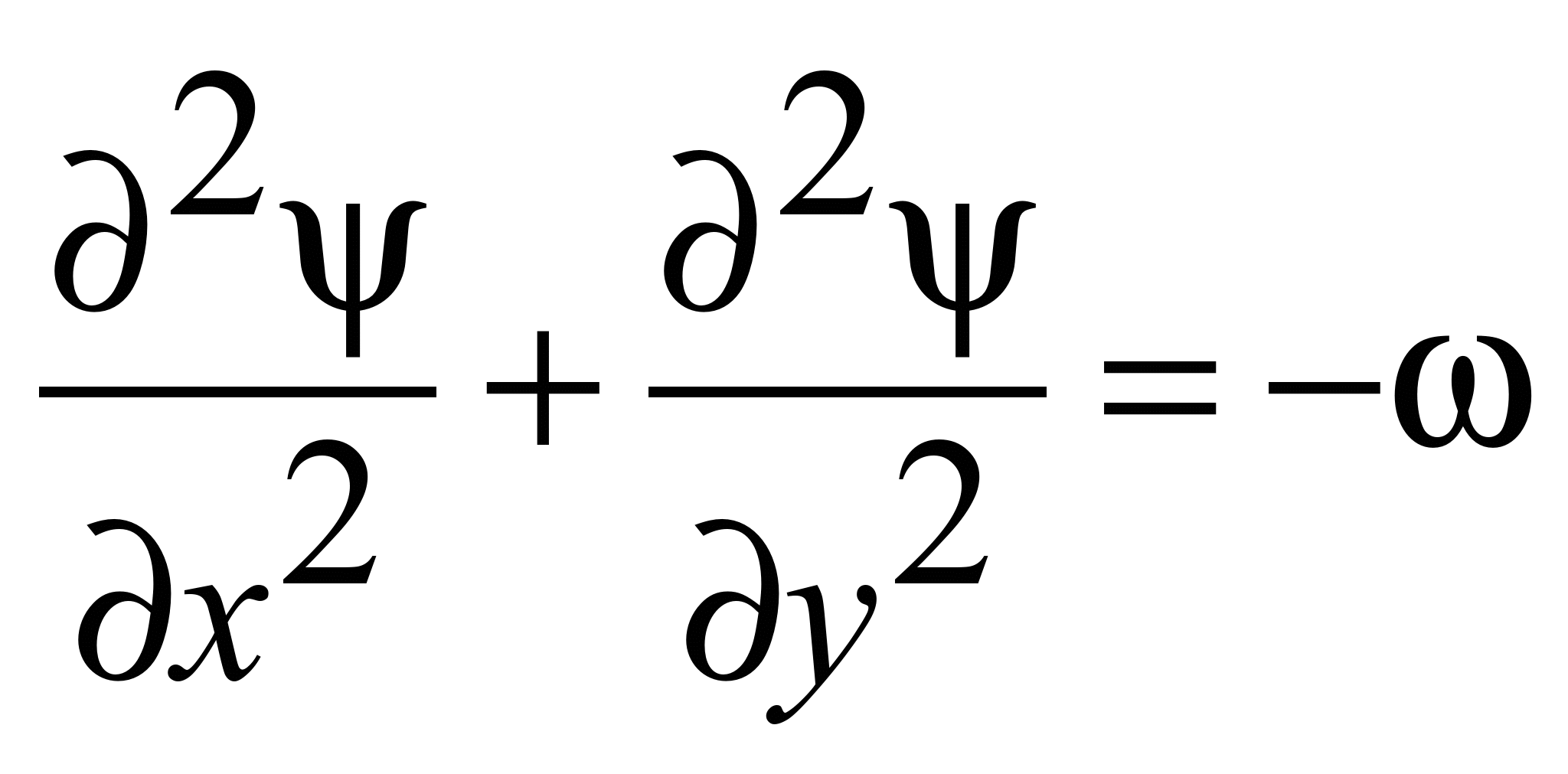 ; (2)
; (2)
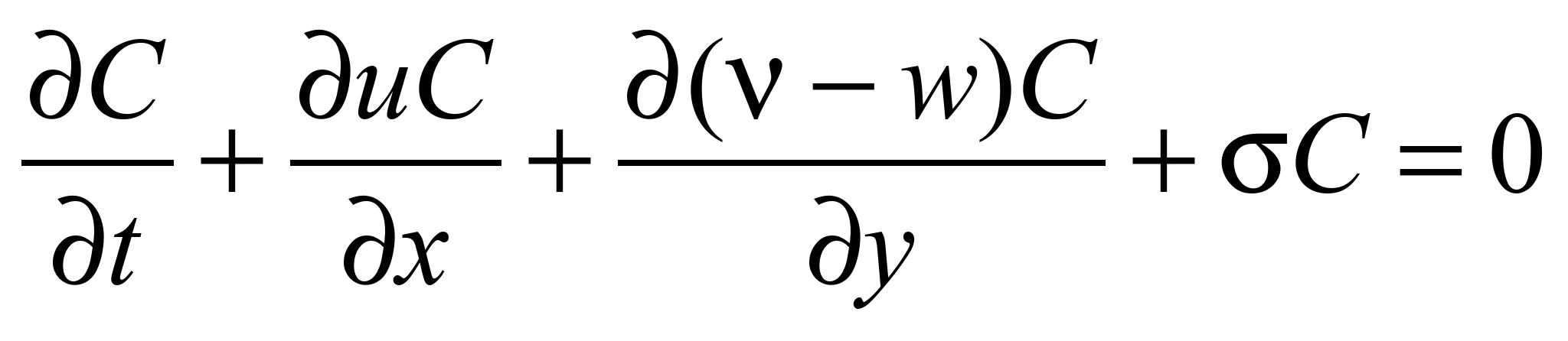 . (3)
. (3)
де
С –
концентрація домішки в піскоуловлювачі;
u, v –
швидкість течії в піскоуловлювачі;
w – гідравлічна
крупність домішки; σ – коефіцієнт, що
враховує процеси трансформації домішки
в піскоуловлювачі; y
– функція потоку; Re
= V0L/x
– число Рейнольдса; ω
= ∂v/∂x – ∂u/∂y – вихор;
u = ∂y/∂y,
v = –∂y/∂x
– компоненти вектора
швидкості потоку в піскоуловлювачі.
Рівняння Нав’є–Стокса
(1) – (2) використано для розрахунку поля
швидкості потоку в піскоуловлювачі.
Рівняння масопереносу (3) дозволяє
розрахувати процес руху важкої домішки
в піскоуловлювачі.
Постановку граничних
умов для моделювальних рівнянь розглянуто
в [1, 2].
Розглянемо методи
чисельного інтегрування моделювальних
рівнянь. Для чисельного інтегрування
рівняння масопереносу використовуємо
апроксимацію [1, 2].
Похідну
за часом моделюємо так:
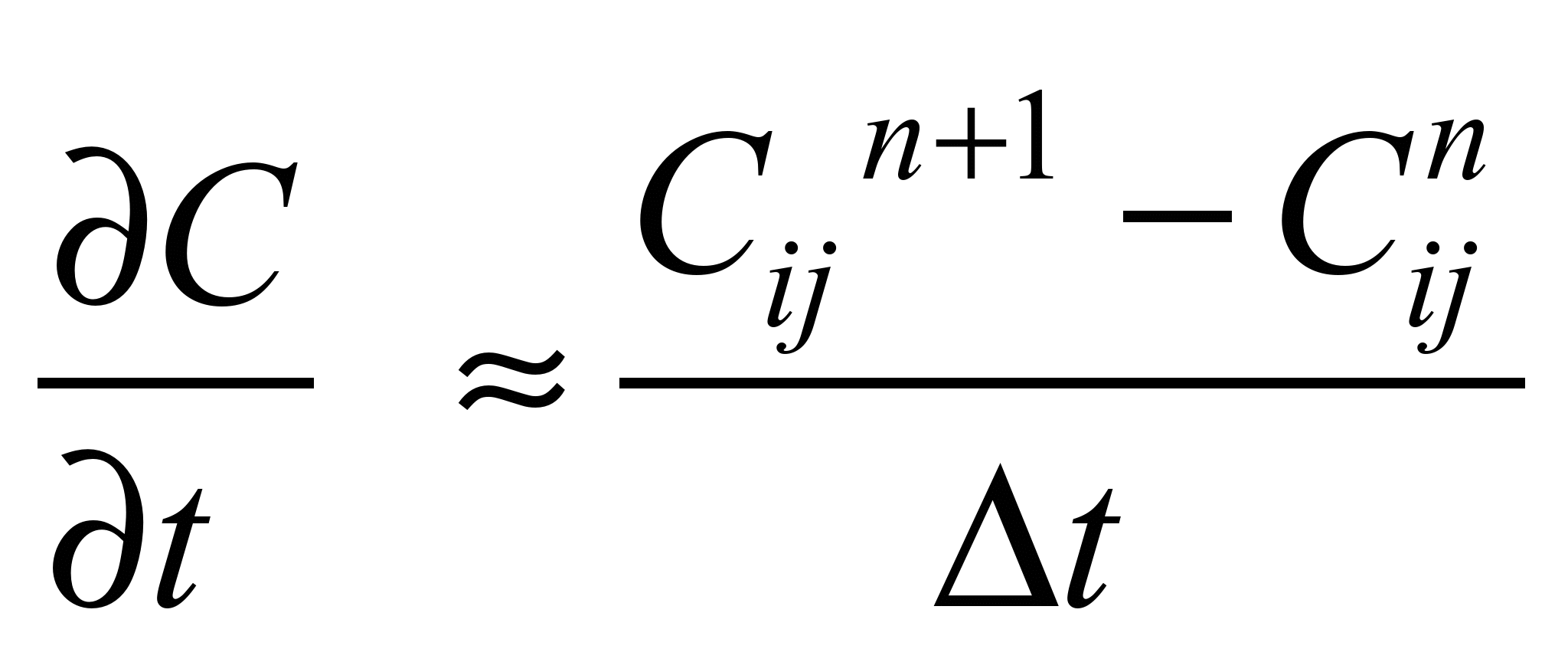 .
.
Конвективні
похідні записуємо таким чином [2]:
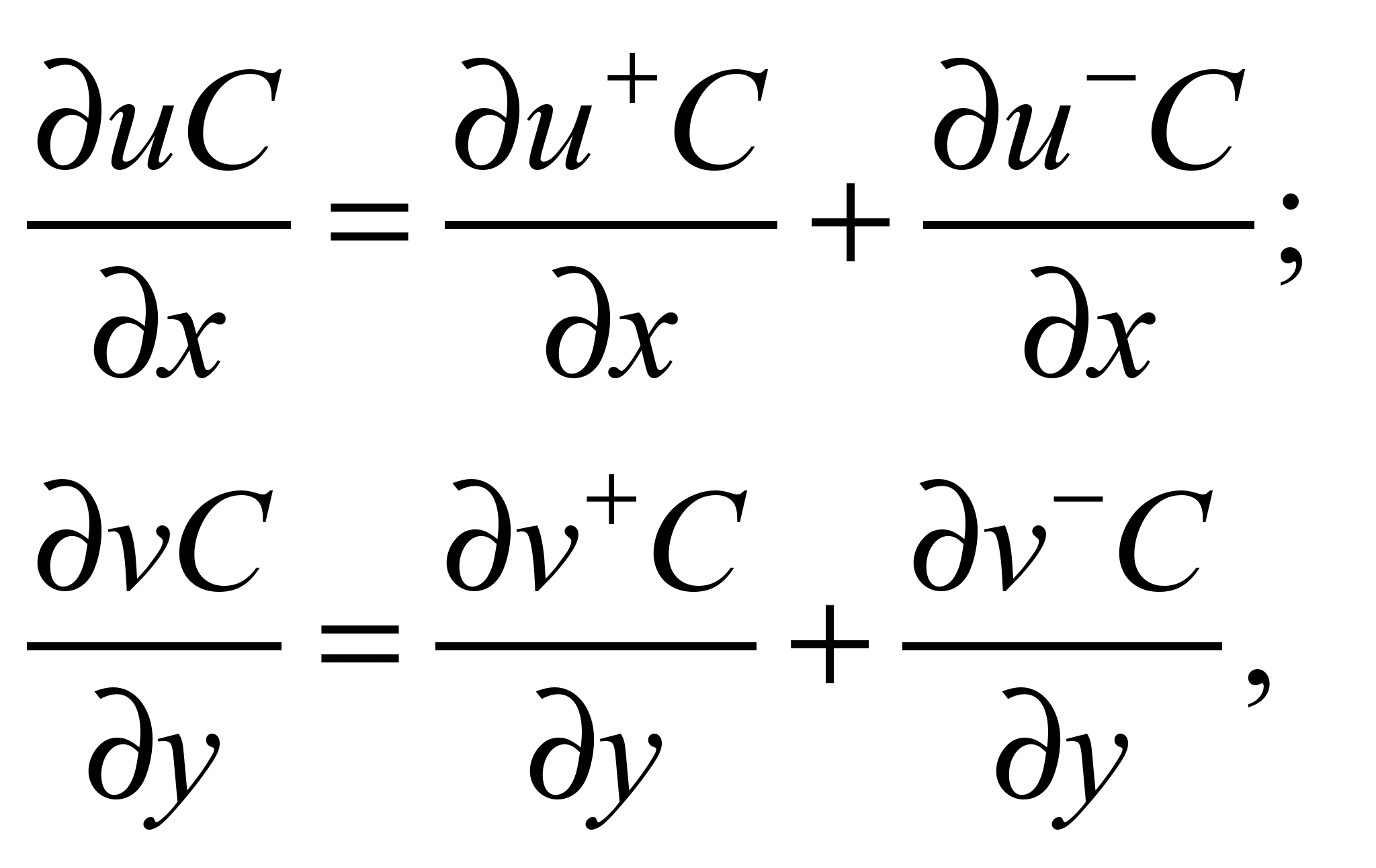
де
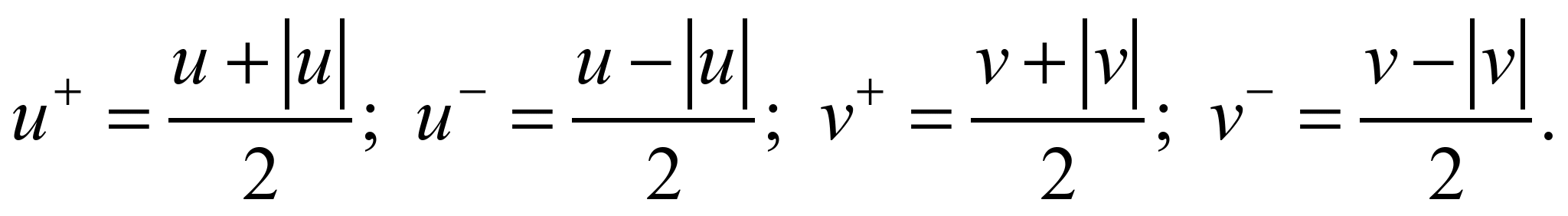
Далі
конвективні та другі похідні моделюємо
так [1, 2]:
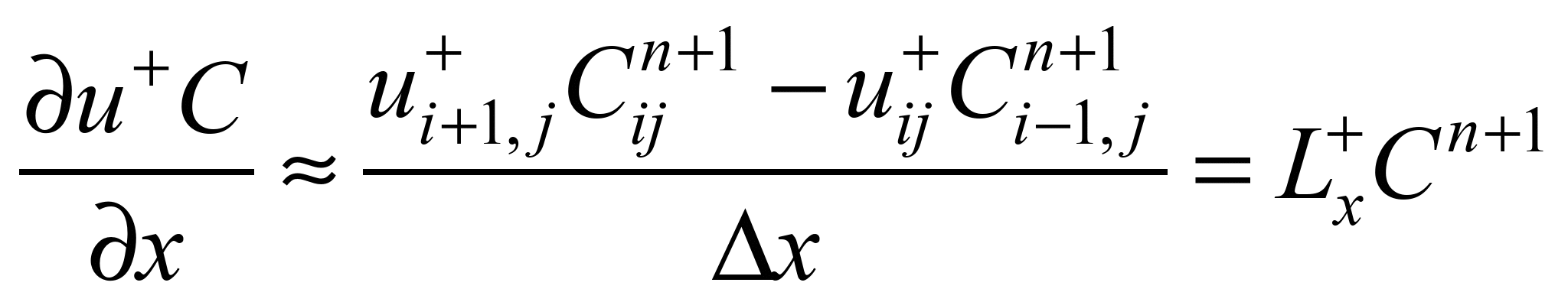 ;
;
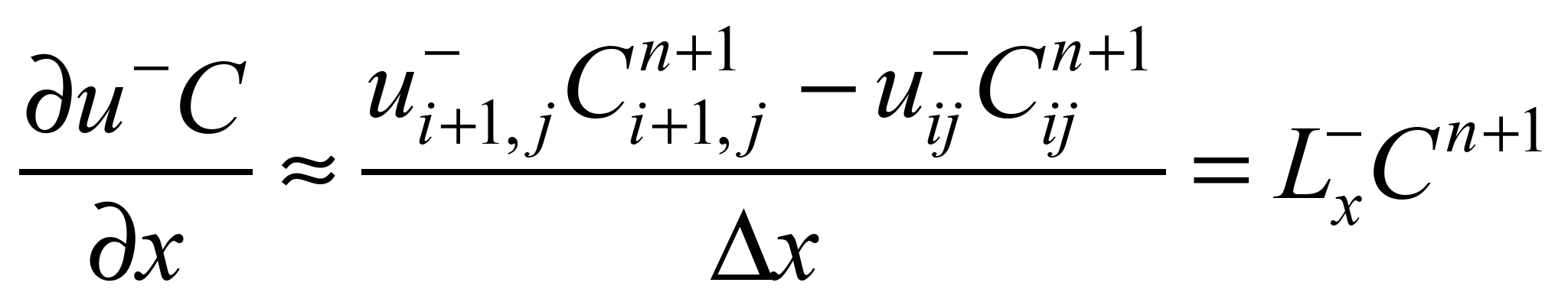 ;
;
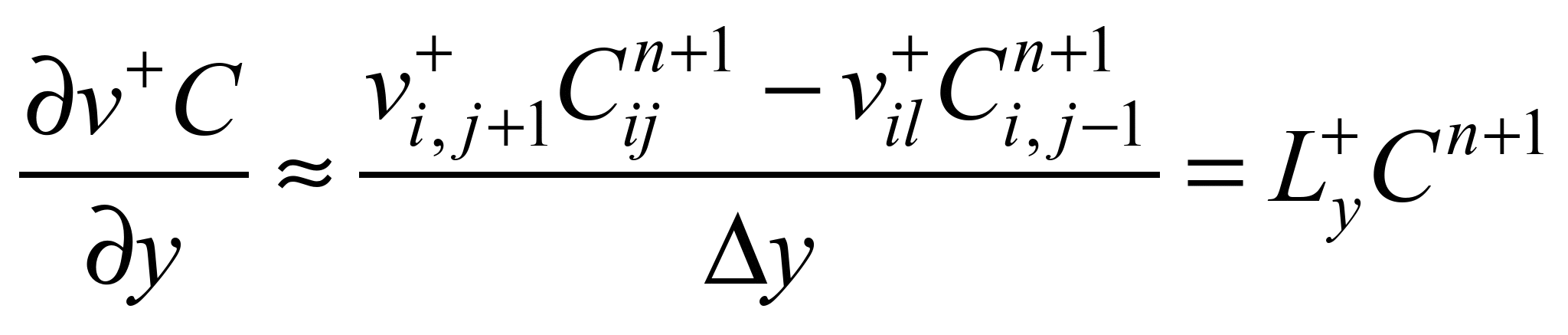 ;
;
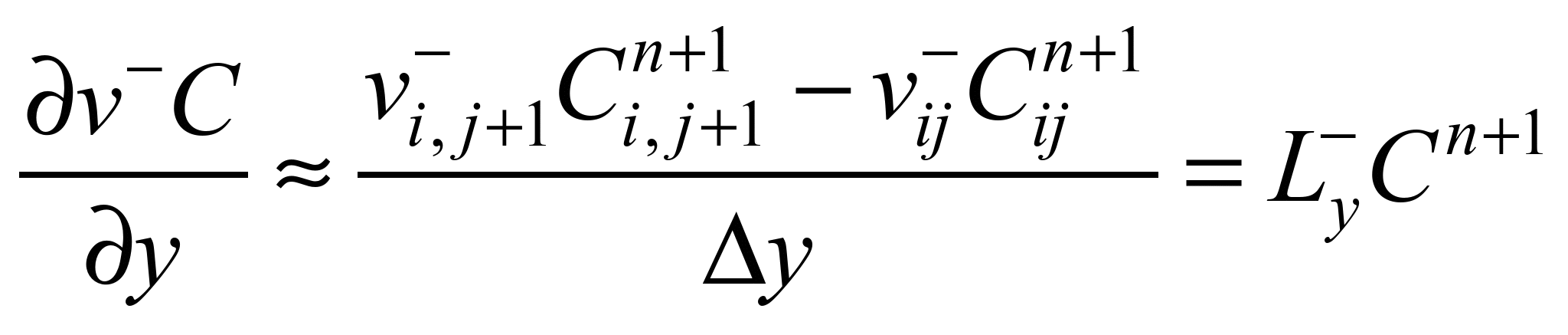 ;
;
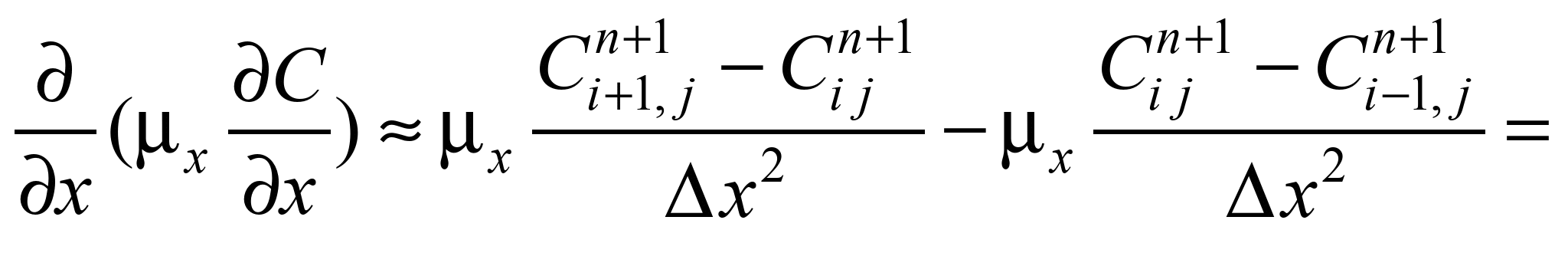
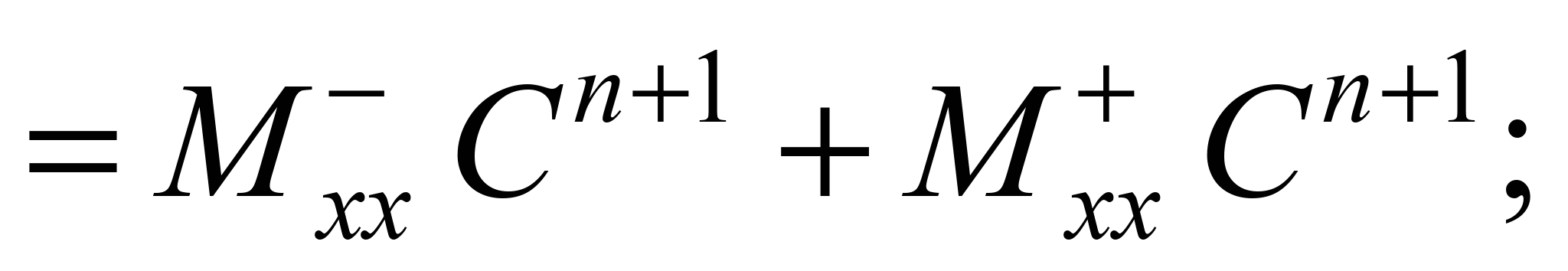
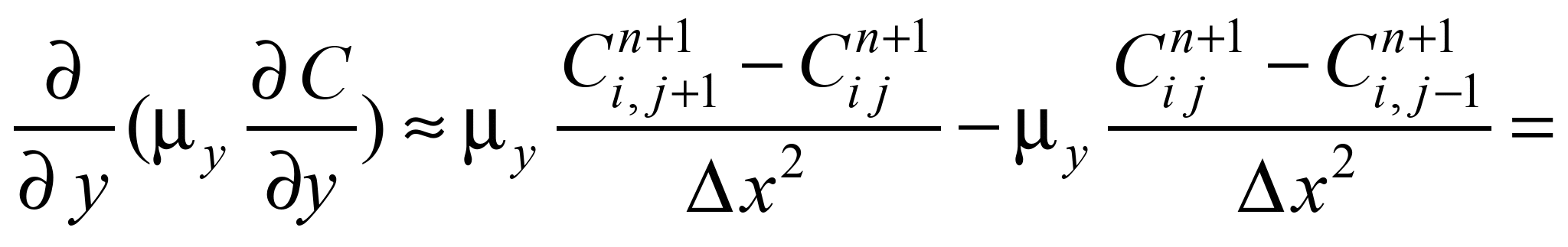
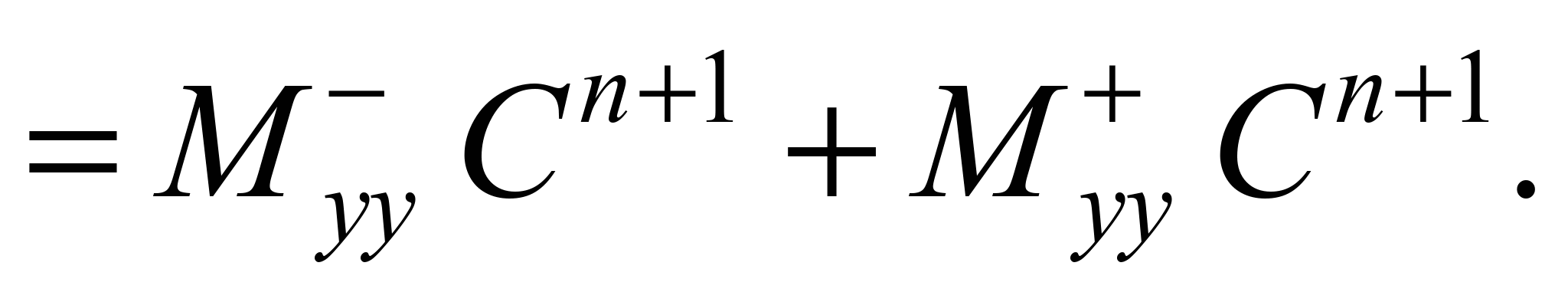
Після
такої апроксимації різницевий аналог
рівняння масопереносу має вигляд:
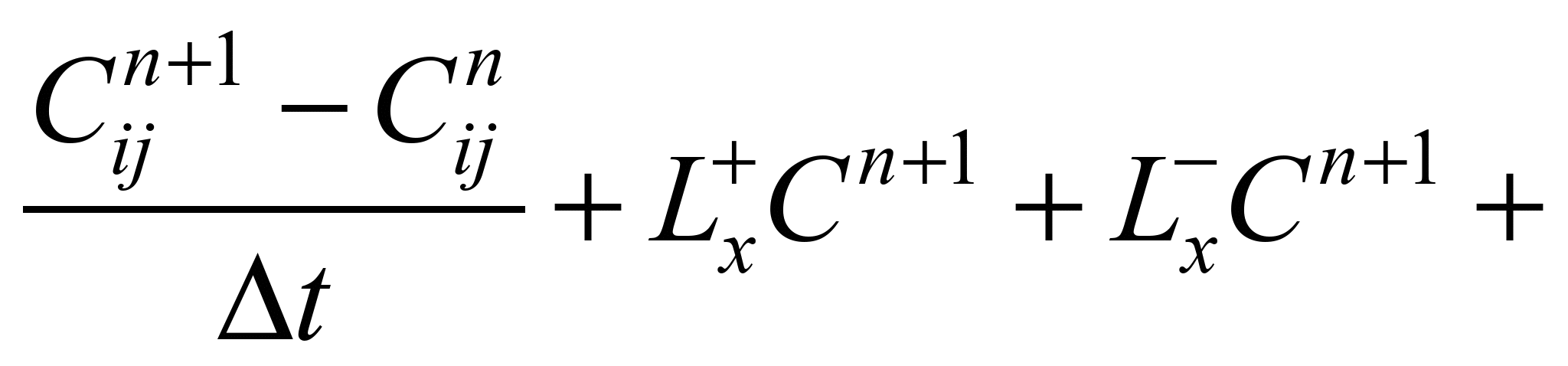
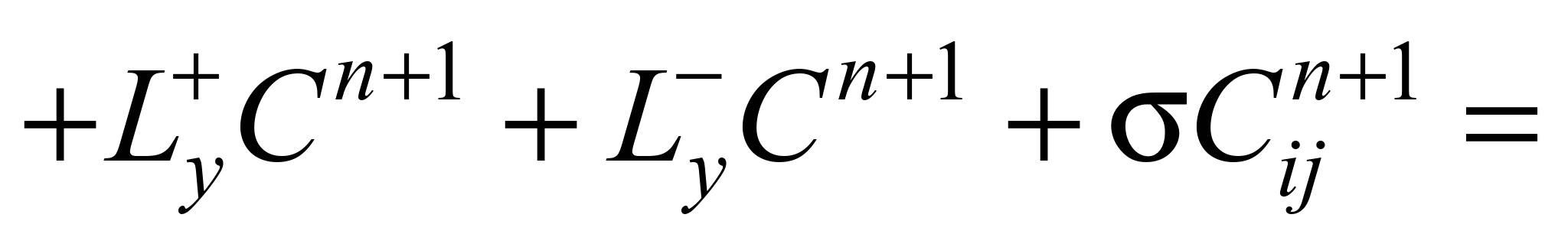
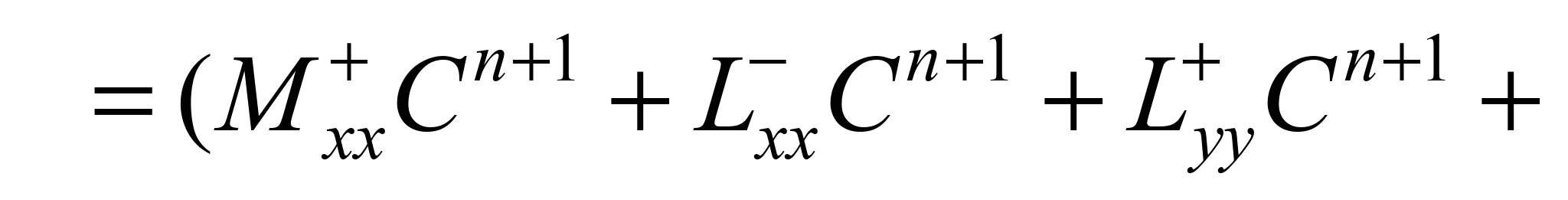
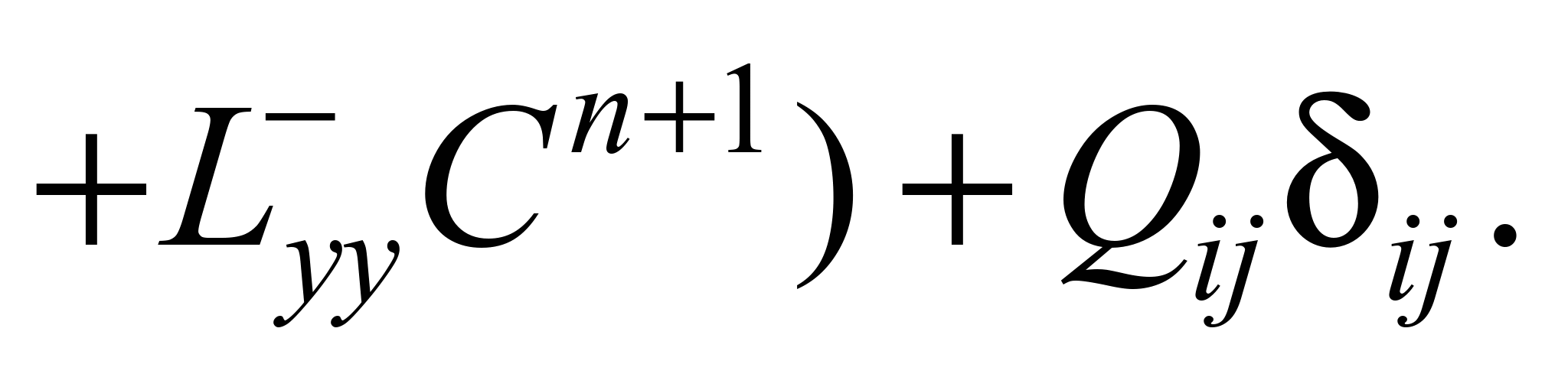 (4)
(4)
На
наступному етапі здійснимо розщеплення
цього рівняння на послідовність таких
рівнянь:
– на
першому кроці розщеплення (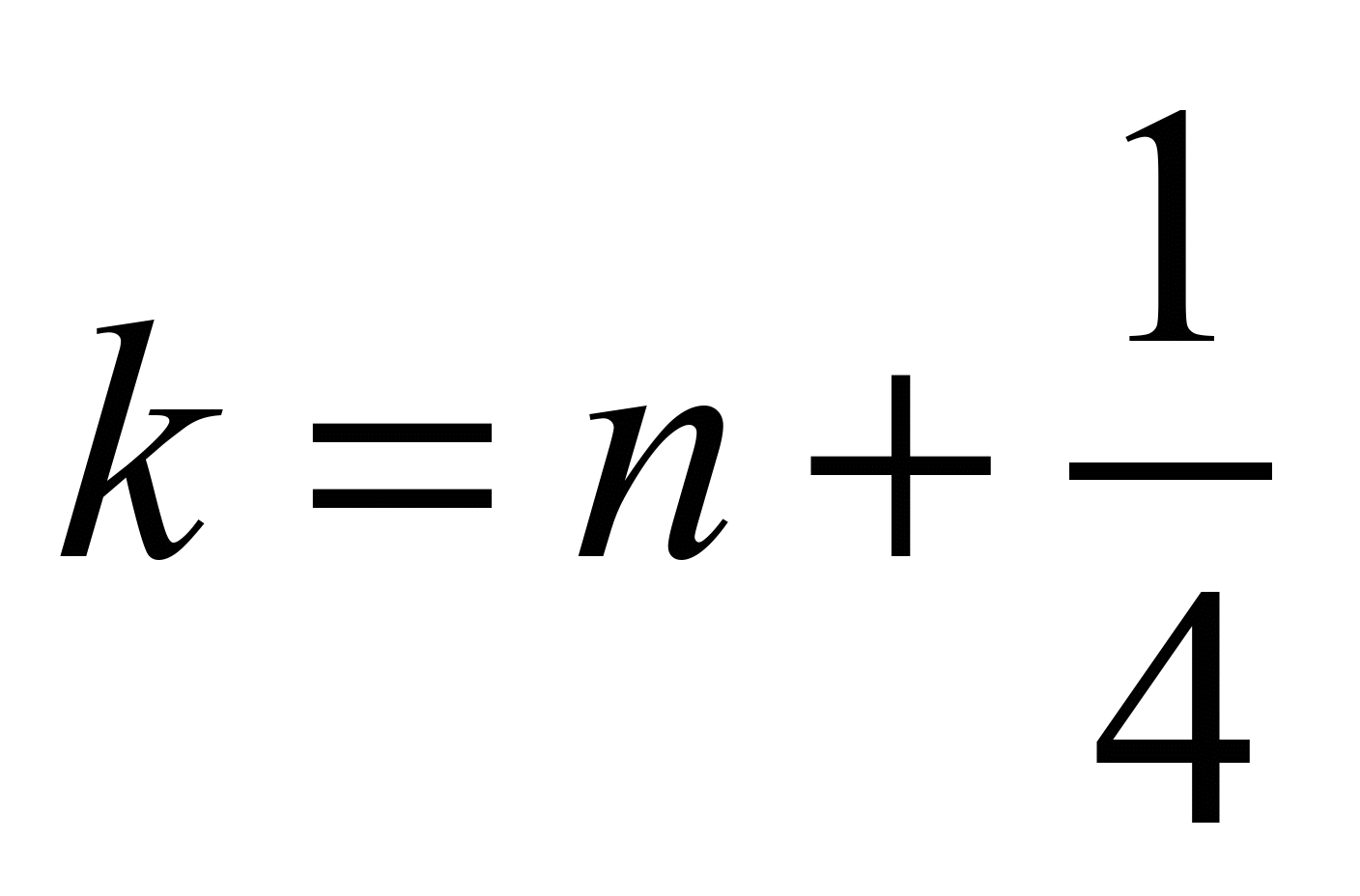 ):
):
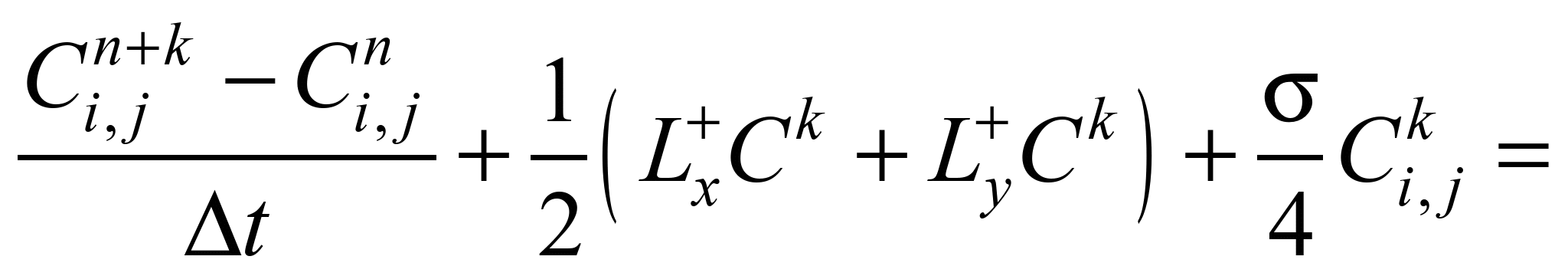
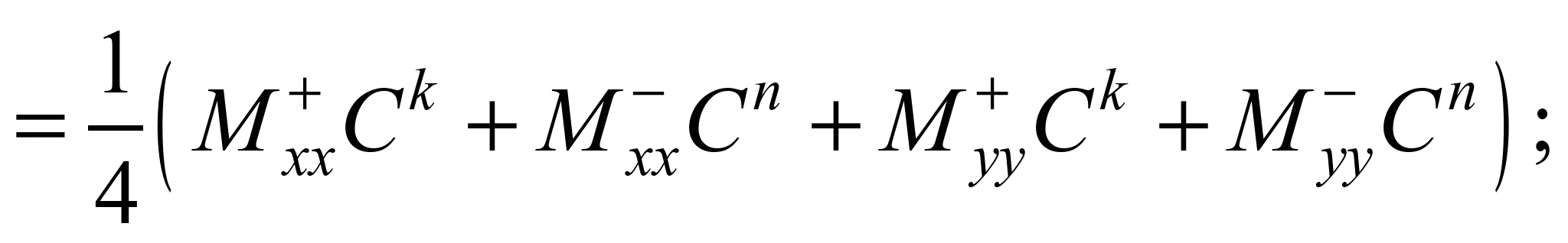 (5)
(5)
– на
другому кроці розщеплення (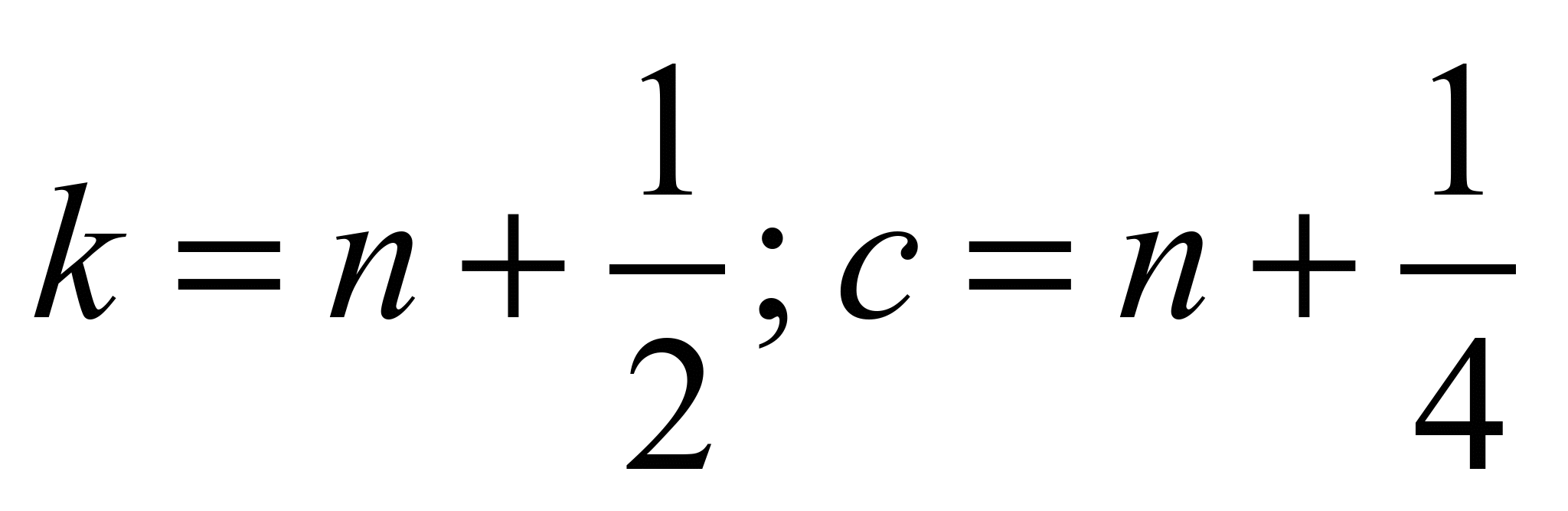 ):
):
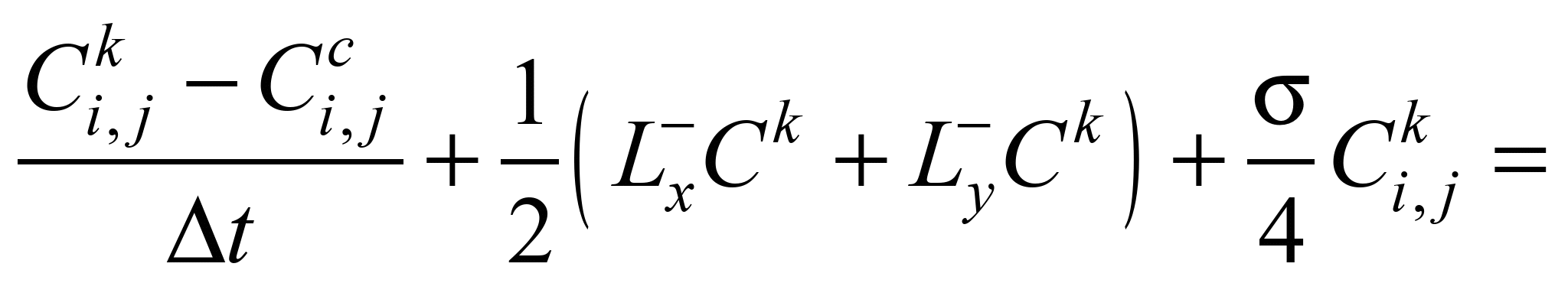
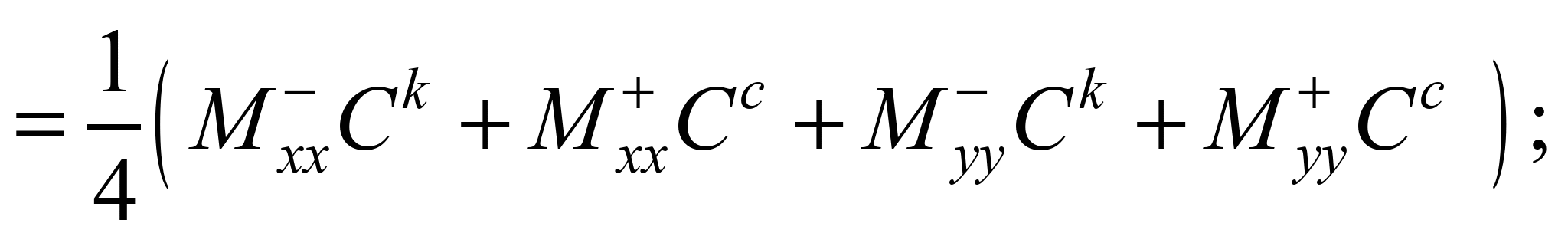 (6)
(6)
– на
третьому кроці ( )
використовуємо залежність (6);
)
використовуємо залежність (6);
– на
четвертому кроці (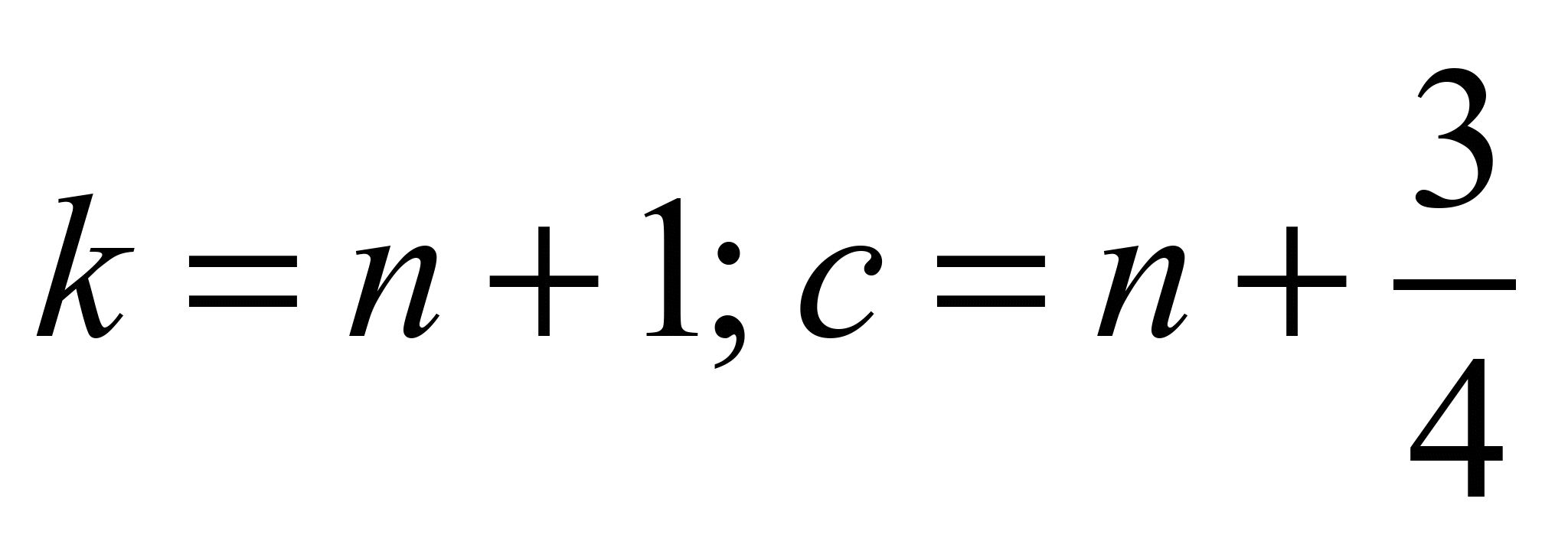 )
застосовуємо залежність (5).
)
застосовуємо залежність (5).
Для чисельного
інтегрування рівнянь гідродинаміки
виконуємо таку апроксимацію рівнянь
[1]:
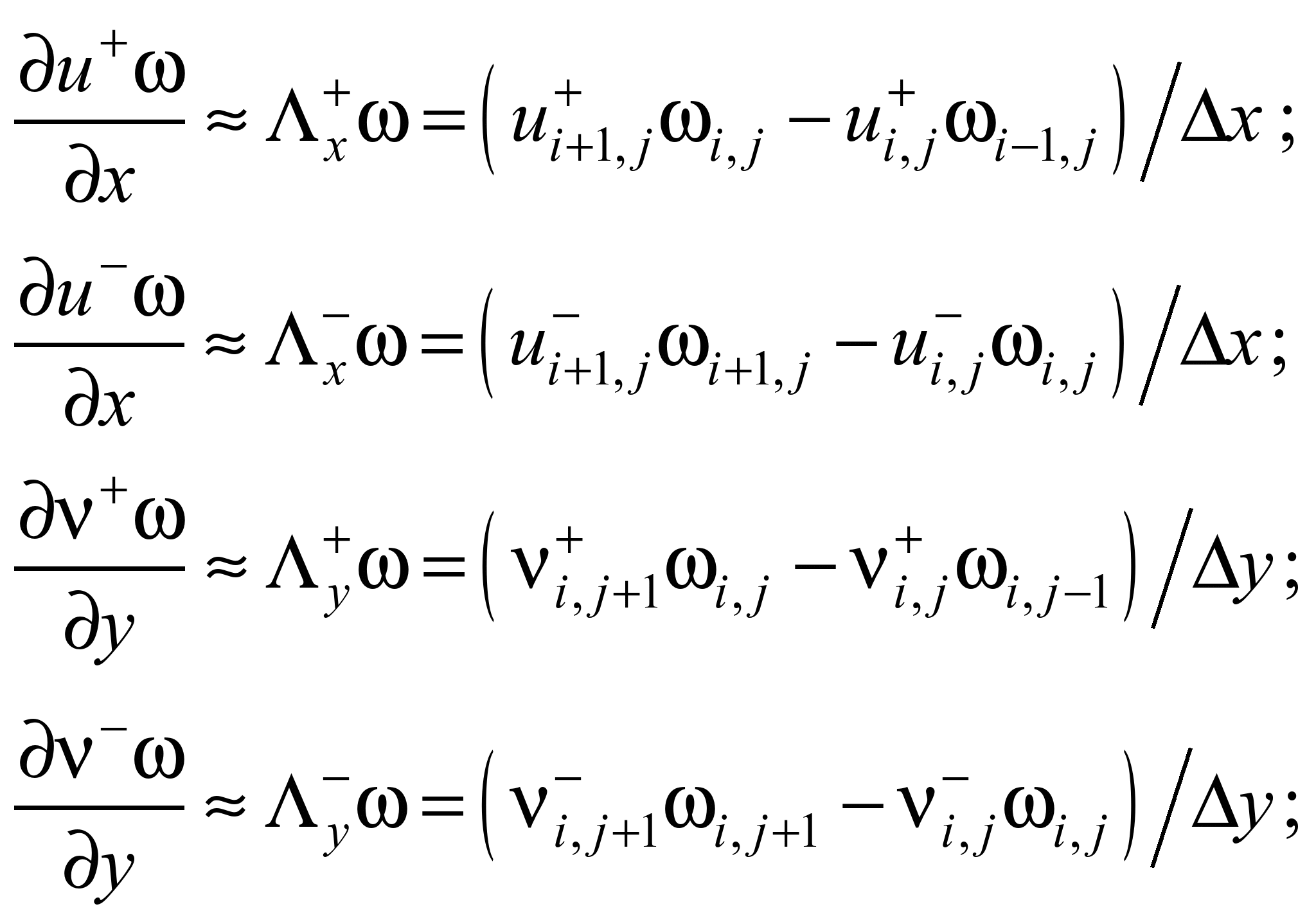
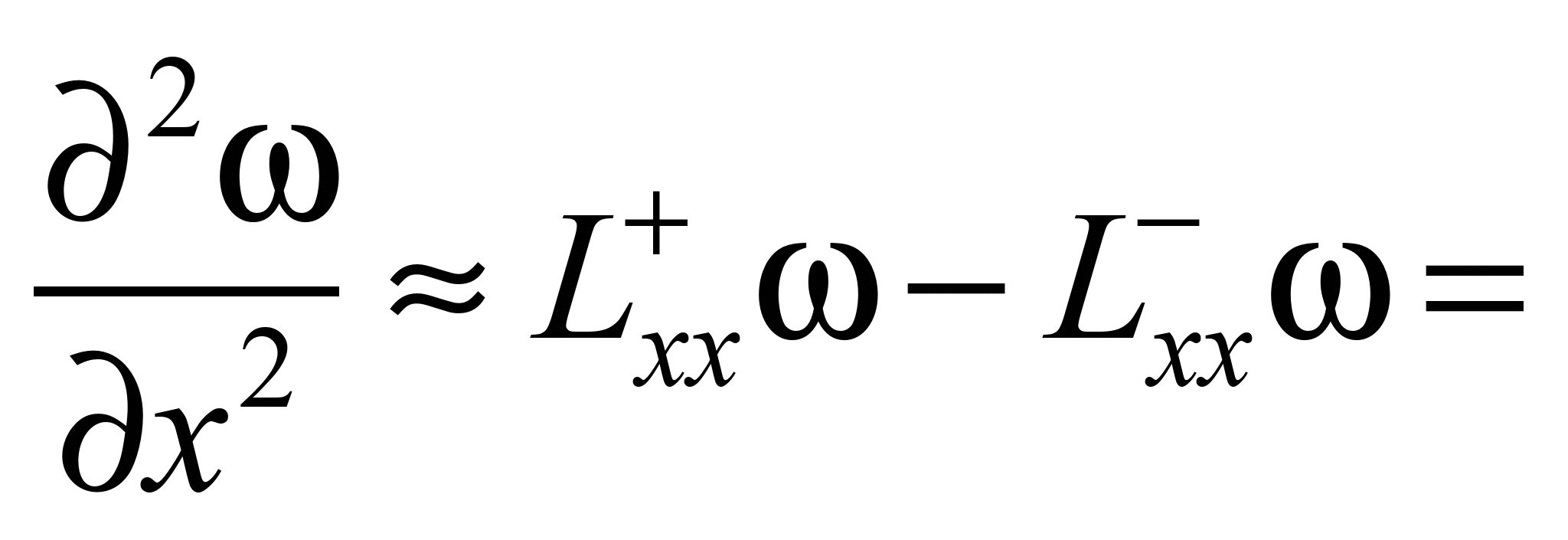
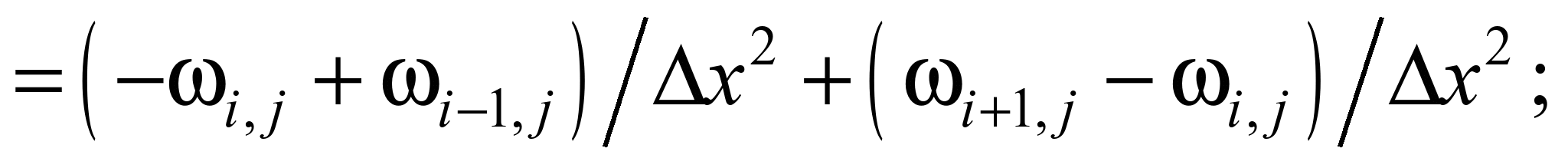
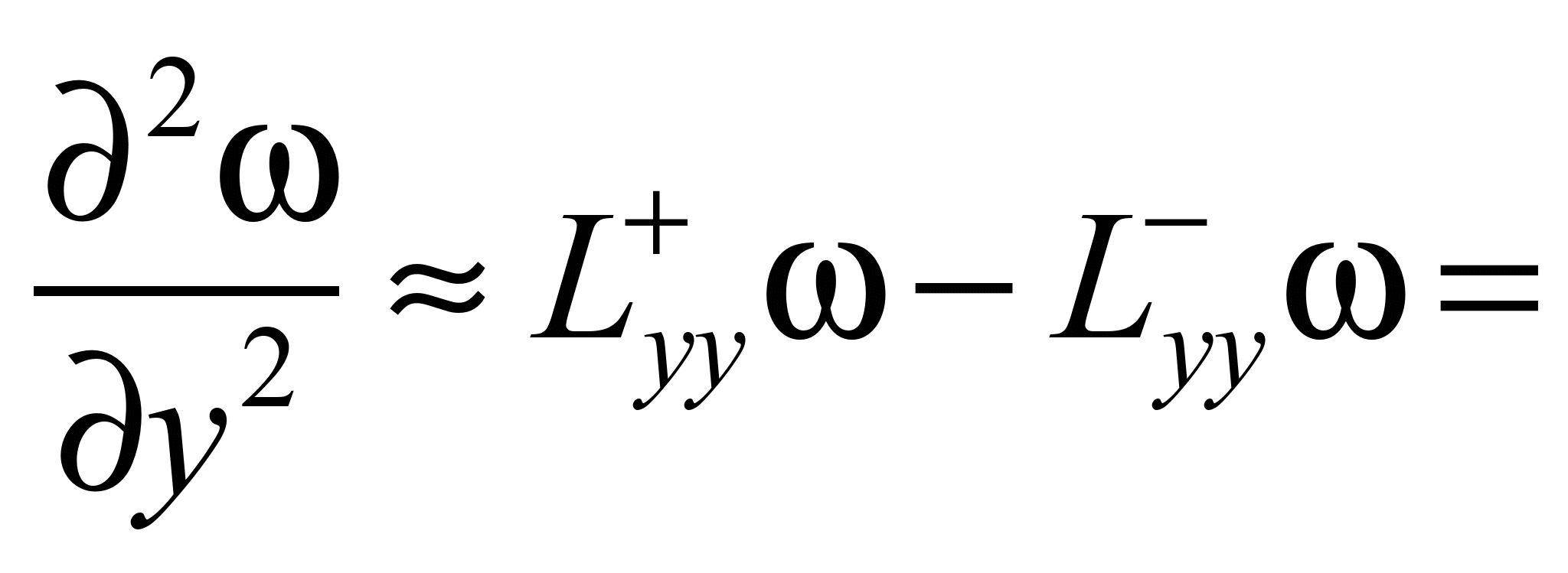
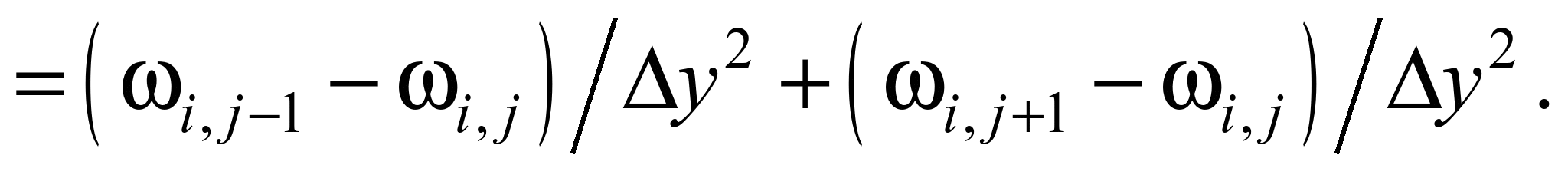
Апроксимувальні
рівняння мають вигляд:

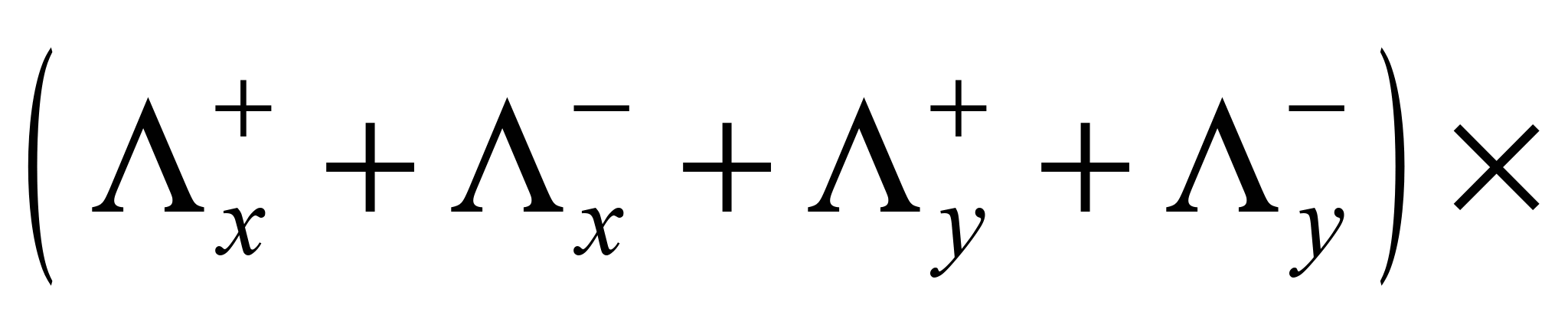
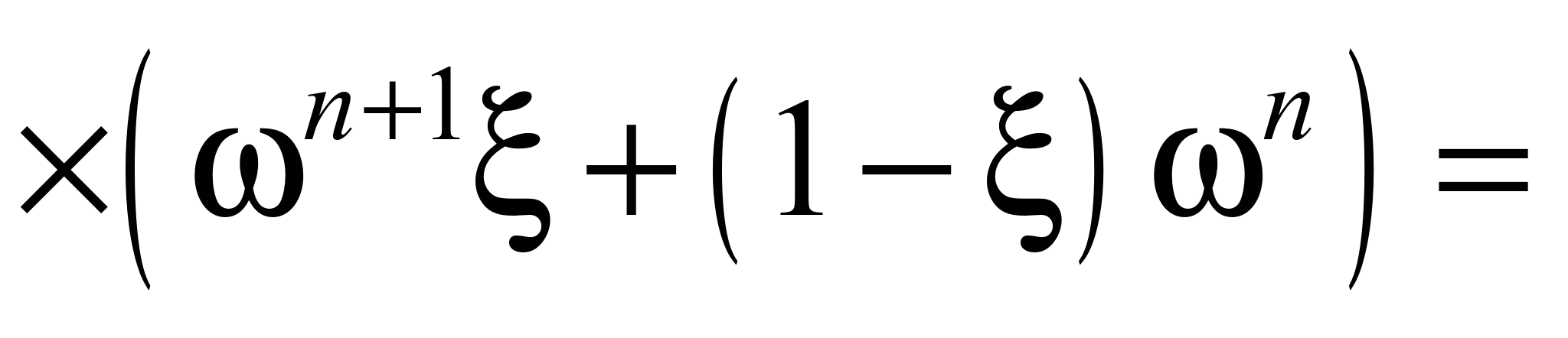
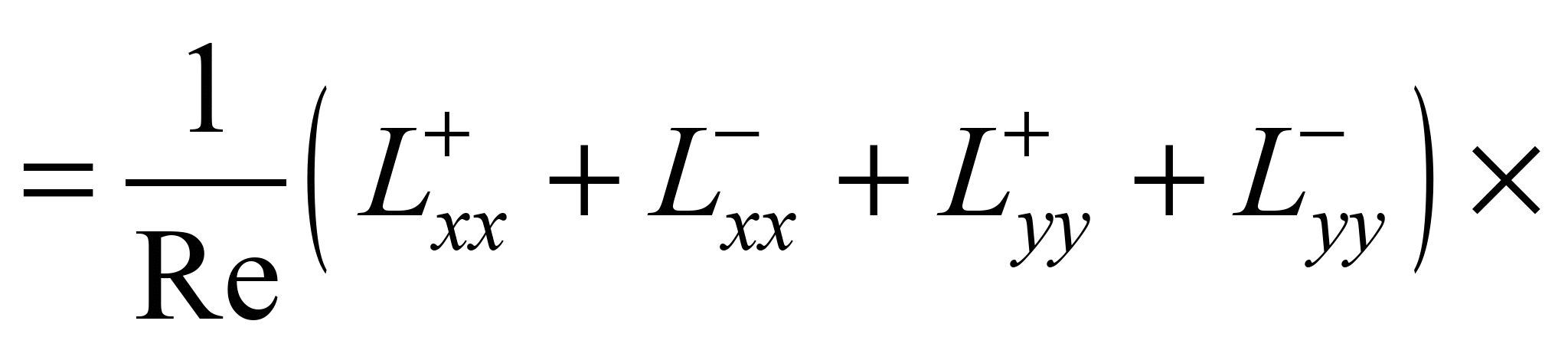
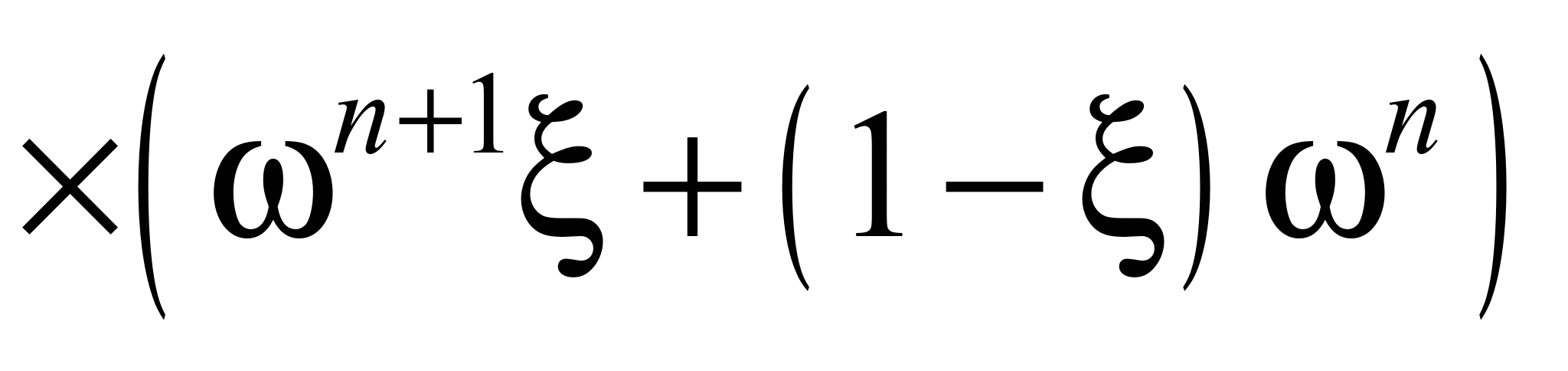
або
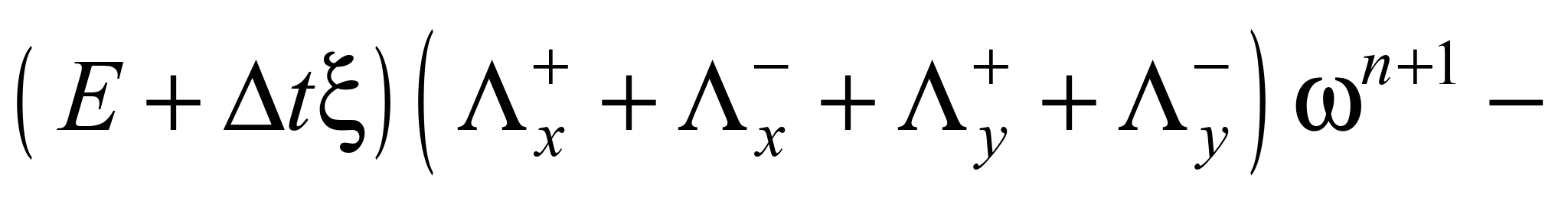
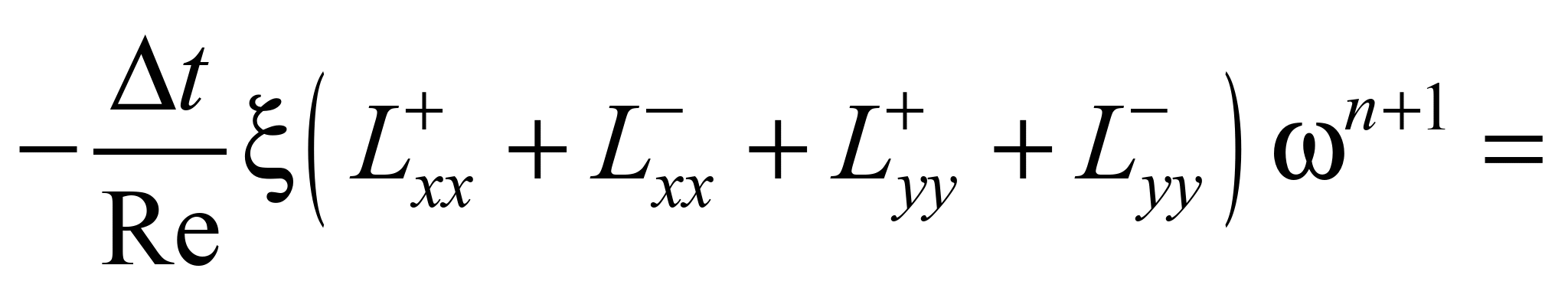
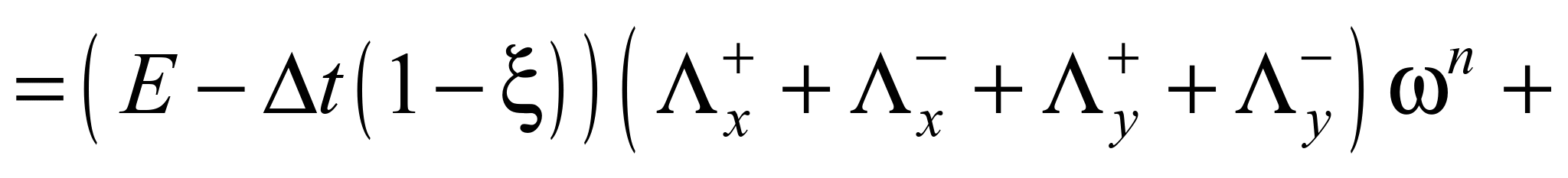
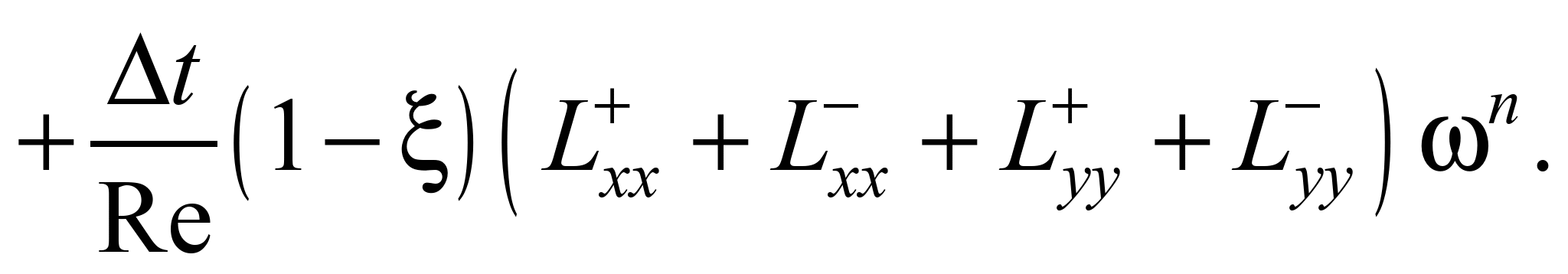
Змінюючи параметр
ξ, можемо змінювати порядок точності
схеми. Так, за ξ = ½ різницева схема має
другий порядок точності за часовою
координатою.
Різницева схема
розщеплення має вигляд [1]:
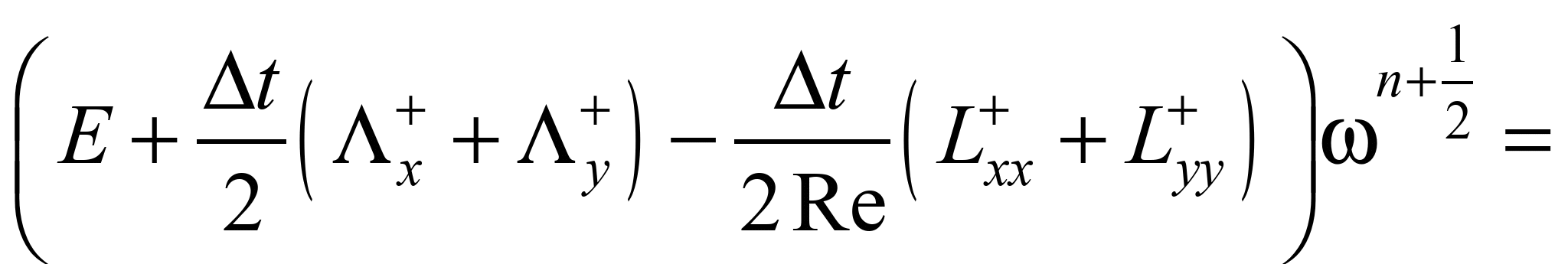
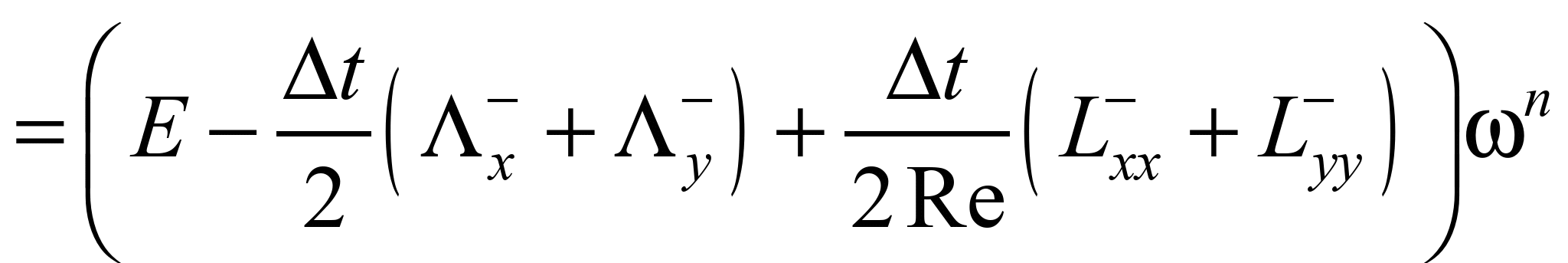 ;
;
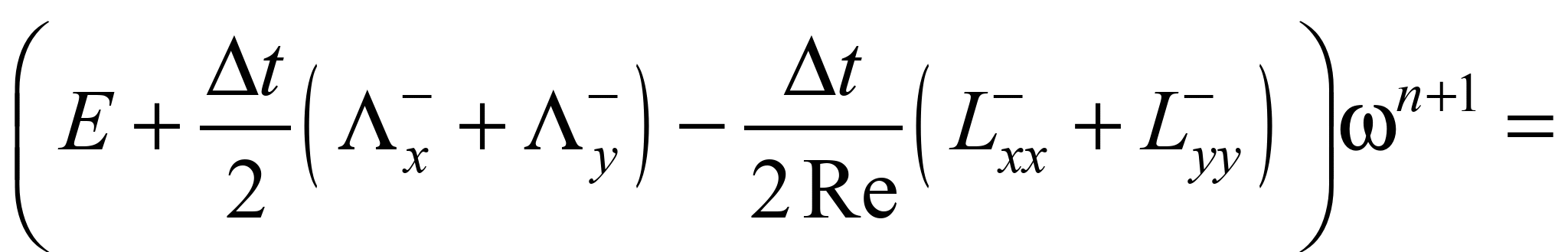
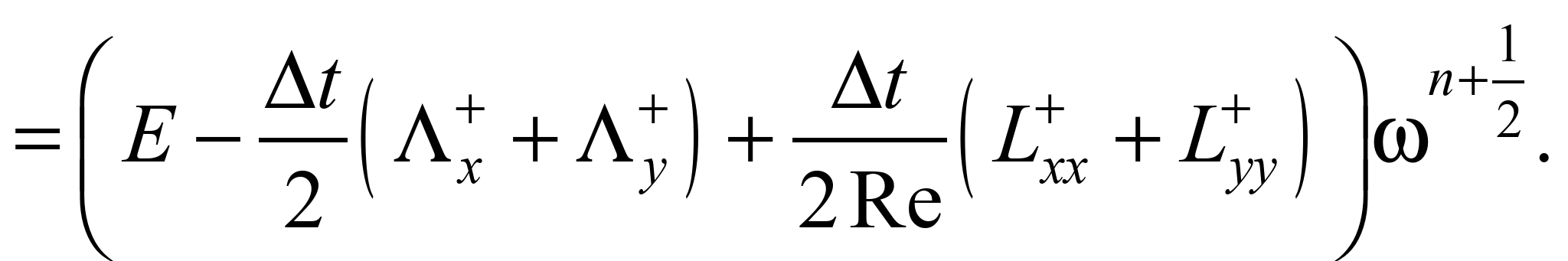
На базі цих формул
можна визначати значення вихору в
піскоуловлювачі.
Для чисельного
інтегрування рівняння функції потоку
на першому кроці зводимо його до вигляду:
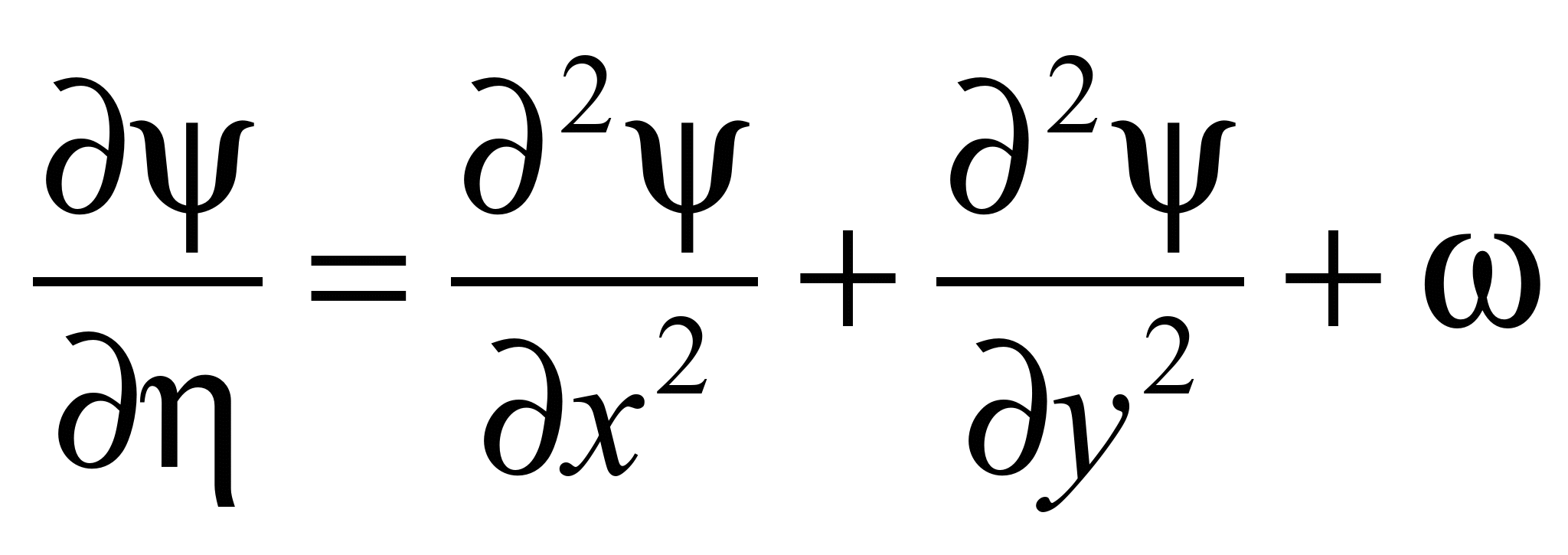 , (7)
, (7)
де η – фіктивний
час.
Далі використовуємо
таку схему розщеплення:
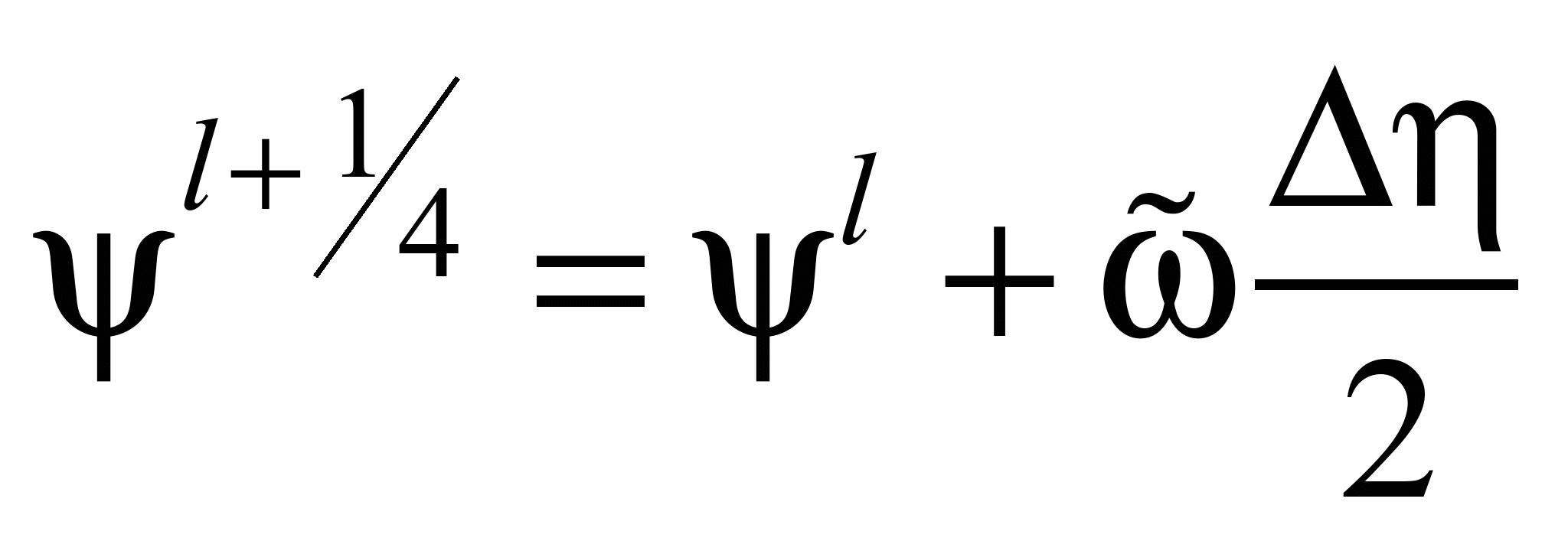 ;
;
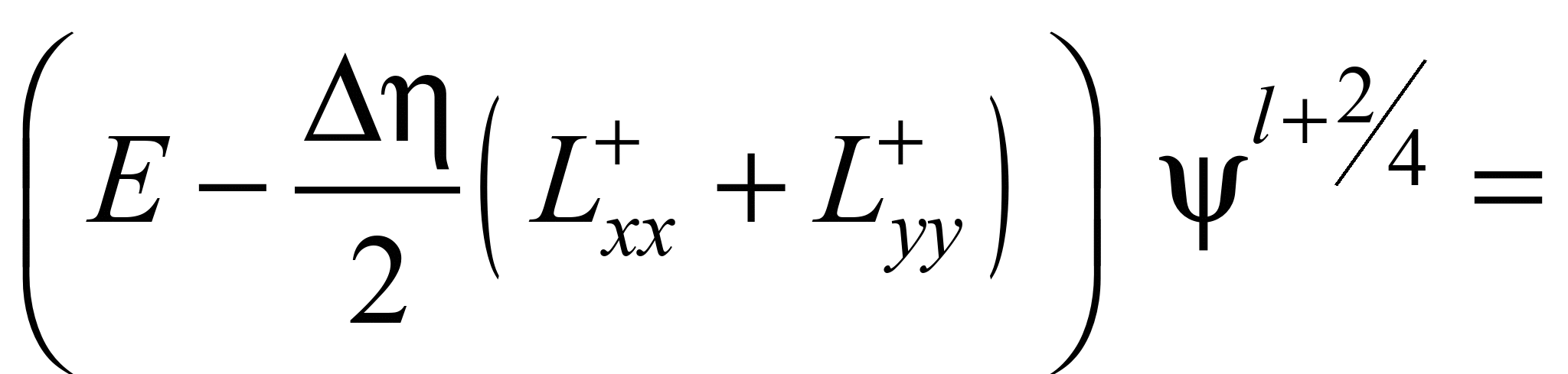
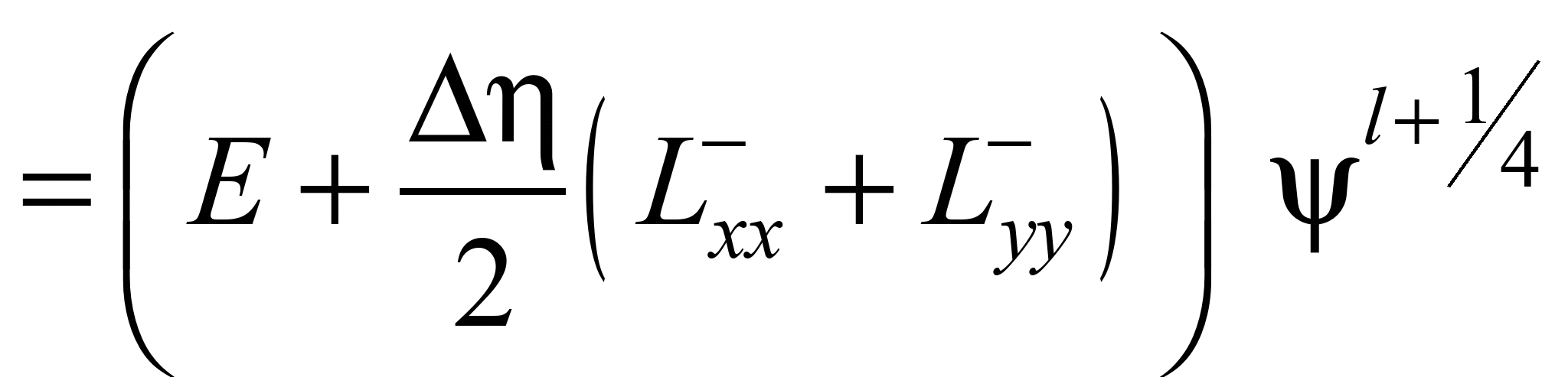 ;
(8)
;
(8)
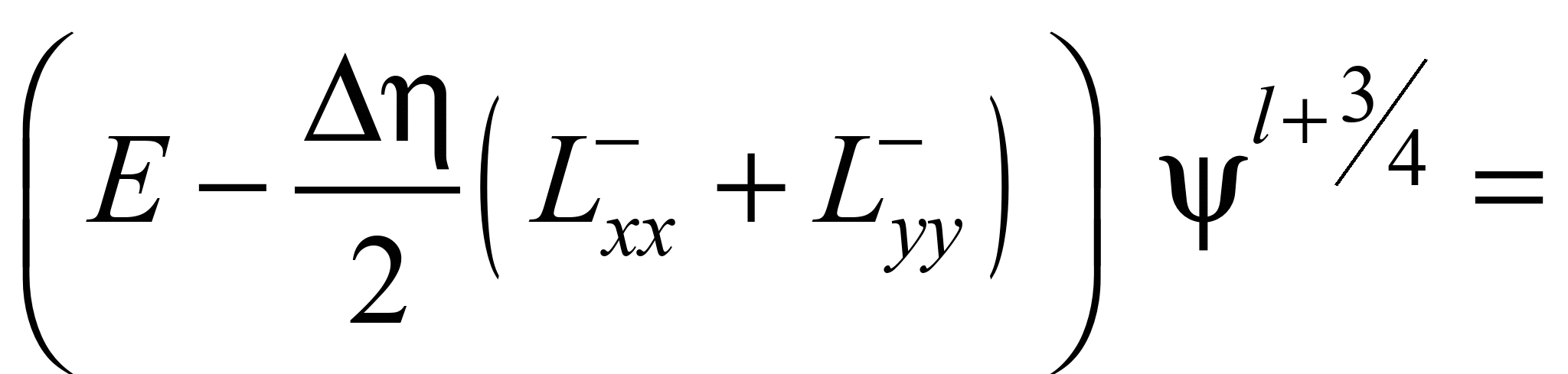
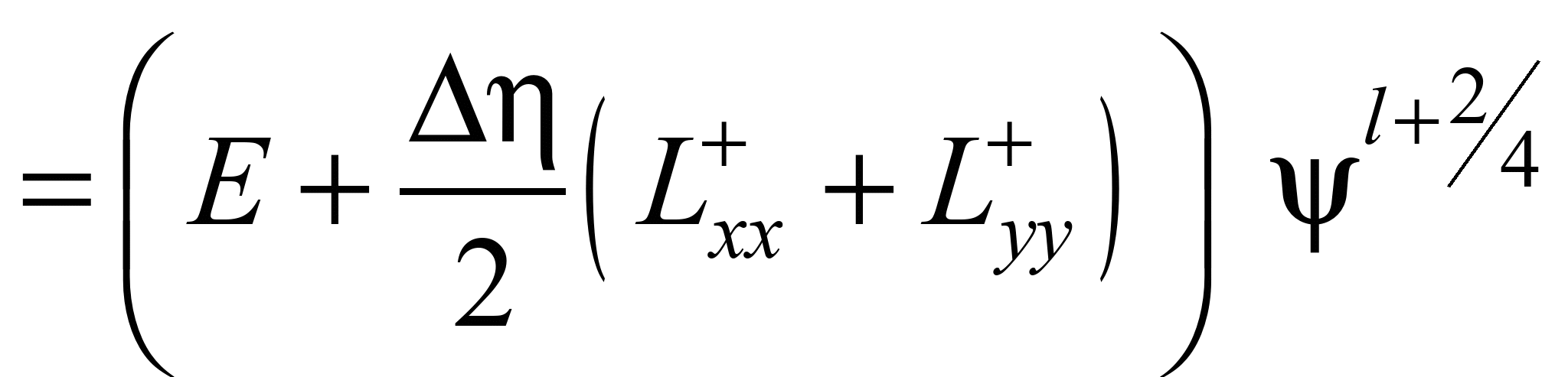 ;
;
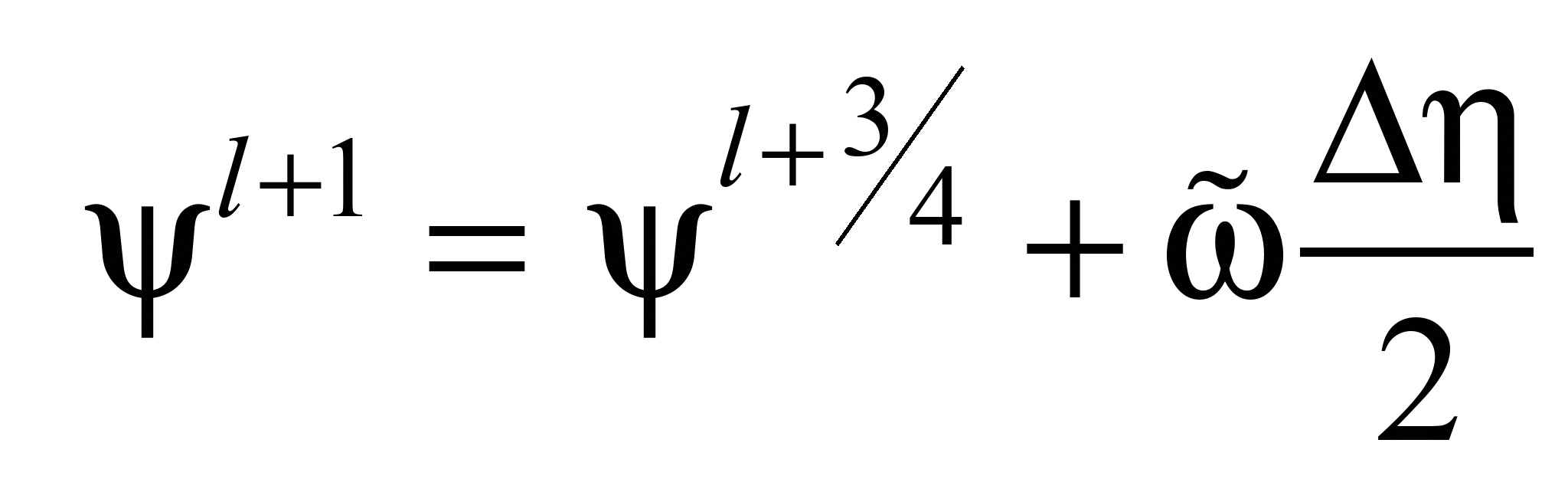 .
.
Особливістю
розглянутих різницевих схем є те, що
розрахунок невідомої величини на
кожному кроці розщеплення здійснено
на базі явних залежностей.
Після розрахунку
значення функції потоку розраховуємо
компоненти вектора швидкості потоку
в піскоуловлювачі:
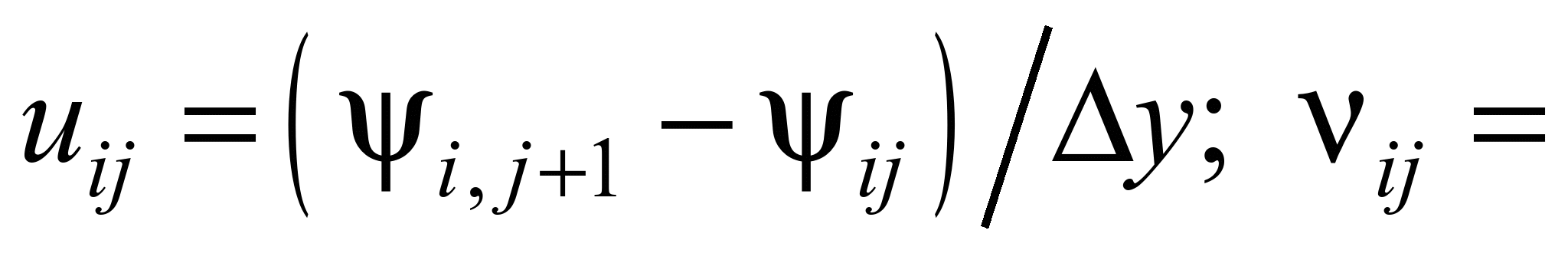
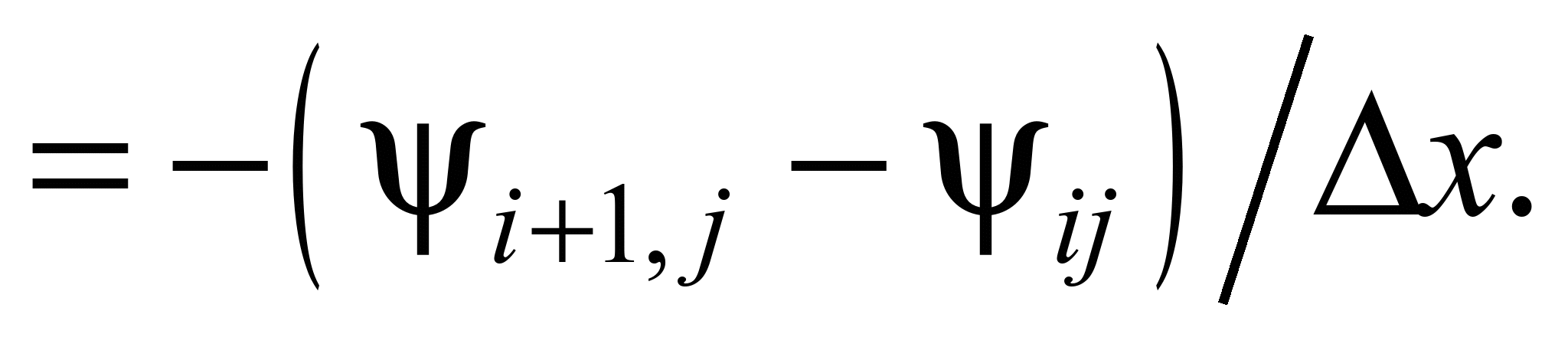
Результати
Для кодування
рівнянь чисельної моделі використано
FORTRAN. Нижче показано результати чисельного
моделювання на базі побудованої
чисельної моделі. Розглянуто три
сценарії. Перший сценарій – у
піскоуловлювачі є додатковий елемент
на дні. Другий сценарій – використаємо
два елемента на дні. Третій сценарій
– використовуємо три додаткових
елемента на дні. Ефективність очищення
визначаємо за концентрацією на виході
з піскоуловлювача. Ця концентрація
показана на рис. 1–3 у відсотках від
концентрації домішки на вході в
піскоуловлювач (концентрація в
безрозмірному вигляді дорівнює
100 одиницям).
На рис. 1 показано
розподіл концентрації вагомої домішки
в піскоуловлювачі, що має додатковий
елемент на дні.
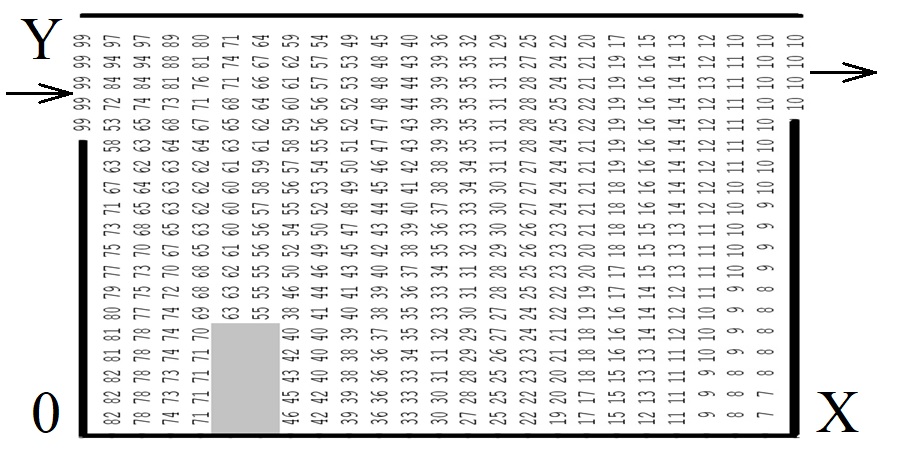
Рис.
1. Концентрація домішки в горизонтальному
піскоуловлювачі (додатковий елемент
на дні)
Fig.
1. Impurity concentration in the horizontal-flow
sand trap (additional element at the bottom)
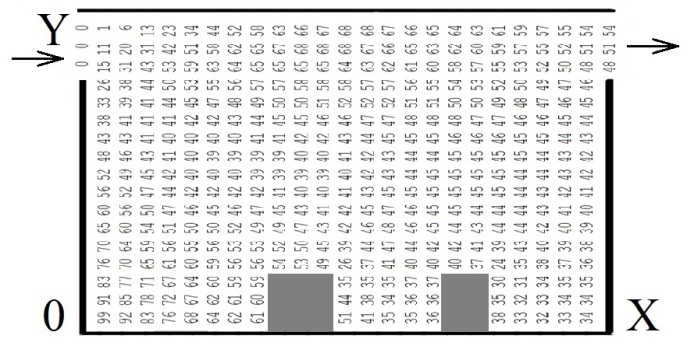
Рис.
2. Концентрація домішки в горизонтальному
піскоуловлювачі (два додаткових
елемента)
Fig. 2.
Impurity concentration in the horizontal-flow sand trap (two
additional elements at the bottom)
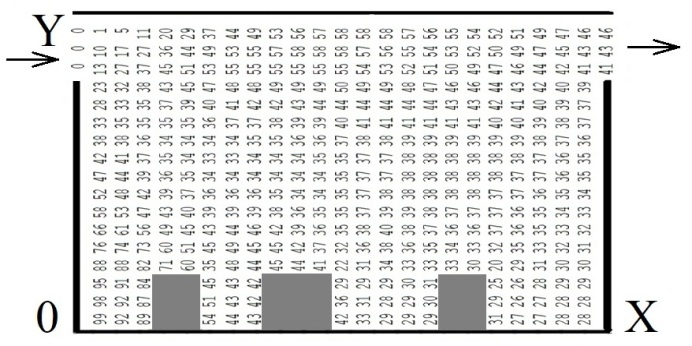
Рис.
3. Концентрація домішки в горизонтальному
піскоуловлювачі (три додаткових
елемента)
Fig. 3.
Impurity concentration in the horizontal-flow sand trap (three
additional elements at the bottom)
Як бачимо з наведених
рисунків, ефективність очищення води
змінюється у випадку збільшення
кількості додаткових елементів на дні
піскоуловлювача. Так, для першого
варіанта, у якому є один додатковий
елемент на дні піскоуловлювача, ефект
очищення становить 10 %. А коли
використано два додаткових елемента,
спостерігається зменшення ефекту
очищення: для третього сценарію ефект
очищення становить вже 43 %.
Відзначимо, що час
розрахунку склав приблизно 12 сек.
Наукова
новизна та практична значимість
Запропоновано
математичну модель для оперативного
розрахунку процесу масопереносу в
піскоуловлювачі. Для моделювання
процесу очищення води використано
рівняння в’язкої нестисливої рідини
та рівняння масопереносу. Побудовані
чисельні моделі дозволяють проводити
обчислювальні експерименти для
піскоуловлювачів, які мають складну
геометричну форму, що дуже важливо для
практики.
Запропоновані
чисельні моделі можуть бути використані
для проведення пілотних розрахунків
на етапі проведення проектних робіт
із підвищення ефективності роботи
систем очищення води.
Висновки
У статті запропоновано
чисельні моделі, що дають можливість
швидко аналізувати, як проходить процес
масопереносу в піскоуловлювачах, які
мають складну геометричну форму. Основою
моделей є фундаментальні рівняння
механіки суцільного середовища.
У подальшому цей
науковий напрям слід розвивати в галузі
побудови тривимірних чисельних моделей
для аналізу процесів масопереносу в
спорудах систем каналізації та
водопостачання.
СПИСОК використаних
джерел
Беляев
Н. Н., Нагорная Е. К. Математическое
моделирование массопереноса в
отстойниках систем водоотведения
: монография.
Днепропетровск : Новая идеология, 2012.
112 с.
Беляев
Н. Н., Козачина В. А.
Математическое моделирование
массопереноса в горизонтальных
отстойниках :
монография. Днепропетровск : Акцент
ПП, 2015. 115 с.
Василенко
О. А., Грабовський П. О., Ларкіна Г. М.,
Поліщук О. В., Прогульний В. Й. Реконструкція
і інтенсифікація споруд водопостачання
та водовідведення :
навч. посіб. Київ : ІВНВКП «Укргеліотек»,
2010. 272 с.
ДБН
В.2.5-75:2013. Каналізація. Зовнішні мережі
та споруди. Основні положення
проектування. [Чинний від 2014-01-01].
Київ : Мінрегіон України, 2013. 128 с.
Епоян
С. М., Колотило В. Д., Друшляк О. Г.
Водопостачання та
очистка природних вод
: навчальний посібник. Харків
: Фактор, 2010. 192
с.
Олійник
О. Я, Айрапетян Т. С. Моделювання очисних
стічних вод від органічних забруднень
в біореакторах-аеротенках зі зваженим
(вільно плаваючим) і закріпленим
біоценозом. Доповідь
НАН України. 2015. № 5.
С. 55–60. DOI: 10/15407/dopovidi2015.05.055
Alharbi,
A. O. M. The biological treatment of wastewater: mathematical
models. Bulletin of the Australian
Mathematical Society.
2016. Vol. 94. Іss. 2. P. 347–348.
DOI: 10.1017/S0004972716000411
Bakiri Z., Nacef S. A simple model
for secondary clarifier: Application to wastewater treatment plant.
Desalination and Water Treatment.
2013. Vol. 51. Iss. 7–9. P. 1571–1576.
DOI: 10.1080/19443994.2012.715073
Bomba A., Klymiuk Y.,
Prysiazhniuk I., Prysiazhniuk O., Safonyk A.
Mathematical modeling of wastewater treatment from multicomponent
pollution by through microporous filling.
AIP Conference Proceedings.
2016. Vol. 1773.
P. 040003-1–040003-11. DOI: 10.1063/1.4964966
Griborio
A. Secondary Clarifier Modeling: A
Multi-Process Approach. Dissertation
and Theses. University of New Orleans
: USA, 2004. 440 p.
Młyński
D., Bugajski P., Młyńska A. Application
of the Mathematical Simulation Methods for the Assessment of the
Wastewater Treatment Plant Operation Work Reliability. Water.
2019. Vol. 11.
Iss. 5. P. 1–17. DOI: 10.3390/w11050873
В. Д. Петренко1,
Н. И. Нетеса2,
А. Л. ТютькИн3,
Е. В. Громова4,
В. И. Шинкаренко5,
В. А. козачина6*
1Каф.
«Мосты и туннели», Днипровский
национальный университет железнодорожного
транспорта имени академика В. Лазаряна,
ул. Лазаряна, 2, Днипро, Украина, 49010, тел.
+38 (056) 373 15 53, эл. почта petrenko.diit@gmail.com, ORCID
0000-0003-2201-3593
2Каф.
«Строительное производство и геодезия»,
Днипровский национальный университет
железнодорожного транспорта имени
академика В. Лазаряна, ул. Лазаряна,
2, Днипро, Украина, 49010, тел. +38 (067) 195 50 27,
эл. почта andreynetesa@meta.ua, ORCID
0000-0003-1730-7642
3Каф.
«Мосты и туннели», Днипровский
национальный университет железнодорожного
транспорта имени академика В. Лазаряна,
ул. Лазаряна, 2, Днипро, Украина, 49010, тел.
+38 (056) 373 15 53, эл. почта alexeytutkin@gmail.com, ORCID
0000-0003-4921-4758
4Каф.
«Архитектурное проектирование,
землеустройство и строительные
материалы», Днипровский национальный
университет железнодорожного транспорта
имени академика В. Лазаряна, ул.
Лазаряна, 2, Днипро, Украина, 49010, тел.
+38 (095) 304 73 33, эл. почта Gromova_Elen_upbbm_diit@i.ua,
ORCID 0000-0002-5149-4165
5Каф.
«Компьютерные информационные технологии»,
Днипровский национальный университет
железнодорожного транспорта имени
академика В. Лазаряна, ул. Лазаряна, 2,
Днипро, Украина, 49010, тел. +38 (056) 373 15 35,
эл. почта shinkarenko_vi@ua.fm, ORCID
0000-0001-8738-7225
6*Каф.
«Гидравлика и водоснабжение», Днипровский
национальный университет железнодорожного
транспорта имени академика В. Лазаряна,
ул. Лазаряна, 2, Днипро, Украина, 49010, тел.
+38 (056) 273 15 09, эл. почта v.kozachyna@gmail.com,
ORCID 0000-0002-6894-5532
экспресс модель для расчета
процесса очистки воды
Цель.
Использование физического эксперимента
для исследования процессов массопереноса
в сооружениях систем водоснабжения и
канализации требует значительного
времени и является весьма дорогостоящим.
Поэтому целью работы является разработка
численных моделей для проведения
вычислительного эксперимента по
исследованию процесса массопереноса
в песколовки. Методика.
Для математического моделирования
процесса массопереноса в песколовки
использованы двумерные уравнения
Навье–Стокса и двумерное уравнение
массопереноса примеси. Для численного
интегрирования уравнений, описывающих
движение вязкой несжимаемой жидкости,
использованы неявные разностные схемы
расщепления. Неизвестные параметры на
каждом шагу расщепления найдены по
явным зависимостям. Для численного
интегрирования двумерного уравнения
массопереноса использована
попеременно-треугольная разностная
схема расщепления. Результаты.
Для проведения вычислительного
эксперимента на базе построенной
численной модели создан специализированный
код. Представлены результаты вычислительных
экспериментов по исследованию процесса
массопереноса в песколовки с
дополнительными элементами. Определено,
что эффективность очистки воды изменяется
при использовании дополнительных
элементов на дне песколовки. Научная
новизна. Построены
численные модели, которые дают возможность
оперативно анализировать и
прогнозировать эффективность работы
песколовок, имеющих сложную геометрическую
форму. Эти модели позволяют учесть
также гидродинамику течения в очистном
сооружении. Практическая
значимость. Предложенные
численные модели можно использовать
на этапе проектирования очистных
сооружений систем канализации.
Ключевые слова:
очистка воды; численное моделирование;
разностные схемы; песколовка;
водопользование; математическое
моделирование
V. D.
Petrenko1,
M.
I. Netesa2,
o.
l. Tiutkin3,
O.
V. Gromova4,
V. І.
shynkarenko5,
V. А.
Kozachyna6*
1Dep.
«Bridges and Tunnels», Dnipro
National University of Railway Transport named after Academician V.
Lazaryan, Lazaryana St., 2, Dnipro, Ukraine, 49010,
tel. +38 (056) 373 15 53, e-mail
petrenko.diit@gmail.com,
ORCID 0000-0003-2201-3593
2Dep.
«Build Production and Geodesy»,
Dnipro National University of
Railway Transport named after Academician V. Lazaryan, Lazaryana
St., 2, Dnipro, Ukraine, 49010,
tel. +38 (067) 195 50 27, e-mail
andreynetesa@meta.ua,
ORCID 0000-0003-1730-7642
3Dep.
«Bridges and Tunnels», Dnipro
National University of Railway Transport named after Academician V.
Lazaryan, Lazaryana St., 2, Dnipro, Ukraine, 49010,
tel. +38 (056) 373 15 53, e-mail
alexeytutkin@gmail.com,
ORCID 0000-0003-4921-4758
4Dep.
«Аrchitectural Design, Land Management and Building Materials»,
Dnipro National University of
Railway Transport named after Academician V. Lazaryan, Lazaryana
St., 2, Dnipro, Ukraine, 49010,
tel. +38 (095) 304 73 33, e-mail
Gromova_Elen_upbbm_diit@i.ua,
ORCID 0000-0002-5149-4165
5Dep.
«Computer and Information Technologies», Dnipro National
University of Railway Transport named after Academician V. Lazaryan,
Lazaryana St., 2, Dnipro, Ukraine, 49010,
tel.
+38 (056) 373 15 35, e-mail shinkarenko_vi@ua.fm,
ORCID 0000-0001-8738-7225
6*Dep.
«Hydraulics and Water Supply», Dnipro National University of
Railway Transport named after Academician V. Lazaryan, Lazaryana
St., 2, Dnipro, Ukraine, 49010, tel. +38 (056) 273 15 09, e-mail
v.kozachyna@gmail.com, ORCID 0000-0002-6894-5532
Express model for water
treatment process
calculation
Purpose. The use of a physical experiment to
study mass transfer processes in structures used in water supply and
sewage systems requires considerable time and is very expensive. The
aim of the work is to develop numerical models for a computational
experiment to study the mass transfer process in sand traps.
Methodology. For mathematical modeling of the mass transfer
process in sand traps, the two-dimensional Navier-Stokes equations
and the two-dimensional impurity mass transfer equation are used.
For numerical integration of equations describing the motion of a
viscous incompressible fluid, implicit difference splitting schemes
are used. The unknown parameters at each step of the splitting were
found by explicit dependencies. For the numerical integration of the
two-dimensional mass transfer equation, an alternately triangular
difference splitting scheme is used. Findings. To conduct a
computational experiment, a specialized code was created on the
basis of the constructed numerical model. The results of
computational experiments on the study of mass transfer in sand
traps with additional elements are presented. It was determined that
water purification efficiency changes with installation of
additional elements at the bottom of the sand trap.
Originality. The constructed numerical models make
it possible to quickly analyze and predict the efficiency of sand
traps having a complex geometric shape. They also make it possible
to take into account the flow hydrodynamics in the treatment plant.
Practical value. The proposed numerical models can be used at
the design stage of sewage treatment plants.
Keywords: water purification; numerical
simulation; difference schemes; sand trap; water use;
mathematical modeling
References
Biliaiev,
N. N., & Nagornaya, E. K. (2012). Matematicheskoye
modelirovaniye massoperenosa v otstoynikakh sistem vodootvedeniya:
monografiya. Dnepropetrovsk: Novaya ideologiya. (in Russian)
Biliaiev,
N. N., & Kozachina, V. A. (2015). Modelirovaniye
massoperenosa v gorizontalnykh otstoynikakh:
monografiya. Dnepropetrovsk: Aktsent PP. (in Russian)
Vasylenko,
O. A., Hrabovskyi, P. O., Larkina, H. M., Polishchuk, O. V., &
Prohulnyi, V. Y. (2010). Rekonstruktsiia
i in-tensyfikatsiia sporud vodopostachannia ta vodovidvedennia:
navchalnyi posibnyk.
Kyiv: IVNVKP «Ukrheliotek». (in Ukrainian)
Kanalizatsiia.
Zovnishni merezhi ta sporudy. Osnovni polozhennia proektuvannia,
128 DBN V.2.5-75-2013 (2013). (in Ukrainian)
Epoian,
S. M., Kolotylo, V. D., & Drushliak, O. H. (2010).
Vodopostachannia ta ochystka
pryrodnykh vod: navchalnyi posibnyk.
Xarkiv : Faktor. (in Ukrainian)
Oleynik,
A. Y., & Airapetyan, T. S. (2015). The modeling of the
clearance of waste waters from organic pollutions in
bioreactors-aerotanks with suspended (free flow) and fixed
biocenoses. Reports of the National
Academy of Sciences of Ukraine, 5,
55-60. DOI: 10.15407/dopovidi2015.05.055 (in
Ukrainian)
Alharbi, A. O. M. (2016). The
biological treatment of wastewater: mathematical models. Bulletin
of the Australian Mathematical Society, 94(2),
347-348. DOI:10.1017/s0004972716000411 (in
English)
Bakiri,
Z., & Nacef, S. (2013). A simple model for secondary clarifier:
application to wastewater treatment plant. Desalination
and Water Treatment, 51(7-9),
1571-1576. DOI: 10.1080/19443994.2012.715073
(in English)
Bomba,
A., Klymiuk, Y., Prysiazhniuk, I., Prysiazhniuk, O., & Safonyk,
A. (2016). Mathematical modeling of wastewater treatment from
multicomponent pollution by through microporous filling. AIP
Conference Proceedings, 1773,
040003-1-040003-11. DOI: 10.1063/1.4964966 (in
English)
Griborio,
A. (2004). Secondary Clarifier
Modeling: A Multi-Process Approach. Dissertation and Theses.
USA, University of New Orleans Publ. (in English)
Młyński,
D., Bugajski, P., & Młyńska, A. (2019). Application of the
Mathematical Simulation Methods for the Assessment of the
Wastewater Treatment Plant Operation Work Reliability. Water,
11(5), 873.
DOI: 10.3390/w11050873
(in English)
Надійшла до
редколегії: 02.12.2019
Прийнята до друку:
03.04.2020
; (1)
; (2)
. (3)
;
;
;
;
(4)
):
(5)
):
(6)
)
використовуємо залежність (6);
)
застосовуємо залежність (5).
;
, (7)
;
;
(8)
;
.