ISSN 2307–3489 (Print), ІSSN 2307–6666 (Online)

Наука та прогрес транспорту. Вісник Дніпропетровського
національного університету залізничного транспорту, 2020, № 1 (85)



ЕКОЛОГІЯ ТА ПРОМИСЛОВА БЕЗПЕКА

УДК 628.16.067.1:519.87

В. Д. Петренко1, М. І. Нетеса2, О. Л. Тютькін3, О. В. Громова4,
В. А. козачина5*

1Каф. «Мости та тунелі», Дніпровський національний університет залізничного транспорту імені академіка В. Лазаряна, вул. Лазаряна, 2, Дніпро, Україна, 49010, тел. +38 (056) 373 15 53, ел. пошта petrenko.diit@gmail.com, ORCID 0000-0003-2201-3593
2Каф. «Будівельне виробництво та геодезія», Дніпровський національний університет залізничного транспорту імені академіка В. Лазаряна, вул. Лазаряна, 2, Дніпро, Україна, 49010, тел. +38 (067) 195 50 27,
ел. пошта andreynetesa@meta.ua, ORCID 0000-0003-1730-7642
3Каф. «Мости та тунелі», Дніпровський національний університет залізничного транспорту імені академіка В. Лазаряна, вул. Лазаряна, 2, Дніпро, Україна, 49010, тел. +38 (056) 373 15 53, ел. пошта alexeytutkin@gmail.com, ORCID 0000-0003-4921-4758
4Каф. «Архітектурне проєктування, землеустрій та будівельні матеріали», Дніпровський національний університет залізничного транспорту імені академіка В. Лазаряна, вул. Лазаряна, 2, Дніпро, Україна, 49010, тел. +38 (095) 304 73 33,
ел. пошта Gromova_Elen_upbbm_diit@i.ua, ORCID 0000-0002-5149-4165
5*Каф. «Гідравліка та водопостачання», Дніпровський національний університет залізничного транспорту імені академіка В. Лазаряна, вул. Лазаряна, 2, Дніпро, Україна, 49010, тел. +38 (056) 273 15 09, ел. пошта v.kozachyna@gmail.com, ORCID 0000-0002-6894-5532

МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ

ОЧИЩЕННЯ ВОДИ У фільтрі

Мета. Для аналізу ефективності очищення води в системах водопідготовки важливим завданням є розробка математичних моделей, що дозволяють визначати ступінь очищення води на етапі проведення проєктних робіт. Основною метою роботи є побудова чисельних моделей для розрахунку процесу фільтрації та масопереносу у фільтрі. Методика. Розрахунок процесу фільтрації забрудненої води у фільтрі проведено у два етапи. На першому етапі розраховано поле швидкості потоку у фільтрі. Для розв’язання цієї задачі використано класичне рівняння фільтрації. На другому етапі розрахунку змодельовано течію забрудненої води у фільтрі. Для розв’язання цієї задачі використано рівняння масопереносу, що виражає закон збереження маси. Це рівняння враховує перенос домішки фільтраційним потоком, перенос домішки за рахунок дисперсії та сорбцію домішки в завантаженні фільтра. Розв’язання рівняння фільтрації проведено за допомогою поперемінно-трикутного методу О. А. Самарского. Визначення невідомого значення напору на базі цього методу проведено за явною формулою біжучого розрахунку. Для чисельного інтегрування моделювального рівняння масопереносу у фільтрі використано різницеву схему розщеплення. Результати. Сучасною тенденцію в галузі водопостачання та водовідведення є створення багатовимірних та багатофакторних математичних моделей. Таки моделі дозволяють замінити фізичний експеримент на обчислювальний. До комплексу споруд водопідготовки обов’язково належать фільтри очищення води. Ефективність роботи фільтрів впливає на ефективність роботи інших очисних споруд технологічної схеми очищення. Розроблено математичниу модель, що дозволяє аналізувати процес очищення води у фільтрі. На базі цієї чисельної моделі розроблено пакет прикладних програм для проведення комп’ютерного експерименту з моделювання процесу очищення води у фільтрі. Наведено результати обчислювального експерименту з моделювання процесу фільтрації забрудненої води у фільтрі. Наукова новизна. У роботі запропоновано чисельну двовимірну модель фільтра, що базується на рівнянні фільтрації та рівнянні масопереносу. Особливістю цієї моделі є можливість моделювання поля швидкості та процесу переносу домішки з урахуванням геометричної форми фільтрів. Практична значимість. Час розрахунку одного варіанта завдання на базі побудованої чисельної моделі складає декілька секунд, що є важливим для проведення серійних розрахунків на практиці. Моделі можна використовувати як альтернативу проведення лабораторних експериментів.

Ключові слова: очищення води; математичне моделювання; фільтр; чисельна модель

Вступ

Актуальною проблемою в галузі водопостачання та водовідведення є розробка математичних моделей для визначення ефективності роботи різних систем та споруд очищення води [1, 2, 3, 5–13]. Важливість цього завдання пов’язана з тим, що використання методу фізичного моделювання є дуже коштовним та потребує значного часу на отримання результатів. Тому постає необхідність у створенні математичних моделей, що дозволяли б оперативно визначати ефективність роботи очисного обладнання для різних умов експлуатації.

У наш час значну увагу приділяють завданням підвищення ефективності роботи очисних споруд на станціях водопідготовки та підприємствах. На цих станціях широко використовують різного роду очисні споруди: відстійники, змішувачі та ін. Слід підкреслити, що практично на кожній станції водопідготовки є фільтри. Ефективність роботи фільтрів залежать від різних факторів. У випадку побудови нових станцій водо підготовки або реконструкції наявних виникає проблема визначення ефективності роботи фільтрів для нових умов експлуатації.

Для вирішення цього завдання широко використовуються емпіричні [4] та аналітичні моделі [6, 7]. Вони дозволяють досить швидко розрахувати необхідні параметри фільтра, але не враховують просторові процеси фільтрації. Тому для практичних цілей важливо розробляти моделі, що дають можливість розв’язувати задачі фільтрації у дво- або тривимірній постановці.

Мета

Як основну мету роботи ми передбачаємо розробку двовимірної чисельної моделі процесу масопереносу у фільтрі. Чисельна модель має бути застосовною для розрахунку як безнапірних, так і напірних фільтрів. Крім цього, має бути реалізована можливість моделювання процесу фільтрації для різного завантаження та різних розмірів, форми фільтра, витрати забрудненої води. Також розроблена чисельна модель повинна дозволяти проведення серійних розрахунків із невеликою витратою комп’ютерного часу.

Методика

Ставимо завдання розробки математичної моделі, що дозволяє розраховувати процес фільтрації забрудненої води у фільтрі.

Процес розрахунку масопереносу у фільтрі складається з двох етапів. На першому етапі розраховуємо поле швидкості фільтрації у фільтрі. Моделювальне рівняння на цьому етапі має вигляд:

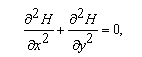(1)

де H – п’єзометричний напір.

Постановку граничних умов для рівняння фільтрації (1) наведено в роботі [3].

Після визначення поля п’єзометричного напору розраховуємо компоненти вектора швидкості фільтраційного потоку у фільтрі так:

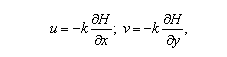
де k – коефіцієнт фільтрації.

Чисельний розв’язок рівняння фільтрації (1) знаходимо за допомогою поперемінно-трикутного методу О. А. Самарського. На кожному кроці розщеплення різницеві рівняння для чисельного інтегрування (1) записуюємо так:

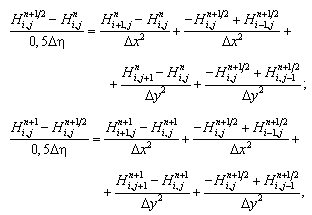
де η – фіктивний час.

Ця різницева схема є неявною, але розрахунок значення потенціалу швидкості Pi,j на кожному кроці розщеплення здійснюємо також за явною формулою – методом біжучого рахунку.

Процес розрахунку закінчується в разі виконання умови:

,

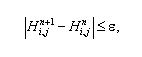де 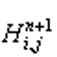– нове наближення величини напору; 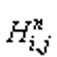– попереднє значення величини напору;
ε – мале число.

Після розрахунку у фільтрі поля напору визначаємо компоненти вектора швидкості фільтраційного потоку на гранях різницевих комірок:

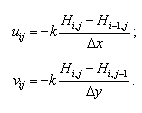
На другому етапі моделювання розраховуємо процес масопереносу домішки у фільтрі. Для розрахунку цього процесу використовуємо наступне рівняння [2, 3]:

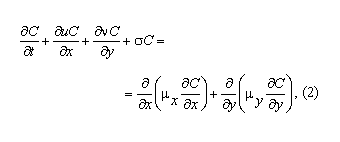
де С – концентрація домішки у фільтраційному потоці; u, v – компоненти вектора швидкості фільтраційного потоку ; μх, μy – коефіцієнти дисперсії; х, у – декартові координати; σ – коефіцієнт, що враховує процес сорбції.

Граничні умови для рівняння (2) розглянуто у [2, 3].

Для чисельного інтегрування рівняння (2) використовуємо неявну схему розщеплення [2, 3].

Результати

Для кодування розробленої чисельної моделі використано FORTRAN. До складу побудованого пакета програм «FILTR–UN» входять підпрограми розрахунку процесу фільтрації та масопереносу. Основні модулі цього пакета такі:

1) підпрограма FUNX – розрахунок поля напору у фільтрі на базі методу О. А. Самарського;

2) підпрограма FUNYY – розрахунок поля швидкості фільтраційного потоку у фільтрі;

3) підпрограма FUNDOM – розрахунок поля концентрації домішки у фільтрі;

4) підпрограма FUNPR – друк поля напору, фільтраційної швидкості та концентрації домішки у фільтрі.

На рис. 1–3 наведено результати обчислювального експерименту щодо моделювання фільтрації забрудненої води у фільтрі, зокрема дані щодо розподілу концентрації домішки
у воді, яку фільтрують. Концентрація домішки у воді подана в безрозмірному вигляді (на вході дорівнює 1) .

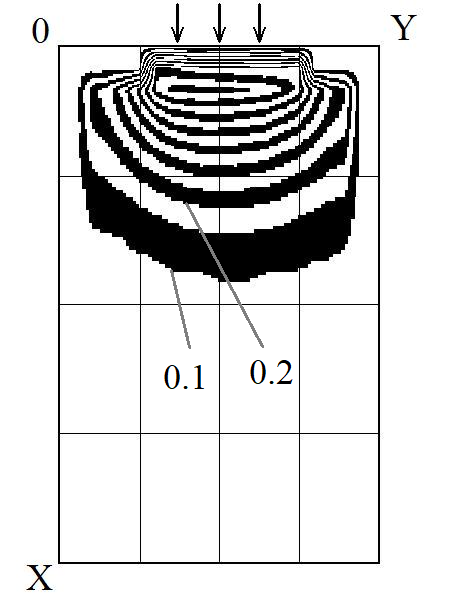
Рис. 1. Ізолінії концентрації домішки в фільтрі
t = 1,8 (час безрозмірний)

Fig. 1. Isolines of impurity concentration in the filter
t = 1.8 (time is dimensionless)

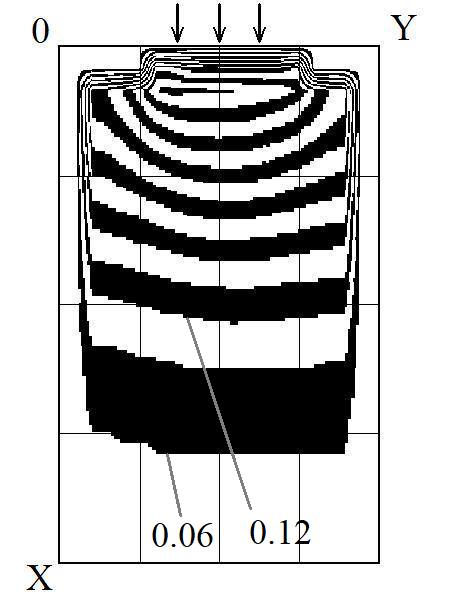
Рис. 2. Ізолінії концентрації домішки в фільтрі
t = 3,1 (час безрозмірний)

Fig. 2. Isolines of impurity concentration in the filter
t = 3.1 (time is dimensionless)

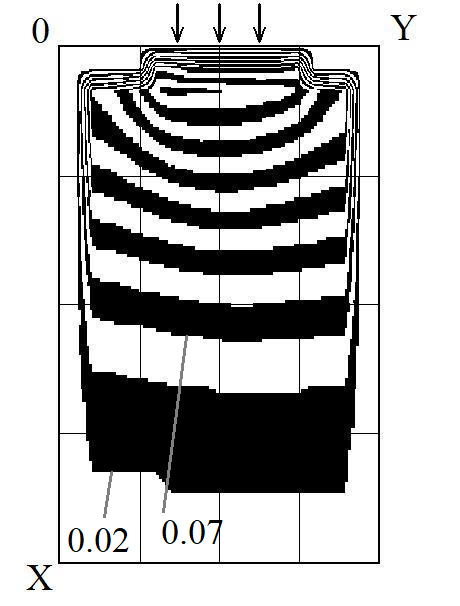
Рис. 3. Ізолінії концентрації домішки в фільтрі
t = 3,4 (час безрозмірний)

Fig. 3. Isolines of impurity concentration in the filter
t = 3.4 (time is dimensionless)

Як видно з наведених рисунків, концентрація домішки у воді, яку фільтрують, зменшується з часом, що обумовлено роботою завантаження фільтра. Ми бачимо, що концентрація домішки для моменту часу 3,4 значно менша, ніж концентрація домішки на початку фільтрування (рис. 1). Тобто вода з фільтра буде виходити зі значно меншою концентрацією домішки, ніж на вході у фільтр.

Відзначимо, що час розрахунку склав близько 5 сек.

Наукова новизна та практична
значимість

У роботі запропонована чисельна 2D-модель фільтра, що базується на рівнянні фільтрації та рівнянні масопереносу. Розроблена модель дозволяє розраховувати нерівномірне поле концентрації домішки у фільтрі.

Представлена чисельна модель може бути використана для розрахунку як безнапірних, так і напірних фільтрів, для різного типу та крупності завантаження, різної кількості шарів завантаження. Перевагою розробленої моделі є те, що можна задавати різні розміри, форму фільтра, різну витрату забрудненої води. Також за допомогою цієї чисельної моделі можна проводити серійні розрахунки з невеликою витратою комп’ютерного часу.

Модель може бути застосована на етапах проєктування, реконструкції очисних споруд систем водопостачання.

Висновки

У статті розглянуто ефективну чисельну модель, що дозволяє оперативно розраховувати процес фільтрації забрудненої води у фільтрі. Модель базується на використанні фундаментального рівняння фільтрації та рівнянні збереження маси забруднювача у фільтраційному потоці.

Подальший розвиток цього наукового напряму слід проводити в області створення 3D-моделі фільтрації та масопереносу у фільтрі.



СПИСОК використаних джерел

  1. Айрапетян Т. С., Карагяур А. С. Теоретические исследования биологической очистки в комбинированных аэротенках с прикрепленным биоценозом. Науковий Вісник Будівництва. 2018. T. 91. No. 1. С. 200–205. DOI: 10.29295/2311-7257-2018-91-1-200-205.

  2. Беляев Н. Н., Козачина В. А. Математическое моделирование массопереноса в горизонтальных отстойниках: монография. Днипро : Акцент ПП, 2015. 115 с.

  3. Беляев Н. Н., Нагорная Е. К. Математическое моделирование массопереноса в отстойниках систем водоотведения: монография. Днипро: Новая идеология, 2012. 112 с.

  4. ДБН В.2.5-75:2013. Каналізація. Зовнішні мережі та споруди. Основні положення проектування. [Чинний від 2014-01-01]. Київ : Мінрегіон України, 2013. 128 с.

  5. Козачина В. А., Шинкаренко В. І., Бондаренко І. О., Габрінець В. О, Горячкін В. М. Моделювання очищення води у горизонтальному відстійнику. Наука та прогрес транспорту. 2019. № 5 (83). P. 36–42. DOI: 10.15802/stp2019/184467

  6. Олійник О. Я, Айрапетян Т. С. Моделювання очисних стічних вод від органічних забруднень в біо-реакторах-аеротенках зі зваженим (вільно плаваючим) і закріпленим біоценозом. Доповідь НАН України. 2015. № 5. С. 55–60. DOI: 10/15407/dopovidi2015.05.055

  7. Поляков В. Л. О моделировании удаления фильт рованием растворенного железа из подземных вод. Доповідь НАН України. 2018. № 12. С. 37–45. DOI: 10.15407/dopovidi2018.12.037

  8. Поляков В. Л., Мартынов С. Ю. Расчет обезжелезивания подземных вод на скором фильтре. Доповідь НАН України. 2019. № 3. С. 35–45. DOI: 10.15407/dopovidi2019.03.035

  9. He, Y., Uehara S., Takana H., Hideya Nishiyama. Numerical Modelling and Simulation of Chemical Reactions in a Nano-Pulse Discharged Bubble for Water Treatment. Plasma Science and Technology. 2016. Vol. 18. No 9. P. 924–932. DOI: 10.1088/1009-0630/18/9/09

  10. Nadezhdin I., Papasidero D., Goryunov A., Manenti F. Optimisation of EDM process for water purification. Chemical Engineering Transactions. 2016. Vol 52. P. 325–330. DOI: 10.3303/CET1652055

  11. Oleynik O., Airapetian T., Kurganska S. Evaluation of the performance of aerotanks due to add-on attached biocenosis. Science and Transport Progress. 2019. № 4 (82). P. 37–46. DOI: 10.15802/stp2019/175883

  12. Rezakazemi M., Ghafarinazari A., Shirazian S., Khoshsima A. Numerical Modeling and Optimization of Wastewater Treatment Using Porous Polymeric Membranes. Polymer Engineering and Science. 2013. Vol. 53. Iss. 6. P. 1272–1278. DOI: 10.1002/pen.23375

  13. Viccione G., Evangelista S. Experimental and numerical analysis of the hydraulic performance of filtering cartridges for water treatment. EPiC Series in Engineering. 2018. Vol. 3. P. 2187–2195. DOI: 10.29007/b26c

В. Д. Петренко1, Н. И. Нетеса2, А. Л. ТютькИн3, Е. В. Громова4,
В. А. козачина5*

1Каф. «Мосты и туннели», Днипровский национальный университет железнодорожного транспорта имени академика В. Лазаряна, ул. Лазаряна, 2, Днипро, Украина, 49010, тел. +38 (056) 373 15 53, эл. почта petrenko.diit@gmail.com, ORCID 0000-0003-2201-3593
2Каф. «Строительное производство и геодезия», Днипровский национальный университет железнодорожного транспорта имени академика В. Лазаряна, ул. Лазаряна, 2, Днипро, Украина, 49010, тел. +38 (067) 195 50 27, эл. почта andreynetesa@meta.ua, ORCID 0000-0003-1730-7642
3Каф. «Мосты и туннели», Днипровский национальный университет железнодорожного транспорта имени академика В. Лазаряна, ул. Лазаряна, 2, Днипро, Украина, 49010, тел. +38 (056) 373 15 53, эл. почта alexeytutkin@gmail.com, ORCID 0000-0003-4921-4758
4Каф. «Архитектурное проектирование, землеустройство и строительные материалы», Днипровский национальный
университет железнодорожного транспорта имени академика В. Лазаряна, ул. Лазаряна, 2, Днипро, Украина, 49010, тел. +38 (095) 304 73 33, эл. почта Gromova_Elen_upbbm_diit@i.ua, ORCID 0000-0002-5149-4165
5*Каф. «Гидравлика и водоснабжение», Днипровский национальный университет железнодорожного транспорта имени академика В. Лазаряна, ул. Лазаряна, 2, Днипро, Украина, 49010, тел. +38 (056) 273 15 09, эл. почта v.kozachyna@gmail.com, ORCID 0000-0002-6894-5532

МАТЕМАТИЧеское МОДЕЛИРОВАНИЕ

ОЧИСТКИ ВОДЫ В фИльтрЕ

Цель. Для анализа эффективности очистки воды в системах водоподготовки важной задачей является разработка математических моделей, которые позволяют определять степень очистки воды на этапе проведения проектных работ. Основной целью работы является построение численных моделей для расчета процесса фильтрации и массопереноса в фильтре. Методика. Расчет процесса фильтрации загрязненной воды в фильтре проведен в два этапа. На первом этапе рассчитано поле скорости потока в фильтре. Для решения этой задачи использовано классическое уравнений фильтрации. На втором этапе расчета смоделировано течение загрязненной воды в фильтре. Для решения этой задачи использовано уравнение массопереноса, которое выражает закон сохранения массы. Это уравнение учитывает перенос примеси фильтрационным потоком, перенос примеси за счет дисперсии и сорбцию примеси в загрузке фильтра. Решение уравнения фильтрации проведено с помощью попеременно-треугольного метода А. А. Самарского. Определение неизвестного значения напора на базе этого метода проведено по явной формуле бегущего счета. Для численного интегрирования моделирующего уравнения массопереноса в фильтре использована разностная схема расщепления. Результаты. Современной тенденцией в области водоснабжения и водоотведения является создание многомерных и многофакторных математических моделей. Такие модели позволяют заменить физический эксперимент на вычислительный. В комплекс сооружений водоподготовки обязательно входят фильтры очистки воды. Эффективность работы фильтров влияет на эффективность работы других очистных сооружений технологической схемы очистки. Разработана математическая модель, которая позволяет анализировать процесс очистки воды в фильтре. На базе этой модели разработан пакет прикладных программ для проведения компьютерного эксперимента по моделированию процесса очистки воды в фильтре. Приведены результаты вычислительного эксперимента по моделированию процесса фильтрации загрязненной воды в фильтре. Научная новизна. В работе предложена численная двумерная модель фильтра, базирующаяся на уравнении фильтрации и уравнении массопереноса. Особенностью этой модели является возможность моделирования поля скорости и процесса переноса примеси с учетом геометрической формы фильтров. Практическая значимость. Время расчета одного варианта задания на базе построенной численной модели составляет несколько секунд, что является важным для проведения серийных расчетов на практике. Модели можно использовать в качестве альтернативы проведения лабораторных экспериментов.

Ключевые слова: очистка воды; математическое моделирование; фильтр; численная модель

V. D. Petrenko1, M. I. Netesa2, o. l. Tiutkin3, O. V. Gromova4,
V. А. Kozachyna5*

1Dep. «Bridges and Tunnels», Dnipro National University of Railway Transport named after Academician V. Lazaryan, Lazaryana St., 2, Dnipro, Ukraine, 49010, tel. +38 (056) 373 15 53, e-mail petrenko.diit@gmail.com, ORCID 0000-0003-2201-3593
2Dep. «Build Production and Geodesy», Dnipro National University of Railway Transport named after Academician
V. Lazaryan, Lazaryana St., 2, Dnipro, Ukraine, 49010, tel. +38 (067) 195 50 27, e-mail andreynetesa@meta.ua, ORCID 0000-0003-1730-7642
3Dep. «Bridges and Tunnels», Dnipro National University of Railway Transport named after Academician V. Lazaryan, Lazaryana St., 2, Dnipro, Ukraine, 49010, tel. +38 (056) 373 15 53, e-mail alexeytutkin@gmail.com, ORCID 0000-0003-4921-4758
4Dep. «Аrchitectural Design, Land Management and Building Materials», Dnipro National University of Railway Transport named after Academician V. Lazaryan, Lazaryana St., 2, Dnipro, Ukraine, 49010, tel. +38 (095) 304 73 33, e-mail Gromova_Elen_upbbm_diit@i.ua, ORCID 0000-0002-5149-4165
5*Dep. «Hydraulics and Water Supply», Dnipro National University of Railway Transport named after Academician V. Lazaryan, Lazaryana St., 2, Dnipro, Ukraine, 49010, tel. +38 (056) 273 15 09, e-mail v.kozachyna@gmail.com, ORCID 0000-0002-6894-5532

MATHEMATICAL MODELING

of WATER PURIFICATION WITH FILTER

Purpose. To analyze the effectiveness of water purification in water treatment systems, an important task is the development of mathematical models that allow determining the degree of water purification at the design stage. The main purpose of the work is to construct numerical models for calculating the filtration process and mass transfer in the filter. Methodology. The calculation of the filtering process of contaminated water in the filter is carried out in two stages. At the first stage, the flow rate field in the filter is calculated. To solve this problem, the classical filtration equations are used. At the second stage of the calculation, the flow of contaminated water in the filter is simulated. To solve this problem, the mass transfer equation is used, which expresses the law of mass conservation. This equation takes into account the transfer of impurities by the filtration flow, the transfer of impurities due to dispersion and the sorption of impurities in the filter material. The solution of the filtration equation is carried out using the alternating triangular method of A. A. Samarskyi. The unknown pressure value based on this method is determined by the explicit formula of point-to-point computation. For numerical integration of the mass transfer equation in the filter, a difference splitting scheme is used. Findings. The current trend in the field of water supply and sanitation is the creation of multidimensional and multifactor mathematical models. Such models make it possible to replace a physical experiment with a computational one. The complex of water treatment facilities necessarily includes water purification filters. The filter efficiency affects the efficiency of other treatment facilities of the technological treatment scheme. A mathematical model has been developed that allows analyzing the water purification process in the filter. Based on the developed numerical model, a package of application programs has been developed for computer simulation of the filter water purification process. The results of a computational experiment on modeling the filtering process of contaminated water in a filter are presented. Originality. The paper proposes a numerical two-dimensional filter model based on the filtration equation and the mass transfer equation. A feature of the developed mathematical models is the possibility of modeling the velocity field and the process of impurity transfer taking into account the geometric shape of the filter. Practical value. The calculation time for one variant of the task based on the developed numerical model is several seconds, which is important for conducting serial calculations in practice. Models can be used as an alternative to laboratory experiments.

Keywords: water purification; mathematical modeling; filter; numerical model

LIST OF Reference LINKS

  1. Airapetian, T. S., & Karahiaur, A. S. (2018). Theoretical studies of biological purification in combined aerotanks with fixed biocenosis. Scientific Bulletin of Civil Engineering, 91(1), 200-205. DOI: 10.29295/2311-7257-2018-91-1-200-205 (in Russian).

  2. Biliaiev, N. N., & Kozachina, V. A. (2015). Modelirovaniye massoperenosa v gorizontalnykh otstoynikakh: monografiya. Dnepropetrovsk: Aktsent PP. (in Russian)

  3. Biliaiev, N. N., & Nagornaya, E. K. (2012). Matematicheskoye modelirovaniye massoperenosa v otstoynikakh sistem vodootvedeniya: monografiya. Dnepropetrovsk: Novaya ideologiya. (in Russian)

  4. Kanalizatsiia. Zovnishni merezhi ta sporudy. Osnovni polozhennia proektuvannia, 128 DBN V.2.5-75-2013 (2013). (in Ukrainian)

  5. Kozachyna, V. A., Shynkarenko, V. I., Bondarenko, I. O., Gabrinets, V. A., & Horiachkin, V. M. (2019). Water Cleaning Modeling in a Horizontal Settler. Science and Transport Progress, 5(83), 36-42. DOI: 10.15802/stp2019/184467 (in Ukrainian)

  6. Oleynik, A. Y., & Airapetyan, T. S. (2015). The modeling of the clearance of waste waters from organic pollutions in bioreactors-aerotanks with suspended (free flow) and fixed biocenoses. Reports of the National Academy of Sciences of Ukraine, 5, 55-60. DOI: 10.15407/dopovidi2015.05.055 (in Ukrainian)

  7. Polyakov, V. L. (2018). On the modeling of a dissolved iron removal from underground water by filtration. Reports of the National Academy of Sciences of Ukraine, 12, 37-45. DOI: 10.15407/dopovidi2018.12.037 (in Russian)

  8. Polyakov, V. L., & Martynov, S. Yu. (2019). Calculation of the removal of iron from groundwater in a fast filter. Reports of the National Academy of Sciences of Ukraine, 3, 35-45. DOI: 10.15407/dopovidi2019.03.035 (in Russian)

  9. He, Y., Uehara, S., Takana, H., & Nishiyama, H. (2016). Numerical Modelling and Simulation of Chemical Reactions in a Nano-Pulse Discharged Bubble for Water Treatment. Plasma Science and Technology, 18(9), 924-932. DOI: 10.1088/1009-0630/18/9/09 (in English)

  10. Nadezhdin, I., Papasidero, D., Goryunov, A., & Manenti, F. (2016). Optimisation of EDM process for water purification. Chemical Engineering Transactions, 52, 325-330. DOI: 10.3303/CET1652055 (in English)

  11. Oleynik, O., Airapetian, T., & Kurganska, S. (2019). Evaluation of the performance of aerotanks due to add-on attached biocenosis. Science and Transport Progress, 4(82), 37-46. DOI: 10.15802/stp2019/175883 (in English)

  12. Rezakazemi, M., Ghafarinazari, A., Shirazian, S., & Khoshsima, A. (2012). Numerical modeling and optimization of wastewater treatment using porous polymeric membranes. Polymer Engineering & Science, 53(6), 1272-1278. DOI: 10.1002/pen.23375 (in English)

  13. Giacomo, V., & Evangelista, S. (2018). Experimental and numerical analysis of the hydraulic performance of filtering cartridges for water treatment. EPiC Series in Engineering, 3, 2187-2195. DOI: 10.29007/b26c (in English)


Поступила в редколегию: 01.10.2019

Принята к печати: 03.02.2020

Creative Commons Attribution 4.0 International © В. Д. Петренко, М. І. Нетеса,

doi: https://doi.org/10.15802/stp2020/199710 О. Л. Тютькін, О. В. Громова, В. А. Козачина, 2020