ISSN 2307–3489 (Print), ІSSN 2307–6666 (Online)

Наука та прогрес транспорту. Вісник Дніпропетровського
національного університету залізничного транспорту, 2019, № 4 (85)

ЕКОЛОГІЯ НА ТРАНСПОРТІ

Вступ

Відстійники відіграють дуже суттєву роль у системах водопостачання та водовідведення. На практиці використовують різні типи відстійників, але в системах очищення стічних вод найчастіше вертикальні, у які вода потрапляє після аеротенків. Для оцінки ефективності роботи відстійників за різних навантажень, потрібно мати математичні моделі, що дозволяють визначати ступінь очищення забруднених вод від різних споживачів, в тому числі підприємств [1–3, 5, 7–12].

Для розв’язання задач з оцінки ефективності роботи очисних споруд використовують різні математичні моделі, зокрема емпіричні [4, 13] й аналітичні [3, 7–11]. Недоліком цих моделей є неможливість врахування нерівномірного потоку в споруді та її геометричної форми. Тому більш ефективними є чисельні моделі [1, 2, 6, 14], що дозволяють проводити розрахунки з урахуванням геометричної форми споруд. Проте на їх практичну реалізацію потрібні у деяких випадках, значні затрати комп’ютерного часу [14].

Мета

Зважаючи на викладене, метою цієї статті є побудова математичної моделі для розрахунку гідродинаміки течії та переносу забруднювача у відстійнику, що має складну геометричну форму.

Методологія

Дослідження процесу очистки води у відстійниках відноситься до задач масопереносу в областях зі складною геометричною формою. Для проведення таких досліджень будемо використовувати фундаментальні рівняння гідродинаміки та переносу забруднюючих речовин.

Модель гідродинаміки. Надважливою задачею під час розрахунку очисних споруд систем водопостачання та водовідведення є визначення поля швидкості водного потоку. Це пов’язано з тим, що рух домішок у споруді визначають, переважно конвекцією. Тому для створення моделей оцінки ефективності роботи очисних споруд розв’язання задачі гідродинаміки постає на першому місці. У роботі будемо використовувати модель рівнянь Нав’є–Стокса. Моделювальні рівняння мають вигляд [2]:

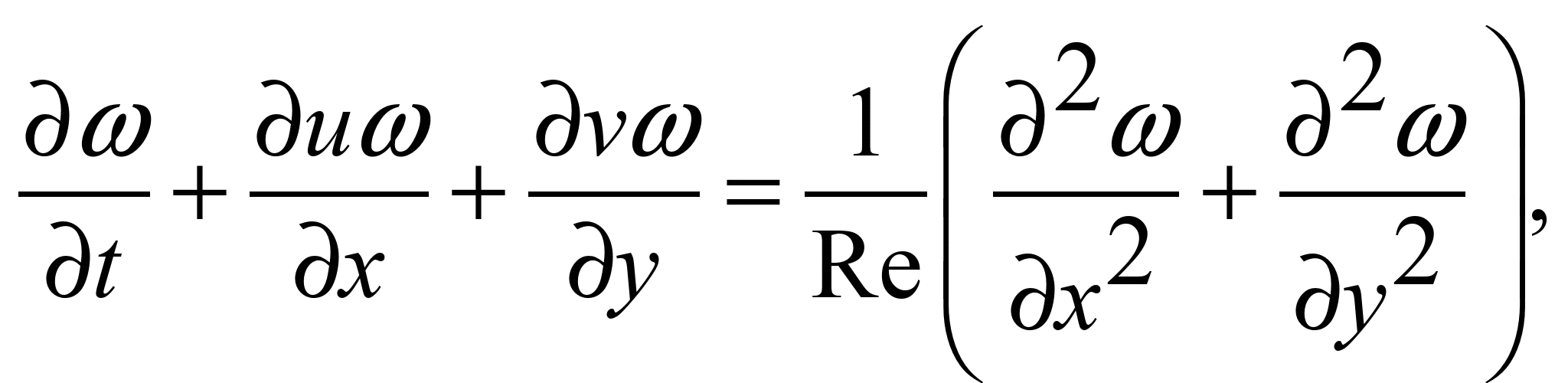(1)

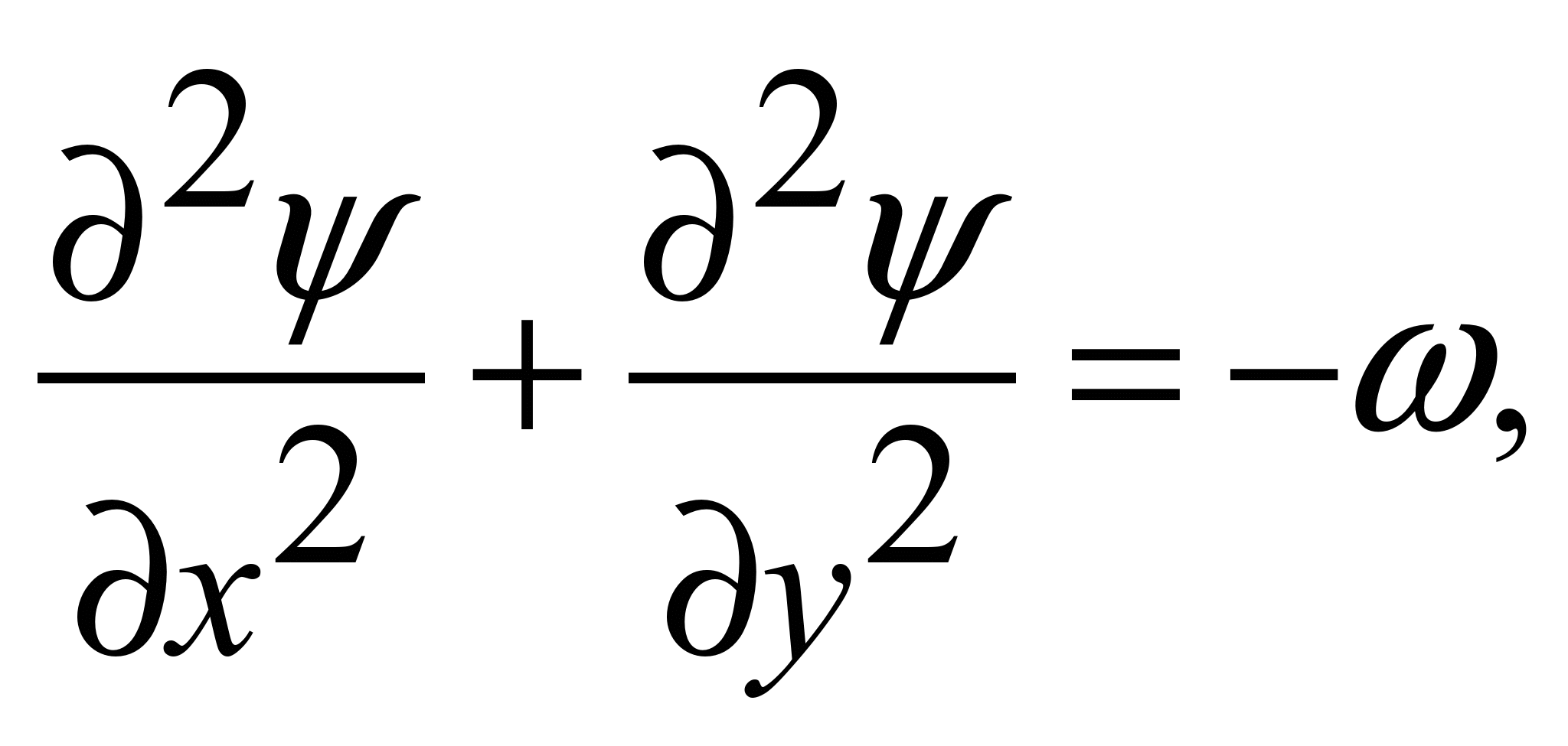(2)

де y – функція потоку; Re = V₀L/x – критерій Рейнольдса; ω = ∂v/∂x – ∂u/∂y – вихор; u = ∂y/∂y, v = –∂y/∂x – компоненти вектора швидкості водного потоку. Для використання рівняння (1) потрібно визначити характерні величини V₀, L для відстійника.

Постановку граничних умов для системи рівнянь (1)–(2) розглянуто в праці [2].

Для загального розуміння запропонованої математичної моделі, потрібно привести основні апроксимуючі залежності, що створюють основу для чисельного інтегрування рівнянь гідродинаміки. Виконаємо наступні перетворення, щоб перейти до чисельного інтегрування рівнянь течії в’язкої рідини:

;

.

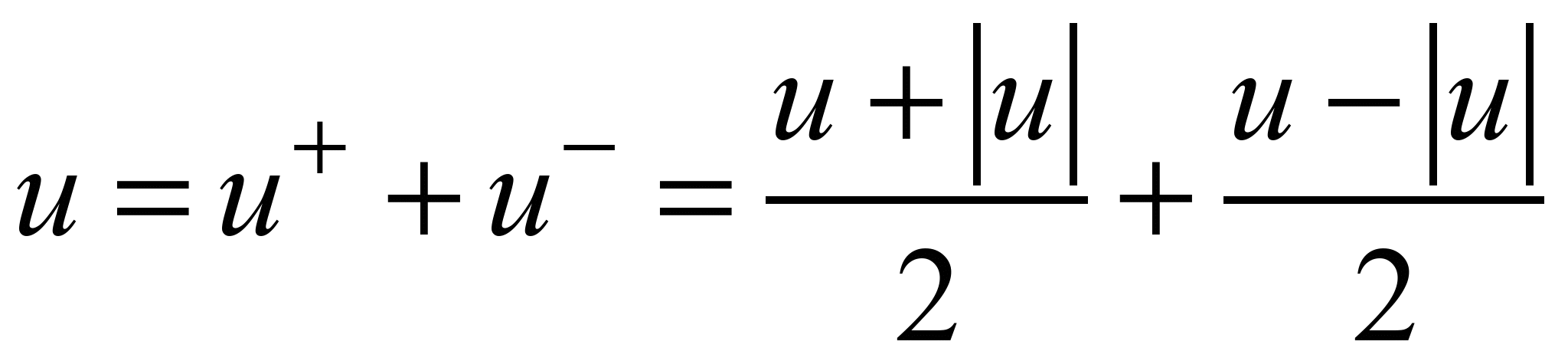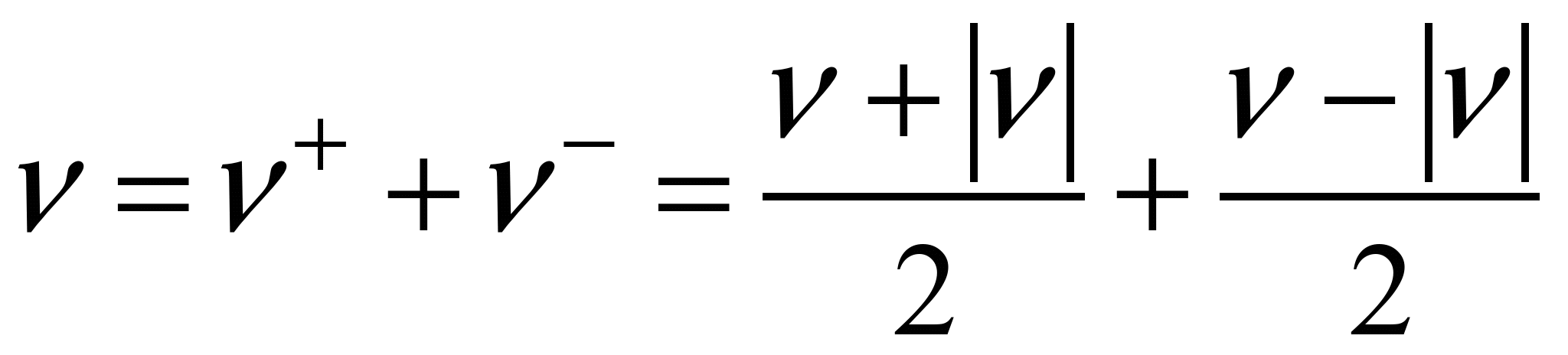Далі здійснюється наступна апроксимація [2]:

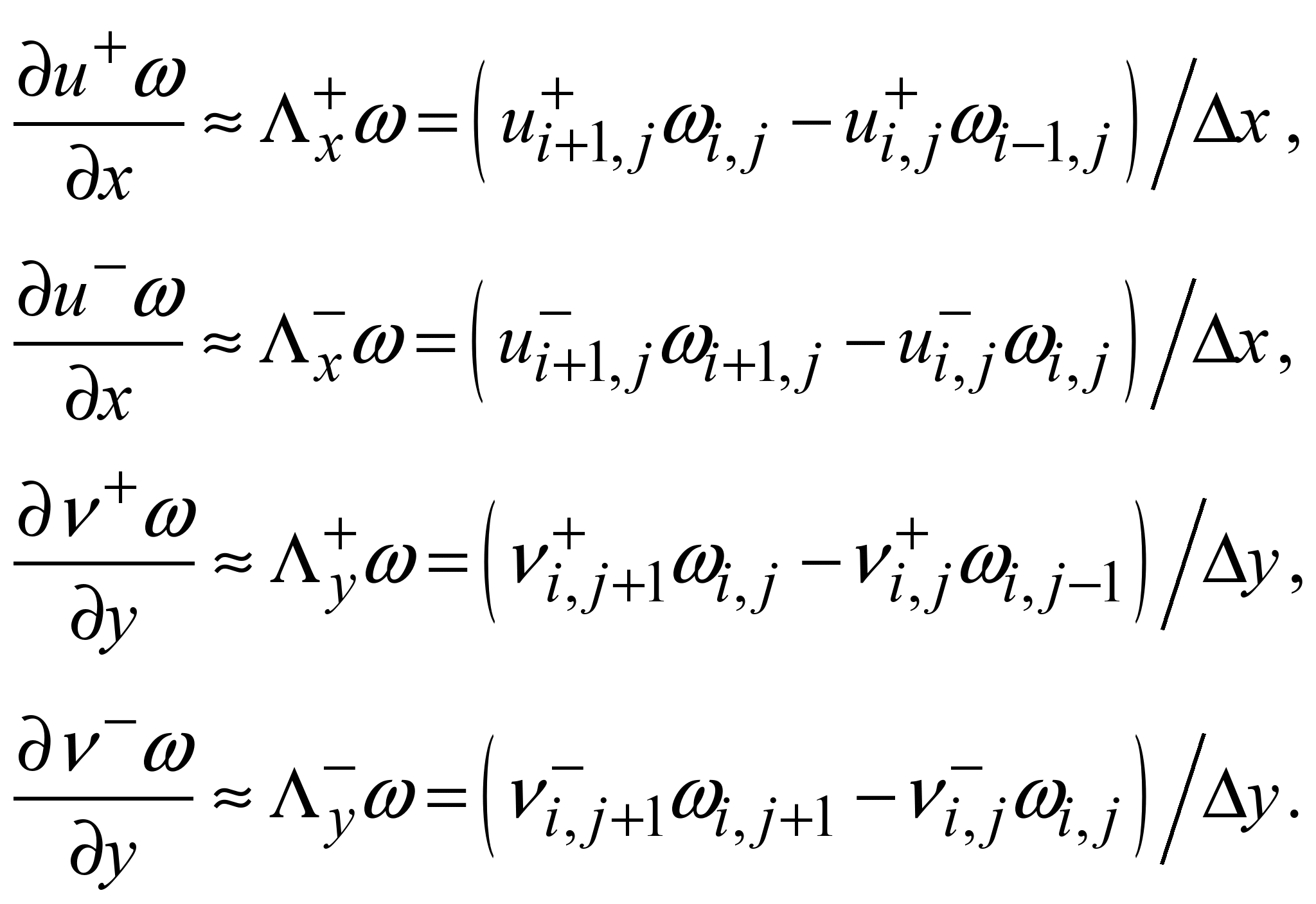(3)

Заміна інших похідних здійснюється так [2]:

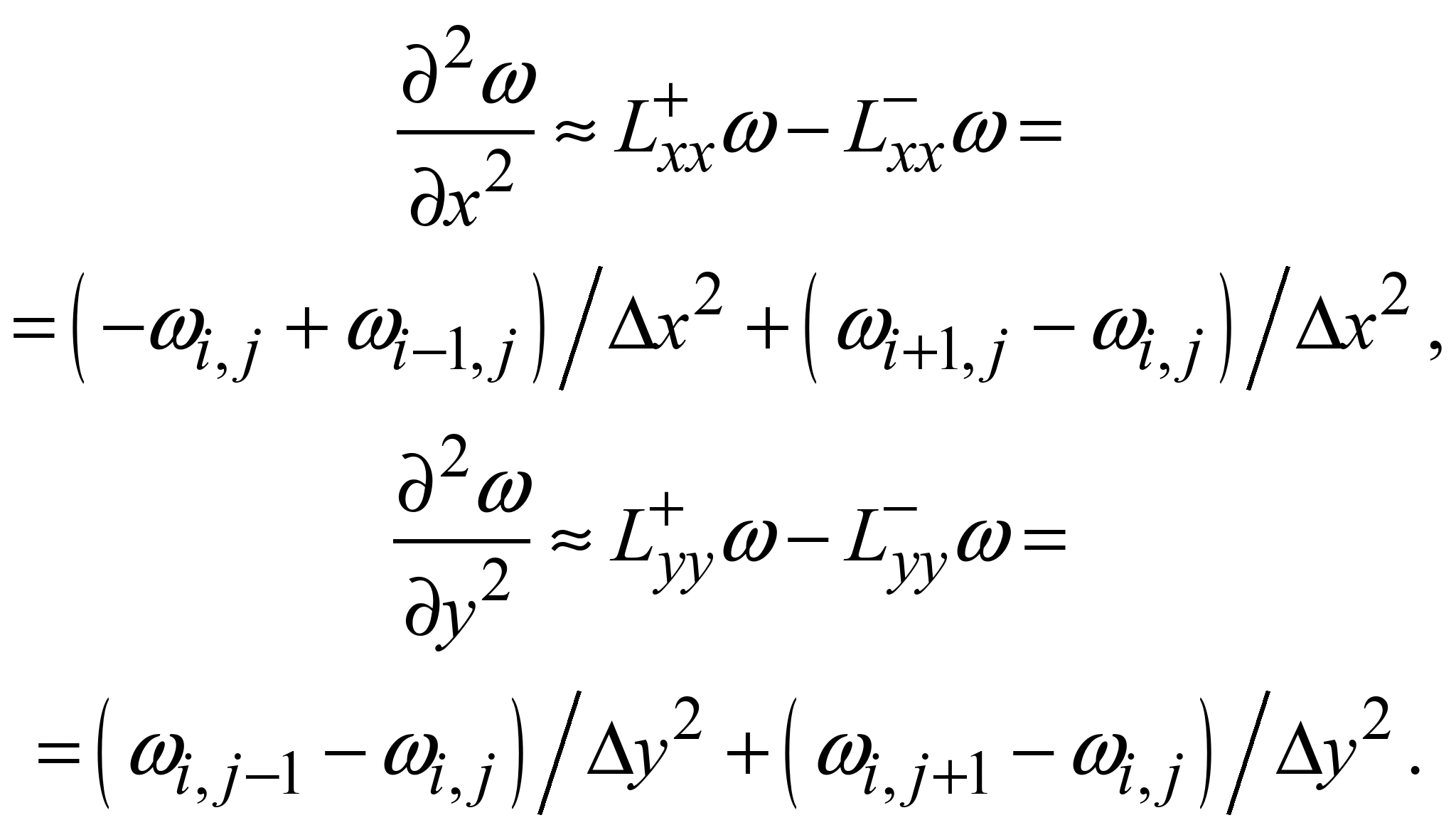(4)

При практичному використанні різницевих залежностей (4) будуть задіяні як нижній, так і верхній часовий шар. Для розрахунку будуть використовуватися наступні різницеві залежності [2]:

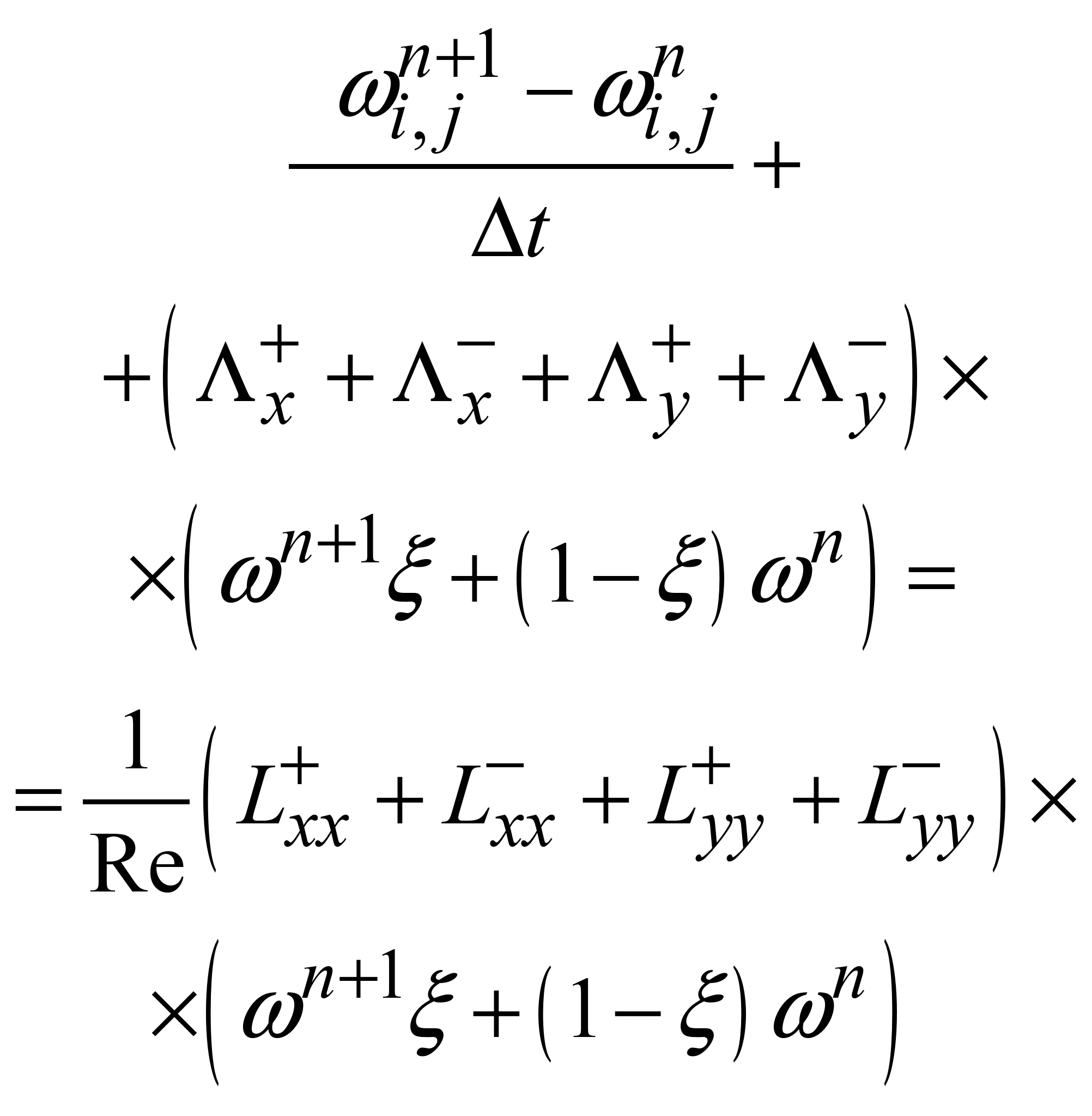(5)

або

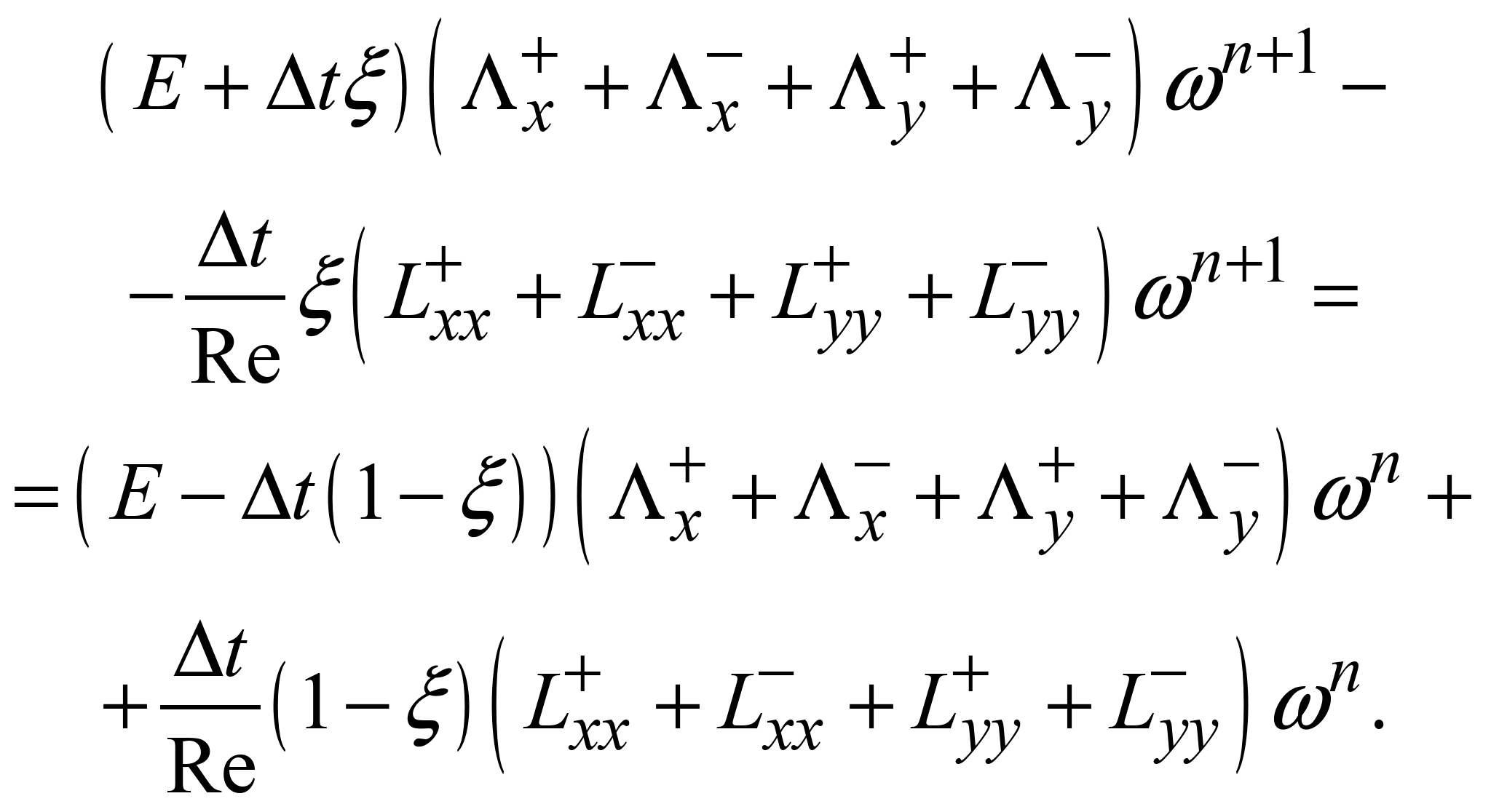(6)

Слід відзначити, що за рахунок зміни параметру ξ можна змінювати порядок точності різницевої схеми, наприклад: за ξ = 1/2 має другий порядок точності за часовою координатою.

Далі записуємо різницеву схему розщеплення [2]:

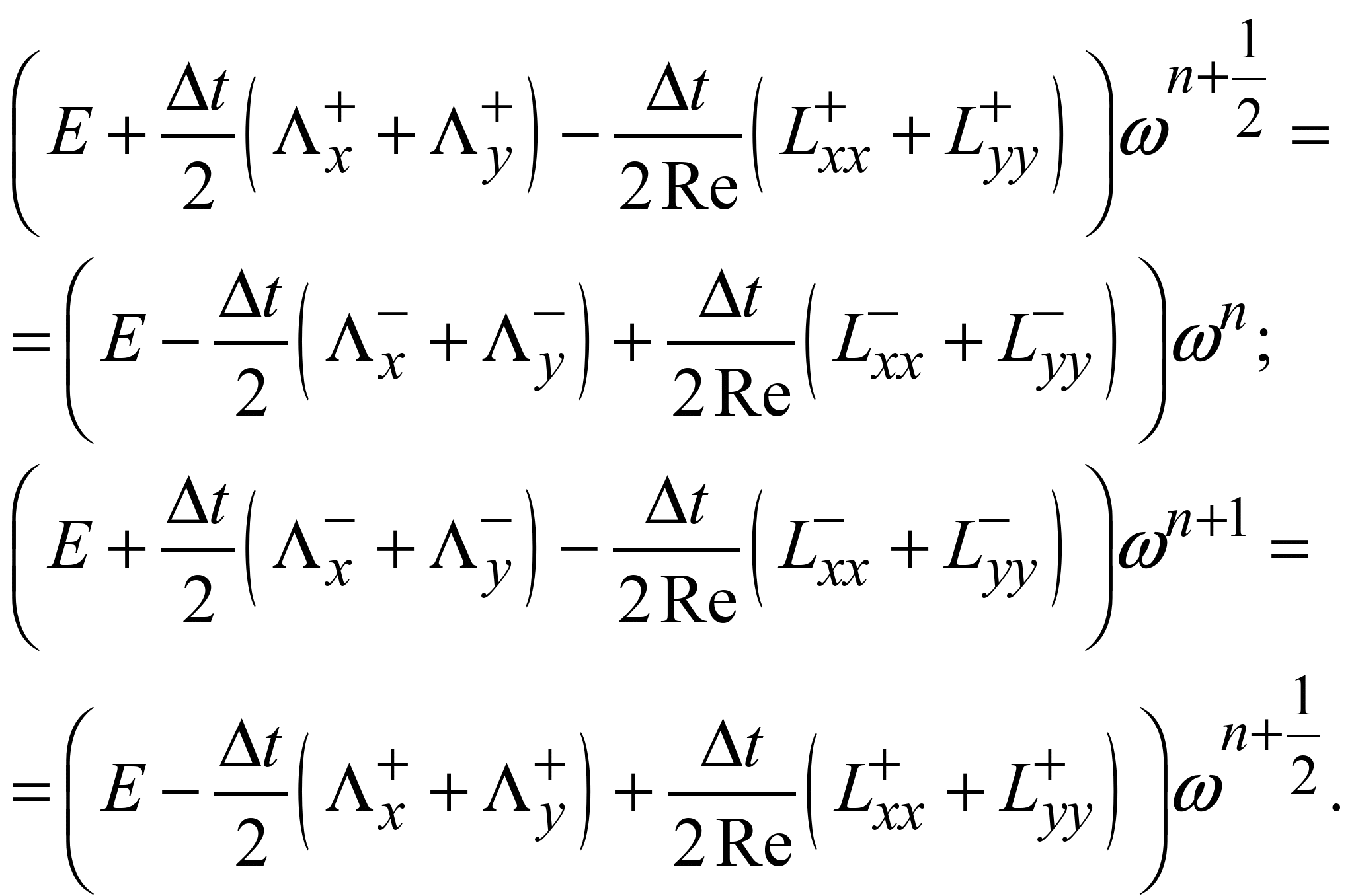(7)

На базі залежностей (7) визначається значення вихору всередині очисної споруди. При цьому використовується явна формула розрахунку.

У випадку чисельного інтегрування рівняння для функції потоку використовують метод ітерацій. Для цього рівняння Пуассона зводимо до вигляду:

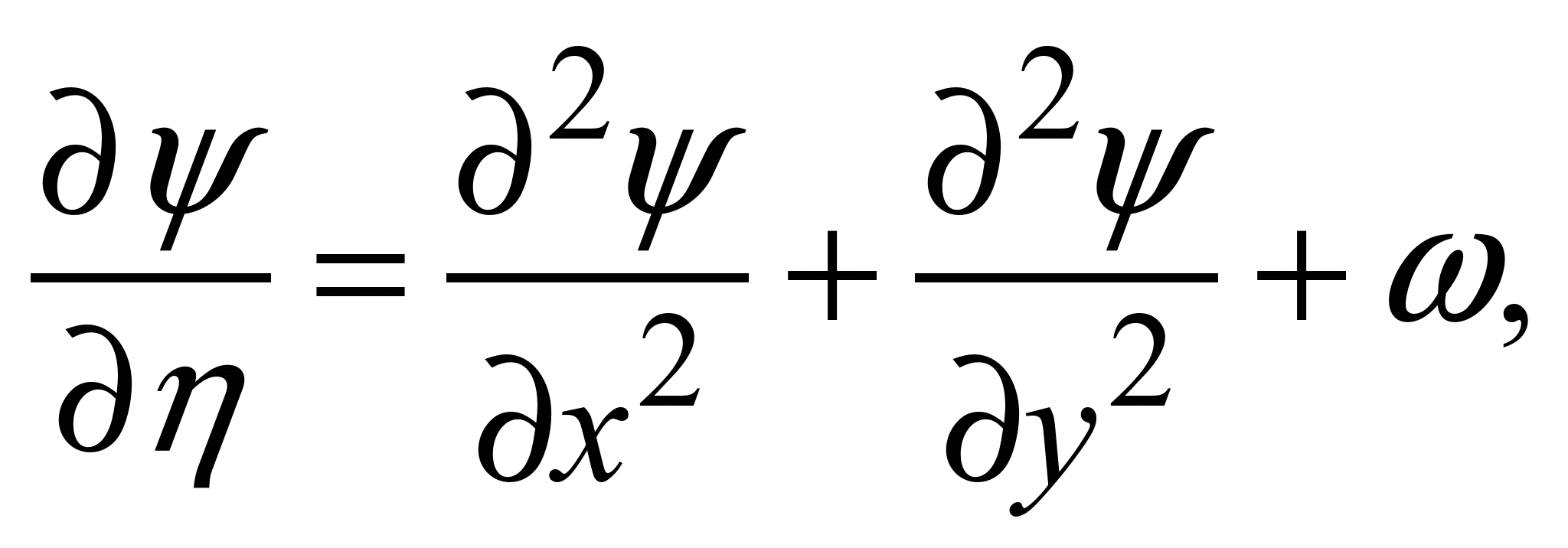(8)

де η – фіктивний час. Функція ψ (x, y, η), будучи розв’язком нестаціонарного рівняння (8), буде розв’язком рівняння Пуассона за η →∞.

Використовувана різницева схема має вигляд [2]:

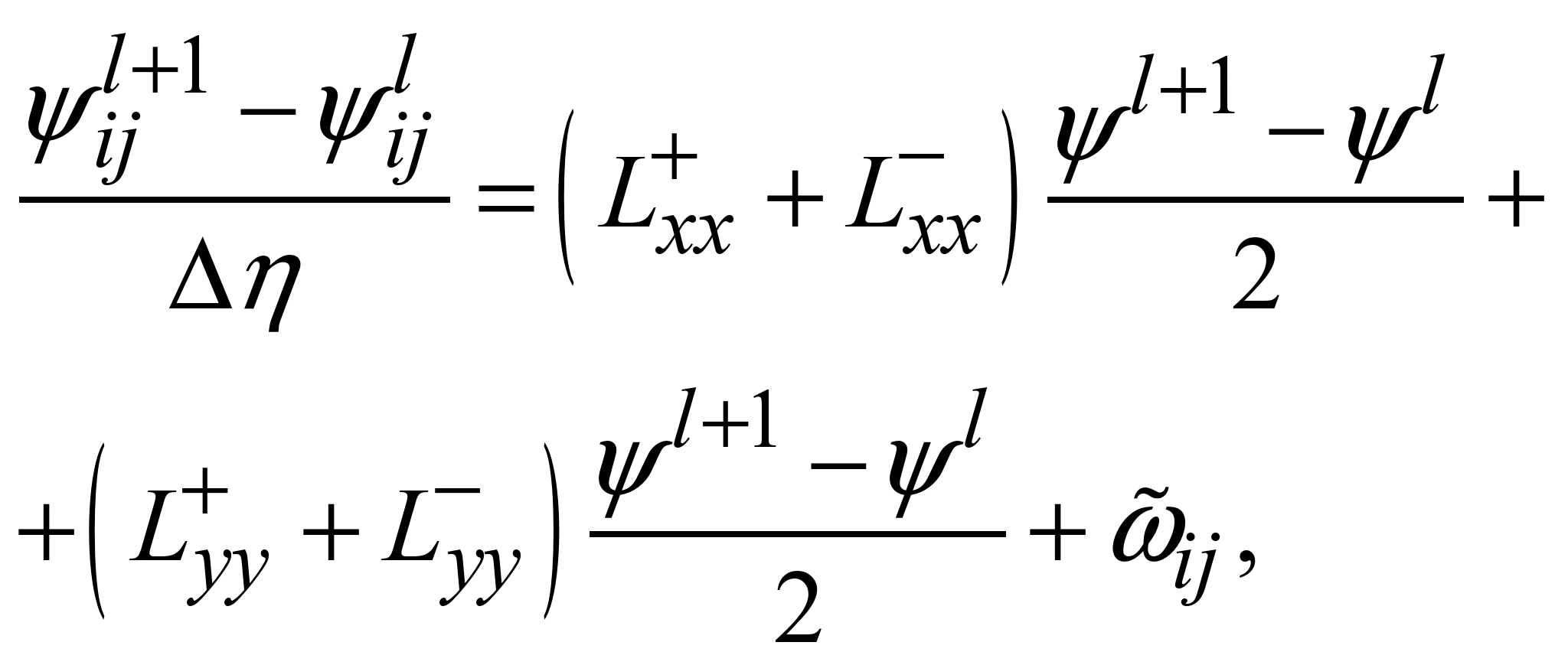(9)

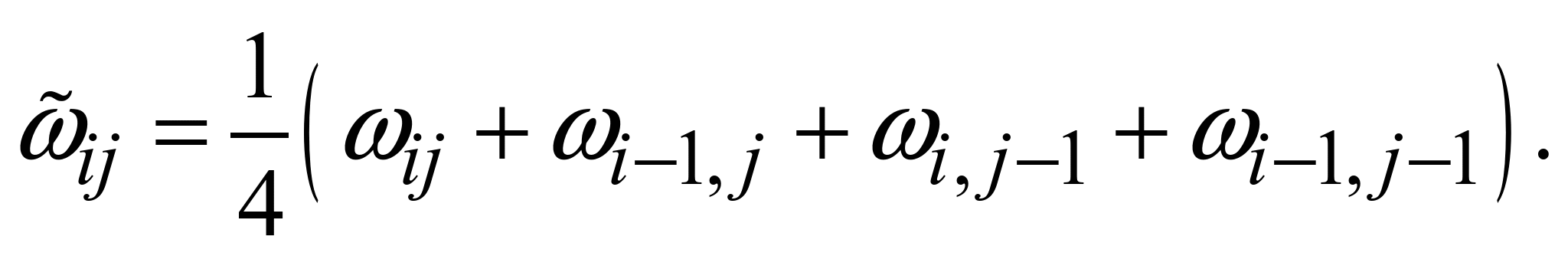
Схема розщеплення має вигляд:

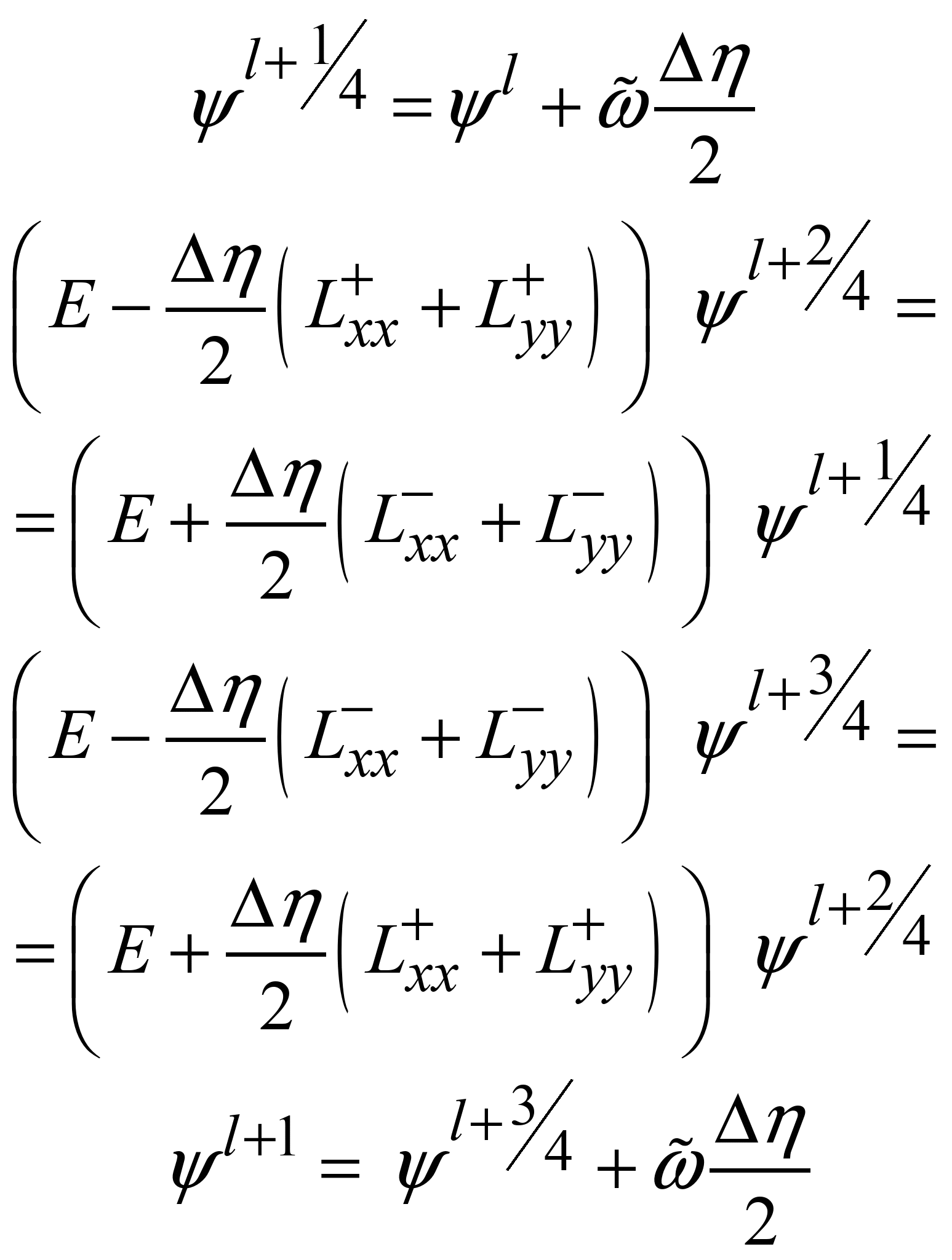(10)

Значення функції потоку ψ^l+2/4, ψ^l+3/4 визначаємо за методом біжучого рахунку на другому та третьому кроках розщеплення.

Компоненти вектора швидкості визначаємо так:

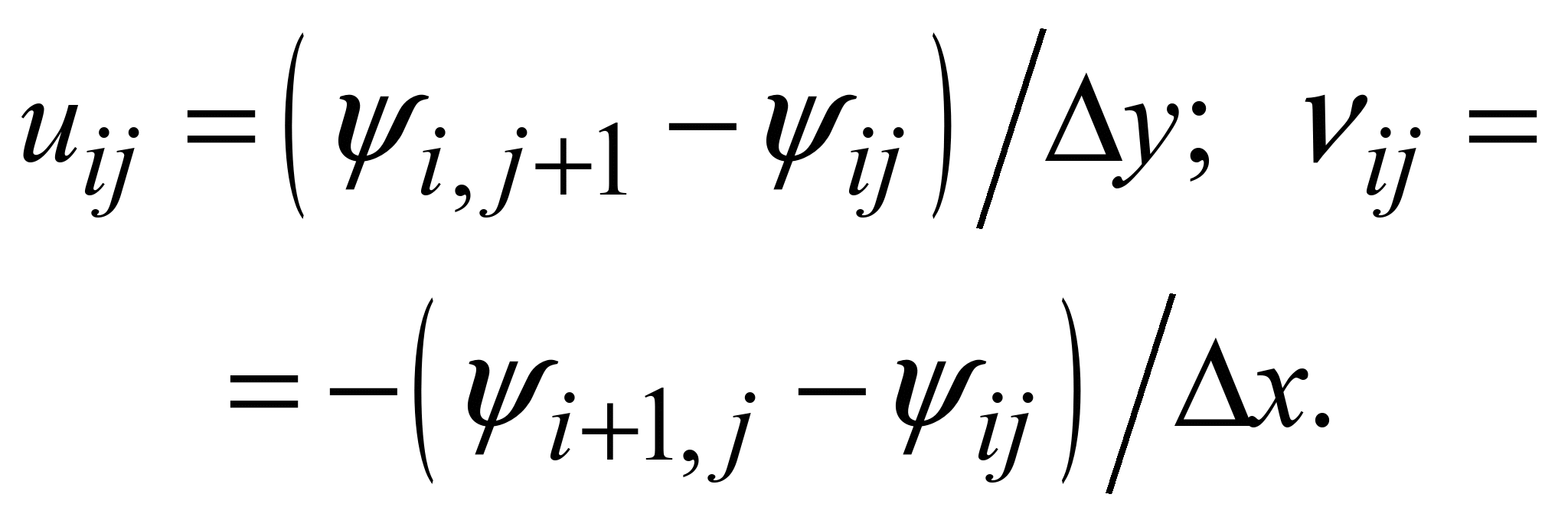
Для формування вигляду розрахункової області використовуємо маркери.

Модель масопереносу у відстійник. Після розрахунку нерівномірного поля швидкості потоку у відстійнику необхідно розрахувати рух домішки. Для математичного описання переносу домішки в очисній споруді будемо використовувати рівняння балансу маси [1, 2, 6, 14]:

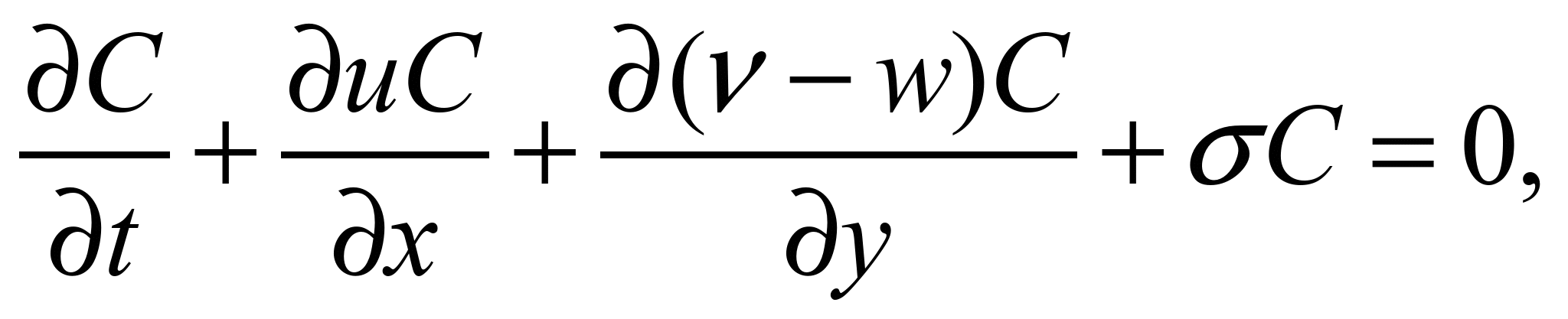(11)

де С – кількість забруднювача в об’ємі рідини; u, v – швидкість течії по координатам х, у; w – гідравлічна крупність забруднювача; σ – емпіричний коефіцієнт, що враховує додаткові процеси окислення та ін. в очисній споруді.

Крайові умови для рівняння (11) розглянуто в [1, 2].

Для чисельного інтегрування рівняння (11) використовуємо неявну змінно–трикутна схему розщеплення [1, 2].

Результати

Для практичного використання розробленої математичної моделі була виконана її програмна реалізація. Розроблено програму, що включає в себе декілька підпрограм, що вирішують окремі специфічні задачі:

1. SUBROUTINE EVORZ – визначення значення вихору всередині відстійника;

2. SUBROUTINE EFUZ – визначення функції току всередині відстійника;

3. SUBROUTINE ECOZ – визначення концентрації забруднювача в очисній споруді;

4. SUBROUTINE ЕPRZ – презентація поля швидкості та концентрації в очисній споруді.

Розроблена комп’ютерна програма була використана для визначення розподілу концентрації забруднювача в вертикальному відстійнику, що характеризувався наявністю додаткових пластин, що були встановлені на бокових сторонах очисної споруди. Використання цих додаткових елементів значно ускладнюють процес математичного моделювання гідродинаміки течії та переносу забруднювача в очисній споруді. Розглянута задача відноситься до класу модельних задач, розв’язок яких дозволяє визначити працездатність розробленої математичної моделі. Рис. 1 ілюструє зону забруднення в очисній споруді. Концентрацію забруднювача наведено у безрозмірному вигляді.

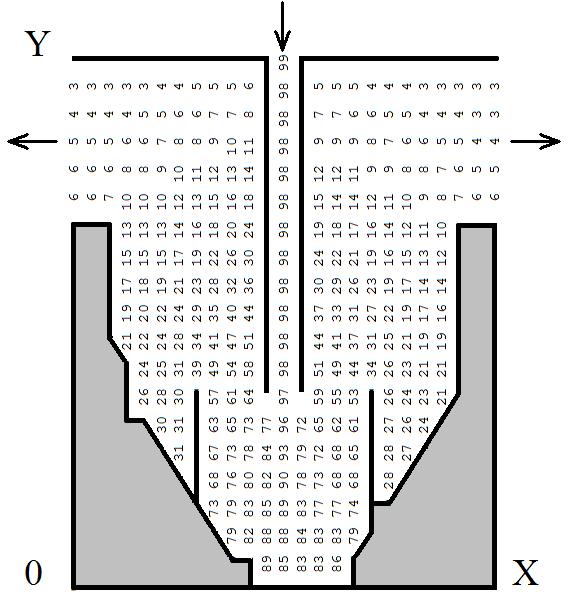
Рис. 1. Концентрація домішки у вертикальному відстійнику

Fig. 1. Impurity concentration in the vertical settler

Як бачимо з рис. 1 ефективність очищення води в цій споруді становитиме близько 90 %.

Відзначимо, що час розрахунку склав приблизно 15 сек.

Наукова новизна та практична значимість

Автори розробили чисельну модель, що базується на рівняннях Нав’є–Стокса та рівнянні переносу домішки у вертикальному відстійнику. Побудовані розрахункові залежності дозволяють швидко визначати розподіл забруднювача у вертикальному відстійнику з урахуванням його форми.

Розроблена методологія розрахунку може бути використана для експертної оцінки ефективності роботи відстійників, що використовуються в системах каналізації.

Висновки

У статті розглянуто чисельну модель, що дозволяє оперативно оцінювати ефективність роботи вертикальних відстійників. Побудовані розрахункові залежності використовують закони збереження для потоку рідини та домішки.

В подальшому цей науковий напрям слід проводити в галузі створення 3D–моделей оцінки ефективності роботи очисних споруд.

СПИСОК використаних джерел

1. Беляев, Н. Н. Математическое моделирование массопереноса в отстойниках систем водоотведения / Н. Н. Беляев, Е. К. Нагорная. – Днепропетровск : Новая идеология, 2012. – 112 с.

2. Беляев, Н. Н. Математическое моделирование массопереноса в горизонтальных отстойниках / Н. Н. Беляев, В. А. Козачина. – Днепропетровск : Акцент ПП, 2015. – 115 с.

3. Горносталь, С. А. Аналіз результатів моделювання процесу біологічного очищення стічних вод / С. А. Горносталь, О. А. Петрухов // Науковий вісник будівництва. – ХНУБА, 2014. – № 1. – С. 112–114.

4. ДБН В.2.5-75-2013. Каналізація. Зовнішні мережі та споруди. Основні положення проектування. – Київ : Мінрегіон України, 2013. – 128 с.

5. Епоян, С. М. Особливості роботи пористої полімербетонної перегородки водопровідного горизонтального відстійника і її регенерація / С. М. Епоян, Д. Г. Сухоруков // Науковий вісник будівництва. – Харків : ХНУБА. – 2012. – Вип. 69. – С. 327–331.

6. Козачина, В. А. Моделирование процесса массопреноса в отстойнике при импульсной подаче примеси / В.А. Козачина // Науковий вісник будівництва. – ХНУБА, 2015. – № 1 (79). – С. 162–165.

7. Олійник, О. Я. Моделювання очистки стічних вод від органічних забруднень в біореакторахаеротенках зі зваженим (вільно плаваючим) і закріпленим біоценозом / О. Я. Олійник, Т. С. Айрапетян // Доповіді НАН України. – 2015. – № 5. – С. 55–60. doi: 10.15407/dopovidi2015.05.055.

8. Олійник, О. Я. Підвищення ефективності біологічного очищення стічних вод в аеротенках за рахунок зваженого та закріпленого біоценозу / О. Я. Олійник, Т. С. Айрапетян // Науковий вісник будівництва. – Харків : ХНУБА, 2015. – № 3 (81). – С. 106–109.

9. Олійник, О. Я. Підвищення ефективності роботи аеротенків-витискувачів за рахунок завислого і зваженого біоценозу / О. Я. Олійник, Т. С. Айрапетян // Проблеми водопостачання, водовідведення та гідравліки : наук.-техн. зб. – Київ, 2016. – Вип. 26. – С. 123–130.

10. Олійник, О. Я. Моделювання і розрахунки біологічної очистки стічних вод на краплинних біофільтрах / О. Я. Олійник, О. А. Колпакова // Екологічна безпека та природокористування : зб. наук.-техн. пр. – Київ, 2014. – Вип. 16. – С. 68–86

11. Олейник, О. Я. Повышение эффективности роботы аеротенков / О. Я. Олейник, Т. С. Айрапетян // Вісник Одеської державної академії будівництва та архітектури. – Одеса : Optimum, 2015. – № 59. – С. 214-222.

12. Олійник, О. Я. Розрахунок кисневого режиму при біологічному очищенні стічних вод в аеротенкахзмішувачах з закріпленим і зваженим біоценозом / О. Я. Олейник, Т. С. Айрапетян // Науковий вісник будівництва. – Харків : ХНУБА, 2018. – № 4 (98). – С. 187–191.

13. Реконструкція і інтенсифікація споруд водопостачання та водовідведення: навч. посіб. / О. А. Василенко, П. О. Грабовський, Г. М. Ларкін та ін. – К.: ІВНВКП «Укргеліотек «, 2010. – 272 с.

14. Griborio, A. Secondary Clarifier Modeling: A Multi-Process Approach / A. Griborio // Dissertation and Theses (for the degree of Doctor of Philosophy in The Engineering and Applied Sciences Program). – University of New Orleans : USA, 2004. – 440 p.

В. И. Шинкаренко¹, В. А. Козачина^2*, И. А. Бондаренко³, В. А. Габринец⁴,
В. Н. Горячкин⁵

¹Каф. «Компьютерные информационные технологии», Днипровский национальный университет железнодорожного транспорта имени академика В. Лазаряна, ул. Лазаряна, 2, Днипро, Украина, 49010, тел. +38 (056) 373 15 35, эл. почта shinkarenko_vi@ua.fm, ORCID 0000-0001-8738-7225
^2*Каф. «Гидравлика и водоснабжение», Днипровский национальный университет железнодорожного транспорта имени академика В. Лазаряна, ул. Лазаряна, 2, Днипро, Украина, 49010, тел. +38 (056) 273 15 09, эл. почта v.kozachyna@gmail.com, ORCID 0000-0002-6894-5532
³Каф. «Путь и путевое хозяйство», Днипровский национальный университет железнодорожного транспорта имени академика В. Лазаряна, ул. Лазаряна, 2, Днипро, Украина, 49010, тел. +38 (056) 373 15 31, эл. почта v.kozachyna@gmail.com, ORCID 0000-0003-4717-3032
^4*Каф. «Теплотехника», Днипровский национальный университет железнодорожного транспорта имени академика В. Лазаряна, ул. Лазаряна, 2, Днипро, Украина, 49010, тел. +38 (056) 373 15 87, эл. почта gabrin62@gmail.com, ORCID 0000-0002-6115-7162^5*Каф. «Теплотехника», Днипровский национальный университет железнодорожного транспорта имени академика В. Лазаряна, ул. Лазаряна, 2, Днипро, Украина, 49010, тел. +38 (056) 373 15 87, эл. почта vgora@ukr.net, ORCID 0000-0002-8952-952X

МОДЕЛирование ОЧИСТКИ ВОДЫ

В ВЕРТИКАЛЬНОМ ОТСТОЙНИКЕ

Цель. Повышение эффективности работы очистных сооружений в системах водоснабжения и водоотведения является важно технической задачей. Для анализа эффективности очистки воды конкретного сооружения, на этапе проектирования, нужно иметь специальные математические модели. Целью работы является построение математических моделей для оценки эффективности работы отстойников с дополнительными конструктивными элементами, которые используют в системах очистки сточных вод. Методика. Процесс распространения загрязнителя в очистном сооружении (отстойнике) рассчитывают с помощью уравнений гидродинамики течения вязкой, несжимаемой жидкости. Дополнительным уравнением является уравнение распространения загрязнителя в вертикальном отстойнике. Уравнения, используемые для расчета вертикального отстойнике, учитывают наиболее существенные физические факторы, влияющие на эффективность работы отстойника. Для численного интегрирования моделирующего уравнения переноса примеси в сооружении используют разностные схемы расщепления. Численное решение уравнения, описывающего процесс движения загрязнителя в вертикальном отстойнике, базируется на расщеплении этого уравнения в уравнение более упрощенной структуры. Для численного интегрирования моделирующих уравнений течения невязкой жидкости используют неявные разностные схемы расщепления. Численный расчет совершают на прямоугольной разностной сетке. Результаты. На базе разработанных численных моделей создан пакет прикладных программ. Этот пакет позволяет оперативно, методом вычислительного эксперимента, определить эффективность работы отстойника. Приведены результаты проведенного вычислительного эксперимента по определению эффективности работы отстойника с двумя пластинами. Научная новизна. Разработанные математические модели дают возможность определять поле скорости и процесс переноса примеси с учетом геометрической формы отстойника и использования в них пластин, которые влияют на гидродинамику потока в сооружении, а значит – на эффективность очистки воды. Практическая значимость. Время расчета одного варианта задания на базе построенных математических моделей составляет несколько секунд. Модели можно использовать для получения экспертной оценки работы очистных сооружений, которые проектируют.

Ключевые слова: очистка сточных вод; численное моделирование; вертикальный отстойник

V. І. shynkarenko¹, V. А. Kozachyna^2*, І. О. Bondarenko³, V. О. GABRINETS⁴, V. M. Horiachkin⁵

¹Dep. «Computer and Information Technologies», Dnipro National University of Railway Transport named after Academician V. Lazaryan, Lazaryana St., 2, Dnipro, Ukraine, 49010, tel. +38 (056) 373 15 35, e-mail shinkarenko_vi@ua.fm, ORCID 0000-0001-8738-7225
^2*Dep. «Hydraulics and Water Supply», Dnipro National University of Railway Transport named after Academician V. Lazaryan, Lazaryana St., 2, Dnipro, Ukraine, 49010, tel. +38 (056) 273 15 09, e-mail.org/ v.kozachyna@gmail.com,ORCID 0000-0002-6894-5532
³Dep. «Railway Track and Track Facilities», Dnipro National University of Railway Transport named after Academician V. Lazaryan, Lazaryana St., 2, Dnipro, Ukraine, 49010, tel. +38 (056) 373 15 31, е-mail irina_bondarenko@ua.fm,ORCID 0000-0003-4717-3032
⁴Dep. «Heat Engineering», Dnipro National University of Railway Transport named after Academician V. Lazaryan, Lazaryana St., 2, Dnipro, Ukraine, 49010, tel. +38 (056) 373 15 87, e-mail gabrin62@gmail.com, ORCID 0000-0002-6115-7162
⁵Dep. «Heat Engineering», Dnipro National University of Railway Transport named after Academician V. Lazaryan, Lazaryana St., 2, Dnipro, Ukraine, 49010, tel. +38 (056) 373 15 87, e-mail vgora@ukr.net,ORCID 0000-0002-8952-952X

MODELING of waste WATER

TREATMENT IN VERTICAL SETTLER

Purpose. Increasing the effectiveness of water treatment plants is an urgent technical problem. To obtain the efficiency analysis of certain facility of water treatment plant, at the design stage, it is necessary to have special mathematical models. In the paper, the development of mathematical models for assessing the performance of vertical settler having additional structural elements and used in wastewater treatment systems is considered. Methodology. The pollutant distribution in the settler has been computed using the hydrodynamics equation for the viscous incompressible fluid. Additional equation is the equation for the spread of contaminants in a vertical settler. The equations used to calculate the vertical settler take into account the most significant physical factors affecting efficiency of the settler. For numerical integration of the modeling impurity transfer equation in the water treatment plant, difference splitting schemes are used. The numerical solution of the equation describing the process of pollutant movement in a vertical settler is based on splitting this equation into the equation of a more simplified structure. For numerical integration of the modeling equations of the inviscid fluid flow, implicit difference splitting schemes are used. Numerical calculation is performed on a rectangular difference grid. Findings. On the basis of the developed numerical models, a package of application programs was created. This package allows quick determining the settler efficiency using a computational experiment. The results of a computational experiment to determine the efficiency of the settler with two plates are presented. Originality. The developed mathematical models make it possible to determine the velocity field and the impurity transfer process, taking into account the geometric shape of the settler and the use of plates, which affect the flow hydrodynamics in the water treatment plant, and therefore the efficiency of water treatment. Practical value. The calculation time for one version of the task based on the constructed mathematical models is several seconds. The models can be used to obtain an expert assessment of the operation of water treatment plants that are being designed.

Keywords: wastewater treatment; numerical simulation; vertical settler

References

1. Biliaiev, N. N., & Nagornaya, E. K. (2012). Matematicheskoye modelirovaniye massoperenosa v otstoynikakh sistem vodootvedeniya. Dnepropetrovsk: Novaya ideologiya. (in Russian)

2. Biliaiev, N. N., & Kozachina, V. A. (2015). Modelirovaniye massoperenosa v gorizontalnykh otstoynikakh: Monografiya. Dnepropetrovsk: Aktsent PP. (in Russian)

3. Gornostal, S. A., & Petrukhov, O. A. (2014). Analysis of simulation results of biological wastewater treatment process. Scientific Bulletin of Construction, 1, 112-114. (in Ukrainian)

4. Kanalizatsiia. Zovnishni merezhi ta sporudy. Osnovni polozhennia proektuvannia, 128 DBN V.2.5-75-2013 (2013). (in Ukrainian)

5. Epoian, S. M., & Sukhorukov, D. G. (2012). Osoblyvosti roboty porystoi polimerbetonnoi perehorodky vodoprovidnoho horyzontalnoho vidstiinyka i yii reheneratsiia. Scientific Bulletin of Construction, 69, 327- 331. (in Ukrainian)

6. Kozachina, V. A. (2015). Modeling of the mass transfer process in a sump during impulse supply of impurities. Scientific Bulletin of Construction, 1(79), 162-165. (in Russian)

7. Oleynik, A. Y., & Kolpakova, O. A. (2014). Modelling and calculation of bioiligical wastewater treatment to trickling biofilters. Environmental safety and natural resources, 16, 68-86. (in Ukrainian)

8. Oleynik, A. Y., & Airapetyan, T. S. (2015). The modeling of the clearance of waste waters from organic pollutions in bioreactors-aerotanks with suspended (free flow) and fixed biocenoses. Reports of the National Academy of Sciences of Ukraine, 5, 55-60. doi: 10.15407/dopovidi2015.05.055 (in Ukrainian)

9. Oliinyk, O. Ya. & Airapetian, T. S. (2015). Pidvyshchennia efektyvnosti biolohichnoho ochyshchennia stichnykh vod v aerotenkakh za rakhunok zvazhenoho ta zakriplenoho biotsenozu. Scientific Bulletin of Construction, 3(81), 106-109. (in Ukrainian)

10. Oliinyk, O. Ya, & Airapetyan, T. S. (2016). Pidvyshchennia efektyvnosti roboty aerotenkiv-vytyskuvachiv za rakhunok zavysloho i zvazhenoho biotsenozu. Problemy vodopostachannia, vodovidvedennia ta hidravliky, 26, 123-130. (in Ukrainian)

11. Oliinyk O. Ya., & Airapetian T. S. (2015). Povyshenie effektivnosti roboty aerotenkov. Visnyk Odeskoi derzhavnoi akademii budivnytstva ta arkhitektury, 59, 214-222.

12. Oliinyk, O. Ya. & Airapetian, T. S. Rozrakhunok kysnevoho regymu pry biolohichnomu ochyschenni stichnykh vod v aerotenkakh-zmishuvachakh z zakriplenym I zvagenym biotsenozom. Scientific Bulletin of Construction, 4(98), 187-191. (in Ukrainian)

13. Vasylenko, O. A., Hrabovskyi, P. O., Larkin, H. M., & others. (2010). Rekonstruktsiia i intensyfikatsiia sporud vodopostachannia ta vodovidvedennia: navch.posib. K.: IVNVKP «Ukrheliotek». (in Ukrainian)

14. Griborio, A. (2004). Secondary Clarifier Modeling: A Multi-Process Approach. Dissertation and Theses. USA, University of New Orleans Publ. (in English)

Надійшла до редколегії: 30.07.2019

Прийнята до друку: 04.11.2019