ISSN
2307–3489 (Print), ІSSN
2307–6666
(Online)
Наука
та прогрес транспорту. Вісник
Дніпропетровського
національного університету залізничного
транспорту, 2019, № 4 (85)
ЕКОЛОГІЯ
НА ТРАНСПОРТІ
УДК
628.35:519.87
В.
А. козачина1*,
В. І. ШИНКАРЕНКО2*,
І. о.
Бондаренко3*,
в. о.
габрінець4*,
В. М. ГОРЯЧКІН5*
1*Каф.
«Гідравліка та водопостачання»,
Дніпровський національний університет
залізничного транспорту імені академіка
В. Лазаряна, вул. Лазаряна, 2, Дніпро,
Україна, 49010, tel. +38 (056) 273
15 09, ел. пошта water.supply.treatment@gmail.com,
ORCID 0000-0002-6894-5532
2*Каф.
«Комп’ютерні інформаційні технології»,
Дніпровський національний університет
залізничного транспорту імені академіка
В. Лазаряна, вул. Лазаряна, 2, Дніпро,
Україна, 49010, тел. +38 (056) 373 15 35, ел. пошта
shinkarenko_vi@ua.fm, ORCID 0000-0001-8738-7225
3*Каф.
«Колія та колійне господарство»,
Дніпровський національний університет
залізничного транспорту імені акаде-міка
В. Лазаряна, вул. Лазаряна, 2, Дніпро,
Україна, 49010, тел. +38 (063) 802 21 80, ел. пошта
irina_bondarenko@ua.fm, ORCID 0000-0003-4717-3032
4*Каф.
«Теплотехніка», Дніпровський національний
університет залізничного транспорту
імені академіка В. Лазаряна, вул. Лазаряна,
2, Дніпро, Україна, 49010, тел. +38 (056) 373 15 87,
ел. пошта gabrin62@gmail.com, ORCID 0000-0002-6115-7162
5*Каф.
«Теплотехніка», Дніпровський національний
університет залізничного транспорту
імені академіка В. Лазаряна, вул. Лазаряна,
2, Дніпро, Україна, 49010, тел. +38 (056) 373 15 87,
ел. пошта vgora@ukr.net, ORCID 0000-0002-6115-7162
МОДЕЛЮВАННЯ
ОЧИЩЕННЯ ВОДИ
У ГОРИЗОНТАЛЬНОМУ ВІДСТІЙНИКУ
Мета.
Підвищення ефективності роботи очисних
споруд у системах водопостачання та
водовідведення є важливою технічною
задачею. Для аналізу ефективності
очищення води конкретної споруди, на
етапі проектування, потрібно мати
спеціальні математичні моделі. Метою
цієї роботи є розробка чисельної моделі
процесу масопереносу у вертикальному
відстійнику для оцінки ефективності
його роботи. Методика.
Процес розповсюдження забруднювача в
очисній споруді (відстійнику) розраховують
на базі рівняння розповсюдження домішки,
що виражае закон збереження маси.
Моделювальне рівняння враховує
конвективний перенос домішки та перенос
домішки за рахунок турбулентної дифузії.
Математична модель враховує нерівномірне
поле швидкості потоку в споруді. Для
визначення цього нерівномірного поля
швидкості потоку використано математичну
модель течії
ідеальної рідини. При цьому враховано
вихрову природу потоку. Результати.
Розв’язання
моделювальних рівнянь знайдено чисельним
шляхом.
Для
чисельного інтегрування моделювального
рівняння переносу в споруді використано
різницеві схеми розщеплення. Базове
рівняння масопереносу попередньо
розщеплено на рівняння, що враховує рух
домішки у відстійнику за рахунок
конвекції, та на рівняння, що враховує
перенос домішки за рахунок дифузії. Для
чисельного інтегрування моделювальних
рівнянь течії нев’язкої рідини
використано неявні різницеві схеми
розщеплення. Чисельний розрахунок
здійснено на прямокутній різницевій
сітці.
Наукова
новизна.
Особливістю розробленої математичної
моделі є можливість визначення поля
швидкості та процесу переносу домішки
з урахуванням геометричної форми
відстійників та можливістю використання
в них пластин, що впливають на гідродинаміку
потоку
в споруді, а значить – на ефективність
очищення води. Практична
значимість. Час
розрахунку одного варіанта завдання
на базі побудованих математичних моделей
складає кілька секунд. Моделі можна
використати для отримання експертної
оцінки роботи очисних споруд, які
проектують. Зазначено результати
проведеного обчислювального експерименту
з визначення ефективності роботи
відстійника з двома пластинами.
Ключові
слова:
очищення
води;
математичне моделювання;
очисні споруди
Вступ
Відстійники
відіграють суттєву роль
у системах водопостачання
та водовідведення. На практиці
використовують різні типи відстійників,
але в системах очищення дуже часто
стічні води після аеротенків потрапляють
на вертикальні відстійники. Для оцінки
ефективності роботи відстійників за
різних навантажень, потрібно мати
математичні моделі, що дозволяють
визначати ступінь очищення стічних
вод для конкретних умов експлуатації
[1–3, 5, 7–9].
Для
розв’язання задач з оцінки ефективності
роботи очисних споруд використовують
математичні моделі, а саме емпіричні
[4, 11] й аналітичні [3, 4, 7,
9, 10, 12].
Недоліком цих моделей є неможливість
урахування нерівномірного потоку в
споруді та геометричної форми споруди.
Тому більш ефективними є чисельні
моделі [1, 2, 6, 13], що
дозволяють проводити розрахунки з
урахуванням геометричної форми споруд.
Але недоліком цих моделей є, у деяких
випадках, значні витрати комп’ютерного
часу їх на практичну реалізацію [13].
Мета
Зважаючи
на викладене, метою нашої
роботи є розробка
чисельної моделі процесу масопереносу
у вертикальному відстійнику для оцінки
ефективності його роботи.
Методика
Будемо розглядати
рух води з домішками в очисній споруді,
наприклад, у вертикальногму відстійнику.
Ставимо задачу розробки математичної
моделі, що дозволяе визначати ефектівність
роботи споруди з урахуванням її
геометричної форми та гідродинаміки
потоку.
Модель
гідродинаміки.
Найважливішою задачею під час розрахунку
очисних споруд систем водопостачання
та водовідведення є визначення поля
швидкості водного потоку. Це пов’язано
з тим, що рух домішок у споруді визначається
переважно, конвекцією. Тому під час
створення моделей оцінки ефективності
роботи очисних споруд розв’язання
задачі гідродинаміки постає на першому
місці. У роботі будемо використовувати
модель рівнянь Нав’є–Стокса
для розв’язання задачі гідродинаміки.
Моделювальні рівняння мають вигляд:
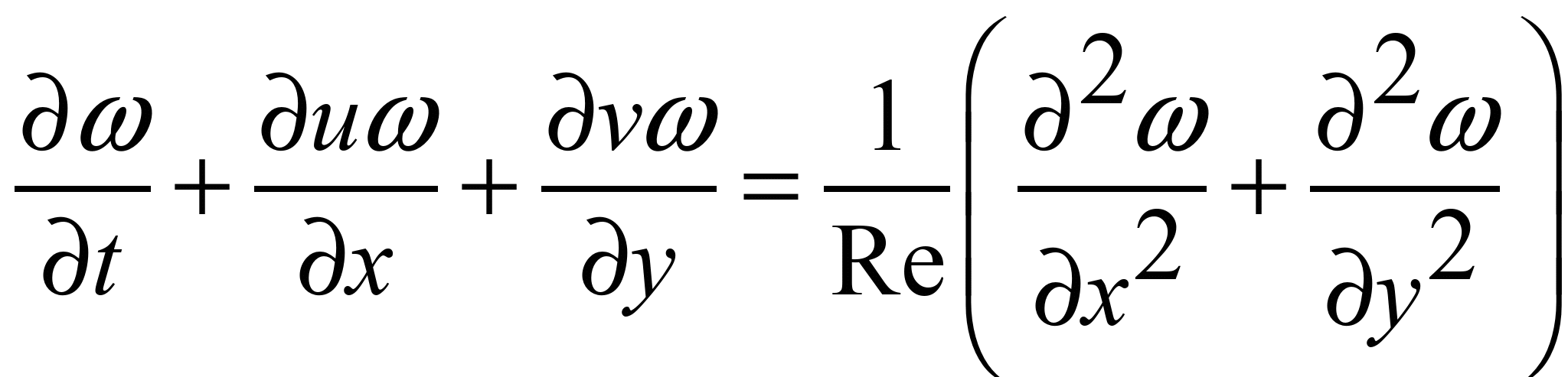 ; (1)
; (1)
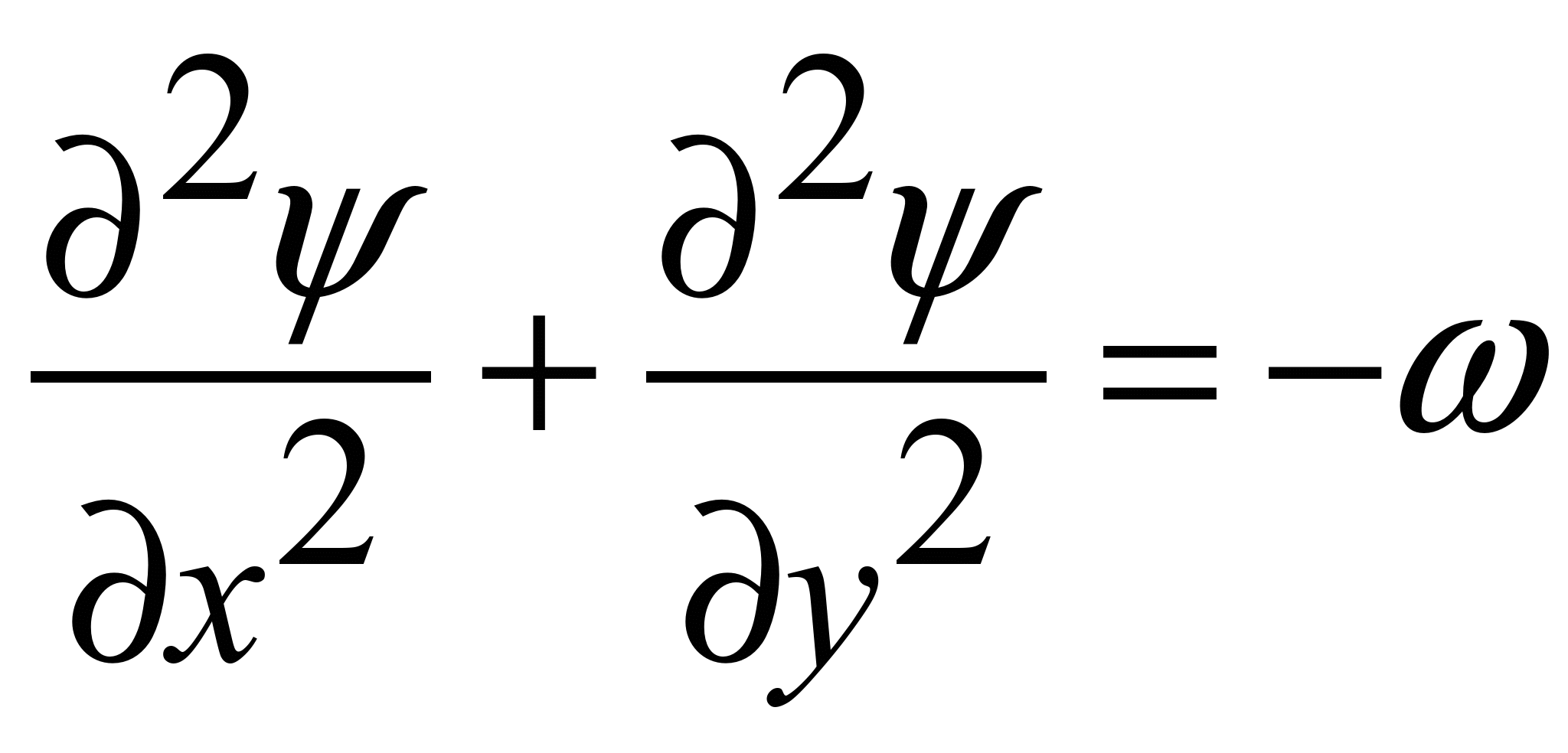 , (2)
, (2)
де y
– функція потоку;
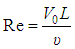 – число Рейнольдса;
– число Рейнольдса;
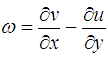 –
завихореність;
–
завихореність;
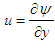 ,
,
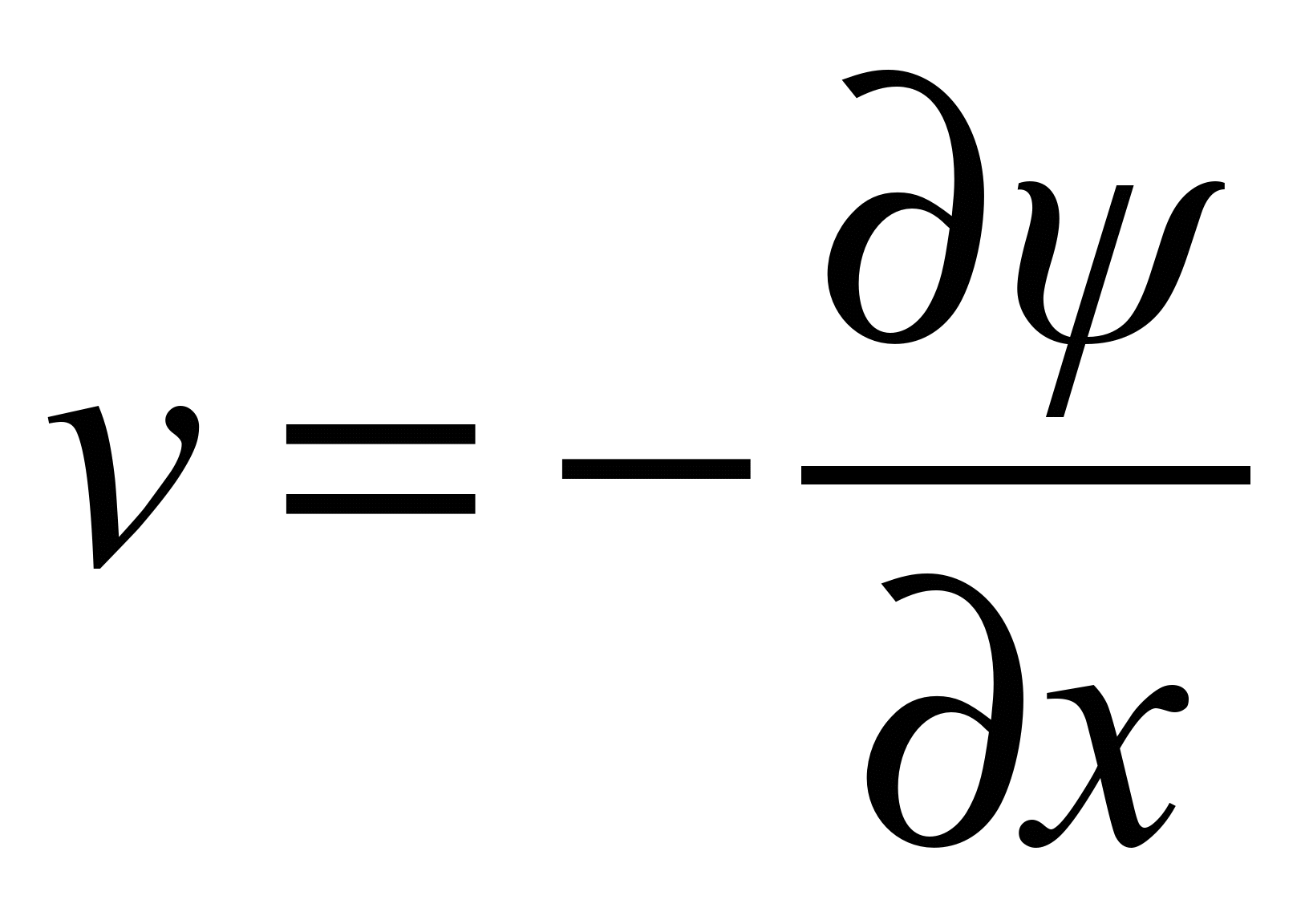 – компоненти вектора швидкості водного
потоку;
L
– характерний лінійний розмір;
– компоненти вектора швидкості водного
потоку;
L
– характерний лінійний розмір;
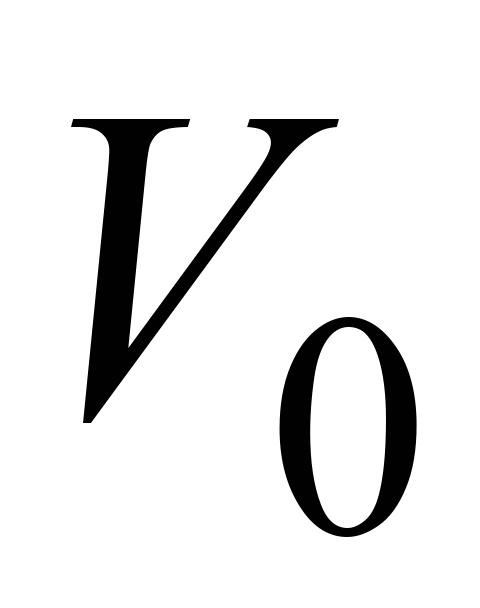 – характерна швидкість.
– характерна швидкість.
Постановку
граничних умов для системи рівнянь
(2)–(3) наведено в роботі [2].
Розглянемо
побудову різницевих схем для чисельного
інтегрування рівнянь Нав’є–Стокса.
Представимо
швидкість потоку в такому вигляді:
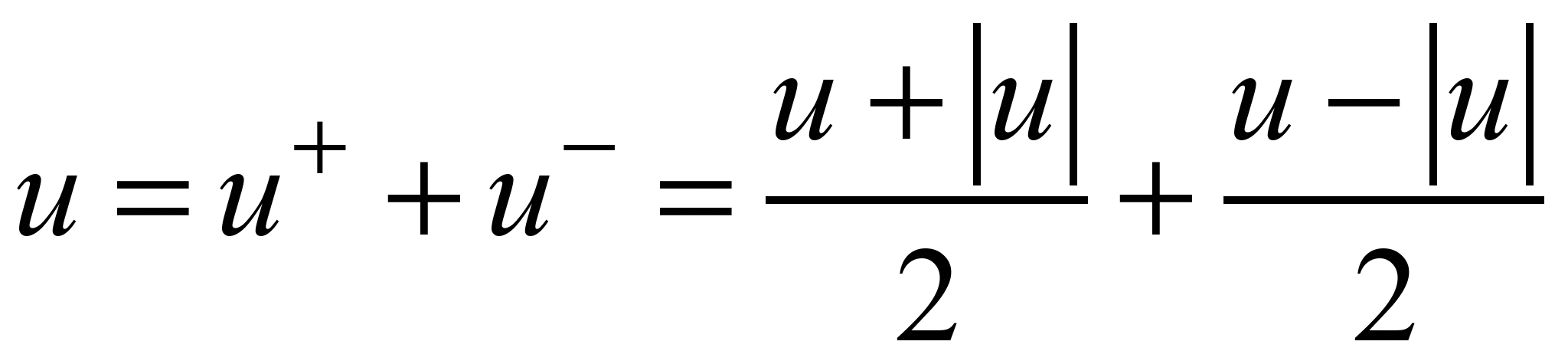 ;
;
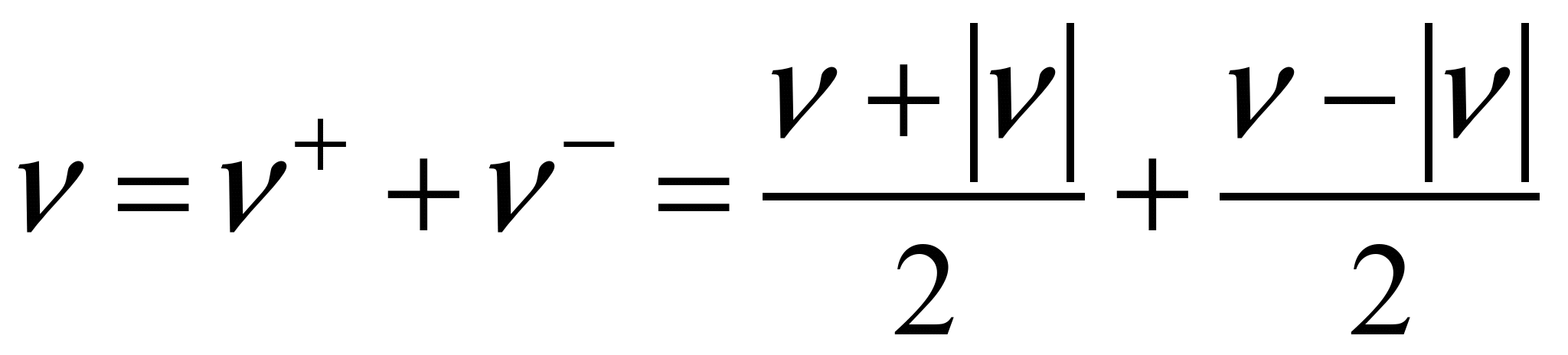 .
.
Виконаємо
заміну конвективних похідних так [1]:
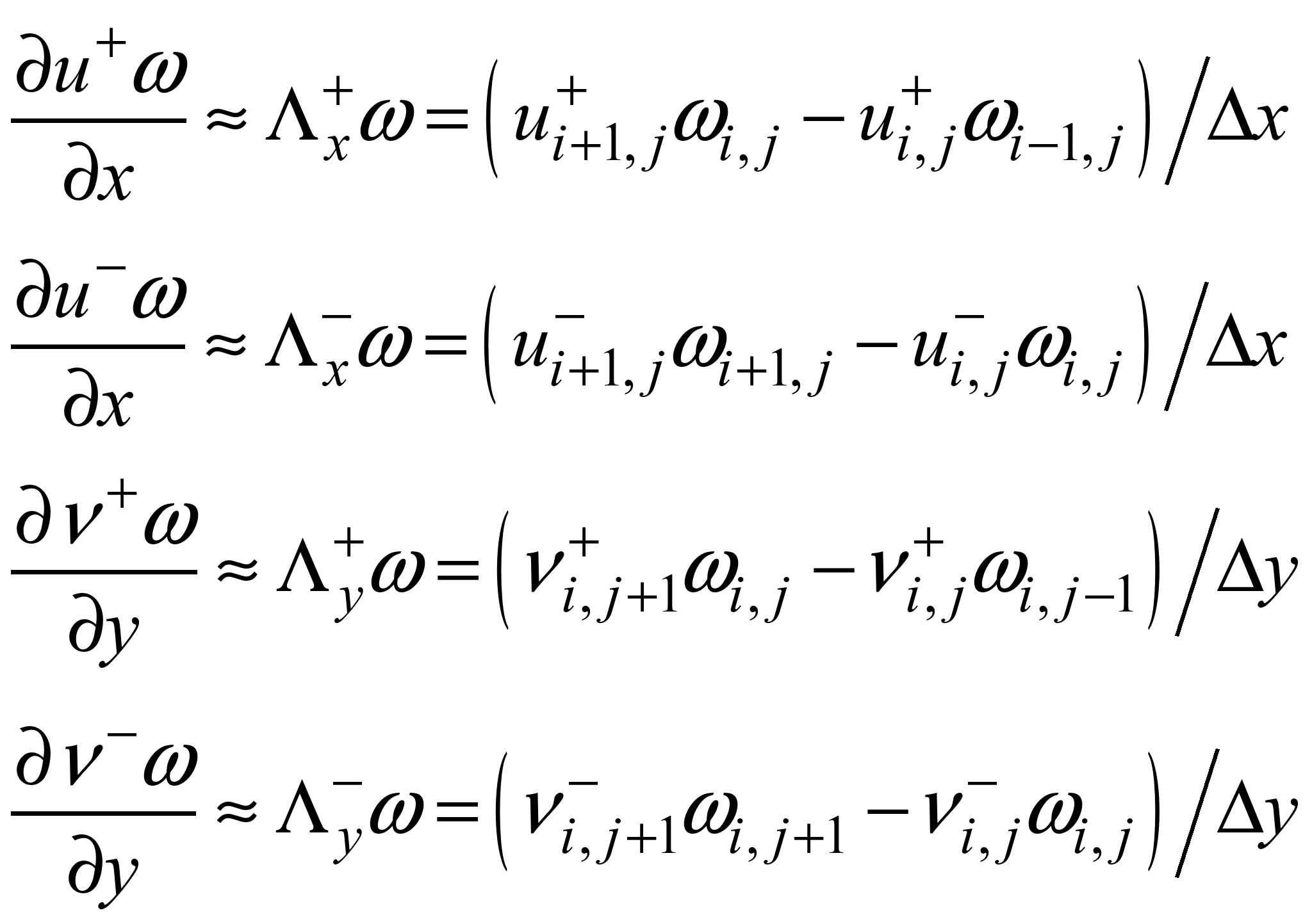 , (3)
, (3)
Для
апроксимації других похідних
використовуємо залежності [1]:
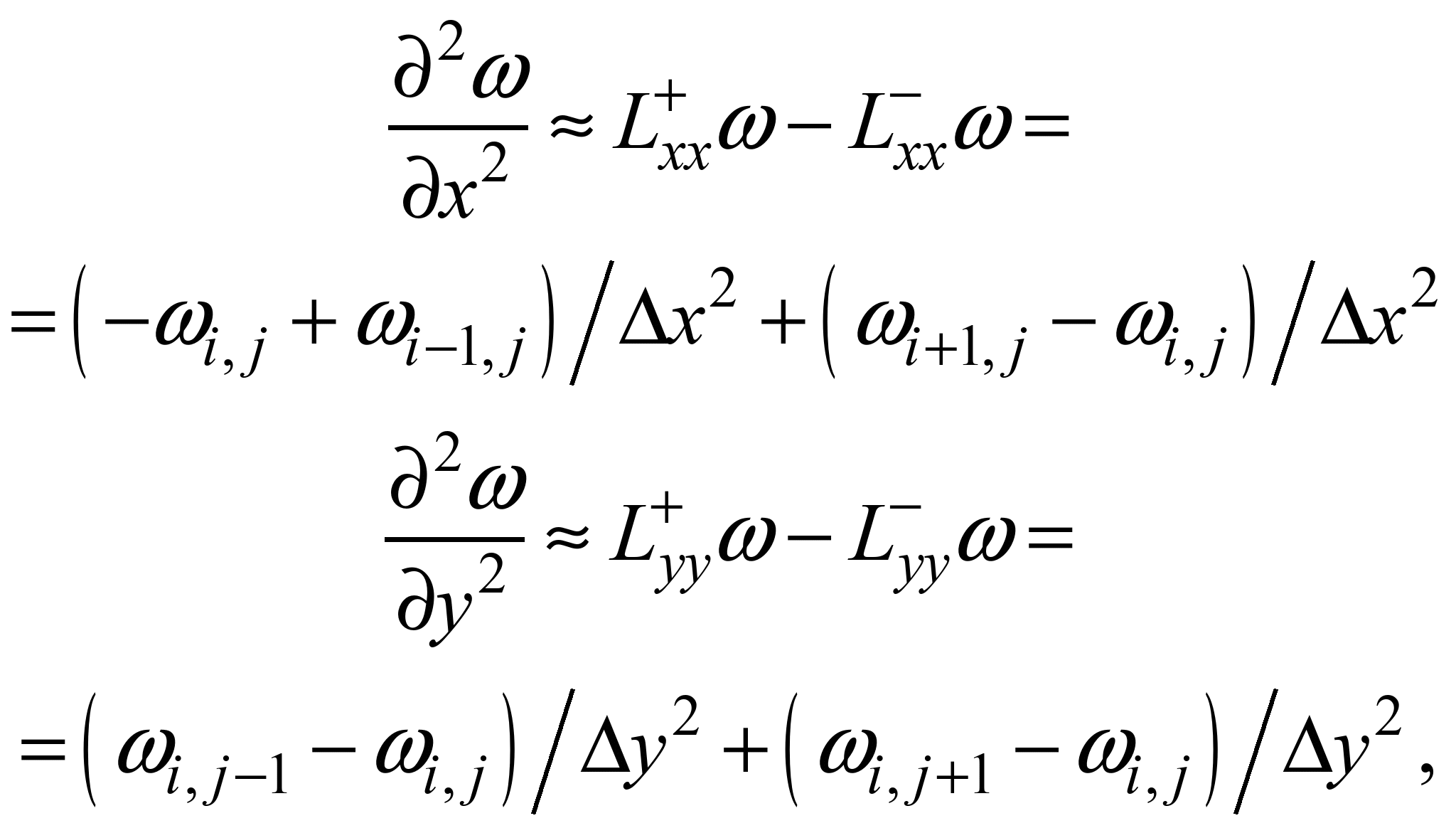 , (4)
, (4)
де в
подальшому різницеві оператори
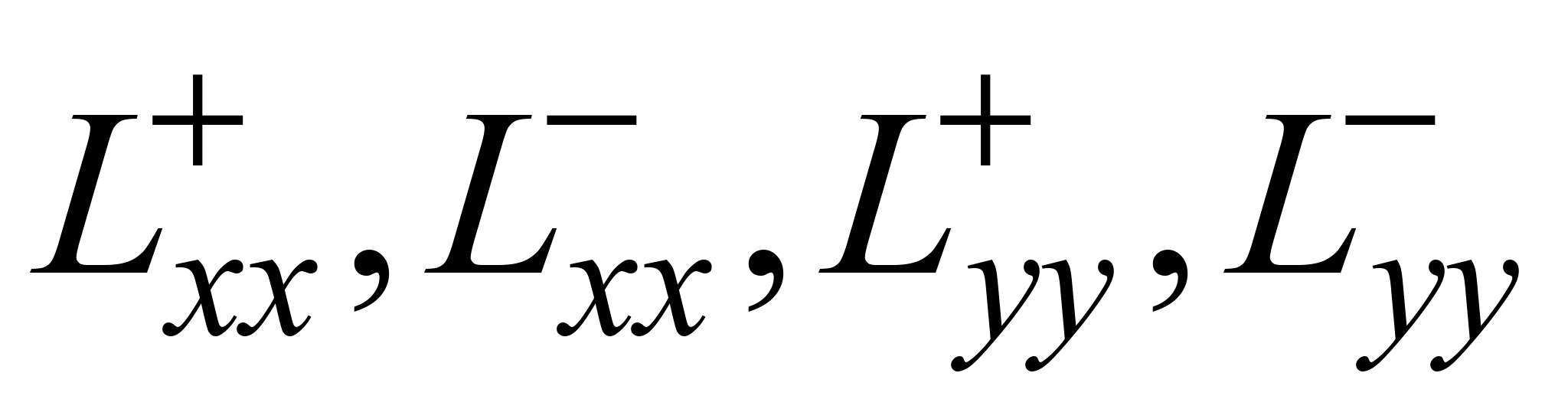 визначатимуться на різних розрахункових
шарах. Замінюючи похідні розділеними
різницями (3)–(4), отримуємо наступну
різницеву схему [8]:
визначатимуться на різних розрахункових
шарах. Замінюючи похідні розділеними
різницями (3)–(4), отримуємо наступну
різницеву схему [8]:
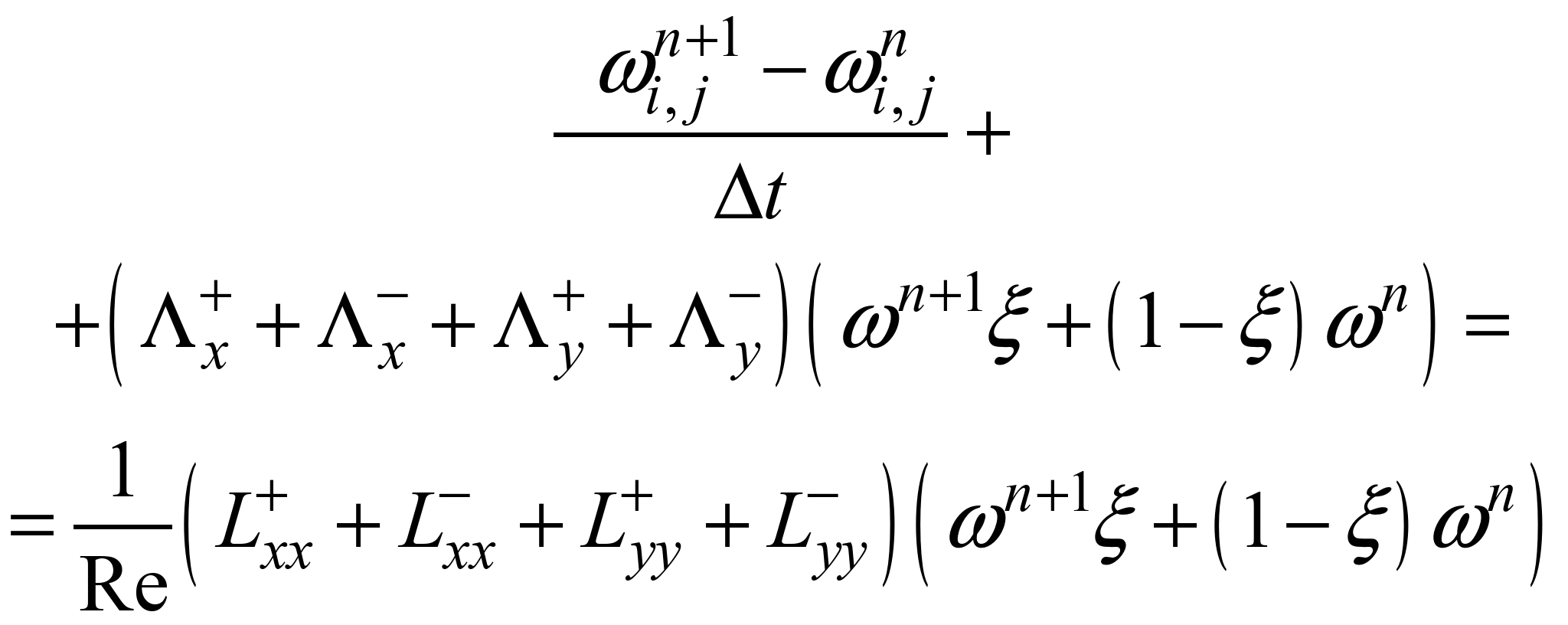 (5)
(5)
або
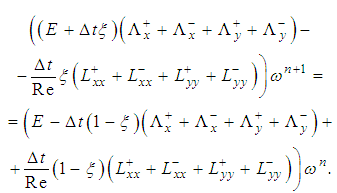 (6)
(6)
Схема
(6) за
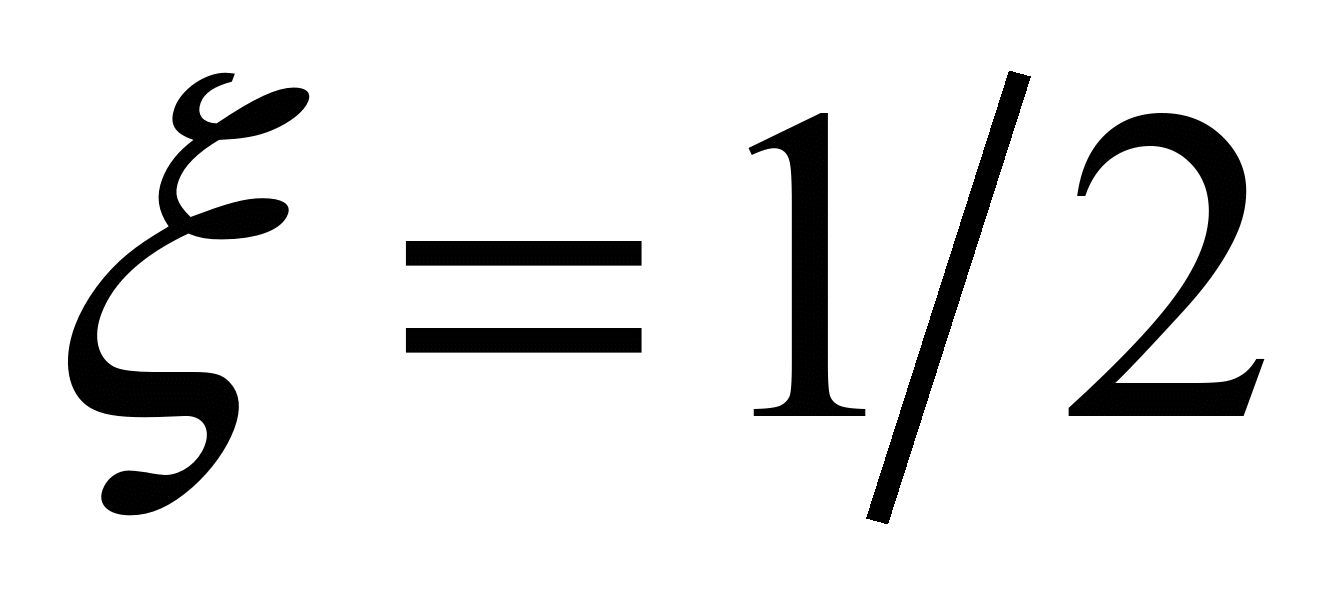 має другий порядок точності за часовою
координатою, однак для визначення
невідомих
має другий порядок точності за часовою
координатою, однак для визначення
невідомих
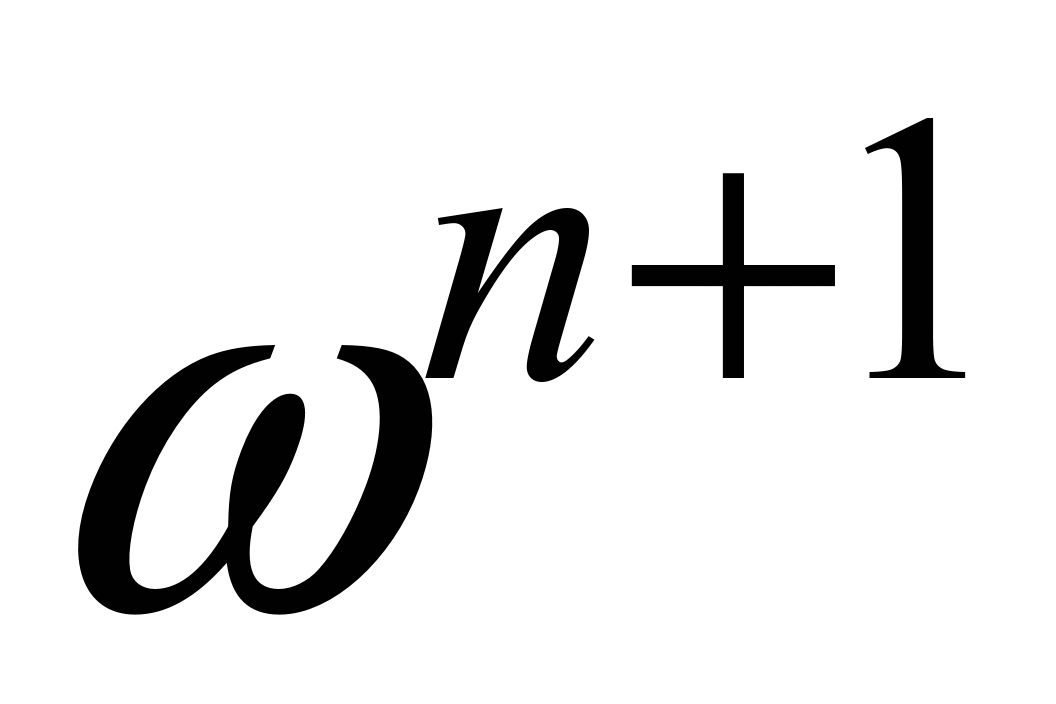 необхідно розв’язувати систему
алгебраїчних рівнянь великої розмірності.
необхідно розв’язувати систему
алгебраїчних рівнянь великої розмірності.
Далі
записуємо різницеву схему розщеплення
[1]:
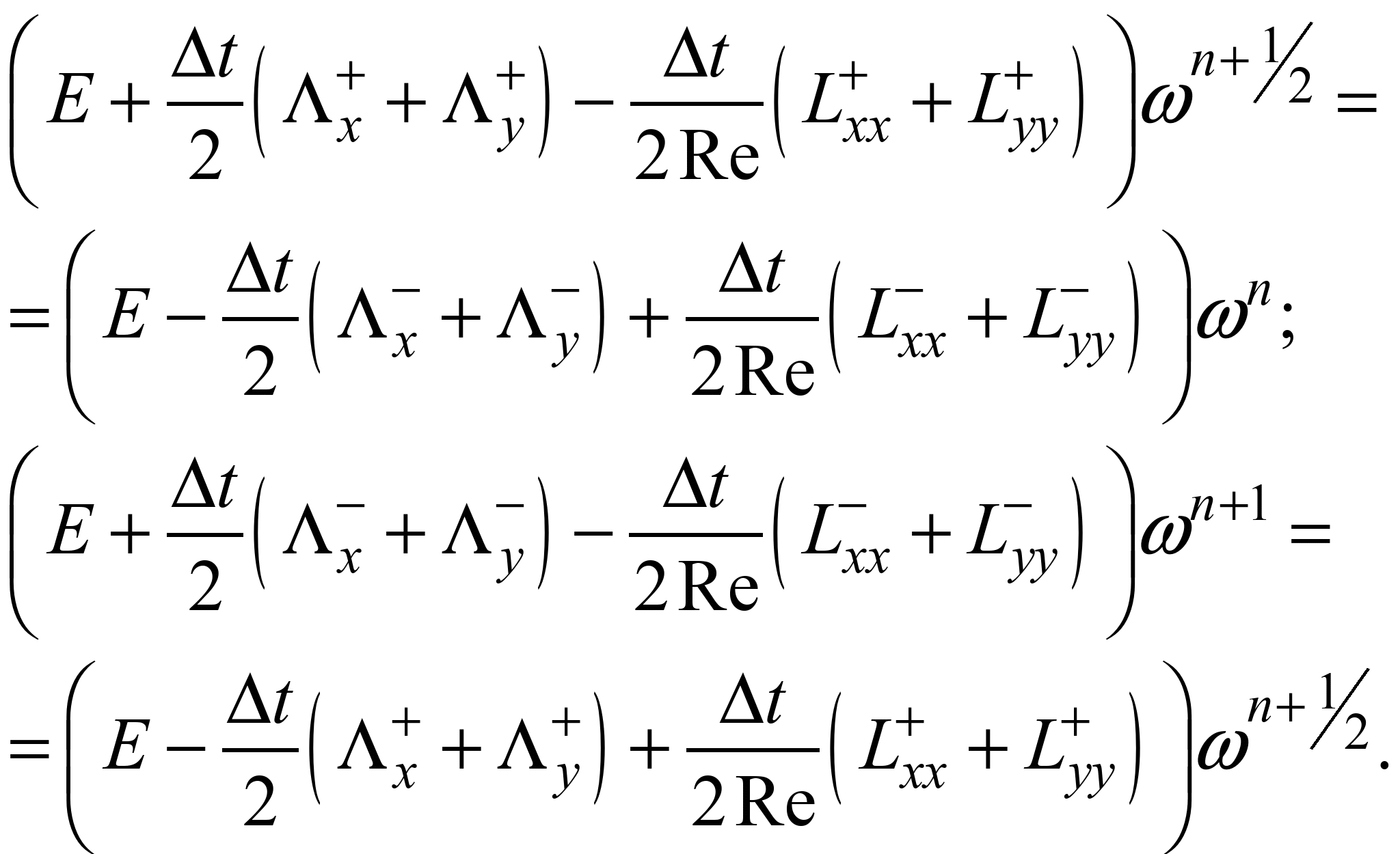 (7)
(7)
Розрахунок
невідомого значення
 на кожному кроці розщеплення визначаємо
за методом біжучого рахунку.
на кожному кроці розщеплення визначаємо
за методом біжучого рахунку.
Для
чисельного інтегрування рівняння для
функції потоку використовуємо метод
ітерацій. Для цього рівняння Пуассона
приводимо до вигляду:
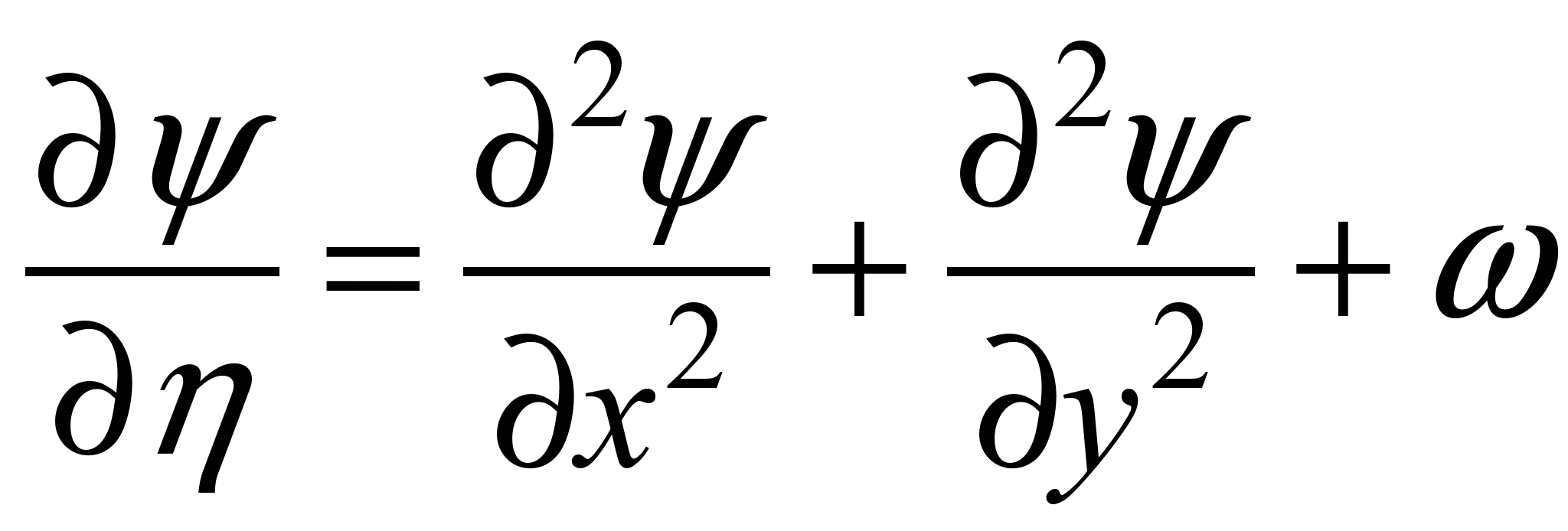 , (8)
, (8)
де
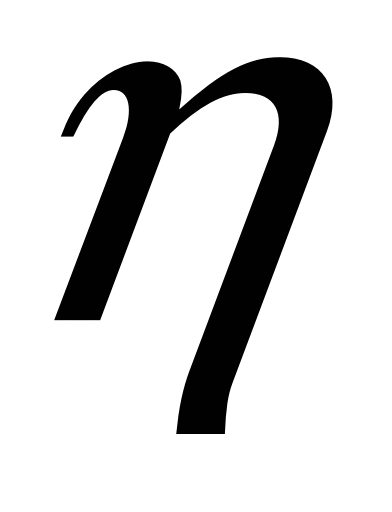 – фіктивний час. Функція
– фіктивний час. Функція
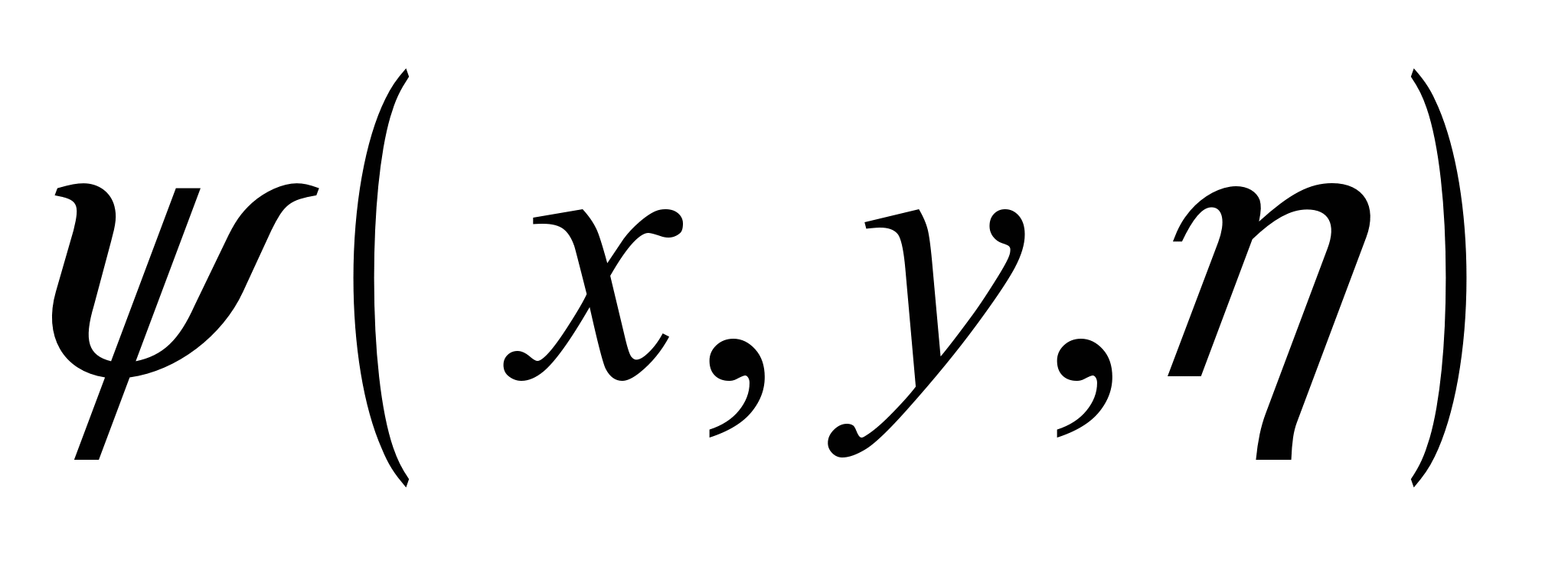 ,
будучи розв’язком нестаціонарного
рівняння (3.14), буде розв’язком рівняння
Пуассона за
,
будучи розв’язком нестаціонарного
рівняння (3.14), буде розв’язком рівняння
Пуассона за
 .
.
Використана
різницева схема має вигляд [1]:
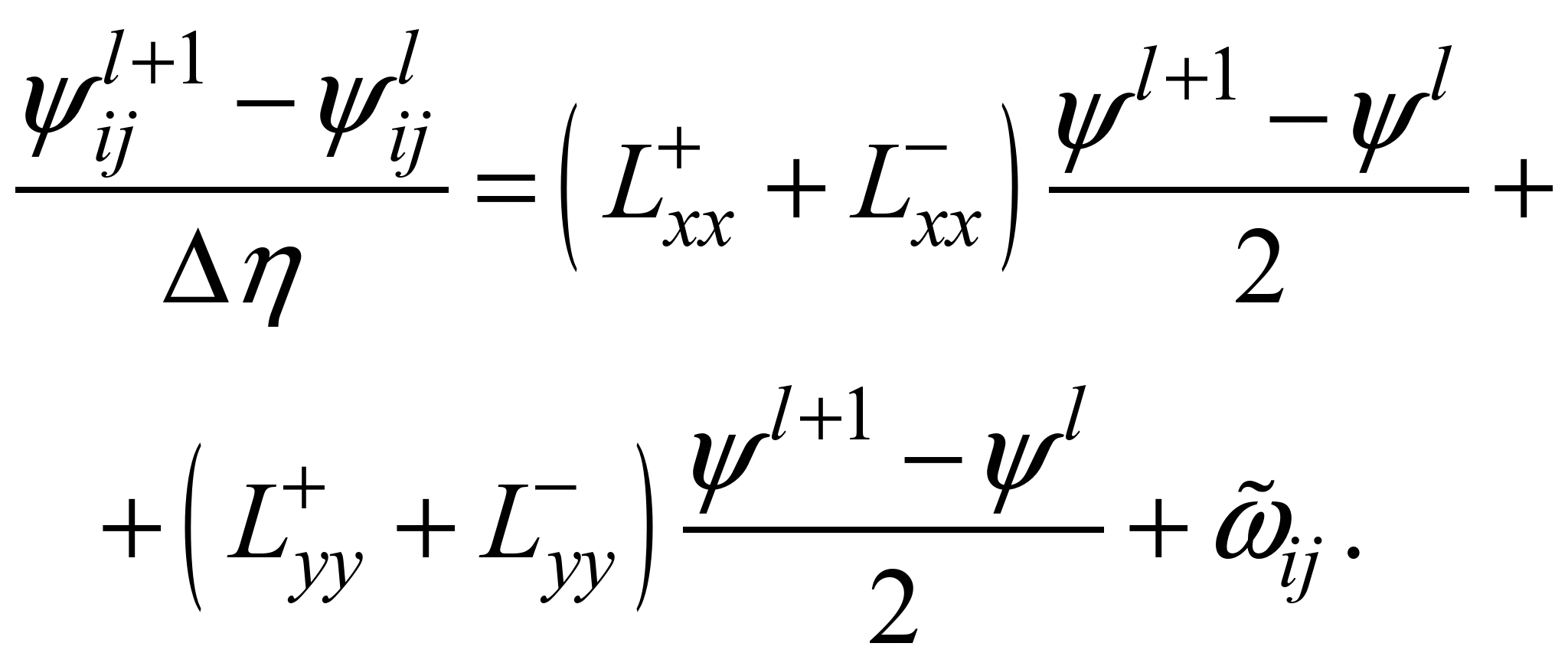 , (9)
, (9)
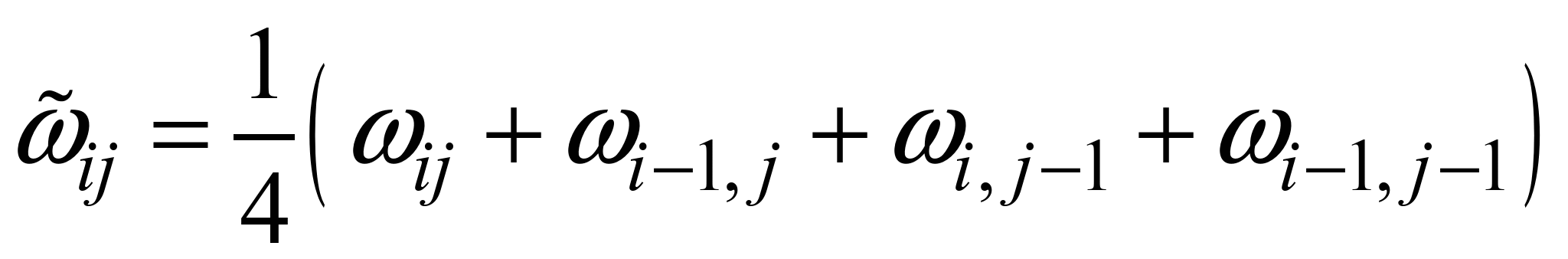 .
.
Схема
розщеплення має вигляд:
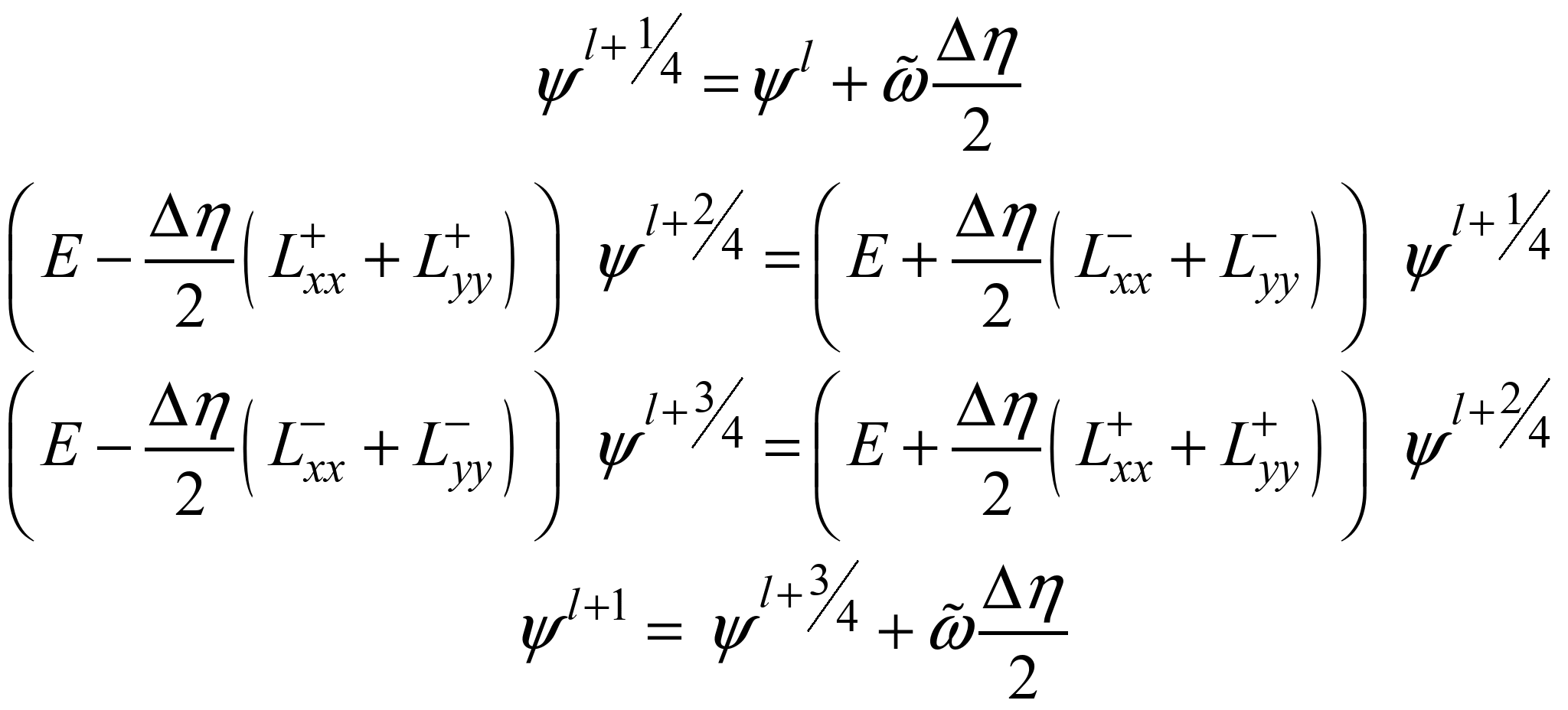 (10)
(10)
Значення
функції потоку
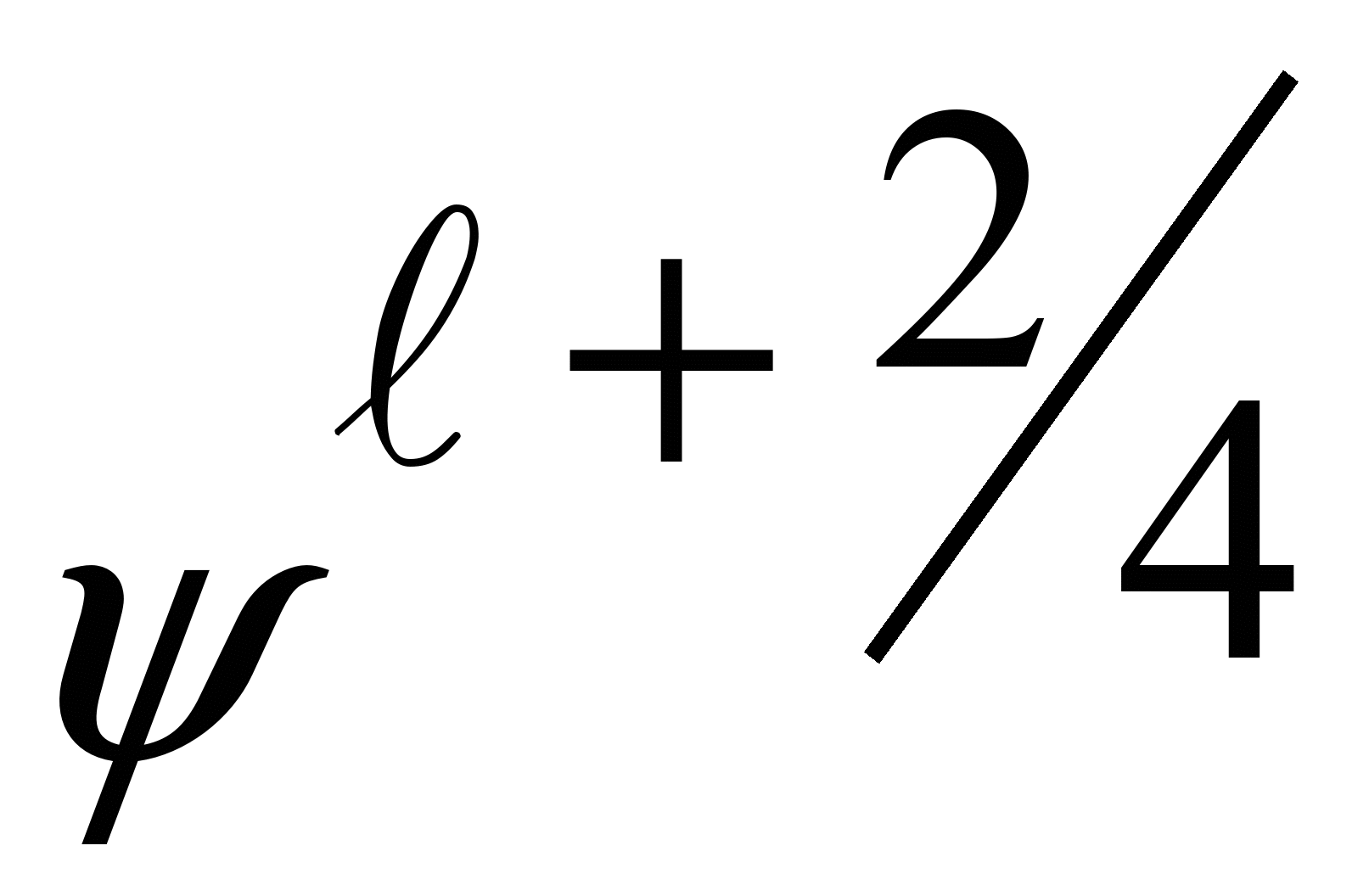 ,
,
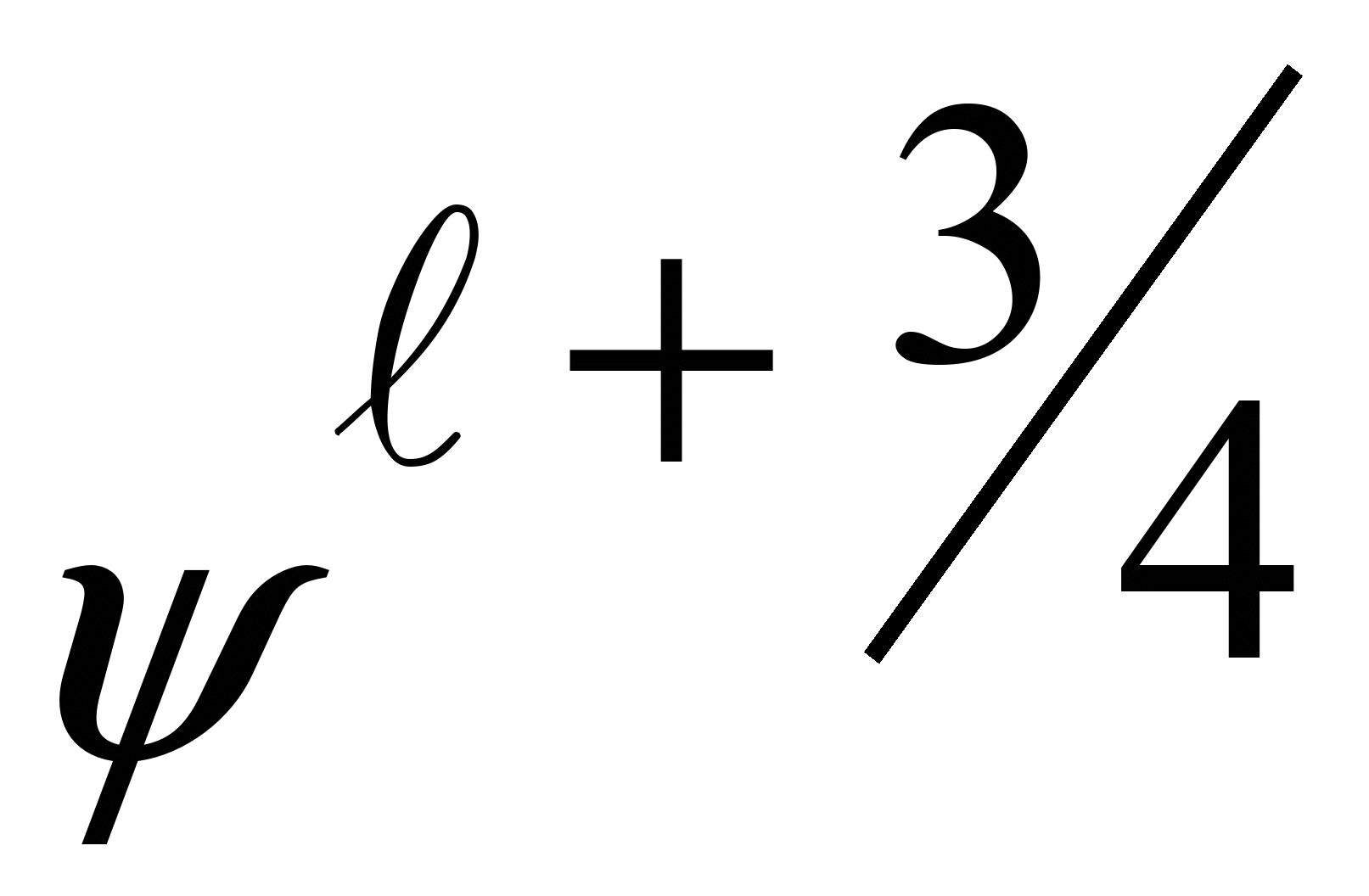 визначаємо методом біжучого рахунку
на другому та третьому кроках розщеплення.
визначаємо методом біжучого рахунку
на другому та третьому кроках розщеплення.
Компоненти
вектора швидкості визначаємо так:

Для
формування вигляду розрахункової
області використовуємо маркери.
Модель
масопереносу у відстійнику.
Після
розрахунку нерівномірного поля швидкості
потоку у відстійнику необхідно
розрахувати рух домішки.
Для математичного
опису переносу
домішки в очисній споруді будемо
використовувати рівняння балансу маси
[1, 2, 6, 13]:
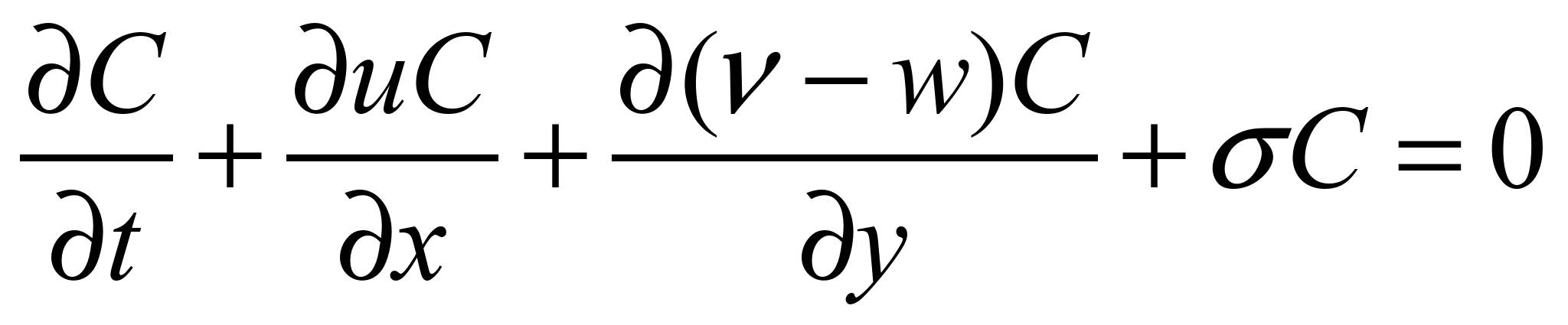 , (11)
, (11)
де С
– концентрація домішки; u,
v –
компоненти вектора швидкості потоку
в напрямку осей х
і у;
w
–
гравітаційна швидкість осадження
домішки; х,
у
– Декартові координати; σ – коефіцієнт,
що враховує процес флокуляції і розпаду
частинок, а також біохімічне окислення.
Крайові
умови для рівняння (11) розглянуто в
[11].
Для
чисельного інтегрування рівняння (11)
використовуємо неявну змінно-трикутну
схему розщеплення [11].
Результати
На базі
побудованої чисельної моделі створено
пакет програм. Основні модулі цього
пакета наступні:
1)
підпрограма EVORZ – розрахунок поля
вихору на базі рівнянь
Нав’є–Стокса;
2)
підпрограма EFUZ– розрахунок функції
потоку на базі рівнянь
Нав’є–Стокса;
3)
підпрограма ECOZ – розрахунок концентрації
домішки у відстійнику;
4)
підпрограма ЕPRZ – друк результатів
обчислювального експерименту.
На рис.
1 показано розподіл домішки у вертикальному
відстійнику. Обчислювальний експеримент
на базі побудованої чисельної моделі
проведено для відстійника, що має дуже
складну геометричну форму. Як відомо,
для таких розрахункових областей ряд
чисельних методів втрачає стійкість,
але побудована чисельна модель не має
такого недоліку. Числа на рис.1 показують
у процентах концентрацію домішки від
значення концентрації домішки на вході
у відстійник (С
= 99 %). На базі такої технології можна
швидко анулізувати, яка концентрація
домішки буде на виході з відстійника.
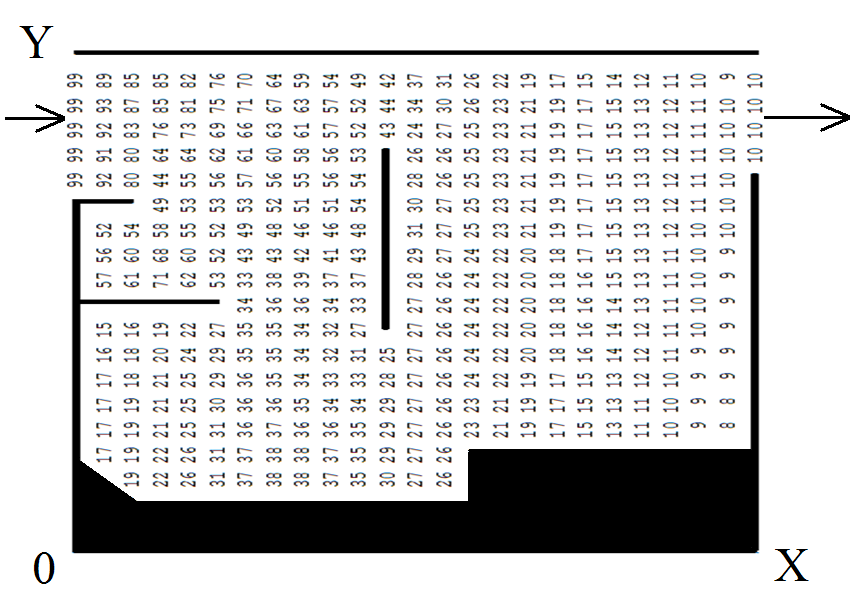
Рис.
1. Концентрація домішки у вертикальному
відстійнику
Fig. 1.
Impurity concentration in a vertical settler
Як ми
бачимо з рис. 1,
ефективність очищення води в цій споруді
буде близько 90 %.
Відзначимо,
що час розрахунку склав близько 15 сек.
Наукова
новизна та практичне значення
Запропоновано
чисельну модель, що базується на
рівнянні Нав’є–Стокса та рівнянні
переносу домішки у вертикальному
відстійнику. Розроблена модель дозволяє
оперативно розраховувати нерівномірне
поле швидкості потоку в споруді та
розподіл концентрації домішки в споруді.
Модель може бути застосована на етапі
проектуванням очисних споруд систем
водовідведення.
Висновки
У статті
розглянуто чисельну модель, що дозволяє
оперативно оцінювати ефективність
роботи вертикальних відстійників.
Модель базується на використанні
фундаментальних рівнянь механіки
суцільного середовища.
Подальший
розвиток цього наукового напрямку слід
проводити в галузі створення 3D- моделей
для оцінки ефективності роботи очисних
споруд.
СПИСОК
ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
Беляев, Н. Н. Математическое
моделирование массопереноса в
горизонтальных отстойниках /
Н.
Н. Беляев, В. А. Козачина.
– Днепропетровск : Акцент ПП, 2015. – 115
с.
Беляев, Н. Н. Математическое
моделирование массопереноса в
отстойниках систем водоотведения / Н.
Н. Беляев, Е. К. Нагорная. – Днепропетровск
: Новая идеология, 2012. – 112 с.
Горносталь, С. А. Аналіз результатів
моделювання процесу біологічного
очищення стічних вод / С. А. Горносталь,
О. А. Петрухов // Науковий вісник
будівництва. – ХНУБА, 2014.
– № 1. – С. 112–114.
ДБН В.2.5-75-2013. Каналізація.
Зовнішні мережі та споруди. Основні
положення проектування. – Київ :
Мінрегіон України, 2013. – 128 с.
Епоян, С. М. Особливості роботи
пористої полімербетонної перегородки
водопровідного горизонтального
відстійника і її регенерація / С.
М. Епоян, Д.
Г. Сухоруков // Науковий
вісник будівництва. – Харків
: ХНУБА. – 2012. – Вип. 69. – С. 327–331.
Козачина, В. А.
Моделирование процесса массопреноса
в отстойнике при импульсной подаче
примеси / В.А. Козачина // Науковий вісник
будівництва. – ХНУБА, 2015. – № 1 (79). –
С. 162–165.
Олійник, О. Я. Моделювання і
розрахунки біологічної очистки стічних
вод на краплинних біофільтрах / О. Я.
Олійник, О. А. Колпакова // Екологічна
безпека та природокористування : зб.
наук.-техн. пр. – Київ, 2014. – Вип. 16. –
С. 68–86.
Олійник, О. Я.
Моделювання очистки стічних вод від
органічних забруднень в
біореакторах-аеротенках зі зваженим
(вільно плаваючим) і закріпленим
біоценозом / О. Я. Олійник, Т. С. Айрапетян
// Доповіді НАН України. – 2015. – № 5. –
С. 55–60. doi:
10.15407/dopovidi2015.05.055
Олійник, О. Я. Підвищення
ефективності біологічного очищення
стічних вод в аеротенках за рахунок
зваженого та закріпленого біоценозу
/ О. Я. Олійник, Т. С. Айрапетян // Науковий
вісник будівництва. – Харків
: ХНУБА, 2015. – № 3 (81). – С. 106–109.
Олійник, О. Я. Підвищення
ефективності роботи аеротенків-витискувачів
за рахунок завислого і зваженого
біоценозу / О. Я. Олійник, Т. С. Айрапетян
// Проблеми водопостачання, водовідведення
та гідравліки : наук.-техн. зб. – Київ,
2016. – Вип. 26. – С. 123–130.
Олійник, О. Я. Розрахунок
кисневого режиму при біологічному
очищенні стічних вод в аеротенках-змішувачах
з закріпленим і зваженим біоценозом
/ О. Я. Олейник, Т. С. Айрапетян // Науковий
вісник будівництва. – Харків : ХНУБА,
2018. – № 4 (98). – С. 187–191.
Реконструкція і інтенсифікація
споруд водопостачання та водовідведення:
навч.посіб. / О. А. Василенко, П. О.
Грабовський, Г. М. Ларкін та ін. – К.:
ІВНВКП «Укргеліотек », 2010. – 272 с.
Griborio,
A. Secondary Clarifier Modeling: A
Multi-Process Approach / A. Griborio // Dissertation and Theses
(for the degree of Doctor of Philosophy in The Engineering and
Applied Sciences Program). – University of New Orleans : USA,
2004. – 440 p.
В.
А. КОЗАЧИНА1*,
В. И. ШИНКАРЕНКО2*,
И. А. БОНДАРЕНКО3*,
В.
А. ГАБРИНЕЦ4*,
В. Н. ГОРЯЧКИН5*
1*Каф.
«Гидравлика и водоснабжение», Днипровский
национальный университет железнодорожного
транспорта имени академика В. Лазаряна,
ул. Лазаряна, 2, Днипро, Украина, 49010, тел.
+38 (056) 273 15 09, эл. почта
water.supply.treatment@gmail.com, ORCID 0000-0002-6894-5532
2*Каф.
«Компьютерные информационные технологии»,
Днипровский национальный университет
железнодорожного транспорта имени
академика В. Лазаряна, ул. Лазаряна, 2,
Днипро, Украина, 49010, тел. +38 (056) 373 15 35,
эл. почта shinkarenko_vi@ua.fm, ORCID 0000-0001-8738-7225
3*Каф. «Путь
и путевое хозяйство», Днипровский
национальный университет железнодорожного
транспорта имени академика В. Лазаряна,
ул. Лазаряна, 2, Днипро, Украина, 49010, тел.
+38 (063) 802 21 80, эл. почта irina_bondarenko@ua.fm, ORCID
0000-0003-4717-3032
4*Каф.
«Теплотехника», Днипровский национальный
университет железнодорожного транспорта
имени академика В. Лазаряна, ул.
Лазаряна, 2, Днипро, Украина, 49010, тел.
+38 (056) 373 15 87, эл. почта gabrin62@gmail.com,ORCID
0000-0002-6115-7162
5*Каф.
«Теплотехника», Днипровский национальный
университет железнодорожного транспорта
имени академика В. Лазаряна, ул. Лазаряна,
2, Днипро, Украина, 49010, тел. +38 (056) 373 15 87,
эл. почта vgora@ukr.net, ORCID 0000-0002-8952-952X
МОДЕЛИРОВАНИЕ ОЧИСТКИ ВОДЫ
В
ГОРИЗОНТАЛЬНОМ отстойнике
Цель.
Повышение
эффективности работы очистных сооружений
в системах водоснабжения и водоотведения
– важная техническая задача. Для анализа
эффективности очистки воды конкретного
сооружения, на этапе проективання,
нужно иметь специальные математические
модели. Целью
данной работы является разработка
численной модели процесса массопереноса
в вертикальном отстойнике для оценки
эффективности его работы. Методика.
Процесс
распространения загрязнителя в очистном
сооружении (отстойнике) рассчитывают
на базе уравнения распространения
примеси, что выражает закон сохранения
массы. Моделирующее уравнение учитывает
конвективный перенос примеси и перенос
примеси за счет турбулентной диффузии.
Математическая модель учитывает
неравномерное поле скорости потока в
сооружении. Для определения этого
неравномерного поля скорости потока
используют математическую модель
течения идеальной жидкости. При этом
учитывают вихревую природу потока.
Результаты.
Решение
моделирующих уравнений найдено численным
путем. Для численного интегрирования
моделирующего уравнения переноса в
сооружении использованы разностные
схемы расщепления. Базовое уравнение
массопереноса предварительно расщеплено
на уравнения, учитывающие движение
примеси в отстойнике за счет конвекции,
и на уравнения, учитывающие перенос
примеси за счет диффузии. Для численного
интегрирования моделирующих уравнений
течения невязкой жидкости использованы
неявные разностные схемы расщепления.
Численный расчет осуществлен на
прямоугольной разностной сетке. Научная
новизна.
Особенностью
разработанной математической модели
является возможность определения поля
скорости и процесса переноса примеси
с учетом геометрической формы отстойников
и возможностью использования в них
пластин, влияющих на гидродинамику
потока в сооружении, а значит – на
эффективность очистки воды. Практическая
значимость. Время
расчета одного варианта задания на
базе построенных математических моделей
составляет несколько секунд. Модели
можно применить для получения экспертной
оценки работы проектируемых очистных
сооружений. Описаны результаты
проведенного вычислительного эксперимента
по определению эффективности работы
отстойника с двумя пластинами.
Ключевые
слова:
очистка
воды; математическое моделирование;
очистные сооружения
V. a.
Kozachyna1*,
V. I. SHYNKARENKO4*,
I. O. BONDARENKO2*,
V.
A. gabrinets5*,
V. M. HORIACHKIN5
1*Dep.
«Hydraulics and Water Supply», Dnipro National University of
Railway Transport named after Academician V. Lazaryan, Lazaryana
St., 2, Dnipro, Ukraine, 49010, tel. +38 (056) 273 15 09, e-mail
water.supply.treatment@gmail.com,ORCID 0000-0002-6894-5532
2*Dep.
«Computer and Information Technologies», Dnipro National
University of Railway Transport named after Academician V. Lazaryan,
Lazaryana St., 2, Dnipro, Ukraine, 49010, tel. +38 (056) 373 15 35,
e-mail shinkarenko_vi@ua.fm,ORCID 0000-0001-8738-7225
3*Dep.
«Track and Track Facilities», Dnipro National University named
after Academician V. Lazaryan, Lazaryana St., 2, Dnipro, Ukraine,
49010, tel. +38 (063) 802 21 80, e-mail irina_bondarenko@ua.fm,
ORCID 0000-0003-4717-3032
4*Dep.
«Heat Engineering», Dnipro National University of Railway
Transport named after Academician V. Lazaryan, Lazaryana St., 2,
Dnipro, Ukraine, 49010, tel. +38 (056) 373 15 87, e-mail
vgora@ukr.net,ORCID 0000-0002-8952-952X
5*Dep.
«Heat Engineering», Dnipro National University of Railway
Transport named after Academician V. Lazaryan, Lazaryana St., 2,
Dnipro, Ukraine, 49010, tel. +38 (056) 373 15 87, e-mail
vgora@ukr.net,ORCID 0000-0002-8952-952X
WATER
CLEANING MODELING IN A HORIZONTAL SETTLER
Purpose.
Improving
the efficiency of wastewater treatment plants in water supply and
sanitation is an important technical task. To analyze the
effectiveness of water treatment of a particular structure, at the
design stage, you need to have special mathematical models. The
work is aimed to develop a numerical model of the mass transfer
process in a vertical settler to assess its performance.
Methodology.
The
spread of the pollutant in the treatment plant (settler) is
calculated on the basis of the distribution equation of the
impurity, which expresses the law of mass conservation. The modeling
equation takes into account the convective transfer of impurities
and the transfer of impurities due to turbulent diffusion. The
mathematical model takes into account the uneven flow velocity field
in the building. To determine this uneven flow velocity field, a
mathematical model of the flow of an ideal fluid is used. In this
case, the vortex nature of the flow is taken into account.
Findings.
The solution of
modeling equations is found numerically. For numerical integration
of the modeling transport equation in the structure, difference
splitting schemes were used. The basic mass transfer equation is
preliminarily split into equations that take into account the
movement of an impurity in a settling tank due to convection, and
into equations that take into account the transfer of an impurity
due to diffusion. For numerical integration of the modeling
equations of the inviscid fluid flow, implicit difference splitting
schemes are used. The numerical calculation is carried out on a
rectangular difference grid.
Originality.
A
feature of the developed mathematical model is the possibility of
modeling the velocity field and the process of impurity transfer
taking into account the geometric shape of the settlers and the
possibility of using plates in them, which affect the flow
hydrodynamics in the structure and, therefore, the efficiency of
water treatment.
Practical
value.
The
calculation time for one version of the task based on the
constructed mathematical models is a
few
seconds. The models can be used to obtain an expert assessment of
the operation of treatment facilities designed. The results of a
computational experiment in determining the efficiency of the
settler with two plates are presented.
Keywords:
water treatment;
mathematical modeling; wastewater treatment plants
References
Biliaiev, N. N.,
& Kozachina, V. A. (2015).
Modelirovaniye massoperenosa v
gorizontalnykh otstoynikakh: Monografiya.
Dnepropetrovsk: Aktsent
PP. (in
Russian)
Biliaiev, N. N.,
& Nagornaya, E. K. (2012).
Matematicheskoye modelirovaniye
massoperenosa v otstoynikakh sistem vodootvedeniya.
Dnepropetrovsk: Novaya ideologiya. (in
Russian)
Gornostal,
S. A.,
& Petrukhov,
O. A.
(2014). Analysis of simulation results of
biological wastewater treatment process.
Scientific Bulletin of Construction,
1,
112-114.
(in Ukrainian)
Kanalizatsiia. Zovnishni merezhi ta
sporudy. Osnovni polozhennia proektuvannia, 128 DBN V.2.5-75-2013
(2013). (in Ukrainian)
Epoian, S. M., &
Sukhorukov, D.
G. (2012). Osoblyvosti
roboty porystoi polimerbetonnoi perehorodky vodoprovidnoho
horyzontalnoho vidstiinyka i yii reheneratsiia.
Scientific Bulletin of Construction,
69,
327-331. (in
Ukrainian)
Kozachina,
V. A.
(2015). Modeling of the mass transfer
process in a sump during impulse supply of impurities.
Scientific Bulletin of Construction,
1(79),
162-165.
(in
Russian)
Oleynik, A. Y., & Kolpakova, O.
A. (2014). Modelling and calculation of bioiligical wastewater
treatment to trickling biofilters.
Environmental safety and natural resources, 16,
68-86. (in Ukrainian)
Oleynik, A. Y., & Airapetyan,
T. S. (2015). The modeling of the clearance of waste waters from
organic pollutions in bioreactors-aerotanks with suspended (free
flow) and fixed biocenoses. Reports
of the National Academy of the Sciences of the Ukraine, 5,
55-60. doi:
10.15407/dopovidi2015.05.055(in Ukrainian)
Oliinyk, O. Ya. & Airapetian,
T. S.
(2015). Pidvyshchennia efektyvnosti
biolohichnoho ochyshchennia stichnykh vod v aerotenkakh za rakhunok
zvazhenoho ta zakriplenoho biotsenozu.
Scientific Bulletin of Construction,
3(81),
106-109. (in
Ukrainian)
Oliinyk, O. Ya, & Airapetyan,
T. S. (2016). Pidvyshchennia efektyvnosti roboty
aerotenkiv-vytyskuvachiv za rakhunok zavysloho i zvazhenoho
biotsenozu. Problemy
vodopostachannia, vodovidvedennia ta hidravliky,
26, 123-130. (in Ukrainian)
Oliinyk, O. Ya. & Airapetian,
T. S.
Rozrakhunok kysnevoho regymu pry
biolohichnomu ochyschenni stichnykh vod v aerotenkakh-zmishuvachakh
z zakriplenym I zvagenym biotsenozom. Scientific
Bulletin of Construction, 4(98),
187-191. (in
Ukrainian).
Vasylenko,
O. A., Hrabovskyi, P. O. Larkin,
H. M. &
others. (2010).
R
Rekonstruktsiia i intensyfikatsiia
sporud vodopostachannia ta vodovidvedennia: navch.posib.
K.: IVNVKP «Ukrheliotek».
Griborio,
A. (2004).
Secondary Clarifier Modeling: A
Multi-Process Approach. Dissertation and Theses.
USA, University
of New
Orleans Publ.
(in English)
Надійшла
до редколегії: 13.05.2019
Прийнята
до друку: 16.09.2019
; (1)
, (2)
– число Рейнольдса;
–
завихореність;
,
– компоненти вектора швидкості водного
потоку;
L
– характерний лінійний розмір;
– характерна швидкість.
;
.
, (3)
, (4)
визначатимуться на різних розрахункових
шарах. Замінюючи похідні розділеними
різницями (3)–(4), отримуємо наступну
різницеву схему [8]:
(5)
(6)
має другий порядок точності за часовою
координатою, однак для визначення
невідомих
необхідно розв’язувати систему
алгебраїчних рівнянь великої розмірності.
(7)
на кожному кроці розщеплення визначаємо
за методом біжучого рахунку.
, (8)
– фіктивний час. Функція
,
будучи розв’язком нестаціонарного
рівняння (3.14), буде розв’язком рівняння
Пуассона за
.
, (9)
.
(10)
,
визначаємо методом біжучого рахунку
на другому та третьому кроках розщеплення.
, (11)