ISSN 2307–3489 (Print), ІSSN 2307–6666 (Online)

Наука та прогрес транспорту. Вісник Дніпропетровського
національного університету залізничного транспорту, 2019, № 4 (82)

ЕКОЛОГІЯ ТА ПРОМИСЛОВА БЕЗПЕКА

Introduction

Explosions in open pit mine yield in large amount of different pollutants emission into the atmosphere [3]. Assessment of risk as a result of air pollution in case of such emissions or others at the different enterprises is of great interest [1,2, 4, 5, 11, 14, 15]. Under the influence of atmospheric diffusion and wind flow, dust clouds are removed from the pit. During explosions in the open pit mines, the territory adjacent to the open pit mine is contaminated. An important problem is prediction of air pollution after explosions in an open pit mine. In Ukraine, at present, the OND-86 method is used to predict the process of atmospheric pollution during explosions in open pit mine. However, this technique has a number of significant drawbacks. It does not take into account the geometric shape of the open pit mine, the wind velocity profile, and atmospheric diffusion.

In this regard, the urgent task is to create efficient numerical models for analyzing the effects of emissions on atmospheric pollution. The use of numerical models, commercial codes like ANSYS® for the prediction of air pollution requires the use of powerful computers and much computer time [7, 8, 12, 13]. For practice, it is important to have numerical models that would take into account the main physical factors influencing the formation of contaminated areas, and on the other hand could be quickly implemented on computers of low and medium power [2, 4, 5].

Purpose

The aim of the work is to develop an efficient, fast computing numerical model for prediction of dust cloud dispersion after explosion in open pit mine.

Methodology

As it is known, the application of the Navier-Stokes equations to calculate the wind flow in open pit mine takes computing time. The calculation may take several days. Therefore, to create a fast-calculating computer model, the inviscid fluid model will be used.

Modeling equations. Introducing the assumption that airflow is potential, the basic equation of aerodynamics has the form [6, 9, 10]:

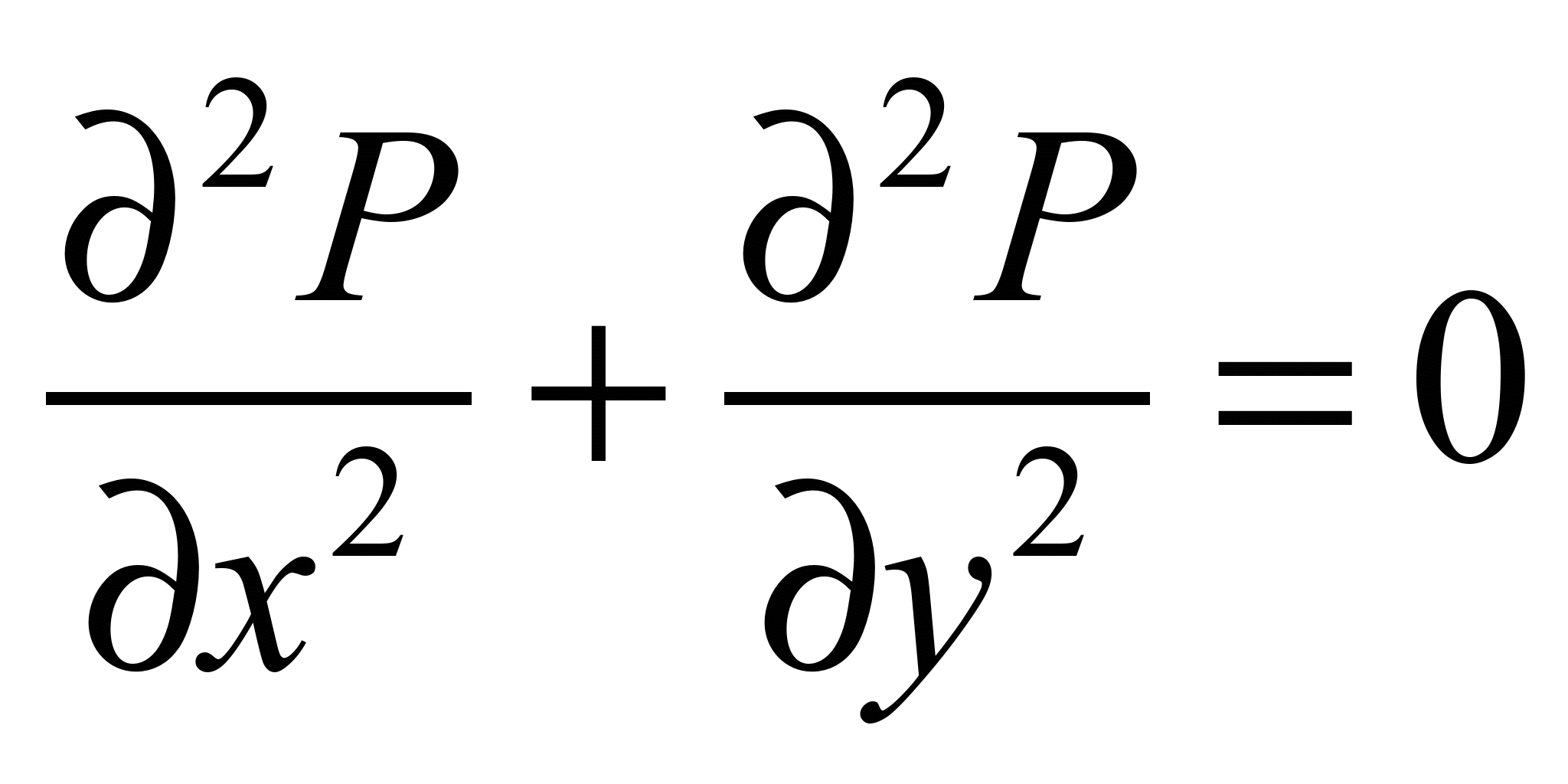, (1)

where Р – is velocity potential, x, y – are Cortesian coordinates, m.

When applying this equation, it is assumed that the Y axis is directed vertically upwards.

To solve the equation (1) the following boundary conditions are used [6]:

1) on the walls of the open pit mine, as well as on other solid surfaces located inside it, a following boundary condition is set: P/n = 0, where n – is unit vector of external normal to solid wall;

2) at the inlet boundary we set: P/n = V_n, where V_n – known airflow velocity, m·s^-1;

3) at the outlet boundary we set: P = P₀ +const, P₀ – is arbitrary number (Dirichlet condition).

To simulate the dispersion of dust in open pit mine, the mass transfer equation (Marchuk equation) is used [6, 9, 10]:

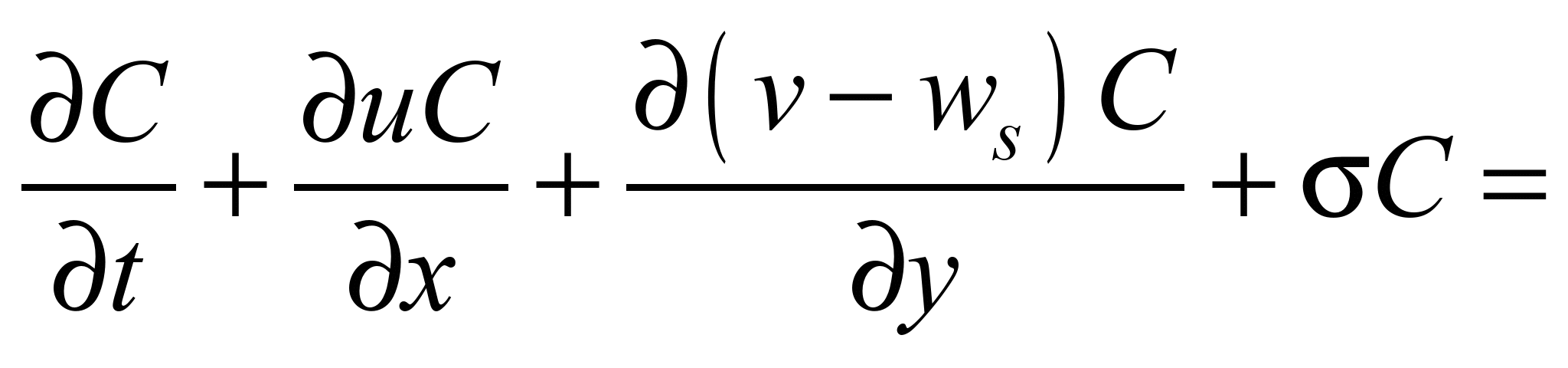
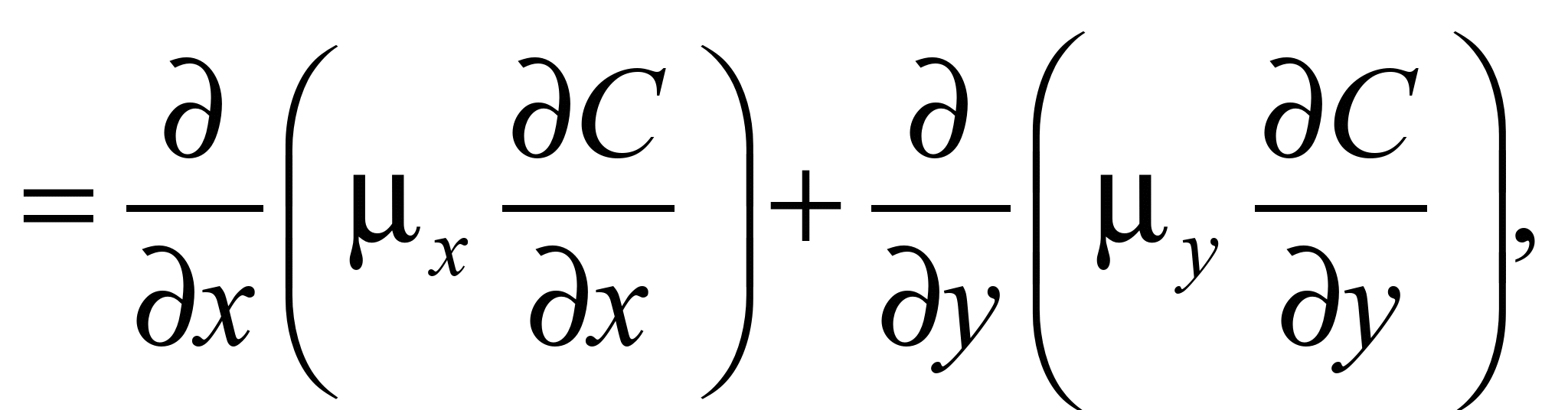(2)

where С – is dust concentration in the atmosphere, g·m^-3; u, v – are wind flow velocity components, m·s^-1; w_s – is dust fallout speed, m·s^-1;
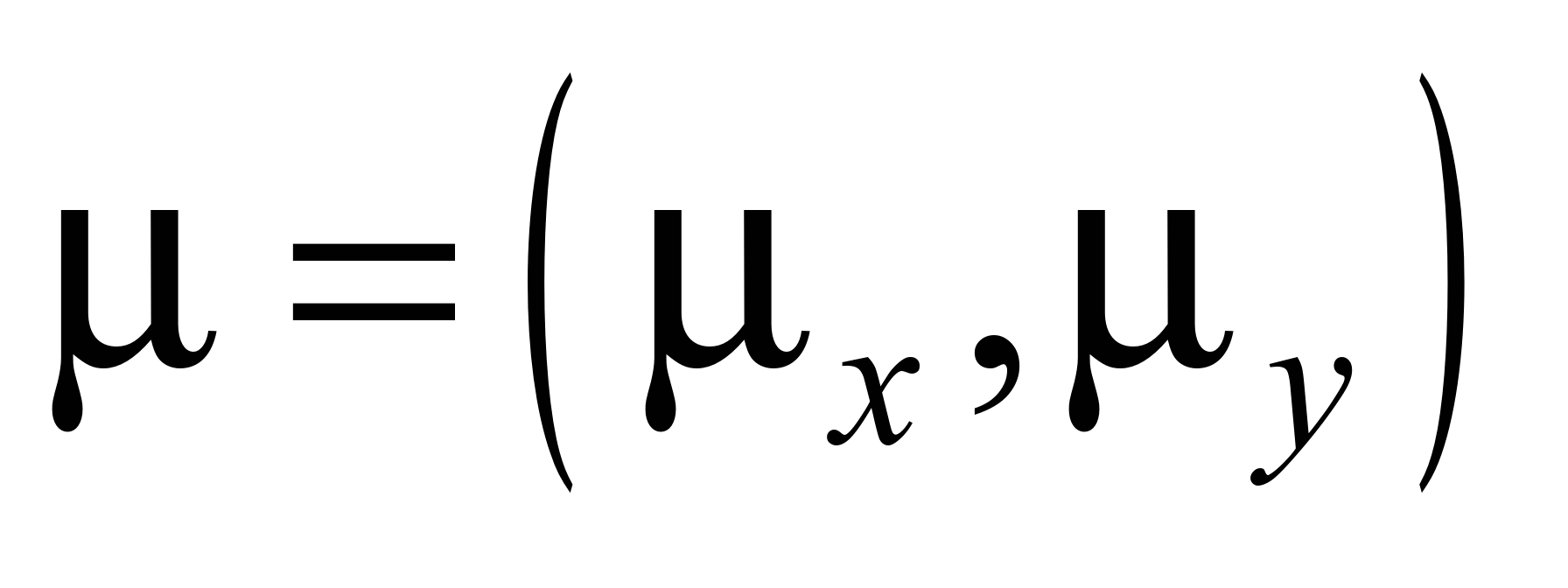– are turbulent diffusion coefficients, m²·s^-1, x, y – are Cortesian coordinates, m; σ – coefficient of pollutant chemical decay, s^-1.

Initial and boundary conditions for (2) are discussed in [6].

Numerical model. Numerical integration of modeling equations is carried out using a rectangular difference grid.

Convective derivatives are represented as [6]:

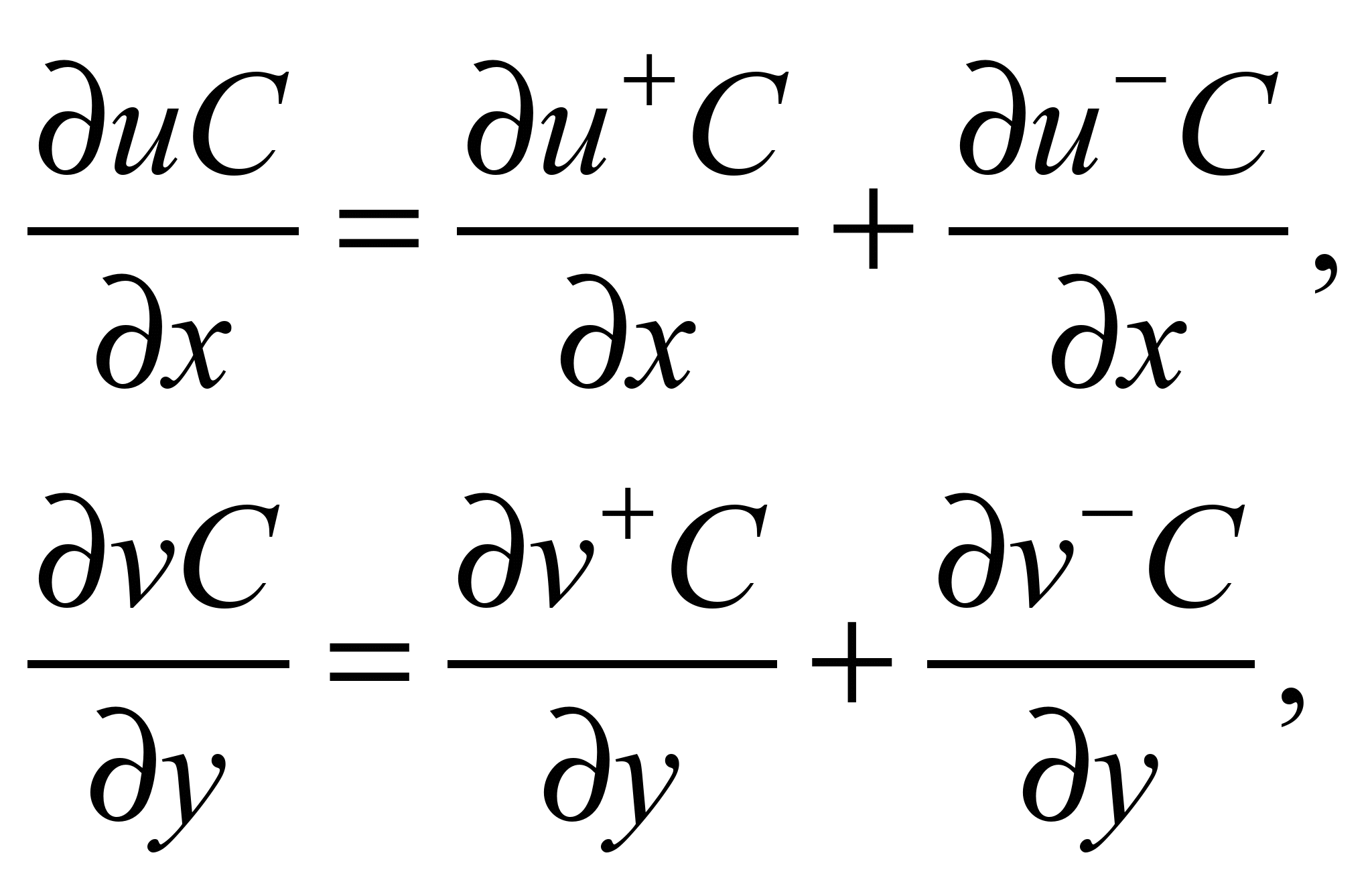
where

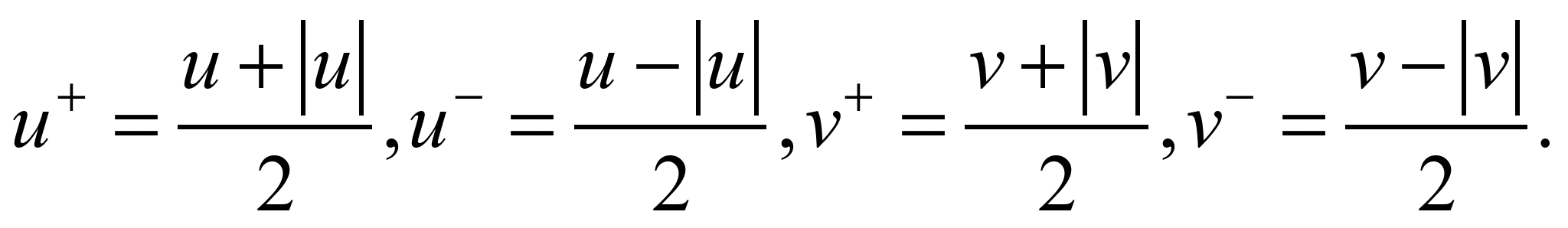
The approximation of these derivatives is carried out according to the formulas [6]:

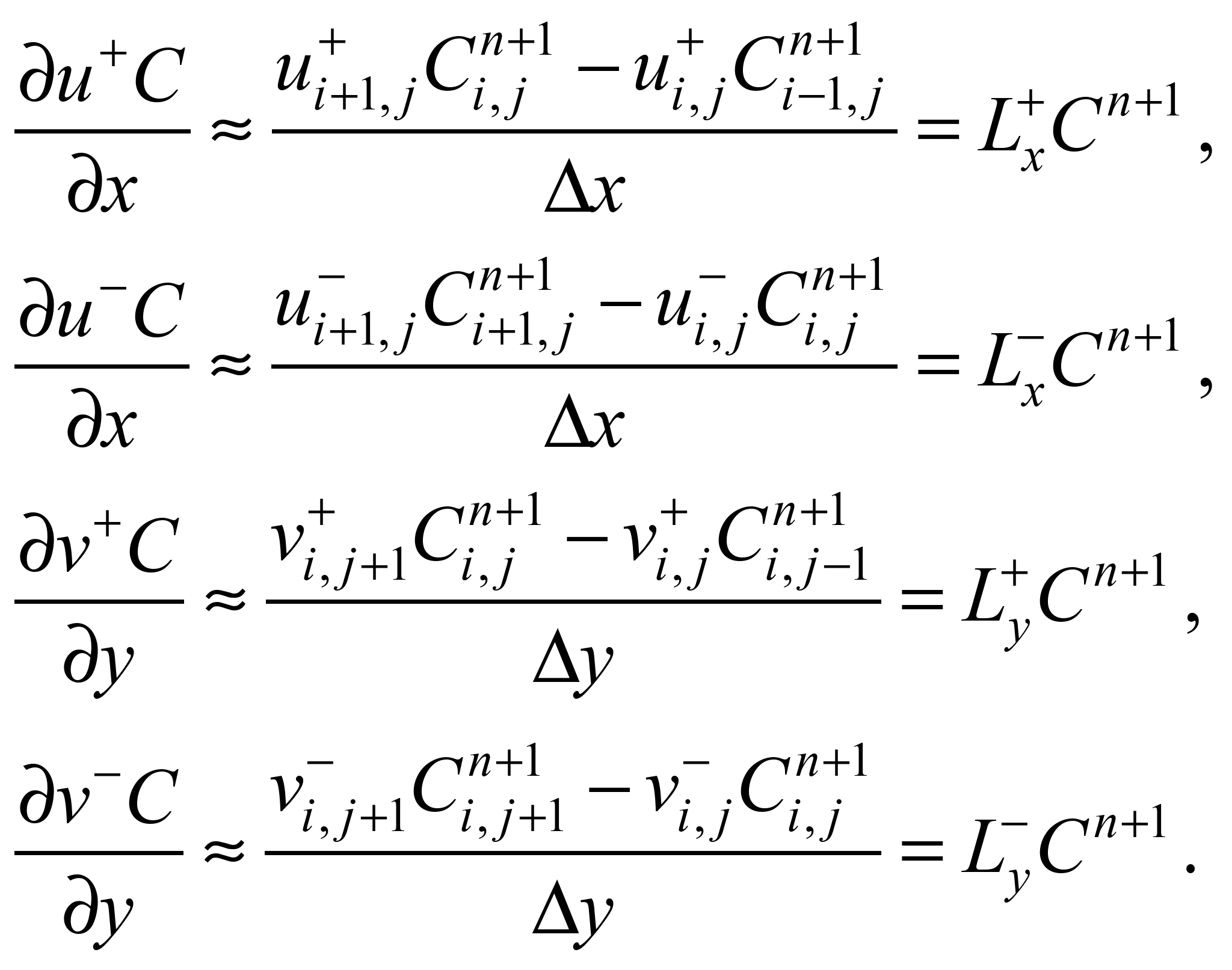
The time derivative is approximated as follows:

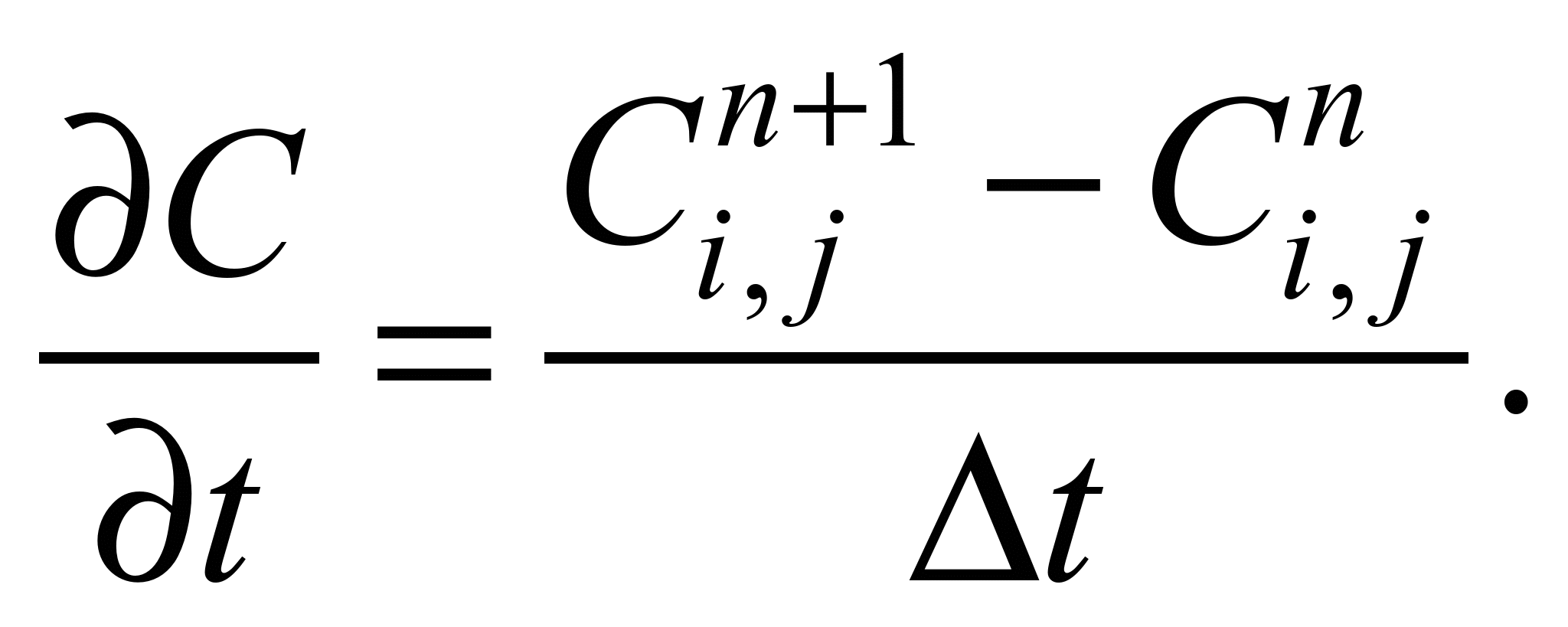
To approximate the second derivatives, the following formulas are used [5]:

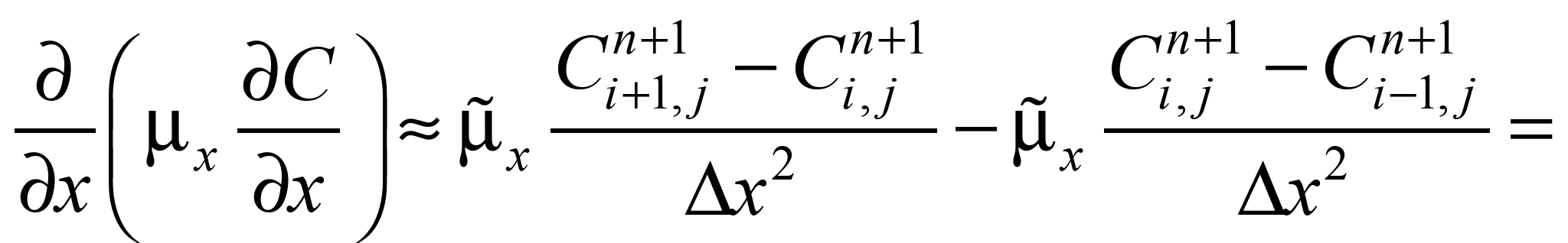
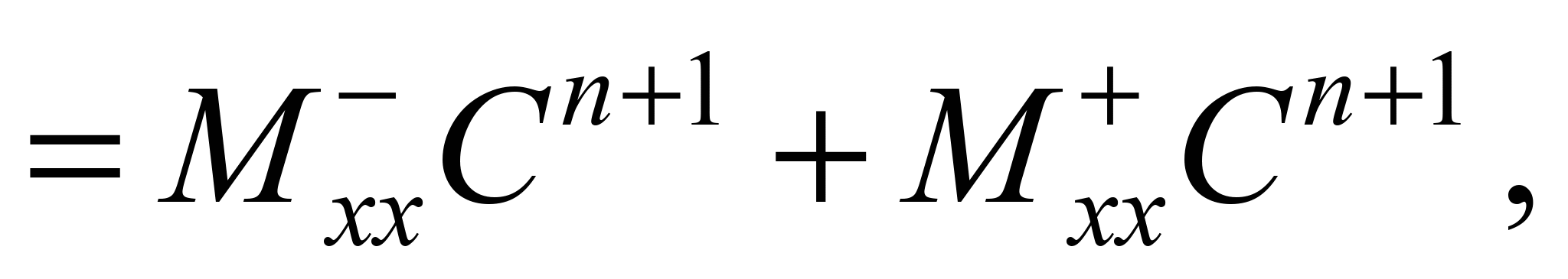
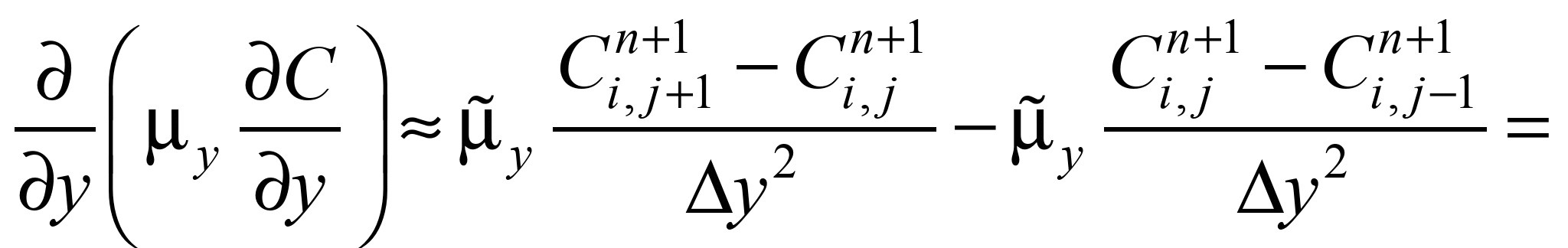
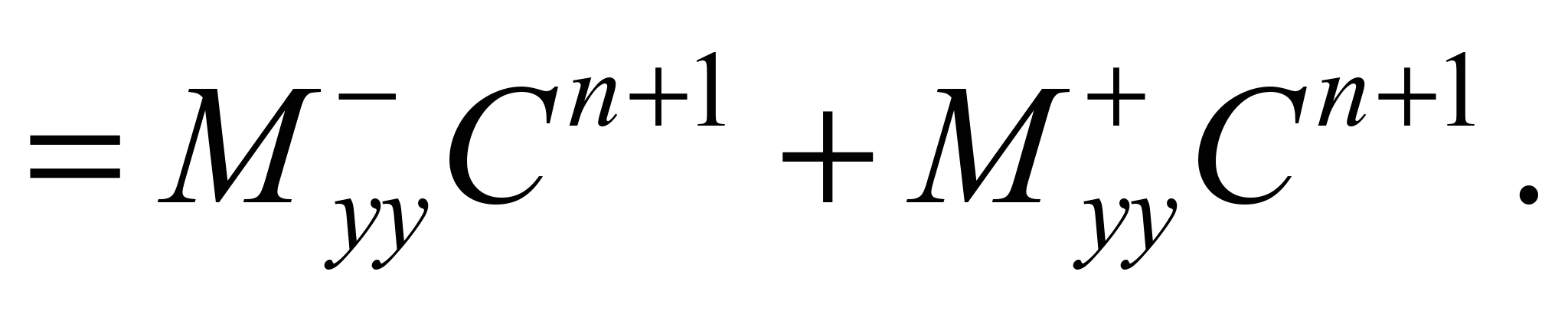
Taking into account the above notation for difference operators, the original mass transfer equation is represented as:

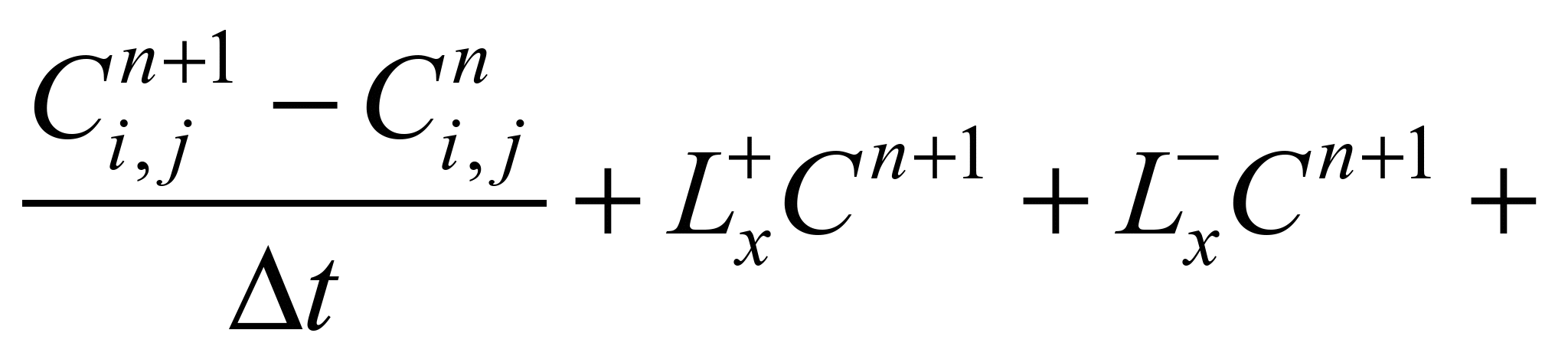
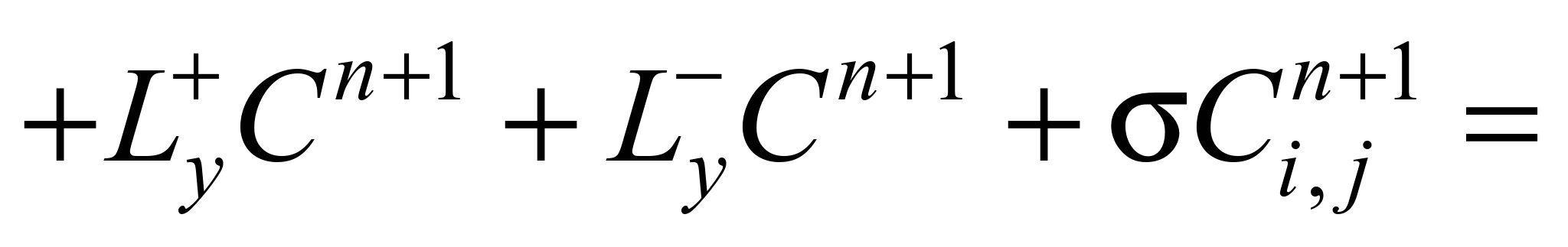
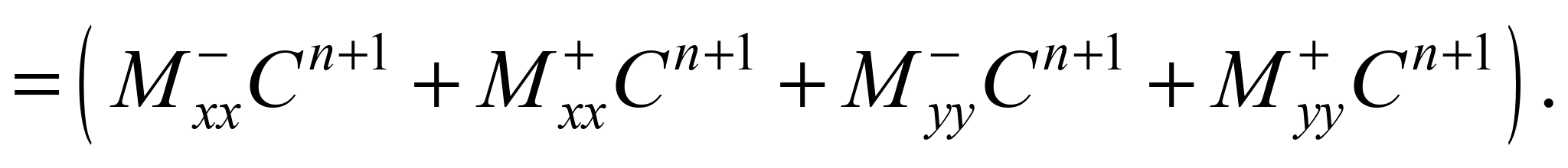
Further, splitting of this difference equation is carried out as following:

1) on the first step of splitting (k = n+1/4) the difference equation has the appearance:

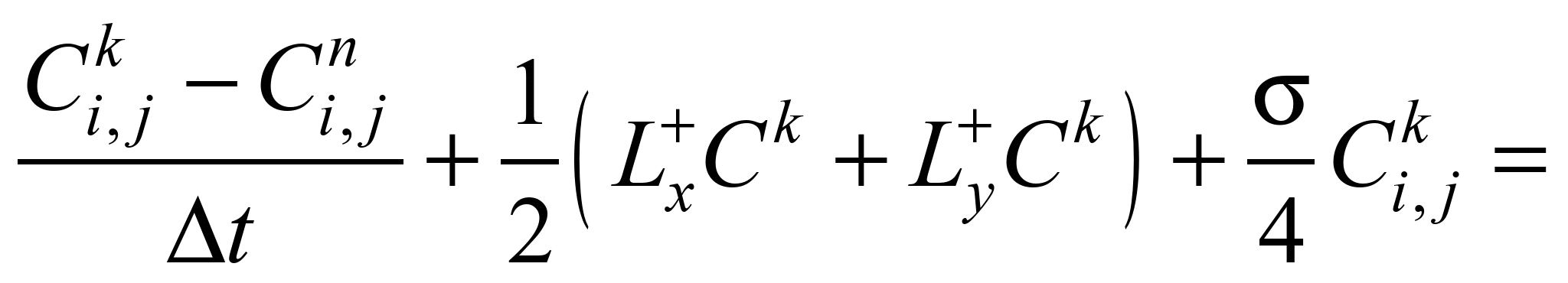
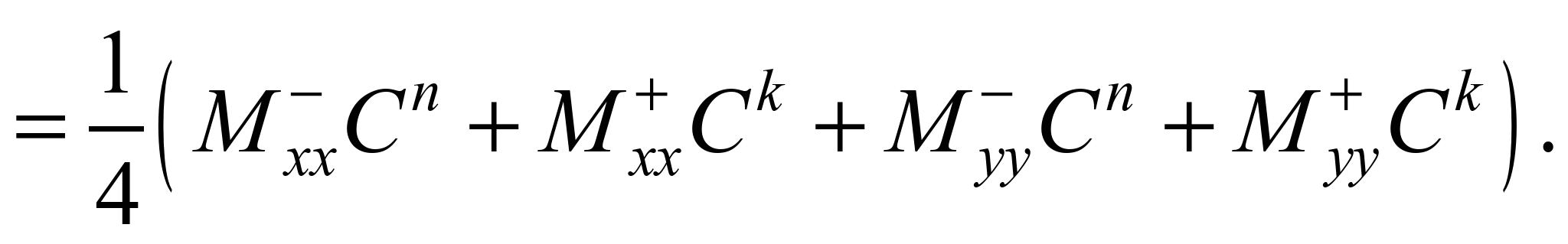(3)

2) on the second step of splitting (k = n+1/2; c = n+1/4) the difference equation has the appearance:

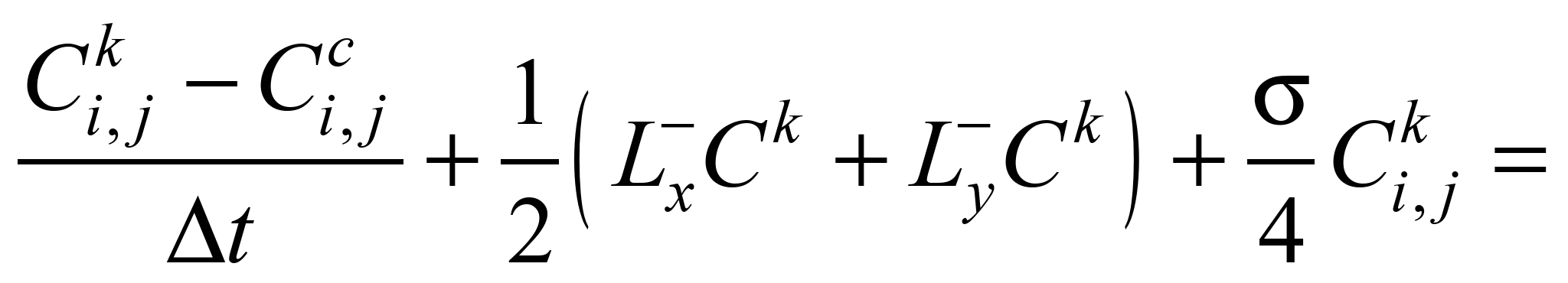
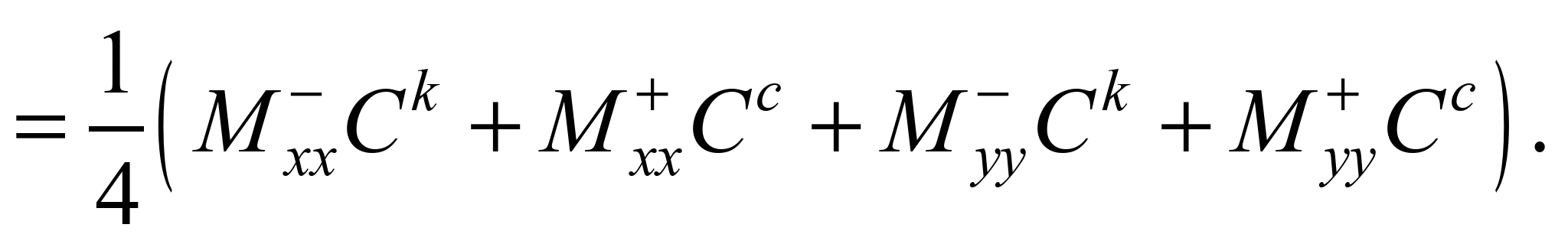(4)

3) on the third step of splitting (k = n+3/4; c = n+1/2) the equation (4) is used;

4) on the fourth step of splitting (k = n+1; c = n+3/4) the equation (3) is used.

From equations (3) and (4) the unknown value of the dust concentration is calculated by explicit formula of running calculation.

For the numerical integration of velocity potential equation, Richards method was used. To solve the two-dimensional equation for the velocity potential, first of all, this equation was written in evolutionary form [6]:

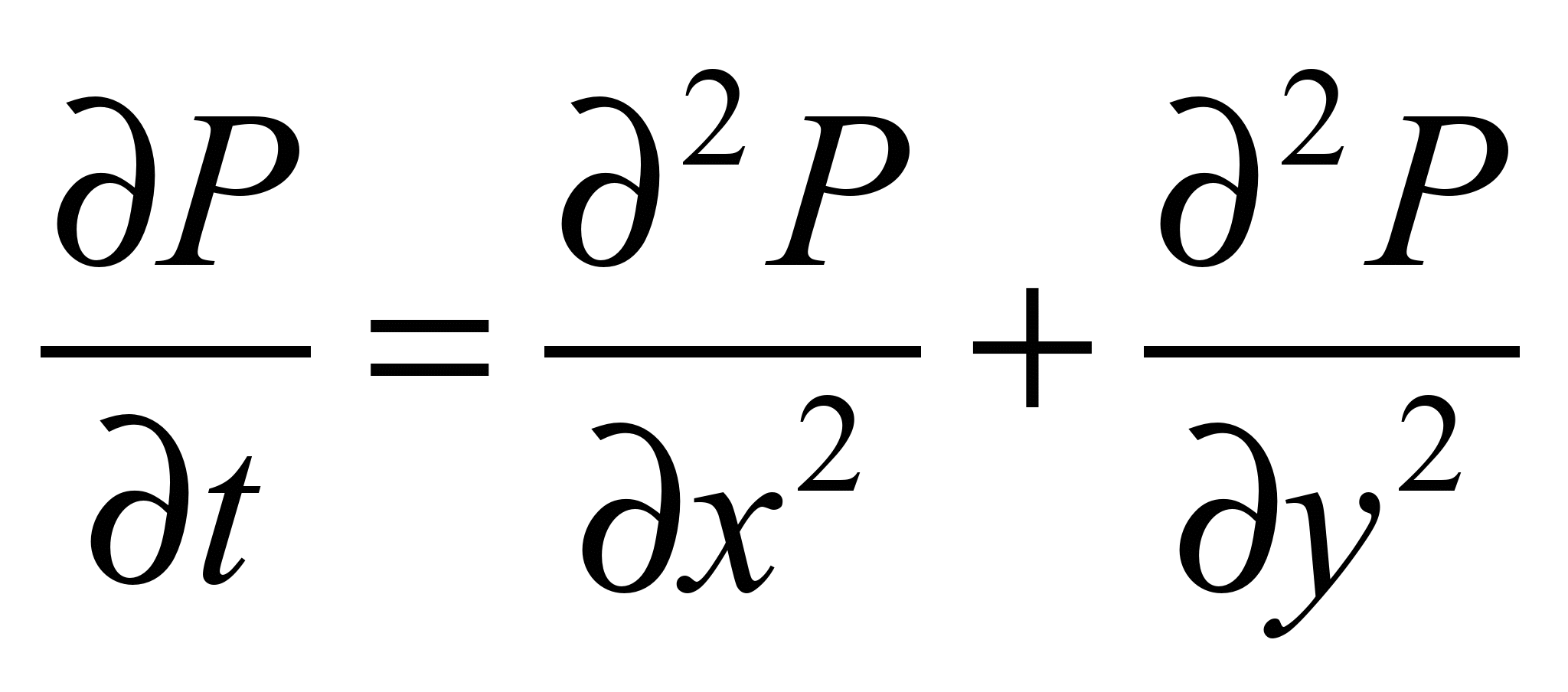, (5)

where t – fictitious time (dimensionless).

It is known, that when 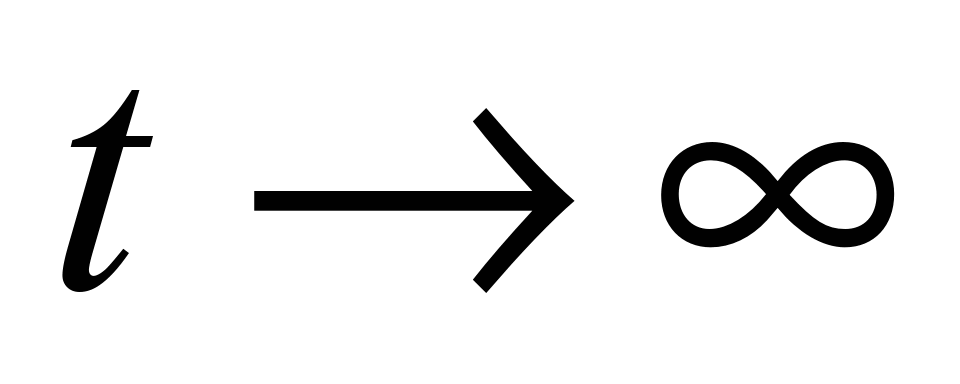the solution of this equation will approach to the Laplace equation solution for the velocity potential. To solve equation (5), it is necessary to set “initial’ field of velocity in computational region at t = 0. For example, before starting the calculation, you can set P = 0 in the entire computational domain for t = 0.

Numerical integration of equation (5) is carried out on a rectangular grid. Function P is determined in the center of the difference cells.

Differential scheme (Richardson’s method) for numerical integration of the evolutional equation (5) is written as:

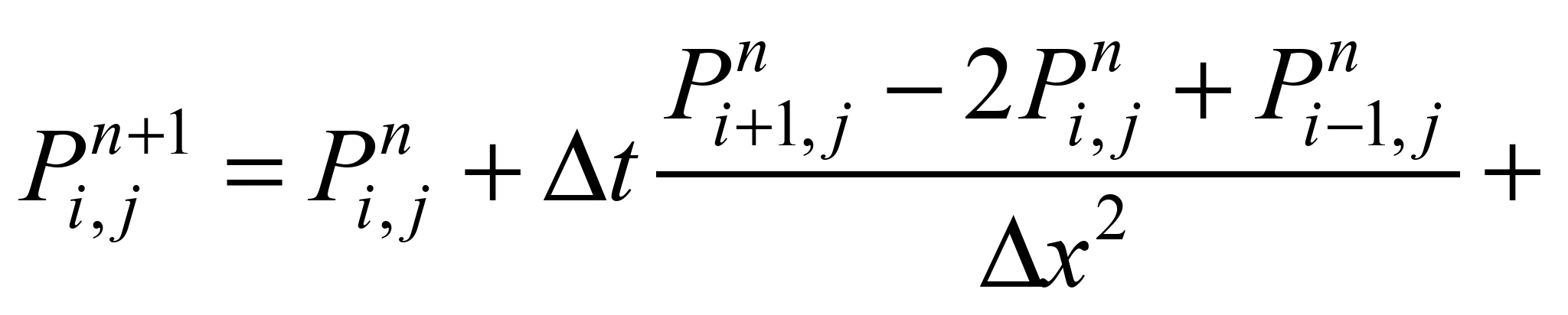
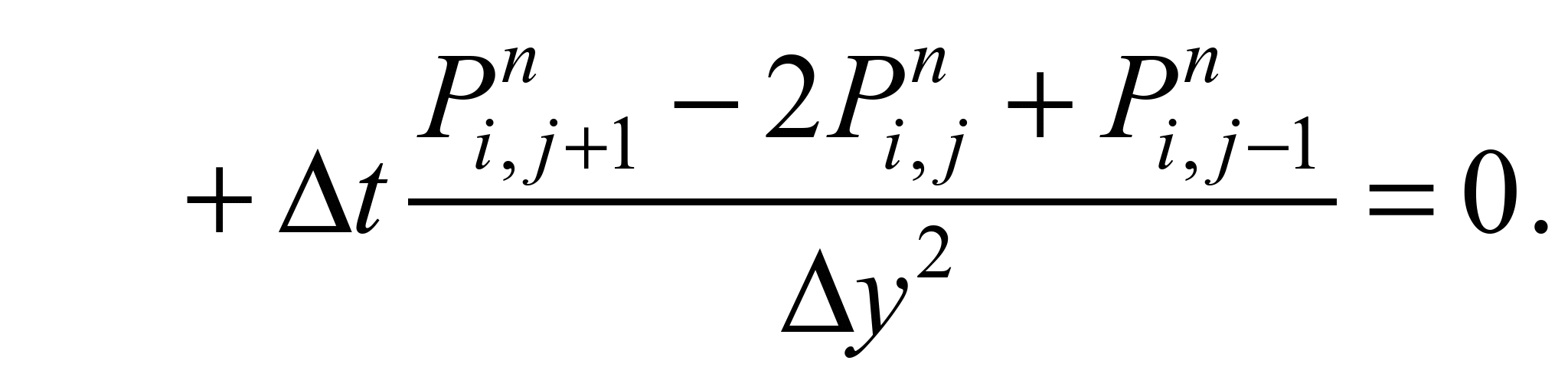
The unknown value of the velocity potential is determined by the explicit running calculation formula. The calculation is completed when the following condition is fulfilled:

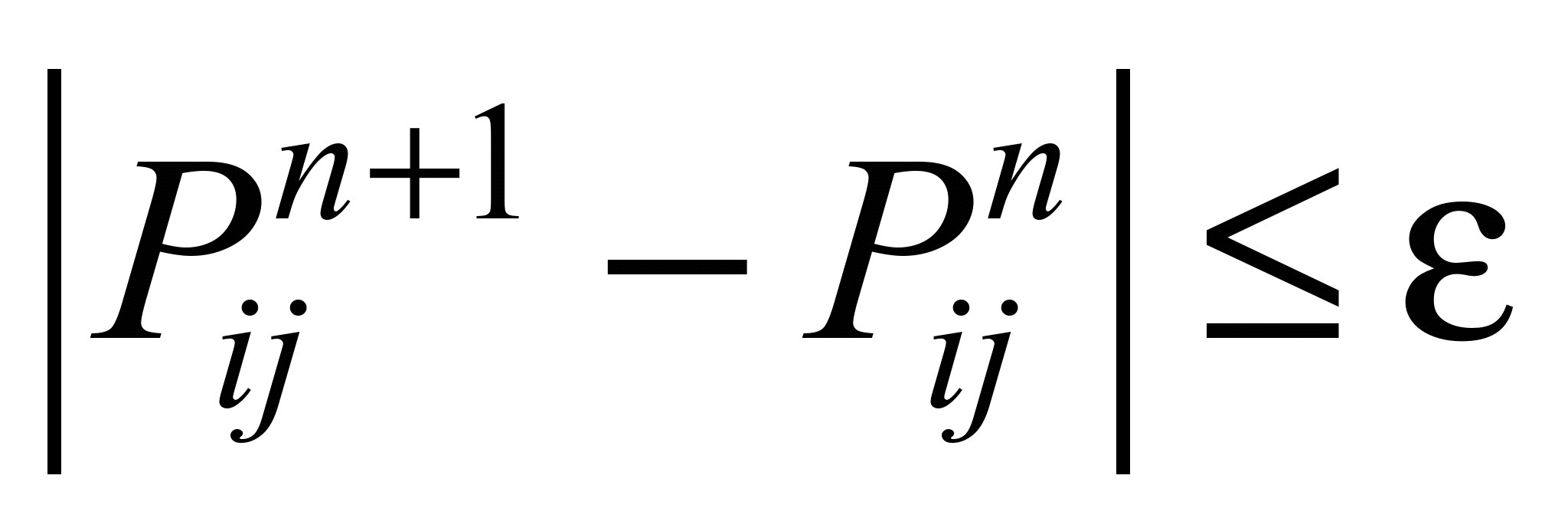, (6)

where ε – is a small number (e.g., ε =0.001); n – iteration number.

After determining the velocity potential field, the components of the air velocity vector are calculated at the sides of the computational cell using formulae:

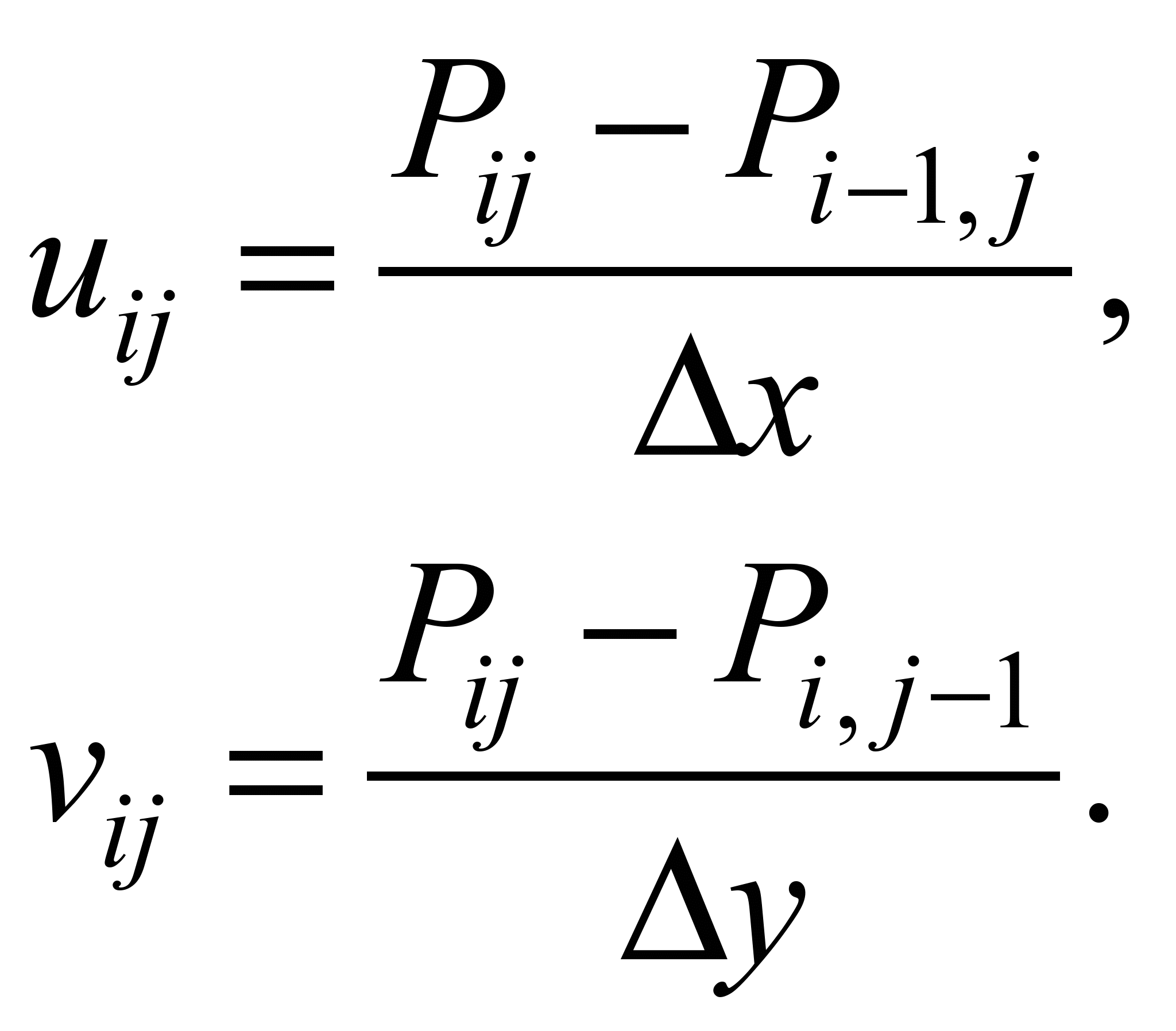
This approach to compute velocity components on the sides of computational cells allows constructing a conservative difference scheme for the mass transfer equation.

For practice, it is extremely important to reproduce the geometric form of the open pit mine. For this, in the numerical model we used porosity technique (‘markers’ method). The computational domain is divided using a rectangular difference grid (Figure 1). Using markers, we constructed open pit mine boundaries. Using other markers, we constructed the initial geometrical form of dust cloud in open pit mine. Other markers were used to construct the geometrical form of obstacle near open pit mine. This technique for computational region formation in numerical model allows to change quickly this form during numerical experiments. In Figure 1 the arrow indicates the wind direction.

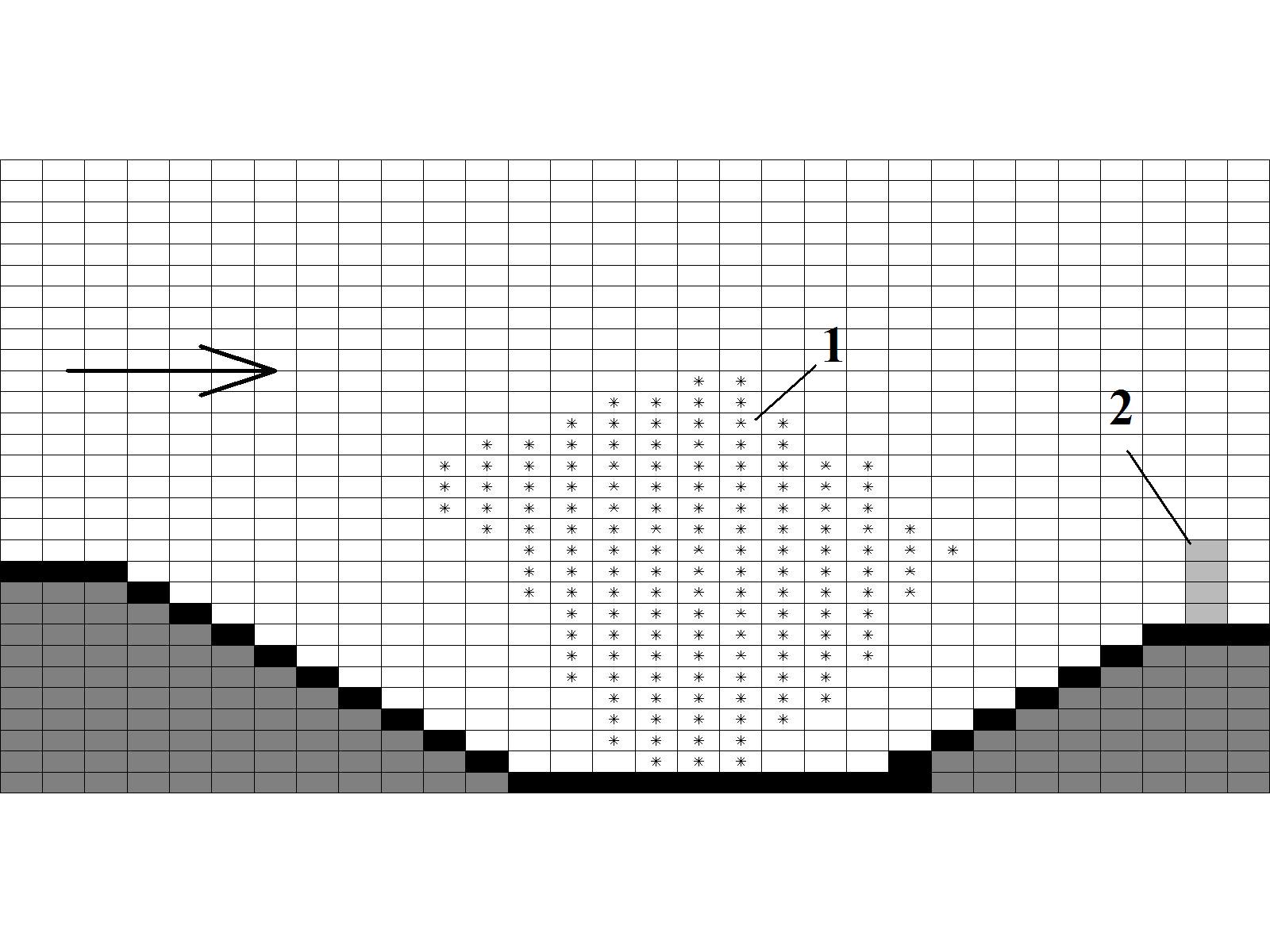
Fig. 1. Sketch of computational domain scheme:
1 – dust-gas cloud; 2 – obstacle (trees position)

The developed numerical model was coded using Fortran language.

Findings

Developed numerical model was used to compute dust cloud movement in open pit mine.

To make all parameters dimensionless, we have chosen the following scales [2]:

1) 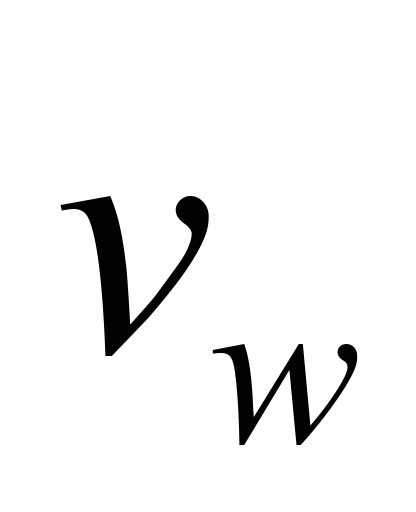is the wind velocity at the left boundary, ;

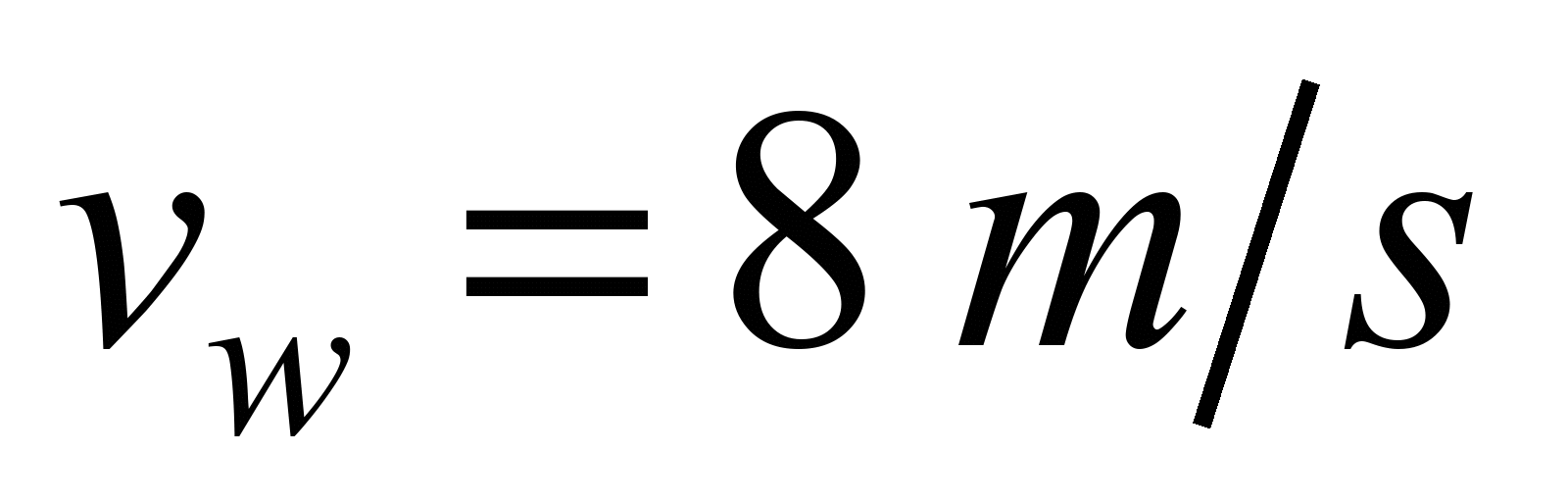2) 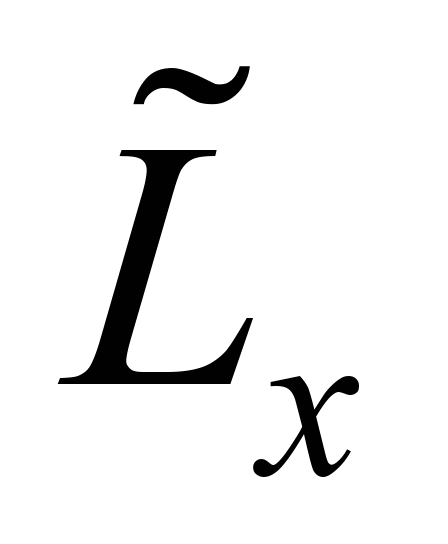, m is the length of the computational domain;

3) 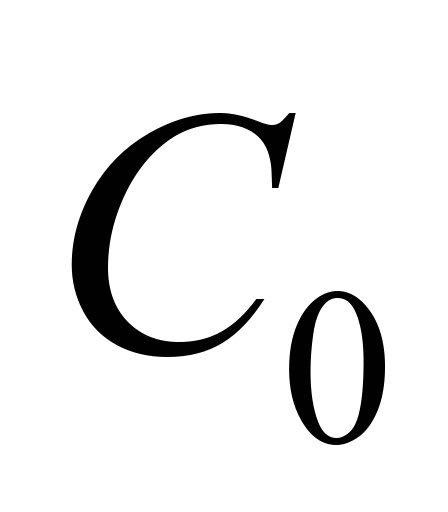, μg·m-3 is the initial dust concentration in the cloud for .

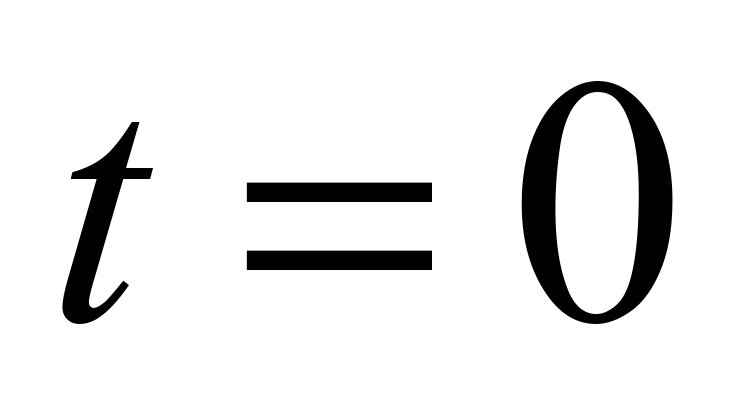The dimensionless parameters are calculated as follows:

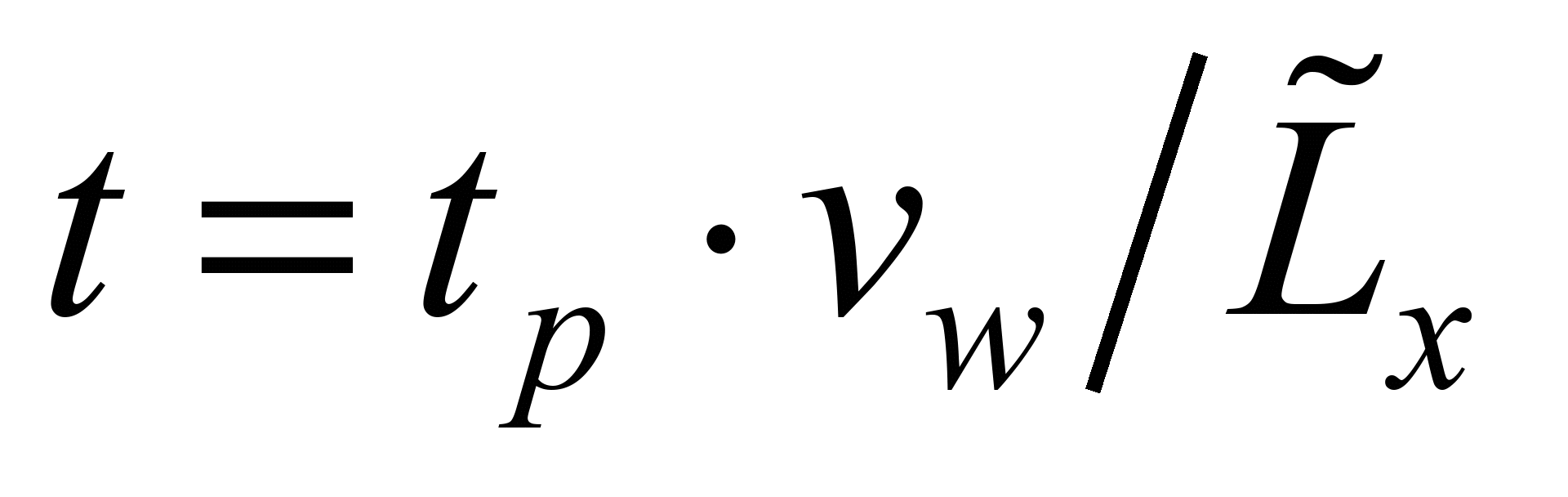1. , where 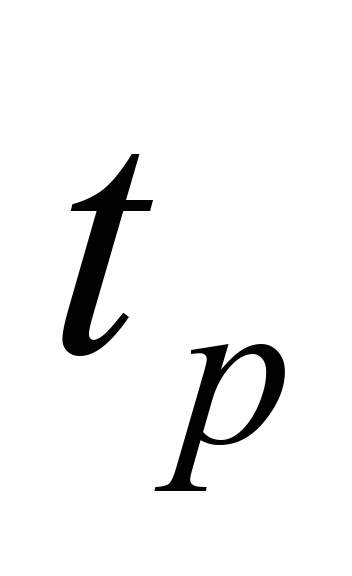is time, s;

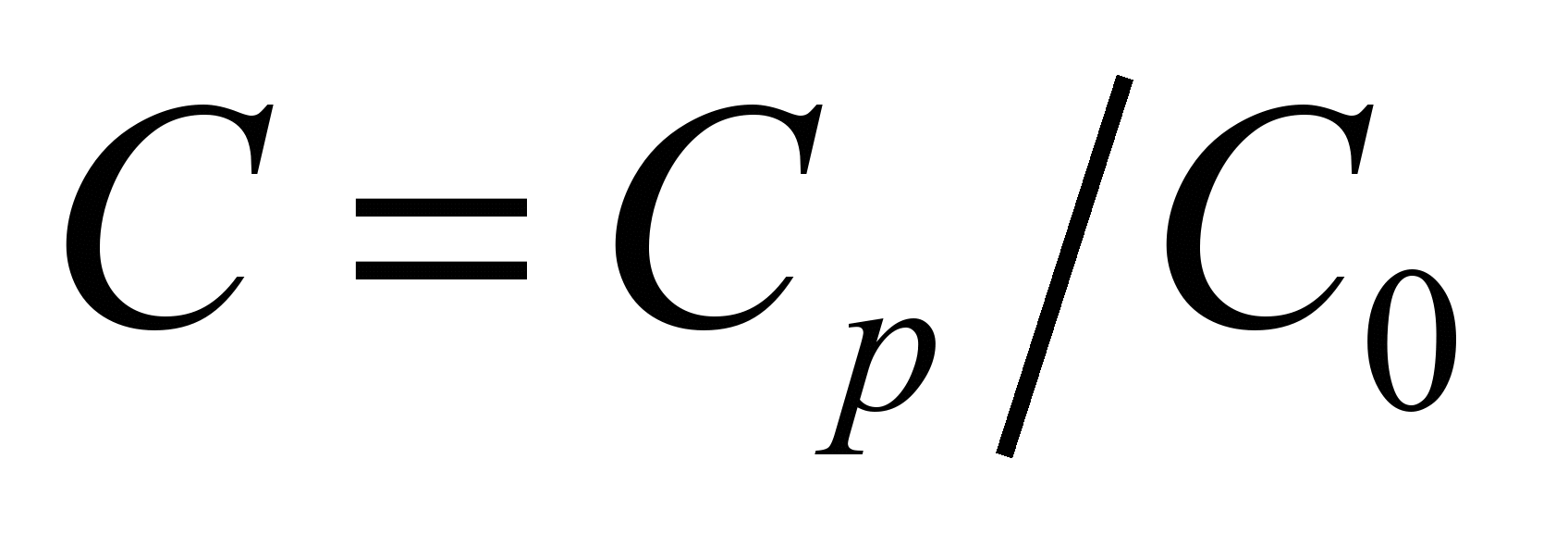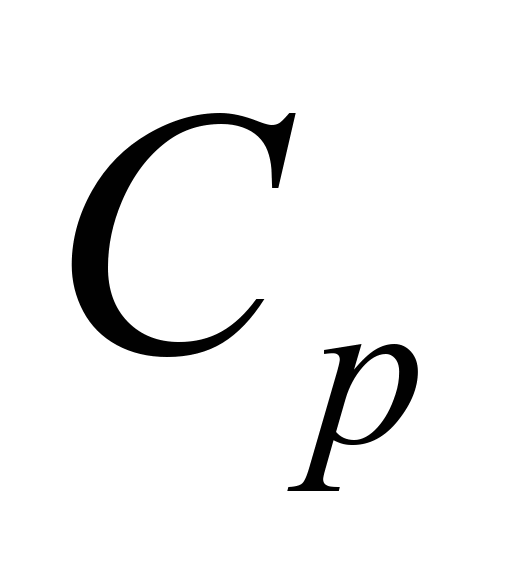2) , where is dust concentration, μg·m-3;

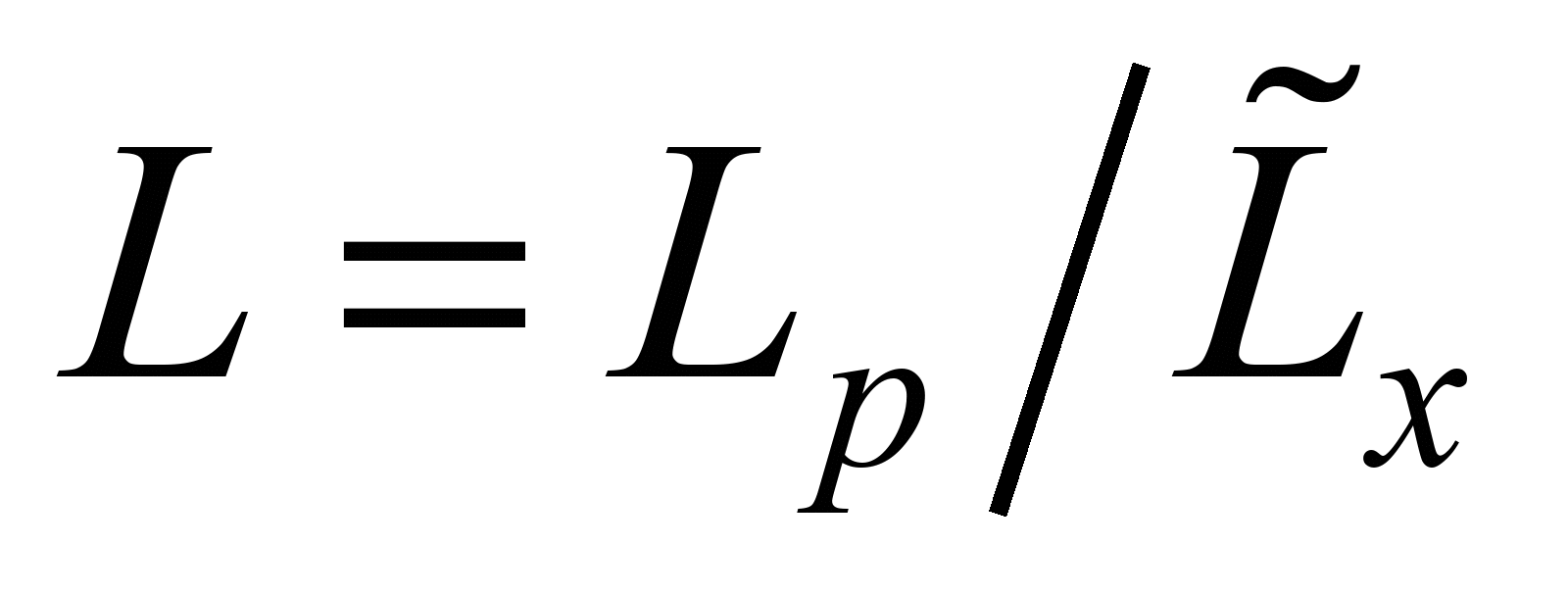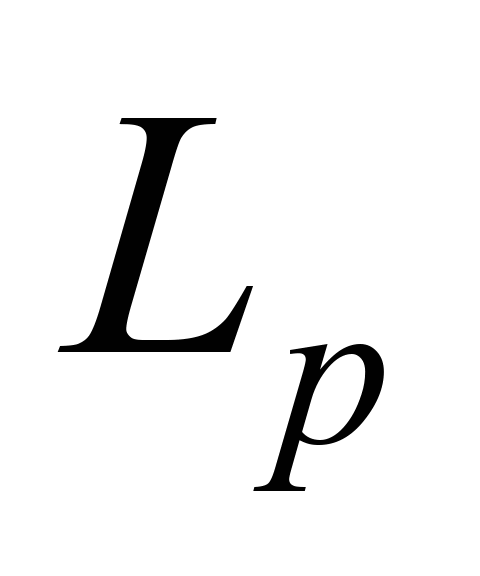3) , where is length, m;

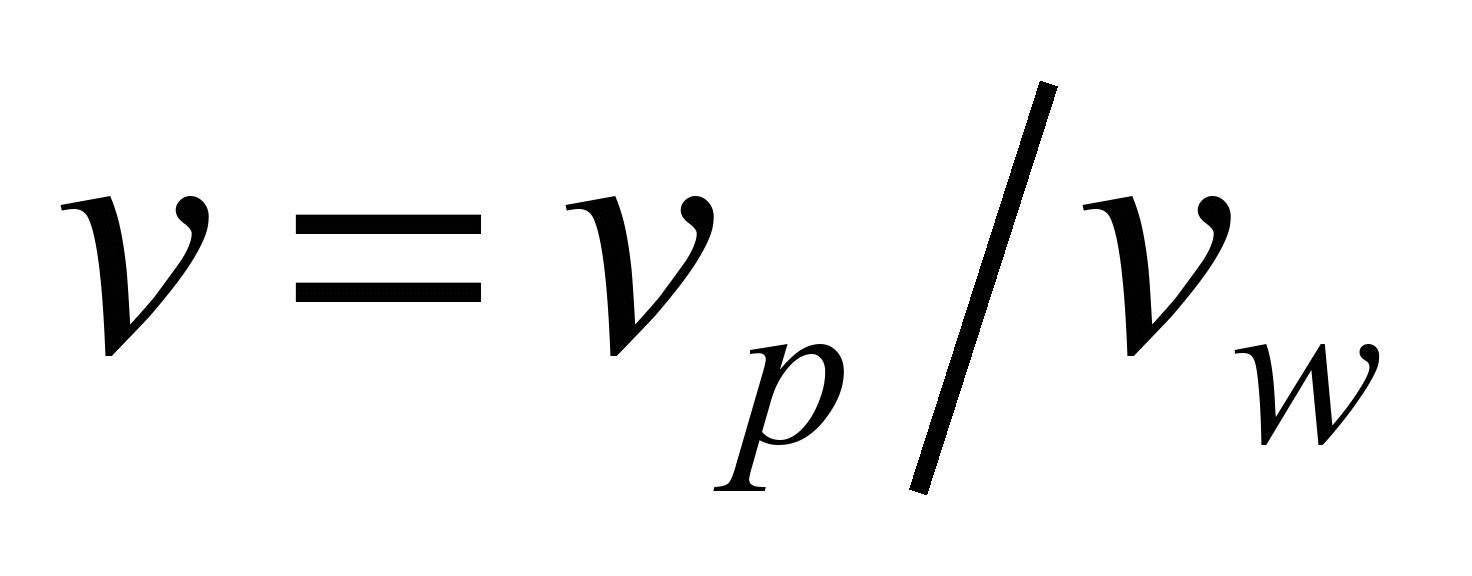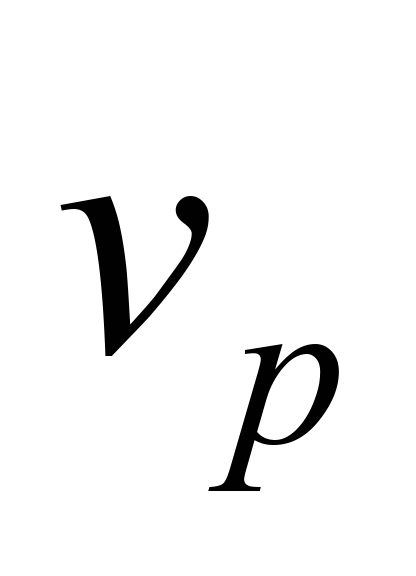4) , where is local wind velocity, m/s.

The length of the computational domain is 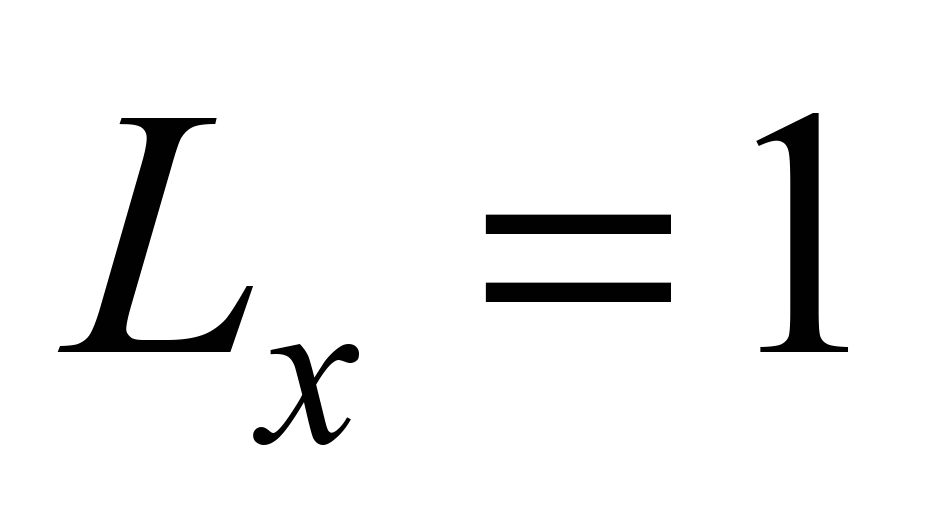(dimensionless), the height of the computational domain is 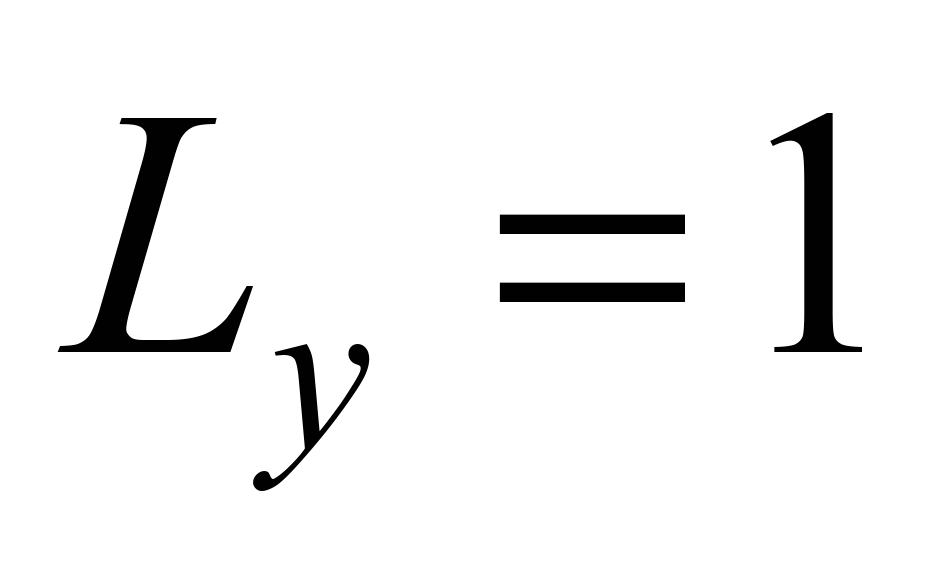(dimensionless). The initial concentration of dust in the cloud is 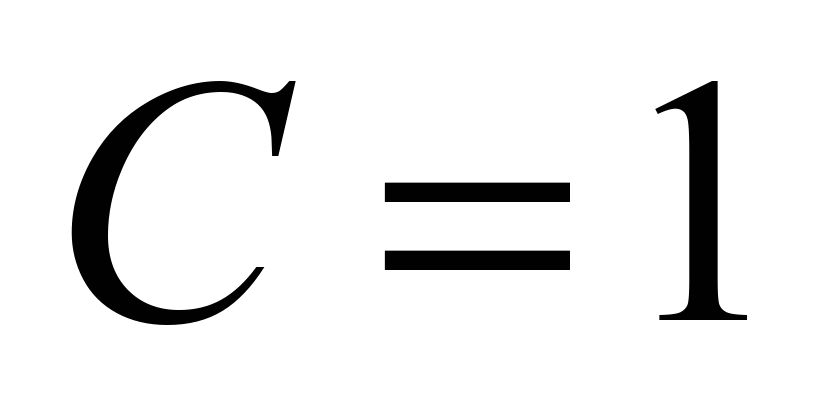(dimensionless) for .

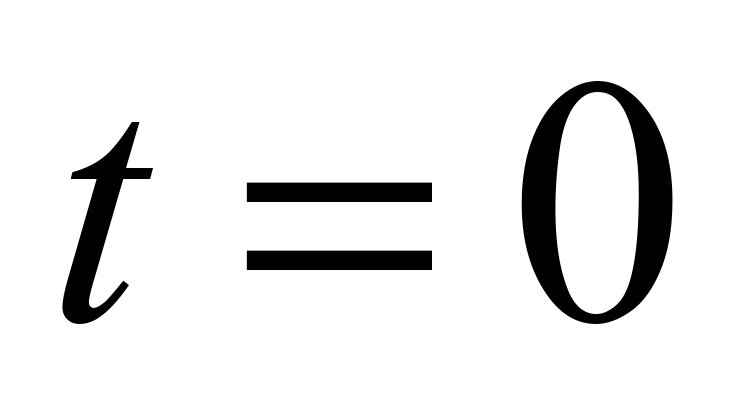Figures 2-8 show dust concentration field for different time after explosion in open mine. In Figures 2-8 the arrow indicates the wind direction.

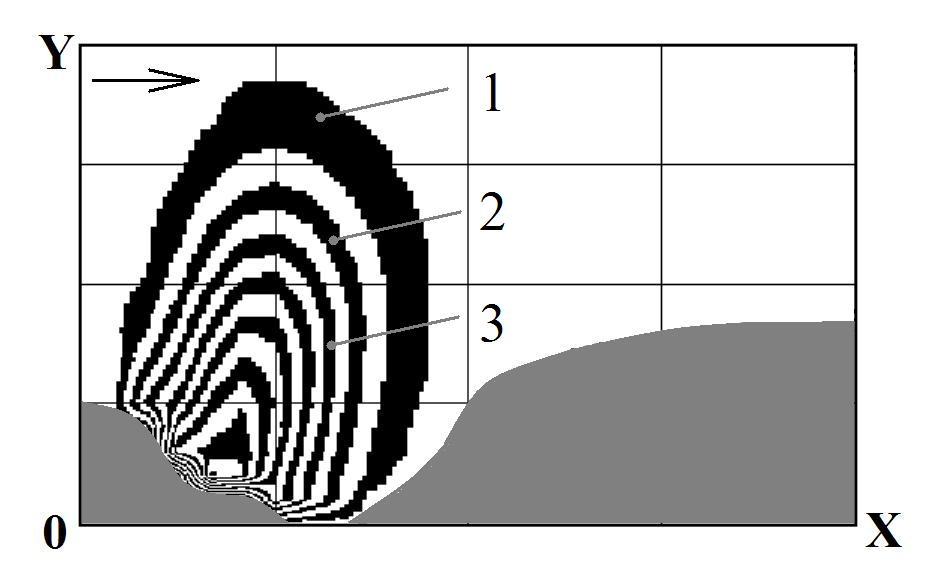
Fig. 2. Pollution zone: t=0.1 (time is dimensionless):
1 – C=0.82; 2 – C=0.88; 3 – C=0.94

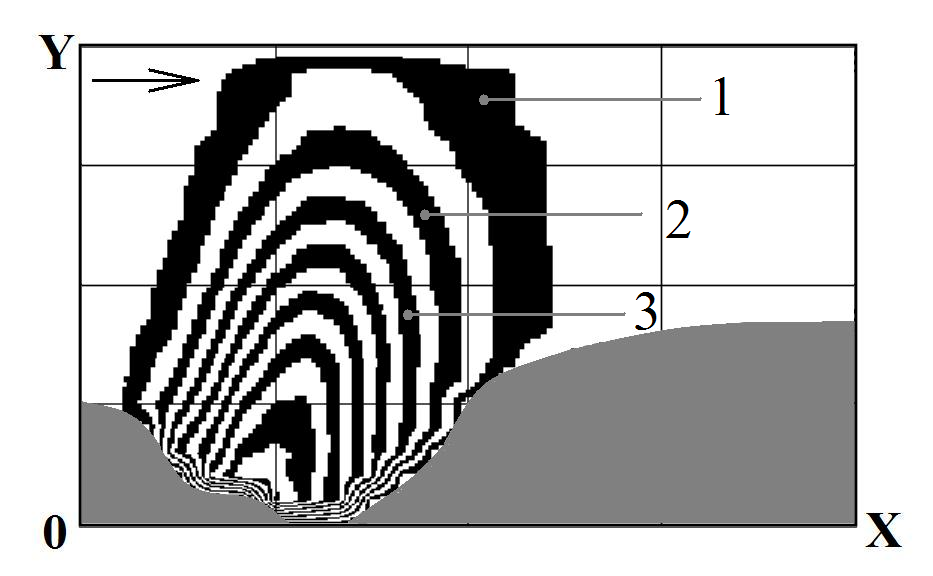
Fig. 3. Pollution zone: t=10 (time is dimensionless):
1 – C=0.67; 2 – C=0.73; 3 – C=0.81

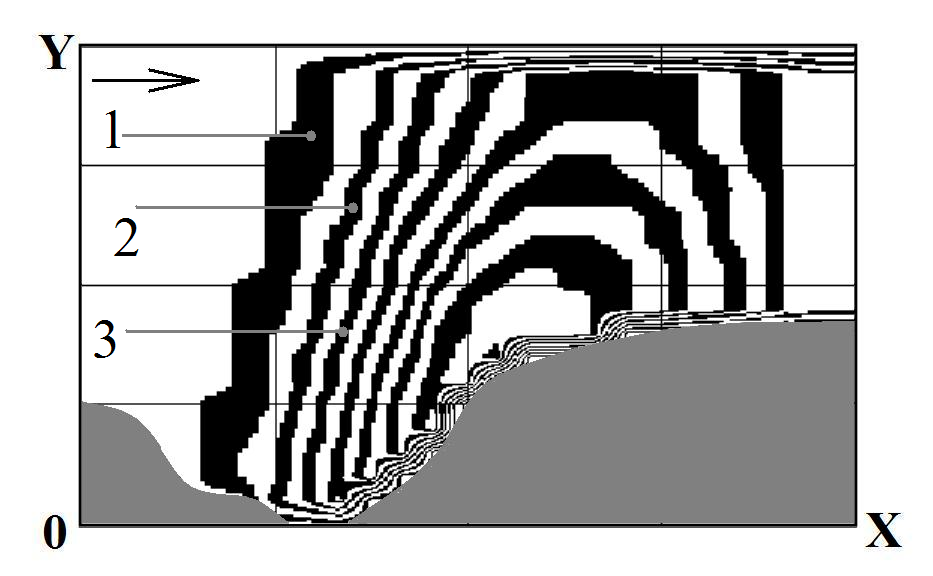
Fig. 4. Pollution zone: t=35 (time is dimensionless):
1 – C=0.51; 2 – C=0.59; 3 – C=0.64

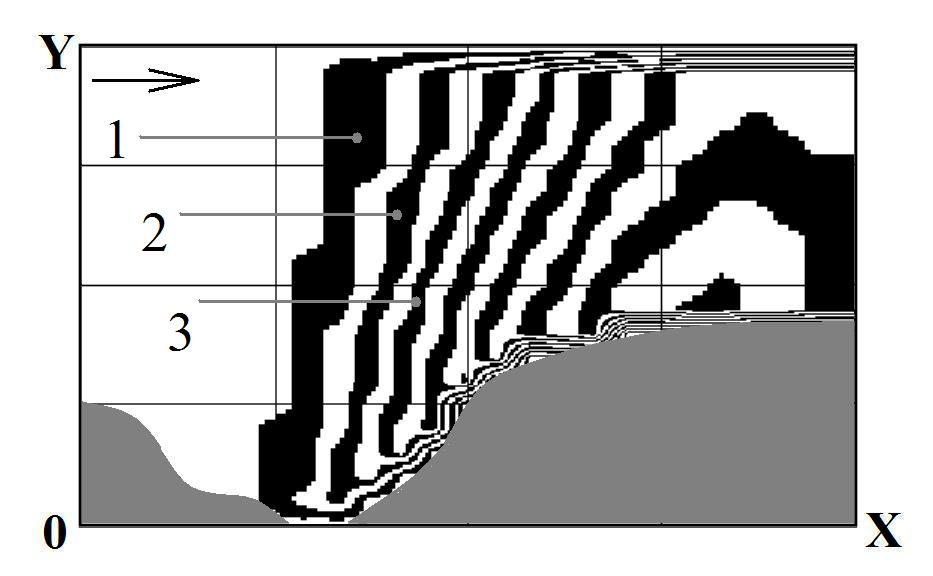
Fig. 5. Pollution zone: t=48
(time is dimensionless):
1 – C=0.42; 2 – C=0.48; 3 – C=0.55

From Figures 2-5 we see deformation of dust cloud form in open pit mine. This dust cloud is expanding during the time as a result of atmospheric diffusion action.

Figures 6-8 show dust concentration field for different time after explosion in open mine but when obstacle was introduced at one side of the open pit mine.

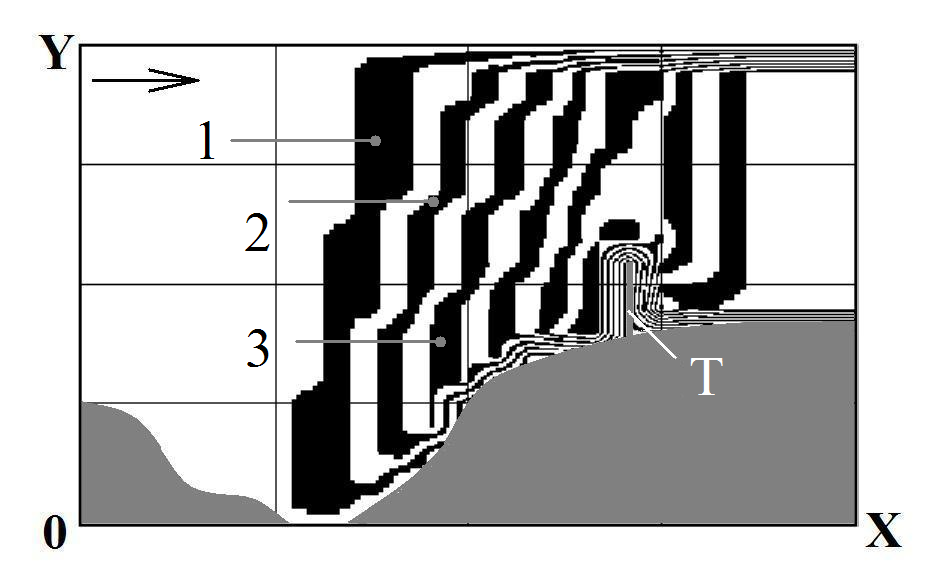
Fig. 6. Pollution zone: t=39
(time is dimensionless):
T – obstacle, 1 – C=0.48; 2 – C=0.56; 3 – C=0.61

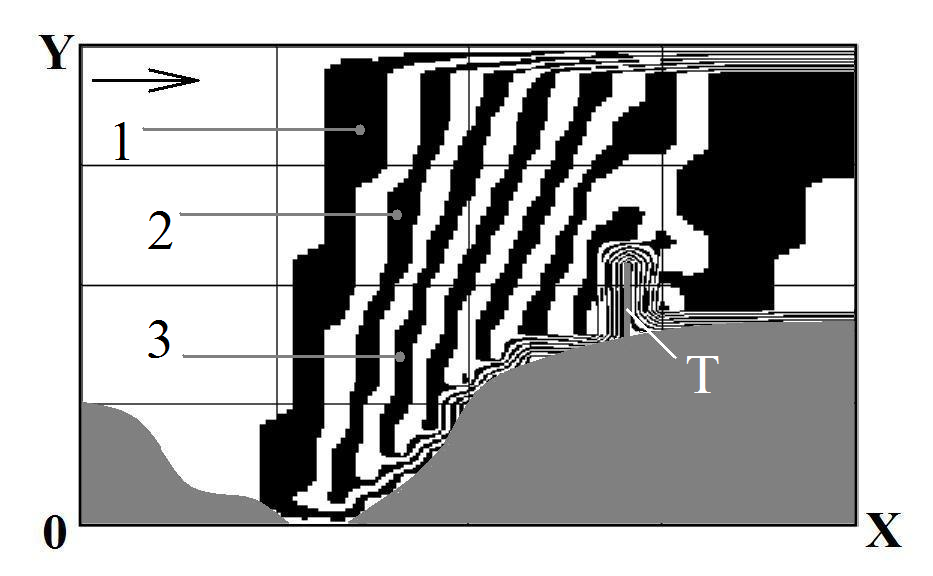
Fig. 7. Pollution zone: t=48
(time is dimensionless):
T – obstacle, 1 – C=0.40; 2 – C=0.46; 3 – C=0.53

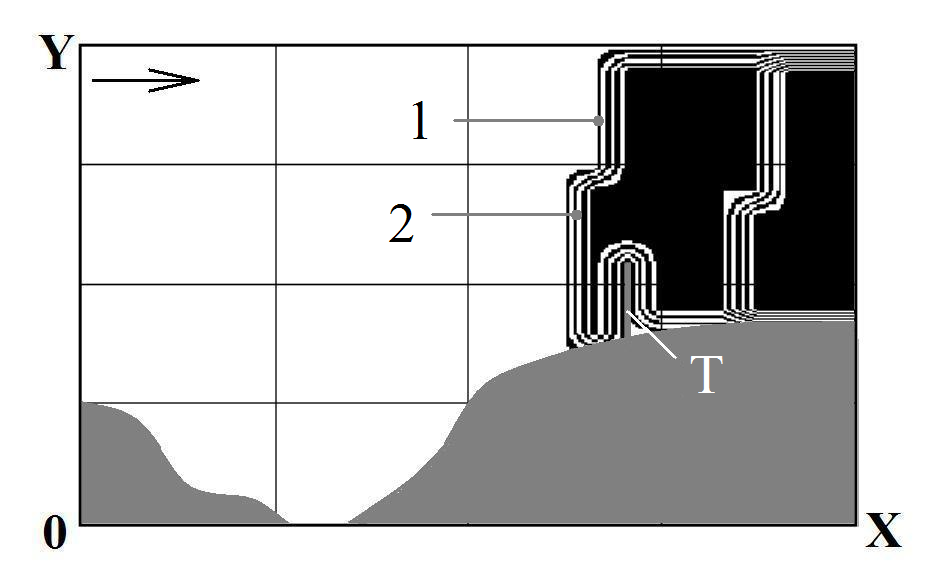
Fig. 8. Pollution zone: t=67 (time is dimensionless):
T – obstacle, 1 – C=0.32; 2 – C=0.41

Figures 6-8 illustrate the process of dust cloud diffraction on the obstaclе, the height of the obstacle is L=0.2 (dimensionless). This obstacle (see Figures 6-8, position T) simulates trees position near the open pit mine [7].

Worthy of note that computational time was 5 s.

Originality and practical value

New numerical model was developed to predict atmosphere pollution after blasts in open pit mines. The model is based on equation of dust dispersion in the atmosphere and equation for speed potential. To solve governing equations difference schemes of splitting were used. Proposed numerical model can be used for predictive calculations to assess the impact of explosions in open pit mines on the environment.

Conclusions

In this paper an effective numerical model for calculating the process of atmospheric pollution after explosion in open pit mine was developed. The model is based on the numerical integration of the equation for the velocity potential and the Marchuk equation. The difference schemes used have logical simplicity and convenient for programming. The calculation of the process of atmospheric pollution on the basis of the developed numerical model requires about 5 seconds of computer time. This allows to carry out serial calculations within one working day. Further development of this direction is associated with the creation of
a three-dimensional numerical model of the atmospheric pollution process during explosion in open pit mine.

LIST OF REFERENCE LINKS

1. Алымов, В. Т. Техногенный риск: Анализ и оценка : учеб. пособие для вузов / В. Т. Алымов, Н. П. Та-расова. – Москва : Академкнига, 2004. – 118 с.

2. Беляев, Н. Н. Защита зданий от проникновения в них опасных веществ : монография / Н. Н. Беляев,
   Е. Ю. Гунько, Н. В. Росточило. – Днепропетровск : Акцент ПП, 2014. – 136 с.

3. Бересневич, П. В. Аэрология карьеров : справочник / П. В. Бересневич, В. А. Михайлов, С. С. Филатов. – Москва : Недра, 1991. – 280 с.

4. Оценка техногенного риска при эмиссии опасных веществ на железнодорожном транспорте / Н. Н. Бе-ляев, Е. Ю. Гунько, П. С. Кириченко, Л. Я. Мунтян. – Кривой Рог : Р. А. Козлов, 2017. – 127 с.

5. Стоецкий, В. Ф. Оценка риска при авариях техногенного характера / В. Ф. Стоецкий, В. И. Голинько, Л. В. Дранишников // Наук. вісн. НГУ. – 2014. – № 3. – С. 117–124.

6. Численное моделирование распространения загрязнения в окружающей среде / М. З. Згуровский, В. В. Скопецкий, В. К. Хрущ, Н. Н. Беляев. – Киев : Наук. думка, 1997. – 368 с.

7. Alvarez, J. T. Dust Barriers In Open Pit Blasts. Multiphase Computational Fluid Dynamics (CFD) Simulations /
   J. T. Alvarez, I. D. Alvarez, S. T. Lougedo // WIT Transactions on Ecology and the Environment. – 2008. – 116 p.

8. Bai, Y. Grey Mathematics Model for Atmospheric Pollution Based on Numerical Simulation / Y. Bai // Chem-ical Engineering Transactions. – 2018. – Vol. 71. – P. 679–684. doi: 10.3303/CET1871114

9. Berlov, O. V. Atmosphere protection in case of emergency during transportation of dangerous cargo / O. V. Berlov // Наука та прогрес транспорту. – 2016. – № 1 (61). – С. 48–54. doi: 10.15802/stp2016/60953

10. Biliaiev, M. M. Numerical Simulation of Indoor Air Pollution and Atmosphere Pollution for Regions Having Complex Topography / M. M. Biliaiev, M. M. Kharytonov // NATO Science for Peace and Security. Series C: Environmental Security. – Dordrecht, 2012. – P. 87–91. doi: 10.1007/978-94-007-1359-8_15

11. Cefic Guidance on safety Risk Assessment for Chemical Transport Operations [Electronic resource] / Croner-i. – Available at: http://clc.am/OnkmUw – Title from the screen. – Accessed : 29.03.2019.

12. Effect of barriers on the status of atmospheric pollution by mathematical modeling / Z. Naserzadeh, F. Atabi, F. Moattar, N. M. Nejad // Bioscience Biotechnology Research Communications. – 2017. – Vol. 10 (1). – P. 192–204.

13. Oyjinda, P. Numerical Simulation to Air Pollution Emission Control near an Industrial Zone / P. Oyjinda, N. Pochai // Advances in Mathematical Physics. – 2017. – Vol. 2017. – P. 1–7. doi: 10.1155/2017/5287132

14. Protective Action Criteria. A Review of Their Derivation, Use, Advantages and Limitations [Electronic resource] // Environmental Public Health Science Unit, Health Protection Branch, Public Health and Compli-ance Division, Alberta Health. – Edmonton, Alberta, 2017. – Available at: http://open.alberta.ca/publications/9781460131213 – Title from the screen. – Accessed : 23.04.2019.

15. The analysis of the use of mathematical modeling for emergency planning purposes [Electronic resource] / O. Zavila, P. Dobes, J. Dlabka, J. Bitta // The science for population protection. – 2015. – № 2. – Available at: http://www.population-protection.eu/prilohy/casopis/eng/22/112.pdf – Title from the screen. – Accessed : 23.04.2019.

В. В. БІЛЯЄВа^1*, п. с. кіріченко^2*, О. В. Берлов^3*, в. о. габрінець^4*,
В. м. горячкін^5*

^1*Каф. «Аерогідромеханіка та енергомасоперенос», Дніпровський національний
університет імені Олеся Гончара, пр. Гагаріна, 72, Дніпро, Україна, 49000,
тел. +38 (056) 374 98 22, ел. пошта water.supply.treatment@gmail.com,
ORCID 0000-0003-2399-3124
^2*Каф. «Теплогазопостачання, водовідведення та вентиляція», Криворізький
національний університет, вул. Віталія Матусевича, 11, Кривий Ріг, Україна,
50027, тел. +38 (056) 409 06 06, ел. пошта pasha_129@ukr.net,
ORCID 0000-0002-0793-9593
^3*Каф. «Безпека життєдіяльності», Придніпровська державна академія
будівництва та архітектури, вул. Чернишевського, 24а, Дніпро, Україна,
49600, тел. +38 (056) 756 34 57, ел. пошта berlov@pgasa.dp.ua,
ORCID 0000-0002-7442-0548
^4*Каф. «Теплотехніка», Дніпровський національний університет залізничного
транспорту імені академіка В. Лазаряна, вул. Лазаряна, 2, Дніпро, Україна,
49010, тел. +38 (056) 373 15 87, ел. пошта gabrin62@gmail.com,
ORCID 0000-0002-6115-7162
^5*Каф. «Теплотехніка», Дніпровський національний університет залізничного
транспорту імені академіка В. Лазаряна, вул. Лазаряна, 2, Дніпро, Україна,
49010, тел. +38 (056) 373 15 87, ел. пошта vgora@ukr.net,
ORCID 0000-0002-8952-952X

КОМП'ЮТЕРНЕ МОДЕЛЮВАННЯ забруднення

атмосферного повітря ПІД ЧАС руХУ

пилової хмари В кар'єрі

Мета. Вибухи в кар’єрах призводять до утворення пилових хмар, які інтенсивно забруднюють атмосферне повітря. Метою цієї роботи є розробка чисельної моделі для прогнозування забруднення атмосфери після вибуху в кар’єрі. Така чисельна модель повинна під час розрахунку враховувати геометричну форму кар'єру, параметри метеорологічної ситуації (швидкість вітру, стан атмосфери), форму пилової хмари, що утворюється в кар’єрі на місці вибуху. Методика. Математичне моделювання розсіювання пилової хмари під час вибуху в кар’єрі ґрунтується на використанні фундаментальних рівнянь аеродинаміки й масопереносу. Поле швидкості повітряного потоку в кар’єрі моделюється за допомогою рівняння Лапласа для потенціалу швидкості. Формування концентраційного поля пилу моделюється на основі рівняння конвективно-дифузійного розсіювання домішки. Для чисельного інтегрування моделювальних рівнянь використано різницеві схеми. Рівняння Лапласа для потенціалу швидкості чисельно інтегрується за допомогою методу Річардсона. Для чисельного інтегрування рівняння конвективно-дифузійного розсіювання домішки використано неявну різницеву схему розщеплення. Результати. Розроблено CFD – модель, яка дозволяє виконати розрахунок формування зон забруднення під часу руху пилової хмари в кар’єрі. Особливістю розробленої моделі є швидкість розрахунку. Для її практичного використання необхідна стандартна вхідна інформація. Наукова новизна. На відміну від наявних в Україні моделей, розроблена чисельна модель дозволяє враховувати геометричну форму кар’єра й геометричну форму пилової хмари для проведення прогнозних розрахунків з оцінки рівня забруднення атмосферного повітря під час вибухів у кар’єрах. Практична значимість. Розроблена чисельна модель може бути імплементована на комп’ютерах малої й середньої потужності використанням стандартної інформації про метеоумови в кар’єрі. Цю модель можна використовувати для екологічної оцінки впливу вибухів у кар’єрі на забруднення навколишнього середовища й робочих зон.

Ключові слова: пилова хмара; кар’єр; забруднення атмосфери; комп'ютерне моделювання

В. В. БЕЛЯЕВА^1*, П. С. КИРИЧЕНКО^2*, А. В. БЕРЛОВ^3*, В. А. ГАБРИНЕЦ^4*,
В. Н. ГОРЯЧКИН^5*

^1*Каф. «Аэрогидромеханика и энергомассопереноса», Днипровский национальный
университет имени Олеся Гончара, пр. Гагарина, 72, Днипро, Украина, 49000,
тел. +38 (056) 374 98 22, эл. почта water.supply.treatment@gmail.com,
ORCID 0000-0003-2399-3124
^2*Каф. «Теплогазоснабжение, водоотведение и вентиляция», Криворожский
национальный университет, ул. Виталия Матусевича, 11, Кривой Рог,
Украина, 50027, тел. +38 (056) 409 06 06, эл. почта pasha_129@ukr.net,
ORCID 0000-0002-0793-9593
^3*Каф. «Безопасность жизнедеятельности», Приднепровская государственная
академия строительства и архитектуры, ул. Чернышевского, 24а, Днипро,
Украина, 49600, тел. +38 (056) 756 34 57, эл. почта berlov@pgasa.dp.ua,
ORCID 0000-0002-7442-0548
^4*Каф. «Теплотехника», Днипровский национальный университет
железнодорожного транспорта имени академика В. Лазаряна, ул. Лазаряна, 2,
Днипро, Украина, 49010, тел. +38 (056) 373 15 87, эл. почта gabrin62@gmail.com,
ORCID 0000-0002-6115-7162
^5*Каф. «Теплотехника», Днипровский национальный университет железнодорожного
транспорта имени академика В. Лазаряна, ул. Лазаряна, 2, Днипро, Украина,
49010, тел. +38 (056) 373 15 87, эл. почта vgora@ukr.net,
ORCID 0000-0002-8952-952X

КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ

ЗАГРЯЗНЕНИЯ АТМОСФЕРНОГО

ВОЗДУХА ПРИ ДВИЖУЩЕМСЯ

ПЫЛЕВОМ ОБЛАКЕ В КАРЬЕРЕ

Цель. Взрывы в карьерах приводят к образованию пылевых облаков, которые интенсивно загрязняют атмосферный воздух. Целью данной работы является разработка численной модели для прогнозирования загрязнения атмосферы после взрыва в карьере. Эта численная модель должна при расчете учитывать геометрическую форму карьера, параметры метеорологической ситуации (скорость ветра, состояние атмосферы), форму пылевого облака, которое образуется в карьере на месте взрыва. Методика. Математическое моделирование рассеивания пылевого облака при взрыве в карьере основывается на использовании фундаментальных уравнений аэродинамики и массопереноса. Поле скорости воздушного потока в карьере моделируется с помощью уравнения Лапласа для потенциала скорости. Формирование концентрационного поля пыли моделируется на базе уравнения конвективно-диффузионного рассеивания примеси. Для численного интегрирования моделирующих уравнений использованы разностные схемы. Уравнение Лапласа для потенциала скорости численно интегрируется с помощью метода Ричардсона. Для численного интегрирования уравнения конвективно-диффузионного рассеивания примеси использована неявная разностная схема расщепления. Результаты. Разработана CFD – модель, которая позволяет выполнить расчет формирования зон загрязнения при движении пылевого облака в карьере. Особенностью разработанной модели является быстрота расчета. Для её практического использования необходима стандартная входная информация. Научная новизна. В отличие от существующих в Украине моделей, разработанная численная модель позволяет учитывать геометрическую форму карьера и геометрическую форму пылевого облака для проведения прогнозных расчетов по оценке уровня загрязнения атмосферного воздуха при взрывах в карьерах. Практическая значимость. Разработанная численная модель может быть имплементирована на компьютерах малой и средней мощности с использованием стандартной информация о метеоусловиях в карьере. Эту модель можно использовать для экологической оценки влияния взрывов в карьере на загрязнение окружающей среды и рабочих зон.

Ключевые слова: пылевое облако; карьер; загрязнение атмосферы; компьютерное моделирование

References

1. Alymov, V. T., & Tarasova, N. P. (2004). Tekhnogennyy risk: Analiz i otsenka: Uchebnoe posobie dlya vuzov. Moscow: Akademkniga. (in Russian)

2. Biliaiev, N. N., Gunko, E. Y., & Rostochilo, N. V. (2014). Zashchita zdaniy ot proniknoveniya v nikh opasnykh veshchestv: Monografiya. Dnepropetrovsk: Aktsent PP. (in Russian)

3. Beresnevich, P. V., Mikhaylov, V. A., & Filatov, S. S. (1991). Aerologtya karerov: spravochnik. Moskva: Nedra. (in Russian)

4. Biliaiev, N. N., Gunko, E. Y., Kirichenko, P. S., & Muntian, L. Y. (2017). Otsenka tekhnogennogo riska pri emissii opasnykh veshchestv na zheleznodorozhnom transporte. Krivoy Rog: Kozlov R. A. (in Russian)

5. Stoetsky, V. F., Golinko, V. I., & Dranishnikov, L. V. (2014). Risk assessment in man-caused accidents. Sci-entific Bulletin of National Mining University, 3, 117-124. (in Russian)

6. Zgurovskiy, M. Z., Skopetskiy, V. V., Khrushch, V. K., & Biliaiev, N. N. (1997). Chislennoe modelirovanie rasprostraneniya zagryazneniya v okruzhayushchey srede. Kyiv: Naukova dumka. (in Russian)

7. Alvarez, J. T., Alvarez, I. D., & Lougedo, S. T. (2008). Dust Barriers in Open Pit Blasts. Multiphase Computational Fluid Dynamics (CFD) Simulations. WIT Transactions on Ecology and the Environment. (in English)

8. Bai, Y. (2017). Grey Mathematics Model for Atmospheric Pollution Based on Numerical Simulation. Chemi-cal Engineering Transactions, 71, 679-684. doi: 10.3303/CET1871114 (in English)

9. Berlov, O. V. (2016). Atmosphere protection in case of emergency during transportation of dangerous cargo. Science and Transport Progress, 1(61), 48-54. doi: 10.15802/stp2016/60953 (in English)

10. Biliaiev, M. M., & Kharytonov, M. M. (2012). Numerical Simulation of Indoor Air Pollution and Atmosphere Pollution for Regions Having Complex Topography. NATO Science for Peace and Security. Series C: Envi-ronmental Security. Dordrecht. doi: 10.1007/978-94-007-1359-8_15 (in English)

11. Cefic Guidance on safety Risk Assessment for Chemical Transport Operations. Croner-i. Retrieved from http://clc.am/OnkmUw (in English)

12. Naserzadeh, Z., Atabi, F., Moattar, F., & Nejad, N. M. (2017). Effect of barriers on the status of atmospheric pollution by mathematical modeling. Bioscience Biotechnology Research Communications, 10(1), 192-204. (in English)

13. Oyjinda, P., & Pochai, N. (2017). Numerical Simulation to Air Pollution Emission Control near an Industrial Zone. Advances in Mathematical Physics, 2017, 1-7. doi: 10.1155/2017/5287132 (in English)

14. Government of Alberta. (2017). Protective Action Criteria: A Review of Their Derivation, Use, Advantagesand Limitations. Environmental Public Health Science Unit, Health Protection Branch, Public Health and Compliance Division, Alberta Health. Edmonton, Alberta. Retrieved from http://open.alberta.ca/publications/9781460131213 (in English)

15. Zavila, О., Dobes, Р., Dlabka, J., & Bitta, J. (2015). The analysis of the use of mathematical modeling foremergency planning purposes. The Science for Population Protection, 2. Retrieved from http://www.population-protection.eu/prilohy/casopis/eng/22/112.pdf (in English)

Received: March 18, 2019

Accepted: July 26, 2019

Creative Commons Attribution 4.0 International © V. V. Biliaieva, P. S. Kirichenko, O. V. Berlov,

doi: 10.15802/stp2019/178556 V. O. Gabrinets, V. M. Horyachkin, 2019