ISSN 2307–3489 (Print), ІSSN 2307–6666 (Online)

Наука та прогрес транспорту. ВісникДніпропетровського
національного університету залізничного транспорту, 2019, № 3 (81)

Електричний транспорт, енергетичні системи та комплекси

Вступ

Залізниця як складна система є одним із найбільших споживачів палива, електроенергії та інших матеріальних і нематеріальних ресурсів. Основна проблема залізничного транспорту – ефективне управління потоками вантажів і пасажирів на всіх етапах – від їх формування до місць доставки. Ефективність функціонування такої системи вимагає забезпечити організацію потоків вагонів і їх упорядкованого руху в складах поїздів згідно з графіками руху, з максимальною безпекою, економічністю тощо. У багатьох випадках виникає необхідність забезпечити максимальну реалізацію пропускної й перевізної здатності, оперативного коригування, за потреби, потоків вагонів і поїздів, відповідно і графіків руху в разі виникнення нештатних ситуацій тощо. Усі процеси на мережі залізниць є взаємопов’язаними, тому їх потрібно аналізувати в комплексі. Системний аналіз таких процесів вимагає наявності певних інструментів – систем оперативної розробки плану формування, оперативного планування роботи станцій і прокладання ниток графіка руху поїздів тощо. На жаль, таких систем, які б у реальному часі забезпечували оптимальне розв’язання згаданих задач, на залізниці України не існує. Відсутність системного підходу до проведення наукових досліджень не сприяє реалізації наявного наукового кадрового потенціалу як загалом в Україні, так і в самій структурі залізниці зокрема.

Список використаних джерел [1–24] містить роботи, у яких наведено розроблення алгоритмічного забезпечення для розв’язування оптимізаційних задач на мережах [1–2, 10–11]; моделі руху поїзда й результати їх апробації [3–9]; дослідження з теми роботи за кордоном [10–22].

У наведеному списку є небагато завершених робіт, присвячених тяговим розрахункам на залізничній мережі України. В оглядовій роботі [3] подано перелік наявних методів визначення енергооптимальних режимів руху електричного рухомого складу без порівняльного аналізу їх використання й апробації із залученням реальних даних. Зазначено, що зазвичай для побудови оптимального управління рухом поїзда застосовують принцип максимуму академіка Л. С. Понтрягіна. Одночасно в роботі наведені й аргументи неефективності його використання саме для розв’язування тягових задач.

У дослідженнях, які проведені за межами України [12–24], проблему оптимізації траєкторії швидкості руху поїздів розглядають у сукупності з проблемами оптимізації графіків руху, експлуатації поїздів за умови оптимального коригування режимів руху в разі їх затримки (максимальне наближення до запланованого розкладу), побудови ефективної інформаційно-дорадчої системи машиніста тощо. При цьому для оптимізації траєкторії руху поїздів використовують оптимальні стратегії й методи нелінійного й динамічного програмування для забезпечення енергоефективних режимів руху з обмеженнями швидкостей і пропускною здатністю тощо.

У багатьох вищезгаданих роботах наведена інформація щодо апробації розробленого математичного забезпечення в окремих країнах, а також національні особливості експлуатації й функціонування залізничного транспорту. Безперечно, свої особливості існують і в Україні, які полягають у наступному:

- централізоване управління перевізним процесом на залізничній мережі;

- незначна частка приватного капіталу в управлінні інфраструктурою української залізниці;

– значна протяжність залізничних колій і розвиненість станційної інфраструктури;

– відмінності за параметрами й технологією управління від європейської колійної системи;

– неповна електрифікація залізниць, що зумовлює зміну тяги на роздільних пунктах.

Окремі особливості впливають як на технологію функціонування залізниці, так і на постановку оптимізаційних задач. Тому певні технологічні рішення для іноземних залізниць не можна безпосередньо переносити на українську залізницю.

У сучасних умовах господарювання досить актуальною проблемою є отримання максимального прибутку. Один із можливих шляхів полягає у створенні системи формування обґрунтованих тарифів на вантажні й пасажирські перевезення, наприклад, збільшення тарифів або зменшення собівартості перевезень і, відповідно, тарифів на них. Тягово-енергетичні розрахунки на мережі залізниць дозволяють: досягати максимальної маси поїздів; управляти швидкістю перевезень у певних діапазонах; перерозподіляти потоки в системі залізниць, що приводить до зростання ступеня використання потужності локомотивів; нарощувати пропускну й перевізну здатність ділянок і напрямків.
У кінцевому підсумку знижується собівартість перевезень.

Мета

Основна мета роботи – запропонувати методи використання тягово-енергетичних розрахунків на залізничній мережі для ефективного управління перевізним процесом. Одним із можливих підходів щодо забезпечення ефективного управління є виявлення та максимальна реалізація наявного потенціалу оптимізації.

Для досягнення поставленої мети необхідно: розробити інтегроване інформаційне забезпечення для тягово-енергетичних розрахунків на залізничній мережі; поставити основні оптимізаційні задачі розрахунку режимних параметрів; розробити алгоритми знаходження енергооптимальних маршрутів руху поїздів із різними типами тяги.

Методика

Для розв’язання поставлених задач використано засоби математичного та імітаційного моделювання із застосуванням класичних фундаментальних алгоритмів на зважених графах. Розроблену математичну модель руху поїзда в просторових координатах із розподіленою масою вздовж траєкторії руху реалізовано числовим інтегрування моделі методом скінченних різниць. Розрахунок оптимальних траєкторій швидкості руху на граф-схемі залізниці проведено згідно із заданими критеріями оптимальності методами комбінаторної оптимізації.

Результати

Розроблено графічний редактор, який забезпечив формування математичної моделі структури залізничних колій, інформаційного забезпечення для розв’язування тягово-енергетичних задач на мережі залізниці, прокладання оптимальних за заданими критеріями шляхів між різними роздільними пунктами, автоматизацію процесу розв’язування режимних задач для потреб оперативного формування та зміни графіків руху тощо [4–9]. Наведені приклади розв’язування основних наборів задач підтверджують високу ефективність розробленого математичного й програмного забезпечення. Розширення сфери експлуатації програмного комплексу дозволить приймати обґрунтовані рішення для організації руху пасажирських і вантажних поїздів у реальних постійно змінюваних ситуаціях.

Мережа залізничних колій. Задання залізничної мережі в термінах графів дозволяє формалізувати об’єкт. Для розв’язування оптимізаційних задач на залізничній мережі використовують відомі фундаментальні алгоритми на графах [1–2]. Різне вагове «навантаження» об’єктів графа на схемі залізниць уможливлює постановку та розв’язування різних оптимізаційних задач. Вага ребра може вказувати на довжину перегону між двома станціями; найбільшу вагу рухомого складу, яка допустима для цієї ділянки шляху; затратні ресурси на тягу; пропускну здатність (середнє число поїздів, що проходять по цій ділянці протягом доби) тощо. У процесі руху поїздів змінюється їх взаємне розташування, потужність тяги і швидкість, оскільки вони в окремі моменти часу знаходяться на різних частинах поздовжнього профілю. Усе це викликає змінне навантаження на тягові підстанції і впливає на величину втрат електроенергії в контактній мережі.

Розглянемо розроблену систему інформаційної підтримки режимних тягових задач. Структуру залізниць (рис. 1) задано частково орієнтованим мультиграфом із можливими паралельними (у парному чи непарному напрямках) або частково орієнтованими ребрами. Структура в основному є планарною (плоскою). Планарність порушується в окремих частинах граф-схеми та на окремих об’єктах типу роздільного пункту.

Розроблена інформаційна база для оптимізації режимів руху поїздів включає:

– перелік роздільних пунктів (станцій, роз’їздів, блок-постів, ключових парків станцій);

– основні технічні характеристики роздільних пунктів (належність до залізниці, код ЄСР, назва, спеціалізація за родом роботи, система управління стрілочними переводами);

– основні технічні характеристики перегонів (колійність, орієнтованість руху поїздів (уперед, назад, неорієнтоване), наявність електрифікації, межі станцій);

– поздовжній профіль і план колій, допустимі швидкості руху, наявність обмежень швидкості руху поїздів, координати нейтральних вставок;

– перелік, координати, класифікація поїзних світлофорів;

– графоаналітичні схеми роздільних пунктів.

Для всіх видів тяги й точок на колії задана максимальна швидкість. Будь-яке обмеження швидкості має початок дії (координата кілометражу) й повернення до максимального значення. У випадку редагування обмежень швидкостей користувач задає/змінює задані параметри. Довжина й координата кінця обмеження обчислюється автоматично. Система дозволяє копіювання та присвоєння обмеження швидкостей з іншого виду руху. Додаткове обмеження швидкості має початок дії (координата кілометражу), довжину й повернення до максимальної швидкості. Інтервали додаткових обмежень швидкості не можуть перетинатись між собою. Система дозволяє скопіювати додаткові обмеження швидкостей з іншого виду руху.

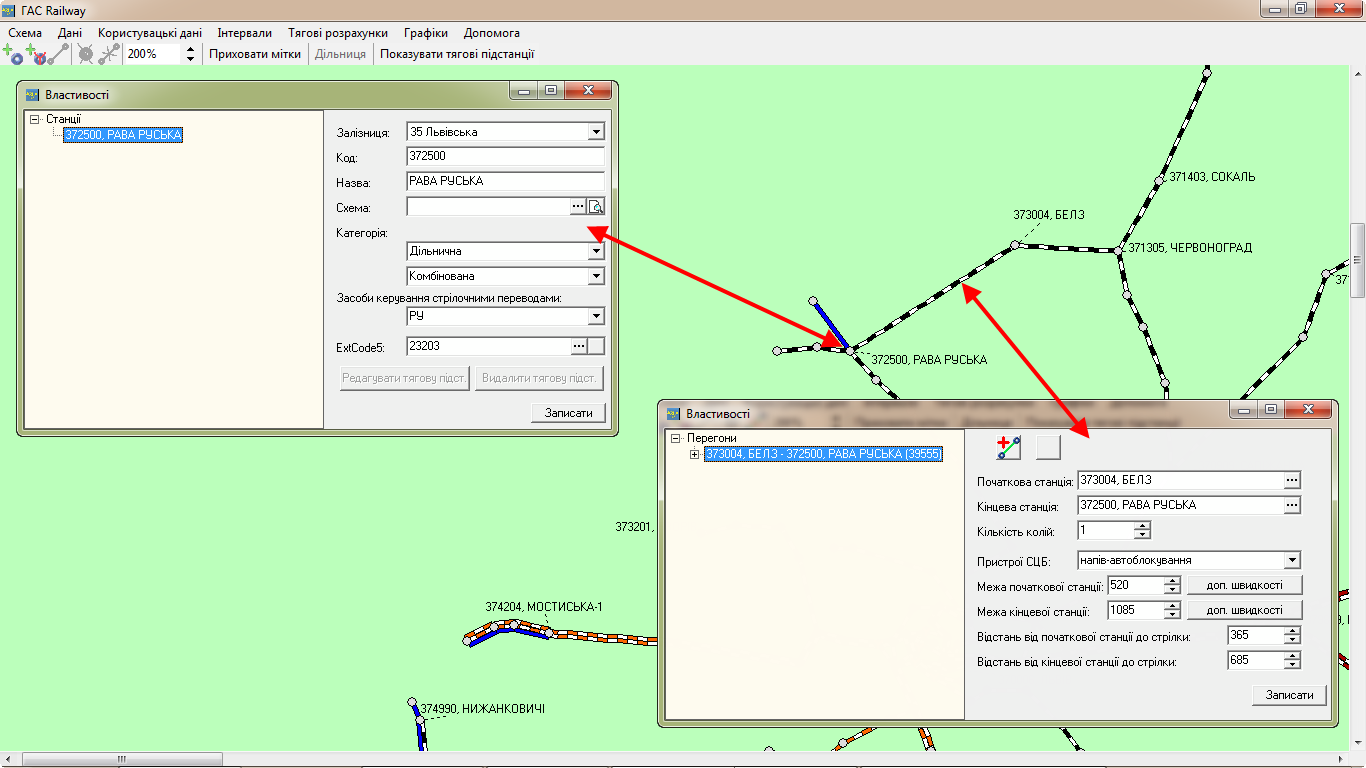
Рис. 1. Частина граф-схеми залізниці України

Fig. 1. Part of the graph-scheme of the Ukrainian railways

Таблиця 1

Основні об’єкти і їх атрибути

Table 1

The main objects and their attributes

Об’єкти	Атрибути
Станції	код; назва; залізниця, до якої належить станція; категорії станції: проміжна, дільнична, вузлова, сортувальна, комбінована, пасажирська, вантажна; засоби керування стрілочними переводами на станції: ДЦ, МРЦ, ЕЦ, МЦ, РУ; код у довіднику станцій
Перегони	інформація про початкову та кінцеву станції: відстань від осі до межі станції, відстань від осі до вхідної стрілки, обмеження швидкостей у горловині станції (для головної/бічної колії в обох напрямках для всіх видів руху); пристрої СЦБ на перегоні: автоблокування, напівавтоматичне блокування, ключ-жезл; інші; інформація про колії перегону: довжина, орієнтація (двобічна, непарна, парна); ширина: 1520; 1435; електрифікація: неелектрифікована, змінного струму, постійного струму; властивості колії: кілометраж, профіль, криві, швидкості. нейтральні вставки, додаткові обмеження швидкості, ізоляційні стики, платформи
Дільниці	«ідентифікатор» – для швидшого пошуку потрібної дільниці

У таблиці позначено:
ДЦ – диспетчерська централізація; МРЦ – маршрутно-релейна централізація; ЕЦ – електрична централізація;
МЦ – механічна централізація; РУ – ручне управління

Таблиця 2

Основні складові об’єктів і їх характеристика

Table 2

The main components of objects and their characteristics

Основні складові об’єктів	Характеристика
Профіль	Профіль має набір елементів із певною довжиною й ухилом. Під час редагування профілю користувач задає довжини й ухили нових елементів або змінює значення наявних. Поля «Початок», «Кінець» (абсолютні координати) й «Початок (кілометраж)», «Кінець (кілометраж)» обчислюються автоматично. Сума довжин усіх елементів повинна бути рівною довжині колії, яку редагують.
Криві	Параметри елементів кривої: початок (задають координатою кілометражу), довжина, радіус, підвищення зовнішньої рейки. Криві не можуть перетинатись.
Нейтральні вставки	Нейтральні вставки – це набір неперетинних інтервалів, які задають координатами кілометражу.
Платформи	Кожна колія перегону може містити набір платформ. Платформу задають координатою й назвою.
Ізоляційні стики	Ізоляційні стики можуть бути прив’язаними до світлофорів, які, у свою чергу, бувають односторонніми або двосторонніми. Тобто ізоляційний стик задають наступними параметрами: координата, тип, тип для зворотного напрямку. Розрізняються наступні типи ізоляційних стиків: вхідний світлофор, вихідний світлофор, попереджувальний світлофор, прохідний світлофор, ізоляційний стик.
Горловини станцій	Система дозволяє відображати й редагувати інформацію про горловини станцій окремої дільниці. Інформація про кожну горловину включає: відстань від осі до межі станції, відстань від осі до вхідної/вихідної стрілки станції, обмеження швидкостей у горловині (швидкості задають окремо для кожного напрямку, для головної/бічної колії, для кожного виду руху).
Станційні колії	Станційна колія, окрім властивостей, які характерні для всіх колій (довжина, орієнтація, ширина, електрифікація, профіль, криві, обмеження швидкості тощо), мають ще і наступні: номер, тип (головна, приймальна, відправна, приймально-відправна, сортувальна, сортувально-відправна, деповська, з’єднувальна, завантажувально-розвантажувальна та ін.); призначення (пасажирська, завантажувально-розвантажувальна, комбінована, маневрова), корисна довжина.
Cтрілочні переводи	Cтрілочні переводи мають такі властивості: код, тип (правий, лівий, симетричний, перехресний, глухий перетин), марка хрестовини (1/6; 1/9; 1/11; 1/18; 1/18п; 1/22). Кожен тип стрілочного переводу визначає кількість станційних колій, які він з’єднує, і правила руху поїздів по цих коліях.
Точки входу на станцію	Точки входу на станцію – це межі її схеми. Вони відповідають координатам меж, які задані у властивостях перегонів, що прилягають до станції.
Тупики	До тупика може бути під’єднана тільки одна станційна колія.
Фіктивні вершини	Фіктивні вершини використовують для більш наочного графічного представлення схеми станції (відповідають зміні напрямку прокладання станційних колій). Від фіктивної вершини можуть виходити рівно дві станційні колії.

Схема станції

Scheme of the station

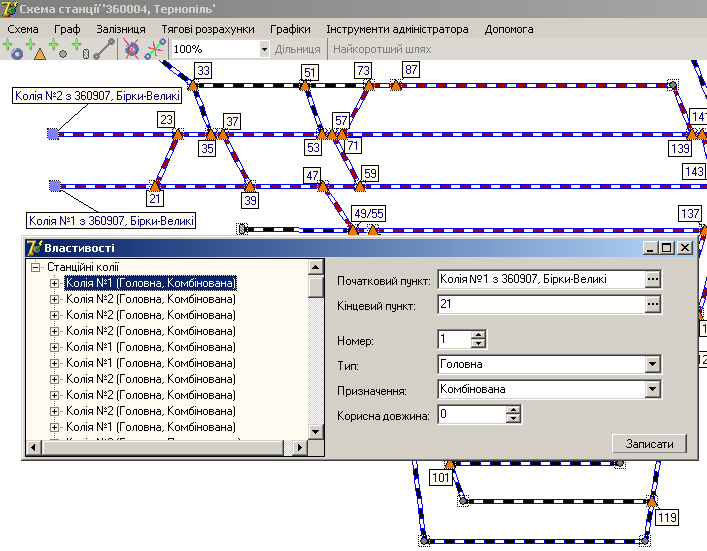
Рис. 2. Властивості станційних колій

Fig. 2. Properties of station tracks

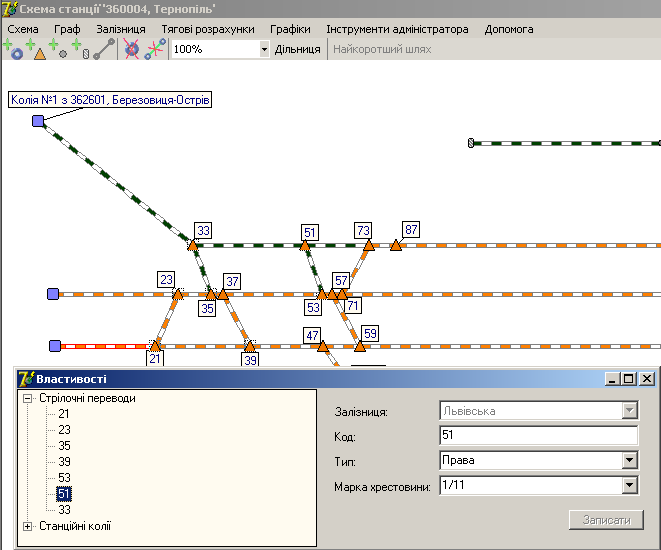
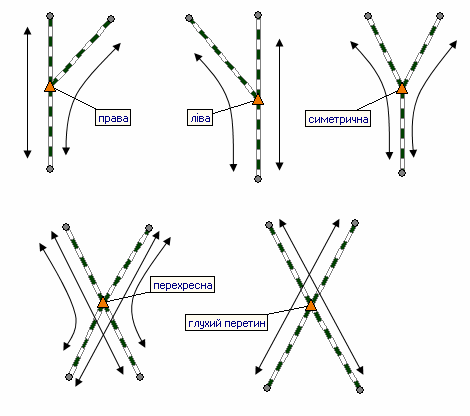
Рис. 3. Правила руху через стрілочні переводи

Fig. 3. Rules of movement through railroad switches

На мережі залізниць можуть виникати різноманітні штатні й нештатні ситуації, які вимагають прокладання замість попереднього нового оптимального шляху руху за тим чи іншим критерієм. Довжиною шляху у зваженому графі називають суму ваги ребер (дуг). Реалізовано можливість задавати, вибирати з бази даних чи розраховувати вагу перегонів – відстань, максимальна маса поїзда заданої довжини, коефіцієнт стану полотна, коефіцієнт завантаженості за пропускною здатністю, середня швидкість, коефіцієнт економічності тощо. Під час трасування шляхів (виділення послідовності роздільних пунктів) можна також використовувати додаткові умови на тип тяги, мінімальні ухили, включення/виключення окремих наборів роздільних пунктів тощо. Можливі ще й інші види ваг роздільних пунктів – пропускна та переробна здатність (максимальна і оперативна на заданому інтервалі часі) за видами операцій, максимальна кількість та довжина приймальних станційних колій тощо. Встановлення ваги об’єктів граф-схеми залізничної мережі дозволяє знаходити оптимальні шляхи за заданими критеріями. У разі прокладання траєкторій руху поїздів за тими чи іншими критеріями передбачена можливість урахування їх взаємного впливу на режим руху, графік руху тощо. Також є можливість синхронізувати в часі режими руху поїздів на перегонах і роздільних пунктах. Детальніше розглянемо ці задачі уже в роботах з автоматизації побудови оптимальних графіків руху поїздів.

Алгоритми на граф-схемі залізниці. Основна характеристика алгоритмів на графах – це їх складність. Вона в основному пов’язана з параметрами графа (кількість вершин, ребер, розподіл величини степеня вершин, зв’язність графа (вершинна та реберна) тощо. У нашому випадку степінь вершин є незначним, і тому складність більшості фундаментальних алгоритмів на таких графах буде незначною, що дозволяє організовувати перебірні процедури пошуку оптимальних варіантів за декількома зваженими параметрами. Так, для зв’язного графа з невеликим максимальним степенем вершин 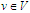, із точністю до деякої константи, складність алгоритмів знаходження найкоротших шляхів є рівною 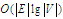[18–19]. Позитивною властивістю найкоротших шляхів є те, що будь-яка частина найкоротшого шляху є найкоротшою. Цю властивість використовують у задачах динамічного програмування. Зокрема, алгоритм знаходження найкоротшого шляху Флойда–Воршелла [20] ґрунтується на методі динамічного програмування, що дозволяє ставити й розв’язувати окремі оптимізаційні задачі математичного програмування за відповідної постановки. Значний набір оптимізаційних задач із пошуку максимальної пропускної здатності й потоку мінімальної вартості розв’язують із використанням алгоритмів пошуку мінімального розрізу в графі транспортної мережі (теорема Форда–Фалкерсона) [21]. Для цього досить подати залізницю як транспортну мережу.

Тягово-енергетичні розрахунки на граф-схемі залізниці. Система розрахунку режимів руху поїздів складається з інформаційного забезпечення, системи задання розрахунку, алгоритмічного й програмного забезпечення, табличного й графічного представлення результатів моделювання [14]. Усі режимні задачі поставлені й розв’язані як задачі оптимального керування, що забезпечило ефективне розв’язання достатньо повного набору прямих та обернених режимних задач [14]. Математична модель тягових засобів є максимально адекватною: використано повну множину тягових, струмових, енерговитратних, теплових, опірних характеристик для всіх типів приводів і вагонів, а також розподілену масу вздовж довжини поїзда, яка прив’язана до центра мас тягових засобів і вагонів. У розрахунках застосовано траєкторію руху поїздів без її спрямлення та враховано вплив основних зовнішніх факторів: температури повітря, сил зустрічного вітру, підвагонних генераторів тощо. Розроблене алгоритмічне забезпечення дозволило поставити та розв’язати достатньо повний набір прямих та обернених задач оптимізації [14–15].

Критерії оптимізації та ресурси на їх реалізацію. Одним із перспективних засобів підвищення енергоефективності є оптимізація руху поїздів за допомогою стратегій керування. Витрати енергії на окремих операціях чи ділянках руху поїзду, загальні енергетичні витрати всієї залізничної мережі є значними. Дослідження енергоефективних стратегій керування проведено з використанням теорії оптимального керування для пошуку траєкторій (кривих швидкості), які гарантують безпечну й енергозбережну роботу поїзда. Процес пошуку оптимальної траєкторії швидкості руху називають оптимізацією траєкторії поїзда. Оптимальна траєкторія є основою для оптимізації процесу експлуатації поїздів.

Оптимізація роботи залізниць у першу чергу пов’язана з розробленням графіків і розкладів руху поїздів. Процесу розроблення графіка руху поїздів передують тягові розрахунки. Проблеми розроблення розкладу руху поїздів є складними для великомасштабних транспортних мереж. Якість режиму руху поїзда та його графіка безпосередньо впливає на вартість і якість послуг. Оцінка графіка за стабільністю й пунктуальністю його реалізації у великомасштабній залізничній мережі є дуже вартісною й трудомісткою процедурою. Ідеальний рух поїздів – це дотримання заздалегідь розробленого графіка, а несподівані події можуть призвести до його порушення. У такому випадку поїзд повинен якомога швидше повернутися до свого графіка з мінімальними затратами, щоб уникнути конфліктів з іншими поїздами.

Оптимальне керування складається з послідовності руху в режимі тяги, вибігу, гальмування й оптимальних координат, їх зміни (перемикання) з урахуванням усіх наявних обмежень. Додатковими обмеженнями можуть бути час прибуття (відправлення), час або швидкість проходження через проміжні станції й конфліктні місця на перегонах і роздільних пунктах. Також траєкторію поїзда обмежують деякі часові й швидкісні параметри щодо розміщення сигналізації. Наприклад, певні проміжки часу між суміжними поїздами потрібні для спрацювання сигналів, які необхідні для дотримання безпеки руху. Так, жовті сигнали обов’язково вимагають, щоб поїзд зменшив свою швидкість. Не менш важливим критерієм оптимізації за умови затримки поїзда є зменшення часу затримки, відповідно, і споживання енергії.

Основний недолік наявних класичних методів оптимального керування полягає в тому, що вони вимагають значного часу на обчислення через труднощі з пошуком оптимальних точок перемикання. На складність обчислення впливають обмеження швидкості й розрахунок градієнтів. Формування оптимального керування в реальних умовах вимагає розроблення більш ефективних методів.

Числові експерименти. Приклади розв’язування задач. Маршрут прямування поїзда будемо задавати як послідовність роздільних пунктів. Для кожного поїзда будемо вважати, що його початкова й кінцева швидкості є нульовими. Об’єкт «поїзд» можна задати, якщо є відомим такий набір параметрів: початкова й кінцева станції; перелік типів локомотивів; кількість вагонів; сумарна чи повагонна маса вантажу тощо. Уважатимемо також відомими параметри зовнішніх умов: температуру
й густину повітря, напрям вітру й ін.

Для прокладання шляхів на граф-схемі мережі залізниць реалізовано відомі фундаментальні алгоритми на графах – пошук оптимального маршруту за заданим критерієм і заданою вагою ребер і вершин.

Приклад 1. Прокладання траєкторії руху поїзда через вузлові станції Львівського вузла.

Відмінність маршрутів на схемах (рис. 4) пов’язана зі спеціалізацією колій. Так, дільниця колії від станції Скнилів до стрілочного переводу № 44 станції Львів дозволяє рух поїздів тільки в парному напрямку, що унеможливлює її включення в маршрут дільниці Підбірці–Комарне.

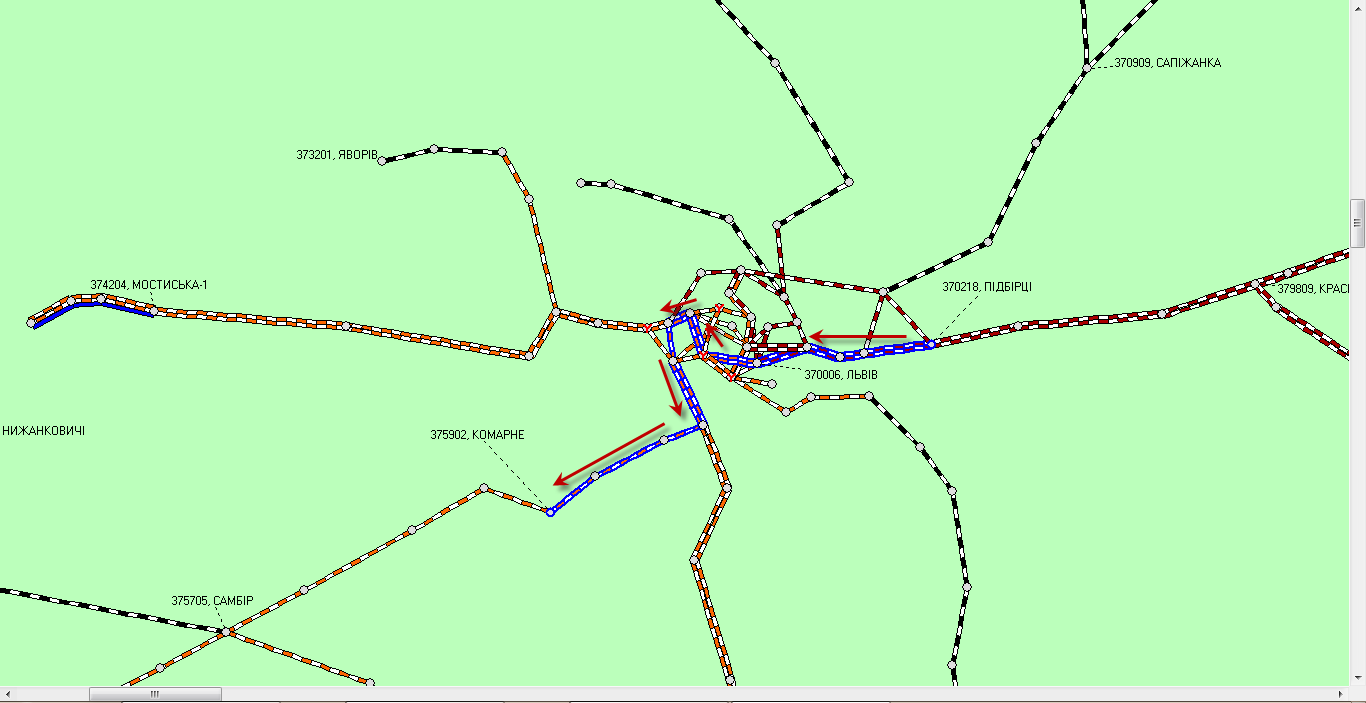
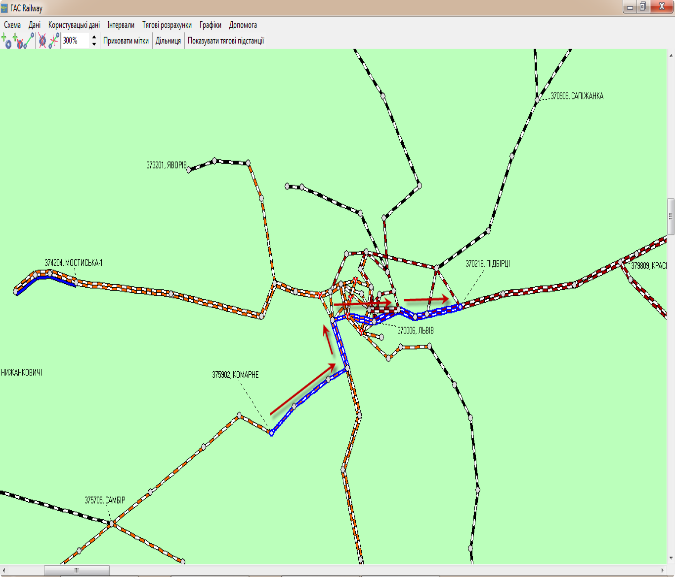
Рис. 4. Найкоротший маршрут між станціями Підбірці й Комарне:
а – від Підбірців до Комарного; б – від Комарного до Підбірців

Fig. 4. The shortest route between Pidbirtsi and Komarne stations:
a – from Pidbirtsi to Komarne; b – from Komarne to Pidbirtsi

Приклад 2. Розрахунок режиму ведення вантажного поїзда. Візьмемо дільницю Ковель–Сарни–Коростень і склад поїзда – 57 порожніх піввагонів, тяговий локомотив – тепловоз серії 2М62. Основні умови ведення поїзда:

– відправлення з транзитного парку станції Ковель із бічної колії;

– прямування із зупинкою на станції Сарни;

– прибуття із зупинкою на станції Коростень;

– швидкість руху – розрахункова для графіка руху поїздів на 2018 рік.

Для першого варіанта розрахунок буде проведено для прямування за умови мінімального часу перебування поїзда на перегоні, у дугому візьмемо режим максимального використання холостого ходу з пригальмовуванням на спусках.

На рис. 8–9 наведено режим руху поїзда за мінімальний час, а на рис. 10–11 – режим руху поїзда за час, що на 5 хв більший за мінімальний,.

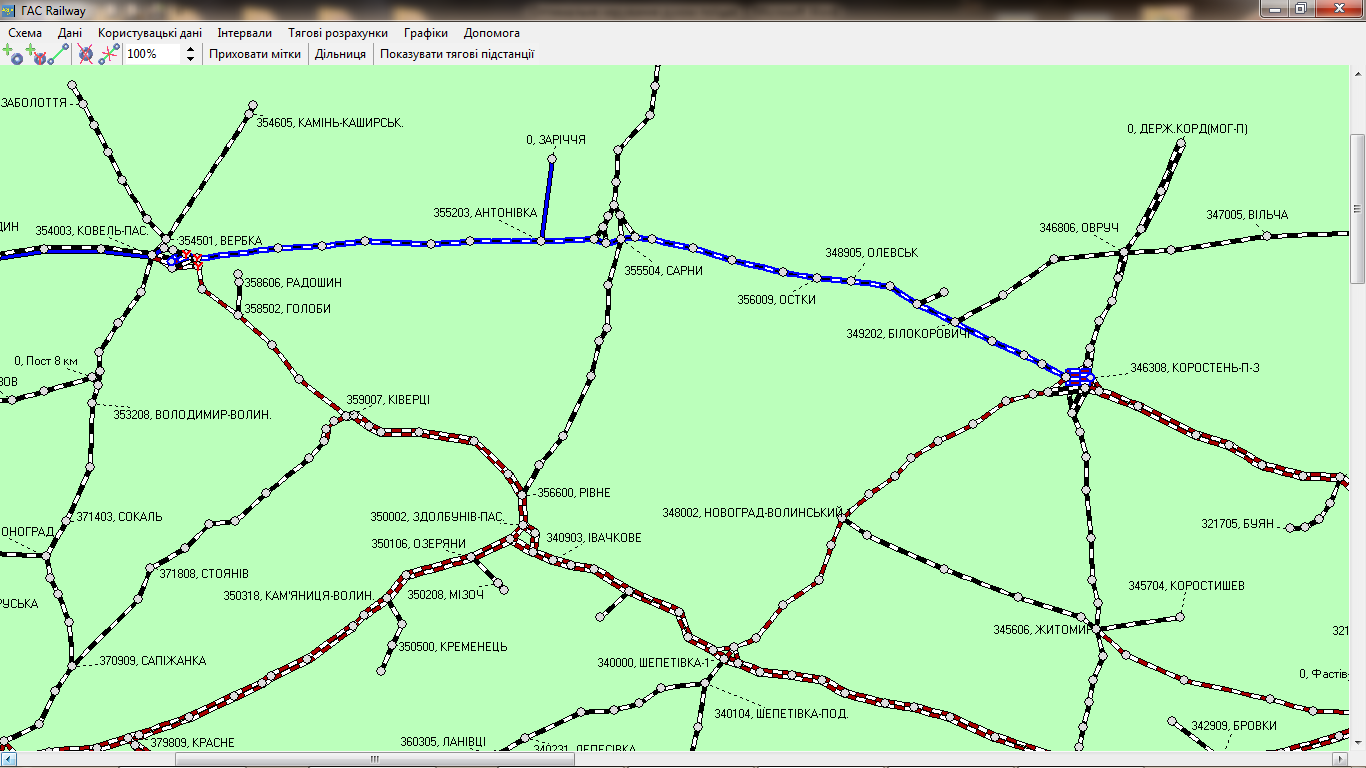
Рис. 5. Вибір дільниці розрахунку на полігоні

Fig. 5. Selection of the calculation section at the operating domain

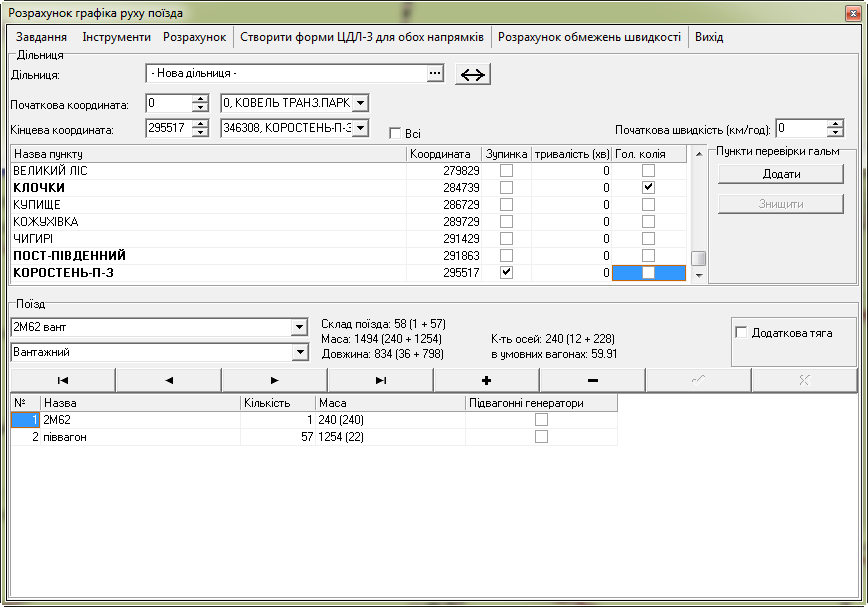
Рис. 6. Задання складу поїзда й умов прямування на дільниці у вікні
«Розрахунок графіка руху поїзда» модуля «Тягові розрахунки» програмного комплексу ГАС «Railway»

Fig. 6. Train formation and the conditions of running along the section
in the «Calculation of train movement» window, «Traction calculations»
module of the GAS «Railway» software complex

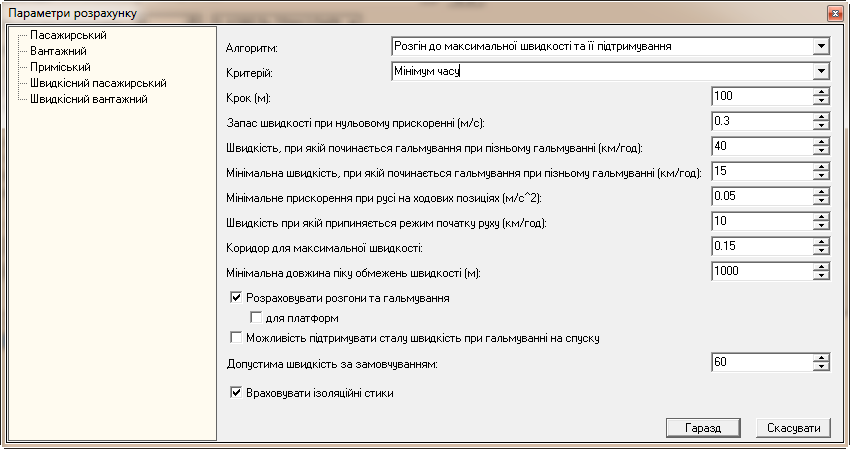
Рис. 7. Формування параметрів для тягово-енергетичних розрахунків

Fig. 7. Formation of parameters for traction-energy calculations

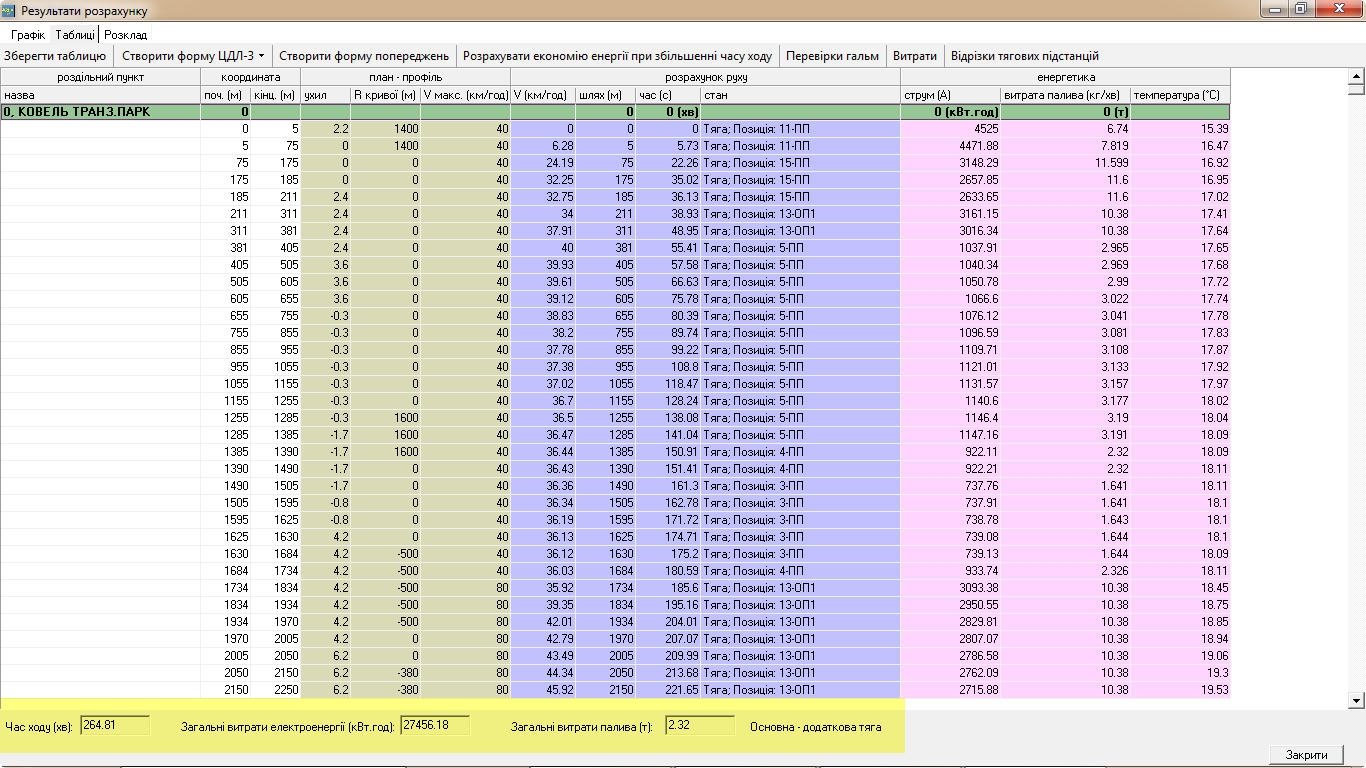
Рис. 8. Результати першого варіанта тягово-енергетичного розрахунку
ведення поїзда на дільниці Ковель–Сарни–Коростень

Fig. 8. Results of the first option of the traction-energy calculation in the train
running on the Kovel-Sarny-Korosten section

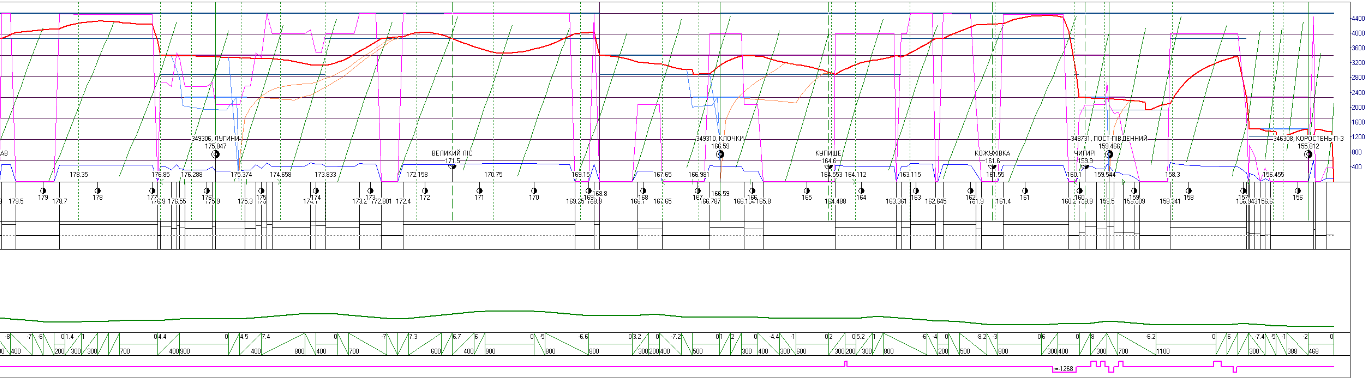
Рис. 9. Графічний фрагмент розрахункової режимної карти ведення поїзда
на дільниці Ковель–Сарни–Коростень за першим варіантом

Fig. 9. Graphic fragment of the calculated mode map in the train running
on the Kovel-Sarny-Korosten section by the first option.

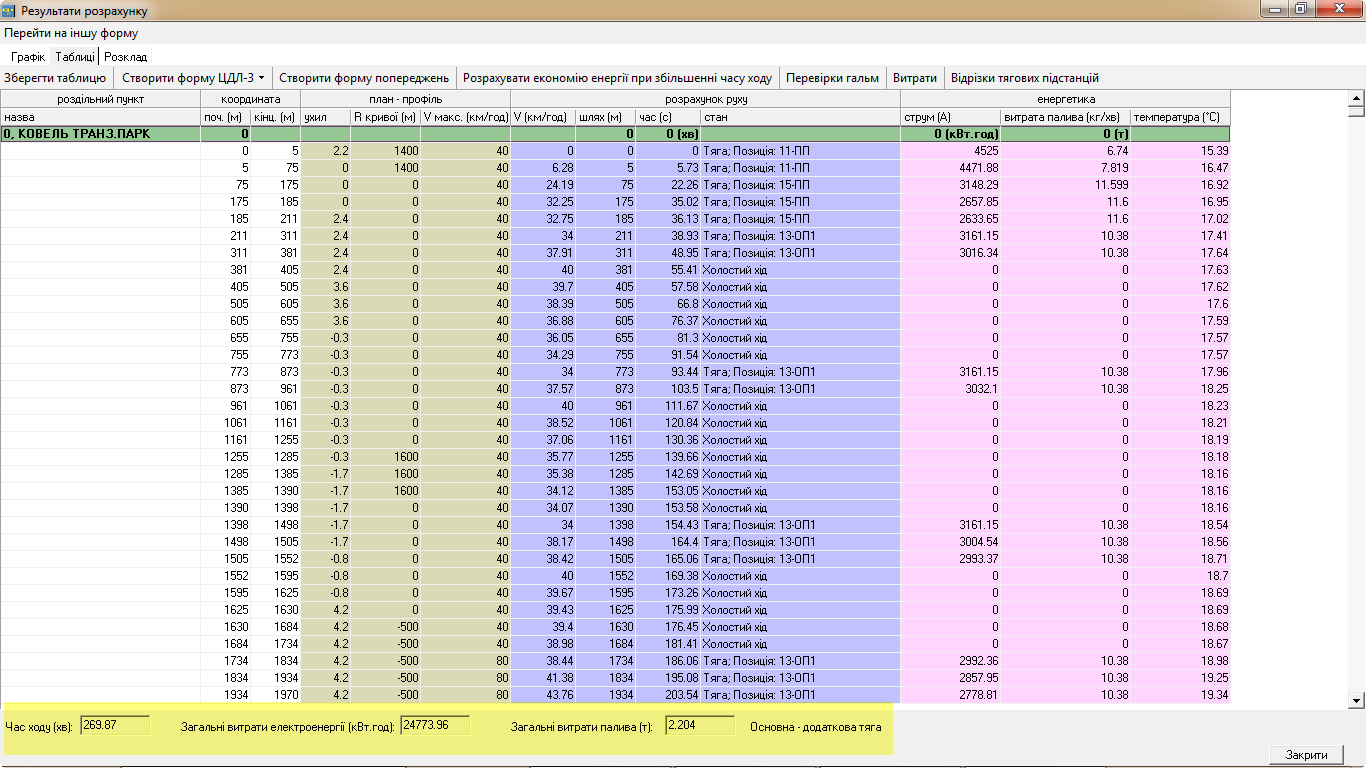
Рис. 10. Результати другого варіанта тягово-енергетичного розрахунку ведення
поїзда на дільниці Ковель–Сарни–Коростень

Fig. 10. Results of the second option of the traction-energy calculation
in the train running on the Kovel-Sarny-Korosten section

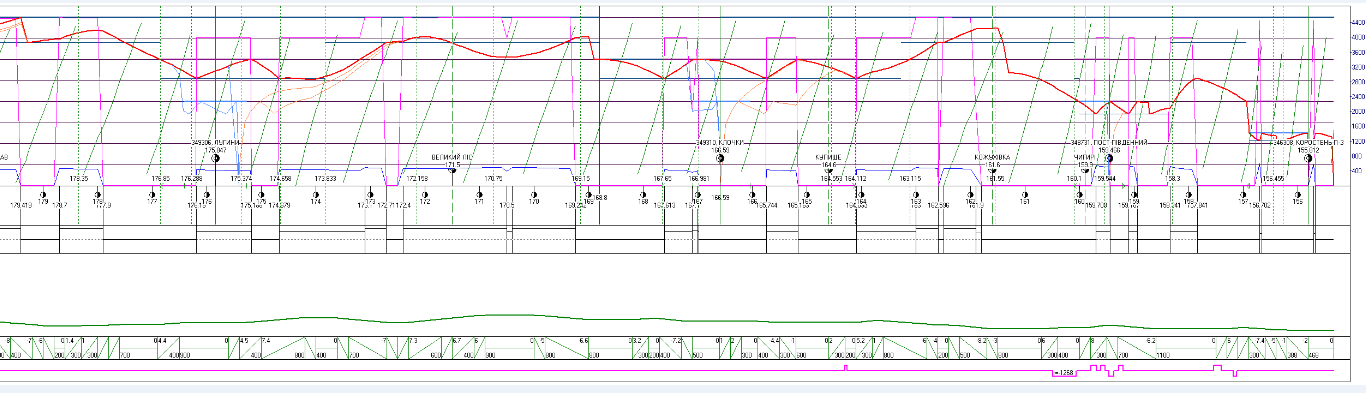
Рис. 11. Графічний фрагмент розрахункової режимної карти ведення
поїзда на дільниці Ковель–Сарни–Коростень за другим варіантом

Fig. 11. Graphic fragment of the calculated mode map in the train
running on the Kovel-Sarny-Korosten section by the second option.

У першому випадку розрахунковий час прямування поїзда без урахування часу стоянки складає 272 хв, витрата дизельного палива на тягу поїзда – 2 350 кг. У другому варіанті розрахунковий час прямування поїзда без урахування часу стоянки складає 277 хв, витрата дизельного палива на тягу поїзда – 2 260 кг. У цьому випадку збільшення часу руху поїзда на дільниці на 5 хв забезпечує економію в 90 кг дизельного палива.

Приклад 3. Розрахунок часу на рух та мінімальних паливно-енергетичних витрат із різними типами локомотивів. Задано параметри: початкова станція – Жмеринка, кінцева – П’ятихатки–Стикова, склад поїзда – 50 піввагонів по 40 т, локомотиви – ВЛ-80 і М62.

Розглянемо два варіанти.

Варіант 1. Найкоротший шлях між станціями Жмеринка й П’ятихатки–Стикова можна забезпечити рухом: на змінному струмі між станціями Жмеринка–Вапнярка, на тепловозній тязі між станціями Вапнярка–Цвіткове, та на змінному струмі між станціями Цвіткове–П’ятихатки–Стикова.

Результат моделювання: час на переміщення – 591 хв (64+330+196); вартість енерговитрат – 14 648 грн (1 365+9 130+4 153).

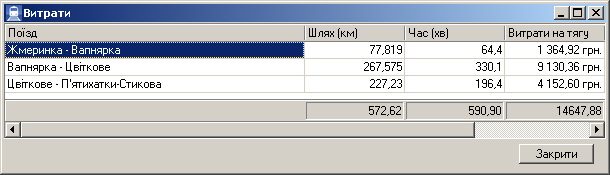
Рис. 12. Розрахунок часу й витрат (у грн) на переміщення поїзда в разі використання комбінованої тяги

Fig. 12. Calculation of time and expenses (in UAH) for the train movement in case of combined traction usage

Варіант 2. Найкоротший шлях для електричної тяги змінного струму між станціями Жмеринка–П’ятихатки–Стикова пролягає через Фастів.

Результат: час на переміщення – 514 хв; вартість енерговитрат – 10 311 грн.

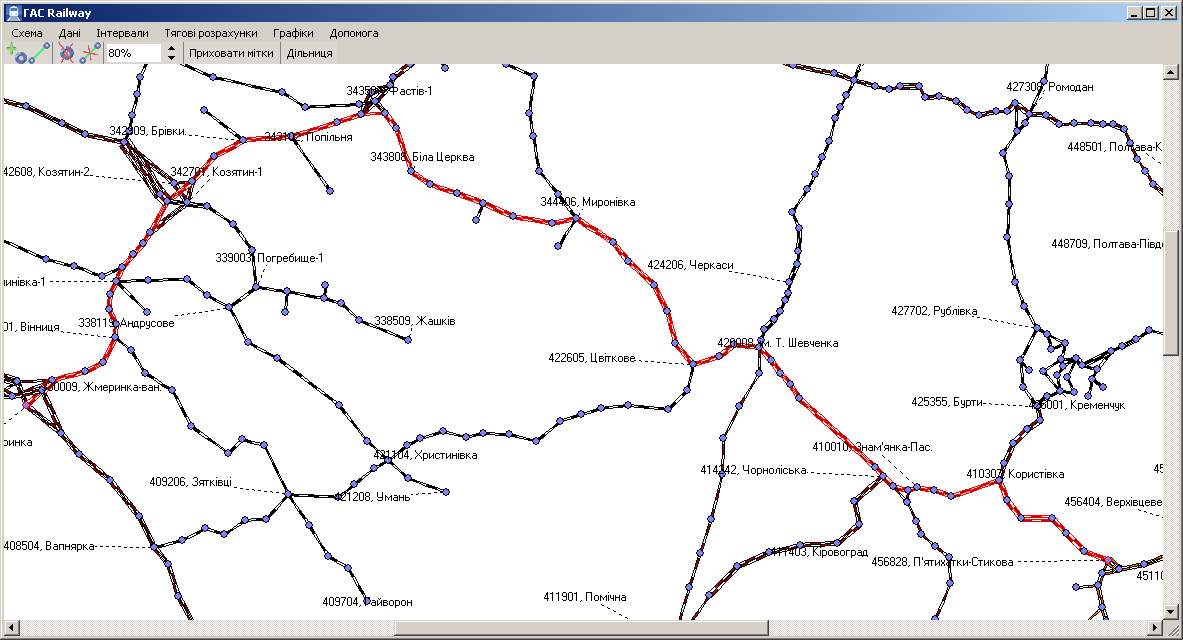
Рис. 13. Знаходження найкоротшого шляху для певного виду тяги

Fig. 13. Finding the shortest track for a particular type of traction

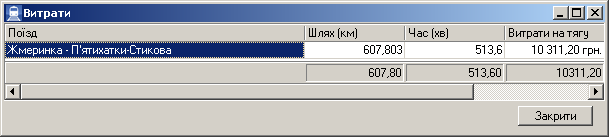
Рис. 14. Розрахунок часу й витрат на переміщення поїзда

Fig. 14. Calculation of time and expenses for the train movement

Шлях між станціями електровоз змінного струму пройде швидше і з меншими на 42 % затратами у гривнях на енергетичні ресурси.

Приклад 4. Розрахунок витрат на тягу поїзда на дільниці Мостиська–Львів–Красне–Рівне–Сарни. На граф-схемі (рис. 15) можна виділити три дільниці, які відрізняються типом тягового електропостачання. Так, на дільниці Мостиська–Львів колії електрифіковано постійним струмом напругою 3 кВ. На дільниці Львів–Красне–Рівне діє система тягового електропостачання змінного струму напругою 27 кВ, а дільниця колій Рівне–Сарни неелектрифікована.

Розрахунок на дільницях проведемо для попередньо визначеного складу поїзда й заданих серій локомотивів. У результаті отримуємо відстань, час ходу, витрати на тягу поїзда, сумарні витрати на ведення й організацію пропускання поїздів із розподілом по дільницях.

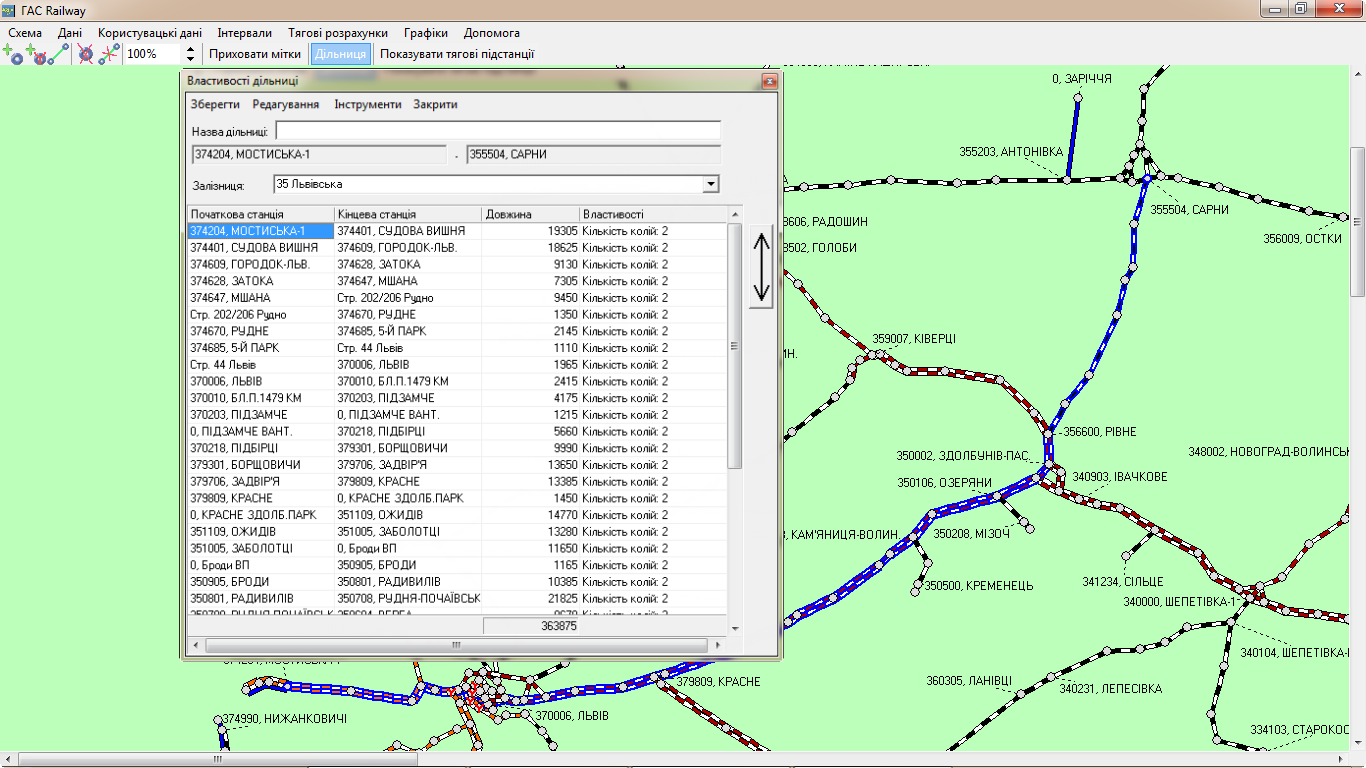
Рис. 15. Дільниця Мостиська–Львів–Красне–Рівне–Сарни

Fig. 15. Mostyska-Lviv-Krasne-Rivne-Sarny section

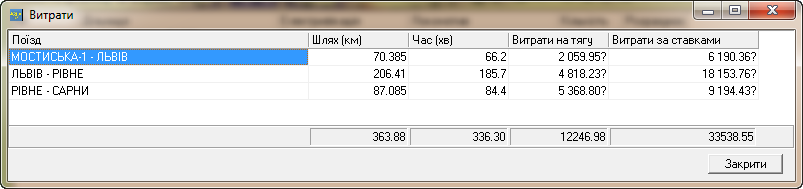
Рис. 16. Вартість енергетичних та за витратними ставками на тягу поїзду

Fig. 16. Cost of energy and the expense of traction train

У наш час правління Укрзалізниці вивчає можливість закупівлі нових локомотивів. Для цього аналізують їх тягові й струменеві характеристики. Для прикладу, на рис. 17 наведено номінальні тягові й струменеві характеристики локомотивів двох фірм – Alstom (робоча назва Альстом 8 (UA)) й КНР (назва БКГ–2 – адаптація (китайського) електровоза серії HXD2 виробництва для Республіки Білорусь).

Високу якість локомотивів із наведеними тягово-струменевими параметрами характеризує пропорційний зв’язок між величинами струму, силою тяги й швидкістю руху.

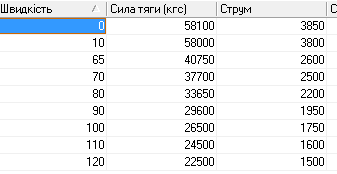
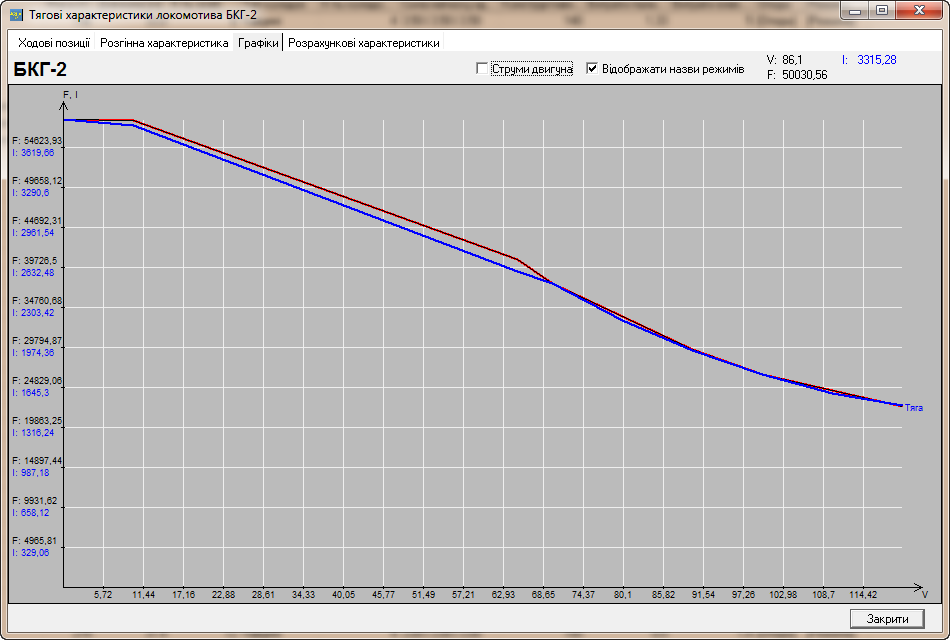
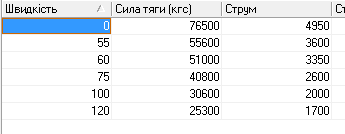
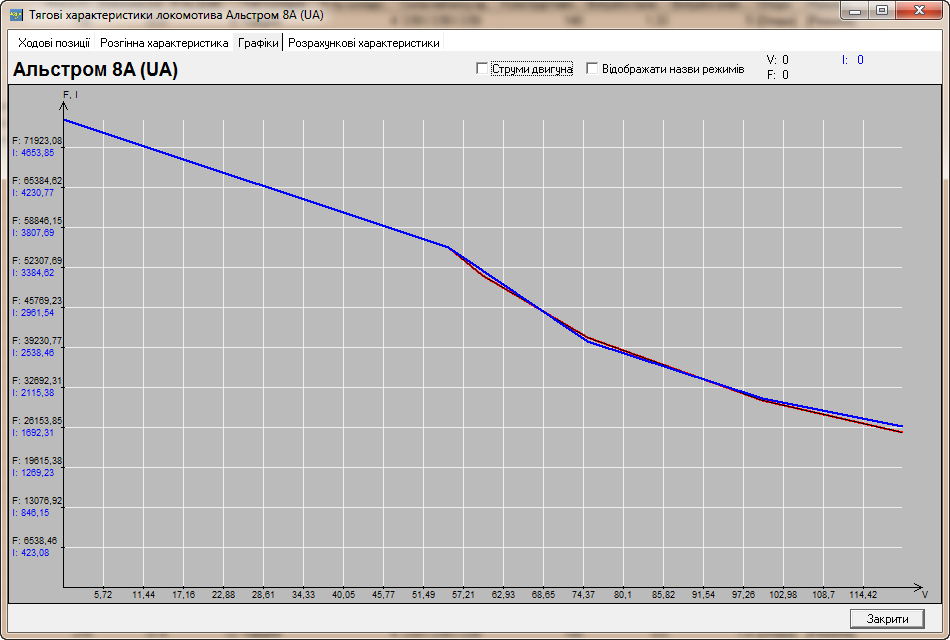
Рис. 17. Тягові й струменеві характеристики локомотивів:
а – БКГ–2; б – Альстром 8 UA

Fig. 17. Traction and jet characteristics of locomotives:
а – BKG–2; б – Alstrom 8 UA

Приклад 5. Дослідження номінальних та екстремальних техніко-економічних властивостей нових перспективних локомотивів для залізниці України.

Дослідження проведено засобами моделювального комплексу у складі вантажних поїздів на дільниці П’ятихатки–Миронівка. Розрахункова швидкість (взята для цієї категорії дільниці) – 55 км/год. За визначенням, розрахункова швидкість – шлях, який проходить повноваговий поїзд на розрахунковому підйомі за 1 год й повного використання потужності локомотива. Розрахунковий підйом – це найбільш важкий для руху в цьому напрямку елемент профілю колії, на якому досягається розрахункова швидкість, що відповідає розрахунковій силі тяги локомотива. Досить довгий і найбільш крутий підйом ділянки беремо за розрахунковий.

У прикладі 5 використано параметри: склад поїзда – 70 вагонів; навантаження – критична вага. На рис. 18 графічні залежності наведено для поїздів із різними типами локомотивів і маси (у правому куточках зверху та знизу). Розраховані максимальні маси наведено зліва у верхньому кутку. Розрахунок показав, що для локомотива фірми Skoda (робоча назва Шкода-8) склад поїзда за вагою може бути більшим.

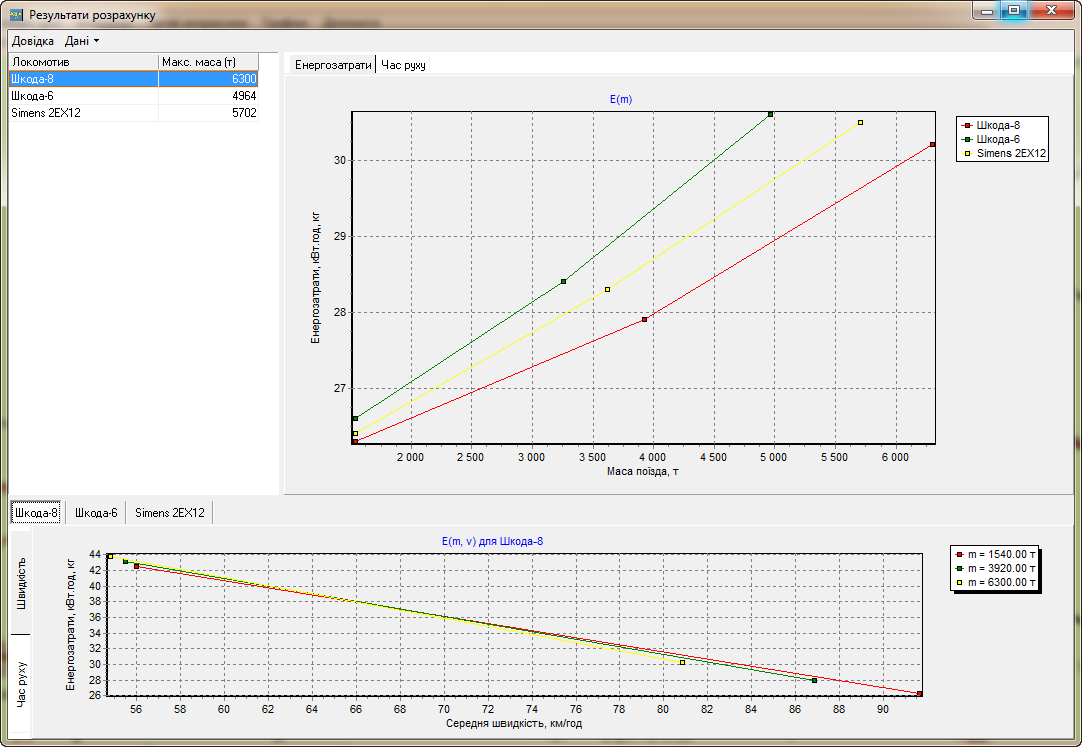
Рис. 18. Результати дослідження енергозатрат як функцій маси і швидкості поїздів
на дільниці П’ятихатки–Миронівка

Fig. 18. Results in the research of energy costs as functions of mass and speed of trains
at the Piatykhatky-Mironovka section

Аналогічні дослідження проведено для інших локомотивів – БКГ–2, Альстом 8А (UA) тощо.

Приклад 6. Знаходження критичних ухилів. Визначено складні для ведення поїзда дільниці колії – перегони з максимальним значенням ухилу на підйомі (спуску) за довжини ухилу, яка має перевищувати загальну довжину складу поїзда (рис. 19).

П’ятихатки–Знам’янка Знам’янка–Миронівка

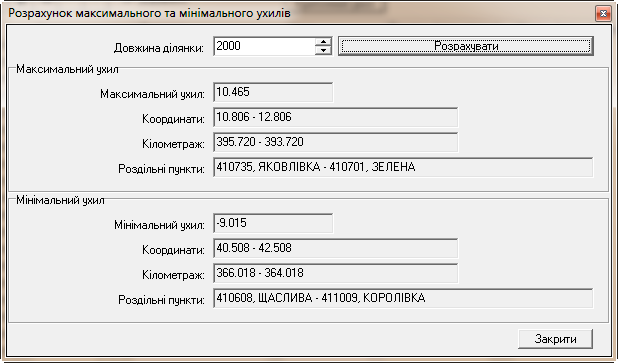
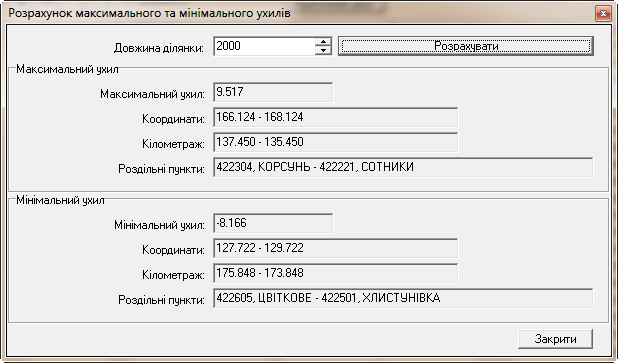
Рис. 19. Результати знаходження екстремальних ухилів

Fig. 19. Results of finding extreme gradients

Наукова новизна та практична
значимість

У роботі запропоновано математичне й програмне забезпечення для: прокладання шляхів за встановленими критеріями оптимальності між виділеними роздільними пунктами; розв’язування режимних задач ведення поїздів із різними типами тяги як задачі оптимального керування рухом на мережі залізниць. У всіх випадках забезпечена автоматизація процесу розв’язування основних режимних задач із різними критеріями оптимальності.

Розроблений програмний комплекс пройшов апробацію і для розрахунку основних складових формування графіків руху, вибору оптимальних параметрів реконструкції полотна й аналізу якісних параметрів руху нових швидкісних локомотивів у складі пасажирських і вантажних поїздів.

Висновки

Мережний варіант тягових розрахунків дає можливість постановки й розв’язання економічних задач, задач формування нормативної бази та проведення числових експериментів для пошуку оптимальних рішень за умови реконструкції полотна, оцінки ефекту від використання нових локомотивів за тягово-енергетичними й ходовими характеристиками тощо.

Розроблений мережний варіант тягових розрахунків забезпечує:

– оптимізацію траєкторії руху поїздів для заданого графіка;

– формування якісних (оптимальних за безпекою, стійкістю й інтегральними ресурсними затратами) графіків руху;

– експлуатацію поїздів за умови оптимального коригування режиму руху у випадках їх затримки (максимально точна реалізація запланованого розкладу);

– інтеграцію тягових, безпекових параметрів на перегонах і роздільних пунктах під час прокладання графіка руху;

– побудову інформаційно-дорадчої системи машиніста.

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1. Алгоритмы: построение и анализ / Т. Кормен, Ч. Лейзерсон, Р. Ривест, К. Штайн ; пер. с англ. – 2-е изд. – Москва : Вильямс, 2005. – 1296 с.

2. Кристофидес, Н. Теория графов. Алгоритмический подход / Н. Кристофидес. – Москва : Мир, 1978. – 432 с.

3. Мугиншейн, Л. А. Энергооптимальные методы управления движением поездов / Л. А. Мугиншейн,
   А. У. Илютович, И. А. Ябко. – Москва : Интекст, 2012. – 80 с.

4. Притула, М. Г. Алгоритм побудови графіка руху поїздів / М. Г. Притула, Р. Р. Шпакович // Вісн. Нац. ун-ту «Львівська політехніка». Серія: Комп’ютерні науки та інформаційні технології : зб. наук. пр. – Львів, 2008. – № 629. – С. 146–152.

5. Притула, М. Г. Моделювання та розрахунок оптимальних параметрів руху поїздів / М. Г. Притула,
   Р. Р. Шпакович // Фізико-математичне моделювання та інформаційні технології. – 2007. – Вип. 5. –
   С. 139–145.

6. Притула, М. Г. Ідентифікація параметрів моделі руху поїзда / М. Г. Притула, Р. Р. Шпакович // Вісн. Нац. ун-ту «Львівська політехніка». Серія: Комп’ютерні науки та інформаційні технології : зб. наук. пр. – Львів, 2008. – № 629. – С. 105–110.

7. Притула, М. Г. Розроблення алгоритмів формування енергооптимальних режимів руху поїздів /
   М. Г. Притула, О. А. Пасечник // Наука та прогрес транспорту. – 2018. – № 6 (78). – С. 82–100.
   doi: https://doi.org/10.15802/stp2018/154641

8. Комп’ютерне моделювання залізничних транспортних засобів : метод. вказівки до виконання практичних робіт, курсового та дипломного проектування / М. Капіца, Я. Калівода, Л. Недужа, О. Очкасов,
   Д. Черняєв. – Дніпро : Дніпропетр. нац. ун-т залізн. трансп. ім. акад. В. Лазаряна, 2018. – 59 с.

9. Седжвик, Р. Фундаментальные алгоритмы на С++: Алгоритмы на графах / Р. Седжвик ; пер. с англ. – Санкт-Петербург : Диасофт, 2002. – 496 с.

10. Троелсен, Э. С# и платформа. NET 3.0 / Э. Троелсен. – Санкт-Петербург : Питер, 2008. – 1456 с.

11. An overview of recovery models and algorithms for real-time railway rescheduling / V. Cacchiani, D. Huisman, M. Kidd [at al.] // Transportation Research. Part B: Methodological. – 2014. – Vol. 63. – P. 15–37.
    doi: https://doi.org/10.1016/j.trb.2014.01.009

12. Application of an iterative framework for real-time railway rescheduling / T. Dollevoet, D. Huisman,
    L. Kroon, L. Veelenturf, J.Wagenaar // Computers & Operations Research. – 2017. – Vol. 78. – P. 203–217. doi: doi.org/10.1016/j.cor.2016.08.011

13. Corman, F. A Review of Online Dynamic Models and Algorithms for Railway Traffic Management / F. Corman, L. Meng // IEEE Transactions on Intelligent Transportation Systems. – 2015. – Vol. 16. – Iss. 3. –
    P. 1274–1284. doi: https://doi.org/10.1109/tits.2014.2358392 

14. Gholamian, S. A. A discrete-event optimization framework for mixed-speed train timetabling problem /
    S. A. Gholamian // Journal of Industrial Engineering and Management Studies. – 2017. – Vol. 4, No. 2. –
    P. 64–84.

15. http://orbit.dtu.dk/en/persons/joergen-thorlund-haahr(c3e6850e-3c3f-4a02-b903-4fd6e7ee696e).html Haahr, J. T. http://orbit.dtu.dk/en/publications/a-dynamic-programming-approach-for-optimizing-train-speed-profiles-with-speed-restrictions-and-passage-points(ea1633f1-4e92-438c-82c9-f82f6de65865).html A dynamic programming approach for optimizing train speed profiles with speed restrictions and passage points / J. T. Haahr, D. Pisinger, M. Sabbaghian // http://orbit.dtu.dk/en/journals/transportation-research-part-b-methodological(98af7cd8-0d34-48aa-88ed-306990ff5573).html Transportation Research. Part B: Methodological. – 2017. – Vol. 99. – P. 167–182. doi: https://doi.org/10.1016/j.trb.2016.12.016

16. Joint optimization of high-speed train timetables and speed profiles: A unified modeling approach using space-time-speed grid networks / L. Zhou, Lu (Carol) Tong, J. Chen, J. Tang, X. Zhou // Transportation Research. Part B: Methodological. – 2017. – Vol. 97. – P. 157–181. doi: https://doi.org/10.1016/j.trb.2017.01.002

17. Klimenko, I. Parameter optimization of the locomotive running gear / I. Klimenko, J. Kalivoda, L. Neduzha // Transport Means 2018 : Proceedings of 22nd International Scientific Conference (October 3–5, 2018) / Kaunas University of Technology. – Trakai, Klaipėda, 2018. – Р. 1095–1098.

18. Review of energy efficient train control and timetabling / G. Scheepmaker, M. Gerben, R. Goverde, L. Kroon // European Journal of Operational Research. – 2017. – Vol. 257. – Iss. 2. – P. 355–376.
    doi: https://doi.org/10.1016/j.ejor.2016.09.044

19. Skiena, S. S. The Algorithm Design Manual / S. S. Skiena. – London : Springer,2008. – 730 p.
    doi: https://doi.org/10.1007/978-1-84800-070-4

20. The key principles of optimal train control. Part 1: Formulation of the model, strategies of optimal type, evolutionary lines, location of optimal switching points / A. Albrecht, P. Howlett, P. Pudney, X. Vu, P. Zhou // Transportation Research. Part B: Methodological. – 2016. – Vol. 94. – P. 482–508.
    doi: https://doi.org/10.1016/j.trb.2015.07.023

21. The key principles of optimal train control. Part 2: Existence of an optimal strategy, the local energy minimization principle, uniqueness, computational techniques / A. Albrecht, P. Howlett, P. Pudney, X. Vu, P. Zhou // Transportation Research. Part B: Methodological. – 2016. – Vol. 94. – P. 509–538.
    doi: https://doi.org/10.1016/j.trb.2015.07.024

22. Wang, P. Train Trajectory Optimization Methods for Energy-Efficient Railway Operations : doctoral thesis [Електронний ресурс] / P. Wang ; Delft University of Technology. – Delft, 2017. – Режим доступу: https://repository.tudelft.nl/islandora/object/uuid%3Ace04a07d-89fc-470a-9d1a-b6fae9182dae. – Назва
    з екрана. – Перевірено : 18.06.2019.

23. Warg, J. The use of railway simulation as an input to economic assessment of timetables / J. Warg, M. Bohlin // Journal of Rail Transport Planning & Management. – 2016. – Vol. 6. – Iss. 3. – P. 255–270.
    doi: https://doi.org/10.1016/j.jrtpm.2016.08.001

24. Ye, H. Nonlinear programming methods based on closed-form expressions for optimal train control / H. Ye,
    R. Liu // Transportation Research. Part C: Emerging Technologies. – 2017. – Vol. 82. – P. 102–123.
    doi: https://doi.org/10.1016/j.trc.2017.06.011

М. Г. ПРИТУЛА^1*, А. А. ПАСЕЧНИК^2*

^1*Центр математического моделирования НАНУ, ул. Дудаева, 15,
Львов, Украина, 79053, тел. +38 (032) 261 18 85,
эл. почта myroslav.prytula@gmail.com , ORCID 0000-0001-9259-4114
^2*ГП «Проектно-конструкторское технологическое бюро
по автоматизации систем управления на железнодорожном
транспорте Украины», ул. Жилянская, 97, Киев,
Украина, 01135, тел. +38 (044) 226 24 82,
эл. почта sasha1101@ukr.net, ORCID 0000-0001-7303-0145

ОПТИМИЗАЦИОННЫЕ ТЯГОВЫЕ ЗАДАЧИ

НА ЖЕЛЕЗНОДОРОЖНОЙ СЕТИ

Цель. Работа предусматривает разработку информационного и алгоритмического обеспечения для проведения оптимизационных тягово-энергетических расчетов на железнодорожной сети с целью их дальнейшего использования в системах эффективного управления перевозочным процессом. Методика. В основе исследования – графоаналитическая система, модель движения поезда с различными типами тяги, методы оптимального управления поездом и фундаментальные алгоритмы на взвешенных графах с возможными параллельными ребрами (дугами). В комплексе эти составляющие системы обеспечивают нахождение на граф-схеме путей по заданным критериям, проведение оптимизационных тягово-энергетических расчетов, а также сравнительного анализа полученных результатов. Достоверность результатов неоднократно проверена имеющимися способами для различной сложности перегонов по плану и профилю трассы. Для этого использованы данные, полученные в результате проведения контрольных поездок с применением динамометрических вагонов, а также проведен сравнительный анализ режимов работы поездов, рассчитанных и полученных квалифицированными машинистами на различных перегонах. Результаты. Рассмотрена проблема эффективной эксплуатации различных типов и модификаций локомотивов, задействованных в реализации графиков движения поездов различного назначения и нагрузки. Приведена постановка прямых и обратных оптимизационных, по различным критериям, режимных задач на железнодорожной сети и варианты их эффективного решения. Приведен анализ результатов разработанного математического обеспечения и идеи реализованных алгоритмов. Научная новизна. В работе предложена постановка сетевых оптимизационных задач, возникающих на этапах разработки плана формирования поездов, построения графиков движения, оценки пропускной способности, расчета оптимальных параметров составляющих графиков движения и др. Важным является системный подход, который обеспечил сочетание разработанной модели сети в универсальных терминах теории графов с системой актуализации их параметров. Тягово-энергетические расчеты проведены методами комбинаторной оптимизации, что обеспечило максимальный уровень автоматизации процесса решения большого набора прямых и обратных режимных задач с различными критериями оптимальности. Практическая значимость. Разработано информационное и алгоритмическое обеспечение для автоматизации процесса решения прямых и обратных режимных тягово-энергетических задач на железнодорожной сети, которое прошло апробацию в процессе расчета основных составляющих для формирования графиков движения, анализа режимов ведения поездов, оценки выбора оптимальных параметров реконструкции путевого полотна для скоростных и новых типов поездов (локомотивов).

Ключевые слова: тяговые расчеты; железнодорожная сеть; фундаментальные алгоритмы; режим движения; оптимальный режим; график движения; безопасность движения; математическое обеспечение

M. G. PRYTULA^1*, О. А. PASECHNYK^2*

^1*Center of Mathematical Modelling NASU, Dudaev St., 15,
Lviv, Ukraine, 79053, tel. +38 (032) 261 18 85,
e-mail myroslav.prytula@gmail.com,
ORCID 0000-0001-9259-4114
^2*SE «Design and Development Bureau of Automation
of Control Systems in the Railway Transport of Ukraine»,
Zhylianska St., 97, Kyiv, Ukraine, 01135,
tel. +38 (044) 226 24 82, e-mail sasha1101@ukr.net,
ORCID 0000-0001-7303-0145

OPTIMIZATIONAL TRACTION TASKS

ON THE RAILWAY NETWORK

Purpose. The paper involves the development of information and algorithmic support for conducting the optimization traction and energy calculations on the railway network for their further use in decision-making systems – systems for efficient management of the transport process. Methodology. The system is based on the graph-analytic system, the model of the train with different types of traction, the methods of optimal control of the train and the fundamental algorithms on the weighted graphs with possible parallel ribs (arcs). In the complex, these components of the system provide finding the tracks on the chart-diagram according to the given criteria, conducting the optimization traction-energy calculations according to different criteria, as well as conducting a comparative analysis of the obtained results. The reliability of the results has been repeatedly checked by available methods for varying complexity of race according to the plan and profile of the course. For this purpose, data obtained as a result of control visits using dynamometric cars were used. Also a comparative analysis of the modes in operation of trains, calculated and received by qualified drivers on different races was conducted. Findings. The problem of efficient operation of various types and modifications of locomotives, involved in the implementation of trains schedules for different purposes and loads is considered. Presentations of direct and inverse optimization, according to various criteria, of the regime tasks on the railway network and variants of their effective solution are given. The analysis of the results of the developed mathematical support and the ideas of implemented algorithms is given. Originality. The paper proposes the establishment of the network optimization problems that arise at the stages of the developing the plan for the formation, construction of traffic schedules, transmission capacity assessment and the calculation of optimal parameters for the composite graphs of motion, etc. The system approach is important to ensure the combination of the developed network structure in the universal terms of the graph theory with the system of actualization of their parameters. Pull and energy efficiency calculations are carried out by combinatorial optimization methods, which ensured the maximum level of automation of the process in solving a large set of direct and inverse regime problems with different optimality criteria. Practical value. The information and algorithmic support for the automation of the process in solving the direct and reverse regime traction-energy problems on the railway network was developed. It was tested in the process of calculating the main components for the formation of traffic schedules, analysis of train driving modes, assessment in choosing the optimal parameters of the track reconstruction for high-speed and new types of trains (locomotives).

Keywords: traction calculations; railway network; fundamental algorithms; mode of movement; optimal mode; schedule; traffic safety; mathematical support

REFERENCES

1. Kormen, T. K., Leyzerson, C. I., Rivest, R. L., & Shtayn, K. (2011). Algoritmy: Postroenie i analiz. Moskow: Williams. (in Russian)

2. Kristofides, N. (1978). Teoriya grafov. Algoritmicheskiy podkhod. Moskow: Mir. (in Russian)

3. Muginsheyn, L. A., Ilyutovich, A. U., & Yabko, I. A. (2012). Energooptimalnye metody upravleniya dvizheniem poezdov. Moskow: Intext. (in Russian)

4. Prytula, M. H., & Shpakovych, R. R. (2008). Alhorytm pobudovy hrafika rukhu poizdiv. Bulletin of the National University «Lviv Polytechnic». Series: Computer Science and Information Technologies, 629, 146-152. (in Ukrainian)

5. Prytula, M. H., & Shpakovych, R. R. (2007). Modeliuvannia ta rozrakhunok optymalnykh parametriv rukhu poizdiv. Physical-mathematical modeling and information technologies, 5, 139-145. (in Ukrainian)

6. Prytula, M. H., & Shpakovych, R. R. (2008). Identyfikatsiia parametriv modeli rukhu poizda. Bulletin of the National University «Lviv Polytechnic». Series: Computer Science and Information Technologies, 629, 105-110. (in Ukrainian)

7. Prytula, M. G., & Pasechnyk, O. A. (2019). Development of the algorithms formation of energy-optimized trains traffic modes. Science and Transport Progress, 6(78), 82-100.
   doi: https://doi.org/10.15802/stp2018/154641 (in Ukrainian)

8. Kapіtsa, M. І., Kalіvoda, J., Neduzha, L. O., Ochkasov, O. B., & Chernyayev, D. V. (2018). Komp’yuterne modelyuvannya zalіznichnikh transportnikh zasobіv: metodychni vkazivky do vykonannia praktychnykh robit, kursovoho ta dyplomnoho proektuvannia. Dnipro. (in Ukranian)

9. Sedzhvik, R. (2002). Fundamentalnye algoritmy na S++: Algoritmy na grafakh. St. Petersburg: Diasoft. (in Russian)

10. Troelsen, E. (2008). S# i platforma. NET 3.0. St. Petersburg: Piter. (in Russian)

11. Cacchiani, V., Huisman, D., Kidd, M., Kroon, L., Toth, P., Veelenturf, L., & Wagenaar, J. (2014). An overview of recovery models and algorithms for real-time railway rescheduling. Transportation Research. Part B: Methodological, 63, 15-37. doi: https://doi.org/10.1016/j.trb.2014.01.009 (in English)

12. Dollevoet, T., Huisman, D., Kroon, L. G., Veelenturf, L. P., & Wagenaar, J. C. (2017). Application of an iterative framework for real-time railway rescheduling. Computers & Operations Research, 78, 203-217.
    doi: doi.org/10.1016/j.cor.2016.08.011 (in English)

13. Corman, F., & Meng, L. (2015). Review of Online Dynamic Models and Algorithms for Railway Traffic Management. IEEE Transactions on Intelligent Transportation Systems, 16(3), 1274-1284.
    doi: https://doi.org/10.1109/tits.2014.2358392  (in English)

14. Gholamian, S. A. (2017). A discrete-event optimization framework for mixed-speed train timetabling problem. Journal of Industrial Engineering and Management Studies, 4(2), 64-84. (in English)

15. http://orbit.dtu.dk/en/persons/joergen-thorlund-haahr(c3e6850e-3c3f-4a02-b903-4fd6e7ee696e).html Haahr, J., Pisinger, D., & Sabbaghian, M. (2017). http://orbit.dtu.dk/en/publications/a-dynamic-programming-approach-for-optimizing-train-speed-profiles-with-speed-restrictions-and-passage-points(ea1633f1-4e92-438c-82c9-f82f6de65865).html A dynamic programming approach for optimizing train speed profiles with speed restrictions and passage points. Transportation Research Part B: Methodological, 99, 167-182. doi: https://doi.org/10.1016/j.trb.2016.12.016  (in English)

16. Zhou, L., Tong, Lu (Carol), Chen, J., Tang, J., & Zhou, X. (2017). Joint optimization of high-speed train timetables and speed profiles: A unified modeling approach using space-time-speed grid networks. Transportation Research. Part B: Methodological, 97, 157-181. doi: https://doi.org/10.1016/j.trb.2017.01.002 (in English)

17. Klimenko, І, Kalivoda, J., & Neduzha, L. (2018). Parameter Optimization of the Locomotive Running Gear, Transport Means 2018: Proceedings of 22nd International Scientific Conference. Trakai, Klaipėda. (in English)

18. Scheepmaker, G. M., Goverde, R. M. P., & Kroon, L. G. (2017). Review of energy-efficient train control and timetabling. European Journal of Operational Research, 257(2), 355-376.
    doi: https://doi.org/10.1016/j.ejor.2016.09.044 (in English)

19. Skiena, S. S. (2008). The Algorithm Design Manual. London: Springer. doi: https://doi.org/10.1007/978-1-84800-070-4 (in English)

20. Albrecht, A., Howlett, P., Pudney, P., Vu, X., & Zhou, P. (2016). The key principles of optimal train control. Part 1: Formulation of the model, strategies of optimal type, evolutionary lines, location of optimal switching points. Transportation Research. Part B: Methodological, 94, 482-508.
    doi: https://doi.org/10.1016/j.trb.2015.07.023 (in English)

21. Albrecht, A., Howlett, P., Pudney, P., Vu, X. & Zhou P. (2016). The key principles of optimal train control. Part 2: Existence of an optimal strategy, the local energy minimization principle, uniqueness, computational techniques. Transportation Research. Part B: Methodological, 94, 509-538.
    doi: https://doi.org/10.1016/j.trb.2015.07.024 (in English)

22. Wang, P. (2017). Train Trajectory Optimization Methods for Energy-Efficient Railway Operations. (Doctoral thesis). Delft University of Technology, Delft. Retrieved from https://repository.tudelft.nl/islandora/object/uuid%3Ace04a07d-89fc-470a-9d1a-b6fae9182dae (in English)

23. Warg, J., & Bohlin, M. (2016). The use of railway simulation as an input to economic assessment of timetables. Journal of Rail Transport Planning & Management, 6(3), 255-270.
    doi: https://doi.org/10.1016/j.jrtpm.2016.08.001 (in English)

24. Ye, H., & Liu, R. (2017). Nonlinear programming methods based on closed-form expressions for optimal train control. Transportation Research. Part C: Emerging Technologies, 82, 102-123.
    doi: https://doi.org/10.1016/j.trc.2017.06.011 (in English)

Надійшла до редколегії: 16.01.2019

Прийнята до друку: 14.05.2019

Creative Commons Attribution 4.0 International

doi: https://doi.org/10.15802/stp2019/171774 © М. Г. Притула, О. А. Пасечник, 2019