ISSN 2307–3489 (Print), ІSSN 2307–6666 (Online)

Наука та прогрес транспорту. Вісник Дніпропетровського
національного університету залізничного транспорту, 2019, № 2(80)

Інформаційно-комунікаційні технології та
математичне моделювання

Introduction

Until recently, the work of the railway transport of Ukraine was the interaction of six railways, on each of which an appropriate information and telecommunication system (ITS) was implemented. The main focus of the development of ITS rail networks is the use of Ethernet (Ethernet, Fast Ethernet, Gigabit Ethernet) family technologies that provide a 10/100/1000 Mbps hierarchy and the use of the TCP/IP protocol stack [9]. The most important part of ITS of railway transport is the data transmission network, which is a three-level hierarchical structure and has the following levels: trunk, road, linear. The node of the data transmission network belongs to the trunk level, if it includes, besides the connections to the nodes of the data transmission network of a particular railway, a connection to the nodes of the data transmission network of other railways. Local enterprise networks belong to the linear level, all other nodes of the data network – to the road level.

To build a unified data transmission network of Ukrzaliznytsia, the network equipment of Cisco [13], which is an integrated software and hardware complex, was selected. One of the key tasks is the organization of routing in the railway transport ITS network. The current routing protocol (OSPF protocol) uses the search for the shortest path on the graph, the real-time implementation of which causes some difficulties, so it is advisable to find solutions to the routing problem using the methods of artificial intelligence [10, 13-20] and study them [1-4, 7]. For example, for the search of the shortest path on the route graph in the railway transport ITS, we analyzed the possibility of using the Hopfield network, ant colony and genetic methods [8], for the integrated network of ITS of railway transport, that in the prospect should work on different technologies, we defined the optimal route by the means of the software model «MLP34-2-410-34», the input of which is an array of bandwidth network channels [17]. In addition to the parameters studied (distance between routers, channel bandwidth) it is appropriate to conduct
a study of other parameters, such as: service availability; line losses; router delays.

Purpose

To develop a routing methodology in the ITS network of rail transport at the trunk level using the neural network technology.

Methodology

Let us consider a fragment of a hypothetical network of railway transport ITS presented in Fig. 1.

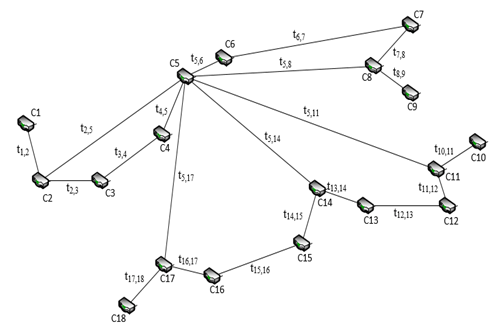
Fig. 1. Graph of routers connections of hypothetical network of information and telecommunication system (ITS) of railway transportDesignations: C1 – Rivne; С2 – Lviv; C3 – Ternopil; C4 – Khmelnytskyi; С5 – Kyiv; C6 – Nizhyn; С7 – Poltava; С8 – Kharkiv; С9 – Sumy; С10 – Luhansk; C11 – Donetsk; C12 – Krasnoarmiisk; C13 – Chaplyne; С14 – Dnipro; С15 – Zaporizhzhia; C16 – Znamianka; С17 – Odesa; C18 – Izmail

The ITS network of rail transport may be represented as a weighted graph G (V, W), where V is the set of vertices of the graph whose number is equal to B (B = 18), with each vertex modeling a node (router) of the network; W is the set of edges of the graph, each edge simulates the relationship between the nodes, the number of graph edges is equal to M (M = 21).

Each edge of the graph is assigned with a certain weight t_ij. Since the channel transmission time is much smaller, it is expedient to use the router delay time when transmitting data from the i-th to j-th router of the ITS network of railway transport, as a weight, in μs.

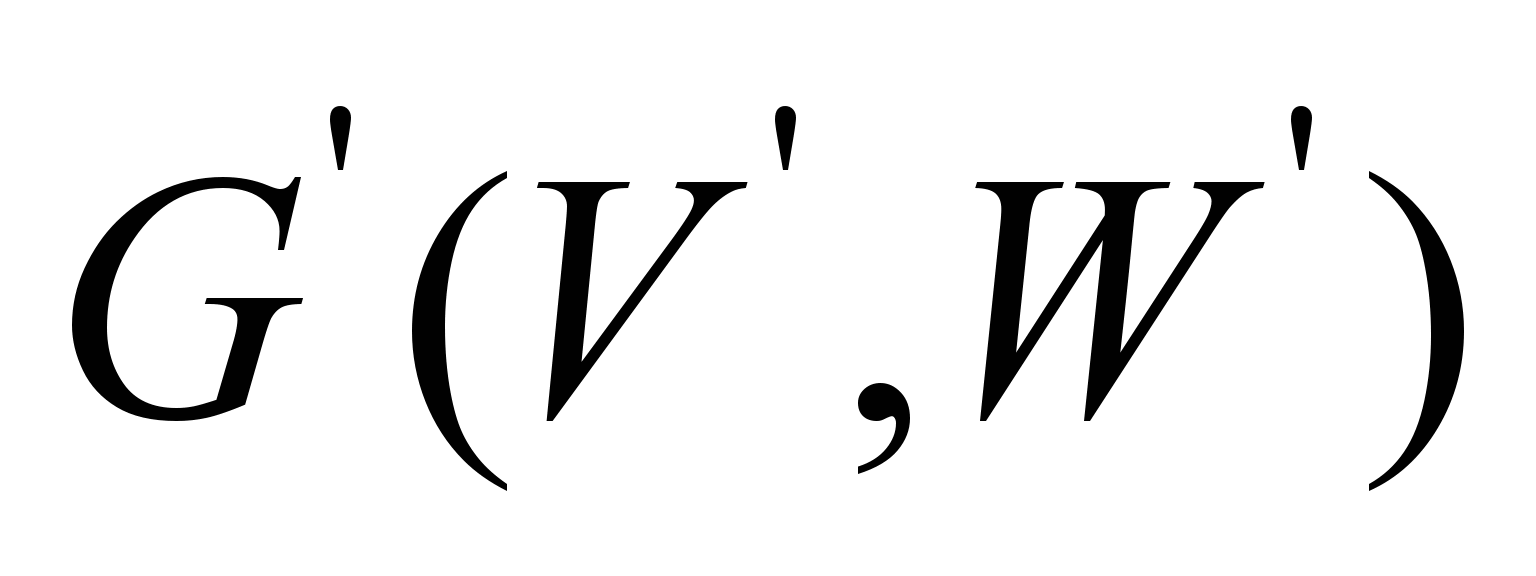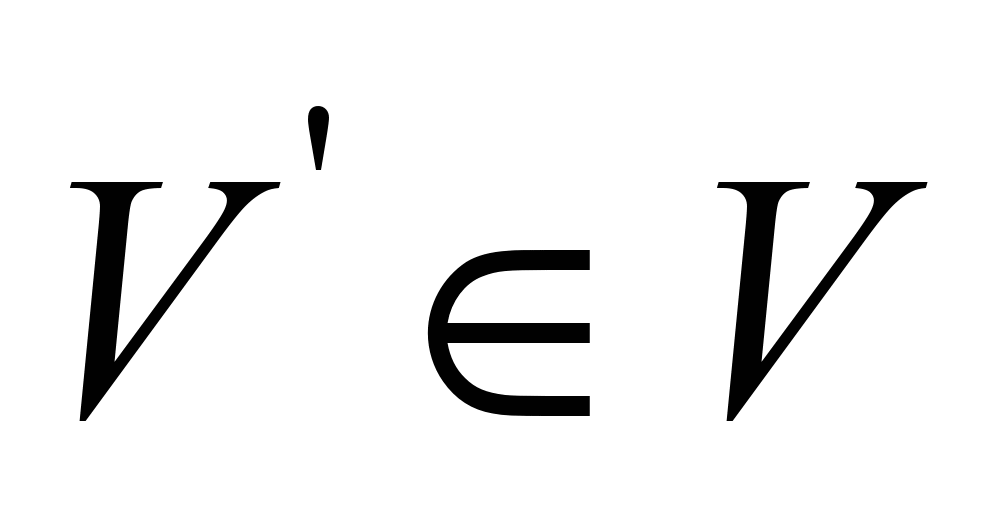It is necessary to determine the minimal spanning tree (MST) of the rail transport ITS network, that is, to find such a graph , where and 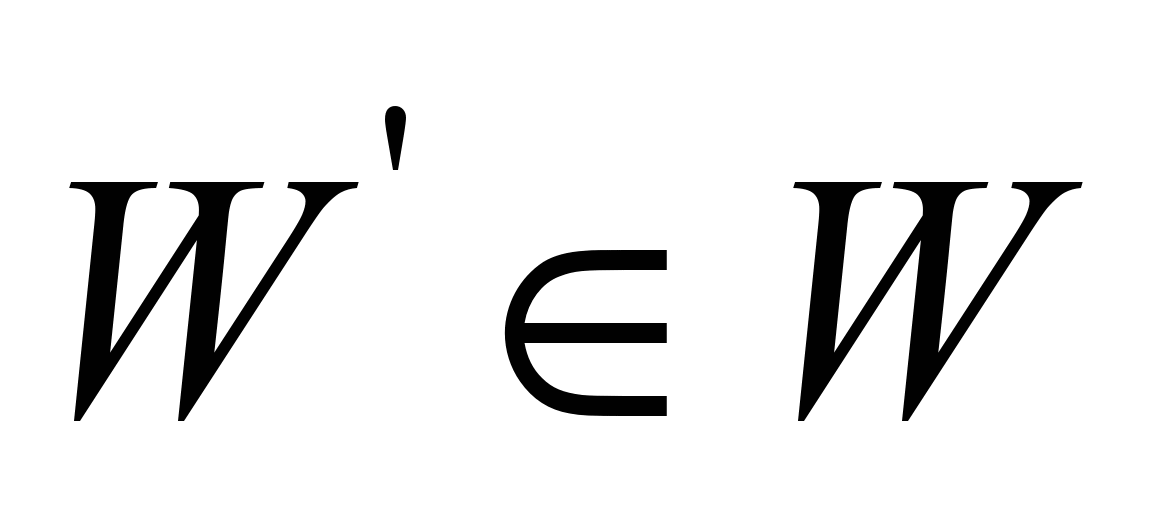, in addition

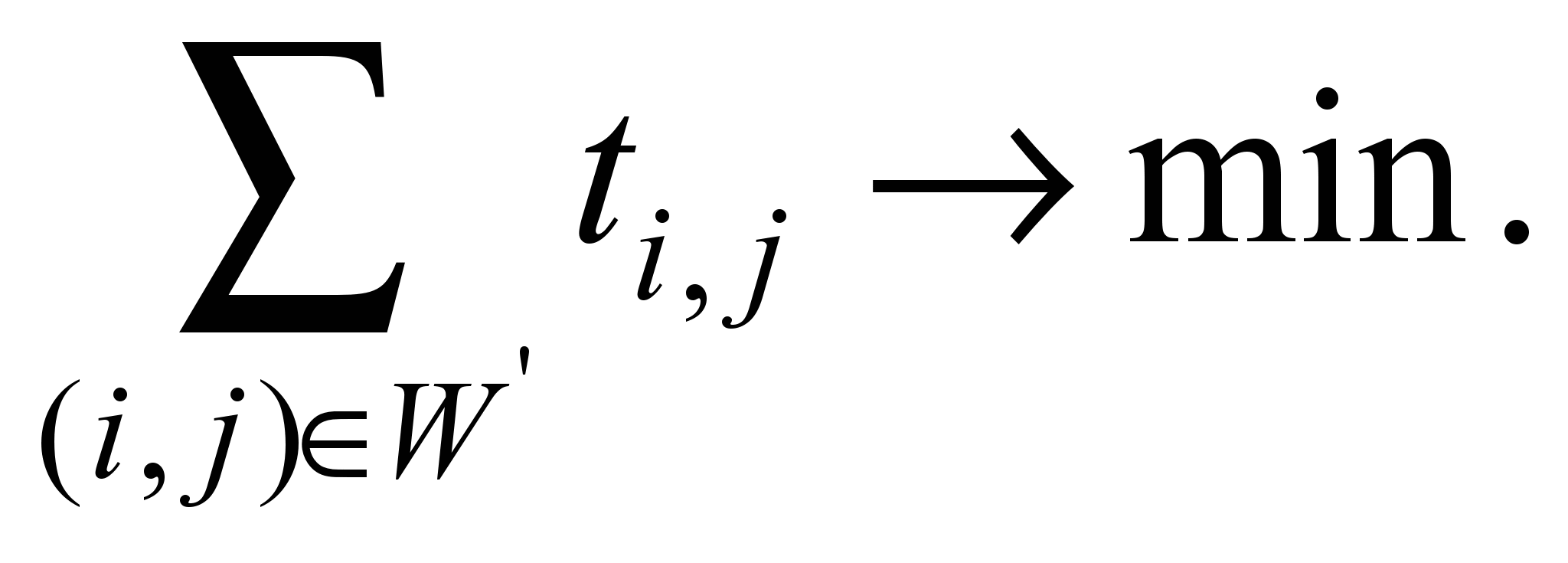(1)

The construction of MST is useful for distributing messages addressed to all nodes of the ITS network of rail transport at the trunk level, for example, the control messages from the main node (Kyiv), then the weight of the whole spanning tree is the cost of sending a message to all its nodes. It should also be noted that if all the weights of the graph edges are different then there is only one MST of the network.

Neural network as the main mathematical device for solving the problem. To determine the MST in the ITS network of rail transport, we used a two-layer neural network (NN), the input vector of which is a plurality of delays on routers and consists of 21 neurons, the resulting vector is build tags of communication channels to the routes, and also consists of 21 neurons. The corresponding NN structure is shown in Fig. 2.

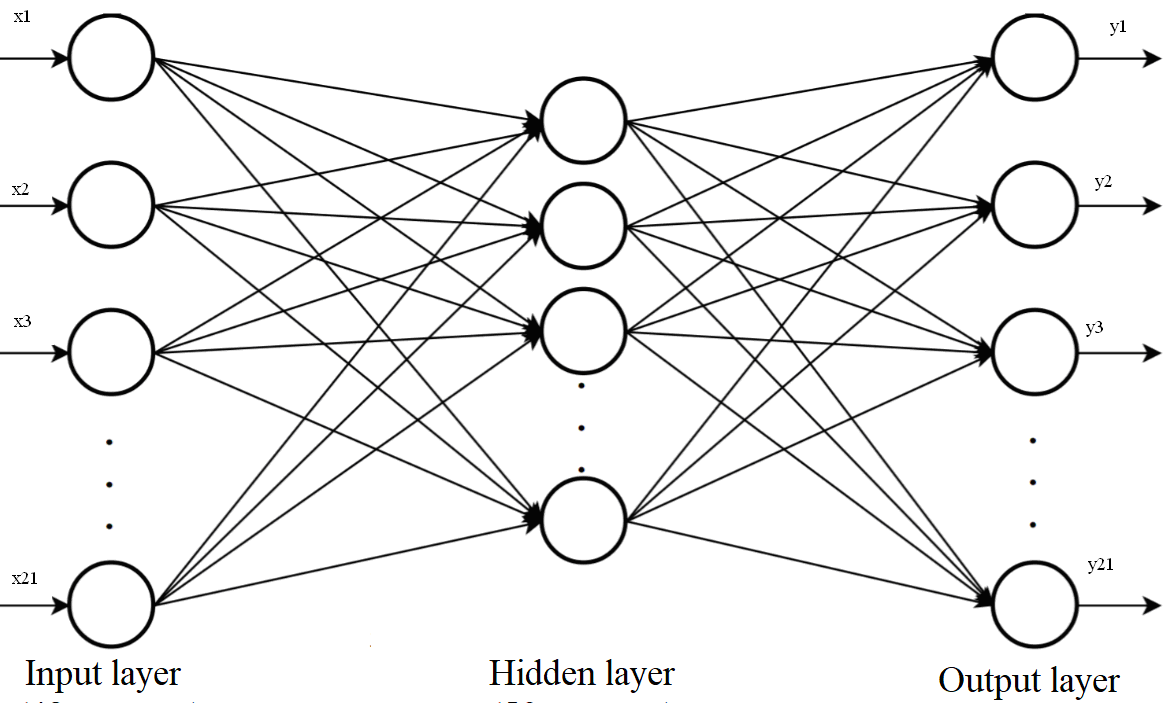
Fig. 2. Structure of the two-layer neural network (NN)

As an activation function of a hidden layer it is appropriate to use the sigmoidal function, which is presented in Fig. 3, a, in the resulting layer – a linear function shown in Fig. 3, b.

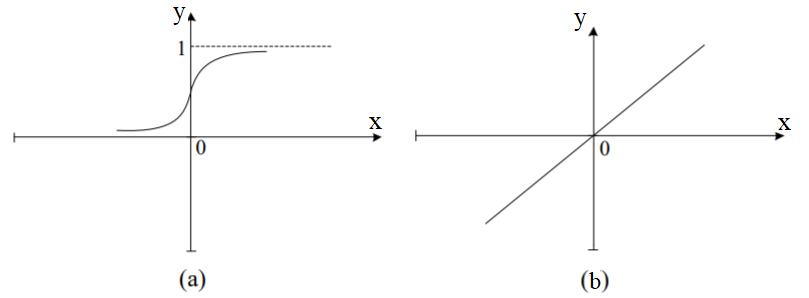
Fig. 3. Activation function graphs:
а – sigmoid; b – linear

Determination of the number of neurons in NN layers is performed using the following formula:

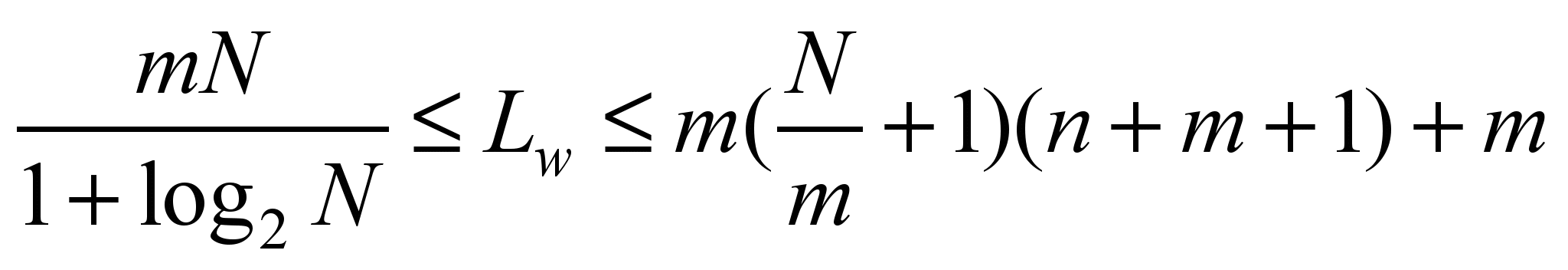(2)

where – the number of synaptic weights; n –input signal dimension; m – output signal dimension; N – the number of sample elements.

In this case 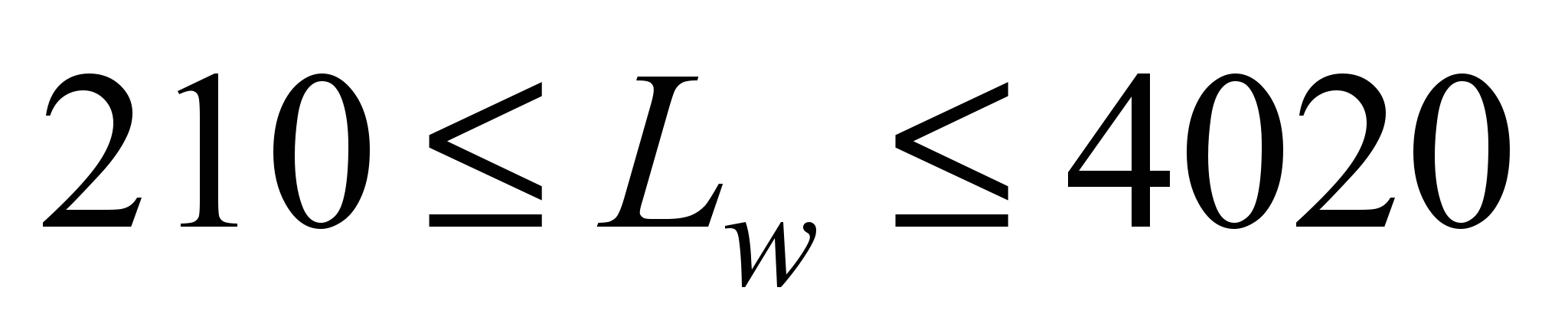. Having estimated the required number of synaptic weights , we calculate the required number of neurons in the hidden layer k according to the known formula:

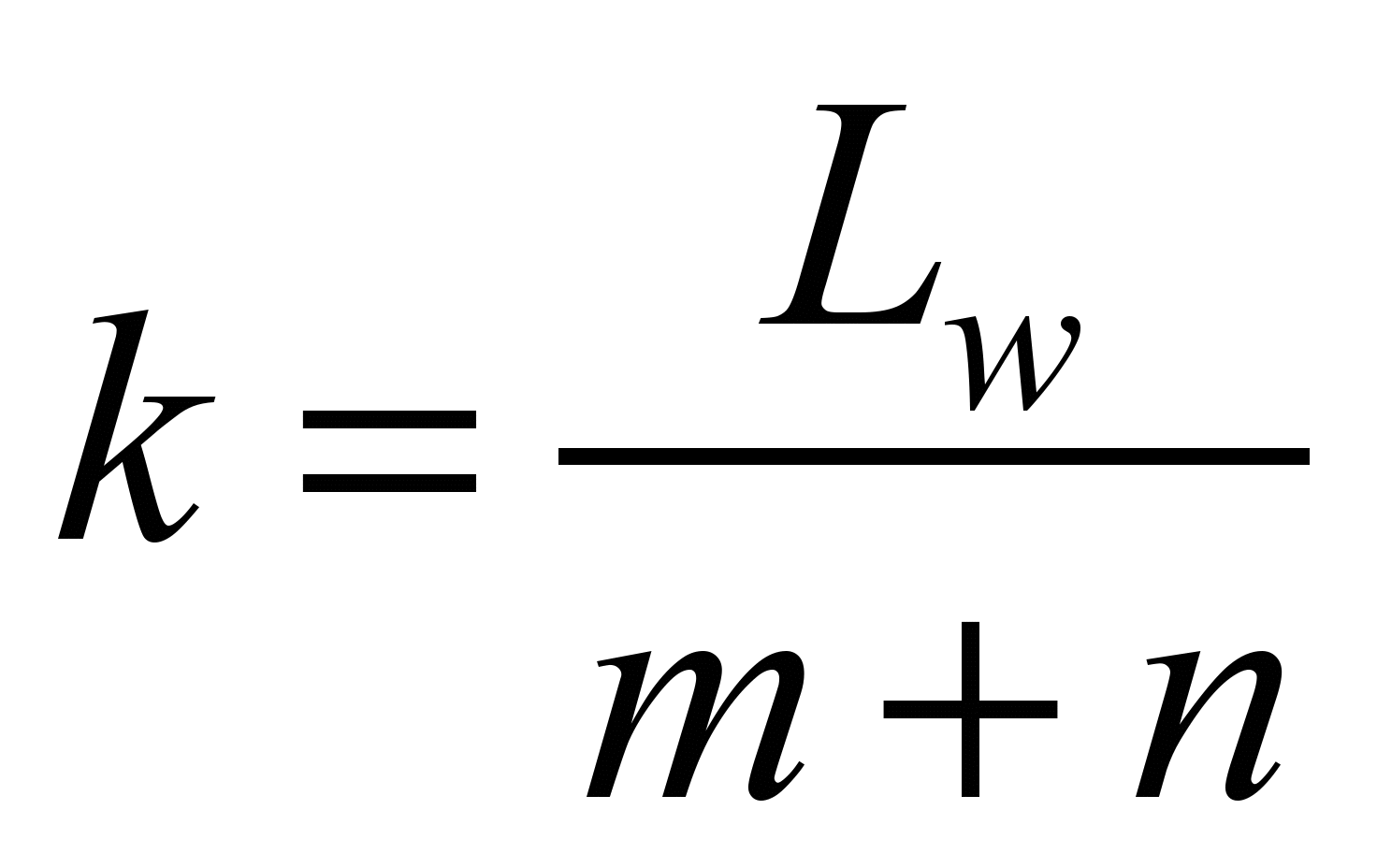. (3)

If you take 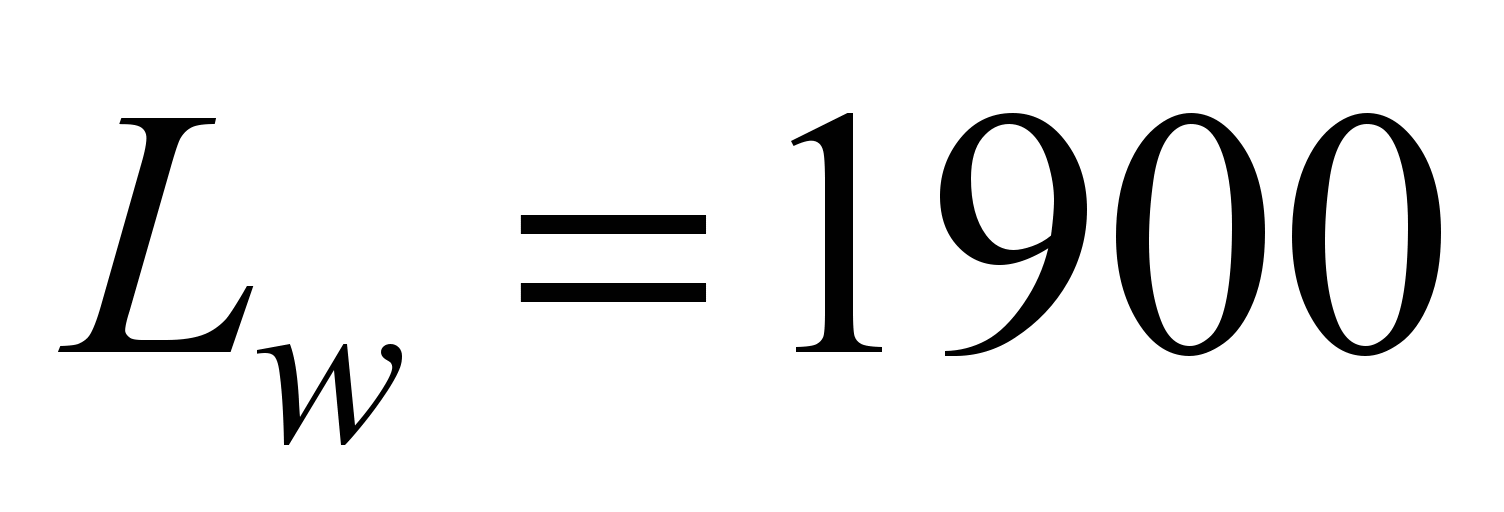, then the number of neurons in the hidden layer will be 45.

The training of a multi-layered NN involves the use of the reverse error propagation algorithm. The training samples are used for learning. The basis of NM training is the minimization of some target function, which depends on the parameters of the neurons and infinity of training samples. As a minimizing target error function of a multilayer NN, the function of the following type is taken:

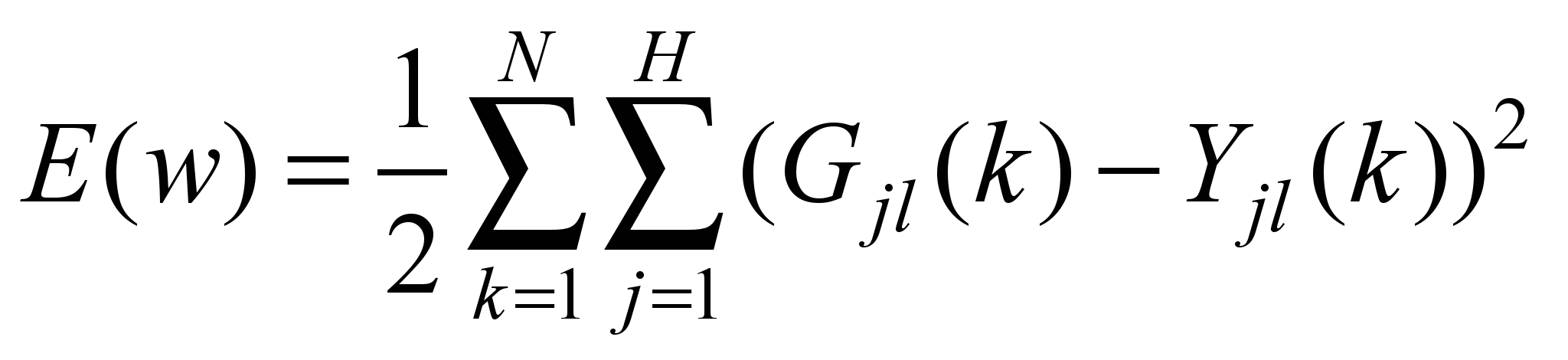, (4)

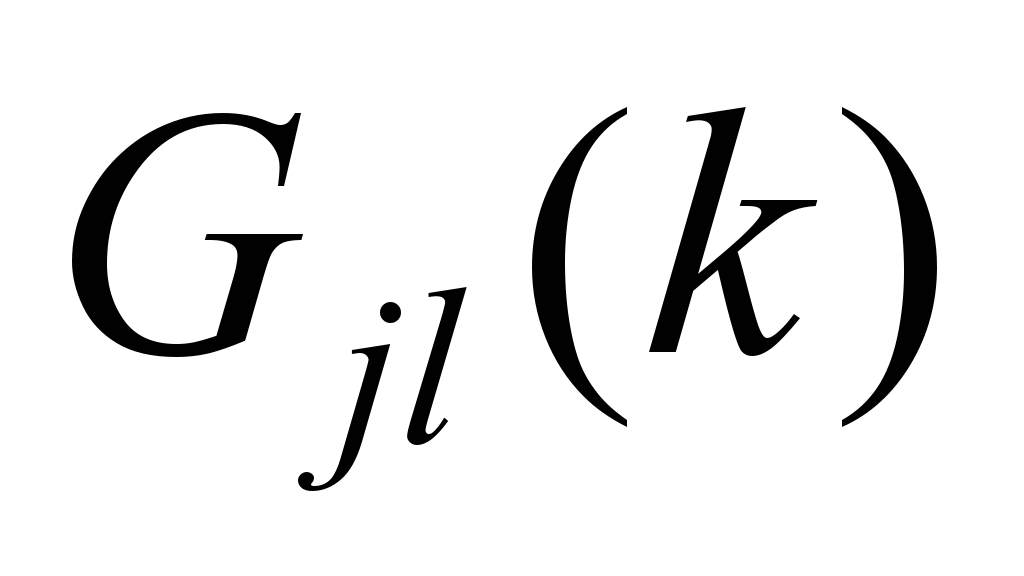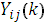where – desired output of the j-th neuron of the l-th output layer for k-th sample of the reference set; – actual output of the j-th neuron of the l-th output layer when supplied to the k-th sample network input from the reference set.

Preparation of the general sample (preparatory stage). The formation of a general sample of NN was carried out for a fragment of a hypothetical network of railway ITS (see Fig. 1). Sample data are obtained on the corresponding simulation model of the ITS network of rail transport, created with assistance of the Master A. Piskun in modelling system OpNet Modeler [6] using Gigabit Ethernet technology under the following conditions: protocol – TCP; type of traffic – FTP; traffic intensity – 600 MB/s; package length – 700 bytes; operation time of the network simulation model – 14 min. Learning vectors are formed in the form of tables using the Excel package in two files. In the first file «input.xml», the data submitted to the NN input, are presented in the form of 21 vectors;
a fragment of contents of the file «input.xml» is shown in Fig. 4.

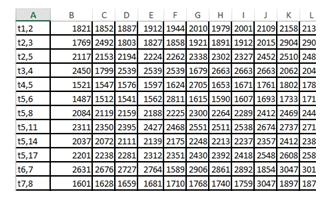
Fig. 4. Fragment of contents of the file «input.xml»

In the second file «target.xml», the data submitted to the NN output are also represented as 21 vectors; a fragment of contents of the «target.xml» file is shown in Fig. 5.

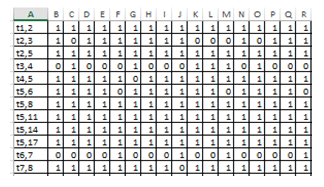
Fig. 5. Fragment of contents of the file «target.xml»

Creating a neural network. Neural Network Toolbox for the MatLab environment was chosen as a neural package to solve the problem of routing the rail transport ITS network. Using Import Data on the Matlab toolbar, the data were imported from the created Excel-table. Training, testing and analysis of NN work are carried out on appropriate samples (Training, Testing and Validation), whose percentage from the general sample is shown in Fig. 6.

The «Network Architecture» window provides the required number of hidden neurons (Figure 7).

Fig. 8 shows the structure of the created neural network.

Fig. 6. Data validation and testing window

Fig. 7. Setting the hidden neurons

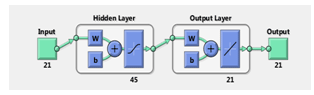
Fig. 8. Structure of the created NN

Teaching and testing of neural network. In the Train Network window, one of the three proposed learning algorithms for the NN (Levenberg-Marquardt, Bayesian Regularization, and Scaled Conjugate Gradient) is selected. For example, learning of the 21-1-45-21 configuration NN by the Levenberg-Marquardt algorithm took place during 11 epochs, the time spent was 26 s (Fig. 9).

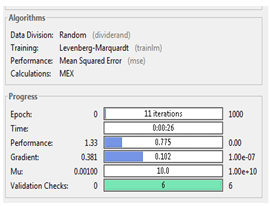
Fig. 9. Characteristics of the NN training

Mean Squared Error (MSE) is the mean square deviation between output and target; the lower the value, the better; zero means no error. The value of regression R means the correlation between output and target. If R = 1, this means close correlation, zero is a random relationship. The MSE values of training, validation and testing of the neural network made 0.204, 0.186 and 0.183, respectively; R has a value of 0.38, 0.43 and 0.44, respectively (Fig. 10).

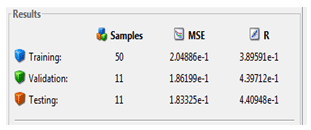
Fig. 10 Results of the NN 21–1–45–21

Regression diagrams and error histograms of the 21-1-45-21 configuration NN by the Levenberg-Marquardt algorithm are presented in Fig. 11.

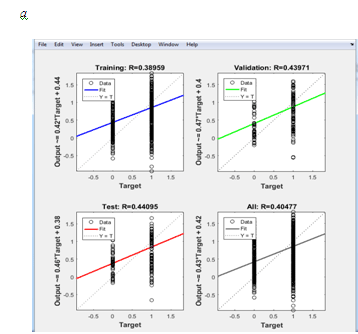
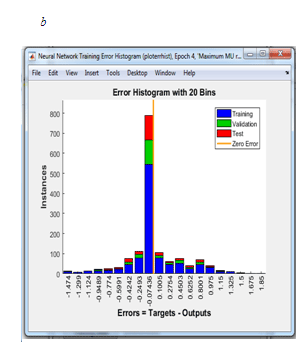
Fig. 11. Graphical presentation of results of NN 21-1-45-21:

а – regression diagrams; б – error histogram

Findings

Analysis of the neural network operation. Based on the results obtained on the 21-1-45-21 configuration NN, the MST of the ITS network of railway transport was built and presented in Fig. 12 (the bold line shows the route for sending control messages from Kyiv).

According to the Kruskal algorithm [5] (without using NN), the MST of the ITS network of railway transport was built, as shown in Fig. 13.

As can be seen from Fig. 12-13, the results coincided, that is, the NN of configuration 21-1-45-21 works correctly. Ten launches were conducted on this NN, the data obtained are summarized in Table 1.

From the table it is clear that the probability of building the MST of the ITS network of rail transport is 0.9 (experiments No. 1-2, 4-10), herewith in experiment No. 7 another MST was obtained (different edges had the same value of weight), but the solution is correct (Fig. 14), but in experiment No. 3, the solution provided by the NN is, unfortunately, incorrect (gap in the route: separation of C1-C2-C3 fragment from C5, which is the source of sending control messages), Fig. 15.

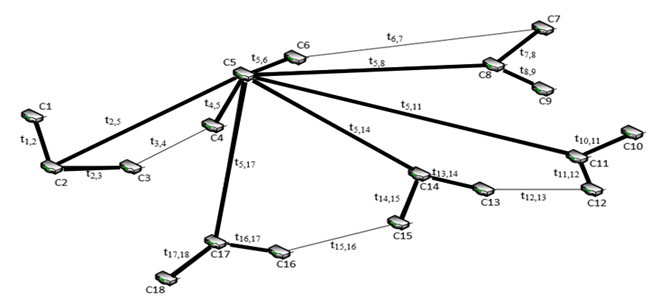
Fig. 12. MST of the ITS network based on NN

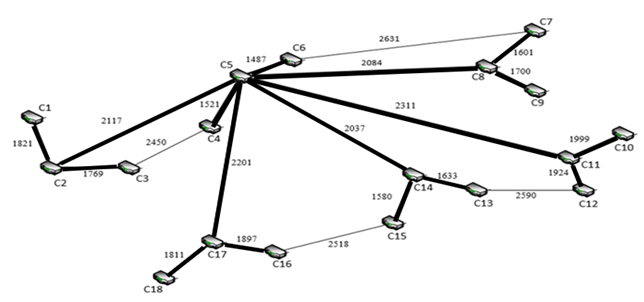
Fig. 13. MST the ITS network, built by the Kruskal algorithm

Designations: edge weights – delays on ITS network routers, µs

Table 1

Analysis of operation of 21-1-45-21configuration NN

Edge weight	Organization of experiments on NN
		1		2		3		4		5		6		7		8		9		10
		x	y	x	y	x	y	x	y	x	y	x	y	x	y	x	y	x	y	x	y
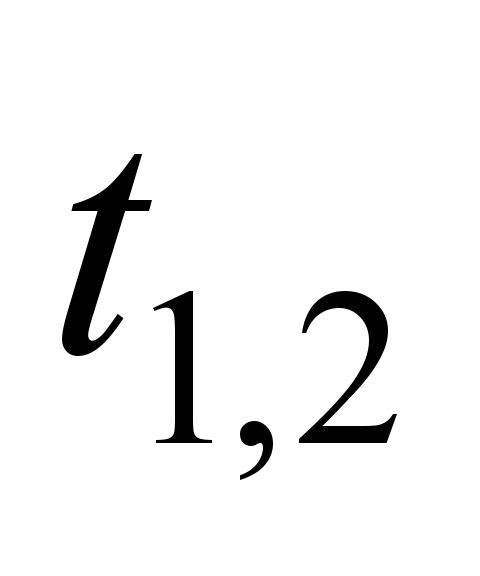
	1 828	1	1 859	1	1 895	1	2 549	1	2 549	1	1 686	1	2 674	1	2 674	1	2 674	1	2 070	1
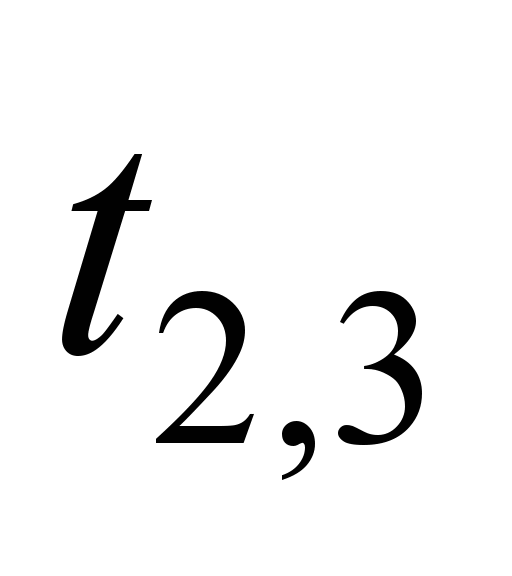
	1 776	1	2 502	1	1 810	1	1 603	1	1 630	1	2 716	1	1 660	1	1 678	1	1 768	1	1 809	1
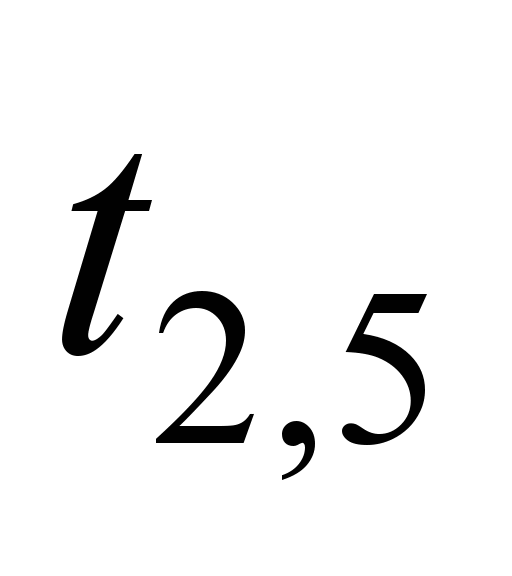
	2 125	1	2 162	1	2 549	1	1 568	1	2 822	1	1 621	1	1 596	1	1 613	1	1 700	1	1 740	1
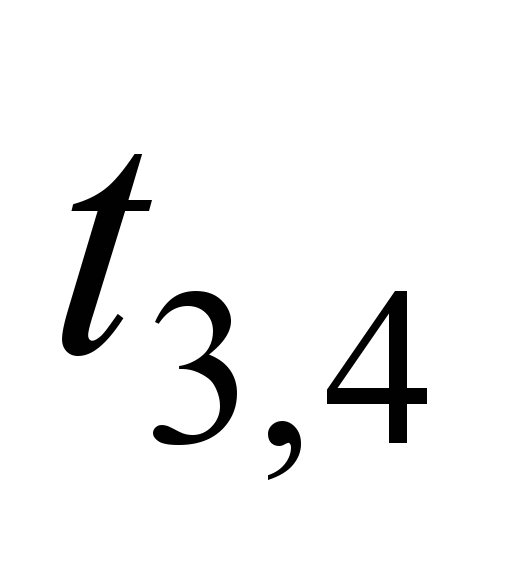
	2 460	0	1 806	0	2 598	0	2 197	0	2 234	0	2 309	0	2 273	0	2 298	0	2 422	0	2 479	0
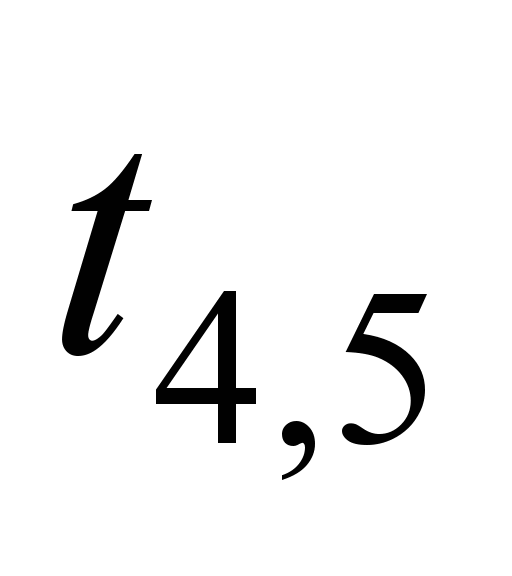
	1 527	1	1 553	1	1 582	1	2 437	1	2 478	1	2 561	1	2 521	1	2 548	1	2 685	1	2 748	1
	1 493	1	1 518	1	1 547	1	2 148	1	2 184	1	2 257	1	2 222	1	2 246	1	2 366	1	2 422	1
	2 092	1	2 127	1	2 168	1	2 321	1	2 360	1	2 440	1	2 402	1	2 428	1	2 558	1	2 618	1
	2 320	1	2 359	1	2 405	1	2 775	1	1 595	1	2 918	1	2 872	1	2 904	1	1 861	1	3 059	1
	2 045	1	2 080	1	2 119	1	1 688	1	1 717	1	1 775	1	1 747	1	1 766	1	3 059	1	1 905	1
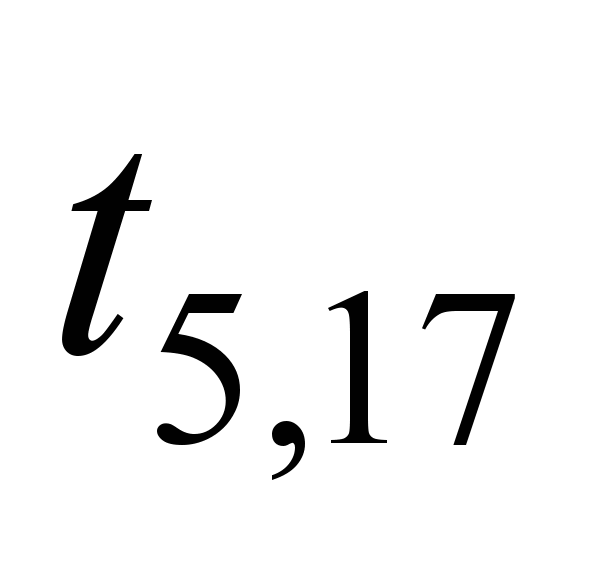
	2 210	1	2 247	1	2 290	1	1 793	1	1 823	1	1 885	1	1 855	1	1 875	1	1 976	1	2 022	1
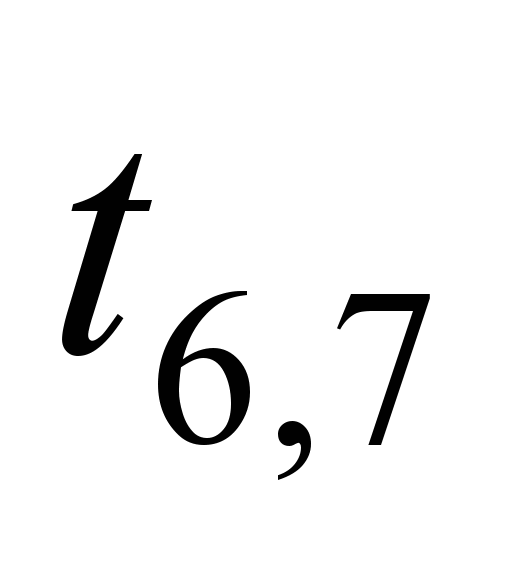
	2 642	0	2 687	0	2 738	0	2 108	0	2 145	0	2 217	0	2 183	0	2 207	0	2 325	0	2 379	0
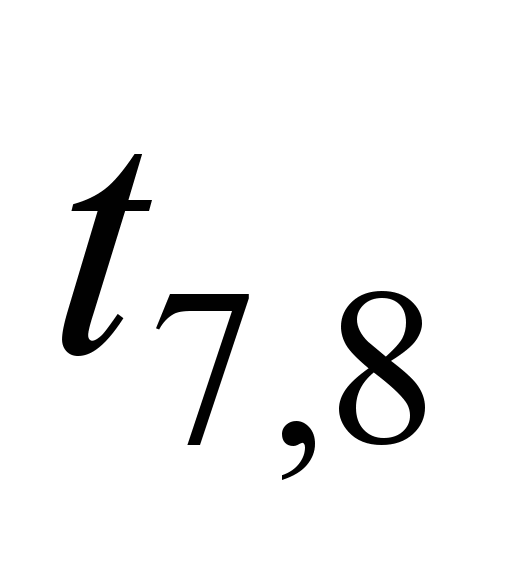
	1 607	1	1 635	1	1 666	1	2 029	1	2 063	1	2 132	1	2 099	1	2 856	1	2 237	1	2 289	1
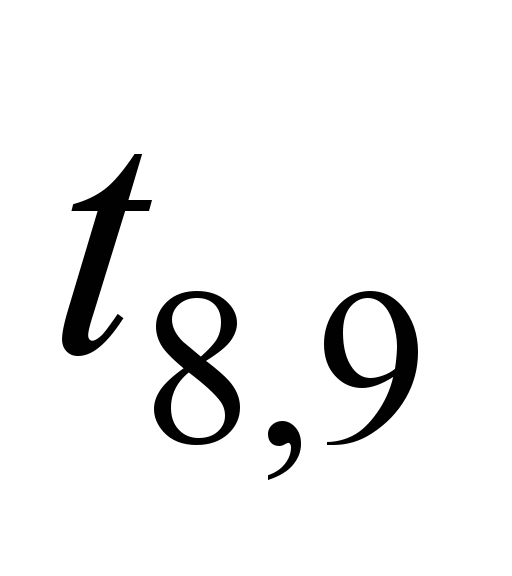
	1 707	1	1 736	1	1 769	1	1 723	1	1 752	1	2 870	1	2 825	1	2 122	1	3 010	1	3 080	1
	2 007	1	2 041	1	2 080	1	2 731	1	2 777	1	1 811	1	1 783	1	1 802	1	1 899	1	1 943	1
	1 932	1	1 965	1	2 002	1	1 667	1	1 695	1	1 752	1	2 749	1	1 744	1	1 837	1	1 880	1
	2 600	0	2 645	0	2 695	0	2 656	0	2 701	0	2 792	0	1 725	0	2 779	0	2 929	0	2 255	0
	1 640	1	1 668	1	1 700	1	2 000	1	2 034	1	2 102	1	2 069	1	2 091	1	2 204	1	2 997	1
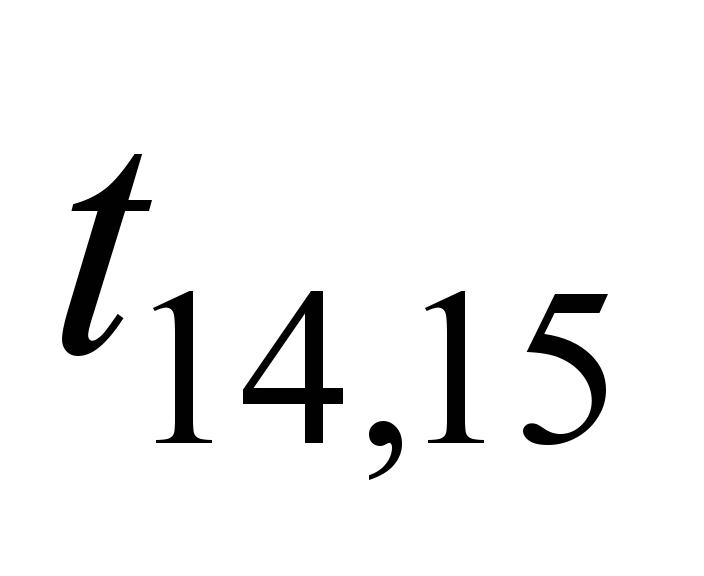
	1 586	1	1 613	1	1 645	1	1 910	1	1 942	1	2 007	1	1 976	0	1 997	1	2 104	1	2 154	1
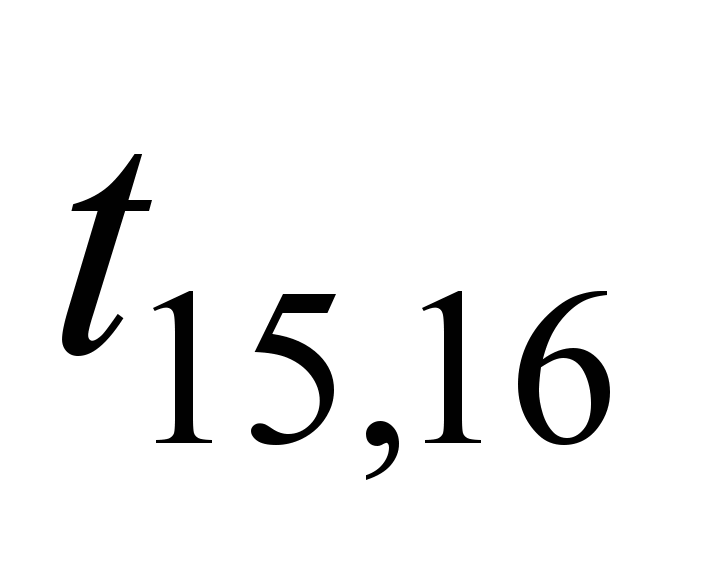
	2 528	0	2 571	0	1 974	1	2 549	0	2 549	0	1 686	0	2 692	1	2 564	0	2 642	0	2 070	0
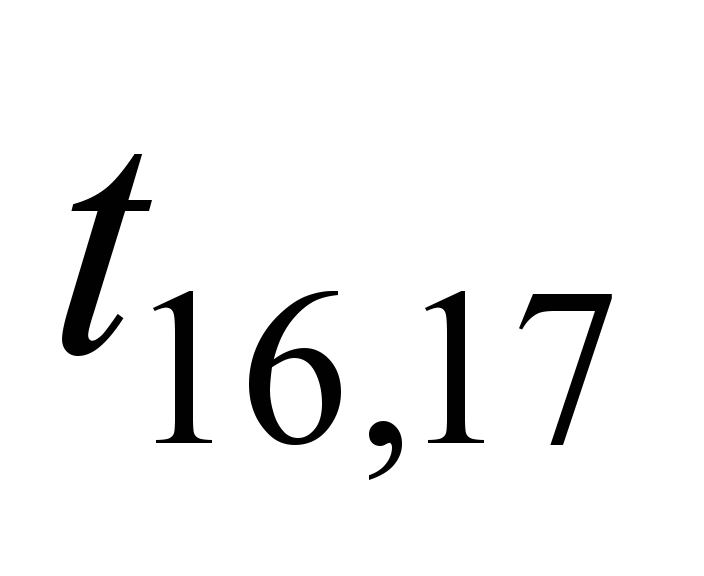
	1 905	1	1 937	1	2 620	0	1 628	1	1 647	1	2 756	1	1 658	1	1 678	1	1 771	1	1 816	1
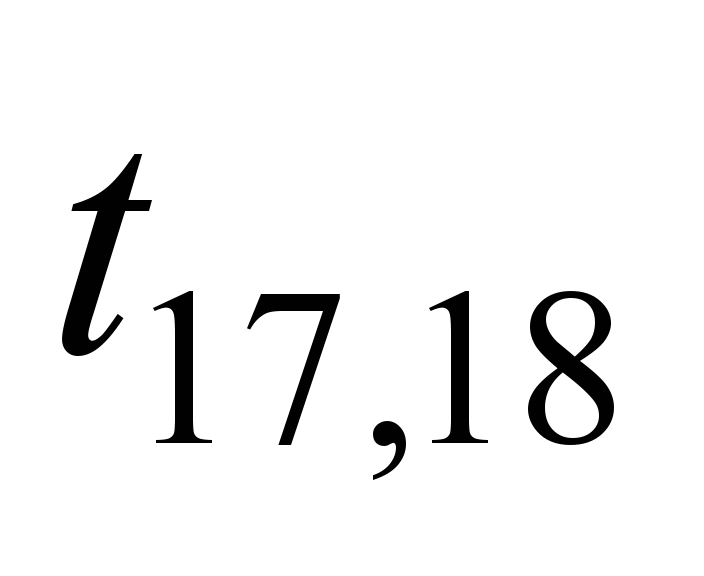
	1 818	1	1 849	1	1 885	1	1 583	1	2 872	1	1 692	1	1 596	1	1 627	1	1 707	1	1 756	1
MAS	+		+				+		+		+				+		+		+
Correct solution													+
Incorrect solution					+
Note: Delay values on routers in the ITS network of rail transport are given in μs

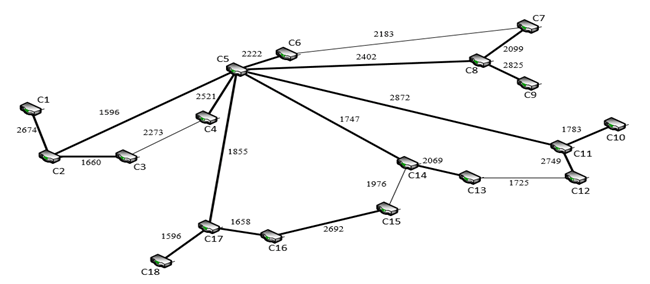
Fig. 14. MST of the ITS network built on the basis of NN (experiment No. 7)

Designations: edge weights – delays on ITS network routers, µs

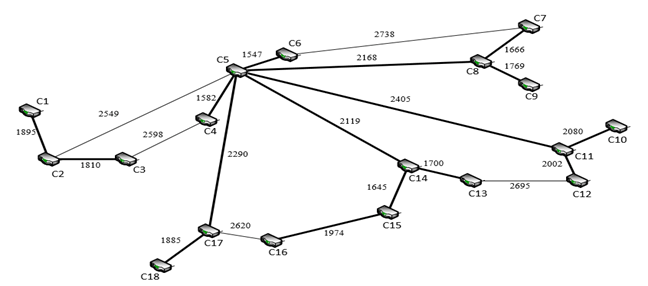
Fig. 15. Incorrect solution obtained on NN (experiment No. 3)

Designations: edge weights – delays on ITS network routers, µs

Originality and practical value

Study of the error and time of NN training on the number of hidden neurons by different learning algorithms. Experiments were performed on the NN of 21-1-X-21 configuration with a sigmoidal activation function in the hidden layer and a linear activation function in the output layer at 10, 45 and 90 hidden neurons using the following algorithms: Levenberg-Marquardt; Bayesian Regularization; Scaled Conjugate Gradient. The results obtained are summarized in Table 2.

Table 2

Error and time of NN training on the number of hidden neurons

Number of hidden neurons	Levenberg-Marquardt		Bayesian Regularization		Scaled Conjugate Gradient
	MSE	Number of epochs	MSE	Number of epochs	MSE	Number of epochs
10	0.775	2	0.392	4	0.00770	125
45	0.204	11	0.870	5	0.00015	154
90	0.991	29	1.270	6	0.00004	302

The dependence of error and time of NN training on the number of hidden neurons by different learning algorithms is presented in Fig. 16.

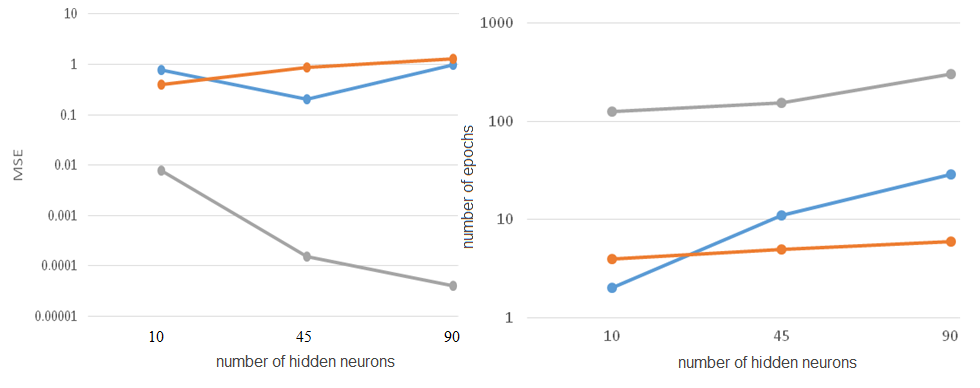
Fig. 16. MSE and NN training time versus the number of hidden neurons

Designations:

From Fig.16 it can be seen that with the increased number of neurons in the hidden layer, the time of training for the 21-1-X-21 configuration NN increases, with 45 neurons in the hidden layer being optimal by the Levenberg-Marquardt algorithm.

Study of the error and time of training NN on the length of the training sample by the Levenberg-Marquardt algorithm. Experiments were performed on the 21-1-45-21 configuration NN with a sigmoid activation function in the hidden layer and a linear activation function in the output layer, while the length of the training sample was 50, 100 and 152 examples. Dependence of the error and time of training of the NN on the length of the training sample is presented in Fig. 17. The Figure shows that the increased length of the training sample results in decrease in the root mean square error, while the training time of NN increases rapidly, but the use of the sample with 100 examples for the NN training is sufficient.

The use of a multilayered neural model, to the entry of which the delay values of routers are supplied, will make it possible to determine the corresponding routes of transmission of control messages from Kyiv (minimum value graph) in the ITS network of railway transport at the trunk level in the real time.

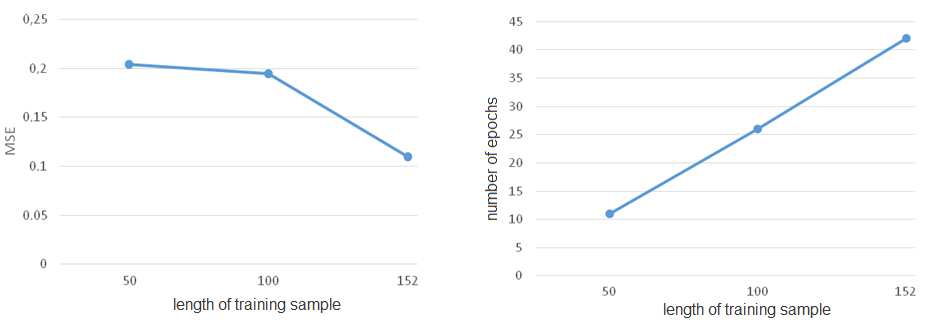
Fig. 17. MSE and NN training time versus the training sample length

Conclusions

1. To determine routes for sending the control messages in the ITS network (at the trunk level) of railway transport using the Neural Network Toolbox of the Matlab environment the neural network of configuration 21-1-45-21 is created, to the input of which an array of delays on the routers is supplied; as a result vector – build tags of communication channels to the routes.

2. The neural network of configuration
   21-1-45-21 with a sigmoidal activation function in the hidden layer and a linear function in the resulting layer under the learning algorithm of Levenberg-Marquardt for 11 epochs gives the MSE value of 0.204, 0.186 and 0.183 in the training, validation and testing samples, respectively. The result given by the neural network coincides with the graph obtained by the Kruskal algorithm. In addition, 10 experiments on the neural network were conducted: the correct result is achieved with a probability of 0.9.

3. On the 21-1-X-21 neural network, a study was made of the mean square error and time of training on the number of hidden neurons (10, 45 and 90) under different learning algorithms: Levenberg-Marquardt, Bayesian Regularization, and Scaled Conjugate Gradient. It is determined that the optimal variant is the configuration 21-1-45-21 by the Levenberg-Marquardt algorithm.

4. On the 21-1-45-21configuration neural network, there was conducted the study of the mean square error and the time of training depending on the length of the training sample: 50, 100 and 152 examples using the Levenberg-Marquardt algorithm. It is determined that the increased length of the training sample results in decrease in the root mean square error, while the training time of the neural network increases rapidly, but the use of the sample with 100 examples for its training is sufficient.

LIST OF REFERENCE LINKS

1. Асланов, А. М. Исследование интеллектуального подхода в маршрутизации компьютерных сетей /
   А. М. Асланов, М. С. Солодовник // Электротехнические и компьютерные системы. – 2014. – № 16 (92). – С. 93–100.

2. Білоус, Р. В. Особливості прикладного застосування генетичного алгоритму пошуку оптимальних шляхів / Р. В. Білоус, С. Д. Погорілий // Реєстрація, зберігання і обробка даних. – 2010. – Т. 12, № 2. – C. 81–87.

3. Колесников, К. В. Нейросетевые модели оптимизации маршрутов доставки данных в динамических сетях / К. В. Колесников, А. Р. Карапетян, А. С. Курков // Международный научный журнал. – 2015. – № 6. – С. 74–77.

4. Колесніков, К. В. Аналіз результатів дослідження реалізації задачі маршрутизації на основі нейронних мереж та генетичних алгоритмів / К. В. Колесніков, А. Р. Карапетян, В. Ю. Баган // Вісн. Черкас. держ. технол. ун-ту. Серія: Технічні науки : зб. наук. пр. – Черкаси, 2016. – № 1. – C. 28–34.

5. Минимальное остовное дерево. Алгоритм Крускала [Electronic resource] // MAXimal. – 2008. – Available at: http://e-maxx.ru/algo/mst_kruskal – Title from the screen. – Accepted : 15.05.2018.

6. Никитченко, В. В. Утилиты моделирующей системы Opnet Modeler / В. В. Никитченко. – Одесса : Одес. нац. акад. связи им. А. С. Попова, 2010. – 128 с.

7. Павленко, М. А. Анализ возможностей искусственных нейронных сетей для решения задач однопутевой маршрутизации в ТКС [Electronic resource] / М. А. Павленко // Проблеми телекомунікацій. – 2011. – № 2 (4). – Available at: http://pt.journal.kh.ua/index/0-139 – Title from the screen. – Accepted : 20.11.2018.

8. Пахомова, В. М. Аналіз методів з природними механізмами визначення оптимального маршруту в комп’ютерній мережі Придніпровської залізниці / В. М. Пахомова, Р. О. Лепеха // Інформ.-керуючі системи на залізн. трансп. – 2014. – № 4. – С. 82–91.

9. Пахомова, В. М. Дослідження інформаційно-телекомунікаційної системи залізничного транспорту з використанням штучного інтелекту : монографія / В. М. Пахомова. – Дніпро : Стандарт-Сервіс, 2018. – 220 с.

10. Погорілий, С. Д. Генетичний алгоритм розв’язання задачі маршрутизації в мережах / С. Д. Погорілий, Р. В. Білоус // Проблеми програмування. – 2010. – № 2-3. – С. 171–178.

11. Реалізація задачі вибору оптимального авіамаршруту нейронною мережею Хопфілда / А. М. Бриндас, П. І. Рожак, Н. О. Семенишин, Р. Р. Курка // Наук. вісн. НЛТУ України : зб. наук.-техн. пр. – Львів, 2016. – Вип. 26.1. – С. 357–363.

12. CiscoTips [Electronic resource] : [веб-сайт]. – Електрон. текст. дані. – Available at: http://ciscotips.ru/ospf/ – Title from the screen. – Accepted : 20.05.2018.

13. Dorigo, M. Ant Colony System: A Cooperative Learning Approach to the Traveling Salesman Problem /
    M. Dorigo, L. M. Gambardella // IEEE Trans. on Evolutionary Compytation. – 1997. – Vol. 1. – Iss. 1. –
    Р. 53–66. doi: 10.1109/4235.585892

14. Hopfield, J. J. Neural networks and physical systems with emergent collective computational abilities /
    J. J. Hopfield // Proceedings of National Academy of Sciences. – 1982. – Vol. 79. – Іss. 8. – P. 2554–2558. doi: 10.1073/pnas.79.8.2554

15. Neural Network Based Near-Optimal Routing Algorihm / Chang Wook Ahn, R. S. Ramakrishna, In Chan Choi, Chung Gu Kang // Neural Information Processing – ICONIP’02 : Proc. of the 9th Intern. Conf. (18–22 Nov. 2002). – Singapore, 2002. – P. 1771–1776.

16. New algorithm for packet routing in mobile ad-hoc networks / N. S. Kojić, M. B. Zajeganović-Ivančić,
    I. S. Reljin, B. D. Reljin // Journal of Automatic Control. – 2010. – Vol. 20. – Іss. 1. – P. 9–16.
    doi: 10.2298/JAC1001009K

17. Pakhomova, V. M. Optimal route definition in the network based on the multilayer neural model /
    V. M. Pakhomova, I. D. Tsykalo // Наука та прогрес транспорту. – 2018. – № 6 (78). – P. 126–142.
    doi: 10.15802/stp2018/154443

18. Schuler, W. H. A novel hybrid training method for hopfield neural networks applied to routing in communications networks / W. H. Schuler, C. J. A. Bastos-Filho, A. L. I. Oliveira // International Journal of Hybrid Intelligent Systems. – 2009. – Vol. 6. – Іss. 1. – P. 27–39. doi: 10.3233/his-2009-0074

19. Towards QoS-aware routing for DASH utilizing MPTCP over SDN / K. Herguner, R. S. Kalan, C. Cetinkaya, M. Sayit // IEEE Conference on Network Function Virtualization and Software Defined Networks (NFV-SDN) (6–8 Nov. 2017). – Berlin, Germany, 2017. – P. 1–6. doi: 10.1109/nfv-sdn.2017.8169844 

20. Zhukovyts’kyy, I. Research of Token Ring network options in automation system of marshalling yard /
    I. Zhukovyts’kyy, V. Pakhomova // Transport Problems. – 2018. – Vol. 13. – Iss. 2. – P. 145–154.
    doi: 10.20858/tp.2018.13.2.14

В. М. ПАХОМОВА^1*, Т. І. СКАБАЛЛАНОВИЧ^2*, В. С. БОНДАРЕВА^3*

^1*Каф. «Електронні обчислювальні машини», Дніпровський національний університет залізничного
транспорту імені академіка В. Лазаряна, вул. Лазаряна, 2, Дніпро, Україна, 49010, тел. +38 (056) 373 15 89,
ел. пошта viknikpakh@gmail.com, ORCID 0000-0002-0022-099X
^2*Каф. «Електронні обчислювальні машини», Дніпровський національний університет залізничного
транспорту імені академіка В. Лазаряна, вул. Лазаряна, 2, Дніпро, Україна, 49010, тел. +38 (056) 373 15 89,
ел. пошта sti19447@gmail.com, ORCID 0000-0001-9409-0139
^3*Каф. «Електронні обчислювальні машини», Дніпровський національний університет залізничного
транспорту імені академіка В. Лазаряна, вул. Лазаряна, 2, Дніпро, Україна, 49010, тел. +38 (056) 373 15 89,
ел. пошта bond290848@gmail.com, ORCID 0000-0002-4016-1656

ІНТЕЛЕКТУАЛЬНИЙ ПІДХІД ДО ВИЗНАЧЕННЯ МАРШРУТІВ

У МЕРЕЖІ ІНФОРМАЦІЙНО-ТЕЛЕКОМУНІКАЦІЙНОЇ

СИСТЕМИ ЗАЛІЗНИЧНОГО ТРАНСПОРТУ

Мета. На сучасному етапі стратегія інформатизації залізничного транспорту України передбачає перехід на трирівневу структуру керування зі створенням єдиного інформаційного простору, тому однією із ключових задач залишається організація маршрутизації в мережі інформаційно-телекомунікаційної системи (ІТС). У зв’язку з цим метою статті є розроблення методики визначення маршрутів у мережі інформаційно-телекомунікаційної системи залізничного транспорту на магістральному рівні з використанням нейромережної технології. Методика. Для визначення маршрутів у мережі інформаційно-телекомунікаційної системи залізничного транспорту, що на сучасному етапі працює за технологіями родини Ethernet, створено нейронну модель 21–1–45–21, на вхід якої подають масив затримок на маршрутизаторах. За результуючий вектор взяті ознаки входження каналів зв’язку до маршрутів. Результати. Оптимальним варіантом є нейронна мережа (НМ) конфігурації 21–1–45–21 із сигмоїдальною функцією активації у прихованому шарі й лінійною функцією активації у результуючому шарі, що навчається за алгоритмом Levenberg-Marquardt. Нейронна мережа навчається найбільш швидко на вибірках різної довжини, менше за інші піддається перенавчанню, досягає значення середньоквадратичної помилки в 0,2 і на контрольній вибірці визначає оптимальний шлях з імовірністю 0,9, при цьому достатньо довжини навчальної вибірки зі 100 прикладів. Наукова новизна. Побудовані залежності середньоквадратичної похибки й часу навчання нейронної мережі (кількості епох) від кількості прихованих нейронів за алгоритмами навчання Levenberg-Marquardt, Bayesian Regularization, Scaled Conjugate Gradient на вибірках різної довжини. Практична значимість. Використання багатошарової нейронної моделі, на вхід якої подають значення затримок на маршрутизаторах, дозволить у масштабі реального часу визначити відповідні маршрути передачі керівних повідомлень (граф мінімальної вартості) в мережі інформаційно-телекомунікаційної системи залізничного транспорту на магістральному рівні.

Ключові слова: інформаційно-телекомунікаційна система; ІТС; затримка на маршрутизаторі; нейронна мережа; НМ; вибірка; функція активації; алгоритм навчання; епоха; похибка

В. Н. ПАХОМОВА^1*, Т. И. СКАБАЛЛАНОВИЧ^2*, В. С. БОНДАРЕВА^3*

^1*Каф. «Электронные вычислительные машины», Днипровский национальный университет железнодорожного
транспорта имени академика В. Лазаряна, ул. Лазаряна, 2, Днипро, Украина, 49010, тел. +38 (056) 373 15 89,
эл. почта viknikpakh@gmail.com., ORCID 0000-0002-0022-099X
^2*Каф. «Электронные вычислительные машины», Днипровский национальный университет железнодорожного
транспорта имени академика В. Лазаряна, ул. Лазаряна, 2, Днипро, Украина, 49010, тел. +38 (056) 373 15 89,
эл. почта sti19447@gmail.com, ORCID 0000-0001-9409-0139
^3*Каф. «Электронные вычислительные машины», Днипровский национальный университет железнодорожного
транспорта имени академика В. Лазаряна, ул. Лазаряна, 2, Днипро, Украина, 49010, тел. +38 (056) 373 15 89,
эл. почта bond290848@gmail.com, ORCID 0000-0002-4016-1656

ИНТЕЛЛЕКТУАЛЬНЫЙ ПОДХОД К ОПРЕДЕЛЕНИЮ МАРШРУТОВ

В СЕТИ ИНФОРМАЦИОННО-ТЕЛЕКОММУНИКАЦИОННОЙ

СИСТЕМЫ ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА

Цель. На современном этапе стратегия информатизации железнодорожного транспорта Украины предусматривает переход на трехуровневую структуру управления с созданием единого информационного пространства, поэтому одной из ключевых задач остается организация маршрутизации в сети информационно-телекоммуникационной системы (ИТС). В связи с этим целью статьи является разработка методики определения маршрутов в сети информационно-телекоммуникационной системы железнодорожного транспорта на магистральном уровне с использованием нейросетевой технологии. Методика. Для определения маршрутов в сети информационно-телекоммуникационной системы железнодорожного транспорта, которая на данном этапе работает по технологиям семейства Ethernet, создано нейронную модель 21–1–45–21, на вход которой подают массив задержек на маршрутизаторах сети. В качестве результирующего вектора приняты признаки включения каналов связи до маршрутов. Результаты. Оптимальным вариантом является нейронная сеть (НС) конфигурации 21–1–45–21 с сигмоидальной функцией активации в скрытом слое и линейной функцией активации в результирующем слое, обучаемая по алгоритму Levenberg-Marquardt. Нейронная сеть обучается наиболее быстро на выборках любой длины, менее других подвержена переобучению, достигает значения среднеквадратичной ошибки в 0,2 и на контрольной выборке определяет оптимальный путь с вероятностью 0,9, при этом достаточно длины обучающей выборки со 100 примеров. Научная новизна. Построены зависимости среднеквадратичной погрешности и времени обучения нейронной сети (количества эпох) от количества скрытых нейронов по алгоритмам обучения Levenberg-Marquardt, Bayesian Regularization, Scaled Conjugate Gradient на выборках различной длины. Практическая значимость. Использование многослойной нейронной модели, на вход которой подают значения задержек на маршрутизаторах, позволит в масштабе реального времени определить соответствующие маршруты передачи управляющих сообщений (граф минимальной стоимости) в сети информационно-телекоммуникационной системы железнодорожного транспорта на магистральном уровне.

Ключевые слова: информационно-телекоммуникационная система; ИТС; задержка на маршрутизаторе; нейронная сеть; НС; выборка; функция активации; алгоритм обучения; эпоха; погрешность

REFERENCES

1. Aslanov, A. M., & Solodovnik, M. S. (2014). Issledovanie intellektualnogo podkhoda v marshrutizatsii kompyuternykh setey. Elektrotekhnicheskie i kompyuternye sistemy, 16(92), 93-100. (in Russian)

2. Bilous, R. V., & Pohorilyi, S. D. (2010). Features of the Application of Genetic Algorithm for Searching Optimal Paths on the Graph. Reiestratsiia, zberihannia i obrobka danykh, 12(2), 81-87. (in Ukrainian)

3. Kolesnikov, K. V., Karapetyan, A. R., & Kurkov, A. S. (2015). Neural network modelsof data delivery route optimization in dynamic networks. International Scientific Journal, 6, 74-77. (in Russian)

4. Kolesnikov, K. V., Karapetian, A. R., & Bahan, V. Y. (2016). Analiz rezultativ doslidzhennia realizatsii zadachi marshrutyzatsii na osnovi neironnykh merezh ta henetychnykh alhorytmiv. Visnyk Cherkaskogo derzhavnogo tehnologichnogo universitetu. Seria: Tehnichni nauky, 1, 28-34. (in Ukrainian)

5. Minimalnoe ostovnoe derevo. Algoritm Kruskala. MAXimal. Retrieved from http://e-maxx.ru/algo/mst_kruskal (in Russian)

6. Nikitchenko, V. V. (2010). Utility modeliruyushchey sistemy Opnet Modeler. Odessa: Odesskaya nats-ionalnaya akademiya svyazi im. A. S. Popova. (in Russian)

7. Pavlenko, M. A. (2011). Analysis opportunities of artificial neural networks for solving single-path routing in telecommunication network. Problemy telekomunikatsii, 2(4). Retrieved from
   http://pt.journal.kh.ua/index/0-139 (in Russian)

8. Pakhomova, V. M., & Lepekha, R. O. (2014). Analiz metodiv z pryrodnymy mekhanizmamy vyznachennia optymalnoho marshrutu v komp’iuternii merezhi Prydniprovskoi zaliznytsi. Informatsiino-keruiuchi systemy na zaliznychnomu transporti, 4, 82-91. (in Ukrainian)

9. Pakhomova, V. M. (2018). Doslidzhennia informatsiino-telekomunikatsiinoi systemy zaliznychnoho transportu z vykorystanniam shtuchnoho intelektu: monohrafiia. Dnipro: Standart-Servis. (in Ukrainian)

10. Pohorilyi, S. D., & Bilous, R. V. (2010). Henetychnyi alhorytm rozviazannia zadachi marshrutyzatsii v merezhakh. Problemy prohramuvannia, 2-3, 171-178. (in Ukrainian)

11. Bryndas, A. M., Rozhak, P. I., Semenyshyn, N. O., & Kurka, R. R. (2016). Realizatsiia zadachi vyboru optymalnoho aviamarshrutu neironnoiu merezheiu Khopfilda. The Scientific Bulletin of UNFU, 26.1, 357-363. (in Ukrainian)

12. CiscoTips. Retrieved from http://ciscotips.ru/ospf (in English)

13. Dorigo, M., & Gambardella, L. M. (1997). Ant colony system: a cooperative learning approach to the traveling salesman problem. IEEE Transactions on Evolutionary Computation, 1(1), 53-66. doi: 10.1109/4235.585892 (in English)

14. Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational abilities. Proceedings of the National Academy of Sciences, 79(8), 2554-2558. doi: 10.1073/pnas.79.8.2554 (in English)

15. Chang Wook Ahn, Ramakrishna, R. S., In Chan Choi, & Chung Gu Kang. (n.d.). Neural network based near-optimal routing algorithm, Proceedings of the 9th International Conference on Neural Information Pro-cessing, 2002, ICONIP’02. Singapore. doi: 10.1109/iconip.2002.1198978 (in English)

16. Kojic, N., Zajeganovic-Ivancic, M., Reljin, I., & Reljin, B. (2010). New algorithm for packet routing in mobile ad-hoc networks. Journal of Automatic Control, 20(1), 9-16. doi: 10.2298/jac1001009k (in English)

17. Pakhomova, V. M., & Tsykalo, I. D. (2018). Optimal route definition in the network based on the multilayer neural model. Science and Transport Progress, 6(78), 126-142. doi: 10.15802/stp2018/154443 (in Ukrainian)

18. Schuler, W. H., Bastos-Filho, C. J. A., & Oliveira, A. L. I. (2009). A novel hybrid training method for hopfield neural networks applied to routing in communications networks. International Journal of Hybrid Intelligent Systems, 6(1), 27-39. doi: 10.3233/his-2009-0074 (in English)

19. Herguner, K., Kalan, R. S., Cetinkaya, C., & Sayit, M. (2017). Towards QoS-aware routing for DASH utilizing MPTCP over SDN, 2017 IEEE Conference on Network Function Virtualization and Software Defined Networks (NFV-SDN). Berlin, Germany. doi: 10.1109/nfv-sdn.2017.8169844 (in English)

20. Zhukovyts’kyy, I., & Pakhomova, V. (2018). Research of Token Ring network options in automation system of marshalling yard. Transport Problems, 13(2), 145-154. doi: 10.20858/tp.2018.13.2.14 (in English)

Received: Nov. 05, 2018

Accepted: March 14, 2019

Creative Commons Attribution 4.0 International

doi: 10.15802/stp2019/ © В. М. Пахомова, Т. І. Скабалланович, В. С. Бондарева, 2019