ISSN 2307–3489 (Print), ІSSN 2307–6666 (Online)

Наука та прогрес транспорту. ВісникДніпропетровського
національного університету залізничного транспорту, 2019, № 1 (79)

мАШИНобудування

Вступ

Захоплювальні пристрої (захоплювачі)промислових роботів, які призначені для захоплення й утримання об’єкта маніпулювання, –це окремі нескладні виконавчі механізми з індивідуальним приводом. Кінематичні схеми механічних стрижньових захоплювачів із невеликою кількістю рухомих ланок мають,переважно, один ступінь свободи і відповідно один двигун приводу. Переважна більшість таких механізмів є діадними з однорухомими кінематичними з’єднаннями.

Останнім часом опубліковано багато робіт із дослідження й проектування схем і конструкцій захоплювачів різного призначення, у тому числі й механічних стрижньових. Широко висвітлені результати розробок нових кінематичних схем захоплювачів, методики й результати кінематичних і кінетостатичних розрахунків, проблеми компонування й конструювання вузлів і деталей захоплювальних пристроїв[1, 3, 8, 9, 11, 17, 18]. Проте залишаються поза увагою питання метричного синтезу схеми механізму, хоча визначення його оптимальних розмірів і положень ланок, встановлення залежностей між швидкостями й пришвидшеннями точок є початковою й важливою задачею проектувальника [5, 10].

Під час проектування схеми захоплювального механізму важливо забезпечити, щоб швидкість затискних елементів у момент контакту з об’єктом маніпулювання була сталою й мінімально можливою для уникнення динамічних перенавантажень. З цієї ж причини кутові швидкості й кутові пришвидшення вихідних ланок механізму також повинні бути мінімальні. Для захоплювачів, побудованих на основі стрижньових схем, доцільне оптимальне проектування з використанням критеріїв передавання руху або індексів передачі[5, 12–15,19,20]. Існує декілька критеріїв якості передачі руху, і останнім часом таких показників пропонується більше: на основі геометричної кінематики, відносних величин сил і реакцій у кінематичних парах, кутів тиску й передавання, погрішностей, чутливості до зміни розмірів ланок механізму, коефіцієнта корисної дії, існування збірок механізму, швидкостей, пришвидшень та ривка окремих і вихідних ланок механізму. Між більшістю критеріїв існує безумовний зв’язок. Великі кути передачі(малі кути тиску) практично гарантують невисокі швидкості й пришвидшення і відсутність ривків, нечутливість механізму до відхилення розмірів ланок від номінальних, інших погрішностей. Щодо енергетичних та силових критеріїв якості руху, то між ними також існує певний зв’язок.

Отримати механізм, параметри якого задовольняють усім критеріям передавання руху, неможливо. При проектуванні у першу чергу задовольняються вимоги необхідних (більш вагомих) критеріїв, і, по можливості, – вимоги інших критеріїв.

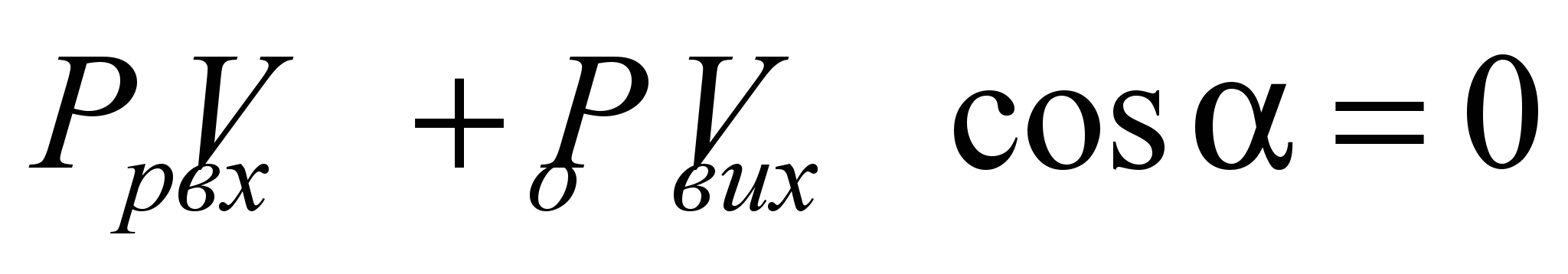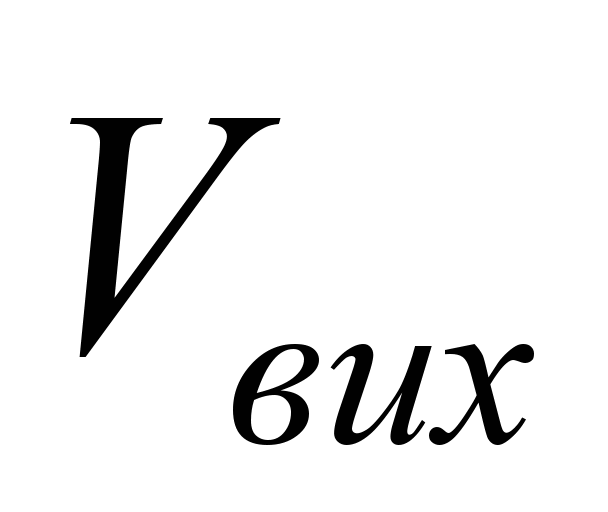У механізмах захоплювачів для забезпечення постійного зусилля затискання для об’єктів різної товщини бажано, щоб потужність приводу була сталою, а енергетичні витрати мінімальними. За умови рівності потужностей рухомих сил Р_р і сил опору Р_о (зневажаючи силами інерції рухомих мас механізму), маємо , де α – кут між вектором сили Р_ой вектором швидкості точки прикладання цієї сили. За бажаного 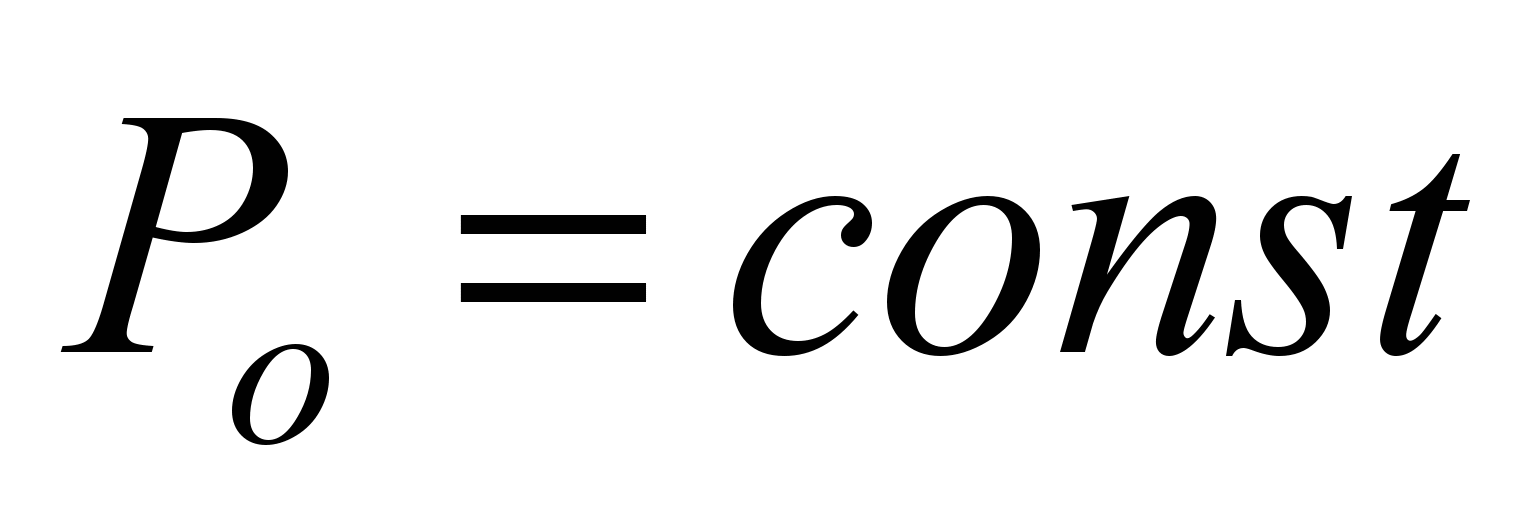зусилля Р_р на вході механізму змінюються за законом зміни 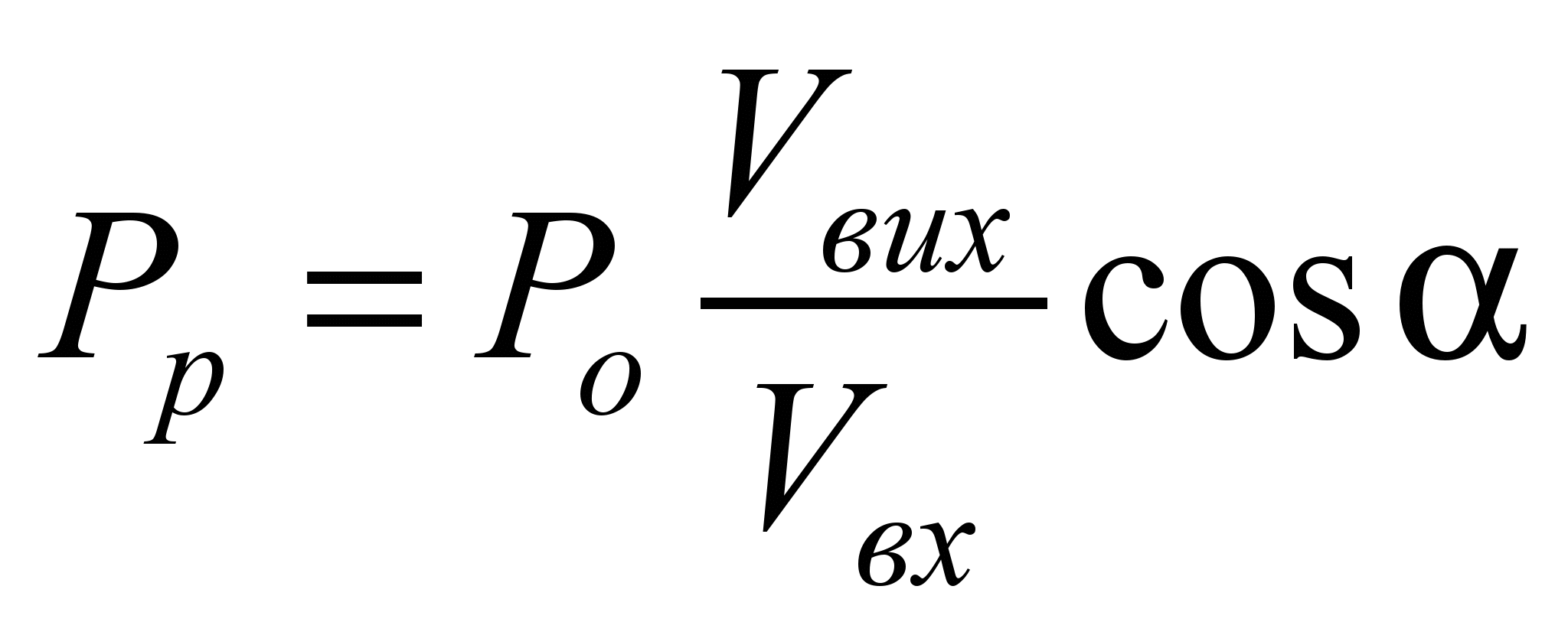й енергетичні витрати тим менші, чим менше це відношення відрізняється від одиниці 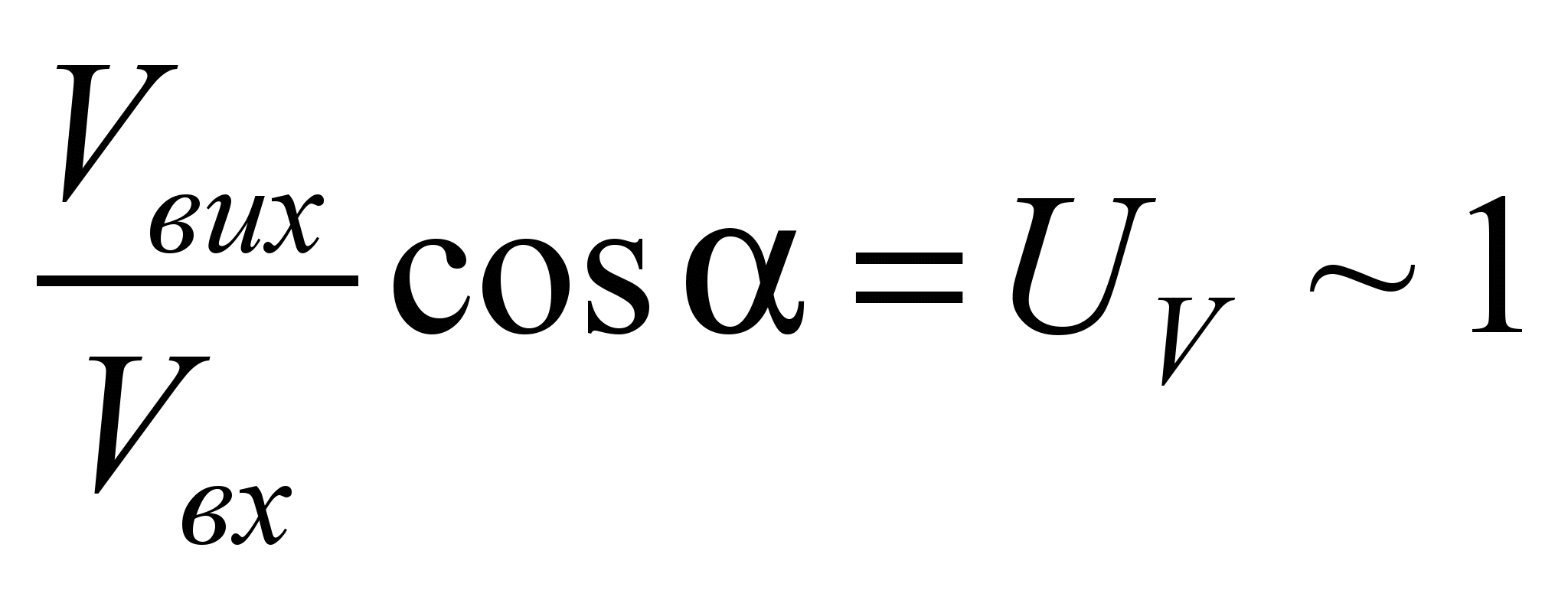. 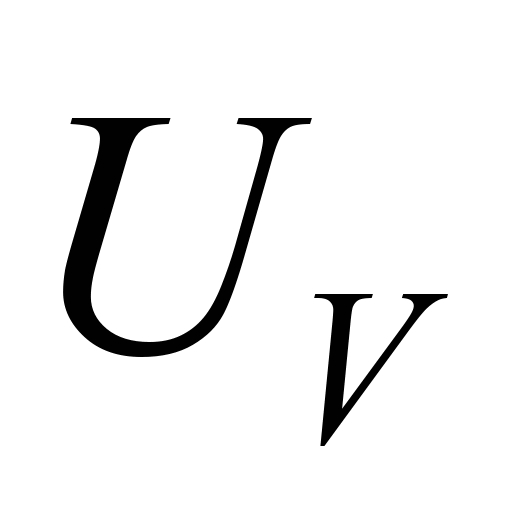Тобто бажано, щоббуло не тільки постійним, але ще й близьким до одиниці. 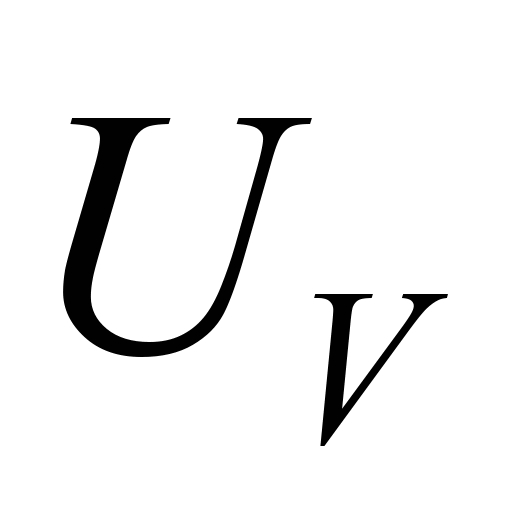Доцільно ввести енергетичний критерій якості передавання руху: відхиленнявід одиниці назвемо енергетичним індексом передачі руху(енергетичний трансмісійний індекс).

Як відомо, критерії передавання руху повинні бути суто геометричними [5, 19, 20], швидкісна передавальна функція від швидкостей не залежить, а залежить від розташування та відносних розмірів ланок механізму.

Кінематичний синтез за подібним критерієм передавання руху для інших механізмів стрижньових захоплювачів виконаний у роботах[7, 8].

Мета

Основна мета роботи – виконати геометричний синтез схем кривошипно-повзункового захоплювального пристрою за критерієм сталості потужності приводу.

Методика

Досягнення поставленої мети здійснюється засобами теорії механізмів і машин за допомогою аналітичного методу трикутників Озолса кінематики пласких механізмів і математичним моделюванням руху ланок захоплювального пристрою.

Результати

Десятиланковий стрижньовий механізм захоплювача побудований на основі спареного паралелограмного центрального кривошипно-повзункового механізму з ведучим повзуном. Ведучий повзун 1 (рис.1) впливає на шатуни 2 і 6, що з’єднані коромислами 3 і 7 зі станиною 0. На кінці шатунів шарнірно закріплені ланки 4 й 8, що містять затискні елементи захоплювача. Додані діади 4–5 і 8–9 утворюють паралелограм і забезпечують плоскопаралельний рух затискних елементів.

У разі затискання об’єктів різної товщини орієнтація затискних елементів захоплювача залишається незмінною, однак його центр переміщується вздовж поздовжньої осі. Тому використання захоплювача, побудованого на цій схемі, для базування об’єкта обмежене.

Структурний аналіз такого механізму захоплювача виконаний у роботі [6].

Рис.1. Кінематична схема й плани швидкостей
і пришвидшень центрального
кривошипно-повзункового механізму захоплювача

Fig. 1. Kinematic scheme and plans for velocities
and accelerations of the central crank-slider
mechanism of the gripping device

Аналітичні дослідження кінематики найпростіших механізмів, до яких належить кривошипно-повзунковий механізм, добре алгоритмізовані[2, 4, 16] і мають високу точність результатів. У складі механізму захоплювача є тільки двоповідкові структурні групи, і механізм має станину, а в основі діадних механізмів лежить змінна форма діади, яка є змінним трикутником. Тому аналітичні кінематичні залежності, отримані на основі методу трикутників, нескладні. Аналітична кінематика кривошипно-повзункового механізму добре описана у класичних підручниках із теорії механізмів, однак для визначення параметрів руху залежності містять, крім незалежного кута нахилу кривошипа φ,ще й кут між напрямом кривошипа й шатуна. Методом трикутників [4] отримана формула визначення швидкості в функції тільки параметра φ:

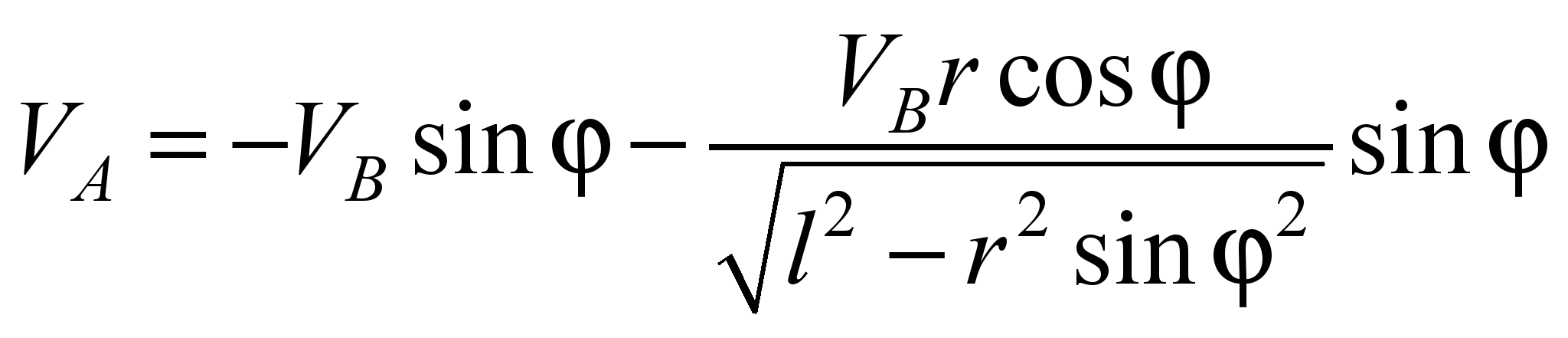(1)

або

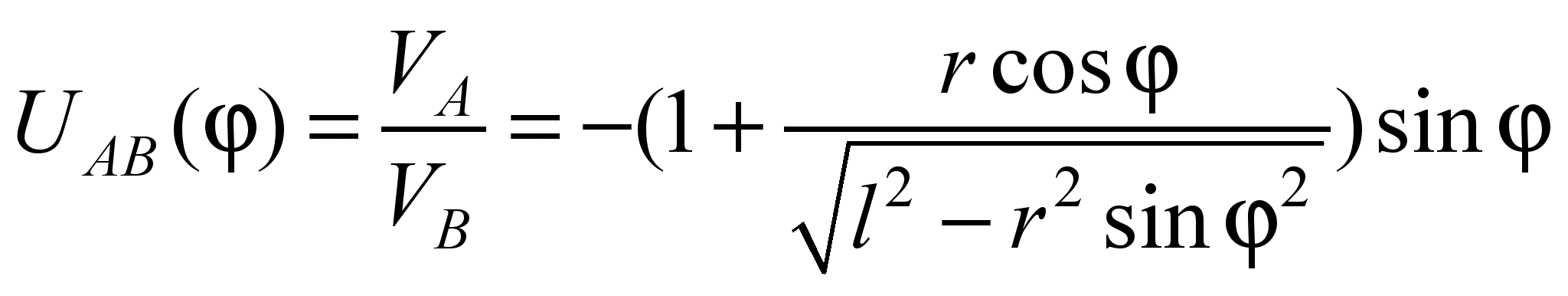, (2)

Введемо відносний параметр розмірів ланок – σ = r/l, тоді залежність (2) прийме форму, зручну для синтезу й моделювання:

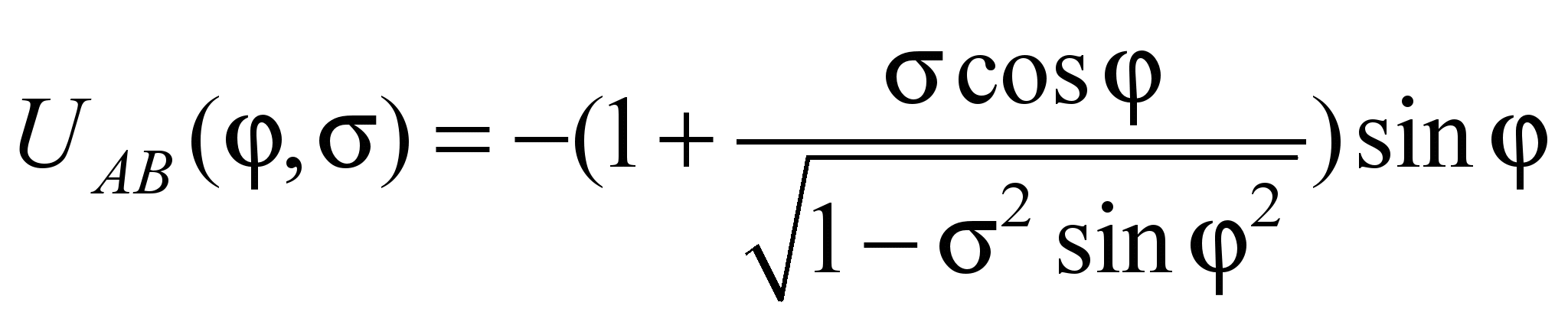. (3)

Сформуємо індекс передачі руху (рис. 1):

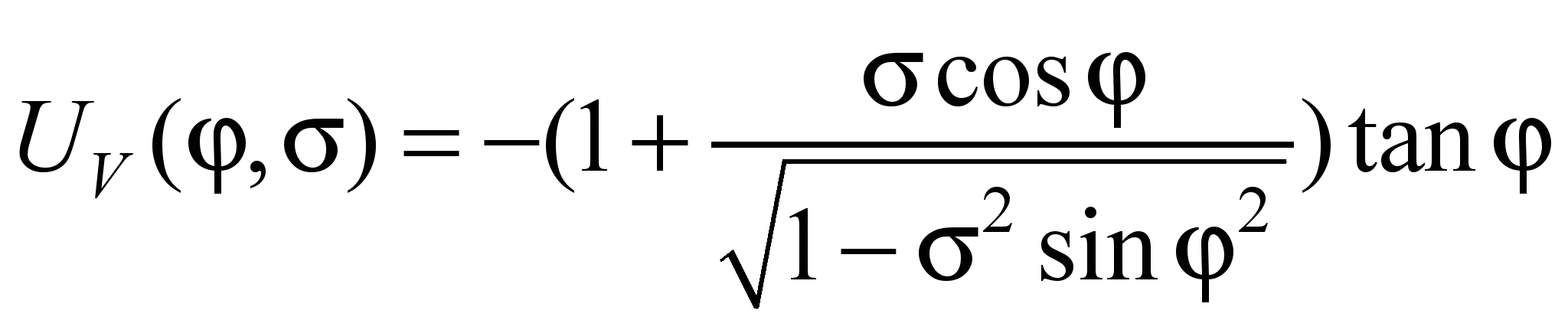. (4)

Як бачимо,індекс залежить від двох параметрів, графік його раціональних і невід’ємних значень представлений на рис. 2, а.

На рис. 2 просторова поверхня залежності (4) перетнута площиною U_V= 1, де лінія перетину задовольняє умові оптимізації. Як видно, функція перетину не має локальних екстремумів і має лише одне рішення для кожного окремого значення σ. Для розповсюджених значень σ на рис. 2, б побудовані залежності індексу передачі у можливому робочому діапазоні φ експлуатації захоплювача. Зон, де |U_V|= 1, по дві симетричні, і всі вони нетривалі (рис. 2, в). За припущення симетричного відхилення Δ/2 від |U_V| = 1 стає можливим визначення діапазону зміни кута повороту кривошипа для взятого σ. Механізм можна експлуатувати у діапазоні 0° <φ < 180°, і нижча межа цього діапазону φ_min відповідає нижньому Δ/2, а значення швидкісної функції у цьому діапазоні будуть симетрично змінюватися від (1 + Δ/2) до (1 – Δ/2).

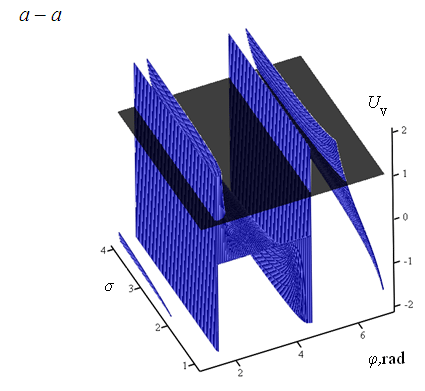
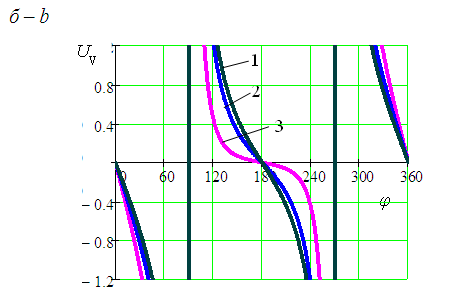
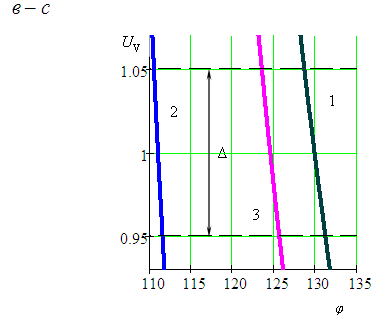
Рис.2. Перетин об’ємної фігури залежності 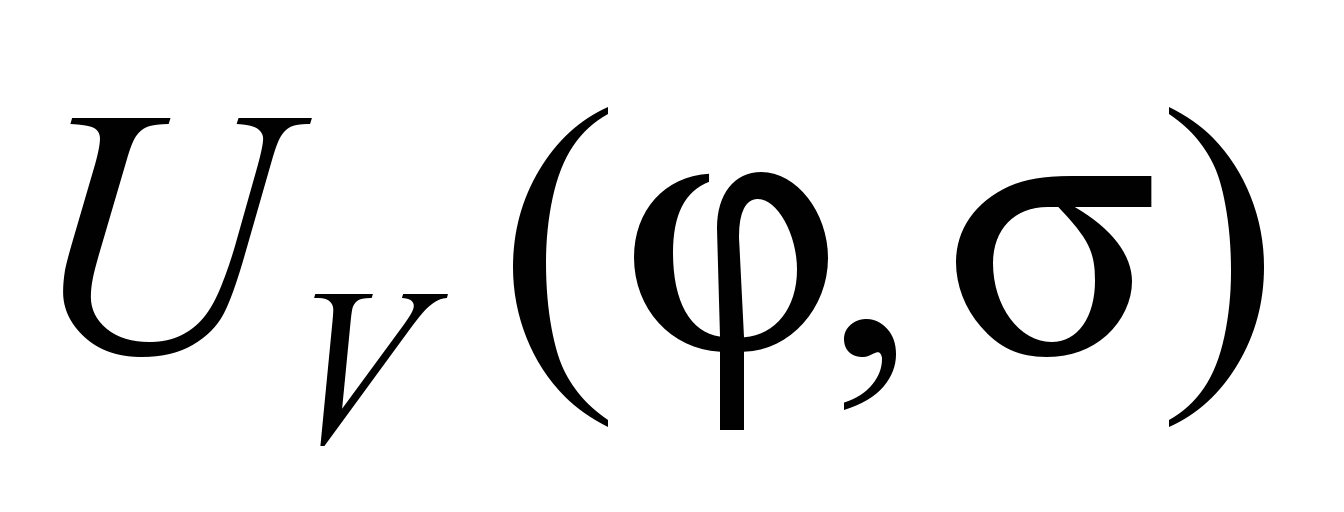центрального кривошипно-повзункового механізму площиною критерію оптимізації(а),
графіки функції U_V(φ,σ) для деяких розповсюджених значень σ(б), для робочої зони експлуатації (в)

Fig. 2. Intersection of the volume figure of the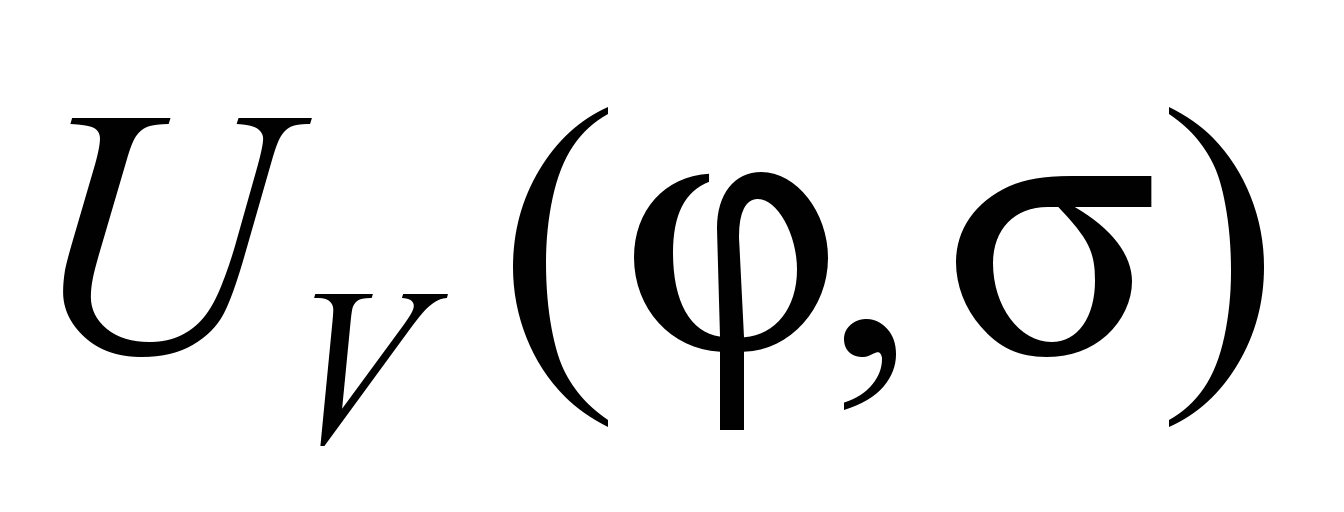 dependence of the central crank-slider mechanism by the plane of the optimization criterion (a), the graphic of the U_V(φ, σ) functions for somecommon values of σ (b), for the working area of operation (c)

Якщо прийняти припустиме відхилення 10 % від критерію оптимізації |U_V|= 1, тобто 1±0,05, то реалізувати таку вимогу зможуть механізми з різними параметрами σ (рис. 2, в), однак кут їх експлуатації φ не перевищує 2°, що є недостатнім, і практичне використання такого механізму за даним критерієм неможливе.

Суттєво розширює можливості захоплювача використання у його схемі дезаксіального кривошипно-повзункового механізму(рис. 3).

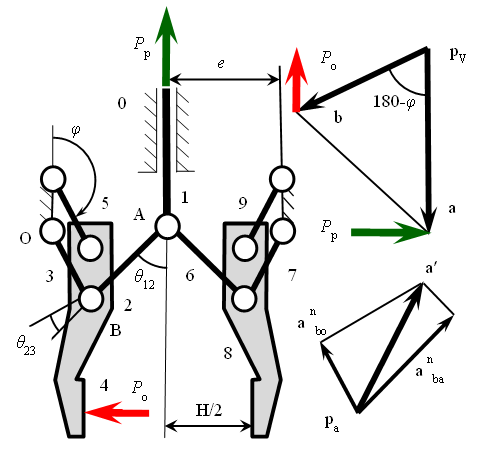
Рис. 3. Кінематична схема й плани швидкостей
і пришвидшень дезаксіального кривошипно-повзункового механізму захоплювача

Fig. 3. Kinematic scheme and plans for velocities and accelerations of the de-axial crank-slider mechanism of the gripping device

Методом трикутників[4] отримана аналітична залежність визначення швидкості для такого механізму:

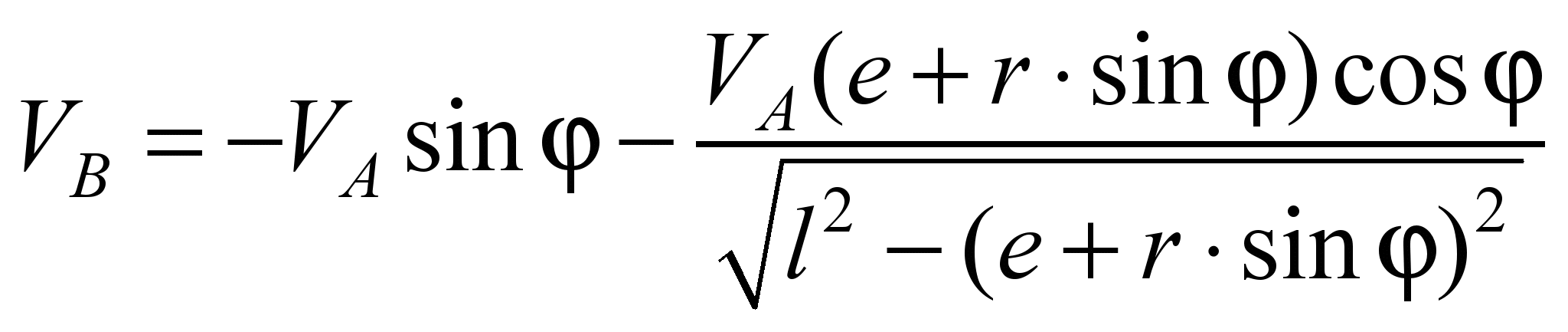, (5)

.

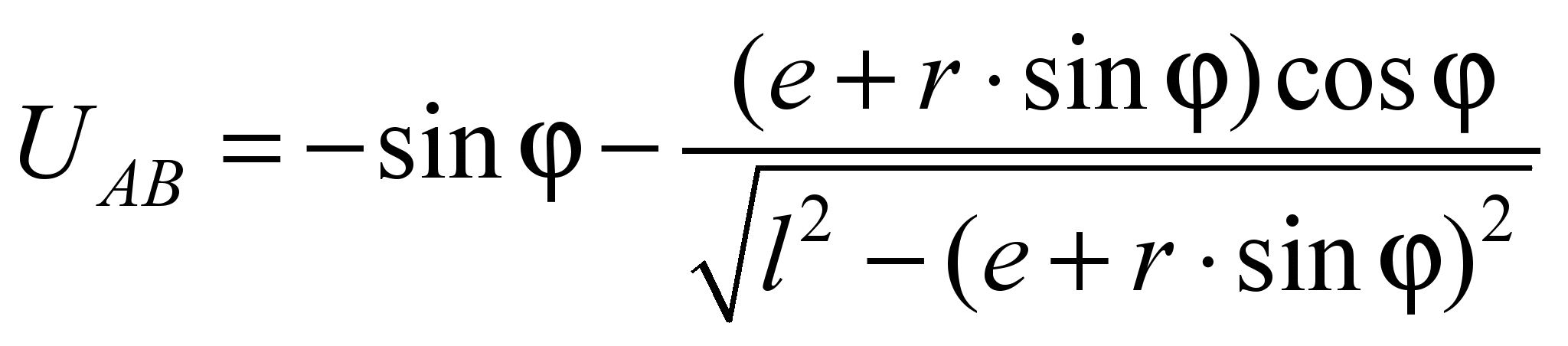Після введення безрозмірного параметра дезаксіала γ=e/l та алгебраїчних перетворень отримаємо залежність для визначення трансмісійного індексу:

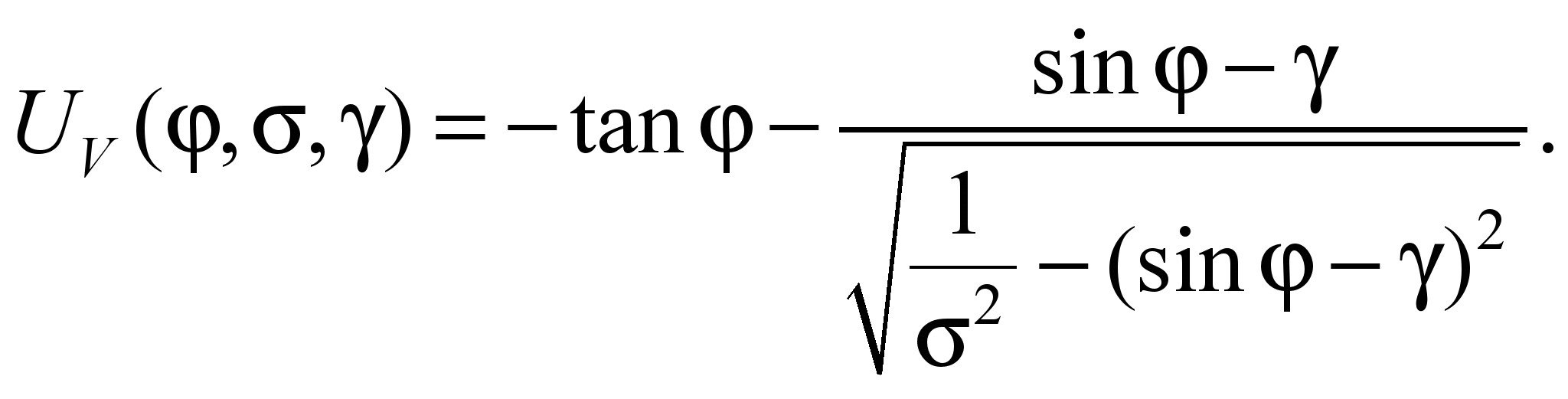(6)

Функція (6) залежить від трьох геометричних параметрів механізму. Для механізму, в якому радіус кривошипа дорівнює дезаксіалу r=e або σ = γ, формула (6) спрощується до залежності від двох параметрів:

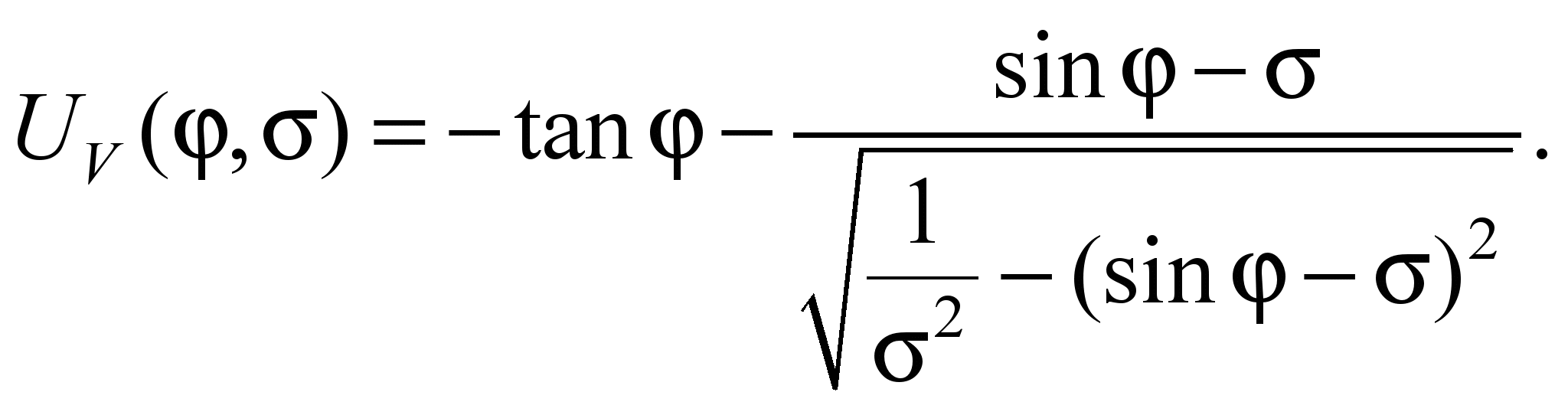(7)

Об’ємний графік цієї залежності представлений на рис. 4, а. Для деяких значень σ, де функції U_V мають локальний мінімум поблизу критерію оптимізації, побудовані графіки на рис. 4, б. Як видно, що такі функції існують тільки в другому квадранті. Графік функції, що задовольняє умові десятивідсоткового відхилення від критерію оптимізації, представлений на рис. 4, в. Останній побудований для єдиного можливого значення σ = 0,905, а діапазон кута експлуатації механізму лежить межах 142° < φ < 170°.

Додаткові обмеження синтезу здійснює дотримання припустимої величини кутів тиску, які в деяких положеннях механізму можуть виходити за межі дозволених. Кут тиску – гострий кут між вектором сили, прикладеної до веденої ланки, і вектором швидкості точки прикладання рушійної сили. Чим він менший, тим якість передачі руху вища. Значення кута тиску в поступальній парі повзун – напрямна визначимо за залежністю (8), його допустиме значення прийнято [θ₁₂] ≤ 30^°[2].

Припустимий кут тиску в обертальній парі 2–3 може бути прийнятий більшим [θ₂₃] ≤ 45° [2].

З урахуванням обмежень за допустимим кутом тиску кут експлуатації механізму звужується до 12° (142° < φ < 154°), де нижню границю діапазону обмежує критерій оптимізації,
а верхню – допустимий кут тиску в парі 0 – 1.
У цьому діапазоні кут тиску в обертальній парі 2 – 3 не перевищує допустимого.

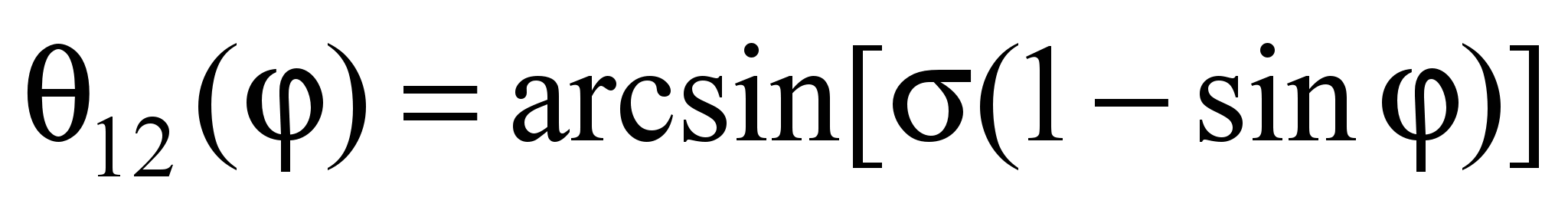. (8)

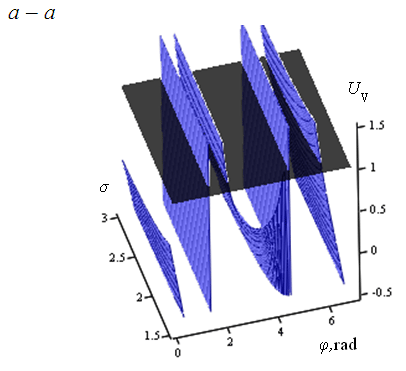
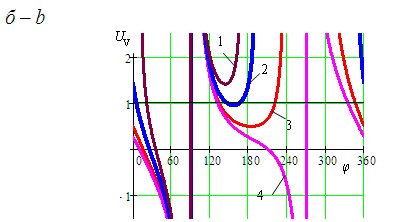
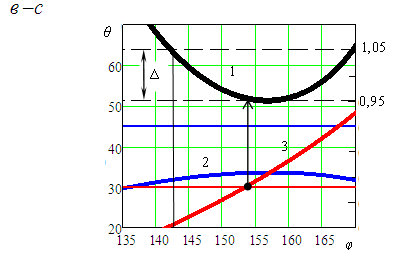
Рис. 4. Перетин об’ємної фігури залежності U_V(φ,σ) дезаксіального кривошипно-повзункового механізму (r=e)площиною критерію оптимізації (а),
деякі функції U_V з локальним мінімумом поблизу критерію оптимізації (1–σ = 1,1; 2–σ = 0,905;
3– σ = 0,67) і без локального мінімуму(4–σ = 0,5) (б), графіки U_V й кутів тиску для механізму з параметром σ =γ =0,905 і визначення для нього кута експлуатації (1– U_V, 2–θ₁₂, 3– θ₂₃) (в)

Fig. 4. Intersection of the volume figure of the U_V (φ, σ)dependence of de-axial crank-slider mechanism (r = e) by the plane of the optimization criterion (a), some U_V functions with a local minimum near the opti-mization criterion (1 – σ = 1.1; 2 –σ = 0.905; 3 – σ = 0.67)and without the local minimum (4 – σ = 0.5) (b), U_V graphs and pressure angles for the mechanism with the parameter σ = γ = 0.905 and determination of the angle for its operation(1 – U_V, 2 – θ₁₂, 3 – θ₂₃) (c)

Найбільш широкі можливості проектування надає розрахунок геометричних параметрів механізму за залежністю (6). Ця залежність є функцією трьох змінних,тому об’ємних поверхонь може бути побудовано багато. Одна з них представлена на рис.5, а. Симетричне відхилення від U_V = 1 може бути підібране комбінацією параметрів σ й γ. Пошук оптимального рішення для мінімальних габаритів механізму слід шукати у схемі, де дезаксіал менший за радіус кривошипа. На рис. 5, б представлені графіки таких комбінацій із параметром e/r <1 для практичного діапазону існування механізму. Усі криві зміни U_V мають локальний мінімум, який відповідає значенню U_V =1,05, що дозволяє знаходити тільки одне симетричне рішення для заданого Δ. 5 %симетричне відхилення задовольняє багато функцій, однак діапазон кута повороту кривошипа, що задовольняє такому відхиленню, становить не більше 35° і тільки
у другому квадранті.

       а – а                                                                                  б – b

       в – c                                                                                            г – d

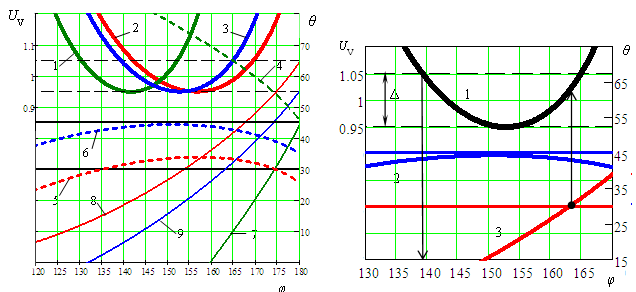
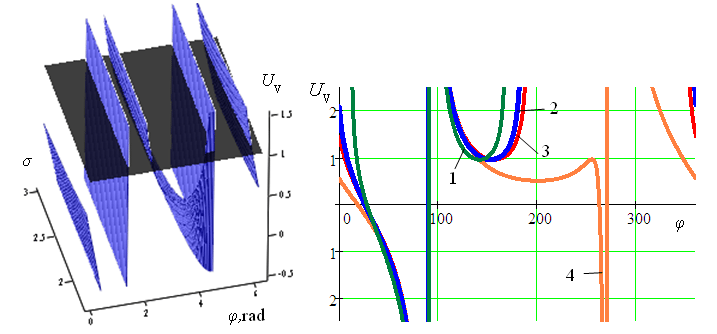
Рис. 5. Перетин об’ємної фігури залежності U_V(φ, σ, γ) дезаксіального кривошипно-повзункового
механізму площиною критерію оптимізації(γ = 0,8) (а), графіки U_V у робочому діапазоні φ
експлуатації захоплювача з симетричним відхиленням від критерію оптимізації для деяких
відносних параметрів механізму (1–σ = 2 і γ=0,7; 2–σ = 1,1і γ=0,82; 3– σ = 0,908 і
γ=0,902; 4– σ = 0,524 і γ=0,902) (б), кути тиску:в обертальній парі шатун – кривошип (4,5,6),
у поступальній парі напрямна –повзун(7,8,9) (в), графіки U_V й кутів тиску для механізму з параметром
σ =1,1і γ=0,82 й визначення для нього кута експлуатації (1– U_V, 2– θ₁₂, 3– θ₂₃) (г)

Fig. 5. Cross section of the volume figure of the U_V(φ, σ, γ) dependence of the de-axial crank-slider
mechanism by the plane of the optimization criterion (γ = 0.8) (a), the U_V graphs in the operating
range φ of the gripping device operation with a symmetric deviation from the optimization criterion
for some relative parameters of the mechanism (1 –σ = 2 and γ = 0.7; 2 –σ = 1.1 and γ = 0.82; 3 – σ = 0.908
and γ = 0.902; 4 – σ = 0.524 and γ = 0.902) (b), angles of pressure: in the rotating pair connecting rod – crank
(4, 5, 6), in thesliding pair a guide – a slider(7, 8, 9) (c), graphs of U_V and pressure angles for the mechanism
with the parameter σ = 1.1 and γ = 0.82 and the definition of operation angle for it(1 – U_V, 2 – θ₁₂, 3 – θ₂₃)(d)

Кут тиску в поступальній парі визначимо за залежністю:

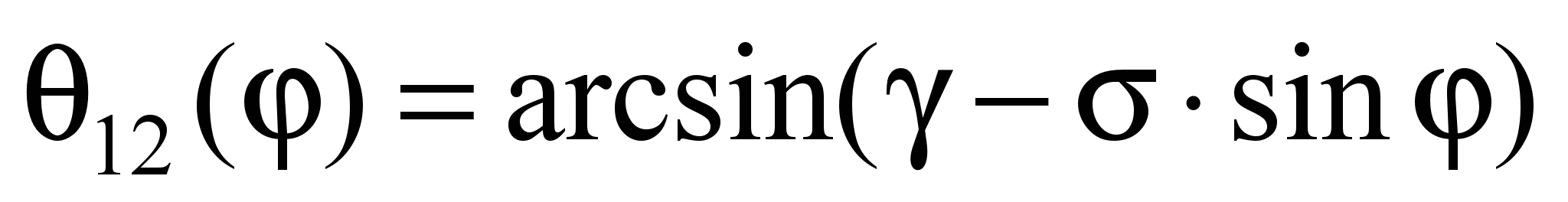, (9)

а в парі шатун – кривошип – за залежністю:

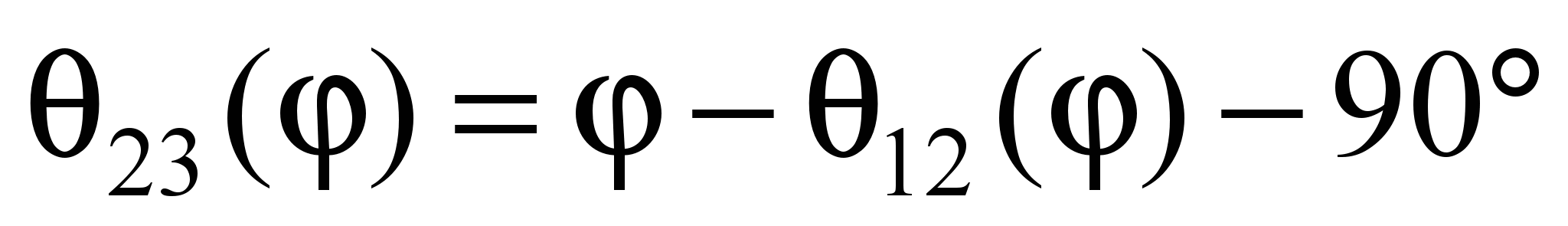. (10)

Як видно з графіків, ці обмеження зменшують верхню межу й діапазон φ роботи механізму.

Механізм із параметрами σ = 0,908, γ=0,902 (рис. 5, г) відповідає граничному стану схеми, де e/r =1.Зміна цих параметрів викликає або збільшення відношення e/r, або збільшення відхилення від нижнього граничного значення критерію оптимізації 0,95. Діапазон кута експлуатації такого механізму лежить у достатньо широких межах 142° <φ< 170°, однак обмеження за кутом тиску у поступальній парі звужують цей діапазон до величини 142° <φ < 154°.Пошук рішення в області зростання σ й зменшення γ призводить до невиконання умови припустимого кута тиску у парі 2–3.

Єдиний варіант схеми, що найкраще задовольняє умовам оптимізації, –це механізм із параметрами σ = 1,1 й γ=0,82, діапазон кута експлуатації якого лежить у межах 139° < φ < 165°. В усьому цьому діапазоні дотримується критерій оптимізації та умова допустимого кута тиску в обертальній парі. Зменшується кут експлуатації механізму до 24° (139° <φ < 163°) за рахунок дотримання допустимого кута тиску в поступальній парі.

Таким чином, механізм захоплювача, побудований за схемою дезаксіального кривошипно-повзункового механізму, що забезпечує відхилення в діапазоні U_V= 0,95…1,05, повинен мати наступні геометричні параметри:
l = r/σ = 0,91r, e = (γ·r)/σ = 0,745r. У такому механізмі в діапазоні кута повороту кривошипа 139° < φ < 163° сила затискання об’єкта буде сталою й дорівнюватиме номінальній рушійній силі приводу в усьому діапазоні товщин деталей, які затискають.

Наприклад, якщо прийняти для максимальної товщини затискуваного об’єкта Н=100мм компактний варіант схеми з e =Н/2, то розміри механізму будуть: r = 67мм, l = 60,98мм, e = 50 мм. У напрямку затискання об’єкта затискні елементи перемістяться на величину 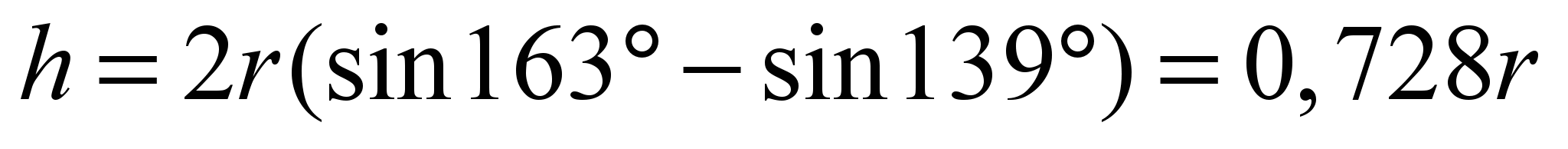, а діапазон товщин об’єктів маніпулювання без заміни затискних елементів складе 49…100 мм.

Характер кривих (рис.4, б; 5, б) показує, що збільшення кута експлуатації механізму відбувається за рахунок збільшення межі відхилення Δ від критеріального параметра й дозволяє знайти рішення симетричного відхилення від U_V = 1 для широкого діапазону Δ, а п’ятивідсоткове обмеження відхилення може бути змінене до заданого.

Наукова новизна та практична значимість

Уведене поняття «енергетичний індекс передачі руху».

Уперше проведений енергетичний синтез захоплювального пристрою, побудованого на основі спареного кривошипно-повзункового механізму,за критерієм рівності одиниці енергетичного індексу передачі руху. Визначені оптимальні відносні розміри ланок і їх розташування для кривошипно-повзункового механізму, що задовольняють вимозі геометричного синтезу за енергетичним індексом передачі руху.

Запропоновані практичні рекомендації щодо розмірів і розташування ланок механізму для центрального й дезаксіального кривошипно-повзункового механізму захоплювача.

Висновки

У роботі виконаний енергетичний синтез геометричних параметрів кривошипно-повзункового механізму захоплювального пристрою за критерієм найменшого відхилення від одиниці швидкісної функції (енергетичний трансмісійний індекс).

Визначені конкретні значення відносних параметрів довжин ланок і діапазони повороту кривошипа центрального й дезаксіального кривошипно-повзункового механізму захоплювача, що найкраще відповідають критерію оптимізації й задовольняють обмеженням за кутами тиску. Найкращі результати синтезу отримані для схеми дезаксіального кривошипно-повзункового механізму з позитивним дезаксіалом, меншим за довжину кривошипа.

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1. Боренштейн, Ю. П. Исполнительные механизмы захватывающих устройств / Ю. П. Боренштейн.–Ленинград: Машиностроение, 1982. –232 с.

2. Кіницький, Я.Т. Теорія механізмів і машин: підручник / Я.Т. Кіницький. – Київ : Наук. думка, 2002. – 650 с.

3. Механика промышленных роботов: учеб. пособие для втузов: в 3 кн. / под ред. К.В.Фролова,
   Е.И. Воробьева. – Москва: Высш. шк, 1988. – Кн. 2 : Расчет и проектирование механизмов / Е. И. Воробьев, О. Д. Егоров, С. А. Попов. – 367с.

4. Озол, О.Г. Основы конструирования и расчета механизмов / О. Г. Озол. – Рига : Звайгзне, 1979.–
   360 с.

5. Пейсах, Э. Е. Система проектирования плоских рычажных механизмов / Э. Е. Пейсах, В. А. Нестеров ; под ред. К.В.Фролова.– Москва : Машиностроение, 1988.– 232с.

6. Погребняк, Р. П. Повторювані зв’язки у схемах стрижньового повзунно-шатунного механізму захоплювального пристрою / Р. П. Погребняк // Наука та прогрес транспорту. – 2018. – № 4 (76). – С. 81–88.
   doi: 10.15802/stp2018/140547

7. Погребняк, Р. П. Структурний аналіз і кінематичний синтез стрижньового кулісного механізму захвата / Р. П. Погребняк // Підйомно-транспортна техніка. – 2017. – № 2 (54).– С. 47–56.

8. Погребняк, Р. П. Структурний аналіз і кінематичний синтез спареного стрижньового кулісного механізму захвата робота / Р. П. Погребняк // Підйомно-транспортна техніка. – 2017. – № 4 (56). – С. 57–66.

9. Челпанов, И. Б. Схваты промышленных роботов / И. Б. Челпанов, С. Н. Колпашников. – Ленинград : Машиностроение, 1989. – 287 с.

10. Atarer, F. Design alternatives of network of Altmann linkages / F. Atarer, K. Korkmaz, G. Kiper // Interna-tional Journal of Computational Methods and Experimental Measurements. – 2017. – Vol. 5. – Iss. 4. –
    P. 495–503. doi: 10.2495/CMEM-V5-N4-495-503

11. Bai, G. Kinematic Analysis and Dimensional Synthesis of a Meso-Gripper / G. Bai, X. Kong, J. M. Ritchie // Journal of Mechanisms and Robotics. – 2017. – Vol. 9. – Iss. 3. – P. 1–59. doi: 10.1115/1.4035800

12. Balli, S. S. Transmission angle in mechanisms (Triangle in mech) / S. S. Balli, S. Chand // Mechanism and Machine Theory. – 2002. – Vol. 37. – Iss. 2. – P. 175–195. doi: 10.1016/S0094-114X(01)00067-2

13. Chen, C. Generalized transmission index and transmission quality for spatial linkages / С. Chen, J. Angeles // Mechanism and Machine Theory. – 2007. – Vol. 42. – Iss. 9. – P. 1225–1237. doi: 10.1016/j.mechmachtheory.2006.08.001

14. Gosselin, C. Optimization of Planar and Spherical Function Generators as Minimum-Defect Linkages /
    C. Gosselin, C. Angeles // Mechanism and Machine Theory. – 1989. – Vol. 24. – Iss.4. – Р. 293–307.
    doi:10.1016/0094-114x(89)90049-9

15. Lin, C.-C. The force transmissivity index of planar linkage mechanisms / C.-C. Lin, W.-T. Chang // Mechanism and Machine Theory. – 2002. – Vol. 37. – Iss. 12. – P. 1465–1485.
    doi: 10.1016/s0094-114x(02)00070-8

16. Pfurner, М. Algebraic analysis of overconstrained single loop four link mechanisms with revolute and prismatic joints / M. Pfurner, T. Stigger, M. L. Husty // Mechanism and Machine Theory. – 2017. – Vol. 114. – P. 11–19. doi: 10.1016/j.mechmachtheory.2017.03.014

17. Pogrebnyak, R. P. Structural analysis and rational design parallelogram arm gripping device/
    R. P. Pogrebnyak // Теория и практика металлургии. – 2015. – № 1/2. – С. 124–126.

18. Robot grippers / Gareth J. Monkman, Stefan Hesse, Ralf Steinmann, Henrik Schunk. – Weinheim : Wiley-VCH, 2007. – 463 р. doi: 10.1002/9783527610280

19. Sutherland, G. Transmission Index for Spatial Mechanisms / G. Sutherland, В. Roth // Journal of Engineering for Industry. – 1973. – Vol. 95. – Iss. 2. – P. 589–597. doi: 10.1115/1.3438195

20. Sutherland, G. H. Quality of Motion and Force Transmission / G. H. Sutherland // Mechanism and Machine Theory. –1981. – Vol.16. –Iss. 3. – P. 221–225. doi: 10.1016/0094-114x(81)90037-9

Р. П. ПОГРЕБНЯК^1*, М. Р. ПОГРЕБНЯК^2*

^1*Каф. «Прикладная механика», Национальная металлургическая академия Украины,
пр. Гагарина, 4, Днипро, Украина, 49005, тел. +38 (056) 743 32 76,
эл. почта pogrebnyakk@ukr.net, ORCID 0000-0002-4685-1818
^2*Каф. «Автоматизация и компьютерные системы», Национальный технический
университет «Днепровская политехника», пр. Дмитрия Яворницкого, 19,
Днипро, Украина, 49005, тел. +38 (056) 743 32 76,
эл. почта mpogrebnyakk@gmail.com, ORCID 0000-0002-2961-3383

кинематический СИНТЕЗ кривошипно-ползунного

механизма захватывающего устройства по

энергетическому индексу передачи движения

Цель.Основная цельработы – провести кинематический синтез схемкривошипно-ползунного захватывающего устройствапо критериюпостоянства мощности привода механизма с ограничениями по допустимым углам давления в кинематических парах. Методика.Достижение поставленной цели осуществляется средствами теории механизмов и машин с помощью аналитического метода треугольников Озолса кинематики плоских стержневых механизмов и математическим моделированием движения звеньев. Результаты. Десятизвенный стержневой механизм схвата построен на основе спаренного параллелограммного кривошипно-ползунного механизма с ведущим ползуном. Для схвата, который построен на основе стержневой схемы, целесообразно оптимальное проектирование с использованием критериев передачи движения, или индексов передачи. В качестве критерия оптимизации принято отношение скорости ведущего звена механизма к проекции вектора скорости точки ведомого звена на направление вектора силы зажатия (энергетический трансмиссионный индекс). Наименьшие энергетические затраты могут быть достигнуты при условии, что это отношение будет близко к единице. Получены аналитические зависимости для определения скоростных функций центрального и дезаксиального кривошипно-ползунного механизма схвата, которые удобны для анализа и моделирования. На их основе выполнен энергетический синтез геометрических параметров механизма захватывающего устройства по критерию наименьшего отклонения от единицы энергетического трансмиссионного индекса. Возможности схвата расширяются при использовании в его схеме дезаксиального кривошипно-ползунного механизма, а наилучшие результаты могут быть получены в схеме, где дезаксиал меньше, чем кривошип. Определены конкретные значения относительных параметров длин звеньев и диапазоны поворота кривошипа центрального и дезаксиального кривошипно-ползунного механизма схвата, которые наилучшим образом отвечают критерию оптимизации и удовлетворяют ограничениям по углам давления. Научная новизна. Впервые введен новый критерий передачи движения – энергетический трансмиссионный индекс. По этому критерию проведен кинематический синтез захватывающего устройства, построенного на основе спаренного кривошипно-ползунного механизма. Практическая значимость. Предложены практические рекомендации по относительным размерам и расположению звеньев механизма для центрального и дезаксиального кривошипно-ползунного механизма схвата, которые удовлетворяют требованиям критерия оптимизации и реализуют ограничения по допустимым углам давления.

Ключевые слова: механический схват; передача движения; энергетический трансмиссионный индекс; скоростная функция; угол давления

R.P. POGREBNYAK^1*, M.R. POHREBNIAK^2*

^1*Dep.«Applied Mechanics», National Metallurgical Academy of Ukraine, Gagarin Av., 4, 49005, Dnipro,
tel. +038 (056) 743 32 76, e-mail pogrebnyakk@ukr.net, ORCID 0000-0002-4685-1818
^2*Dep. «Automation and Computer Systems», National Technical University «Dnipro Polytechic»,
Dmitro Yavornytskyi Av., 19, Dnipro, Ukraine, 49005, e-mail mpogrebnyakk@gmail.com,
ORCID 0000-0002-2961-3383

KINEMATIC SYNTHESIS OF CRANK-slider MECHANISM

OF THE gripping DEVICE based ON THE power

transmission index

Purpose. The main purpose of the work is to carry out a kinematic synthesis of a crank-slider gripping device in accordance to the criterion of the constancy of the drive power of the mechanism with restrictions on permissible pressure angles in kinematic pairs. Methodology. Achieving this purpose is carried out by means of the theory of mechanisms and machines using the analytical method of the Ozols triangles of kinematics of plane rod mechanisms and mathematical modeling of the movement of links. Findings. The ten-bar mechanism of the gripping device is built on the basis of a paired parallelogram of a crank-slider mechanism with a leading slider. For gripping device, which is built on the basis of the rod scheme, it is advisable optimal design using the criteria for the transfer of motion or transmission indices. The criterion of optimization is the ratio of the speed of the leading link to the projection of the velocity vector of the driven point on the direction of the clamping force vector (power transmission index). The lowest energy costs can be achieved, provided that this ratio is equal to one. Analytical dependences are obtained for determining the velocity function of the central and de-axial crank-slider gripping device, which are convenient for analysis and modeling. On their basis, an energy synthesis of the geometrical parameters of the mechanism of the gripping device in accordance with the criterion of the smallest deviation from the unit ofpower transmission index is performed. The possibilities of the gripping device are enhanced by using it in a de-axial crank-slider mechanism, and the best results can be obtained in a scheme where the de-axial value is larger than the crank length. It is determined the specific values of the relative parameters of the lengths of the links and the ranges of rotation of the crank of the central and de-axial crank-slider of the grippingdevice, which best meet the optimization criterion and satisfy the pressure angle constraints. Originality. For the first time, a new criterion for the transmission of motion was introduced –power transmission index. According to this criteria, a kinematic synthesis of the gripping device built on the basis of a paired crank slider mechanism was carried out. Practical value. Practical recommendations are proposed on the size and location of the links of the mechanism for the central and de-axial crank-slider mechanism, which satisfy the requirements of the optimization criterion and implement restrictions on permissible pressure angles.

Keywords: mechanical gripping device; motion transmission; power transmission index; speed function; pressure angle

REFERENCES

1. Borenshteyn, Y. P. (1982). Ispolnitelnye mekhanizmy zakhvatyvayushchikh ustroystv. Leningrad: Ma-shinostroyeniye. (in Russian)

2. Kinytskyi, Y. T.(2002). Teoriya mekhanizmiv i mashyn: pidruchnyk. Kyiv: Naukova dumka. (in Ukraіnian)

3. Vorobov, Y. I., Yegorov, O. D., & Popov, S. A. (1988). Raschet i proyektirovanie mekhanizmov. In
   K. V. Frolov, Y. I. Vorobеv (Eds.), Mekhanika promyshlennykh robotov. (Vol. 2). Moscow: Vysshaya shkola. (in Russian)

4. Ozol, O. G. (1979). Osnovy konstruirovaniya i rascheta mekhanizmov. Riga: Zvaygzne. (in Russian)

5. Peysakh, E. Y., & Nesterov, V. A. (1988). Sistema proyektirovaniya ploskikh rychazhnykh mekhanizmov. Moscow: Mashinostroyeniye. (in Russian)

6. Pogrebnyak, R. P. (2018). Repeated Connections in the Schemes of Link Slider-crank Mechanism of Gripping Device. Science and Transport Progress. 4(76), 81-88. doi: 10.15802/stp2018/140547 (in Ukraіnian)

7. Pogrebnyak, R. P. (2017). Strukturniy analiz i kinematychniy sintez strizhnovogo kulisnogo mekhanizmu zakhvata. Pidyomno-transportna tekhnika,2(54), 47-56. (in Ukraіnian)

8. Pogrebnyak, R. P. (2017). Strukturniy analiz i kinematychniy sintez sparenogostrizhnovogo kulisnogo mekhanizmu zakhvata robota. Pidyomno-transportna tekhnika,4(56), 57-66. (in Ukraіnian)

9. Chelpanov, I. B., & Kolpashnikov, S. N. (1989). Skhvaty promyshlennykh robotov. Leningrad: Ma-shinostroyenie. (in Russian)

10. Atarer, F., Korkmaz, K., & Kiper, G. (2017). Design alternatives of network of altmann linkages. International Journal of Computational Methods and Experimental Measurements, 5(4), 495-503.
    doi:10.2495/CMEM-V5-N4-495-503 (in English)

11. Bai, G., Kong, X., & Ritchie, J. M. (2017). Kinematic Analysis and Dimensional Synthesis of a Meso-Gripper. Journal of Mechanisms and Robotics, 9(3), 1-59. doi: 10.1115/1.4035800 (in English)

12. Balli, S. S., & Chand, S. (2002). Transmission angle in mechanisms (Triangle in mech). Mechanism and Machine Theory, 37(2), 175-195. doi: 10.1016/s0094-114x(01)00067-2 (in English)

13. Chen, C., & Angeles, J. (2007). Generalized transmission index and transmission quality for spatial linkages. Mechanism and Machine Theory, 42(9), 1225-1237. doi: 10.1016/j.mechmachtheory.2006.08.001 (in English)

14. Gosselin, C., & Angeles, J. (1989). Optimization of planar and spherical function generators as minimum-defect linkages. Mechanism and Machine Theory, 24(4), 293-307. doi:10.1016/0094-114x(89)90049-9(in English)

15. Lin, C.-C., & Chang, W.-T. (2002). The force transmissivity index of planar linkage mechanisms. Mechanism and Machine Theory, 37(12), 1465-1485. doi: 10.1016/s0094-114x(02)00070-8 (in English)

16. Pfurner, M., Stigger, T., & Husty, M. L. (2017). Algebraic analysis of overconstrained single loop four link mechanisms with revolute and prismatic joints. Mechanism and Machine Theory,114, 11-19.
    doi: 10.1016/j.mechmachtheory.2017.03.014 (in English)

17. Pogrebnyak, R. P. (2015). Structural analysis and rational design parallelogram arm gripping device. Theory and Practice Steel Industry,1/2, 124-126. (in English)

18. Monkman, G. J., Hesse, S., Steinmann, R., & Schunk, H. (2007). Robot Grippers.Weinheim: Wiley-VCH. doi: 10.1002/9783527610280 (in English)

19. Sutherland, G., & Roth, B. (1973). A Transmission Index for Spatial Mechanisms. Journal of Engineering for Industry, 95(2), 589-597. doi: 10.1115/1.3438195 (in English)

20. Sutherland, G. H. (1981). Quality of motion and force transmission. Mechanism and Machine Theory, 16(3), 221-225. doi: 10.1016/0094-114x(81)90037-9 (in English)

Надійшла до редколегії: 21.09.2018

Прийнята до друку:09.01.2019

Creative Commons Attribution 4.0 International

doi: 10.15802/stp2019/ © Р. П. Погребняк, М. Р. Погребняк, 2018