ISSN
2307–3489 (Print), ІSSN 2307–6666 (Online)
Наука
та прогрес транспорту. Вісник
Дніпропетровського
національного університету залізничного
транспорту, 2018, №
6 (78)
Експлуатація
та ремонт засобів транспорту
УДК 656.078.5
Б.
О. Цейко1*
1*Каф.
«Управління процесами перевезень»,
Державний університет
інфраструктури та технологій,
вул. Котельникова, 29/18, Київ,
Україна,
03115, тел. +38 (093) 811 09 20, ел. пошта
boris16@bigmir.net,
ORCID 0000-0002-2636-6321
ОЦІНКА
ЯКОСТІ ДОСТАВКИ ВАНТАЖІВ
ЗА ДОПОМОГОЮ
КОЕФІЦІЄНТА
ВІДХИЛЕННЯ ЧАСУ
ПРИБУТТЯ поїзда
Мета.
Дослідження спрямовано на розгляд
особливостей обчислення коефіцієнта
відхилення часу прибуття поїзда на
станцію від запланованого по відношенню
до очікуваного відхилення. На
теперішній час для управління перевезеннями
вантажів застосовуються підходи, в яких
такий показник як коефіцієнт відхилення
не обчислюється та не враховується. В
практичній реалізації це зумовлює те,
що залізниця, здійснюючи перевезення
вантажу, не отримує інформацію щодо
відношення номінальних часових відхилень
до реальних. Ця ситуація вимагає вирішення
задач удосконалення діючих технологій
перевізного процесу, пов’язаних із
формуванням, організацією та відправленням
вантажів. Тому потреби в розрахунках
таких коефіцієнтів є актуальними.
Методика.
Для досягнення мети потрібно
ранжувати зібрані
статистичні дані, згрупувати й
проаналізувати їх. Запропоновано
математичну модель розрахунку відхилення
часу прибуття поїздів від запланованого
та залежність даного відхилення від
етапу доставки (станції) й кількості
поїздів (у відсотках від загального їх
числа). Результати.
Уведено поняття «коефіцієнт відхилення»,
який характеризує відхилення часу
прибуття поїзда на станцію від
запланованого по відношенню до очікуваного
відхилення. Спираючись на результати
аналізу відхилення часу прибуття поїздів
на станцію залежно від прогону, можна
зазначити, що простежується прямий
взаємозв’язок між запізненням потягів
у годинах та номером станції (тобто
відстанню). Результат залишається
справедливим для довільної кількості
поїздів (було розглянуто 0, 25, 50, 75 та
100 %). Наукова новизна.
Автор уперше ввів
поняття «коефіцієнт відхилення»,
який характеризує
відхилення часу прибуття поїзда на
станцію від запланованого по відношенню
до очікуваного відхилення. Практична
значимість. На основі
наведеної математичної моделі можна
передбачити приблизну величину запізнення
поїздів для залізничної лінії з більшою
кількістю станцій, якщо основні
характеристики вантажоперевезення
залишаться без суттєвих змін, наприклад,
значного поліпшення або погіршення
технічних характеристик залізничної
інфраструктури.
Ключові
слова: відхилення;
коефіцієнт відхилення; середнє відхилення;
загальний коефіцієнт відхилення; поїзд
Вступ
На теперішній час
для управління перевезеннями вантажів
застосовують підходи, у яких такий
показник, як коефіцієнт відхилення, не
обчислюється й не враховується. У
практичній реалізації це зумовлює те,
що залізниця, здійснюючи перевезення
вантажу, не отримує інформації щодо
відношення номінальних часових відхилень
до реальних. Тому потреби в розрахунках
таких коефіцієнтів є актуальними.
Мета
Ураховуючи
вищезгадане, автор має за мету розглянути
особливості обчислення коефіцієнта
відхилення часу прибуття поїзда на
станцію від запланованого по відношенню
до очікуваного відхилення.
Методика
Обсяги
вантажоперевезень постійно збільшуються,
отже зростає і конкуренція між
перевізниками. Тому виникає потреба у
науковому підході до аналізу, планування
та здійснення залізничних вантажних
перевезень.
Завдання
організації логістики, як відомо,
полягає в тому, щоб відносини між
окремими видами логістичної діяльності,
особами та ресурсами забезпечували
оптимальне досягнення цілі. Основною
ціллю вантажного перевезення як
логістичної системи є максимізація
прибутків за мінімізації часу й
витратності
перевезення. Для її досягнення необхідно
врахувати багато факторів, які впливають
на якість транспортування.
Своєчасність
відіграє велику роль під час оцінювання
якості перевезення. Вона підвищує імідж
і конкурентоспроможність як перевізників,
так і їх клієнтів на ринку й дає змогу
зменшити додаткові витрати на зберігання
вантажу [2], втрати під час перевезення,
іммобілізацію товарно-матеріальних
цінностей зі сфери виробництва на час
перевезення, можливе пониження
ефективності виробництва, подовження
оренди вантажно-розвантажувального
обладнання та ін. [9].
Таким чином, оцінка
ефективності доставки, розподілу
відхилень та складання його математичної
моделі є актуальним завданням
клієнто-орієнтовного перевезення
вантажів.
У цій статті
розглянуто відхилення прибуття поїздів
на станції від плану, залежність цих
відхилень від кількості станцій та
досліджуваних поїздів. І першим кроком
буде ранжувати зібрані статистичні
дані, згрупувати й проаналізувати їх,
скласти математичну модель розподілу
відхилень, оцінити основні параметри
й визначити вид такого розподілу з
певною ймовірністю. Це, у свою чергу,
дасть можливість спрогнозувати
відхилення на кожному етапі руху й
остаточне відхилення в кінці маршруту.
Після чого можна буде передбачити
можливі втрати й надалі розробити
стратегію їх поступового зменшення.
Для правильної
оцінки всіх факторів та прогнозування
можливих витрат [10] запропоновано
математичну модель розрахунку відхилення
часу прибуття поїздів на станції лінії
Кривий Ріг – Одеса (К – О) від запланованого
та залежність цього відхилення від
етапу доставки (станції) й кількості
поїздів (у відсотках від загального їх
числа). Модель базується на статистичних
оцінках розподілу відхилення за часом.
Результати
Оцінка відхилень
на всіх етапах транспортування з
використанням статистичних методів
[1, 7, 9] дозволяє точніше кваліфікувати
такий показник, як якість транспортування
[3]. Потреба приділяти увагу більш
якісному транспортному обслуговуванню
зумовлена зростанням рівня
конкурентоспроможності транспортних
послуг [4–6, 8, 14].
Отримані результати
дають змогу зробити припущення стосовно
закономірності зростання відхилень у
разі збільшення кількості станцій за
порівняно близьких технічних умов
транспортування. Це дає змогу передбачити
можливі витрати через порушення графіка
перевезень та його наслідки.
Річні дані стосовно
кількості поїздів (у відсотках), для
яких наявне відхилення від запланованого
графіка руху, наведено в табл. 1 [8].
Таблиця
1
Відхилення
прибуття поїздів на станції лінії К –
О залежно від етапу
з кроком 25 %
від кількості поїздів
Table 1
Deviation
in the arrival of trains to
the stations of
K – O line
depending on the
stage
with a step of 25% of the trains
number
|
№ зп
|
Станція
|

|
0 %
|
25 %
|
50 %
|
75 %
|
100 %
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
1
|
Кривий
Ріг
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
|
2
|
Кривий
Ріг–Західний
|
0,48
|
–0,07
|
0,10
|
0,15
|
0,27
|
40,65
|
|
3
|
Мусіївка
|
0,53
|
–0,20
|
0,12
|
0,17
|
0,32
|
40,70
|
|
4
|
Гейківка
|
0,58
|
0,00
|
0,13
|
0,21
|
0,36
|
40,73
|
|
5
|
Висунь
|
0,78
|
–0,03
|
0,15
|
0,29
|
0,55
|
41,22
|
|
6
|
Тимкове
|
3,37
|
–0,22
|
0,79
|
1,81
|
4,00
|
44,71
|
Продовження
табл.1
Continuation
of Table 1
|
№ зп
|
Станція
|

|
0 %
|
25 %
|
50 %
|
75 %
|
100 %
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
7
|
Червоне
Озеро
|
3,36
|
–0,05
|
0,90
|
2,10
|
4,17
|
24,57
|
|
8
|
Бобринець
|
4,01
|
0,25
|
1,57
|
2,68
|
4,73
|
25,69
|
|
9
|
Кропивницька
|
6,46
|
–0,57
|
2,50
|
4,16
|
7,86
|
63,73
|
|
10
|
Олійникове
|
6,67
|
–0,05
|
2,70
|
4,33
|
8,38
|
50,18
|
|
11
|
Кавуни
|
7,49
|
0,22
|
3,12
|
4,74
|
8,77
|
50,77
|
|
12
|
Южноукраїнська
|
7,25
|
0,23
|
3,13
|
4,75
|
9,37
|
50,77
|
|
13
|
Трикратне
|
7,40
|
0,81
|
3,36
|
4,85
|
9,45
|
50,78
|
|
14
|
Олександрівка
|
7,35
|
0,65
|
3,34
|
4,86
|
9,19
|
50,78
|
|
15
|
Вознесенськ
|
7,63
|
0,86
|
3,56
|
5,03
|
8,97
|
64,78
|
|
16
|
Мартинівська
|
7,90
|
1,02
|
3,90
|
5,37
|
9,94
|
51,45
|
|
17
|
Веселинове
|
8,04
|
1,01
|
3,92
|
5,42
|
10,15
|
51,46
|
|
18
|
Колосівка
|
16,85
|
0,10
|
3,52
|
6,40
|
14,20
|
237,77
|
|
19
|
Березівка
|
18,63
|
0,08
|
3,84
|
6,83
|
14,59
|
237,85
|
|
20
|
Раухівка
|
18,87
|
0,15
|
3,90
|
7,13
|
14,83
|
237,93
|
|
21
|
Сербка
|
19,03
|
0,25
|
4,04
|
7,34
|
14,95
|
238,03
|
|
22
|
Буялик
|
19,29
|
0,05
|
3,91
|
7,17
|
14,87
|
237,86
|
|
23
|
Чорноморська
|
18,69
|
0,10
|
4,02
|
7,14
|
15,04
|
237,90
|
|
24
|
Кулиндрове
|
21,66
|
0,20
|
4,84
|
8,39
|
18,52
|
237,95
|
|
25
|
Одеса–Східна
|
26,91
|
1,10
|
6,39
|
11,78
|
27,78
|
310,22
|
|
26
|
Одеса–Сортувальна
|
26,41
|
1,35
|
7,53
|
14,12
|
27,87
|
310,47
|
|
27
|
Одеса–Порт
|
45,08
|
7,05
|
22,61
|
33,13
|
49,91
|
337,88
|
Тут
 –
середнє відхилення
для кожної станції, обчислене за річною
інформацією з кроком у 25 %.
–
середнє відхилення
для кожної станції, обчислене за річною
інформацією з кроком у 25 %.
Знайдемо
очікуване відхилення
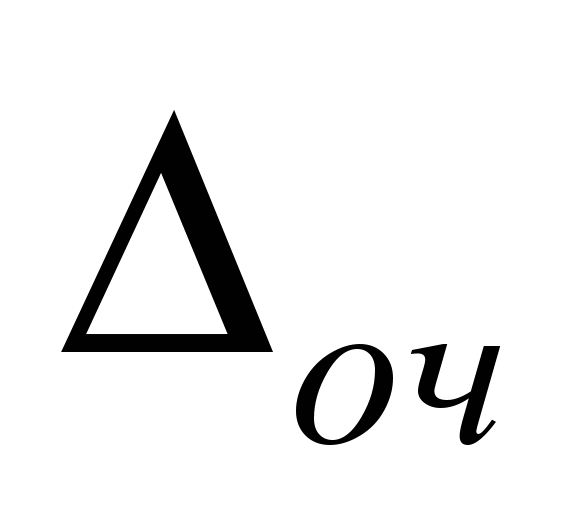 для кожної станції як середнє
відхилення
для кожної станції як середнє
відхилення
 для 25, 50 та 75 % поїздів,
округлене до цілих [11].
для 25, 50 та 75 % поїздів,
округлене до цілих [11].
Відхилення прибуття
поїзда на станції лінії К – О залежно
від етапу з кроком 25 % від кількості
поїздів та очікуване відхилення наведено
в табл. 2 [8].
Графічне зображення
відхилення прибуття поїздів на лінії
К – О наведено на рис. 1 [8].
Як бачимо, відхилення
зростають зі збільшенням кількості
станцій, тобто для перших 5 станцій
графіки коливаються біля 0, на середині
маршруту – близько 5, а в кінці вже
перевищують 20. Для різної кількості
поїздів остаточні результати розташовані
між 20 та 50 год.
Таблиця 2
Очікуване
відхилення прибуття поїздів
на
станції лінії К – О
Table
2
Expected
deviation in the arrival of trains
to the stations of K - O line
|
№
зп
|
Станція
|

|
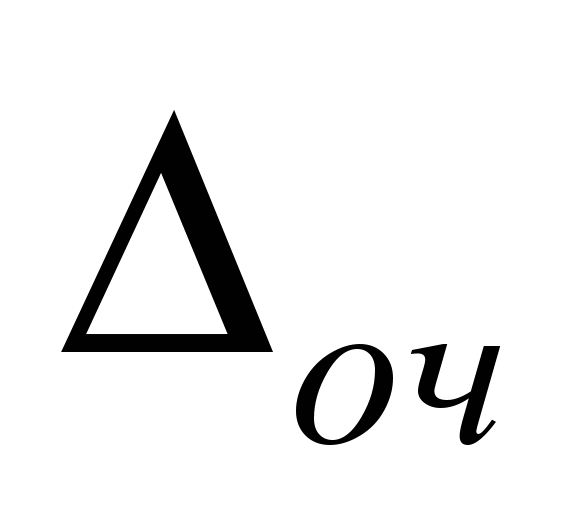
|
|
1
|
Кривий
Ріг
|
0,00
|
0
|
|
2
|
Кривий
Ріг–Західний
|
0,17
|
0
|
|
3
|
Мусіївка
|
0,20
|
0
|
|
4
|
Гейківка
|
0,23
|
0
|
|
5
|
Висунь
|
0,33
|
0
|
|
6
|
Тимкове
|
2,20
|
2
|
|
7
|
Червоне
Озеро
|
2,39
|
2
|
|
8
|
Бобринець
|
2,99
|
3
|
|
9
|
Кропивницька
|
4,84
|
5
|
|
10
|
Олійникове
|
5,14
|
5
|
|
11
|
Кавуни
|
5,54
|
6
|
|
12
|
Южноукраїнська
|
5,75
|
6
|
Продовження
табл.2
Continuation
of Table 2
|
№
зп
|
Станція
|

|
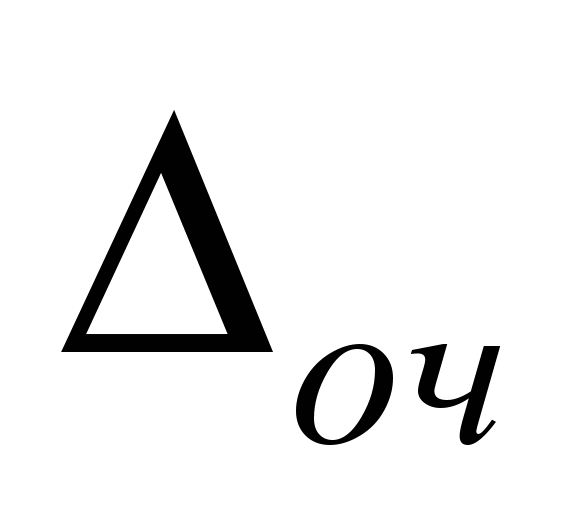
|
|
13
|
Трикратне
|
5,89
|
6
|
|
14
|
Олександрівка
|
5,80
|
6
|
|
15
|
Вознесенськ
|
5,85
|
6
|
|
16
|
Мартинівська
|
6,40
|
6
|
|
17
|
Веселинове
|
6,50
|
6
|
|
18
|
Колосівка
|
8,04
|
8
|
|
19
|
Березівка
|
8,42
|
8
|
|
20
|
Раухівка
|
8,62
|
9
|
|
21
|
Сербка
|
8,78
|
9
|
|
22
|
Буялик
|
8,65
|
9
|
|
23
|
Чорноморська
|
8,74
|
9
|
|
24
|
Кулиндрове
|
10,58
|
11
|
|
25
|
Одеса–Східна
|
15,31
|
15
|
|
26
|
Одеса–Сортувальна
|
16,51
|
17
|
|
27
|
Одеса–Порт
|
35,22
|
35
|
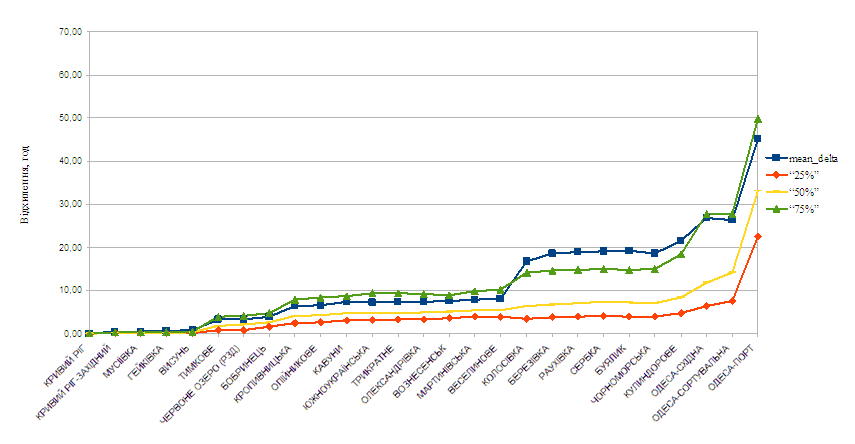
Рис. 1.
Відхилення прибуття поїздів на лінії
К – О
Fig.
1. Deviation in the arrival of trains on the K – O line
Уведемо
коефіцієнт
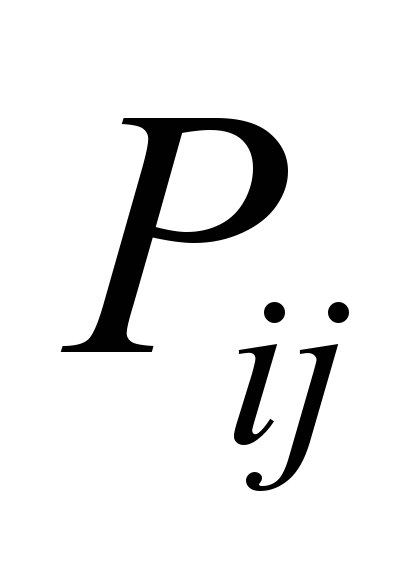 ,
який характеризує відхилення часу
прибуття поїзда на станцію від
запланованого по відношенню до
очікуваного відхилення за формулою:
,
який характеризує відхилення часу
прибуття поїзда на станцію від
запланованого по відношенню до
очікуваного відхилення за формулою:
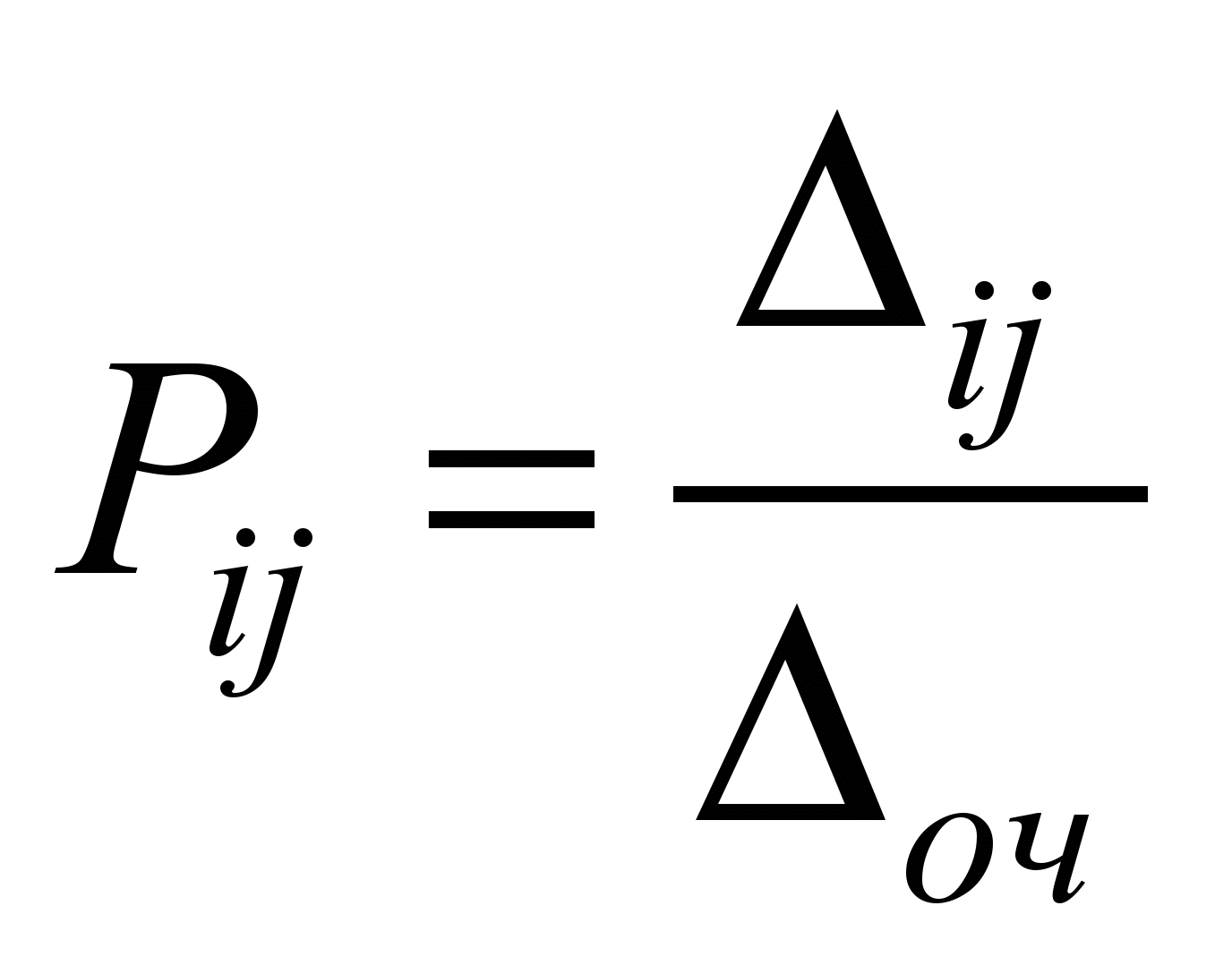 , (1)
, (1)
де
 – номер станції, а
– номер станції, а
 –
номер кроку (0, 25, 50, 75, 100 %);
–
номер кроку (0, 25, 50, 75, 100 %);
 – відхилення
часу прибуття поїзда на відповідну
станцію;
– відхилення
часу прибуття поїзда на відповідну
станцію;
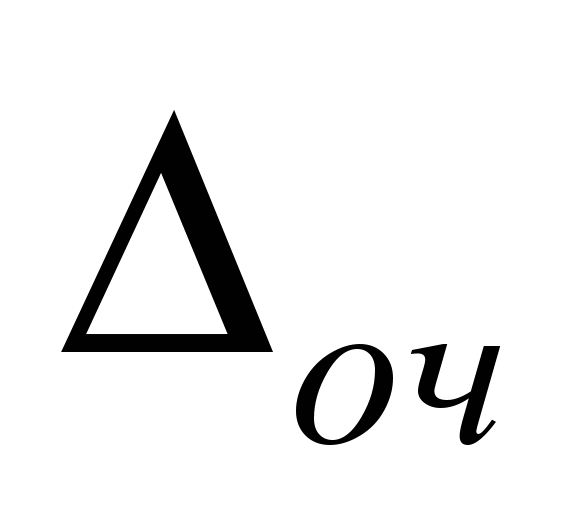 – середнє
відхилення часу.
– середнє
відхилення часу.
Чим
ближче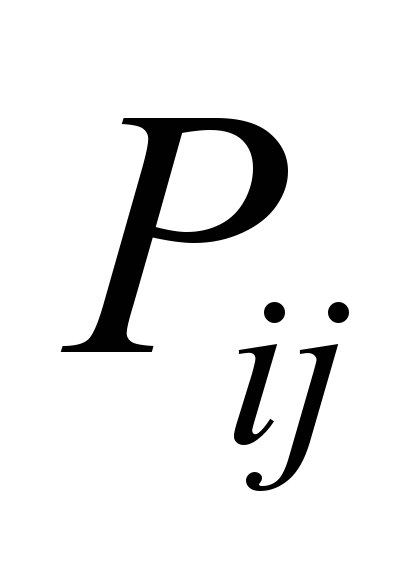 до 0, тим ближчим є реальний графік руху
до запланованого. Якщо коефіцієнт
коливається між 0 та 1, то відхилення
до 0, тим ближчим є реальний графік руху
до запланованого. Якщо коефіцієнт
коливається між 0 та 1, то відхилення
є, але вони не перевищують очікуваних
значень [12]. Коли коефіцієнт більший за
1, графік руху помітно порушений. Оскільки
відхилення накопичуються, то коефіцієнт
зростає як зі збільшенням кількості
станцій, так і зі збільшенням кількості
поїздів [11].
Знайдемо
коефіцієнти
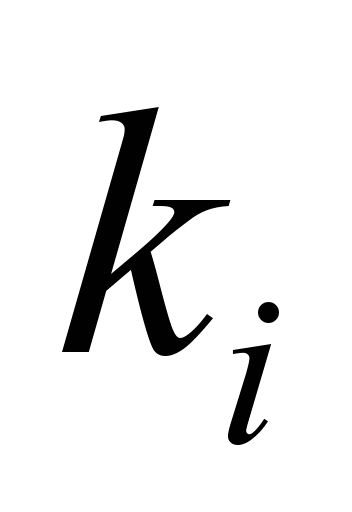 та
та
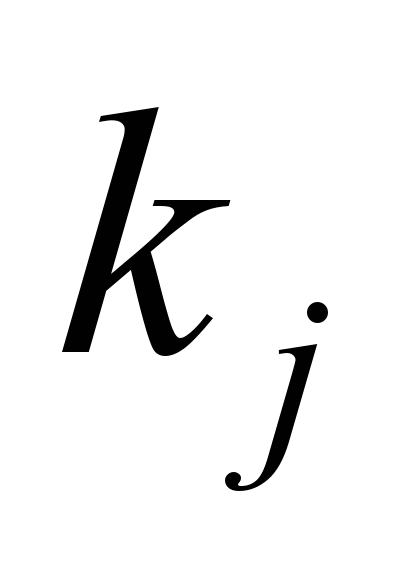 ,
які характеризують рівень
відхилення для кожної станції та для
кожного кроку (0, 25, 50, 75, 100 %) за
формулами:
,
які характеризують рівень
відхилення для кожної станції та для
кожного кроку (0, 25, 50, 75, 100 %) за
формулами:
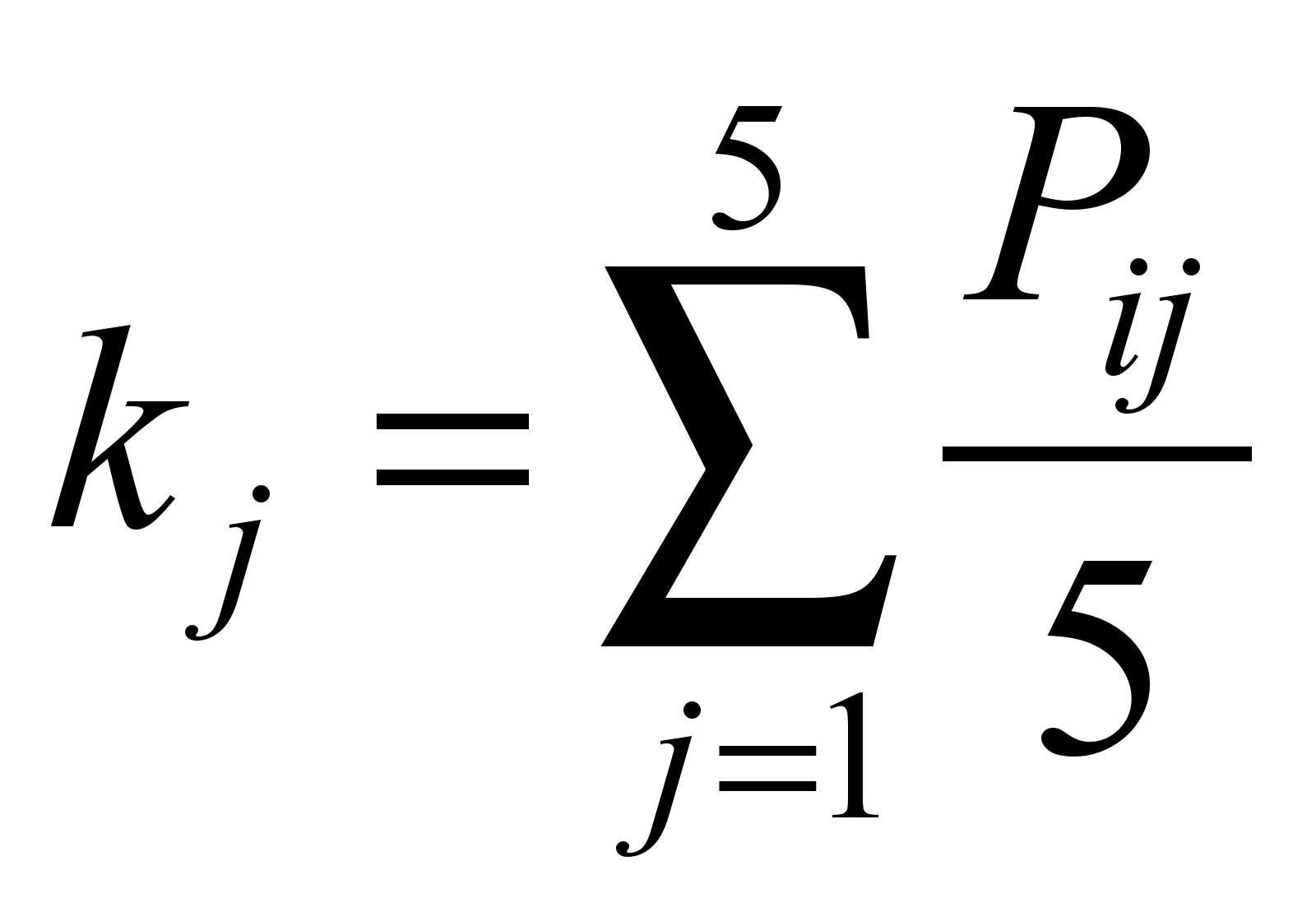 ; (2)
; (2)
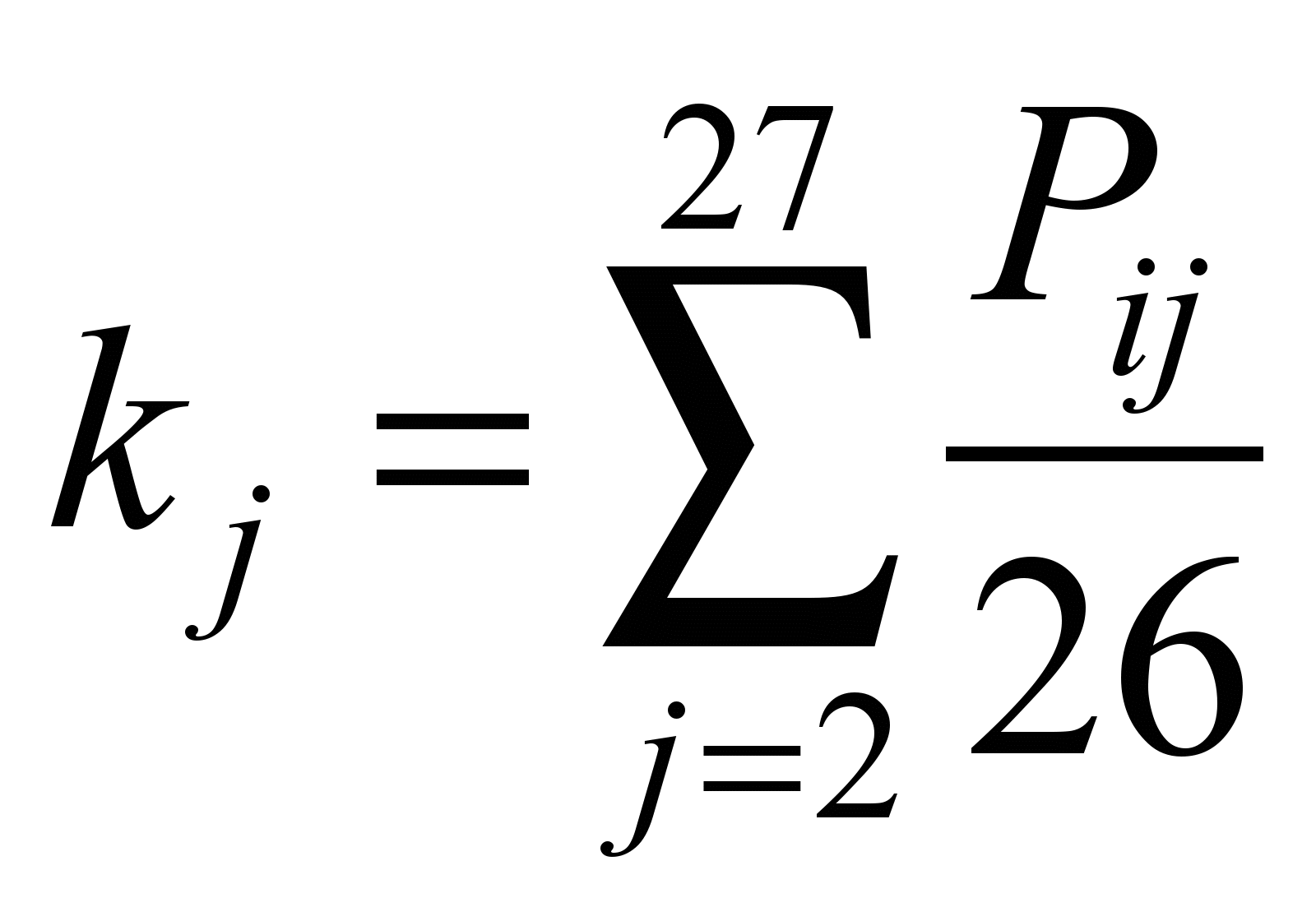 . (3)
. (3)
Коефіцієнти
відхилення прибуття поїздів на станції
лінії К – О наведено в табл. 3.
Таблиця 3
Коефіцієнти
відхилення прибуття поїздів на станції
лінії К – О
Table
3
The
coefficients of deviation in the arrival of trains
to the
stations of K - O line
|
№
зп
|
Станція
|
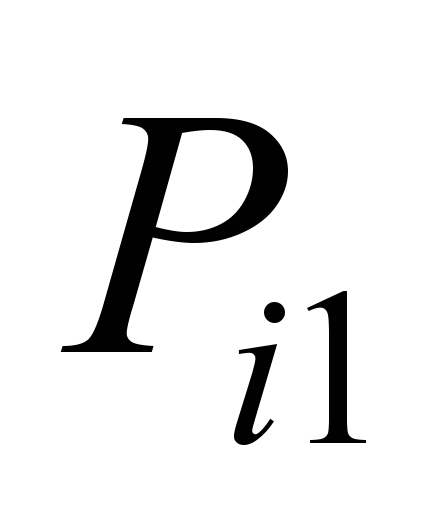
|
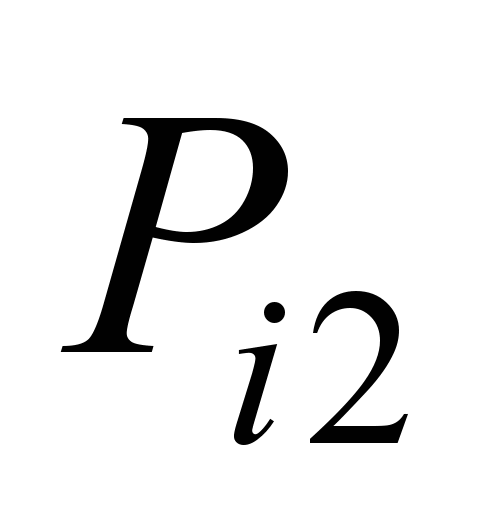
|
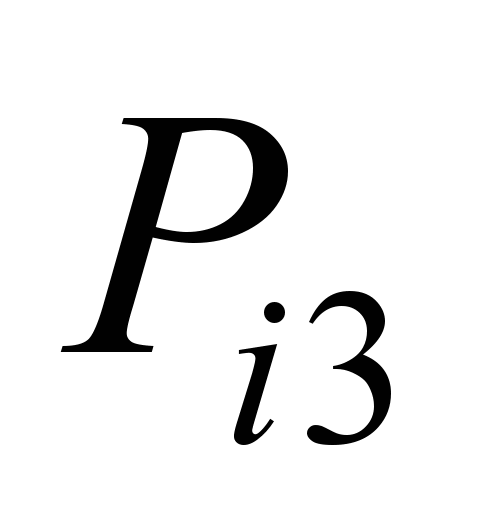
|
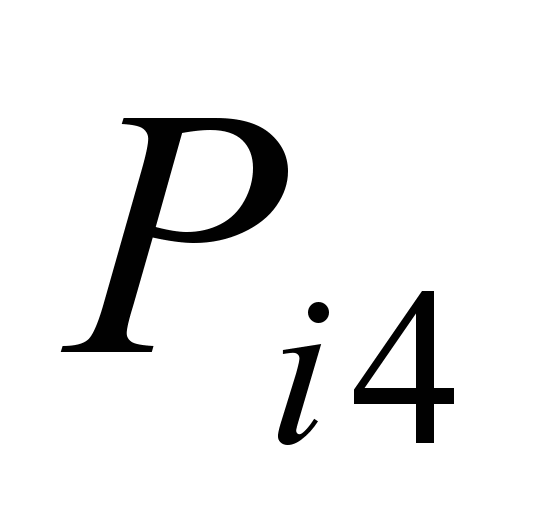
|
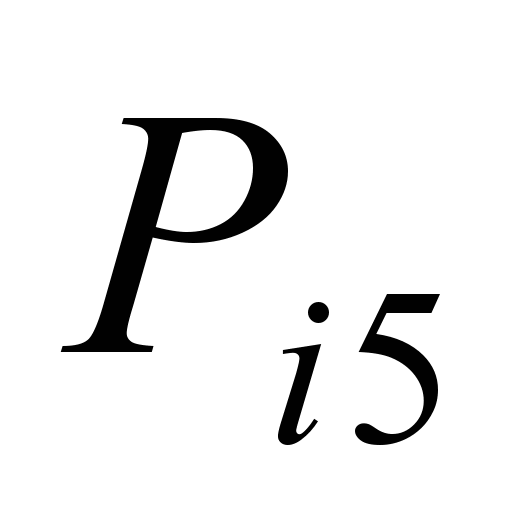
|
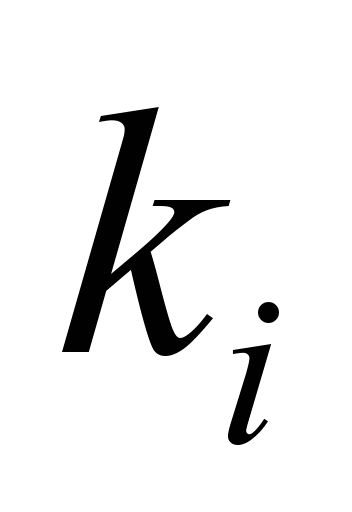
|
|
1
|
Кривий
Ріг
|
–
|
–
|
–
|
–
|
–
|
–
|
|
2
|
Кривий
Ріг–Західний
|
–0,40
|
0,57
|
0,87
|
1,56
|
234,52
|
47,42
|
|
3
|
Мусіївка
|
–0,99
|
0,57
|
0,84
|
1,59
|
201,82
|
40,77
|
|
4
|
Гейківка
|
0,00
|
0,56
|
0,90
|
1,54
|
174,56
|
35,51
|
|
6
|
Висунь
|
–0,09
|
0,45
|
0,88
|
1,67
|
124,91
|
25,56
|
|
7
|
Тимкове
|
–0,10
|
0,36
|
0,82
|
1,82
|
20,32
|
4,64
|
|
8
|
Червоне
Озеро
|
–0,02
|
0,37
|
0,88
|
1,75
|
10,28
|
2,65
|
|
9
|
Бобринець
|
0,08
|
0,52
|
0,90
|
1,58
|
8,58
|
2,33
|
|
10
|
Кропивницька
|
–0,12
|
0,52
|
0,86
|
1,62
|
13,18
|
3,21
|
|
11
|
Олійникове
|
–0,01
|
0,53
|
0,84
|
1,63
|
9,77
|
2,55
|
|
12
|
Кавуни
|
0,04
|
0,56
|
0,85
|
1,58
|
9,16
|
2,44
|
|
13
|
Южноукраїнська
|
0,04
|
0,54
|
0,83
|
1,63
|
8,83
|
2,37
|
|
14
|
Трикратне
|
0,14
|
0,57
|
0,82
|
1,61
|
8,63
|
2,35
|
|
15
|
Олександрівка
|
0,11
|
0,58
|
0,84
|
1,59
|
8,76
|
2,37
|
Продовження
табл.3
Continuation
of Table 3
|
№
зп
|
Станція
|
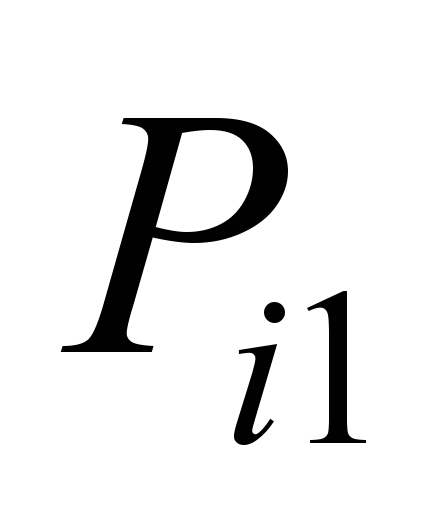
|
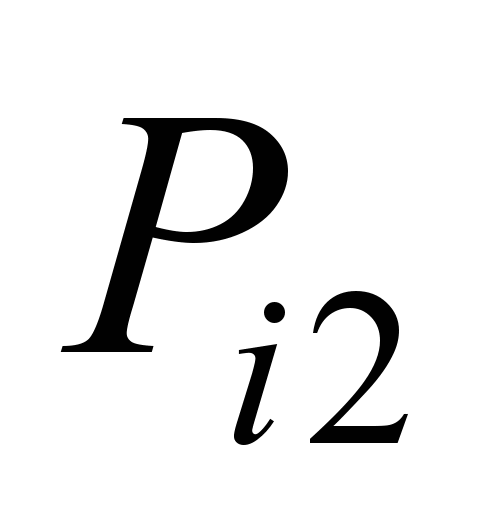
|
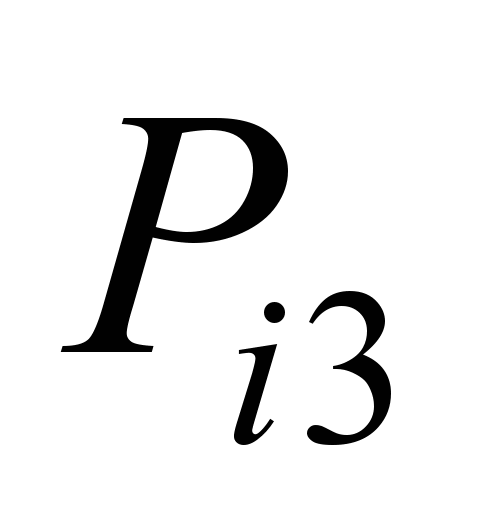
|
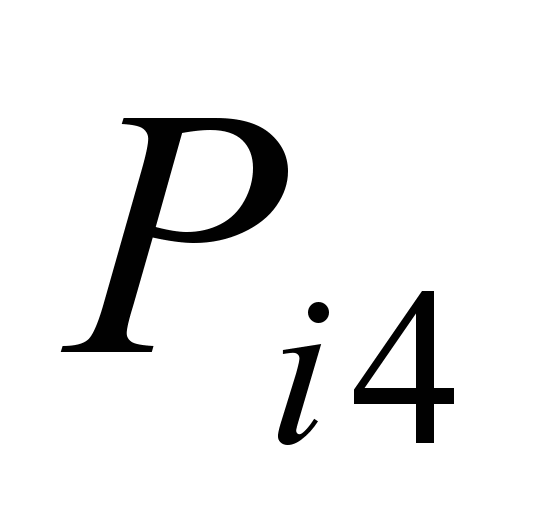
|
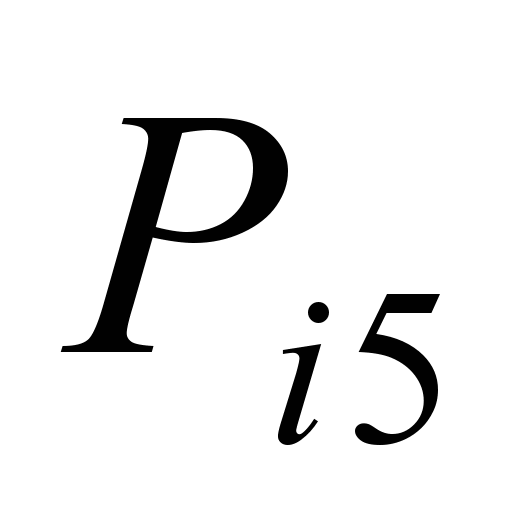
|
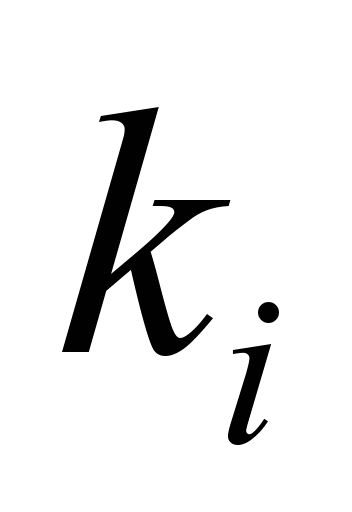
|
|
16
|
Вознесенськ
|
0,15
|
0,61
|
0,86
|
1,53
|
11,07
|
2,84
|
|
17
|
Мартинівська
|
0,16
|
0,61
|
0,84
|
1,55
|
8,03
|
2,24
|
|
18
|
Веселинове
|
0,16
|
0,60
|
0,83
|
1,56
|
7,92
|
2,22
|
|
19
|
Колосівка
|
0,01
|
0,44
|
0,80
|
1,77
|
29,58
|
6,52
|
|
29
|
Березівка
|
0,01
|
0,46
|
0,81
|
1,73
|
28,26
|
6,25
|
|
21
|
Раухівка
|
0,02
|
0,45
|
0,83
|
1,72
|
27,60
|
6,12
|
|
22
|
Сербка
|
0,03
|
0,46
|
0,84
|
1,70
|
27,13
|
6,03
|
|
23
|
Буялик
|
0,01
|
0,45
|
0,83
|
1,72
|
27,50
|
6,10
|
|
24
|
Чорноморська
|
0,01
|
0,46
|
0,82
|
1,72
|
27,24
|
6,05
|
|
25
|
Кулиндрове
|
0,02
|
0,46
|
0,79
|
1,75
|
22,48
|
5,10
|
|
26
|
Одеса–Східна
|
0,07
|
0,42
|
0,77
|
1,81
|
20,26
|
4,67
|
|
27
|
Одеса–Сортувальна
|
0,08
|
0,46
|
0,86
|
1,69
|
18,81
|
4,38
|
|
24
|
Одеса–Порт
|
0,20
|
0,64
|
0,94
|
1,42
|
9,59
|
2,56
|
|
25
|
Висунь
|
–0,09
|
0,45
|
0,88
|
1,67
|
124,91
|
25,56
|
|
26
|
Тимкове
|
–0,10
|
0,36
|
0,82
|
1,82
|
20,32
|
4,64
|
|
27
|
Червоне
Озеро
|
–0,02
|
0,37
|
0,88
|
1,75
|
10,28
|
2,65
|
|
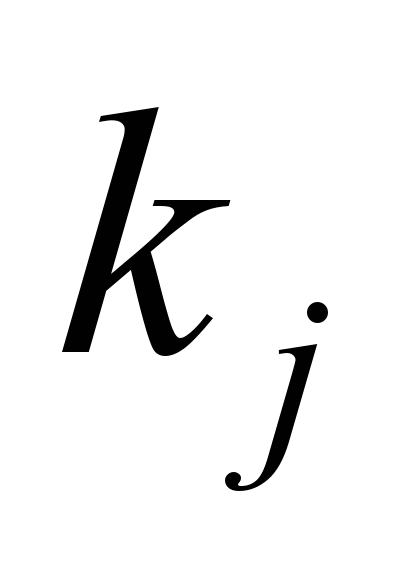
|
–0,02
|
0,51
|
0,84
|
1,65
|
42,26
|
|
Обчислимо значення
загального коефіцієнта відхилення у
рядках та стовпчиках (відповіді мають
співпасти) за формулами [10]:
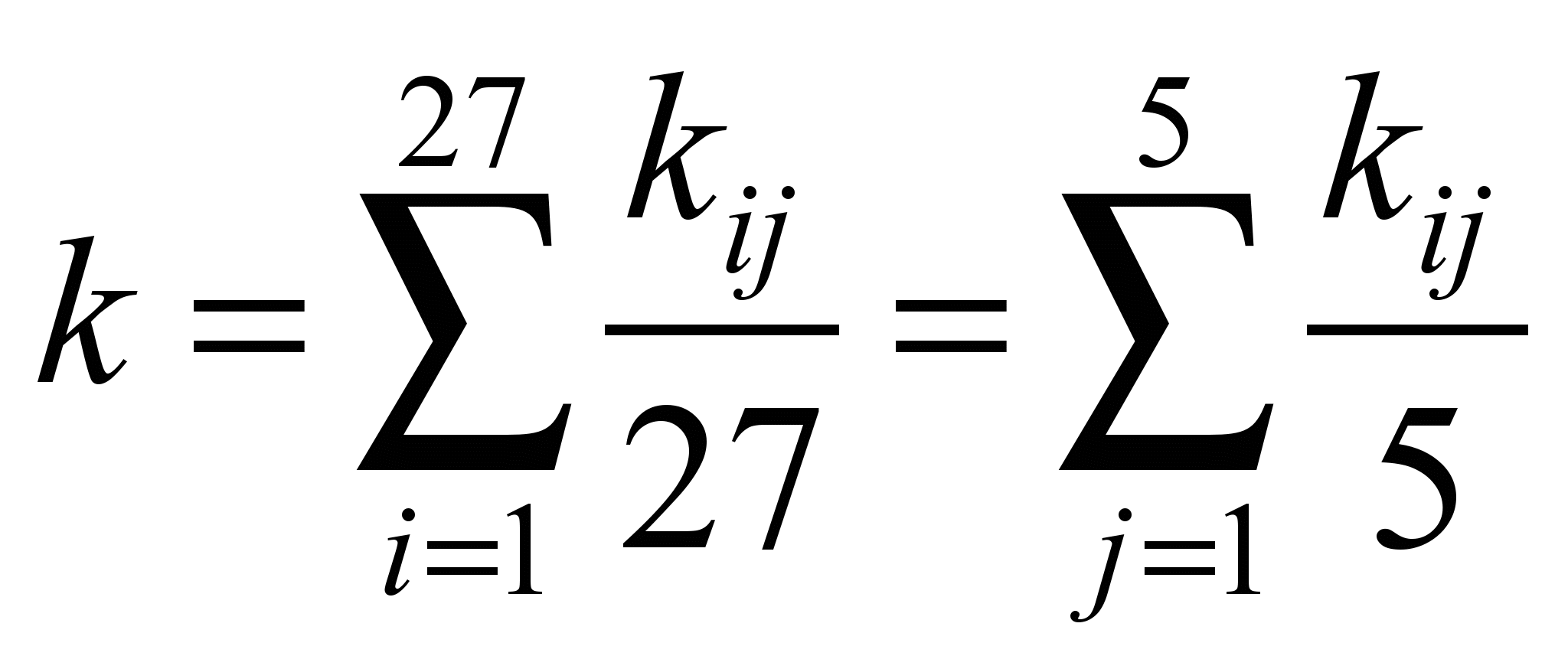 ; (4)
; (4)
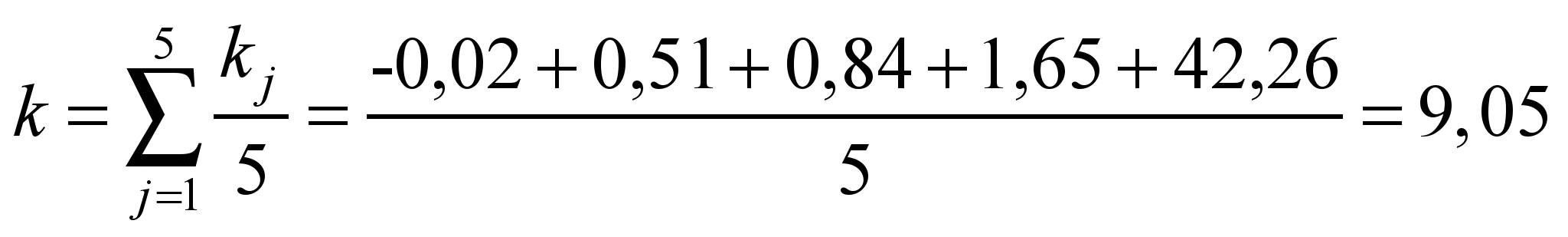
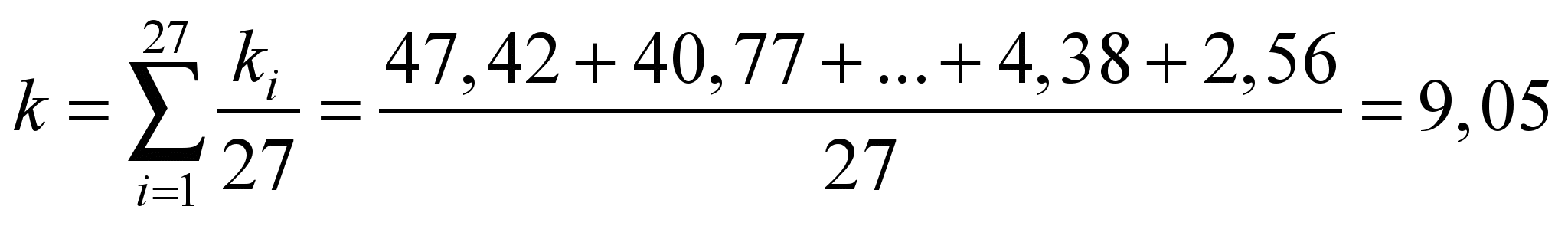
Графічне зображення
цих коефіцієнтів відхилення відображено
на рис. 2.
Як бачимо, коефіцієнти
відхилення зростають зі збільшенням
кількості поїздів, тобто для 0 %
поїздів коефіцієнти коливаються близько
0, для 25 % – близько 0,5, а для 75 % вже
перевищують 1,5 [13].
Проаналізуємо всі
дані про відхилення часу прибуття
поїздів від запланованого, що подані
в табл. 1.
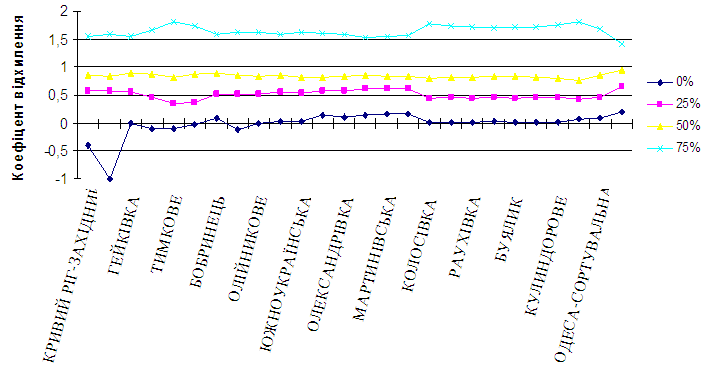
Рис. 2.
Коефіцієнти відхилення прибуття поїздів
на станції лінії К – О
Fig. 2. The
coefficients of deviation in the arrival of trains to the stations
of K – O line
Оскільки загальна
кількість значень досить велика (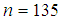 ),
спочатку згрупуємо всі отримані
статистичні дані [1].
),
спочатку згрупуємо всі отримані
статистичні дані [1].
Кількість груп
наближено визначаємо за формулою
Стерджеса:
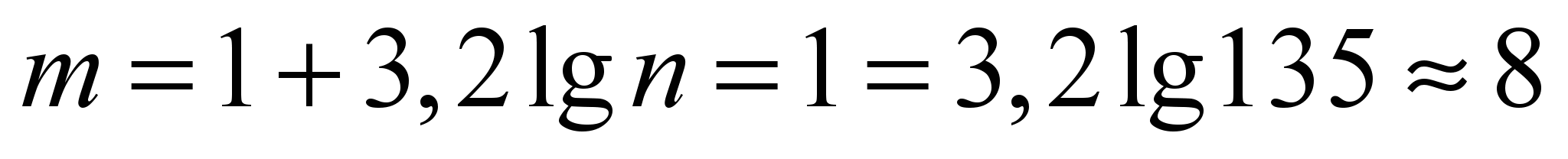
Тоді довжина
інтервалу буде:
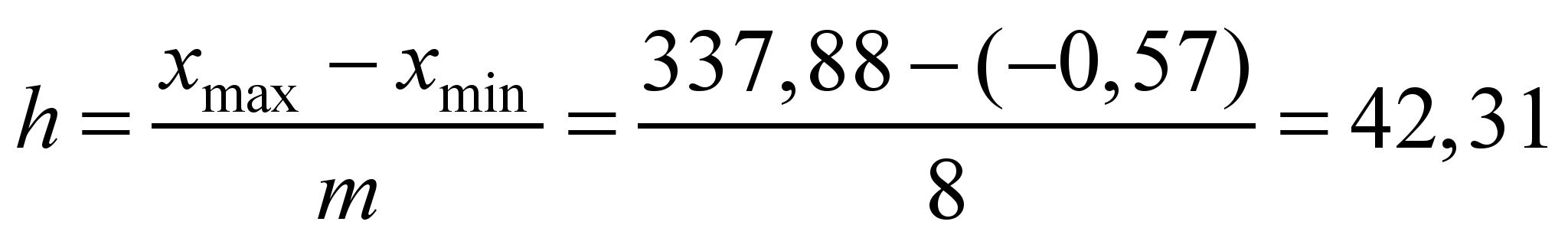 ,
,
де
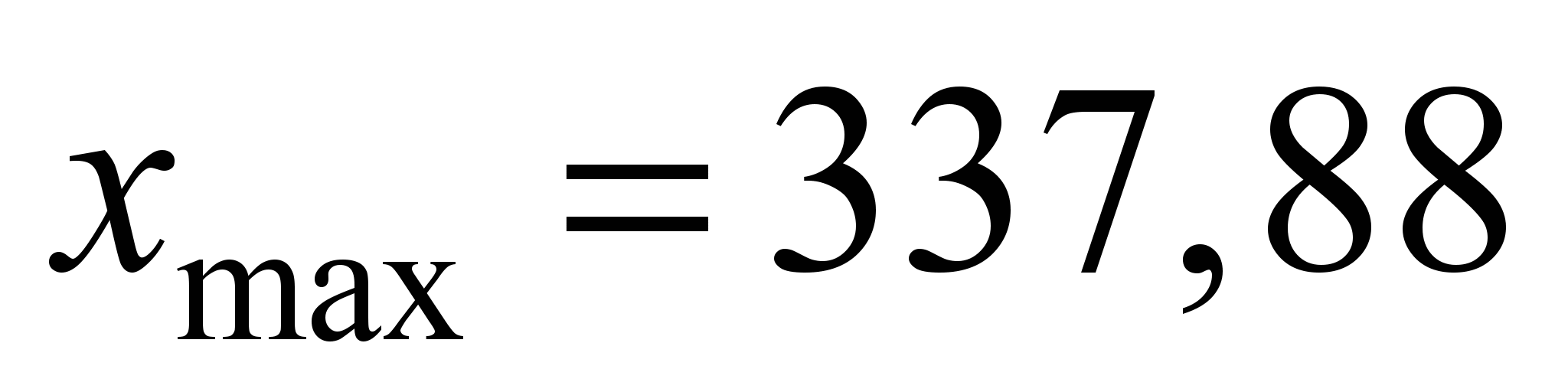 – максимальне значення
відхилення;
– максимальне значення
відхилення;
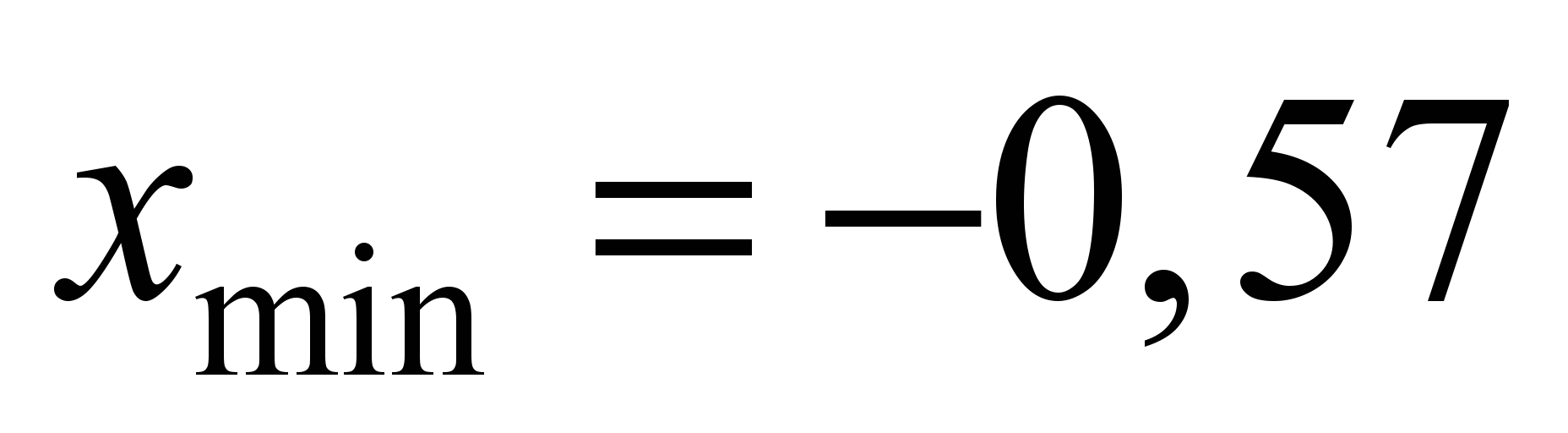 – мінімальне значення відхилення.
– мінімальне значення відхилення.
Отже, усі
дані розбиваємо на 8 інтервалів по 42,31
години. За початок першого інтервалу
для спрощення обчислень візьмемо
мінімальне значення
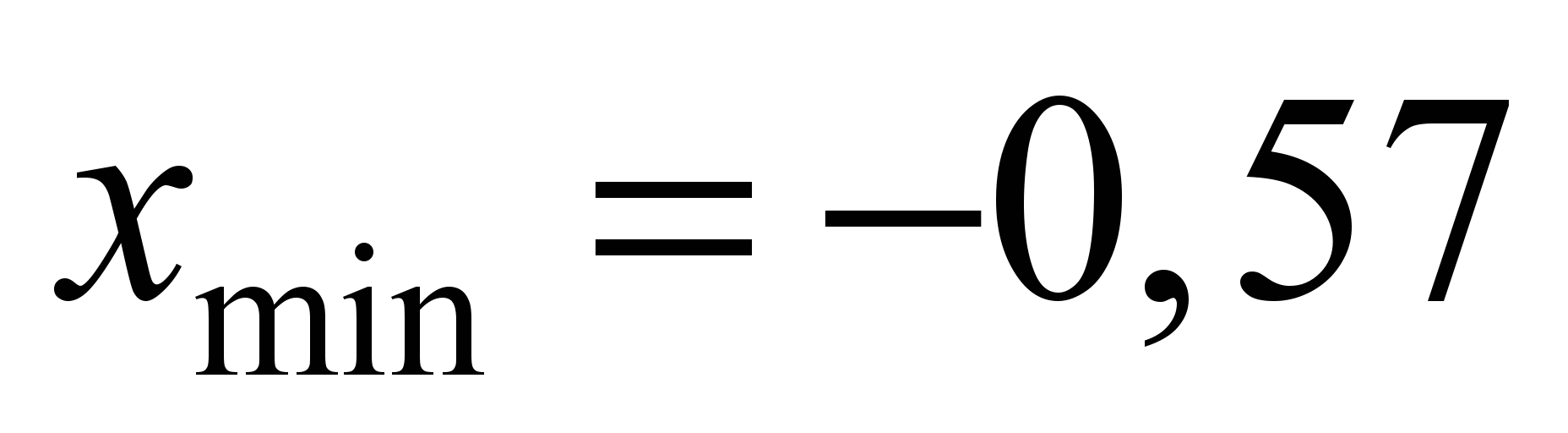 [18]. Для кожного частинного інтервалу
[18]. Для кожного частинного інтервалу
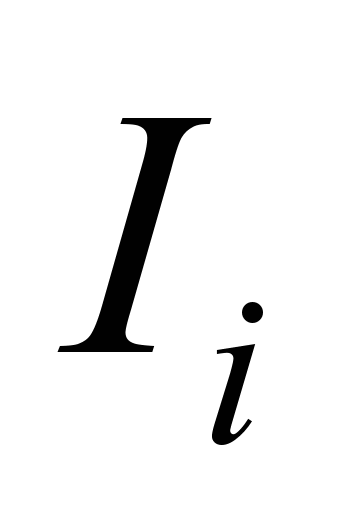 ,
,
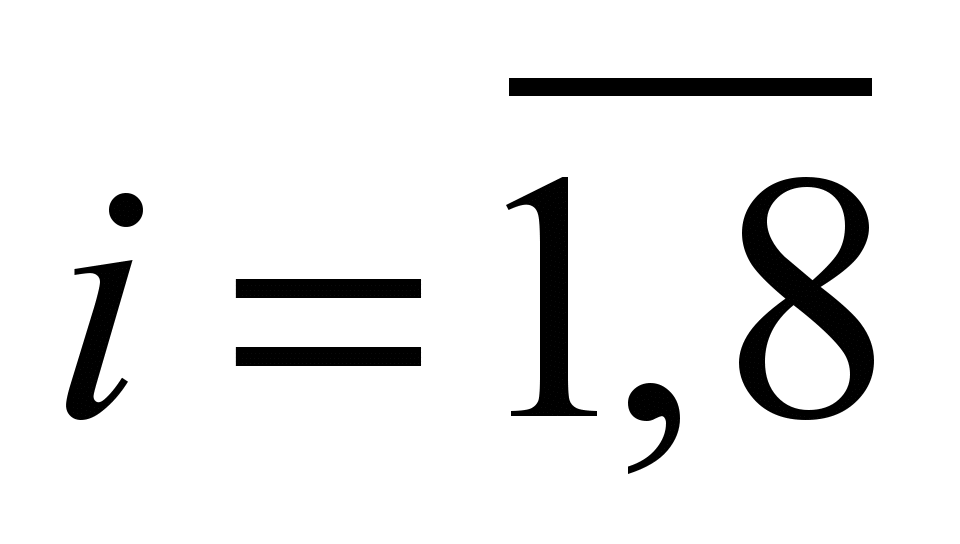 підрахуємо частоти
підрахуємо частоти
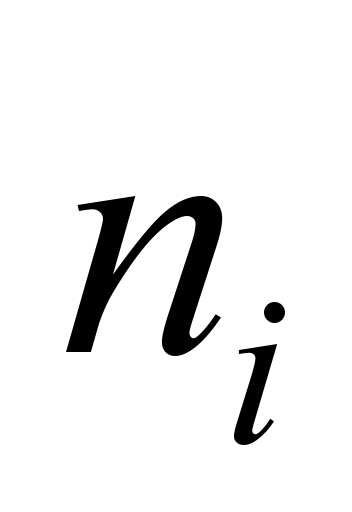 (кількість значень, які потрапляють у
вказаний інтервал). Оскільки і кількість
інтервалів, і крок були обчислені
наближено, перевіримо охоплення
інтервалами всіх значень. Найбільше
значення
(кількість значень, які потрапляють у
вказаний інтервал). Оскільки і кількість
інтервалів, і крок були обчислені
наближено, перевіримо охоплення
інтервалами всіх значень. Найбільше
значення
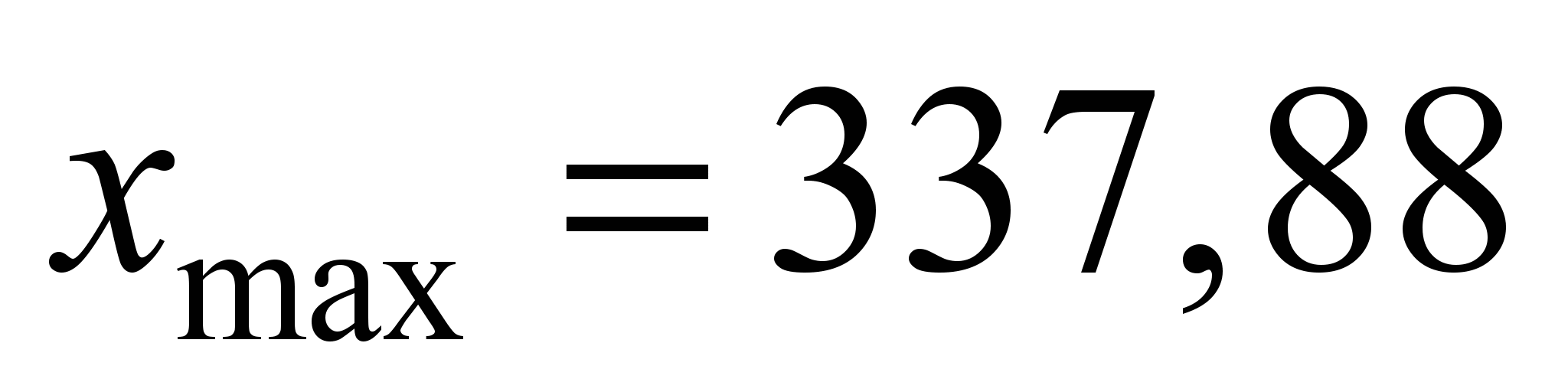 належать до останнього
інтервалу.
належать до останнього
інтервалу.
Інтервальний
статистичний ряд розподілу відхилень
наведено в табл. 4.
Таблиця 4
Інтервальний
статистичний ряд розподілу відхилень
Table
4
Interval
statistical series of distribution of deviations
|
|
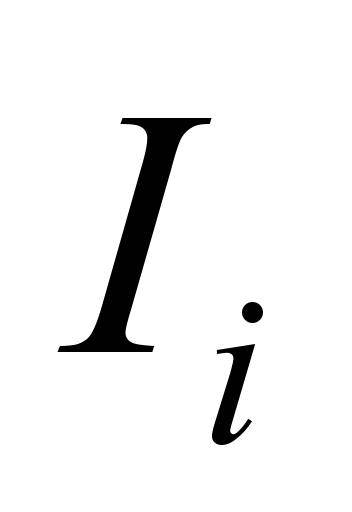
|
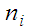
|
|
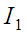
|
–0,57
– 41,74
|
114
|
|
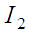
|
41,74
– 84,05
|
11
|
|
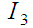
|
84.05
– 126,36
|
0
|
|
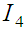
|
126,36
– 168,67
|
0
|
|

|
168,67
– 210.98
|
0
|
|
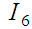
|
210,98
– 253,29
|
7
|
|
|
253,29
– 295,6
|
0
|
|
|
295,6
– 337,91
|
3
|
Графічне
зображення інтервального статистичного
ряду показано на рис. 3.
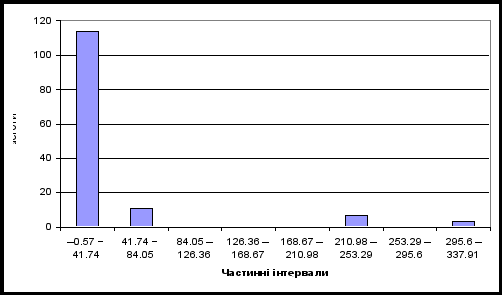
Рис. 3.
Гістограма частот
Fig. 3. Histogram
of frequencies
Наукова новизна
та практична
значимість
У статті
вперше було введено
поняття «коефіцієнт
відхилення», який характеризує відхилення
часу прибуття поїзда на станцію від
запланованого по відношенню до
очікуваного відхилення.
Висновки
На основі наведеної
математичної моделі можна передбачити
приблизну величину запізнення поїздів
для залізничної лінії з більшою кількістю
станцій, якщо основні характеристики
вантажоперевезення залишаться без
суттєвих змін (наприклад, значного
поліпшення або погіршення технічних
характеристик залізничної інфраструктури).
Спираючись
на результати аналізу відхилення часу
прибуття поїздів на станцію залежно
від прогону, можна зазначити, що
простежується прямий взаємозв’язок
між запізненням поїздів у годинах та
номером станції (тобто відстанню)
[15–17]. Результат залишається
справедливим для довільної кількості
поїздів (було розглянуто 0, 25, 50, 75 та
100 %).
СПИСОК ВИКОРИСТАНИХ
ДЖЕРЕЛ
Гмурман,
В. Е. Теория вероятностей и математическая
статистика : учеб.
пособие для вузов /
В. Е. Гмурман. –
10-е изд.,
стереот.
– Москва : Высш.
шк., 2004. –
479 с.
Економічна
енциклопедія :
у 3 т. /
відп. ред. С. В. Мочерний.
– Київ :
Академія, 2000. –
Т. 1.
– 864 с.
Елисеева,
И. И. Общая теория статистики
: учебник
/ И. И. Елисеева,
М. М. Юзбашев
; под ред.
И. И. Елисеевой. – 4-е изд.,
перераб.
и доп. – Москва :
Финансы и Статистика, 2001.
– 480 с.
Кириченко,
Г. І.
Проблематика застосування інформаційних
технологій в управлінні
процесами доставки
вантажу / А.
І. Кириченко
// Проблеми
транспорту :
зб. наук. пр. – Київ, 2012.
– Вип. 9.
– С. 17–27.
Кириченко,
Г. І. Інтелектуальна система управління
процесом доставки вантажу
/ Г. І.
Кириченко // Інформ.-керуючі
системи на залізн.
трансп. –
2015. – №
5 (114). –
С. 3–6.
Кириченко,
Г. І. Концепція інтелектуальної
транспортної системи управління
процесами доставки вантажу //
Залізничний транспорт
України. –
2013. – №
1. –
С. 37–40.
Мармоза,
А. Т. Теорія статистики
: підручник
/ А. Т. Мармоза. – 2-е вид,
перероб. та
доп. – Київ :
Центр
учбової літератури, 2013. – 592
с.
Методологічний
аспект формування критеріїв ефективного
управління залізничною транспортною
системою / М. І. Данько, Т. В. Бутько, Д.
В. Ломотько, В. В. Козак //
Зб. наук. пр. Укр. держ. акад. залізн.
трансп. – Харків, 2010.
– Вип. 113.
– С. 5–9.
Общая
теория статистики : учебник / под
ред. Р. А. Шмойловой. – 3-е изд., перераб.
– Москва : Финансы и Статистика, 2002. –
560 с.
Титов,
Б. А.
Транспортная логистика [Електронний
ресурс] : электрон. учеб. пособие / Б. А.
Титов //
docplayer.ru.
– Самара, 2012. –
Режим доступу:
https://docplayer.ru/25930451-B-a-titov-transportnaya-logistika.html
– Назва з екрана. –
Перевірено : 22.12.2018.
Удосконалення
технічного нормування показників
експлуатаційної роботи в умовах
перерозподілу повноважень структурних
вертикалей ПАТ «Укрзалізниця» :
матеріали семінару-наради (05–06 черв.
2018 р.). – Львів, 2018. – С. 1–16.
Усков,
А. А.
Интеллектуальные
технологии управления. Искусственные
нейронные сети и нечёткиая логика
/ А. А. Усков, А.
В. Кузьмин.
– Москва
: Горячая линия-Телеком. 2004. –
143 с.
Analysis
of Various Approaches to Modeling of Dynamics of Lifting-Transport
Vehicles / O. Grigorov,
E. Druzhynin, G. Anishchenko, M.
Strizhak, V. Strizhak // International Journal of Engineering &
Technology. – 2018. – Vol. 7. – Iss.
4.3. – P. 64–70. doi: 10.14419/ijet.v7i4.3.19553
Assessment
of cargo delivery quality using fuzzy set apparatus
/ Н. Kyrychenko, Y.
Statyvka, О.
Strelko,
Y.
Berdnychenko, Н.
Nesterenko //
International
Journal of Engineering & Technology.
– 2018.
–
Vol.
7. –
Iss. 4.3.
– P. 262–265. doi:
10.14419/ijet.v7i4.3.19800
A
standardised language code for rail freight operations / M.
Marinov, T. Zunder, R. Arnoldus, C. Moolen // Transport Problems. –
2012. – Vol. 7.
– Iss.
2. – Р.
141–148.
Kirit
Mehta, A. Adopting
pade approximation for first order plus dead time models for
blending process /
A. Kirit Mehta,
R. Swarnalatha
// International Journal of Engineering &
Technology. – 2018. –
Vol.
7. – Iss.
4. – P.
2800–2805.
doi:
10.14419/ijet.v7i4.18089
Simulation
Technique of Kinematic Processes in the Vehicle Steering Linkage /
S. Chernenko, E. Klimov,
A. Chernish, O. Pavlenko, V. Kukhar //
International Journal of Engineering & Technology. – 2018. –
Vol. 7. – Iss.
4.3. – P. 120–124. doi:
10.14419/ijet.v7i4.3.19720
Strutynskyi,
S. Mathematical Modelling of a Specialized Vehicle Caterpillar
Mover Dynamic Processes Under Condition of the Distributing the
Parameters of the Caterpillar / S. Strutynskyi, V. Kravchuk, R.
Semenchuk // International Journal of Engineering & Technology.
– 2018. – Vol. 7. – Iss.
4.3. – P. 40–46.
doi: 10.14419/ijet.v7i4.3.19549
Б.
А. Цейко1*
1*Каф.
«Управление процессами перевозок»,
Государственный университет
инфраструктуры
и технологий, ул. Котельникова, 29/18,
Киев, Украина,
03115, тел. +38 (093) 811 09 20, эл.
почта boris16@bigmir.net,
ORCID 0000-0002-2636-6321
ОЦЕНКА
КАЧЕСТВА ДОСТАВКИ ГРУЗОВ
С ПОМОЩЬЮ
КОЭФФИЦИЕНТА
ОТКЛОНЕНИЯ ВРЕМЕНИ
ПРИБЫТИЯ ПОЕЗДА
Цель.
Исследование направлено на рассмотрение
особенностей исчисления коэффициента
отклонения времени прибытия поезда на
станцию от запланированного по отношению
к ожидаемому отклонению. В настоящее
время для управления перевозками грузов
применяются подходы, в которых такой
показатель как коэффициент отклонения
не исчисляется и не учитывается. В
практической реализации это приводит
к тому, что железная дорога, осуществляя
перевозки груза, не получает информацию
по отношению номинальных временных
отклонений к реальным. Эта ситуация
требует решения задач совершенствования
действующих технологий перевозочного
процесса, связанных с формированием,
организацией и отправкой грузов. Поэтому
потребности в расчетах таких коэффициентов
являются актуальными. Методика.
Для достижения цели необходимо
ранжировать собранные статистические
данные, сгруппировать и проанализировать
их. Предложена математическая модель
расчета отклонения времени прибытия
поездов от запланированного и зависимость
данного отклонения от этапа доставки
(станции) и количества поездов (в
процентах от общего их числа). Результаты.
Введено понятие «коэффициент отклонения»,
характеризующий отклонение времени
прибытия поезда на станцию от
запланированного
по отношению к ожидаемому отклонению.
Опираясь на результаты анализа отклонения
времени прибытия поездов на станцию в
зависимости
от прогона,
можно
отметить,
что
прослеживается
прямая
взаимосвязь
между
опозданием
поездов в
часах и
номером
станции (то есть расстоянием). Результат
остается справедливым для произвольного
количества поездов (было рассмотрено
0, 25, 50, 75 и 100 %). Научная
новизна. Автор впервые
ввел понятие «коэффициент отклонения»,
характеризующий отклонение времени
прибытия поезда на станцию от
запланированного
по отношению
к ожидаемому
отклонению.
Практическая
значимость.
На
основании
представленной
математической
модели
можно
предвидеть
приблизительную
величину
опоздания
поездов
для
железнодорожной
линии с
большим
количеством
станций,
если основные характеристики
грузоперевозки останутся без существенных
изменений, например, значительного
улучшения или ухудшения технических
характеристик железнодорожной
инфраструктуры.
Ключевые
слова: отклонение;
коэффициент отклонения; среднее
отклонение; общий коэффициент отклонения;
поезд
B.
A. Tseyko1*
1*Dep.
«Transportation Management»,
State University of Infrastructure
and Technologies, Kotelnikov
St.,
29/18, Kyiv, Ukraine, 03115,
tel. +38 (093) 811 09 20, e-mail
boris16@bigmir.net,
ORCID 0000-0002-2636-6321
EVALUATIng
THE QUALITY OF CARGO
DELIVERY USING THE COEFFICIENT
OF DEVIATION IN
THE ARRIVAL TIME
OF TRAINS
Purpose.
The research is aimed at considering the features of calculating the
coefficient of deviation in the arrival time of trains to the
station from the planned one relative to the expected deviation.
Currently, for the management of cargo
transportation, one uses the approaches in which such an indicator
as the coefficient of deviation is not calculated and not taken into
account. In practical implementation, this leads to the fact that
the railway transporting cargo does not receive information on the
ratio of nominal time deviations to real ones. This situation
requires solving the problems of improving the current technologies
of the transportation process related to the formation, organization
and shipment of cargoes. Therefore, the requirements for the
calculation of such factors are relevant. Methodology.
To achieve the purpose, it is necessary to rank
the collected statistics, group them and analyze them. A
mathematical model is proposed for calculating the deviation of the
train arrival time from the planned one and the dependence of this
deviation from the delivery stage (station) and the number of trains
(as a percentage of their total number).
Findings. The
concept of «deviation
coefficient»
has been introduced, which characterizes the deviation of the time
of train arrival to a station from the planned relative to the
expected deviation. Based on the results of the analysis of the
deviation of the train arrival time at the station depending on the
run, it can be noted that there is a direct relationship between the
lateness of trains in hours and the station number (that is,
distance). The result remains valid for an arbitrary number of
trains (0, 25, 50, 75 and 100% were considered). Originality.
The author first introduced the concept of “deviation
coefficient”, which characterizes the deviation of the time of
train arrival to a station from the planned relative to the expected
deviation. Practical value.
Based on the presented mathematical model, it is possible to foresee
an approximate value of the lateness of trains for a railway
line with a large number of stations, if the main characteristics of
cargo transportation remain without significant changes, for
example, a significant improvement or deterioration of the technical
characteristics of the railway infrastructure.
Keywords:
deviation; deviation coefficient; mean deviation; total coefficient
of deviation; train
REFERENCES
Gmurman,
V. Y. (2004). Teoriya veroyatnostey i
matematicheskaya statistika: uchebnoe posobie dlya vuzov.
Moscow: Vyisshaya shkola.
(in Russian)
Mochernyi,
S. V. (Ed.). (2000). Ekonomichna
entsyklopediia (Vol. 1-3).
Kyiv: Akademiia.
(in Ukrainian)
Yeliseeva,
I. I.
(Ed.),
& Yuzbashev,
M. M. (2001).
Obshchaya teoriya statistiki.
Moscow: Finansy i Statistika.
(in Russian)
Kyrychenko,
H. I. (2012). Problematyka zastosuvannia informatsiinykh
tekhnolohii v upravlinni protsesamy dostavky vantazhu. Transport
Problems, 9, 17-27.
(in
Ukrainian)
Kyrychenko,
H. I. (2015). Intelligence system of a cargo delivery process
management.
Information and Management Systems of Railway Transport, 5(114),
3-6. (in Ukrainian)
Kyrychenko,
H. I. (2013). Kontseptsiia intelektualnoi transportnoi systemy
upravlinnia protsesamy dostavky vantazhu. Zaliznychnyi
transport Ukrainy, 1,
37-40. (in Ukrainian)
Marmoza,
A. T. (2013). Teoriia statystyky:
Pidruchnyk.
Kyiv: Tsentr uchbovoi literatury.
(in Ukrainian)
Danko,
M. I., Butko,
T. V., Lomotko,
D. V., &
Kozak, V. V.
(2010). Metodolohichnyi aspekt formuvannia kryteriiv efektyvnoho
upravlinnia zaliznychnoiu transportnoiu systemoiu.
Collected Scientific Works of
Ukrainian State University of Railway Transport,
113, 5-9.
(in Ukrainian)
Shmoylova,
R. A. (Ed.). (2002).
Obshchaya teoriya statistiki.
Moscow: Finansy i Statistika.
(in
Russian)
Titov,
B. A. (2012). Transportnaya logistika. docplayer.ru.
Retrirved from
https://docplayer.ru/25930451-B-a-titov-transportnaya-logistika.html
(in Russian)
Udoskonalennia
tekhnichnoho normuvannia pokaznykiv ekspluatatsiinoi roboty v
umovakh pererozpodilu povnovazhen strukturnykh vertykalei PAT
«Ukrzaliznytsia»: materialy seminaru-narady (05–06 chervnia
2018 r.).
Lviv. (in Ukrainian)
Uskov,
A. A., &
Kuzmin, A.
V. (2004).
Intellektualnye tekhnologii
upravleniya. Iskusstvennye neyronnye seti i nechetkiaya logika.
Moscow: Goryachaya liniya-Telekom.
(in Russian)
Grigorov,
O., Druzhynin, E., Anishchenko, G., Strizhak, M., & Strizhak,
V. (2018). Analysis of Various Approaches to Modeling of Dynamics
of Lifting-Transport Vehicles.
International Journal of Engineering & Technology, 7(4.3),
64-70. doi: 10.14419/ijet.v7i4.3.19553 (in English)
Kyrychenko,
H., Statyvka, Y., Strelko, O., Berdnychenko, Y., & Nesterenko,
Н. (2018). Assessment of Cargo Delivery Quality Using Fuzzy Set
Apparatus. International Journal of
Engineering & Technology, 7(4.3),
262-265. doi: 10.14419/ijet.v7i4.3.19800 (in
English)
Marinov,
М., Zunder, Т., Arnoldus, R., & Moolen, С. (2012). A
standardised language code for rail freight operations.
Transport Problems, 7(2),
141-148. (in English)
Kirit
Mehta, A., & Swarnalatha, R. (2018). Adopting pade
approximation for first order plus dead time models for blending
process. International Journal of
Engineering & Technology, 7(4),
2800-2805. doi: 10.14419/ijet.v7i4.18089 (in
English)
Chernenko,
S., Klimov,
E., Chernish,
A., Pavlenko,
O., &
Kukhar,
V. (2018).
Simulation Technique of Kinematic
Processes in the Vehicle Steering Linkage.
International Journal of Engineering &
Technology, 7(4.3), 120-124. doi:
10.14419/ijet.v7i4.3.19720 (in
English)
Strutynskyi,
S., Kravchu, V., & Semenchuk, R. (2018). Mathematical Modelling
of a Specialized Vehicle Caterpillar Mover Dynamic Processes Under
Condition of the Distributing the Parameters of the Caterpillar.
International
Journal of Engineering & Technology, 7(4.3),
40-46. doi: 10.14419/ijet.v7i4.3.19549 (in English)
Надійшла до
редколегії: 27.07.2018
Прийнята до друку:
21.11.2018