ISSN
2307–3489 (Print), ІSSN
2307–6666
(Online)
Наука
та прогрес транспорту. Вісник
Дніпропетровського
національного університету залізничного
транспорту, 2018, № 6 (78)
Електричний
транспорт
ЕЛЕКТРИЧНИЙ
ТРАНСПОРТ
УДК
519.87:[656.22:621.331]
М. Г. ПРИТУЛА1*,
О. А. ПАСЕЧНИК2*
1*Центр
математичного моделювання НАНУ, вул.
Дудаєва, 15,
Львів, Україна, 79053, тел. +38
(032) 261 18 85,
ел. пошта myroslav.prytula@gmail.com,
ORCID
0000-0001-9259-4114
2*ДП
«Проектно-конструкторське
технологічне бюро з
автоматизації
систем управління на залізничному
транспорті України»,
вул. Жилянська, 97, Київ, Україна,
01135, тел.
+38 (044) 226 24 82,
ел. пошта sasha1101@ukr.net,
ORCID 0000-0001-7303-0145
РОЗРОБЛЕННЯ
АЛГОРИТМІВ ФОРМУВАННЯ
ЕНЕРГООПТИМАЛЬНИХ
РЕЖИМІВ РУХУ ПОЇЗДІВ
Мета.
Робота передбачає розроблення
алгоритмічного забезпечення для
моделювання й оптимізації режимів руху
поїздів. Методика.
Для описання процесу руху поїзда в
просторових координатах із розподіленою
масою вздовж траєкторії руху запропонована
системна модель. Вона враховує тягові
й опірні параметри та їх зміну залежно
від зовнішніх і внутрішніх факторів.
Для числового інтегрування моделі
системи використаний метод скінченних
різниць. Крім цього, розроблені ітераційні
процедури для задоволення крайових
умов, формування послідовності з режимів
тяги, гальмування й холостого ходу з
відповідними параметрами, щоб забезпечити
виконання критерію оптимальності руху
й технічних обмежень із достатньою
точністю. Критерій оптимальності містить
паливно-енергетичні ресурси, частоту
зміни режимів роботи тягових засобів
(суттєво впливає на зношеність приводів),
затратні ставки тощо. Результати.
Розроблене алгоритмічне, програмне й
інформаційне забезпечення дозволило
проведення: розрахунків режимів ведення
довільних поїздів, зокрема нормативних,
для формування графіків руху, розрахунок
міжпоїзних і станційних інтервалів,
дослідження впливу екстремальних
параметрів поїздів на режими їх ведення.
У системі передбачена можливість
адаптації параметрів моделі руху поїзда
за результатами дослідних поїздок.
Наукова новизна.
У роботі запропонована постановка
розрахунку режимів ведення поїздів як
задачі оптимального керування, з’ясований
швидкий метод її розв’язування. Це
забезпечило автоматизацію процесу
розв’язування великого набору прямих
та обернених режимних, із різними
критеріями оптимальності, задач.
Практична значимість.
Запропонований підхід щодо постановки
й розв’язування задач моделювання та
оптимізації режимів ведення поїздів
пройшов апробацію в процесі розрахунку
основних складових для формування
графіків руху, вибору оптимальних
параметрів реконструкції полотна для
всіх, швидкісних і нових, типів поїздів.
Ключові
слова: тягово-енергетичні розрахунки;
оптимальний режим; математичне
забезпечення; математична модель поїзда;
ідентифікація параметрів моделі; прямі
й обернені задачі
Вступ
Тягово-енергетичні
розрахунки – одна з центральних
проблем ефективного управління
перевізними процесами на залізниці.
Над постановкою та розв’язуванням
цієї проблеми працювали й продовжують
роботу багато колективів [1–11].
Протягом усього часу постановка задач
і методи їх розв’язування були тісно
прив’язані до розвитку обчислювальної
техніки й інформаційних технологій.
Тому перші підходи вимагали суттєвого
спрощення постановок задач і спеціально
поданих вхідних даних, які б дозволили
знайти аналітичне представлення
розв’язку чи побудувати прості «ручні»
ітераційні методи розв’язування
відповідних рівнянь. Так, довідники з
тягових розрахунків [4] пропонували
зображення поїзда у вигляді фізичної
точки, рекомендували використовувати
тільки номінальні тягові й
паливно-енергетичні характеристики
приводів локомотивів, а для зменшення
вхідних даних проводити спрямлення
плану та профілю траєкторії руху
(колій). Ці та інші спрощення забезпечували
постановку однієї задачі – за мінімальний
час проходження поїзда між роздільними
пунктами. У таких випадках точність
моделювання суттєво залежала від
діапазону зміни параметрів траєкторії
руху поїзда. Тягово-енергетичні
розрахунки проводили тільки для певного
набору нормативних поїздів не більше
ніж один чи два рази на рік. Довідники
з тягово-енергетичних розрахунків
рекомендували багато обмежень, які
спрощували алгоритм розрахунку. Серед
рекомендацій було багато варіантів
аналітичних і геометричних підходів,
які дозволяли проводити розрахунок
кривої діаграми швидкості руху «ручним»
способом. Перші програмні комплекси
були створені з урахуванням рекомендацій
щодо наявних вимог до тягових розрахунків.
Під час спроби провести оцінку
паливно-енергетичних ресурсів за
знайденими кривими швидкостей виявилося,
що їх величина є суттєво вищою від
результатів, отриманих із використанням
динамометричних вагонів. У випадку
швидкого нарощення вартості
паливно-енергетичних ресурсів такі
розрахунки уже були незадовільними.
Сказане зумовило проведення досліджень
для побудови адекватних моделей та
алгоритмічного забезпечення, яке б
враховувало всі основні фактори впливу
на режим руху поїзда й дозволило
поставити максимально повний набір
прямих та обернених оптимізаційних
задач.
Підвищення
ефективності експлуатації наявного й
перспективного тягового рухомого
складу в умовах дефіциту паливно-енергетичних
ресурсів (ПЕР) і постійно змінних
нормативів становить важливу
науково-технічну проблему. Її практична
реалізація полягає у створенні
комплексної системи оптимального
планування та керування рухом поїзда.
Крім того, розв’язок названої проблеми
пов’язаний із вирішенням низки важливих
питань, таких як формування оптимальних
режимів ведення поїздів, розроблення
оптимального графіка руху поїздів,
створення тренажерних навчальних
систем та автоматизованих комп’ютерних
систем нормування витрат ПЕР.
Розробленню методів
формування оптимальних режимів руху
поїздів присвячена значна кількість
робіт [1–11]. У них можна виділити такі
напрямки досліджень: оптимальні
стратегії й методи нелінійного
програмування для оптимізації траєкторії
швидкості руху поїздів; підходи щодо
розроблення дорадчих систем для
машиністів; інтегровані моделі для
оптимізації режимів і графіків руху
поїздів; методи динамічного програмування
для забезпечення енергоефективних
режимів руху поїздів з обмеженнями
швидкостей і пропускною здатністю;
основні принципи оптимального управління
рухом поїзда; розроблення моделі і
розрахунок оптимальних координат зміни
режиму роботи локомотивів тощо.
Практично всі
згадані методи й підходи не пройшли
апробацію в реальних умовах експлуатації,
тому наведені результати в цих роботах
є чисто теоретичними. Розроблення
максимально універсальних програмних
комплексів, які б об’єднували засоби
моделювання, планування, ідентифікації,
адаптації й оптимального керування
процесами та були інтегрованими з
інформаційним забезпеченням і засобами
їх постійної актуалізації, вимагає
наявності досвіду в побудові математичних
та імітаційних моделей, методів та
алгоритмів мінімальної складності,
розподілених інформаційних систем
тощо. Крім цього, ще необхідні системні
знання (технічні, технологічні,
економічні), які стосуються об’єкта
дослідження. Досвід реалізації
широкомасштабних проектів показав, що
традиційні підходи й відомі класичні
методи не дають змоги ставити й ефективно
розв’язувати задачі, які б задовольнили
сучасні вимоги щодо їх якості за
функціональністю, надійністю, зручністю
використання, продуктивністю, адаптивністю
тощо. У зв’язку з цим завершені наукоємні
програмні продукти промислового
значення, необхідні для практичного
використання, в основному є відсутніми.
В окремих
роботах [7] запропоновано, для розв’язування
задач оптимізації режимів руху поїздів
використовувати класичні математичні
інструменти; проте не наведено будь-яких
прикладів їх використання. Результати
приведені в монографії [1, 186–191] дають
розуміння того, що для
розв’язування задач
такого рівня складності реалізувати
класичні підходи практично нереально.
Для отримання результатів необхідно
розробляти нові методи, які б максимально
використовували особливості об’єкта
дослідження: фізику процесів, наявні
емпіричні залежності, результати
аналізу замірів отриманих із використанням
динамометричних вагонів, тощо.
Розв’язати
задачу оптимального керування рухом
поїзда не вдається класичними методами,
оскільки всі змінні, які
його характеризують, є нелінійними,
багатопараметричними, зі змінними
обмеженнями, а деякі вхідні дані є
слабо прогнозованими. Крім цього,
важливим є унікальність
об’єкта за набором факторів впливу,
зосереджених і розподілених, дискретних
і неперервних, які нелінійним чином
впливають на процес руху [14].
Мета
Ураховуючи
вищезазначене, метою статті є: побудувати
математичні моделі основних типів
тягових засобів і поїздів із розподіленою
масою вздовж траєкторії руху; розробити
ефективне алгоритмічне забезпечення
для моделювання й оптимізації процесу
руху поїздів за заданими критеріями
оптимальності; розв’язати необхідний
набір прямих та обернених тягових і
енергетичних задач для систем побудови
оптимальних графіків і розрахунку
параметрів безпечного руху на перегонах
і роздільних пунктах.
Методика
Для досягнення
поставленої мети використані засоби
математичного й імітаційного моделювання.
Розроблена математична модель руху
поїзда в просторових координатах із
розподіленою масою вздовж траєкторії
руху реалізується за допомогою числового
інтегрування методом скінченних
різниць. Для процесу керування
локомотивами розроблені детальні
імітаційні моделі, які відтворюють їх
роботу з урахуванням реальних тягових,
енергетичних характеристик і наявних
зовнішніх впливів тощо. Поставлені
оптимізаційні задачі розв’язані
розробленими методами дискретної
(комбінаторної) оптимізації.
Результати
Математичне
описання моделі поїзда ґрунтується на
класичних положеннях теорії локомотивної
тяги, уявленні про поїзд як об’єкт
керування, а також враховує основні
розрахункові залежності, визначені в
нормативній літературі [12].
Питання теоретичного описання руху
поїзда докладно розроблені у згаданих
джерелах. Однак у них багато положень,
які стосуються руху поїзда як фізичної
точки з використанням тільки номінальних
тягових характеристик. Певні обмежувальні
рекомендації довелося видозмінити, бо
вони не дозволяли поставити коректно
математичну задачу оптимального
керування поїздом із розподіленою
масою вздовж його складу з урахуванням
повної множини важливих обмежень і
тягово-енергетичних характеристик. У
більшості випадків рекомендації,
наведені в нормативній літературі,
дозволяли постановку тільки однієї
задачі, як вже було сказано, руху поїзда
за мінімальний час.
Параметри
руху поїзда
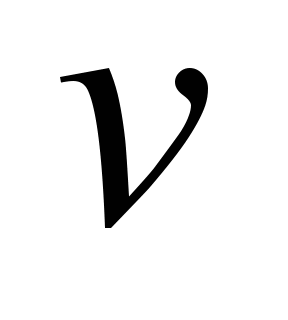 ,
,
 ,
,
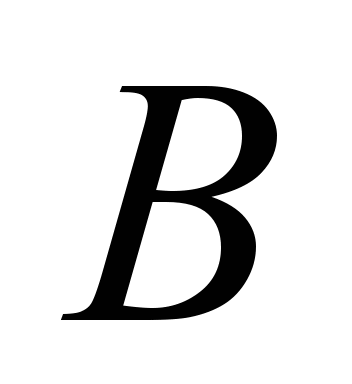 (швидкість руху, сила тяги й гальмівна
сила) задовольняють рівняння:
(швидкість руху, сила тяги й гальмівна
сила) задовольняють рівняння:
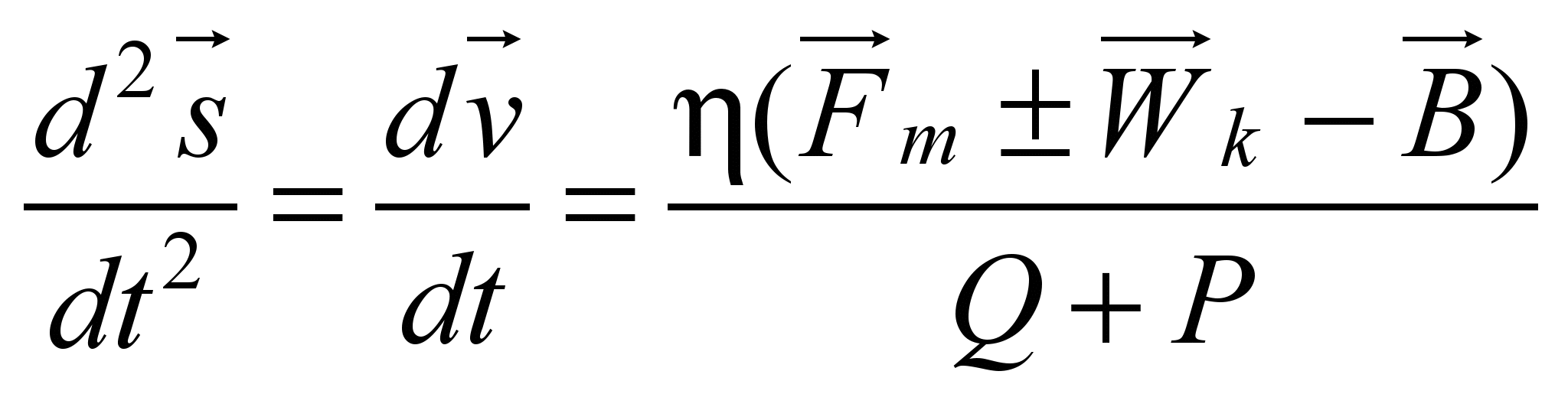 (1)
(1)
за обмежень
 ,
,
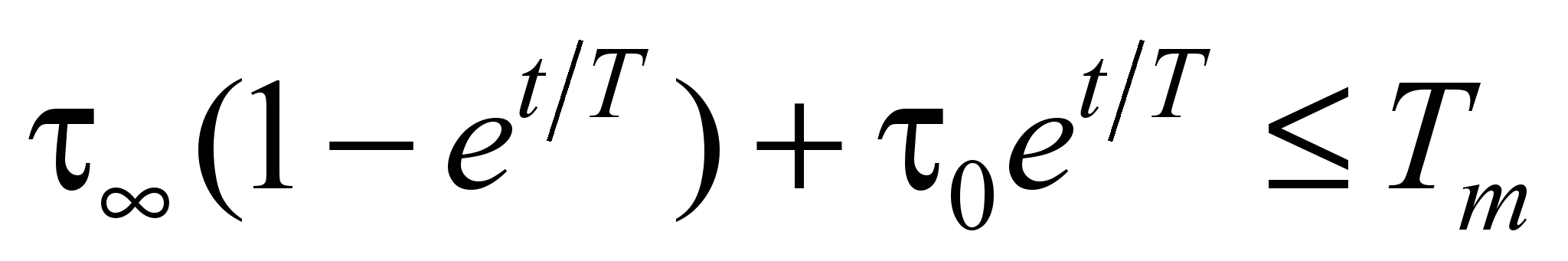 , (2)
, (2)
тут
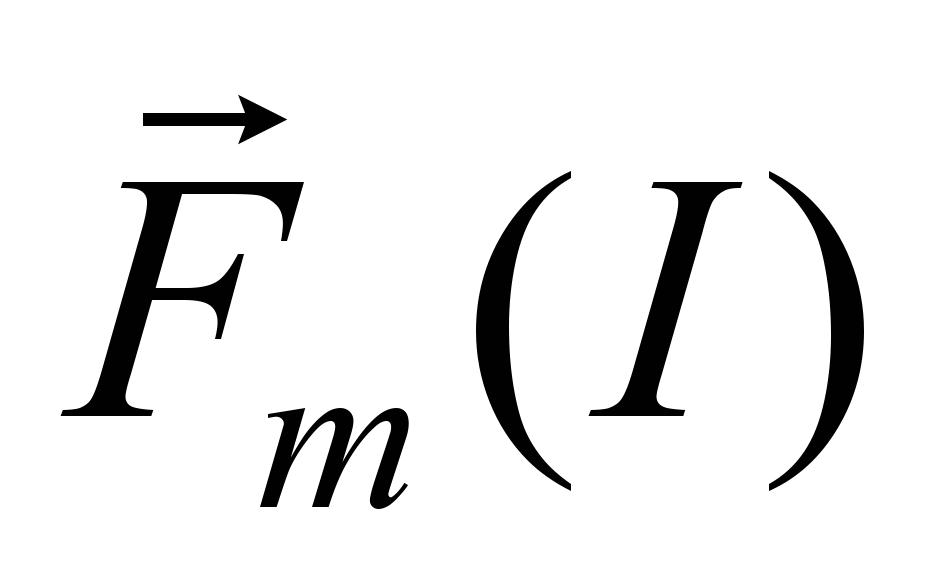 – тягова сила, Н;
– тягова сила, Н;
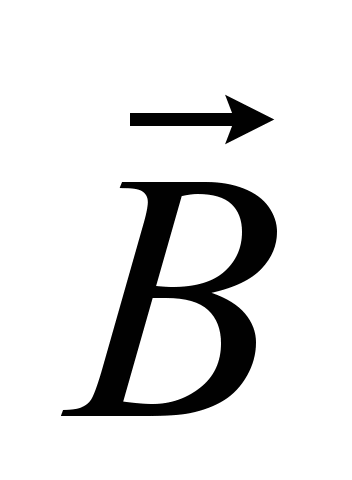 – гальмівна сила, Н;
– гальмівна сила, Н;
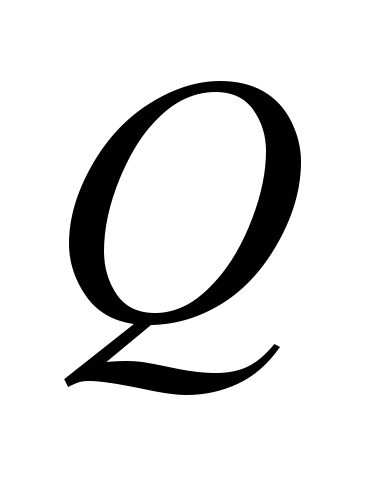 – маса вагонів, Н;
– маса вагонів, Н;
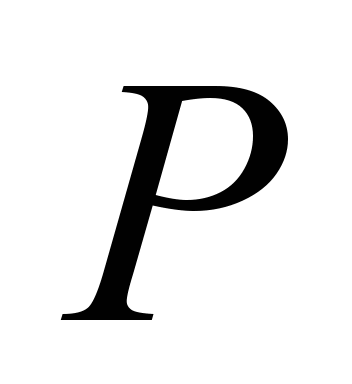 – маса локомотива, т;
– маса локомотива, т;
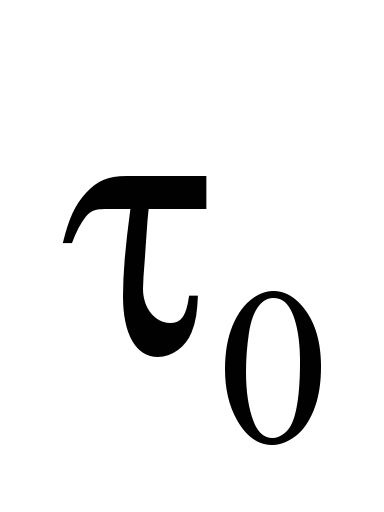 – різниця між температурою обмоток
тягових двигунів і температурою повітря,
оС;
– різниця між температурою обмоток
тягових двигунів і температурою повітря,
оС;
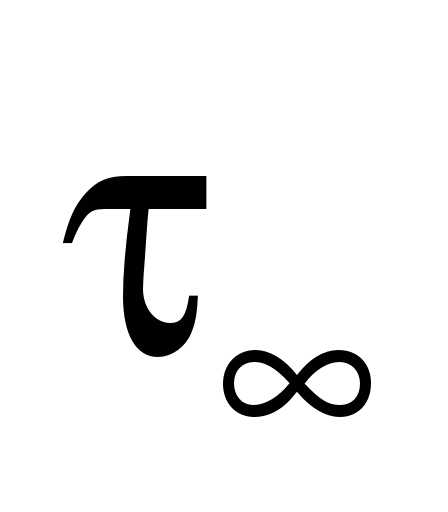 ,
,
 – значення теплових
параметрів, що залежать від величини
струму, який використовує тяговий
двигун;
– значення теплових
параметрів, що залежать від величини
струму, який використовує тяговий
двигун;
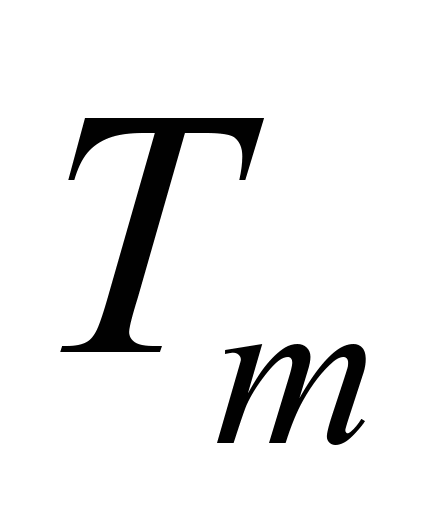 – максимально допустима
температура нагрівання обмоток тягових
двигунів, оС;
– максимально допустима
температура нагрівання обмоток тягових
двигунів, оС;
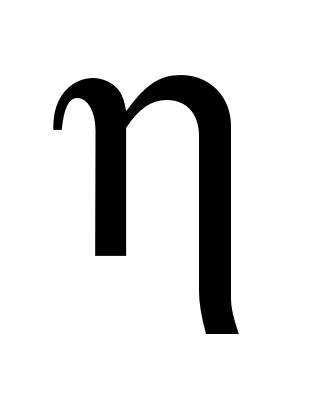 – коефіцієнт інерції обертових мас
поїзда, км/год2;
– коефіцієнт інерції обертових мас
поїзда, км/год2;
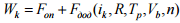 ,
де
,
де
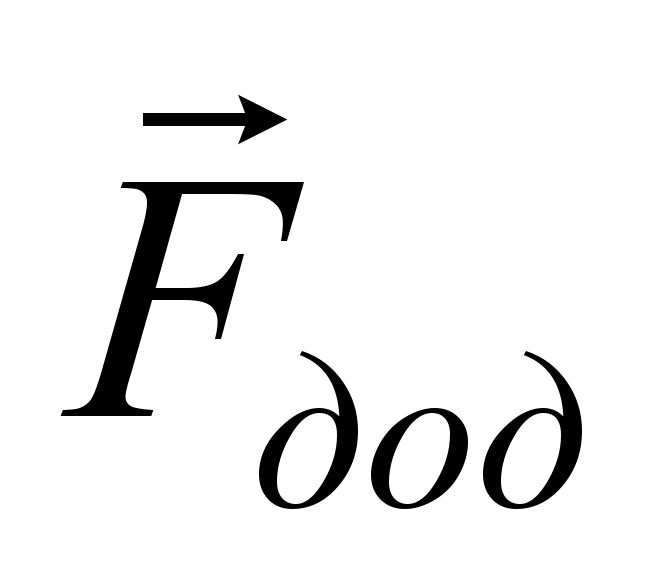 – сила додаткового опору, яка залежить
від ухилу,
– сила додаткового опору, яка залежить
від ухилу,
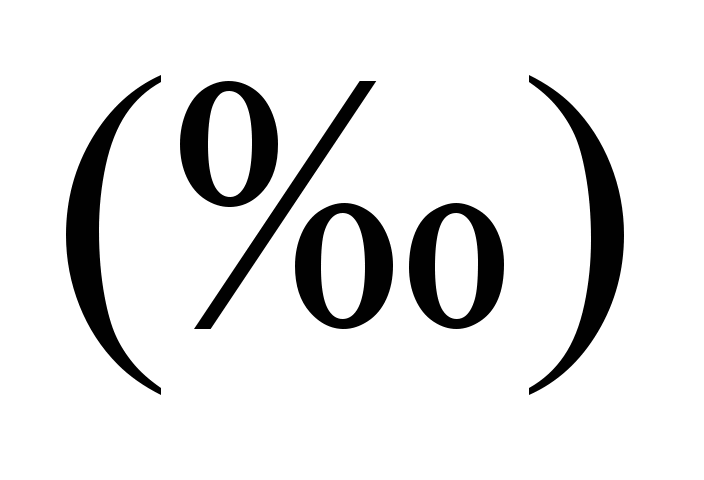 ;
радіуса кривизни
;
радіуса кривизни
 траєкторії переміщення, м; температури
повітря
траєкторії переміщення, м; температури
повітря
 ,
оС;
швидкості зустрічного вітру
,
оС;
швидкості зустрічного вітру
 ,
м; кількості увімкнених підвагонних
генераторів
,
м; кількості увімкнених підвагонних
генераторів
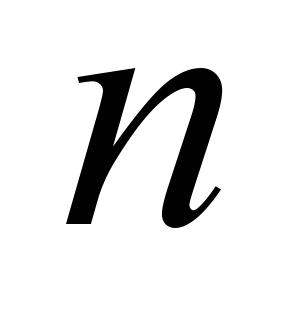 ;
;
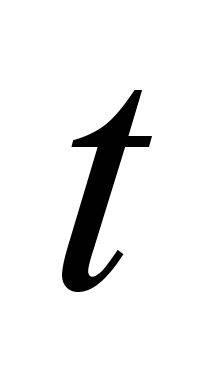 – час, год.
– час, год.
Поїзд –
це упорядкований набір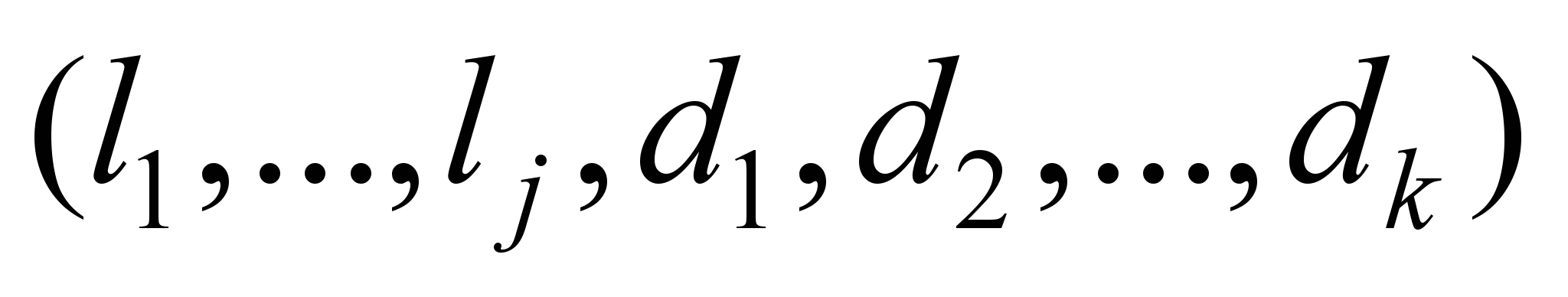 однотипних
локомотивів
однотипних
локомотивів
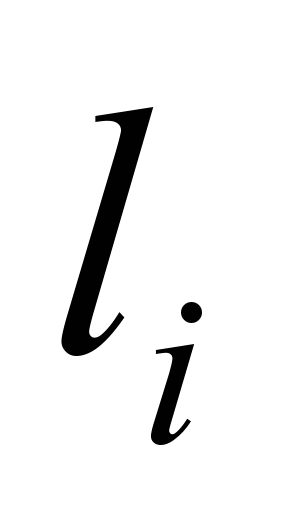
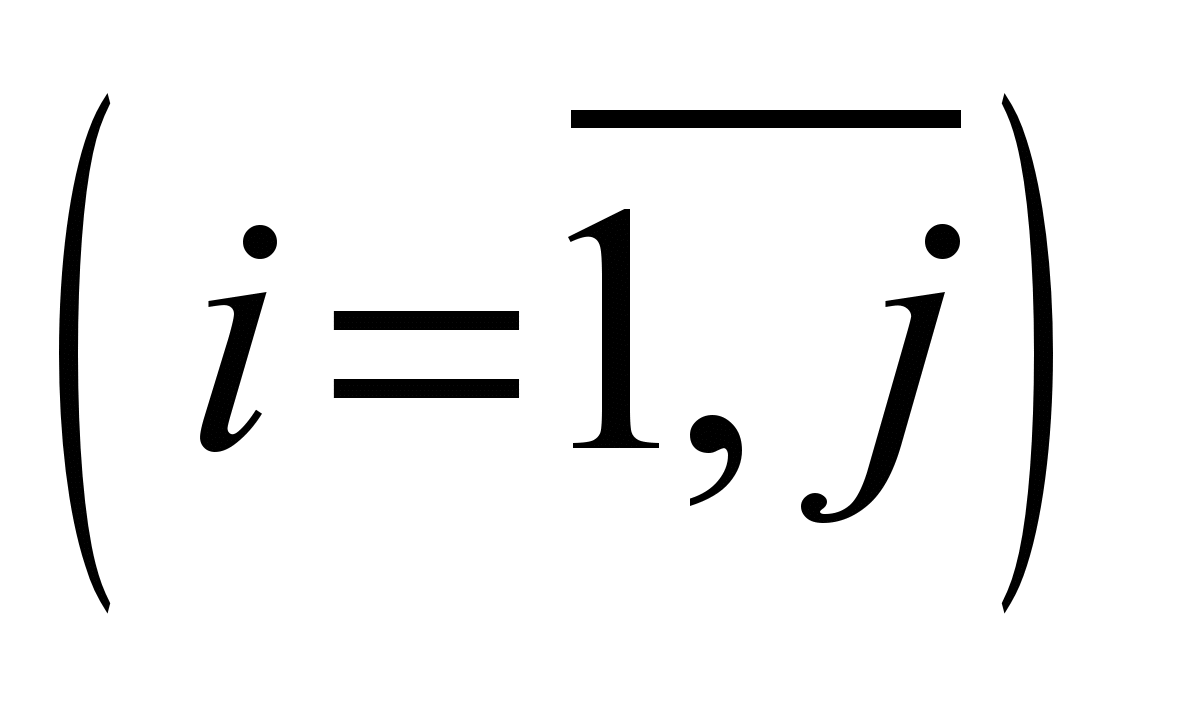 і вагонів
і вагонів

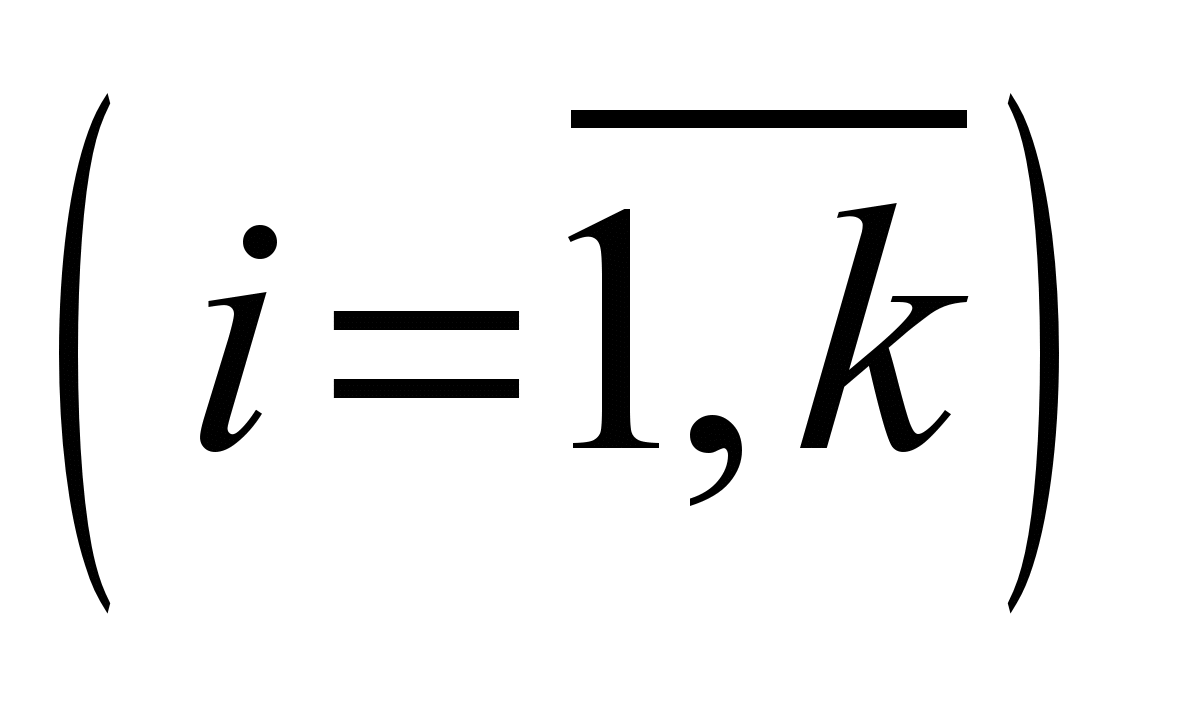 .
Порядок розміщення локомотивів у поїзді
може бути різним.
.
Порядок розміщення локомотивів у поїзді
може бути різним.
Локомотиви
є різних типів. Тип
локомотива визначають за параметрами:
масою
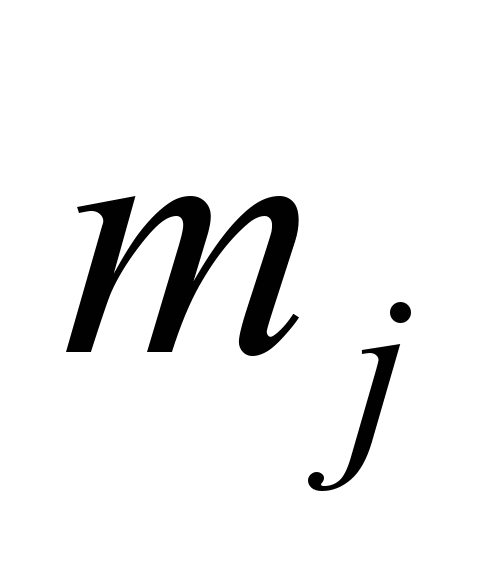 ,
довжиною
,
довжиною
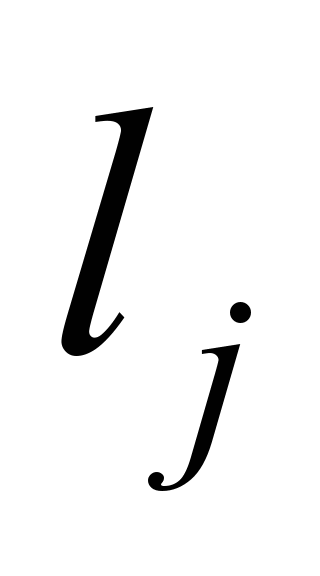 ,
кількістю осей
,
кількістю осей
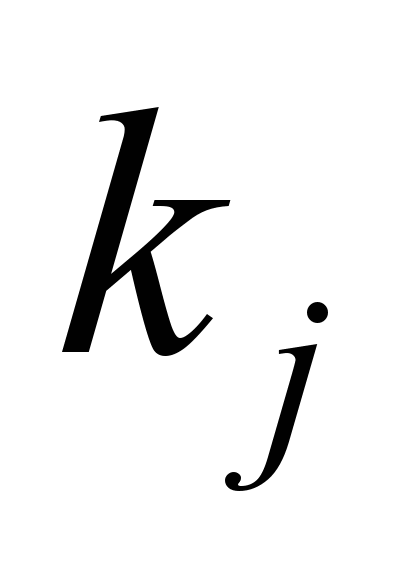 ,
силою натиску гальмівних колодок на
вісь
,
силою натиску гальмівних колодок на
вісь
 ,
конструктивною швидкістю
,
конструктивною швидкістю
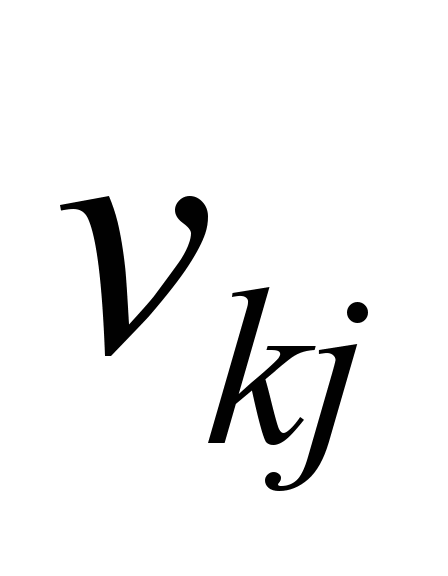 ,
затратами палива в режимі холостого
ходу
,
затратами палива в режимі холостого
ходу
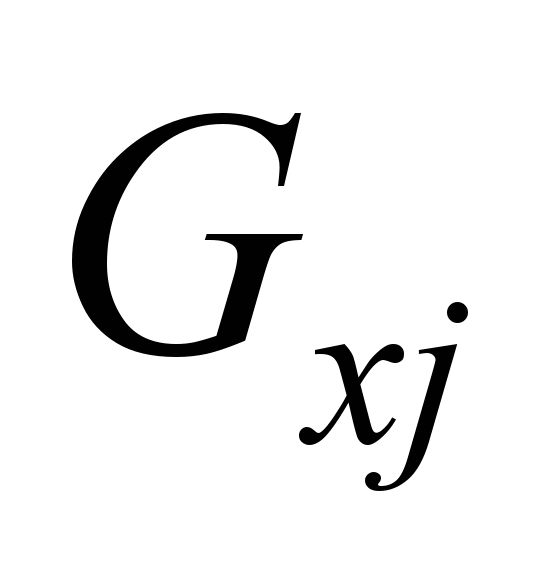 (для тепловозів і
дизель-поїздів), затратами електроенергії
на внутрішні потреби
(для тепловозів і
дизель-поїздів), затратами електроенергії
на внутрішні потреби
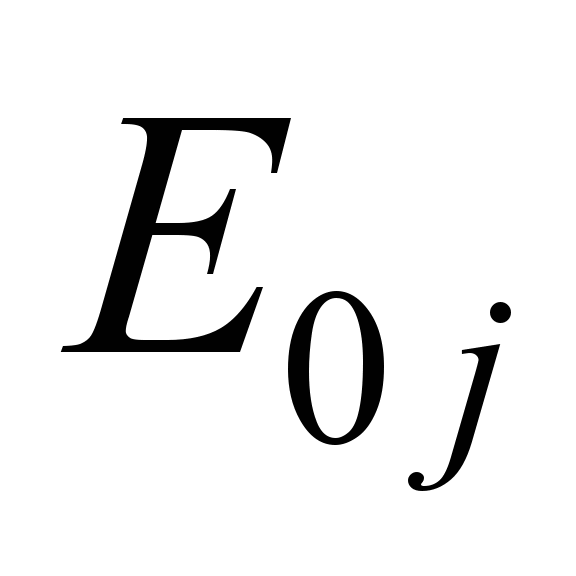 ,
коефіцієнтом зчеплення коліс із рейками
дороги
,
коефіцієнтом зчеплення коліс із рейками
дороги
 .
.
Повна
гальмівна сила поїзда є такою:
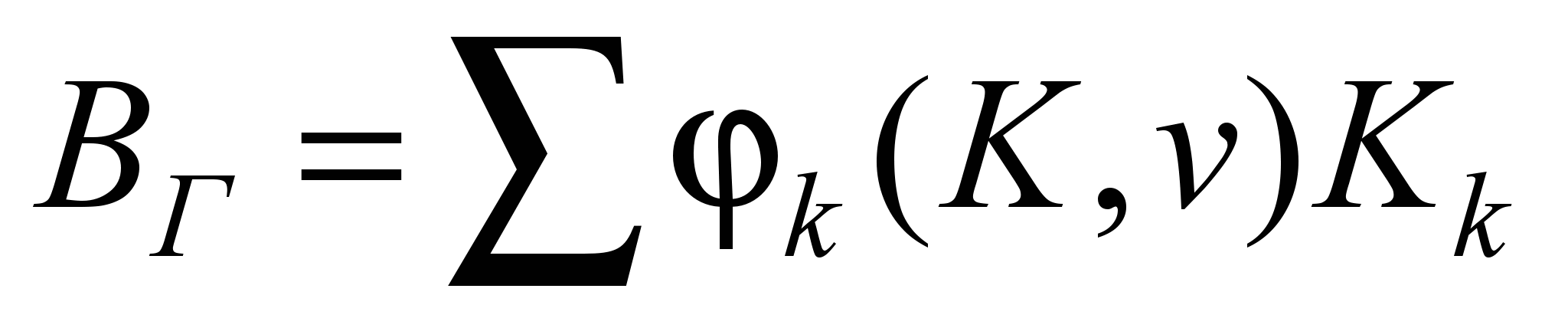 ,
,
де
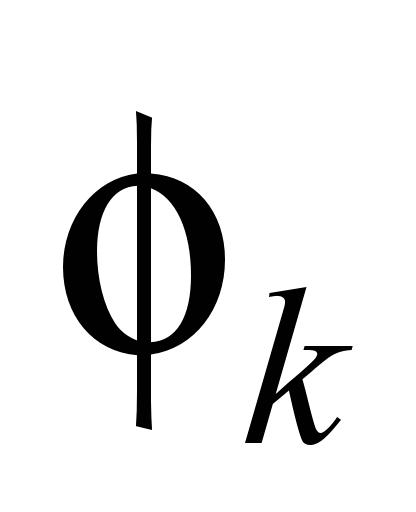 – коефіцієнт тертя гальмівних колодок;
– коефіцієнт тертя гальмівних колодок;
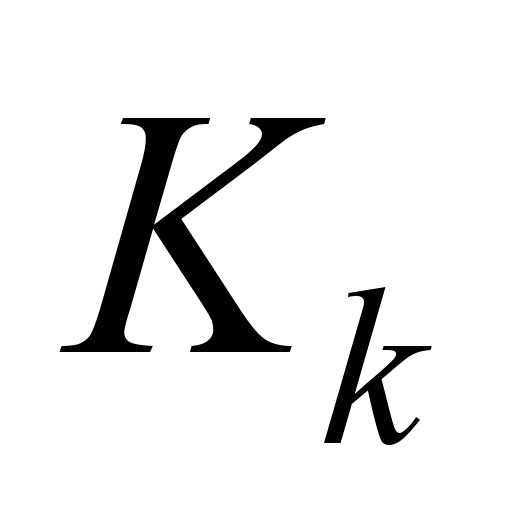 – сила натиску
гальмівних колодок на бандаж.
– сила натиску
гальмівних колодок на бандаж.
Основний опір рухові
локомотива в режимі тяги визначають
за емпіричною формулою:
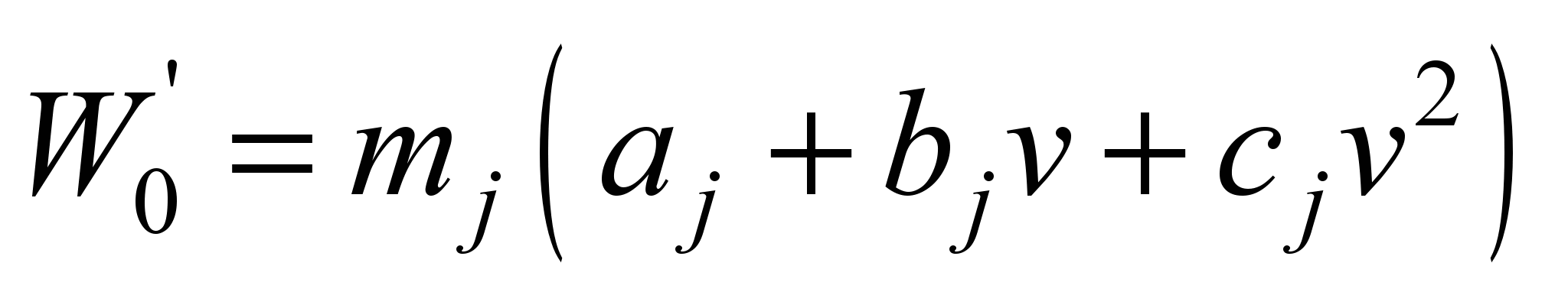 ,
,
опір рухові в режимі
холостого ходу:
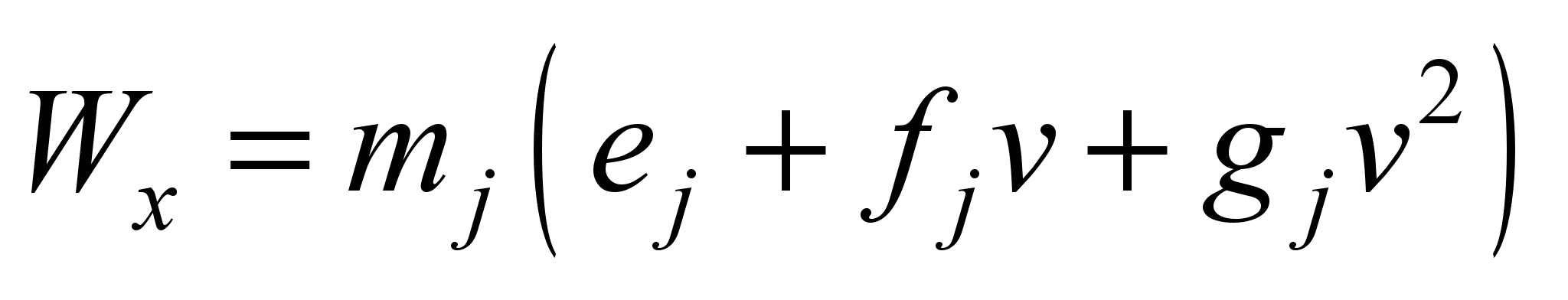 ,
,
де
 ,
,
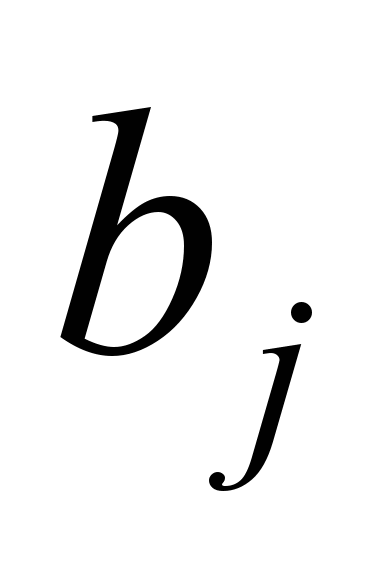 ,
,
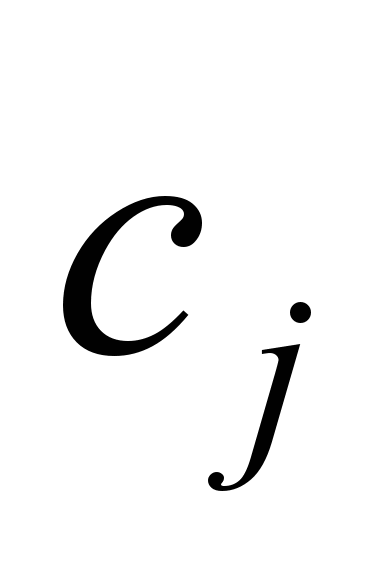 ,
,
 ,
,
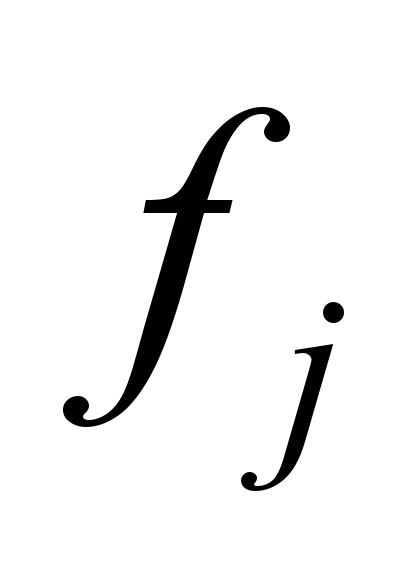 ,
,
 – коефіцієнти для певного типу локомотива
й типу колії (ланкова або безстикова).
– коефіцієнти для певного типу локомотива
й типу колії (ланкова або безстикова).
Коефіцієнт
зчеплення коліс із рейками
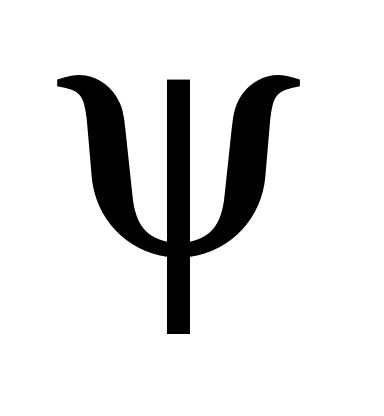 обмежує максимальну силу тяги локомотива
обмежує максимальну силу тяги локомотива
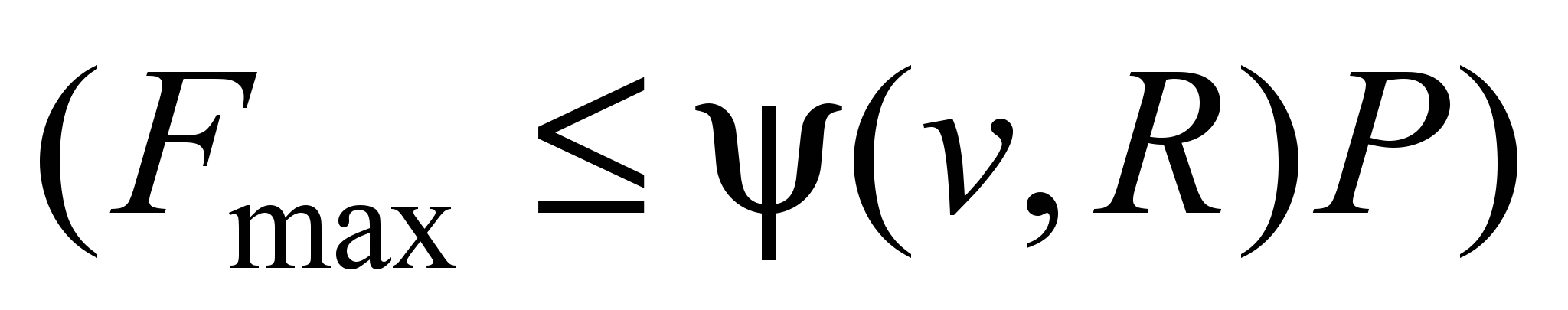 .
Цей коефіцієнт є різним для різних
типів локомотивів.
.
Цей коефіцієнт є різним для різних
типів локомотивів.
Привід
кожного локомотива має набір із
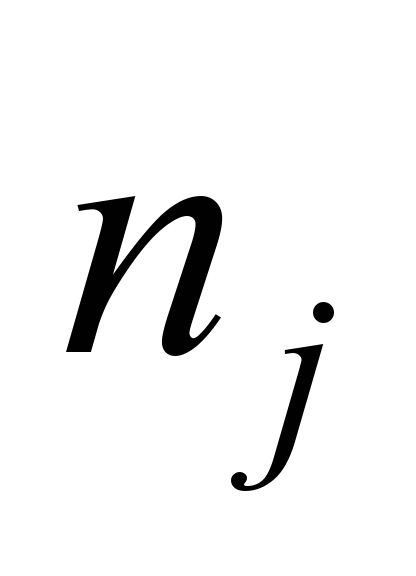 позицій
позицій 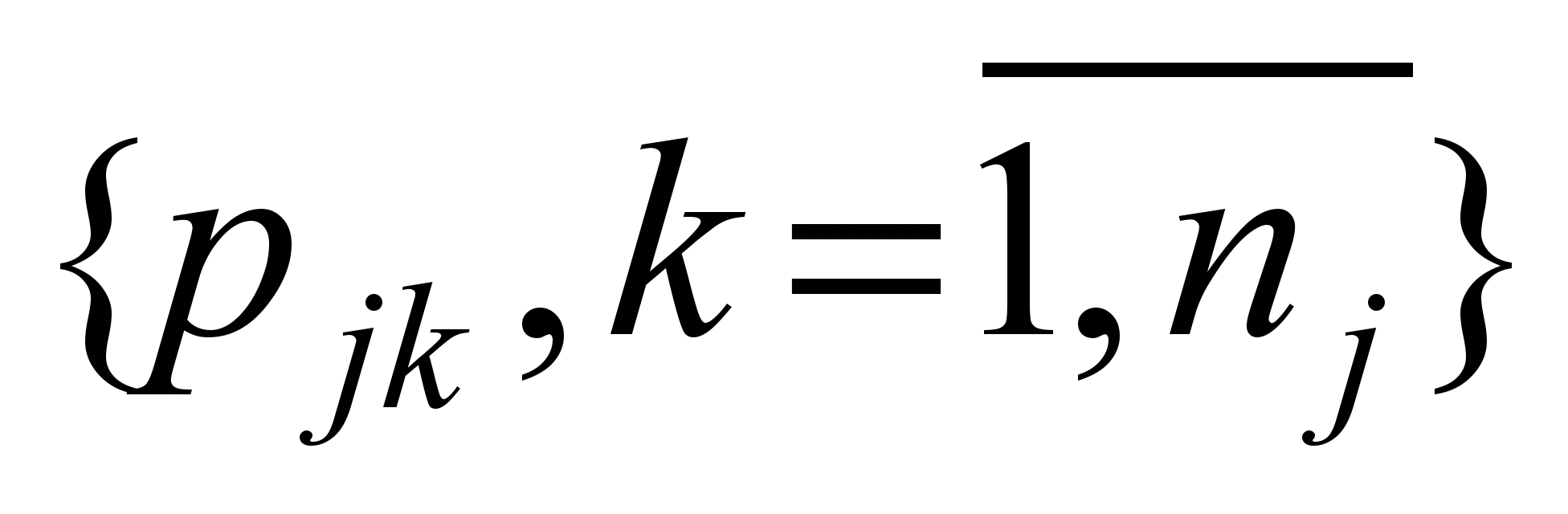 .
Для кожної позиції відомі інтервали
її дії за швидкістю, силою тяги
.
Для кожної позиції відомі інтервали
її дії за швидкістю, силою тяги
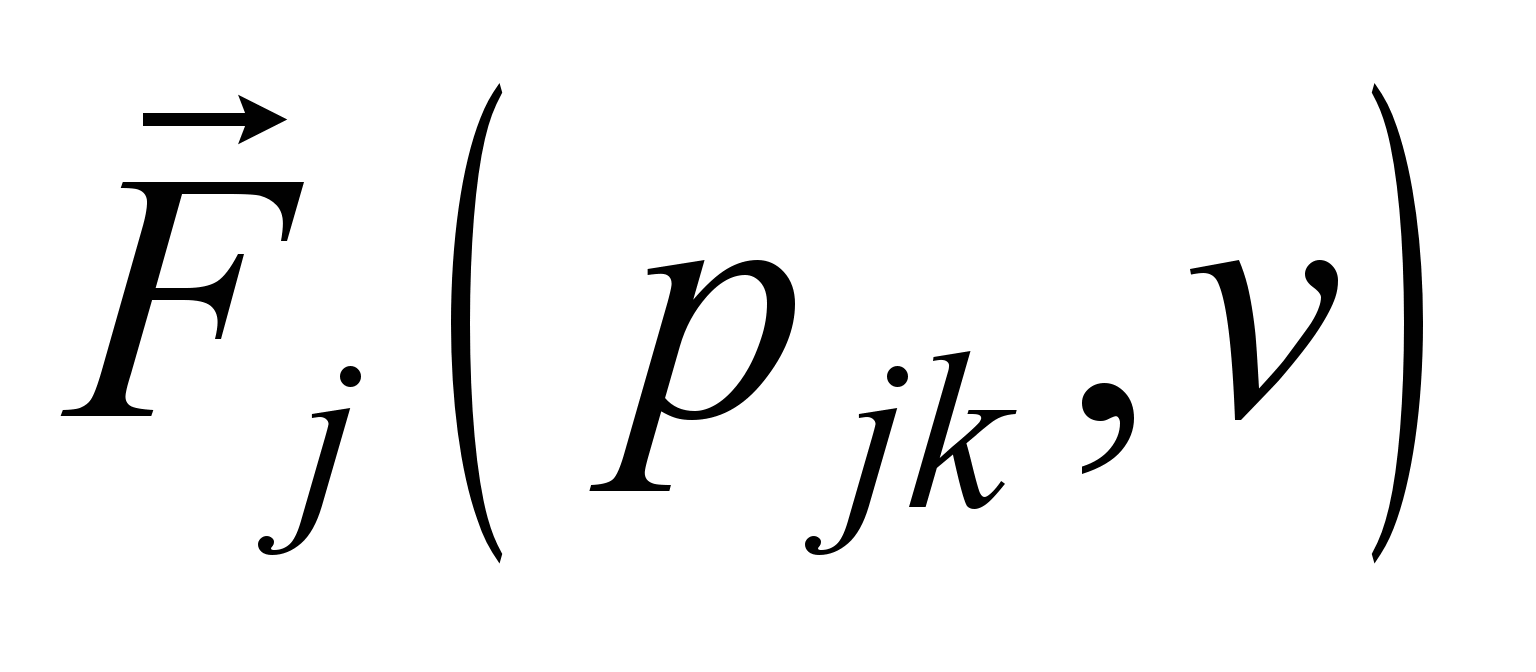 ,
струмом
,
струмом
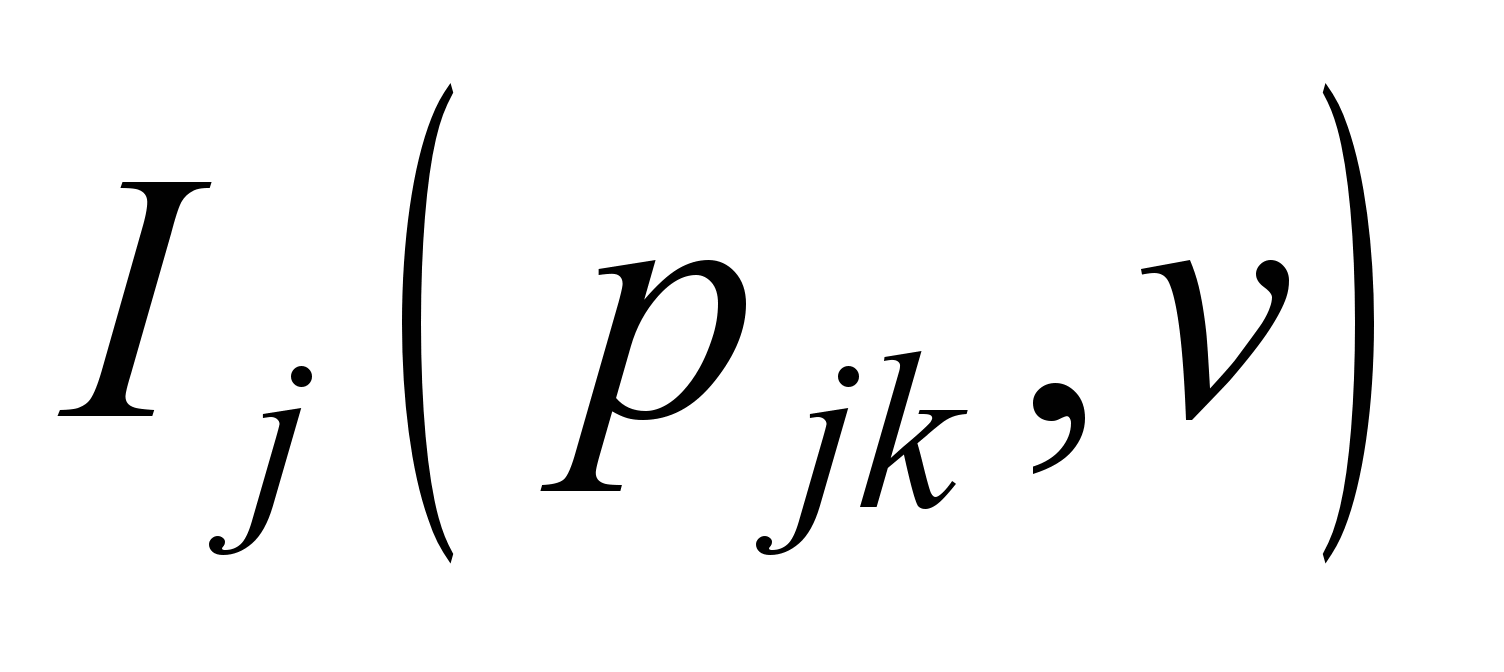 .
Для силових позицій є відомими теплові
характеристики двигунів: температура
перегріву
.
Для силових позицій є відомими теплові
характеристики двигунів: температура
перегріву
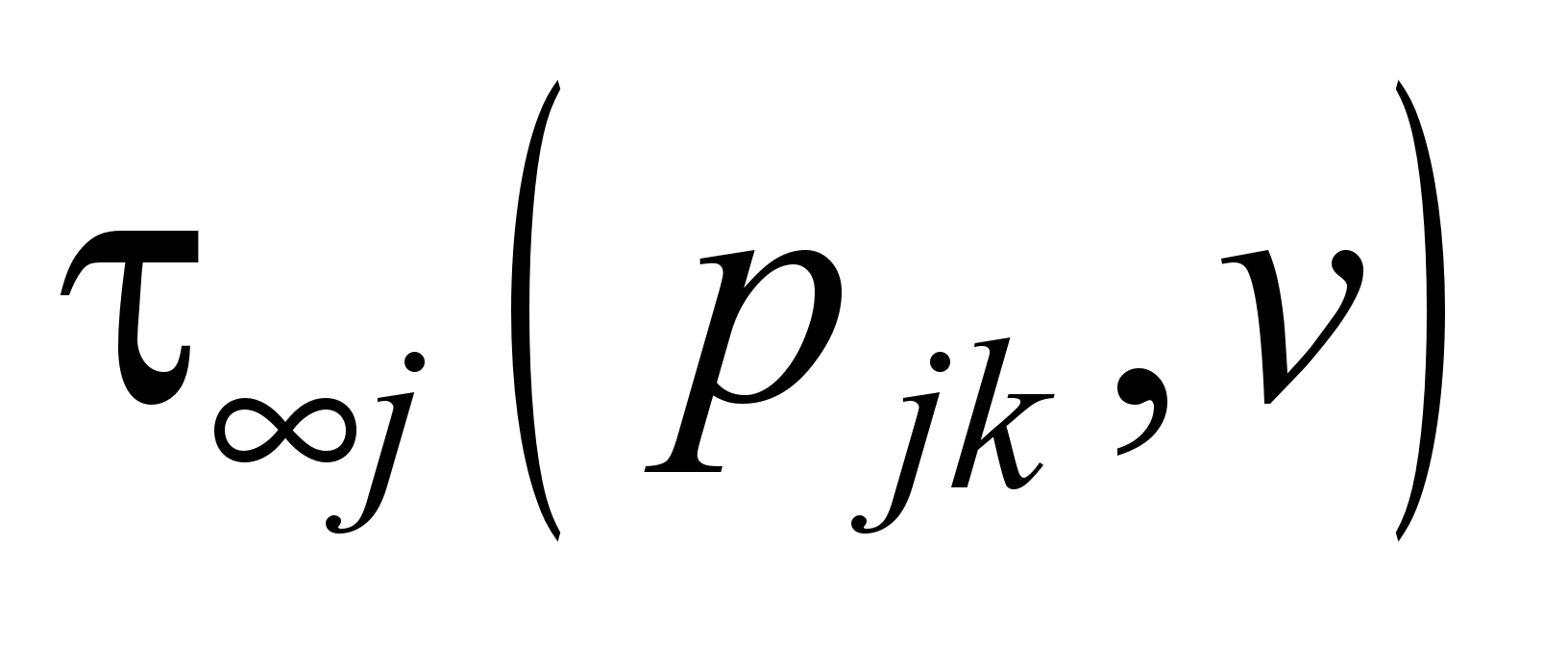
й теплова постійна
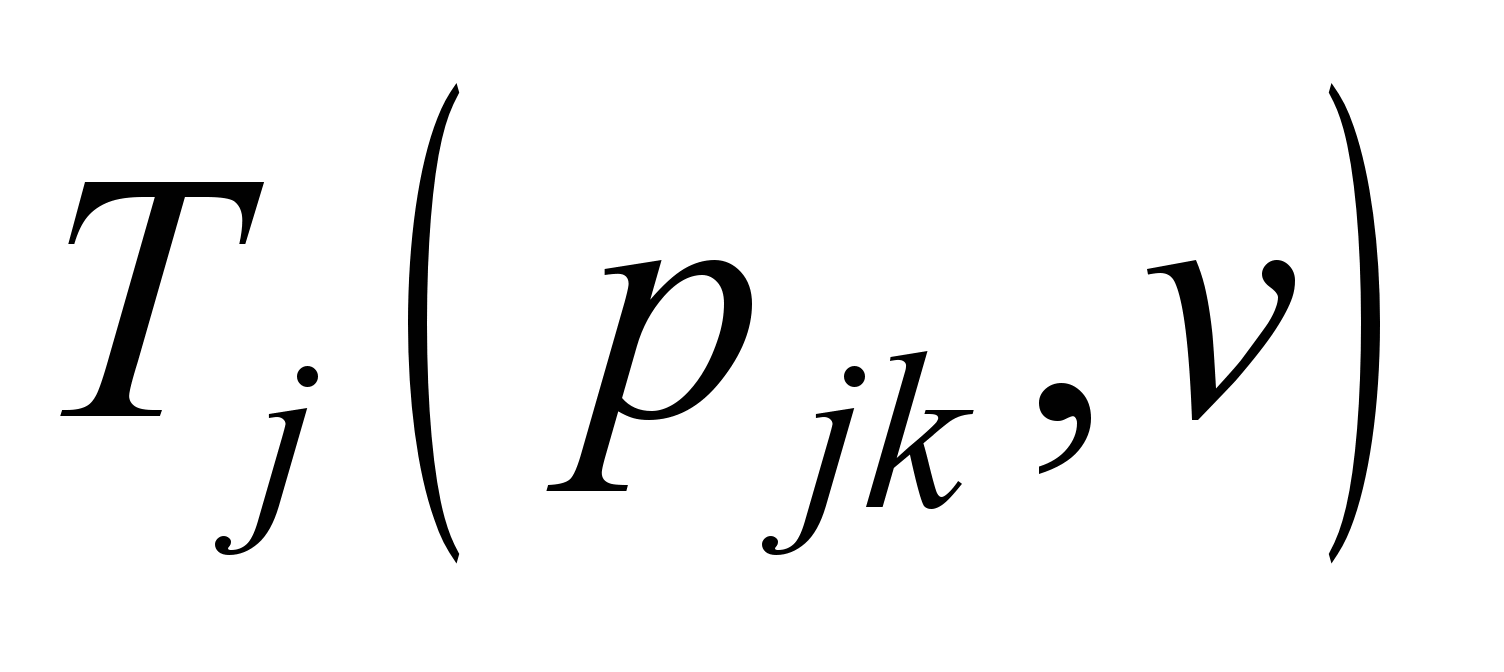 (для електровозів,
моторних вагонів електропоїздів,
тепловозів, моторних вагонів
дизель-поїздів), паливні характеристики
(для електровозів,
моторних вагонів електропоїздів,
тепловозів, моторних вагонів
дизель-поїздів), паливні характеристики
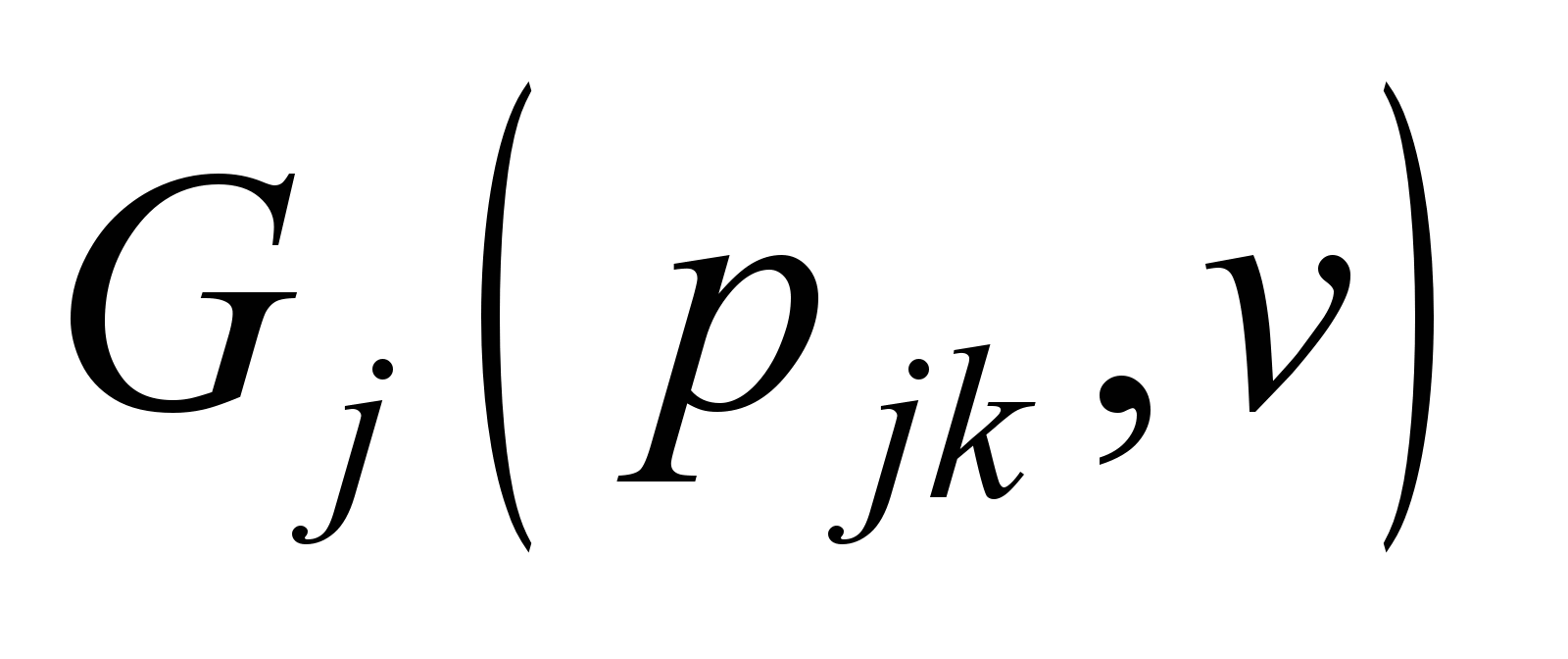 (для тепловозів, тепловозів із гідравлічною
передачею, моторних вагонів дизель-поїздів,
моторних вагонів дизель-поїздів із
гідравлічною передачею).
(для тепловозів, тепловозів із гідравлічною
передачею, моторних вагонів дизель-поїздів,
моторних вагонів дизель-поїздів із
гідравлічною передачею).
Тягові характеристики
локомотивів мають обмеження за ресурсами
й надійністю роботи; тепловозів – за
конструктивною швидкістю й параметрами
дизеля, тягової передачі, зчеплення;
електровозів – за конструктивною
швидкістю й параметрами тягових
двигунів, зчеплення.
Характеристики
тягового режиму електровоза поділяють
на електромеханічні, електротягові й
тягові. Електромеханічні характеристики
називають характеристиками тягових
двигунів, віднесених до валу якоря, а
саме:
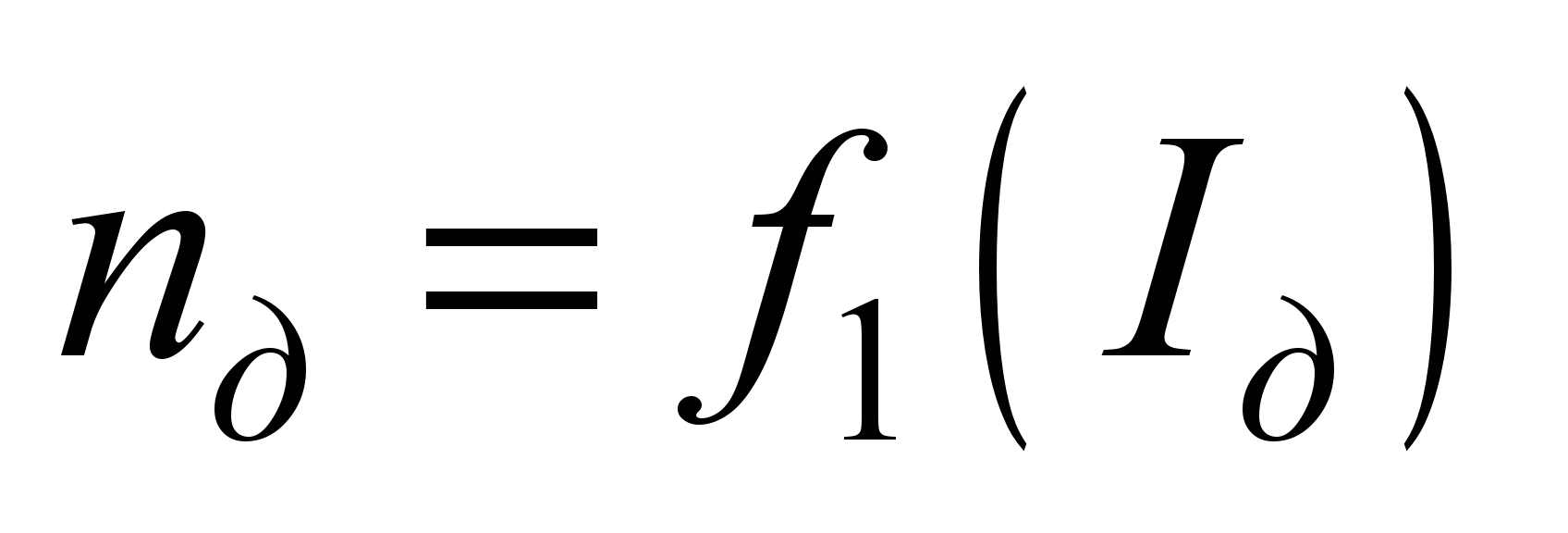 ;
;
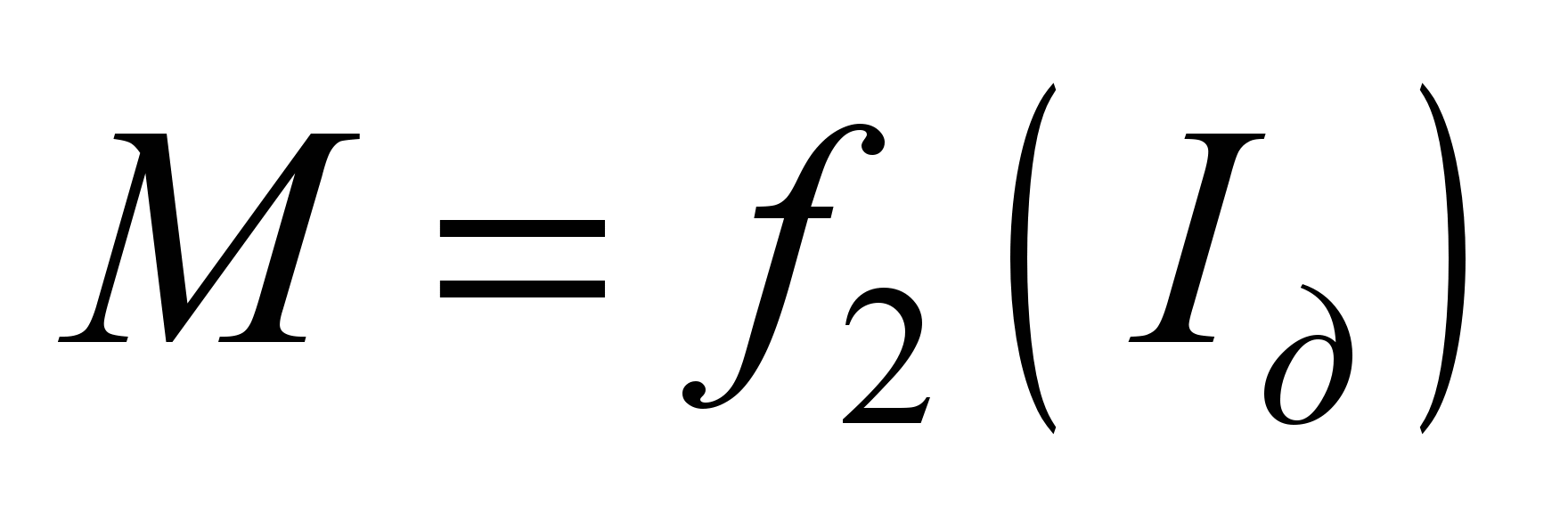 ;
;
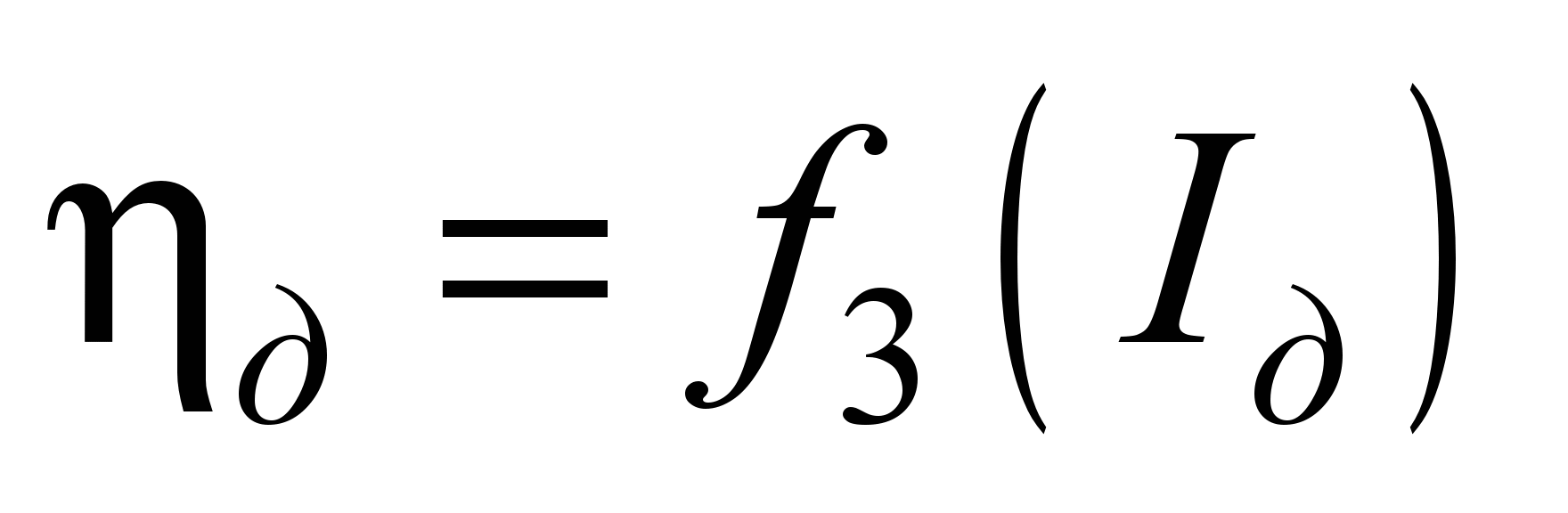 ,
,
тобто,
залежність числа обертання якоря
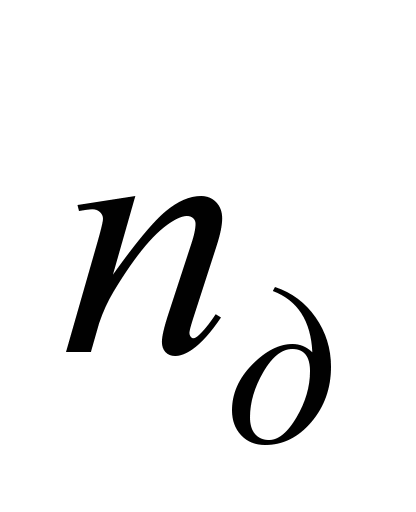 ,
моменту
,
моменту
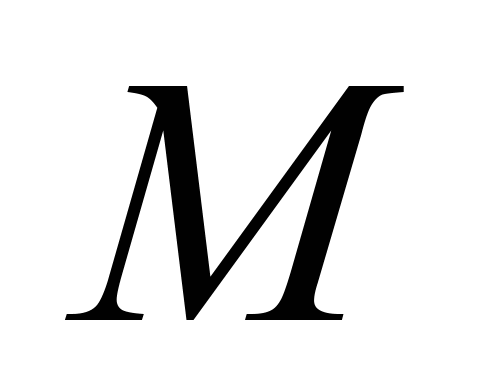 і ККД
і ККД
 від струму
від струму
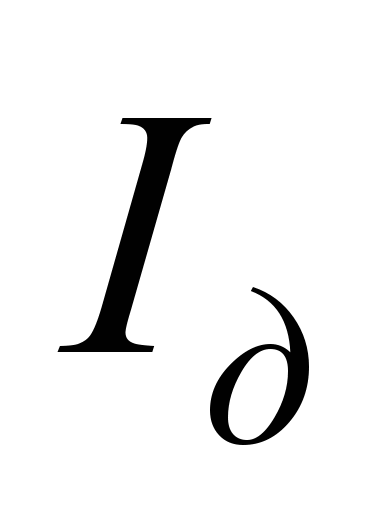 за постійного значення
за постійного значення
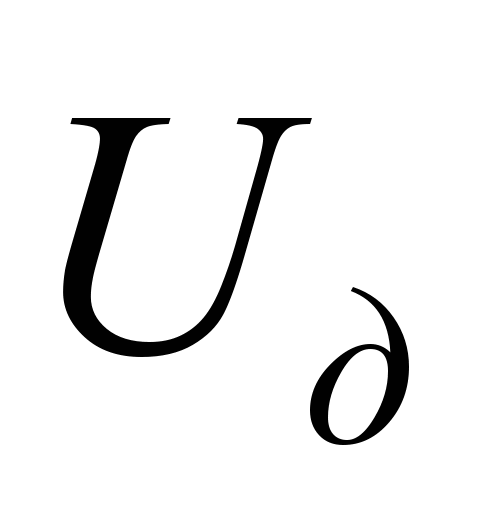 на клемах двигуна.
на клемах двигуна.
Електротягові
характеристики є віднесеними до ободу
рухомого колеса:
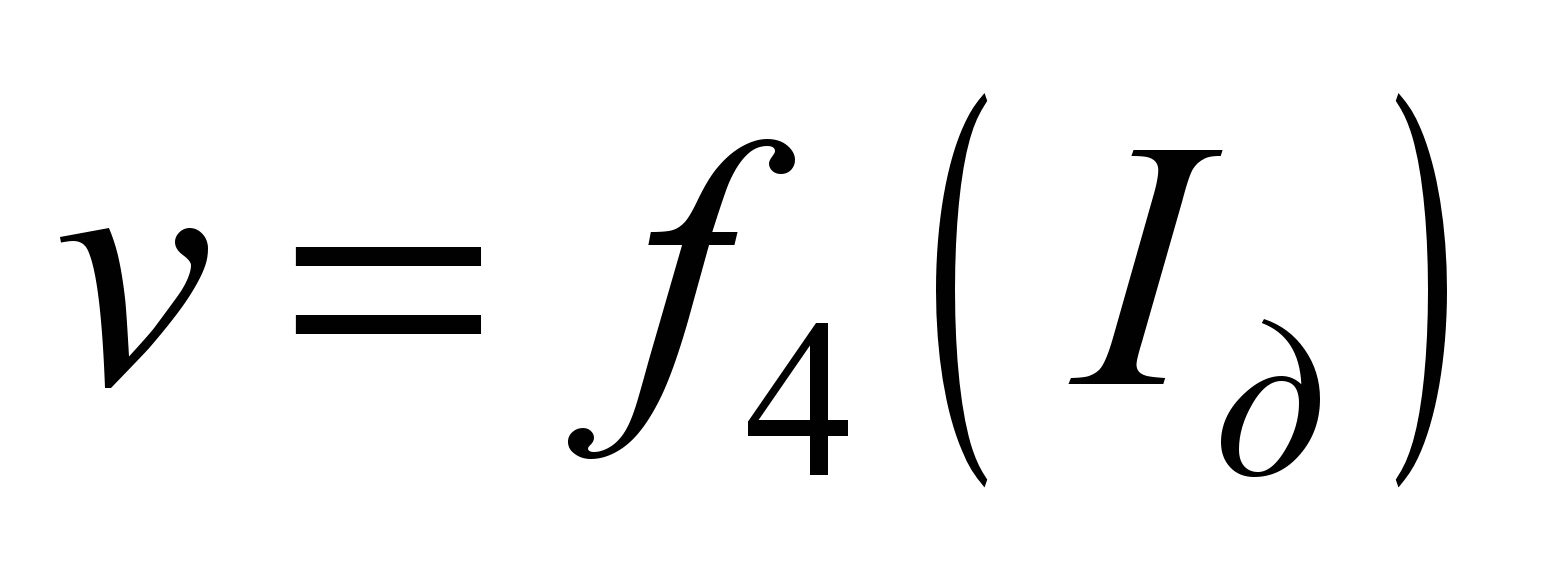 ;
;
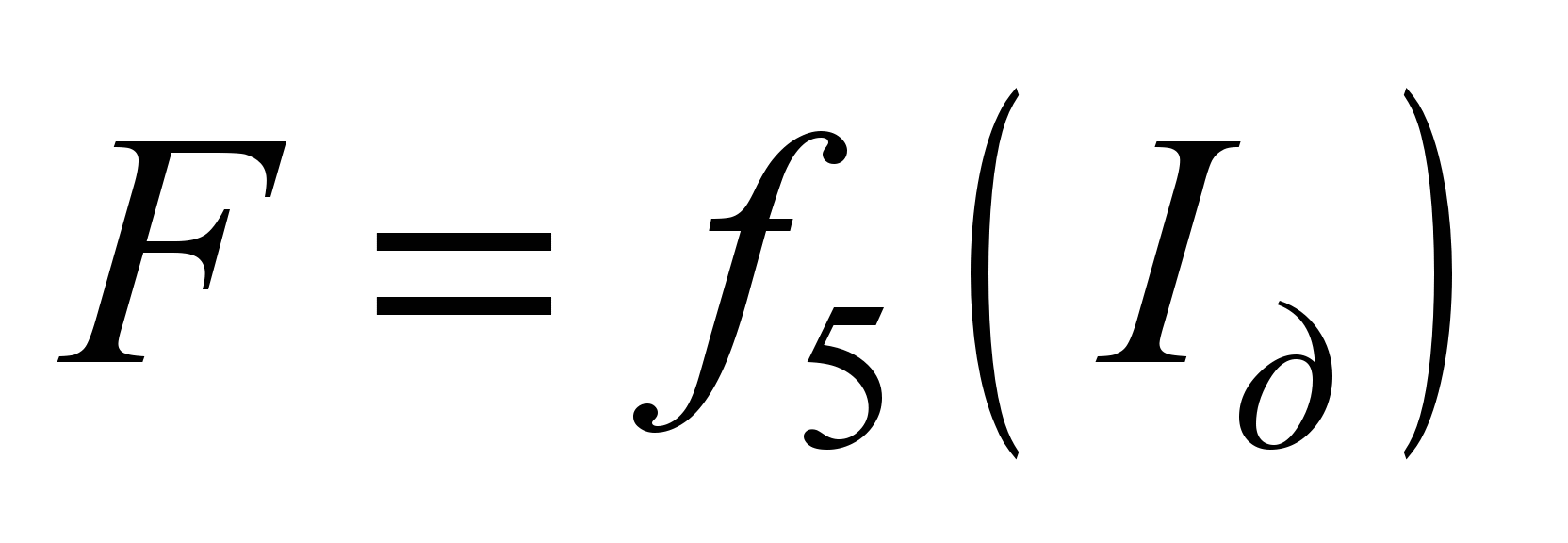 і
і
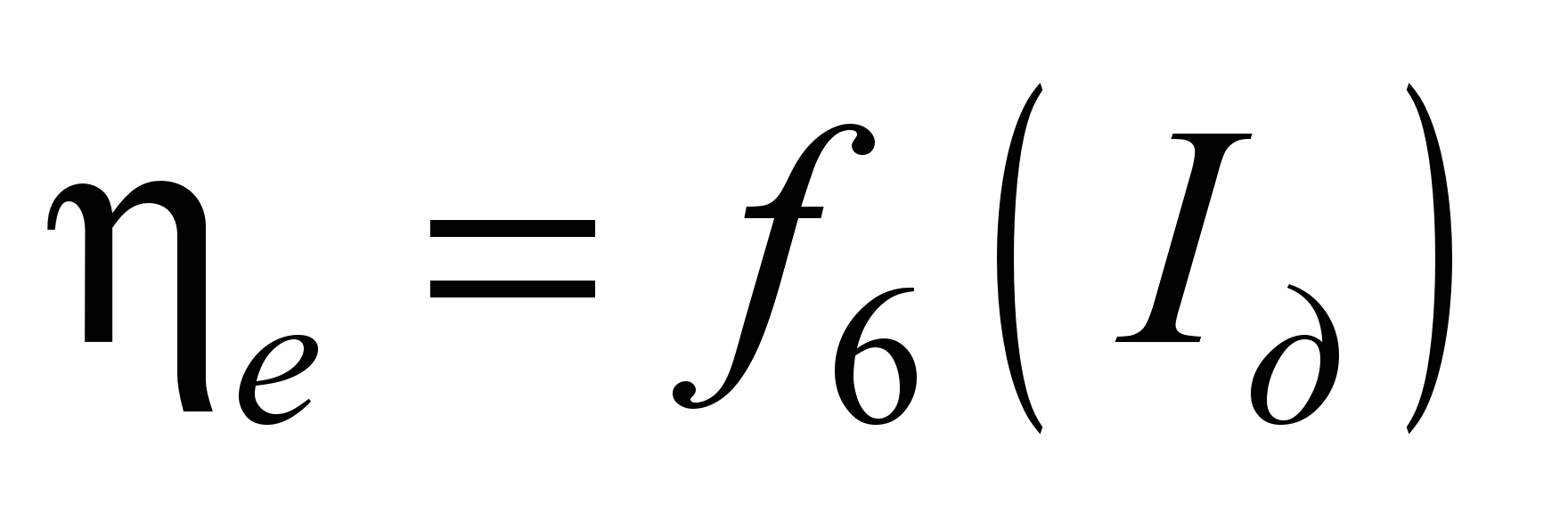 ,
,
тобто, залежність
швидкості
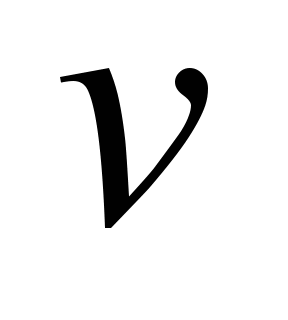 ,
сили тяги
,
сили тяги
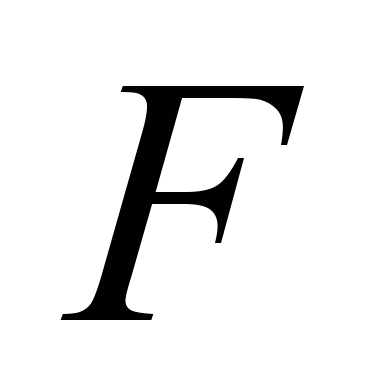 і ККД двигуна з передачею
і ККД двигуна з передачею
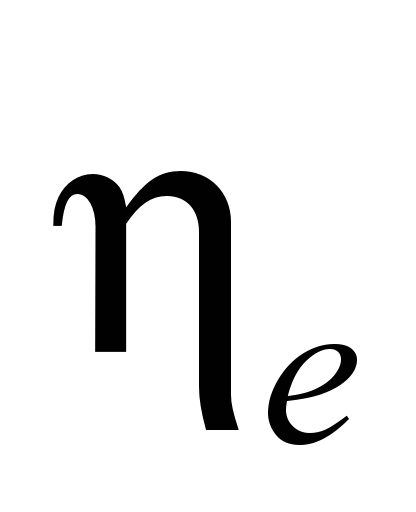 від струму якоря
від струму якоря 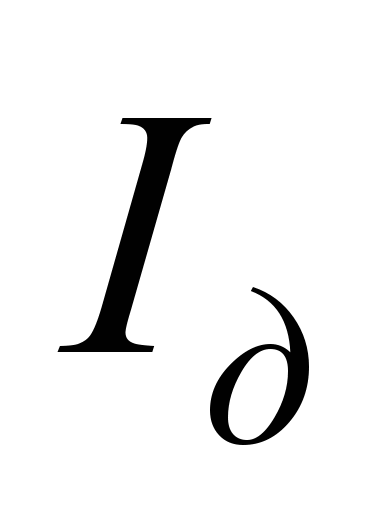 .
.
Електротягові
характеристики розраховують на основі
електромеханічних характеристик
тягового двигуна, заданого діаметру
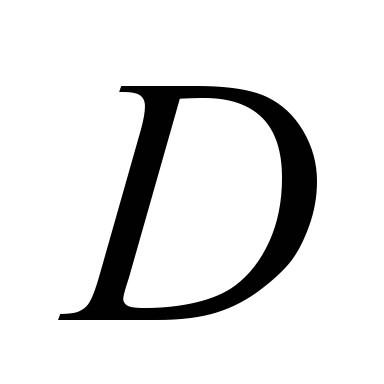 рухомих коліс, передаточного числа
рухомих коліс, передаточного числа
 і
і
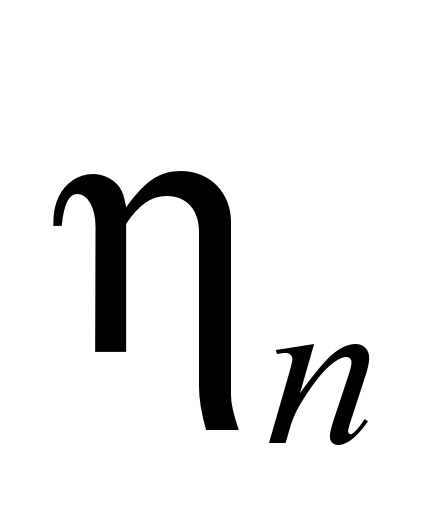 – ККД передачі або
– ККД передачі або
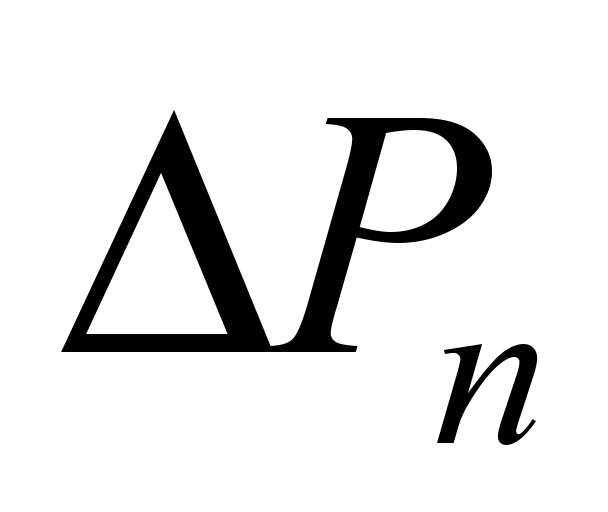 – втрат у передачі. Швидкісну
характеристику локомотива розраховують
за формулою:
– втрат у передачі. Швидкісну
характеристику локомотива розраховують
за формулою:
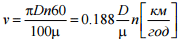 ,
,
а дотичну силу тяги
можна знайти із рівняння:
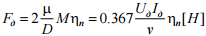 ,
,
а
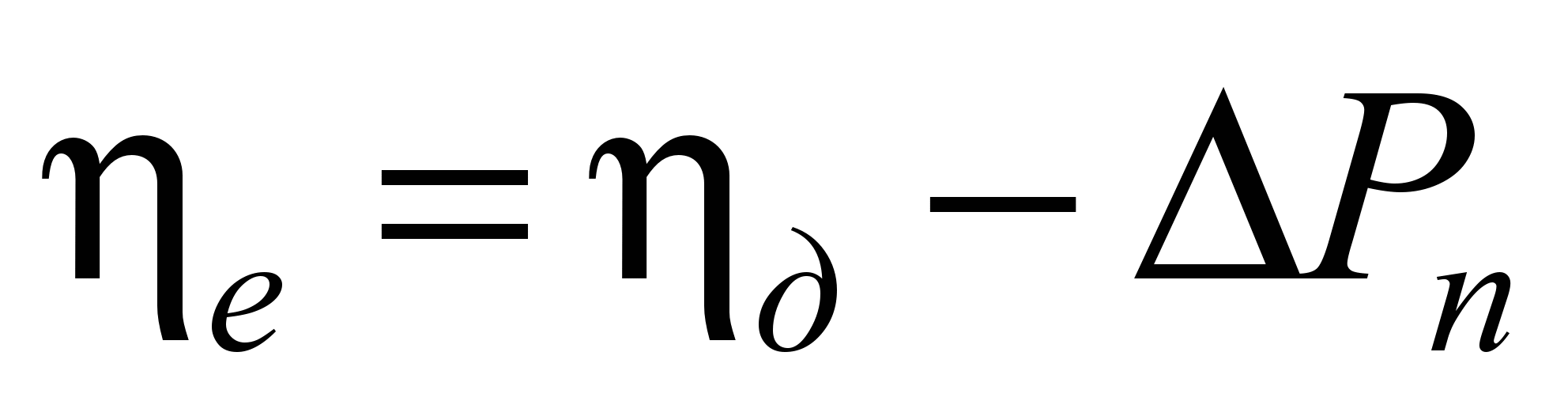 .
Втрати енергії в передачі можна знайти
на основі даних табл. 1 [5].
.
Втрати енергії в передачі можна знайти
на основі даних табл. 1 [5].
Таблиця 1
Втрати
енергії в передачі від тягових двигунів
до коліс
Table
1
Energy
losses in the transmission from the traction motors to the wheels
|
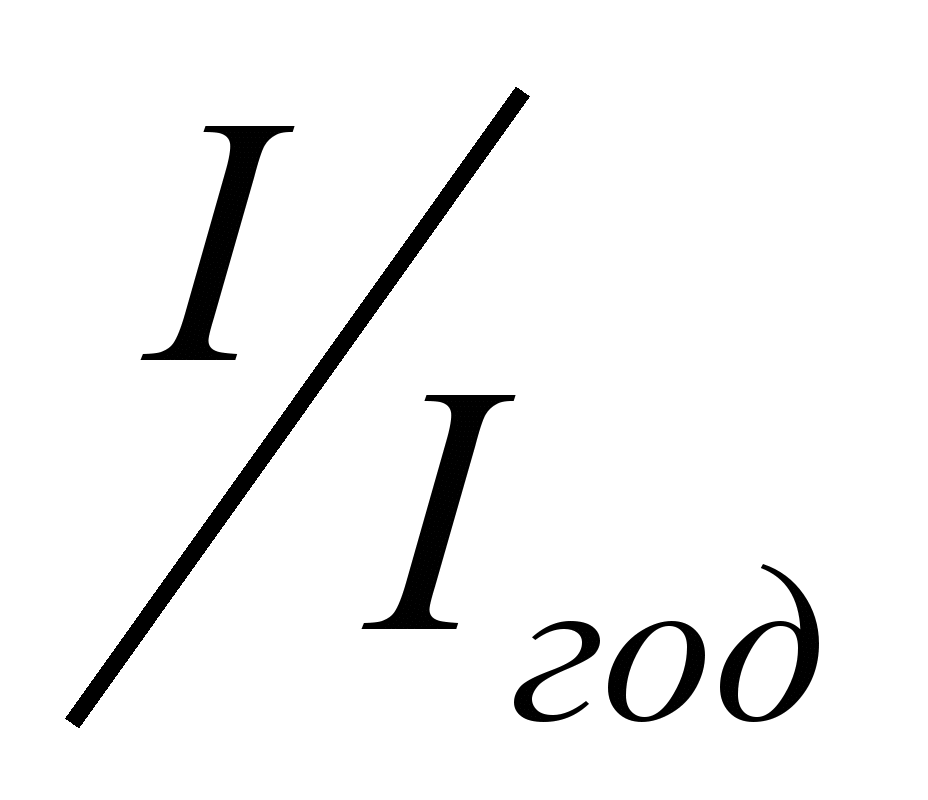
|
0,25
|
0,30
|
0,40
|
0,50
|
0,60
|
0,70
|
1
|
1,25
|
1,5
|
2
|
|
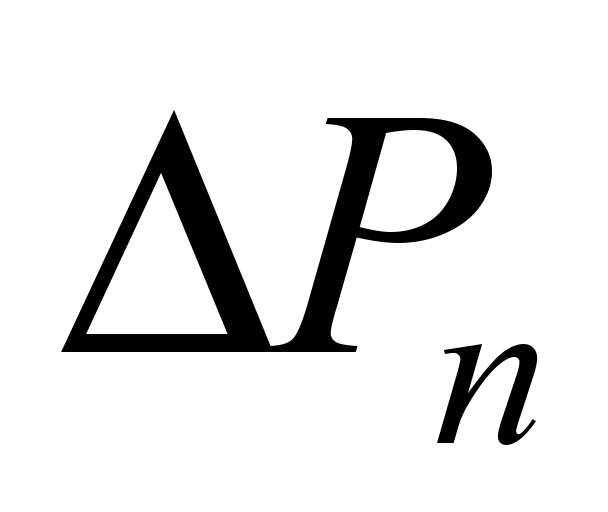
|
0,085
|
0,067
|
0,044
|
0,032
|
0,027
|
0,025
|
0,025
|
0,027
|
0,030
|
0,035
|
Тягові
характеристики
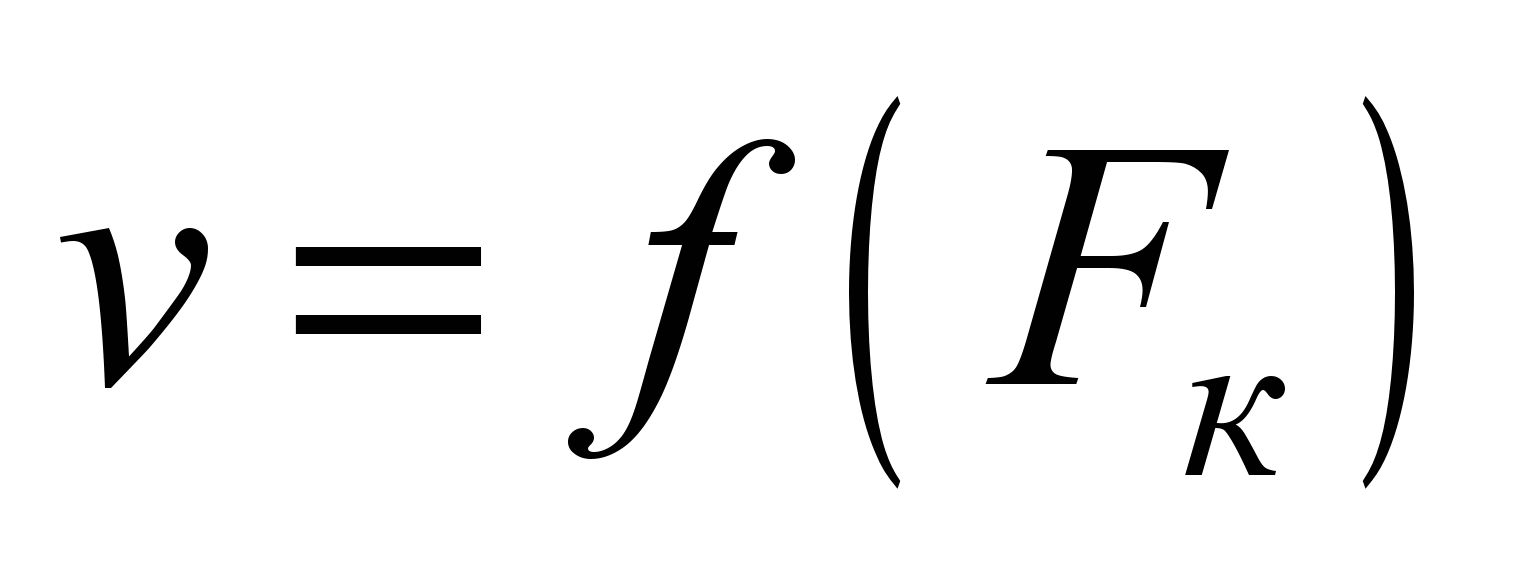 отримують із електротягових виключенням
отримують із електротягових виключенням
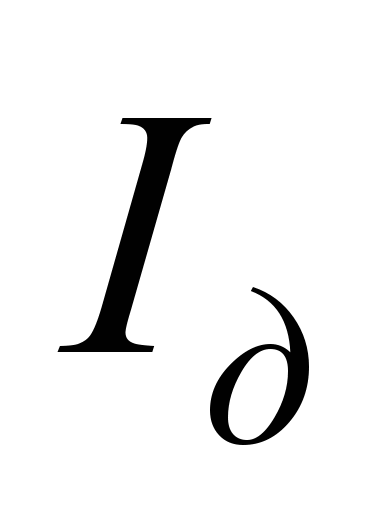 .
За усталеного електричного режиму
швидкість руху електровоза знаходять
за формулою:
.
За усталеного електричного режиму
швидкість руху електровоза знаходять
за формулою:
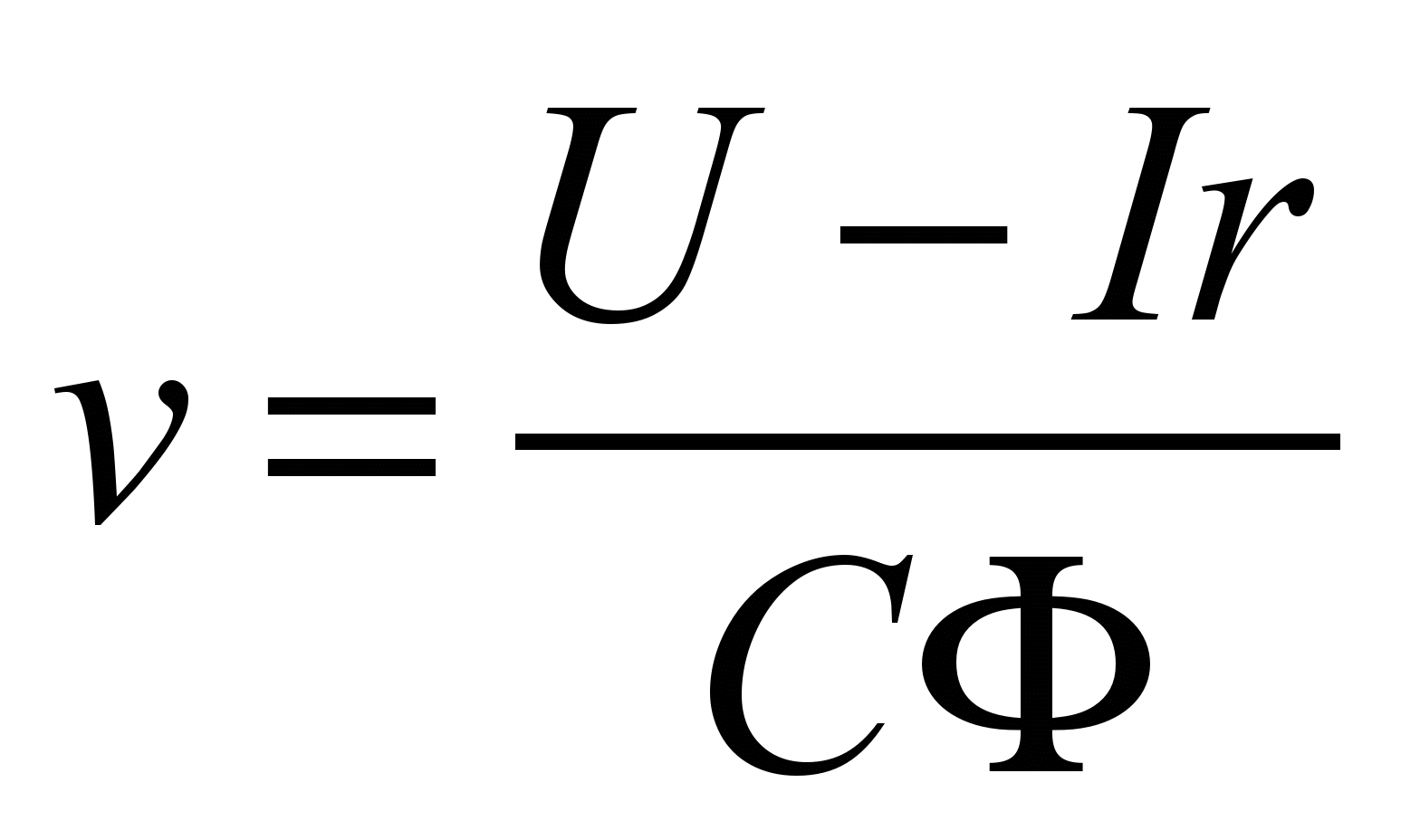 .
.
За даного
струму на вході двигуна його швидкість
можна міняти зміною напруги
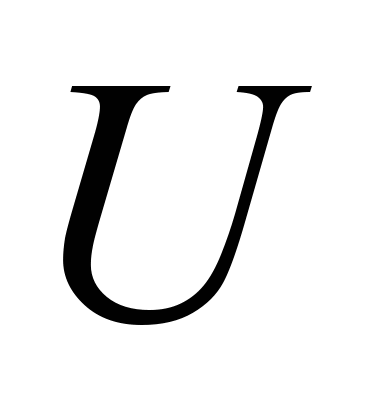 на колекторі або зміною магнітного
потоку
на колекторі або зміною магнітного
потоку
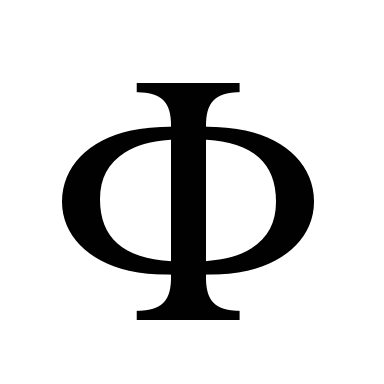 тягового двигуна.
тягового двигуна.
Вагони
характеризуються типом
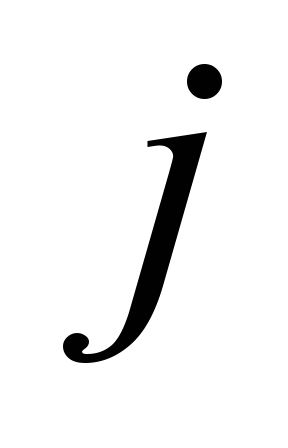 ,
масою
,
масою
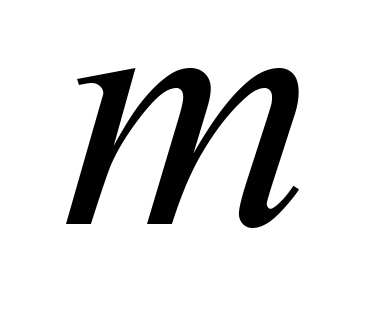 ,
типом гальмівних колодок, габаритами,
довжиною
,
типом гальмівних колодок, габаритами,
довжиною
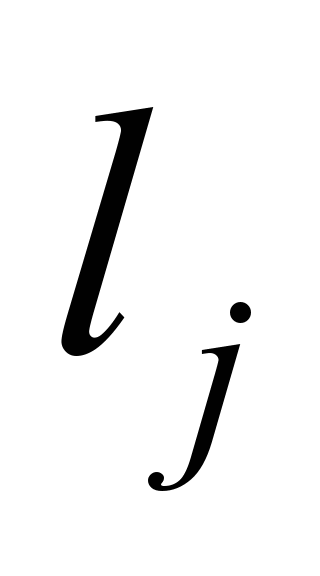 ,
масою тари
,
масою тари 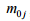 , кількістю осей
, кількістю осей 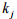 , силою
натиску колодок на бандаж
, силою
натиску колодок на бандаж 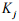 .
.
Основний
опір руху вагонів на ланковій і
безстиковій
коліях визначають такою емпіричною
формулою:
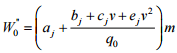 ,
,
де
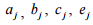 – коефіцієнти, залежні від типу
вагона,
– коефіцієнти, залежні від типу
вагона,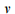 – швидкості руху,
– швидкості руху, 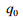 – маси, яка
припадає на одну вісь колісної пари.
– маси, яка
припадає на одну вісь колісної пари.
Розглянемо сили,
які протидіють рухові. Розрізняють
основний і додатковий опір рухові. За
основний беруть опір, який діє на поїзд
під час руху вздовж прямого горизонтального
шляху з рівномірною швидкістю за
нормальних метеорологічних умов. Для
локомотива розрізняють ще опори руху
в режимі тяги й за її відсутності. До
основного належать також опори внаслідок:
тертя між шийками осей і підшипниками,
кочення коліс по рейках, ударів коліс
об стики рейок, повітряного середовища.
До додаткових відносять опори внаслідок:
ухилу та кривизни траєкторії руху,
зміни метеорологічних умов, роботи
підвагонних генераторів, руху з місця.
Силу опору рухові
обчислюють за формулою:
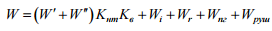 ,
,
де
 – основні опори локомотивів
і вагонів відповідно;
– основні опори локомотивів
і вагонів відповідно;
 – коефіцієнти
опору внаслідок низької температури
й наявності вітру (залежать від
температури
– коефіцієнти
опору внаслідок низької температури
й наявності вітру (залежать від
температури 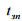 , густини повітря
, густини повітря
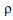 , швидкості
вітру
, швидкості
вітру 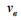 та
швидкості руху поїзда
та
швидкості руху поїзда 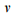 );
);
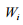 –
опір від
ухилу (
–
опір від
ухилу (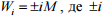 – значення ухилу ділянки
руху в проміле
– значення ухилу ділянки
руху в проміле 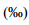 ,
,
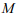 -
маса вагона (локомотива);
-
маса вагона (локомотива);
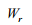 –
опір, зумовлений кривизною траєкторії;
–
опір, зумовлений кривизною траєкторії;
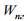 – опір
від підвагонних генераторів;
– опір
від підвагонних генераторів;
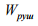 – опір
під час рушання з місця.
– опір
під час рушання з місця.
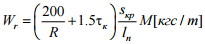 ,
,
де
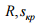 – радіус та довжина
кривої відповідно, м;
– радіус та довжина
кривої відповідно, м;
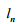 – довжина поїзда,
м;
– довжина поїзда,
м; 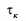 – непогашене прискорення в кривій,
яке обчислюють за наступною формулою:
– непогашене прискорення в кривій,
яке обчислюють за наступною формулою:
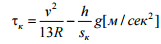 ,
,
де 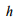 – підвищення зовнішньої рейки,
мм;
– підвищення зовнішньої рейки,
мм; 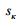 – відстань між кругами кочення
коліс, мм;
– відстань між кругами кочення
коліс, мм; 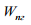 – опір від підвагонних
генераторів.
– опір від підвагонних
генераторів.
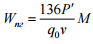 ,
,
де 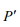 – середня потужність
пдвагонного генератора, кВт.
– середня потужність
пдвагонного генератора, кВт.
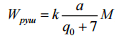 , де
, де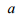 – коефіцієнт,
який залежить від типу підшипників
вагона (локомотива);
– коефіцієнт,
який залежить від типу підшипників
вагона (локомотива); 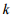 – коефіцієнт, який
залежить від кількості вагонів у поїзді.
– коефіцієнт, який
залежить від кількості вагонів у поїзді.
Для всіх
типів вагонів (локомотивів) встановлені
емпіричні залежності, які дозволяють
визначати основну й додаткову сили
опору руху. Під час розрахунків уважають,
що всі сили, які діють на вагон чи
локомотив, зосереджені в його центрі
мас. Координати центра мас дають
можливість ідентифікувати (встановити
координати) місце розташування вагона
чи локомотива на траєкторії руху.
Режим руху поїзда
здійснюється чергуванням режимів тяги,
холостого ходу (за відсутності режиму
тяги) й гальмування. Режим тяги може
відбуватися за різних тягових позицій.
Тяговим відповідають відповідні
струменеві позиції. Режим гальмування
визначається величиною гальмівної
сили, яка залежить від сумарної сили
притискання гальмівних колодок до
бандажів коліс або до дисків, встановлених
на осях. Гальмівна сила виникає також
у процесі переведення тягових
електродвигунів у генератори струму
(електричне гальмування). Гальмування
може супроводжуватися рекуперацією
(поверненням електроенергії в мережу)
й роботою тягових електродвигунів на
опір рухові (реостатне гальмування).
Траєкторія
руху поїзда 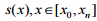 , де
, де
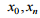 –
початкова й кінцева координати сусідніх
роздільних пунктів (станцій). Траєкторія
руху представлена як послідовність
–
початкова й кінцева координати сусідніх
роздільних пунктів (станцій). Траєкторія
руху представлена як послідовність 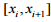 лінійних
лінійних 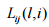 , які визначаються ухилом й
довжиною
, які визначаються ухилом й
довжиною 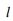 ,
та криволінійних елементів
,
та криволінійних елементів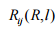 , що
визначаються довжиною
, що
визначаються довжиною 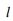 і радіусом
кривизни
і радіусом
кривизни 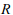 . Уздовж траєкторії руху
. Уздовж траєкторії руху 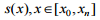 задають максимально допустиму швидкість
руху
задають максимально допустиму швидкість
руху 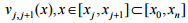 .
.
Будемо
вважати, що типи локомотивів і їх
технічні, тягово-енергетичні й опірні
параметри
є відомі, також для
кожного вагона заданий тип, маса вантажу
та його опірні параметри.
Інтегрування
диференціального рівняння руху (1)
вимагає багатократного розв’язування
прямих та обернених задач. Ітераційний
процес побудовано таким чином, що він
проходить за траєкторією руху необхідний
шлях уперед, потім повертається необхідну
кількість разів назад, поки не задовольнить
усі умови на оптимальність, виконання
технічних і технологічних обмежень,
неперервність траєкторії швидкості.
Важливо, що такий алгоритм не вимагає
заздалегідь знання
всіх умов, які впливають на оптимальність
руху, і тому він є адаптивним до можливих
змін у процесі руху. Алгоритм у
максимальній мірі реалізовує наявний
потенціал оптимізації.
Траєкторія
швидкості режиму руху поїзда за
мінімальний час є максимально близькою
до максимально допустимої. Такий режим
руху формується під час використання
максимально можливих силових характеристик
тяги й гальмівної сили та мінімально
можливої частоти зміни тягових позицій.
Для цього критерію оптимальності
економія паливно-енергетичних ресурсів
не передбачена.
Оптимізація
режиму здійснюється тільки у випадку
наявності задання часу на переміщення,
який перевищує мінімальний. Енергетичні
затрати нелінійно залежать від швидкості
руху. У разі зміни швидкості руху (зміни
силових позицій) у напрямку її збільшення
затратні величини зростають на значну
величину. Тому для зменшення затрат
проводять мінімізацію кількості й
величини перехідних режимів. Втрати
інерції руху й, відповідно, енергії
відбуваються в режимі використання
гальмівної сили. Якщо дозволяє час,
варто економити інерційний потенціал
у режимі холостого руху й гальмування
(пригальмовування) проводити максимально
пізніше і тільки для того, щоб забезпечити
рух за заданий час.
Алгоритм
оптимізації вимагає багатократних
розрахунків режиму руху. Зменшення
енергетичних затрат проводять за
допомогою: коригування в сторону
зменшення максимальних швидкостей на
окремих ділянках перегону (при цьому
зменшується кількість і величини
перехідних режимів), використання
мінімально можливих тягових позицій
і режиму гальмування; використання в
максимальній мірі інерції руху на
підйомах і спусках тощо. Процес розрахунку
завершується за умови достатньої
близькості розрахованого часу руху до
заданого.
Для
забезпечення максимального рівня
автоматизації процесу розв’язування
оптимізаційних задач формування
оптимальних режимів поставлена як
задача оптимального керування рухом
поїзда. Розроблення підходів щодо її
розв’язування дозволило забезпечити
максимальний рівень автоматизації
процесу розв’язування великого набору
оптимізаційних задач. Керування –
послідовний набір параметрів зміни
режимів тяги, холостого
ходу й гальмування. Зміна керування
формується за умов досягнення меж
коридору швидкостей 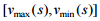 на
заданому інтервалі траєкторії руху
на
заданому інтервалі траєкторії руху 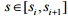 .
Вибір ширини меж зміни швидкостей
дозволяє регулювати частоту зміни
керування. Корегування верхньої межі
швидкості в напрямку її зменшення, для
окремих додаткових умов, є одним із
важливих складових алгоритму розв’язування
оптимізаційних задач. Холостий хід на
інтервалі часу характеризується
координатою початку й швидкістю в
кінцевій координаті
.
Вибір ширини меж зміни швидкостей
дозволяє регулювати частоту зміни
керування. Корегування верхньої межі
швидкості в напрямку її зменшення, для
окремих додаткових умов, є одним із
важливих складових алгоритму розв’язування
оптимізаційних задач. Холостий хід на
інтервалі часу характеризується
координатою початку й швидкістю в
кінцевій координаті 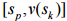 ,
гальмування визначається силою натиску
гальмівних колодок на бандаж, початок
– координатою чи швидкістю руху, а
завершення – координатою і швидкістю
руху.
,
гальмування визначається силою натиску
гальмівних колодок на бандаж, початок
– координатою чи швидкістю руху, а
завершення – координатою і швидкістю
руху.
У загальному
випадку задача розрахунку режимів
ведення поїздів вимагає задання:
– траєкторії
руху поїзда 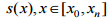 у просторових
координатах;
у просторових
координатах;
– поїзда,
тобто впорядкованого набору (l1,
..., lj, d1, d2,
..., dk)
однотипних локомотивів li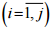 і вагонів di
і вагонів di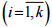 ;
;
– зовнішніх
умов – напрям вітру, температура
повітря, стан підвагонних генераторів
тощо;
– додаткових
умов – час руху, частота зміни силових
позицій тощо;
– крайових
умов для початкової й кінцевої координати
траєкторії руху на швидкість.
За заданими
даними необхідно знайти:
– траєкторію
швидкості руху поїзда 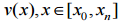 ;
;
– траєкторію зміни
паливно-енергетичних параметрів уздовж
траєкторії руху;
– режим роботи
тягових засобів;
– траєкторію зміни
температури нагрівання обмоток якорів
двигунів за електричної тяги;
–
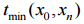 – мінімальний час на
проходження траєкторії руху;
– мінімальний час на
проходження траєкторії руху;
– мінімальні
паливно-енергетичні затрати й раціональну
експлуатацію тягових засобів за заданого
часу 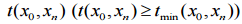 на переміщення;
на переміщення;
– сумарні затрати
паливно-енергетичних параметрів (за
витратними ставками на перевезення);
– максимальну
масу поїзда;
– залежність
між масою, часом руху й енергетичними
затратами поїзда для різних типів
локомотивів;
– оптимальний
час руху тільки за енергетичним
критерієм;
– необхідну
мінімальну додаткову тягу під час
проходження перевалів;
– мінімальну
швидкість на окремих перегонах руху,
яка гарантує рух без зупинки та без
додаткової тяги.
Система
розрахунку режимів руху поїздів
складається з інформаційного забезпечення,
задання розрахунку, алгоритмічного й
програмного забезпечення, табличного
й графічного представлення результатів
моделювання (рис. 1–5).
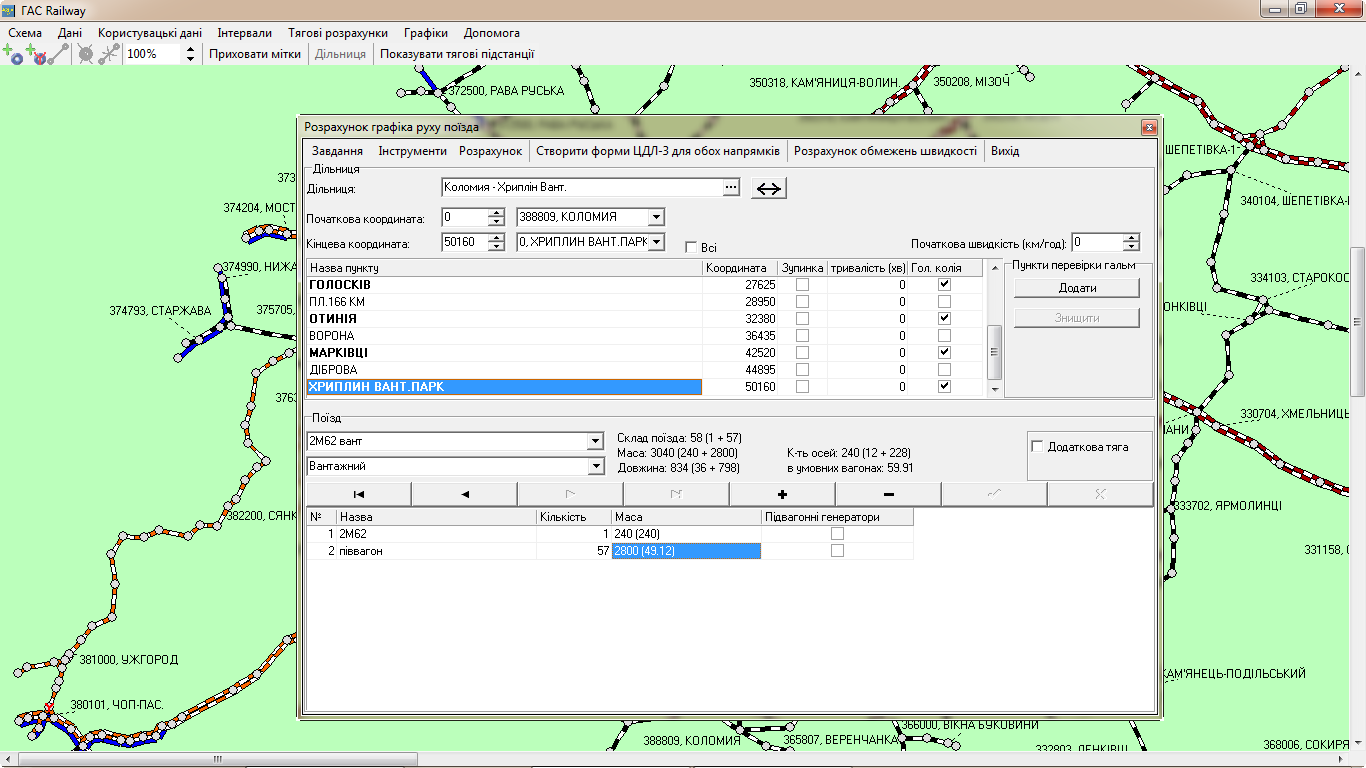
Рис.
1. Діалогове вікно
вибору шляху руху й задання на розрахунок
режиму руху поїзда
Fig.
1. Dialog box for choosing a way of motion and task for calculation
of the train’s operating condition
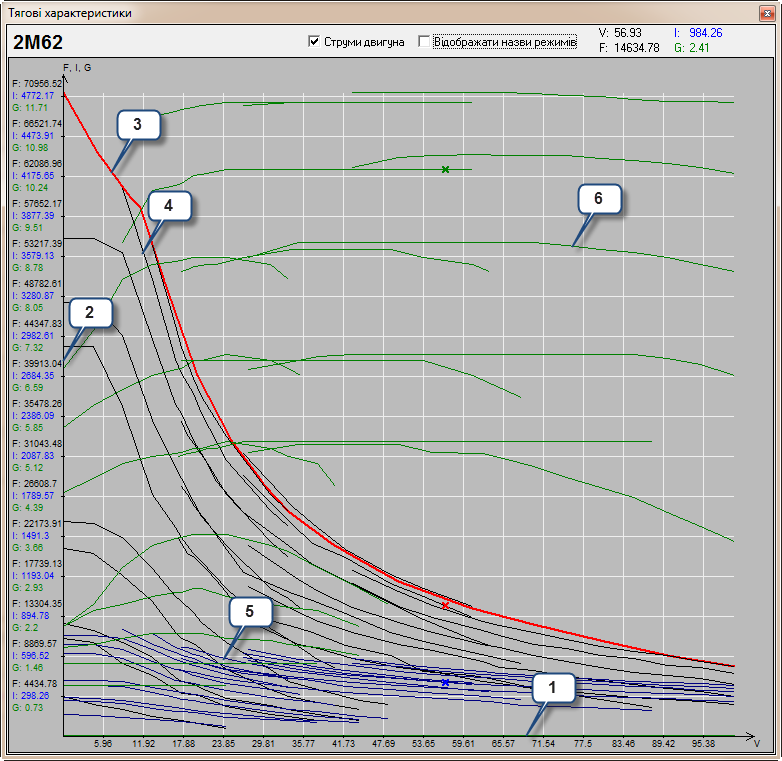
Рис. 2. Тягові
(2, 3, 4), струменеві (1, 5) і паливні (6)
характеристики локомотива 2М62
Fig.
2. Traction (2, 3, 4), jet (1, 5) and fuel (6) characteristics of
the locomotive 2M62
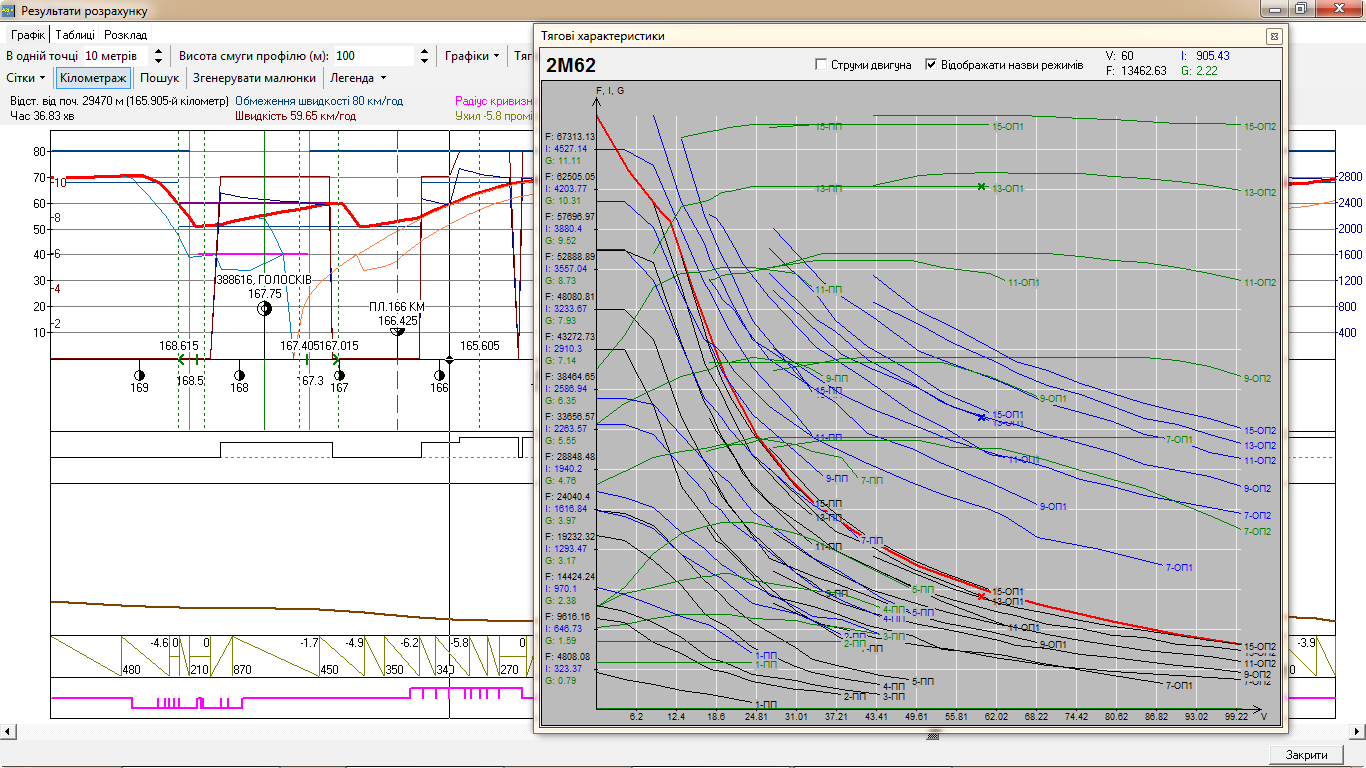
Рис. 3. Графічне
представлення результатів і робочих
точок на схемі – тягові
й струменеві
характеристики локомотива 2М62
Fig.
3. Graphical presentation of results and operating points at the
scheme - traction
and
jet characteristics of the locomotive 2M62
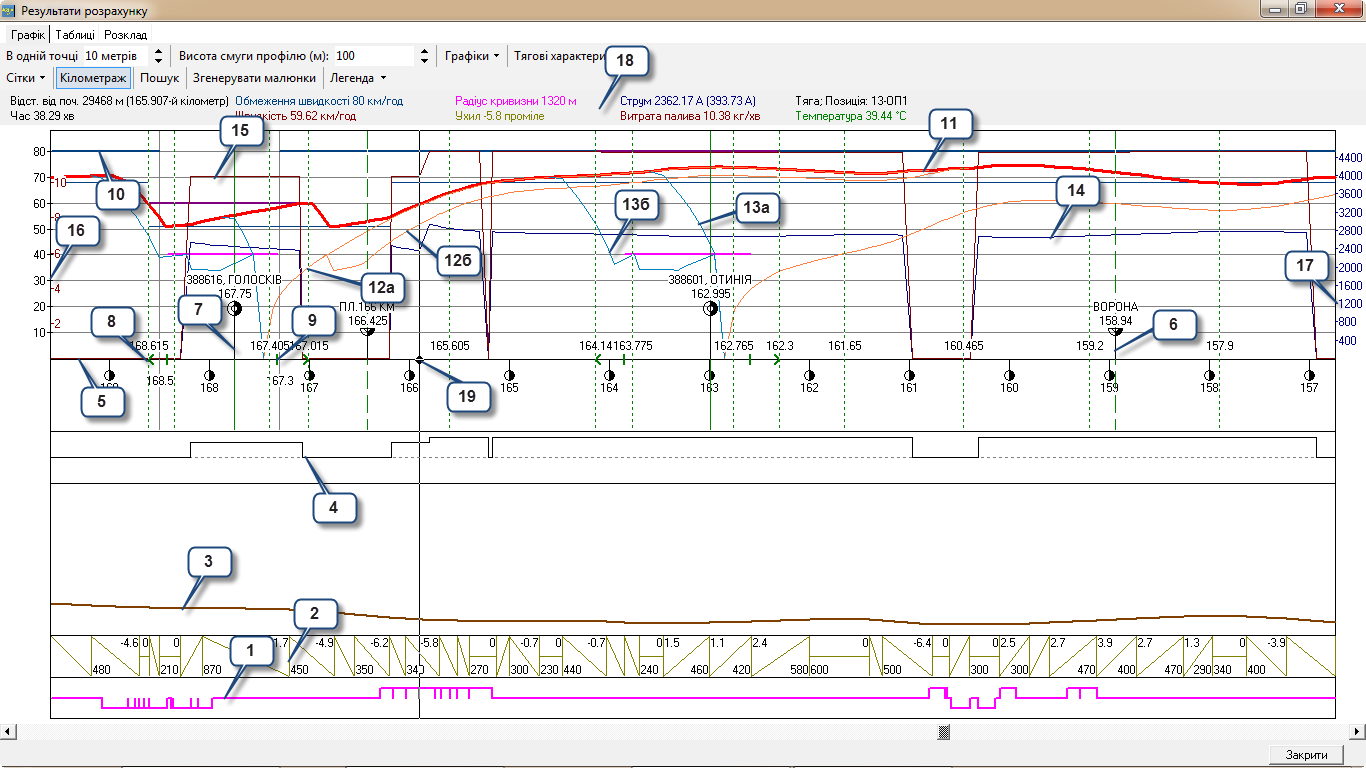
Рис. 4.
Представлення інформаційного забезпечення
й результатів моделювання
за заданим
критерієм оптимальності
Fig.
4. Presentation of information support and simulation results
by
the given criterion of optimality
На рис.
4 наведена наступна
графічна формація:
поздовжній
план колії в елементах (прямі, криві
ділянки);
елементи
профілю колії (довжина елемента, ухил);
поздовжній
профіль колії;
діаграма
режимів ведення локомотива (використання
тяги по позиціях);
кілометрова
розмітка лінії;
посадкова
платформа на перегоні;
роздільний
пункт (станція, блокпост, роз’їзд);
вхідна
стрілка роздільного пункту;
межа
роздільного пункту;
допустима
швидкість руху;
діаграма
швидкості руху поїзда;
діаграма
сповільнення поїзда за умови зупинки
на роздільному пункті:
а)
слідування по головній колії;
б)
слідування по бічній колії;
діаграма
розгону поїзда за умови зупинки на
роздільному пункті:
а)
слідування по головній колії;
б)
слідування по бічній колії;
діаграма
сили струму, А;
діаграма
миттєвих витрат палива, кг/хв;
шкала
осі сили струму;
шкала
осі швидкостей руху;
інформаційне
вікно;
бігунок
курсора (за яким відображають дані в
інформаційному вікні й у вікні тягових
характеристик).
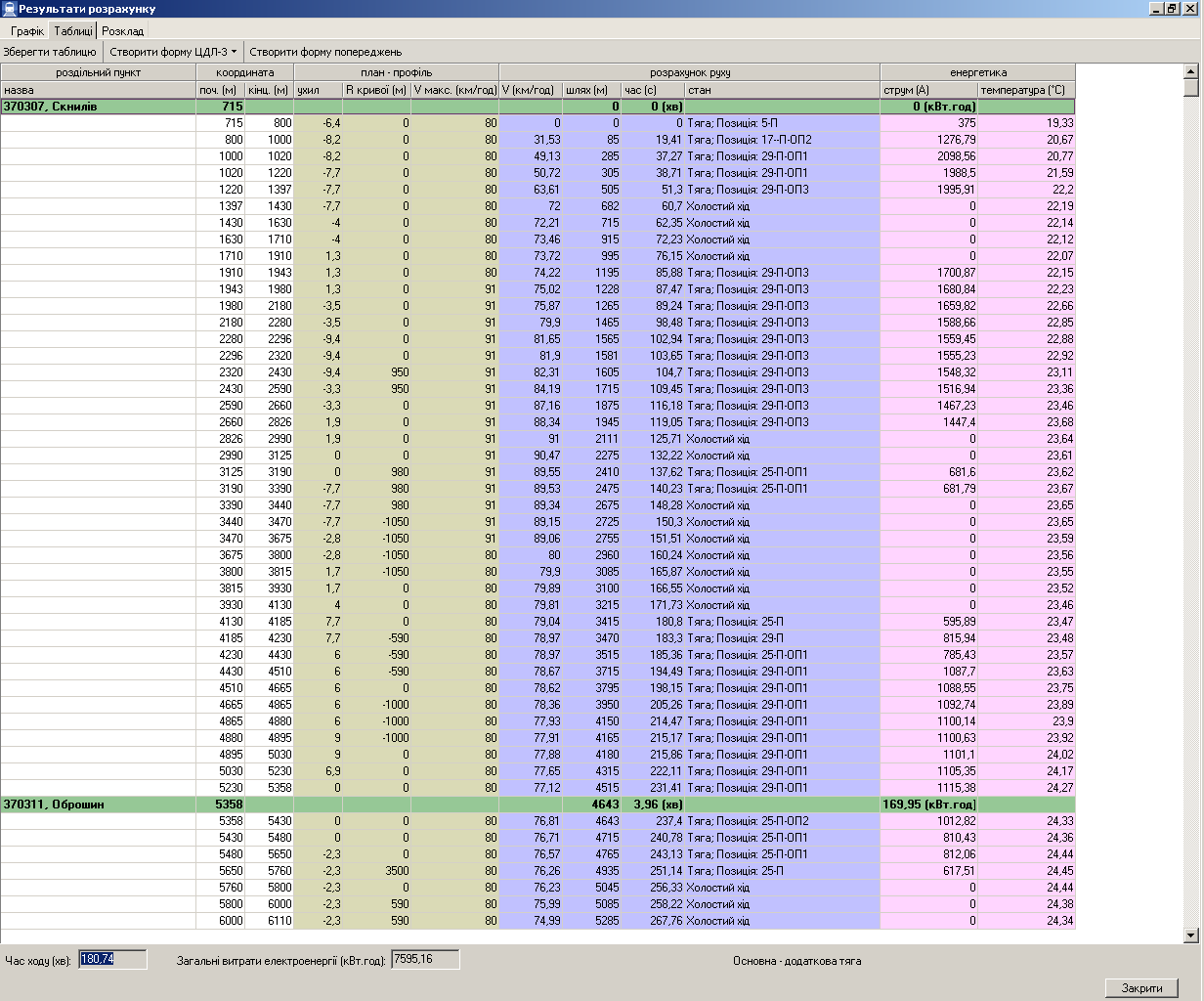
Рис. 5.
Розрахована режимна карта руху поїзда
в табличному вигляді
Fig.
5. Calculated mode map of the train motion in a tabular form
Наведемо
приклади розв’язування основних
режимних оптимізаційних задач.
Приклад
1 – розрахунок
максимальної маси поїзда.
Розрахунок максимальної маси поїзда
проведено для заданої серії локомотивів,
розрахункової дільниці за умов
максимальної реалізації кінетичної
енергії руху поїзда і його тягових
характеристик. На рис. 6 наведені
результати числового експерименту.
У результаті
розрахунку отримано, що для локомотивів
типу 2М62 й М62 максимальна допустима
маса є рівною – 1 782 й 892 відповідно.
Збільшення маси призведе до зупинки
поїзда у вказаних координатах траєкторії
руху (рис. 6 ). Для збільшення маси
поїзда необхідна додаткова тяга.
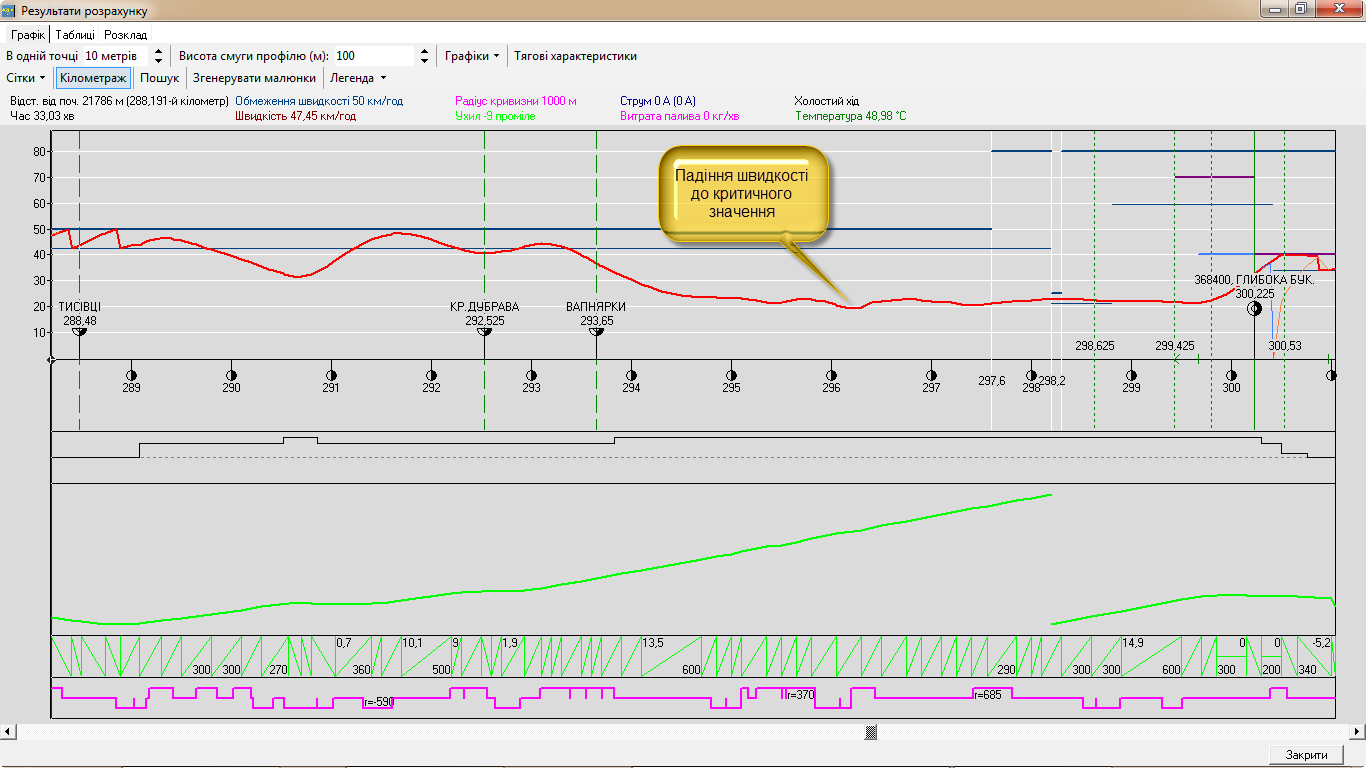
Рис. 6.
Графічне представлення результатів
числового експерименту
Fig.
6. Graphical representation of the results of the numerical
experiment
Приклад
2 – розрахунок
поїздів із
різною кількістю
вагонів. Розрахунки
проведені на
дільницях
Чернівці Південні
– Великий Кучурів
і Вигнанка
– Гадинківці – Копичинці.
Траєкторії швидкості руху наведені
на рис. 7.
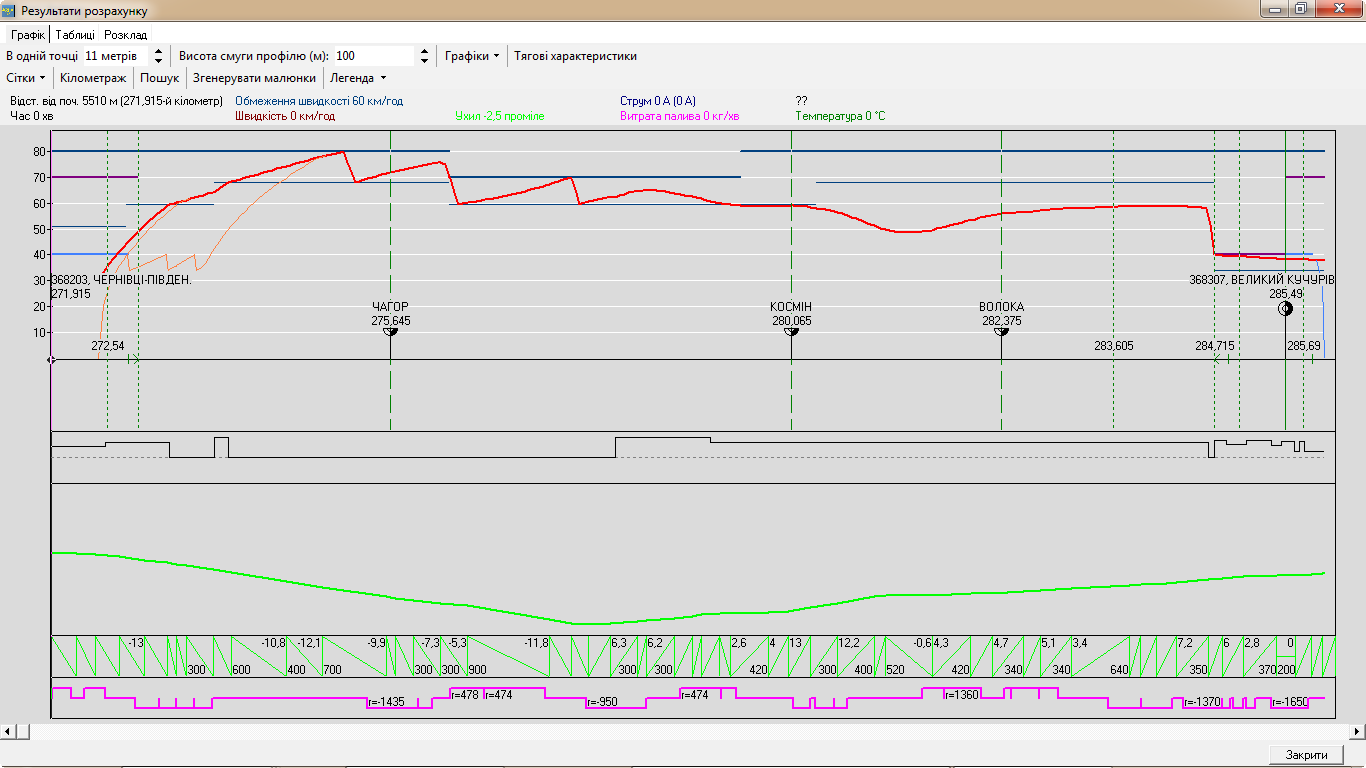
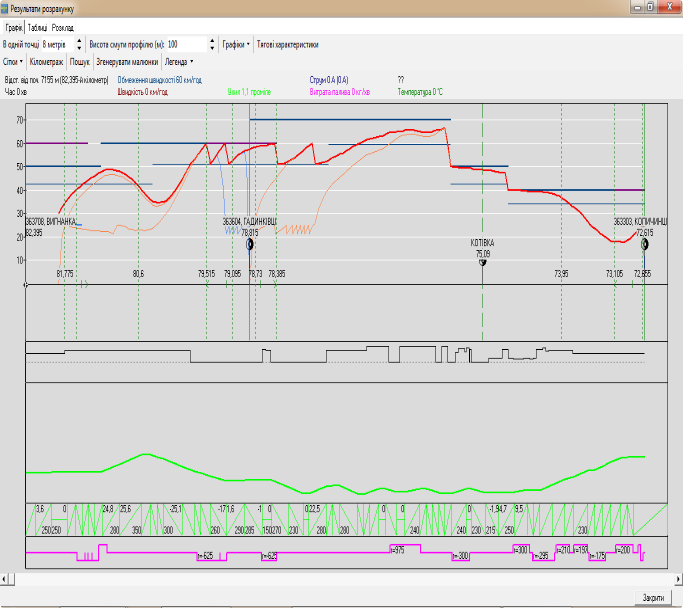
Рис. 7.
Траєкторія швидкості руху проїзду: 57
вагонів – зліва, 15 вагонів – справа
Fig.
7. Trajectory of the speed of trains: 57 cars - left, 15 cars -
right
Наведено по два
приклади ведення поїзда на різних
дільницях із різною кількістю вагонів.
В обох випадках використаний локомотив
серії 2М62, склад поїзда масою 1 250 т,
режим ведення поїзда – з максимально
допустимою швидкістю (мінімум часу). У
першому варіанті розрахунку склад
поїзда 57 вагонів, у другому – 15 вагонів.
На дільниці Чернівці Південні – Великий
Кучурів час ходу поїзда зі складом у
57 вагонів на 2 хв більший, ніж у короткого
складу, витрата палива також збільшена
на 12 %. На дільниці Вигнанка –
Гадинківці – Копичинці час ходу обох
складів поїздів практично не відрізняється,
а витрата палива у довшого складу поїзда
виявилася меншою на 3,8 %. Для поїзда
з більшою кількістю вагонів необхідна
менша тяга для руху по місцевості зі
значними перепадами висот.
Приклад
3 – вплив окремих обмежень на режим
руху. Проведені числові
експерименти для оцінки впливу на режим
руху поїзда окремих обмежень. Для цього
взяті дільниця Здолбунів – Ківерців
і поїзд із 57 вагонів загальною масою
1 438 т і локомотивом ВЛ-80к. Довжина
шляху дорівнює 81,130 км. Кількість зупинок
на проміжних станціях – 4. Переходити
в режим гальмування дозволили за
швидкості 60 км/год. Отримані такі
результати розрахунків:
зміна
частоти тягових позицій величинами
інтервалу швидкості руху в межах 5–15 %
збільшує на 2,8 % час руху і зменшує
енергетичні затрати на 2,35 %;
використання
режиму гальмування за швидкостей 40 і
20 км/год збільшує час руху на 4 й 10 хв і
зменшує затрати електроенергії в межах
5 і 7,5 % відповідно;
зменшення
верхніх обмежень на швидкість до 15 %
призводить до зменшення енерговитрат
на 3,5 % і збільшення часу на рух на
9,7 %.
Приклад
4 – вплив зміни тяги.
Розрахунки проведені на дільниці
Чернівці Південні – Великий Кучурів
із зміною типу тяги. Склад поїзда – 57
вагонів, маса – 1 254 т. Критерій руху
– за мінімальний час ходу.
Заміна тепловоза
2М62 (час ходу 14 хв, витрата палива 100 кг,
витрати на паливо – 696 грн, за витратними
ставками 1 423 грн) на тепловоз 2ТЕ10л,
згідно з розрахунком, дозволяє незначно
пришвидшити рух поїзда по перегону,
але збільшення витрати палива складе
24 %. При цьому витрати на тягу складуть
873 грн, а за витратними ставками –
1 423 грн. Для тепловоза ТЕ33а час
ходу зменшено на 1 хв, а витрата палива
– на 17,6 %. Витрати на тягу складуть
598 грн, а за витратними ставками –
1 422 грн. Для електровоза ВЛ-80к час
ходу зменшено на 1 хв, а витрата
електроенергії на тягу поїзда становить
446 кВт/год. Витрати на тягу складуть 245
грн, а за витратними ставками – 1 185
грн.
Приклад
5 – оптимізаційні розрахунки
на перегоні.
Проведені числові експерименти для
різних типів тяги, маси поїздів і
середньої швидкості. Отримані затратні
величини на рух поїздів і максимальні
маси поїздів (рис. 8).
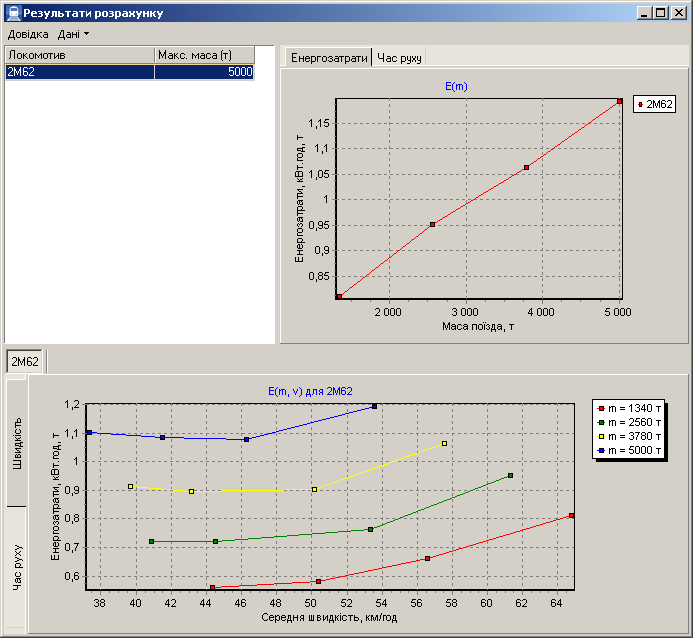
Рис. 8. Графічне
представлення результатів проведених
експериментів
Fig.
8. Graphical representation of the results of the experiments
conducted
Результати
експерименту показали, що:
– максимальна маса
поїзда залежить від типу тяги;
– зі
збільшенням маси поїзда зростуть і
енергетичні затрати;
– енергетичні
затрати зростають зі збільшенням
середньої швидкості руху поїзда
нелінійно;
– за незначних мас
поїздів енерговитрати можуть бути
непропорційними їх зростанню, це
пов’язано як із дискретністю тягових
силових позицій, так із формалізацією
поняття «режим (оптимальний режим) руху
поїзда».
Приклад
6 – сумарні витрати, розраховані за
витратними ставками на вантажні й
пасажирські перевезення.
Були задані витратні ставки, дільниця,
початкова й кінцева станції, зупинки,
поїзд і час на його переміщення від
початкової до кінцевої станції. Потрібно
знайти такий режим руху поїзда, який
задовольняє задані умови й забезпечує
мінімальні витрати на його переміщення.
Перелік витратних ставок наведений на
рис. 9, а результати досліджень – у табл.
2.
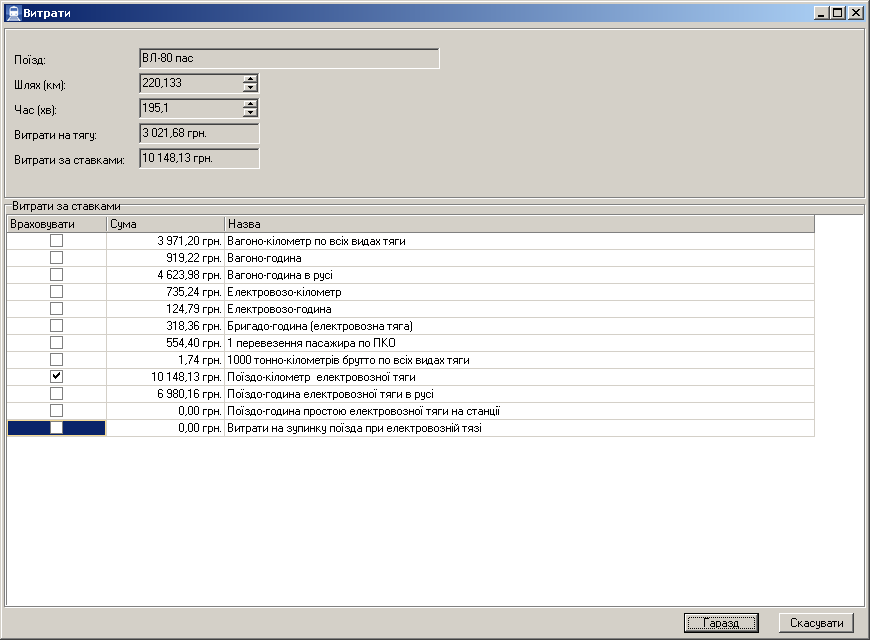
Рис. 9. Форма
представлення розрахунку сумарних
витрат за витратними ставками
Fig.
9. Form of presentation of calculation of total expenses at cost
rates
Таблиця 2
Енергетичні
витрати та витрати за ставками
Table 2
Energy
costs and costs at rates
-
|
Енергетичні
витрати,
грн
|
Витрати
за витратними
ставками,
грн
|
Сумарні
витрати,
грн
|
Час
руху,
хв
|
|
2 776,67
|
18 332,89
|
21 109,56
|
195
|
|
2 629,09
|
19 310,1
|
21 939,19
|
226
|
|
2 631,59
|
20 571,88
|
23 203,47
|
254
|
Як бачимо, сумарні
витрати за ставками зі збільшенням
часу руху поїзда зростають, а суми
паливно-енергетичних витрат і витрати
за ставками, як правило, завжди будуть
зі збільшенням часу руху поїзда зростати.
Приклад 7
– характер
зміни енергетичних витрат від типу
тяги й часу руху.
На рис.10 наведені результати розрахунку
зміни енергетичних витрат для різних
типів тяги як функції від заданого часу
на рух, який є більшим за мінімальний.
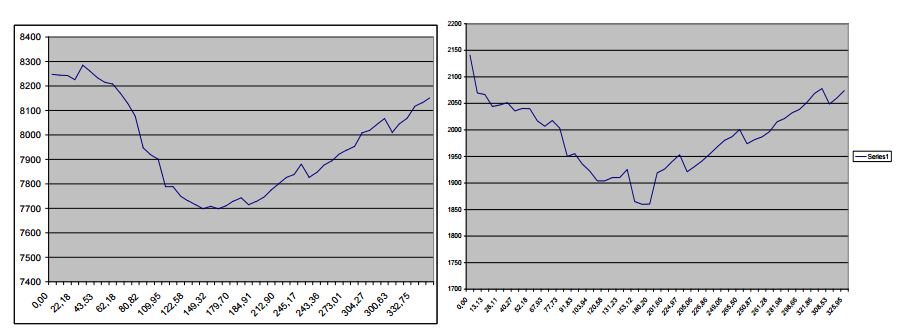
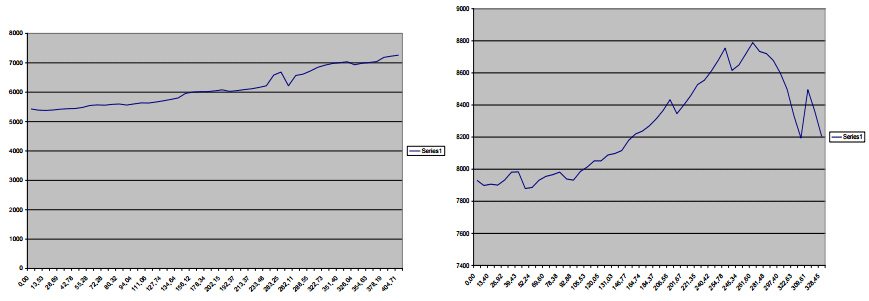
Рис. 10.
Характер зміни енергетичних витрат
залежно від заданого на рух часу по
дільниці Івано-Франківськ – Рахів для
заданих типів поїздів і локомотивів:
вантажний, 2М62; вантажний, ВЛ-11; вантажний,
ВЛ-80, 3 000 т; вантажний, 2М62
Fig.
10. Nature of the change in energy costs depending on the defined
time for the motion in the Ivano-Frankivsk-Rakhiv section for the
specified types of trains and locomotives: cargo, 2M62; cargo,
VL-11; cargo, VL-80, 3000 tons; cargo, 2М62
Як бачимо, характер
залежності паливних та енергетичних
величин від часу руху для різних типів
тяги суттєво відрізняється. Частково
на такий характер залежності вплинув
наявний план і профіль траєкторії руху.
Приклад
8 – використання для системи проектування
й модернізації колії.
Запропоновано алгоритм розрахунку
обмежень швидкостей на незаданих
інтервалах траєкторії руху за заданого
часу на рух і визначення прийнятності
проектованих радіусів кривих за
розрахованими швидкостями руху й
необхідне для цього підвищення зовнішньої
рейки в кривій і довжину перехідної
кривої з урахуванням допустимого
непогашеного прискорення. Указавши
допустиме значення непогашеного
прискорення, можна отримати інформацію
про прийнятність радіуса кожної кривої.
Якщо запроектовані радіуси будуть
неприйнятними, користувач отримає
зручну форму для вибору параметрів
кривої (радіус кривої, підвищення
зовнішньої рейки або допустиму
швидкість). Користувачеві потрібно
буде вказати, які параметри є незмінними
(фіксованими), а система запропонує
решту параметрів автоматично.
Для розрахунку
значення непогашеного прискорення
використана формула [4]:
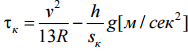
.
Довжина
перехідної кривої
повинна задовольняти
наступні умови:
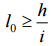 , обмеження на
ухил зовнішньої рейки, мм;
, обмеження на
ухил зовнішньої рейки, мм;
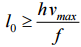 , обмеження
на швидкість підйому колеса на підвищення
зовнішньої рейки, м/сек2;
, обмеження
на швидкість підйому колеса на підвищення
зовнішньої рейки, м/сек2;
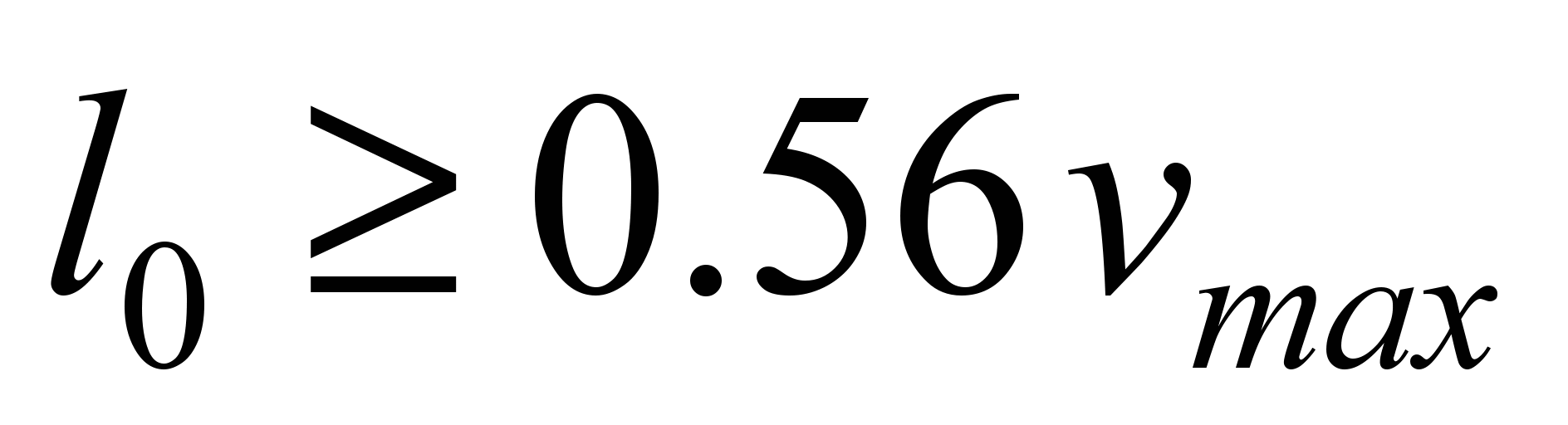 ,
обмеження на швидкість збільшення
непогашеного прискорення, м/сек2;
,
обмеження на швидкість збільшення
непогашеного прискорення, м/сек2;
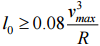 , обмеження на удар
об зовнішню рейку гребеня першої осі;
, обмеження на удар
об зовнішню рейку гребеня першої осі;
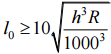 , обмеження на
величину непогашеного прискорення;
, обмеження на
величину непогашеного прискорення;
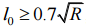 , обмеження, яке
випливає з можливості практичної
розбивки кривої на місцевості.
, обмеження, яке
випливає з можливості практичної
розбивки кривої на місцевості.
Тут 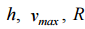 –
відповідно висота підняття зовнішньої
рейки, мм; максимально допустима
швидкість у кривій (м/сек2)
й радіус кривої, м. Нормативні величини
i та f
– ухил зовнішньої
рейки та найбільша допустима швидкість
підйому колеса по зовнішній рейці. Для
кожної кривої цієї дільниці система
обчислить мінімальну довжину перехідної
кривої. При цьому користувач зможе
настроювати, які із заданих шести
обмежень враховувати. Також користувач
зможе редагувати значення нормативних
констант, які входять у формули.
–
відповідно висота підняття зовнішньої
рейки, мм; максимально допустима
швидкість у кривій (м/сек2)
й радіус кривої, м. Нормативні величини
i та f
– ухил зовнішньої
рейки та найбільша допустима швидкість
підйому колеса по зовнішній рейці. Для
кожної кривої цієї дільниці система
обчислить мінімальну довжину перехідної
кривої. При цьому користувач зможе
настроювати, які із заданих шести
обмежень враховувати. Також користувач
зможе редагувати значення нормативних
констант, які входять у формули.
Процес встановлення
обмежень на максимальну швидкість на
певних ділянках, проведення
тягово-енергетичних розрахунків за
заданим критерієм та автоматична оцінка
затрат на можливі ремонтні роботи дають
можливість з’ясувати мінімальні
ресурси для забезпечення заданої
швидкості на заданому перегоні для
заданого набору поїздів.
Наукова новизна
та практична
значимість
У роботі запропонована
постановка задачі розрахунку режимів
ведення поїздів як задача оптимального
керування. Розроблено алгоритм
мінімальної складності, який забезпечив
ефективне розв’язання прямих та
обернених нелінійних оптимізаційних
задач у всій галузі їх паливних,
енергетичних і тягових характеристик.
Це забезпечило автоматизацію процесу
розв’язування великого набору прямих
та обернених режимних, із різними
критеріями оптимальності, задач.
Розроблено програмний комплекс, який
пройшов апробацію в процесі розрахунку
основних складових для формування
графіків руху, вибору оптимальних
параметрів реконструкції полотна й
формування режимних параметрів руху
нових швидкісних поїздів.
Висновки
Запропонована
модель та алгоритмічне забезпечення
дають можливість урахувати сумарний
вплив на екстремальні параметри руху
поїздів різних факторів: зміну коефіцієнта
(залежить від багатьох зовнішніх
факторів) зчеплення коліс локомотива
з колійним полотном; силу й напрямку
вітру; температуру повітря; відхилення
напруги в контактних мережах від
номінальних характеристик; коефіцієнт
технічного стану локомотива за тягою;
зміну радіусу тягових коліс тощо.
Кожна задача
оптимізації вимагає певного ресурсу
(часового, можливості вибору локомотива
із заданої множини локомотивів,
корегування маси поїздів, вибору
траєкторії руху між заданими роздільними
пунктами, можливості встановлювати чи
коригувати обмеження за швидкістю на
певних ділянках тощо), ефективне
використання якого забезпечує мінімізацію
витрат на переміщення між двома
роздільними пунктами.
Більшість задач
оптимізації можна звести до ефективного
використання наявного часового ресурсу.
Для цього необхідно ефективно використати
кінетичну енергію руху поїздів і
мінімізувати затрати на перехідні
режими способом їх зменшення за кількістю
й величиною. Для розв’язання задач
оптимізації (прямих та обернених)
основна увага була приділена центральній
задачі – оптимізація за заданих умов
на часовий ресурс.
Для
розробленого алгоритмічного й програмного
забезпечення характерно:
– математична
модель тягових засобів є максимально
повною – використана повна множина
тягових, струмових, енерговитратних,
теплових, опірних характеристик для
всіх типів приводів і вагонів, а також
розподілена маса вздовж довжини поїзда,
яка прив’язана до центру мас тягових
засобів і вагонів;
– врахований
вплив основних зовнішніх факторів –
температури повітря, сил зустрічного
вітру, підвагонних генераторів тощо;
– для
розрахунків застосована траєкторія
руху поїздів без її спрямлення;
– усі
задачі поставлені як задачі оптимального
керування;
– запропоноване
алгоритмічне забезпечення дозволило
поставити й розв’язати достатньо
повний набір прямих та обернених задач
оптимізації;
– забезпечена
повна автоматизація задання вхідних
даних і процесу розв’язування поставлених
задач;
– створені
засоби для проведення числових
експериментів та порівняльного аналізу
результатів;
– усі
задачі можуть бути розв’язані в
оптимізаційній постановці за
паливно-енергетичними ресурсами без
додаткових умов;
– алгоритмічне
забезпечення дозволяє розв’язати
оптимізаційні задачі з додатковими
умовами і врахуванням усіх суттєвих
технологічних обмежень;
– розроблена
ефективна система графічного й табличного
представлення результатів розв’язування
задач.
СПИСОК ВИКОРИСТАНИХ
ДЖЕРЕЛ
Афанасьев,
В. Н. Математическая теория конструирования
систем управления: учеб.
для вузов / В. Н. Афанасьев, В. Б.
Колмановский, В. Р. Носов. – Москва:
Высш. шк., 2003. – 615 с.
Визначення
енергозаощаджуючих режимів розгону
поїздів / Б. Є. Боднар, М. І. Капіца, А. М.
Афанасов,
Д.
М. Кислий //
Наука та прогрес транспорту. – 2015. –
№ 5 (59). – С. 40–52. doi:
10.15802/stp2015/55359
Кульбашна,
Н. І. Нові підходи щодо складання
раціональних режимів водіння рухомого
складу по маршрутах / Н. І. Кульбашна,
А. Г. Тарновецька, О. І. Балас // Проблеми
та перспективи розвитку техн. засобів
трансп. та систем автоматизації :
матеріали міжнар. наук.-практ. конф.
(1.10–3.10.2014) / Харк. нац. ун-т міськ. госп-ва
ім. О. М. Бекетова. – Харків, 2014. – С.
84–85.
Правила
тяговых расчетов для поездной работы.
– Москва: Транспорт, 1985. – 289 с.
Притула, М.
Г. Моделювання та розрахунок оптимальних
параметрів руху поїздів / М. Г. Притула,
Р. Р. Шпакович // Фізико-математичне
моделювання та інформаційні технології
: наук. зб. – Львів, 2007. – Вип. 5. – С.
139–145.
Сорока, К.
О. Змістовна модель та рівняння руху
електричного транспорту / К. О. Сорока,
Д. О. Личов // Наука та прогрес транспорту.
– 2015. – № 3 (57). – С. 97–106. doi:
10.15802/stp2015/46056
Сорока,
К. О. Система автоматизованого вибору
швидкісного режиму руху засобів
електротранспорту з метою зменшення
витрат електроенергії / К. О. Сорока,
Т. П. Павленко, Д. О. Личов // Наука та
прогрес транспорту. – 2017. – № 3 (69). –
С.
77–91.
doi: 10.15802/stp2017/104360
Individual
driving style impact on traction energy consumption in railway
lines: A simulation model / A. Capasso, R. Lamedica, F. M. Gatta
[et al.] // Intern. Symposium on Power Electronics, Electrical
Drives, Automation and Motion (SPEEDAM) (22.06–24.06.2016)
:
Conf. Paper. – Anacapri, Italy, 2016. – P. 665–670. doi:
10.1109/SPEEDAM.2016.7525929
Wang,
P. Train Trajectory Optimization Methods for Energy-Efficient
Railway Operations:
doctoral
thesis
[Електронний
ресурс] / Pengling Wang ; Delft University of Technology. –
Delft, 2017. – 197
p.
– Режим доступу: http://clc.am/2oMizA
–
Назва з екрана. – Перевірено : 28.12.2018.
Haahr,
J.
T.
A
dynamic programming approach for optimizing train speed profiles
with speed restrictions and passage points /
J. T. Haahr, D. Pisinger, M. Sabbaghian // Transportation
Research.
Part B: Methodological.
– 2017. –
Vol. 99.
–
Р.
167–182.
doi: 10.1016/j.trb.2016.12.016
Scheepmaker,
G. M. Review of energy efficient train control and timetabling /
G. M. Scheepmaker, R. M. P. Goverde, L. G. Kroon // European
Journal of Operational Research.
– 2017. – Vol. 257.
– Іss.
2.
–
Р.
355–376.
doi:
10.1016/j.ejor.2016.09.044
The
key principles of optimal train control
–
Рart
1: Formulation of the model, strategies of optimal type,
evolutionary lines, location of optimal switching points
/ Amie Albrecht, Phil Howlett, Peter Pudney, Xuan Vu, Peng Zhou //
Transportation Research.
Part B: Methodological.
– 2016. –
Vol.
94.
– Р.
482–508. doi: 10.1016/j.trb.2015.07.023
The
key principles of optimal train control
–
Рart
2: Existence of an optimal strategy, the local energy minimization
principle, uniqueness, computational techniques
/ Amie Albrecht,
Phil Howlett, Peter Pudney, Xuan Vu, Peng Zhou
//
Transportation
Research.
Part B: Methodological.
–
2016.
– Vol. 94.
– Р.
509–538. doi: 10.1016/j.trb.2015.07.024
Ye,
H. Nonlinear programming methods based on closed-form expressions
for optimal train control /
Hongbo Ye, Ronghui Liu // Transportation
Research.
Part
C:
Emerging
Technologies.
– 2017. – Vol. 82. – Р. 102–123.
doi: 10.1016/j.trc.2017.06.011
М.
Г.
ПРИТУЛА1*,
А.
А.
ПАСЕЧНИК2*
1*Центр
математического
моделирования
НАНУ, ул. Дудаева,
15, Львов,
Украина,
97053,
тел.
+38
(032) 261
18
85,
эл.
почта
myroslav.prytula@gmail.com,
ORCID0000-0001-9259-4114
2*ГП
«Проектно-конструкторское технологическое
бюро по автоматизации
систем управления
на железнодорожном транспорте Украины»,
ул. Жилянская, 97, Киев, Украина,
01135,
тел.
+38 (044) 226
24
82,
эл.
почта
sasha1101@ukr.net,
ORCID 0000-0001-7303-0145
РАЗРАБОТКА
АЛГОРИТМОВ ФОРМИРОВАНИЯ
ЭНЕРГООПТИМАЛЬНЫХ
РЕЖИМОВ
ДВИЖЕНИЯ ПОЕЗДОВ
Цель.
Работа предусматривает разработку
алгоритмического обеспечения для
моделирования и оптимизации режимов
движения поездов. Методика.
Для описания процесса движения поезда
в пространственных координатах с
распределенной массой вдоль траектории
движения предложена системная модель.
Она учитывает тяговые и опорные параметры
и их изменение в зависимости от внешних
и внутренних факторов. Для численного
интегрирования модели системы использован
метод конечных разностей. Кроме этого,
разработаны итерационные процедуры
для удовлетворения краевых условий,
формирования последовательности из
режимов тяги, торможения и холостого
хода с соответствующими параметрами,
чтобы обеспечить выполнение критерия
оптимальности движения и технических
ограничений с достаточной точностью.
Критерий оптимальности включает
топливно-энергетические ресурсы,
частоту смены режимов работы тяговых
средств (существенно влияет на износ
приводов), затратные ставки и тому
подобное. Результаты.
Разработанное алгоритмическое,
программное и информационное обеспечение
позволило проведение: расчетов режимов
ведения произвольных поездов, в том
числе нормативных, для формирования
графиков движения, расчет между поездными
и станционными интервалами, исследование
влияния экстремальных параметров
поездов на режимы их ведения. В системе
предусмотрена возможность адаптации
параметров модели движения поезда по
результатам исследовательских поездок.
Научная
новизна.
В работе предложена постановка расчета
режимов ведения поездов как задачи
оптимального управления, определён
быстрый метод ее решения. Это обеспечило
автоматизацию процесса решения большого
набора прямых и обратных режимных, с
различными критериями оптимальности,
задач. Практическая
значимость.
Предложенный подход к постановке и
решению задач моделирования и оптимизации
режимов ведения поездов прошел апробацию
в процессе расчета основных составляющих
для формирования графиков движения,
выбора оптимальных параметров
реконструкции полотна для всех,
скоростных и новых, типов поездов.
Ключевые
слова:
тягово-энергетические расчеты;
оптимальный режим; математическое
обеспечение; математическая модель
поезда; идентификация параметров
модели, прямые и обратные задачи
M.
G. PRYTULA1*,
O.
A. PASECHNYK2*
1*Center
of Mathematical Modelling NASU,
Dudaev St.,
15, Lviv,
Ukraine,
79053,
tel.
+38
(032) 261
18
85,
e-mail myroslav.prytula@gmail.com,
ORCID 0000-0001-9259-4114
2*SE
«Design
and Development Bureau of Automation of Control Systems
in the
Railway Transport of Ukraine»,
Zhylianska St.,
97, Kyiv,
Ukraine,
01135,
tel.
+38 (044) 226
24
82,
e-mail
sasha1101@ukr.net,
ORCID 0000-0001-7303-0145
DEVELOPMENT
OF THE ALGORITHMS
FORMATION OF ENERGY-
OPTIMIZED
TRAINS TRAFFIC MODES
Purpose. The
paper involves the development of algorithmic support for simulation
and optimization of train traffic modes. Methodology. To
describe the process of the train movement in spatial coordinates
with the distributed mass along the trajectory of motion, a system
model is proposed. The model takes into account traction and support
parameters and their changes depending on external and internal
factors. For a numerical integration of a system model, a
finite-difference method is used. In addition, iterative procedures
are developed to meet the boundary conditions, the formation of a
sequence of traction, braking and idling modes with appropriate
parameters to satisfy the criterion of optimality of traffic and
technical limitations with sufficient accuracy. The criterion of
optimality includes fuel and energy resources, the frequency of
changes in the modes of work of traction means (significantly affect
the wear of drives), cost rates, etc. Findings. The developed
algorithmic, software and information support provided: calculation
of driving modes of arbitrary, including standard ones for formation
of traffic schedules, calculation of inter-station and station
intervals, and research of influence of extreme parameters of trains
on their modes of operation. The system provides for the adaptation
of the parameters of the train model based on the results of
experimental trips. Originality. The paper proposes the task
of calculating train driving modes as a problem of optimal control
and proposes a quick method for its solution. This ensured the
automation of the process of solving a large set of direct and
inverse modes with different optimality criteria. Practical
value. The proposed approach to the formulation and solution of
tasks of modeling and optimization of train driving modes was tested
in the process of calculating the main components for the formation
of traffic schedules, the selection of optimal parameters for the
reconstruction of the roadbed for high-speed and new types of
trains.
Key words:
traction–energy calculations; optimal mode; mathematical support;
mathematical model of train; identification of model parameters;
direct and inverse problems
REFERENCES
Afanasev,
V. N., Kolmanovskiy, V. B., & Nosov, V. R. (2003).
Matematicheskaya teoriya konstruirovaniya sistem upravleniya:
uchebnik dlya vuzov.
Moscow: Vysshaya shkola. (in Russian)
Bodnar, B. Y.,
Kapitsa, M. I., Afanasov, A. M., & Kyslyi, D. N. (2015).
Definition of Energy Saving Acceleration Modes of Trains. Science
and Transport Progress, 5(59),
40-52. doi: 10.15802/stp2015/55359
(in
Ukrainian)
Kulbashna, N. I.,
Tarnovetska, A. H., & Balas, O. І. (2014). Novi pidkhody
shchodo skladannia ratsionalnykh rezhymiv vodinnia rukhomoho skladu
po marshrutakh. Proceedings
of the International Conference Problemy ta perspektyvy rozvytku
tekhnichnykh zasobiv transportu ta system avtomatyzatsii, October,
01-03, 2014,
Kharkiv. 84-85. Kharkiv: O. M. Beketov National University of Urban
Economy in Kharkiv.
(in
Ukrainian)
Pravila
tyagovykh raschetov dlya poezdnoy raboty.
(1985). Moscow: Transport. (in Russian)
Prytula,
M. H., & Shpakovych, R. R. (2007). Modeliuvannia ta rozrakhunok
optymalnykh parametriv rukhu poizdiv. Fizyko-matematychne
modeliuvannia ta informatsiini tekhnolohii, 5,
139-145. (in Ukrainian)
Soroka, K. O., &
Lychov, D. A. (2015). The Content Model and the Equations of Motion
of Electric Vehicle. Science
and Transport Progress. 3(57),
97-106. doi: 10.15802/stp2015/46056
(in
Ukrainian)
Soroka, K. O.,
Pavlenko, T. P., & Lychov, D. A. (2017). System for Automatic
Selection of the Speed Rate of Electric Vehicles for Reducing the
Power Consumption. Science
and Transport Progress, 3(69),
77-91. doi: 10.15802/stp2017/104360
(in
Ukrainian)
Capasso, A.,
Lamedica, R., Gatta, F. M., Geri, A., Maccioni, M., Ruvio, A., …
Carones, N. (2016). Individual driving style impact on traction
energy consumption in railway lines: A simulation model. 2016
International Symposium on Power Electronics, Electrical Drives,
Automation and Motion (SPEEDAM). doi: 10.1109/speedam.2016.7525929
(in
English)
Wang,
P. (2017). Train
Trajectory Optimization Methods for Energy-Efficient Railway
Operations:
doctoral thesis.
Retrived from http://clc.am/2oMizA
(in
English)
Haahr, J. T.,
Pisinger, D., & Sabbaghian, M. (2017). A dynamic programming
approach for optimizing train speed profiles with speed
restrictions and passage points. Transportation
Research Part B: Methodological, 99, 167-182.
doi: 10.1016/j.trb.2016.12.016 (in
English)
Scheepmaker, G.
M., Goverde, R. M. P., & Kroon, L. G. (2017). Review of
energy-efficient train control and timetabling. European
Journal of Operational Research, 257(2), 355-376.
doi: 10.1016/j.ejor.2016.09.044 (in
English)
Albrecht, A.,
Howlett, P., Pudney, P., Vu, X., & Zhou, P. (2016). The key
principles of optimal train control – Part 1: Formulation of the
model, strategies of optimal type, evolutionary lines, location of
optimal switching points. Transportation
Research Part B: Methodological, 94,
482-508. doi: 10.1016/j.trb.2015.07.023 (in
English)
Albrecht, A.,
Howlett, P., Pudney, P., Vu, X., & Zhou, P. (2016). The key
principles of optimal train control –Part 2: Existence of an
optimal strategy, the local energy minimization principle,
uniqueness, computational techniques. Transportation
Research Part B: Methodological, 94,
509-538. doi: 10.1016/j.trb.2015.07.024 (in
English)
Ye, H., & Liu,
R. (2017). Nonlinear programming methods based on closed-form
expressions for optimal train control. Transportation
Research Part C: Emerging Technologies, 82,
102-123. doi: 10.1016/j.trc.2017.06.011 (in
English)
Надійшла
до редколегії: 28.07.2018
Прийнята до друку:
30.11.2018
,
,
(швидкість руху, сила тяги й гальмівна
сила) задовольняють рівняння:
(1)
,
, (2)
– тягова сила, Н;
– гальмівна сила, Н;
– маса вагонів, Н;
– маса локомотива, т;
– різниця між температурою обмоток
тягових двигунів і температурою повітря,
оС;
,
– значення теплових
параметрів, що залежать від величини
струму, який використовує тяговий
двигун;
– максимально допустима
температура нагрівання обмоток тягових
двигунів, оС;
– коефіцієнт інерції обертових мас
поїзда, км/год2;
,
де
– сила додаткового опору, яка залежить
від ухилу,
;
радіуса кривизни
траєкторії переміщення, м; температури
повітря
,
оС;
швидкості зустрічного вітру
,
м; кількості увімкнених підвагонних
генераторів
;
– час, год.
однотипних
локомотивів
і вагонів
.
Порядок розміщення локомотивів у поїзді
може бути різним.
,
довжиною
,
кількістю осей
,
силою натиску гальмівних колодок на
вісь
,
конструктивною швидкістю
,
затратами палива в режимі холостого
ходу
(для тепловозів і
дизель-поїздів), затратами електроенергії
на внутрішні потреби
,
коефіцієнтом зчеплення коліс із рейками
дороги
.
,
– коефіцієнт тертя гальмівних колодок;
– сила натиску
гальмівних колодок на бандаж.
,
,
,
,
,
,
,
– коефіцієнти для певного типу локомотива
й типу колії (ланкова або безстикова).
обмежує максимальну силу тяги локомотива
.
Цей коефіцієнт є різним для різних
типів локомотивів.
позицій
.
Для кожної позиції відомі інтервали
її дії за швидкістю, силою тяги
,
струмом
.
Для силових позицій є відомими теплові
характеристики двигунів: температура
перегріву
(для електровозів,
моторних вагонів електропоїздів,
тепловозів, моторних вагонів
дизель-поїздів), паливні характеристики
(для тепловозів, тепловозів із гідравлічною
передачею, моторних вагонів дизель-поїздів,
моторних вагонів дизель-поїздів із
гідравлічною передачею).
;
;
,
,
моменту
і ККД
від струму
за постійного значення
на клемах двигуна.
;
і
,
,
сили тяги
і ККД двигуна з передачею
від струму якоря
.
рухомих коліс, передаточного числа
і
– ККД передачі або
– втрат у передачі. Швидкісну
характеристику локомотива розраховують
за формулою:
,
,
.
Втрати енергії в передачі можна знайти
на основі даних табл. 1 [5].