ISSN 2307–3489 (Print), ІSSN 2307–6666 (Online)

Наука та прогрес транспорту. Вісник Дніпропетровського
національного університету залізничного транспорту, 2018, № 6 (7)

ЕКОЛОГІЯ НА ТРАНСПОРТІ

Introduction

Acts of terrorism with the use of chemical (biological) agents in the streets of cities are not a groundless threat. One of the variants to emit a hazardous chemical agent into the atmosphere, which is sufficiently hidden from an observer, can be its discharge into the ventilation system of various cafes, which are located in city streets (Fig. 1). Emission of polluted air from the ventilation system of a cafe is usually carried out on the roof. Scientifically, it is the emission from a low source.

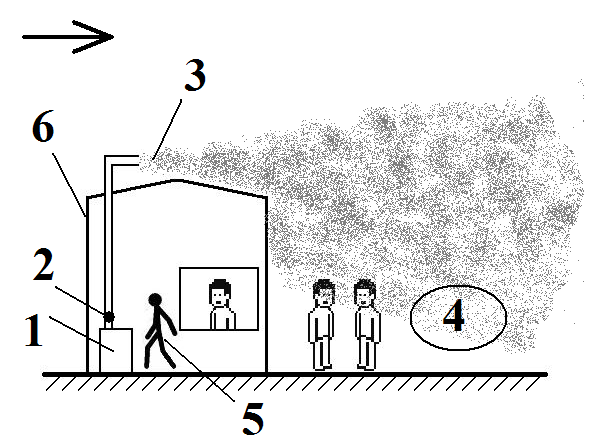
Fig. 1. Scheme of outdoor chemical air contamination
at initiated entry of hazardous substances in
a cafe ventilation system:
1 – process equipment; 2 – place of hazardous
substance entry into the ventilation system;
3 – polluted air discharging device on the cafe roof;
4 – outdoor chemical contamination zone;
5 – initiator of hazardous substance discharge into
the ventilation system; 6 – cafe building

With such an emission of a chemical agent through a ventilation system, a sufficiently large area of chemical contamination can form behind the building. For example, Fig. 2 shows a photo of the contamination zone near the mini-cafe. Emission is combustion process products from the kitchen. It is clearly seen that the pollution zone covers not only the sidewalk, but also part of the roadway. If people get into this chemical contamination zone, the risk of their toxication is extremely high. We emphasize that people will definitely fall into the contamination zone, because cafes are public places. In addition, such a scenario of a terrorist attack ensures unexpectedness and secrecy. In this regard, the question arises about the development of engineering methods to protect people from damage by reducing the concentration of a hazardous substance in the street during a possible terrorist attack.

The theoretical solution to this problem is quite complicated. When emitting a chemical agent from a low source, it is necessary, first, to take into account the influence of the building on the formation of the chemical contamination zone. Secondly, it is important that the mathematical model would also make it possible to calculate the effectiveness of the use of specific engineering solutions to reduce the intensity of chemical contamination of the air environment near the facility. To estimate the level of air pollution in case of a possible terrorist act, for example, Gaussian

Fig. 2. Air contamination zone near the cafe:
1 – polluted air discharging device on the cafe roof;
2 – visible boundary of the contamination zone
(Heroev Avenue, Dnipro)

models can be used as a zero approximation. But these models do not allow to take into account the influence of the building and various engineering elements on the formation of chemical contamination zones, that is, they cannot be used to assess the effectiveness of various anti-terror methods. The normative methods used in Ukraine for solving problems of assessing the size of chemical contamination zones (for example, the OND-86 technique), for this reason, also cannot be applied. The only theoretical method for solving problems of this class is CFD modeling. Within this scientific direction, specialized software packages «ANSYS Fluent», «FAST», etc. have been created. These packages are a powerful tool for solving a wide class of problems. It should be noted that the cost of licensed packages for research is very high, so access to such packages is limited. It is also known that the use of these packages requires the use of powerful computers and large consumption of computer time when solving a practical problem – several days to calculate one variant of the problem. This is
a definite obstacle, as the organizations of a special focus conduct numerous serial calculations.

Purpose

This work aims to develop a method of local outdoor reduction of the concentration of a chemically hazardous substance, which entered the atmosphere through a cafe roof vent. It also involves the creation of a numerical model for evaluating the effectiveness of engineering methods for air contamination protection during a terrorist attack with a highly toxic chemical agent.

Methodology

The process of dispersing a highly toxic chemical agent outdoor can be described on the basis of the following equation (profile task) [2–5, 7, 8]:

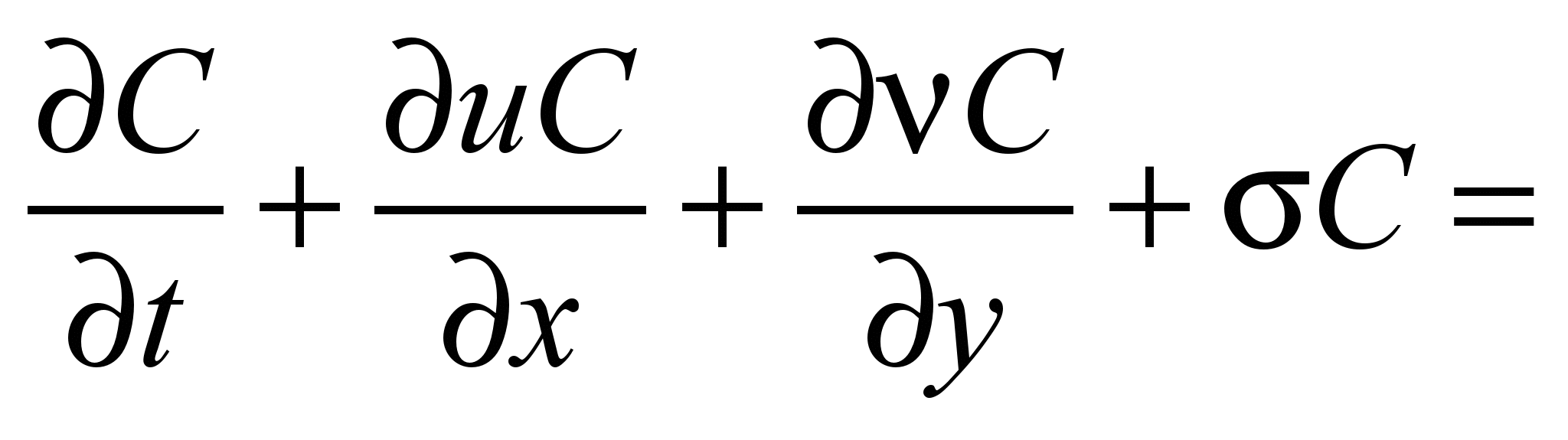
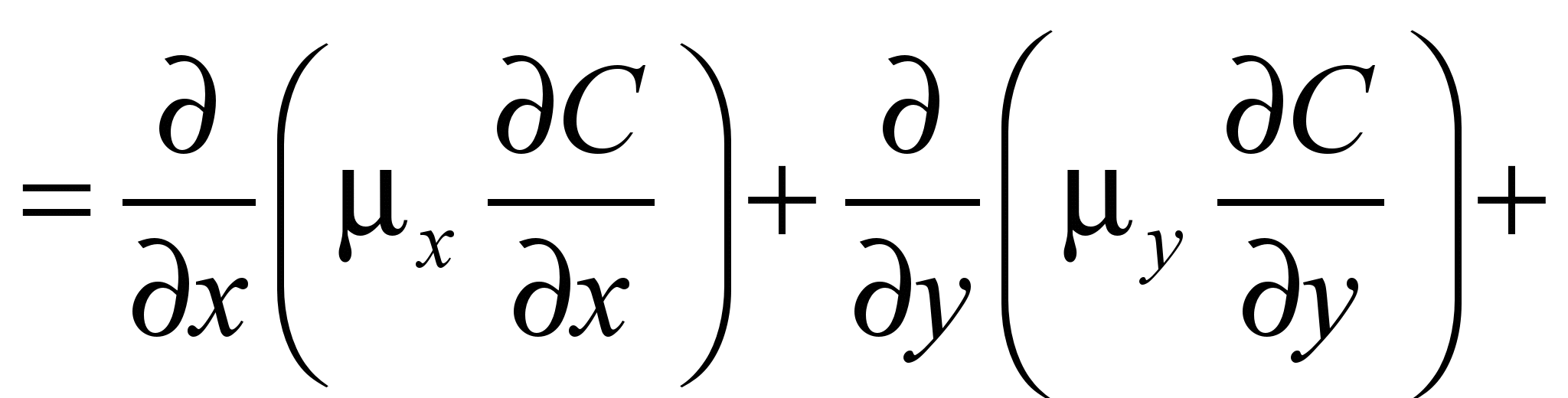
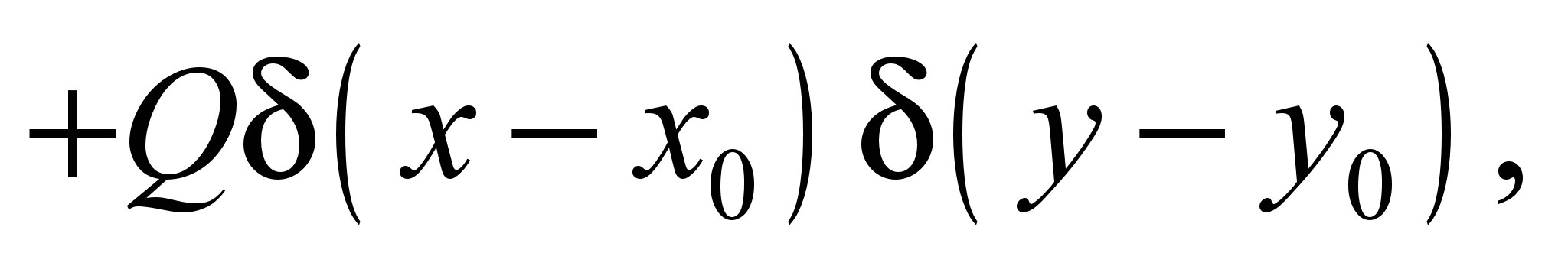(1)

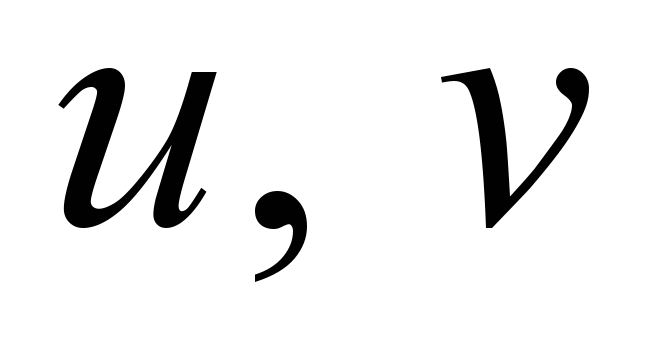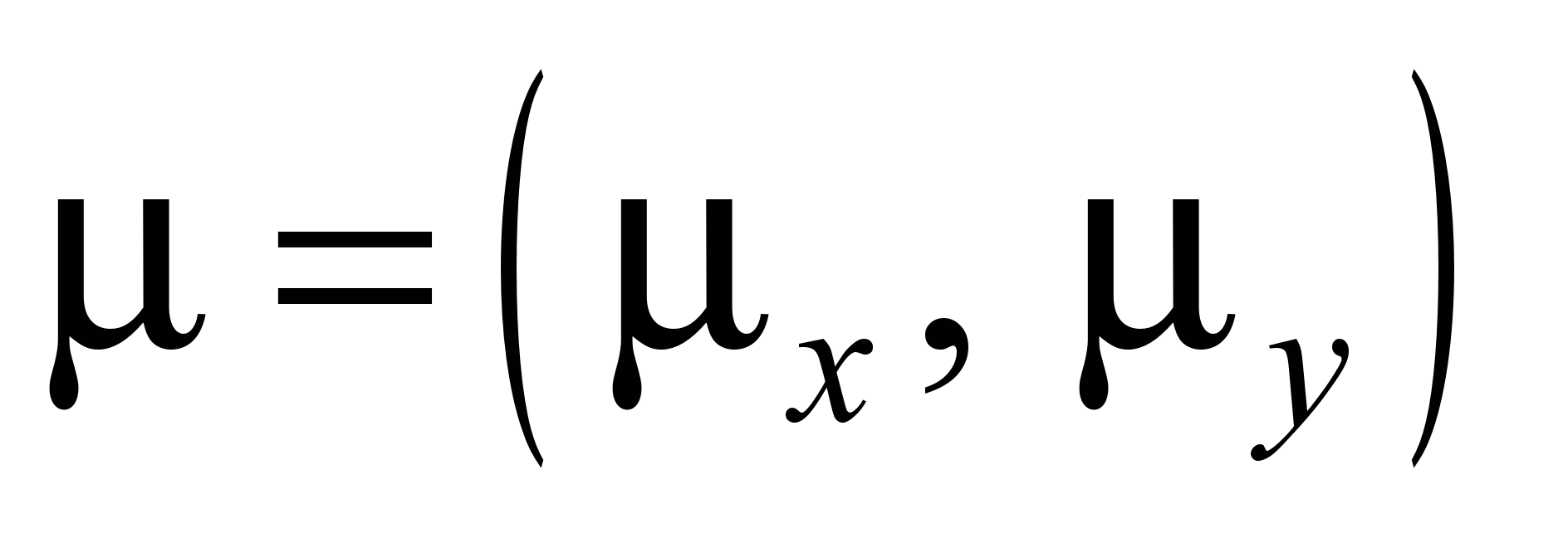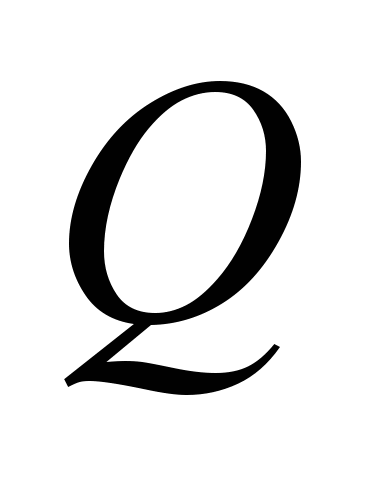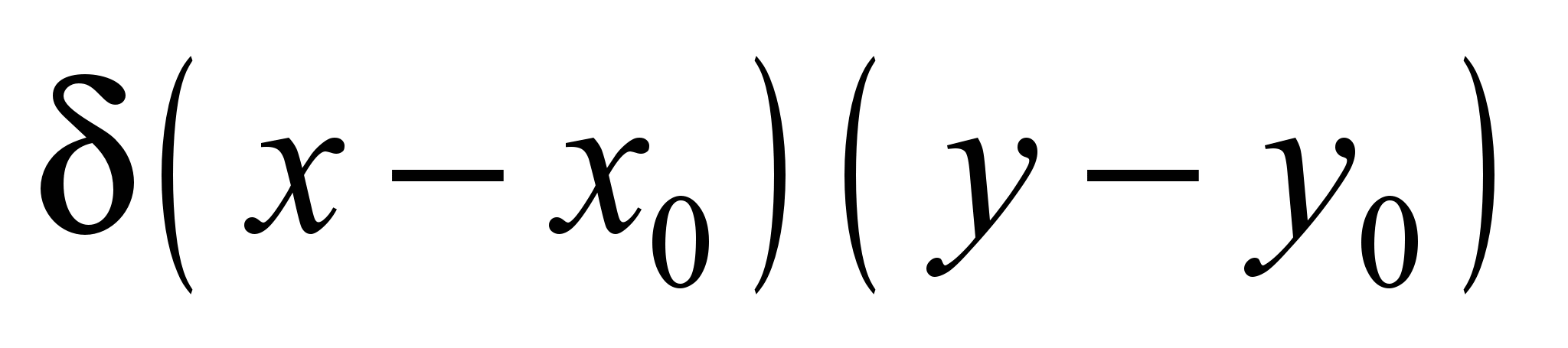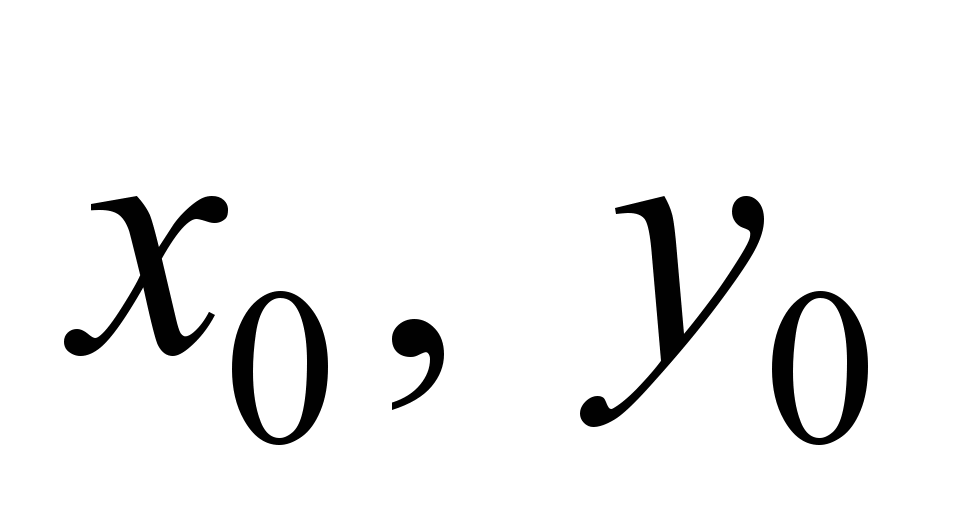where – average concentration of chemical (biological) agent in outdoor air; – coefficient taking into account the agent decomposition in the atmosphere; – components of the air flow velocity vector; – coefficients of atmospheric turbulent diffusion; – agent emission intensity during the terrorist attack; – Dirac delta function; –agent emission source coordinates during the terrorist attack; t – time.

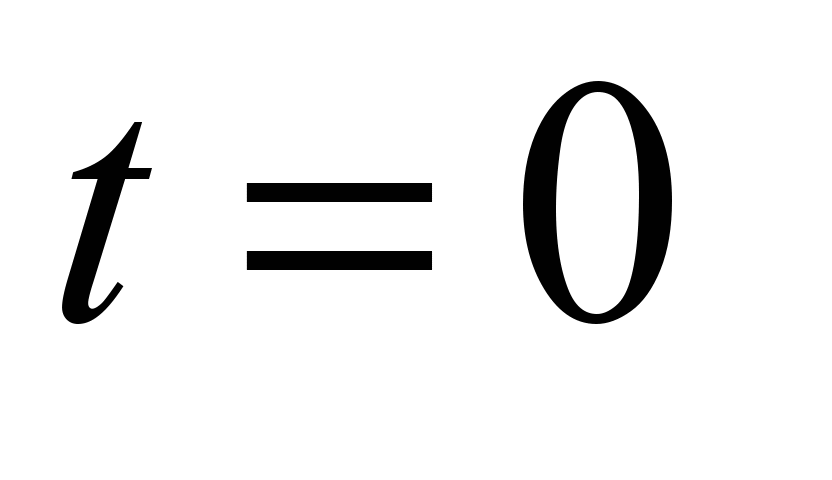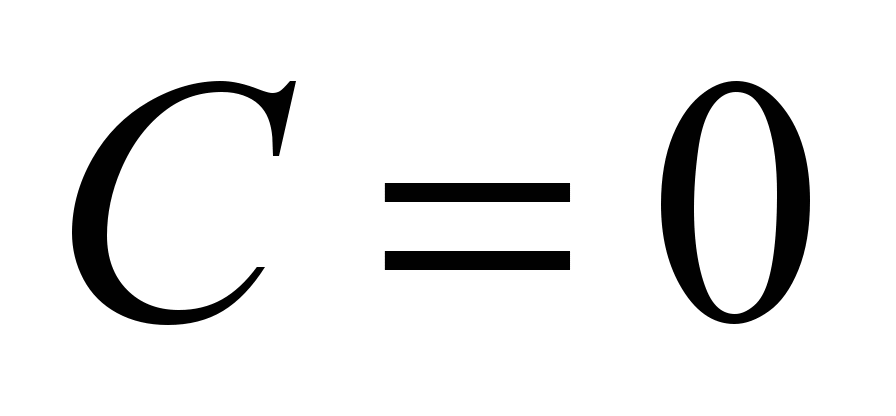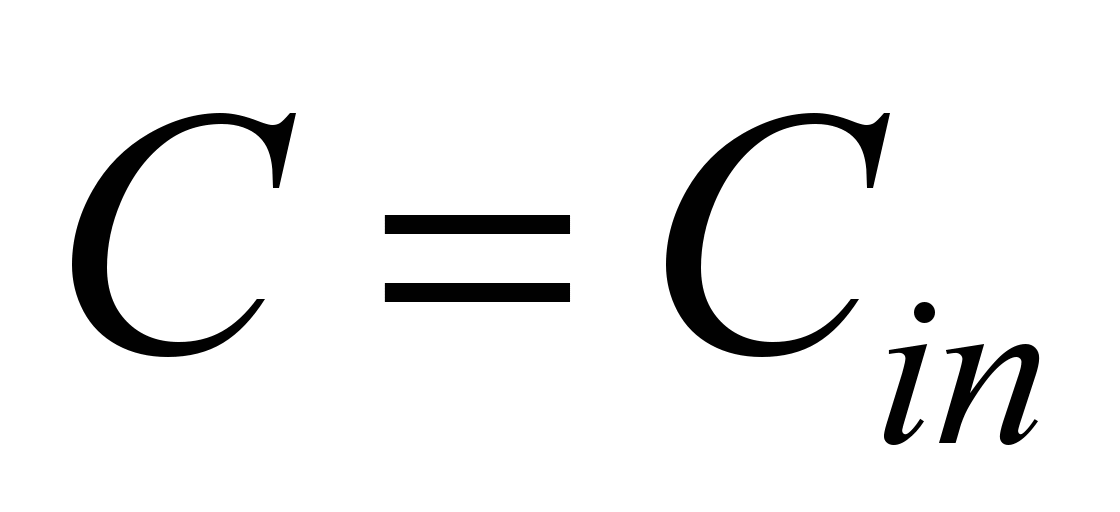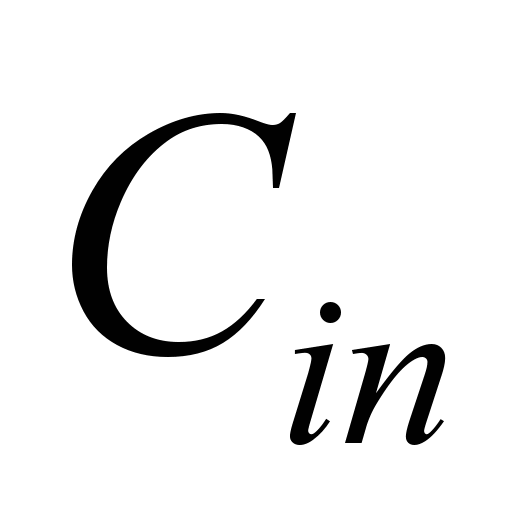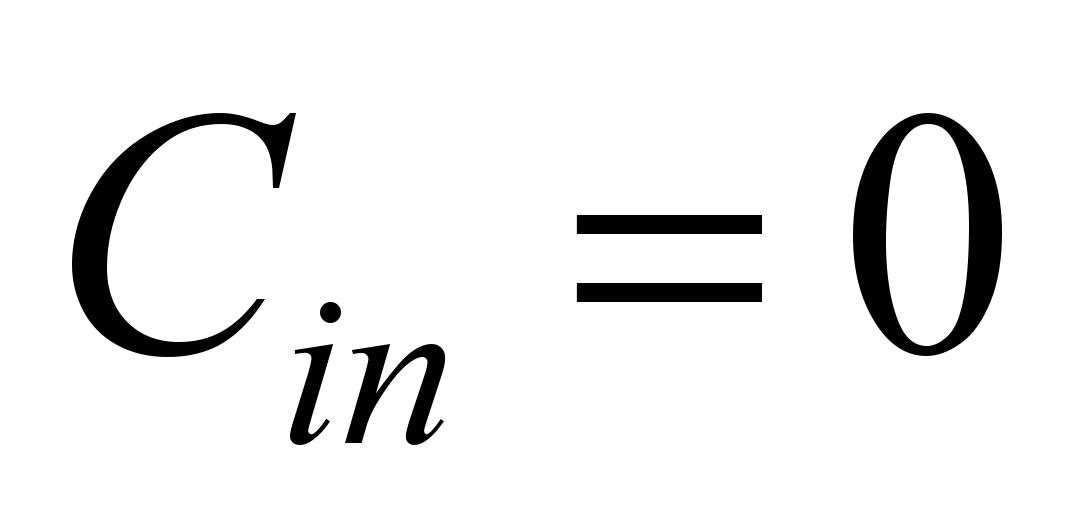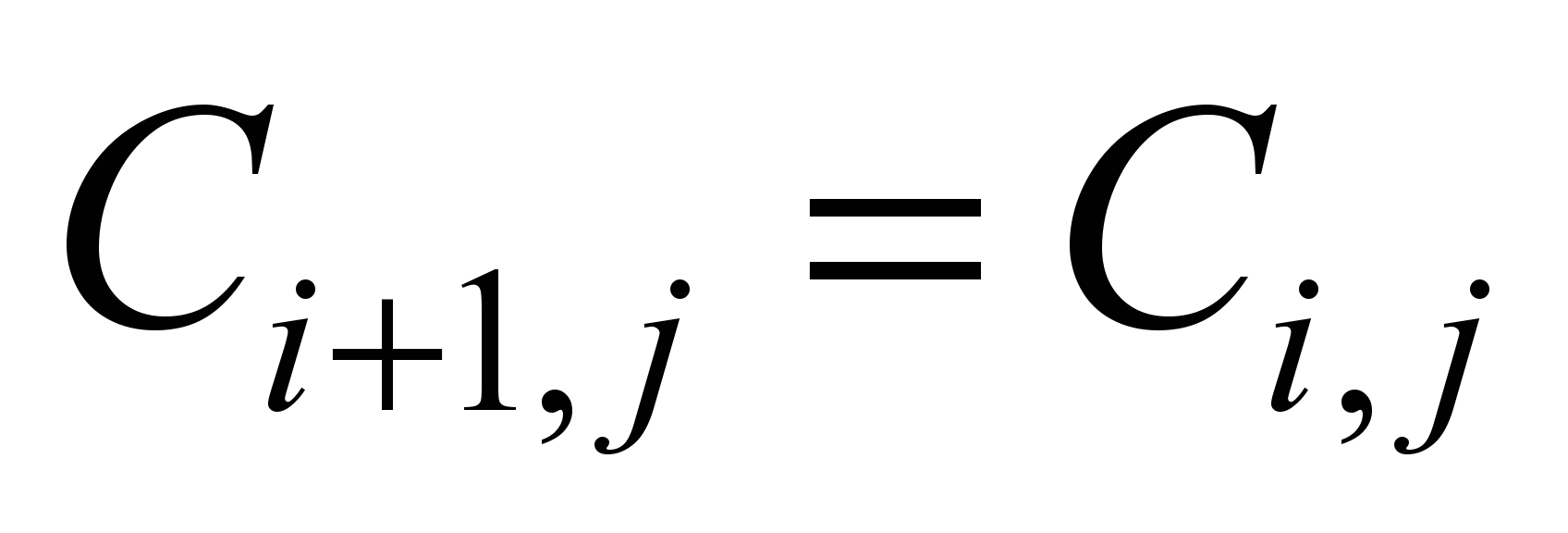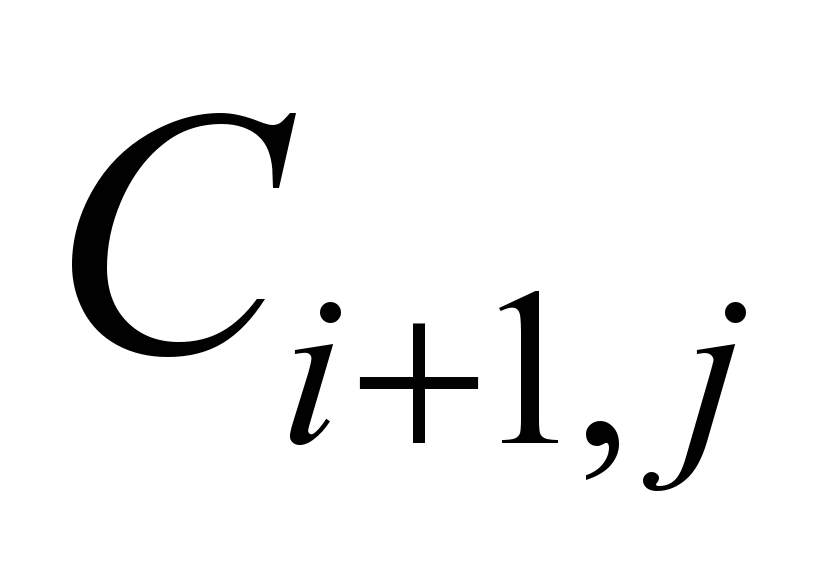The boundary conditions for equation (2) are written as [3]: at , . At the boundaries where the air flow enters the calculation area, , here is the known value. We assume that . In the area where the air flow exits the computational domain, in the numerical model we set a «soft» boundary condition of the form: , here is the pollutant concentration in the boundary (last) cell.

Aerodynamics model. To apply equation (1) in the case of dispersion of a chemical (biological) agent in the presence of a building, it is necessary to know the uneven velocity field of the wind flow. To determine the wind flow velocity field u = f(x, y), v = f(x, y), we will use the ideal fluid irrotational flow model [5]:

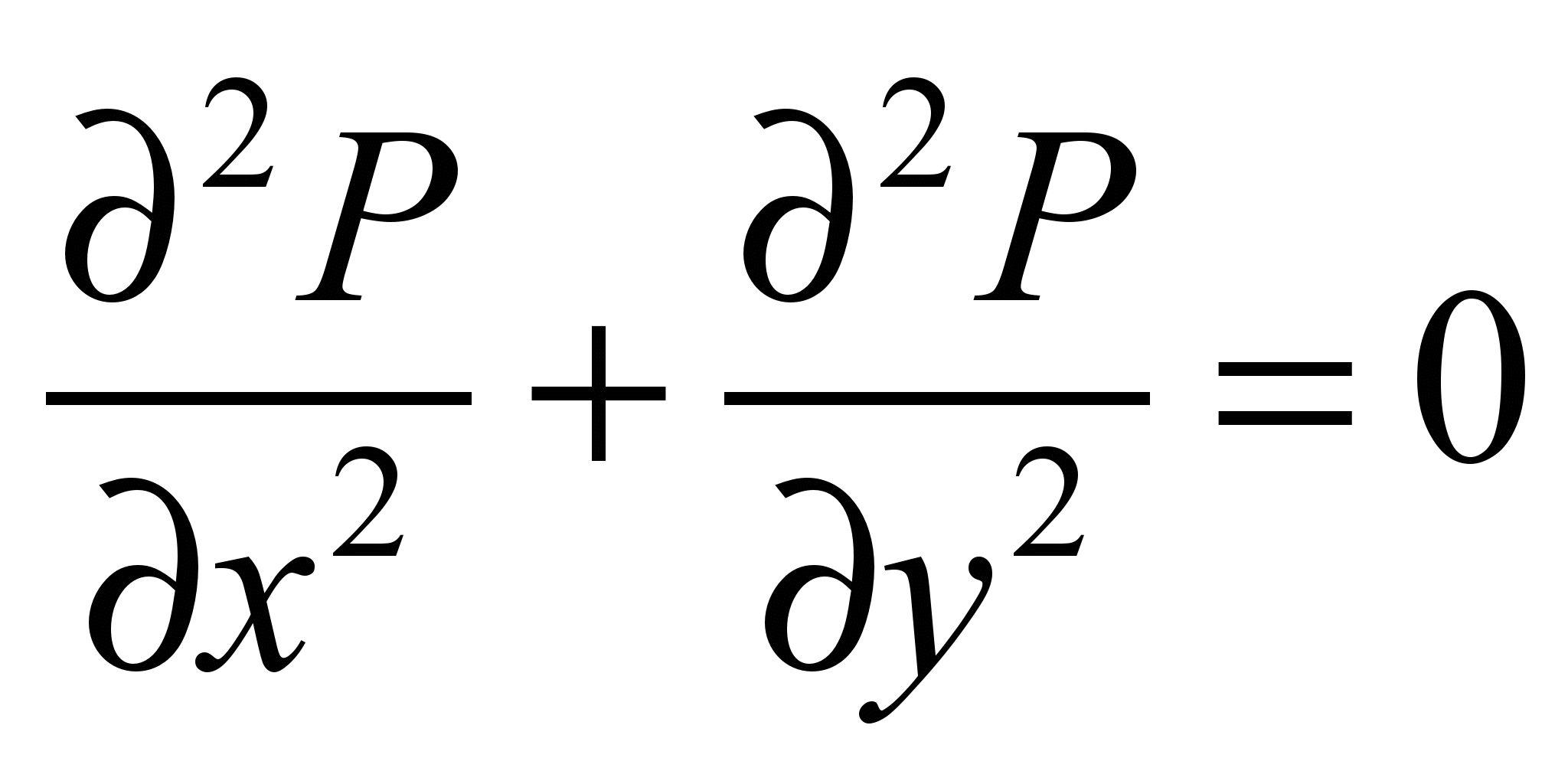, (2)

where Р – velocity potential.

The components of the air flow velocity vector are determined by the dependence of the form:

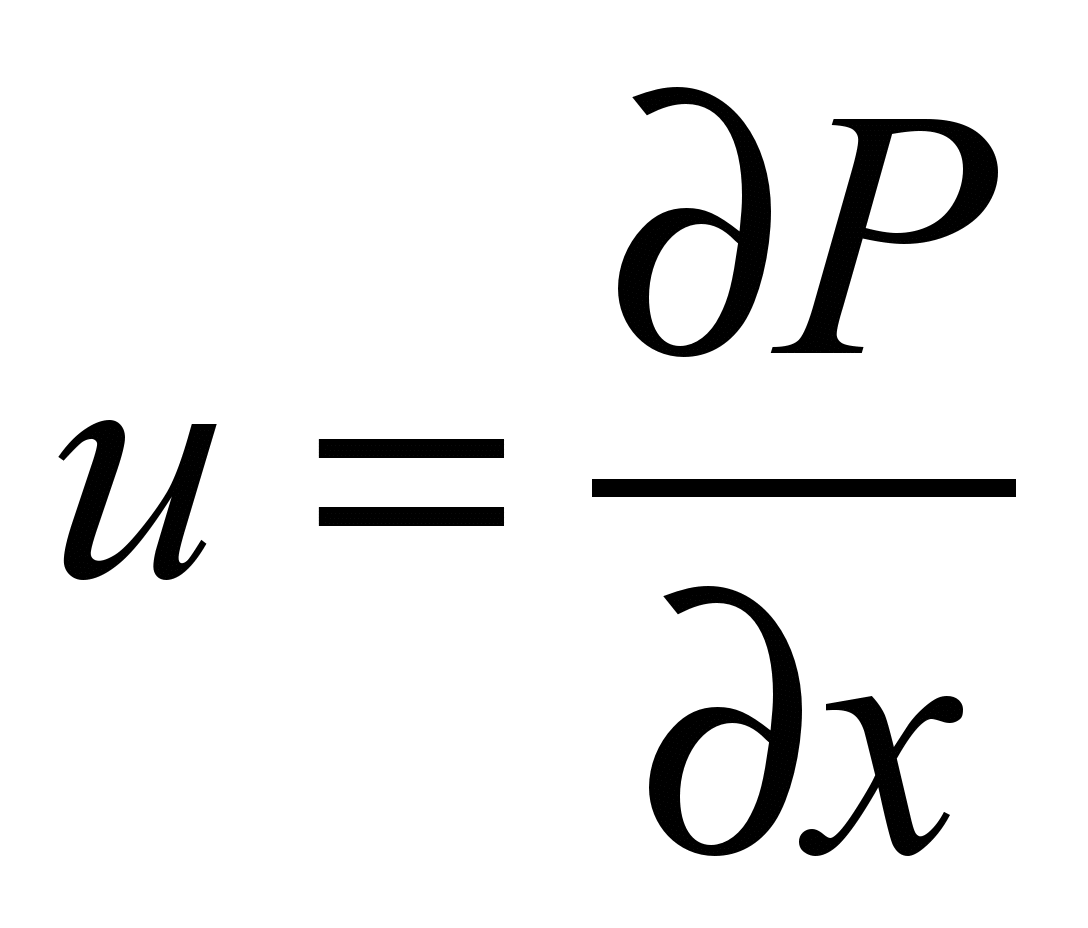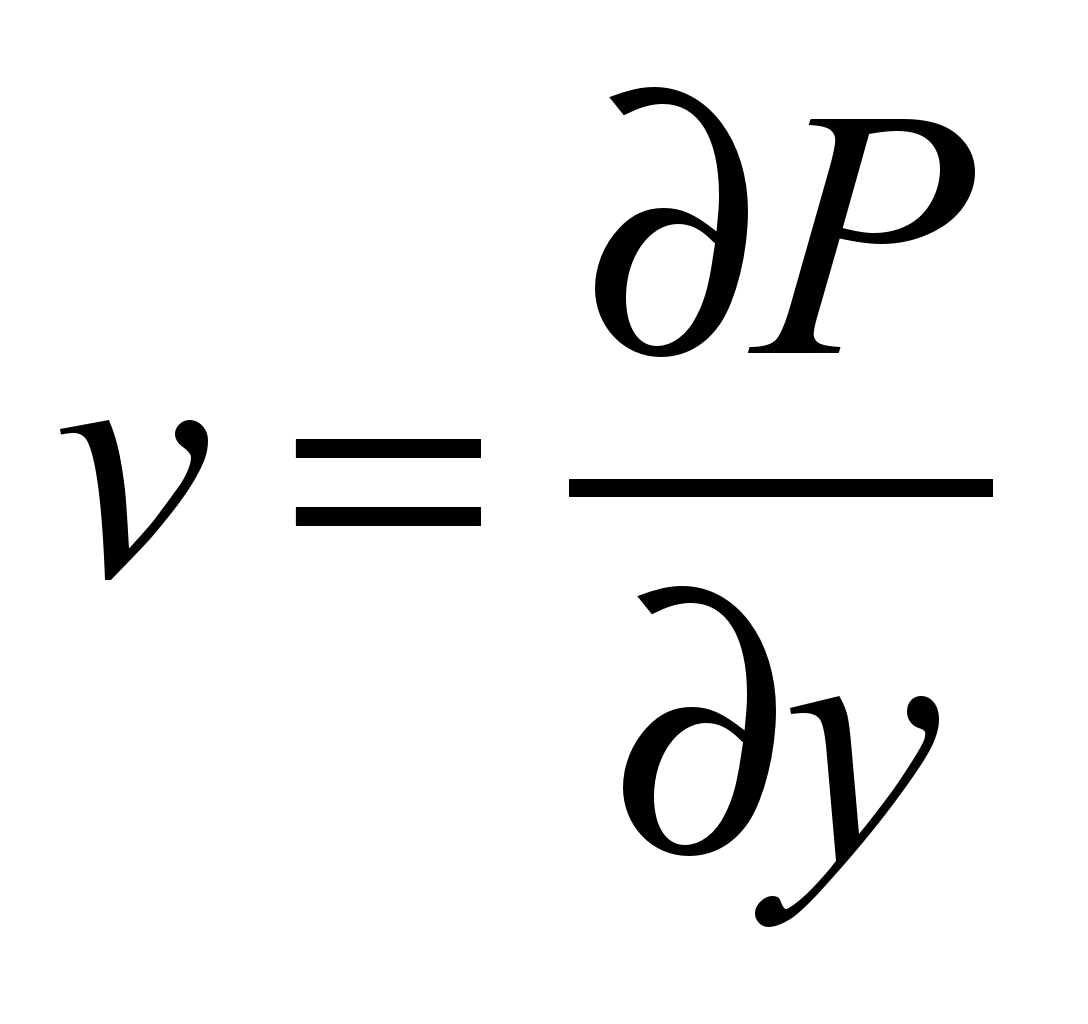, . (3)

For equation (2) there are such boundary conditions:

– on solid boundaries we set the condition of the form:

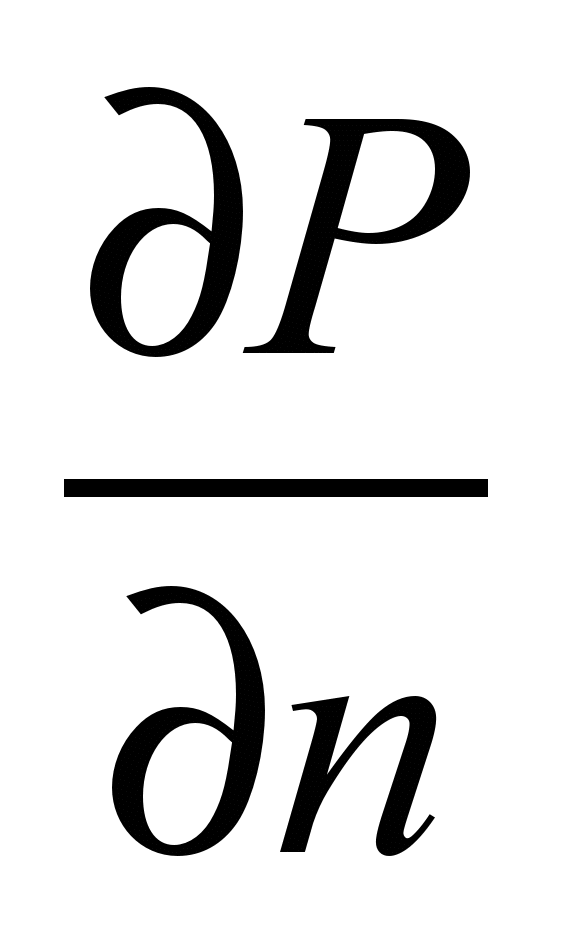= 0,

where n – unit outer normal vector to the boundary;

– on the boundary of the airflow exit from the computational domain, we set the boundary condition P = const;

– on the boundaries where the inflow of air occurs, we set the boundary condition of the form: 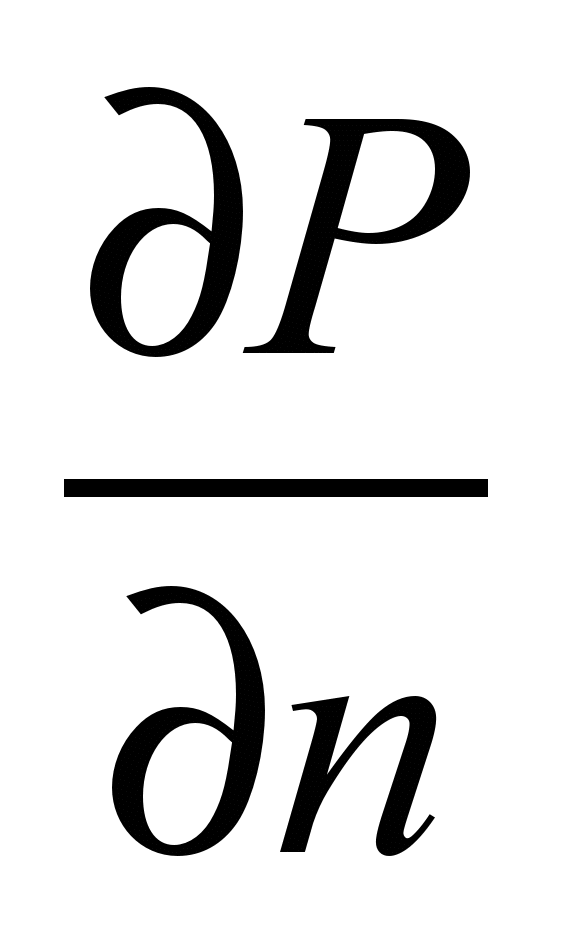 = V, where V – the known wind flow velocity.

Numerical solution to the task. For the numerical integration of the modeling equations we will use finite-difference solution methods.

We will carry out the approximation of derivatives, following [2, 5]. Approximation of the time derivative is carried out as follows:

.

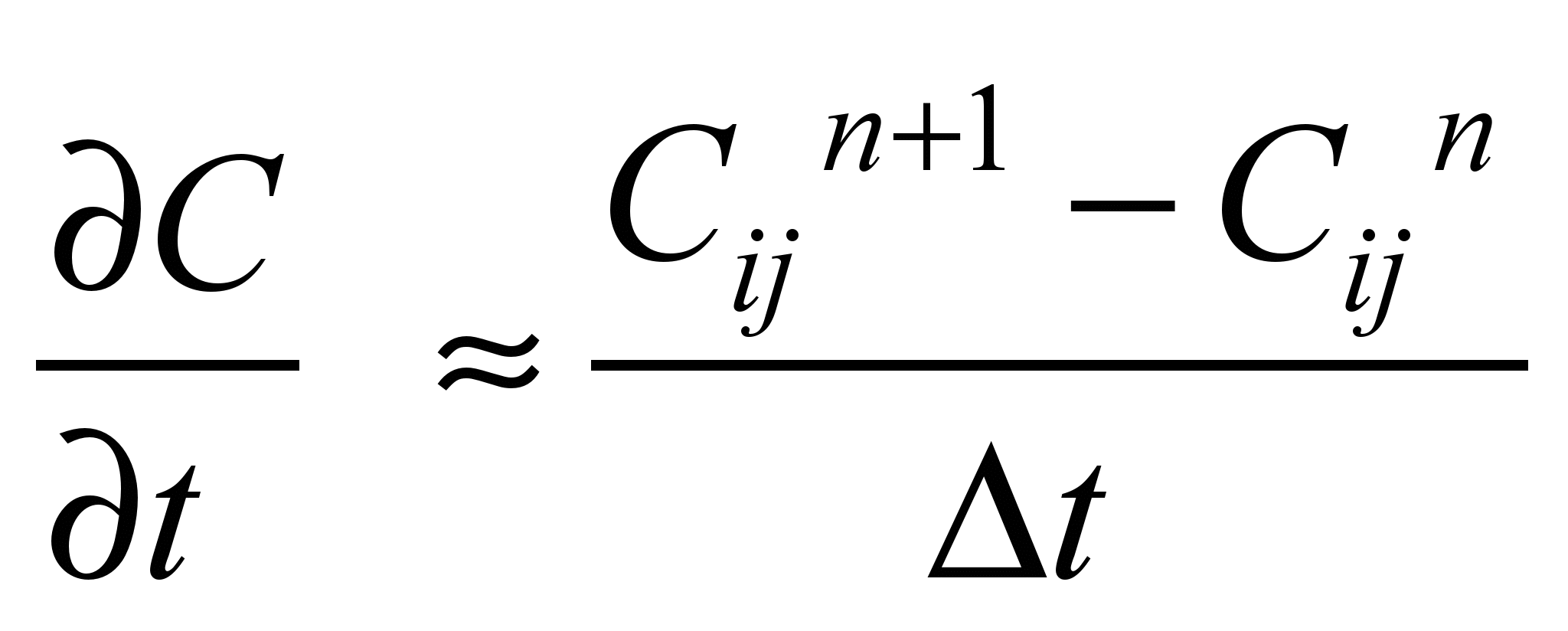The first derivatives are approximated by co-relations [5]:

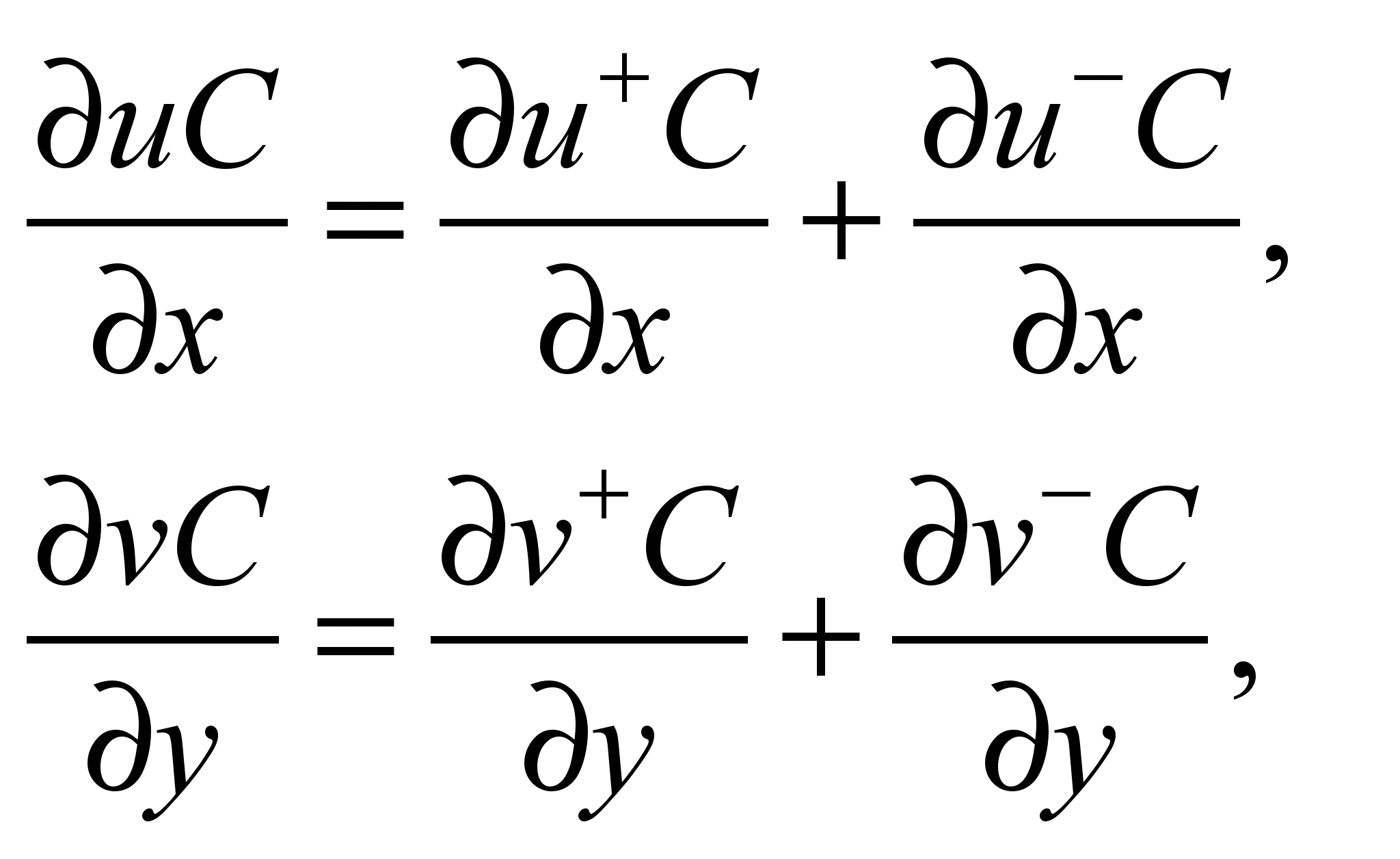
where 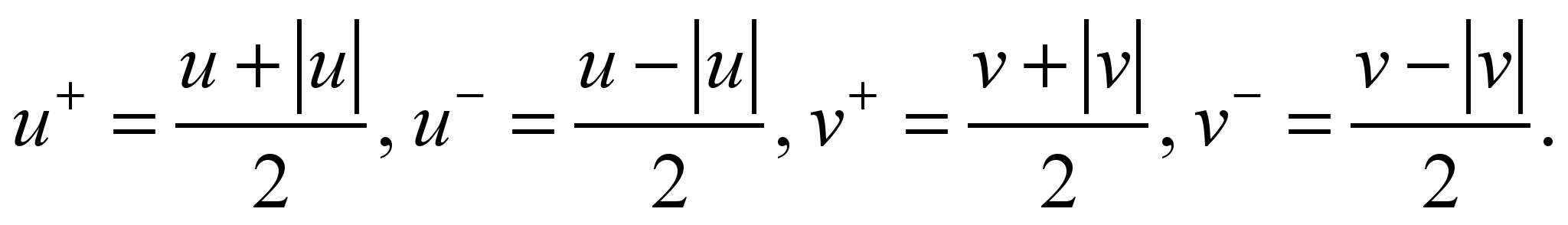For approximation of the first derivatives, we use the formulas [2, 5]:

;

;

;

.

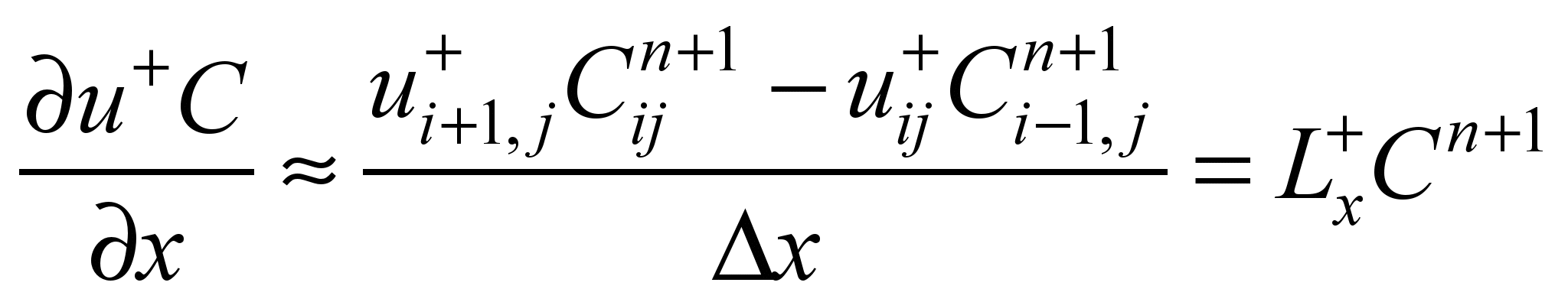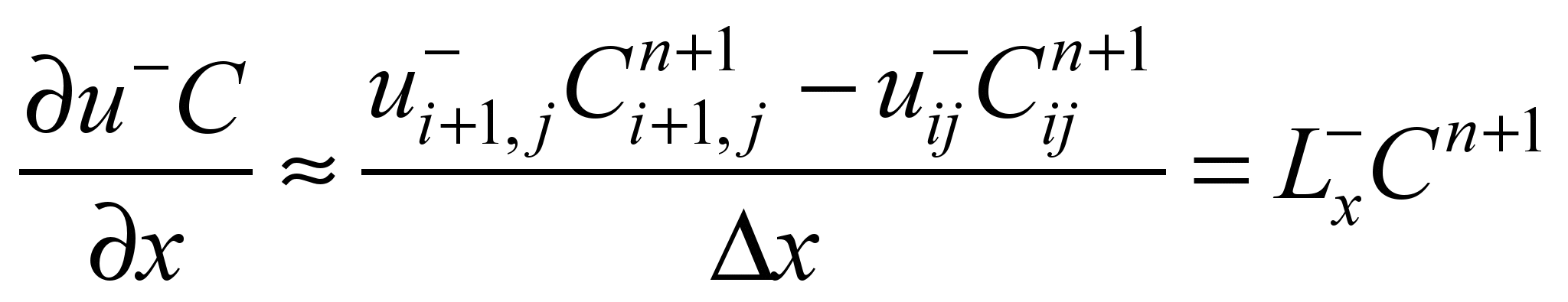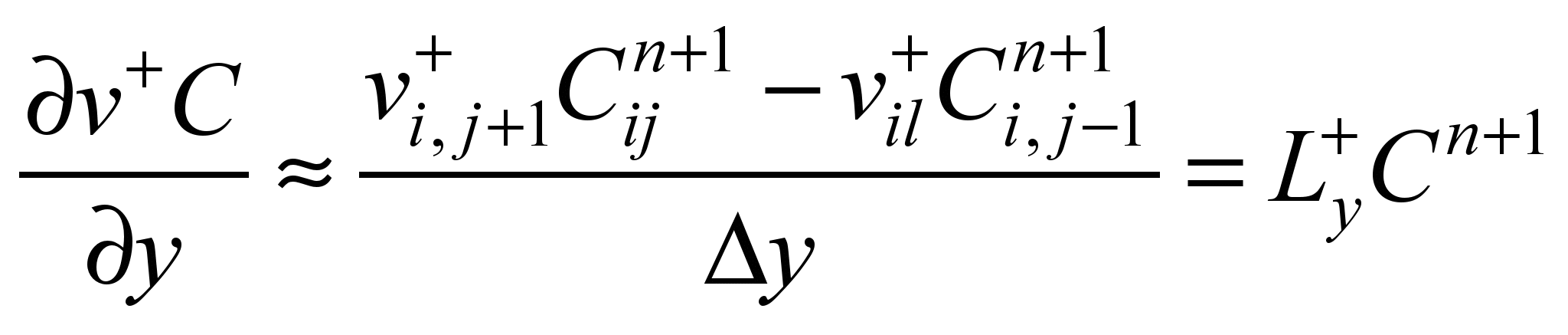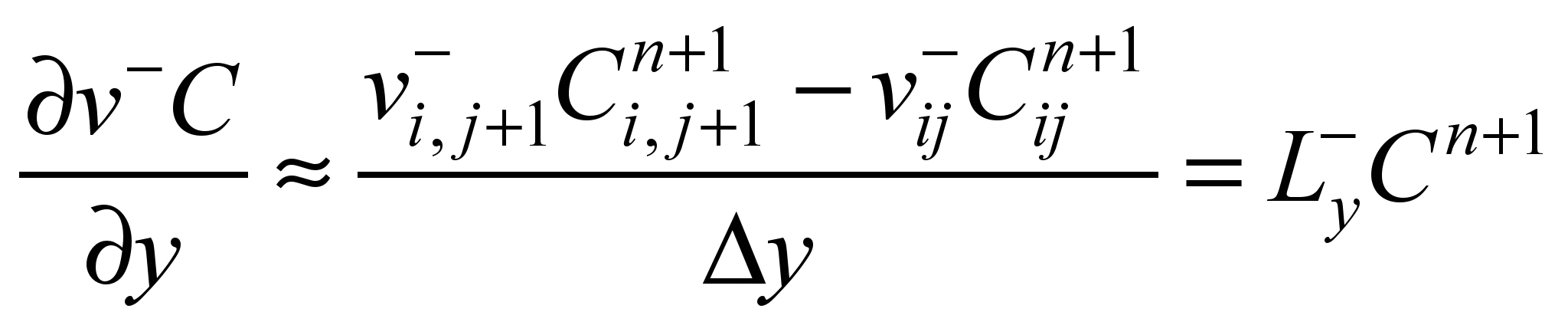For approximation of the second derivatives, we use the dependencies [5]:

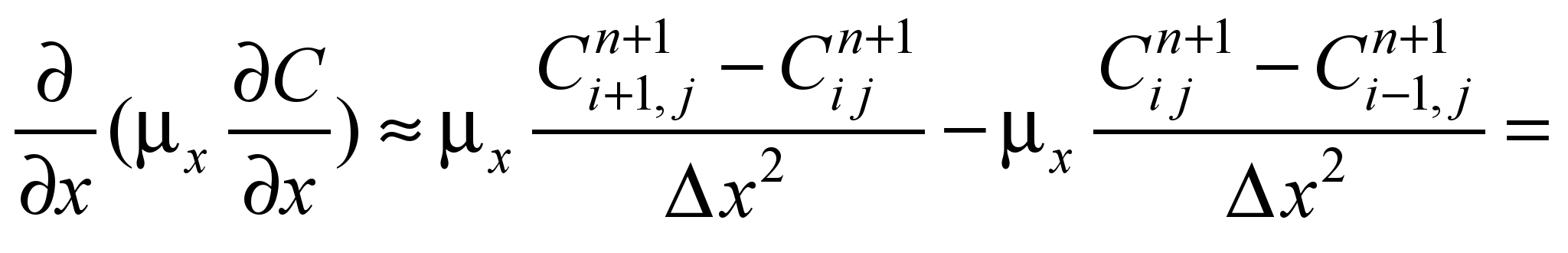
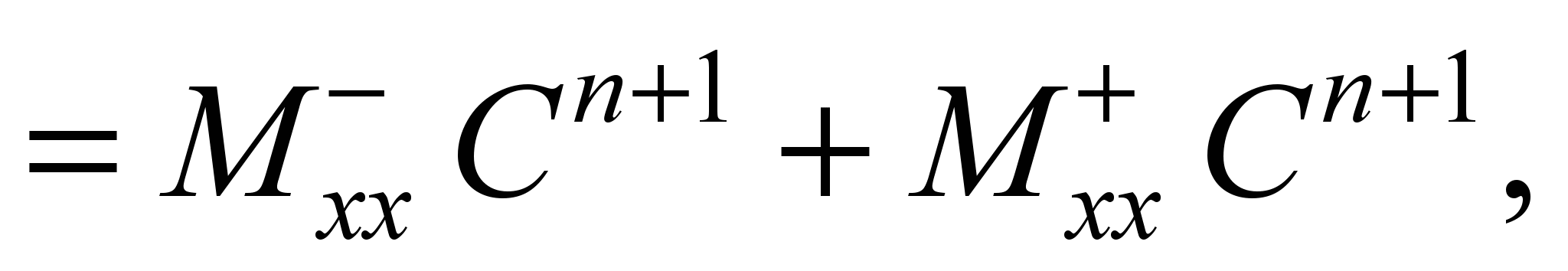
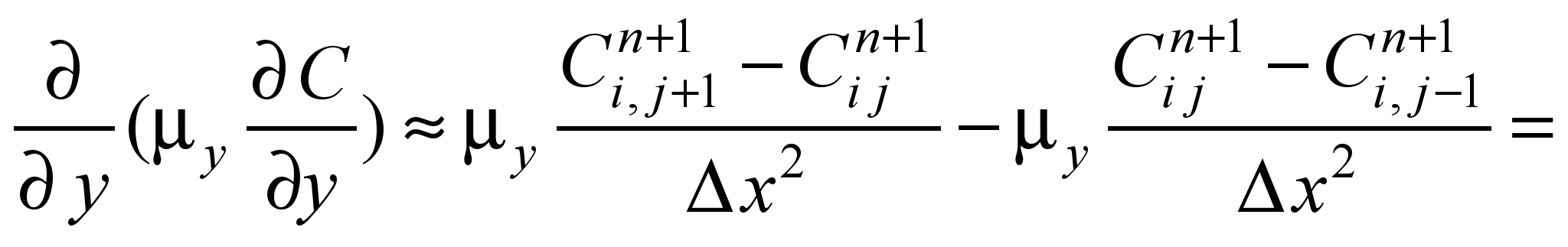
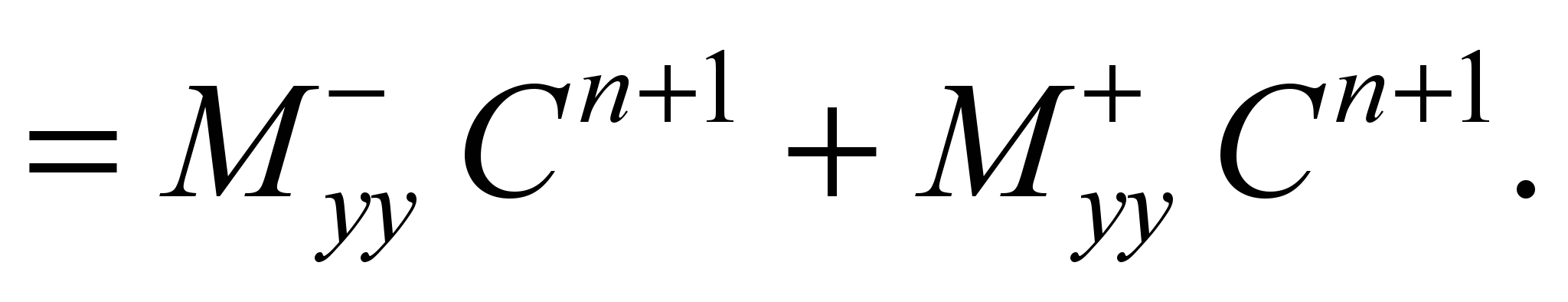
Taking into account the above designations of difference operators, we write the difference analogue of equation (1):

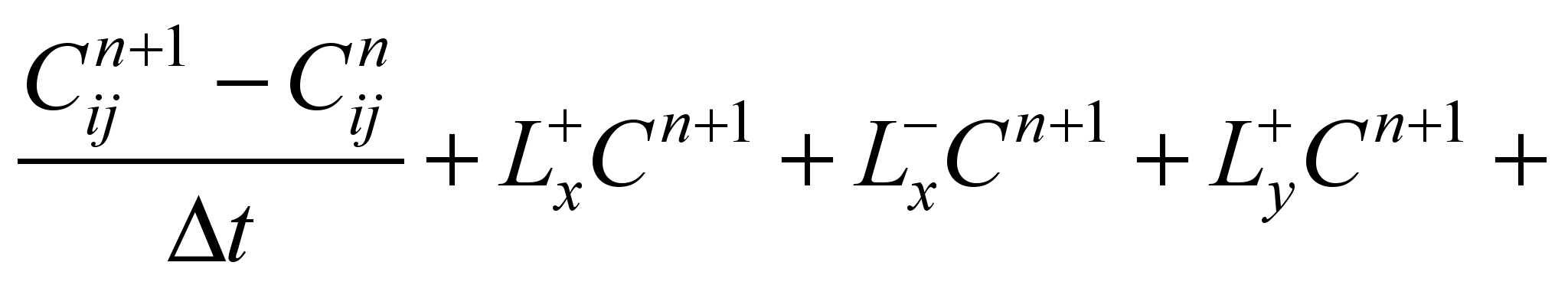
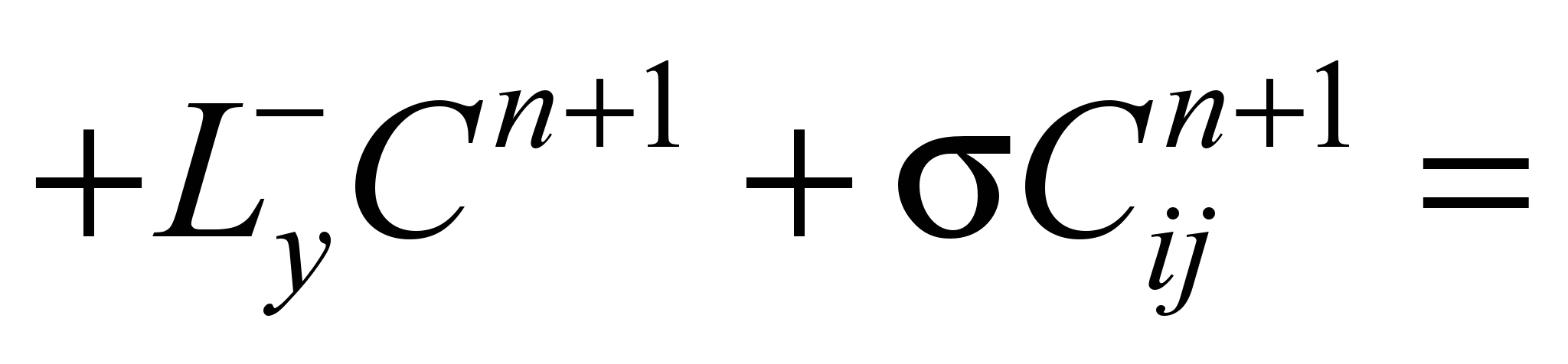
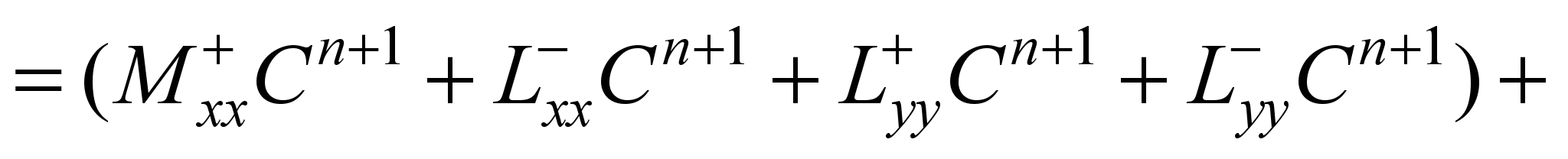
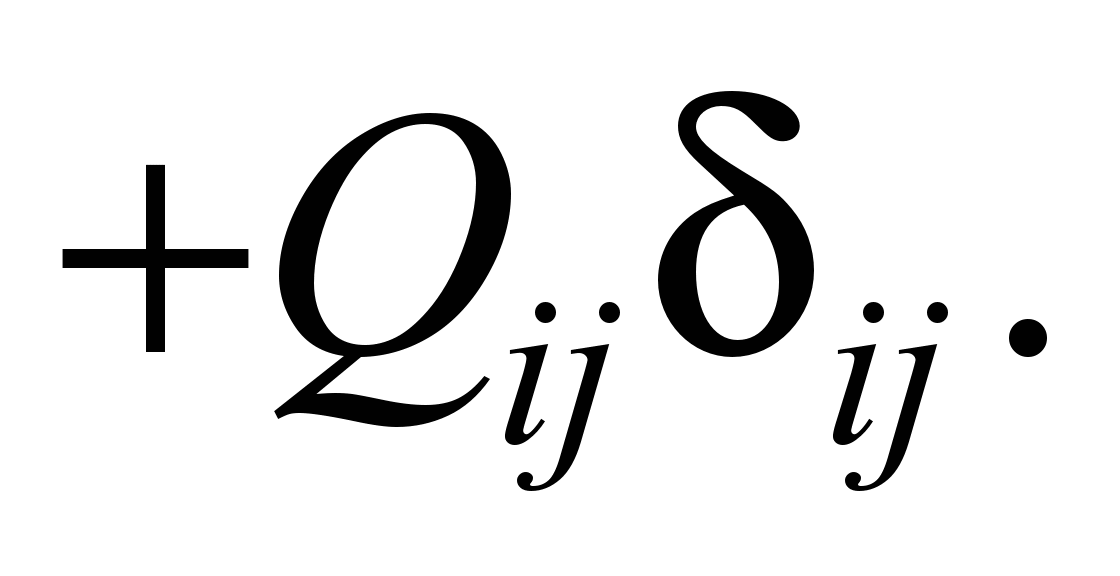(4)

We perform the splitting of the difference equation (4). The splitting equations at each step are written as follows:

• in the first step ():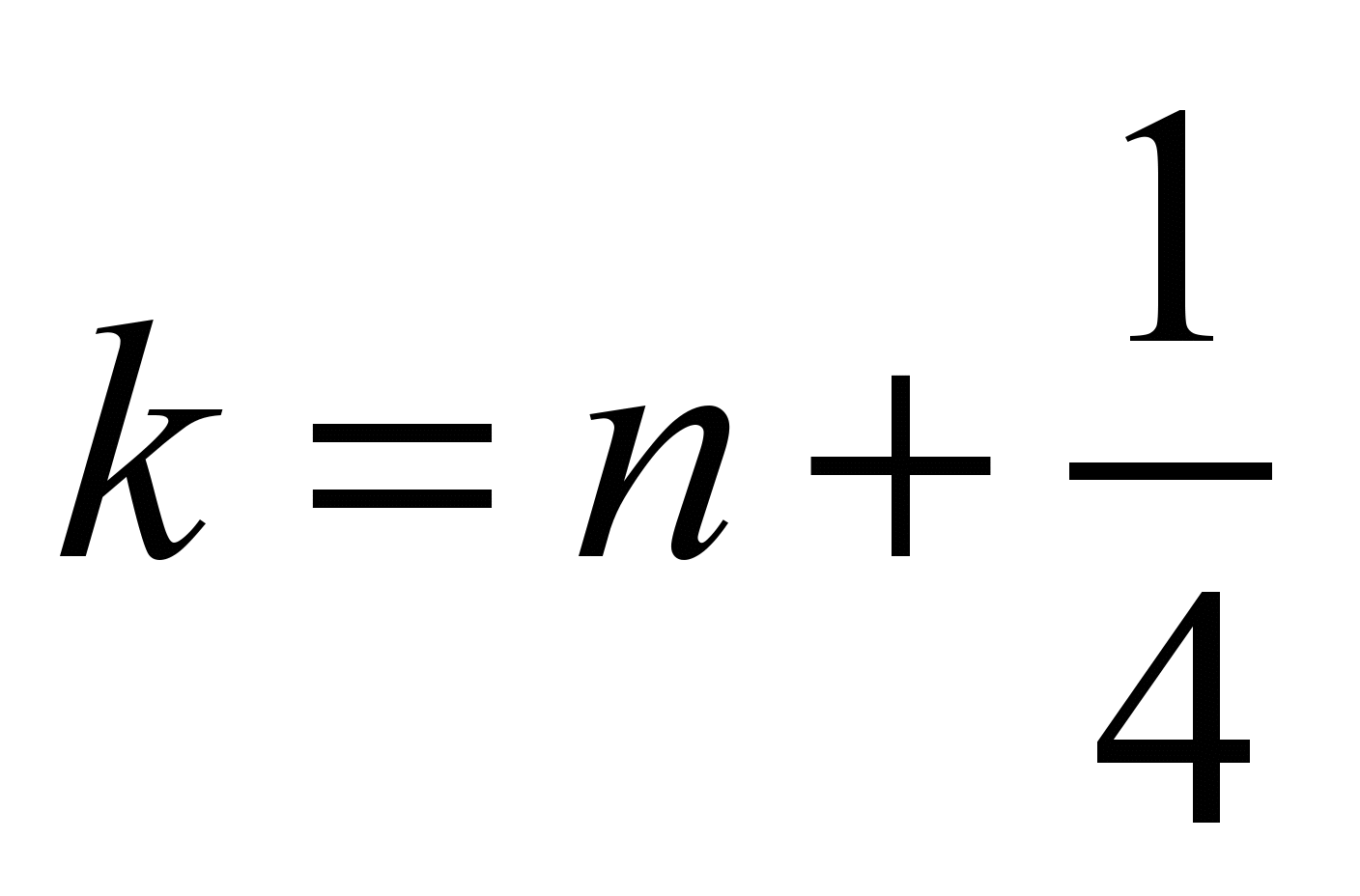

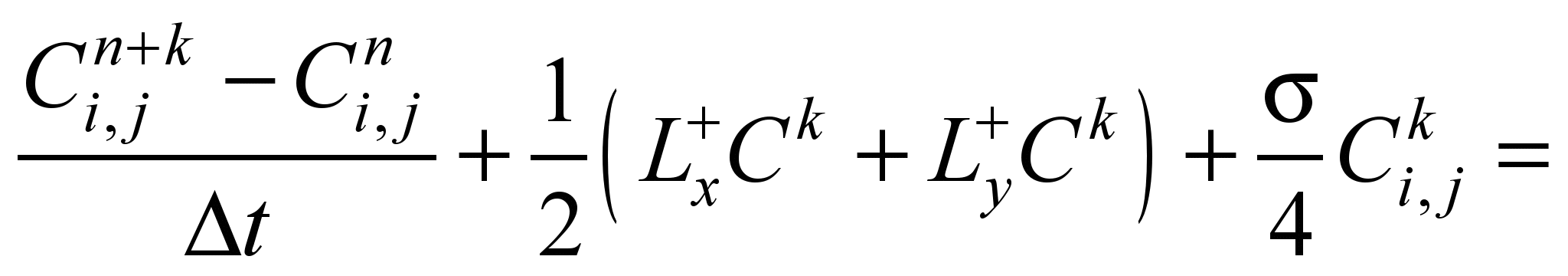
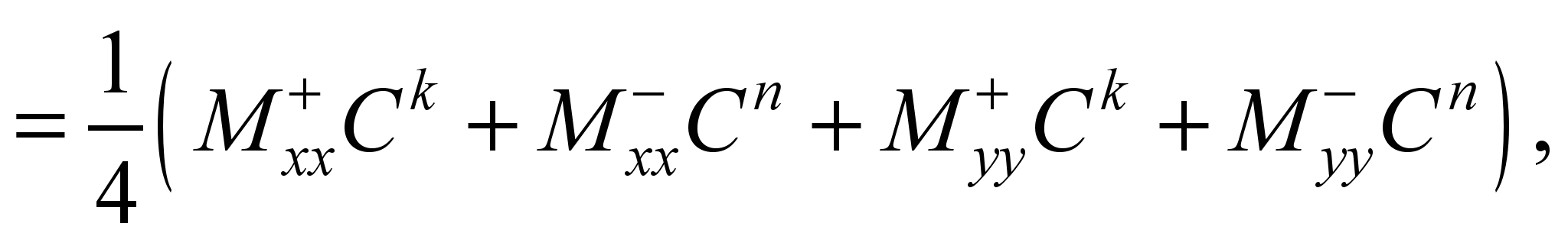(5)

– in the second step ():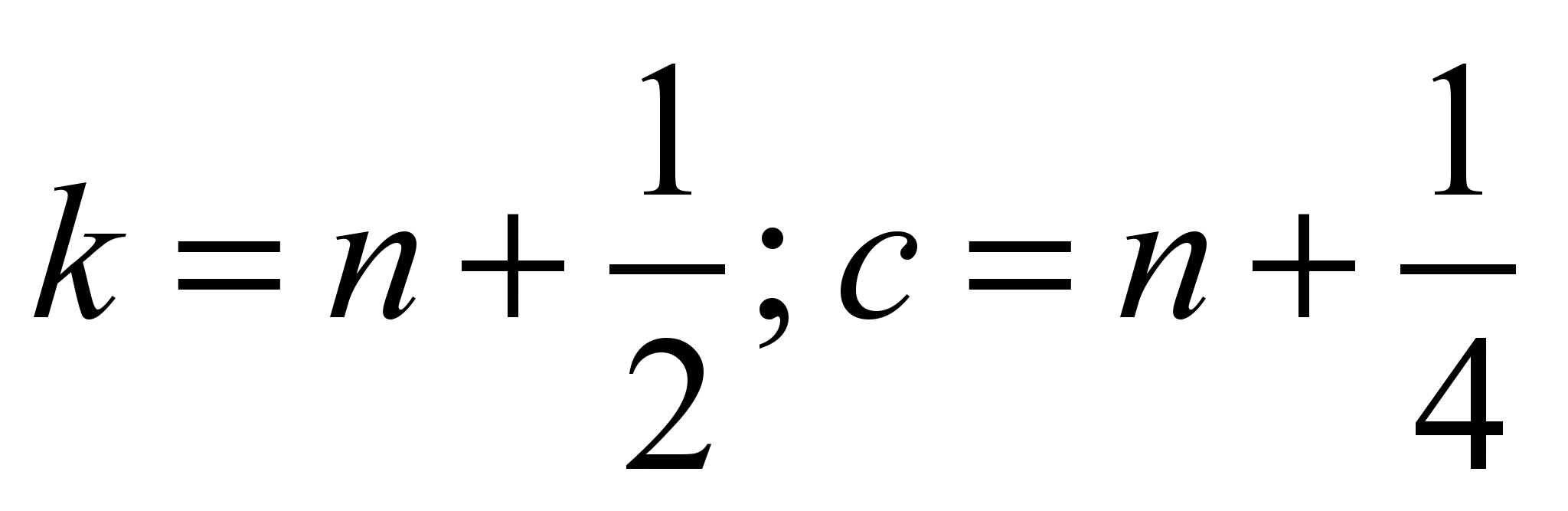

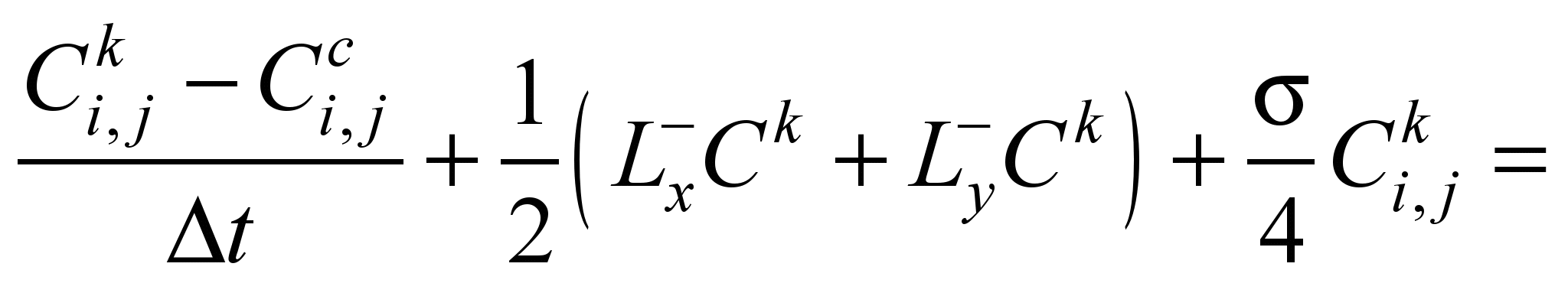
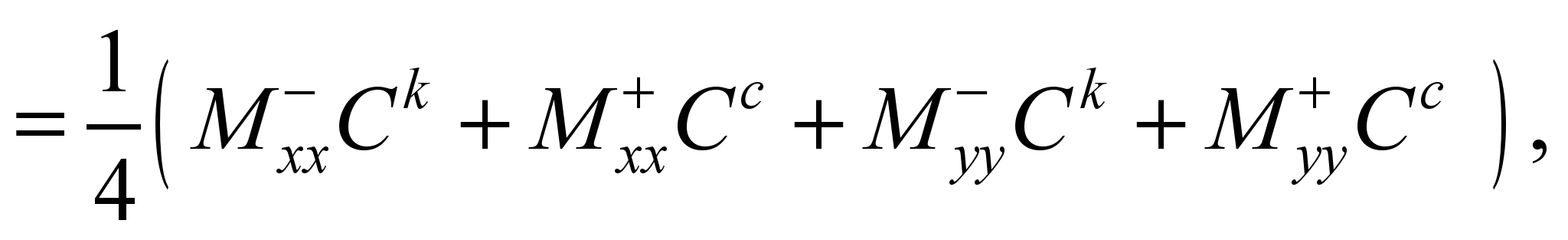(6)

– in the third step (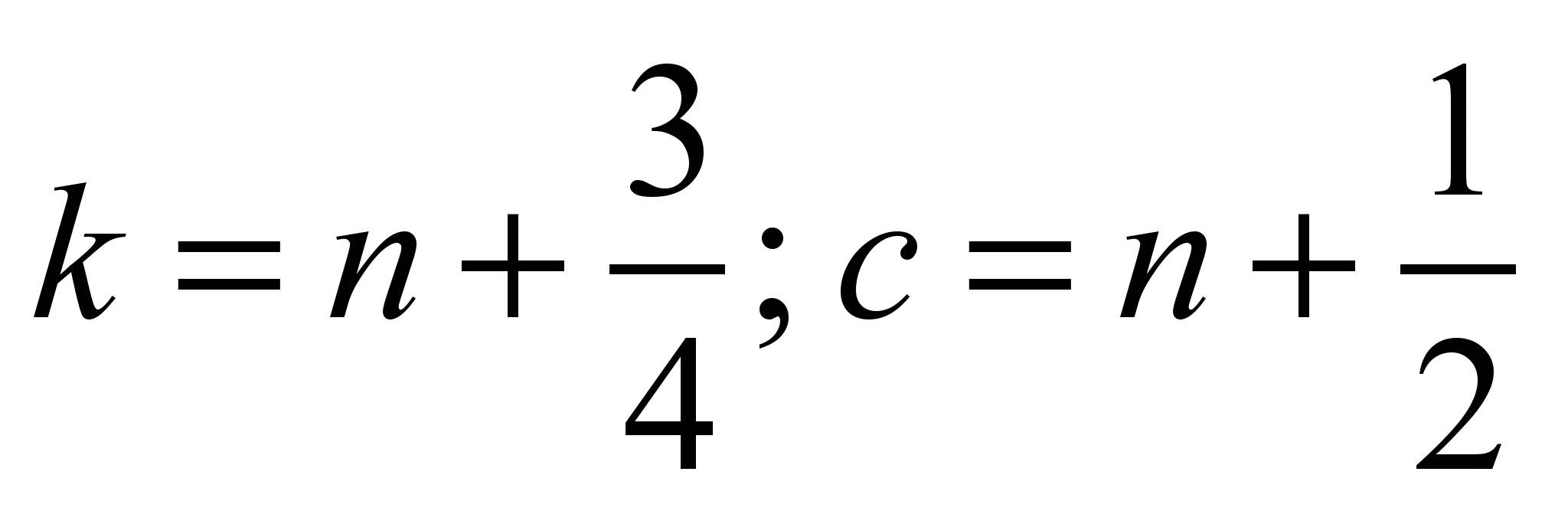) we apply the dependence (6);

– in the fourth step (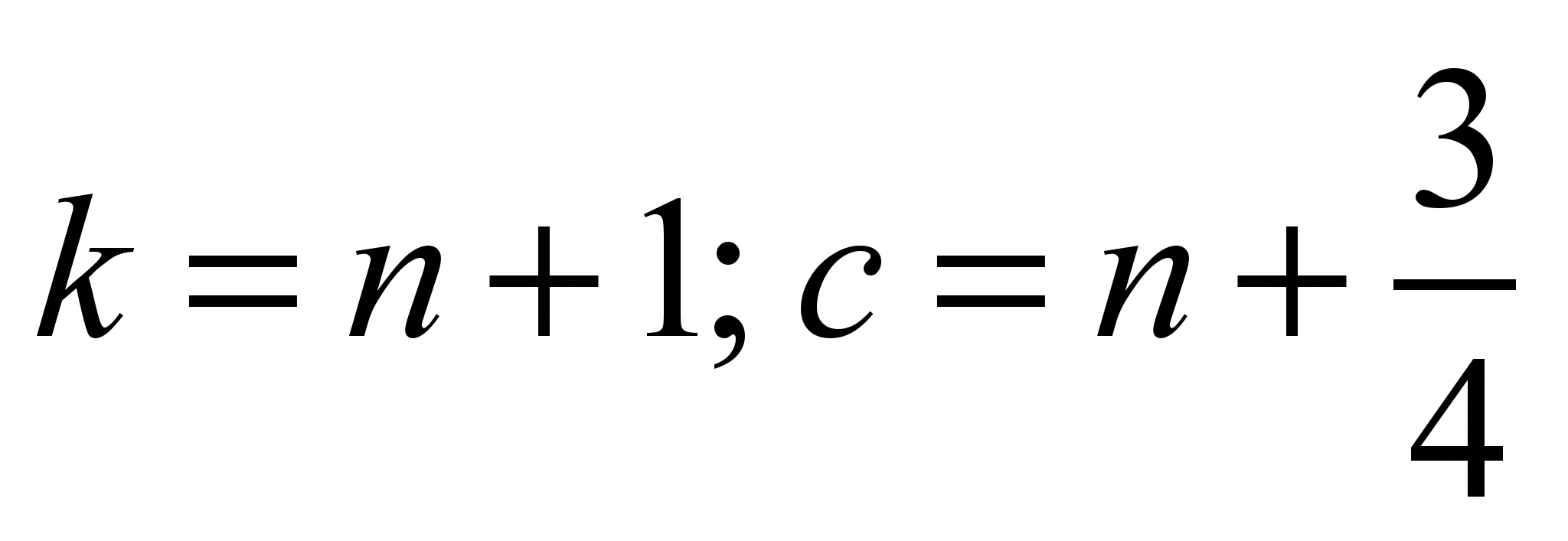) we use the dependence (5).

The desired value of the function C at each fractional step (5), (6) is determined by the point-to-point computation formula.

In the last step, we solve the equation:

.

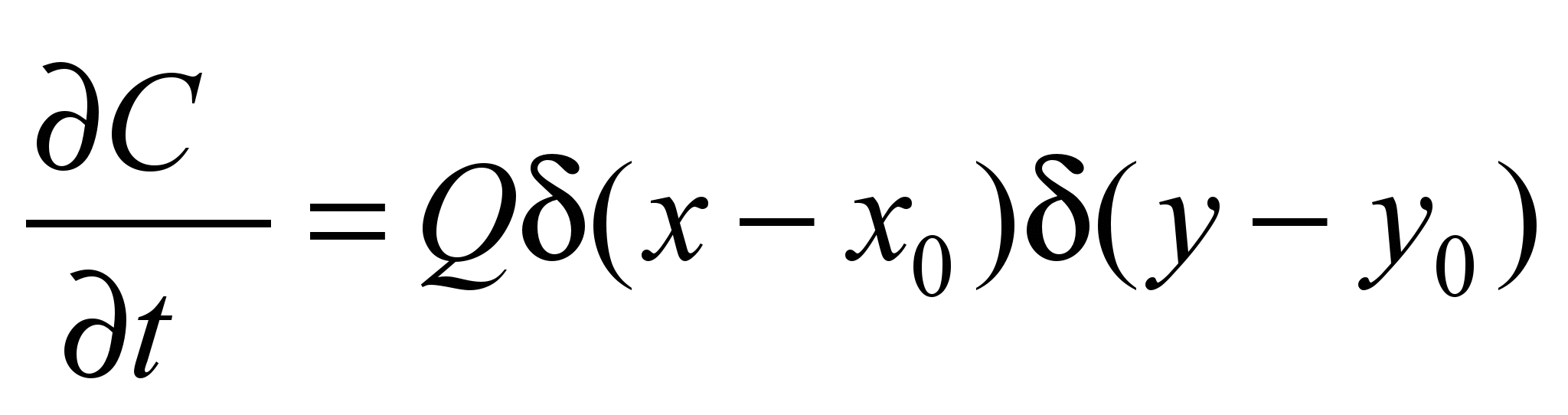To solve this equation, the Euler method is used.

For the numerical solution of equation (2), we use the Liebmann method. The approximate equation for the velocity potential in this case is written in the form:

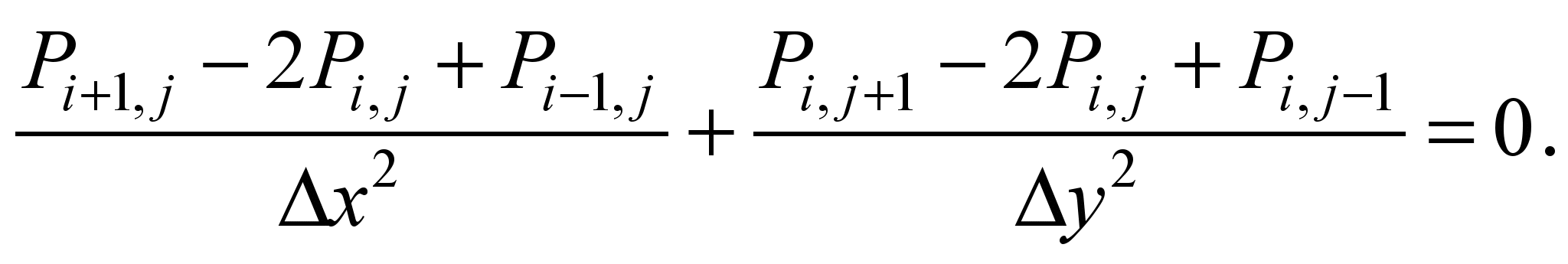
The value of the velocity potential 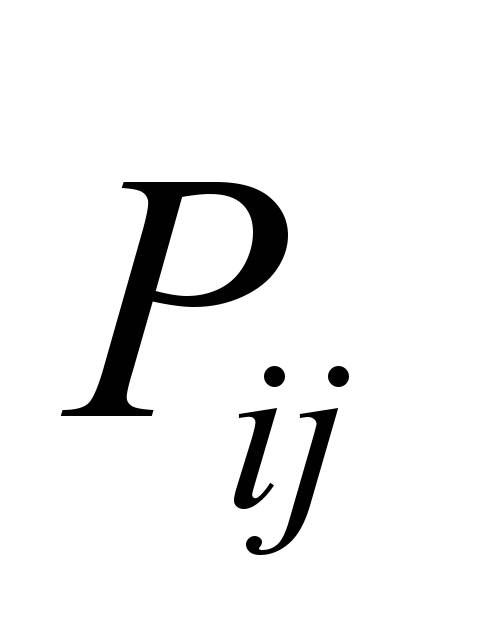is calculated in the centers of the difference cells by the formula:

,

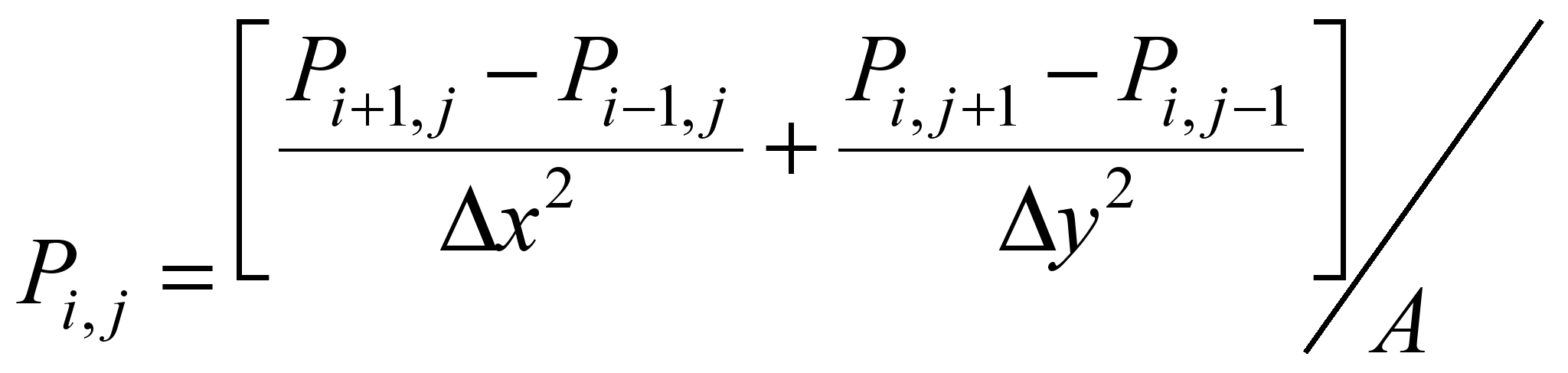where .

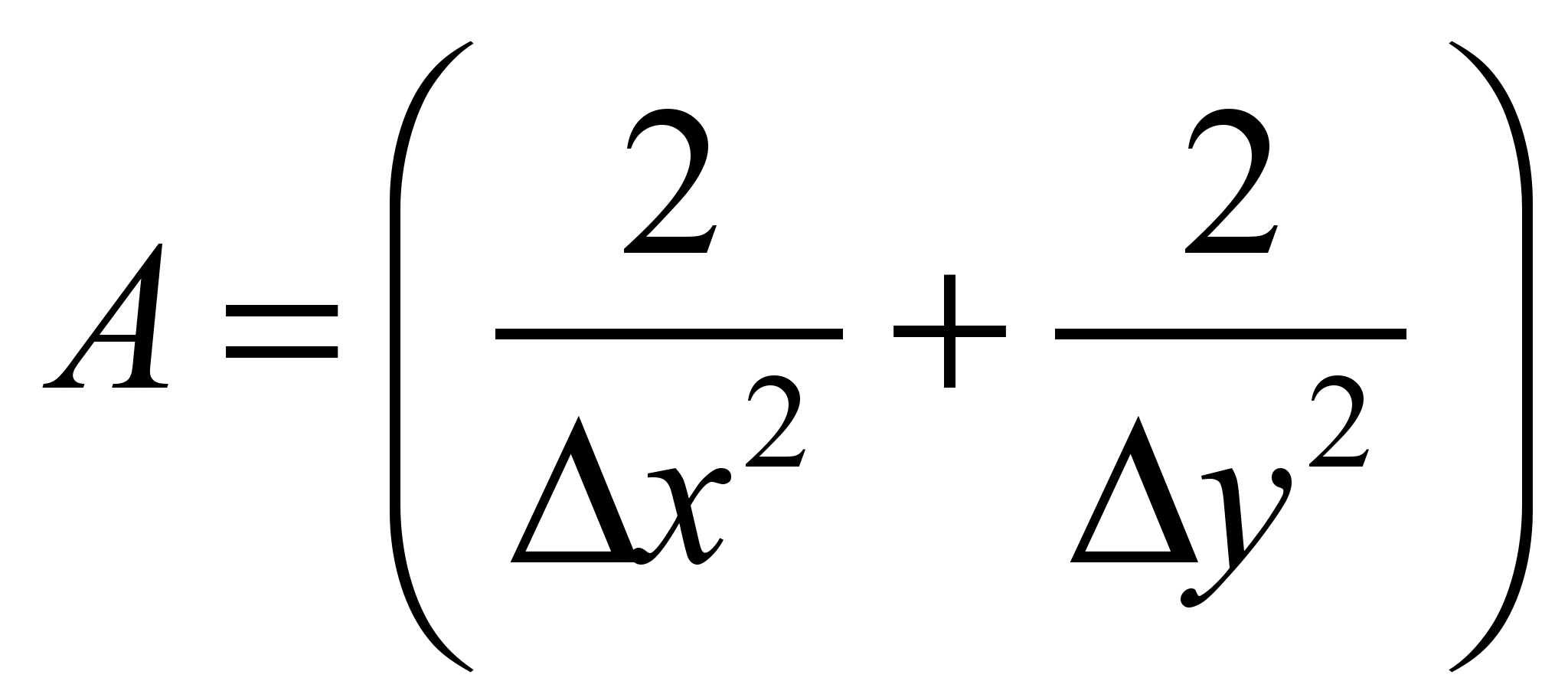For the software implementation of the constructed numerical model, we used FORTRAN.

Findings

The developed CFD model was used to solve the following model problem. We consider the emission of highly toxic chemical agent through the ventilation system, the outlet of which is located on the cafe roof. The scetch of the computational domain is shown in Fig.3.

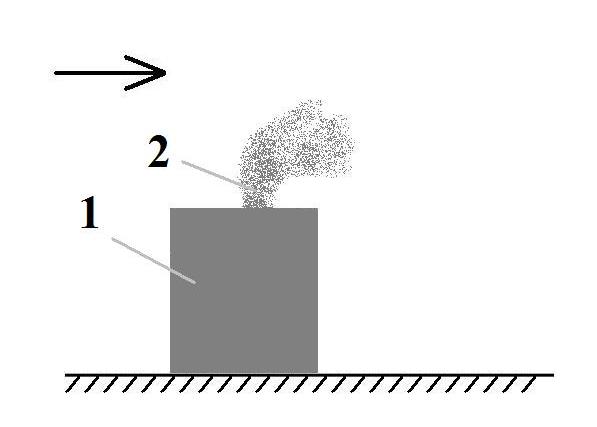
Fig. 3. Sketch of emission of a chemical agent
on the cafe roof (no protection element):
1 –cafe building; 2 – point of chemical
agent emission

To minimize the air contamination level near the cafe, as an anti-terrorist method, we use the installation of a vertical (Fig. 4) or inclined screen (Fig. 6) on the roof.

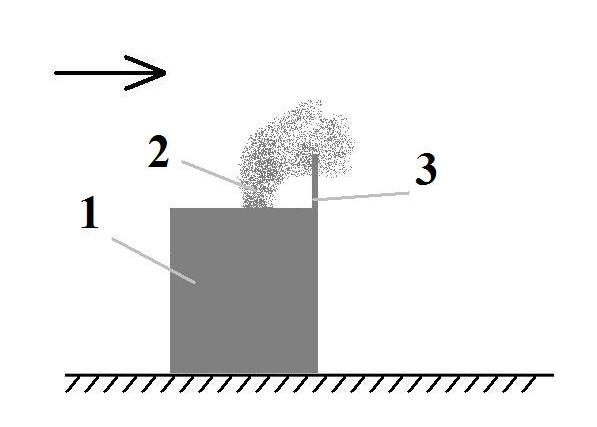
Fig. 4. Sketch of computational region (vertical screen on the café roof is a protection measure, scenario #2):
1 – café building; 2 – point of high toxic chemical emission;
3 – vertical screen

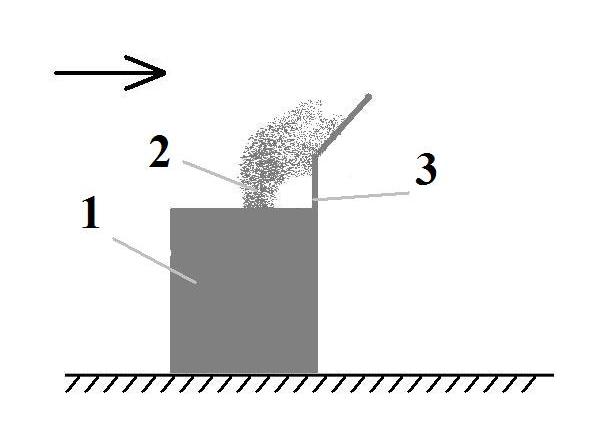
Fig. 5. Sketch of computational region (inclined screen on the café roof is a protection measure, scenario #3):

1 – café building; 2 – point of high toxic chemical
emission; 3 – inclined screen

It is necessary to evaluate the effectiveness of the used screens to minimize the air contamination level near the cafe.

The air contamination zone near the cafe for each working scenario is shown in Fig. 6–8.

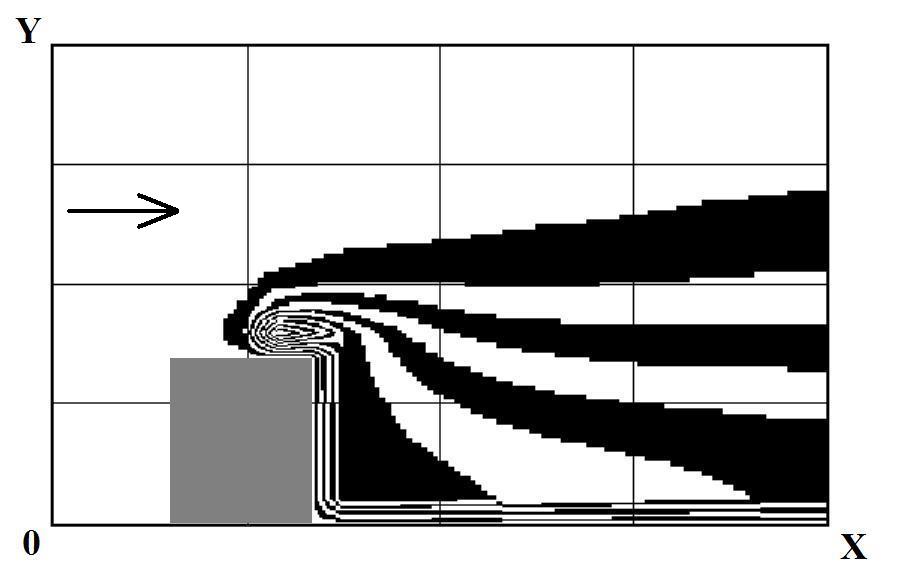
Fig. 6. Isolines of toxic chemical concentration
near café building (no protection measures
are used, scenario #1)

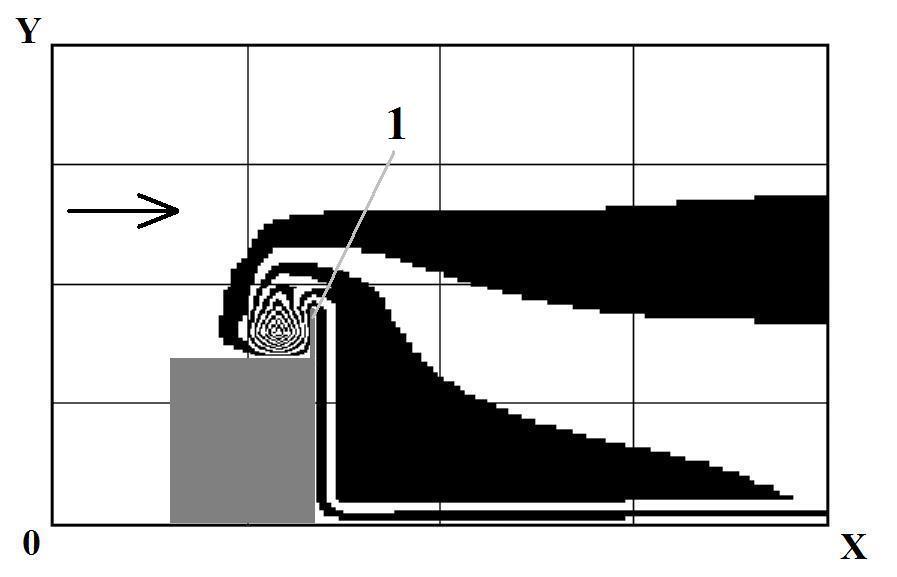
Fig. 7. Isolines of toxic chemical concentration near café building (vertical screen on the roof is a protection measure, scenario #2):
1 – vertical screen

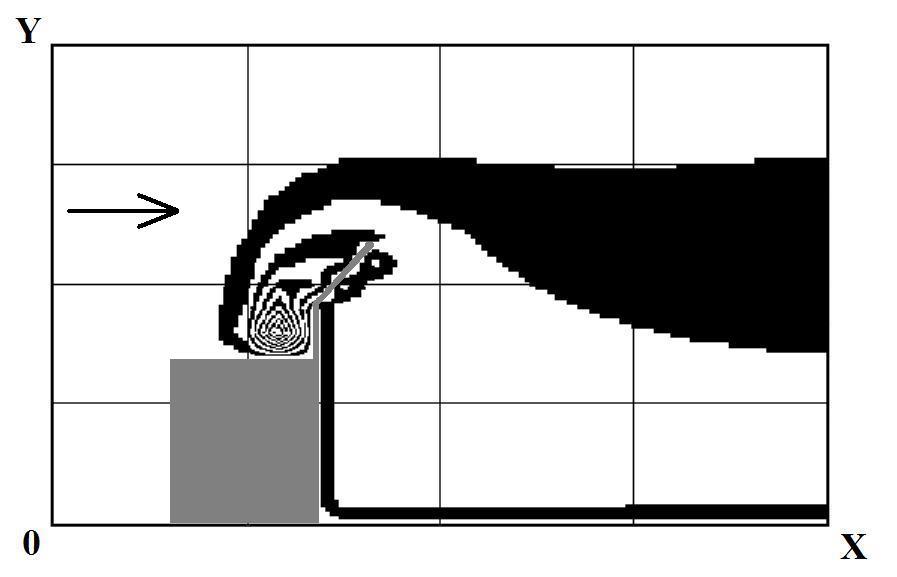
Fig. 8. Isolines of toxic chemical concentration near café building (inclined screen on the roof is
a protection measure, scenario #3)

Fig. 8 shows that the use of the inclined screen makes it possible to take a stream of contaminated air away from the cafe. For a more detailed analysis of the effectiveness of the used screens, the Table 1 shows the concentration of the contaminant at different distances from the building, the level of 1.7 m – the height of a person for all the scenarios under consideration.

Table 1

Dimensionless concentration of toxic chemical
at different distance from the cafe building

Distance from the café building, m	Concentration, scenario # 1	Concentration, scenario # 2	Concentration, scenario #3
2.5 m	1.26	0.98	0.78
4.5 m	1.16	0.93	0.75
5.5 m	1.12	0.91	0.74
9.5 m	1.02	0.86	0.70
11.5 m	0.98	0.83	0.68

As can be seen from the Table 1, the use of screens on the building roof allows to reduce the concentration of a chemically hazardous substance outdoor and thereby minimize the risk of toxic damage to people during the terrorist attack. Obviously, for the case under consideration, it is more effective to use the inclined screen (scenario No. 3).

It should be noted that the task solution time is about 5 seconds.

Originality and practical value

The numerical model has been developed that allows to determine the effectiveness of engineering methods for minimizing the outdoor air contamination level in the event of an initiated (terrorist attack) pollution with a highly toxic chemical agent.

The distinctive feature of the constructed model is the use of the equation of convective-diffusive dispersion of a chemical agent together with the equation for calculating the wind flow velocity field near the building (potential flow model). Computer time spent on the implementation of the developed numerical model is a few seconds.

Studies conducted on the basis of numerical simulation have shown that the use of screens on the roof of a building can reduce the air contamination level in a certain area near the building.

Conclusions

The numerical model has been developed for assessing the air contamination level near the building in the event of the chemical agent emission on its roof. The model makes it possible to assess the effect of screens on the protection of atmospheric air against contamination during such an emission. The basis for solving the problem is numerical simulation based on the equations describing the dispersion of impurities and aerodynamics.

Further improvement of this approach should be carried out in the direction of developing a three-dimensional numerical model focused on solving the tasks of this class.

LIST OF REFERENCE LINKS

1. Алымов, В. Т. Техногенный риск. Анализ и оценка : учеб. пособие для вузов / В. Т. Алымов, Н. П. Тарасова. – Москва : Академкнига, 2004. – 118 с.

2. Беляев, Н. Н. Защита зданий от проникновения в них опасных веществ : монография / Н. Н. Беляев,
   Е. Ю. Гунько, Н. В. Росточило. – Днепропетровск : Акцент ПП, 2014. – 136 с.

3. Марчук, Г. И. Математическое моделирование в проблеме окружающей среды / Г. И. Марчук. – Москва : Наука, 1982. – 320 с.

4. Оценка техногенного риска при эмиссии опасных веществ на железнодорожном транспорте / Н. Н. Беляев, Е. Ю. Гунько, П. С. Кириченко, Л. Я. Мунтян. – Кривой Рог : Р. А. Козлов, 2017. – 127 с.

5. Численное моделирование распространения загрязнения в окружающей среде / М. З. Згуровский,
   В. В. Скопецкий, В. К. Хрущ, Н. Н. Беляев. – Киев : Наук. думка, 1997. – 368 с.

6. Barret, A. M. Mathematical Modeling and Decision Analysis for Terrorism Defense: Assessing Chlorine Truck Attack Consequence and Countermeasure Cost Effectiveness : Degree of Doctor of Philosophy / Anthony Michael Barret ; Carnegie Mellon University. – Pittsburg, Pennsylvania, 2009. – 123 p.

7. Berlov, O. V. Atmosphere protection in case of emergency during transportation of dangerous cargo /
   O. V. Berlov // Наука та прогрес транспорту. – 2016. – № 1 (61). – С. 48–54. doi: 10.15802/stp2016/60953

8. Biliaiev, M. M. Numerical Simulation of Indoor Air Pollution and Atmosphere Pollution for Regions Having Complex Topography / M. M. Biliaiev, M. M. Kharytonov // NATO Science for Peace and Security. Series C: Environmental Security. – Dordrecht, 2012. – P. 87–91. doi: 10.1007/978-94-007-1359-8_15

9. CEFIC Guidance on safety Risk Assessment for Chemical Transport Operations [Электронный ресурс] // Croner-i. – Режим доступа: https://app.croneri.co.uk/news/cefic-guidance-safety-risk-assessment-chemical-transport-operations?product=139 – Загл. с экрана. – Проверено : 29.01.2018.

10. Development of advanced mathematical predictive models for assessing damage avoided accidents on potentially-dangerous sea-based energy facility / Aleksandr Tumanov, Vasily Gumenyuk, Vladimir Tumanov // IOP Conf. Series: Earth and Environmental Science. – 2017. – Vol. 90.
    doi: 10.1088/1755-1315/90/1/012027

11. Effect of barriers on the status of atmospheric pollution by mathematical modeling / Zahra Naserzadeh, Farideh Atabi, Faramarz Moattar, Naser Moharram Nejad // Bioscience Biotechnology Research Communication. – 2017. – Vol. 10 (1). – P. 192–204.

12. Multi-Objective Optimization Model of Emergency Organization Allocation for Sustainable Disaster Supply Chain / Cejun Cao, Congdong Li, Qin Yang, Fanshun Zhang // Sustainability. – 2017. – Vol. 9. – Іss. 11.
    doi: 10.3390/su9112103

13. Protective Action Criteria. A Review of Their Derivation, Use, Advantages and Limitations [Электронный ресурс] // Environmental Public Health Science Unit, Health Protection Branch, Public Health and Compliance Division, Alberta Health. – Edmonton, Alberta, 2017. – Режим доступа: http://open.alberta.ca/publications/9781460131213 – Загл. с экрана. – Проверено : 14.06.2018.

14. The analysis of the use of mathematical modeling for emergency planning purposes / Ondrej Zavila, Pavel Dobes, Jakub Dlabka, Jan Bitta // The Science for Population Protection. – 2015. – No. 2.

М. М. БІЛЯЄВ^1*, О. В. Бєрлов^2*, І. В. КАЛАШНІКОВ^3*, В. А. КОЗАЧИНА^4*

^1*Каф. «Гідравліка та водопостачання», Дніпропетровський національний
університет залізничного транспорту імені академіка В. Лазаряна,
вул. Лазаряна, 2, Дніпро, Україна, 49010, тел. +38 (056) 273 15 09,
ел. пошта water.supply.treatment@gmail.com , ORCID 0000-0002-1531-7882

2^*Каф. «Безпека життєдіяльності», Державний вищий навчальний заклад
«Придніпровська державна академія будівництва та архітектури»,
вул. Чернишевського, 24 а, Дніпро, Україна, 49600, тел. +38 (056) 756 34 57,
ел. пошта berlov@mail.pgasa.dp.ua, ORCID 0000-0002-7442-0548

^3*ДП «Проектно-вишукувальний інститут залізничного транспорту
України «Укрзалізничпроект», вул. Конарєва, 7,
Харків, Україна, 61052, тел. +38 (057) 724 41 25,
ел. пошта uzp38@ukr.net, ORCID 0000-0002-2814-380X

^4*Каф. «Гідравліка та водопостачання», Дніпропетровський національний
університет залізничного транспорту імені академіка В. Лазаряна,
вул. Лазаряна, 2, Дніпро, Україна, 49010, тел. +38 (056) 273 15 09,
ел. пошта v.kozachyna@gmail.com, ORCID 0000-0002-6894-5532

АНТИТЕРОРистичний ІНЖИНІРИНГ

ПРИ можливОМУ терактІ

З ВИКОРИСТАННЯМ ХІМІЧНОГО

АГЕНТА НА ВУЛИЦІ

Мета. Дана робота передбачає розробку методу локального зниження на вулиці концентрації хімічно небезпечної речовини, яка надійшла в атмосферу через вентиляційний викид на даху кафе, а також створення чисельної моделі для розрахунку зони хімічного зараження, яка дозволяє оцінити ефективність застосування екранів, що мінімізують його рівень. Методика. Для вирішення поставленого завдання використано рівняння для потенціалу швидкості, на базі якого визначено поле швидкості повітряного потоку, і рівняння конвективно-дифузійного розсіювання хімічно небезпечного агента в атмосферному повітрі, викинутого в разі теракту через систему вентиляції. При моделюванні були враховані нерівномірне поле швидкості вітрового потоку, атмосферна дифузія, інтенсивність викиду хімічно небезпечного агента. При чисельному інтегруванні рівняння для потенціалу швидкості використаний метод Лібмана. Для чисельного рішення рівняння конвективно-дифузійного розсіювання домішки використана неявна поперемінно-трикутна різницева схема розщеплення. Результати. На основі розробленої чисельної моделі подана оцінка ефективності застосування екранів на будівлі для зниження концентрації небезпечної речовини та мінімізації ризику токсичного ураження людей на вулиці при ініційованому викиді хімічного агента. Побудована чисельна модель може бути реалізована на комп’ютерах малої та середньої потужності, що дозволяє широко використовувати її для вирішення завдань даного класу при розробці стратегії антитерористичного інжинірингу. Наукова новизна. Запропоновано ефективну чисельну модель для розрахунку зони зараження людей на вулиці при можливому теракті з використанням хімічного (біологічного) агента. Модель також може бути застосована для оцінки ефективності деяких захисних заходів, спрямованих на зниження рівня забруднення повітряного середовища під час теракту. Практична значимість. Розроблена чисельна модель може бути використана для організації захисних заходів біля соціальних об’єктів можливої хімічної атаки терориста.

Ключові слова: теракт; хімічне забруднення атмосфери; антитерористичний інжиніринг; чисельне моделювання

Н. Н. БЕЛЯЕВ^1*, А. В. БЕРЛОВ², И. В. КАЛАШНИКОВ^3*, В. А. КОЗАЧИНА^4*

^1*Каф. «Гидравлика и водоснабжение», Днепропетровский национальный
университет железнодорожного транспорта имени академика В. Лазаряна,
ул. Лазаряна, 2, Днипро, Украина, 49010, тел. +38 (056) 273 15 09,
эл. почта water.supply.treatment@gmail.com, ORCID 0000-0002-1531-7882
^2*Каф. «Безопасность жизнедеятельности», Государственное высшее
учебное заведение «Приднепровская государственная академия
строительства и архитектуры», ул. Чернышевского, 24 а,
Днипро, Украина, 49600, тел. +38 (056) 756 34 57,
эл. почта berlov@mail.pgasa.dp.ua, ORCID 0000-0002-7442-0548
^3*ГП «Проектно-изыскательный институт железнодорожного транспорта
«Укрзализнычпроект», ул. Конарева, 7, Харьков, Украина, 61052,
тел. +38 (057) 724 41 25, эл. почта uzp38@ukr.net, ORCID 0000-0002-2814-380X
^4*Каф. «Гидравлика и водоснабжение», Днепропетровский национальный
университет железнодорожного транспорта имени академика В. Лазаряна,
ул. Лазаряна, 2, Днипро, Украина, 49010, тел. +38 (056) 273 15 09,
эл. почта v.kozachyna@gmail.com, ORCID 0000-0002-6894-5532

АНТИТЕРРОРистический ИНЖИНИРИНГ

ПРИ ВОЗМОЖНОМ ТЕРАКТЕ С

ПРИМЕНЕНИЕМ ХИМИЧЕСКОГО АГЕНТА

НА УЛИЦЕ

Цель. Данная работа предусматривает разработку метода локального снижения на улице концентрации химически опасного вещества, которое поступило в атмосферу через вентиляционный выброс на крыше кафе, а также создание численной модели для расчета зоны химического заражения, позволяющей оценить эффективность применения экранов, минимизирующих его уровень. Методика. Для решения поставленной задачи использовано уравнение для потенциала скорости, на базе которого определено поле скорости воздушного потока, и уравнение конвективно-диффузионного рассеивания химически опасного агента в атмосферном воздухе, выброшенного в случае теракта через систему вентиляции. При моделировании были учтены неравномерное поле скорости ветрового потока, атмосферная диффузия, интенсивность выброса химически опасного агента. При численном интегрировании уравнения для потенциала скорости использован метод Либмана. Для численного решения уравнения конвективно-диффузионного рассеивания примеси использована неявная попеременно-треугольная разностная схема расщепления. Результаты. На основе разработанной численной модели дана оценка эффективности применения экранов на здании для снижения концентрации опасного вещества и минимизации риска токсичного поражения людей на улице при инициированном выбросе химического агента. Построенная численная модель может быть реализована на компьютерах малой и средней мощности, что позволяет широко использовать ее для решения задач рассматриваемого класса при разработке стратегии антитеррористического инжиниринга. Научная новизна. Предложена эффективная численная модель для расчета зоны заражения людей на улице при возможном теракте с использованием химического (биологического) агента. Модель также может быть применена для оценки эффективности некоторых защитных мероприятий, направленных на снижение уровня загрязнения воздушной среды при теракте. Практическая значимость. Разработанная численная модель может быть использована для организации защитных мероприятий возле социальных объектов возможной химической атаки террориста.

Ключевые слова: теракт; химическое загрязнение атмосферы; антитеррористический инжиниринг; численное моделирование

References

1. Alymov, V. T., & Tarasova, N. P. (2004). Tekhnogennyy risk. Analiz i otsenka: Uchebebnoe posobie dlya vuzov. Moscow: Akademkniga. (in Russian)

2. Belyaev, N. N., Gunko, Y. Y., & Rostochilo, N. V. (2014). Zashchita zdaniy ot proniknoveniya v nikh opasnykh veshchestv: Monografiya. Dnepropetrovsk: Aktsent PP. (in Russian)

3. Marchuk, G. I. (1982). Matematicheskoye modelirovaniye v probleme okruzhayushchey sredy. Moscow: Nauka. (in Russian)

4. Belyaev, N. N., Gunko, Y. Y., Kirichenko, P. S., & Muntyan, L. Y. (2017). Otsenka tekhnogennogo riska pri emissii opasnykh veshchestv na zheleznodorozhnom transporte. https://www.multitran.ru/c/m.exe?t=4605566_1_2&s1=(%E3.)%20%CA%F0%E8%E2%EE%E9%20%D0%EE%E3 Krivoi Rog: Kozlov R. A. (in Russian).

5. Zgurovskiy, M. Z., Skopetskiy, V. V., Khrushch, V. K., & Belyaev, N. N. (1997). Chislennoe modelirovanie rasprostraneniya zagryazneniya v okruzhayushchey srede. Kуiv: Naukova dumka. (in Russian)

6. Barret, A. M. (2009). Mathematical Modeling and Decision Analysis for Terrorism Defense: Assessing Chlorine Truck Attack Consequence and Countermeasure Cost Effectiveness. (Dissertation of Doctor of Philosophy). Carnegie Mellon University, Pittsburg. (in English)

7. Berlov, O. V. (2016). Atmosphere protection in case of emergency during transportation of dangerous cargo. Science and Transport Progress, 1(61), 48-54. doi: 10.15802/stp2016/60953 (in English)

8. Biliaiev, M. M., & Kharytonov, M. M. (2012). Numerical Simulation of Indoor Air Pollution and Atmosphere Pollution for Regions Having Complex Topography. NATO Science for Peace and Security. Series C: Environmental Security, 87-91. doi: 10.1007/978-94-007-1359-8_15 (in English)

9. CEFIC Guidance on safety Risk Assessment for Chemical Transport Operations. Croner-i. Retrived from https://app.croneri.co.uk/news/cefic-guidance-safety-risk-assessment-chemical-transport-operations?product=139 (in English)

10. Tumanov, A., Gumenyuk, V., & Tumanov, V. (2017). Development of advanced mathematical predictive models for assessing damage avoided accidents on potentially-dangerous sea-based energy facility. IOP Conf. Series: Earth and Environmental Science, 90. doi: 10.1088/1755-1315/90/1/012027 (in English)

11. Zahra Naserzadeh, Farideh Atabi, Faramarz Moattar, & Naser Moharram Nejad. (2017). Effect of barriers on the status of atmospheric pollution by mathematical modeling. Bioscience Biotechnology Research Communication, 10(1), 192-204. (in English)

12. Cao, C., Li, C., Yang, Q., & Zhang, F. (2017). Multi-Objective Optimization Model of Emergency Organization Allocation for Sustainable Disaster Supply Chain. Sustainability, 9(11). doi: 10.3390/su9112103 (in English)

13. Government of Alberta. (2017). Protective Action Criteria: A Review of Their Derivation, Use, Advantages and Limitations. Environmental Public Health Science Unit, Health Protection Branch, Public Health and Compliance Division, Alberta Health. Edmonton, Alberta. Retrived from http://open.alberta.ca/publications/9781460131213 (in English)

14. Ondrej Zavila, Pavel Dobes, Jakub Dlabka, & Jan Bitta. (2015). The analysis of the use of mathematical modeling for emergency planning purposes. The Science for Population Protection, 2. (in English)

Received: July 30, 2018

Accepted: Nov. 14, 2018

Creative Commons Attribution 4.0 International

doi: 10.15802/stp2018/ © M. M. Biliaiev, O. V. Berlov, I. V. Kalashnikov, V. A. Kozachyna, 2018