ISSN
2307–3489 (Print), ІSSN 2307–6666 (Online)
Наука
та прогрес транспорту. Вісник
Дніпропетровського
національного університету залізничного
транспорту, 2018, №
6(78)
ЗАЛІЗНИЧНА
КОЛіЯ
ЗАЛІЗНИЧНА
КОЛІЯ
УДК 539.3:625.12
Л. П. ТЕЛИПКО1*,
Л. М. МАМАЕВ2, С.
В. РАКША3
1*Каф.
«Теоретическая и прикладная механика»,
Днепровский государственный технический
университет, ул. Днепро-строевская,
2, Каменское, Украина, 51918, тел.
+38 (0569)
53
85
23,
эл. почта leo46din@gmailcom,
ORCID 0000-0003-3165-3920
2Каф. «Теоретическая
и прикладная механика», Днепровский
государственный технический
университет,
ул. Днепро-строевская, 2,
Каменское, Украина, 51918, тел. +38 (0569)
53
85
23,
эл. почта leo46din@gmailcom,
ORCID 0000-0002-6421-4396
3Каф.
«Прикладная механика и материаловедение»,
Днепропетровский национальный
университет
железнодорожного транспорта имени
академика В. Лазаряна, ул. Лазаряна, 2,
Днипро, Украина, 49010, тел. +38 (056) 47 15 18, эл.
почта raksha@ukr.net,
ORCID 0000-0002-4118-1341
УЧЕТ
НЕОДНОРОДНОСТИ ЗЕМЛЯНОГО ПОЛОТНА
ЖЕЛЕЗНОДОРОЖНОГО ПУТИ ПРИ ОПРЕДЕЛЕНИИ
ЕГО НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО
СОСТОЯНИЯ
Цель.
Увеличение скорости движения и
грузоподъемности поездов приводит к
увеличению нагрузки на железнодорожный
путь и, в свою очередь, нагрузки на
земляное полотно. Это вызывает
необходимость уточнения методов расчета,
как верхнего строения, так и земляного
полотна железнодорожного пути. Целью
работы является разработка метода
определения напряженно-деформированного
состояния земляного полотна железнодорожного
пути на основании учета ограниченной
распределительной способности, конечности
зоны деформирования по глубине земляного
полотна и его неоднородности. Методика.
На основании смешанного метода Б. Н.
Жемочкина, согласно с которым действительную
криволинейную эпюру отпоров по нижней
постели шпал заменяют ступенчатой,
рассмотрена совместная работа
рельсо-шпальной решетки и земляного
полотна железнодорожного пути. Результаты.
Дано развитие
осесимметричной столбчатой
модели грунтового основания, которая
учитывает такие важные его свойства,
как ограниченная распределительная
способность, конечность зоны деформирования
и неоднородность (слоистость). На
основании дискретного метода Л. П.
Винокурова и осесимметричной столбчатой
модели грунтового основания получены
уравнения для перемещений и напряжений
для i-го
слоя основания. В результате решения
системы дифференциальных уравнений
дискретного метода численным методом,
в котором функции от матриц представляют
рядами, определены вертикальные и
радиальные перемещения слоистого
основания, после чего определены
нормальные и касательные напряжения в
основании. Реализация смешанного метода
Б. Н. Жемочкина позволяет определить
отпор по подошве шпал и прогибы центральных
сечений балок-шпал. Научная
новизна. Разработан
метод расчета напряженно-деформированного
состояния земляного полотна железнодорожного
пути при их совместной работе на основании
осесимметричной столбчатой модели. При
этом учтены ограниченная распределительная
способность, конечность зоны деформирования
и неоднородность по глубине грунтового
основания. Практическая
значимость. Полученные
результаты позволяют повысить точность
решений при проектировании земляного
полотна железнодорожного пути, что, в
свою очередь, приведет к повышению его
надежности и долговечности.
Ключевые
слова: напряженно-деформированное
состояние;
земляное полотно;
железнодорожный путь;
напряжения;
перемещения;
осадка
Введение
Интенсификация
грузоперевозок на железных дорогах
возможна за счет увеличения скорости
и грузоподъемности подвижного состава.
Это приводит к увеличению нагрузок на
железнодорожный путь, что, в свою
очередь, вызывает необходимость
уточнения методов расчета как верхнего
строения, так и земляного полотна
железнодорожного пути [1, 2].
Следует отметить, что прочность и
долговечность железнодорожного пути
во многом зависит от прочности земляного
полотна.
Для определения
напряженно-деформированного состояния
земляного полотна железнодорожного
пути строят математическую модель,
которая призвана отражать реальное
поведение грунта под нагрузкой.
Разработаны различные расчетные модели
грунтовых оснований, сравнительный
анализ некоторых из них приведен в
[10]. Чаще всего применяют модели Винклера
или упругого полупространства. Первая
модель совсем не учитывает распределительную
способность, то есть способность
деформироваться вне зоны приложения
нагрузки, а модель упругого полупространства
сильно преувеличивает ее. Различные
аспекты определения напряженно-деформированного
состояния земляного полотна
железнодорожного пути приведены в
работах [7, 9, 12, 13, 20, 21]. Учет начальных
напряжений в полупространстве при
воздействии кольцевых штампов рассмотрено
в [14]. Вопросы волновых процессов в
грунтовой среде отражены в работах [8,
15, 18]. Влияние конфигурации фундаментов
на напряженно-деформированное состояние
основания рассмотрено в [16, 17]. Исследование
различных моделей коэффициента несущей
способности грунта отражено в [19]. Однако
в наведенных работах не учтены
ограниченность зоны деформирования и
неоднородность грунтового основания
по глубине. Результаты многочисленных
экспериментов свидетельствуют, что
реальные грунты обладают ограниченной
распределительной способностью и
конечностью толщины деформированного
слоя. Учет этих характеристик реальных
грунтов повысит точность проектных
решений, что, в свою очередь, приведет
к повышению надежности и долговечности
железнодорожного пути.
Цель
Нагрузку от подвижного
состава через рельсо-шпальную решетку
балластный слой воспринимает и упруго
передает на основную площадку земляного
полотна. Поскольку толщина балластного
слоя, как правило, незначительна по
сравнению с толщиной грунтового
основания, в котором происходит
локализация напряжений и деформаций,
то влиянием последнего на
напряженно-деформированное состояние
земляного полотна можно пренебречь.
Для определения
осадок земляного полотна под нижней
постелью шпал и его напряженно-деформированного
состояния привлекаем осесимметричную
столбчатую модель основания [3, 4], которая
учитывает как конечность толщины
деформированного слоя, так и его
ограниченную распределительную
способность. Однако в работах [3, 4] она
построена для однородного по глубине
основания, в то время как реальным
основаниям, как уже отмечалось выше,
свойственна неоднородность по глубине,
слоистость.
Поэтому целью работы
является обобщение осесимметричной
столбчатой модели для определения
напряженно-деформированного
состояния земляного полотна
железнодорожного пути на основании
учета ограниченной распределительной
способности, конечности зоны деформирования
по глубине земляного полотна и его неоднородности.
Методика
Земляное полотно
железнодорожного пути в большинстве
случаев представлено связанными
грунтами, модуль деформации Е и
коэффициент Пуассона µ которых переменны
по глубине или они являются слоистыми
с различными значениями Е и µ для
каждого слоя. При решении задачи о
перемещениях и напряжениях неоднородного
по глубине основания кривую изменения
модуля деформации Е(x)
аппроксимируем ступенчатой прямой.
Такая аппроксимация точно соответствует
слоистому основанию с тем только
отличием, что для реального слоистого
основания может быть такое обстоятельство,
что модуль деформации нижележащих
слоев будет меньшим, чем вышележащих.
Рассмотрим совместную
работу рельсо-шпальной решетки, состоящей
(исходя из ограниченной способности
грунта) из трех шпал с расположением
оси колесной пары тележки вагона над
продольной осью средней шпалы. Шпалы
рассматриваем как гибкие балки на
податливом основании. Для их расчета
привлекаем смешанный метод Б. Н. Жемочкина
[6], согласно с которым действительную
криволинейную эпюру отпоров заменяют
ступенчатой. Непрерывный контакт шпалы
с основанием заменяют контактом в
отдельных точках путем введения между
шпалой и основанием шарнирно прикрепленных
вертикальных стержней-связей,
расположенных в середине участков
ступенчатой эпюры.
Крайние шпалы
находятся в силовой и геометрической
симметрии относительно средней, поэтому
будем рассматривать среднюю шпалу и
одну из крайних. Разбиваем длины
балок-шпал на участки с размерами,
равными ширине шпал, в серединах которых
ставим опорные стержни-связи. Посередине
балок-шпал вводим добавочные связи
против линейного и углового перемещений.
Расчетная схема приведена на рис. 1.
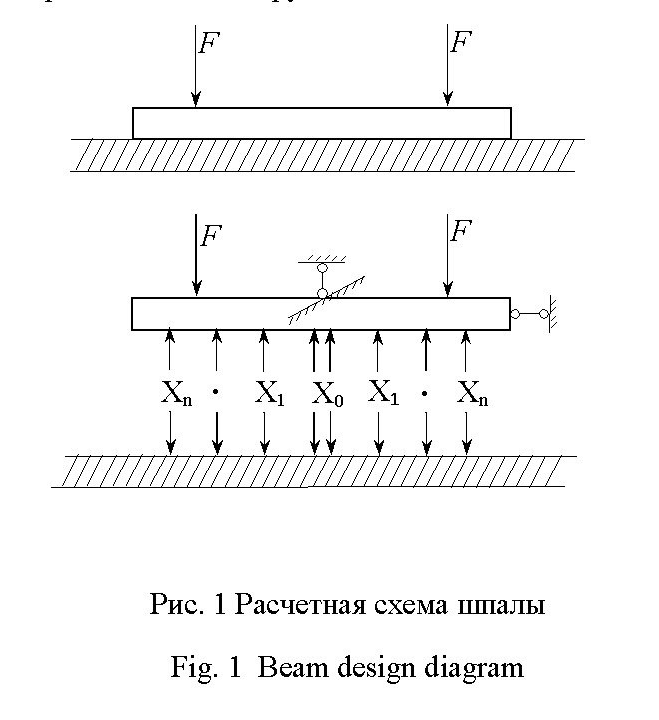
Вследствие симметрии
левые и правые неизвестные силы Xi
попарно равны между собой, а угловое
перемещение сечения середины балок-шпал
равно нулю. Неизвестными будут усилия
в стержневых связях Xi
(i = 0, 1, 2,
…, n) и
прогибы δ центральных сечений балок-шпал.
Система канонических
уравнений смешанного метода в матричной
форме имеет вид:
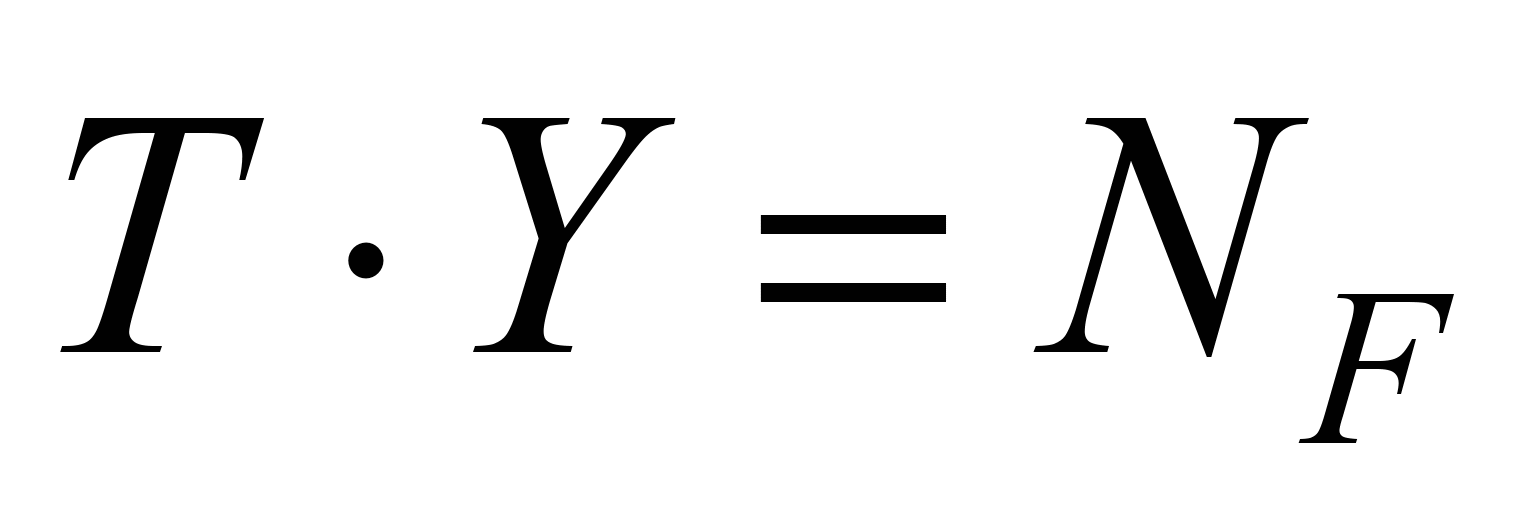 , (1)
, (1)
где
T – матрица коэффициентов,
которая составляет:
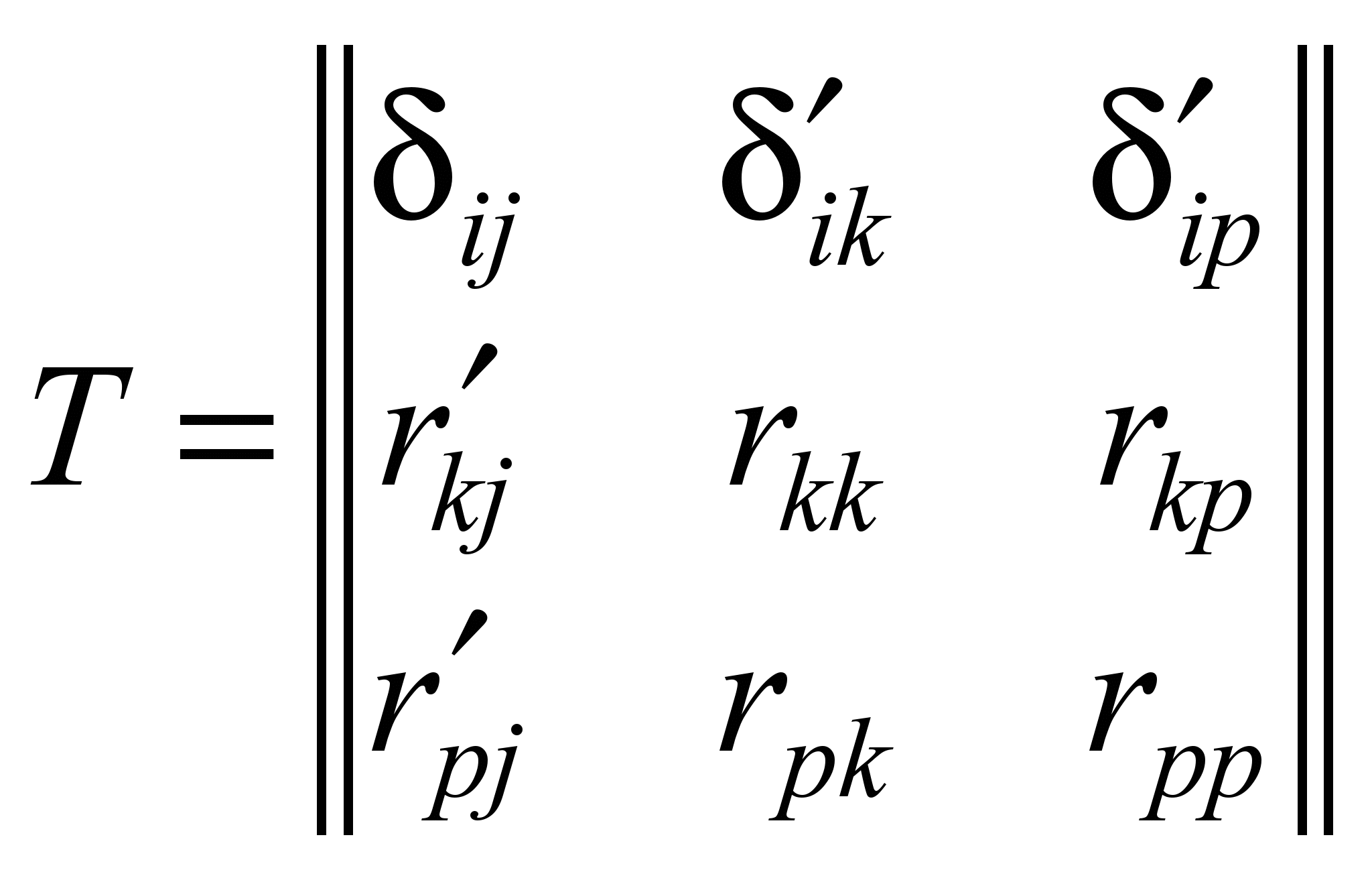 ,
,
здесь i
= 0, 1, 2, 3, …, n;
j = 0, 1, 2, 3, …,
n; k,
p – соответственно
номера стержней-связей, расположенных
посередине шпал; Y,
NF
– соответственно вектор неизвестных
и вектор правых частей.
Таким образом:
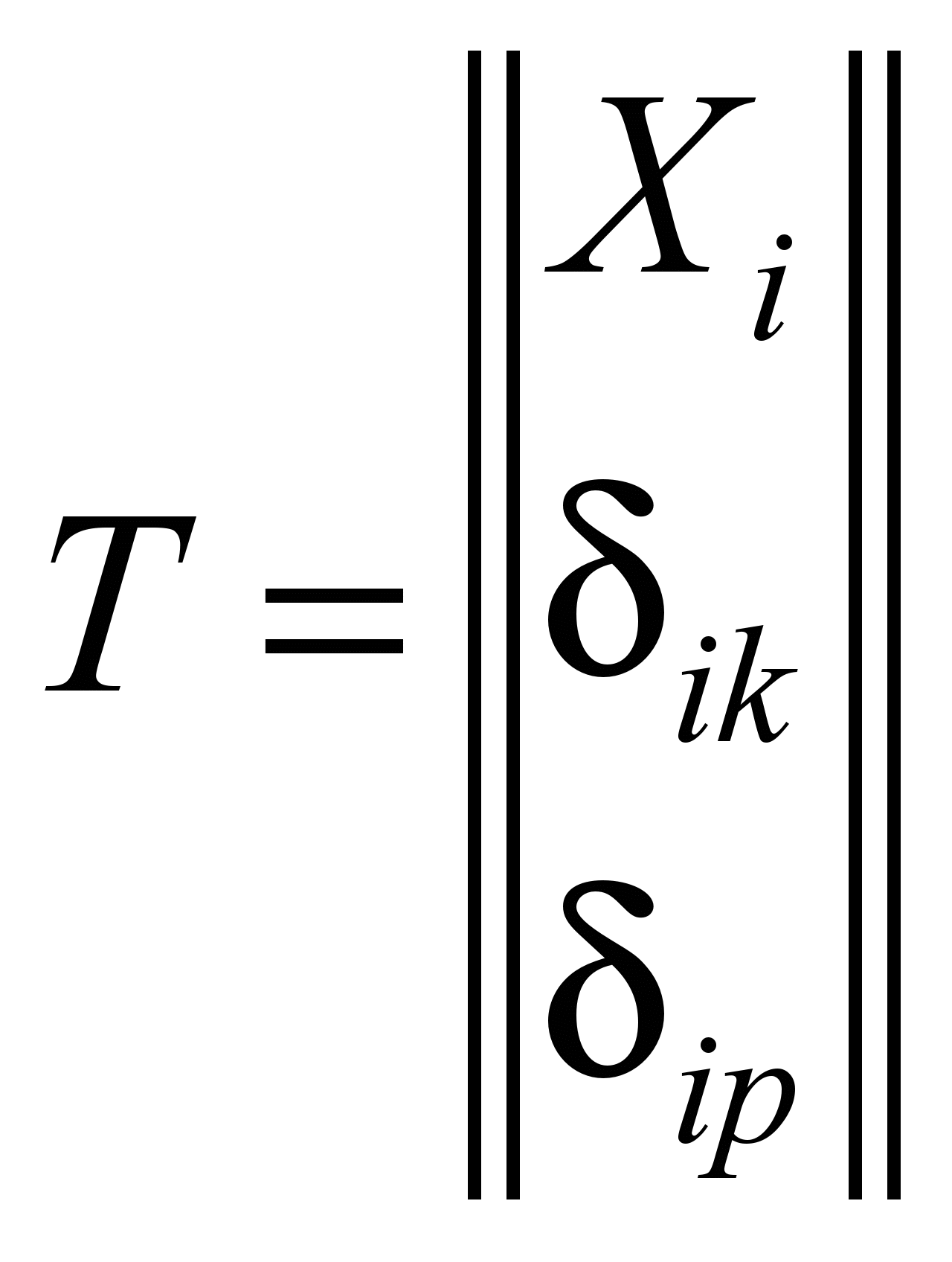 ;
;
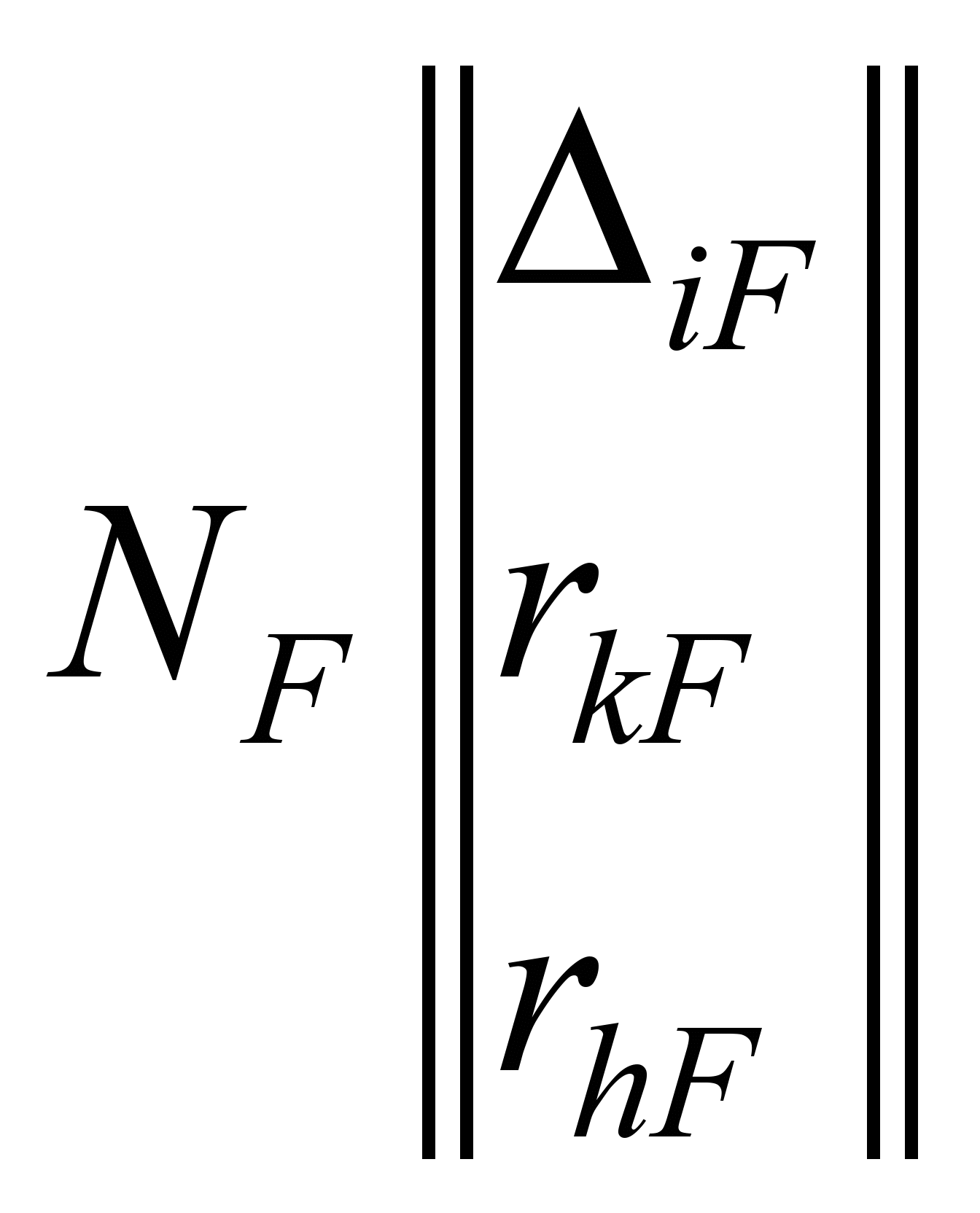 ,
,
здесь
 – перемещение точки i
(по направлению силы Xi)
от единичного усилия
– перемещение точки i
(по направлению силы Xi)
от единичного усилия
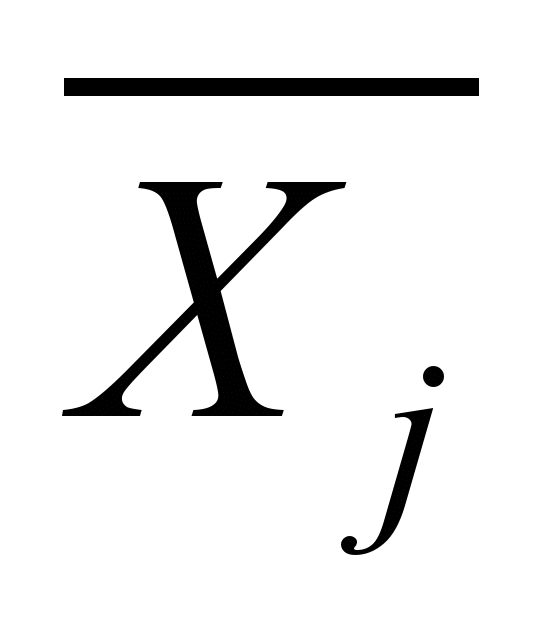 ,
равное сумме перемещений балки
,
равное сумме перемещений балки
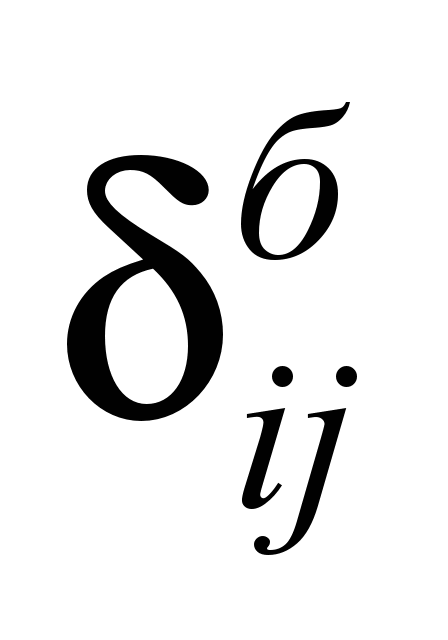 (в основной системе) и податливого
основания
(в основной системе) и податливого
основания
 (на основание действует единичная сила,
равномерно распределенная по участку
j):
(на основание действует единичная сила,
равномерно распределенная по участку
j):
 =
=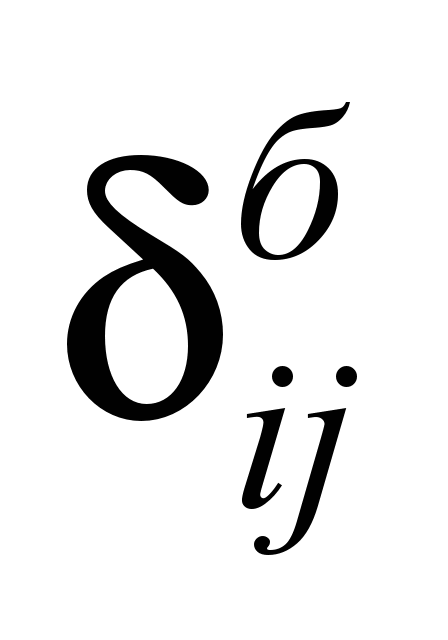 +
+ ;
;
δ′ik,
δ′ip
– соответственно перемещение точки
в основной системе от единичного
перемещения связей k
и p;
r′kj,
r′pj
– соответственно реакции в связях
k и p
от единичного усилия, приложенного к
основной системе в связи j;
rkk,
rkp,
rpk,
rpp
– соответственно реакции в связях
k и p
от единичного перемещения этих связей;
∆iF –
перемещение балки-шпалы в основной
системе от внешней нагрузки; rkF,
rpF
– соответственно реакции в связях k
и p от внешней нагрузки.
При определении
осадок земляного полотна под подошвами
шпал δоij
и его напряженно-деформированного
состояния, согласно осесимметричной
столбчатой модели основания [3, 4], зону,
в которой происходит локализация
перемещений и напряжений от равномерно
распределенной нагрузки
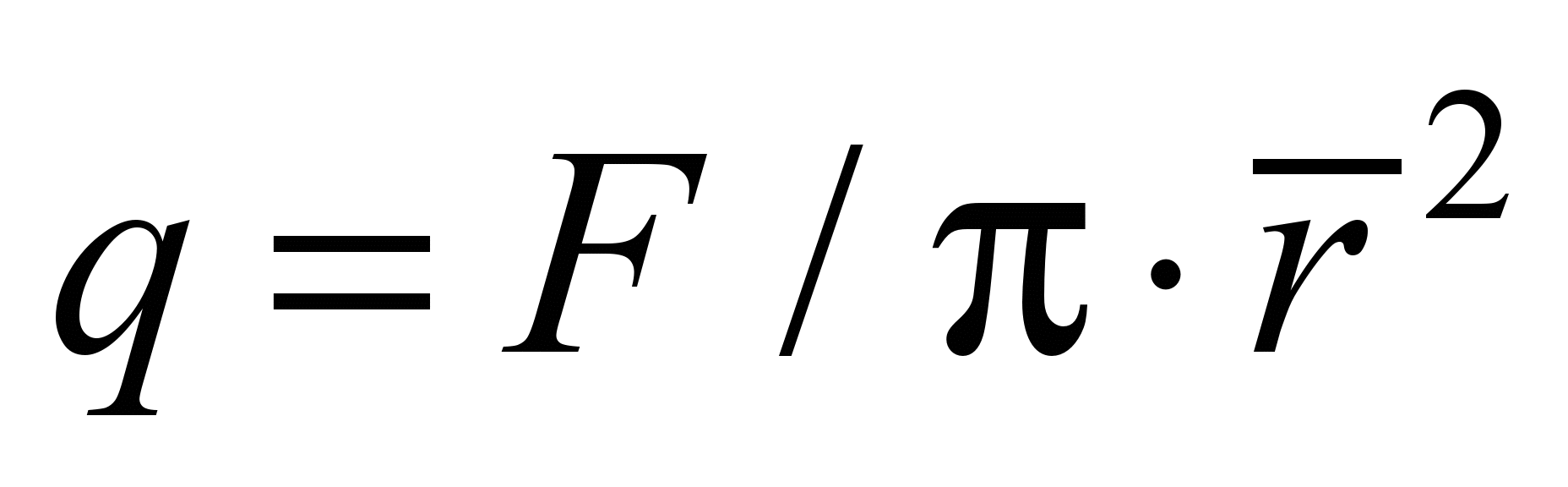 в пределах центрально расположенной
площадки радиусом
в пределах центрально расположенной
площадки радиусом 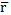 ,
моделируем круговым цилиндрическим
слоистым столбом высотой Н и конечным
радиусом
,
моделируем круговым цилиндрическим
слоистым столбом высотой Н и конечным
радиусом
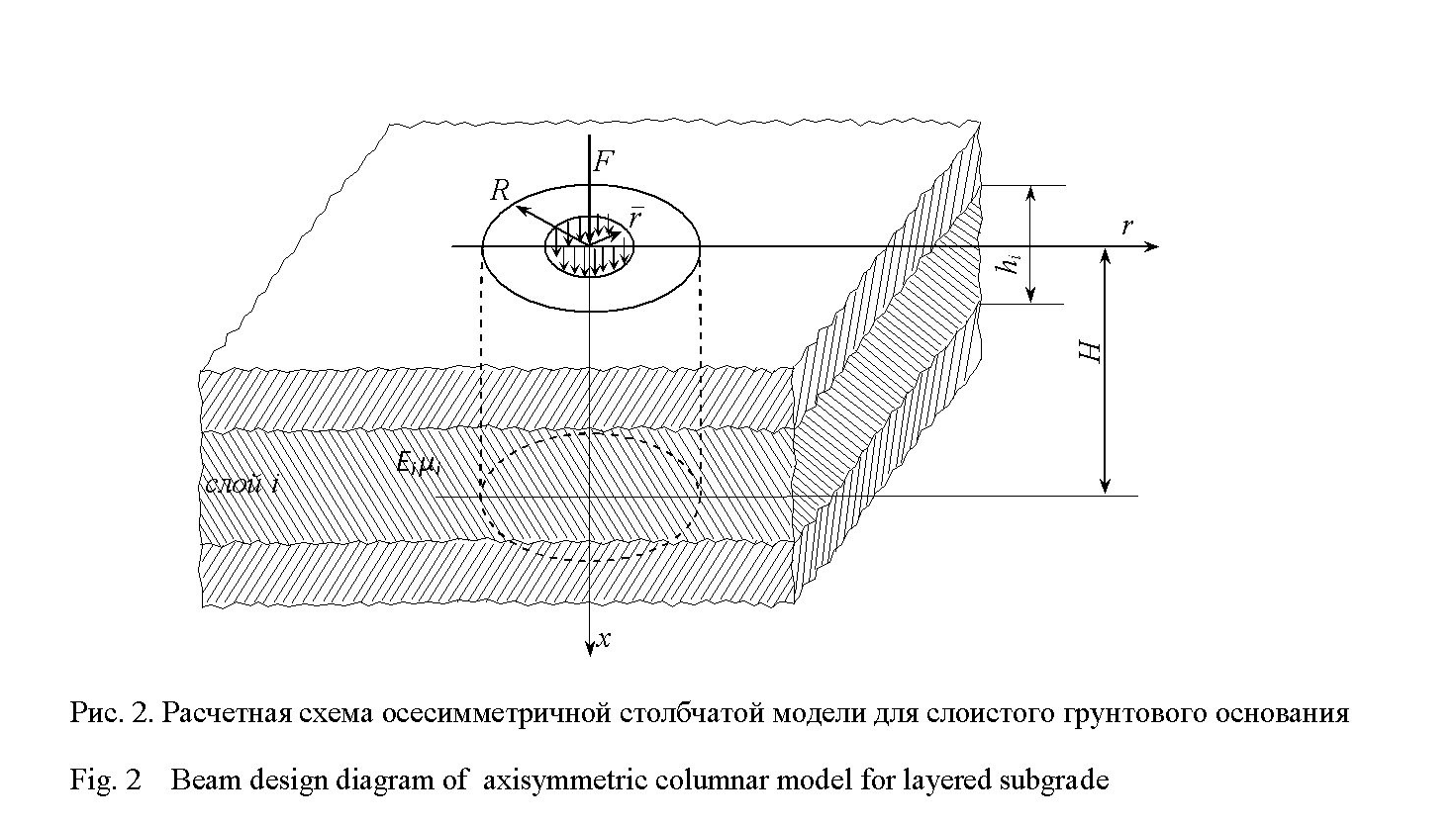
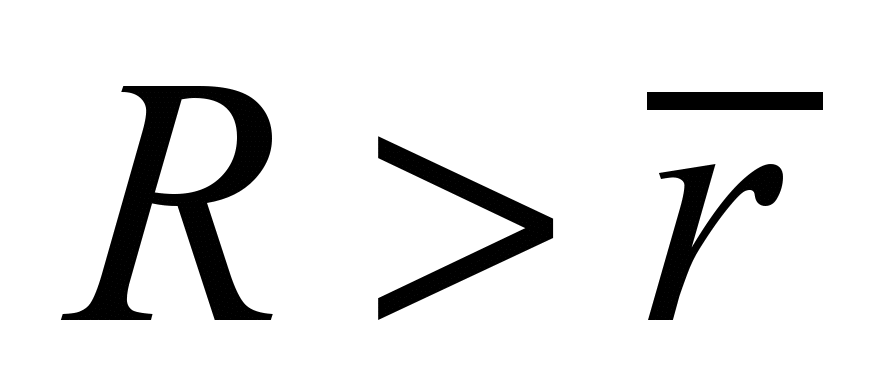 в поперечном сечении (рис. 2), совпадающим
с радиусом затухания перемещений на
граничной плоскости основания. Площадь
грузовой площадки радиусом
в поперечном сечении (рис. 2), совпадающим
с радиусом затухания перемещений на
граничной плоскости основания. Площадь
грузовой площадки радиусом
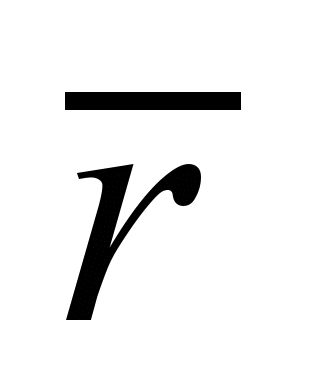 согласуется с площадью участков, на
которые разбита подошва балки-шпалы.
согласуется с площадью участков, на
которые разбита подошва балки-шпалы.
Совместим начало
цилиндрической системы координат x,
y, θ с точкой
приложения силы F,
причем вертикальную ось x
направим по направлению силы F
к нижнему торцу цилиндра. Рассматриваемое
слоистое цилиндрическое тело находится
в условиях осевой симметрии, поэтому
будут наблюдаться только радиальные
w и вертикальные u
перемещения (тангенциальные v
= 0), являющиеся функциями переменных x
и r.
Решение уравнений
Ляме, которыми описывают деформирование
каждого слоя цилиндрического тела,
будем проводить дискретным методом Л.
В. Винокурова [5]. По переменной x
решение ищем в аналитической форме, а
по переменной r – в
конечно-разностной. Объем рассматриваемого
слоистого цилиндрического тела
аппроксимируем призмами путем деления
его продольными сечениями, проходящими
через вертикальную ось x
и составляющими между собой углы θ, и
концентрическими окружностями.
Перемещения ребер призм принимаем в
качестве независимых неизвестных. Так
как рассматриваемое слоистое
цилиндрическое тело находится в условиях
осевой симметрии, то в дифференциальных
уравнениях дискретного метода будут
содержаться перемещения на вертикальных
линиях-ребрах (линиях, образующихся в
результате пересечения продольного
сечения с концентрическими окружностями),
расположенных в одной диаметральной
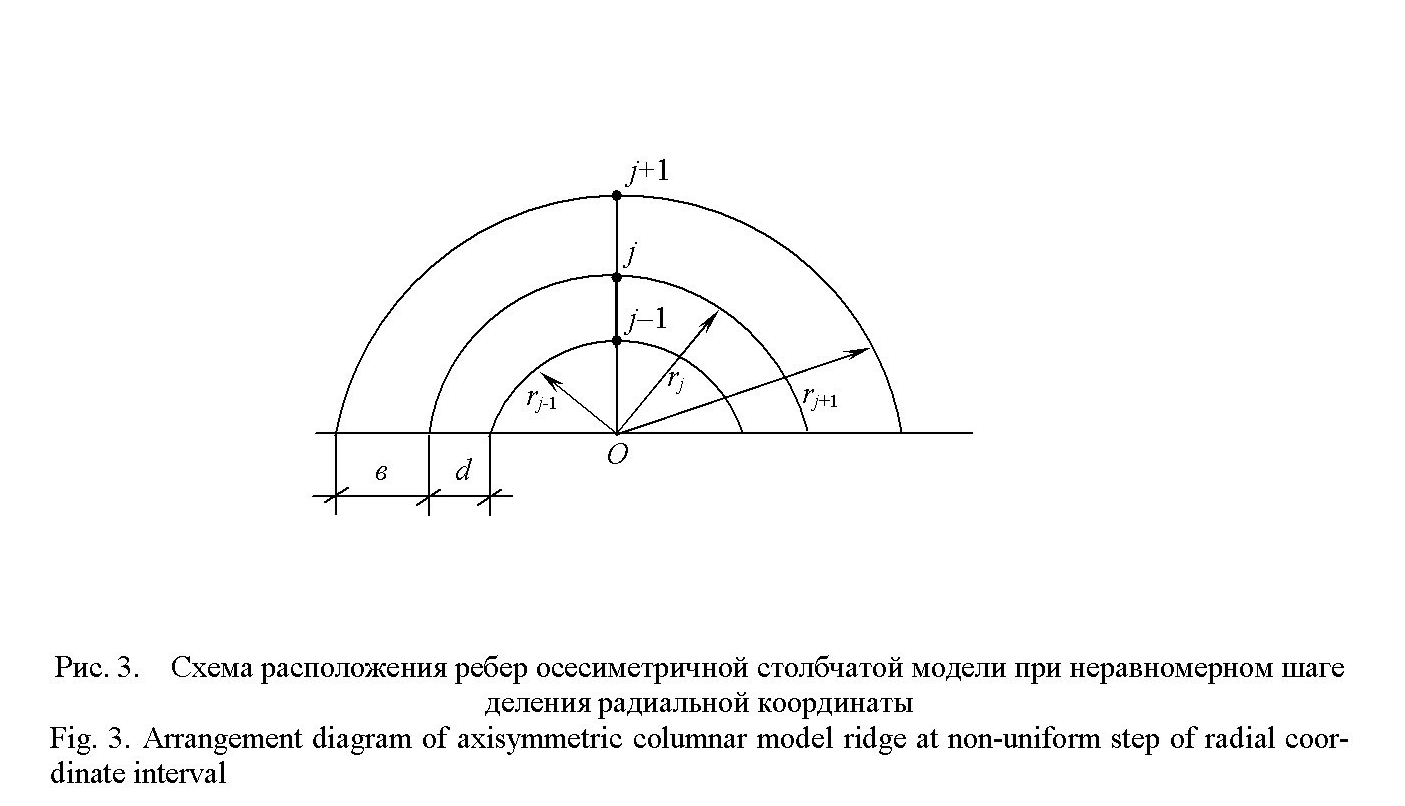
плоскости. Для ребра
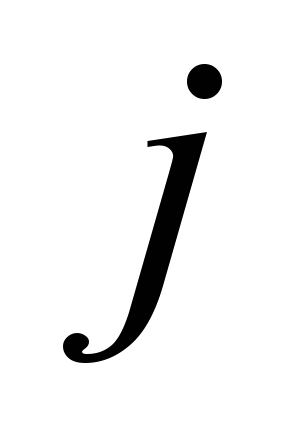 i-го слоя основания
при неравномерном шаге деления радиальной
координаты (рис. 3) мы получили следующие
уравнения дискретного метода для
перемещений и напряжений:
i-го слоя основания
при неравномерном шаге деления радиальной
координаты (рис. 3) мы получили следующие
уравнения дискретного метода для
перемещений и напряжений:
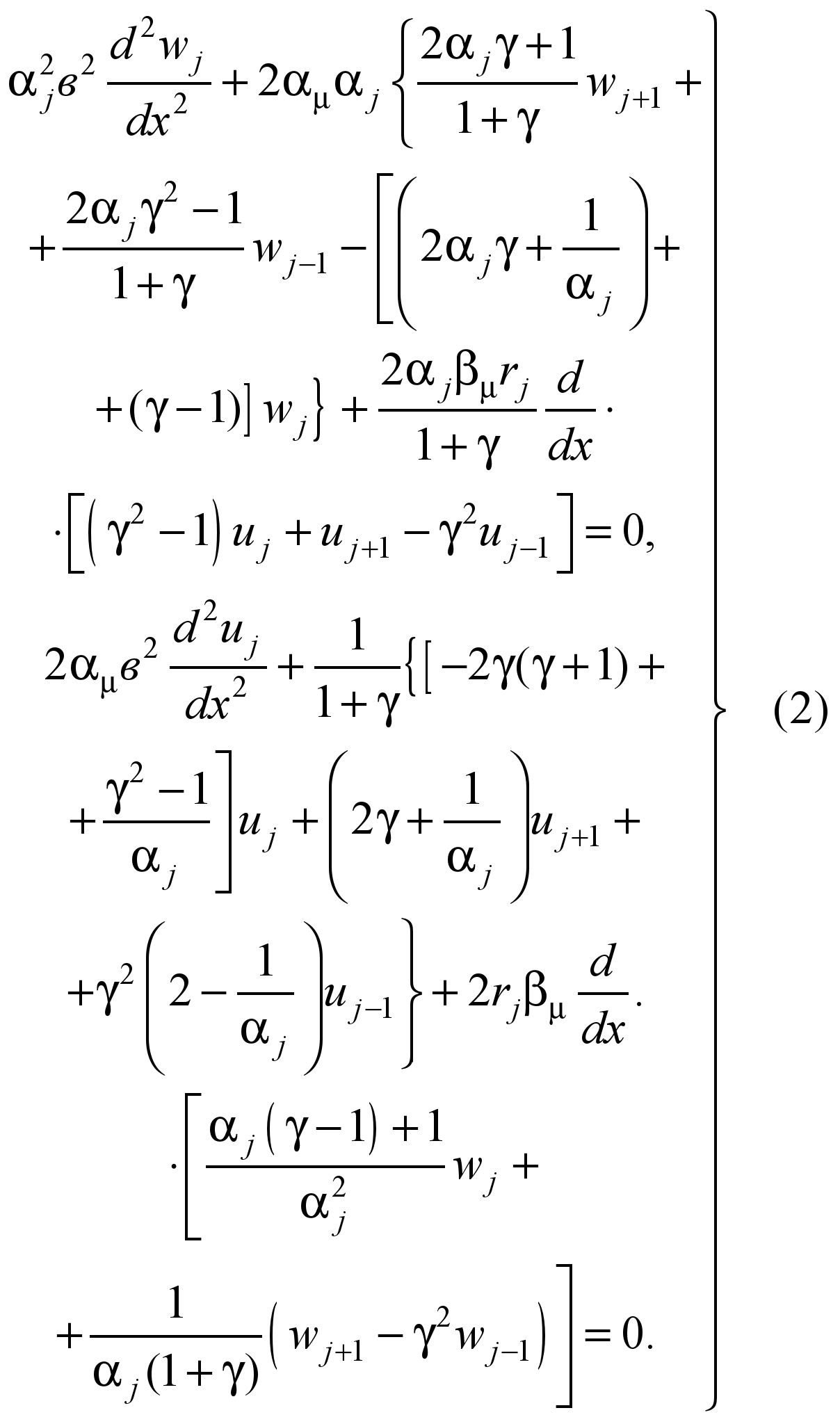
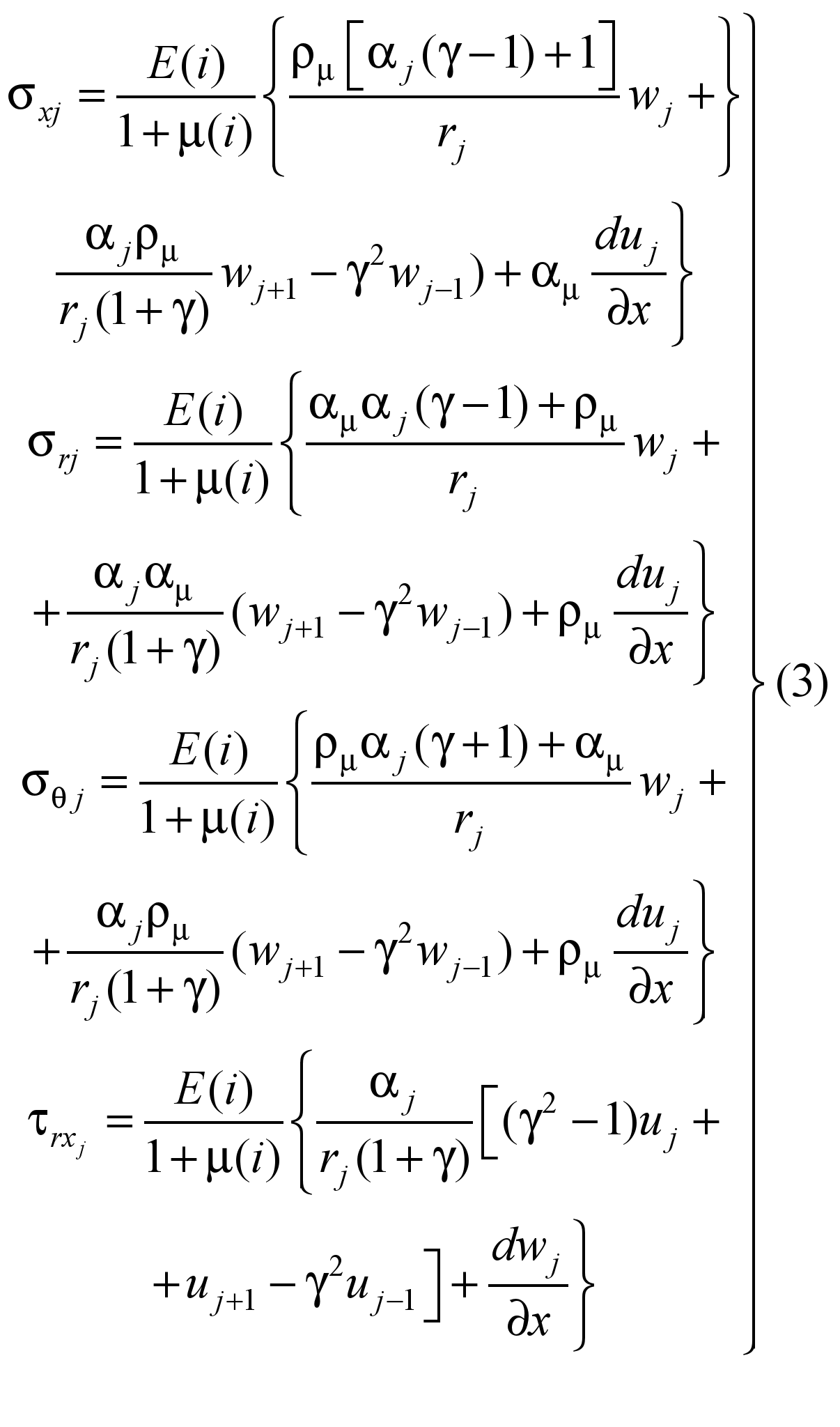
где
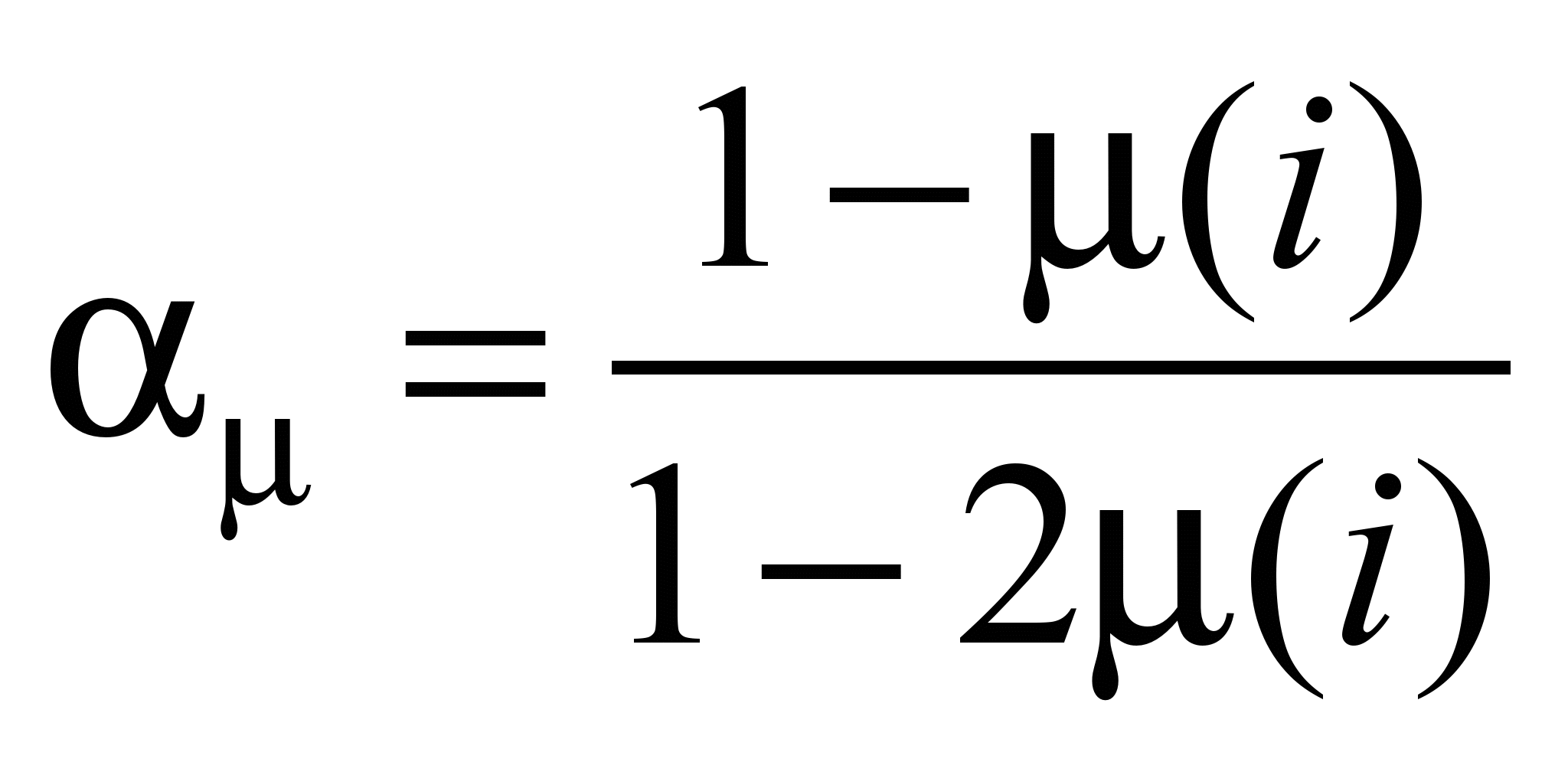 ;
;
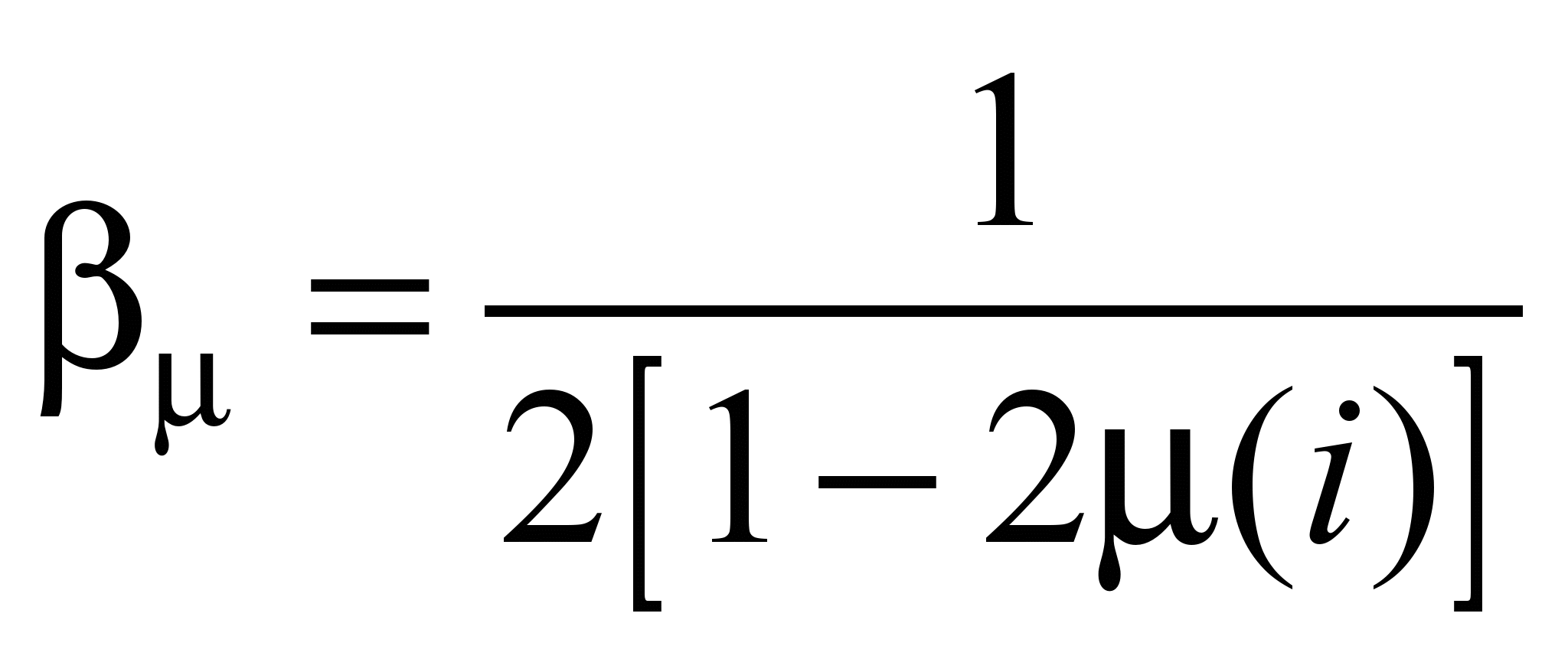 ;
;
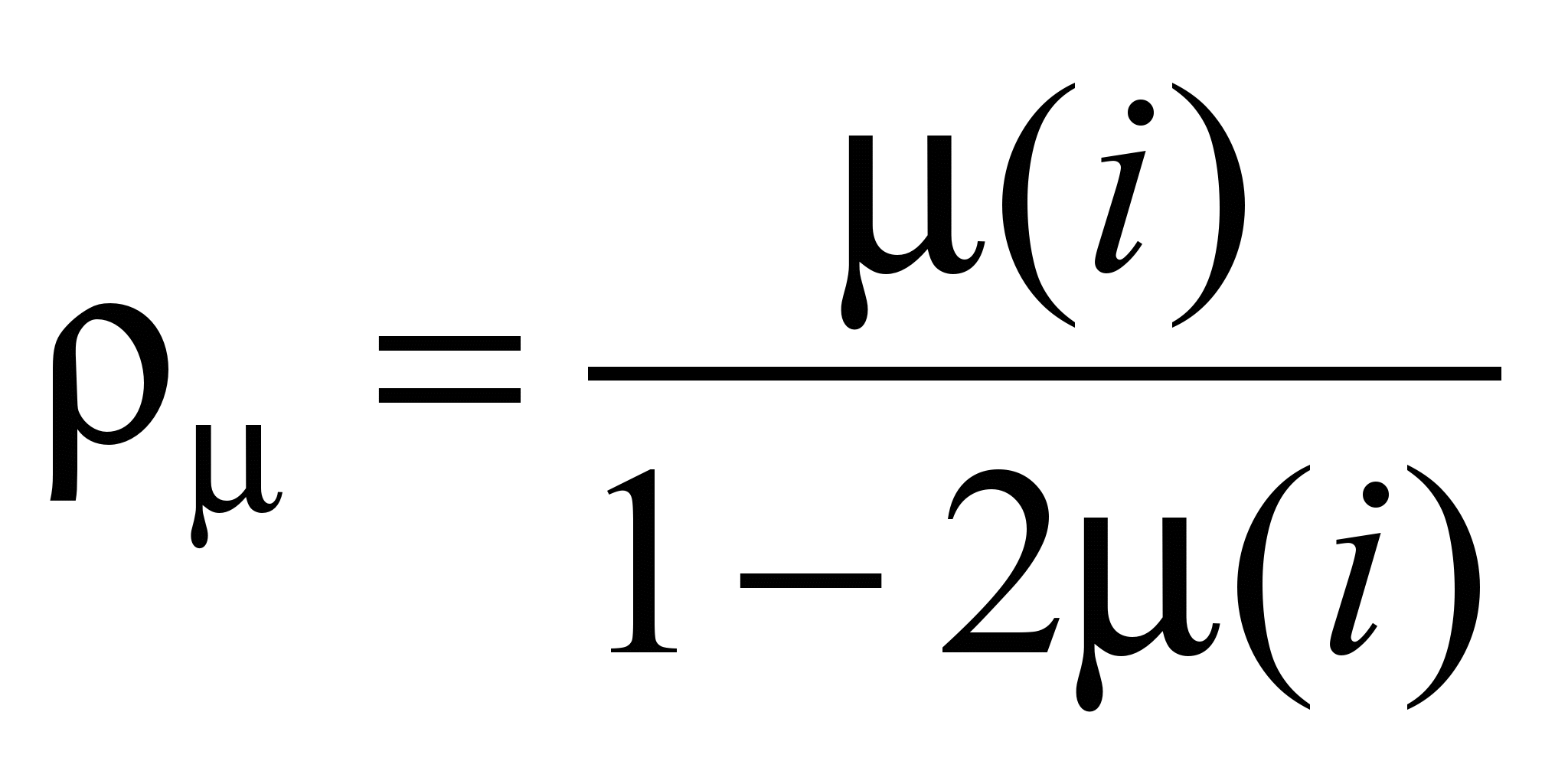 ;
;
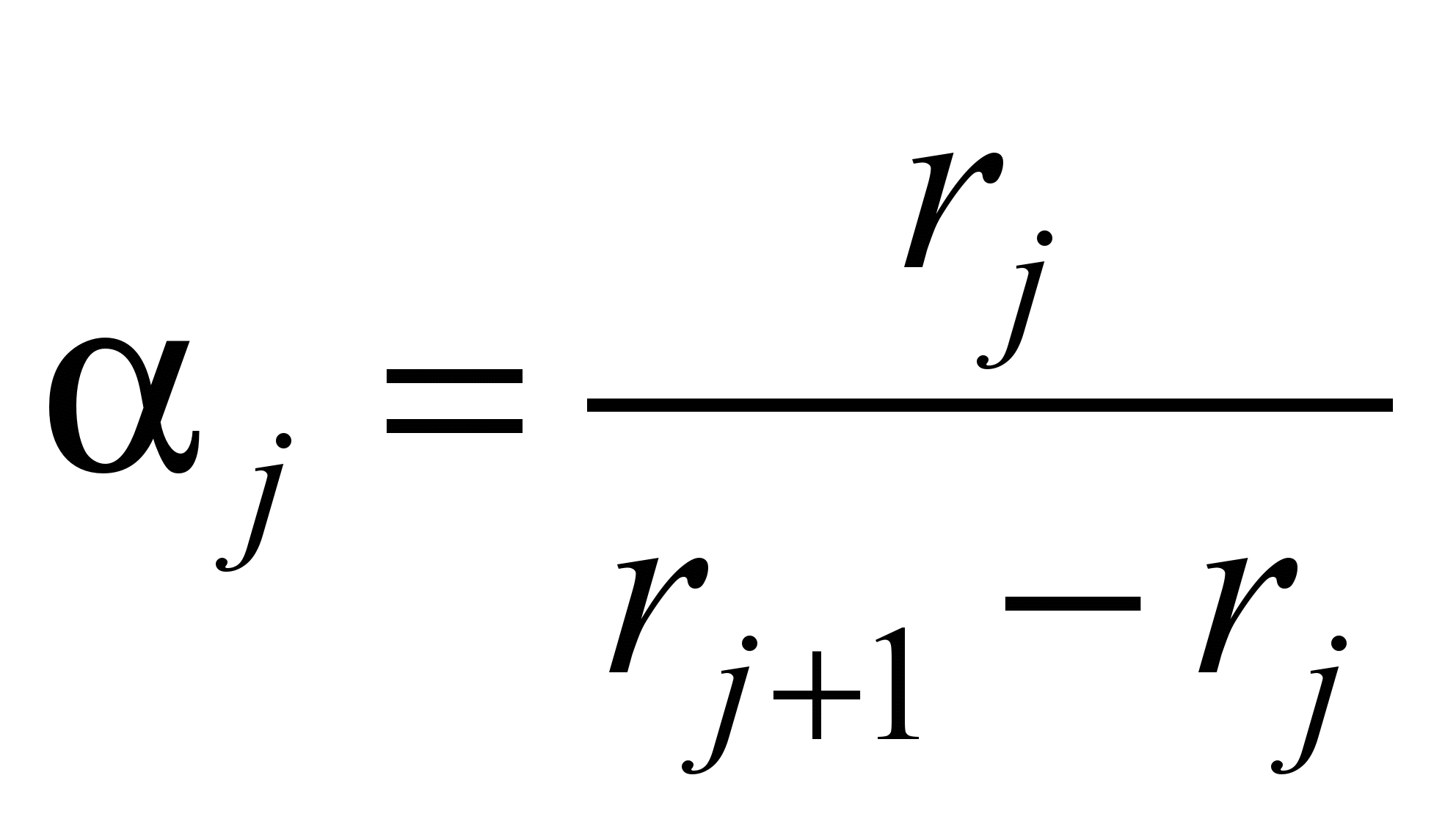 ;
;
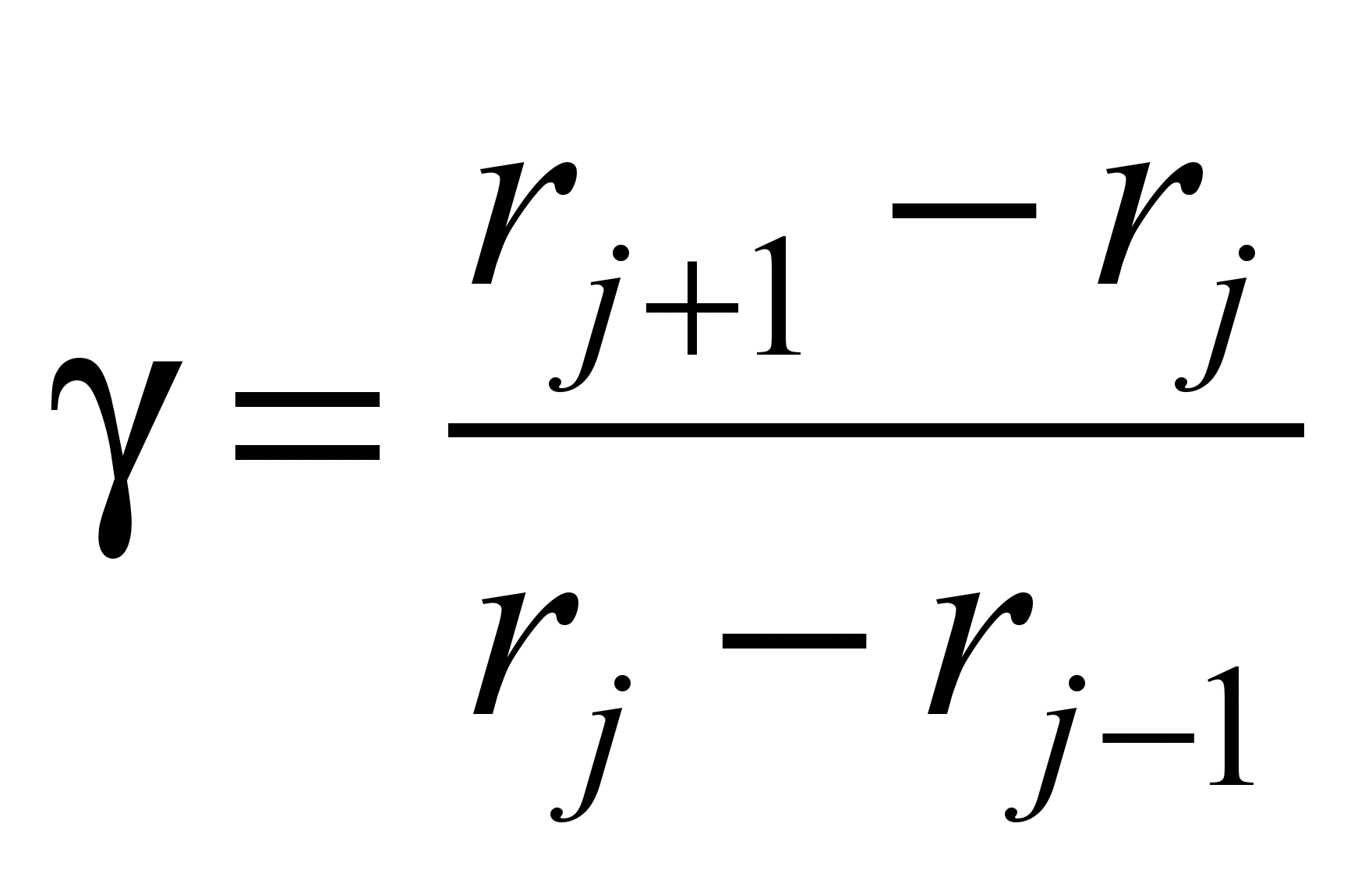 ;
;
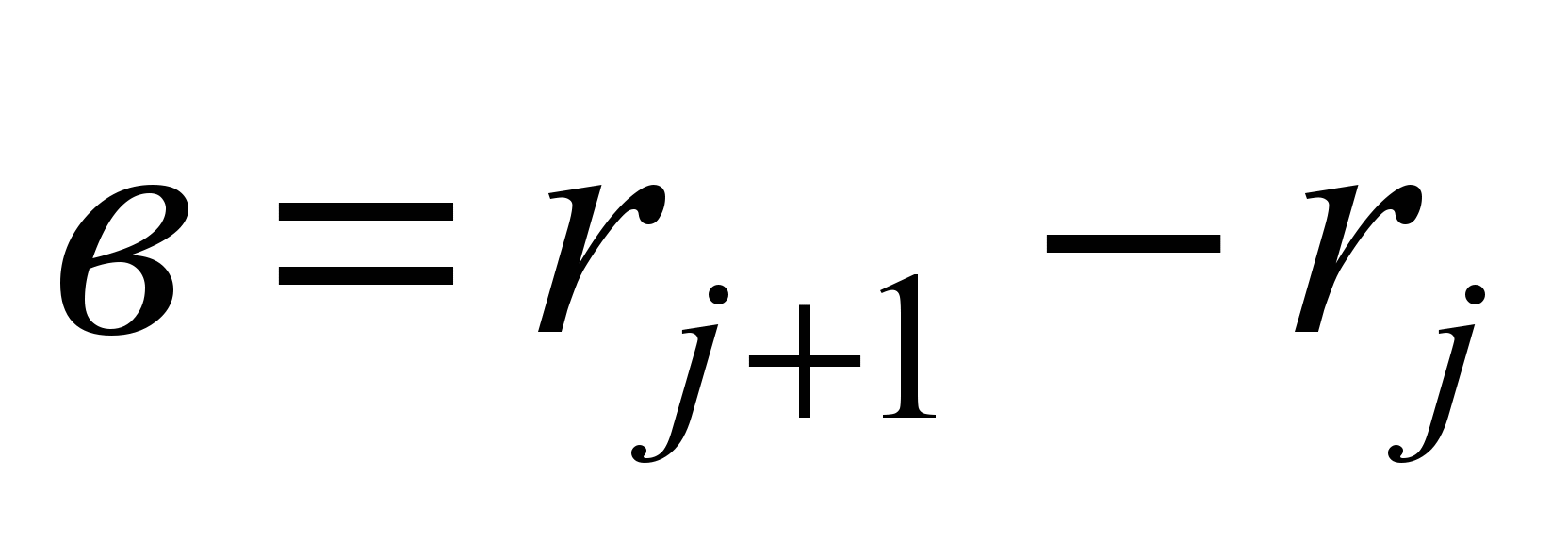 ,
,
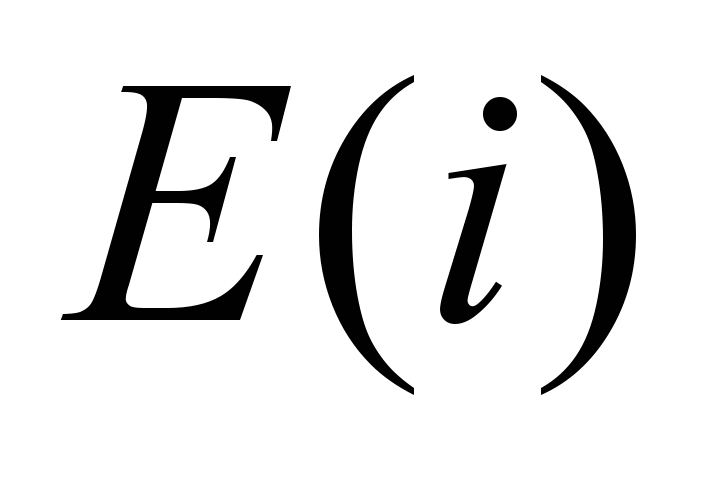 ,
,
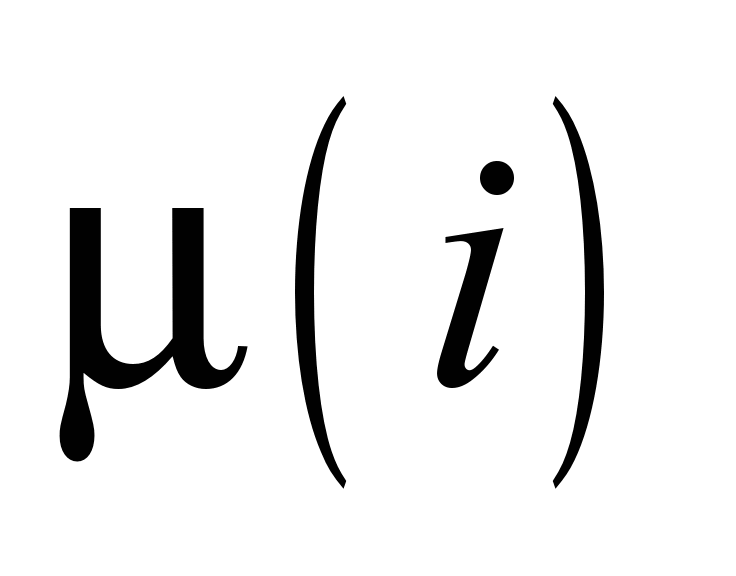 – соответственно модуль упругости и
коэффициент Пуассона материала i-го
слоя основания.
– соответственно модуль упругости и
коэффициент Пуассона материала i-го
слоя основания.
При равномерном
шаге деления радиальной координаты
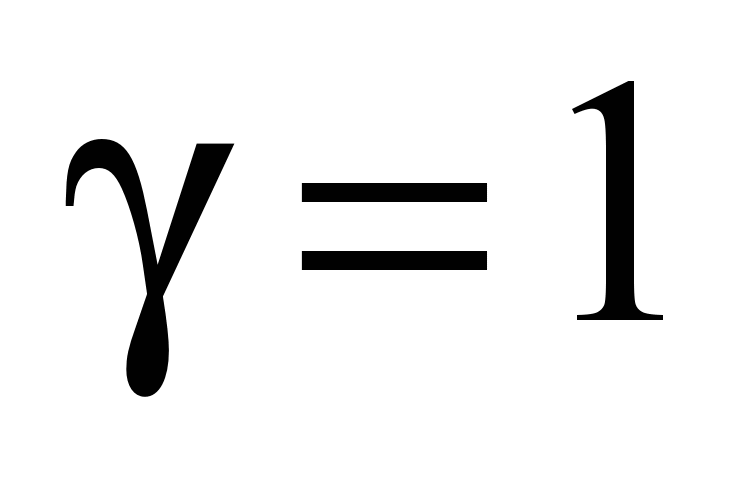 уравнения (2) и (3) принимают вид:
уравнения (2) и (3) принимают вид:
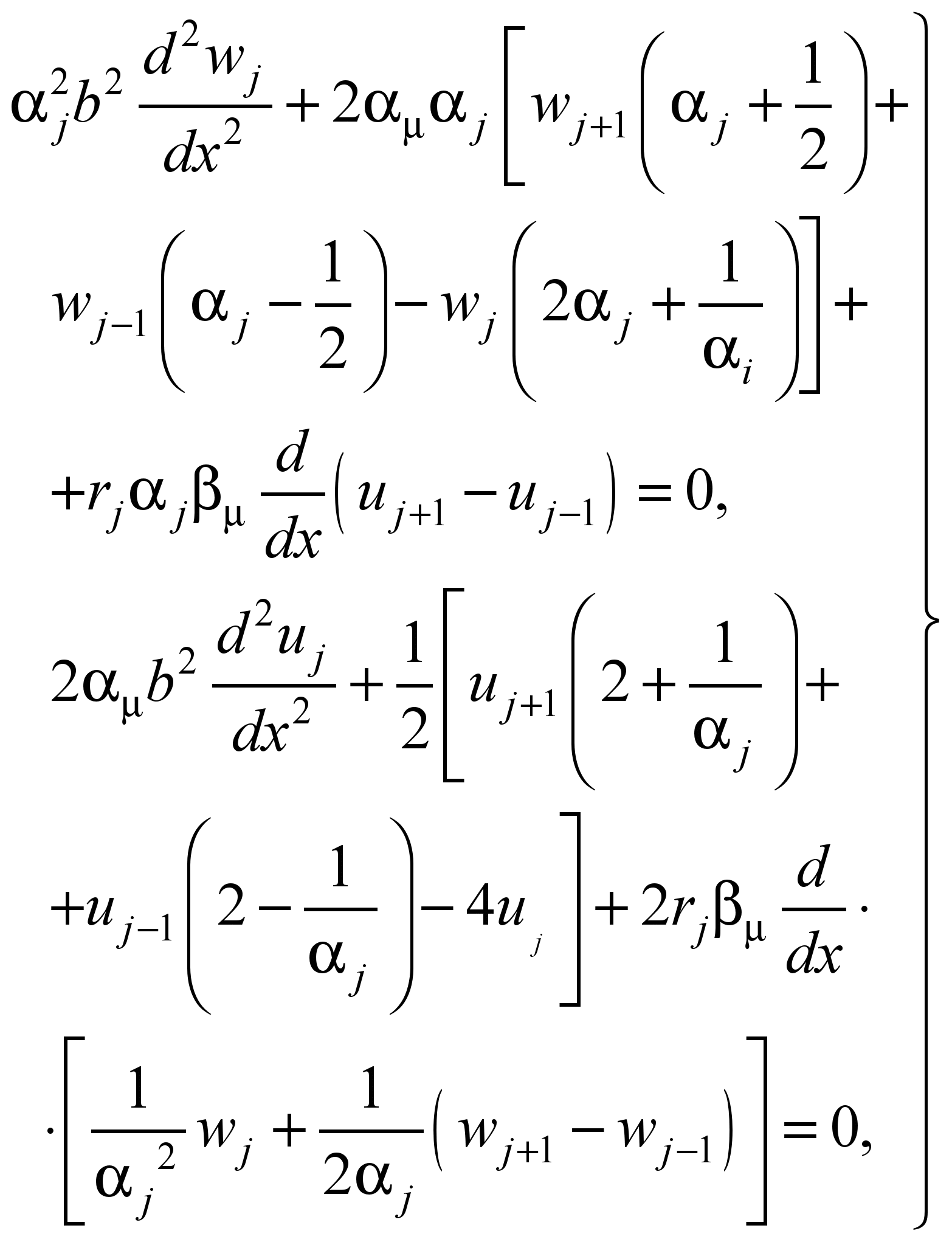 (4)
(4)
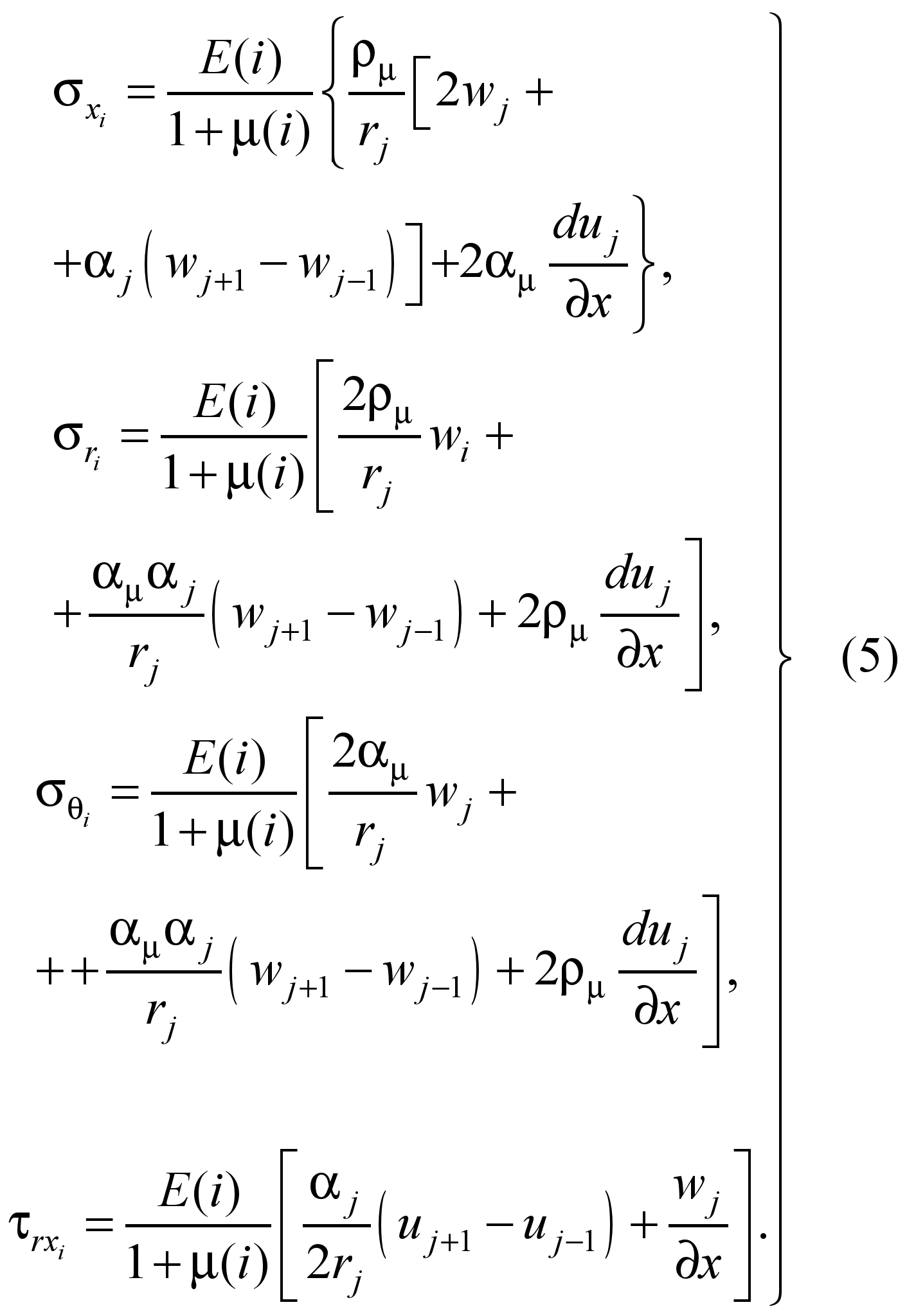
Дифференциальные
уравнения и выражения напряжений для
центрального ребра 0 (цилиндрической
поверхности, для которой r0 =
0) теряют смысл, так как радиальная
координата rj входит в
знаменатели некоторых слагаемых.
Поэтому уравнения перемещений и
напряжений для центрального ребра 0
составлены в прямоугольных координатах,
при этом первая аппроксимирующая
цилиндрическая поверхность заменена
призматической поверхностью, которая
имеет в плане форму многоугольника.
После перехода от прямоугольных
координат к цилиндрическим уравнения
для перемещений и напряжений для
центрального ребра 0 имеют вид:
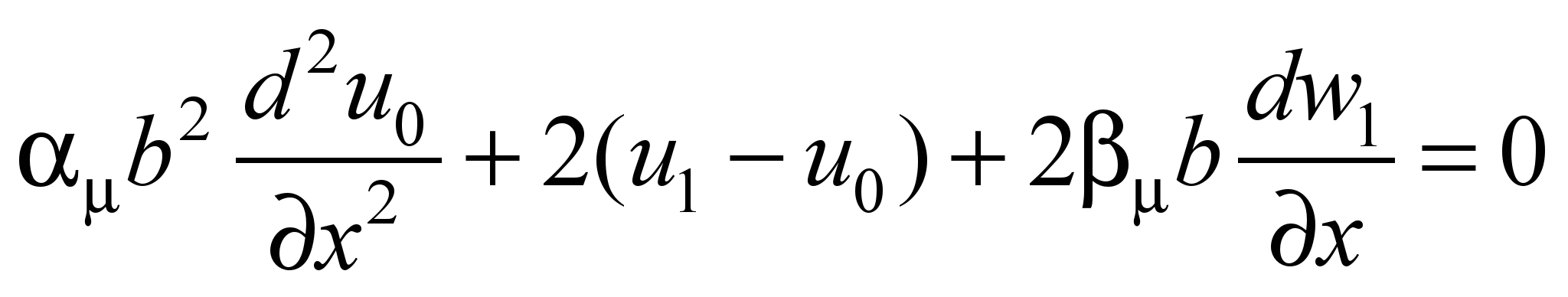 , (6)
, (6)
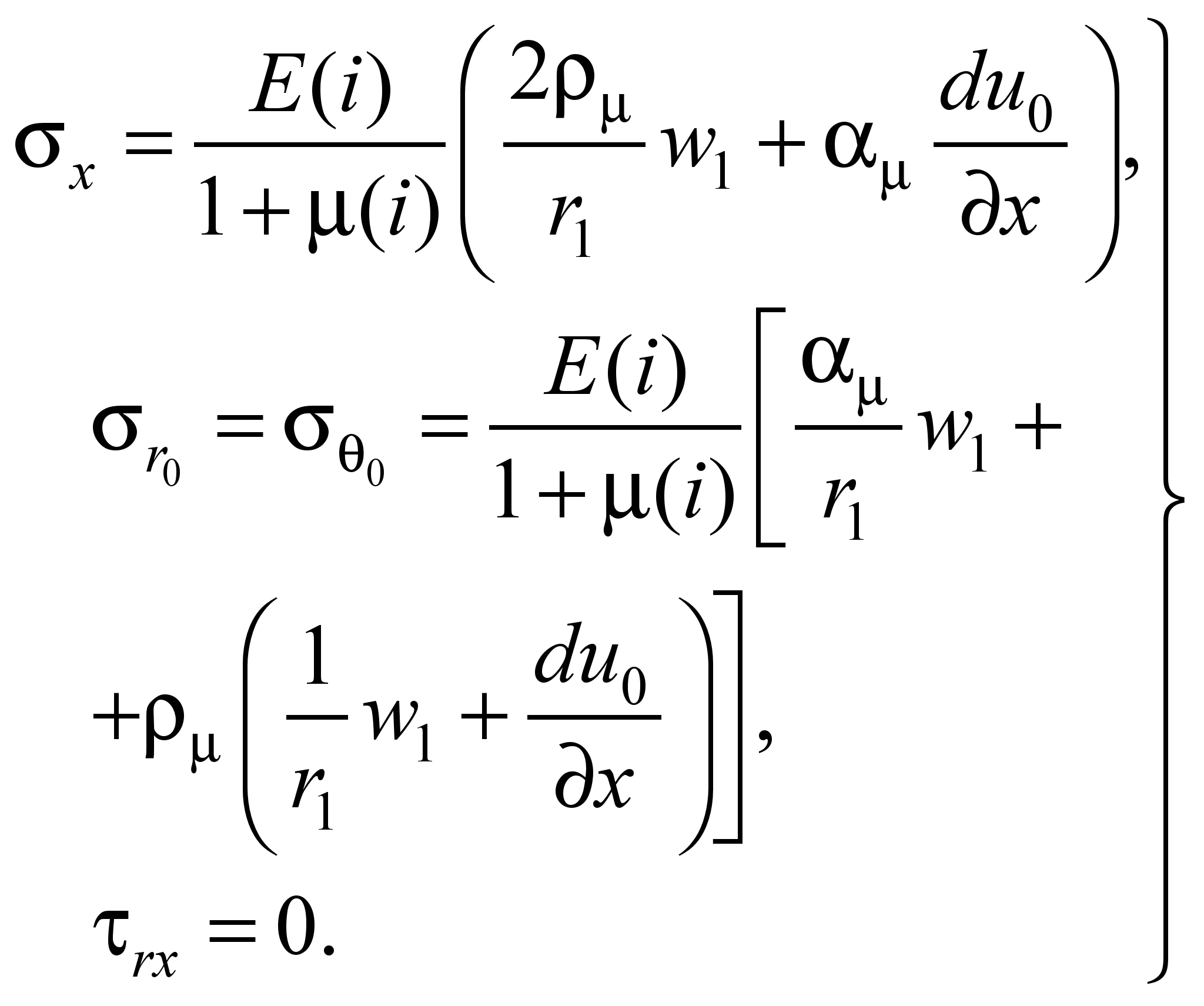 . (7)
. (7)
Результаты
Решая задачу о
напряженно-деформированном состоянии
земляного полотна железнодорожного
пути, представленного осесимметричной
столбчатой моделью, берем четыре
линии-ребра, расположенных на
цилиндрических поверхностях в одной
диаметральной плоскости, окружности
которых в поперечных сечениях имеют
радиусы r0 =
0, r1 = b,
r2 = 2b,
r3 = 3b
= R.
Записывая уравнения
(3) и (5) для ребер 0, 1, 2 (для ребра 3,
расположенного на наружной цилиндрической
поверхности при r3
= R, уравнения
перемещений не составляем, так как
согласно условию затухания перемещений
при r = R,
w = 0, u
= 0), получаем для i-го
слоя основания систему линейных
однородных дифференциальных уравнений
с постоянными коэффициентами, которая
после перехода к безразмерной координате
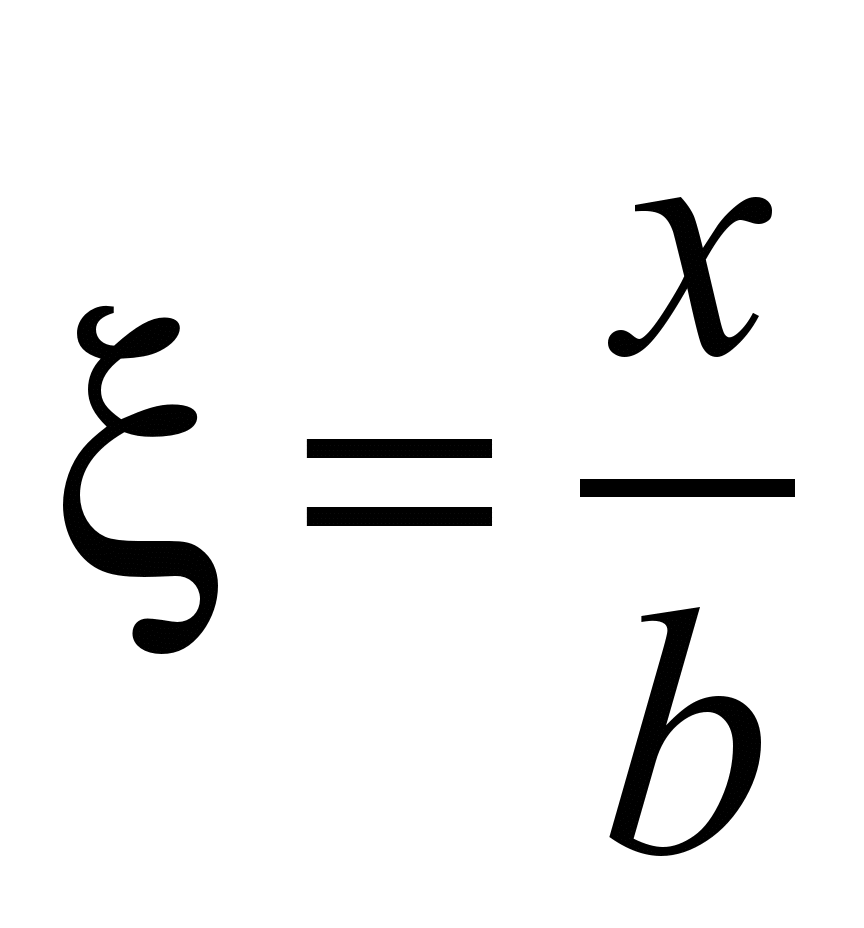 с учетом rj
= jb, αj
= j имеет вид:
с учетом rj
= jb, αj
= j имеет вид:
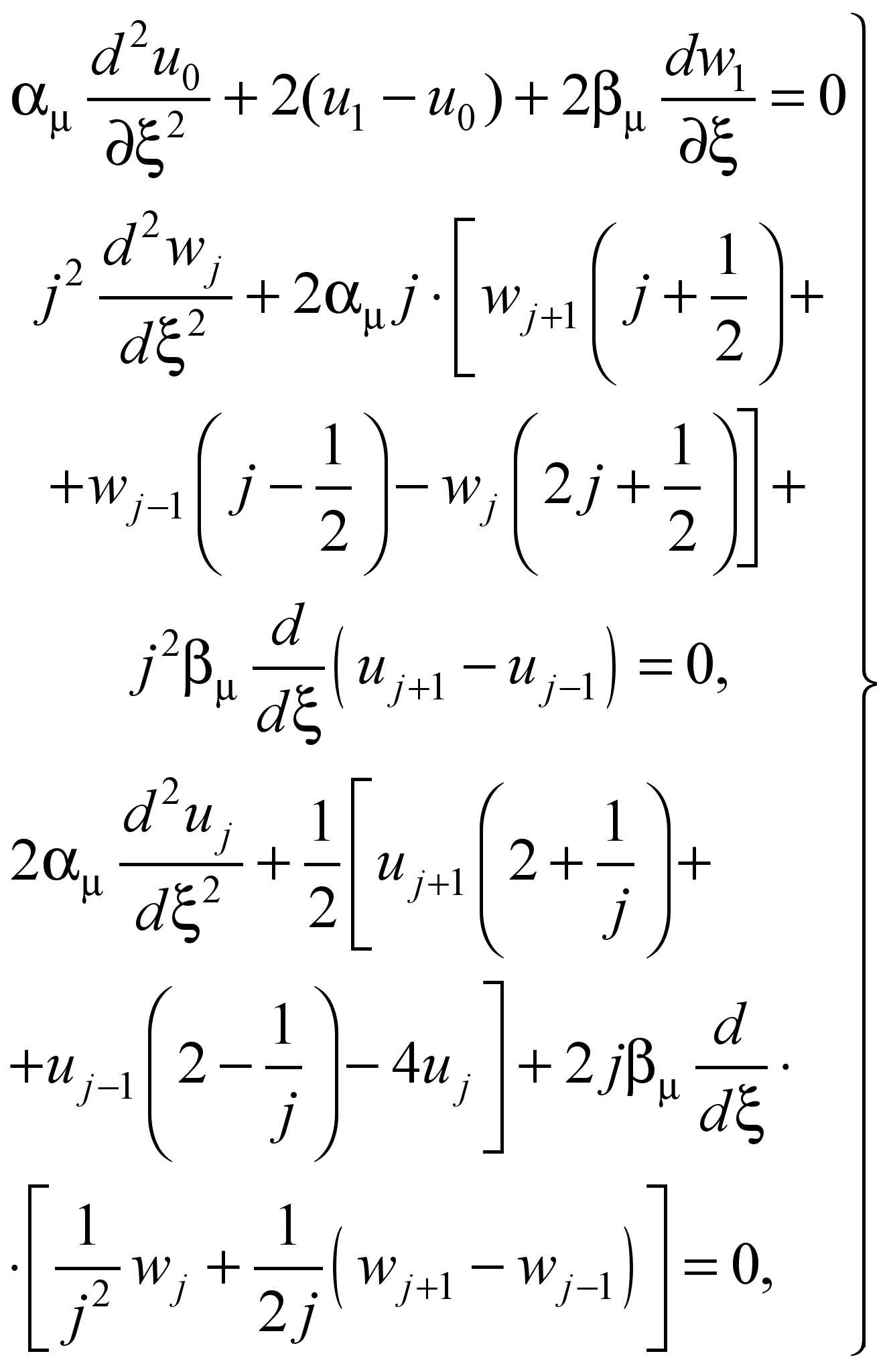 (8)
(8)
(j
= 1, 2).
Интегрирование
системы уравнений (8) целесообразно
проводить численным методом [11], в
котором функции от матриц представляют
рядами. После приведения системы
дифференциальных уравнений (8) к
нормальному виду последнюю запишем в
виде одного матричного уравнения:
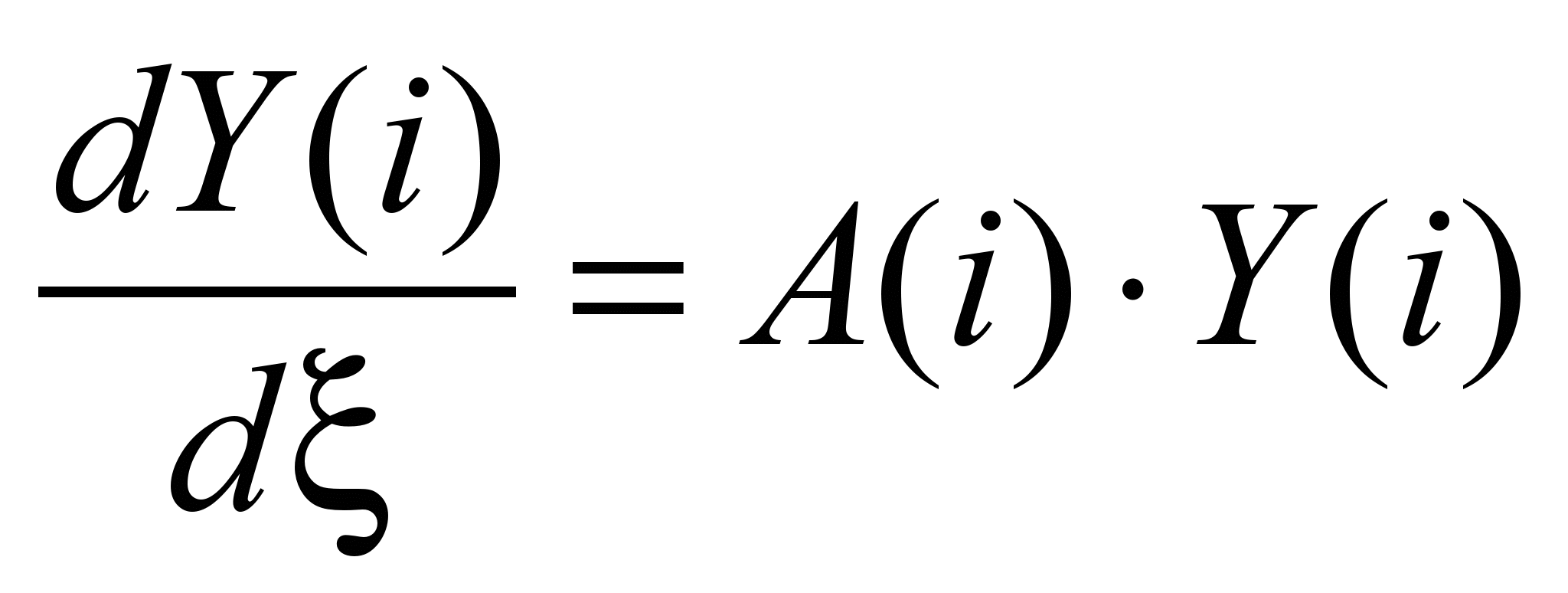 , (9)
, (9)
где
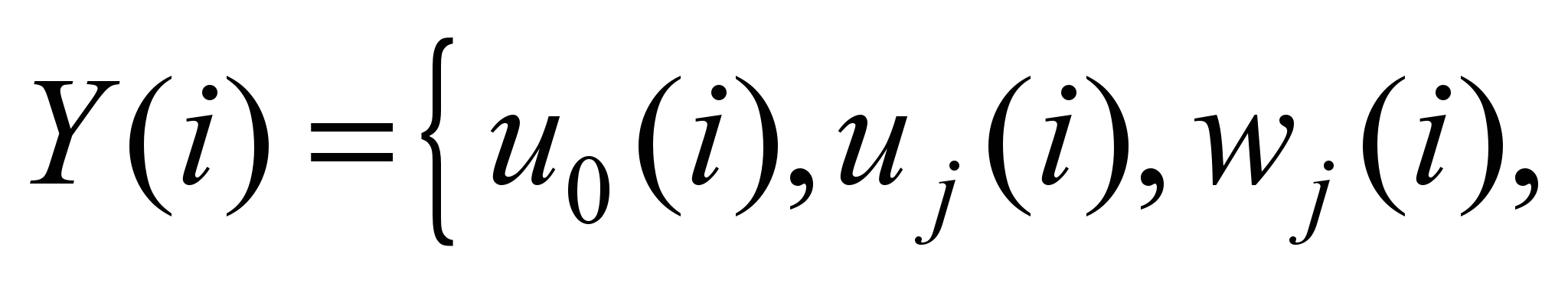
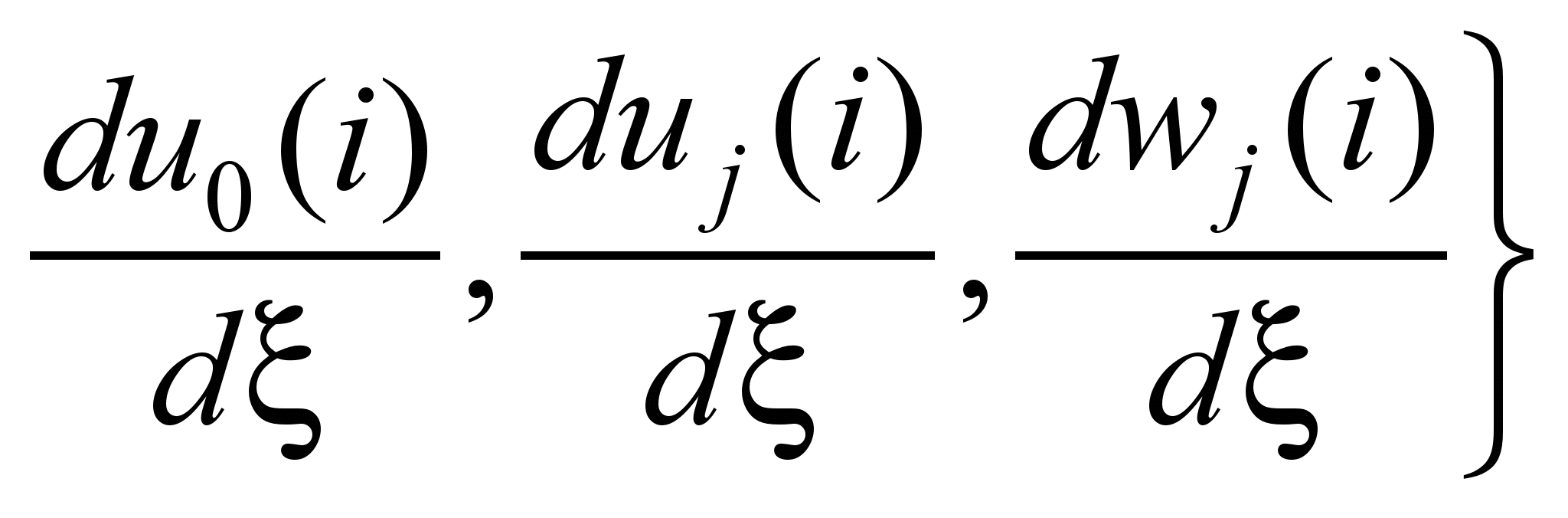 – столбцовая матрица
искомых функций и их производных;
– столбцовая матрица
искомых функций и их производных;
 –
квазиматрица вида:
–
квазиматрица вида:
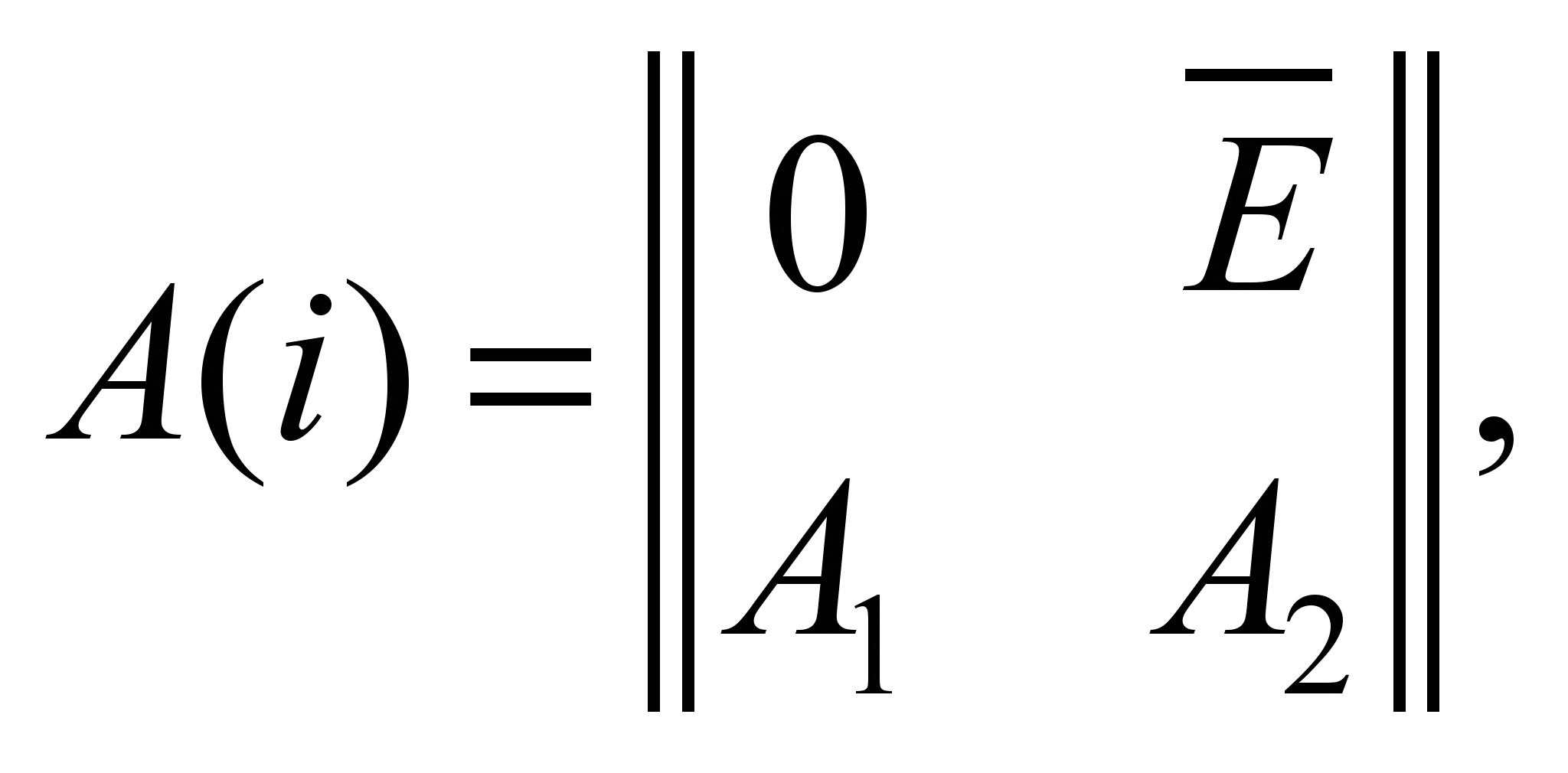
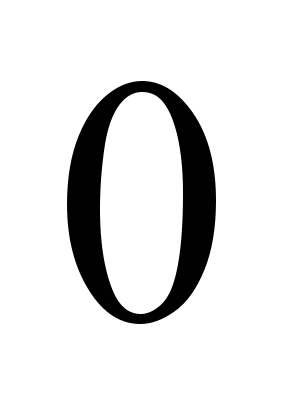 и
и
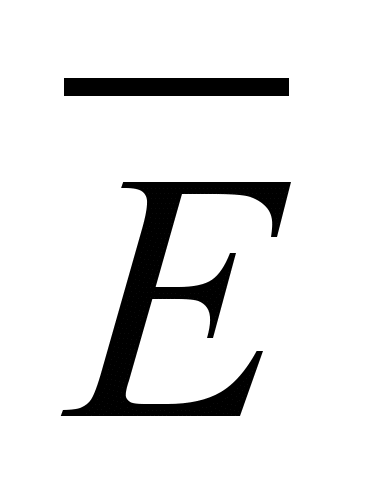 – соответственно нулевая и единичная
матрицы;
– соответственно нулевая и единичная
матрицы;
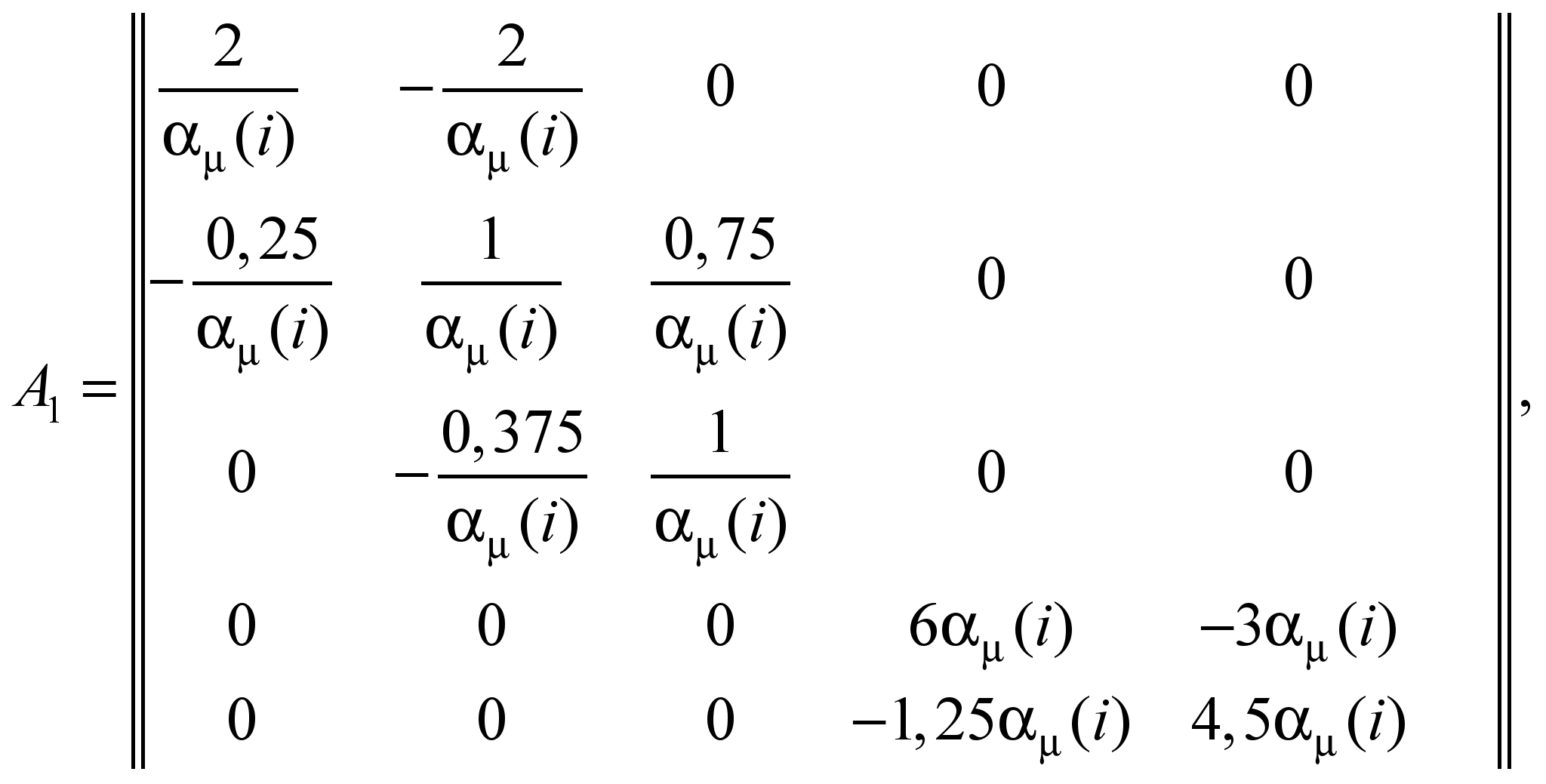
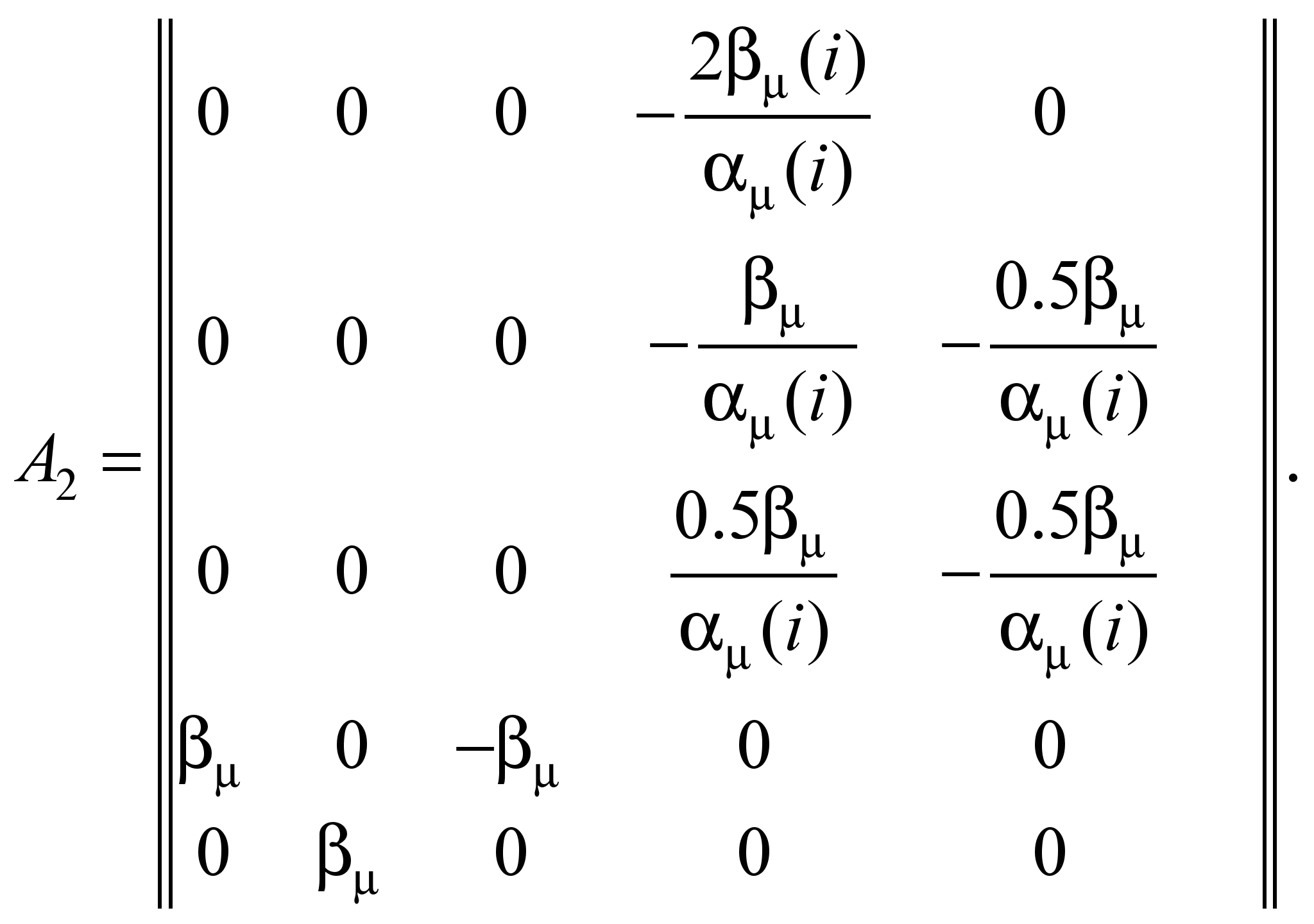
Для каждого слоя
записывают свою систему уравнений (9).
Решение системы
уравнений (9) будем отыскивать в виде:
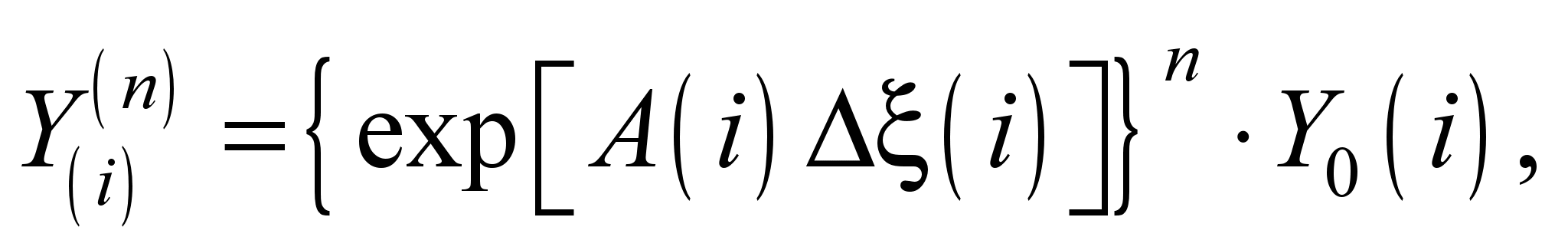 (10)
(10)
где
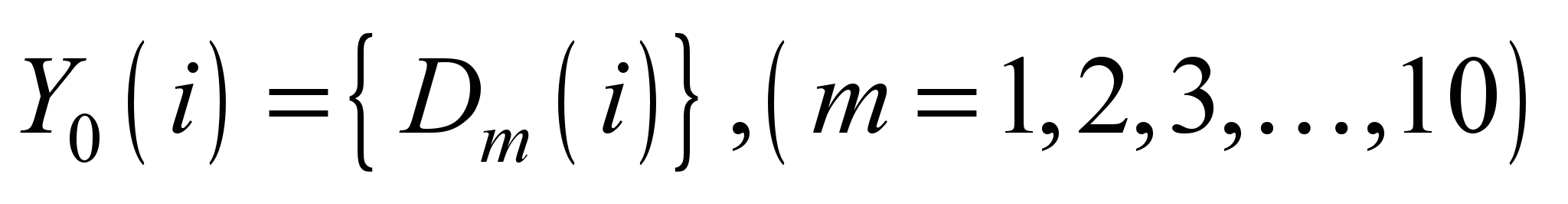 – столбцовая матрица постоянных
интегрирования;
– столбцовая матрица постоянных
интегрирования;
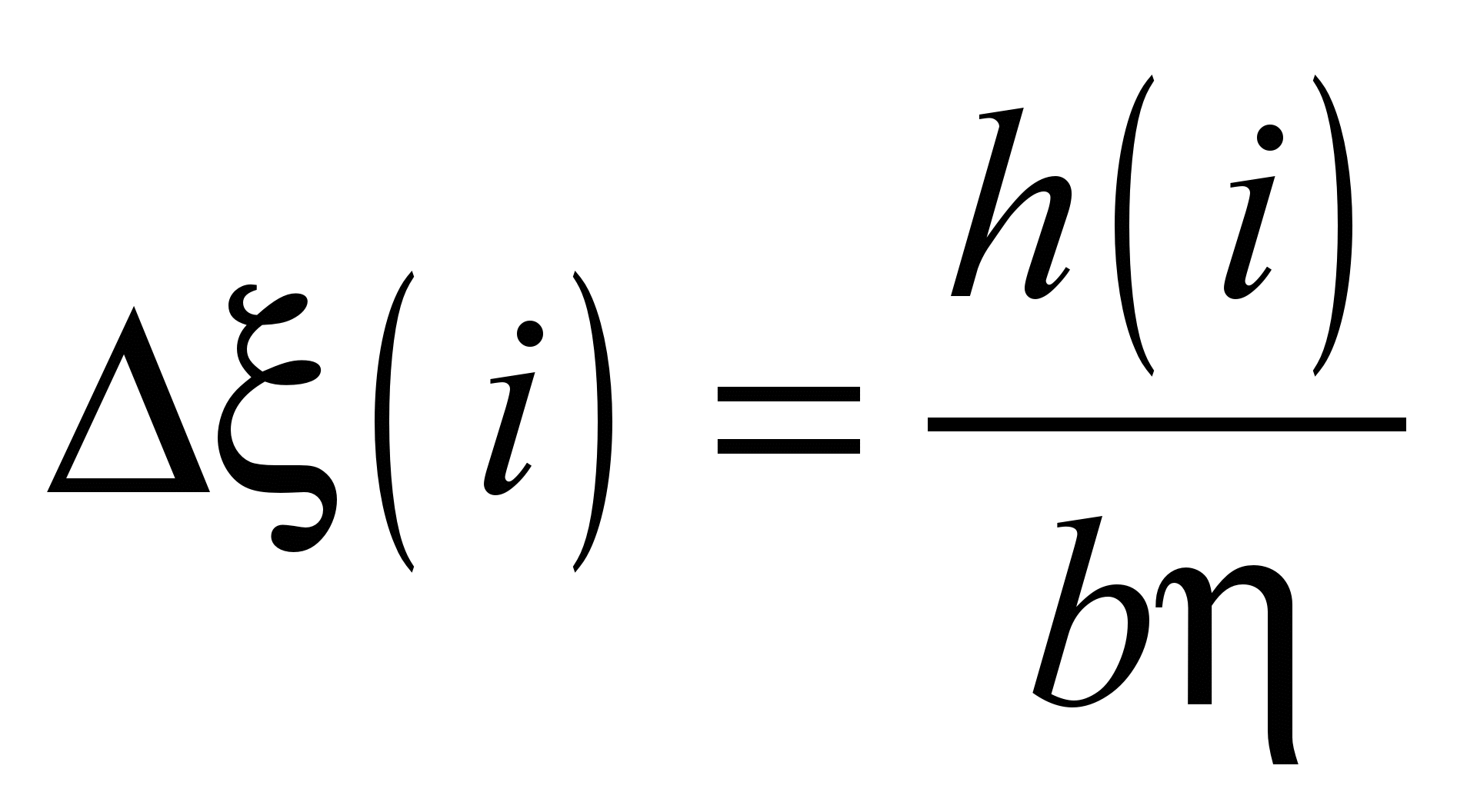 – шаг интегрирования; h(i) –
толщина i-го слоя; (n = 1, 2, 3,
– число точек на отрезке интегрирования
– шаг интегрирования; h(i) –
толщина i-го слоя; (n = 1, 2, 3,
– число точек на отрезке интегрирования
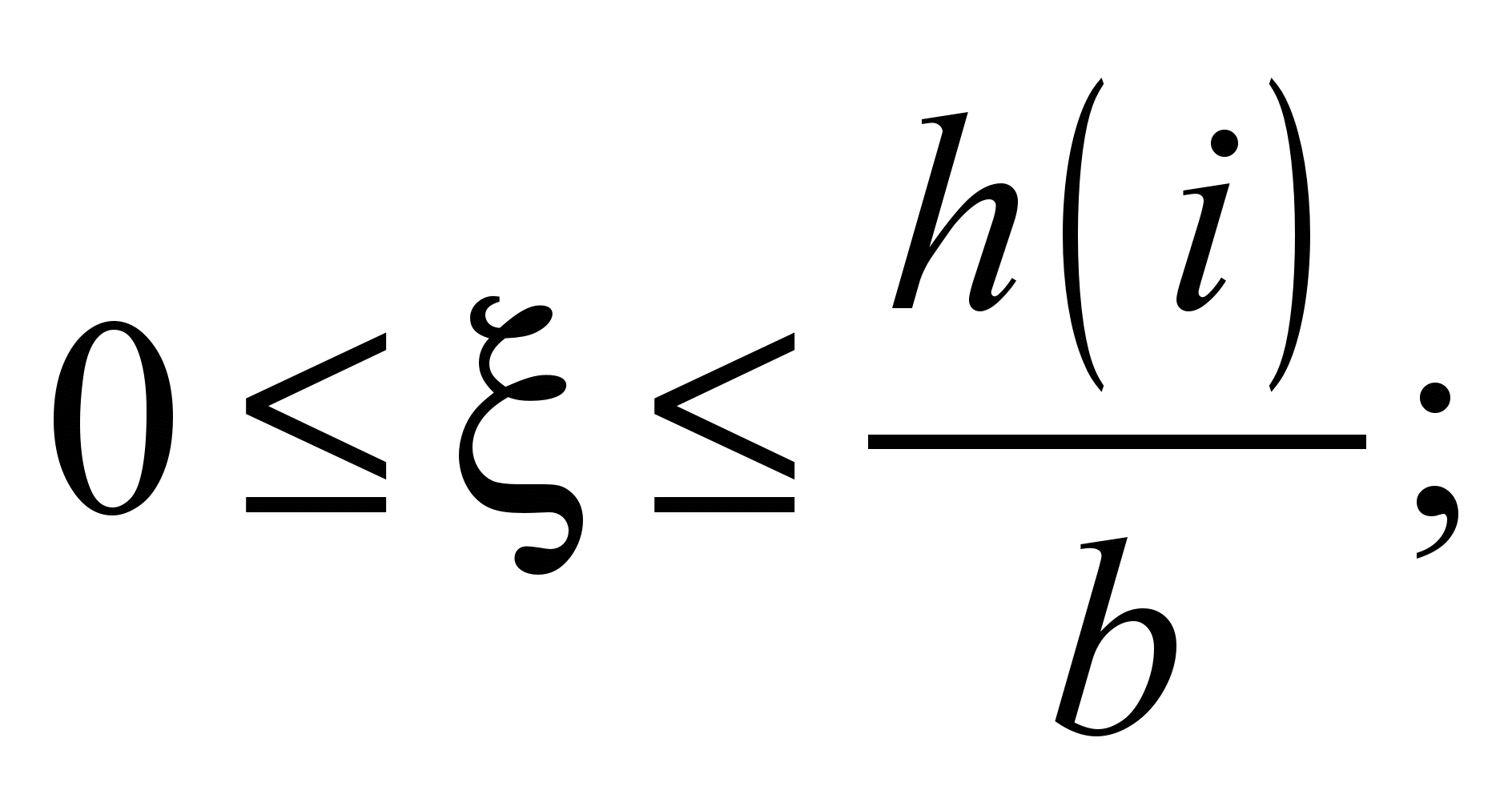
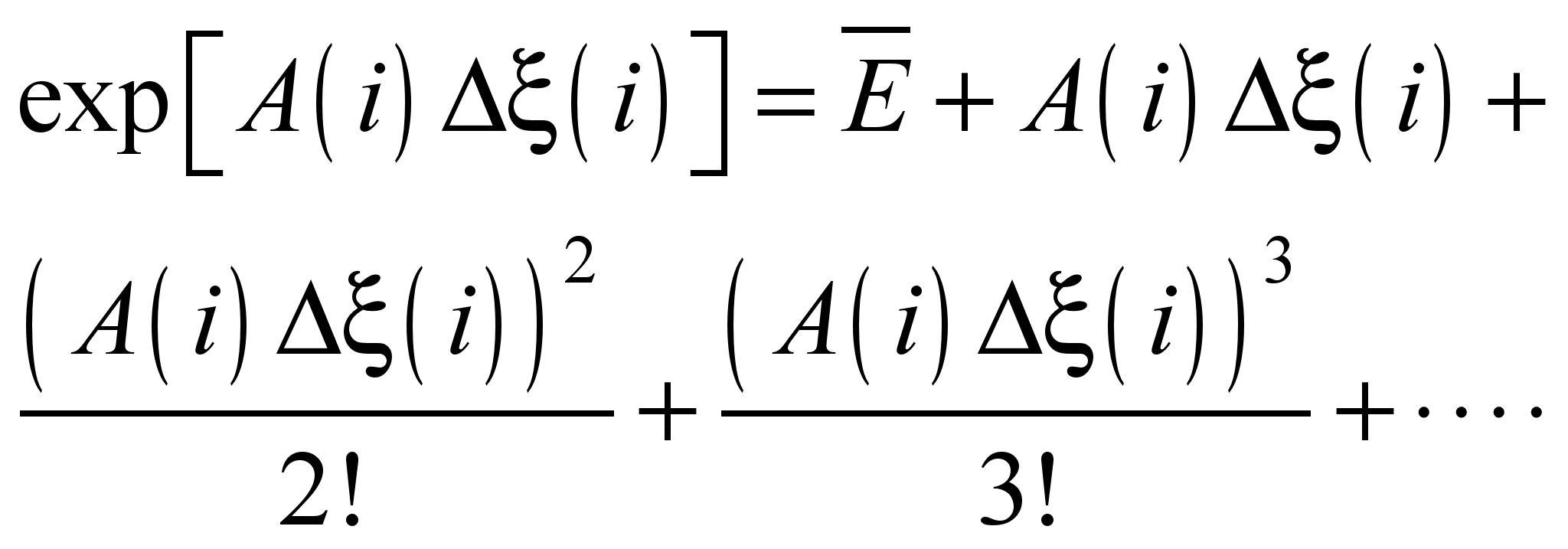
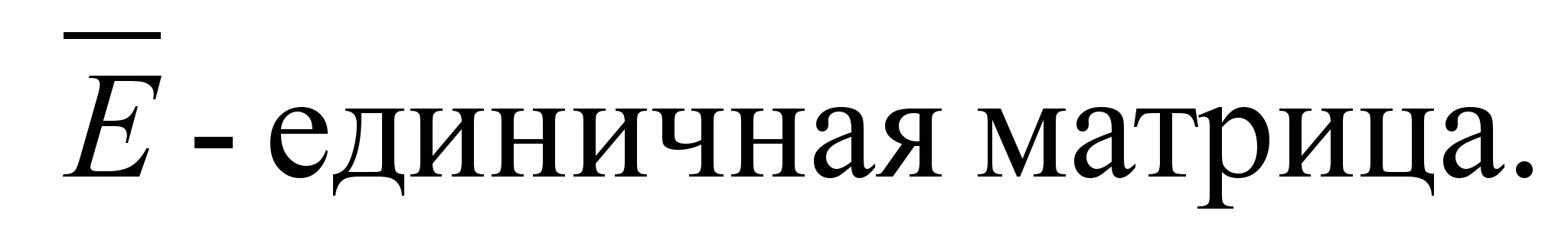
При ξ(i) = 0,
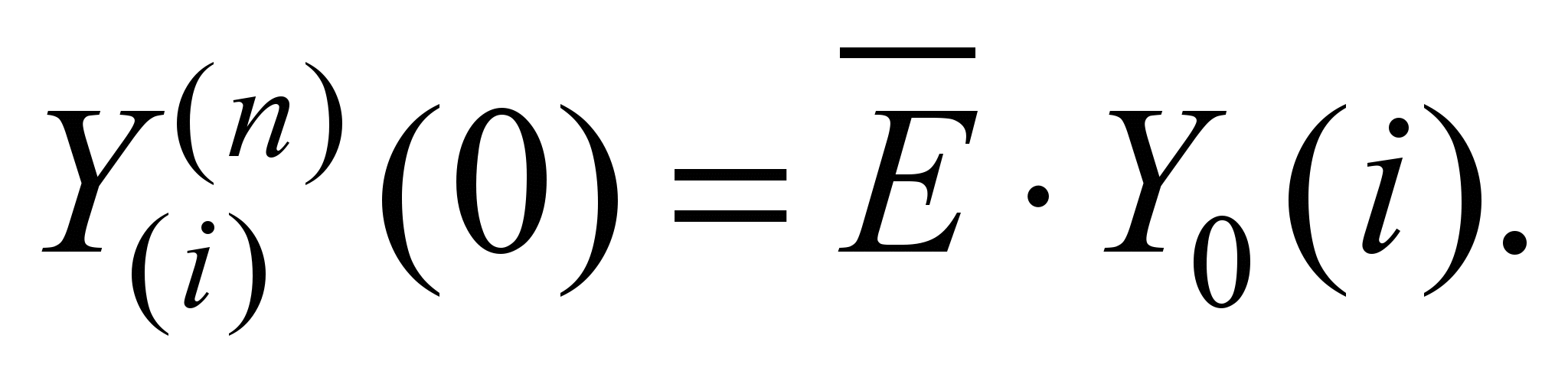 (11)
(11)
Из выражения (11)
следует:

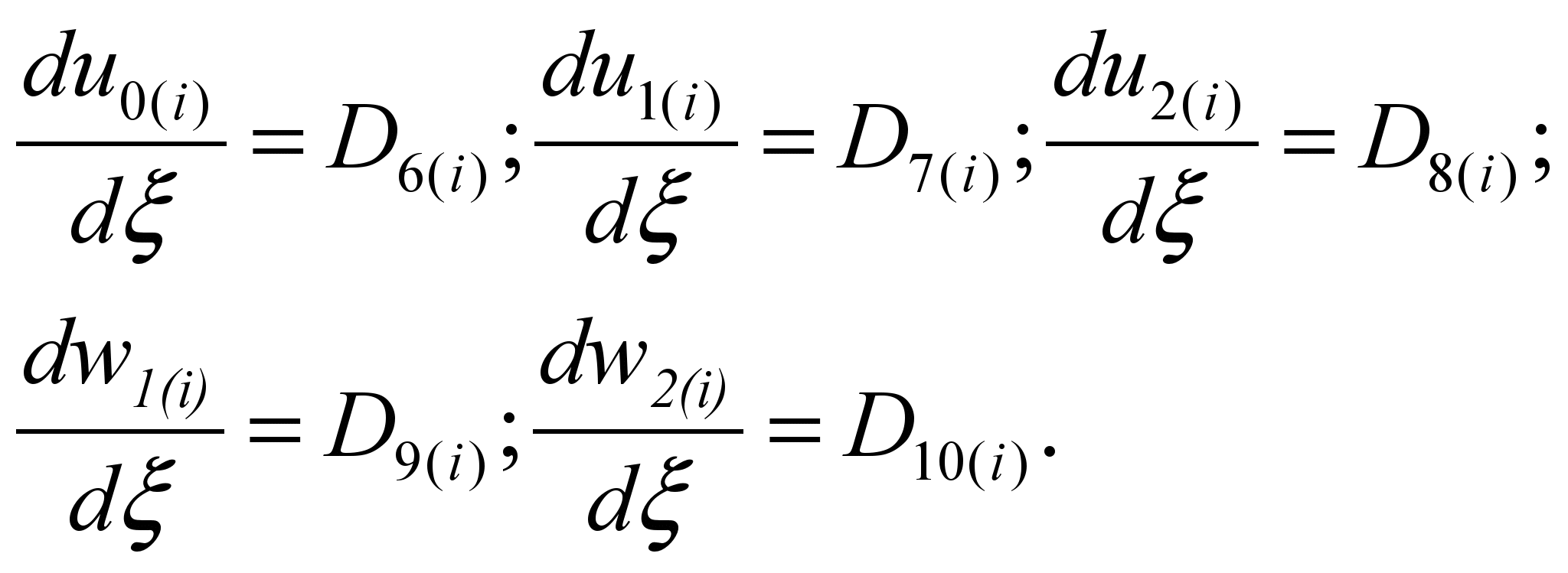

Таким образом, для
каждого слоя решается своя система
дифференциальных уравнений, и общее
число неизвестных постоянных
интегрирования составляет и
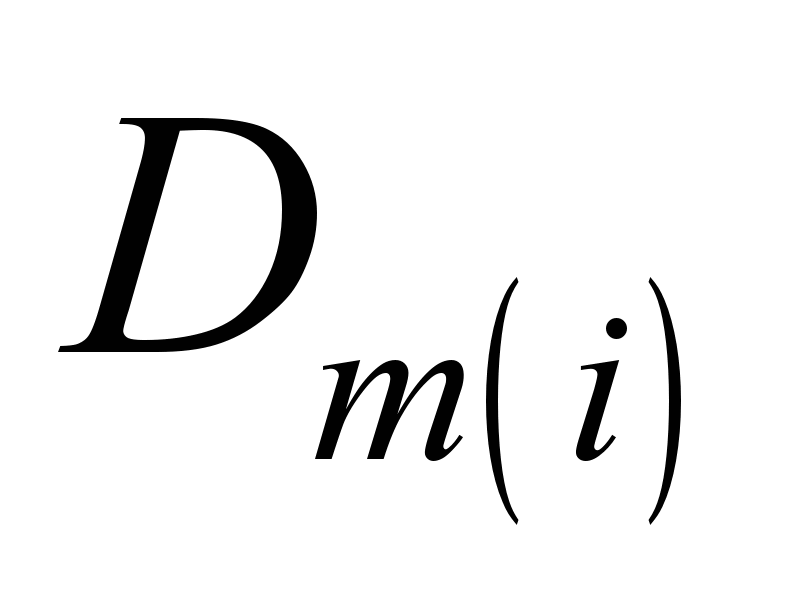 .
Для их определения привлекаем условия
на граничных плоскостях основания и
условия сопряжения слоев на линии их
контакта:
.
Для их определения привлекаем условия
на граничных плоскостях основания и
условия сопряжения слоев на линии их
контакта:
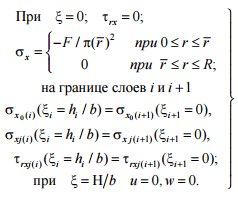 (12)
(12)
Следует отметить,
что равенство нормальных и касательных
напряжений на линии сопряжения слоев
неоднородного основания позволяет
учесть разную деформативность слоев
основания.
Удовлетворяя
граничным условиям (12), получим систему
алгебраических уравнений:
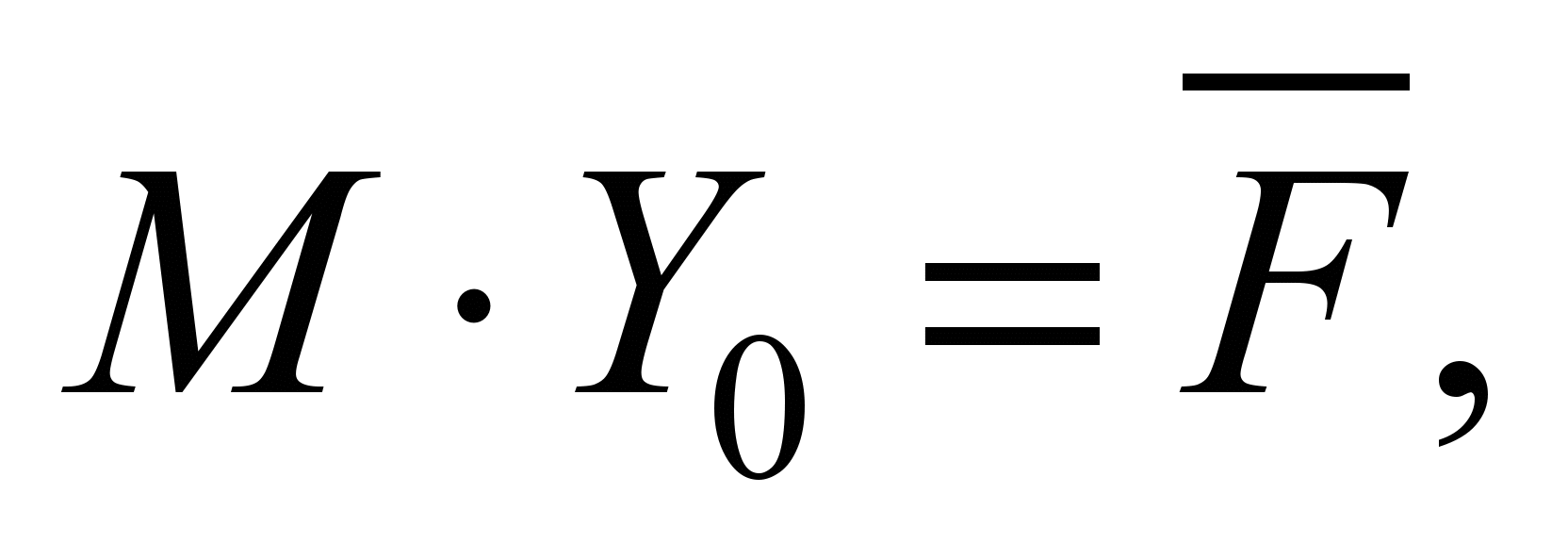 (13)
(13)
где
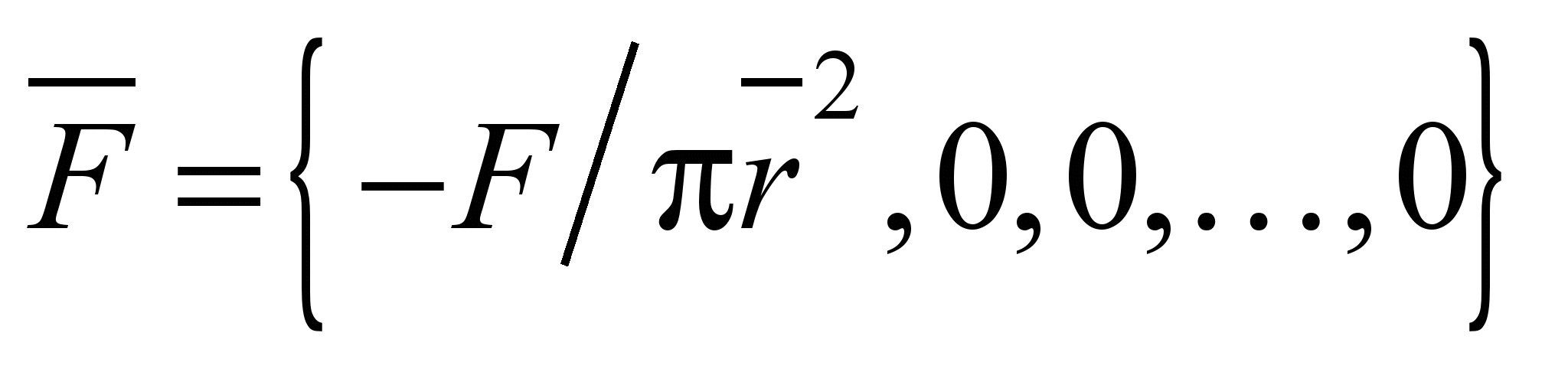 – вектор правых частей;
– вектор правых частей;
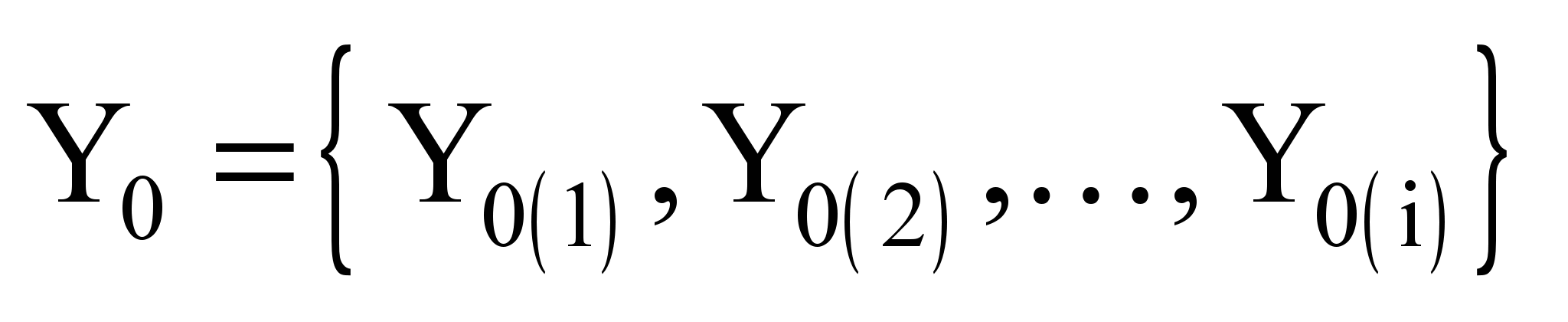 – столбцовая
квазиматрица постоянных интегрирования;
– столбцовая
квазиматрица постоянных интегрирования;
М – квазиматрица
коэффициентов.
Так как квазиматрица
М имеет ленточную структуру, то
система (13) хорошо обусловлена.
После решения
системы (9) составляющие перемещений
u(i), w(i) и их производные
определяем при помощи зависимости:
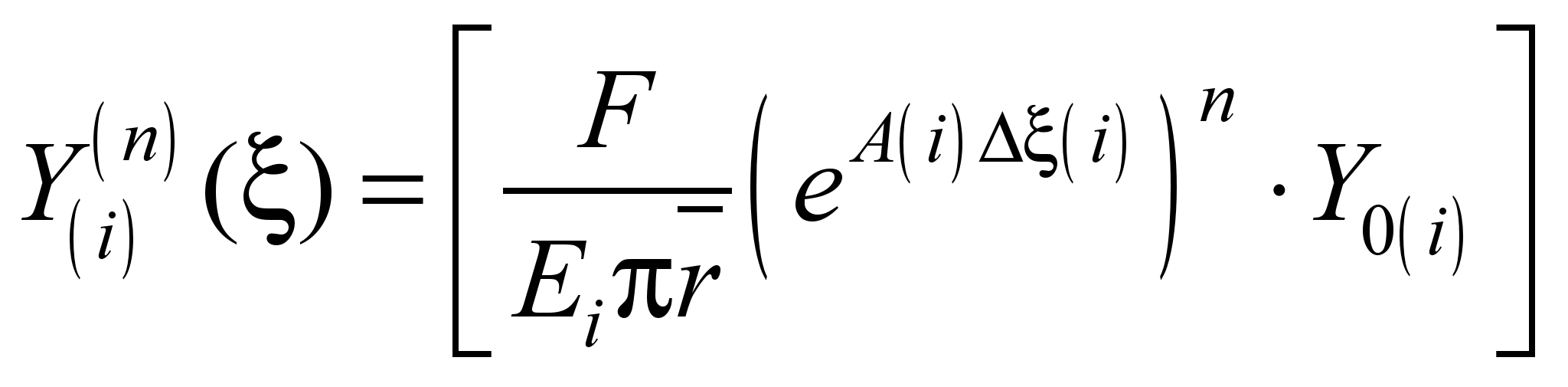 . (14)
. (14)
Подстановкой
значений
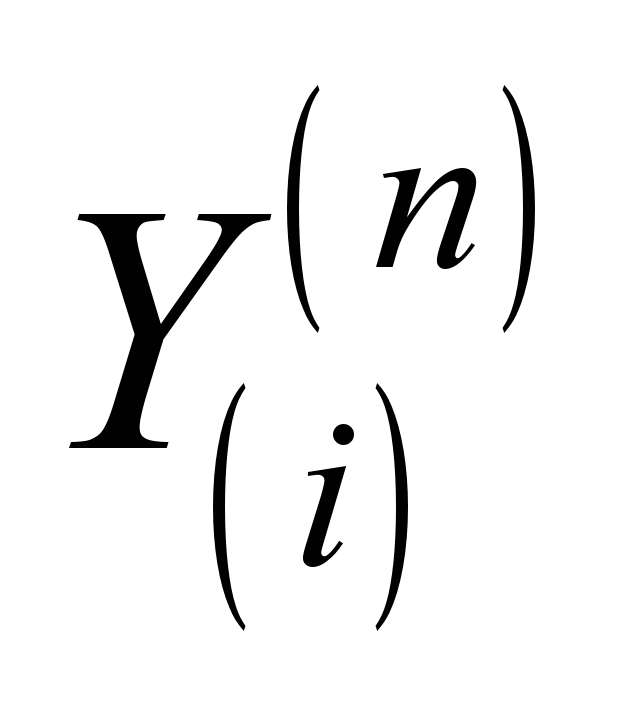 в (5) и (7) определяем напряжения в i-том
слое основания.
в (5) и (7) определяем напряжения в i-том
слое основания.
Изложенный алгоритм
определения напряженно-деформированного
состояния неоднородного по глубине
основания легко может быть реализован
при помощи компьютерных программ.
При проектировании
и проверке прочности земляного полотна
железнодорожного пути необходимо
рассматривать совместную работу
рельсо-шпальной решетки и основной
площадки земляного полотна. Будем
учитывать только вертикальную
составляющую поездной нагрузки,
передаваемой на основную площадку
земляного полотна через элементы
верхнего строения пути.
Поездную нагрузку
через рельсо-шпальную решетку балластный
слой воспринимает и упруго передает
на основную площадку земляного полотна.
Балластный слой под рельсо-шпальной
решеткой находится в неоднородном
напряженном состоянии, т. к. давление
по нижней постели шпалы различно. В
сечении поперек шпалы давление больше
под продольной осью и уменьшается к
краям постели. Зона распределения
давления от шпалы по глубине балластного
слоя постепенно расширяется, что говорит
о его некоторой распределительной
способности, при этом давление по
глубине изменяется нелинейно.
Экспериментальные исследования
показывают, что при эпюре шпал 1 600
шт/км (при расстоянии между осями шпал
60 см) полное выравнивание напряжений
происходит на глубине 75 см под шпалами.
Балластный слой,
воспринимая часть поездной нагрузки,
снижает давление на земляное полотно
со стороны рельсо-шпальной решетки.
Поэтому при определении напряжений в
теле земляного полотна необходимо
рассматривать совместную работу
балластного слоя и земляного полотна.
Это приводит к расчетной схеме
двухслойного упругого основания с
разными значениями параметров Ляме
при однородности по глубине земляного
полотна. Если же земляное полотно по
глубине неоднородно, то приходим в
расчетной схеме к многослойному
основанию. Толщина верхнего слоя
основания соответствует толщине
балластного слоя, а нижних согласуется
с условием затухания деформаций и
напряжений по глубине грунтового
основания.
Ниже
рассмотрена практическая реализация
изложенного алгоритма при
проверке прочности земляного
полотна железнодорожного пути в районе
складов ЛВЖ цеха полистирола на одном
химическом заводе. Путь выполнен из
рельсов типа Р-43, уложенных на деревянные
обрезные шпалы первого типа. Эпюра шпал
1 600 шт/км. Балласт из гранитного щебня
средней крупности толщиной 20 см.
Промежуточное крепление костыльного
типа. Путь выполнен из звеньев 12,5 м.
Подвижной состав – это тепловозы с
осевой нагрузкой 200 кН и цистернами
трех типов с разными значениями колесной
базы и с одинаковыми значениями жесткой
базы, которая составляет 1 800 мм.
Осевая нагрузка составляла от 217,5 кН
до 237,05 кН. Земляное полотно сложено из
суглинков мощностью 6 м со следующими
нормативными значениями основных
характеристик:
– коэффициент
пористости
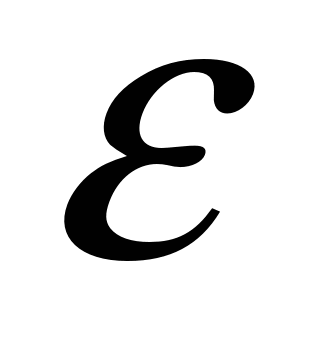 = 0,65;
= 0,65;
– модуль деформации
Е = 19 МПа;
– угол внутреннего
трения
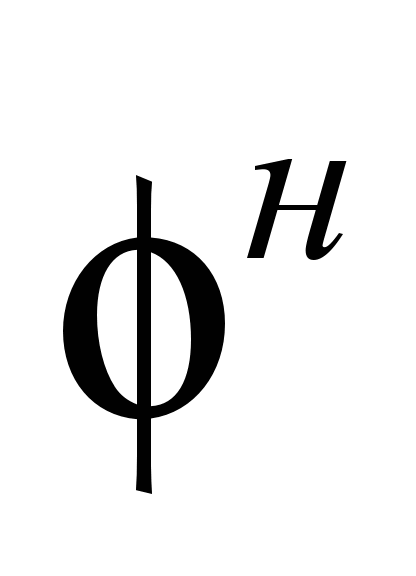 = 220;
= 220;
– удельное сцепление
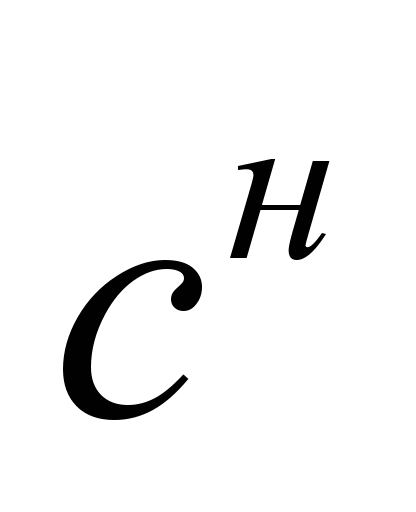 = 0,028 МПа.
= 0,028 МПа.
Связные грунты, к
которым относятся и суглинки, обладают
распределительной способностью, т. е.
способностью деформироваться вне зоны
приложения нагрузки. Данные экспериментов
свидетельствуют, что при нагрузке,
распределенной равномерно по кругу
радиусом
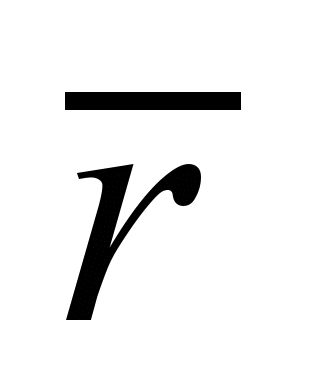 ,
затухание перемещений и напряжений на
граничной поверхности основания
происходит на расстоянии
,
затухание перемещений и напряжений на
граничной поверхности основания
происходит на расстоянии
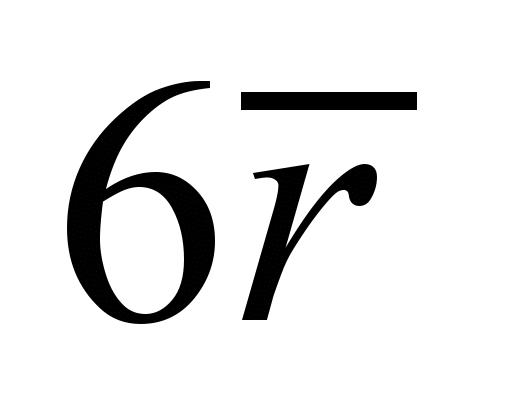 ,
по глубине основания − на расстоянии
,
по глубине основания − на расстоянии
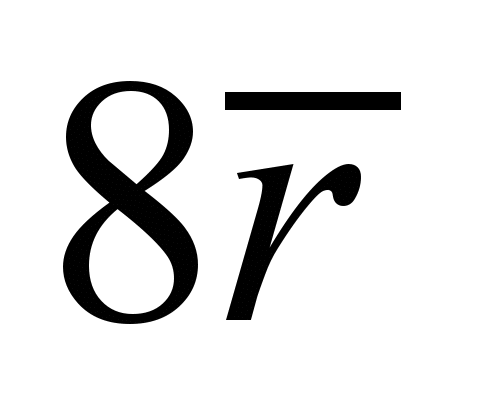 .
.
Учитывая, что в
данном случае толщина балластного слоя
незначительна (20 см) по сравнению с
толщиной грунтового основания, й и
деформаций, влиянием последнего на
напряженно-деформированное состояние
земляного полотна можно пренебречь.
Малая толщина балластного слоя приводит
к значительной неравномерности, в
продольном направлении пути его давления
на земляное полотно. При этом основная
часть давления приходится на площадку,
совпадающую с проекцией нижней постели
шпалы под подошвой рельса на основную
площадку земляного полотна. Это также
говорит о возможности в данном случае
не учитывать влияние балластного слоя
при определении осадок и напряжений
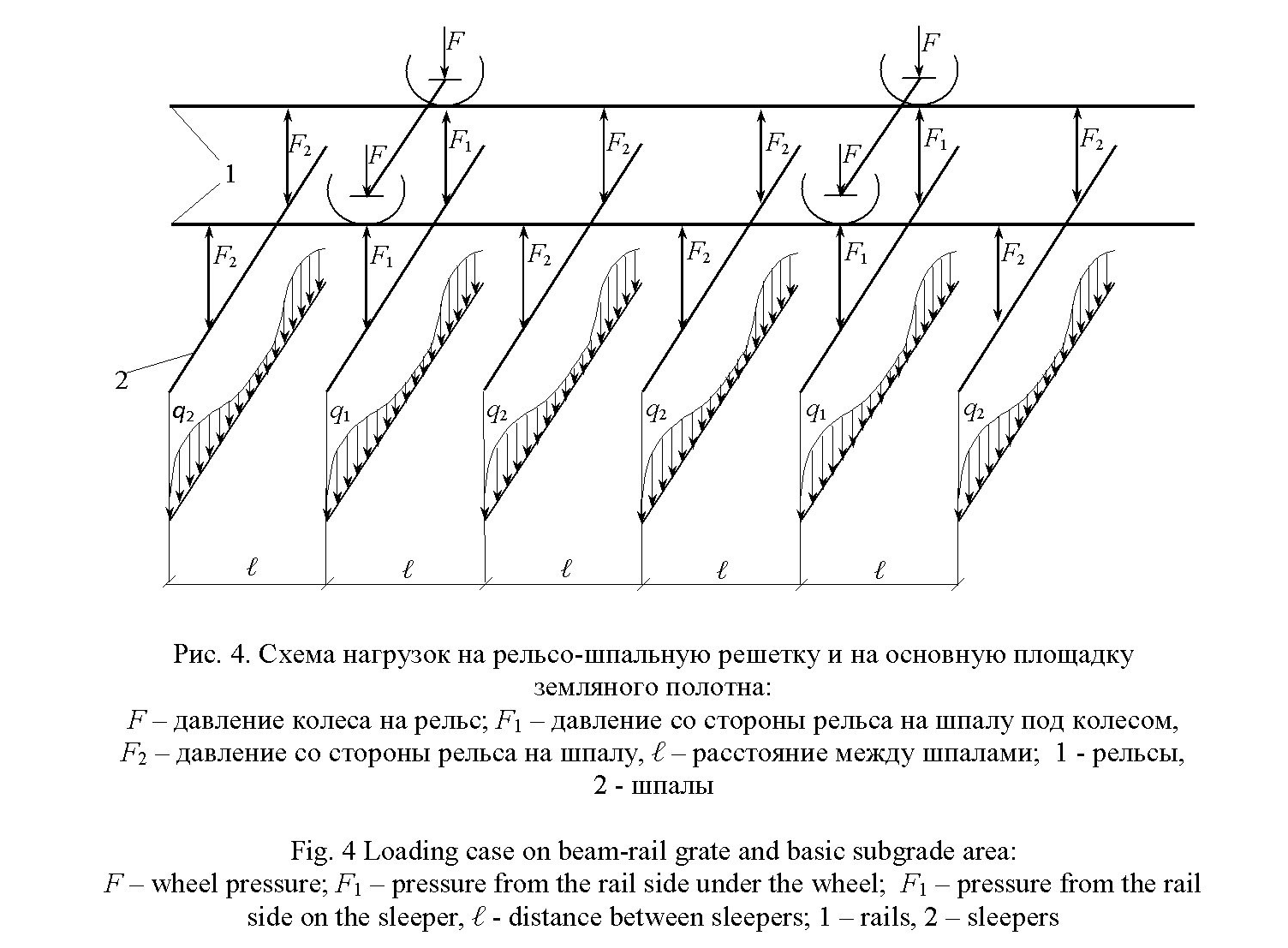
земляного полотна. Схема нагрузок на
рельсо-шпальную решетку и на основную
площадку земляного полотна приведена
на рис. 4. При решении задачи смешанным
методом нижнюю постель шпалы разбиваем
на прямоугольные участки, размеры
которых согласуем с шириной шпалы и
длиной путевой прокладки для рельса
Р-43, т. е. на участки с размерами
250 x 290 мм. Из эквивалентности
площадей участка шпалы и круга
радиусом
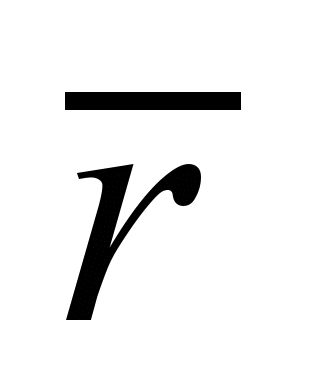 ,
получаем
,
получаем
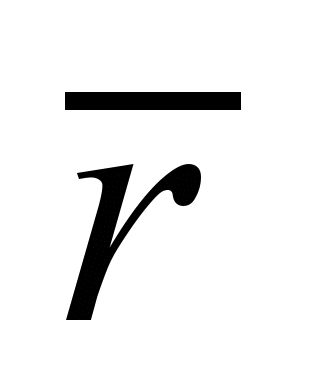 = 15,1 см. Тогда R
= 6,
= 15,1 см. Тогда R
= 6,
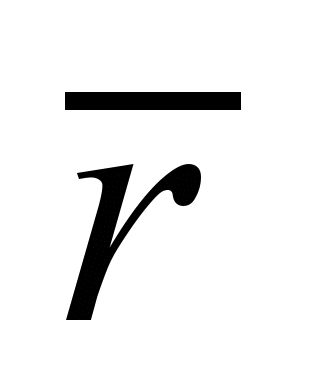 = 90,6 см, H = 8,
= 90,6 см, H = 8,
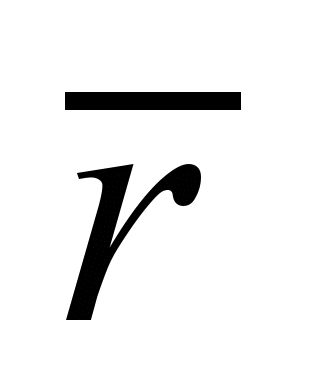 = 120,8 см.
= 120,8 см.
Расстояние между
шпалами при эпюре шпал 1 600 шт/км
составляет 60 см, поэтому рассматриваем
совместную работу трех шпал с
расположением оси тележки цистерны
над средней шпалой (рис. 5). Опорные
реакции по схеме а (рис. 5) определить
весьма затруднительно, т. к. опоры
(шпала на балластном слое) являются
упругоподатливыми, и при действии
нагрузки на опору В происходит ее
смещение по вертикали. Это смещение
зависит и от осадки земляного полотна,
которая на этой стадии расчета еще
неизвестна. Если опоры рассматривать
как жесткие, то всю нагрузку будет
воспринимать опора В, а реакции в
опорах А и В будут равны нулю,
что противоречит действительности.
Поэтому расчетную схему на рис. 5, а
заменяем расчетной схемой рис. 5, б.
Опоры считаем жесткими. Представляя
рельс на трех опорах как неразрезную
балку и привлекая уравнения трех
моментов, находим: RB
= 1,375 F1/2 = 0,69
F1; RA
= 0,313; F1/2
= 0,1565 F1.
Длину балки шпалы разбиваем на девять
участков, тогда расстояния между
стержнями-связями будет составлять
с = 2,75/9 = 0,306 м.
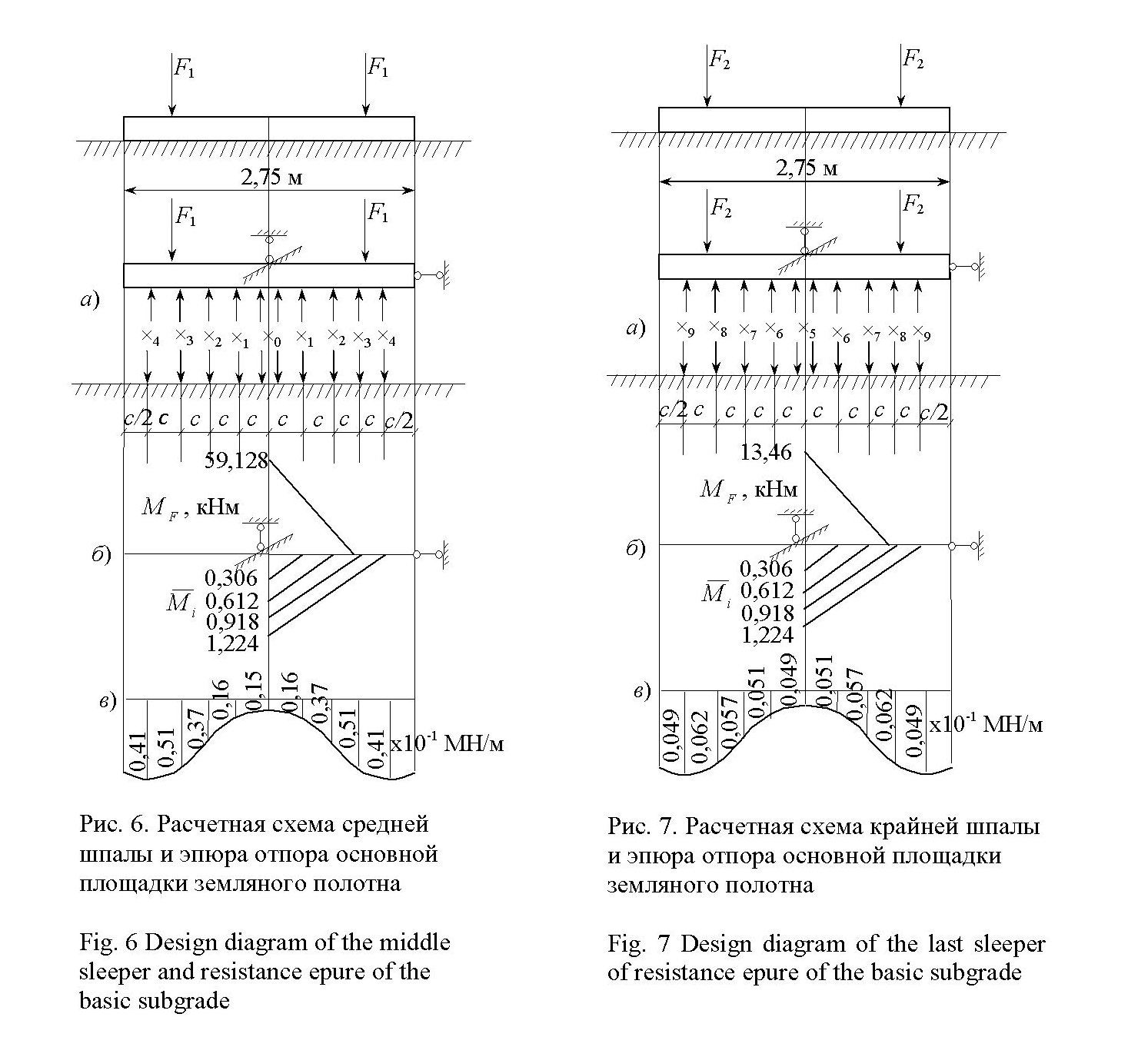
Расчетная схема
средней шпалы приведена на рис. 6, крайней
– на рис. 7. Неизвестными будут усилия
в стержневых связях X0, X1,
…, X9, а также прогибы
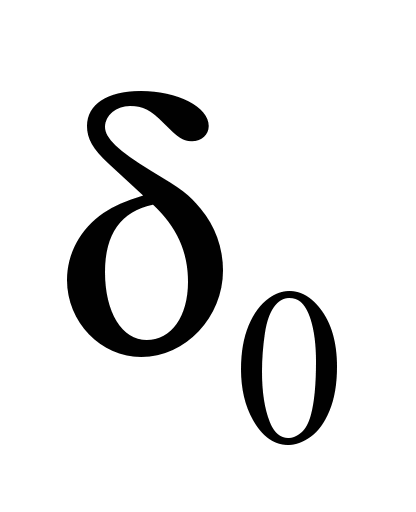 и
и
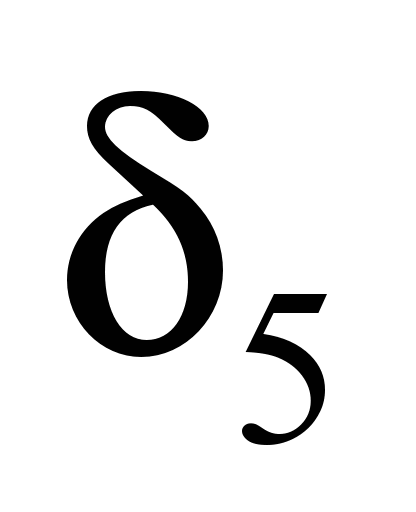 центральных сечений балок-шпал. Матрица
коэффициентов Т и векторы неизвестных
Y и правой части NF системы
канонических уравнения смешанного
метода (1) имеют вид:
центральных сечений балок-шпал. Матрица
коэффициентов Т и векторы неизвестных
Y и правой части NF системы
канонических уравнения смешанного
метода (1) имеют вид:
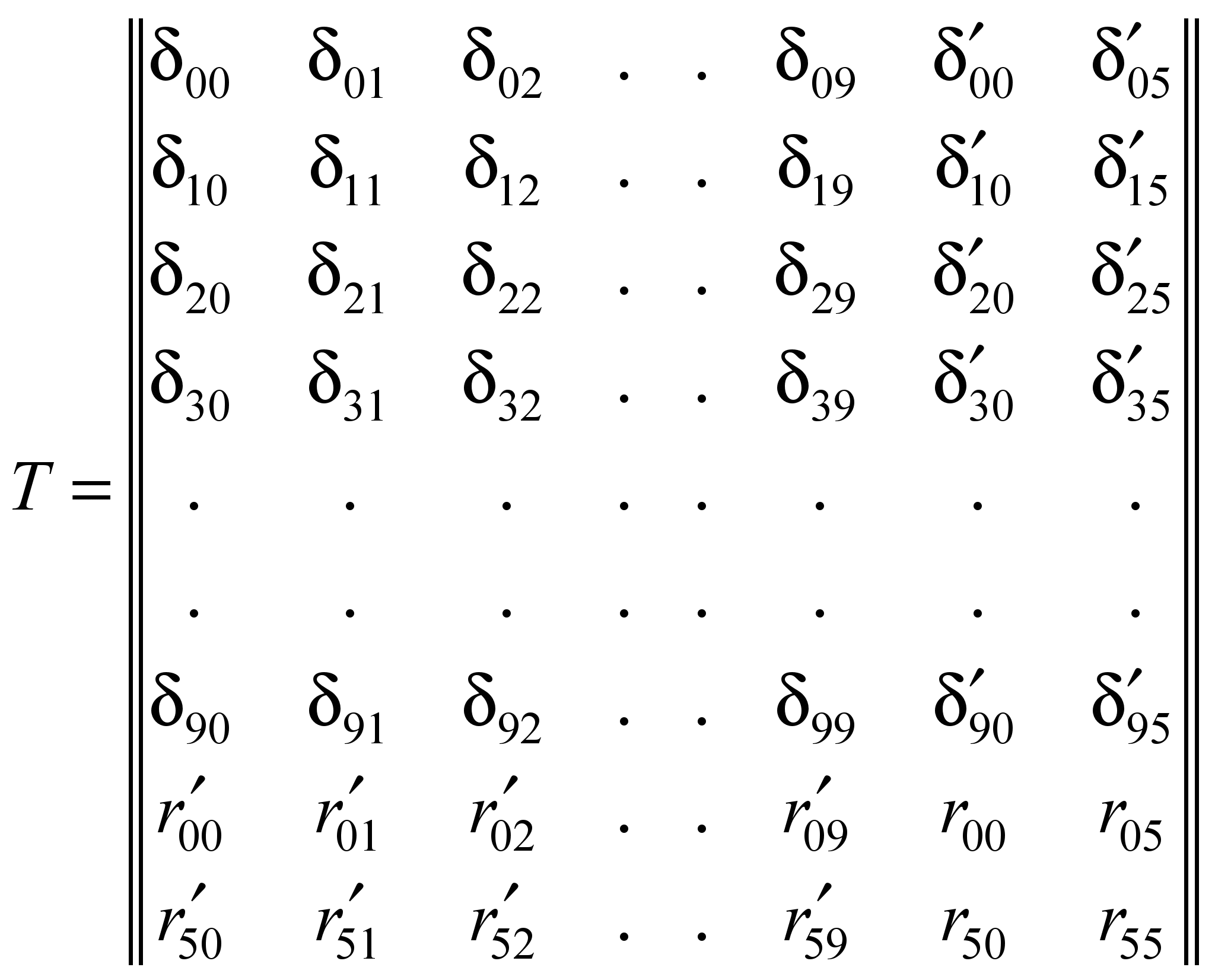
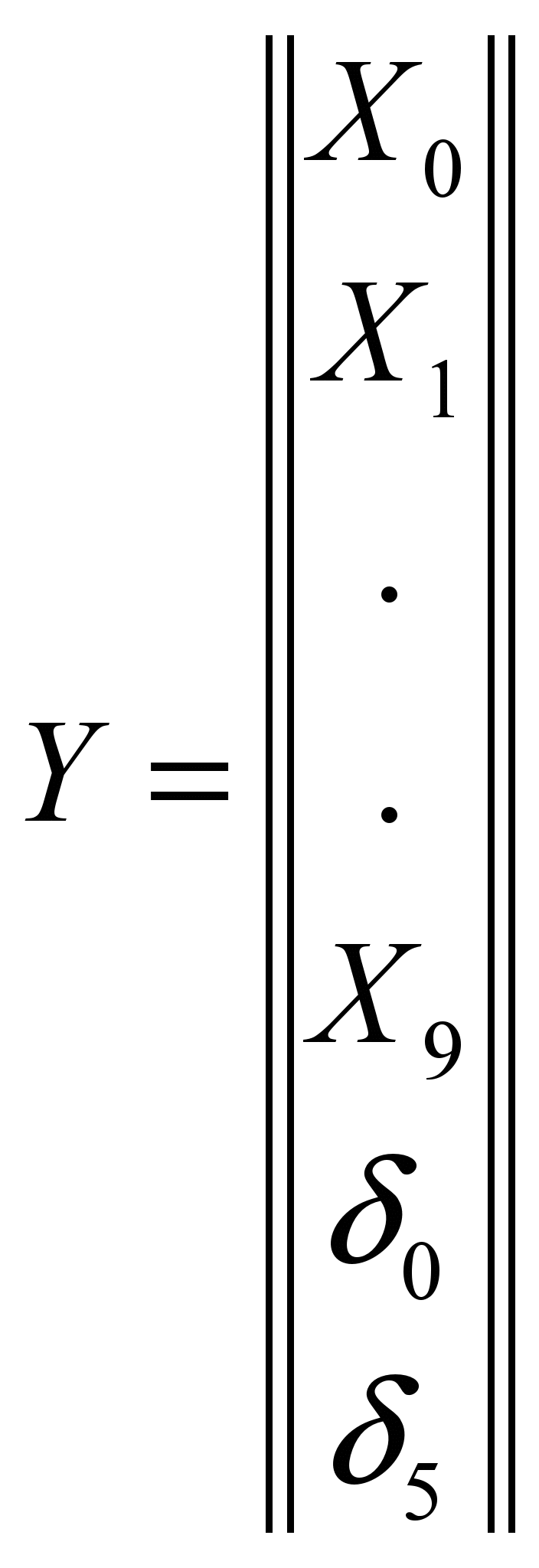 ,
,
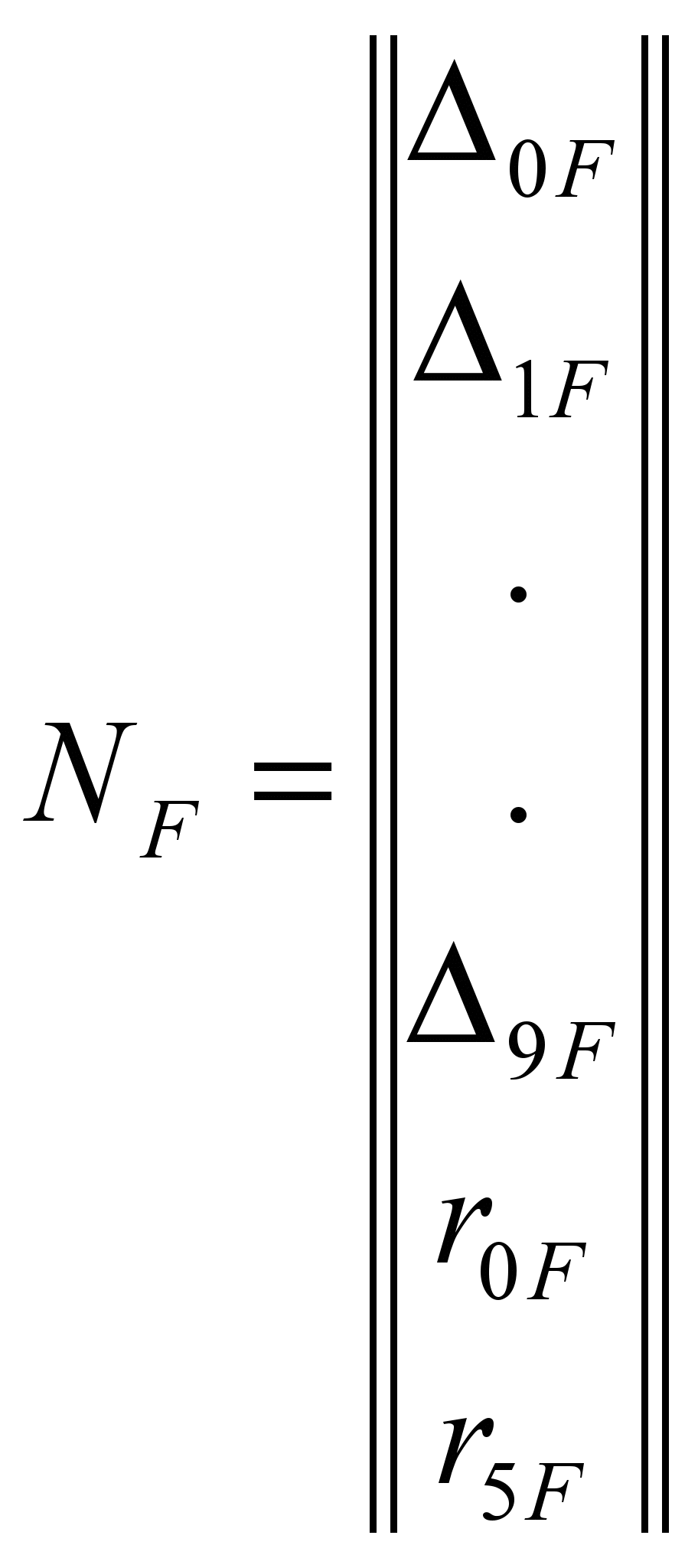 .
.
Перемещения
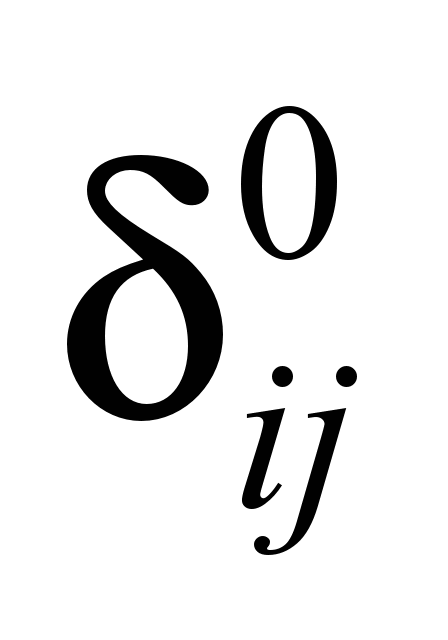 земляного полотна железнодорожного
пути определяем при помощи осесимметричной
столбчатой модели при F = 1. Из
равенства площадей прямоугольного
участка (0,306 x 0,23) подошвы шпалы и
круга радиусом
земляного полотна железнодорожного
пути определяем при помощи осесимметричной
столбчатой модели при F = 1. Из
равенства площадей прямоугольного
участка (0,306 x 0,23) подошвы шпалы и
круга радиусом
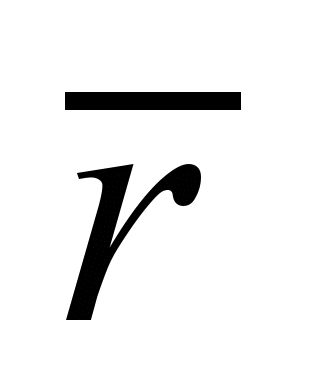 имеем
имеем
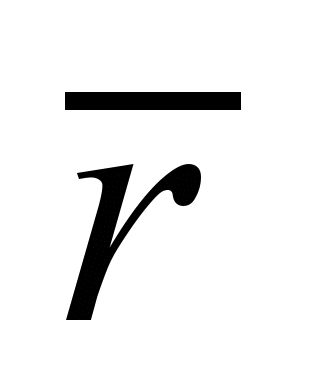 = 0,15 м.
= 0,15 м.
Перемещения
поверхности земляного полотна на ребрах
осесимметричной столбчатой модели 0,
1 и 2, которые получены при реализации
изложенного алгоритма при
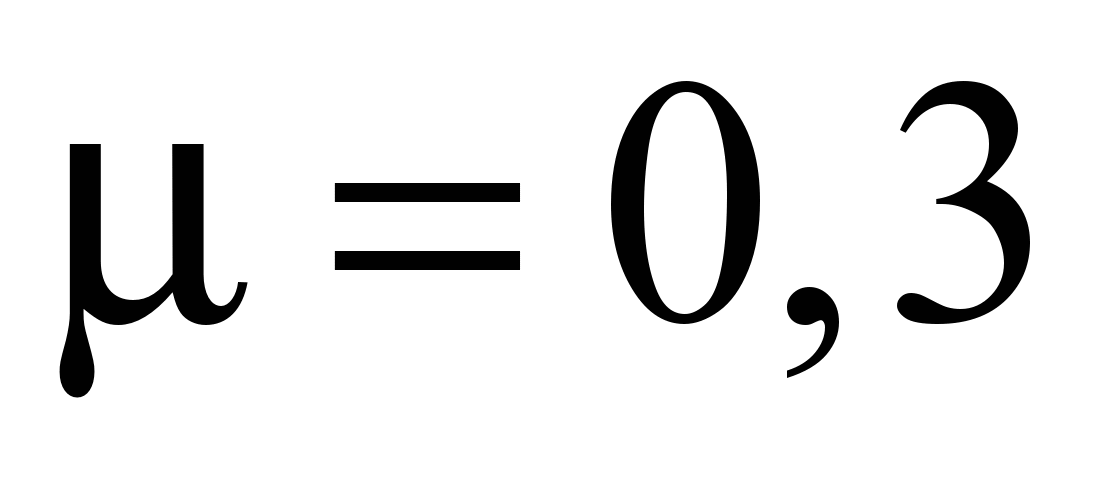 ,
приведены в табл. 1.
,
приведены в табл. 1.
Таблица 1
Относительные
перемещения поверхности земляного
полотна на ребрах осесимметричной
столбчатой модели
Table
1
Relative
displacement of the subgrade surface on the ridges of axisymmetric
columnar model
|
r
|
0
|
c = b
|
2c = 2b
|
3c = 3b
|
4c = 4b
|
|
(r)
|
1,7771
|
0,3054
|
0,0641
|
0
|
0
|
В данном случае
расстояние между стержнями-связями с
= 0,305 м≈ 0,30 м
совпадает с расстоянием между ребрами
(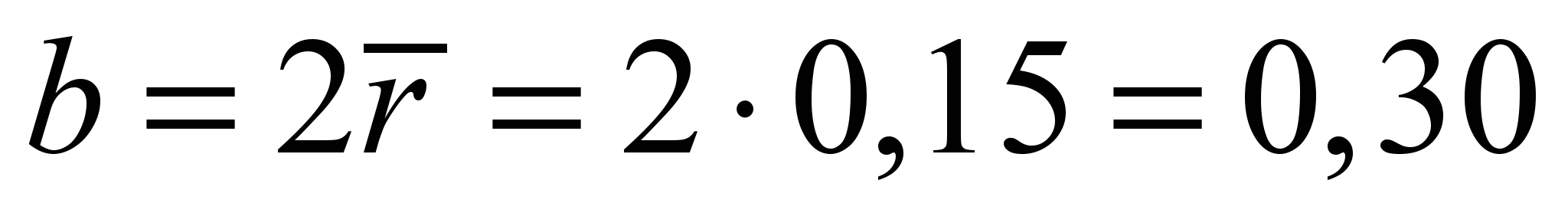 м). Тогда при Е = 19 МПа имеем:
м). Тогда при Е = 19 МПа имеем:
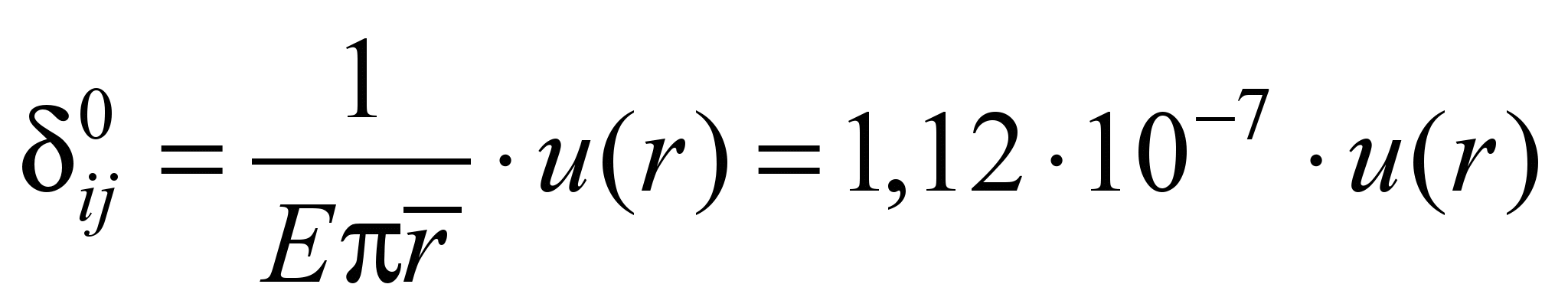 .
.
При принятом радиусе
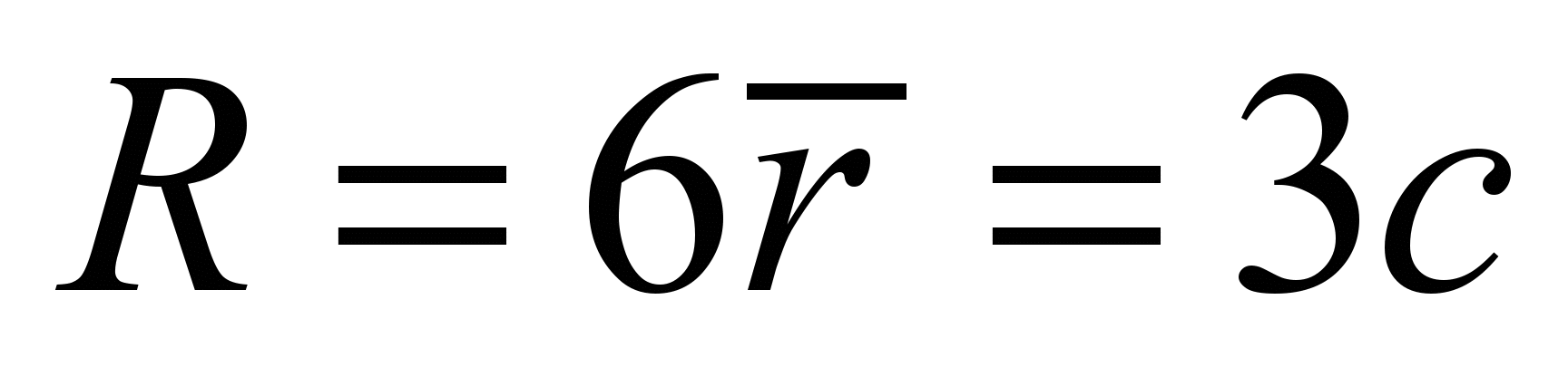 затухания перемещений на граничной
плоскости земляного полотна перемещения
крайних шпал не оказывают взаимного
влияния на свои перемещения. Поэтому
при совместном расчете трех балок-шпал
нужно учитывать влияние крайних шпал
на среднюю и наоборот – влияние средней
шпалы на крайние.
затухания перемещений на граничной
плоскости земляного полотна перемещения
крайних шпал не оказывают взаимного
влияния на свои перемещения. Поэтому
при совместном расчете трех балок-шпал
нужно учитывать влияние крайних шпал
на среднюю и наоборот – влияние средней
шпалы на крайние.
Единичная осадка
основания равна:
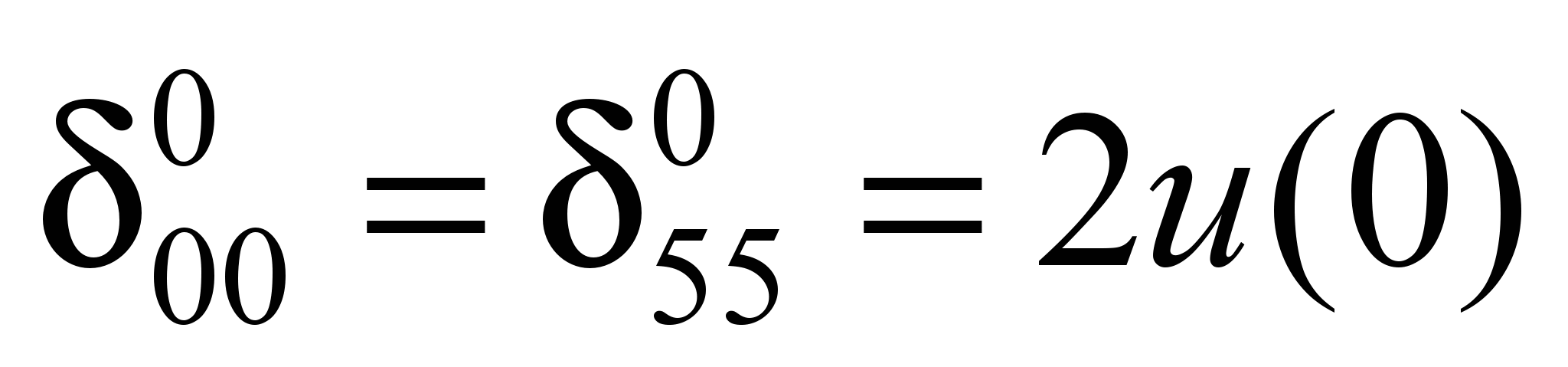 ;
;
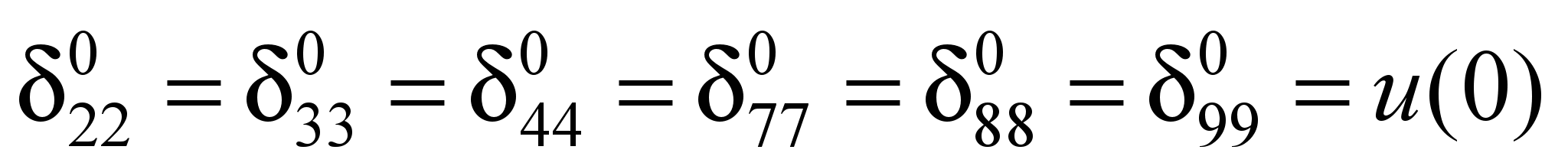 ;
;
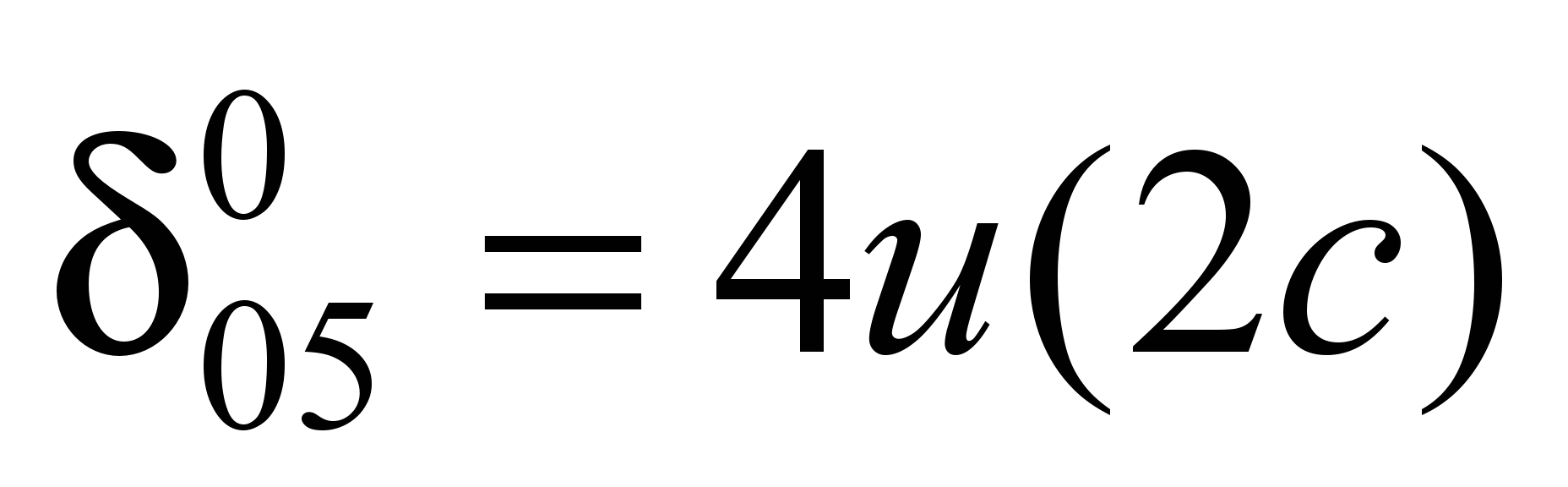 ;
;
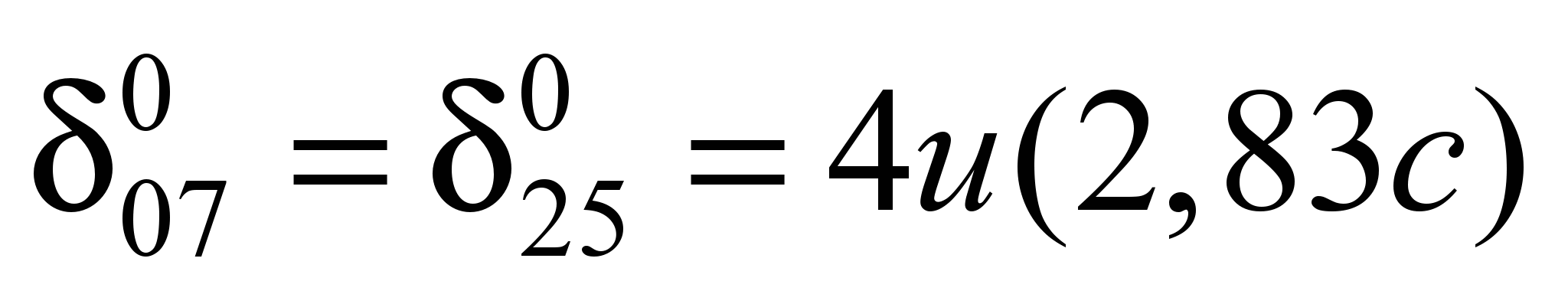 ;
;
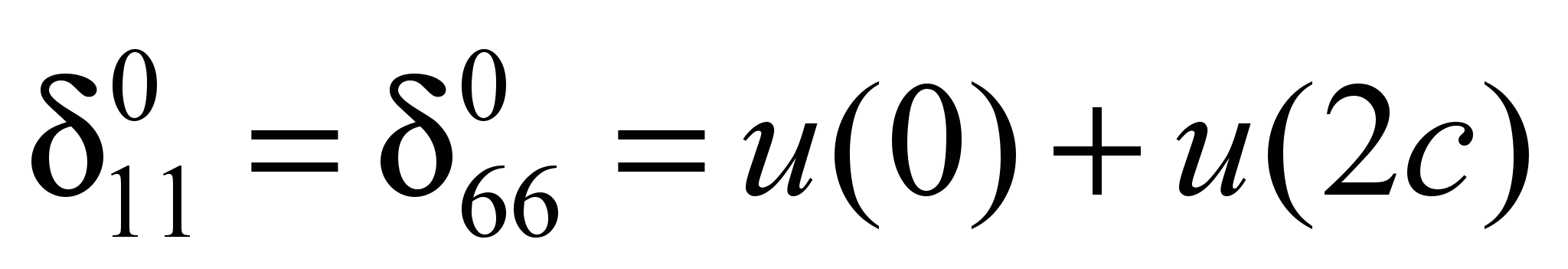 ;
;
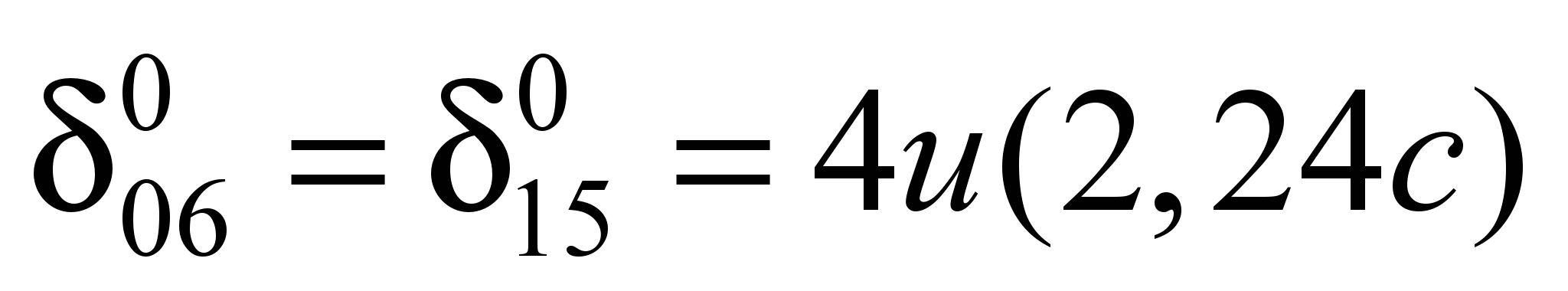 ;
;
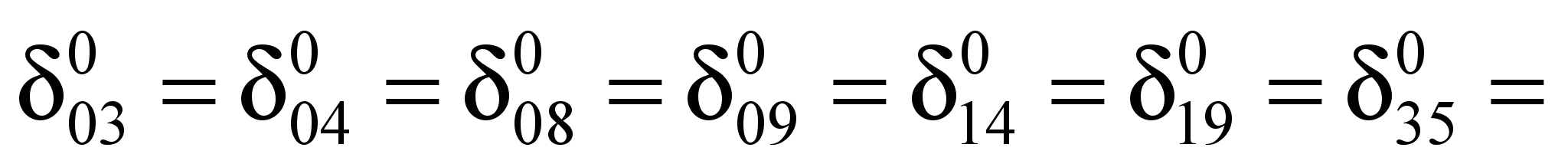
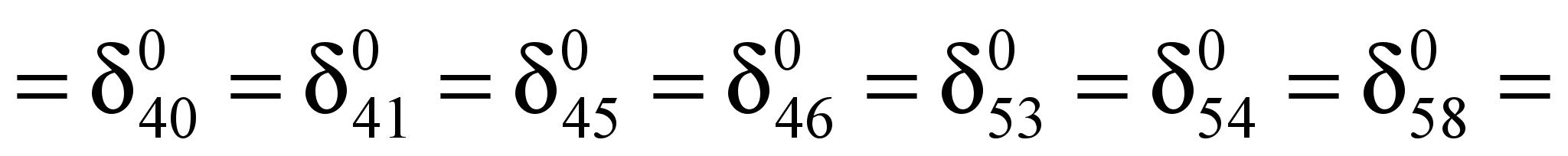
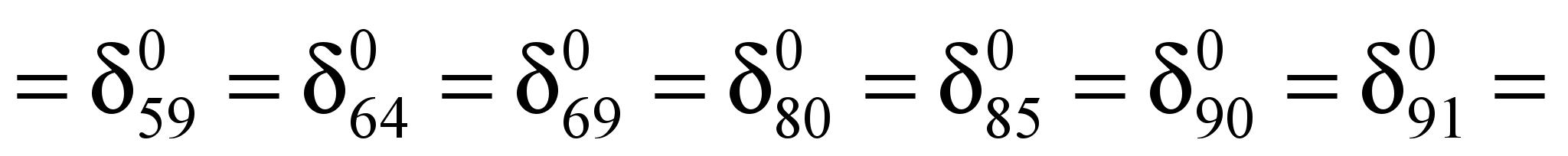
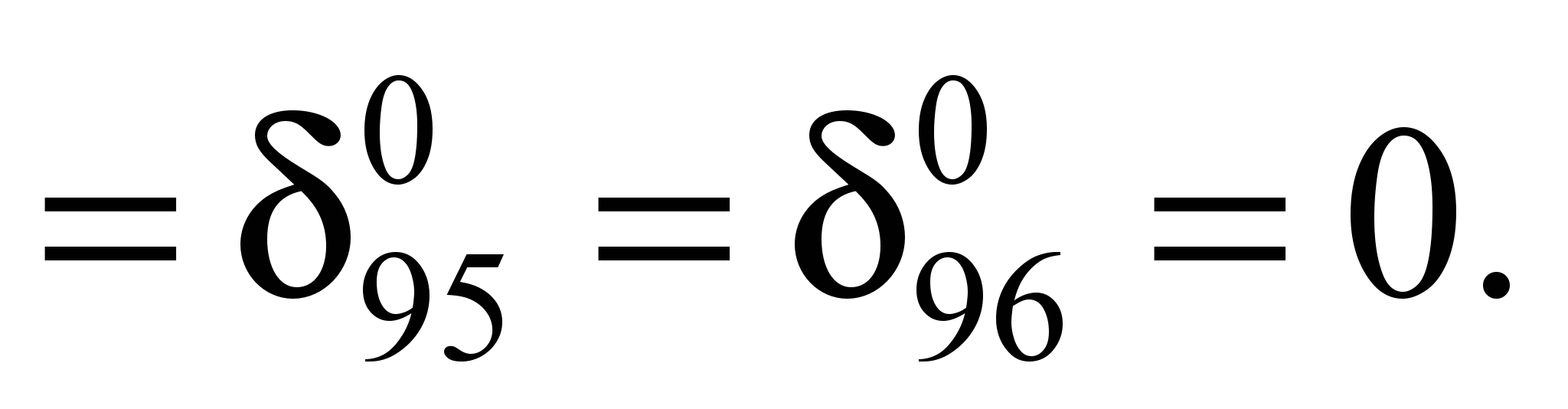
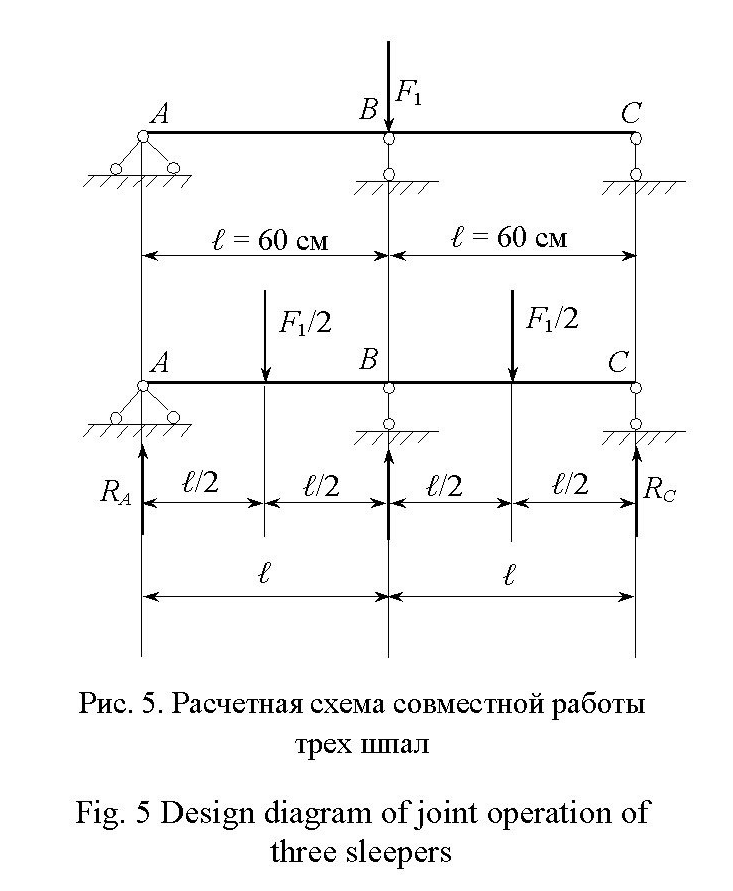
Аналогично определяют
остальные перемещения основания
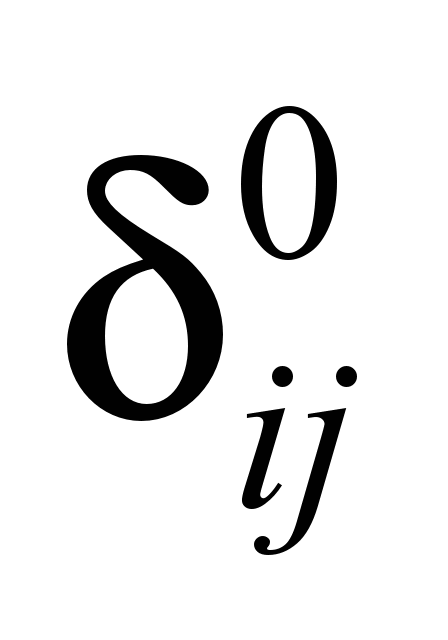 .
.
Единичные перемещения
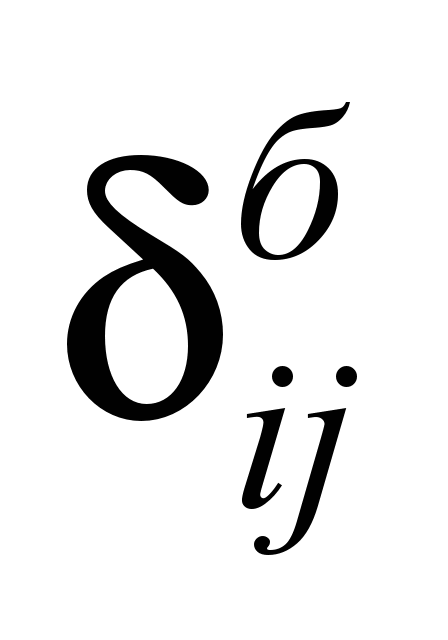 балки-шпалы определены по таблице IV
(4) Б. Н. Жемочкина [6] (ниже приведены
значения некоторых из них):
балки-шпалы определены по таблице IV
(4) Б. Н. Жемочкина [6] (ниже приведены
значения некоторых из них):
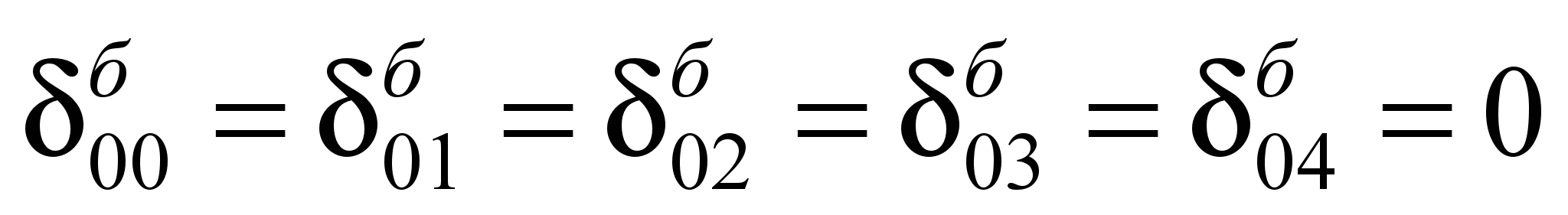 ;
;
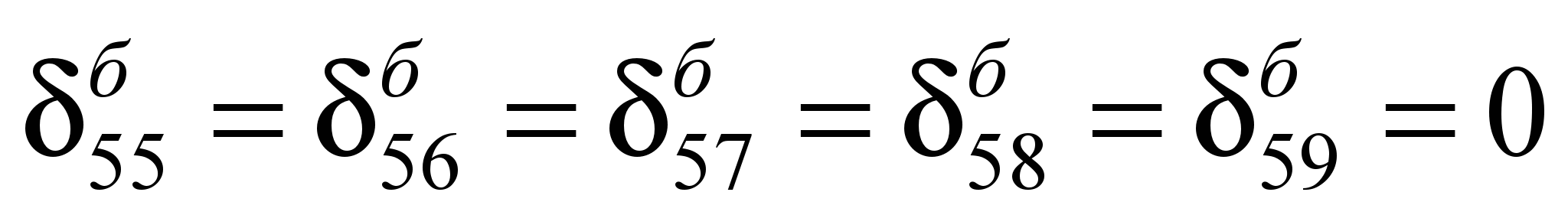 ;
;
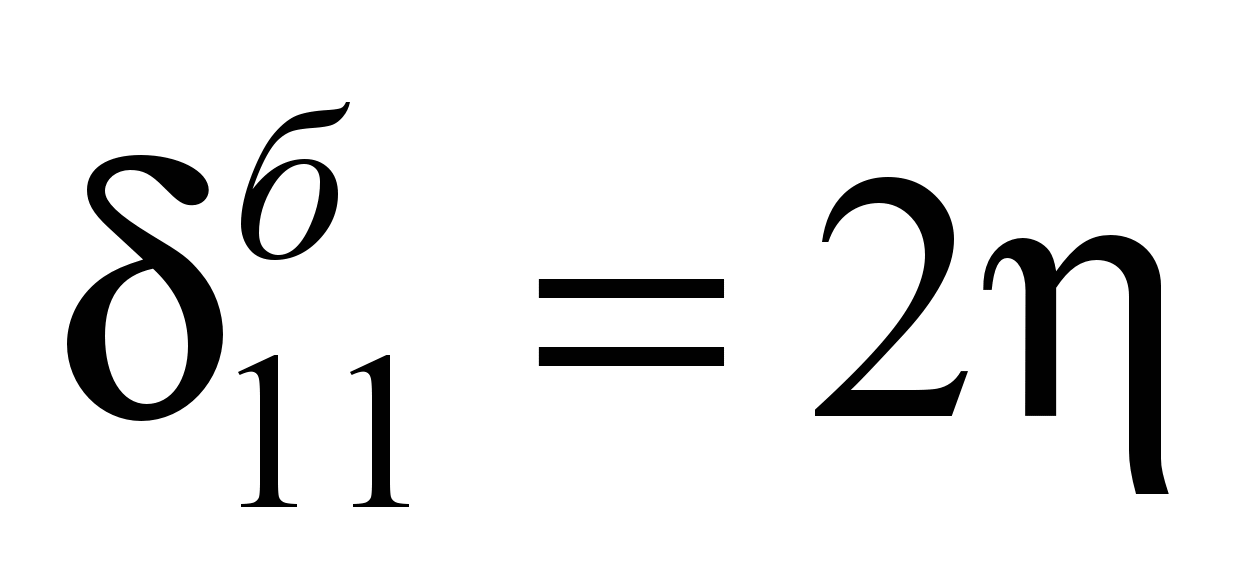 ;
;
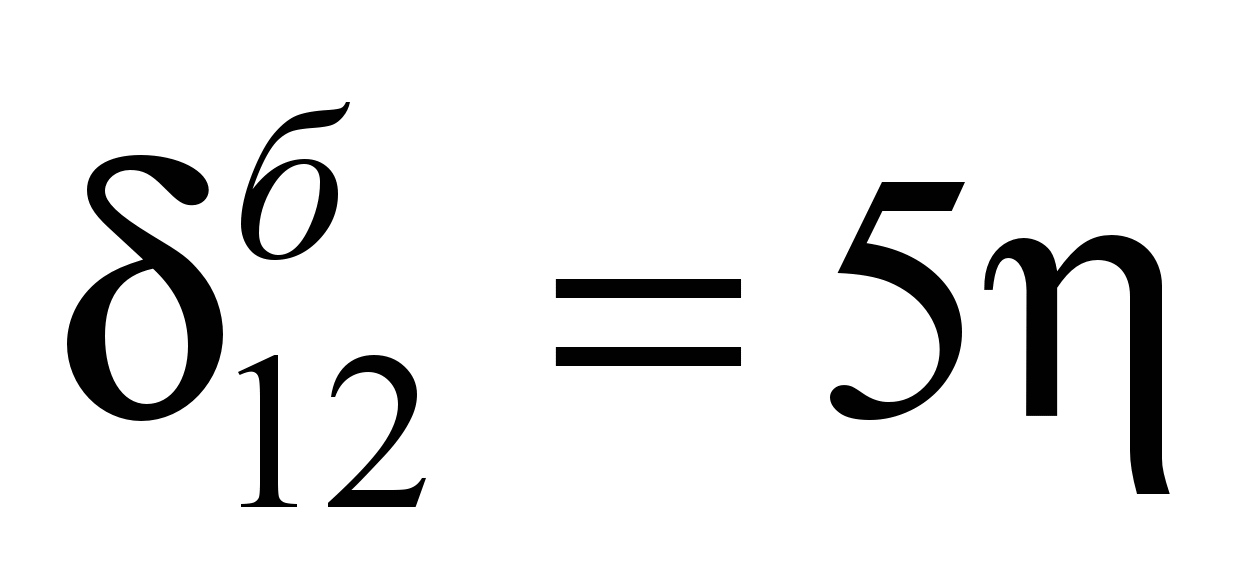 ;
;
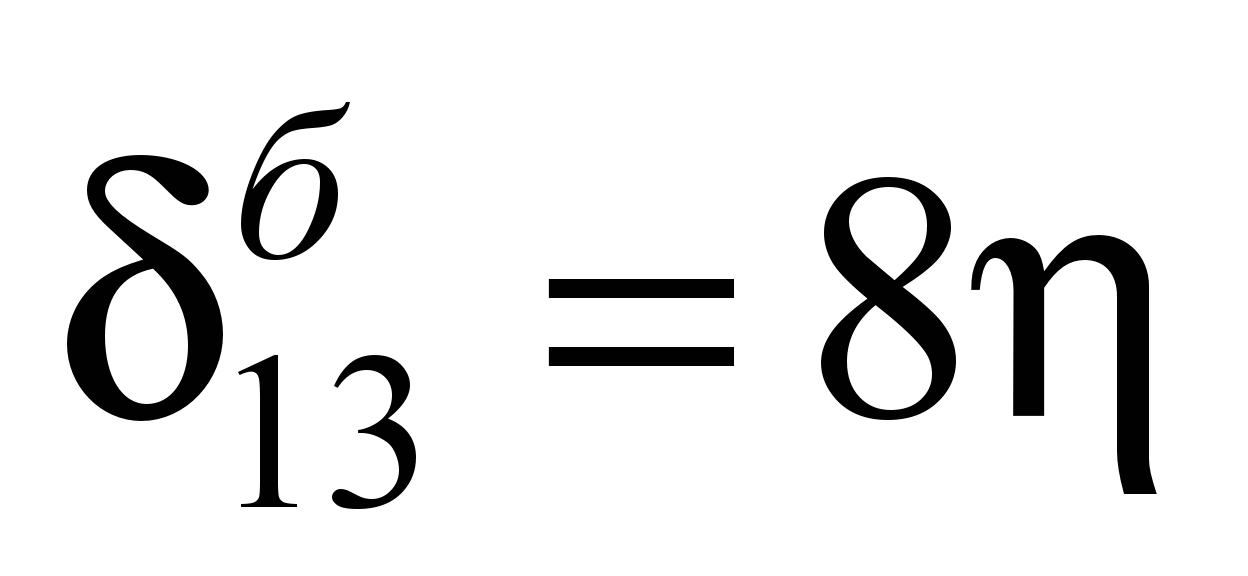 ;
;
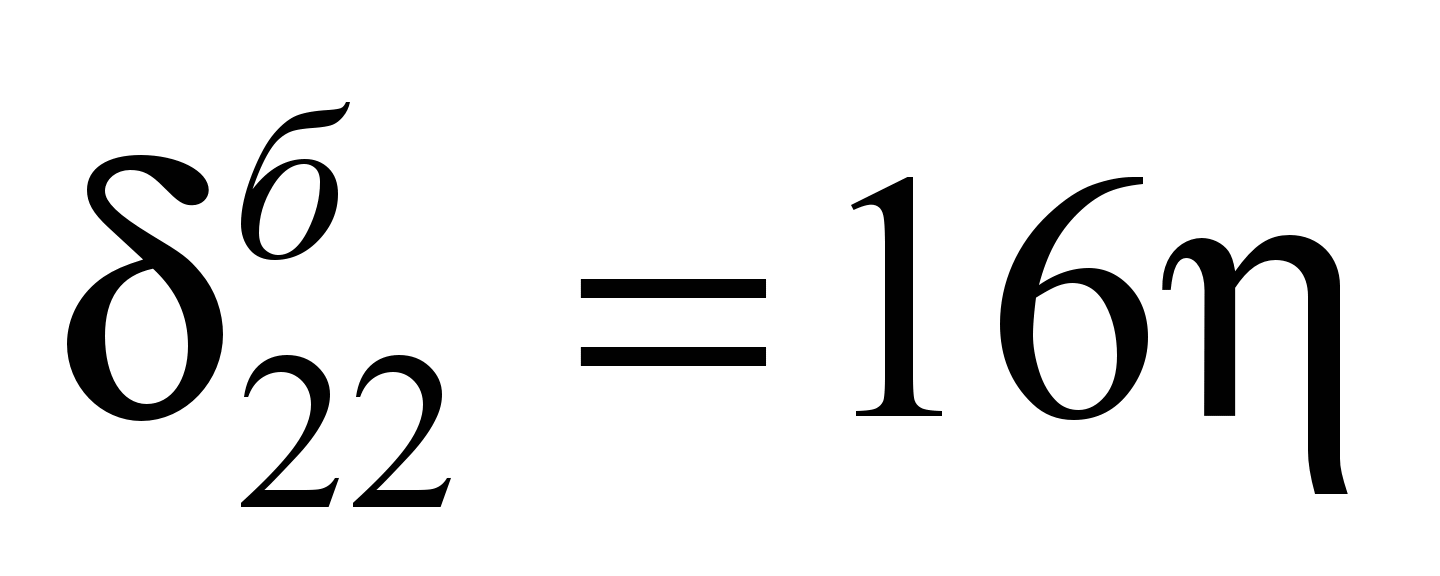 ;
;
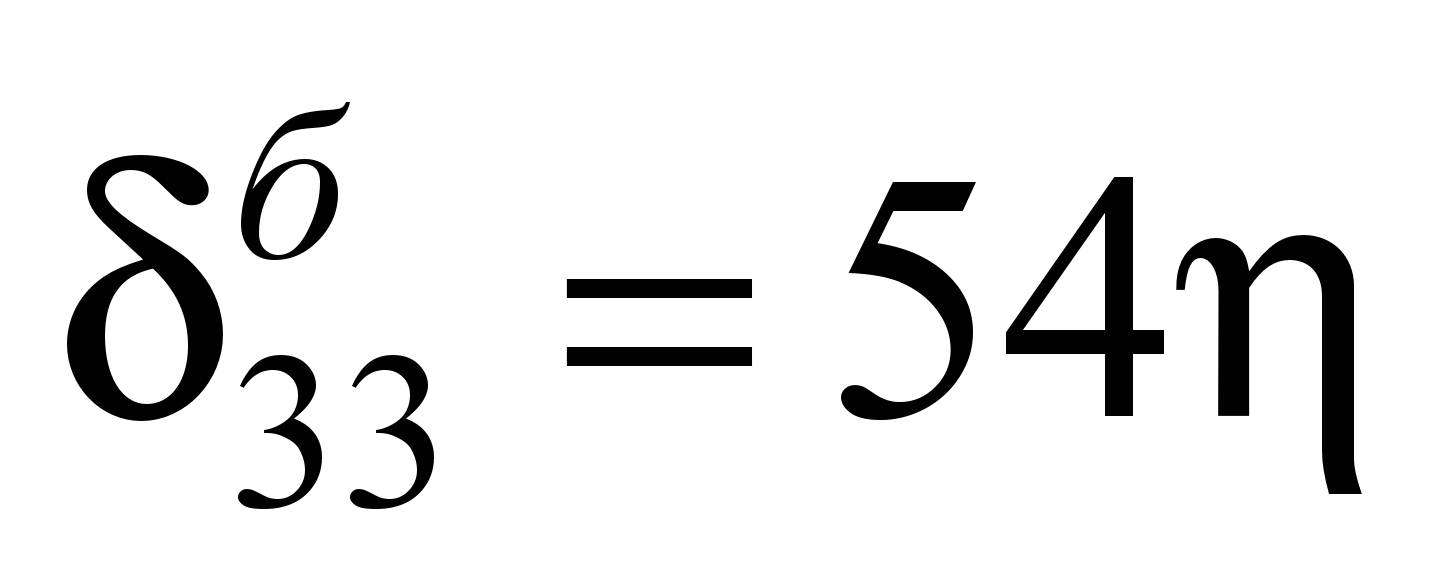 ;
;
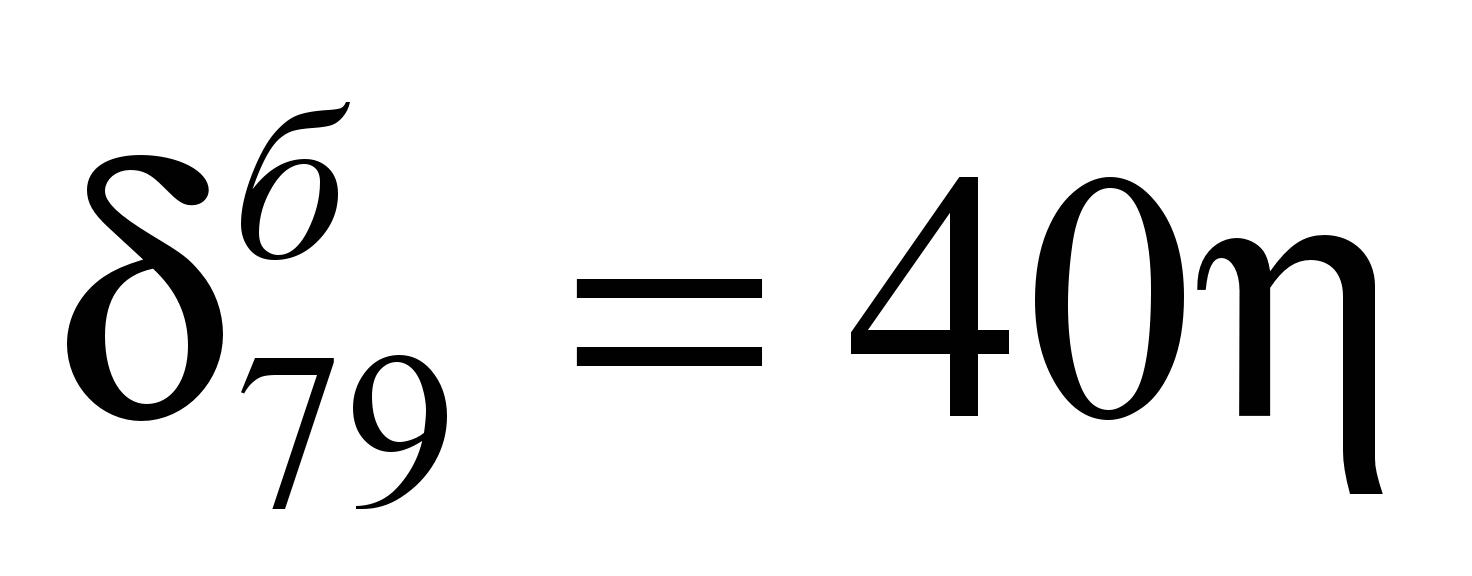 ;
;
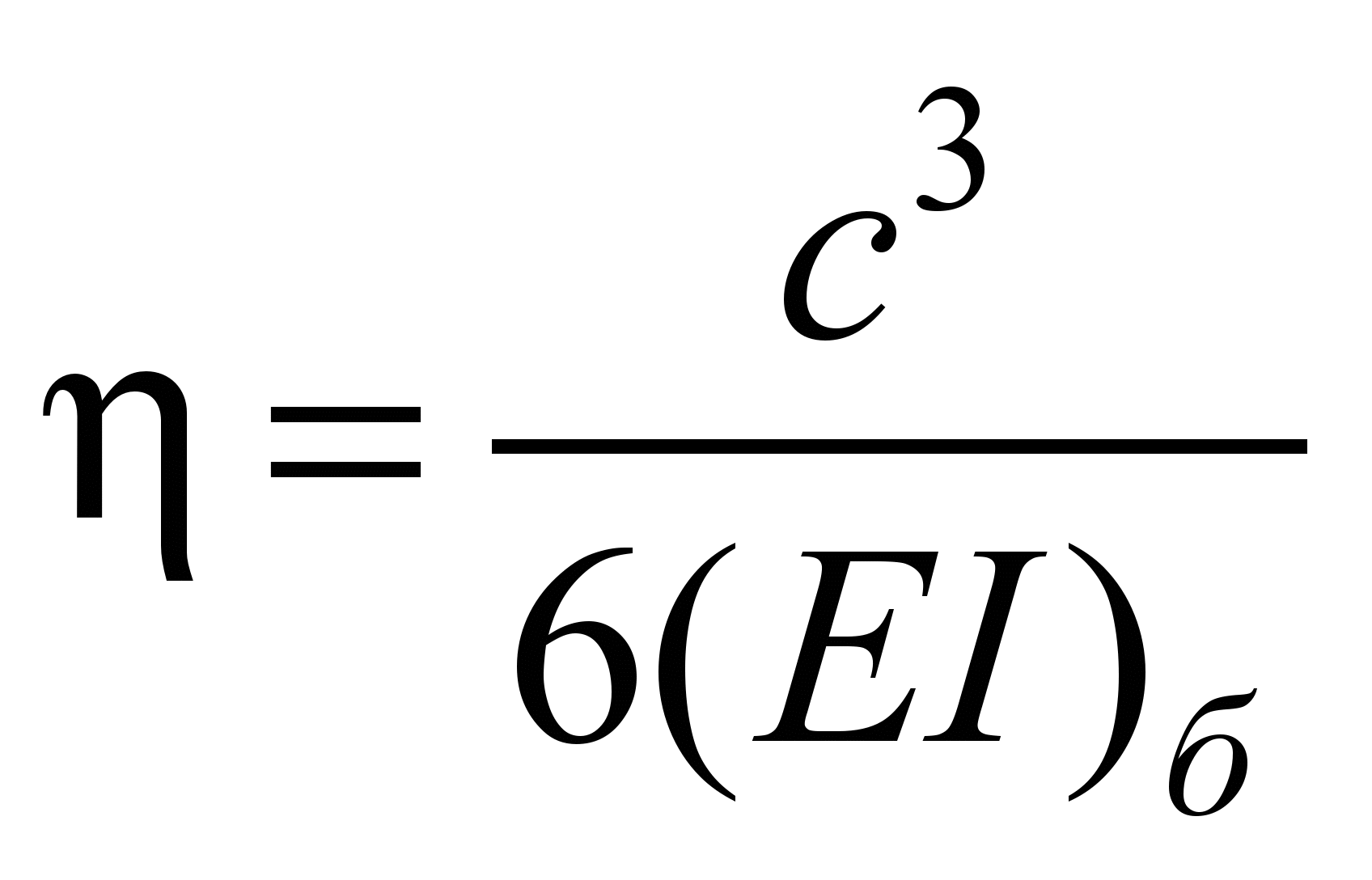 .
.
Грузовые перемещения
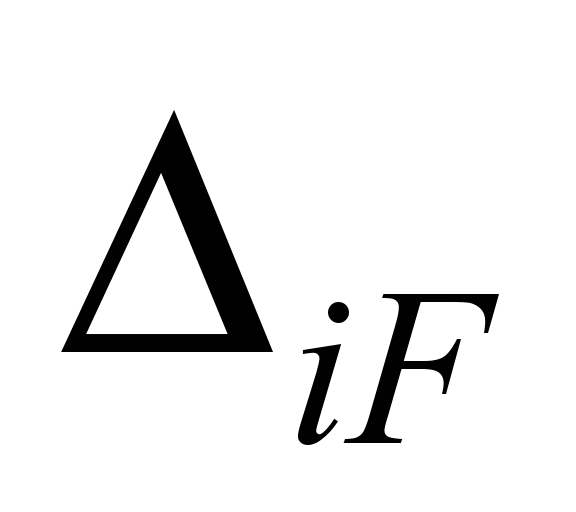 определены по способу Верещагина (рис.
6, б и рис. 7, б).
определены по способу Верещагина (рис.
6, б и рис. 7, б).
Для данной основной
системы перемещение точки i основной
системы от единичного перемещения
связи «0» или «5» равны:
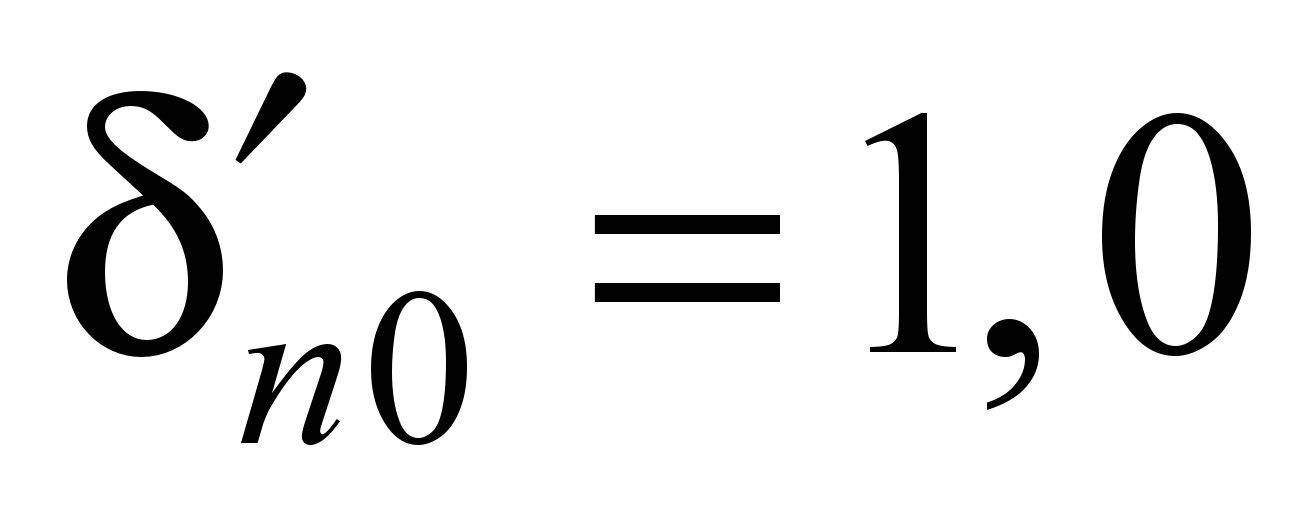 (п = 0, 1, …, 4);
(п = 0, 1, …, 4);
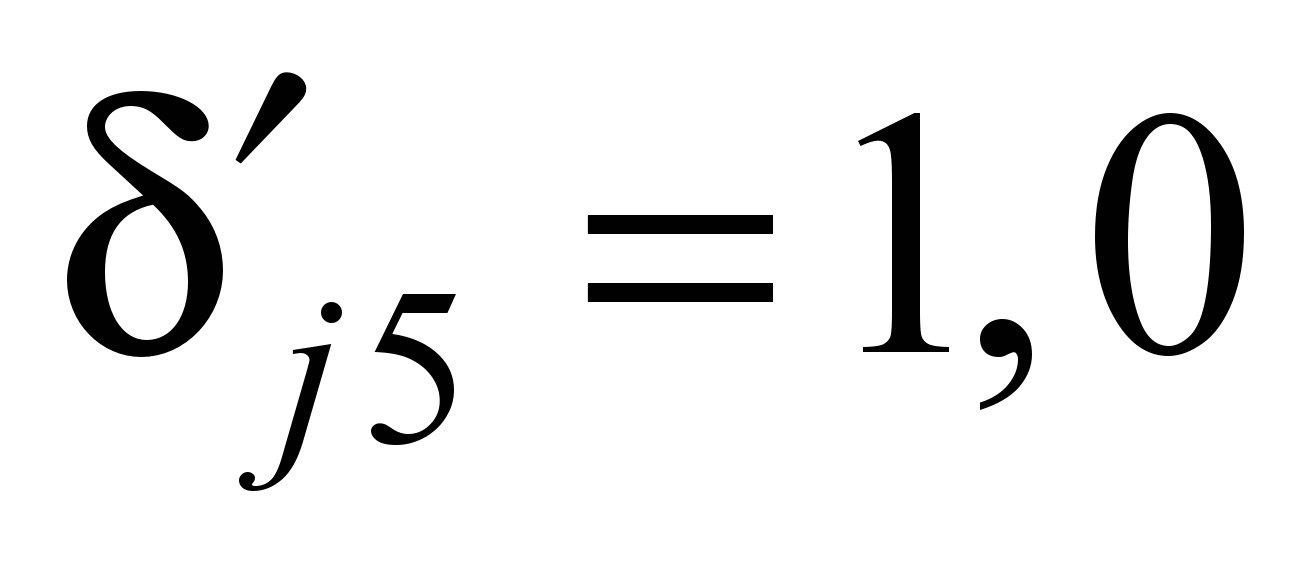 (j = 5, 6, …, 9).
(j = 5, 6, …, 9).
В нашем случае
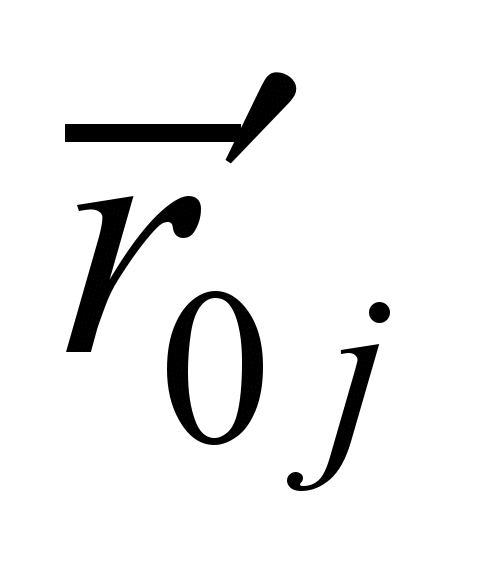 является реакцией в линейной связи
основной системы от единичного усилия,
приложенного в связи j:
является реакцией в линейной связи
основной системы от единичного усилия,
приложенного в связи j:
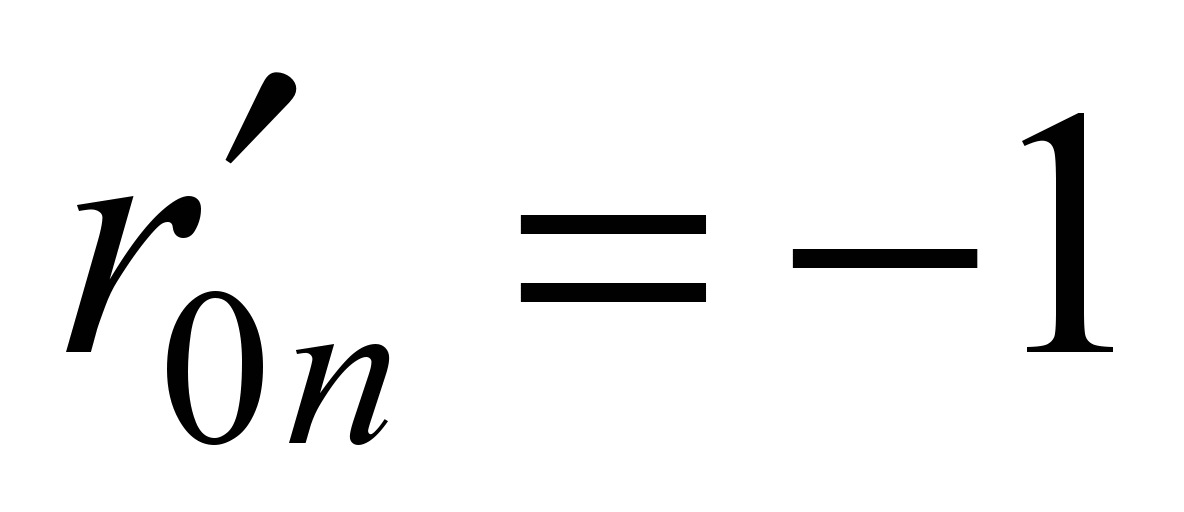 (п = 0, 1, …, 4);
(п = 0, 1, …, 4);
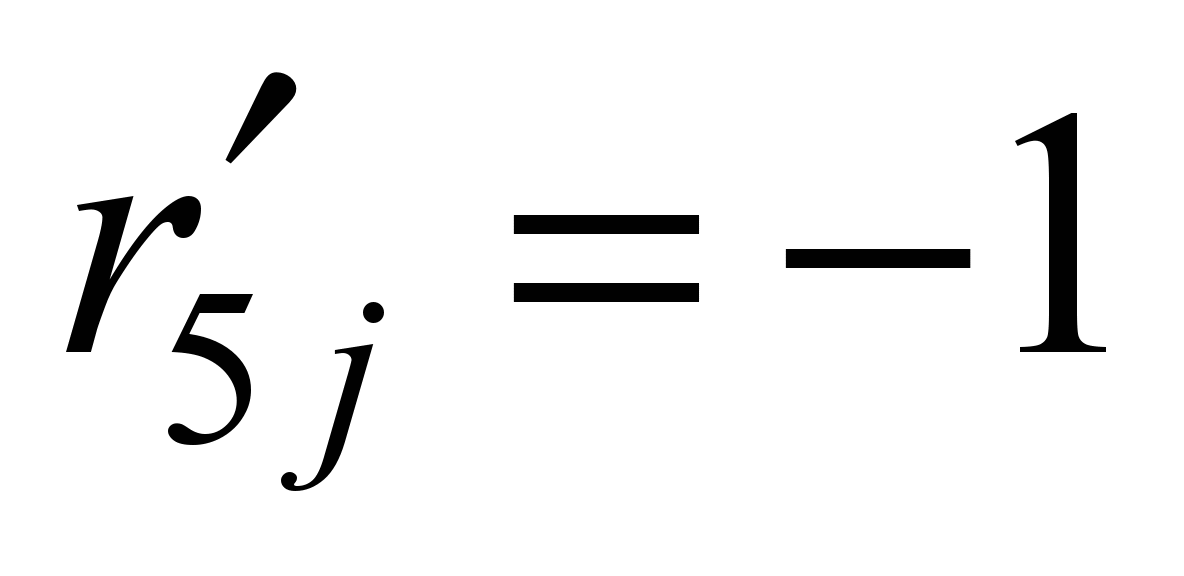 (j = 5, 6,
…, 9);
(j = 5, 6,
…, 9);
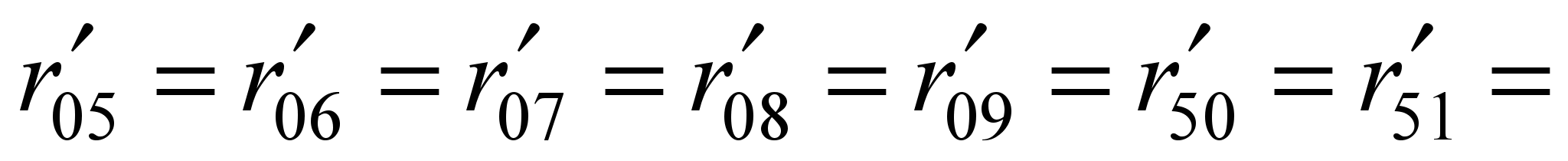
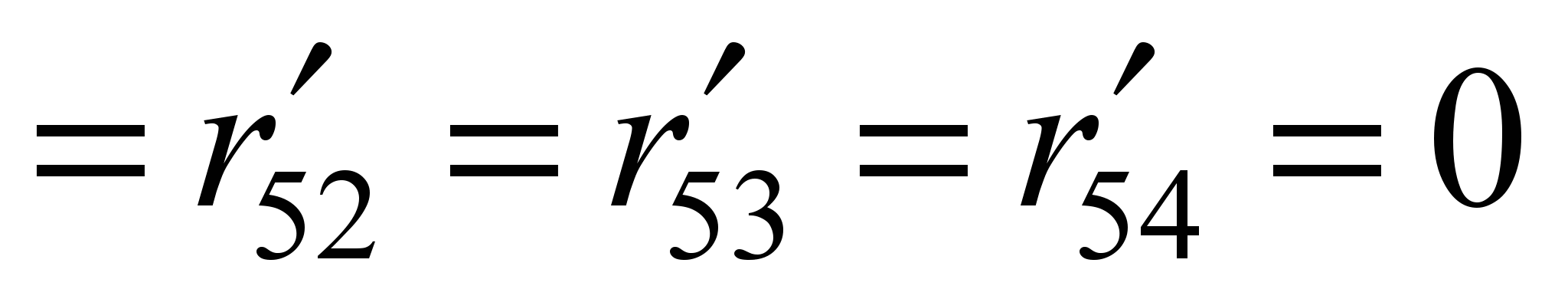 .
.
Вертикальная реакция
в защемлении основной системы от
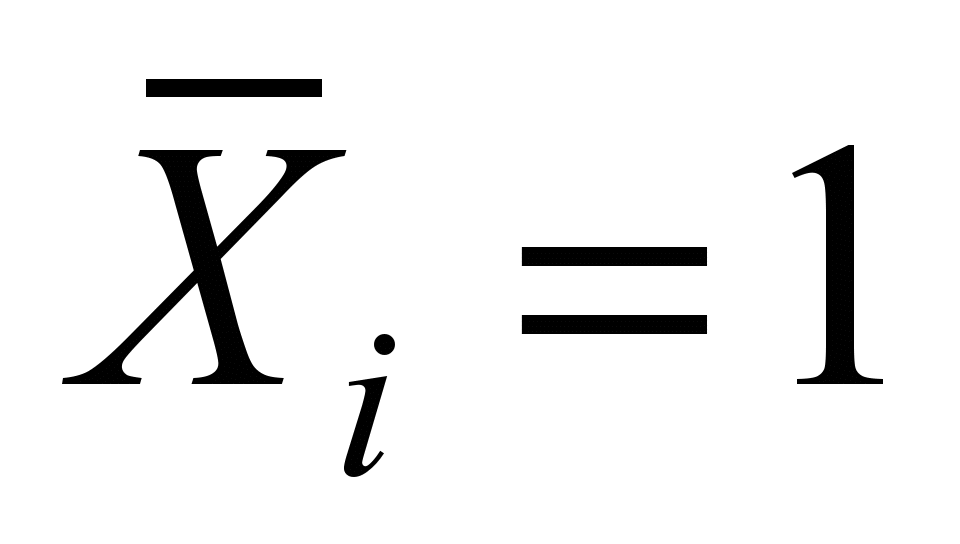 направлена вниз.
направлена вниз.
Коэффициенты r00
и r55, представляющие собой
реакцию в линейной связи «0» и «5» от
единичного перемещения этих
связей, равны:
r00
= r55 = 0.
Реакции в линейных
связях «0» и «5» основной системы от
внешней нагрузки равны сумме внешней
нагрузки:
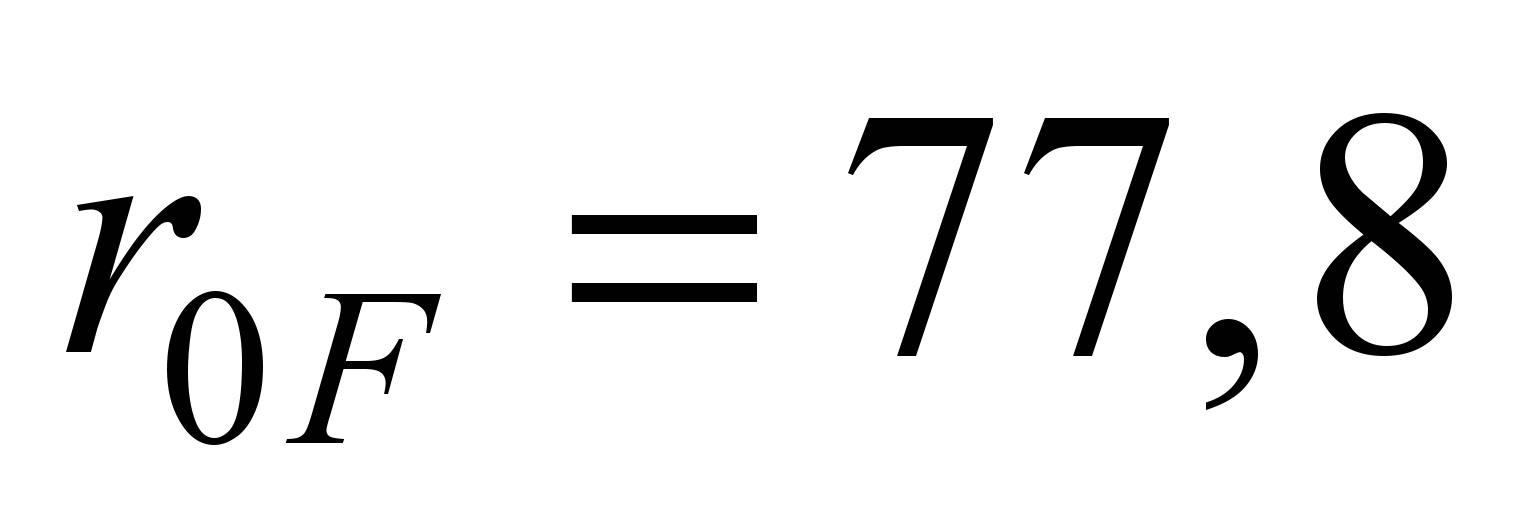 кН;
кН;
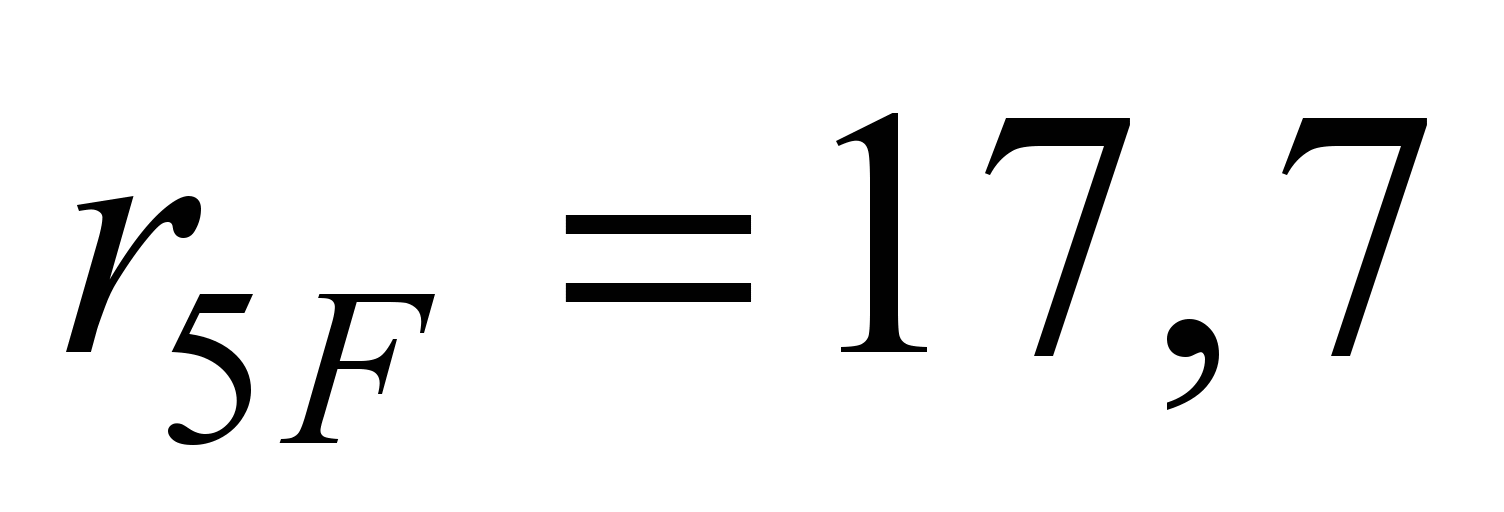 кН.
кН.
В результате решения
системы алгебраических уравнений (1)
определяем усилия Xi в
стержневых связях и прогибы
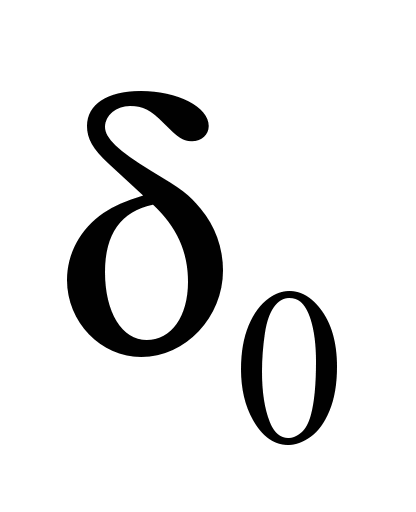 и
и
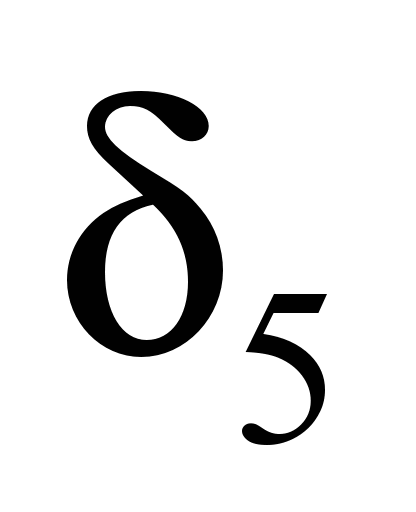 центральных сечений средней и крайней
шпал.
центральных сечений средней и крайней
шпал.
Интенсивность
отпора по нижней постели шпалы получим,
разделив Xi на длину участка
с.
Осадку основания
под шпалами определяем с привлечением
принципа суперпозиции:
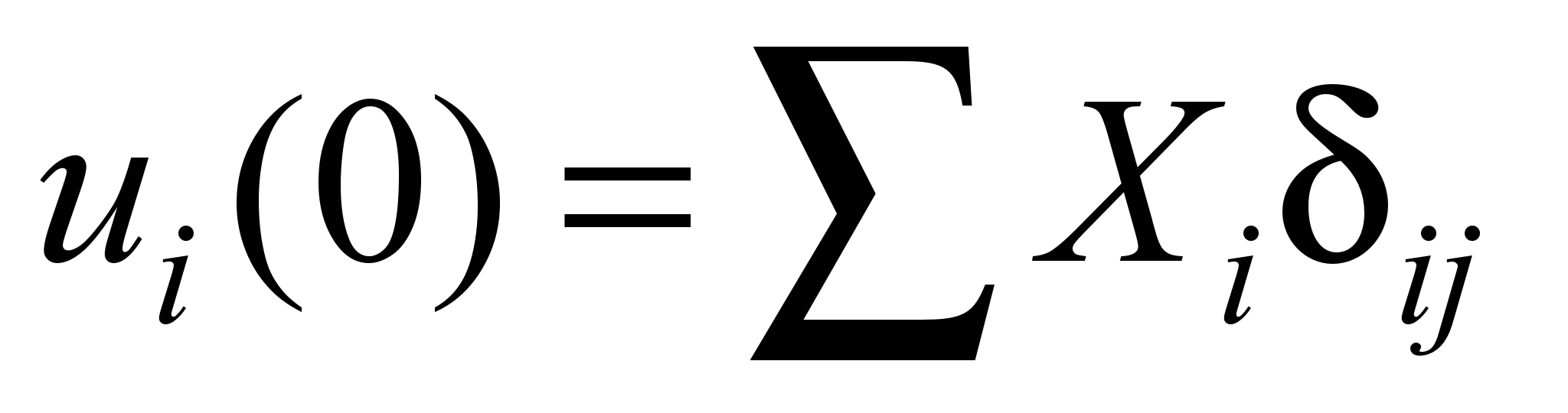
Эпюры отпоров
земляного полотна под средней и крайней
шпалами приведены соответственно на
рис. 6, в и рис. 7, в.
Максимальные
нормальные напряжения на поверхности
земляного полотна под средней шпалой
составили
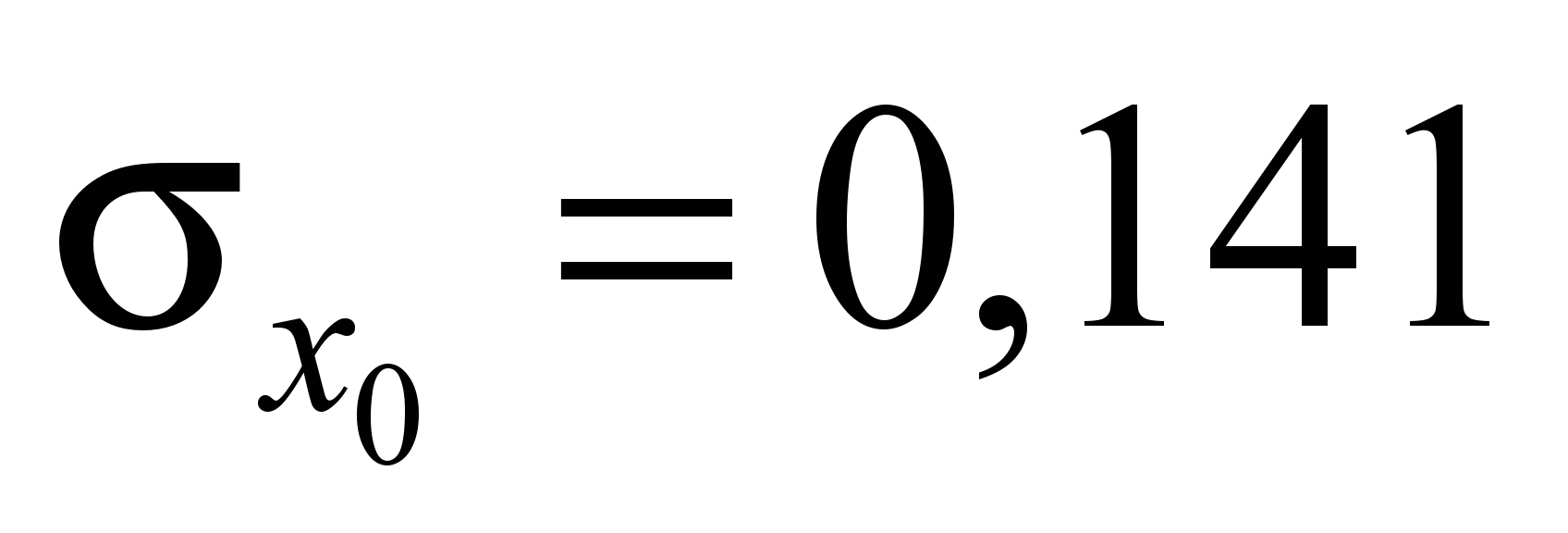 МПа. Максимальные касательные напряжения
в грунте составили
МПа. Максимальные касательные напряжения
в грунте составили
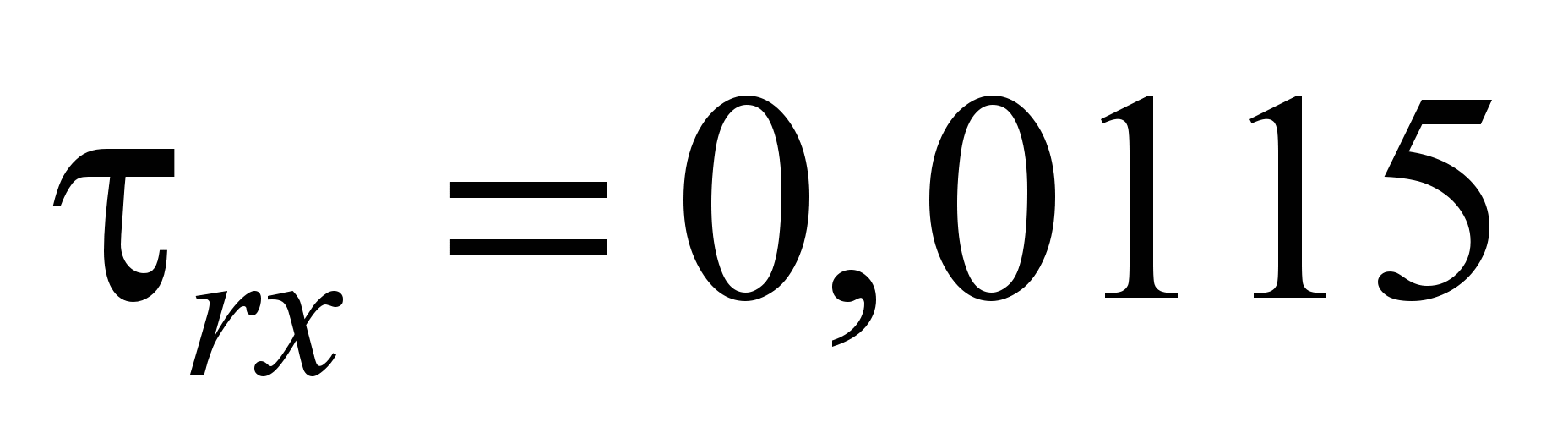 МПа. Приняв в качестве критерия прочности
условие Кулона, при данных характеристиках
грунта, получим
МПа. Приняв в качестве критерия прочности
условие Кулона, при данных характеристиках
грунта, получим
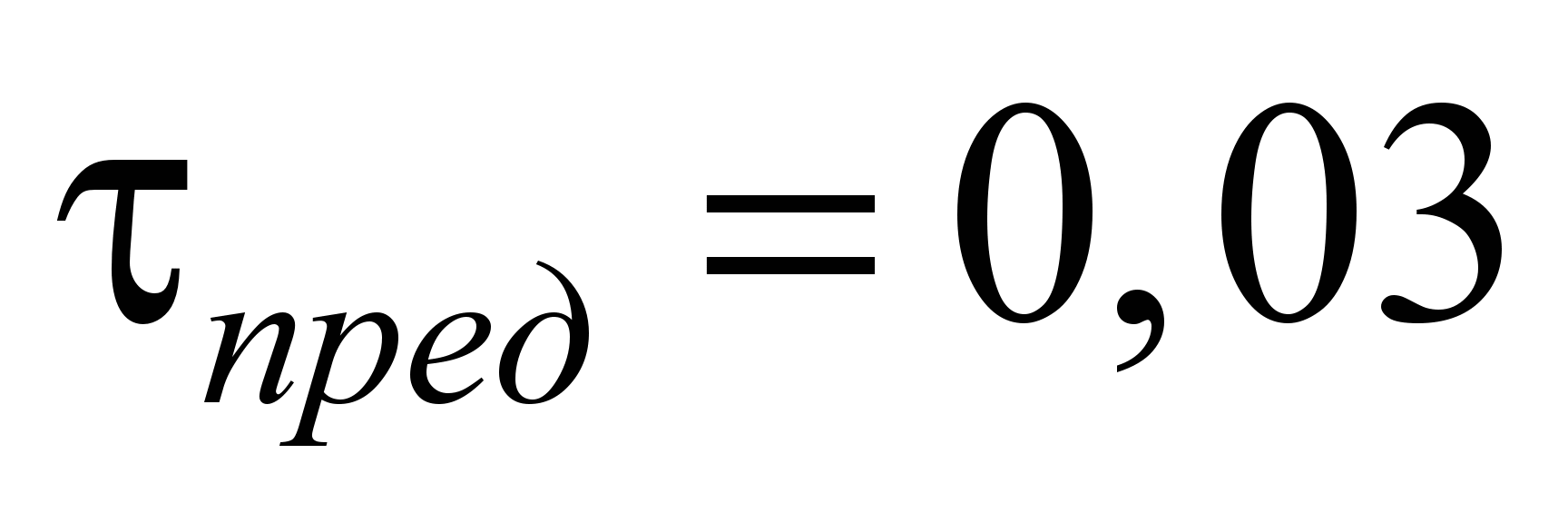 МПа. Сопоставление расчетных напряжений
с нормативными показывает выполнение
условия прочности земляного полотна
железнодорожного пути.
МПа. Сопоставление расчетных напряжений
с нормативными показывает выполнение
условия прочности земляного полотна
железнодорожного пути.
Научная новизна
и практическая
значимость
Разработан метод
расчета напряженно-деформированного
состояния земляного полотна
железнодорожного пути при учете их
совместной работы на основании
осесимметричной столбчатой модели
грунтового основания, которая учитывает
такие важные свойства реального
грунтового основания, как ограниченная
распределительная способность,
конечность зоны деформирования и
неоднородность (слоистость) по
глубине основания. При этом предложенный
алгоритм позволяет определять как
перемещения основания, так и его
напряженное состояние, что,
в свою очередь, позволяет
оценить его прочность при проектировании
железнодорожного пути.
Приведено дальнейшее
развитие осесимметричной столбчатой
модели грунтового основания.
Разработан алгоритм
расчета верхнего строения и земляного
полотна железнодорожного пути при
учете их совместной работы.
В качестве
математической модели грунтового
основания принята осесимметричная
столбчатая модель, которая учитывает
такие важные параметры грунтового
основания, как ограниченную
распределительную способность,
конечность толщины деформирования по
глубине.
Выводы
В данной работе
осесимметричная столбчатая модель
развита на слоистое (неоднородное по
глубине) основание, которое больше
отвечает реальности. Следует отметить,
что осесимметричная столбчатая модель
позволяет определять как перемещения
основания, так и его напряженное
состояние, что, в свою
очередь, позволяет оценить
его прочность при проектировании
железнодорожного пути.
В дальнейшем
целесообразно развить рассмотренный
алгоритм на действие динамического
нагружения, так как поездная нагрузка
при движении подвижного состава
представляет собой именно динамическую
нагрузку.
СПИСОК
ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
Бондаренко,
І. О. Рекомендації щодо проектування
конструкцій нижньої будови залізничної
колії / І. О. Бондаренко
// Вісн. Дніпропетр. нац. ун-ту залізн.
трансп. ім. акад. В. Лазаряна. –
Дніпропетровськ, 2011. – Вип. 36. – С.
100–103.
Бондаренко,
І. О. Щодо забезпечення якості проектування
конструкції земляного полотна
залізничної колії / І. О. Бондаренко //
Вісн. Дніпропетр. нац. ун-ту залізн.
трансп. ім. акад. В. Лазаряна. –
Дніпропетровськ, 2011. – Вип. 37. – С.
120–123.
Винокуров,
Л. П. Решение динамической контактной
задачи для балок, лежащих на весомом
податливом слое, с привлечением
осесимметричной столбчатой модели
/ Л. П. Винокуров,
Л. П. Телипко // Изв.
высш. учеб.
заведений. Стр-во и
архитектура. – 1977. –
№ 2. –
С. 31–36.
Винокуров,
Л. П. Решение контактной задачи для
статически и динамически нагруженных
фундаментов на податливом основании,
представленном осесимметричной
столбчатой моделью / Л. П.
Винокуров, Л. П.
Телипко // Сопротивление
материалов и теория сооружений : респ.
межвед. науч. техн. сб. –
Киев, 1978. – Вып. XXXII.
– С. 31–38.
Винокуров,
Л. П. Прямые методы решения пространственных
и контактных задач для массивов и
фундаментов / Л. П.
Винокуров. – Харьков :
Изд-во Харьк. ун-та, 1956.
– 280 с.
Жемочкин,
Б. Н. Практические методы расчета
фундаментных балок и плит на упругом
основании / Б. Н. Жемочкин,
А. П. Синицын. –
Москва : Госстройиздат,
1962. – 239 с.
Исследование
параметров модернизированного земляного
полотна / В. Д. Петренко, А. М. М. Алхдур,
А. Л. Тютькин, В. В. Ковалевич // Вісн.
Дніпропетр. нац. ун-ту залізн. трансп.
ім. акад. В. Лазаряна. – Дніпропетровськ,
2012. – Вип. 41. – С. 164–169.
Курган,
Д. М. Основи математичного опису
хвильової моделі поширення напружень
у залізничній колії / Д.
М. Курган //
Наука та прогрес транспорту. – 2016. –
№ 5 (65). – С. 101–113.
doi:
10.15802/stp2016/84032
Петренко,
В. Д. Дослідження впливу деформаційних
характеристик шару посилення на НДС
залізничного насипу при під’їзді до
мостового переходу / В. Д. Петренко, В.
Т. Гузченко, А. М. М. Алхдур // Вісн.
Дніпропетр. нац. ун-ту
залізн. трансп. ім. акад. В. Лазаряна. –
Дніпропетровськ, 2010. – Вип. 32. – С.
101–105.
Петренко,
В. Д. Порівняльний аналіз розрахункових
моделей залізничного земляного полотна
/ В. Д. Петренко, Д. О. Ямпольський, І. О.
Святко // Наука та прогрес транспорту.
– 2013. – № 4 (46). – С. 56–62. doi:
10.15802/stp2013/16619
Подольский,
Е. Н. О матричном методе исследования
и решения однородной системы линейных
обыкновенных дифференциальных уравнений
с постоянными коэффициентами на
электронно-цифровых машинах
/ Е. Н. Подольский, В. И.
Пустынников // Труды
ХИСИ. – Харьков,
1961. –
Вып. 17. – С.
89–100.
Порівняльний
аналіз напружено-деформованого стану
двох варіантів підсилення конструкції
земляного полотна / В. Д.
Петренко, В. Т.
Гузченко, О. Л.
Тютькін, А.
М. М. Алхдур
// Вісн. Дніпропетр. нац. ун-ту залізн.
трансп. ім. акад. В. Лазаряна. –
Дніпропетровськ, 2009. – Вип. 29. – С.
107–111.
Тютькін, О.
Л. Теоретичні основи визначення
напружено-деформованого стану глинистого
породного масиву як в’язко-пружно-пластичного
середовища / О. Л. Тютькін // Вісн.
Дніпропетр. нац. ун-ту залізн. трансп.
ім. акад. В. Лазаряна. – Дніпропетровськ,
2008. – Вип. 21. – С. 201–206.
Ярецкая, Н.
А. Контактная задача для жесткого
кольцевого штампа и полупространства
с начальными (остаточными) напряжениями
/ Н. А. Ярецкая // Прикладная механика.
– 2018. – № 5 (54). –
С. 55–60.
Connolly,
D. Numerical
modeling of
ground borne
vibrations from
high speed
rail lines
on embankments
/ D. Connolly, A. Giannopoulos, M.
C. Forde // Soil Dynamics and Earthquake
Engineering. – 2013. – Vol. 46.
– P. 13–19. doi: 10.1016/j.soildyn.2012.12.003
Evtushenko,
S. I. Investigation of the Behavior of Strip Foundations with
Complex Configuration of the Base /
S. I. Evtushenko,
T. A. Krakhmal’nyi // Soil Mechanics and Foundation Engineering.
– 2017.
– Vol. 54.
– Іss.
3. – P. 169–172.
doi: 10.1007/s11204-017-9452-6
Glushkov,
V. Influence of the form and size of the isolated foundations on
the stress-strain state of the soil base / V. Glushkov, A.
Bartolomey // Journal of Applied Engineering Science.
– 2016. – Vol. 14. – Іss.
1. –
P. 28–35.
doi: 10.5937/jaes14-9136
Lugovoi,
P. Z. Nojnstationary Dynamics of a System Consisting of a
Cylindrical Shell and a Soil Medium of Periodic Structure / P. Z.
Lugovoi, V. F. Meish, Y. A. Meish // International
Applied Mechanics. – 2016. – Vol. 52.
– Іss.4.
– P. 350–353. doi: 10.1007/s10778-016-0758-2
Motra,
H. B. Quality assessment of soil bearing capacity factor models of
shallow foundations
/
H. B. Motra,
H. Stutz,
F.
Wuttke
// Soils
and Foundations.
– 2016. – Vol. 56.
– Іss.
2. – P.
265–276.
doi:
10.1016/j.sandf.2016.02.009
Petrenko,
V. D. Simulation of subgrade embankment on weak base / V. D.
Petrenko, I. O. Sviatko // Наука та
прогрес транспорту. – 2015. – № 4 (58). –
С. 198–204. doi:
10.15802/stp2015/49286
The
basing of stabilization parameters of a fortified railway
bed / V. D. Petrenko,
O. L. Tіutkin,
O. M. Kulazhenko, A. M. M. Alkhdour // Наука
та прогрес транспорту. – 2015. – № 1 (55).
– С. 165–172.
doi:
10.15802/stp2015/38269
Л. П. ТЕЛІПКО1*,
Л. М. МАМАЄВ2, С. В.
РАКША3
1*Каф.
«Теоретична та прикладна механіка»,
Дніпровський державний технічний
університет, вул. Дніпробудівська, 2,
Кам’янське, Україна, 51918,
тел. +38 (0569)
53 85 23, ел. пошта leo46din@gmail.com, ORCID
0000-0003-3165-3920
2Каф. «Теоретична та
прикладна механіка», Дніпровський
державний технічний
університет, вул.
Дніпробудівська, 2, Кам’янське, Україна,
51918,
тел. +38 (0569)
53 85 23, ел. пошта leo46din@gmail.com,
ORCID 0000-0002-6421-4396
3Каф. «Прикладна
механіка та матеріалознавство»,
Дніпропетровський національний
університет залізничного транспорту
імені академіка В. Лазаряна, вул.
Лазаряна, 2,
Дніпро, Україна, 49010, тел.
+38 (056) 47 15 18,
ел. пошта raksha@ukr.net, ORCID
0000-0002-4118-1341
УРАХУВАННЯ
НЕОДНОРІДНОСТІ ЗЕМЛЯНОГО
ПОЛОТНА
ЗАЛІЗНИЧНОЇ КОЛІЇ ПРИ
ВИЗНАЧЕННІ
ЙОГО
НАПРУЖЕНО-ДЕФОРМОВАНОГО СТАНУ
Мета.
Збільшення швидкості руху й
вантажопідйомності потягів призводить
до збільшення навантаження на залізничну
колію і, у свою чергу, навантаження на
земляне полотно. Це викликає необхідність
уточнення методів розрахунку як верхньої
будови, так і земляного полотна
залізничної колії. Метою роботи є
розробка методу визначення
напружено-деформованого стану земляного
полотна залізничної колії на підставі
врахування обмеженої розподільної
здатності, кінцевості зони деформації
по глибині земляного полотна і його
неоднорідності. Методика. На підставі
змішаного методу Б. Н. Жемочкіна,
згідно з яким дійсну криволінійну епюру
відпору по нижній площині шпал замінюють
ступінчастою, розглянута спільна робота
рейко-шпальної решітки й земляного
полотна залізничної колії. Результати.
Отримала розвиток вісесиметрична
стовпчаста модель ґрунтової основи,
яка враховує такі важливі її властивості,
як обмежена розподільна здатність,
кінцевість зони деформування й
неоднорідність (шаруватість). На підставі
дискретного методу Л. П. Винокурова
й вісесиметричної стовпчастої моделі
ґрунтової основи отримані рівняння
для переміщень і напружень для i-го шару
основи. У результаті розв’язання
системи диференціальних рівнянь
дискретного методу чисельним методом,
в якому функції від матриць представляють
рядами, визначені вертикальні й радіальні
переміщення шаруватої основи, після
чого визначені нормальні й дотичні
напруження в основі. Реалізація змішаного
методу Б. Н. Жемочкіна дозволяє
визначити відпору по підошві шпал та
прогини центральних перерізів балок-шпал.
Наукова новизна. Розроблений
метод розрахунку напружено-деформованого
стану земляного полотна залізничної
колії при їх спільній роботі на підставі
вісесиметричної стовпчастої моделі.
При цьому враховані обмежена розподільна
здатність, кінцевість зони деформування
й неоднорідність по глибині ґрунтової
основи. Практична значимість.
Отримані результати дозволяють підвищити
точність рішень під час проектування
земляного полотна залізничної колії,
що, у свою чергу, призведе до підвищення
її надійності й довговічності.
Ключові
слова: напружено-деформований стан;
земляне полотно; залізнична колія;
напруження; переміщення; осідання
L.
P. TELIPKO1*,
L. M. MAMAEV2,
S. V. RAKSHA3
1*⃰Dep.
«Theoretical and Applied Mechanics», Dniprovsk State Technical
University,
Dniprobudivska St., 2, Kamenskoye, Ukraine, 51918, tel.
+38 (0569)
53 85 23,
e-mail leo46din@gmail.com,
ORCID 0000-0003-3165-3920
2Dep. «Theoretical and
Applied Mechanics», Dniprovsk State Technical University,
Dniprobudivska St., 2, Kamenskoye, Ukraine, 51918. tel. +38 (0569)
53 85 23,
e-mail leo46din@gmail.com, ORCID
0000-0002-6421-4396
3Dep. «Applied Mechanics
and Material Science», Dnipropetrovsk National University
of
Railway Transport named after Aca-demician V. Lazaryan, Lazaryan
St., 2, Dnipro,
Ukraine, 49010, tel. +38 (056) 47 15 18, e-mail raksha@ukr.net,
ORCID 0000-0002-4118-1341
THE SUBGRADE
HETEROGENEITY CONSIDERATION
OF A RAILWAY TRACK WHEN DETERMINING ITS
STRESS-STRAIN STATE
Purpose.
Increase of the speed and train carrying capacity causes the
increase in the load on the railway track and, in turn, loads on the
subgrade. This makes it necessary to clarify the calculation
methods, both the upper structure and the subgrade of the railway
track. The purpose of the paper is the development of a method for
determining the stress-strain state of railway subgrade on the basis
of taking into account the limited distribution capacity, the
extremity of the deformation area along the subgrade depth and its
heterogeneity. Methodology. Based on the mixed method of B.
N. Zhemochkin, according to which the actual curvilinear resistance
diagram on the lower flat of the sleepers is replaced by a stepwise
one, the joint operation of the rail-sleeper grate and the subgrade
of the railway track is considered. Findings. The development
of an axisymmetric columnar model of the subgrade is considered,
which takes into account such important properties of the subgrade
as the limited distribution capacity and the extremity of the
deformation area on heterogeneous (layered) base. Based on the
discrete method of L. P. Vinokurov and the subgrade axisymmetric
columnar model, the equations for displacements and stresses for
i-th foundation layer have been obtained. As a result of
differential equation system solution of the discrete method by a
numerical method in which the functions of the matrices are
represented by series, the vertical and radial displacements of the
layered base are determined, after which the normal and shearing
stresses at the base are determined. The implementation of B. N.
Zhemochkin mixed method allows to determine the resistance from the
bottom of sleepers and the deflections of the central sections of
the sleepers-beams. Originality. Method for calculating the
stress-strain state of railway subgrade during their joint operation
on the basis of an axisymmetric columnar model has been developed.
At this the limited distribution capacity, the extremity of the
deformation area and the heterogeneity according to the depth of the
base have been taken into account. Practical value. The
results obtained make it possible to increase the accuracy of design
solutions in the design of the railway subgrade, which in turn,
resulting in increased reliability and service life of the railway
track.
Keywords:
stress-strain state; subgrade; railway track; stress; displacement;
settling
REFERENCES
Bondarenko,
I. O. (2011). Rekomendatsii shchodo proektuvannia konstruktsii
nyzhnoi budovy zaliznychnoi kolii.
Bulletin of Dnipropetrovsk National
University of Railway Transport named after Academician V.
Lazaryan,
36, 100-103. (in Ukraіnian)
Bondarenko
I. O. (2011). Shchodo zabezpechennia yakosti proektuvannia
konstruktsii zemlianoho polotna zaliznychnoi kolii.
Bulletin of Dnipropetrovsk National
University of Railway Transport named after Academician V.
Lazaryan,
37,
120-123. (in
Ukraіnian)
Vinokurov,
L. P.,
& Telipko,
L. P.
(1977). Reshenie
dinamicheskoy
kontaktnoy
zadachi dlya
balok,
lezhashchikh na
vesomom
podatlivom
sloe, s
privlecheniem
osesimetrichnoy
stolbchatoy
modeli.
Izvestiya vysshikh uchebnykh
zavedeniy. Stroitelstvo i arkhitektura,2,
31-36. (in
Russian)
Vinokurov,
L. P., &
Telipko, L.
P. (1978).
Reshenie kontaktnoy zadachi dlya staticheski i dinamicheski
nagruzhennykh fundamentov na podatlivom osnovanii, predstavlennom
osesimmetrichnoy stolbchatoy modelyu.
Soprotivlenie materialov i teoriya
sooruzheniy, XXXII, 31-38.
(in Russian)
Vinokurov,
L. P. (1956). Pryamye
metody resheniya prostranstvennykh i kontaktnykh zadach dlya
massivov i fundamentov.
Kharkov: Izdatelstvo Kharkovskogo universiteta.
(in Russian)
Zhemochkin,
B. N., & Sinitsyn,
A. P. (1962). Prakticheskie metody
rascheta fundamentnykh balok i plit na uprugom osnovanii.
Moscow:
Gosstroyizdat. (in
Russian)
Petrenko,
V. D., Alkhdur,
A. M. M., Tyutkin,
A. L., & Kovalevich,
V. V. (2012). Issledovanie parametrov modernizirovannogo zemlyanogo
polotna. Bulletin of Dnipropetrovsk
National University of Railway Transport named after Academician V.
Lazaryan,
41, 164-169.
(in Russian)
Kurhan,
D. M. (2016). The Basis of Mathematical Description for Wave Model
of Stresses Propagation in Railway Track. Science
and Transport Progress, 5(65),
101-113. doi: 10.15802/stp2016/84032 (in
Ukraіnian)
Petrenko,
V. D.,
Huzchenko,
V. T.,
& Alkhdur,
A. M.
M. (2010). The
Study of the Influence of the Deformation Characteristics of the
Layer of Reinforcement on Vat Railway Embankment at the Entrance to
the Bridge Crossing. Bulletin
of Dnipropetrovsk National University of Railway Transport named
after Academician V. Lazaryan,
32,
101-105. (in
Ukraіnian)
Petrenko,
V. D., Yampolskiy, D. O., & Sviatko, I. O. (2013). Comparative
analysis of calculation models of railway subgrade. Science
and Transport Progress, 4(46), 56-62.
doi: 10.15802/stp2013/16619 (in
Ukraіnian)
Podolskiy,
Y. N., & Pustynnikov,
V. I. (1961). O
matrichnom
metode
issledovaniya i
resheniya
odnorodnoy
sistemy
lineynykh
obyknovennykh
differentsialnykh
uravneniy s
postoyannymi
koeffitsientami
na
elektronno-tsifrovykh
mashinakh.
Trudy KhISI,
17, 89-100. (in
Russian)
Petrenko,
V. D.,
Huzchenko, V.
T., Tiutkin,
O. L.,
& Alkhdur,
A. M.
M. (2009).
Comparative Analysis of the
Stress-Strain State of the Two Variants of Reinforcement Design
Subgrade.
Bulletin of
Dnipropetrovsk National University of Railway Transport named after
Academician V. Lazaryan, 29,
107-111.
(in Ukraіnian)
Tyutkin,
O. L.
(2008). The Theoretical Basis for Determining the Stress-Strain
State of the Clay Rock Mass as a Visco-Elasto-Plastic Environment.
Bulletin of Dnipropetrovsk National
University of Railway Transport named after Academician V.
Lazaryan,
21,
201-206. (in
Ukraіnian)
Yaretskaya,
N. A. (2018)
Contact
problem for the stiff annular punch and semispace with initial
(residual) stresses. International
Applied Mechanics,
5(54),
55-60. (in
Russian)
Connolly,
D., Giannopoulos, A., & Forde, M. C. (2013). Numerical
modelling of ground borne vibrations from high speed rail lines on
embankments. Soil Dynamics and
Earthquake Engineering, 46, 13-19.
doi: 10.1016/j.soildyn.2012.12.003 (in
English)
Evtushenko,
S. I., & Krakhmal’nyi, T. A. (2017). Investigation of the
Behavior of Strip Foundations with Complex Configuration of the
Base. Soil Mechanics and Foundation
Engineering, 54(3), 169-172. doi:
10.1007/s11204-017-9452-6 (in English)
Glushkov,
V., & Bartolomey,
A. (2016). Influence of the form and size
of the isolated foundations on the stress-strain state of the soil
base. Journal of Applied Engineering
Science, 14(1),
28-35. doi: 10.5937/jaes14-9136 (in
English)
Lugovoi,
P. Z., Meish, V. F., & Meish, Y. A. (2016). Nonstationary
Dynamics of a System Consisting of a Cylindrical Shell and a Soil
Medium of Periodic Structure. International
Applied Mechanics, 52(4), 350-353.
doi: 10.1007/s10778-016-0758-2 (in
English)
Motra,
H. B., Stutz, H., & Wuttke, F. (2016). Quality assessment of
soil bearing capacity factor models of shallow foundations. Soils
and Foundations, 56(2), 265-276.
doi: 10.1016/j.sandf.2016.02.009 (in
English)
Petrenko,
V. D., & Sviatko, I. O. (2015). Simulation of Subgrade
Embankment on Weak Base. Science and
Transport Progress, 4(58), 198-204.
doi: 0.15802/stp2015/49286 (in
English)
Petrenko,
V. D., Tiutkin, O. L., Kulazhenko, O. M., & Alkhdour, A. M. M.
(2015). The Basing of Stabilization Parameters of a Fortified
Railway Bed. Science and Transport
Progress, 1(55), 165-172.
doi: 10.15802/stp2015/38269 (in
English)
Поступила
в редколлегию: 30.07.2018
Принята
к печати: 14.11.2018
, (1)
;
,
– перемещение точки i
(по направлению силы Xi)
от единичного усилия
,
равное сумме перемещений балки
(в основной системе) и податливого
основания
(на основание действует единичная сила,
равномерно распределенная по участку
j):
=
+
;
в пределах центрально расположенной
площадки радиусом
,
моделируем круговым цилиндрическим
слоистым столбом высотой Н и конечным
радиусом
в поперечном сечении (рис. 2), совпадающим
с радиусом затухания перемещений на
граничной плоскости основания. Площадь
грузовой площадки радиусом
согласуется с площадью участков, на
которые разбита подошва балки-шпалы.
i-го слоя основания
при неравномерном шаге деления радиальной
координаты (рис. 3) мы получили следующие
уравнения дискретного метода для
перемещений и напряжений: