ISSN
2307–3489 (Print), ІSSN
2307–6666
(Online)
Наука
та прогрес транспорту. Вісник
Дніпропетровського
національного університету залізничного
транспорту, 2018, № 5 (77)
рухомий
склад залізниць і тяга поїздів
UDC 629.45.027.3
A.
G. Reidemeister1*,
S. I. LevYtska2*
1*Dep.
«Cars and Car Facilities», Dnipropetrovsk National University of
Railway Transport named after Academician
V. Lazaryan, Lazaryan
St., 2, Dnipro,
Ukraine, 49010, tel. +38 (056) 373 15 19,
e-mail
reidemeister.a@gmail.com,
ORCID 0000-0001-7490-7180
2*Dep.
«Foreign Languages», Prydniprovsk State
Academy of Civil Engineering and Architecture,
Chernyshevsky
St., 24 A, Dnipro, Ukraine, 49000, tel. +38 (056) 756 33 56, e-mail
svetik23com@ukr.net,
ORCID 0000-0001-6725-0280
STABILITY
OF MOTION OF RAILWAY VEHICLES
DESCRIBED WITH LAGRANGE EQUATIONS
OF
the first KIND
Purpose.
The article aims to estimate
the stability of
the railway
vehicle motion,
whose oscillations
are described by
Lagrange equations
of the first
kind under the
assumption that
there are no
nonlinearities with
discontinuities of
the right-hand
sides. Methodology. The study
is based on the Lyapunov’s stability method of linear
approximation. The equations of motion are compiled in a matrix form.
The creep forces are calculated in accordance with the Kalker linear
theory. Sequential differentiations of the constraint equations
reduced the equation system index from 2 to 0. The coefficient matrix
eigenvalues of the system obtained in such a way are found by means
of the QR-algorithm. In accordance with Lyapunov's criterion of
stability in the linear approximation, the motion is stable if the
real part of all eigenvalues is negative. The presence of
«superfluous» degrees of freedom, which the mechanical system does
not have (in whose motion equations there are left only independent
coordinates) is not trivial. Herewith the eigenvalues and
eigenvectors correspond to these degrees of freedom and have no
relation to the stability. In order to find a rule that allows
excluding them, we considered several models of a bogie, with rigid
and elastic constraints of high rigidity at the nodes. In the
limiting case of high rigidities, the results for a system without
rigid constraints must coincide with the results for a system with
rigid constraints. Findings. We carried out the analysis and
compared the frequencies (with decrements) and the vibration modes of
a three-piece bogie with and without constraints. When analysing
the stability of the system with constraints, only those eigenvalues
are of interest whose eigenvectors do not break the constraints. The
values of these numbers are limits for the eigenvalues of the system,
in which rigid constraints are replaced by elastic elements of high
rigidity, which allows us to leave the Lyapunov’s criterion
unchanged. Originality consists in the adaptation of
Lyapunov's stability method of linear approximation to the case when
the equations of railway vehicle motion are written in the form of
differential-algebraic Lagrange equations of the first kind.
Practical value. This written form of the equation of motion
makes it possible to simplify the stability study by avoiding the
selection of a set of independent generalized coordinates with the
subsequent elimination of dependent ones and allows for the
coefficient matrix calculation in an easily algorithmized way.
Information on the vehicle stability is vitally important, since the
truck design must necessarily exclude the loss of stability in the
operational speed range.
Keywords: railway
vehicle; motion stability; differential-algebraic equations
Introduction
Studies on
the railway vehicle motion stability have been under the spotlight
since the 1950s. Loss of stability is accompanied by the emergence
of large transverse forces that threaten the safety of movement,
which prevents from operating cars at high speeds. Among the
extensive literature devoted to this issue, we point out [1–14].
In accordance with modern concepts, loss of stability is a very
complex phenomenon, which near the critical speeds is described by
the subcritical Hopf bifurcation. Up to a certain velocity
v1
there is only one attractor corresponding to a straight-line motion,
then a periodic attractor appears, while the original one remains
and disappears at the velocity 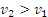 .
At high velocities, chaotic attractors may appear. There may be
cases when they occur already at the velocity
.
At high velocities, chaotic attractors may appear. There may be
cases when they occur already at the velocity 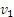 [5]. The following methods of motion stability analysis are used
[15]:
[5]. The following methods of motion stability analysis are used
[15]:
1) Linearization of the motion
equations (Lyapunov’s stability criterion of linear approximation
[1]);
2) Quasi-linearization;
3) Galerkin-Urabe method [12,
13] (quasi-linearization by several frequencies, a large amount of
computational work is required);
4) «Brute
force» method,
when one reduces the movement speed and waits for the
auto-oscillations to disappear; to determine the unstable limit
cycle, one gradually increases the disturbance range [14];
5) Trajectory
tracing method (the motion is assumed to be periodic, and the
equation 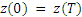 is solved; it is not suitable for the study of quasi-periodic and
chaotic oscillations).
is solved; it is not suitable for the study of quasi-periodic and
chaotic oscillations).
Despite the obvious
unsuitability to analyze the complex picture of the emergence and
disappearance of attractors, Lyapunov's stability criterion of
linear approximation retains its attractiveness due to its
simplicity and ability to do the main thing – to evaluate the
critical velocity. It is formulated for the systems that describe
ordinary differential equations. In the present paper we will extend
it to the systems whose motion is defined by Lagrange
differential-algebraic equations (DAE) of the first kind. Nowadays,
due to the spread of standard integration programs (for example,
DASSL), DAE are increasingly used in modeling railway vehicle
oscillations, since they make it possible to do both without
dependent generalized coordinates and without replacing rigid
constraints between the car parts with high rigidity elastic
elements.
Purpose
To estimate
the stability of the railway vehicle motion, whose oscillations are
described by Lagrange equations of the first kind under the
assumption that there are no nonlinearities with discontinuities of
the right-hand sides.
Methodology
The
structure of
the railway
vehicle motion
equations is
as follows:
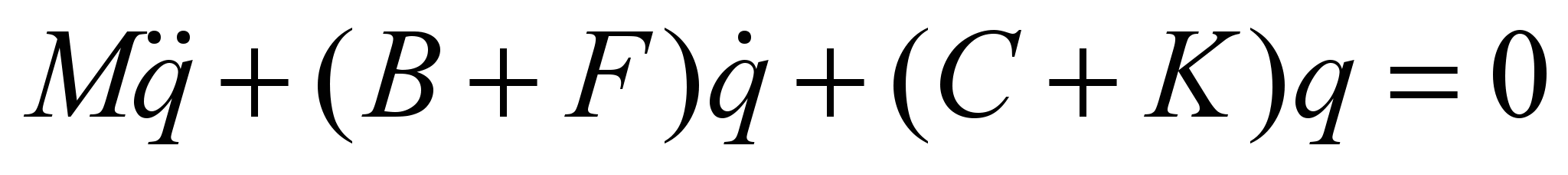 , (1)
, (1)
(without
nonlinear and non-uniform terms describing the movement along a
curve). Here q
is the generalized coordinate vector; M
is the inertial coefficient matrix; C,
B are the
rigidity and viscosity matrices; K,
F are the
matrices describing the wheel-rail interaction. Equation (1) is
obtained if we remove the dependent generalized coordinates from the
vector q
using the equations of constraints. When applying the Lagrange
equation of the I kind, another approach is used: instead of
eliminating the elements of the vector
q,
they are all remained, the constraint equations are included in the
full set of equations describing the system motion, and additional
unknowns λ are introduced (in the amount equal to the number of
constraint equations) so that all these equations can be solved. The
result is the following system of equations:
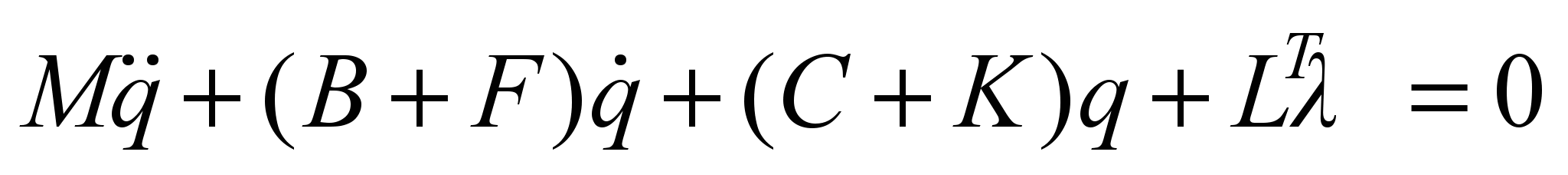 ; (2)
; (2)
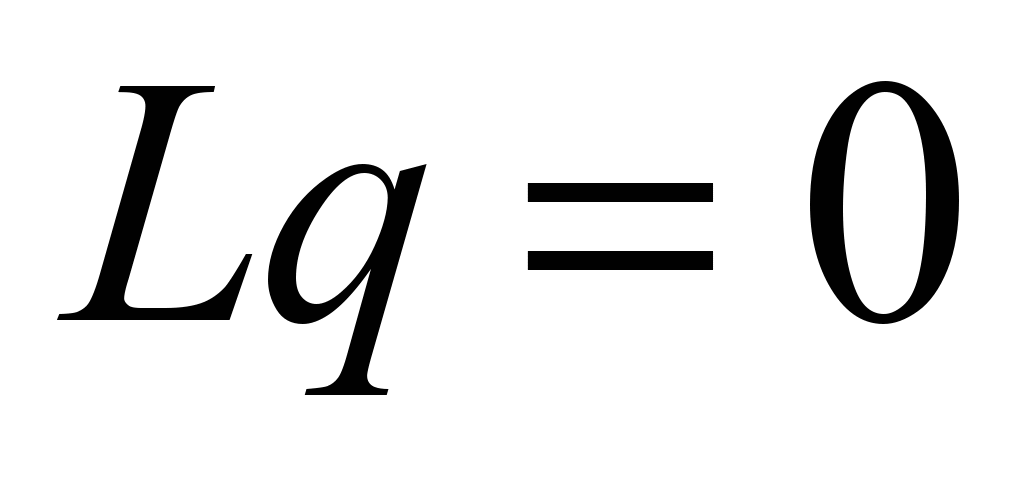 . (3)
. (3)
The last
expression is the equation of the constraints which the mechanical
system is subject to. We will assume that the matrix L
is constant (depends neither on time nor on system phase
coordinates). The system of equations (2) and (3) is linear, so its
solution is:
 ,
,
where
the constants
 are found from the initial conditions.
The indices
are found from the initial conditions.
The indices
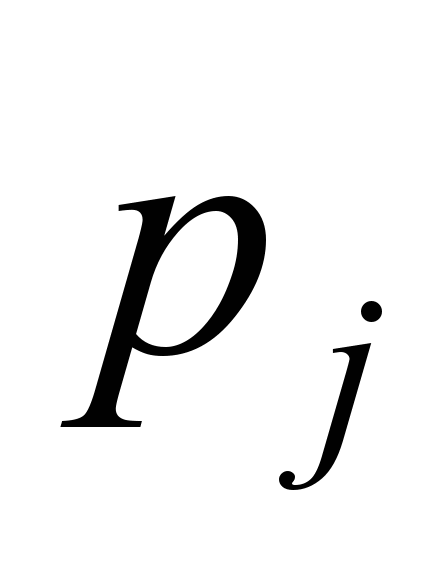 together with nonzero eigenvectors
together with nonzero eigenvectors
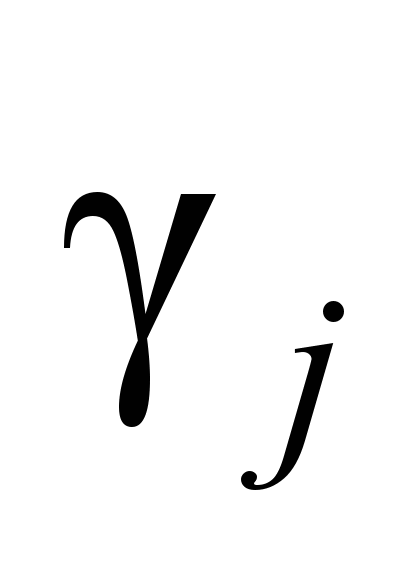 ,
,
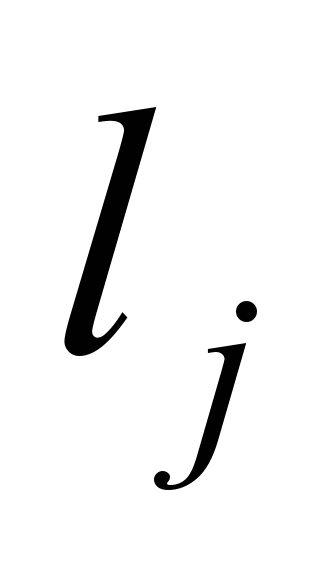 are solutions of the equation
are solutions of the equation
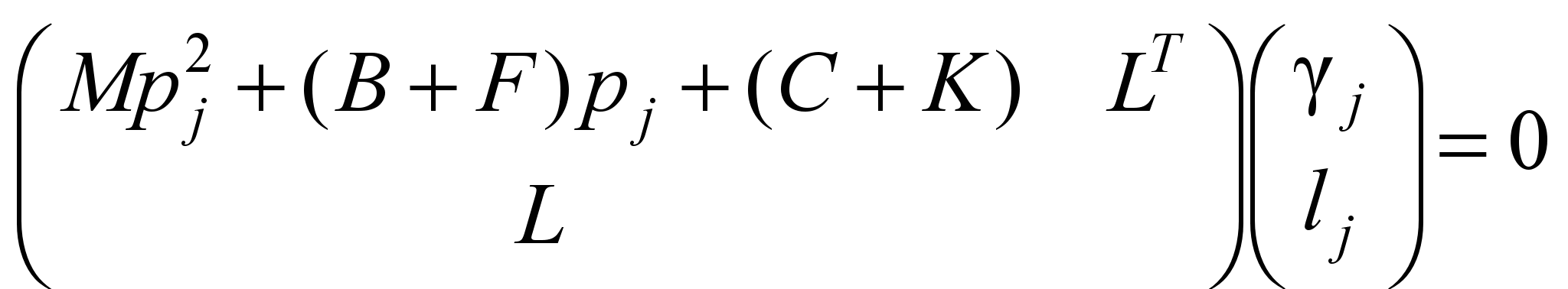 , (4)
, (4)
It is
possible to understand whether motion is stable or not, by the sign
of the real part of the values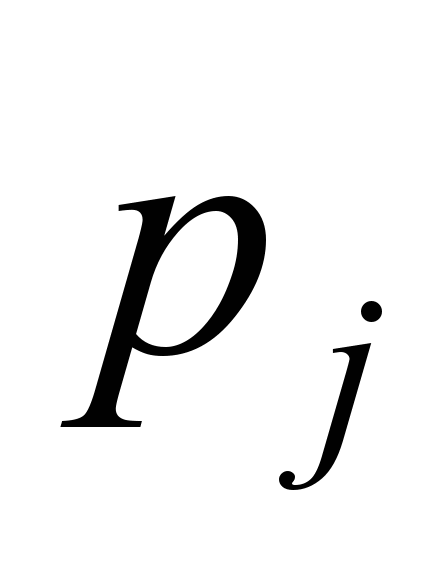 – if there are positive numbers among them, the motion is stable.
It is inconvenient to search for numbers
– if there are positive numbers among them, the motion is stable.
It is inconvenient to search for numbers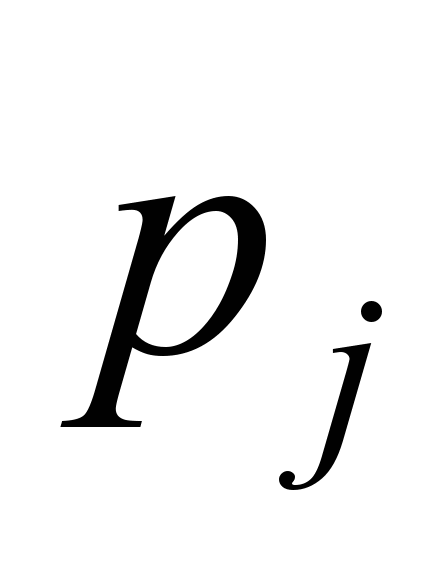 ,
equating the determinant of the left matrix to zero. Instead, we
reformulate the problem so that the indices
,
equating the determinant of the left matrix to zero. Instead, we
reformulate the problem so that the indices
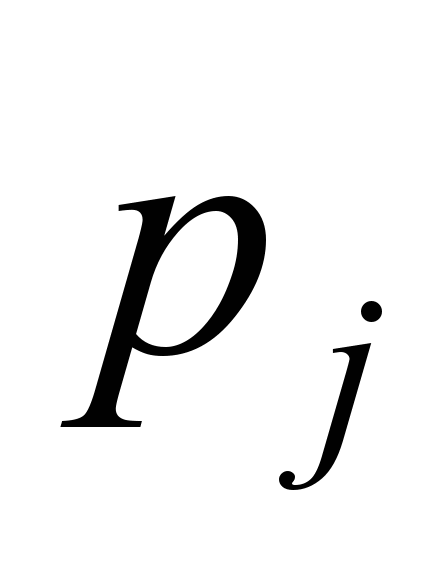 turn out to be eigenvalues of a certain matrix. From (2) it follows
that
turn out to be eigenvalues of a certain matrix. From (2) it follows
that
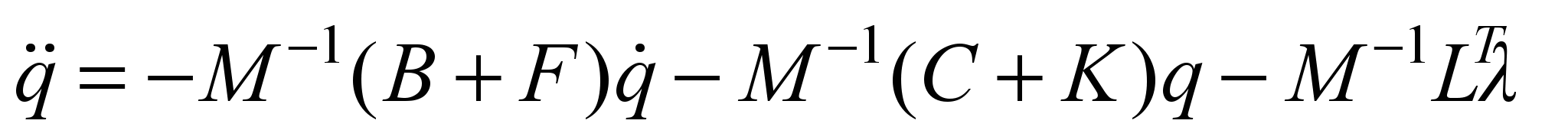 ,
,
Multiplying
the resulting
expression by
L and
using the
fact that
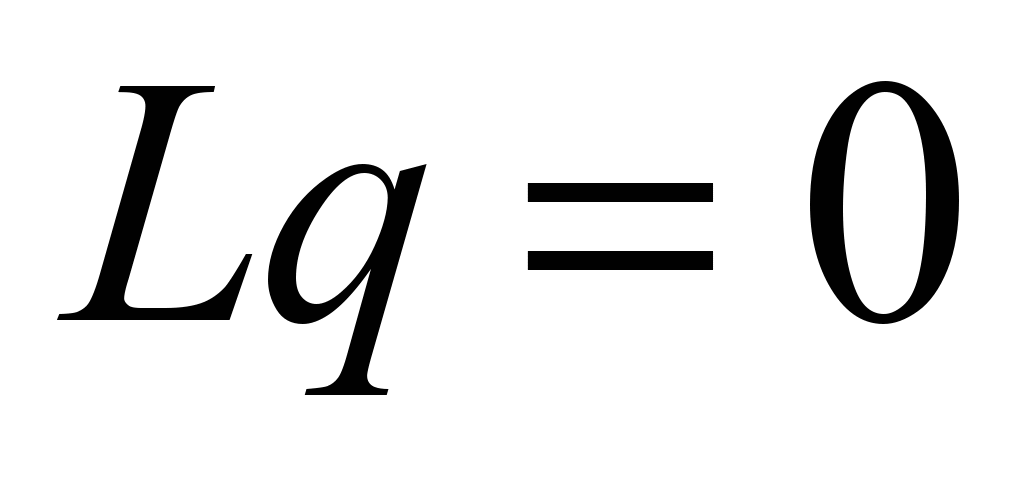 ,
we get
,
we get
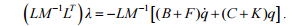
The
matrix
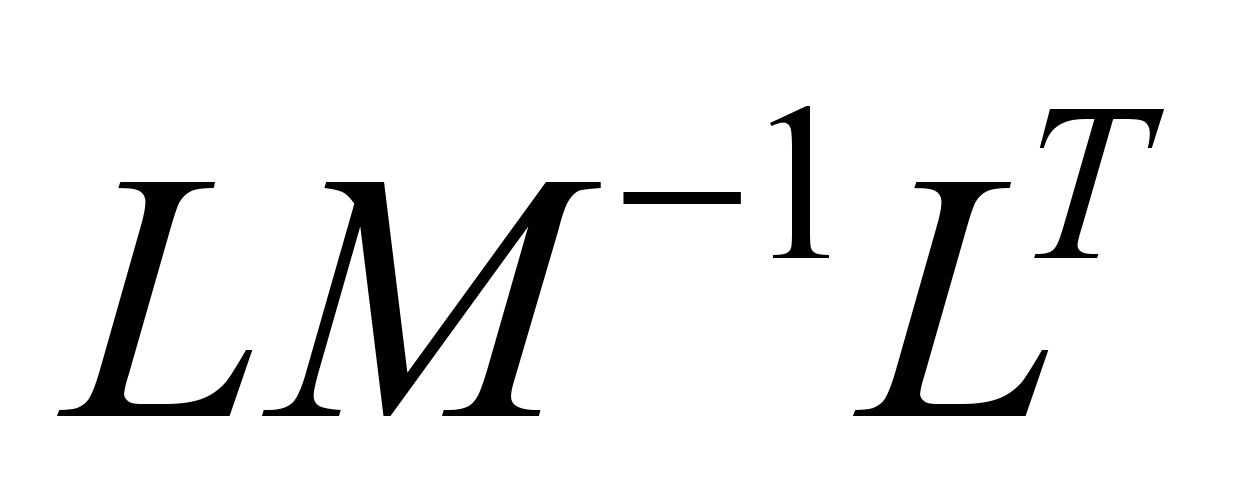 is
non-degenerate
(if the
constraint
coefficient
matrix L
has less rows
than columns,
and the
rank is
equal to
the number
of rows,
which we
assume),
therefore
is
non-degenerate
(if the
constraint
coefficient
matrix L
has less rows
than columns,
and the
rank is
equal to
the number
of rows,
which we
assume),
therefore
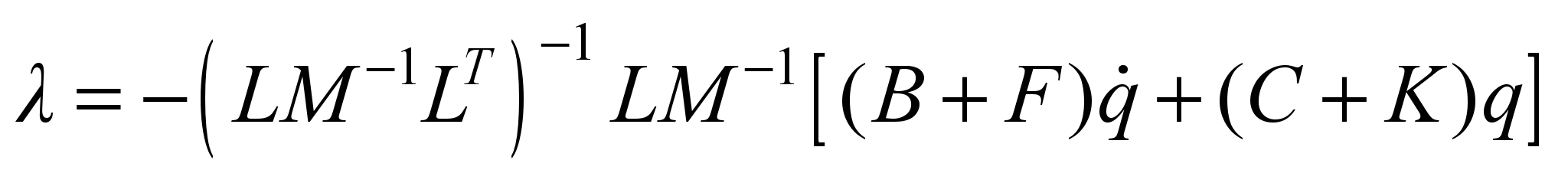 .
.
Substituting
this expression into the original equation, we get
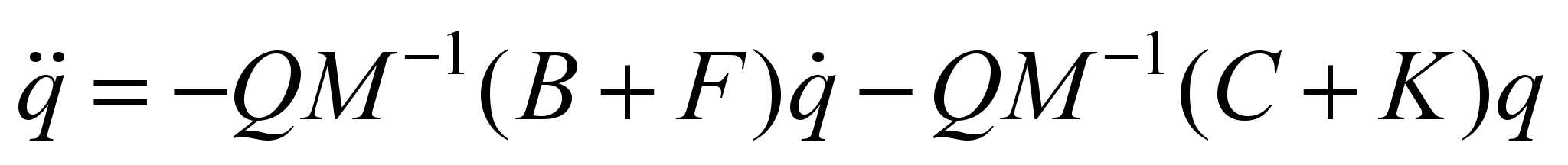 ;
;
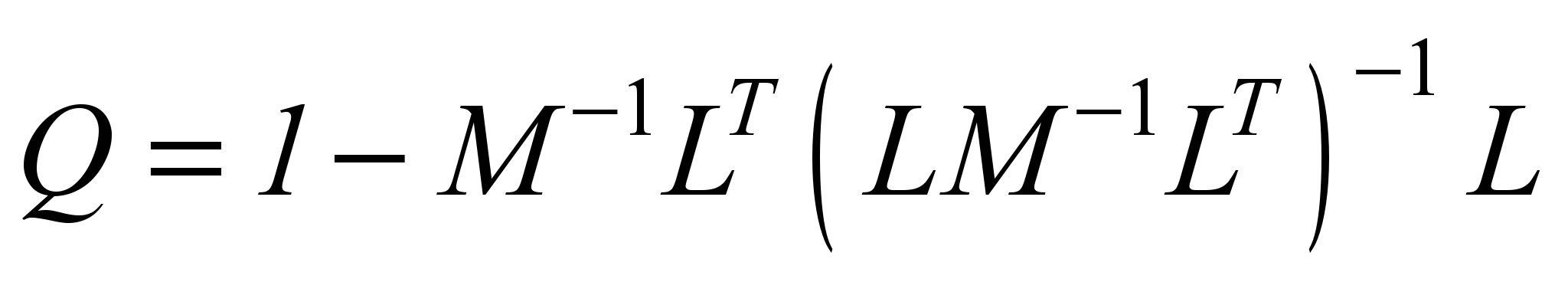 .
.
Thus,
the vector
of phase
coordinates
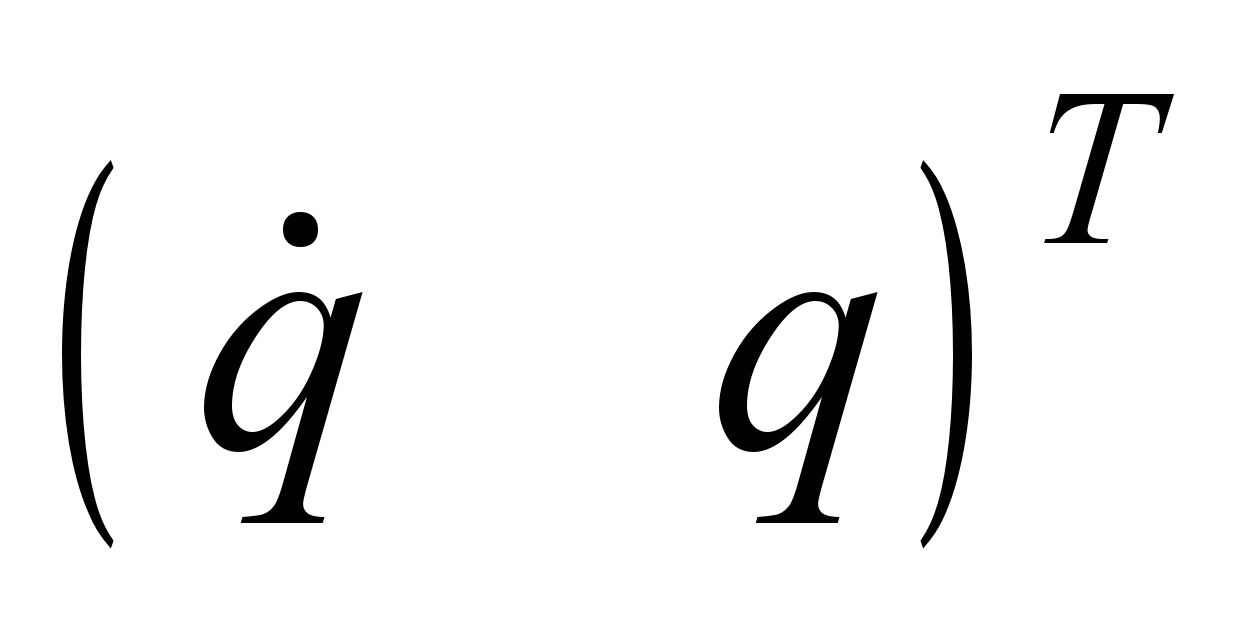 satisfies the
differential
equation
satisfies the
differential
equation
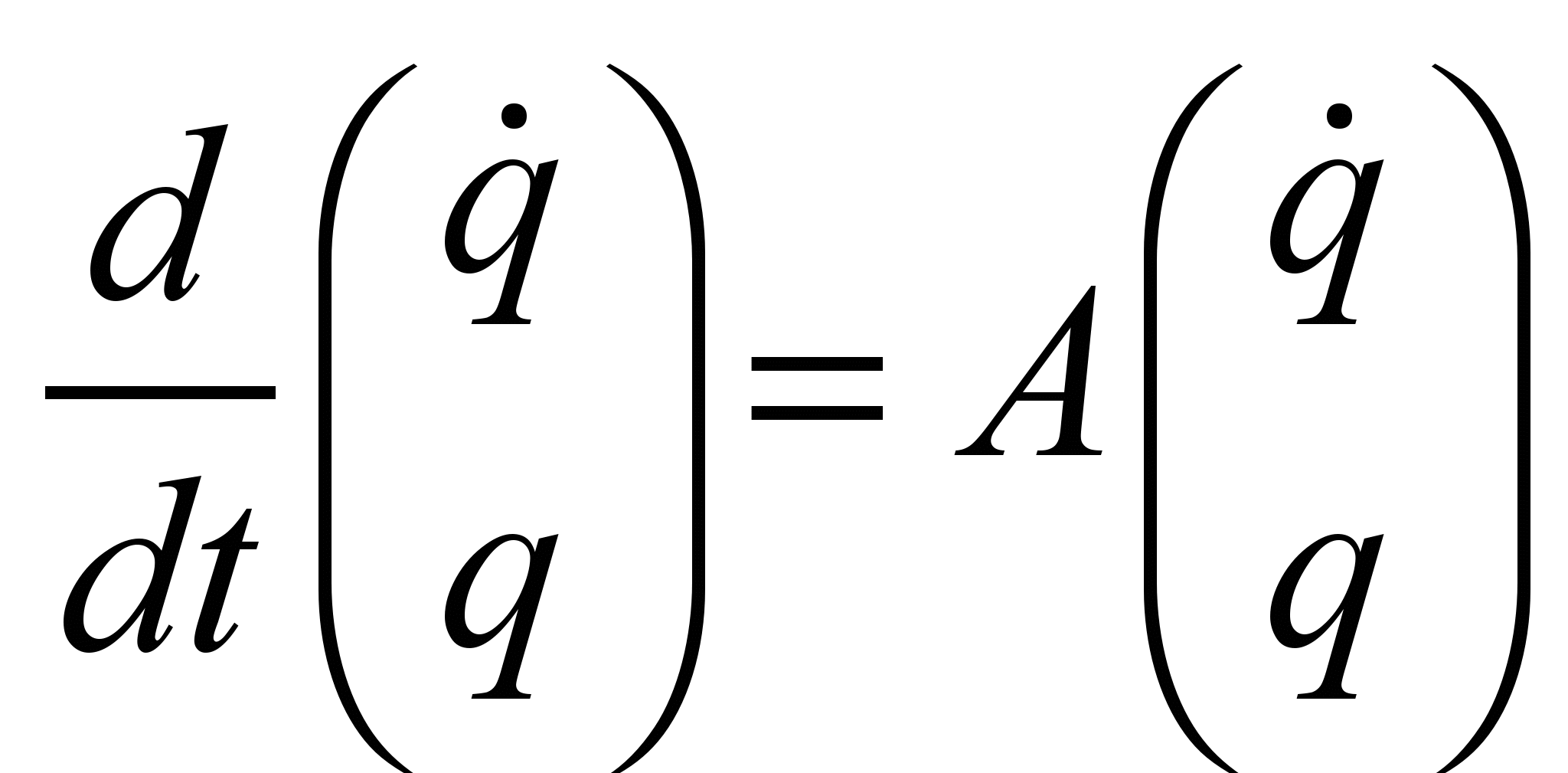 ;
;
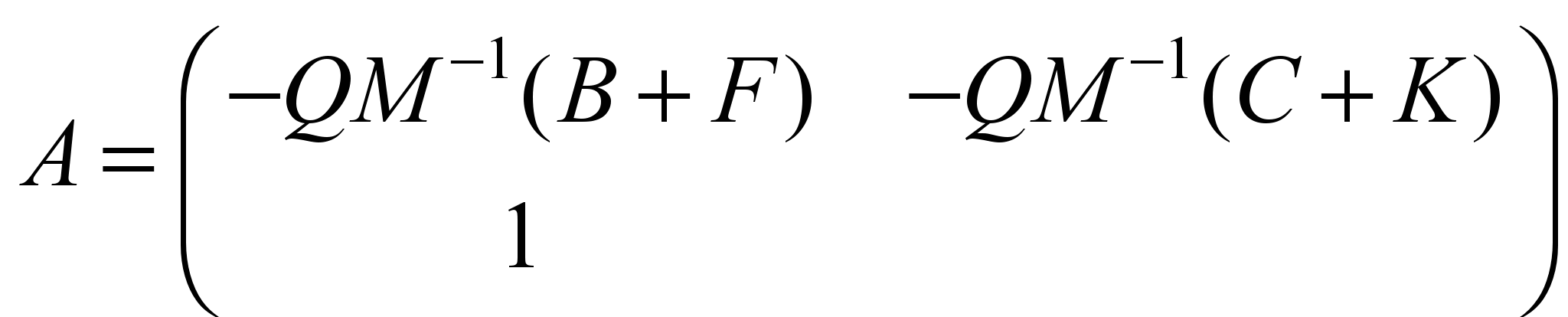 .
.
The
eigenvectors of the matrix A,
corresponding to the eigenvalues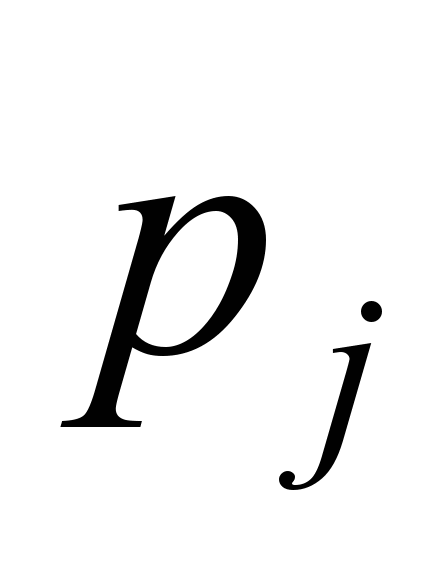 ,
has the form
,
has the form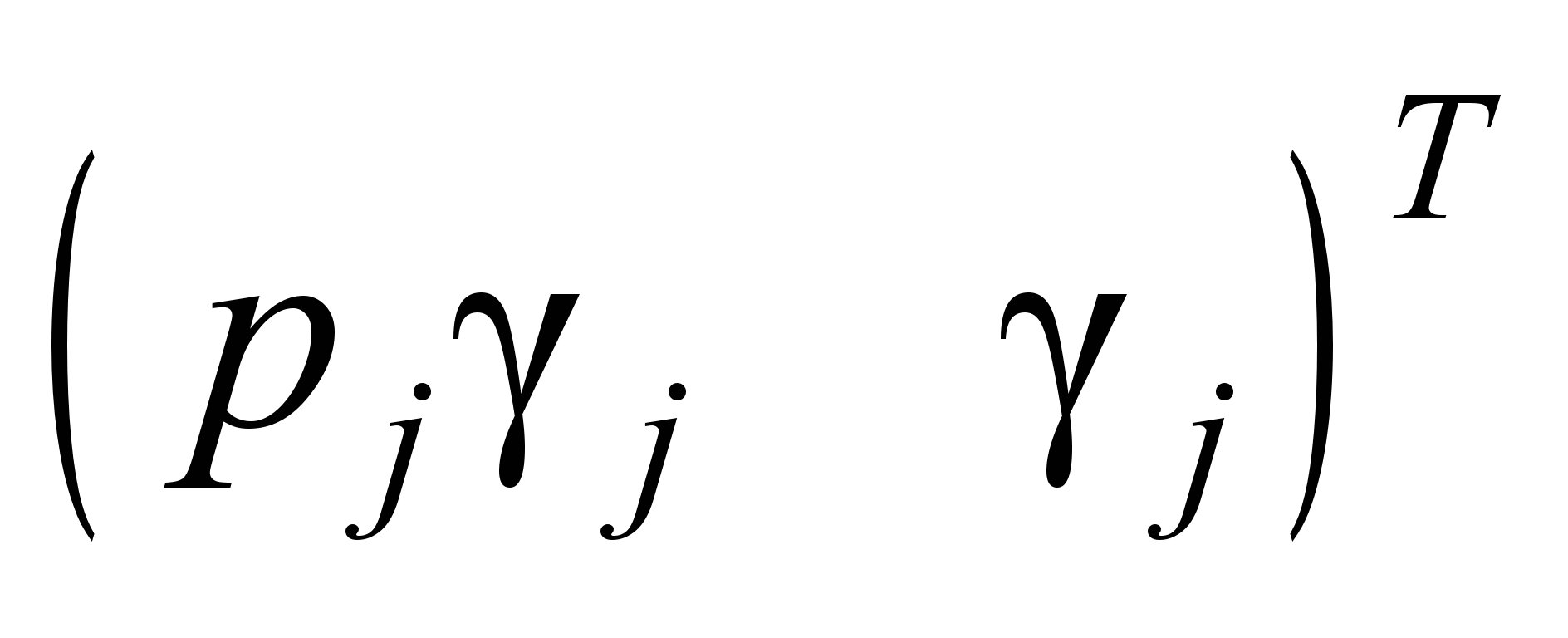 .
Let us consider how they are related to
the eigenvalues and eigenvectors of the original system with
constraints, that is, if they satisfy the equation (4) with a
suitable choice of the vector of Lagrange multipliers
.
Let us consider how they are related to
the eigenvalues and eigenvectors of the original system with
constraints, that is, if they satisfy the equation (4) with a
suitable choice of the vector of Lagrange multipliers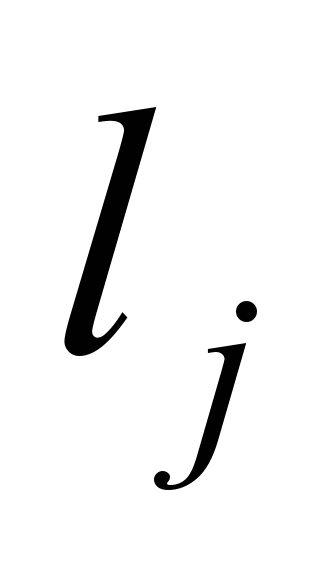 .
We will need an obvious correlation
.
We will need an obvious correlation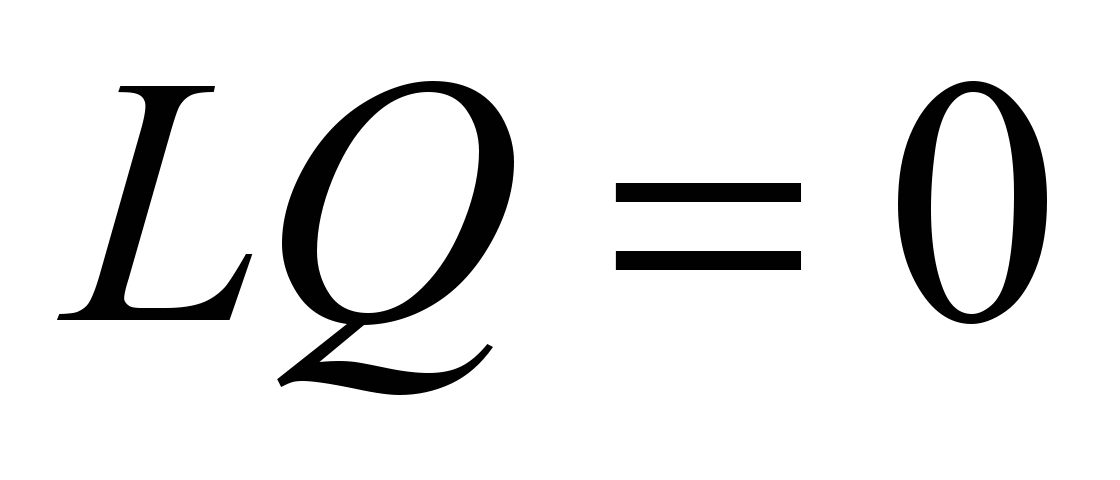 .
Multiplying the left expression by L
.
Multiplying the left expression by L
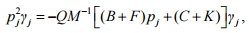 (5)
(5)
we will get
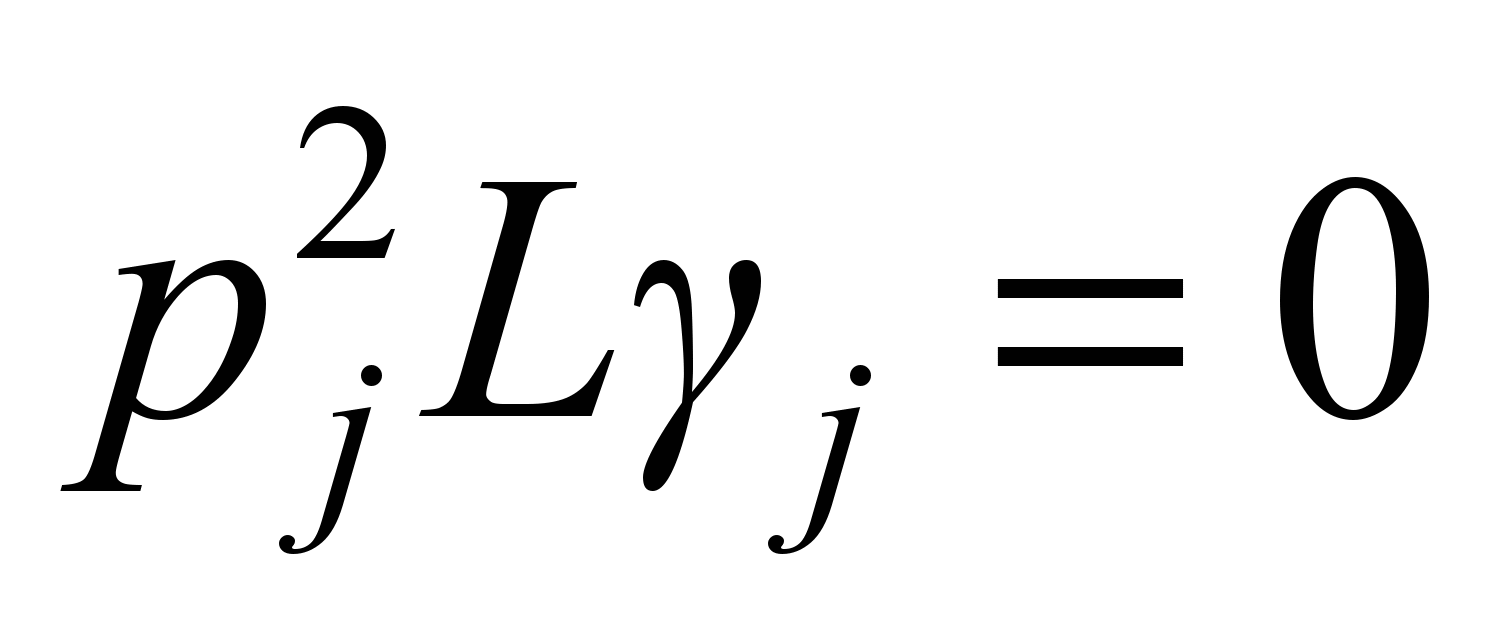 .
.
Therefore,
for nonzero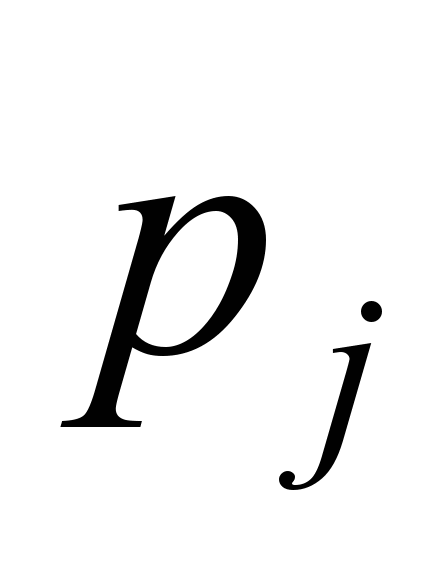 the vector
the vector
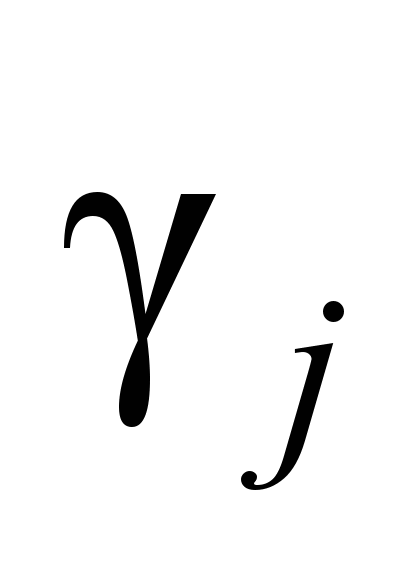 satisfies the constraint equation
satisfies the constraint equation
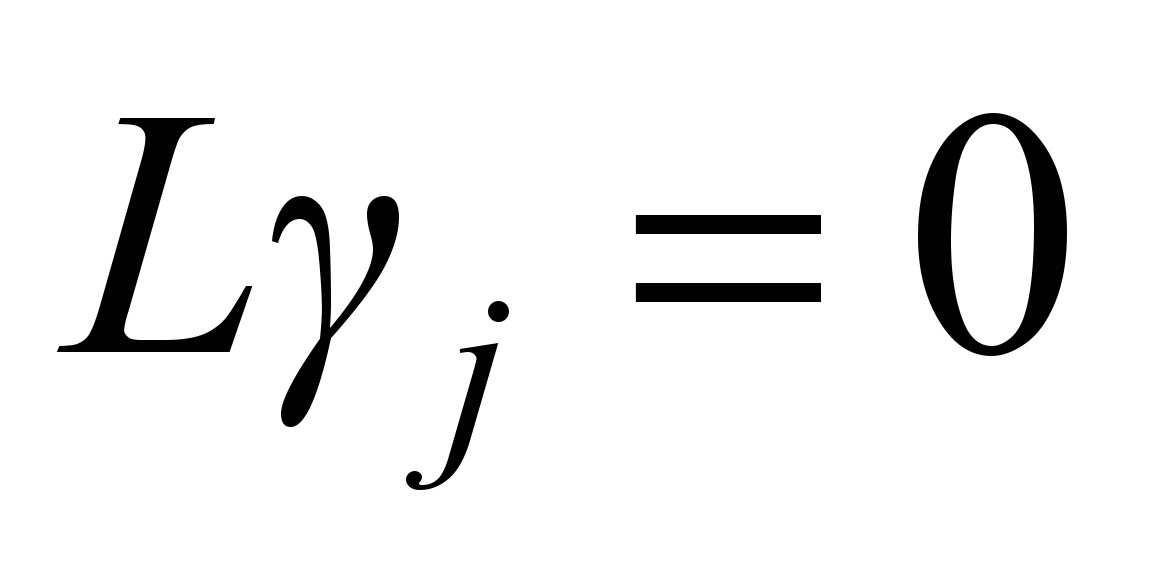 .
Equation (4) is easy to rewrite as
.
Equation (4) is easy to rewrite as
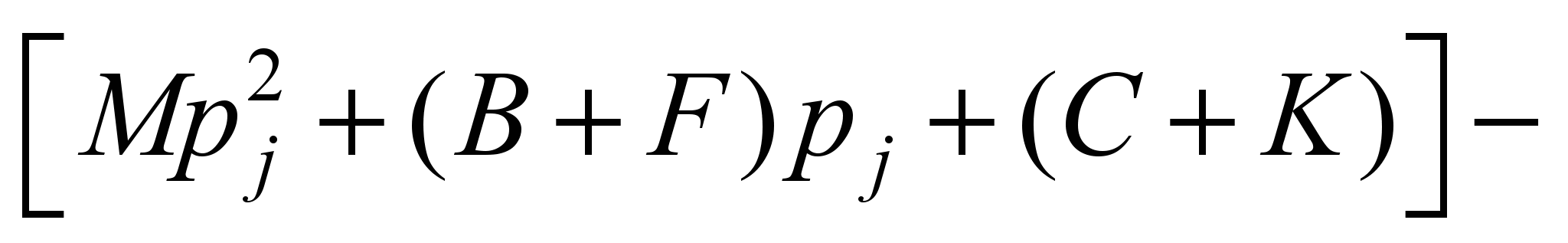
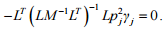
Thus, with
nonzero
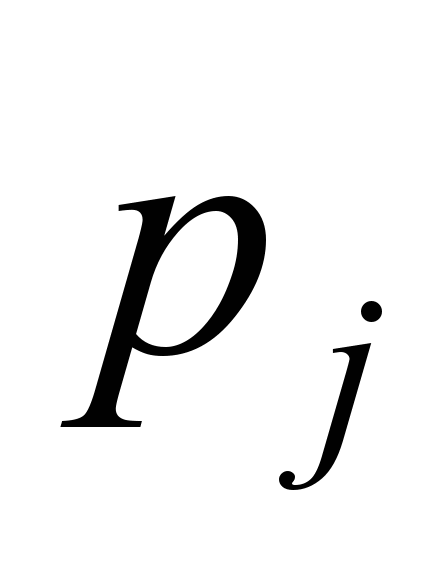 the vectors
the vectors
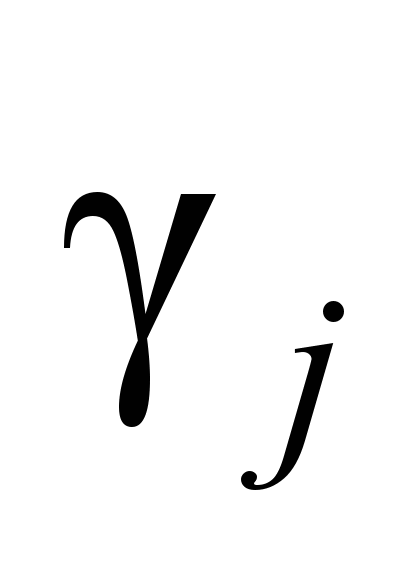 satisfy the equation (4) with
satisfy the equation (4) with
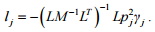 .
.
It is not
clear whether the vectors 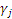 satisfy the equation (4) for
satisfy the equation (4) for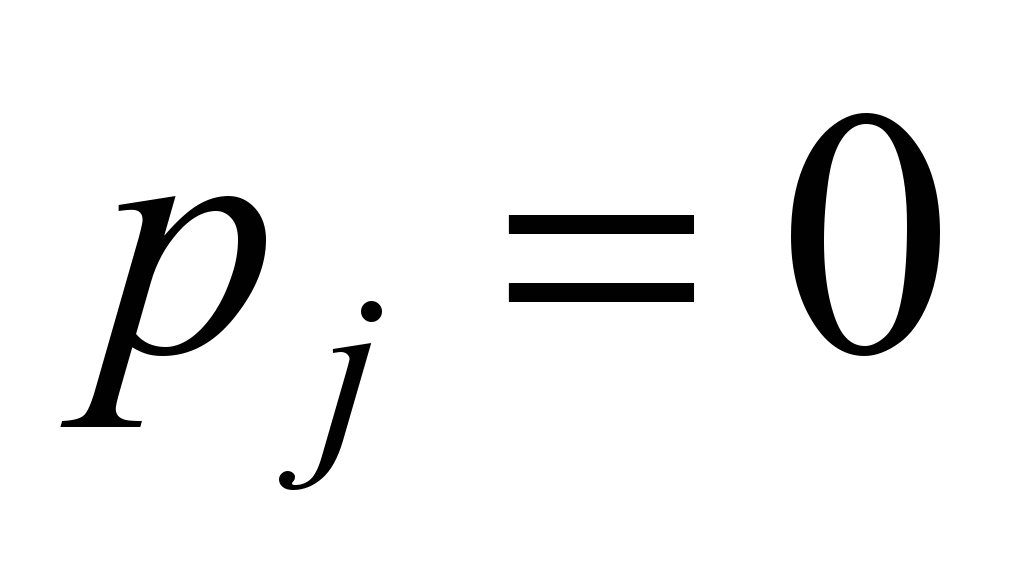 ,
but, since these solutions correspond to constant processes that are
of no interest, we will not deal with them.
,
but, since these solutions correspond to constant processes that are
of no interest, we will not deal with them.
Thus, the stability condition of
the system with constraints is as follows:
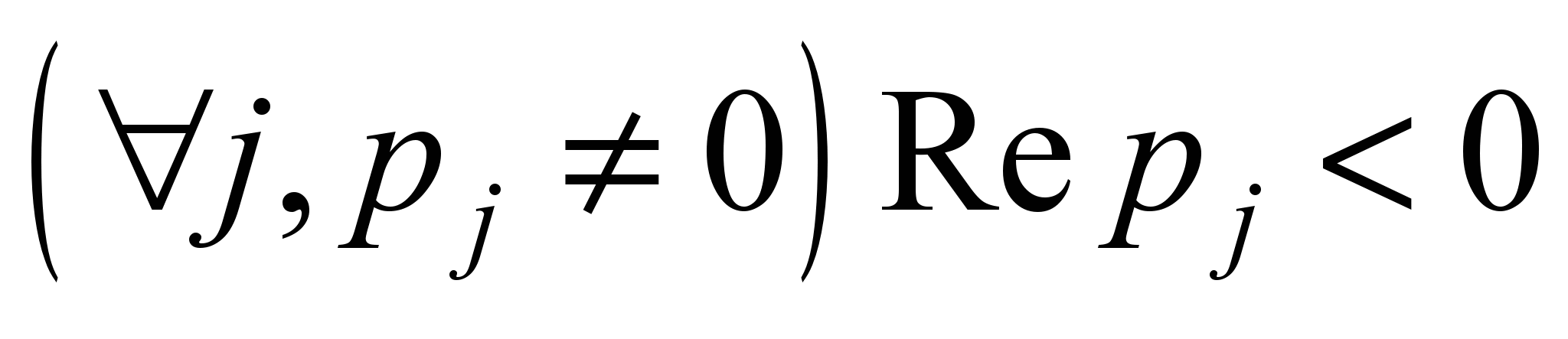 ,
,
where
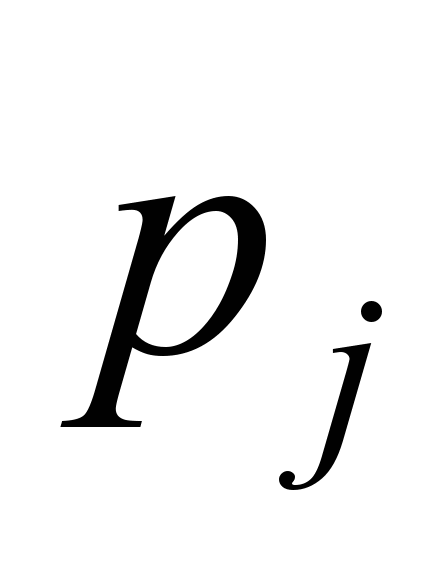 are eigenvalues of matrix A.
are eigenvalues of matrix A.
Let us apply the above theory to
the study of stability, natural frequencies and vibration modes of a
simplified mechanical system consisting of half a car body and a
3-piece bogie, on which it rests (Fig. 1).
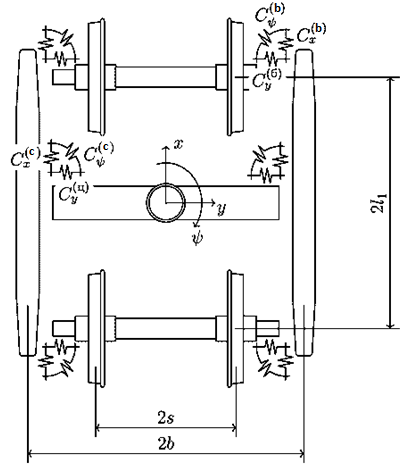
Fig.
1. 3 –
piece bogie
Table 1
Degrees
of freedom and
generalized coordinates
|
Body
|
Degrees
of freedom
|
Generalized
coordinates
|
|
Body
with bolster
|
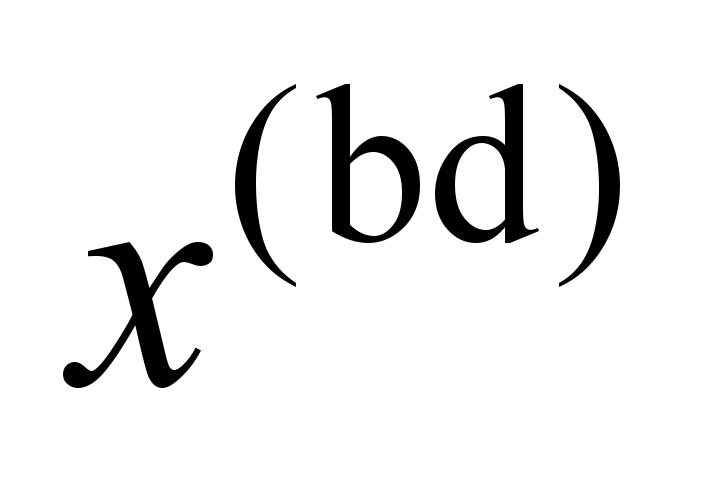 , ,
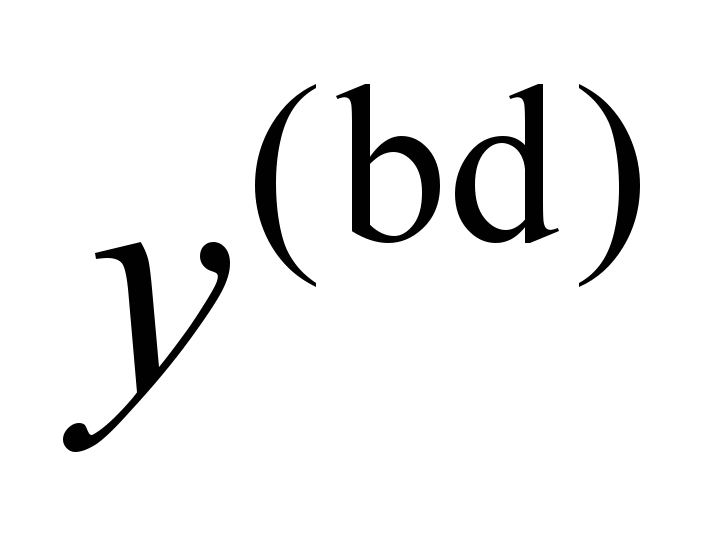 , ,
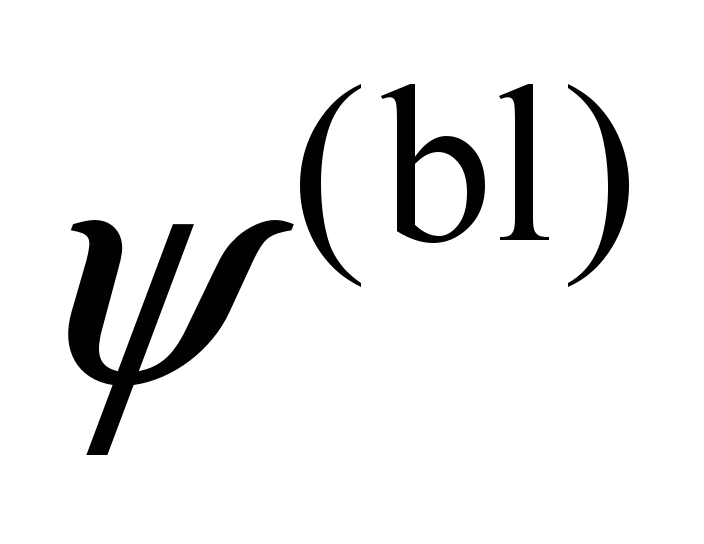
|
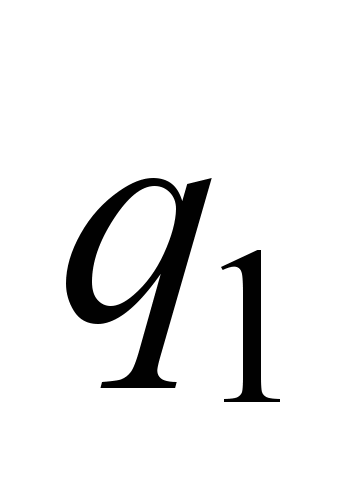 , ,
 , ,
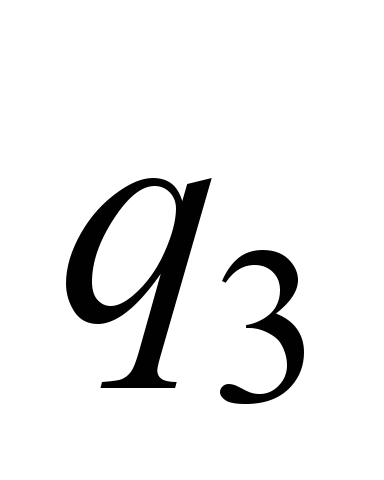
|
|
Left
side frame (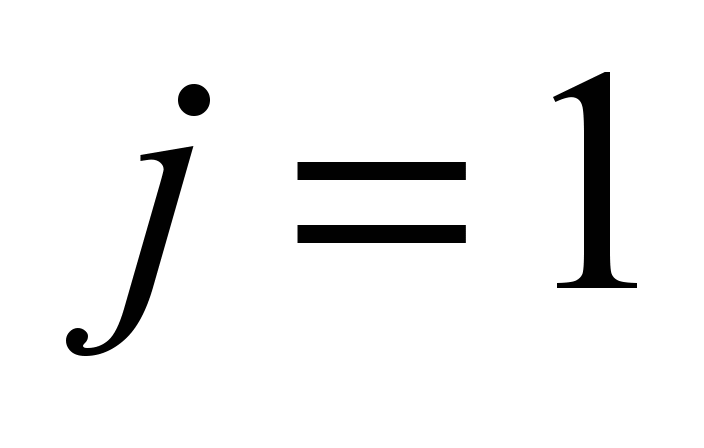 ) )
|
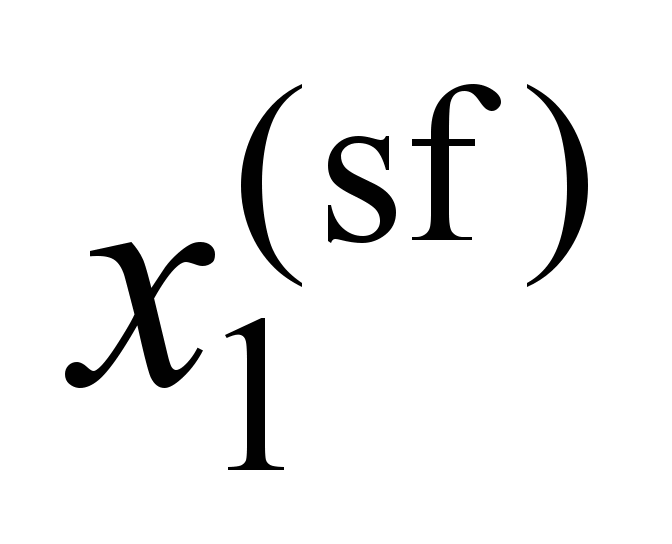 , ,
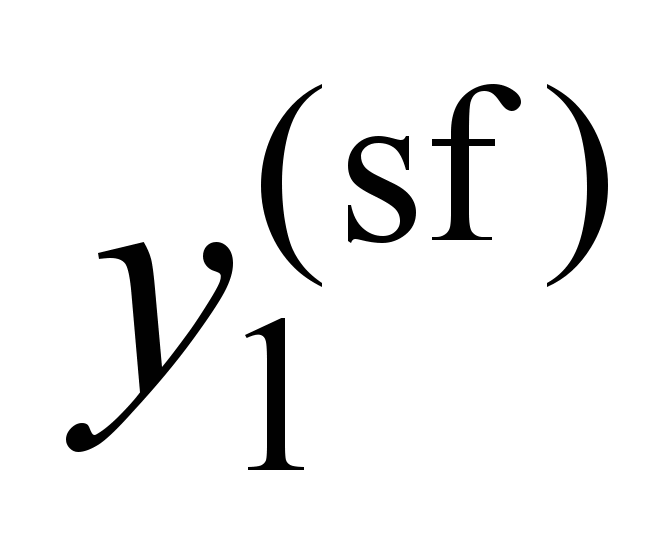 , ,
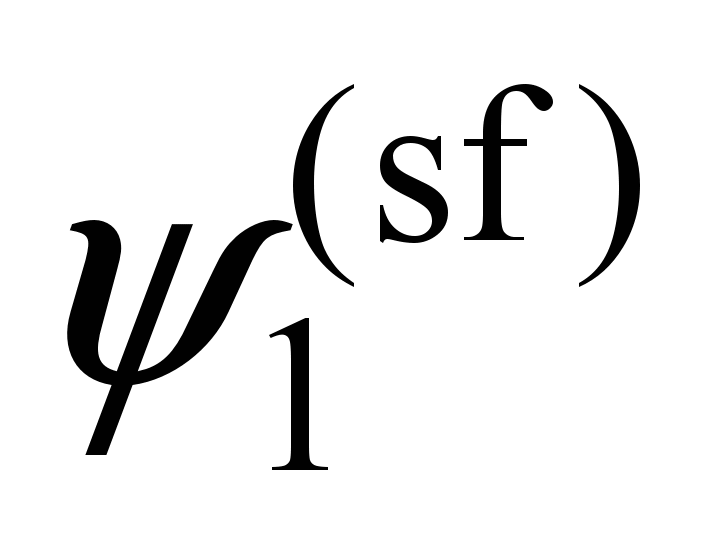
|
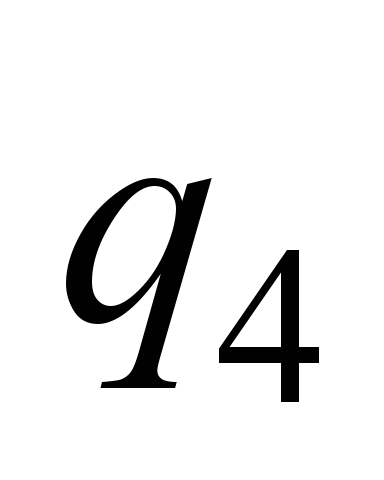 , ,
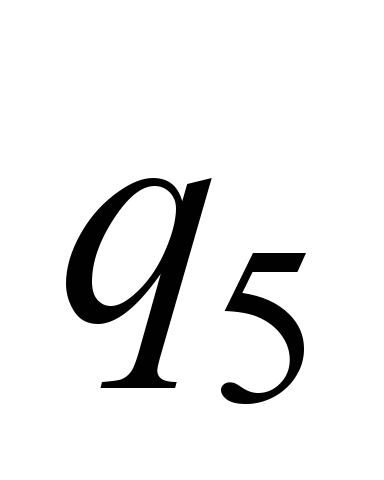 , ,
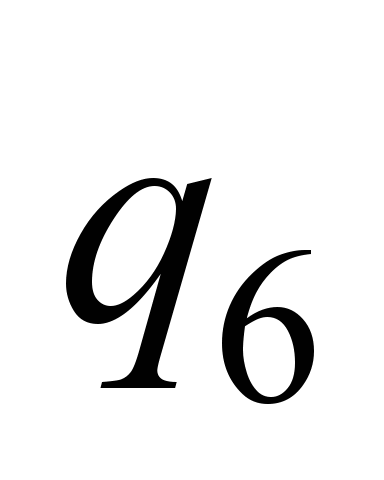
|
|
Right
side frame (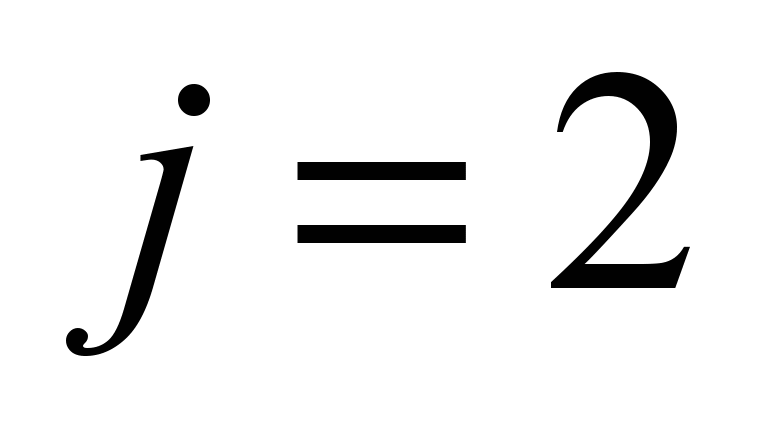 ) )
|
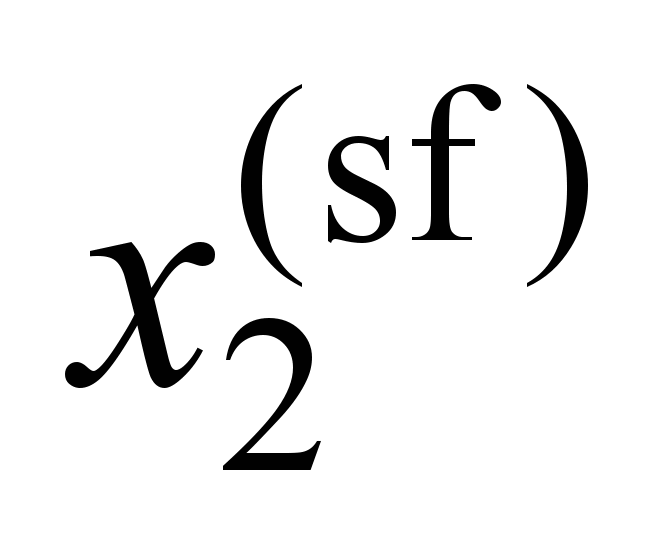 , ,
 , ,

|
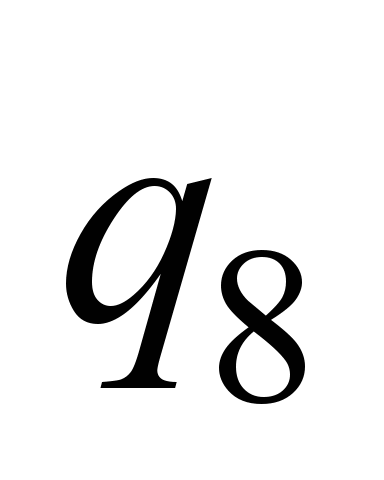 , ,
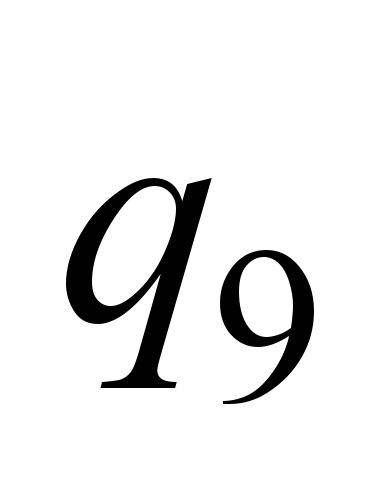 , ,
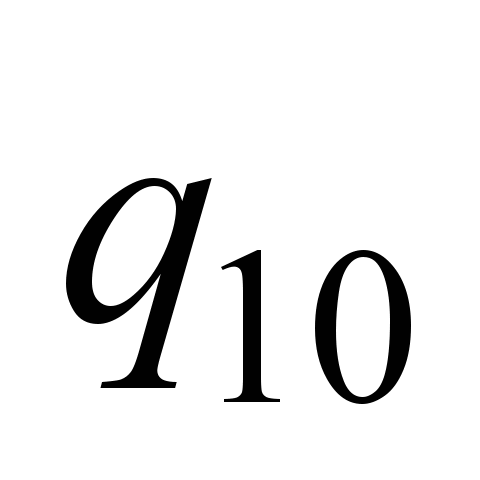
|
|
First
wheel set
(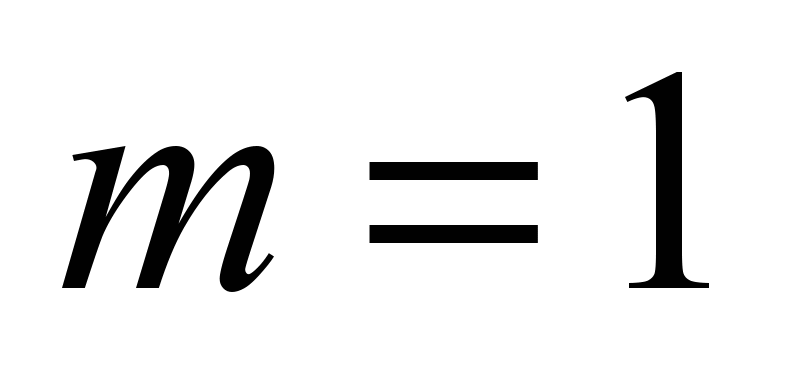 ) )
|
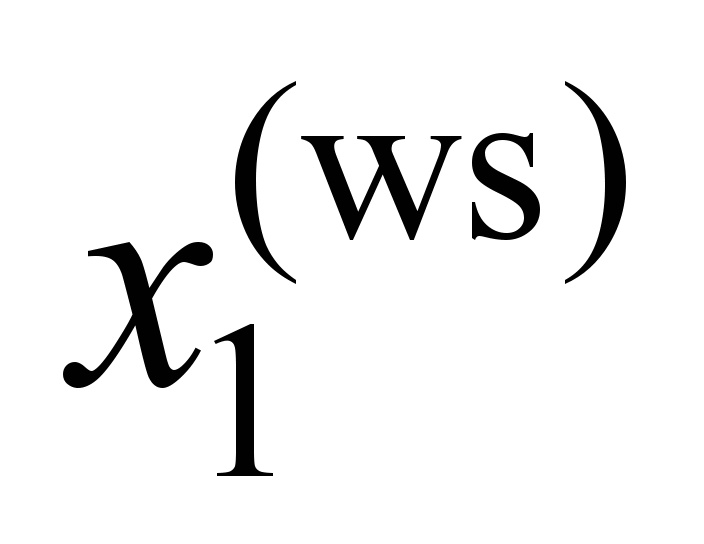 , ,
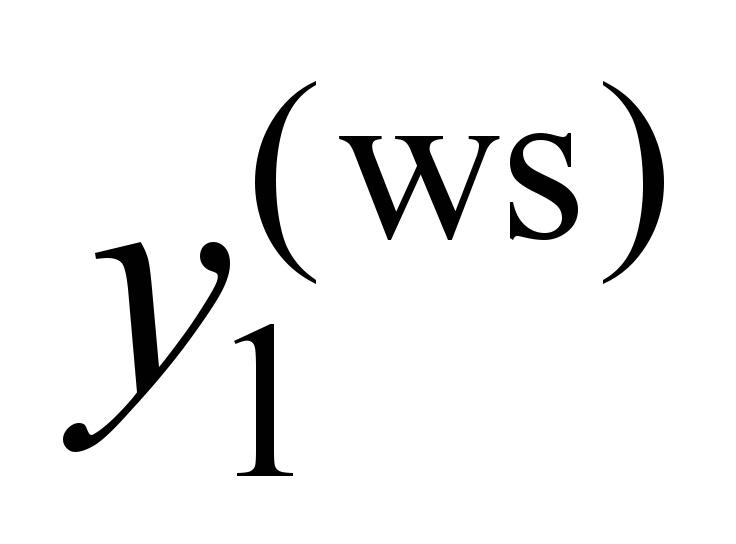 , ,
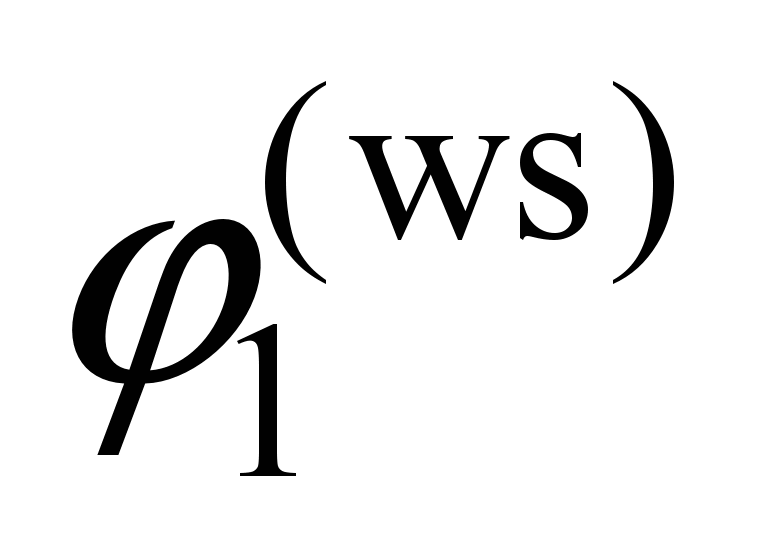 , ,
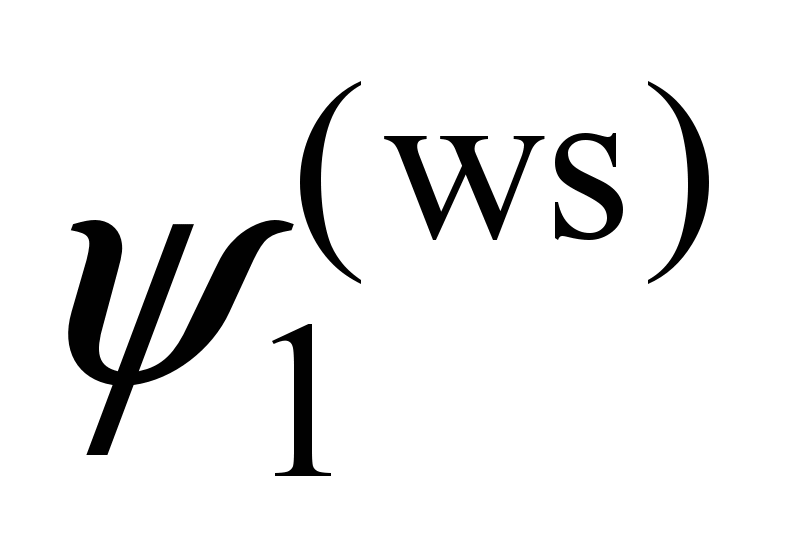
|
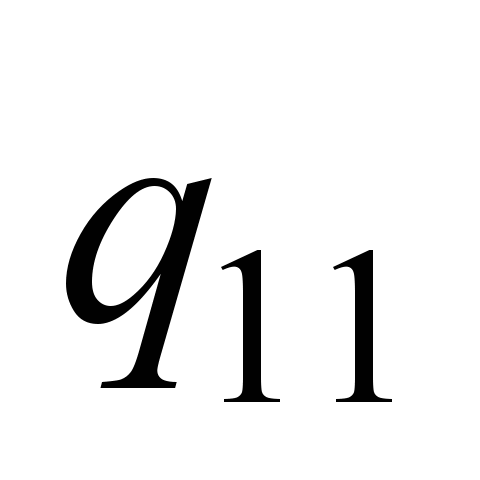 ,
…, ,
…,
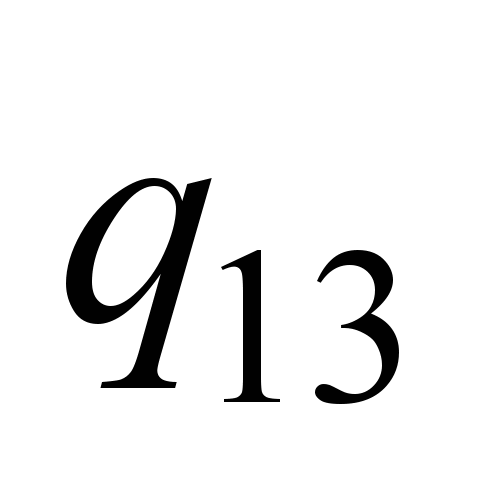
|
|
Second
wheel set
(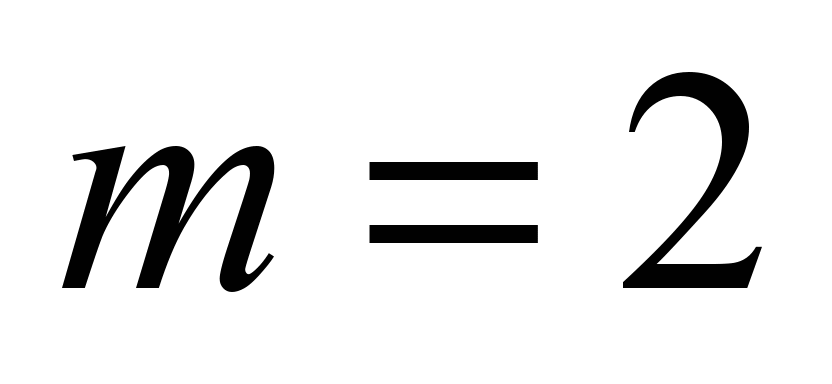 ) )
|
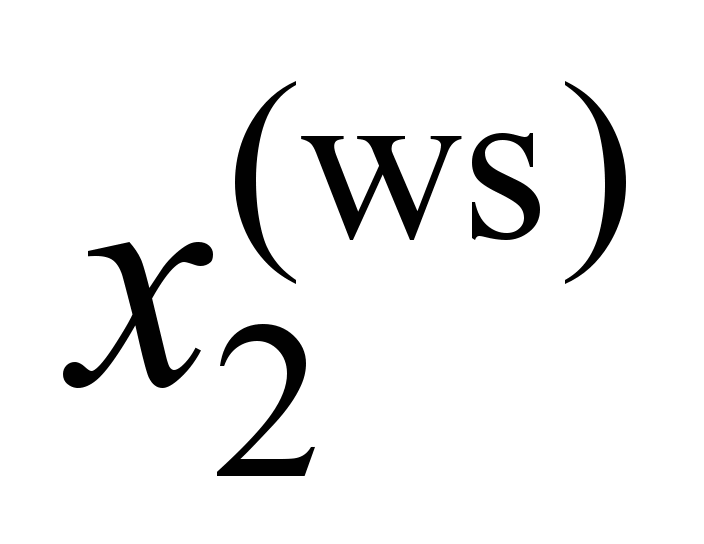 , ,
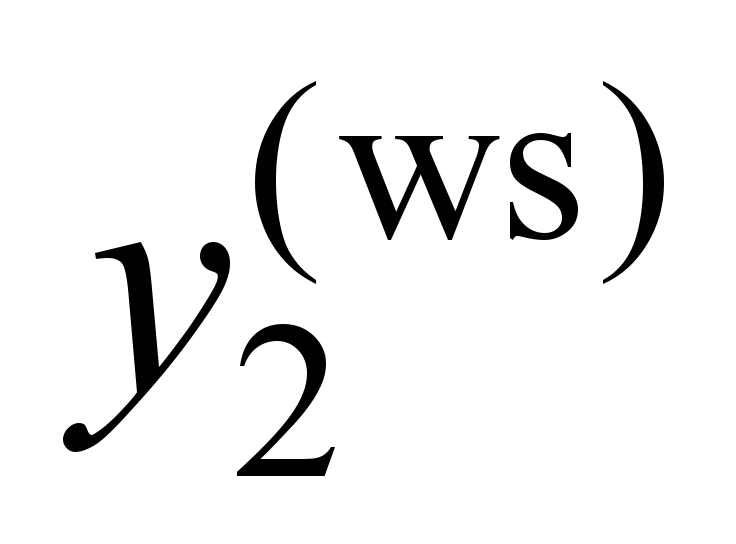 , ,
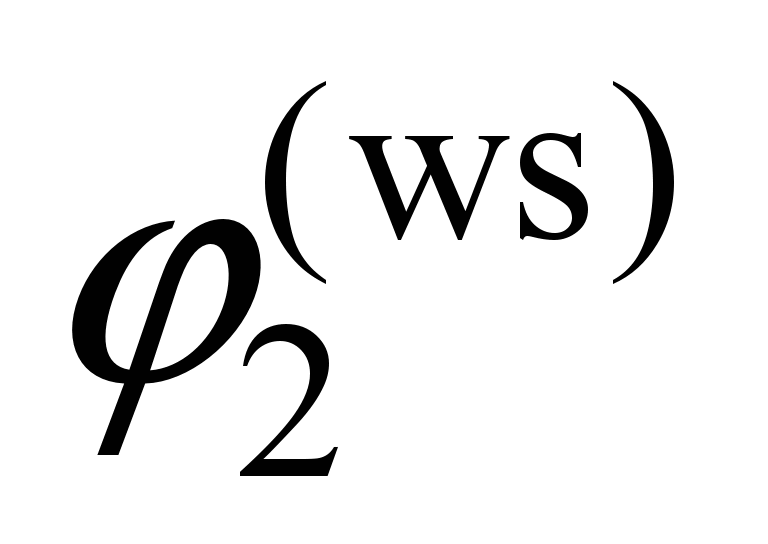 , ,
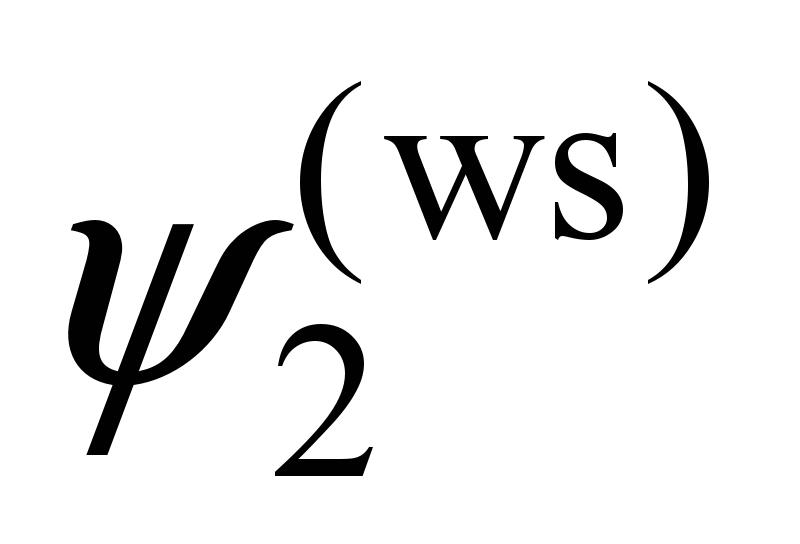
|
 ,
…, ,
…,
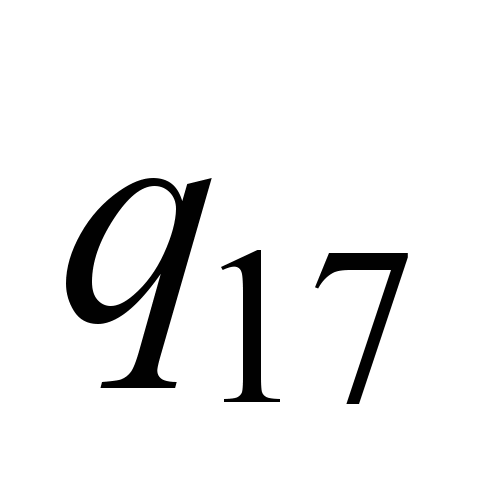
|
We
will be
interested in
how the
frequencies and
forms of
oscillations of
the system
without
constraints (SF)
and systems,
whose
displacement is
subject to
the following
restrictions,
correlate:
SCX –
it is prohibited to move the
bolster relative
to the
side frames (in
the spring
suspension
openings) in
the longitudinal
direction;
SAJ –
it is
prohibited to
move the
pedestal
openings of
the side
frames relative
to the
wheel set
axle journals
(side frames are
pivotally
connected to
the wheel
sets).
As for system
parameters, the
meaning of
the notation
for rigidity
coefficients and
basic dimensions
is clear
from Figure
1: the
letters m,
I
with
corresponding
indices denote
the masses
and central
moments of
body inertia,
the coefficients
in the
expressions for
the interaction
forces are
explained below,
the capital
letters X,
Y,
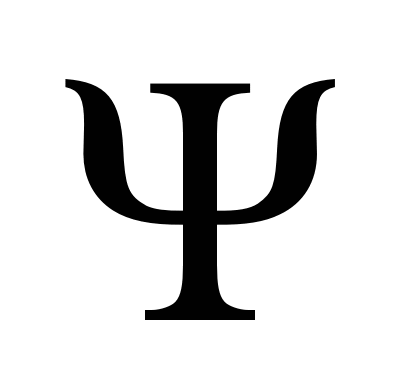 denote the
force components
and the
system body
interaction force
moments. Without
giving a complete derivation of the expressions for the matrices M,
L, etc, let us dwell only on certain
points that may be of methodical interest. The elements of the
matrix C
are coefficients for the products of generalized coordinates and
their variations in the expression for the virtual work of forces in
elastic elements
denote the
force components
and the
system body
interaction force
moments. Without
giving a complete derivation of the expressions for the matrices M,
L, etc, let us dwell only on certain
points that may be of methodical interest. The elements of the
matrix C
are coefficients for the products of generalized coordinates and
their variations in the expression for the virtual work of forces in
elastic elements
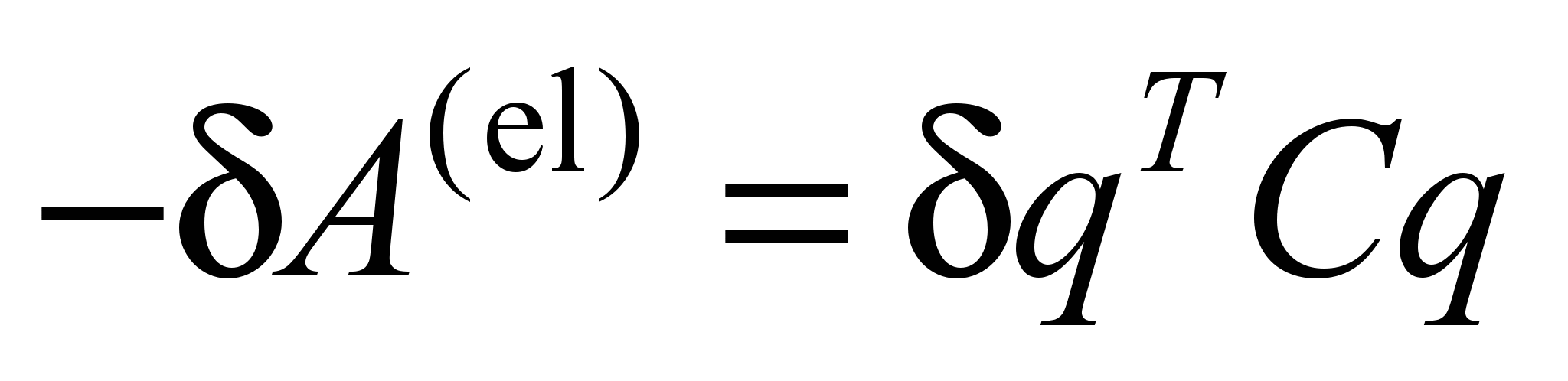 . (6)
. (6)
Let
us
consider
the
contribution
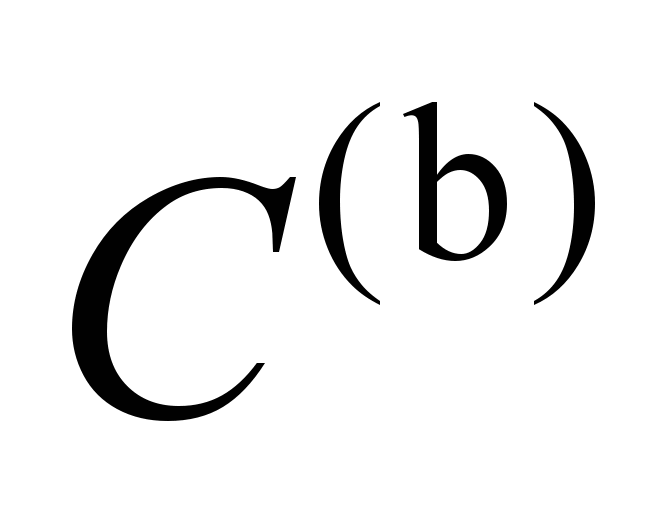 to
the
matrix
C
from
the
elastic
elements
that
are
in
axle boxes.
The
components of the displacement of the side frame pedestal opening
relative to the wheel set axle box are combined into a vector
to
the
matrix
C
from
the
elastic
elements
that
are
in
axle boxes.
The
components of the displacement of the side frame pedestal opening
relative to the wheel set axle box are combined into a vector
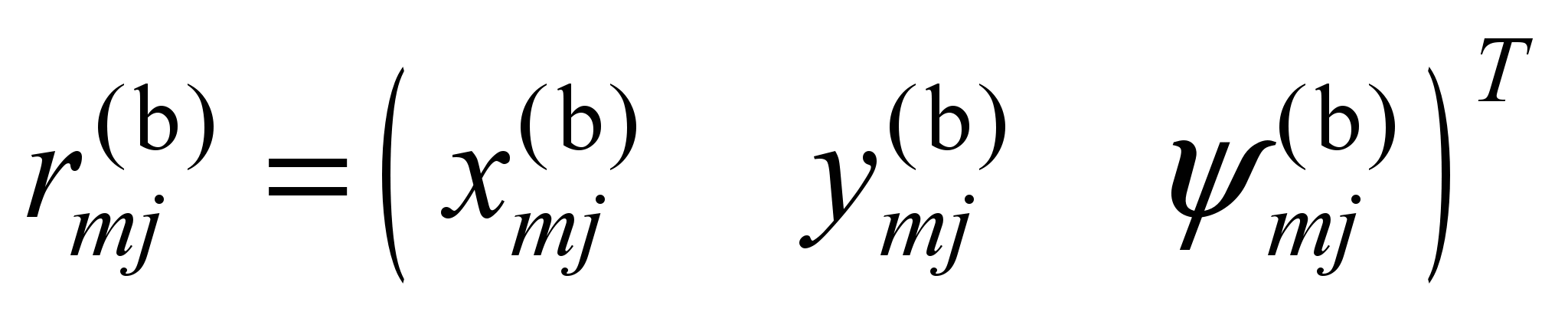 .
.
They are linear combinations of
the generalized coordinates
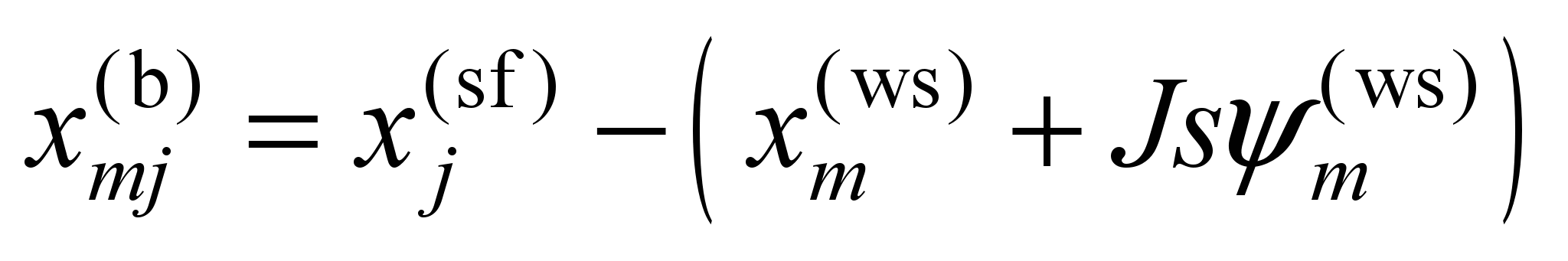 ,
,
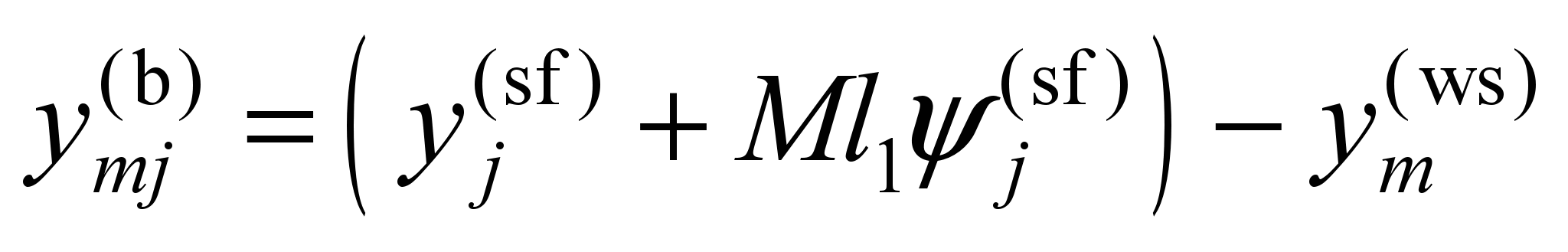 ,
,
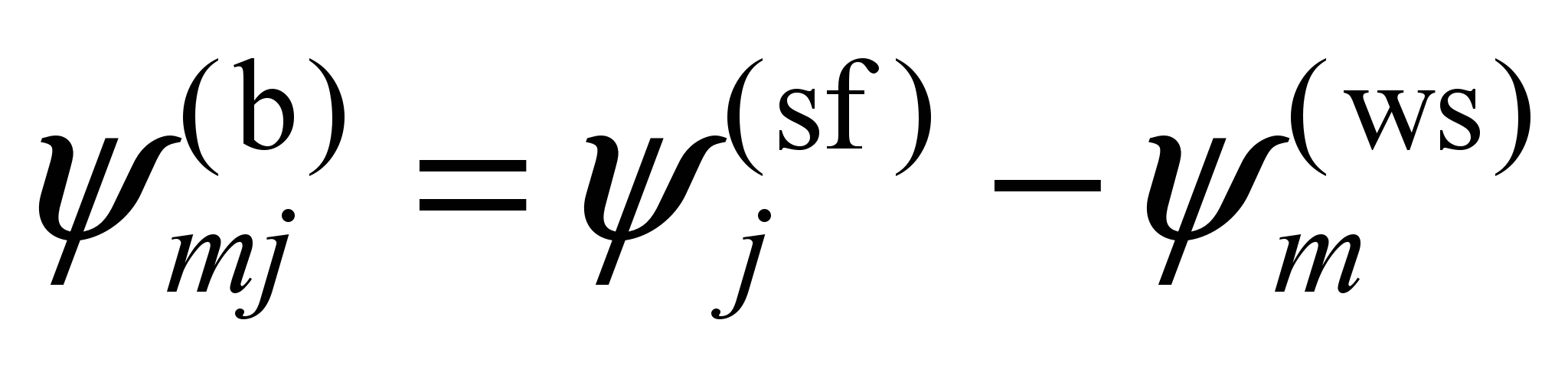 ,
,
This
means that
it is
possible to
choose such
matrices
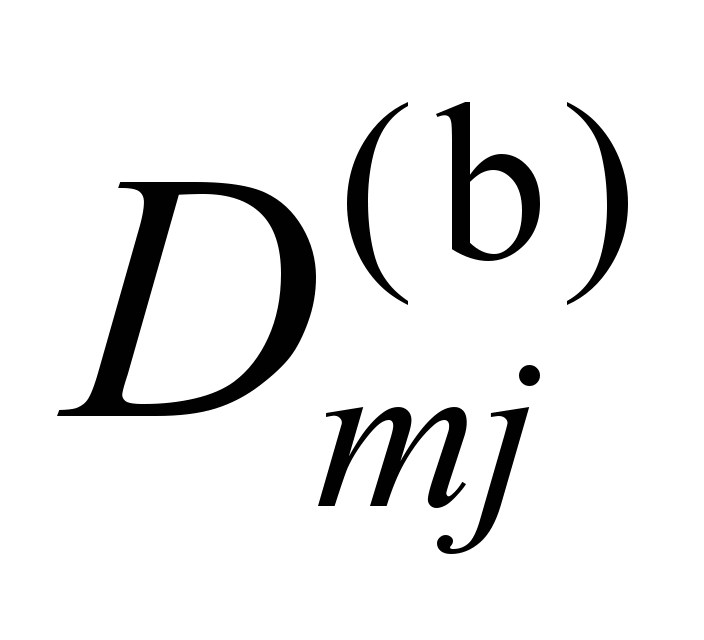 with constant
coefficients
that
with constant
coefficients
that
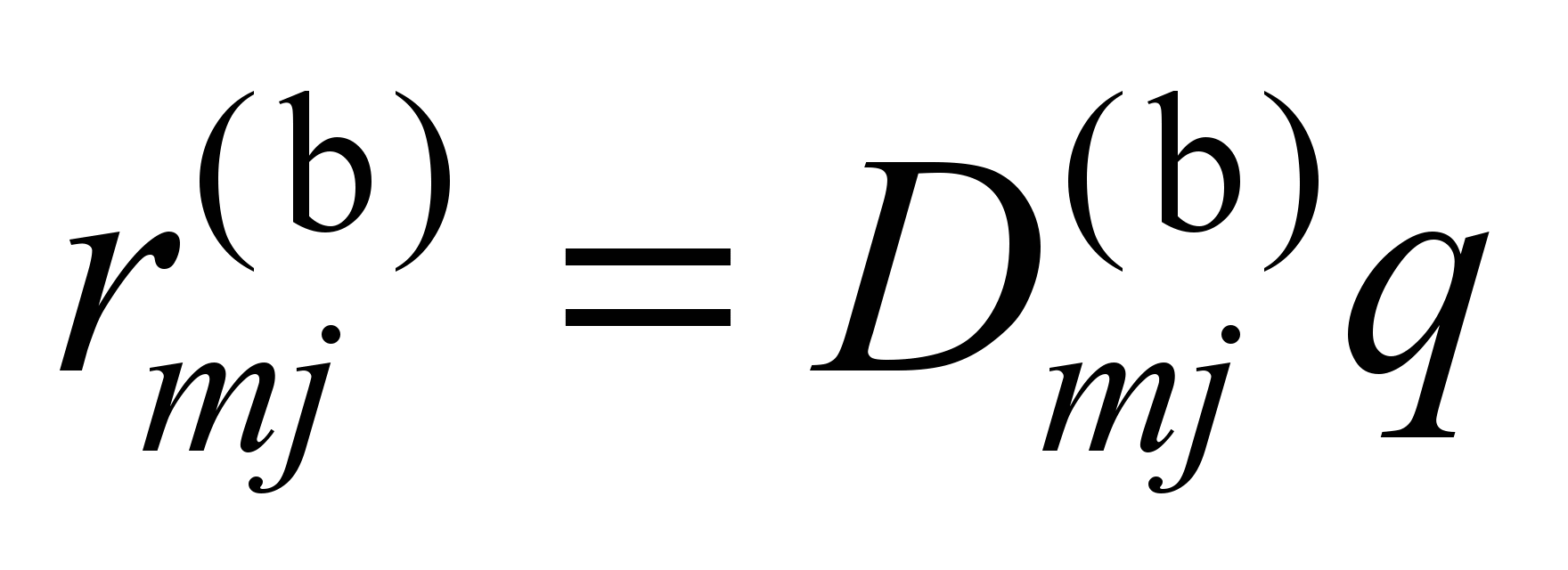 .
.
The force
components in the elastic element are proportional to the vector
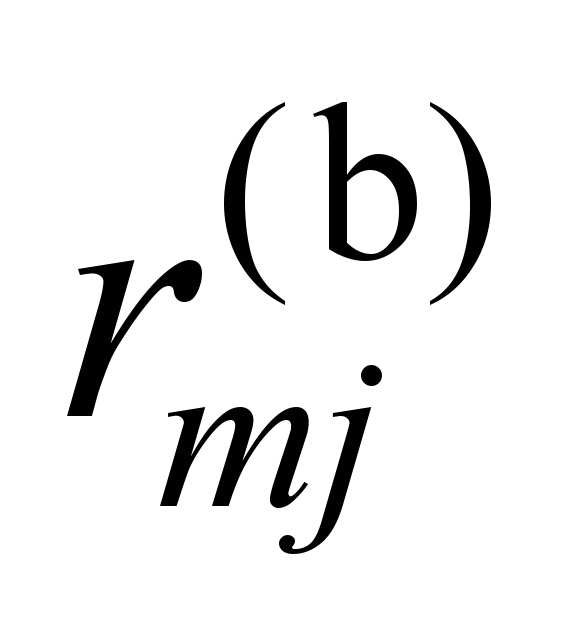 ,
,
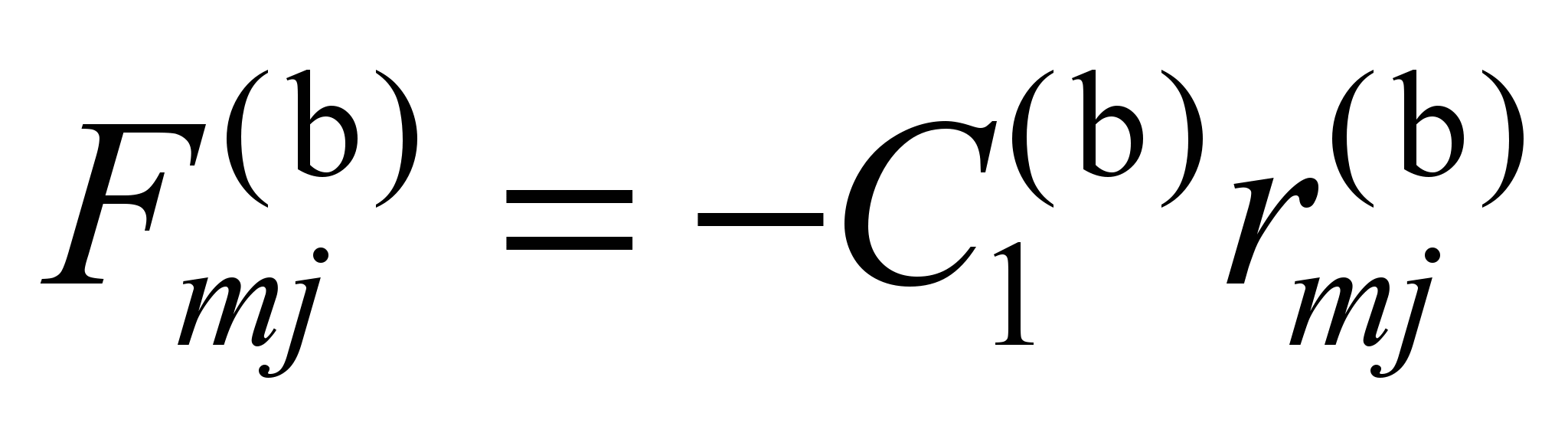 ,
,
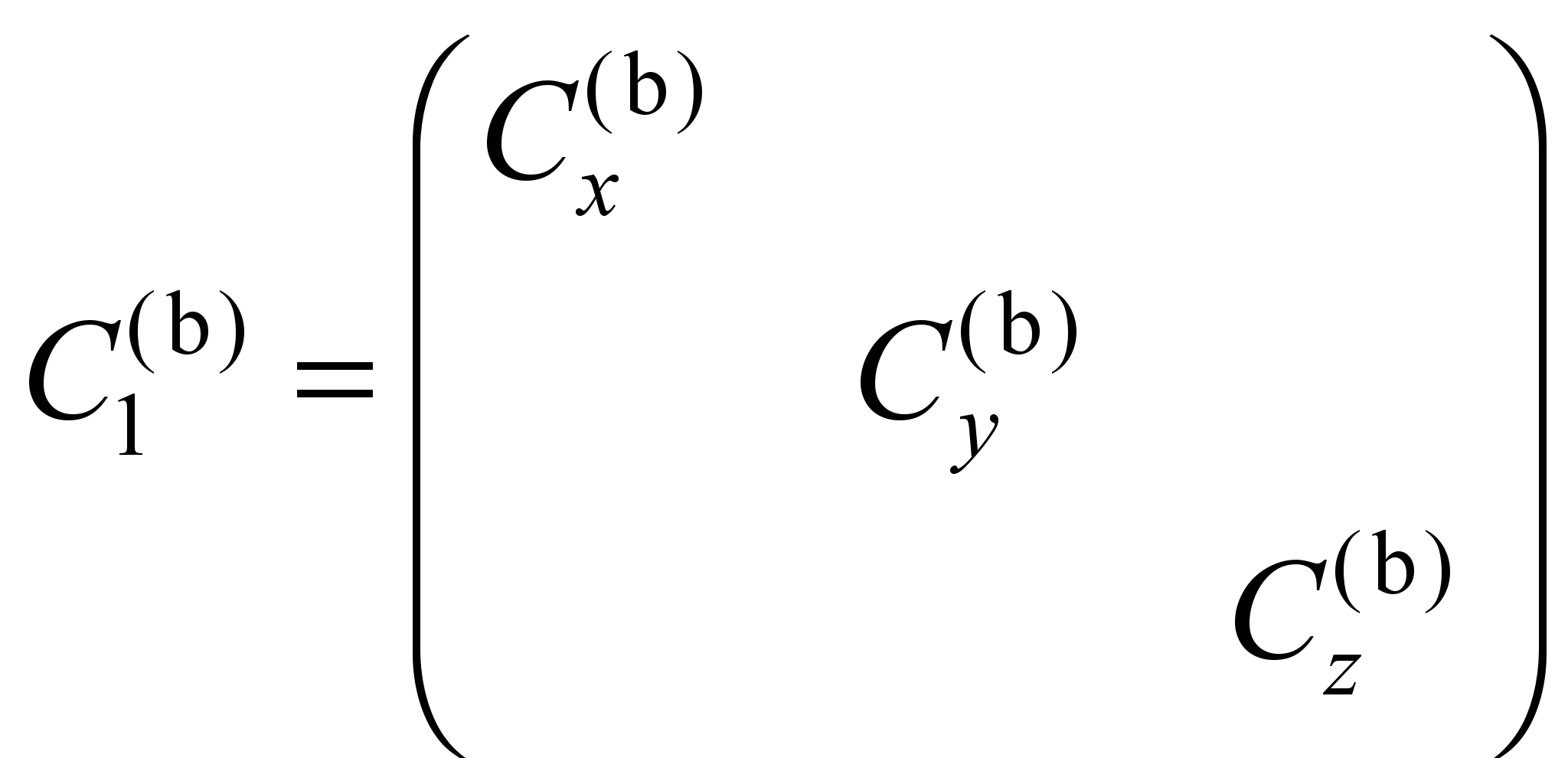
The virtual
work of the forces
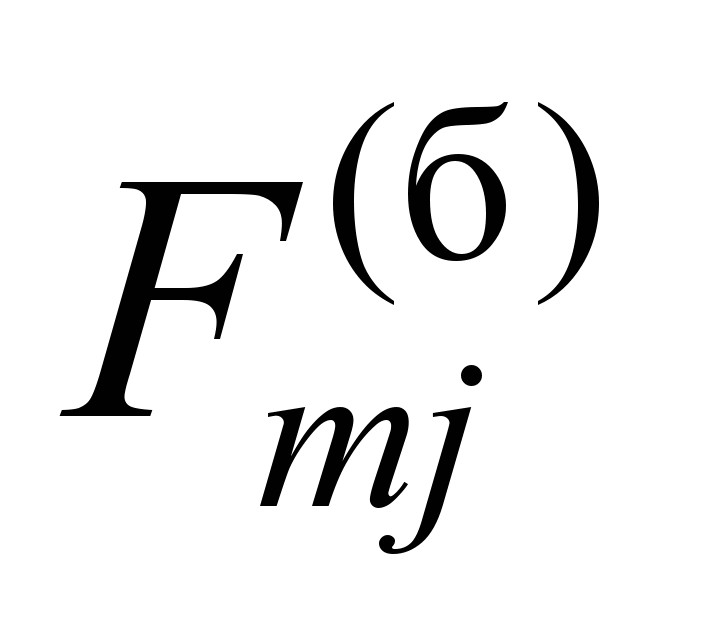 is equal to
is equal to
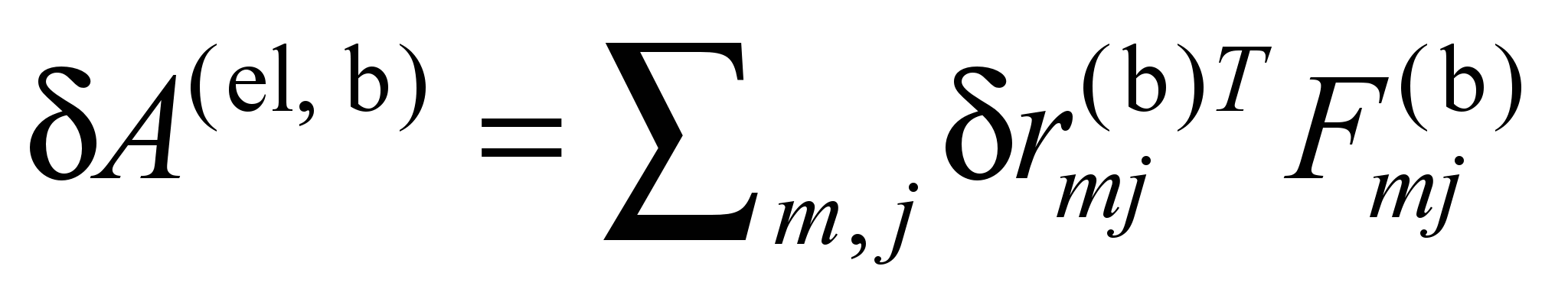 . (7)
. (7)
Comparing
the expressions (6) and (7), we get:
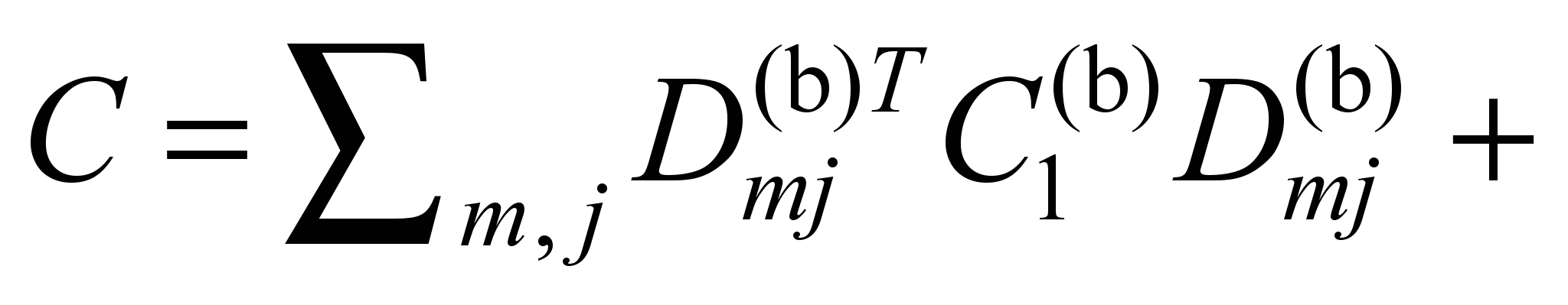 (contributions
from other elastic elements).
(contributions
from other elastic elements).
In order to prohibit linear
movements of the pedestal openings of the side frames relative to
wheel set axle boxes, it is necessary to require the fulfillment of
the conditions:
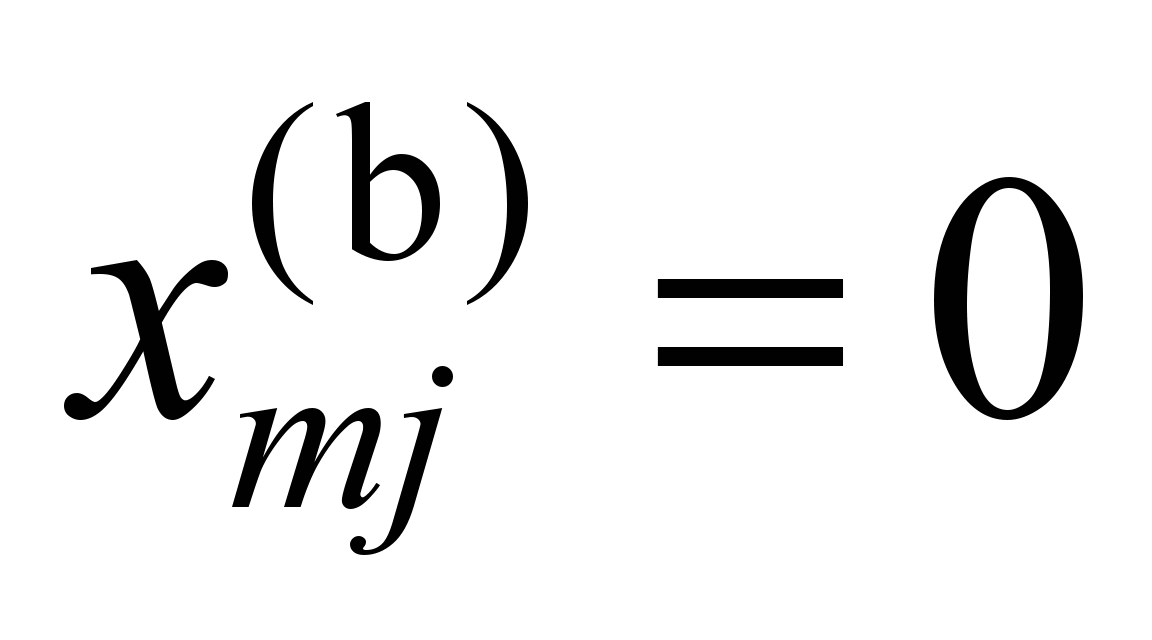 ,
,
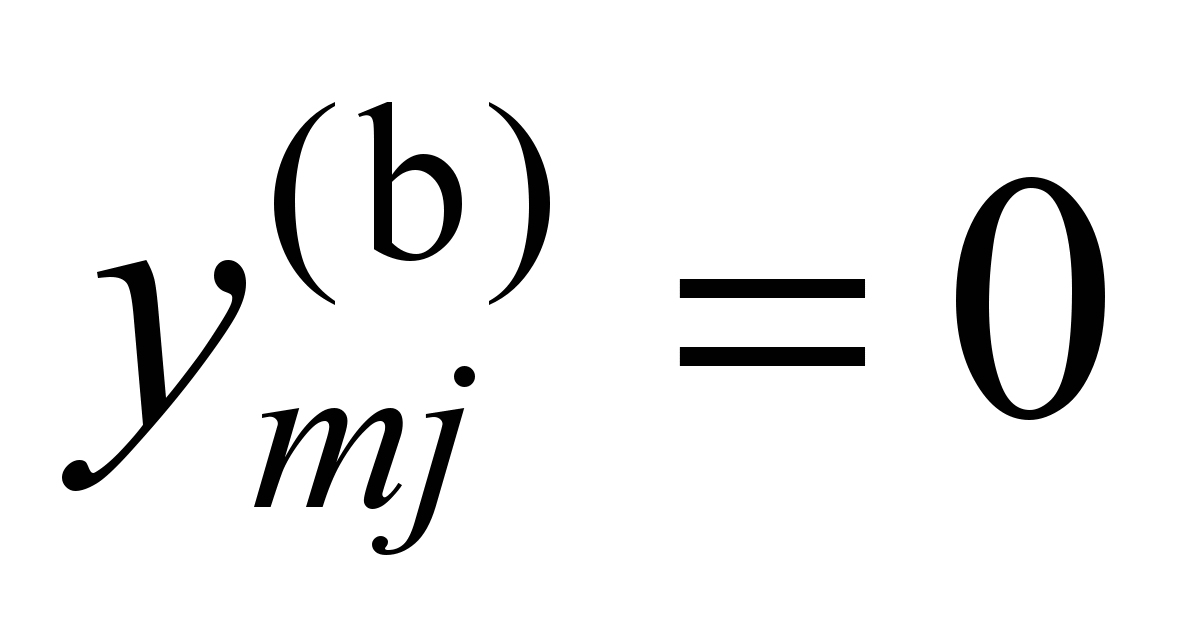 .
.
There are 8
rows in the L
matrix, which we get by writing the first two rows of each matrix
under each other. Thus, the compilation of a system of equations
describing the motion of a mechanical system with constraints does
not practically require additional calculations – in our case, the
matrices
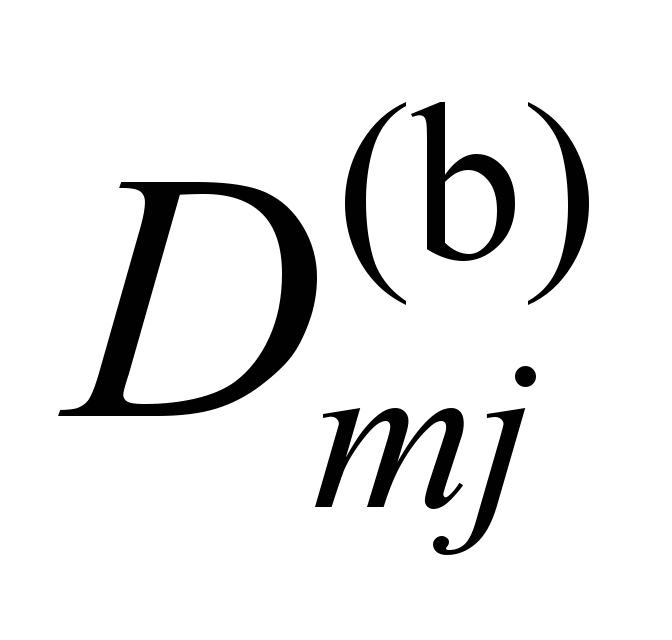 were written out at the stage of working with the system without
constraints.
were written out at the stage of working with the system without
constraints.
The wheel-rail interaction is
described by Kalker linear theory [16 par. 2.2.2] with the following
simplifications:
1) spin is neglected;
2) the
coefficients
 ,
,
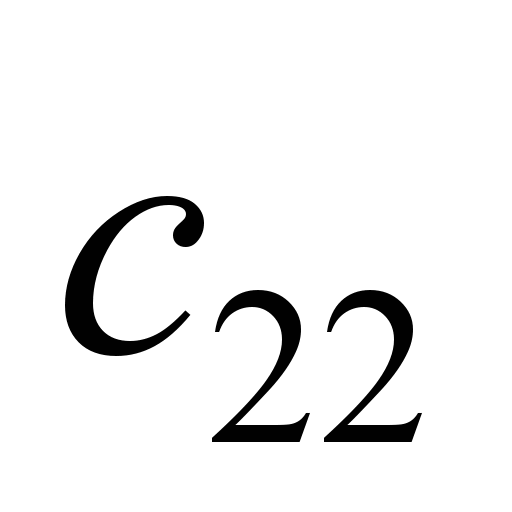 for the longitudinal and transverse
directions are considered equal to 3.90.
for the longitudinal and transverse
directions are considered equal to 3.90.
The
expression for longitudinal sliding additionally contains terms
proportional to the velocities
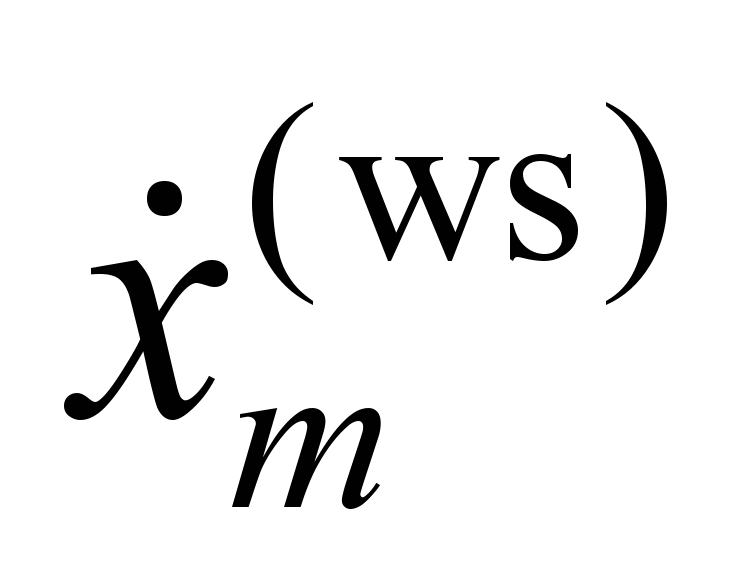 ,
,
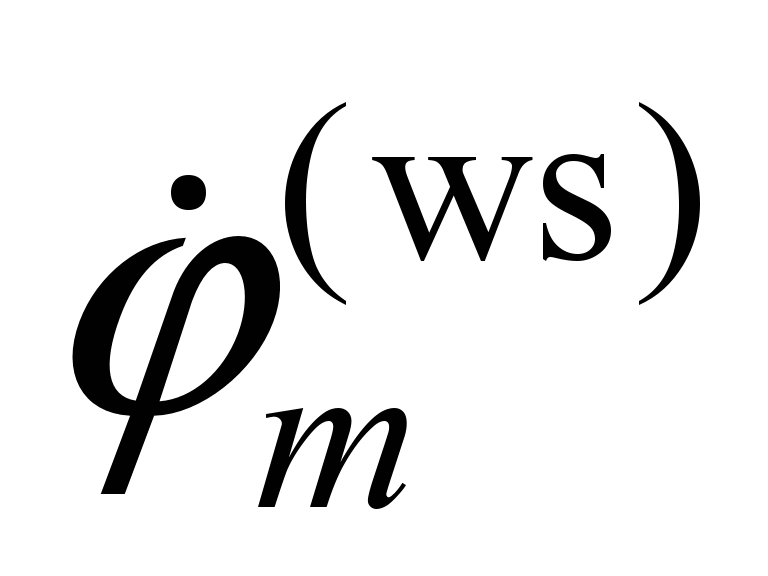 .
.
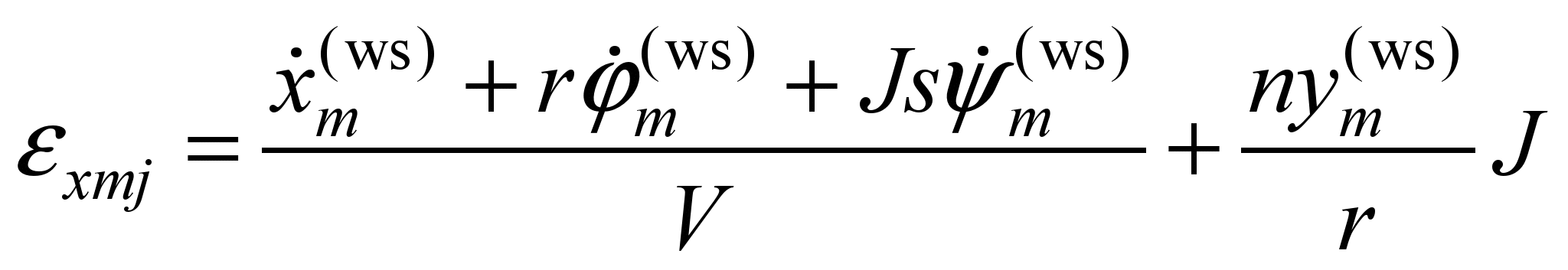 ,
,
The
expression for transverse sliding retains the usual look
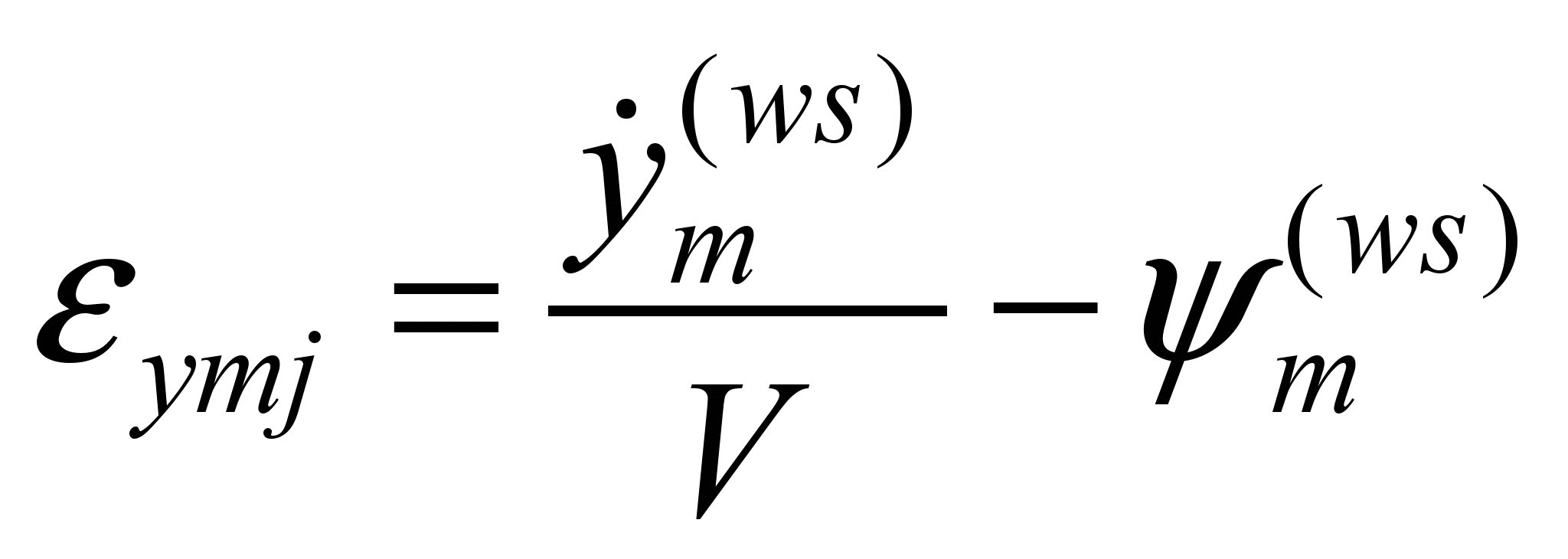 .
.
Findings
Let us
consider the results of the calculation of the eigenvalues and
eigenvectors describing the 3–piеce
bogie oscillations. Our goal is to understand how the eigenvalues
and eigenvectors of SF system with constraints and SCX and SAJ
systems without constraints are related.
We expect that the results for SF with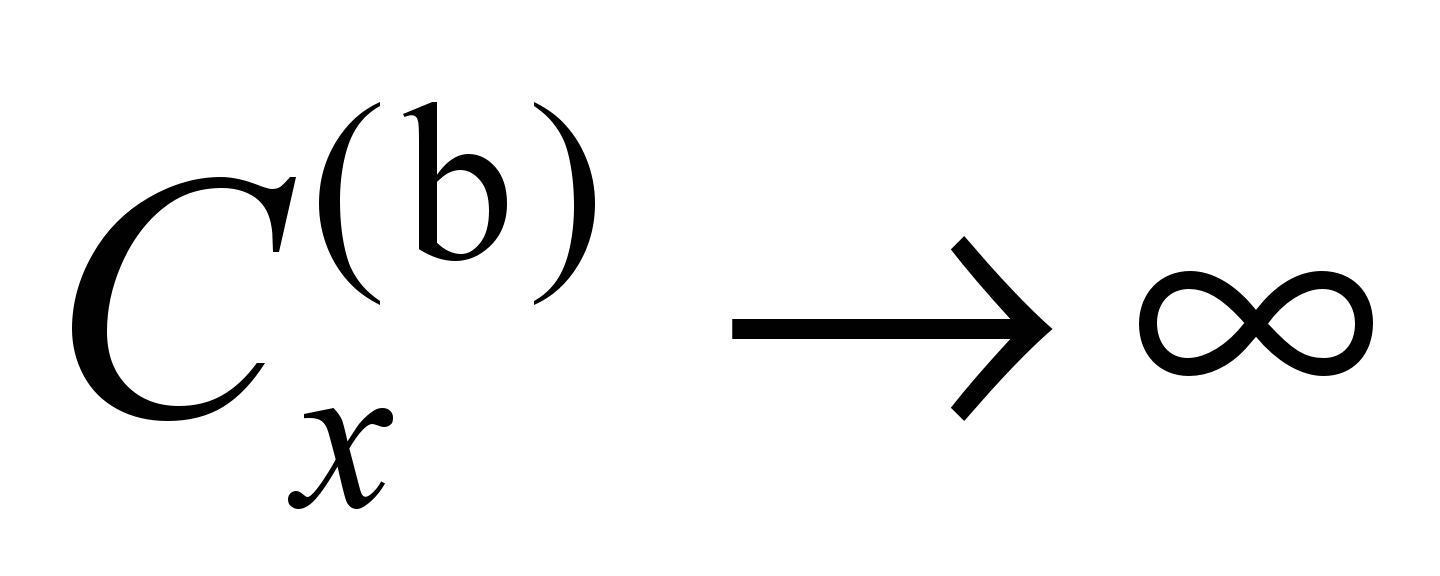 ,
,
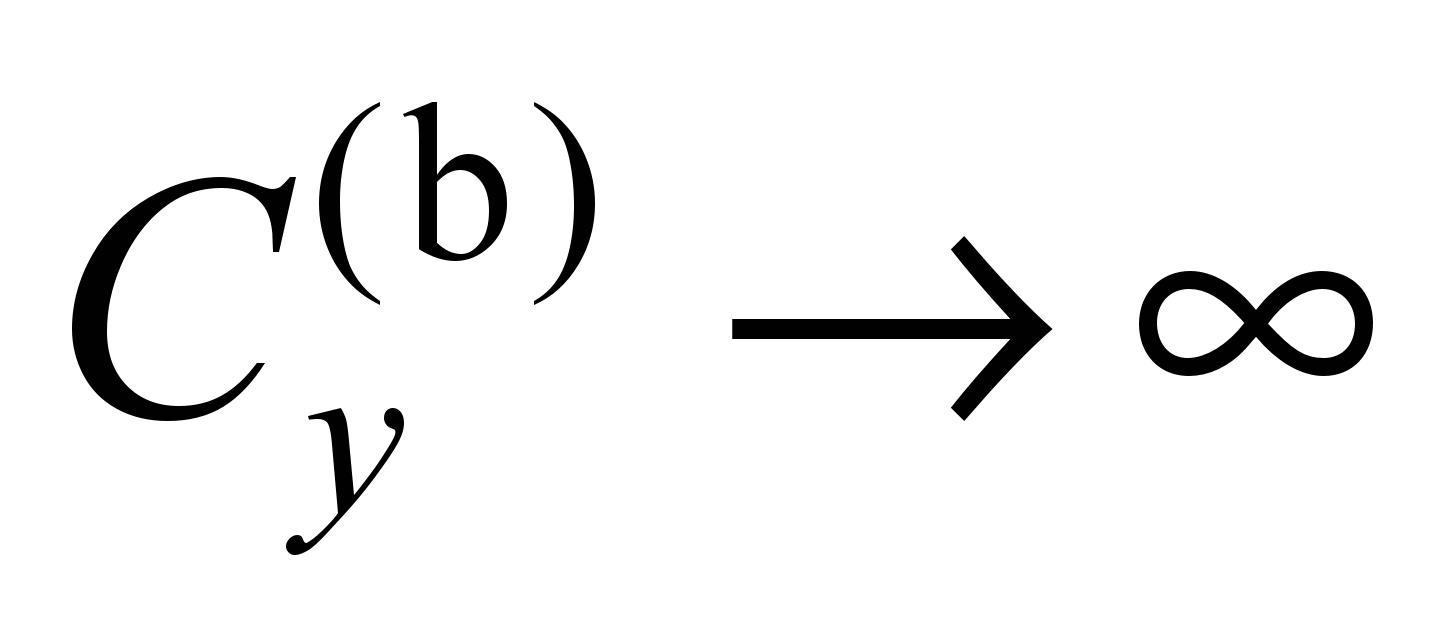 will tend to the results for SAJ, and the results for SF with
will tend to the results for SAJ, and the results for SF with
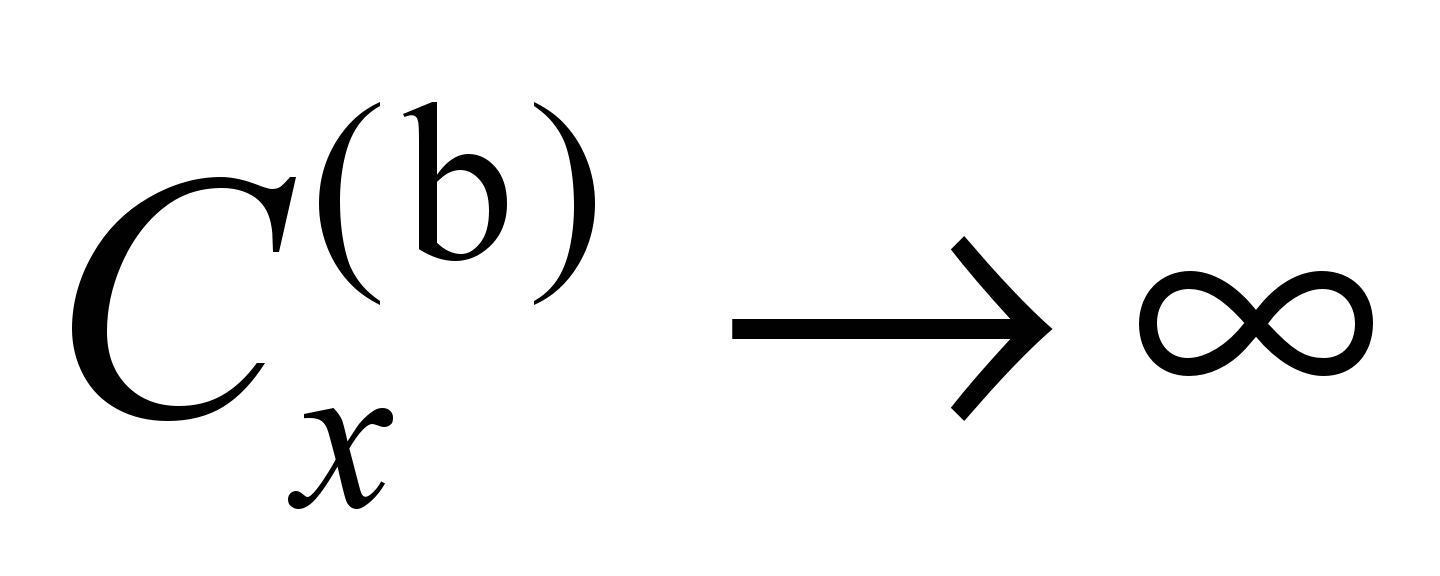 – to the results for SCX. The subject of
the study will be the confirmation of this expectation and a
detailed description of the limiting transition nature.
– to the results for SCX. The subject of
the study will be the confirmation of this expectation and a
detailed description of the limiting transition nature.
The
eigenvalues of the matrix 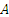 for the SF and SAJ systems are listed in
Table 2. The system parameters correspond to the 4-axle car loaded
up to deadweight capacity on 18–100 bogies (with an axle load of
23.5 tf). The motion speed
for the SF and SAJ systems are listed in
Table 2. The system parameters correspond to the 4-axle car loaded
up to deadweight capacity on 18–100 bogies (with an axle load of
23.5 tf). The motion speed
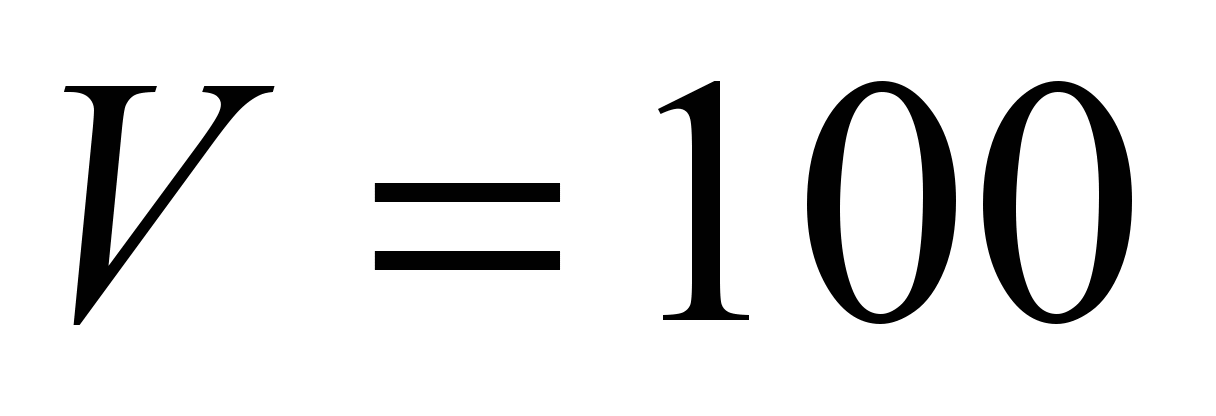 km/h.
km/h.
The
eigenvalues were ordered by the QR algorithm, so they can be
compared only by values. Even without analyzing the eigenvectors, it
is clear that the numbers with
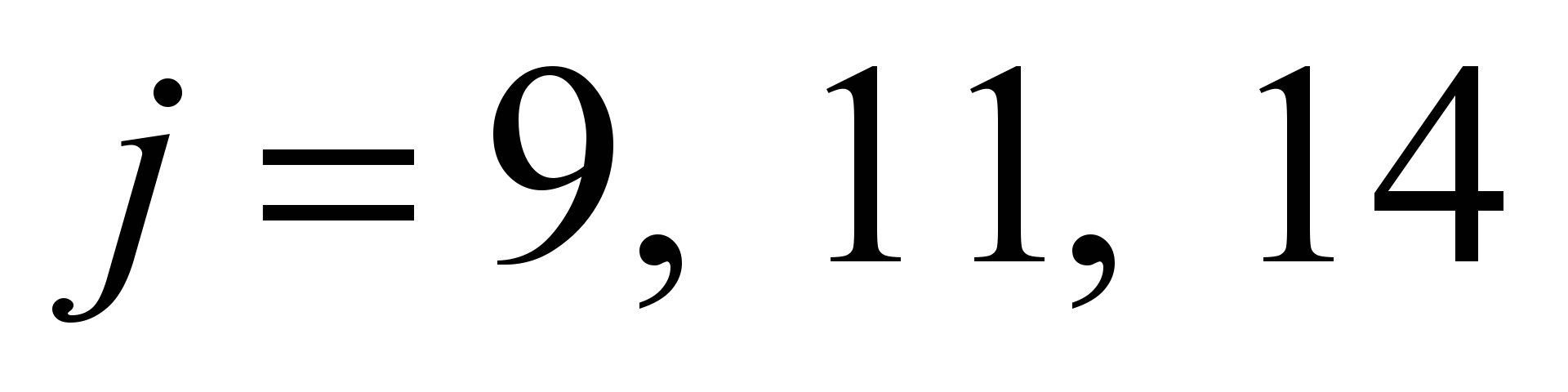 of
the SAJ system are the limits for the eigenvalues
of
the SAJ system are the limits for the eigenvalues
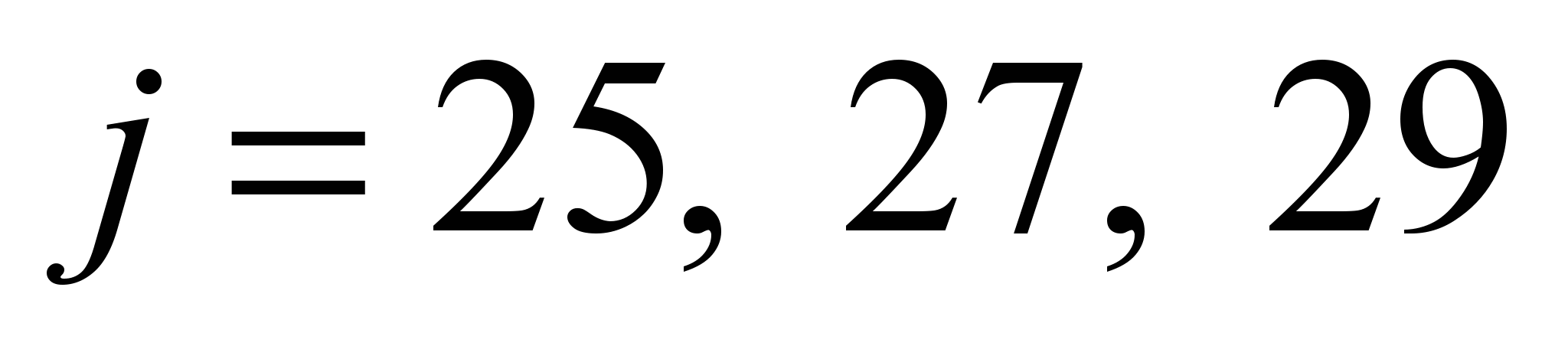 of the SAF system. It seems plausible to
assume that large negative numbers of one system go into large
negative numbers of the other system, both systems have five such
numbers, but the correspondence between them is not obvious. It is
not quite clear which of the numbers of the SF system goes into the
number
of the SAF system. It seems plausible to
assume that large negative numbers of one system go into large
negative numbers of the other system, both systems have five such
numbers, but the correspondence between them is not obvious. It is
not quite clear which of the numbers of the SF system goes into the
number
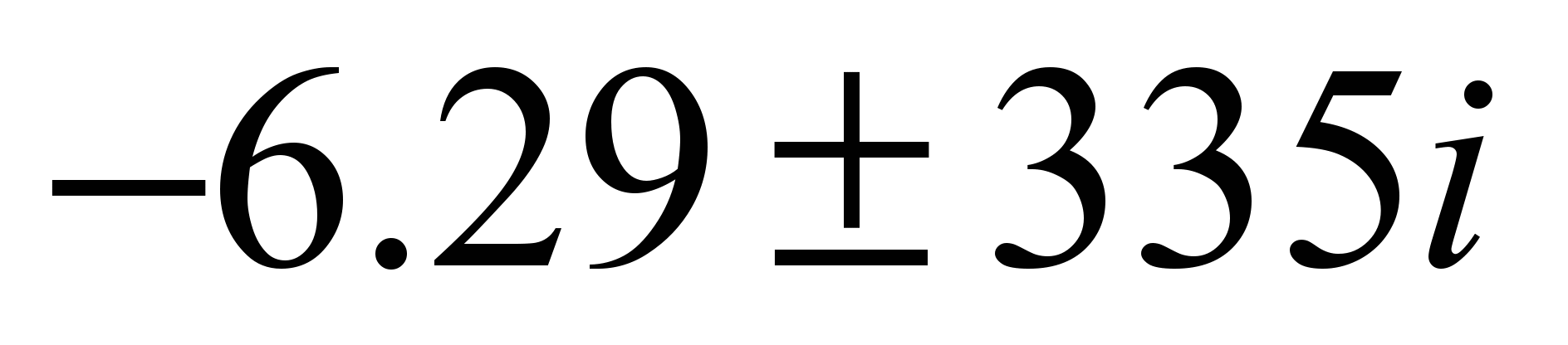 of the SAJ system. The numbers
of the SAJ system. The numbers
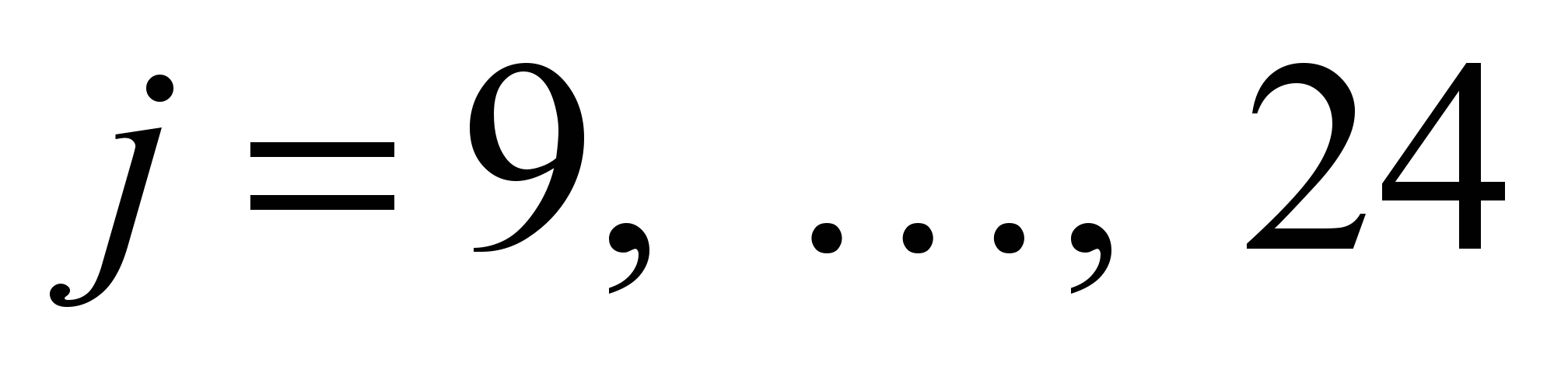 of
SF, except
for one pair, apparently correspond to the side frame oscillations
on the high rigidity elastic elements in the axle boxes, since these
numbers have a large imaginary component.
of
SF, except
for one pair, apparently correspond to the side frame oscillations
on the high rigidity elastic elements in the axle boxes, since these
numbers have a large imaginary component.
The study of eigenvectors
confirms the conclusions made and allows for some refinements. Let
us consider the SAJ system with hinges in axle boxes. Equations of
constraints do not violate the first 15 eigenvectors:
1, 2)
non-physical solutions, which appeared due
to the fact that there are no variables
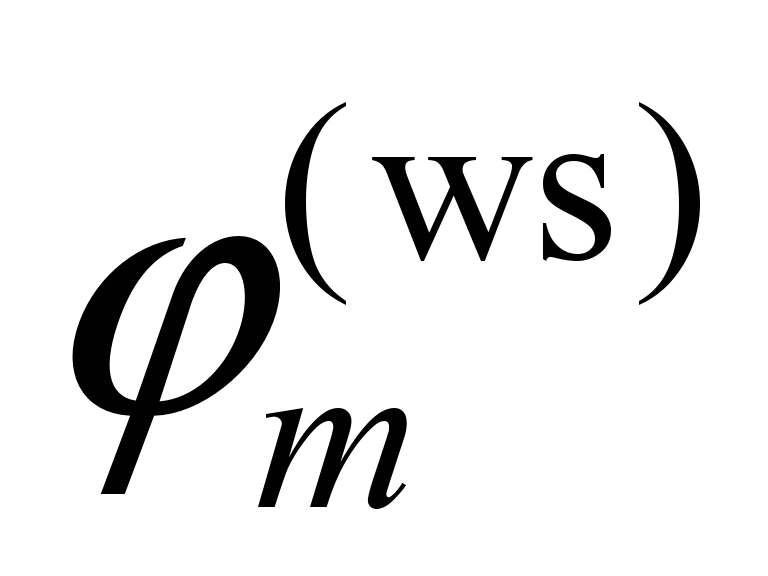 in the equations of motion, there are only
their derivatives;
in the equations of motion, there are only
their derivatives;
3, 4, 13)
extremely rapidly decaying solutions
describing the motion of wheel sets
against pseudo-slip forces (for example, bogie
swaying without hunting);
5, 6)
bolster hunting
oscillations;
7, 8) the
same as 3, 4 – rotation of the wheel
sets about their
axis without longitudinal displacement;
9, 10) body
swaying oscillations (wheel
sets also have
swaying and
hunting oscillations,
but the ratio of amplitude values
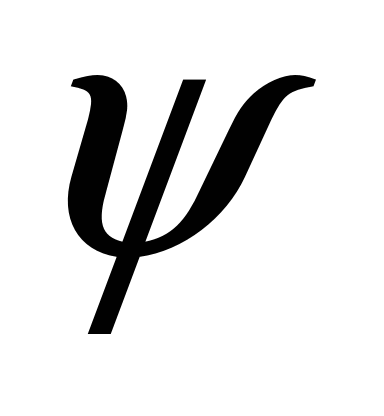 and y
is less by about 20% than Klingel
solution provides);
and y
is less by about 20% than Klingel
solution provides);
11, 12)
joint oscillations of the wheel set
swaying and
hunting (amplitude of body oscillations is
less than with the forms 9 and
10);
14, 15)
bogie oscillations
under the body in the longitudinal direction (spring suspension sets
are deformed in the longitudinal direction).
Table 2
Eigenvalues
for systems SF, SAJ, and SCX
|
j
|
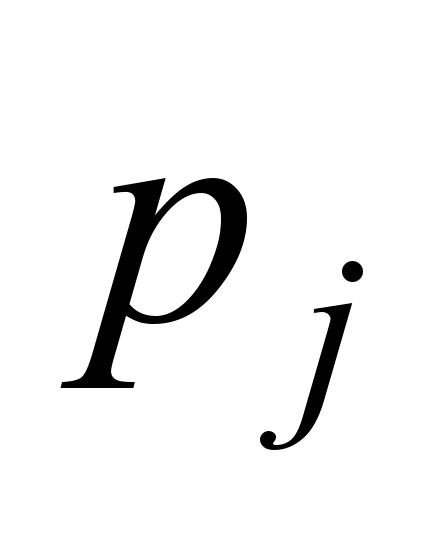 ,
1/с ,
1/с
|
j
|
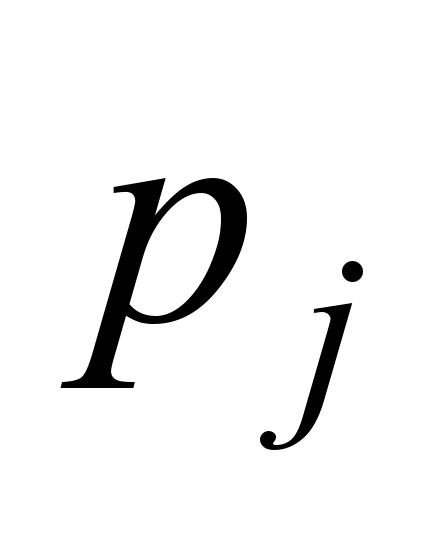 ,
1/с ,
1/с
|
|
SF
|
SAJ
|
|
1,
2
|
0
|
1,
2
|
0
|
|
3
|
–1800
|
3
|
–990
|
|
4
|
–1640
|
4
|
–1140
|
|
5,
6
|
–5610
|
5,
6
|
–6.29±335i
|
|
7
|
–1790
|
7
|
–5040
|
|
8
|
–1650
|
8
|
–3900
|
|
9,
10
|
–56.5±585i
|
9,
10
|
–2.33±17.3i
|
|
11,
12
|
–38.2±554i
|
11,
12
|
1.24±11.9i
|
|
13,
14
|
–11.9±314i
|
13
|
–1440
|
|
15,
16
|
–34.1±874i
|
14,
15
|
–0.21±91.1i
|
|
17,
18
|
±857i
|
16,
…, 34
|
0
|
|
19,
20
|
–3.64±638i
|
SAJ
+ SCX
|
|
21,
22
|
±542i
|
1,
2
|
0
|
|
23,
24
|
–3.89±315i
|
3
|
–4000
|
|
25,
26
|
–2.31±17.1i
|
4
|
–3900
|
|
27,
28
|
1.25±11.9i
|
5
|
–891
|
|
29,
30
|
–0.21±88.6i
|
6
|
–1440
|
|
31
|
–148
|
7
|
–1440
|
|
32,
33
|
0
|
8,
9
|
–2.33±17.,3i
|
|
34
|
–1.14
|
10,
11
|
1.24±11.9i
|
|
|
|
12,
…, 34
|
0
|
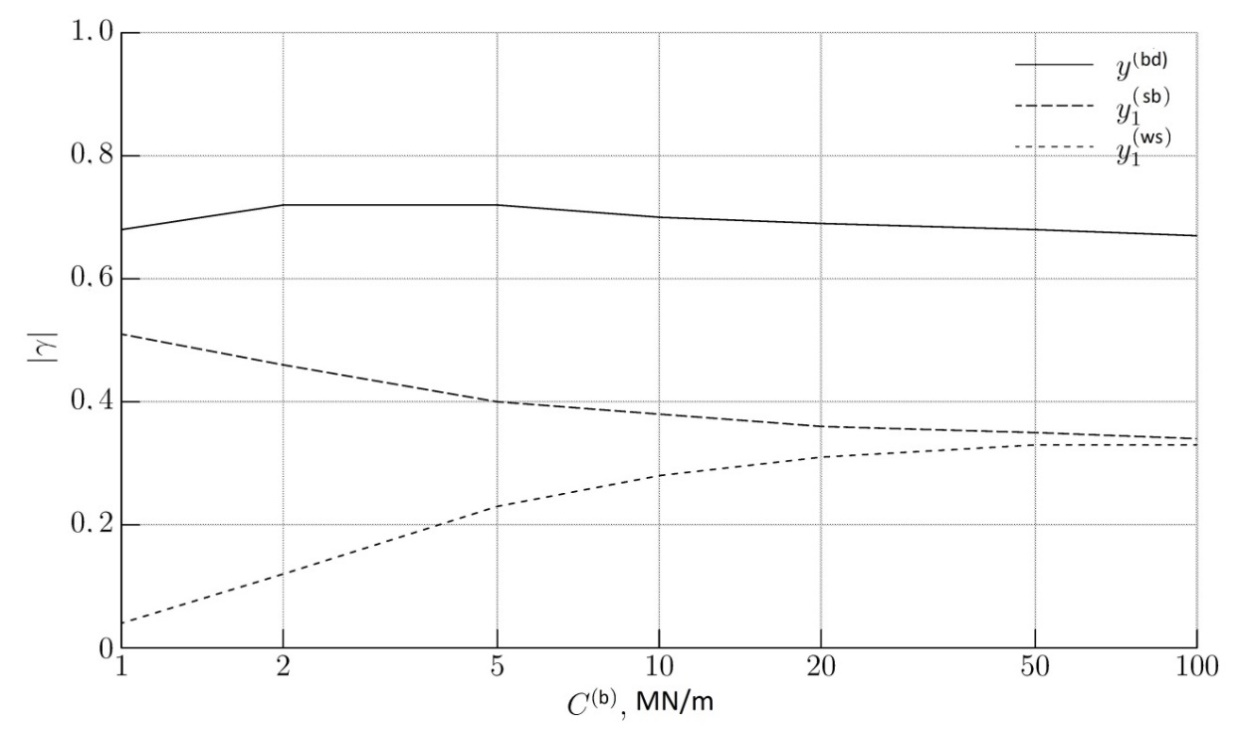
Fig.
2. The principal mode of unstable motion
Table
3
Components
of eigenvectors
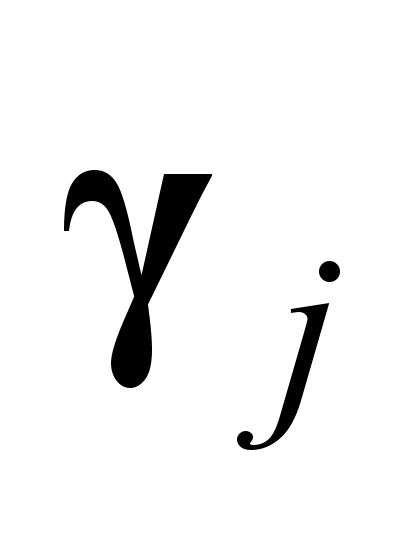
|
Compo-
|
SF
|
SAJ
|
|
nent
|
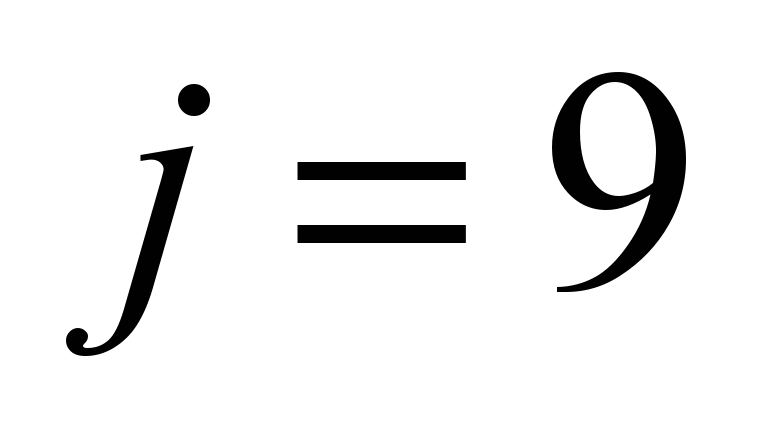
|
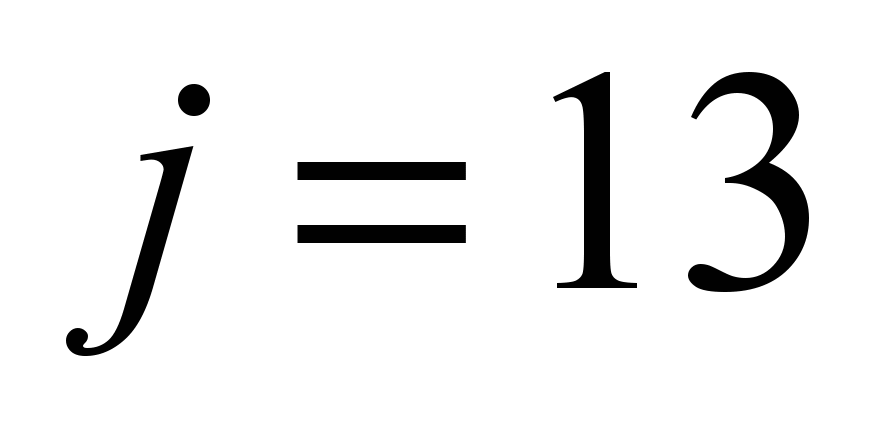
|
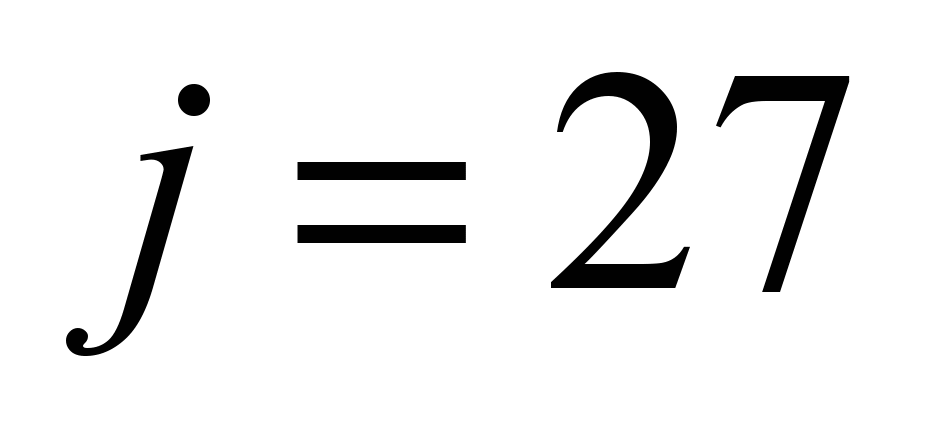
|
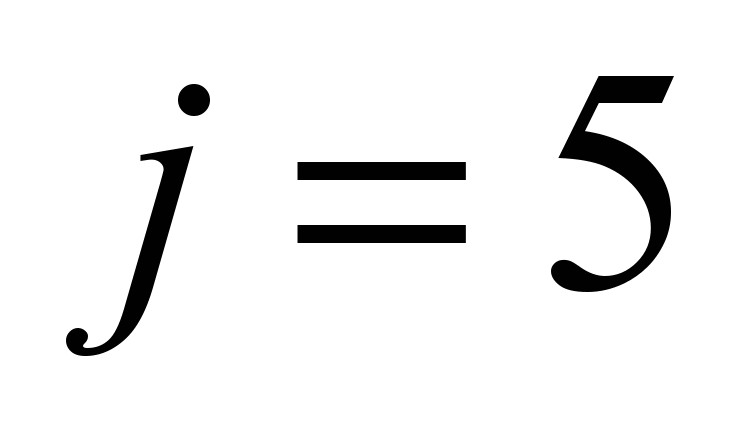
|
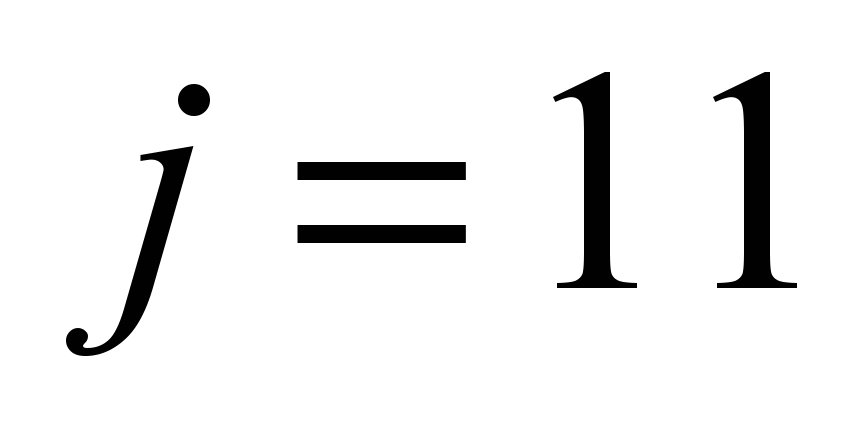
|
|
|
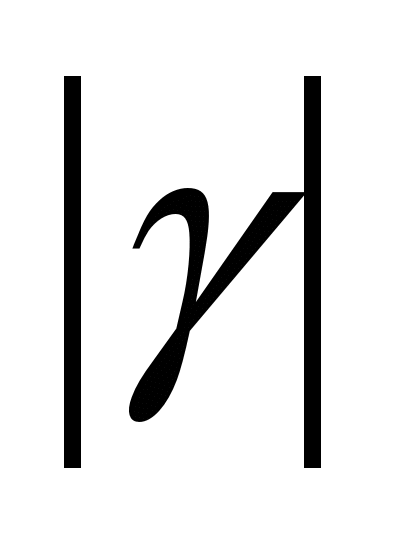
|
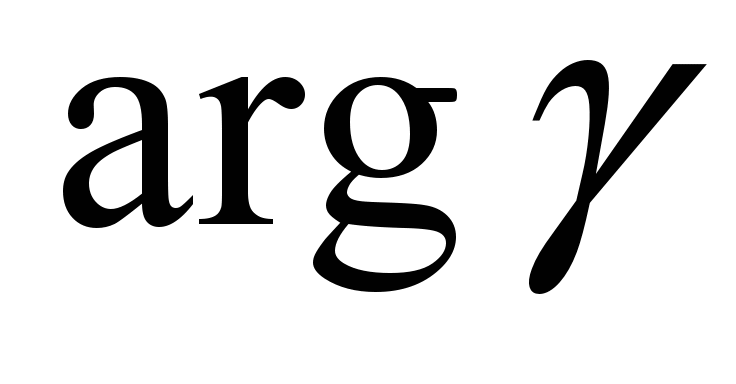
|
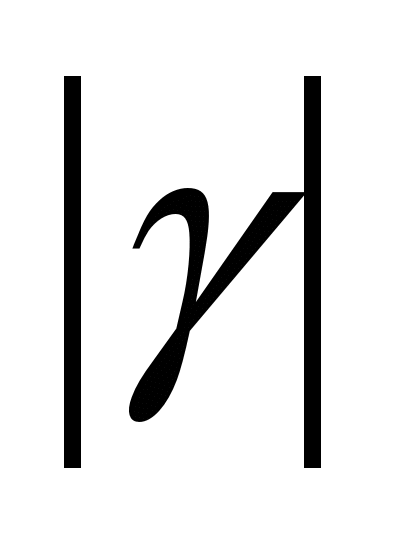
|
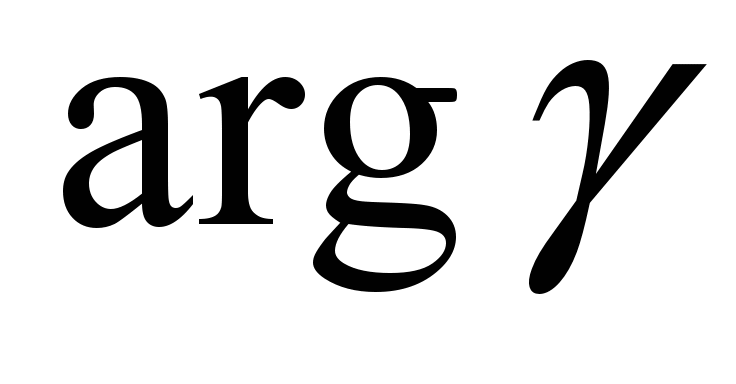
|
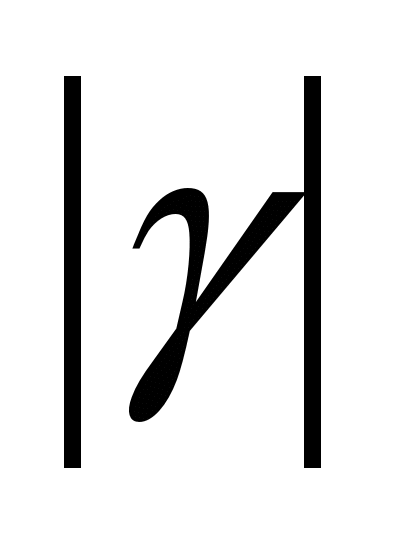
|
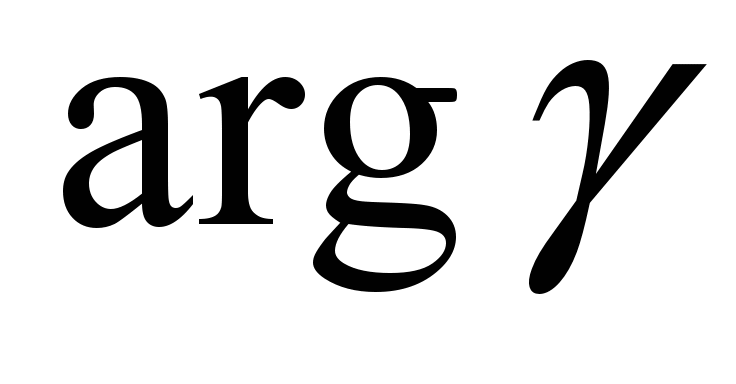
|
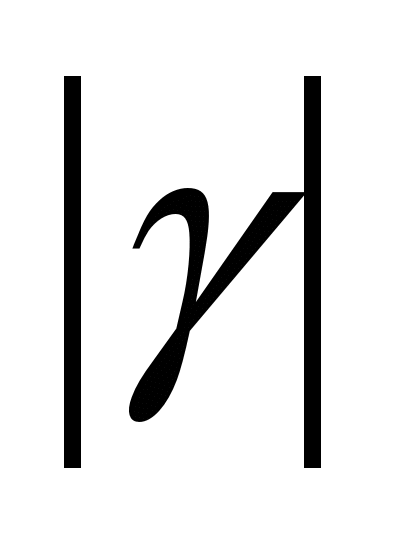
|
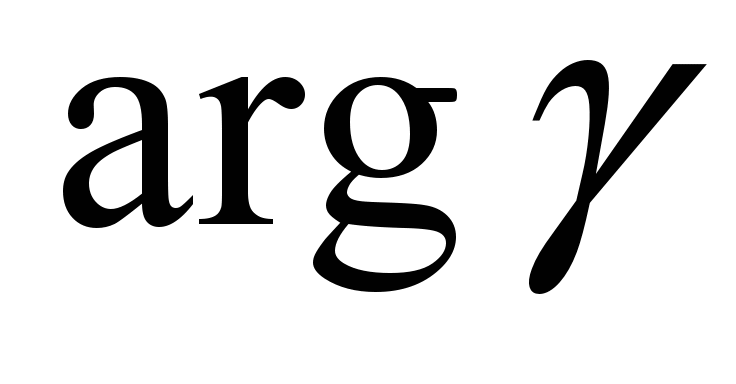
|
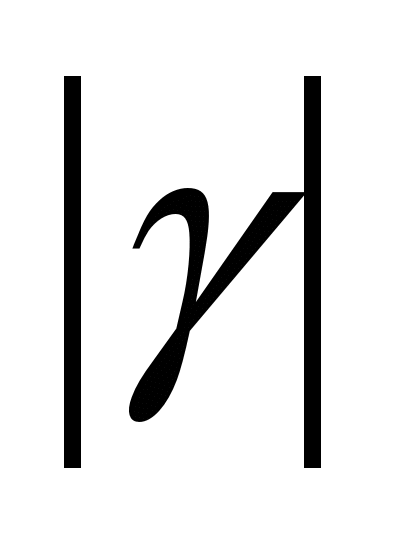
|
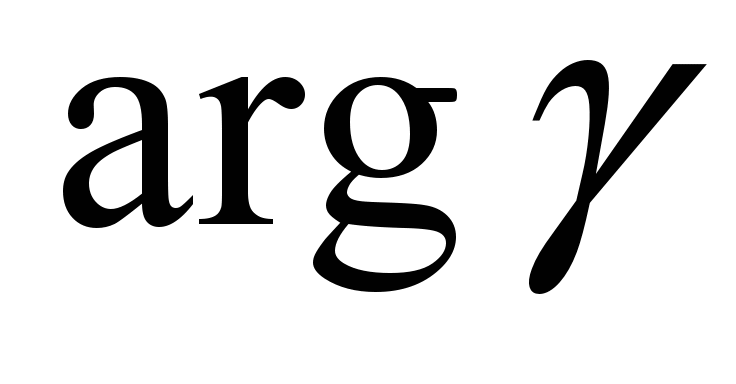
|
|
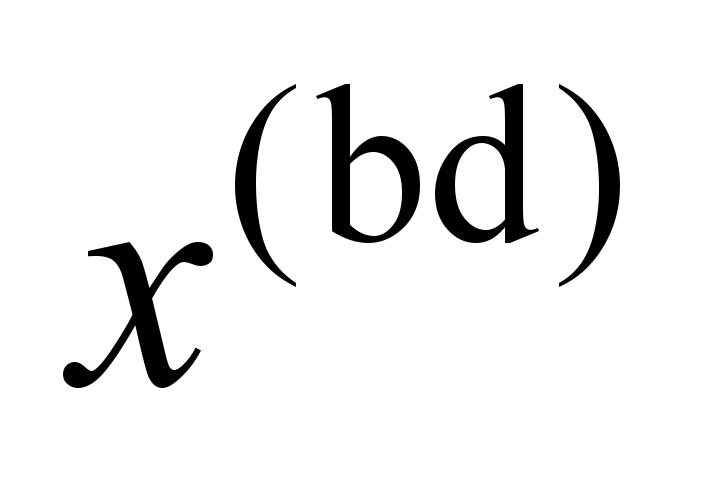
|
|
|
|
|
|
|
|
|
|
|
|
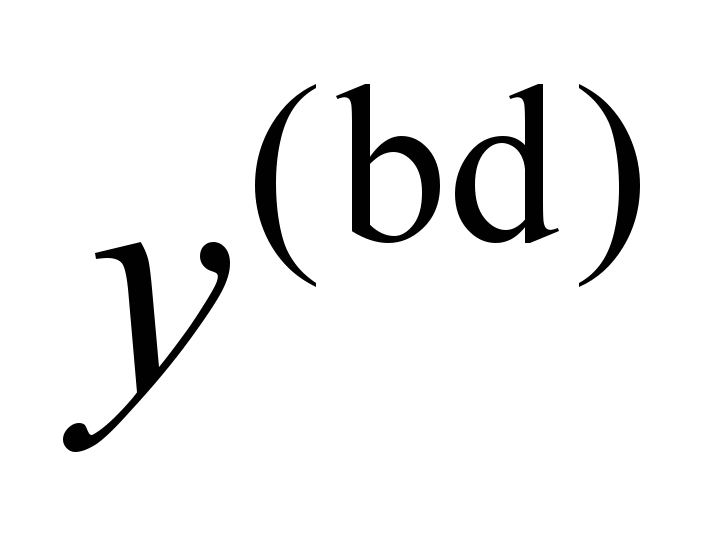
|
|
|
|
|
0.67
|
–1.47
|
|
|
0.67
|
–1.47
|
|
|
0.30
|
1.19
|
0.98
|
–1.61
|
0.13
|
0.42
|
1.00
|
–1.59
|
0.13
|
0.40
|
|
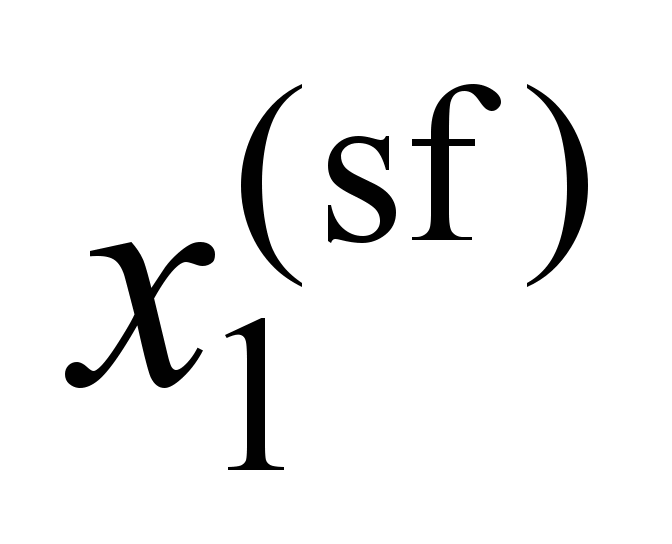
|
0.65
|
–1.67
|
0.13
|
–2.15
|
0.13
|
0.42
|
0.04
|
2.82
|
0.14
|
0.40
|
|
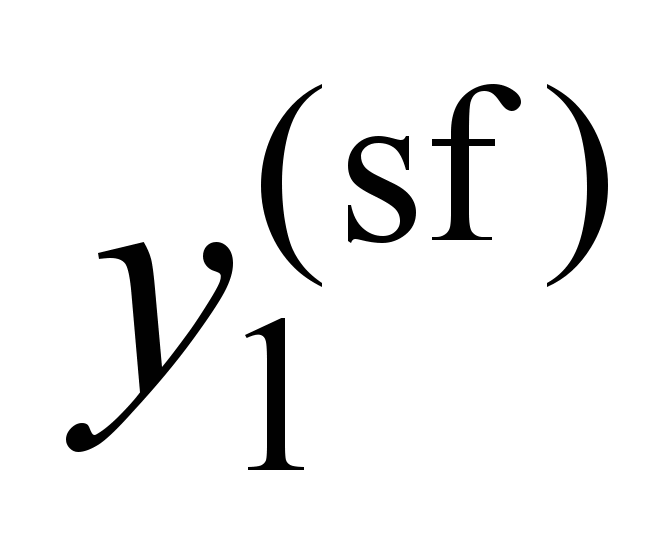
|
0.06
|
–2.82
|
|
|
0.34
|
–1.26
|
|
|
0.34
|
–1.26
|
|
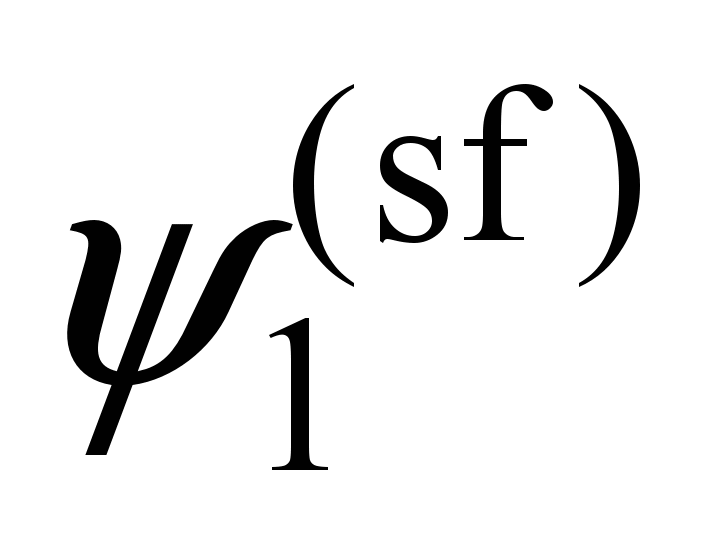
|
|
|
|
|
|
|
|
|
|
|
|
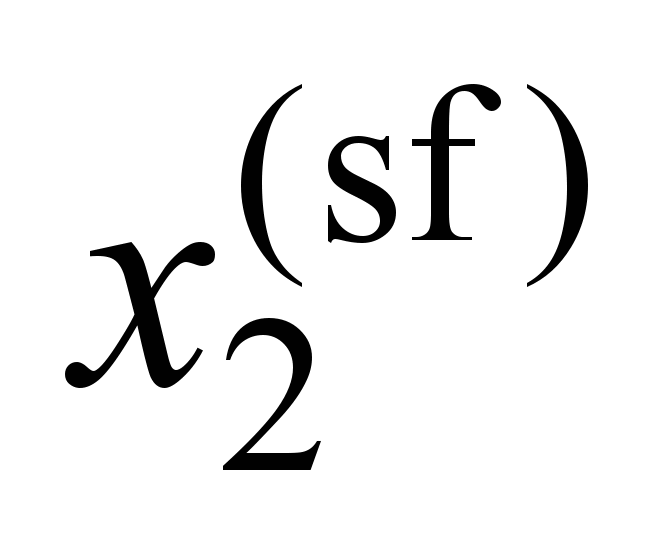
|
0.65
|
1.47
|
0.13
|
0.99
|
0.13
|
–2.73
|
0.04
|
–0.33
|
0.14
|
–2.74
|
|

|
0.06
|
–2.82
|
|
|
0.34
|
–1.26
|
|
|
0.34
|
–1.26
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.02
|
1.29
|
|
|
0.33
|
–1.25
|
|
|
0.34
|
–1.26
|
Continuation of the
table 3
|
Compo-
|
SF
|
SAJ
|
|
nent
|
|
|
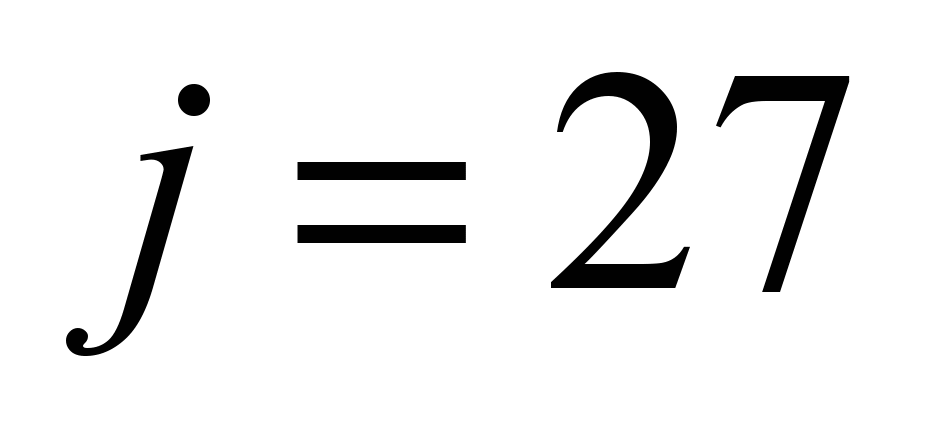
|
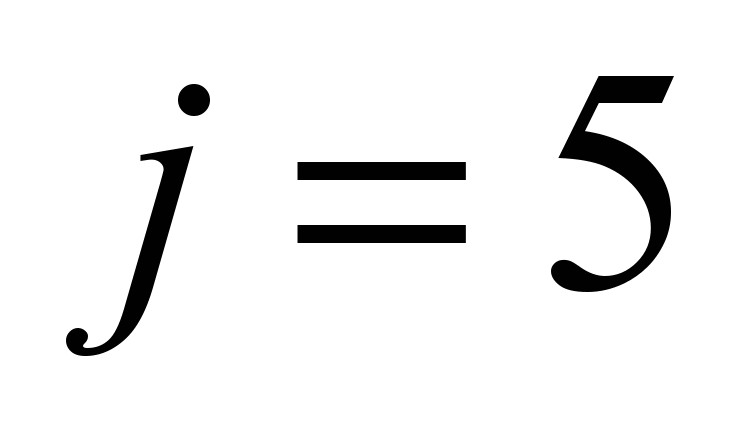
|
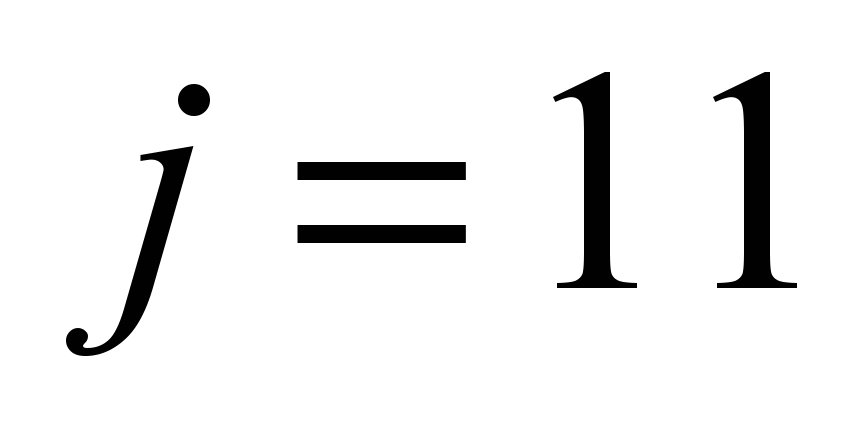
|
|
|
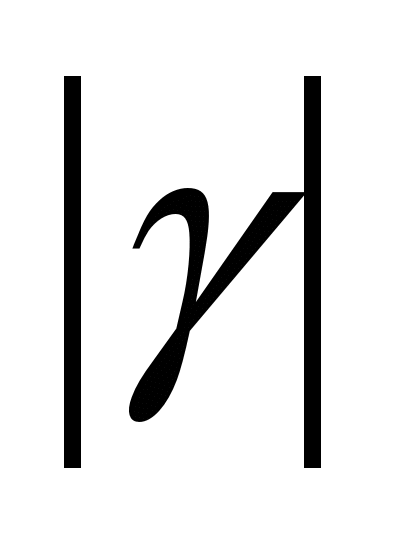
|
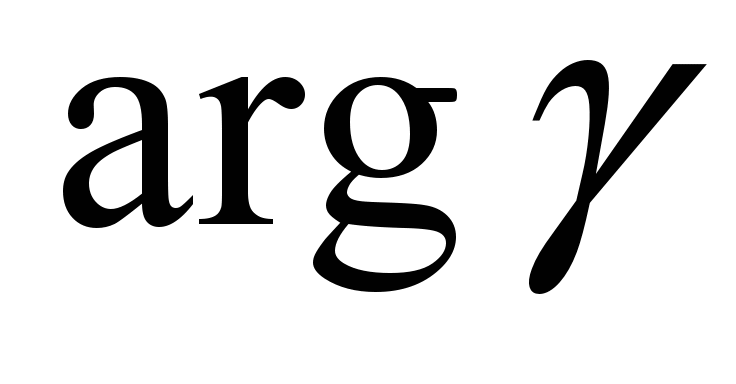
|
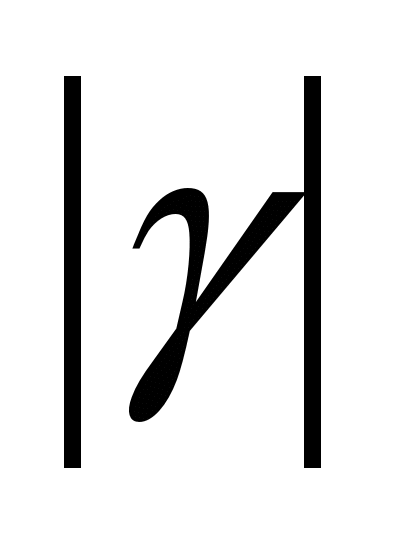
|
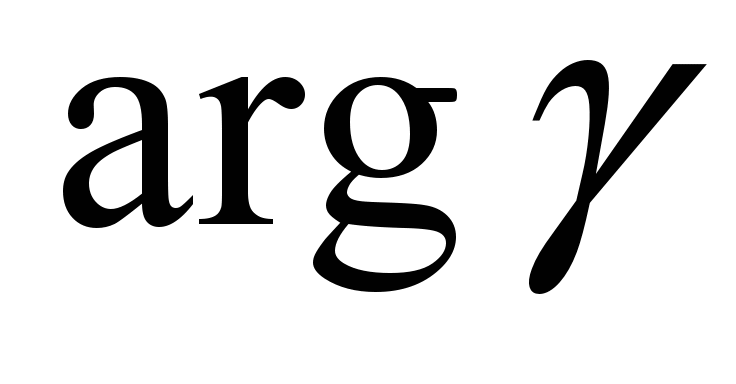
|
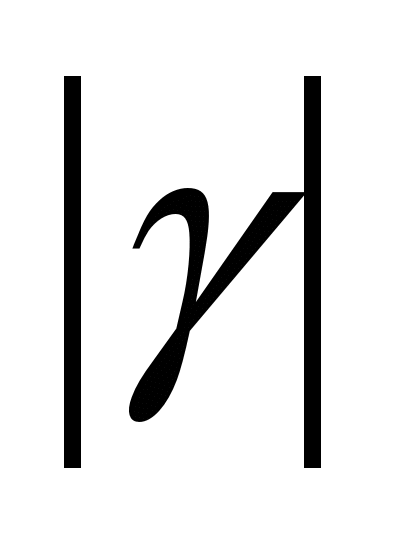
|
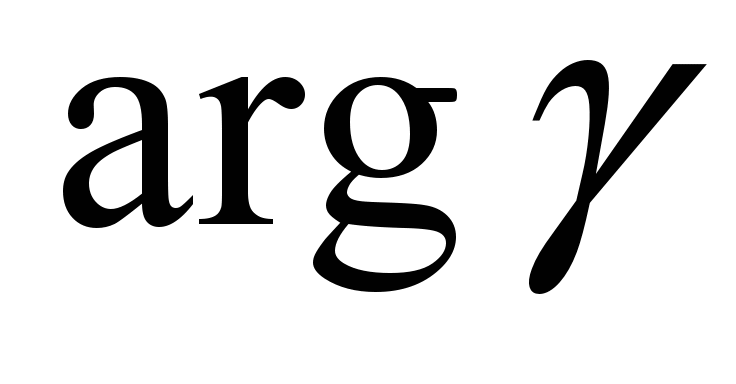
|
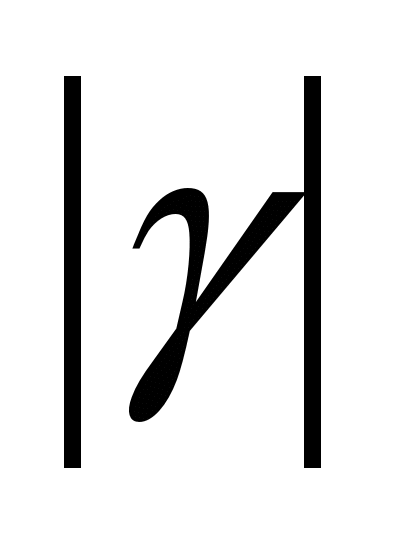
|
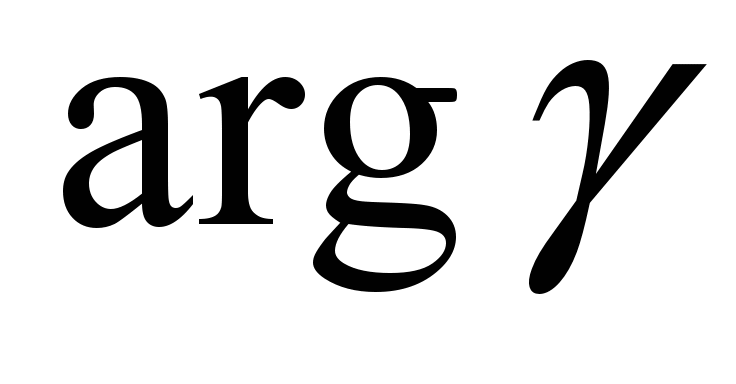
|
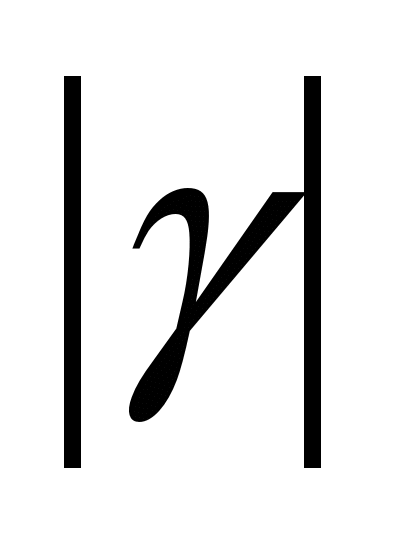
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.16
|
2.88
|
0.06
|
2.80
|
0.13
|
0.42
|
0.04
|
2.82
|
0.13
|
0.40
|
|
|
|
|
|
|
|
|
|
|
|
|
|
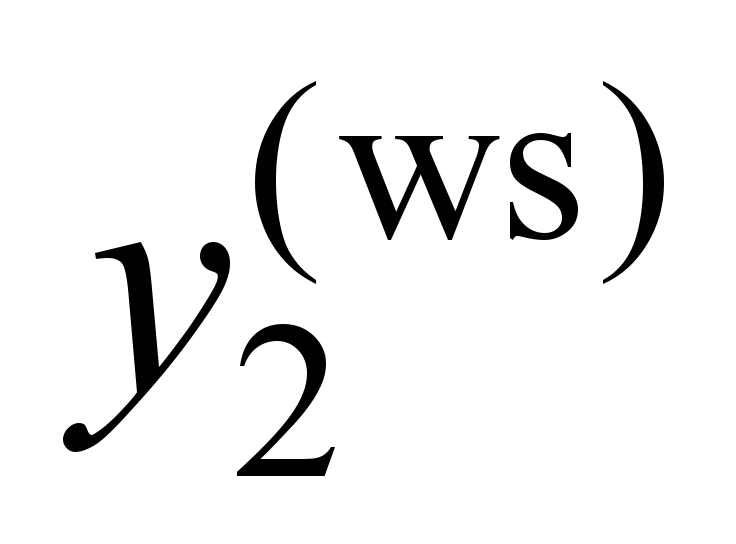
|
0.02
|
1.29
|
|
|
0.33
|
–1.25
|
|
|
0.34
|
–1.26
|
|
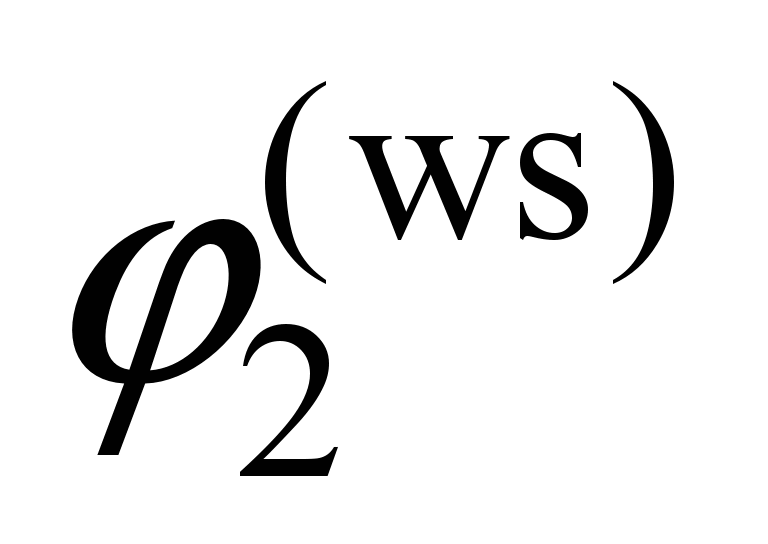
|
|
|
|
|
|
|
|
|
|
|
|
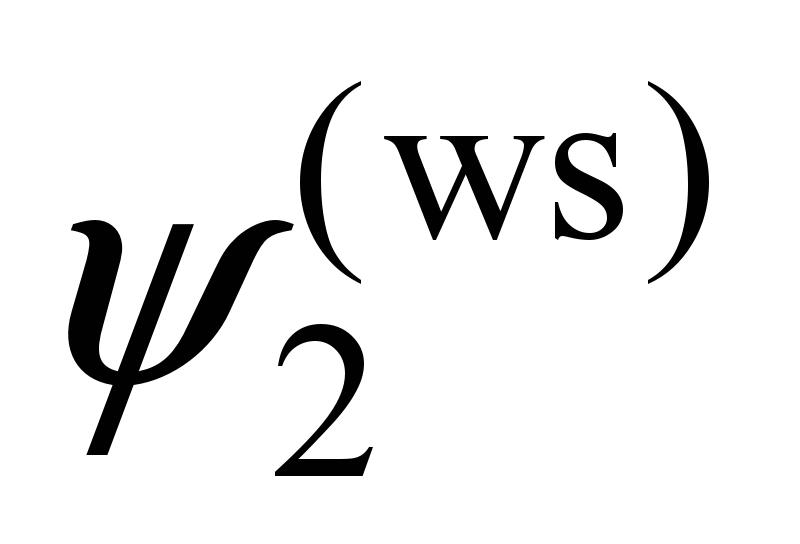
|
0.16
|
2.88
|
0.06
|
2.80
|
0.13
|
0.42
|
0.04
|
2.82
|
0.13
|
0.40
|
If a rigid
longitudinal constraint
in the spring suspension is added to the hinges in the axle
box (Table 2, column SAJ + SCX),
then the oscillation patterns 5, 6, 14, 15 in the SAJ system, which
are accompanied by deformations of the spring groups in the
longitudinal direction will disappear and four more eigenvectors,
corresponding to zero eigenvalues and violating equations of
constraints, will be. Other eigenvalues will change slightly.
Originality and practical
value
Originality consists in the
adaptation of Lyapunov's stability method of linear approximation to
the case when the equations of railway vehicle motion are written in
the form of differential-algebraic Lagrange equations of the first
kind. This written form of the equation of motion makes it possible
to simplify the stability study by avoiding the selection of a set
of independent generalized coordinates with the subsequent
elimination of dependent ones and allows for the coefficient matrix
calculation in an easily algorithmized way. Information on the
vehicle stability is vitally important, since the truck design must
necessarily exclude the loss of stability in the operational speed
range.
Conclusions
1. An
effective method for studying the stability of railway vehicle
motion, described by the Lagrange equations of the first kind, has
been proposed. Stability criterion – the real numbers of
exponential functions that satisfy the equations of motion –
should not be greater than zero. The indicators themselves can be
found as eigenvalues of a certain matrix A,
depending on the matrices of physical parameters M,
B, F, C, K and the matrix of
constraint coefficients L,
using the QR algorithm [2, chapter 4].
2. The eigenvectors of this
matrix, corresponding to nonzero eigenvalues, satisfy the equations
of constraints. The advantage of the proposed method is the easy
algorithmization of the motion equation derivation (no need to
choose independent generalized coordinates).
LIST OF REFERENCE LINKS
1.Деммель, Дж.
Вычислительная линейная алгебра. Теория
и приложения / Дж. Деммель
; пер. с англ. Х. Д. Икрамова. – Москва
: Мир, 2001. – 435 с.
2.Лазарян,
В. А. Устойчивость движения рельсовых
экипажей / В. А. Лазарян, Л. А. Длугач, М.
Л. Коротенко. – Киев : Наук. думка, 1972. –
198 с.
3.Орлова,
А. М. Влияние конструктивных схем и
параметров тележек на устойчивость,
ходовые качества и нагруженность
грузовых вагонов : автореф. дис. ... д-ра
техн. наук : 05.22.07 / Орлова Анна Михайловна
; Петербург. гос. ун-т путей сообщения.
– Санкт-Петербург, 2008. – 32 с.
4.Bigoni,
D. Sensitivity analysis of the critical speed in railway vehicle
dynamics / D. Bigoni,
H. True,
A. P. Engsig-Karup
//
Vehicle System Dynamics. – 2014. – Vol. 54. – Iss. supp1. –
P. 272–286.
doi: 10.1080/00423114.2014.898776
5.Critical
speed of a Korean high-speed train through optimization with
measured wheel profiles / C.-S.
Jeon, H.-S. Cho, C.-S. Park, S.-W. Kim, T.-W. Park //
Proceedings
of the Institution of Mechanical Engineers, Part F: Journal of Rail
and Rapid Transit. – 2018. – Vol. 232.
– Iss. 1. – P. 171–181.
doi: 10.1177/0954409716662091
6.Gasch,
R. Non-linear bogie hunting / R. Gasch, W. Kik, D. Moelle // Vehicle
System Dynamics. – 1981. – Vol. 10. – Iss. 2-3. – P.
145–148. doi: 10.1080/00423118108968657
7.Influence
of vehicle parameters on critical hunting speed based on Ruzicka
model / D. Cui,
Li
Li,
X. Jin,
X. Xiao,
J. Ding
// Chinese Journal of Mechanical Engineering. – 2012. – Vol. 25.
– Iss. 3. –
P. 536–542. doi: 10.3901/cjme.2012.03.536
8.Kalker,
J. J. Three-dimensional elastic bodies in rolling contact / J. J.
Kalker. – Dordrecht
: Springer,
1990. – 314 p. doi: 10.1007/978-94-015-7889-9
9.Mao,
X. A design method for rail profiles based on the geometric
characteristics of wheel-rail contact /
X. Mao, G. Chen //
Proceedings of the Institution of Mechanical Engineers, Part F:
Journal of Rail and Rapid Transit. – 2018. – Vol. 232.
– Iss. 5. – P. 1255–1265. doi: 10.1177/0954409717720346
10.Mazzola,
L. Evaluation of the hunting behavior of a railway vehicle in a
curve / L. Mazzola,
S. Alfi,
S. Bruni
//
Proceedings of the Institution of Mechanical Engineers, Part F:
Journal of Rail and Rapid Transit. – 2014. – Vol. 229.
– Iss. 5. – P. 530–541. doi: 10.1177/0954409713517379
11.Moelle,
D. Computation of Limit Cycles of a Wheelset Using a Galerkin Method
/ D. Moelle,
H. Steinborn,
R. Gasch
//
Vehicle System Dynamics. – 1979. – Vol. 8. – Iss. 2-3. – P.
168–171.
doi: 10.1080/00423117908968592
12.Molatefi,
H. Critical speed and limit cycles in the empty Y25-freight wagon /
H. Molatefi,
M. Hecht,
M. H. Kadivar
// Proceedings of the Institution of Mechanical Engineers, Part F:
Journal of Rail and Rapid Transit. – 2006. – Vol. 220. – Iss.
4. – P. 347–359. doi: 10.1243/09544097jrrt67
13.Polach,
O. Bogie design for better dynamic performance:
example of a locomotive bogie
/ O. Polach // European Railway Review.
– 2003. – No. 1. – P. 69–77.
14.Polach,
O. Comparison of Methods Analyzing Bifurcation and Hunting of
Complex Rail Vehicle Models /
O. Polach,
I. Kaiser
//
Journal of Computational and Nonlinear Dynamics. – 2012. – Vol.
7. – Iss. 4.
doi: 10.1115/1.4006825
15.Polach,
O. Compatibility of the non-linear and linearized stability
assessment during railway vehicle design / O.
Polach
// Vehicle System Dynamics. – 2006. – Vol. 44. – Iss. sup1. –
P. 129–138.
doi: 10.1080/00423110600869537
16.True,
H. The Dynamics of a Railway Freight Wagon Wheelset with Dry
Friction Damping / H. True,
R. Asmund
//
Vehicle System Dynamics. – 2002. – Vol. 38. – Iss. 2. – P.
149–163. doi: 10.1076/vesd.38.2.149.5617
17.Xia,
F. On the dynamics of the three-piece-freight truck / F. Xia,
H. True
//
Proceedings of the 2003 IEEE/ASME Joint Rail Conference. – 2003. –
P. 149–159. doi: 10.1109/rrcon.2003.1204661
О.
Г. РЕЙДЕМЕЙСТЕР1*, С. І.
Левицька2*
1*Каф.
«Вагони та вагонне господарство»,
Дніпропетровський національний
університет залізничного
транспорту
імені академіка В. Лазаряна, вул.
Лазаряна, 2, Дніпро, Україна, 49010,
тел. +38 (056) 373 15 19,
ел. пошта
reidemeister.a@gmail.com,
ORCID 0000-0001-7490-7180
2*Каф.
«Іноземні мови», Придніпровська державна
академія будівництва та архітектури,
вул. Чернишевського, 24А, Дніпро, Україна,
49000, тел. +38 (056) 756 33 56,
ел. пошта svetik23com@ukr.net,
ORCID 0000-0001-6725-0280
Стійкість
руху залізничних екіпажів,
ЯКИЙ
описують рівняння Лагранжа I
роду
Мета.
У статті необхідно оцінити стійкість
руху залізничних екіпажів, коливання
яких описані рівняннями Лагранжа I
роду, в припущенні, що відсутні
нелінійності з розривами правих частин.
Методика.
За основу прийнято метод дослідження
стійкості руху Ляпунова за лінійним
наближенням. Рівняння руху складено в
матричній формі. Сили кріпа обчислені
у відповідності з лінійної теорією
Калкера. Послідовними диференціюваннями
рівнянь зв’язків індекс системи рівнянь
знижений з 2 до 0. Власні числа матриці
коефіцієнтів отриманої таким чином
системи знайдені за допомогою
QR-алгоритму. Відповідно до критерію
Ляпунова про стійкість за лінійним
наближенням рух стійкий, якщо у всіх
власних чисел дійсна частина негативна.
Нетривіальним є наявність «зайвих»
ступенів свободи, яких немає у механічної
системи (в її рівняннях руху залишили
тільки незалежні координати). Цим
ступеням свободи відповідають власні
числа і власні вектори, що не мають
відношення до стійкості. Щоб знайти
правило, що дозволяє їх виключити, ми
розглянули кілька моделей візків, із
жорсткими і пружними зв’язками великої
жорсткості у вузлах. У граничному
випадку великих жорсткостей результати
для системи без жорстких зв’язків
повинні співпасти з результатами для
системи з жорсткими зв’язками.
Результати.
Проведено аналіз і зіставлені частоти
(з декрементом) і форми коливань
3-елементного візка зі зв’язками і без
них. При аналізі стійкості системи зі
зв’язками становлять інтерес тільки
ті власні числа, власні вектори яких
не порушують зв’язків. Значення цих
чисел є межами для власних чисел системи,
в якій жорсткі зв’язки замінені пружними
елементами великої жорсткості, що
дозволяє залишити критерій Ляпунова
незмінним. Наукова
новизна полягає в
адаптації методу дослідження стійкості
руху Ляпунова за лінійним наближенням
до випадку, коли рівняння руху залізничних
екіпажів записані в формі
диференційно-алгебраїчних рівнянь
Лагранжа I роду. Практична
значимість. Зазначена
форма запису рівняння руху дозволяє
спростити дослідження стійкості за
рахунок відмови від виділення безлічі
незалежних узагальнених координат із
наступним виключенням залежних і
допускає обчислення матриці коефіцієнтів
легко алгоритмізованим способом.
Інформація про стійкість екіпажів
украй важлива, оскільки конструкція
ходових частин повинна в обов’язковому
порядку виключати втрату стійкості в
експлуатаційному діапазоні швидкостей.
Ключові
слова: залізничний
екіпаж; стійкість руху; диференційно-алгебраїчні
рівняння
А. Г.
РЕЙДЕМЕЙСТЕР1*, С. И. ЛЕВИЦКАЯ2*
1*Каф.
«Вагоны и вагонное хозяйство»,
Днепропетровский национальный
университет железнодорожного
транспорта
имени академика В. Лазаряна, ул. Лазаряна,
2, Днипро, Украина, 49010, тел. +38 (056) 373 15 19,
эл. почта reidemeister.a@gmail.com, ORCID 0000-0001-7490-7180
2*Каф.
«Иностранные языки»,
Приднепровская государственная академия
строительства и архитектуры,
ул.
Чернышевского, 24А, Днипро,
Украина, 49000,
тел. +38 (056) 756 33 56,
эл. почта svetik23com@ukr.net,
ORCID 0000-0001-6725-0280
УСТОЙЧИВОСТЬ
ДВИЖЕНИЯ ЖЕЛЕЗНОДОРОЖНЫХ
ЭКИПАЖЕЙ,
ОПИСЫВАЕМого УРАВНЕНИЯМИ
ЛАГРАНЖА I
РОДА
Цель.
В статье необходимо оценить устойчивость
движения железнодорожных экипажей,
колебания которых описаны уравнениями
Лагранжа I рода, в
предположении, что отсутствуют
нелинейности с разрывами правых частей.
Методика.
За
основу принят метод исследования
устойчивости движения Ляпунова по
линейному приближению. Уравнения
движения составлены в матричной форме.
Силы крипа вычислены в соответствии
с линейной теорией Калкера. Последовательными
дифференцированиями уравнений связей
индекс системы уравнений понижен с 2
до 0. Собственные числа матрицы
коэффициентов полученной таким образом
системы найдены с помощью
QR–алгоритма.
В соответствии с критерием Ляпунова
об устойчивости по линейному приближению
движение устойчиво, если у всех
собственных чисел действительная часть
отрицательна. Нетривиальным является
наличие «лишних» степеней свободы,
которых нет у механической системы (в
ее уравнениях движения оставили только
независимые координаты). Этим степеням
свободы соответствуют собственные
числа и собственные векторы, к устойчивости
отношения не имеющие. Чтобы найти
правило, позволяющее их исключить, мы
рассмотрели несколько моделей тележки,
с жесткими и упругими связями большой
жесткости в узлах. В предельном случае
больших жесткостей результаты для
системы без жестких связей должны
совпасть с результатами для системы с
жесткими связями.
Результаты. Проведен
анализ и сопоставлены частоты (с
декрементами) и формы колебаний
3–элементной тележки со связями и без
них. При анализе устойчивости системы
со связями представляют интерес только
те собственные числа, собственные
векторы которых не нарушают связей.
Значения этих чисел являются пределами
для собственных чисел системы, в которой
жесткие связи заменены упругими
элементами большой жесткости, что
позволяет оставить критерий Ляпунова
неизменным. Научная
новизна состоит в
адаптации метода исследования
устойчивости движения Ляпунова по
линейному приближению к случаю, когда
уравнения движения железнодорожных
экипажей записаны в форме
дифференциально-алгебраических
уравнений Лагранжа I
рода. Практическая
значимость. Указанная
форма записи уравнения движения
позволяет упростить исследование
устойчивости за счет отказа от выделения
множества независимых обобщенных
координат с последующим исключением
зависимых и допускает вычисление
матрицы коэффициентов легко
алгоритмизируемым способом. Информация
об устойчивости экипажей крайне важна,
поскольку конструкция ходовых частей
должна в обязательном порядке исключать
потерю устойчивости в эксплуатационном
диапазоне скоростей.
Ключевые
слова: железнодорожный экипаж;
устойчивость движения;
дифференциально-алгебраические
уравнения
REFERENCES
Demmel,
D. (2001). Vychislitelnaya lineynaya
algebra. Teoriya i prilozheniya.
Moscow: Mir.
(in Russian)
Lazaryan,
V. A., Dlugach, L. A., & Korotenko, M. L. (1972). Ustoychivost
dvizheniya relsovykh ekipazhey. Kyiv:
Naukova
dumka. (in
Russian)
Orlova,
A. M. (2008). Vliyanie konstruktivnykh
skhem i parametrov telezhek na ustoychivost, khodovye kachestva i
nagruzhennost gruzovykh vagonov.
(Avtoreferat dissertatsii doktora tekhnicheskikh nauk). Emperor
Alexander I St. Petersburg State Transport University, Saint
Petersburg. (in
Russian)
Bigoni,
D., True, H., & Engsig-Karup, A. P. (2014). Sensitivity
analysis of the critical speed in railway vehicle dynamics. Vehicle
System Dynamics, 52(sup1), 272-286.
doi: 10.1080/00423114.2014.898776
(in English)
Jeon,
C.-S., Cho, H.-S., Park, C.-S., Kim, S.-W., & Park,
T.-W.
(2018). Critical speed of a Korean
high-speed train through optimization with measured wheel profiles.
Proceedings
of the Institution of Mechanical Engineers, Part F: Journal of Rail
and Rapid Transit, 232(1),
171-181. doi: 10.1177/0954409716662091
(in English)
Gasch,
R., Kik, W., & Moelle, D. (1981). Non-Linear Bogie Hunting.
Vehicle System Dynamics, 10(2-3),
145-148. doi: 10.1080/00423118108968657 (in English)
Cui,
D., Li, L., Jin, X., Xiao, X., & Ding, J. (2012). Influence of
vehicle parameters on critical hunting speed based on Ruzicka
model. Chinese Journal of Mechanical
Engineering, 25(3), 536-542.
doi: 10.3901/cjme.2012.03.536
(in English)
Kalker,
J. J. (1990). Three-Dimensional Elastic Bodies in Rolling Contact.
Dordrecht:
Springer.
doi:
10.1007/978-94-015-7889-9 (in English)
Mao,
X., & Chen, G. (2018). A design method for rail profiles based
on the geometric characteristics of wheel-rail contact. Proceedings
of the Institution of Mechanical Engineers, Part F: Journal of Rail
and Rapid Transit, 232(5), 1255-1265.
doi: 10.1177/0954409717720346
(in English)
Mazzola,
L., Alfi, S., & Bruni, S. (2014). Evaluation of the hunting
behavior of a railway vehicle in a curve. Proceedings
of the Institution of Mechanical Engineers, Part F: Journal of Rail
and Rapid Transit, 229(5), 530-541.
doi: 10.1177/0954409713517379 (in English)
Moelle,
D., Steinborn, H., & Gasch, R. (1979). Computation of Limit
Cycles of a Wheelset Using a Galerkin Method. Vehicle
System Dynamics, 8(2-3), 168-171.
doi: 10.1080/00423117908968592
(in English)
Molatefi,
H., Hecht, M., & Kadivar, M. H. (2006). Critical speed and
limit cycles in the empty Y25-freight wagon. Proceedings
of the Institution of Mechanical Engineers, Part F: Journal of Rail
and Rapid Transit, 220(4), 347-359.
doi: 10.1243/09544097jrrt67 (in English)
Polach,
O. (2003). Bogie design for better dynamic performance:
example of a locomotive bogie.
European Railway
Review, 1, 69-77. (in
English)
Polach,
O., & Kaiser, I. (2012). Comparison of Methods Analyzing
Bifurcation and Hunting of Complex Rail Vehicle Models. Journal
of Computational and Nonlinear Dynamics, 7(4),
041005.
doi:
10.1115/1.4006825 (in
English)
Polach,
O. (2006). Comparability of the non-linear and linearized stability
assessment during railway vehicle design. Vehicle
System Dynamics, 44(sup1), 129-138.
doi: 10.1080/00423110600869537 (in
English)
True,
H., & Asmund, R. (2003). The Dynamics of a Railway Freight
Wagon Wheelset With Dry Friction Damping. Vehicle
System Dynamics, 38(2), 149-163.
doi: 10.1076/vesd.38.2.149.5617 (in
English)
Fujie
Xia, & True, H. (n.d.). (2003). On
the dynamics of the three-piece-freight truck.
Proceedings of the 2003 IEEE/ASME Joint Railroad Conference.
doi:
10.1109/rrcon.2003.1204661 (in
English)
Received:
June 25,
2018
Accepted:
Oct. 03,
2018
d oi
10.15802/stp2018/ ©
A. G. Reidemeister, S. I. Levytska,
2018
oi
10.15802/stp2018/ ©
A. G. Reidemeister, S. I. Levytska,
2018
.
At high velocities, chaotic attractors may appear. There may be
cases when they occur already at the velocity
[5]. The following methods of motion stability analysis are used
[15]:
is solved; it is not suitable for the study of quasi-periodic and
chaotic oscillations).
, (1)
. (3)
,
are found from the initial conditions.
The indices
together with nonzero eigenvectors
,
are solutions of the equation
, (4)
– if there are positive numbers among them, the motion is stable.
It is inconvenient to search for numbers
,
equating the determinant of the left matrix to zero. Instead, we
reformulate the problem so that the indices
turn out to be eigenvalues of a certain matrix. From (2) it follows
that
,
,
we get
is
non-degenerate
(if the
constraint
coefficient
matrix L
has less rows
than columns,
and the
rank is
equal to
the number
of rows,
which we
assume),
therefore
.
;
.
satisfies the
differential
equation
;
.
,
has the form
.
Let us consider how they are related to
the eigenvalues and eigenvectors of the original system with
constraints, that is, if they satisfy the equation (4) with a
suitable choice of the vector of Lagrange multipliers
.
We will need an obvious correlation
.
Multiplying the left expression by L
(5)
.
the vector
satisfies the constraint equation
.
Equation (4) is easy to rewrite as
the vectors
satisfy the equation (4) with
.
satisfy the equation (4) for
,
but, since these solutions correspond to constant processes that are
of no interest, we will not deal with them.
,
are eigenvalues of matrix A.