ISSN
2307–3489 (Print), ІSSN
2307–6666
(Online)
Наука та прогрес
транспорту. Вісник
Дніпропетровського
національного університету
залізничного транспорту, 2018, № 5
(77)
Експлуатація
та ремонт засобів транспорту
Експлуатація
та ремонт засобів транспорту
UDC
629.42.083-047.58
B. E.
BODNAR1,
O. B.
ОCHKАSОV2*,
Е. B. BODNAR3,
Т. S.
HRYSHECHKINA4,
М. V. OCHERETNYUK5
1Dep.
«Locomotives», Dnipropetrovsk National University named after
Academician V. Lazaryan, Lazaryan St., 2, Dnipro, Ukraine, 49010,
tel. + 38 (056) 733 19 01, e-mail bodnarz@nz.diit.edu.ua, ORCID
0000-0002-3591-4772
2*Dep.
«Locomotives», Dnipropetrovsk National University named after
Academician V. Lazaryan, Lazaryan St., 2, Dnipro, Ukraine, 49010,
tel. + 38 (056) 733 19 61, e-mail abochkasov@gmail.com, ORCID
0000-0002-7719-7214
3Dep.
«Locomotives», Dnipropetrovsk National University named after
Academician V. Lazaryan, Lazaryan St., 2, Dnipro, Ukraine, 49010,
tel. + 38 (056) 733 19 61, e-mail Melnar78@gmail.com,
ORCID 0000-0001-6040-913X
4Dep.
«Higher Mathematics», Dnipropetrovsk National University named
after Academician V. Lazaryan, Lazaryan St., 2, Dnipro, Ukraine,
49010, tel. +38 (0562) 36 26 04, e-mail grishechkina.tatiana@gmail.com, ORCID
0000-0003-1570-4150
5Dep.
«Locomotives», Dnipropetrovsk National University named after
Academician V. Lazaryan, Lazaryan St., 2, Dnipro, Ukraine, 49010,
tel. + 38 (056) 733 19 61, e-mail ocheretniukmaksym@gmail.com, ORCID
0000-0002-9032-8602
SIMULATION
OF LOCOMOTIVE REPAIR
ORGANIZATION BY THE METHODS
OF QUEUE SYSTEMS
THEORY
Purpose.
The article is aimed to evaluate the influence
of locomotives` operation and reliability indicators on the system of
locomotives repair organization in depot, using the methods of queue
theory. Methodology.
The article describes the locomotive repair workshop using the terms
and concepts of the queue systems
theory (QST).
The tasks solved during simulation of the repair workshop operation
are formulated, the list of initial data and simulation results is
given. A graphical simulation environment Simulink was used as a
software simulation tool. Findings.
It was established that the main indicators of locomotive depot
operation are affected by the volume of traffic, the reliability of
locomotives, the rule used to select locomotives from the queue, the
number of operating repair bays. The developed model of the depot
repair workshop will make possible rational planning of the repair
workshop`s equipment use, the human capital, the time of putting the
locomotives into repair taking into account the workshop loading
uniformity, as well as to improve the repair parts supply logistics.
This model in a simplified form describes the repair process of the
main diesel locomotive fleet, and can be supplemented depending on
the repair type performed in the depot. Originality.
The paper presents the locomotive repair depot as an object of the
queue systems theory. The simulation model of the locomotive repair
depot was developed. It allows analyzing the influence of various
factors on the system of locomotives` repair organization in the
depot. Practical value. The obtained results make it possible
to determine the influence of locomotives` operation and reliability
indicators on the organization of the locomotive repair depot
operation. In further studies, the developed model can be used to
improve the system of repair organization on the railway network when
introducing new series of locomotives and changing the strategy of
their maintenance.
Keywords: locomotive
repair workshop; simulation; queue system theory; organization of the
repair workshop operation
Introduction
Improvement
of the locomotives` repair system organization is one of the ways to
reduce operating costs. Management system restructuring of
Ukrzaliznytsia`s locomotive facilities involves the separation of
operation and repair functions of traction rolling stock. Such an
approach is already used at large industrial transport enterprises
(metallurgical enterprises, ore mining and processing enterprises).
Foreign railway companies (RR, Lithuanian Railways, etc.) also
carried out the functions` separation of locomotive operation and
their repairs between the locomotive depots. On the basis of the
largest depots, the repairs of locomotives allocated not only in
this depot, but also in the other ones, are performed. Another part
of the depots performs solely the locomotive maintenance during
operation. At this stage in Ukrzaliznytsia operate locomotive depots
specialized in locomotive series and repair types (CR-2, CR-3).
Separation
of depots into operational and repair ones requires careful
consideration, as the repair program is changing, which can lead to
the formation of locomotives queue waiting for repairs, and this in
turn will lead to increase in their downtime. On the one hand, when
using this approach, the enterprise`s costs increase, this is due to
the locomotive's withdrawal from operation and the costs of their
transportation from the operating depot to the repair one. On the
other hand, there may be a low loading of repair enterprises, which
leads to the idle of repair facilities waiting for the locomotives
supply. The described situations eventually lead to the maintenance
costs increase for both the locomotives and the technological
equipment. The positive thing is that the creation of specialized
depots reduces the capital costs for the repairs organization,
increases the equipment use efficiency, increases the labor
productivity, and, as a consequence, the repair quality. The
distribution task of the repair program between the repair depots of
the railway network and the methodology of selecting the specialized
depots is an urgent task [7,
10, 16]. Solution of this task involves the development of general
model for the locomotives` repair organization at a level not less
than that of the Ukrzaliznytsia`s regional branch. The part of this
model is the model of locomotives` repair organization at the level
of repair depot. This article is devoted to the analysis of methods
and approaches to simulating the operation organization of the
repair locomotive depot.
The
initial data when simulating the repair organization in the
locomotive depot is the need for locomotive repairs. From the point
of view of the operating company, the locomotive is a part of the
overall locomotive fleet management system. To maintain a given
level of locomotive reliability, the transport companies use a
certain maintenance system. In this case, the choice of the
locomotive maintenance system is influenced by such factors as the
repair enterprise characteristics, the type of service and operating
conditions, the performance history of each locomotive (electronic
passport), the level of equipment and loading of the repair
enterprise, the failure statistics (reliability) of locomotive units
and the locomotives of this series, as well as a number of other
factors.
Based on
the analysis [7,
12, 14, 19, 20] of the existing systems of locomotive fleet
management, the main tasks are formulated that need to be addressed
when choosing a system of technical maintenance of locomotives.
Among them are as follows:
– development
of the methodology for repair units loading planning, taking into
account the technical condition of the locomotive fleet and the
volume of planned repair works;
– development
of methodology for planning logistical support for repair units,
taking into account the technical condition of the locomotive fleet
and the volume of planned repair works.
Solution
of the set tasks also requires the creation of the model for the
locomotive repair organization in the repair depot, taking into
account the repair units loading planning, the technical condition
of the locomotive fleet, and the volume of the performed works.
The
methods of the queue system theory [5, 7,
8, 11, 13], optimization [2,
4, 9, 15], the theory of economic and
mathematical modeling [1, 4],
analysis of the large amounts of data and simulation modeling are
used during the development of the repair organization model in the
locomotive depot [18].
Purpose
To analyze
the influence of locomotives` operation and reliability indicators
on the locomotive repair system organization in the depot with the
use of the queue theory methods.
Methodology
The task
of planning the locomotive putting into repair is to reduce the idle
time of locomotives in repair and waiting for repairs, which
significantly affects the locomotive availability. At the same time,
it is necessary to ensure the loading uniformity of the repair
units, the possibility of planning the supply of components and
consumables, as well as to ensure a given level of the locomotive
fleet reliability.
The
existing system of repair planning is based on the control of
overhaul periods. It determines the need for repair or maintenance
on the basis of comparison with the normative values of the
between-repair mileages of locomotives (first of all, when working
in trains) or the operating time (for example, when used for
shunting or export works). Typical standards for between-repair
mileages according to locomotive series can be set individually for
different locomotive series.
The need
for repair or maintenance for this locomotive is fixed in the event
the between-repair mileage, or the operating time, have become more
than the normative ones for the corresponding repair type. In this
case, according to regulatory documents, for the loading uniformity
of the depot repair workshops and locomotive repair plants, it is
possible to regulate the overhauls (usually within -10% + 25%). That
is, fixing of the need for repair or maintenance takes place for a
certain interval of values of between-repair mileage or the
operating time of locomotive.
Current
values of between-repair mileages or locomotive operating time are
determined based on the accounting for their work (by processing the
running schedules of the drivers). At the same time, since the
determination of the need for repair or maintenance should be
carried out for the future, forecasting of changes in these
parameters is used. As a rule, forecasting is carried out based on
their average values.
Planning
of locomotives` putting into repair can be of two types: the
calendar planning and the planning by mileage. When planning
according to calendar time one proceeds from the average daily
mileage during this period or the planned task in order to determine
a planned day of locomotive putting into repair. The disadvantage of
this method of planning is that the actual daily mileage of
locomotives greatly varies due to their different technical
condition, different idle times in the current repair, different
degrees of use at work and other things and it is significantly
different from the planned one. More expedient is the planning
according to the mileage, since in this case the locomotives are put
into repair according to the established frequency. The disadvantage
of this method of planning is possible uneven performance of the
daily maintenance plan. The maintenance schedule of an individual
locomotive is based on the established periodicity of maintenance,
repair cycle and daily mileage of locomotive.
This
approach is used in the case of the planned-preventive locomotive
repair system. However, its use when implementing the combined
repair system or the one, which takes into account the technical
condition of the locomotives, is not rational, since in this case
the repair volume and the overhaul periods are determined for each
individual locomotive taking into account the reliability
characteristics of the locomotive units.
For the
operational planning of putting the locomotives into repair, one has
to know the probabilities of locomotives being in different
conditions (operation, repair type, idle time when waiting for
repair, etc.).
When
solving this problem, it is expedient to use the tools of queue
theory.
Let us
consider in more detail the possibility of using the queue theory
approaches to simulate the processes of putting the locomotive into
repair and its implementation, analyzing the loading of repair bays
and calculating their required quantity.
In the
queue theory the methods of probability theory and mathematical
statistics are used. The queue theory considers the theoretical
basis of rational design and operation of queue systems (QS). The
queue system operation consists in performing the flow of
applications received by it. The subject of the queue theory is the
establishment of a relationship between the nature of the
application flow, the performance of certain channels, the number of
channels and the service efficiency.
The
following indicators can be the efficiency characteristics of
services:
– the
average idle-time of certain channels;
– the
average time of waiting in the queue;
– the
probability that the received application will be accepted for
service immediately;
etc.
The
given characteristics describe the degree of the system's
suitability to perform the application flow (i.e., its capacity).
The average number of applications that a system can serve per unit
of time is considered as capacity.
Maintenance of requirements
in the system is performed by the service channels. A classical
queue system contains from one to an infinite number of channels.
Depending
on the availability of the possibility for the beginning of
servicing the QS are divided into:
– lossy
systems in which the claims that did not find any free handler at
the time of receipt are lost;
– the
systems with waiting, which have an infinite capacity storage for
buffering the received requirements, while the waiting requirements
form a queue;
– the
systems with end capacity storage (with waiting and restrictions),
in which the queue length cannot exceed the storage capacity. At the
same time, the requirement received by the overflow system in which
there is no free place for waiting is lost.
The
selection of the application from the queue is made using the
discipline of service. Its examples are: FIFO (first in, first out),
random, SF (short forward). In systems with waiting, a storage in
the general case can have a complex structure. The system can be
single-channel and multi-channel.
To
simulate the locomotive fleet repair under conditions of locomotive
depot, a waiting system that has infinite capacity storage for
buffering the received requirements is suitable. At this the waiting
locomotives form a queue. Also in this case, from our point of view,
it is most appropriate to choose a requirement from the queue
according to the FIFO system.
In
this system, the repair bays are the service facilities (channels),
the flow of applications is the number of locomotives received by
the service system for a certain time: year, month, week, shift,
hour, minute. The application flow serves as the basis for planning
the production program of the repair bays.
Due
to the randomness of the incoming application flow and the duration
of their execution, there is always some average number of idle
locomotives. Therefore, it is necessary to distribute the number
of repair bays between different subsystems so that the idle time
and, therefore, the losses would be minimal. Note that the
locomotive queue system is
a discrete type physical system S
with a countable set of states:
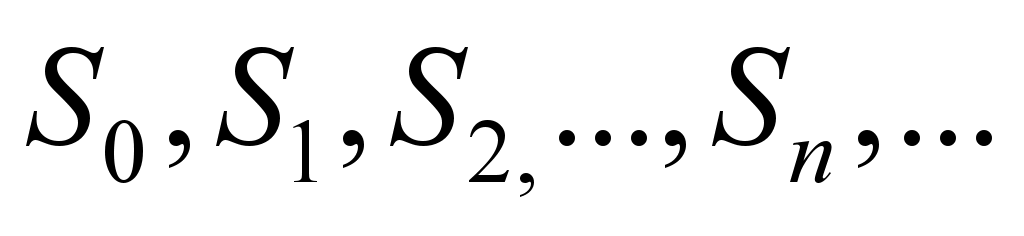 .
.
At any
moment of time t
the system S can
be in one of these states. Then for any t:
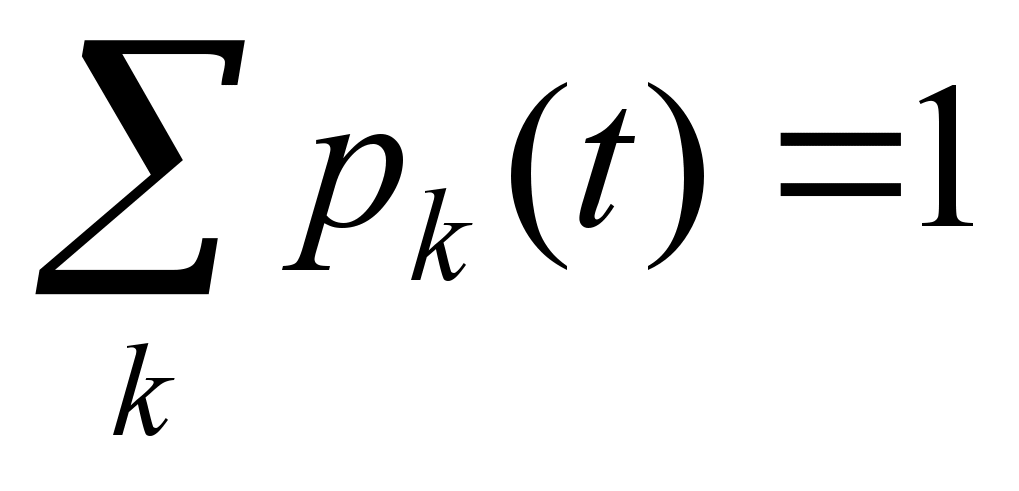 ,
,
where
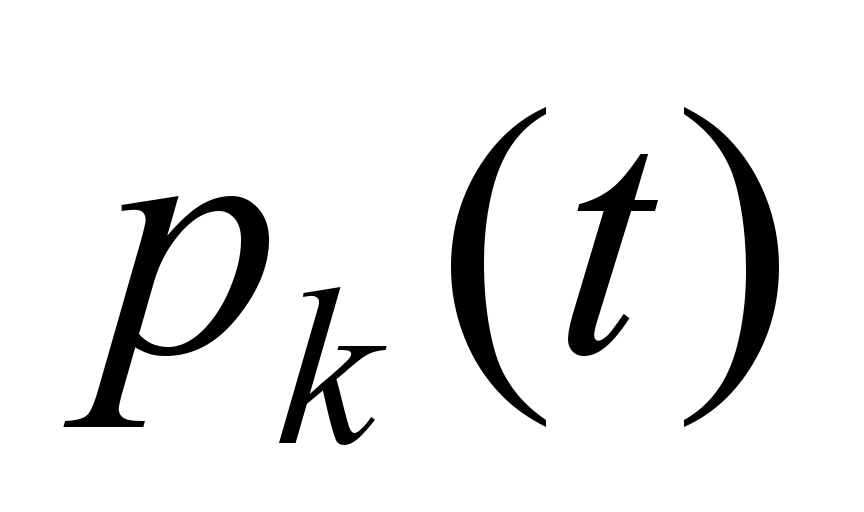
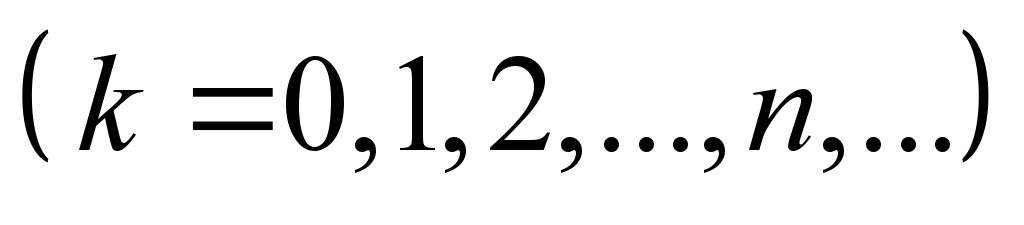 – is the probability that at the moment of time t
the system will be in the state
– is the probability that at the moment of time t
the system will be in the state
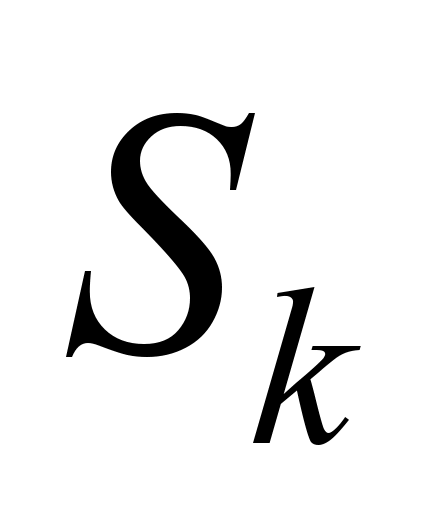 .
.
Let us
consider in more detail the repair workshop of the locomotive depot,
in which all types of depot repairs are performed, as a queue system
for locomotives.
Repair
workshop with repair bays, in terms of queue theory, has the
following characteristics:
– it is
an open system, since the source of applications is outside the
system (operation depot) and has an infinite number of them;
– by the
nature of the queue creation it is a waiting system with an infinite
queue. Non-preferential service discipline, the service system can
be adopted any of the previously considered ones;
– by the
number of channels it is a multi-channel system with parallel
channel arrangement. In this paper, we consider the depot as a
system with heterogeneous channels, since when performing repairs in
the depot, the bays specialized according to the repair types are
used (M-3, CR-1, etc.).
For the
repair workshop as a queue system, the main factor that determines
the processes occurring in it is the input application flow – the
number of locomotives that need one or another type of repair. The
Poisson application flow was considered during the simulation. The
service time of one application is accepted as distributed according
to the demonstrative law.
To analyze
the random processes with discrete states it is convenient to use
the so-called graph of states and transitions. For further
calculation of the efficiency characteristics of the QS operation,
it is necessary to determine the possible states of the system, as
well as the probability of occurrence of these states (pi),
which are called the limit probabilities of the system.
The graph
of the states of the repair workshop with repair positions n
and places in the queue m
is shown in Fig. 1.

Fig.
1. The graph of the repair workshop states
with n repair positions and a limited queue
Let us
introduce the following designations:
i
– is the number of locomotive sections (applications) in the queue
system (in the queue and on the service);
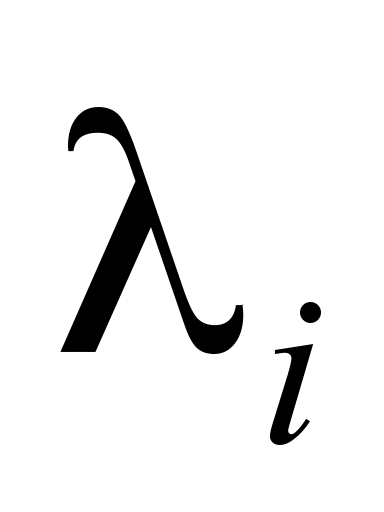 – is the intensity of sections receipt into the system, provided
that there are already i
sections in the system;
– is the intensity of sections receipt into the system, provided
that there are already i
sections in the system;
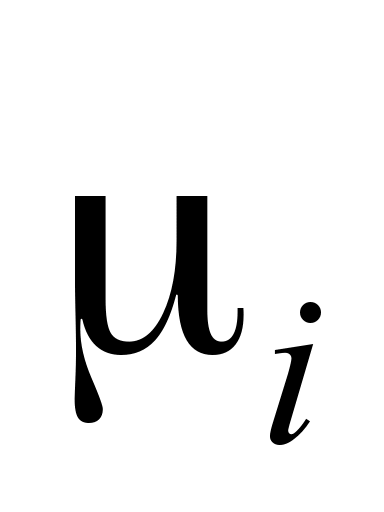 – is the output flow intensity of the served sections, provided
that there are i
sections in the system;
– is the output flow intensity of the served sections, provided
that there are i
sections in the system;
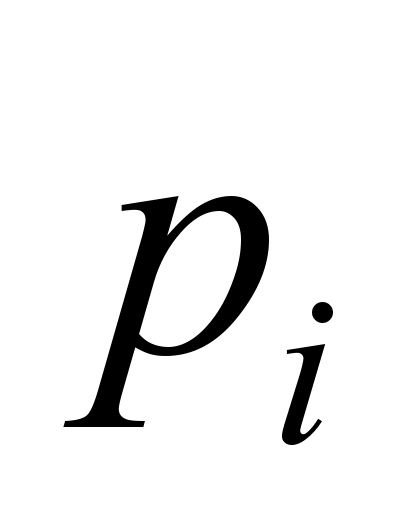 – is the probability that there are i
sections in the system;
– is the probability that there are i
sections in the system;
 – is the summary bay loading intensity (or the channel loading
intensity)
– is the summary bay loading intensity (or the channel loading
intensity)
The repair
workshop of locomotives can take one of the following states:
– 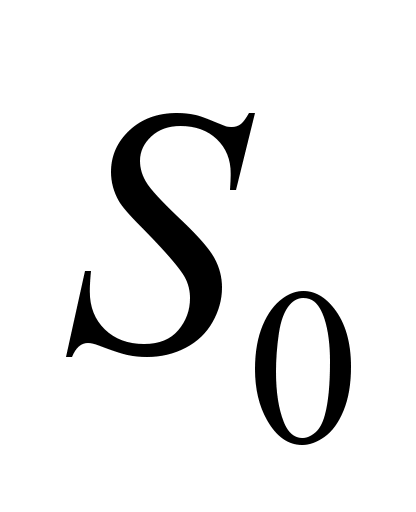 – all positions are free;
– all positions are free;
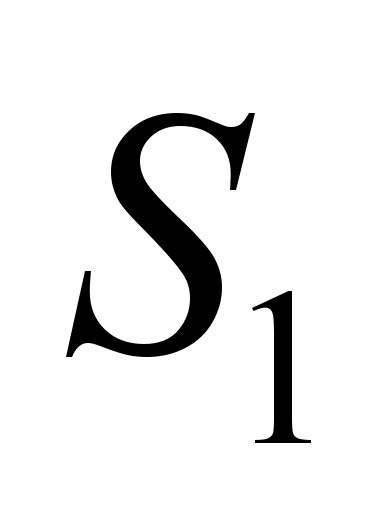 – the one position is occupied, and the rest ones
– the one position is occupied, and the rest ones
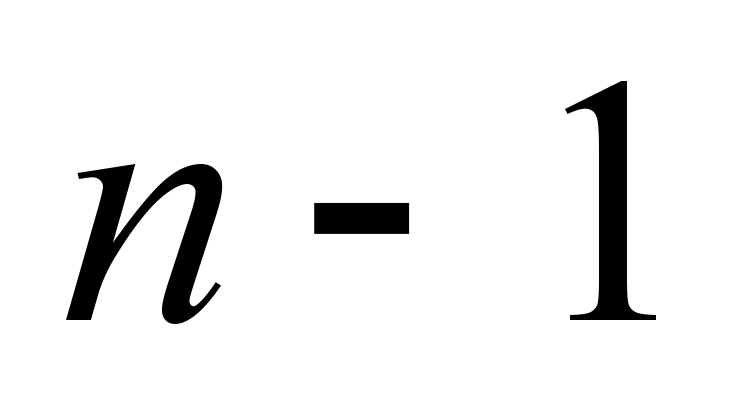 are free;
are free;
– 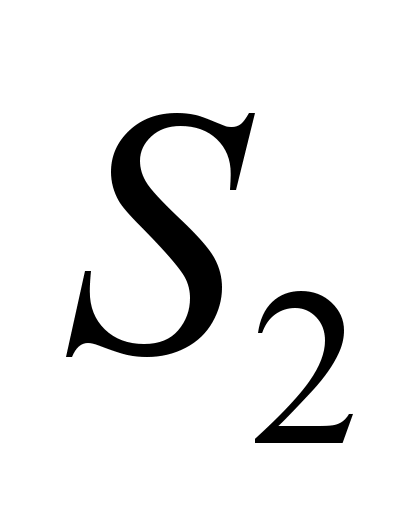 – two positions are occupied, and the rest ones
– two positions are occupied, and the rest ones
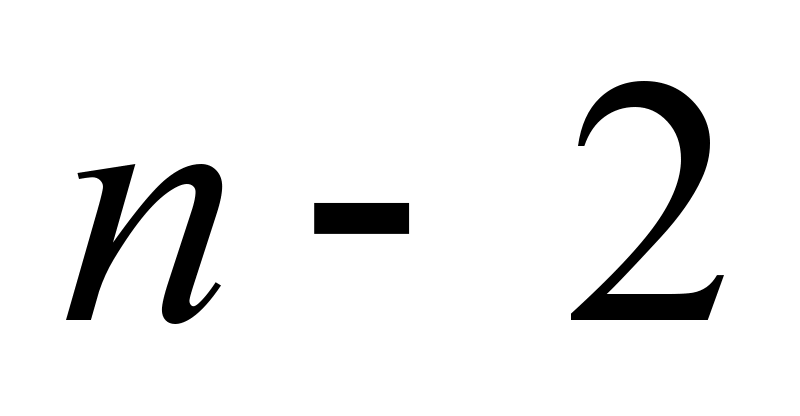 are free;
are free;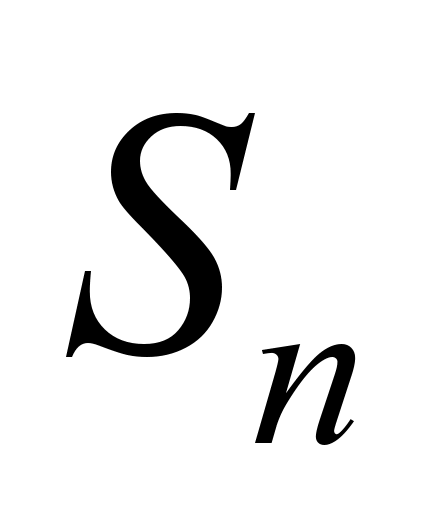 – all positions are occupied, but there is no queue;
– all positions are occupied, but there is no queue;
– 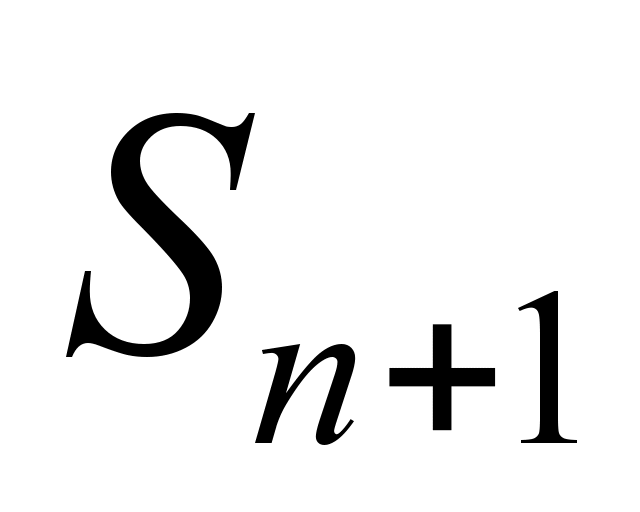 – all positions are occupied,
one locomotive (section) is in the queue;
– all positions are occupied,
one locomotive (section) is in the queue;
– 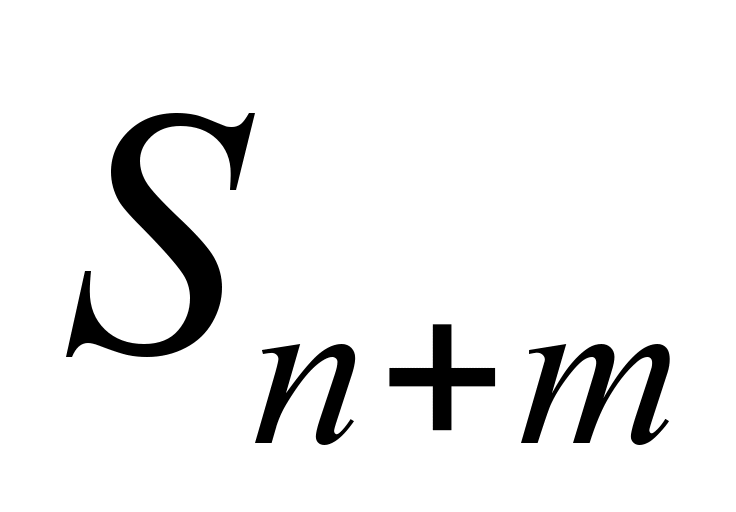 – all positions are occupied,
– all positions are occupied,
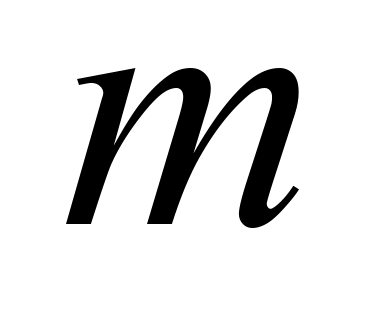 locomotives (sections) are in the
queue.
locomotives (sections) are in the
queue.
It should
be noted that in this system the service flow intensity will
increase from
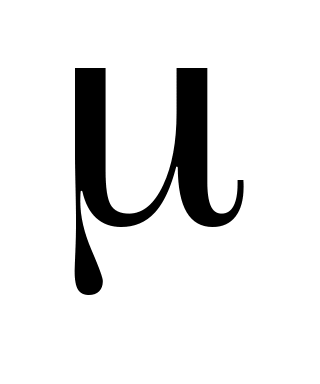 to
to
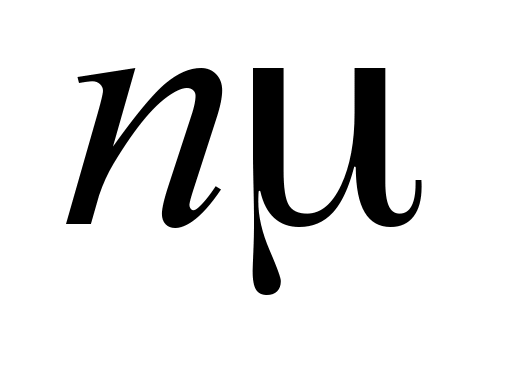 with
the increase in the number of applications from 0 to
with
the increase in the number of applications from 0 to
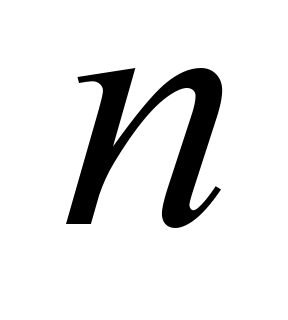 .
Accordingly, the number of service channels is increased. With the
number of requirements exceeding
.
Accordingly, the number of service channels is increased. With the
number of requirements exceeding
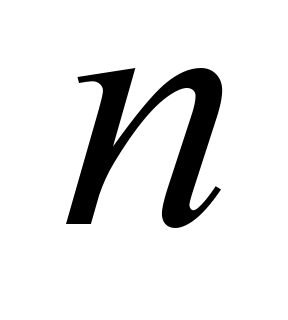 ,
the service intensity remains equal to
,
the service intensity remains equal to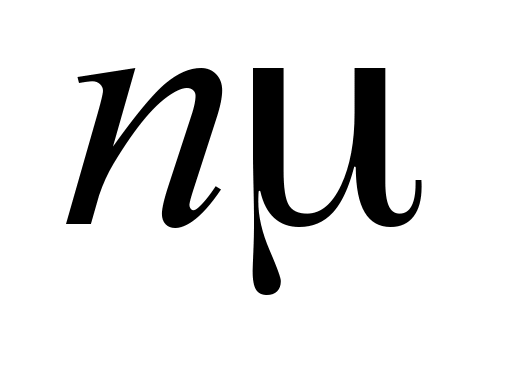 .
.
When
simulating, the following tasks need to be solved: simulating the
repair workshop operation for a specified number of hours;
determining the probabilities of the repair workshop conditions
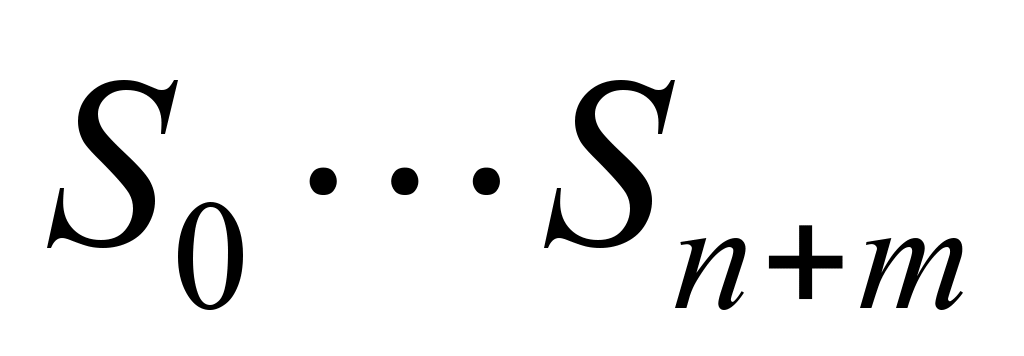 ;
determining the average number of applications (locomotives) in the
service queue; determining the average number of applications for
service; determining the average number of applications in the
system; determining the average duration of the application stay in
the queue; determining the average duration of the application stay
in the system; determining the system relative capacity; determining
the absolute system capacity.
;
determining the average number of applications (locomotives) in the
service queue; determining the average number of applications for
service; determining the average number of applications in the
system; determining the average duration of the application stay in
the queue; determining the average duration of the application stay
in the system; determining the system relative capacity; determining
the absolute system capacity.
For the
probabilities p1(t),
p2(t),…,
pn(t)
the system of linear differential equations (Erlang equations) will
be:
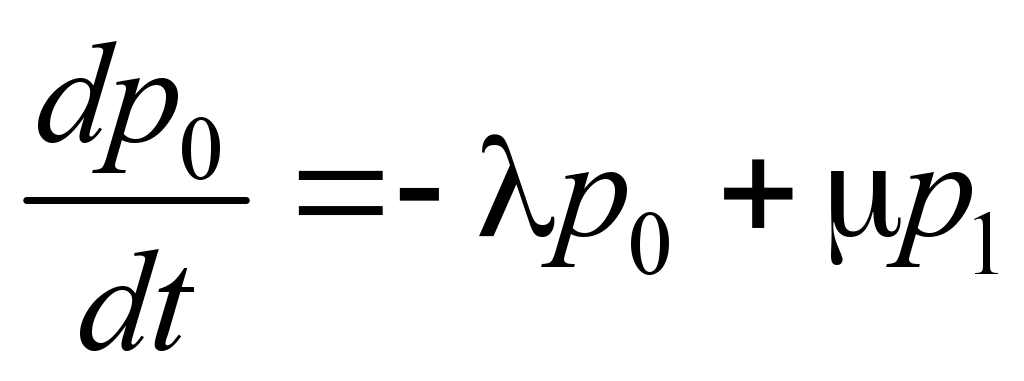 ;
;
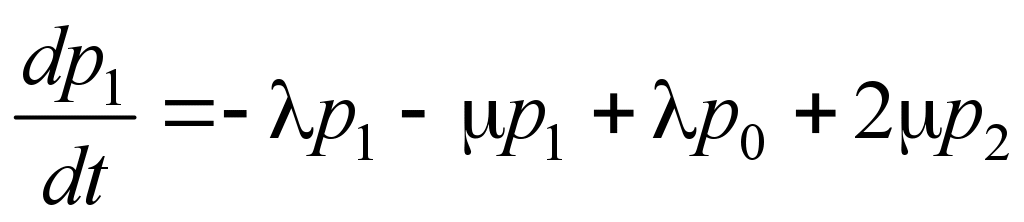 ;
;
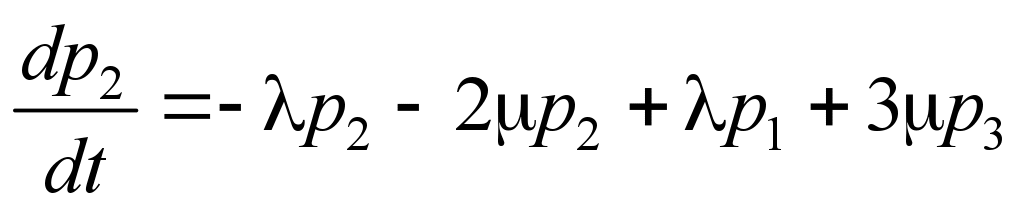 ;
;
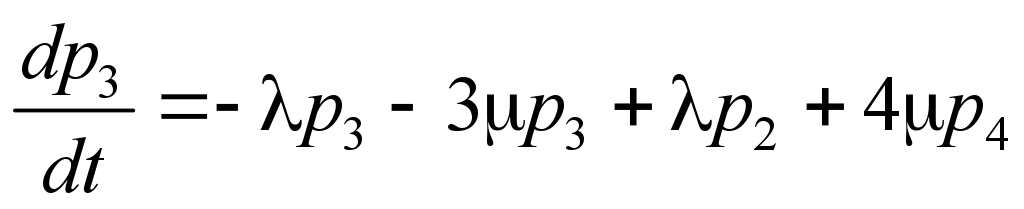 ;
;
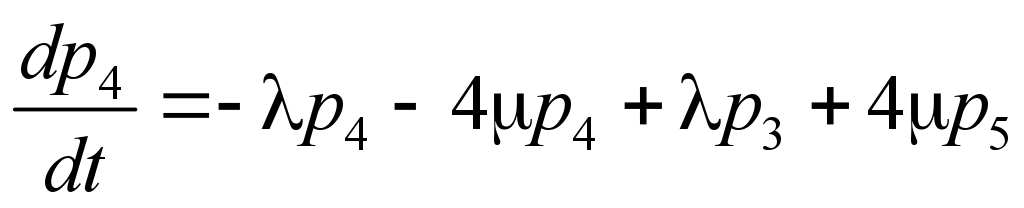 ;
;
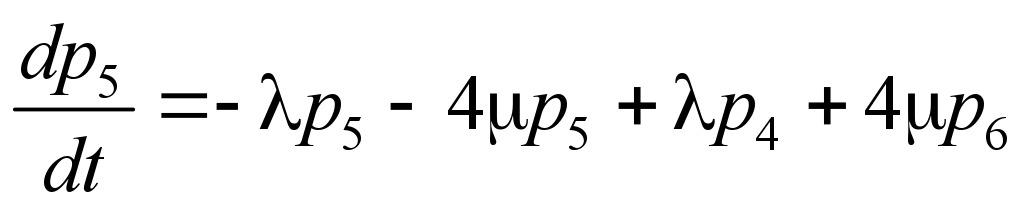 . (1)
. (1)
In the
steady (stationary) state (with
 )
the system of equations takes the form:
)
the system of equations takes the form:
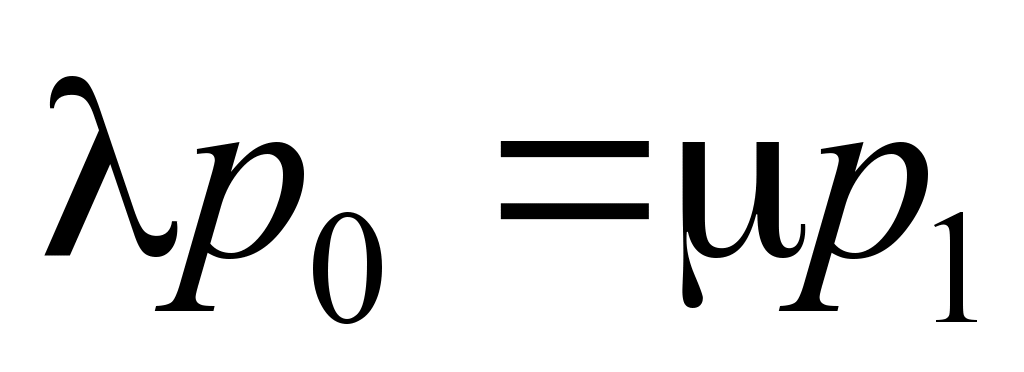 ;
;
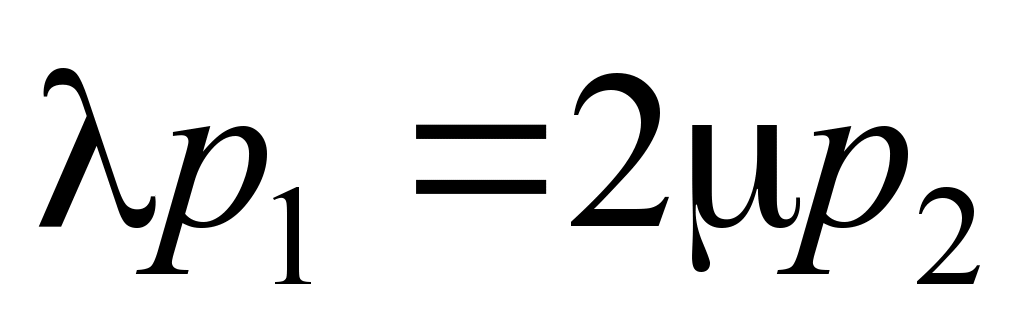 ;
;
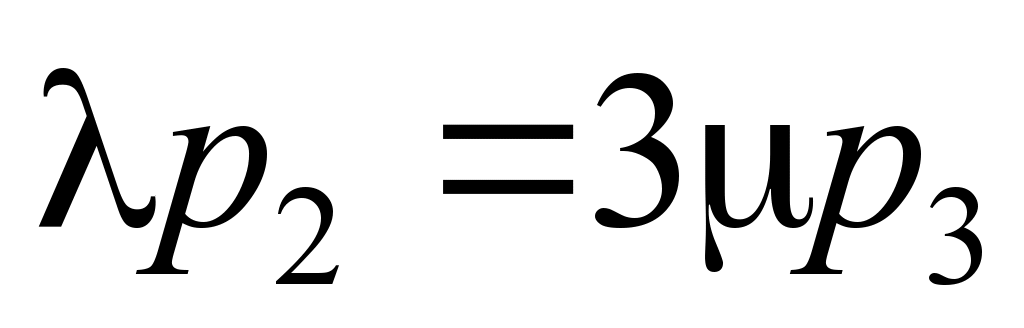 ;
;
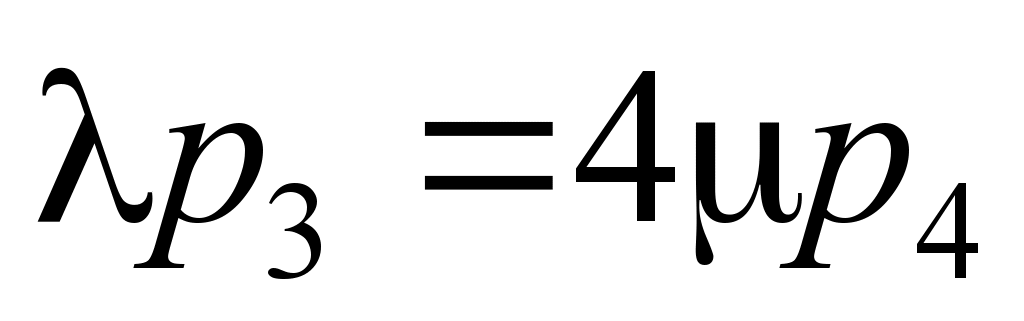 ;
;
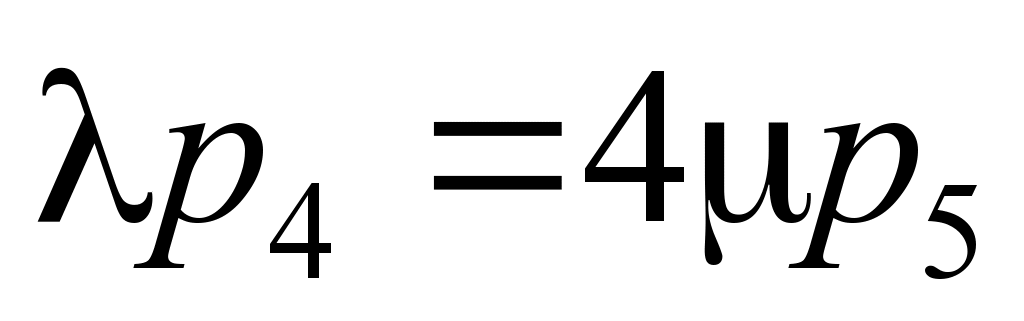 .
(2)
.
(2)
Let us add
a normalizing condition:
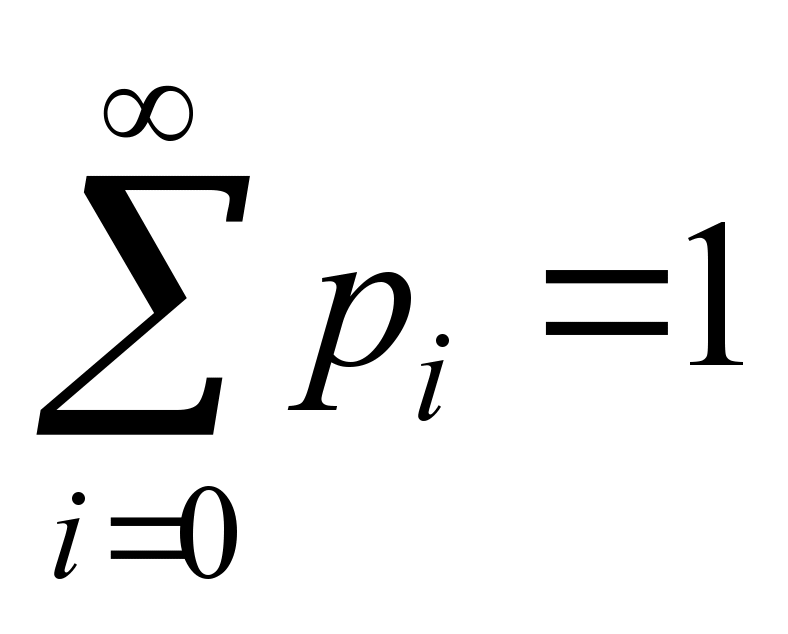 . (3)
. (3)
Its
meaning is that at any moment the workshop must be in one of its
states (idle, operation, operation with a queue).
The
initial data for the simulation of the repair workshop operation
are: the number of repair positions; simulation time; the intensity
of the incoming application flow (including the scheduled and
unscheduled repairs); the duration of service at each repair
position for each repair type.
As a
result of simulation, the following indicators of the QS (locomotive
repair workshop) are determined: the probability of the system
conditions
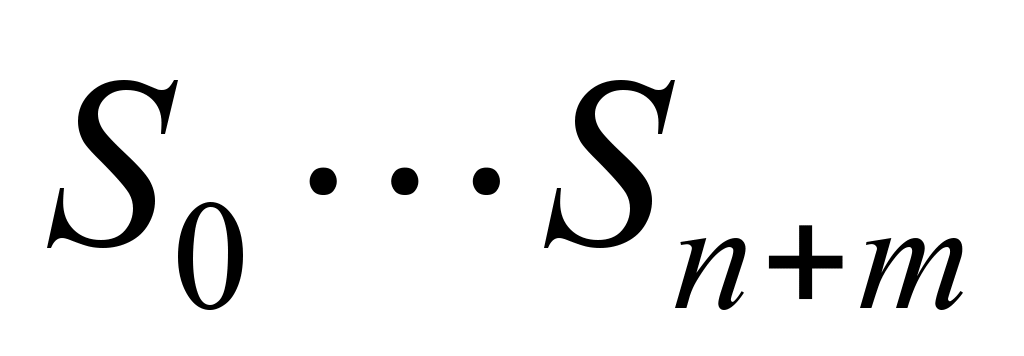 ;
the average number of applications (locomotives) in the queue for
service; the average number of applications in the system; the
average duration of stay in the queue; the average duration of
application stay in the system. The simulation results of the repair
workshop operation for a given time include the number of the
received applications and the number of hours spent for service.
;
the average number of applications (locomotives) in the queue for
service; the average number of applications in the system; the
average duration of stay in the queue; the average duration of
application stay in the system. The simulation results of the repair
workshop operation for a given time include the number of the
received applications and the number of hours spent for service.
To
determine the probability of finding a QS in one of the possible
conditions, we use formulas
4–6:
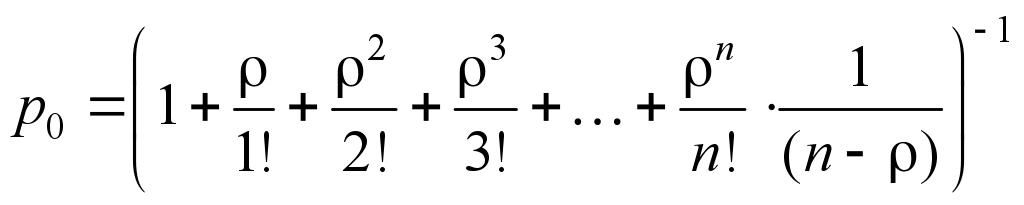 (4)
(4)
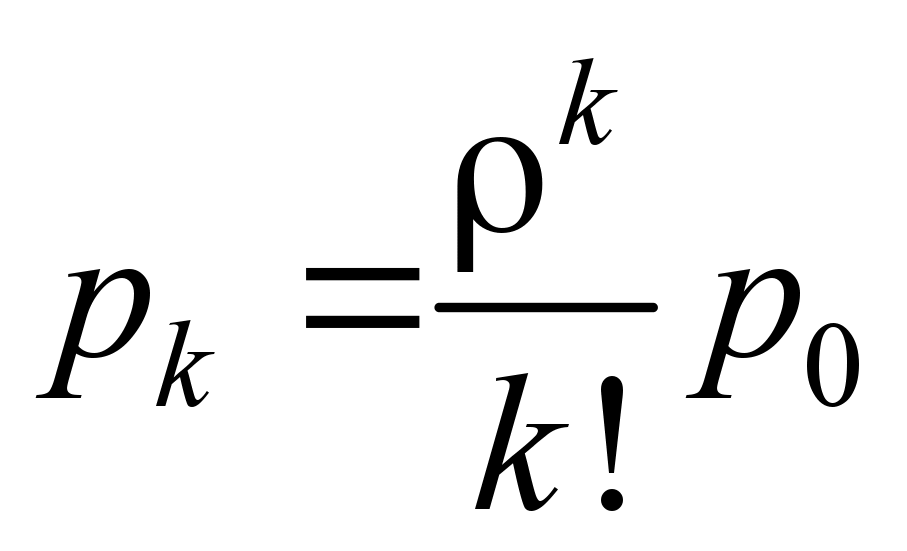 ,
,
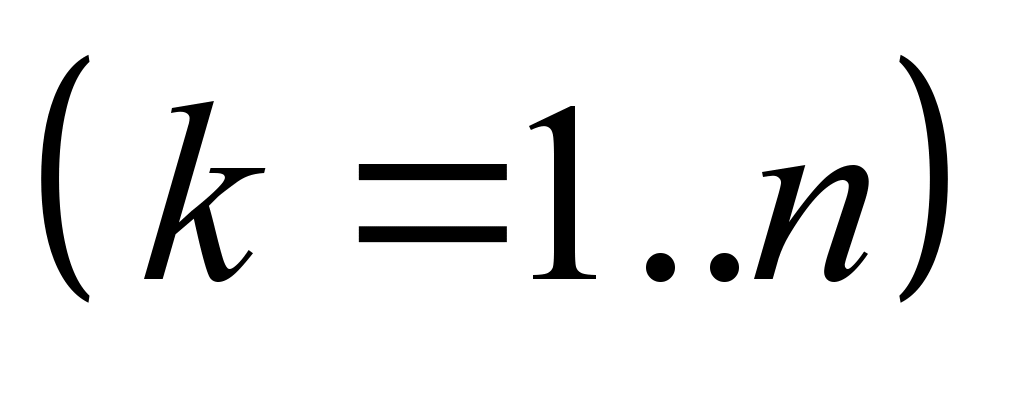 , (5)
, (5)
where k –
is the number of the occupied repair bays;
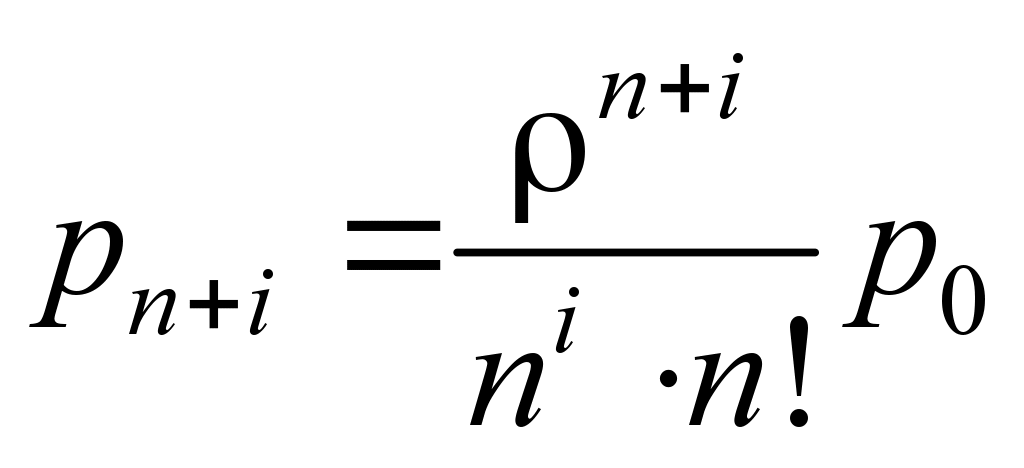 ,
,
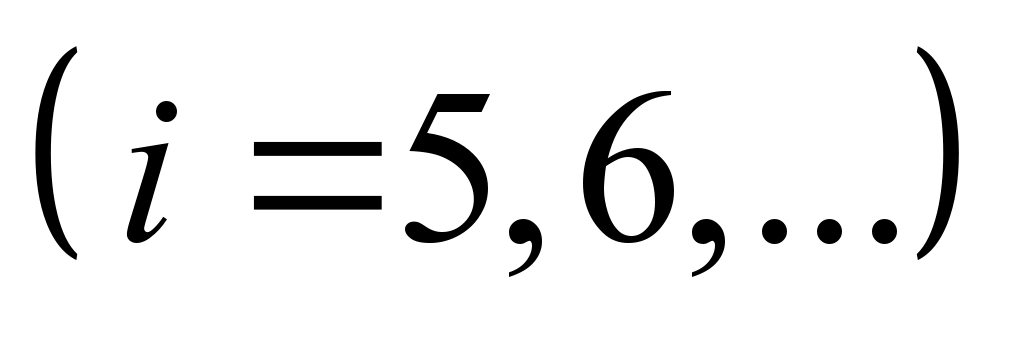 (6)
(6)
The probability of queue
formation is determined by the formula:
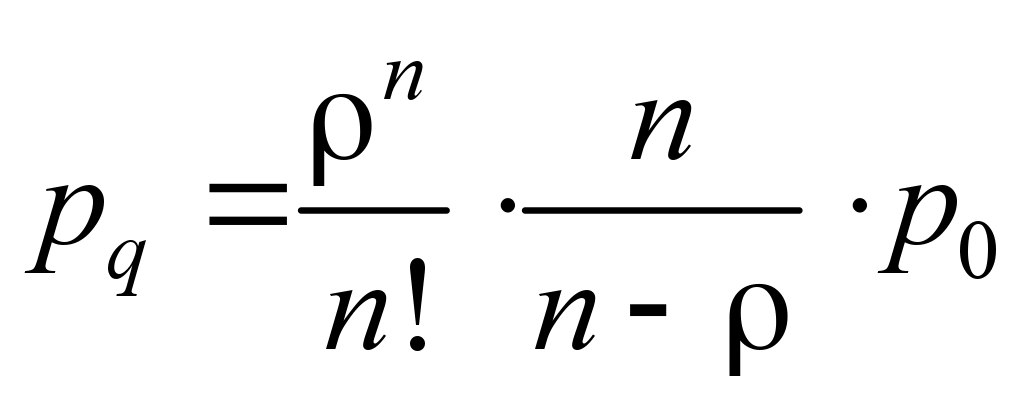 . (7)
. (7)
The
average application number in a queue:
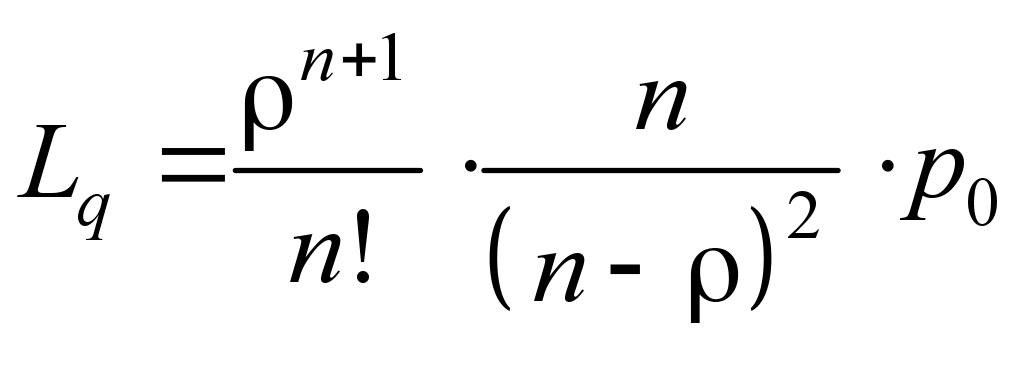 (8)
(8)
Average
number of applications served:
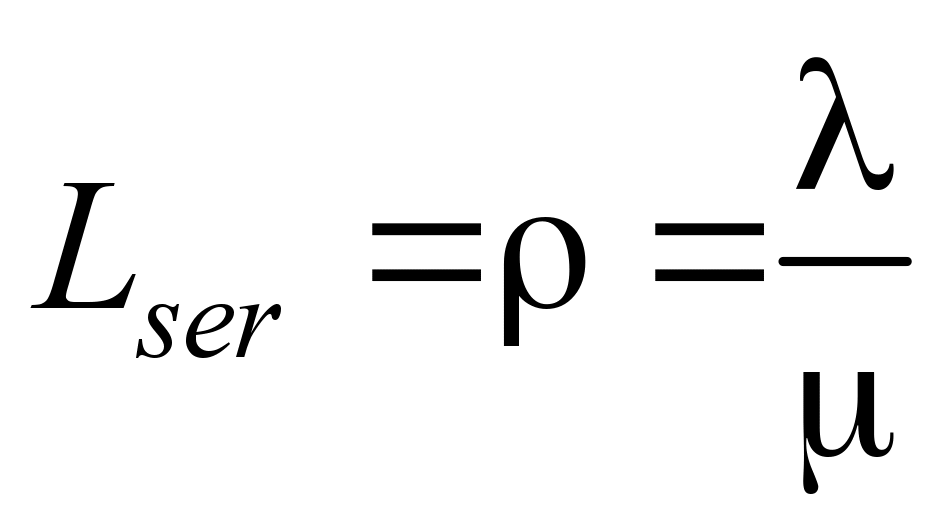 . (9)
. (9)
The
average number of application stay in the system:
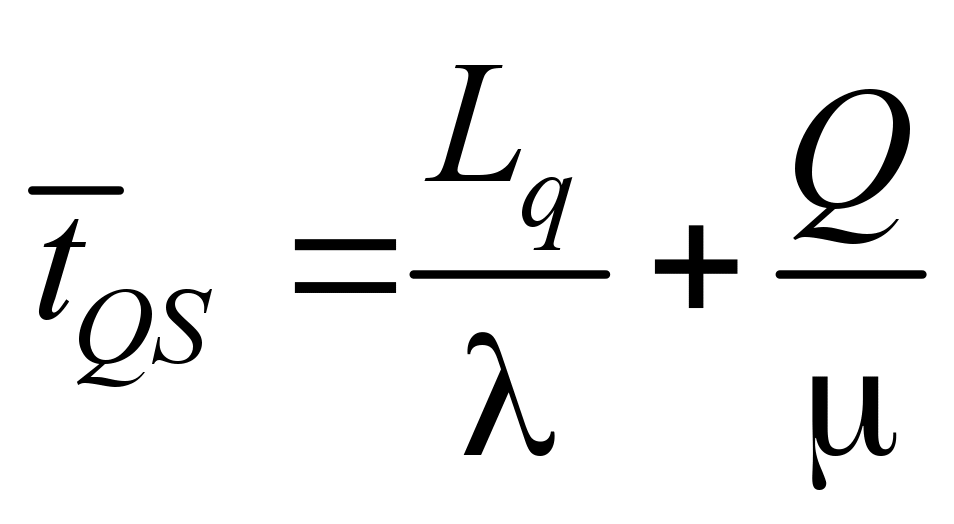 , (10)
, (10)
where Q
– is the relative QS capacity (in this case it is equal to one).
Average
time in the queue:
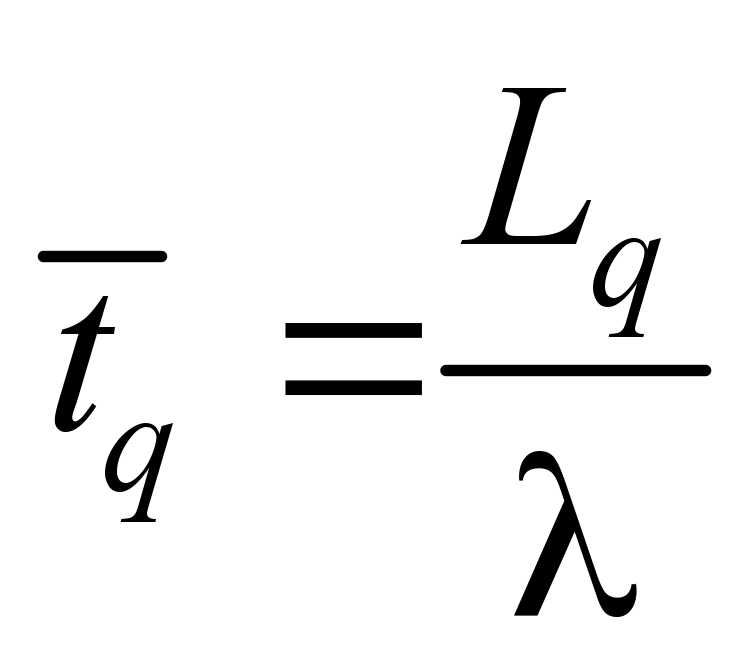 . (11)
. (11)
Findings
To study
the influence of the system of maintenance, operation and repair
organization of locomotives, as well as their reliability level, a
model was developed and the operation of the main diesel locomotive
repair workshop at the repair depot was simulated. When simulating,
it was taken the performance of all types of depot repair of diesel
locomotives TM-3, CR-1, CR-3 and unscheduled repairs in the repair
workshop. When organizing the applications servicing (locomotive
repair simulation), specialization of repair bays by the repair type
was taken. There are two groups of repair bays. Unscheduled repairs
and CR-3 are performed in one group, CR-1 and TM-3 are performed in
another group of repair bays.
A
graphical environment Simulink was used as a simulation software.
The block diagram of the repair workshop model of the locomotive
depot is presented in Fig. 2
The blocks
1 and 2 form the applications for the diesel locomotives repair
interspaced in time in a random manner. Block 3 forms the time for
performing repair in a random manner. The calculation of application
number and the service time of diesel locomotives is made in
accordance with the current regulatory documentation. In this case,
it is allowed the deviation of the receipt time 20%
from the norm. The block 4 «repair position» was used as a repair
depot in the model. The time required to perform the corresponding
repair type is determined by this block depending on the repair type
20%.
FIFO discipline has been adopted as the discipline for servicing the
applications. The queue of diesel locomotives waiting for repair is
organized by the block 5.
A
simulation of the repair workshop for the allocated locomotive fleet
of
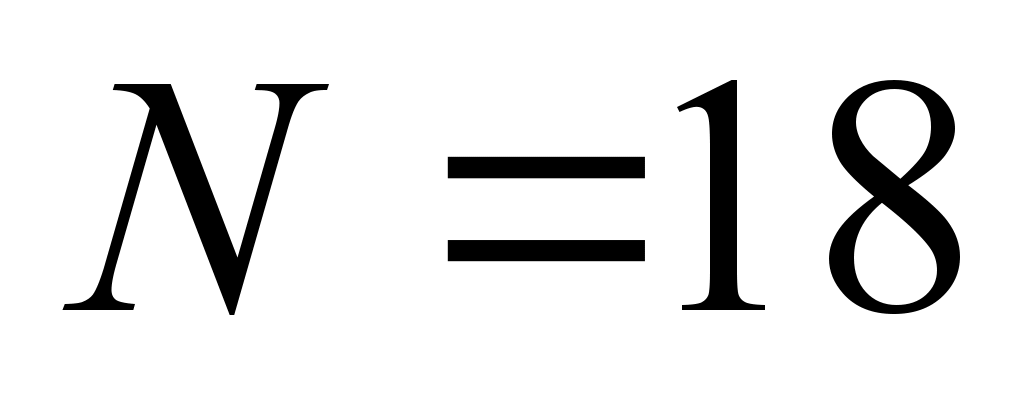 diesel locomotives (36 sections) of the 2TE116 series was performed.
The average daily mileage of diesel locomotives was taken
diesel locomotives (36 sections) of the 2TE116 series was performed.
The average daily mileage of diesel locomotives was taken
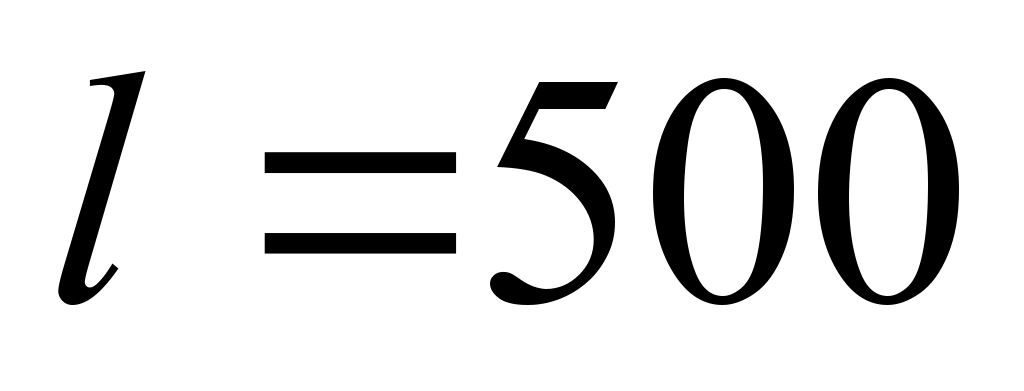 ,
the simulation time is 365 days, the share of unscheduled repairs is
5%. The simulation results are shown in Table 1–3.
,
the simulation time is 365 days, the share of unscheduled repairs is
5%. The simulation results are shown in Table 1–3.
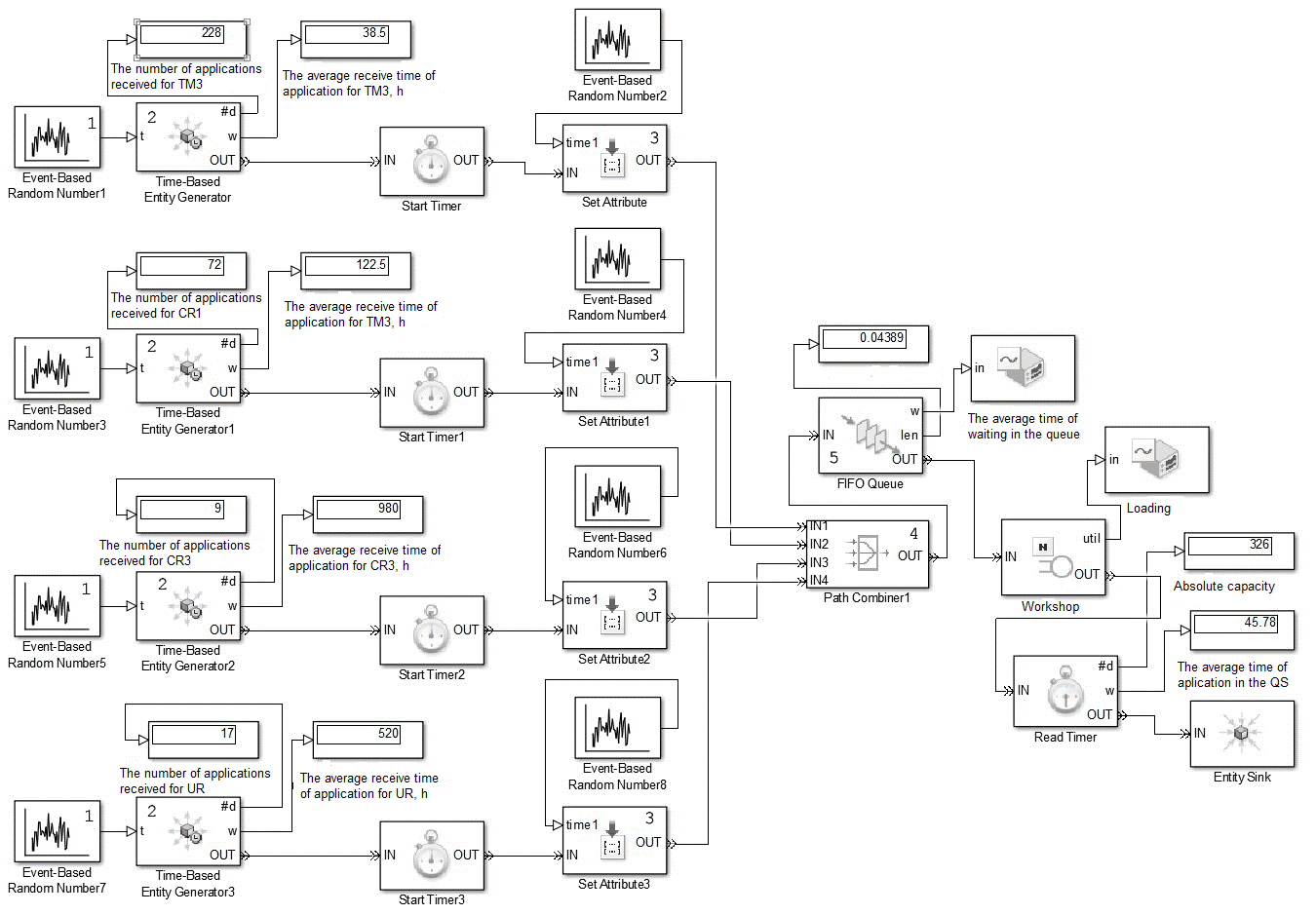
Fig. 2. Repair workshop model
of diesel locomotives in the form of QS:
1
– former of the receipt time of locomotives for repair;
2
– block of the former of the application distribution in time;
3
– former of diesel locomotive service time at repair position;
4
– diesel locomotive repair positions; 5
– queue of locomotives waiting for repair
In tab. 1
shows the simulation results with a different number of repair
stalls. As can be seen from the obtained results, with the accepted
initial data, the use of three repair stalls is the most rational,
while the loading of the depot workshop is 0.6%.
The Tab. 1
shows the simulation results with a different number of repair bays.
As one can see from the obtained results, with the accepted initial
data the use of three repair bays is the most rational, at this the
loading of the depot workshop is 0.6%.
Table
1
The simulation results of
the repair workshop operation for diesel locomotives on change
of
the repair bays number
Number
of repair bays, pcs.
|
The
average time of waiting in the queue, h.
|
The
average queue length, sect.
|
Workshop/depot
loading, %
|
The average time of
application in the QS, h
|
2
|
60
|
1.439
|
0.88
|
83.18
|
3
|
1.5
|
0.044
|
0.59
|
45.78
|
4
|
0
|
0
|
0.45
|
44.6
|
The Tab. 2
shows the simulation results when using in the depot three repair
bays and changing the average daily mileage of diesel locomotives
from 400 to 700 km/day. As one can see from the obtained results,
increase in the average daily mileage leads to an increase in the
repair workshop loading to 0.79%, while the queue length increases
by 10 times, and the average waiting time – by 5.6 times. This is
explained by the fact that with increase in the average daily
mileage, the number of applications for repairs is increasing.
The Tab. 3
shows the simulation results when using in the depot three repair
bays and changing the number of unscheduled repairs from 5 to 10%.
The results show that increase in the percentage of unscheduled
repairs leads to a slight increase in the repair workshop loading,
at this, the queue length and average waiting time change slightly
as well.
Table
2
The
simulation results of the repair workshop when changing the
average daily mileage of diesel locomotives
The
average daily mileage of locomotive, km
|
The
average time of waiting in the queue, h
|
The
average queue length, locomotives
|
Workshop/depot
loading, %
|
The average time of
application in the QS, h
|
400
|
0.8
|
0.02
|
0.48
|
44.94
|
500
|
1.5
|
0.04
|
0.59
|
45.78
|
600
|
2.1
|
0.08
|
0.68
|
45.58
|
700
|
4.5
|
0.22
|
0.79
|
48.22
|
Table
3
The
simulation results of the repair workshop when changing the
unscheduled repair percentage
Percentage
of unscheduled repairs of locomotives, %
|
Locomotive average daily
mileage, km
|
The average waiting time
in the queue, h
|
The average queue length,
locomotives
|
Workshop/depot
loading, %
|
The average time of
application in the QS, h
|
5
|
500
|
1.4
|
0.032
|
0.57
|
44.3
|
8
|
500
|
1.5
|
0.044
|
0.59
|
45.78
|
10
|
500
|
1.5
|
0.048
|
0.6
|
46.68
|
Originality and practical
value
The work originality lies in
the presentation of the locomotive depot as the queue system object.
A simulation model of a locomotive repair depot has been developed.
It allows analyzing the influence of various factors on the system
of organizing the locomotive repair in depot.
The use of the developed
model and simulation results allows determining the influence of
operation and reliability indicators of locomotives on the work
organization of the locomotive repair depots. In further studies,
the proposed model can be used to improve the organization of repair
on the road network when introducing new series of locomotives and
changing their maintenance strategy.
Conclusions
The paper
presents the locomotive repair workshop description using the terms
and concepts of the queue system. The tasks for modeling the repair
work workshop operation are formulated, a list of the initial data
and the results of the simulation are given. Based on the simulation
results analysis, it is possible to optimize the repair workshop
structure and the required number of personnel, based on the
transportations volume, locomotive reliability indicators, the
locomotive selection rule used, the number of operating repair bays,
etc. It is established that the listed parameters influence the main
indicators of the locomotive repair depot. The proposed models of
the repair workshop make possible the rational planning of the
equipment use, human capital, the time for putting the locomotive
into repair, taking into account the uniform loading of the
workshop, as well as providing the opportunity to improve the spare
parts supply logistics. The model in a simplified form describes the
process of the mainline locomotive fleet repair and can be
supplemented depending on the repair type performed at the depot.
The
problem of accounting the reliability indicators when simulating the
locomotive putting into unplanned repair types, determining the
probability of locomotive transition from one state to another, as
well as taking into account the reliability indicators when
determining the repair work amount, requires further development.
LIST OF REFERENCE LINKS
Берестовой,
А. М. Моделирование системы технического
обслуживания и ремонта локомотивов /
А.
М. Берестовой,
А.
А.
Лямзин // Вісн. Приазов.
держ.
техн.
ун-ту.
Серія:
Технічні
науки
:
зб.
наук. пр. –
Маріуполь,
2003. – Вип.
13.
– С. 276–280.
Босов,
А. А. Теоретические основы рационального
содержания подвижного состава железных
дорог : монография
/ А. А. Босов, П. А. Лоза.
– Днепропетровск
:
Дриант,
2015.
– 252 с.
Гришечкіна,
Т. С. Побудова математичної моделі
раціональної системи утримання
технічних об’єктів залізничного
транспорту / Т. С. Гришечкіна
// Транспортні системи та технології
перевезень
:
зб.
наук.
пр.
Дніпропетр.
нац.
ун-ту
залізн.
трансп.
ім.
акад.
В. Лазаряна.
– Дніпропетровськ,
2017. – Вип.
14. – С. 30–35.
doi:
10.15802/tstt2017/123165
Гурьева,
А. Г. Основы моделирования процессов
технического обслуживания локомотивов
/
А. Г. Гурьева, Н. Б. Чернецкая-Белецкая
// Вісн.
Східноукр. нац. ун-ту ім. В. Даля. – 2015.
– № 1 (218). – С. 262–265.
Зіненко, О. Л.
Підвищення ефективності використання
локомотивного парку шляхом вдосконалення
управління експлуатаційною роботою
: дис. ... канд. техн. наук : 05.22.20 / Зіненко
Ольга Леонідівна ; Дніпропетр. нац.
ун-т залізн. трансп. ім. акад. В. Лазаряна.
– Дніпропетровськ, 2010. – 200 с.
Исследование
процесса эксплуатации и ремонта
электровозов с использованием
инструментов BIG
DATA
и имитационного моделирования / А. В.
Скребков, А. А. Воробьев, А. Г. Ламкин,
Д. И. Бодриков // Бюллетень результатов
научных исследований. – 2017. – № 4. –
С. 190–198.
Кудаяров,
М. М. Выбор оптимальной организации
ремонта локомотивов на полигоне
железной дороги / М. М. Кудаяров //
Изв.
Петербург. ун-та путей сообщения.
– 2012. – №
3
(32). – С. 99–103.
Кудаяров,
М. М. Оптимизация системы технологического
процесса ремонта тягового подвижного
состава /
М. М. Кудаяров, И. С. Цихалевский //
Современные проблемы транспортного
комплекса России : межвуз. сб.
науч. тр. молодых ученых, магистрантов
и аспирантов. – Магнитогорск,
2012.
–
Вып.
2.
– С. 14–22.
Лоза,
П. А. Оценка
качества выполнения системы содержания
парка электроподвижного состава /
П.
А. Лоза,
Т.
С. Гришечкина // Електрифікація
транспорту.
– 2015. – № 9. – С. 87–93.
Методика
и алгоритм оптимального распределения
локомотивов по ремонтным предприятиям
/
А.
В. Горский, А. В. Скребков, Т. О. Чигамбаев,
И. С. Цихалевский // Транспорт Урала. –
2008. –
№
3 (18). – С. 25–27.
Моделювання
процесу оперативного планування роботи
локомотивного парку і локомотивних
бригад
/ І. В.
Жуковицький, В. В. Скалозуб, О. В. Вєтрова,
О. Л. Зіненко
// Вісн.
Дніпропетр. нац. ун-ту залізн. трансп.
ім. акад. В. Лазаряна. – Дніпропетровськ,
2006.
–
Вип.
12.
– С. 74–78.
Моделювання
зміни коефіцієнту технічного використання
маневрового тепловозу для різних
систем утримання / А. П. Фалендиш, А. Л.
Сумцов, О. В. Артеменко, О. В. Клецька //
Восточно-Европейский журнал передовых
технологий. – 2016. – № 1/3 (79). – С. 24–31.
doi: 10.15587/1729-4061.2016.60640
Очкасов,
А. Б. Подходы
к моделированию системы технического
обслуживания локомотивов
/
O.
Б.
Очкасов,
Т.
С.
Гришечкина, М.
В. Очеретнюк
// Актуальні проблеми автоматизації
та управління
: тези доп. V
міжнар. наук.-практ. інтернет-конф.
молодих учених і аспірантів (Луцьк,
28–30 бер. 2017 р.) / Луцьк. нац. техн. ун-т,
НУ «Львівська політехніка», Київ. нац.
ун-т харчових технологій, Нац. гірн.
ун-т, Херсон. нац. техн. ун-т, Люблінська
політехніка. – Луцьк, 2017. – № 5. –
С. 99–104.
Сумцов,
А. Л. Удосконалення методів та
моделей визначення системи технічної
експлуатації модернізованих маневрових
тепловозів : дис. … канд. тех. наук :
05.22.07 / Сумцов Андрій Леонідович
; Укр. держ. ун-т залізн. трансп. – Харків,
2017. –
165
с.
Шантаренко,
С. Г. Моделирование процессов технического
обслуживания локомотивов /
С. Г.
Шантаренко // Изв. Томск. политехн.
ун-та.
Инжиниринг
георесурсов. – 2005. – Т. 308, № 5. –
С.
169–171.
Bodnar,
B.
Improving
Operation
and
Maintenance
of
Locomotives
of
Ukrainian
Railways
/ B.
Bodnar,
A.
Ochkasov,
D.
Bobyr
// Technologijos
ir Menas = Technology and Art. –
2016. –
№ 7. –
P. 109–114.
Bodnar,
B. System Choice of the Technical Maintenance of Locomotives
Equipped with on-Board Diagnostic Systems / B. Bodnar, O. Ochkasov
// Transport Means : Proc.
of 21st Intern.
Sci.
Conf.
(Sept.
20–22, 2017)
/ Kaunas University of Technology,
Klaipėda University. – Juodkrante, Kaunas, Lithuania. – 2017.
– Pt.
I. – P. 43–47.
Development
of an Integrated Model for the Evaluation and Planning of Railroad
Track Maintenance
/
Alexander H. Lovett, C. Tyler Dick, Conrad Ruppert, M. Rapik Saat,
Christopher Barkan //
Proc.
of the 2013 Joint Rail Conf.
(Apr.
15–18,
2013, Knoxville, Tennessee, USA).
– Knoxville,
2013.
doi: 10.1115/jrc2013-2407
Ochkasov,
O. Usage of Intelligent Technologies in Choosing the Strategy of
Technical Maintenance of Locomotives / O. Ochkasov, O. Shvets, L.
Černiauskaitė
//
Technologijos ir Menas = Technology and Art. – 2017. – № 8. –
P. 68–71.
Wu,
J. Study on Adjustment
Evaluation of Locomotive Affair Productivity Layout / Jun Wu, Hua
Fei Jia // Applied Mechanics and Materials. – 2013. – Vol.
401–403.
– P. 2120–2126.
doi:
10.4028/www.scientific.net/amm.401-403.2120
Б. Є. БОДНАР1,
О. Б. ОЧКАСОВ2*,
Є. Б. БОДНАР3,
Т. С. ГРИШЕЧКИНА4,
М. В. ОЧЕРЕТНЮК5
1Каф.
«Локомотиви», Дніпропетровський
національний університет залізничного
транспорту імені академіка
В.
Лазаряна, вул. Лазаряна,
2, Дніпро, Україна, 49010, тел. +38 (056) 733 19 01,
ел. пошта bodnarz@nz.diit.edu.ua,
ORCID
0000-0002-3591-4772
2*Каф. «Локомотиви»,
Дніпропетровський національний
університет залізничного транспорту
імені академіка
В. Лазаряна, вул.
Лазаряна, 2, Дніпро, Україна, 49010, тел.
+38 (056) 733 19 61, ел. пошта abochkasov@gmail.com,
ORCID
0000-0002-7719-7214
3Каф. «Локомотиви»,
Дніпропетровський національний
університет залізничного транспорту
імені академіка
В. Лазаряна, вул.
Лазаряна, 2, Дніпро, Україна, 49010, тел.
+38 (056) 733 19 61, ел. пошта Melnar78@gmail.com,
ORCID 0000-0001-6040-913X
4Каф.
«Вища математика», Дніпропетровський
національний університет залізничного
транспорту імені академіка
В.
Лазаряна, вул. Лазаряна, 2, Дніпро, 49010,
Україна, тел. +38 (0562) 36 26 04, ел. пошта
grishechkina.tatiana@gmail.com, ORCID 0000-0003-1570-4150
5Каф.
«Локомотиви», Дніпропетровський
національний університет залізничного
транспорту імені академіка
В.
Лазаряна, вул. Лазаряна, 2, Дніпро,
Україна, 49010, тел. +38 (056) 733 19 61, ел. пошта
ocheretniukmaksym@gmail.com,
ORCID 0000-0002-9032-8602
МОДЕЛЮВАННЯ
ОРГАНІЗАЦІЇ РЕМОНТУ
ЛОКОМОТИВІВ
МЕТОДАМИ ТЕОРІЇ
СИСТЕМ МАСОВОГО
ОБСЛУГОВУВАННЯ
Мета.
У науковій роботі необхідно
оцінити вплив показників експлуатації
та надійності локомотивів на систему
організації їх ремонту в депо з
використанням методів теорії масового
обслуговування.
Методика.
У роботі представлено опис цеху з
ремонту локомотивів за допомогою
термінів і понять системи масового
обслуговування (СМО). Сформульовано
завдання, які вирішуються при моделюванні
роботи ремонтного цеху, наведено перелік
вихідних даних і результатів моделювання.
У якості програмного
засобу
моделювання використане графічне
середовище імітаційного моделювання
Simulink.
Результати.
Встановлено, що на основні показники
роботи локомотивного депо впливає
обсяг перевезень, надійність локомотивів,
що використовуються, правило відбору
локомотивів із черги, кількість працюючих
ремонтних стійл. Розроблена модель
ремонтного цеху депо дозволяє раціонально
планувати використання обладнання,
фонду робочої сили, часу постановки
локомотивів у ремонт із урахуванням
рівномірності завантаження цеху, а
також удосконалити логістику поставок
запасних частин. Ця модель у спрощеному
вигляді описує процес виконання ремонту
парку магістральних тепловозів і може
бути доповнена
в залежності від
виду виконуваних у депо ремонтів.
Наукова новизна.
У роботі локомотиворемонтне депо
представлене як об’єкт системи масового
обслуговування. Розроблено імітаційну
модель локомотиворемонтного депо, яка
дозволяє проводити аналіз впливу різних
чинників на систему організації ремонту
локомотивів у депо. Практична
значимість. Отримані
результати дозволяють визначити вплив
показників експлуатації та надійності
локомотивів на організацію роботи
локомотиворемонтного депо.
У
подальших дослідженнях розроблена
модель може бути використана для
удосконалення системи організації
ремонту на мережі доріг при впровадженні
нових серій локомотивів та зміні
стратегії їх технічного обслуговування.
Ключові
слова: цех ремонту
локомотивів; моделювання; система
масового обслуговування; організація
роботи ремонтного цеху
Б. Е. БОДНАРЬ1,
А. Б. ОЧКАСОВ2*,
Е. Б. БОДНАРЬ3,
Т. С. ГРИШЕЧКИНА4,
М. В. ОЧЕРЕТНЮК5
1Каф.
«Локомотивы», Днепропетровский
национальный университет железнодорожного
транспорта имени академика
В.
Лазаряна, ул. Лазаряна, 2, Днипро, Украина,
49010, тел. +38 (056) 733 19 01, эл. почта
bodnarz@nz.diit.edu.ua,
ORCID 0000-0002-3591-4772
2*Каф.
«Локомотивы», Днепропетровский
национальный университет железнодорожного
транспорта имени академика
В.
Лазаряна, ул. Лазаряна, 2, Днипро, Украина,
49010, тел. +38 (056) 733 19 61, эл. почта
abochkasov@gmail.com,
ORCID 0000-0002-7719-7214
3Каф.
«Локомотивы», Днепропетровский
национальный университет железнодорожного
транспорта имени академика
В.
Лазаряна, ул. Лазаряна, 2, Днипро, Украина,
49010, тел. +38 (056) 733 19 61, эл. почта
Melnar78@gmail.com,
ORCID 0000-0001-6040-913X
4Каф.
«Высшая математика», Днепропетровский
национальный университет железнодорожного
транспорта имени академика
В. Лазаряна,
ул. Лазаряна, 2, Днипро, Украина, 49010, тел.
+38 (0562) 36 26 04, эл. почта
grishechkina.tatiana@gmail.com,
ORCID 0000-0003-1570-4150
5Каф.
«Локомотивы», Днепропетровский
национальный университет железнодорожного
транспорта имени академика
В.
Лазаряна, ул. Лазаряна, 2, Днипро, Украина,
49010, тел. +38 (056) 733 19 61, эл. почта
ocheretniukmaksym@gmail.com,
ORCID 0000-0002-9032-8602
МОДЕЛИРОВАНИЕ
ОРГАНИЗАЦИИ РЕМОНТА
ЛОКОМОТИВОВ МЕТОДАМИ
ТЕОРИИ
СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ
Цель.
В
научной работе необходимо оценить
влияние показателей эксплуатации и
надежности локомотивов на систему
организации их ремонта в депо с
использованием методов теории массового
обслуживания. Методика.
В работе представлено
описание цеха по ремонту локомотивов
с помощью терминов и понятий системы
массового обслуживания (СМО). Сформулированы
задачи, решаемые при моделировании
работы ремонтного цеха, приведен
перечень исходных данных и результатов
моделирования. В качестве программного
средства моделирования использована
графическая среда имитационного
моделирования Simulink.
Результаты.
Установлено, что
на основные показатели работы
локомотивного депо влияет объем
перевозок, надежность локомотивов,
используемое правило отбора локомотивов
из очереди, количество работающих
ремонтных стойл. Разработанная модель
ремонтного цеха депо позволяет
рационально планировать использование
оборудования, фонда рабочей силы,
времени постановки локомотивов в ремонт
с учетом равномерности загрузки цеха,
а также усовершенствовать логистику
поставок запасных частей. Эта модель
в упрощенном виде описывает процесс
выполнения ремонта парка магистральных
тепловозов и может быть дополнена в
зависимости от вида выполняемых
в
депо ремонтов. Научная
новизна. В работе
локомотиворемонтное депо представлено
как объект системы массового обслуживания.
Разработана имитационная модель
локомотиворемонтного депо, которая
позволяет проводить анализ влияния
различных факторов на систему организации
ремонта локомотивов
в депо.
Практическая значимость.
Полученные результаты позволяют
определить влияние показателей
эксплуатации и надежности локомотивов
на организацию работы локомотиворемонтного
депо.
В дальнейших исследованиях
разработанная модель может быть
использована для усовершенствования
системы организации ремонта на сети
дорог при внедрении новых серий
локомотивов и изменении стратегии их
технического обслуживания.
Ключевые
слова: цех ремонта
локомотивов; моделирование; система
массового обслуживания; организация
работы ремонтного цеха
REFERENCES
Berestovoy,
A. M., & Lyamzin, A. A. (2003). Modelirovanie sistemy
tekhnicheskogo obsluzhivaniya i remonta lokomotivov. Visnyk
Pryazovskoho derzhavnoho tekhnichnoho universytetu. Seriia:
Tekhnichni nauky,
13,
276-280. (in Russian)
Bosov,
A. A.,
& Loza, P. A. (2015). Teoreticheskie
osnovy ratsionalnogo soderzhaniya podvizhnogo sostava zheleznykh
dorog: monografiya.
Dnepropetrovsk: Driant. (in Russian)
Hryshechkina,
T. S. (2017). Mathematical Model
of the Rational Maintenance System of Railway Transport Technical
Objects.
Transport
Systems and Transportation Technologies.
Collection of Scientific Works of Dnepropetrovsk National
University of Railway Transport named after Academician Lazaryan,
14,
30-35. doi: 10.15802/tstt2017/123165
(in Ukrainian)
Hureva,
А. Н., &
Chernetskaia-Beletskaia,
N. B. (2015).
Fundamentals of Modeling of
Processes of Maintenance of Locomotives. Visnyk
Skhidnoukrainskoho natsionalnoho universytetu imeni Volodymyra
Dalia,
1(218),
262-265.
(in Russian)
Zinenko,
O. L. (2010). Pidvyshchennia
efektyvnosti vykorystannia lokomotyvnoho parku shliakhom
vdoskonalennia upravlinnia ekspluatatsiinoiu robotoiu.
(Dysertatsiia kandydata tekhnichnykh nauk). Dnipropetrovsk National
University of Railway Transport named after Academician V.
Lazaryan, Dnipropetrovsk. (in Ukranian)
Skrebkov,
A. V., Vorobiyov, A. A., Lamkyn, A. G.,
& Bodrikov,
D. I.
(2017).
The
Study of Running and Maintenance Process of Electric Locomotives
with Big Data and Simulation Modeling Tools. Byulleten
rezultatov nauchnykh issledovaniy,
4,
190-198.
(in Russian)
Kudayarov,
M. M. (2012). Vybor optimalnoy organizatsii remonta lokomotivov na
poligone zheleznoy dorogi Izvestiya
Peterburgskogo universiteta putey soobshcheniya, 3(32),
99-103.
(in Russian)
Kudayarov,
M. M. (2012). Optimizatsiya sistemy tekhnologicheskogo protsessa
remonta tyagovogo podvizhnogo sostava. Sovremennye
problemy transportnogo kompleksa Rossii, 2,
14-22.
(in Russian)
Loza,
P. A., &
Hryshechkyna, T. S. (2015). Estimation of the quality of
implementation electric rolling stock maintenance system.
Elektryfikatsiia
transportu,
9,
87-93. (in Russian)
Gorskiy,
A. V.,
Skrebkov, A.
V., Chigambaev,
T. O.,
&
Tsikhalevskiy,
I. S.
(2008). Methods
and Algorithm of Optimum Sending of Locomotives to Repair
Enterprises.
Transport Urala, 3(18),
25-27.
(in Russian)
Zhukovytskyi,
I. V., Skalozub, V. V., Vietrova, O. V., & Zinenko, O. L.
(2006). Modeliuvannia protsesu operatyvnoho planuvannia roboty
lokomotyvnoho parku i lokomotyvnykh bryhad. Visnyk
Dnipropetrovskoho natsionalnoho universytetu zaliznychnoho
transportu imeni akademika V. Lazariana, 12,
74-78.
(in Ukrainian)
Falendysh,
A. P., Sumtsov, A. L., Artemenko, O. V., & Kletska, O. V.
(2016). Simulation of changes in the steady state availability
factor of shunting locomotives for various maintenance systems.
Eastern-European
Journal of Enterprise Technologies, 1/3(79),
24-21.
doi: 10.15587/1729-4061.2016.6064040
(in Ukrainian)
Ochkasov,
O. B., Hryshechkina,
T. S., &
Ocheretnyuk, M. V. (2017).
Approaches to
the system
simulation of
maintenance
operations for
locomotives.
Aktualni problemy avtomatyzatsii ta
upravlinnia : tezy dopovidei V mizhnarodnoi naukovo-praktychnoi
internet-konferentsii molodykh uchenykh i aspirantiv (Lutsk, 28–30
bereznia 2017 r.), 5, 99-104.
(in
Russian)
Sumtsov,
A. L. (2017). Udoskonalennia
metodiv ta modelei vyznachennia systemy tekhnichnoi ekspluatatsii
modernizovanykh manevrovykh teplovoziv.
(Dysertatsiia kandydata
tekhnichnykh nauk).
Ukrainskyi derzhavnyi universytet zaliznychnoho transport,
Kharkiv.
(in Ukraininan)
Shantarenko,
S.
G.
(2005). Modelirovanie
protsessov
tekhnicheskogo
obsluzhivaniya
lokomotivov.
Izvestiya
Tomskogo
politekhnicheskogo
universitetata. Inzhiniring georesursov, 308(5),
169-171. (in Russian)
Bodnar,
B., Ochkasov, A. & Bobyr, D. (2016). Improving Operation and
Maintenance of Locomotives of Ukrainian Railways. Technologijos
ir Menas = Technology and Art, 7,
109-114. (in English)
Bodnar,
B., &
Ochkasov,
О. (2017). System
Choice of the Technical Maintenance of Locomotives Equipped with
on-Board Diagnostic Systems.
Transport Means: Proceedings
of 21st International Science
Conference
(Sept.
20–22, 2017).
Juodkrante, Kaunas, Lithuania,
Pt. I,
43-47.
(in English)
Lovett,
A. H., Dick, C. T., Ruppert, C., Saat, M. R., & Barkan, C.
(2013). Development of an Integrated Model for the Evaluation and
Planning of Railroad Track Maintenance. 2013 Joint
Rail Conference.
doi: 10.1115/jrc2013-2407
(in English)
Ochkasov,
O., Shvets, O.,
& Černiauskaitė, L. (2017). Usage of Intelligent Technologies
in Choosing the Strategy of Technical Maintenance of Locomotives.
Technologijos
ir Menas = Technology and Art, 8,
68-71. (in English)
Wu,
Jun,
& Jia, Hua Fei (2013). Study on Adjustment Evaluation of
Locomotive Affair Productivity Layout. Applied
Mechanics and Materials, 401-403,
2120-2126. doi: 10.4028/www.scientific.net/amm.401-403.2120 (in
English)
Received:
June 20, 2018
Accepted:
October 03, 2018
d
oi
10.15802/stp2018/ ©
B.
E.
Bodnar, A.
V.
Оchkаsоv,
Е. B.
Bodnar, Т. S.
Hryshechkina,
М. V.
Ocheretnyuk,
2018
.
,
– is the probability that at the moment of time t
the system will be in the state
.