UDC 624.953.014.2.004.15

Introduction

Inadequate design reliability of technical systems leads to a significant increase in the share of operating costs in total expenditures for their design, fabrication and application. At the same time, the cost of operation can many times exceed the cost of designing and manufacturing the system [1, 3, 10]. Therefore, the reliability of technical systems should be ensured, first of all, at the design stage [2, 12, 13].

One of the main methods for ensuring the reliability of the technical systems being designed is the method of structural redundancy [6-8], which involves the use of redundant elements in the system. The essence of structural redundancy lies in the fact that in addition to the main (reserved) object containing the minimum required number of elements for the normal performance of the system's functions, in the system structure the additional identical (in terms of performed operational functions and reliability) elements are introduced. These redundant elements are designed to perform the work functions of the main elements. Thus, a system with redundancy is a system containing redundant structural components with respect to being reserved object that perform the same work functions as the corresponding components of the main object. The redundant system remains operable after subsequent failure of any element if the number of operable elements does not become less than the minimum required number provided for by regulatory requirements for the main object.

The problem of rational choice of one of the several variants of the system composition always arises during the structural redundancy. On the one hand, to increase reliability it is desirable to provide each of the system elements with maximum possible number of redundant elements, and, on the other hand, it is impossible to design a system with too large cost, weight or dimensions. Therefore, the actual task is how to reserve the system in such a way as to provide the required level of system reliability at acceptable costs. The choice of the cost characteristic is determined by the type of the system and its purpose. For example, for aircrafts the essential factor is weight, and for the ground system – the cost. Regardless of the physical essence, the selected cost characteristic for brevity below will be referred to as cost. Usually, the problems of optimal structural redundancy of technical systems are formulated as non-linear programming problems, and to solve them, depending on the complexity and required accuracy, the special algorithms are used. They are based primarily on the dynamic programming method [6]. In this article, the initial optimization model is represented in terms of the problem of non-linear integer programming with binary variables, which greatly simplifies its numerical implementation.

Purpose

The purpose of the article is to give the designers of highly reliable technical systems that do not know modern optimization methods and programming skills, a simple mathematical tool for choosing the optimal structure of a redundant system.

Methodology

During problem definition of the optimal structural redundancy, the main object is considered as a system consisting of 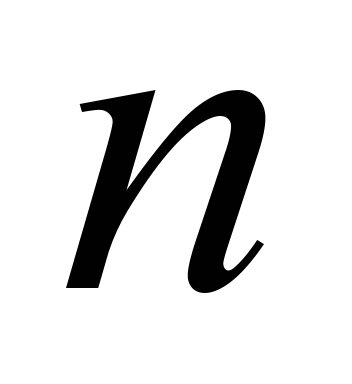of various elements that have a coherent connection [4] (see Fig. 1).

Fig. 1. Structural diagram of reliability
of the main object

As the main indicator of reliability of the redundant system, the probability of its fail-safe operation is assumed. It is believed that the failure flow of elements put into operation is described by the Poisson arrival [5]. Possible variants of the main object redundancy are limited to the consideration of typical schemes of separate «cold» backup with an integer multiplicity with an ideal switch (see Fig. 2) and «hot» backup with parallel connection of elements (see Fig.3) [7].

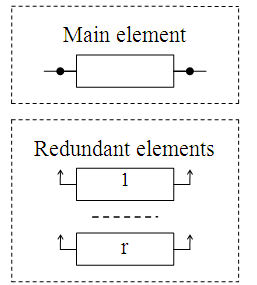
Fig. 2. Structural scheme of reliability at «cold» backup

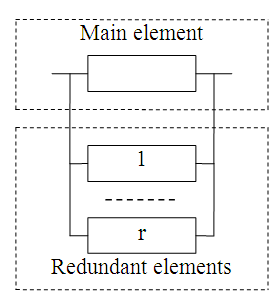
Fig. 3. Structural scheme of reliability at «hot» backup

Note that, taking into account the assumptions made, the probability of failure-free operation of the redundant group of elements, the scheme of structural reliability of which is shown in Fig. 2, is determined by the Erlangian formula [5, 9]

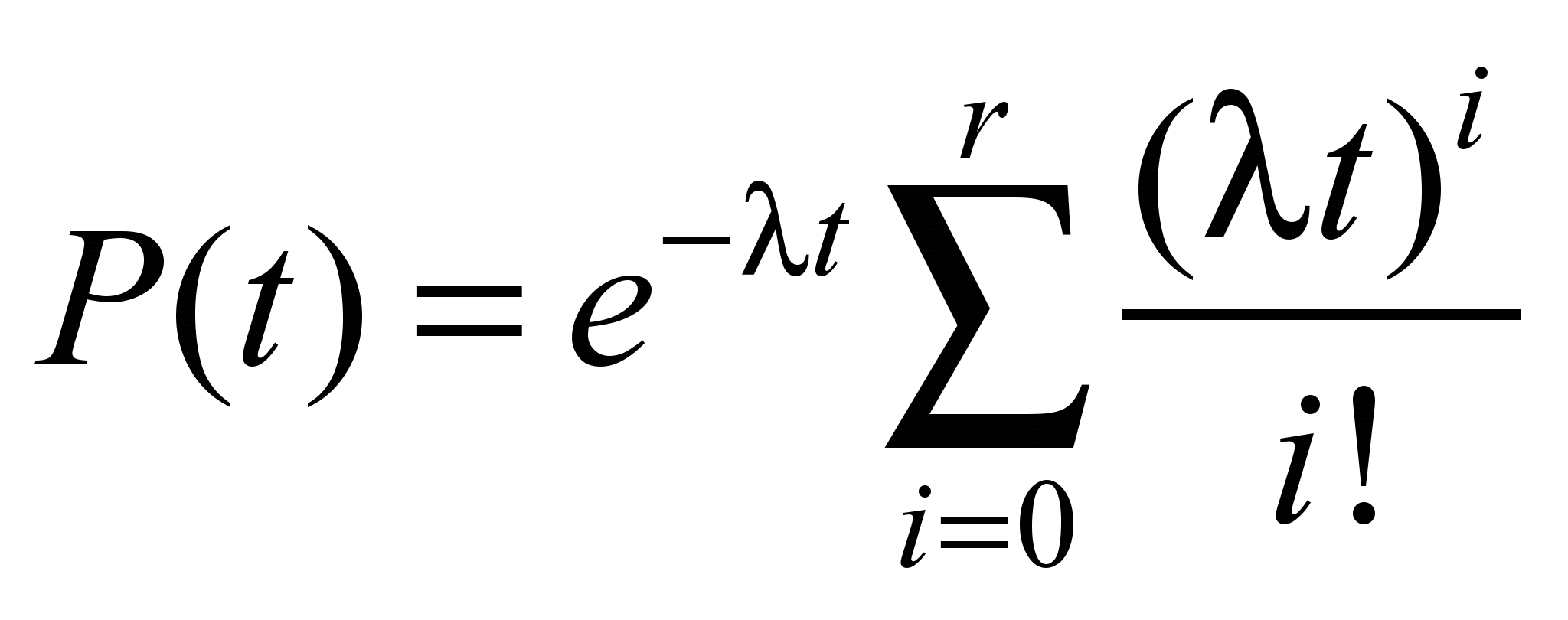, (1)

and the formula for calculating the probability of failure-free operation of a redundant group of elements, the structural scheme of reliability of which is shown in Fig. 3, has the form

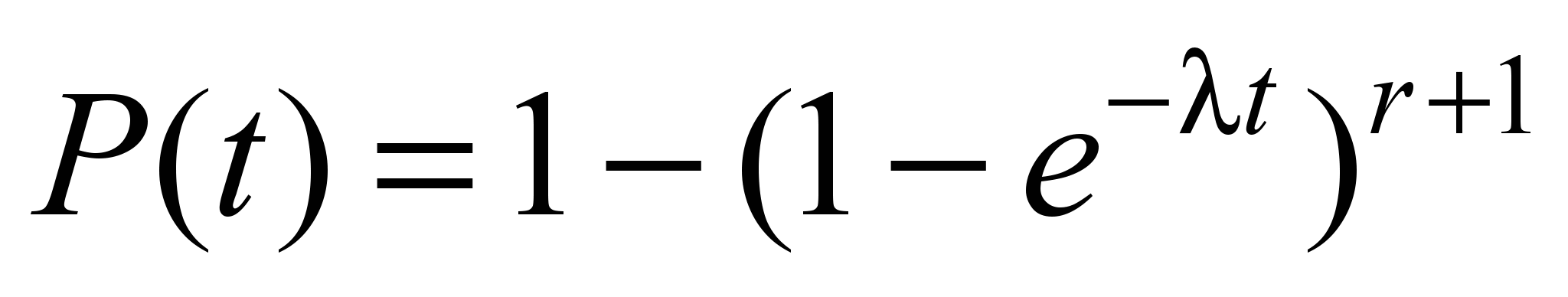, (2)

where 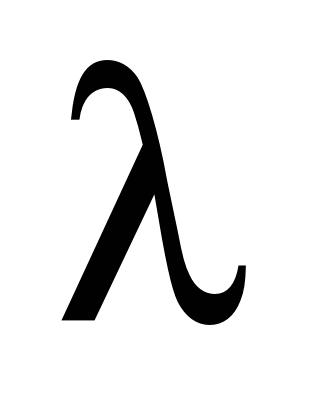– is the failure rate of the element put into operation; 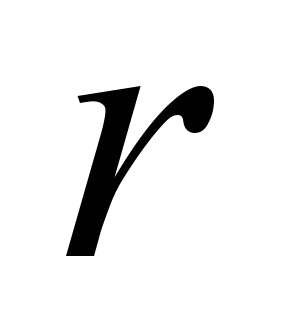– is the redundancy rate.

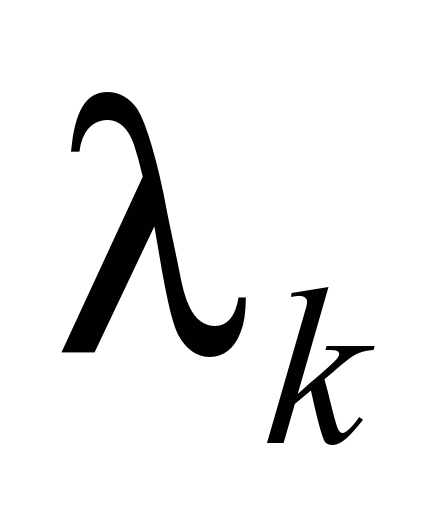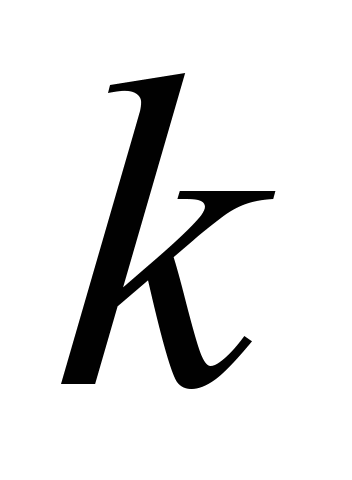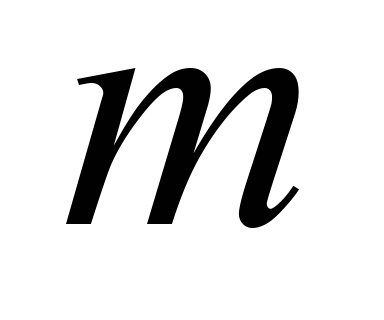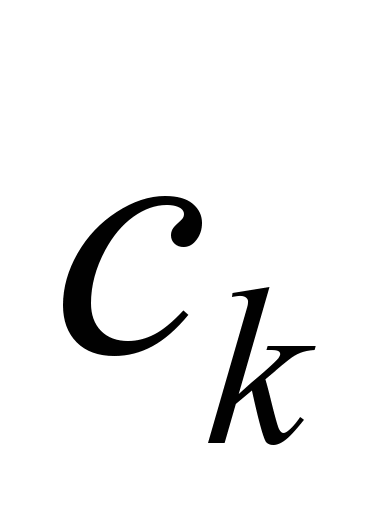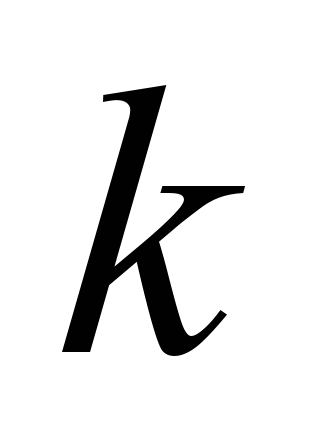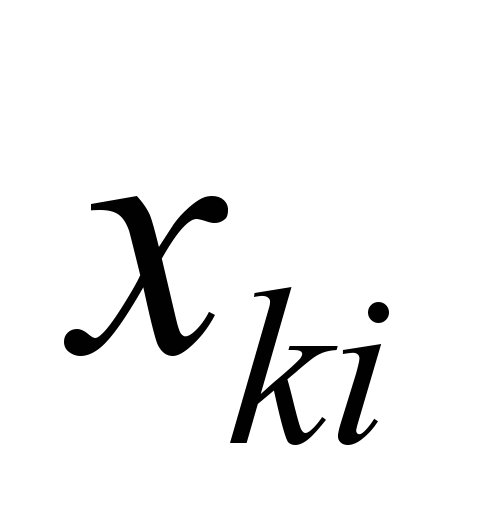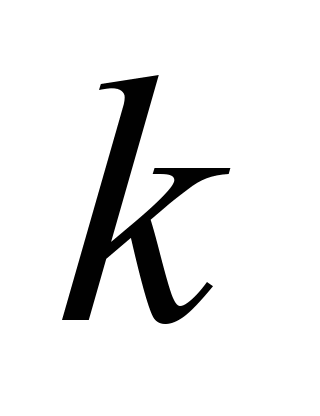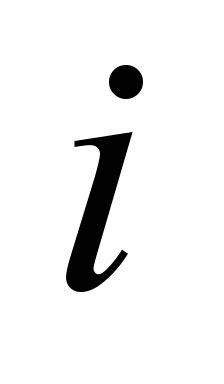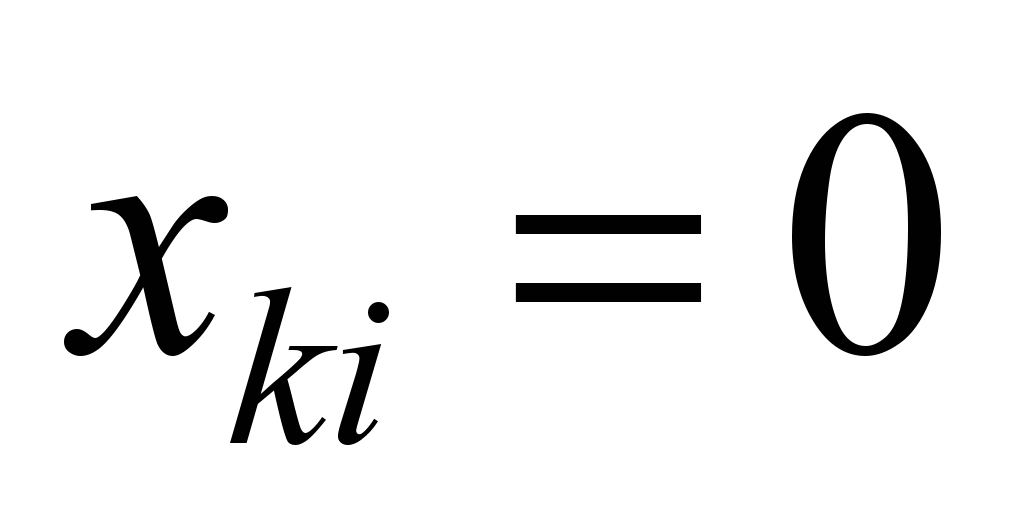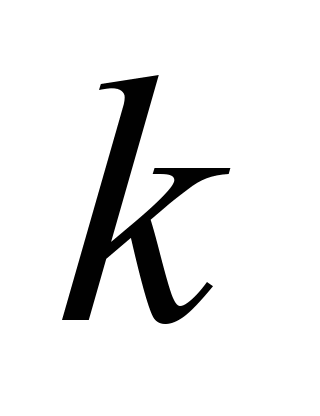Let us introduce the following designations: – is the failure rate of the element of the -th type put into operation; – is the maximum allowable redundancy rate of main elements; – is the cost of one element of the -th type; – is the binary variable, equal to 1, if the number of redundant elements of the -th is equal to , and , f the number of redundant elements of the -th type is not equal to 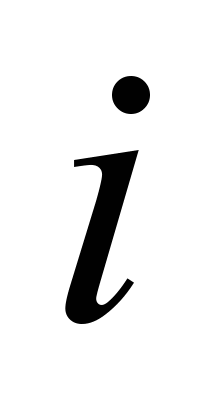; 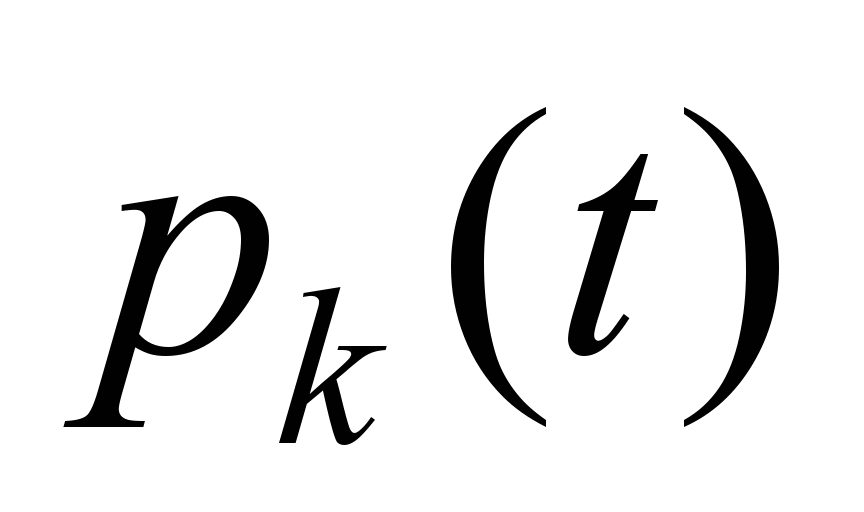– is the probability of fail-safe operation of the main element of the -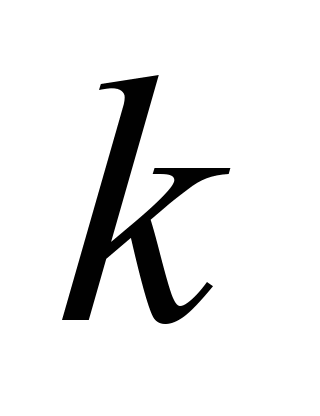th type, over the time

.

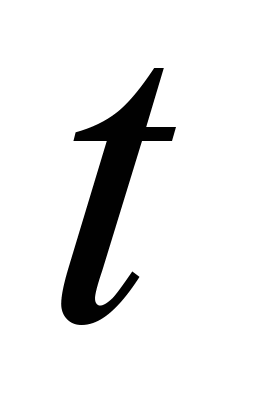
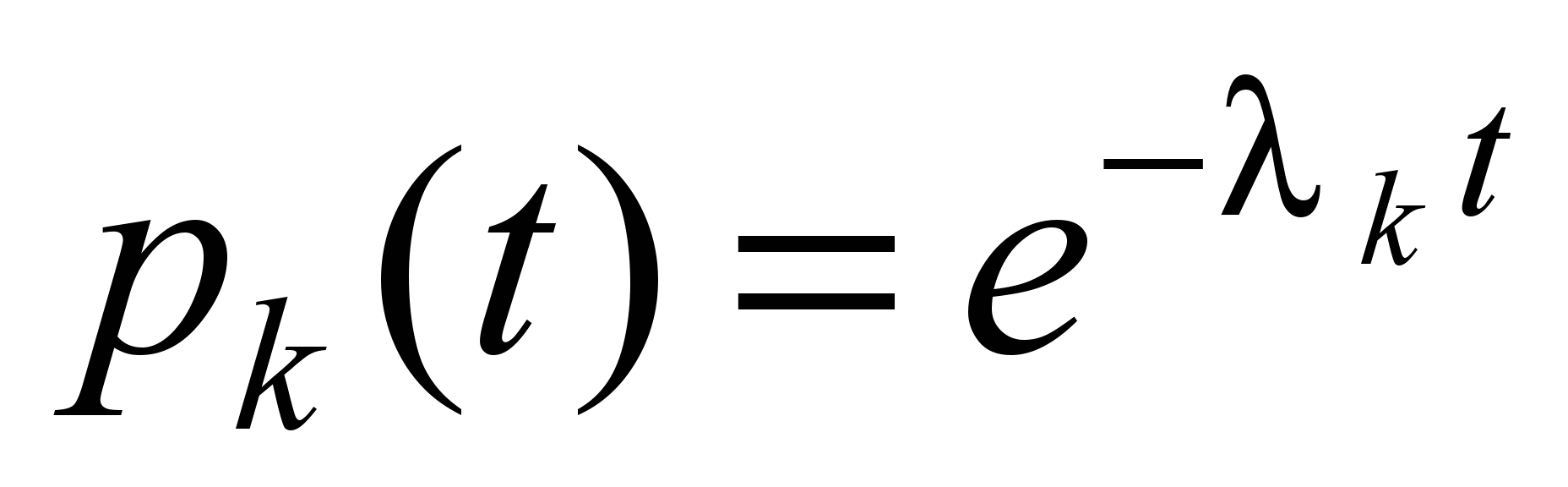Let us consider a redundant group of elements, consisting of the elements of the 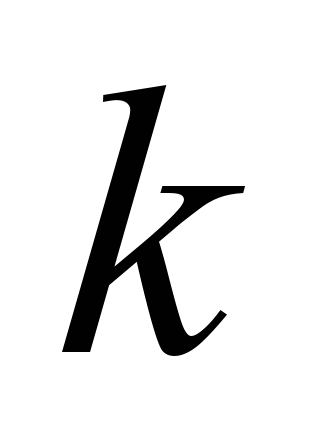-th type. Taking into account the introduced designations, the probability of failure-free operation of a redundant group at «cold» backup is estimated by formula

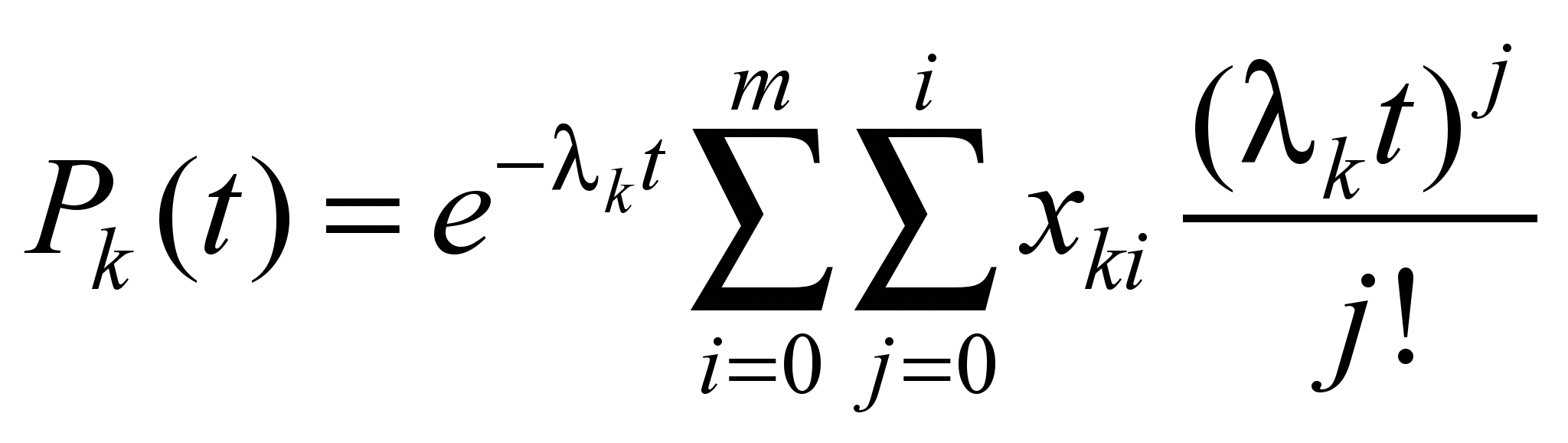, (3)

and when using the «hot» backup scheme, this probability is represented as follows

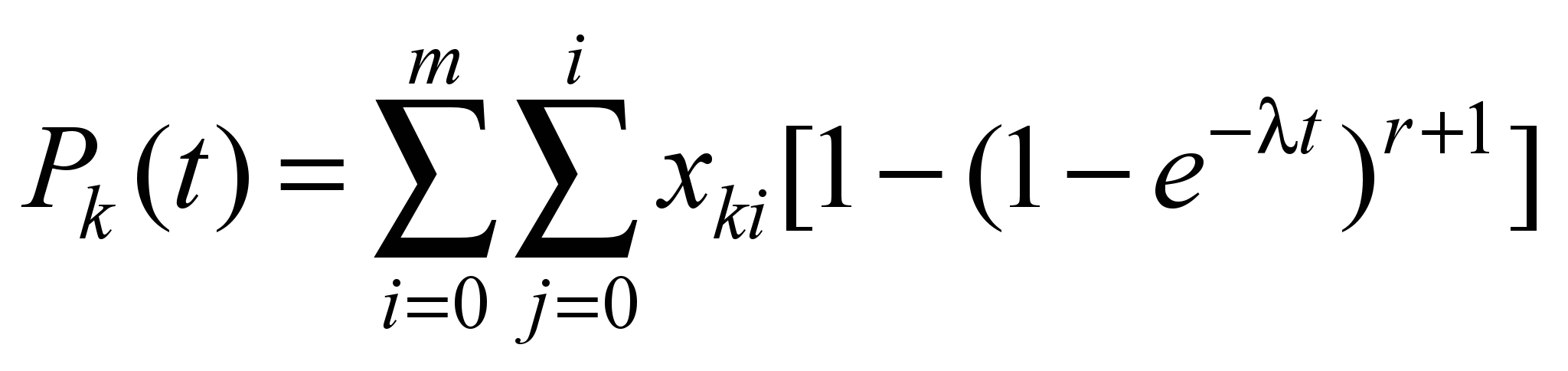. (4)

With neglect of the cost of switching equipment in case of «cold» backup, the cost of the redundant group consisting of the elements of the 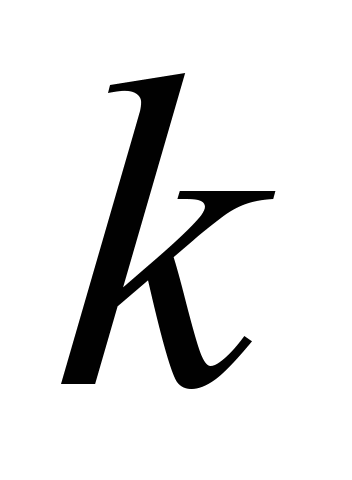-th type in both backup schemes can be found using formula

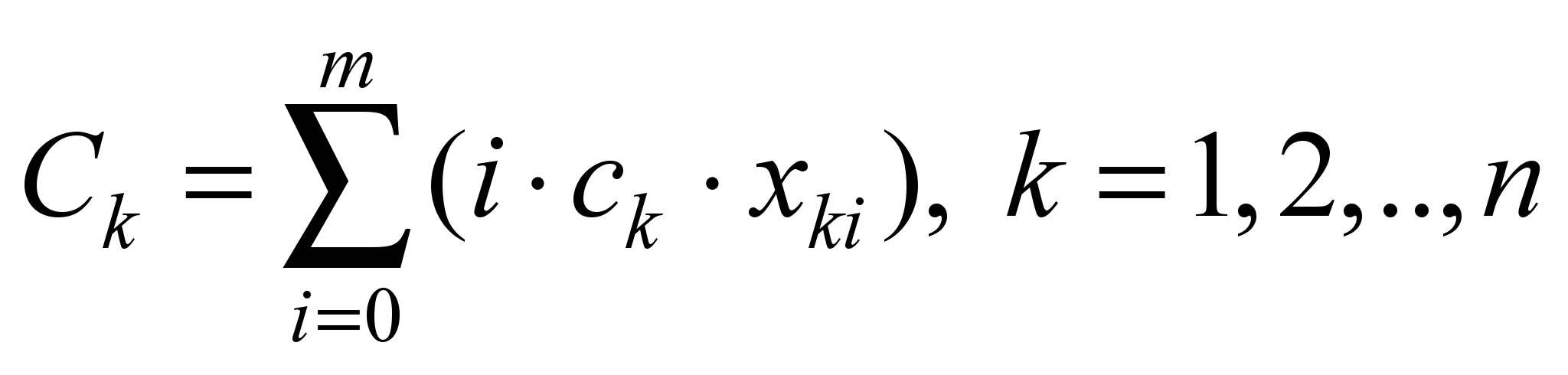. (5)

Taking into account the coherent connection of the main elements and the product rule, the probability of failure-free operation and the cost of the entire redundant system are determined as follows:

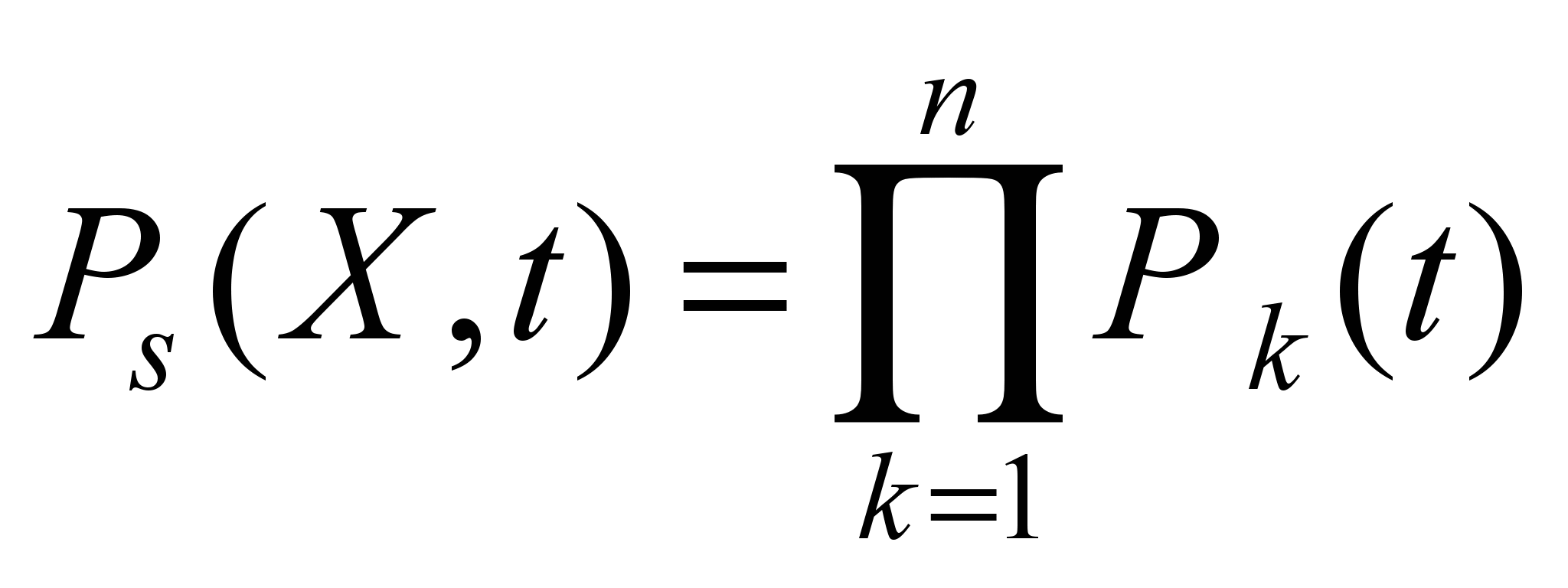; (6)

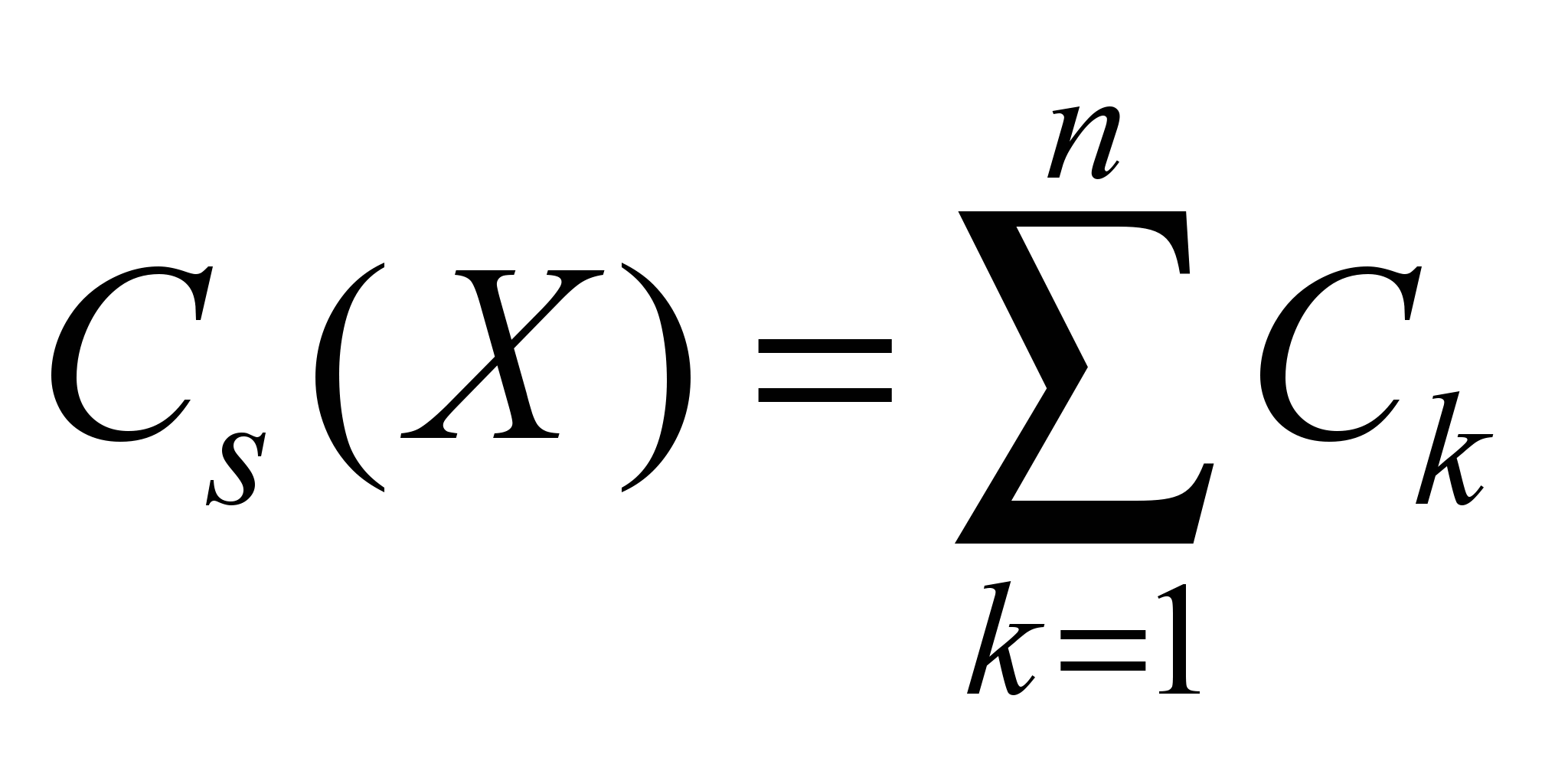, (7)

where 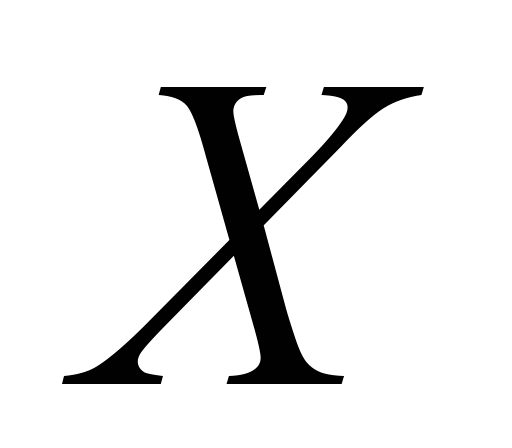– is the matrix describing composition of the elements of the redundant system

,

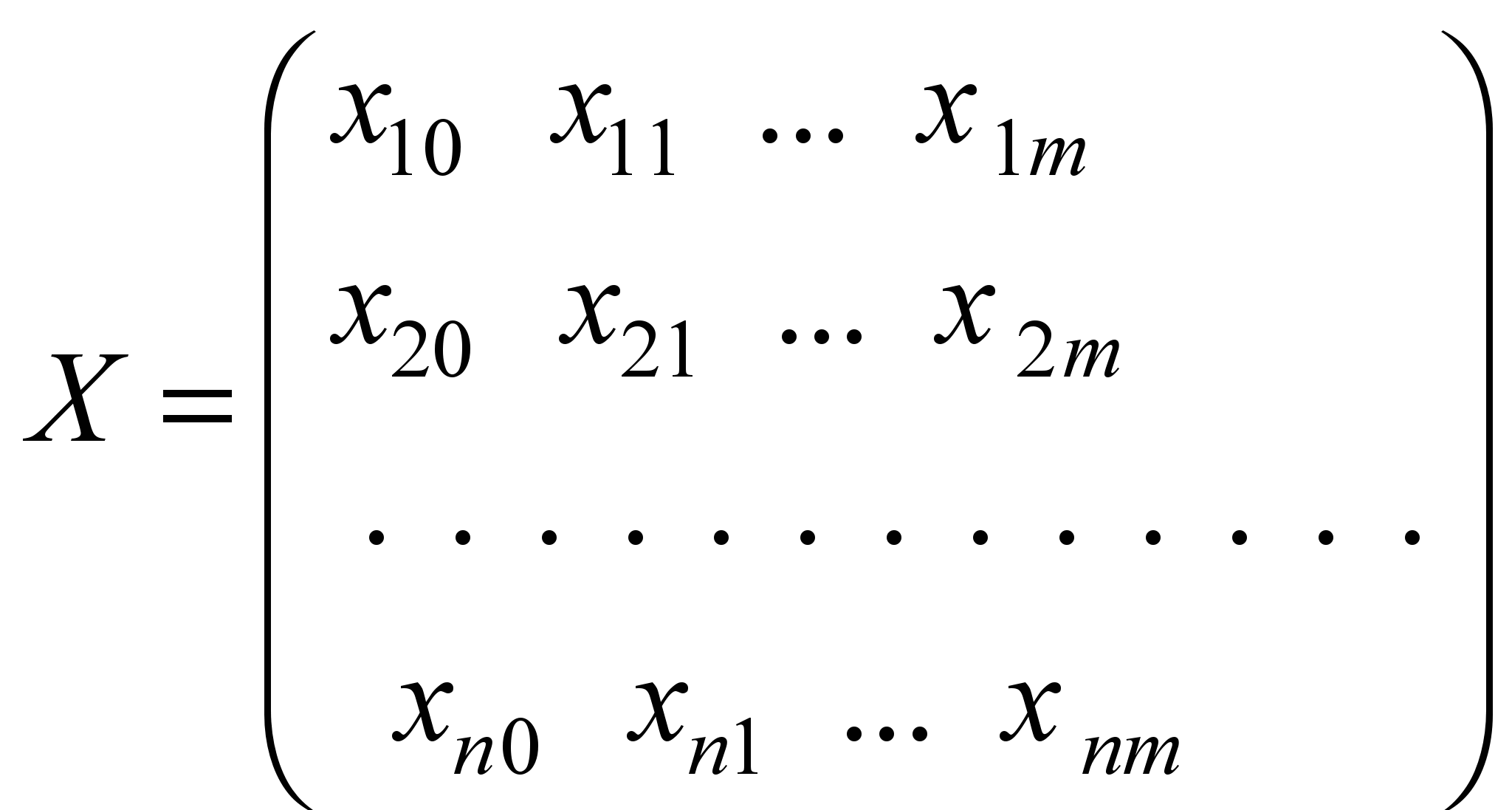and the probabilities 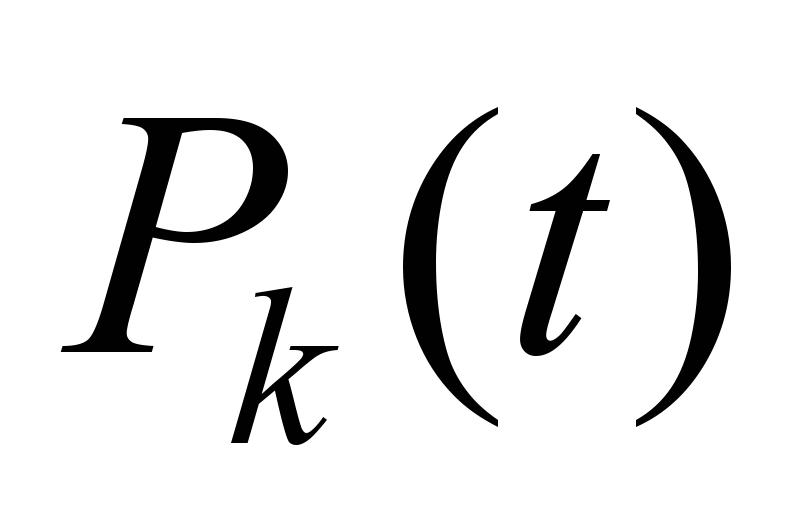are determined using formulas (3) and (4) depending on the backup scheme used.

In terms of the mathematical programming problem, the following two typical statements of the task of optimal structural redundancy are possible.

The problem 1: it is required to find the composition of redundant elements (matrix elements 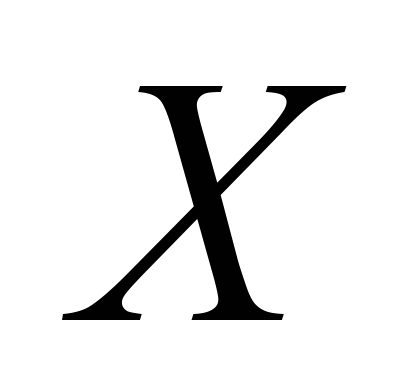) that provides the required level of system reliability for a given time at the lowest possible cost

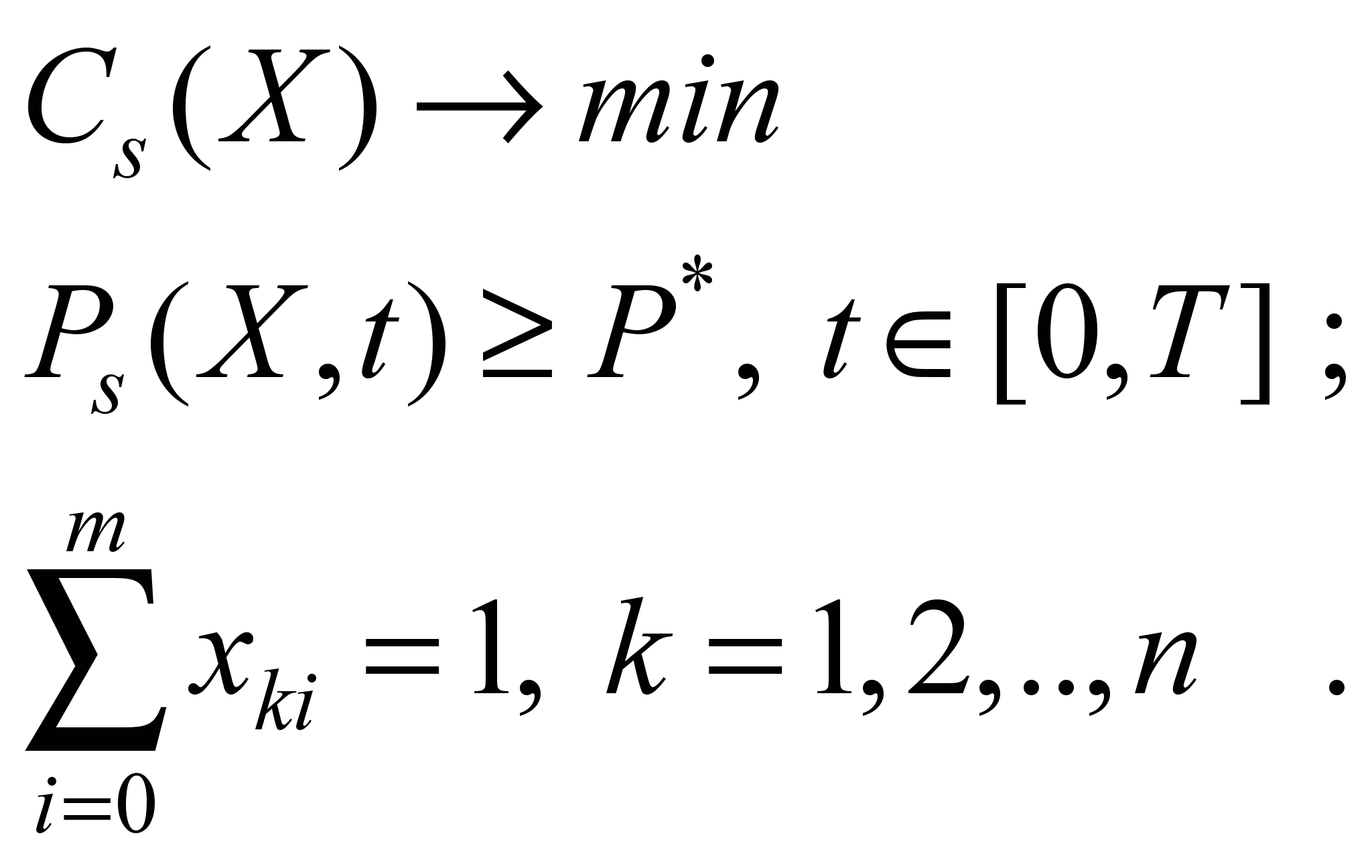(8)

The problem 2: it is required to find the composition of redundant elements, which provides the highest possible level of system reliability for a given time , with a restriction on its cost

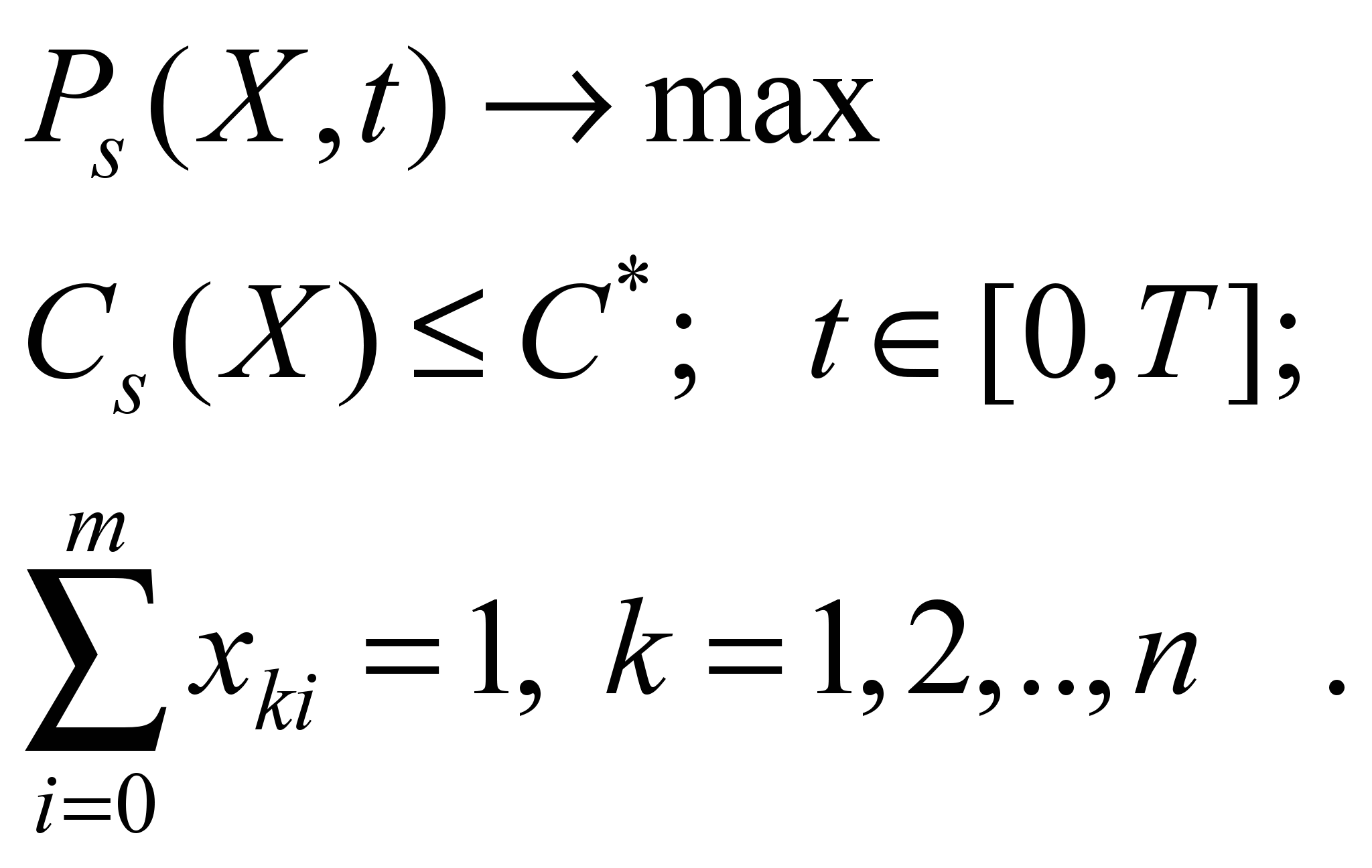(9)

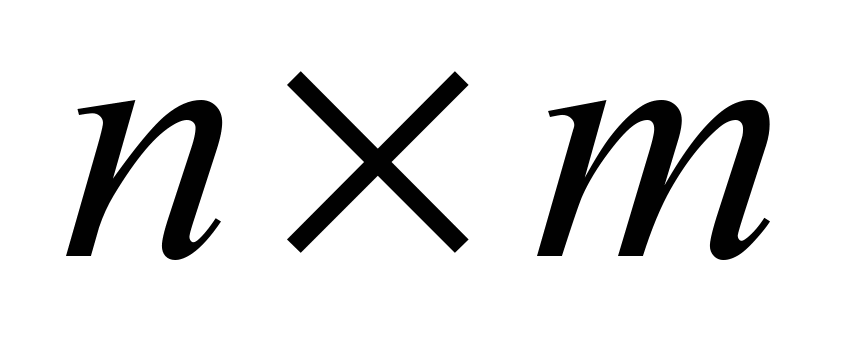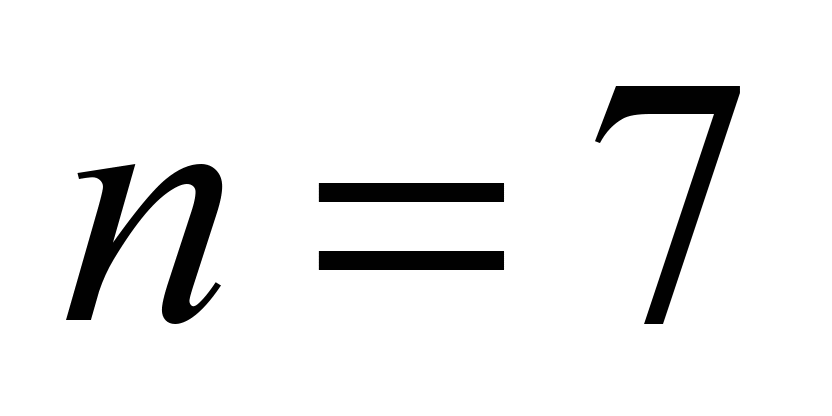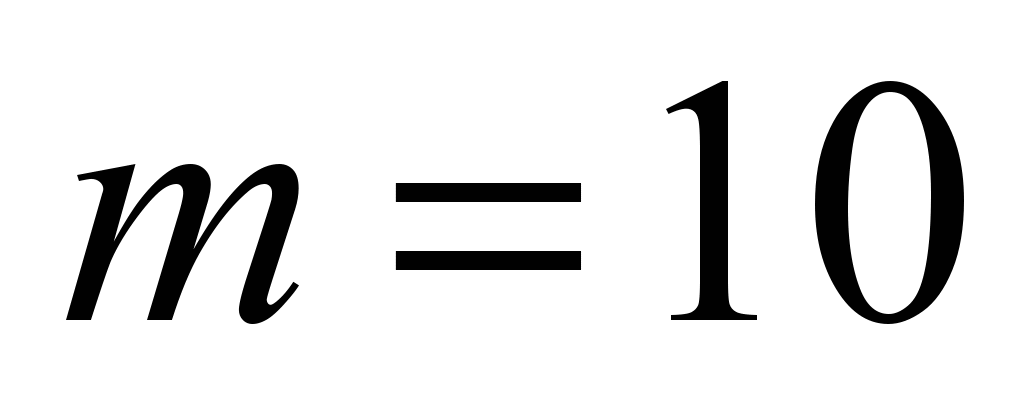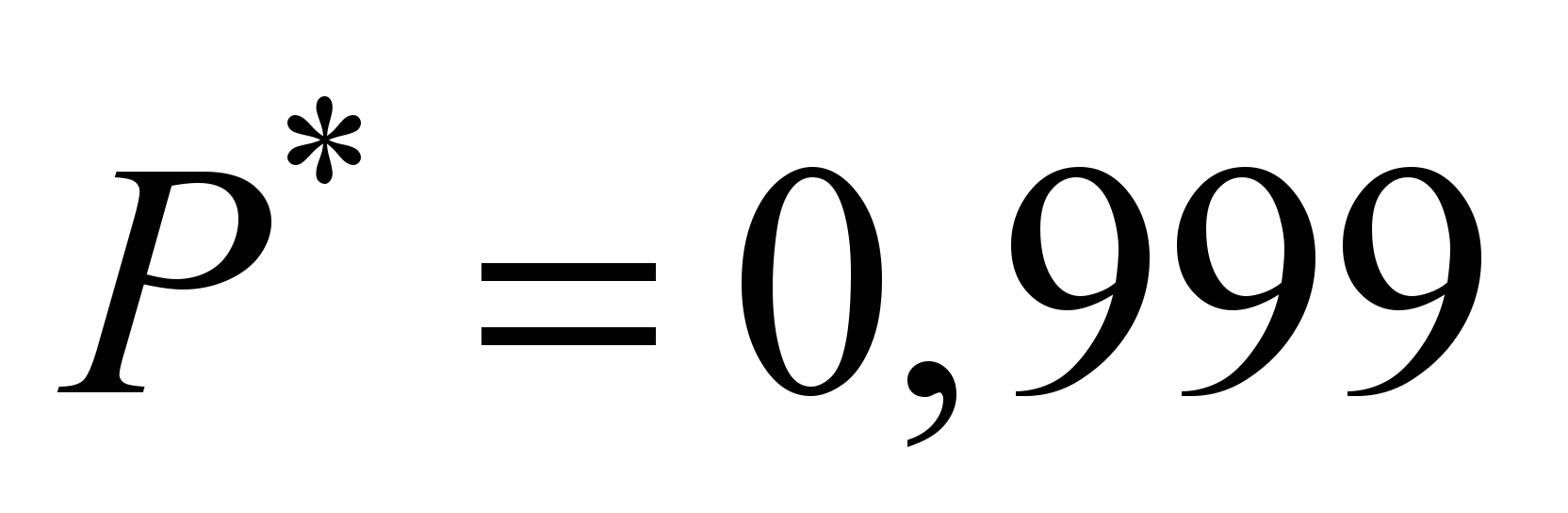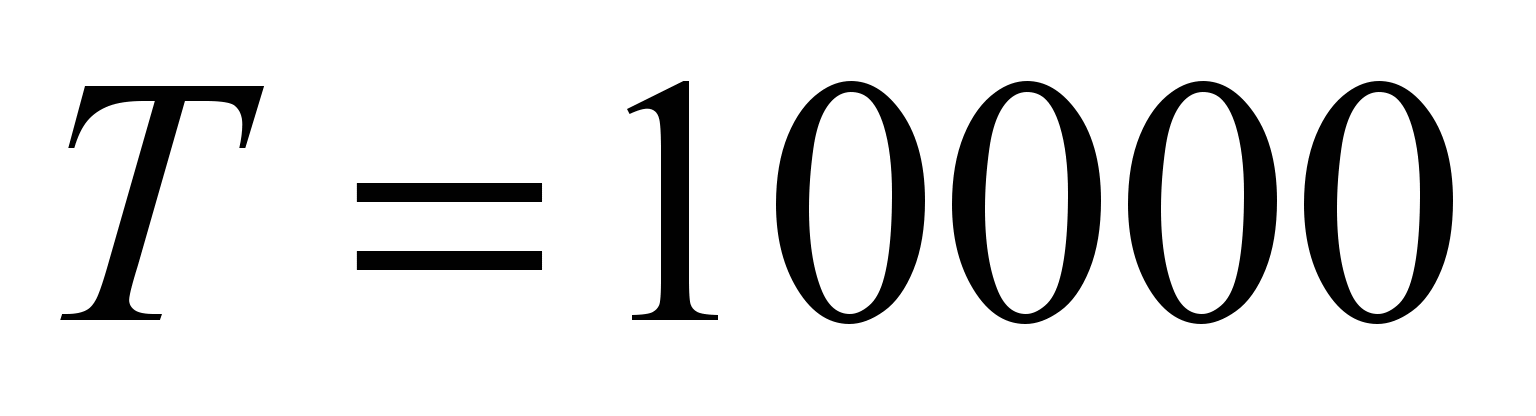The optimization models (8) and (9) have dimensions and belong to the class of problems of integer nonlinear programming with binary variables. The model (8) was numerically realized for cases of «cold» and «hot» separate backup using the MS Excel Solver add-in. The problem was solved with the following initial data: ; ; ; h. The failure rates and cost of elements were taken using Table 1.

Table 1

Initial data

Number of element	Failure rate (hour-1)	Cost (thous. UAH)
1	0.02·10-4	25
2	0.014·10-4	52
3	0.09·10-4	12
4	0.30·10-4	17
5	0.11·10-4	29
6	0.01·10-4	43
7	0.07·10-4	34

The optimal values of the unknowns 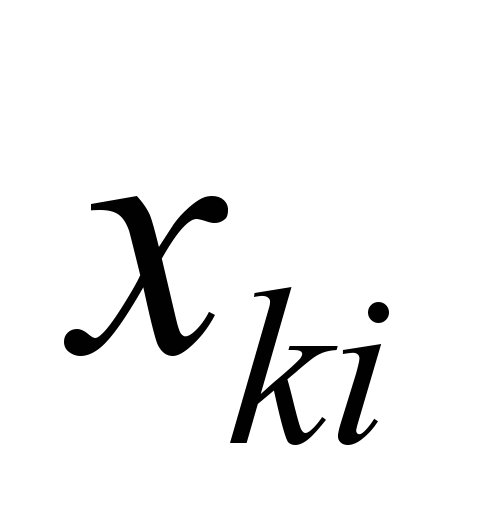in cases of «cold» and «hot» backup are found in Tables, respectively, 2 and 3, and the corresponding structural diagrams of the system reliability are shown in Figures 4 and 5. The calculated reliability estimates and the cost of the optimal system for «cold» and «hot» backup are listed in Table 4.

Table 2

Optimal parameters of the «cold» backup

k\i	0	1	2	3
1	0	1	0	0
2	0	1	0	0
3	0	0	1	0
4	0	0	1	0
5	0	0	1	0
6	0	1	0	0
7	0	0	1	0

Table 3

Optimal parameters of the «hot» backup

k\i	0	1	2	3	4	5	6
1	0	0	1	0	0	0	0
2	0	0	1	0	0	0	0
3	0	0	0	1	0	0	0
4	0	0	0	0	0	0	1
5	0	0	0	0	1	0	0
6	0	0	1	0	0	0	0
7	0	0	0	0	1	0	0

Table 4

The reliability parameters and the cost of optimal system

Backup type	P1	P2	P3	P4	P5	P6	P7	Ps	Cs
cold	0.99982	0.99995	0.99982	0.99983	0.99981	0.99992	0.99993	0.99908	533
hot	0.99999	0.99999	0.99994	0.99992	0.99988	0.99999	0.99997	0.99971	718

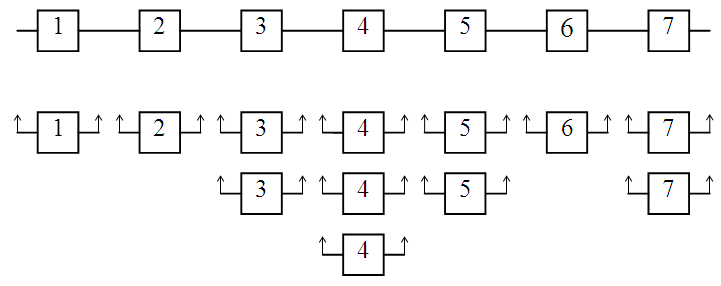
Fig. 4. Optimal structural scheme of the system reliability with «cold» redundancy

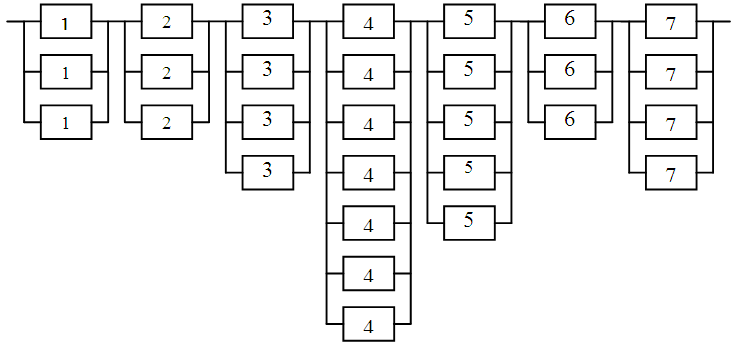
Fig. 5. Optimal structural scheme of the system reliability with «hot» redundancy

Findings

The calculated models for estimating reliability, as well as the optimization models for the redundant systems according to the «hot» and «cold» separate backup schemes, have been developed. The optimal options for reserving the 7 element object at separate «cold» and «hot» backup using the Excel spreadsheet were found.

Originality and practical value

New calculation models for estimating the reliability of redundant systems are proposed, as well as the optimization models developed on their basis, which are formulated using the unknown decomposition of initial problem of structural redundancy into binary components. The obtained optimization models belong to the class of problems of non-linear mathematical programming with binary variables, for the numerical solution of which (even for a sufficiently large dimensions) the well-known packages of applied computer programs, in particular, the MS Excel spreadsheet, are well adapted. Thus, the process of solving the initially very complicated problem of optimal structural redundancy is greatly simplified and reduced to performing elementary actions in the corresponding programming interfaces. The proposed calculation models for estimating the reliability of redundant systems, the models of optimal structural redundancy, and the methodology for their formation in order to simplify further numerical implementation can be useful in solving the problems of ensuring the reliability of technical systems at the early stages of their design.

Conclusions

The results obtained in the article using the specific examples show the efficiency and sufficient generality of the considered approach to solving the problems of optimal structural redundancy. The optimization models (8) and (9) belong to the class of non-linear programming problems with binary variables and are easily implemented numerically in the operating environment of the Excel spreadsheet. The obtained calculation models for estimating the reliability of redundant systems (3) – (6), the models for optimal structural redundancy (8) and (9), and the methodology for their formation can be used in practical problems of ensuring the reliability of technical systems at the early stages of their design.

LIST OF REFERENCE LINKS

1. Афанасьев, В. П. Надежность тонкостенной оболочки в условиях коррозионного износа / В. П. Афанасьев, Г. И. Семенец // Вісн. Дніпропетр. нац. ун-ту залізн. трансп. ім. акад. В. Лазаряна. – Дніпропетровськ, 2006. – Вип. 11. – С. 171–174.

2. Безопасность и надежность сложных систем : учеб. пособие / Л. Н. Александровская, И. З. Аронов, В. И. Круглов [и др.]. – Москва : Логос, 2017. – 376 с.

3. Бородин, А. В. Технико-экономическое обоснование варианта резервирования сетевой компоненты отказоустойчивой масштабируемой вычислительной системы специального назначения / А. В. Бородин // Кибернетика и программирование. – 2015. – № 6. – С. 55–70.

4. Капур, К. Надежность и проектирование систем : [пер. с англ.] / К. Капур, Л. Ламберсон. – Москва : Мир, 1980. – 604 с.

5. Каштанов, В. А. Теория надежности сложных систем / В. А. Каштанов, А. И. Медведев. – Москва : Физматлит, 2010. – 606 с.

6. Насонова, С. С. Оптимизация риска отказа в задачах управления надежностью стальных резервуаров для нефтепродуктов / С. С. Насонова // Вісн. Дніпропетр. нац. ун-ту залізн. трансп. ім. акад. В. Лазаряна. – Дніпропетровськ, 2008. – Вип. 20. – С. 126–130.

7. Обеспечение надежности сложных технических систем / А. Н. Дорохов, В. А. Керножицкий, А. Н. Миронов, О. Л. Шестопалова. – Санкт-Петербург : Лань, 2011. – 352 с.

8. Половко, А. М. Основы теории надежности / А. М. Половко, С. В. Гуров. – Санкт-Петербург : БХВ, 2006. – 704 с.

9. Рябинин, И. А. Надежность и безопасность структурно-сложных систем / И. А. Рябинин. – Санкт-Петербург : Политехника, 2000. – 248 с.

10. Трошин, А. В. Оптимизация резервирования в коммутируемых пакетных сетях / А. В. Трошин // Инфокоммуникационные технологии. – 2017. – Т. 15, № 4. – С. 354–360.

11. Шишмарев, В. Ю. Надёжность технических систем : учебник / В. Ю. Шишмарев. – Москва : Юрайт, 2018. – 306 с.

12. Chanda, N. Redundant Transmitting System in Aircraft (RTSA) / N. Chanda // SAE Technical Paper Series 2015-01-2443. – 2015. doi: 10.4271/2015-01-2443

13. Jaberipur, G. Redundant Number System-Based Arithmetic Circuits / G. Jaberipur // Arithmetic Circuits for DSP Applications. – Hoboken : John Wiley & Sons, 2017. – P. 273–312. doi: 10.1002/9781119206804.ch8

с. м. семенець^1*, с. с. насонова^2*, Г. І. семенець^3*

^1*Каф. «Прикладна математика та інформаційні технології», Придніпровська державна академія будівництва та архітектури, вул. Чернишевського, 24-а, Дніпро, Україна, 49600, тел. +38 (067) 639 60 64, ел. пошта Ssemenets28@gmail.com, ORCID 0000-0002-6359-1069
^2*Каф. «Вища математика», Український державний хіміко-технологічний університет, пр. Гагаріна, 8, Дніпро, Україна, 49005, тел. +38 (097) 940 98 56, ел. пошта ms.nasonova.s@gmail.com, ORCID 0000-0002-0920-7417
^3*Каф. «Вища математика», Дніпропетровський національний університет залізничного транспорту імені академіка В. Лазаряна, вул. Лазаряна, 2, Дніпро, Україна, 49010, тел. +38 (096) 879 48 19, ел. пошта semga1952@gmail.com,
ORCID 0000-0003-2693-3282

ОПТИМАЛЬНЕ СТРУКТУРНЕ РЕЗЕРВУВАННЯ ТЕХНІЧНИХ СИСТЕМ

Мета. Основна мета статті – дати проектувальникам високонадійних технічних систем, які не володіють спеціальними знаннями в галузі оптимізації та навичками програмування, простий і доступний математичний інструмент для вибору оптимального рішення під час структурного резервуванні систем. Методика. За головний показник надійності резервованої системи прийнята ймовірність її безвідмовної роботи. Розглянуті дві типові схеми резервування: 1) схема роздільного «гарячого» резервування; 2) схема роздільного «холодного» резервування. Сформульовані розрахункові моделі оцінки надійності резервованих систем.
Результати. У роботі запропоновані оптимізаційні моделі, що дозволяють знайти раціональний варіант резервування проектованої системи з урахуванням суперечливих вимог до її надійності й вартості. Ці моделі чисельно реалізуються в операційному середовищі табличного процесора Excel стосовно основного об’єкта, який складається із 7 елементів. Наведені оптимальні варіанти резервування цього об’єкта за схемами «гарячого» й «холодного» роздільного резервування. Наукова новизна. Запропоновані нові розрахункові моделі оцінки надійності резервованих систем, а також розроблені на їх основі оптимізаційні моделі, які сформульовані з використанням розкладання невідомих вихідної задачі структурного резервування на бінарні складові. При цьому отримані оптимізаційні моделі відносяться до класу задач нелінійного математичного програмування з двійковими змінними, для чисельного вирішення яких (навіть за досить великої розмірності) добре пристосовані широко відомі пакети прикладних комп’ютерних програм, зокрема табличний процесор MS Excel. Таким чином, процес вирішення спочатку досить складної задачі оптимального структурного резервування значно спрощується і зводиться до виконання елементарних дій у відповідних програмних інтерфейсах. Практична значимість. Запропоновані розрахункові моделі оцінки надійності резервованих систем, моделі оптимального структурного резервування, а також методологія їх формування з метою спрощення подальшої чисельної реалізації можуть бути корисні при вирішенні задач забезпечення надійності технічних систем на ранніх стадіях їх проектування.

Ключові слова: система; проектування; надійність; структурне резервування; модель; оптимізація; бінарні змінні

с. н. семенец^1*, с. с. насонова^2*, Г. И. семенец^3*

^1*Каф. «Прикладная математика и информационные технологии», Приднепровская государственная академия строительства и архитектуры, ул. Чернышевского, 24-а, Днипро, Украина, 49600, тел. +38 (067) 639 60 64,
эл. почта Ssemenets28@gmail.com, ORCID 0000-0002-6359-1069
^2*Каф. «Высшая математика», Украинский государственный химико-технологический университет, пр. Гагарина, 8, Днипро, Україна, 49005, тел. +38 (097) 940 98 56, эл. почта ms.nasonova.s@gmail.com, ORCID 0000-0002-7228-7499
^3*Каф. «Высшая математика», Днепропетровский национальный университет железнодорожного транспорта имени академика В. Лазаряна, ул. Лазаряна, 2, Днипро, Украина, 49010, тел. +38 (096) 879 48 19, эл. почта semga1952@gmail.com,
ORCID 0000-0003-2693-3282

ОПТИМАЛЬНОЕ СТРУКТУРНОЕ РЕЗЕРВИРОВАНИЕ ТЕХНИЧЕСКИХ СИСТЕМ

Цель. Основная цель статьи – дать проектировщикам высоконадежных технических систем, не обладающим специальными знаниями в области оптимизации и навыками программирования, простой и доступный математический инструмент для выбора оптимального решения при структурном резервировании систем. Методика. В качестве главного показателя надежности резервированной системы принята вероятность ее безотказной работы. Рассмотрены две типовые схемы резервирования: 1) схема раздельного «горячего» резервирования; 2) схема раздельного «холодного» резервирования. Сформулированы расчетные модели оценки надежности резервированных систем. Результаты. В работе предложены оптимизационные модели, позволяющие найти рациональный вариант резервирования проектируемой системы с учетом противоречивых требований к ее надежности и стоимости. Данные модели численно реализуются в операционной среде табличного процессора Excel применительно к основному объекту, состоящему из 7 элементов. Приведены оптимальные варианты резервирования этого объекта по схемам «горячего» и «холодного» раздельного резервирования. Научная новизна. Предложены новые расчетные модели оценки надежности резервированных систем, а также разработанные на их основе оптимизационные модели, которые сформулированы с использованием разложения неизвестных исходной задачи структурного резервирования на бинарные составляющие. При этом полученные оптимизационные модели относятся к классу задач нелинейного математического программирования с двоичными переменными, для численного решения которых (даже при достаточно большой размерности) хорошо приспособлены широко известные пакеты прикладных компьютерных программ, в частности табличный процессор MS Excel. Таким образом, процесс решения изначально весьма сложной задачи оптимального структурного резервирования значительно упрощается и сводится к выполнению элементарных действий в соответствующих программных интерфейсах. Практическая значимость. Предложенные расчетные модели оценки надежности резервированных систем, модели оптимального структурного резервирования, а также методология их формирования с целью упрощения дальнейшей численной реализации могут быть полезны при решении задач обеспечения надежности технических систем на ранних стадиях их проектирования.

Ключевые слова: система; проектирование; надежность; структурное резервирование; модель; оптимизация; бинарные переменные

REFERENCES

1. Afanasev, V. P., & Semenets, G. I. (2006). Reliability of a thin-walled shell under conditions of corrosive wear. Bulletin of Dnipropetrovsk National University of Railway Transport named after Academician V. La-zaryan, 11, 171-174. (in Russin)

2. Aleksandrovskaya, L. N., Aronov, I. Z., & Kruglov, V. I. (2017). Bezopasnost i nadezhnost slozhnykh sistem: uchebnoe posobie. Moscow: Logos. (in Russian)

3. Borodin, A. V. (2015). Tekhniko-ekonomicheskoe obosnovanie varianta rezervirovaniya setevoy komponenty ot-kazoustoychivoy masshtabiruemoy vychislitelnoy sistemy spetsialnogo naznacheniya. Kibernetika i programmirovanie, 6(6), 55-70. doi: 10.7256/2306-4196.2015.6.17523 (in Russian)

4. Kapur, K., & Lamberson, L. (1980). Reliability in engineering design. Moscow: Peace. (in Russian)

5. Kashtanov, V. A., & Medvedev, A. I. (2010). Teoriya nadezhnosti slozhnykh system. Moscow: Fizmatlit. (in Russian)

6. Nasonova, S. S. (2008). The optimization of failure risk in management tasks reliability of steel storage tanks for petroleum products. Bulletin of Dnipropetrovsk National University of Railway Transport named after Academician V. Lazaryan, 20, 126-130. (in Russian)

7. Dorokhov, A. N., Kernozhitskiy, V. A., Mironov, A. N., & Shestopalova, O. L. (2011). Obespechenie nadezhnosti slozhnykh tekhnicheskikh system. Saint Petersburg: Lan. (in Russian)

8. Polovko, A. M., & Gurov, S.V. (2006). Fundamentals of the theory of reliability. Saint Petersburg: BHV. (in Russian)

9. Ryabinin, I. A. (2000). Reliability and safety of structurally complicated systems. Saint Petersburg: Politekhnika. (in Russian)

10. Troshin, A. V. (2017). Optimizatsiya rezervirovaniya v kommutiruemykh paketnykh setyakh.
    Infokommunikatsionnye tekhnologii, 15(4), 354-360. (in Russian)

11. Shishmarev, V. Y. (2018). Nadezhnost tekhnicheskikh sistem: uchebnik dlya bakalavriata i magistratury. Moscow: Yurayt. (in Russian)

12. Chanda, N. (2015). Redundant Transmitting System in Aircraft (RTSA). SAE Technical Paper Series, 2015-01-2443. doi: 10.4271/2015-01-2443 (in English)

13. Jaberipur, G. (2017). Redundant Number System-Based Arithmetic Circuits. In Arithmetic Circuits for DSP Applications (рр. 273-312). Hoboken: John Wiley & Sons. doi: 10.1002/9781119206804.ch8 (in English)

Received: April 30, 2018

Accepted: August 02, 2018

doi : 10.15802/stp2018/141008 © s. n. semenets, s. s. nasonova, G. I. semenets, 2018