ISSN
2307–3489 (Print), ІSSN
2307–6666
(Online)
Наука
та прогрес транспорту. Вісник
Дніпропетровського
національного університету залізничного
транспорту, 2018, № 3 (75)
МОДЕЛЮВАННЯ
ЗАДАЧ ТРАНСПОРТУ ТА ЕКОНОМІКИ
УДК 004.421.2:519.17
В. В. скалозуб1*,
Л. А. Паник2*
1*Каф.
«Компьютерные информационные технологии»,
Днепропетровский
национальный университет железнодорожного
транспорта имени академика В. Лазаряна,
ул. Лазаряна, 2, Днипро, Украина, 49010, тел.
+38 (056) 373 15 35,
эл. почта skalozhubtk@gmail.com,
ORCID 0000-0002-1941-4751
2*Каф.
«Компьютерные информационные технологии»,
Днепропетровский
национальный университет железнодорожного
транспорта имени академика В. Лазаряна,
ул. Лазаряна, 2, Днипро, Украина, 49010, тел.
+38 (056) 373 15 35,
эл. почта leon140377@gmail.com,
ORCID 0000-0003-1343-3000
Реализация
динамических, коНКУРЕНТНЫХ и нечетких
моделей планирования многопродуктовых
потоков в транспортных сетях
Цель.
Главной целью статьи является разработка
новой унифицированной процедуры
планирования нечетких многопродуктовых
и динамических, а также конкурентных
потоков в транспортных сетях и сетевых
информационных системах. Процедура
основана на использовании параллельных
синхронных алгоритмов расчета неоднородных
максимальных потоков. Методика.
В работе предложена
классификация математических моделей
задач по планированию потоков в
транспортных сетях. Исследованы
возможности использования унифицированной
процедуры и параллельного синхронного
алгоритма расчета максимальных
неоднородных потоков для реализации
задач планирования многопродуктовых,
нечетких, динамических и конкурентных
потоков.
Результаты.
Эффективность и универсальность
предложенных методов планирования
неоднородных потоков установлена путем
сравнения полученных в статье результатов
расчетов с известными в литературе.
Разработана унифицированная процедура
и параллельный синхронный алгоритм для
планирования нечетких
многопродуктовых, динамических и
конкурентных потоков в транспортных
сетях, а также реализованы задачи
оптимального распределения этих потоков
в транспортных сетях. Научная
новизна. В статье
разработана новая унифицированная
процедура планирования нечетких
многопродуктовых, динамических и
конкурентных потоков в транспортных
сетях информационных систем, использующая
параллельные синхронные алгоритмы
расчетов максимальных потоков. Процедура
позволяет вычислить локальные экстремумы
моделей оптимального распределения
потоков. Практическая
значимость. Практическая
ценность полученных результатов
определяется унифицированными
возможностями и эффективностью процедуры
и параллельного синхронного алгоритма,
предназначенного для расчета максимальных
многопродуктовых потоков в транспортных
сетях. Разработанная процедура
обеспечивает возможность решения задач
анализа и планирования многопродуктовых
потоков в сетях для динамических,
нечетких и конкурентных моделей
распределения транспортных и информационных
потоков.
Ключевые
слова: транспортные
сети; модели планирования;
максимальные неоднородные потоки;
нечеткие и динамические потоки;
конкурентные информационные потоки;
параллельные алгоритмы
Введение
В различных
современных сферах деятельности
(транспортные, энергетические и сетевые
информационные структуры и т. д.
[6, 8, 12]) чрезвычайно широко распространенными
являются задачи анализа и оптимального
планирования и управления потоками в
сетях [2, 3, 14] или задачи,
приведенные к ним. Отметим, что на
практике во многих случаях потоки в
транспортных и других сетях являются
неоднородными, динамическими (существенный
срок передачи, изменение параметров
сети по периодам суток [2, 7, 11]), с
неопределенными параметрами (пропускная
способность ребер сети, действительные
условия передачи потоков [2, 13]).
Неоднородные потоки в сетях могут
содержать объекты с различными свойствами
по функциональному назначению,
требованиям к процессу транспортировки,
сервисам и др. [3, 4]. Развитие сетевых
технологий также требует совершенствования
методов управления потоками.
В связи с необходимостью
передачи и обработки все возрастающих
объемов информации важное значение
приобретают вопросы организации и
оптимизации функционирования сетевых
информационных систем (СИС) [2, 11]. В
СИС присутствует неопределенность,
вызванная рядом факторов: невозможностью
точных измерений значений информационных
потоков (ИП); влияние внешней среды на
параметры элементов структуры СИС; при
оценках функционирования СИС неизвестны
требования пользователей к передаче
ИП [4]. При изменяющихся требованиях к
процессу передачи ИП внутри СИС, а также
конфликтах между ИП, снижается
эффективность функционирования СИС.
Поиск эффективных распределений ИП в
СИС (с учетом требований множества
клиентов, динамических параметров
потоков, неопределенности пропускных
способностей элементов СИС, объемов
передаваемых информационных потоков
и др.) является актуальной задачей
управления СИС. В [2] разработана
процедурная модель распределения ИП
в СИС на основе совместного использования
вполне полиномиальной аппроксимационной
схемы (FPTAS) [8] и генетического алгоритма.
Модель обеспечивает решение задачи
определения максимального конкурентного
потока путем разрешения конфликтов
между потоками. В [2, 11] исследованы
оптимизационные задачи о потоках в
нечетких сетях применительно к
транспортным и энергетическим структурам.
Задачи нахождения
максимального потока и потока
минимальной стоимости в транспортных
сетях (ТС) широко освещались [6, 10, 14]. При
учете факторов неопределенности
(пропускные способности, стоимости
перевозок и др.) возникают менее
исследованные потоковые задачи в
нечетких условиях [7, 11, 14]. При учете
затрат времени, а не мгновенного
прохождения потока по дугам сети,
получают «стационарно-динамические»
модели задач [2, 11], а при изменениях
параметров ТС во времени получают
динамические модели задач о потоках.
В [7] исследована задача расчета потока
минимальной стоимости в нечеткой
динамической ТС, которая решается на
основе предложенного авторами алгоритма
и процедуры «растяжения вершин графа
во времени». В динамической ТС
требовалось переместить определенное
число единиц потока с минимальными
затратами так, чтобы последний элемент
вошел в сток в момент времени не позднее
заданного.
Цель
Развитие методов
и средств анализа свойств элементов
потоков, а также создание современных
информационно-коммуникационных
технологий и систем дают возможность
для все более полного учета требований
отдельных категорий объектов транспортных
потоков, а также параметров их
взаимодействия.
Целью статьи является
разработка новой унифицированной
процедуры планирования нечетких
многопродуктовых и динамических, а
также конкурентных потоков в транспортных
сетях и сетевых информационных системах.
Для достижения поставленной цели
необходимо решить следующие задачи:
разработать классификацию моделей
взаимодействия транспортных потоков;
разработать унифицированный параллельный
синхронный алгоритм расчета максимального
потока в транспортных сетях; реализовать
нечеткие динамические модели планирования
многопродуктовых потоков в транспортных
сетях; разработать конкурентные модели
планирования многопродуктовых потоков.
Методика
Анализ публикаций
позволил классифицировать математические
модели взаимодействия транспортных
потоков.
В табл. 1 приведена
классификация математических моделей
задач о потоках в транспортных сетях
с учетом числа «серверов» и «клиентов»
(отдельных потоков или продуктов).
Другими характеристиками
моделей (табл. 1) являются свойства
их параметров (детерминированные,
стохастические, интервальные, нечеткие,
неоднородно-неопределенные [3, 4]),
временные характеристики (статические,
стационарно-динамические, динамические).
Учет специфических
категорий требований или свойств
объектов транспортных потоков существенно
влияет на содержание и сложность
соответствующих моделей и методов их
анализа и планирования [3, 6, 12]. В табл.
2 представлены данные, характеризующие
возрастающую сложность математических
моделей детерминированных потоковых
задач в ТС. Классы моделей можно
развивать, учитывая динамические
свойства ТС, различные виды условий
неопределенности параметров ТС и
данных.
Таблица 1
Классификация
моделей взаимодействия транспортных
потоков
Table
1
Classification
of models of transport flows interaction
|
Свойства
Тип
взаимодействия
|
Инфраструктура
(сервисы)
|
Клиенты
(потоки)
|
Примеры
моделей
|
|
Т1
|
1
|
1
|
Однопродуктовые
потоки
|
|
Т2
|
1
|
n
|
Многопродуктовые
потоки
|
|
Т3
|
m
|
1
|
Конкуренция
за потоки
|
|
Т4
|
m
|
n
|
Кооперация
(поездка с пересадками)
|
Представленная
классификация задач анализа транспортных
потоков исходит из свойств математических
моделей и алгоритмов реализации. Все
последующие классы включают требования
предыдущих, дополняя их специальными
условиями, указанными в табл. 2.
В
исследованиях [10, 12, 14] описан широкий
круг алгоритмов анализа и планирования
потоков в транспортных и других сетях,
среди них также указаны алгоритмы
расчета максимальных потоков. Эти
исследования в большинстве рассматривают
однородные потоки. В то же время
отмечается, что задачи совершенствования
и развития методов анализа и планирования
неоднородных потоков в ТС становятся
все более актуальными.
Таблица 2
Классы
математических моделей задач анализа
транспортных потоков
Table
2
Classes
of mathematical models of traffic flow analysis tasks
|
Класс
модели
|
Название
|
Условия
потоков
|
Свойства
|
Модель
|
|
К1
|
Однопродуктовые
|
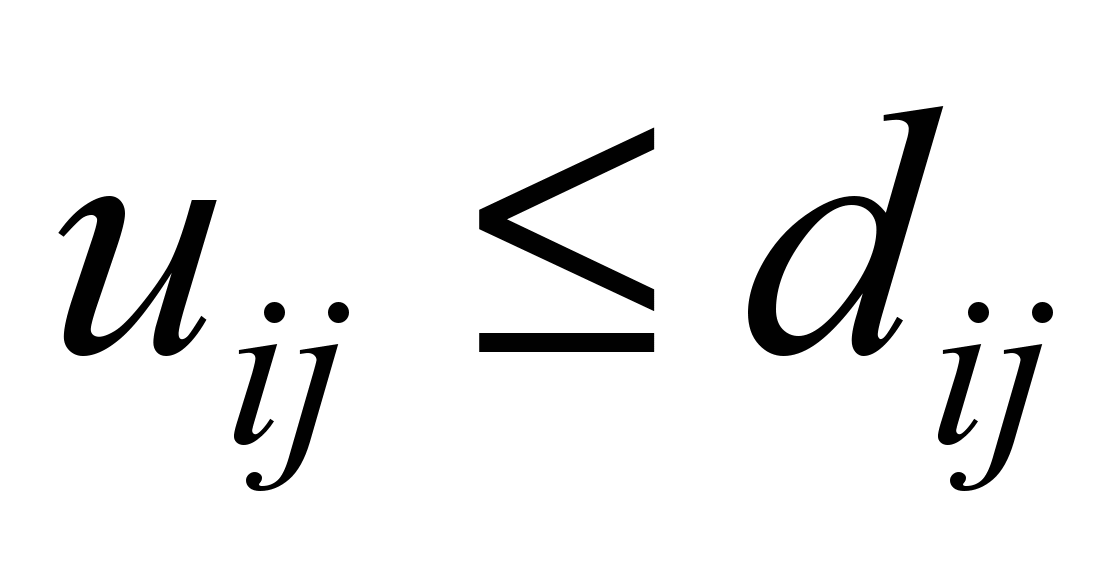
|
Неразрывность
потока
|
Минимальный
разрез
|
|
К2
|
Многопродуктовые
|
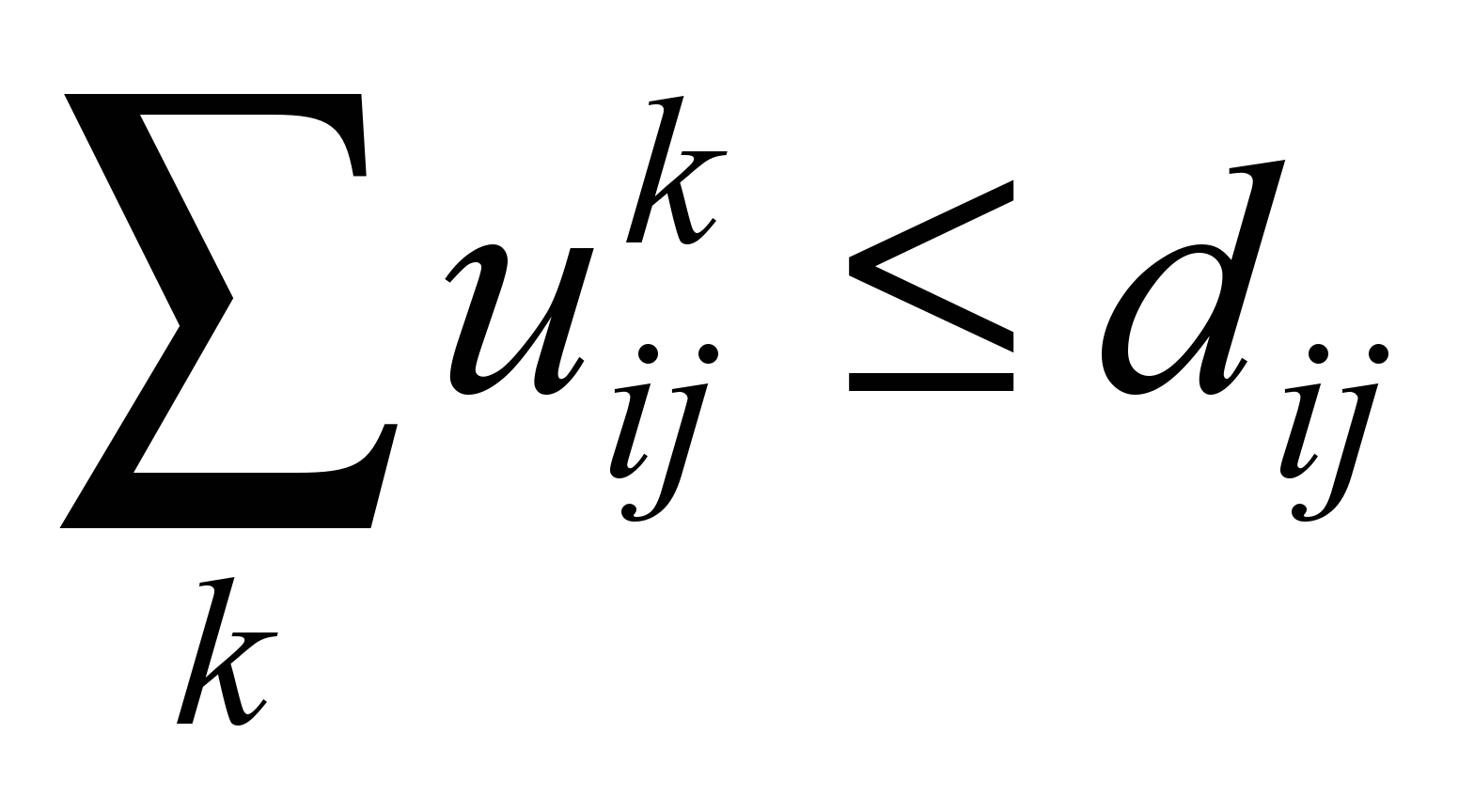
|
Множество
сетей для потока
|
Минимальное
разделяющее множество
|
|
К3
|
Компромиссные
многопродуктовые
|
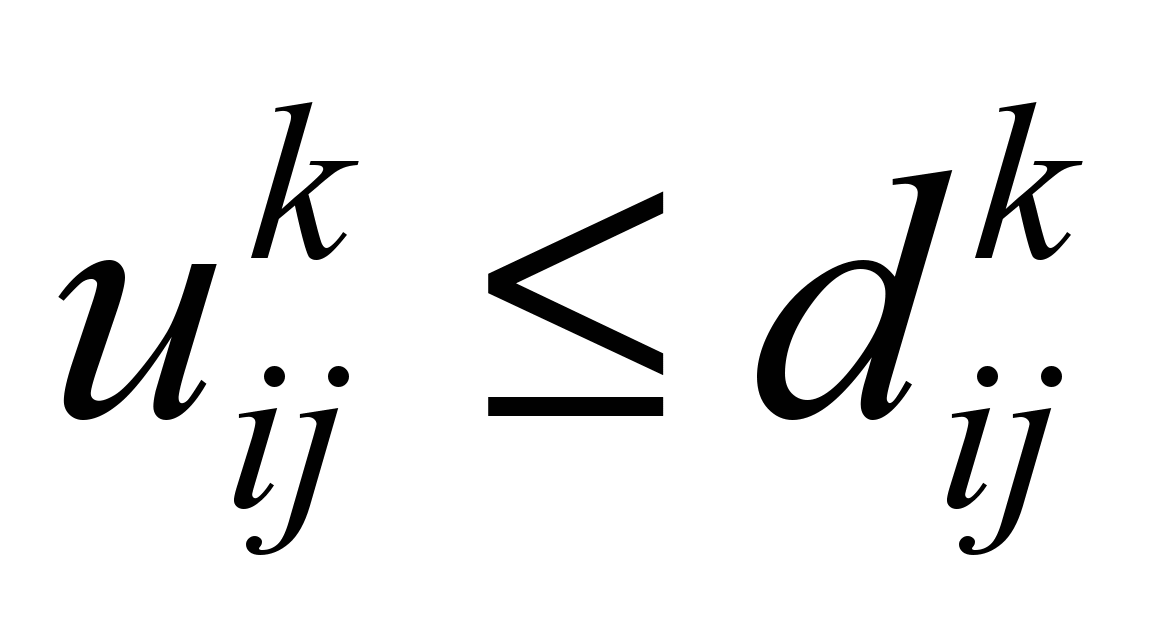
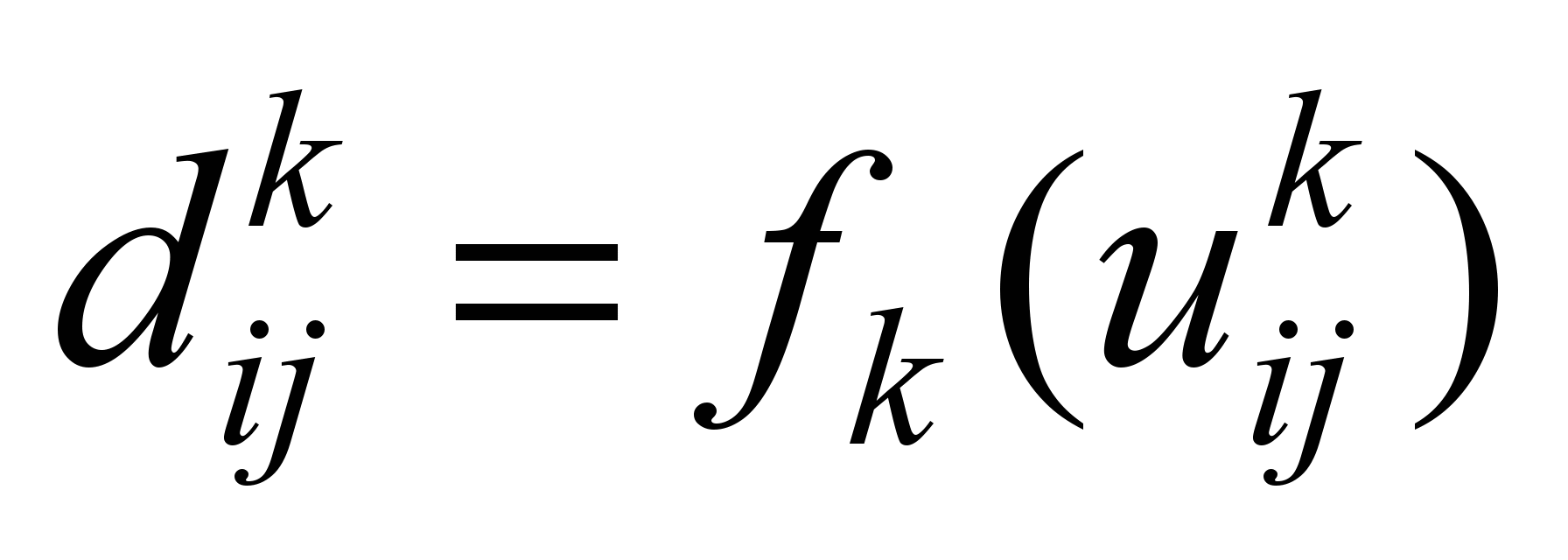
|
Сепарабельность
ограничений потоков
|
Компромисс
потоков на дугах
|
|
К4
|
Структурные
требования к потокам продуктов
|
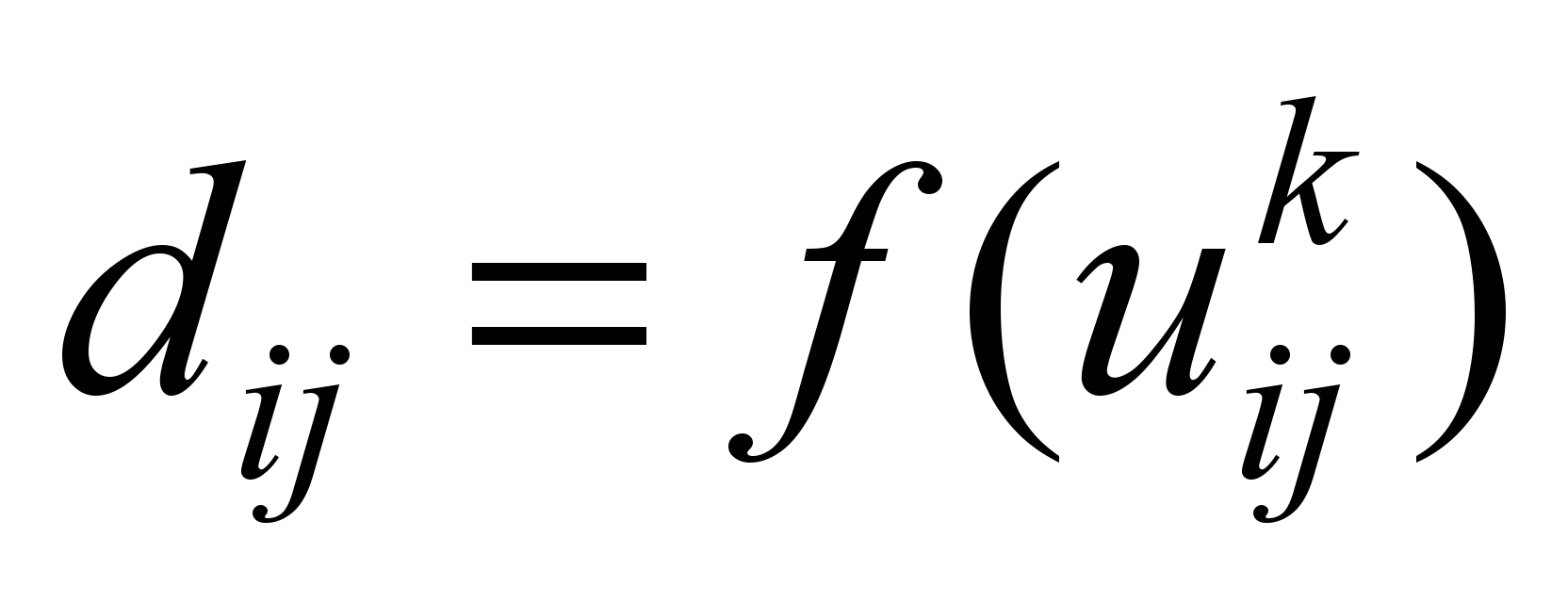
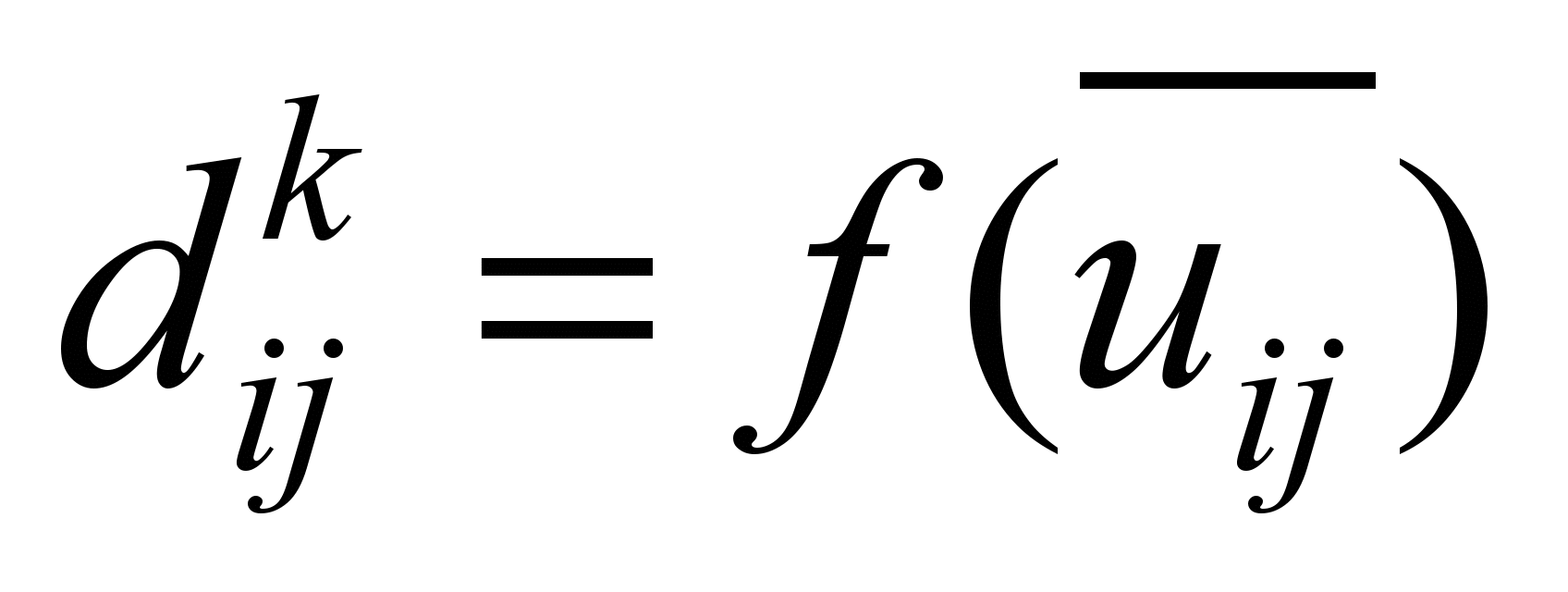
|
Несепарабельность
связей в потоках
|
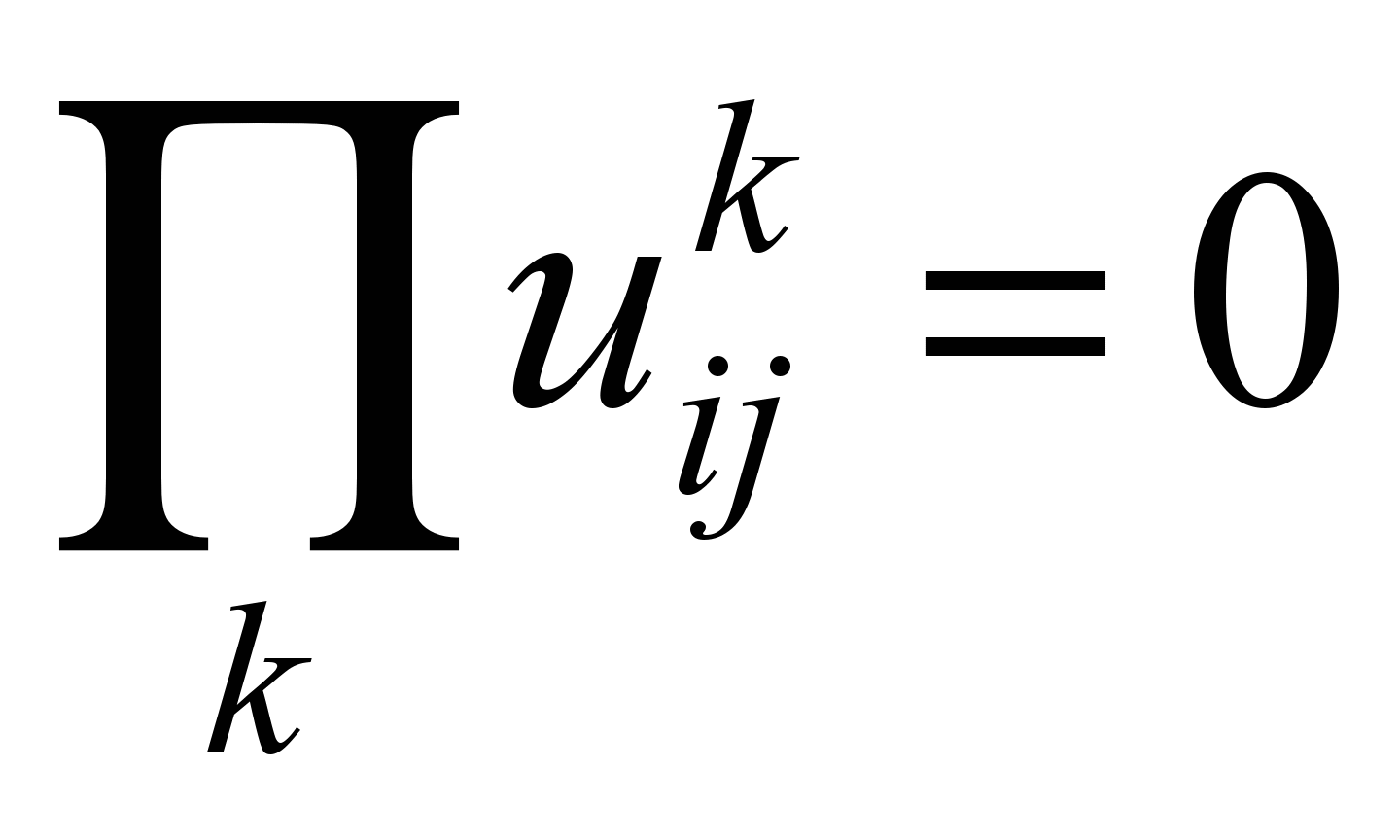
|
Среди задач анализа
и планирования потоков в ТС выделяется
задача по определению максимальных
потоков в качестве основы при формировании
и анализе ТС, результаты которой широко
применяются на практике [1, 6, 10, 14].
В связи с всесторонним
развитием сетевых технологий, созданием
и функционированием интеллектуальных
транспортных систем (ИТС) [3] формируются
новые задачи оптимального планирования
неоднородных транспортных потоков
(многопродуктовые, многокритериальные,
с учетом индивидуальных потребностей
элементов-носителей потоков и др.) [3,
4], которые все больше учитывают требования
отдельных участников потоков. Решение
таких задач базируется на определении
наборов количественных и качественных
оценок свойств сетей. Реализация
многопродуктовых, компромиссных,
динамических и др. моделей планирования
потоков в ТС [1, 5, 6] использует расчеты
максимальных потоков, потоков минимальной
стоимости, анализ разделяющих множеств
ребер ТС и т. д. [1, 2], что требует
применения отдельных численных методов
и алгоритмов. В работе [5] предложен
новый унифицированный параллельный
синхронный алгоритм анализа и планирования
потоков (ПСАП) в ТС, пригодный для
реализации различных классов моделей
потоков. Этот алгоритм применен для
расчета максимальных одно- и
многопродуктовых потоков. В предлагаемой
статье ПСАП применяется для исследования
нечетких динамических и конкурентных
моделей планирования многопродуктовых
потоков в ТС.
Задача расчета
максимального потока (МП) в ТС является
достаточно затратной, также существуют
определенные структуры сетей, для
которых известные алгоритмы имеют
слабую сходимость [1, 10]. Отметим, что в
настоящее время существует более
двадцати алгоритмов для расчета
максимальных потоков в сетях, среди
которых наиболее распространены
алгоритмы Форда–Фалкерсона,
Эдмондса–Карпа, Диница [1]. При анализе
многопродуктовых (неоднородных) потоков
сложности построения и реализации
алгоритмов оценки параметров максимальных
потоков существенно возрастают [2, 6,
8].
Формально ТС – это
ориентированный
граф G = (V, E), в котором
каждое ребро (u, v) имеет положительную
пропускную способность c (u, v) > 0
и поток f (u, v) [1, 6]. Выделяют две
вершины (исток
s и сток t) такие, что любая другая
вершина сети лежит на пути из вершины
s к вершине t. Обозначим через
G = ((V, E),
c, s, t)} (1)
транспортную
сеть (далее сеть), в которой c (u, v)
– пропускная способность; f (u, v)
– поток через ребро (u, v); V –
множество узлов, E – множество
ребер.
Параллельный
синхронный алгоритм анализа параметров
максимальных потоков в сетях (ПСАП),
подобно алгоритму Эдмондса–Карпа
(А–ЭК) [1], использует стратегию поиска
в ширину при одновременном определении
возможных путей потоков через сеть с
известными на определенном шаге расчета
пропускными способностями дуг (ребер)
остаточной сети (ОС). ОС формируется
итерациями, как сеть, пропускные
способности ребер которой модифицируются
на основе величин определенных и
увеличивающих потоков [1, 6]. В А–ЭК на
каждой итерации в построенном дереве
возможных путей выбирается кратчайший
по числу ребер путь, по которому
пропускается дополнительный увеличивающий
поток. В отличии от А–ЭД и других
подобных алгоритмов, в предлагаемом
ПСАП за счет синхронизации процессов
формирования узлов дерева в них также
одновременно выполняется анализ
возможных значений дополнительных,
увеличивающих потоков, которые могут
распространяться по следующим ребрам
ОС. При этом возникает возможность
параллельно (на одной итерации) выполнять
анализ нескольких увеличивающих потоков
через ОС.
В работе принято,
что узловые процедуры могут выполняться,
если к ним по схеме сети (1) поступили
все входящие потоки. Для управления
процессами синхронизации узловых
процедур вводится шаговый параметр
поступления потоков
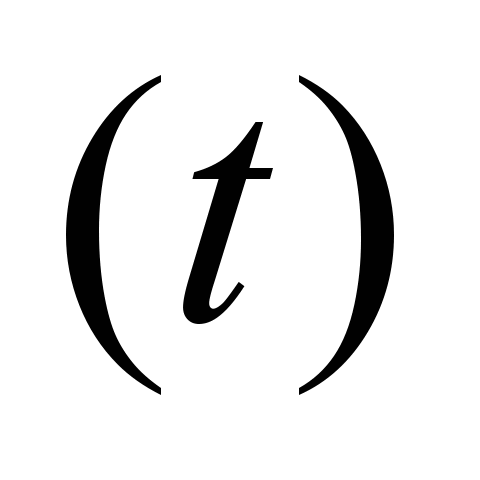 .
Значение параметра указывает «длину
в шагах
.
Значение параметра указывает «длину
в шагах
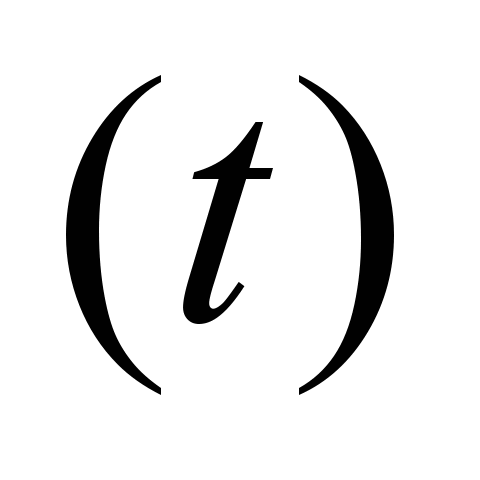 »
пути от истока до соответствующего
узла в ОС. Узлам транспортной сети
назначают состояния в зависимости от
этапов расчета потоков. Сначала все
узлы имеют состояние «Ожидает». Если
на этапе
»
пути от истока до соответствующего
узла в ОС. Узлам транспортной сети
назначают состояния в зависимости от
этапов расчета потоков. Сначала все
узлы имеют состояние «Ожидает». Если
на этапе
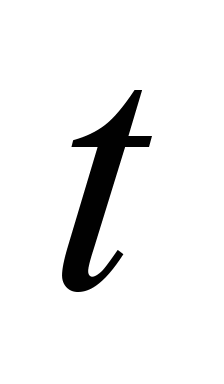 к узлу поступил некоторый входной
поток, узел переходит в состояние
«Активный», а при поступлении всех
входных потоков становится «Готов».
При этом параллельно выполняется вызов
всех выходных узлов, передавая им
рассчитанные параметры возможных
потоков по соответствующим путям. После
передачи потоков сам узел переходит в
состояние «Выполнено», а число активных
узлов в сети
к узлу поступил некоторый входной
поток, узел переходит в состояние
«Активный», а при поступлении всех
входных потоков становится «Готов».
При этом параллельно выполняется вызов
всех выходных узлов, передавая им
рассчитанные параметры возможных
потоков по соответствующим путям. После
передачи потоков сам узел переходит в
состояние «Выполнено», а число активных
узлов в сети
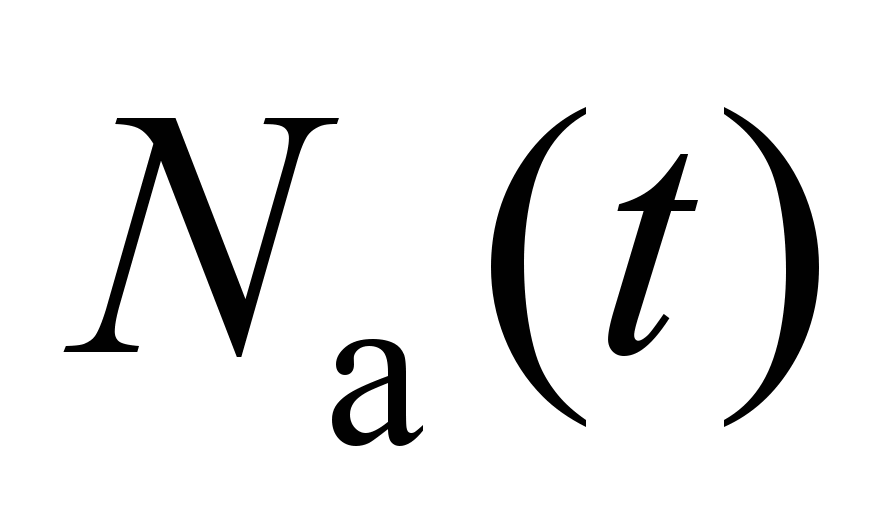 уменьшается на единицу. Система
синхронизации контролирует число
активных узлов на шаге
уменьшается на единицу. Система
синхронизации контролирует число
активных узлов на шаге
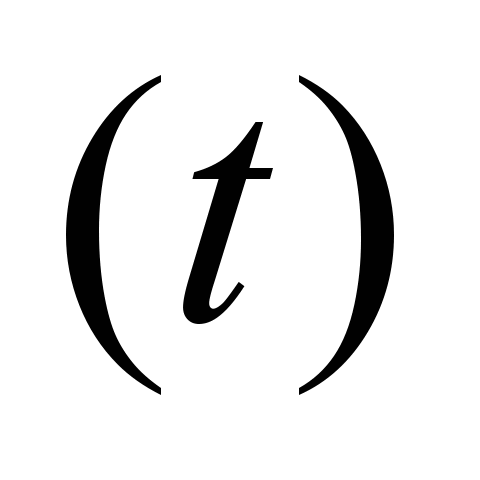 .
По параметру
.
По параметру
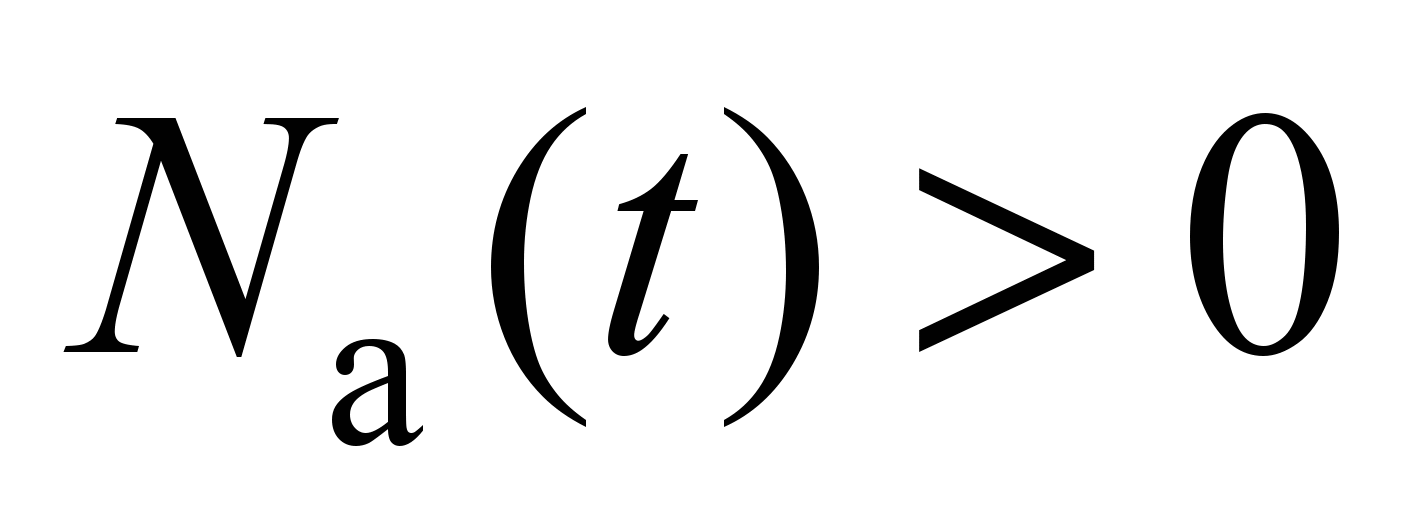 также выполняется контроль возможного
блокирования процессов формирования
маршрутов через ОС. Блокировка
синхронизированных потоков возникает,
если в ТС нет ни одного узла, к которому
на шаге
также выполняется контроль возможного
блокирования процессов формирования
маршрутов через ОС. Блокировка
синхронизированных потоков возникает,
если в ТС нет ни одного узла, к которому
на шаге
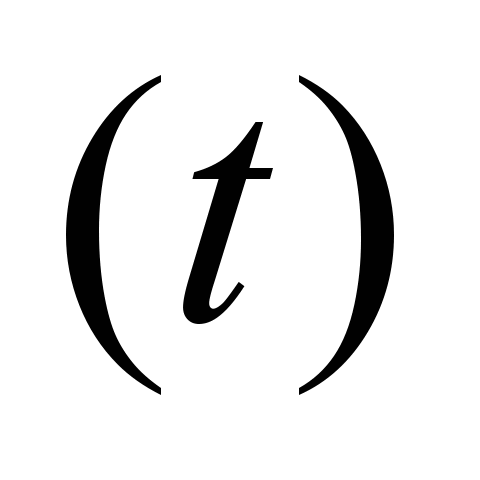 поступили все входящие потоки, то
есть в состоянии «Готов». В таком случае
предусмотрена передача синхронизирующего
потока «нулевого» объема. Выбор узла
для разблокировки синхронизированных
потоков определяется по следующим
признакам: минимальное количество
отсутствующих входных потоков, при
равенстве – минимальность номера шага
активизации процедуры
поступили все входящие потоки, то
есть в состоянии «Готов». В таком случае
предусмотрена передача синхронизирующего
потока «нулевого» объема. Выбор узла
для разблокировки синхронизированных
потоков определяется по следующим
признакам: минимальное количество
отсутствующих входных потоков, при
равенстве – минимальность номера шага
активизации процедуры
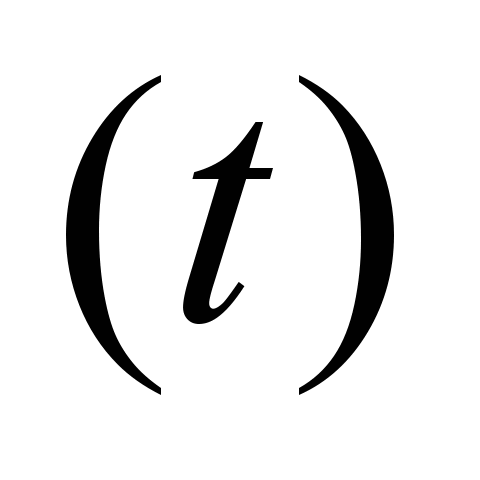 ,
при равенстве этих параметров – меньшее
количество выходных узлов. Возникновение
отмеченных процессов блокировки может
быть при анализе многопродуктовых
потоков. В дальнейших процедурах
синхронизирующий поток учитывается в
алгоритме, как и все остальные.
,
при равенстве этих параметров – меньшее
количество выходных узлов. Возникновение
отмеченных процессов блокировки может
быть при анализе многопродуктовых
потоков. В дальнейших процедурах
синхронизирующий поток учитывается в
алгоритме, как и все остальные.
В статье [5] разработаны
параллельные синхронные алгоритмы, а
также приведены примеры расчета
максимальных однопродуктовых и
многопродуктовых потоков (МПСАП) в ТС.
Алгоритмы расчета многопродуктовых
потоков часто формируют решения путем
поочередного расчета общего потока
через ТС [6]. Пример компромиссного
потока двух продуктов (рис. 1) показывает
дополнительные возможности применения
ПСАП, который выполняет одновременный
анализ потоков всех продуктов. За счет
этого можно применять различные модели
компромиссного анализа потоков продуктов
на ребрах ТС. На рис. 1 приведена схема
сети для пропуска двух продуктов с
заданными величинами пропускных
способностей дуг.
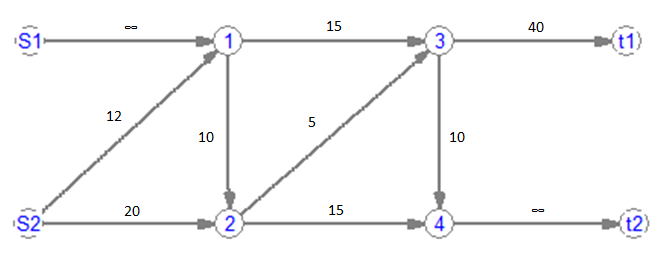
Рис.
1. Схема сети для расчета максимального
и компромиссного потоков двух
продуктов
Fig.
1. Network diagram for calculating
the maximum and trade-off
flows of two products
При применении
классических алгоритмов [1, 6] получают
различные структуры максимальных
потоков продуктов S1 и S2 в
зависимости от очередности их
распределения. Например, максимальный
поток продуктов Р1 (S1) и Р2
(S2) при расчете от S1 является
следующим:
Р1:
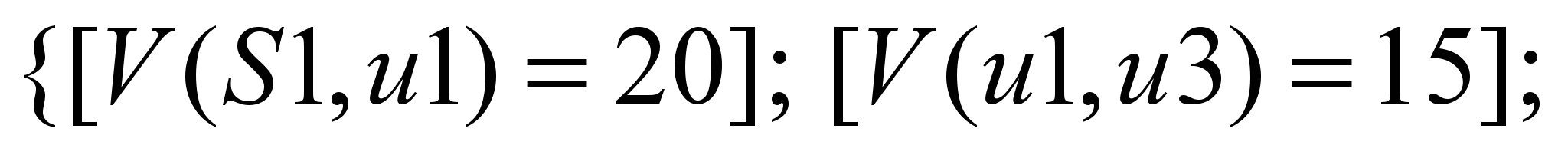
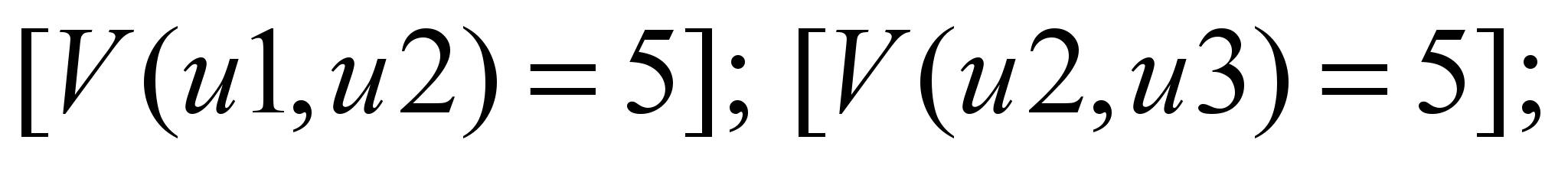

Р2:
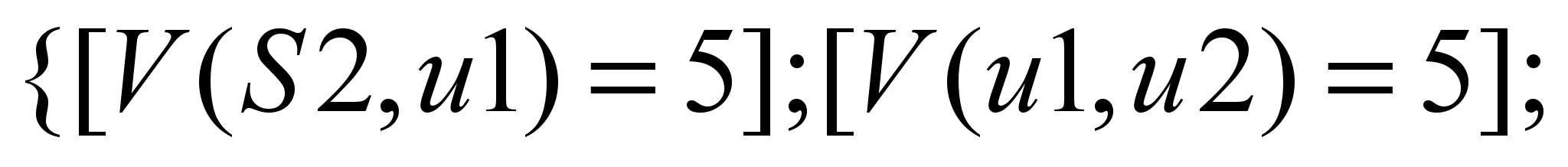
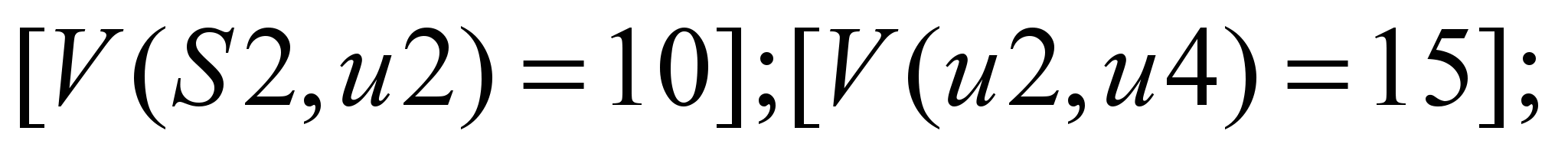
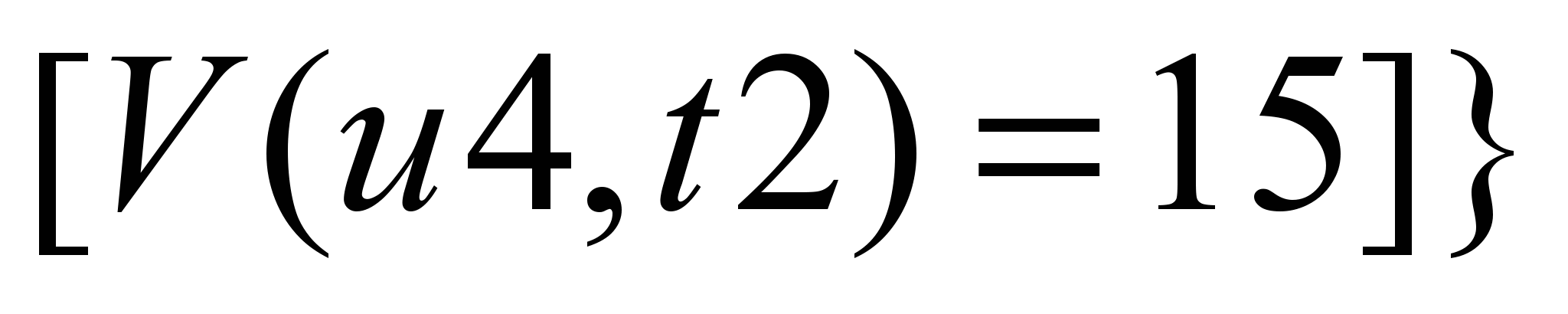 .
.
При
расчете от S2, максимальный
двухпродуктовый поток следующий:
Р1:
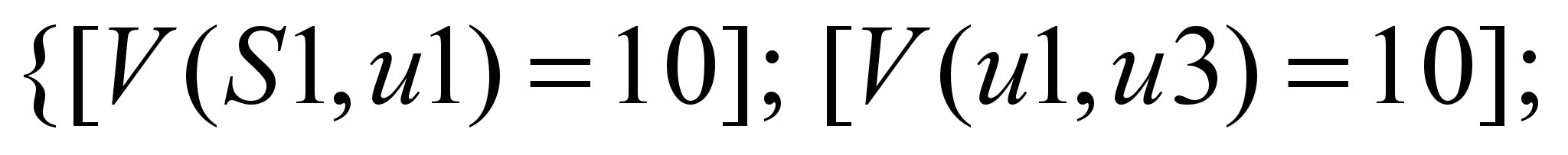
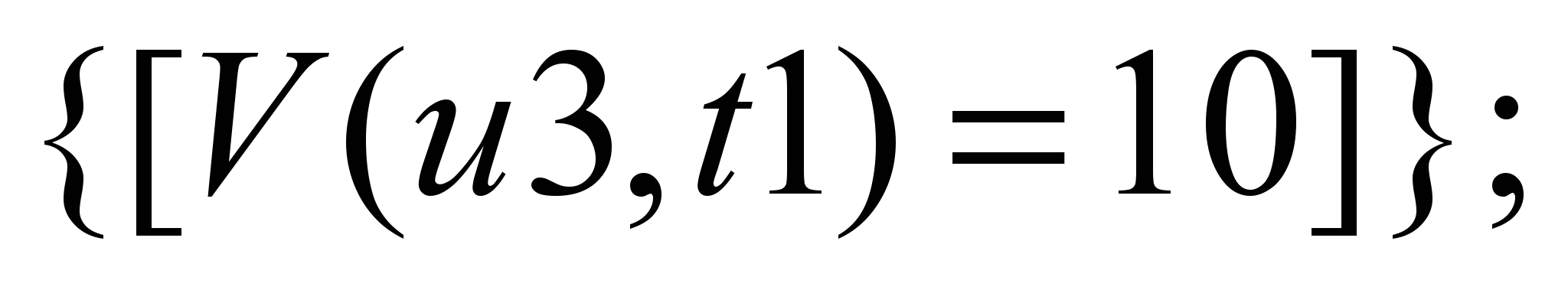
Р2:
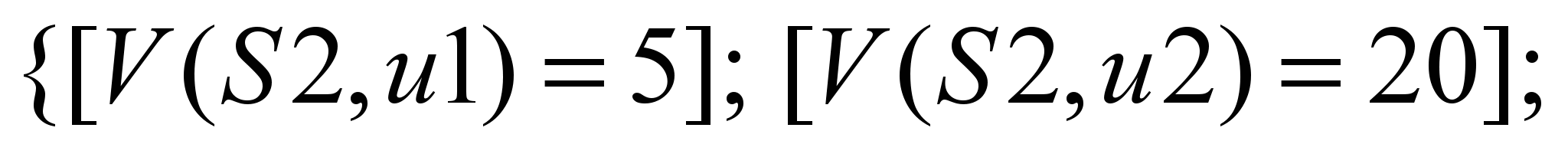
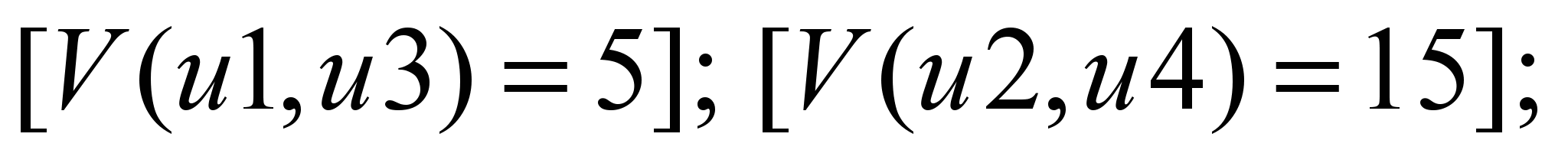
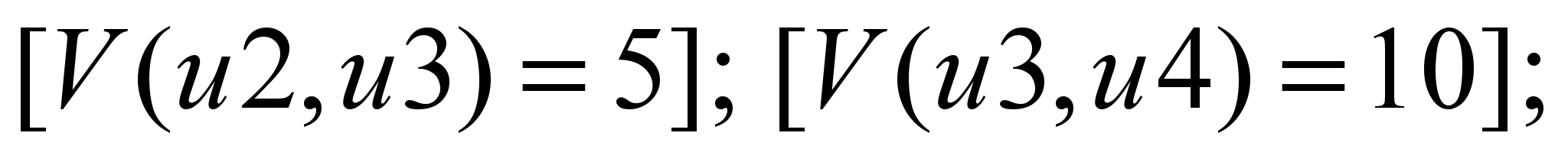
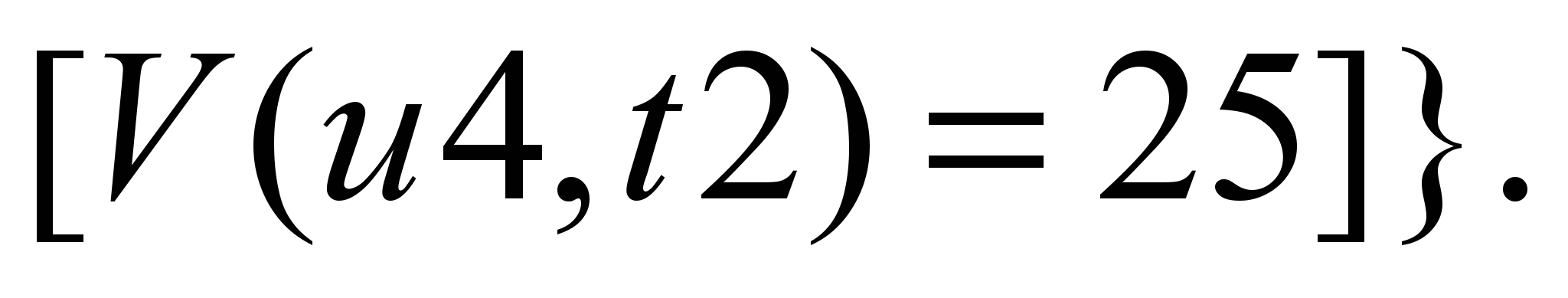
В обоих вариантах
максимальный поток через ТС равен 35,
но имеет существенно различную структуру.
Такие варианты могут быть не приемлемыми
в условиях конкуренции потоков продуктов
Р1 (S1) и Р2 (S2). Поэтому
даже для двух продуктов применения
известных алгоритмов в условиях модели
компромисса как равноценности дает
существенно разные, многозначные,
решения. Алгоритм МПСАП позволяет
одновременно формировать решения для
всех продуктов отдельно, а при анализе
компромиссного множества ребер
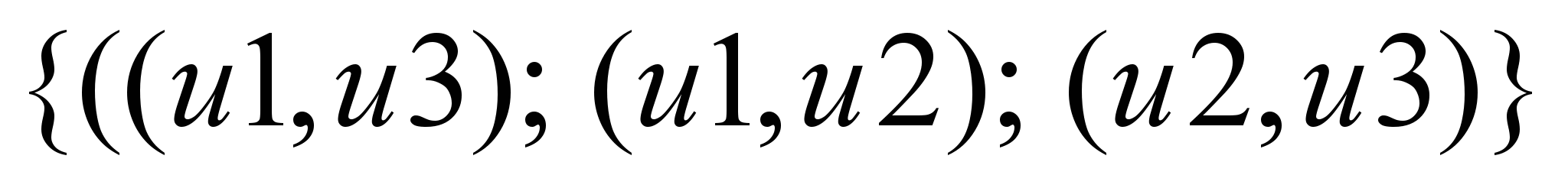 применять нужные модели выбора
решений. Реализацию компромиссных
потоков представлено в следующих
разделах.
применять нужные модели выбора
решений. Реализацию компромиссных
потоков представлено в следующих
разделах.
Результаты
Рассмотрим применение
МПСАП к нечеткой многопродуктовой
модели планирования потоков в ТС (рис.
1).
Таблица 3
Нечеткие
пропускные способности дуг
Table
3
Fuzzy
carrying capacities of the arcs
|
Нечеткие
пропускные способности по дугам
графа
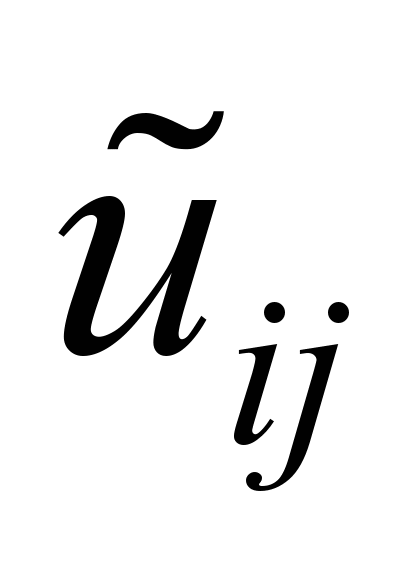 ,
ед. ,
ед.
|
|
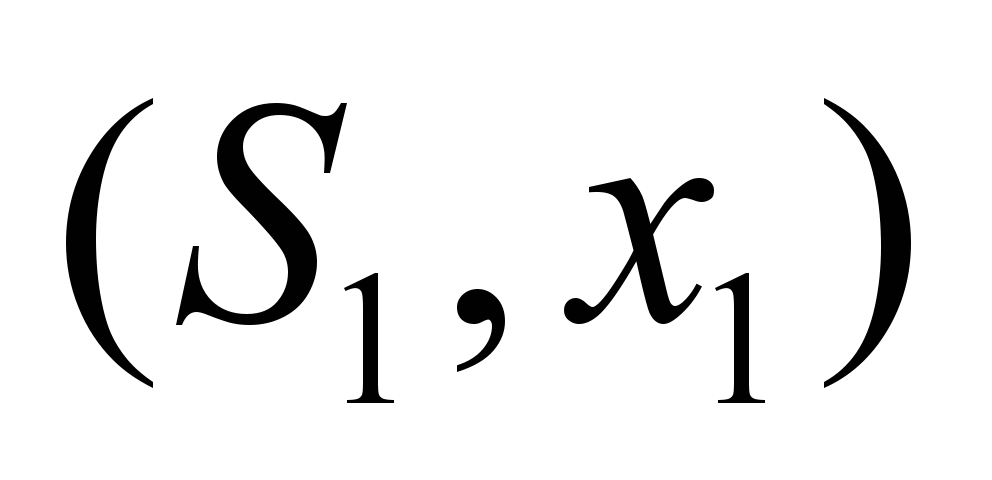
|
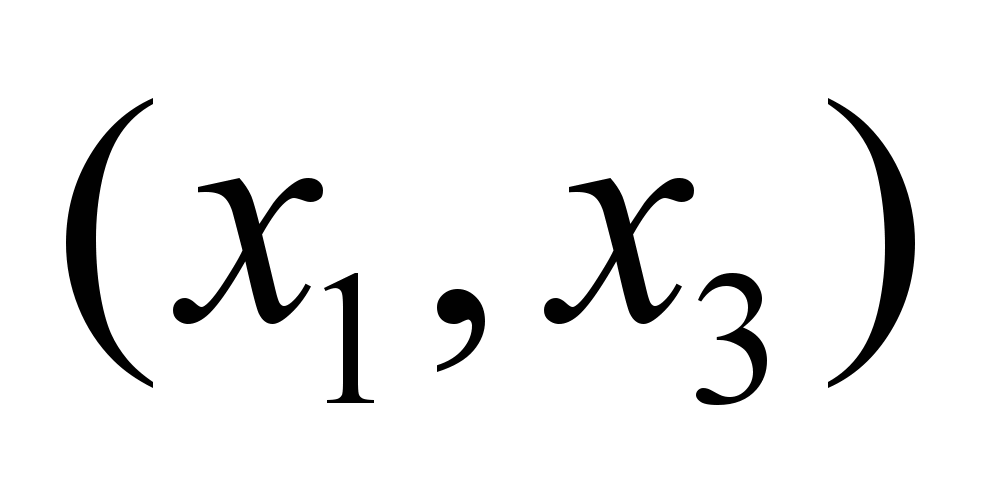
|
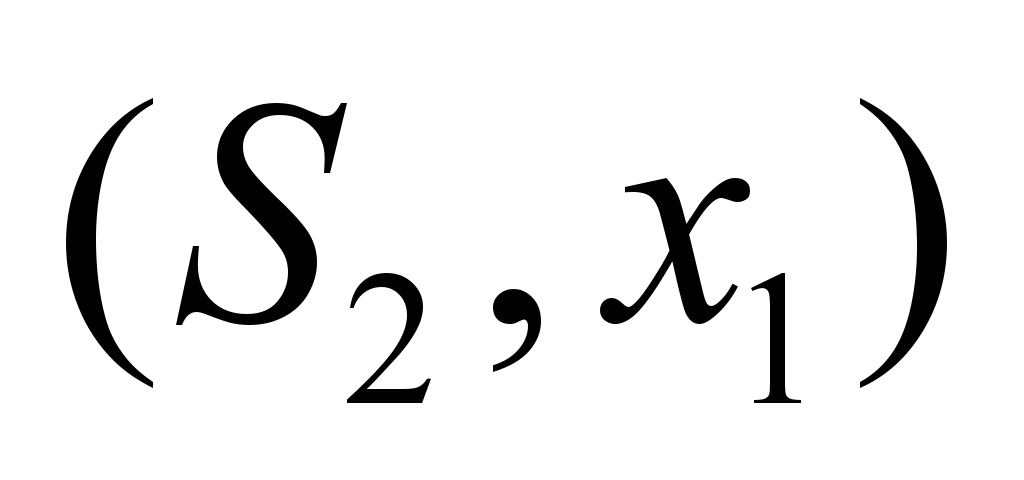
|
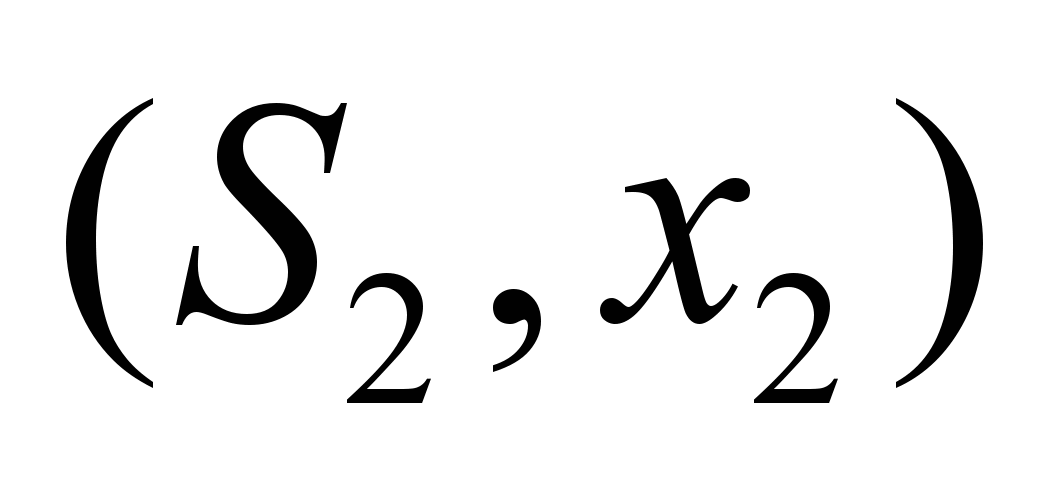
|

|
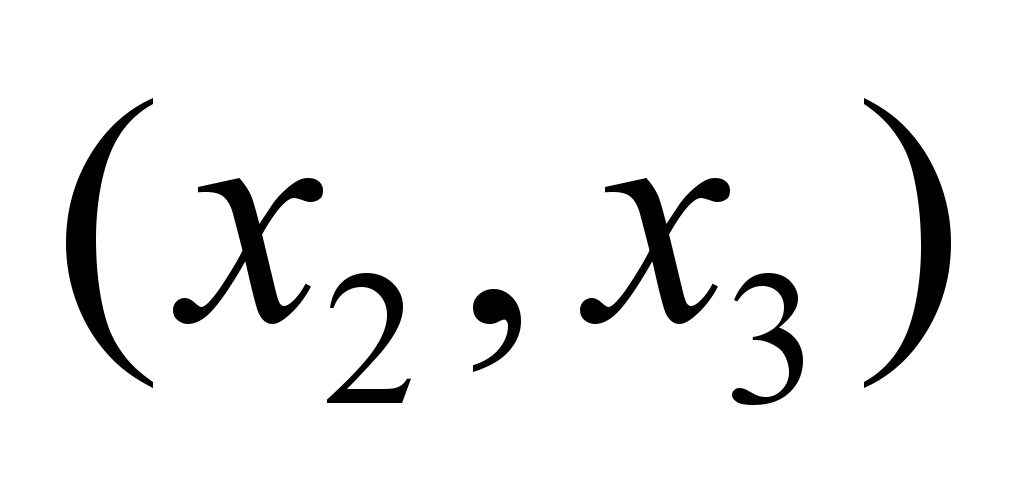
|
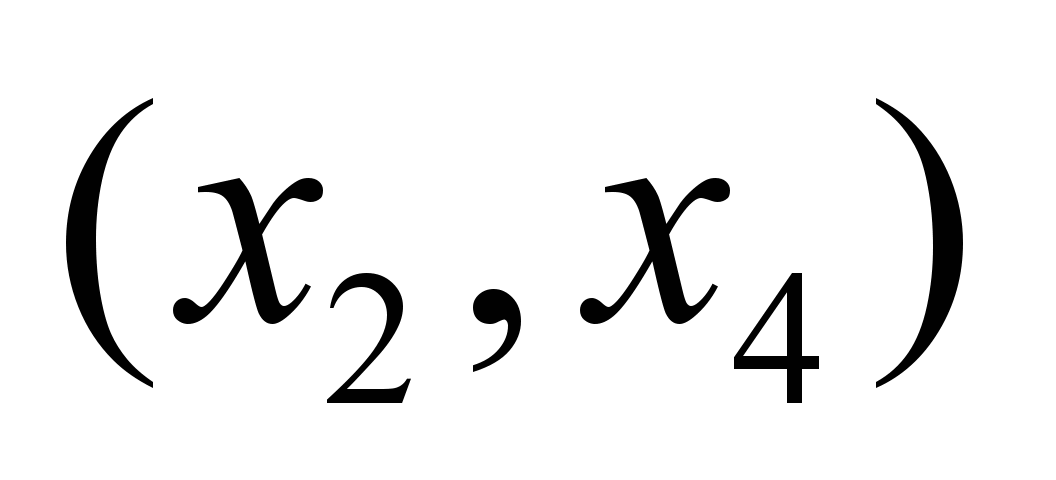
|
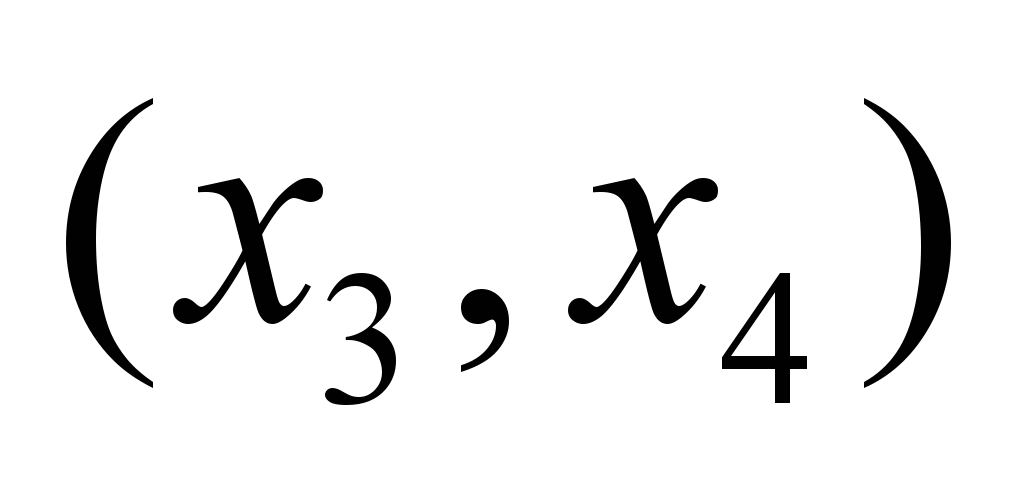
|
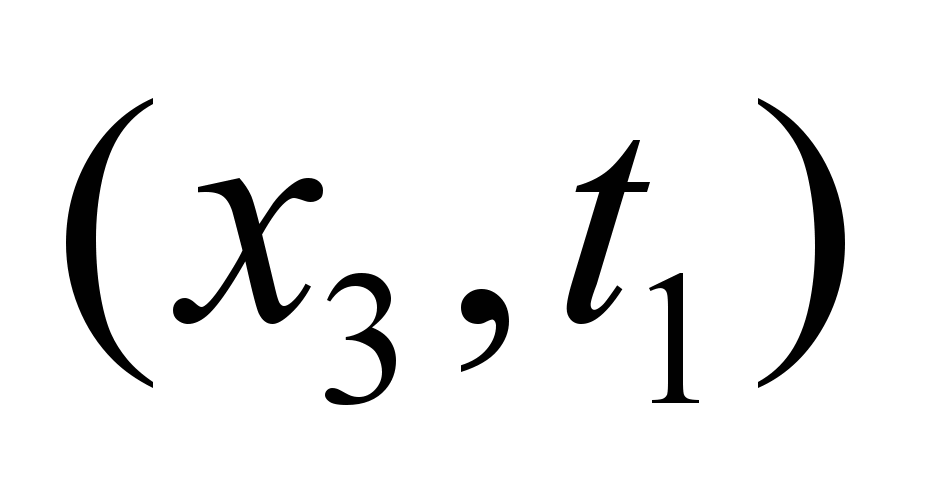
|
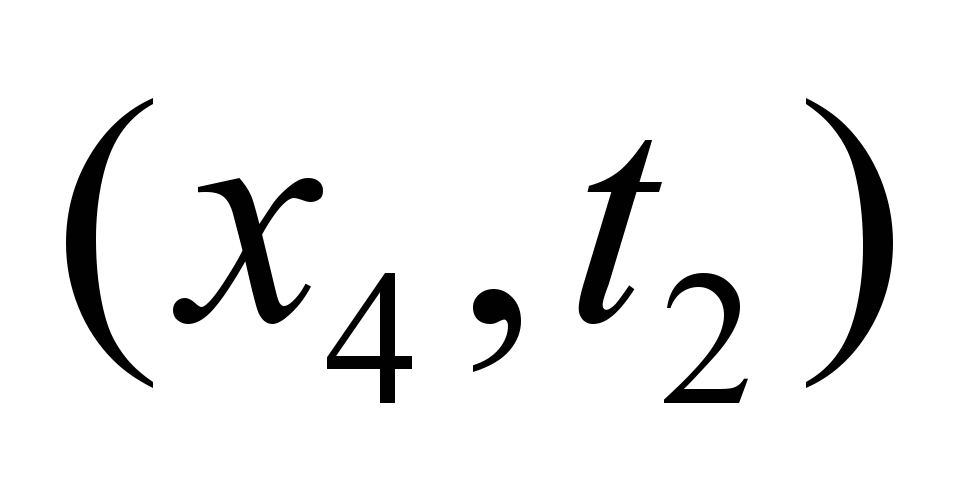
|
|
|
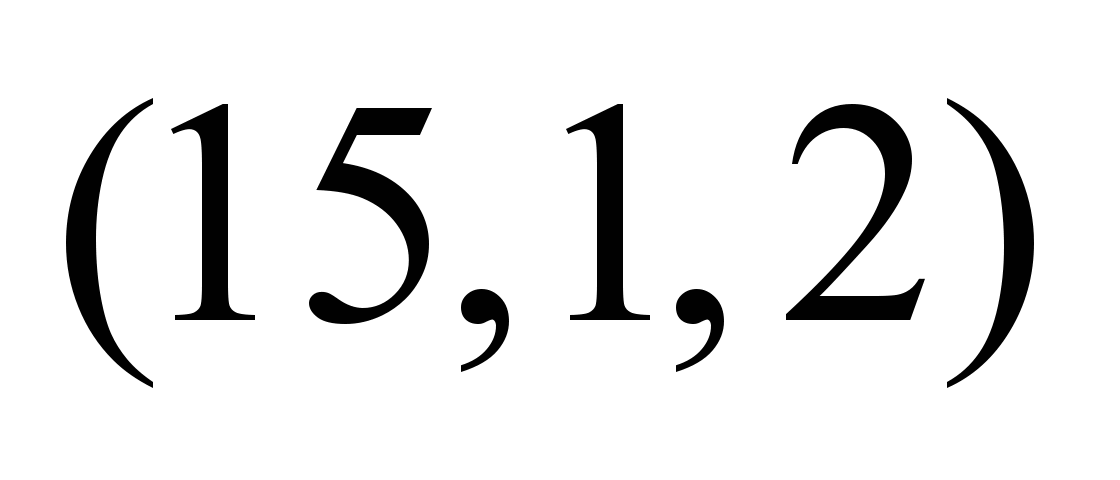
|
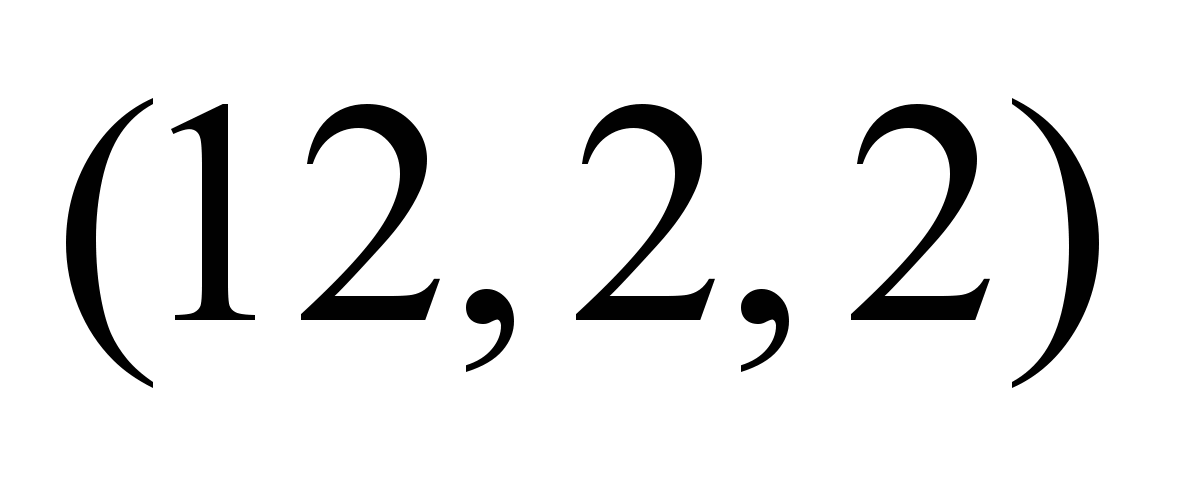
|
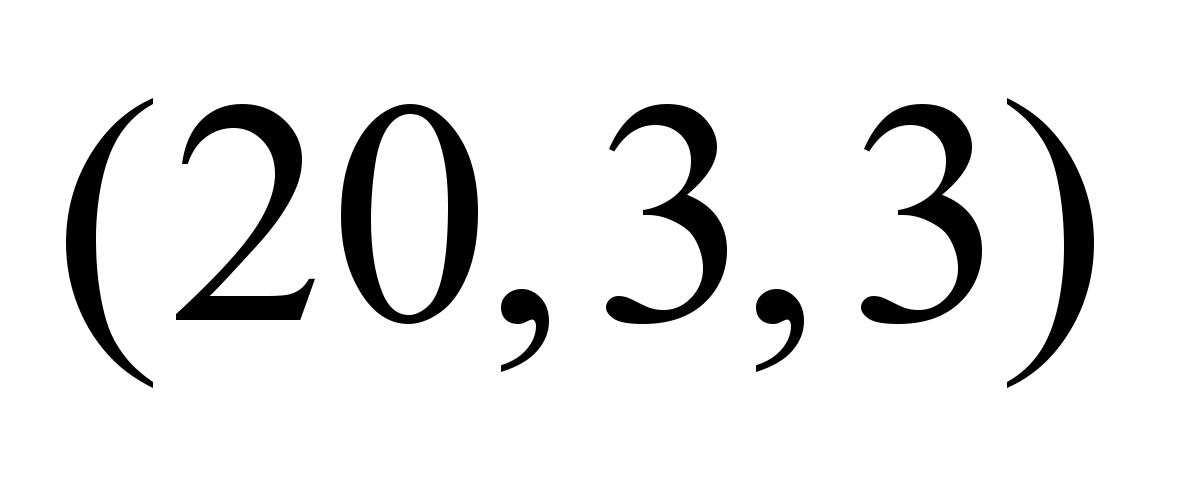
|
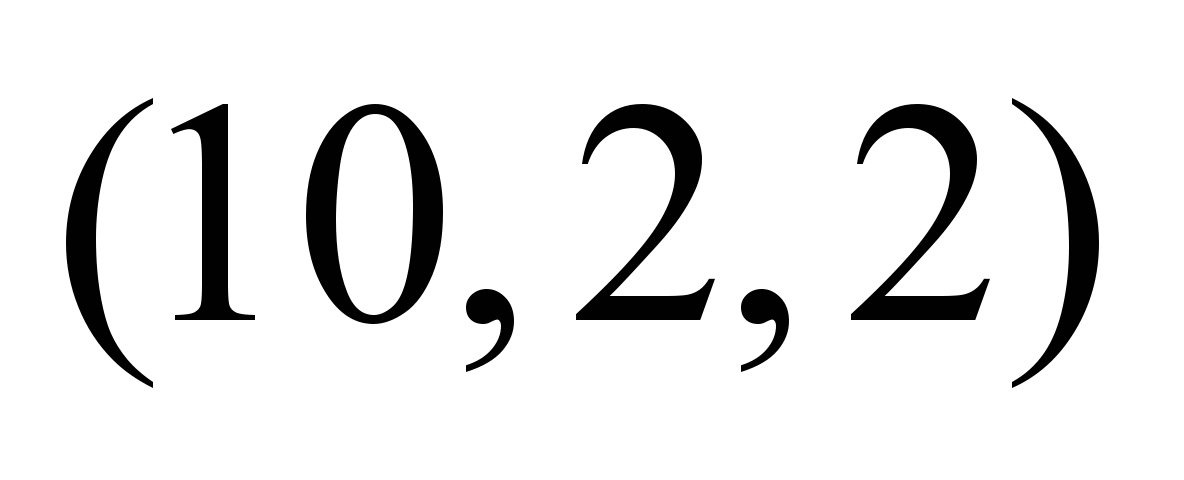
|
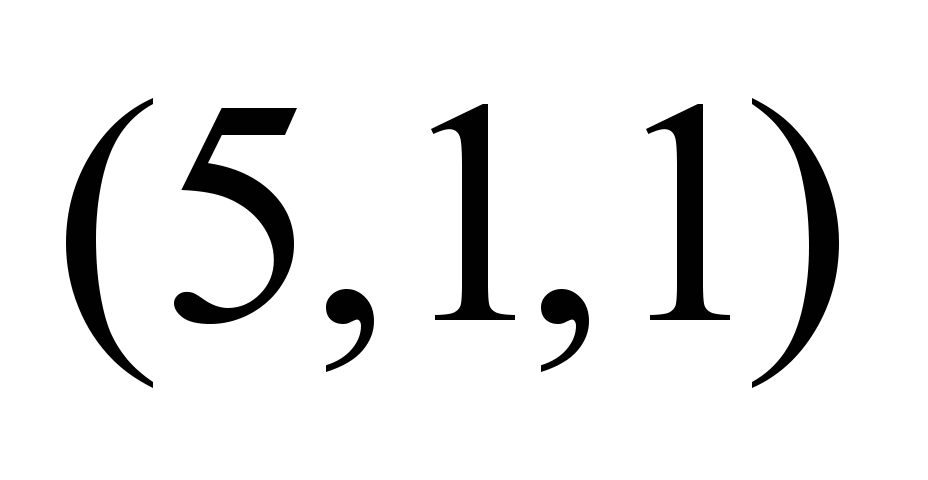
|
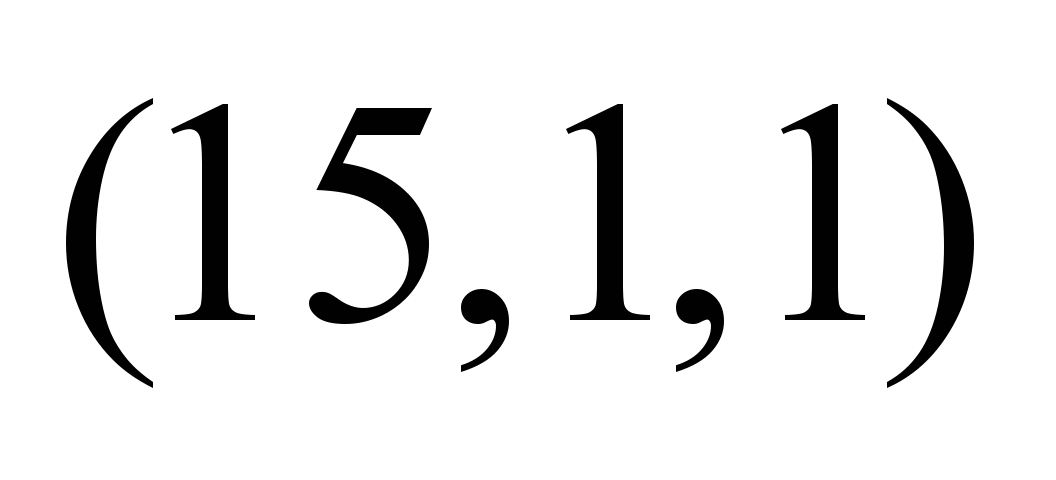
|
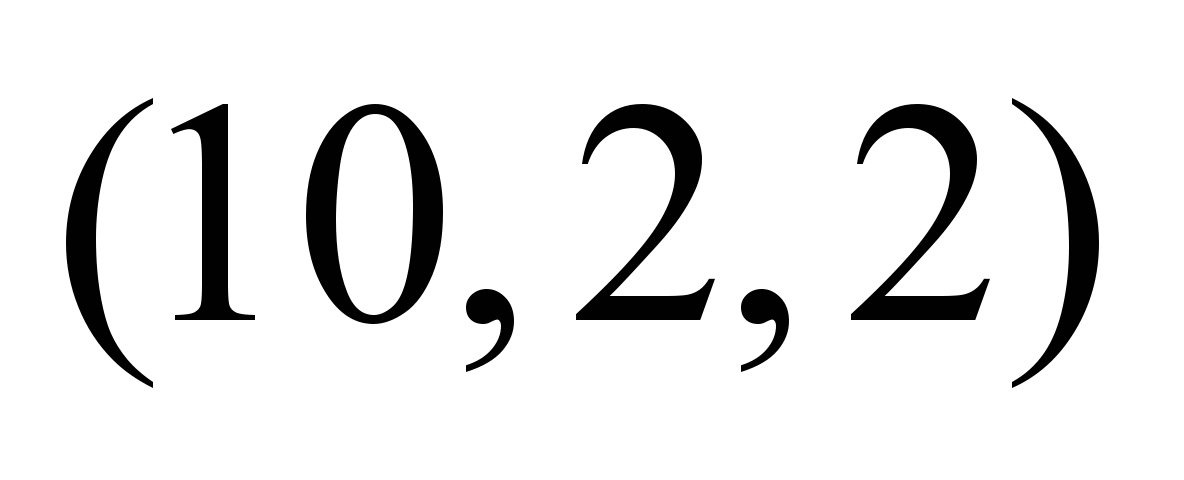
|
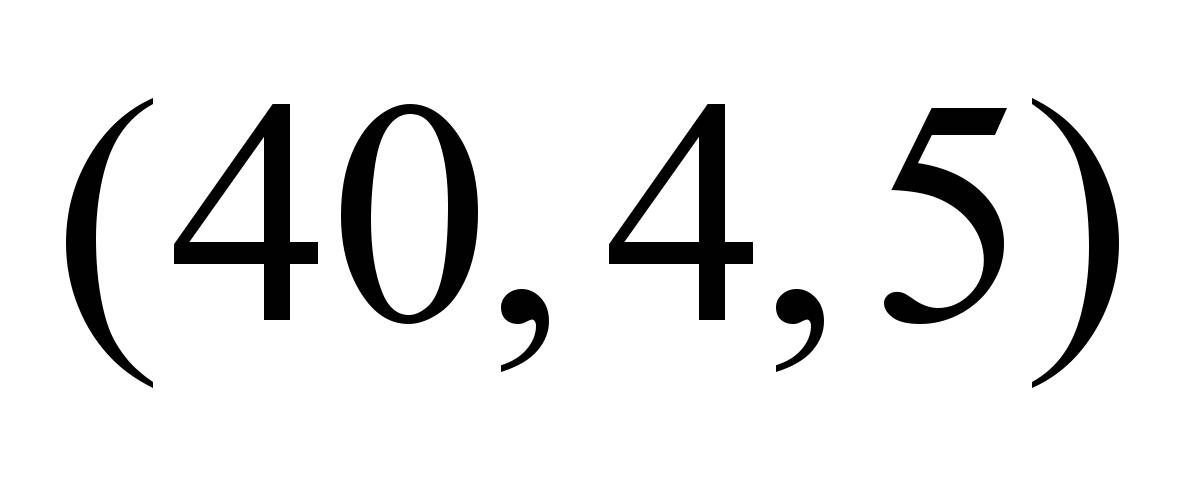
|
|
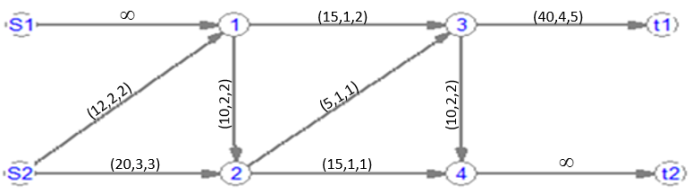
Рис. 2. Схема
сети для расчета максимального нечеткого
и компромиссного потоков двух продуктов
Fig.
2. Network diagram for calculating the maximum fuzzy and trade-off
flows of two products
Максимальный поток
продукта Р1 (S1) для нечетких
пропускных способностей представлен
на рис. 3. Таким
образом, максимальный нечеткий поток
для продукта Р1 равен
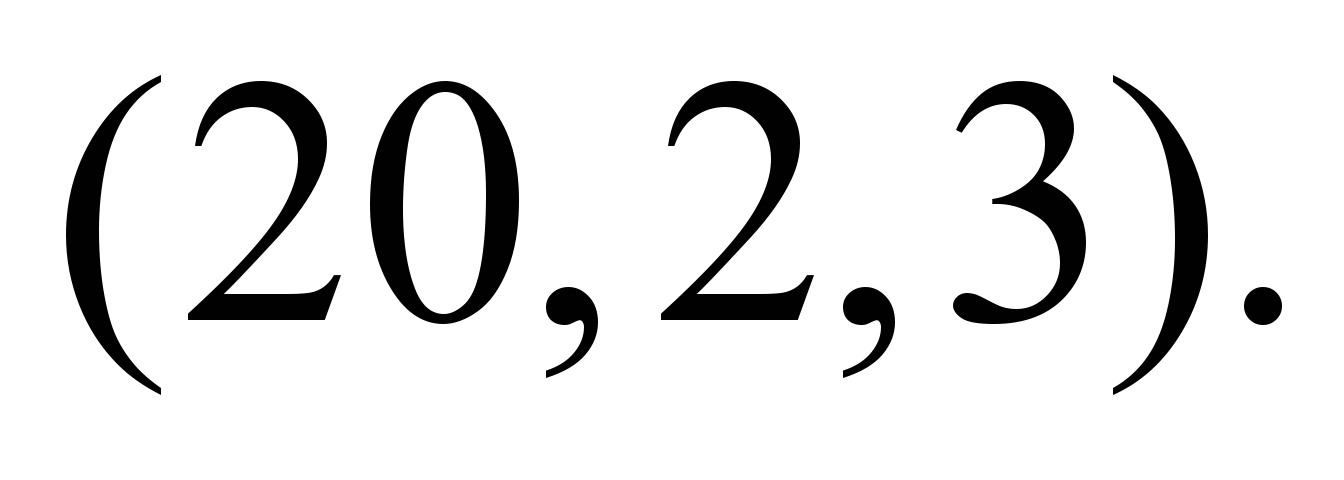
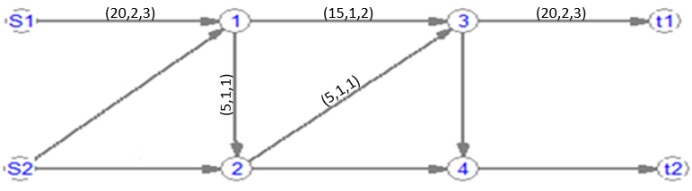
Рис.
3. Схема сети для расчета нечеткого
максимального потока для первого
продукта
Fig.
3. Network diagram for calculating fuzzy maximum flow for the first
product
Максимальный поток
продукта Р2 (S2) для нечетких
пропускных способностей представлен
на рис. 4.
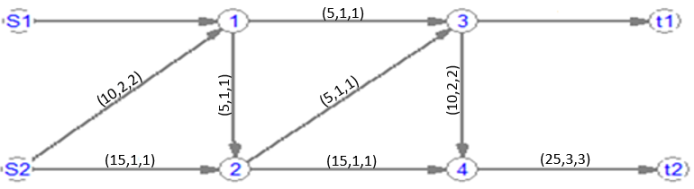
Рис.
4. Схема сети для расчета нечеткого
максимального потока для второго
продукта
Fig.
4. Network diagram for calculating fuzzy maximum flow for the second
product
При этом максимальный
нечеткий поток для продукта Р2 равен
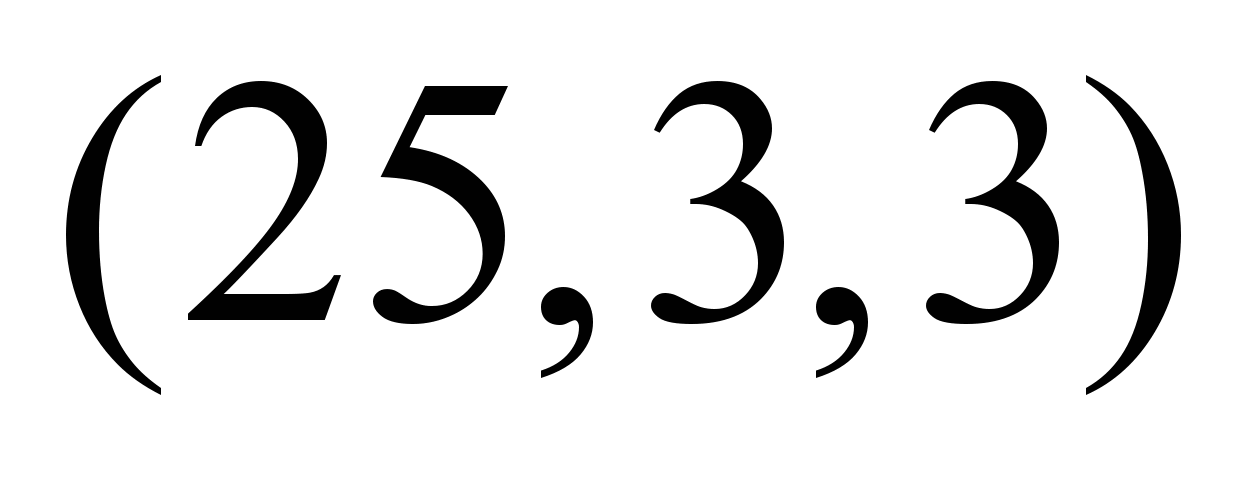 ,
что соответствует результатам расчетов
[11].
,
что соответствует результатам расчетов
[11].
Задачи нахождения
максимального потока и потока
минимальной стоимости в транспортных
сетях могут содержать параметры
(пропускные способности, стоимости
перевозок и др.), значения которых
известны не точно в силу различных
видов неопределенности [2, 9, 11]. Для
анализа таких потоков могут быть
использованы модели ТС в нечетких
условиях [7]. При учете времени прохождения
потока по дугам, а также возможности
изменения параметров ТС во времени
получают математические модели потоковых
задач в динамических ТС при нечетких
условиях (ДТСНУ) [2, 11]. В разделе рассмотрено
применение алгоритма ПСАП для нахождения
максимального потока минимальной
стоимости в нечеткой динамической
транспортной сети. А именно: требуется
пропустить
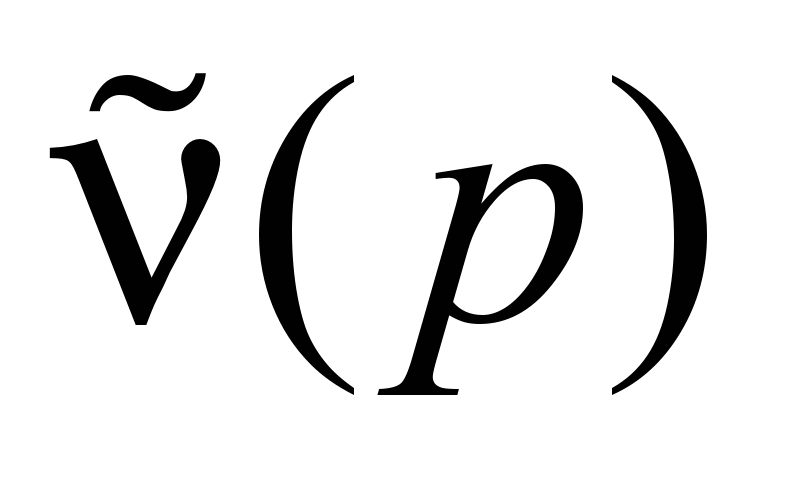 единиц потока с минимальными затратами
в динамической транспортной сети так,
чтобы последняя единица потока вошла
в сток в момент времени не позднее
заданного
единиц потока с минимальными затратами
в динамической транспортной сети так,
чтобы последняя единица потока вошла
в сток в момент времени не позднее
заданного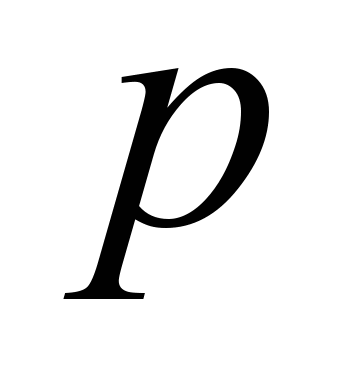 .
.
Математическая
постановка задачи ДТСНУ, следуя [11],
имеет вид:
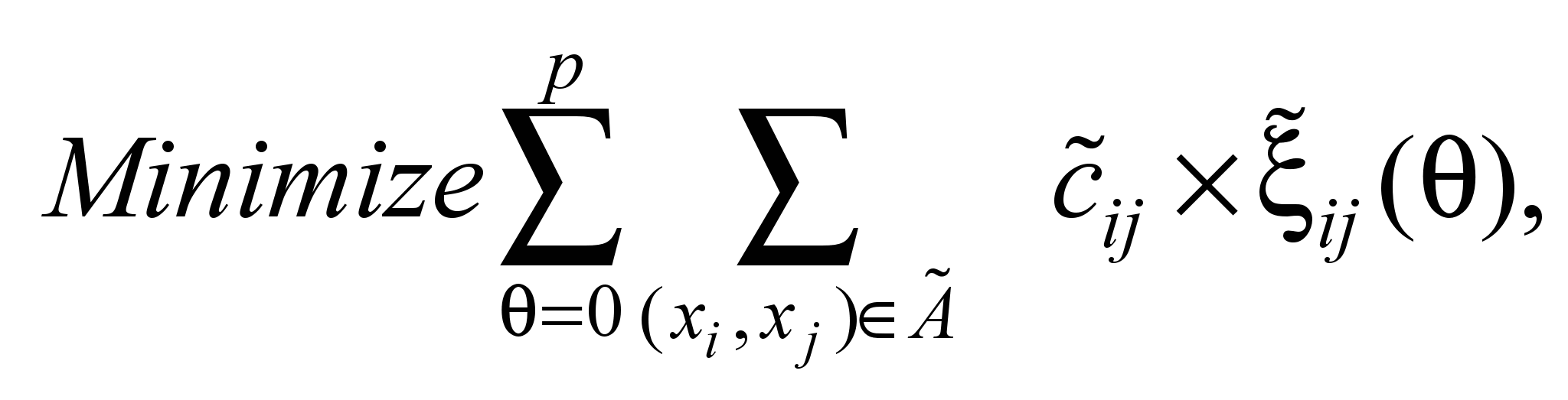 (2)
(2)
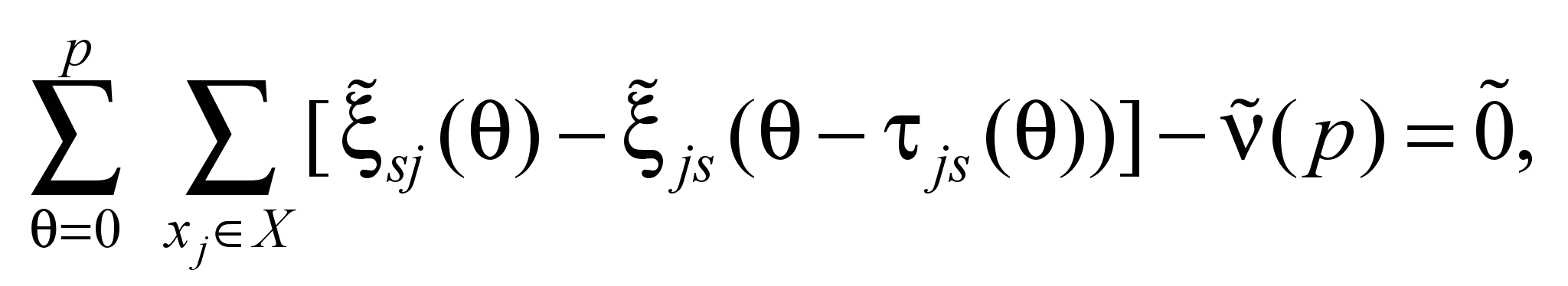 (3)
(3)
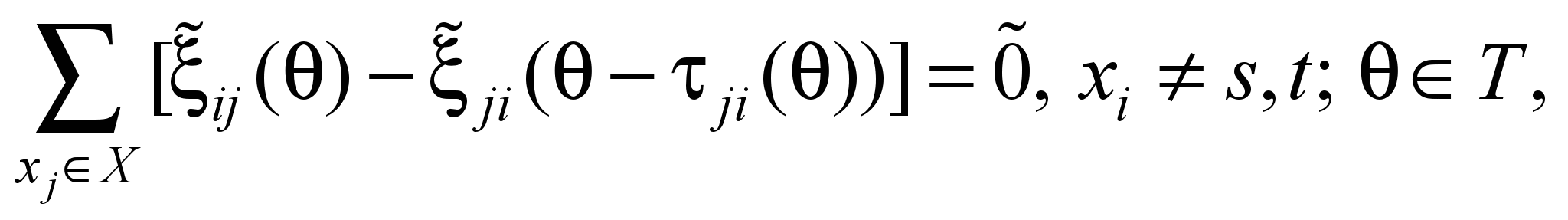 (4)
(4)
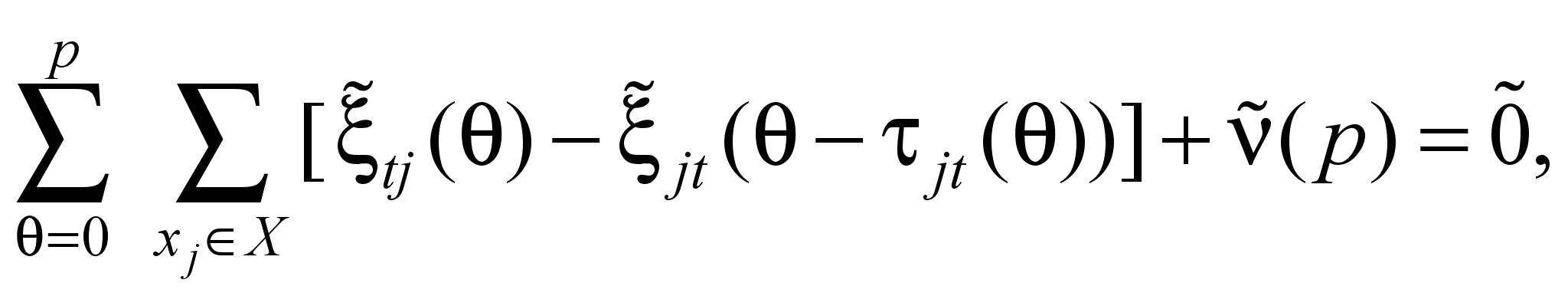 (5)
(5)
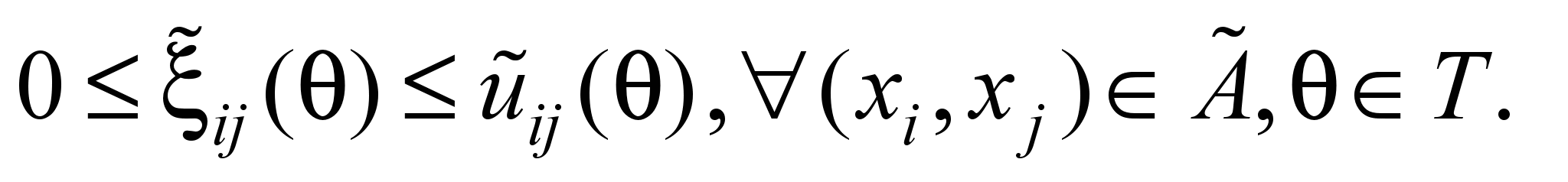 (6)
(6)
Согласно (2), требуется
найти минимальный маршрут перевозки
максимального количества единиц потока
в ТС за заданное число моментов времени
p, что равно потоку, выходящему из
источника
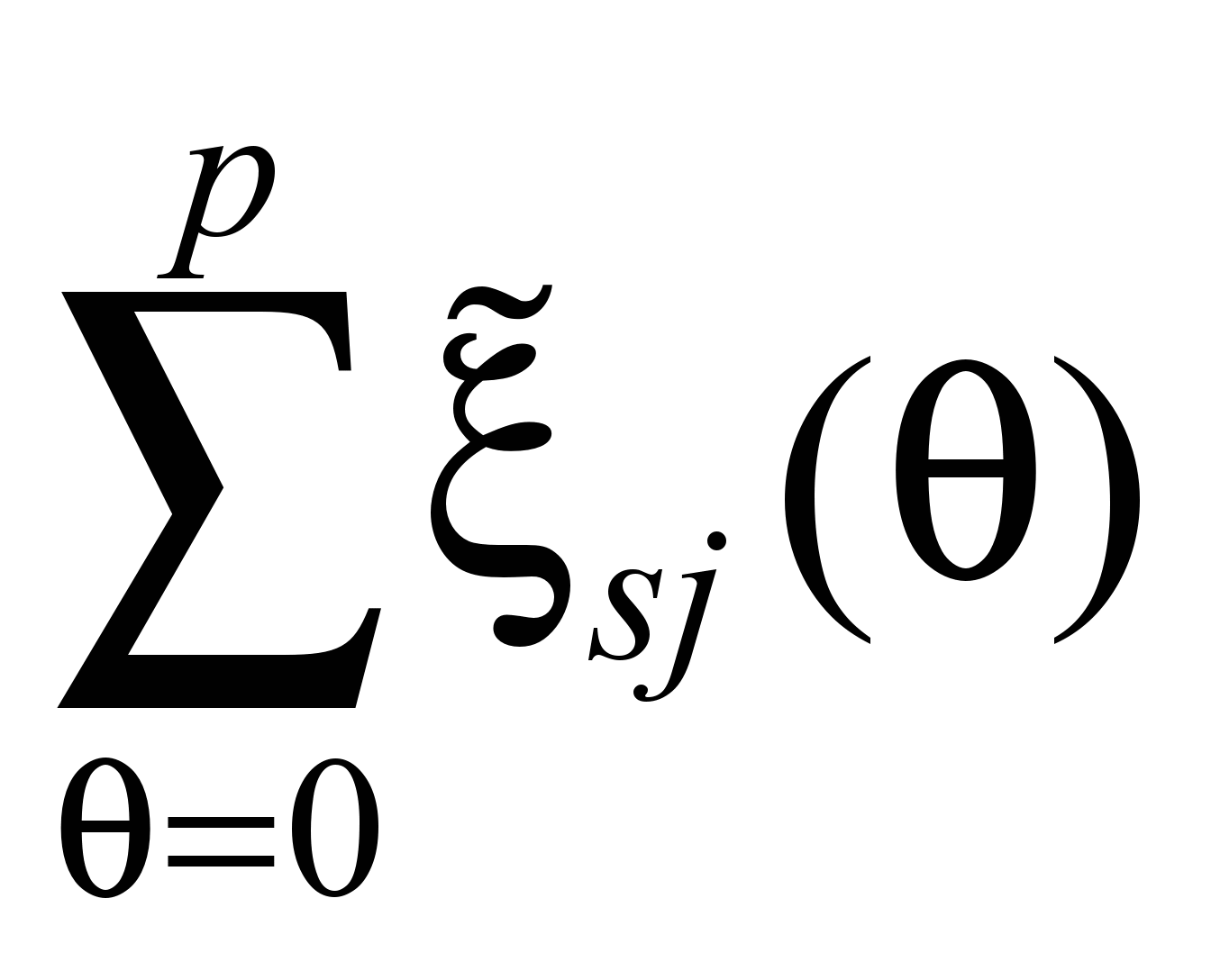 (3). Уравнения (5) обеспечивают непрерывность
потока: максимальное число единиц
потока
(3). Уравнения (5) обеспечивают непрерывность
потока: максимальное число единиц
потока
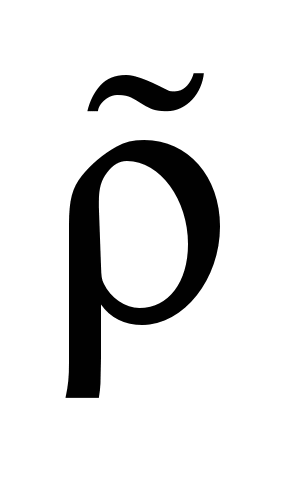 за p периодов равно потоку, входящему
в сток за p периодов времени
за p периодов равно потоку, входящему
в сток за p периодов времени
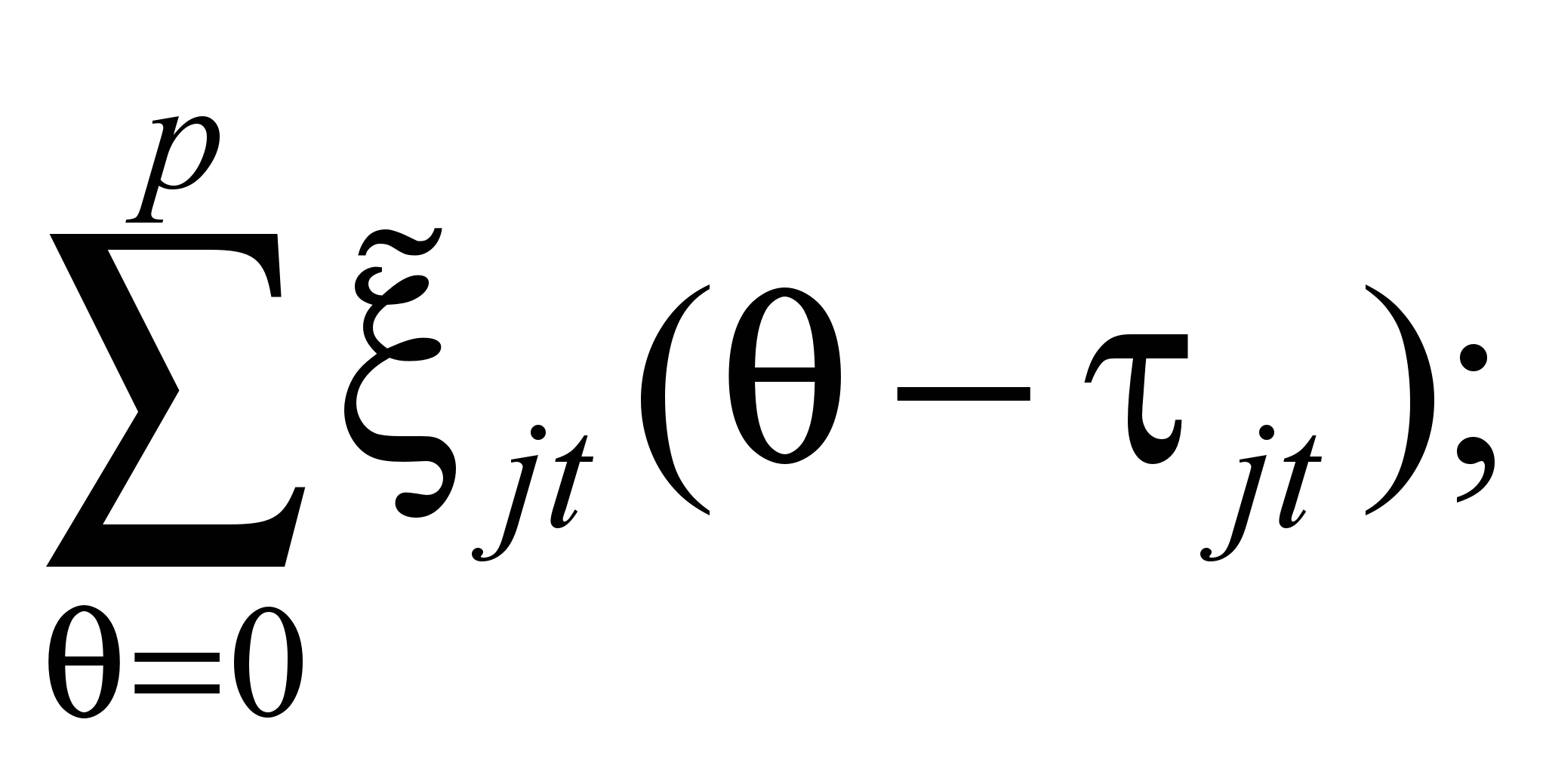 поток
поток
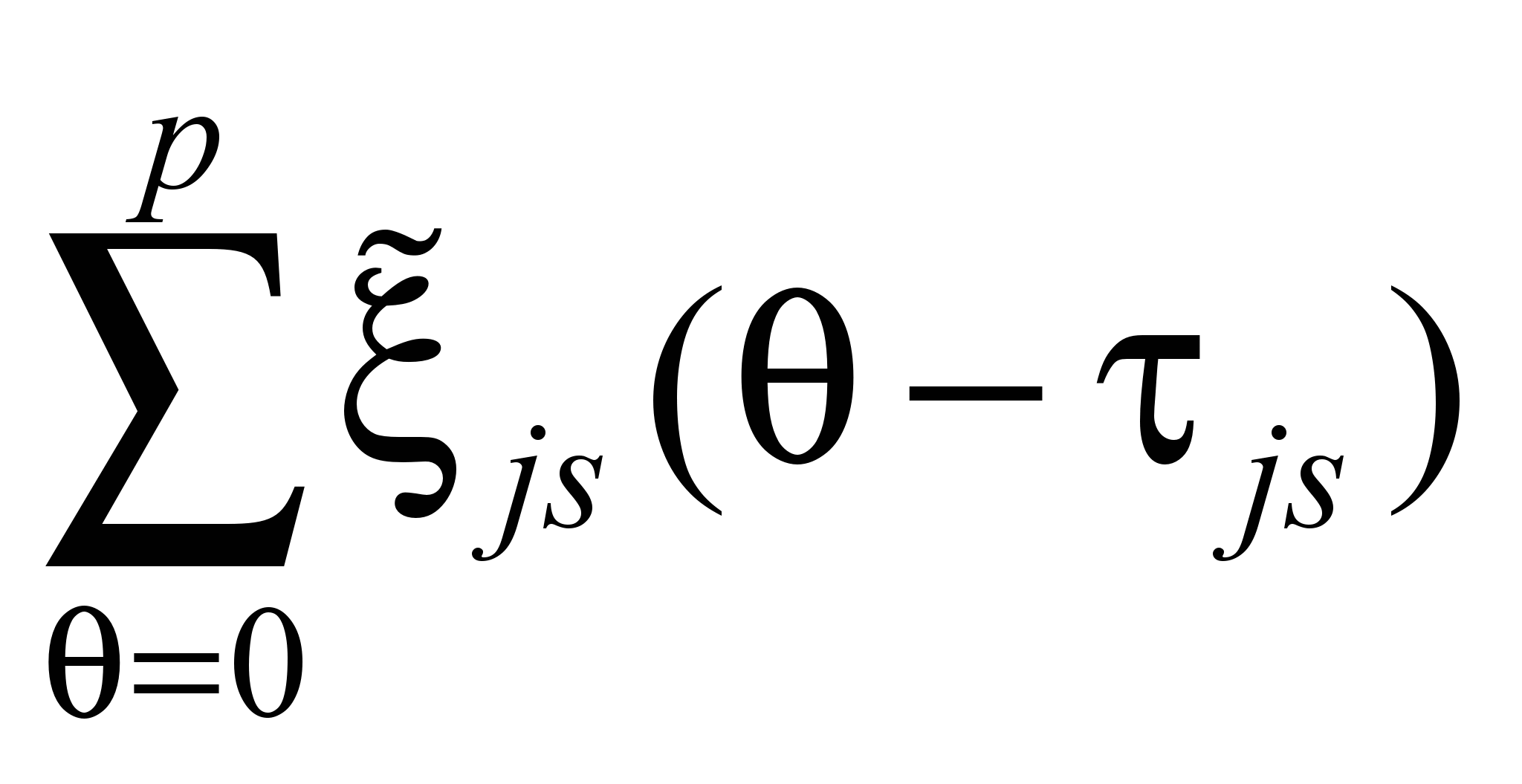 ,
входящий в источник за p периодов,
равен потоку, покидающему сток
,
входящий в источник за p периодов,
равен потоку, покидающему сток
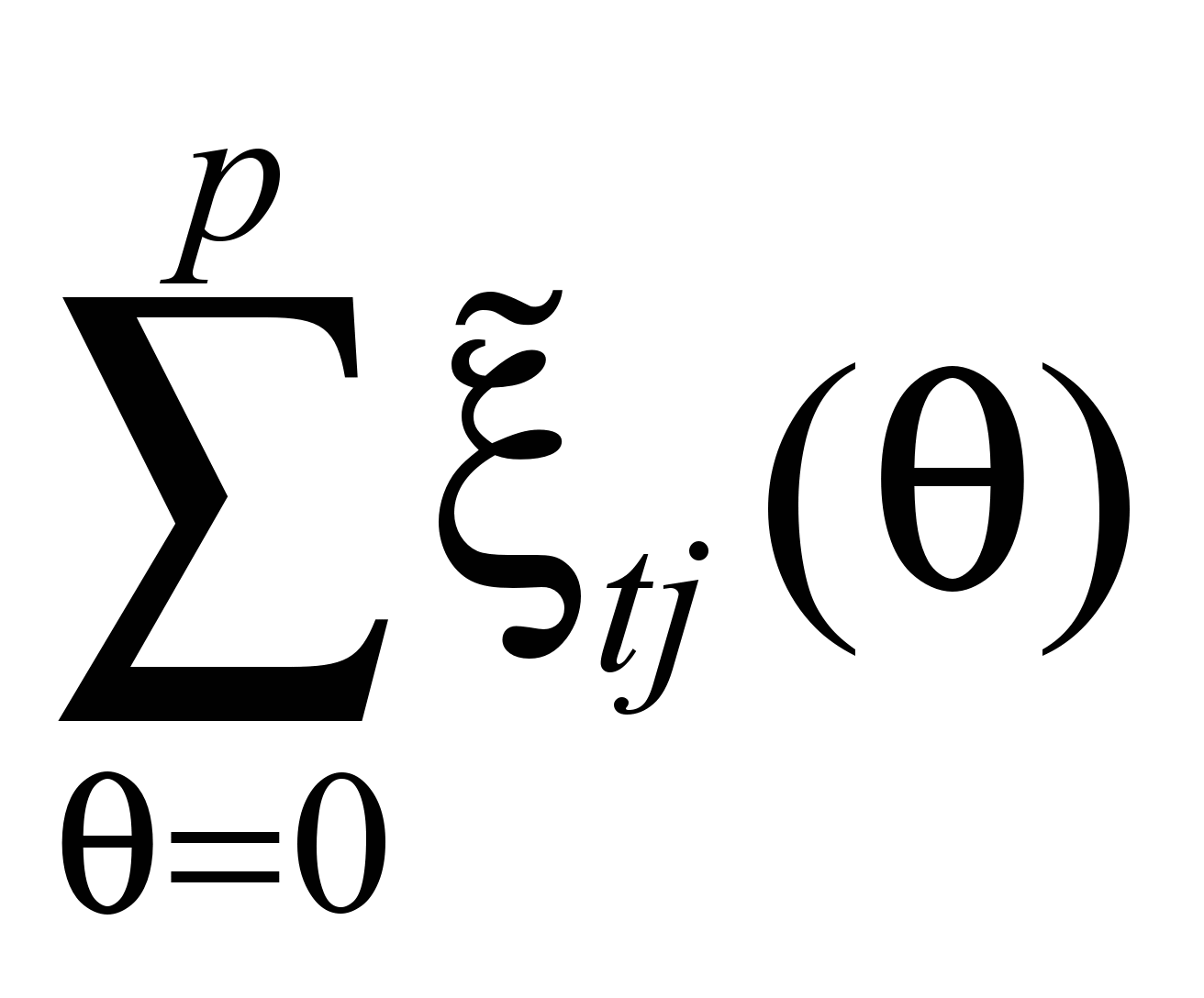 .
.
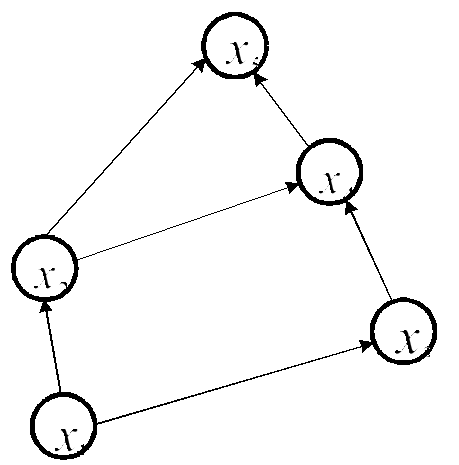
Рис.
5. Исходный динамический граф
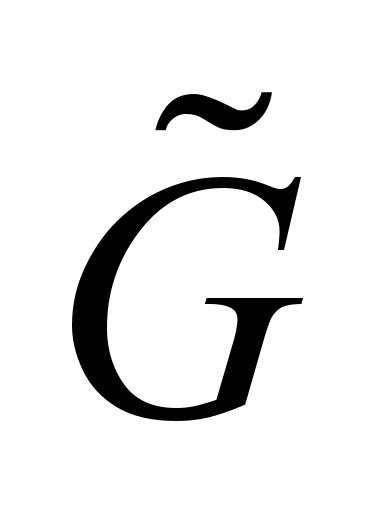
Fig.
5. Initial dynamic graph
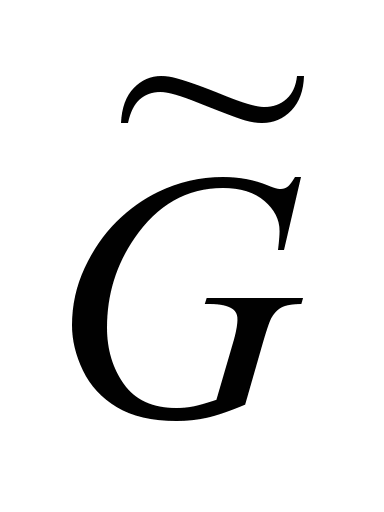
Уравнения (4)
обеспечивают условия непрерывности
потока для каждого узла
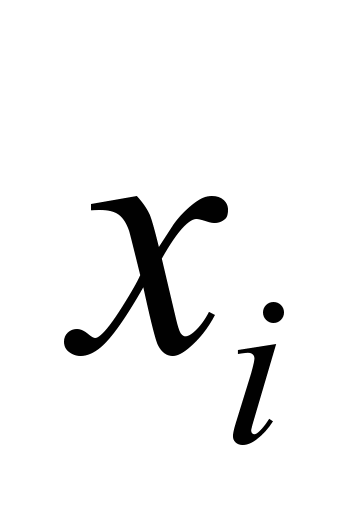 и каждого момента времени
и каждого момента времени
 ,
кроме источника и стока. Неравенства
(5) ограничивают потоки пропускными
способностями дуг ТС.
,
кроме источника и стока. Неравенства
(5) ограничивают потоки пропускными
способностями дуг ТС.
Алгоритм решения
задачи (2–6) [11] основан на переходе к
«растянутому во времени» на p
интервалов нечеткому статическому
графу
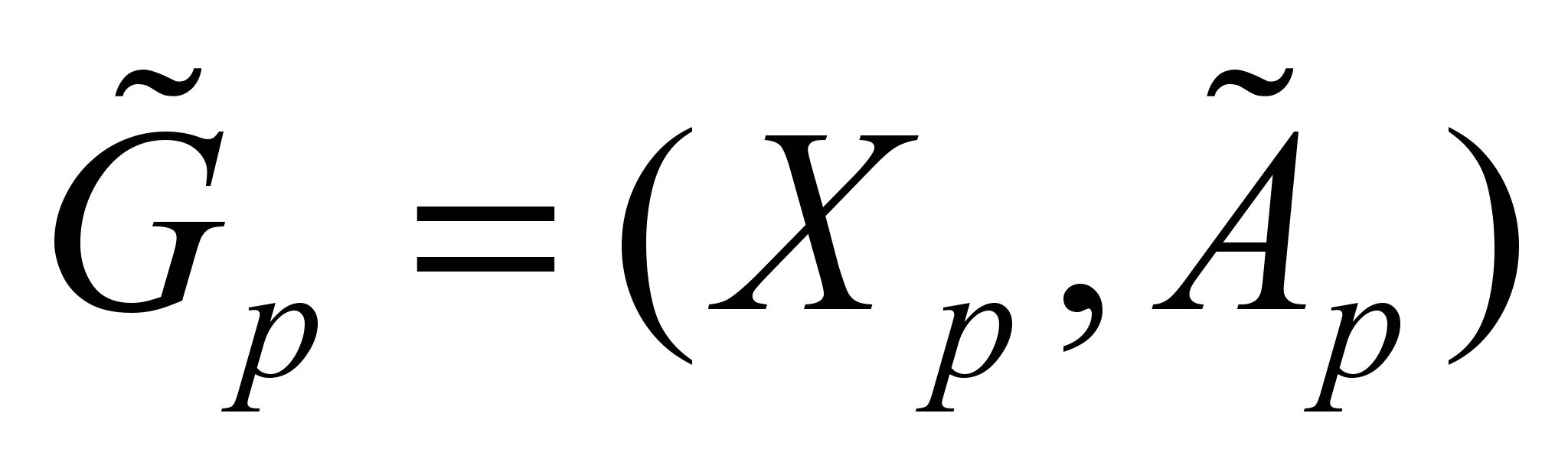 .
Переход выполняется путем создания
отдельной копии каждой вершины
.
Переход выполняется путем создания
отдельной копии каждой вершины
 в каждый рассматриваемый момент времени
в каждый рассматриваемый момент времени
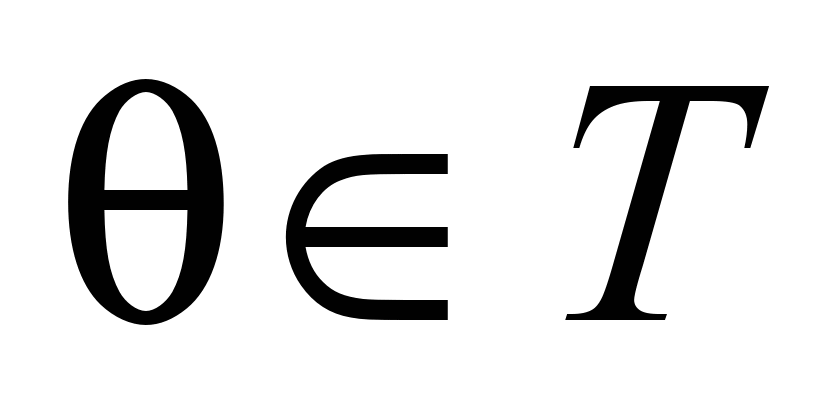 .
Подробная процедура формирования
эквивалентной статической модели
задачи ДТСНУ, а также пример расчета
оптимальных параметров исходной ТС
приведены в [7, 11]. Рассмотрим реализацию
этой задачи на основе алгоритма ПСАП
[5]. На рис. 5 показана часть железнодорожной
сети, далее представленная в форме
нечеткой ТС. Здесь вершина
.
Подробная процедура формирования
эквивалентной статической модели
задачи ДТСНУ, а также пример расчета
оптимальных параметров исходной ТС
приведены в [7, 11]. Рассмотрим реализацию
этой задачи на основе алгоритма ПСАП
[5]. На рис. 5 показана часть железнодорожной
сети, далее представленная в форме
нечеткой ТС. Здесь вершина 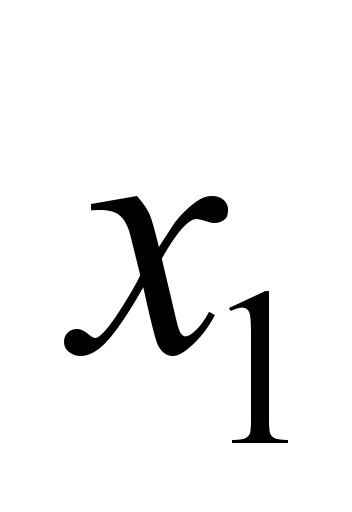 – это источник, вершина
– это источник, вершина
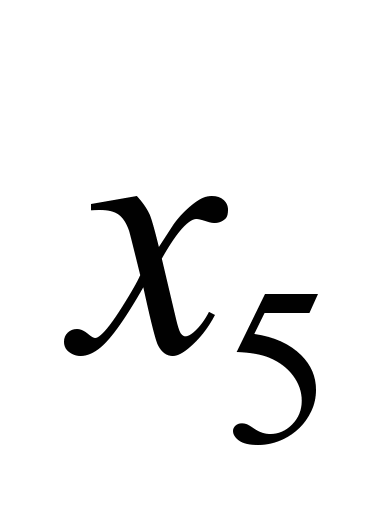 – сток. Нечеткие пропускные способности
и стоимости, а также параметры времени
прохождения потока по дугам, зависящие
от момента отправления потока,
представлены в виде таблиц 4, 5 и 6.
Необходимо найти минимальную стоимость
перевозки максимального числа единиц
потока
– сток. Нечеткие пропускные способности
и стоимости, а также параметры времени
прохождения потока по дугам, зависящие
от момента отправления потока,
представлены в виде таблиц 4, 5 и 6.
Необходимо найти минимальную стоимость
перевозки максимального числа единиц
потока
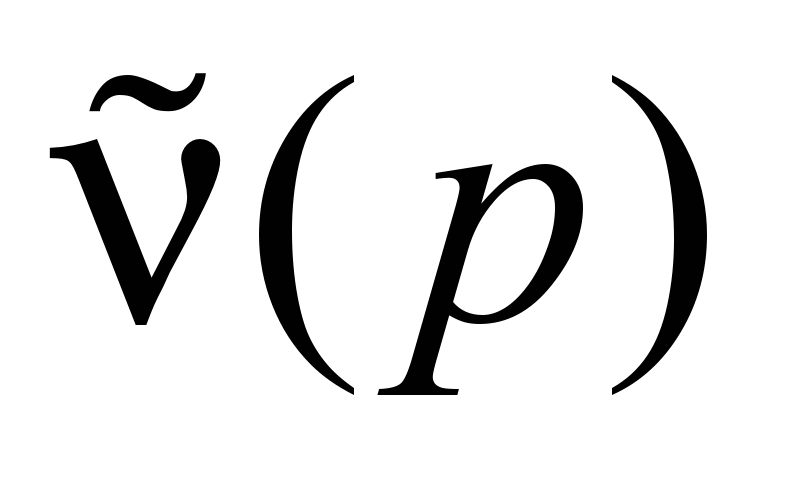 .
Правила оперирования с нечеткими
треугольными числами представлены в
[2].
.
Правила оперирования с нечеткими
треугольными числами представлены в
[2].
На рис. 6 показана
остаточная сеть после нахождения потока
согласно (2–6). В отличие от [11], максимальный
поток минимальной стоимости (рис. 6) на
основе ПСАП получен за одну итерацию.
Отбрасывая искусственные вершины и
дуги с потоком, соединяющие их с
другими вершинами, получаем максимальный
поток
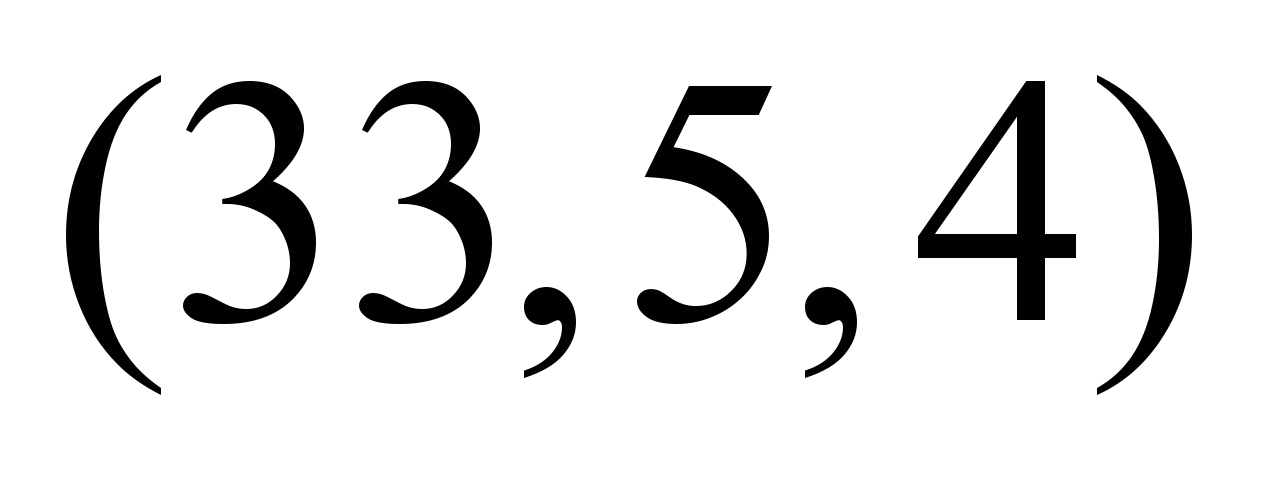 единиц минимальной стоимости
единиц минимальной стоимости
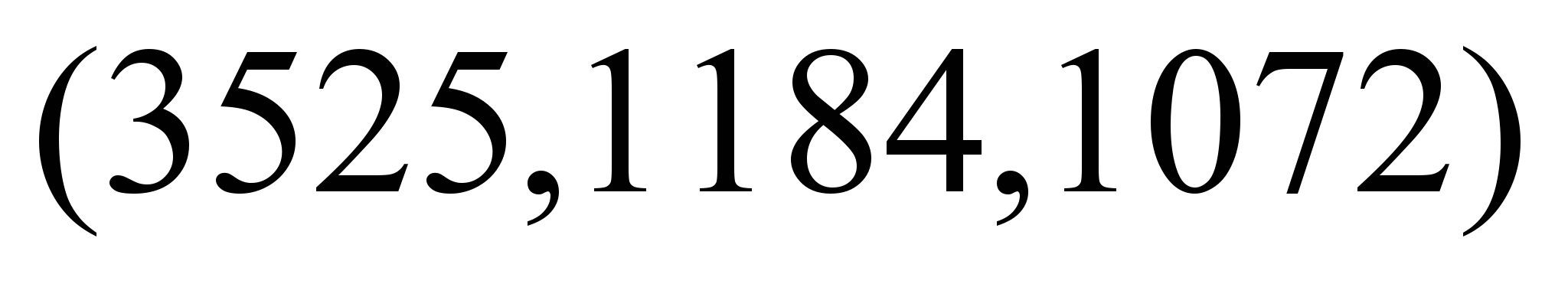 условных единиц. Переходя к динамическому
графу
условных единиц. Переходя к динамическому
графу
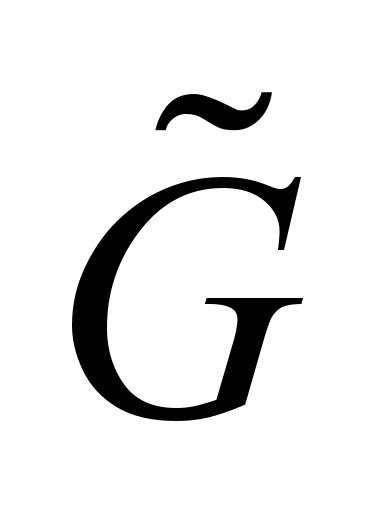 от «растянутого во времени» статического
графа
от «растянутого во времени» статического
графа
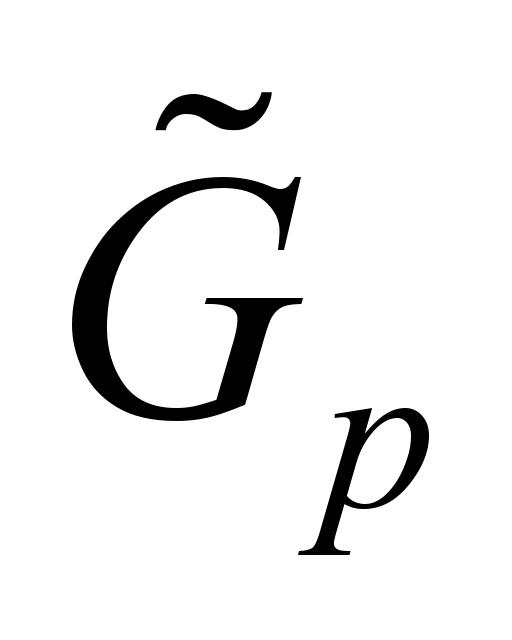 ,
получаем, что максимальный поток
,
получаем, что максимальный поток
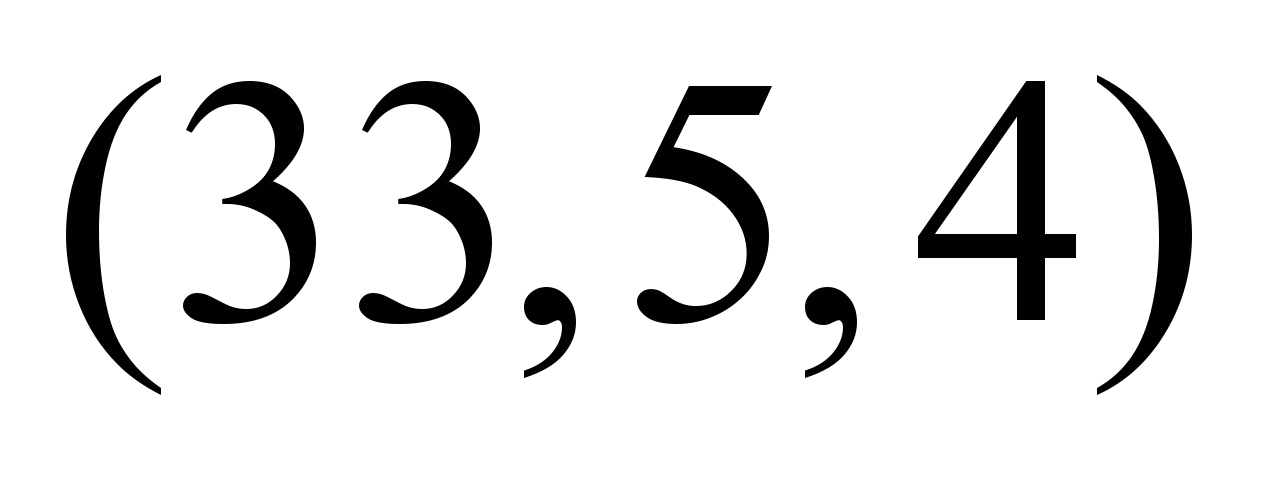 за 3 интервала времени равен потоку,
выходящему из пар «вершина–время»
за 3 интервала времени равен потоку,
выходящему из пар «вершина–время»
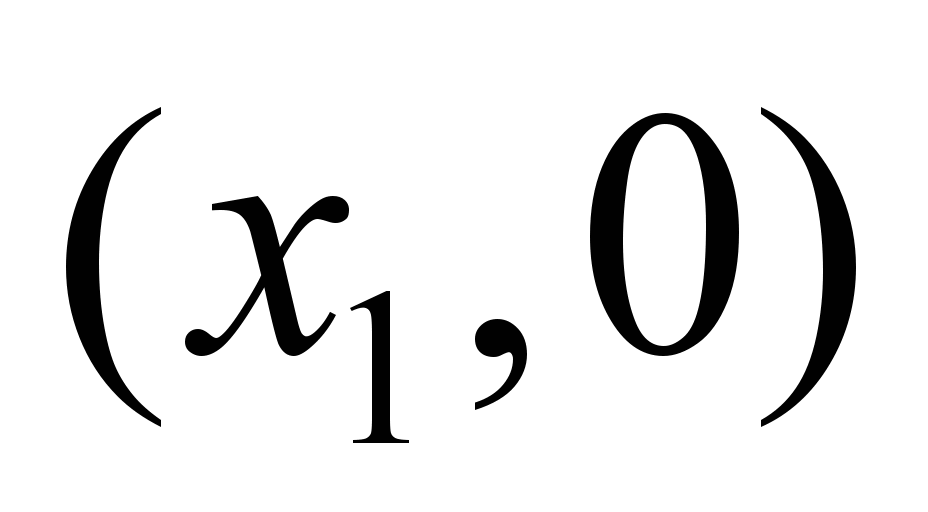 и
и
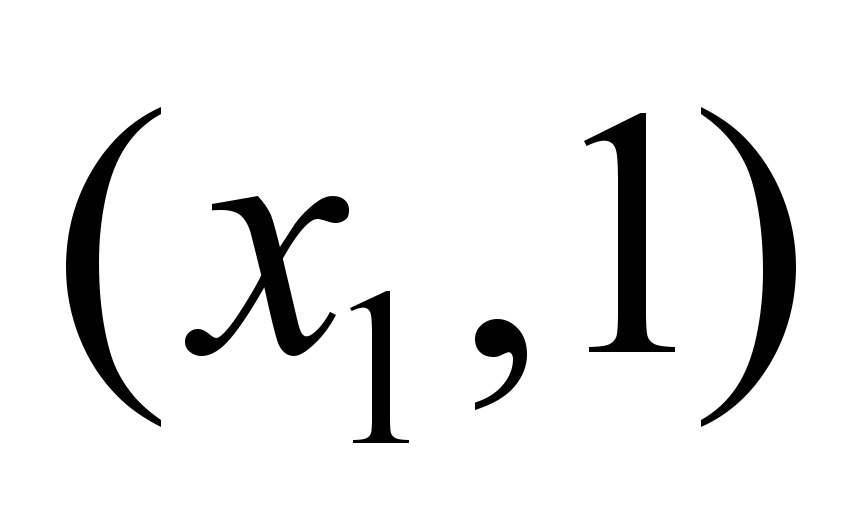 и входящему в пару «вершина–время»
и входящему в пару «вершина–время»
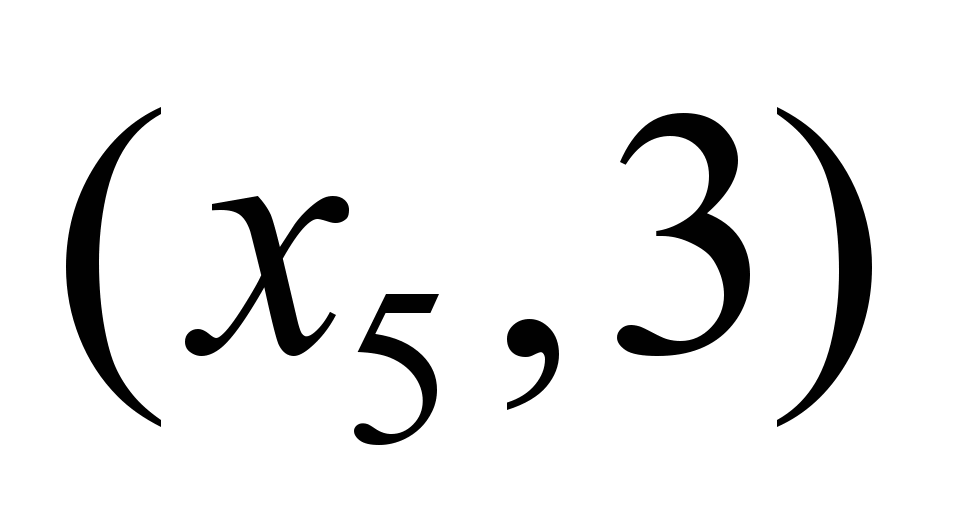 .
Таким образом, получаем нечеткий
динамический поток в
.
Таким образом, получаем нечеткий
динамический поток в
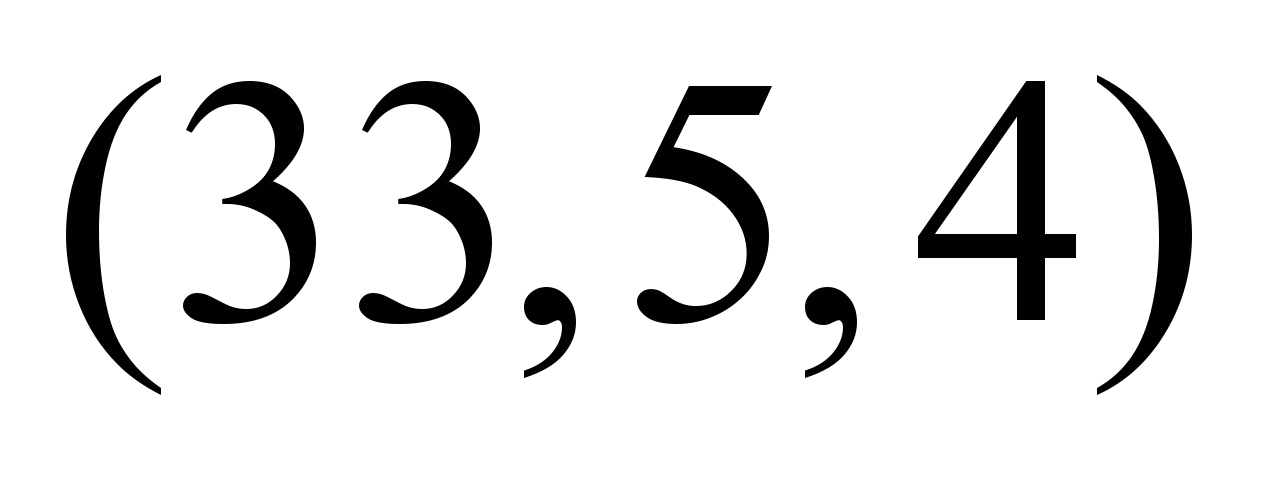 единиц с путем
единиц с путем
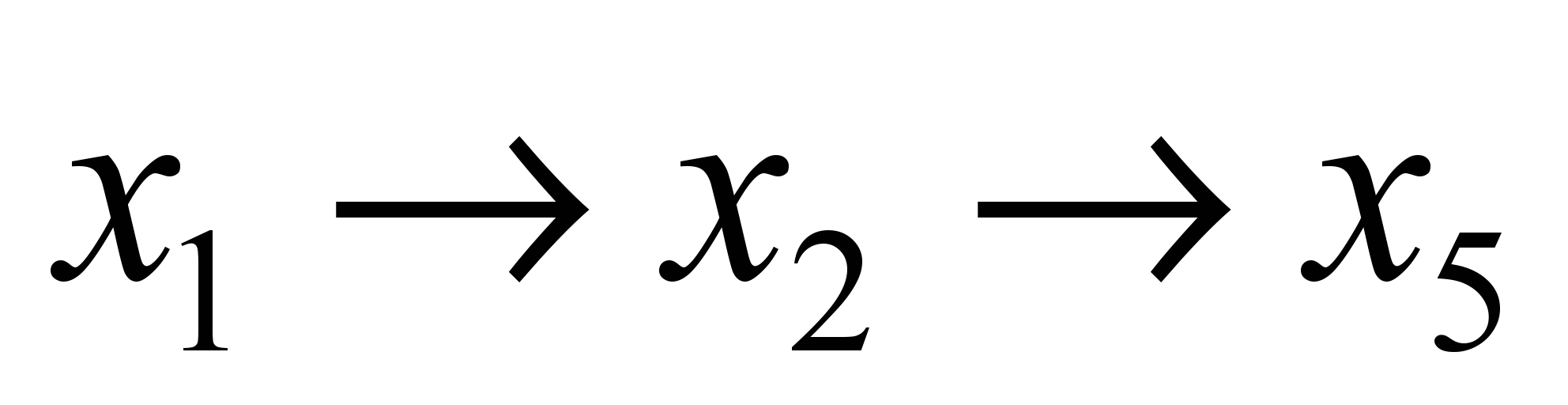 ,
который отправляется в момент времени
,
который отправляется в момент времени
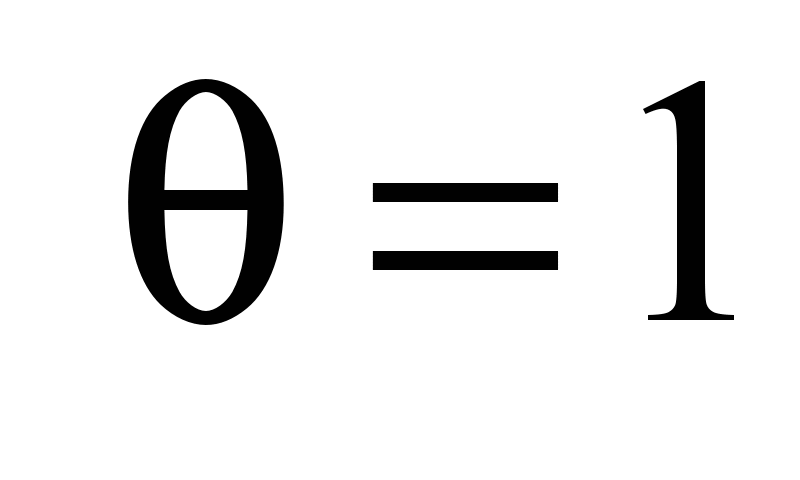 и прибывает в сток в момент времени
и прибывает в сток в момент времени
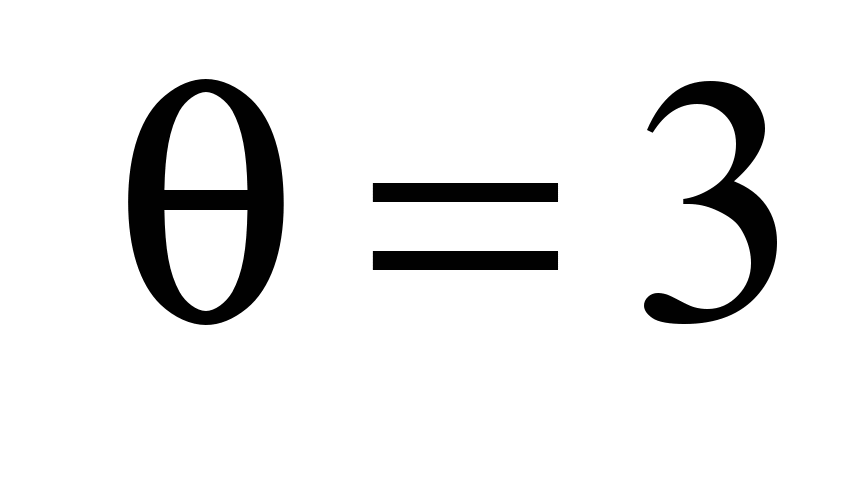 ,
а также путем
,
а также путем
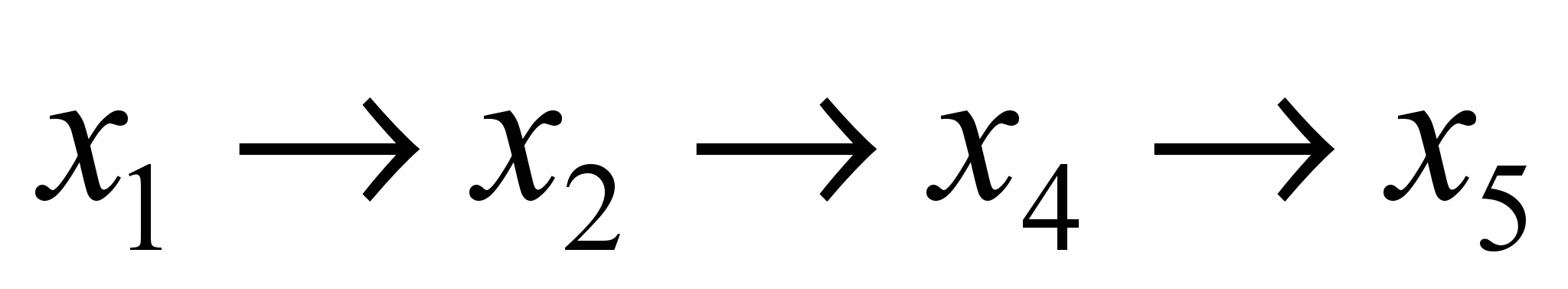 ,
который отправляется в момент времени
,
который отправляется в момент времени
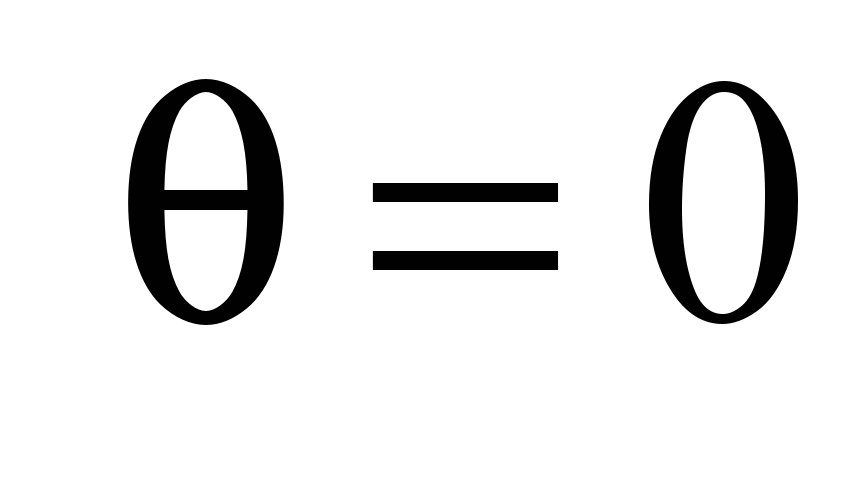 и прибывает в сток в момент
и прибывает в сток в момент
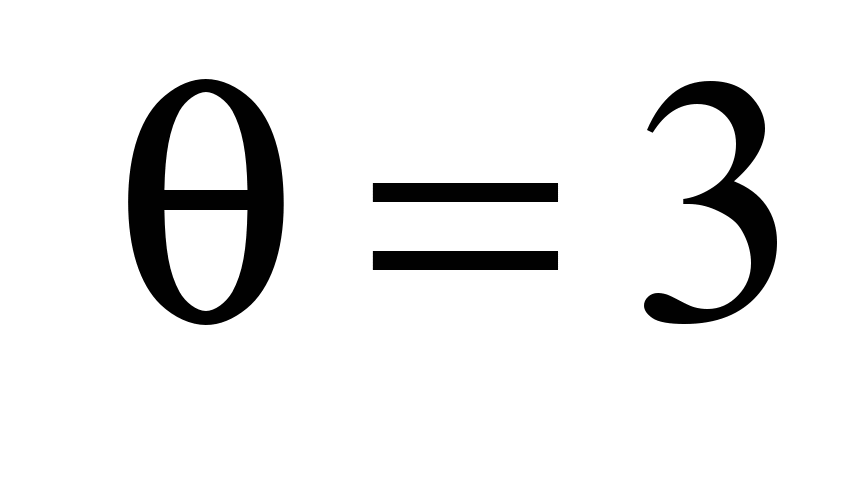 .
.
Таблица 4
Нечеткие,
зависящие от момента отправления
потока, пропускные способности ТС
Table
4
Fuzzy, depending
on the moment of flow departure, network capacity of the TN
|
Момент
времени
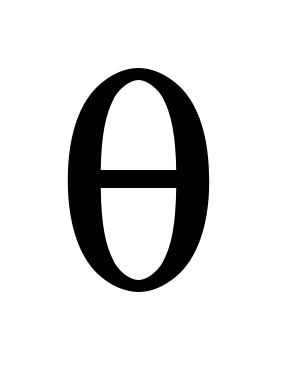
|
Нечеткие
пропускные способности по дугам
графа
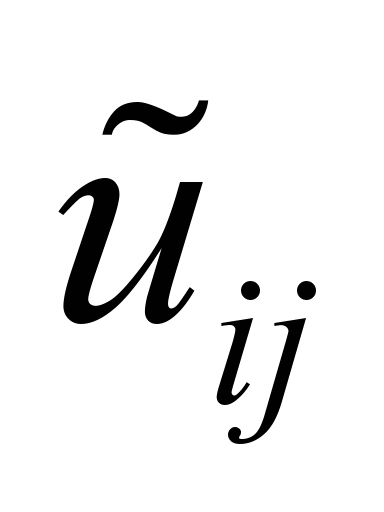 ,
ед. ,
ед.
|
|
|

|
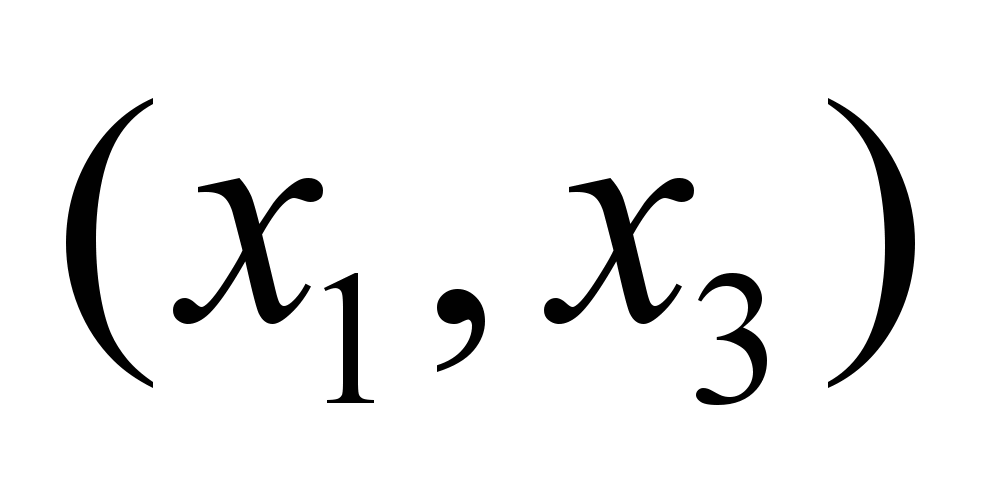
|
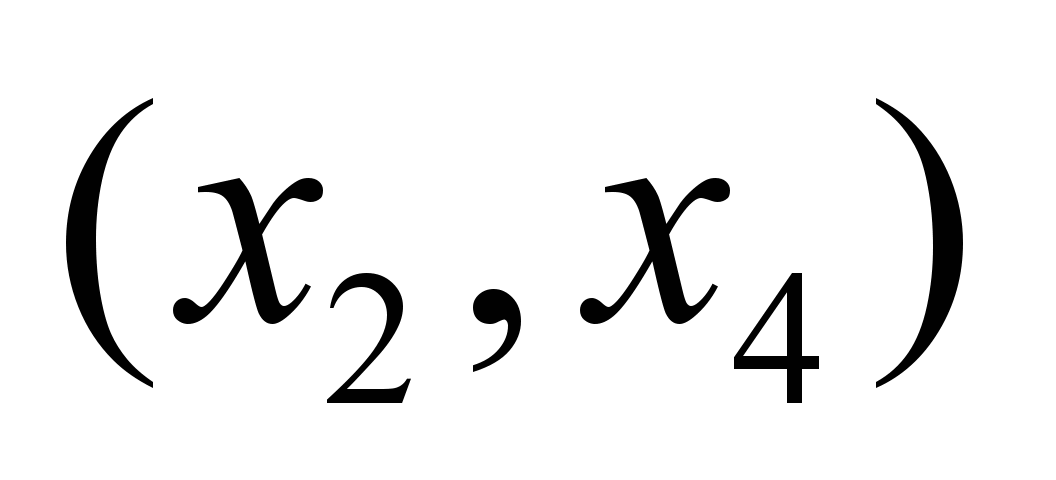
|
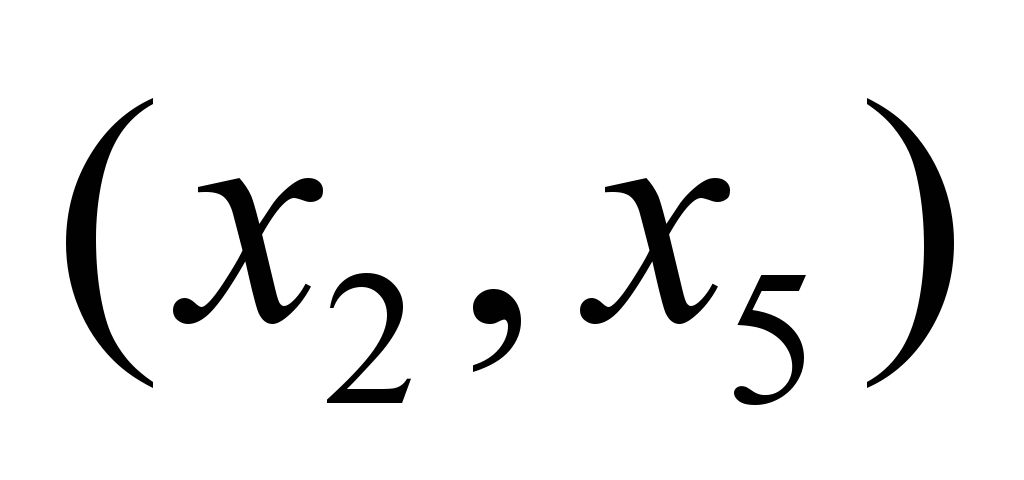
|
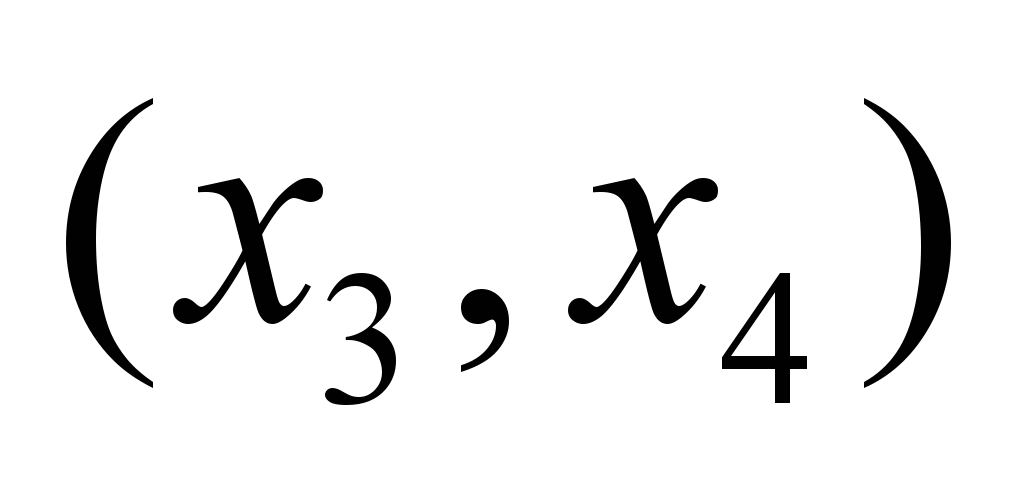
|
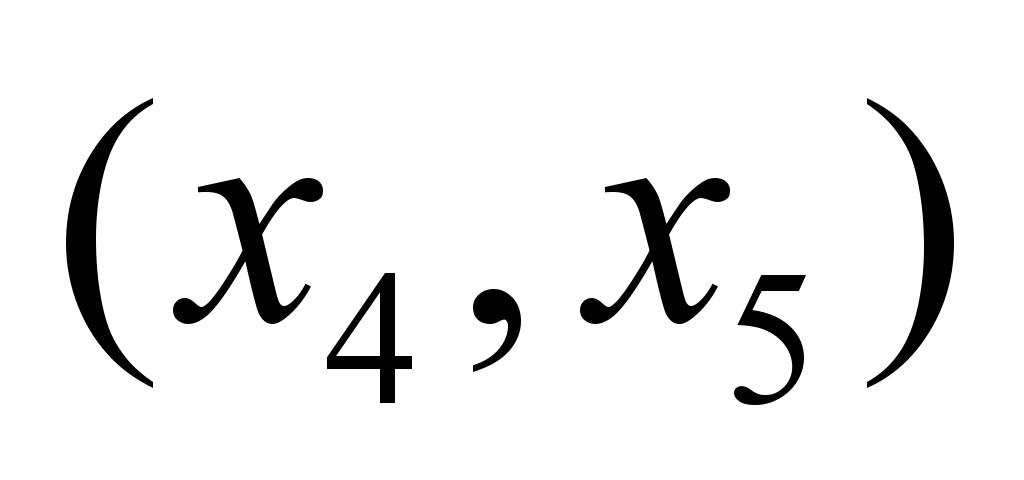
|
|
0
|
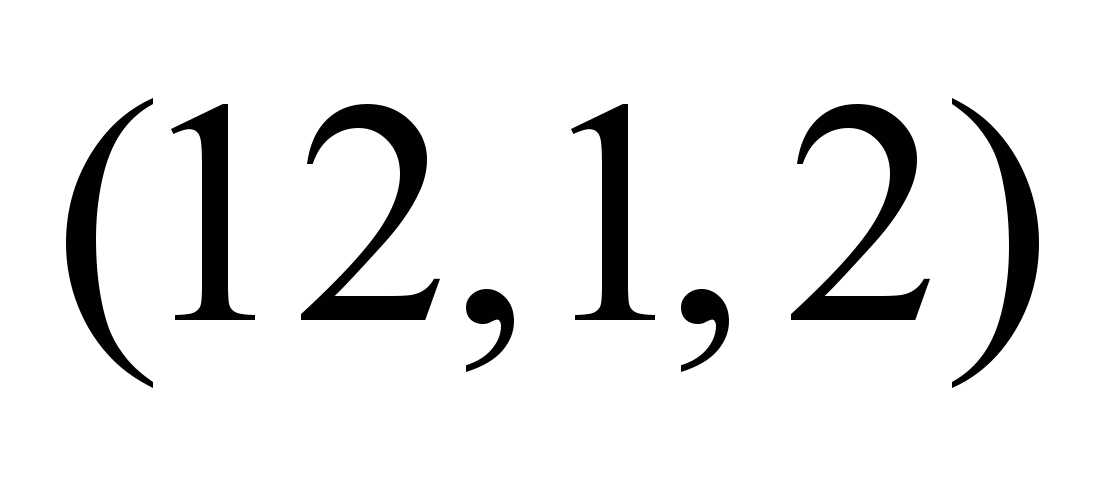
|
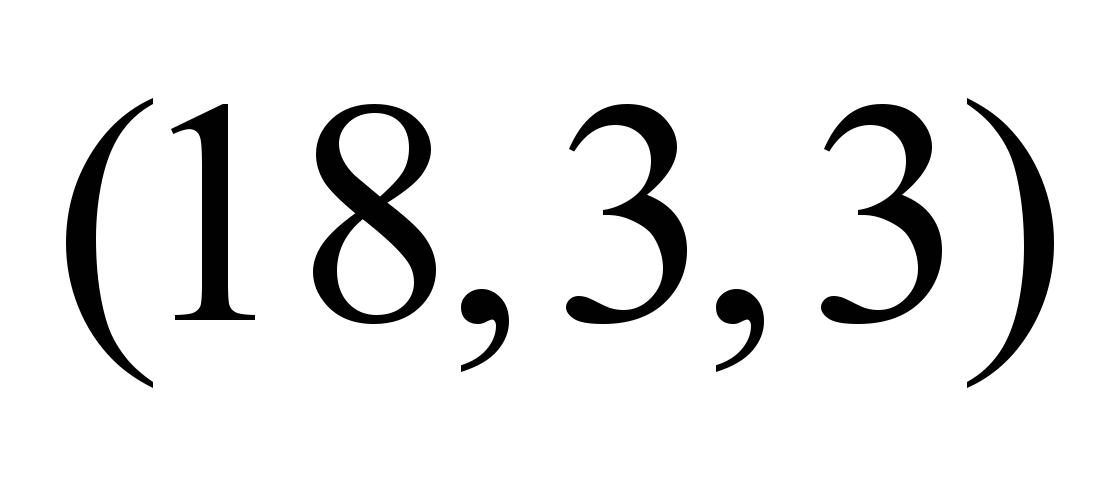
|
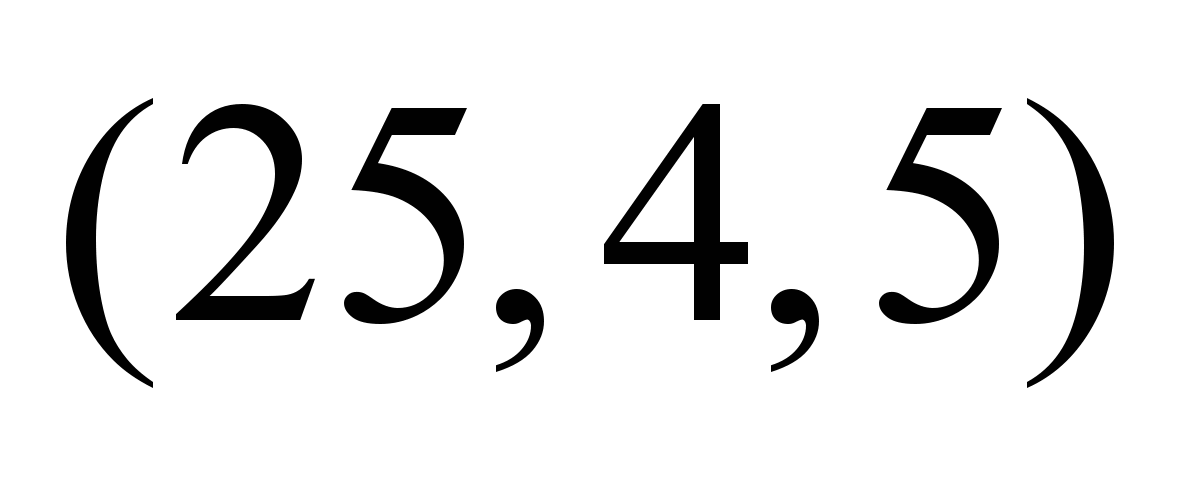
|
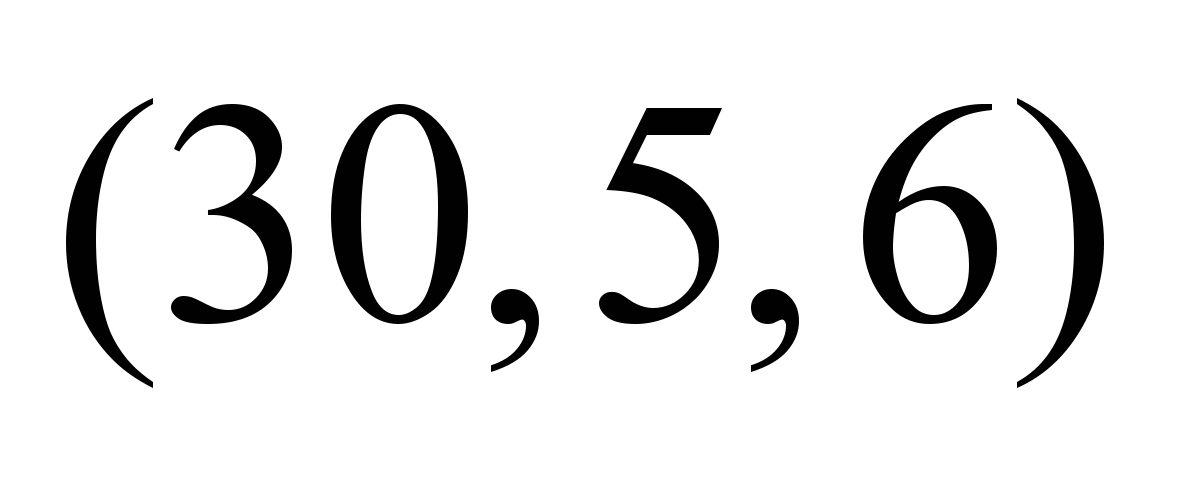
|
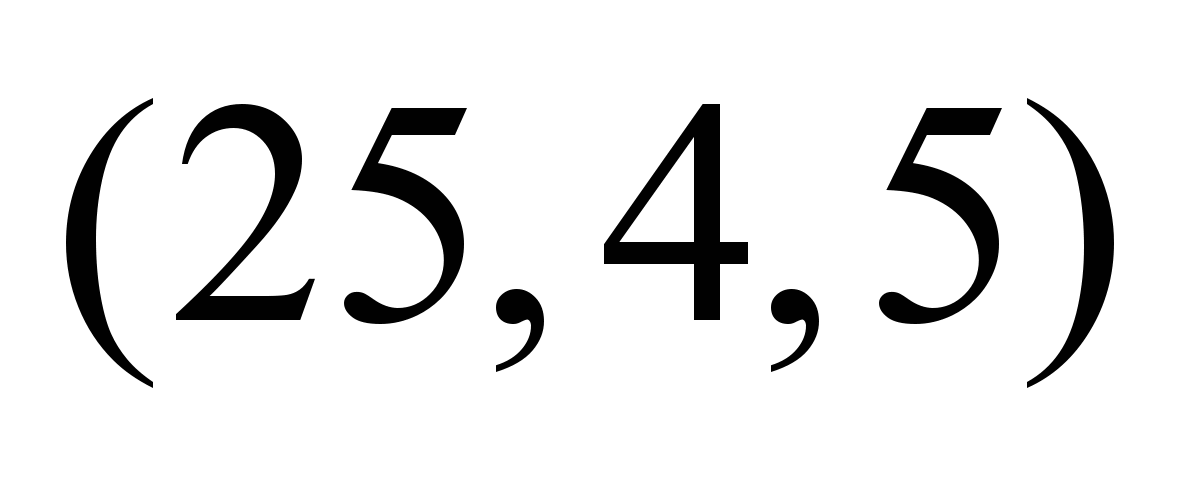
|
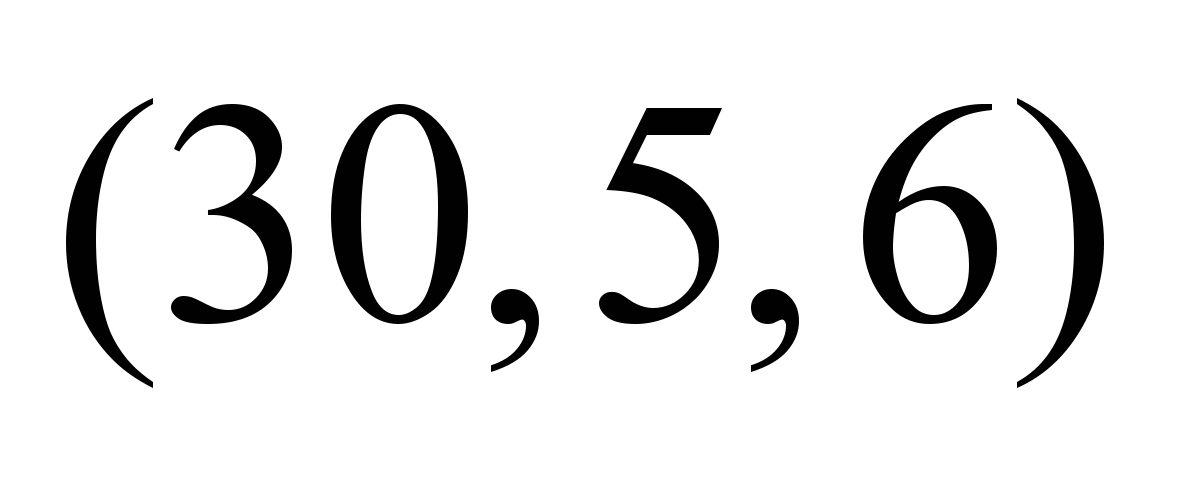
|
|
1
|
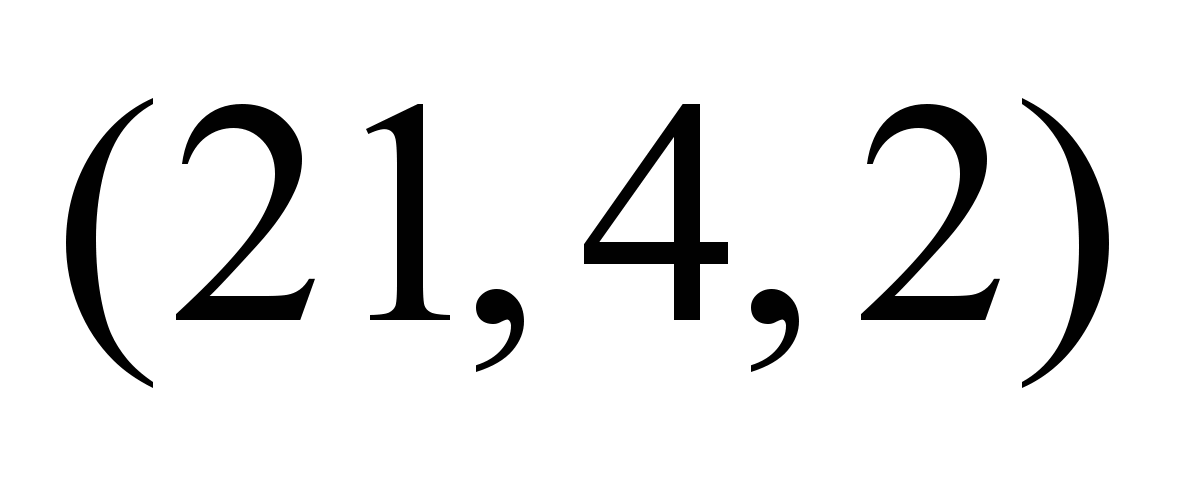
|
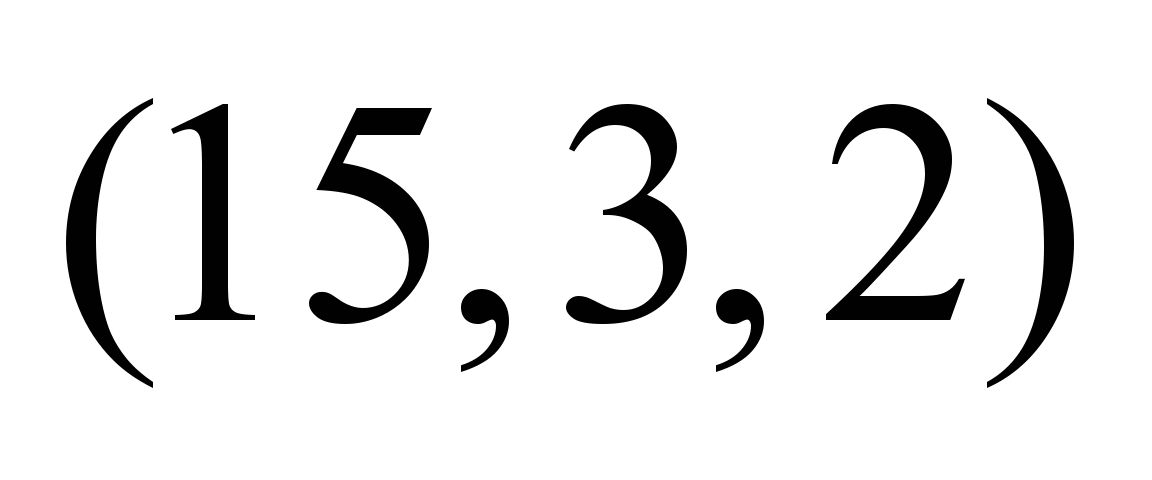
|
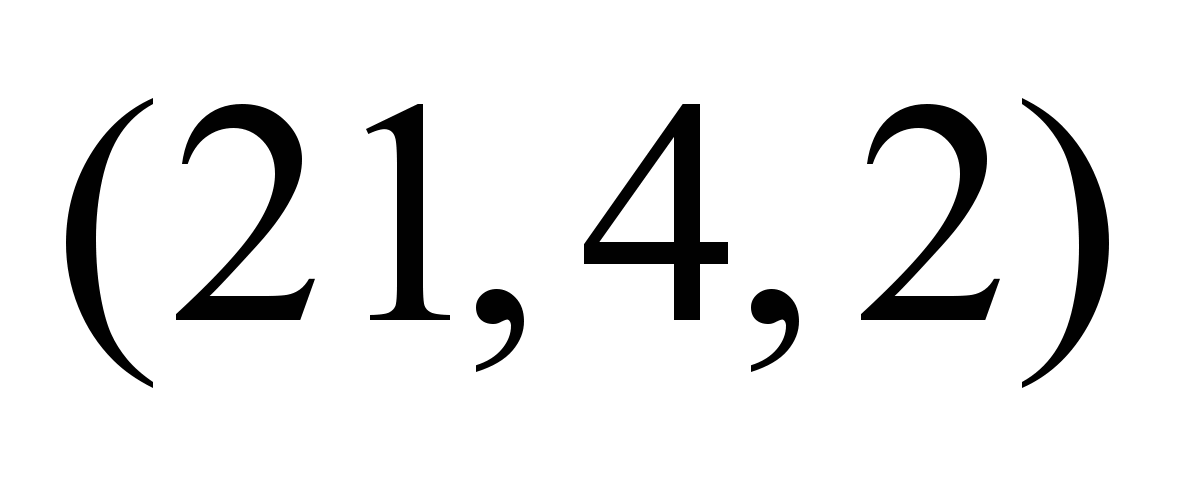
|
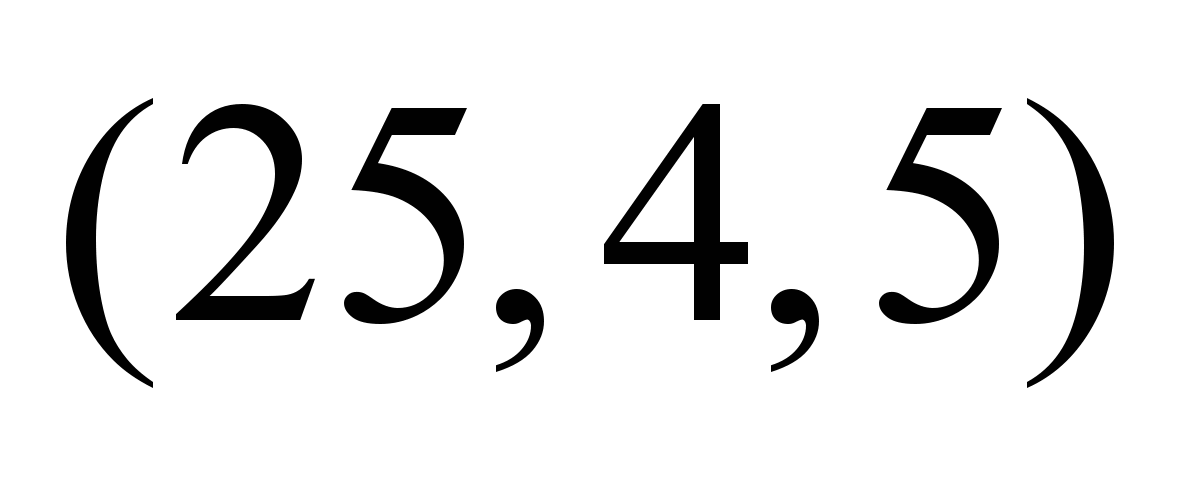
|
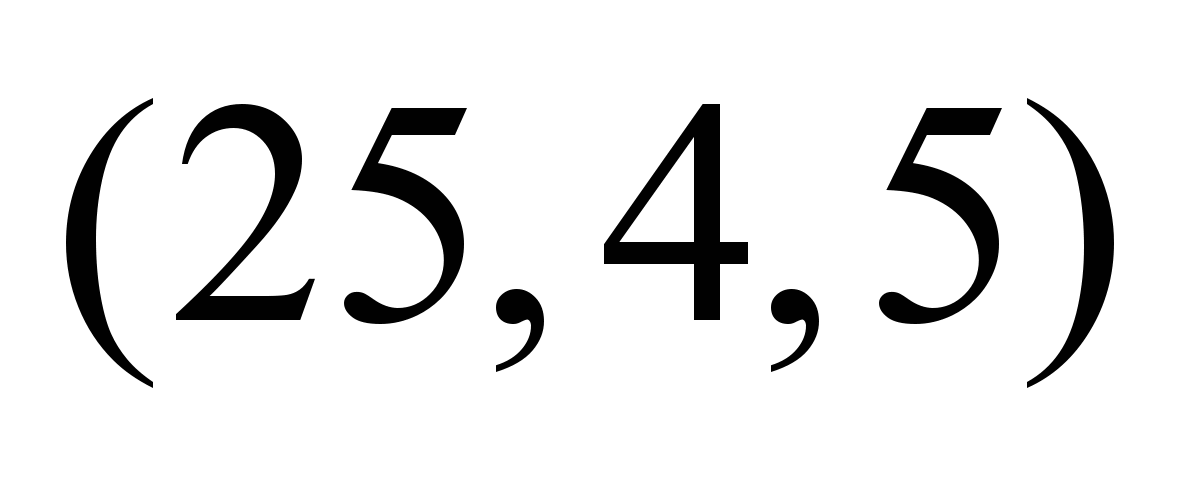
|
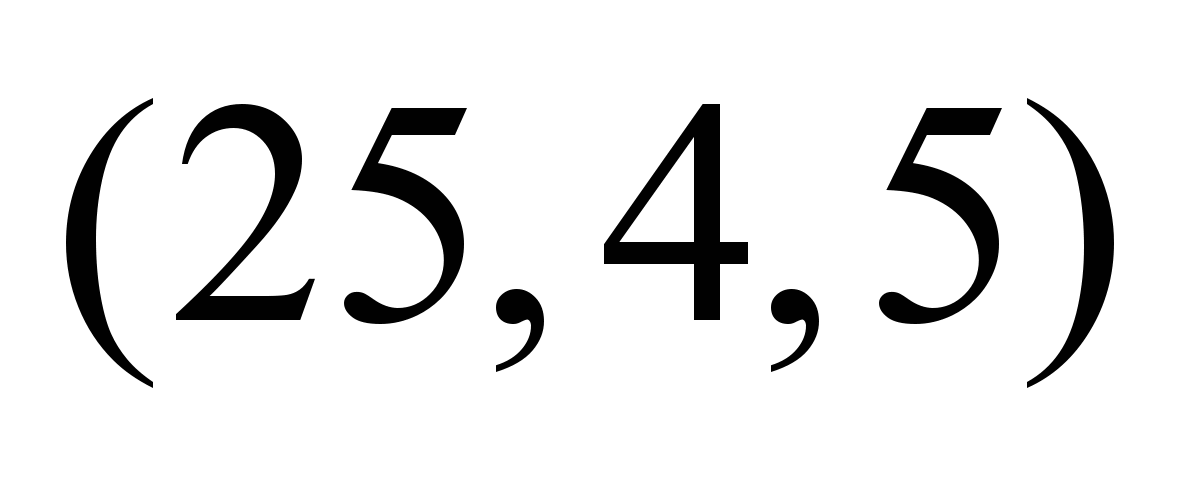
|
|
2
|
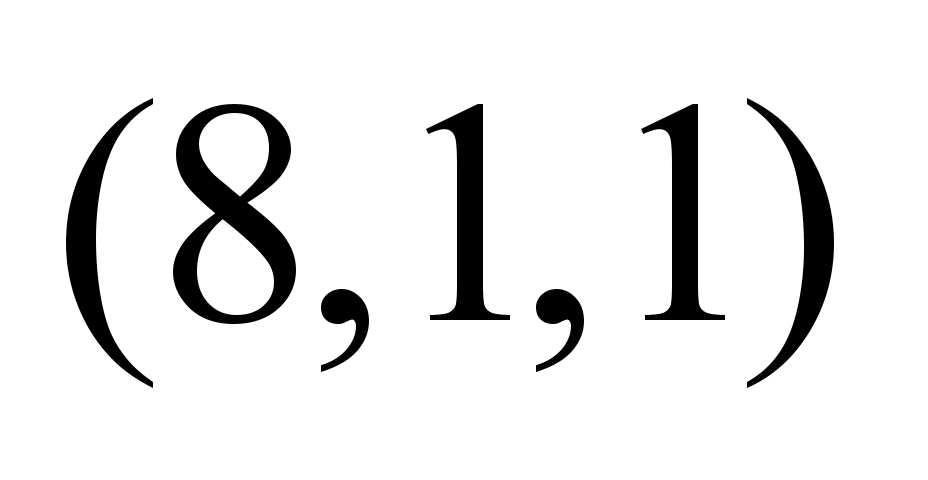
|
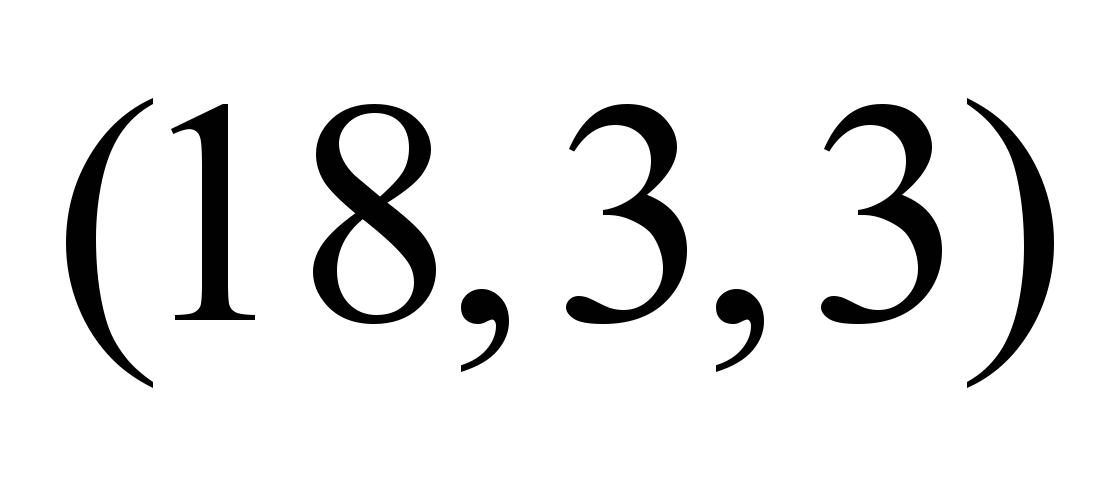
|
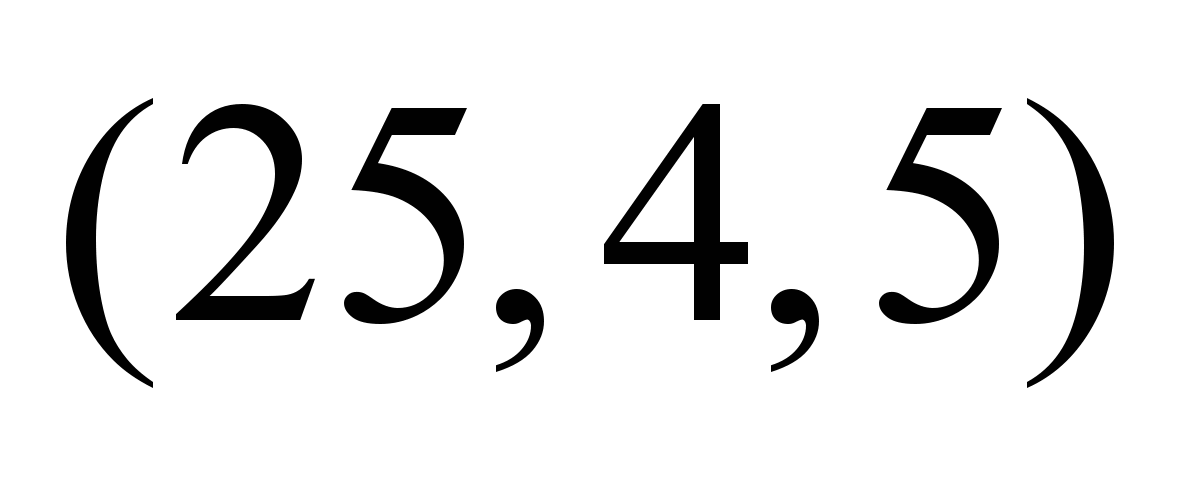
|
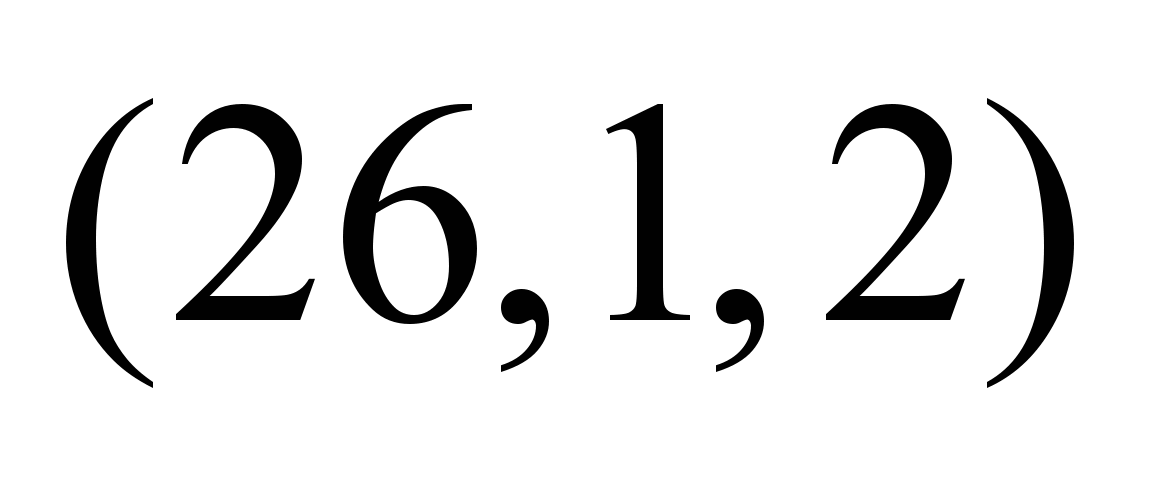
|
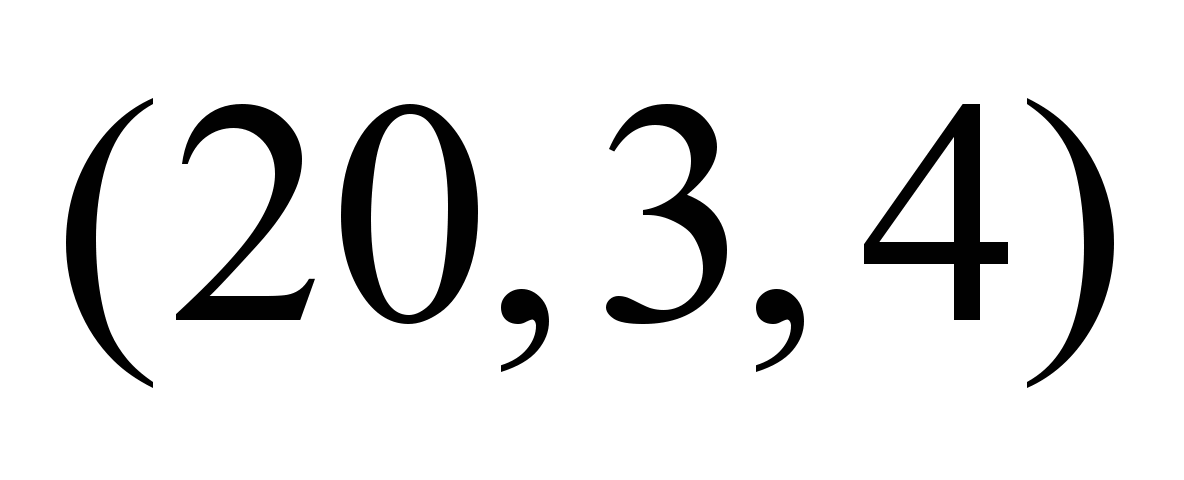
|
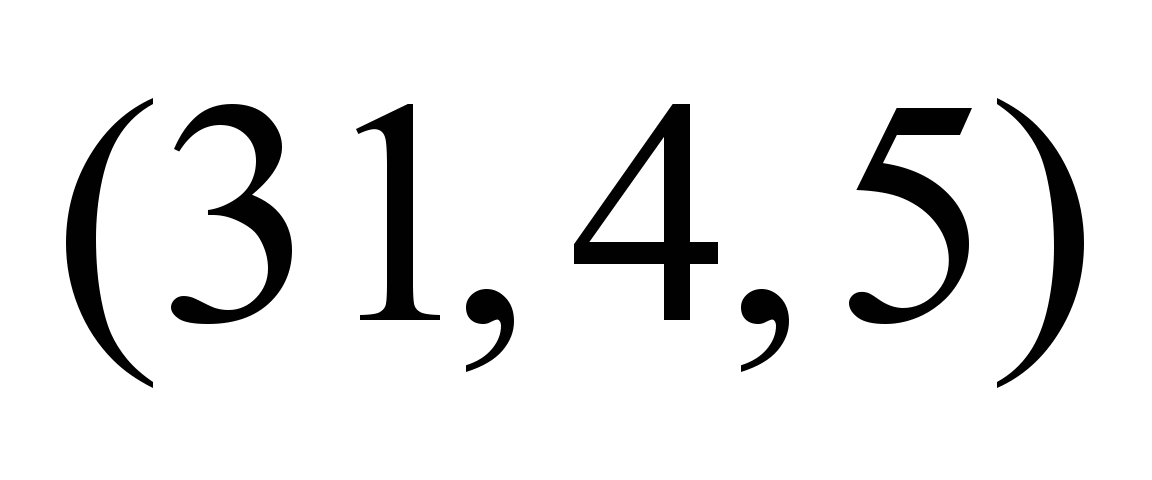
|
|
3
|
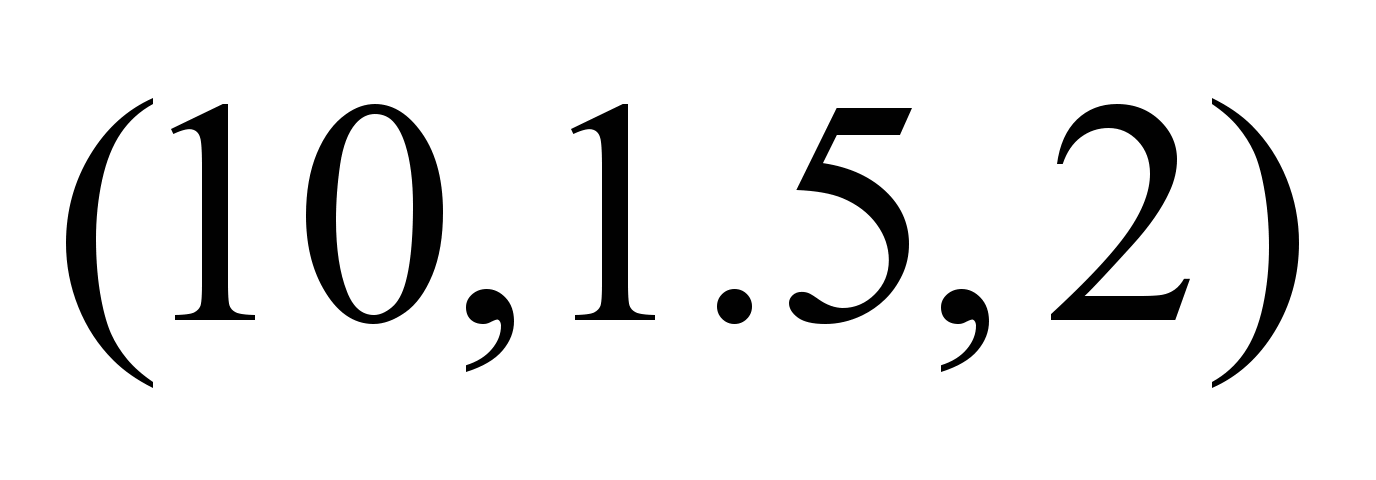
|
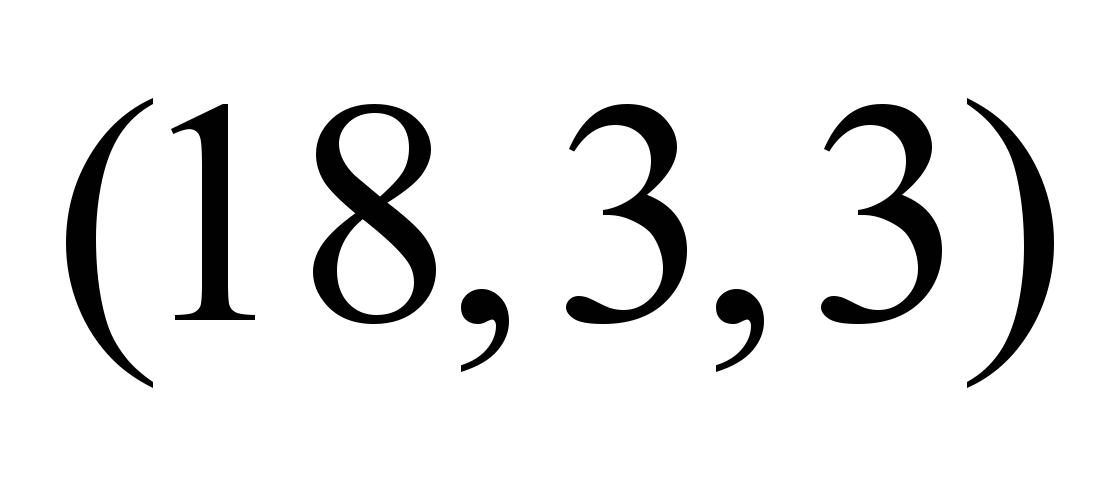
|
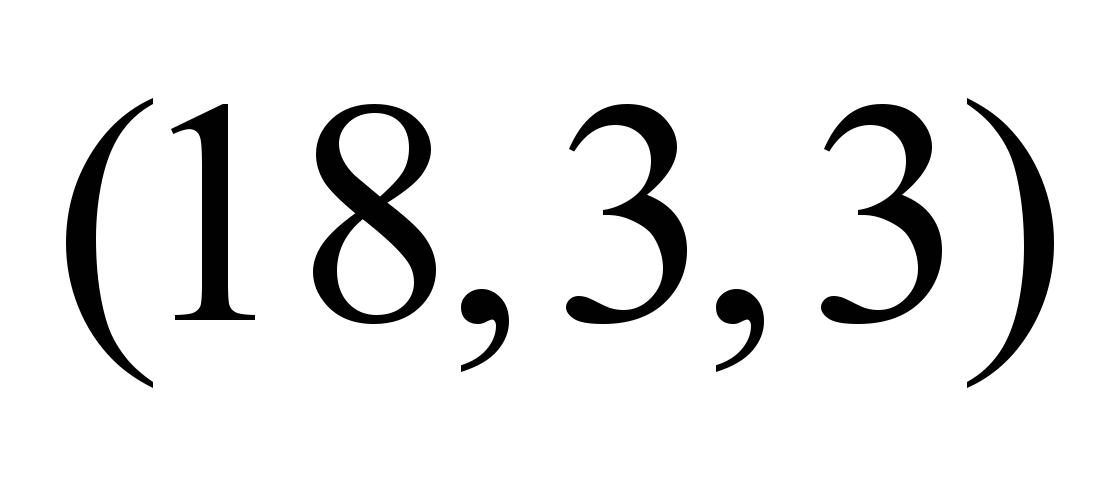
|
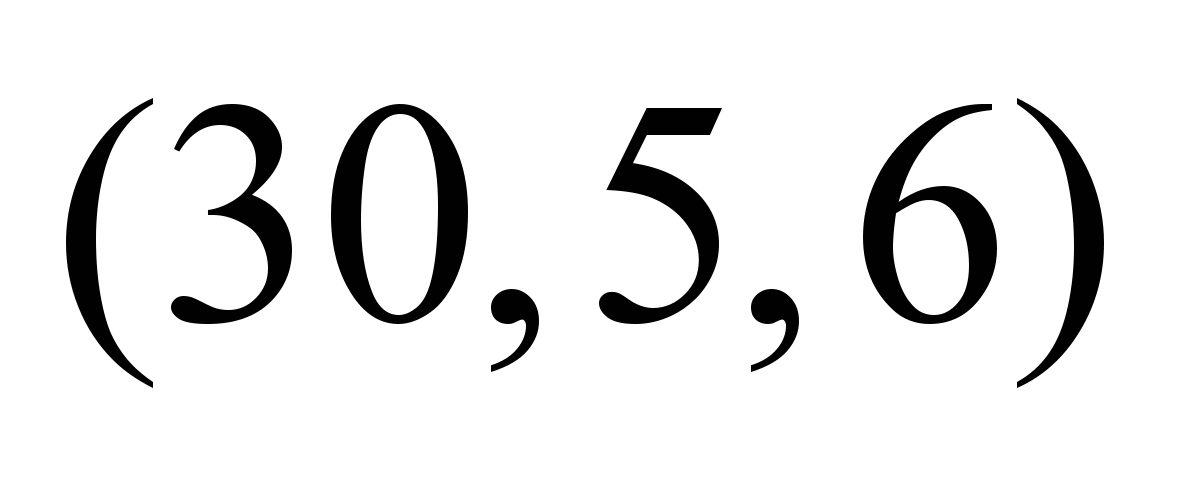
|
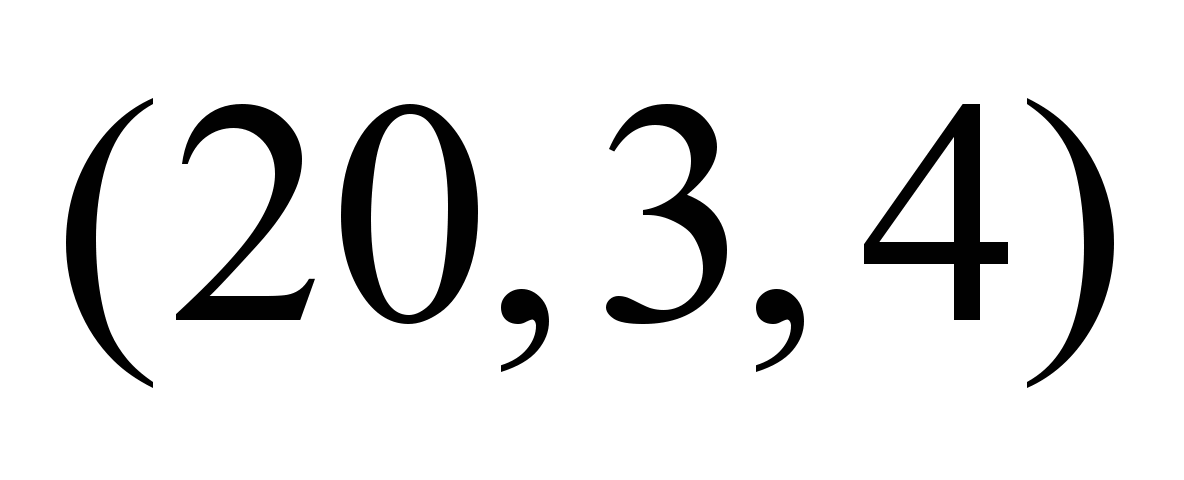
|
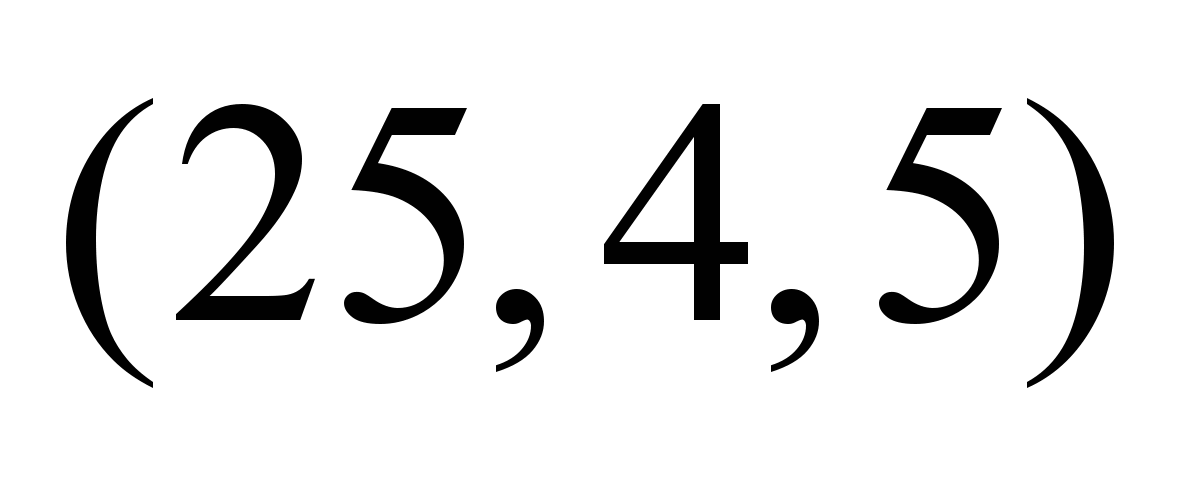
|
Таблица 5
Нечеткие,
зависящие от момента отправления
потока, стоимости
Table 5
Fuzzy
values, depending on the moment of flow departure
|
Момент
времени
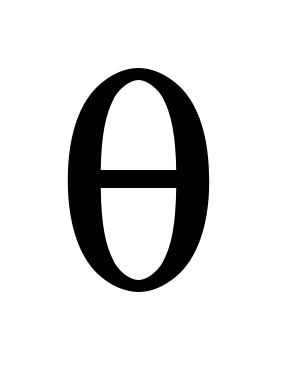
|
Нечеткие
стоимости по дугам графа
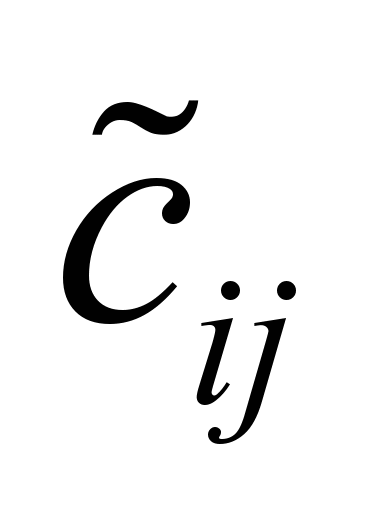 ,
условные ед. ,
условные ед.
|
|
|

|
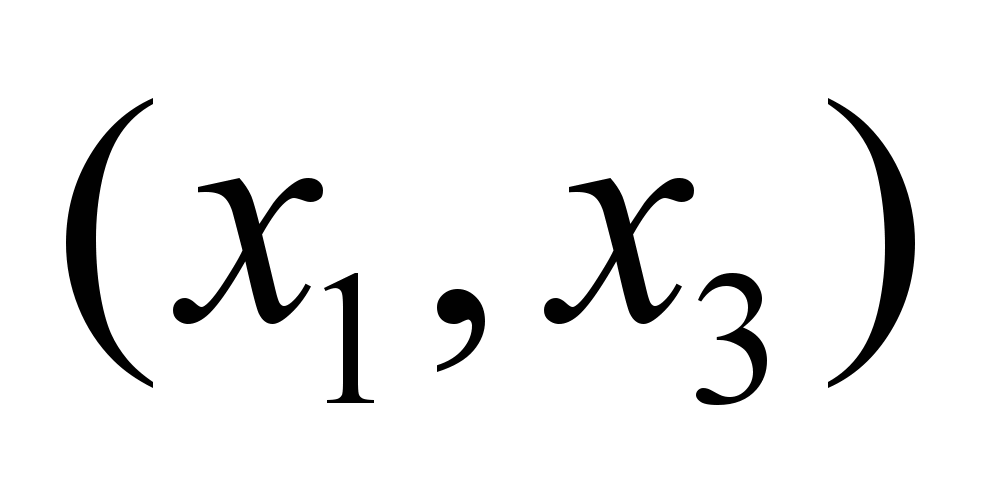
|
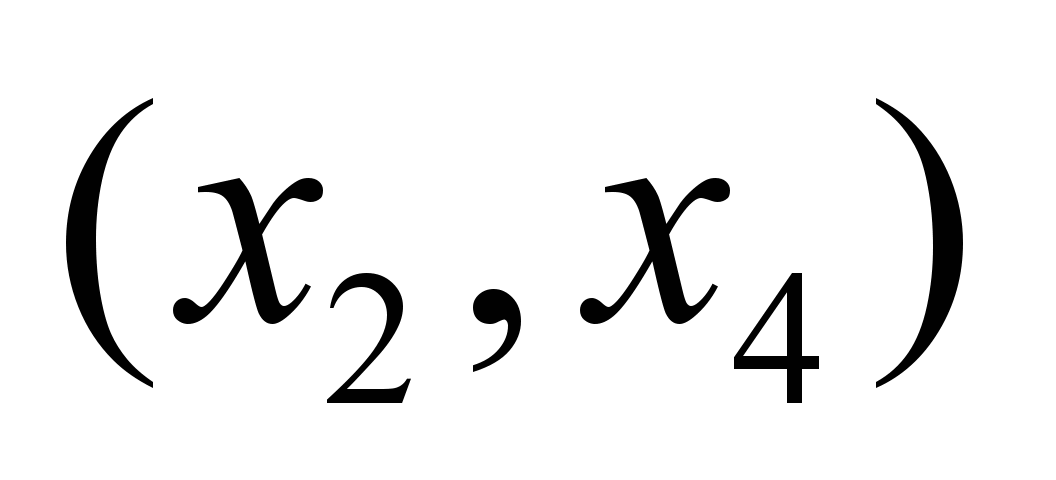
|
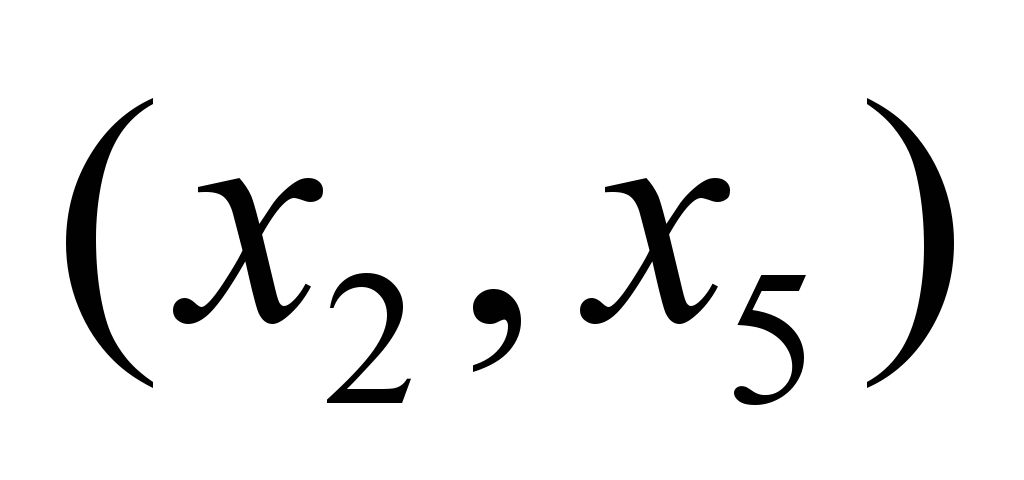
|
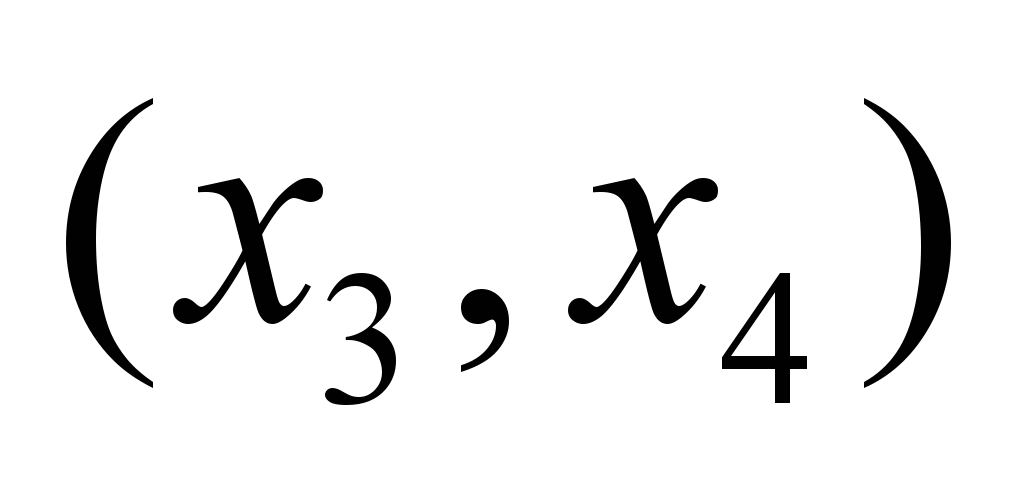
|
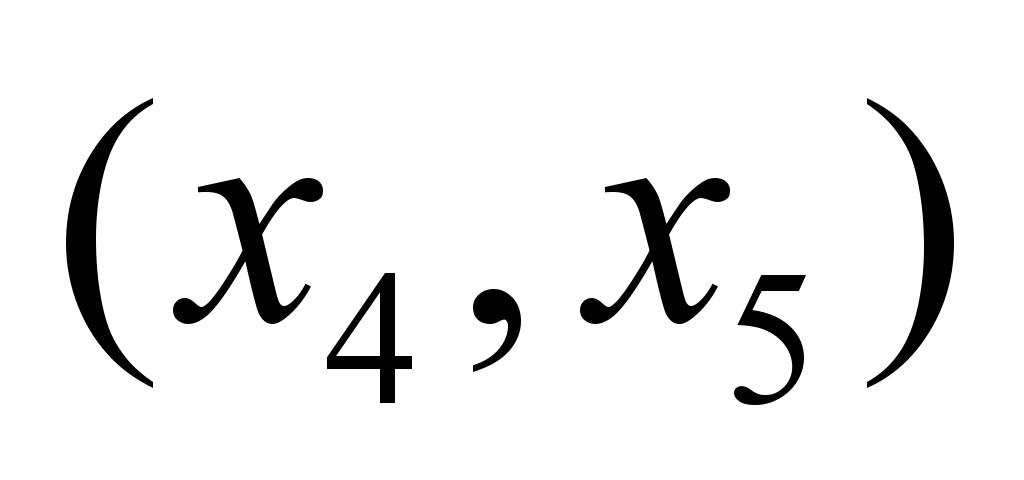
|
|
0
|
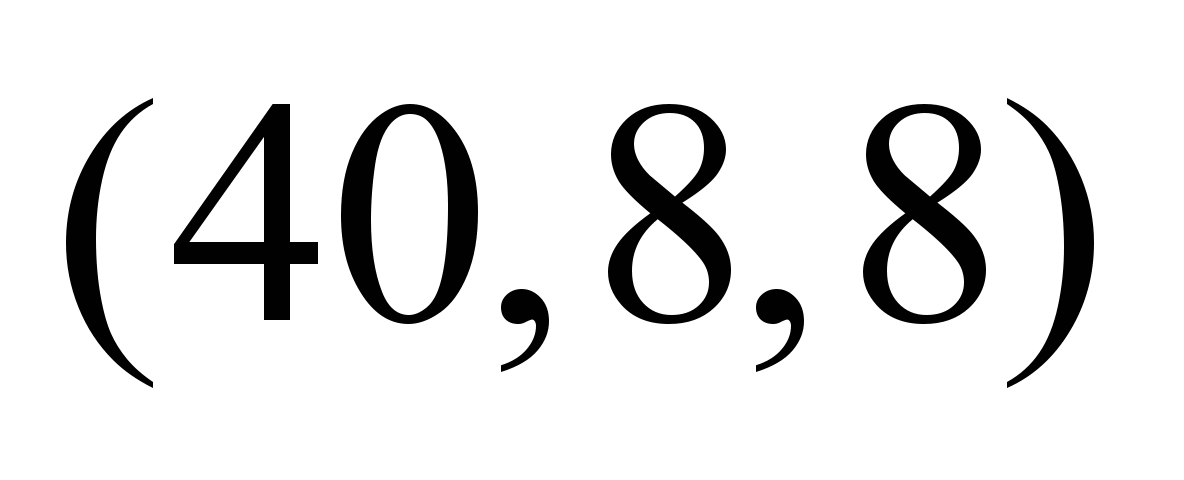
|
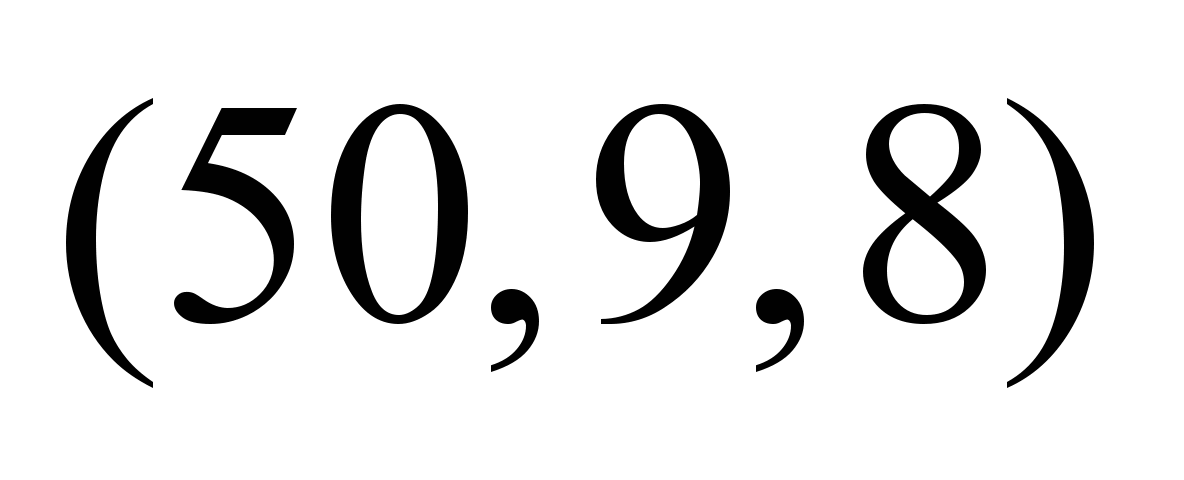
|
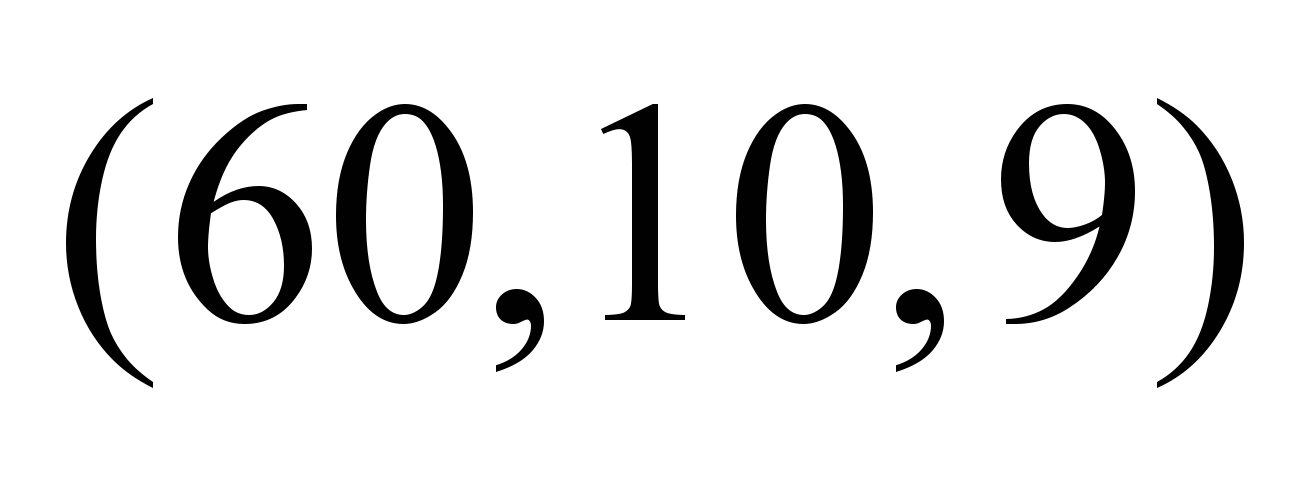
|
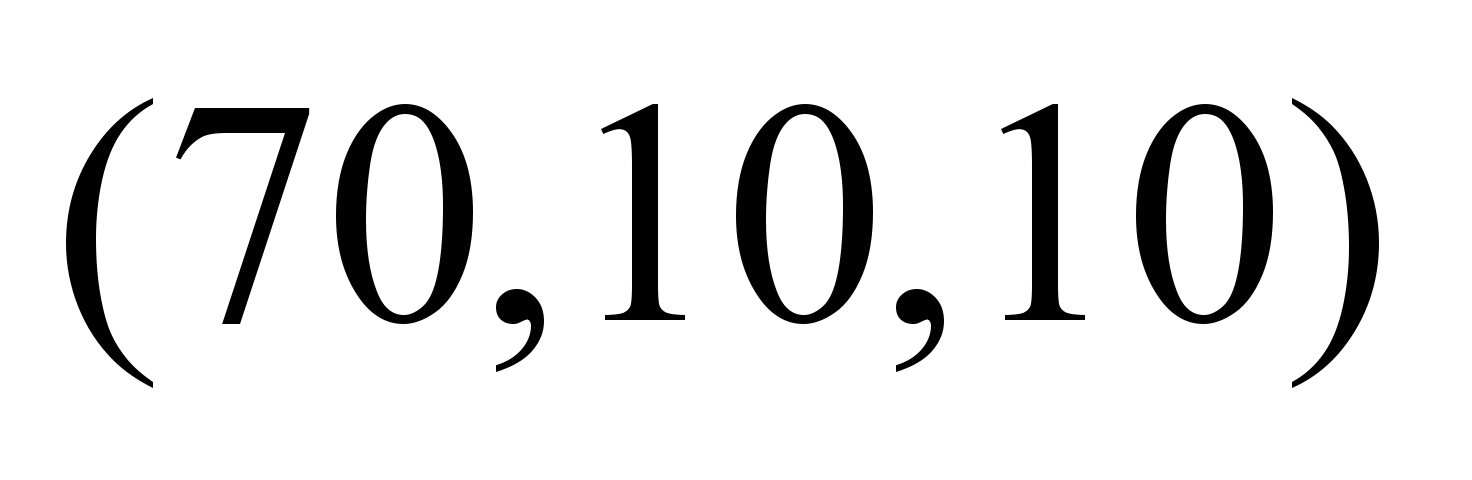
|
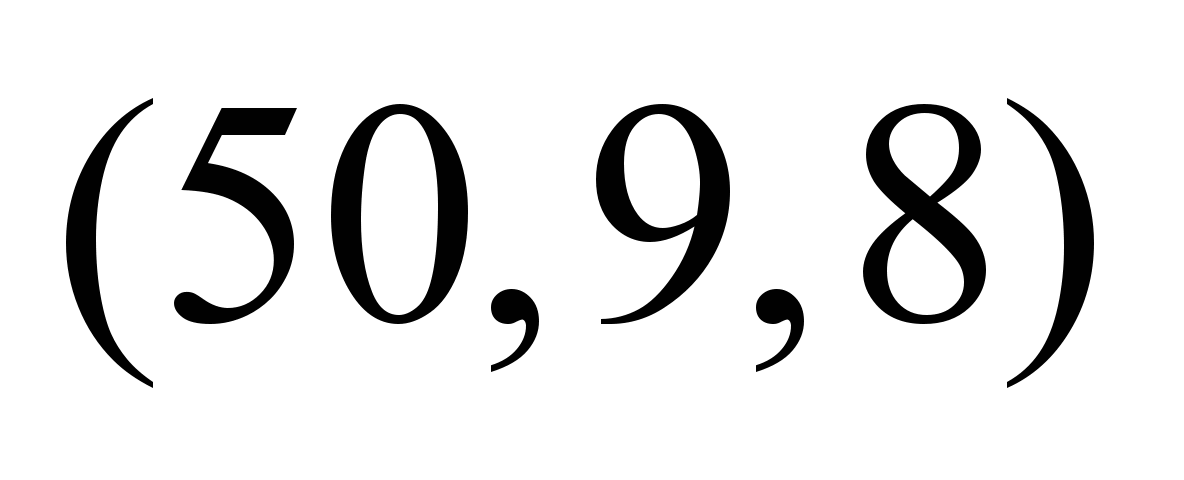
|
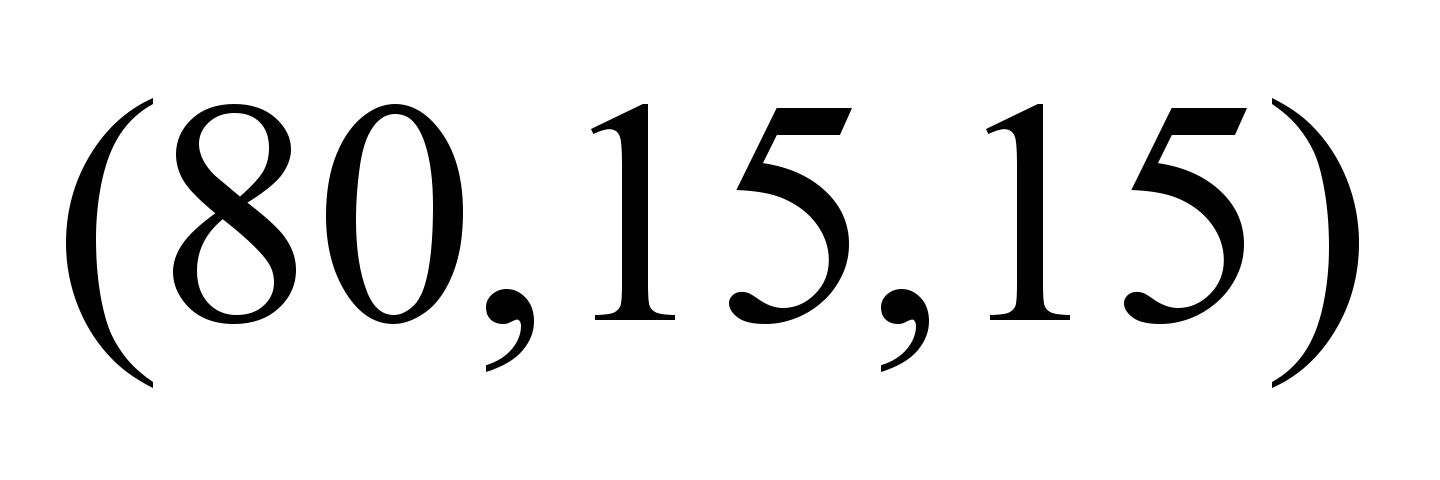
|
|
1
|
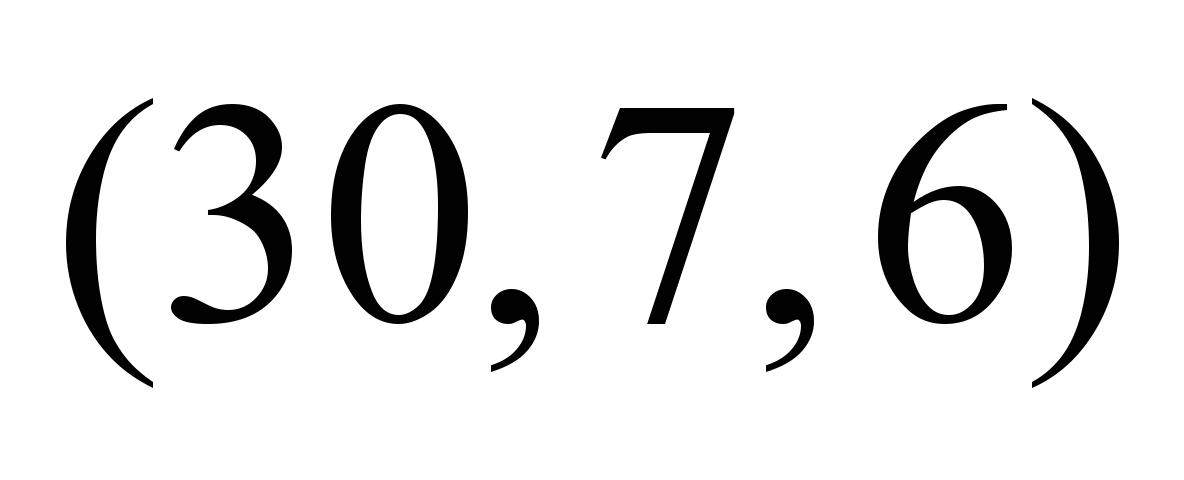
|
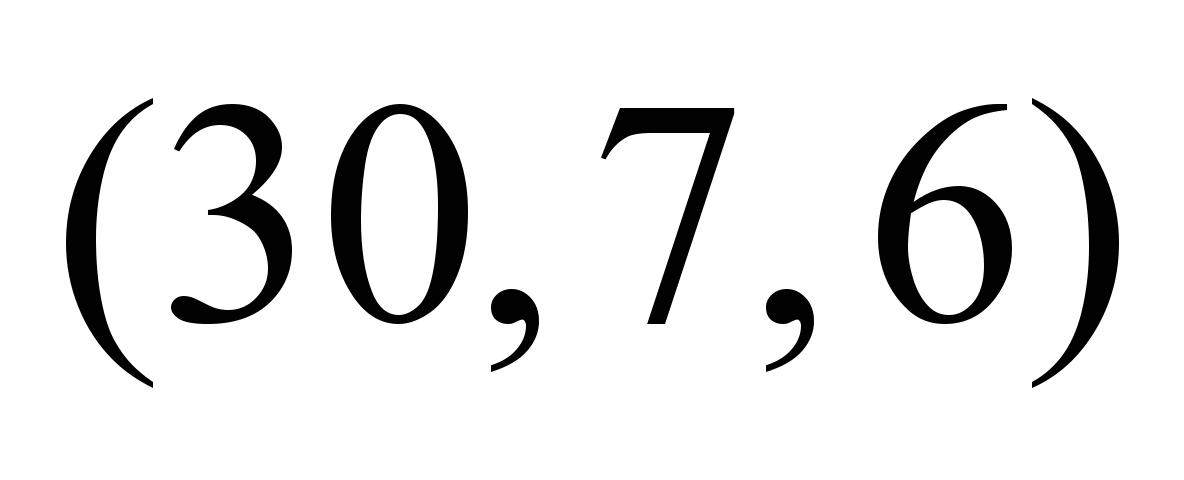
|
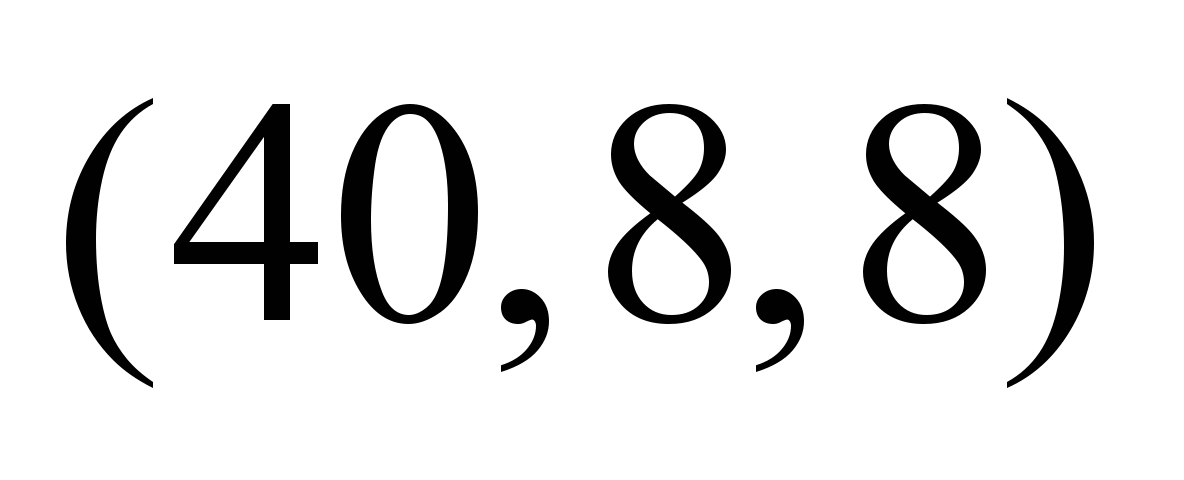
|
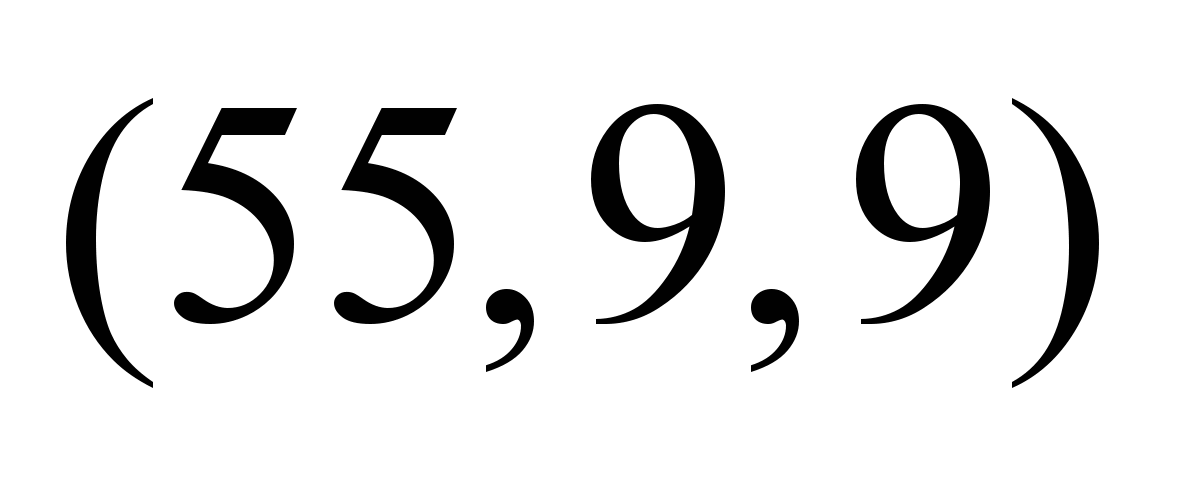
|
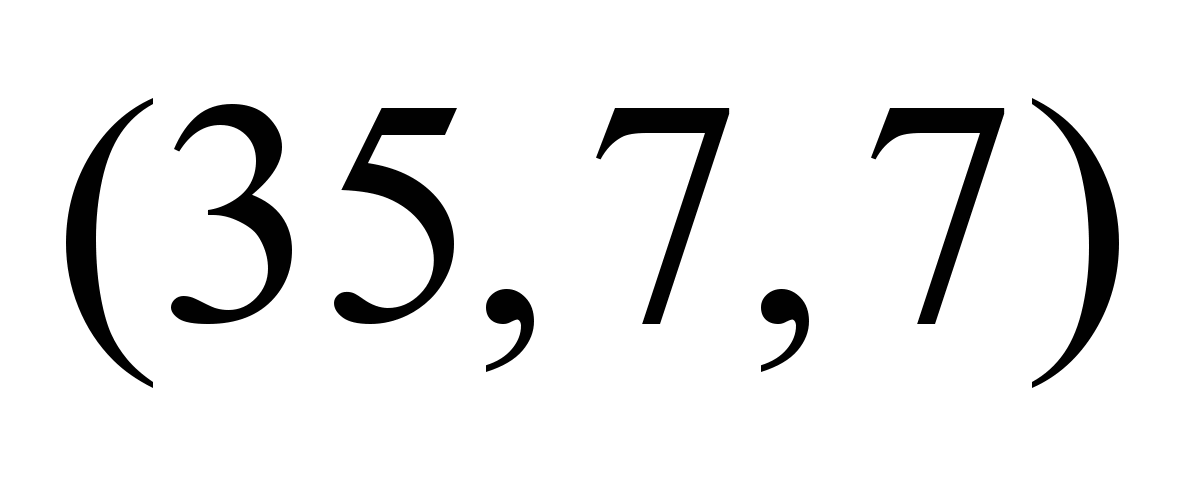
|
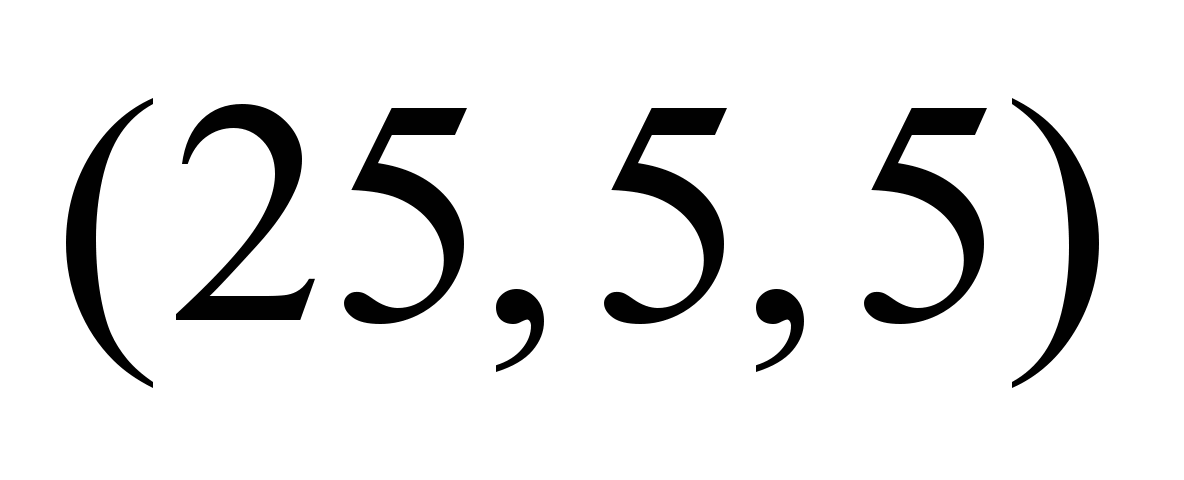
|
|
2
|
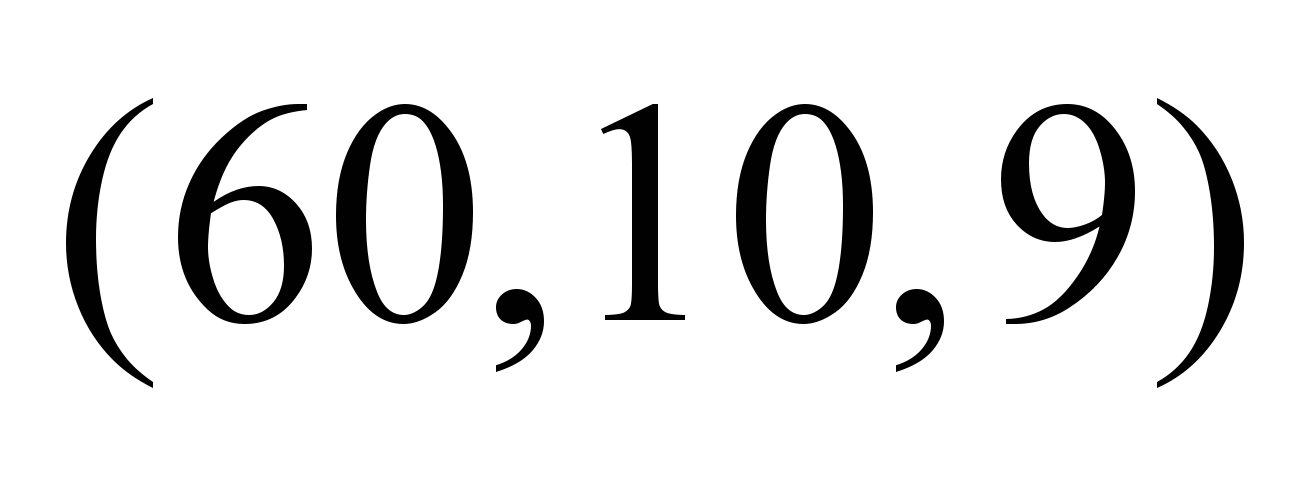
|
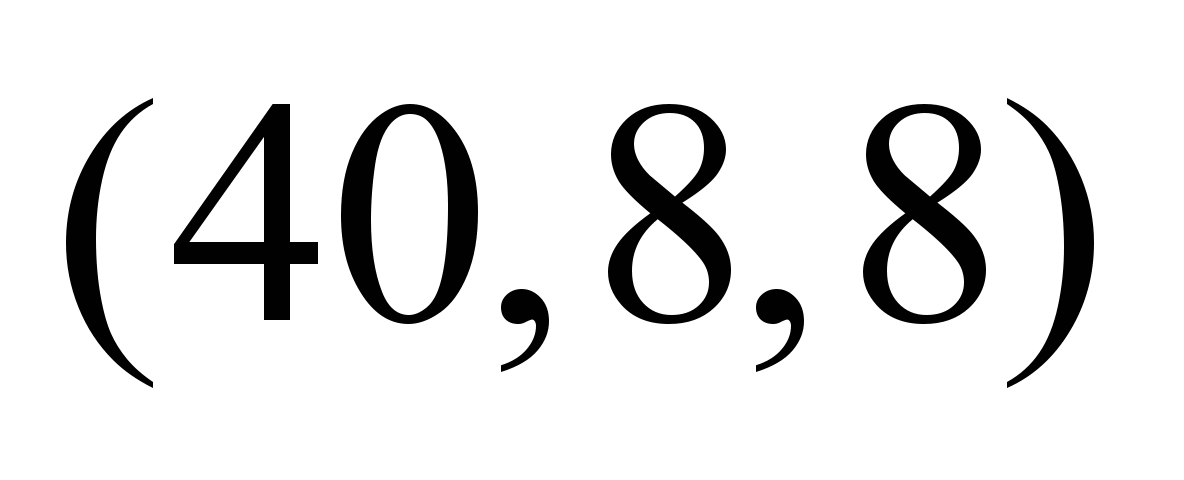
|
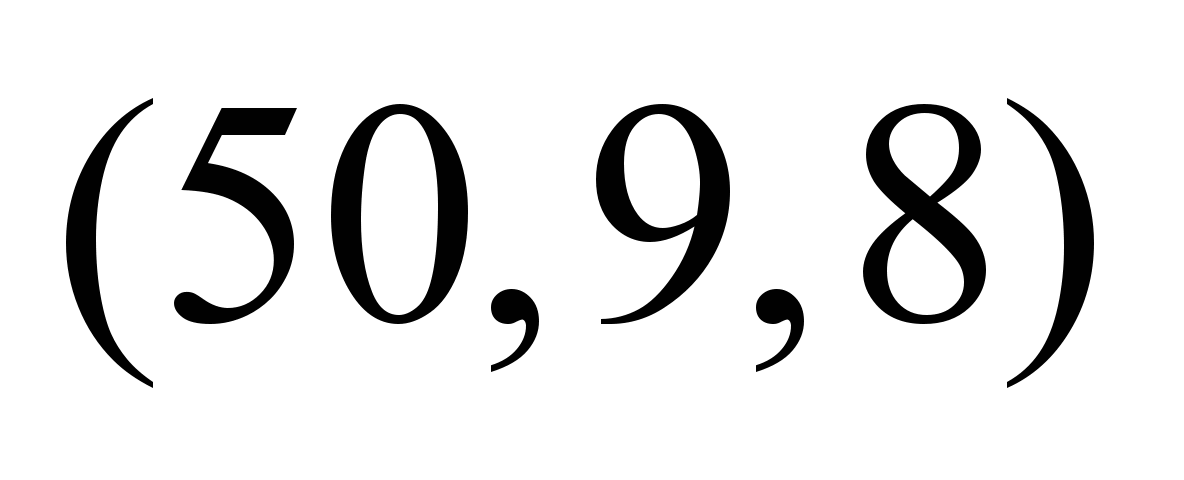
|
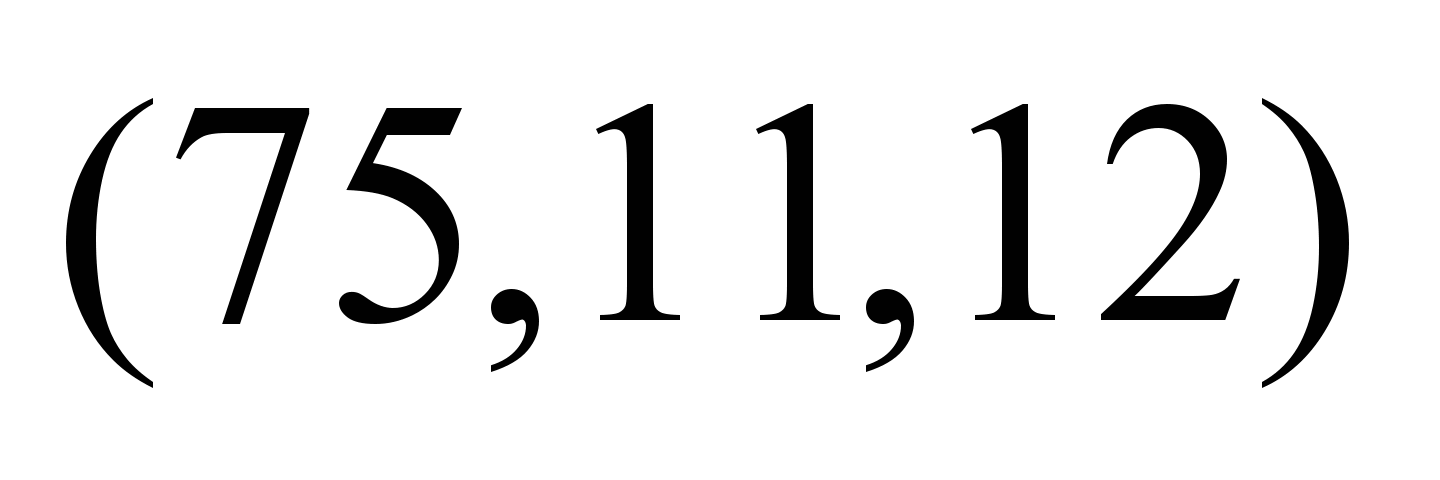
|
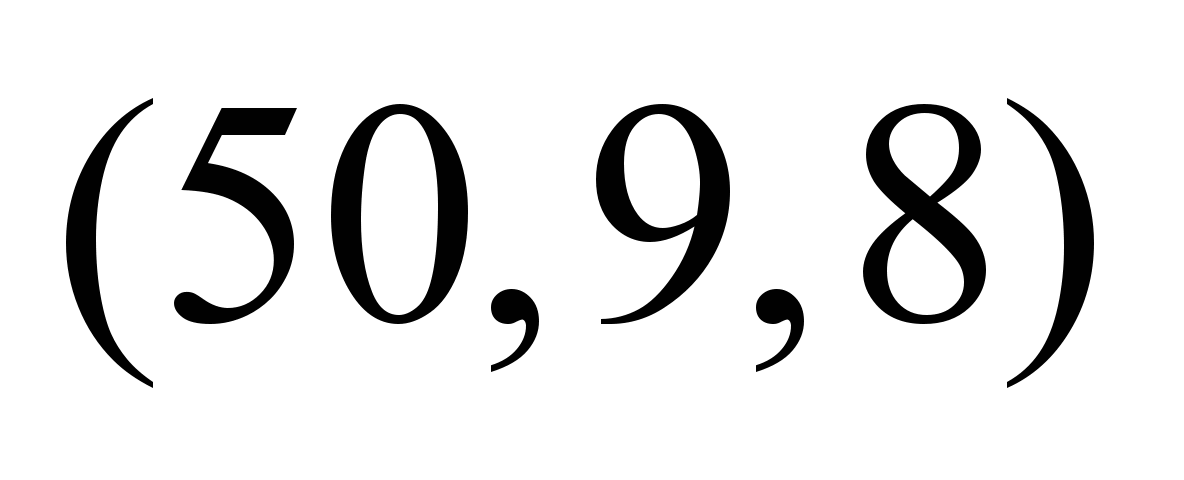
|
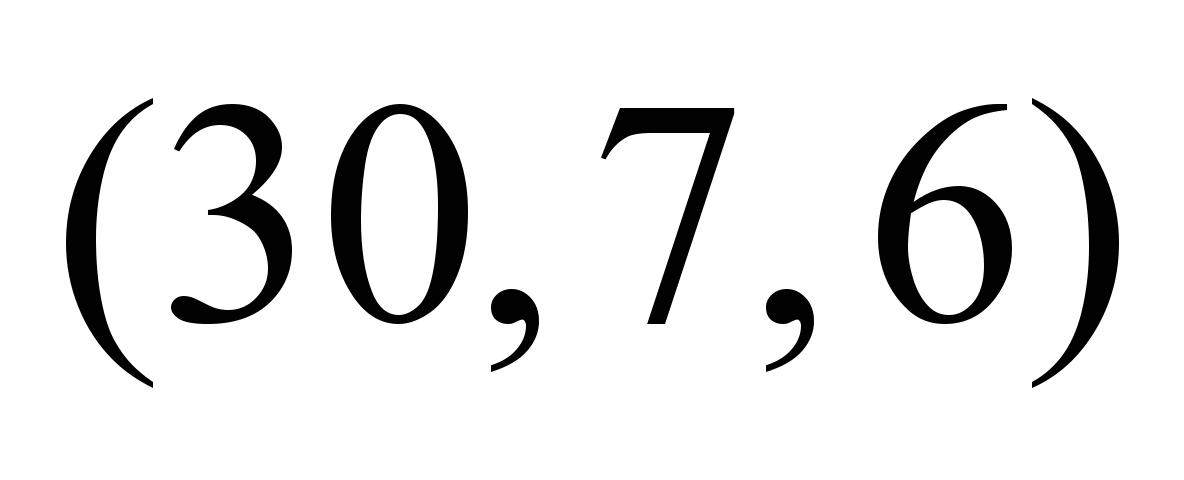
|
|
3
|
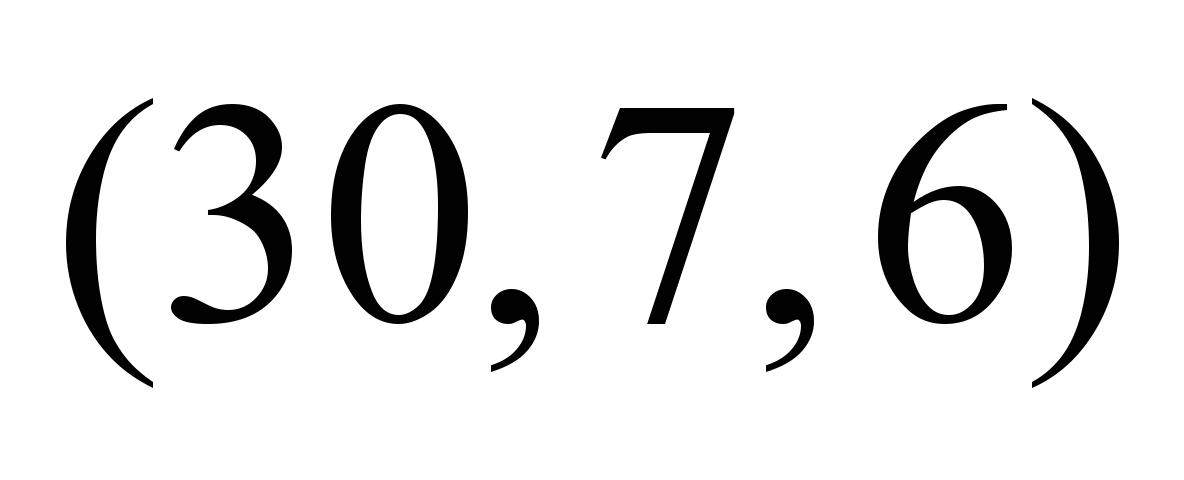
|
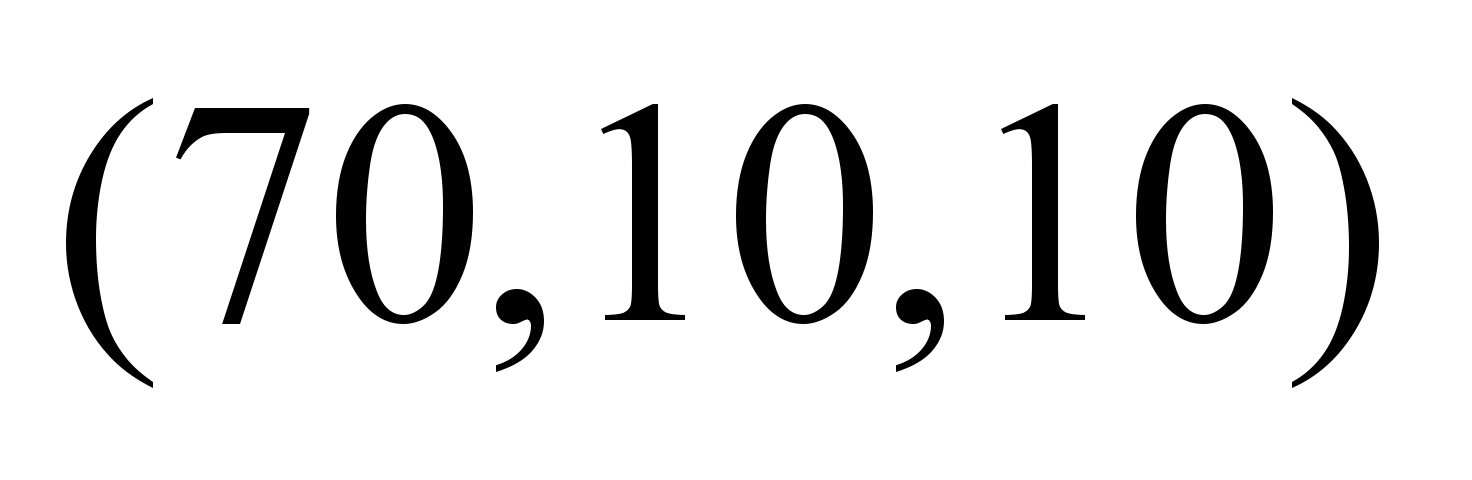
|
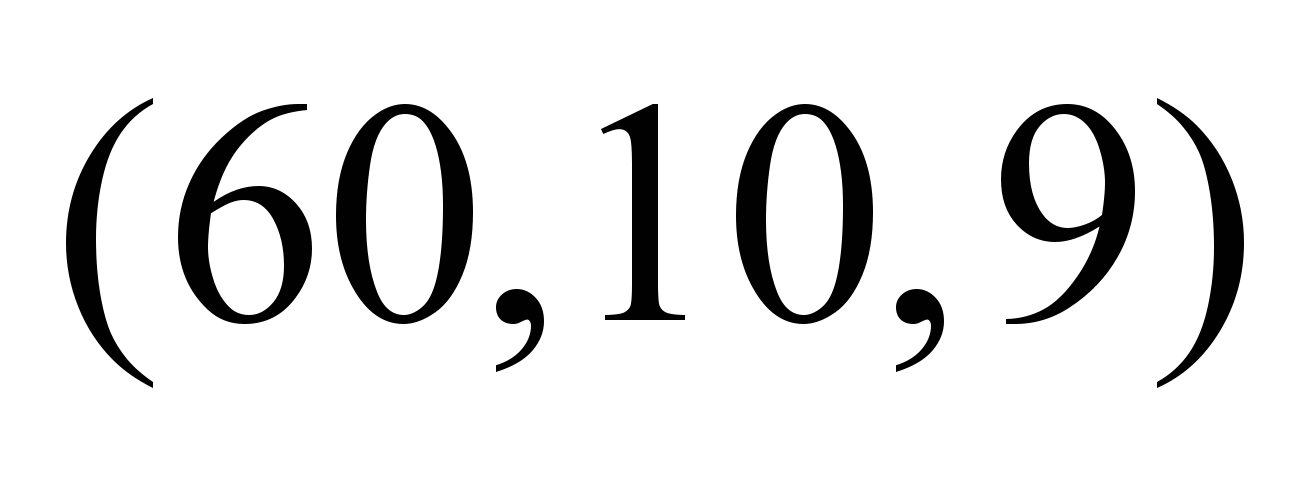
|
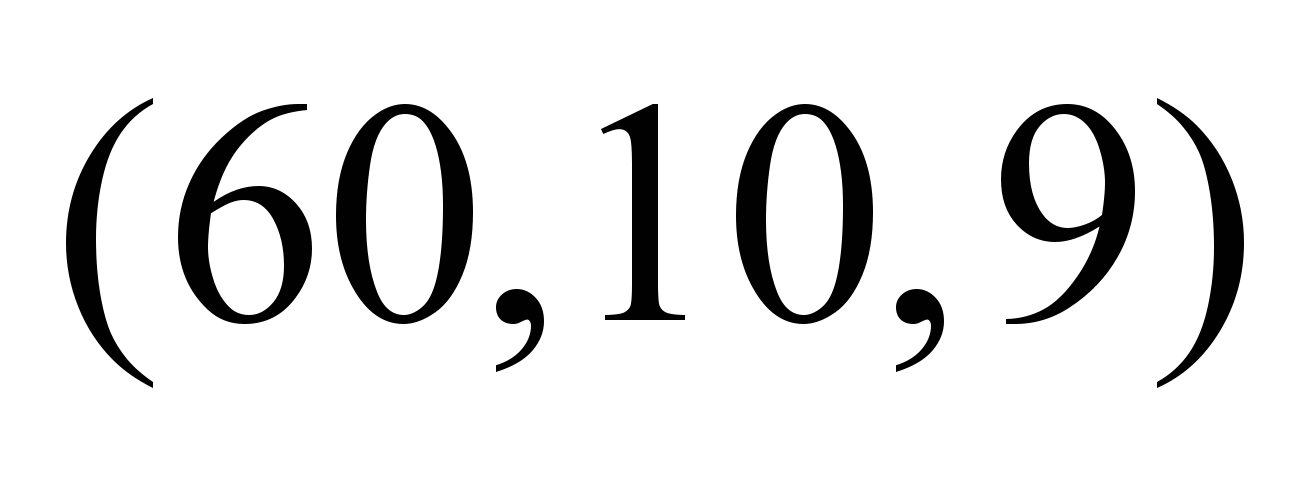
|
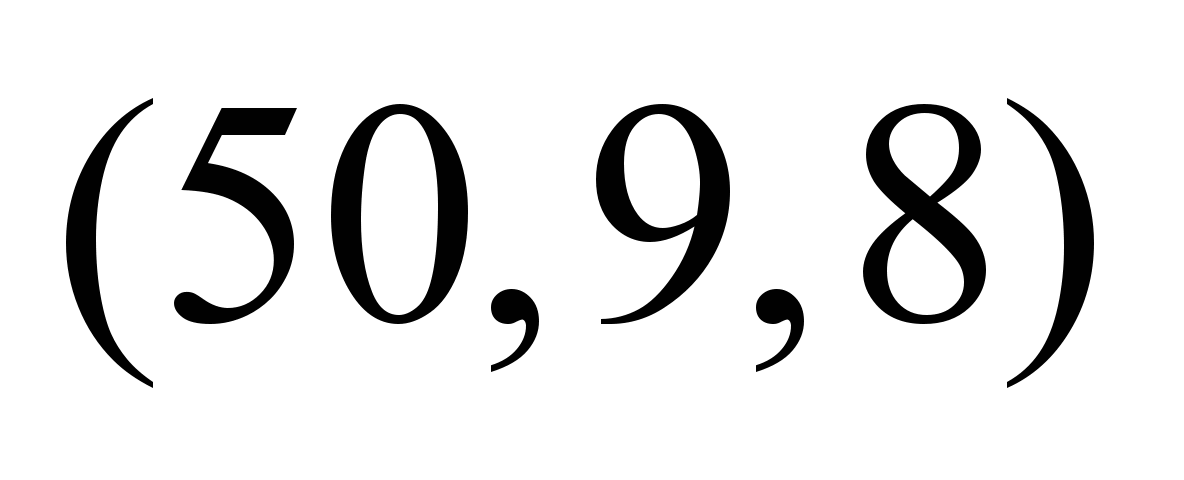
|
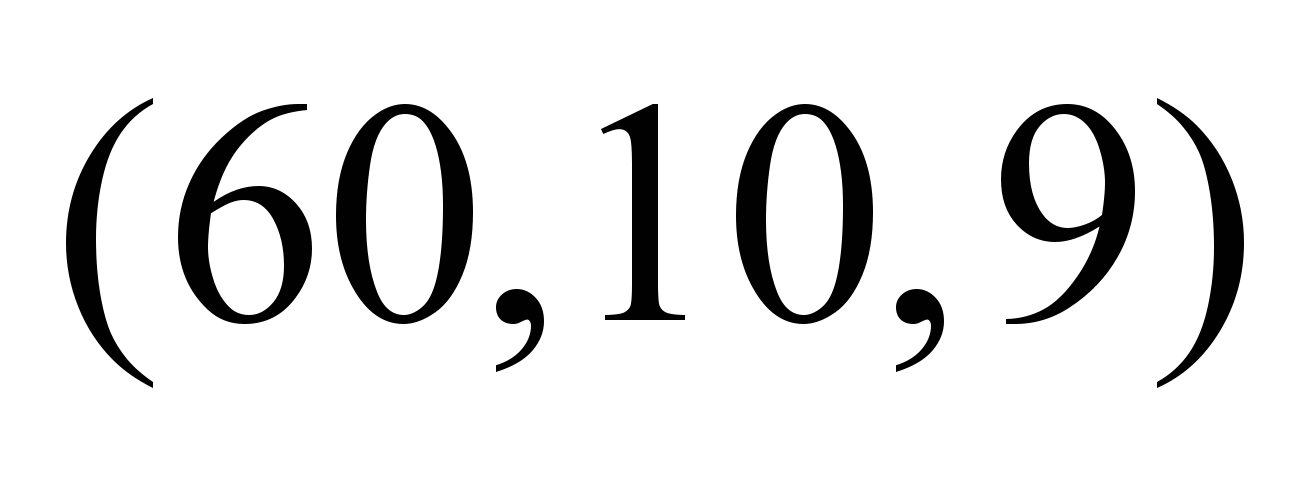
|
Таблица 6
Параметры
времен прохождения потока по дугам ТС
Table 6
Times
parameters of the flow passing along the transport networks arcs
|
Момент
времени
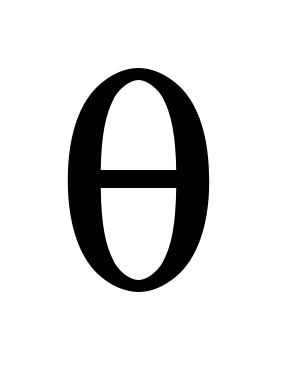
|
Время
прохождения потока по дугам графа
 ,
ед. времени ,
ед. времени
|
|
|

|
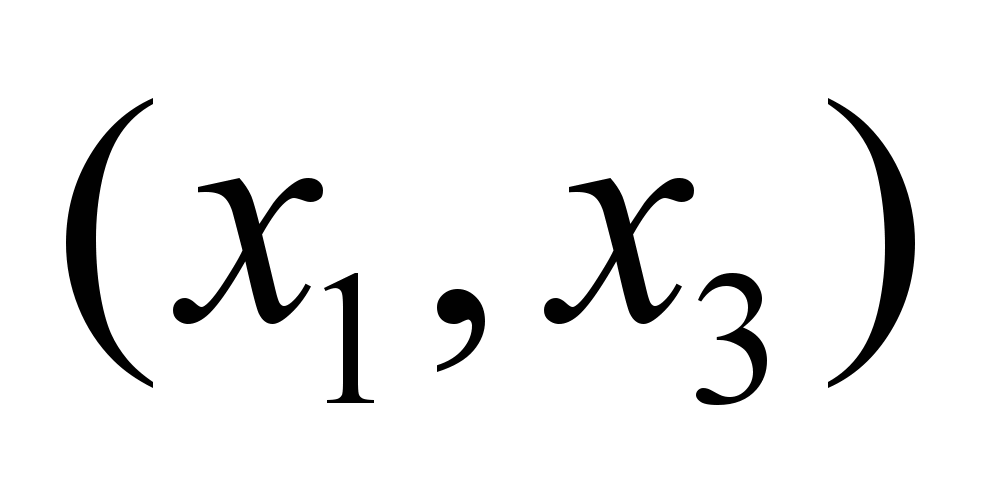
|
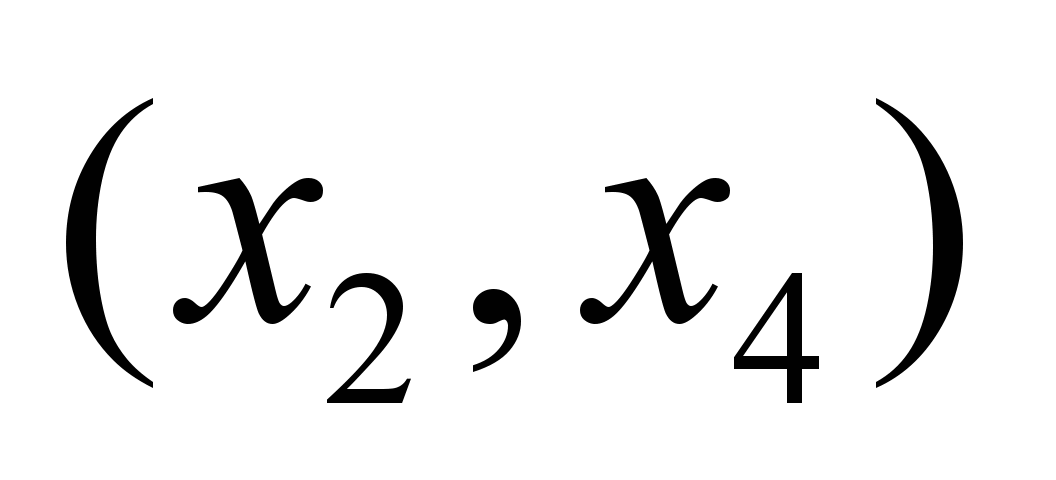
|
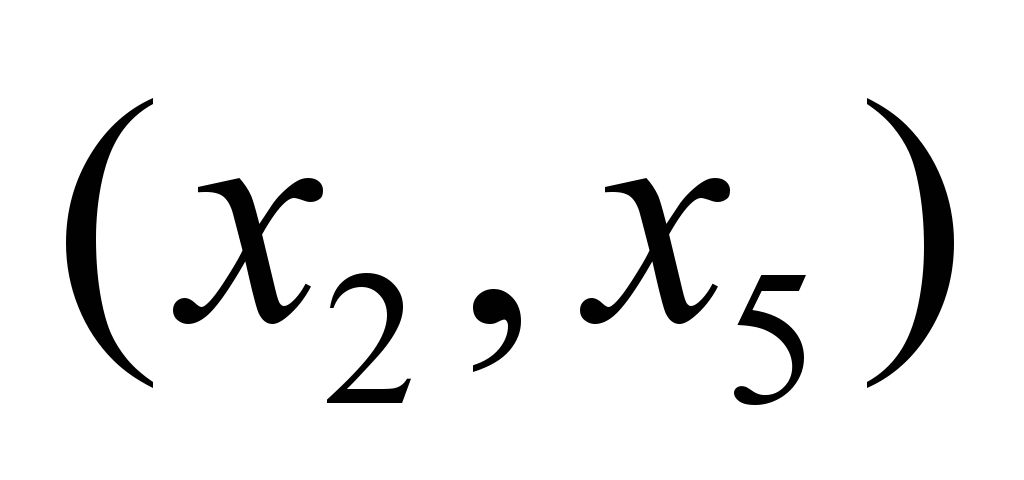
|
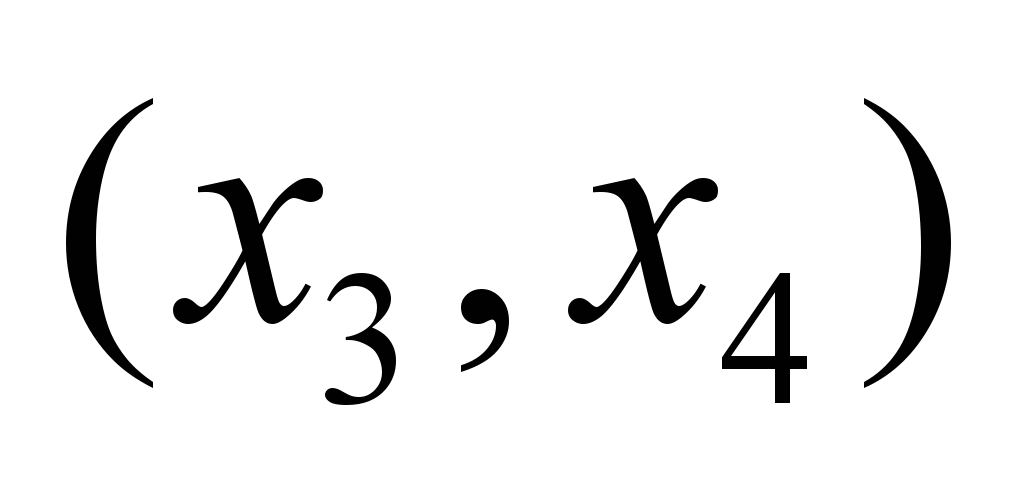
|
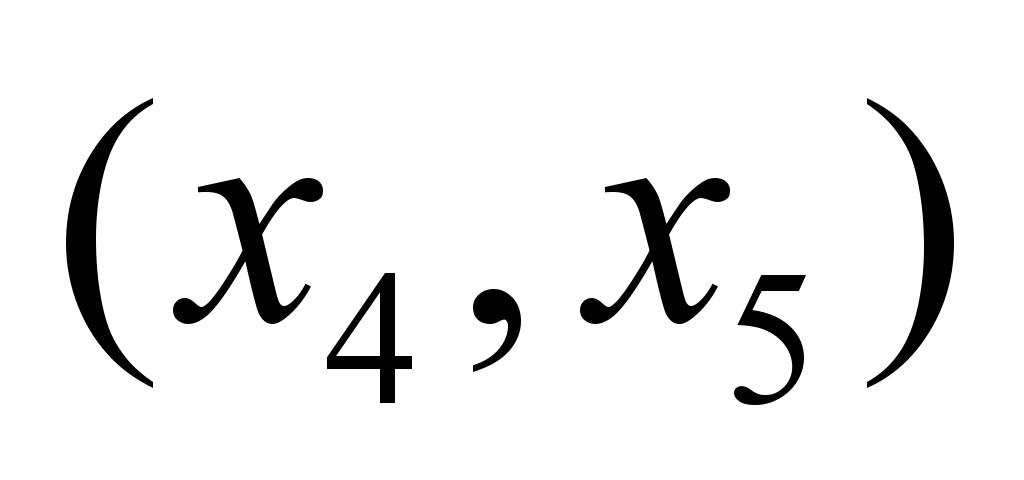
|
|
0
|
1
|
4
|
4
|
2
|
5
|
1
|
|
1
|
1
|
3
|
1
|
4
|
4
|
4
|
|
2
|
3
|
1
|
3
|
1
|
3
|
1
|
|
3
|
2
|
1
|
3
|
2
|
3
|
1
|
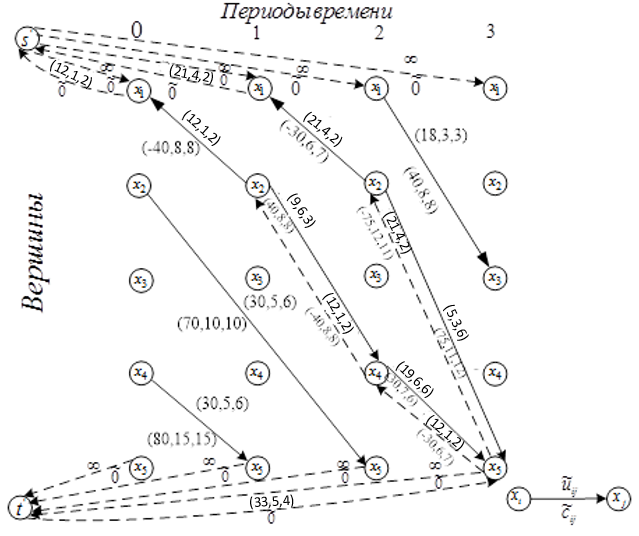
Рис.
6. Остаточная сеть
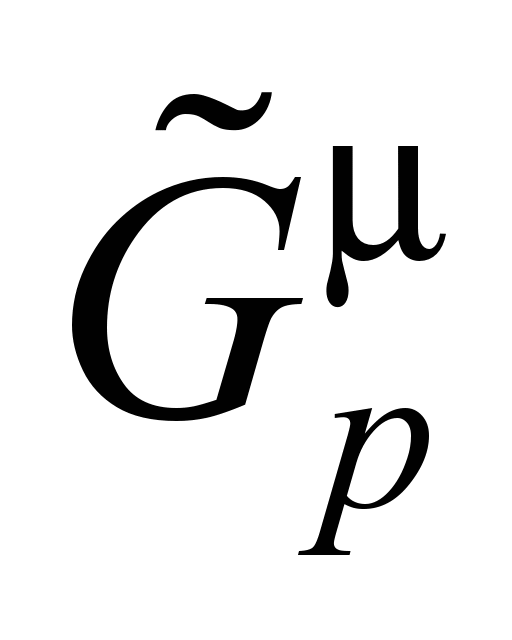 после нахождения потока
после нахождения потока
Fig.
6. Residual network
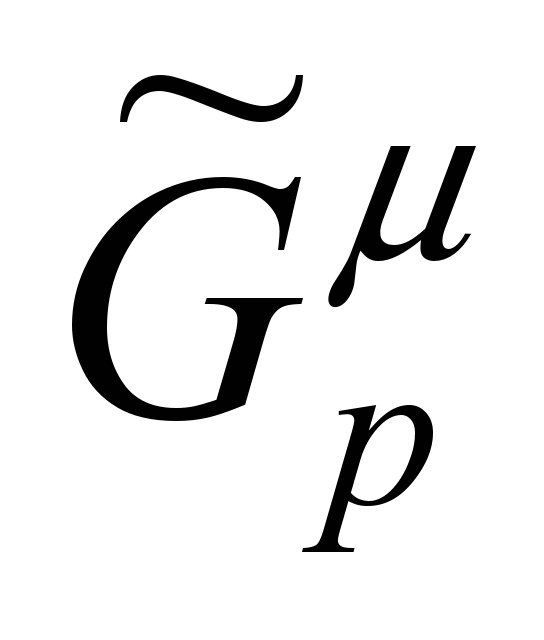 after
flow finding
after
flow finding
Приведенный выше
алгоритм ПСАП является пригодным и для
исследования компромиссных
(детерминированных и нечетких) моделей
планирования многопродуктовых потоков.
В разделе приводится процедура и
результаты планирования потоков трех
продуктов (для сети на рис. 1, источник
продукта 3 – S2, а сток – t1) на
основе принципа компромисса:
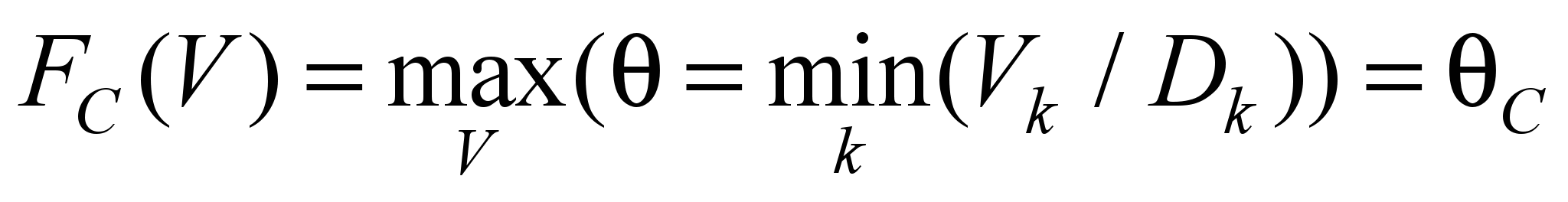 , (7)
, (7)
где

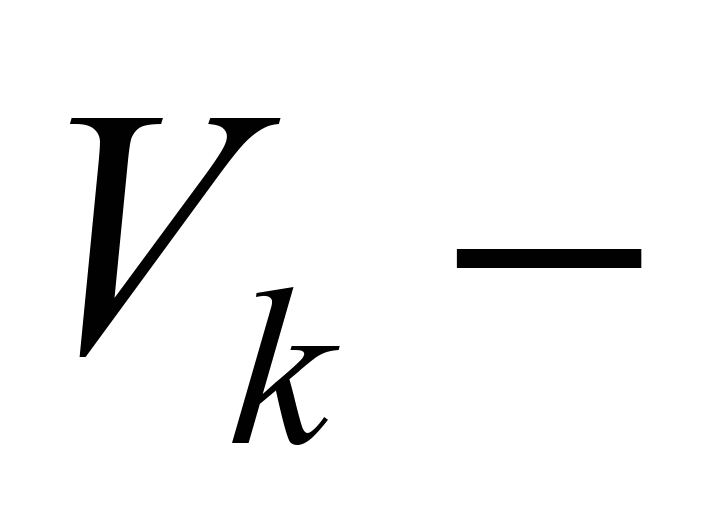 величина компромиссного потока k-ого
продукта, а
величина компромиссного потока k-ого
продукта, а
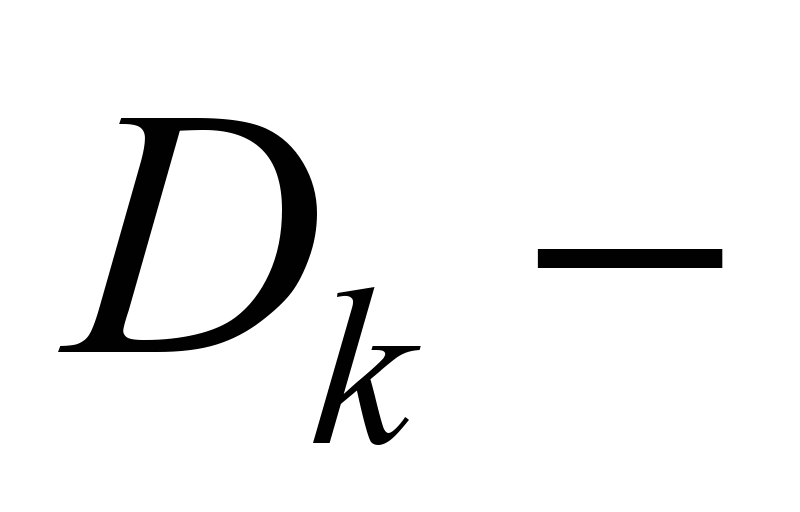 его максимальный поток в сети (рис. 1).
Укажем, что в ТС может быть несколько
максимальных потоков, функция (7) является
недифференцированной, имеет насколько
локальных экстремумов. Поэтому в
общем случае на основе ПСАП и приведенных
ниже процедур находится локальный
экстремум (7) для ТС на рис. 1.
его максимальный поток в сети (рис. 1).
Укажем, что в ТС может быть несколько
максимальных потоков, функция (7) является
недифференцированной, имеет насколько
локальных экстремумов. Поэтому в
общем случае на основе ПСАП и приведенных
ниже процедур находится локальный
экстремум (7) для ТС на рис. 1.
Реализация модели
планирования (7) класса К3 (табл. 2) на
основе ПСАП выполняется по следующим
процедурам (П).
П1. На основе ПСАП
параллельными вычислениями независимо
рассчитывают максимальные потоки
каждого из продуктов
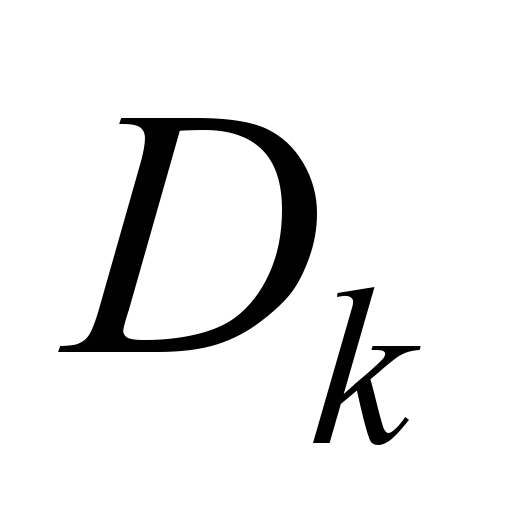 .
При этом также определяют деревья
потоков каждого продукта
.
При этом также определяют деревья
потоков каждого продукта
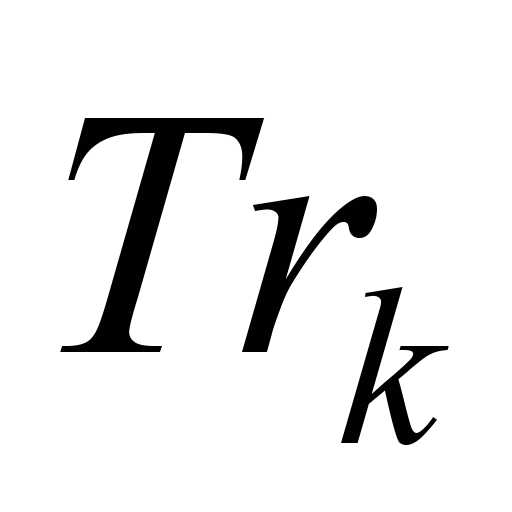 ,
ветви которых помечают величинами
соответствующих потоков
,
ветви которых помечают величинами
соответствующих потоков
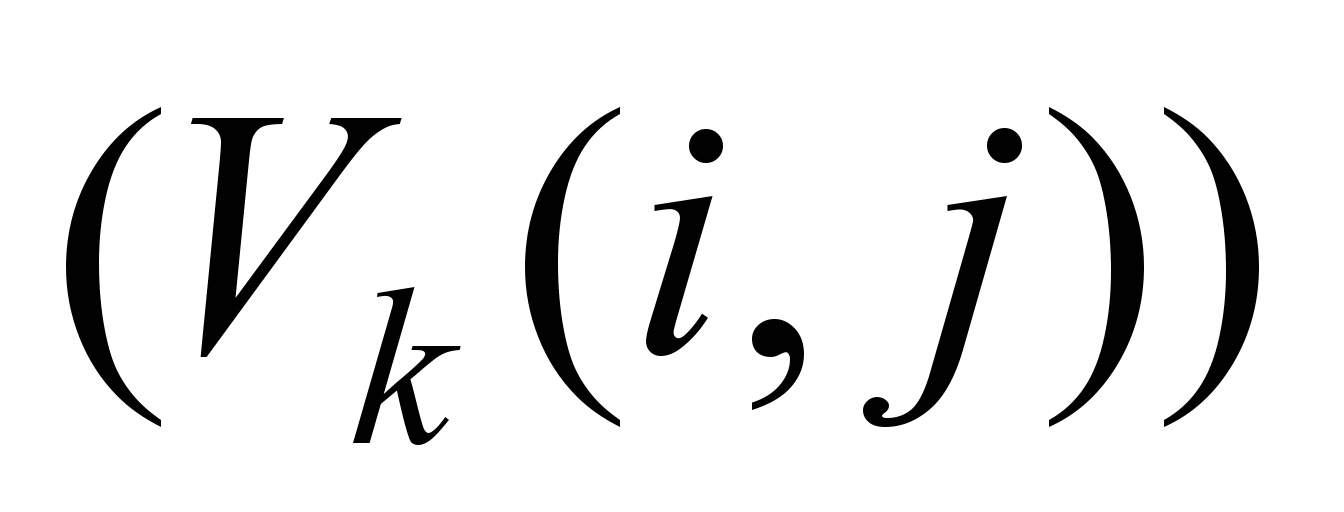 .
.
П2. Расчет максимального
многопродуктового потока
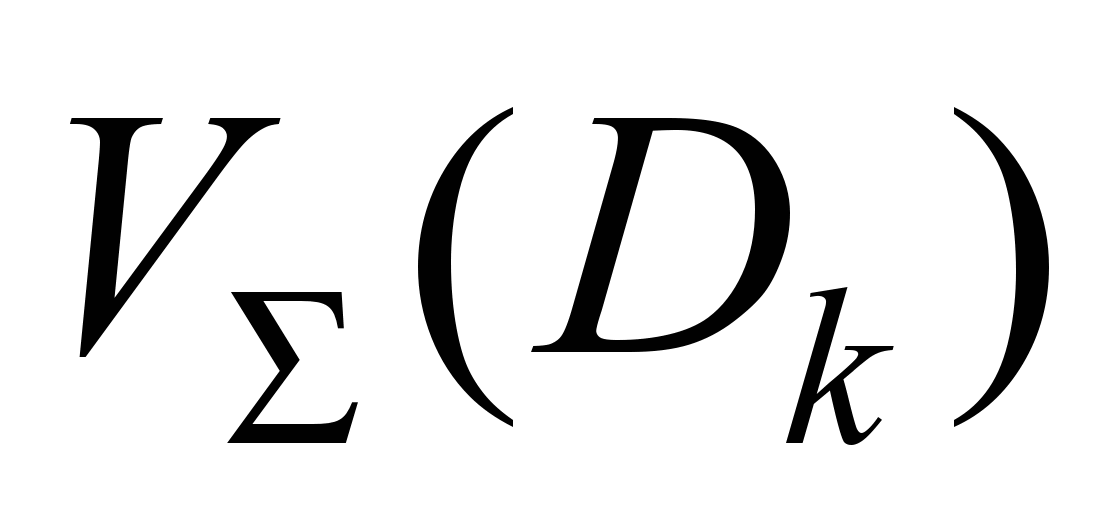 по
сети путем наложения деревьев величин
потоков
по
сети путем наложения деревьев величин
потоков
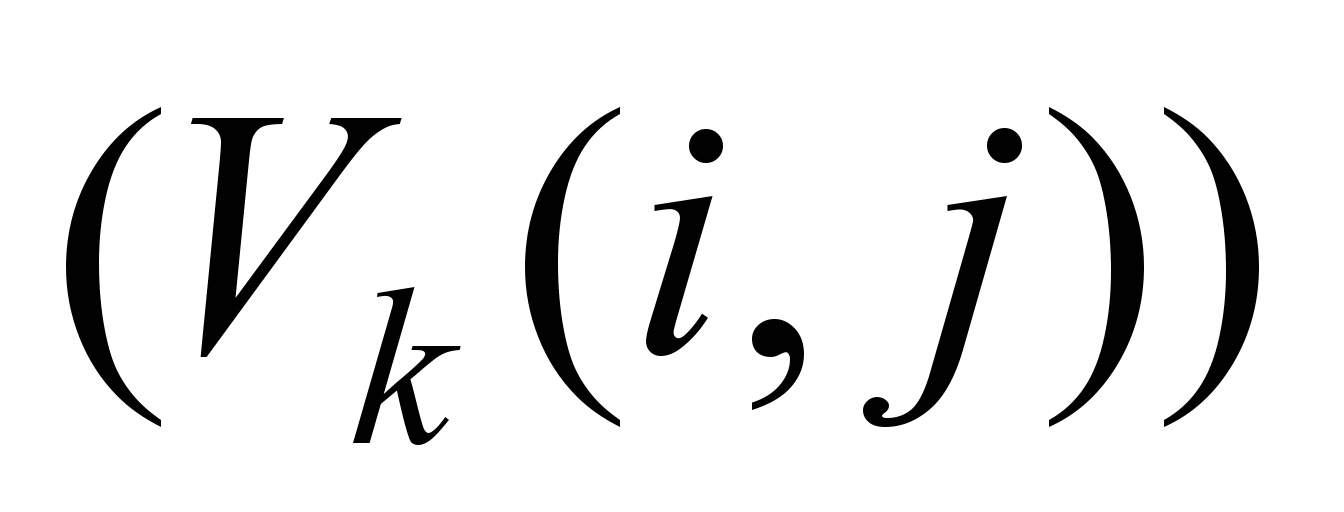 .
При этом дугам потока
.
При этом дугам потока
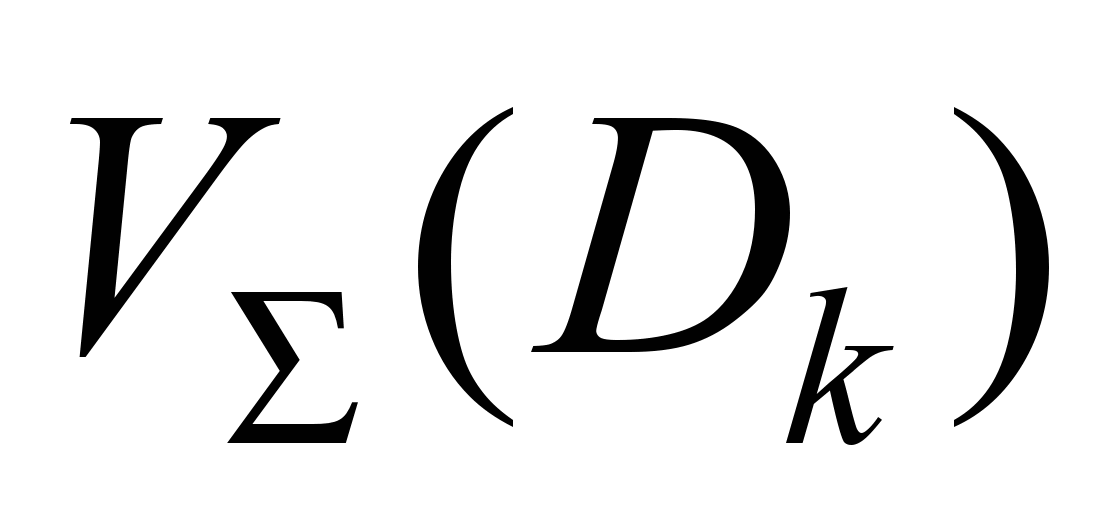 присваивают величины потоков (
присваивают величины потоков (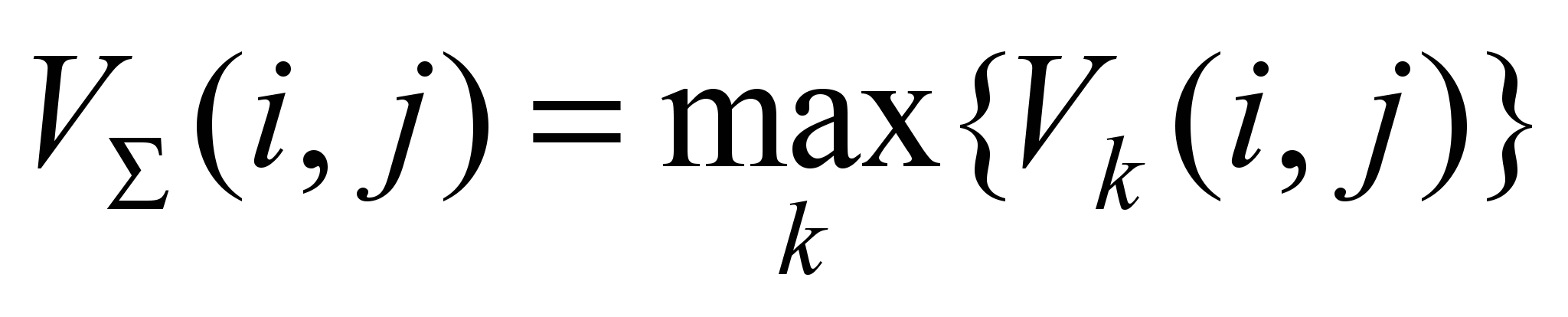 ).
В деревьях
).
В деревьях
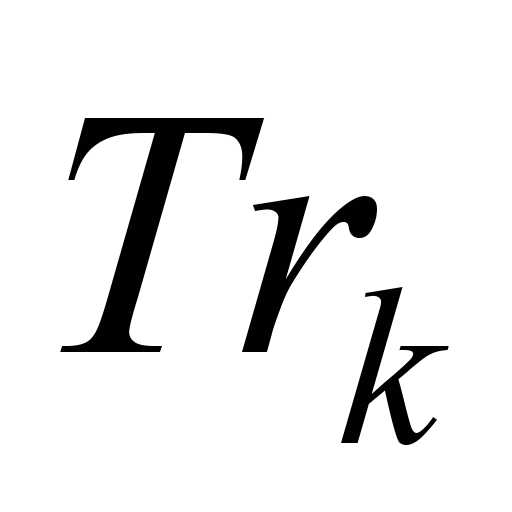 ,
на которых не был реализован максимум
,
на которых не был реализован максимум
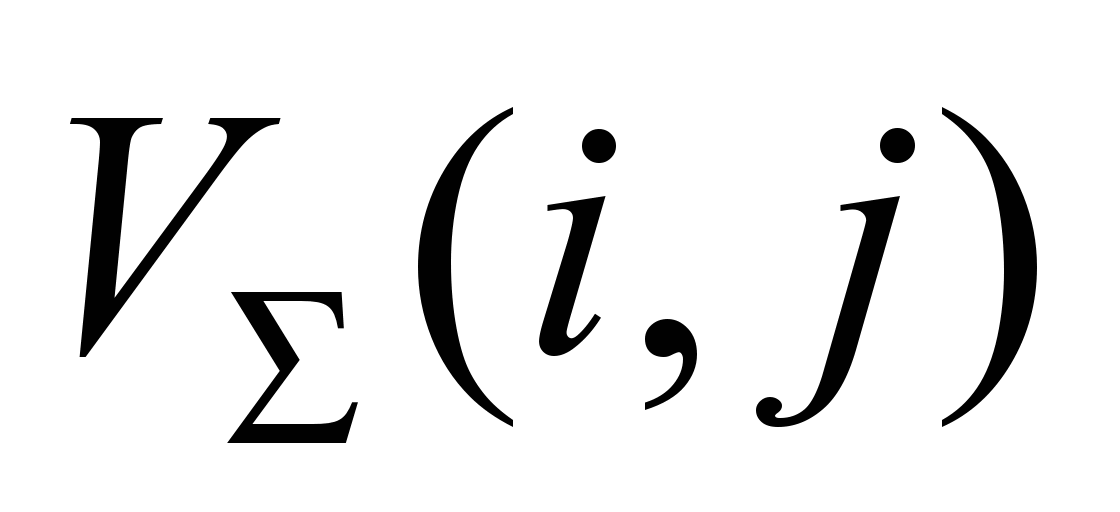 ,
потоки продуктов уменьшаются на значения
,
потоки продуктов уменьшаются на значения
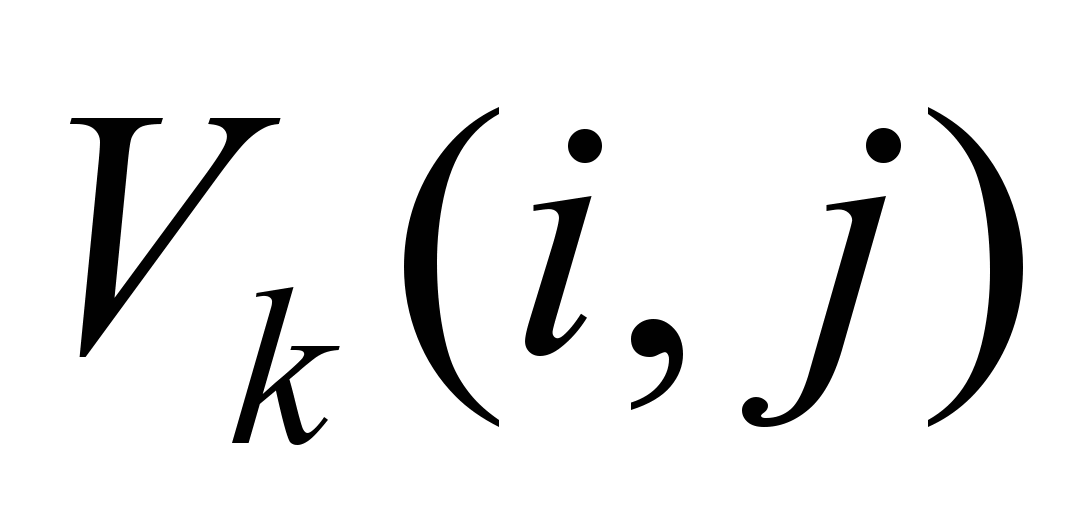 ,
корректируя на эту величину оценки
,
корректируя на эту величину оценки
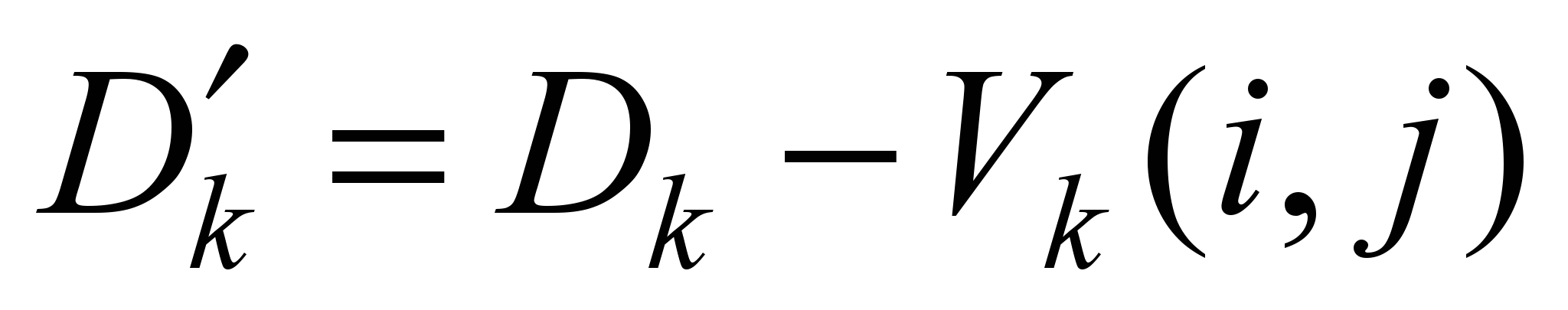 .
В результате выполнения процедуры
наложения величины
.
В результате выполнения процедуры
наложения величины
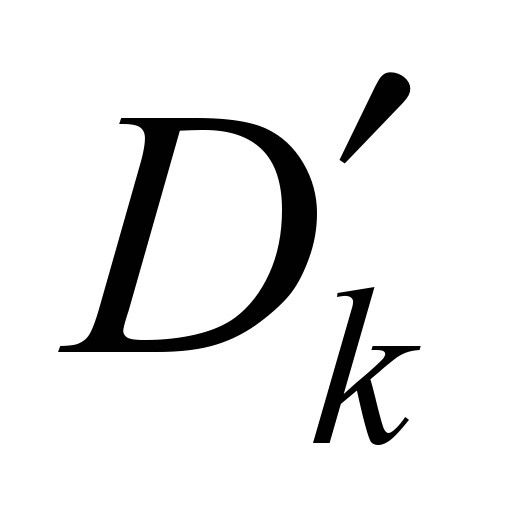 равны компромиссным оценкам потоков
продуктов «k», а их сумма – общему
максимальному потоку
равны компромиссным оценкам потоков
продуктов «k», а их сумма – общему
максимальному потоку
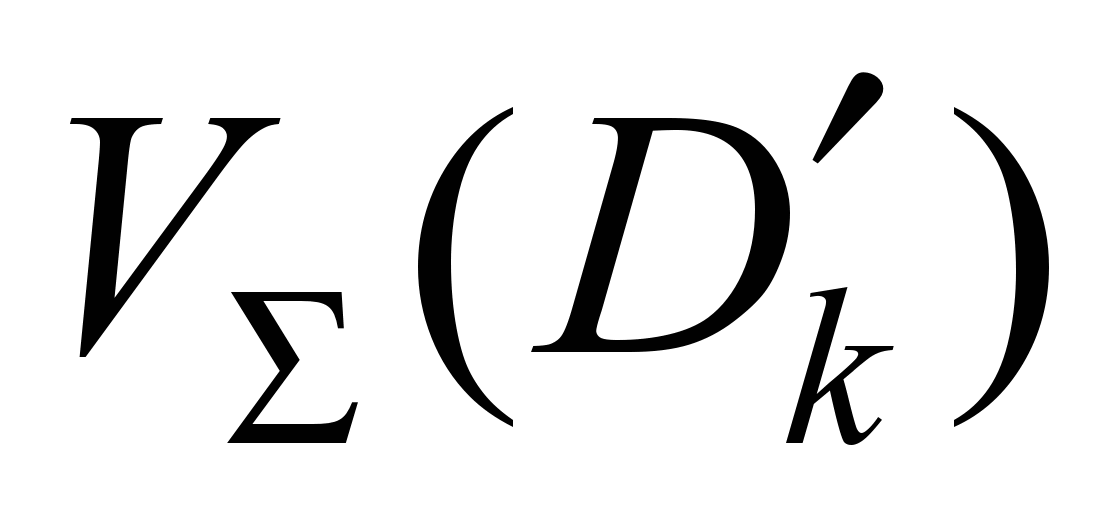 .
.
П3. Максимальное
значение (7) рассчитывают согласно
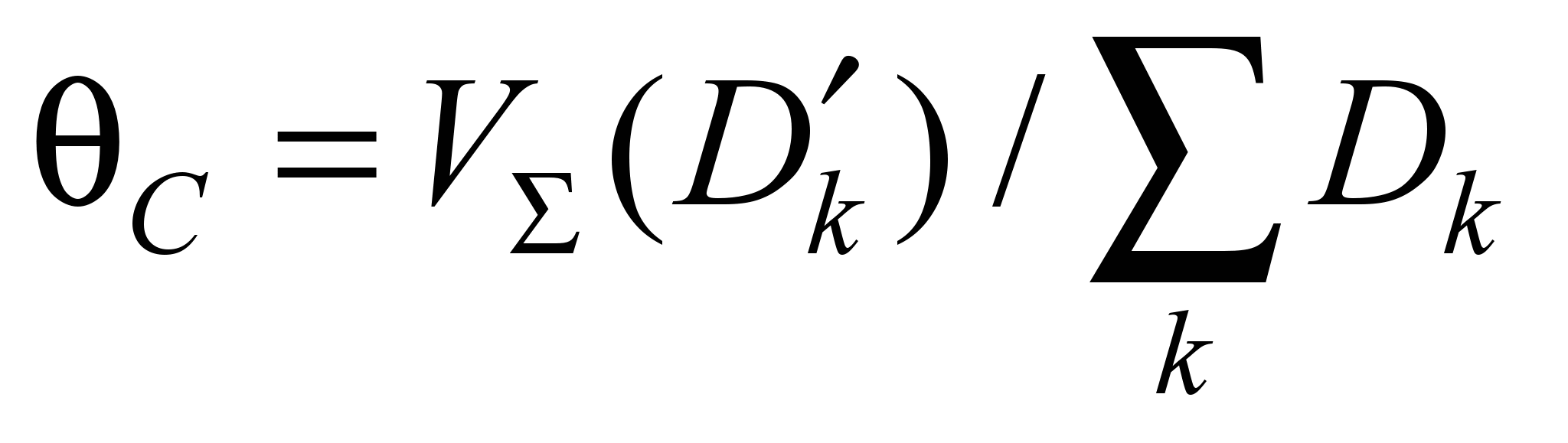 .
Далее решают задачу разделения суммарного
потока
.
Далее решают задачу разделения суммарного
потока
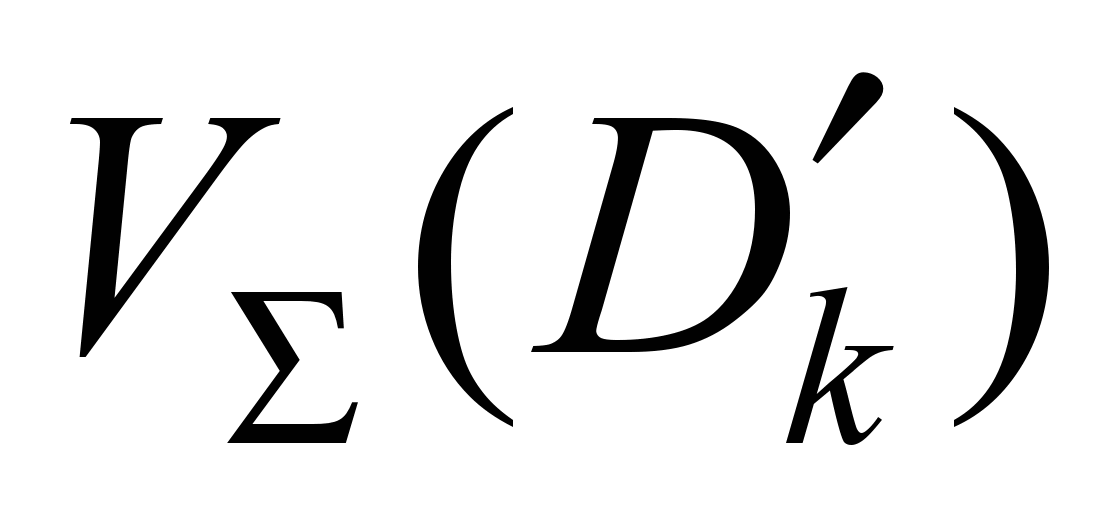 в соответствии с
в соответствии с
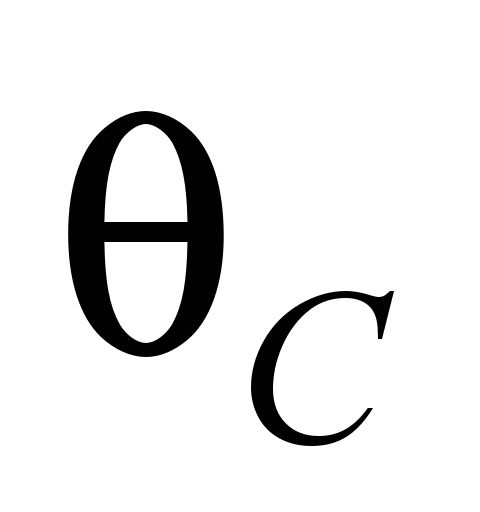 и набором
и набором
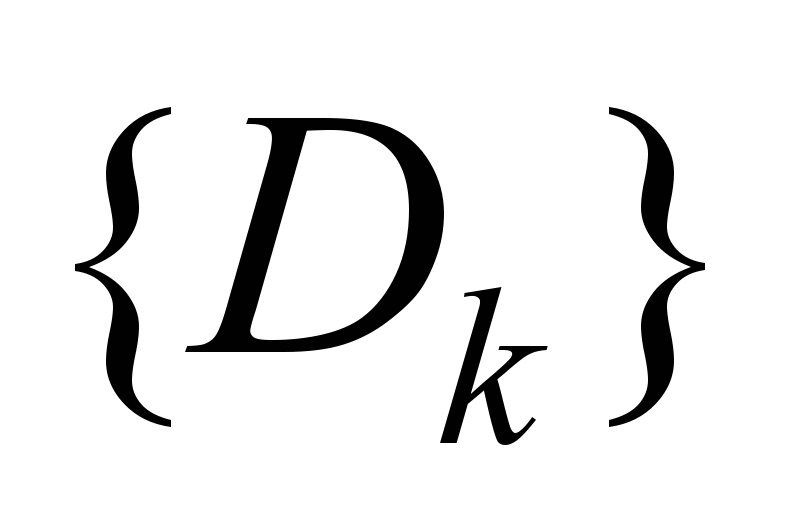 :
:
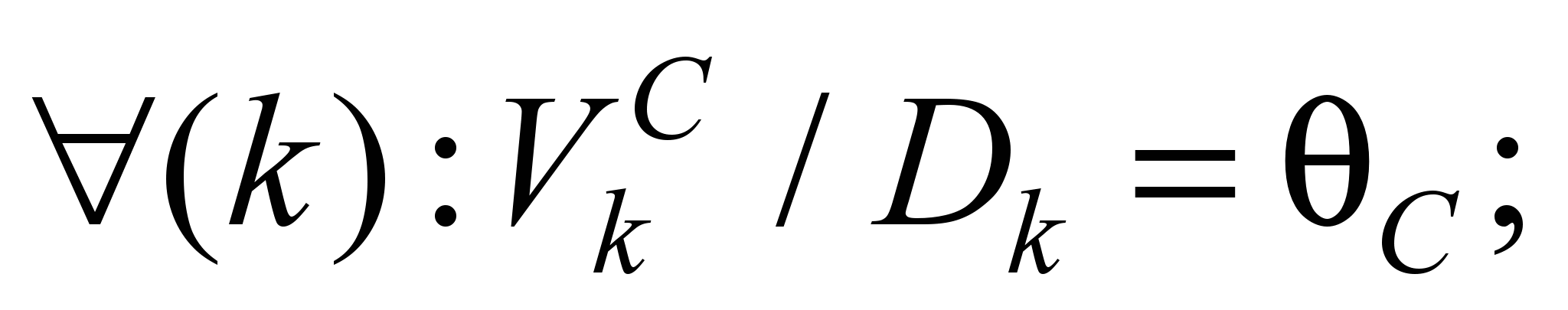
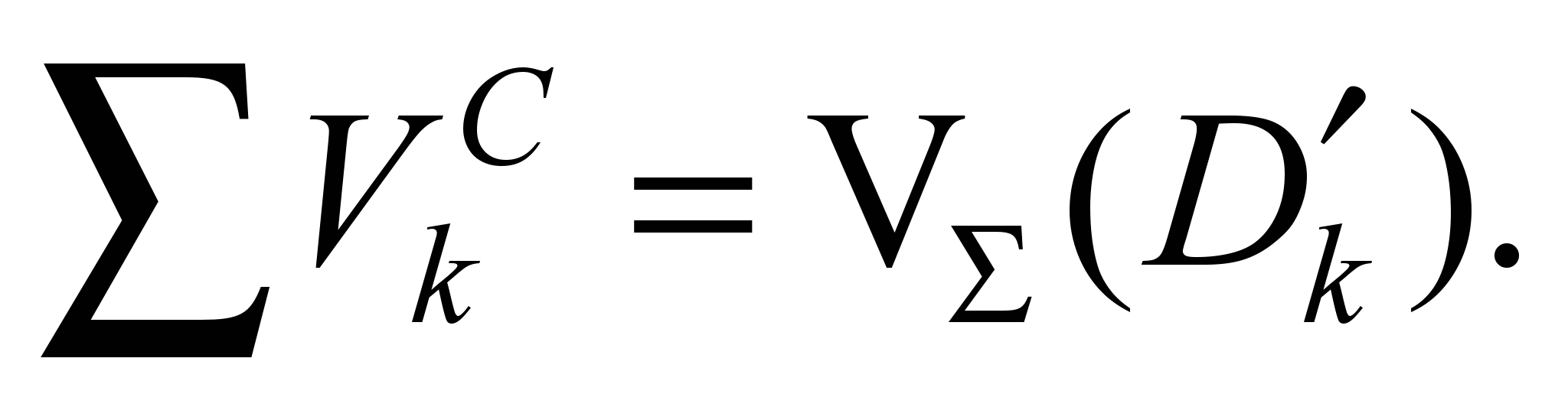 (8)
(8)
П4. На основе
сопоставления деревьев потоков
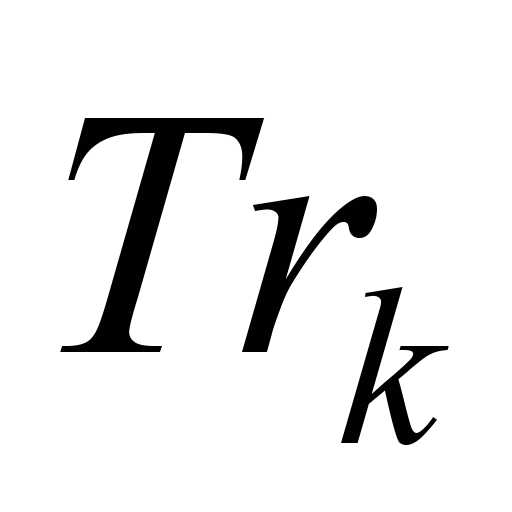 выделяют множество дуг
выделяют множество дуг 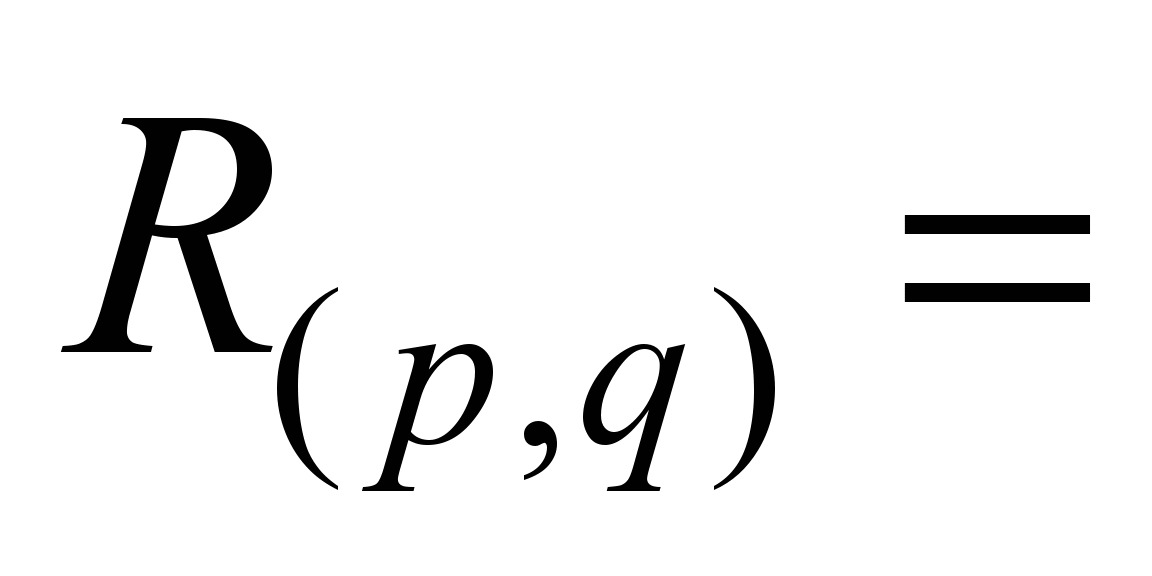 (
(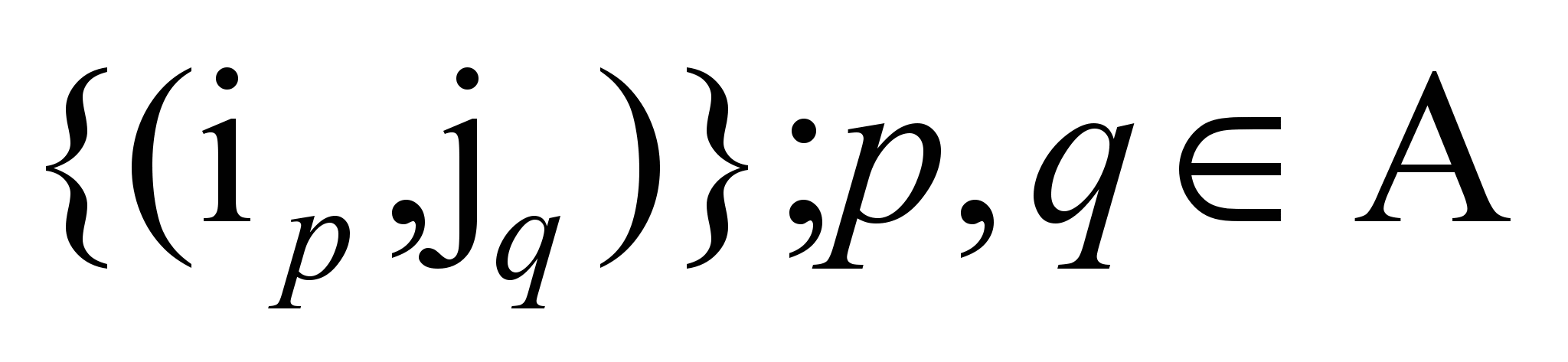 )
транспортной сети, на которых требуется
разделить конкурирующие потоки
продуктов. Здесь знак А соответствует
множеству дуг транспортной сети.
)
транспортной сети, на которых требуется
разделить конкурирующие потоки
продуктов. Здесь знак А соответствует
множеству дуг транспортной сети.
П5. На основе решения
системы линейных уравнений для дуг
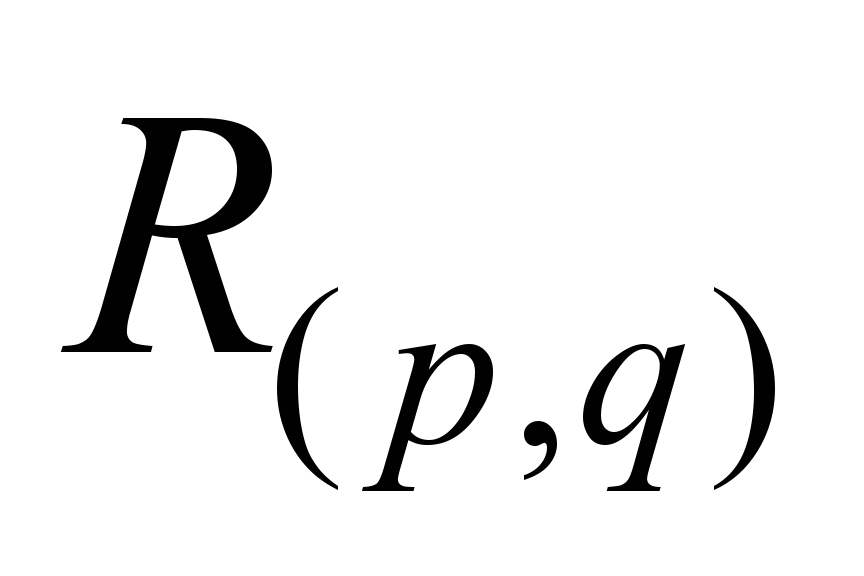 разделяющего множества (РМ) выполняют
расчет величин компромиссных потоков
продуктов «k» по дугам транспортной
сети. При этом структура системы
уравнений детализирует (8), а также
учитывает ограничения пропускных
способностей дуг
разделяющего множества (РМ) выполняют
расчет величин компромиссных потоков
продуктов «k» по дугам транспортной
сети. При этом структура системы
уравнений детализирует (8), а также
учитывает ограничения пропускных
способностей дуг
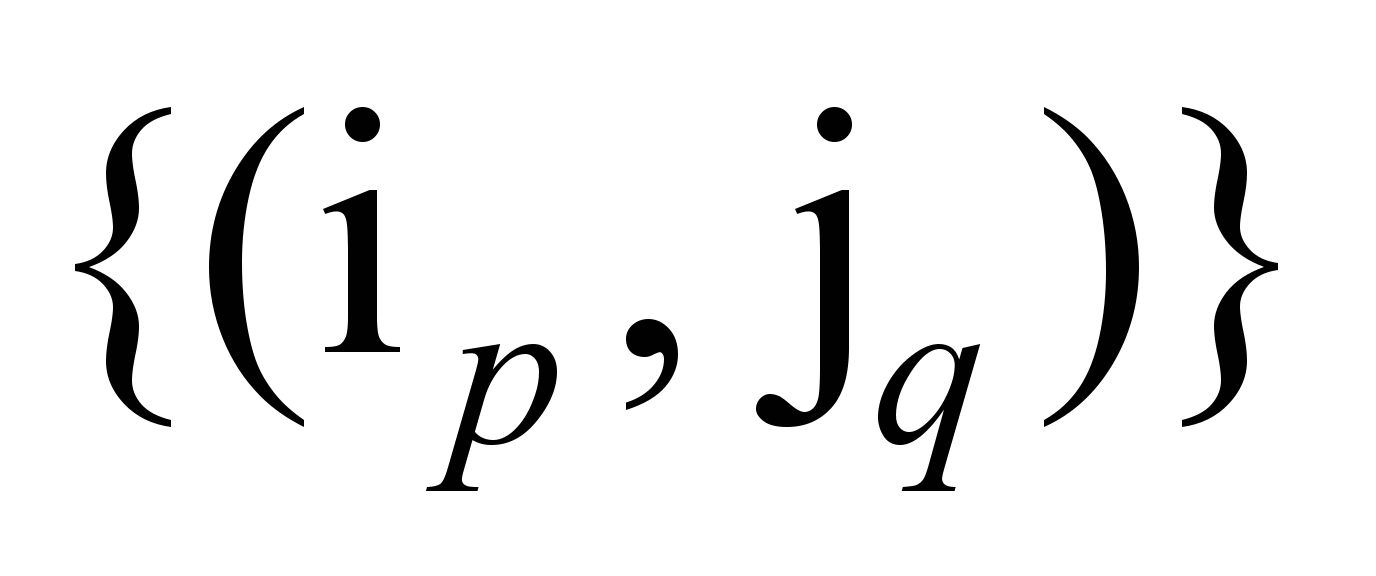 и имеет вид:
и имеет вид:
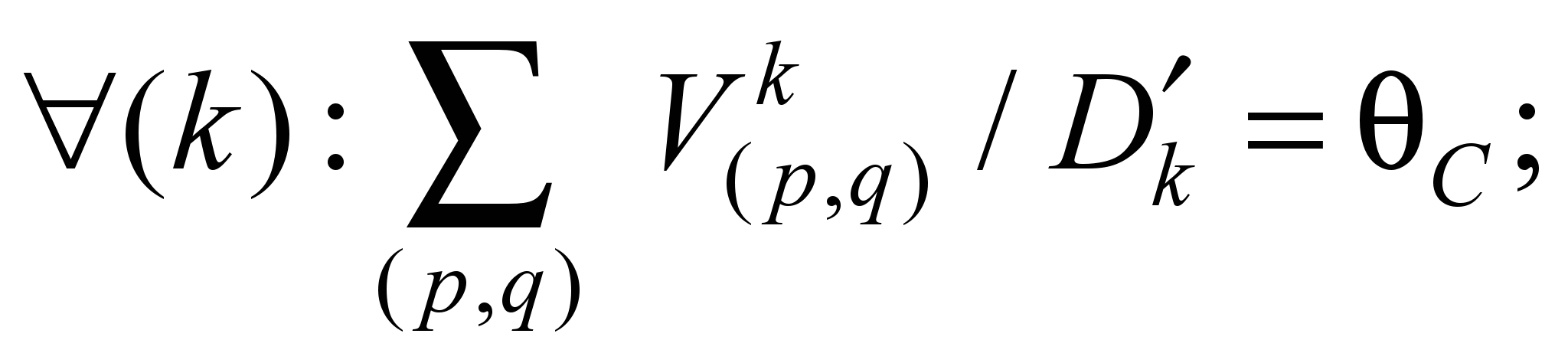
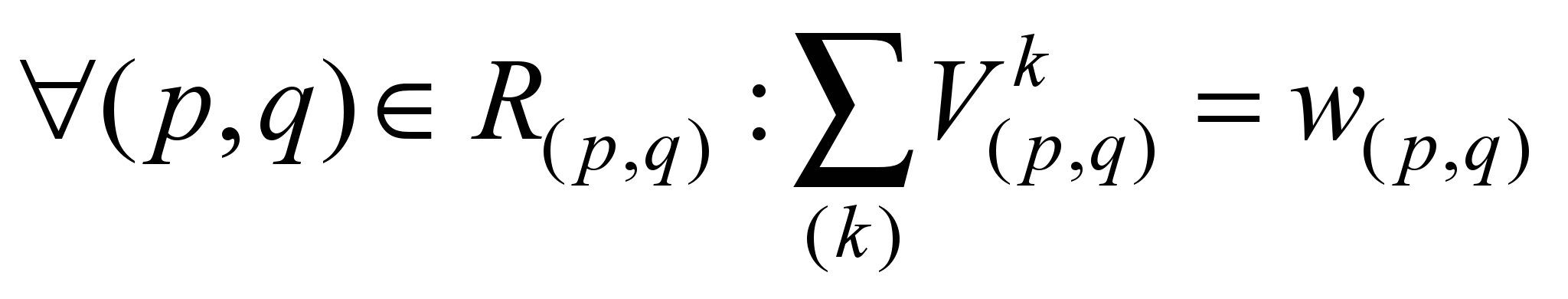 . (9)
. (9)
Таблица 7
Планирование
компромиссных многопродуктовых потоков
Table
7
Planning
trade-off multi-product flows
|
Сеть
|
W(i,j)
|
P1
|
P2
|
P3
|
Pc(1)
|
Pc(2)
|
P2(2)
|
P3(2)
|
P3–К4
|
Pc–K4
|
|
Ws1,1
|
50
|
20
|
0
|
0
|
10
|
10
|
0
|
0
|
0
|
9,2668
|
|
W1,3
|
15
|
15
|
10
|
12
|
15
|
15
|
0
|
8,5
|
12
|
13
|
|
W1,2
|
5
|
5
|
0
|
0
|
5
|
3,5
|
0
|
0
|
0
|
5
|
|
W2,3
|
5
|
5
|
0
|
5
|
5
|
5
|
1,5
|
0
|
4
|
5
|
|
W2,4
|
7
|
0
|
7
|
0
|
7
|
7
|
7
|
0
|
0
|
7
|
|
W34
|
10
|
0
|
10
|
0
|
1,5
|
1,5
|
1,5
|
0
|
0
|
0,8666
|
|
Ws2,1
|
12
|
0
|
10
|
12
|
10
|
8,5
|
0
|
8,5
|
12
|
8,7332
|
|
Ws2,2
|
20
|
0
|
7
|
5
|
7
|
8,5
|
8,5
|
0
|
4
|
7
|
|
W3,t1
|
50
|
20
|
0
|
17
|
18,5
|
18,5
|
0
|
8,5
|
16
|
17,1334
|
|
W4,t2
|
50
|
0
|
17
|
0
|
8,5
|
8,5
|
8,5
|
0
|
0
|
7,8666
|
|
Vmax
|
|
20
|
17
|
17
|
27
|
27
|
8,5
|
8,5
|
16
|
25
|
|
|
|
|
|
|
0,5
|
0,5
|
|
|
|
0,4627
|
В уравнениях (9)
параметры

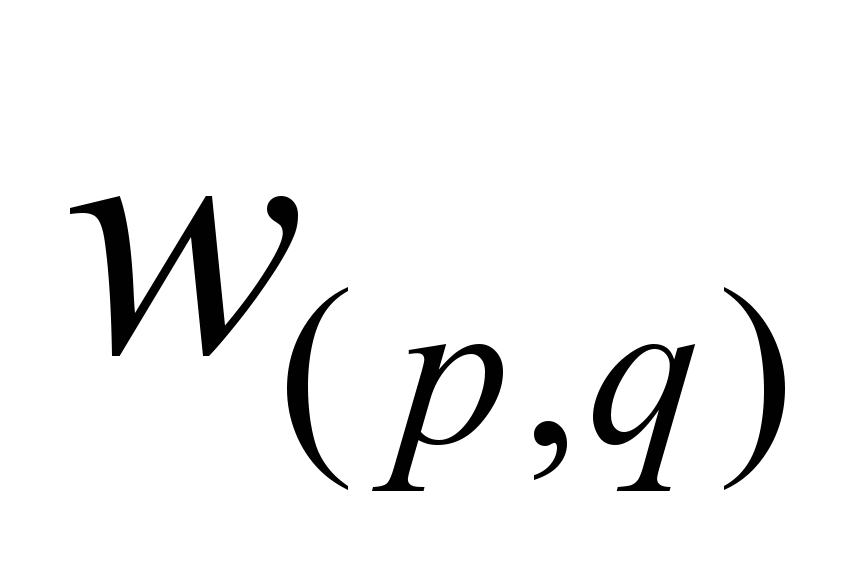 равны пропускным способностям
соответствующих дуг.
равны пропускным способностям
соответствующих дуг.
Реализация процедур
П1–П5 завершает компромиссное планирование
многопродуктовых потоков на основе
ПСАП. Приведем примеры планирования
потоков согласно модели (7) для транспортной
сети на рис. 1.
В табл. 7 приведены
результаты планирования согласно (6)
потоков трех продуктов для сети на рис.
1. Здесь в столбце «Сеть» указаны дуги,
в столбце W(i, j) их пропускные
способности, а в строках величины
потоков. В строке Vmax указаны
максимальные потоки продуктов Р1,
Р2, Р3, а также компромиссные
значения (столбцы Рс (1), Рс (2),
Рс–К4), а под ними даны значения
показателей компромисса (7). Решения
Р3–К4 и Рс–К4
соответствуют моделям типа К4,
(табл. 2), остальные модели соответствуют
классу К3, допускающему независимый
расчет каждого из потоков продуктов.
Столбцы Рс (1) и Рс (2)
показывают возможность существования
нескольких компромиссных решений (7).
Столбцы Р2 (2) и Р3 (2) содержат
величины компромиссных потоков продуктов
типа два (Р2) и три (Р3), которые
имеют существенные отличия от отдельных
максимальных потоков Р2, Р3.
Отметим, что значение (7) соответствует
уравнениям (8).
Решения для моделей
класса К4 получены при задании
условных пропускных способностей дуг,
зависящих от значений величин различных
потоков. Это свойство модели не позволяет
выполнять расчет максимальных потоков
каждого из «k» продуктов независимо от
других, а требует применения ПСАП ко
всей совокупности одновременно. Как
указано в таблице, наличие нескольких
потоков уменьшило пропускную способность
дуги W(1,3) и привело к уменьшению
общего потока до 25.
Рассмотрим вопросы
планирования ИП на основе алгоритма
ПСАП в СИС, используя постановку [2]. В
этой работе решается задача передачи
ИП известных величин между наборами
абонентских пар (исток–сток). Требуется
распределить ресурс пропускной
способности СИС таким образом, чтобы
в максимально возможной степени
удовлетворить требованиям всех
абонентских пар в передаче ИП (как
продуктов), при условии удовлетворения
ограничениям пропускной способности.
Задача распределения и перераспределения
ИП в СИС обычно сводится к решению
задачи о максимальном потоке в сети.
Многопродуктовые потоковые задачи
могут быть решены за полиномиальное
время методами линейного программирования.
При недостаточности
пропускной способности элементов
структуры СИС требования пользователей
не могут быть удовлетворены в полной
мере.
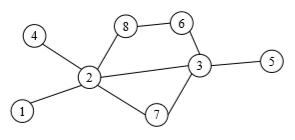
Рис.
7. Структура
сети
передачи
сообщений
Fig.
7. Structure of the messaging network
Таблица 8
Характеристики
ребер графа сети передачи данных
Table
8
Characteristics
of graph edges of the data transmission network
|
ri(ui,
vi)
|
ci
|
ri(ui,
vi)
|
ci
|
pi(si,
ti)
|
di
|
|
r1(1,2)
|
200
|
r10(2,1)
|
190
|
p1(1,5)
|
150
|
|
r2(2,3)
|
220
|
r11(3,2)
|
280
|
p2(1,6)
|
100
|
|
r3(2,4)
|
250
|
r12(4,2)
|
290
|
p3(7,2)
|
50
|
|
r4(2,7)
|
200
|
r13(7,2
|
210
|
p4(8,3)
|
100
|
|
r5(2,8)
|
250
|
r14(8,2)
|
270
|
p5(5,1)
|
110
|
|
r6(3,5)
|
260
|
r15(5,3)
|
290
|
p6(2,4)
|
70
|
|
r7(3,6)
|
300
|
r16(6,3)
|
210
|
p7(5,1)
|
140
|
|
r8(3,7)
|
210
|
r17(7,3)
|
200
|
p8(2,7)
|
100
|
|
r9(6,8)
|
230
|
r18(8,6)
|
240
|
|
|
Таблица 9
Результаты
планирования компромиссных путей и
величин потоков
Table
9
The
results of planning trade-off ways and flow values
|
pi(si,
ti)
|
wi
|
zi
|
zi
/di (%)
|
|
p1(1,5)
|
1-2-6
|
120
|
80,00 %
|
|
p2(1,6)
|
1-4-17-7
|
80
|
80,00 %
|
|
p3(7,2)
|
17-7-9-14
|
50
|
100,00 %
|
|
p4(8,3)
|
18-16
|
100,00
|
100,00 %
|
|
p5(5,1)
|
15-11-10
|
83,6
|
76,00 %
|
|
p6(2,4)
|
3
|
70
|
100,00 %
|
|
p7(5,1)
|
15-7-9-14-10
|
106,4
|
76,00 %
|
|
p8(2,7)
|
5-18-16-8
|
100
|
100,00 %
|
Поэтому рассчитывают
распределение потоков в СИС, которое
не дискриминирует абонентские пары и
наилучшим образом использует все
имеющиеся ресурсы сети – суперконкурентный
мультипоток. Для решения задачи в
[2] разработан специализированный
генетический алгоритм, а результаты
получены за счет осреднения многократных
расчетов. На рис. 8 приведена сеть
передачи сообщений, граф которой имеет
8 вершин и 9 ребер, которым соответствуют
18 дуг. Начало ui
и конец vi каждой
дуги ri, а также
их пропускные способности ci
указаны в табл. 8.
Через сеть (рис. 7)
необходимо пропустить многопродуктовый
поток, в наибольшей степени выполняющий
запросы 8-ми продуктов pi,
источники si,
стоки ti и
требования di
которых приведены в табл. 8.
Полученный
компромиссный поток с помощью алгоритма
МПСАП в рамках процедур П1–П5 представлен
в табл. 9, где wi
– путь для пары узлов, между которыми
передаются сообщения. В примере
наименьшая величина критерия (7),
соотношение поток/запрос zi/di,
имеют пары № 5 и № 7 (zi/di = 76,00 %).
Результаты планирования распределения
ИП основе МПСАП (табл. 9) полностью
совпадают с работой [2], что подтверждает
достоверность и эффективность
предлагаемых методов расчета
многопродуктовых потоков.
Научная
новизна и практическая
значимость
В работе на основе
анализа известных постановок задач о
потоках в транспортных сетях предложены
два вида классификаций математических
моделей таких задач: на основе учета
числа «серверов» и «клиентов» (отдельных
потоков или продуктов); исходя из
структурных свойств математических
моделей и алгоритмов реализации. В
классификации все последующие классы
моделей включают требования предыдущих,
дополняя их специальными условиями.
Указано, что другими характеристиками
предложенных классов моделей являются
свойства их параметров (детерминированные,
стохастические, интервальные, нечеткие),
а также временные характеристики
(статические, стационарно-динамические,
динамические и др.).
В данной статье
впервые разработанный нами параллельный
синхронный алгоритм был использован
для реализации нечетких моделей
планирования многопродуктовых потоков
в транспортных сетях. Также на основе
ПСАП были реализованы нечеткие
динамические модели планирования
многопродуктовых потоков. При этом за
счет процедур распараллеливания был
получен вычислительный эффект по
сравнению с известными результатами.
В статье разработана
новая процедура планирования конкурентных
потоков в сетях информационных систем,
использующая параллельные синхронные
алгоритмы расчетов максимальных
потоков. Применение процедуры планирования
позволяет вычислить локальные экстремумы
модели распределения потоков. Это
объясняется тем, что функция распределения
конкурентных потоков является
недифференцированной, кроме того
возможно существование нескольких
максимальных потоков в транспортных
сетях.
Практическая
ценность результатов работы определяется
унифицированными возможностями ПСАП
для эффективной реализации задач
анализа и планирования многопродуктовых
потоков в сетях на основе динамических,
нечетких и конкурентных моделей
распределения транспортных и
информационных потоков.
Выводы
В статье исследованы
вопросы анализа и планирования
многопродуктовых потоков в сетях на
основе динамических, нечетких и
компромиссных моделей транспортных
потоков. Для расчета оптимальных потоков
указанных категорий разработана
унифицированная процедура на основе
параллельных синхронных алгоритмов
расчетов максимальных потоков и потоков
минимальной стоимости.
Предложена новая
классификация математических моделей
анализа и оптимального планирования
транспортных потоков.
Выполненные на
основе разработанных процедур и
унифицированного параллельного
синхронного алгоритма реализации
нечетких моделей планирования
многопродуктовых потоков в транспортных
и информационных сетях, а также нечетких
динамических и конкурентных моделей
распределения потоков показали
эффективность и универсальность
предложенных методов.
СПИСОК ИСПОЛЬЗУЕМЫХ
ИСТОЧНИКОВ
Алгоритмы:
построение и анализ : [пер. с
англ.] /
Клиффорд Штайн, Рональд Линн
Ривест, Томас Кормен, Чарльз Эрик
Лейзерсон. – 2-е изд.
– Москва : Вильямс, 2010. –
1296 с.
Осин, В. Н.
Эффективное распределение информационных
потоков в сетевой информационной
системе на основе нечетких моделей
: автореф. дис. … канд.
техн. наук : 05.25.05 / Осин Вячеслав Николаевич
; Тамбов. гос. техн. ун-т. – Тамбов, 2014. –
20 с.
Скалозуб,
В. В. Интеллектуальные информационные
технологии и системы железнодорожного
транспорта / В. В. Скалозуб, С. Ю. Цейтлин,
М. С. Чередниченко // Системные технологии
моделирования сложных процессов
: монография / под общ.
ред. А. И.
Михалёва. – Днепр, 2016. –
C. 560–589.
Скалозуб,
В. В. Моделирование и анализ потоковых
задач с неоднородными носителями /
В. В. Скалозуб, Л. А. Паник // Вісн.
Дніпропетр. нац. ун-ту залізн. трансп.
ім. акад. В. Лазаряна. – Дніпропетровськ,
2007. – Вип. 19. – C. 125–133.
Скалозуб,
В. В. Паралельні синхронні алгоритми
аналізу та планування неоднорідних
потоків у транспортних мережах / В. В.
Скалозуб, Л. О. Панік // Системні технології
: регіон. міжвуз. зб. наук. пр. –
Дніпро, 2017. – № 5 (112). –
С. 183–197.
Филлипс, Д.
И. Методы анализа сетей / Д. И. Филлипс,
А. Гарсиа-Диас. – Москва : Мир, 1984. – 496
с.
Bozhenyuk,
А. Algorithm
for Monitoring
Minimum Cost
in Fuzzy
Dynamic Networks
/ Alexander Bozhenyuk, Evgeniya
Gerasimenko // Information
Technology and Management Science. –
2013. – Vol. 16. – Iss. 1. – P. 53–59.
doi:
10.2478/itms-2013-0008
Grigoriadis,
M. D.
Approximate minimum-cost
multicommodity flows in $$\tilde O$$ (ɛ −2 KNM) timetime
/ M. D. Grigoriadis, L. G.
Khachiyan // Mathematical Programming. – 1996. – Vol. 75. –
Iss. 3. – P. 477–482. doi: 10.1007/BF02592195
Holzhauser,
M. Maximum flows in generalized processing networks / Michael
Holzhauser, Sven O. Krumke, Clemens Thielen // Journal of
Combinatorial Optimization. – 2016. – Vol. 33. – Iss. 4. –
P. 1226–1256.
doi:
10.1007/s10878-016-0031-y
Kovacs,
P. Minimum-cost flow algorithms: An experimental evaluation EGRES
Technical Report [Электронный
ресурс] / P. Kovacs // EGRES
Technical Report. – 2013. – No. 2013-04. – P. 1–40. –
Режим доступа:
https://web.cs.elte.hu/egres/tr/egres-13-04.pdf – Загл.
с экрана.
– Проверено : 17.05.2018.
Maximum
and Minimum Cost Flow Finding in Networks in Fuzzy Conditions / A.
V. Bozhenyuk, E. M. Gerasimenko, J. Kacprzyk, I. N. Rozenberg
// Flows
in Networks Under Fuzzy Conditions. –
Cham : Springer,
2016. – P. 23–75.
doi: 10.1007/978-3-319-41618-2_2
Nasrabadi,
E. Minimum cost time-varying network flow problems / E. Nasrabadi,
S. M. Hashemi //
Optim. Methods and Software. – 2010. – Vol. 25. – Iss. 3. –
P. 429–447.
doi:
10.1080/10556780903239121
Schiopu,
C. The Maximum Flows in Planar Dynamic Networks / C. Schiopu, E.
Ciurea // Intern. Journal of Computers Communications&Control. –
2016. – Vol. 11. – Iss. 2. – P. 282–291.
doi:
10.15837/ijccc.2016.2.2444
Sifaleras,
A. Minimum cost network flows: problems, algorithms, and software /
A. Sifaleras // Yugoslav Journal of Operations Research. – 2013. –
Vol. 23. – Iss. 1. – Р. 3–17.
doi:
10.2298/YJOR121120001S
В. в. скалозуб1*,
Л. О. панік2*
1*Каф.
«Комп’ютерні інформаційні технології»,
Дніпропетровський національний
університет залізничного транспорту
імені академіка В. Лазаряна, вул.
Лазаряна, 2, Дніпро, Україна, 49010, тел.
+38 (056) 373 15 35,
ел. пошта
skalozhubtk@gmail.com,
ORCID 0000-0002-1941-4751
2*Каф.
«Комп’ютерні інформаційні технології»,
Дніпропетровський національний
університет залізничного транспорту
імені академіка В. Лазаряна, вул.
Лазаряна, 2, Дніпро, Україна, 49010, тел.
+38 (056) 373 15 35,
ел. пошта leon140377@gmail.com,
ORCID 0000-0003-1343-3000
РЕАЛІЗАЦІЯ
ДИНАМІЧНИХ, КОНКУРЕНТНИХ І НЕЧІТКИХ
МОДЕЛЕЙ ПЛАНУВАННЯ багатопродуктових
ПОТОКІВ
У
ТРАНСПОРТНИХ МЕРЕЖАХ
Мета.
Головною метою статті є розробка нової
уніфікованої процедури планування
нечітких багатопродуктових, динамічних,
а також конкурентних потоків у
транспортних мережах і мережевих
інформаційних системах. Процедура
заснована на використанні паралельних
синхронних алгоритмів розрахунку
неоднорідних максимальних потоків.
Методика.
В роботі запропонована класифікація
математичних моделей задач із планування
потоків у транспортних мережах.
Досліджено можливості використання
уніфікованої процедури і паралельного
синхронного алгоритму розрахунку
максимальних неоднорідних потоків для
реалізації завдань планування
багатопродуктових, нечітких, динамічних
і конкурентних потоків. Результати.
Ефективність і універсальність
запропонованих методів планування
неоднорідних потоків встановлена
шляхом порівняння отриманих у статті
результатів розрахунків із відомими
в літературі. Розроблено уніфіковану
процедуру і паралельний синхронний
алгоритм для планування нечітких
багатопродуктових, динамічних і
конкурентних потоків у транспортних
мережах, а також реалізовано завдання
оптимального розподілу цих потоків у
транспортних мережах. Наукова
новизна. У статті
розроблена нова уніфікована процедура
планування нечітких багатопродуктових,
динамічних і конкурентних потоків у
транспортних мережах інформаційних
систем, що використовує паралельні
синхронні алгоритми розрахунків
максимальних потоків. Процедура дозволяє
обчислити локальні екстремуми моделей
оптимального розподілу потоків.
Практична значимість.
Практична цінність отриманих результатів
визначається уніфікованими можливостями
та ефективністю процедури і паралельно
синхронного алгоритму, призначеного
для розрахунку максимальних
багатопродуктових потоків у транспортних
мережах. Розроблена процедура забезпечує
можливість вирішення завдань аналізу
і планування багатопродуктових потоків
у мережах для динамічних, нечітких і
конкурентних моделей розподілу
транспортних та інформаційних потоків.
Ключові
слова: транспортні мережі; моделі
планування; максимальні неоднорідні
потоки; нечіткі й динамічні потоки;
конкурентні інформаційні потоки;
паралельні алгоритми
V.
V. skalozub1*,
L. O. panik2*
1*Dep.
«Computer Information Technologies », Dnipropetrovsk National
University of Railway Transport named after Academician V. Lazaryan,
Lazaryan St., 2, Dnipro, Ukraine, 49010, tel. (056) 373 15 35,
e-mail skalozhubtk@gmail.com,
ORCID 0000-0002-1941-4751
2*Dep.
«Computer Information Technologies », Dnipropetrovsk National
University of Railway Transport named after Academician V. Lazaryan,
Lazaryan St., 2, Dnipro, Ukraine, 49010, tel. (056) 373 15 35,
e-mail leon140377@gmail.com,
ORCID
0000-0003-1343-3000
IMPLEMENTATION
OF THE DYNAMIC, COMPETITIVE AND
FUZZY MODELS FOR PLANNING OF THE
MULTI-PRODUCT
FLOWS IN TRANSPORT NETWORKS
Purpose. The
purpose of the article is to develop a new unified procedure for
planning of the fuzzy multi-product, dynamic and competitive flows
in the transport networks and in the information network systems.
The procedure is based on the use of the parallel synchronous
algorithms for inhomogeneous maximum flows calculating.
Methodology. The paper proposes the mathematical models’
classification of the tasks for planning the flows in transport
networks. The possibilities of using the unified procedure and the
parallel synchronous algorithm for calculating the maximum
inhomogeneous flows for implementation of the tasks for planning
multi-product, fuzzy, dynamic and competitive flows are
investigated. The efficiency and universality of the proposed
methods for the planning inhomogeneous flows is established by
comparing the results of the calculations obtained in the article
with the known results. Findings. The article proposes
classification of the mathematical models for the planning
inhomogeneous flows in the transport networks. The unified procedure
and the parallel synchronous algorithm for planning fuzzy
multi-product, dynamic and competitive flows in the transport
networks have been developed. The tasks of the optimal distribution
of the fuzzy multi-product, dynamic and competitive flows in the
transport networks are realized. Originality. The article
describes the new unified procedure for planning fuzzy
multi-product, dynamic and competitive flows in the transport and
information systems, using the parallel synchronous algorithms for
calculating maximum flows. The procedure allows us to calculate the
local extrema of the optimal flows distribution models. Practical
value. The practical value of the obtained results is determined
by the unified capabilities and the procedure efficiency, as well as
the parallel synchronous algorithm designed to calculate the maximum
multi-product flows in transport networks. The developed procedure
provides the possibility to solve the analysis and planning problems
of the multi-product flows in the networks for dynamic, fuzzy and
competitive models for the distribution of the transport and
information flows.
Keywords:
transport networks, planning models for maximum inhomogeneous flows,
fuzzy and dynamic flows, competitive information flows, parallel
algorithms
REFERENCES
Shtayn,
K., Rivest, R., Kormen, T., & Leyzerson, C. (2010). Algoritmy:
postroenie i analiz. Moscow: Publisher
Vilyams. (in Russian)
Osin,
V. N. (2014) Effektivnoe raspredelenie
informatsionnykh potokov v setevoy informatsionnoy sisteme na osnove
nechetkikh modeley. (Avtoreferat
dysertatsii kandydata tekhnicheskikh nauk). Tambov State Technical
University, Tambov. (in Russian)
Skalozub,
V. V., Tseytlin, S. Y., & Cherednichenko, M. S. (2016).
Intellektualnye informatsionnye tekhnologii i sistemy
zheleznodorozhnogo transporta. In A. I. Mikhaleva (Ed.),
Sistemnye tekhnologii modelirovaniya slozhnykh protsessov:
Monografiya (pp. 560-589). Dnipro. (in
Russian)
Skalozub,
V. V., &
Panik, L. A. (2007). Modelirovanie i analiz potokovykh zadach s
neodnorodnymi nositelyami. Bulletin
of Dnipropetrovsk National University of Railway Transport named
after Academician
V. Lazaryan, 19,
125-133. (in Russian)
Skalozub,
V. V., & Panik,
L. O.
(2017). Paralelni
synkhronni alhorytmy analizu ta planuvannia neodnoridnykh potokiv
u transportnykh merezhakh.
System technology: Regional
intercollegiate collection of scientific works, 5(112), 183-197.
(in
Ukranian)
Fillips,
D. I., & Garsia-Dias, A. (1984).
Metody analiza setey.
Moscow: Publisher Mir. (in Russian)
Bozhenyuk,
А. & Gerasimenko,
E.
(2013). Algorithm for
Monitoring
Minimum Cost
in Fuzzy
Dynamic
Networks.
Information
Technology and Management Science,
16(1),
53-59. doi: 10.2478/itms-2013-0008
(in English)
Grigoriadis,
M. D., & Khachiyan, L. G. (1996). Approximate minimum-cost
multicommodity flows in $$\tilde O$$ (ɛ
−2 KNM) timetime. Mathematical
Programming, 75(3), 477-482.
doi: 10.1007/bf02592195 (in English)
Holzhauser,
M., Krumke, S. O., & Thielen, C. (2016). Maximum flows in
generalized processing networks. Journal
of Combinatorial Optimization, 33(4),
1226-1256. doi: 10.1007/s10878-016-0031-y
(in English)
Kovacs,
P. (2013). Minimum-cost flow algorithms: An experimental evaluation
EGRES Technical Report. EGRES Technical
Report, 4, 1-40.
Retrieved from https://web.cs.elte.hu/egres/tr/egres-13-04.pdf (in
English)
Bozhenyuk,
A. V., Gerasimenko, E. M., Kacprzyk, J., & Rozenberg, I. N.
(2016). Maximum and Minimum Cost Flow Finding in Networks in Fuzzy
Conditions. Flows
in Networks Under Fuzzy Conditions,
23-75. Cham:
Springer. doi:
10.1007/978-3-319-41618-2_2 (in
English)
Nasrabadi,
E., & Hashemi, S. M. (2010). Minimum cost time-varying network
flow problems. Optimization Methods and
Software, 25(3), 429-447. doi
:10.1080/10556780903239121 (in
English)
Schiopu,
C., & Ciurea, E. (2016). The Maximum Flows in Planar Dynamic
Networks. International Journal of
Computers Communications & Control, 11(2),
282-291. doi: 10.15837/ijccc.2016.2.2444
(in English)
Sifaleras,
A. (2013). Minimum cost network flows: Problems, algorithms, and
software. Yugoslav Journal of
Operations Research, 23(1), 3-17. doi:
10.2298/YJOR121120001S (in English)
Статья рекомендована
к публикации д.т.н.,
проф. В. И. Шинкаренко
(Украина)
Поступила в
редколегию: 15.02.2017
Принята к печати:
24.05.2018
doi:
10.15802/stp2018/133742 ©
В. В. Скалозуб, Л. А. Паник, 2018