ISSN 2307–3489 (Print), ІSSN 2307–6666 (Online)

Наука та прогрес транспорту. Вісник Дніпропетровського
національного університету залізничного транспорту, 2017, № 5 (71)

рухомий склад залізниць і тяга поїздів

Introduction

At present, the approach to constructing models of car oscillations is well known and tested for assessing the car running qualities and dynamic loading of elements [12]. The car is considered as a set of solid bodies [1], connected by rigid, elastic, viscous, dissipative elements [10, 11, 13]. As a rule, the angles of rotation are considered small values, after which the compilation of the equations of motion becomes a routine procedure, which it is advisable to deliver into charge of the computer.

Let us consider one of the possible approaches to the solution of this problem, for this we will present a semi-formal way of describing the model and the rules of compiling the equations of motion. Actually, we will not be interested in the solution of the equations, since for these purposes there are universal packages of applied programs Simulink [6], Simscape, OpenModelica, Dymola (the last two packages implement the language of the description of dynamical systems Modelica [9]) and so on.

Purpose

To develop a methodology for describing the structure of the railway vehicles (they are con-sidered as a system of rigid bodies connected by rigid, elastic and dissipative elements), which would allow us to obtain the equations of motion in an easily algorithmized way.

Methodology

When building a model, we strive to ensure that its structure reflects the structure of the mechanical system (car), that is, parts of the model must cor-respond to parts of the car. In this case, the model takes the form of a hierarchically organized graph whose vertices correspond to the bodies and connecting elements, and the edges describe the sets of processes that that are related to the incident to edge vertices [7]. An example of the general structure of the model is shown in Figure 1.

Fig. 1. Car body: a – vertex representing, b – its internal structure. Pt1 and Pt2 are attachment points of pairs «Centre plate - Centre pad»

As a rule, a set of generalized displacements and corresponding generalized forces correspond to the edge.

For the edge, causality conditions can be defined (for example, if the force is considered as a function of displacements) or not (forces and displacements are related by implicit relations). The difference between the two types of edges is not fundamental and, if desired, one can write down the formal rules for determining the causality relation.

To describe the model-building rules, we use the inductive approach and consider the basic types of subsystems and the corresponding equations. In doing so, we will try to match the set of equations to the node, and the set of variables to the edge.

Fig. 2. Fragment of «Bogie» subsystem

Figure 2 shows a fragment of the «Bogie» subsystem, in which the bolster NB is connected to the solebars BR1, BR2 with the spring suspension unit RP1, RP2. The motion of such a subsystem is described by the equations that can be conveniently divided into the following groups:

1) Equations of motion of bodies;

2) Equations expressing the movement of the attachment points of the connecting elements through the movements of the bodies;

3) Equation of the relationship between the deformation of the connecting element and the force that arises in it.

The last group of equations refers to the connecting elements, the first two to the bodies. In view of the fact that the parameters of the equations of the first two groups are different, it is advisable to equip each body with an internal structure, as shown in Fig. 3, using the example of bolster.

Fig. 3. Bolster.
Internal structure of the node

The inner vertex «Body» corresponds to the body motion equations. Internal vertices RP1, RP2, PP, SK1, SK2 - to the attachment points of corresponding connecting elements: spring suspension, pair «Centre plate - Centre pad», side bearing. These classes of vertices (for the body, for attachment points of the connecting element and for the connecting element itself) are the basic ones for building the car model. We will dwell in detail on each of them.

The vertex representing the motion equations of the body, whose principal central axes of inertia are parallel to the coordinate axes, is shown in Fig. 4.

This vertex can be incident with several edges, each of which is associated with a set of gene-ralized displacements 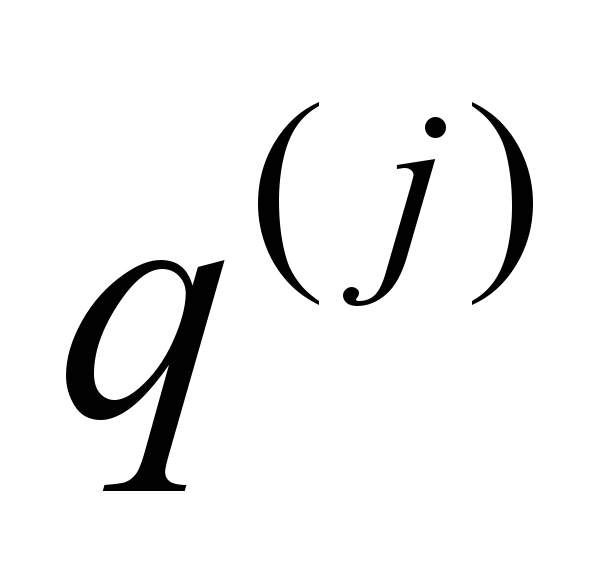and generalized forces 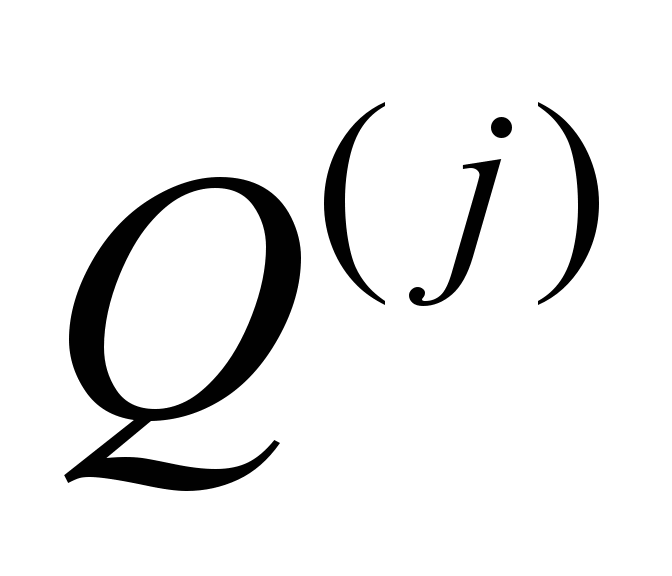. The edges connect the vertex «Body» with the vertex «Point».

The physical meaning of the processes 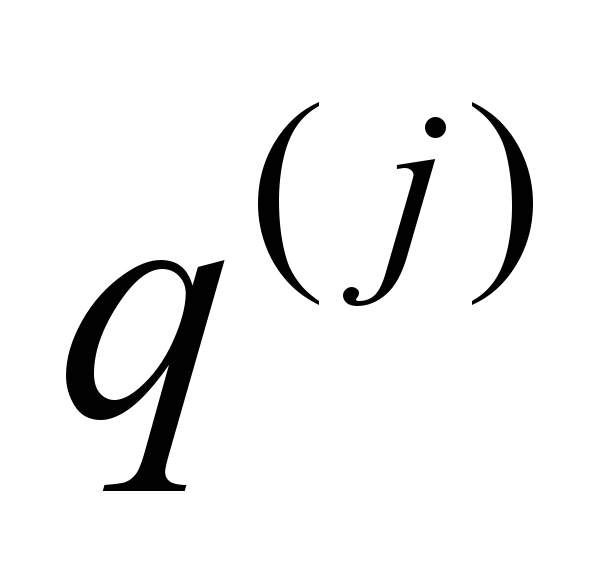–is the generalized displacements of the body.

The vectors 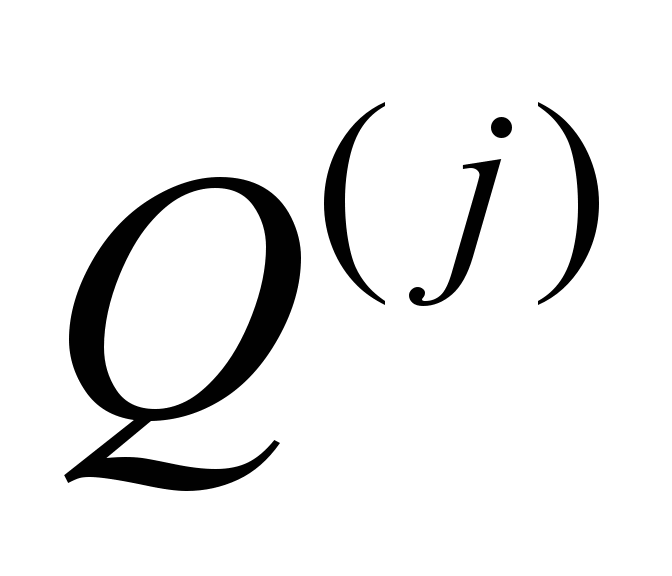correspond to generalized forces acting on the body at the j-th point. The body motion equation includes the sums of the components of these vectors, and the motion equations themselves take the form:

(1)

where – body mass, – main central moments of inertia.

Variables corresponding to displacements are called variables of the potential type, and processes corresponding to the forces are variables of the current type. These names refer to Kirchhoff's laws for electrical circuits and to the fact that the movements in the edges incident to one vertex are equated to each other, and the forces are added together.

Fig. 4. Vertex «Body motion equations»

The vertex representing the «Point» (Figure 5) is responsible for transforming the displacements and forces acting on the body (superscript «0») into the displacements of the point and the force applied to it (superscript «1»). The parameters of the vertex are the coordinates of the point in the coordinate system, whose origin is in the center of gravity of the body. At small angles of rotation, the expressions that determines the relationship between the values and 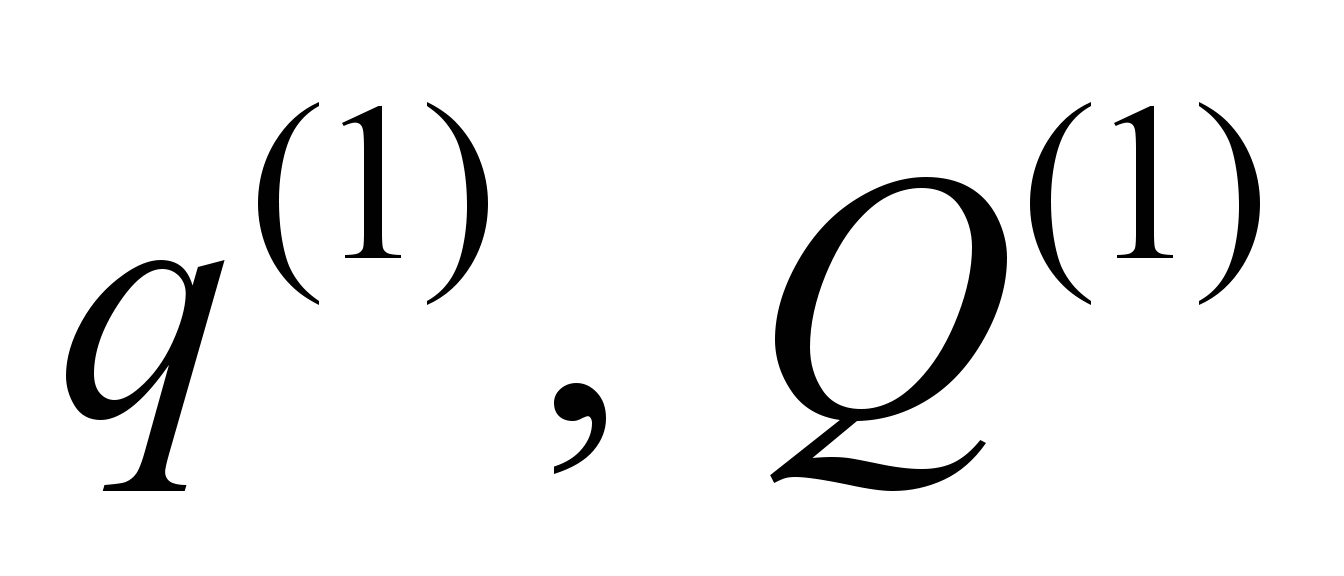take the form:

(2)

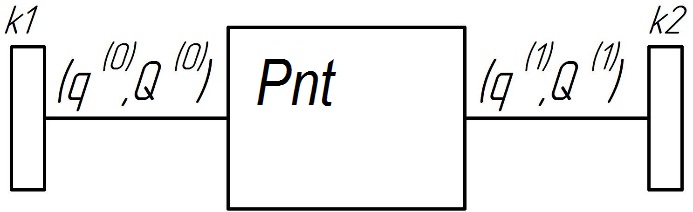
Fig. 5. Vertex «Point»

The «Connecting element» connects the «Points» of two «Bodies», Figure 6.

Fig. 6. Vertex «Connecting element»

The deformation of the connecting element is the difference

(3)

The force , arising in the connecting element depends on the deformation . The expression for the force depends on the type of the connecting element. For example, for a linear spring of rigidity , operating in a vertical direction

(4)

It is convenient to assume that the force acts on the Body-0 from the side of the Body-1. In this case , .

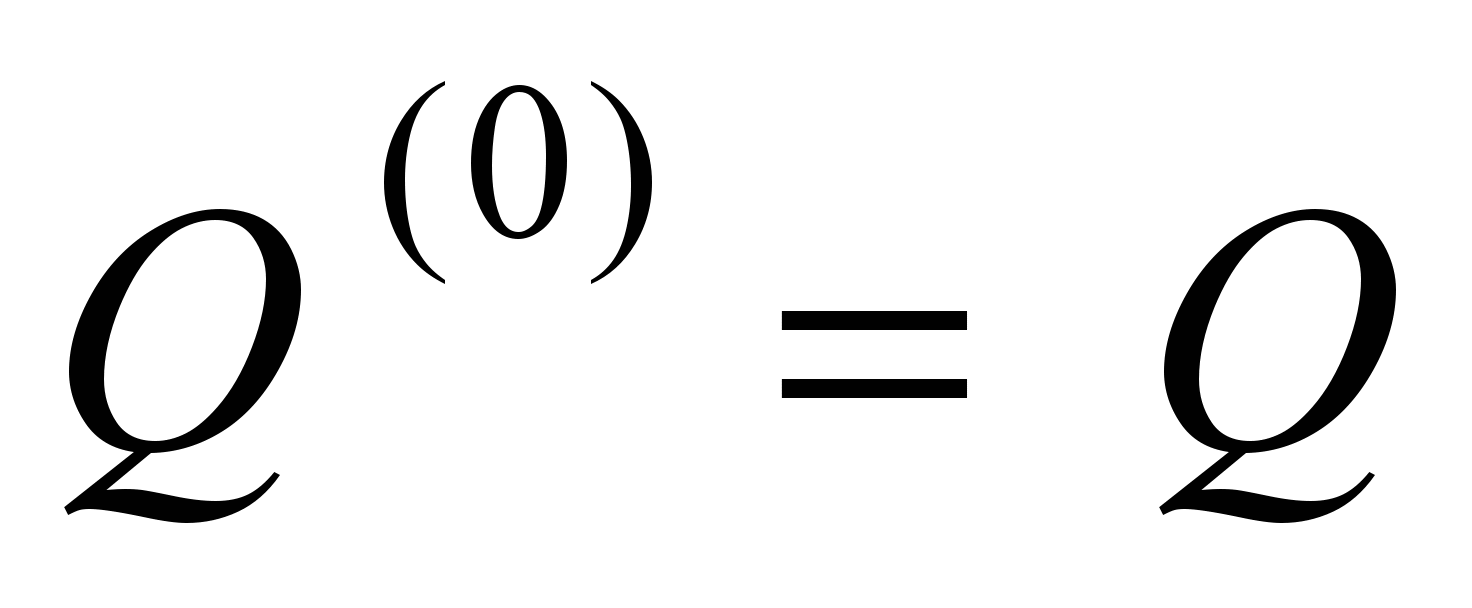By combining the described types of vertices, it is possible to present in a compact and visual form a model of car oscillations, suitable for direct formation of the motion equations.

Let us consider the implementation of the described approach for building a model in the Simulink package. In this case, the body, point and connecting element are conveniently represented as subsystems. As an example, Figure 7 shows the Simulink scheme for the subsystem «Bolster».

Fig. 7. Subsystem «Bolster» in Simulink model

A non-trivial matter is the question of comparing each edge with the direction of signal propagation, which is chosen so that for explicit expression of some values through other the argument is the input, and the function is the output.

Having examined the expression (2), we see that the directions for displacements and the directions for forces in one edge are opposite to each other. The direction of propagation for different signals is given in Table 1.

Table 1

Directions of signal propagation

Vertex class	Process	Direction
Body	q(j)	output
	Q(j)	input
Point	q(0)	input
	Q(0)	output
	q(1)	output
	Q(1)	input
Connecting element	q(0), q(1)	input
	Q(0), Q(1)	output

Findings

The use of the proposed method resulted in creation of a freight car model, which consists of a body and two bogies. The bogies were considered as a construction consisting of the following subsystem-elements [2, 3]:

­ wheel sets with box;

– solebars;

– bolster;

– springs of the central spring unit (each two-row spring separately);

– friction vibration dampers;

– axle-box suspension;

– centre pad;

– side bearing.

Each of these subsystems is independent and can be replaced with the condition of preserving the geometric parameters of the connection points of the element. This feature of the model is convenient to use for changing the parameters in order to select their optimal values.

The bodies, with the exception of bolsters and bogie solebars, have 6 degrees of freedom; the angles of rotation are small. To better estimate the dynamic loading of the bogie cast parts, the detailed models of spring suspension (up to individual springs and friction wedges, which are consi-dered as separate bodies of the system) and axle box were developed.

The model will be used to evaluate the dynamic loading of bogie elements of the car with an axial load of 25 tons [8], in order to clarify the loads arising during operation [4, 5, 14]. Vertical forces acting in the axle box when the car moves along a straight section of the track at 120 km/h speed are shown in Figure 8.

Originality and practical value

For the first time, a methodical approach to creating dynamic models of railway vehicles based on their description using hierarchically organized graphs was proposed.

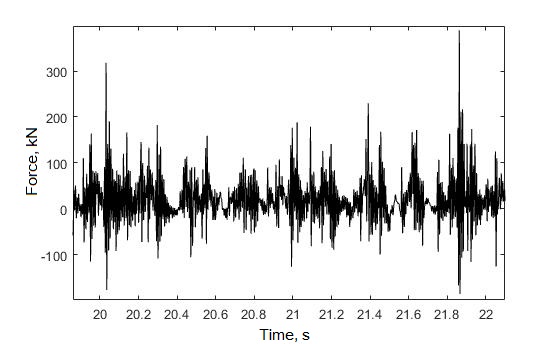
Fig. 8. Vertical forces in the axle box of gondola car with axle load of 25 tons, speed of 120 km/h

This methodological approach will allow, after creating a library of bodies and connecting elements, to significantly reduce the time spent on modeling the oscillations of different vehicles.

Conclusions

A technique has been developed for describing the structure of a railway vehicle using a hierarchical graph, which makes it possible to obtain equations of motion in an easily algorithmized manner. The vehicle is a system of rigid bodies connected by rigid, elastic and dissipative elements. The technique was tested to construct a model of spatial oscillations of a 4-axle freight car in the Simulink package. Directions of further development: creation of the library of bodies and connecting elements, detailed presentation of the geometry of track, the models of track superstructure and wheel-rail interaction.

LIST OF REFERENCE LINKS

1. Виттенбург, Й. Динамика систем твердых тел / Й. Виттенбург. – Москва : Мир, 1980. – 294 с.

2. Динамические качества грузовых вагонов, имеющих тележки с диагональными связями / Е. П. Блохин, К. Т. Алпысбаев, Р. Б. Грановский [и др.] // Вісн. Східноукр. нац. ун-ту ім. Володимира Даля. – 2012. – № 5, ч. 1. – С. 12–16.

3. Определение допускаемых скоростей движения грузовых вагонов по железнодорожным путям колеи 1520 мм / В. Д. Данович, В. В. Рыбкин, С. В. Мямлин, А. Г. Рейдемейстер, А. П. Трякин, Н. В. Халипова // Вісн. Дніпропетр. нац. ун-ту залізн. трансп. ім. акад. В. Лазаряна. – Дніпропетровськ, 2003. – Вип. 2. – С. 77–86.

4. Определение параметров пространственного нагружения литых деталей тележки 18-9855 при проведении стендовых испытаний / Д. В. Шевченко, Т. С. Куклин, А. М. Орлова [и др.] // Техника железных дорог. – 2016. – № 1 (33). – С. 68–74.

5. Рейдемейстер, А. Г. Способы увеличения прочности боковых рам трехэлементных тележек / А. Г. Рейдемейстер, А. А. Шикунов // Наука та прогрес транспорту. – 2015. – № 5 (59). – С. 141–149.
   doi: 10.15802/stp2015/55351.

6. Черных, И. В. Simulink: Инструмент моделирования динамических систем [Electronic resource] /
   И. В. Черных. – Available at: http://matlab.exponenta.ru/simulink/book1/index.php. – Title from the screen. – Accessed : 31.08.2017.

7. Borutzky, W. Bond graph methodology: development and analysis of multidisciplinary dynamic system models / W. Borutzky. – Sankt Augustin : Springer Science & Business Media, 2009. – 662 p.

8. Bubnov, V. M. Dynamic performance of freight cars on bogies model 18-1711 / V. M. Bubnov,
   S. V. Myamlin, N. B. Mankevych // Наука та прогрес транспорту. – 2013. – № 4 (46). – С. 118–126.
   doi: 10.15802/stp2013/16616.

9. Fritzson, P. Introduction to modeling and simulation of technical and physical systems with Modelica /
   P. Fritzson. – Hoboken : John Wiley & Sons, 2011. – 211 p.

10. Handbook of railway vehicle dynamics / Edited by S. Iwnicki. – Boca Raton : CRC press, 2006. – 526 p.

11. Knothe, K. Rail vehicle dynamics / K. Knothe, S. Stichel. – Cham : Springer, 2017. – 321 p.

12. Shabana, A. A. Dynamics of multibody systems / A. A. Shabana. – Cambridge : Cambridge university press, 2013. – 374 p.

13. Shabana, A. A. Railroad vehicle dynamics: a computational approach / A. A. Shabana, K. E. Zaazaa,
    H. Sugiyama. – Boca Raton : CRC press, 2007. – 343 p.

14. Shykunov, O. A. Three-Element Bogie Side Frame Strength / O. A. Shykunov // Наука та прогрес транспорту. – 2017. – № 1 (67). – С. 183–193. doi: 10.15802/stp2017/92535.

О. Г. РЕЙДЕМЕЙСТЕР¹, В. О. КАЛАШНИК², О. А. ШИКУНОВ^3*

¹Каф. «Вагони та вагонне господарство», Дніпропетровській національний університет залізничного
транспорту імені академіка В. Лазаряна, вул. Лазаряна, 2, Дніпро, Україна, 49010, тел. +38 (056) 373 15 04,
ел. пошта reidemeister@mail.ru, ORCID 0000-0001-7490-7180
²Каф. «Вагони та вагонне господарство», Дніпропетровській національний університет залізничного
транспорту імені академіка В. Лазаряна, вул. Лазаряна, 2, Дніпро, Україна, 49010, тел. +38 (056) 793 19 16,
ел. пошта kv47@i.ua, ORCID 0000-0002-8073-4631
^3*Каф. «Вагони та вагонне господарство», Дніпропетровській національний університет залізничного
транспорту імені академіка В. Лазаряна, вул. Лазаряна, 2, Дніпро, Україна, 49010, тел. +38 (056) 373 15 04,
ел. пошта tri_s@ua.fm, ORCID 0000-0002-8256-2634

МЕТОДИКА ПОБУДОВИ ДИНАМІЧНОЇ МОДЕЛІ

РУХУ БАГАТОМАСОВИХ СИСТЕМ

Мета. У науковій роботі необхідно розробити методику опису структури залізничних екіпажів (розглядаються як система твердих тіл, з’єднаних жорсткими, пружними та дисипативними елементами), яка дозволила б отримати рівняння руху способом, що легко алгоритмізується. Методика. При побудові моделі автори прагнуть до того, щоб її структура відображала структуру механічної системи, тобто частини моделі повинні відповідати частинам вагона. При цьому модель набуває форму ієрархічно організованого графа, вершини якого відповідають тілам, точкам кріплення з’єднувальних елементів та самим з’єднувальним елементам, а ребра описують сукупності процесів, які мають відношення до інцидентних ребру вершин. Як правило, це переміщення та сили: для ребра між тілом і точкою кріплення – узагальнені переміщення тіла та діючі на нього узагальнені сили; для ребра між точкою кріплення й з’єднувальним елементом – переміщення точки і сили, що виникають в елементі. Кожній вершині відповідає група рівнянь, що описують рух системи. Характер рівнянь залежить від типу вершини. Для тіла – рівняння руху тіла; для точки – вирази переміщень точки через узагальнені переміщення тіла й узагальнених сил, що діють на тіло, через сили, що виникають у з’єднувальному елементі; для з’єднувального елемента – вирази для сил, що виникають в ньому, через деформації елемента. Граф може розглядатися як орієнтований. Напрямок ребра обирають таким чином, щоб для кожної вершини величини, що стоять у правій частині зіставлених вершині рівнянь, відповідали ребру, що входить, а в лівій – виходить. Результати. Розроблено методику побудови динамічної моделі коливань залізничних екіпажів як системи твердих тіл на основі їх опису за допомогою ієрархічно організованих графів. Методика випробувана для побудови моделі просторових коливань 4-вісного вантажного вагона з осьовим навантаженням 25 тс в пакеті Simulink. Наукова новизна. Вперше розроблено методику опису структури залізничного екіпажу за допомогою ієрархічного графа, яка дозволяє отримати рівняння руху способом, що легко алгоритмізується. Практична значимість. Запропонований методичний підхід дозволить, після створення бібліотеки тіл та з’єднувальних елементів, значно скоротити витрати часу на моделювання коливань різних екіпажів.

Ключові слова: модель коливань; залізничний екіпаж; багатомасова система; граф

А. Г. РЕЙДЕМЕЙСТЕР¹, В. А. КАЛАШНИК², А. А. ШИКУНОВ^3*

¹Каф. «Вагоны и вагонное хозяйство», Днепропетровский национальный университет железнодорожного
транспорта имени академика В. Лазаряна, ул. Лазаряна, 2, Днипро, Украина, 49010, тел. +38 (056) 373 15 04,
эл. почта reidemeister@mail.ru, ORCID 0000-0001-7490-7180
²Каф. «Вагоны и вагонное хозяйство», Днепропетровский национальный университет железнодорожного
транспорта имени академика В. Лазаряна, ул. Лазаряна, 2, Днипро, Украина, 49010, тел. +38 (056) 793 19 16,
эл. почта kv47@i.ua, ORCID 0000-0002-8073-4631
^3*Каф. «Вагоны и вагонное хозяйство», Днепропетровский национальный университет железнодорожного
транспорта имени академика В. Лазаряна, ул. Лазаряна, 2, Днипро, Украина, 49010, тел. +38 (056) 373 15 04,
эл. почта tri_s@ua.fm, ORCID 0000-0002-8256-2634

МЕТОДИКА ПОСТРОЕНИЯ ДИНАМИЧЕСКОЙ МОДЕЛИ

ДВИЖЕНИЯ МНОГОМАССОВОЙ СИСТЕМЫ

Цель. В научной работе необходимо разработать методику описания структуры железнодорожных экипажей (рассматриваются как система твердых тел, соединенных жесткими, упругими и диссипативными элементами), которая позволила б получить уравнения движения легко алгоритмизируемым способом. Методика. При построении модели авторы стремятся к тому, чтобы ее структура отражала структуру механической системы, то есть части модели должны соответствовать частям вагона. При этом модель приобретает форму иерархически организованного графа, вершины которого соответствуют телам, точкам крепления соединительных элементов и самим соединительным элементам, а ребра описывают совокупности процессов, которые имеют отношение к инцидентным ребру вершинам. Как правило, это перемещения и силы: для ребра между телом и точкой крепления – обобщенные перемещения тела и действующие на него обобщенные силы; для ребра между точкой крепления и соединительным элементом – перемещения точки и силы, возникающие в элементе. Каждой вершине соответствует группа уравнений, описывающих движение системы. Характер уравнений зависит от типа вершины. Для тела – уравнения движения тела; для точки – выражения перемещений точки через обобщенные перемещения тела и обобщенных сил, действующих на тело, через силы, возникающие в соединительном элементе; для соединительного элемента – выражения для сил, возникающих в нем, через деформации элемента. Граф может рассматриваться как ориентированный. Направление ребра выбирают таким образом, чтобы для каждой вершины величины, стоящие в правой части сопоставленных вершине уравнений, соответствовали входящему ребру, а в левой – исходящему. Результаты. Разработана методика построения динамической модели колебаний железнодорожных экипажей как системы твердых тел на основе их описания с помощью иерархически организованных графов. Методика опробована для построения модели пространственных колебаний 4-осного грузового вагона с осевой нагрузкой 25 тс в пакете Simulink. Научная новизна. Впервые разработана методика описания структуры железнодорожного экипажа с помощью иерархического графа, которая позволяет получить уравнения движения легко алгоритмизируемым способом. Практическая значимость. Предложенный методический подход позволит, после создания библиотеки тел и соединительных элементов, значительно сократить затраты времени на моделирование колебаний различных экипажей.

Ключевые слова: модель колебаний; железнодорожный экипаж; многомассовая система; граф

REFERENCES

1. Vittenburg, Y. (1980). Dinamika sistem tverdykh tel. Moscow: Mir.

2. Blokhin, Y. P., Alpysbaev, K. T., Granovskiy, R. B., Dzichkovskiy, Y., Krivchikov, A., Fedorov, Y. F. (2012). Dinamicheskie kachestva gruzovykh vagonov, imeyushchikh telezhki s diagonalnymi svyazyami. Visnik of the Volodymyr Dahl East Ukrainian National University, 5 (1), 12-16.

3. Danovich, V. D., Rybkin, V. V., Myamlin, S. V., Reydemeyster, A. G., Tryakin, A. P., Khalipova,
   N. V. (2003). Determination of permissible speeds of freight cars on railroad tracks 1520 mm. Bulletin of Dnipropetrovsk National University of Railway Transport, 2, 77-86.

4. Shevchenko, D. V., Kuklin, T. S., Orlova, A. M., Savushkin, R. A., Dmitriev, S. V., & Belyankin,
   A. V. (2016). Opredeleniye parametrov prostranstvennogo nagruzheniya litykh detaley telezhki 18-9855 pri provedenii stendovykh ispytaniy. Railway Equipment Magazine, 1 (33), 68-74.

5. Reidemeister, O. H., & Shykunov, O. A. (2015). Strength increase methods of the side frame of the bogie in three-piece trucks. Science and Transport Progress, 5 (59), 141-149. doi:10.15802/stp2015/55351

6. Chernykh, I. V. (n.d.). Simulink: Instrument modelirovaniya dinamicheskikh system. MATLAB.Exponenta! Retrieved from http://matlab.exponenta.ru/simulink/book1/index.php

7. Borutzky, W. (2010). Bond graph methodology: development and analysis of multidisciplinary dynamic system models. Sankt Augustin: Springer Science & Business Media. doi:10.1007/978-1-84882-882-7

8. Bubnov, V. M., Myamlin, S. V., & Mankevych, N. B. (2013). Dynamic performance of freight cars on bogies model 18-1711. Science and Transport Progress, 4 (46), 118-126. doi:10.15802/stp2013/16616

9. Fritzson, P. (2011). Introduction to modeling and simulation of technical and physical systems with Modelica. Hoboken: John Wiley & Sons. doi:10.1002/9781118094259

10. Iwnicki, S. (Ed.). (2006). Handbook of railway vehicle dynamics. Boca Raton: CRC press.

11. Knothe, K., & Stichel, S. (2017). Rail vehicle dynamics. Cham: Springer. doi:10.1007/978-3-319-45376-7

12. Shabana, A. A. (2013). Dynamics of multibody systems. Cambridge: Cambridge university press.

13. Shabana, A. A., Zaazaa, K. E., & Sugiyama, H. (2007). Railroad vehicle dynamics: A computational approach. Boca Raton: CRC press.

14. Shykunov, O. A. (2017). Three-element bogie side frame strength. Science and Transport Progress, 1 (67), 183-193. doi:10.15802/stp2017/92535

Prof. S. V. Myamlin, D. Sc. (Tech.), (Ukraine); PhD Tech., Senior Research Associate T. V. Sheleiko (Ukraine) recommended this article to be published

Received: May 17, 2017

Accessed: Sept. 21, 2017

doi 10.15802/stp2017/112921 © O. H. Reidemeister, V. O. Kalashnyk, O. A. Shykunov, 2017