ISSN 2307–3489 (Print), ІSSN 2307–6666 (Online)

Наука та прогрес транспорту. Вісник Дніпропетровського
національного університету залізничного транспорту, 2017, № 4 (70)

ЕКОЛОГІЯ НА ТРАНСПОРТІ

Introduction

Pollution from vehicles in urban streets is very intensive and can cause harm to humans. For this purpose, it is necessary to predict the level of pollution in streets. Physical modeling, in this case, is very expensive [8]. For quick prediction empirical models are used [1]. These models are convenient in practice, especially when we must run many «pilot» calculations. But these models do not take into account some important properties of pollutant dispersion process in streets. The main problem is that the process of air pollution in streets takes part in the region having comprehensive geometrical form (presence of buildings, different obstacles, etc). The alternative way is the numerical simulation of this process. Many authors apply CFD simulation to solve the problem [1, 3, 6, 8–10]. As a rule, to obtain flow pattern in streets foreign authors use Navier – Stokes equations (this is the model of viscous fluid) coupled with turbulent models. Very often commercial codes are used for this purpose. Worthy of note, that application of Navier – Stokes equations needs application of very fine computational grid during the computational experiment to simulate in detail the process of vortexes formation and their dispersion and interaction in the region. Using the model of viscous fluid, we must use very fine grid inside the boundary layers. This is a real problem if we have big dimensions of the buildings, obstacles in streets. So, in case of Navier – Stokes equations application it is necessary to use powerful PC and every computational experiment consumes much time. This is not convenient when we must run a lot of practical calculations considering different scenario of air pollution in streets and, especially, when we try to find the effective protection measures because in this case we must consider many alternative variants of protection. In this case it would be better to split the study in two steps. At the first step we may find the «satisfying» variant using numerical model which does not consume much time and not take into account some physical features of the process. After that, at the second step, we may use more powerful model to compute in detail the variant of protection which has been chosen. So, for quick calculations at the first step it is important to have CFD models which consume not much computational time but they allow to take into account such important features as obstacles, emission rate, etc.

Purpose

The purpose of this paper is development a numerical model for quick computing of the local air quality near roads.

Aerodynamic equation

To simulate the wind pattern near the road we use model of potential flow. In this case the governing equation is [5]:

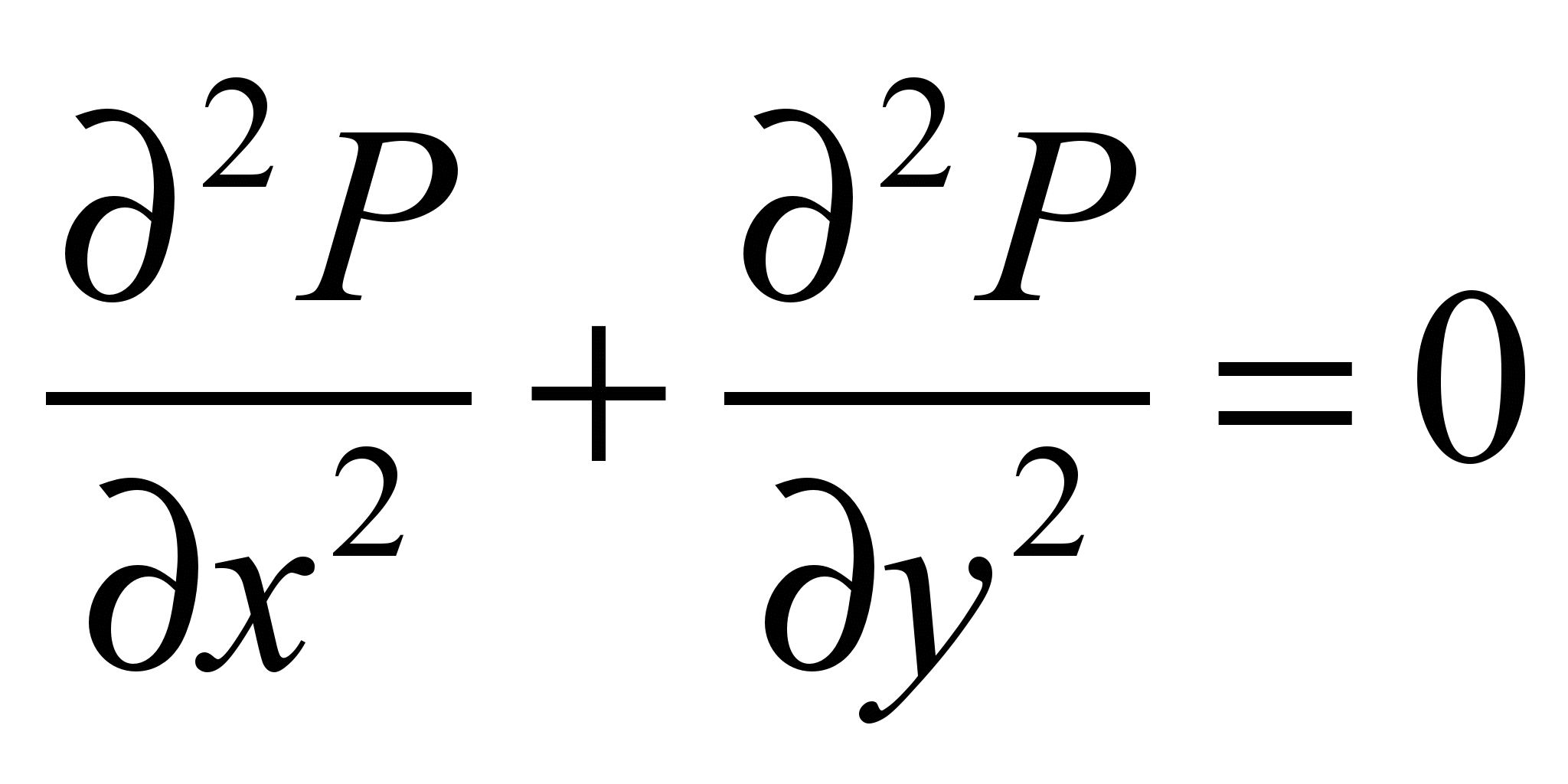, (1)

where Р is the potential of speed.

The wind velocity components are calculated as follows:

.

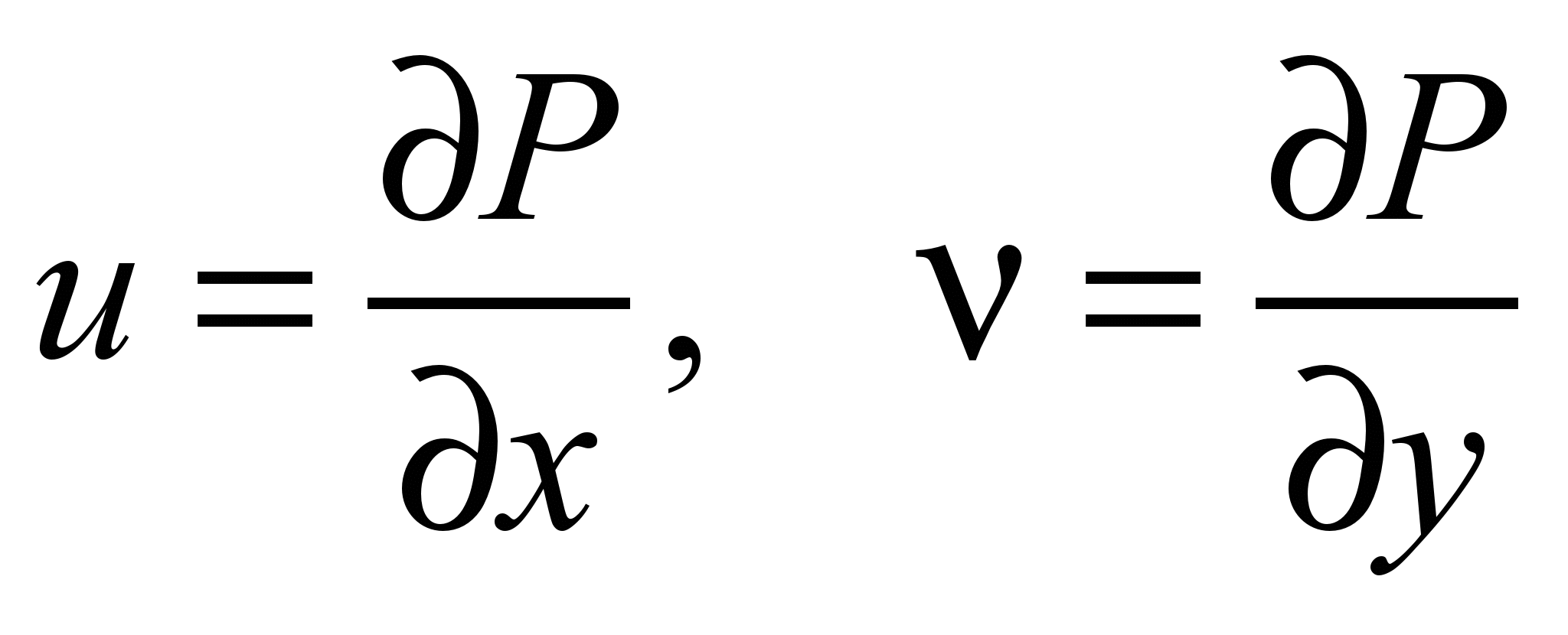Boundary conditions equation (1) are discussed in [1]. To perform numerical integration of this equation rectangular grid was used.

To solve equation of potential flow (1) we used the difference scheme of «conditional approximation». In this case, first of all, we transformed Eq. 1 to equation having «evolution type» [5]

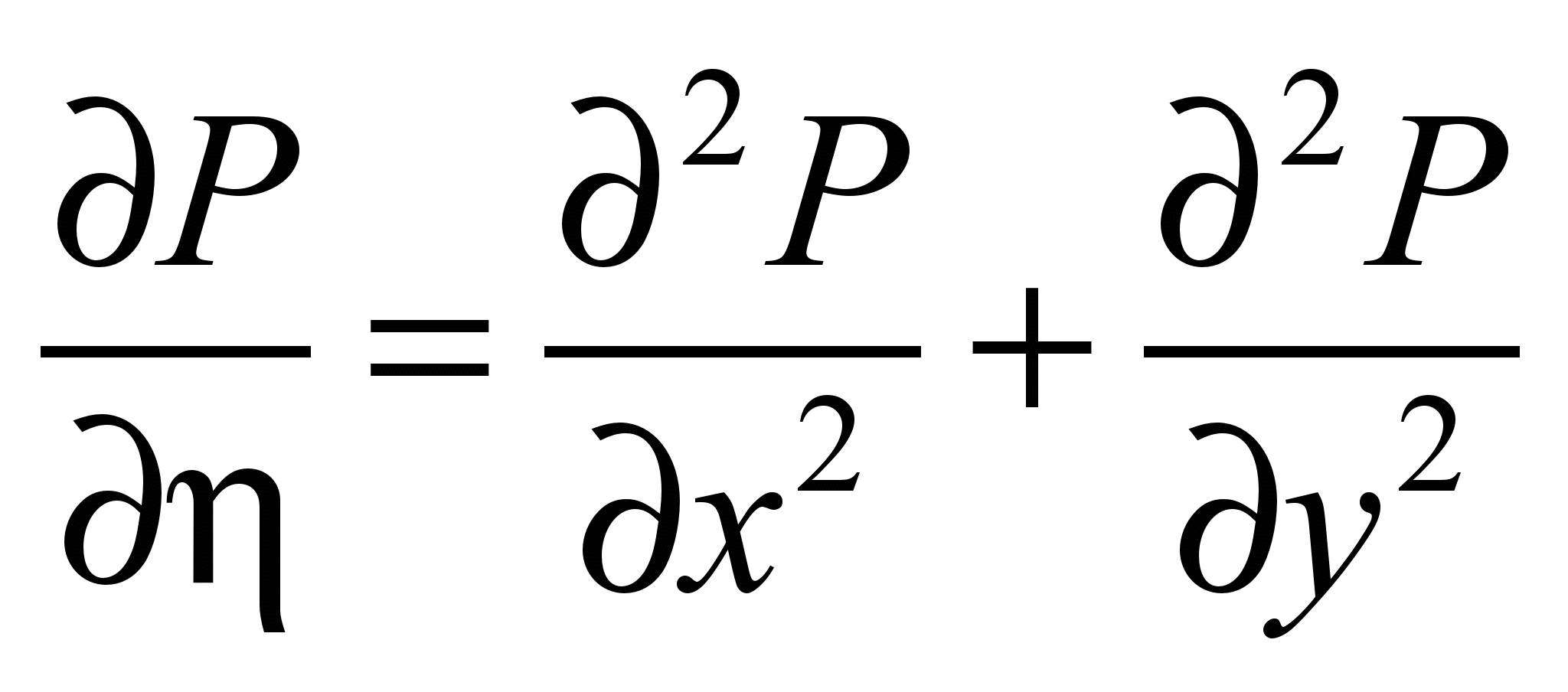, (2)

where 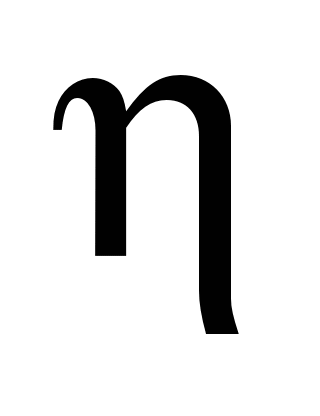is «fictitious» time.

For the solution of equation (2) tends to the solution of equation (1).

After approximation of Eq. 2, we split it in the sequence of two difference equations having implicit form [5]

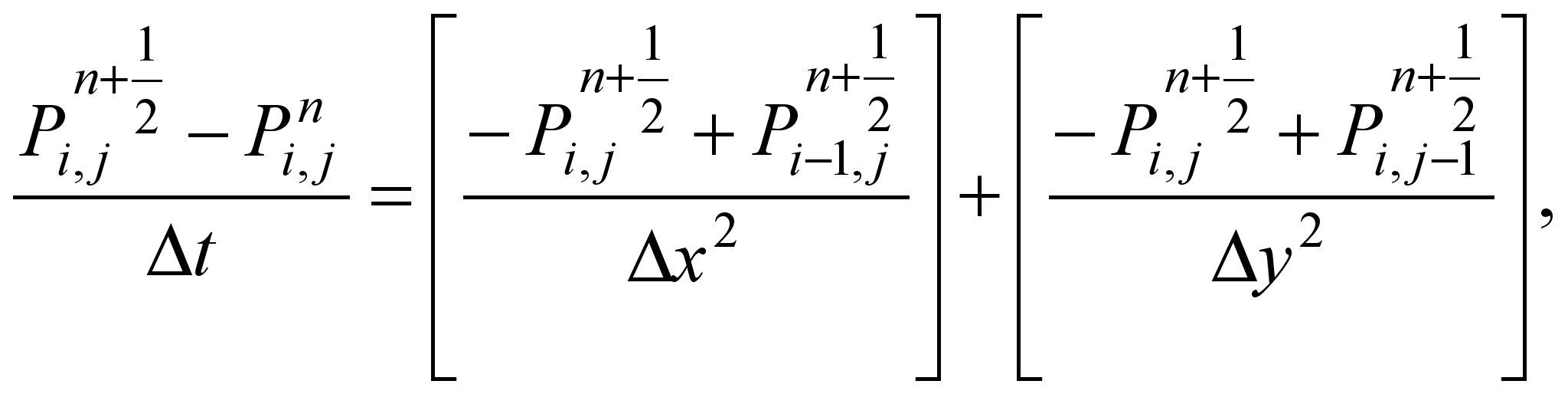
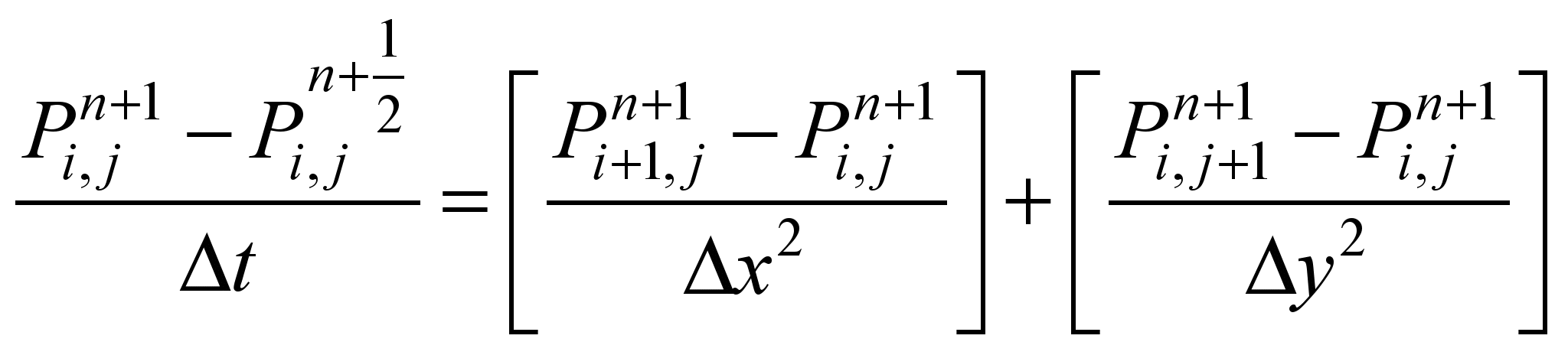.(3)

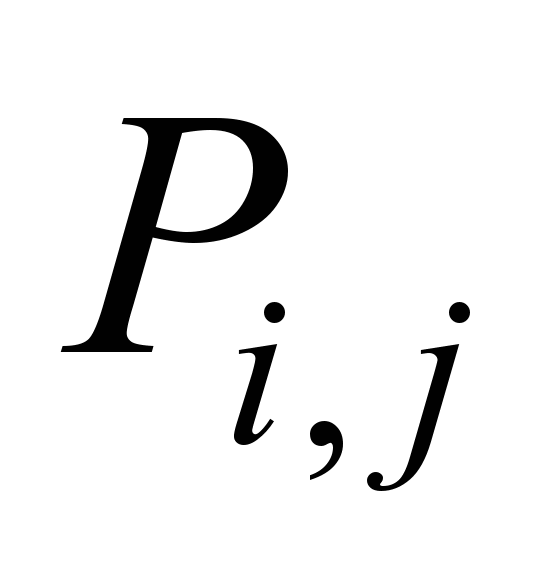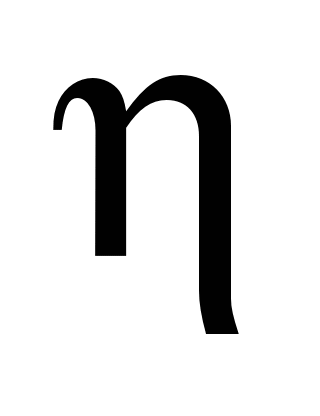Unknown value of can be easily determined from each difference equation (3) using explicit formulae of «running calculation». As the «initial» condition for Eq. 2 we may use, for, example, P=0 for =0.

Pollutant Transport Equation

To simulate the pollutant dispersion near road equation of convective – diffusive transfer is used [1, 4, 7]

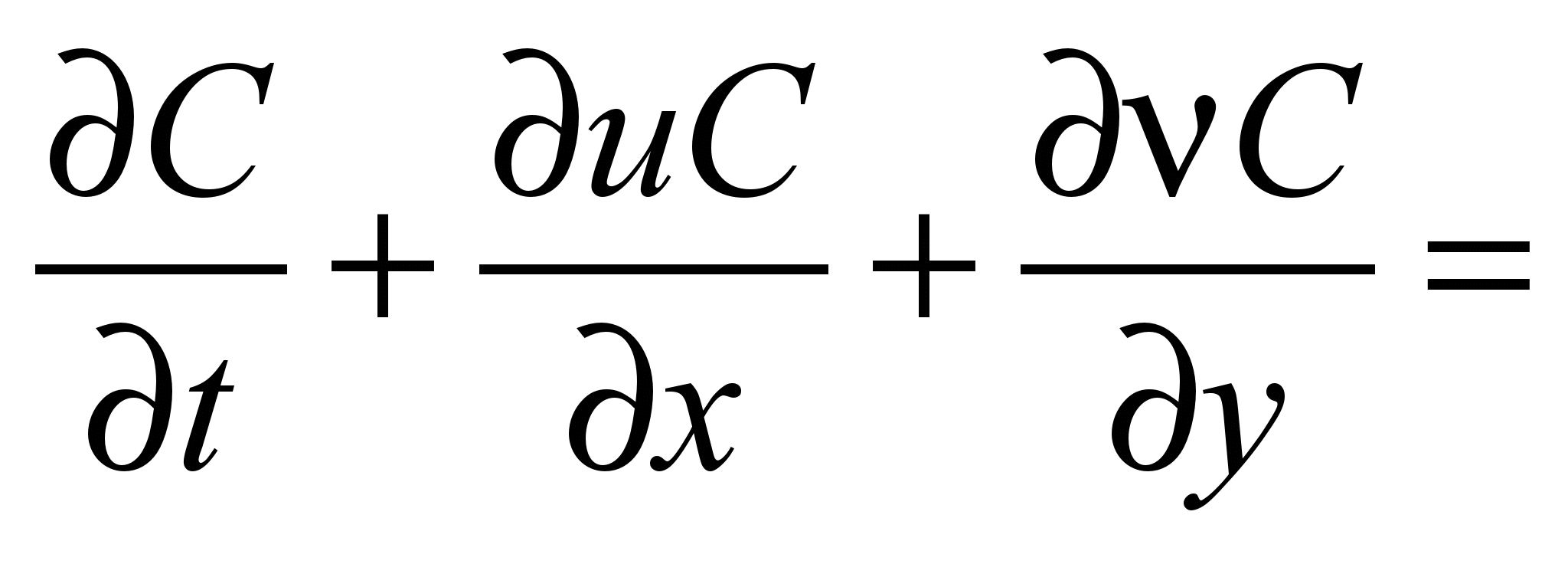
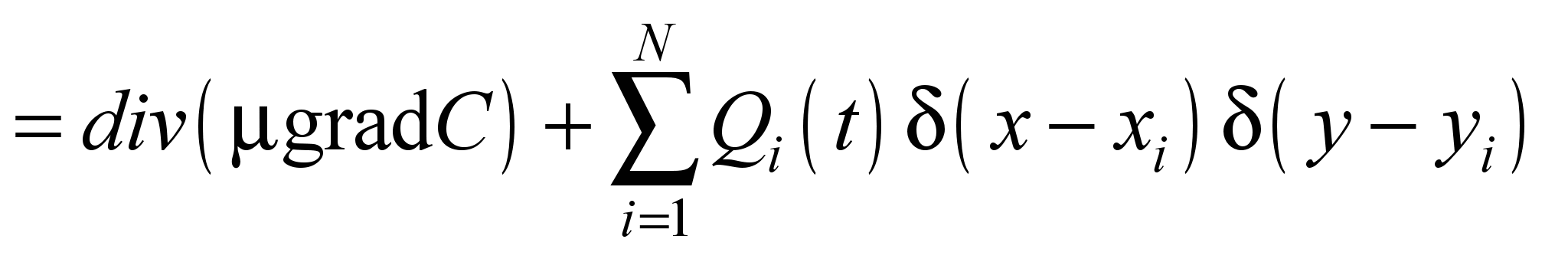, (4)

where С is mean concentration

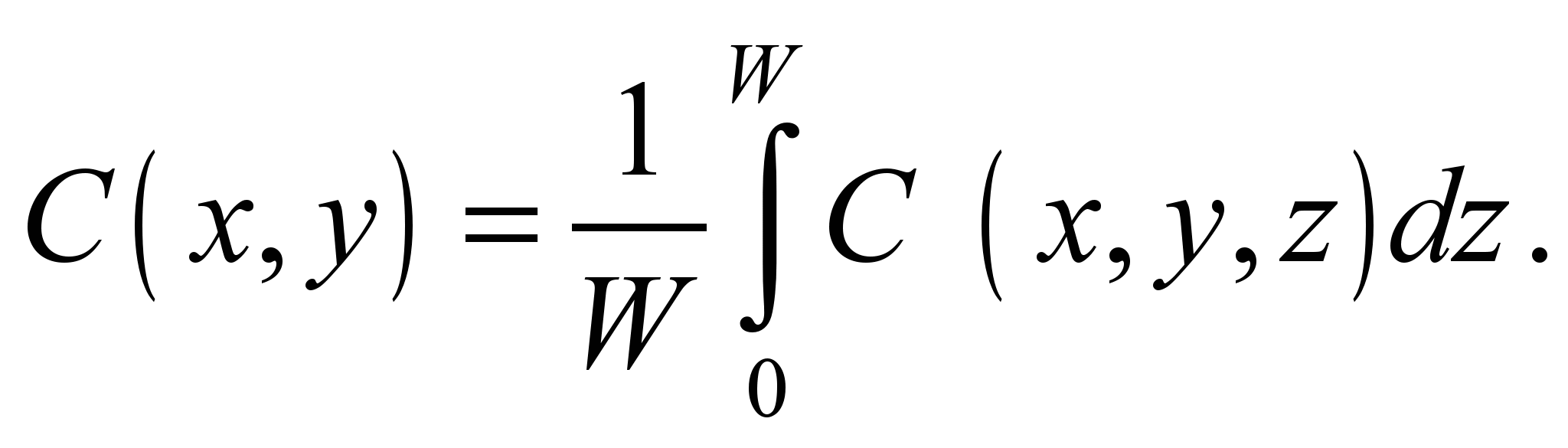
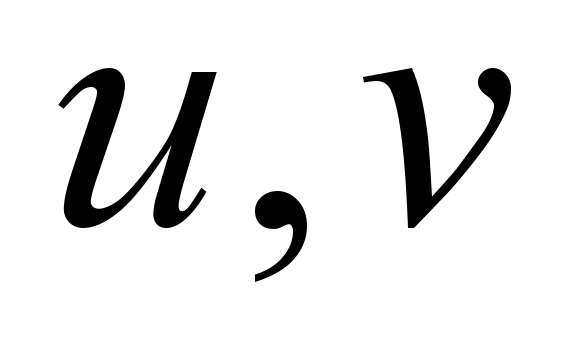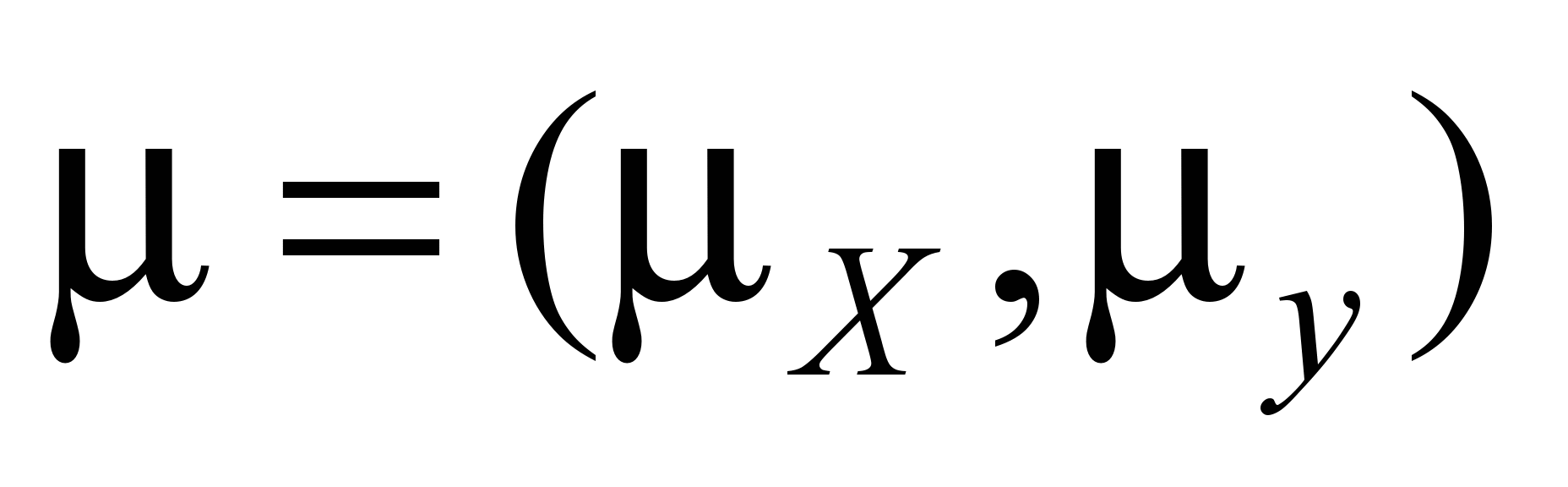W is width of the computational region; are the wind velocity components; are the diffusion coefficients; 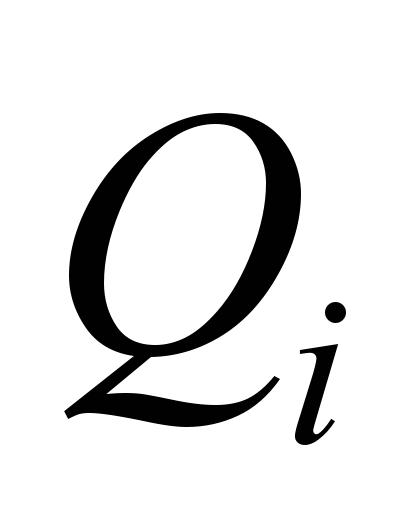is rate of emission; 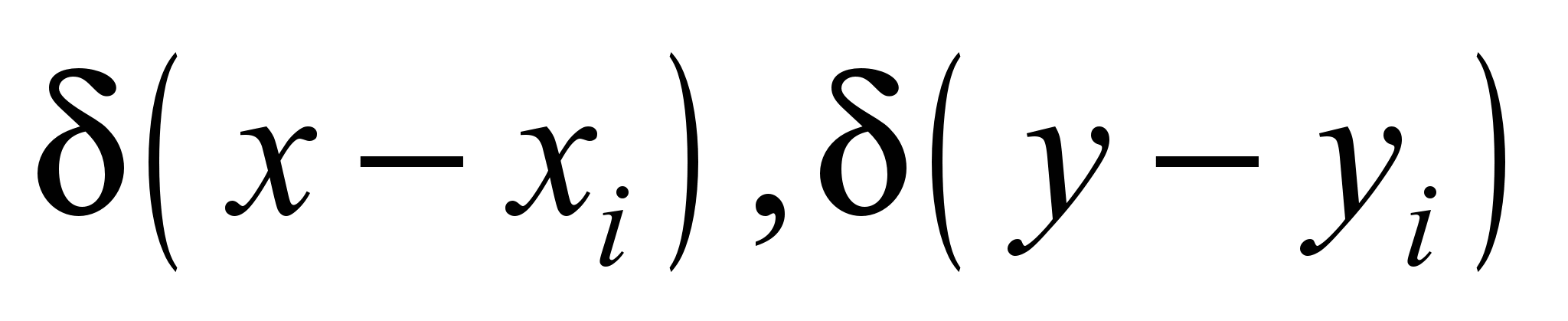– are Dirac delta function; t is time.

Initial and boundary conditions for Eq. 4 are described in [1, 4].

Before solving Eq. (2) we made it’s physical splitting into the sequence of three equations. These are the following equations:

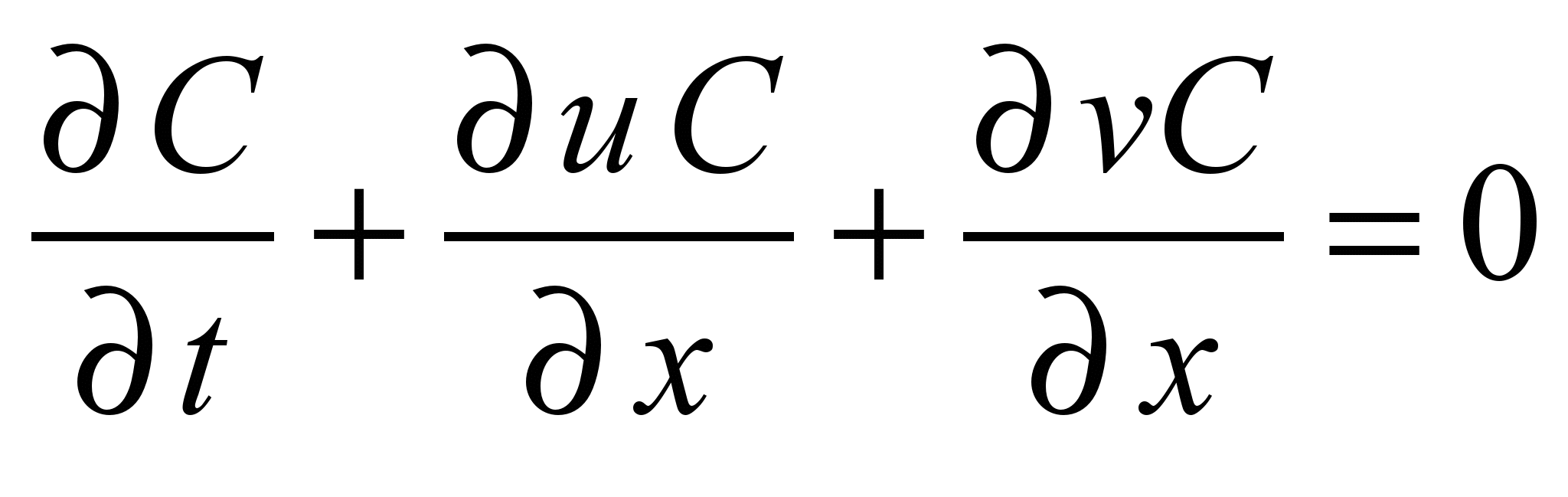, (5)

,

,

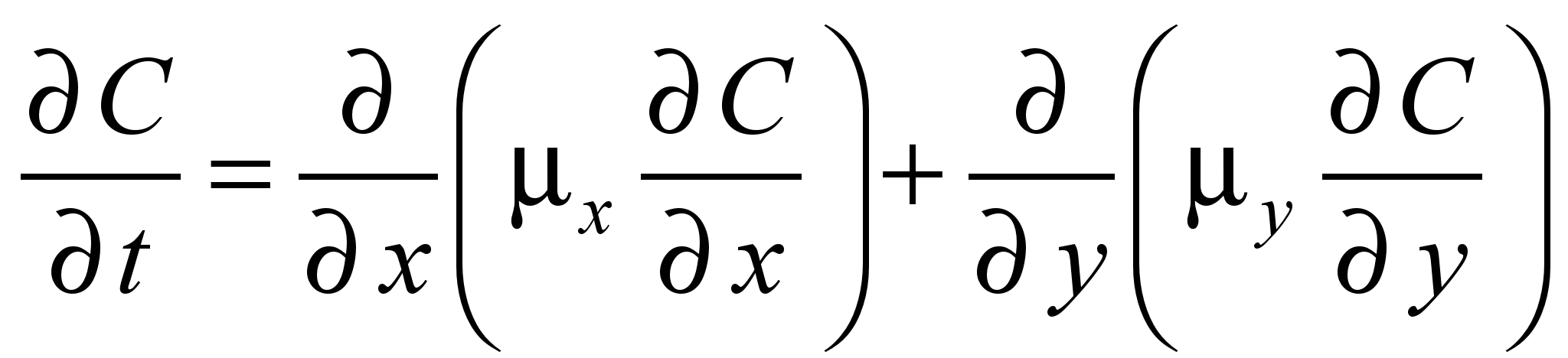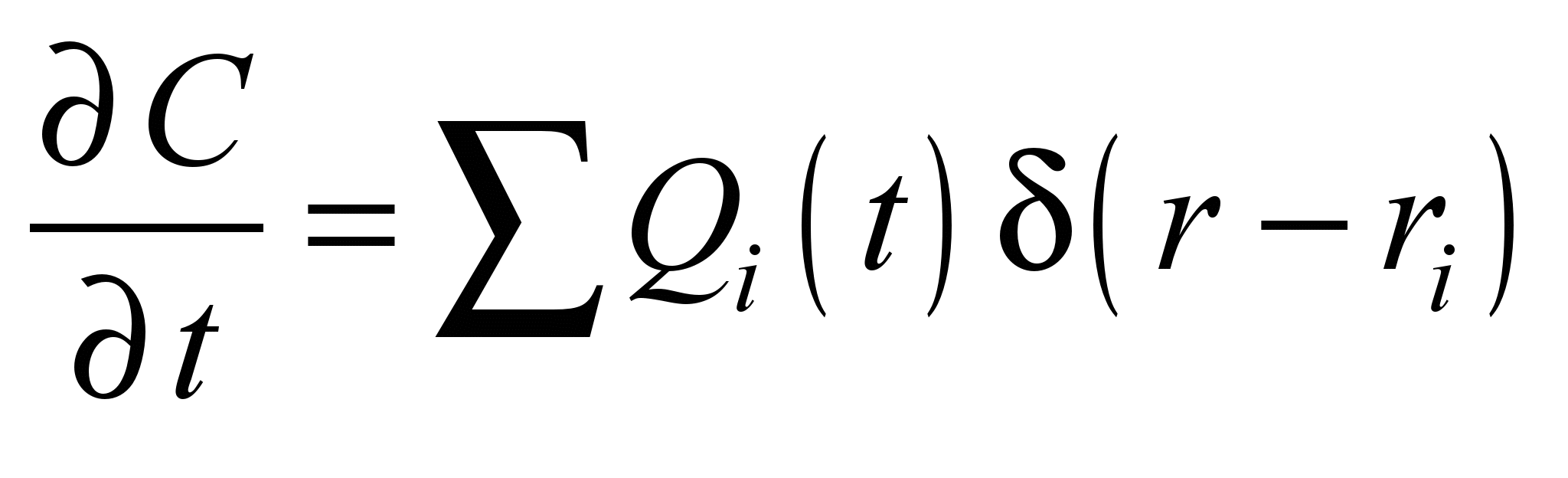where 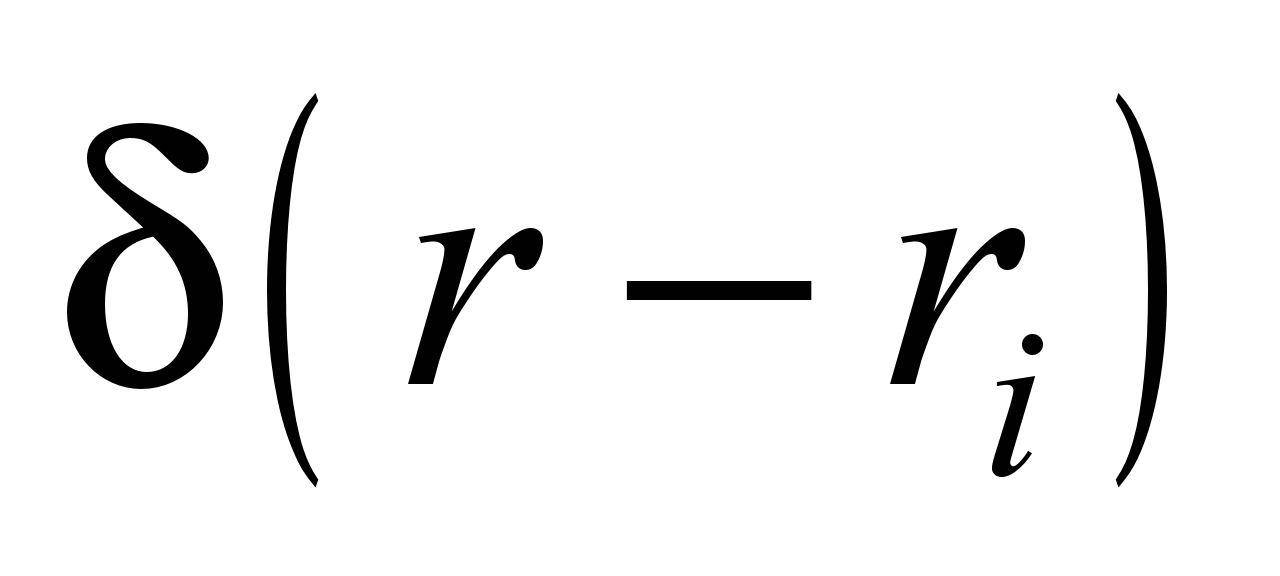is Dirac delta function; 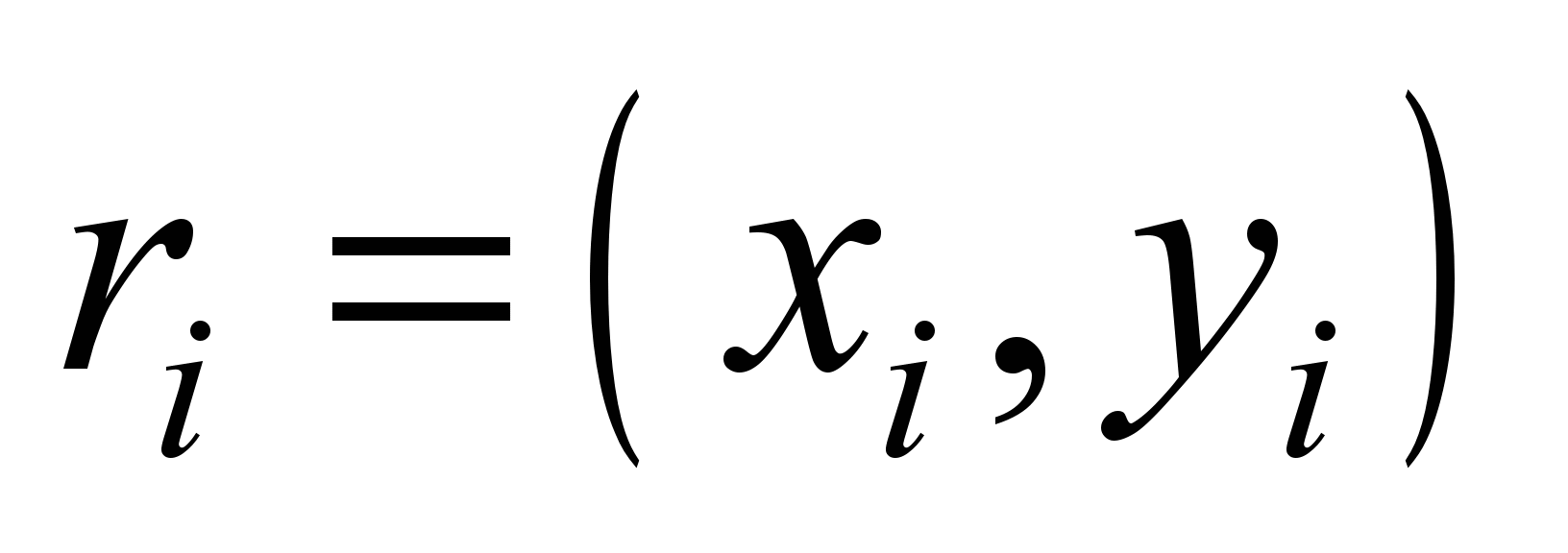are the coordinates of the point source.

The first equation in (5) describes pollutant transfer along trajectories. The second equation in (5) describes the diffusive dispersion of pollutant. The third equation in (5) describes concentration change under the action of source .

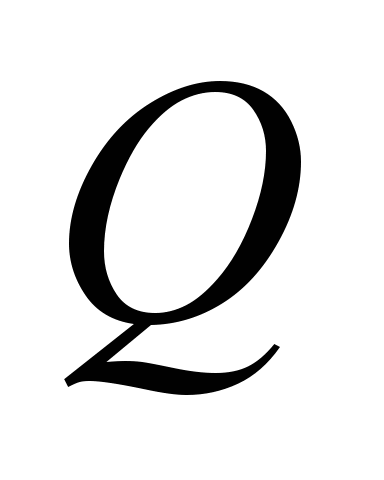To solve the first and the second equations in (5) the implicit change – triangle difference scheme was used [1]. To solve the third equation from (5) Euler method was used [5].

Numerical integration of difference equations is performed using rectangular grid. Values of P, C are determined in the centers of computational cells, values of u, v are determined at the sides of the computational cells. For coding difference equations, we used FORTRAN language.

Findings

Developed numerical model and code were used to compute CO concentrations near road which has barrier at the curb. Numerical simulation was performed for two scenarios. The first one is scenario where barrier has a form of vertical plate (Fig. 1). The second scenario is application of barrier which has additional «short wing» at the top (Fig. 2). «Body» of the vehicle is represented as rectangular. Its form and form of the curb, barrier is represented in numerical model using «markers» (porosity technique). Outlet opening of the vehicle is a passive source of emission. It means that we don’t take into account speed of gases which move from it. Arrow indicates the wind direction.

Results of numerical simulations are shown in Fig. 3–5. Fig. 3, 4 represent CO concentration field near road. We can see that application of barrier with «short wing» allows to reduce the width of contaminated zone behind the barrier.

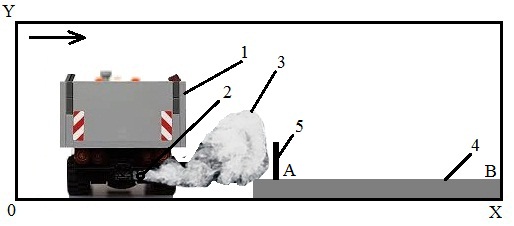
Fig. 1. Sketch of computational region (the first
scenario): 1 – vehicle; 2 – source of emission
(outlet opening); 3 – plume; 4 – curb; 5 – barrier

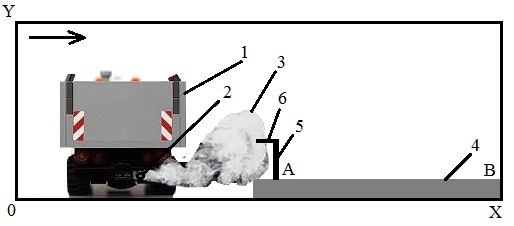
Fig. 2. Sketch of computational region
(the second scenario):
1 – vehicle; 2 – source of emission (outlet
opening); 3 – plume; 4 – curb; 5 – barrier; 6 – «short wing»

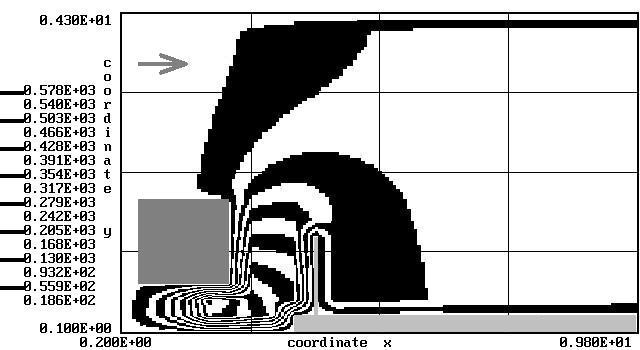
Fig. 3. Computed CO concentration
(barrier without «wing»)

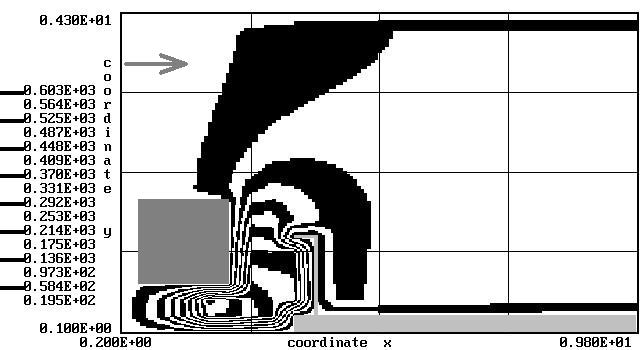
Fig. 4. Computed CO concentration
(barrier with «short wing»)

In Table 1 we present computed CO concentration behind barriers at height h=1,7 m.

Table 1

Computed CO concentration at height h =1.7 m

Distance from barrier	Concentration (scenario: no wing)	Concentration (scenario: short wing)
0.6 m	1.01 mg/m3	0.94 mg/m3
1.0 m	0.95 mg/m3	0.88 mg/m3
1.4 m	0.89 mg/m3	0.82 mg/m3
1.8 m	0.85 mg/m3	0.78 mg/m3

As we can see from Table 1 application of barrier having «short wing» allows reduce CO concentrations near the road.

Worthy of note that computational time was about 5 sec. for each scenario. It allows to use the developed numerical model for practical application when series of computational experiments must be run.

Originality and practical value

A model has been developed to compute concentrations near roads. Numerical model is based on application of mass transfer equation and equation of potential flow.

The peculiarity of the developed model is the use quick calculation of contaminated zones and account of geometrical form of vehicle, curb, barriers near the road.

Conclusions

Numerical model for estimating the level of atmospheric air pollution near roads is proposed. Proposed numerical model allows to predict level of pollution with account of geometrical form of vehicle, curb, barriers near the road, intensity of emission rate. The solution of the aerodynamic problem is based on the numerical integration of equation for potential flow. This allows to perform quick calculation of wind pattern near road using PC which are available now in Ukraine. To predict toxic gases concentrations near road convective – diffusive equation is used. Numerical integration of this equation is performed using implicit difference scheme. Using the developed numerical model some numerical experiments were performed to study the influence of barrier form on intensity of local contamination near road.

Further improvement of the model should be carried out in the direction of creating a 3D numerical model.

LIST OF REFERENCE LINKS

1. Беляев, Н. Н. Моделирование загрязнения атмосферного воздуха выбросами автотранспорта на улицах городов : монография / Н. Н. Беляев, Т. И. Русакова, П. С. Кириченко. – Днепропетровск : Акцент ПП, 2014. – 159 с.

2. Беляев, Н. Н. Прогноз загрязнения атмосферного воздуха выбросами автотранспорта с учетом химической трансформации вредных веществ / Н. Н. Беляев, Е. С. Славинская, Р. В. Кириченко // Наука та прогрес транспорту. – 2017. – № 3 (69). – С. 15–22. doi: 10.15802/stp2017/104549.

3. Беляев, Н. Н. CFD прогнозирование процесса загрязнения воздушной среды на улицах / Н. Н. Беляев, Т. И. Русакова // Екологія і природокористування : зб. наук. пр. Ін-ту проблем природокористування та екології НАН України. – Київ, 2013. – Вип. 17. – С. 188–194.

4. Марчук, Г. И. Математическое моделирование в проблеме окружающей среды / Г. И. Марчук. – Москва : Наука, 1982. – 320 с.

5. Самарский, А. А. Теория разностных схем / А. А. Самарский. – Москва : Наука, 1983. – 616 с.

6. A new simplified NO/NO₂ conversion model under consideration of direct NO₂-emissions / I. Düring, W. Bächlin, M. Ketzel, A. Baum, U. Friedrich, S. Wurzler // Meteorologische Zeitschrift. – 2011. – Vol. 20. – Iss. 1. – P. 67–73. doi: 10.1127/0941-2948/2011/0491.

7. Berlov, O. V. Atmosphere protection in case of emergency during transportation of dangerous cargo /
   O. V. Berlov // Наука та прогрес транспорту. – 2016. – № 1 (61). – С. 48–54. doi: 10.15802/stp2016/60953.

8. Nguyen, T. N. Numerical simulation of wind flow and pollution transport in urban street canyons / T. N. Nguyen, T. C. Nguyen, V. T. Nguyen // Advanced Science and Technology Letters. – 2015. – Vol. 120. – P. 770–777. doi: 10.14257/astl.2015.120.152.

9. Numerical simulations and wind tunnel studies of pollutant dispersion in the urban street canyons with different height arrangements / Ch.-H. Chang, J.-S. Lin, C.-M. Cheng, Y.-S. Hong //
   J. of Marine Science and technology. – 2013. – Vol. 21, No. 2. – P. 119–126.

10. Overman, H. T. J. Simulation model for NO_x distributions in a street canyon with air purifying pavement: мaster thesis / H. T. J. Overman ; University of Twente. – Enschede, Netherlands, 2009. – 69 р.

М. М. БІЛЯЄВ^1*, О. С. СЛАВІНСЬКА^2*, Р. В. КИРИЧЕНКО^3*

^1*Каф. «Гідравліка та водопостачання», Дніпропетровський національний університет залізничного транспорту
імені академіка В. Лазаряна, вул. Лазаряна, 2, Дніпро, Україна, 49010, тел. +38 (056) 273 15 09,
ел. пошта water.supply.treatment@gmail.com, ORCID 0000-0002-1531-7882
^2*Каф. «Управління виробництвом та майном», Національний транспортний університет, вул. Суворова, 1, Київ,
Україна, 01010, тел. +38 (044) 280 82 03, ел. пошта water.supply.treatment@gmail.com, ORCID 0000-0001-5163-5645
^3*Каф. «Управління виробництвом та майном», Національний транспортний університет, вул. Суворова, 1, Київ,
Україна, 01010, тел. +38 (044) 280 82 03, ел. пошта water.supply.treatment@gmail.com, ORCID 0000-0001-9918-3895

Чисельне моделювання розповсюдження забруднення

на міській вулиці

Мета. У науковій статті необхідно вирішити питання щодо розробки 2D чисельної моделі, яка дозволила б швидко розрахувати процес забруднення атмосферного повітря викидами автотранспорту. Передбачено також створити чисельну модель, що давала б можливість прогнозувати рівень забруднення атмосферного повітря при використанні захисних бар’єрів біля дороги. Методика. Використано розроблену модель, яка базується на рівнянні нев’язкої рідини та рівнянні масопереносу. Рівняння для потенціалу швидкості використовується для розрахунку поля швидкості повітряного потоку при експлуатації бар’єрів. При вирішенні рівняння для потенціалу швидкості задіяна неявна різницева схема «умовної апроксимації». Для чисельного рішення задачі масопереносу вживається неявна поперемінно-трикутна різницева схема. Чисельне інтегрування здійснюється на прямокутній різницевій сітці. Для формування складної форми розрахункової області використовуються маркери, а для моделювання джерела емісії – модель точкового джерела, яка формується за допомогою дельта-функції Дірака. Результати. Авторами розроблено 2D чисельну модель, яка враховує основні фізичні фактори, що впливають на процес розсіювання шкідливих речовин в атмосфері при викидах від автотранспорту з урахуванням розміщення захисних бар’єрів біля дороги. На основі побудованих чисельних моделей проведено обчислювальний експеримент із оцінки рівня забруднення повітряного середовища на вулиці. Наукова новизна. Створено чисельну модель, яка дозволяє розрахувати 2D аеродинаміку вітрового потоку в умовах наявності перешкод та процес масопереносу викидів токсичних газів від автотраси. Модель дозволяє враховувати наявність автомобіля на дорозі, форму захисного бар’єру, присутність бордюру. Виконано розрахунки по визначенню зони забруднення, що формується біля захисного бар’єру, розташованого біля автомагістралі. Практична значимість. Розглянута ефективна чисельна модель, яка може бути застосована при розробці заходів із охорони навколишнього середовища при експлуатації автомобільного транспорту в місті. Розроблена модель дозволяє оцінити розміри, форму та інтенсивність зони забруднення біля автомагістралі.

Ключові слова: забруднення атмосфери; міські вулиці; поширення забруднень; чисельне моделювання

Н. Н. БЕЛЯЕВ^1*, О. С. СЛАВИНСКАЯ^2*, Р. В. КИРИЧЕНКО^3*

^1*Каф. «Гидравлика и водоснабжение», Днепропетровский национальный университет железнодорожного
транспорта имени академика В. Лазаряна, ул. Лазаряна, 2, Днипро, Украина, 49010, тел. +38 (056) 273 15 09,
эл. почта water.supply.treatment@gmail.com , ORCID 0000-0002-1531-7882
^2*Каф. «Управление производством и имуществом», Национальный транспортный университет,
ул. Суворова, 1, Киев, Украина, 01010, тел. +38 (044) 280 82 03,
эл. почта water.supply.treatment@gmail.com, ORCID 0000-0001-5163-5645
^3*Каф. «Управление производством и имуществом», Национальный транспортный университет,
ул. Суворова, 1, Киев, Украина, 01010, тел. +38 (044) 280 82 03,
эл. почта water.supply.treatment@gmail.com, ORCID 0000-0001-9918-3895

Численное моделирование распространения

загрязнения на городской улице

Цель. В научной статье необходимо решить вопрос разработки 2D численной модели, которая позволила бы быстро рассчитать процесс загрязнения атмосферного воздуха выбросами автотранспорта. Предполагается также создать численную модель, которая давала б возможность прогнозировать уровень загрязнения атмосферного воздуха при использовании защитных барьеров у дороги. Методика. Использована разработанная модель, основанная на уравнении невязкой жидкости и уравнении массопереноса. Уравнение для потенциала скорости используется для расчета поля скорости воздушного потока при эксплуатации барьеров. При решении уравнения для потенциала скорости задействована неявная разностная схема «условной аппроксимации». Для численного решения задачи массопереноса употребляется неявная попеременно-треугольная разностная схема. Численное интегрирование осуществляется на прямоугольной разностной сетке. Для формирования сложной формы расчетной области применяются маркеры. А для моделирования источника эмиссии – модель точечного источника, которая моделируется с помощью дельта-функции Дирака. Результаты. Авторами разработана 2D численная модель, которая учитывает основные физические факторы, влияющие на процесс рассеивания вредных веществ в атмосфере при выбросах от автотранспорта с учетом размещения защитных барьеров у дороги. На основе построенных численных моделей проведен вычислительный эксперимент по оценке уровня загрязнения воздушной среды на улице. Научная новизна. Создана численная модель, которая позволяет рассчитать 2D аэродинамику ветрового потока в условиях наличия помех и процесс массопереноса выбросов токсичных газов от автотрассы. Модель позволяет учитывать наличие автомобиля на дороге, форму защитного барьера, присутствие бордюра. Выполнены расчеты по определению зоны загрязнения, формируемой у защитного барьера, который расположен у автомагистрали. Практическая значимость. Рассмотрена эффективная численная модель, которая может быть применена при разработке мероприятий по охране окружающей среды при эксплуатации автомобильного транспорта в городе. Разработанная модель позволяет оценить размеры, форму и интенсивность зоны загрязнения у автомагистрали.

Ключевые слова: загрязнение атмосферы; городские улицы; распространение загрязнений; численное моделирование

REFERENCES

1. Biliaiev, M. M., Rusakova, T. I., & Kirichenko, P. S. (2014). Modelirovaniye zagryazneniya atmosfernogo vozduha vybrosami avtotransporta na ulicah gorodov [Monograph]. Dnipropetrovsk: Aktsent PP.

2. Biliaiev, M. M., Slavinska, O. S., & Kyrychenko, R. V. (2017). Prediction of atmospheric air pollution by emissions of motor transport taking into account the chemical transformation of harmful substances. Science and Transport Progress, 3(69), 15-22. doi:10.15802/stp2017/104549

3. Biliaiev, M. M., & Rusakova, T. I. (2013). CFD prediction of air pollution in the streets. Ecology and Nature Management, 17, 188-194.

4. Marchuk, G. I. (1982). Matematicheskoye modelirovaniye v probleme okruzhayushchey sredy. Moscow: Nauka.

5. Samarskiy, A. A. (1983). Teoriya raznostnykh skhem. Moscow: Nauka.

6. Düring, I., Bächlin, W., Ketzel, M., Baum, A., Friedrich, U., & Wurzler, S. (2011). A new simplified NO/NO₂ conversion model under consideration of direct NO₂-emissions. Meteorologische Zeitschrift, 20 (1), 67-73. doi:10.1127/0941-2948/2011/0491

7. Berlov, O. V. (2016). Atmosphere protection in case of emergency during transportation of dangerous cargo. Science and Transport Progress, 1(61), 48-54. doi:10.15802/stp2016/60953

8. Nguyen, T. N., Nguyen, T. C., & Nguyen, V. T. (2015). Numerical simulation of wind flow and pollution transport in urban street canyons. Advanced Science and Technology Letters, 120, 770-777.
   doi:10.14257/astl.2015.120.152

9. Chang, C.-H., Lin, J.-S., Cheng, C.-M., & Hong, Y.-S. (2013). Numerical simulations and wind tunnel studies of pollutant dispersion in the urban street canyons with different height arrangements. Journal of Marine Science and Technology, 21(2), 119-126.

10. Overman, H. T. J. (2009). Simulation model for NO_x distributions in a street canyon with air purifying pavement. (Master thesis). University Twente, Netherlands.

Prof. S. A. Pichugov, Dr. Sc. in Phys.-and-Math. (Ukraine); Prof. S. Z. Polishchuk, D. Sc. (Tech.), (Ukraine) recommended this article to be published

Received: April 10, 2017

Accessed: July 21, 2017

doi 10.15802/stp2017/109526 © M. M. Biliaiev, O. S. Slavinska, R. V. Kyrychenko, 2017