ISSN
2307–3489 (Print), ІSSN
2307–6666
(Online)
Наука
та прогрес транспорту. Вісник
Дніпропетровського
національного університету залізничного
транспорту, 2017, № 4 (70)
НЕТРАДИЦІЙНІ
ВИДИ ТРАНСПОРТУ. МАШИНИ ТА МЕХАНІЗМИ
нетрадиційні
види транспорту. машини
та
механізми
УДК 621.86/87(075.8)
В. Н. Богомаз1*, Л. Н.
Бондаренко2*, М. В. ОЧЕРЕТНЮК3*,
А. А. ТКАЧОВ4*
1*Каф. «Военная
подготовка специалистов Государственной
специальной службы транспорта»,
Днепропетровский
национальный
университет железнодорожного транспорта
имени академика В. Лазаряна, ул. Лазаряна,
2, Днипро,
Украина, 49010, тел. +38 (056) 373 19
09, эл. почта wbogomas@i.ua, ORCID 0000-0001-5913-2671
2*Каф.
«Прикладная механика и материаловедение»,
Днепропетровский национальный университет
железнодорожного
транспорта имени
академика В. Лазаряна, ул. Лазаряна, 2,
Днипро, Украина, 49010, тел. +38 (056) 373 15 18,
эл. почта bondarenko-l-m2015@yandex.ua, ORCID
0000-0002-2212-3058
3*Каф.
«Военная подготовка специалистов
Государственной специальной службы
транспорта», Днепропетровский
национальный университет железнодорожного
транспорта имени академика В. Лазаряна,
ул. Лазаряна, 2, Днипро,
Украина, 49010,
тел. +38 (056) 373 19 09, эл. почта atleteba@gmail.com,
ORCID 0000-0002-9032-8602
4*Каф. «Военная
подготовка специалистов Государственной
специальной службы транспорта»,
Днепропетровский
национальный
университет железнодорожного транспорта
имени академика В. Лазаряна, ул. Лазаряна,
2, Днипро,
Украина, 49010, тел. +38 (056) 373 19
09, эл. почта otkachov@i.ua, ORCID 0000-0002-1857-7567
СООТНОШЕНИЯ МЕЖДУ ЖЕСТКОСТНЫМИ
ПОТЕРЯМИ И
ПОТЕРЯМИ В ПОДШИПНИКАХ
КАНАТНЫХ БЛОКОВ
Цель. Для
уточнения величин коэффициента полезного
действия (КПД)
канатных блоков необходимо определить
коэффициент жесткости канатов блоков
с учетом классификационной группы
механизма и угла обхвата канатом
блока. Предполагается использовать при
этом хорошо опробованные значения
коэффициентов полезного действия
канатных блоков с учетом углов обхвата
канатами блоков и аналитически найденные
величины коэффициента трения подшипников
качения, приведенных к цапфе.
Методика.
В работе используется аналитический
метод определения коэффициента
сопротивления подшипника блока при
вращении его как внутренней, так и
наружной обойм, а также расчетная схема
подшипника блока. Результаты.
Для канатных блоков
проведен анализ влияния способа смазки,
режима работы механизма и угла обхвата
канатом блока на потери в подшипниках.
Приведены соответствующие сравнительные
таблицы значений потерь. Анализ полученных
результатов расчетов позволяет
установить: 1) главным сопротивлением,
влияющим на коэффициент полезного
действия канатных блоков, является
сопротивление в подшипниках; 2) второй
по величине составляющей является
жесткостные потери, зависящие от режима
работы, угла обхвата канатом блока, вида
смазки подшипника; 3) КПД блока при
вращении внутренней обоймы выше, чем
при вращении наружной примерно, на 3 %
при густой смазке и режиме 1М; 4) при
последовательном расположении узлов
с подшипником качения необходимо
стремиться к конструкции узла, в котором
вращается внутренняя обойма;
5) при числе блоков до
5 можно пользоваться рекомендуемыми в
литературе значениями подшипников
блоков с ошибкой в величине КПД до 10 %.
Научная новизна. Авторы
получили значения сопротивлений в
шариковых подшипниках канатных блоков
и жесткостные потери, обусловленные
обхватом блока канатом.
Использовали
при этом зависимости по определению
коэффициента трения качения, полученные
с применением аналитических зависимостей
Герца по установлению контактных
напряжений и деформаций, а также
экспериментальных величин коэффициента
трения качения для блоков. Практическая
значимость. Полученные
авторами значения сопротивлений могут
быть использованы для уточненных
расчетов механизмов машин.
Ключевые слова: блок; канат; потери;
подшипник; жесткость
Введение
Коэффициент
жесткости ξ показывает, какую часть
рабочего натяжения составляет
сопротивление растяжению каната. Такой
коэффициент входит в формулу, определяющую
коэффициент полезного действия блока
[10]:
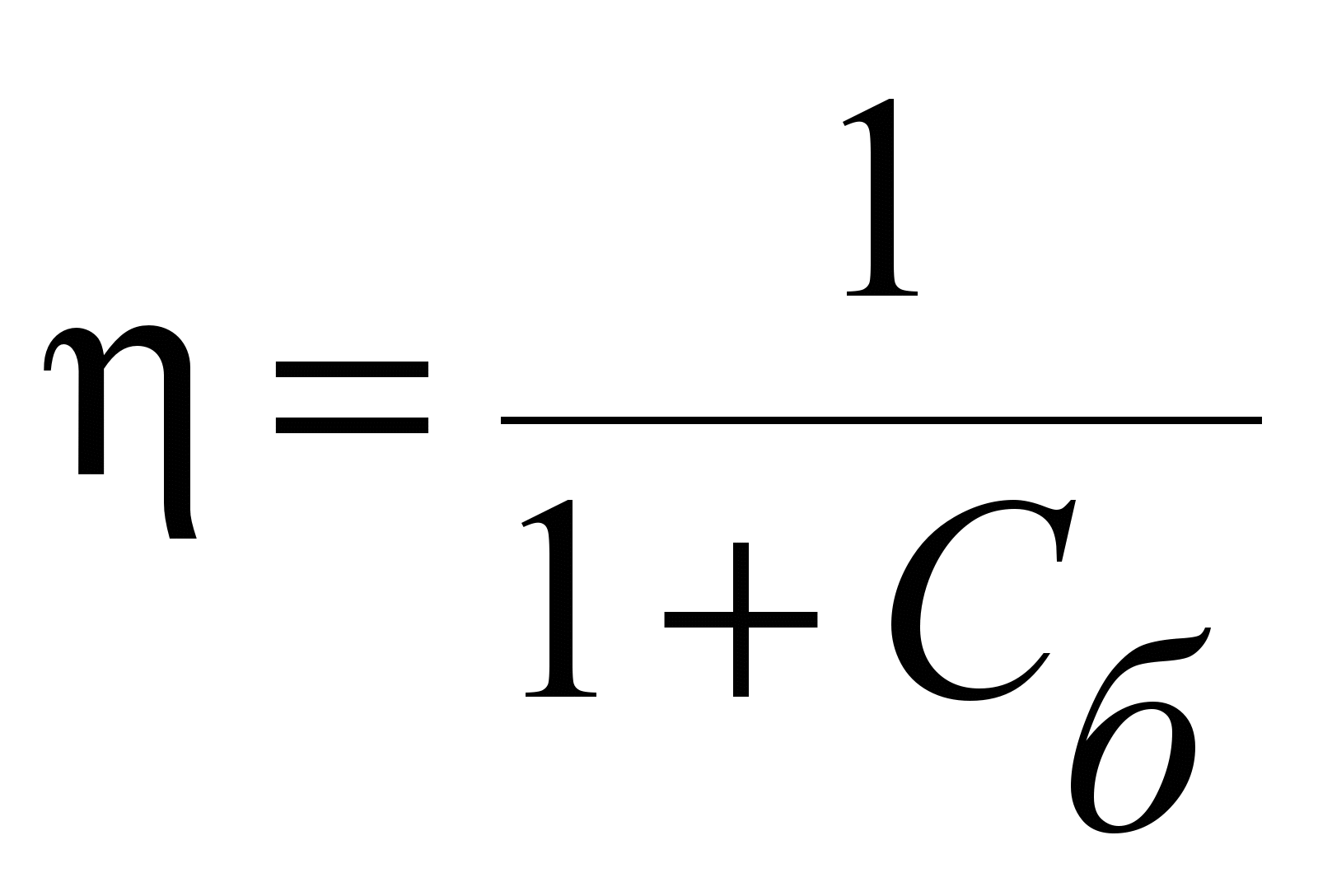 , (1.1)
, (1.1)
где
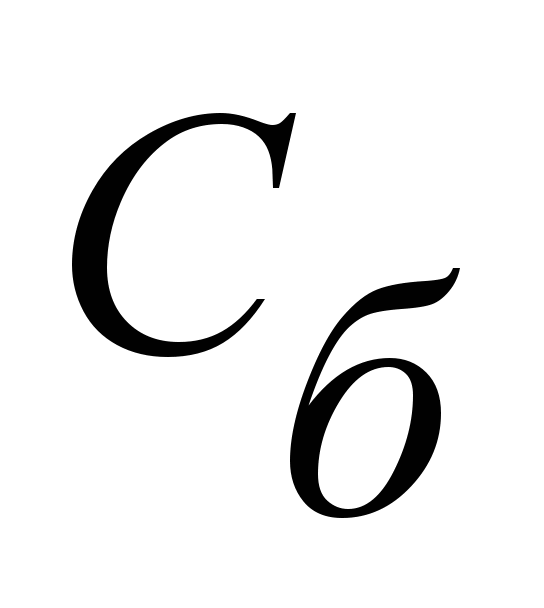 – коэффициент сопротивления блока,
– коэффициент сопротивления блока,
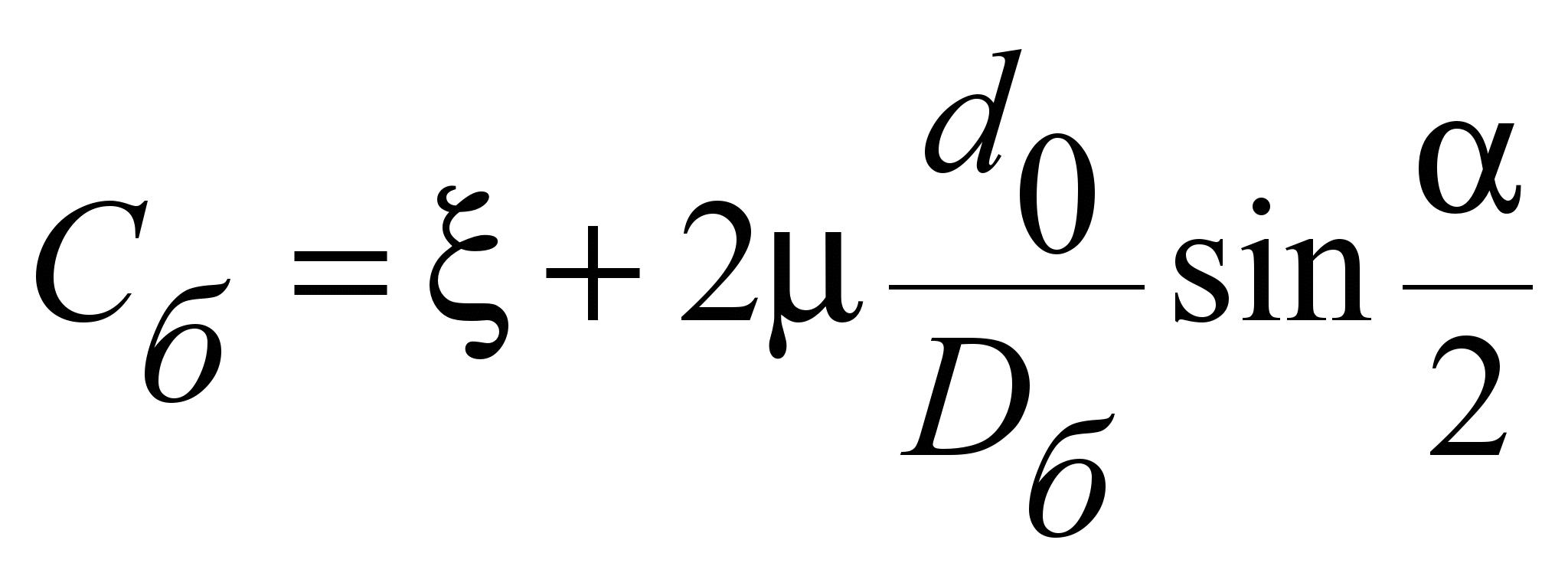 , (1.2)
, (1.2)
где
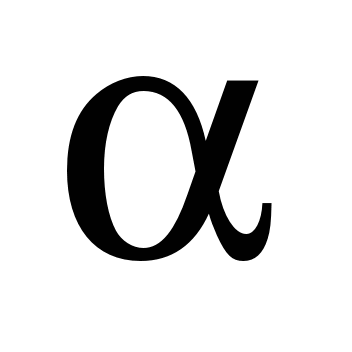 – угол обхвата канатом блока в радианах;
– угол обхвата канатом блока в радианах;
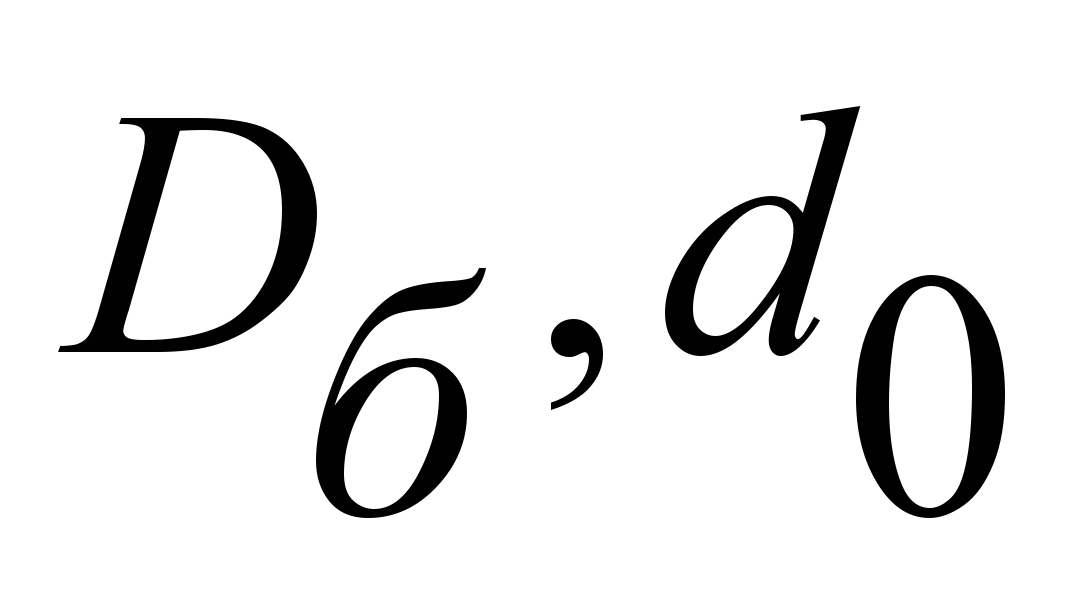 – диаметры блока и упора в сантиметрах;
– диаметры блока и упора в сантиметрах;
 – коэффициент трения подшипника,
приведенный к цапфе;
– коэффициент трения подшипника,
приведенный к цапфе;
 –
коэффициент жесткости.
–
коэффициент жесткости.
Коэффициент
жесткости находится с использованием
экспериментальных величин по формулам,
приведенным в [10] и [3]:
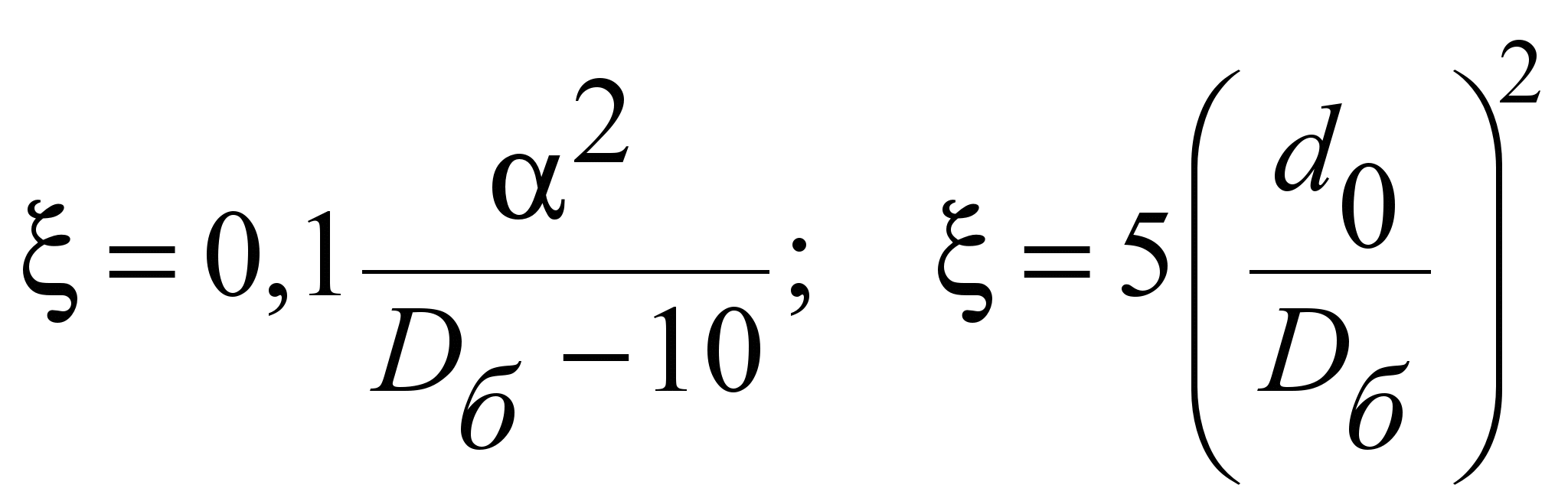 . (1.3)
. (1.3)
Поскольку коэффициент
полезного действия (КПД) блоков известен
до третьего знака после запятой [15], то
при известных уравнениях для определения
коэффициента трения качения при линейном
и точечном контактах можно определить
и коэффициент жесткости
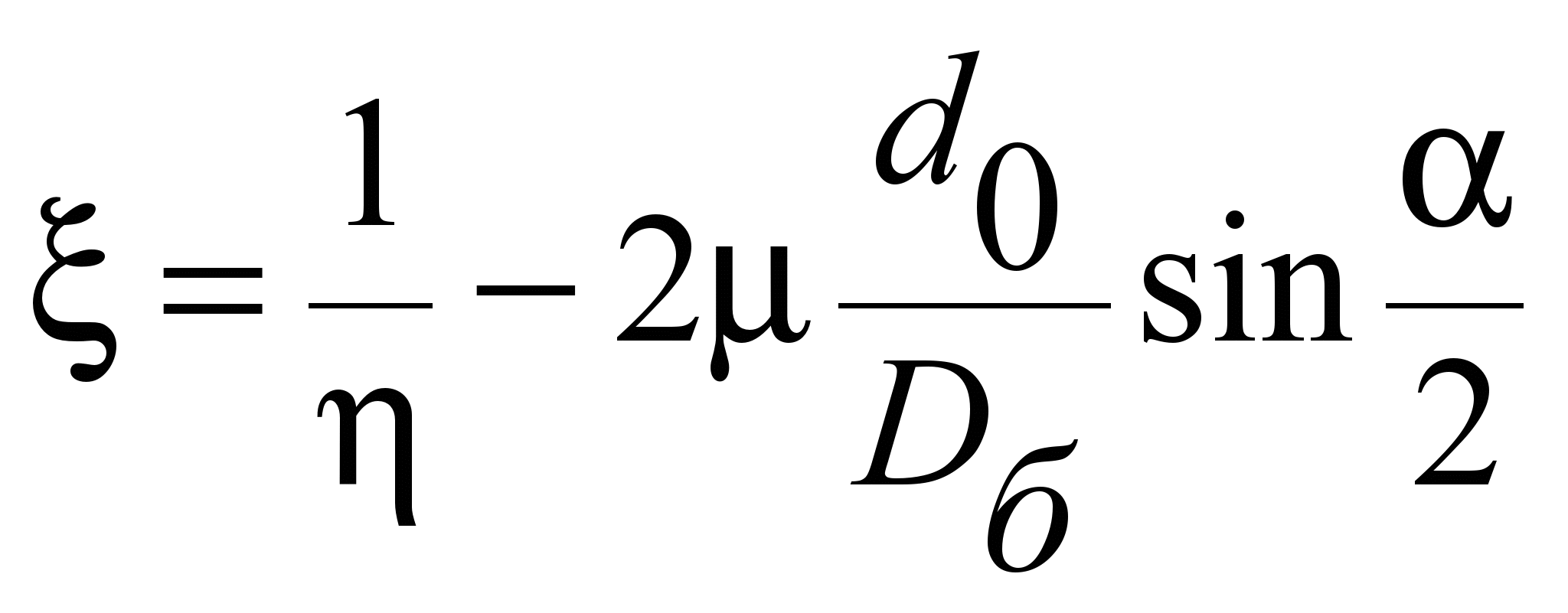 . (2)
. (2)
Проблемы определения
коэффициента жесткости каната блока
и его влияния на общую величину
коэффициента полезного действия блоков,
а также задачи, связанные с
ними, рассматривались в разной мере
в работах разных авторов [1, 2,
4–7, 9, 11–14].
Цель
Определить
коэффициент жесткости канатов блоков
с учетом классификационной группы
механизма и угла обхвата канатом блока,
используя хорошо опробованные
значения коэффициентов полезного
действия канатных блоков с учетом угла
обхвата канатом блока и найденные
аналитически величины коэффициента
трения подшипников качения, приведенных
к цапфе.
Методика
Многие
авторы получили большое количество
формул для определения сопротивлений
движению, особенно качению. Но они
обычно содержали величины, которые
определялись экспериментально и часто
требовали большего труда и времени,
чем определение самого сопротивления.
Аналитические
зависимости не могли быть получены до
решения основных задач о контактных
напряжениях и деформациях методами
теории упругости Г. Герцем в 1881–1882 г.г.
Только через 60 лет после исследований
Герца Д. Табором [15]
получены аналитические зависимости
по определению коэффициентов трения
качения при линейном и точечном
контактах. Им установлены следующие
зависимости для определения коэффициента
трения качения:
– при линейном
контакте:
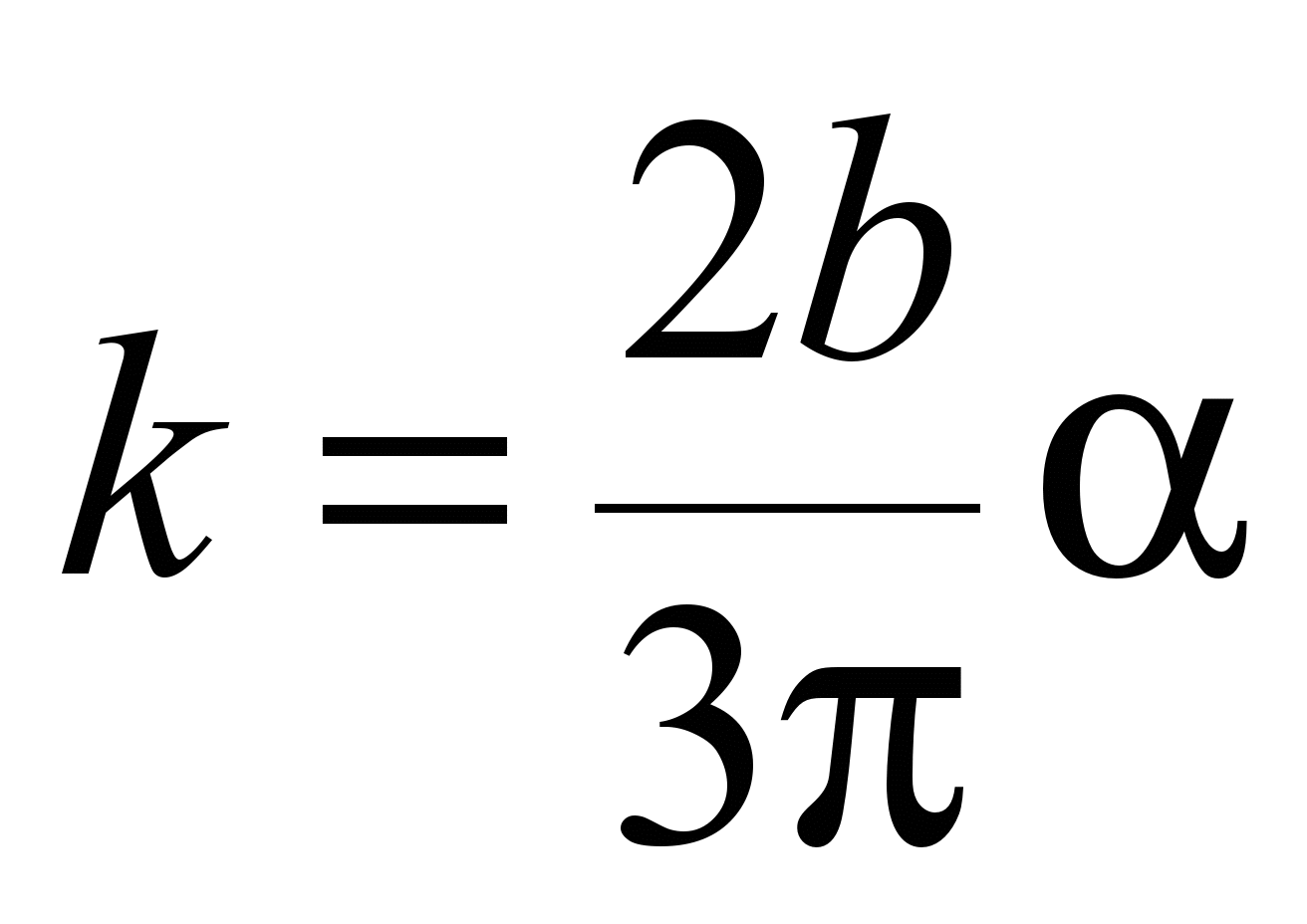 , (3)
, (3)
– при точечном
контакте:
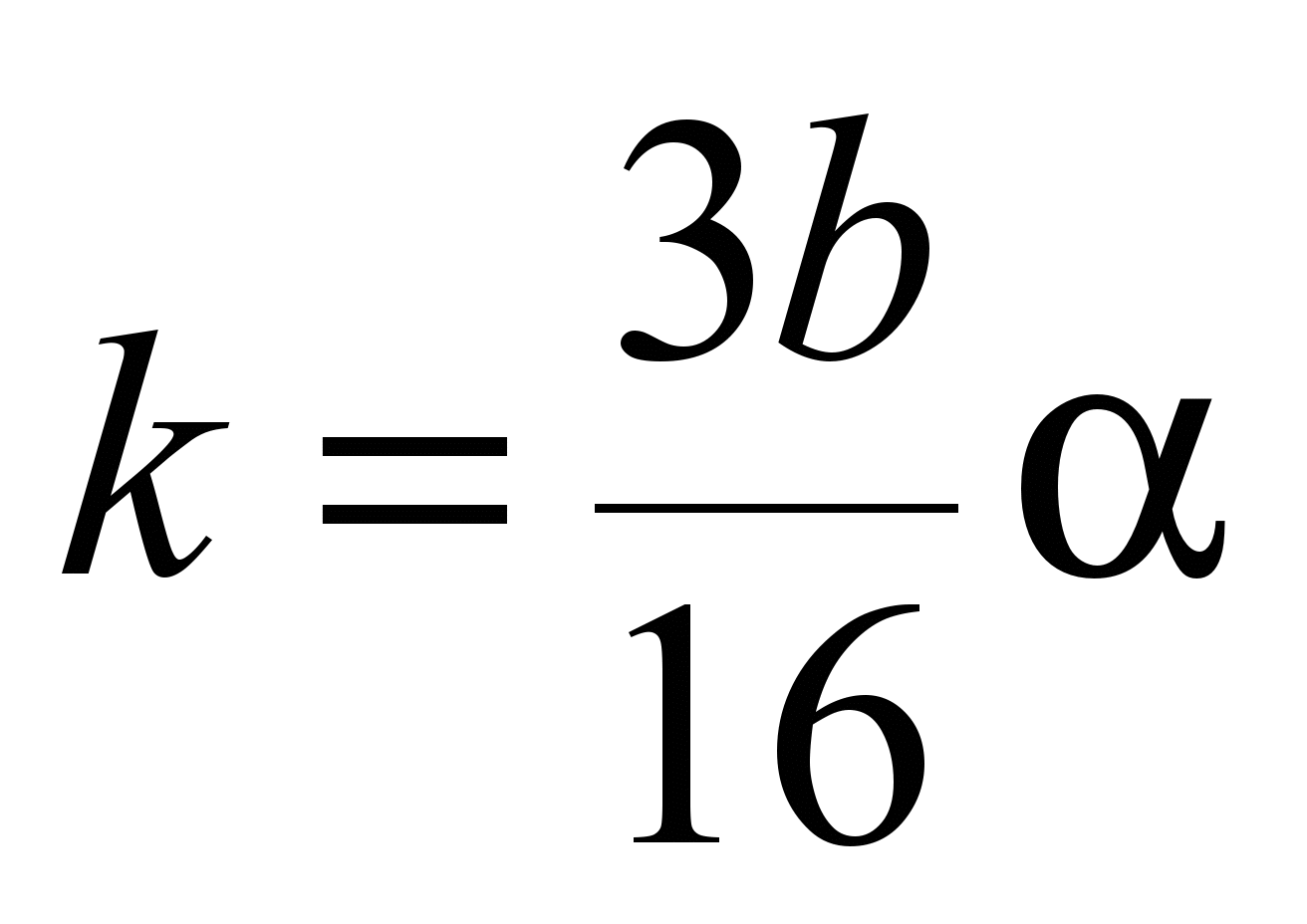 ,
(4)
,
(4)
где
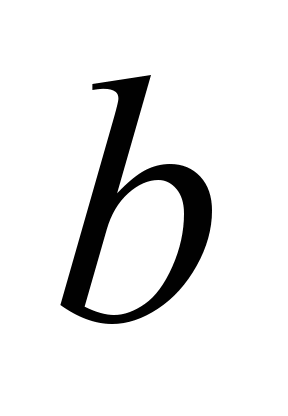 – полуширина пятна контакта, определяемая
согласно теории Герца;
– полуширина пятна контакта, определяемая
согласно теории Герца;
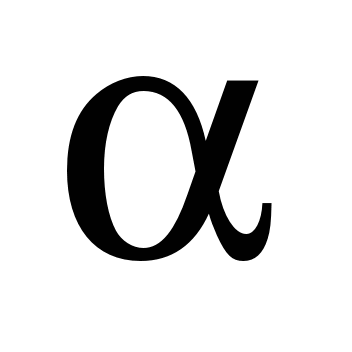 – коэффициент гистерезисных потерь.
– коэффициент гистерезисных потерь.
Но поскольку
коэффициент
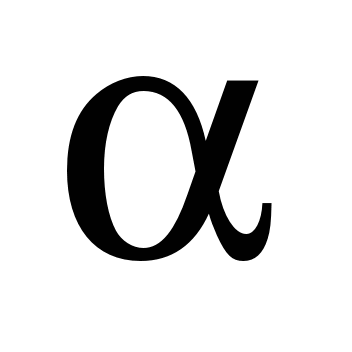 имеет молекулярно-механическую природу,
то определить его для практического
использования вряд ли возможно. Как
следствие, эти формулы не получили
практического применения.
имеет молекулярно-механическую природу,
то определить его для практического
использования вряд ли возможно. Как
следствие, эти формулы не получили
практического применения.
С использованием
формул (3) и (4), хорошо опробованных
величин коэффициента трения качения
для крановых колес [1] найдены значения
коэффициента
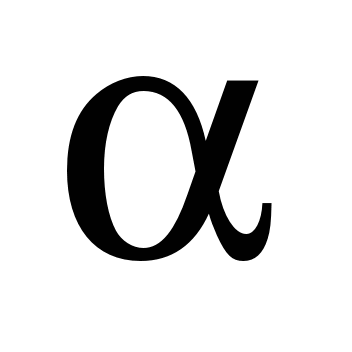 [2].
[2].
Аналогично формулам
(3) и (4) эти формулы получены в виде:
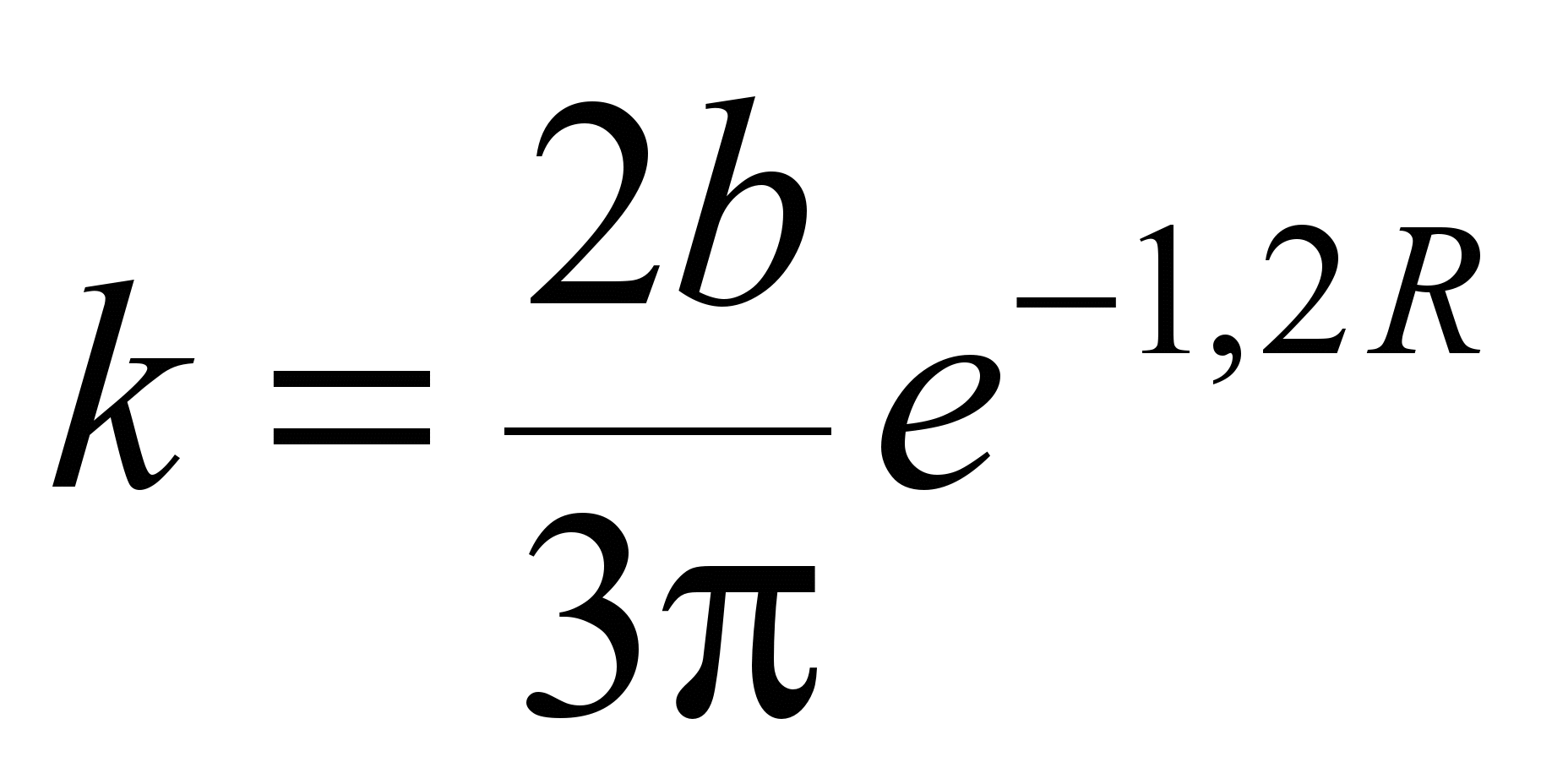 , (5)
, (5)
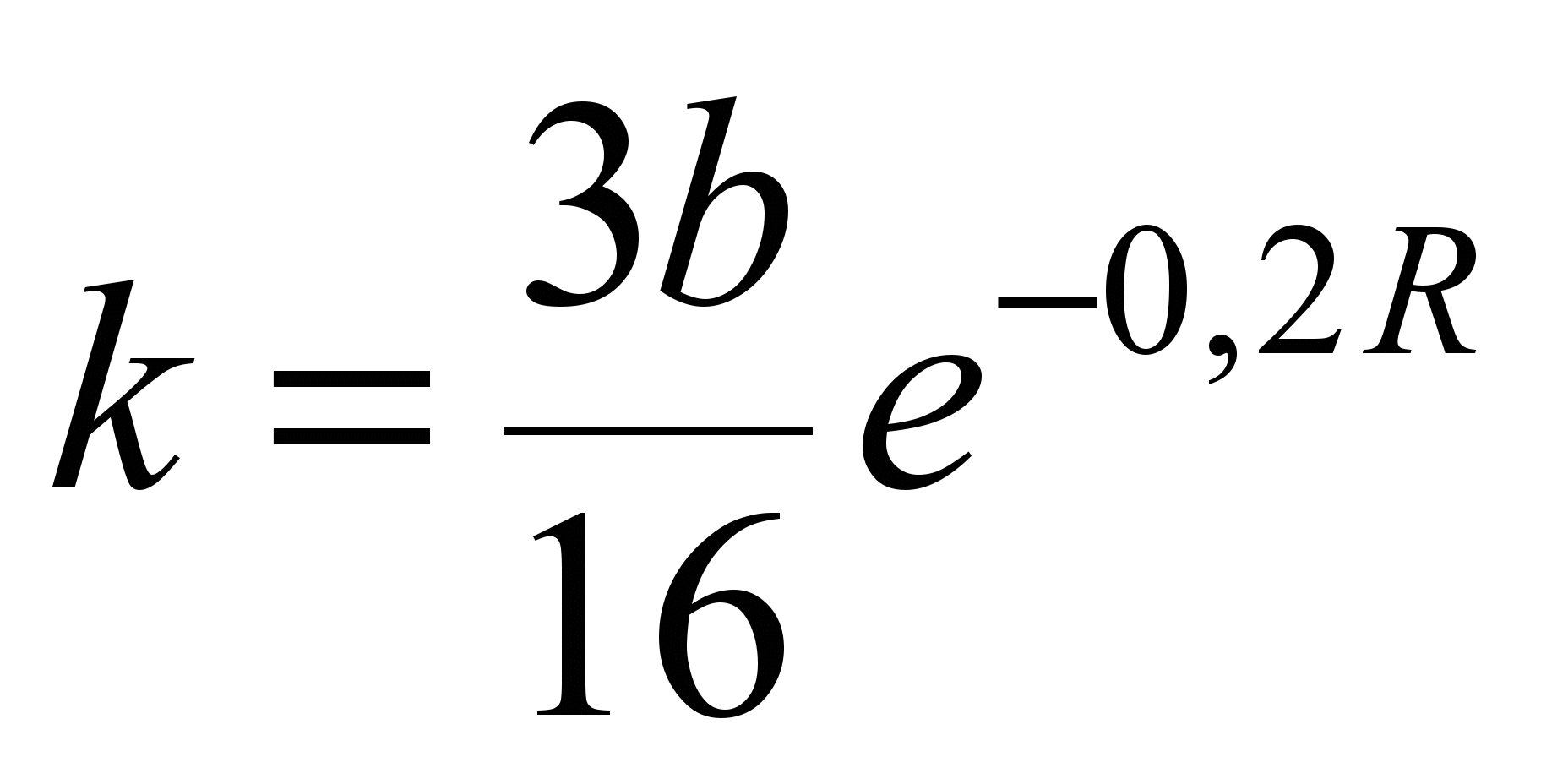 , (6)
, (6)
где
 – радиус качения тела в метрах.
– радиус качения тела в метрах.
Естественно, эти
формулы пригодны для металлов, а для
других материалов требуют уточнений
в величине
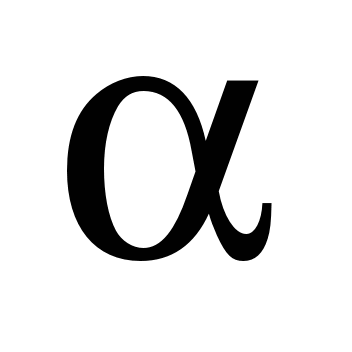 .
.
На рис. 1 приведена
схема одного подшипника блока. Приложенная
к блоку сила
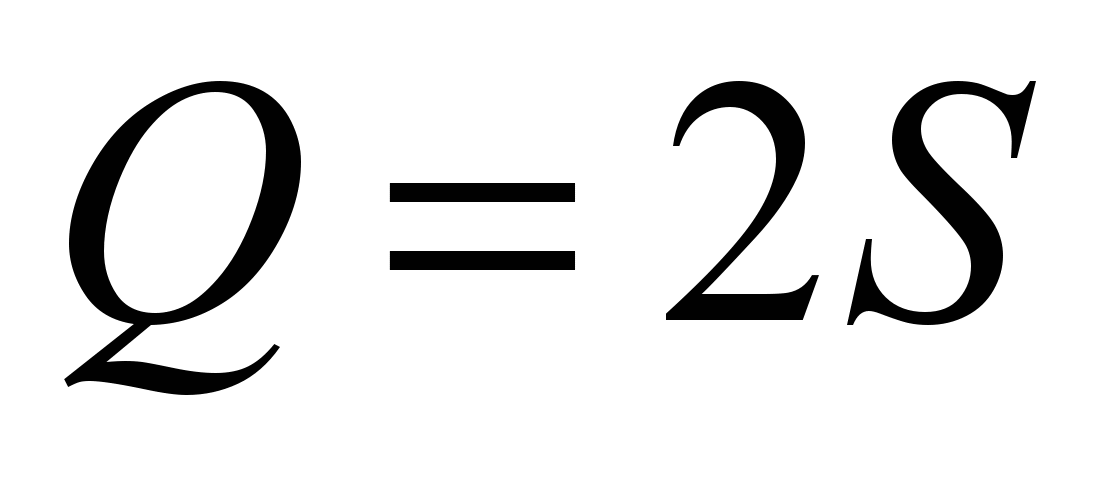 через внутреннюю обойму передается
шарикам, которые нагружаются неравномерно.
через внутреннюю обойму передается
шарикам, которые нагружаются неравномерно.
Наибольшую нагрузку
воспринимает шарик с центром, расположенным
на линии действия силы
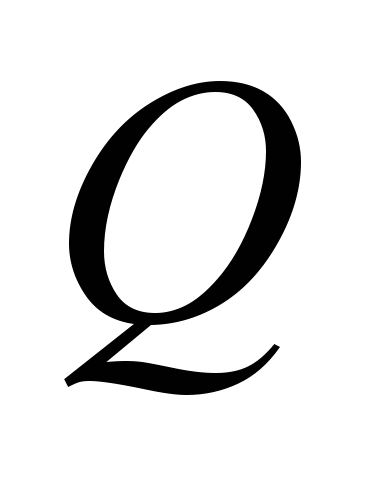 ,
а наименьшую – шарик с центром,
расположенным на линии, перпендикулярной
направлению силы
,
а наименьшую – шарик с центром,
расположенным на линии, перпендикулярной
направлению силы
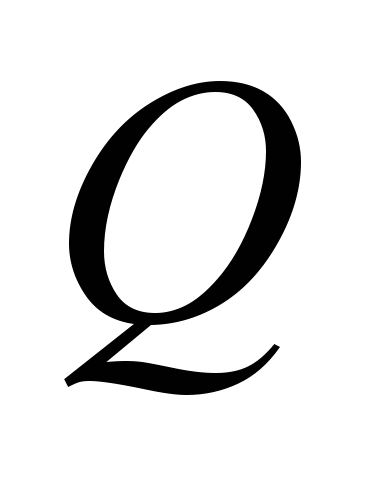 .
Нагрузку воспринимают только те шарики,
которые располагаются ниже горизонтального
диаметра. Силы
.
Нагрузку воспринимают только те шарики,
которые располагаются ниже горизонтального
диаметра. Силы
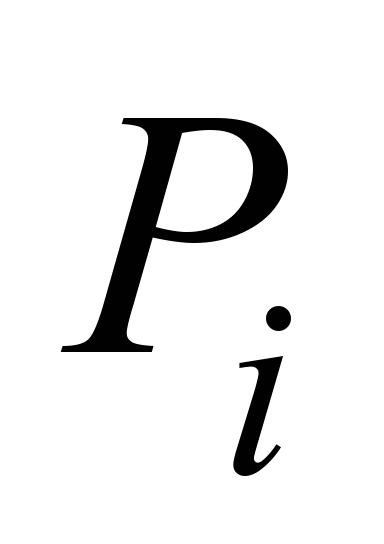 ,
координированные углами
,
координированные углами
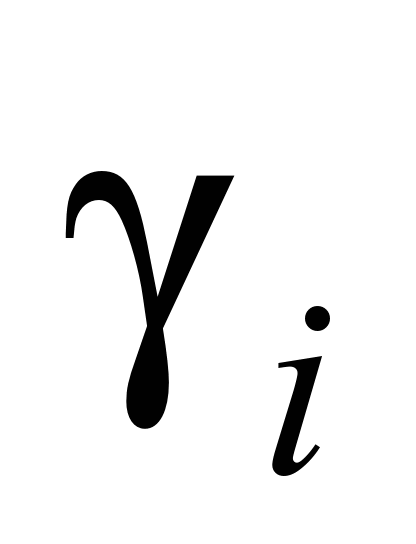 относительно линии где действия
силы
относительно линии где действия
силы
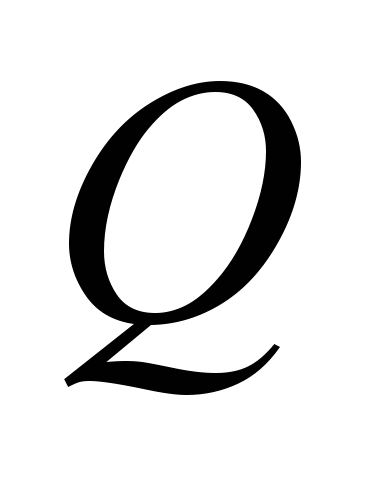 ,
будем считать симметричными.
,
будем считать симметричными.
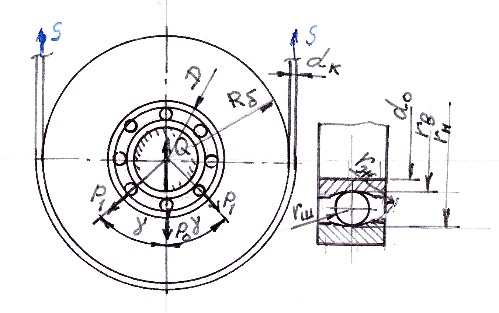
Рис. 1. Расчетная схема подшипника блока
и принятые обозначения
Fig. 1. Calculation
scheme of the
bearing of the
block and
accepted designations
Нагрузка,
приходящаяся на
наиболее загруженный
шарик, находится
по формуле
из [3]:
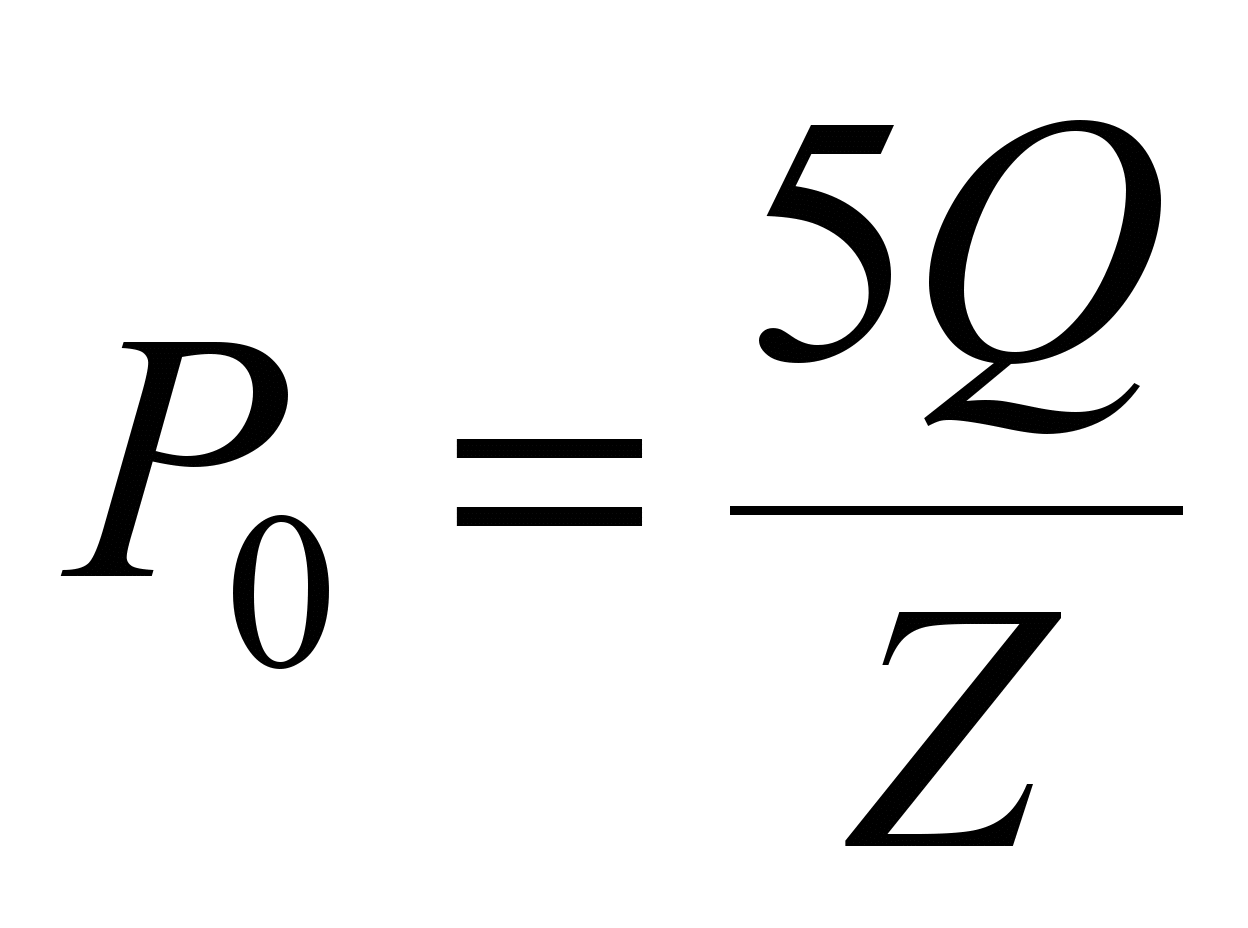 , (7)
, (7)
где
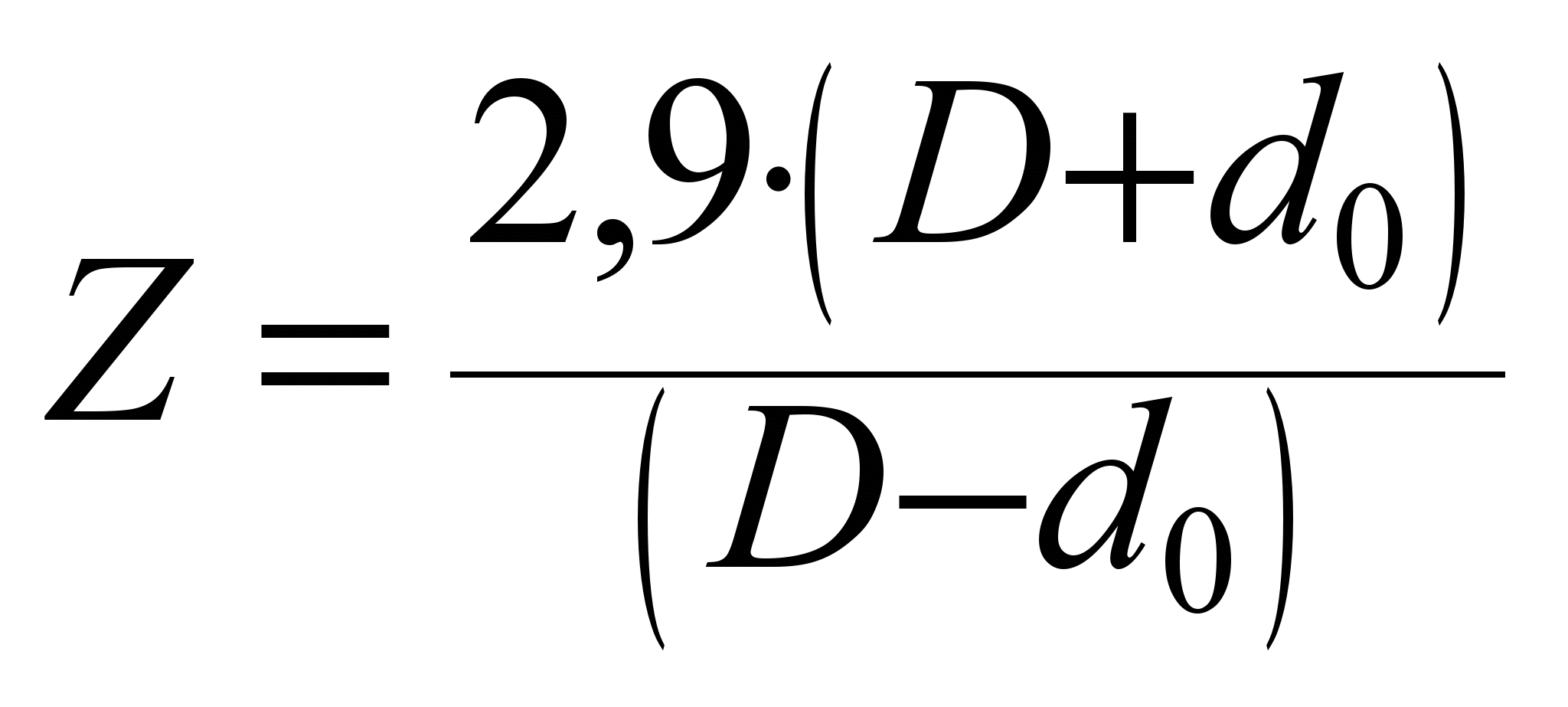 – число шариков по условиям сборки.
– число шариков по условиям сборки.
На один боковой
шарик действует сила
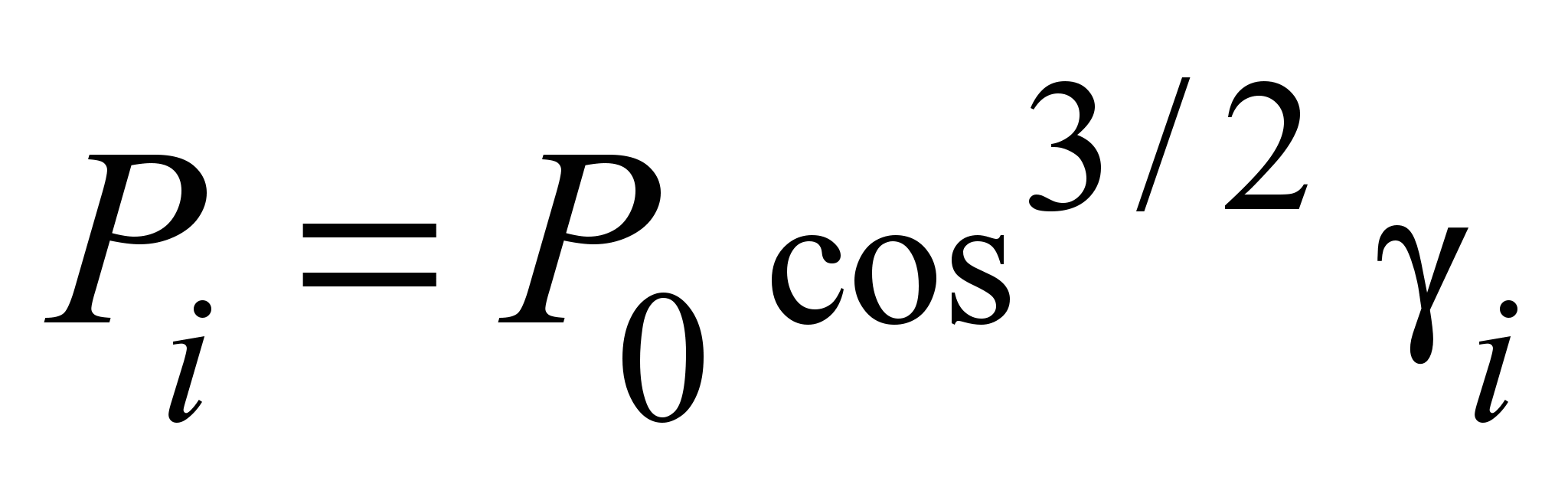 . (8)
. (8)
Имея нагрузки на
шарики и принятые размеры, определим
сопротивления качению двух различных
типов шариков.
Рассмотрим движение
наиболее загруженного шарика по
внутренней и наружной обоймам, определив
сначала полуширину пятна контакта. При
равенстве коэффициентов Пуассона для
шариков обойм, равном 0,3, и равенстве
модулей упругости полуширина пятна
контакта [4]:
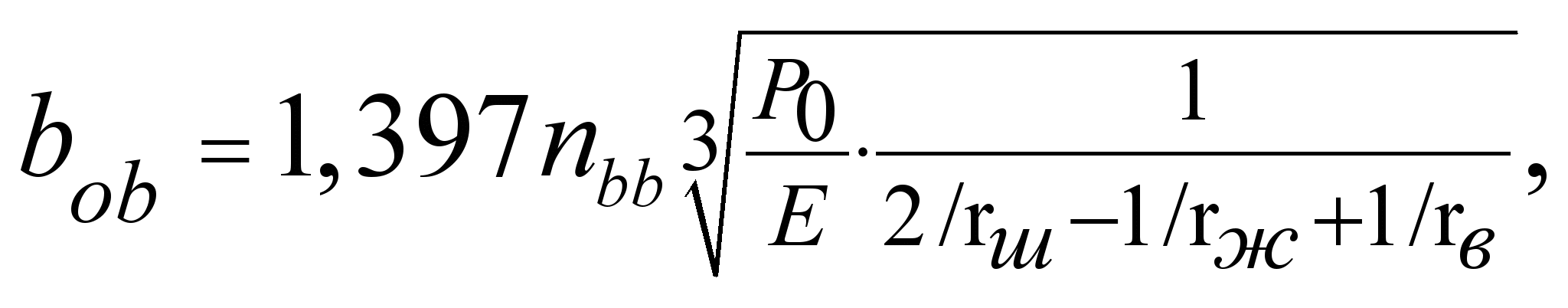 (9)
(9)
где
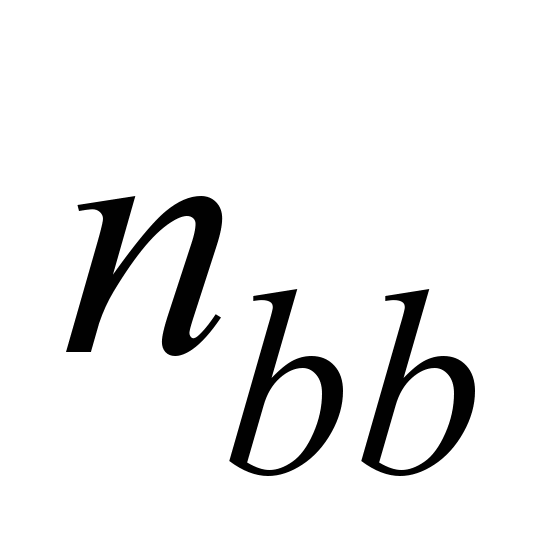 – величина, зависящая от отношения
коэффициентов уравнения эллипса
касания.
– величина, зависящая от отношения
коэффициентов уравнения эллипса
касания.
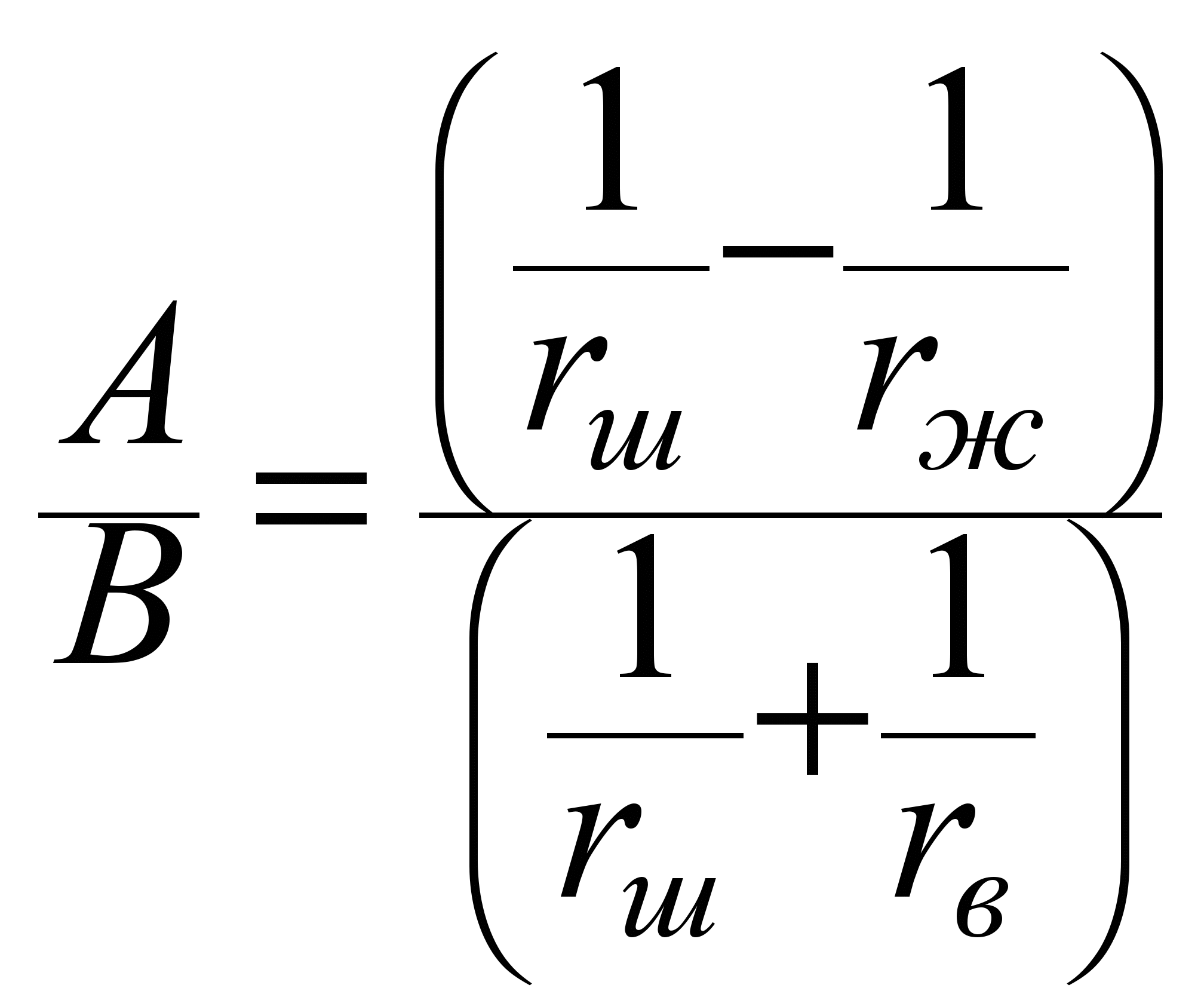 ,
,
где
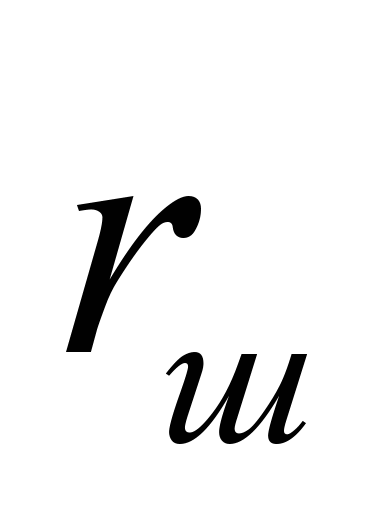 – радиус шарика;
– радиус шарика;
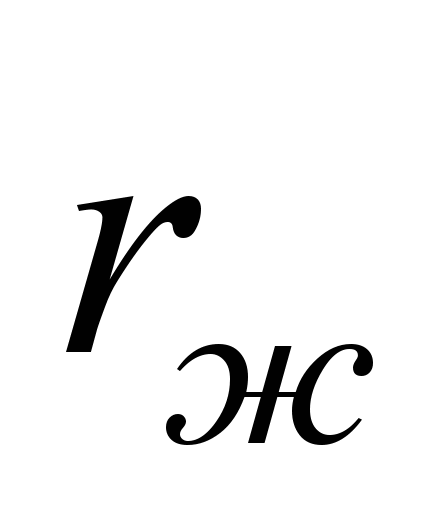 – радиус желоба;
– радиус желоба;
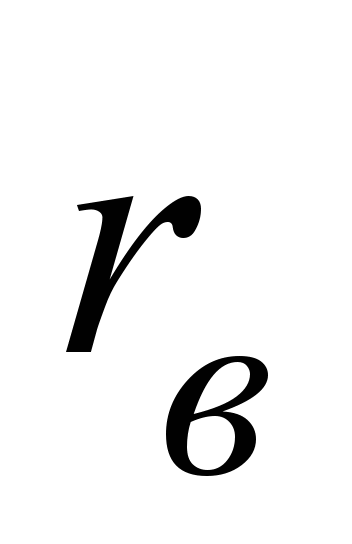 – радиус беговой дорожки внутренней
обоймы, который определяется по формуле
– радиус беговой дорожки внутренней
обоймы, который определяется по формуле
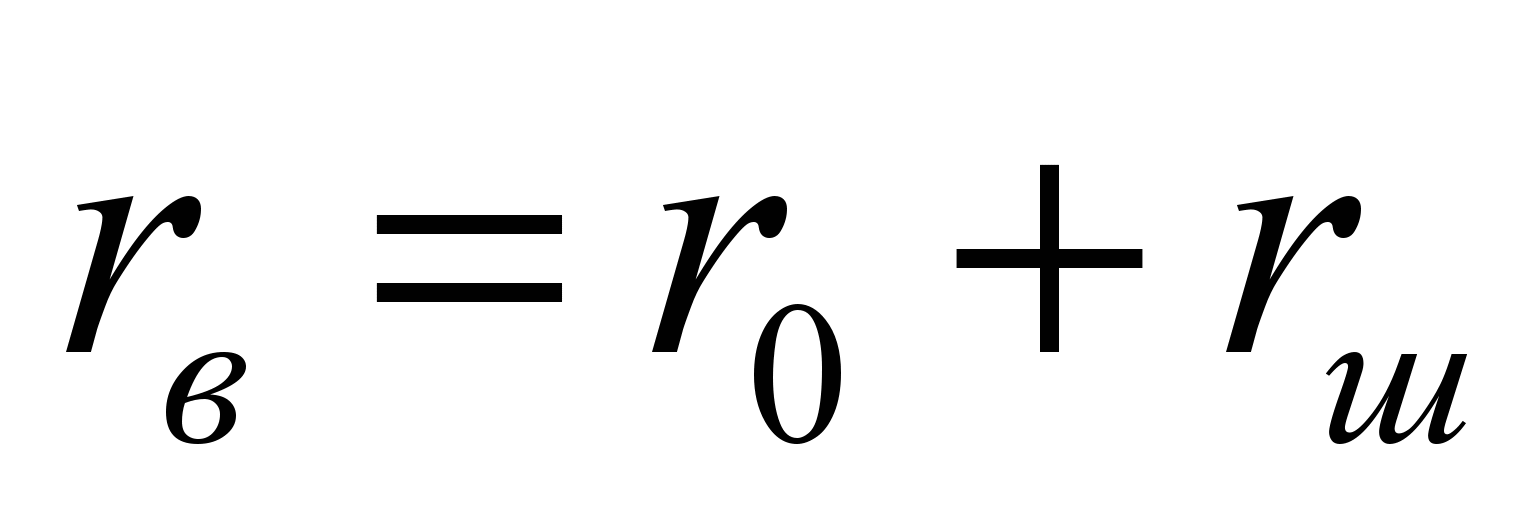 .
.
При известной
величине
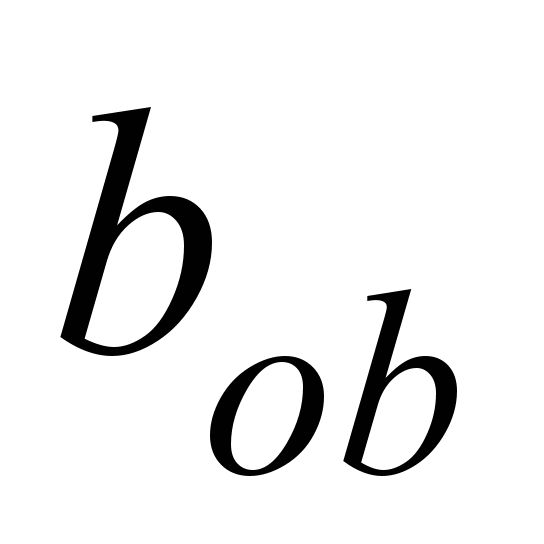 коэффициент трения качения выводится
из формулы (6):
коэффициент трения качения выводится
из формулы (6):
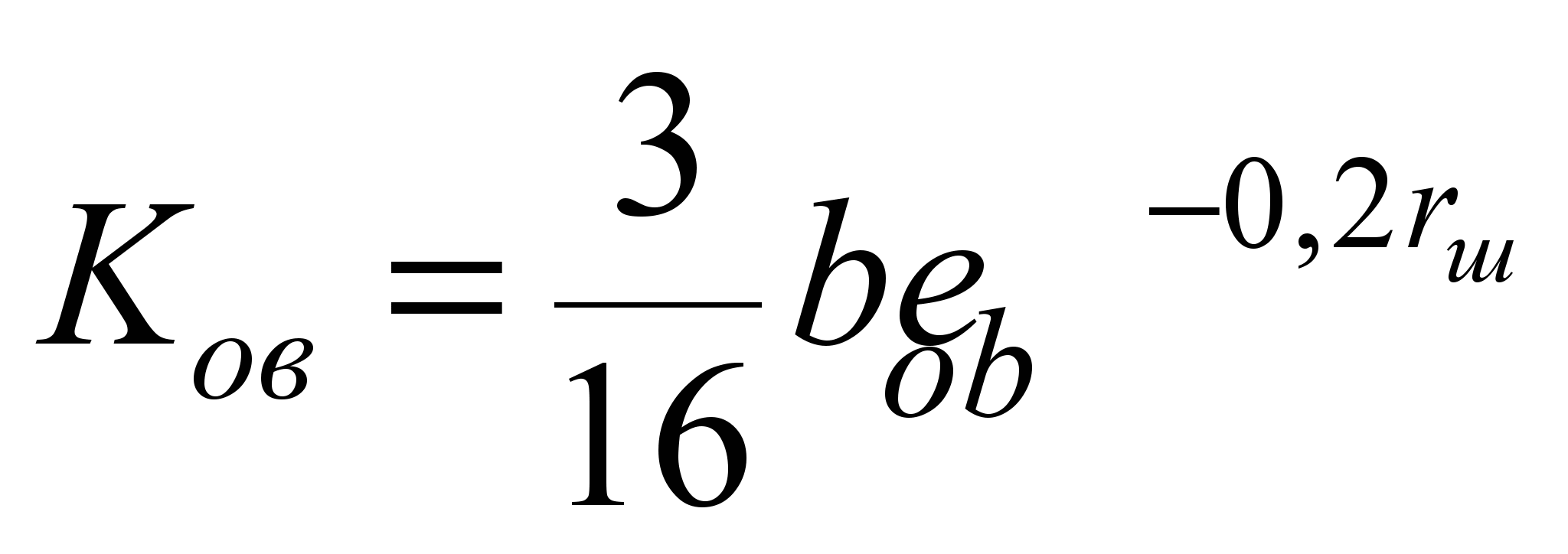 , (10)
, (10)
а сопротивление
качению наиболее загруженного шарика
по внутренней обойме
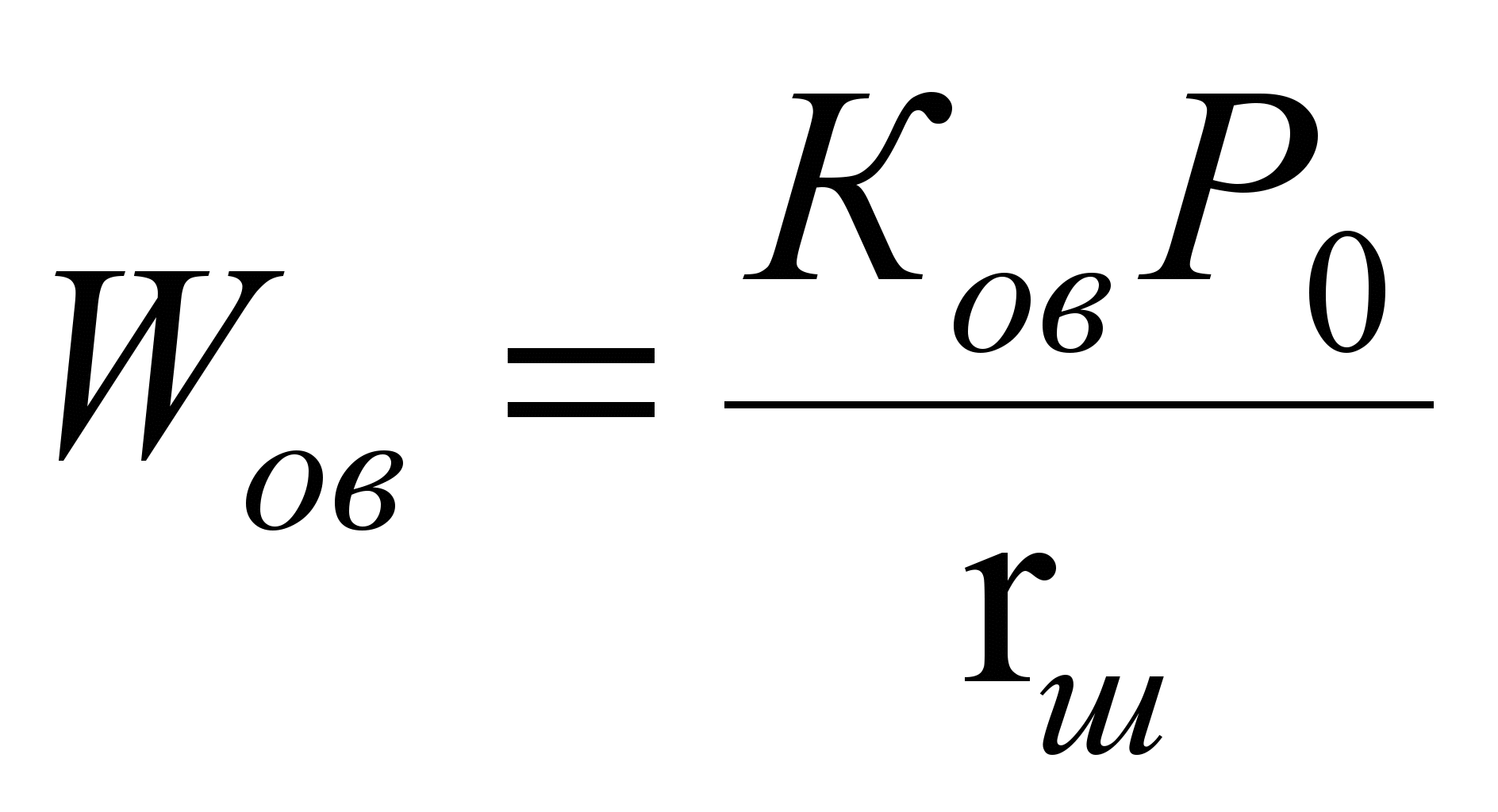 . (11)
. (11)
Полуширина пятна
контакта наиболее загруженного шарика
с наружной обоймой
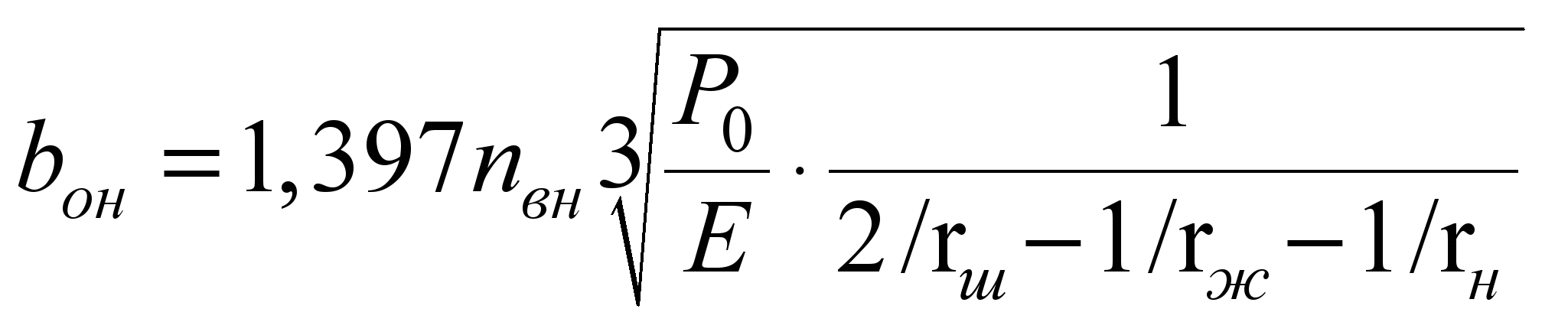 , (12)
, (12)
Рассмотрим подобную
задачу для боковых шариков. В
шарикоподшипниках блоков полиспастов
число шариков 7 или 8 зависит от диаметров
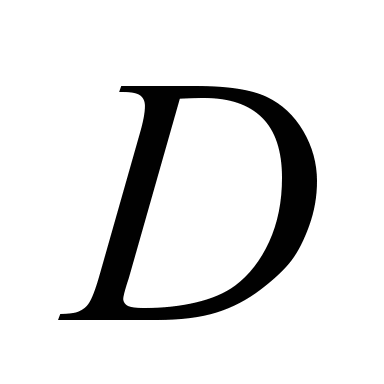 и
и
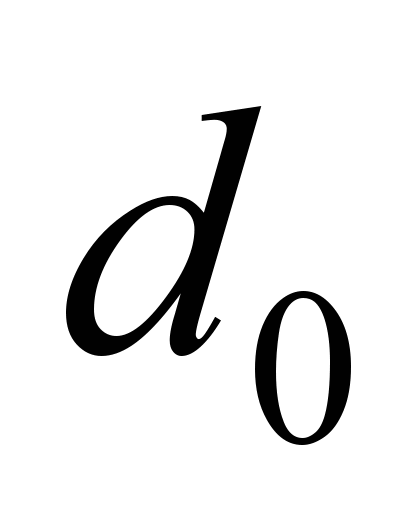 ,
поэтому боковых роликов два: расположенных
под углом
,
поэтому боковых роликов два: расположенных
под углом
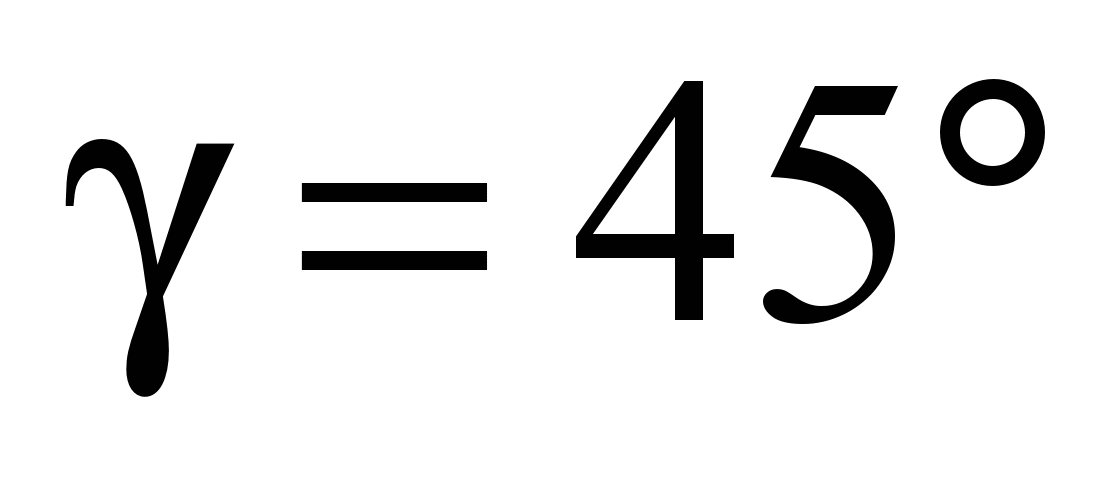 при
при
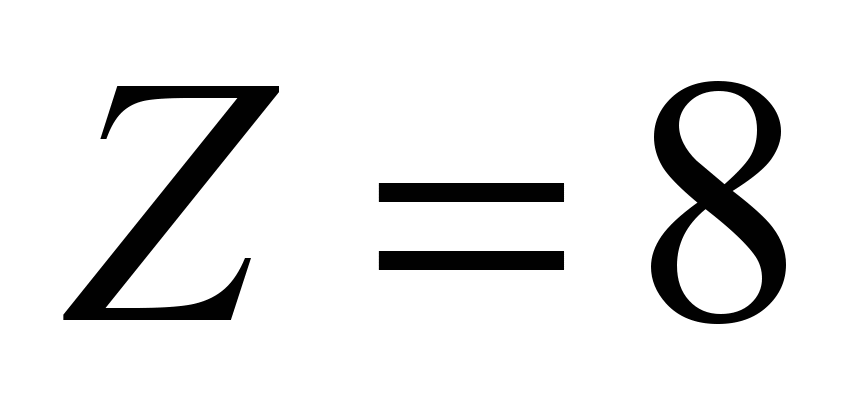 или
или
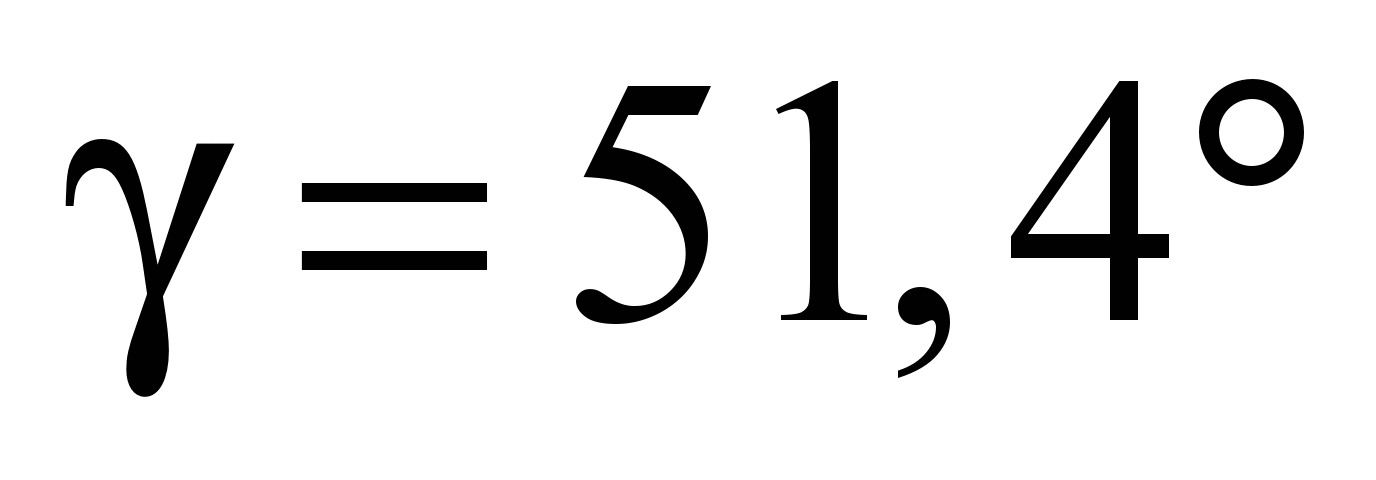 при
при
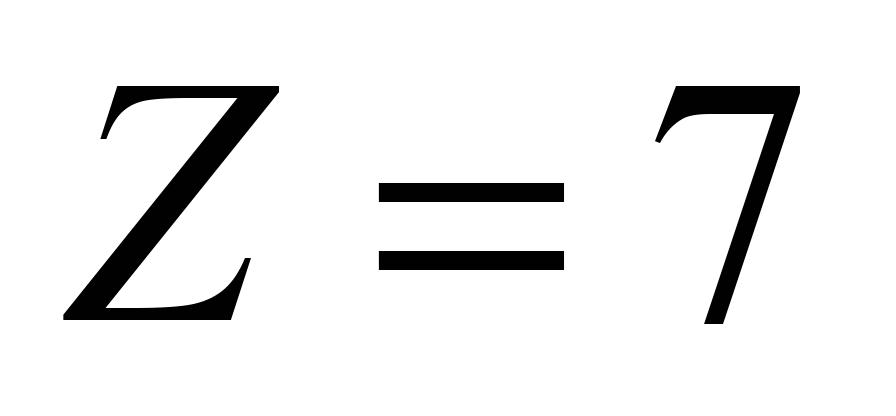 .
Поэтому сопротивление их качению по
внутренней и наружной обоймам определяется
по формулам (9) – (12) с удвоением
сопротивления (11).
.
Поэтому сопротивление их качению по
внутренней и наружной обоймам определяется
по формулам (9) – (12) с удвоением
сопротивления (11).
Для определения
коэффициента трения подшипников блока,
приведенных к цапфе при неподвижной
наружной обойме, найдем работу сил
трения качения по внутренней и наружной
обоймам на расстоянии, равном длине
беговой дорожки внутренней обоймы на
одном ее повороте, т.е.
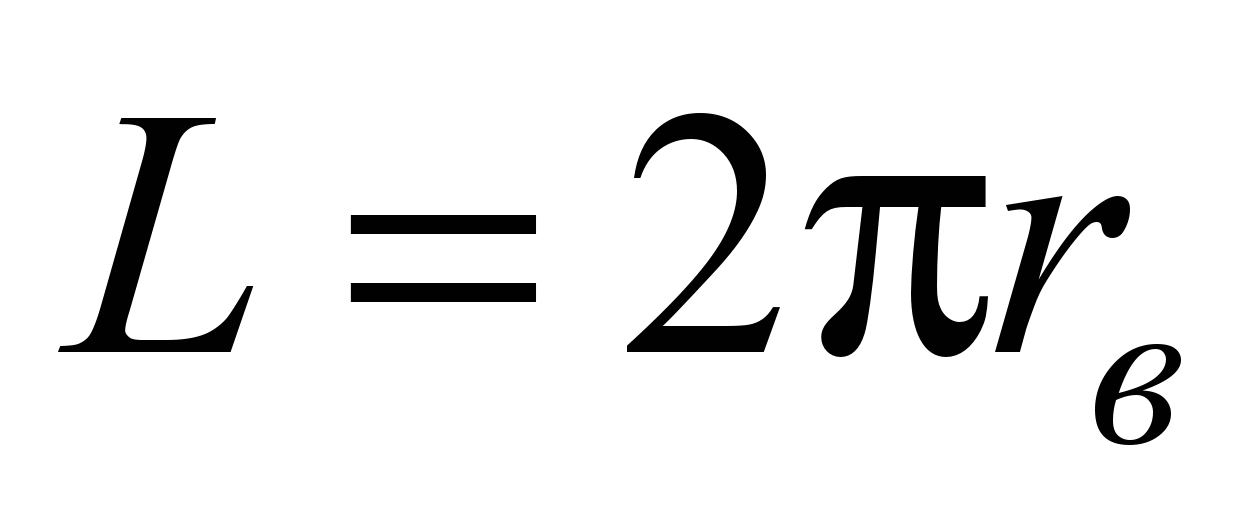 .
.
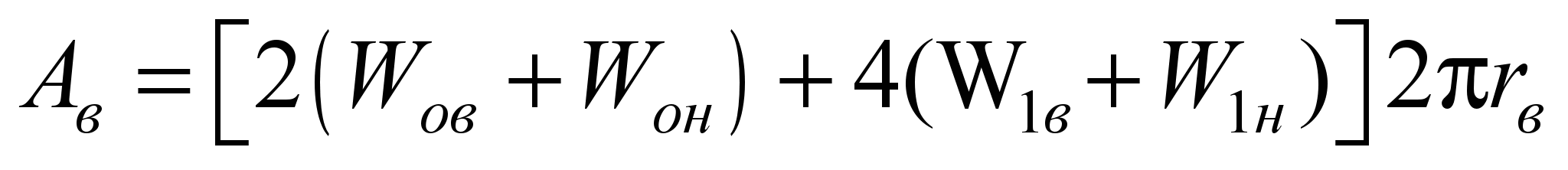 .
.
Работа условной
силы
 ,
приложенной к радиусу цапфы,
,
приложенной к радиусу цапфы,
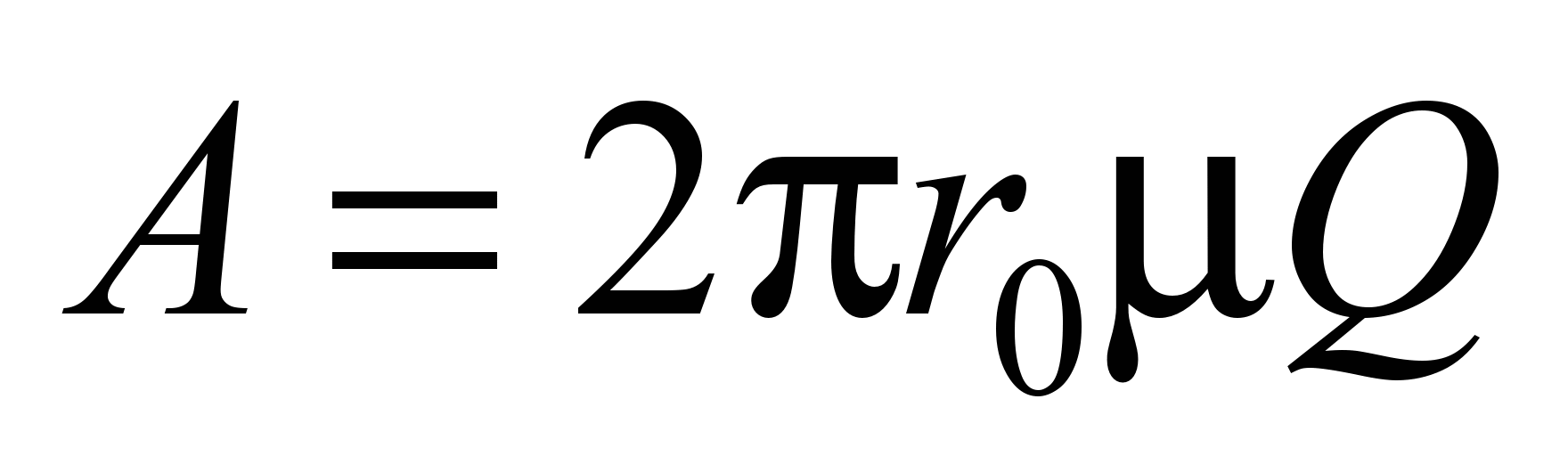 .
.
Приравняв работы,
получим:
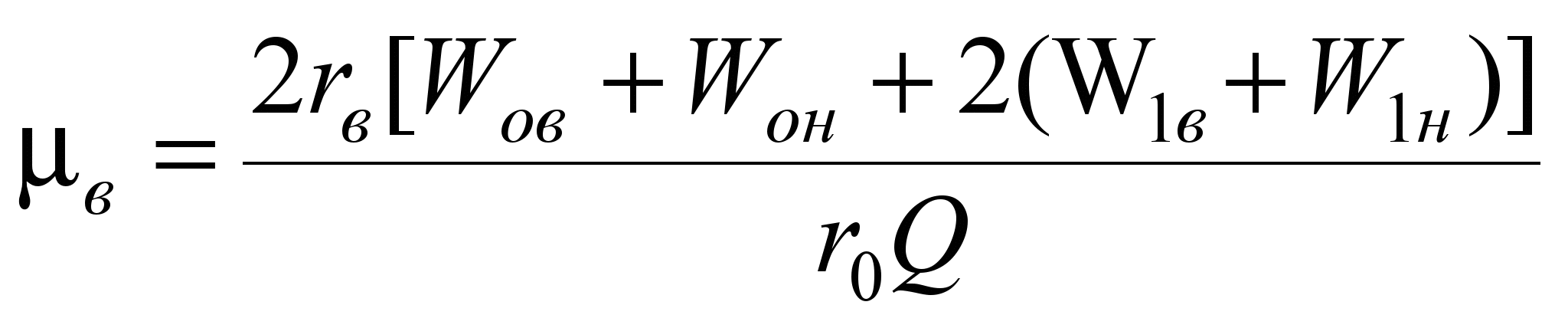 . (13)
. (13)
Рассмотрим случай,
когда вращается наружная обойма
подшипника.
Существенное
отличие в работе блока этого исполнения
состоит в том, что если в первом случае
шарик за один оборот не доходил по
наружной обойме расстояние
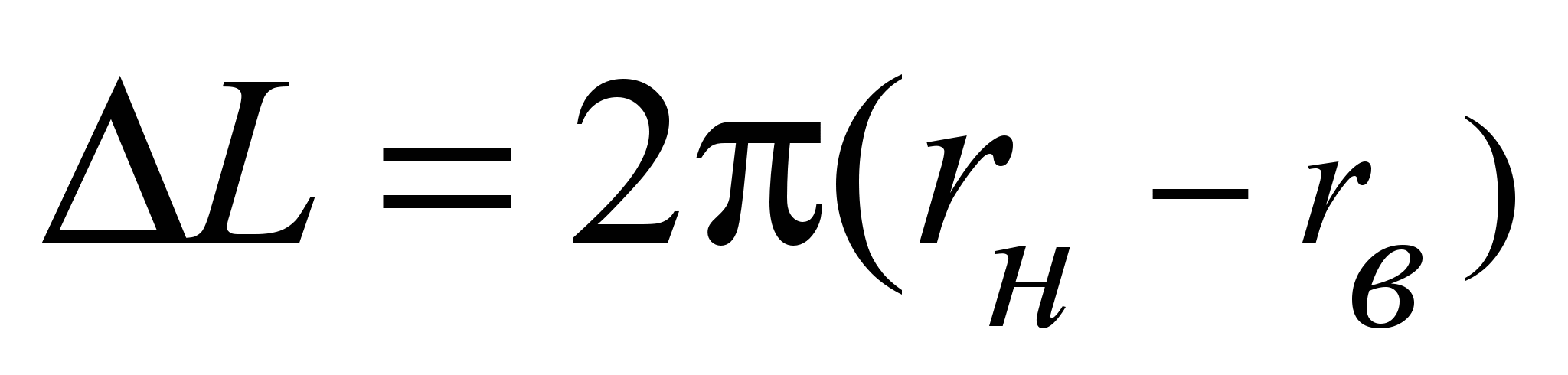 ,
то в этом случае, на этом расстоянии,
шарики будут скользить по внутренней
обойме ввиду большего их сопротивления
качению по наружной обойме, являющегося
движущей силой скольжения.
,
то в этом случае, на этом расстоянии,
шарики будут скользить по внутренней
обойме ввиду большего их сопротивления
качению по наружной обойме, являющегося
движущей силой скольжения.
По аналогии с первым
случаем, но с учетом скольжения шариков,
формула для определения приведенного
к цапфе коэффициента сопротивления
подшипника при вращении наружной обоймы
имеет вид:
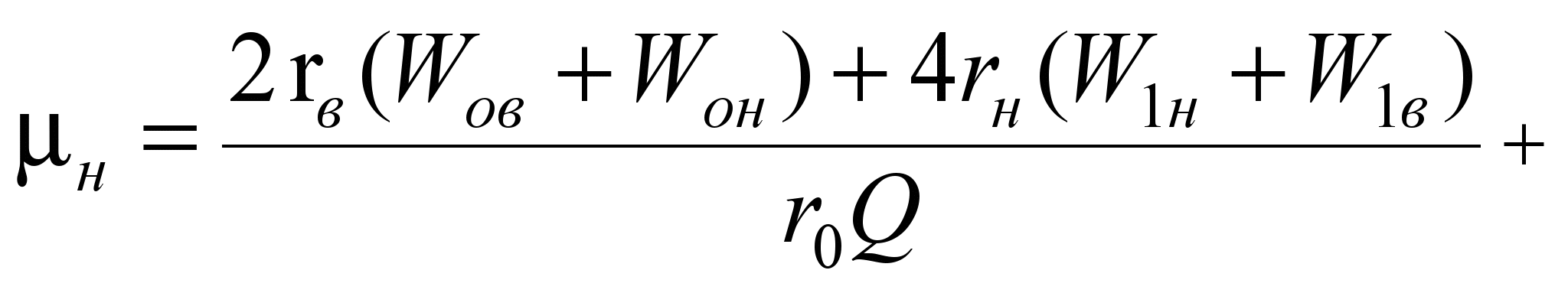
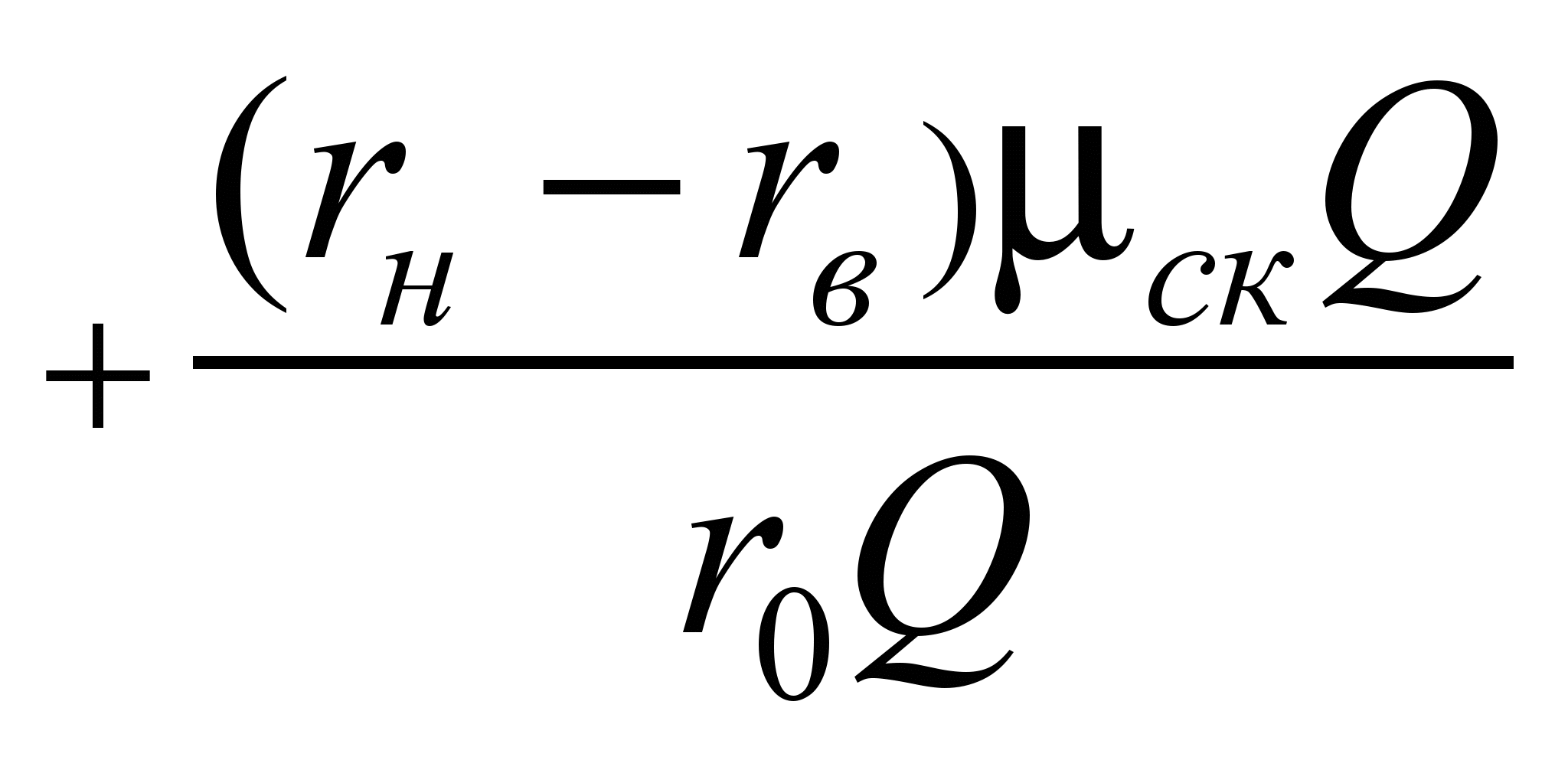 ,
(14)
,
(14)
где
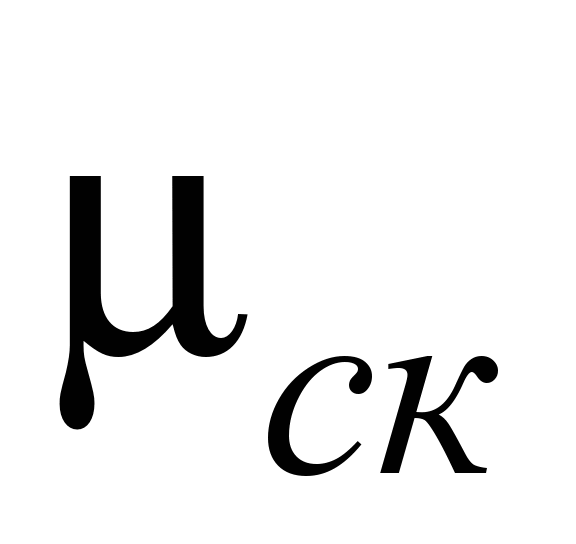 – коэффициент трения скольжения
между шариками и обоймой.
– коэффициент трения скольжения
между шариками и обоймой.
Рассмотрим пример
расчета
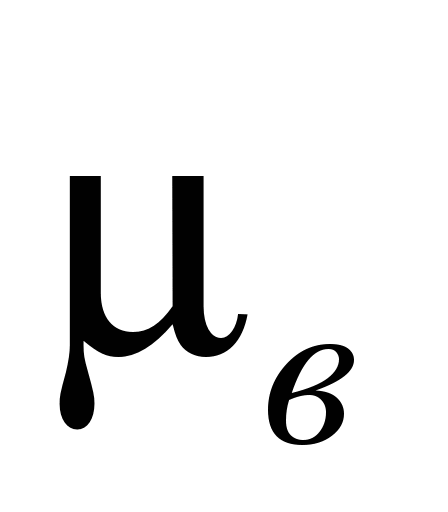 и
и
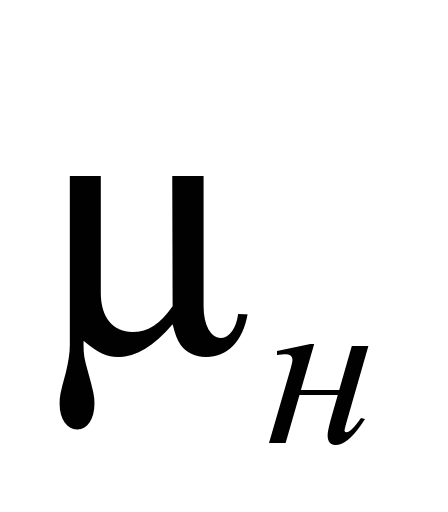 ,
определив затем КПД подшипника, сначала
без учета жесткостных потерь [10]:
,
определив затем КПД подшипника, сначала
без учета жесткостных потерь [10]:
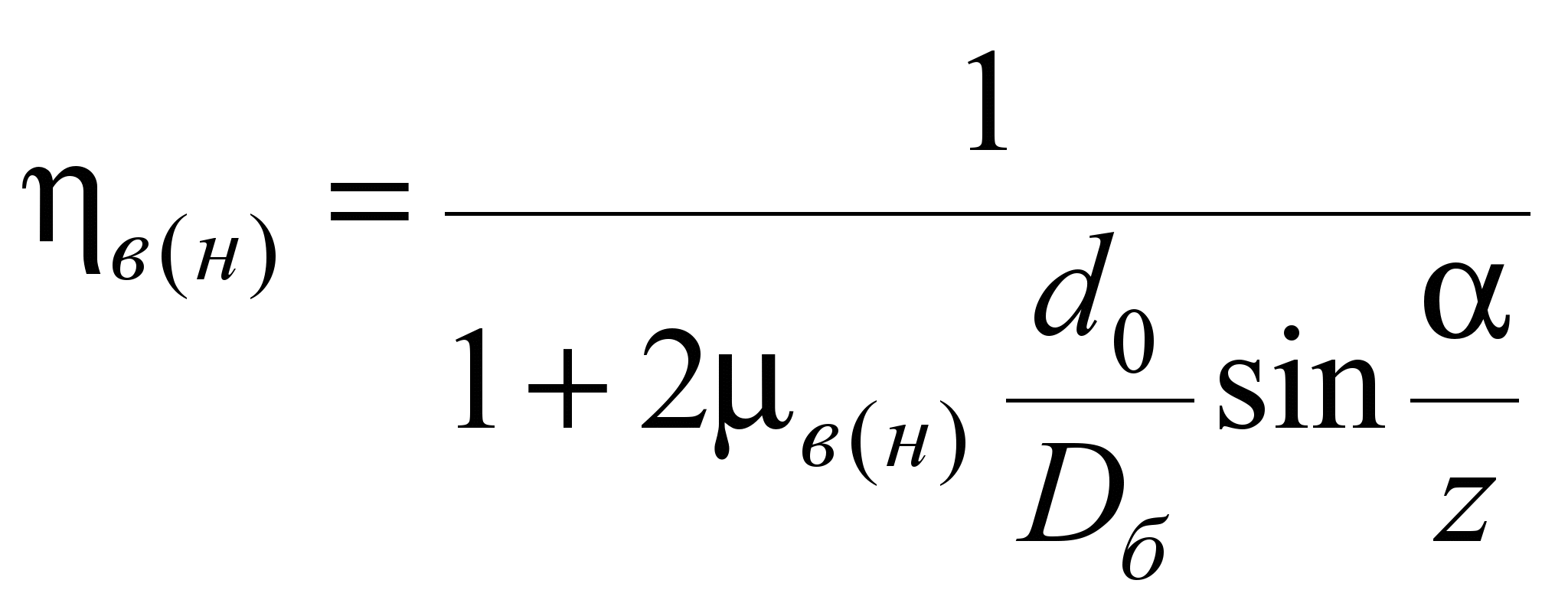 . (15)
. (15)
Результаты
Рассмотрим влияние
классификационной группы механизма
подъема на потери в подшипниках.
Максимальную
нагрузку на один из двух подшипников
примем равной
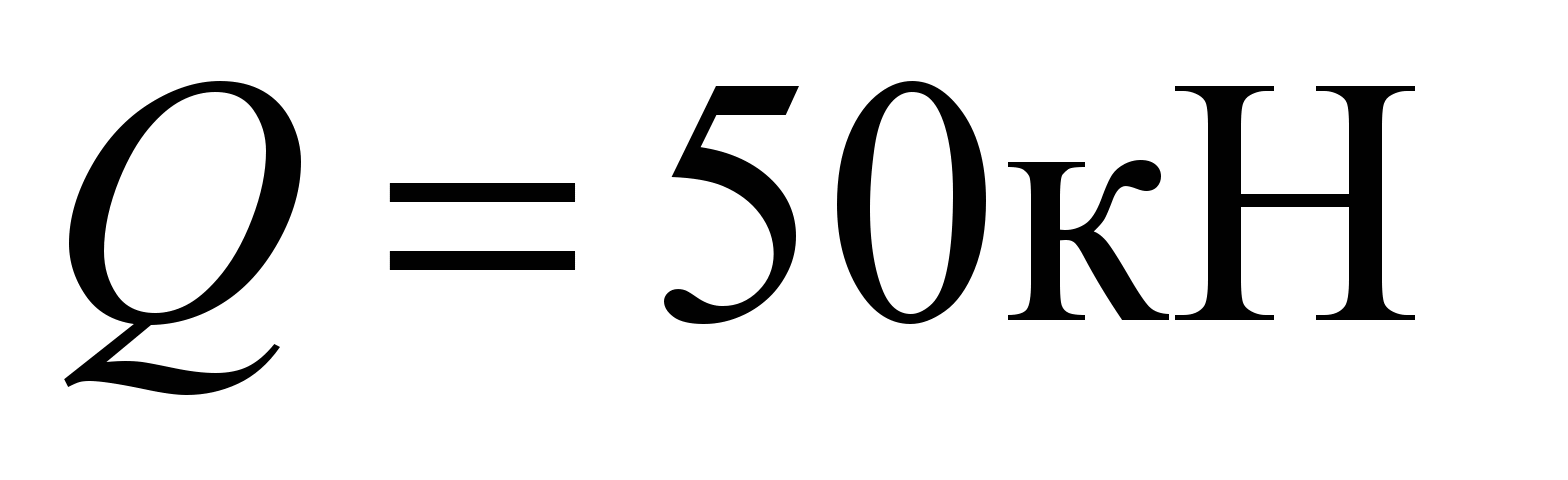 ,
которой соответствует шариковый
подшипник № 313 со статической нагрузкой
,
которой соответствует шариковый
подшипник № 313 со статической нагрузкой
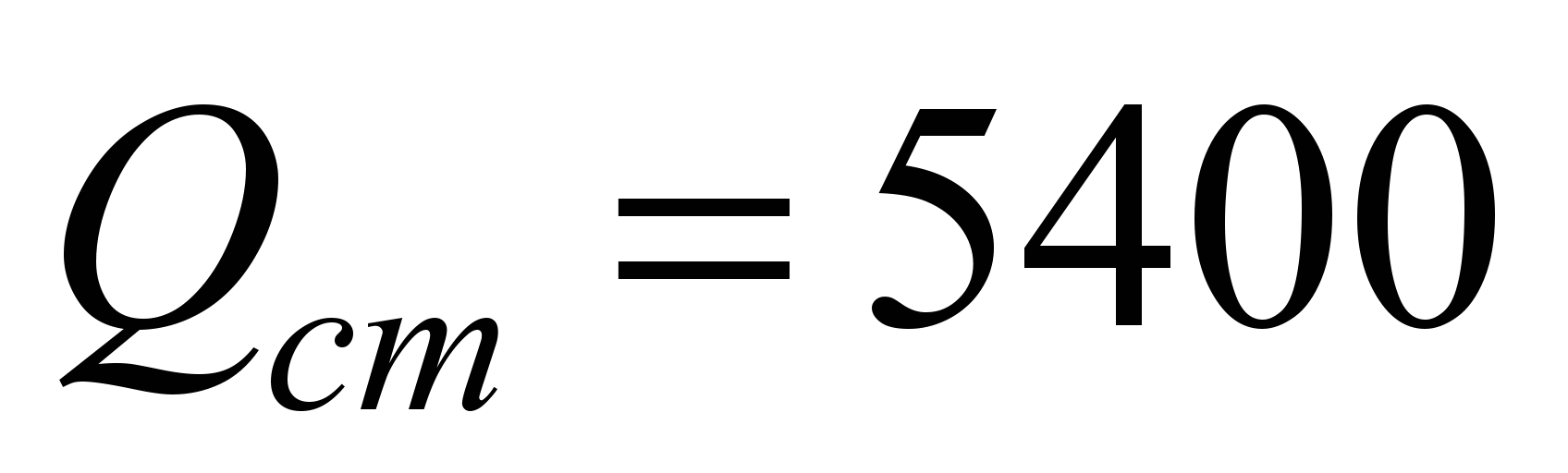 кг массы,
кг массы,
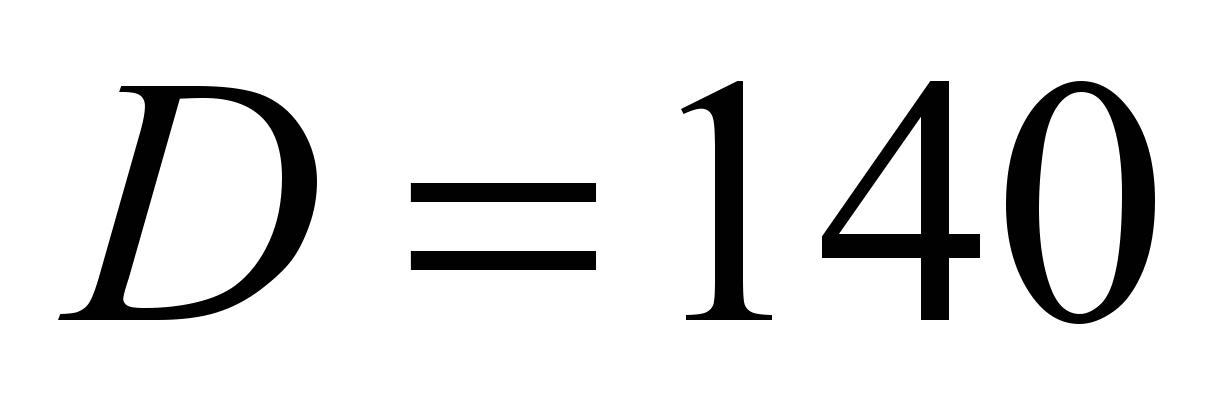 и
и
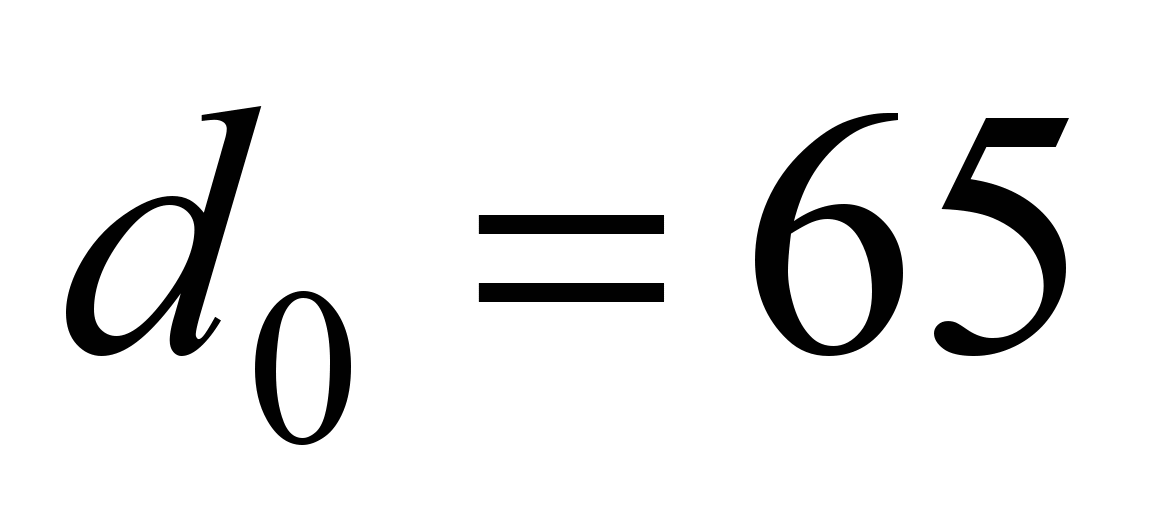 мм
(рис. 1). Остальные данные примем следующими
[4]:
мм
(рис. 1). Остальные данные примем следующими
[4]:
диаметр шариков
(без округления до стандартных размеров)
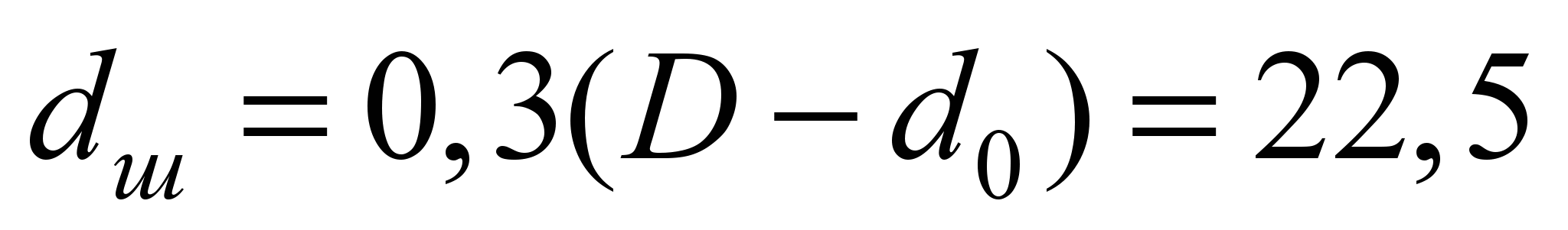 мм;
мм;
радиус желоба беговых дорожек
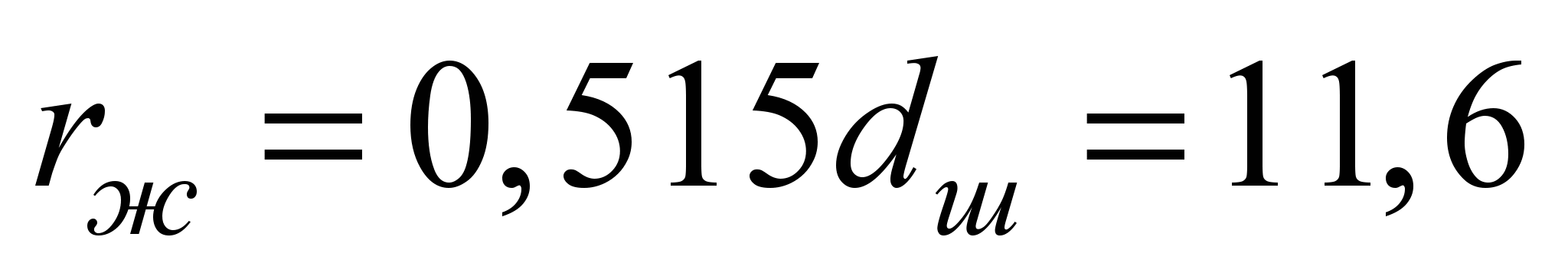 мм;
количество шариков
мм;
количество шариков
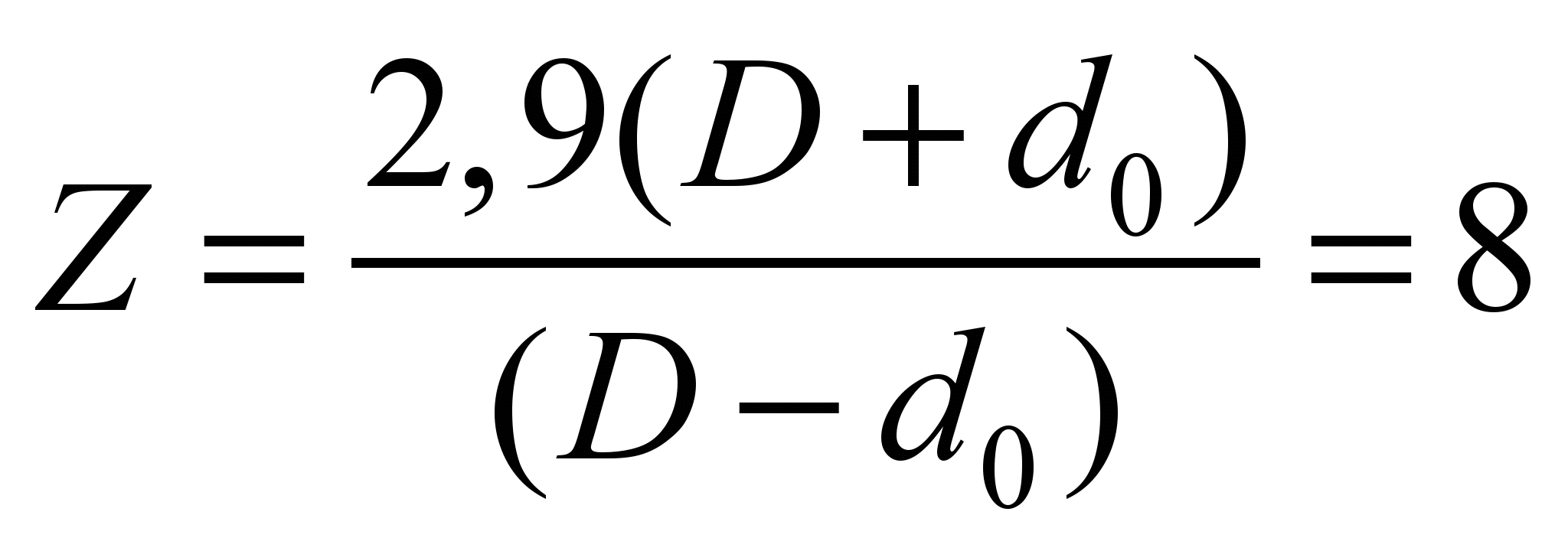 при угле между шариками
при угле между шариками
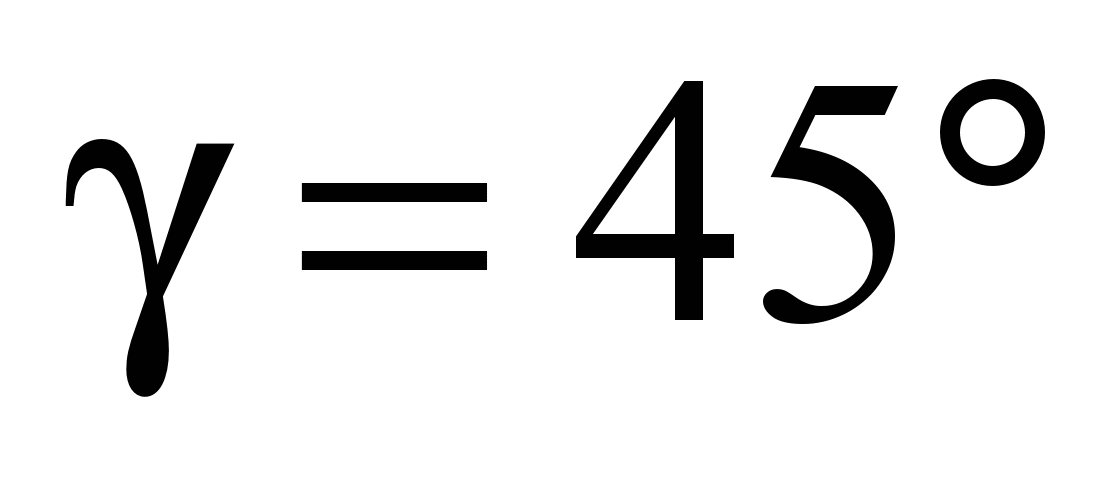 .
.
Нагрузка на наиболее
загруженный шарик согласно формуле
(7) составляет
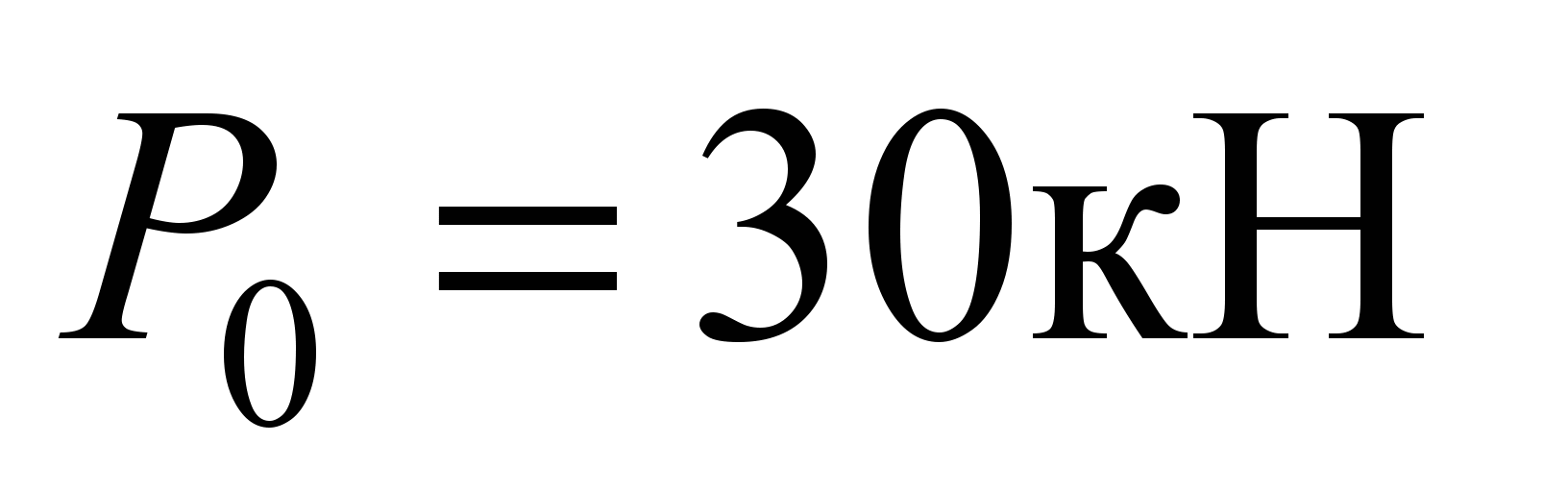 .
На один боковой шарик согласно формуле
(8) действует
.
На один боковой шарик согласно формуле
(8) действует
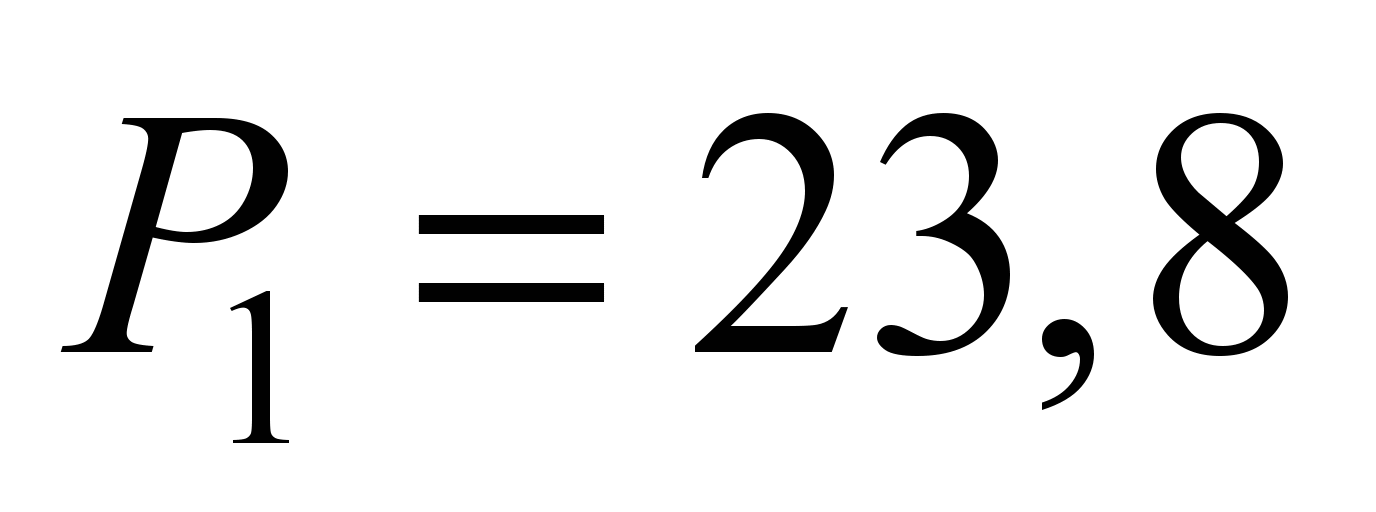 кН.
кН.
Коэффициенты трения
качения наиболее загруженного шарика
по внутренней и наружной обоймам
составляют соответственно
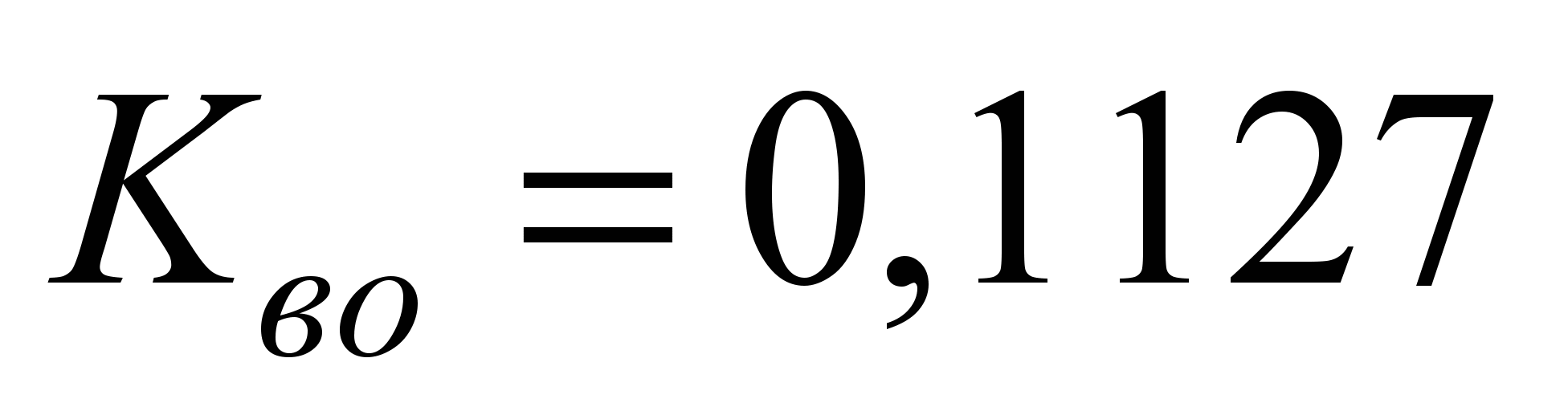 мм,
мм,
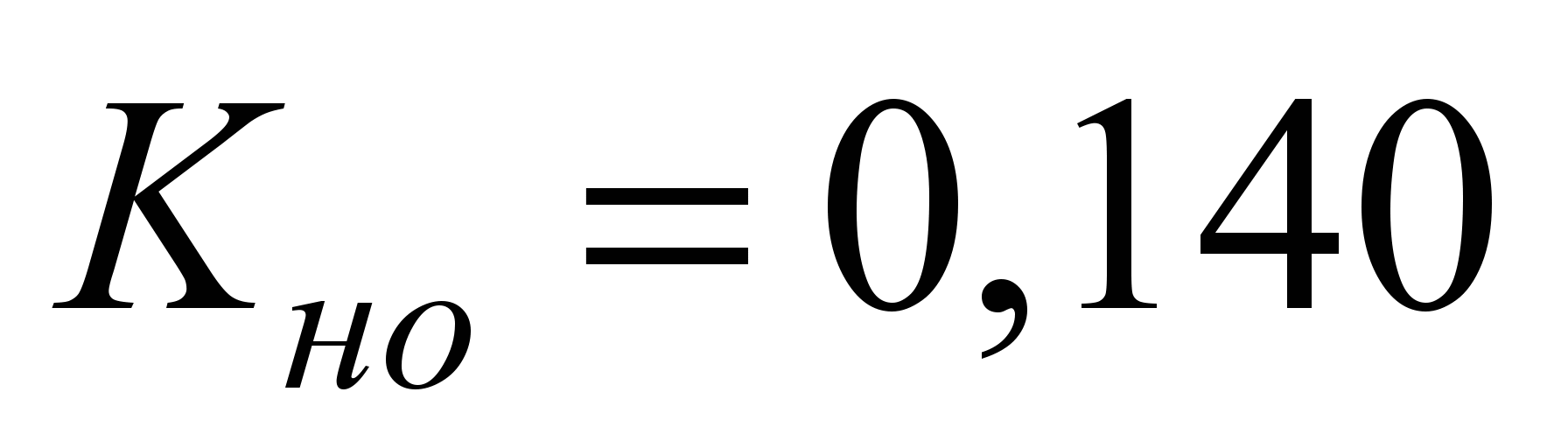 мм,
а сопротивление качению одного шарика
составит
мм,
а сопротивление качению одного шарика
составит
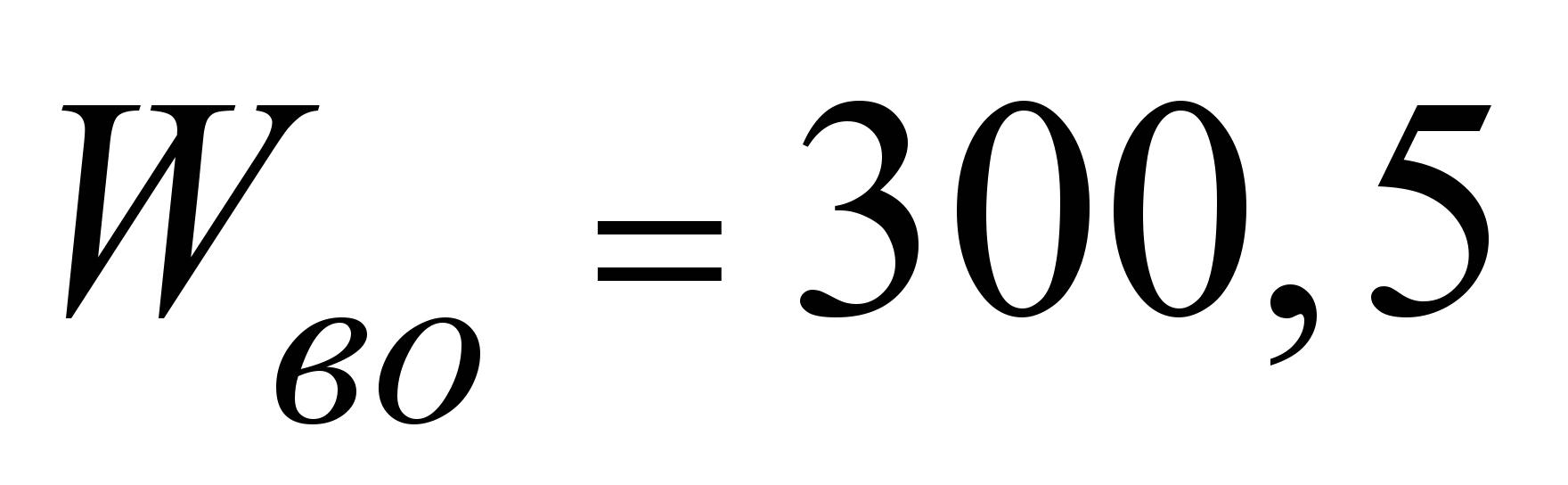 Н;
Н;
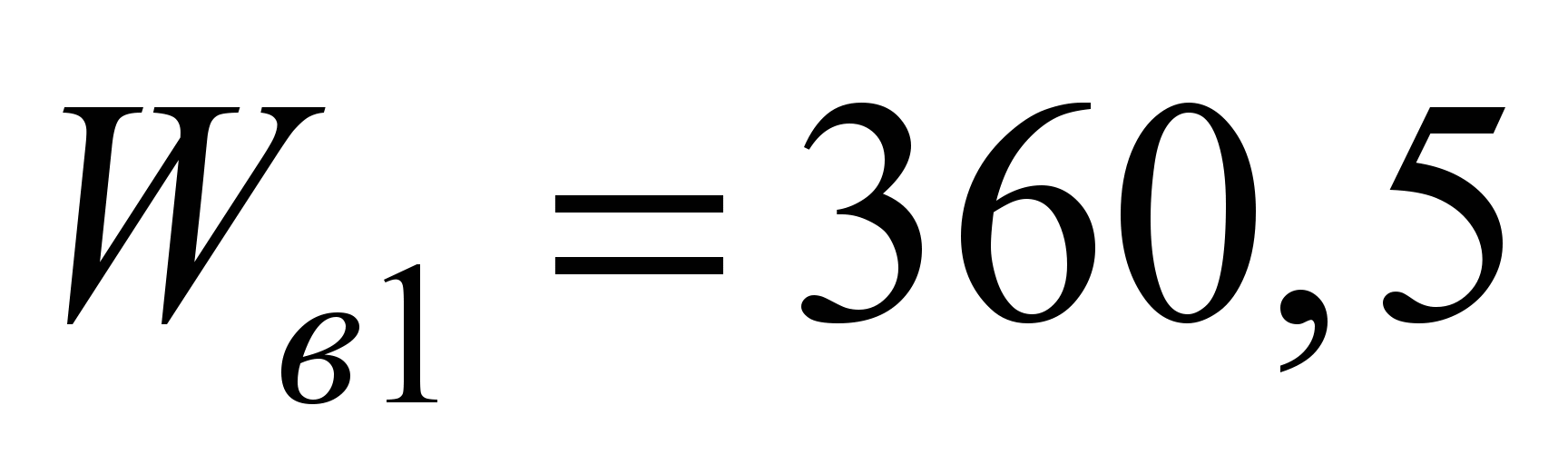 Н;
Н;
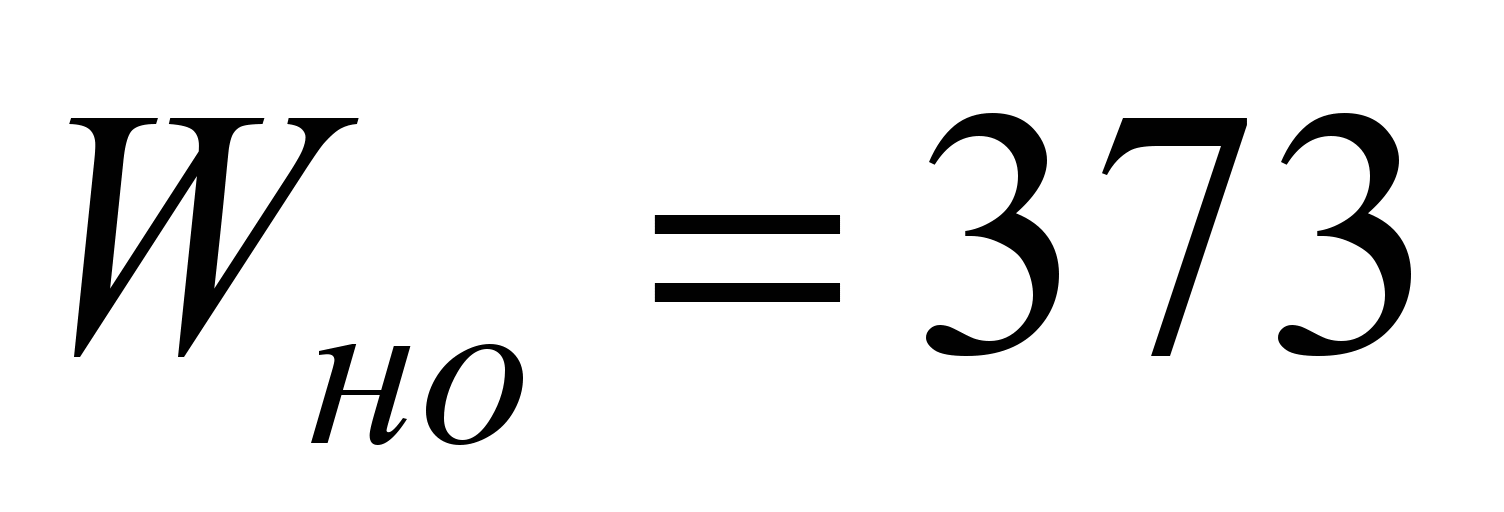 Н;
Н;
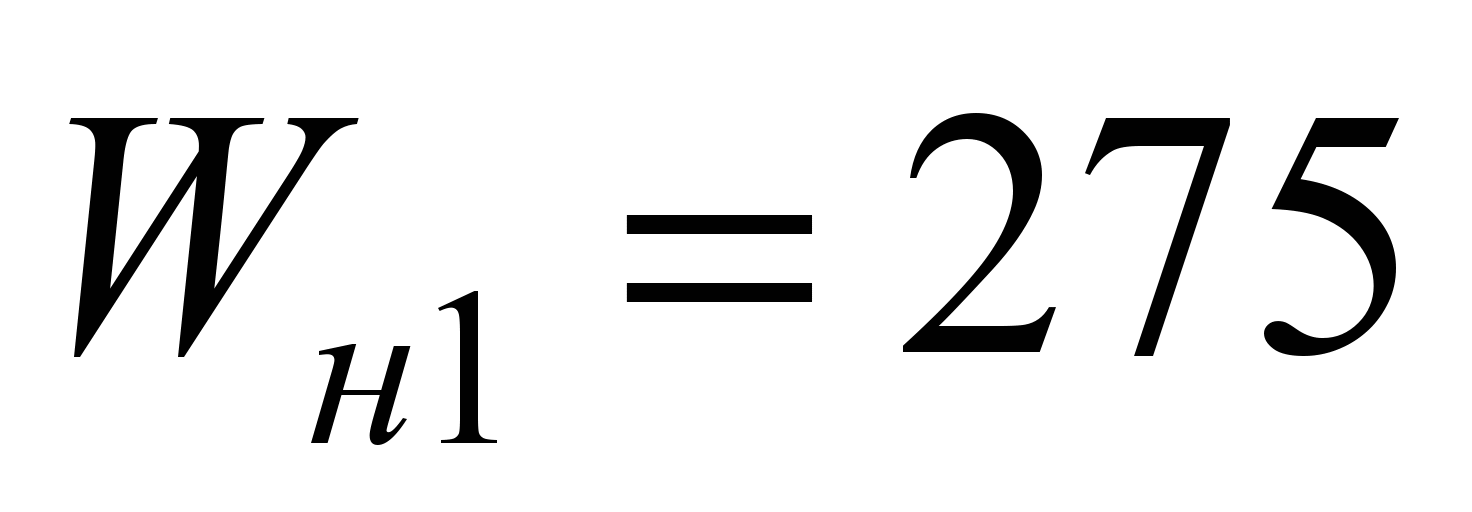 Н.
Н.
Приведенный к оси
блока коэффициент трения двух подшипников
составляет (при
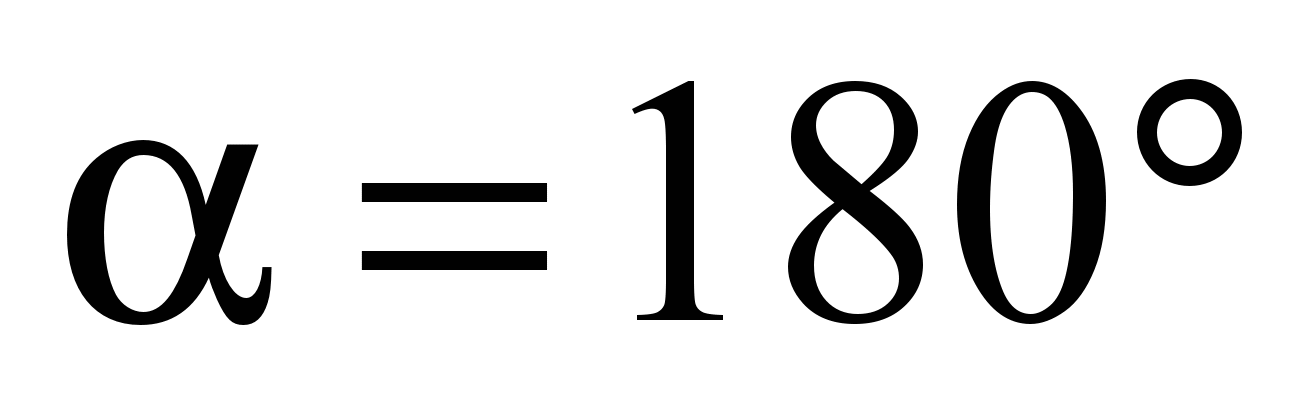 ):
при вращении наружной обоймы подшипников
при жидкостной смазке
):
при вращении наружной обоймы подшипников
при жидкостной смазке
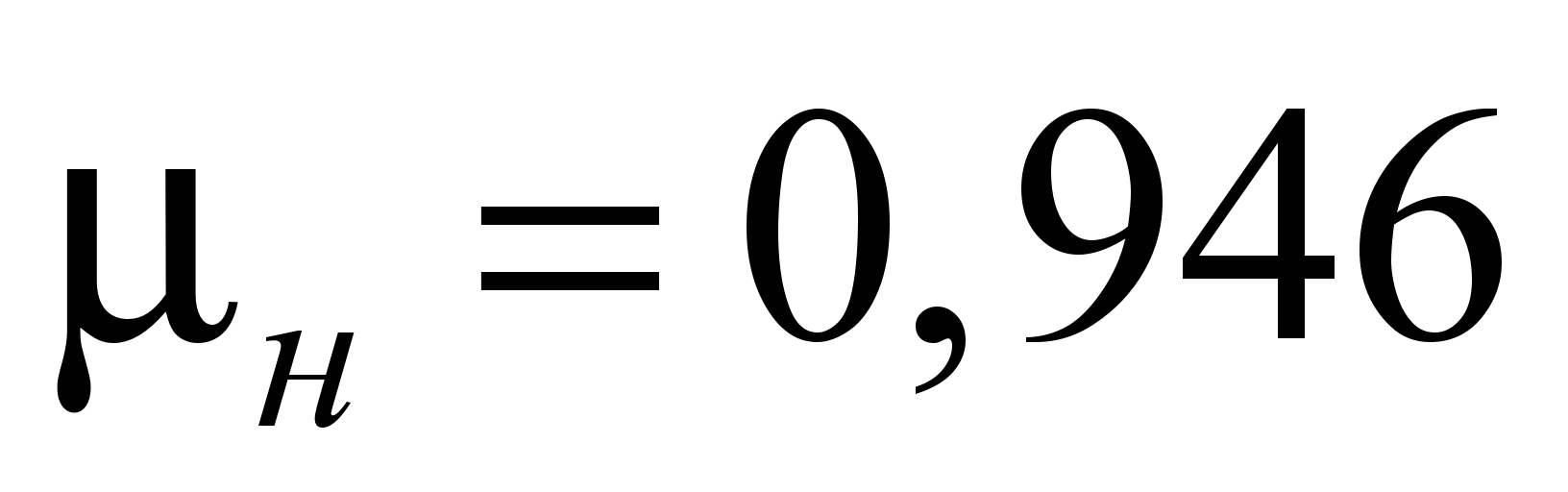 и при густой смазке
и при густой смазке
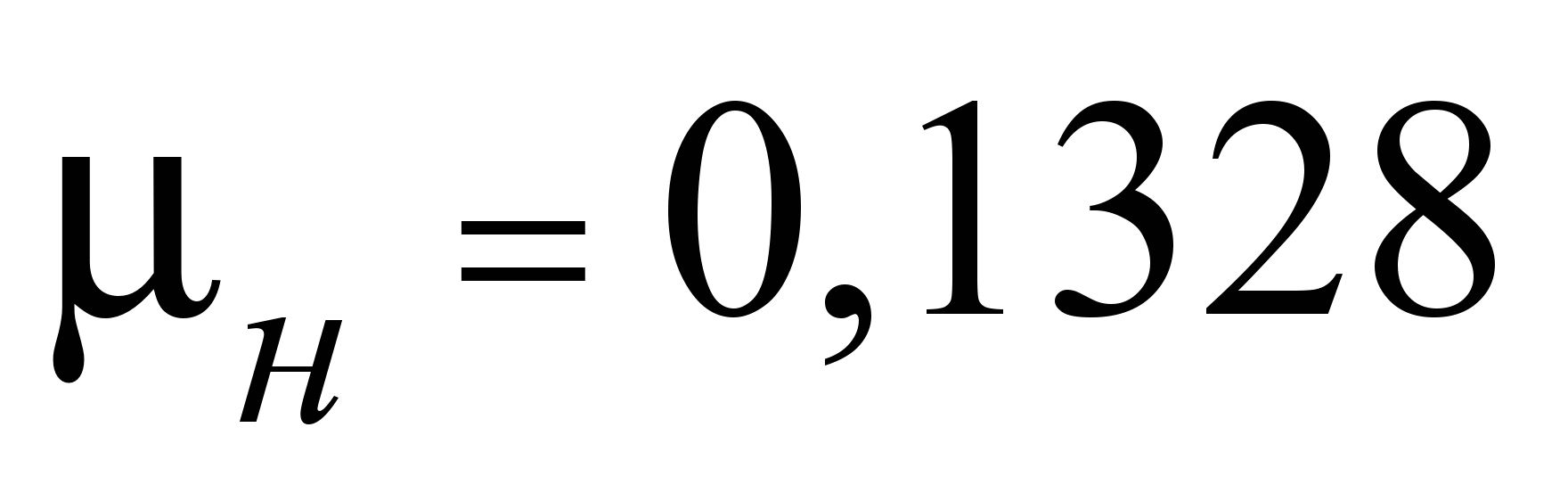 ,
при отсутствии смазки
,
при отсутствии смазки
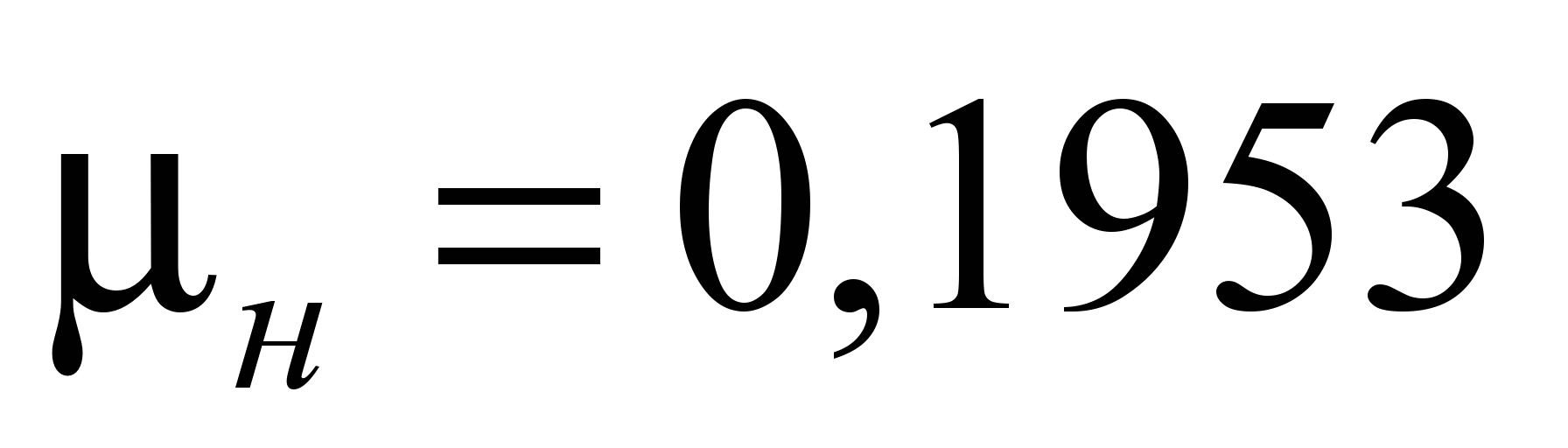 .
Отметим, что при вращении внутренней
обоймы эта величина составит
.
Отметим, что при вращении внутренней
обоймы эта величина составит
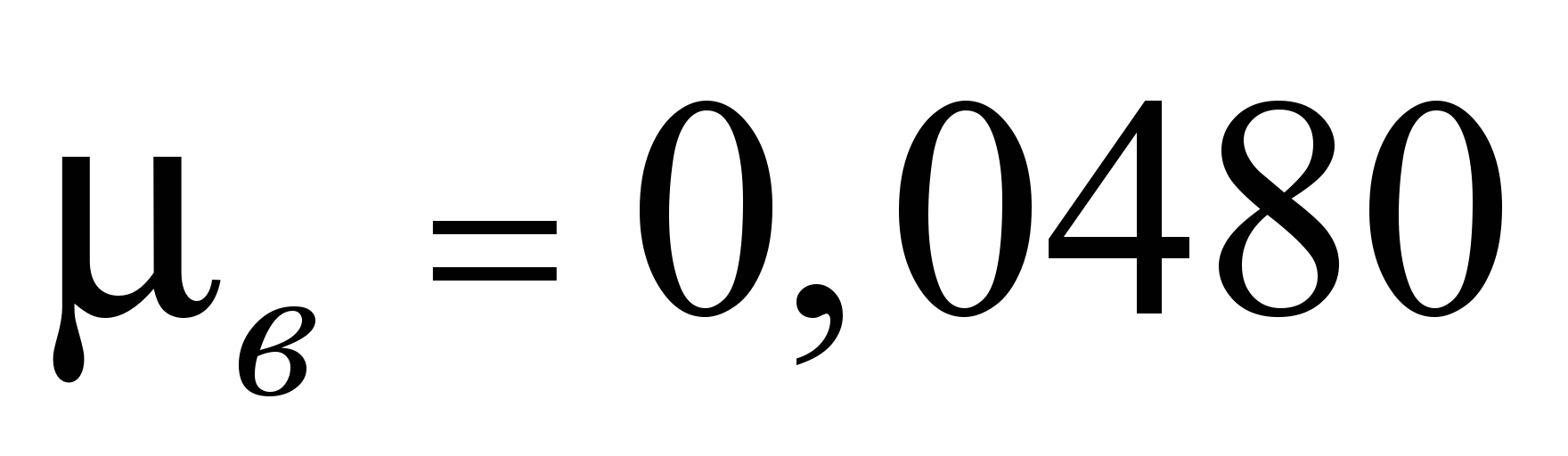 .
.
Зависимость КПД
блока (15) от режима работы механизма
при густой и жидкостной (см. цифру в
скобках) смазке приведена в табл. 1
(без учета жесткости каната).
Коэффициенты
полезного действия блоков (КПД) в
зависимости от угла обхвата канатом
блока и вида смазки, без учета жесткостных
потерь, приведены в табл. 2.
В табл. 3 приведены
значения жесткостных потерь в зависимости
от режима работы и вида смазки подшипника
при справочной величине
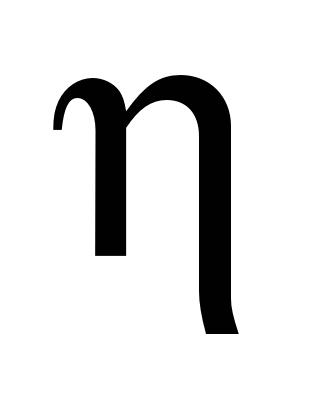 =0,980.
=0,980.
Анологично табл.
3 приведем коэффициент полезного
действия блока при угле обхвата
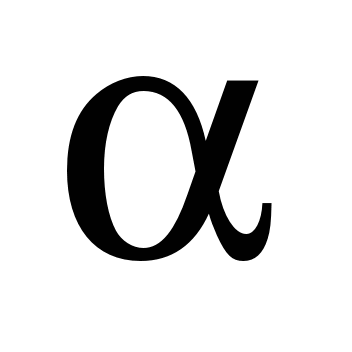 =180
=180 и густой смазке (
и густой смазке ( =0,1328)
– табл. 4.
=0,1328)
– табл. 4.
Таблица
1
Зависимость КПД блока от режима работы
механизма при густой и жидкостной
(в
скобках) смазке (без учета жесткости
каната)
Table 1
Dependence of
block efficiency
on operation
mode of
the mechanism
at thick
and liquid
(in parentheses)
lubrication
(without considering the rope
rigidity)
|
Режим
работы
|
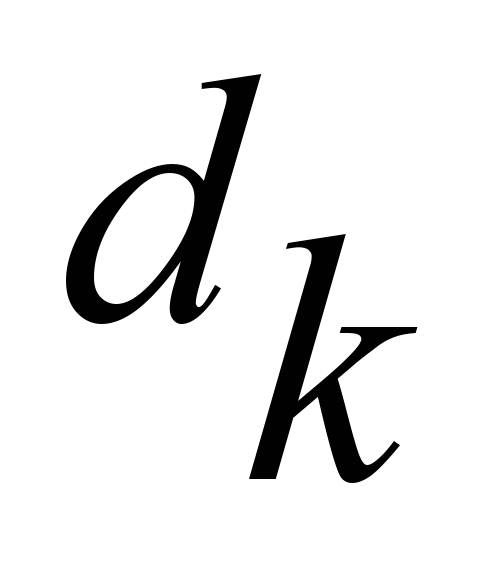
|
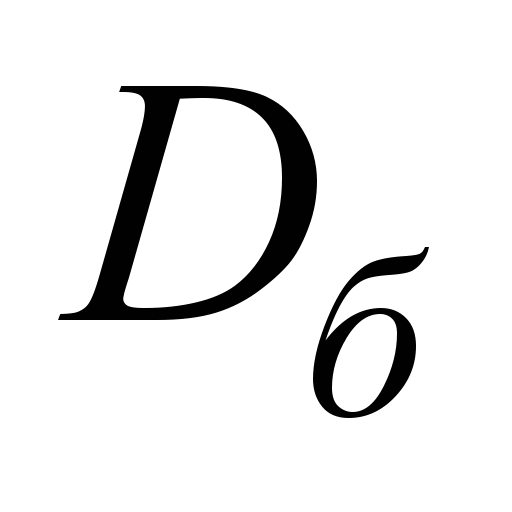
|
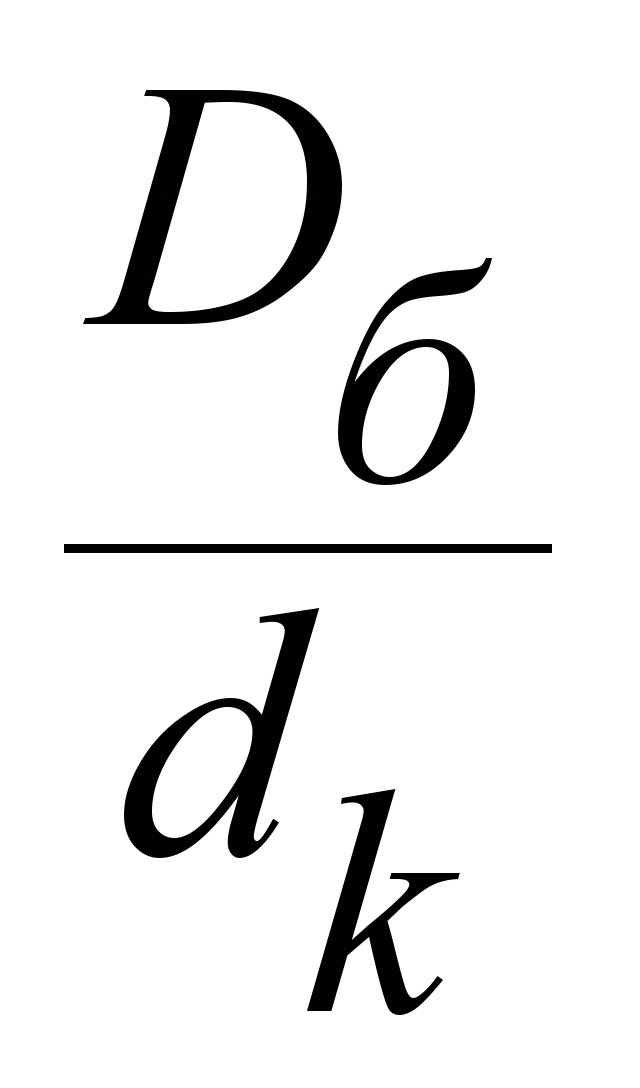
|
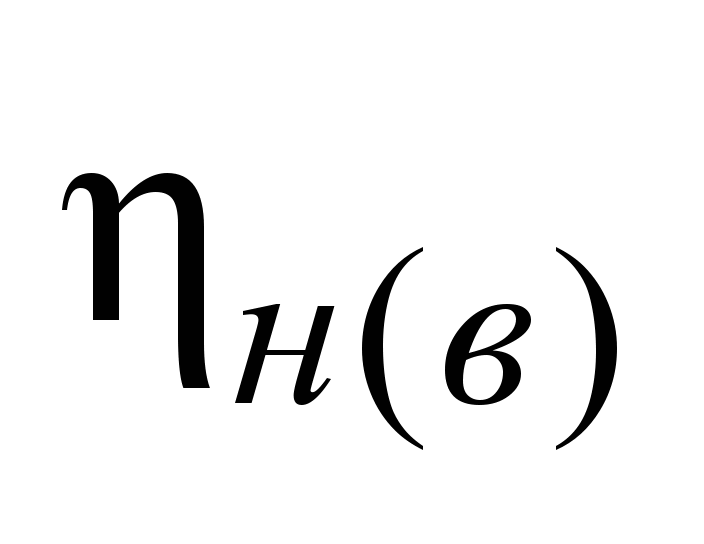 при вращении
при вращении
|
|
по наружной
обойме
|
по внутренней
обойме
|
|
1М
|
22,5
|
382,5
|
17
|
0,9568 (0,9689)
|
0,9840
|
|
2М, 3М
|
24,0
|
456,0
|
19
|
0,9635 (0,9737)
|
0,9865
|
|
4М
|
25,0
|
600,0
|
24
|
0,9720 (0,9800)
|
0,9897
|
|
5М, 6М
|
27,0
|
783,0
|
29
|
0,9785 (0,9845)
|
0,9920
|
Коэффициент полезного действия блоков
в зависимости
от угла обхвата канатом
блока и вида
смазки (без учета
жесткостных потерь)
Table 2
Blocks efficiency depending on the wrapping
angle of a block by a rope
and the type of lubrication without
considering
the stiffening losses
|
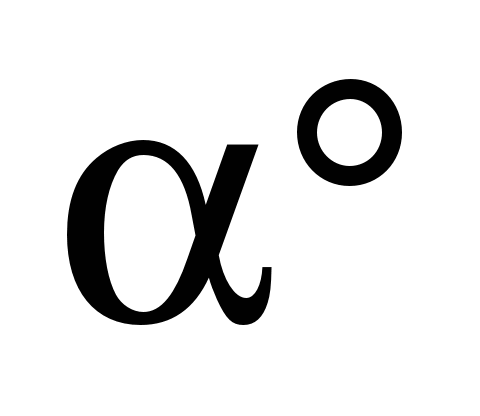
|
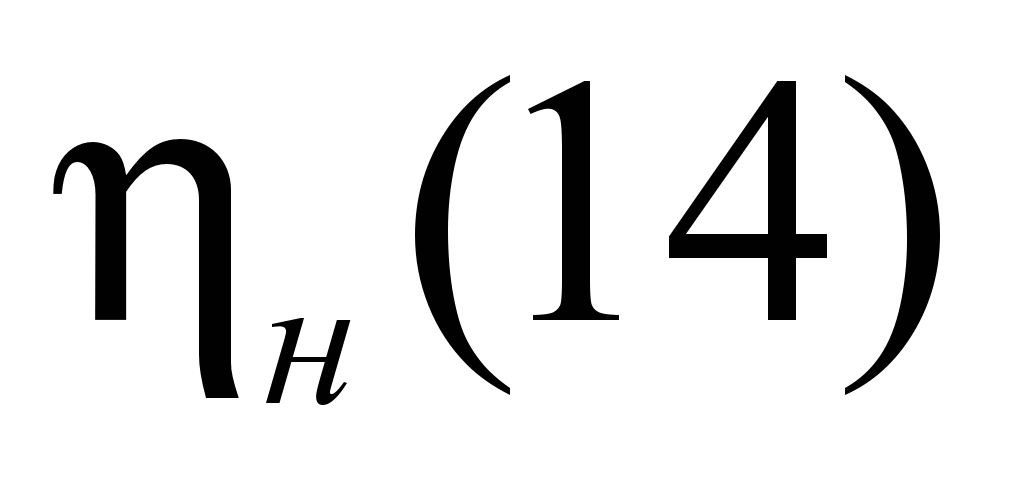
|
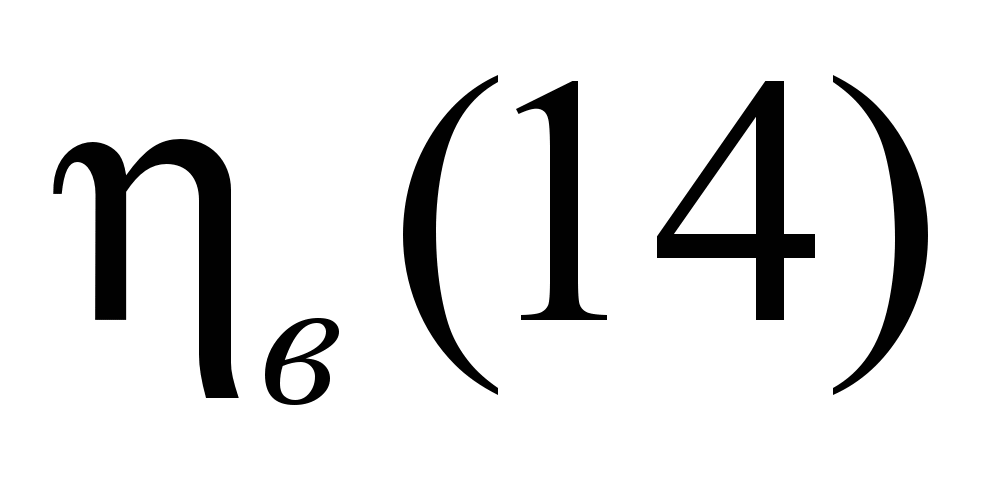
|
Справочная
величина
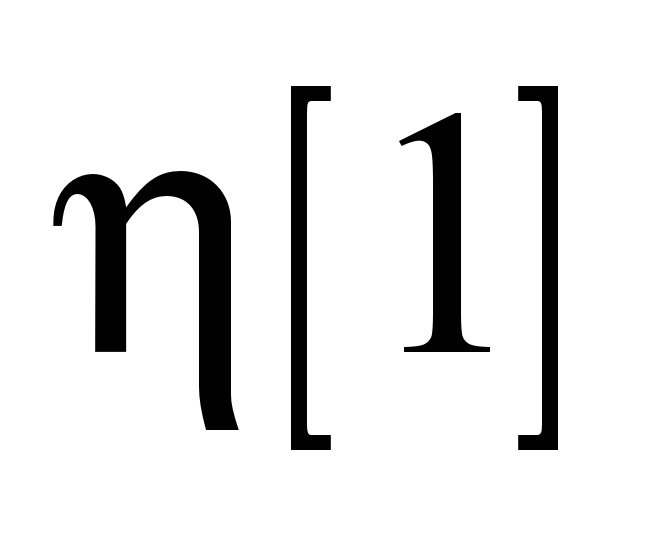
|
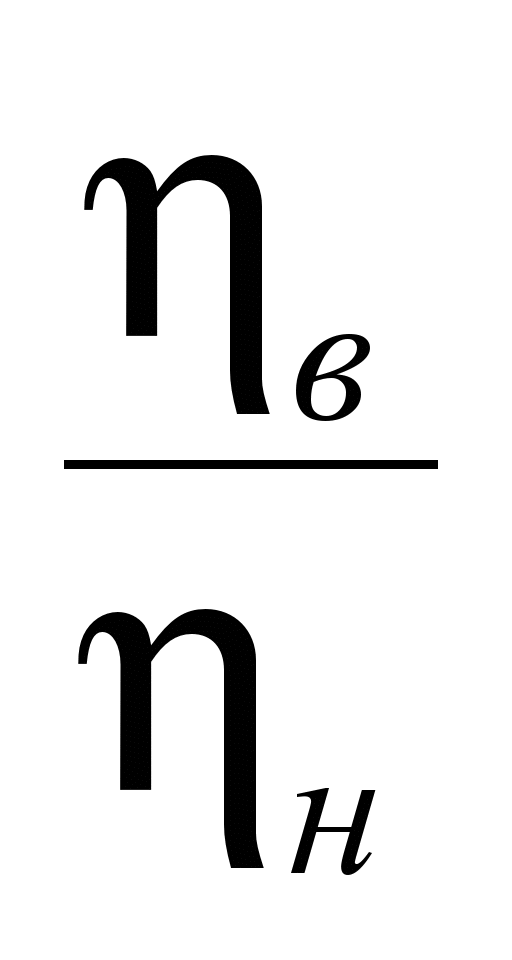
|
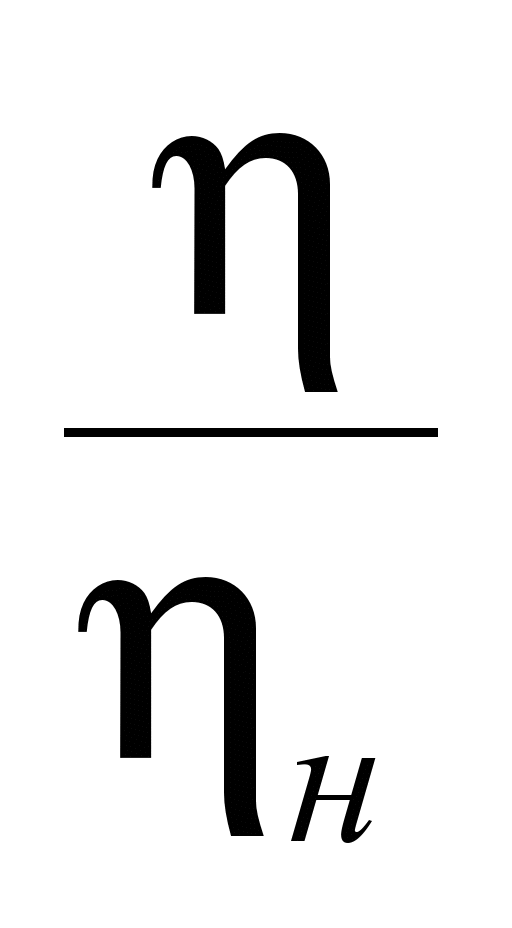
|
|
 =0,1328 =0,1328
|
 =0,0946
=0,0946
|
 =0,1328
=0,1328
|
 =0,1328
=0,1328
|
 =0,1328 =0,1328
|
|
180
|
0,9720
|
0,9800
|
0,9897
|
0,980
|
1,018
|
1,008
|
|
90
|
0,9800
|
0,9857
|
0,9927
|
0,985
|
1,013
|
1,005
|
|
40
|
0,9891
|
0,9922
|
0,9960
|
0,987
|
1,007
|
0,998
|
|
15
|
0,9963
|
0,9973
|
0,9986
|
0,990
|
1,002
|
0,994
|
Таблица 3
Значения жесткостных потерь в
зависимости от режима работы
и вида
смазки подшипника при справочной
величине
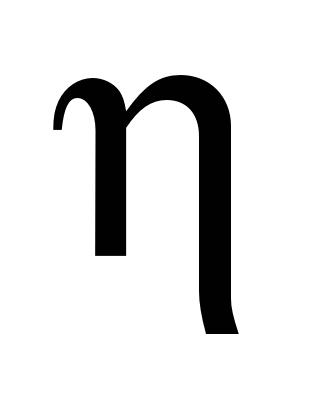 =0,980
=0,980
Table 3
Values of the stiffness losses depending on
the operation mode and the type of bearing
lubrication at the
reference value
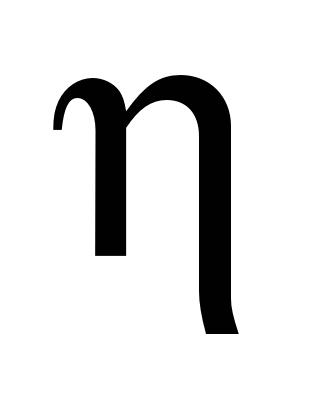 = 0,980
= 0,980
|
Режим
работы
|
 [1]
[1]
|
 [2]
[2]
|
 [1]
[1]
|
 [1]
[1]
|
|
1М
|
0,0349
|
0,029
|
0,0636(0,0513)
|
0,0307
|
|
2М, 3М
|
0,0277
|
0,020
|
0,0404(0,0347)
|
0,0277
|
|
4М
|
0,0197
|
0,017
|
0,0313(0,0282)
|
0,0244
|
|
5М, 6М
|
0,0144
|
0,0069
|
0,0241(0,023)
|
0,0218
|
Таблица 4
Коэффициент полезного действия блока
при
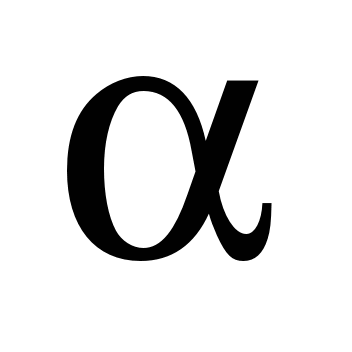 =180˚
и густой смазке (
=180˚
и густой смазке ( =0,1328)
=0,1328)
Table 4
Block efficiency at
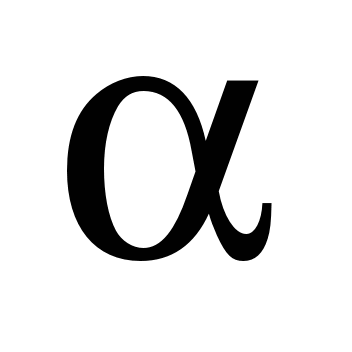 = 180˚ and thick lubrication (
= 180˚ and thick lubrication ( = 0,1328)
= 0,1328)
|
Режим
работы
|
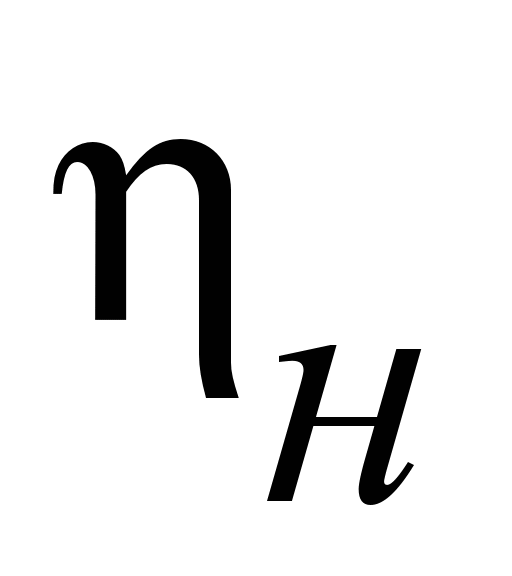
|
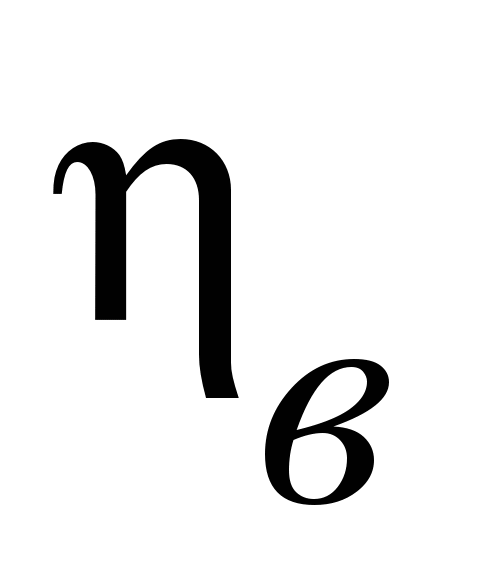
|
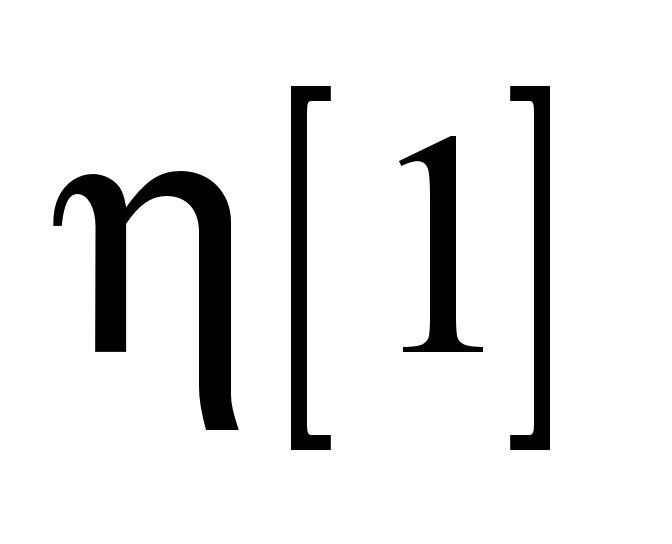
|
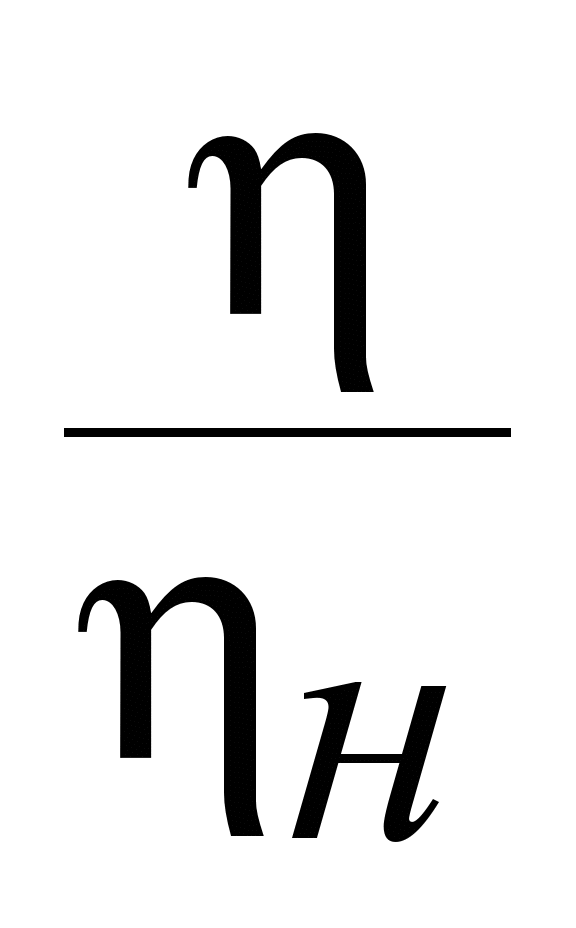
|
|
1М
|
0,8564
|
0,8607
|
0,8358
|
0,976
|
|
2М, 3М
|
0,8617
|
0,8674
|
0,8524
|
0,989
|
|
4М
|
0,8676
|
0,8750
|
0,8590
|
0,990
|
|
5М, 6М
|
0,8717
|
0,8774
|
0,8644
|
0,992
|
Научная
новизна и практическая
значимость
С помощью зависимостей
по определению коэффициента трения
качения, полученных с использованием
аналитических зависимостей Герца по
определению контактных напряжений и
деформаций, а также экспериментальных
величин коэффициента трения качения
для крановых колес получены значения
сопротивлений в шариковых подшипниках
канатных блоков и жесткостные потери,
обусловленные обхватом блока канатом.
Получение значения
сопротивлений могут быть использованы
для уточненных расчетов механизмов
машин.
Выводы
Анализ полученных
и существующих формул, результатов
расчетов позволяет сделать следующие
выводы и рекомендации:
– главным
сопротивлением, влияющим на КПД канатных
блоков, является сопротивление в
подшипниках (до 70 % при густой смазке и
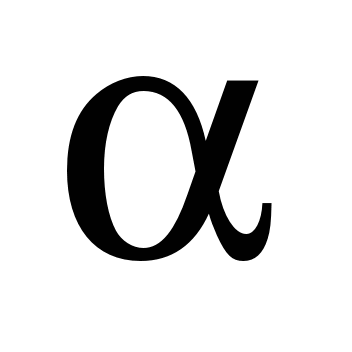 =1800)
(до 100 %);
=1800)
(до 100 %);
– второй
по величине составляющей КПД блоков
являются жесткостные потери, зависящие
от режима работы, угла обхвата канатом
блока, вида смазки подшипника (до 30 %
при густой смазке и
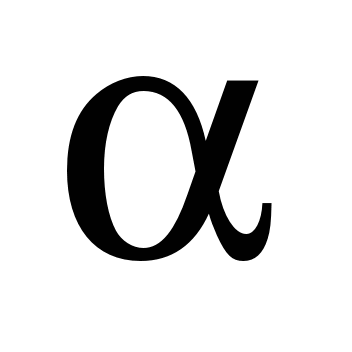 =1800);
=1800);
– КПД
блока при вращении внутренней обоймы
выше, чем при вращении наружной (примерно
на 3 % при густой смазке, режиме 1М и на
1,4 % при режиме 5М);
– при
последовательном расположении узлов
с подшипником качения необходимо
стремиться к конструкции узла, в котором
вращается внутренняя обойма (при
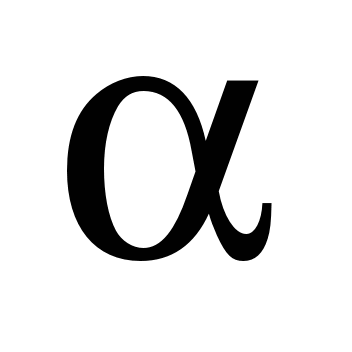 =10
и густой смазке разница в КПД примерно
25 %);
=10
и густой смазке разница в КПД примерно
25 %);
– при
числе блоков до 5 можно пользоваться
рекомендуемыми в литературе КПД
подшипников блоков с погрешностью в
величине КПД до 10 %.
СПИСОК ИСПОЛЬЗОВАННЫХ
ИСТОЧНИКОВ
Вплив
коефіцієнта тертя ковзання та кута
обхвату колодкою та стрічкою гальмівного
шківа на рівновагу важільної системи
/ В. М. Богомаз, М. Г.
Брильова, Л. М. Бондаренко,
К. Ц. Главацький //
Вісн. нац. ун-ту водного
госп-ва та природокористування. –
Рівне : Вид-во НУВГПК, 2015. – № 2. – С.
120–125.
Довбня,
М. П. Теоретичне
визначення сили ковзання при коченнi
/ М. П. Довбня // Проблеми
трибологiї. –
2002. – № 2.
– С. 103–106.
Ковальский,
Б. С. Потери на блоках канатных полиспастов
/ Б. С. Ковальский // Строительные
и дорожные машины. – 1986. –
№ 8. – С. 34–37.
Кожевников,
С. Н. Теория машин и
механизмов / С. Н. Кожевников. –
Москва : Машиностроение, 1969. – 584
с.
Механика.
Сопротивление материалов (теория и
практика) : учеб. пособие
/ О. М.
Болтенкова,
О. Ю. Давыдов,
В. Г. Егоров,
С. В. Ульшин.
– Воронеж : Изд-во ВГУИТ, 2013. – 121
с.
Прикладная
механика : учеб. пособие
/ Х. С. Гумерова,
Н. П. Петухов,
В. М. Котляр,
С. Г. Сидорин.
– Казань : Изд-во КНИТУ, 2014. – 142 с.
Применение
и прочность полимерных материалов при
изготовлении и ремонте машин и
оборудования / Б. А. Грязнов [и др.]. –
Киев : Ин-т проблем
прочности имени Г. С. Писаренко НАН
Украины, 2013. – 296 с.
Синенко,
Е. Г. Механика : учеб. пособие
/ Е. Г. Синенко,
О. В. Конищева.
– Красноярск : Изд-во СФУ,
2015. – 236 с.
Способ
определения мощности привода механизма
передвижения мостового крана при учете
трения качения / В. М. Богомаз, Л. М.
Бондаренко, К. Ц. Главацкий, К. О. Сокол
// Наука та прогрес транспорту. – 2015. –
№ 5 (59). – С. 123–131. doi:
10.15802/stp2015/55335.
Справочник
по кранам : в
2 т / М. П.
Александров, М. М. Гохберг,
А. А. Ковин [и др.].
– Ленинград :
Машиностроение, 1988. –
Т. 2. – 559
с.
Яковлев, С.
А. Соотношения между
показателями сопротивления качению
и скольжению в узлах машин /
С. А. Яковлев, Л. Н. Бондаренко //
Гірничі, будівельні, дорожні та
меліоративні машини : зб. наук. пр. /
Київ. нац. ун-т буд-ва і архітектури.
– Київ, 2003. – Вип. 62. –
С. 88–92.
A
general friction model of discrete interactions for tendon actuated
dexterous manipulators / A. Gao, Y. Zou, Z. Wang, H. Liu // J. of
Mechanisms and Robotics. – 2017. –
Vol. 9. – Iss. 4. – P. 041019.
doi:
10.1115/1.4036719.
Makhkamov,
K. Kh. Energy analysis of wear of sliding friction units / K. Kh.
Makhkamov // J. of Friction and Wear. – 2017. – Vol. 38. –
Iss. 2. – P.
168–172. doi:
0.3103/s1068366617020143.
Rahaman,
M. L. Size effect on friction and wear mechanisms of bulk metallic
glass / M. L. Rahaman, L. Zhang // Wear. – 2017. – Vol.
376–377. –
P. 1522–1527. doi: 10.1016/j.wear.2017.01.068.
Tabor,
D. The mechanism of rolling friction. II. The elastic range / D.
Tabor // Proceedings
of the Royal Society A: Mathematical, Physical and Engineering
Sciences. – 1955. – Vol. 229.
– Iss. 1177. – P. 198–220.
doi: 10.1098/rspa.1955.0082.
В. М. БОГОМАЗ1*,
Л. М. БОНДАРЕНКО2*,
М. В. ОЧЕРЕТНЮК3*,
О. О. ТКАЧОВ4*
1*Каф.
«Військова підготовка спеціалістів
Державної спеціальної служби транспорту»,
Дніпропетровський національний
університет залізничного транспорту
імені академіка В. Лазаряна, вул.
Лазаряна, 2, Дніпро, Україна, 49010,
тел.
+38 (056) 373 19 09, ел. пошта wbogomas@i.ua, ORCID
0000-0001-5913-2671
2*Каф.
«Прикладна механіка та матеріалознавство»,
Дніпропетровський національний
університет залізничного
транспорту
імені академіка В. Лазаряна, вул.
Лазаряна, 2, Дніпро, Україна, 49010, тел.
+38 (056) 373 15 18,
ел. пошта bondarenko-l-m2015@yandex.ua, ORCID 0000-0002-2212-3058
3*Каф.
«Військова підготовка спеціалістів
Державної спеціальної служби транспорту»,
Дніпропетровський національний
університет залізничного транспорту
імені академіка В. Лазаряна, вул.
Лазаряна, 2, Дніпро, Україна, 49010,
тел.
+38 (056) 373 19 09, ел. пошта atleteba@gmail.com, ORCID
0000-0002-9032-8602
4*Каф.
«Військова підготовка спеціалістів
Державної спеціальної служби транспорту»,
Дніпропетровський національний
університет залізничного транспорту
імені академіка В. Лазаряна, вул.
Лазаряна, 2, Дніпро, Україна, 49010,
тел.
+38 (056) 373 19 09, ел. пошта otkachov@i.ua, ORCID
0000-0002-1857-7567
СПІВВІДНОШЕННЯ МІЖ ЖОРСТКІСНИМИ
ВТРАТАМИ ТА
ВТРАТАМИ В ПІДШИПНИКАХ
КАНАТНИХ БЛОКІВ
Мета. Для
уточнення величин коефіцієнта корисної
дії (ККД) канатних блоків необхідно
визначити коефіцієнт жорсткості канатів
блоків із урахуванням класифікаційної
групи механізму та кута обхвату канатом
блоку. Передбачається використовувати
при цьому добре випробувані значення
коефіцієнтів корисної дії канатних
блоків із урахуванням кутів обхвату
канатами блоків та аналітично знайдені
величини коефіцієнта тертя підшипників
кочення, наведених до цапфи. Методика.
В роботі вживається аналітичний метод
визначення коефіцієнта опору підшипника
блоку при обертанні його як внутрішньої,
так і зовнішньої обойм, а також
розрахункова схема підшипника блоку.
Результати.
Для канатних блоків проведено аналіз
впливу способу змазки, режиму роботи
механізму та кута обхвату канатом на
втрати в підшипниках. Наведено відповідні
порівняльні таблиці значень втрат.
Аналіз отриманих результатів розрахунків
дозволяє встановити: 1) головним опором,
який впливає на коефіцієнт корисної
дії канатних блоків, є опір у підшипниках;
2) другою за величиною його складовою
є жорсткісні втрати, що залежать від
режиму роботи, кута обхвату канатом
блоку, виду мастила підшипника; 3) ККД
блоку при обертанні внутрішньої обойми
вище, ніж при обертанні зовнішньої
приблизно на 3 % при густому мастилі та
режимі 1М; 4) при послідовному розташуванні
вузлів із підшипником кочення необхідно
прагнути до конструкції вузла, в якому
обертається внутрішня обойма; 5) при
числі блоків до 5 можна користуватися
рекомендованими в літературі ККД
підшипників блоків із помилкою в
величині ККД до 10 %. Наукова
новизна. Автори отримали
значення опорів у кулькових підшипниках
канатних блоків та жорсткісні втрати,
зумовлені обхватом блоку канатом.
Застосовували при цьому залежності
для рішення коефіцієнта тертя кочення,
отримані з використанням аналітичних
залежностей Герца з визначення контактних
напружень і деформацій, а також
експериментальних величин коефіцієнта
тертя кочення для блоків. Практична
значимість. Застосування
отриманих значень опорів можуть бути
використані для уточнених розрахунків
механізмів машин.
Ключові слова: блок; канат; втрати;
підшипник; жорсткість
V. M. BOHOMAZ1*,
L. M. BONDARENKO2*,
M. V. OCHERETNIUK3*,
O. O. TKACHOV4*
1*Dep.
«Military Training of Specialists of the State Special Service of
Transport», Dnipropetrovsk National University of Railway
Transport
named after Academician V. Lazaryan,
Lazaryan St., 2, Dnipro, Ukraine, 49010, tel. +38
(056) 373 19 09,
e-mail wbogomas@i.ua, ORCID
0000-0001-5913-2671
2*Dep.
«Applied Mechanics and Material Science»,
Dnipropetrovsk National University of Railway
Transport named
after Academician V. Lazaryan,
Lazaryan St., 2, Dnipro,
Ukraine, 49010, tel.
+38 (056) 373 15
18,
e-mail
bondarenko-l-m2015@yandex.ua, ORCID
0000-0002-2212-3058
3*Dep.
«Military Training of Specialists of the
State Special Service of Transport»,
Dnipropetrovsk National University of Railway
Transport named
after Academician V. Lazaryan,
Lazaryan St., 2, Dnipro,
Ukraine, 49010, tel.
+38 (056) 373 19
09,
e-mail
atleteba@gmail.com,
ORCID 0000-0002-9032-8602
4*Dep.
«Military Training of Specialists of the
State Special Service of Transport»,
Dnipropetrovsk National University of Railway
Transport named
after Academician V. Lazaryan,
Lazaryan St., 2, Dnipro,
Ukraine, 49010, tel.
+38 (056) 373 19 09,
e-mail otkachov@i.ua, ORCID
0000-0002-1857-7567
the RELATIONSHIP BETWEEN STIFFNESS LOSSES AND
LOSSES
IN BEARINGS OF ROPE BLOCKS
Purpose. To determine the efficiency of rope blocks, it is
necessary to determine the stiffness coefficient of the ropes of
blocks, taking into account the classification group of the
mechanism and the wrapping angle of a block by a rope. At this one
should use well-tested values of the efficiency coefficients of the
rope blocks, taking into account the wrapping angle of a block by a
rope and the analytically found friction coefficients of the rolling
bearings given to the trunnion. Methodology. The work
presents the analytical method of determining the coefficient of
bearing resistance of the block when it is rotated by both the inner
and outer cages, as well as the design scheme of the bearing of the
block. Findings. The analysis of the lubrication method
effect, the operating mode of the mechanism and the wrapping angle
of a block by a rope on losses in bearings was carried out for rope
blocks. The corresponding comparative tables of losses are given.
Analysis of the obtained calculation results allows us to establish:
1) the main resistance affecting the cable blocks efficiency is the
resistance in bearings; 2) the second largest component is the
stiffness losses, depending on the operating mode, the wrapping
angle of a block by a rope, the type of bearing lubrication; 3)
the block efficiency when rotating the inner cage is higher than
rotating the outer one by about 3% with thick lubrication and 1M
mode; 4) in the sequential location of assemblies with a rolling
bearing, it is necessary to strive for the design of the assembly in
which the inner cage rotates; 5) with the number of blocks up to 5,
one can use the recommended definitions of block bearings in the
literature with an error in the efficiency value of up to 10%.
Originality. The authors obtained values of resistances in
the rolling bearings of the rope blocks and stiffness losses due to
the girth of the block by the rope. In this case, dependences were
used to determine the coefficient of rolling friction, obtained
using the Hertz analytic dependences on determination of contact
stresses and deformations, as well as the experimental values of
the coefficient of rolling friction for the blocks. Practical
value. The resistance values obtained by the authors can be used
for refined calculations of the mechanisms of machines.
Key words: block; rope; losses; bearing; stiffness
REFERENCES
Bogomas,
V. M., Briljova, M. G., Bondarenko, L. M., & Glavatskij, K. C.
(2015). Vplyv koefitsiienta tertia kovzannia ta kuta obkhvatu
kolodkoiu ta strichkoiu halmivnoho shkiva na rivnovahu vazhilnoi
systemy. Bulletin National University
of Water and Environmental Engineering, Technical Sciences,
2,
120-125.
Dovbnia,
M. P. (2002). Teoretychne vyznachennia syly kovzannia pry kochenni.
Problems of Tribology,
2,
103-106.
Kovalskiy,
B. S. (1986). Poteri na blokakh kanatnykh polispastov. Construction
and Road Building Machines, 8,
34-37.
Kozhevnikov,
S. N. (1969). Teoriya mashin i
mekhanizmov. Moscow:
Mashinostroeniye.
Boltenkova,
O. M., Davydov, O. Y., Yegorov, V. G., & Ulshin, S. V. (2013).
Mekhanika. Soprotivleniye materialov
(teoriya i praktika). Voronezh:
Voronezh State University of Engineering Technologies.
Gumerova,
K. S., Petukhov, N. P., Kotlyar, V. M., & Sidorin S. G. (2014).
Prikladnaya mekhanika.
Kazan: Kazan National Research Technological University.
Gryaznov,
B. A., Bukhtiyarov, V. K., Kakuevitskiy, V. A., Aronovich, D. A., &
Nalimov, Y. S. (2013). Primeneniye
i prochnost polimernykh materialov pri izgotovlenii i remonte
mashin i oborudovaniya. B. A.
Lyashenko (Ed.). Kyiv: G.S. Pisarenko Institute for Problems of
Strength of the National Academy of Sciences of Ukraine.
Sinenko,
Y. G., & Konishcheva, O. V. (2015). Mekhanika.
Krasnoyarsk: SibFU.
Bohomaz,
V. M., Bondarenko, L. M., Hlavatskyi, K. T., & Sokol,
K. O.(2015). Method
of the drive power determination of the mechanisms of the bridge
crane movement considering the rolling friction. Science
and Transport Progress, 5
(59), 123-131. doi:10.15802/stp2015/55335
Aleksandrov,
M. P., Gokhberg, M. M., Kovin, A. A., Kulkova, N. N., Mazover, I.
S., Nevzorov, L. A., & … Sokolov S.A. (1988). Spravochnik po
kranam (Vol. 1-2). Kharakteristiki i
konstruktivnyye
skhemy kranov. Kranovyye
mekhanizmy, ikh detali i uzly. Tekhnicheskaya ekspluatatsiya kranov
(Vol. 2). M. M. Gokhberg (Ed.). Moscow: Mashinostroeniye.
Yakovlev,
S. A., Bondarenko, L. N. (2003). Sootnosheniya mezhdu pokazatelyami
soprotivleniya kacheniyu i skolzheniyu v uzlakh mashin. Mining,
constructional, road and melioration machines,
62,
88-92.
Gao,
A., Yun, Z., Zhidong, W., & Hao, L. (2017). A general friction
model of discrete interactions for tendon actuated dexterous
manipulators. Journal of Mechanisms
and Robotics, 9
(4), 041019. doi:10.1115/1.4036719
Makhkamov,
K. K. (2017). Energy analysis of wear of sliding friction units.
Journal of Friction and Wear,
38 (2),
168-172. doi:0.3103/s1068366617020143
Rahaman,
M. L., & Zhang, L. (2017). Size effect on friction and wear
mechanisms of bulk metallic glass. Wear,
376-377,
1522-1527. doi:10.1016/j.wear.2017.01.068
Tabor
D. (1955). The mechanism of rolling friction: The elastic range.
Proceedings of the Royal Society A:
Mathematical, Physical and Engineering Sciences,
229
(1177), 198-220. doi:10.1098/rspa.1955.0082
Статья рекомендована
к публикации д.т.н., проф. С. В. Ракшой
(Украина);
д.т.н., проф. В. Г. Заренбиным
(Украина)
Поступила
в редколлегию: 22.03.2017
Принята
к печати: 06.07.2017
doi 10.15802/stp2017/109453 ©
В. Н. Богомаз, Л. Н. Бондаренко, М. В.
Очеретнюк, А. А. Ткачов, 2017
, (1.1)
– коэффициент сопротивления блока,
, (1.2)
– угол обхвата канатом блока в радианах;
– диаметры блока и упора в сантиметрах;
– коэффициент трения подшипника,
приведенный к цапфе;
–
коэффициент жесткости.
. (1.3)
. (2)
, (3)
,
(4)
– полуширина пятна контакта, определяемая
согласно теории Герца;
– коэффициент гистерезисных потерь.
имеет молекулярно-механическую природу,
то определить его для практического
использования вряд ли возможно. Как
следствие, эти формулы не получили
практического применения.
[2].
, (5)
, (6)
– радиус качения тела в метрах.
.
через внутреннюю обойму передается
шарикам, которые нагружаются неравномерно.
,
а наименьшую – шарик с центром,
расположенным на линии, перпендикулярной
направлению силы
.
Нагрузку воспринимают только те шарики,
которые располагаются ниже горизонтального
диаметра. Силы
,
координированные углами
относительно линии где действия
силы
,
будем считать симметричными.
, (7)
– число шариков по условиям сборки.
. (8)
(9)
– величина, зависящая от отношения
коэффициентов уравнения эллипса
касания.
,
– радиус шарика;
– радиус желоба;
– радиус беговой дорожки внутренней
обоймы, который определяется по формуле
.
коэффициент трения качения выводится
из формулы (6):
, (10)
. (11)
, (12)
и
,
поэтому боковых роликов два: расположенных
под углом
при
или
при
.
Поэтому сопротивление их качению по
внутренней и наружной обоймам определяется
по формулам (9) – (12) с удвоением
сопротивления (11).
.
.
,
приложенной к радиусу цапфы,
.
. (13)
,
то в этом случае, на этом расстоянии,
шарики будут скользить по внутренней
обойме ввиду большего их сопротивления
качению по наружной обойме, являющегося
движущей силой скольжения.
,
(14)
– коэффициент трения скольжения
между шариками и обоймой.
и
,
определив затем КПД подшипника, сначала
без учета жесткостных потерь [10]:
. (15)
,
которой соответствует шариковый
подшипник № 313 со статической нагрузкой
кг массы,
и
мм
(рис. 1). Остальные данные примем следующими
[4]:
мм;
мм;
количество шариков
при угле между шариками
.
.
На один боковой шарик согласно формуле
(8) действует
кН.
мм,
мм,
а сопротивление качению одного шарика
составит
Н;
Н;
Н;
Н.
):
при вращении наружной обоймы подшипников
при жидкостной смазке
и при густой смазке
,
при отсутствии смазки
.
Отметим, что при вращении внутренней
обоймы эта величина составит
.
=0,980.
=180
и густой смазке (
=0,1328)
– табл. 4.