ISSN 2307–3489 (Print), ІSSN
2307–6666 (Online)
Наука та прогрес
транспорту. Вісник Дніпропетровського
національного університету залізничного
транспорту, 2017, № 3 (69)
електричний
ТРАНСПОРТ
електричний
ТРАНСПОРТ
UDC
629.423.2:621.313.333
H. K. Hetman1,
S. l. Marikutsa2*
1Dep.
«Electric Rolling Stock of Railways», Dnipropetrovsk National
University
of Railway Transport named after Academician V. Lazaryan,
Lazaryan St., 2,
Dnipro,
Ukraine, 49010, tel. +38 (056) 373 15 31,
e-mail getman-gk@i.ua,
ORCID
0000-0002-3471-6096
2*Dep. «Electric Rolling Stock of
Railways», Dnipropetrovsk National University
of Railway Transport
named after Academician V. Lazaryan, Lazaryan St., 2,
Dnipro,
Ukraine, 49010, tel. +38 (056) 373 15 31,
e-mail
marikutsasergei@gmail.com,
ORCID 0000-0002-0429-6633
selection of rational parameters
of the nominal mode
electric
trains with asynchronous
traction drive
Purpose.
Parameters of the nominal mode are related to the most
important performance indicators of traction means, therefore, the
problems of choosing their optimal values always inevitably arise
when forming technical requirements for a new rolling stock. The
paper describes the features of solving the above-mentioned problems
for electric trains with an asynchronous traction drive in the case
of two-zone and three-zone frequency control of power. Methodology.
Power of nominal mode of the rolling stock should be
chosen in such a way that it would be possible to realize a
predetermined travel time along in the section or the movement speed.
On that basis, and also taking into account the fact that the
important operational characteristics of electric trains include the
acceleration value during the start-up and acceleration at the design
speed, we will formulate the problem of
determining the nominal power. In the task for a given range of
traction, it is necessary to find such a value of the nominal mode
power and the corresponding force value to ensure the ability to
carry out transportations with the given level of average speed with
minimal energy consumption for traction. At the same time, it is
necessary to fulfill the following conditions: a) the speed of
the electric train on the section does not exceed the established
limits; b) it is possible to realize the given values of
accelerations. A more detailed consideration of the problem shows
that in real conditions, when the starting acceleration and the mass
of the train are given, the problem of determining electric train
power is practically reduced to determining the optimal value of the
nominal mode speed. Findings.
The task of choosing the optimal values of the nominal
mode speed is solved by determining the electric power consumption
with the variation of the possible values of starting speed.
Therefore, only those values that ensure the implementation of
the given starting and residual accelerations should be taken into
account. The work shows that the traction force value increases with
the design speed increase and other equal conditions, if the starting
speed is increased. Originality.
Authors developed the methodology for determining the optimal values
of the nominal mode parameters of electric trains with an
asynchronous traction drive, with two-zone and three-zone frequency
power regulation. Practical value.
The above mentioned methodology can be the basis when forming
technical requirements for new rolling stock for Ukraine’s
railways.
Keywords: electric train; starting and residual
acceleration; starting speed; motion equation; traction
characteristic; power regulation zone;
specific force
Introduction
Parameters of the nominal mode
are related to the most important performance indicators of the
electric rolling stock. Therefore, the problems of determining their
optimal values always inevitably arise when forming technical
requirements for a new rolling stock. For the railways of Ukraine,
these tasks are currently particularly relevant in connection with
the need to renovate morally and physically obsolete locomotive
fleet in conditions of acute shortage of funds, when it is
especially important to avoid the acquisition of inefficient
equipment.
Determining the parameters of
the nominal mode (traction force, speed of movement and power) of
traction means is the main objective of the so-called traction
supply problems. Review of the papers on this topic is given in [1,
5, 6]. There one can find the ways of solving such problems with
regard to freight and passenger electric locomotives, mainly with a
collector traction drive.
Purpose
In the case of electric trains,
the tasks of determining the parameters of nominal mode were
considered in a smaller volume and only with reference to the
collector traction drive [3, 4, 9]. In this article, the features of
these traction supply problems for electric trains with an
asynchronous traction drive are described.
Methodology
The nominal mode power should
be selected in such a way that it would be possible to realize the
predetermined travel time along the section (or movement speed).
With such a «blurred» statement of the problem, its solution
contains many variants, and when determining the rules for selecting
the best ones the work [6] proposes to apply the following
indicators for a comparative evaluation of the variants:
– specific
power consumption for train traction;
– excess
capacity of the required locomotive fleet;
– the mean
value of the traction multiplicity required for transportations.
Last two indicators make sense
for freight and passenger traffic, as the weight (composition) of
trains varies widely.
In the case of electric trains
only the first of the above-mentioned indicators is used:
electricity consumption, since in the general case, when the
specific power is distributed along the length of the train, i.e.
which accounts for 1 ton of train weight, it does not depend on
train composition. For electric trains, where the traction motors
are located in the end cars, the maximum train weight should be
taken into account.
Based on the
above and taking into account that the acceleration value during
starting period (acceleration) аs
and acceleration at the design speed аr
(residual acceleration) refers to the important operational
characteristics, the problem of determining the nominal power of the
electric train is formulated as follows: for the given traction
polygon, it is necessary to find such a value of the nominal mode
power and corresponding traction value, so that it would be possible
to carry out transportations with a given level of average speed
with minimum electricity consumption for traction and the following
conditions would be met:
– the
speed of the train movement in the section does not have to exceed
the established limits;
– it is
possible to realize the given values of acceleration at start (аs)
and the residual one (аr).
A more detailed consideration
of the problem shows that in real conditions, when the starting
acceleration and the train weight are given, the task of traction
supply of electric trains practically reduces to determining the
optimal value of the nominal mode speed.
To be convinced of the validity
of the foregoing, let us determine the factors defining the nominal
mode power.
The traction
force in N,
required to realize the given acceleration а,
is determined on the basis of the equation of the train motion used
for traction calculations [2, 12] as
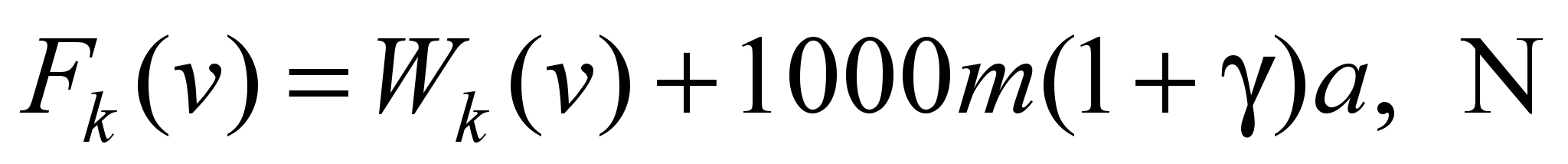 , (1)
, (1)
where
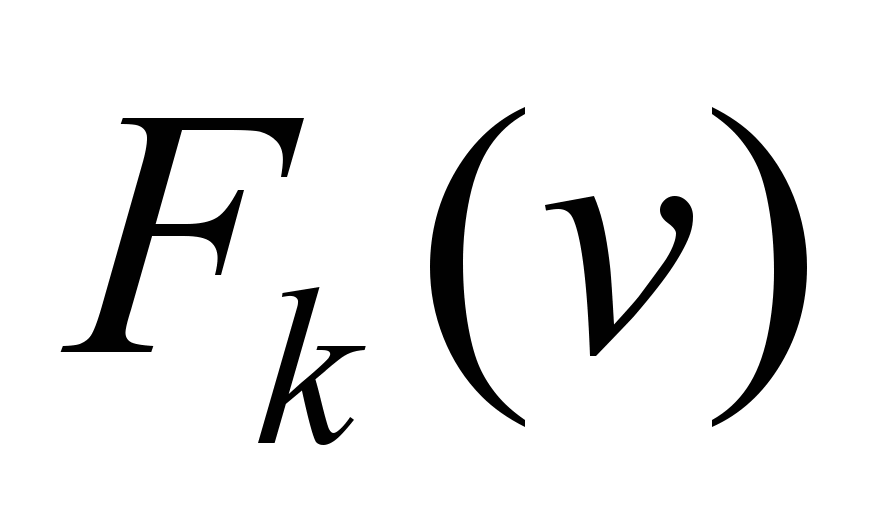 – tangential traction force (on the rim of the driving wheels) of
the motor cars, N;
– tangential traction force (on the rim of the driving wheels) of
the motor cars, N;
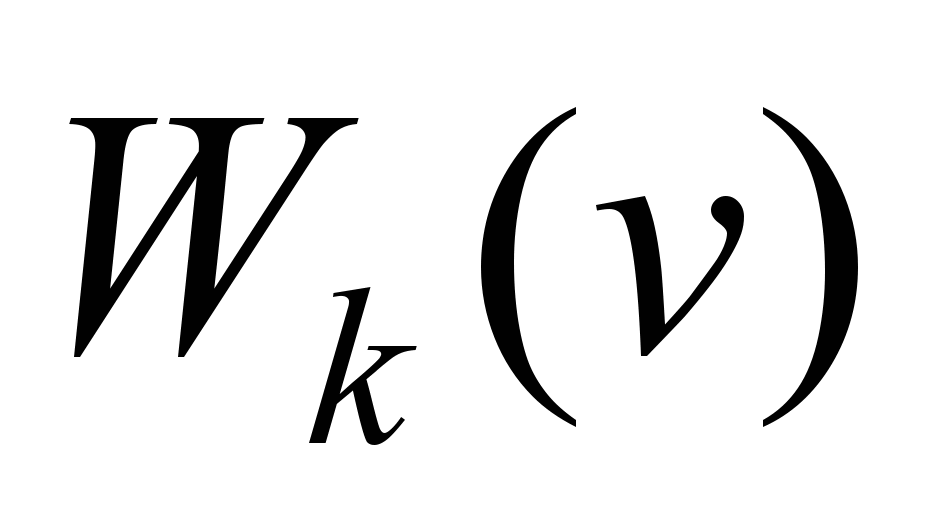 – total movement resistance, N;
– total movement resistance, N;
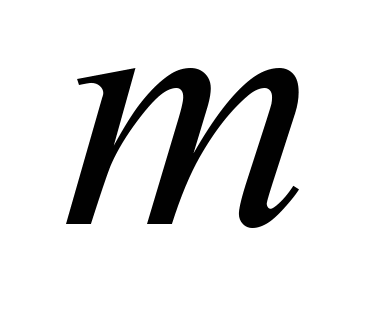 – train weight, t;
– train weight, t;
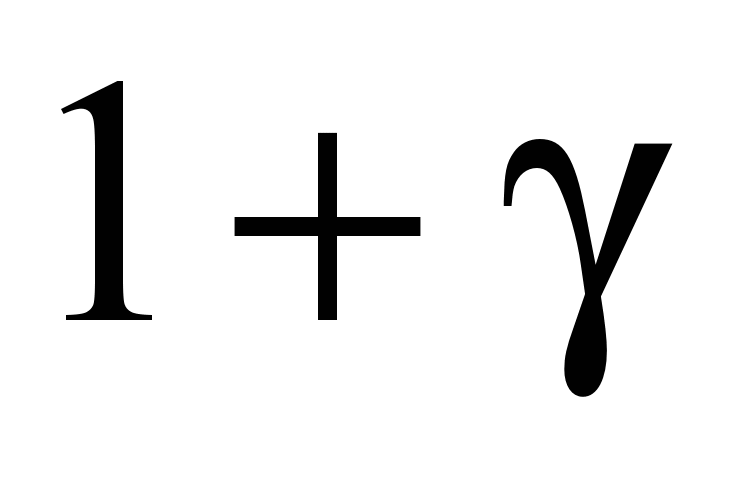 –
inertia coefficient of the rotating masses of the train;
–
inertia coefficient of the rotating masses of the train;
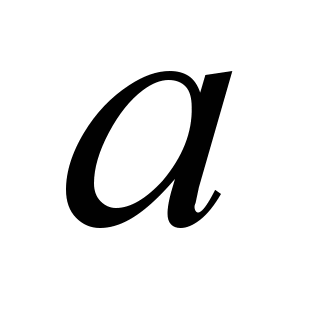 – acceleration, m/s2.
– acceleration, m/s2.
Given that the train movement
resistance
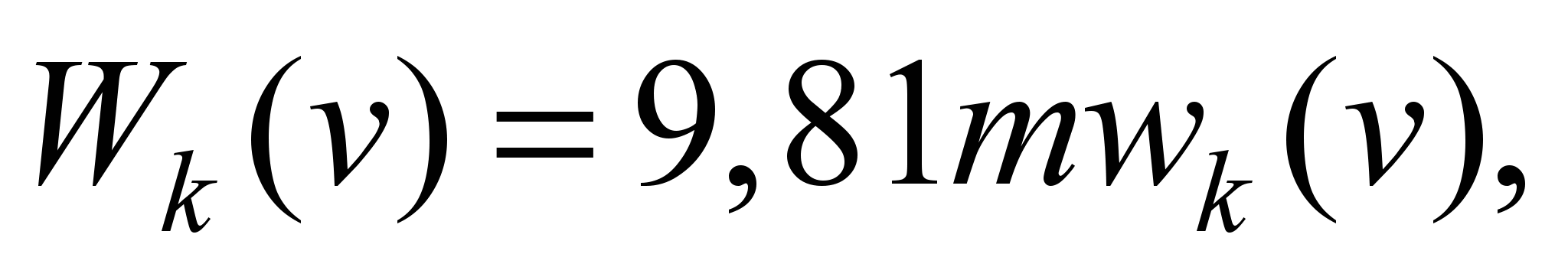 (2)
(2)
where
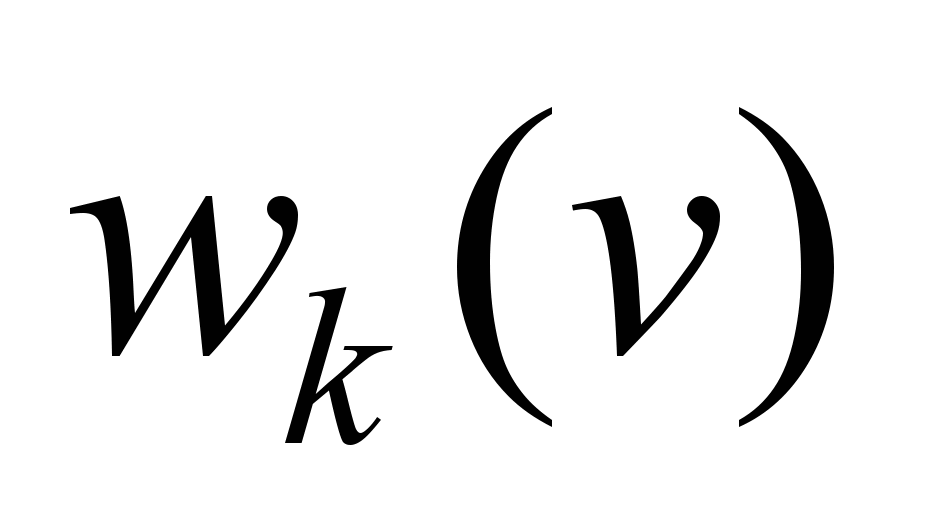 – specific total resistance to train movement, N/kN.
– specific total resistance to train movement, N/kN.
Taking into account (2), we
transform (1) to the form
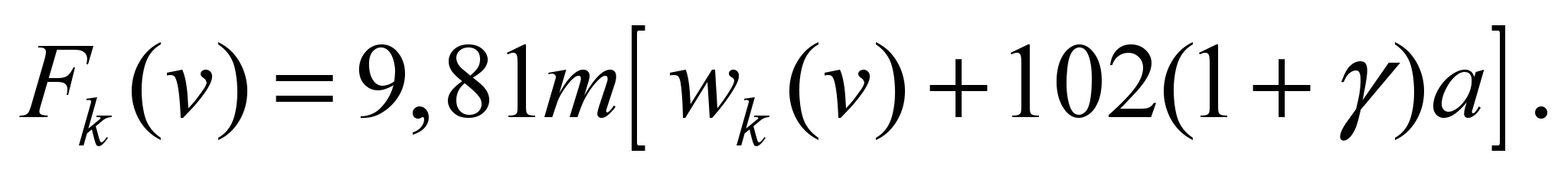 (3)
(3)
When measuring the movement
speed in (km/h) the nominal mode power is defined as
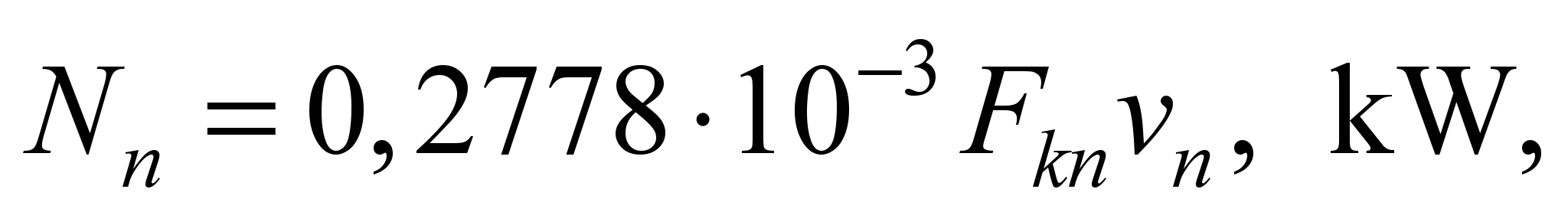 (4)
(4)
where
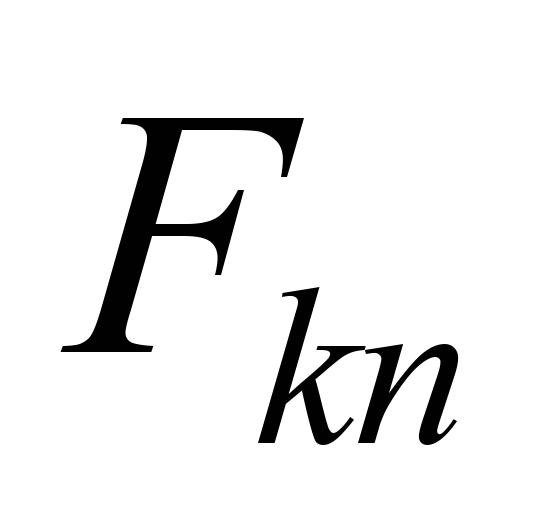 – tangential traction force related to one traction motor, N; the
index «n» – means the value of the parameter corresponding to
the nominal mode.
– tangential traction force related to one traction motor, N; the
index «n» – means the value of the parameter corresponding to
the nominal mode.
Substitution of (3) into (4)
gives
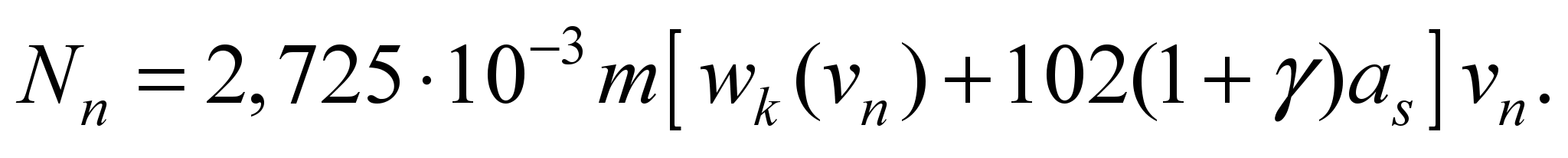 (5)
(5)
Expression
(5) shows that the power of nominal mode at the given values
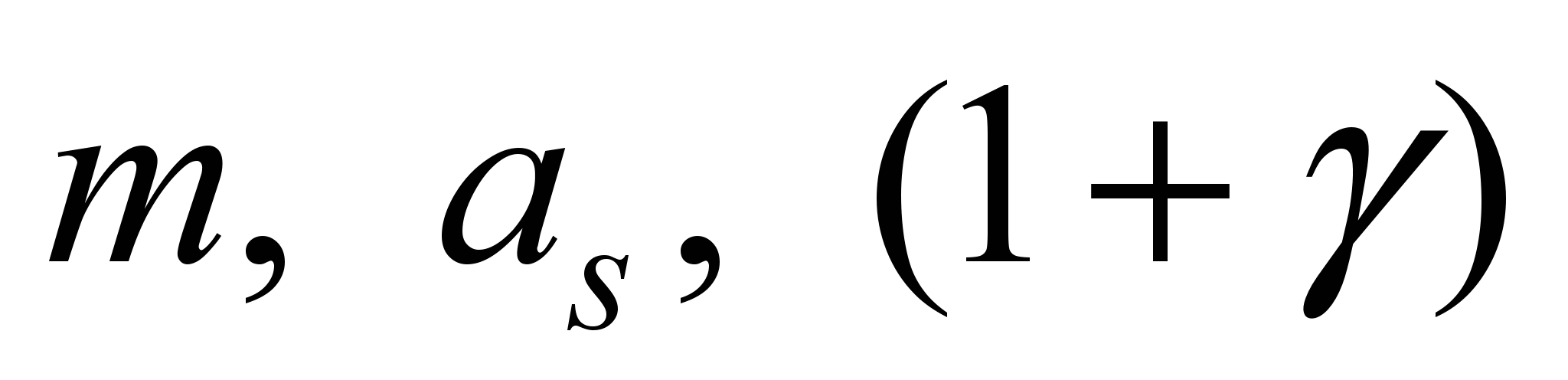 and
and
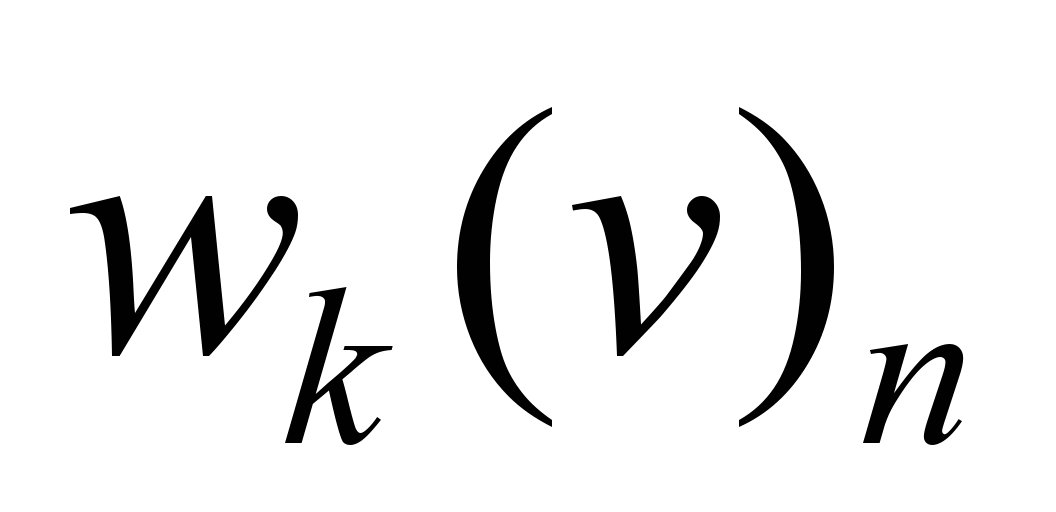 dependencies is definitely determined by the value of the optimal
mode speed, and thus the problem of choosing the optimal parameters
of nominal mode of electric trains reduces to the choice of the
movement speed in the nominal power mode from the condition of
minimizing the electricity consumption for traction of trains.
dependencies is definitely determined by the value of the optimal
mode speed, and thus the problem of choosing the optimal parameters
of nominal mode of electric trains reduces to the choice of the
movement speed in the nominal power mode from the condition of
minimizing the electricity consumption for traction of trains.
To solve the problem, one can
use the method proposed in [6]. Its implementation is carried out by
successively solving the following tasks:
– determination
of control parameters of the train movement equation;
– optimization
of train traffic control for minimal electric power consumption;
– determination
of the nominal mode speed, corresponding to the minimum power
consumption when implementing the given travel time.
To solve the last two of the
problems posed above, it is possible to apply the approaches used in
solving similar problems for passenger electric locomotives [1, 5,
11]. Therefore, we will dwell only on the problem of determining the
control parameters of the motion equation.
Traction calculations are based
on the integration of the motion equation (6).
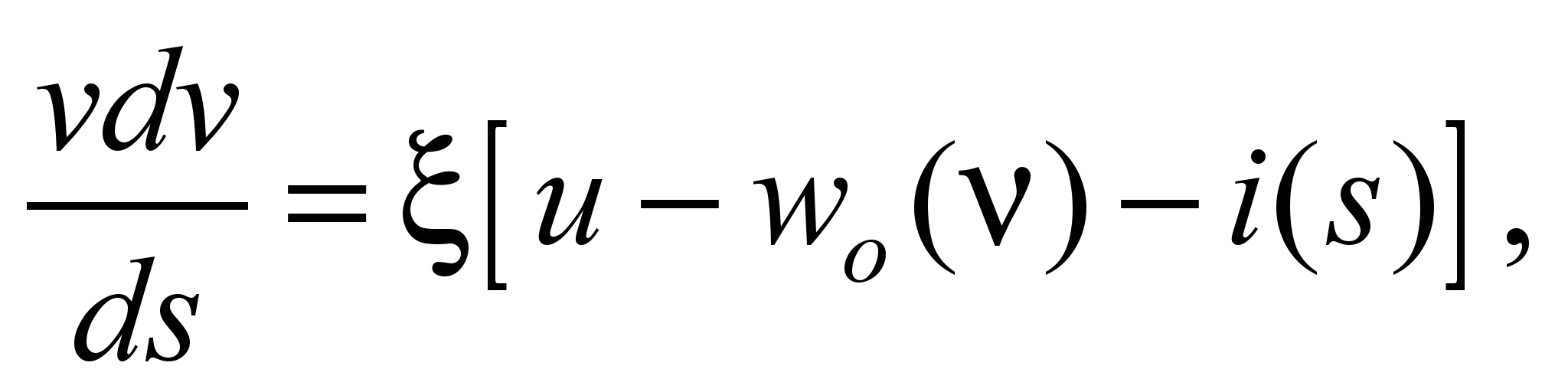 (6)
(6)
where
 − is dimensional coefficient, the value of which depends on the
accepted units of measurement of physical quantities;
− is dimensional coefficient, the value of which depends on the
accepted units of measurement of physical quantities;
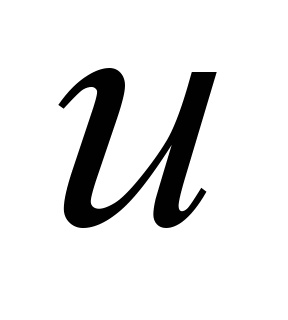 − control parameter;
− control parameter;
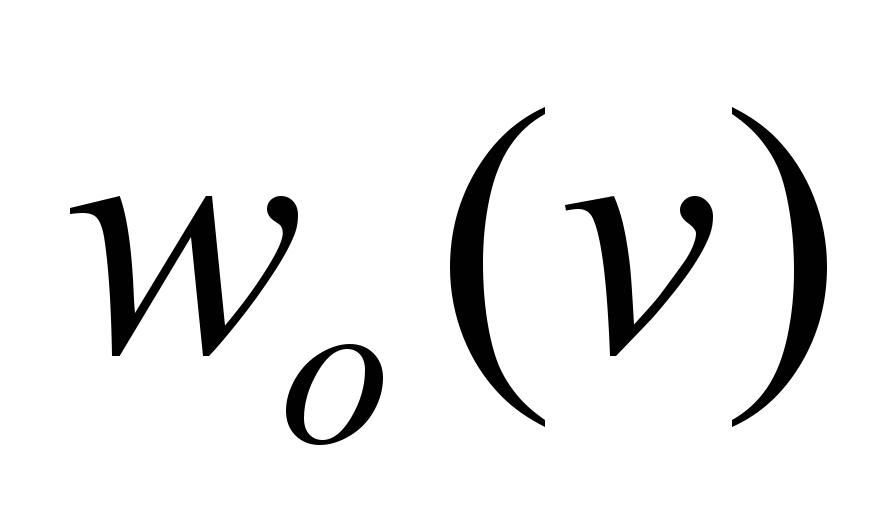 – basic specific
net train resistance;
– basic specific
net train resistance;
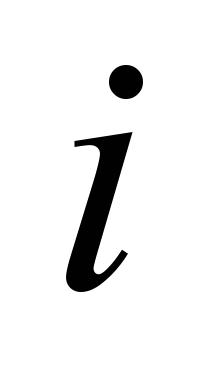 − the value of the longitudinal path gradient, which is a function
of the path
− the value of the longitudinal path gradient, which is a function
of the path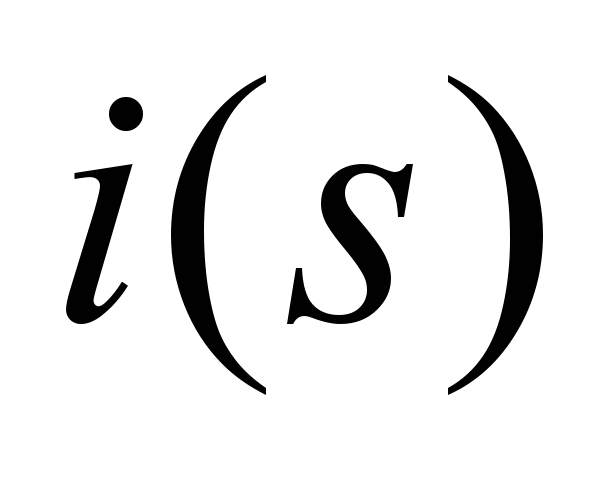 .
.
The value
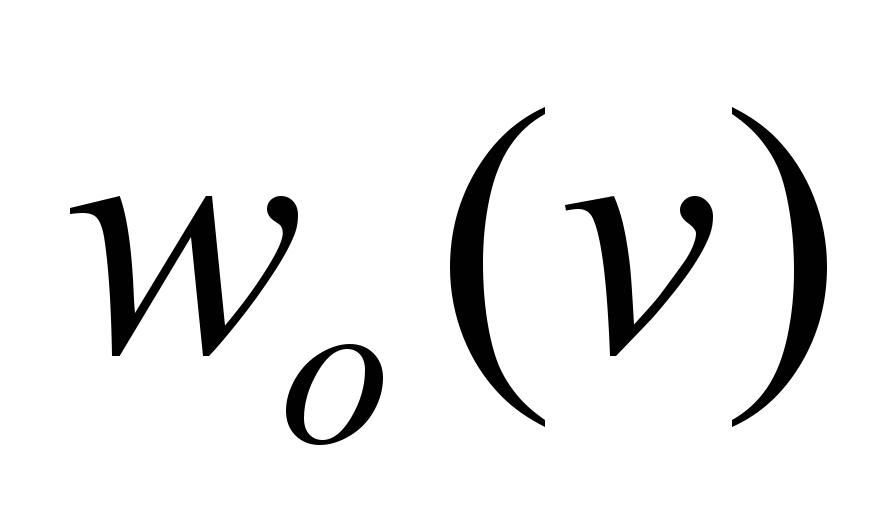 is determined as
is determined as
 (7)
(7)
The
dependences
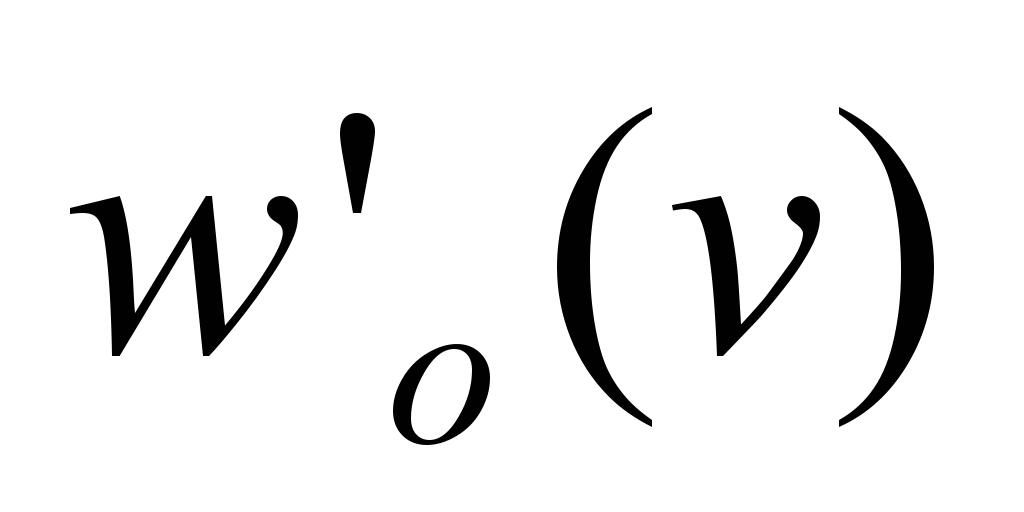 and
and
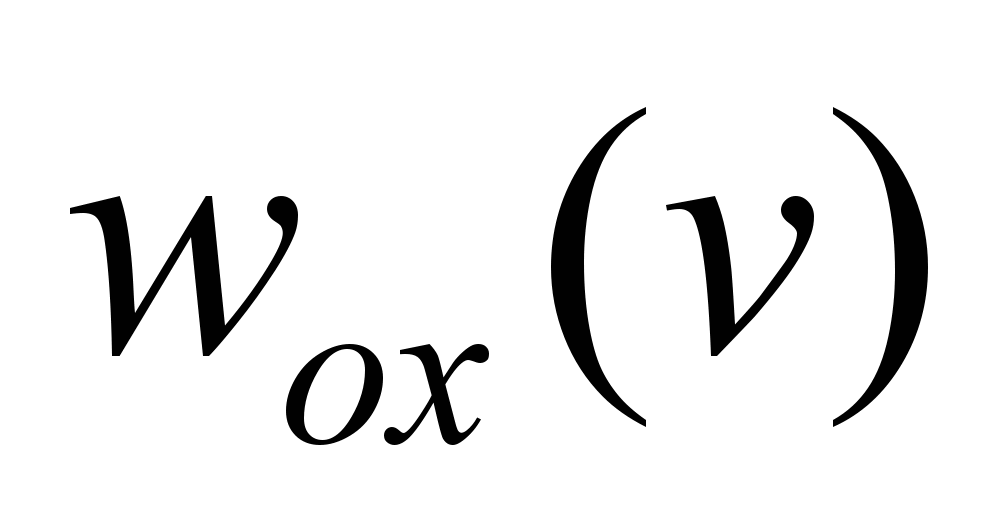 are determined by the corresponding dependences obtained on the
basis of the experimental data [7, 8, 10].
are determined by the corresponding dependences obtained on the
basis of the experimental data [7, 8, 10].
The control
parameter depends on the operation mode of the electric train:
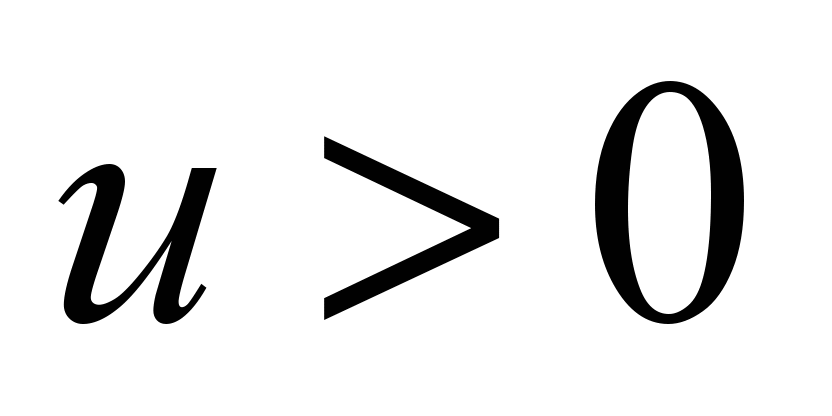 corresponds to the traction mode;
corresponds to the traction mode;
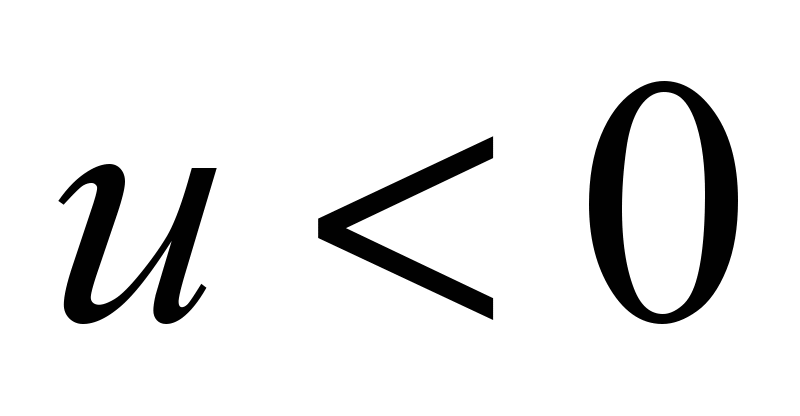 – to the braking mode;
– to the braking mode;
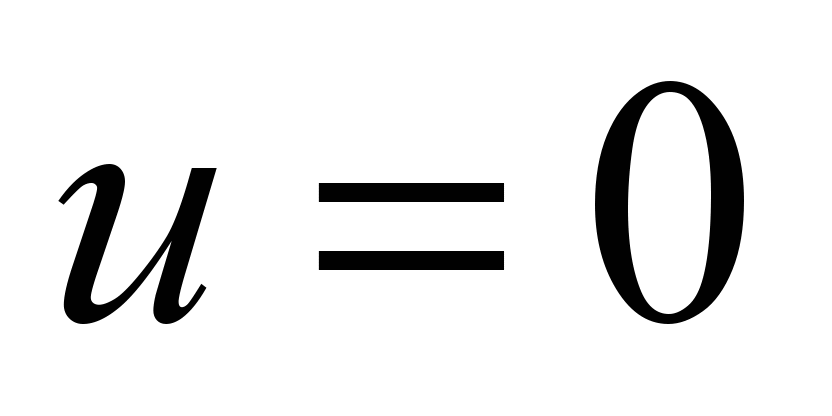 to
the run-out mode.
to
the run-out mode.
Let us consider the traction
drive with a smooth control of the traction power. Then, in the
power calculation the control parameters that satisfy the following
conditions are adopted:
– traction
mode
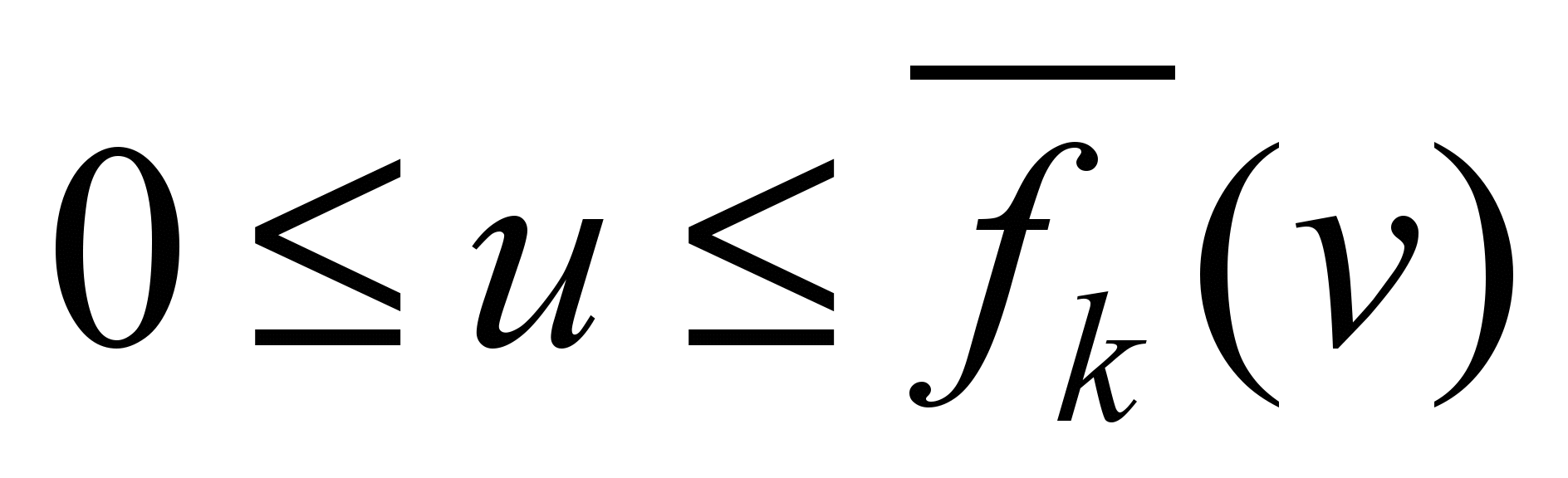 ;
;
– breaking
mode
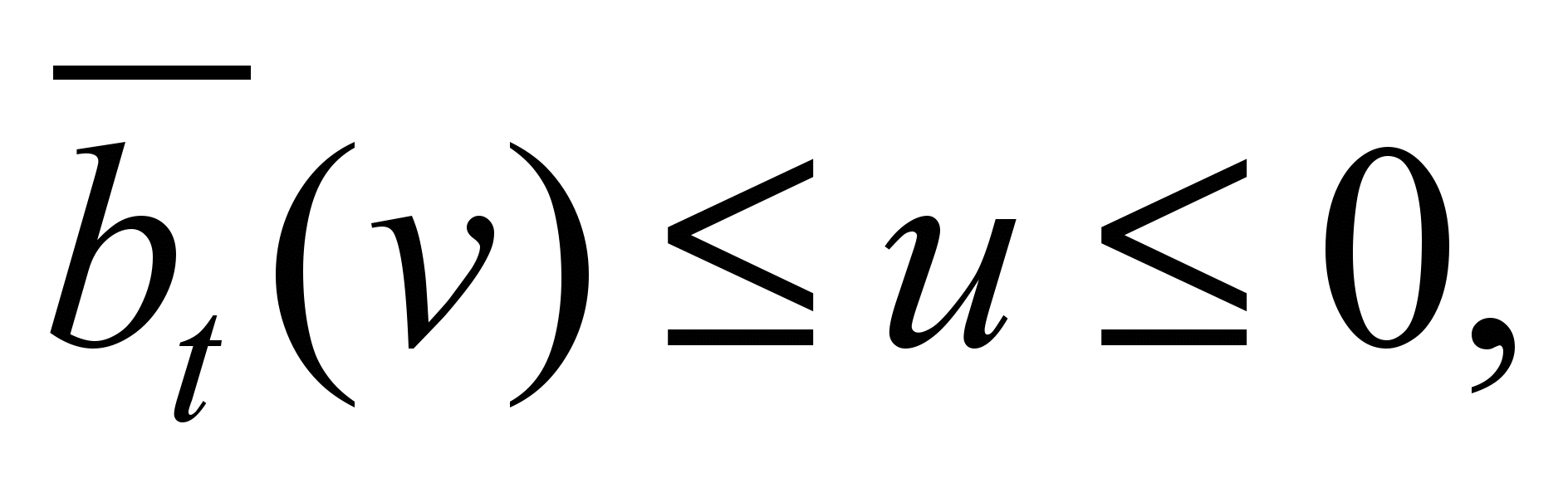
where
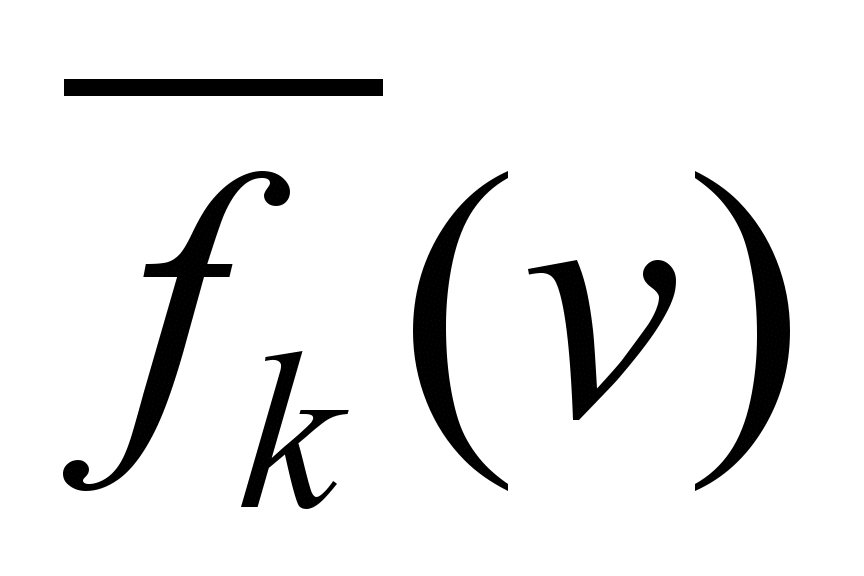 и
и
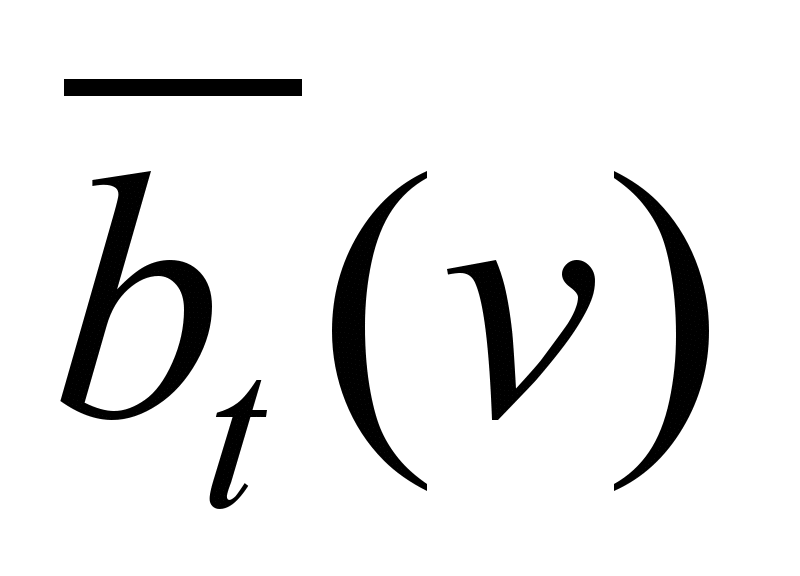 − limiting traction and braking characteristics respectively,
referred to 1 kN of the train weight.
− limiting traction and braking characteristics respectively,
referred to 1 kN of the train weight.
Let us
consider the problem of calculating dependencies
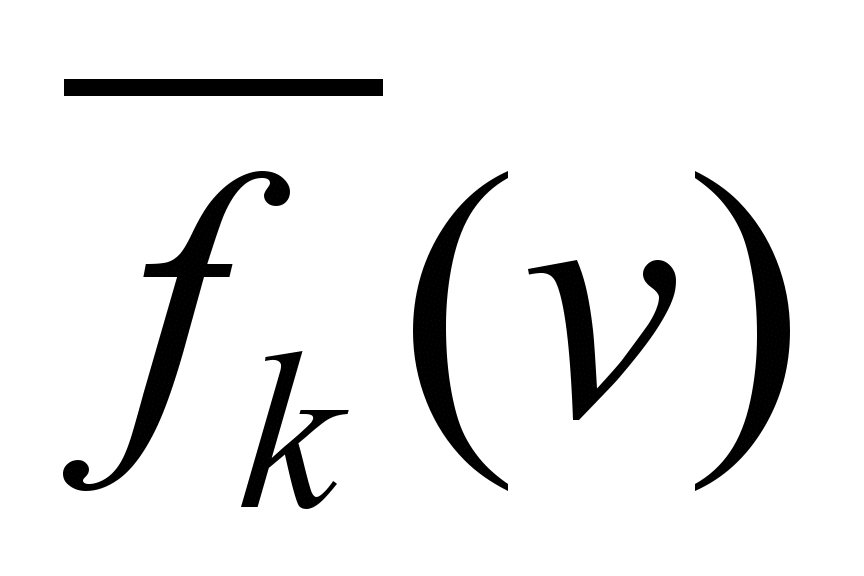 for the two most frequently encountered methods of 3-zone (Fig. 1,
a) and 2-zone (Fig. 1, b) frequency control of the asynchronous
traction drive power for electric trains.
for the two most frequently encountered methods of 3-zone (Fig. 1,
a) and 2-zone (Fig. 1, b) frequency control of the asynchronous
traction drive power for electric trains.
In the case of 3-zone
regulation, there is a possibility:
– in the
zone 1
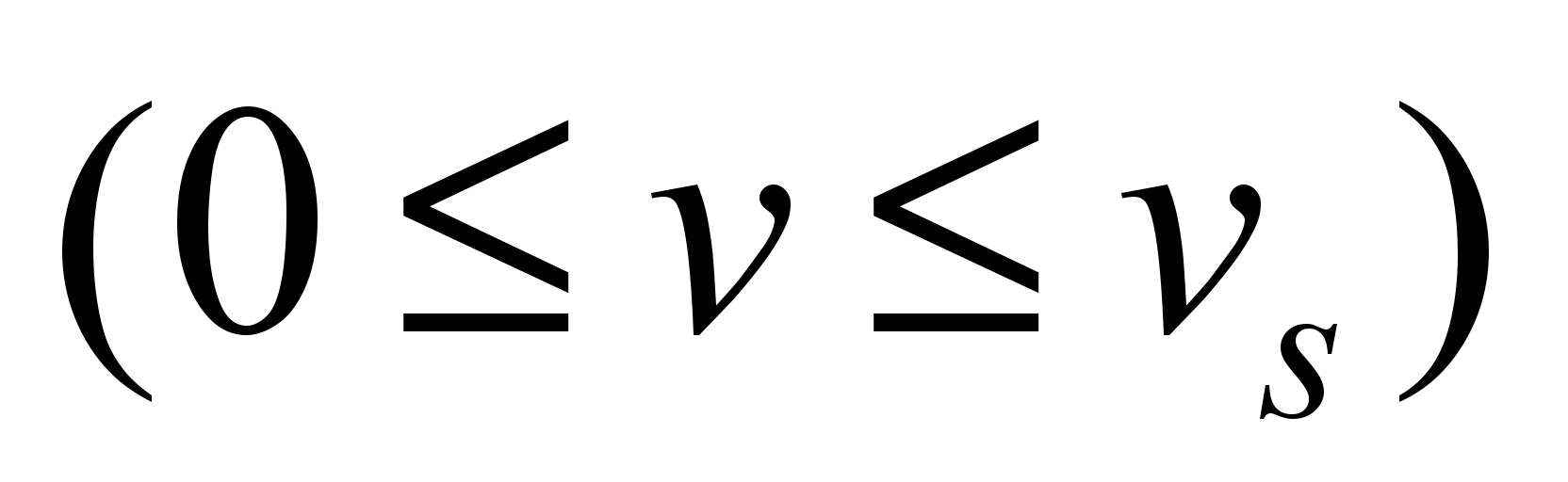 – acceleration with the given starting traction force;
– acceleration with the given starting traction force;
− in zone
2
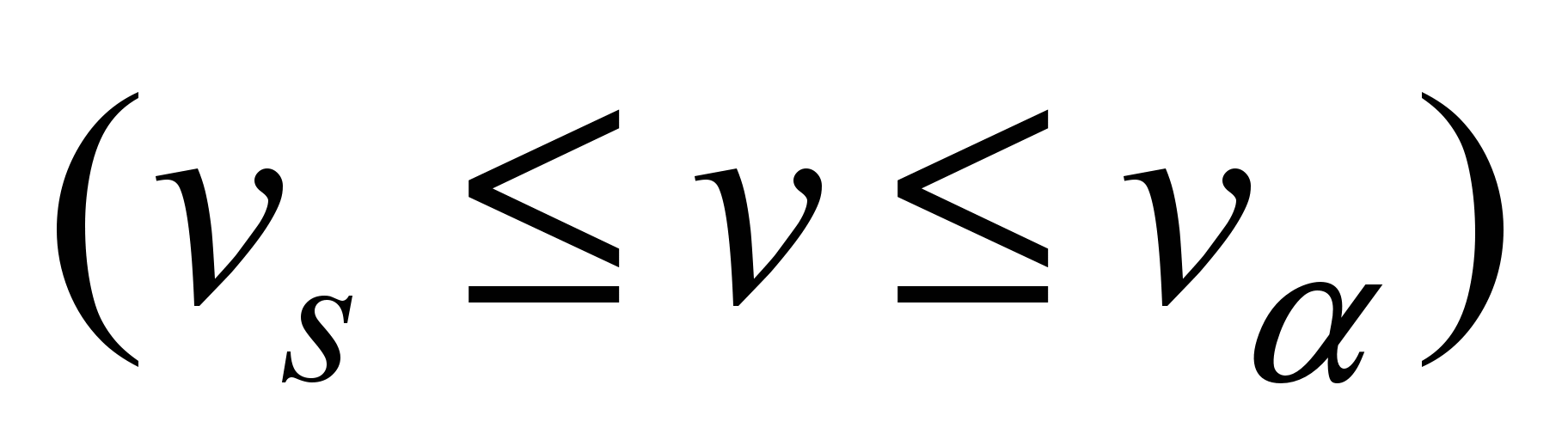 – the realization of the constant traction power;
– the realization of the constant traction power;
− in zone
3
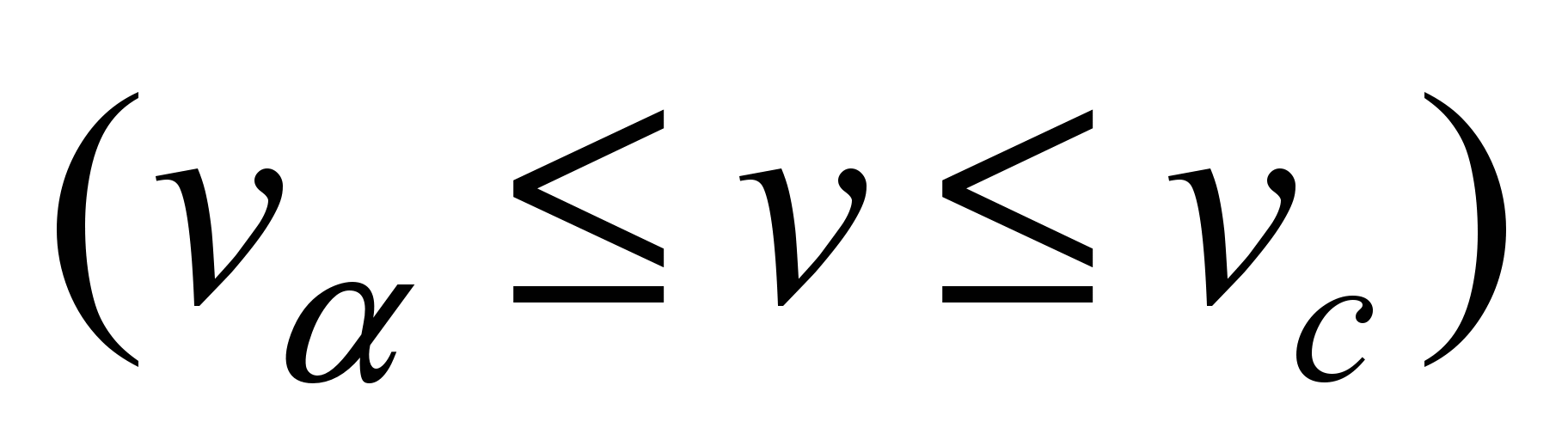 – the traction power control is inversely proportional to the
movement speed.
– the traction power control is inversely proportional to the
movement speed.
In the
acceleration zone
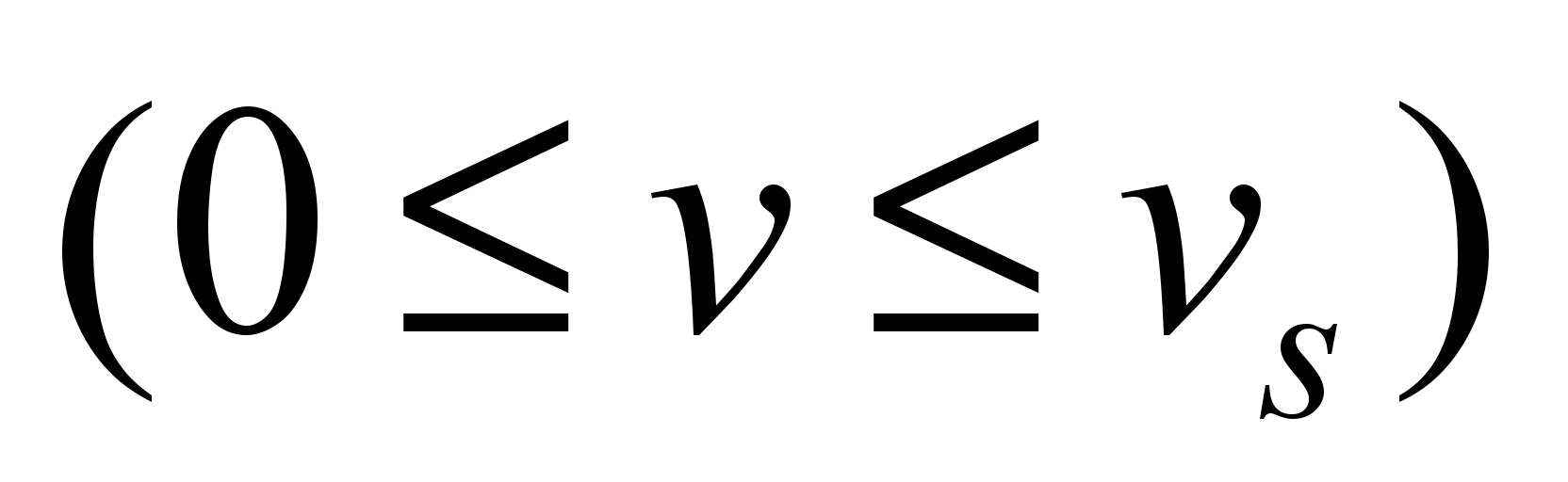 ,
the starting traction force of thrust in specific units (3)
,
the starting traction force of thrust in specific units (3)
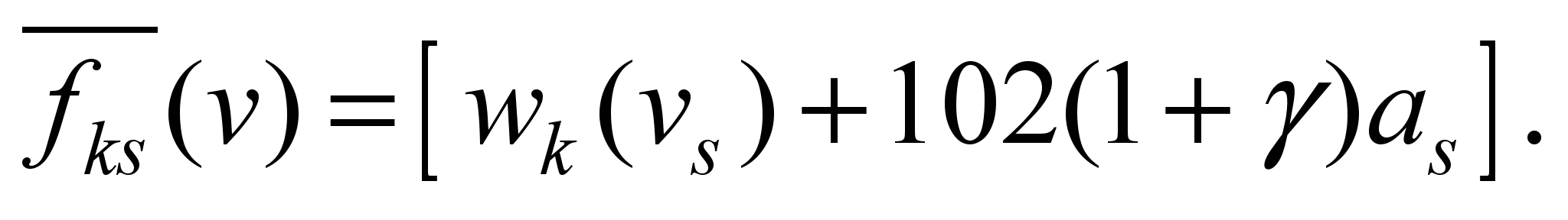 (8)
(8)
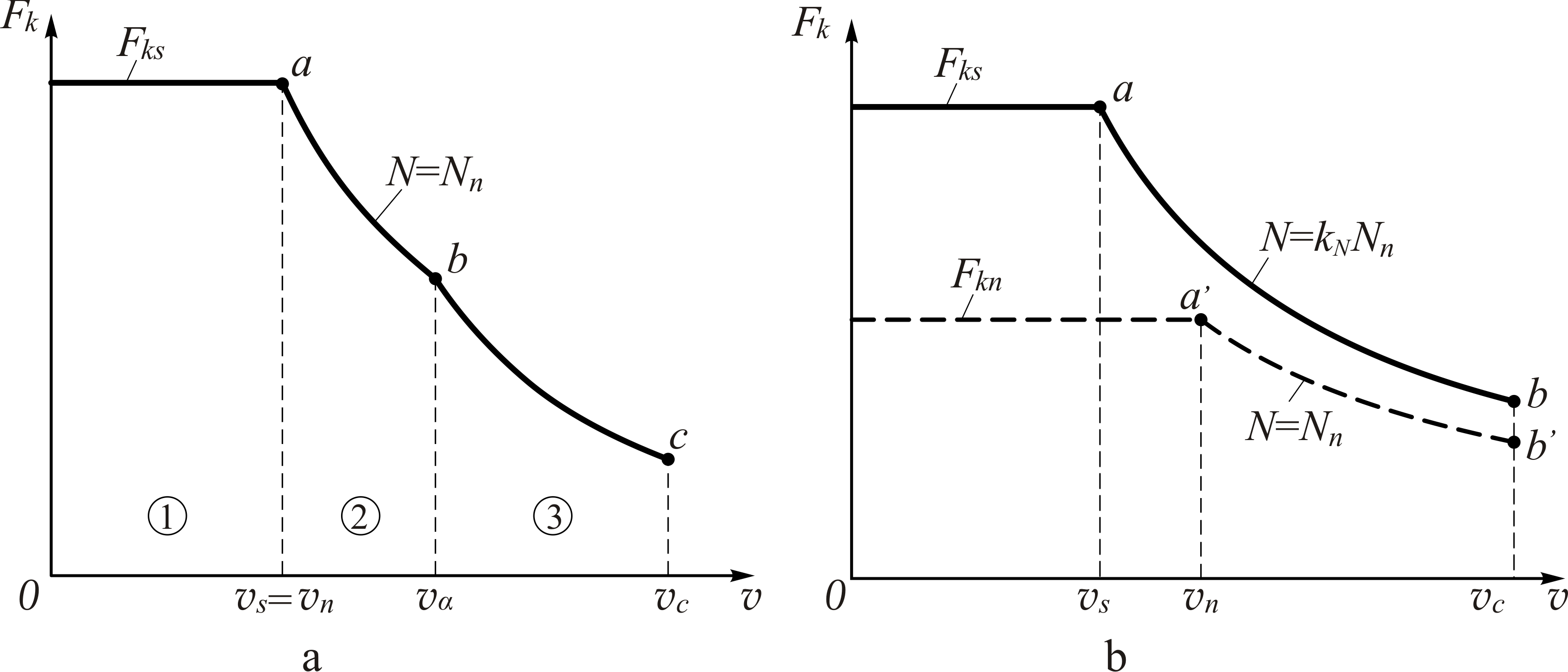
Fig.
1. The limiting traction characteristics of the electric trains,
HRCS2 series:
a
– the Hyundai-Rotem Company and b – EJ675 of SKODA Vagonka
.
In zone 2
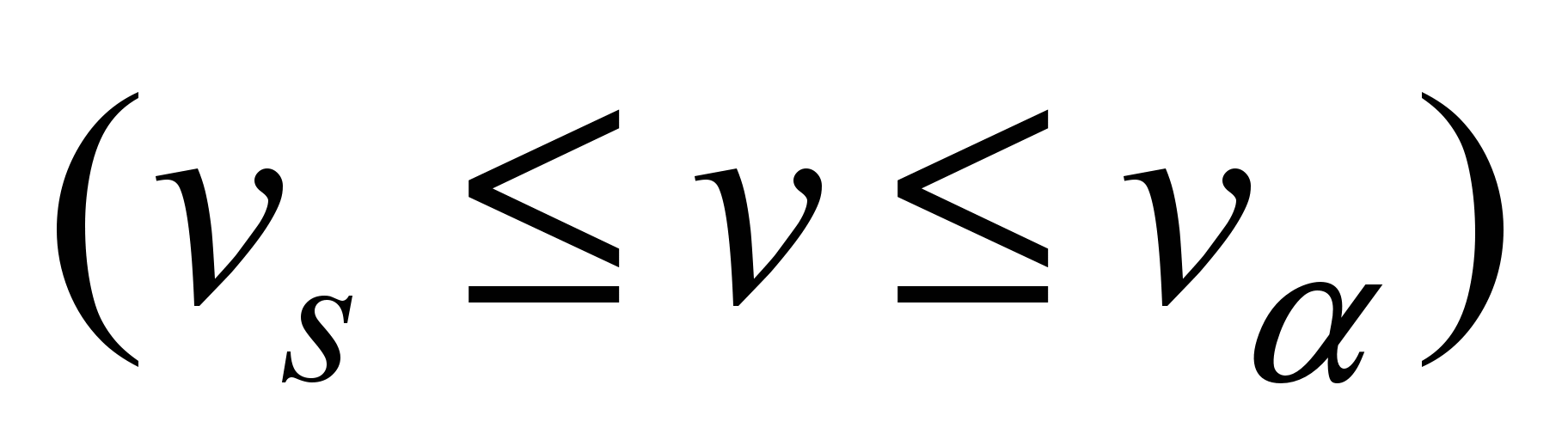
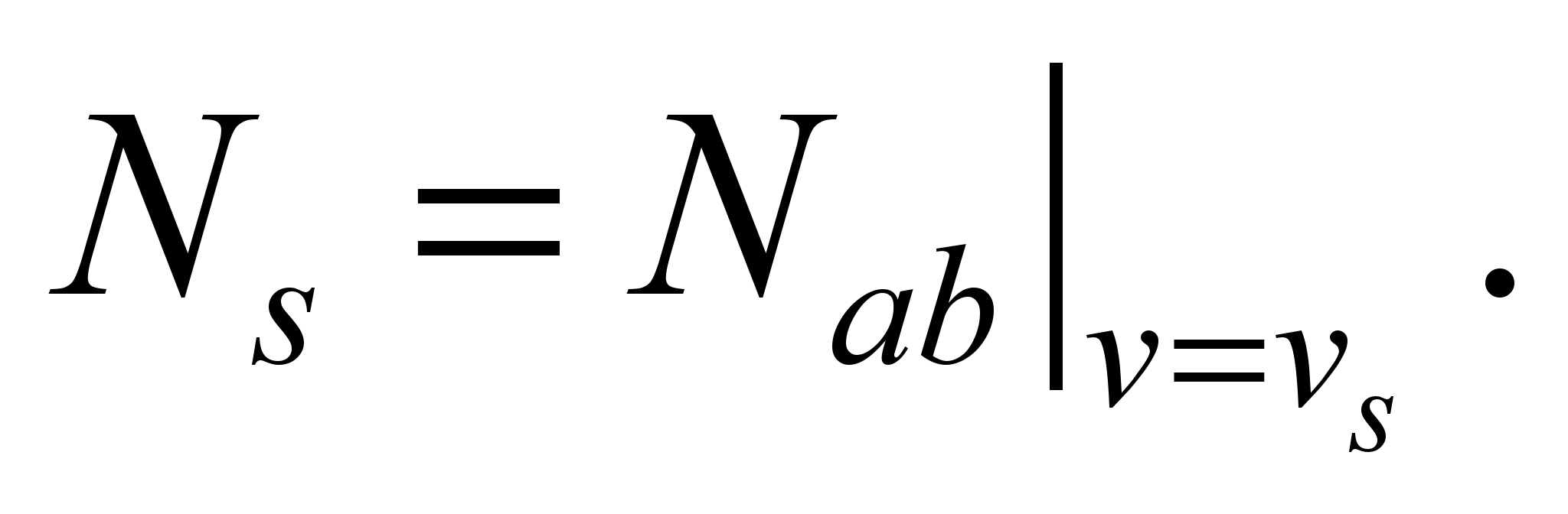
Since
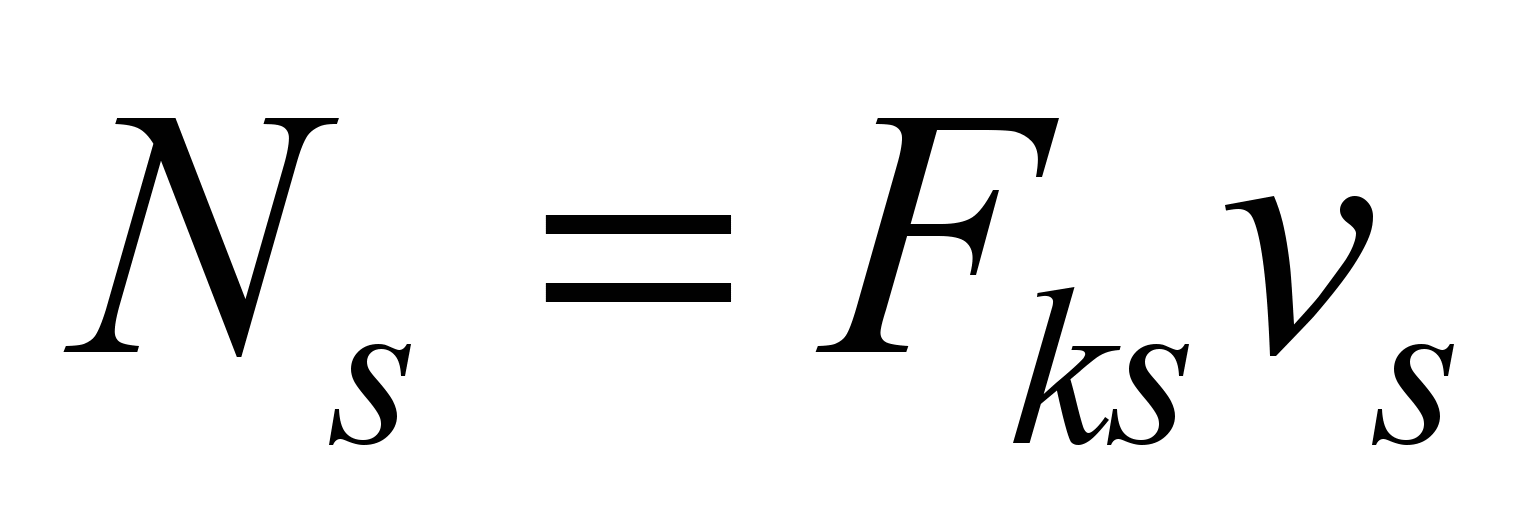 and
and
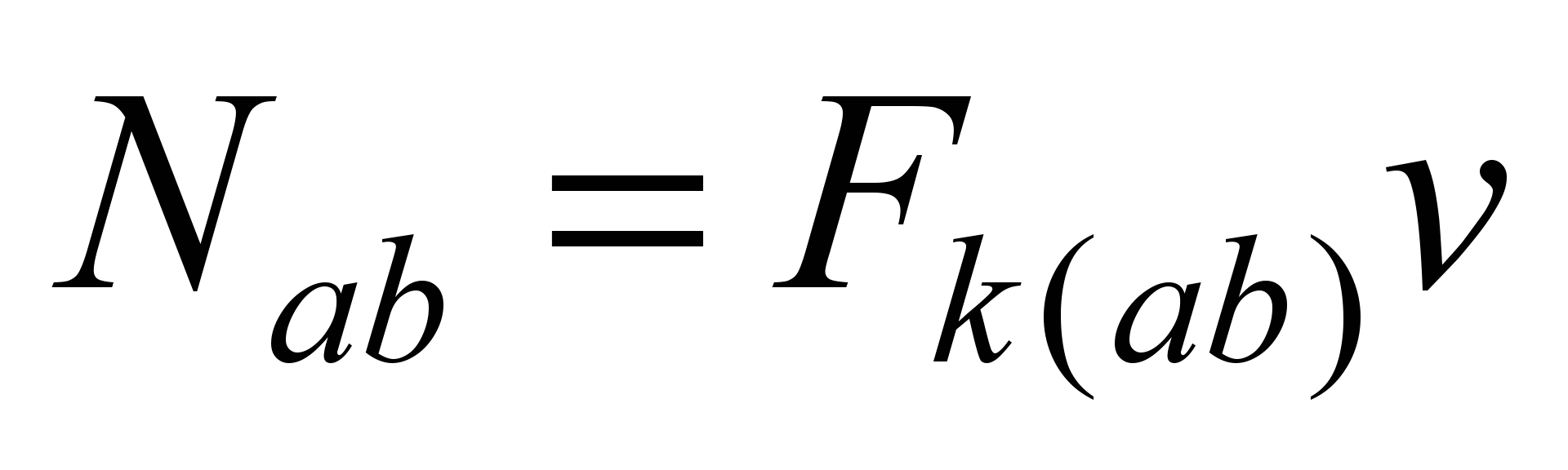 then
then
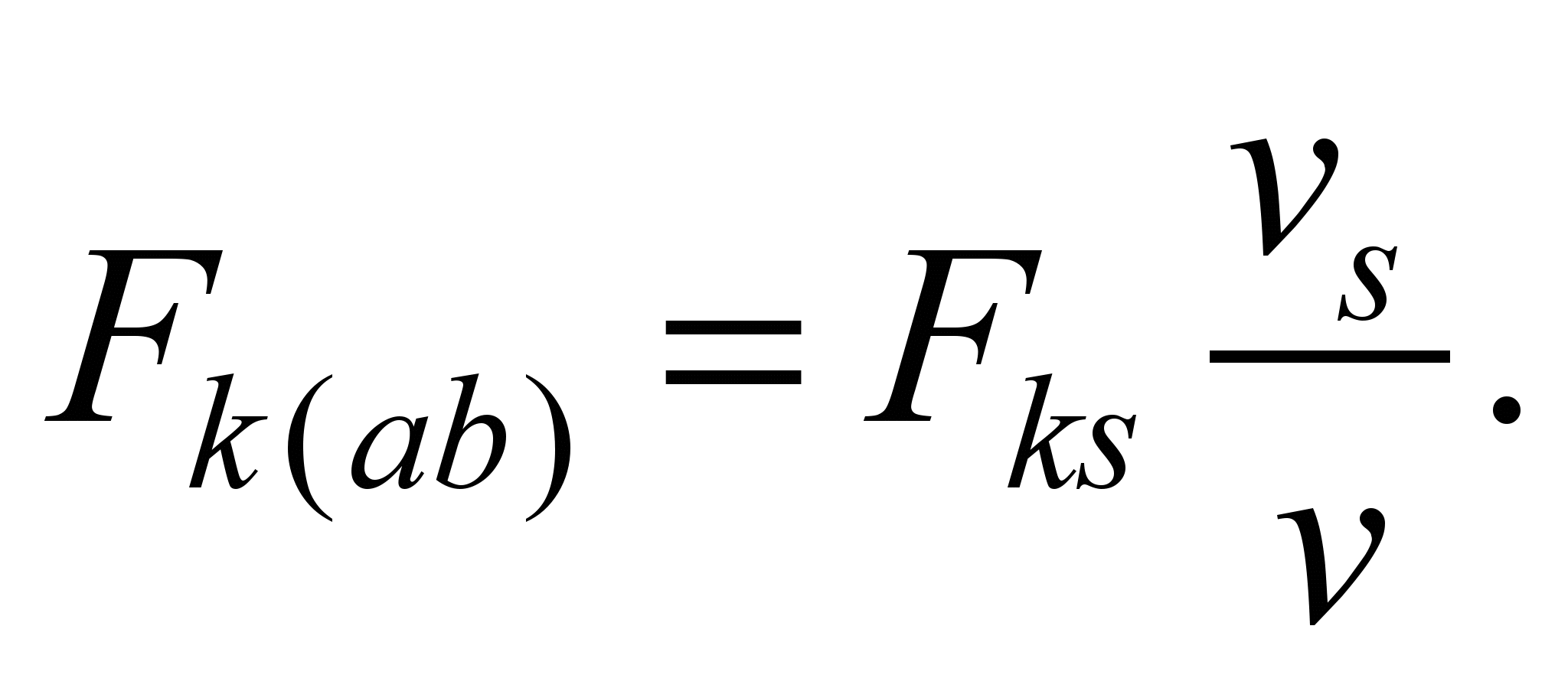 (9)
(9)
Taking into account (8)
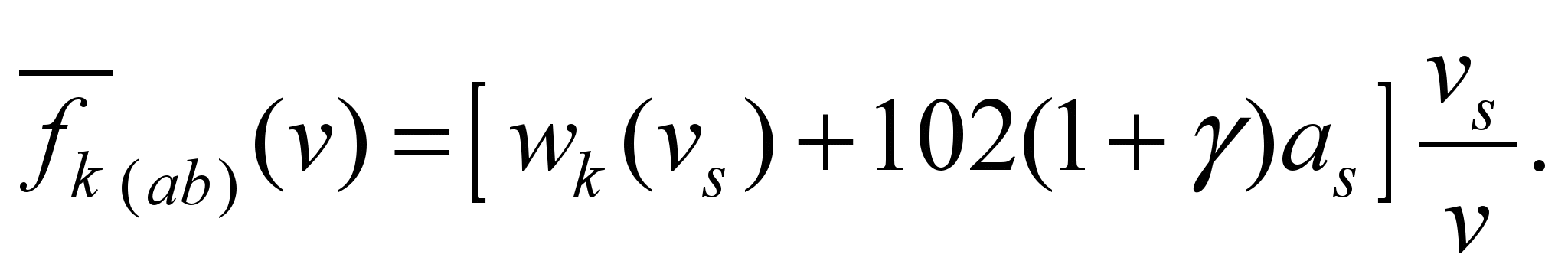 (10)
(10)
In the 3rd
regulation zone
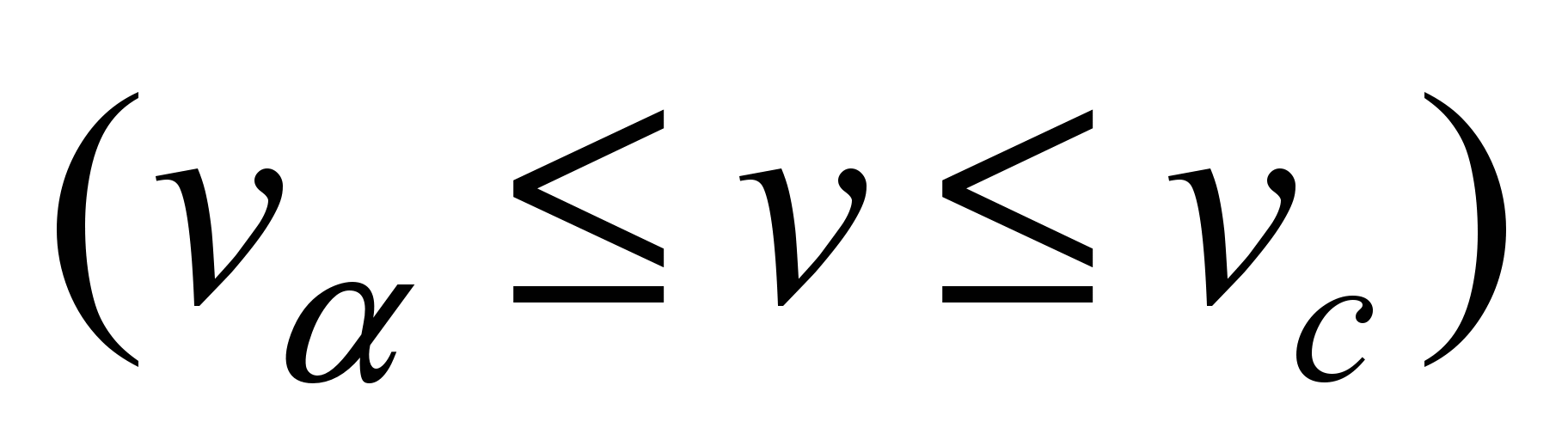 the ultimate traction power
the ultimate traction power
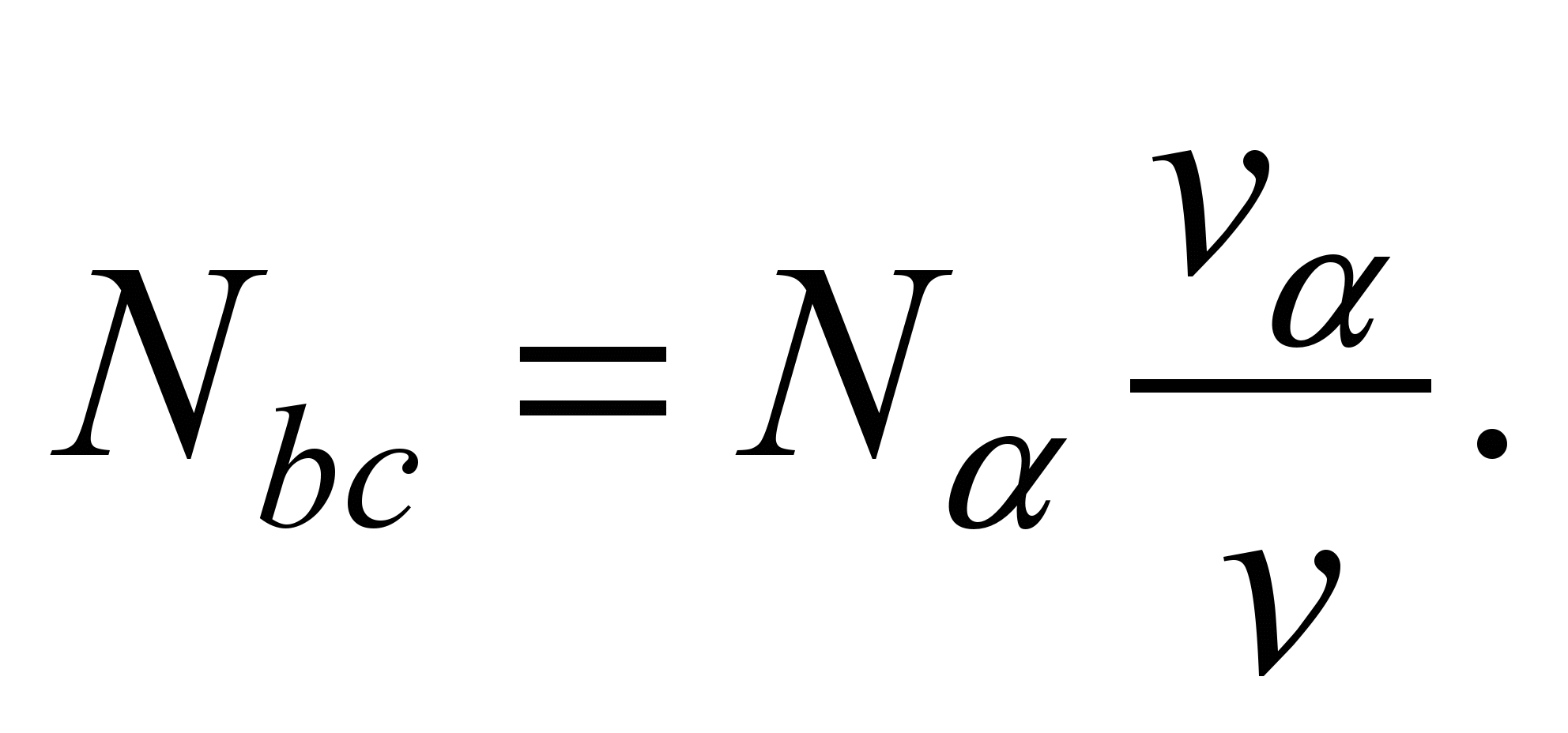
Since
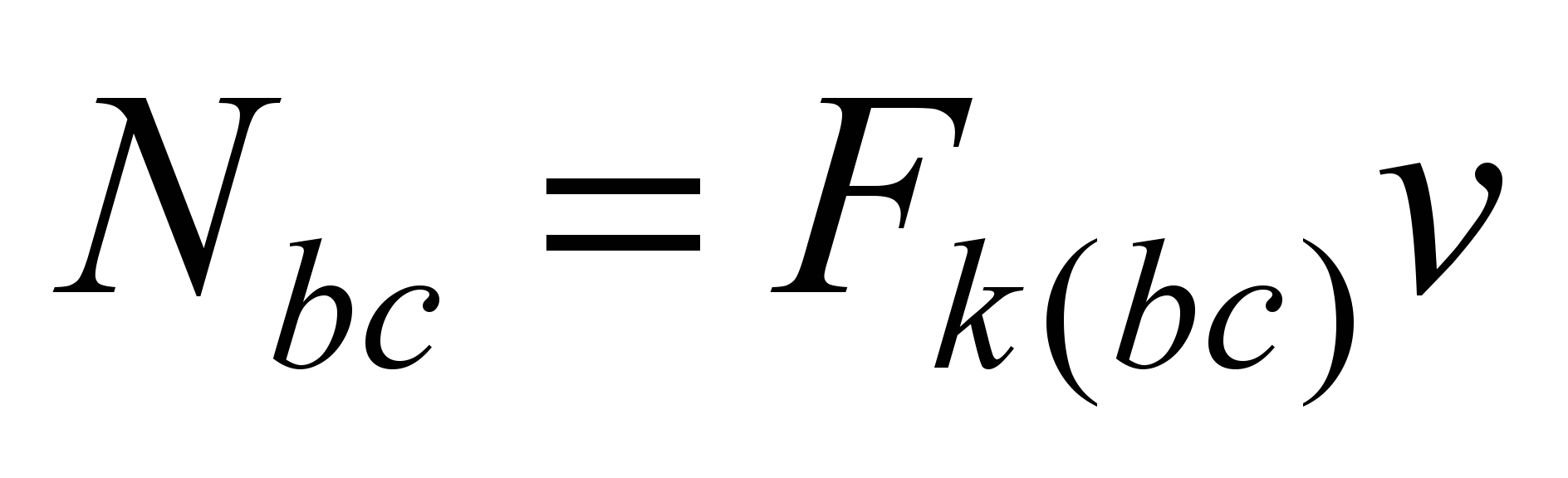 or
or
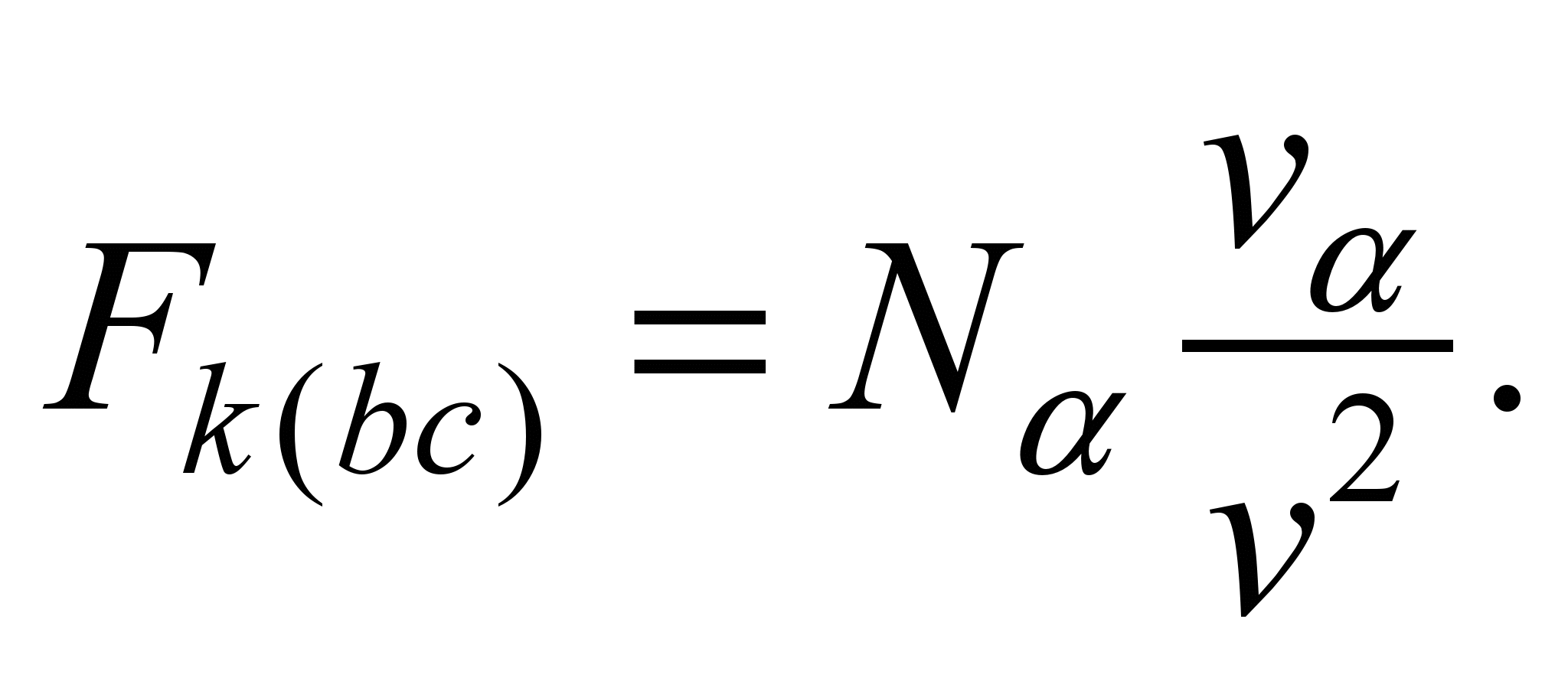 (11)
(11)
But since
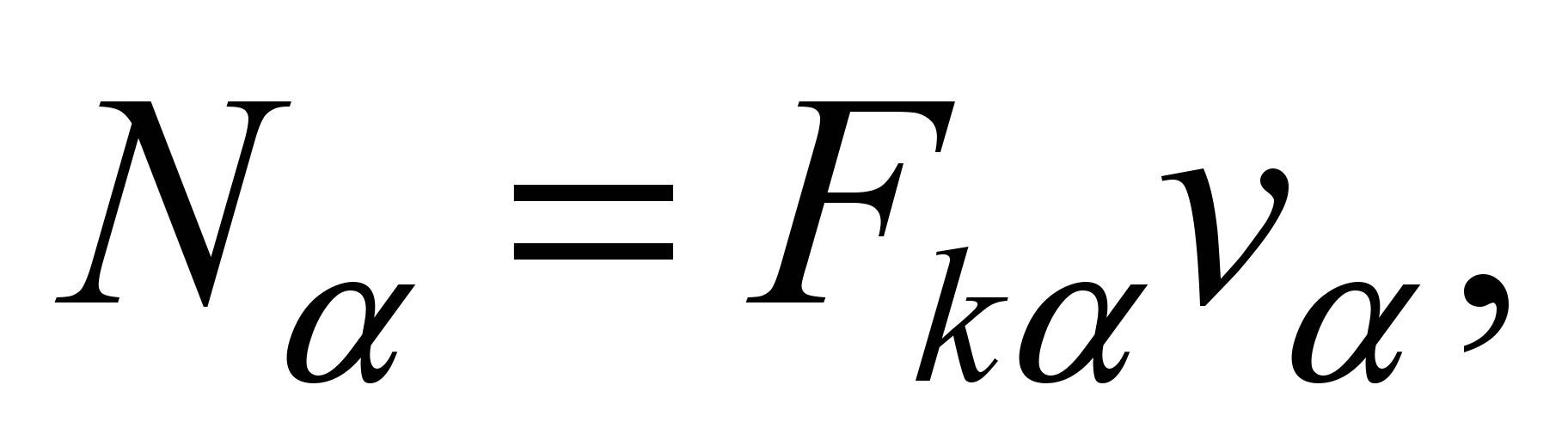 where
where
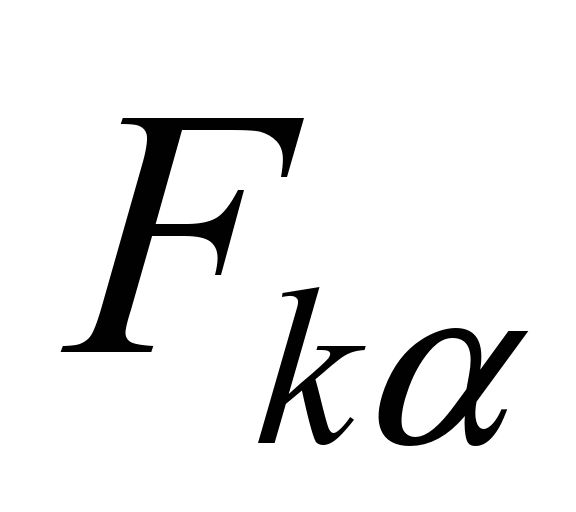 – is the value
– is the value
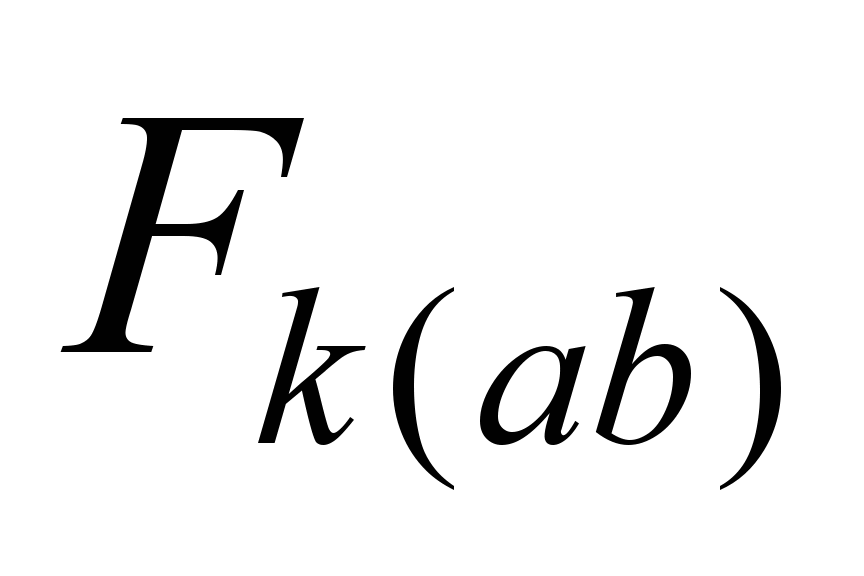 at
at
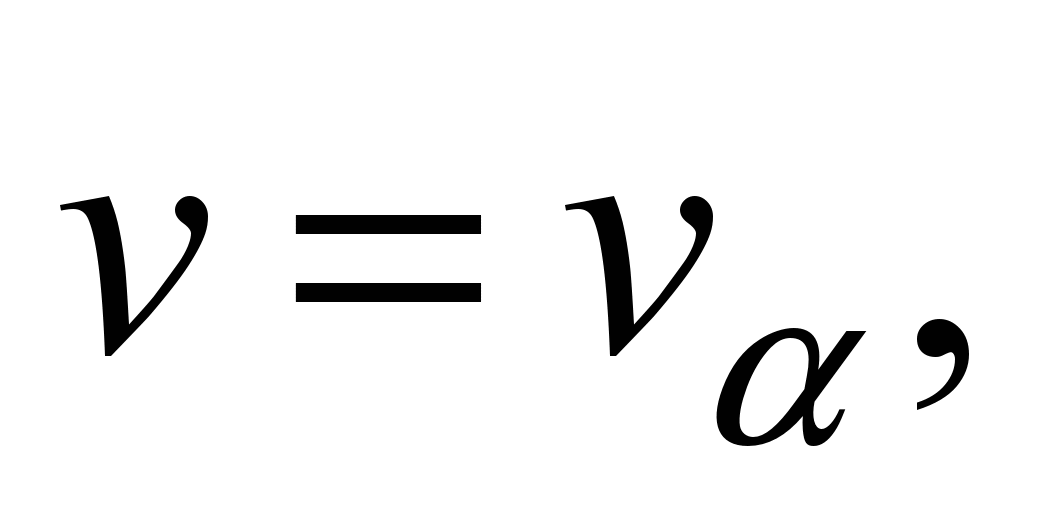 then
then
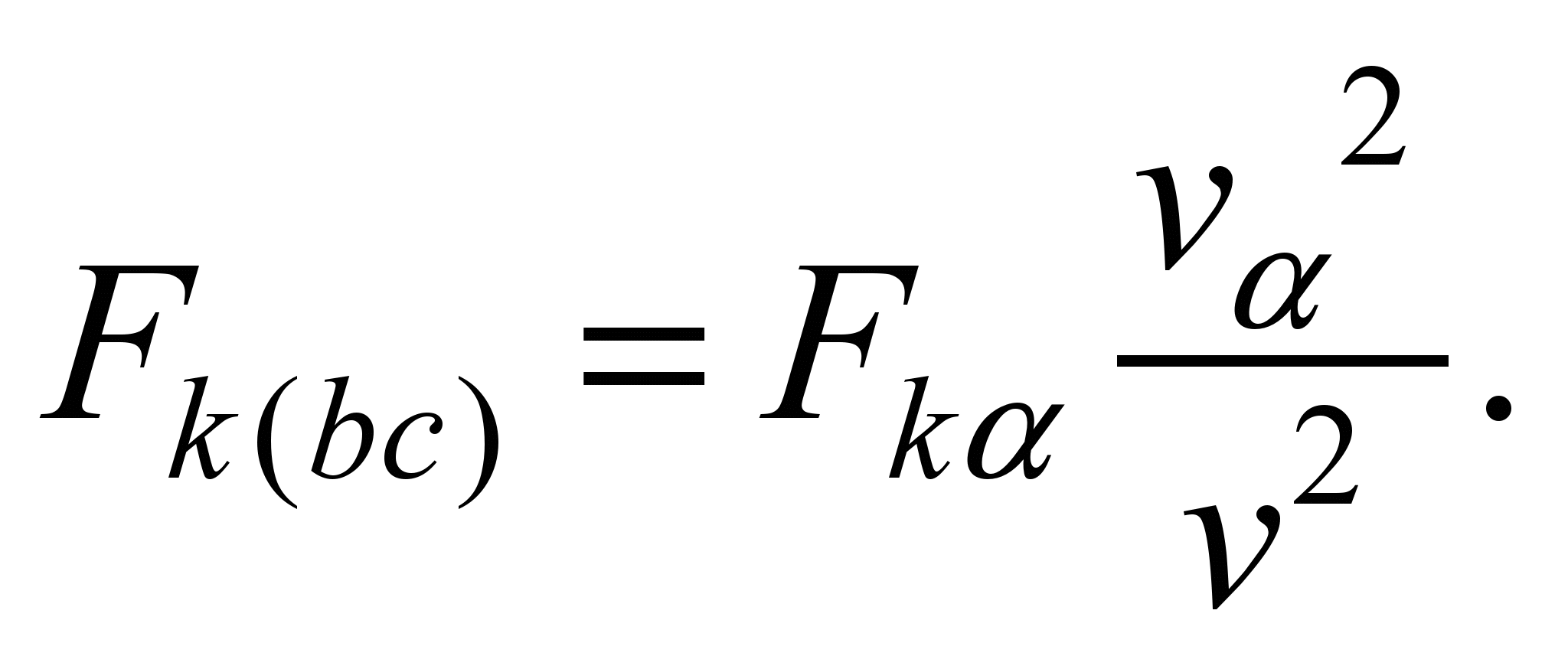 (12)
(12)
From the (9) we have the
following
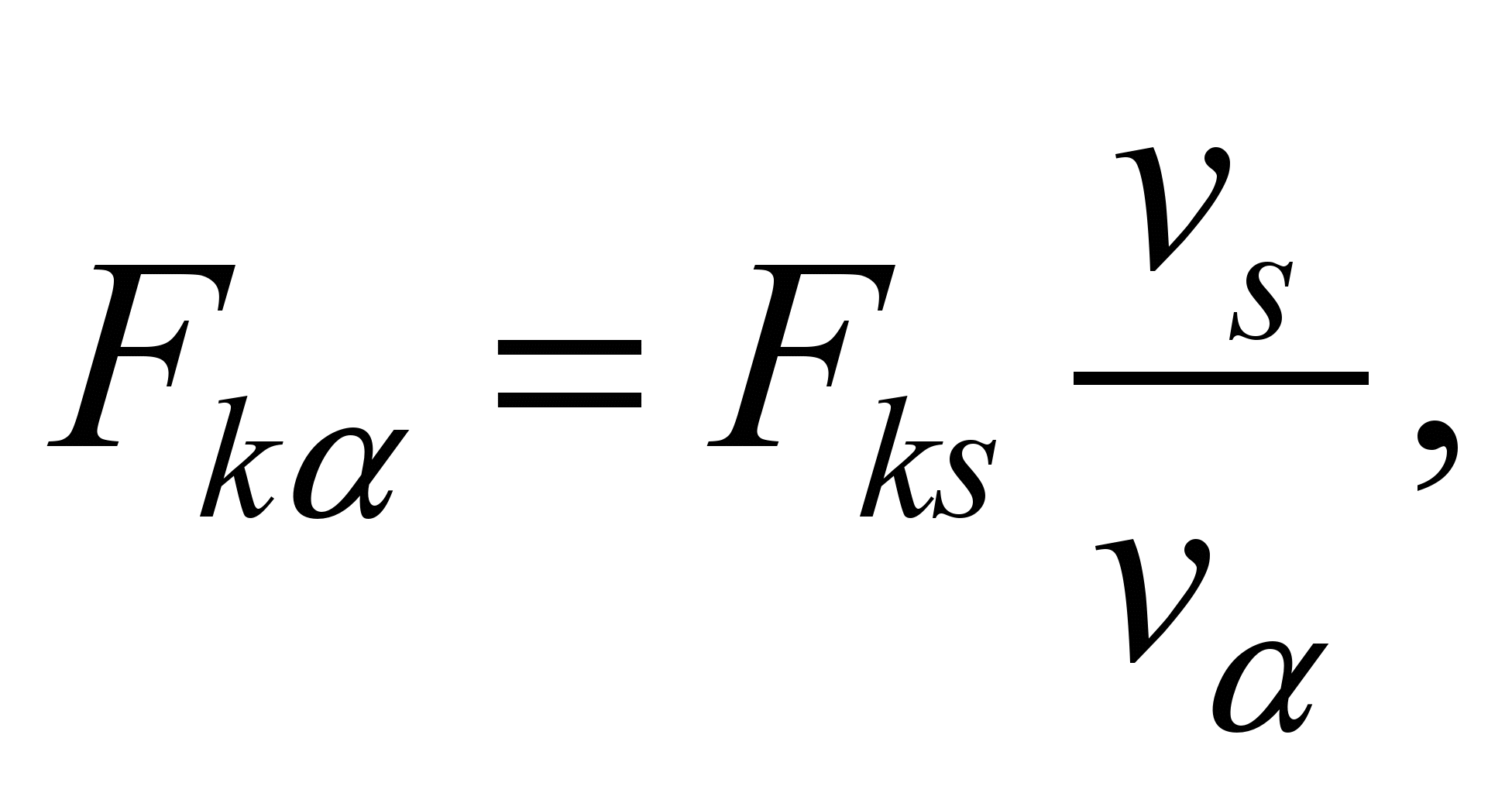
that
is why
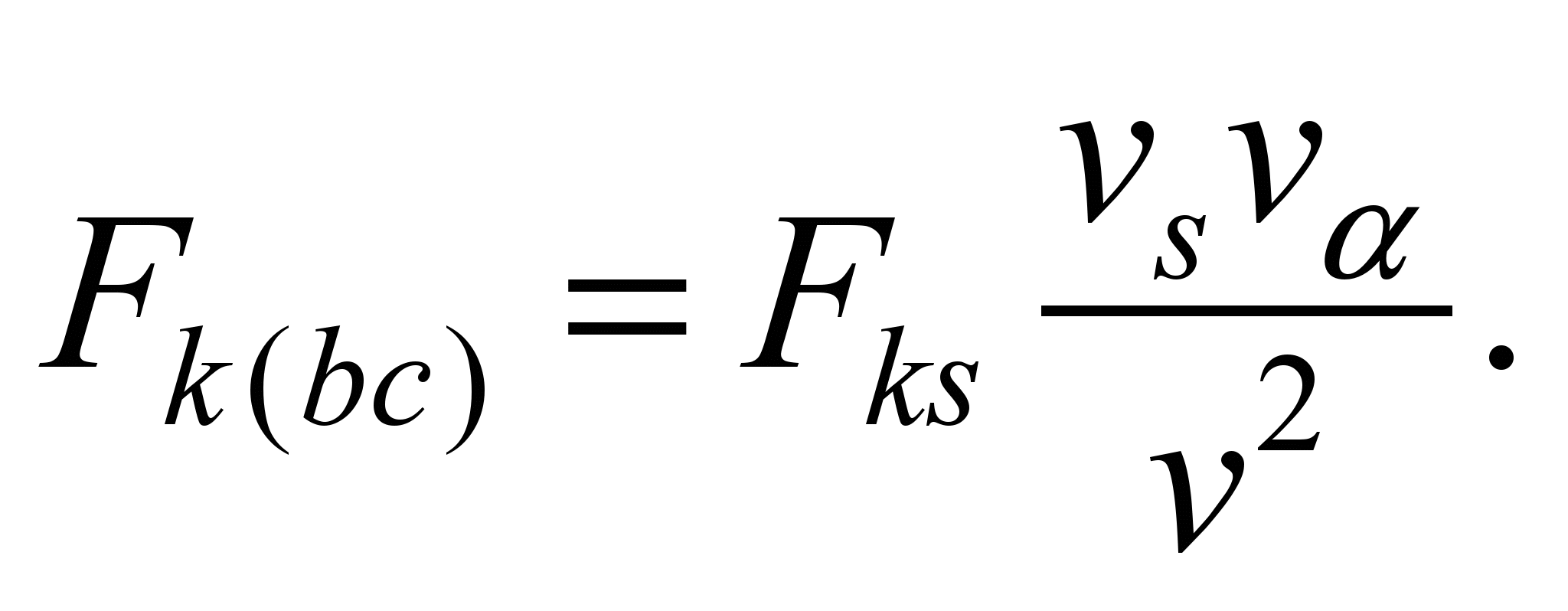 (13)
(13)
We
designate
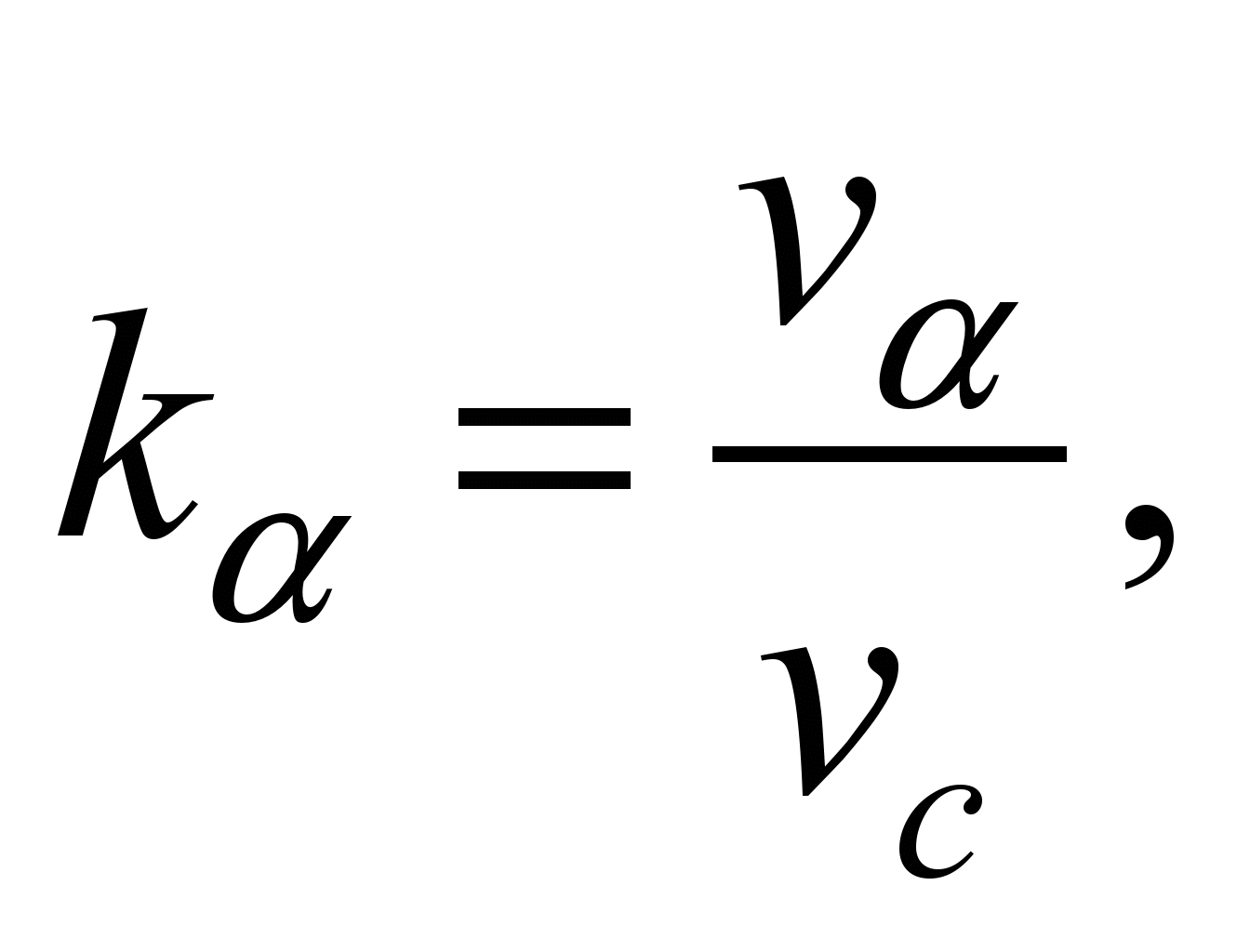 then
then
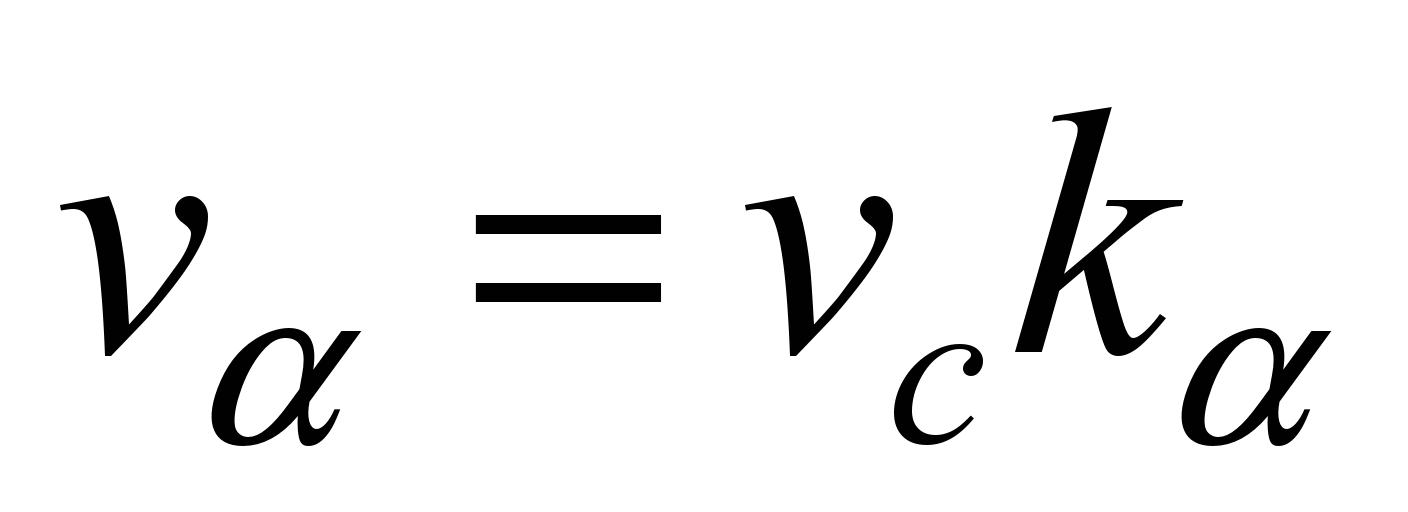 and
and
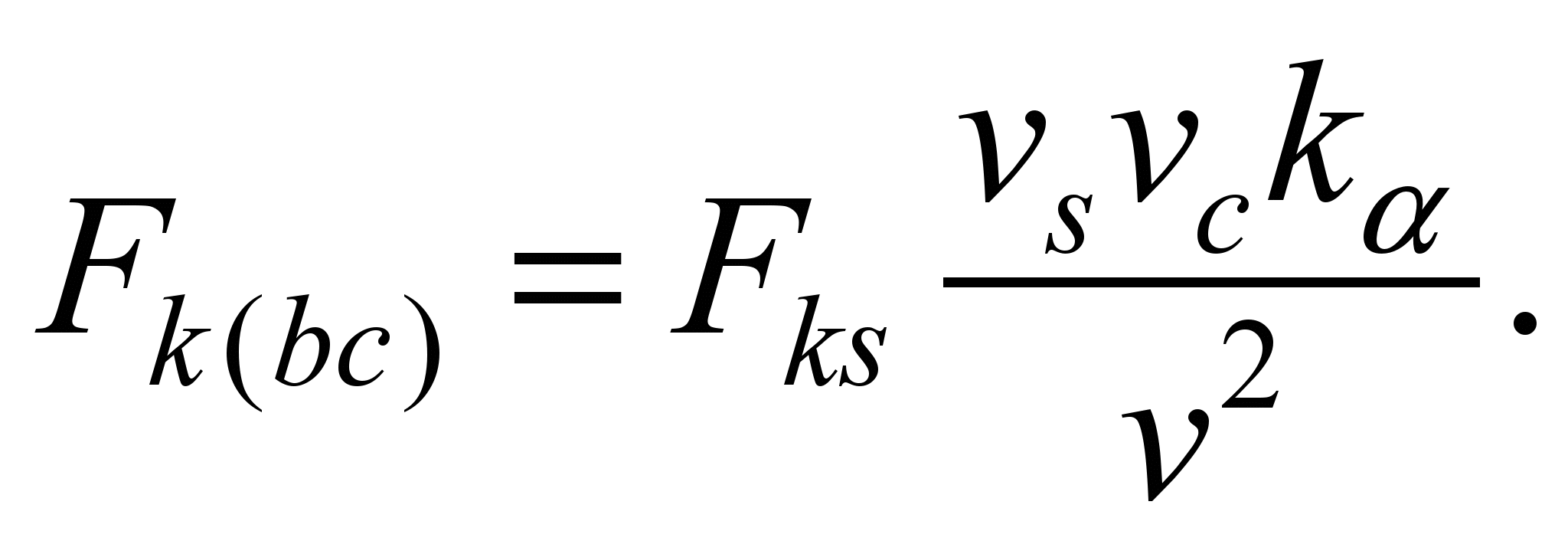 (14)
(14)
where
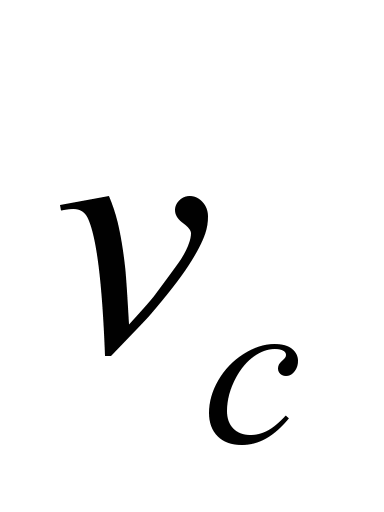 – constructional speed of the train, km/h.
– constructional speed of the train, km/h.
Taking into account the
specific quantities, we obtain
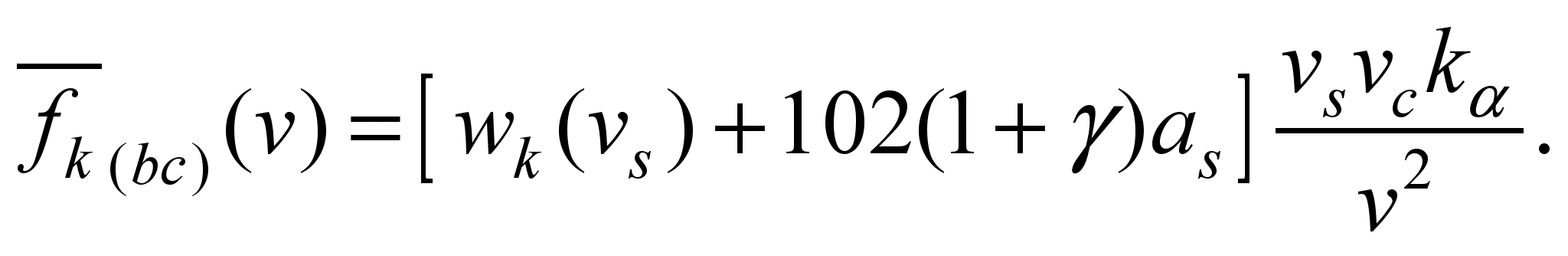 (15)
(15)
Let us
consider the case of two-zone regulation using booster modes, i.e.
when the implementation of loading modes providing for the
realization of traction forces exceeding the values corresponding to
the nominal mode is provided. This mode of operation is used, for
example, on the Skoda electric train. In this case, the traction
characteristic corresponds to that shown in the Fig. 1, b.
Let us introduce the
designations
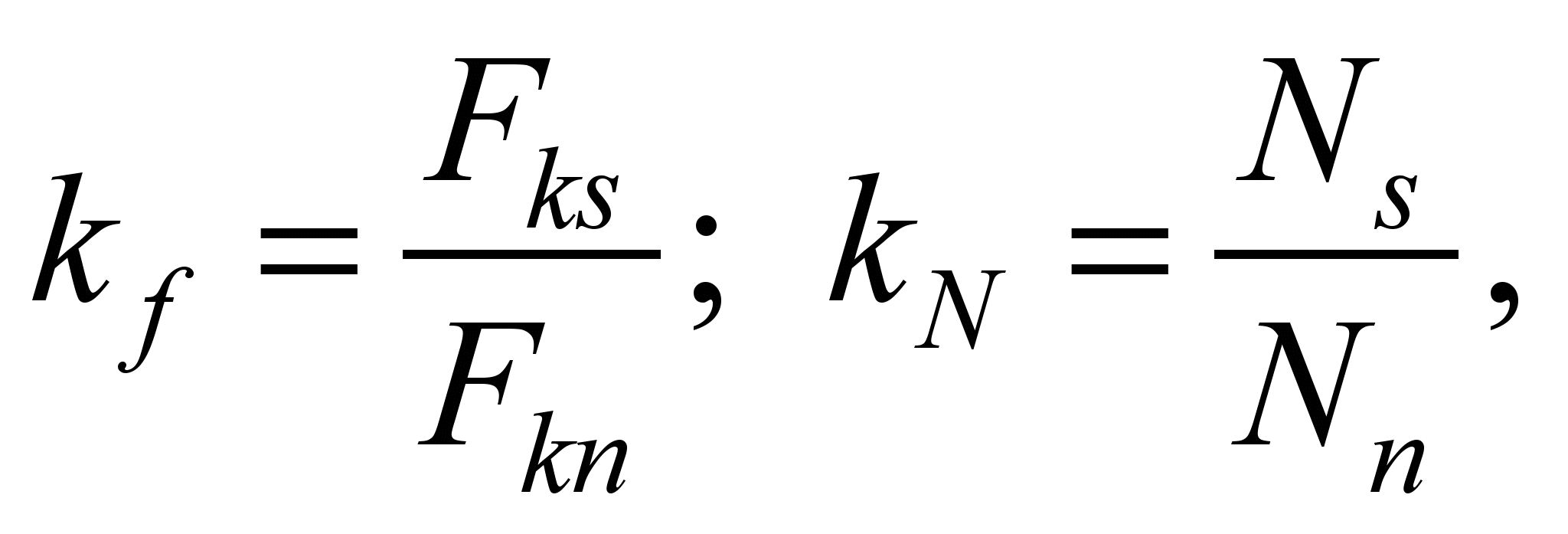 (16)
(16)
where
 – is the maximal traction force, at
– is the maximal traction force, at
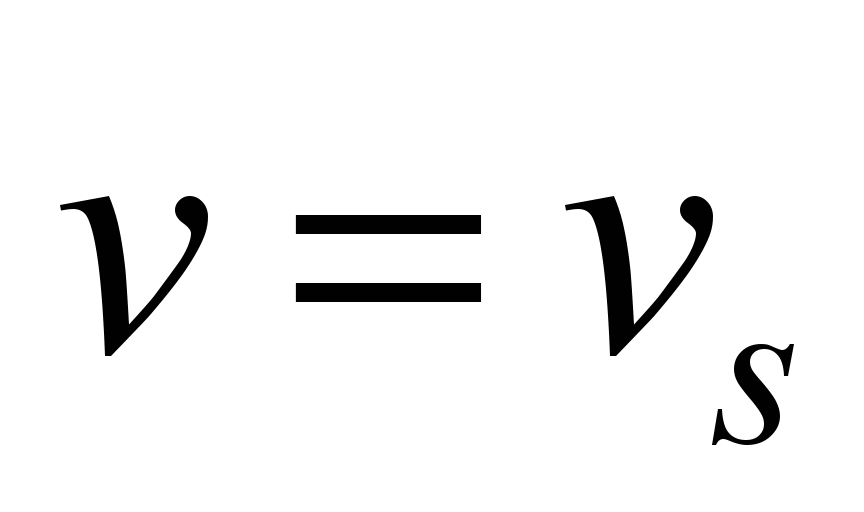 .
.
The limiting
traction characteristic for the acceleration section is determined
by the expression (8), and
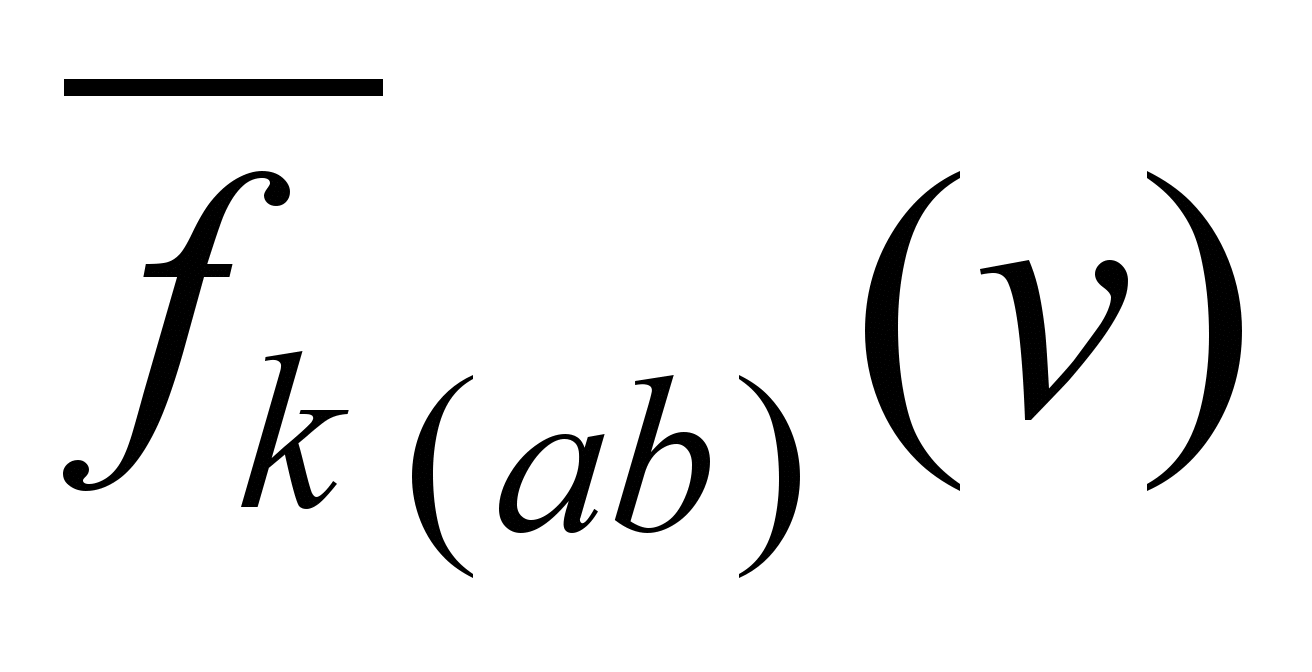 – according to the formula (10).
– according to the formula (10).
Nominal traction force
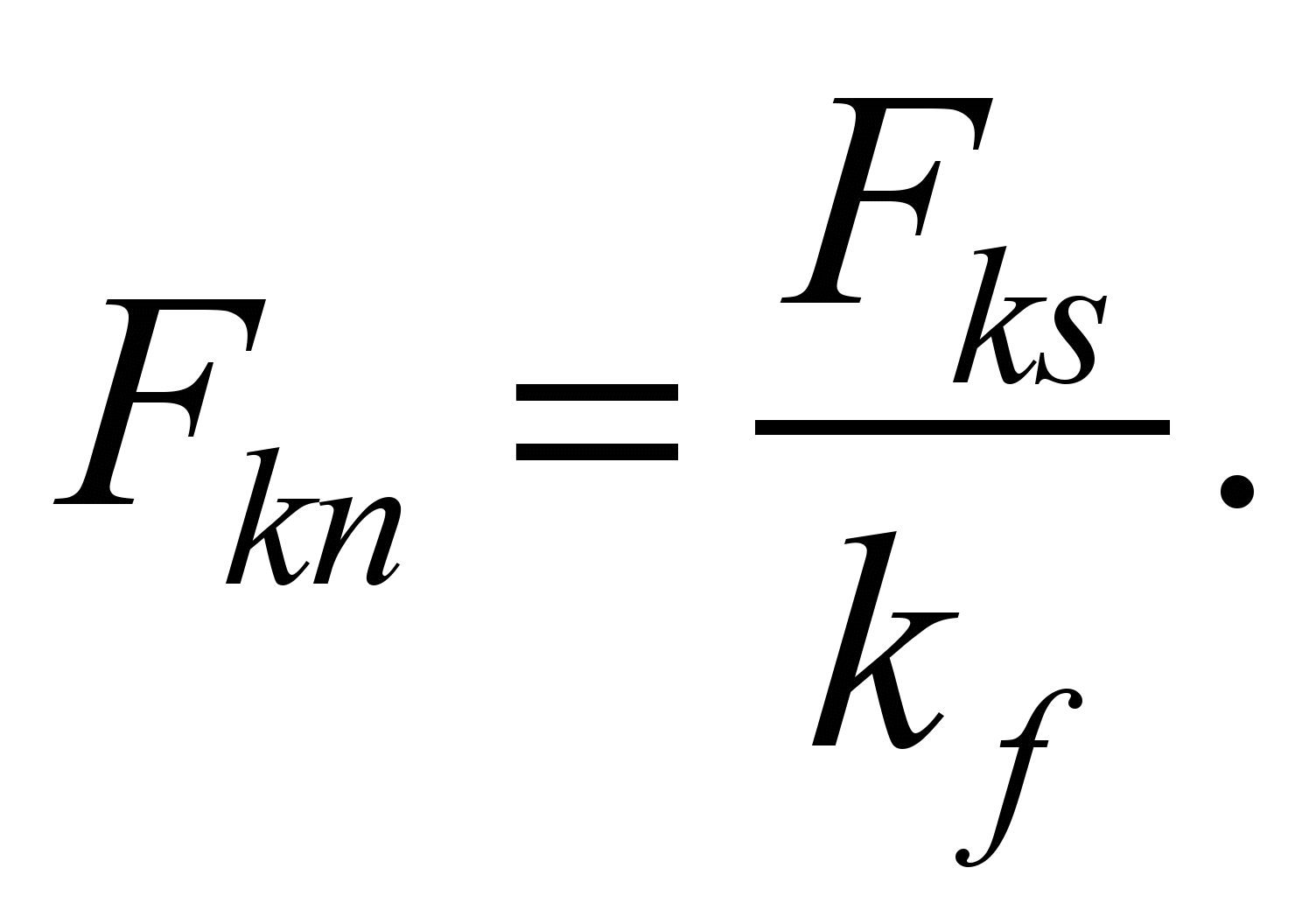 (17)
(17)
The value of
the nominal mode speed is obtained on the basis of the relation
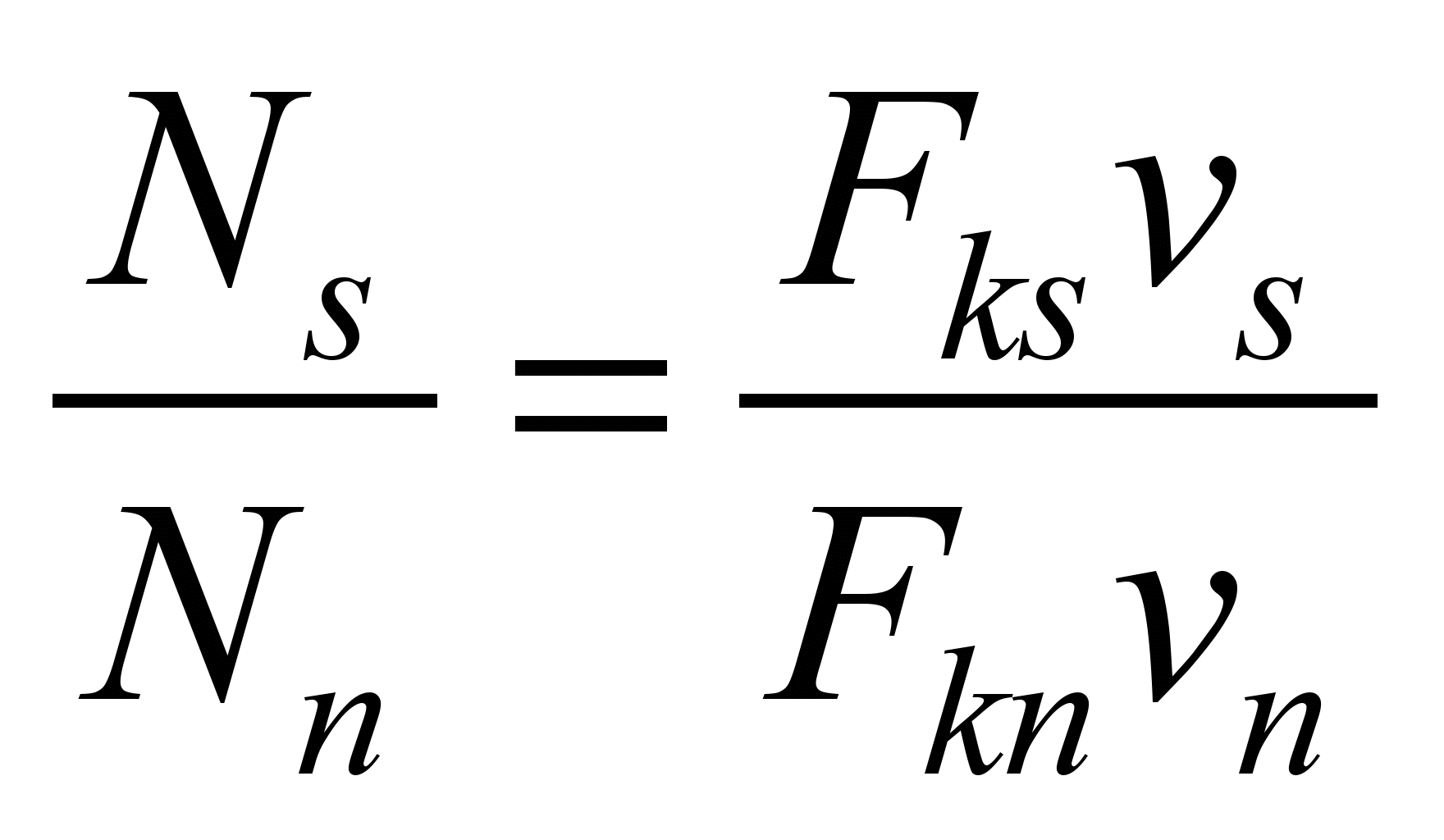 ,
taking into account the expressions (16).
,
taking into account the expressions (16).
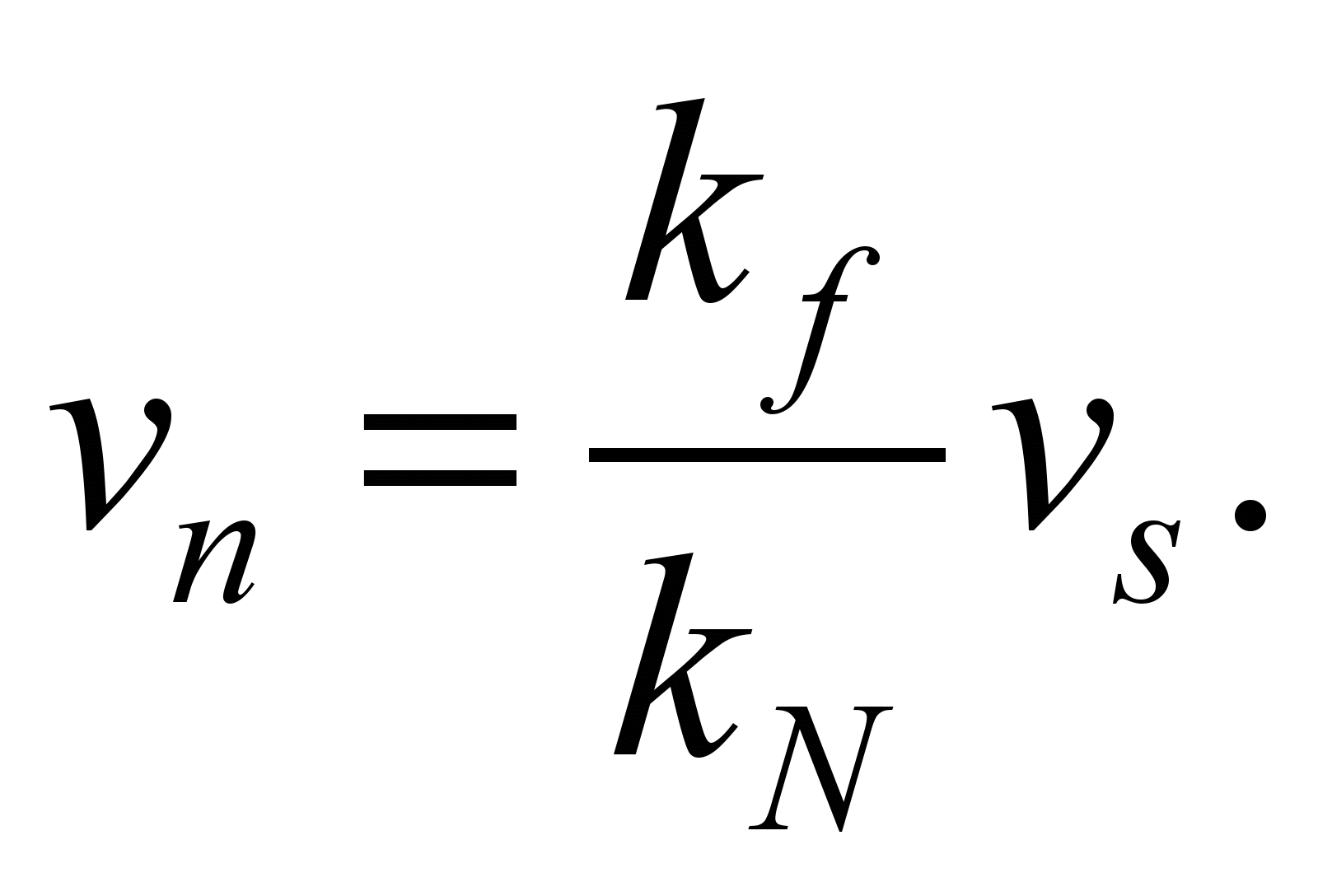 (18)
(18)
Findings
The task of
choosing the optimal values of the nominal mode speed
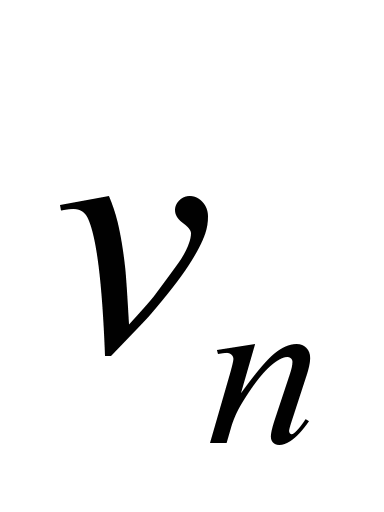 is solved by determining the electric power consumption with the
variation of the possible values of the starting speed
is solved by determining the electric power consumption with the
variation of the possible values of the starting speed
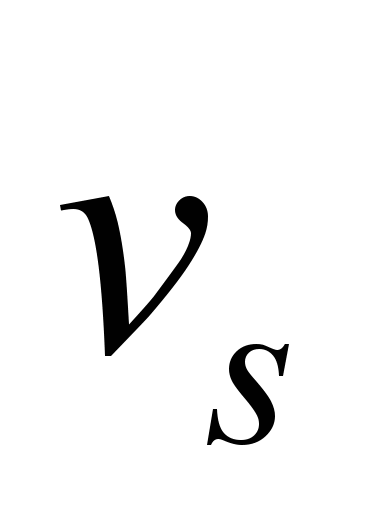 ,
therefore one should take into account only those its values that
ensure the implementation of the given starting
,
therefore one should take into account only those its values that
ensure the implementation of the given starting
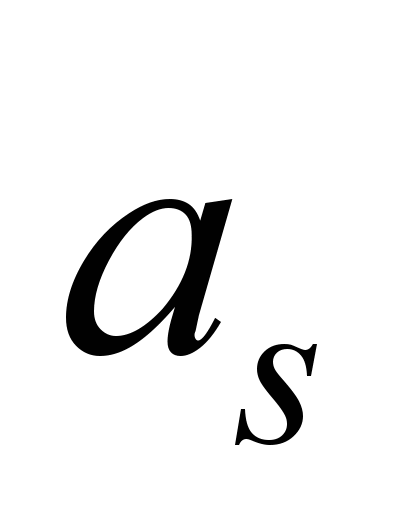 and residual
and residual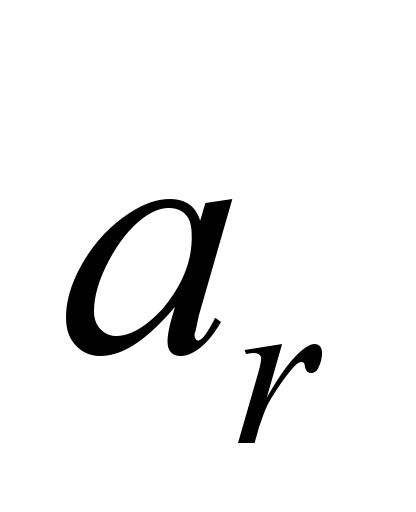 accelerations at the selected control method.
accelerations at the selected control method.
As it can be
seen from the Fig. 1a and Fig. 1b, the value of traction force at
the design speed, other things being equal, increases with
increasing starting speed. Therefore, in order to exclude variants
that do not match the conditions of the problem solution, it is
necessary to determine the minimal values
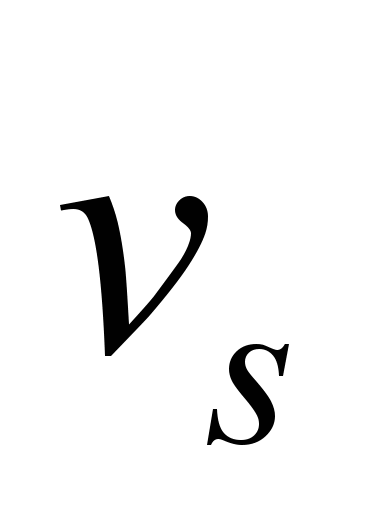 corresponding to the given starting and residual accelerations.
corresponding to the given starting and residual accelerations.
Since the traction force at the
design speed:
– from the
one side
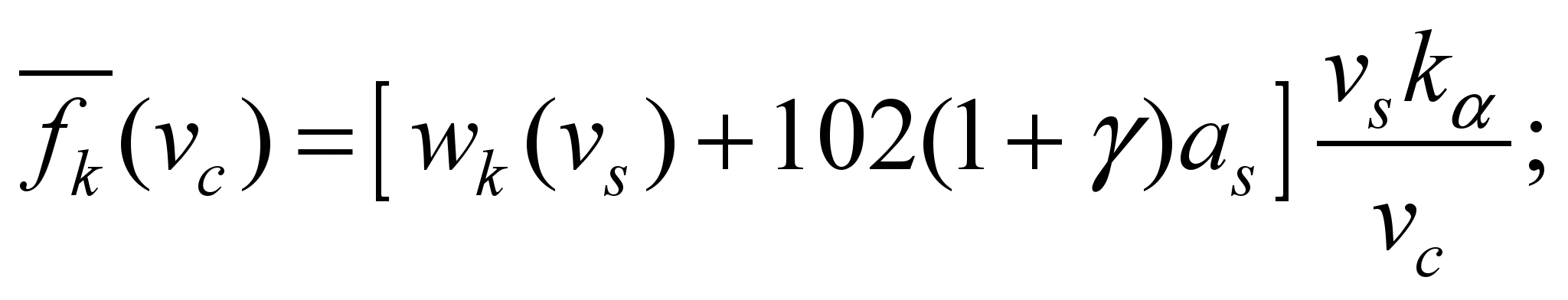
– and from
the other side
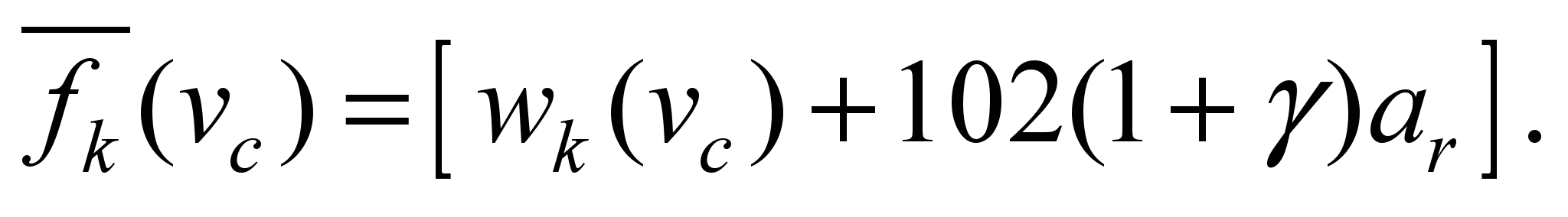
Neglecting
the dependence of
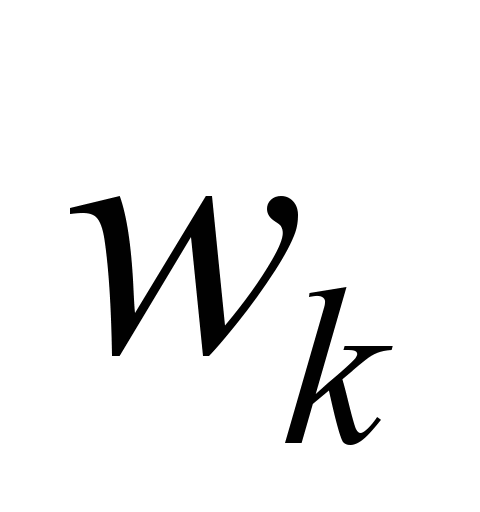 on
on
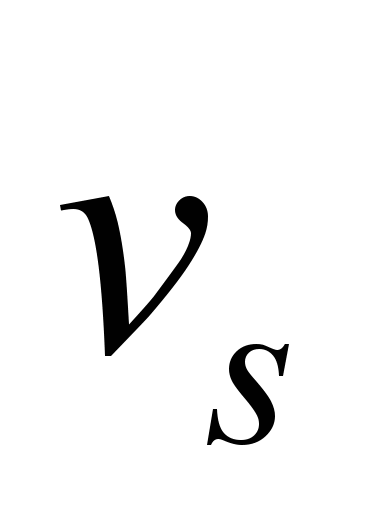 ,
we obtain
,
we obtain
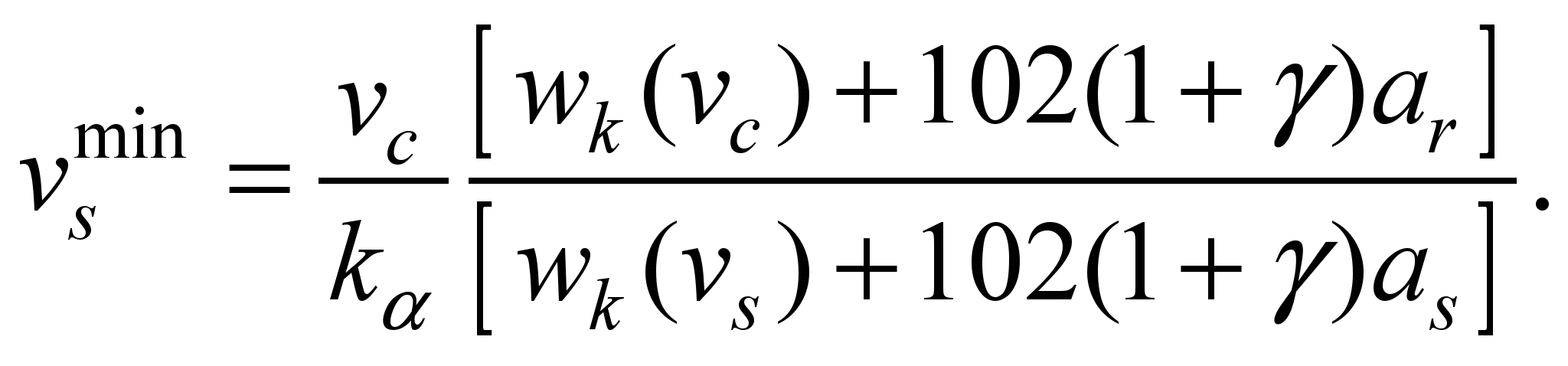 (19)
(19)
For the case
of two zone regulation in the presented expression it should be
taken
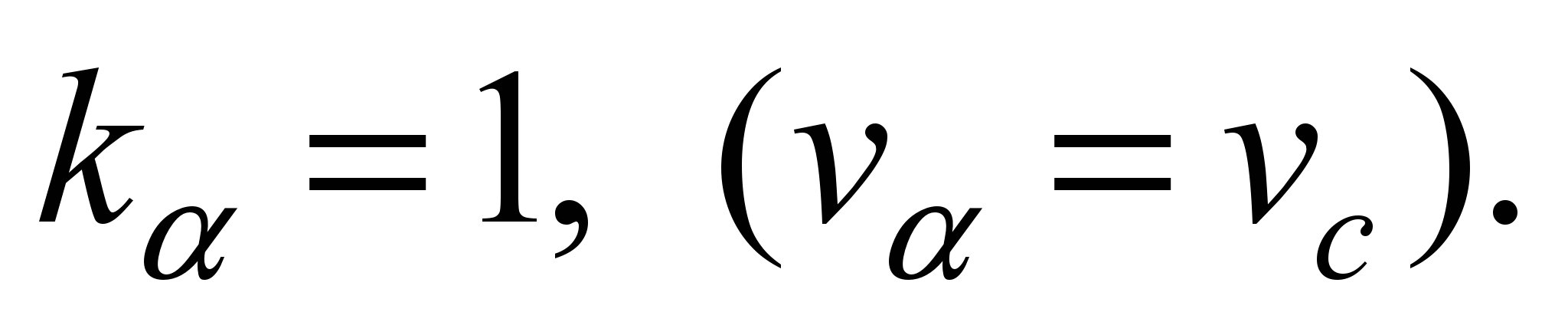
In the
calculations one should take only the values
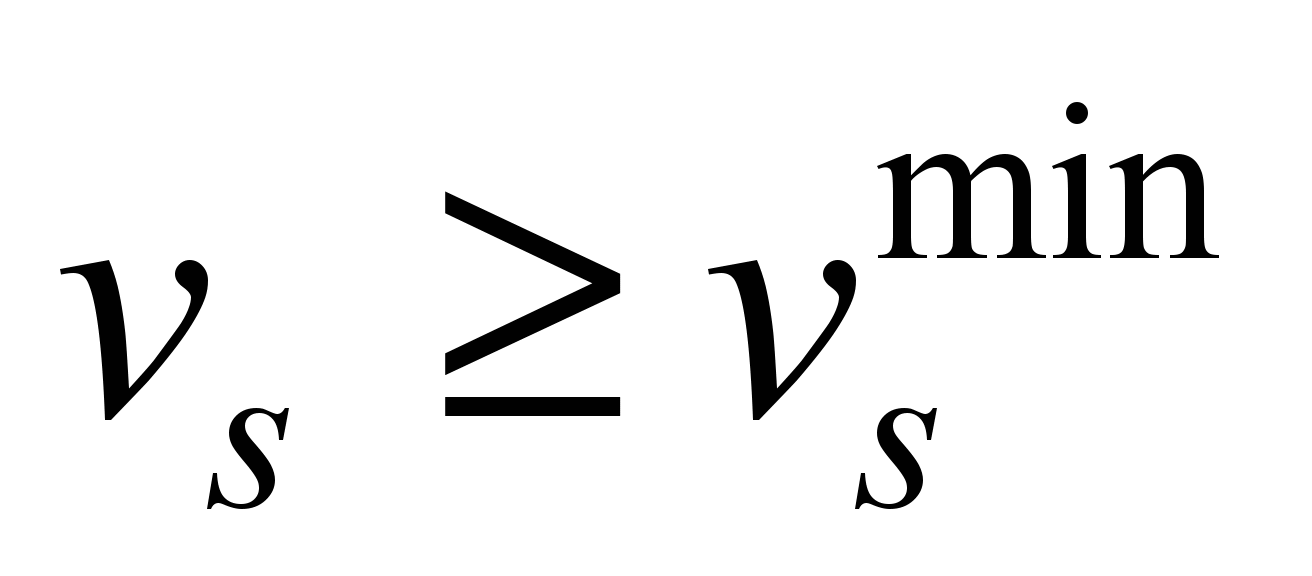 .
Dependencies
.
Dependencies
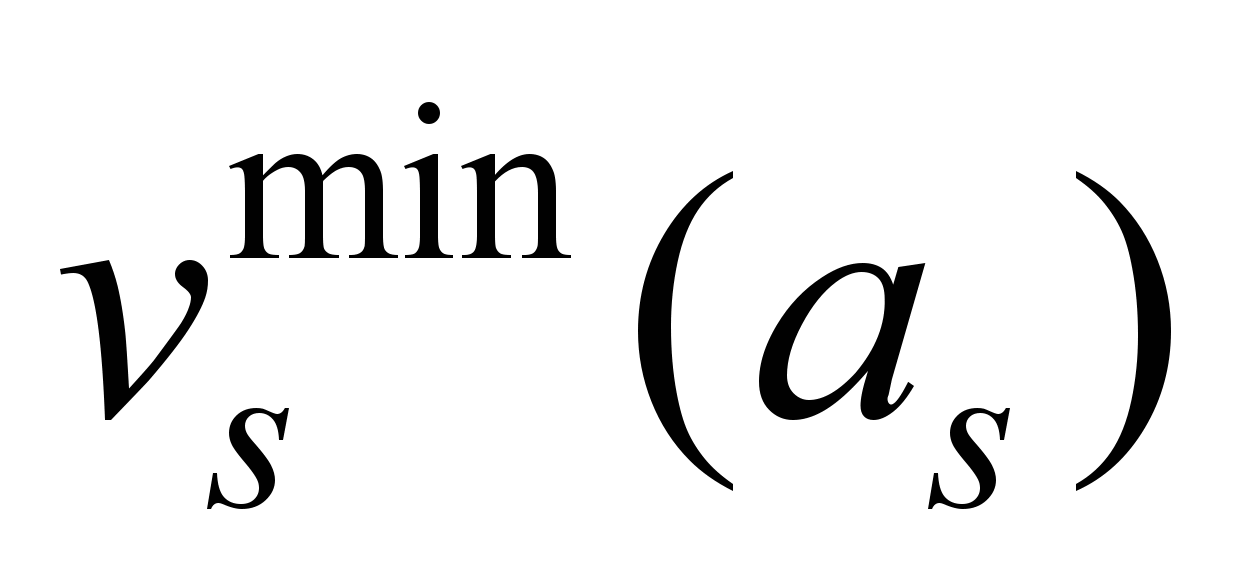 for different values
for different values
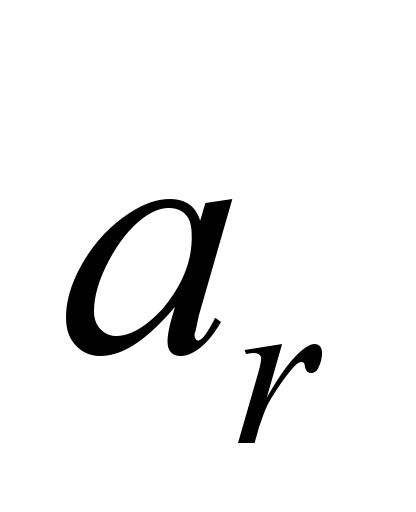 are shown in the Fig. 2.
are shown in the Fig. 2.
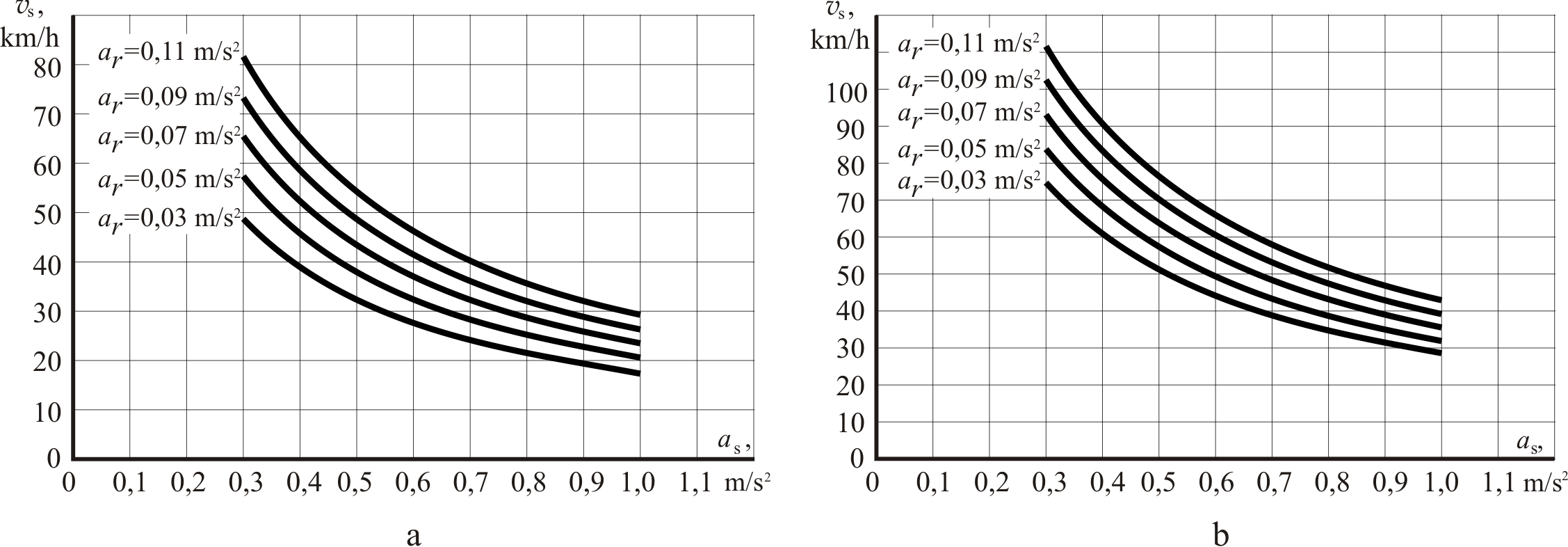
Fig.
2. The family of dependencies of the minimum starting speed on the
starting acceleration with the variation of values of residual
acceleration and design speed is: a
– 160 km/h and b
– 200 km/h
The value of the starting
acceleration at the given train weight determines the tractive
effort, and hence the use of the «wheel-rail» contact
capabilities to realize the traction creepage. In order to
exclude from consideration, the variants, when the traction force
cannot be reliably realized according to the adhesion conditions, it
is expedient to set the maximum permissible values of the
starting acceleration according to the adhesion conditions, i.e.
corresponding to the specified design coefficient of adhesion.
Estimated adhesive force
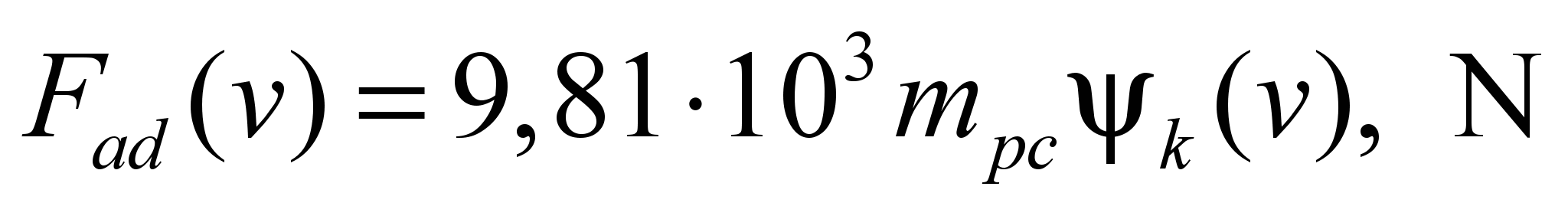 (20)
(20)
where
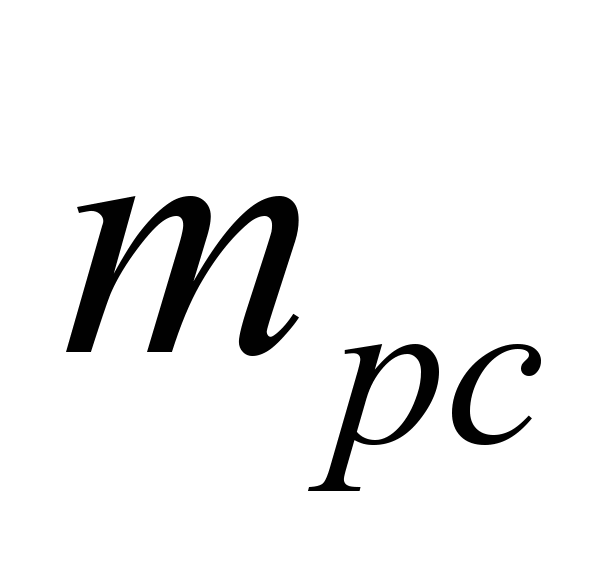 –
adhesive weight (weight of power cars), t;
–
adhesive weight (weight of power cars), t;
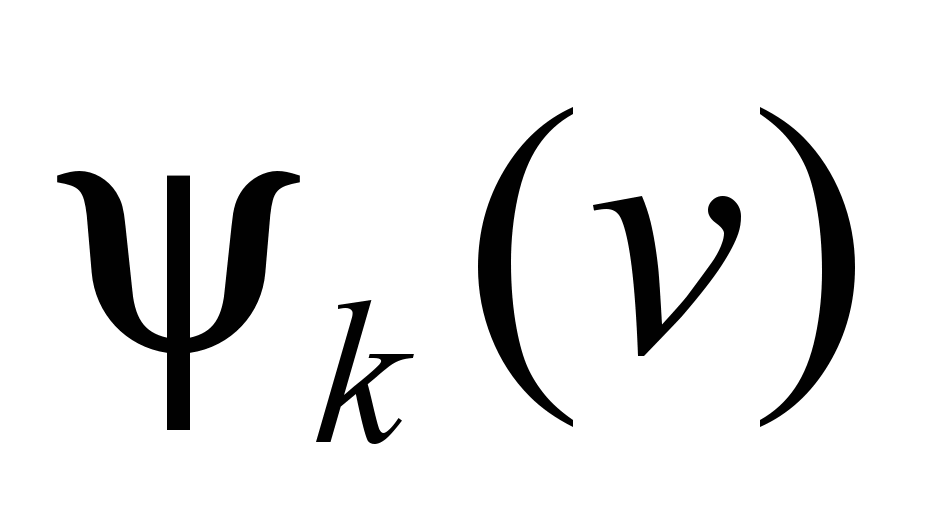 – estimated coefficient of adhesion.
– estimated coefficient of adhesion.
Specific value of the adhesion
force
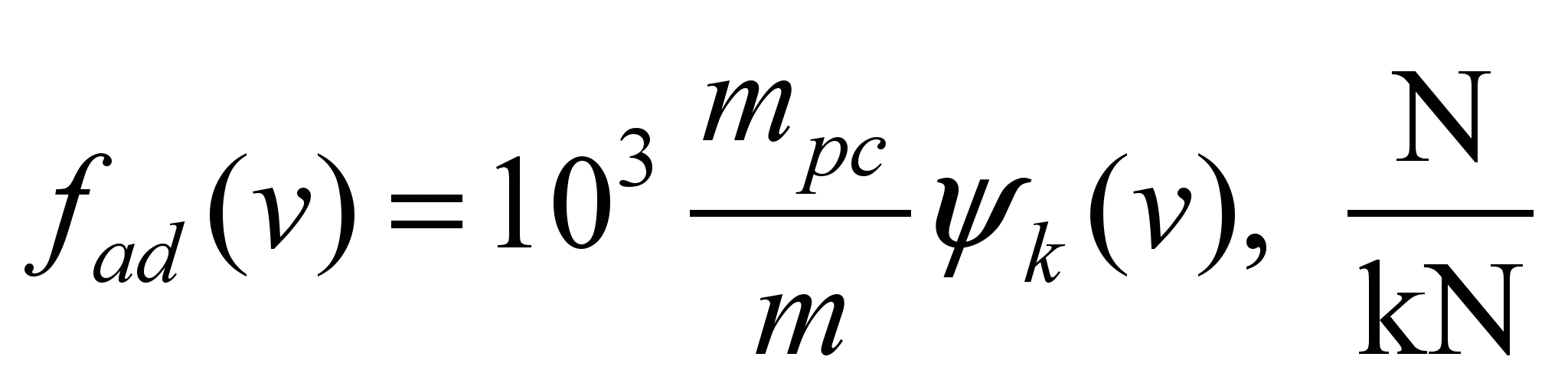 (21)
(21)
The necessary acceleration
value is obtained from the well-known law of locomotive traction
[2], according to which for the reliable operation of a wheel-rail
vehicle, it is necessary to fulfill the condition
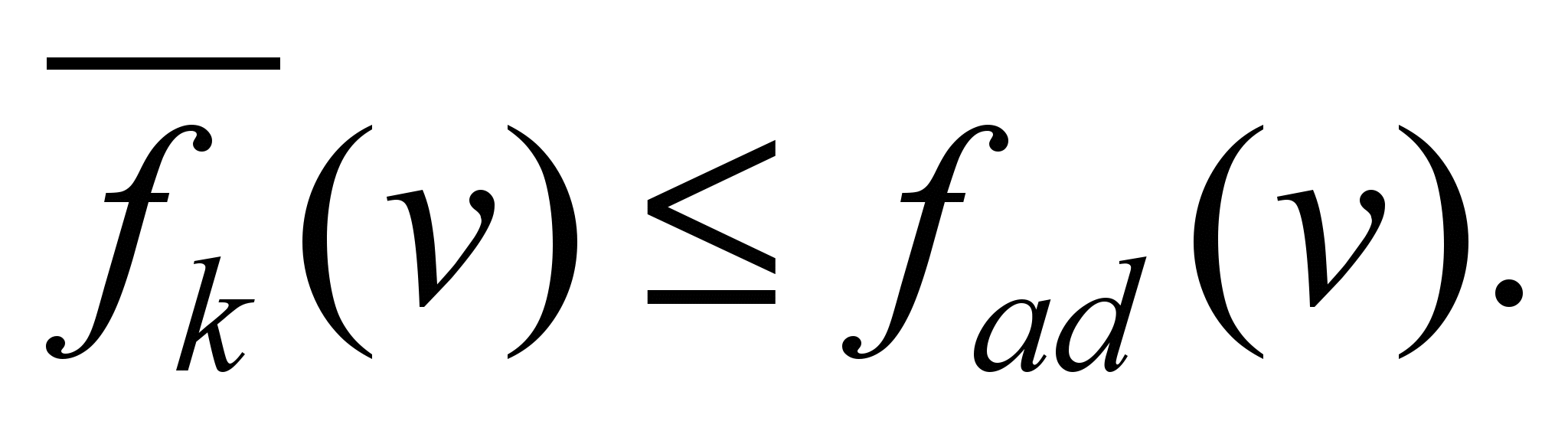
Based on the expression (8) and
(21) we obtain
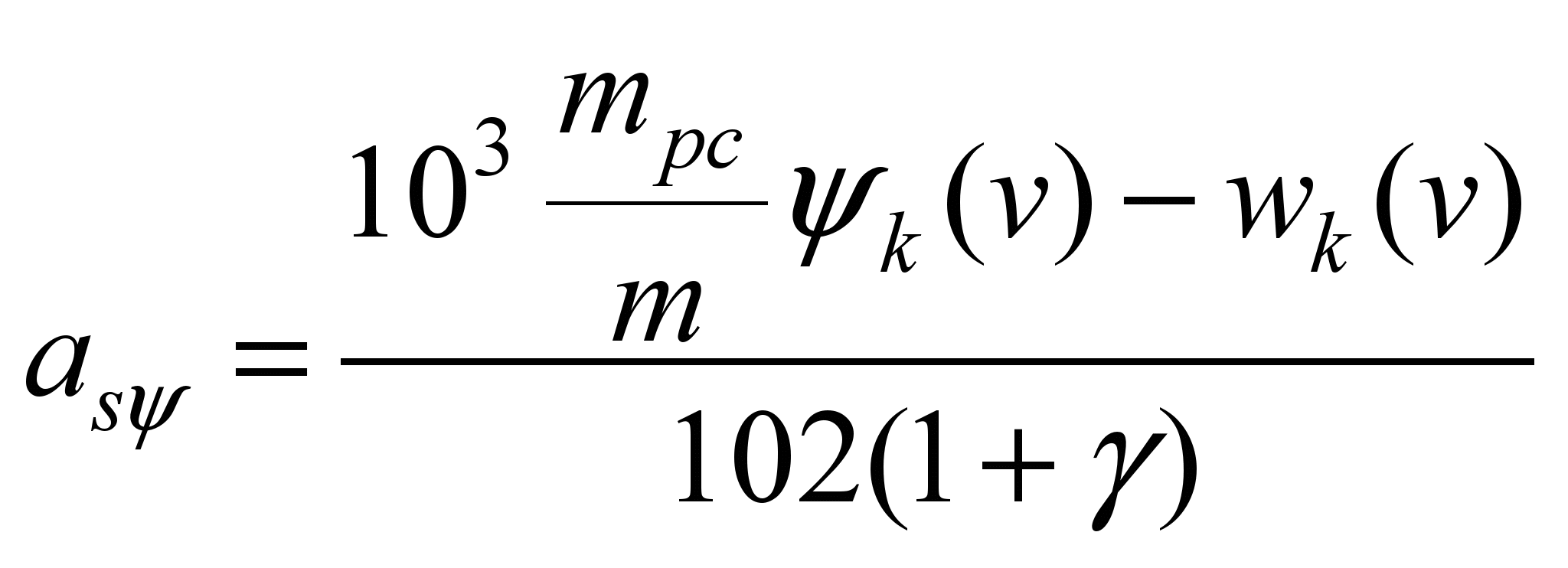 . (22)
. (22)
where
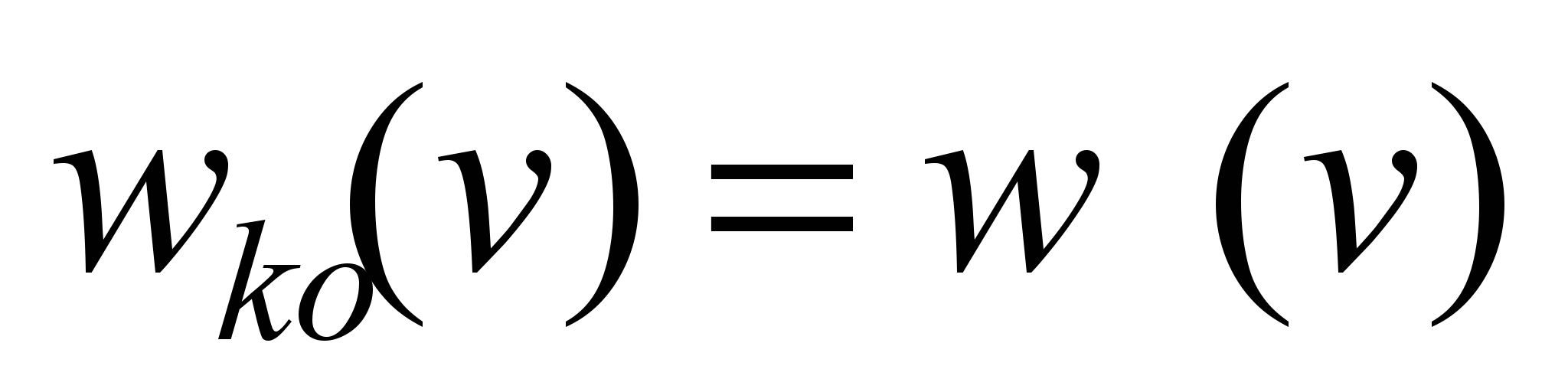 upon the condition that the electric train moves at the section,
i.e.
upon the condition that the electric train moves at the section,
i.e.
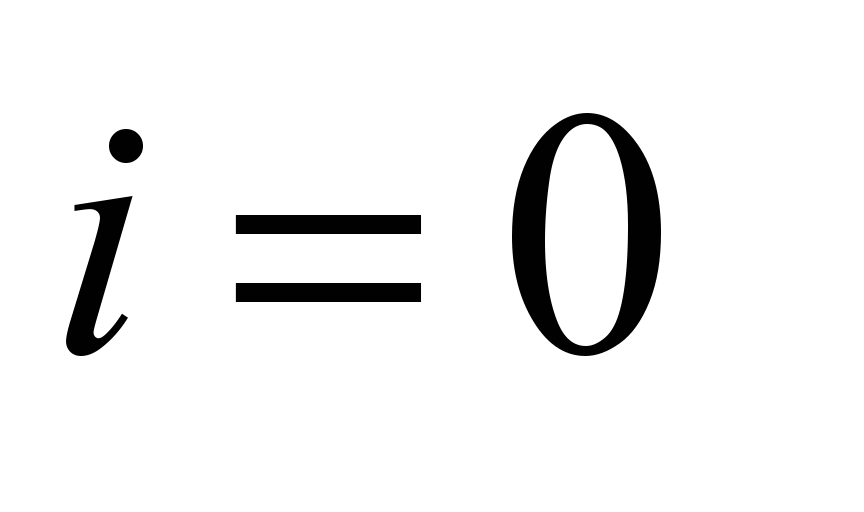 ‰.
‰.
Obviously,
only values
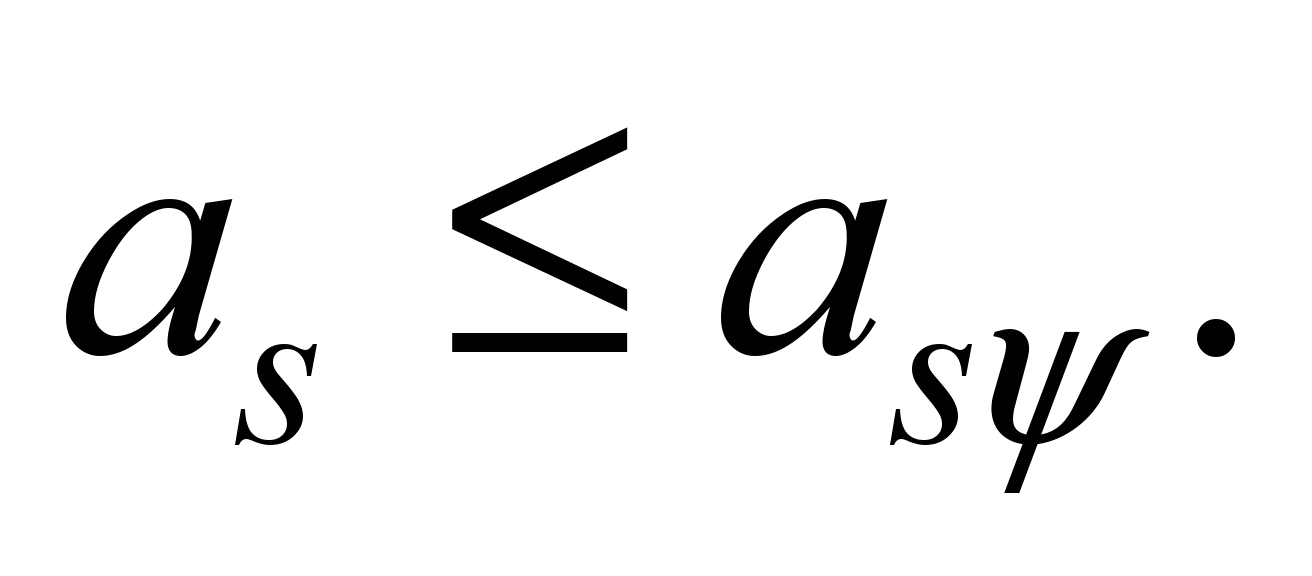 can be taken into account.
can be taken into account.
The
dependences
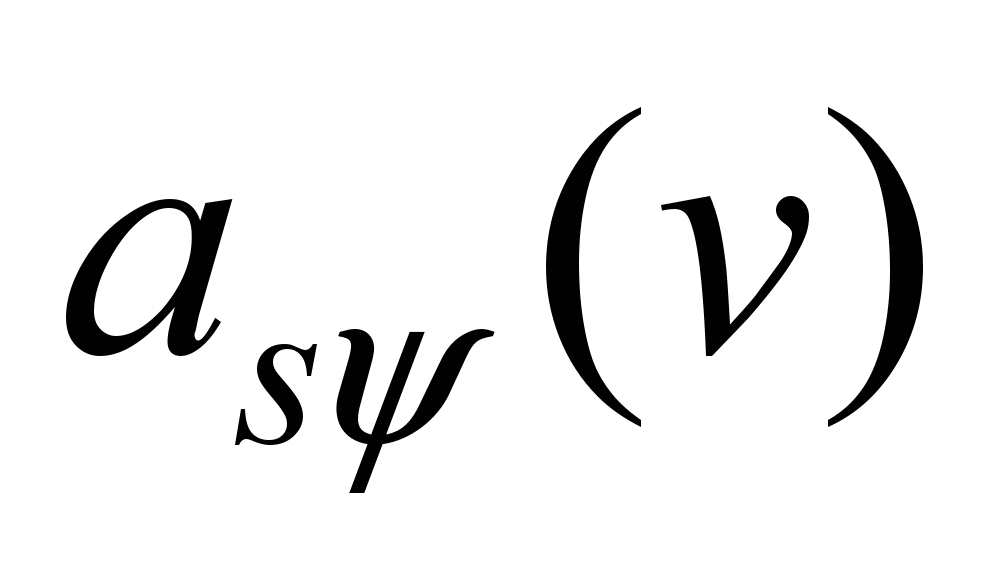 for the variants of the concentrated and distributed traction are
shown in the Fig. 3. They are considered for these electric trains
of HRCS2 series by Hyundai-Rotem Company«and EJ675 of «SKODA
Vagonka». The calculations were performed with the initial data
given in the Table 1.
for the variants of the concentrated and distributed traction are
shown in the Fig. 3. They are considered for these electric trains
of HRCS2 series by Hyundai-Rotem Company«and EJ675 of «SKODA
Vagonka». The calculations were performed with the initial data
given in the Table 1.
Table 1
Initial
data for calculating the dependencies of the minimum permissible
starting
acceleration using the conditions of adhesion on the speed
of motion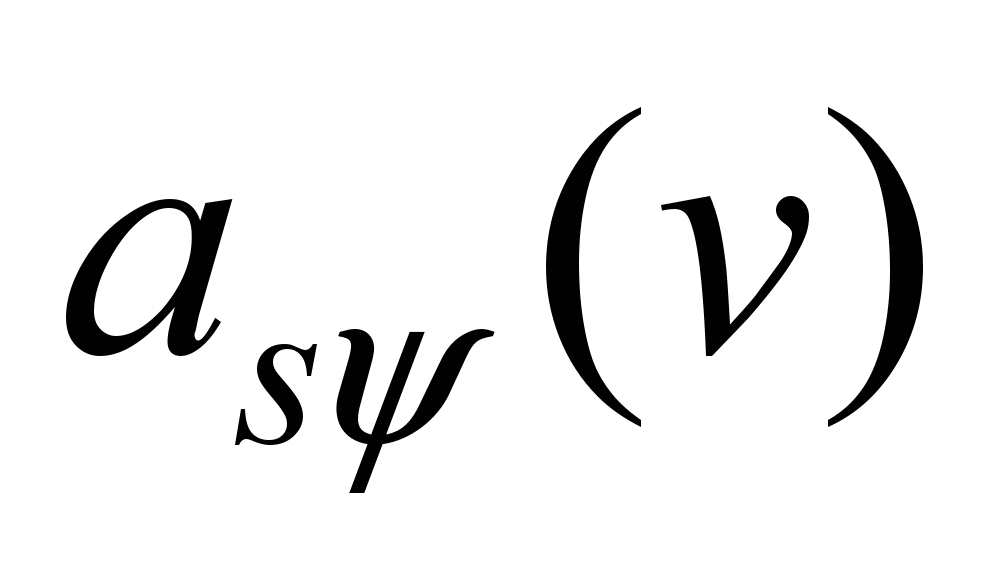 .
.
|
Electric
train range
|
Weight,
t
|
The
inertia coefficient of the rotating masses of the train,
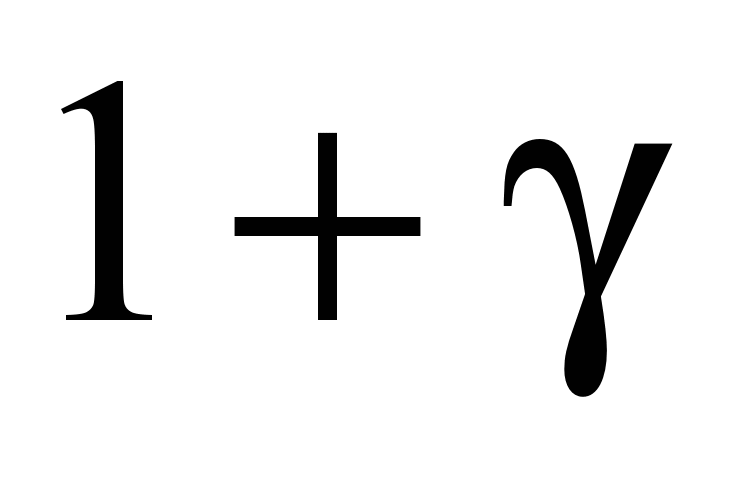
|
Dependence
of the adhesion coefficient on the speed
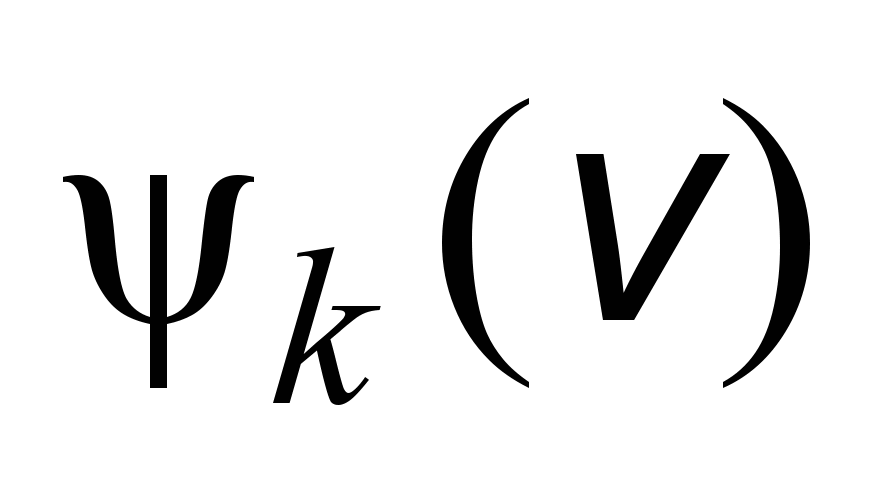
|
Dependence
of the total specific movement resistance on the speed,
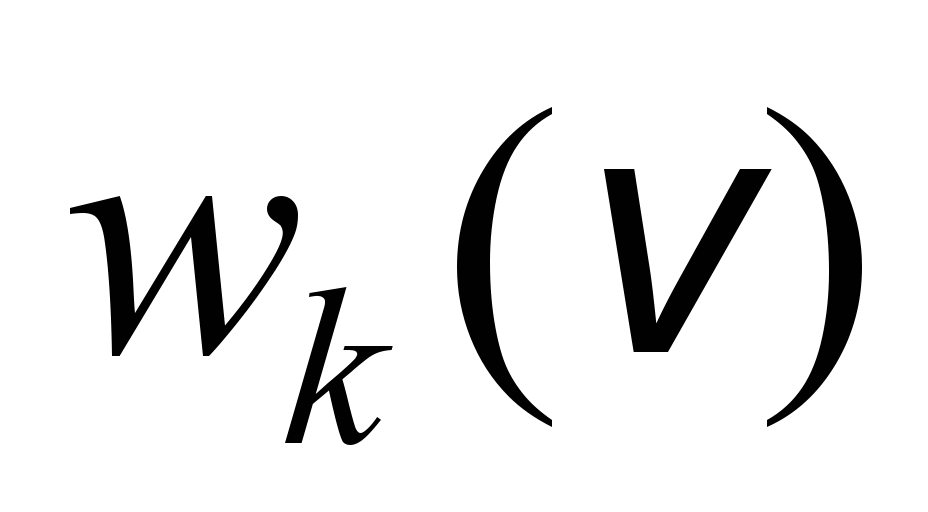 2 2
|
|
adhesive,
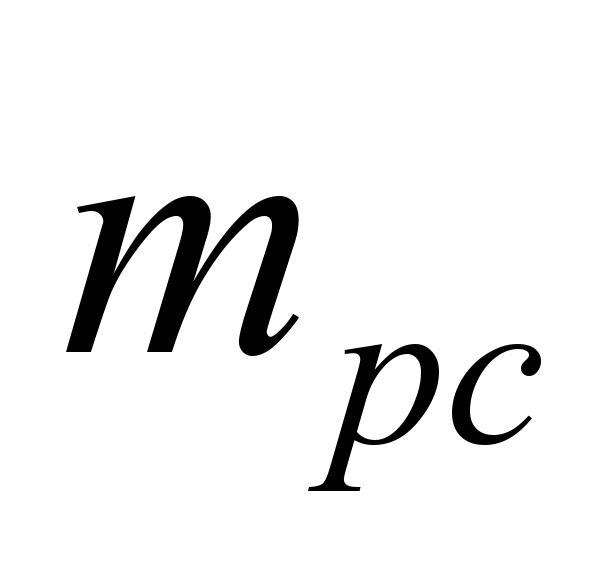
|
train,
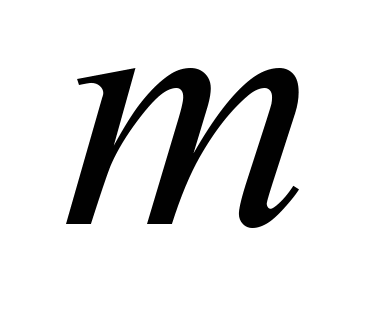
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
HRCS2
(distributed traction)
|
438
|
640
|
1.115
|
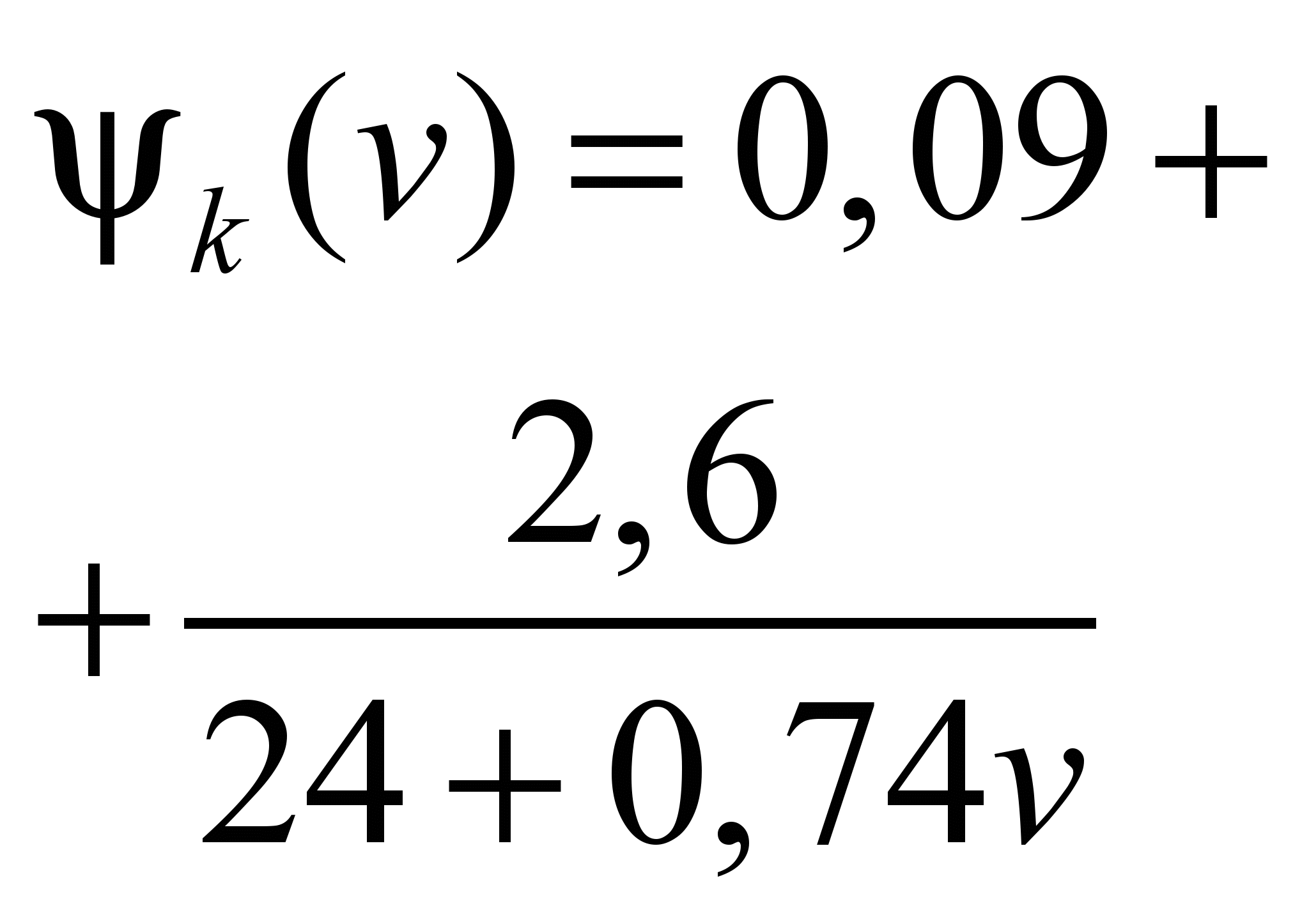
|
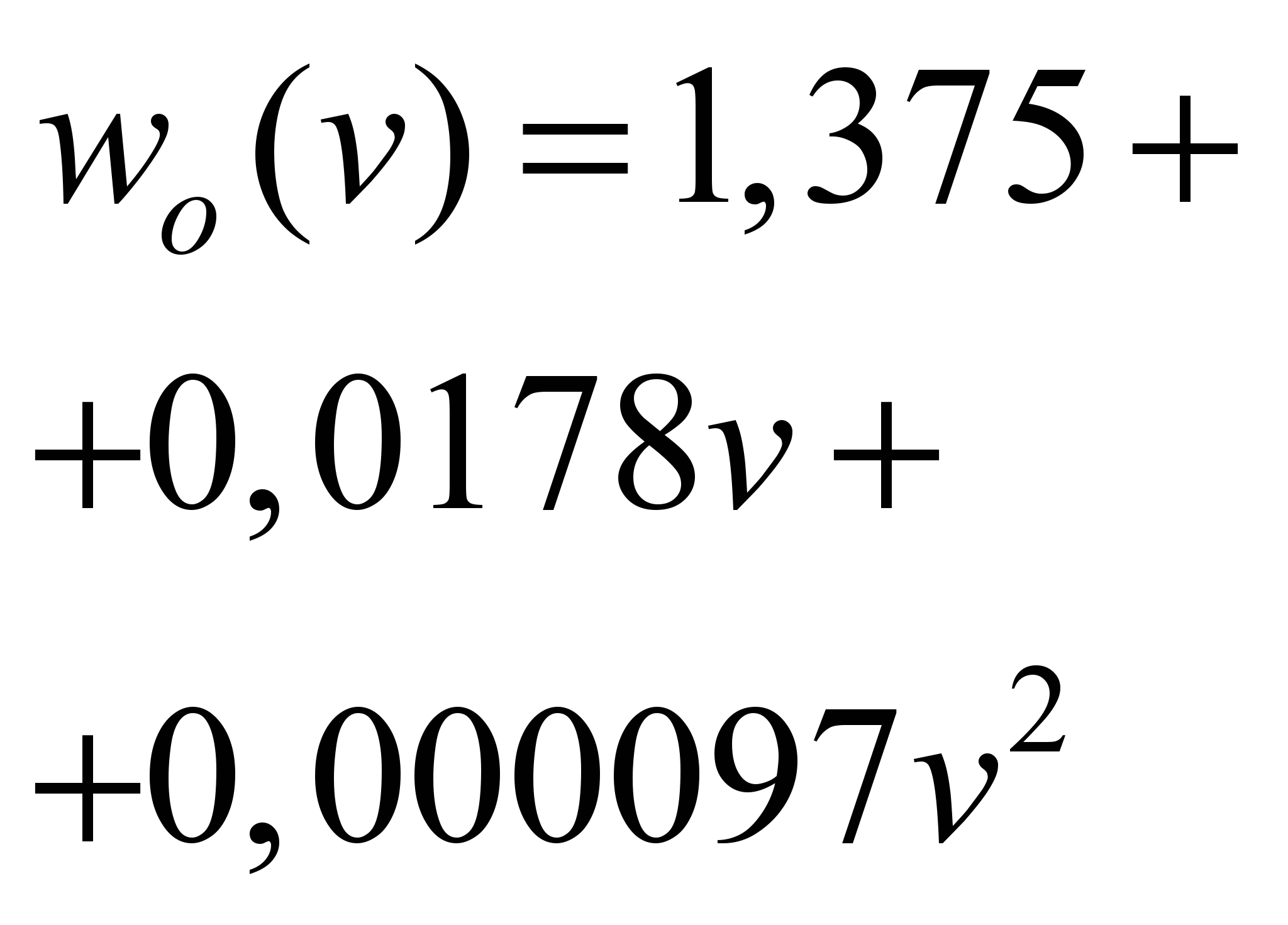
|
|
EJ675
(concentrated
tracrion)
|
172
|
456
|
1.08
|
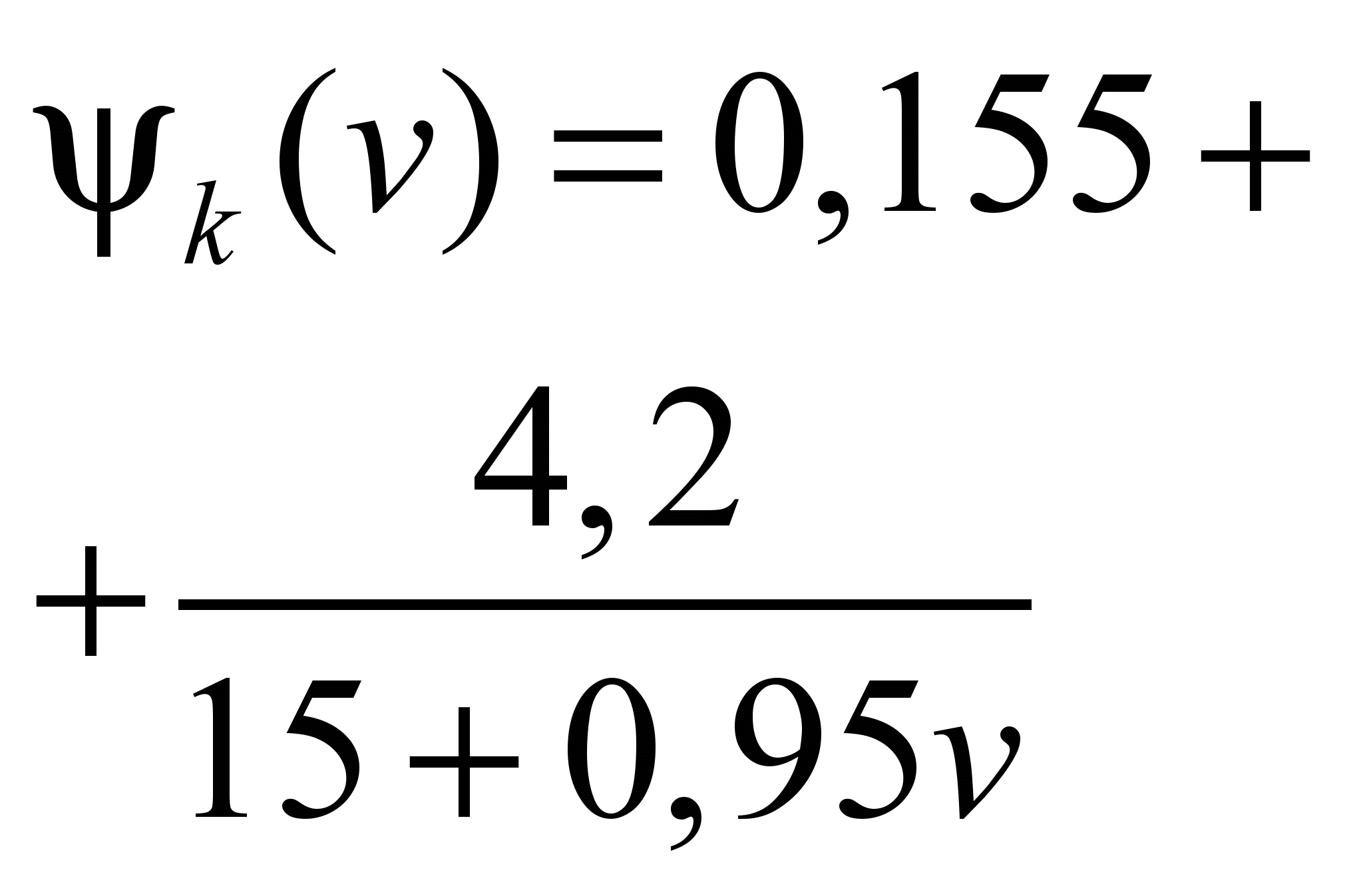
|
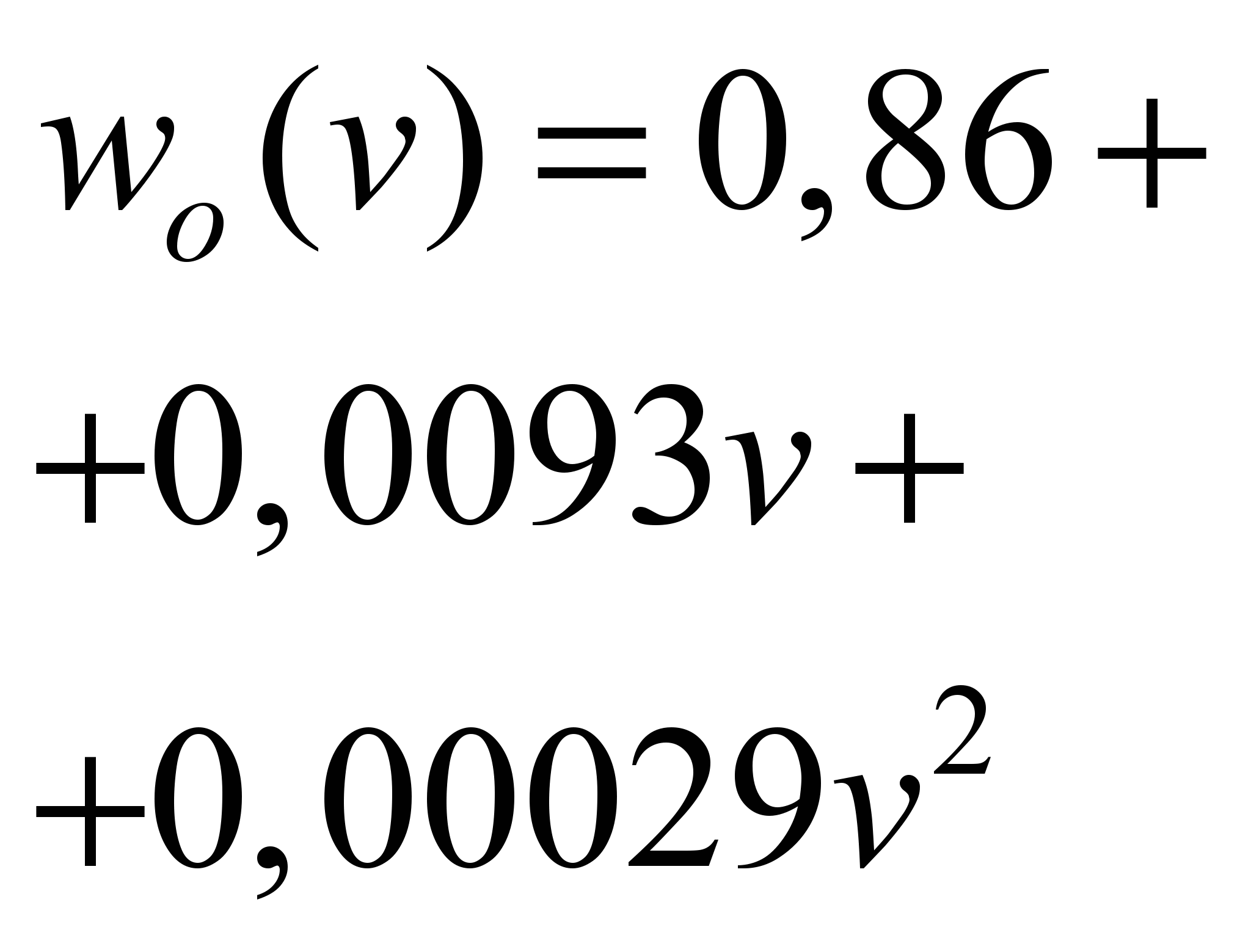
|
Notations.
1 The value of weight is presented with the maximum
loading of cars by passengers.
2
Total specific movement resistance is determined on condition
of movement at the section.
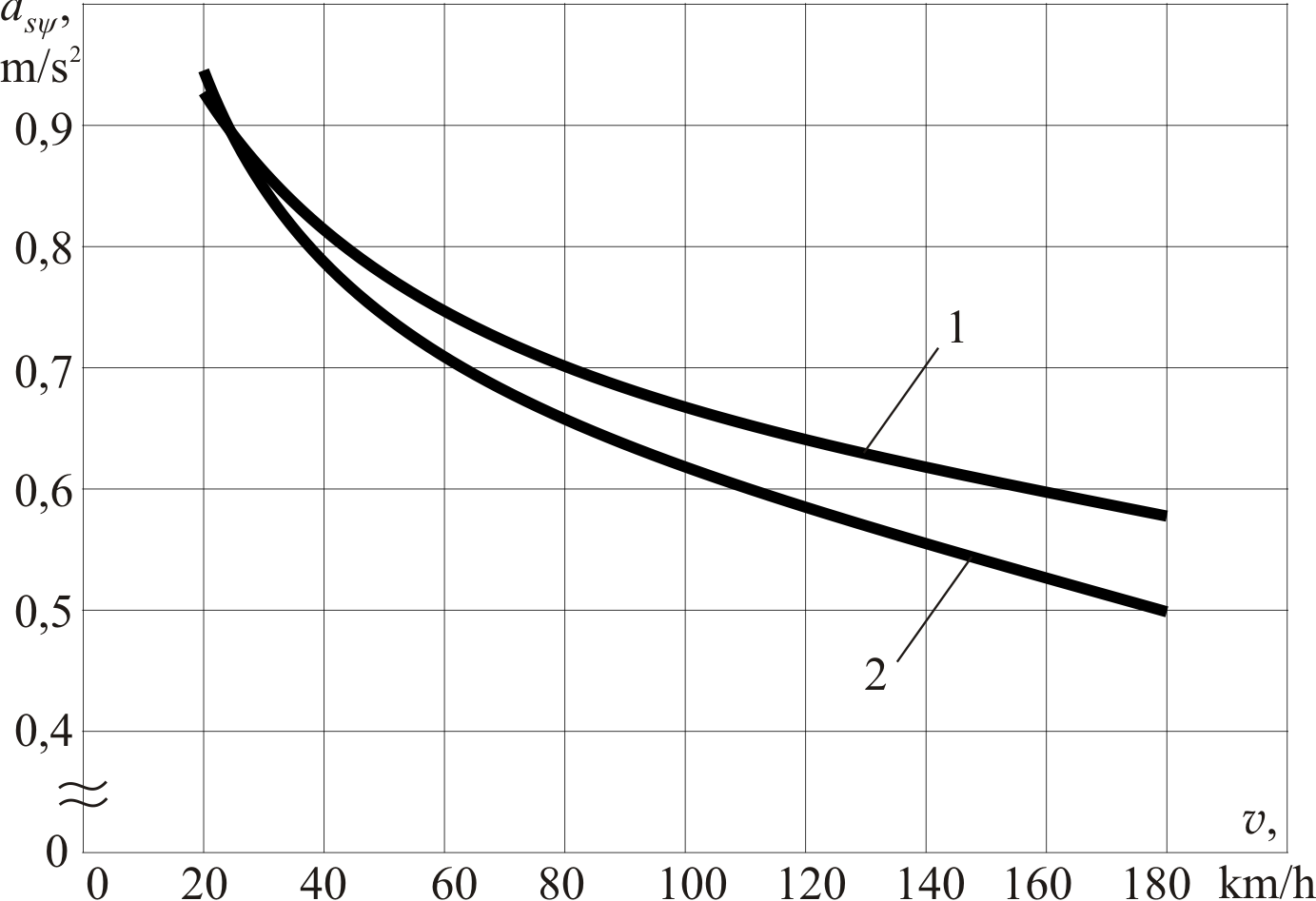
Fig.
3. Dependencies
 for the variants of the distributed (curve 1) and concentrated
(curve 2) traction
for the variants of the distributed (curve 1) and concentrated
(curve 2) traction
Originality and Practical
Value
Originality consists in
developing a methodology for determining the optimum values for the
parameters of the nominal mode of electric trains with asynchronous
traction drive, with two-zone and three-zone frequency regulation of
power.
The resulted methodology can
serve as a basis at formation of technical requirements for a new
rolling stock for railways of Ukraine.
Conclusions
The materials presented in the
article provide for the implementation of traction calculations (in
terms of plotting the motion curves), in solving problems, selecting
parameters for the nominal mode of electric trains with asynchronous
traction drive.
LIST OF REFERENCE LINKS
Арпуль,
С. В. Выбор рациональных параметров
тягового электроподвижного состава
/ С. В. Арпуль // Электрификация транспорта.
– 2014. – № 8. – С. 66–72.
Бабичков,
А. М. Тяга поездов и
тяговые расчеты : учеб.
для вузов ж.-д. трансп.
/ А. М. Бабичков, П.
А. Гурский, А. П.
Новиков. – Москва :
Транспорт, 1971. – 280 с.
Бещева,
Н. И. Пригородное движение на
электрифицированных линиях / Н.
И. Бещева // Тр. ВНИИЖТа.
– Москва, 1961. – Вып.
223. – 372 с.
Бещева,
Н. И. Сравнение отдельных видов тяги в
пригородном пассажирском движении /
Н. И. Бещева //
Труды ЦНИИ МПС. –
Москва, 1968. – Вып. 358.
– 363 с.
Гетьман,
Г. К. Вибір раціональних параметрів
номінального режиму електровозів / Г.
К. Гетьман, С. Л. Марікуца // Наука та
прогрес транспорту. –
2017. – № 1 (67).
– С. 96–105. doi:
10.15802/stp2017/92615.
Гетьман,
Г. К. Научные основы определения
рационального мощностного ряда тяговых
средств железнодорожного транспорта
: монография / Г.
К. Гетьман.
– Дніпропетровськ :
Вид-во Дніпропетр. нац.
ун-ту залізн. трансп. ім. акад. В.
Лазаряна, 2008. – 444 с.
Гетьман,
Г. К. Теорія електричної
тяги : підручник : у 2 т.
/ Г. К. Гетьман. – Дніпропетровськ
: Вид-во Дніпропетр. нац. ун-ту залізн.
трансп. ім. акад. В. Лазаряна, 2014. – Т.
1. – 578 с.
Правила
тяговых расчетов для поездной работы.
– Москва : Транспорт,
1985. – 287 с.
Розенфельд,
В. Е. Электрическая тяга
поездов / В. Е. Розенфельд, Ю. Е. Равкин,
И. А. Лакштовский. – Москва
: Гос. трансп.
ж.-д. изд-во,
1940. – 799 с.
Fischer,
Sz: Traction Energy Consumption of Electric Locomotives and
Electric Multiple Units at Speed Restrictions
/ Sz: Fischer
// Acta Technica Jauriensis.
– 2015. –
Vol. 8, No. 3.
– Р.
240–256.
doi: 10.14513/actatechjaur.v8.n3.384.
Optimization
of Train Operation in Multiple Interstations with Multi-Population
Genetic Algorithm /
Y. Huang,
X.
Ma,
S. Su, T.
Tang //
Energies. –
2015.
– Vol.
8 (12).
– Р.
14311–14329.
doi: 10.3390/en81212433.
Sarsembayev,
B. Analyze of
Impact of Track Alignment on the Energy Consumption Level
/ B.
Sarsembayev,
T. Suleimenov, M.
Arpabekov // Intern.
J. of Traffic and Transportation Engineering.
– 2015. –
Vol. 4,
No. 2. – Р. 45–59.
doi: 10.5923/j.ijtte.20150402.02.
Г. К. Гетьман1, С. Л. Марікуца2*
1Каф.
«Електрорухомий склад залізниць»,
Дніпропетровський національний
університет
залізничного транспорту
імені академіка В.
Лазаряна, вул. Лазаряна, 2, Дніпро,
Україна,
49010,
тел. +38 (056) 373 15 31, ел. пошта getman-gk@i.ua,
ORCID 0000-0002-3471-6096
2*Каф. «Електрорухомий
склад залізниць», Дніпропетровський
національний університет
залізничного
транспорту імені академіка В. Лазаряна,
вул. Лазаряна, 2, Дніпро, Україна,
49010, тел. +38 (056) 373 15 31, ел. пошта
marikutsasergei@gmail.com,
ORCID 0000-0002-0429-6633
ВиБіР РАЦіОНАЛЬНиХ ПАРАМЕТРіВ
НОМіНАЛЬНОГО
РЕЖИМу еЛЕКТРОПоїзДіВ
із АСИНХРОННиМ
ТЯГОВиМ
ПРИВОДОМ
Мета.
Параметри номінального режиму відносяться
до найважливіших експлуатаційних
показників тягових засобів, тому
задачі вибору їх оптимальних значень
завжди неминуче виникають при формуванні
технічних вимог на новий рухомий склад.
У роботі необхідно викласти особливості
рішення зазначених задач для
електропоїздів із асинхронним тяговим
приводом при двозонному та тризонному
частотному регулюванні потужності.
Методика.
Потужність номінального режиму
електрорухомого складу повинна бути
обрана таким чином, щоб забезпечувалася
можливість реалізації заданого часу
ходу по ділянці або швидкості руху.
Виходячи із цього, а також враховуючи,
що до важливих експлуатаційних
характеристик електропоїздів відноситься
величина прискорення в період пуску й
прискорення при конструкційній
швидкості, сформулюємо задачу визначення
номінальної потужності. В задачі для
заданого полігона тяги необхідно знайти
таке значення потужності номінального
режиму й відповідне їй значення сили
тяги, щоб забезпечувалася можливість
здійснювати перевезення із заданим
рівнем середньої швидкості руху при
мінімальній витраті електроенергії
на тягу. При цьому необхідно, щоб
виконувалися умови: а) швидкість руху
електропоїзда на ділянці не перевищує
встановлених обмежень; б) забезпечується
можливість реалізації заданих значень
прискорень. Більш детальний розгляд
питання показує, що в реальних умовах,
коли задані пускове прискорення й
маса поїзда, задача визначення потужності
електропоїзда практично зводиться
до визначення оптимального значення
швидкості номінального режиму.
Результати.
Задача вибору
оптимальних значень швидкості
номінального режиму вирішується шляхом
визначення витрати електроенергії при
варіації можливих значень пускової
швидкості, тому в розрахунки слід
приймати тільки ті її значення, які
забезпечують реалізацію заданих
пускового й залишкового прискорень.У
роботі показано, що величина сили тяги
при збільшенні конструкційної швидкості
й інших рівних умовах зростає, якщо
збільшувати пускову швидкість. Наукова
новизна. Авторами
розроблена методика для визначення
оптимальних значень параметрів
номінального режиму електропоїздів
із асинхронним тяговим приводом, при
двозонному та тризонному частотному
регулюванні потужності. Практична
значимість. Наведена
методика може бути основою при формуванні
технічних вимог на новий рухомий склад
для залізниць України.
Ключові слова:
електропоїзд; пускове й залишкове
прискорення; пускова швидкість; рівняння
руху; тягова характеристика;
зона регулювання потужності; питома
сила
Г. К. Гетьман1, С. Л. Марикуца2*
1Каф.
«Электроподвижной состав железных
дорог», Днепропетровский национальный
университет железнодорожного транспорта
имени академика В. Лазаряна,
ул. Лазаряна,
2, Днипро, Украина, 49010, тел.
+38 (056) 373 15 31,
эл. почта getman-gk@i.ua, ORCID
0000-0002-3471-6096
2*Каф.
«Электроподвижной
состав железных дорог», Днепропетровский
национальный
университет железнодорожного
транспорта имени академика В. Лазаряна,
ул. Лазаряна, 2, Днипро, Украина, 49010, тел.
+38 (056) 373 15 31,
эл. почта
marikutsasergei@gmail.com, ORCID 0000-0002-0429-6633
ВЫБОР РАЦИОНАЛЬНЫХ ПАРАМЕТРОВ
НОМИНАЛЬНОГО РЕЖИМА ЭЛЕКТРОПОЕЗДОВ
С
АСИНХРОННЫМ ТЯГОВЫМ ПРИВОДОМ
Цель.
Параметры номинального
режима относятся к важнейшим
эксплуатационным показателям тяговых
средств, поэтому задачи выбора их
оптимальных значений всегда неизбежно
возникают при формировании технических
требований на новый подвижной состав.
В работе необходимо изложить особенности
решения указанных задач для электропоездов
с асинхронным тяговым приводом при
двухзонном и трехзонном частотном
регулировании мощности. Методика.
Мощность
номинального режима электроподвижного
состава должна быть выбрана
таким образом, чтобы обеспечивалась
возможность реализации заданного
времени хода по участку или скорости
движения. Исходя из этого, а также
учитывая, что к важным эксплуатационным
характеристикам электропоездов
относится величина ускорения в период
пуска и ускорения при конструкционной
скорости, сформулируем задачу определения
номинальной мощности. В задаче для
заданного полигона тяги необходимо
найти такое значение мощности номинального
режима и соответствующее ей значение
силы тяги, чтобы обеспечивалась
возможность осуществлять перевозки
с заданным уровнем средней скорости
движения при минимальных затратах
электроэнергии на тягу. При этом
необходимо чтобы выполнялись условия:
а) скорость движения
электропоезда на участке не превышает
установленных ограничений; б)
обеспечивается возможность реализации
заданных значений ускорений. Более
детальное рассмотрение вопроса
показывает, что в реальных условиях,
когда задано пусковое ускорение и
масса поезда, задача определения
мощности электропоезда практически
сводится к определению оптимального
значения скорости номинального режима.
Результаты.
Задача
выбора оптимальных значений скорости
номинального режима решается путем
определения расхода электроэнергии
при вариации возможных значений пусковой
скорости, поэтому в расчет следует
принимать только те ее значения, которые
обеспечивают реализацию заданных
пускового и остаточного ускорений. В
работе показано, что величина силы тяги
при увеличении конструкционной скорости
и прочих равных условиях возрастает,
если увеличивать пусковую скорость.
Научная
новизна.
Авторами разработана
методика для определения оптимальных
значений параметров номинального
режима электропоездов с асинхронным
тяговым приводом, при
двухзонном и трехзонном частотном
регулировании мощности. Практическая
значимость.
Приведенная методика может служить
основой при формировании технических
требований на новый подвижной состав
для железных дорог Украины.
Ключевые слова:
электропоезд; пусковое и остаточное
ускорение; пусковая скорость; уравнение
движения; тяговая характеристика;
зона регулирования мощности; удельная
сила
REFERENCES
Arpul,
S. V. (2014). The choice of rational parameters of the traction
electric rolling stock. Electrification of Transport,
8, 66-72.
Babichkov,
A. M., Gurskiy, P. A., & Novikov, A. P. (1971). Tyaga
poezdov i tyagovyye raschety. Moscow:
Transport.
Beshcheva,
N. I. (1961). Prigorodnoye dvizheniye
na elektrifitsirovannykh liniyakh.
Moscow: Railway research institution of railway transport.
Beshcheva,
N. I. (1968). Sravneniye otdelnykh
vidov tyagi v prigorodnom passazhirskom dvizhenii.
Moscow: Transport.
Hetman,
H. K., & Marikutsa, S. L. (2017). Selection of rational
parameters of the nominal mode of electric locomotives. Science
and Transport Progress, 1(67),
96-105. doi:
10.15802/stp2017/92615
Hetman,
H. K. (2008). Nauchnyye osnovy
opredeleniya ratsionalnogo moshchnostnogo ryada tyagovykh sredstv
zheleznodorozhnogo transporta
[Monograph]. Dnipropetrovsk: Dnipropetrovsk National University of
Railway Transport named after Academician V. Lazaryan.
Hetman,
H. K. (2014). Teoriia elektrychnoi
tiahy (Vol. 1). Dnipropetrovsk:
Dnipropetrovsk National University of Railway Transport named after
Academician V. Lazaryan.
Pravila
tyagovykh raschetov dlya poyezdnoy raboty.
(1985). Moscow: Transport.
Rozenfeld,
V. Y., Ravkin, Y. Y., & Lakshtovskiy, I. A. (1940).
Elektricheskaya tyaga poyezdov.
Moscow: Transzheldorizdat.
Fischer,
S. (2015). Traction Energy Consumption of Electric Locomotives and
Electric Multiple Units at Speed Restrictions. Acta
Technica Jauriensis, 8(3),
240-256. doi: 10.14513/actatechjaur.v8.n3.384
Huang,
Y., Ma, X., Su, S., & Tang, T. (2015). Optimization of Train
Operation in Multiple Interstations with Multi-Population Genetic
Algorithm. Energies, 8(12),
14311-14329. doi: 10.3390/en81212433
Sarsembayev,
B., Suleimenov, T., & Arpabekov, M. (2015). Analyze of Impact
of Track Alignment on the Energy Consumption Level. International
Journal of Traffic and Transportation Engineering,
4(2),
45-59. doi: 10.5923/j.ijtte.20150402.02
Prof.
A. M. Afanasov, D. Sc. (Tech.), (Ukraine);
Prof. O. O.
Beihul, D. Sc. (Tech.), (Ukraine)
recommended this article to be published
Received:
Feb. 10, 2017
Accessed:
May 17, 2017
, (1)
– tangential traction force (on the rim of the driving wheels) of
the motor cars, N;
– total movement resistance, N;
– train weight, t;
–
inertia coefficient of the rotating masses of the train;
– acceleration, m/s2.
(2)
– specific total resistance to train movement, N/kN.
(3)
(4)
– tangential traction force related to one traction motor, N; the
index «n» – means the value of the parameter corresponding to
the nominal mode.
(5)
and
dependencies is definitely determined by the value of the optimal
mode speed, and thus the problem of choosing the optimal parameters
of nominal mode of electric trains reduces to the choice of the
movement speed in the nominal power mode from the condition of
minimizing the electricity consumption for traction of trains.
(6)
− is dimensional coefficient, the value of which depends on the
accepted units of measurement of physical quantities;
− control parameter;
– basic specific
net train resistance;
− the value of the longitudinal path gradient, which is a function
of the path
.
is determined as
(7)
and
are determined by the corresponding dependences obtained on the
basis of the experimental data [7, 8, 10].
corresponds to the traction mode;
– to the braking mode;
to
the run-out mode.
;
и
− limiting traction and braking characteristics respectively,
referred to 1 kN of the train weight.
for the two most frequently encountered methods of 3-zone (Fig. 1,
a) and 2-zone (Fig. 1, b) frequency control of the asynchronous
traction drive power for electric trains.
– acceleration with the given starting traction force;
– the realization of the constant traction power;
– the traction power control is inversely proportional to the
movement speed.
,
the starting traction force of thrust in specific units (3)
(8)