ISSN
2307–3489 (Print), ІSSN
2307–6666
(Online)
Наука
та прогрес транспорту. Вісник
Дніпропетровського
національного університету залізничного
транспорту, 2017,
№
3
(69)
електричний
транспорт
УДК
629.423.31:621.313.222.013
А. Е. ДРУБЕЦКИЙ1*
1*Каф.
«Электроподвижной состав железных
дорог», Днепропетровский национальный
университет железнодорожного транспорта
имени академика В. Лазаряна, ул. Лазаряна,
2,
Днипро, Украина, 49010, тел. +38 (0562) 33 55 38,
эл. почта drubetskiy.ae@gmail.com,
ORCID 0000-0001-5691-0925
расчет магнитных характеристик
тягового
электродвигателя с помощью
усовершенствованной универсальной
магнитной характеристики
Цель.
В исследовании предполагается разработать
методику расчета магнитных характеристик
некомпенсированных тяговых электродвигателей
(ТЭД) при любой степени ослабления
возбуждения на базе аппроксимирующего
выражения для усовершенствованной
универсальной магнитной характеристики
(УМХ). Необходимо также осуществить
анализ выражений для усовершенствованной
УМХ с целью нахождения выражения,
наиболее полно удовлетворяющего
требованиям разработки методики
определения индуктивных параметров
ТЭД. Методика.
Для построения характеристик по
усовершенствованной УМХ необходимо
для каждой степени ослабления возбуждения
определить коэффициент насыщения. Это
возможно осуществить только аналитически.
Для упрощения аналитического нахождения
коэффициента насыщения предложен метод,
основанный на решении системы из двух
уравнений, одним из которых является
сама УМХ, а вторым – уравнение прямой,
угловой коэффициент которой пропорционален
коэффициенту насыщения. Получающиеся
в результате расчетов значения
коэффициента насыщения для степеней
возбуждения β < 1 по сути являются
коэффициентами формы магнитной
характеристики. Чтобы избавиться от
необходимости каждый раз при расчете
характеристик определять коэффициенты
аппроксимации, предложена форма
усовершенствованной УМХ, у которой роль
аргумента выполняет магнитодвижущая
сила (МДС) обмотки возбуждения. Результаты.
Доказано, что с помощью усовершенствованной
УМХ возможен расчет характеристик
некомпенсированных ТЭД для любых
степеней ослабления возбуждения.
Точность расчета при β = 1 не отличается
от таковой при расчете по УМХ, предложенной
проф. М. Д. Находкиным. Такая же точность
сохраняется при степенях возбуждения,
отличных от единицы. Научная
новизна. Предложена
аналитическая методика расчета магнитных
(скоростных) характеристик некомпенсированных
ТЭД для любой степени ослабления
возбуждения с помощью усовершенствованной
УМХ. Также предложена аналитическая
методика определения коэффициента
насыщения для усовершенствованной УМХ
при любой степени ослабления возбуждения.
Благодаря введению в качестве аргумента
МДС обмотки возбуждения отпадает
необходимость в определении
коэффициентов аппроксимации для каждого
конкретного ТЭД. Практическая
значимость. Разработанная
методика позволяет производить расчеты
магнитных характеристик некомпенсированных
ТЭД для любой степени ослабления
возбуждения. На ее базе
возможна разработка методики определения
индуктивных параметров ТЭД, использующей
в качестве исходных данных коэффициент
насыщения машины.
Ключевые слова: универсальная
магнитная характеристика; аппроксимация;
тяговый электродвигатель; магнитные
характеристики
Введение
Рабочие характеристики
тяговых электродвигателей (ТЭД) и их
поведение при переходных процессах
определяются их магнитными характеристиками
[14]. Кроме того, благодаря широкому
использованию ЭВМ при расчетах,
проектировании и моделировании ТЭД
все более актуальными становятся
различные методы аппроксимации магнитных
характеристик [1, 2, 5, 13, 18–22].
В представленных
работах аппроксимация магнитных
характеристик вычисляется выражением
с одной переменной в виде МДС обмотки
возбуждения или тока обмотки возбуждения.
Тем не менее, несмотря на всю простоту
такого подхода, он оказывается неприменим
для некомпенсированных ТЭД в случае,
если аппроксимирующее выражение
необходимо использовать для режима
ослабления возбуждения отличного от
того, при котором выполнялась
аппроксимация. Это происходит из-за
того, что в некомпенсированных ТЭД
сильное влияние на основной магнитный
поток оказывает реакция якоря [4, 8, 10,
16]. В таком случае необходима методика,
позволяющая учесть размагничивающее
действие реакции якоря при аппроксимации
основного магнитного потока. Этим
требованиям полностью соответствует
методика, описанная в работе [3]. Данная
методика для определения основного
магнитного потока требует наличия
характеристики намагничивания
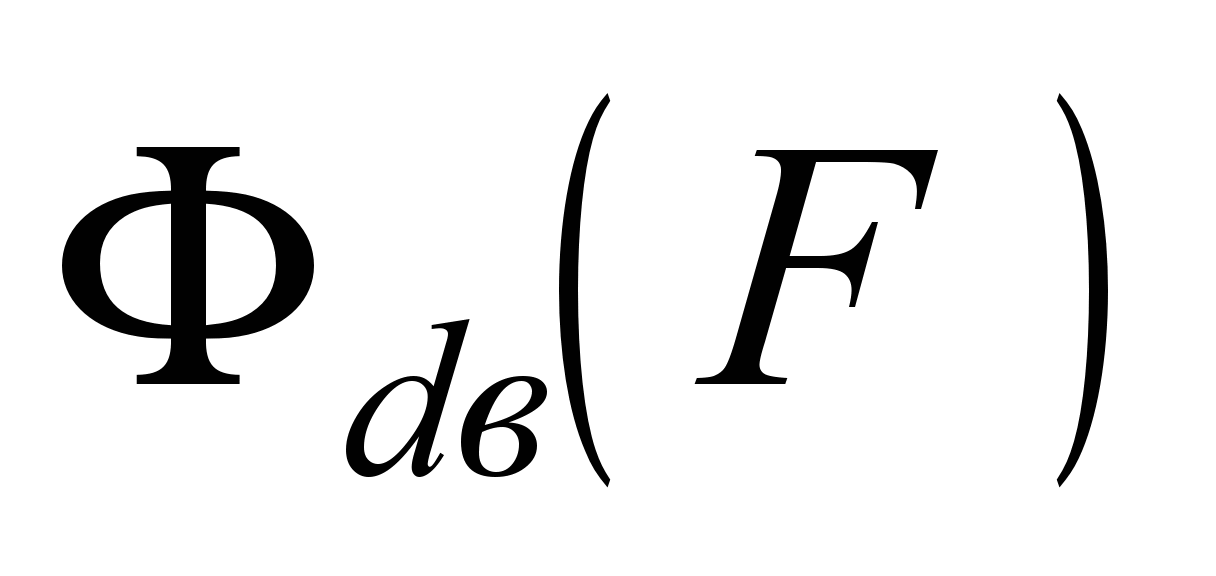 ,
т.е. зависимости основного магнитного
потока от МДС обмотки возбуждения
,
т.е. зависимости основного магнитного
потока от МДС обмотки возбуждения
 ,
определенной на холостом ходу. Как
правило, эта характеристика не приводится
в справочной литературе. В этом случае
очень удобным для аппроксимации
магнитных характеристик является
использование коэффициента насыщения
,
определенной на холостом ходу. Как
правило, эта характеристика не приводится
в справочной литературе. В этом случае
очень удобным для аппроксимации
магнитных характеристик является
использование коэффициента насыщения
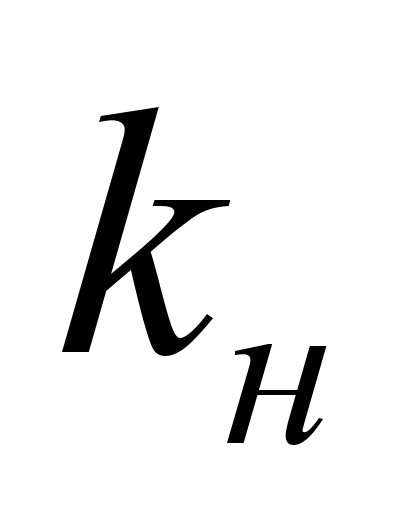 и УМХ [1].
и УМХ [1].
В работе [7] выполнен
анализ возможности определения магнитной
характеристики ТЭД с учетом
размагничивающего действия реакции
якоря с использованием достоинства
методик, описанных в [3]
и [1, 14, 16].
Цель
Целью данной работы
является разработка методики
аналитического расчета магнитных
характеристик некомпенсированных ТЭД
при любой степени ослабления возбуждения
на базе аппроксимирующего выражения
для УМХ. А также, проведение анализа
выражений для усовершенствованной УМХ
с целью нахождения выражения, наиболее
полно удовлетворяющего требованиям
для разработки методики определения
индуктивных параметров ТЭД.
Методика
Как было указано
в [7], процесс разработки методики для
определения индуктивных параметров
по УМХ разделен на пять пунктов, четыре
из которых были описаны в [7]. В данной
работе рассмотрим пятый пункт «Определение
на базе аппроксимирующего выражения
для УМХ универсальных формул для
индуктивных параметров машины».
Для сохранения
смысловой структуры статьи сохраним
нумерацию пунктов разработки методики,
принятую в [7]. Так как освещение всего
пункта 5 выходит за объем одной статьи,
разобьем его на два подпункта:
5.1. расчет характеристик
некомпенсированных ТЭД с помощью
усовершенствованной УМХ;
5.2. определение
универсальных формул для индуктивных
параметров некомпенсированных ТЭД.
В данной работе
будет рассмотрен подпункт «Определение
на базе аппроксимирующего выражения
для УМХ универсальных формул для
индуктивных параметров машины»,
а именно:
5.1. расчет
характеристик некомпенсированных ТЭД
с помощью усовершенствованной УМХ.
В работе [7] было
получено аппроксимирующее выражение
для УМХ применительно
к некомпенсированным
ТЭД, оно имеет вид:
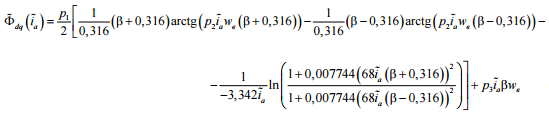 ,(1)
,(1)
где
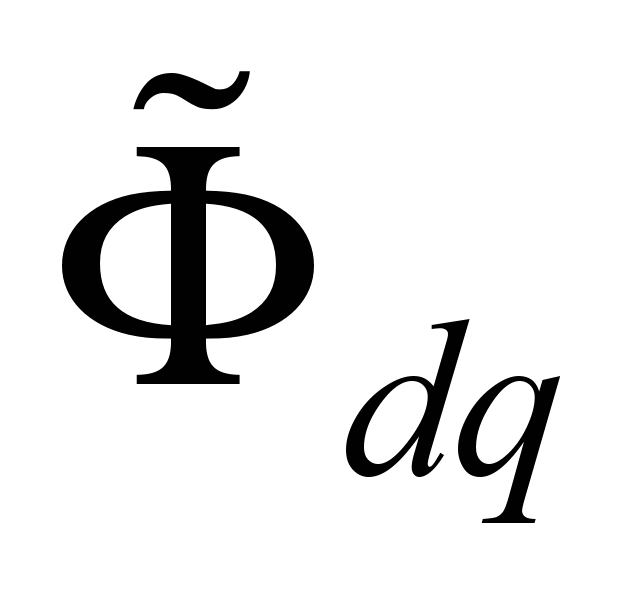 и
и
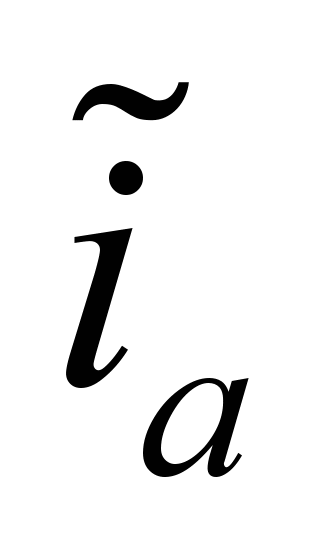 – основной магнитный поток и ток якоря
машины в относительных единицах;
– основной магнитный поток и ток якоря
машины в относительных единицах;
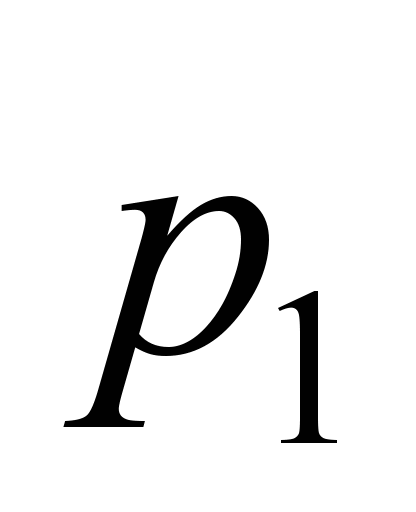 ,
,
 ,
,
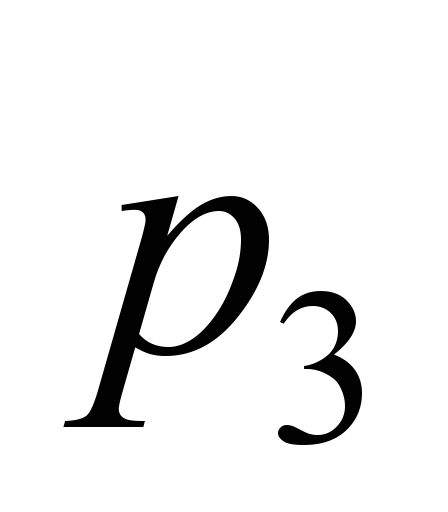 – коэффициенты аппроксимации;
– коэффициенты аппроксимации;
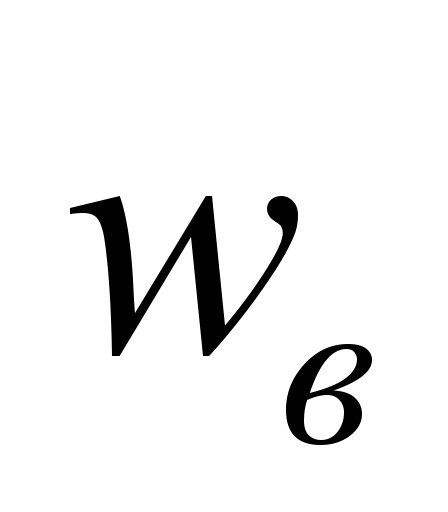 – число витков обмотки возбуждения
машины, для которой выполняется
построение магнитной характеристики;
– число витков обмотки возбуждения
машины, для которой выполняется
построение магнитной характеристики;
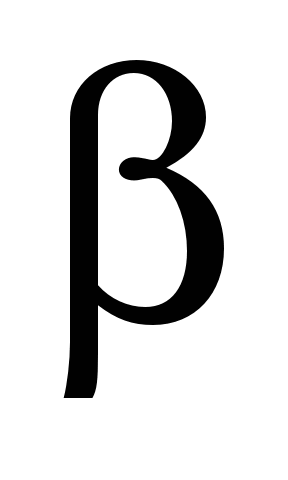 – степень ослабления возбуждения.
– степень ослабления возбуждения.
Основные принципы
построения магнитных характеристик
по усовершенствованной УМХ не отличаются
от тех, которые описаны в литературе
по проектированию тяговых электрических
машин [14, 16]. То есть для определения
реальных характеристик машины необходимо
определить масштабы для магнитного
потока и МДС (тока). Однако, есть
существенные различия в способах
построения реальных характеристик.
Различия заключаются в том, что для
каждой степени ослабления возбуждения
необходимо определить свои масштабы.
Также, в случае проектирования новой
машины, усовершенствованную УМХ для
ослабленного возбуждения невозможно
заранее изобразить графически, как это
сделано для
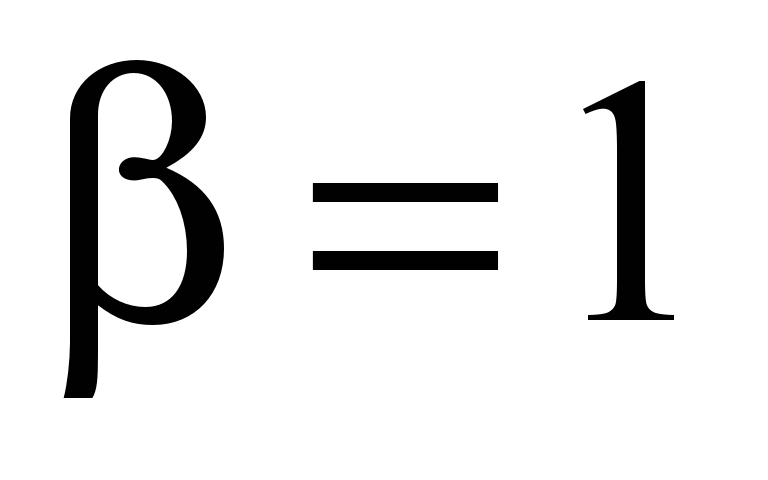 .
Это происходит из-за того, что значения
степеней ослабления возбуждения, в том
числе и минимальные, определяются в
процессе расчета проектируемой машины.
Поэтому единственно возможным способом
построения характеристик по
усовершенствованной УМХ является
аналитический.
.
Это происходит из-за того, что значения
степеней ослабления возбуждения, в том
числе и минимальные, определяются в
процессе расчета проектируемой машины.
Поэтому единственно возможным способом
построения характеристик по
усовершенствованной УМХ является
аналитический.
Чтобы проверить
адекватность выражения (1) необходимо
выполнить построение магнитных
характеристик любого некомпенсированного
ТЭД для различных степеней ослабления
возбуждения. В качестве примера
рассмотрим двигатели НБ-406 и РТ-51Д.
Коэффициенты
аппроксимации для НБ-406
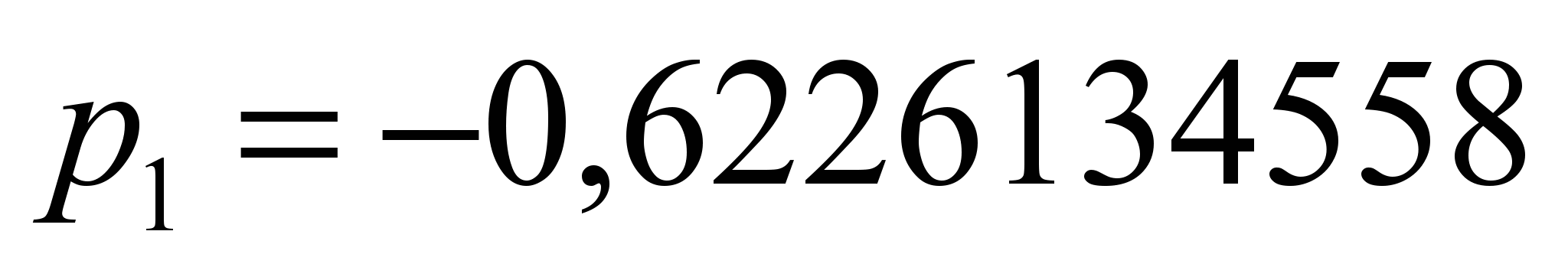 ,
,
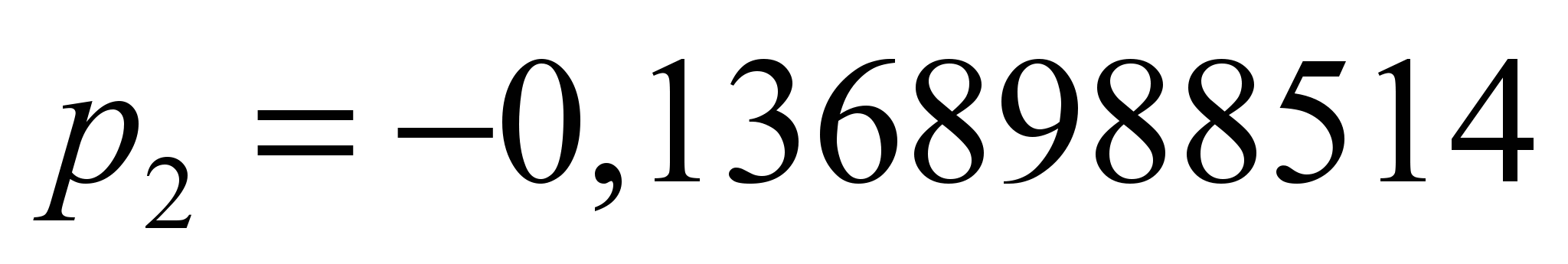 ,
,
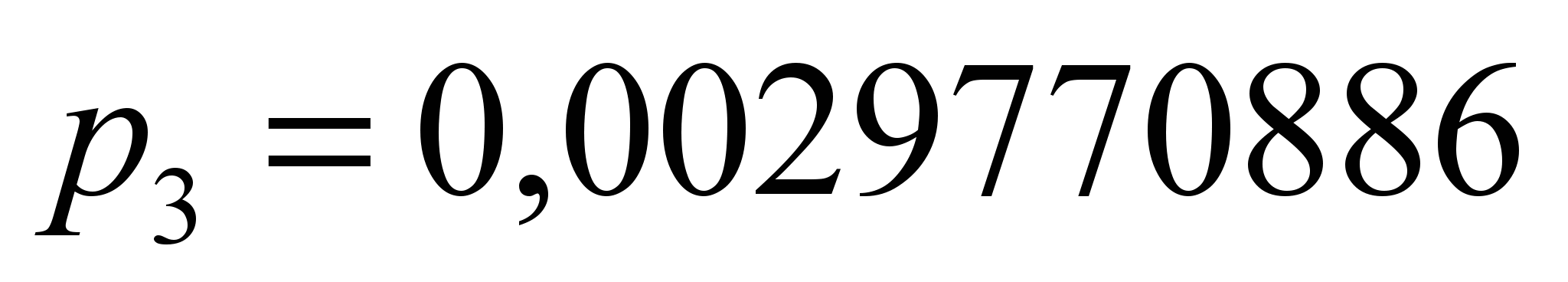 .
.
Коэффициент
насыщения для НБ-406, соответствующий
номинальному часовому режиму,
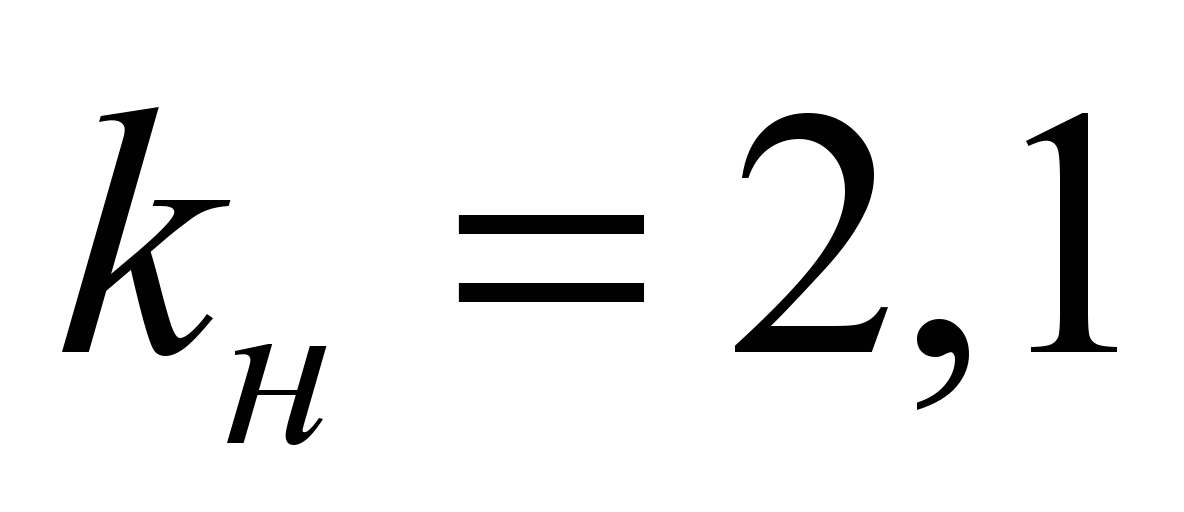 .
Он определен при
.
Он определен при
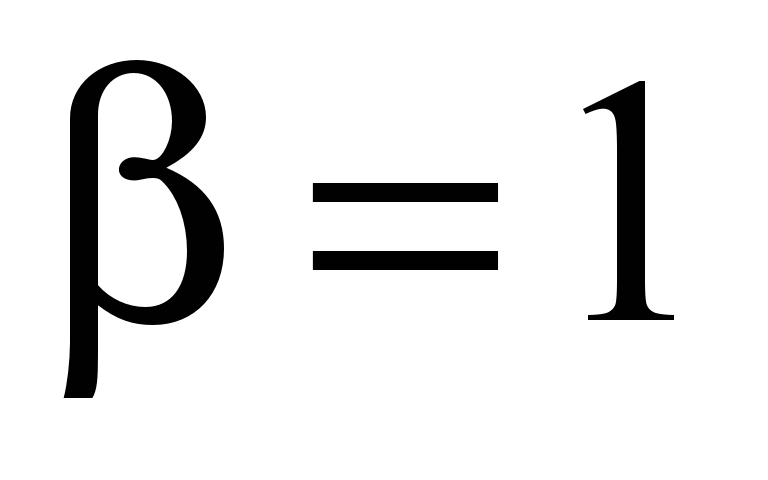 .
Аналитически определим точку на УМХ,
соответствующую данному
.
Аналитически определим точку на УМХ,
соответствующую данному
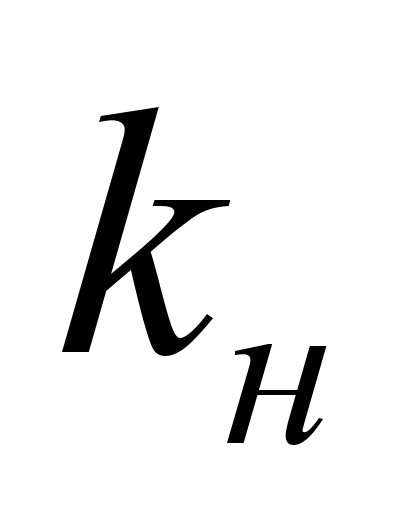 ,
как точку пересечения прямой, угловой
коэффициент которой пропорционален
,
как точку пересечения прямой, угловой
коэффициент которой пропорционален
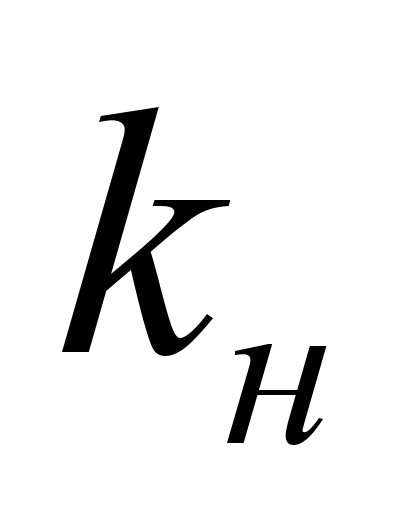 и самой УМХ. Назовем такую прямую прямой
коэффициента насыщения (ПКН). Определить
угловой коэффициент ПКН можно, зная
угловой коэффициент прямой, соответствующей
магнитному напряжению воздушного
зазора. Уравнение прямой магнитного
напряжения воздушного зазора согласно
[5] имеет вид:
и самой УМХ. Назовем такую прямую прямой
коэффициента насыщения (ПКН). Определить
угловой коэффициент ПКН можно, зная
угловой коэффициент прямой, соответствующей
магнитному напряжению воздушного
зазора. Уравнение прямой магнитного
напряжения воздушного зазора согласно
[5] имеет вид:
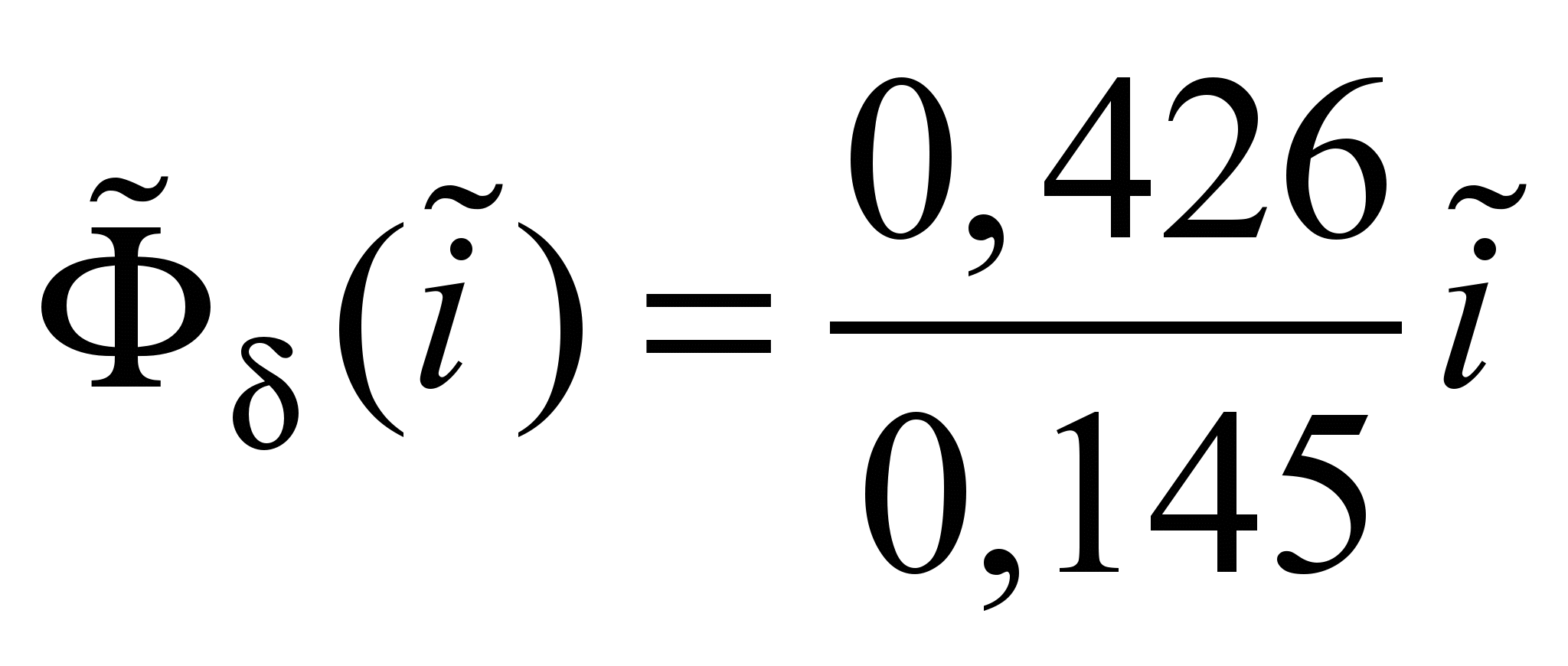 , (2)
, (2)
С помощью
математических преобразований находим,
что угловой коэффициент ПКН
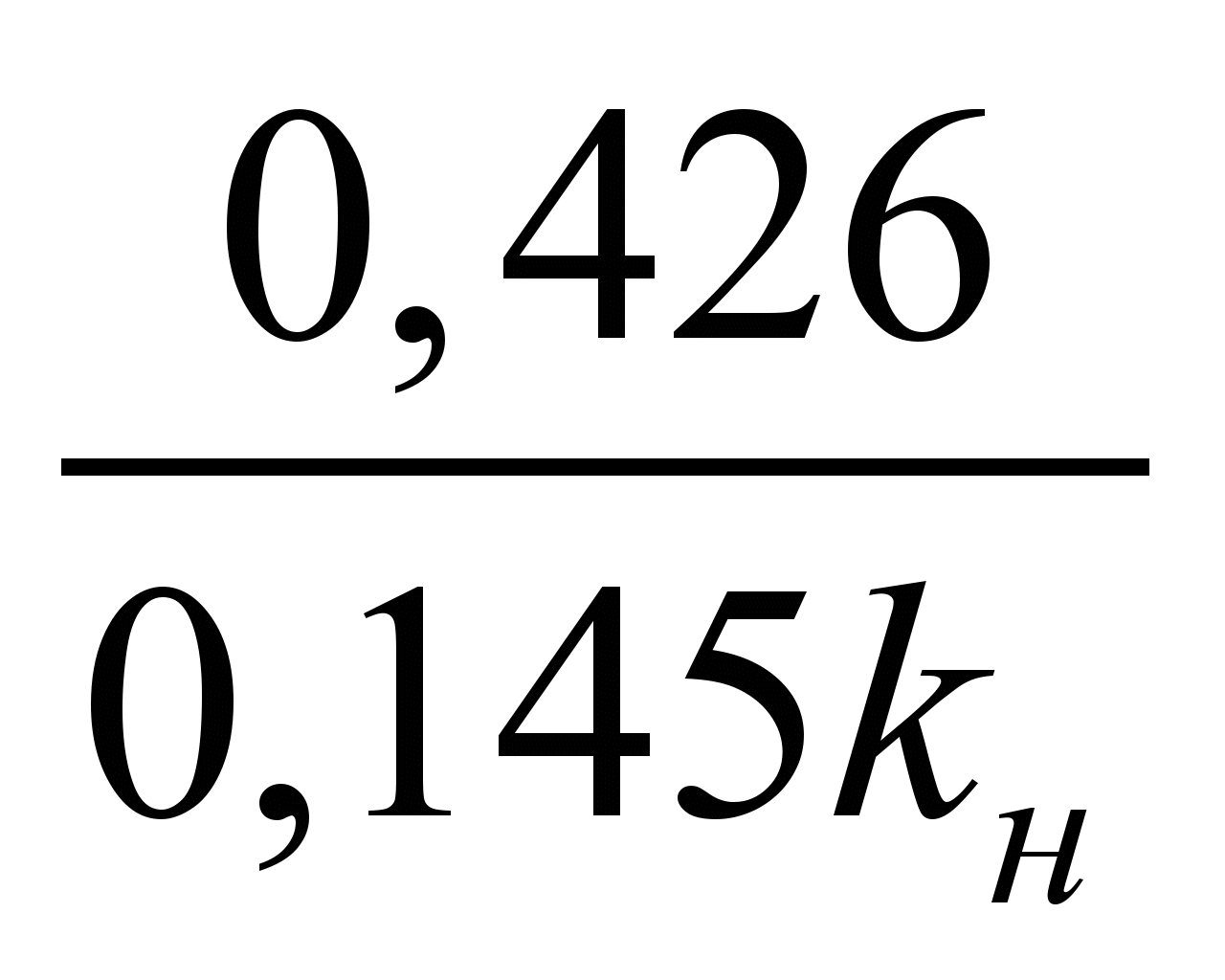 , (3)
, (3)
Далее точка
пересечения УМХ и ПКН определяется
аналитически, путем решения соответствующей
системы из двух уравнений:
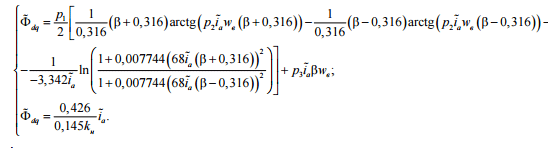 (4)
(4)
Для удобства решения
системы (4) можно воспользоваться одним
из прикладных математических пакетов
программного обеспечения, например,
MathCAD.
Координаты точки
пересечения УМХ и ПКН для НБ-406 при
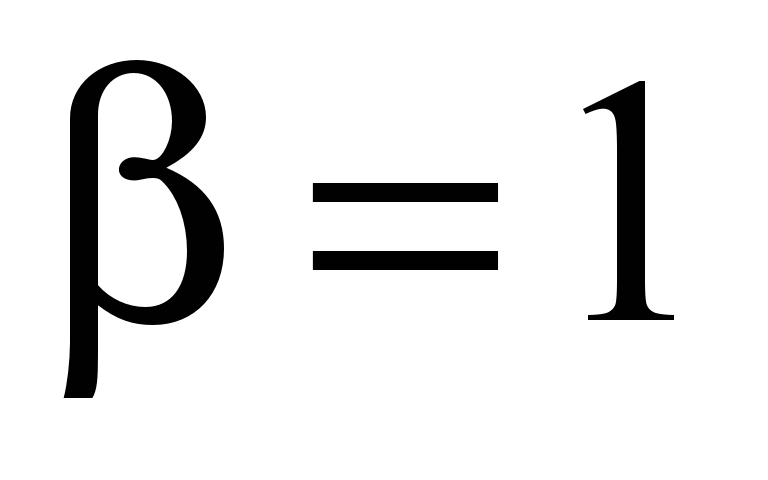 ,
,
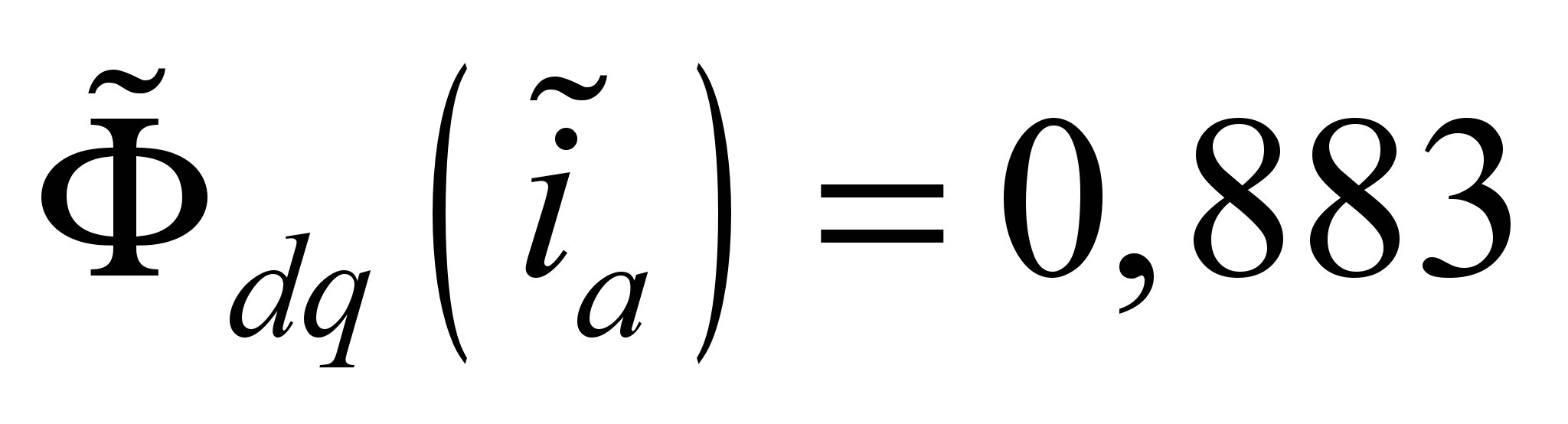 и
и
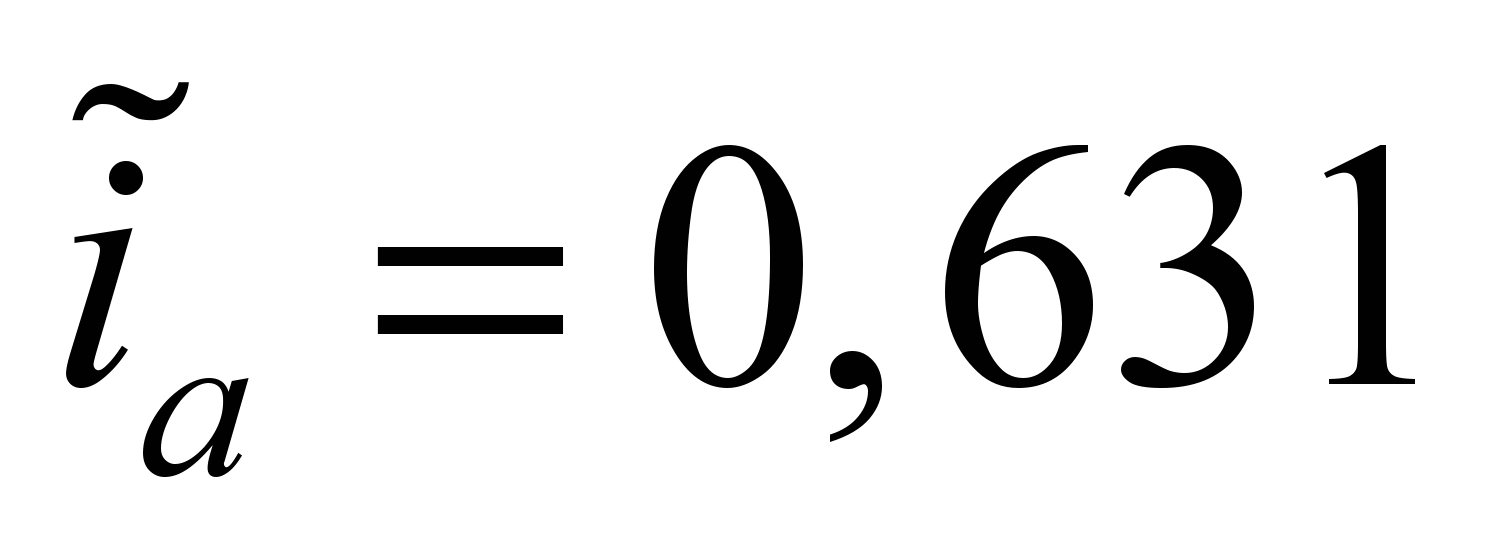 являются также и масштабами для
магнитного потока и тока. Определив
масштабы, можно рассчитать магнитные
характеристики в абсолютных единицах
[14, 16].
являются также и масштабами для
магнитного потока и тока. Определив
масштабы, можно рассчитать магнитные
характеристики в абсолютных единицах
[14, 16].
Отдельно следует
рассмотреть расчет магнитных характеристик
для ослабленного поля. Здесь следует
обратить внимание и на вид усовершенствованной
УМХ для ослабленного возбуждения, и на
изменения при этом коэффициента
насыщения. Вид усовершенствованной
УМХ при различных степенях ослабления
возбуждения, соответствующих степеням
ослабления возбуждения НБ-406, показан
на рис. 1. На этом же рисунке указаны
точки пересечения УМХ и ПКН для
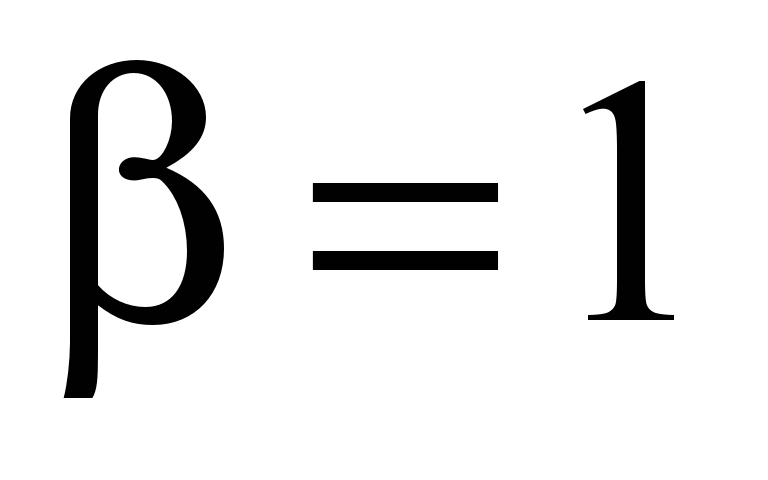 и
и
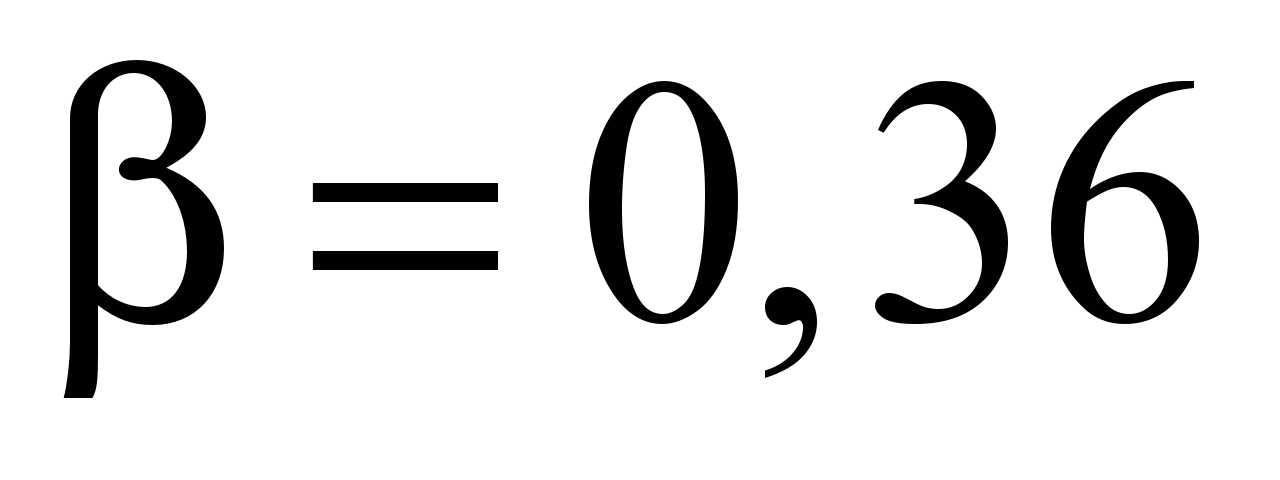 .
.
Как видно из рис.
1, отношение отрезков
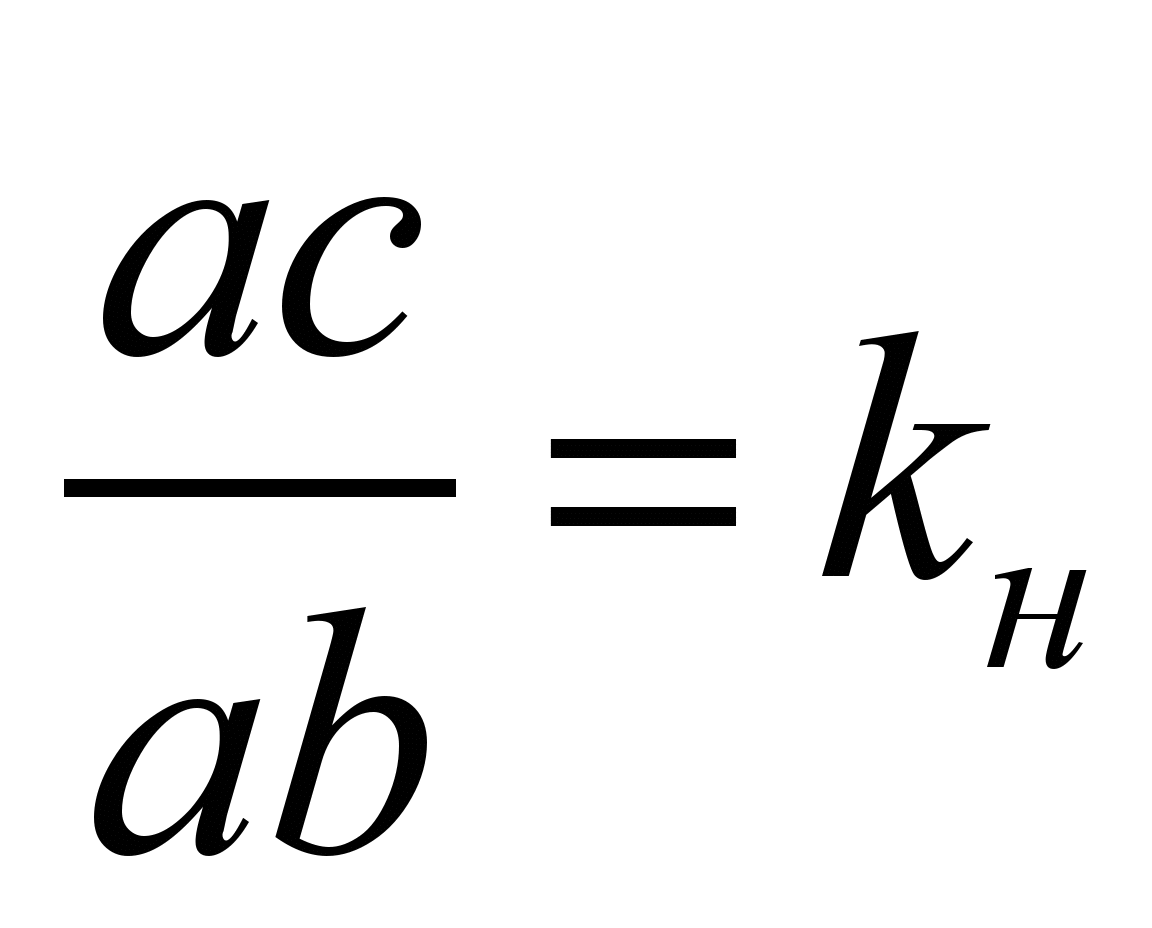 при
при
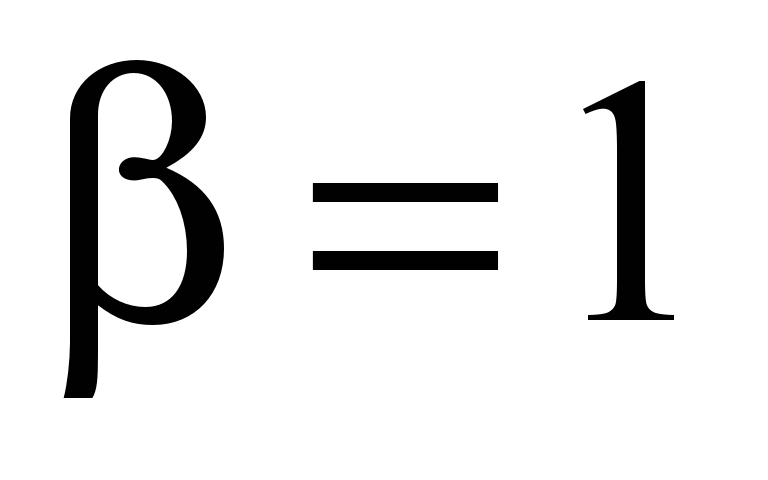 не равно отношению
не равно отношению
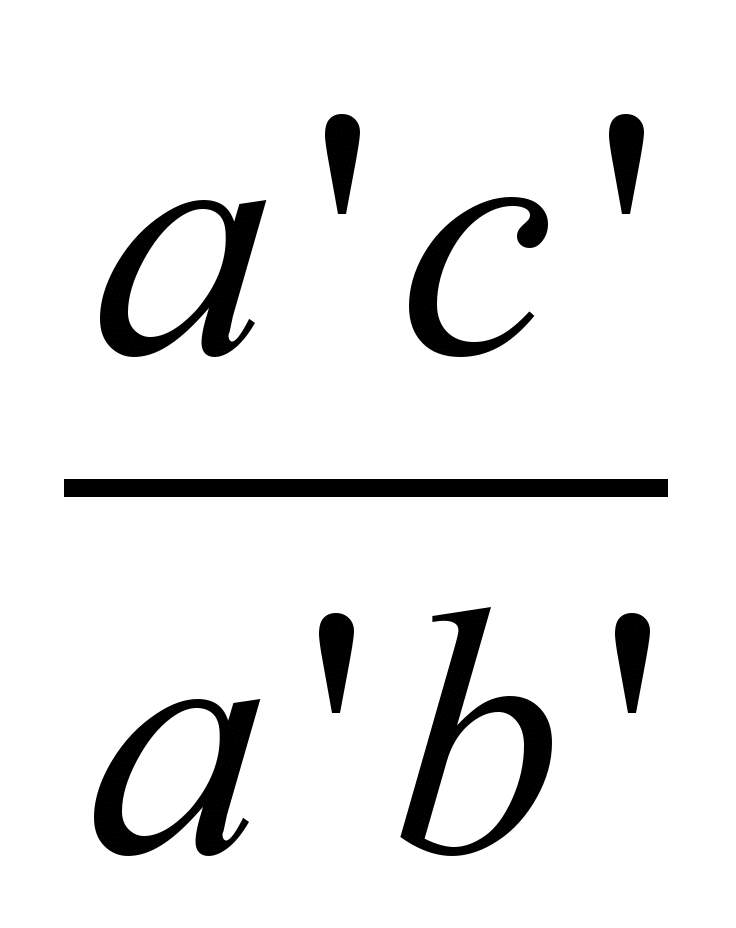 при
при
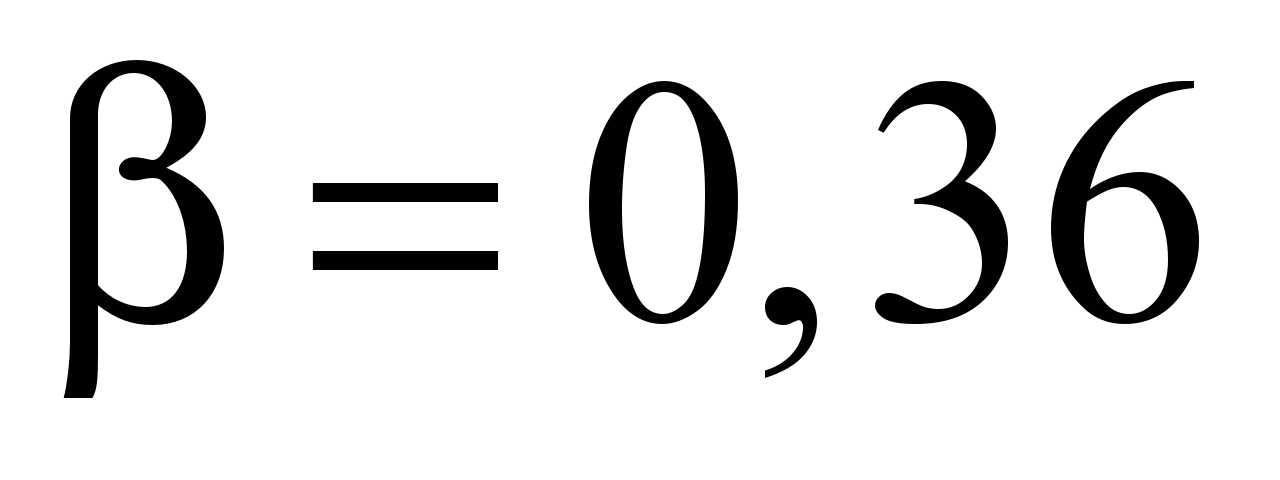 ,
это связанно с тем, что в качестве
аргумента в выражении (1) принят ток
якоря. Чтобы не вносить путаницу в
объяснения, отношение абсцисс точек
пересечения ПКН и УМХ при любых
степенях ослабления возбуждения в
дальнейшем будет сохранять название
«коэффициент насыщения», хотя, строго
говоря, оно таковым не является. Очевидно,
что коэффициент насыщения по мере
уменьшения
,
это связанно с тем, что в качестве
аргумента в выражении (1) принят ток
якоря. Чтобы не вносить путаницу в
объяснения, отношение абсцисс точек
пересечения ПКН и УМХ при любых
степенях ослабления возбуждения в
дальнейшем будет сохранять название
«коэффициент насыщения», хотя, строго
говоря, оно таковым не является. Очевидно,
что коэффициент насыщения по мере
уменьшения
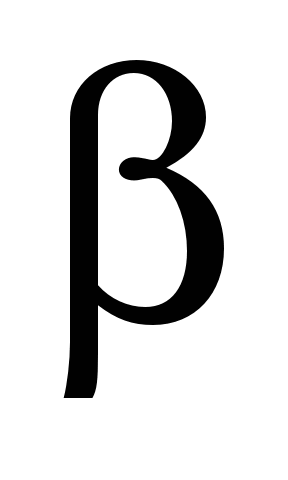 растет. В данном случае были получены
такие значения коэффициента насыщения:
растет. В данном случае были получены
такие значения коэффициента насыщения:
Затем для полученных
коэффициентов насыщения по системе
уравнений (4) определяются масштабы и
строятся магнитные характеристики для
ослабленного поля [14, 16].
Хотелось бы отметить,
что, несмотря на утерю физического
значения коэффициента насыщения при
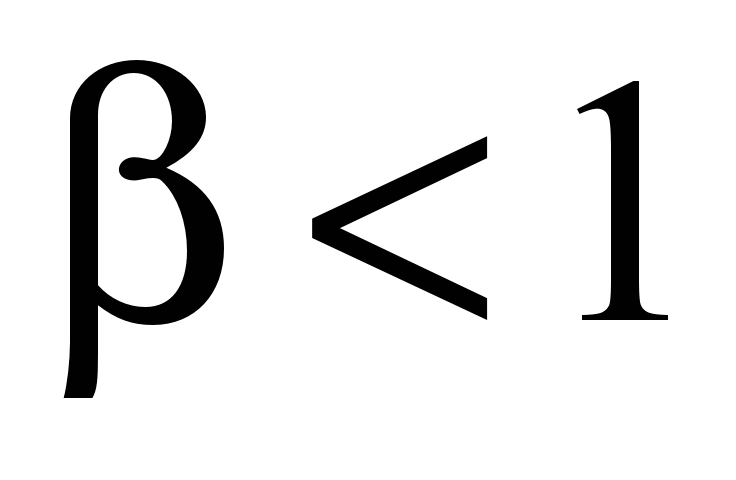 ,
а именно из отношения МДС обмотки
возбуждения к падению магнитного
напряжения в воздушном зазоре, он
полностью соответствует своему
определению как коэффициент формы
магнитной характеристики [14].
,
а именно из отношения МДС обмотки
возбуждения к падению магнитного
напряжения в воздушном зазоре, он
полностью соответствует своему
определению как коэффициент формы
магнитной характеристики [14].
Магнитные
характеристики НБ-406 в абсолютных
единицах приведены на рис. 2.
Сплошными линиями
на рис. 2 показаны магнитных характеристики,
полученные из скоростных характеристик
[15], пунктирными линиями – полученные
по усовершенствованной УМХ. Некоторое
расхождение характеристик при
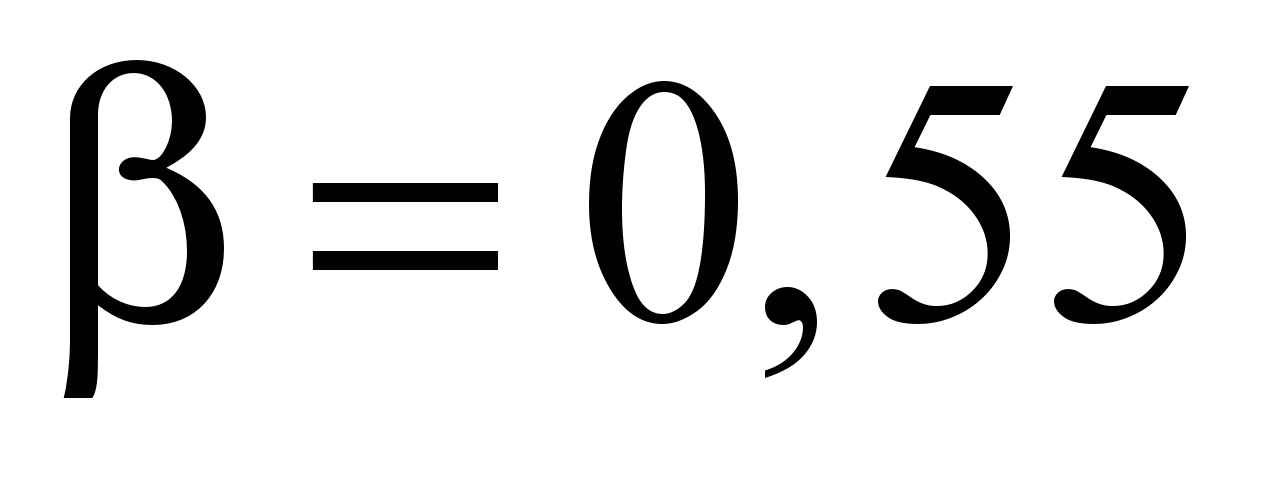 и
и
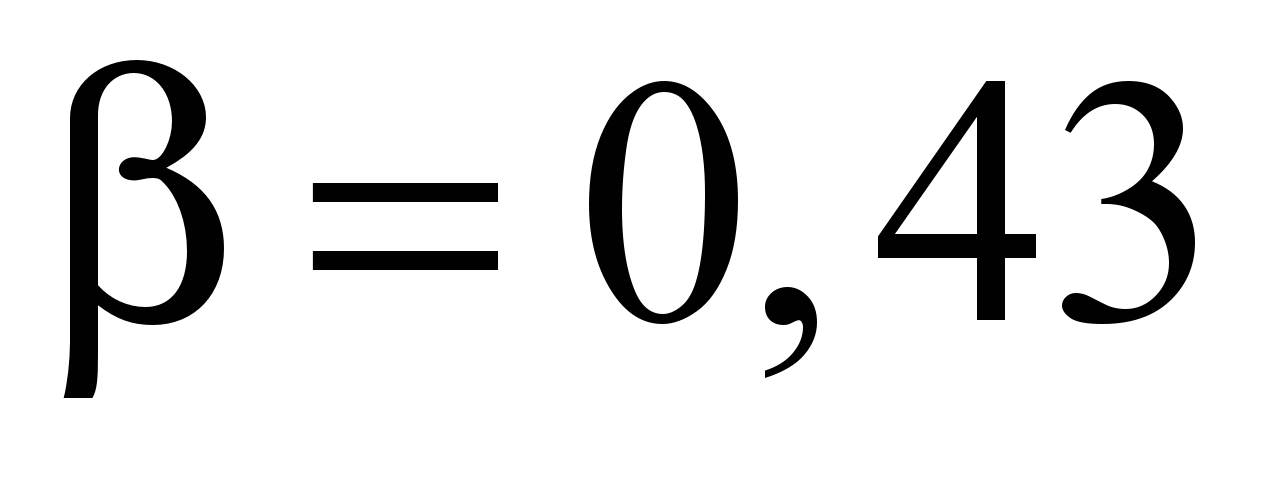 обусловлено неточным определением
коэффициента насыщения в этих режимах
(неточность ПТР).
обусловлено неточным определением
коэффициента насыщения в этих режимах
(неточность ПТР).
Таким же образом
выполнено построение характеристик
для двигателя РТ-51Д. Коэффициенты
аппроксимации, рассчитанные для (1) при
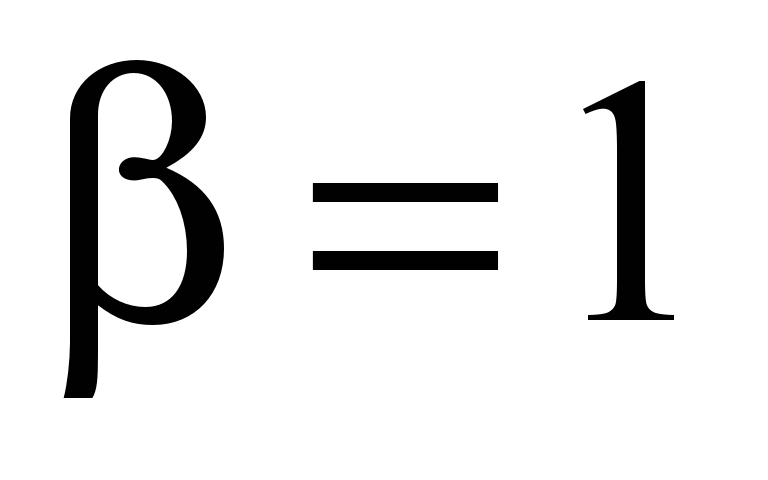 :
:
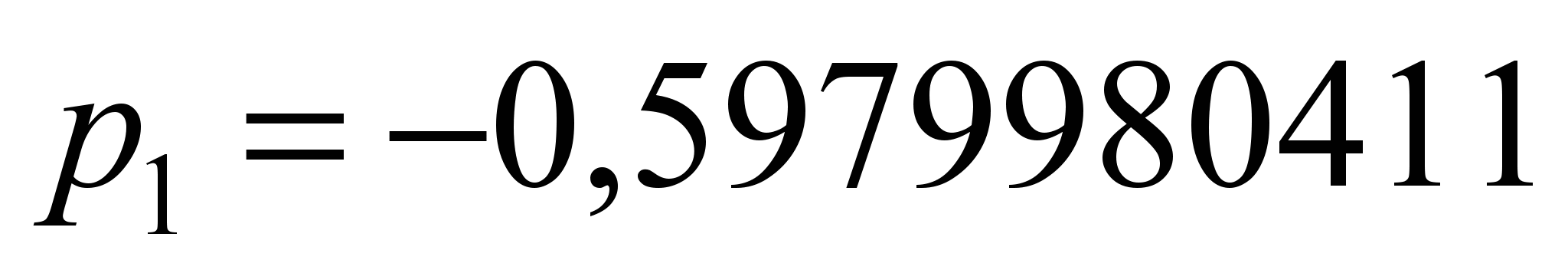 ,
,
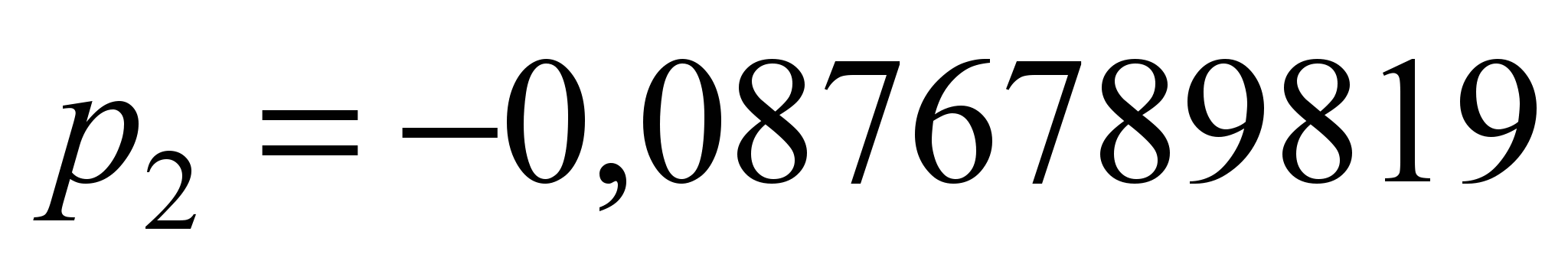 ,
,
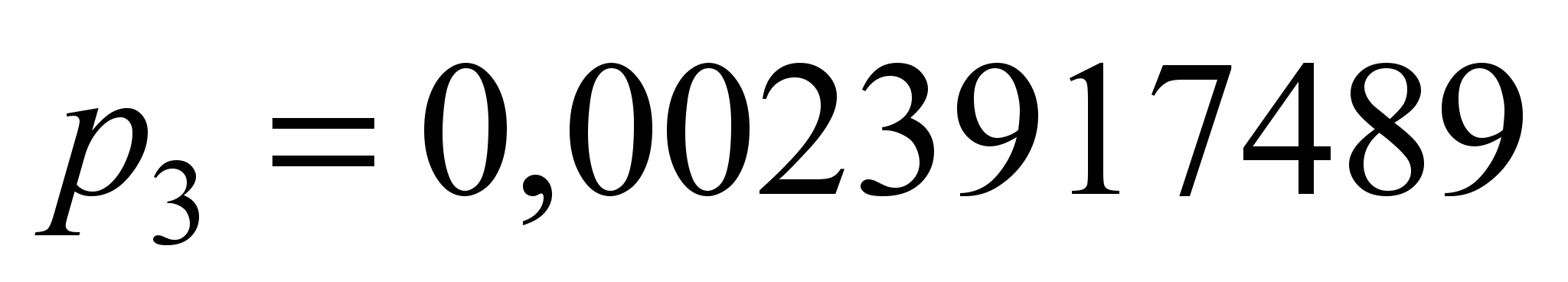 .
Заметим, что коэффициенты аппроксимации
рассчитываются при
.
Заметим, что коэффициенты аппроксимации
рассчитываются при
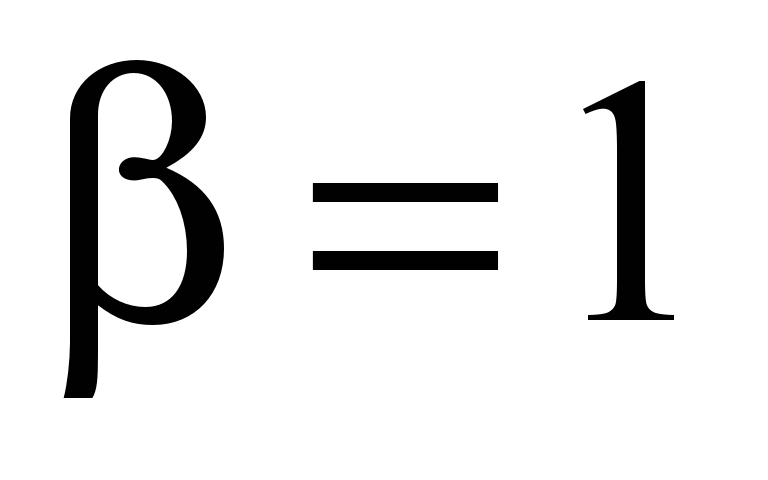 независимо от того, какой режим
возбуждения является номинальным для
данной машины. Значения коэффициента
насыщения при различных степенях
ослабления возбуждения:
независимо от того, какой режим
возбуждения является номинальным для
данной машины. Значения коэффициента
насыщения при различных степенях
ослабления возбуждения:
Магнитные
характеристики в абсолютных единицах
для двигателя РТ-51Д построены на рис.
3.
Как видно, визуализация
в процессе расчетов по выражению (1)
имеет хорошую наглядность, так как
построение ведется в зависимости от
тока якоря, который остается неизменным
при ослаблении возбуждения. Однако,
как видно из примеров расчетов
характеристик по выражению (1), для
каждой конкретной машины необходимо
определять коэффициенты аппроксимации.
Такой подход неприемлем для инженерной
практики, так как даже при наличии
современных прикладных математических
программных пакетов нахождение
коэффициентов аппроксимации занимает
весьма длительное время. Особенно
сильно это проявляется при проектировании
тяговых электрических машин, когда во
время расчета приходится несколько
раз уточнять параметры машины.
Следовательно, выражению (1) необходимо
придать такую форму, при которой отпадает
необходимость в определении коэффициентов
аппроксимации отдельно для каждой
тяговой электрической машины. Для
решения этой задачи подходит форма
выражения усовершенствованной УМХ, в
которой в качестве аргумента выступает
МДС обмотки возбуждения.
В работе [7] показано,
что исходную формулу для усовершенствованной
УМХ, которая является функцией двух
переменных, можно привести к функции
одной переменной. Исходная формула для
усовершенствованной УМХ в абсолютных
единицах имеет вид:
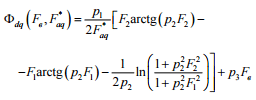 ,
(5)
,
(5)
где
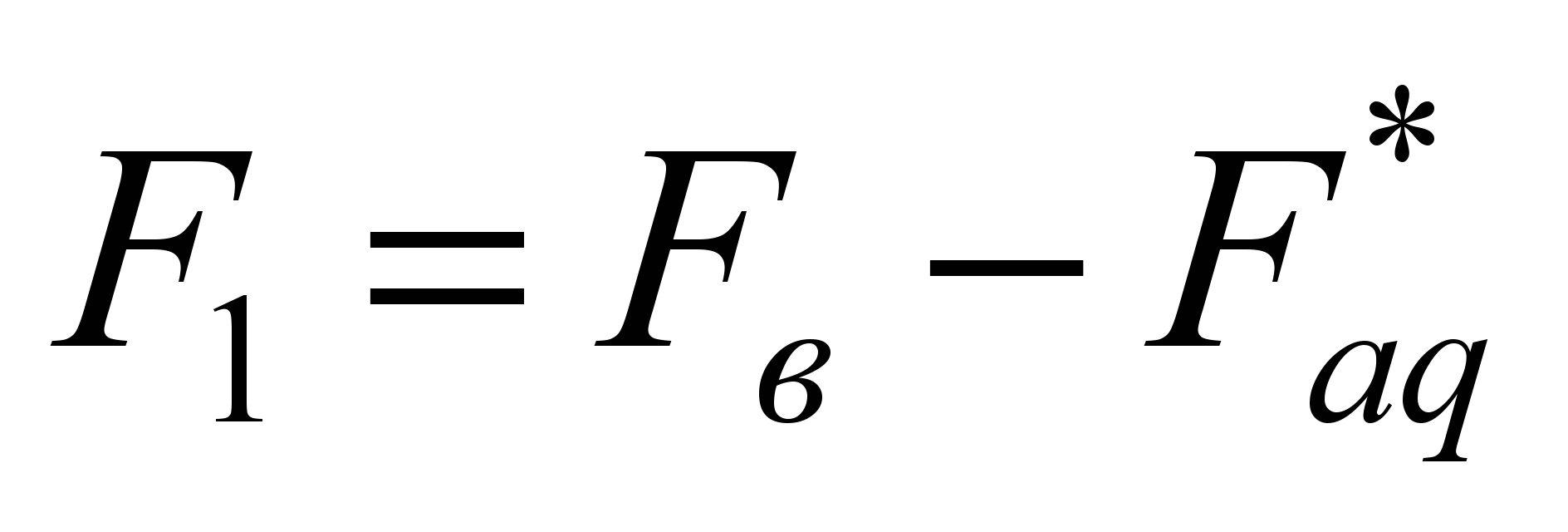 и
и
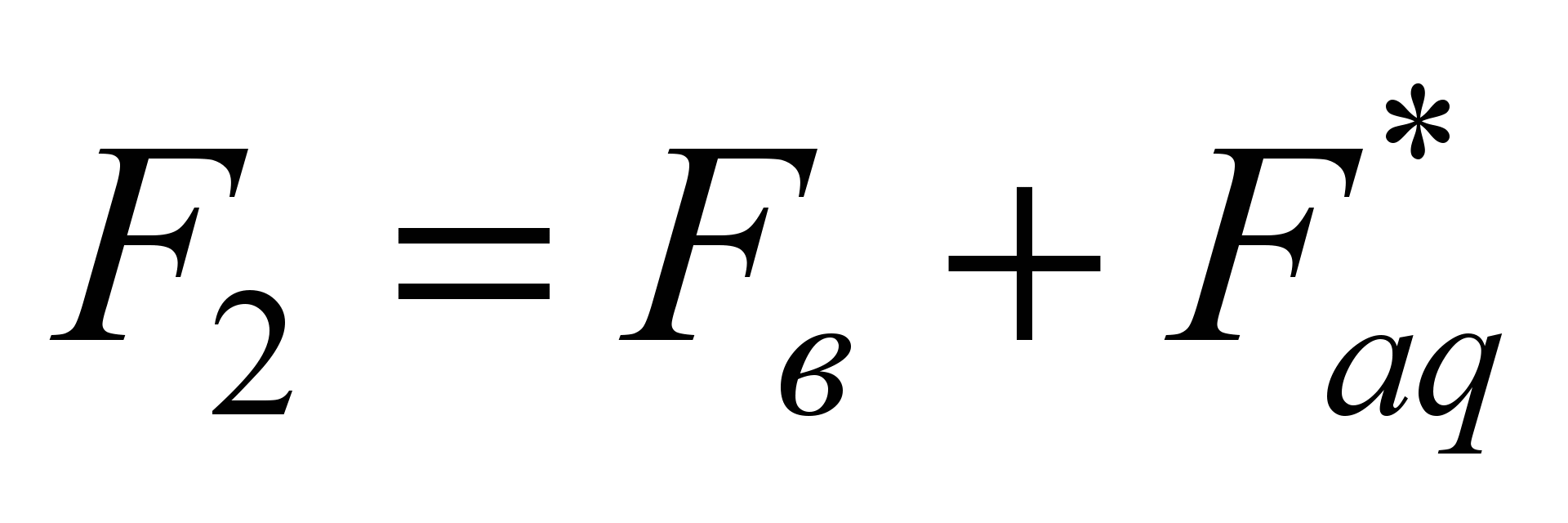 ;
;
 – МДС обмотки возбуждения;
– МДС обмотки возбуждения;
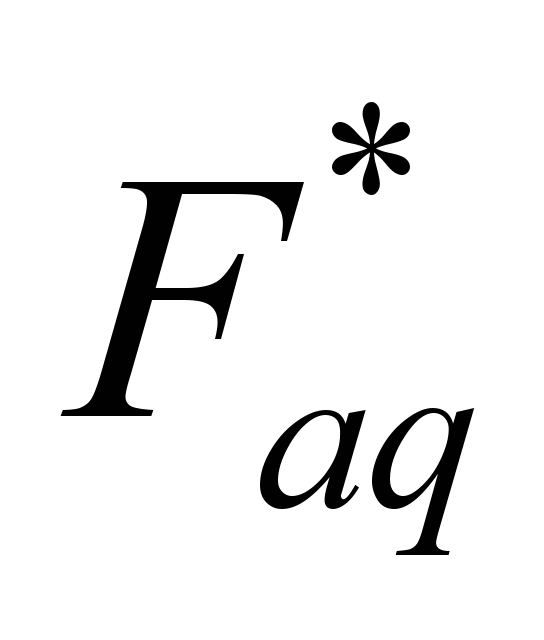 – МДС обмотки якоря, действующая в
пределах расчетного полюсного деления.
– МДС обмотки якоря, действующая в
пределах расчетного полюсного деления.
Применим методы
приведения выражения (5) к функции одной
переменной, описанные в [7]. Принимая
во внимание, что вид полученного
выражения в относительных единицах
аналогичен виду выражения в абсолютных,
получим выражение для усовершенствованной
УМХ с МДС обмотки возбуждения в качестве
аргумента:
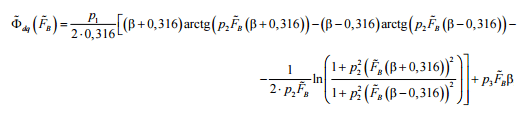 , (6)
, (6)
где
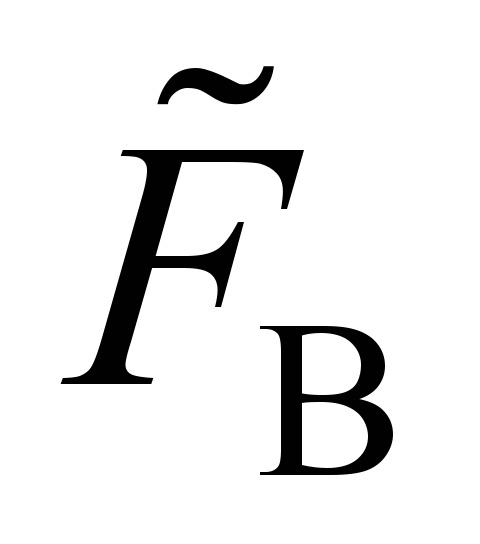 – МДС обмотки возбуждения в относительных
единицах.
– МДС обмотки возбуждения в относительных
единицах.
Коэффициенты
аппроксимации для выражения (6) имеют
значения
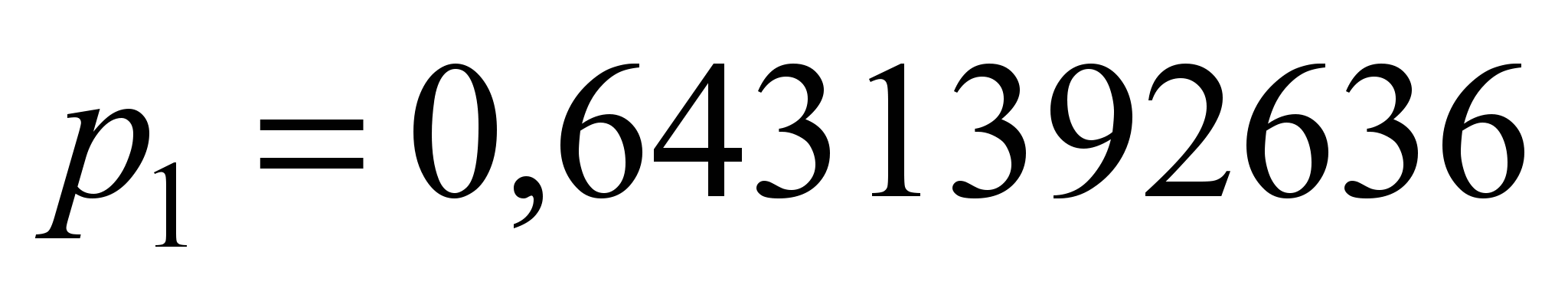 ,
,
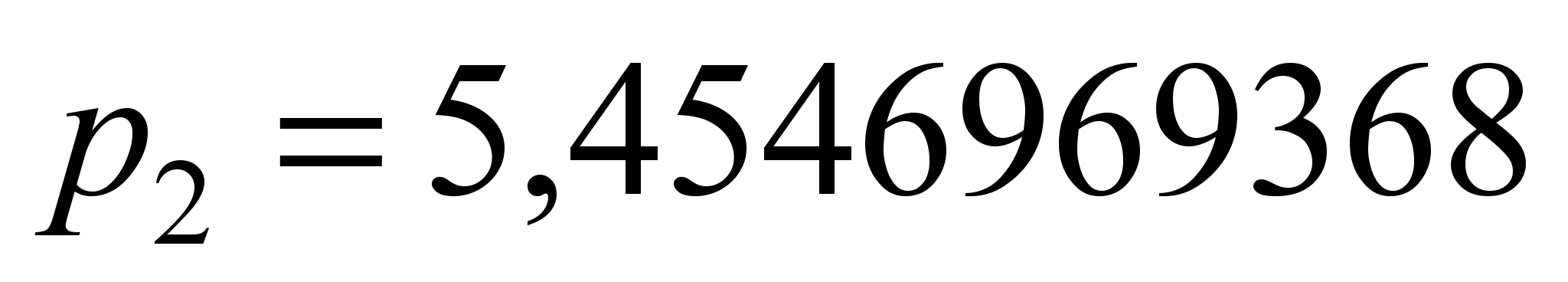 ,
,
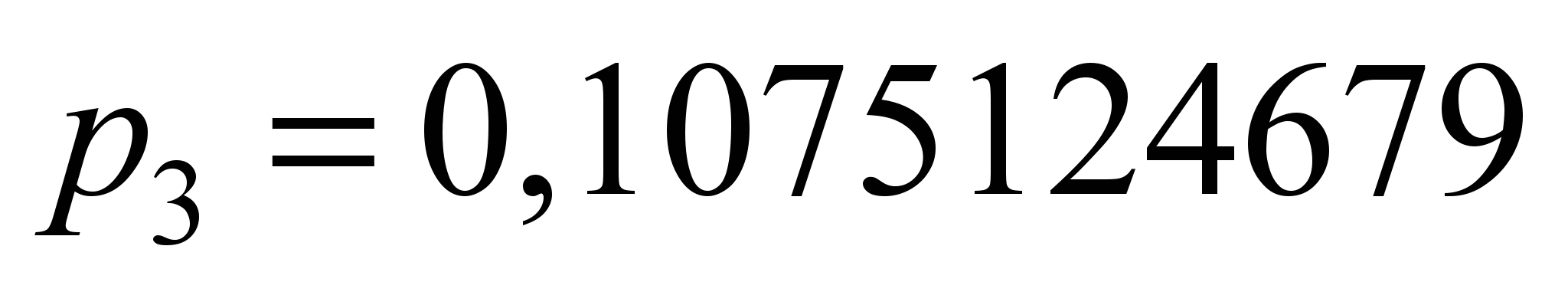 и являются едиными для всех типов
некомпенсированных тяговых
электродвигателей.
и являются едиными для всех типов
некомпенсированных тяговых
электродвигателей.
Здесь стоит отметить,
что если в качестве аргумента по оси
абсцисс откладывается МДС обмотки
возбуждения, то изображение семейства
характеристик (магнитных или скоростных)
для разных степеней ослабления
возбуждения является затруднительным.
Это происходит из-за того, что невозможно,
как в случае с током якоря, для одного
и того же значения МДС определить
несколько значений магнитного потока.
Чтобы преодолеть
это затруднение в методику построения
магнитных характеристик по выражению
(6) введено допущение, что МДС обмотки
возбуждения не изменяется при изменении
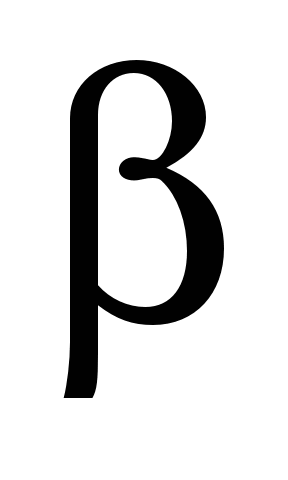 ,
то есть она пропорциональна току якоря,
а не возбуждения. В остальном методика
расчета характеристик по выражению
(6) аналогична той, которая была рассмотрена
для выражения (1).
,
то есть она пропорциональна току якоря,
а не возбуждения. В остальном методика
расчета характеристик по выражению
(6) аналогична той, которая была рассмотрена
для выражения (1).
Выполним построение
магнитных характеристик по выражению
(6) для тяговых двигателей НБ-406 и РТ-51Д.
Значения коэффициентов насыщения были
определены в предыдущем расчете. На
рис. 4 и 5 показаны магнитные характеристики
для НБ-406 и РТ-51Д соответственно.
Как видно из рис.
4 и 5 точность расчета по выражению (6)
такая же, как и по выражению (1). Однако,
выражение (6), в отличие от выражения
(1), может быть применено для всех типов
некомпенсированных ТЭД постоянного
тока без определения коэффициентов
аппроксимации для каждой машины в
отдельности.
Очевидно, чтобы
получить магнитные характеристики в
функции тока якоря необходимо полученную
МДС обмотки возбуждения разделить на
количество ее витков
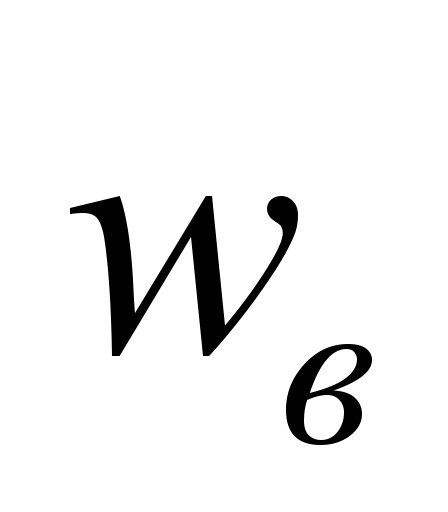 .
.
Научная
новизна и практическая
значимость
В выражении для
усовершенствованной УМХ удалось
избавиться от необходимости пересчета
коэффициентов аппроксимации для каждой
конкретной машины. Это стало возможным
благодаря замене тока в качестве
аргумента на МДС обмотки возбуждения.
Таким образом, появилась возможность
избавиться от влияния конструктивных
особенностей конкретной машины (а
именно, влияние количества витков
обмотки возбуждения) на результат
определения коэффициентов аппроксимации.
Выводы
Выполнен анализ
аппроксимирующей функции усовершенствованной
УМХ для различных аргументов. На базе
усовершенствованной УМХ с аргументом
в виде МДС обмотки возбуждения возможно
выполнить расчет магнитных (скоростных)
характеристик без необходимости
определять коэффициенты аппроксимации
для каждого типа некомпенсированных
ТЭД в отдельности.
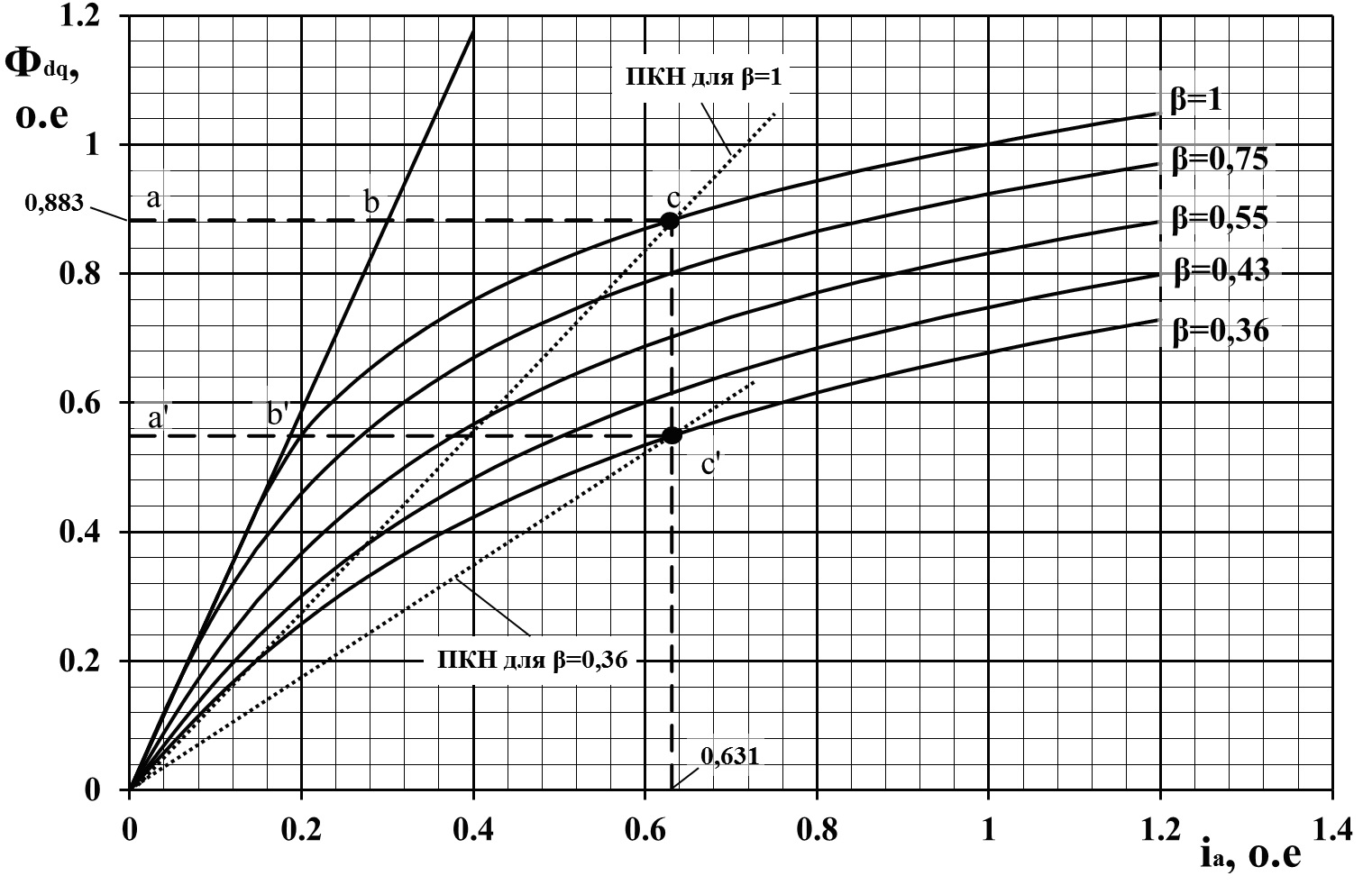
Рис. 1. Вид усовершенствованной
УМХ при различных степенях
ослабления возбуждения для НБ-406
Fig. 1. Type of improved of universal magnetic
characteristic at various degrees
of
attenuation of excitation of NB-406
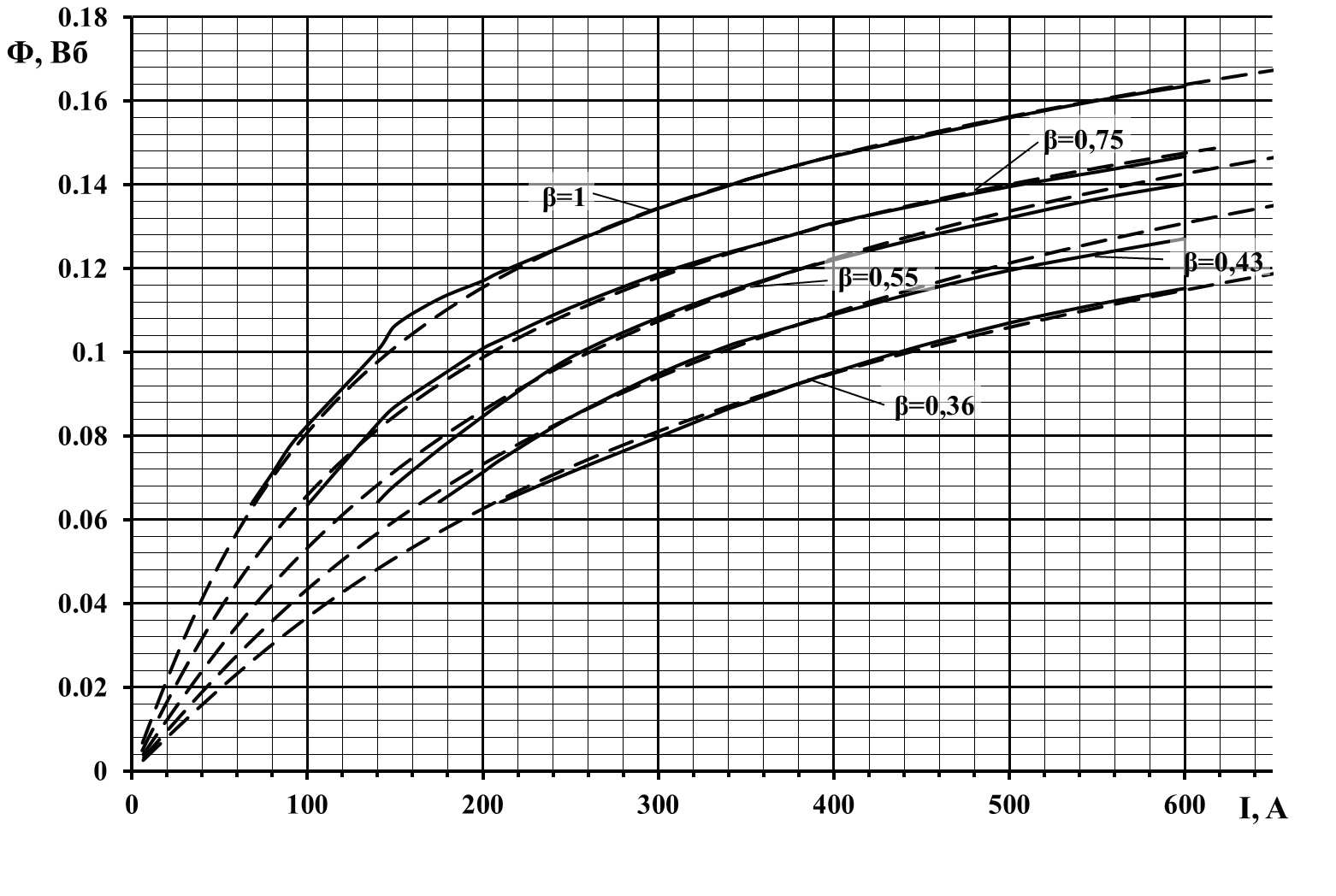
Рис. 2. Магнитные
характеристики НБ-406, построенные по
выражению (1)
Fig. 2. Magnetic characteristics of NB-406, constructed
according to the expression (1)
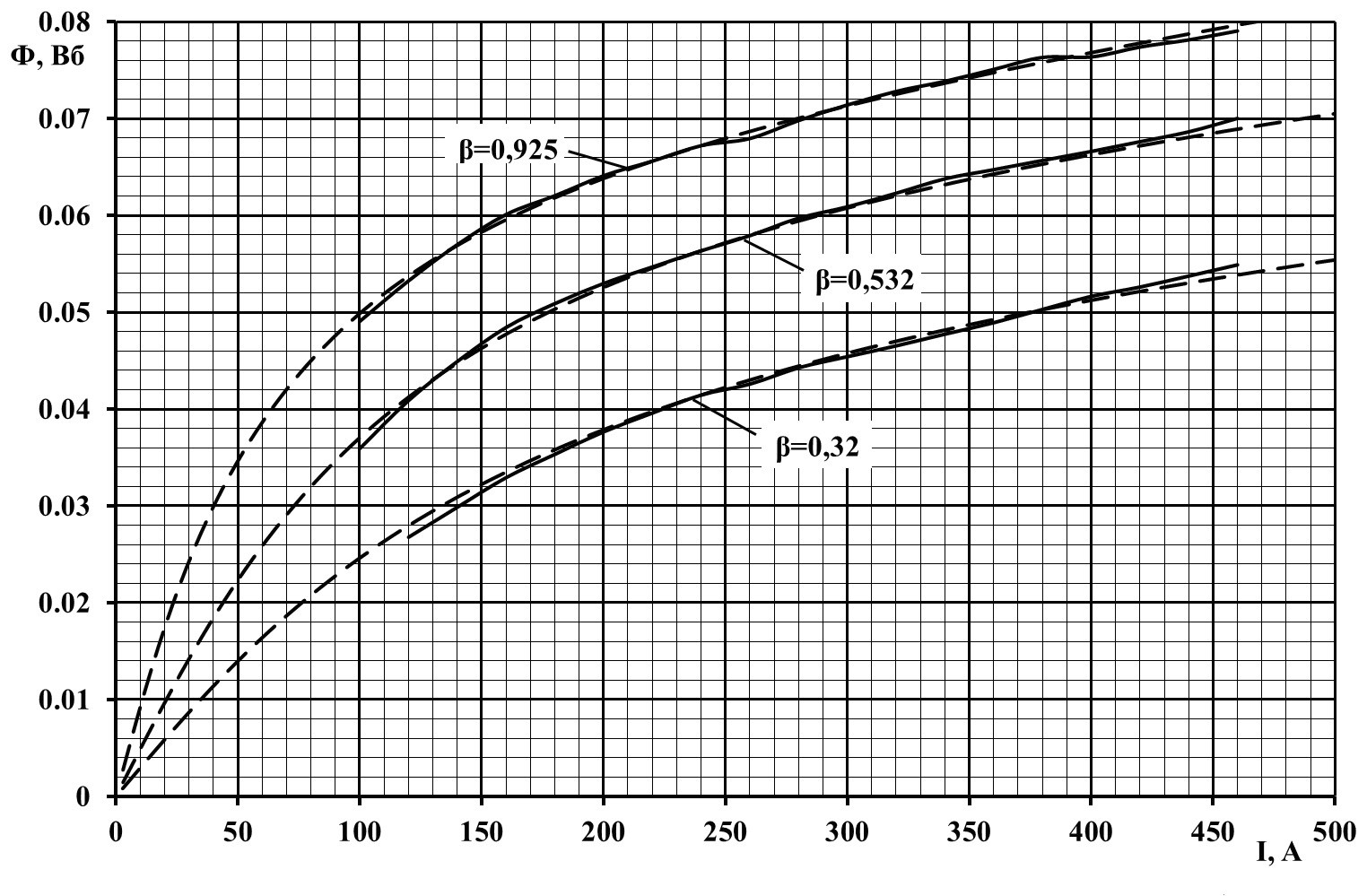
Рис. 3. Магнитные характеристики
РТ-51Д, построенные по выражению (1)
Fig. 3. The magnetic characteristics of RT-51D,
constructed according to the expression (1)

Рис. 4. Магнитные
характеристики НБ-406, построенные по
выражению (6)
Fig. 4. Magnetic characteristics of NB-406, constructed
according to the expression (6)
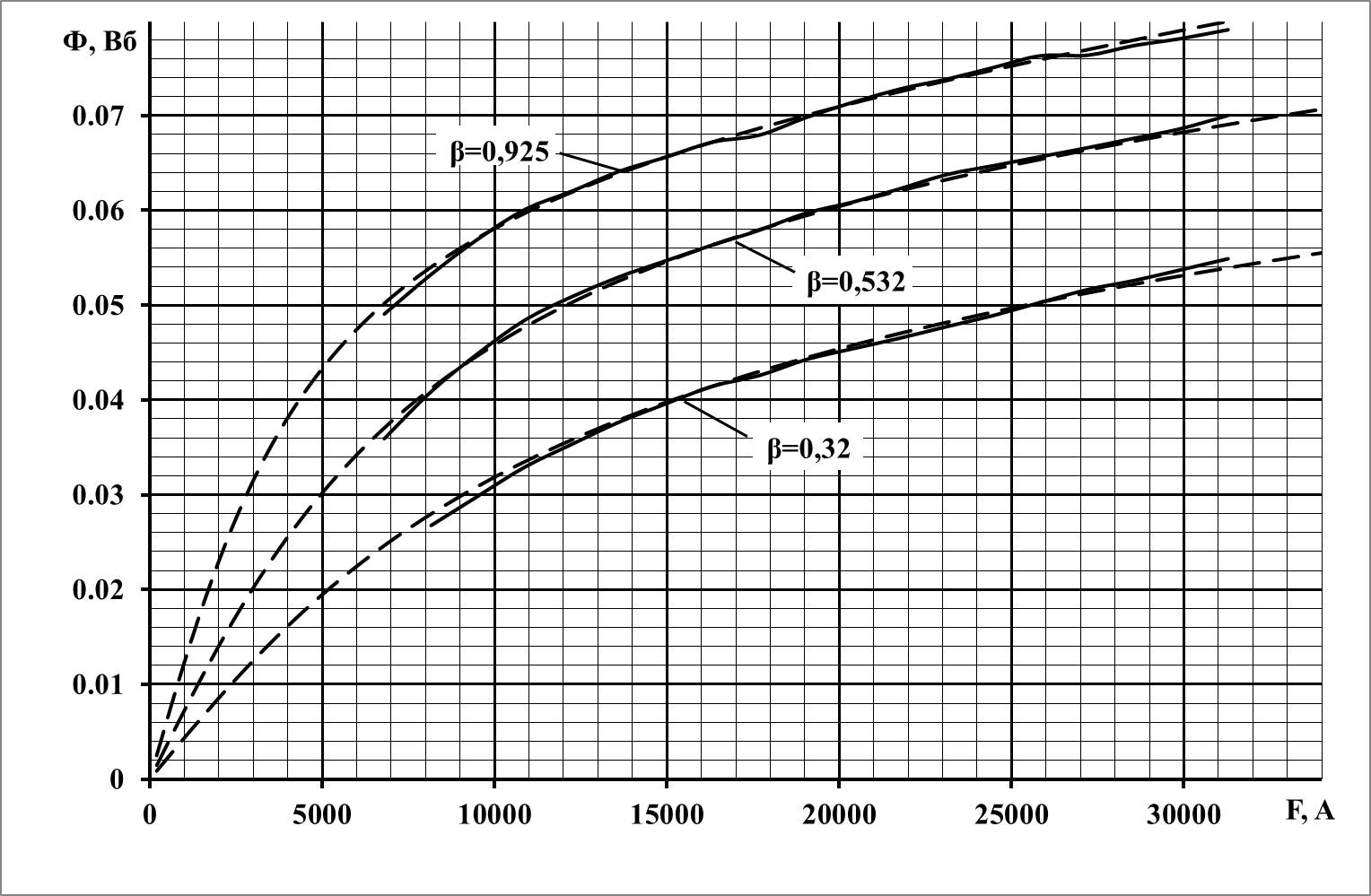
Рис. 5. Магнитные характеристики
РТ-51Д, построенные по выражению (6)
Fig. 5. Magnetic characteristics of RT-51D, constructed
according to the expression (6)
СПИСОК использованных
источников
Афанасов, А. М. Аппроксимация
магнитных характеристик тяговых
двигателей электроподвижного состава
/ А. М. Афанасов // Електромагнітна
сумісність та безпека на залізничному
транспорті. – 2012. – № 4. – С. 25–29.
Белкина, Е. Н. Aнализ
способов аппроксимации кривой
намагничивания электротехнической
стали / Е. Н. Белкина, С. А. Жуков //
Инновационная наука. – 2015. – № 5-2. – С.
22–27.
Бельман, М. Х. Переходные процессы
в микродвигателях постоянного тока
при импульсном питании / М. Х.
Бельман. – Ленинград : Энергия, 1975. –
184 с.
Вольдек, А. И. Электрические
машины : учеб. для студ. высш. техн. учеб.
заведений / А. И. Вольдек. – 3-е изд.,
перераб. – Ленинград : Энергия, 1978. –
832 с.
Гетьман, Г. К. Аналіз аналітичних
функцій для апроксимації універсальної
магнітної характеристики тягових
двигунів постійного та пульсуючого
струму / Г. К. Гетьман, С. Л. Марікуца //
Вісн. Дніпропетр. нац. ун-ту залізн.
трансп. ім. акад. В. Лазаряна. –
Дніпропетровськ, 2011. –
Вип. 37. – С. 63–71.
Гетьман, Г. К. Об использовании
универсальной магнитной характеристики
для расчета электромеханических
характеристик тяговых двигателей / Г.
К. Гетьман, С. Н. Голик // Вісн. Дніпропетр.
нац. ун-ту залізн. трансп. ім. акад. В.
Лазаряна. – Дніпропетровськ,
2007. – Вип. 16. – С. 21–25.
Друбецкий, А. Е. Аппроксимация
универсальной магнитной характеристики
для моделирования тяговых электрических
машин / А. Е. Друбецкий // Наука та прогрес
транспорту. – 2017. – № 1 (67).
– С. 106–116. doi:
10.15802/stp2017/94031.
Иванов-Смоленский, А. В.
Электрические машины : учеб. для вузов
/ А. В. Иванов-Смоленский. – Москва :
Энергия, 1980. – 928 с.
Калантаров, П. Л. Расчет
индуктивностей : справ. книга / П. Л.
Калантаров, Л. А Цейтлин. – 3-е изд.
перераб. и доп. – Ленинград : Энергоатомиздат,
1986. – 488 с.
Костенко, М. П. Электрические
машины : учеб. для студ. высш. техн. учеб.
заведений : в 2 ч. /
М. П. Костенко, Л. М.
Пиотровский. – 3-е изд., перераб. –
Ленинград : Энергия, 1972. – Ч. 1 : Машины
постоянного тока. Трансформаторы. –
544 с.
Костін, М. О. Теоретичні основи
електротехніки : підручник : в 3 т. / М.
О. Костін, О. Г. Шейкіна. – Дніпропетровськ
: Вид-во Дніпропетр. нац. ун-ту залізн.
трансп. ім. акад. В. Лазаряна, 2006. – 336 с.
Матюк, В. Ф. Математические модели
кривой намагничивания и петель магнитного
гистерезиса. Ч. I. Анализ моделей / В. Ф.
Матюк, А. А. Осипов // Неразрушающий
контроль и диагностика. – 2011. – № 2
– С. 3–35.
Моделирование тягового
электропривода с двигателями постоянного
тока последовательного возбуждения /
А. А. Шавелкин, И. А. Костенко, В. А.
Герасименко, А. Н. Мовчан // Вост.-Европ.
журн. передовых технологий. – 2016. – №
1 (2). – С. 42–48.
Находкин, М. Д. Универсальная
магнитная характеристика / М. Д.
Находкин, В. С. Хвостов // Вестник
электропромышленности. – 1958. – № 1. –
С. 44–48.
Правила тяговых расчетов для
поездной работы. – Москва : Транспорт,
1985. – 287 с.
Проектирование тяговых
электрических машин : учеб. пособие для
вузов ж.-д. трансп. / М. Д. Находкин, Г. В.
Василенко, В. И. Бочаров, М. А. Козорезов.
– Москва : Транспорт, 1976. – 624 с.
Справочник по электроподвижному
составу, тепловозам и
дизель-поездам / под ред. А. И. Тищенко.
– Москва : Транспорт, 1976. – 432 с.
Discrete-Time Neural Sliding-Mode
Block Control for a DC Motor With Controlled Flux / C. E. Castaneda,
A. G. Loukianov, E. N. Sanchez, C.-T.
Bernardino
// IEEE Transactions on Industrial Electronics. – 2012. – Vol.
59. – Iss. 2. – P. 1194–1207.
doi:
10.1109/TIE.2011.2161246.
Castañeda,
C. E. Direct current motor control based on high order neural
networks using stochastic estimation / C. E. Castañeda,
P. Esquivel // The 2010 Intern. Joint Conf.
on Neural Networks (IJCNNI)
(18.07–23.07.2010). – Barcelona, Spain, 2010. – P. 1515–1520.
Hayek, El. J. Experiences with a traction drive
laboratory model / El. J. Hayek, T. J. Sobczyk, G. Skarpetowski //
Electromotion. – 2010. – Vol. 17. – Iss. 1. – P. 30–36.
Design and Simulation of Heavy Haul Locomotives and
Trains / M. Spiryagin, P. Wolfs, C. Cole [et al.]. – Boca Raton ;
London ; New York : Taylor & Francis Group, 2017. – 465 p.
Electromechanical Coupled Vibration
between Traction Motor and Bogie of High-Speed Train / Z. Zhang,
X. Zhao, X. Li [et al.] // Proc. of the 6th
Intern. Conf. on Mechatronics, Materials, Biotechnology and
Environment ICMMBE-2016 (13.08–14.08.2016). – Yinchuan, China,
2016. – P. 153–158.
doi:
10.2991/icmmbe-16.2016.30.
А. Ю. ДРУБЕЦЬКИЙ1*
1*Каф.
«Електрорухомий склад залізниць»,
Дніпропетровський національний
університет залізничного транспорту
імені академіка В.
Лазаряна, вул. Лазаряна, 2,
Дніпро, Україна,
49010, тел. +38 (0562) 33 55 38,
ел.
пошта drubetskiy.ae@gmail.com,
ORCID 0000-0001-5691-0925
РОЗРАХУНОК МАГНІТНИХ ХАРАКТЕРИСТИК
ТЯГОВОГО ЕЛЕКТРОДВИГУНА за допомогою
вдосконаленої УНІВЕРСАЛЬНОЇ магнітної
ХАРАКТЕРИСТИКИ
Мета.
У дослідженні передбачається розробити
методику розрахунку магнітних
характеристик некомпенсованих тягових
електродвигунів (ТЕД) для будь-якого
ступеня ослаблення збудження на базі
апроксимуючих виразів для вдосконаленої
універсальної магнітної характеристики
(УМХ). Необхідно також провести аналіз
виразів для вдосконаленої УМХ із метою
знаходження виразу, що найбільш повно
задовольняє вимогам розробки методики
визначення індуктивних параметрів ТЕД.
Методика.
Для побудови характеристик за вдосконаленою
УМХ необхідно для кожного ступеня
ослаблення збудження визначити коефіцієнт
насичення. Це можливо здійснити тільки
аналітично. Для спрощення аналітичного
знаходження коефіцієнта насичення
запропонований метод, заснований на
рішенні системи з двох рівнянь, одним
із яких є сама УМХ, а другим – рівняння
прямої, кутовий коефіцієнт якої
пропорційний коефіцієнту насичення.
Значення коефіцієнта насичення, отримані
в результаті розрахунків для різних
ступенів збудження β <
1, по суті є коефіцієнтами
форми магнітної характеристики. Щоб
позбутися від необхідності кожного
разу при розрахунку характеристик
визначати коефіцієнти апроксимації,
запропонована форма вдосконаленою УМХ,
в якій роль аргументу виконує магніторушійна
сила (МРС) обмотки збудження. Результати.
Доведено, що за допомогою вдосконаленої
УМХ можливий розрахунок характеристик
некомпенсованих ТЕД для будь-яких
ступенів ослаблення збудження. Точність
розрахунку при β = 1 не
відрізняється від такої при розрахунку
по УМХ, запропонованій проф. М. Д.
Находкіним. Така ж точність зберігається
при ступенях збудження, відмінних від
одиниці. Наукова новизна.
Запропонована аналітична методика
розрахунку магнітних (швидкісних)
характеристик некомпенсованих ТЕД для
будь-якого ступеня ослаблення збудження
за допомогою вдосконаленої УМХ. Також
запропонована аналітична методика
визначення коефіцієнта насичення
вдосконаленої УМХ для будь-якого ступеня
ослаблення збудження. Завдяки введенню
в якості аргументу МРС обмотки збудження
відпадає необхідність у визначенні
коефіцієнтів апроксимації для кожного
конкретного ТЕД. Практична
значимість. Розроблена
методика дозволяє проводити розрахунки
магнітних характеристик некомпенсованих
ТЕД для будь-якого ступеня ослаблення
збудження. На її базі можлива розробка
методики визначення індуктивних
параметрів ТЕД, використовуючи в якості
вихідних даних коефіцієнт насичення
машини.
Ключові слова: універсальна
магнітна характеристика; апроксимація;
тяговий електродвигун; магнітні
характеристики
A. Y. DRUBETSKYI1*
1*Dep.
«Electric Rolling Stock of Railways», Dnipropetrovsk National
University of Railway Transport named after
Academician V. Lazaryan, Lazaryan St., 2,
Dnipro, Ukraine, 49010,
tel. +38 (0562) 33 55 38,
e-mail
drubetskiy.ae@gmail.com,
ORCID 0000-0001-5691-0925
CALCULATION OF MAGNETIC CHARACTERISTICS
OF Traction ELECTRIC Engine
USING THE IMPROVED
UNIVERSAL MAGNETIC CHARACTERISTICS
Purpose. The article is aimed to develop a
technique for calculating the magnetic characteristics of
uncompensated traction electric motors (TEM) at any degree of
attenuation of excitation based on the approximating expression for
improved universal magnetic characteristics (UMC). It is also
necessary to conduct an analysis of expressions for improved UMC with
the aim of finding an expression that most fully satisfies the
requirements for developing a technique for determining the inductive
parameters of TEM. Methodology. It is necessary to determine
the saturation coefficient for each degree of attenuation of the
excitation for building the characteristics with the improved UMC.
This can only be done analytically. To simplify the analytical
finding of the saturation coefficient, the method based on solving a
system of two equations is proposed, one of which is UMC itself, and
the second one is a straight line whose angular coefficient is
proportional to the saturation coefficient. Resulting values of the
saturation coefficient for the excitation degrees β < 1 are
essentially the coefficients of the shape of the magnetic
characteristic. To get rid of the need to determine the coefficients
of approximation each time in the calculation of characteristics a
form of improved UMC is proposed, in which the magnetomotive force
(MMF) of the excitation winding serves as the argument's role.
Findings. Using the improved UMC it is possible to calculate
the characteristics of uncompensated TEMs for any degree of
attenuation of excitation. The accuracy of the calculation at
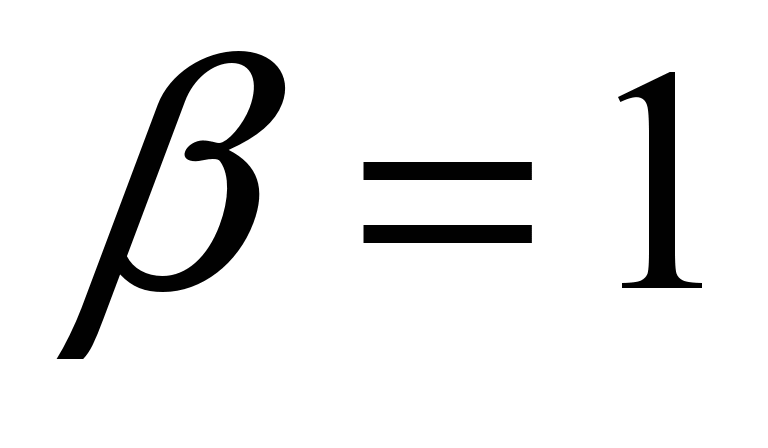 does not differ from that in the calculation for UMC, proposed by
Prof. M. D. Nakhodkin. The same accuracy is preserved at excitation
degrees that are different from unity. Originality. An
analytical technique for calculating the magnetic (speed)
characteristics of uncompensated TEM for any degree of attenuation
with the help of an improved UMC is proposed. The analytical
technique for determining the saturation coefficient for an improved
UMC at any degree of attenuation of excitation is also proposed. Due
to the introduction of an excitation winding as an argument, there is
no need to determine the approximation coefficients for each specific
TEM. Practical value. The developed methodology let
calculate magnetic characteristics of uncompensated REMs for any
degree of attenuation of excitation. On the basis of this technique,
it is possible to develop a technique for determining the inductive
parameters of the TEM, using the saturation coefficient of the
machine as initial data.
does not differ from that in the calculation for UMC, proposed by
Prof. M. D. Nakhodkin. The same accuracy is preserved at excitation
degrees that are different from unity. Originality. An
analytical technique for calculating the magnetic (speed)
characteristics of uncompensated TEM for any degree of attenuation
with the help of an improved UMC is proposed. The analytical
technique for determining the saturation coefficient for an improved
UMC at any degree of attenuation of excitation is also proposed. Due
to the introduction of an excitation winding as an argument, there is
no need to determine the approximation coefficients for each specific
TEM. Practical value. The developed methodology let
calculate magnetic characteristics of uncompensated REMs for any
degree of attenuation of excitation. On the basis of this technique,
it is possible to develop a technique for determining the inductive
parameters of the TEM, using the saturation coefficient of the
machine as initial data.
Keywords: universal magnetic characteristic;
approximation; traction motor; magnetic characteristics
REFERENCES
Afanasov, A. M. (2012). Approximation of the magnetic
characteristics of the traction motors of electric rolling stock.
Electromagnetic Compatibility and Safety on the Railway
Transport, 4, 25-29.
Belkina, Y. N., & Zhukov, S. A. (2015). Analiz
sposobov approksimatsii krivoy namagnichivaniya elektrotekhnicheskoy
stali. Innovatsionnaya nauka, 5 (2),
22-27.
Belman, M. K. (1975). Perekhodnyye protsessy v
mikrodvigatelyakh postoyannogo toka pri impulsnom pitanii.
Leningrad: Energiya.
Voldek, A. I. (1978). Elektricheskiye mashiny
(3rd ed.). Leningrad: Energiya.
Hetman, H. K., & Marikutsa, S. L. (2011). The
analysis of analytical functions for approximative do-all magnetic
characteristic of direct – current and undulated – current
traction motors. Bulletin of Dnipropetrovsk National University
of Railway Transport, 37, 63-71.
Hetman, H. K., & Golik, S. M. (2007). About the use
of universal magnetic characteristics to calculate the
electromechanical characteristics of traction motors. Bulletin of
Dnipropetrovsk National University of Railway Transport, 16,
21-25.
Drubetskyi, A. Y. (2017). Approximation of universal
magnetic characteristic for modelling electric traction machines.
Science and Transport Progress, 1 (67), 106-116. doi:
10.15802/stp2017/94031
Ivanov-Smolenskiy, A. V. (1980). Elektricheskiye
mashiny. Moscow: Energiya.
Kalantarov, P. L., & Tseytlin, L. A. (1986).
Raschet induktivnostey: spravochnaya kniga (3rd ed.).
Leningrad: Energoatomizdat.
Kostenko, M. P., & Piotrovskiy, L. M. (1972).
Mashiny postoyannogo toka. Transformatory: Elektricheskiye
mashiny (3rd ed.). Leningrad: Energiya.
Kostin, M. O., & Sheikina, O. H. (2006).
Teoretychni osnovy elektrotekhniky (Vol. 1-3).
Dnipropetrovsk: Dnipropetrovsk National University of Railway
Transport named after Academician V. Lazaryan Press.
Matyuk,
V. F., & Osipov,
A. A. (2011). The mathematical models of the magnetization curve and
the magnetic hysteresis loops, Part 1: Analysis of models.
Nerazrushayushchiy kontrol i diagnostika, 2, 3-35.
Shavelkin, A., Gerasimenko, V.,
Kostenko, I., & Movchan, A. (2016). Modeling of traction
electric drive with DC series motors. Eastern-European
Journal of Enterprise Technologies,
1-2(79),
42-48.
doi: 10.15587/1729-4061.2016.60322
Nakhodkin, M. D., & Khvostov, V.
S. (1958). Universalnaya magnitnaya kharakteristika. Vestnik
elektropromyshlennosti, 1, 44-48.
All-Soviet Union Research Institute
of Railway Transport. (1985). Pravila
tyagovykh raschetov dlya poyezdnoy raboty.
Moscow: Transport.
Nakhodkin, M. D., Vasilenko, G. V.,
Bocharov, V. I., & Kozorezov, M. A. (1976). Proyektirovaniye
tyagovykh elektricheskikh mashin.
Moscow: Transport.
Tishchenko, A. I. (Ed.). (1976).
Spravochnik po elektropodvizhnomu
sostavu teplovozam i dizel-poyezdam.
Moscow: Transport.
Castaneda, C. E., Loukianov, A. G.,
Sanchez, E. N., & Castillo-Toledo, B. (2012). Discrete-Time
Neural Sliding-Mode Block Control for a DC Motor With Controlled
Flux. IEEE Transactions on Industrial Electronics, 59 (2),
1194-1207. doi: 10.1109/TIE.2011.2161246
Castañeda, C. E., & Esquivel,
P. (2010). Direct current motor control based on high order neural
networks using stochastic estimation. Proceedings
of the 2010 International Joint Conference on Neural Networks
IJCNNI, July 18-23, 2010, Barcelona, Spain.
1515-1520. doi: 10.1109/IJCNN.2010.5596331
Hayek, El. J., Sobczyk, T. J., &
Skarpetowski, G. (2010). Experiences with a traction drive
laboratory model. Electromotion,
17 (1),
30-36.
Spiryagin, M., Wolfs P., Cole, C.,
Sun, Y. Q., McClanachan, M., Spiryagin, V., & McSweeney, T.
(2017). Design and Simulation of Heavy
Haul Locomotives and Trains. New York:
Taylor & Francis Group.
Zhang, Z., Zhao, X., Li, X., Lin,
F., & Yang, Z. (2016). Electromechanical Coupled Vibration
between Traction Motor and Bogie of High-Speed Train. Proceedings
of the 6th
International Conference on Mechatronics, Materials, Biotechnology
and Environment ICMMBE-2016, August 13-14, 2016, Yinchuan, China.
153-158. doi:
10.2991/icmmbe-16.2016.30
Статья рекомендована
к публикации д.т.н., проф. Г. К. Гетьманом
(Украина); д.т.н., проф.
Ф. П. Шкрабцом
(Украина)
Поступила в
редколлегию: 10.03.2017
Принята к печати:
18.05.2017
,
т.е. зависимости основного магнитного
потока от МДС обмотки возбуждения
,
определенной на холостом ходу. Как
правило, эта характеристика не приводится
в справочной литературе. В этом случае
очень удобным для аппроксимации
магнитных характеристик является
использование коэффициента насыщения
и УМХ [1].