ISSN 2307–3489 (Print), ІSSN 2307–6666 (Online)

Наука та прогрес транспорту. Вісник Дніпропетровського
національного університету залізничного транспорту, 2017, № 3 (69)



ЕКОЛОГІЯ НА ТРАНСПОРТІ

екологія на ТРАНСПОРТі

UDC [502.3:504.5]:519.872

L. V. AMELINA1*, M. M. BILIAIEV2

1*Dep. «Hydraulics and Water Supply», Dnipropetrovsk National University
of Railway Transport named after Academician V. Lazaryan, Lazaryan St., 2,
Dnipro, Ukraine, 49010, tel. +38 (056) 273 15 09, e-mail gidravlika2013@mail.ru,
ORCID 0000-0002-8525-7096
2Dep. «Hydraulics and Water Supply», Dnipropetrovsk National University
of Railway Transport named after Academician V. Lazaryan, Lazaryan St., 2,
Dnipro, Ukraine, 49010, tel. +38 (056) 273 15 09, e-mail gidravlika2013@mail.ru,
ORCID 0000-0002-1531-7882

NUMERICAL SIMULATION OF AIR POLLUTION

IN CASE OF UNPLANNED AMMONIA RELEASE

Purpose. Development fast calculating model which takes into account the meteorological parameters and buildings which are situated near the source of toxic chemical emission. Methodology. The developed model is based on the equation for potential flow and equation of pollutant dispersion. Equation of potential flow is used to compute wind pattern among buildings. To solve equation for potential flow Samarskii implicit difference scheme is used. The implicit change – triangle difference scheme is used to solve equation of mass transfer. Numerical integration is carried out using the rectangular difference grid. Method of porosity technique («markers method») is used to create the form of comprehensive computational region. Emission of ammonia is modeled using Delta function for point source. Findings. Developed 2D numerical model belongs to the class of «diagnostic models». This model takes into account the main physical factors affecting the process of dispersion of pollutants in the atmosphere. The model takes into account the influence of buildings on pollutant dispersion. On the basis of the developed numerical models a computational experiment was carried out to estimate the level of toxic chemical pollution in the case of unplanned ammonia release at ammonia pump station. Originality. Developed numerical model allows to calculate the 2D wind pattern among buildings and pollutant dispersion in the case unplanned ammonia release. Model allows to perform fast calculations of the atmosphere pollution. Practical value. The model can be used when developing the PLAS (Emergency Response Plan).

Keywords: air pollution; unplanned release; toxic chemical; numerical modeling

Introduction

The ammonia pipeline Toliatti–Odessa was built in the late 70s–early 80s specifically for the transportation of the main products of the Toliatti nitrogen plant for export. The end point of ammonia pipeline is Odessa Port. There are several pumping stations along the route of this pipeline (Fig. 1). These pump stations support the correct pressure in ammonia pipeline. From the point view of industrial safety these pump stations are the chemically dangerous objects [4, 6, 15]. According to the Law of Ukraine for high-risk objects, a PLAS (Emergency Response Plan) document should be developed for such industrial object. Prediction of contaminated zones and detection of Dangerous Level of Contamination is the basis of this document. Therefore, the actual task is to estimate the level of contamination in working areas of the pump station in the case of unplanned ammonia release.

Review of literature sources

To solve the problem of chemical contamination zones formation in the case of unplanned ammonia emissions analytical models are widely used. For example, Berland model was used to predict air pollution in the case of ammonia pipe rupture [6]:

,

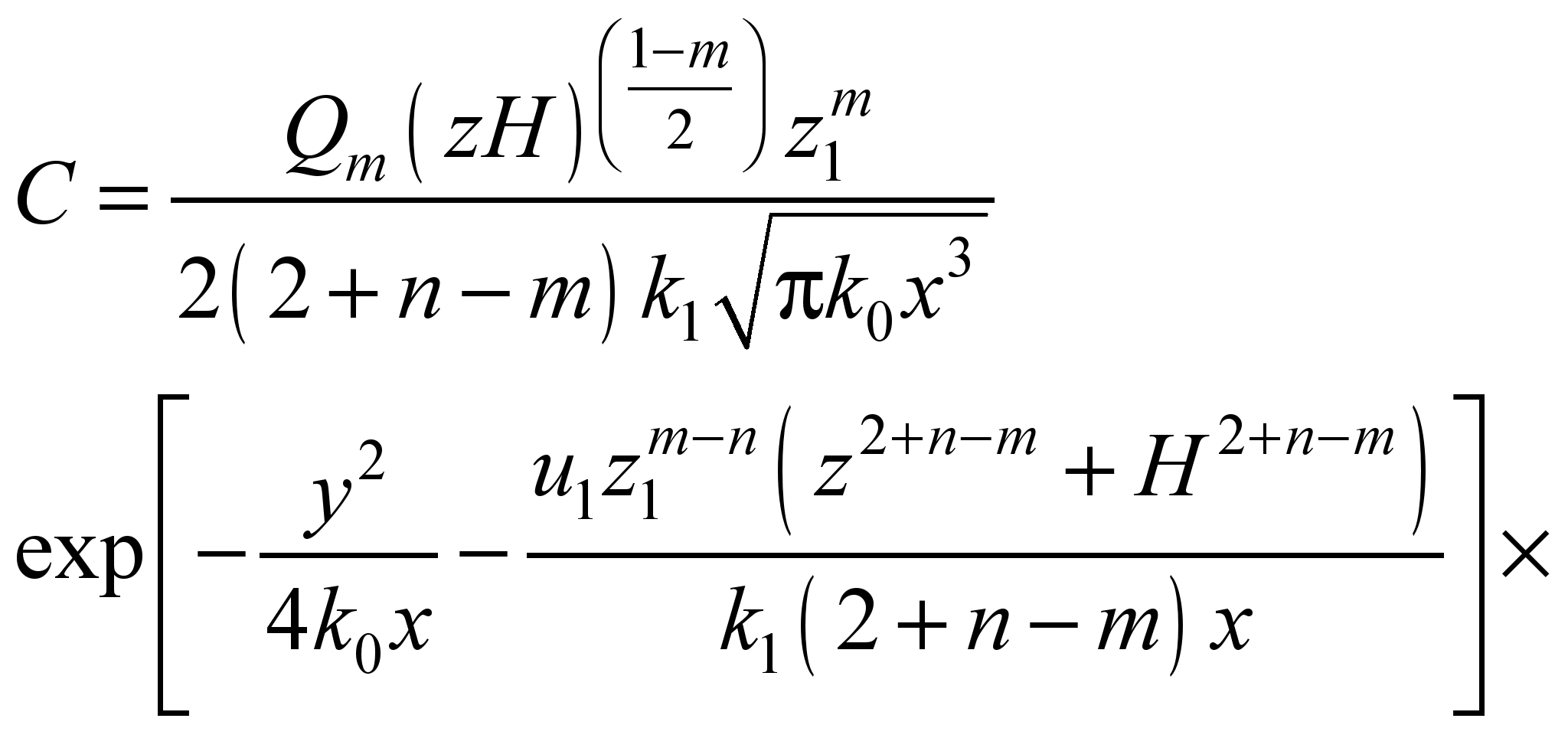
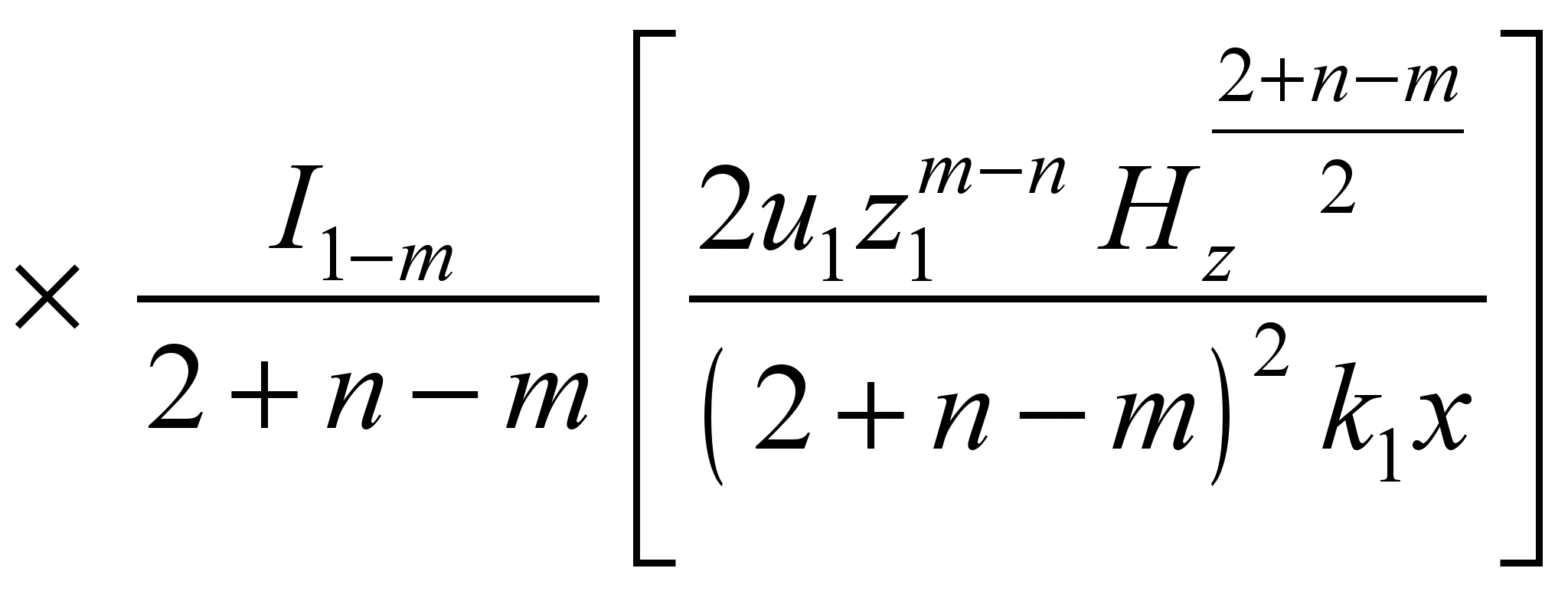Qт – emission rate; H – height of emission source; k0, k1, m – empirical constants; I – Bessel function; C-concentration.

Another approach for assessing the zones of chemical contamination is the application of the Gaussian plume model [2, 3, 10-14]. The use of the analytical models or Gaussian models allow to calculate quickly zones of chemical contamination. On the other hand, these models have significant lacks because they cannot be used when we model toxic chemical dispersion among buildings. For this purpose, it is necessary to use numerical models [1, 8, 9] which are based on Fluid Dynamics equations. In Ukraine, there is a certain deficit of such models [8, 9]. Worthy of note that the application Navier–Stokes equations for this purpose demands using of very fine computational grid and much computational time.

Purpose

The purpose of this paper is to develop a numerical model for computing the chemical contamination of air on the territory of the ammonia pump station for unplanned ammonia release (accidental release or terror act).

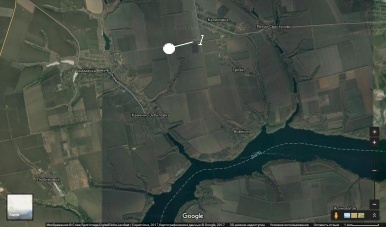
Fig. 1. GOOGLE’s image of Ammonia Pump Station:
1 – pump station

Mathematical formulation

To simulate the pollutant dispersion in the atmosphere 2D transport model is used [5, 7]

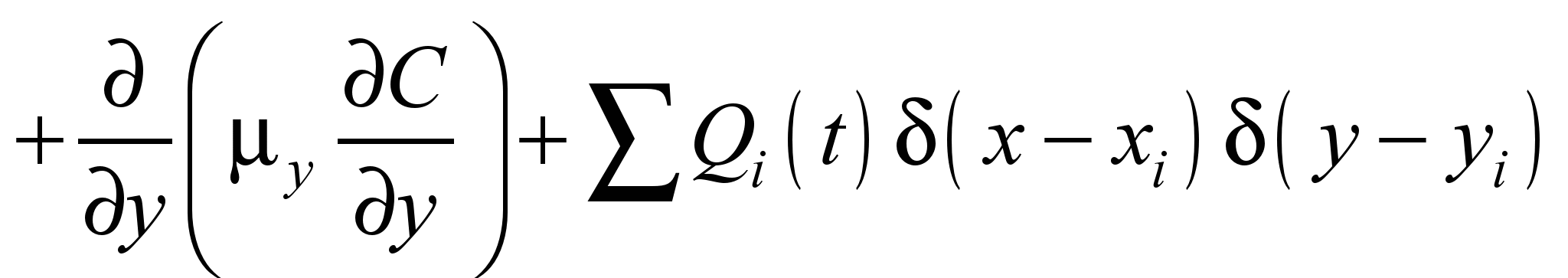, (1)

where С is mean concentration; u, v are the wind velocity components; is the parameter taking into account the process of pollutant chemical decay or washout; μ=(μх , μy ) are the diffusion coefficients; Q is intensity of point source emission; 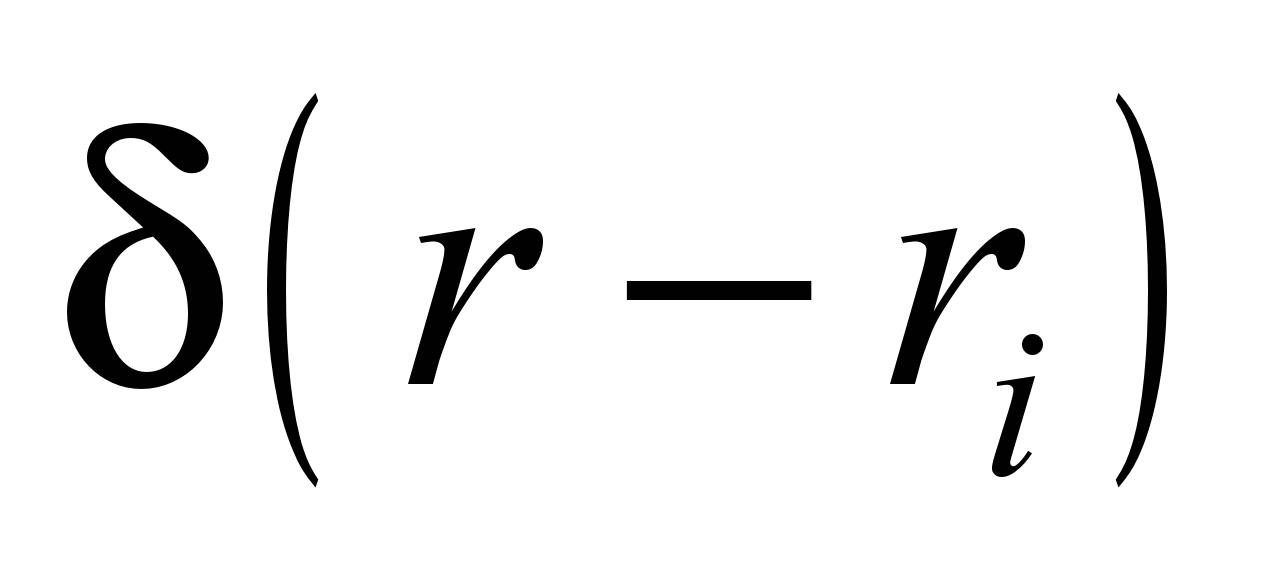are Dirak delta function; ri= (xi , yi ) are the coordinates of the point source .

To simulate the wind flow in the case of the buildings at the territory of Pump Station the 2D model of potential flow is used [7]

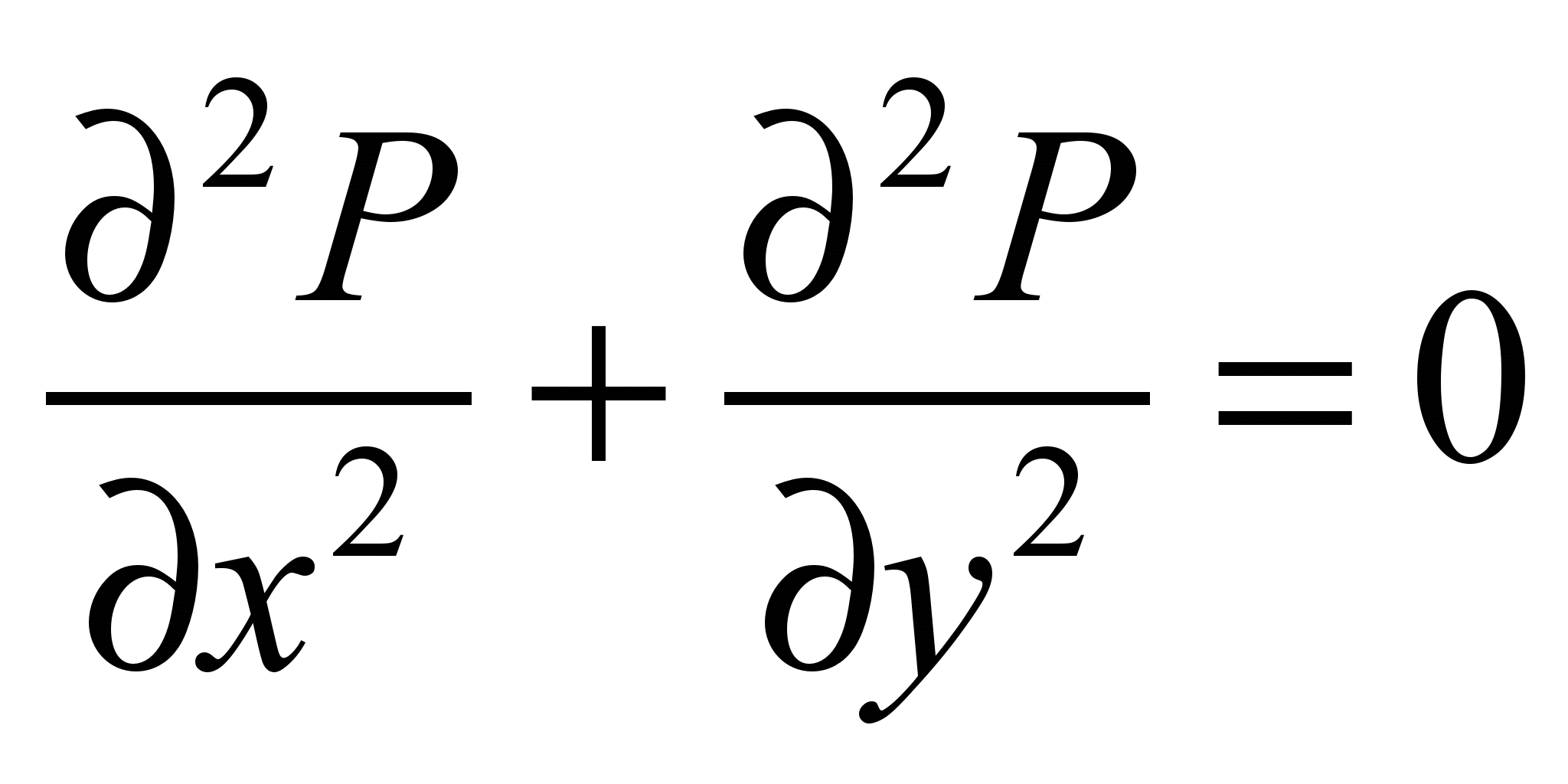, (2)

where Р is the potential of velocity.

The wind velocity components are calculated as follows:

.

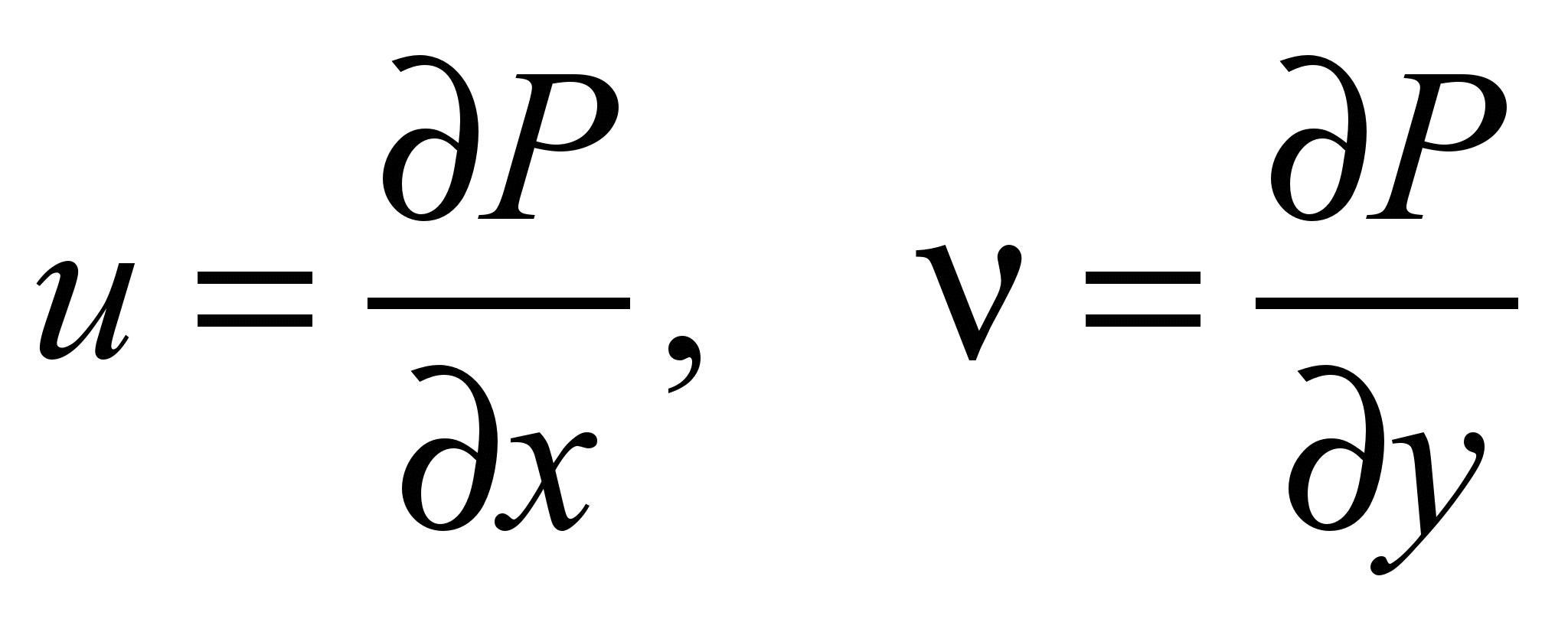Boundary conditions for modeling equations are discussed in [5, 7].

Numerical model

The computation of wind pattern and pollutant dispersion is carried out on rectangular grid. To create the form of buildings we use porosity technique or so called «markers method» [1, 7]. Markers are used to separate the computational cells where flow takes place from the cells which correspond to buildings.

Main features of the finite difference schemes which we use for the numerical integration of modeling equations are shown below.

To solve equation (1) we use change – triangle difference scheme [1, 7]. The time dependent derivative in Eq. (1) is approximated as follows:

.

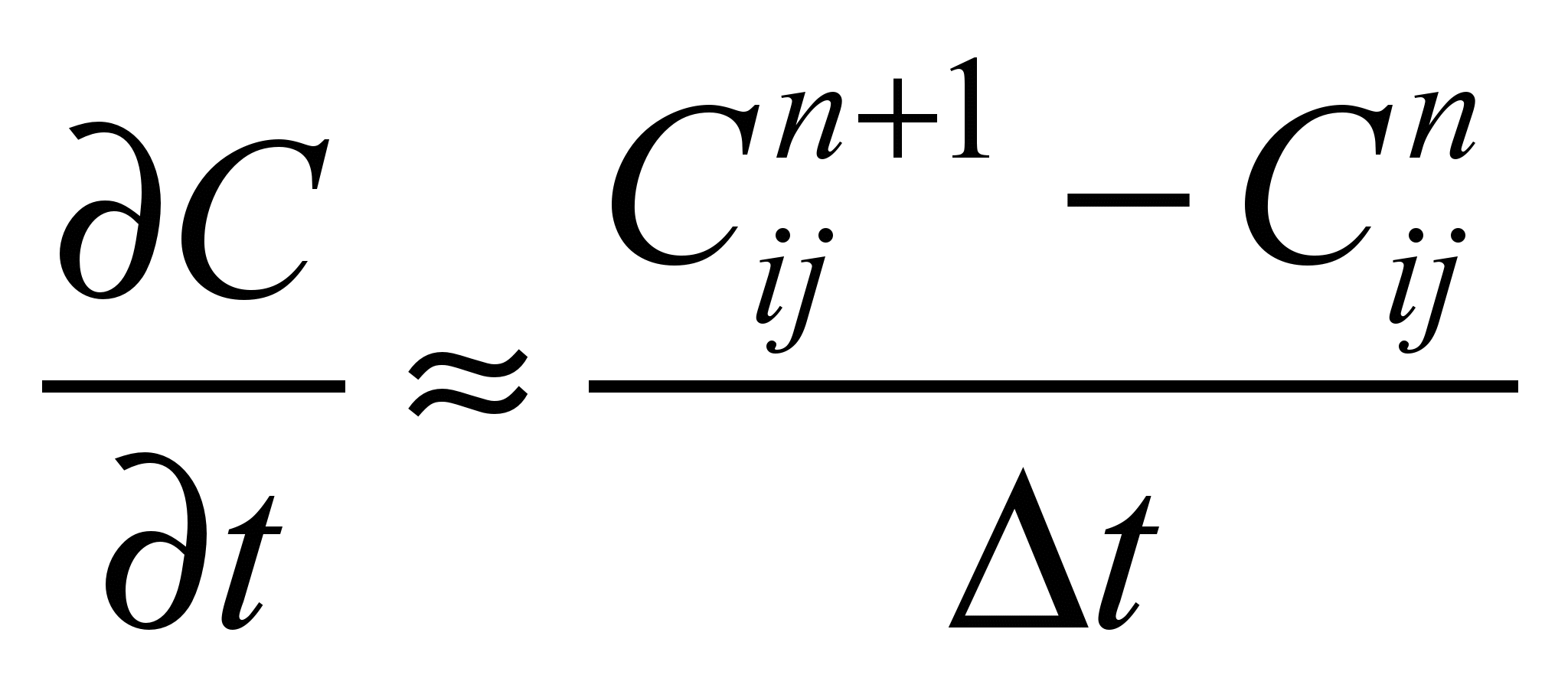At the first step convective derivatives are represented in the following way:

;

;

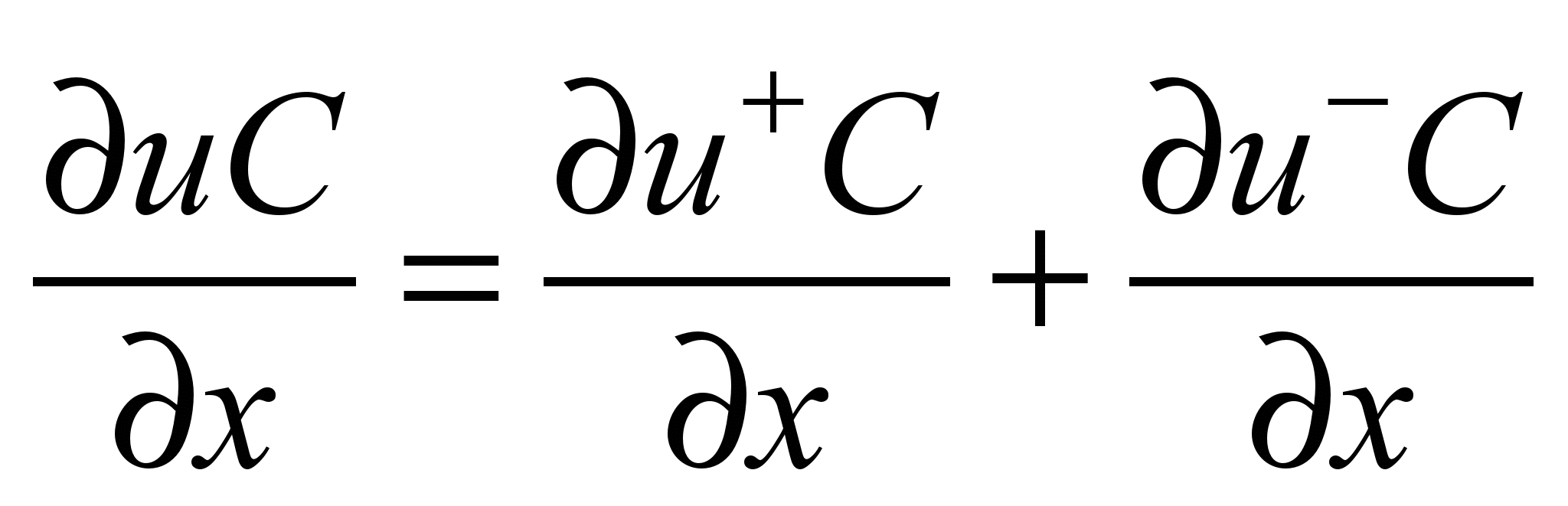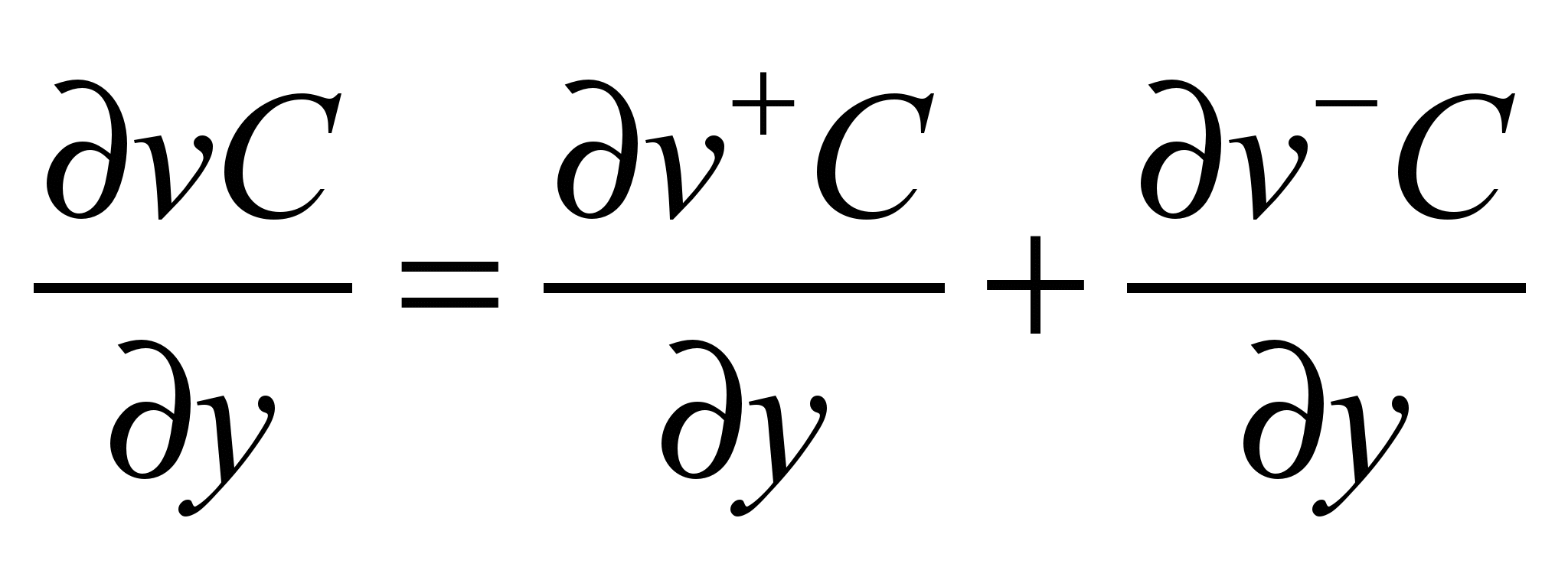where ; , ; .

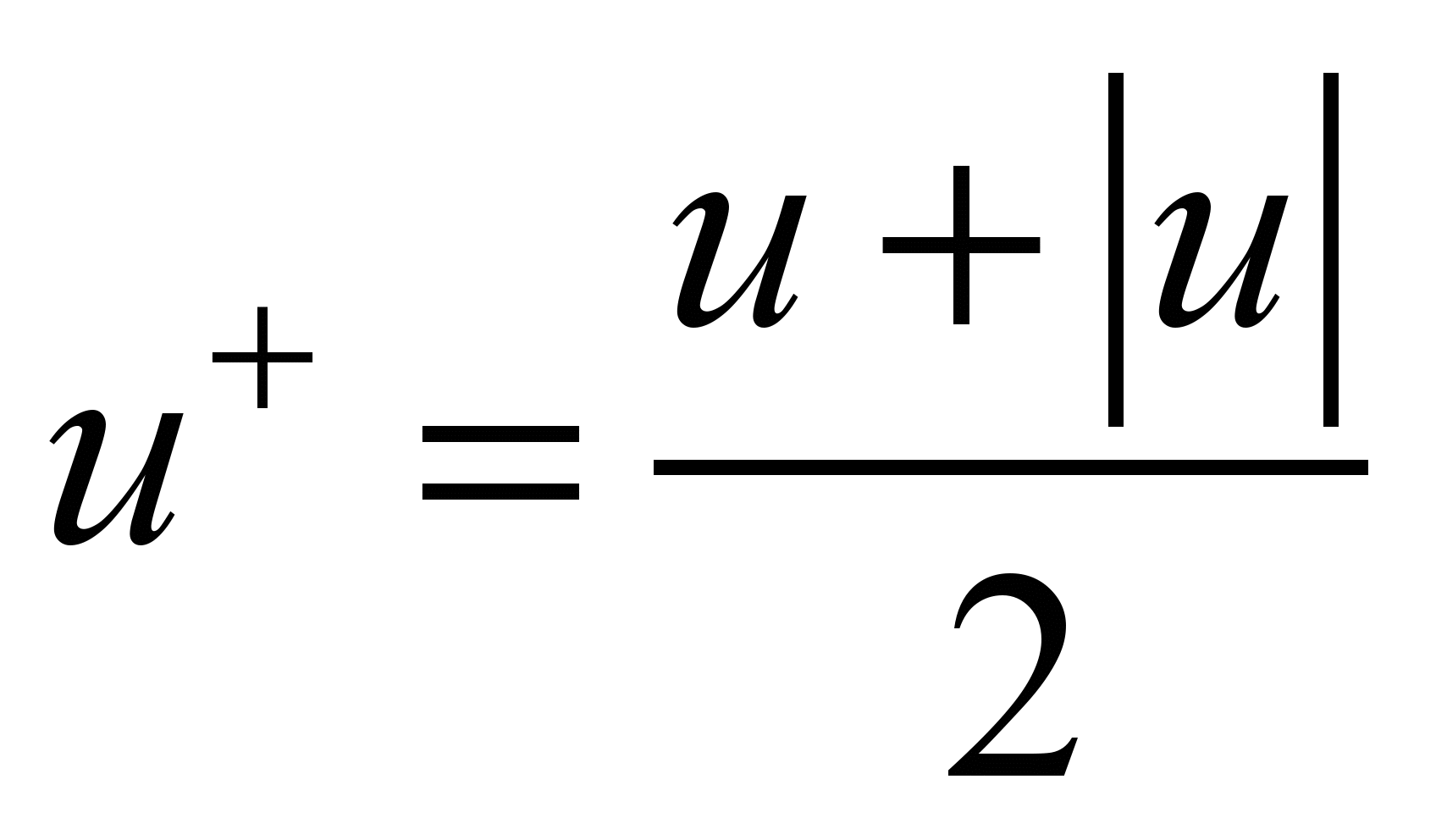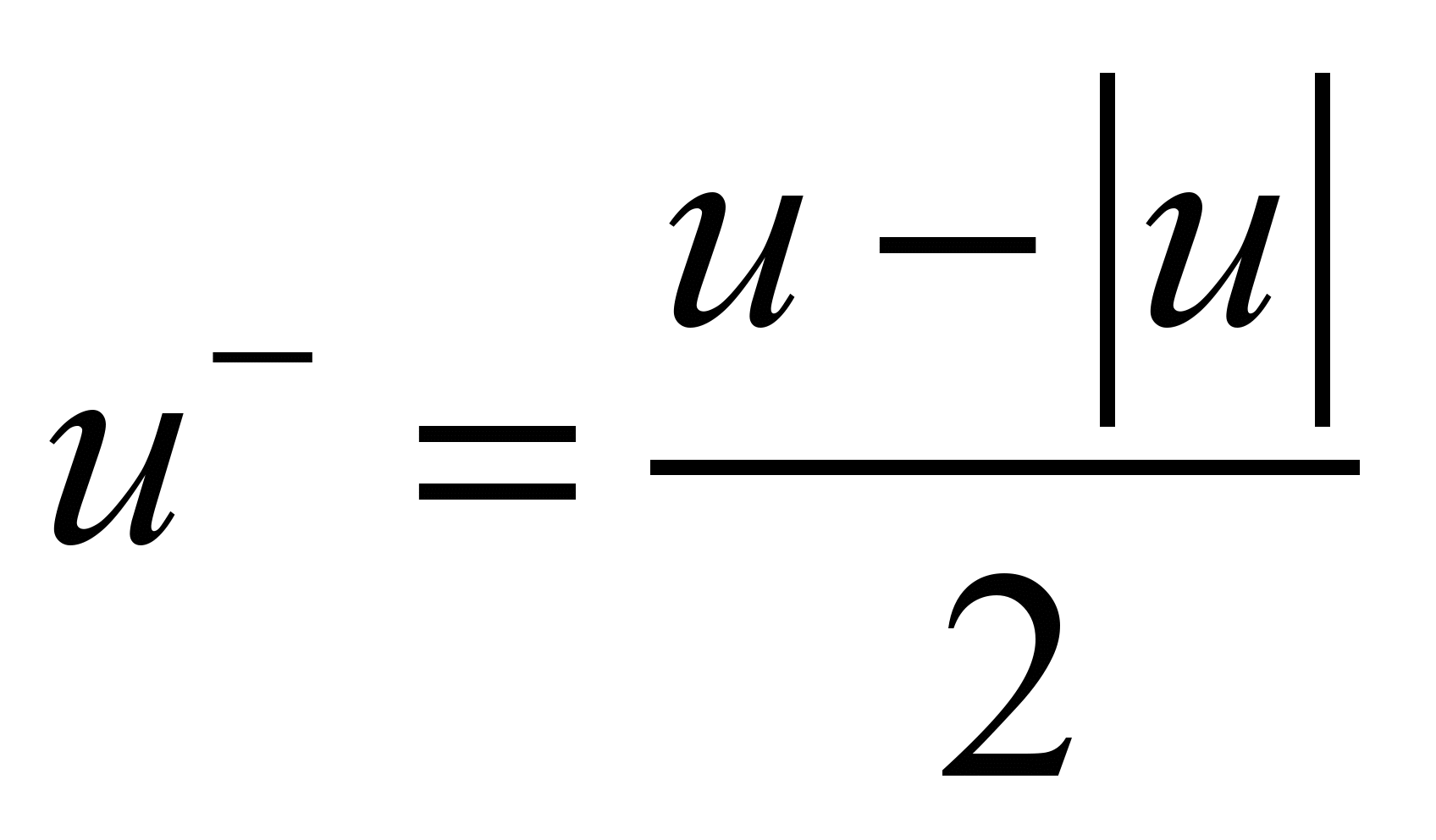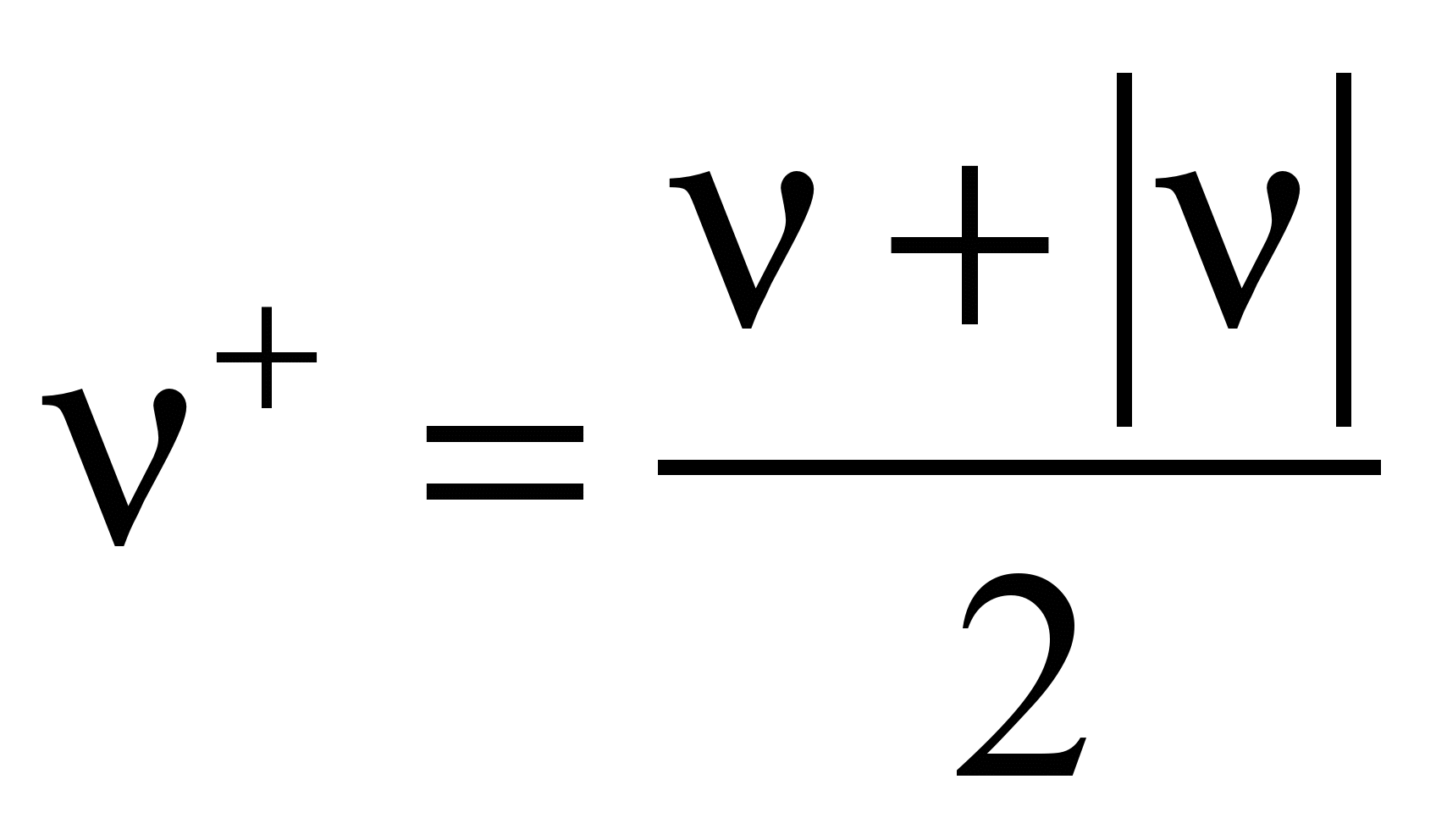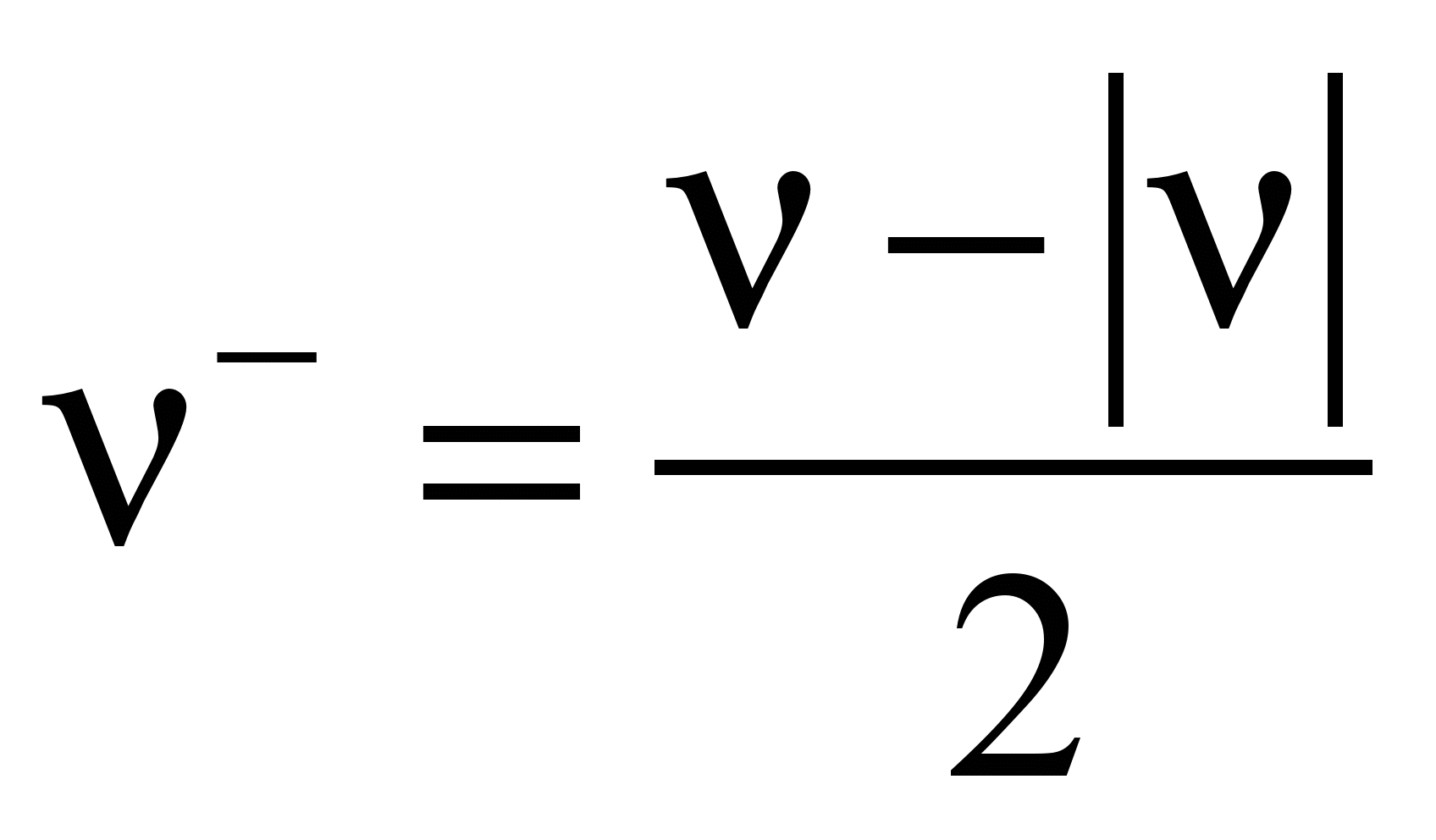At the second step the convective derivatives are approximated as follows:

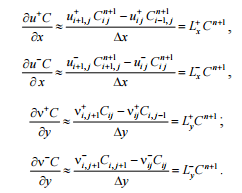
The second order derivatives are approximated as follows:

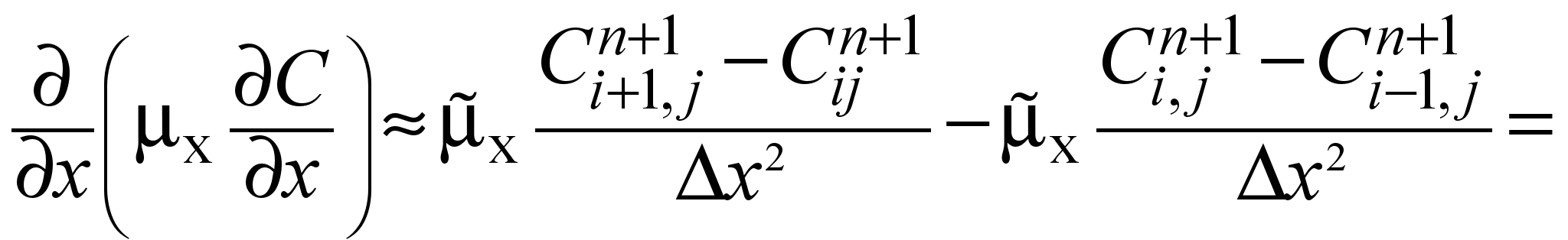
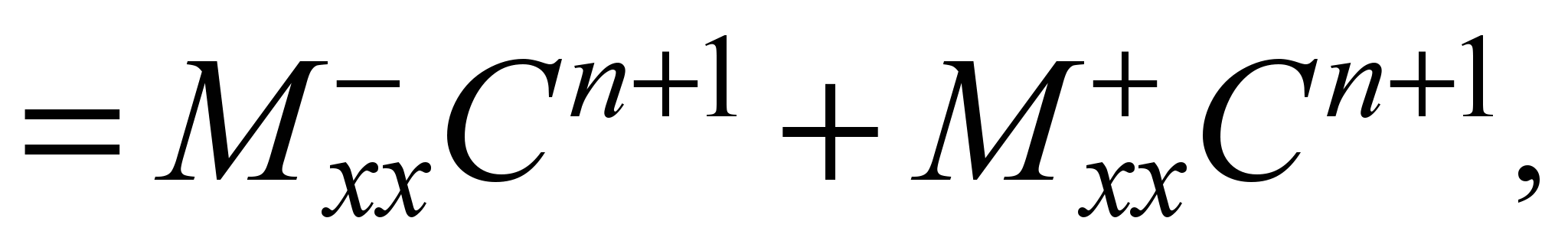
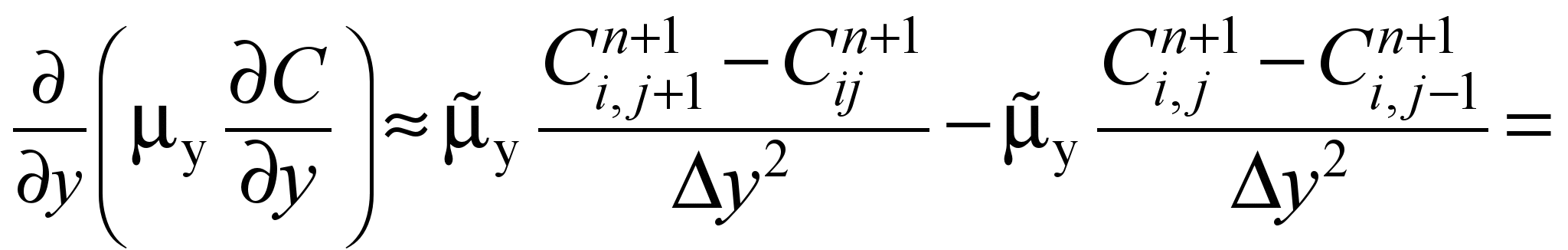
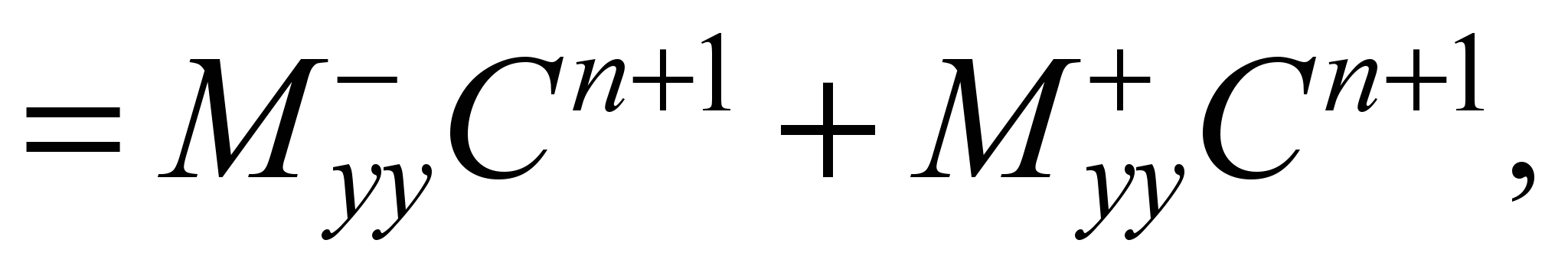
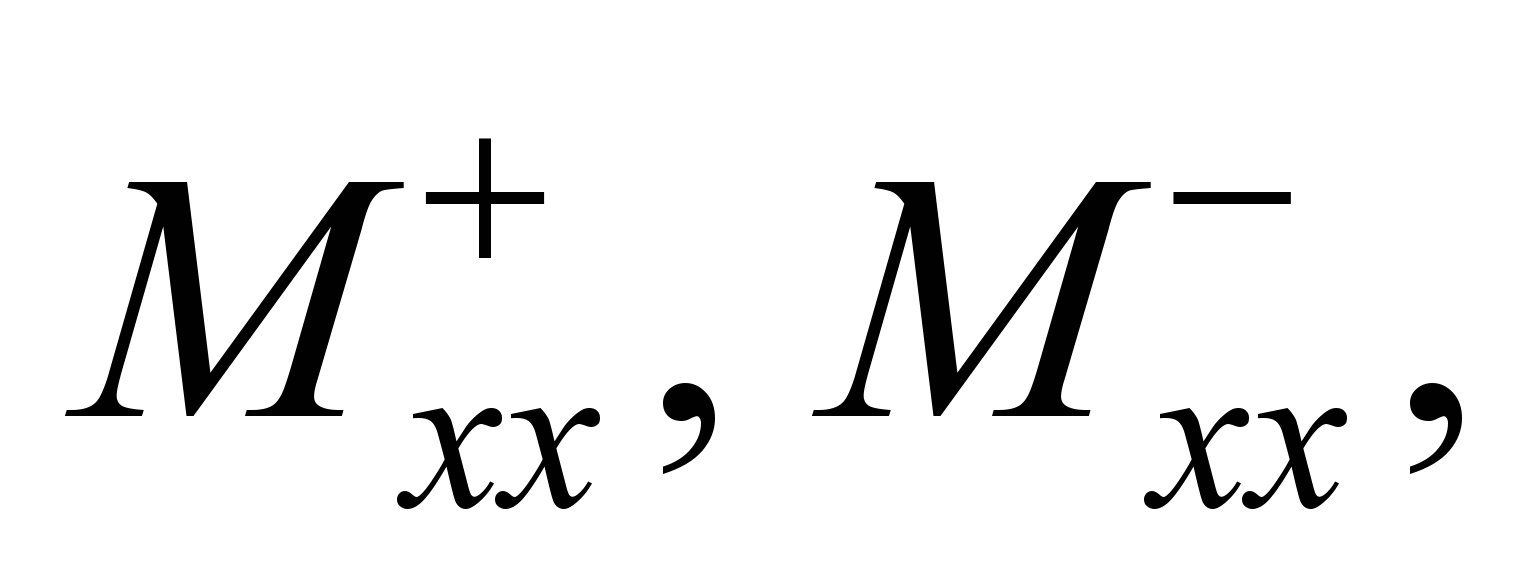
In these expressions 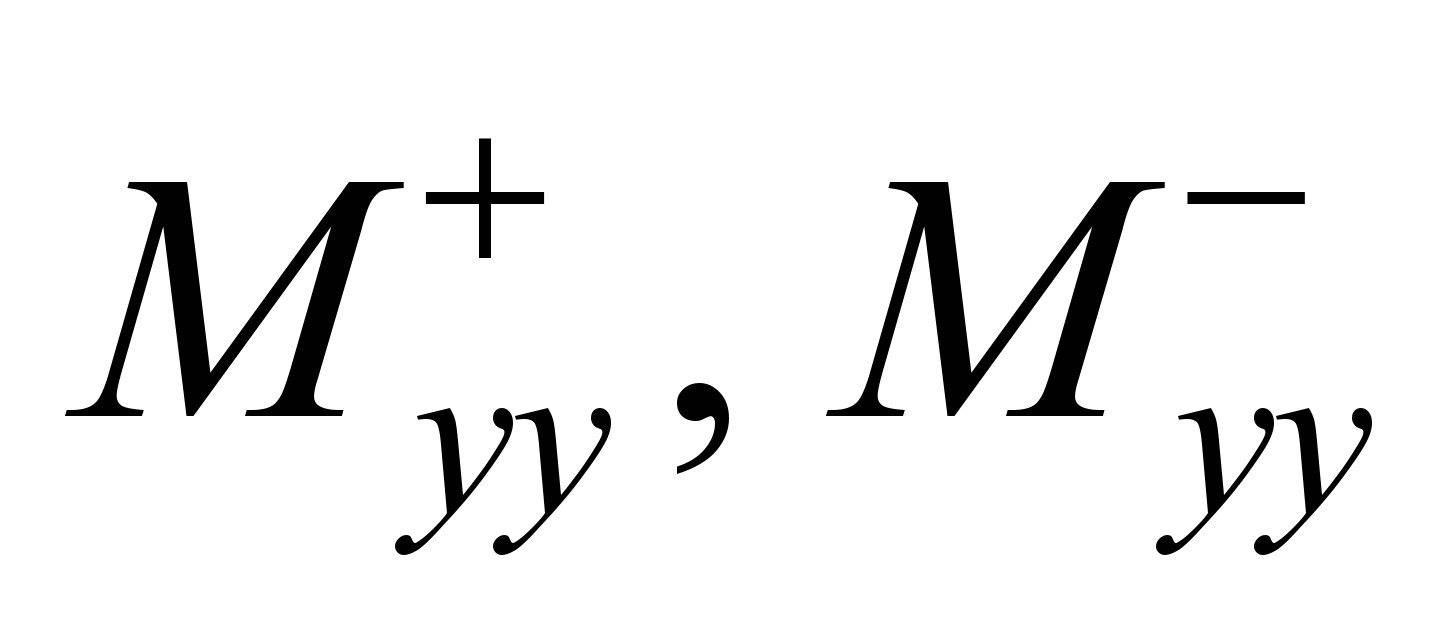are the difference operators. Using these expressions, the difference scheme for the transport equation can be written as follows:

Solution of the transport equation in finite – difference form is split in four steps on the time step of integration dt:

– at the first step (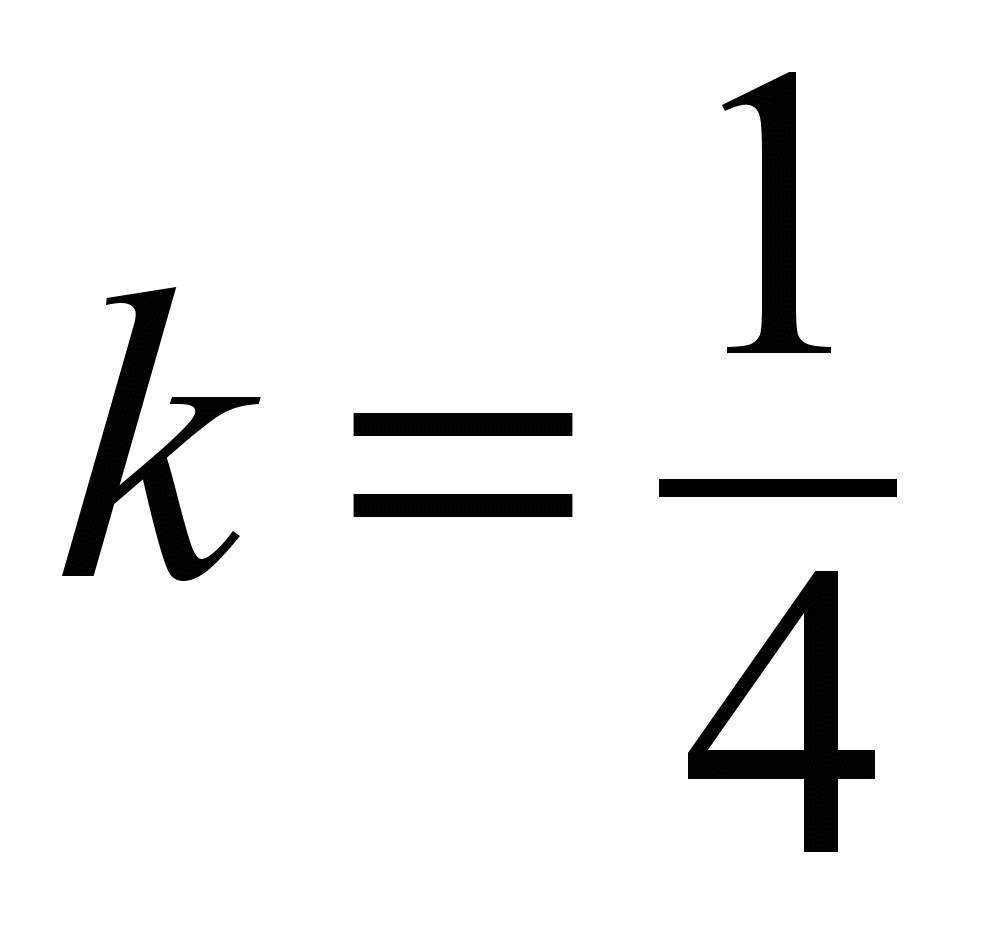) the difference equation is:

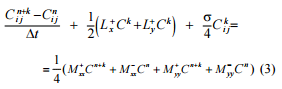
– at the second step (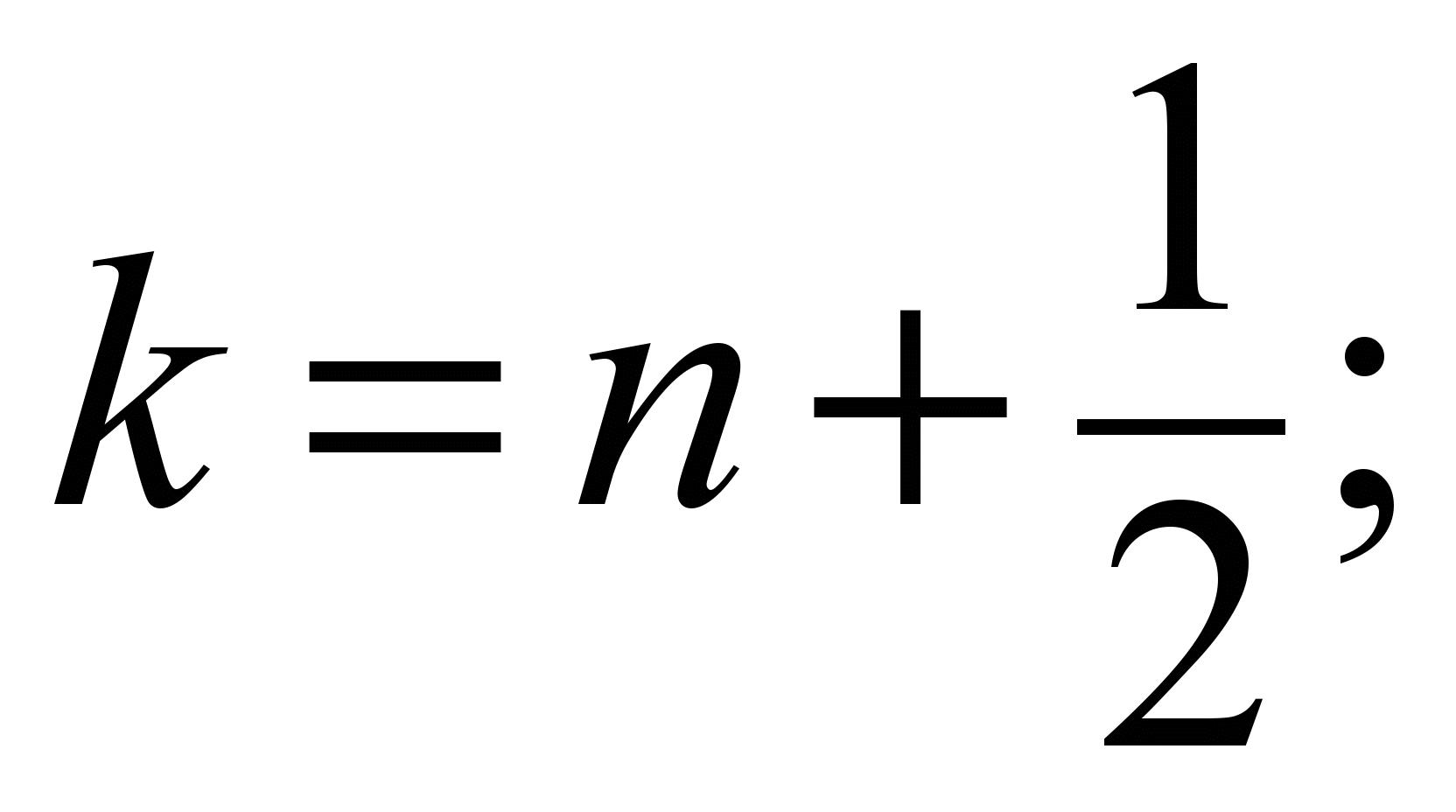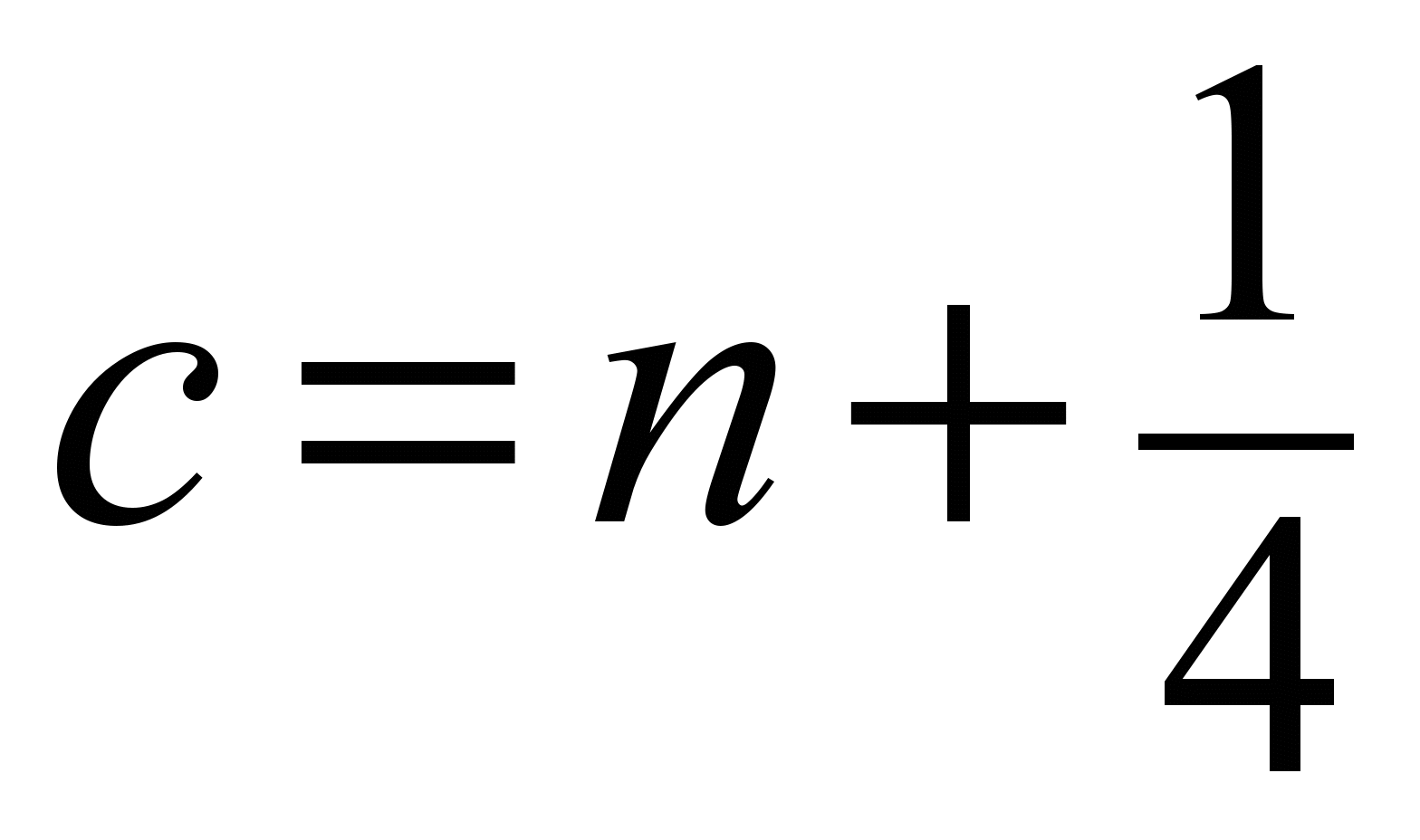) the difference equation is:

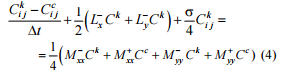
– at the third step (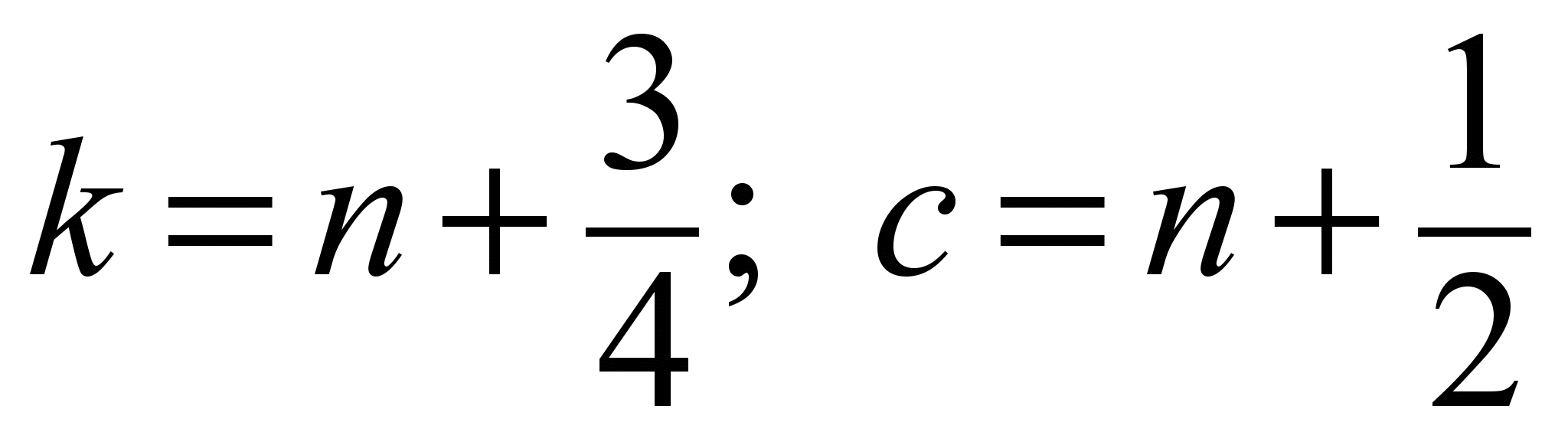) the expression (4) is used;

– at the fourth step (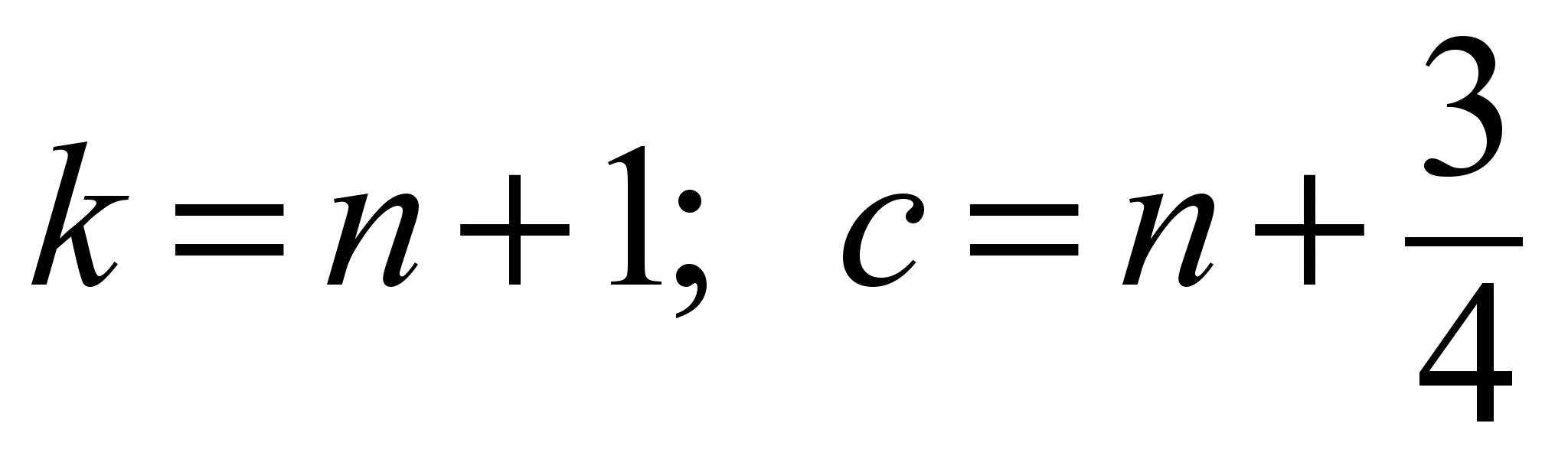) the expression (3) is used.

At the fifth step (at this step the influence of the source of pollutant emission is taken into account) the following approximation is used:

.

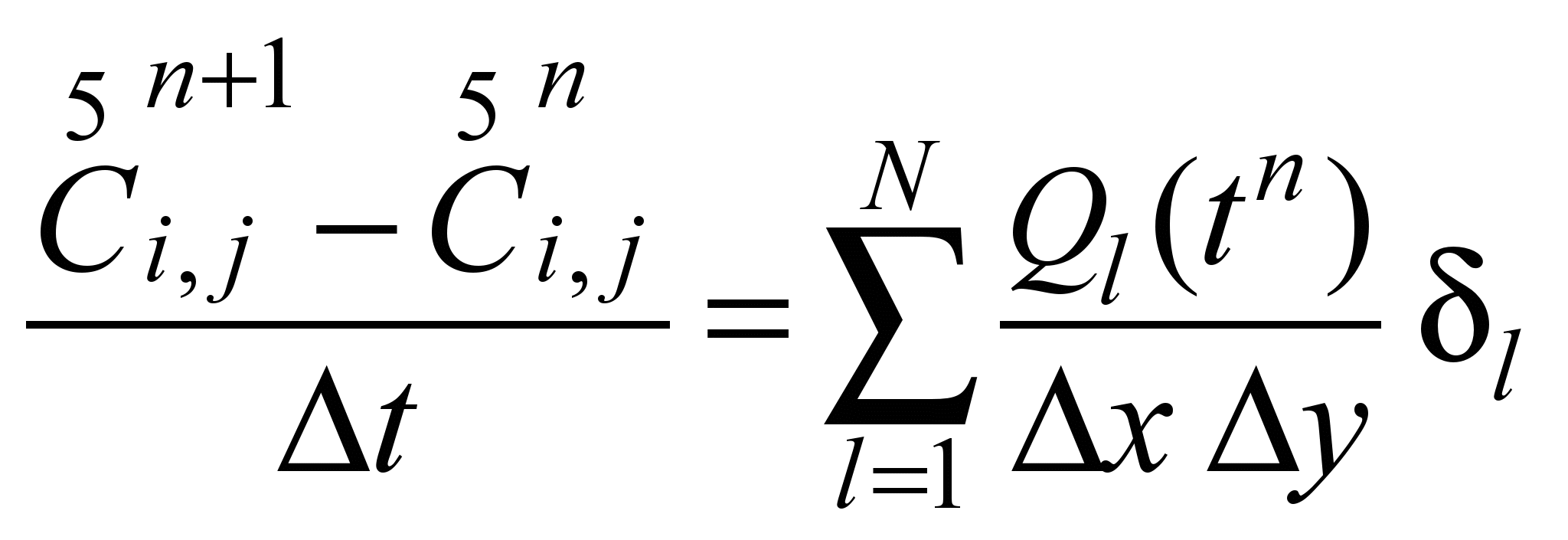Function l is equal to zero in all cells accept the cells where source of emission is situated.

This difference scheme is implicit and absolutely steady but the unknown concentration C is calculated using the explicit formulae at each step (so called «method of running calculation»).

To solve equation (2) we transform it to the «evolution type»

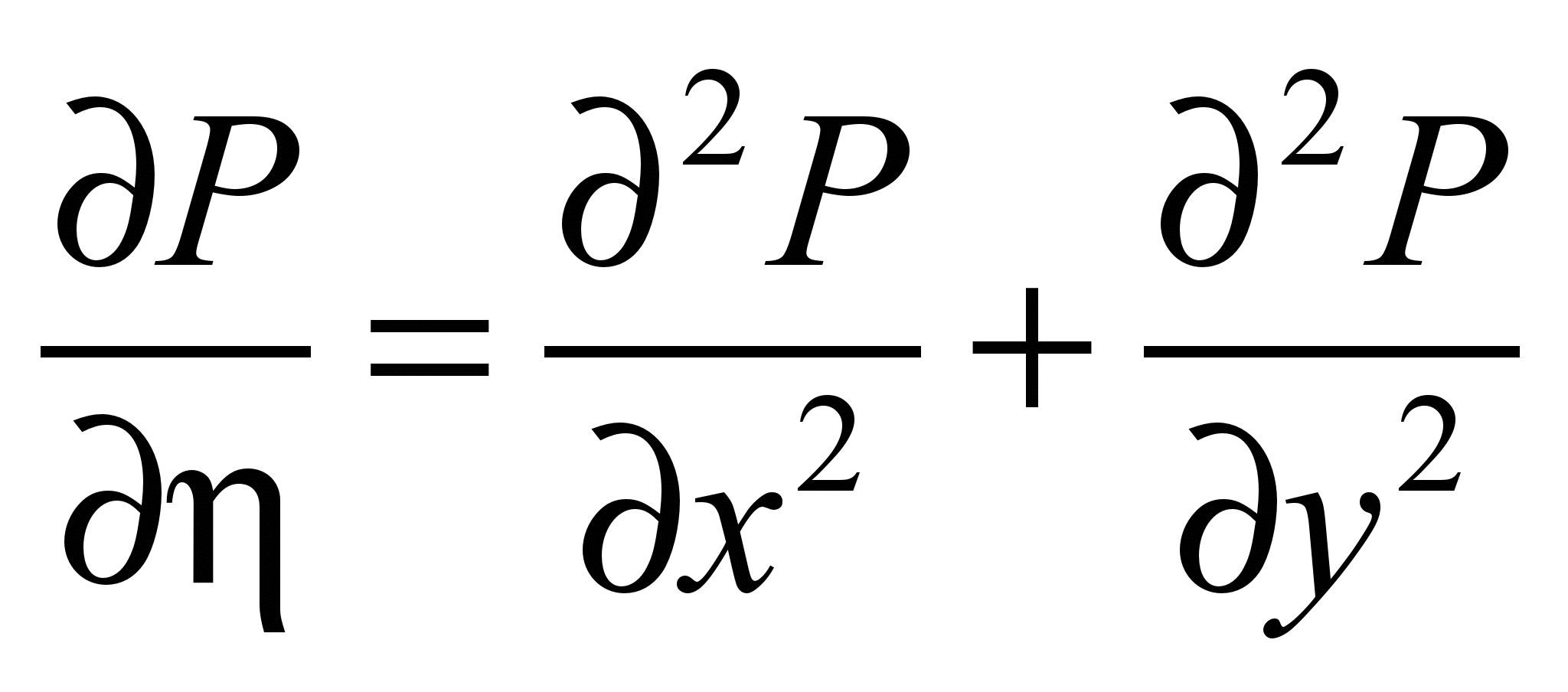, (3)

where 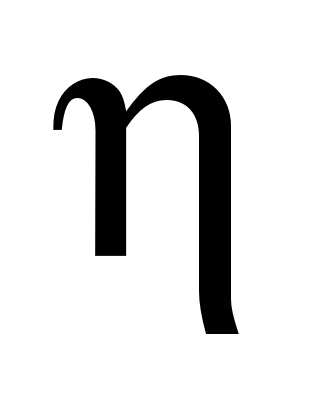is ’fictitious’ time.

For the solution of equation (3) tends to the solution of equation (2).

To solve equation (3) A. A. Samarskii’s change-triangle difference scheme is used. According to this scheme the solution of equation (3) is split into two steps:

– at the first step the difference equation is

– at the second step the difference equation is

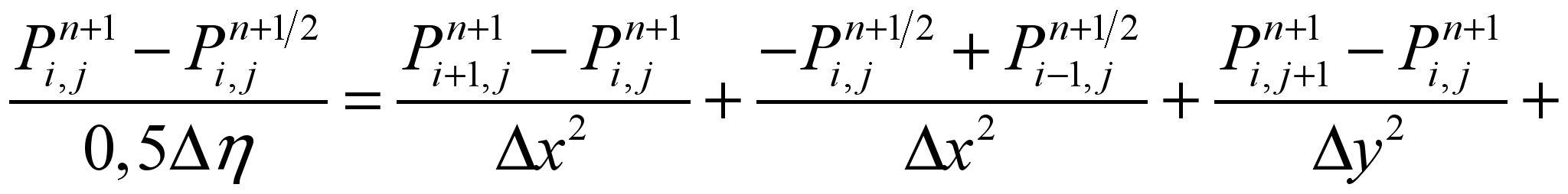
From these expressions the unknown value Pi,j is determined using the explicit formulae at each step of splitting («method of running calculation»). The calculation is completed if the condition

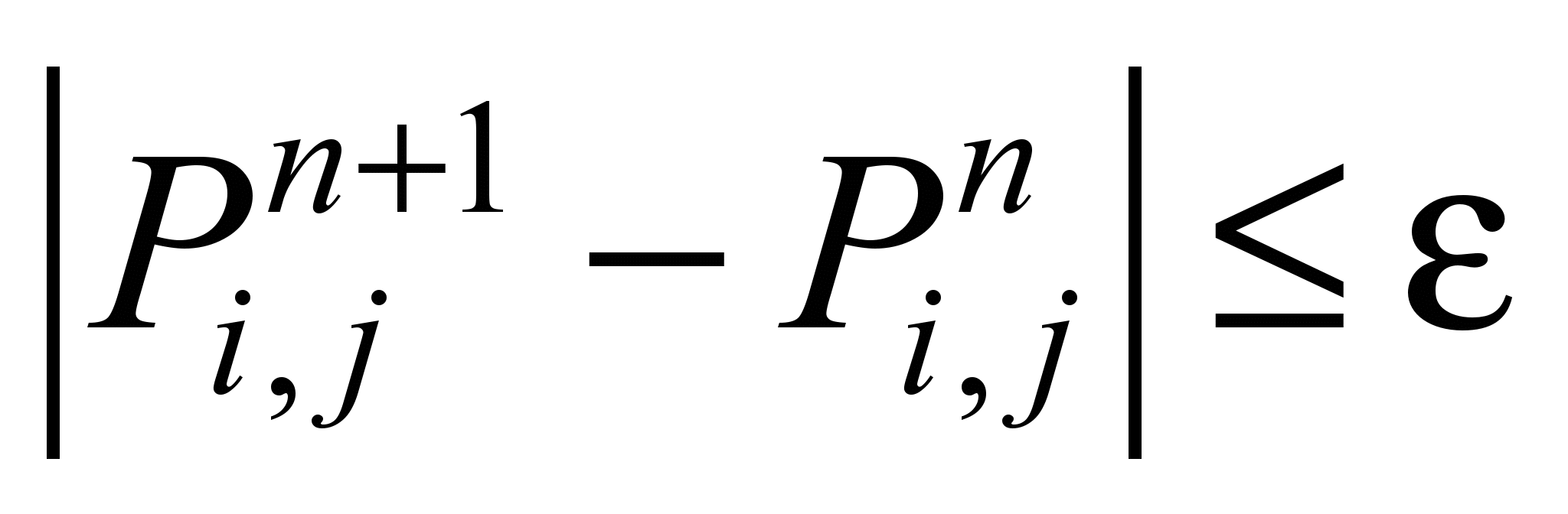
is fulfilled (where 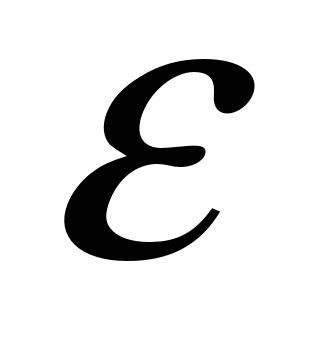is a small number, n is the number of iteration). The components of velocity vector are calculated on the sides of computational cell as follows

,

.

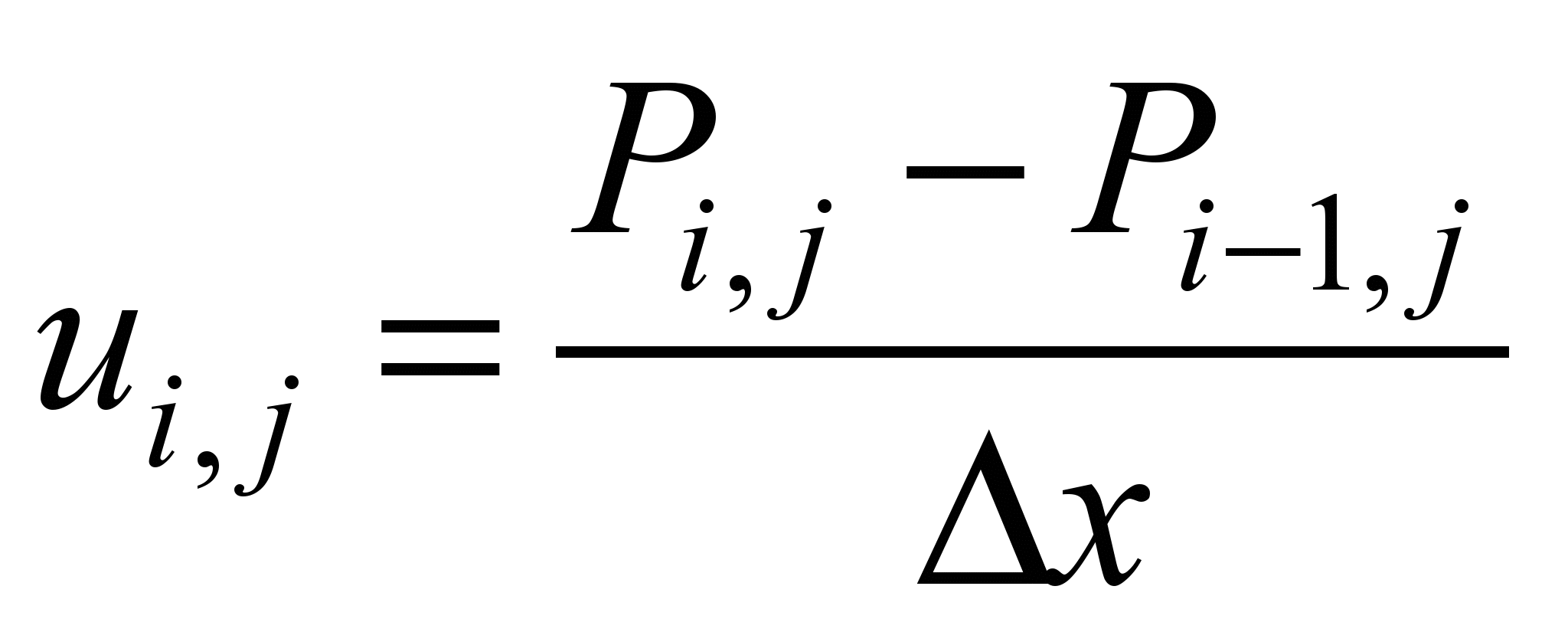Calculation of velocity components on the sides of computational cell allows to develop the conservative numerical scheme for pollutant dispersion.

For coding of difference formulae, we used FORTRAN language.

Findings

Developed numerical model and code were used to compute ammonia concentrations at the territory of ammonia pump station in the case of unplanned release (Fig.2). It was supposed that release takes place near building with ammonia pumps (Fig. 3, 4). Sketch of computational region is shown in Figure 4. Figures 5, 6 show modeling results for ammonia emission. Emission rate is Q=17 kg/s and was chosen from literature [6].

Fig. 2. Ammonia pump station

Fig. 3. Buildings with ammonia pumps

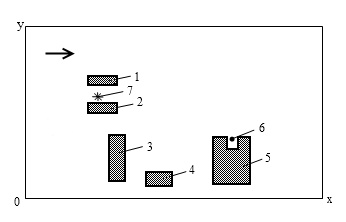
Fig. 4. Sketch of computational region
(ammonia pump station): 1, 2 – buildings with ammonia pumps, 3, 4, 5 – industrial buildings on the territory of station; 6 – receptor position; 7 – position of ammonia release
at the territory of pump station

Fig. 5. Computed ammonia concentration, t=250 s

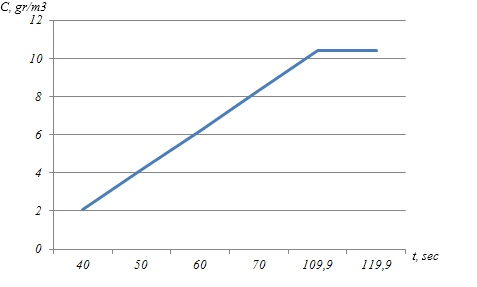
Fig. 6. Ammonia concentration at receptor
 spot (position No. 6, Fig. 4)

As we can see from Fig. 5 plume of toxic chemical quickly covers all the territory of ammonia pump station. To estimate the danger of such unplanned release we computed the ammonia concentration near one building at the territory of this station. Receptor position (position of person) is shown in Fig.4. Dynamics of ammonia concentration at this spot is shown in Fig.6. It is clear that the people affected will die at the territory in the case of this unplanned release because the ammonia concentration exceeds Level of Concern which is 20 mg/m3.

Worthy of note that computational time was 5 sec. It allows to use the developed model for prediction of air pollution during PLAS development.

Originality and practical value

A 2D numerical model has been developed to compute contamination zones among buildings during the accidental emission of a hazardous substance. The presented 2D numerical model is based on the application of the fundamental equations of aerodynamics and mass transfer.

The peculiarity of the developed model is the use of standard meteorological information and quick calculation.

Conclusions

Numerical 2D numerical model for estimating the level of atmospheric air pollution during the emergency emission of hazardous substances is proposed. Proposed numerical model allows to predict level of pollution of atmospheric air among buildings. The solution of the aerodynamic problem is based on the numerical integration of the equation for the velocity potential. To predict the air pollution, the equation of mass transfer is used. The mass transfer equation takes into account the convective and diffusive transport of pollutants in atmosphere, taking into account buildings situated near the source of emission. Emission of a dangerous substance is simulated by a point source, which is modeled using Dirac’s delta function.

Further improvement of the model should be carried out in the direction of creating a 3D numerical model that takes into account the formation of vortices in the air flow.


LIST OF REFERENCE LINKS

  1. Беляев, Н. Н. Моделирование нестационарных процессов аварийного загрязнения атмосферы : монография / Н. Н. Беляев, А. В. Берлов, П. Б. Машихина. – Днепропетровск : Акцент ПП, 2014. – 127 с.

  2. Берлянд, М. Е. Прогноз и регулирование загрязнения атмосферы / М. Е. Берлянд. – Ленинград : Гидрометеоиздат, 1985. – 273 с.

  3. Бруяцкий, Е. В. Теория атмосферной диффузии радиоактивных выбросов / Е. В. Бруяцкий. – Киев : Ин-т гидромеханики НАН Украины, 2000. – 443 с.

  4. Заказнов, В. Ф. Распространение аммиака при разгерметизации аммиакопровода, емкостей /В. Ф. Заказнов, Л. А. Куршева // Исследования и разработки по созданию магистральных аммиакопроводов и складов жидкого аммиака : тр. ГИАП. – Москва, 1985. – С. 57.

  5. Марчук, Г. И. Математическое моделирование в проблеме окружающей среды / Г. И. Марчук. – Москва : Наука, 1982. – 320 с.

  6. Цыкало, А. Л. Испарение и рассеивание аммиака при его разливах и утечках. Серия: Азотная промышленность / А. Л. Цыкало, И. И. Стрижевский, А. Д. Баглет. – Москва : НИИТЭХИМ, 1982. – 48 с.

  7. Численное моделирование распространения загрязнения в окружающей среде / М. З. Згуровский, В. В. Скопецкий, В. К. Хрущ, Н. Н. Беляев. – Київ : Наук. думка, 1997. – 368 с.

  8. Biliaiev, M. M. Numerical simulation of the atmosphere pollution after accident at the «Tolliaty-Odessa» ammonia pipe / M. M. Biliaiev, L. V. Amelina, M. M. Kharytonov // NATO Science for Peace and Security. Series C: Environmental security. – 2013. – P. 391–395. doi: 10.1007/978-94-007-5577-2_66.

  9. Biliaiev, M. M. The Numeric Forecast of Air Pollution Caused by a Blasting Accident in the Enterprise Responsible for Rocket Fuel Utilization in Ukraine / M. M. Biliaiev, M. M. Kharytonov // NATO Science for Peace and Security. Series C: Environmental Security. – 2012. – P. 313–327. doi: 10.1007/978-94-007-5034-0_25.

  10. Daly, A. Accident reconstruction and plume modeling of an unplanned ammonia release / A. Daly, P. Zanetti, M. Jennings // Air Pollution XX. WIT Transactions on Ecology and The Environment. – 2013. – Vol. 174. – P. 3–13. doi:10.2495/AIR130011.

  11. Dispersion Modeling of Hydrogen Sulfide at Cimarex Rands Butte Project Using ALOHA / Bureau of Land Management Pinedale Field Office, SWCA Environmental Consultants. – Wyoming, 2010. – 26 p.

  12. Janos, T. Atmostheric spreading model for ammonia released from the poultry house [Electronic resource] / T. Janos. E. Gorliczay, J. Borbely // Ecotoxicologie, Zootehnie si Tehnologii de Industrie Alimentara. – 2016. – Vol. XV/B. – P. 331–337. – Available at: http://protmed.uoradea.ro/facultate/publicatii/ecotox_zooteh_ind_alim/2016B/ipa/17%20Tamas_Janos.pdf. – Title from the screen. – Accessed : 30.05.2017.

  13. Mellsen, S. B. A Fortran Program for Calculating Chemical Hazards Using the NATO Stanag 2103/ATP-45 Algorithm [Electronic resource] / S. B. Mellsen // Suffield memorandum No. 1275. – Alberta : Defence Research Establishment Suffield, 1989. – 34 p. – Available at: http://oai.dtic.mil/oai/oai?verb=getRecord&metadataPrefix=html&identifier=ADA214763. – Title from the screen. – Accessed : 30.05.2017.

  14. The analysis of the use of mathematical modeling for emergency planning purposes [Electronic resource] / O. Zavila, P. Dobeš, J. Dlabka, J. Bitta // Bezpecnostni vyzkum. The science for population protection. – 2015. – No. 2. – P. 1–9. – Available at: http://www.population-protection.eu/prilohy/casopis/30/213.pdf. – Title from the screen. – Accessed : 30.05.2017.

  15. The Pentagon Shield Field Program: Toward Critical Infrastructure Protection / T. Warner, P. Benda, S. Swerdlin [et al.] // Bulletin of the American Meteorological Society. – 2007. – Vol. 88. – Iss. 2. – P. 167–176. doi: 10.1175/BAMS-88-2-167.

Л. В. АМЕЛІНА1*, М. М. БІЛЯЄВ2

1*Каф. «Гідравліка та водопостачання», Дніпропетровський національний університет
залізничного транспорту імені академіка В. Лазаряна, вул. Лазаряна, 2, Дніпро,
Україна, 49010, тел. +38 (056) 273 15 09,
ел. пошта gidravlika2013@mail.ru, ORCID 0000-0002-8525-7096
2*Каф. «Гідравліка та водопостачання», Дніпропетровський національний університет
залізничного транспорту імені академіка В. Лазаряна, вул. Лазаряна, 2, Дніпро,
Україна, 49010, тел. +38 (056) 273 15 09,
ел. пошта gidravlika2013@mail.ru, ORCID 0000-0002-1531-7882

ЧИСЕЛЬНЕ МОДЕЛЮВАННЯ ЗАБРУДНЕННЯ

ПОВІТРЯ В РАЗІ РАПТОВОГО ВИКИДУ АММІАКУ

Мета. Дослідження спрямоване на розробку моделі швидкого обчислення, яка враховувала б метеорологічні параметри та будівлі, котрі знаходяться поблизу джерела токсичного викиду. Методика. Розроблена модель заснована на рівнянні для потенційного потоку та рівнянні розсіювання забруднюючих речовин. Рівняння потенційного потоку використовується для обчислення моделі вітру між будівлями, а для вирішення рівняння потенційної течії – неявна різницева схема Самарського. Неявна поперемінно-трикутна різницева схема застосовується для вирішення рівняння масопереносу. Чисельне інтегрування здійснюється за допомогою прямокутної різницевої сітки. Метод маркування («метод маркерів») вживається для створення форми великої розрахункової області. Викид аміаку моделюється з використанням Дельта функції для точкового джерела. Результати. Розроблена двомірна чисельна модель відноситься до класу «діагностичні моделі». Ця модель має на увазі основні фізичні фактори, що впливають на процес розсіювання забруднюючих речовин в атмосфері. Модель враховує вплив будівель на розсіювання забруднюючих речовин. На основі розроблених чисельних моделей був проведений обчислювальний експеримент для оцінки рівня токсичного хімічного забруднення в разі раптового викиду аміаку на аміачній насосній станції. Наукова новизна. Розроблена авторами чисельна модель дозволяє розрахувати двомірну модель вітру серед будівель та розсіювання забруднюючих речовин у разі раптового викиду аміаку. Модель дозволяє виконувати швидкі розрахунки забруднення атмосфери. Практична значимість. Модель можливо використовувати при розробці ПЛАСа (план ліквідації аварійних ситуацій).

Ключові слова: забруднення повітря; раптовий викид; токсичні хімічні речовини; чисельне моделювання

Л. В. АМЕЛИНА1*, Н. Н. беляев2

1*Каф. «Гидравлика и водоснабжение», Днепропетровский национальный университет
железнодорожного транспорта имени академика В. Лазаряна, ул. Лазаряна, 2, Днипро,
Украина, 49010, тел. +38 (056) 273 15 09,
эл. почта gidravlika2013@mail.ru, ORCID 0000-0002-8525-7096
2Каф. «Гидравлика и водоснабжение», Днепропетровский национальный университет
железнодорожного транспорта имени академика В. Лазаряна, ул. Лазаряна, 2, Днипро,
Украина, 49010, тел. +38 (056) 273 15 09,
эл. почта gidravlika2013@mail.ru, ORCID 0000-0002-1531-7882

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ЗАГРЯЗНЕНИЯ

ВОЗДУХА В СЛУЧАЕ ВНЕЗАПНОГО ВЫБРОСА

АММИАКА

Цель. Исследование направлено на разработку быстрой расчетной модели, которая учитывала б метеорологические параметры и здания, расположенные вблизи источника токсического химического выброса. Методика. Разработанная модель основана на уравнении для потенциального потока и уравнении дисперсии загрязняющих веществ. Уравнение потенциального потока используется для вычисления модели ветра между зданиями, а для решения уравнения потенциального течения – неявная разностная схема Самарского. Неявная попеременно-треугольная разностная схема применяется для решения уравнения массопереноса. Численное интегрирование осуществляется с помощью прямоугольной разностной сетки. Метод маркировки («метод маркеров») используется для создания формы большой расчетной области. Эмиссия аммиака моделируется с использованием Дельта функции для точечного источника. Результаты. Разработанная двумерная численная модель относится к классу «диагностические модели». Эта модель имеет в виду основные физические факторы, влияющие на процесс рассеивания загрязняющих веществ в атмосфере. Модель учитывает влияние зданий на дисперсию загрязняющих веществ. На основе разработанных численных моделей был проведен вычислительный эксперимент для оценки уровня токсического химического загрязнения в случае внезапного выброса аммиака на аммиачной насосной станции. Научная новизна. Разработанная авторами численная модель позволяет рассчитать двумерную модель ветра между зданиями и дисперсию загрязняющих веществ в случае внезапного выброса аммиака. Модель позволяет выполнять быстрые расчеты загрязнения атмосферы. Практическая значимость. Модель можно применять при разработке ПЛАСа (план ликвидации аварийных ситуаций).

Ключевые слова: загрязнение воздуха; внезапный выброс; токсичные химические вещества; численное моделирование

REFERENCES

  1. Biliaiev, M. M., Berlov, A. V., & Mashikhina, P. B. (2014). Modelirovaniye nestatsionarnykh protsessov avariynogo zagryazneniya atmosfery [Monograph]. Dnipropetrovsk: Aktsent PP.

  2. Berlyand, M. Y. (1985). Prognoz i regulirovaniye zagryazneniya atmosfery. Leningrad: Gidrometeoizdat.

  3. Bruyatskiy, Y. V. (2000). Teoriya atmosfernoy diffuzii radioaktivnykh vybrosov. Kyiv: Institut gidromekhaniki NAN Ukrainy.

  4. Zakaznov, V. F., & Kursheva, L. A. (1985). Rasprostraneniye ammiaka pri razgermetizatsii ammiakoprovoda, emkostey. In Issledovaniya i razrabotki po sozdaniyu magistralnykh ammiakoprovodov i skladov zhidkogo ammiaka. Moscow: The State Research and Design Institute of the Nitric Industry and Organic Synthesis Products.

  5. Marchuk, G. I. (1982). Matematicheskoye modelirovaniye v probleme okruzhayushchey sredy. Moscow: Nauka.

  6. Tsykalo, A. L., Strizhevskiy, I. I., & Baglet, A. D. (1982). Azotnaya promyshlennost: Ispareniye i rasseivaniye ammiaka pri ego razlivakh i utechkakh. Moscow: NIITEKHIM.

  7. Zgurovskiy, M. Z., Skopetskiy, V. V., Khrushch, V. K., & Biliaiev M. M. (1997). Chislennoye modelirovaniye rasprostraneniya zagryazneniya v okruzhayushchey srede. Kyiv: Naukova dumka.

  8. Biliaiev, M. M., Amelina, L.V., & Kharitonov, M. M. (2013). Numerical simulation of the atmosphere pollution after accident at the “Tolliaty-Odessa” ammonia pipe. NATO Science for Peace and Security Series C: Environmental Security, 391-395. doi: 10.1007/978-94-007-5577-2_66

  9. Biliaiev, M. M., & Kharytonov, M. M. (2012). The Numeric Forecast of Air Pollution Caused by a Blasting Accident in the Enterprise Responsible for Rocket Fuel Utilization in Ukraine. NATO Science for Peace and Security Series C: Environmental Security, 313-327. doi: 10.1007/978-94-007-5034-0_25

  10. Daly, A., Zanetti, P., & Jennings, M. (2013). Accident reconstruction and plume modeling of an unplanned ammonia release. Air Pollution XXI. WIT Transactions on Ecology and the Environment, 174, 3-13.
    doi: 10.2495/AIR130011

  11. SWCA Environmental Consultants. (2010). Dispersion Modeling of Hydrogen Sulfide at Cimarex Rands Butte Project Using ALOHA. Wyoming.

  12. Janos, T., Gorliczay, E., & Borbely, J. (2016). Atmostheric spreading model for ammonia released from the poultry house. Ecotoxicologie, Zootehnie si Tehnologii de Industrie Alimentara, XV/B, 331-337. Retrieved from http://protmed.uoradea.ro/facultate/publicatii/ecotox_zooteh_ind_alim/2016B/ipa/17%20Tamas_Janos.pdf

  13. Mellsen, S. B. (1989). A Fortran Program for Calculating Chemical Hazards Using the NATO Stanag 2103/ATP-45 Algorithm: Suffield memorandum 1275. Alberta: Defence Research Establishment Suffield.
    Retrieved from http://oai.dtic.mil/oai/oai?verb=getRecord&metadataPrefix=html&identifier=ADA214763

  14. Zavila, O., Dobeš, P., Dlabka, J., & Bitta, J. (2015). The analysis of the use of mathematical modeling for emergency planning purposes. Bezpecnostni vyzkum, 2. Retrieved from http://www.population-protection.eu/prilohy/casopis/30/213.pdf.

  15. Warner, T., Benda, P., Swerdlin, S., Knievel, J., Copeland, J., Crook, A., …, & Weil, J. (2007). The Pentagon Shield Field Program: Toward Critical Infrastructure Protection. Bulletin of the American Meteorological Society, 88 (2), 167-176. doi: 10.1175/BAMS-88-2-167


Prof. S. A. Pichugov, Dr. Sc. in Phys.-and-Math. (Ukraine); Prof. S. Z. Polishchuk, D. Sc. (Tech.), (Ukraine) recommended this article to be published


Accessed: Feb. 10, 2017

Received: May 18, 2017


doi 10.15802/stp2017/104142 © L. V. Amelina, M. M. Biliaiev 2017